Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра
электроснабжения промышленных предприятий
Основы использования
возобновляемых источников энергии и энергосбережение
Методические указания и задания к выполнению
расчетно-графических работ № 1, 2 для студентов специальности
5В081200 - Энергобеспечение сельского хозяйства
Алматы 2013
СОСТАВИТЕЛИ: Умбетов Е.С., Живаева О.П. Основы использования возобновляемых источников энергии и энергосбережение. Методические указания и задания к выполнению расчетно-графических работ № 1,2 для студентов специальности 5В081200-Энергобеспечение сельского хозяйства. – Алматы: АУЭС, 2013.- 13 с.
Данная разработка включает в себя задания на расчетно-графические работы, методические указания по их выполнению и перечень рекомендуемой литературы.
Табл. 7, библиогр. - 9 назв.
Рецензент: Курпенов Б.К.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013 г.
© НАО «Алматинский университет энергетики и связи», 2013 г.
1 Расчетно-графическая работа № 1
1.1 Задание
Задача 1.
На солнечной электростанции башенного типа установлено п гелиостатов, каждый из которых имеет поверхность Fг, м2. Гелиостаты отражают солнечные лучи на приемник, на поверхности которого зарегистрирована максимальная энергетическая освещенность Нпр = 2,5 МВт/мг. Коэффициент отражения гелиостата Rг = 0,8. коэффициент поглощения приемника Апр =0,95. Максимальная облученность зеркала гелиостата Hг=600 Вт/мг. Исходные данные выбираются по таблице 1.1.
Определить площадь поверхности приемника Fпр и тепловые потери в нем, вызванные излучением и конвекцией, если рабочая температура теплоносителя составляет t °С. Степень черноты приемника εпр = 0,95. Конвективные потери вдвое меньше потерь от излучения.
Таблица 1.1
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
n |
243 |
253 |
263 |
273 |
283 |
293 |
303 |
313 |
323 |
333 |
|
|
Численные значения величин, выбираемые по предпоследней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
Fг ,м2 |
64 |
61 |
58 |
55 |
52 |
49 |
46 |
43 |
40 |
37 |
|
|
Численные значения величин, выбираемые по последней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
t ,o C |
700 |
680 |
660 |
640 |
620 |
580 |
560 |
540 |
520 |
600 |
Задача 2.
Считается, что действительный КПД η океанической ТЭС, использующей температурный перепад поверхностных и глубинных вод (T1-T2)= ∆T и работающей по циклу Ренкина, вдвое меньше термического КПД установки, работающей по циклу Карно, ηtk. Оценить возможную величину действительного КПД ОТЭС, рабочим телом которой является аммиак, если температура воды на поверхности океана t, °С, а температура воды на глубине океана t2, °С. Исходные данные выбираются по таблице 1.2.
Какой расход теплой воды V, m/ч потребуется для ОТЭС мощностью N МВт? Считать, что плотность воды = 1·103 кг/м3 , а удельная массовая теплоемкость Сp = 4,2·103 Дж/(кг·К).
Таблица 1.2
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
N ,МВт |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
Численные значения величин, выбираемые по предпоследней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
t1 , o C |
30 |
30 |
28 |
28 |
26 |
26 |
24 |
23 |
21 |
20 |
|
|
Численные значения величин, выбираемые по последней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
t2 ,° C |
4 |
5 |
4 |
5 |
4 |
5 |
4 |
5 |
4 |
5 |
Задача 3.
Определить начальную температуру t0 и количество геотермальной энергии Еo, Дж водоносного пласта толщиной h км при глубине залегания z км, если заданы характеристики породы пласта: плотность rгр = 2700 кг/м3; пористость а = 5 %; удельная теплоемкость Сгр =840 Дж/(кг·К). Температурный градиент (dT/dz) в °С/км выбрать по таблице вариантов задания. Среднюю температуру поверхности tср принять равной 10°С. Удельная теплоемкость воды Св = 4200 Дж/(кг·К); плотность воды ρ= 1·103 кг/м3. Расчет произвести по отношению к площади поверхности F = 1 км2. Минимально допустимую температуру пласта принять равной t1 =40° С.
Исходные данные выбираются по таблице 1.3.
Определить также постоянную времени извлечения тепловой энергии τo(лет) при закачивании воды в пласт и расходе ее V =0,1 м3/(с·км2). Какова будет тепловая мощность, извлекаемая первоначально (dE/dz)τ=0 и через 10 лет (dE/dz)τ=10 ?
Таблица 1.3
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
h, км |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
|
|
Численные значения величин, выбираемые по предпоследней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
z, км |
2,5 |
3,0 |
3,5 |
4,0 |
3,5 |
3,0 |
2,5 |
4 |
3,5 |
3 |
|
|
Численные значения величин, выбираемые по последней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
(dT/dz), °C/км |
75 |
70 |
65 |
60 |
55 |
50 |
45 |
40 |
35 |
30 |
1.2 Методические указания к расчетно-графической работе № 1
В задаче 1 рассмотрены вопросы использования солнечной энергии на электростанции башенного типа с использованием гелиостатов, отправляющих солнечные лучи на приемник, в котором, в конечном счете, получают перегретый водяной пар для работы в паровой турбине.
Энергия, полученная приемником от солнца через гелиостаты (Вт), может быть определена по уравнению [2]:
|
|
Q = Rг·Апр·Fг Нг ·п, |
(1.1) |
где Нг – облученность зеркала гелиостата в Вт/м2 (для типичных условий Hг= 600 Вт/м2);
Fг – площадь поверхности гелиостата, м2 ;
п – количество гелиостатов;
Rг – коэффициент отражения зеркала концетратора, Rг =0,7÷0,8;
Aпр – коэффициент поглощения приемника, Апр < 1.
Площадь поверхности приемника может быть определена, если известна энергетическая освещенность на нем Нпр Вт/ мг,
|
|
Fпр=Q/Hпр. |
(1.2) |
В общем случае температура на поверхности приемника может достигать tпов= 1160 К, что позволяет нагреть теплоноситель до 700 оС. Потери тепла за счет излучения в теплоприемнике можно вычислить по закону Стефана-Больцмана:
|
|
qлуч = εпр·Co·(T/100)4, Вт/м2 , |
(1.3) |
где T – абсолютная температура теплоносителя, К;
εпр – степень черноты серого тела приемника;
Co – коэффициент излучения абсолютно черного чела, Вт/(м2·K4).
В задаче 2 рассмотрены вопросы использования перепада температур поверхностных и глубинных вод океана для получения электроэнергии на ОТЭС, работающей по известному циклу Ренкина. В качестве рабочего тела предполагается использование легкокипящих веществ (аммиак, фреон). Вследствие небольших перепадов температур (∆T=15÷26 oC) термический КПД установки, работающей по циклу Карно, составляет всего 5-9 %. Реальный КПД установки, работающей по циклу Ренкина, будет вдвое меньше [6]. В результате для получения доли относительно небольших мощностей на ОТЭС требуются большие расходы "теплой" и "холодной" воды и, следовательно, огромные диаметры подводящих и отводящих трубопроводов.
Если считать теплообменники (испаритель и конденсатор) идеальными, то тепловую мощность, полученную от теплой воды Q0, Вт можно представить как
|
|
Q0=r·V·Cp·∆T, |
(1.4) |
где r – плотность морской воды, кг/м3;
Ср – массовая теплоемкость морской воды, Дж/(кг · К);
V – объемный расход воды, м3/с ;
∆T = T1-T2 – разность температур поверхностных и глубинных вод (температурный перепад цикла) в °С или К.
В идеальном теоретическом цикле Карно механическая мощность N0 (Вт) может быть определена как:
|
|
N0=ηtk·Q0 , |
(1.5) |
или с учетом (1.2) и выражения для термического КПД цикла Карно ηtk:
|
|
N0=r·Cp·V·(∆T)2/T1. |
(1.6) |
Задача 2 посвящена тепловому потенциалу геотермальной энергии, сосредоточенной в естественных водоносных горизонтах на глубине z (км) от земной поверхности. Обычно толщина водоносного слоя h (км) меньше глубины его залегания. Слой имеет пористую структуру - скальные породы имеют поры, заполненные водой (пористость оценивается коэффициентом α). Средняя плотность твердых пород земной коры rгр =2700 кг/м3 , а коэффициент теплопроводности λгр =2 Вт/(м·К). Изменение температуры грунта по направлению к земной поверхности характеризуется температурным градиентом (dT/dz), измеряемым в °С/км или К/км .
Наиболее распространены на земном шаре районы с нормальным температурным градиентом (менее 40 °С/км) с плотностью исходящих в направлении поверхности тепловых потоков ≈ 0,06 Вт/м2 (например, Алматинская область). Экономическая целесообразность извлечения тепла из недр Земли здесь маловероятна.
В полутермальных районах температурный градиент равен 40-80 °С/км (например, Северный Кавказ). Здесь целесообразно использовать тепло недр для отопления, в теплицах, в бальнеологии.
В гипертермальных районах (вблизи границ платформ земной коры) градиент более 80 °С/км. Здесь целесообразно строить ГеоТЭС [2].
При известном температурном градиенте можно определить температуру водоносного пласта перед началом его эксплуатации:
|
|
Tг=To+(dT/dz)·z, |
(1.7) |
где Тo - температура на поверхности Земли, К (°С).
В расчетной практике характеристики геотермальной энергетики обычно относят к 1 км 2 поверхности F.
Теплоемкость пласта Спл (Дж/К) можно определить по уравнению
|
|
Cпл=[α·ρв·Cв+(1 – α)·ρгр·Cгр]·h·F, |
(1.8) |
где ρв и Св – соответственно плотность и изобарная удельная теплоемкость
воды;
ρгр и Сгр – плотность и удельная теплоемкость грунта (пород пласта); обычно ρгр = 820-850 Дж/(кг·К).
Если задать минимально допустимую температуру, при которой можно использовать тепловую энергию пласта Т1 (К), то можно оценить его тепловой потенциал к началу эксплуатации (Дж):
|
|
E0=Cпл·(T2-T1). |
(1.9) |
Постоянную времени пласта τ0 (возможное время его использования, лет) в случае отвода тепловой энергии путем закачки в него воды с объемным расходом V (м3/с) можно определить по уравнению:
|
|
τ0=Cпл/(V·ρв·Св). |
(1.10) |
Считают, что тепловой потенциал пласта во время его разработки изменяется по экспоненциальному закону:
|
|
|
(1.11) |
где τ - число лет с начала эксплуатации;
е - основание натуральных логарифмов.
Тепловая мощность геотермального пласта в момент времени τ (лет с начала разработки) в Вт (МВт):
|
|
|
(1.12) |
2 Расчетно-графическая работа № 2
2.1 Задание
Задача 1.
Определить объем биогазогенератора Vб и суточный выход биогаза Vг в установке, утилизирующей навоз от п коров, а также обеспечиваемую ею тепловую мощность N (Вт). Время цикла сбраживания навоза τ = 14 сут при температуре t = 25 ° С; подача сухого сбраживаемого материала от одного животного идет со скоростью W = 2 кг/сут; выход биогаза из сухой массы νг= 0,24 м3/кг. Содержание метана в биогазе составляет 70 %. КПД горелочного устройства η. Плотность сухого материала, распределенного в массе биогазогенератора, ρсух ≈ 50 кг/мг. Теплота сгорания метана при нормальных физических условиях Qнр =28 МДж/м3. Исходные данные выбираются по таблице 2.1.
Таблица 2.1
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
n |
24 |
20 |
18 |
16 |
14 |
12 |
10 |
8 |
6 |
4 |
|
|
Численные значения величин, выбираемые по последней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
η |
0,7 |
0,7 |
0,68 |
0,68 |
0,66 |
0,66 |
0,64 |
0,62 |
0,6 |
0,6 |
Задача 2.
Используя формулу Л.Б. Бернштейна, оценить приливный потенциал бассейна Э пот (кВт·ч), если его площадь F км2, а средняя величина прилива Rср м. Исходные данные выбираются по таблице 2.3.
Таблица 2.3
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
F ,км2 |
400 |
700 |
1000 |
1500 |
2000 |
2200 |
2500 |
3000 |
3500 |
4000 |
|
|
Численные значения величин, выбираемые по предпоследней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
R ср ,м |
8,0 |
7,5 |
7,2 |
7,0 |
6,8 |
6,5 |
6,0 |
5,4 |
5,2 |
5,0 |
Задача 3.
Для отопления дома в течение суток потребуется Q ГДж теплоты. При использовании для этой цели солнечной энергии тепловая энергия может быть запасена в водяном аккумуляторе. Допустим, что температура горячей воды t1°С. Какова должна быть емкость бака аккумулятора V (м3), если тепловая энергия может использоваться в отопительных целях до тех пор, пока температура воды не понизится до t2 °C? Величины теплоемкости и плотности воды взять из справочной литературы. Исходные данные выбираются по таблице 2.2.
Таблица 2.2
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
Q, ГДж |
0,56 |
0,58 |
0,60 |
0,62 |
0,64 |
0,56 |
0,64 |
0,62 |
0,60 |
0,58 |
|
|
Численные значения величин, выбираемые по предпоследней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
t1 , oC |
52 |
50 |
54 |
50 |
52 |
54 |
52 |
50 |
52 |
50 |
|
|
Численные значения величин, выбираемые по последней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
t2,°C |
31 |
30 |
29 |
28 |
27 |
31 |
30 |
29 |
28 |
27 |
Задание 4.
Как изменится мощность малой ГЭС, если напор водохранилища Н в засушливый период уменьшится в п раз, а расход воды V сократится на m %? Потери в гидротехнических сооружениях, водоводах, турбинах и генераторах считать постоянными. Исходные данные выбираются по таблице 2.4.
Таблица 2.4
|
Величины и единицы их измерения |
Численные значения величин, выбираемые по начальной букве фамилии студента |
|||||||||
|
А, К Ф |
Б, Л, Х |
В, М, Ц |
Г, Н, Ч |
Д, О, Ш |
Е, П, Щ |
Ё, Р, Э |
Ж, С, Ю |
З, Т Я |
И, У |
|
|
n |
3 |
2 |
1,2 |
1,5 |
3 |
2 |
1,2 |
1,5 |
3 |
2 |
|
|
Численные значения величин, выбираемые по последней цифре номера зачетной книжки |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
m |
30 |
10 |
20 |
30 |
50 |
30 |
10 |
20 |
40 |
20 |
2.2 Методические указания к расчетно-графической работе № 2
В задаче 1 рассмотрены вопросы использования биотоплива для преобразования его энергии в тепловую или электрическую в сельскохозяйственных предприятиях и на фермах. Одним из видов биотоплива являются отходы жизнедеятельности животных (навоз), при переработке которых (сбраживание) в биогазогенераторах можно получать биогаз, в состав которого (70 % по объему) входит метан; теплота сгорания метана при НФУ Qнp =28 МДж/м3 . Время полного сбраживания субстрата, состоящего из воды, навоза и ферментов, в зависимости от температуры изменятся от 8 до 30 сут. Плотность сухого материала в субстрате составляет ρсух ≈50 кг/m3 . Выход биогаза от 1 кг сухого материала в сутки составляет примерно νг =0,2 ÷ 0,4 м3/кг. Скорость подачи сухого сбраживаемого материала в биогазогенератор (метантенк) W зависит от вида животных и их количества на ферме [1].
Если обозначить через т0 (кг/сут) подачу сухого сбраживаемого материала, то суточный объем жидкой массы, поступающей в биогазогенерагор (м3/сут), можно определить по формуле:
|
|
Vсут=m0/ρсух. |
(2.1) |
Объем биогазогенератора, необходимого для фермы (м3):
|
|
Vб=τ·Vсут. |
(2.2) |
Суточный выход биогаза:
|
|
Vг=m0·ν г . |
(2.3) |
Тепловая мощность устройства, использующего биогаз (МДж/сут) или (Вт),
|
|
N=η·Qнр·Vг·ƒм |
(2.4) |
где fм – объемная доля метана в биогазе;
η – КПД горелочного устройства (≈ 60%).
В задаче 2 рассмотрен расчет энергетического потенциала Эпот (кВт·ч) приливной энергии океанического бассейна, имеющего площадь F км2, если известна средняя величина приливной волны Rср м. В научной литературе существует несколько уравнений, позволяющих определить приливный потенциал бассейна. Для расчета используем уравнение, предложенное ученым Л.Б. Бернштейном [6]:
|
|
Эпот =1,97·106·R2ср·F, |
(2.6) |
В задаче 3 рассмотрен расчет емкости водяного аккумулятора тепловой энергии, предназначенного для отопления, горячего водоснабжения и кондиционирования воздуха в жилом доме. Источником тепловой энергии может быть, например, солнечная энергия, улавливаемая солнечными панелями па крыше дома. Циркулирующая в панелях вода после нагрева направляется в бак - аккумулятор, а оттуда насосом в отопительные батареи и к водоразборным кранам горячего водоснабжения. Могут быть и более сложные, комплексные системы аккумулирования тепла с использованием засыпки из гравия и др. [2].
Необходимый объем бака - аккумулятора V (м3) для воды – можно определить по известному уравнению для изобарного процесса, если знать: суточную потребность в тепловой энергии для дома Q (ГДж); температуру горячей воды, получаемой в солнечных панелях t1 0С; наименьшую температуру в баке t2 °C, при которой еще возможно действие отопительной системы:
|
|
Q=ρ·V·Cр·(t1-t2), |
(2.5) |
где р - плотность морской воды, кг/м3;
Ср - удельная массовая теплоемкость воды при ρ = const, Дж/(кг · К).
В задаче 4 рассмотрены вопросы оценки изменения мощности малой ГЭС при колебаниях расхода воды и напора. Известно, что мощность ГЭС (Вт) можно определить по простому уравнению [13]:
|
|
Эпот =1,97·106· V2ср·Н, |
(2.7) |
где V – объемный расход воды в м3/с ;
Н – напор ГЭС в м ;
η – КПД ГЭС, учитывающий потери в гидравлических сооружениях,
водоводах, турбинах, генераторах. Для малых ГЭС η≈0,5;
КПД гидротурбин изменяется в пределах 0,5 ÷ 0,9.
Список литературы
1. Ресурсы и эффективность использования возобновляемых источников энергии в России / П.П. Безруких, Ю.Д. Арбузов, Г.А. Борисов и др. - СПб.: Наука, 2002.
2. Твайделл Д. Возобновляемые источники энергии/Д.Твайделл, А.Уэйр. - М.: Эиергоатомиздат, 1990.
3. Девинс Д. Энергия: Пер. с англ / Д.Девинс. - М.: Энергоатомиздат, 1985.
4. Виссарионов В.И. Экологические аспекты возобновляемых источников энергии / В.И.Виссарионов, Л.А.Золотов. - М.: МЭИ, 1996.
5. Шефтер Я.Н. Использование энергии ветра / Я.Н.Шефтер. – М.: Энергоатомиздат, 1983.
6. Коробков В.А. Преобразование энергии океана / В.А.Коробков. - Л.: Судостроение, 1986.
7. Геотермальное теплоснабжение / А.Г. Гаджиев, Ю.Н. Султанов, П.Н. Ригер и др. – М.: Энергоатомиздат, 1984.
8. Вымороков Б.М. Геотермальные электростанции / Б.М.Вымороков. – М.,Л.: Энергия, 1966.
9. Оборудование нетрадиционной и малой энергетики: справочник — каталог / Ю.Д. Арбузов, П.П. Безруких и др. - АО «Новые и возобновляемые источники энергии», 2002.
Содержание
|
1 Расчетно-графическая работа № 1 |
3 |
|
1.1 Задание |
3 |
|
1.2 Методические указания к расчетно-графической работе № 1 |
5 |
|
2 Расчетно-графическая работа № 2 |
8 |
|
2.1 Задание |
8 |
|
2.2 Методические указания к расчетно-графической работе № 2 |
10 |
|
Список литературы |
12 |
Сводный план 2013 г., поз. 10
Еркин Сериккалиевич Умбетов
Ольга Петровна Живаева
Основы использования
возобновляемых источников энергии и энергосбережение
Методические указания и задания к выполнению
расчетно-графических
работ № 1, 2 для студентов специальности
5В081200 - Энергобеспечение сельского хозяйства
Редактор Л.Т. Сластихина
Специалист по стандартизации
Н.К. Молдабекова
Подписано в печать ________
Формат 60х84 1/16
Тираж 50 экз.
Бумага типографская №1
Объем 0,81
уч.-изд.л.
Заказ ______. Цена 81 тг.
Копировально-множительное бюро
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
050013, Алматы, ул. Байтурсынова, 126
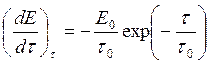 .
.