АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ

КОММЕРЦИЯЛЫҚ ЕМЕС АКЦИОНЕРЛІК ҚОҒАМЫ

«Өндіріс кәсіпорындарын электрмен жабдықтау» кафедрасы

 

                                                                 

 

 

Электрэнергетикадағы математикалық есептер және компьютерлік моделдеу 

5В071800 – Электр энергетика мамандығының студенттерінің №1 есептік-графикалық жұмыстарына әдістемелік нұсқаулар

 

 

 

Алматы 2010 

ҚҰРАСТЫРУШЫ:  К.А.Бакенов, M.А.Тергеусизова. Электрэнергетикадағы математикалық есептер және компьютерлік моделдеу. 5В071800 – Электр энергетика мамандығының студенттерінің №1 есептік-графикалық жұмыстарына әдістемелік нұсқаулар. – Алматы: АЭжБУ, 2010.-20 б.

 

Мазмұны 

Кіріспе	4
1 Тапсырма №1. Графикалық    әдіспен    сызықты   теңдеулер   жүйесін шешу. Фунция экстремумының нүктесін анықтау және рұқсатты шешім ауданыны тұрғызу	4
2 Тапсырма №2. Синхронды қозғалтқыштардың оңтайлы реактивті қуатын  Лагранждың анықталмаған көбейткіштер әдісімен анықтау	7
3 Тапсырма №3.  Қореқтендіретін қосалқы стансаның трансформатор жүктемесінің ықтималдығын анықтау; математикалық күту, дисперция, трансформатор жүктемесінің лездік шамасының ортаквадраттық ауытқуы; 0,4 кВ шинасына қатысты электржабдықтау жүйесінің сенімділік көрсеткіштері; 0,4 кВ шинасына қатысты бір жылғы жіберілмеген электроэнергия шамасы	12
Әдебиеттер тізімі	17

 

Кіріспе

 

Оқу жоспарына сәйкес, 5В071800 – Электрэнергетика  мамандығы бойынша оқытылатын  студенттер «Электроэнергетикадағы компютерлік моделдеу және математикалық есептер»  курсын оқиды, онда студенттердің өткен пәндер бөлімінен өзіндік қайталауға мүмкіндік беретін әрқайсысы үш тапсырмадан тұратын екі есептік-графикалық жұмыс қарастырылған.

Курс бойынша  емтиханға тек  есептік-графикалық жұмысты  жақсы орындап қорғаған студенттер жіберіледі.

 

1  Тапсырма №1. Графикалық әдіспен  сызықты теңдеулер жүйесін шешу. Тапсырмаға сәйкес функция экстремумының нүктесін анықтау және рұқсатты шешім ауданын тұрғызу

 

Есепке алғашқы мәліметтер 1.1, кесте бойынша нұсқаларды таңдау ережесіне сәйкес жүргізіледі.

 

Кесте 1.1 – Алғашқы мәліметтер

Студент тегінің алғашқы әрпі	А, Д	Б, Е	В, Г, Я	Ж, З, И, Л	К, Ю	М, О	Н, П	Р, Т, У, Ф	С, Ч, Ц	Х, Ш, Щ, Э
Мақсаттық функция элементтері
С1	1	2	1	-1	5	2	2	1	-4	5
С2	-2	1	5	3	2	1	3	-2	5	1
С3	3	-1	4	2	-1	-1	6	-3	6	3
С4	10	-1	-6	-	-	-1	3	-	-	1
f(х)	max	min	max	min	max	min	max	min	max	min

 

1.1 Әдістемелік нұсқаулар

 

Сызықты теңдеулер жүйесін графикалық әдіспен шешу. х₂×х₁ координат жүйесінде теңсіздікті а₁х₁+а₂х₂=а₀  шекті түзу жарты жазықтықты анықтайды. 

Егер теңсіздіктер жүйесі берілген болса, онда  рұқсатты шешімдер ауданын (РША) тұрғызу үшін шекаралық  түзулер тұрғызады, содан  теңсіздіктер мәліметтері орындалатын  жартылай жазықтықтар орындалады.

РША  (төбе) координаттарын алу үшін, осы төбелерде түйісетін түзулер теңдеулер жүйесін шешу керек.

n>2  санынында теңсізді

а₁х₁+ а₂х₂ +........+ а_nх_nа₀  теңдеуге эквивалентті

а₁х₁+ ........+ а_nх_n +х_n+1 = а₀; х_n+1 ≥0 және

а₁х₁+ ........+ а_nх_n≥0.

сәйкесінше  а₁х₁+ ........+ а_nх_n -х_n+1 =0.

х_n+1 айнымалысын қосымша ( баланстық) деп атайды.

Егер теңсіздік жүйесі берілсе

 

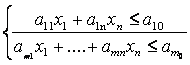
онда  оны  эквиваленнті сызықты теңдеулер жүйесінің (n+m) айнымалылармен алмастыруға болады.

 

 

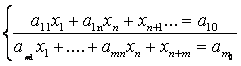
мұнда

 

Вектор–потенциал , тура басизті айнымалыларға перпендикуляр, ол f функциясының жылдам өсу бағытын көрсетеді, ал вектор   f функциясының жылдам төмендеуіне бағытталған.

Берілген есеп  Mathcad программасының көмегімен шешіледі. Бұл үшін функция теңдеуіне сәйкес 1.1, кестесінен берілген мәліметтерді енгізу қажет, ал 1.2, кестесінен шектеу теңдеуіне сәйкес мәліметтерді алу қажет. Алынған шешімдерді теріс емес принцип бойынша орындауға талаптар қою.

 

1.2 кесте – Алғашқы мәліметтер

		Сынақ кітапшасының соңғы  № мәні
		Элеменнтер Аi.Bi.Cii	0	1	2	3	4	5	6	7	8	9
Тұтыну қуаты және қуат бірлігінің  берілу құны	Қорек көздері нің қуаты, Аi.j	а11	1	2	1	1	2	1	2	-1	1	6
		а12	1	3	-1	1	1	1	-1	1	2	-1
		а13	2	-4	2	2	1	2	1	2	-3	4
		а14	-6	-5	-1	-	-	-1	2	-	-	2
		а21	1	5	2	2	3	2	2	1	4	-9
		а22	1	-6	1	-3	2	1	1	-5	6	8
		а23	4	1	-3	1	1	-3	1	-1	2	7
		а24	-8	-1	1	-	-	1	1	-	-	1
		а31	4	4	1	2	5	1	-1	1	2	4
		а32	2	1	1	-5	3	1	4	1	-3	5
		а33	1	-2	1	6	4	1	-2	3	1	6
		а34	-4	3	1	-	-	1	-2	-	-	1
	Тұтынушылар қуаты B j	b1	1	1	2	-5	5	2	1	2	4	5
		b2	1	3	6	3	6	6	2	1	10	7
		b3	3	2	7	5	7	7	3	5	1	8
		b4	-	-	-	-	-	-	-	-	-	-
	Шектеу белгілері (    )	1	=		=			=			=
		2	=		=		=	=			=
		3	=		=			=			=

Графикте рұқсатты шешімдер және векторпотенциал ауданын тұрғызу, оның бағыты бойынша функцияның экстремум нүктелерін және оның координаттарын анықтау. Экстремум нүктесінде айнымалыларды және функция мәнін анықтау.

 

1.2  Мысал

f( х_4,х₅)= 4х₄+х₅

Given

5х₁-2х₂+2х₃+х₄-х₅ = 13

2х₁-2х₂+х₃-х₄+х₅ = 5

х₁+2х₂+4х₄-2х₅ = 5

 

Find (х_1, х_2, х_3, х_4, х₅)      

 

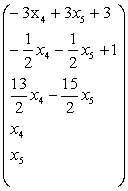
Ары қарай  х₄ және х₅ тәуелділігінен шектеулі теңдеу өрнегін тұрғызу қажет.

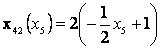
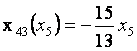
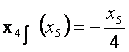
График бойынша потенциал-вектор бағытын анықтаймыз, қазіргі жағдайда оның координаттары (0,0) және (4,1); содан кейін осы векторға перепендикуляр тұрғызамыз, ол арқылы біз функцияның жылдам өсу бағытын анықтаймыз.

Перпендикулярдың ОДР мен қилысқан бірінші нүктесі min функция болып табылады, ал соңғысы – max.  Біздің жағдайда: min ƒ (0,0), ал max ƒ (1,1). 

Алынған мәндермен барлық айнымалылар және экстремум нүктесіндегі фунция мәні анықталады.

 

График саламыз.

  

 

 

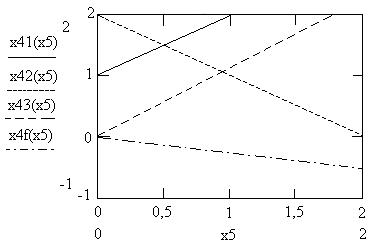
х₁(х_4,х₅) = 3: х₂(х_4,х₅) = 0: х₃(х_4,х₅) = -1;

махƒ(х_4,х₅)→ 5; minƒ(х_4,х₅) = 0.

 

 

2 Тапсырма №2. Синхронды қозғалтқыштардың оңтайлы реактивті қуатын  Лагранждың анықталмаған көбейткіштер әдісімен анықтау

 

Өндірістік өнеркәсіптің ТҚ 6-10 шиналарына  N синхронды электрқозғалтқыштар қосылған, Лагранждың анықталмаған көбейткіштер  әдісі арқылы  кәбілдер кедергісін ескермей әрбір синхронды қозғалтқышының тиімді реактивті қуатын анықтау керек. 6-10 кВ жағындағы  компенсацияға жататын реактивті жүктеме  есеп нұсқасымен анықталады.

Әрбір нұсқаның есепке берілген мәліметтері 2.1, 2.2 және 2.3 кестесінен анықталады. Қозғалтқыштардың техникалық сипаттамалары 2.4 кестесінде берілген.

 

2.1 Кесте – Алғашқы мәліметтер

Меншікті құн	Сынақ  кітапшасының соңғы нөмірінің алдындағы сан
	0	1	2	3	4	5	6	7	8	9
с0 (ш.б./кВт)	55	60	65	70	75	50	72	68	80	73

 

2.2 Кесте – Алғашқы мәліметтер

Компенсацияға жататын қуат	Сынақ  кітапшасының соңғы саны
	0	1	2	3	4	5	6	7	8	9
QA,Мвар	1,4	1,6	1,3	1,5	1,2	0,8	0,9	1,5	1,2	0,8

 

 

2.3 Кесте – Алғашқы мәліметтер

СҚ параметрі және саны	Студент тегінің алғашқы әрпі
	А, Д	Б, Е	В, Г, Я	Ж, З, И, Л	К, Ю	М, О	Н, П	Р, Т, У, Ф	С, Ч, Ц	Х, Ш, Щ, Э
N	4	5	6	4	5	5	4	4	4	4
Uн(кВ)	6	6	10	6	6	10	10	10	6	6
Рн(кВт)	1000	2500	3200	6300	800	1250	4000	1600	400	6300
n айн/мин	1000	750	750	1000	750	1000	750	1000	500	1000
	600	500	600	750	500	600	600	600	300	750
	500	600	500	600	375	500	500	375	187	600
	250	250	375	500	300	300	1000	250	167	500
		300	300		167	250
			250

 

2.1 Әдістемелік нұсқау

Есепті  Лагранж көбейткіштері тәсілімен шығарғанда  f  мақсаттық функциясы және φ_i  шектуі беріледі.  Есеп  шектеулі  φ_i (х_1.........х_n ) = b_i   функция экстремум нүктесінде х₁,  х_2........., х_n,  табу болып табылады.

Әдістің  негізгі мақсаты фунция кейбір бір шешімге түрлендіру, ол үшін есеп шешімі шығарылып және шартты экстремум анықталады. Функцияны, айнымалылар саны екіге тең кезінде қарастырамыз.

 

                                                  f(x₁, x₂),                                                               (2.1)

                                             φ_i (х_1.........х_n ) = 0.                                                       (2.2)

 

Берілген шартқа Лагранж функциясының  түрі келесідей болады

 

                                           L (x₁, x_2, λ)= f(x₁, x₂ )+ λ[b-φ(x₁, x₂ )]                        (2.3)

 

мұнда  λ – Лагранж  көбейткіші, шартсыз экстремум, ол шартты экстремуммен  f (x₁, x₂) және λ мән саны шектеу санына тәуелді.

 

2.4 Кесте – Алғашқы  мәліметтер

Кернеу Uн,кВ	Айналу жиілігі n, айн/мин	Номиналды қуат		Шамалар (кВт)
		Активті Рн, кВт	Реактивті Qн, квар	Д1	Д2
1	2	3	4	5	6
10	1000	1250 1600 4000	645 817 2010	6,77 7,58 10,6	6,98 7,56 11,8
	750	4000 3200	2010 1615	14,2 12,2	13,0 12,3

            2.4 кестенің жалғасы

1	2	3	4	5	6
10	600	1250 1600 3200 4000	637 820 1620 2010	8,6 9,43 10,3 11,3	6,05 8,24 13,6 13,6
	500	1250 3200 4000	642 1620 2039	9,08 9,72 16,4	8,53 11,2 15,4
	375	1600 3200	825 1625	10,3 14,7	10,4 14,7
	300	1250 3200	645 1620	9,71 14,0	8,07 15,1
	250	1250 1600 3200	650 825 1635	9,96 11,1 18,2	8,83 9,51 14,4
6	1000	1000 6300	511 3150	5,09 14,6	3,99 13,1
	750	6300 2500 800	3150 1265 407	18,1 11,2 4,9	14,8 10,2 4,57
	600	6300 2500 1000	3150 1265 511	17,1 10,9 7,66	14,4 8,46 5,38
	500	6300 2500 1000 800 400	3160 1265 511 412 209	21,0 11,5 6,61 6,48 3,88	16,3 9,36 5,88 5,54 2,97
	250	1000 2500	520 1270	10,0 15,9	7,19 11,7
	300	2500 800 400	1270 416 211	15,3 7,76 5,13	10,7 6,00 5,08
	375	800	415	7,07	5,25
	187	400	216	5,97	5,38
	167	800 400	423 216	10,5 7,64	8,3 4,25

 

Осындай жағдайда  f(x₁, x₂) шартты функция экстремумының анықтауда, жылдам L функциясының экстремумын табу болып табылады, өйткені ОДР-де  f(x₁, x₂) функциясын Лагранж функциясымен ауыстыруға болады.

Лагранж функциясын шешу үшін x₁, x_2, λ  жеке туындылары алынады және 0-ге теңестіріледі. Бұл экстремумның қажетті шарты.

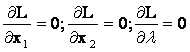                                                .                                     (2.4)

 

(2.4) жүйесін шешу есепті шығаруға қажеттті шарттты береді. Экстремум нүктесін табу үшін 2-ші туындыны талдау қажет d²L < 0 (max), d²L > 0 (max). Бұл әдістің кемшілігі мақсатты функцияны теңсіздік ретінде шектеулі шешу мүмкіндігі жоқ.

Шығару реттілігі:

а) Лагранж функциясы құрылады      

L (x₁……..x_n, λ₁……, λ_m)= f (x₁….x_n)+[b_i-φ_i(x₁….x_n)];

б) экстремум нүктесін табу үшін жеке туындылар теңдеу жүйесі құрылады:

 

;

                                                                      ;

;

 

в) ары қарай барлық нүктелерден,  берілген  шектеуде экстремум нүктесі бар функция таңдап алынады.

Энергетикада  Лагранж көбейткіштері әдісі  реактивті қуат компенсациясы сұрақтарында, электрэнергия өндірісіндегі  шығындарға т.б. қолданылады;

а) жалпы жағдайда реактивті қуат өндіруге кеткен шығынның айнымалы бөлігі  анықталуы мүмкін болады.

 

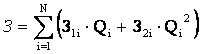                                                                                    (2.5)

мұнда  Q_i - қорек  көздерден өндірілетін реактивті қуат;

   З_1i - 1 Мвар өндірілетін қуаттың меншікті шығыны (у.е./Мвар);

   З_2i - 1 Мвар² өндірілетін қуаттың меншікті шығыны (у.е./Мвар²);

б)  Синхронды қозғалтқыштан алуға болатын реактивті қуаттың максималды шамасы

                                      

                                                   Q_Mi= _MMQ_Mi                                                    (2.6)

 

мұнда _M 1,39

М-қуаты және айналу жылдамдығы бірдей топтағы синхронды қозғалтқыштар саны;

в) шығынды құраушылар келесі формулалар бойынша анықталады

 

,

                                                                                            

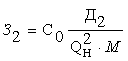                                                   ;                                                (2.7)

 

г) есепті шешу үшін Лагранж функциясын келесі түрде құру қажет:

                   (2.8)

мұнда  m-шектеу теңдеуінің саны.

Берілген есепке Лагранж функциясының түрі келесідей болады.

 

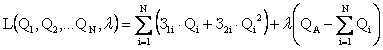                    .                          (2.9)

 

Экстремумның шартты нүктесін табу үшін  жеке туындыларды анықтаймыз

 

                                                   ,                              (2.10)

 

          .

 

Алынған теңдеулер жүйесінен анықтаймыз

 

                                                                                               (2.11)

  

және

 

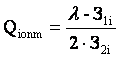                                                  ;                                            (2.12)

 

 

д) Тиімді реактивті қуатты Q_oпmi-ді  Q_mi-мен салыстыру қажет. Егер кезкелген СҚ үшін Q_oптК>Q_МК, онда  Q_oптК ретінде Q_МК алынады. Мұндай жағдайда қалған СҚ–тар үшін анықталмаған Лагранж көбейткішін λ¹ қайта  анықтау қажет.

 

                                                                                                      (2.13)

 

мұнда Q¹_A=Q_A-Q_М   және қалған СҚ-дан тиімді реактивті қуатты  анықтаймыз

 

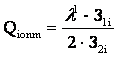                                                        .                                       (2.14)

 

Егер Q_ioптQ_im, онда Q_ioпт мәнінің шамасы алынады. Бұл кезде Лагранж көбейткішінің шамасы λ өзгермейді;

е)  Q_ioпт есебінің  дұрыстығы түйіндегі реактивті қуаттың теңдік шарты бойынша тексеріледі

 

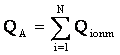
.                                        (2.15)

3 Тапсырма №3. Қореқтендіретін қосалқы стансаның трансформатор жүктемесінің ықтималдығын анықтау; математикалық күту, дисперция, трансформатор жүктемесінің лездік шамасының ортаквадраттық ауытқуы; 0,4 кВ шинасына қатысты электржабдықтау жүйесінің сенімділік көрсеткіштері; 0,4 кВ шинасына қатысты бір жылғы жіберілмеген электроэнергия шамасы

 

Кіші кернеу шинасынан (3.1 суретті қара) цех қосалқы стансасынан (ТҚС) үш топ (n₁,n₂,n₃) электрқозғалтқыштары қоректенеді, тұтынатын қуаты n₁хS₁,n₂ хS₂,n₃ хS₃ (3.1 кестені қара) және бірдей cosφ=0,85. Әрбір қозғалтқыштың қосылу ықтималдығы  бірінші топ – р₁, екінші топ – р₂, үшінші топ- р₃, (3.2 кестені қара). Жұмысқа қосылу оқиғасы және әрбір топтағы кезкелген қозғалтқыштың өшіп қалу оқиғасы  тәуелсіз ретінде қарастырылады. Электр жабдықтаудың жүйесінің сенімділік элемент көрсеткіштері  3.4 және 3.5, кестелерінде көрсетілген.

Анықтау қажет:

а)  қоректендіретін қосалқы стансаның  (ТҚС) трансформаторларының жүктемелерін:

1) S₁=0кВА;

2) S₂=60кВА;

3) S₃=100кВА;

4) тұтынушының максималды қуат шамасына;

 

б)  математикалық күту, дисперсия, трансформатор жүктемесінің кезкелген шамасының ортаквадраттық ауытқуы;

в)   3.1, суретте көрсетілген  0,4 кВ шинасына қатысты  (алдын-ала ажыратуды ескермей) электржабдықтау жүйесінің сенімділік көрсеткіштерін анықтау.

1) істен шығу жиілігі λ_с, 1/г;

2) қалыптасудың орташа уақыты t_aвc, сағ;

3) істен шығу орташа жұмысы Т_с, жыл ;

4) тоқтап қалу коэффициенті g_c, дайындық коэффициенті р_с;

 

г)  0,4 кВ шинаға қатысты жіберілмей қалған электрэнергияның шамасын  бір жылға (8760сағ)  анықтау.

 

 

 

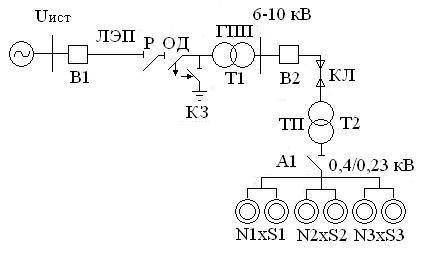
                                              3.1 сурет – Электржабдықтау сұлбасы

 

3.1 Әдістемелік нұсқаулар:

 

а)  трансформатордың берілген жүктеме ықтималдығын анықтау үшін тәуелсіз сынау сұлбасы қолданады-биноминалды таралу заңы

 

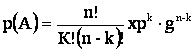                                                                                    (3.1)

 

мұнда  n – тәуелсіз  сынақ саны;

            к – А оқиғасы n-тәуелсіз  сынақ  сериясынан шыққан сынақ саны;

            р – қозғалтқышты қосу ықтималдығы;

                      g – қозғалтқышты өшіру ықтималдығы.       

         б)  математикалық күту, дисперсия, трансформатор жүктемесінің кезкелген шамасының ортаквадраттық ауытқуын  анықтау үшін келесі өрнектер қолданылады;

, кВА,

 

                                             , кВА²,                                   (3.2)

                                                 

                                                , кВА

 

мұнда m – электрқозғалтқыштар тобының саны;

в)  0,4 кВ шинасына қатысты тізбектей жалғанған сұлба элементтеріне  электржабдықтау жүйесінің сенімділік көрсеткіштерін анықталады:

1) істен шығу жиілігі

 

                                                   ;                                               (3.3)

 

2) қалыптасудың орташа уақыты

 

                                                       ;                                     (3.4)

 

3) істен шығу орташа жұмысы

                                        

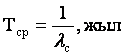
;                                        (3.5)

 

4) тоқтап қалу коэффициенті

 

                                        ;                              (3.6)        

 

5) дайындық коэффициенті

 

                                                    .                                 (3.7)

 

г)  0,4 кВ шинаға қатысты жіберілмей қалған электрэнергияның шамасын  бір жылға анықтау.

 

                                           .                     (3.8)

3.1 Кесте – Алғашқы мәліметтер

Сынақ кітапшасы ның соңғы саны	0	1	2	3	4	5	6	7	8	9
n1xS1,кВт	3x10	3x15	2x15	4x10	4x15	3x40	3x40	2x25	4x35	4x25
n2xS2,кВт	2x20	3x20	3x10	2x20	2x20	3x20	3x20	4x15	4x10	5x10
n3xS3,кВт	3x30	2x40	3x40	3x30	2x40	4x10	4x10	2x35	3x20	2x20

 

3.2 Кесте – Алғашқы мәліметтер

Сынақ  кітапшасының соңғы нәмірінің алдындағы сан	0	1	2	3	4	5	6	7	8	9
р1	0,6	0,9	0,5	0,7	0,9	0,8	0,4	0,4	0,3	0,5
р2	0,7	0,8	0,6	0,6	0,5	0,7	0,3	0,9	0,8	0,6
р3	0,5	0,7	0,7	0,5	0,8	0,6	0,5	0,6	0,5	0,4

 

3.3 Кесте – Алғашқы мәліметтер

Студент тегінің алғашқы әрпі	А, Д	В, Г, Я	Б, Щ, Е	Ж, З, И,	К, Ф Э	Л М, О	Н, П Ю	Р, Т, У,	С, Ч, Ц	Х, Д Ш,
Жүйе кернеуі,кВ	330	220	110	35	330	220	110	35	220	110
ЭБЖ ұзындығы,км	110	150	200	30	150	100	80	20	100	140
а) Ауа ажыратқышы	ВВ	ВВ	ВВ	ВВ	ВВ	-	-	-	-	-
б) Майлы ажыратқышы	-	-	-	-	-	МВ	МВ	МВ	МВ	МВ
Кәбіел желі (КЖ) ұзындығы, км	1	2	3	4	5	0,4	0,5	0,6	0,7	0,8
Кәбіелді желілерді төсеу тәсілдері	траншеяда	туннелде	блокта	траншеяда	туннелде	блокта	траншеяда	туннелде	блокта	траншеяда

3.4 Кесте – Электржабдықтау жүйе элементтерінің істен шығу жиілігі , 1/жыл

Электржабдықтау жүйесінің элементтері	Кернеу, кВ
	330	220	110	35	6-10	1-дейін
Біртізбекті ЭБЖ (100 км-ге)	1,23	1,4	2,1	2,2	2,5
КЖ  (100 км-ге)
- траншеяда	-	-	-	-	8,0
-туннелде	-	-	-	-	1,3
-блокта	-	-	-	-	10,0
Трансформаторлар	0,03	0,02	0,02	0,018	0,023
Ауа ажыратқыштар	0,05	0,06	0,04	0,02	0,02
Майлы ажыратқыштар	-	0,02	0,05	0,05	0,05
Айырғыштар және қысқа тұйықтағыштар	0,03	0,03	0,02	0,01	-
Айырғыштар	0,03	0,03	0,03	0,02	-
Автоматтар	-	-	-	-	-	0,14

 

3.5 Кесте- Электржабдықтау жүйесінің элементтерінің қалыптасуының орта уақыты t_авi, сағ

Электржабдықтау жүйесінің элементтері	Кернеу, кВ
	330	220	110	35	6-10	1-дейін
Біртізбекті ЭБЖ	8,1	6,5	4,2	5,6	12,0
КЖ :
- траншеяда	-	-	-	-	7,0
-туннелде	-	-	-	-	11,5
-блокта	-	-	-	-	4,0
Трансформаторлар	200	150	100	90	15
Ауа ажыратқыштар	60	40	30	24	20
Майлы ажыратқыштар	-	24	20	10	10
Айырғыштар және қысқа тұйықтағыштар	15	15	15	10	-
Айырғыштар	15	15	15	10	10
Автоматтар	-	-	-	-	-	4,0

 

Әдебиеттер тізімі

1.  Электрические системы. Математические задачи электроэнергетики        /Под ред, В.А. Веникова. - М.: Высшая школа, 1981. - 288 с.

2.  Веников        В.А.        и        др.        Регулирование        напряжения        в электроэнергетических системах. - М.: Энергоатомиздат, 1985. - 216 с.

3.  Вентцель    Е.С.    Исследование    операций:         задачи,    принципы, методология. - М.: Наука, 1988. - 208 с.

4.  Вентцель Е.С., Овчарова Л.А. Теория вероятности и ее инженерные приложения. - М.: Наука, 1988. - 480 с.

5.  Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию. - Минск: Высшая школа, 1978. - 256 с.

6. Гук Ю.Б. Анализ надежности электроэнергетических установок. - Л.: Энергоатомиздат, 1988. - 224 с.

7.       Гордиевский И.Г., Лордкипанидзе В. Д.  Оптимизация  параметров электрических сетей / Под ред. Г.В. Сэрбйновского. - М.: Энергия, 1978.

8.       Фокин Ю.А. Вероятностно-статические методы  в расчетах систем электроснабжения. - М.: Энергоатомиздат, 1985.

9.       Арзамасцев Д.А.,  Липес А.В., Мызин А.Л. Модели  оптимизации развития энергосистем. - М.: Высш. шк., 1987.

10.  Электрические сети и системы в примерах и иллюстрациях: Учеб.пособие для электроэнерг. спец. / В.В. Ежков. Г.К., Зарудский. Э.Н., Зуев и др.; Под ред. В.А. Строева. - М.: Высш. шк., 1999. - 352 с.

11.  Беллман А. Динамическое программирование / Пер. с англ. - М.; Изд-во иностр. лит., 1960.

12. Строев В.А., Рокотян И.С. Методы математической оптимизации в задачах электроснабжения. - М.: МЭИ, 1993.