Коммерциялық емес акционерлік қоғамы
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
«Электр станциялары, тораптары мен жүйелері»,
«Электржетегі және өндірістік қондырғылардың автоматизациясы»,
«Өндіріс кәсіпорындарын электрмен жабдықтау» кафедралары
ЭЛЕКТР ЭНЕРГЕТИКАДАҒЫ МАТЕМАТИКАЛЫҚ ЕСЕПТЕР ЖӘНЕ КОМПЬЮТЕРЛІК МОДЕЛДЕУ
5В071800 – Электр энергетика мамандығының барлық
оқу түрі бойынша оқитын студенттер үшін
Дәрістер жинағы
Алматы 2011
ҚҰРАСТЫРУШЫЛАР: 1 бөлім - Ж. К. Оржанова, , 2 бөлім - Н.К. Алмуратова, Қ.Ө. Гали, 3 бөлім – Қ. А. Бакенов. Электр энергетикадағы математикалық есептер және компьютерлік моделдеу. 5В071800 – Электр энергетика мамандығының барлық оқу түрі бойынша оқитын студенттер үшін арналған дәрістер жинағы. Алматы: КЕАҚ АЭжБУ, 2010.- 57б.
Дәрістер жинағында электрлік жүйелер тораптарын анализдеуде графтар теориясын және матрица алгебраларын қолдану, автоматты реттелуші энергетикалық жүйелердегі өтпелі процестерді математикалық зерттеудің негізгі кіріспесі қарастырылды.
Без.- 9, кесте 4, әдебиетті - 7 атау.
Пікір беруші: техн. ғыл. канд., профессор Борисов В.Н.
«Алматы энергетика және байланыс институті» коммерциялық емес акционерлік қоғамының 2010 ж. баспа жоспары бойынша басылады.
© Алматы энергетика және байланыс университеті, КЕАҚ 2011 ж.
Мазмұны
|
1 бөлім. Электрлік жүйелерді математикалык моделдеу |
4 |
|
1 дәріс. Электр энергетикасындағы математикалық есептеулер мен компьютерлік моделдеу. Курстың негізгі міндеттері мен қойылымы және оларды шешудің математикалық әдістері |
4 |
|
2 дәріс. Электр жүйелерінің орнықты режімдерінің математикалық моделі. Электр жүйесінің орнықты режімінің теңдеуі |
7 |
|
3 дәріс. Электр жүйесі күйінің теңдеуін шешу әдістері |
10 |
|
4 дәріс. Энергетикада сызықтық бағдарламалауды қолдану |
15 |
|
2 бөлім. Математикалык моделдеу |
19 |
|
1 дәріс. Моделдеу теориясының негізгі ұғымдары |
19 |
|
1.1 Моделдеу принциптері |
20 |
|
1.2 Математикалық моделдеу кезеңдері |
21 |
|
2 дәріс. Аналитикалық моделдеу. Жалпыланған электрмеханикалық түрлендіргіштерді моделдеу (ЖЭМТ) |
22 |
|
2.1 ЖЭМТ математикалық моделін құру |
22 |
|
3 дәріс. Моделді бағдарламалық іске асыру |
25 |
|
4 дәріс. Дифференциалдық теңдеулер жүйесін қолданып шешуді үйрену |
27 |
|
4.1 Бірінші реттік дифференциалдық теңдеуді Рунге-Кутта әдісімен шешу |
27 |
|
4.2 Дифференциалдық теңдеулер жүйесін Рунге-Кутта әдісімен шешу |
28 |
|
3 бөлім. Электр энергетикасындағы оңтайландыру (оптимизационные) есептері |
29 |
|
1 дәріс. Оңтайландыру есептерінің қойылуы және оларды шешу жолдары |
29 |
|
2 дәріс. Оңтайландыру (оптимизационные) есептерді шешу үшін сызықтық жобалауды қолдану |
32 |
|
3 дәріс. Электрэнергетикадағы тасымалдау есептері |
36 |
|
4 дәріс. Сызықты емес оңтайлы есептерді шешу |
41 |
|
5 дәріс. Айнымалы дискреттік және бүтінсанды оптимизациялық есептер |
44 |
|
6 дәріс. Кездейсоқ шыққан бағдарламалар кезіндегі оңтайландырылған есептер |
47 |
|
7 дәріс. Берілген анықталмаған ақпараты бар оңтайландырулық есептер |
49 |
|
8 дәріс. Көпкритерилі оңтайландырулық есептер |
52 |
|
Әдебиеттер тізімі |
55 |
1 бөлім. Электрлік жүйелерде математикалык моделдеу
1 дәріс. Электр энергетикасындағы математикалық есептеулер мен компьютерлік моделдеу. Курстың негізгі міндеттері мен қойылымы және оларды шешудің математикалық әдістері
Дәріс мазмұны:
– электр энергетикалық жүйелердің параметрлерін анықтау, электр энергетикадағы орнықтылыққа түсініктеме, жүйенің жеке элементтеріне математикалық модель құру.
Дәріс мақсаты:
– электрлік сұлбаларды, принципиальды сұлбаларды, орынбасу сұлбаларын оқып үйрену.
Электрлік жүйе (ЭЖ) деп энергетикалық жүйенің электрлік бөлігін түсінеміз, яғни өндіруші, түрлендіруші, беріліс, таратушы және электр энергетикасын (ээ) тұтынушы элементтердің жиынтығы.
Электрлік торап – бұл қосалқы станциядан, таратушы құрылғылардан, әуелік және кәбілдік электр беріліс желілерінен тұратын электр энергиясын таратуға арналған электр қондырғыларының жиынтығы. Электр торабымен электр станциясынан тұтынушыларға электр энергиясын тарату атқарылады.
Электр беріліс желісі (ЭБЖ) (әуелік немесе кәбілдік) – электр берілісі үшін арналған электр қондырғысы.
Электр энергетикалық жүйенің математикалық сипаттамасы өзіне тән қасиетке ие және жүйенің жылу энергетика мен су энергетикалық бөлігінен ерекшеленеді. Математикалық сипаттамасын құрастыру барысында, электрлік жүйелерге күштік элементте – генераторлар, трансформаторлар, түрлендіргіштер, жүктемелер және электрлік тораптар (жоғары кернеулі беріліс желісі бар, салыстырмалы төмен кернеуді таратушы орташа кернеулі) кіретіні ескеріледі.
Электрлік жүйе құрамына сонымен қатар жүйе жағдайын немесе жүйенің режімін өзгертетін және реттейтін басқару элементтері кіреді. Жүйенің режімін есептеу үшін математикалық аспап қажет. Өзара байланыса отырып, жүйенің элементтері кез келген уақытта электрлік энергияны тұтыну, тарату, беріліс және өндіріс үрдістерінің бірлігімен байланысты. Оның ішінде үрдістер деп, жүйенің (немесе режімнің) қазіргі күйіне сәйкес құбылыстарға жауап беретін айнымалы шамалар арасындағы кейбір байланыстарды бейнелейтін құбылыстардың жеке құраушыларын түсінеді.
Жүйеге математикалық сипаттама беру үшін үрдістердің айнымалы шамаларының арасындағы барлық байланыстарды математикалық модель түрінде көрсету керек. Бұл үрдістерді оқып үйренудің негізгі міндеті болып, электр энергиясын өндіру, жүйенің жақсы жұмысын қамтамасыз етуге бағытталған.
Энергия – бұл электр жүйесі жұмысының сандық көрсеткіші. Энергия сапасы басты рөлде тұтынушыдағы кернеудің жиілігі және шамасымен сипатталады. Жүйе режімі – бұл оның кез келген уақыт мезетіндегі немесе кейбір уақыт интервалдарындағы күйі. Жүйе режімі көрсетілген көрсеткіштер және басқа көрсеткіштермен анықталады. Режім параметрлері – режімнің өзгеруіне тәуелді көрсеткіштер. Режімнің параметрлеріне жүйенің әртүрлі нүктелеріндегі кернеулері, оның элементтеріндегі токтары, кернеу мен ЭҚК векторларының айрылу бұрыштары, активтік және реактивтік қуаттары және т.б. жатады.
Математикалық сипаттаманы талдауда және құрастыруда электр жүйелер режімінің үш негізгі түрін ажыратады:
қалыпты орнықты режім, оны қолданумен электр жүйесі жобаланады және технико-экономикалық сипаттамасы анықталады;
апаттан кейінгі орнықты режім, ол қандайда бір элементтің немесе жүйенің бірқатар элементінің апаттық сөндірілуінен кейін пайда болады. Аталған орнықты режімдер уақыт байланысты өзгермейтін параметрлермен сипатталады. Соның ішінде режім параметрлерінің арасындағы байланыс алгебралық теңдеумен көрсетіледі;
өтпелі режім, онда жүйе бір күйден екінші күйге өтеді. Оған уақытпен оның барлық параметрлерінің өзгеруі тән және ол дифференциальдық теңдеумен сипатталады.
Кез келген режім көптеген түрлі үрділерден тұрады.
Электр жүйесіндегі режімдер параметрлері жүйе параметрлері деп аталатын қатынастармен өзара байланысты.
Жүйе параметрлері – бұл жүйе элементтерінің, олардың қосылу сұлбасының физикалық қасиеттерімен анықталатын сандық көрсеткіштері. Жүйе параметрлеріне кедергілер, элементтер өткізгіштіктері, трансформация коэффициенттері, уақыт тұрақтылығы және т.б. мәндері жатады.
Егер, жүйе параметрлері оның режімінің өзгеруіне тәуелді болса, онда жүйе сызықты емес деп аталады. Барлық шынайы электрлік жүйелер параметрлері сызықты емес. Бірақ математикалық аспап, оларды зерттеу үшін әлі толық өңделмеген. Сондықтан, кейбір зерттелетін бөліктерде жүйені сызықтық деп есептегендіктен, жүйе параметрлерін көбінесе тұрақты деп алады.
Орынбасу сұлбасы инженердің математикалық құралы болып табылады. Инженер қандай электр торабы және қандай үрдістің қызықтыратынына тәуелді зерттелетін тораптың орынбасу сұлбасын таңдайды. Орынбасу сұлбасын таңдағаннан кейін электр жүйесінің (режімнің) күйін есептеу, электр тізбегінің есебіне келтіріледі.
Өтпелі режімдер қалыпты (қалпына келетін) және апатты болып бөлінеді. Қалыпты өтпелі үрдістер жүйе жүктемесінің өзгеруіне және оларға реттеуіш құрылғылардың реакциясына негізделген. Кәдімгі қалпына келтірілетін операциялар кезінде туатын қалыпты өтпелі үрдістер: трансформаторлардың, сонымен бірге жеке электр беріліс желілерінің қосылу мен ажыратылуы; жүйенің коммутация сұлбасының қайта қалпына келу өзгерістері; жеке генераторлардың және жүктемелердің қосылуы мен ажыратылуы немесе олардың қуатының өзгерісі. Қалыпты өтпелі үрдістер кезінде жүйені сипаттау үшін сызықтық дифференциальдық теңдеу қолданылады.
Апаттық өтпелі үрдістер режімнің қандай да бір шұғыл апаттық өзгерісі нәтижесінде туады: жүйе элементтерінің қысқа тұйықталуы кезінде, жүйенің қосылу сұлбасының өзгеруінен, үлкен жүктемені тасымалдаушы электр беріліс желісінің немесе агрегаттардың кездейсоқ ажыратылумен. Электрлік жүйенің математикалық теориясында үлкен қарсылықтар немесе әсерлер деп аталынатын, мұндай өзгерістер режім параметрлерінің бастапқы күйінен біраз ауытқуына алып келеді.
Өтпелі режімдерді зерттеу барысында электр жүйесінің төзімділік проблемасы ерекше мәнге ие. Орнықты режім деп аталатын электрлік жүйенің жұмыс күйі төзімділік қасиетіне ие болуы тиіс, яғни қандай да бір оның өзгерісінен, ауытқудан кейін (қарсылық: электр берілістерінің ажыратылуы, қысқа тұйықталу кезінде генераторлардан берілетін қуаттың үлкен өзгерісі, жүктеме қуатының кіші өзгерісі және т.б.) бастапқы орнықты режім немесе оған жақын режім қалпына келу қасиеті. Жүйенің төзімділік дәрежесі жүктеменің өсуімен (оның генераторларынан берілетін қуат) және кернеудің түсуімен (тұтынушылар қуаты көбеюімен, генераторлар қоздыруының азаюынан) төмендейді. Әрбір жүйе үшін төзімділік шегін сипаттайтын режім параметрлерінің кейбір - шама мәндерімен анықталады.
Жүйе осы шектен аспай, яғни апаттан кейінгі жағдай немесе арнайы нормативтермен анықталатын кейбір төзімділік қорымен жұмыс істеуі тиіс.
Электрлік жүйе төзімділігін анализдеу кезінде оны үш түрге бөледі: статикалық, динамикалық және қорытынды.
Статикалық төзімділік – оның кіші ауытқулардан (қарсылық) кейін жүйенің бастапқы күйіне қайта келу қасиеті. Кіші ауытқу деп, төзімділік облысы шектерін құратын түрлі әдістерді қоса отырып, жиіліктік сипаттамаларды қолдануды және сипаттамалық теңдеулерді зерттеуді қарастыратын, кіші тербелістер әдістерін және Ляпунов жалпы әдісін қолданумен сызықтық дифференциальдық теңдеулер жүйесі негізінде зерттелуі мүмкін саналатын электрлік жүйені түсінеміз.
Динамикалық төзімділік – ол үлкен ауытқудан (қысқа тұйықталу, желінің ажыратылуы және т.б.) кейінгі жүйенің бастапқы немесе оған практикалық жақын режімге қайта келу қасиеті. Динамикалық төзімділікті анализдеу кезінде режім параметрлері өзгерістерінің көрінуі үшін, жоғары ретті трансценденттік, сызықты емес теңдеулер құрайды. Оның үшін аналогтық есептеу машиналарын және автоматикамен жабдықталған айнымалы ток есептеу моделі қолданылады.
Қорытынды төзімділік – ол жүйенің бастапқы режім немесе оған практикалық жақын режім қалпына, істен шыққаннан кейін біраз уақыт синхронды жұмыс істеуімен, жүйенің негізгі жұмыс элементтерінің сөндірілмей қайта қалпына келу қасиеті.
2 дәріс. Электр жүйелерінің орнықты режімдерінің математикалық моделі. Электр жүйесінің орнықты режімінің теңдеуі
Дәріс мазмұны:
– орынбасу сұлбасын, желілі электр тораптарының теңдескен күйі, электр тізбектер күйінің матрицалық теңдеуінің қалыптасуы.
Дәріс мақсаты:
– электр жүйесінің режімін, матрицалық формадағы Ом және Кирхгоф заңдарын, электрэнергетикадағы өтпелі үрдістердің математикалық моделін зерттеу.
Электр жүйесінің жұмыс күйін талдау орнықты режімін есептеуді талап етеді, оның мақсаты режімнің: түйін нүктелердегі кернеу, жеке элементтерінде жүретін қуат пен ток параметрлерін анықтау.
Орнықты режімнің есебіндегі электр жүйесінің негізгі элементтері электр тізбегінің элементтерінен тұратын орынбасу сұлбасы ретінде: кернеу немесе ток және кедергі көздері көрсетілген. Орынбасу сұлбасына тармақ, түйін және контур сияқты түсініктер қолданылады. Контуры бар орынбасу сұлбалары тұйықталған, ал керісінше жағдайда – тұйықталмаған деп аталады.
Желілі электрлік тізбектің күйі Ом және Кирхгоф теңдеуінде сипатталады.
Ом заңы тізбектің әрбір тармағының параметрлерінің өзара байланысын анықтайды. Zi кедергімен сипатталатын, i- тармағы үшін, онда әсер ететін ЭҚК Еi және оның бойымен ағатын ток Ii, ұштарының арасындағы потенциалдар айырмасы (тармақтардағы кернеудің құлауы) UBi мына теңдеуге сәйкес анықталады
![]() (1.2.1)
(1.2.1)
Кирхгофтың бірінші заңы тізбектің әрбір түйініндегі токтың байланысын анықтайды, түйіндегі токтың алгебралық қосындысы нөлге тең. Ток көзі бар J ерікті түйін және байланыстырғыш k тармақтар үшін теңдеу мына түрде болады
![]() (1.2.2)
(1.2.2)
Кирхгофтың екінші заңы тізбектің контурындағы кернеудің балансын анықтайды, контур тармақтарындағы кернеудің құлауының алгебралық қосындысы нөлге тең. 1 тармақты ерікті контурдың теңдеуі мына түрде болады
![]() . (1.2.3)
. (1.2.3)
Электр жүйесінің орынбасу сұлбасы көбінесе байланысты бағытталған граф болып табылады. Ол түйінге біріккен (төбе) тармақтардан (қабырға) тұрады. Тармақтар тізбек (граф жолы) түзеді, ол тұйық болуы мүмкін. Тармақтардың (ЭҚК, токтар, кернеудің құлауы) күйін сипаттайтын барлық шамалар белгілі бағытқа ие.
Бағытталған граф үшін мыналар анықталуы мүмкін: 1) түйіндегі тармақтардың қосылу матрицасы (инциденцияның бірінші матрицасы); 2) тәуелсіз контурда тармақтардың қосылу матрицасы (инциденцияның екінші матрицасы).
Түйінде тармақтардың қосылу матрицасы –бұл жол саны графтың төбе санына n тең, ал бағана саны – қабырға санына m тең тік бұрышты матрица.
MS =(mij), i=1,...,n; j=1,....,m..
Тәуелсіз контурларға тармақтардың қосылу матрицасы – бұл жол саны графтың тәуелсіз контур санына k, ал бағана саны – тармақ санына m тең тік бұрышты матрица.
N=(nij), i=1,……..k; j=1,……. m.
М және N матрицалары электр тізбегінің матрицалы формадағы теңдеу күйін жазуға мүмкіндік береді.
Кирхгофтың матрицалық формадағы бірінші заңы:
![]() (1.2.4)
(1.2.4)
мұндағы ![]() - тармақтардағы токтың
бағандары мен сәйкесінше түйіндерде берілетін ток.
- тармақтардағы токтың
бағандары мен сәйкесінше түйіндерде берілетін ток.
Кирхгофтың матрицалық формадағы екінші заңы:
![]() (1.2.5)
(1.2.5)
мұндағы ![]() - сұлбаның тармақтарындағы
кернеудің құлау бағаны.
- сұлбаның тармақтарындағы
кернеудің құлау бағаны.
Орынбасу сұлбасының тармақтарындағы токтарды Кирхгофтың екінші заң теңдеуіне енгізу үшін матрицалық теңдеумен көрсетілетін Ом заңын қолданамыз:
![]() (1.2.6)
(1.2.6)
мұндағы ZB – тармақ кедергілерінің диагоналды матрицасы; Е – тармақтарындағы ЭҚК.
Күйдің толықтырылған теңдеуін құрастыру үшін, аналитикалық формада электр тораптарының орын басу сұлбасының конфигурациясын бейнелейтін М және N қосылыс матрицаларын шамамен анықтау қажет.
МS матрицасын құрастыру үшін сұлбаның барлық түйіндер мен сұлба тармақтарын нөмірлеп, матрицаның әрбір бағанында (+1) және (-1) деп берілген тармақпен сәйкес келетін түйіндерге, ал бағананың басқа элементтерінде «0» деп жазу жеткілікті. Баланстық түйінге сәйкес жолды сызып тастаумен, іздеген М матрицасын аламыз.
N матрицасын құрастыру үшін
алдын ала тәуелсіз контурды бөліп алу керек, олардың саны ![]() көбірек болуы мүмкін. N матрицасында жалпы
алғанда тораптың конфигурациясы туралы толық ақпарат
болмайды, өйткені тұйық емес тармақтар онда
көрінбейді.
көбірек болуы мүмкін. N матрицасында жалпы
алғанда тораптың конфигурациясы туралы толық ақпарат
болмайды, өйткені тұйық емес тармақтар онда
көрінбейді.
Электр жүйесінің
орнықты режімін есептеу міндетіне орынбасу сұлбасының
тармағындағы токты анықтау, оның түйін
нүктелеріндегі кернеуді және оған сәйкесті қуатты
анықтау болып табылады. Ол үшін тармақтағы токтарға
салыстырмалы шешілетін жалпылама теңдеуі құрастырылады.
Алынған матрица ![]() бойынша (1.2.6) теңдеуіне сәйкес
сұлбаның тармақтарындағы
бойынша (1.2.6) теңдеуіне сәйкес
сұлбаның тармақтарындағы ![]() кернеудің құлауы
анықталады, одан кейін баланстылыққа
кернеудің құлауы
анықталады, одан кейін баланстылыққа ![]() салыстырмалы түрде түйіндердің кернеуі табылады.
салыстырмалы түрде түйіндердің кернеуі табылады.
Баланстыққа
салыстырмалы түрде барлық түйіндердегі кернеулерді,
яғни түйіндер кернеуі және барлық қалған
тармақтардағы кернеудің құлауын анықтау
үшін сұлба тармақтарындағы кернеу құлауын
білген жеткілікті, егер баланстық түйін кернеуі ![]() берілген болса
берілген болса
![]()
Егер есепті
баланстыққа салыстырмалы сұлбаның (![]() матрицасы)
түйіндеріндегі кернеуді анықтаудан бастаса, онда шешілетін
жүйенің теңдеуі
n-1 –ге тең болады. Баланстық берілген токты
түйіндерде және тармақтардағы ЭҚК –ға
салыстырмалы түрде түйін кернеулерін байланыстыратын
теңдеулерден тұратын жүйе, түйіндік теңдеулер
жүйесі деп аталады.
матрицасы)
түйіндеріндегі кернеуді анықтаудан бастаса, онда шешілетін
жүйенің теңдеуі
n-1 –ге тең болады. Баланстық берілген токты
түйіндерде және тармақтардағы ЭҚК –ға
салыстырмалы түрде түйін кернеулерін байланыстыратын
теңдеулерден тұратын жүйе, түйіндік теңдеулер
жүйесі деп аталады.
Белгілейміз
![]() (1.2.7)
(1.2.7)
Реттің (n-1) төртбұрышты матрицасы (7) түйіндік өткізгіштіктің матрицасы деп аталады. Ол түйіндік теңдеу жүйесінің соңғы жазба формасын алуға мүмкіндік береді
![]() (1.2.8)
(1.2.8)
Теңдеуді
(1.2.8) шешу арқылы салыстырмалы түрде ![]() , сұлбаның тармақтарындағы кернеудің
құлауын алуға болады және (1.2.6)
сұлбасының тармақтарынан токты табуға болады
, сұлбаның тармақтарындағы кернеудің
құлауын алуға болады және (1.2.6)
сұлбасының тармақтарынан токты табуға болады
Түйіндік теңдеулер жүйесін матрицалық әдіспен есептеу ережесі алынған сұлбаға құрастырылады:
- сұлбаның түйіндік токтарының диагоналды матрицасы;
- тармақтардың өткізгіштігінің диагоналды матрицасы.
- инциденция матрицасы нөлдермен, бірліктермен толтырылады.
3 дәріс. Электр жүйесі күйінің теңдеуін шешу әдістері
Дәріс мазмұны:
– сызықтық алгебралық теңдеулерді шешудің дәл және келтірілген әдістерін анықтау;
– Гаусс әдісімен күдің теңдеуін шешу.
Дәріс мақсаты:
– күй теңдеуінің матрица коэффицентіне қатынасы;
– күй теңдеуін итерациялық әдіспен шешу.
Орнықты режімнің есептеулері электр жүйесінің сұлба конфигурациясын және оның элементтерінің параметрлерін таңдауда, тұрақтылық анализі мен қысқа тұйықталу тогын бағалауда, оның жұмысының экономикалық режімін анықтау үшін қажет.
Кез келген орнықты режімнің есебін жасау үшін электр жүйелері тораптарының параметрлері мен сұлбасы туралы, тұтынушылар (жүктеме) мен электр энергия көздері туралы (электрстанциясы) ақпарат керек.
Түйіндерде токты және кернеуді пайда ететін, қуатты байланыстырғыш электр жүйесінің орнықты режімінің теңдеуі, тармақтарда ЭҚК болмаса, мына түрге ие
![]() (1.3.1)
(1.3.1)
![]() (1.3.2)
(1.3.2)
мұндағы ![]() - орынбасу жүйесінің
түйіндеме сұлбасына қосылған қуатты
көздердің немесе тұтынушылардың бағаны;
- орынбасу жүйесінің
түйіндеме сұлбасына қосылған қуатты
көздердің немесе тұтынушылардың бағаны;
![]() - орынбасу сұлбасының
түйіндемесіндегі кернеудің диагоналды матрицасы;
- орынбасу сұлбасының
түйіндемесіндегі кернеудің диагоналды матрицасы;
![]() - сұлба түйіндемесіндегі кернеу
бағаны;
- сұлба түйіндемесіндегі кернеу
бағаны;
![]() - әрбір элементі балансты түйіндегі
кернеуге тең бағана;
- әрбір элементі балансты түйіндегі
кернеуге тең бағана;
![]() - түйінде ток беретін бағана (Ù белгісімен кешенді-қиылысатын шамалар).
- түйінде ток беретін бағана (Ù белгісімен кешенді-қиылысатын шамалар).
Түйіннің берілген қуатындағы сызықсыз (1.3.1) және сызықты (1.3.2) теңдеулер жүйесі, жалпы алғанда тек итерациялық әдіспен шешілуі мүмкін. Оның екі жолы бар:
- теңдеуді кезекпен (1.3.1) және (1.3.2) жалпы итерациялық циклде шешу;
- бұл теңдеулері сызықтық емес теңдеулердің біртұтас жүйесіне біріктіріп және артынан оны шешу.
Бірінші жағдайда шешу келесі сұлба бойынша жүргізіледі:
1) түйін кернеулеріне бастапқы жақын мәндер беріледі;
2) берілген қуат мәні (1.3.1) және кернеу мәні бойынша берілу тогы анықталады;
3) сызықтық теңдеу жүйесі (1.3.2) түйіндегі кернеуге салыстырмалы түрде берілген токтар мәндері белгілі болған кезде шешіледі;
4) түйіндердегі алынған кернеу мәні негізінде п.2.-ден бастап итерациялық үрдістің келесі қадамы орындалады.
Итерациялық үрдістің аяқталу шарты болып, екі соңғы қатар келетін итерациялар кернеулерінің жақын ұқсастығы табылады, сонымен қатар (1.3.1) бойынша есептелген түйіндердегі қуаттар мәні берілген мәнге ұқсастығы.
Екінші жағдайда (1.3.1) және (1.3.2) теңдеулері беріліс токтарын бірінен – біріне қою жолымен біріктіріледі, (1.3.2) ден (1.3.1) ге көшіргенде жүйе мына түрге келеді
![]() (1.3.3)
(1.3.3)
(1.3.1) ден (1.3.2) ге көшіргенде
![]() (1.3.4)
(1.3.4)
Біріншідегідей екінші жүрісте де итерациялық үрдістің әрбір қадамында сызықтық алгебралық теңдеу, не болмаса тікелей түйіндік теңдеу түрінде (1.3.2), не болмаса (1.3.3) және (1.3.4) линеаризовандық теңдеу түрінде шешіледі.
Сызықтық алгебралық теңдеу жүйесін шешу әдістері екі топқа бөлінеді: тікелей және итерациялық, Тікелейге есептегіш сұлбаларға тәуелді арифметикалық операциялар соңғы санының нәтижесіне, сонымен бірге теңдеу жүйесі матрица коэффиценттерінің құрылымына және ретіне сәйкес шешім алуға мүмкіндік беретін әдістер жатады. Бұл топтың әдістері нақты болып табылады, өйткені бастапқы берілген мәліметтер мен есептер нақты болса, алынатын шешімі де нақты болады
Итерациялыққа сызықты алгебралық теңдеулер жүйесін шешу біртекті операциялармен есептелетін тізбектік жақындасулардың шегіндегідей қарастырылуға мүмкіндік беретін әдістер жатады. Бұл әдістер жақынырақ болып табылады, өйткені есептер дөңгелектенбей теңдеулер жүйесінің шешімін тек берілген нақтылықпен алуға көмектеседі.
Электр жүйесі орнықты режімінің (ОРТ) сызықтық алгебралық теңдеуін шешудің барлық тікелей әдістері негізінде Гаусс әдісі жатады. Бұл әдіске тән есептегіш сұлбалар қатарына кері жүрісті және кері жүріссіз алгоритмдер жатады.
Кері жүрісі бар Гаусс әдісінің алгоритмі. Сызықтық теңдеулер жүйесінің шешімі n
![]() .
.
Сондықтан алгоритм екі кезеңнен тұрады. Бірінші кезеңде (тікелей жүріс) біртекті қадамдар n үшін бастапқы жүйе мына түрде түрлендіріледі, түрлендірілген жүйе матрица коэффиценттері жоғарғы үшбұрыш болады, яғни бас диагоналынан төмен орналасқан барлық элементтер нөлге тең. Екінші кезеңде (кері қадам) бір –бірлеп белгісіздердің мәні анықталады хn ден х1-ге дейін.
Тікелей жүріс кезінде орындалатын операциялардың тізбектілігі:
Бастапқы теңдеу жүйесінің бірінші қадамында жаңа теңдеу а11-ге бөлінеді
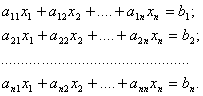
Әрі қарай бірінші теңдеуді әрбір рет аi1-ге көбейту жолымен барлық келесі теңдеулерден (i=2,....,n) х1 алынып тасталынады және i-ші теңдеуден алынады. Бұл операциялардың нәтижесінде А(1) матрица коэффиценті теңдеу жүйесі алынады:
![]()
![]()
………………………..
![]()
мұндағы
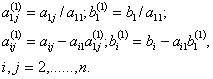
Бірінші қадамның операциясын орындау жетекші деп аталатын а11 элементінің нөлден ажыратылуын талап етеді.
Екінші қадам жетекші элемент ретінде ![]() қолдану кезінде ұқсас операциялар жүргізу
жолымен бірінші қадам жүйесінен алынған 3,……,n теңдеуінен
х2–ні алып тастаудан тұрады. Нәтижесінде жүйе
қолдану кезінде ұқсас операциялар жүргізу
жолымен бірінші қадам жүйесінен алынған 3,……,n теңдеуінен
х2–ні алып тастаудан тұрады. Нәтижесінде жүйе ![]() түріне келеді.
түріне келеді.
Үшінші және келесі қадамдарында алдыңғыларға сәйкес жүреді. Еркін қадамда (k-м) теңдеу жүйесінің коэффиценттерін есептеу үшін формулалар былайша жазылады
![]()
![]() (1.3.5)
(1.3.5)
![]()
Соңғы қадамда (k=n) (1.3.5) өрнектің екіншісі ![]() анықтайды. Осылайша, тікелей жүріс кезінде жетекші
элементтер мен тізбектей
анықтайды. Осылайша, тікелей жүріс кезінде жетекші
элементтер мен тізбектей ![]() жүреді және олардың нөлден
айырмашылығы есептеу үрдісінің орындалу шарты болып табылады.
жүреді және олардың нөлден
айырмашылығы есептеу үрдісінің орындалу шарты болып табылады.
Жалпы түрде формулалар кері жүріс үшін былай жазылады
![]() (1.3.6)
(1.3.6)
Сызықтық алгебралық теңдеулер жүйесін шешудің итерациялық әдісі итерациялық немесе тізбекті жақындасу деп аталатын біртекті есептеу қадамдарын бірқатар орындау нәтижесінде іздеген белгісіздер мәнін алуға мүмкіндік береді. Сызықтық алгебралық теңдеулер жүйесін шешудің екі итерациялық әдісін қарастырамыз (жай итерация әдісі және Зейдел әдісі). Бұл әдістер электр жүйелері түйіндеріндегі кернеулермен қуатты байланыстыратын орнықты режімнің сызықты емес теңдеулерін шешуді қамтиды.
Жай итерация әдісі. Бастапқы сызықтық алгебралық теңдеулер жүйесі

![]() болжамда мына түрге келтіріледі:
болжамда мына түрге келтіріледі:
 (1.3.7)
(1.3.7)
(1.3.7) теңдеулер жүйесі жай итерация әдісіне сәйкес келесі түрде шешіледі:
1) белгісіздерді
бастапқы (нөлдік) жақындасумен беріледі ![]()
2) ![]() мәні (1.3.7) теңдеудің оң
бөлігіне қойылады және келесі белгісіздердің
жақындасуы
мәні (1.3.7) теңдеудің оң
бөлігіне қойылады және келесі белгісіздердің
жақындасуы ![]() анықталады;
анықталады;
3) алынған мәндерді қоюмен ![]() келесі жақындасулар және т.б. табылады. Осыған
орай, итерациялық үрдістің k қадамында
жүйе (1.3.7) былайша жазылады:
келесі жақындасулар және т.б. табылады. Осыған
орай, итерациялық үрдістің k қадамында
жүйе (1.3.7) былайша жазылады:
 (1.3.8)
(1.3.8)
Итерациялық үрдіс екі аралас
итерациядан алынған ![]() мәні берілген қателік e шешімінен аз шамасынан айырмасы болмайды, яғни
шарт орындалғанға дейін жалғасады
мәні берілген қателік e шешімінен аз шамасынан айырмасы болмайды, яғни
шарт орындалғанға дейін жалғасады
![]() (1.3.9)
(1.3.9)
Кез келген берілген дәлдікті шешім, яғни аз мәндердегі e кезінде (1.3.9) шарттың орындалуы үшін қажет
![]() (1.3.10)
(1.3.10)
мұндағы ![]() - бастапқы теңдеулер
жүйесінің дәлдік шешімі.
- бастапқы теңдеулер
жүйесінің дәлдік шешімі.
(1.3.10) орындау кезінде ерікті бастапқы
жақындасу үшін ![]() итерациялық үрдіс қосылған
деп аталады. Қарама қарсы жағдайда итерациялық
үрдіс шешімге алып келмейді және айырылысқан болып табылады.
итерациялық үрдіс қосылған
деп аталады. Қарама қарсы жағдайда итерациялық
үрдіс шешімге алып келмейді және айырылысқан болып табылады.
Зейдел әдісі. Бұл әдіс, жай итерация әдісі сияқты, (1.3.7)-де келтірілген теңдеулерді пайдалануға негізделеді. Жай итерация әдісінен ерекшелігі итерациялық үрдістің әрбір k қадамындағы i айнымалыларын есептеу үшін алдыңғы (k-1) қадамында есептелген айнымалылар мәні қолданылады, келесі қадамды есептеу осылай жүреді. Соның ішінде итерациялық үрдістің k қадамында жүйе (1.3.7) мына түрге ие:
 (1.3.11)
(1.3.11)
Зейдел әдісі бойынша итерациялық үрдістердің ұқсастығын анықтайтын шарттарды түсіндіру үшін, алдыңғыдай матрицалық (1.3.7) жазба түрінде көрсетеміз:
![]()
мұндағы В – бағана; С – нөлдік диагоналды элементтері бар квадратты матрица.
Жоғарғы (Сж) және төменгі (Ст) үшбұрышты матрицалардың қосындысын С түрінде көрсетіп, аламыз:
![]()
Осыған сәйкес итерациялық үрдісті (3.16) матрицалық түрде көрсетеміз:
![]()
немесе ![]() (1.3.12)
(1.3.12)
мұндағы ![]()
(1.3.11) өрнек жәй итерация әдісі үшін алынған (1.3.11) өрнекке ұқсас. Әрі қарай, Зейдел әдісі бойынша итерациялық үрдістердің ұқсастығы үшін С/ матрицасының өз мәні абсолюттік шамасы бойынша бірден аз болуы тиіс және жеткілікті. С және С/ матрицалары А матрицасының компоненттері арқылы түрліше өрнектелетіндіктен, Зейдел әдісі және жәй итерация әдісінің ұқсастық шарттары жалпы жағдайда әртүрлі көрінеді, яғни А Зейдел әдісі бойынша итерациялық әдістері ұқсас, жай итерация әдісі бойынша ұқсамайтын және керісінше болатын матрицалар бар.
Жай итерация әдісінің ұқсастығына жеткілікті шарттар Зейдел әдісі үшін де жеткілікті. Егер осы шарттар орындалса, онда Зейдел әдісі бойынша үрдіс ұқсастырылады.
Оң-белгілі
А матрицасы кезінде Зейдел
әдісі бойынша итерациялық үрдіс барлық уақытта
ұқсастырылатыны белгілі. Егер, А матрицасы оң- белгілі
болса, онда ұқсастық кепілденеді; егер олай болмаса,
бастапқы жүйенің сол бөлігін транспонирленген А
матрицасына көбейту арқылы оң-белгілі коэффицентті матрицалы
эквивалентке келтіруге болады, яғни Ах=b жүйесінен ![]() жүйесіне өту арқылы немесе
жүйесіне өту арқылы немесе
![]()
мұндағы ![]()
Егер бастапқы жүйе шешімге ие болса, басқаша айтқанда егер А –ерекше емес болса, онда А/ - матрицасы оң-белгілі және Зейдел әдісі бойынша итерациялық үрдіс шешімге келеді.
4 дәріс. Энергетикада сызықтық бағдарламалауды қолдану
Дәріс мазмұны:
- қолдану облысы және шешудің негізгі тәсілдері. Математикалық моделді құрастыру және транспорттық есебінің тіректік жоспарын табу жолдары. Потенциалдар әдісі;
- ашық транспорттық есептер және аралық тасымалдаушы транспорттық есептер шешімі. Тармақ және шекара әдісін қолданумен, тораптық бекітпедегі транспорттық есептер.
Дәріс мақсаты:
- энергетикадағы сызықтық бағдарламалау міндетін, экстрималдық есептерді транспорттық түрге келтірілуін, олардың шешімі әдістерін оқып үйрену.
Сызықтық бағдарламалау есебі математикалық түрде былай келтірілуі мүмкін. Математикалық модель сызықтық қатынас түрінде былай жазылсын:
![]()
Мына шектеулер кезінде, Ц(х) фунуциясының экстремальды мәнін қамтамасыз етуі мүмкін болатын х1, ……,хn, мәнін табу қажет
![]()
![]()
![]()
Сызықтық бағдарламалау есептеулерінде кездесетін шектеулерге, сонымен қатар кейде айнымалылардың xj≥0, j=1,....,p толық немесе бөліктерінің кері еместігі шарты түрінде шектеулер енгізіледі.
Мақсаттық Ц(а,х) функцияны кейбір жағдайларда сызықтық бағдарламалау міндетінің функционалы немесе критерийлері деп аталады.
Сызықтық бағдарламалау есебінің ең көп таралғандарының бірі транспорттық есеп болып табылады. Осы есепті шешу барысында қоймалардан тұтынушыларға қандай да бір өнімдерді тасымалдаудың ең тиімді экономикалық тәсілдері ізделеді. Берілген пункт реализацияларында өнімді тұтынатын тұтынушыға өнімнің бірлігін тасымалдауға кететін шығындар белгілі.
Транспорттық есепті матрицалық түрде құру. Транспорттық есепті баға критерийлері бойынша құрастыру төмеде көрсетілген. m пунктіндегі А1, …..,Аm өндірісте а1,…..,аm санына сәйкес біртекті өнім бар (қант, көмір, картоп және т.б.), олар b1,…..,bn көлемінде n тұтынушыларға В1,….,Вn жеткізілуі тиіс. Аi пунктінен Вj пунктіне өнім бірлігін тасымалдауға байланысты транспорттық шығындар сij белгілі.
Берілген есепті шешу үшін сұраныстың барлық пункттерінің қосындысы қорлардың қосындысына тең болуы қажет және жеткілікті, яғни
![]()
Транспорттық есепті көрнекілік үшін таратушы (1.4.1 кесте) деп аталатын кесте түрінде келтіреміз.
1.4.1 к е с т е
|
Өнімді жеткізуші |
Тұтынушы |
Жүктің қоры |
|||
|
В1 |
В2 |
…. |
Вn |
|
|
|
А1 |
с11 х11 |
с12 х12 |
…. |
с1n х1n |
а1 |
|
А2 |
с21 х21 |
с22 х22 |
…. |
с2n х2n |
а2 |
|
…… |
…… |
…… |
…… |
…… |
…… |
|
Аm |
сm1 хm1 |
сm2 хm2 |
…… |
сmn хmn |
аm |
|
Жүкке қажеттілік |
b1 |
b1 |
…… |
bn |
|
(Сij)mxn матрицасы тарифтер (транспорттық шығындар) матрицасы деп аталады, ал сij саны тарифтер деп аталады.
Транспорттық есеп жоспары деп ![]() аталады, онда әрбір хij саны жіберілетін i-пунктінен қабылданатын
j- пунктіне берілетін жүктің бірлік санын көрсетеді. Х матрицасын басқаша, тасымалдау
матрицасы деп атайды.
аталады, онда әрбір хij саны жіберілетін i-пунктінен қабылданатын
j- пунктіне берілетін жүктің бірлік санын көрсетеді. Х матрицасын басқаша, тасымалдау
матрицасы деп атайды.
Тасымалдау жоспарын іске асыруға байланысты жалпы шығындар қосындысын мақсатты функция түрінде көрсетуге болады.
![]() (1.4.1)
(1.4.1)
хij айнымалылары кері еместік шарты және тұтыну бойынша, қорлар бойынша шектерді қанағаттандыруы қажет. Математикалық түрде бұл шектеулік шарттарды мына түрде келтіруге болады:
 (1.4.2)
(1.4.2)
![]() (1.4.3)
(1.4.3)
(1.4.2) шарты мына шектеулер жүйесін түзеді. Бұл жүйені қанағаттандыратын компоненттердің кез-келген жоспары іске жарамды болып табылады.
Осылайша транспорттық есептің
математикалық қойылымы мына түрде жазылады. (1.4.3) шарты
кезінде (1.4.2) шектеулер жүйесі және (1.4.1) мақсаттық
функция берілген, көптеген жүйе шешімдері арасынан (1.4.1)
мақсаттық функцияны минималдайтын кері емес тасымалдау жоспарын
табу керек. Транспорттық есептер үшін маңыздысы келесі
теорема болып табылады: Транспорттық есептер матрицасының рангы
теңдеулер санынан бір бірлікке аз, яғни ![]()
Транспорттық есептер келесі негізгі этаптардан тұратын жоспарлардың жалпы тізбектей жақсартылуы көмегімен шешіледі: 1) бастапқы тіректік жоспарын анықтау; 2) осы жоспарды бағалау; 3) бір базистік айнымалыны еркінге біртекті ығыстыру жолымен жоспарды келесі түрге өткеру.
Бастапқы тіректік жоспарды анықтау.
1. «Солтүстік-батыс бұрышы» ережесі. Бастапқы тасымалдау жоспарын құру үшін «солтүстік-батыс бұрышы» ережесін қолданған ыңғайлы. Ол келесілерден тұрады.
Кестені жоғарғы сол жақтағы (солтүстік-оңтүстік) бұрышынан бастап, жол бойынша оңға қарай немесе бағана бойынша төменге қарай жылжу арқылы толтырамыз. (1, 1) торға а1 және b1 сандарының кішісін енгіземіз, яғни
![]()
Егер a1>b1, онда х11= b1 және оның басқа торларын толтыру үшін бірінші бағана «жабық», яғни i=2,3,….,m үшін хi1=0 (бірінші тұтынушының қажеттілігі толықтай қанағаттандырылды). Бірінші жол бойымен ары қарай жылжи отырып, (1, 2) көрші торына а1-b1 және b2 сандарының кішісін жазамыз, яғни
![]()
Егер b1>a1, онда осыған сәйкес бірінші жол «жабылады», яғни k=2,3,….,n үшін x1k=0. (2, 1) көрші торды толтыруға өтеміз, онда мынаны енгіземіз
![]()
(1, 2) немесе (2, 1) торларын толтырғаннан кейін екінші жол немесе екінші бағана бойынша келесі үшінші торды толтыруға көшеміз. Үрдіс жүктің толық берілгеніне дейін немесе тұтынушының толық қанағаттандырылуына дейін жалғасады. Соңғы толтырылған тор (m, n) соңғы жатқан n-м бағанасында және соңғы m-й жолында көрінеді.
2. «Минимальды элемент» ережесі. Сандарды және терацияларды қысқартуға болады, егер бастапқы жоспар жаңартылған «минимальды элемент» ережесі бойынша құрылған болса. Оның болмысы мынадай, онда әрбір қадамда торға сik минимальды тарифімен максимальды мүмкін болатын жүкті тасымалдау жүргізіледі. Кестені толтыруды барлық матрица тарифтерінің ең кіші сik элементіне сәйкес келетін тордан бастаймыз. Содан кейін бағана немесе жол бойынша қалған қалдықты, келесі сik шамасының мәні бойынша сәйкес келетін сол бағанаға немесе жолға орналастырамыз және т.б. Толтырылатын торлардың тізбектігі сik шамасы бойынша, ал сол торларда орналастырылатын xik шамасы «солтүстік-оңтүстік бұрышы» ережесіндегідей анықталады.
Транспорттық есептерді потенциалдар
әдісімен шешу. Потенциалдар
әдісінің болмысы келесіден тұрады. Тасымалдаудың
бастапқы тіректік жоспары табылғаннан кейін, әрбір Аi
жүк тасымалдаушыға (әрбір жолға) сәйкес кейбір ui
![]() сандары қойылады, ал әрбір Bj
тұтынушыға (әрбір бағанаға) кейбір nj
сандары қойылады. ui және nj
сандары Аi жүк тасымалдаушы және Вj
тұтынушыларға сәйкес потенциалдық деп аталады,
және оларды таңдағанда кез-келген жүктелген торда
олардың қосындысы сол тордың тарифіне тең болады, яғни
ui +nj =сij. Бос емес торлардың m+n
барлық ui және nj
потенциалдарын анықтау үшін ui +nj
=сij теңдеуі қолданылады.
сандары қойылады, ал әрбір Bj
тұтынушыға (әрбір бағанаға) кейбір nj
сандары қойылады. ui және nj
сандары Аi жүк тасымалдаушы және Вj
тұтынушыларға сәйкес потенциалдық деп аталады,
және оларды таңдағанда кез-келген жүктелген торда
олардың қосындысы сол тордың тарифіне тең болады, яғни
ui +nj =сij. Бос емес торлардың m+n
барлық ui және nj
потенциалдарын анықтау үшін ui +nj
=сij теңдеуі қолданылады.
Жоспар оптималды деп әрбір бос (i, j)
торларындағы sij айырмасы кері емес шамаға
тең болуы саналады, яғни ![]()
Алынған айырмалар бос торлардың бағасы (сипаттамасы) деп аталады.
Транспорттық есепті потенциалдар әдісімен шешу үшін келесілер қажет:
1) алдында көрсетілген ережелердің біреуі бойынша тіректік тасымалдау жоспарын құру;
2) жүк тасушылар мен тұтынушыларға сәйкес ui және nj потенциалдарын есептеу;
3) ui +nj =сij бос торлары үшін потенциалдар қосындысын (жанама тарифтер) есептеу;
4) sij=cij - cij. айырмасын тексеру.
2 бөлім. Математикалык моделдеу
1 дәріс. Моделдеу теориясының негізгі ұғымдары
Дәріс мақсаты:
1) Моделдеу теориясының негізгі ұғымдары. Моделдеу анықтамасы.
2) Моделдеу принципі.
3) Математикалық моделдеу кезеңдері.
4) Аналитикалық және еліктеулік моделдеу.
Моделдеу – ол зерттелетін объектіні оның шартты бейнесімен немесе басқа кескінмен ауыстыру және түп нұсқаның қасиеттерін бейненің қасиеттері зерттеу жолымен оқып білу.
Сірә, моделдеуден келетін нақты пайда тек қана екі шартты сақтаған кезде ғана болуы мүмкін:
- зерттеу операциясының көзқарасы бойынша модель түпнұсқа қасиетіне барабар кескінмен қамтамасыз етеді;
- модель жоғарыда айтылған, нақты объектілерді өлшеу кезінде болатын қиындықтарды жоюға мүмкіндік береді.
Орындалу әдістеріне байланысты, бүкіл моделдерді екі үлкен классқа бөоуге болады: физикалық және математикалық.
Физикалық моделдер түп нұсқаның керекті физикалық қасиеттерін нақты түрде іске асыруды болжайды. Мысалы, жаңа ұшақты жобалаған кезде шын ұшақтың аэродинамикалық қасиеттеріндей қасиеті бар, оның макеті жасалады; құрылысты жобалаған кезде архитекторлар оның элементтерінің кеңістікте қалай орналасуы керектігін көрсететін макет дайындайды. Осыған байланысты физикалық моделдеуді сонымен қатар макеттендіру деп те атайды.
Математикалық модель жүйені
(немесе операцияларды) қандайда бір абстракталық тілдегі
өрнектер түрінде жазуды көрсетеді, мысалы математикалық
қатынастардың немесе алгоритмдер сұлбасының
жиынтықтары түрінде. Сондықтан, оларда физикалық
шамалар ескерілетін кез-келген математикалық өрнектерді сол немесе
басқа үрдістердің немесе құбылыстардың
математикалық моделі ретінде қарастыруға болады. Мысалы,
бәрімізге бастапқы мектептен белгілі ![]() теңдеуі бірқалыпты түзу
сызықты қозғалыстың моделін көрсетеді. Атап
айтқанда математикалық моделдерді біз мұнан былай балама
стратегияларды тиімді бағалайтын негізгі құрал ретінде
қарастыратын боламыз.
теңдеуі бірқалыпты түзу
сызықты қозғалыстың моделін көрсетеді. Атап
айтқанда математикалық моделдерді біз мұнан былай балама
стратегияларды тиімді бағалайтын негізгі құрал ретінде
қарастыратын боламыз.
Компьютерлік моделдеу – бұл есептеу техникаларын пайдаланатын математикалық моделдеу.
Аналитикалық моделдеу шектеу жүйелерімен толықтырылған, шықпалық айнымалыларды кірмелікпен байланыстыратын нақты объектінің математикалық моделін алгебралық, дифференциалдық, интегралдық және де басқа теңдеулер түрінде қолдануды болжайды. Бұл кезде теңдеу дәл шешіледі деп болжанылады.
Өліктеулік моделдеу кезінде пайдаланылатын математикалық модель зерттелетін жүйенің уақыт бойынша, жүйенің және сыртқы ортаның параметрлерінің үйлесімді әртүрлі мәндері кезіндегі жұмыс алгоритмін жасайды.
Қарапайым аналитикалық моделге бірқалыпты түзу сызықты қозғалыстың теңдеуі мысал болуы мүмкін. Мұндай үрдісті имитациялық моделдің көмегімен зерттеген кезде уақыттың өтуімен жүрілген жолдың өзгеруін бақылауды іске асыру керек. Кейбір жағдайларда аналитикалық моделдеуді пайдаланған тиімді болса, басқа бір жағдайларда имитациялық (немесе екеуін сәкестендіріп) моделдеуді қолдану тиімді болады. Таңдау сәтті болу үшін, екі сұраққа жауап беру қажет.
Нақты модель жасағанда моделдеу мақсаты, ресурстар мен уақытқа және операцияның пайдалы тиімділігіне жұмсалатын қаржыны ескеретін, пайдаланылатын тиімділіктің өлшемін анықтап алу.
Сонымен қатар, моделдеу мақсаты зерттеу операциясының мақсатымен және зерттеу нәтижесін пайдалану әдісін жоспарлауды анықтау.
1.1 Моделдеу принциптері
Ақпараттық жеткіліктілік принципі. Зерттелетін жүйе жөнінде толық ақпарат болмаған кезде оның моделін құру мүмкін емес. Жүйе жөнінде ақпарат толық болған кезде оны моделдеудің мағынасы жоқ. Жүйе жөніндегі априорлық мәліметтің кейбір аумалы деңгейі болады (ақпараттың жеткіліктілік деңгейі), осыған жеткен кезде оған барабар модель құрылуы мүмкін.
Іске асырылу принципі. Жасалатын модель
зерттеуге қойылІске асырылу принципі. Жасалатын модель зерттеуге
қойылған мақсатқа жету мүмкіндігінің
нөлден өзгеше және шектелген уақытта болуын
қамтамасыз етуі қажет. әдетте моделдеу мақсатына жету
мүмкіндігі ![]() болатын
қандайда бір
болатын
қандайда бір ![]() мәні,
сондай-ақ осы мақсатқа жету уақытының
қабылданған шекарасы беріледі. Егер
мәні,
сондай-ақ осы мақсатқа жету уақытының
қабылданған шекарасы беріледі. Егер ![]() шартының орындалуы мүмкін
болса, моделді іске асыруға болады деп есептейді.
шартының орындалуы мүмкін
болса, моделді іске асыруға болады деп есептейді.
Моделдердің көптік принципі. Бұл кілттік принцип болады. Жаслатын модель бірінші кезекте нақты жүйенің (немесе құбылыстың) таңдалған тиімділіктің көрсеткішіне әсер ететін қасиеттерін көрсету керек. Осыған сәйкес кез келген нақты моделді пайдаланған кезде шындықтың кейбір жақтары ғана білінеді. Оны толығырақ зерттеу үшін, қарастырылатын үрдісті жан-жақты және әртүрлі деңгейде көрсетуге мүмкіндік беретін бірнеше моделдер керек болады.
Агрегаттау принципі. Көптеген жағдайда күрделі жүйені агрегаттардан құралатын етіп көрсетуге болады, оларды бірдей математикалық түрде бейнелеуге біраз стандартты математикалық сұлбалар жарамды болады екен. Агрегаттау принципі, бұдан басқа, моделді зерттеу мақсатына байланысты қайта жасауға мүмкіндік береді.
Параметрлеу принципі. Көптеген жағдайда моделдендіретін жүйенің құрамына белгілі параметрлермен, соның ішінде векторлармен сипатталатын кейбір оқшауландырылған қосалқы жүйелер болады. Мұндай қосалқы жүйелерді моделде, олардың жұмыстың үрдістерін баяндап жатпай, оларға сәйкес сандық шамалармен ауыстыруға болады. Бұл шамалардың жағдайға байланысты мәндерінің тәуелділігі қажет болған жағдайда оларды кесте түрінде, график немесе аналитикалық өрнектер түрінде беруге болады. Параметрлеу принципі моделдеу көлемін және мерзімін ықшамдауға мүмкіндік береді. Дегенмен параметрлеу моделдің түп нұсқасымен бірдей болуын төмендететінін ескеру керек.
1.2 Математикалық моделдеу кезеңдері
Компьютерлік моделдеу технологиясы келесідей әрекеттерді орындау керек деп болжайды.
1. Моделдеу мақсатын анықтау.
2. Мазмұнды модел дайындау.
3. Моделдерді түрлендіру.
4. Моделді бағдарламалық іске асыру.
5. Моделдік эксперименттерді жоспарлау.
6. Эксперимент жоспарын жүзеге асыру.
7. Моделдеу нәтижелерін талдау және түсіндіру.
Бірінші екі кезеңнің мазмұны іс жүзінде, моделдеу негізінде алынған, математикалық әдіске тәуелсіз болады (керісінше – олардың нәтижесі әдісті таңдайды).
Ал соңғы бес кезеңді іске асыру модель құратын негізгі екі әдістің әрқайсысы үшін елеулі айырмашылықта болады.
Мысалы, шешім қабылдауды қажет ететін, проблемалық жағдай, келесі түрде тұжырымдалады:өнімділігі бойынша және сенімділігі бойынша қойылатын талаптарды сақтаған кезде оның құны ең аз болатын, есептеу желілерін құру нұсқаларын табу. Бұл жағдайда моделдеудің мақсаты тиімділік көрсеткішінің (ТЭ) ең аз мәнін қамтамасыз ететін желінің параметрлерін іздестіру болады, яғни құнын.
Мақсат басқаша тұжырымдалуы мүмкін: есептеу желілерінің бірнеше құрылымдық нұсқаларының ішінен ең сенімдісін таңдап алу. Мұнда тиімділік көрсеткіші ретінде сенімділік көрсеткішінің бірі алынады (токтап қалғанға дейінгі орташа жұмыс істеуі, токтамай жұмыс істеу мүмкіндігі және т.б.), ал моделдеу мақсаты осы көрсеткіш бойынша желінің нұсақаларын салыстырып бағалауға болады.
Келтірілген мысалдар, тиімділік көрсеткішін таңдау келешек моделдің «архитектурасын» анықтамайтынын, себебі бұл кезеңде ол туралы негізгі пікір қалыптаспайтынын, немесе, былайша айтқанда, зерттелетін жүйенің мазмұнды моделі анықталмайтынын еске салуға мүмкіндік береді.
Мазмұнды модель – бұл моделдендірілетін жүйенің құрылымын, оның элементтерінің және моделдеу мақсатына жету үшін маңызды қасиеттерін анықтайтын абстрактты модель.
Аналитикалық моделдеу нақты объектінің алгебралық, дифференциалдық, интегралдық және шықпалық айнымалыны кірмелікпен байланыстыратын, шектеу жүйелерімен толықтырылған басқа да теңдеулер түріндегі математикалық моделін пайдалануды болжайды. Бұл кезде теңдеуді дәл шешетін есептеу жолдары болуын болжайды.
2 дәріс. Аналитикалық моделдеу. Жалпыланған электромеханикалық түрлендіргіштерді моделдеу (ЖЭМТ)
2.1 ЖЭМТ математикалық моделін құру
Моделдеу мақсаты: ЖЭМТ динамикалық және статикалық қасиеттерін есептегіш машиналармен зерттеу үшін математикалық модель дайындау.
2.1.1 ЖЭМТ концептуалдық моделі.
ЖЭМТ – статорда немесе роторда екі-екіден орамалары бар, екіполюсті және екі фазалы симметриялы идеалды электрлік машина (2.1 суретті қара).
Идеалдау (ұйғару):
1) Машина толықтай симметриялы;
2) Магниттік тізбектің қанығуы ескерілмейді;
3) Статор мен ротордың тістері ескерілмейді;
4) Полюстің айқындалмауы магниттік индукцияның остер бойынша бірдей болмай таралуымен ескеріледі.
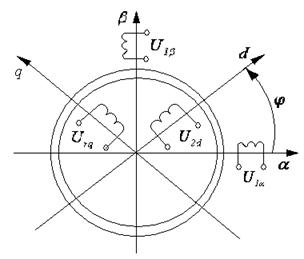
2.1 сурет – ЖЭМТ кеңістіктік моделі
Суретте: α, β – машина статорымен қатаң байланысқан, ортогоналдық координат жүйесі. d, q – машинаның роторымен қатаң байланысқан, ортогоналдық координат жүйесі.
![]() - статордың және
ротордың остері бойынша кернеулері.
- статордың және
ротордың остері бойынша кернеулері.
2.1.2 Моделдің сыртқы пішіні.
Объектінің математикалық моделі аналитикалық болады, яғни дифферциалдық және алгебралық теңдеулер жүйелері түрінде құрылады.
ЖЭМТ электрлік тепе-теңдігінің дифференциалдық теңдеулер жүйесі төрт орама үшін жазылған Кирхгофтың төрт теңдеуінен тұрады
![]() (2.2.1)
(2.2.1)
![]()
![]()
![]() ,
,
мұнда ![]() -
статор мен ротордың активті кедергілері;
-
статор мен ротордың активті кедергілері;
![]() -
статор және ротор орамаларының токтары.
-
статор және ротор орамаларының токтары.
Толық магниттік ағындар остер бойынша келесідей өрнекпен анықталады:
![]() (2.2.2)
(2.2.2)
![]()
![]()
![]()
Индуктивтіліктердегі ![]() индекстер, қандай орамада
және қандай ораманың (
индекстер, қандай орамада
және қандай ораманың (![]() ) тоғымен толық магнит
ағыны пайда болғанын белгілейді. Теңдеулерді келесі
түрде қайта жазуға болады:
) тоғымен толық магнит
ағыны пайда болғанын белгілейді. Теңдеулерді келесі
түрде қайта жазуға болады:
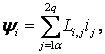 (2.2.3)
(2.2.3)
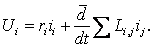 (2.2.4)
(2.2.4)
(2.2.1) теңдеулер жүйесін бірге шешу мүмкін емес, себебі теңдеулер әртүрлі координат жүйелерінде жазылған. (2.2.1), (2.2.2) теңдеулерді статордың координат жүйесінде көшіріп жазуға болады:
![]() (2.2.5)
(2.2.5)
![]()
![]()
![]() ,
,
мұнда ![]() -
дифферециалдау операторы.
-
дифферециалдау операторы.
![]() -
статордың, ротордың толық индуктивтілігі және
өзара индуктивтілік.
-
статордың, ротордың толық индуктивтілігі және
өзара индуктивтілік.
Матрица түрінде жазылуы:

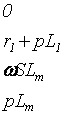

 . (2.2.6)
. (2.2.6)
ЭМТ статоры мен роторының өрістері өзара әрекеттесіп электромагниттік момент туғызады.
![]() (2.2.7)
(2.2.7)
(2.2.6), (2.2.7) теңдеулер қозғалыс теңдеуімен бірге
 (2.2.8)
(2.2.8)
энергияның электромеханикалық түрлену үрдісін бейнелейді.
3 дәріс. Моделді бағдарламалық іске асыру
Дәріс мақсаты:
- дифференциалды теңдеуді аналитикалық жолмен шешу.
Математикалық моделді пішіндеген кезде берілген динамикалық үрдісті бейнелейтін дифференциалдық теңдеуді (немесе теңдеулер жүйесін) шешетін әдіс таңдау керек. Символдық (аналитикалық) әдістер ең дәл және артықшылығы бар, бірақ әрқашан іске асырылмайды. Символдық әдіспен есептеу жүргізуге символдық математика пакеттерін «Maple» немесе «Mathematica» пайдалану үлкен көмек көрсетуі мүмкін.
Қазіргі есептік әдістерді пайдалану жуықтап есептейтін сандық әдістердің дәлдігін, олардың тездігін айтарлықтай өсірді. Көптеген математикалық компьютерлік қосымшалар сандық есептеу әдістерін қолдануды ықшамдайды және оларды әмбебап жасайды. Модельді аналитикалық әдіспен қарапайым түрде бейнелеп және шешетін жағдай болса, онда соңғысына жол берген дұрыс. Қазіргі кезде, инженерлік есептеулер үшін ең көп таралған математикалық қолтаңбалы бағдарламамен «Mathcad» және «Matlab».
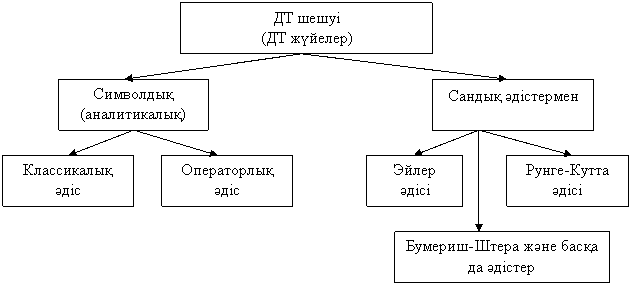
Дифференциалдық теңдеулерді аналитикалық шешуге мысалды қарапайым электрлік схемаға (2.3.1 – суретті қара) қарастырамыз.
а) Классикалық әдіс.
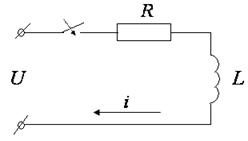
2.3.1 сурет
Бірінші реттік дифференциал теңдеумен бейнеленетін, қарапайым звеноны қарастырамыз
![]() .
.
Кілт тұйықталған кезде токтың қалыптасқан мәніне дифференциал теңдеудің жеке шешімі сәйкес келеді деп қабылдаймыз
![]() .
.
Бұл шешімді қалыптаспаған үрдісті бейнелейтін, бір текті дифференциал теңдеудің шешімімен қосады:
![]() .
.
Шешуі
![]() ,
,
мұнда ![]() -
уақыт тұрақтысы.
-
уақыт тұрақтысы.
Уақыт ![]() болған кезде, осыған дейін
нөлге тең болған ток, лезде өзгере алмайды деген шартты
ескеріп, бұл екі шешімді қосамыз:
болған кезде, осыған дейін
нөлге тең болған ток, лезде өзгере алмайды деген шартты
ескеріп, бұл екі шешімді қосамыз:
![]() .
.
Сондықтан, ![]()
және толық шешуі
 .
.
б) Операторлық әдіс.
ДТ операторлық әдіспен шешу теңдеудің функцияларын – түп нұсқаларды Лапластың түрлендірулеріне сәйкес олардың бейнелерімен ауыстыруды қарастырады, алынған алгебралық теңдеуді шешеді (мұнда дифференциалдау және интегралдау көбейтумен және бөлумен ауыстырылады) және алынған нәтиже кері қарай түрлендіріледі.
Екі жағдайда да, тіпті қарапайым теңдеуді шешу үшін де көп уақыт кетеді. ЖЭМТ үшін жазылған Кирхгофтың теңдеулерін аналити калық әдіспен шешу статор мен ротор фазаларындағы өзара индуктивтіліктерді есептеуге байланысты қиындайды. (2.2.6) - (2.2.8) теңдеулерді, момент теңдеуі сызықсыз болатындықтан, біріктіріп аналитикалық түрде шешу мүмкін емес. ДТ бұл жүйелерін сандық жолмен шешуге альтернатив жоқ.
4 дәріс. Дифференциалдық теңдеулер жүйесін қолданып шешуді үйрену
Дәріс мақсаты:
- дифференциалдық теңдеулерді және дифференциалдық теңдеулер жүйесін сандық әдіспен жуықтап шешуді үйрену.
Іс жүзінде динамикалық жүйені және олардың математикалық моделдерін талдауға қатысты барлық есептер, ДТ жүйесін сандық әдістерді қолданып шешуге негізделген.
Жалғыз дифференциал теңдеуді шешетін қарапайым сандық әдіс Эйлер әдісі болады
![]() .
.
Ол келесі рекурренттік формуламен іске асырылады:
![]() ,
,
мұнда ![]() –
шешу қадамы. Бұл әдістің қателігі
айтарлықтай, сондықтан ол іс жүзінде қолданылмайды десе
де болады.
–
шешу қадамы. Бұл әдістің қателігі
айтарлықтай, сондықтан ол іс жүзінде қолданылмайды десе
де болады.
Суретте модификацияланған Эйлер
әдісін «Mathcad»та пайдаланып іске асыру берілген, оның қателігі
![]() жақын
(яғни
жақын
(яғни ![]() болған
кезде 1% болады), бұл бірінші реттегі дифференциал теңдеуді шешуге
сирек қолданылатынын білдіреді.
болған
кезде 1% болады), бұл бірінші реттегі дифференциал теңдеуді шешуге
сирек қолданылатынын білдіреді.
Бұл әдісті қолданған кезде есептеу дәлдігін жақсартуға, интегралдауды тікбұрыштар әдісінің орнына трапеция әдісін қолдану арқылы қол жеткізуге болады.
4.1 Бірінші реттік дифференциалдық теңдеуді Рунге-Кутта әдісімен шешу
Енді дифференциалдық теңдеуді ![]() шешуді іске асыру
үшін жақсы белгілі басқа әдіске токталамыз – Рунге-Кутта
әдісі. Егер
шешуді іске асыру
үшін жақсы белгілі басқа әдіске токталамыз – Рунге-Кутта
әдісі. Егер ![]() -
айнымалы х өсу қадамы, і – 1-ден N дейін
өзгеретін индекс делік. Төртінші реттік Рунге-Кутта әдісі
шешу қателігі
-
айнымалы х өсу қадамы, і – 1-ден N дейін
өзгеретін индекс делік. Төртінші реттік Рунге-Кутта әдісі
шешу қателігі ![]() реттік
болады, бұл сандық әдістердің дәлдігіне
қойылатын талаптарды қанағаттандырады.
реттік
болады, бұл сандық әдістердің дәлдігіне
қойылатын талаптарды қанағаттандырады.
Шешу үшін ![]() функциясын, х айнымалының
өзгеру қадамын
функциясын, х айнымалының
өзгеру қадамын ![]() , шешу нүктелер санын N
және х пен у бастапқы мәндері берілуі керек.
, шешу нүктелер санын N
және х пен у бастапқы мәндері берілуі керек.
N –ші реттік дифференциалдық теңдеу, шешкен кезде бірінші реттік дифференциалдық теңдеулер жүйесіне келтіріледі және көптеген математикалық жүйелерге кіретін стандартты шешу әдістерімен шешіледі.
4.2 Дифференциалдық теңдеулер жүйесін Рунге-Кутта әдісімен шешу
Жалғыз дифференциалдық
теңдеулерді шешуден дифференциалдық теңдеулер жүйесін
шешуге өткенде шешу күрделілігі тез өседі. Екі
дифференциалдық теңдеулерден тұратын жүйені шешкен
кездің өзінде, Рунге-Кутта коэффициенттерін анықтайтын
рекурренттік формулалар айтарлықтай қиындайды. Бұл кезде
әрқашан кезектегі теңдеулерді қосу оларды
векторлық түрде жазған кезде теңдеулер санын
өсіреді. Әрине, бұл шешуді қиындатады, ![]() коэффициенттері
беретін функциядағы айнымалылар санының өсуіне әкеледі,
бірақ есептеу алгоритмінің іске асырылуын өзгертпейді.
коэффициенттері
беретін функциядағы айнымалылар санының өсуіне әкеледі,
бірақ есептеу алгоритмінің іске асырылуын өзгертпейді.
Дифференциалдық теңдеулер
жүйесін бірден шешкен кезде теңдеулердің тез
қиындауынан және олардың жеке сипаттарына байланысты
бұл жол тұйық жол болады. «Mathcad»
құрамындағы дифференциал теңдеулер жүйесін шешуге
арналған функциялар бұл қиындықтарды болдырмайды,
себебі дифференциал теңдеулер жүйесін шешу үшін формулалар
құруды қажет етпейді және мұндай шешімдерді жалпы
түрде береді. Дегенмен, дифференциал теңдеулерді шешетін
нақты алгоритмдердің қарастырылғандардан
айтарлықтай күрделі болатынын ескеру керек. Сонымен, бейімделген
алгоритмдер көп таралды, оларда әрбір қадам сайын шешу
қателігін бақылау орындалады («Mathcad»-ғы Rkadapt
функциясы). Егер қателік берілгеннен төмендесе, ![]() қадамы азаяды. Осылай,
қателік берілгеннен аз болғанша жалғасады. Бұл шешу
тұрақсыздығын едәуір азайтады, бірақ әрбір
қадамдағы және шешімі тұрақсыз болуы мүмкін
аймақтағы есептеу уақытын өсіреді.
қадамы азаяды. Осылай,
қателік берілгеннен аз болғанша жалғасады. Бұл шешу
тұрақсыздығын едәуір азайтады, бірақ әрбір
қадамдағы және шешімі тұрақсыз болуы мүмкін
аймақтағы есептеу уақытын өсіреді.
Компьютерлік математикалық жүйелердің соңғы версиялары жеке дифференциалдық жүйелерді де, сондай-ақ дифференциал теңдеулер жүйесін де сандық шешетін функциялармен жабдықталған. Мұндай класстағы есептерді шешу үшін функциялар қатары кіргізілген.
![]() - у векторында бастапқы
шарты бар, х1 ден х2 дейінгі аралықтағы
қадамдар саны N болатын, қарапайым дифференциал теңдеулер
жүйесін Рунге-Кутта әдісімен шешетін матрица; теңдеулерді
оң бөлігі Д векторына жазылған.
- у векторында бастапқы
шарты бар, х1 ден х2 дейінгі аралықтағы
қадамдар саны N болатын, қарапайым дифференциал теңдеулер
жүйесін Рунге-Кутта әдісімен шешетін матрица; теңдеулерді
оң бөлігі Д векторына жазылған.
![]() - у векторында бастапқы
шарты берілген, х1 ден х2 дейінгі аралықтағы
қадамдар саны N болатын, қарапайым дифференциал
теңдеулер жүйесін Рунге-Кутта әдісімен (айнымалы
қадаммен) шешетін матрица; теңдеулерді оң бөлігі Д
векторына жазылған.
- у векторында бастапқы
шарты берілген, х1 ден х2 дейінгі аралықтағы
қадамдар саны N болатын, қарапайым дифференциал
теңдеулер жүйесін Рунге-Кутта әдісімен (айнымалы
қадаммен) шешетін матрица; теңдеулерді оң бөлігі Д
векторына жазылған.
Мысал ретінде 2.4.1 – суретте көрсетілген электрлік сұлбаның динамикалық моделін қарастырамыз.
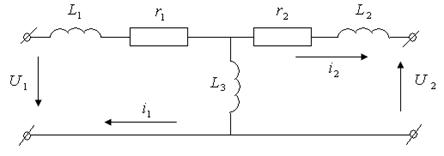
2.4.1 сурет
Берілген сұлбадағы электрлік тепе-теңдік келесі дифференциалдық теңдеулер жүйесімен анықталады:
 .
.
3 бөлім. Электр энергетикасындағы оңтайландырулық (оптимизациялық) есептер
1 дәріс. Оңтайландыру есептердің қойылуы және оларды шешу жолдары
Дәрістің мазмұны:
- негізгі мәліметтерді жинау, математикалық модельдеу, оңтайландыру есептерін шешу әдістері, оңтайландыру есептерін шешу қорытындысы.
Дәрістің мақсаты:
- оңтайландыру есептерді құру және оларды математикалық модельдеуге тәжірибелік дағдылау.
Мамандардың алдында электр техникалық жүйелерді жобалау процесінде тиімді нұсқасын таңдау сұрағы туындайды. Тиімді шешуді іздеу үшін техникалық жүйелердің математикалық модельдерін құруды және оңтайландыру (оптимизационные) есептерді шешу әдістерін білу қажет.
Математикалық программалардың белгілі әдістері кез-келген есепті әр жағдайға өзіндік әдістерді өңдемей-ақ шешуге мүмкіндік береді. Сондықтан маманға тек тиімді әдісті таңдау ғана қалады.
Алынған шешімнің оңтайлылығын анықтайтын көрсеткіш оптималдылық критерийі деп аталады.
Электр энергетикасындағы оңтайлылық критерийі ретінде келесі критерийлер таңдалынуы мүмкін: экономикалық, электржабдықтау немесе релелік қорғаныс сенімділігі, электр энергиясының сапасы, экологиялық.
Кез келген есептің шешімі бастапқы мәндерден басталады. Ең біріншіден олардың растылығы соңғы шешімнің дәлдігін қамтамасыз етеді. Сондықтан оның жиынтығы есепті шешудегі маңызды этап болып табылады.
Жинау процесінде оны негізгі және қосымшаға бөлу және бастапқы мәліметтердің категорияларын бағалау қажет. Мәліметтер анықталған, кездейсоқ және детерминдірілген болуы мүмкін.
Технологиялық процесті көрсететін теңестіру жүйесі математикалық модель деп аталады. Оңтайландыру есептерін бейнелейтін математикалық модеоь мақсатты функциядан, шектеуден және шектелген шарттардан тұрады.
Мақсатты функция – оңтайлылық критерийінің математикалық жазбасы.
Оңтайлы шешімді табу мақсатты функцияның экстремумын табуға алып барады. Мақсатты функцияның жалпы жазбасы:
![]() (3.1.1)
(3.1.1)
![]() - ізделінетін айнымалылар;
- ізделінетін айнымалылар;
![]() - айнымалылар саны.
- айнымалылар саны.
Ізделінетін айнымалылар үзіліссіз дискретті және бүтін есептелген болып бөлінеді.Мақсаттық функцияның айнымалыларының арасындағы байланыс сызықтық және сызықтық емес сипатты болуы мүмкін.
Сызықтық емес мақсатты функция бір экстремалды және көп экстремалды функцияда әрбір экстремум локалды, ал ең кішісі немесе ең үлкені глобалды деп аталады.
Шектеу деп есепті шешу кезінде ескерілетін әртүрлі техникалық, экономикалық немесе экологиялық шарттарды айтады. Олар айнымалылар арасындағы байланысты көрсетеді.
 , (3.1.2)
, (3.1.2)
мұндағы ![]() - шектеулердің жалпы саны
- шектеулердің жалпы саны
![]() - тұрақты коэфициенттер, ал еркін
мүшесі -
- тұрақты коэфициенттер, ал еркін
мүшесі -![]() .
.
Теңсіздік немесе толық емес теңдік түрі бар шектеу орнықтыру есебінің шешімін қиындатады. Соендықтан теңсіздікті теңдікке түрлендіру үшін теңсіздіктің сол бөлігіне формуланың оң және сол бөлігін теңестіретін қосымша айнымалыларды енгізеді. Осыдан кейін теңсіздік қатал тепе-теңдікте көрсетіледі. Мұнымен қоса айнымалылар саны артады.
Егер ![]() болғса теңдікте бір ғана шешім
болатыны белгілі және орнықтылау мүмкін емес.
болғса теңдікте бір ғана шешім
болатыны белгілі және орнықтылау мүмкін емес. ![]() жағдайында жүйеде шешім жоқ, ал
жағдайында жүйеде шешім жоқ, ал ![]() болғанда жүйе шексіз көп шешімге ие және
тиімдісін таңдауға болады. Шектік шарттармен ізделінетін
айнымалылардың өзгеру диапазоны қойылады.
болғанда жүйе шексіз көп шешімге ие және
тиімдісін таңдауға болады. Шектік шарттармен ізделінетін
айнымалылардың өзгеру диапазоны қойылады.
![]() ,
, ![]() , (3.1.3)
, (3.1.3)
![]() - айнымалылардың өзгеру диапазонының төменгі
және жоғарғы шегі.
- айнымалылардың өзгеру диапазонының төменгі
және жоғарғы шегі.
Егер орнықтылау есебінде шектік шарттар болса, онда салыстырмалы экстремум ізделінеді. 3.1.1 суретте бір айнымалының Z(x) кейбір функциялары көрсетілген.
Х айнымалысының өзгеру диапазоны көрсетілген(төменгі шек d және жоғарғы шек D). Фуекцияның абсолютті минимумы 1-нүктеге, салыстырмалы минимумы 2-нүктеге сәйкес келеді.
Орнықтылау есептерін шешу үшін математикалық жобалауды қолданады. Бұл көп қайталанбалы есептеу тәртібі, яғни ізделінетін шешімге әкеледі.
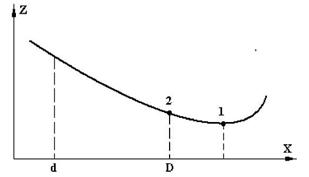
3.1.1 сурет – Абсолютті(1нүкте)және салыстырмалы (2 нүкте) функцияның абсолютті минимумыдары
Шектеудің түрі, ізделінетін айнымалының сипаты, бастапқы мәндердің категориялары және критерийлерінің саны математикалық жобалау әдісін таңдауды анықтайды. Математикалық жобалаудың келесі түрлерін анықтайды: сызықтық және сызықтық емес, бүтін сандық және дискретті, стохастикалық.
Оңтайлылық шешімді қабылдау параметрлік, структуралық, көпкритерийлік нәтиженің анализін келтіреді. Параметрлік анализ деп кейбір бастапқы параметрлердің әртүрлі мәнінде көп мәрте есептелінетін есеп кезіндегі анализді айтады.
Есептелудің нәтижесінде осы параметрлердің әсер етуі бағаланады.
Структуралық анализ кезінде есептің көп мәрте есептелінуі шектік шарт және шектеулердің әртүрлі структурасы кезінде жүреді. Бұл жағдайда есептің нәтижесіне шектік шартпен шектің әсері бағаланады.
Есептің соңғы шешімі барлық есептеулерді зерттегеннен соң қабылданады.
2 дәріс. Оңтайландыру(оптимизационный) есептерді шешу үшін сызықтық жобалауды қолдану
Дәрістің мазмұны:
- дәрісте сұлбалық, алгебралық және симплекс-әдіс, сызықты жобалаулы оңтайландыру есептердің есептелу әдістері келтірілген.
Дәрістің мақсаты:
- сызықтық жобалаулы оңтайландыру есептерді шешу әдістері сұлбалық, алгебралық, симплекс-әдісін қолдануға дағдылау.
Сызықты жобалау әдістері мақсатты фуекция және шектеу жүйесінің ізделінетін айнымалыларын сызықты тәуелділігі бар болған жағдайда қолданылады.
Сызықты математикалық модель жалпы жағдайда мына түрде болады:
![]() ,
,
 (3.1.4)
(3.1.4)
![]() - берілген тұрақты шамалар,
- берілген тұрақты шамалар, ![]()
Сызықты жобалау есебі келесі түрде тұжырымдалады: сызықтық теңдік немесе теңсіздік түрінде берілген шектеу кезіндегі және айнымалылардың өзгеру диапазонын көрсететін шектік шарттар кезіндегі сызықты мақсатты функцияның экстремалды (айырықша) мәнін табу.
Шынайы оңтайландырылған (оптимизационных) есептерде мақсатты функцияның минимумы мен максисусы ізделінеді. Сызықты жобалау әдістері мақсатты функцияның минимумын іздеуде де, максимумын іздеуде де бірдей жұмыс істейді.
Мақсатты функцияның минимумы ізделінетін математикалық модельді қарастырамыз.
![]() .
.
Егер осы математикалық модель бойынша мақсатты функцияның максимумын табу керек болса, онда мақсатты функцияның коэфициенттерінің таңбасы қарама-қарсы таңбаға өзгеріп, тағыда Z функциясының минимумы ізделінеді.
![]() .
.
Осылайша,
![]()
Сызықты жобалау есептерін шешудің сұлбалық әдісі қарапайым және көрнекі әдіс болып табылады. Көлемінің үлкен еместігі бұл әдістің қолданылуын шектейді.
Мысал ретінде мақсатты функцияның минимумын табу қажет сызықты жобалаудың математикалық моделін қарастыралық
![]()
Шектеу кезінде
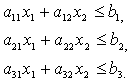
Айнымалылардың теріс еместігінің шектік шарттарында
![]()
![]()
Қосымша айнымалылардың х3, х4, х5 енгізгеннен кейін шектеу –теңсіздігінен теңдікке өтеді.
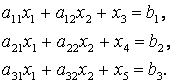 (3.1.5)
(3.1.5)
Айнымалылардың теріс еместігінің
шектік шарттары қосымша айнымалыларға да таралатынын ескереміз. ![]() , i = 3, 4, 5.
, i = 3, 4, 5.
Горизонталь осі бойынша ![]() айнымалысының манін, ал вертикаль осі бойынша
айнымалысының манін, ал вертикаль осі бойынша ![]() айнымалының мәнін қоямыз (3.2.1
сурет). Шектік шарттарды ескере отырып (
айнымалының мәнін қоямыз (3.2.1
сурет). Шектік шарттарды ескере отырып (![]() ,
, ![]() ),
), ![]() және
және![]() айнымалыларының мәндерін жарты
жазықтықта штрихпен ерекшелейміз.
айнымалыларының мәндерін жарты
жазықтықта штрихпен ерекшелейміз.
Шектеу – теңдіктерінің бірі, мысалы, біріншісі
![]()
Келесідей түрде жазамыз
![]()
х3 айнымалыны нолге теңестіреміз
![]() .
.
Соңғы қатынас ![]() жазықтығындағы тік сызық
теңдеуін корсетеді. Мұнда
жазықтығындағы тік сызық
теңдеуін корсетеді. Мұнда ![]() . Осыдан, тік сызықтың
бір жағына х3>0, ал
басқа жағына х3<0.
шектік шартты ескере отырып
. Осыдан, тік сызықтың
бір жағына х3>0, ал
басқа жағына х3<0.
шектік шартты ескере отырып ![]() , х3>0 болатын жарты жазықтықты штрихпен
ерекшелейміз
, х3>0 болатын жарты жазықтықты штрихпен
ерекшелейміз
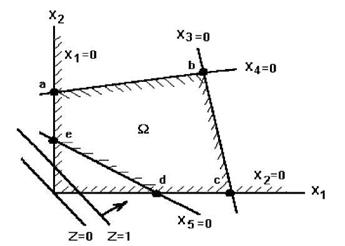
3.2.1 сурет – Есепті шешудің сұлбалық иллюстрацияс
Аналогтық сұлбалық тұрғызуды 2-ші және 3-ші шектеу жүйелеріне орындаймыз.
![]() жазықтықтарында орындалған
сұлбалық тұрғызулар нәтижесінде
жазықтықтарында орындалған
сұлбалық тұрғызулар нәтижесінде ![]() айнымалыларының рұқсат етілген
мәндерінің
айнымалыларының рұқсат етілген
мәндерінің ![]() ерекшеленеді (3.2.1 суретті қара).
Бұл аймақ дөңес көпжақты abcde
көрсетеді. Есептің
барлық рұқсат етілген шешімдері,сонымен қатар
оңтайлы шешім де осы
ерекшеленеді (3.2.1 суретті қара).
Бұл аймақ дөңес көпжақты abcde
көрсетеді. Есептің
барлық рұқсат етілген шешімдері,сонымен қатар
оңтайлы шешім де осы ![]() аймаққа жатады.
аймаққа жатады.
Мақсатты фуекцияның көрінісін қарастырамыз және оны нолге теңестіреміз.
![]()
Мақсатты функцияның
көрінісін кез келген 0-ден басқа мәнге теңестіреміз,
мысалы, бірге ![]() және
және
![]() жазықтығына сәйкес түзуді
тұрғызамыз (3.2.1 суретті қара)
жазықтығына сәйкес түзуді
тұрғызамыз (3.2.1 суретті қара)
Түзулер ![]() тең деңгейде мақсатты
функцияның сызықты болып табылады. Тең деңгейдегі
сызықтар өзара паралель.
тең деңгейде мақсатты
функцияның сызықты болып табылады. Тең деңгейдегі
сызықтар өзара паралель.
Z=0 және Z=l тең деңгейдегі сызықтың өзара орналасуы бойынша мақсатты функцияның Z өсу бағытын қадағалаймыз. Бұл бағыт 3.2.1 суретте стрелкамен көрсетілген.
Мақсатты функцияның
түзуін өзіне паралель өсу бағытына қарай ауыстырсақ
айнымалылардың рұқсат етілген мәндерінің
аймағына![]() жататын жақын нүктені
анықтаймыз.
жататын жақын нүктені
анықтаймыз.
Сұлбаның тұрғызуымен байланысты мұндай нүкте көпжақтың Q шыңы болып табылады. Бұл шың мақсатты функцияның минимумына, есептің шешіміне сәкес келеді.
Мақсатты функцияның минималды мәні айнымалының келесідей мәнінде болады.
![]()
Үш айнымалылар нолден ерекшеленеді,екі айнымалылар нолге тең. Нолге тең емес айнымалылардың саны шектеулер санына тең. Қалған айнымалылар нолге тең.
Максимумды табу үшін коэфициенттердің таңбасын өзгертеміз және аналогты түрде минимумын табамыз.
Шешудің әртүрлі жолдарын іздеудің алгебралық түрлендірулердің көмегімен алуға болады.
Бастапқы шектеу – теңдік жүйелерінің математикалық модельге бір шешімнен басқа шешімге өтуі кезіндегі, еркін айнымалылардың біреуі базис разрядына, ал базисті айнымалылардың біреуі бос разрядқа өту кезіндегі түрленуін қарастырамыз.
Жүйені қайта қарастырамыз (3.1.5):
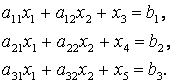 (3.1.6)
(3.1.6)
Еркін
және базисті айнымалыларының бастапқы таңдалынуы еркін
бола алады. Бірақ жүйенің структурасында базисті айнымалылар
ретінде ![]()
айнымалыларын
қабылдаған ыңғайлы, ал еркін айнымалылар ретінде ![]() және
және![]() . Бұл жағдайда
жүйенің бастапқы шешімін (3.1.6) табамыз:
. Бұл жағдайда
жүйенің бастапқы шешімін (3.1.6) табамыз:
1)
Еркін айнымалылар ![]() ,
,
2)
Базисті айнымалылар ![]() .
.
Әр бір базисті айнымалылы жүйенің бір ғана теңдеуіне кіреді және 1-ге тең коэфициентке ие. Сондықтан, базисті айнымалылар саны шектеулер санына тең. Қалған айнымалылар еркін.
Айнымалылар коэфициенттерін ескере отырып теңдеулер жүйесін (3.1.6) келесідей жазуға болады
 (3.1.7)
(3.1.7)
Базисті
айнымалыларды еркінге айналдыру шарасын өткізуде бірнеше базисті шешім
қажет. Еркін айнымалыны ![]() базистер разрядына, ал базисті
айнымалыларды еркін разрядқа ауыстыру керек делік. Бұл үшін
жүйенің бірінші теңдеуінен
базистер разрядына, ал базисті
айнымалыларды еркін разрядқа ауыстыру керек делік. Бұл үшін
жүйенің бірінші теңдеуінен ![]() алынып, 2-ші және 3-ші
теңдеулерге қойылады. Мұндай түрленудің
нәтижесінде
алынып, 2-ші және 3-ші
теңдеулерге қойылады. Мұндай түрленудің
нәтижесінде ![]() еркін айнымалы базисті болып, ал базисті
айнымалы
еркін айнымалы базисті болып, ал базисті
айнымалы ![]() еркінге ауысады.
еркінге ауысады.
Түрлендірудің нәтижесінде жаңа базисті шешім аламыз.
 (3.1.8)
(3.1.8)
Жүйенің жаңа коэфициенттері штрихпен көрсетілген. Жаңа шешім келесі түрде
1) Еркін айнымалылар ![]() .
.
2) Базисті айнымалылар ![]() .
.
Бұл әдісте шешімнің ізделуі хаотикалық болады.
Симплекс - әдіс универсалды әдіс болып табылады.
Симплекс - әдіс алгоритмі 9 қадамнан тұрады.
1) Шектеу жүйесі айнымалыларды еркін және базистыға бөлуге ыңғайлы түрге түрленеді (3.1.6).
2) Шектеу жүйесі және мақсатты функция кесте түрінде жазылады.
3.2.1 кесте
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
0 |
1 |
0 |
|
|
|
|
0 |
0 |
1 |
|
|
|
|
0 |
0 |
0 |
- |
3) Еркін айныцмалылары нолге тең, базисті айнымалылары шектеудің еркін мүшелеріне тең, мақсаттық функцияның мәні нолге тең бастапқы шешім жазылады.
4)
bj бос мүшелерінің бағаны
қарастырылады. Егер барлық ![]() , онда шешім рұқсат
етілген болып табылады. Егер еркін мүшелері
, онда шешім рұқсат
етілген болып табылады. Егер еркін мүшелері ![]() болса, онда олардың кез келгені таңдалынады.
болса, онда олардың кез келгені таңдалынады.
5) Рұқсат ететін бағанның aji коэффициенті қарастырылады. Егер осы коэффициенттің барлығы оң болса есептің шешуі болмайды. Егер aji коэффициенттерінің ішінде терісі болса, онда олардың кез келгені таңдалады және сәйкес келетін баған шешуші болып табылады.
6) Кестенің барлық коэффициенттері қайта есептелінеді, қарама – қарсы таңбалы мақсатты функция да қайта есептелінеді.
7)
Мақсатты функцияның бағанындағы ![]() коэфициенттері қарастырылады. Егер бұл
коэфициенттердің
коэфициенттері қарастырылады. Егер бұл
коэфициенттердің ![]() (Z
минимумын іздеген кезде) немсе
(Z
минимумын іздеген кезде) немсе ![]() (Z максимумын іздеген
кезде) онда, шешім тиімді болады.
(Z максимумын іздеген
кезде) онда, шешім тиімді болады.
8) Егер ![]() коэффициенті (минимум Z –ті іздеген
кезде) немесе
коэффициенті (минимум Z –ті іздеген
кезде) немесе ![]() (максимум Z –ті
іздегенде),онда әрқайсысының біреуі таңдалады
және бағана рұқсат етілген болады. Бос
мүшелердің bj рұқсат етілген
бағанадағы
(максимум Z –ті
іздегенде),онда әрқайсысының біреуі таңдалады
және бағана рұқсат етілген болады. Бос
мүшелердің bj рұқсат етілген
бағанадағы ![]() қатынасы есептелінеді.Осы минимал
қатынасқа жауапты бағана рұқсат етілген болады.
қатынасы есептелінеді.Осы минимал
қатынасқа жауапты бағана рұқсат етілген болады.
9) Кестедегі барлық коэффициенттерге қайта есептеу жүргізіледі. 7 пунктіге өту орындалады.
3 дәріс. Электрэнергетикадағы тасымалдау есептері
Дәрістің мазмұны:
- тасымалдау есептерінің қойлымы және оларды электрэнергетикада қолдану, тасымалдау есептерін шешу әдістері,транзиттік қуаттың анықтамасын түсіндіру, желінің өткізу қабілетін анықтау әдістерін оқып үйрену.
Дәрістің мақсаты:
- электрэнергетикадағы тасымалдау есептерін шешу әдістерін қолдануды дағдыландыру.
Энергия көздерінің тұтынушыларға электр энергиясын тарату есептерін іздеу жолы бойынша шешу үшін таратудың минимал шығынын есептеуде, тасымалдау есептерін шешуде қолданылатын математикалық аппарат қолданылады. Бұл жерде оңтайландыру (оптимизация) қорек көздерінің түйіндерін тұтынушы түйіндерімен байланыстыратын электр беріліс желілерінен тұратын электр тораптарының сұлбаларындағы шығындарға жатады.
Тасымалдау
есептерін шешуде бірінші кезеңде математикалық үлгілерді
(моделдерді) құрастыру болып табылады. Мысал
қарастырайық. Электрмен жабдықтауды жобалау жүйесінде
екі қорек көзі түйіні және 3 тұтынушы
түйіні болады. Қоректердің қуатын ![]() және
және
![]() , ал тұтынушылардың қуатын
, ал тұтынушылардың қуатын ![]() және
және ![]() е.м. құрайды.
Түйіндердің өзара орналасуы және электр
тораптарындағы желінің құрылысы 3.3.1 суретте
көрсетілген.Қорек пен тұтынушы түйіндерінің
арасындағы меншікті шығын қуаттарын желі бойынша тарату
е.м. құрайды.
Түйіндердің өзара орналасуы және электр
тораптарындағы желінің құрылысы 3.3.1 суретте
көрсетілген.Қорек пен тұтынушы түйіндерінің
арасындағы меншікті шығын қуаттарын желі бойынша тарату![]() у.е/е.м. құрайды.
у.е/е.м. құрайды.
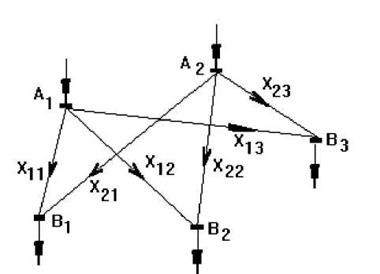
3.3.1 сурет – Электр тораптарындағы түйіндердің өзара орналасуы және желі құрылысының нұсқалары
Мақсаттық функция келесідей болады:
![]()
Электр тораптарындағы түйіндер шектегіш баланстық қуаттарды көрсетеді және теңдік мынандай түрде болады:

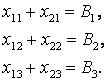
Шекаралық теңдіктер былай жазылады:
![]()
Келесі кезеңде шектік есептеу табылады. Бастапқы шектік есептеу минималды алгоритмнің меншікті баға бойынша алынуы мүмкін:
1) Тасымалдау матрицасында минималды
мәні![]() бар тор (клетка) алынады. Егер осындай бірнеше торлар
болса, онда біреуі таңдалады.
бар тор (клетка) алынады. Егер осындай бірнеше торлар
болса, онда біреуі таңдалады.
2) Алынған торға (клеткаға)
сапалық ретінде базистік ауысудың екі өлшемінің
орташасы![]() немесе
немесе ![]() алынады, яғни
алынады, яғни ![]() . Сонымен қатар
. Сонымен қатар ![]() ауысуына кіретін
ауысуына кіретін ![]() жолына немесе
жолына немесе ![]() бағанасы арқылы
базистік қуат орындалады.
бағанасы арқылы
базистік қуат орындалады.
3) Қалған
торларға ![]() жолы немесе
жолы немесе ![]() бағанасы баланс қуаты
орындалған бос ауысуларға сәйкес нөлдер алынады. Екі
өлшемнің үлкені
бағанасы баланс қуаты
орындалған бос ауысуларға сәйкес нөлдер алынады. Екі
өлшемнің үлкені ![]() мен
мен ![]() осы өлшемнің
әртүрлі болу шартымен ауыстырылады.
осы өлшемнің
әртүрлі болу шартымен ауыстырылады.
4) Қалған
толтырылмаған торларда тасымалдау матрицасында қайтадан минималды
мәнімен ![]() торы таңдалады. Ары қарай
2-ші және 3-ші пункттер тасымалдау матрицасының барлық
торлары толығымен толтырылғанша қайталанады.
торы таңдалады. Ары қарай
2-ші және 3-ші пункттер тасымалдау матрицасының барлық
торлары толығымен толтырылғанша қайталанады.
Атап айтқан жөн, ауысудың толық саны пт-ны құрайды. Нөлден кейігнгі базистік ауыспалының саны (n+m-1) құрайды. Нөлге тең бос ауыспалының саны (nm-(n+m-1)) құрайды.
Тасымалдау есептерінің шектік оңтайландыруын (оптимизациясын) шешу тарату әдісін қолдану жолы арқылы немесе потенциалдар әдісі арқылы шығарылады. Тасымалдау есептерін шешу алгоритміне потенциалдар әдісін қолданғанда ол мынандай түрде болады:
1) Сәйкесінше бастапқы берілгендердің тасымалдау матрицасы көлемдікті nm-ны құрайды, мұндағы п-қорек көзінің саны; m-тұтынушылар саны.
2) Шектік шешудің орташа меншікті бағасы табылады.
3) Шектікті шешу үшін
әр i-ші жолдағы және әр j-ші
бағандағы тасымалдау матрицасына потенциалдар мәні Vi және
Uj (i=1,2,...n; j=1,2,...m) жүктеледі. Әр
базистік ауысу үшін потенциалдар қосындысы меншікті
бағаға ![]() тең.
тең.
4) Потенциалдар біреуінің
еркінше берілген мәні мына теңдеу бойынша ![]() орындалады, ол базистік ауысу үшін тиімді,
қалған потенциалдардың мәні есептелінеді.
орындалады, ол базистік ауысу үшін тиімді,
қалған потенциалдардың мәні есептелінеді.
5) Барлық бос
ауыспалылардың меншікті бағасы бар потенциалдар қосындысымен
тексеріледі. Егер барлық бос ауыспалылар үшін ![]() болса, онда алынған шешім оңтайлы болып
табылады.
болса, онда алынған шешім оңтайлы болып
табылады.
6) Егер бос ауыспалылар ![]() болса, онда осы бос ауыспалылардың біреуі алынады
және базиске ауыстырылады. Осы үшін қайта есептеу циклі
жүргізіледі (тұйық желі), бастапқы биіктік
таңдалған бос ауыспалының торында жатады. Қалған
циклің биіктігі базистік ауыспалыға сәйкес торда жатады.
Бастапқы циклддің биіктігіне ауыспалының өсуіне
сәйкес "+" белгісі беріледі. Ары қарай белгілер
жалғасады. "+" белгісі базистік ауыспалының өсуіне,
ал "-" белгілері кемуіне сәйкес келеді.
болса, онда осы бос ауыспалылардың біреуі алынады
және базиске ауыстырылады. Осы үшін қайта есептеу циклі
жүргізіледі (тұйық желі), бастапқы биіктік
таңдалған бос ауыспалының торында жатады. Қалған
циклің биіктігі базистік ауыспалыға сәйкес торда жатады.
Бастапқы циклддің биіктігіне ауыспалының өсуіне
сәйкес "+" белгісі беріледі. Ары қарай белгілер
жалғасады. "+" белгісі базистік ауыспалының өсуіне,
ал "-" белгілері кемуіне сәйкес келеді.
7) Циклдың теріс биіктігінен базистік ауыспалының орташа мәнімен биіктік таңдалады және осы өлшемге циклдың биіктігінде жатқан барлық ауыспалылар өлшенеді. Оң биіктіктегі ауыспалылар көбейеді, ал терісте азаяды. Таңдалған бос ауыспалылар базистік болады, ал орташа өлшемдегі циклдың теріс биіктігіндегі базистік ауыспалылар бос болады (нөлге тең).
8) Қайтадан алынған шешім үшін 3 пункттен бастап қайтадан есептелу жүргізіледі.
Шектелген өткізу қабілеті бар тасымалдау есебі келесідей шешіледі:
1) Тасымалдау матрицасындағы
![]() бағанасы беріліс қуаты шектелген және
тұтынушыға жауапты қуат Bj екі бағанға
немесе екі шартпен
бағанасы беріліс қуаты шектелген және
тұтынушыға жауапты қуат Bj екі бағанға
немесе екі шартпен ![]() және
және![]() тұтынушы қуатына
бөлінеді, мұндағы
тұтынушы қуатына
бөлінеді, мұндағы ![]() -шектелген қуат.
-шектелген қуат.
2) Қорек i мен ![]() тұтынушы арасындағы ауыспалы қуатты
тарату үшін қорғаныс орындалады, яғни осы
ауыспалыға үлкен меншікті баға көрсеткіші
қолданылады.
тұтынушы арасындағы ауыспалы қуатты
тарату үшін қорғаныс орындалады, яғни осы
ауыспалыға үлкен меншікті баға көрсеткіші
қолданылады.
Ары қарай тасымалдау есебін
шешу желінің өткізу қабілетінің шектеуінсіз септеуден
ешқандай айырмашылығы жоқ. Осыны көрсеткен жөн,
барлық шекті шешулнр үшін, сонымен бірге оңтайлы шешуге i
қоректен ![]() тұтынушыға берілетін
қуат мәнінен аспайды.
тұтынушыға берілетін
қуат мәнінен аспайды.
Жоғарыда қарастырылған тасымалдау есебінде қуатты тарату қоректен тұтынушыға тікелей іске асырылады.Бұл тасымалдау есебі классикалық қойылымға жатады. Электр тораптаындағы шынайы сұлбалар әдетте қуатты тарату аралық (транзиттік) түйіндері арқылы болады. Осындай транзиттік түйіндер қорек көзінің түйіндері, тұтынушылар түйіндері бола алады. 3.3 суретте мысал ретінде "транзиттік қуат" анықтамасын білдіретін электр тораптарының қарапайым сұлбалары көрсетілген.
3.3.2 сурет – «транзиттік қуат» анықтамасын көрсететін сұлбалар
3.3.2 а суретінде қорек
түйіндерінің ![]() және тұтынушының
және тұтынушының ![]() мен
мен ![]() өзара орналасуы көрсетілген.
Классикалық қойлымда тасымалдау есебінң электр
торабының оңтайлы сұлбасы 3.3.2 б суретіндегідей түрде
болады. Әдетте бұл сұлба 3.3 в суретіне қарағанда
қуаты тұтынушыға
өзара орналасуы көрсетілген.
Классикалық қойлымда тасымалдау есебінң электр
торабының оңтайлы сұлбасы 3.3.2 б суретіндегідей түрде
болады. Әдетте бұл сұлба 3.3 в суретіне қарағанда
қуаты тұтынушыға![]() аралық түйіндер
арқылы
аралық түйіндер
арқылы ![]() тұтынушысына берілетін
қуаттан қымбаттырақ болады.
тұтынушысына берілетін
қуаттан қымбаттырақ болады. ![]() түйіні арқылы
берілетін транзиттік қуаттың өлшемі
түйіні арқылы
берілетін транзиттік қуаттың өлшемі ![]() тұтынушының қуатына тең,
яғни
тұтынушының қуатына тең,
яғни ![]() .
.
Түйіннің нөміріне сәйкес осы түйін арқыл өтетін транзиттік қуат ауысудың екі бірдей индексімен белгіленеді.Транзиттік түйін ретінде қорек көзінің түйіні де болатынын көрсетуге болады.
Осы арқылы, транзиттік қуаты бар тасымалдау есебі толық есеп болып табылады және электр торабының сұлбаларының оңтайландырылуы классикалық қойлымға қарағанда тасымалдау есебі үлкен мүмкіншілдікке ие.
Транзиттік қуаты бар тасымалдау есептерін алгоритмді шешудің классикалық тасымалдау есебінен ешқандай айырмашылығы жоқ.Транзиттік қуаты бар тасымалдау есептерінің ерекшеліктерін атап айтуға болады, олар жоғарыда қарастырылған.
1. Барлық «n» түйіндер қорегі және «m» тұтынушылар түйіндеріне сквозная нөмірленуі 1, 2,... (n+m) беріледі.
2. Әр i - ші түйін бойынша транзиттік хij қуат берілуі мүмкін деп есептелінеді.
3. Транзиттік қуаттарды таратудың
меншікті бағасы ![]() тең.
тең.
4. Тасымалдау матрицасы квадрат болып табылады және мынандай өлшемге (n+m)(n+m) ие.
5. Транзиттік ауысу ![]() теріс белгісі бар есепті шешуге кіреді.
теріс белгісі бар есепті шешуге кіреді.
Мәнге тәуелді емес барлық транзиттік ауысулар базистік болып есептелінеді.
Бос ауысулар үшін мына
теңдік ![]() орындалмайынша тиімді шешуді іздестіру
жалғаса береді.
орындалмайынша тиімді шешуді іздестіру
жалғаса береді.
4 дәріс. Сызықты емес оңтайлы есептерді шешу
Дәрістің мазмұны:
- математикалық моделдердің оңтайлы есептерін шешу әдістерін іздестіру, сызықты емес тәуелділілікпен сипатталатын градиент әдісін сипаттау, анықталмаған Лагранж көйбейткіш әдісі арқылы электрэнергетикадағы оңтайлы есептерді шешуде қолдану.
Дәрістің мақсаты:
- энергожүйелерінде активті және реактивті қуаттарды таратуда оңтайлы есептерді шешуде программалаудың сызықты емес әдісін қолдануды дағдыландыру.
Шынайы оңтайлы есептер сызықты емес болады және олардың шешу жолын іздестіру қиын есеп болып табылады. Сондықтан градиенттік әдістер кең қолданысқа ие. Оңтайлы есептердің мақсаты шартты және шартты емес экстремумдарды табу болып есептелінеді.
Программалаудың
сызықты емес есептерінің графикалық суреттелуін екі айнымалы бар
мақсатты функция мысалында қарастырамыз. Мақсатты функция ![]() 3.4.1 суретте көрсетілген.
3.4.1 суретте көрсетілген.
3.4.1 сурет – Сызықты
емес мақсатты функция ![]() және оның сызықтары
және оның сызықтары ![]() теңдігіне тең теңдеумен
көрсетілген
теңдігіне тең теңдеумен
көрсетілген
Егер ![]() функциясын жазықтықпен кесіп өтсе,
горизонталды жазықтыққа параллель
функциясын жазықтықпен кесіп өтсе,
горизонталды жазықтыққа параллель ![]() және
және ![]() жазықтығына
құрастыру,онда осы жазыққтықта
шоғырланған тұйық қисықтарды аламыз, ол 3.4.2
суретте көрсетілген.Осы әр тұйық
қисықтардың мәні мақсатты функцияда
жазықтығына
құрастыру,онда осы жазыққтықта
шоғырланған тұйық қисықтарды аламыз, ол 3.4.2
суретте көрсетілген.Осы әр тұйық
қисықтардың мәні мақсатты функцияда ![]() өзгермейді.
өзгермейді.
3.4.2 сурет – Z функциясының минимум және ауысудың
шекті мәндерінің ![]() облысында суреттелуі.
облысында суреттелуі.
Алынған
тұйық қисықтар Z мақсатты функцияның ![]() теңдігіне тең сызықтар деп аталады. Сол
себепті, екі ауысудың сызықты емес фунуциясын
теңдігіне тең сызықтар деп аталады. Сол
себепті, екі ауысудың сызықты емес фунуциясын ![]() сызықты теңдікке тең
сызықты теңдікке тең ![]() екі жазықтықта
екі жазықтықта ![]() көрсетуге болады. Осы
шоғырланған сызықтар мақсатты функцияның минимумы
болып есептелінетін
көрсетуге болады. Осы
шоғырланған сызықтар мақсатты функцияның минимумы
болып есептелінетін ![]() және
және ![]() координата нүктесіне
созылады.
координата нүктесіне
созылады.
Енді ![]() жазықтықтарына шек қою сызықтарын
жүргізуге және шектік мәннің
жазықтықтарына шек қою сызықтарын
жүргізуге және шектік мәннің ![]() облысын табуға болды. 3.4.2 – суретте екі шек
қоюдың 1 мен 2 тепе-тең емес сызықты болатын және
3 шек қою тепе-тең емес сызықты емес жағдайы
көрсетілген. Әр шек қоюдың штрихталудың ауысуы
шектік мәнге қарай бағытталған.
облысын табуға болды. 3.4.2 – суретте екі шек
қоюдың 1 мен 2 тепе-тең емес сызықты болатын және
3 шек қою тепе-тең емес сызықты емес жағдайы
көрсетілген. Әр шек қоюдың штрихталудың ауысуы
шектік мәнге қарай бағытталған.
Сызықты есепті
қарастырған кезде, оңтайлы шешу әрқашан ![]() көпжақтылық биіктігінің біреуінде
жатады. Сызықты емес оңтайлы есептерде бұл шарт орындалмауы
мүмкін. Оңтайлы шешу
көпжақтылық биіктігінің біреуінде
жатады. Сызықты емес оңтайлы есептерде бұл шарт орындалмауы
мүмкін. Оңтайлы шешу ![]() облысының біреуінде немесе
осы облыстың ішінде жатуы мүмкін.
облысының біреуінде немесе
осы облыстың ішінде жатуы мүмкін.
Оңтайлы
есептерді шешу кезінде градиенттік әдіс қолданылады. Градиенттік
әдісте градиенттік функция қолданылады. Функцияның градиентін
![]() вектор деп атайды
вектор деп атайды
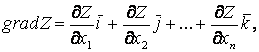 (3.4.1)
(3.4.1)
мұндағы i, j, ...k – бірлік векторлар.
Осы вектордың өлшемі мына теңдікпен анықталады.
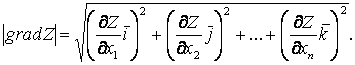 (3.4.2)
(3.4.2)
(3.4.1) және (3.4.2) теңдеуінен функцияның n айнымалылардаң барлық градиенттері дифференциалдануы керек.
Функция градиентінің
физикалық мәні бағыттылылықты (3.4.2) және
жылдамдықты (3.4.1) қарастырылатын
нүктедегі функцияның аз өзгеруін көрсетеді. Егер кейбір
нүктеде ![]() онда функция бұл нүктеде
өзгермейді. Бұл нүкте функция экстремумына сәйкес.
онда функция бұл нүктеде
өзгермейді. Бұл нүкте функция экстремумына сәйкес.
Есептелу нәтижесі мақсатты функцияның өзгеруі бастапқы i-ші және (i+1)-ші іздермен ε берілген нақты шешуден аз болады:
![]() (3.4.3)
(3.4.3)
Градиенттік әдістің келесідей түрлері болады: координаталық түсудің тұрақты ізі, тез түсу градиентін жобалау. Барлық аталған әдістер көпжақты шешудің экстремумының ақырындап қадаммен жақындауы, ол осы әдістерді қиындатады.
Аныкталмаған Лагранж көбейткіші әдісінде шартты оңтайлы есебінде шартты емес жеңіл есепке келтіріледі. Осы әдістің мәнін қарастырайық.
Сызықты емес функцияның шартты емес экстремумын табу керек:
![]() (3.4.4)
(3.4.4)
m-ға шек қою кезіндегі n айнымалы
 (3.4.5)
(3.4.5)
Тең емес шек қою тепе-теңдікке түрленеді, ал бос мүшелері шек қоюдың сол бөлігіне өтеді, яғни жүйе (3.4.5) түріне келтіріледі
 (3.4.6)
(3.4.6)
Лагранж әдісінің сәйкестігіне байланысты, функцияның экстремумымен (3.4.4) бірге шек қоюда (3.4.6) Лагранж функциясының абсолюттік экстремумы іздестіріледі, ол мынандай түрде болады:
 (3.4.7)
(3.4.7)
мұндағы ![]() - Лагранж функциясының белгісіз
көбейткіштері, сонымен бірге ол айнымалыларі
- Лагранж функциясының белгісіз
көбейткіштері, сонымен бірге ол айнымалыларі ![]() болып табылады.
болып табылады.
Көріп отырғанымыздай, Лагранж функциясына мақсатты функция, қосымша әр шек қою және Лагранж көбейткішіне көбейту жатады.
Мақсаттық функцияның қатысты экстремумы (3.4.4) шектеу кезінде (3.4.6). Лагранж функциясының абсолюттік экстремумымен сәйкес келетіндігі дәлелденген (4.1.7). Функцияның абсолюттік экстремумын анықтау (4.1.7) белгілі тәсілдермен орындалады. Сонымен қатар, Лагранж функциясының дербес туындысы болып табылады және дербес туындысы нөлге тең.


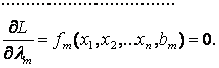
Алынған жүйе оптимизациялық есептердың шектеуі болып табылады, ал оның шешімі Лагранж функциясының абсолютті минимумдік координатасын береді (3.4.7) немесе мақсаттық функциясының қатыстық минимумын (3.4.4) шектеу кезінде (3.4.6).
Бұл тәсіл оптимизациялық тапсырмаларды шешу үшін яғни активті қуаттың тұтынушы энергожүйесін мен электрлік станция жүйелері арасында таратуы, сонымен қатар реактивті қуат көздерін қою мақсатында.
5 дәріс. Айнымалы дискреттік және бүтінсанды оптимизациялық есептер
Дәріс мазмұны:
- бүтінсанды, екілік және дискреттік айнымалы есептерді шешу тәсілдері.
Дәріс мақсаты:
- оңтайландырылған есептерді бүтінсанды екілік және дискреттік айнымалылар арқылы шешілуіне мысал келтіру.
Әдетте оптимизациялық есептерді шешу кезінде шыққан айнымалылар немесе олардың бөлігі тек бүтін санды қабылдауы тиіс, мұндай есептердің математикалық моделі сызықты және сызықсыз моделі секілдіжәне бүтін функцияны, шектелген жүйені және шектеу шартын құрайды. Олар ерекшеленеді, бүтінсанды айнымалы есептерде шектелген жүйе мынадай шектеулермен толтырылады. Бұндай есептің математикалық моделі жоғарыдағы сызықты және сызықсыз модельдерінің ұқсастығы қаралып мақсаттық функцияның шектелген және шектелмеген жүйе шартын құрайды. Дегенмен, шектелмеген жүйелер бүтінсанды айнымалылар есебін түрді шектеумен толтырады
![]() - бүтін, k=1, 2, … l,
(3.5.1)
- бүтін, k=1, 2, … l,
(3.5.1)
мұндағы l - бүтінсанды айнымалылар саны, l ≤ n;
n – айнымалылардың жалпы саны.
Оптимизацияланған есептердің, ізделінген айнымалылары немесе олардың бөлшегі бүтін сан болуы қажет және бүтінсандардың бағдарламалау әдісімен шешіледі.
Қосымша шектеуді енгізгенде бүтінсанды айнымалылар есептеу көлемін елеулі ұлғайтып және оңтайлы шешімді іздеу кезінде есептеуіш процедураны қиындатады. Берілген диапазондағы айнымалының өзгеруі, үзіліссіз айнымалыға қарағанда бүтінсанды айнымалының мәні аз болады. Көп жағдайда, 0 ≤ х ≤ 3 диапазонында х бүтінмәнді айнымалының төрт мәні болады (х=0, 1, 2, 3), ал үзіліссіз айнымалыда –шексіз мәндер саны.
Бүтінсанды оптимизацияланған есепті толық іріктеу әдісімен шешуге әрекетін жасауда айнымалылар мәні өте үлкен көлемді есептеуге алып келеді. Мысалы, үш бүтінсанды айнымалы және диапазонды есебінің өзгеруінде 0 ≤ хк ≤ 10, k=1, 2, 3 бүтінсандар көлемінің шешімі 113=1331 құрайды. Бұл нақты оптимизацияланған есептер үшін толық іріктеу әдісі қолайсыз екені анық.
Бүтінсанды есептерді шығарудың басқалай шешу әрекеті (3.4.1) шектеу түрін қолданусыз шығарудан тұрады. Бұл жағдайда үзіліссіз айнымалылармен қарапайым есеп шығарылады, ал алынған үзіліссіз айнымалылар бүтін сан болғанға дейін жұықтамыз.
Бүтінсанды есептерді шешудің басқа түрлі әдістері бар: Беллман әдісі,тармақталу мен шектеу әдісі, тармақтау мен шектеу әдісімен белгіленген шешімдерге негізделген, бірақ бөлек шешімді енгізуге емес, олардың топтарын енгізу арқылы орындалады. Қосымша шектерді енгізгенде (x1 , x2, x3 ) – бүтін сан. Бүтін сан функциясы нашарлайды, үзіліссіз айнымалыларды бүтін санға дейін дөңгелектеу керек, орнықсыз және белгісіз шешімдерге дейін алып келеді. Бүтінсандарды есептеу орнықты шешімге жақындамауы да мүмкін.
Көп жағдайда бүтінсандық есептердің есебі болып, ізделініп отырған айнымалының бүтін мәні, әртүрлі мәнді емес, тек бір ғана мәнді қабылдай алады: не 0, не 1. Бұндай айнымалылар екілік немесе бульдік деп аталады.
Берілген шешім саны ішінде оңтайлы шешімін(нұсқасының) таңдау есептері екілік айнымалылы есептерінің көп таралған түріне жатады. Егер нұсқа оңтайлы шешімге кірсе, онда бұл нұсқаға сәйкес, екілік айнымалы, 1-ге тең болады. Егер нұсқа оңтайлы шешімге кірмесе, онда бұл нұсқаға сәйкес, екілік айнымалы, 0-ге тең болады. Мысалы, егер электротарату желісі оңтайлы электр желісіне кірсе, онда бұл сызыққа сәйкес екілік айнымалысы 1-ге тең; егер электротарату сызығы оңтайлы электр желісіне кірмесе, онда бұл сызыққа сәйкес екілік айнымалысы 0-ге тең.
хі дәстүрлі айнымалысына қарағанда δі екілік айнымалысы десек, бұнда і=1, 2, …, n.
Екілік айнымалылыны қолдануда шешілетін есептерге логикалық шарттар «егер ... , онда ... » қатарының түрін қоюға рұқсат етеді.
Егер оңтайлы шешімге (i және j) нұсқаларының біреуі ғана кіретін болса, онда айнымалылардың қосынды саны
δi +δj=1. (3.5.2)
Егер оңтайлы шешімге i-ші және j-ші нұсқалар кіретін болса, онда айнымалылардың қосынды саны
δi +δj=2. (3.5.3)
Егер оңтайлы шешімге екеуіде ( i және j) нұсқалары, кіретін немесе кірмейтін болса, онда айнымалылардың қосынды саны
δi +δj≥0. (3.5.4)
Егер кірісінде(шығысында) оңтайлы шешімнің i-ші нұсқасына бұл шешімге j-ші нұсқасы кіретін(кірмейтін) болуы қажет, онда
δi =δj. (3.5.5)
Ұқсас шартты үш немесе одан да көп нұсқаларға жазуға болады. Егер n мүмкін нұсқасының оңтайлы шешіміне тек m нұсқасы (m<n) кіретін болса, онда
δ1 +δ2+...+ δn =m.
«егер ..., онда ...» түрдегі логикалық шарттардың саны шектелмегені анық.
Оңтайландырылған тәжірбиелік есептер қатарында жіберілетін шешісдер алдын-ала белгілі, осылардан оңтайлы шешімді таңдау қажет. Мысалы, орын толтыру қуатымен берілген Qi электрожабдықтау жүйесінде 1, 2, ... , n түйіндеріне орналастыруға болады. Орын толтыру құрылғысының түйінді оңтайлы орналастыруын таңдалған белгісіне сәйкес таңдау қажет.
Басқа қатардағы ізделініп отырған есептерде айнымалылар әртүрлі емес, тек анықталған мәнді ғана қабылдай алады, оның ішінде оңтайландыру шешіміне жауап беретін айнымалыларды таңдау қажет. Мысалы, берілген түйіндегі электрожабдықтау жүйесіне, қуаты Qк1,Qк2, ... Qkn мәніне тең болатын компенсацияланған құрылғыны орнату қажет. Бұл қатардан таңдалған критерии бойынша, компенсацияланған құрылғы қуатының оңтайлы мәнін таңдау қажет.
Көрсетілген есептер берілген есептер санының таңдау нұсқасына жатады және дискретті бағдарламалау әдісімен шешіледі. Бұл әдістерде дәстүрлі айнымалылармен қатар екілік айнымалылар қолданылады, олардың мүмкіндіктері берілген логикалық шарттары м.5.2. қарастырылған.
Дискретті бағдарламалаудың есебінің математикалық моделі жоғарғы модельдермен ұқсас қаралған және мақсаттық функциясын, шектелген жүйесін және шартты шекарасын құрайды. Айнымалылары арасындағы тәуелділікте, мақсаттық функциядағы жүйелер сызықты секілді, сызықты емес болуы мүмкін. Дискретті айнымалылардың берілген мәні әртүрлі бола беруі мүмкін, яғни бүтінсандық кезіндеде.
Оптимизацияланған есепте п ізделінген айнымалысы хі(і=1, 2, ... , п) болсын. Әрбір айнымалының дискретті мәні берілген. Оңтайлындырылған шешімге k айнымалысы кіруі керек (k<п). Әрбір хі айнымалысына сәйкес δі екілік айнымалылысын қоямыз. Егер есепті шығару кезінде δі=1, онда хі айнымалысы оңтайландыру есебіне кіреді; егер δі=0, онда хі айнымалысы оңтайландыру есебіне кірмейді.
Мақсаттық функция х1,х2, ... , хп дискретті және δ1,δ2, ... , δп екілік айнымалыны өзіне қосады
Z(х1,х2, ... , хп, δ1,δ2, ... , δп)→extr.
Шектеу жүйесіне дискретті және екілік айнымалылар жатады
f1(х1,х2, ... , хп, δ1,δ2, ... , δп,b1 )=0,
f2(х1,х2, ... , хп, δ1,δ2, ... , δп,b2)=0,
…………………………………
fm(х1,х2, ... , хп, δ1,δ2, ... , δп,bm )=0.
Бұл жүйеге шектеу түрлері қосылады
δ1+δ2+...+ δп=k,
δi – екілік, і =1, 2,..., п.
Шектеу шарттары, осылай дискретті айнымалылардың мәні берілгендей болған, ал екілік айнымалылардың мәні тек 0 немесе 1 болады.
6 дәріс. Кездейсоқ шыққан бағдарламалар кезіндегі оңтайландырылған есептер
Дәріс мақсаты:
- кездейсоқ шаманы түсіну, математикалық күту,орташаквадраттық ауытқу, функцияны тарату мүмкіндігі. Оңтайладырылған есептерді шешуге арналған стохастикалық бағдарлама.
Дәріс мазмұны:
- шыққан мәліметтердегі кездейсоқ элементтердің оңтайландырылған есептерді шешуге арналған стохастикалық бағдарламасын қолдануға дағдылану.
Жоғарыдағы лекцияларда оптимизациялық есептерді шешкенде барлық берілген шығнындылары айқындалған болатын. Ондай мәліметтер детермироваланған деп аталады. Оған мысал болатын:
![]() ,
, ![]() и bj (i=1, 2,...n; j=1, 2,...m) Практикалық есептерде шыққан
мәліметтер детермировалық болмайды. Шыққан
мәліметтер немесе оның бөлігі кездейсоқ шама немесе
кездейсоқ функция болады. Электржабдықтау жүйесінде
жүктеме қуатын кездейсоқ шама деп қабылдауға
болады. Оңтайландырылған есептерді шешу кезінде
стохастикалық бағдарламаны қолдану.
и bj (i=1, 2,...n; j=1, 2,...m) Практикалық есептерде шыққан
мәліметтер детермировалық болмайды. Шыққан
мәліметтер немесе оның бөлігі кездейсоқ шама немесе
кездейсоқ функция болады. Электржабдықтау жүйесінде
жүктеме қуатын кездейсоқ шама деп қабылдауға
болады. Оңтайландырылған есептерді шешу кезінде
стохастикалық бағдарламаны қолдану.
Кездейсоқ шамалармен жоғарға математика пәнінің ықтималдық теория жұмыс жасайды. Сол себептен бұл есепті шешпес бұрын осы математика бөліміне көңіл аударғанымыз дұрыс болар.
Кездейсоқ шама деп сол немесе басқа шаманы қабылдайтскреткінті болуы мүмын, яғни алдын ала белгісіз болатыныншаманы айтамыз.
Кездейсоқ шама үзіліссіз немесе дискретті болуы мүмкін. Берілген диапазондағы кездейсоқ өзгерген шаманың дискреттік кездейсоқ шаманың мәні шектеулі болады, ал узіліссіз кездейсоқ шаманың мәні шектелмеген болады. Үзіліссіз кездейсоқ шамаға мысал ретінде электржабдықтау жүуйесіндегі кейбір түйіндердегі кернеу шамасын айтуға болады. Ал дискретті кездейсоқ шамаға мысал ретінде, энергожүйедегі бірмезгілде жұмыс іспеп тұрған генераторлар санын айтуға болады.
Кездейсоқ шаманың математикалық тосуы деп оның орташа мәнін айтуға болады, n айқындауы арқылы
![]() . (3.6.1)
. (3.6.1)
Орташа квадраттық ауытқу кездейсоқ шамаға қатысты математикалық тосуды анықтайды:
 (3.6.2)
(3.6.2)
Кездейсоқ шаманың маңызды мінездемесі Р ықтималы қызмет етеді, мұндай кездейсоқ шаманың кездесуі нақты интервал мәнінде.
Кездейсоқ шаманың ықтималды қосынды бағасы үшін тарату функция шамасы енгізіледі. Кездейсоқ шама s мәндерді қабылдауы мүмкін (-∞ ; +∞).
Тарату функциясы Р(s) кездейсоқ шаманың шексіздіктен s дейінгі ықтималын көрсетеді.
![]() (3.6.3)
(3.6.3)
Практикада қалыпты тарату заңы бар, ықтималдылықпен сәйкес 0,999 кедейсоқ шама s (-∞<s<+∞) интервалынан табылады
![]() (3.6.4)
(3.6.4)
Практикалық есептерді шешу үшін қалыпты стандартты тарату заңын қолданған жеткілікті.

3.6 сурет – Қалыпты стандартты заңның тарату функциясы
Осының көмегеімен кездейсоқ шаманың мәнін анықтауға болады η, яғни белгілі мән беруі үшін. Осы тарату функциясы арқылы басқа функцияға өтуге болады.
![]() (3.6.5)
(3.6.5)
Оңтайландырылған есептерді шешуге арналған стохастикалық бағдарлама атты сұраққа көшелік. Оны шешудің универсалды әдісі жоқ. Сол себептен оны сызықты бағдарлама арқылы шешуге болады.
![]()

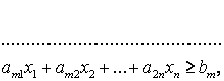 (3.6.6)
(3.6.6)
![]()
Мақсаттық функцияның
коэффициенті ![]() ,
, ![]() и bj (i=1, 2,...n; j=1, 2,...m) кездейсоқ шама болса,
мақсаттық функцияның математикалық тосуының
экстремалдық мәнін іздесе
и bj (i=1, 2,...n; j=1, 2,...m) кездейсоқ шама болса,
мақсаттық функцияның математикалық тосуының
экстремалдық мәнін іздесе
![]() (3.6.7)
(3.6.7)
Егер ![]() немесе bj
коэффициенттері жүйесінің шектеуі кездейсоқ шама болса, онда
әр бір j шектеуге
немесе bj
коэффициенттері жүйесінің шектеуі кездейсоқ шама болса, онда
әр бір j шектеуге ![]() ықтималын
енгіземіз. Әр бір ықтималдылықтың орындалуы s шектеуі
берілген шамадан аспайуы тиіс
ықтималын
енгіземіз. Әр бір ықтималдылықтың орындалуы s шектеуі
берілген шамадан аспайуы тиіс
![]()
Шектік талаптар графикалық оңтайлы тапсырмаларда ережедегідей, кездейсоқ шаманы құрамайды және өзгеріссіз жазылады.
Математикалық есептік моделдер стохастикалық бағдарлама бойынша келесідей жазылады:
 (3.6.8)
(3.6.8)
Стохастикалық есептер жоғарыда көрсетілгендей (3.65) матаматикалық модельдің түрлері тікелей шешімі болмайды. Тәртіп бойынша есепке кездейсоқ берілген ақпарат олардың детермерленген эквиваленті кіреді. Бұл үшін кездейсоқ шама олардың мінездемесінің орнын басады. (Математикалық кідіру мен стандартты өшу) және есептеледі, кездейсоқ шама қалыпты заңды таратады.
Егер
кездейсоқ шама толық функцияның коэффициенті ![]() болады, бұл
коэффициент математикалық кідірудің орнын басады. Осындай орын
басудың арқасында детермирленген эквивалентті толық
функциямен аламыз.
болады, бұл
коэффициент математикалық кідірудің орнын басады. Осындай орын
басудың арқасында детермирленген эквивалентті толық
функциямен аламыз.
![]() (3.6.9)
(3.6.9)
Әрқасысына j-ге дейінгі шектеу беріледі,ықтималдылығы Рij осы шектеу орындалуы керек. Мәні бойынша Рберj стандарт кездейсоқ шама η мәнін табамыз. Стандартты кездейсоқ шаманың η оңтайлы тапсырманың аij және bj кездейсоқ шамаға ауысуы жүзеге асырылады, ол байланысты ескеру керек. Егер кездейсоқ шама дедермирленген j коэффициенті болатын болса эквивалентті j туріндегі шектеулер болады.Если случайной величиной являются коэффициенты bj, то детерминированный эквиваленту j-го ограничения будет иметь вид
![]() ,
,
![]() (3.6.10)
(3.6.10)
Егер кездейсоқ шама аij коэффициент болатын болса, онда дитермирленген эквивалент түріндегі шектеулер болады.
 (3.6.11)
(3.6.11)
Шекаралық шарт өзгеріссіз қалады
![]() (3.6.12)
(3.6.12)
Осындай математикалық модельдеу стохастикалық есептеу дитермирленген эквивалентке (3.6.9.) (3.6.10) және (3.6.11) әкеледі.
Негізгі бөлігі стохастикалық есептеудің кездейсоқ шамасы бір немесе бірнеше коэффициент аij - bj болып табылады.
7 дәріс. Берілгені анықталмаған ақпараты бар оңтайландырулық есептер
Дәріс мазмұны:
- ойындар теориясы, орташа шығын минимумының стратегиясы, минималды және максималды стратегия, Гурвиц стратегия.
Дәріс мақсаты:
- ойын тоериясын және шешімді таңдаудың негізгі стратегиясын қарастырамыз.
Нақты оңтайландырылған есептерде көбінесе анықталмаған шарттағы шешімді іздеуге тура келеді. Анықталмағандықтаң негізгі себебі берілген ақпараттың жетіспеушілігі. Электроэнергетика саласында қолданылатын анықталмаған ақпараттың мысалы ретінде, дамып келе жатқан электроэнергетика жүйесінде перспективалы қуаттың өсуі қызмет етуі мүмкін.
Анықталмаған ақпаратты оңтайландырылған есепті шешеу үшін математикалық бағдарламалау әдісі қолайлы емес. Бұнда ойын теориясын есептейтін аппарат қолданылады.
Осыған сәйкес оңтайландырылған теория есебі екі ойыншының ойынын ұсынады. Бірінші – шешім қабылдайтын адам. Келтірілген мысалда адам жаңа электростанцияда,электроберілу сызығының құрылысы және кіші станцияда, энергожүйесін орналастыру туралы шешім қабылдауы қажет. Адам – ақылды ойыншы. Оның стратегиясы – максималды ұтыс және минималды жеңіліс. Басқа сөзбен - адам өз шығынын минималдайды.
Екінші ойыншы – энергожүйе, анығырақ айтқанда энерия тұтынушыларының перспективті қуаты. Энергожүйе қалай дамиды, перспективтағы тұтынушылардың қуаты қандай болады – бірыңғай белгісіз. Энергожүйе стратегиясы – кездейсоқ. Ол максмалды ұтысқа ұмытылмайды. Демек, энергожүйені ақылды ойыншы деп санауға болмайды.
Оңтайландырылған есебін шешкенде төлемді матирца құралады, ол екі ойыншы арасындағы шығын кестесін көрсетеді. Матрица жолдары шешімге(қадамға) сәйкес келеді, оны бірінші ойыншы қабылдай алады. Бағандар – қадамдарға, оны екінші ойыншы қабылдай алады. Төлем матрицасын құру процессі біршама қиын және әрбір нақты жағдайда әртүрлі болады.
Мысалы, (3.7 кестеге қара) төлем матрицасын құрылған. Адам қадамдарының жиыны бар, олар x1,x2, … xn белгіленген. Энергожүйенің қадамдарының у1,у2, … уm жиыны бар. Егер адам хі қадамын таңдаса, ал жүйе уj қадамымен жауап берсе, онда бұндай таратуда шығын zij құрайды. Оңтайлы шешім төлем матрицасының талдау нәтижесінен таңдалады.
3.7 Кесте
|
|
y1 |
y2 |
… |
yj |
… |
ym |
|
x1 |
z11 |
z12 |
… |
z1j |
… |
z1m |
|
x2 |
z21 |
z22 |
… |
z2j |
… |
z2m |
|
… |
… |
… |
… |
… |
… |
… |
|
xi |
zi1 |
zi2 |
… |
zij |
… |
zim |
|
… |
… |
… |
… |
… |
… |
… |
|
xn |
zn1 |
zn2 |
… |
znj |
… |
znm |
Ойындар теориясы ұсынған, шешудің негізгі таңдау стратегиясын карастырайық.
1. Орташа шығынның минимум стратегиясы. Осы стратегияға сәйкес әрбір үшін жүйенің барлық мүмкін қадамдарының орташа шығыны анықталады

i=1,2, … n жинағының минимумының минималды шығынына жауап беретін шешімі таңдалады
![]() .
.
Осы стратегияда қолдану кезінде, жүйенің барлық қадамдары бірдей ықтималдықта болады, 1/m тең деп саналады. Нақты тапсырмалар үшін бұндай болжау, ереже ретінде, шындық болып табылмайды.
2. Миниминдік стратегия. Осы стратегияға сәйкес хі адамының әрбір қадамы жүйеның уі қадамымен, минималды стратегияға сәйкес жауап қайтарады деп саналады
![]() .
.
Осы стратегия бойынша шешім қабылдау үлкен есептеуге алып келеді, өйткені бұнда ең қолайлы жағдай қаралып отыр
![]() .
.
Жүйені ақылды ойыншы деп санауға болмайды, дегенмен ол беріп ойнамайды:
3. Минимкасты стратегия. Осы стратегияға сәйкес хі адамының әрбір қадамы жүйенің уі қадамымен, максималды стратегияға сәйкес жауап қайтарады деп саналады
![]() .
.
i=1,2, … n жинағының минимумының максималды шығынына жауап беретін шешімі таңдалады:
![]() .
.
Бұл стратегияда ең қолайсыз жағдай ескеріледі. Бұнда жүйе ақылды ойыншы болып табылады және максималды жеңіске ұмтылады. Бұндай болжам шындыққа сәйкес келмейді.
4. Гурвиц стратегиясы. Бұл стратегия ең қолайлы және ең қолайсыз жағдайды қарастырады. Бұнда шешім шарт бойынша таңдалады
![]() ,
,
мұндағы k – коэффициенті және (1- k) көлемді коэффициенттер ролін ойнайды, демек минимаксты және миниминдық стратегиялар есепке алынады. k=1 кезінде минимаксты статегия, ал k=0 кезінде миниминді стратегия болады.
Бұл стратегияны қолдану кезінде көптеген қиындықты (1- k) және k көлемді коэффициенттерінің шамасын анықтау тудырады. Осы сұраққа ойындар теориясы жауап бермейді. Алынған тәжірибе нәтижесінде, әрбір нақты тапсырма үшін көлемді коэффициенттер жеке анықталады.
Демек, оптимизациялық тапсырманы шешу үшін, берілген анықталмаған ақпараттарда ойын теориясы стратегиялар қатарына апарады. Формальды түрде барлық стратегиялар тең құқықты, соңғы шешім негізде таңдалады:
- әрбір стратегияда алынаған, шешімдер сараптамасы;
- жобалаушы тәжірибесі;
- нақты тапсырмалардың ерекшеліктері.
8 дәріс. Көпкритериялі оңтайландырулық есептер
Дәріс мазмұны:
- көпкритерилі есептер, критерилердің салмақты коэффициенттерінің түсінігі, жалпыланған мақсаттық функцияның оңтайлылығы.
Дәріс мақсаты:
- көпкритерилі есептертерге түсіндіріп және оның шешу әдетін беру.
Жоғарыда қарастырылған оңтайлылық есептердің шешімі бір критеримен орындалған(бір мақсаттық функциямын). Тәжірибеде есептерді бңр критериге келтіру әрдайым орындала бермейді, өйткені алынатын мақсаттар бірнеше болуы мүмкін.
Оңтайландырылған бірнеше критеримен шешілетін есептер, көпкритерилі оңтайландырылған есебі деп аталады. Бұндай оңтайлылық қабылданған критерилер арасында келісімді табуға көмектеседі.
Бұндай келісімді табудағы қажетті кезеңі әрбір критериге кофэффициенттер салмағын тағайындау. Көпкритерилі есептердің қорытынды шешімі жалпыланған критериді оптимизациялауға әкеледі, бұған барлық қабылданған критерилердің салмақты коэффициенттері кіреді.
Тәжірибелік оңтайлылық есептердегі шектік шарттар, ереже ретінде, кездейсоқ шамасы болмайды және еш өзгеріссіз жазылады.
Стохастикалық бағдарламалау есебінің математикалық моделі болады:
Математикалық моделі (3.6.5) түрінде көрсетілген, стохастикалық есептер, яғни шешімі болмайды. Ереже ретінде, яғни кездейсоқ берілген ақпараты бар есептерді апарады. Сол үшін кездейсоқ шамалар сипаттамасына ауыстырылады (, стандартты ақаулар) және кездейсоқ шамаларда қарапайым тарату заңы болады.
Егер xi мақсаттық функция коэффициенті кездейсоқ шама болса, онда бұл коэффициенттер математикалық үмітпен ауыстырылады. Яғни осындай ауыстыру нәтижесінде мақсаттық функцияның анықталмаған эквивалентін аламыз.
Әрбір у- ші шектеуіне осы шектеу
орындалатын Рбері ықтималдығының беріледі. Рбері
мәні бойынша ![]() стандартты кездейсоқ шамасының
мәні табылады. (3.6.5) өрнегінің қатынасы бойынша
стандартты кездейсоқ шамасының
мәні табылады. (3.6.5) өрнегінің қатынасы бойынша ![]() стандартты кездейсоқ шамасынан аіj
және bj оптимизациялық есеп шамасына ауысады.
стандартты кездейсоқ шамасынан аіj
және bj оптимизациялық есеп шамасына ауысады.
Егер кездейсоқ шамасы bj коэффициенті болса, онда анықталмаған эквивалентінің j-ші шектеуі мынадай түрде болады
Егер кездейсоқ шамасы аіj коэффициенті болса, онда j-ші шектеуі мынадай түрде болады
Шектік шарттар мына түрде өзгеріссіз болады
Демек,стохастикалық есептің математикалық моделі анықталмаған эквивалентіне апарады (3.6.9), (3.6.10) және (3.6.11).
Стохастикалық есептің негізгі салмағында кездейсоқ шамалы есептердің бір немесе бірнеше аіj және bj коэффициенттері болады.
Салмактық коэффициенттердің көптеген түрлері бар. Солардың біреуін қарастырайык, эксперттік бағалау тәсілі . Бұл тәсілдің негізі келесілерге негізделген:
Оңтайлылық есебін шешу үшін мысалға: үш критерий қабылдансын (А критериі,В критериі,С критериі). Оңтайлылық есебіне катысты аймактағы мамандар – эксперттер тобы жиналады. Эксперттер тобы мысалыға үш адамнан тұрсын (1-ші эксперт, 2-ші эксперт,3-ші эксперт) Әрбір экспертке әр критериді 0-1дейінгі баллмен бағалау ұсынылады. Бұл жағдайда мынадай шарт қойылады: барлық критерий бойынша әр эксперттің баллдарының косындысы 1-ге тең болуы керек.
Экспертизаның қортындысы кестеде көрсетілген. i-ші критеридің (i=А,Б,С) салмактық коэффициенті ретінде осы критерий бойынша әрбір эксперттің бағасының орташа мәні қабылданады. (3.8 кестеде соңғы жол)
3.8 Кестес
|
|
Критериялар |
|
||
|
Эксперты |
А |
В |
С |
Сумма |
|
1-й |
0,2 |
0,2 |
0,6 |
1,0 |
|
2-й |
0,4 |
0,3 |
0,3 |
1,0 |
|
3-й |
0,3 |
0,2 |
0,5 |
1,0 |
|
Коэф.веса |
0,3 |
0,23 |
0,47 |
1,0 |
Жалпылы максаттық функция бойынша оңтайлылық
Көп параметрлі есептің мүмкін болатын шешімдерінің бірі жалпылы максатты функция бойынша оңтайлылық болып табылады, оған өздерінің салмақтық коэффициенттерімен қарастыруға қаралған критерилар кіреді. Бұл жалпы функция келесі түрде жазылады.
 ,
,
мұндағы zк – k-ші критерий максаты мұнда к-ші критериді көрсетеді;
zкнорм – к-ші максатты функцияның нормаланған мәні;
αк – к-ші максаттық функцияның салмактық коэффициенті;
S – максаттық функцияның саны (қабылданған критерилердің саны).
Егер k-ші мақсаттық функция максималданса, оның алдында қосынды белгісі (+) таңбасы қойылады.
Егер k-ші мақсаттық функцияны минималдаса, оның алдында қосынды белгісінің астына (±) таңбасы қойылады.
Салмақтық коэффициенті мысалы: эксперттік бағалау көмегімен анықталуы мумкін.
Мақсаттық функцияның k-ші мақсаттық функциясы нормаланған мәні zкнорм бір ғана k-ші критерий бойынша оңтайлы есебінің шешімінің қортындысы бойынша қабылданады.
Жалпы жағдайда мақсаттық фунқциялардың әртүрлі өлшем бірліктері болады. Сондықтан (3.28-де) әрбір мақсаттық функцияның оның нормаланған мәнінің бөліндісі енгізілген.
Бұл әрекет барлық мақсаттық функциялардың бірдей өлшемге әкеледі.(Салыстырмалы бірліктерге, С,В).
Бір критериялды есеппен салыстырғанда, көп критериалды есептер үшін шекаралық шарттармен шектеулердің құрастырылудың спецификалық ерекшелігі жоқ.
Әдебиеттер тізімі
1. Гордиевский И.Г. Критериальный анализ некоторых технико-экономических задач энергетики. – М.: «Высшая школа», 2002.
2. Волков Л.Т. Математические задачи энергетики. Типовые задачи: Учеб.пос. / Энергия, 2003.
3. Электрические системы. Математические задачи электроэнергетики: Учебник для студентов вузов / Под ред. В.А. Веникова. - М.: Высшая школа, 1986 - 288 с.
4. Астраханов Ю.А., Веников В.А., Ежков В.В. Электроэнергетические системы в примерах и иллюстрациях. - М.: Высшая школа, 1989.
5. Электрические системы и сети, Ежков В.В. и др. Учебное пособие для электроэнергетических спец./Учебная литература/Технические науки.-М.: «Высшая школа», 2005.
6. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями. Шапкин А.С. - Изд.: «Издательский дом Дашков и К», 2004.
7. Акулич И.Л. Математическое програмирование в примерах и задачах. - М.: «Высшая школа», 1986.
2010 ж. жиынтық жоспары, рет.10