НЕКОММЕРЧЕСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра Электроснабжения промышленных предприятий
КОСПЕКТ ЛЕКЦИЙ
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ И
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
В ЭЛЕКТРОЭНЕРГЕТИКЕ
АЛМАТЫ 2007
СОСТАВИТЕЛИ: Н.А. Туканова, К.А. Бакенов. Математические задачи и компьютерное моделирование в электроэнергетике. Конспект лекций для студентов всех форм обучения специальности050718 – Электроэнергетика. – Алматы: АИЭС, 2007. – 23 с.
Данная разработка включает конспект лекций по дисциплине «Математические задачи и компьютерное моделирование в электроэнергетике» для студентов специальности 050718 – Электроэнергетика, а также список рекомендованной литературы.
1 Элементы схем замещения электрических систем
Содержание лекции:
- идеальные источники напряжения и тока;
- реальные источники напряжения и тока;
- комплексные сопротивления и проводимости;
- взаимоиндукция.
Цели лекции:
- изучить основные элементы схем замещения электрических систем и научиться определять их параметры.
Электрическая система, как объект исследования (познания), представляет собой бесконечно сложную систему. Поэтому над изучением будем понимать поведение каких-то выделенных элементов (в настоящем случае связанных с токами к.з.). Если удастся набрать систему логико-математического описания поведения электрической системы, что каждому элементу ai, оригинала будет поставлен в соответствие элемент описания a'i, (a'1,a'2,a'3...a'm ), каждому действию Ок будет поставлена в соответствие некая операция в описании О к, (О1,'О2,'Оз' ...О'п), то можно сказать, что множество аi и Ок оригинала отображаются на соответствующих множествах а'i и О'к модели. При этом, как следствие, реакции оригинала Rк(аi) соответствует реакция модели Rк' (a'i).
Отсюда следует главный вывод, что моделью любого оригинала, в частности электрической системы, может называться такое логико-математическое описание интересующих процессов, для которого можно найти соответствие элементов, возмущений и реакций этого описания и оригинала.
Прежде чем рассматривать расчеты схем электрических систем, необходимо уточнить состав этих схем и дать качественное и количественное определение всех элементов, которые будут использоваться при расчетах.
Схемы замещения электрических систем, по своей сути, являются логико-символическими моделями самих систем. Если, к тому же, найдены соответствующие формулы, уравнения и т.п. их расчета, то схемы замещения можно назвать логико-математическими моделями электрических систем, на элементы которой отображаются различные элементы реальной системы.
В расчетах электрических и электронных схем используется много идеальных элементов [1, 10], а в практике расчетов электрических режимов систем используется несколько из них.
Все используемые идеальные элементы можно разделить на две большие группы. Первую группу элементов характеризует то, что они являются источниками электрической энергии, поэтому их называют активными. Вторую группу представляют те элементы, которые осуществляют различные преобразования электрических величин, не являясь источниками электрической энергии. Иногда, правда, это отличие становится условным.
1.1 Источники напряжения
Источником напряжения - активный элемент,
содержащий в себе источник ЭДС и характеризующийся постоянством напряжения на
его выводах (зажимах) в функции от нагрузки. Выражение "содержит в себе
источник ЭДС" означает способность элемента неограниченное время
поддерживать на своих выводах разность потенциалов в соответствии с заданным
законом его изменения. "Постоянство напряжения в функции нагрузки"
означает, что параметры напряжения не зависят от характеристики цепи, к которой
подключен источник. Это, в свою очередь, означает, что внутреннее сопротивление
источника бесконечно малая величина. Качественное определение можно дополнить
количественным
|
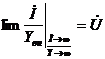
здесь i - ток, который обеспечивает источник напряжения;
Yвн – внутренняя проводимость источника;
![]() -
напряжение
на зажимах источника.
-
напряжение
на зажимах источника.
Таким источником можно отобразить например, трансформатор напряжения, работающий с малой нагрузкой, т.е. в пределах его класса точности. Другой пример: генератор в нормальном нагрузочном режиме, оборудованный автоматическим регулятором напряжения.
1.2 Источники тока
Источник тока - активный элемент, который характеризуется постоянством величины тока. Это означает
независимость тока от величины нагрузки, но может меняться по заданному закону,
например, синусоидальному. Сказанное означает, что источник тока содержит в
себе источник ЭДС и внутреннее сопротивление, которые по величине принимают
бесконечно большие значения, точнее
|
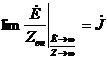
где Ė - ЭДС источника тока, Zвн - его внутреннее сопротивление;
![]() - ток
источника тока.
- ток
источника тока.
Источником тока можно отобразить регулируемую нагрузку, у которой по технологии требуется сохранение постоянства тока, например, электролизные процессы, трансформатор тока.
1.3 Реальные источники тока и напряжения
В схемах замещения реальность заключается
только в вводе в идеальные источники сопротивлений или проводимостей
соизмеримых с сопротивлениями или проводимостями внешних цепей.
|
Реальный источник напряжения ![]() характеризуется
величиной ЭДС Ė и сопротивлением
Z
рассматривается по формуле
характеризуется
величиной ЭДС Ė и сопротивлением
Z
рассматривается по формуле
![]()
|
Реальный источник тока можно представить как идеальный источник тока, зашунтированный проводимостью ненулевой величины, и определяется по формуле
![]() .
.
1.4 Комплексные сопротивления и проводимости
Эти элементы относятся к группе пассивных элементов в том смысле, что они осуществляют преобразование электрических величин цепи, не имея собственных источников электроэнергии.
Известно, что комплексные сопротивления состоят из двух составляющих -активной и реактивной.
За реактивное сопротивление воспринимаются
эффект действия ЭДС самоиндукции индуктивности и эффект действия напряжения
зарядки конденсатора для какой-либо конкретной частоты
|
![]()
где xL и xc - реактивные сопротивления индуктивности и емкости соответственно;
w - угловая частота (w = 2p¦);
L – индуктивность;
С - емкость.
|
Применение комплексных чисел позволяет объединить активное и реактивное сопротивление в одно - комплексное
Z = R+jx
где Z - комплексное сопротивление;
R – активное;
x - реактивное сопротивление;
j=![]() .
.
1.5 Трансформации или идеальные трансформаторы - пассивный элемент, который совершает
преобразование электрических величин при сохранении инвариантности
электрической мощности. Он характеризуется одним параметром - коэффициентом
трансформации.
|
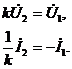
Таким образом, для задания ИТ достаточно
одного параметра ![]() - коэффициента трансформации.
- коэффициента трансформации.
|
В процессе трансформации происходит сдвиг фазы у трансформируемых величин. Более полная идеализация ИТ будет, если придать коэффициенту трансформации значения комплексного числа. Пусть коэффициент трансформации задан в комплексной форме
![]()
где ![]() - модуль коэффициента
трансформации;
- модуль коэффициента
трансформации;
![]() - угол поворота.
- угол поворота.
Далее пусть заданы напряжения ![]() и
и
![]() .
Напряжение
.
Напряжение ![]() расположено по отношению к
напряжению
расположено по отношению к
напряжению ![]() под некоторым углом
под некоторым углом ![]() . Но для того,
чтобы
. Но для того,
чтобы ![]() совместить с
совместить с ![]() , необходимо
, необходимо ![]() повернуть
в положительном направлении на угол
повернуть
в положительном направлении на угол ![]()
![]() ,
т.е.
,
т.е.
|
![]() .
.
|
Токи ИТ трансформирует иначе. Предположим,
что вторичная обмотка ИТ нагружена, а активное сопротивление, которое обеспечивает ток ![]() ,
совпадает по фазе с
,
совпадает по фазе с ![]() . Тогда и ток
. Тогда и ток ![]() должен
совпадать с напряжением
должен
совпадать с напряжением ![]() . Отсюда следует: для того, чтобы
сохранить абсолютную величину
. Отсюда следует: для того, чтобы
сохранить абсолютную величину ![]() , необходимо
, необходимо ![]() разделить
на
разделить
на ![]() ,
но при этом уже
,
но при этом уже ![]() , необходимо развернуть на угол -
, необходимо развернуть на угол -![]() до совпадения с
до совпадения с ![]() , т.е.
, т.е.
![]()
где ![]() - комплексно
сопряженный коэффициент трансформации.
- комплексно
сопряженный коэффициент трансформации.
Используя принцип инвариантности мощности
при преобразованиях осуществляемых ИТ, можно получить тот же результат в общем
виде
|
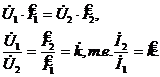
ИТ трансформирует сопротивление в
отношении ![]() , что легко получается из принципа
инвариантности мощности
, что легко получается из принципа
инвариантности мощности
|
![]()
а ![]() и
и ![]() .
.
Проводимость ИТ трансформирует в обратном
отношении
|
![]()
Реальный трансформатор отличается от
идеального тем, что он имеет ряд особенностей. Он при преобразовании
электрической энергии имеет потери (в меди, в стали), индуктивности ![]() ,
, ![]() и
взаимоиндукция имеют конечные значения, а также наличием так называемой
индуктивности рассеяния, потому разность
и
взаимоиндукция имеют конечные значения, а также наличием так называемой
индуктивности рассеяния, потому разность ![]() уже не равна нулю.
Подробнее о реальных трансформаторах см. [12].
уже не равна нулю.
Подробнее о реальных трансформаторах см. [12].
1.6 Взаимоиндукция.
В принципе две воздушные линии
электропередачи (ВЛ) для токов к.з. нулевой последовательности представляют
собой реальный трансформатор без ферромагнитного магнитопровода, у которого
разность ![]() значительно отличается от нуля.
значительно отличается от нуля.
Уравнение двух воздушных линий, связанных
взаимоиндукцией с сопротивлениями ![]() и
и ![]() , с
приложенными к ним напряжениями:
, с
приложенными к ним напряжениями: ![]() , и
, и ![]() ,
и токами текущие по ВЛ:
,
и токами текущие по ВЛ: ![]() и
и ![]() можно описать
уравнением
можно описать
уравнением
|
![]()
Перепишем это уравнение в следующем виде
|
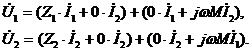
Первая группа скобок формирует составляющую напряжения, обусловленную собственными сопротивлениями ВЛ, а вторая группа скобок - составляющую напряжения, обусловленную взаимоиндукцией.
В результате получаем вариант идеального трансформатора, у которого отсутствует собственная индуктивность, но имеет место взаимоиндукция.
Отметим так же, что взаимоиндукция может восприниматься как некоторое сопротивление (jωM), но сопротивление особого рода. Это сопротивление включается в рассматриваемую ВЛ, но по которому протекает ток другой, параллельной ВЛ.
2 Отображение реальных элементов электрической системы на идеальные
Содержание лекции:
- синхронные генераторы;
- синхронные и асинхронные крупные двигатели;
- прочая нагрузка;
- эквивалентирование нагрузок;
- трансформаторы (Т) и автотрансформаторы (AT);
- воздушные (ВЛ) и кабельные (КЛ) линии электропередачи;
- остальные элементы электрических систем.
Цели лекции:
- изучить основные правила составления схем замещения и их эквивалентирования.
2.1 Синхронные генераторы
Для любого генератора к.з. очень серьезное испытание, тем более серьезное, чем больше единичная мощность генератора. Однако, общие принципы расчета токов к.з. от генератора одинаковые, мало зависящие от его мощности.
Не рассматривая подробно физику
электромагнитных процессов в генераторе при к.з. [см. 13, 14]
сам ток к.з. ненагруженного
генератора
|
![]()
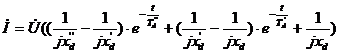
где ![]() - ток к.з.;
- ток к.з.;
![]() -
напряжение
на выводах ненагруженного генератора перед к.з.;
-
напряжение
на выводах ненагруженного генератора перед к.з.;
xd - ненасыщенное значение сопротивления генератора по продольной оси;
x'd -переходное сопротивление по продольной оси;
x''d - сверхпереходное сопротивление по продольной оси;
Td - постоянная времени (переходное значение);
Td" - постоянная времени (сверхпереходное значение);
t - текущее время.
В схемах генератор представляется реальным
источником напряжения или тока, у которых
|
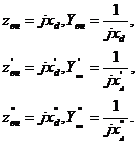
Для нагруженного генератора ток к.з.
рассчитывается по формуле
|
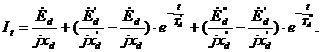
2.2 Синхронные и асинхронные крупные двигатели, в принципе, могут отображаться на источники напряжения и тока по аналогии с генераторами. Разница только в величинах ЭДС и сопротивлений. В [19] имеются рекомендации по принятию этих величин, которые можно принимать к расчету, если нет паспортных данных двигателей.
2.3 Прочая нагрузка
2.3.1 Статическая нагрузка, к которой можно отнести осветительную нагрузку или нагрузку связанную с электролизом, в первом приближении любую нагрузку за выпрямителями, в том числе и электротяговую и т.п. Она отображается на комплексное сопротивление, естественно с преобладанием активной составляющей.
2.3.2 Обобщенная нагрузка, как правило,
это двигательная нагрузка, в основном асинхронная, двигатели которой не
разделить, их много и каждый из них небольшой мощности. [19] рекомендует
представлять ее сверхпереходным реактивным сопротивлением и сверхпереходной
ЭДС, т.е. отображать на реальный источник напряжения. В относительных единицах
x"d = 0,35, это означает, что в реальных именованных величинах
|
![]() .
.
|
ЭДС источника рекомендуется
![]() .
.
2.4 Эквивалентирование нагрузок
Пусть к шинам какой-либо п/ст подключена достаточно мощная двигательная нагрузка и соизмеримая с ней статическая (рис. 2.1), требуется объединить их в некоторую эквивалентную нагрузку, представленную одним элементом.
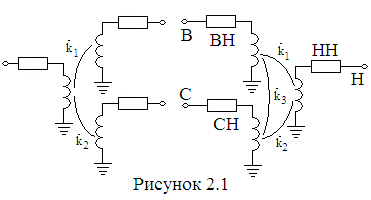
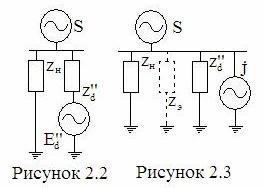
Представим двигательную нагрузку в виде
реального источника тока (рисунок 2.3) с током
|
![]()
Затем соединим в одно сопротивление
Zн
и
Zd"
|
![]()
и снова перейдем к реальному источнику
напряжения с ЭДС
|
![]()
По аналогии можно совершать и более сложные эквивалентирования [19].
2.5 Трансформаторы (Т) и автотрансформаторы (AT)
Двухобмоточные трансформаторы отображаются на реальный трансформатор, состоящий из идеального трансформатора и сопротивления. Трехобмоточные трансформаторы, вообще говоря, отображаются на три ИТ и соответственно на три сопротивления, для которых они изображаются как показано на рисунке 2.1. Аналогично решается вопрос с трансформаторами с расщепленными обмотками см. [12 и 19]. Сложнее дело обстоит с автотрансформаторами и регулировочными трансформаторами (AT - РТ), которые включаются или в нейтраль AT или в качестве линейного РТ на стороне среднего или низшего напряжения. Построение таких схем как для продольного, так и для поперечного, а также для смешанного регулирования дано в [12 и 18].
2.6 Воздушные (ВЛ) и кабельные (КЛ) линии электропередачи
Короткие (единицы, десятки км) ВЛ и КЛ всех напряжений можно представлять одним комплексным сопротивлением
![]()
где R=rL;
X = xL;
r - удельное активное сопротивление;
х - удельное реактивное сопротивление ВЛ или КЛ. В отдельных случаях требуется уточнение схем замещения ВЛ. Например, имеется несколько ВЛ напряжением 220 кВ включенных последовательно, каждая по 40-50 км (типичная схема для электротягового транзита на переменном токе).
Каждую ВЛ в отдельности можно представить упрощенно, но в совокупности (физически это одна ВЛ с отпайками) необходимы уточнения, т.е. учет емкостной проводимости. Второй пример, одиночная ВЛ 35 кВ длиной 50-100 км при малой нагрузке, которую она питает. Не учет емкости может привести к неправильной ориентации относительно реактивной составляющей тока ВЛ и, как следствие, к неправильной фазировке релейных защит. Наконец, ВЛ длиной более 300 км. Здесь даже П и Т образные схемы замещения становятся недостаточно точными. Есть два варианта представления таких ВЛ: в распределенных параметрах, параметрах проводимости (Y-параметрах) и сопротивления (Z-параметрах).
2.7 Остальные элементы электрических систем, как правило, задаются сопротивлениями. При этом не возникает особых трудностей, поэтому имеется возможность рассчитать их схемы замещения по [13 и 19] или другим.
3 Учет взаимоиндукции
Содержание лекции:
- влияние взаимоиндукции при расчете матриц узловых проводимостей;
- влияние взаимоиндукции при расчете матриц узловых сопротивлений.
Цели лекции:
- изучить влияние взаимоиндукции при расчете матриц узловых проводимостей и узловых сопротивлений.
3.1 Учет взаимоиндукции при расчете матрицы узловых проводимостей.
Учет взаимоиндукции значительно усложняет
расчет узловых параметров. В общем виде решение можно найти используя методику
приведенную в [29]. Следуя этой методике составляются две матрицы: элементарная
матрица сопротивлений ![]() и матрица инциденций П.
и матрица инциденций П.
В первой матрице по диагонали располагаются значения самих сопротивлений ветвей, остальные элементы - сопротивления взаимоиндукции между соответствующими ветвями. Вторая матрица состоит из единиц и нулей (незаполненные элементы - нули): положительное направление тока от начала ветви к ее концу, т.е. от узла с меньшим номером к узлу с большим. Таким образом, ток вытекает из узла с меньшим номером, т.е. узловой ток отрицательный, следовательно, на пересечении данной ветви и ее меньшего узла стоит -1, а большего узла +1. Остальные элементы - нули.
Матрица узловых проводимостей определяется
|
![]()
где Пt - транспонированная матрица инциденций.
Полученную матрицу узловых проводимостей можно теперь вписать, точнее просуммировать с матрицей узловых проводимостей, суммируя каждый элемент с одинаковой парой индексов.
3.2 Учет взаимоиндукции при расчете матрицы узловых сопротивлений.
 Учет взаимоиндукции возможен при
последовательном наращивании схемы и соответственно матрицы узловых
сопротивлений. Такой способ изложен подробно в [28]. Однако его реализация
представляет немалые трудности, поскольку связана с очень сложным алгоритмом.
Учет взаимоиндукции возможен при
последовательном наращивании схемы и соответственно матрицы узловых
сопротивлений. Такой способ изложен подробно в [28]. Однако его реализация
представляет немалые трудности, поскольку связана с очень сложным алгоритмом.
Более простым, в смысле простоты алгоритма, являются два других способа.
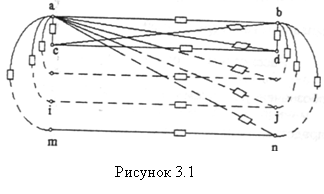
Один из них позволяет представить группу линий, связанных взаимоиндукцией в виде полного многоугольника и этот многоугольник включить в общую схему замещения нулевой последовательности электрической системы.
На первом этапе этот метод требует получения матрицы узловых проводимостей (3.1), а на втором позволяет получить параметры схемы замещения (рисунок 3.1), величины сопротивления которой находятся из соотношения
|
![]() , т.е.
, т.е.
![]()
причем, индексы пробегают все значения узлов при условии, что i < j. В результате получаются все элементы полного многоугольника.
Другой эффективный способ учета взаимоиндукции заключается в пересчете матрицы узловых сопротивлений, рассчитанной без учета взаимоиндукции [29]. Алгоритм пересчета следующий.
![]()
 Итак, на первом этапе рассчитывается
матрица узловых сопротивлений электрической системы так, как будто нет
взаимоиндукции. Обозначим
эту матрицу
zmn, которая соответствует произвольной схеме (рисунок 3.1).
Итак, на первом этапе рассчитывается
матрица узловых сопротивлений электрической системы так, как будто нет
взаимоиндукции. Обозначим
эту матрицу
zmn, которая соответствует произвольной схеме (рисунок 3.1).
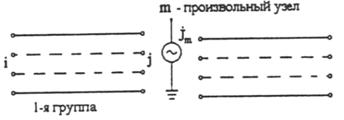
В этой схеме есть несколько групп линий, связанных взаимоиндукцией.
Рассмотрим первую группу линий, связанных взаимоиндукцией, обозначенную узлами i - j (рисунок 3.1), в соответствии
с этим матрицу zmn представим в виде блоков
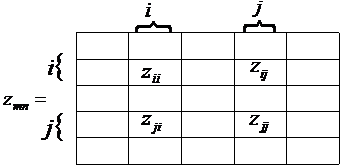
Приложим к произвольному узлу ![]() источник
тока, тогда напряжения в узлах
источник
тока, тогда напряжения в узлах ![]() и
и ![]() можно
определить по формулам
можно
определить по формулам
|
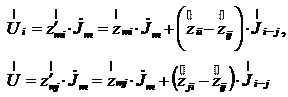 ,
,
и их разность
|
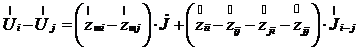 .
.
В этих формулах
![]() -
напряжение
в начале ветвей;
-
напряжение
в начале ветвей;
![]() -
напряжение в конце ветвей;
-
напряжение в конце ветвей;
![]() -
ток
приложенного источника;
-
ток
приложенного источника;
![]() -
взаимные сопротивления, взятые из матрицы, в которой не
учтена взаимоиндукция рассматриваемой группы линий (без штриха), и из новой,
еще неизвестной, но учитывающей эту взаимоиндукцию (со штрихом);
-
взаимные сопротивления, взятые из матрицы, в которой не
учтена взаимоиндукция рассматриваемой группы линий (без штриха), и из новой,
еще неизвестной, но учитывающей эту взаимоиндукцию (со штрихом);
![]()
![]()
![]() -
матрицы сопротивлений, образованные из исходной (не
учитывающей данную группу взаимоиндукции) для всех значений
-
матрицы сопротивлений, образованные из исходной (не
учитывающей данную группу взаимоиндукции) для всех значений ![]() и
и ![]() ,
причем
,
причем ![]() ;
;
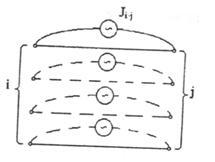
![]() -
ток,
эквивалентный введению взаимоиндукции (рисунок 3.6), который требуется
определить.
-
ток,
эквивалентный введению взаимоиндукции (рисунок 3.6), который требуется
определить.
![]() Кроме
того, приняты следующие дополнительные обозначения: точка над буквой - комплексное
число; "|" - матрица столбец;
"-" - матрица строка;
Кроме
того, приняты следующие дополнительные обозначения: точка над буквой - комплексное
число; "|" - матрица столбец;
"-" - матрица строка; ![]() - квадратная матрица;
- квадратная матрица;
![]() - квадратная
диагональная матрица.
- квадратная
диагональная матрица.
Обозначим
![]() ,
,
тогда выражение (3.2) упростится
|
![]() .
.
|
В свою очередь, ток, эквивалентный введению взаимоиндукции (рисунок 3.3), определяется по следующему выражению
![]()
в котором ![]() - истинный ток ветвей
- истинный ток ветвей ![]() с учетом
взаимоиндукции,
обусловленной
с учетом
взаимоиндукции,
обусловленной
![]() .
Смысл выражения (3.4) заключается в определении ЭДС, наведенных в смежных
ветвях (произведение двух последних матриц) и переходе от ЭДС к эквивалентным
токам (умножение на первую матрицу).
.
Смысл выражения (3.4) заключается в определении ЭДС, наведенных в смежных
ветвях (произведение двух последних матриц) и переходе от ЭДС к эквивалентным
токам (умножение на первую матрицу).
Поскольку произведение двух первых матриц
- тоже квадратная неособая матрица, то возможно представление (3.5) в виде
|
![]() .
.
С другой стороны, эти же токи связаны с
напряжениями ветвей, т.е. разностями напряжений
|
![]() .
.
Подставляя в это выражение значение тока из (3.6), приравняем правые части (3.4 а) и (3.5)
![]() .
.
Ввиду произвольности ![]() , дадим ему
единичное значение и решим это уравнение относительно эквивалентных токов
, дадим ему
единичное значение и решим это уравнение относительно эквивалентных токов
|
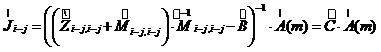
где буквой ![]() обозначен множитель при
обозначен множитель при ![]() .
.
Напряжение в произвольном узле
![]()
![]()
или с учетом, что
![]() = 1
= 1
|
![]()
Если индексам придать следующие значения ![]() -
номера строк, а
-
номера строк, а ![]() -номера элементов в строке, то с
помощью (3.9) можно организовать пересчет всех элементов матрицы.
-номера элементов в строке, то с
помощью (3.9) можно организовать пересчет всех элементов матрицы.
Ввиду линейности рассматриваемых цепей возможен переход к следующей группе взаимоиндукции для которой справедливы все изложенные выше формулы, а исходной будет матрица пересчитанная для предыдущей группы взаимоиндукции.
4 Вопросы эквивалентирования
Содержание лекции:
- эквивалентирование электрических систем, выраженных параметрами узловых проводимостей;
- эквивалентирование электрических систем, выраженных матрицей узловых сопротивлений;
- нахождение продольных эквивалентов.
Цели лекции:
- изучить основные категории эквивалентирования, научиться применять закономерности эквивалентирования при расчете токов к.з.
Современные электрические системы являются сложными образованиями, содержащими десятки и сотни тысяч элементов различного назначения. Сюда входят генераторы, трансформаторы, линии электропередачи, реакторы, двигатели и т.д. и т.п. Соответственно схема замещения электрической системы также должна содержать такое же количество элементов. Если еще добавить, что существуют объединенные энергосистемы, то становиться ясно, что невозможно составить полную схему замещения, необходимо выделить интересующую часть, остальную представить неким эквивалентом.
В [19] достаточно подробно рассмотрены вопросы эквивалентирования и сформулированы общие принципы эквивалентирования. В частности определены три категории эквивалентирования:
- прямое или косвенное функциональное эквивалентирование;
- параметрическое эквивалентирование;
- эквивалентирование в пространстве функций; и три этапа эквивалентирования;
- сбор и обработка информации об эквивалентируемой части электрической системы;
- приведение к существенно меньшему количеству элементов;
- приведение к типовым схемам;
- оценка точности.
4.1 Начнем с эквивалентирования электрической системы, выраженной параметрами узловых проводимостей. Уравнение состояния такой системы описывается уравнением
|
.Из уравнения следует, что система содержит
![]() узлов.
Пусть узлы, обозначенные индексом
узлов.
Пусть узлы, обозначенные индексом
![]() , выделяются тем, что
относительно них требуется произвести эквивалентирование (
, выделяются тем, что
относительно них требуется произвести эквивалентирование (![]() - может означать номер одного узла, или
номера серии узлов, скомпонованных рядом, относительно которых требуется
произвести эквивалентирование). Произвести эквивалентирование в данном случае
означает замену системы, содержащей
- может означать номер одного узла, или
номера серии узлов, скомпонованных рядом, относительно которых требуется
произвести эквивалентирование). Произвести эквивалентирование в данном случае
означает замену системы, содержащей ![]() узлов на схему
содержащую
узлов на схему
содержащую ![]() узлов, причем
узлов, причем![]() . Остальные
узлы необходимо исключить. Но при этом токи и напряжения интересующих нас узлов
должны сохраниться неизменными. Такая группа преобразований схем называется
группой эквивалентных преобразований.
. Остальные
узлы необходимо исключить. Но при этом токи и напряжения интересующих нас узлов
должны сохраниться неизменными. Такая группа преобразований схем называется
группой эквивалентных преобразований.
Итак, суть эквивалентирования с выделением интересующих узлов заключается в том, что токи всех остальных узлов приравниваются нулю и матрица с коэффициентами пропорциональности находится между токами интересующих узлов и напряжениями этих узлов
(4/2)
|
![]()
![]()

где сплошными линиями выделены параметры узлов эквивалентирования (интересующих).
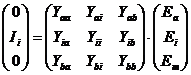 (4/3)
(4/3)
где индексы ![]() и
и ![]() пробегают
значения исчезающих узлов.
пробегают
значения исчезающих узлов.
Уравнение (6.3) представим в виде трех
матричных уравнений, получаемых в соответствии с правилами умножения
матриц
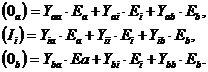 (4.4)
(4.4)
Переставим местами два нижних уравнения и после этого объединим два верхних в одно
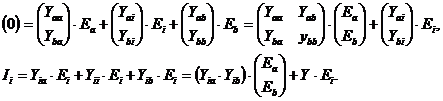 (4.5)
(4.5)
Из первого уравнения находятся величины источников напряжения
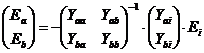 (4.6)
(4.6)
и подставляется во второе
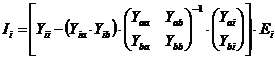 .(4.7)
.(4.7)
Выражение, следующее в квадратных скобках,
есть искомая матрица - коэффициент пропорциональности между матрицей узловых
токов и матрицей узловых напряжений интересующих нас узлов, т.е. это и есть
эквивалент электрической системы узловых проводимостей относительно узлов
![]()
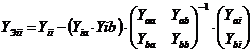 .
.
Во многих широко распространенных программах предусмотрено выделение так называемой зоны расчета, т.е. области, части электрической системы, где возможно задание мест к.з. и расчет требуемых электрических величин. Выделение такой зоны происходит путем эквивалентирования по (4.8) с последующим обращением матрицы узловых проводимостей для получения эквивалентной матрицы узловых сопротивлений
![]() .(4.9)
.(4.9)
4.2 В свою очередь, возможно эквивалентирование электрической системы, представленной матрицей узловых сопротивлений.
Намечаются требуемые узлы эквивалентирования и определяются номера их индексов. Из матрицы узловых сопротивлений выбираются все элементы с определенными индексами, из этих элементов компонуется новая эквивалентная матрица.
Не представляет исключения и эквивалентирование относительно одного узла. В этом случае выбирается только один элемент матрицы узловых сопротивлений.
4.3 Нахождение продольных эквивалентов
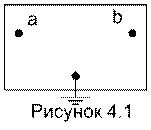 Необходимость получения продольных
эквивалентов диктуется расчетами электрических режимов, связанных с
неполнофазными режимами линий электропередачи, некоторыми видами сложных
повреждений и расчетами электрических величин при рассогласовании РПН по фазам
у трансформаторов и
AT
[12].
Необходимость получения продольных
эквивалентов диктуется расчетами электрических режимов, связанных с
неполнофазными режимами линий электропередачи, некоторыми видами сложных
повреждений и расчетами электрических величин при рассогласовании РПН по фазам
у трансформаторов и
AT
[12].
Пусть требуется найти продольное
эквивалентное сопротивление между узлами ![]() и
и ![]() схемы
замещения (рисунок 6.1). Исходными данными будут элементы матрицы узловых
сопротивлений, пересчитанные для требуемого режима (например, отключение ВЛ,
отключение и подключение с одного конца и т.п.).
схемы
замещения (рисунок 6.1). Исходными данными будут элементы матрицы узловых
сопротивлений, пересчитанные для требуемого режима (например, отключение ВЛ,
отключение и подключение с одного конца и т.п.).
Итак, известна матрица эквивалентных
узловых сопротивлений относительно узлов ![]() и
и
![]()
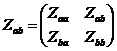 ,(4.10)
,(4.10)
в общем случае ![]() .
.
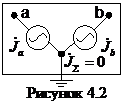 Теперь реализуем следующий прием. Между
узлами
Теперь реализуем следующий прием. Между
узлами ![]() и
и ![]() и общим узлом
включим два источника тока равные по величине, но находящиеся в противофазе
так, что их сумма, определяющая вход тока в общий узел, равна нулю (рисунок
4.2).
и общим узлом
включим два источника тока равные по величине, но находящиеся в противофазе
так, что их сумма, определяющая вход тока в общий узел, равна нулю (рисунок
4.2).
Состояние схемы можно описать следующими уравнениями
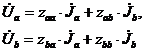 (4.11)
(4.11)
противофазе так, что их сумма,
определяющая вход тока в общий узел, равна нулю (рисунок 4.2).
Произведем очевидную замену
![]() (4.12)
(4.12)
тогда (4.11) получим в следующем виде
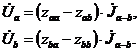
Вычтем из первого уравнения второе
![]() (4.14)
(4.14)
Выражение, стоящее в скобках и есть
искомый продольный эквивалент, ибо он связывает напряжение и ток между
заданными узлами
![]()
Если zab = zba, т.е. если в схеме замещения отсутствуют комплексные коэффициенты трансформации, то формула (4.15) упрощается
![]() (4.16)
(4.16)
5 Расчеты простых видов коротких замыканий
Содержание лекции:
- основные принципы расчета токов к.з.;
- расчеты трехфазных к.з.;
- несимметричные короткие замыкания.
Цели лекции:
- изучить основные методы расчета токов к.з., ив частности метод симметричных составляющих.
5.1 Общие принципы
Существует три координатных метода расчета режимов коротких замыканий: метод симметричных составляющих, метод несимметричных составляющих и метод фазных координат. Подробно все три метода описаны в [28]. Наибольшее распространение получил метод симметричных составляющих. Учитывая, однако, популярность и эффективность метода симметричных составляющих дальнейшее изложение будем основывать на этом методе.
5.2 Трехфазные короткие замыкания (цифровое обозначение (3))
 Рассмотрим схему
электрической системы
прямой последовательности содержащую N узлов. Пусть в произвольном узле к
происходит трехфазное к.з. Узлы в порядке их нумерации обозначим:
i,
j
- узлы до узла
k;
m,
n - узлы после узла к. С учетом этих
обозначений уравнение состояния схемы можно описать следующим уравнением
Рассмотрим схему
электрической системы
прямой последовательности содержащую N узлов. Пусть в произвольном узле к
происходит трехфазное к.з. Узлы в порядке их нумерации обозначим:
i,
j
- узлы до узла
k;
m,
n - узлы после узла к. С учетом этих
обозначений уравнение состояния схемы можно описать следующим уравнением
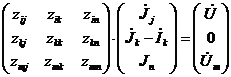 (5.1)
(5.1)
где ![]() - элементы и блоки
матрицы узловых сопротивлений схемы замещения;
- элементы и блоки
матрицы узловых сопротивлений схемы замещения;
![]() - токи
(скомпонованные в матрицы-блоки) эквивалентные источникам напряжения, которые
соответствуют ЭДС всех вращающихся электрических машин;
- токи
(скомпонованные в матрицы-блоки) эквивалентные источникам напряжения, которые
соответствуют ЭДС всех вращающихся электрических машин;
![]() -
ток
в месте, в узле короткого замыкания;
-
ток
в месте, в узле короткого замыкания;
![]() i,
i,
![]() m
- остаточные напряжения в узлах схемы
(кроме узла
k).
m
- остаточные напряжения в узлах схемы
(кроме узла
k).
Учитывая правила операций с матрицами (в частности умножения) выделим среднюю часть уравнения (5.1) и приведем к следующему виду
![]() .(5.2)
.(5.2)
Теперь, используя (7.1) можно найти все или только требуемые остаточные напряжения. В последнем случае задаются конкретные значения индексов i, j или т, n. По найденным напряжениям находятся токи ветвей
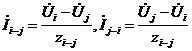 или
или ![]() .(5.3)
.(5.3)
На основе всех этих электрических величин могут вычисляться другие, такие как мощности, сопротивления, углы и т.д.
Тот же результат можно получить другим
способом расчета с использованием метода наложения. В этом случае расчет режима
короткого замыкания раскладывается на две задачи. Первая - расчет (или
использование готовых данных) предаварийного режима. В качестве предаварийного
режима  могут выступать любые нормальные режимы,
но ими могут быть и динамические режимы, точнее какие-либо конкретные моменты
переходного процесса. Вторая - расчет дополнительного режима, в котором
участвует только один активный источник эквивалентный напряжению в точке к.з. в
предварительном режиме, что значительно упрощает задачу.
могут выступать любые нормальные режимы,
но ими могут быть и динамические режимы, точнее какие-либо конкретные моменты
переходного процесса. Вторая - расчет дополнительного режима, в котором
участвует только один активный источник эквивалентный напряжению в точке к.з. в
предварительном режиме, что значительно упрощает задачу.
Рассмотрим процесс расчленения задачи подробнее. Для начала рассмотрим к.з. на выводах нагруженного генератора (рисунок 5.2). Ток генератора определяется по известной формуле
![]()
Из последнего варианта написания ее видно, что истинный ток к.з. генератора можно представить как суперпозицию двух токов - тока к.з., определяемого через напряжение предшествующего режима и тока нагрузки в предаварийном режиме. Включим в ветвь короткого замыкания два источника напряжения (рисунок 5.3 а), включим последовательно и в противофазе. От такого включения режим генератора и электрической системы не изменится, т.к. сумма напряжений этих двух источников равна нулю, также как и их внутреннее сопротивление. Ввиду произвольности величин напряжения этих источников выберем их равными, точнее
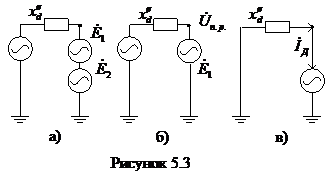
![]() (5.5)
(5.5)
Для перехода к предшествующему режиму
исключим ![]() 2
(рисунок 5.3 б). Поскольку
2
(рисунок 5.3 б). Поскольку ![]() , ток в ветвь с Е, отсасываться
не будет, следовательно, восстанавливается действительно предшествующий режим.
Затем перейдем к дополнительному режиму, для чего подключим только один
источник
, ток в ветвь с Е, отсасываться
не будет, следовательно, восстанавливается действительно предшествующий режим.
Затем перейдем к дополнительному режиму, для чего подключим только один
источник ![]() 2, который создаст ток к.з. дополнительного
режима
2, который создаст ток к.з. дополнительного
режима
![]() .
.
Истинный ток определится как сумма
![]() (5.7)
(5.7)
Такой способ решения задачи расчета токов короткого замыкания можно обобщить на любой узел электрической системы.
5.3 Несимметричные короткие замыкания
Граничные условия для всех несимметричных к.з. приведены в таблице 1. Следует заметить, что несимметричные к.з. образующие только соединение между фазами создают так называемую уравновешенную систему токов, у которой ток нулевой последовательности равен нулю. В расчете участвуют только составляющие прямой и обратной последовательностей. В случаях к.з. на землю в расчете участвуют все три последовательности.
Таблица 1
|
Вид к.з. |
Обозначение |
Особая фаза |
Граничные условия по току |
Граничные условия по напряжению |
|
Трехфазное |
(3) |
А |
|
|
|
Двухфазное без земли |
(2) |
А |
|
|
|
Однофазное на землю |
(1) |
А |
|
|
|
Двухфазное к.з. на землю |
(1.1) |
А |
|
|
Для каждого вида к.з. этих граничных
условий достаточно для построения комплексной схемы замещения. Чтобы перейти к
их построению, необходимо напомнить операцию перехода от представления
электрических величин в фазных координатах к представлению их в координатах
симметричных составляющих (именуемых координатами Фортяскью) и обратно. В [13,
28] дано подробное обоснование метода симметричных составляющих, в [27] дано
оригинальное матрично-тензорское описание перехода от фазных координат к
координатам последовательностей. В обобщенном виде такие переходы можно
выразить следующим образом
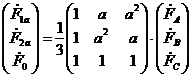 ,
,
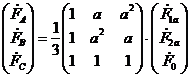 (5.9)
(5.9)
где ![]() -
произвольная электрическая величина, представленная
комплексным вектором;
-
произвольная электрическая величина, представленная
комплексным вектором;
![]() - комплексный трехфазный оператор, поворачивающий комплексный
вектор на угол 1200 в положительном направлении;
- комплексный трехфазный оператор, поворачивающий комплексный
вектор на угол 1200 в положительном направлении;
а
- индекс при
![]() , обозначающий приведение расчета к фазе А
для симметричных составляющих прямой и обратной последовательности;
, обозначающий приведение расчета к фазе А
для симметричных составляющих прямой и обратной последовательности;
А, В, С - индексы фазных составляющих.
5.4 Нахождение ![]() является необходимым и достаточным
для расчета всех других электрических величин в режиме к.з. Для этого можно
воспользоваться формулами (5.1), (5.4).
является необходимым и достаточным
для расчета всех других электрических величин в режиме к.з. Для этого можно
воспользоваться формулами (5.1), (5.4).
Если используется метод наложения, то следует помнить, что составляющие обратной и прямой последовательностей сразу получаются истинными, а величины прямой последовательности получаются истинными после реализации суперпозиции.
Список литературы
1. Сешус И. Рид М. Линейные графы и электрические цепи. - М.: Высшая школа, 1971.
2. Крон Г. Применение тензорного анализа в электротехнике. – М., Л.: ГЭИ, 1955.
3. Быстрое В.П., Кимельман Л.Б. О разработке комплекса программ расчета токов короткого замыкания. – Электричество. – 1988. - № 8.
4. Штоф В.А. Проблемы методологии научного познания. - М.: Высшая школа, 1978. - гл. 4.
5. Морозов К.Е. Математическое моделирование в научном познании. - Мысль, 1969.
6. Честнат Г. Техника больших систем. - Энергия, 1969.
7. Корн Г. и Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1968.
8. Веников В.А. Теория подобия и моделирование применительно к задачам электротехники. - М.: Высшая школа, 1966.
9. Веников В.А., Суханов О.А. Кибернетические модели электрических систем. - М.: Энергоатомиздат, 1982.
10. Ю. Зевеке Г.В., Ионкин ПА, Нетушил А.В., Страхов СВ. Основы теории цепей. - М.: Энергоатомиздат, 1989.
11. Шухов Г.Е. К теории цепей с квазисопротивлениями. Теоретическая электротехника. - Сборник статей. Вып. 3. Из-во Львовского университета. -Львов, 1967.
13. Ульянов С.А. Электромагнитные переходные процессы в электрических системах. - М., Л.: Энергия, 1964.
14. Костенко М.П. и Пиотровский Л.М. - Электрические машины. - ч. 2.- ГЭИ, 1958.
15. Костелянец B.C., Беньковская Г.Я., Качурина Е.М. Оценка погрешности расчета токов к.з. генератора с системой самовозбуждения. - Электрические станции, 1981.- № 6.
16. Бартоломей П.И., Мызин А.Л. Расчетные кривые токов короткого замыкания турбогенераторов, построенные с учетом насыщения. - Труды УПИ, вып. 154, 1966. - С. 143-152.
17. Мельников Н.А. Электрические сети и системы. - М.: Энергия, 1969. -19 с.
18. Беляков Ю.С. Схемы замещения автотрансформаторов с регулировочными трансформаторами. – Электричество. – 1988. - № 5.
19. Щедрин Н.Н. Упрощение электрических систем при моделировании. - М., Л.: Энергия, 1966.
20. Брацлавский С.Х., Гершенгорн А.И., Лосев СБ. Специальные расчеты электропередач сверхвысокого напряжения. - М.: Энергоатомиздат, 1985.
21. Демидович Б.П., Маран И.А. Основы вычислительной математики.
22. Байли Р.Т., Ланг Р.В., Болдуин С.Я., Кинг СВ. Расчеты коротких замыканий в сетях электрических систем с помощью цифровых вычислительных машин. Сборник статей "Применение счетно-решающих устройств в электрических системах. - М., Л.: ГЭИ, 1960.
23. Хрущева Е.В. Особенности расчета токов короткого замыкания в электрических системах при автоматическом чередовании вариантов изменений в схеме сети. - Проблемы технической электродинамики, Вып. 17. - Киев, 1968.
24. Хрущова Е.В, Крылов В.А., Федченко В.А. Определение независимых контуров путем преобразования матриц при расчетах на ЦВМ режимов сложных электрических сетей. - Проблемы технической электродинамики, Вып.4. - Киев, 1966.
25. Милях А.Н., Шидловский А.К. Принципы взаимности и обратимости в электротехнике. - Киев, 1967.
26. Атабеков Г.И. Основы теории цепей. - М.: Энергия, 1969.
28. Мельников Н.А. Матричный метод анализа электрических цепей. - М.: Энергия, 1972.
29. Максимович Н.Г. Линейные электрические цепи и их преобразования. - М.,Л.: ГЭИ, 1961.
Содержание
|
1 Элементы схем замещения электрических систем |
3 |
|
2 Отображение реальных элементов электрической системы на идеальные |
7 |
|
3 Учет взаимоиндукции |
10 |
|
4 Вопросы эквивалентирования |
14 |
|
5 Расчеты простых видов коротких замыканий |
17 |
Список литературы |
21 |
Наталья Анатольевна Туканова
Кайрат Асенгалиевич Бакенов