Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра Электрических станций, сетей и систем
ЭЛЕКТРОТЕХНИЧЕСКОЕ МАТЕРИАЛОВЕДЕНИЕ
Методические указания к выполнению
лабораторных работ
для студентов специальности 5В071800 –
Электроэнергетика
Алматы 2010
СОСТАВИТЕЛИ: К.Х. Бекмагамбетова, Р.М. Кузембаева, А.А. Дусимов. Электротехническое материаловедение. Методические указания к выполнению лабораторных работ для студентов специальности 5В071800 - Электроэнергетика. – Алматы: АУЭС, 2010 г.- 30 с.
Методические указания содержат рекомендации по оформлению и защите отчетов, в них приведены описания к лабораторным работам по всем разделам курса ЭТМ, дана методика проведения и обработки опытных данных, перечень литературы и контрольные вопросы.
Ил.12, таблиц 5, библиограф.-7 назв.
Рецензент: канд.техн.наук, доцент Оржанова Ж.К.
Печатается по плану издания НАО «Алматинского института энергетики и связи» на 2010 г.
© НАО «Алматинский университет энергетики и связи», 2011 г.
Правила работы в лаборатории электротехнических материалов
1) Студенческая группа, явившись на первое занятие, разбивается на бригады по указанию преподавателя. Бригады выполняют лабораторные работы в соответствии с графиком.
2) К работе в лаборатории допускаются студенты, прошедшие инструктаж по технике безопасности, расписавшиеся в специальном журнале учета инструктажа.
3) В случае нарушения дисциплины и правил безопасного ведения работ в лаборатории студенты отстраняются от работы и к последующим занятиям допускаются только после разрешения декана факультета (заведующего кафедрой) и повторной сдачи зачета по правилам техники безопасности.
4) К следующему занятию каждый член бригады составляет отчет по выполненной работе, удовлетворяющий всем основным требованиям. Небрежно оформленные отчеты преподавателем не принимаются. Студенты, не представившие отчет по выполненной работе, к занятиям не допускаются.
5) Для защиты отчета по выполненной работе студенты должны подготовиться в соответствии с требованиями, предъявляемыми кафедрой.
Требования к отчету по лабораторной работе
1) Отчет должен быть оформлен аккуратно и технически грамотно. Неправильно оформленные отчеты к защите не принимаются.
2) Оформление отчета может производиться на листах бумаги формата А4 или близкого к этому формату.
3) Текст и таблицы в отчете должны быть написаны шариковой ручкой.
4) Графики должны быть построены по экспериментальным точкам на клеточной бумаге.
5) Отчет должен содержать:
- название работы и ее цель;
- схемы установки;
- рабочее задание и расчетные формулы;
- таблицы экспериментальных и расчетных данных;
- графики полученных зависимостей;
- короткое письменное объяснение полученных закономерностей и величин.
Требования, предъявляемые при защите лабораторных работ
При защите работы студент должен знать:
- разделы теоретической части курса, относящиеся к защищаемой работе;
- свойства и области применения в электротехнике исследованных материалов;
- принцип работы и схему установки, назначение ее элементов;
- методику проведения эксперимента и правила безопасной работы;
Лабораторная работа 1
Определение тангенса угла диэлектрических потерь и диэлектрической проницаемости диэлектриков
Цель работы:
- изучение явлений поляризации и диэлектрических потерь в диэлектрике, находящемся в электрическом поле;
- определение ε и tg δ для твердых изоляционных материалов.
1.1 Теоретическое введение
Диэлектрическая проницаемость ε и tg угла диэлектрических потерь tg δ являются важнейшими характеристиками диэлектриков, так как характеризуют: ε количественно определяет свойство диэлектрика поляризоваться и образовывать электрическую емкость, tg δ величину мощности, теряемой в диэлектрике. Однако в связи с тем, что tg δ не дает количественного определения величины рассеиваемой мощности в диэлектрике, для вычисления последней обычно пользуются формулами общих (Р) или удельных (р) потерь.
![]() , [Вт],
(1.1)
, [Вт],
(1.1)
![]() , [Вт/м3]
(1.2)
, [Вт/м3]
(1.2)
где U - напряжение, В;
w - угловая частота, с-1;
Сх - емкость образца диэлектрика, Ф;
Е - напряженность электрического поля, В/м;
d - угол диэлектрических потерь (угол, дополняющий до 90°, угол сдвига фаз между током и напряжением).
Наиболее широко применяемые на практике методы определения e и tgd дают возможность непосредственно измерять и рассчитывать, зная форму и геометрические размеры образца диэлектрика, величины Сх и e.
Зависимости e и tgd от температуры для электрорадиоматериалов, предназначенных для работы в электрических и температурных полях, особенно для полярных, являются достаточно важными характеристиками этих материалов.
1.2 Принципиальная схема высоковольтного моста
Рассмотрим порядок измерения tgd и Сх на высоковольтном мосте, представленном на рисунке 1.1, дающий возможность определить величины
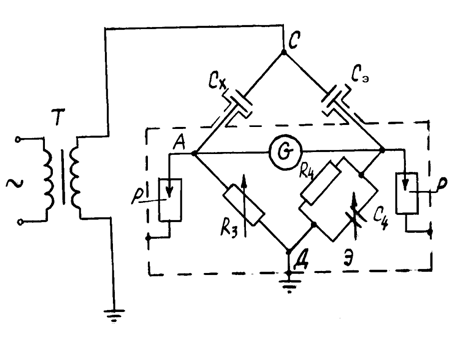 |
этих характеристик при частотах порядка 25―600 Гц.
Рисунок 1.1 - Принципиальная схема высоковольтного моста
Работа на мосте переменного тока сводится к подбору регулируемого сопротивления R3 и емкости С4, при которых нульиндикатор G будет показывать нуль.
При достигнутом равновесии моста искомая величина емкости Сх вычисляется по формуле:
Сх = Сэ![]() (1.3)
(1.3)
где Сэ ― емкость образцового (воздушного) конденсатора, пФ (указана на конденсаторе).
По величине емкости Сх и известным величинам S и h подсчитывают диэлектрическую проницаемость электроизоляционного материала:
e=![]()
![]() (1.4)
(1.4)
где h - толщина образца, м;
S - площадь обкладок конденсатора с данным диэлектриком, м2;
e0 =8.85×10-12, Ф/м ― электрическая постоянная.
tgd при достигнутом равновесии моста численно равен величине регулируемой емкости С4 моста, т.е:
tgd = çС4ç (1.5)
Испытуемый диэлектрик или конденсатор Сх соединяется в схему моста с образцовым конденсатором Сэ, емкость которого равна 100 ± 10 пФ и тангенс угла не превышает 5×10-5, магазином сопротивления R3 и магазином емкости С4 в точках А,В,С,Д.
Питание моста подведено к точкам С и Д от повысительного трансформатора типа НОМ ― 10.
Плечо R3 представляет собой безреактивное сопротивление на 10х(1000+100+10+0.1) Ом. Сопротивление R4 включено параллельно емкости С4, состоит из двух разных безреактивных сопротивлений, соединенных между собой последовательно.
Величина
R4
составляет ![]()
1.3 Описание установки
1.3.1 Мост переменного тока автоматический с цифровым отсчетом Р5010 (в дальнейшем мост) является быстродействующим универсальным измерителем параметров комплексного сопротивления на частоте 1000 Гц и предназначен для измерения:
- емкости / С / и
тангенса угла потерь / ![]() /;
/;
- индуктивности / L / и сопротивления потерь / Rn /;
- активного сопротивления / RL / и остаточной индуктивности / L0 /;
- активного сопротивления / RC / и постоянной времени / τС /.
1.3.2 Диапазон измерений моста:
- по С от 0,1 пф до 100 мкФ,
при ![]() от 0 до
0,5;
от 0 до
0,5;
- по
L
от 1 мкГн до 10 Гн, при
Rп от 0 до 40 кОм при ![]() ≤0,5;
≤0,5;
- по
RL,
RC от 0,1 Ом до 1 Мом, при
остаточной индуктивности от 0 до 0,1 Гн и τ ≤ 1∙10-5
с, где ![]() для
RL
от 0,1 Ом до 100 кОм и
постоянной времени / τ =
RC / от 0 до 1∙10-5 с для
RС от 100 Ом до 1 Мом.
для
RL
от 0,1 Ом до 100 кОм и
постоянной времени / τ =
RC / от 0 до 1∙10-5 с для
RС от 100 Ом до 1 Мом.
1.3.3 Эквивалентная схема замещения при измерении С, L, и RL – последовательная при измерении RС – параллельная.
1.3.4 Максимальное время уравновешения с учетом времени выбора поддиапазона измерения не превышает 0,3 с.
1.3.5 Схема и конструкция моста обеспечивают автоматический выбор диапазонов измерения и полное уравновешивание моста при следующих видах запуска:
- ручной, осуществляемый кнопкой запуска;
- автоматический, с регулируемым временем цикла в пределах 1-10 с ручкой «время индикации»;
- вид запуска устанавливается нажатием соответствующей кнопки переключателя «запуск».
1.3.6 При нормальных условиях эксплуатации допускается непрерывная работа моста в течение 8 ч с момента его включения без снижения его технических характеристик.
Рекомендуемый перерыв между непрерывной работой 1 ч.
1.3.7 питание моста осуществляется от сети переменного тока напряжением 220±22 В частоты 50±1 Гц.
1.3.8 Потребляемая мостом мощность при нормальном напряжении сети не превышает 200 ВА.
1.4 Рабочее задание
1.4.1 Проверьте наличие и целестность предохранителя перед включением моста в сеть.
1.4.2 Установите переключатель «запуск» в нужное положение нажатием кнопки: «ручн»-для ручного запуска;
«внешн»-для внешнего запуска.
Установить переключатель в положение «автом» допускается после осуществления ручного запуска.
При установке переключателя вида «запуск» в положение «внешн» подсоедините к гнезду внешнего запуска посредством кабеля источник запускающих импульсов.
При установке переключателя в положение «ручн» запуск моста производите нажатием кнопки.
При установке переключателя а положение «автом» запуск должен осуществляться автоматически от внутреннего источника запускающих импульсов, а длительность цикла работы прибора /время измерения и время индикации результатов измерения/ регулируйте поворотом ручки «время индикации».
1.4.3 Установите переключатель «измерение» в положение, соответствующее характеру комплексного сопротивления измеряемого объекта, нажатием кнопки:
«С» - емкостной характер комплексного сопротивления;
«L» - индуктивный характер комплексного сопротивления;
«RL» - активное сопротивление с индуктивной составляющей;
«RС» - активное сопротивление с емкостной составляющей и постоянной времени τ = RC;
1.4.4 Заземлите зажим «![]() ».
».
1.4.5 Подсоедините к штепсельным разъемам «ZX» с учетом маркировки кабель для соединения измеряемого объекта.
1.4.6 Подсоедините измеряемый объект к зажимам кабеля.
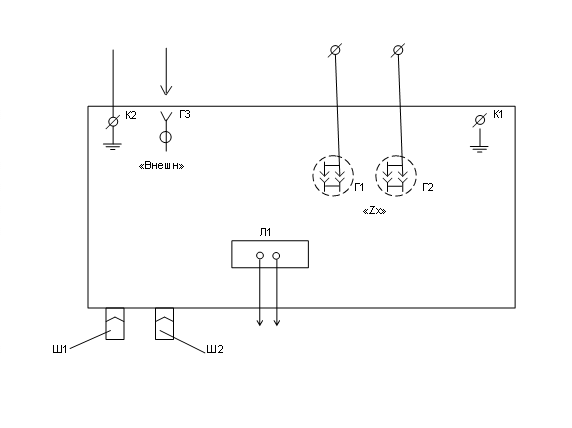
Рисунок 1.2 - Схема электрическая подключения моста переменного тока Р5010
1.4.7 Вставьте вилку шнура питания в розетку сети 220В±10% и включите тумблер «сеть», как показано стрелкой.
1.4.8 Запустите подготовленный к работе мост в соответствии с п.1.5.2.
1.4.9 Считывайте результаты измерения на табло отсчетного устройства, а при необходимости автоматической фиксации результатов измерения постредством печатающего устройства, подключите последнее к выходным разъемам моста «Ш1» и «Ш2», расположенным на задней стенке прибора, согласно схеме подключения.
Схема подключения представлена на рисунке 1.2.
1.4.10 По формулам (1.3, 1.4,1.5,1.1) определить Сх, e, tgd, Р.
1.4.11 По ε и tgδ сделать выводы о качестве изоляционных материалов и возможности их применения в конденсаторах, электрических машинах, проводах и кабелях.
1.5 Контрольные вопросы
1.5.1 Что характеризует e и tgd?
1.5.2 Какой метод использован при измерении e и tgd у диэлектриков?
1.5.3 В каком пределе находится величина e для технических диэлектриков?
1.5.4 Единицы измерения e, tgd, Р.
1.5.5 Какая кривая выражает зависимость e = ¦(Т) для полярных диэлектриков?
1.5.6 До какого максимального напряжения можно снимать e и tgd?
1.5.7 Как можно рассчитать диэлектрическую проницаемость?
Лабораторная работа 2
Определение электрической прочности технических диэлектриков
![]()
Цель работы:
- определение электрической прочности твердых диэлектриков;
- исследование статистических закономерностей распределения электрической прочности технических диэлектриков.
2.1 Краткие теоретические сведения
При повышенных значениях напряженности поля в твердом диэлектрике наблюдается значительное возрастание тока, причем возрастает ток по экспоненциальному закону. При достижении некоторой разности потенциалов между электродами происходит пробой твердого диэлектрика и последний теряет свои изолирующие свойства. Напряжение, приложенное к диэлектрику и вызывающее его пробой, называется пробивным напряжением: Uпр.
Нарушение стационарного режима электропроводности, возникающее при достижении определенного напряжения, называют нарушением электрической прочности. За меру электрической прочности твердого диэлектрика принимают напряженность однородного среднего макроскопического поля ― Епр.. Однако, достижение высокой однородности среднего макроскопического поля непосредственно перед пробоем в ряде случаев невозможно. Вследствие указанного пробивная напряженность является несколько условным понятием и рассчитывается по формуле
![]()
![]()
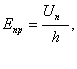 (2.1)
(2.1)
где Uпр -напряжение, при котором произошел пробой, кВ;
h ― толщина испытуемого диэлектрика, мм.
При определении пробивного напряжения Uпр или электрической прочности Е пр технических диэлектриков, даже изготовленных в одних и тех же условиях, всегда можно наблюдать более или менее значительный разброс величин U пр и Е пр , что обусловлено наличием примесей, газовых включений и неоднородностей в объеме диэлектрика, распределение которых имеет статистическую природу. Кроме того, в диэлектрике есть дефекты структуры самого материала (неравномерность упаковки молекул в объеме, дисперсии молекулярных весов и т.д.), что также вызывает разброс отдельных значений электрической прочности.
Для более объективной оценки величины электрической прочности изоляционных материалов или конструкций, испытания проводятся на достаточно большом числе образцов. После испытания проводят статистическую обработку результатов.
2.2 Основные статистические характеристики распределения электрической прочности
Простейшей характеристикой совокупности значений электрической прочности любой выборки образцов является среднее значение Епр, которое определяется по формуле:
![]() , (2.2)
, (2.2)
где k―число интервалов;
Епрi― значение электрической прочности для i―го интервала;
ni ―число образцов, пробитых в i―м интервале;
N―общее число образцов.
Характеристикой, определяющей разброс значений Епр, является среднеквадратичное отклонение s, равное:
s=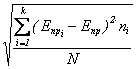 . (2.3)
. (2.3)
Более наглядное представление результатов определения Епр можно получить после построения гистограмм и интегральных кривых распределения электрической прочности.
2.3 Определение Епр и s. Построение гистограммы и интегральной кривой
Первым шагом при статистической обработке полученных результатов является составление сводки, в которой определяется значение электрической прочности для каждого интервала / Епрi / и число образцов в каждом интервале /ni/.
Порядок составления сводки следующий:
2.3.1 Результаты наблюдений располагаются в порядке возрастания от минимального значения Епр до максимального (вариационный ряд).
2.3.2 Вариационный ряд значений Епр разбивается на равные интервалы, число которых обычно выбирается от 8 до 12.
2.3.3 Определяется число образцов для каждого интервала ni. В качестве примера приводится таблица 1.1 и схема вычисления Епр и s по формулам (2.2) и (2.3) для двух слоев пропитанной кабельной бумаги.
Таблица 2.1-Cводная таблица и схема вычисления Епр и s
|
Епрi, кВ/мм |
ni |
|
Wi |
|
ni Епрi |
Епрi―Епр |
(Епрi―Епр)2 |
(Епрi―Епр)2ni |
|
18.0 |
2 |
2 |
0.012 |
0.012 |
36.0 |
―10.7 |
114.5 |
229.0 |
|
20.5 |
8 |
10 |
0.048 |
0.060 |
164.0 |
―8.2 |
67.24 |
537.9 |
|
23.0 |
5 |
15 |
0.030 |
0.090 |
115.0 |
―5.7 |
32.5 |
162.5 |
|
25.5 |
24 |
39 |
0.143 |
0.233 |
612.0 |
―3.2 |
10.24 |
245.8 |
|
28.0 |
52 |
91 |
0.314 |
0.547 |
1456.0 |
―0.7 |
0.49 |
25.5 |
|
30.5 |
43 |
134 |
0.258 |
0.805 |
1311.5 |
1.8 |
3.24 |
139.3 |
|
33.0 |
27 |
161 |
0.162 |
0.970 |
891.0 |
4.3 |
18.5 |
499.5 |
|
35.5 |
5 |
166 |
0.03 |
1.00 |
177.5 |
6.8 |
36.24 |
231.2 |
|
|
166 |
|
|
|
4763 |
|
|
2070.7 |
Епр=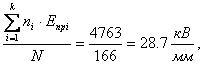
s=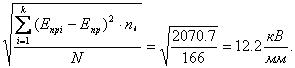
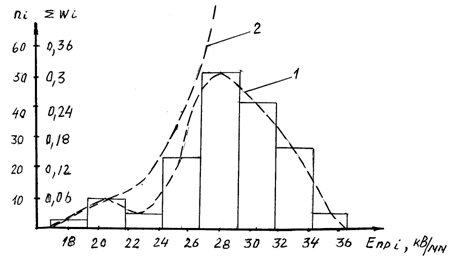 |
Для наглядности данные представляются в виде гистограммы и интегральной кривой в соответствии с рисунком 2.1.
Рисунок 2.1 - 1-Гистограмма и 2- интегральная кривая
При построении гистограммы горизонтальная ось разбивается на равные отрезки, соответствующие интервалам Е пр. На этих отрезках, как основаниях, строятся прямоугольники высотой, пропорциональной количеству пробоев образца в данном интервале. Затем соединяют середины прямоугольников плавной кривой. Полученная фигура называется гистограммой. Далее строится кривая сумм или интегральная кривая. При построении интегральной кривой производится последовательное суммирование образцов для соответствующих интервалов. Затем полученные величины наносятся против средних значений каждого интервала и нанесенные точки соединяются плавной кривой.
На рисунке 2.1 приведены примеры построения гистограммы и интегральной кривой в соответствии с данными, приведенными в таблице 1.1. Если построить интегральную кривую и гистограмму в относительных единицах, то по результатам наблюдений можно оценить вероятность, с которой произойдет пробой образца при той или иной напряженности. Для этого нужно частоты определить в относительных единицах. Частота разряда, выраженная в относительных единицах, носит название частости―W:
Wi=![]() (2.4)
(2.4)
Таким образом, при
построении интегральной кривой в соответствии с рисунком 2.1 по оси ординат
откладывается накопленная частость, т.е. ![]() , а при построении гистограммы частость
Wi при данной
напряженности (ni=Wi, при данной напряженности).
, а при построении гистограммы частость
Wi при данной
напряженности (ni=Wi, при данной напряженности).
Практикой установлено, что с увеличением числа опытов, частость принимает определенное устойчивое значение, которое характеризует вероятность появления пробоя в заданном интервале напряженности DЕi.
Следовательно,
вероятность можно определить как ![]() lim
lim![]() при
N®¥. Имея интегральную кривую, по
вертикальной оси которой отложена накопленная частость, можно определить
вероятность, с которой произойдет пробой образца при данной напряженности.
Например, в соответствии с рисунком 2.1 при напряженности 37 кВ/мм вероятность
пробоя равна 1 , а при напряженности поля 28 кВ/мм―0.5 и т.д.
при
N®¥. Имея интегральную кривую, по
вертикальной оси которой отложена накопленная частость, можно определить
вероятность, с которой произойдет пробой образца при данной напряженности.
Например, в соответствии с рисунком 2.1 при напряженности 37 кВ/мм вероятность
пробоя равна 1 , а при напряженности поля 28 кВ/мм―0.5 и т.д.
Имея гистограмму, можно определить вероятность, с которой произойдет пробой в данном интервале. Например, в соответствии с рисунком 2.1 при напряженности электрического поля в интервале /26.5―29.5/ кВ/мм вероятность пробоя составляет―0.33, в интервале /29.5―31.5/ кВ/мм вероятность пробоя составляет―0.26.
2.4 Описание испытательной установки
Установка для испытания служит для определения электрической прочности изоляционных лаков, плитообразных изоляционных материалов, например, гетинакса и т.п., а также для испытания изолированных лаком проводов.
Все приборы для получения, регулировки и измерения высокого напряжения, а также и место испытаний с испытательными электродами находятся в первичном корпусе, облицованном листовой сталью, что обеспечивает надежную защиту от прикосновения. Камера для испытаний становится доступной после открытия передней стенки и крышки корпуса. Предусмотренное в крышке окошко допускает наблюдение за исследуемым материалом во время испытания.

1-устройство для плавного регулирования напряжения;
2-трансформатор для повышения напряжения;
3-испытуемый образец;
4-сигнальная лампа;
5-камера;
6-ключ.
Рисунок 2.2 - Принципиальная схема установки
Выходное напряжение можно плавно регулировать регулировочным трансформатором. Высокое напряжение получается на высоковольтном трансформаторе, выполненном в литой изоляции. Для выпрямления используются селеновые выпрямители, включенные по однофазной мостиковой схеме. Переменное высокое напряжение измеряется вольтметром, включенным в первичную сторону высоковольтного трансформатора. Для измерения постоянного напряжения на выходе предусмотрен вольтметр с последовательно включенным сопротивлением.
В случае пробоя на испытуемом объекте или при протекании слишком большого тока через испытуемый объект высокое напряжение немедленно отключается при помощи реле максимального тока.
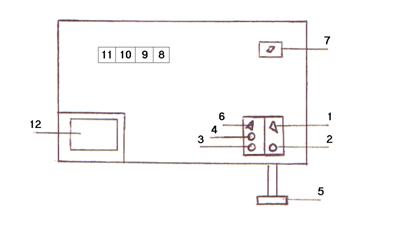 |
Рисунок 2.3- Расположение элементов обслуживания и измерительных приборов на панели обслуживания
Таблица 2.2-Символы, используемые на панели обслуживания
|
Пози― ция |
Символ |
Значение |
|
1 |
220 В 01 |
Выключатель «силовой выключатель 0―1» |
|
2 |
1 |
Кнопка «рабочий контактор―1» |
|
3 |
0 |
Кнопка «рабочий контактор―0» |
|
|
|
Кнопка «нулевой выключатель» |
|
5 |
|
Ручка напряжение повышение―понижение |
|
6 |
1 кВ, 2кВ. 5кВ, 10 кВ. |
Переключатель ступеней |
|
7 |
110В, 1кВ, 10 кВ, 0 |
Переключатель напряжения |
|
8 |
|
Прибор «постоянное напряжение―выход» |
|
9 |
|
Прибор «переменный ток ― выход» |
|
10 |
|
Прибор «первичное напряжение» |
|
11 |
|
Прибор «первичный ток» |
|
12 |
|
Прибор «испытательное напряжение» |
2.5 Работа на установке при испытаниях
2.5.1 Установить требуемое испытательное напряжение переключателем /7/. При испытаниях переменным напряжением включить переключателем /6/ требуемое напряжение /1/ 2/5/10 кВ/.
2.5.2 Включить силовой выключатель /1/. Зажигается зеленая сигнальная лампа, находящаяся в кнопочном выключателе /2/ .
2.5.3 Выключить рабочий контактор кнопочным выключателем /2/. Гаснет зеленая сигнальная лампа /2/, и загорается красная сигнальная лампа в кнопочном выключателе /3/.
2.5.4 Установить выходное напряжение вращением вправо ручки /5/. В случае пробоя на испытуемом объекте или при слишком большом потребляемом токе выключается рабочий контактор.
2.6 Снятие показаний измерительных приборов
2.6.1 Измерение переменного напряжения.
Выходное напряжение получается произведением первичного напряжения на коэффициент в соответствии с таблицей 2.3.
Таблица 2.3
|
|
Коэффициент при выходе на |
|
|
Клеммах U-Y |
Клеммах Y- |
|
|
1 кВ |
5 |
2.5 |
|
2 кВ |
10 |
5 |
|
5 кВ |
25 |
12.5 |
|
10 кВ |
50 |
25 |
2.6.2 Измерение постоянного напряжения.
Выходное напряжение показывает прибор /8/ с учетом положения выключателя /7/.
2.6.3 Измерение тока.
Прибор показывает следующие значения:
выходной ток регулировочного трансформатора (11);
выходной ток высоковольтного трансформатора (9).
2.7 Выключение устройства
Выключение испытательного устройства производится, как правило, по следующей схеме:
2.7.1 Установить испытательное напряжение вращением ручки /5/ до левого упора на нуль.
2.7.2 Выключить рабочий контактор кнопочным выключателем /3/.
2.7.3 Выключить силовой выключатель /1/.
2.7.4 В случае опасности выключить силовой выключатель (1).
Выключать силовой выключатель размыканием двух контактов не допускается.
2.8 Рабочее задание
2.8.1 Пробить указанное преподавателем количество образцов.
2.8.2 Результаты определения Епр представить в виде вариационного ряда и сводной таблицы аналогично таблице 1.1.
2.8.3 Вычислить Епр и s.
2.8.4 Построить гистограмму и интегральную кривую.
2.8.5 Объяснить полученные результаты.
2.8.6 По результатам пробоя разных изоляционных материалов сделать выводы о зависимости электрической прочности от состава и структуры материала.
2.9 Контрольные вопросы
2.9.1 Что такое электрическая прочность диэлектрика? Единицы измерения в системе СИ.
2.9.2 Виды пробоя твердых диэлектриков.
2.9.3 Как происходит электрический пробой?
2.9.4 Как происходит электротепловой пробой?
2.9.5 Как происходит электрохимический пробой?
2.9.6 Зависимость электрической прочности диэлектрика от его толщины.
2.9.7 Как проводят статистическую обработку результатов эксперимента?
2.9.8 Что такое среднеквадратичное отклонение?
2.9.9 Цель статистической обработка результатов?
2.9.10 Описание установки для испытания электрической прочности.
2.9.11 Как строится гистограмма и интегральная кривая?
Лабораторная работа 3
Проводниковые материалы
Цель работы:
- изучение физических явлений в проводниковых материалах и экспериментальное определение основных электрических характеристик проводниковых материалов - удельного сопротивления, температурного коэффициента сопротивления, термоэлектродвижущей силы.
3.1 Краткие теоретические сведения
К проводниковым материалам относятся вещества с удельным сопротивлением менее 10-5 Ом×м. Важнейшими проводниковыми материалами, применяемыми в электротехнике, являются металлы и их сплавы. Из металлических проводниковых материалов могут быть выделены металлы высокой проводимости, имеющие удельное сопротивление (r) при нормальной температуре не более 0.1 мкОм×м и сплавы высокого сопротивления с r, при нормальной температуре, не менее 0.3 мкОм×м. Металлы высокой проводимости используют для проводов, токопроводящих жил кабелей, обмоток электрических машин и трансформаторов. Сплавы высокого сопротивления применяют при изготовлении резисторов, электронагревательных элементов и т.п.
Согласно классической электронной теории металлов твердый проводник представляют в виде узлов кристаллической ионной решетки, внутри которой находится «электронный газ», состоящий из коллективизированных (свободных) электронов. Так как механизм прохождения тока в металлах под действием электрического поля обусловлен движением указанных свободных электронов, то металлы называют проводниками с электронной электропроводимостью или проводниками первого рода.
К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся:
- удельное сопротивление (r) или обратная ему величина - удельная проводимость (Ã);
- температурный коэффициент удельного сопротивления (ТКr);
-контактная разность потенциалов и термоэлектродвижущая сила (термо -э.д.с.).
Для проводника, имеющего сопротивление - R, длину - l и постоянное поперечное сечение - S, удельное сопротивление вычисляют по формуле
r = ![]() (3.1)
(3.1)
Для измерения r, кроме единицы СИ - Ом×м, часто используют внесистемную единицу - Ом.мм2/м. Удельная проводимость (Ã) проводников часто выражается в единицах, обратных единицам r, - См/м. Удельные сопротивления наиболее распространенных проводников - меди и алюминия - составляют соответственно 0.0172 и 0.028 мкОм×м.
Удельное сопротивление металлических проводников согласно классической теории металлов может быть выражено следующим образом:
r = ![]() , (3.2)
, (3.2)
где m - масса электрона;
V т - средняя скорость теплового движения электрона;
![]() - заряд электрона;
- заряд электрона;
N - концентрация электронов;
l - средняя длина свободного пробега электрона.
Для различных металлов скорости хаотического теплового движения электронов (при определенной температуре) примерно одинаковы. Незначительно различается также и концентрация свободных электронов N, поэтому значение r в основном зависит от средней длины свободного пробега электронов в данном проводнике - l, которая в свою очередь определяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению r.
Для проводников имеют место понятия температурных коэффициентов сопротивления:
ТКR = ![]() ,
(3.3)
,
(3.3)
удельного сопротивления:
ТКr =![]() ,
(3.4)
,
(3.4)
и линейного расширения:
ТКl=![]() (3.5)
(3.5)
где l- произвольный линейный параметр изделия из данного материала.
В конечных приращениях любой из этих коэффициентов, например, температурный коэффициент сопротивления, можно записать:
ТКR=![]() (3.6.)
(3.6.)
где R1 _- сопротивление при температуре Т1;
R2 - сопротивление при температуре Т2.
Температурный коэффициент сопротивления ТКR характеризует зависимость изменения сопротивления от температуры и численно показывает, во сколько раз по сравнению с первоначальным сопротивлением R1изменяется сопротивление проводника при его нагревании на 1 градус. Размерность ТК обратная размерности температуры, и все ТК выражаются в (К-1). Согласно классической теории ТК чистых металлов в твердом состоянии должен быть близок к ТК объема идеальных газов, т.е. к 1\273 = 0.00367 К-1. Температурные коэффициенты проводника связаны между собой зависимостью:
ТКR=TKr-TKl. (3.7)
Для чистых металлов обычно TKl << TKr, т.е для них можно считать приближенно ТКR» TKr. Для меди и алюминия TKr составляет соответственно 0.0043 и 0.0042 К-1, а TKl - 0.000016 и 0.000024 К-1. При повышении температуры проводника из чистого металла число носителей заряда (концентрация свободных электронов) практически не изменяется. Однако, вследствие усиления колебаний узлов кристаллической решетки, с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т.е. уменьшается средняя длина свободного пробега (l) и, как следствие, возрастает удельное сопротивление металлов в соответствии с рисунком 3.1.
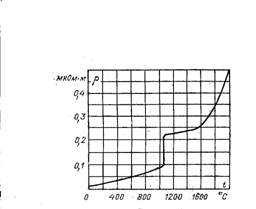 |
Иными словами, температурный коэффициент удельного сопротивления металлов положителен. Однако для сплавов TKr может приобретать и отрицательные значения.
Рисунок 3.1- Зависимость удельного сопротивления меди от температуры
При изменении температуры в узких диапазонах на
практике допустима линейно - кусочная аппроксимация зависимости
r=![]() f(Т°),
в этом случае принимают, что:
f(Т°),
в этом случае принимают, что:
r2=r1[1+ТКr(Т2―Т1)], (3.8)
где r1 и r2 - удельные сопротивления проводника при температурах Т1и Т2
соответственно ( при этом Т2> Т1);
ТКr - средний коэффициент удельного сопротивления при температуре
от Т1 до Т2.
При соприкосновении двух различных металлов между ними возникает контактная разность потенциалов, обусловленная различием значений концентраций свободных электронов соприкасающихся металлов. Если один из спаев (для случая цепи из двух металлов А и Б) имеет температуру Т1, а другой Т2, причем Т1¹Т2, между спаями возникает термо - э.д.с.:
Ит = k×( Т1 - Т2), (3.9)
где k― постоянный для проводников коэффициент термо―э.д.с.
3.2 Описание установки
Установка, приведенная в соответствии с рисунком 3.2, состоит из
электропечи и моста одинарного РЗЗЗ. Электропечь состоит из прямоугольного корпуса, выполненного из листовой стали и окрашенного коррозостойкой краской. Внутри корпуса помещается разборная футеровка шахты, выполненная из шамота и ультралегковеса и установлено на подставке из шамотного кирпича ― легковеса. Пространство между стенками шахты и кожухом заполнено теплоизоляционным материалом. Между подставкой и дном кожуха находится асбестовая прокладка.
В качестве нагревательных элементов применены карборундовые стержни, расположенные по двум противоположным стенкам. В крышке электропечи, выполненной из шамота, имеется отверстие для термометра в рабочее пространство и отверстие для проводника. Сопротивление карборудновых стержней при температуре 1200°С резко падает, при этом резко возрастает сила тока, а следовательно, и температура, что может вывести стержни из строя. Поэтому при работе на максимальной температуре необходимо непрерывное наблюдение за током.
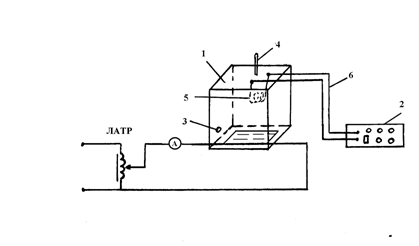 |
1 - электропечь ШП - 1, 2 - мост одинарный РЗЗЗ, 3 - контактный винт, 4 - термометр, 5 - испытуемый проводник, 6 - подводящие проводники.
Рисунок 3.2- Схема установки для измерения r и ТКr проводников
3.3 Рабочее задание
3.3.1 Закоротить подводящие проводники и замерить их сопротивление Rп.п измерительным мостом.
3.3.2 С помощью линейки и микрометра определить длину l и диаметр испытуемого проводника.
3.3.3 Подключить к подводящим проводникам испытуемый проводник и замерить их суммарное сопротивление Rå при комнатной температуре. Сопротивление испытуемого проводника будет равно:
R= Rå-Rпп.
Удельное сопротивление определить по формуле (3.1).
3.3.4 Поместить испытуемый проводник в нагревательную печь и замерить суммарное сопротивление через каждые 20°С, при нагревании до 160°С.
3.3.5 Напряжение на нагревательном элементе печи - Uп поддерживать таким, чтобы ток Iп не превышал 9А.
Записать значение термо - э.д.с. для тех же значений температуры.
Результаты занести в таблицу 3.1 (графы 2,3,6,8).
Таблица 3.1
|
№ пп |
Т°С |
Rå,, Ом |
R, Ом |
r, мкОм.м |
Uп, Ом |
Rп, Ом |
Uт, mV |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
3.4 Расчетное задание
3.4.1 На одном графике построить экспериментальную зависимость удельного сопротивления испытуемого проводника от температуры и теоретическую, рассчитав ее по закону Видемана - Франца:
r=![]() , (3.10)
, (3.10)
где К=385 Вт/(м.К) ― коэффициент теплопроводности меди;
Т° ― температура °К;
L=2.45×10-8 В2/К2 - число Лоренца.
3.4.2 Построить график зависимости сопротивления нагревательного элемента печи от температуры:
Rп=![]() .
(3.11)
.
(3.11)
3.4.3 По формулам (3.6, 3.7) определить температурные коэффициенты сопротивления и удельного сопротивления испытуемого проводника при максимальной разнице температур.
3.4.4 Используя полученную величину ТКr, подсчитать по формуле (3.8) удельное сопротивление проводника при 0 °С и 180°С. Расчетные точки нанести на график.
3.4.6 Построить график зависимости термо - э.д.с. от температуры. Определить из формулы (3.9) величину коэффициента k для максимальной разницы температур.
3.4.7 Сравнить графики, построенные в соответствии с п.п. 3.5.1 и 3.5.6 и сделать выводы о проводимости проводников и полупроводников.
По результатам вычисления ρи ТКρ дать рекомендации о возможности использования данных проводников в электрических машинах и аппаратах.
3.5 Контрольные вопросы
3.5.1 Какова физическая природа сопротивления?
3.5.2 Что представляет собой температурный коэффициент удельного сопротивления? Чем он отличается от температурного коэффициента сопротивления?
3.5.3 Почему с увеличением температуры удельное сопротивление металлов возрастает, а удельное сопротивление сплавов уменьшается?
3.5.4 Как выглядят графики зависимости удельного сопротивления от температуры при ТКr больше 0, меньше 0, равном 0?
3.5.5 Как изменяются r и ТКr сплава двух металлов?
3.5.6 Какова физическая природа термоэлектродвижущей силы?
3.5.7 Свойства меди и алюминия.
3.5.8 Явления сверхпроводимости и криопроводимости.
Лабораторная работа 4
Магнитные характеристики материалов
Цель работы:
- изучение магнитных характеристик ферромагнитных материалов и методов определения этих характеристик.
4.1 Краткие теоретические сведения
Основной характеристикой магнитного поля является вектор магнитной индукции В, определяющий величину (интенсивность) магнитного поля и его направление. В системе СИ В измеряется в теслах [Тл].
1 Тл= 1 В с/м2=1 Вб/ м2 (в системе СГСМ в гауссах).
1 Гс= 10―8 Вб\см2.
В магнитных измерениях и расчетах широко пользуются величиной потока вектора магнитной индукции ( магнитного потока), равной интегралу вектора магнитной индукции по некоторой поверхности:
Ф=![]() (4.1)
(4.1)
В однородном поле:
Ф=В×S (4.2)
где S ― площадь плоской площадки, ограниченной замкнутым
контуром, плоскость которого перпендикулярна к направлению
вектора магнитной индукции.
В системе СИ Ф измеряется В.с или веберах, в СГСМ - в максвеллах
1 Мкс=10-8Вб.
Для описания поведения ферромагнитных сред в магнитном поле вводится параметр, называемый напряженностью магнитного поля Н - вектор напряженности магнитного поля определяет магнитное поле, создаваемое внешними по отношению к данному объему тела источниками.
В системе СИ Н измеряют
в А/м, в СГСМ в эрстедах ![]() . Основной характеристикой ферромагнитных
материалов является связь между вектором магнитной индукции и вектором
напряженности магнитного поля В=f(Н). Эти зависимости не имеют точного
аналитического выражения и обычно определяются экспериментально.
. Основной характеристикой ферромагнитных
материалов является связь между вектором магнитной индукции и вектором
напряженности магнитного поля В=f(Н). Эти зависимости не имеют точного
аналитического выражения и обычно определяются экспериментально.
Отношение индукции к напряженности поля называют магнитной проницаемостью материала:
µ=![]() ,
(4.3)
,
(4.3)
где ![]() - постоянная, характеризующая магнитные
свойства вакуума;
- постоянная, характеризующая магнитные
свойства вакуума;
![]() - относительная
магнитная проницаемость.
- относительная
магнитная проницаемость.
В СИ ![]() =4p×
10-7 Гн/м = 1.256 ×10-6Гн/м.
=4p×
10-7 Гн/м = 1.256 ×10-6Гн/м.
В СГСМ ![]() =1.
=1.
При исследовании ферромагнитных материалов важную роль играют измерения в постоянных магнитных полях.
Измерение магнитных характеристик в постоянных полях необходимо в тех случаях, когда исследуемый материал применяется в аналогичных условиях, например, в качестве магнитопровода электромагнита постоянного тока, полюсных наконечников, постоянного магнита, магнитного шунта и т.д. В ряде случаев по магнитным характеристикам, определенным в постоянных магнитных полях, можно судить о поведении материала в переменных полях небольшой частоты. Например, кривые индукции листовой электротехнической стали в постоянных магнитных полях до частоты примерно 50 Гц для толщины листа 0,35 мм и тоньше практически совпадают.
Наконец, только по магнитным характеристикам материала в постоянных магнитных полях - можно судить о его качестве, о физическом состоянии, правильности технологии обработки и применения, т.к. его характеристики в переменных магнитных полях в сильной степени зависят от частоты поля, толщины и т.п. и могут служить чаще всего лишь относительными характеристиками пригодности его в данном конкретном применении.
4.2 Определение основной кривой индукции и петли гистерезиса на тороидальных образцах
Измерения производятся на предварительно размагниченном образце. Наиболее простой метод измерения кривой индукции состоит в следующем:
-подбирают значения напряженности магнитного поля, для которых необходимо определить магнитную индукцию.
-для образцов замкнутой формы напряженность магнитного поля подсчитывают по известному числу витков намагничивающей обмотки W1, средней длине магнитной линии в образце - l (м) и величине тока -I (А).
В практической системе единиц МКСА:
Н=![]()
![]() . (4.4)
. (4.4)
Для каждого выбранного значения напряженности поля по формуле (4.4.) рассчитывают соответствующую ей величину тока. Затем включают в цепь обмотки W1, первое значение тока и отмечают при этом отброс миллиамперметра - I2.
Величина индукции, соответствующая установленному значению напряженности поля , определяется по формуле:
В=![]() [Тл],
(4.5)
[Тл],
(4.5)
где Сd - постоянная миллиамперметра;
W2 - число витков измерительной обмотки;
S - сечение образца, м2;
I2 - отброс миллиамперметра (А).
После этого скачком увеличивают ток намагничивающей обмотки до второго вычисленного значения и измеряют отброс миллиамперметра I2, который пропорционален приращению индукции.
4.3 Принципиальная схема установки и порядок измерений
Принципиальная схема установки изображена на рисунке 4.1
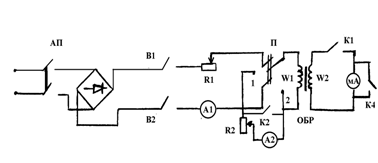 |
R1 - реостат для регулирования тока в намагничивающей обмотке образца;
A 1 - амперметр для измерения тока в намагничивающей обмотке образца;
П - переключатель направления тока;
A2 - амперметр для регулирования тока в размагничивающей цепи;
K2 - ключ, замыкающий накоротко размагничивающую цепь;
Обр.- исследуемый образец;
W1 - намагничивающая обмотка образца;
W2 - измерительная обмотка образца;
mA - микроамперметр (гальванометр);
K1 - ключ для включения измерительной цепи;
K4 - ключ для закорачивания цепи рамки гальванометра.
Рисунок 4.1
 |
Рисунок 4.2 - Построение основной кривой намагничивания
Измерение остальных точек кривой индукции проводится точно так же.
Измеренная таким образом кривая индукции (ступенчатая), только с известным приближением, может характеризовать свойства материала. Поэтому обычно для определения основной кривой индукции применяют коммутационный метод измерения.
Основной кривой индукции называют кривую, совпадающую с геометрическим местом вершин симметричных петель гистерезиса с изменяющимся от 0 до насыщения амплитудным значением магнитной индукции. Определение точек основной кривой на предварительно размагниченном образце начинают с меньших значений напряженности поля: в противном случае после каждой точки пришлось бы производить размагничивание.
Измерение точки основной кривой индукции проводят в следующем порядке:
1) На все время измерений замыкают ключ К2. Переключатель П ставят в положение 2 и при помощи реостатов R1, по амперметру А1, устанавливают ток (поднимая его от нуля), необходимый для получения первого значения напряженности намагничивающегося поля. После установки тока проводят коммутирование направления тока, необходимое для стабилизации магнитного состояния образца. Коммутирование заключается в 10 - 15 кратных переключениях направления тока при неизменной величине в намагничивающей обмотке образца W1. После коммутирования переключатель П оставляют в положении 2, замыканием ключа К1 включают в цепь миллиамперметр и при перебрасывании переключателя в положение 1 отмечают отброс на шкале.
Такое измерение величины отброса миллиамперметра при неизменной величине намагничивающего тока приводят 2 - 3 раза. Если проведенная подготовка (стабилизация) была достаточной, то величины исследуемых отбросов совпадут. При несовпадении повторных отклонений проводят коммутирование дополнительное до тех пор, пока отклонения не будут одинаковыми. Величину магнитной индукции в [Тл] в образце находят по формуле (4.5).
После определения отброса, соответствующего первой измеряемой точке кривой, миллиамперметр отключается и при помощи реостатов R1, по амперметру А1 устанавливается второе значение тока, соответствующее большему значению напряженности поля Н2; проводят коммутирование и измеряют величину второго отброса. По формуле 4.5) вычисляется следующее значение индукции В2. Затем операция повторяется для третьей точки и т.д. до тех пор, пока не будет определена индукция для всех намеченных значений напряженности поля. Полученные результаты заносятся в таблицу.
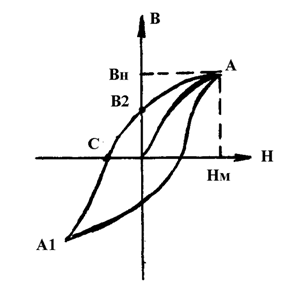 |
2) При определении точек петли гистерезиса обычно измеряют только одну ее половину АВ2СА1 в соответствии с рисунком 4.3, поскольку соответствующие точки второй половины отличаются только знаками индукции и напряженности поля при той же абсолютной величине.
Рисунок 4.3 - Построение петли гистерезиса
При измерениях пользуются несколькими различными приемами для определения участка АВ2 , где напряженность поля положительна и участка В2СА1, где она отрицательна. Измерения на участке АВ2 начинают с точки А ( с координатами Вм и Нм), для чего при положении 1 переключателя П и замкнутом ключе К2 реостатом R1 устанавливают намагничивающий ток, соответствующий максимальной напряженности намагничивающегося поля (обычно это последняя измеренная точка основной кривой индукции; петля гистерезиса может быть определена так, чтобы ее вершина совпадала с любой точкой основной индукции). Затем ключ К2 размыкают и при помощи реостата R2 по амперметру А2 устанавливают значение тока, соответствующее напряженности намагничивающего поля несколько меньше, чем точка Н1 в соответствии с рисунком 4.4.
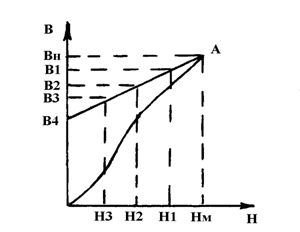 |
Рисунок 4.4- Зависимость В= f(Н) при Н↓0
После этого ключ К2 замыкают, производят коммутирование тока, соответствующего напряженности поля Нм, и оставляют переключатель П в положении 1.
Включают миллиамперметр и отмечают отброс стрелки при замыкании ключа К2 . Величина отброса пропорциональна разности индукции Вм―В1, рассчитываемой по формуле:
Вм―В1=![]() .
(4.6)
.
(4.6)
Индукцию В1 легко определить, так как Вм известно из измерения основной кривой индукции. Аналогичным способом определяют следующую точку В2, соответствующую напряженности намагничивающего поля Н2< Н1. Точка остаточной индукции образца В2 получается при включении переключателя П из положения 1 в нулевое. Измерение на участке петли В2СА1 в соответствии с рисунком 4.5 начинают с установки значения размагничивающего поля ― Н1, для чего при положении 1 переключателя П размыкают ключ К2 и реостатом R2 устанавливают по амперметру А2 ток, соответствующий напряженности поля /Н1/, заведомо много меньшей, чем коэрцитивная сила материала образца Н0. После этого ключ К2 замыкают, проводят коммутирование тока максимальной величины (соответствующей Нм) и оставляют переключатель П в положении 2,размыкают ключом К2 размагничивающую цепь, включают миллиамперметр и, перебрасывая переключатель П в положение 1, отмечают отброс ― I2. Это отклонение пропорционально разности индукции Вм―В1, которая подсчитывается по формуле (4.6) .
Напряженность поля рассчитывается по формуле (4.1.). Аналогично определяется вторая точка участка В2СА1 и т.д. до точки А1 с координатами (―Вм; ―Нм). Перед построением основной кривой индукции и петли гистерезиса необходимо знать данные испытуемого образца, которые задаются преподавателем.
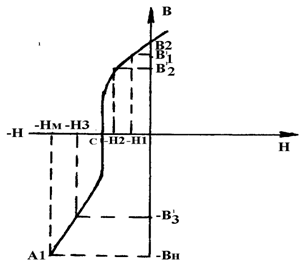 |
Рисунок 4.5- Зависимость В=f (Н) при Н®-Н
4.4 Рабочее задание
4.4.1 Снять и построить по результатам вычислений основную кривую индукции, петлю гистерезиса.
4.4.2 Построить
зависимость ![]() =f(Н).
=f(Н).
4.4.3 Сравнить полученные кривые с кривыми из /1/ и сделать вывод о возможностях применения испытанной стали.
Таблица 4.1-Таблица расчета магнитных характеристик
|
№ |
I1,А |
I2,А |
Н= |
В= |
|
|
|
|
|
|
|
|
4.5 Контрольные вопросы
4.5.1 Где применяются магнитные материалы?
4.5.2 Характеристики магнитных материалов.
4.5.3 Основные характеристики магнитного поля, единицы измерения.
4.5.4 Какие приборы и аппараты применялись для снятия кривой В=f(Н)?
4.5.5 Какой метод определения магнитных характеристик был использован? В чем заключается его сущность?
4.5.6 Схема установки.
4.5.7 Порядок выполнения работы.
Список литературы
1. Богородицкий Н.П., Пасынков В.В., Тареев Б.М. Электротехнические материалы. ―Л.: Энергоатомиздат, 1985.―304 с.
2. Тареев Б.М. Электрорадиоматериалы, ―М.: Высшая школа, 1978. ― 336 с.
3. Казарновский Д.М., Тареев Б.М. Испытание электроизоляционных материалов и изделий. ―Л.: Энергия, 1980. ―214 с.
4. Справочник по электротехническим материалам. /Под ред. Ю.В. Корицкого. ― М.: Энергия, 1988.
5. Кифер И.И. Испытания ферромагнитных материалов. ― М.;Л.: ТЭИ, 1982.― 554 с.
6. Пасынков В.В., Сорокин В.С. Материалы электронной техники. ― М.: Высшая школа, 1986. ―386 с.
7. Бекмагамбетова К.Х. Электротехническое материаловедение: Учебное пособие. - Алматы, 2001.- 258 с.
Содержание
1 Правила работы в лаборатории электротехнических материалов 3
2 Требования к отчету по лабораторной работе 3
3 Требования, предъявляемые при защите лабораторных работ 3
4 Лабораторная работа 1. Определение тангенса угла диэлектрической
проницаемости диэлектриков 4
5 Лабораторная работа 2. Определение электрической
прочности технических диэлектриков 9
5 Лабораторная работа 3 Проводниковые материалы 16
6 Лабораторная работа 4. Магнитные характеристики материалов 22
7 Список литературы 29
Сводный план 2010г., поз 79