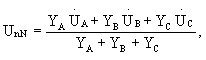АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра теоретических основ электротехники

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ 1,2

Расчет линейных электрических цепей.

Методические указания и задания к выполнению

расчетно-графических работ

для студентов всех форм обучения специальности 050718 - Электроэнергетика

Алматы 2009

СОСТАВИТЕЛИ: Креслина С.Ю, Болдырева Л.П.

Теоретические основы электротехники 1,2. Расчет линейных электрических цепей. Методические указания и задания к выполнению расчетно-графических работ для студентов всех форм обучения специальности 050718 –Электроэнергетика - Алматы: АИЭС, 2009. – 29 стр.

Приводятся методические указания и задания для студентов по курсу “Теоретические основы электротехники 1,2” по темам: “Линейные электрические цепи постоянного тока”,“Расчет линейных электрических цепей однофазного синусоидального тока”, “Расчет трехфазных цепей синусоидальными периодическими э.д.с”. Задания к расчетно-графическим работам соответствуют типовой программе по ТОЭ.

Задания предназначены для студентов электроэнергетических и электротехнических специальностей.

1 Методические указания к выполнению заданий

Одним из основных видов занятий по курсу “Теоретические основы электротехники” является выполнение расчетно-графических заданий.

Номер варианта, который должен быть выполнен студентом, определяется последними двумя цифрами зачетной книжки и первой буквой фамилии студента.

К представленным на рецензию РГР заданиям предъявляются следующие требования:

· Основные положения решения должны быть достаточно подробно пояснены.

· Рисунки, графики, схемы, в том числе и заданные условием задачи, не следует размещать среди текста. Они должны быть выполнены на отдельном листе бумаги, аккуратно и в удобночитаемом масштабе.

· В тетради следует оставлять поля шириной не менее 4 см для замечаний рецензента.

· Вычисления должны быть сделаны с точностью, которая может быть получена при использовании калькулятора.

· Задания должны быть датированы и подписаны студентом.

· Незачтенное задание должно быть выполнено заново и отдано на повторную рецензию вместе с первоначальной работой и замечаниями рецензента. Исправления ошибок в отрецензированном тексте не допускаются. Если неправильно выполнена не вся работа, а только ее часть, то после переработки исправленный текст нужно написать в тетради после первоначального текста, указав, что это исправление ошибок.

РГР засчитываются, если решения не содержат ошибок принципиального характера и если выполнены перечисленные требования.

Работа над контрольным заданием помогает студентам проверить степень усвоения ими курса, вырабатывает у них навык четко и кратко излагать свои мысли. Для успешного достижения этой цели необходимо руководствоваться следующими правилами:

o Начиная решение задачи, указать, какие физические законы или расчетные методы предполагается использовать при решении, привести математическую запись этих законов и методов.

o Тщательно продумать, какие буквенные символы предполагается использовать в решении. Пояснить значение каждого буквенного символа словами или же соответствующими обозначениями на схеме.

o В ходе решения задачи не следует изменять однажды принятые направления токов и наименования узлов, сопротивлений и т. д. Не следует изменять обозначения, заданные условием. При решении одной и той же задачи различными методами одну и ту же величину надлежит обозначать одним и тем же буквенным символом.

o Расчет каждой искомой величины следует выполнять сначала в общем виде, а затем в полученную формулу подставить числовые значения и привести окончательный результат с указанием единиц измерения. При решении системы уравнений целесообразно воспользоваться известными методами упрощения расчета определителей (например, вынесение за знак определителя общего множителя и другими, а ещё проще методом подстановки).

o Промежуточные и конечные результаты расчетов должны быть ясно выделены из общего текста.

o Решение задач не следует перегружать приведением всех алгебраических преобразований и арифметических расчетов.

o Для элементов электрических схем следует пользоваться обозначениями, применяемыми в учебниках по ТОЭ.

o Каждому этапу решения задачи нужно давать пояснения.

o При построении кривых выбирать такой масштаб, чтобы на 1 см оси координат приходилось 1*10^±n или 2*10^±n единиц измерения физической величины, где n-целое число. Градуировку осей выполнять, начиная с нуля, равномерно через один или через два сантиметра. Числовые значения координат точек, по которым строятся кривые, не приводить. Весь график в целом и отдельные кривые на нем должны иметь названия.

2 Задание №1

Линейные электрические цепи постоянного тока

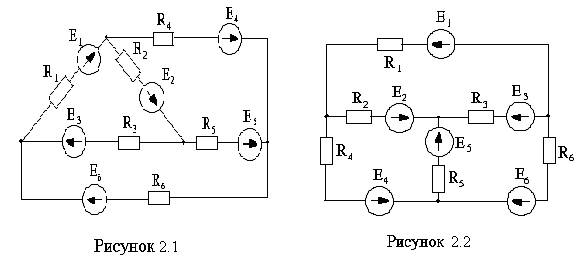
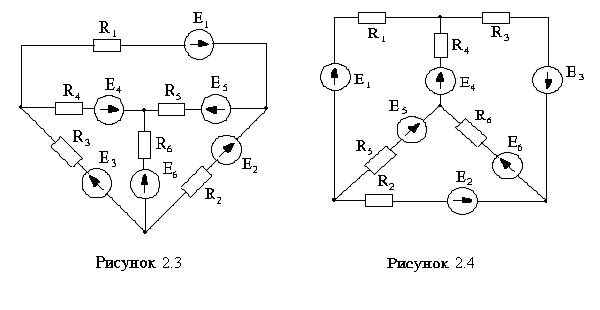
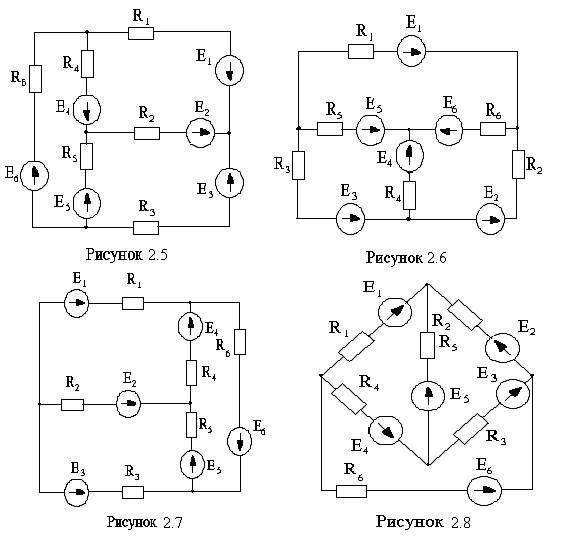
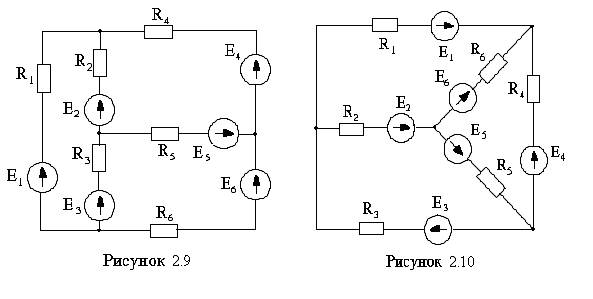
Для электрической схемы, соответствующей номеру варианта (см. рисунки 2.1-2.10, таблицы 2.1-2.3), выполнить следующее:

2.1 Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

2.2 Составить систему уравнений и уравнения для определения токов во всех ветвях схемы методом контурных токов (МКТ).

2.3 Составить систему уравнений и уравнения для определения токов во всех ветвях схемы методом узловых потенциалов (МУП).

2.4 Рассчитать токи в ветвях указанным в таблице 2.3 методом.

2.5 Составить уравнение баланса мощностей.

2.6 Построить потенциальную диаграмму для внешнего контура схемы.

Т а б л и ц а 2.1

Год поступления

Последняя цифра зачетной книжки

Нечетный

№ схемы

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

Четный

№ схемы

2.10

2.9

2.8

2.7

2.6

2.5

2.4

2.3

2.2

2.1

R₁, Ом

R₂,Ом

R₃, Ом

R₄,Ом

R₅, Ом

R₆, Ом

Т а б л и ц а 2.2

Год поступления

Предпоследняя цифра зачетной книжки

Нечетный

Четный

Е₁, В

Е₂,В

Е₃, В

Е₄,В

Е₅, В

Е₆, В

I_К, А

150

100

200

150

100

200

100

250

150

200

100

150

100

200

100

150

250

200

150

100

2,5

100

200

150

3,5

250

100

200

4,5

250

100

150

5,5

Т а б л и ц а 2.3

Год поступления

Первая буква фамилии

Нечетный

АНМЖУ

БСЮЗФ

ВИЯКЦ

ГРЩХЛ

ДОПЧ

ЕТШЭ

Четный

БСЮЗФ

ВИЯКЦ

ДОПЧ

ЕТШЭ

АНМЖУ

ГРЩХЛ

Определить токи

МКТ

МУП

МКТ

МУП

МКТ

МУП

3 Задание №2

Расчет линейных электрических цепей однофазного

синусоидального тока

Содержание задания

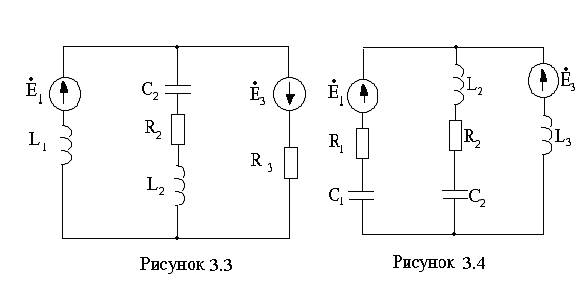
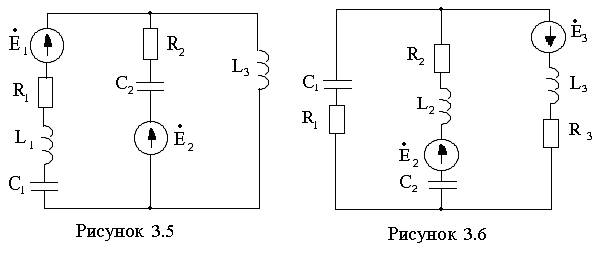
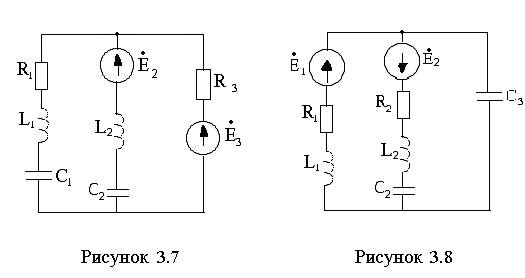
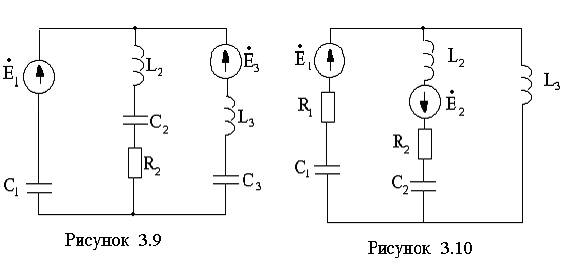
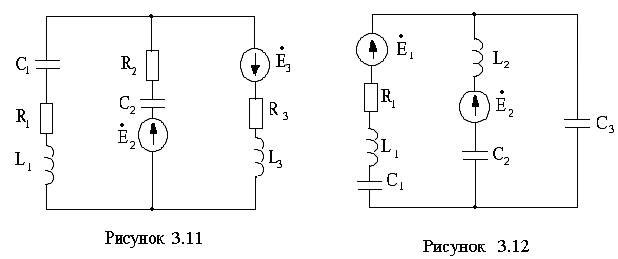
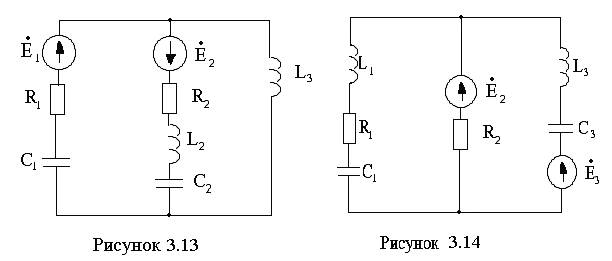
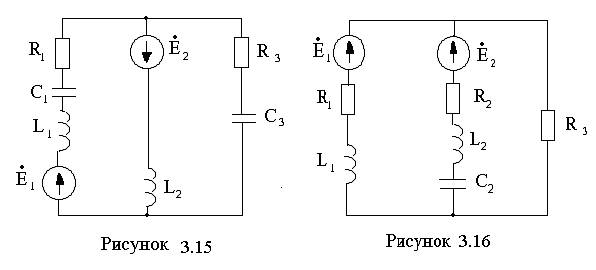
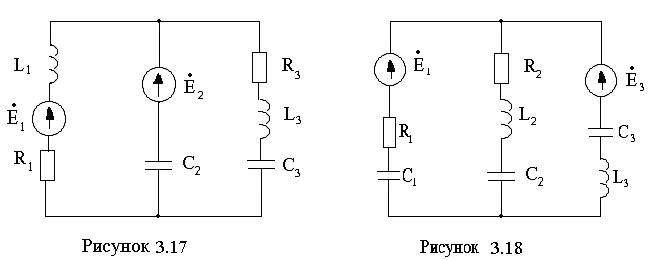
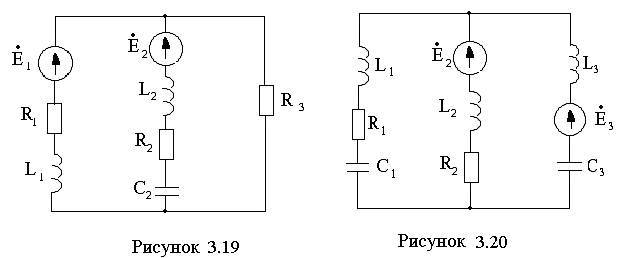
Для электрической цепи (см. рисунки 3.1 –3.20) по заданным в таблицах 3.1 – 3.3 параметрам требуется:

3.1 Составить уравнения по законам Кирхгофа в дифференциальной и комплексной формах.

3.2 Рассчитать заданную цепь одним из методов расчета линейных цепей. Записать выражения мгновенных значений токов в ветвях цепи.

3.3 Проверить выполнение баланса мощностей.

3.4 Построить векторно-топографическую диаграмму токов и напряжений.

Т а б л и ц а 3.1

Год поступления	Последняя цифра зачетной книжки
Нечетный	1	2	3	4	5	6	7	8	9	0
№ схемы	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8	3.9	3.10
Четный	6	7	8	9	0	1	2	3	4	5
№ схемы	3.11	3.12	3.13	3.14	3.15	3.16	3.17	3.18	3.19	3.20
E₁, B	20	10	15	30	40	35	50	45	25	20
j₁,град	0	-30	45	-60	90	0	135	60	-45	30
E₂, B	10	15	20	35	25	10	25	20	20	15
j₂,град	-60	45	90	135	0	60	0	45	60	0
E₃, B	30	40	30	15	45	20	45	50	35	25
j₃,град	90	0	60	0	-30	270	-30	0	90	270

Т а б л и ц а 3.2

Год поступления	Предпоследняя цифра зачетной книжки
Нечетный	1	2	3	4	5	6	7	8	9	0
Четный	0	1	2	3	4	5	6	7	8	9
R₁, Ом	20	25	30	35	40	45	10	15	10	10
R₂, Ом	10	20	15	40	20	20	35	30	30	20
R₃, Ом	40	45	20	15	10	15	20	20	20	25

Т а б л и ц а 3.3

Год поступления	Первая буква фамилии
Нечетный	АЛХ	БМЦ	ВНЧ	ГОЩ	ДПШ	ЕРЭ	ЖСЮ	ЗТЯ	ИУ	КФ
Четный	ЕРЭ	АЛХ	ЖСЮ	БМЦ	ЗТЯ	ВНЧ	ИУ	ГОЩ	КФ	ДПШ
X_L₁, Ом	10	25	8	12	18	5	15	20	13	30
X_L₂, Ом	5	10	10	20	12	10	12	10	15	20
X_L₃, Ом	15	20	25	25	20	12	13	30	18	10
X_C₁, Ом	15	15	15	15	10	18	10	12	10	15
X_C2, Ом	12	5	20	10	20	13	18	15	20	25
X_C₃, Ом	5	18	10	18	15	15	20	18	25	18

4 Задание №3

Расчет трехфазных цепей с синусоидальными периодическими э.д.с.

К симметричному трехфазному генератору с синусоидальными фазными э.д.с подключена симметричная нагрузка.

Для электрических схем с нейтральным проводом и при обрыве нейтрального провода рассчитать:

- мгновенные значения токов в фазах А, В, С;

- мгновенное значение тока в нейтральном проводе;

- активную, реактивную, полную мощности;

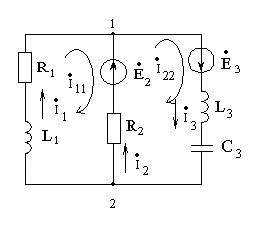
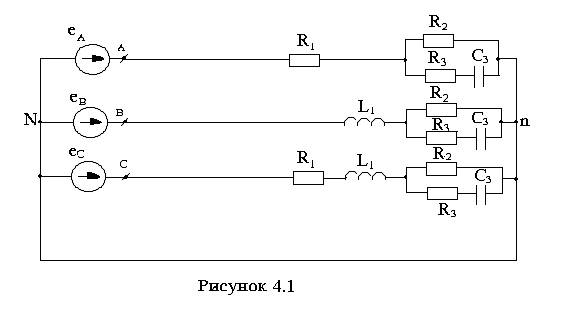
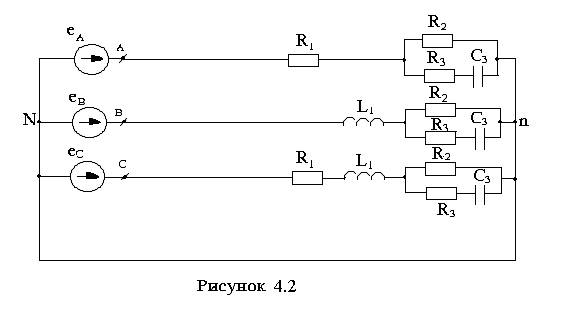
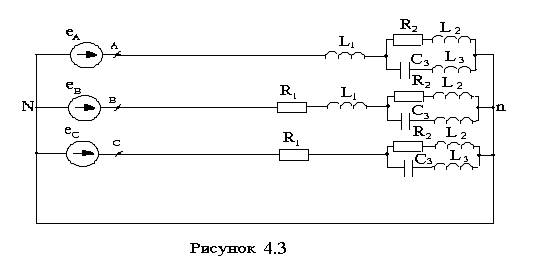
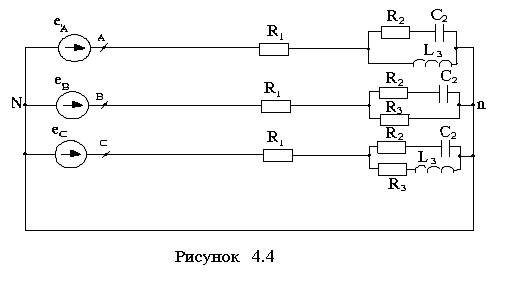
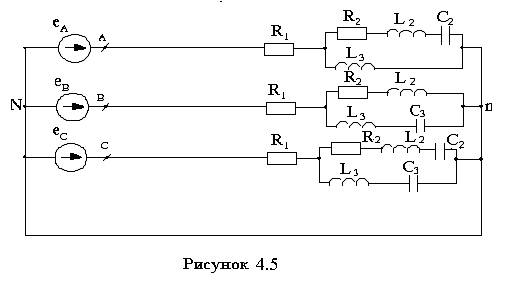
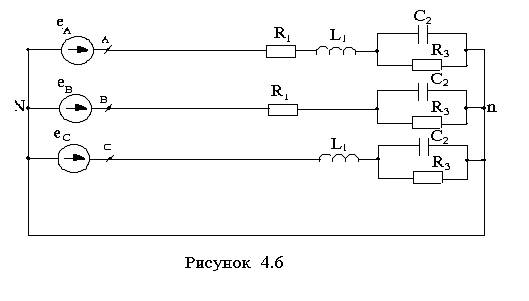
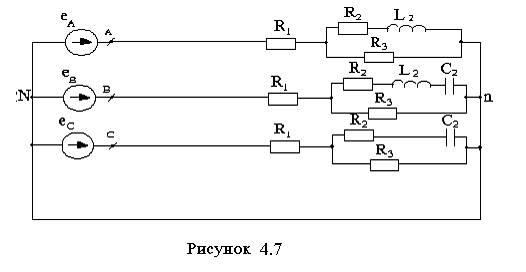
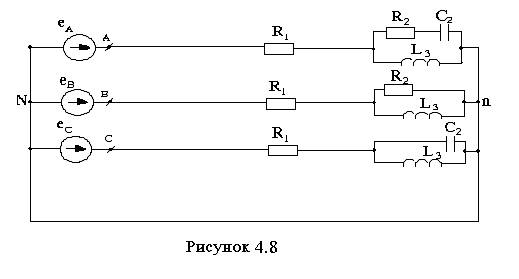
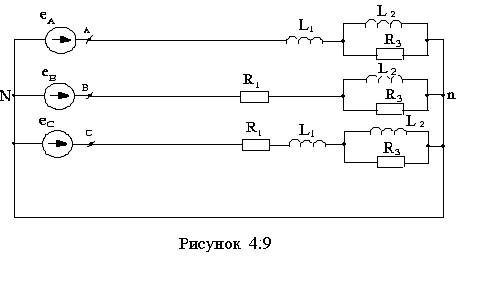
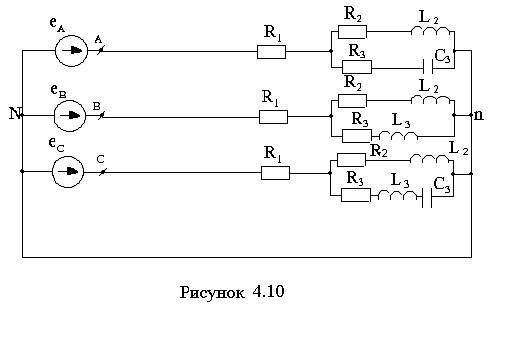
Электрические схемы приведены на рисунках 4.1-4.10.

Максимальные значения фазной э.д.с генератора Е_А_m и параметры цепи приведены в таблицах 4.1-4.3. Основная частота фазных э.д.с. генератора f=50 Гц.

Т а б л и ц а 4.1

Год поступления	Последняя цифра зачетной книжки
Нечетный № схемы	1 4.1	2 4.2	3 4.3	4 4.4	5 4.5	6 4.6	7 4.7	8 4.8	9 4.9	0 4.10
Четный № схемы	0 4.1	9 4.2	8 4.3	7 4.4	6 4.5	5 4.6	4 4.7	3 4.8	2 4.9	1 4.10
R₁, Ом	10	8	14	9	15	20	18	22	16	12
L₁, мГн	50	40	60	30	20	90	95	85	65	80
R₃, Ом	40	30	45	44	35	35	55	45	70	80
L₃, мГн	35	100	80	50	60	75	35	70	75	40
C₃, мкФ	60	60	70	25	40	35	60	40	95	50

Таблица 4.2

Год поступления	Предпоследняя цифра зачетной книжки
Нечетный	0	2	4	6	8	9	7	5	3	1
Четный	8	7	5	3	1	0	2	4	6	9
R₂, Ом	30	45	60	40	25	100	70	80	45	65
L₂, мГн	40	65	90	80	30	85	85	50	70	60
C₂, мкФ	20	80	75	50	60	90	95	85	35	35

Таблица 4.3

Год поступления	Первая буква фамилии
Нечетный	А,КХ	Б,Л,Ц	В,М,Ч	Г,НШ	Д,О,Щ	Е,ПР	Ж,С,З	Т,Э,И	У,Ю	Ф,Я
Четный	Б,ИЗ	Ж, Е	Д,Г,В	А, Ф	У,Т,С	Р,ПО	Н,М,Л	К,ЯЮ	Э,Щ,Ч	Ш,Ц,Х
E_Аm, В	380	120	220	360	270	110	127	200	100	60

5. Методические указания к расчету заданий

5.1 Составление уравнений для расчета токов методом контурных токов для электрической цепи постоянного тока (рисунок 5.1)

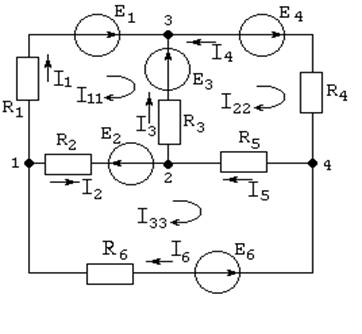
Рисунок 5.1

Выбираем взаимно независимые контуры, в каждом из которых замыкается один контурный ток. Положительные направления контурных токов выбираем произвольно. Число уравнений, составленных по МКТ, равно числу уравнений, составленных по второму закону Кирхгофа.

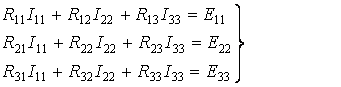
R₁₁, R₂₂, R₃₃ - cобственные сопротивления контуров.

Собственное сопротивление контура равно сумме сопротивлений ветвей, входящих в данный контур:

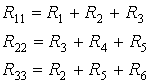
R₁₂=R₂₁; R₁₃=R₃₁; R₂₃=R₃₂ - общие сопротивления контуров.

Общее сопротивление контуров равно сопротивлению ветви, общей для этих контуров. Общее сопротивление берется со знаком «+», если контурные токи рассматриваемых контуров протекают через общие для этих контуров ветви в одинаковом направлении, знак «-», если контурные токи в общих ветвях имеют противоположные направления.

R₁₂ = R₂₁= -R₃

R₁₃ = R₃₁= -R₂

R₂₃ = R₃₂= - R₅

Е₁₁, Е₂₂, Е₃₃ - контурные э.д.с.

Каждая из контурных э.д.с. равна алгебраической сумме э.д.с. всех источников в ветвях, входящих в данный контур. Положительные знаки взяты для э.д.с, положительные направления которых совпадают с положительным направлением контурного тока, замыкающегося в данном контуре.

Е₁₁=Е₁- Е₃+ Е₂

Е₂₂=Е₃ + Е₄

Е₃₃= -Е₂- Е₆

Решая систему при помощи определителей, определим токи I₁₁, I₂₂, I₃₃.

Рассчитаем определитель системы D :

Рассчитаем определители D₁₁, D₂₂, D₃₃ :

;

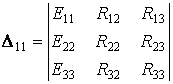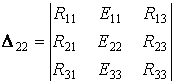Определим контурные токи по формулам:

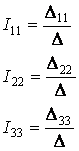
Рассчитаем токи в ветвях электрической цепи.

Токи в ветвях равны контурным токам:

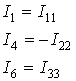
Токи в ветвях , общих для нескольких контуров, равны алгебраической сумме контурных токов, протекающих по этим ветвям:

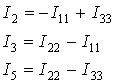
Расчет токов во всех ветвях электрической цепи методом узловых потенциалов.

Определим узловые потенциалы для электрической цепи (рисунок 5.1).

Рассчитаем проводимости каждой ветви:

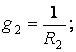
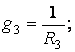
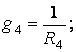
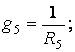
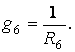
Приравниваем к нулю потенциал любого узла, пусть j₄=0.

Запишем уравнения для определения узловых потенциалов:

g₁₁, g₂₂, g₃₃ - cобственная узловая проводимость, равна сумме проводимостей ветвей, присоединенных к данному узлу.

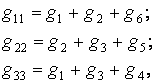
общая узловая проводимость, равна сумме проводимостей ветвей, соединяющих между собой рассматриваемые узлы.

- алгебраическая сумма произведений э.д.с. на соответствующие проводимости для всех ветвей, присоединенных к рассматриваемому узлу. Если э.д.с направлена к рассматриваемому узлу, записывается знак «+», если э.д.с направлена от узла - « -».

;

Рассчитаем потенциалы j₁, j₂, j₃при помощи определителей. Определители для системы уравнений равны:

;

Потенциалы j₁, j₂, j₃ определим по формулам:

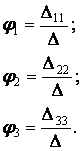
Токи в ветвях электрической цепи определим по закону Ома:

Составление уравнения баланса мощностей.

Суммарная мощность всех источников э.д.с Р_ИСТ в электрической цепи равна суммарной мощности, расходуемой в сопротивлениях Р_ПР :

Р_ИСТ = Р_ПР

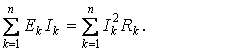
Е_kI_k - мощность источника э.д.с в к-й ветви; мощность положительна, если положительные направления э.д.с Е_Ки тока I_K одинаковы; и отрицательна, если положительные направления э.д.с Е_К и тока I_K противоположны;

- мощность в сопротивлении к-й ветви.

5.2 Составление уравнений для расчета токов во всех ветвях схемы на основании законов Кирхгофа, используя две формы записи: дифференциальную и символическую.

Рисунок 5.2

Произвольно выбираем направление токов в ветвях (рисунок 5.2). Составим уравнения в дифференциальной форме, т.е. для мгновенных значений токов и напряжений. В соответствии с первым законом Кирхгофа алгебраическая сумма мгновенных токов ветвей, сходящихся в узле, равна нулю. В схеме два узла, поэтому по первому закону Кирхгофа составим одно уравнение. По второму закону Кирхгофа алгебраическая сумма мгновенных э.д.с. всех источников напряжения в замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура. В схеме два независимых контура, поэтому составляется два уравнения по второму закону Кирхгофа. Таким образом, получаем систему уравнений, составленных по законам Кирхгофа, в дифференциальной форме:

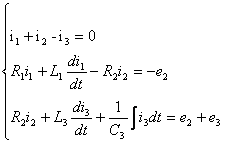
Для записи уравнений в символической форме необходимо мгновенные значения токов, э.д.с. и напряжений заменить изображающими комплексами. Тогда получим систему уравнений по законам Кирхгофа в символической форме:

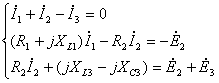
Решение полученной системы уравнений позволяет определить комплексные действующие значения токов в ветвях. Более эффективно эта задача может быть решена с использованием методов контурных токов и узловых потенциалов.

Расчет комплексных токов методом контурных токов

Выберем направления контурных токов по часовой стрелке и составим уравнения по второму закону Кирхгофа для этих токов (рисунок 5.2).

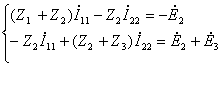
где через Z₁, Z₂, Z₃ обозначены комплексные сопротивления соответствующих ветвей; Z₁=R₁+jX_L₁; Z₂=R₂; Z₃=j(X_L₃-X_C₃). представляют собой комплексные действующие значения э.д.с.

Расчет комплексов токов методом узловых потенциалов

В схеме (рисунок 5.2) два узла, поэтому целесообразно применить метод двух узлов, являющийся частным случаем метода узловых потенциалов. Рассчитываем комплекс напряжения между узлами:

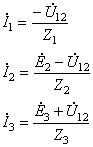
Уравнение баланса комплексных мощностей

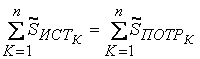Комплексная мощность источника э.д.с.

где - комплекс, сопряженный с комплексным током .

Комплексная мощность потребителя

5.3 При наличии нейтрального провода имеем _,ток в каждой фазе может быть подсчитан по закону Ома независимо от токов остальных фаз.

При отсутствии нейтрального провода определяется в начале U_nN, поскольку Y_N = 0, а именно:

Список литературы

1. Сборник задач по теоретическим основам электротехники/ Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-52с.

2. Бессонов Л.А. Теоретические основы электротехники.-М.: Гардарики,1999. - 638с.

3. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990.- 544с.

4. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.- М.: Энергоатомиздат, 1989. -528с.

5. Денисенко В.И., Зуслина Е.Х ТОЭ. Учебное пособие.- Алматы: АИЭС, 2000, 83 с.

6. В.И. Денисенко, С.Ю. Креслина. Теоретические основы электротехники 1. Конспект лекций. – Алматы: АИЭС, 2006. – 63 с.

7. В.И. Денисенко, С.Ю. Креслина. Теоретические основы электротехники 2. Конспект лекций. – Алматы: АИЭС, 2007. – 62 с.

Содержание

1 Методические указания к выполнению заданий. ...................... …………3

2 Задание №1. Линейные электрические цепи постоянного тока. …………………………………………...5

3 Задание №2. Расчет линейных электрических цепей однофазного синусоидального тока. …………..8

4 Задание №3. Расчет трехфазных цепей с синусоидальными э.д.с…..13

5 Методические указания к расчету заданий. ....................... ………..…..…18

Список литературы. ………………………………………………………….25