Коммерциялық емес акционерлік қоғам
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Электротехниканың теориялық негіздері кафедрасы
ЭЛЕКТРОТЕХНИКАНЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ - 4
5B071800 - Электроэнергетика мамандығының студенттері үшін
Дәріс жинағы
Алматы 2010
Құрастырған: М.М. Аршидинов, Ж.К.Әміров. Электротехниканың теория негіздері 4. 5В071800-Электроэнергетика мамандығының барлық оқу түрлерінің студенттеріне арналған дәрістер жинағы- Алматы: АЭжБУ, 2010-75б
Дәрістер жинағында ЭТН-4 пәні бойынша 15 дәрісте келесі негізгі бөлімдер қарастырылған: «Сызықты электр тізбектеріндегі өтпелі үрдістер» , « Параметрлері таратылған тізбектер» , «Электромагнит өрісінің теориясы»
Дәрістер жинағы 5В071800- Электроэнергетика мамандығының барлық оқу түрінің студентеріне арналған. Безендіру. 42, библиогр. 6 атау
Мазмұны
|
Кіріспе Дәріс 1 Дәріс 2 Дәріс 3 Дәріс 4 Дәріс 5 Дәріс 6 Дәріс 7 Дәріс 8 Дәріс 9 Дәріс 10 Дәріс 11 Дәріс 12 Дәріс 13 Дәріс 14 Дәріс 15 Ұсынылған әдебиеттер |
4 5 10 14 23 26 31 35 36 41 49 55 58 61 64 67 71 |
Кіріспе
Электроэнергетика саласы бойынша бакалаврларды дайындау «Электротехниканың теория негіздері 4» пәні негізгі міндетті базалық курс болып табылады.
Бұл пән электр тізбегінің негізгі элементтері көмегімен баламалы сұлбалада берілген, әртүрлі электротехниканың құрылғыларда байқалатын электромагниттік үрдістер мен құбылыстарды сапалы және сандық жағынан оқыту және сипаттау үшін қабылданады.
Бұл дәріс жинағы 15 дәрістен, 3 бөлімнен тұрады. «Сызықты электр тізбегіндегі өтпелі үрдістер», « Параметрлері таратылған тізбектер» және «Электромагнит өрісінің теориясы» .
Бірінші бөлімінде сызықты электр тізбегіндегі өтпелі үрдістерден классикалық, операторлық, жиіліктік, Дюамель интегралдық негізгі әдістері қарастырылған.
Екінші бөлімінде параметрлері таратылған тізбектер, біртекті желідегі қалыптасқан ереже, желі теориясы жүктемелі және шығынсыз желімен үйлесімді желі жөнінде негізгі түсініктер қарастырылған.
Үшінші бөлімінде электростатикалық өрістің теориясы мен негізгі теңдеулері, электр өрісінің есептеулері, негізгі заңдары мен өлшемдері, тұрақты токтағы электр өрісінің сипаттамалары қарастырылған.
Дәрістер жинағы 5В0718-Электроэнергетика мамандығы бойынша оқып жүрген студенттеріне арналған.
Дәріс 1. Сызықты электр тізбектердегі өтпелі процестер. Өтпелі процестерді классикалық әдіспен есептеу
1.1 Өтпелі процестердің пайда болуы
Жоғарыда сызықты электр тізбектерде қалыптасқан процестер қаралды, яғни токтармен кернеулер уақыт бойынша өзгермейтін (тұрақты ток тізбектер) немесе уақыт бойынша периодикалы синусоидалды функция (айнымалы ток тізбектері) кездегі процестер.
Қалыптасқан процесс басталудың алдында периодикалы емес түрде токтар және кернеулер өзгеретін өтпелі процесс бұрын өтеді.
Жұмыстың бір ережесінен екінші ережеге өтуі тізбектің параметрлері өзгергені немесе тізбектің сүлбесінің өзгергені себеп болады. Бұл өзгерулер коммутация деп аталады.
Тізбектің
коммутациясы, яғни тізбекті қосу, ажырату немесе ауыстырып
қосу лезді емес, оларға уақыт керек. Сонымен, тізбек
қалыптасқан ережеге кейбір уақыт ішінде өтеді.
Бұған себеп болатын жағдай – тізбектің әрбір
күйіне электр және магнит өрістердің
энергияларының белгілі қоры сәйкес. Жаңа ережеге
өту осы өрістердің энергияларының өсумен немесе
кемумен байланысты. L индуктивтіктің магнит өрісінде энергия
қоры ![]() және
С сыйымдылықтың электр өрісінде энергия қоры
және
С сыйымдылықтың электр өрісінде энергия қоры ![]() лезде өзгеруге
мүмкіншіліктері жоқ: энергия үздіксіз, кенет өзгерусіз
өзгеруі мүмкін, себебі қуат энергияның туындысы ретінде
шексіз мәндерге жетеді.
лезде өзгеруге
мүмкіншіліктері жоқ: энергия үздіксіз, кенет өзгерусіз
өзгеруі мүмкін, себебі қуат энергияның туындысы ретінде
шексіз мәндерге жетеді.
Теория бойынша өтпелі процесс аяқталып қалыптасқан процесс басталу үшін шексіз үлкен уақыт керек. Іс жүзінде өтпелі процесс аз уақытпен белгіленеді. Бұл уақыт ішінде токпен кернеу қалыптасқан мәндерге жақындап қалады.
Неғұрлым кедергілерде энергия шашуы қорқынды өтсе, соғұрлым өтпелі процесс жылдам өтеді. Егер де электр тізбек тек кедергілерден құралса, онда өтпелі процесс лезде өтетін еді.
Арнайы сүлбелерді қолданып және тізбектің параметрлерін таңдап өтпелі процесті тездетуге немесе бәсеңдетуге болады.
Сызықты электр тізбектердегі өтпелі процестерді есептеудің бірнеше әдістері бар. Бұл тарауда өтпелі процестерді бейнелейтін дифференциалды теңдеулерді шешетін классикалық әдіске арналған.
1.2 Коммутацияның заңдары және басты жағдайлар
Магнит немесе электр өрістің қоры үздіксіз, ырғақсыз өзгеруі индуктивтіктің ψ ағын ілінісі және сыйымдылықтың q электр заряды уақыт бойынша үздіксіз принципті көрсетеді.
Ψ = Li болғандықтан ағын ілінісудің үздіксіз принципі L тұрақты кезде і ток ырғақты өзгермейтінін көрсетеді.
Сонымен, коммутациядан кейін басты мезгілде индуктивтіктегі ток тікелей коммутация алдындағы шамада қалады да, содан кейін байсалды өзгереді (коммутацияның бірінші заңы).
q = Cuc болғандықтан электр зарядтың үздіксіз принципі С тұрақты кезде uc кернеу ырғақты өзгермейтінін көрсетеді.
Сонымен, коммутациядан кейін басты мезгілде сыйымдылықтағы кернеу тікелей коммутация алдындағы шамада қалады, ал содан кейін байсалды өзгереді (коммутацияның екінші заңы).
Ескерту: кедергіде және сыйымдылықта ток ырғақты өзгеруі мүмкін, кедергіде және индуктивтікте кернеу ырғақты өзгеруі мүмкін.
Коммутация кездегі индуктивтіктегі токтың және сыйымдылықтағы кернеудің мәндері тәуелсіз басты жағдайлар деп аталады. Басқа токтардың және кернеулердің басты мәндері тәуелді басты жағдайлар деп аталады. Тәуелді басты жағдайлар Кирхгофтың бірінші және екінші заңдары бойынша жазылған кернеулердің көмегімен тәуелсіз басты жағдайлар арқылы белгіленеді.
Әдетте, коммутация t = 0 уақыт мезгілде өтеді деп санайды, онда индуктивтіктегі токты және сыйымдылықтағы кернеуді коммутация алдында iL(0-) және uс(0-), ал коммутациядан кейін өтпелі процестің басты кезінде - iL(0) және uс(0) деп белгілейді.
Коммутация заңдары бойынша жазамыз
iL(0-) = iL(0); (1.1)
uс(0-) = uс(0)
Бұл теңдеулер коммутация өтетін тізбектегі басты жағдайларды көрсетеді.
1.3 Өтпелі, қалыптасу және еркін процестер
Жалпы жағдайда параметрлері R, L және C бар сызықты электр тізбектің талдауы Кирхгофтың заңдарын көрсететін сызықты әр текті дифференциалды теңдеулерді шешуге келеді.
Мысалы, уақыт бойынша өзгеретін ЭҚК е(t) тізбектеп қосылған R, L және C элементтері бар тізбекке қосылса, онда бұл тізбек үшін Кирхгофтың екінші заңы:
![]() (1.2)
(1.2)
мұнда і - өтпелі процестің тогы, өтпелі ток деп аталады.
Бұл теңдеу дифференциалдаудан кейін екінші дәрежелі әр текті дифференциалды теңдеуге келеді
![]() (1.3)
(1.3)
мұндай теңдеудің жалпы интегралы әр текті теңдеудің жеке шешуімен бір текті теңдеудің жалпы шешуінің қосындысына тең.
Өтпелі процесс біткеннен кейін көзбен тапсырылатын қалыптасу ереже басталады.Бұны (1.2) теңдеудің жеке шешуі белгілейді.
Қалыптасу ережесі кезіндегі (1.2) теңдеудің түрі:
![]() (1.4)
(1.4)
Мұнда iқ – қалыптасу ток.
(1.2) теңдеуден (1.4) теңдеуді алсақ, және і – іқ = іе деп белгілеп табамыз.
![]() (1.5)
(1.5)
немесе ![]() (1.6)
(1.6)
Өтпелі процестің және қалыптасу ереженің токтар және кернеулер айырымын еркін ток және еркін кернеу деп атайды.
(1.3) теңдеумен жазылатын тізбек үшін бір текті теңдеудің түрі:
![]() ,
(1.7)
,
(1.7)
ал оған сәйкесті сипаттамалы теңдеу
![]() (1.8)
(1.8)
Бұл теңдеудің жалпы шешімі
![]() (1.9)
(1.9)
Мұнда р1 және р2 – сипаттамалы теңдеудің түбірлері,
А1 және А2 – интегралдаудың тұрақтылары.
Тізбектегі толық өтпелі ток қалыптасқан және еркін токтардың қосындысына тең:
![]() (1.10)
(1.10)
Коммутация заңдары бойынша
басты тәуелсіз жағдайларды, яғни ![]() және
және ![]() табуға болады.
табуға болады.
Бұдан кейін жазуға болады.
іL(0) = іLқ(0) + іLe(0);
Uc(0) = Ucқ(0) + Uce(0), ал бұдан шығады:
іLе(0) = іL(0) - іLқ(0);
Ucе(0) = Uc(0) - Ucқ(0) (1.11)
Егер нөлдік басты жағдайлар болса, онда
іLе(0) =- іLқ(0);
Ucе(0) =- Ucқ(0).
1.4 R, L тізбектегі өтпелі процестер
t = 0 уақыт мезгілде тізбектеп қосылған R кедергімен L индуктивтіктен құралған тізбекке ЭҚК көзі e(t) қосылып тұр. (1.1 - сурет)
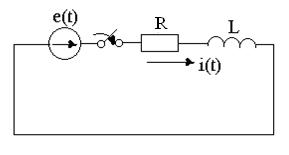
1.1 сурет- R, L тізбекті электр көзіне қосу
t ≥ 0 уақыт үшін дифференциалды таңдау былай жазылады
![]() .
.
Сипаттамалы теңдеудің түрі
R + pL = 0, ал оған
сәйкес теңдеудің түбірі р1= -![]() .
.
Еркін ток ![]() .
.
Тізбектегі
өтпелі ток і![]() .
(1.12)
.
(1.12)
Қалыптасқан токты егер де ЭҚК е(t) берілген болса, онда табуға болады
Үш жағдайды қарайық:
1) r, L тізбекке тұрақты ЭҚК Е қосу;
2) r, L тізбектегі қысқа тұйықталу;
3) r, L тізбекке синусоидалды ЭҚК Е sin(ωt + ψ) қосу.
1. R, L тізбекке тұрақты ЭҚК-ті қосу
ЭҚК Е
тұрақты кезде қалыптасқан ток ![]() ал (1.1) теңдеу бойынша
өтпелі ток тең
ал (1.1) теңдеу бойынша
өтпелі ток тең
![]() .
(1.13)
.
(1.13)
Интегралдаудың А тұрақтысы басты жағдайдан табылады
і(0) = і(0-) = 0
(1.2) теңдеу бойынша t = 0 кезде
![]() ал бұдан
ал бұдан ![]() .
.
Демек, 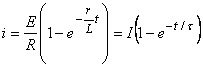 , (1.14)
, (1.14)
мұнда ![]() - қалыптасқан ток,
τ
- қалыптасқан ток,
τ![]() -
уақыт тұрақтысы.
-
уақыт тұрақтысы.
Уақыт тұрақтысы секундамен өлшенеді
![]() .
.
Басты мезгіл t = 0
кезде өздік индукцияның ЭҚК-і ![]() , ол көздің ЭҚК-ін
толық өтемелейді, себебі ток і(0) = 0.
, ол көздің ЭҚК-ін
толық өтемелейді, себебі ток і(0) = 0.
Уақыт озған сайын өздік индукцияның ЭҚК-і азаяды, ал ток үлкейіп қалыптасқан мәніне жетеді.
1.2 суретте қалыптасқан, еркін және өтпелі токтардың қисықтары келтірілген; сол суретте индуктивтегі кернеудің қисығы бейнелеген.

Неғұрлым уақыт тұрақтысы шамалы болса, соғұрлым ток тез өседі.
Әртүрлі уақыт мезгілі үшін тізбектің тоғының (қалыптасқан мәннің % белгіленген) мәні тең.
|
|
t = τ |
2τ |
3τ |
4τ |
5τ |
¥ |
|
|
63,2 |
86,5 |
95 |
98,2 |
99,3 |
100 |
Сондықтан,
R, L тізбектің τ уақыт тұрақтылығы
токтың еркін құрастұрушысы ![]() азайғанға кететін
уақытқа тең, немесе тұрақты кернеуге
қосқанда сол уақытта қалыптасқан
мәнінің 63,2 % жетеді.
азайғанға кететін
уақытқа тең, немесе тұрақты кернеуге
қосқанда сол уақытта қалыптасқан
мәнінің 63,2 % жетеді.
Энергетика жағынан R, L тізбектегі қысқа тұйықталу процесі орауыштың магнит өрісіндегі коммутацияға дейін жиналған энергия R кедергіде жылуға айналады:
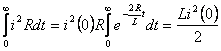 (қысқа тұйықталу
кезде).
(қысқа тұйықталу
кезде).
Іс жүзінде өтпелі процесс t = (4-5)τ уақыт өткенде бітті деп есептеуге болады.
Дәріс 2. R, L тізбектің қысқа тұйықталуы
Тұрақты немесе айнымалы кернеу көзіне қосылып тұрған R, L тізбек t = 0 кезде қысқа тұйықталып қалды. (2.3-сурет).

2.3сурет- R, L тізбектегі қысқа тұйықталу.
А- есептеу сүлбе; б-і токтың және UL кернеудің қисықтары.
Сол себептен құрылған, R және L контурда индуктивтік орауыштың ішінде магнит ағын болғандықтан ток лезде жоқ болып кетпейді: магнит ағынның азаюмен пайда болатын өздік индукцияның ЭҚК-і контурдағы токты магнит өрістің энергиясы есебімен қолдайды. Магнит өрістің энергиясы тарап R кедергіде жылулыққа айналады, ал контурдағы ток нөлге жақындайды, яғни іқ = 0.
(1.3) теңдеуде іқ = 0 деп алғанда, шығады:
![]() .
.
Интегралдаудың тұрақтысы басты жағдайдан табылады
і(0) = і(0-),
![]() .
.
Индуктивтегі кернеудің қисығы
![]() .
.
2.1. R, L тізбекке синусоидалды ЭҚК-ті қосу
R, L тізбекке синусоидалды ЭҚК е = Emsin(ωt + ψ) қосылғанда қалыптасқан ток болады
іқ =Imsin (ωt + ψ - φ),
мұнда 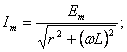
![]() .
.
![]() , мұнда
, мұнда ![]() .
.
Интегралдаудың тұрақтысы басты жағдай і(0) = і(0-) = 0 бойынша белгіленеді.
Сондықтан, 0 = Imsin (ψ - φ) + А, ал бұдан А = -Imsin (ψ - φ).
Өтпелі ток тізбекте
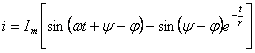 .
.

2.4 сурет- Қалыптасқан, еркін және өтпелі токтар R,
L тізбекті синусоидалды ЭҚк-ке қосқанда
2.5 R, С тізбектегі өтпелі процестер
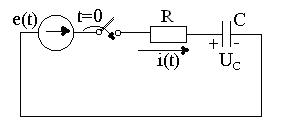
2.5 – сурет. R,С тізбекті электр көзіне қосу
t=0 уақыт кезде тізбектеп қосылған R кедіргімен С сыйымдылықтан құралған тізбекке ЭҚК е(t) қосылып тұр.
t ≥ 0 уақыт үшін дифференциалды теңдеу былай жазылады
е = Ri + Uc
мұнда Uc – сыйымдылықтағы кернеу.
![]() екенін есепке
алып, табамыз
екенін есепке
алып, табамыз
![]()
мұнда ізделіп жатқан шама-сыйымдылықтағы кернеу.
Сипаттамалы теңдеудің түрі 1+ RCP = 0, ал оған сәйкес теңдеудің түбірі
![]() .
.
Сыйымдылықтағы кернеудің еркін құрастырушысы
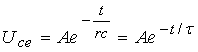
мұнда τ = RC - R,С контурдың уақыт тұрақтысы (секундамен өлшенеді):
[RC] = Oм∙Ф = Ом∙А∙с/В = С).
![]()
![]() - өшу коэффициенті.
- өшу коэффициенті.
Сыйымдылықтағы өтпелі кернеу Uc=Ucқ + Ае -t/t (2.4)
Контурдағы
ток ![]() =
= ![]() . (2.5)
. (2.5)
Үш жағдайды қарайық:
1) R, C тізбекке тұрақты ЭҚК Е қосу;
2) R, C тізбекте қысқа тұйықталу;
3) R, C тізбекке синусоидалды е = Еmsin (wt + ψ) қосу.
2.1 R, C тізбекке тұрақты ЭҚК-ті қосу.
R кедергісі және алдына ала зарядталған С сыйымдылығы бар тізбекке тұрақты ЭҚК-ті қосамыз. Зарядталған сыйымдылықтың полярлығы
2.5 суретте + және – таңбамен көрсетілген. Сыйымдылықтағы Uc(0) басты кернеуді U деп белгілейміз. Сыйымдылықта қалыптасқан кернеу көздің ЭҚК-іне тең, яғни U сқ=Е.
Сондықтан, (1.16) бойынша
U сқ = Е+Ае-t/t
Интегралдаудың тұрақтысы басты жағдайлардан табылады:
t=0 кезде U=E+A, ал бұдан A=U–E.
Олай болса, U с=E–(E–U)е-t/t (2.6)
(1.17) бойынша контурдағы ток
![]() (2.7)
(2.7)
Егер де Е > U болса уақыт озған сайын сыйымдылықтағы кернеу өседі (қалыптасқан Е мәніне дейін), ал ток азаяды (аяғында нөлге дейін). 2.6, а суретте U с өскенін және і азайғанның қисықтары көрсетілген.
Егер де Е < U болса, онда қисықтардың түрі 2.6, б суреттегідей болады.
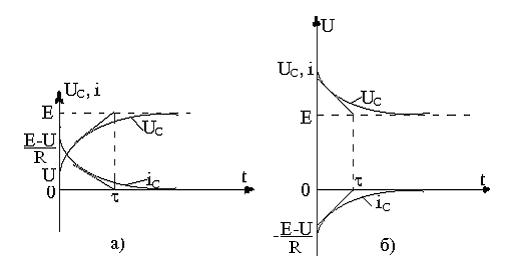
2.6 сурет-R, С тізбекке тұрақты ЭҚК-ті қосқанда ток және кернеу қисықтары.
2.3 R, C тізбекте қысқа тұйықталу
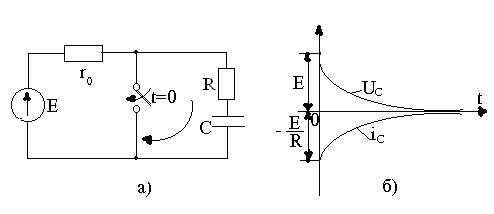
2.7сурет- R, C тізбектің қысқа тұйықталғаны.
а)- есептеу сүлбе; б)- кернеудің және тоқтың қисықтары.
Тұрақты
кернеу көзіне Е жалғанған тізбек ![]() кезде қысқа
тұйықталады (2.7, а-сурет). Сол себептен, R және С
элементтерден құралған контурда лезде
сыйымдылықтағы кернеу жоқ болып кетпейді: электр
ағынның энергия есебімен сыйымдылықтағы кернеудің
өзгеруі байсалды өтеді (2.7, б сурет). Контурдағы
қалыптасқан кернеу және ток нөлге тең болады.
(2.1) теңдеуде
кезде қысқа
тұйықталады (2.7, а-сурет). Сол себептен, R және С
элементтерден құралған контурда лезде
сыйымдылықтағы кернеу жоқ болып кетпейді: электр
ағынның энергия есебімен сыйымдылықтағы кернеудің
өзгеруі байсалды өтеді (2.7, б сурет). Контурдағы
қалыптасқан кернеу және ток нөлге тең болады.
(2.1) теңдеуде ![]() деп
алғанда, шығады
деп
алғанда, шығады
![]() .
.
Конденсатор Е кернеуге дейін қысқа тұйықталу алдында зарядталған. Интегралдаудың тұрақтысын басты жағдайлардан белгілейміз:
![]() кезде
кезде ![]() .
.
Сонымен, конденсатордағы
кернеу ![]() .
(2.7)
.
(2.7)
Ток ![]() .
(2.8)
.
(2.8)
R кедергіде өтпелі процесс кезде таратылатын энергия электр өрісте коммутацияға дейін жиналған энергияға тең:
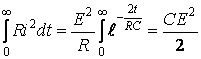 .
.
3. R,C тізбекті синусоидалды кернеуге қосу
Тізбек ![]() кернеуге
қосылады.
кернеуге
қосылады.
Сыйымдылықтағы қалыптасқан кернеу
![]()
мұнда ![]() .
.
Сыйымдылықтағы еркін кернеу
![]() .
.
Сыйымдылықтағы өтпелі кернеу
![]()
басты
жағдайдан шығады ![]() кезде
кезде ![]() .
.
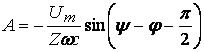 .
.
Сыйымдылықтағы кернеу өзгеруі
![]() (2.9)
(2.9)
Ток ![]() (2.10)
(2.10)
Дәріс 3. Тарамаған R, L,С тізбектегі өтпелі процестер
R, L, С тізбек осы ЭҚК-ке қосылғанда (3.10-сурет) өтпелі процес (1.3) дифференциалды теңдеу бойынша зерттеледі.
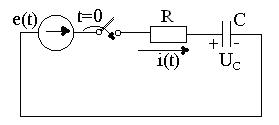
3.1сурет - R, L, С тізбекті е(t) кернеуге қосу
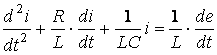 . (3.1)
. (3.1)
Бұған сәйкес сипаттамалы теңдеу
![]() .
.
Оның түбірлері
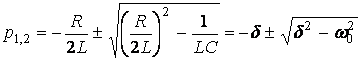 . (3.2)
. (3.2)
мұнда 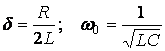 - резонансты жиілік
(2.9) бойынша
- резонансты жиілік
(2.9) бойынша ![]() .
.
Тізбектегі ток қалыптасқан және еркін токтардың қосындысы.
![]() (3.3)
(3.3)
Қалыптасқан тоқ берілген е(t) ЭҚК-ке сәйкес табылады, ал еркін токтың түрі (9.26) көріністік (түбір астындағы) таңбасына тәуелді.
3.1 R, L, С тізбекті тұрақты ЭҚК-ке қосу
Сыйымдылықтың
басты кернеуі ![]() .
.
Тізбекте
индуктивтік болғандықтан токтың басты мәні ![]() .
.
Бастапқы теңдеудің
![]()
коммутация басталған кезге түрі мынадай болады
![]() . (3.4)
. (3.4)
(9.28) теңдеуден табамыз
![]() (3.5)
(3.5)
![]() ток
тұрақталған ереже кезде нөлге тең; сол себептен
(9.27) теңдеуді дифференциалдаудан кейін шығады
ток
тұрақталған ереже кезде нөлге тең; сол себептен
(9.27) теңдеуді дифференциалдаудан кейін шығады
![]() (3.6)
(3.6)
(3.3) және (3.6) теңдеулерді және (3.5) пайдаланып t=0 уақыт үшін жазамыз:
0=A1+A2;
![]()
Бұл теңдеулерден шығады:
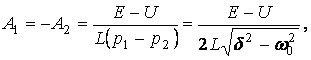 сондықтан
сондықтан
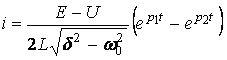 (3.7)
(3.7)
Мүмкін болатын үш жағдайды қарап шығамыз.
1
жағдай.
![]() , яғни
, яғни 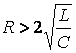 (апериодикалы процесс).
(3.2) бойынша сипатталы теңдеудің түбірлері
(апериодикалы процесс).
(3.2) бойынша сипатталы теңдеудің түбірлері ![]() және
және ![]() - теріс нақтылы
сандар.
- теріс нақтылы
сандар.
2
жағдай.
![]() , яғни
, яғни 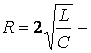 (9.26) бойынша
(9.26) бойынша ![]()
Бұл
жағдайда (8.31) теңдеу түрі ![]() белгісіздікке әкеледі.
белгісіздікке әкеледі.
Белгісіздікті Лопитальдің тәртібі бойынша ашқанда шығады:
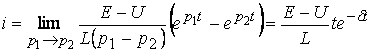 (3.8)
(3.8)
Тоқтың
қисығы 2.1 суреттегі ![]() қисығына сәйкес.
қисығына сәйкес.
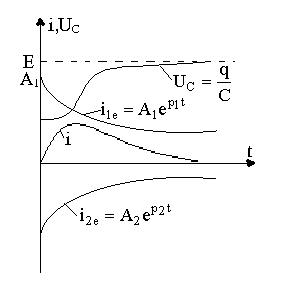
3.2 сурет- R, L, С тізбектегі апериодикалы процесс.

3.3 сурет- Сипаттамалы теңдеудің түбірлерінің комплексті жазықтықта орналасуы.
3
жағдай.
![]() , яғни
, яғни ![]() (тербелену процесс).
(тербелену процесс).
Сипаттамалы теңдеудің түбірлері комплексті және ілестіру:
![]() , (3.9)
, (3.9)
мұнда ![]() (3.10)
(3.10)
Сипаттамалы теңдеудің
түбірлері нақтылы білікке симетриялы сол жартылай
жазықтықта жартылай шеңбердің үстінде орналасады.
Шеңбердің орталығы координат басында, ал радиус тең 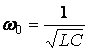 . (9.10, в сурет).
. (9.10, в сурет).
Тізбектегі ток 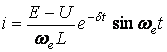 .
.
Сонымен, R, L, С
тізбектегі тұрақты кернеуге қосқанда, егер де ![]() болса тізбекте
сөнетін синусоидалды тербелену пайда болады. Тоқтың
қисығын оралып өтетін қисықтар
болса тізбекте
сөнетін синусоидалды тербелену пайда болады. Тоқтың
қисығын оралып өтетін қисықтар 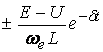 (3.4 – сурет).
Тербелену пайда болу себеп – электр өрістің энергиясын магнит
өрістің энергиясына периодты түрлендіру және кері
өтетін процесс, бұл тербеленулер кедергіде энергия
шығындармен өтеді, яғни тербелену өшеді.
(3.4 – сурет).
Тербелену пайда болу себеп – электр өрістің энергиясын магнит
өрістің энергиясына периодты түрлендіру және кері
өтетін процесс, бұл тербеленулер кедергіде энергия
шығындармен өтеді, яғни тербелену өшеді.
![]() шама (3.4, в сурет)
R, L, С тізбектегі еркін немесе өздік тербеленудің
бұрыштық жиілігі деп, ал
шама (3.4, в сурет)
R, L, С тізбектегі еркін немесе өздік тербеленудің
бұрыштық жиілігі деп, ал 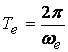 - бұл тербеленудердің периоды
деп атайды.
- бұл тербеленудердің периоды
деп атайды.
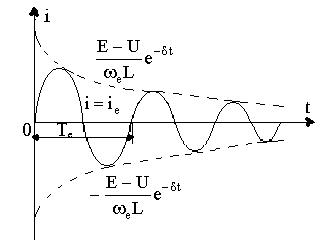
3.4 сурет- R, L, С тізбектегі тұрақты ЭҚК-ке қосқанда тербелену процесс.
3.3, а,б,в – сурет көрсетіп тұр - R, L, С тізбектегі өтпелі процестің түрі тұралы сипаттамалы теңдеудің түбірлерінің орналасуын, яғни Z(р) функцияның комплексті жазықтықта нөлдер бойынша айтуға болады.
Егерде сол жақтағы жартылай жазықтықта орналасқан Z(р) функцияның нөлдері нақтылы білікте жатса, онда апериодикалық процесс болады, нөлдер бір нүктеде болса – аумалы жағдай, егер де Z(р) функцияның нөлдері комплексті ілестіру болса, онда тербелену процесі болады.
![]() болғанда оралып
өтетін қисықтың ординатасы 2,72 есе басты мәнінен
аз болады. Сондықтан
болғанда оралып
өтетін қисықтың ординатасы 2,72 есе басты мәнінен
аз болады. Сондықтан ![]() шаманы тербелену контурдың
уақыт тұрақтысы деп атайды.
шаманы тербелену контурдың
уақыт тұрақтысы деп атайды.
3.2 Тармақталған тізбекте өтпелі процесті есептеу
Тармақталған сызықты тізбекте өтпелі процесс тұрақты коэффициенттері бар сызықты дифференциалды теңдеулер жүйесімен бейнеленеді. Жалпы шешу қалыптасқан және еркін құрастырушылардың қосындысы деп табылады.
Көбінесе
әсер ететін функция, мысалы көздің ЭҚК-і
қорытынды түрде ![]() көрсетіледі, мұнда
көрсетіледі, мұнда ![]() - комплексті сан.
- комплексті сан.
Егер де ![]() болса, онда ЭҚК
гармоникалы болады.
болса, онда ЭҚК
гармоникалы болады.
Егер де ![]() болса, онда
көрсеткіш функция болады; с = 0 кезде ЭҚК
тұрақты болады (9.12 сурет).
болса, онда
көрсеткіш функция болады; с = 0 кезде ЭҚК
тұрақты болады (9.12 сурет).
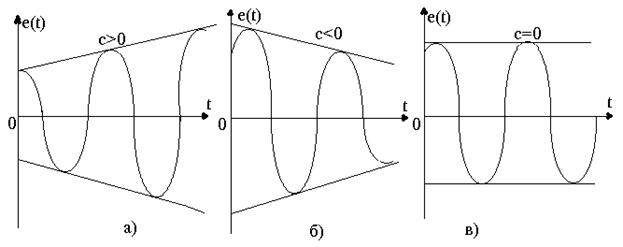
3.5 сурет - Өсетін (а), азайатын (б) және тұрақты (в) амплитудалары бар синусоидалар.
Тармақтардағы токтарды өтпелі процесс кезінде табу үшін (ЭҚК Е және параметрлер R, L, С белгілі кезде) комплексті түрде коммутация алдында және коммутациядан кейін қалыптасқан токтың құрыстырушысын табудан бастаймыз.
Еркін токтарды және кернеулерді белгілеуді тізбектің сипаттамалы теңдеуін құрудан бастаймыз.
Ол үшін 3.6 суреттегі сүлбені қараймыз. Қосқыш Қ тұйықталған кезде еркін құрастырушылардың лезді мәндеріне контурлық токтар әдісімен теңдеулерді жазамыз:
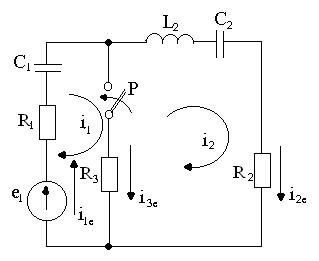
3.6 сурет

R11, R22,
L22, C11, C22 – контурлардың
кедергілері, сыйымдылықтары және индуктивтіктері, ал ![]() - екі көршілес
контурлардың жалпы кедергісі деп белгілейміз, онда
- екі көршілес
контурлардың жалпы кедергісі деп белгілейміз, онда
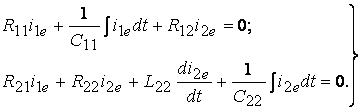 (3.11)
(3.11)
(9.36) теңдеу жүйенің шешуі мынадай болады:
![]() .
.
Онда ![]() ;
;
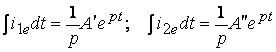 .
.
Туындылардың және интегралдардың мәндерін (9.36) теңдеулерге қойып, табамыз:
 (3.12)
(3.12)
(3.11)
дифференциалды теңдеулер ![]() және
және ![]() функциялар үшін сол
функциялардың (3.12) алгебралық функцияларға айналды.
Мұндай түрлендіру алгебраизация деп аталады.
функциялар үшін сол
функциялардың (3.12) алгебралық функцияларға айналды.
Мұндай түрлендіру алгебраизация деп аталады.
Табылған екі
біртекті екі белгісіз ![]() және
және ![]() токтары бар теңдеулер жүйесі
нөлдік шешімнен бөлек, тек егерде жүйенің
анықтаушы нөлге тең болса, болады:
токтары бар теңдеулер жүйесі
нөлдік шешімнен бөлек, тек егерде жүйенің
анықтаушы нөлге тең болса, болады:
 (3.13)
(3.13)
(3.13)
шығады – р теңдеу ![]() -дің түбірі, ал
-дің түбірі, ал ![]() теңдеу
дифференциалды теңдеулер үшін сипаттамалы теңдеу.
теңдеу
дифференциалды теңдеулер үшін сипаттамалы теңдеу.
Қандайда болған тармақ үшін, мысалы бірінші тармақ үшін, р-ға тәуелді кіріс кедергіні жазайық:
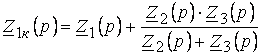 . (3.14)
. (3.14)
Егерде (3.14) ![]() нөлге тең
деп аталсақ, онда бірден сипаттамалы теңдеу шығады.
нөлге тең
деп аталсақ, онда бірден сипаттамалы теңдеу шығады.
Жүйенің сипаттамалы теңдеуінің түбірлерін тапқаннан кейін әрбір контурлық ток үшін жалпы түрін жазамыз.
Бірнеше жағдай болуы мүмкін:
а) ![]() және
және ![]() түбірлер – затты
және әртүрлі:
түбірлер – затты
және әртүрлі:
![]()
б) ![]() және
және ![]() түбірлер – затты
және бірдей, яғни
түбірлер – затты
және бірдей, яғни ![]() :
:
![]()
в) ![]() түбір-затты,
түбір-затты, ![]() және
және ![]() түбірлер –
комплексті және ілесу, яғни
түбірлер –
комплексті және ілесу, яғни ![]()
![]()
Сипаттамалы теңдеудің түбірлерінің түрін есептеу тәртібі тәуелсіз болғандықтан бірінші жағдайды қарайық.
Бірінші тармақтағы өтпелі токтың көрінісін жазайық:
![]() , ал содан (3.15)
, ал содан (3.15)
кейін А1,
А2 және А3 интегралдардың
тұрақтылары белгілейміз. Ол үшін (3.15) екі рет
дифференциалдаймыз және ![]() (9.40) теңдеуге және
табылған дифференциалды көріністерге қоямыз
(9.40) теңдеуге және
табылған дифференциалды көріністерге қоямыз
 (3.16)
(3.16)
Қалыптасқан
ток ![]() және
оның туындылары
және
оның туындылары ![]() кезде және түбірлер
кезде және түбірлер ![]() белгілі
болғандықтан (9.41) теңдеуден
белгілі
болғандықтан (9.41) теңдеуден ![]() табуға болады, егерде
табуға болады, егерде ![]() ток және
оның туындылары
ток және
оның туындылары ![]() кезде белгілі болса.
кезде белгілі болса.
![]() және
және ![]() табу үшін
тармақтардағы токтар үшін Кирхгофтың бірінші және
екінші заңдарды жазамыз:
табу үшін
тармақтардағы токтар үшін Кирхгофтың бірінші және
екінші заңдарды жазамыз:
![]() (3.17)
(3.17)
![]() мұнда
мұнда ![]() (3.18)
(3.18)
![]() , мұнда
, мұнда ![]() (3.19)
(3.19)
Коммутация
заңдары бойынша индуктивтік бар тармақтарда ток және
сыйымдылықтардың кернеулері коммутация басталған кезде (![]() ) ырғақты
өзгермейді. Ондай болса, (3.17)- (3.18.) жүйеде
) ырғақты
өзгермейді. Ондай болса, (3.17)- (3.18.) жүйеде ![]() кезде
кезде ![]() ,
, ![]() және
және ![]() белгілі. Онда (3.17), (3.18)
теңдеулерден
белгілі. Онда (3.17), (3.18)
теңдеулерден ![]() және
және
![]() табамыз.
табамыз.
Содан кейін (3.17) және (3.18) теңдеулерді дифференциалдаймыз, ал (3.19) теңдеуді қайта жазамыз:
![]() (3.20)
(3.20)
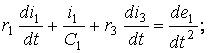 (3.21)
(3.21)
![]() (3.22)
(3.22)
(3.20)-(3.22)
теңдеулердің жүйесін ![]() кезде қарап, барлық
токтардың басты мәндері және
кезде қарап, барлық
токтардың басты мәндері және ![]() белгілі екенін еске алып, (3.22)
теңдеуден
белгілі екенін еске алып, (3.22)
теңдеуден ![]() ,
ал (9.45) және (9.46) теңдеулерден
,
ал (9.45) және (9.46) теңдеулерден ![]() және
және ![]() табамыз.
табамыз.
Бұл жүйені тағы да дифференциялдап, табамыз:
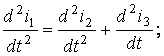 (3.23)
(3.23)
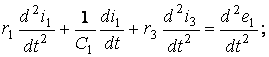 (3.24)
(3.24)
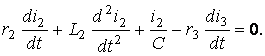 (3.25)
(3.25)
(3.23)-(3.25)
теңдеулердің жүйесін ![]() кезде қарап, барлық
токтардың басты мәндері және
кезде қарап, барлық
токтардың басты мәндері және ![]() белгілі екенін еске алып, (3.22)
теңдеуден
белгілі екенін еске алып, (3.22)
теңдеуден ![]() ,
ал (3.20) және (3.21) теңдеулерден
,
ал (3.20) және (3.21) теңдеулерден ![]() және
және ![]() табамыз.
табамыз.
Енді (3.15) жүйеден А1, А2 және А3 интегралдаудың тұрақтыларын табуға болады.
Сонымен, классикалық әдіспен өтпелі процесті есептеу келесі тәртіп бойынша өткізіледі:
1)
Коммутацияның алдындағы ереже есептеліп, онда ырғақты
өзгермейтін функциялардың (индуктивтегі токтар және
сыйымдылықтағы кернеулер) соңғы мәндері
(яғни ![]() -
кездегі) белгіленеді. Содан кейін, коммутацияның заңдарын
қолданып, тәуелсіз басты жағдайлар, яғни
-
кездегі) белгіленеді. Содан кейін, коммутацияның заңдарын
қолданып, тәуелсіз басты жағдайлар, яғни ![]() және
және ![]() табылады.
табылады.
2)Тізбектегі коммутациядан кейінгі процесті бейнелейтін Кирхгоф заңдары бойынша жазылған дифференциалды теңдеулер жүйесі құрылады.
3) Біртекті дифференциалды теңдеулердің жалпы шешімі табылады.
4) Біртекті емес дифференциалды теңдеулердің жеке шешімі табылады.
5)1 пунктте
табылған тәуелсіз басты жағдайлар және 2 пунктте ![]() кез үшін
қолданған Кирхгофтың теңдеулері бойынша тәуелді
басты жағдайлар белгіленеді.
кез үшін
қолданған Кирхгофтың теңдеулері бойынша тәуелді
басты жағдайлар белгіленеді.
6) Жалпы шешімде болатын интегралдаудың тұрақтыларын басты жағдайлар бойынша белгіленеді.
7) Табылған қалыптасқан және еркін токтар және кернеулер қосылады.
Дәріс 4
Мысал - Тізбектегі
ажыратқыш ажырағаннан кейін ![]() және
және ![]() токтарды табу керек.
токтарды табу керек.
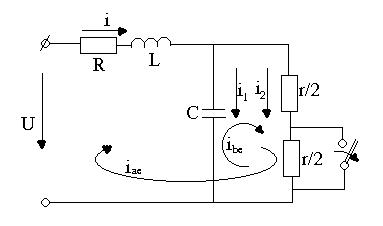
Берілгені:
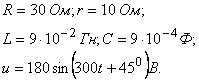
Шешуі
1 Индуктивтіктегі токты және кернеуді коммутация алдында қалыптасқан ережеде табамыз.
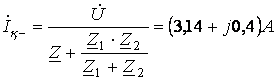 .
.
мұнда
![]()
![]()
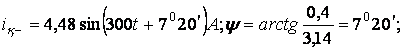
![]()
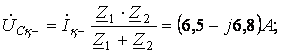
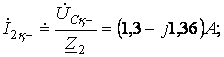
![]()
![]() .
.
2 Қалыптасқан токтарды коммутациядан кейін табамыз.
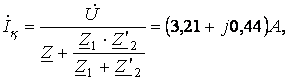 мұнда
мұнда ![]() ;
;
![]()
![]()
![]()
Өтпелі токтарды есептеуге кірісеміз.
Еркін контурлық токтар үшін кернеулерді құрамыз
![]()
![]()
Бұл дифференциалды теңдеулердің алгебраизациясын өткізіп табамыз:
![]()
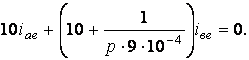
Сипаттамалы теңдеуді құру үшін бұл біртекті алгебралық теңдеулердің анықтауышын нөлге теңдейміз:
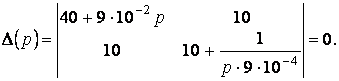
Бұдан
шығады ![]()
Оның
түбірлері ![]()
![]()
Коммутация кезде ![]() индуктивтіктегі ток
ырғақты өзгермейді
индуктивтіктегі ток
ырғақты өзгермейді
![]() бұдан А1=-0,044 A.
бұдан А1=-0,044 A.
![]() кезде
конденсатордағы кернеу
кезде
конденсатордағы кернеу ![]() ырғақты өзгермейді, ал
сол себептен индуктивтегі
ырғақты өзгермейді, ал
сол себептен индуктивтегі ![]() кернеуде ырғақты
өзгермейді, ал бұл жағдай
кернеуде ырғақты
өзгермейді, ал бұл жағдай 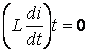 табуға рұқсат етеді
табуға рұқсат етеді
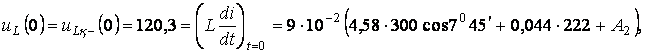 ал бұдан
ал бұдан ![]()
Біржолата ток ![]() үшін.
үшін.
![]()
Сұлбаның сыртқы контуры үшін Кирхгофтың екінші заңы бойынша еркін токтар үшін теңдеуді құрамыз:
![]() , бұдан
шығады
, бұдан
шығады
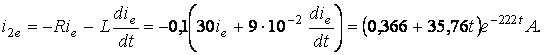
Онда ![]() , ал токтар
, ал токтар
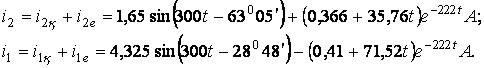
5 Дәріс. Өтпелі процестерді операторлық әдіспен есептеу
5.1 Лапластың түрлендіруін өтпелі процестерді есептеуге қолдану
Өтпелі процестерді классикалық әдіспен есептеу басты жағдай бойынша интегралдаудың тұрақтыларын белгілеу және басты функцияларды және олардың туындыларын табу үшін алгебралық теңдеулердің жүйесін дүркін-дүркін шешуді талап етеді. Бұл жағдай осы әдіспен есептеудің негізгі қиыншылығына жатады. Электр сүлбелер қүрделендірілген сайын және дифференциялды теңдеудің дәрежесі өскен сайын бұл қиыншылықтарда өседі.
Сондықтан, тапсырылған басты жағдайлар бастапқы теңдеулерге кіргізіліп сызықты дифференциалды теңдеулерді шешу әдісті пайдалану қолайлы болады, өйткені бұл әдісте керекті функцияларды табу үшін интегралдаудың тұрақтыларын белгілеудің қажеттігі жоқ болады.
Сызықты дифференциалды теңдеулерді Лапластың түрлендірулерге негізделген операторлық әдіспен интегралдауға болады.
Операторлық
әдістің маңызы – түпнұсқа деп аталатын
кейбір тапсырылған бір қатарлы шектелген заттың
айнымалының ![]() функциясына
басқа бейнесі деп аталатын
функциясына
басқа бейнесі деп аталатын ![]() комплексті айнымалының
комплексті айнымалының ![]() функциясы
салыстырылады. Функция
функциясы
салыстырылады. Функция ![]() әрбір ақырғы уақыт
аралықта Дирихле жағдайын қамтамасыз ету керек және
әрбір ақырғы уақыт
аралықта Дирихле жағдайын қамтамасыз ету керек және ![]() кезде нөлге
тең болу керек.
кезде нөлге
тең болу керек.
Салыстыру мына формула бойынша өткізіледі
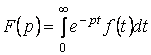 (5.1)
(5.1)
(5.1) кейіптеме - ![]() функцияның
үстінен Лапластың тікелей түрлендіруін көрсетеді.
функцияның
үстінен Лапластың тікелей түрлендіруін көрсетеді.
Оны былай белгілейді:
![]() немесе
немесе ![]() , мұнда
, мұнда ![]() -
- ![]() функцияның
Лапластық бейнесі. Кері, егерде
функцияның
Лапластық бейнесі. Кері, егерде ![]() бейнесі бойынша
бейнесі бойынша ![]() түпнұсқаны
табу керек болса, онда Лапластың кері түрлендіруі қолданады
түпнұсқаны
табу керек болса, онда Лапластың кері түрлендіруі қолданады
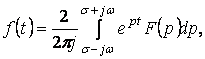 (5.2)
(5.2)
яғни (10.1)
интегралды теңдеуді ![]() функцияға қатысты
шешу.
функцияға қатысты
шешу.
(10.2) интегралды былай белгілеуге болады:
![]() немесе
немесе ![]() .
.
Түпнұсқадан туындылардың және интегралдардың бейнелері үшін кейіптемелерін (шығарусыз) келтірейік:
Егер де ![]() болса, онда (5.3)
болса, онда (5.3)
![]() (5.4)
(5.4)
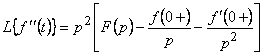 және т.с.с. (5.5)
және т.с.с. (5.5)
Егер де ![]() функция
және оның туындылары
функция
және оның туындылары ![]()
![]() кезде кенет өзгерсе, онда
(9.4) және (9.5) кейіптемелерге олардың мәнін осы кенет
өзгерісті есепке алып қою керек, яғни нөлдің
оң жағында, бұл жағдай олардың аргументтерінде 0+
белгімен көрсетілген. Егер де
кезде кенет өзгерсе, онда
(9.4) және (9.5) кейіптемелерге олардың мәнін осы кенет
өзгерісті есепке алып қою керек, яғни нөлдің
оң жағында, бұл жағдай олардың аргументтерінде 0+
белгімен көрсетілген. Егер де ![]() кезде функцияның және
оның туындыларының басты мәндері нөлге тең болса,
онда бірінші және одан соңғы туындылардың бейнелері
өте жеңіл табылады:
кезде функцияның және
оның туындыларының басты мәндері нөлге тең болса,
онда бірінші және одан соңғы туындылардың бейнелері
өте жеңіл табылады:
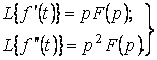 және т.с.с. (5.6)
және т.с.с. (5.6)
Тұп нұсқаның интегралдық бейнелерінің түрі:
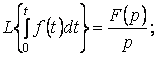 (5.7)
(5.7)
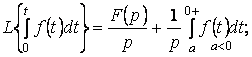 (5.8)
(5.8)
Егерде интеграл 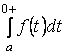
![]() кезде кенет өзгерсе, онда
оның мәнін нөлдік оң жағынан алу керек, бұл
жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
кезде кенет өзгерсе, онда
оның мәнін нөлдік оң жағынан алу керек, бұл
жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
5.2 Жіктеудің теоремасы
Бейне 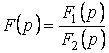 (5.9) дұрыс
бөлшек түрде берілсін, алымның және
бөлгіштің жалпы түбірлері жоқ.
(5.9) дұрыс
бөлшек түрде берілсін, алымның және
бөлгіштің жалпы түбірлері жоқ. ![]() функцияның
полюстерінің орыны
функцияның
полюстерінің орыны ![]() (10.10) теңдеудің
түбірлерімен белгіленеді. (5.10) теңдеудің
(10.10) теңдеудің
түбірлерімен белгіленеді. (5.10) теңдеудің ![]() түбірлерін
түбірлерін ![]() деп белгілейміз.
деп белгілейміз.
Екі жағдай болуы мүмкін: а) барлық түбірлер жай; б) кейбір немесе барлық түбірлер еселі.
а) жай түбірлердің жағдайы
Өте жай жағдайда бейне радионалды бөлшек түрінде болады:
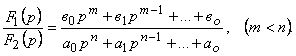 (5.11)
(5.11)
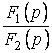 бөлшек
қысқарылмайды, яғни
бөлшек
қысқарылмайды, яғни ![]() және
және ![]() мүшелердің жалпы
түбірлері жоқ, ал
мүшелердің жалпы
түбірлері жоқ, ал ![]() және
және ![]() - заттық сандар. (5.11)
бейненің түпнұсқасын жікте теормасы деп
аталатын кейіптеме бойынша табуға болады:
- заттық сандар. (5.11)
бейненің түпнұсқасын жікте теормасы деп
аталатын кейіптеме бойынша табуға болады:
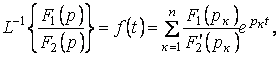 (5.12)
(5.12)
Мұнда pк
сипаттамалы теңдеудің, яғни ![]() теңдеудің жай
түбірлері, бір түбір нөлге тең болуы мүмкін.
теңдеудің жай
түбірлері, бір түбір нөлге тең болуы мүмкін.
Егер де бір түбір нөлге тең болса, яғни бөлгіш ішінде (5.11) р көбейткіш бар болса, онда жіктеу теореманың басқа түрі қолданады.
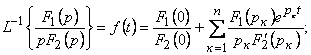 (10.13)
(10.13)
б) еселі түбірлердің жағдайы
Егер де көп
мүшелі ![]() түбірлерінің
ішінде еселі түбірлер болса, онда жіктеу теореманы (5.12) және (5.13)
формулаға ұқсасты жасауға болады, бірақ оң
жағында қосындымен (бір қосынды түбірлер саны бойынша,
ал екінші әрбір түбір үшін оның еселік реттігімен).
түбірлерінің
ішінде еселі түбірлер болса, онда жіктеу теореманы (5.12) және (5.13)
формулаға ұқсасты жасауға болады, бірақ оң
жағында қосындымен (бір қосынды түбірлер саны бойынша,
ал екінші әрбір түбір үшін оның еселік реттігімен).
Сонымен, ![]() теңдеуде еселі
түбірлер болса, онда
теңдеуде еселі
түбірлер болса, онда 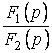 кесінді бойынша тұп
нұсқау мына формула бойынша есептеледі:
кесінді бойынша тұп
нұсқау мына формула бойынша есептеледі:
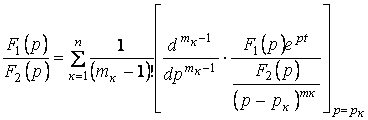 (5.14)
(5.14)
Шаршы
жақшаның бөлгішіндегі көріністі алдымен ![]() шамаға
қысқартып, содан кейін дифференциялдау керек.
шамаға
қысқартып, содан кейін дифференциялдау керек.
Егер де ![]() теңдеуде бір
мезгілде жай және еселі түбірлер болса, онда жай түбірлерге
сәйкесті қосындыларды (5.12) және (5.13) формулалар, ал еселі
түбірлер үшін (5.14) формула қолданады.
теңдеуде бір
мезгілде жай және еселі түбірлер болса, онда жай түбірлерге
сәйкесті қосындыларды (5.12) және (5.13) формулалар, ал еселі
түбірлер үшін (5.14) формула қолданады.
5.3 Операторлық түрдегі Ом және Кирхгофтың заңдары
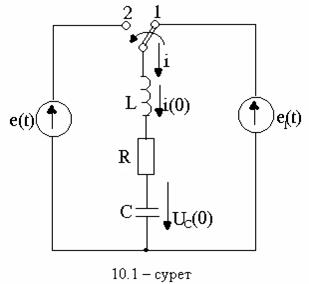 5.1 суреттегі
R, L, C тізбек
5.1 суреттегі
R, L, C тізбек ![]() ЭҚК-ке
қосылып тұрған, ал
ЭҚК-ке
қосылып тұрған, ал ![]() уақыт мезгілде
уақыт мезгілде ![]() ЭҚК-ке ауысып
қосылады.
ЭҚК-ке ауысып
қосылады.
Ауысып қосылғаннан кейін Кирхгофтың екінші заңы лезді мәндер үшін былай жазылады.
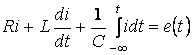 (5.15)
(5.15)
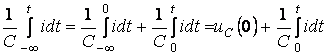 . (5.16)
. (5.16)
мұнда ![]() - сыйымдылықта
ауысып қосу кездегі кернеу, яғни
- сыйымдылықта
ауысып қосу кездегі кернеу, яғни ![]() кезде.
кезде.
Лезді мәндер
үшін жазылған түпнұсқасынан оның
операторлық түрде жазылған бейнесіне өту үшін (5.1)
кейіптемеге сәйкес былай істеледі: (5.15) теңдіктің екі
жағын ![]() шамаға
көбейтіп, нөлден шексіздікке дейін интегралдау керек. Онда
шығады:
шамаға
көбейтіп, нөлден шексіздікке дейін интегралдау керек. Онда
шығады:
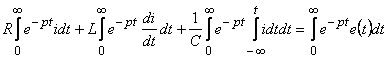 .
.
![]() деп есептеп
және (5.4), (5.7), (5.16) кейіптемелерді есепке алып, шығарамыз:
деп есептеп
және (5.4), (5.7), (5.16) кейіптемелерді есепке алып, шығарамыз:
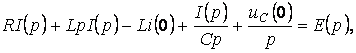 ал бұл
теңдеуден R, L, C тізбек үшін операторлық түрде
Омның заңы шығады
ал бұл
теңдеуден R, L, C тізбек үшін операторлық түрде
Омның заңы шығады
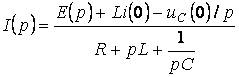 (5.17)
(5.17)
Бөлгіште
тұрған көрініс операторлық кедергі деп аталады 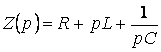 . (5.18)
. (5.18)
Операторлық
кедергіге кері шама операторлық өткізгіш деп аталады 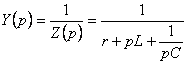 . (5.19)
. (5.19)
Басты
жағдайлар нөлге тең болса, яғни ![]() және
және ![]() болса, онда (5.17)
көрініс:
болса, онда (5.17)
көрініс:
 (5.20)
(5.20)
яғни комплексті түрдегі Ом заңына толық ұқсас.
Тармақталған тізбектің әрбір түйіні үшін
![]() .
.
Сондықтан
токтың кесіндісін ![]() белгілеп Кирхгофтың бірінші
заңын операторлық түрде жазамыз:
белгілеп Кирхгофтың бірінші
заңын операторлық түрде жазамыз:
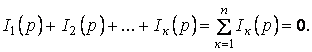 (5.21)
(5.21)
![]() тармақтан
құралған әрбір тұйықталған контур
үшін
тармақтан
құралған әрбір тұйықталған контур
үшін
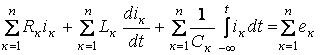 .
.
![]() деп есептеп,
Кирхгофтың екінші заңы операторлық түрде жазылады:
деп есептеп,
Кирхгофтың екінші заңы операторлық түрде жазылады:
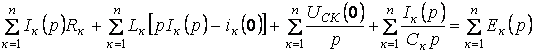 , ал бұны былай
жазуға болады:
, ал бұны былай
жазуға болады:
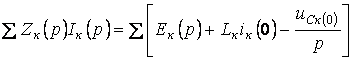 , (5.22)
, (5.22)
Былай
жазылған түрде ![]() және
және ![]() - индуктивтік орауыштардағы
токтың және конденсаторларды кернеудің басты мәндері.
- индуктивтік орауыштардағы
токтың және конденсаторларды кернеудің басты мәндері.
Егер де басты жағдайлар нөлге тең болса, онда Кирхгофтың екінші заңы былай жазылады:
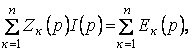 (5.23)
яғни бұл жағдайда ол Кирхгофтың екінші
заңы комплексті түрде жазылғанға толық
ұқсас.
(5.23)
яғни бұл жағдайда ол Кирхгофтың екінші
заңы комплексті түрде жазылғанға толық
ұқсас.
Сонымен Омның және Кирхгофтың заңдары операторлық түрде өздерінің жазылу түрі бойынша синусоидалды ток тізбегі үшін сол заңдардың комплексті түрде жазылғанға ұқсас.
Бірақ есте
ұстау керек, бірінші – басты жағдайлар нөлге тең
болмағанда, яғни ![]() және
және ![]() болғанда әрбір к
тармақта сыртқы ЭҚК
болғанда әрбір к
тармақта сыртқы ЭҚК ![]() -дан басқа ішкі ЭҚК-тер
-дан басқа ішкі ЭҚК-тер ![]() және
және ![]() әсер етеді.
(олардың болымды бағыттары сол тармақтағы токтың
болымды бағытына сәйкес), екінші – тармақтың кедергісі
ретінде операторлық кедергі алынады.
әсер етеді.
(олардың болымды бағыттары сол тармақтағы токтың
болымды бағытына сәйкес), екінші – тармақтың кедергісі
ретінде операторлық кедергі алынады.
6 Дәріс. Баламалы операторлық сүлбелер
Операторлық әдіспен өтпелі процесті есептеген кезде берілген тізбек үшін баламалы операторлық сүлбені құру пайдалы болады.
Басты жағдайлар нөлге тең болмағанда баламалы операторлық сүлбені құруды 6.1 суретте келтірілген сүлбені қарайық.
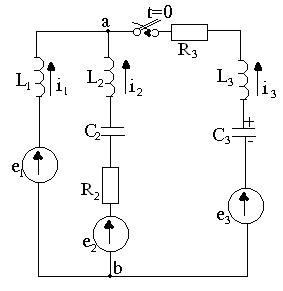
6.1 сурет-Тізбектің электр сұлбасы
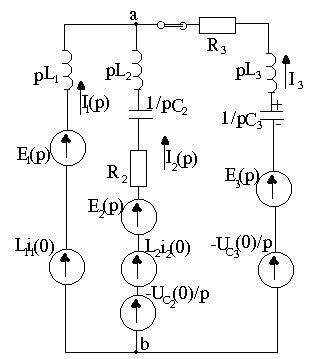
6.2 сурет -Тізбектің баламалы операторлық сұлбасы
Кирхгофтың заңдарын операторлық түрде жазамыз:
![]()
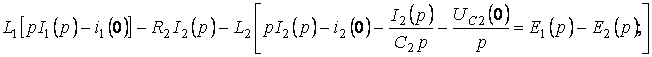
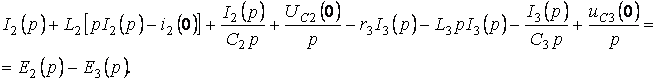
Қайтадан мына түрде жазамыз:
![]()

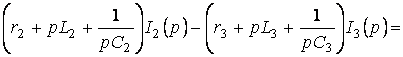
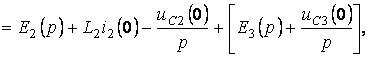 бұл теңдеулер
бойынша 6.1 суретте келтірілген балама операторлық сүлбені
құрамыз.
бұл теңдеулер
бойынша 6.1 суретте келтірілген балама операторлық сүлбені
құрамыз.
Тізбектерді есептеу әдістердің токпен кернеудің кесінділерін есептеу үшін (6.1 сурет) контурлық тоқ, түйінді потенциалдар ж.т.б. әдістерді қолдануға болады.
6.2 Пассивтік екіұштықты үздіксіз өзгеріп тұрған кернеу көзіне қосу (Дюамельдін интегралы)
Мейлі еркінше
пассивтік сызықты екіұштық ![]() уақыттан бастап үздіксіз
өзгеріп тұрған кернеу көзіне қосылсын (6.2 сурет).
Екі ұштықтың қандайда болған тармағында
кілт тұйықталғанда ток
уақыттан бастап үздіксіз
өзгеріп тұрған кернеу көзіне қосылсын (6.2 сурет).
Екі ұштықтың қандайда болған тармағында
кілт тұйықталғанда ток ![]() -ді (немесе
-ді (немесе ![]() -ды) табу керек.
-ды) табу керек.
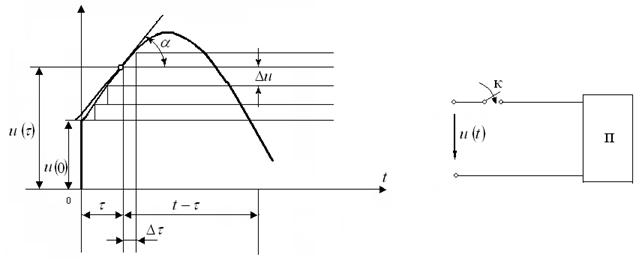
6.2 Сурет
Есепті екі кезеңге бөлеміз. Алдымен керекті шаманы екіұштықты жекелеген кернеудің ырғағына қосқан кезде табамыз (кернеу тұрақты және сан бойынша бірге тең).
Жекелеген ырғақ (жекелеген сатылы әсер ету) жекелеген сатылы функциямен беріледі –6.3-суреттегі бейнеленген 1(t) Хевисайдтың функциясымен.
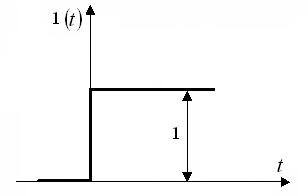
6.3 Сурет
Электр тізбектер
теориясының көзқарасы бойынша тізбектің кірісінде
әрекет істейтін жекелеген тұрақты кернеу (немесе ток) ![]() + уақыт кезінде.
+ уақыт кезінде.
Сонымен ![]() кезінде;
кезінде;
![]() кезінде. (6.3.)
кезінде. (6.3.)
Жекелеген ырғақ
әсер еткендегі сан бойынша ізделіп отырған токқа (немесе
кернеуге) тең ![]() функция
өтпелі функция деп аталады. Бұл тізбектің жекелеген
ырғаққа әсерлістігі.
функция
өтпелі функция деп аталады. Бұл тізбектің жекелеген
ырғаққа әсерлістігі.
Мысалы, R, L –
тізбек үшін кернеудің өтпелі функциясы ![]() ал RC-тізбек үшін
кернеудің өтпелі функциясы
ал RC-тізбек үшін
кернеудің өтпелі функциясы ![]()
Өтпелі
функцияны, қандайда болған екіұштықтық
сүлбесі болғанда, классикалық немесе операторлық
әдіспен табуға болады. Сонымен, есептеу кезде ![]() функция белгілі деп санаймыз.
функция белгілі деп санаймыз.
Пассивтік
екіұштық қосылып тұрғандықтан ![]() кезде токтар
және кернеулер тармақтарда нөлге тең, яғни t<0
кезде
кезде токтар
және кернеулер тармақтарда нөлге тең, яғни t<0
кезде ![]() .
.
Тоқты есептеу жағдайын қарап шығайық.
Үздіксіз
өзгеріп тұрған ![]() кернеуді
кернеуді ![]() тура бұрышты ырғақтары
бар сатылы функциямен алмастырамыз (6.4 сурет).
тура бұрышты ырғақтары
бар сатылы функциямен алмастырамыз (6.4 сурет).
Онда кернеу
өзгерудің процесін ![]() кезде
кезде ![]() тұрақты кернеуді қосу
деп, ал содан кейін бірбірінен
тұрақты кернеуді қосу
деп, ал содан кейін бірбірінен ![]() уақыт аралыққа
ығысқан
уақыт аралыққа
ығысқан ![]() элементарлы
тұрақты кернеулердің қосылуы деп көрсетуге
болады. Кернеудің қисығына өскенде + таңба, ал
төмендегенде – таңба қойылады.
элементарлы
тұрақты кернеулердің қосылуы деп көрсетуге
болады. Кернеудің қисығына өскенде + таңба, ал
төмендегенде – таңба қойылады.
Ізделіп
жатқан токтың ![]() тұрақты кернеуден t
уақыт кездегі құрастырушысы
тұрақты кернеуден t
уақыт кездегі құрастырушысы ![]() тең. Токтың
құрастырушысы t уақыт кезде
тең. Токтың
құрастырушысы t уақыт кезде ![]() уақыт кезде қосылатын
уақыт кезде қосылатын ![]() ырғақты
кернеуге тең
ырғақты
кернеуге тең ![]() .
Мұнда өтпелі функцияның аргументі ретінде уақыт
.
Мұнда өтпелі функцияның аргументі ретінде уақыт ![]() алынады. Оған
себеп болатыны -
алынады. Оған
себеп болатыны - ![]() кернеудің
ырғағының әрекеті кілт тұйықталғаннан
кейін
кернеудің
ырғағының әрекеті кілт тұйықталғаннан
кейін ![]() уақыт
өткенде басталады.
уақыт
өткенде басталады.
Кернеудің элементарлы ырғағы
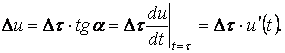
Сондықтан токтың ізделіп жатқан құрастырушысы
![]() (6.4)
(6.4)
Кернеудің
элементарлы ырғақтары ![]() -ден t кездегі уақыт аралықта
қосылады. Сондықтан, барлық ырғақтардан
токтың құрастырушыларын жинақтап,
-ден t кездегі уақыт аралықта
қосылады. Сондықтан, барлық ырғақтардан
токтың құрастырушыларын жинақтап, ![]() кезде шекке өтіп және
кезде шекке өтіп және
![]() басты
кернеудің ырғағынан токтың құрастырушысын
есепке алып табамыз.
басты
кернеудің ырғағынан токтың құрастырушысын
есепке алып табамыз.
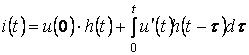 (6.5)
(6.5)
(6.5) кейіптеме Дюамельдің интегралы деп аталады.
7 Дәріс
7.1 Пассивтік екіұштықты еркінше түрі бар кернеу көзіне қосу
Кернеудің еркінше түрі-кесекті-аналитикалық функциясымен белгіленетін кернеудін өзгеруін айтады.
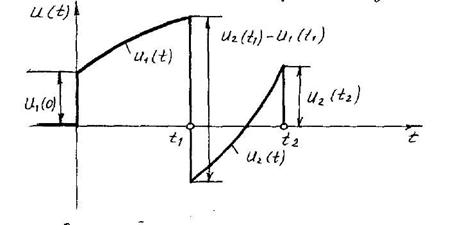
7.4 Сурет
Пассивтік екіұштық, өзгеру қисығы 7.4 суретте берілген, кернеу көзіне қосылады.
Токты белгілеу үшін жоғарыдай h(t) – өтпелі функцияны белгілейміз.
Қосылатын
кернеу 0<t<t1 аралықта ![]() функциямен берілген
болғандықтан (6.5) кейтемені пайдаланып бұл уақыт
аралыққа жазуға болады
функциямен берілген
болғандықтан (6.5) кейтемені пайдаланып бұл уақыт
аралыққа жазуға болады
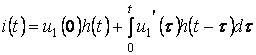 . (7.1)
. (7.1)
Келесі уақыт
аралықта (t1<t<t2) кернеу басқа ![]() функциямен беріледі.
Бұл кернеу t1 мезгілде
функциямен беріледі.
Бұл кернеу t1 мезгілде ![]() мәнінен
мәнінен ![]() мәніне дейін
ырғақты өзгереді. Кернеудің ырғағын есепке
алу үшін t=t1 нүктеде екіұштыққа кері
тұрақты кернеу
мәніне дейін
ырғақты өзгереді. Кернеудің ырғағын есепке
алу үшін t=t1 нүктеде екіұштыққа кері
тұрақты кернеу ![]() бұл мезгілде ынта салынып тұр
деп санайық. Онан басқа, кернеудің бастапқы
ырғағынан
бұл мезгілде ынта салынып тұр
деп санайық. Онан басқа, кернеудің бастапқы
ырғағынан ![]() және кернеудің элементарлы
ырғақтарынан токтардың құрастырушыларын есепке
алып, нәтижесінде табамыз
және кернеудің элементарлы
ырғақтарынан токтардың құрастырушыларын есепке
алып, нәтижесінде табамыз
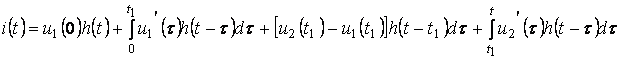
(7.2)
Аяғында, t2<t<![]() уақыт
аралық үшін t=t2 мезгілде -
уақыт
аралық үшін t=t2 мезгілде - ![]() тұрақты кернеу
қосылғанды және
тұрақты кернеу
қосылғанды және ![]() кернеу қисығымен белгіленетін
элементарлы ырғақтар t=t2 уақыт мезгілге дейін
әрекет ететінін есепке алып, табамыз
кернеу қисығымен белгіленетін
элементарлы ырғақтар t=t2 уақыт мезгілге дейін
әрекет ететінін есепке алып, табамыз
 (7.3)
(7.3)
8 Дәріс. Параметрлері таратылған тізбектер
8.1 Ұзын желілердегі токтар және кернеулер
Электр энергетикада үлкен кернеулер кезінде және электр байланыста үлкен жиіліктер кезінде, сонымен бірге электр жеткізу желінің ұзындығы үлкен болғанда ығысу және кему токтармен елемеуге болмайды.
Сымдарғы токтар кедергілерде кернеу түсуді құрады және айнымалы магнит өрісті құрады. Бұл өріс барлық желінің бойында өздік электр қозғаушы күшті өндейді. Сондықтан, сымдарының арасындағы кернеуде тұрақты болып қалмайды.
Желіні бойлай токтың және кернеудің өзгеруін есептеу үшін желінің әрбір қандай да болған кішкентай элементтің кедергісі және индуктивтігі, ал сымдар арасында - өткізштік және сыйымдылығы бар, яғни желіні параметрлері таратылған тізбек деп қарау керек. Мұндай желі ұзын желі деп аталады.
Кедергі, индуктивтік, өткізгіштік және сыйымдылық желінің ұзындығы бойынша біркелкі таратылған деп есептейміз. Мұндай желіні біртекті деп атайды.
8.2 Біртекті екі сымды желінің теңдеулері
Екі сымды желінің кез келген кескіндісінде токтарға және кернеулерге сәйкесті дифференциалды теңдеулерді құрамыз.
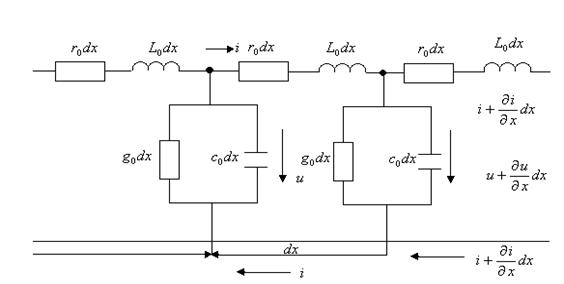
8.1 Сурет
Жоғары сым
тура сым, төменгі сым кері сым деп аталады. Біртекті желінің
оның ұзындық бірлігіне жататын біріншілік параметрлері
белгілі болсын: ![]() -
тура және кері сымдардың кедергілері
-
тура және кері сымдардың кедергілері ![]() ;
; ![]() -тура және кері сымдармен
құрылатын ілмектің индуктивтігі
-тура және кері сымдармен
құрылатын ілмектің индуктивтігі ![]() ;
; ![]() - сымдар арасындағы сыйымдылық
- сымдар арасындағы сыйымдылық
![]() .
.
Ұзын желіні
өте көп ұзындығы ![]() тең элементтердің тізбекті
қосылған түрінде көрсетуге болады. Әрбір
элементтің
тең элементтердің тізбекті
қосылған түрінде көрсетуге болады. Әрбір
элементтің ![]() кедергісі,
кедергісі,
![]() индуктивтігі,
индуктивтігі,
![]() өткізгіштігі
және
өткізгіштігі
және ![]() сыйымдылығы
бар (8.1сурет).
сыйымдылығы
бар (8.1сурет).
Желінің
басынан элементке дейін аралықты ![]() деп белгілейміз. Кирхгофтың
заңдары бойынша
деп белгілейміз. Кирхгофтың
заңдары бойынша ![]() ұзындығы бар элемент
үшін жазамыз:
ұзындығы бар элемент
үшін жазамыз:
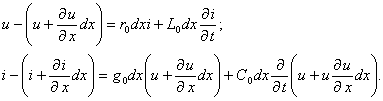
Екіншілік
дәрежелі шамаларды еске алмай және ![]() қысқартып дифферинциалды
теңдеулерді табамыз:
қысқартып дифферинциалды
теңдеулерді табамыз:
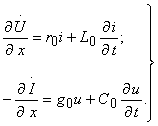 (8.1)
(8.1)
(8.2)
Белгілі басты және шекаралық жағдайлар кезде теңдеулердің жүйесін шешу токты және кернеуді желінің ұзындығының және уақыттың функциялары ретінде белгілеуге рұқсат береді.
8.3 Біртекті желідегі қалыптасқан ереже
(8.1) және (8.2) теңдеулерді қалыптасқан ереже жасап және комплексті токтарды, кернеулерді, кедергілерді және өткізгіштерді кіргізіп табамыз
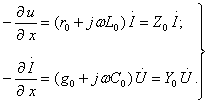 (8.3)
(8.3)
(8.4)
мұндағы
![]() және
және ![]() -
ұзындықтың бірлігінде комплекстік кедергі және
комплекстік өткізгіштік. (8.3) және (8.4) теңдеулерді
дифференциялаймыз:
-
ұзындықтың бірлігінде комплекстік кедергі және
комплекстік өткізгіштік. (8.3) және (8.4) теңдеулерді
дифференциялаймыз:
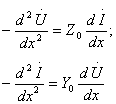 ал содан кейін
ал содан кейін ![]() және
және ![]() (8.3) және (8.4) бойынша
алмастырып табамыз:
(8.3) және (8.4) бойынша
алмастырып табамыз:
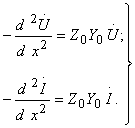
(8.5)
(8.6)
(8.5)- тұрақты коэффициенттері бар екінші дәрежелі сызықты дифференциалды теңдеу. Оның шешуі мына түрде болады:
![]() , (8.7)
, (8.7)
мұндағы
![]() , (8.8)
, (8.8)

![]() -интегралдаудың
комплексті тұрақтылары. (8.3) бойынша ток
-интегралдаудың
комплексті тұрақтылары. (8.3) бойынша ток ![]() тең
тең
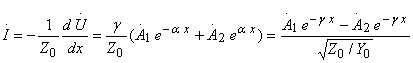 . (8.9)
. (8.9)
Өлшемі
кедергіге тең (8.9) теңдеудің бөлгіші ![]() толқынды кедергі
деп аталады. Біртекті желі үшін (төртұштық үшін)
толқынды кедергі сипаттамалы кедергімен дәл түседі.
толқынды кедергі
деп аталады. Біртекті желі үшін (төртұштық үшін)
толқынды кедергі сипаттамалы кедергімен дәл түседі.
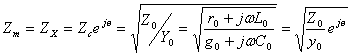 , (8.10)
, (8.10)
мұндағы
![]() .
(8.11)
.
(8.11)
Толқынды
кедергі ![]() және
тарату коэффициент
және
тарату коэффициент ![]() біртекті
желінің екіншілік параметрлері деп аталады.
біртекті
желінің екіншілік параметрлері деп аталады. ![]() (13.9) теңдеуге қойып
жазамыз:
(13.9) теңдеуге қойып
жазамыз:
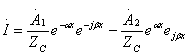 .
(8.12)
.
(8.12)
![]() (өлшемдері –
кернеу) көрсеткіш түрде көрсетіп
(өлшемдері –
кернеу) көрсеткіш түрде көрсетіп ![]() , кернеулерді және токтардың
лезді мәндерін жазамыз:
, кернеулерді және токтардың
лезді мәндерін жазамыз:
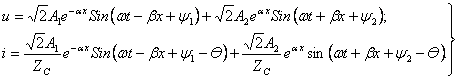
(8.13)
(8.14)
Теңдеулердің
оқ жағындағы әрбір қосындыны координата х
өсу және кему бағытына қарай жүгіріп бара
жатқан толқын деп қарауға болады. Бұл
толқындар қозғалыстың бағытына қарай
сөнеді. Әрбір қосында қандай да болған бекітілген
![]() нүктеде
периодикалы синусоидалы уақыт функциясы болады, ал бекітілген
нүктеде
периодикалы синусоидалы уақыт функциясы болады, ал бекітілген ![]() уақыт мезгілде
бұл қосындылар сөніп бара жатқан желі бойындағы
тербелену болады (яғни х өзгерген кезде).
уақыт мезгілде
бұл қосындылар сөніп бара жатқан желі бойындағы
тербелену болады (яғни х өзгерген кезде).
Жүгіріп бара жатқан толқынның негізгі сипаттамалары фазалық жылдамдық және толқынның ұзындығы.
Толқынның
![]() фазалық
жылдамдығы деп тербеленудің фазасының ауыспалалық
жылдамдығы аталады. Бұл жылдамдық уақыт өзгерген
кезде және х аралық өскен кезде тұрақты болып
қалады, яғни
фазалық
жылдамдығы деп тербеленудің фазасының ауыспалалық
жылдамдығы аталады. Бұл жылдамдық уақыт өзгерген
кезде және х аралық өскен кезде тұрақты болып
қалады, яғни
![]() ал бұдан
шығады
ал бұдан
шығады
![]() және
және ![]() .
(8.15)
.
(8.15)
(8.13) теңдеудің оң жағындағы екінші қосындыны зерттегенде фазалық жылдамдықтың мәні сол сияқты бірақ таңбасы кері болады. Бұдан шығады- қосындылар қарама-қарсы бағыттарда қозғалып бара жатқан толқындар.
Толқынның
ұзындығы ![]() деп
тербелену фазалары
деп
тербелену фазалары ![]() -ге
айырылатын толқынның таралу бағытына қарай
алынған екі ең жақын жатқан нүктелердің
арасындағы аралық.
-ге
айырылатын толқынның таралу бағытына қарай
алынған екі ең жақын жатқан нүктелердің
арасындағы аралық.
![]() .
.
Бұдан
шығады ![]() және
және
![]() ,
(8.16)
,
(8.16)
Яғни период Т тең уақытта толқын толқынның ұзындығына тең аралықты жүгіріп өтеді.
Желінің басынан қозғалап келе жатқан толқынды тура, ал аяғынан қозғалып келе жатқан толқынды кері деп атайды.
8.1 суретте тура сөніп бара жатқан толқын көрсетілген
![]() (8.17)
(8.17)
мұндағы
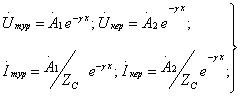 (8.18)
(8.19)
(8.18)
(8.19)
Тура және кері толқындардың токтарымен кернеулері Ом
заңымен байланысқан
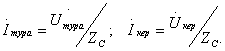 (8.20)
(8.20)
Табылған
нәтижелер үш фазалы желілерге де қолданылады. Бұл
жағдайда U және I – фазалық кернеу және ток, ал ![]() және
және ![]() бір фазаға
жатады.
бір фазаға
жатады.
Мысал. Үш
фазалы электр жеткізу желінің ұзындығы ![]() , кернеуі
, кернеуі ![]() , жиілігі
, жиілігі ![]() . Біріншілік
параметрлердің келесі шамалары бар:
. Біріншілік
параметрлердің келесі шамалары бар:![]() .
.
Екіншілік параметрлерді, толқынның ұзындығы және фазалық жылдамдықты белгілеу керек.
1 шқ. комплекстік кедергі және өткізгіштік:
![]() ;
;
![]() .
.
Жиілік сипаттамалары:

9 Дәріс
9.1 Гиперболикалық функцияларда біртекті желінің теңдеулері
![]() және
және ![]() тұрақтыларын
білу үшін шекаралық жағдайлар белгілі болу керек.
тұрақтыларын
білу үшін шекаралық жағдайлар белгілі болу керек.
Желінің
басында ![]()
![]() кернеу және
кернеу және ![]() ток берілген болсын.
(8.7) және (8.12) теңдеулерден
ток берілген болсын.
(8.7) және (8.12) теңдеулерден ![]() кезде шығады:
кезде шығады:
![]() , ал бұдан
, ал бұдан
 (9.1)
(9.1)
(8.7) және
(8.12) теңдеулерге ![]() және
және ![]() мәндері қойып желінің
қандай да болған нүктесінде (желінің басынан Х
аралықта)
мәндері қойып желінің
қандай да болған нүктесінде (желінің басынан Х
аралықта) ![]() кернеу
және
кернеу
және ![]() үшін
табамыз:
үшін
табамыз:

Оң
жақтағы мүшелерді топтастарып және ![]() пен
пен ![]() гиперболикалық
функцияларды кіргізіп табамыз:
гиперболикалық
функцияларды кіргізіп табамыз:
![]()
 (9.2)
(9.2)
Бұл теңдеулер желінің басындағы шамалары бойынша желінің қандай да болған нүктесіндегі кернеумен токты белгілеуге рұқсат етеді.
Енді
желінің аяғындағы ![]() кернеу және
кернеу және ![]() ток берілген болсын, ал
бұл жағдайда жүктеменің кедергісі
ток берілген болсын, ал
бұл жағдайда жүктеменің кедергісі 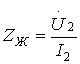 белгілі болады.
белгілі болады.
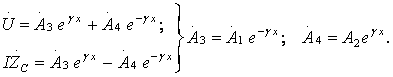 (9.3)
(9.3)
(9.3)
ден ![]() кезде
табамыз:
кезде
табамыз:
![]() , ал
бұдан шығады
, ал
бұдан шығады
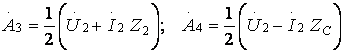 (9.4)
(9.4)
(9.4) ті (9.3) –ге
қойып, мүшелерді топтастырып және ![]() пен
пен ![]() гиперболикалық
функцияларды кіргізіп табамыз:
гиперболикалық
функцияларды кіргізіп табамыз:
 (9.5)
(9.5)
Тұрақты
ток желілер үшін ![]() :
:
![]() (9.6)
(9.6)
 (9.7)
(9.7)
8.2 мысал 8.1 мысалдың нәтижелері бойынша белгілеу керек:
1 желінің аяғында токты;
2 желінің басындағы кернеуді және токты;
3 желінің басында және аяғында кернеумен токтың арасындағы фазалық ығысуды;
4 желінің ПӘК-тің, егер де желінің аяғында белгілі:
![]()
1
Желінің аяғындағы ток ![]()
![]()
2
Комплекстік ауыспалыдан ![]() гиперболикалық функциялардың
мәндерін кестеден немесе калькулятор арқылы табамыз
гиперболикалық функциялардың
мәндерін кестеден немесе калькулятор арқылы табамыз

Желің
басындағы ток кернеуден ![]() бұрышқа озады.
бұрышқа озады.
3
![]() тең
болғандықтан желінің басымен аяғындағы кернеулер
арасындағы фазалық ығысу
тең
болғандықтан желінің басымен аяғындағы кернеулер
арасындағы фазалық ығысу ![]() тең.
тең.
4 Желіге берілетін активтік қуат
![]()
5 Желінің ПӘК-і
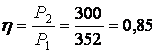 .
.
9.2 Біртекті желінің сипаттамалары
Әлсірету коэффициенті
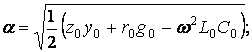 (9.8)
(9.8)
Фазалық коэффициент
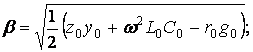 (9.9)
(9.9)
![]() орташа мәні:
орташа мәні:
1.
ауа желілер үшін ![]() ;
;
2.
кәбілдер үшін ![]() .
.
9.1
– суретте (8.11) және (8.11) бойынша салынған ![]() және Ө үшін
жиілік сипаттамалар көрсетілген
және Ө үшін
жиілік сипаттамалар көрсетілген
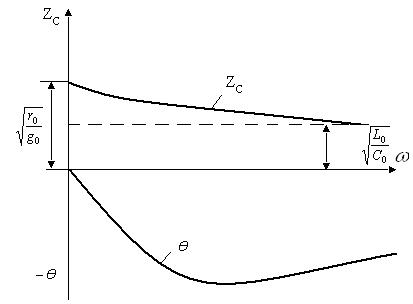
9.1 Сурет
![]() кезінде
кезінде 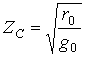 (9.10)
(9.10)
![]() кезінде
кезінде
 (9.11)
(9.11)
Ө
нөлге тең ![]() және
және ![]() кезінде.
кезінде.
![]() (9.12)
(9.12)
мұндағы
![]() -вакуумдағы
жарықтықтың жылдамдығы,
-вакуумдағы
жарықтықтың жылдамдығы, ![]() және
және ![]() -сымды коршайтын кеңістіктің
диэлектрик және магниттік тұрақтылары.
-сымды коршайтын кеңістіктің
диэлектрик және магниттік тұрақтылары.
Ауа
желілер үшін ![]() және
және
![]() толқындардың
жылдамдағы с тең, ал кәбілді желілерде
толқындардың жылдамдығы С –ден 2-2,5 есе төмен.
толқындардың
жылдамдағы с тең, ал кәбілді желілерде
толқындардың жылдамдығы С –ден 2-2,5 есе төмен.
АЭЖ
–лерде ![]() кезінде
толқынның ұзындығы
кезінде
толқынның ұзындығы
![]()
9.2 Желінің кіріс кедергісі және толқынның шағылу коэффициенті
Желінің Zкір кіріс кедергісі ретінде желінің басындағы ережені есептеу кезінде желінің оның аяғында жүктемемен бірге екіұштықтың кедергісімен алмастыруыды ұғады, яғни
 (9.13)
(9.13)
Қандай
да болған ![]() жүктеме
кедергісі кезінде кіріс кедергіні бос жүріс кездегі
жүктеме
кедергісі кезінде кіріс кедергіні бос жүріс кездегі ![]() және қысқа тұйықтау
кездесі
және қысқа тұйықтау
кездесі ![]() кедергілер
арқылы көрсетуге болады
кедергілер
арқылы көрсетуге болады
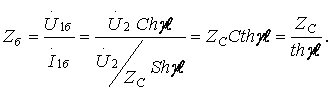 (9.14)
(9.14)
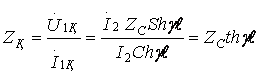 (9.15)
(9.15)
(9.13)
теңдеудің оң жағының алымын және
бөлгішін ![]() бөліп
(9.14) және (9.15) есепке алып, табамыз
бөліп
(9.14) және (9.15) есепке алып, табамыз
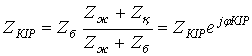 (9.16)
(9.16)
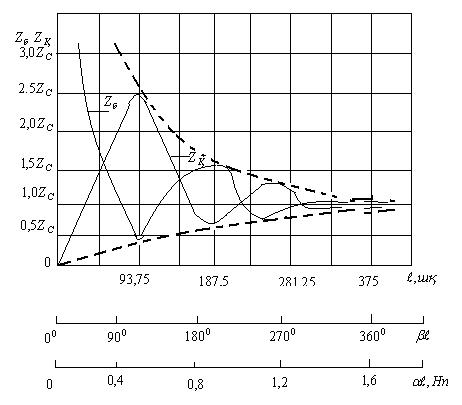
9.2 Сурет
![]() және
және ![]() желінің бос
жүріс және қысқа тұйықталу
тәжірібелер арқылы табылады.
желінің бос
жүріс және қысқа тұйықталу
тәжірібелер арқылы табылады. ![]() және
және ![]() желінің ұзындағы
өзгерген кезде толқында өзгереді (9.2-сурет).
желінің ұзындағы
өзгерген кезде толқында өзгереді (9.2-сурет).
![]() және
және ![]() арқылы
арқылы ![]() және
және ![]() жеңіл табылады.
жеңіл табылады.
(9.14) және (9.15) теңдеулері бір-біріне көбейтіп, содан кейін мүшелер бойынша бөліп және түбір астынан шығарып, табамыз
 (9.16)
(9.16)
Желінің
аяғындағы ![]() жүктеменің кедергісі еркінше
болса
жүктеменің кедергісі еркінше
болса ![]() болады,
яғни желіде кері толқын пайдалы болады.
болады,
яғни желіде кері толқын пайдалы болады.
Бұл
жағдайда комплекстік шағылу коэффициенті арқылы есепке
алуға болады. Комплекстік шағылу коэффициент ![]() - желінің қандай да
болған нүктесіндегі кері және тура толқындардың
комплексті кернеулермен токтардың өзара қатынасы:
- желінің қандай да
болған нүктесіндегі кері және тура толқындардың
комплексті кернеулермен токтардың өзара қатынасы:
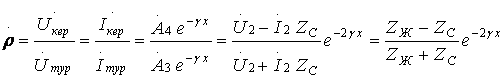 (9.17)
(9.17)
Кері толқын жоқ кезде желінің аяғына тура толқынмен жеткізілетін барлық қуат жүктемеде сіңіріледі. Кері толқын бар кезде тура толқынның қуат бөлігі кері толқынмен энергия көзіне қайтарылады.
9.3 Желінің келіскен жүктемесі
Егер
де желінің аяғында толқынды кедергіге тең
жүктеменің кедергісі қосылған болса, яғни 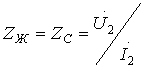 , онда
, онда 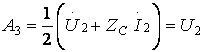 және
және  болады да, кері
толқын тумайды. Мұндай жүктемені келіскен деп атайды.
Бұл жағдайда шағылу коэффициенті
болады да, кері
толқын тумайды. Мұндай жүктемені келіскен деп атайды.
Бұл жағдайда шағылу коэффициенті ![]() .
.
![]() (9.18)
(9.18)
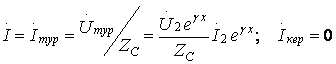 (9.19)
(9.19)
Бұдан
шығады 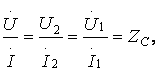
яғни
желінің қандай да болған нүктесі үшін ![]() және
және ![]() комплекстердің
қатынасы
комплекстердің
қатынасы ![]() толқынды
кедергіге тең.
толқынды
кедергіге тең.
(9.13)
теңдеуден шығады: келіскен желі үшін ![]() =
=![]() .
.
Желінің
аяғындағы кернеудің басты фазасы нөлге тең деп
алсақ, яғни ![]() тең деп, (9.18) және (9.19)
негізінде желінің қандай да болған нүктесінде кернеумен
токтың лезді мәндерін жазамыз:
тең деп, (9.18) және (9.19)
негізінде желінің қандай да болған нүктесінде кернеумен
токтың лезді мәндерін жазамыз:
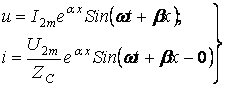 (9.20)
(9.20)
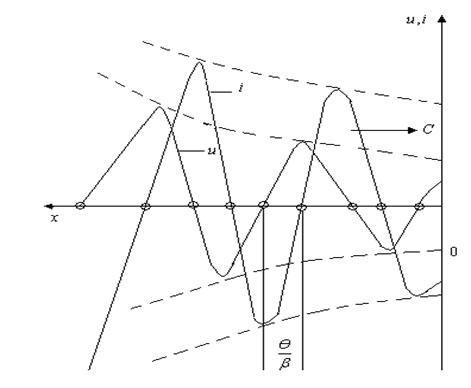
9.3 сурет
Ток
кернеудің ![]() бұрышқа
озады.
бұрышқа
озады.
Желінің қандай да болған кесіндісіндегі қуат
![]() (9.21)
(9.21)
Келіскен желіден берілетін қуат табиғи немесе натуралды деп аталады.
500, 220, 110 және 35 кВ кернеуі бар желілер үшін табиғи қуат 600, 120, 30 және 3 МВт тең.
Желінің
алатын қуаты ![]() ,
желінің аяғындағы қуат
,
желінің аяғындағы қуат ![]()
![]() (9.22)
(9.22)
Желінің ПӘК-і
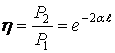 (9.23)
(9.23)
Желінің басынан алыстанған сайын қуат азайды.
Қуат шығындары сымдағы кедергілердегі және оқшаулардың өткізгіштеріндегі шығындардың қосындысына тең.
9.4 Бұрмалауы жоқ желі
Байланыс желісімен берілетін дабылдар әртүрлі жиіліктердің көпшіліктің жиынтығы: егер де синусоидалды периодикалы дабылдар болса, үзінді ал периодикалы емес дабыл болса, үзілмес спектр құрылады.
Егер де желінің басымен аяғындағы дабылдың түрі бірдей болса, онда дабыл берілісі бұрмаланған емес болады.
Бұл
жағдай ![]() әлсіреу
коэффициент және
әлсіреу
коэффициент және ![]() фазалық жылдамдық бірліқ
жиіліктерінде бірдей болса тұрады.
фазалық жылдамдық бірліқ
жиіліктерінде бірдей болса тұрады.
Әртүрлі жиіліктердегі бірдей сөну емес амплитудалық бұрмалауды, толқындардың әртүрлі жиіліктерде жылдамдықтарының бірдей емес болуы фазалық бұрмалауды тудырады.
Бұрмаланған
емес беріліс үшін ![]() жиіліктен тәуелсіз, ал
жиіліктен тәуелсіз, ал ![]() жиілікке тура
пропоционалды болуы керек. Ақырғы жағдайда фазалық
жылдамдық
жиілікке тура
пропоционалды болуы керек. Ақырғы жағдайда фазалық
жылдамдық ![]() жиілікке
тәуелді болмайды. Мұндай жағдайда мынадай теңдік
орындалса болады
жиілікке
тәуелді болмайды. Мұндай жағдайда мынадай теңдік
орындалса болады
![]() (9.24)
(9.24)
Тарату
коэффициенті ![]() тең:
тең:
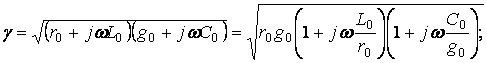
(9.24) есепке алып, табамыз
![]() (9.25)
(9.25)
яғни
әлсірету коэффициент ![]() -жиіліктен тәуелсіз, ал
фазалық коэффициент
-жиіліктен тәуелсіз, ал
фазалық коэффициент ![]() -жиілікке тура пропорционалды.
-жиілікке тура пропорционалды.
Параметрлері (9.24) теңдеуді қанағат ететін желіні бұрмалауы жоқ желі деп атайды.
Бұрмалауы жоқ желінің толқынды кедергісі – нақтылы сан, яғни жиіліктен тәуелсіз активтік кедергі
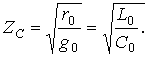 (9.26)
(9.26)
Фазалық жылдамдықта жиіліктен тәуелсіз
![]()
![]() . (9.27)
. (9.27)
Желінің
толқынды кедергісі активтік болғандықтан ![]() .
.
Кернеулердің және токтардың лезді мәндерінің желінің қатынасы болған нүктелерінде тең:
 , ал
бұдан шығады
, ал
бұдан шығады  . (9.28)
. (9.28)
Сондықтан келіскен жүктемесі бар бұрмалауы жоқ желінің қандай да болған бөлігінде әрбір уақытта магнит өрістің энергиясы электр өрістің энергиясына тең.
(9.24) жағдай орындау үшін желіге белгілі аралық сайын жасанды индуктивтікті үлкейту үшін индуктивтік орауыштарды қосу керек немесе өткізгіш талсымдары жоғары магниттік өтімділігі бар заттардан жасалған кәбілдерді қолдану керек.
10 Дәріс
10.1 Шығындары жоқ желі
Желіде
энергия шығындарын азайту үшін активтік кедергі ![]() және
оқшалаудың өткізгіштігі
және
оқшалаудың өткізгіштігі ![]() неғұрлым аз болуы керек.
неғұрлым аз болуы керек.
Ауалық
желілерде индуктивтік кедергі ![]() активтік кедергіден
активтік кедергіден ![]() үлкен болады, ал
сыйымдылық өткізгішті
үлкен болады, ал
сыйымдылық өткізгішті ![]() активтік өткізгіштен
активтік өткізгіштен ![]() үлкен болады.
Жиілік өскен кезде бұл айырмашылық одан әрі
өседі.
үлкен болады.
Жиілік өскен кезде бұл айырмашылық одан әрі
өседі.
Активтік
кедергісі ![]() және
активтік өткізгіштігі
және
активтік өткізгіштігі ![]() нөлге тең деп алынатын
желілер шығындары жоқ желі деп аталады.
нөлге тең деп алынатын
желілер шығындары жоқ желі деп аталады.
Бұл жағдайда желінің екіншілік параметрлерінің түрі:
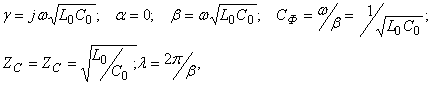
яғни шығыны жоқ желіде толқындар әлсіремейді, толқынды кедергі активтік, ал фазалық жылдамдық жиілікке тәуелді емес.
Екі
сымды желінің ұзындық бірлігінің сыйымдылығы, ![]() :
:
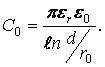 (10.1)
(10.1)
Сол
желінің ұзындық бірлігінің индуктивтігі, ![]() :
:
![]() (10.2)
(10.2)
мұндағы
![]() -
сымның радиусы, d- сымдардың біліктерінің арасындағы
аралық.
-
сымның радиусы, d- сымдардың біліктерінің арасындағы
аралық.
![]() және
және ![]() мәндері
мәндері ![]() қойып, табамыз
қойып, табамыз
![]() (10.3)
(10.3)
мұндағы
![]() және
және ![]() -сымдар
арасындағы ортаның абсолюттік диэлектрикалық және
магниттік өтімділіктері.
-сымдар
арасындағы ортаның абсолюттік диэлектрикалық және
магниттік өтімділіктері.
Вакуумда жарықтық жылдамдығы
![]() (10.4)
(10.4)
онда фазалық жылдамдық үшін жазуға болады
![]() .
(10.5)
.
(10.5)
Толқынды кедергінің аргументі Ө нөлге тең, яғни тура және кері толқынды токтар кернеулермен дәл түседі.
Шығындары жоқ желінің комплекстік аргументтінен гиперболикалық функциялар ұзын желінің теңдеулері нақтылы аргументтен айналма функциялар теңдеулерге көшеді.
Егер
де желінің басындағы кернеу ![]() және ток
және ток ![]() берілсе, онда
берілсе, онда
 (10.6)
(10.6)
Егер
де желінің аяғындағы кернеу ![]() және ток
және ток ![]() берілсе, онда
берілсе, онда
 (10.7)
(10.7)
Желінің кіріс кедергісі
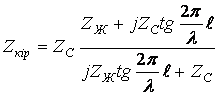 (10.8)
(10.8)
![]() және
және ![]() кезінде лезді
мәндерге өтетін болсақ
кезінде лезді
мәндерге өтетін болсақ  (10.9)
(10.9)
![]() және
және ![]() кезінде, шығады
кезінде, шығады
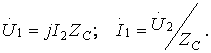 (10.10)
(10.10)
![]() және
және ![]() кезінде,
шығады
кезінде,
шығады
![]() (10.11)
(10.11)
10.2 Тұйық толқындар
Шығыны жоқ желінің аяғында бос жүріс, қысқа тұйықталу кезінде және таза реактивтік жүктеме кезінде активтік қуат нөлге тең болады.
1
Бос жүріс ереже 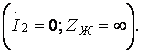
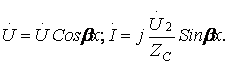 (10.12)
(10.12)
![]() кезінде
кернеудің және токтың лезді мәндері тең
кезінде
кернеудің және токтың лезді мәндері тең
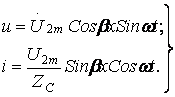 (10.13)
(10.13)
Бұл тұйық толқындардың теңдеулері
Тұйық толқынның теңдеуінің біреуі уақыттан, екіншісі координатадан тәуелді екі функцияның көбейтіндісі.
Тұйық толқын деп амплитудалары бірдей тура және кері толқындардың бір-біріне салу процесін атайды.
Шынында,
![]() және
және ![]()
Кернеуді амплитудалары бірдей тура және кері толқындардың кернеулерінің қосындасы, токтарды-айырма түрінде көрсетуге болады.
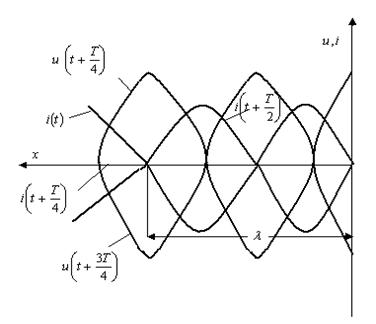
10.1Сурет
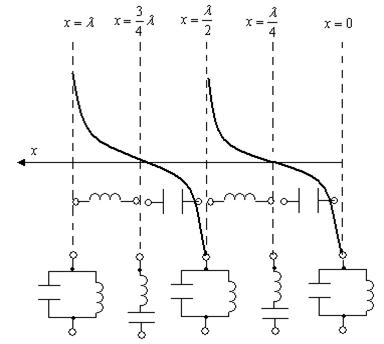
10.2 Сурет
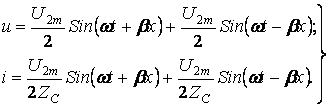 (10.14)
(10.14)
Бос
жүріс ережеде желінің аяғында ![]() және аяқтан
және аяқтан 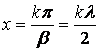 (мұндағы
К- бүтін сан) аралықта тұратын нүктелерде қандай
да болған уақыт мезгілде пучность деп аталатын кернеудің
максимумдары және токтың түйіндері байқалады.
Токтың және кернеудің түйіндері және пучнестері
орындарынан қозғалмайды.
(мұндағы
К- бүтін сан) аралықта тұратын нүктелерде қандай
да болған уақыт мезгілде пучность деп аталатын кернеудің
максимумдары және токтың түйіндері байқалады.
Токтың және кернеудің түйіндері және пучнестері
орындарынан қозғалмайды.
Шығындары жоқ ажыратылған желінің кіріс кедергісі
![]() (10.15)
(10.15)
яғни
таза реактивтік, ал оның мінезі желінің ұзындығымен
және жиілікпен белгіленеді. Абсолюттік шамамен және мінездің
өзгеруінің желінің ұзындығынан тәуелдігі
13.7-суретте көрсетілген х=0 – ден ![]() ге дейін,
ге дейін, ![]() ден
ден ![]() -ге дейін және сол сияқты желі
сыйымдылық кедергі болады, ал
-ге дейін және сол сияқты желі
сыйымдылық кедергі болады, ал ![]() тен,
тен, ![]() дейін,
дейін, ![]() -ден
-ден ![]() және сол сияқты желі
индуктивтік кедергі.
және сол сияқты желі
индуктивтік кедергі. ![]() және
сол сияқты желі-параллельді резонанстық контур, ал
және
сол сияқты желі-параллельді резонанстық контур, ал ![]()
![]() және сол сияқты
желі тізбекті резонанстық контур.
және сол сияқты
желі тізбекті резонанстық контур.
Қысқа
тұйықталу кезде ![]() шығады:
шығады:
![]() (10.16)
(10.16)
Лезді мәндер
![]() (10.17)
(10.17)
яғни кернеумен ток – тұйық толқындар
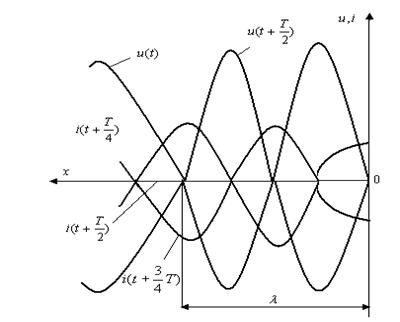
10.3 Сурет
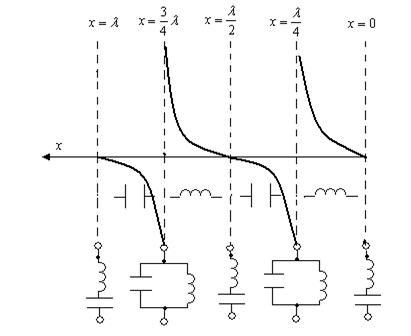
10.4 Сурет
Әртүрлі
уақыт мезгіл үшін желінің аяғында ![]() және аяғынан
және аяғынан ![]() аралықта жататын
нүктелерде кернеудің түйіні және токтың жинағы
болады, ал желінің аяғынан
аралықта жататын
нүктелерде кернеудің түйіні және токтың жинағы
болады, ал желінің аяғынан ![]() аралықта жататын нүктелерде
кернеудің жинағы және токтың түйіндері болады
(10.3 Сурет).
аралықта жататын нүктелерде
кернеудің жинағы және токтың түйіндері болады
(10.3 Сурет).
Кернеудің жинағы және тоқтың түйіні бір-бірінен толқынның ұзындығының бір шірекке ығысқан.
Шығындары жоқ қысқа тұйықталған желінің кіріс кедергісі
![]() (10.18)
(10.18)
яғни
таза реактивтік, желінің ұзындығына және жиіліке
тәуелді индуктивтік немесе сыйымдылықты болуы мүмкін.
Қысқа тұйықталған желінің
ұзындығына тәуелді кіріс кедергінің өзгеруі 10.4-суретте
көрсетілген. Суреттен көрініп тұр: ![]() -ден,
-ден, ![]() ге дейін,
ге дейін, ![]() ден
ден ![]() -ге дейін желі индуктивтік
кедергі, ал
-ге дейін желі индуктивтік
кедергі, ал ![]() тен,
тен,
![]() ,
, ![]() -ден,
-ден, ![]() -ге дейін
–сыйымдылық кедергі,
-ге дейін
–сыйымдылық кедергі, ![]() ж.с.с. желі –параллельді
резонанстық контур.
ж.с.с. желі –параллельді
резонанстық контур.
Жүктемемен келіскен желіні құру үшін қабылдағышқа тізбектеп немесе параллельді индуктивтік немесе сыйымдылық элементтерді қосу керек. Мұндай элементтер ретінде жоғары жиілік кезде қысқа шығыны жоқ тұйықталған немесе ажыратылған желіні пайдалануға болады.
Сыйымдылық
элементі ретінде ұзындығы ![]() тең ажыратылған желіні, ал
индуктивтік элемент ретінде ұзындығы
тең ажыратылған желіні, ал
индуктивтік элемент ретінде ұзындығы ![]() тең қысқы
тұйықталған желіні таңдайды.
тең қысқы
тұйықталған желіні таңдайды.
Шығыны
жоқ ажыратылған желінің х ұзындығын ![]() берілген кезде мына
кейіптеме бойынша анықтауға болады
берілген кезде мына
кейіптеме бойынша анықтауға болады
![]() (10.19)
(10.19)
![]() кезде, яғни
таза реактивтік жүктеме кезінде желіде тағы да тұйық
толқындар болады. Бірақ та желінің аяғында
кернеудің және токтың жинағы және түйіні
болмайды.
кезде, яғни
таза реактивтік жүктеме кезінде желіде тағы да тұйық
толқындар болады. Бірақ та желінің аяғында
кернеудің және токтың жинағы және түйіні
болмайды.
Түйінде ток немесе кернеу нөлге тең, онымен бірге қуатта нөлге тең, ал сол себептен түйін арқылы энергия өтпейді.
Желі
арқылы энергияны тек жүгіріп бара жатқан толқындар
жүзеге асырады. Егер де ![]() болса, онда қысқа
тұйықталған және ажыратылған желіде
энергияның қозғалысы (көзбен желінің
арасындағы энергияның алмасуы) желінің барлық
ұзындығы бойынша өтеді.
болса, онда қысқа
тұйықталған және ажыратылған желіде
энергияның қозғалысы (көзбен желінің
арасындағы энергияның алмасуы) желінің барлық
ұзындығы бойынша өтеді.
11 Дәріс. Электрстатикалық өрісті сипаттайтын негізгі шамалар
Дәрістің мақсаты: Электрстатикалық өрісті сипаттайтын негізгі физикалық шамаларды оқып білу.
11.1 Электр зарядтар. Кулон заңы.
Электрстатикалық өріс-қозғалмайтын электр зарядтардың электр өрісі.
Егерде электр заряд V көлемде
таратылған болса, онда ![]()
![]() - зарядтың көлемдік
тығыздығы.
- зарядтың көлемдік
тығыздығы.
Егерде заряд S беттік бойынша таратылған
болса, онда ![]()
![]() - зарядтың беттік
тығыздығы.
- зарядтың беттік
тығыздығы.
Егерде заряд L сызық бойынша
таратылған болса, онда ![]()
![]() - зарядтың сызықты
тығыздығы.
- зарядтың сызықты
тығыздығы.
Зарядталған дененің мөлшері өрісті қарайтын нүктелердің аралығына қарағанда шамалы болса, онда мұндай зарядты нүктелі деп атайды. Нүктелі зарядтың тығыздығы шексіздікке тең.
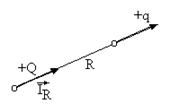
11.1 сурет – Бір текті диэлектриктегі екі нүктелі заряд
Таңбалары бірдей нүктелі зарядтар бір-бірінен итеріледі.
Итерілу күш Кулон заңымен белгіленеді
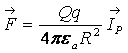 (11.1)
(11.1)
мұнда Q-бірінші нүктелі заряд;
q-екінші нүктелі заряд;
R-нүктелі зарядтар арасындағы аралық;
![]() - Q заряды бар нүктеден q заряды бар нүктеге
бағытталған жекелік вектор;
- Q заряды бар нүктеден q заряды бар нүктеге
бағытталған жекелік вектор;
![]() -абсолюттік диэлектрлік өтімділік;
-абсолюттік диэлектрлік өтімділік;
![]() -салыстырмалы диэлектрлік өтімділік;
-салыстырмалы диэлектрлік өтімділік;
![]() -электрлік тұрақтылық
-электрлік тұрақтылық
11.2 Электростатикалық өрістің кернеулігі және электрлік ығысу
Электростатикалық өрісті бейнелеу және өлшеу үшін бұл өріске орнатылған заряд байқалатын және сыналатын итеру немесе тарту күштің көрнісімен пайдаланады. Электр өрістің кернеулігі сандық тұрғыдан зарядталған бөлшекке әсер етуші күштің осы бөлшек зарядтың қатынасына тең, яғни
![]() (11.2)
(11.2)
Нүктелі зарядталған дененің электр өрістің кернеулігі
![]() (11.3)
(11.3)
Электростатикалық өрісті ![]() кернеуліктің векторлық өрісі
деп қарауға болады.
кернеуліктің векторлық өрісі
деп қарауға болады.
Электрлік ығысу немесе электрлік
индукция деп ![]() векторлық шаманы айтады. Ол біртекті және
изотропты ортада электр өрістің кернеулігіне пропорционалды,
яғни
векторлық шаманы айтады. Ол біртекті және
изотропты ортада электр өрістің кернеулігіне пропорционалды,
яғни
![]() . (11.4)
. (11.4)
СИ жүйеде электр индукцияның өлшемі Кл/м2.
Егерде өріс бірнеше нүктелі
зарядтармен құрылса, онда қандай да болған
нүктедегі өрістің жалпы кернеулігі ![]() геометриялық қосындыға
тең, яғни
геометриялық қосындыға
тең, яғни
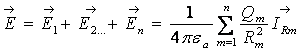 . (11.5)
. (11.5)
11.3 Электростатикалық өрістің потенциалдығы. Электрлік потенциал.
Өрістерді зерттеу кезде, өрістің бейнелеуін білу үшін өрістің құйындыма немесе құйынды емес пе екендігін білу керек.
Өріс құйынды емес немесе потенциалды деп аталады қандай да болған L тұйықталған қисық бойынша вектордың айналымы нөлге тең болса.
Егерде Е кернеулігі бар
электростатикалық өріске ![]() нүктелі зарядты еңгізсек, онда
өрістің күштерінің әсерімен заряд тоғысады.
Заряд
нүктелі зарядты еңгізсек, онда
өрістің күштерінің әсерімен заряд тоғысады.
Заряд ![]() кейбір 1 нүктеден 2 нүктеге ығысуға
жұмсалған өрістің күштерінің жұмысына
тең
кейбір 1 нүктеден 2 нүктеге ығысуға
жұмсалған өрістің күштерінің жұмысына
тең
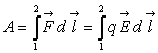 .
(11.6)
.
(11.6)
Тұйықталған қисық бойынша өріс күштердің жұмысы нөлге тең
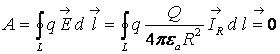 . (11.7)
. (11.7)
Сондықтан, өрістің векторының айналымы
![]() . (11.8)
. (11.8)
яғни электростатикалық өріс-потенциалды өріс.
Стокстың теоремасын қолданып жазуға болады
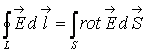 . (11.9)
. (11.9)
Электростатикалық өрісінің кернеулік векторының айналымы нөлге тең болғандықтан, оның роторы нөлге тең
![]() (11.10)
(11.10)
Электростатикалық өріс
құйынды емес болғандықтан, таңбасы минуспен
алынған өрістің кернеулігінің векторына ![]() тең кейбір скалярлы φ бернені табуға болады
тең кейбір скалярлы φ бернені табуға болады
![]() . (11.11)
. (11.11)
φ скалярлы берне потенциал деп аталады.
Өрістің әрбір нүктесінің потенциалын былай белгілеуге болады
![]() . (11.12)
. (11.12)
Потенциалдық айырымы кернеу деп аталады
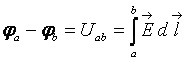 (11.13)
(11.13)
Потенциалдық айырымы интегралдаудың жолының түрінен тәуелсіз, ол нүктелердің бастапқы және аяққы тұратын орындарына тәуелді.
Нүктелі зарядтың өрісінің потенциалы былай табылады:
 (11.14)
(11.14)
![]() болғандықтан
болғандықтан
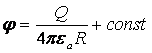 (11.15)
(11.15)
Егерде R =![]() , кезде потенциал φ=0 деп алсақ, онда
интегралдаудың тұрақтысы нөлге айналады.
, кезде потенциал φ=0 деп алсақ, онда
интегралдаудың тұрақтысы нөлге айналады.
Қозғалмас көлемдік, беттік және сызықтық зарядтардың потенциалын беттесу әдіспен табуға болады, яғни
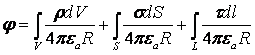 (11.16)
(11.16)
12 Дәріс. Электростатикалық өрістің негізгі теоремалары және теңдеулері
Дәрістің мақсаты: Электрстатикалық өрістің негізгі теоремаларын және теңдеулерін зерттеп тану
12.1 Полярлану векторы
Q зарядпен қоздырылған өрістің кернеулігі ![]() вакуумда және өткізгіш емес затта
бірдей емес, яғни өткізгіш емес орталықта
электростатикалық өрістің кернеулігі вакуумға
қарағанда εr есе аз болады. Кернеуліктің өзгеруі
диэлектриктің полярлануы.
вакуумда және өткізгіш емес затта
бірдей емес, яғни өткізгіш емес орталықта
электростатикалық өрістің кернеулігі вакуумға
қарағанда εr есе аз болады. Кернеуліктің өзгеруі
диэлектриктің полярлануы.
Диэлектрдің молекулалар құрыстырына қарай полярлану әртүрлі өтеді. Егерде сыртқы электростатикалық өріс жоқ болса, онда диэлектрик электрлі бейтарапты болады, ал өріс пайдалы кезде диэлектрик полярланады, яғни бейтарапты болмайды. Полярлану кезінде пайда болған зарядтар молекулалармен байланысты, сол себептен молекулалар ішінде шамалы ығысады. Мұндай зарядтар байланысқан деп аталады. Бір денеден екінші денеге ауыстыруға болатын зарядтарды еркін зарядтар деп аталады.
Байланысқан зарядтар полярлану кезінде
сыртқы өрістің кернеулігіне қарсы
бағытталған өзінің өрісінің кернеулігін
құрады. Сол себептен диэлектрик ішіндегі нәтижелі
өрістің кернеулігі сыртқы өрістің кернеулігінен
аз болады. Диэлектриктің полярлану дәрежесі ![]() полярлану вектормен сипатталады. Бұл
вектор біркелкі және изотропты диэлектртер үшін өрістің
кернеулігіне пропорционалды, яғни
полярлану вектормен сипатталады. Бұл
вектор біркелкі және изотропты диэлектртер үшін өрістің
кернеулігіне пропорционалды, яғни
![]() . (12.1)
. (12.1)
мұнда ![]() -өлшемсіз шама, салыстырмалы диэлектрлік
қабілеттілік деп аталады.
-өлшемсіз шама, салыстырмалы диэлектрлік
қабілеттілік деп аталады.
Ортаның полярлану векторы ![]() осы ортадағы электр ығысудың
осы ортадағы электр ығысудың
![]() вакуумдағы электр ығысудың айырмашылығын
көрсетеді, яғни
вакуумдағы электр ығысудың айырмашылығын
көрсетеді, яғни
![]() . (12.2)
. (12.2)
Сондықтан, ![]()
Полярлану, электр ығысу сияқты, СИ жүйеде Кл/м2 өлшенеді.
12.2 Гаусстың теоремасы интегралды түрде
Гаусстың теоремасы өріс
теориясының бір негізгі теоремасы болып есептеледі. Еркінше
тұйықталған бет арқылы өтетін ![]() ығысудың векторының
ағыны осы бетпен шектелген көлемде орналасқан Q еркін
зарядтардың алгебралық қосындысына тең.
ығысудың векторының
ағыны осы бетпен шектелген көлемде орналасқан Q еркін
зарядтардың алгебралық қосындысына тең.
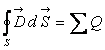 . (12.3)
. (12.3)
Заряд көлемді таратыла
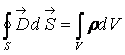 . (12.4)
. (12.4)
Егерде заряд бетпен шектелген
көлемнің сыртында болса, онда ![]() вектордың ағыны бұл бет
арқылы нөлге тең.
вектордың ағыны бұл бет
арқылы нөлге тең.
Гаусстың теоремасы электр өрістерді есептеуде кең қолданады.
12.3 Гаусстың теоремасы дифференциалды түрде
Остроградскийдің теоремасы бойынша электр ығысу вектордың ағынын түрлендіреміз
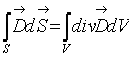 . (12.5)
. (12.5)
Гаусс теоремасы бойынша
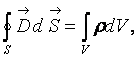
онда
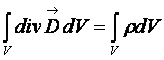 . (12.6)
. (12.6)
Көлем V еркін алынған, сол себептен оның барлық мәндері үшін теңдік (12.6) әділетті. Бұл жағдайда интегралдардың астындағы көріністер тең болады.
![]() . (12.7)
. (12.7)
(12.7) көрініс – Гаусс теоремасының дифференциалды түрі.
Диэлектрлік өтімділік тұрақты орталар үшін
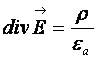 .
(12.8)
.
(12.8)
12.4 Пуассон және Лапластың теңдеулері
Электрстатикалық өрісті беттесу әдіспен немесе Гаустың интегралды теоремасын пайдаланып есептеуге болады. Екі әдіс жай кескін үйлесімі бар өрісті есептеуге ғана қолданады. Жалпы жағдайда өрісті есептеу Пуассон және Лапластың теңдеулерін шешуде жатады.
Есептеу кейіптемені табу үшін 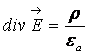 және
және ![]() теңдеулерді пайдаланыңыз.
теңдеулерді пайдаланыңыз. ![]() мәнін қойғаннан кейін
табамыз
мәнін қойғаннан кейін
табамыз
![]() (12.9)
(12.9)
Градиенттің дивергенциясын лапласиан деп
атайды және оны ![]() деп белгілейді.
деп белгілейді.
Сондықтан, (12.9) көріністі былай жазуға болады
![]() (12.10)
(12.10)
Зарядтар жоқ өрістің нүктелерінде
![]() (12.11)
(12.11)
(12.10) кейіптеме – Пуассонның теңдеуі, (8.11) кейіптеме – Лапластың теңдеуі деп аталады. Шешім былай жазылады
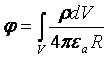 (12.12)
(12.12)
Потенциал ұғымын енгізу электрстатикалық өрісті есептеуді жеңілдетеді. Есептеу φ скалярлы бернені белгілеуге алып барады, ал φ бернені тапқаннан кейін өрістің кернеулігін жеңіл табуға болады
![]()
13 Дәріс. Электростатикалық өрісті есептеу
Дәрістің мақсаты: Шекаралық шарттарды және электростатикалық өрістерді есептеу әдістерді зерттеп тану.
13.1 Электрстатикалық өрісте шекаралық шарттар
Әртүрлі екі орталардың шекарасында өріс векторларын қанағат қылатын шарттар шекаралық шарттар деп аталады.
Диэлектрикалық өтімділіктері ε1 және ε2 тең екі өткізбейтін ортаның шекарасын қарайық.
Бірінші шарт
![]() немесе
немесе 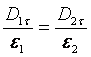 . (13.1)
. (13.1)
Екі өткізбейтін ортаның
шекарасында өрістің кернеулік вектордың тангенциалды
құрастырушылар бір-біріне тең. Екі ортаның бөліну
үстінгі бетте потенциал үздіксіз ![]()
Екінші шарт
![]() (13.2)
(13.2)
![]() . (13.3)
. (13.3)
Екі өткізбейтін ортаның шекарасында электр ығысудың векторының нормаль құрастырушысы еркін зарядтардың беттік тығыздығына тең ырғақты өзгереді.
Егерде ![]() онда
онда ![]()
![]() . (13.4)
. (13.4)
Электр ығысу ![]() вектордың нормаль
құрастырушысы үздіксіз. Егерде бір орта өткізгіш болса,
онда шекаралық шарттар өзгереді. Өткізгіш ортада
өрістің векторлары нөлге тең, ал
өткізгіштің барлық нүктелерінде потенциал бірдей.
вектордың нормаль
құрастырушысы үздіксіз. Егерде бір орта өткізгіш болса,
онда шекаралық шарттар өзгереді. Өткізгіш ортада
өрістің векторлары нөлге тең, ал
өткізгіштің барлық нүктелерінде потенциал бірдей.
Бірінші орта – салыстырмалы өтімділігі ε диэлектрик, екінші орта-өткізгіш.
Шекаралық шарттар келесі түрде жазылады:
![]()
![]()
![]()
![]()
![]() (13.5)
(13.5)
![]()
![]() .
.
13.2 Электростатикалық өрістерді есептеу әдістер
13.2.1 Беттесу әдісі
Егерде кеңістікте зарядтың таратылуы берілген болса, онда бұл зарядты шексіз аз элемент dQ бөліп өрістің потенциалын және кернеулігін белгілеуге болады
 ,
(13.6)
,
(13.6)
 .
(13.7)
.
(13.7)
Алгебралық dφ шамаларды қосып өрістің қандайда болған нүктесінде потенциалды белгілеуге болады
![]() (13.8)
(13.8)
Кернеулік ![]() мынау кейіптемемен белгіленеді
мынау кейіптемемен белгіленеді
![]() (13.9)
(13.9)
13.2.2 Айнымалық бейнелеу әдісі
Егерде электр зарядтар екі әртүрлі ортаның шекарасына жақын орнатылса, онда өрістің векторларын жасанды әдісті қолданып белгілеуге болады. Бұл әдіс айналық бейнелеу әдіс деп аталады.
Бұл әдісте біртекті емес ортаның орнына біртекті орта қаралады, ал біртекті еместікті жалған зарядтарды енгізу арқылы есепке алады. Берілген және жалған зарядтардың бірлесіп әрекет істегеннен өрістің векторларын белгілеп, негізгі есептің шекаралық шарттарды жазып, олармен пайдаланып өрістің ізделіп жатқан векторларын табады.
13.3 Өткізгіш денелер жүйеде потенциалдардың және зарядтардың таратылуы
Электр беріліс желілерде үрдістерді зерттеу кезде келесі мақсат туады. Бірнеше параллельді сым берілген. Өзара орналасуы және олардың үстіндегі зарядтар берілген. Бұл сымдардың потенциалдарын белгілеу керек.
![]() деп
деп ![]() сымның зарядымен себепші болған және
P нүктеде орналасқан потенциалды белгілейік. Заряд
және потенциал пропорционалды болғандықтан
сымның зарядымен себепші болған және
P нүктеде орналасқан потенциалды белгілейік. Заряд
және потенциал пропорционалды болғандықтан
![]() (13.10)
(13.10)
Коэффициент ![]() -тұрақты шама. Егерде барлық
сымдардың санын n деп белгілесек, онда P нүктедегі потенциал,
барлық сымдардың зарядтармен себепші болғанда, беттесу
әдіспен пайдаланып белгілеуге болады
-тұрақты шама. Егерде барлық
сымдардың санын n деп белгілесек, онда P нүктедегі потенциал,
барлық сымдардың зарядтармен себепші болғанда, беттесу
әдіспен пайдаланып белгілеуге болады
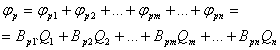 (13.11)
(13.11)
Егерде P нүктені бірінші сымның бетінде болса, онда оның потенциалы
![]() (13.12)
(13.12)
Сол сияқты басқа сымдардың потенциалдары
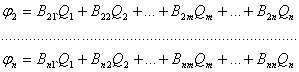 (13.13)
(13.13)
В тұрақтылар потенциалды коэффициенттер деп аталады.
Индекстерді айырбастаған кезде коэффициент өзгермейді, яғни ![]()
Егерде табылған теңдеулер жүйесін зарядтарға қарай шешу болса, онда
 (13.14)
(13.14)
A тұрақтылар сыйымдылық коэффициенттер деп аталады.
Потенциалды және сыйымдылық коэффициенттер арасындағы байланыс келесі
![]() (13.15)
(13.15)
Жүйенің анықтауышы
 (13.16)
(13.16)
ал алгебралық толықтыру
 (13.17)
(13.17)
Индекстері бірдей А коэффициенттер
болымды, әртүрлі индекстер бар – теріс. Индекстерді
айырбастаған кезде коэффициент өзгермейді, яғни ![]()
(19.14) теңдеу жүйелерді басқаша жазуға болады.
![]()
мұнда ![]() (13.18)
(13.18)
С коэффициенттер жарым-жартылай сыйымдылық деп аталады.
Егерде жарым-жартылай сыйымдылықтардың индекстері бірдей болса оны өздік жарым-жартылай сыймдылық деп атайды.
Индекстерді айырбастаған кезде
коэффициент өзгермейді, яғни ![]()
А коэффициенттер тәжірибелі белгілеуге болады. Оларды білгеннен кейін жарым-жартылай сыйымдылықтарды санауға болады.
14 Дәріс. Тұрақты токтың электр өрісі
Дәрістің мақсаты: Электр өрісті сипаттайтын негізгі физикалық шамаларды және олардың өзара байланыстарын оқып білу.
14.1 Ток және токтың тығыздығы
Егерде өткізгіш ортада сыртқы көздердің әсерімен электр өріс туатын болса, онда оларда өткізгіштік электр ток ағады. Электр өрісінің әрекетінен металдағы еркін электрондардың, сұйықтағы иондардың реті түрде қозғалысын өткізгіштік деп атайды. Тұрақты токтың электр өрісі деп өткізгіш ортада қозғалыста болатын зарядтардың жиынтығынан болған өрісті айтады.
Шектік ∆t→ нөлге ұмтылғанда, берілген бетті кейбір ∆t уақыт аралығында тесіп өтетін ∆q зарядының сол ∆t шамасына қатынасының шегі ток өлшемін береді
![]() (14.1)
(14.1)
Ток скалярлы шама. Егер токтың мәні уақыттан тәуелді болмаса, оны тұрақты ток дейміз. Токтың өлшемі (А).
Заряд тасушылар өздерінің бірбеткей қозғалысы кезінде заттың басқа бөлшектерімен көптеген қағысуларға ұшырайды. Бұл қағысулар заряд тасушыларының бірбеткей қозғалыстарын қиындатады және өткізу ортада ток ағуға кедергі жасайды.
Электр өрісіндегі өткізгіш
ортаның негізгі шамасы ![]() -ток тығыздығы саналады.
Бұл векторлық шама электр өрісінің кернеулігі бойынша
бағытталған
-ток тығыздығы саналады.
Бұл векторлық шама электр өрісінің кернеулігі бойынша
бағытталған
![]() (14.2)
(14.2)
Ток және ток тығыздығы келесі қатынас бойынша байланысқан
![]() . (14.3)
. (14.3)
яғни S беті арқылы ағатын ток сол бет арқылы өтетін ток тығыздығы векторының ағынына тең. Ток тығыздығының өлшемі (А/м2).
14.2 Дифференциалды түріндегі Ом заңы
Изотропты өткізгіште өткізгіш
токтың тығыздығы ![]() электр өрістің Е
кернеулігіне пропорционалды
электр өрістің Е
кернеулігіне пропорционалды
![]() (14.4)
(14.4)
Бұл кейіптеме дифференциалды түріндегі Ом заңы.
Коэффициент γ меншікті өткізгіштік
деп аталады, өлшемі (См/м). Өткізгіште ұзақ
уақыт бойынша ток аққан үшін зарядтарды жылжытатын
электр өріс болу керек. Мұнда өріс химиялық,
жылулық, термоэлектрлік үрдістермен құрылады да, шеттік
электр өріс деп аталады. Шеттік электр өрістің кернеулігін Eшек
деп белгілейміз. Егерде өткізгіште бір мезгілде электростатикалық
және шектік күштер әрекет істесе, онда нәтижелі
өрістің кернеулігі ![]() .
.
Өткізгіш а-1-в-2-а (20.1 сурет) контурды қарайық.
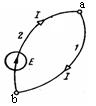
в-2-а салады шеттік күштер әрекет
істейді. Бұл салада ![]()
а-1-в салада шеттік күштер жоқ, сондықтан ![]()
14.1 Сурет
Тұйықталған тізбекте кернеу түсудің қосындысы тең ЭҚК-ке:
![]() немесе
немесе ![]() .
.
Қаралып тұрған контурдың екі нүктелерінің арасындағы потенциалдар айырымы бұл контурда әрекет істейтін ЭҚК-тен кем болады. а-1-в салада ток а нүктеден (жоғары потенциалы бар нүктеден) в нүктеге ағады (төмен потенциалы бар нүкте). Егерде тізбекте шеттік күштер жоқ болса, онда а және в нүктелердің потенциалдары тең болар еді де, ток тоқталар еді. Шеттік күштер зарядтарды в-2-а жолмен в нүктеден а нүктеге жылжытады, ал а және в нүктелерінің потенциалдарын тұрақты қылып ұстайды. Шеткі өрістің энергиясы а-1-в және в-2-а салаларда жылулық шығындарға кетеді.
Шеткі күштер бар өткізгіштің салаларында Ом заңының кейіптемесі
![]() (14.5)
(14.5)
14.3 Дифференциалды түріндегі Джоуль-Ленц заңы
Өткізгіште жылулық
шығындардың қуаты токпен кернеудің көбейтіндісіне
тең, яғни ![]() .
.
Егерде өткізгіш ортада көлемнің dV элементін қарасақ, онда бұл көлемде жылулық шығындарға жұмсалатын қуат тең
![]()
ал бұдан ![]() (14.6)
(14.6)
V көлемде жылылық шығындардың қуаты
![]() (14.7)
(14.7)
(14.7) кейіптеме дифференциалды түріндегі Джоуль-Ленц заңы.
14.4 Дифференциалды түріндегі Кирхгофтың бірінші заңы
Интеграл түрде Кирхгофтың бірінші заңы
![]() (14.8)
(14.8)
Әрбір токты ток тығыздығы
арқылы көрсетсек, яғни ![]() онда
онда ![]() тең болады немесе көлемге кіретін
және көлемнен шығатын токтардың қосындысы
нөлге тең.
тең болады немесе көлемге кіретін
және көлемнен шығатын токтардың қосындысы
нөлге тең.
![]() көрініс тұйықталған
бет арқылы өтетін ток тығыздығының
векторларының сызықтары тұйықталған болады,
яғни тұрақты ток үздіксіз.
көрініс тұйықталған
бет арқылы өтетін ток тығыздығының
векторларының сызықтары тұйықталған болады,
яғни тұрақты ток үздіксіз.
Остроградскийдің теоремасы бойынша
![]() (14.9)
(14.9)
бұдан шығады ![]() (14.10)
(14.10)
Бұл кейіптеме (14.10) дифференциалды түріндегі Кирхгофтың бірінші заңы. Таратылмаған тізбекте әртүрлі кесінділерде тұрақты токтың мәні бірдей.
14.4 Шекаралық шарттар
Меншікті өткізгіштері γ1 және γ2 екі өткізгіш ортаның шекарасын қарайық.
Шекаралық шарттар:
а) екі өткізгіш ортаның шекарасында ток тығыздықтың векторының нормаль құрастырушылары үздіксіз
![]()
б) екі өткізгіш ортаның шекарасында электр өрістің кернеуліктің векторының потенциалды құрастырушылары үздіксіз
![]()
Егерде ![]() және векторлар шекараға
қарай нормальмен бірінші ортада α1 бұрышты, ал
екінші ортада α2 бұрышты құрса (14.2 сурет),
онда
және векторлар шекараға
қарай нормальмен бірінші ортада α1 бұрышты, ал
екінші ортада α2 бұрышты құрса (14.2 сурет),
онда ![]()
![]()
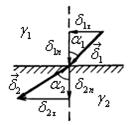
![]()
![]() болғандықтан
болғандықтан
![]() (14.11)
(14.11)
14.2 Сурет
14.5 Тұрақты токтың электр өрісі және электрстатикалық өрісі арасындағы ұқсастық
|
Тұрақты токтың өрісі |
Электростатикалық өріс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 Дәріс. Тұрақты токтың магнит өрісі
Лекцияның мақсаты: Магнит өрісті сипаттайтын негізгі шамаларды және заңдарды оқып білу.
15.1 Магнит өрісті сипаттайтын негізгі шамалар
Магнит өріс- кеңістікте қозғалмай тұрған өткізгіш дене бойында ағын өтетін уақытқа байланысты өзгермейтін токтармен жасалатын өріс. Электр тогы бар өткізгіш айналасын магнит өріс қоршайды. Магнит өрістің негізгі қасиеті – оның ішінде жылжып бара жатқан зарядталған денеге сонымен бірге электр ток өтіп тұрған қозғалмайтын өткізгіштерге күштік әсері. Магнит өрістің белгілі бағыты бар, яғни ол векторлық өріс.
Өрістің қасиеттерін зерттеу
үшін және оны санды бейнелеу үшін кеңістіктің
әрбір нүктесінде өрістің қарқынын
белгілейтін физикалық шаманы кіргізу керек. Мұндай шама магнит
индукцияның векторы ![]() болады.
болады. ![]() білген кезде магнит өрістің
қасиеттерін және онымен байланысты құбылыстарды білуге
болады.
білген кезде магнит өрістің
қасиеттерін және онымен байланысты құбылыстарды білуге
болады.
Егерде магнит өріске тұрақты тогы бар сызықты контурды еңгізсек, онда оған әсер ететін күш тең
![]() (15.1)
(15.1)
мұнда І – L контурдағы ток;
![]() -вакуумдағы магнит индукцияның векторы;
-вакуумдағы магнит индукцияның векторы;
dl – сызықты сымның ұзындықтың элементі
І токтың магнит өрісінің әсерімен орта
магниттеледі. Магниттелген зат индукциясы ![]() тең өзінің магнит
әсерін құрады. Нәтижелі өрістің магнит
индукциясы
тең өзінің магнит
әсерін құрады. Нәтижелі өрістің магнит
индукциясы ![]()
Магнит өрісі ![]() магнит индукциямен,
магнит индукциямен, ![]() магниттелгендігімен және
магниттелгендігімен және ![]() магнит өрістің кернеулігімен
сипатталады. Бұл шамалардың бір-бірімен ара қатынас
байланыстары мынадай
магнит өрістің кернеулігімен
сипатталады. Бұл шамалардың бір-бірімен ара қатынас
байланыстары мынадай
![]() (15.2)
(15.2)
мұнда ![]() -магнителгендіктің
векторы, магнит кернеулікке пропорционалды:
-магнителгендіктің
векторы, магнит кернеулікке пропорционалды:
![]() Гн/м- магниттік
тұрақтысы;
Гн/м- магниттік
тұрақтысы;
![]() - заттың салыстырмалы магнит
өтімділігі;
- заттың салыстырмалы магнит
өтімділігі;
![]() - абсолюттік магнит өтімділігі;
- абсолюттік магнит өтімділігі;
![]() -магнит өрісінің
кернеулігінің векторы, А/м;
-магнит өрісінің
кернеулігінің векторы, А/м;
![]() - магнит индукциясының векторы, Тл;
- магнит индукциясының векторы, Тл;
![]() -магниттелгендіктің векторы, А/м.
-магниттелгендіктің векторы, А/м.
Барлық заттарда магнит қасиеттері
бар. Көбінесінде магнит қасиеттері шамалы. Тек ферромагнит
денелердің ![]() бірден едәуір үлкен болады (болат,
никель). Ферромагнит емес заттардың
бірден едәуір үлкен болады (болат,
никель). Ферромагнит емес заттардың ![]() деп алуға болады. Келешекте ферромагнит
емес орталарда өрістерді қараймыз.
деп алуға болады. Келешекте ферромагнит
емес орталарда өрістерді қараймыз.
15.2 Магнит ағын және оның үздіксіздігі
Магнит индукцияның векторының ағыны
![]() (15.3)
(15.3)
магнит ағыны деп аталады. Өлшем бірлігі – Вебер (Вб). Магнит индукция-магнит ағынының тығыздығы. Егерде индукция В үстіңгі бетке перпендикулярлы болса, онда Ф = BS.
Егерде бет тұйықталған болса, онда
![]() (15.4)
(15.4)
Остроградскийдің теориясын қолданып, келесіні жазуға болады
![]() (15.5)
(15.5)
Бұл теңдік қандай да болған көлемге әділ.
Сондықтан, div![]() = 0
(15.6)
= 0
(15.6)
(15.4) кейіптеме интегралды түрде, ал (21.6) кейіптеме дифференциалды түрде магнит ағынның үздіксіздігін көрсетеді.
div![]() =0
(15.7)
=0
(15.7)
Магнит өрістің суреті ![]() вектордың сызықтары (магнит сызықтары) арқылы
бейнеленеді.
вектордың сызықтары (магнит сызықтары) арқылы
бейнеленеді.
15.3 Интегралды және дифференциалды түріндегі толық токтың заңы
Магнит өрістің қасиеттерін сипатталатын негізгі заңы – толық токтың заңы. Бұл заң магнит өрістің кернеулігімен ток арасындағы байланысты орнатады. Анықтамасы: магнит өрістің кернеулігінің векторының циркуляциясы интегралдау контурмен қамтылған толық токқа тең.
![]() (15.8)
(15.8)
Егерде ![]() деп толық токтың
тығыздығын белгілесек, L қисықпен шектелген, S
бет арқылы өтетін ток
деп толық токтың
тығыздығын белгілесек, L қисықпен шектелген, S
бет арқылы өтетін ток
![]()
Стокстың теоремасын пайдаланып, жазуға болады
![]() (15.9)
(15.9)
Сондықтан
![]() (15.10)
(15.10)
Бұл теңдік барлық S үшін әділетті болғандықтан интегралдаудың астындағы бернелер бір-бірімен тең
![]() (15.11)
(15.11)
Табылған кейіптеме толық ток заңының дифференциалды түрі және Максвеллдің бірінші теңдеуі деп аталады. Бұл теңдеу магнит өріс құйынды екенін көрсетеді.
![]() және
және ![]() кейіптемелермен пайдаланып магнит
өрісті есептеуге болады.
кейіптемелермен пайдаланып магнит
өрісті есептеуге болады.
15.4 Магнит өрістің скалярлы және векторлы потенциалдары
Токтары ток салалар үшін (тогы бар өткізгіштердің сырттарында)
mа= const; ![]() ; rot
; rot ![]() =0; div
=0; div![]() =0.
=0.
Бұл теңдеулер көлемді зарядтар жоқ диэлектрлік ортада (eа = const) электростатикалық өрістің теңдеулеріне ұқсас. Сондықтан тоғы жоқ өрістің саласында потенциалды деп қарауға болады және оны скалярлы φm бернемен сипаттауға болады.
![]() (15.12)
(15.12)
φm шаманы скалярлы магнит потенциал деп атайды.
Егерде магнит өрістің ![]() кернеулігін берілген ток тығыздығы
кернеулігін берілген ток тығыздығы ![]() бойынша, онда Максвеллдің бірінші
теңдеуін
бойынша, онда Максвеллдің бірінші
теңдеуін
![]()
күрделі есептеуге алып келеді.
Кейбір жағдайда
векторлық потенциал деп аталатын ![]() шаманы алдымен белгілеп алу ыңғайлы
болады.
шаманы алдымен белгілеп алу ыңғайлы
болады.
Векторлық потенциал ![]() магнит кернеулік
магнит кернеулік ![]() былай байланысқан
былай байланысқан
![]() (15.13)
(15.13)
![]() деп алайық. Егерде Максвеллдің бірінші теңдеуіне
магнит өрістің
деп алайық. Егерде Максвеллдің бірінші теңдеуіне
магнит өрістің ![]() кернеулігі орнына оған тең шаманы
кернеулігі орнына оған тең шаманы ![]() қойсақ,
табамыз
қойсақ,
табамыз
![]()
Белгілі ![]()
![]() болғандықтан
болғандықтан
![]() (15.14)
(15.14)
Магнит өрістің векторлық
потенциалы Пуассон теңдеумен белгіленеді. Дифференциалды теңдеуді
шешіп ![]() табамыз.
табамыз.
Теңдеудің шешімі интеграл түрде де жазылуға болады
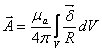 ,
(15.15)
,
(15.15)
мұнда ![]() -векторлық потенциал белгіленетін
нүктеден
-векторлық потенциал белгіленетін
нүктеден ![]() көлем элементіне дейін аралық;
көлем элементіне дейін аралық;
![]() -тұрақты токтың
тығыздығы.
-тұрақты токтың
тығыздығы.
Сызықты ток магнит өрістің векторлық потенциалы
![]() (15.16)
(15.16)
Әдебиеттер тізімі
1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.- М.: Энергоатомиздат, 1989. -528 с.
2. Бессонов Л.А. Теоретические основы электротехники.-М.: Гардарики, 1999. – 638 с.
3. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Т.1. - Л.: Энергоиздат, Ленинградское отделение, 1981. – 536 с.
4. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Т.2. - Л.: Энергоиздат, Ленинградское отделение, 1981. – 416 с.
5. Теоретические основы электротехники. Т.1. Основы теории линейных цепей / Под ред. П.А.Ионкина - М.: Высшая школа, 1976. -544 с.
6. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990.- 544 с.
7. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. - М.: Высшая школа, 1986. – 263 с.
8. Атабеков Г.И., Купалян С.Д. Тимофеев А.Б., Хухриков С.С. Теоретические основы электротехники. ч.2. Нелинейные электрические цепи; ч.3 Электромагнитное поле. - М.: Энергия, 1979. – 432 с.
9. Сборник задач по теоретическим основам электротехники/ Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 1988.-543 с.
10. Сборник задач и упражнений по теоретическим основам электротехники / Под ред. П.А.Ионкина.-М.: Энергоиздат, 1982.-768 с.
11. Данилов И.А., Иванов П.И. Общая электротехника с основами электроники: Учебное пособие – М.: Высшая школа, 2000.-752 с.
12. Денисенко В.И., Зуслина Е.Х. Теоретические основы электротехники: Учебное пособие - Алматы.: АИЭС, 2000.-83 с.