З.И. Жолдыбаева
Е.Х. Зуслина
ПРИМЕНЕНИЕ MATHCAD В ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Учебное пособие
Алматы 2012
УДК 621.3.71:519.6(275.8)
ББК 31.211 Я73
Ж 79. Учебное пособие. З.И. Жолдыбаева, Е.Х. Зуслина.
Применение MathCad в теории электрических цепей.
АУЭС. Алматы, 2012. - 83 с.
I SBN 978-601-7327-18-7
В пособии рассмотрены расчеты сложных разветвленных электрических цепей постоянного и синусоидального токов, расчет переходных процессов классическим, операторным, спектральным методами, с помощью интеграла Дюамеля и построение графиков функций в среде MathCad.
Пособие предназначено для студентов специальностей бакалавриата 5В071900, 5В070400, 5В070300, 5В074600, 5В060200, 5В071600, 5В100200.
Табл.4, ил.74, библиогр. - 16 назв.
ББК 31.211 Я73
РЕЦЕНЗЕНТЫ: КазНТУ канд. техн. наук. доц. Иманбекова Т.Д.
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2012 г.
I SBN 978-601-7327-18-7
©НАО «Алматинский университет энергетики и связи», 2012г.
Введение
Теория электрических цепей является базовым курсом, на который опираются профилирующие дисциплины радиотехнических специальностей, специальностей по вычислительной технике и информационным системам. В соответствии с новыми учебными планами курс ТЭЦ изучается в течение двух семестров. При этом существенно увеличен объем самостоятельной работы студентов (до 60% от общего числа часов). Цель настоящего учебного пособия состоит в оказании помощи студентам в их самостоятельной работе.
В пособии рассмотрены расчеты сложных разветвленных электрических цепей постоянного и синусоидального токов, расчет переходных процессов классическим, операторным, спектральным методами, с помощью интеграла Дюамеля и построение графиков функций в среде MathCad. Расчеты и графики, выполненные в среде MathCad, в тексте выделены прямоугольными рамками.
Данное пособие рассчитано на студентов специальностей бакалавриата 5В071900, 5В070400, 5В070300, 5В074600, 5В060200, 5В071600, 5В100200. Оно ставит задачу помочь студентам в успешном изучении курса «Теория электрических цепей » и выполнении расчетно-графических и курсовых работ.
1 Расчёт сложных разветвленных электрических цепей
постоянного тока
Расчет сложных разветвленных цепей постоянного тока основан на решении системы линейных алгебраических уравнений (СЛАУ), составляемых по законам Кирхгофа, методу контурных токов, методу узловых потенциалов.
В общем случае система линейных алгебраических уравнений имеет вид:
,
(1.1)
где
коэффициенты при неизвестных переменных 
,
свободные члены 
− постоянные
действительные числа.
В MathCad СЛАУ можно решить различными способами.
Способ 1.1. Решение СЛАУ с помощью вычислительного блока given–find (см. пример 1.1):
− напечатать ключевое слово given (дано);
− ввести уравнения, входящие в систему, ниже ключевого слова given, между левой и правой частями уравнения поставить жирный знак логического равенства, для его ввода используют сочетание клавиш Ctrl = или выбирают его в панели Boolean (Булевый, Логический (см. рисунок 1.1));
− напечатать функцию find(x1, x2, x3 …), где x1, x2, x3 — неизвестные переменные;
− после find(x1, x2, x3 …) поставить команду float (численное вычисление) и после запятой ввести число значащих цифр, затем щелкнуть левой кнопкой мыши по пустому месту и нажать знак равенства. Команду float можно напечатать или выбрать на панели Symbolic (Символика) (см. рисунок 1.1 и пример 1.1).
Пример 1.1
Способ 1.2. Решение СЛАУ с помощью оператора solve:
− в математическом меню выбрать кнопку с изображением матрицы. Откроется панель Matrix (Матрица) (см. рисунок 1.1), на которой щелкнуть по кнопке с изображением матрицы;
− откроется окно Insert Matrix (диалоговое окно), открыть диалоговое окно можно также нажатием сочетания клавиш Ctrl+m. В диалоговом окне надо ввести число строк матрицы, равное числу уравнений системы и число столбцов матрицы равное 1 и щелкнуть левой кнопкой мыши по кнопке ОK. На экране появится шаблон матрицы;
− в каждой строке полученной матрицы записать одно уравнение из системы, между левой и правой частями уравнения поставить жирный знак равенства, используя сочетание клавиш Ctrl = или выбрав его в панели Boolean (Булевый, Логический);
− применить к системе уравнений, записанных в виде матрицы оператор solve.
Оператор solve находится на панели Symbolic (Символика) (см. рисунок 1.1) и применяется для решения уравнений или систем уравнений в численном и символьном виде. После solve,x1,x2,x3 можно вставить команду float, записать число значащих цифр, щелкнуть левой кнопкой мыши по пустому месту и нажать знак равенства (см. пример 1.2).
Пример 1.2
Рисунок 1.1 - Панели Символика, Булевый, Математика, Матрица
Рисунок 1.2 - Диалоговое окно Insert Matrix
Способ 1.3. Решение СЛАУ с помощью оператора lsolve (lsolve(А,В) – решение системы линейных уравнений):
− запишем СЛАУ в матричной форме 
, где А – матрица составленная из коэффициентов
(i - номер строки матрицы, а j- номер
столбца) при неизвестных переменных х1,х2,х3…;
В – матрица-столбец (вектор), составленная из свободных членов 
; Х – матрица-столбец (вектор), составленная из неизвестных переменных хi;
− чтобы присвоить значение переменной А,
обозначающей матрицу коэффициентов, запишем сначала «А:=», а затем вставим
матрицу коэффициентов уравнений
;
− чтобы присвоить значение переменной В, обозначающей матрицу свободных членов, запишем сначала «В:=», а затем вставим матрицу-столбец (вектор) свободных членов;
− запишем «Х:=lsolve(А,В)», где X – переменная, обозначающая матрицу-столбец неизвестных переменных хi;
− для получения результата нужно напечатать Х и нажать знак = (см. пример 1.3).
Примечание. Оператор lsolve можно напечатать или щелкнуть левой кнопкой мыши по кнопке f(x) – список встроенных функций (см. рисунок 1.3), или используя сочетание клавиш Ctrl+E. Откроется диалоговое окно, в котором надо выделить оператор (функцию) lsolve и щелкнуть левой кнопкой мыши по кнопке ОK (см. рисунок 1.4);
Рисунок 1.3 - Панель инструментов (Standard)
Рисунок 1.4 - Диалоговое окно Insert Function
Пример 1.3
Способ 1.4. Решение СЛАУ путем обращения матрицы коэффициентов:
− запишем СЛАУ в матричной форме 
, где А – матрица составленная из коэффициентов
(i – номер строки матрицы, а j – номер
столбца) при неизвестных переменных х1,х2,х3…;
В – матрица-столбец, составленная из свободных членов ;
Х – матрица-столбец, составленная из неизвестных
переменных хi;
− решим СЛАУ в матричной форме путем обращения матрицы коэффициентов X
= A-1 ·B (см. пример
1.4).
Пример 1.4
Примеры решения СЛАУ, составленные по МКТ и МУП приведены в задаче 1.1.
Примечание: для решения СЛАУ в MathCad выбирается произвольно один из рассмотренных выше способов.
Задача 1.1.
Для электрической цепи (см. рисунок 1.5), содержащей независимые источники ЭДС 
, 
, 
, 
, независимый
источник тока 
А,
резистивные сопротивления 
Ом, 
Ом, 
Ом, 
Ом, 
Ом,
выполнить следующее:
− рассчитать токи во всех ветвях методом контурных токов (МКТ);
− рассчитать токи во всех ветвях методом узловых потенциалов (МУП).
Рисунок 1.5 - Схема цепи постоянного тока
Расчет токов методом контурных токов.
Один контурный ток выберем так, чтобы он проходил
через источник тока, тогда этот контурный ток совпадёт с током источника тока 
. В двух других независимых контурах цепи
(не содержащих источник тока!) введем контурные токи 
(cм.
рисунок 1.5).
Для
двух неизвестных контурных токов составим уравнения по методу контурных токов:
. (1.2)
Перенесём
в правую часть уравнения, получим:
. (1.3)
Обозначим:
Запишем систему уравнений (1.3) в виде:
 |
, (1.4)
Уравнение контурных токов в матричной форме имеет вид:
R k Ik= Ek , (1.5)
где Rk– квадратная
матрица контурных сопротивлений Rk=
;
Ek– матрица-столбец
контурных ЭДС: Ek=
;
Ik – матрица-столбец
контурных токов: Ik=
.
Решая систему уравнений (1.4), или уравнение контурных
токов в матричной форме (1.5) в MathСad одним из приведенных способов, определим
контурные токи: 
, 
. Токи в ветвях представим в виде алгебраической
суммы контурных токов протекающим по этим же ветвям:
Ниже приведено решение системы контурных уравнений (1.4), (1.5) в MathCad различными способами.
Расчет токов методом узловых потенциалов. Примем 
и запишем уравнения
для определения потенциалов 
:
,
(1.6)
где
Обозначим:
Запишем систему уравнений (1.6) в виде:
(1.7)
Уравнения узловых потенциалов в матричной форме: Gу φу = Jy (1.8)
где Gy – квадратная матрица узловых проводимостей:
Gy =
;
Jy – матрица-столбец узловых
токов: Jy=
;
φу –
матрица-столбец узловых потенциалов: φу=
.
Решая
уравнения узловых потенциалов в MathCad одним из приведенных способов, найдём
потенциалы узлов электрической цепи: 
Токи определим по закону Ома:
Ниже приведено решение системы уравнений по методу узловых потенциалов (1.7), (1.8) в MathCad различными способами.
Решение системы уравнений по методу контурных токов и узловых потенциалов в MathCad различными способами.
Присвоим параметрам цепи и источникам ЭДС и тока, заданные в задаче числовые значения:
Присвоим:
Способ 1.1. Решение СЛАУ с помощью вычислительного блока given–find.
Решение системы уравнений по методу контурных токов (1.4):
, 
.
Решение системы уравнений по методу узловых потенциалов (1.7):
Способ 1.2. Решение СЛАУ с помощью оператора solve.
Решение системы уравнений по методу контурных токов (1.4):
, 
.
Решение системы уравнений по методу узловых потенциалов (1.7):
Способ 1.3. Решение с помощью оператора lsolve.
Решение системы уравнений по методу контурных токов в матричной форме Rk Ik= Ek с помощью оператора lsolve:
, 
Решение системы уравнений по методу узловых потенциалов в матричной форме Gy φу = Jy с помощью оператора lsolve:
Способ 1.4. Решение путем обращения матрицы коэффициентов.
Решение системы уравнений по методу контурных токов в матричной форме Rk Ik= Ek
.
Решение системы уравнений по методу узловых потенциалов в матричной форме Gy φy = Jy
Примечание: 1. Нижний индекс переменной можно задать путем нажатия точки на клавиатуре (язык английский);
2. Простой способ ввода греческих букв: надо с клавиатуры набрать латинский аналог греческой буквы, как правило, первую букву в латинском названии греческой буквы, введя аналог греческой буквы, следует нажать сочетание клавиш Ctrl+G, на экране появится греческое написание буквы, заглавной или строчной в зависимости от того, в верхнем или в нижнем регистре был набран ее латинский аналог.
Греческие буквы и их аналоги (в скобках): α(a), β(b), χ(c), δ(d), ε(e), η(h), γ(g), λ(l), μ(m), ν(n), ω(w), ϕ(f), π(p), ψ(y), ρ(r), σ(s), τ(t), θ(q), ξ(x), ς(z).
2 Расчет линейных электрических цепей синусоидального тока
При расчете линейных электрических цепей синусоидального
тока применяется символический (комплексный) метод, который основан на изображении
синусоидальных функций времени (напряжений 
токов
) комплексными величинами (комплексы
действующих значений 
или комплексные амплитуды 
и 
). Для
определения комплексных напряжений и токов решаются системы линейных комплексных
алгебраических уравнений (СЛКАУ), составленные по законам Кирхгофа, МКТ, МУП.
В MathСad можно выполнять вычисления с комплексными
числами, которые обычно представляются в алгебраическом виде: 
или 
, где
− действительная часть
комплексного числа
, 
– его
мнимая часть, а символы i или j обозначают мнимую единицу,
то есть корень квадратный из –1. В теории цепей мнимая единица обозначается
символом j. Поэтому перед использованием
операций с комплексными числами нужно вначале выбрать символ j для обозначения мнимой единицы,
для этого открываем диалоговое окно “Result Format”, нажимаем “Display Options”
и выбираем Imaginary value j, или можно присвоить j значение
корня квадратного из −1.
Рисунок 2.1 - Диалоговое окно “Result Format”
Чтобы перевести в MathСad комплексное число из показательной в алгебраическую форму достаточно ввести комплексное число в показательной форме и нажать знак =.
Перевод комплексного числа из алгебраической формы в показательную осуществляется
следующим образом: записывают комплексное число в алгебраческой форме 
и, для определения модуля комлексного числа,
вычисляют его абсолютное значение 
, аргумент определяется
по формуле arg(
):
Примечание:
− в MathCad не будем обозначать комплексные величины точкой сверху или подчеркиванием.
− в MathCad значения углов (как аргумента тригонометрических функций, а также, как значение обратных тригонометрических функций), по умолчанию, задаются в радианах. Чтобы перевести значение угла из градусов в радианы, следует значение угла, записанного в градусах, умножить на “deg”:
− чтобы перевести радианы в градусы нужно поделить на “deg”:
0,983 – это значение угла в радианах, соответствующее 56,31градусам.
Преобразовать радианы (
) в
градусы (
) можно так же используя известную пропорцию:
,
отсюда
можно найти угол в радианах (), если задан угол в
градусах():
и
значение угла в градусах () по заданному
значению угла в радианах():
.
Для решения системы линейных комплексных алгебраических уравнений (СЛКАУ) в MathCad применяются те же способы, которые используются
для расчета СЛАУ в линейных электрических цепях постоянного тока, и подробно описанные в разделе 1.
Ниже рассмотрены различные способы решения в MathCad СЛКАУ:
– способ 2.1. Решение с помощью вычислительного блока given–find;
– способ 2. 2. Решение с помощью оператора solve;
– способ 2.3. Решение СЛКАУ с помощью оператора lsolve;
– способ 2.4. Решение путем обращения матрицы коэффициентов.
Задача 2.1. Электрическая цепь (см. рисунок 2.2) содержит синусоидальные источники ЭДС и синусоидальный источник тока:
Параметры
цепи: 
, 
, 
Ом, 
Рисунок 2.2 - Схема цепи синусоидального тока
Требуется выполнить следующее:
− рассчитать комплексные токи во всех ветвях схемы методом контурных токов;
− рассчитать комплексные токи во всех ветвях схемы методом узловых потенциалов.
Расчет комплексных токов в ветвях цепи методом контурных токов
Определим
комплексные сопротивления каждой ветви: 
Нарисуем эквивалентную схему для расчета цепи
синусоидального тока комплексным методом (см. рисунок 2.3). В независимых
контурах цепи введем неизвестные контурные токи 
. Один
контурный ток выберем проходящим через источник тока, тогда этот контурный ток
совпадёт с током источника тока 
.
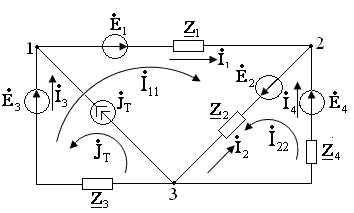
Рисунок 2.3
Для двух неизвестных контурных токов составим уравнения:
(2.1)
Перенесём
в правую часть уравнения, получим:
(2.2)
Комплексные действующие значения ЭДС и комплексное действующее значение тока источника тока равны:
Обозначим:
Подставим в уравнение (2.2), получим:
(
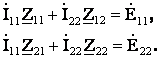2.3)
Уравнение контурных токов в матричной форме имеет вид:
ZkIk=Ek, (2.4)
где Zk= 
– квадратная матрица контурных сопротивлений,
Ek– матрица-столбец контурных ЭДС, учитывающая источники ЭДС и эквивалентные ЭДС от источников тока
Ek=
;
Ik – матрица-столбец контурных токов
Ik=
.
Решая
систему уравнений (2.3), или уравнение контурных токов в матричной форме (2.4)
в MathCad одним из приведенных способов, определим контурные токи: 
(0,703+j1,538)А, 
(-0,465-j1,176)А.
Токи в ветвях представим в виде алгебраической суммы контурных токов:
Расчет комплексных токов методом узловых потенциалов.
Примем потенциал узла 3 электрической цепи (см.
рисунок 2.3) равным нулю: 
и запишем систему
уравнений по методу узловых потенциалов:
(2.5)
где 
,
, 
, 
Обозначим:
Подставим в уравнение (2.5), получим:
(2.6)
Уравнение по методу узловых потенциалов в матричной форме имеет вид:
Yyφy=Jy, (2.7)
где Yy= 
− квадратная матрица узловых проводимостей,
Jy – матрица-столбец узловых
токов: Jy=
; 
– матрица-столбец узловых потенциалов: 
.
Решая уравнения узловых потенциалов в MathCad одним из
ниже приведенных способов, найдём комплексные потенциалы узлов электрической
цепи: 
, 
Токи рассчитаем по закону Ома:
Решение системы контурных (2.3), (2.4) и узловых уравнений (2.6), (2.7) в MathCad различными способами.
Присвоим параметрам цепи и источникам ЭДС и тока числовые значения, заданные в задаче:
Присвоим:
Способ 2.1. Решение СЛКАУ с помощью блока given–find:
− целесообразно задать начальные приближения для всех неизвестных;
− напечатать ключевое слово given (дано);
− ввести уравнения, входящие в систему, ниже ключевого слова given; между левой и правой частями уравнения поставить жирный знак равенства, для его ввода используют сочетание клавиш Ctrl = или выбирают его в панели Boolean (Булевый, Логический);
− напечатать функцию find(x1, x2, x3 …), где x1, x2, x3 … — неизвестные переменные (например, контурные токи или узловые потенциалы) и нажать знак =; можно после find(x1, x2, x3 …) поставить команду float, щелкнуть левой кнопкой мыши по пустому месту, затем нажать знак = (в этом случае можно не задавать начальные приближения для всех неизвестных,) .
Решение системы уравнений по методу контурных токов (2.3).
(0,703+j1,538)А,
(-0,465-j1,176)А.
Решение системы уравнений по методу узловых потенциалов (2.6):
,B; 
,
B
Способ 2.2. Решение СЛКАУ с помощью оператора solve:
− в математическом меню выбрать кнопку с изображением матрицы. Откроется панель Matrix (Матрица) (см. рисунок 1.1), на которой щелкнуть по кнопке с изображением матрицы;
− откроется окно Insert Matrix (диалоговое окно), открыть диалоговое окно можно также нажатием сочетания клавиш. Ctrl+m. В диалоговом окне надо ввести число строк матрицы, равное числу уравнений системы и число столбцов матрицы равное 1 и щелкнуть левой кнопкой мыши по кнопке ОK. На экране появится шаблон матрицы;
− в каждой строке полученной матрицы записать одно уравнение из системы, между левой и правой частями уравнения поставить жирный знак равенства, используя сочетание клавиш Ctrl = или выбрав его в панели Boolean (Булевый, Логический);
− применить к системе уравнений, записанных в виде матрицы оператор solve,
после solve,x1,x2,x3 вставить команду float, записать число значащих цифр и щелкнуть левой кнопкой мыши по пустому месту и нажать знак равенства
Примечание. При решении СЛКАУ с помощью оператора solve получается очень громоздкий промежуточный результат вычислений,и его нецелесообразно приводить в пособии. Решение СЛКАУ предпочтительнее выполнять с помощью оператора (функции) lsolve.
Способ 2.3. Решение СЛКАУ с помощью оператора lsolve:
−
запишем СЛКАУ в матричной форме ZkIk=Ek (МКТ)
или Yyφy=Jy (МУП), Zk и Yy – матрицы контурных сопротивлений 
и,
соответственно, узловых проводимостей 
(i - номер
строки матрицы, а j- номер столбца) при неизвестных переменных контурных токов 
и, соответственно, неизвестных переменных
узловых потенциалов
, Ek, Jy
– матрицы-столбцы, составленные из свободных членов. Ik, φy
– матрицы-столбцы составленные из неизвестных
переменных и ;
−
чтобы присвоить значение переменным Zk или Yy, обозначающим матрицы контурных сопротивлений 
и, соответственно, узловых проводимостей
, запишем сначала «Zk:=» или «Yy:=», а затем вставим матрицы, соответственно, контурных
сопротивлений 
или узловых проводимостей;
− чтобы присвоить значение переменным Ek или Jy, обозначающим матрицы-столбцы свободных членов, запишем сначала «Ek:=» или «Jy:=», а затем вставим соответствующие матрицы-столбцы свободных членов;
−
запишем «Ik:=lsolve(Zk,Ek)» или «φy:=lsolve(Yy,Jy )», где Ik и
φy переменные, обозначающие, соответственно,
матрицы-столбцы неизвестных переменных и ;
− для получения результата нужно напечатать Ik или φy, и нажать знак =.
Решение системы уравнений по методу контурных токов в матричной форме ZkIk=Ek с помощью оператора lsolve:
(0,703+j1,538)А,
(-0,465-j1,176)А.
Решение системы уравнений по методу узловых потенциалов в матричной форме Yyφy=Jy с помощью оператора lsolve:
,B; 
,
B.
Способ 2.4. Решение путем обращения матрицы коэффициентов:
−
запишем СЛКАУ в матричной форме ZkIk=Ek (МКТ)
или Yyφy=Jy (МУП), где Zk и Yy – матрицы контурных сопротивлений 
и,
соответственно, узловых проводимостей (i - номер
строки матрицы, а j- номер столбца) при неизвестных переменных и ; Ek, Jy
– матрицы-столбцы, составленные из свободных членов, Ik, φy
– матрицы-столбцы составленные из неизвестных
переменных и ;
− решим СЛКАУ в матричной форме ZkIk=Ek или Yyφy=Jy путем обращения матрицы коэффициентов Ik= Zk-1 Ek или φy= Yy-1 Jy
Решение системы уравнений по методу контурных токов в матричной форме ZkIk=Ek:
(0,703+j1,538)А,
(-0,465-j1,176)А.
Решение системы уравнений по методу узловых потенциалов в матричной форме Yyφy=Jy:
,B; 
,
B.
Примечание: для решения СЛКАУ в MathCad выбирается произвольно один из предлагаемых способов.
3 Построение графиков функций в Mathcad
При анализе установившихся и переходных режимов в электрических цепях большое значение имеет графическое представление результатов расчетов. Наглядность графиков токов и напряжений в электрических цепях позволяет всесторонне исследовать и интерпретировать полученные результаты.
Для построения графиков в MathCad используются соответствующие шаблоны, перечень которых содержит подменю График (Graph) в пункте главного меню Вставка (Insert) или панель Графики (Graph) — вставка шаблонов графиков (см. рисунок 3.1).
Рисунок 3.1 - Шаблоны для построения графиков и панель «Графики (Graph)»
3.1 Построение двумерных графиков функций, заданных аналитическими выражениями
3.1.1 Ввести аналитическое выражение функции, например:
3.1.2 Задать диапазон значений аргумента, например:
.
Диапазон изменения аргумента состоит из 3-х значений: начальное, второе и конечное. В приведенном примере 0 − начальное значение диапазона аргумента, 0,0001− второе значение диапазона аргумента (0+0.0001 – начальное значение диапазона плюс шаг), 0.02 – конечное значение диапазона аргумента. Многоточие вводится с клавиатуры нажатием кнопки: точка с запятой (язык английский).
3.1.3 Установить курсор (крестик) в то место, где надо построить график.
3.1.4 В подменю График (Graph) или на
математической панели щелкнуть по кнопке 
(см. рисунок 3.1).
3.1.5 На месте курсора появляется шаблон графика (см рисунок 3.2, а)
3.1.6 В шаблоне графика ввести на оси абсцисс имя аргумента, на оси ординат имя функции (см. рисунок 3.2, б).
а б
Рисунок 3.2 - Шаблон графика
3.1.7 Щелкнуть мышью вне шаблона графика. Появится график, построенный в заданном диапазоне изменения аргумента (см. рисунок 3.3).
Рисунок 3.3 - График функции f(t) в заданном диапазоне значений аргумента
Если график не принимает требуемый вид, нужно изменить шаг, диапазон значений аргумента и функции.
3.1.8 Если диапазон значений аргумента предварительно не задан, то предельные значения аргумента (на оси абсцисс) и предельные значения функции (на оси ординат) можно задать путем заполнения крайних меток на шаблоне графика, которые задают масштаб графика (см. рисунок 3.2, б). После заполнения предельных значений аргумента и функции (см. рисунок 3.4, а), щелкнуть мышью вне шаблона графика. Появится график, построенный для заданных предельных значений аргумента и функции (см. рисунок 3.4, б).
Рисунок 3.4 - График функции f(t) для заданных предельных значений аргумента и функции
3.1.9 Если диапазон значений аргумента предварительно не задан или не заполнены крайние метки на шаблоне графика, то график будет построен по умолчанию в диапазоне значений аргумента от −10 до 10, а предельные значения на оси ординат будут установлены больше максимальных расчетных значений функции (см. рисунок 3.5, а).
Рисунок 3.5- График функции f(t), построенный по умолчанию в диапазоне значений от −10 до 10
3.1.10 Диапазон значений аргумента, установленный по умолчанию от −10 до 10 в большинстве случаев не отражает график в требуемом виде, поэтому предельные значения аргумента по оси абсцисс и предельные значения функции по оси ординат изменяются вручную. Для этого график выделяют, щелкнув по графику мышью (см. рисунок 3.5, б).
3.1.11 На выделенном графике заменяют числа −10, например, на 0, а 10 на 0,02. Предельные значения на оси ординат устанавливают, например, − 35, 35 (см. рисунок 3.6, а). После установки нужных интервалов изменения аргумента и функции, щелкают мышью вне шалона графика. Появится график функции f(t), построенный в требуемом диапазоне значений аргумента (см. рисунок 3.6, б).
Рисунок 3.6 - График функции f(t)
3.2 Построение в одном шаблоне графиков нескольких функций
3.2.1 Ввести аналитические выражения функций (см. рисунок 3.7).
Рисунок 3.7 - График функций f1(t) и f2(t)
3.2.2 Набрать на оси ординат имя первой функции, затем установить синий уголок курсора в конце имени функции и нажать клавишу «запятая» (язык английский), на следующей строке появится место ввода (черный квадратик), в которое нужно вписать имя второй функции и так далее, если число функций больше двух. Диапазон значений аргумента и предельные значения функций устанавливаются так же, как написано ранее (см. рисунок 3.7).
3.2.3 Если две функции зависят от разных аргументов, то на оси абсцисс вводят через запятую два аргумента, а на оси ординат вводят, через запятую, имена функций. В этом случае график первой функции будет построен по первому аргументу, график второй функции – по второму аргументу (см. рисунок 3.8).
Рисунок 3.8 - График функций f1(x) и f2(y)
3.3 Построение графиков кусочно-непрерывных функций
Кусочно-непрерывная функция имеет различные аналитические выражения для различных интервалов значений аргумента, как, например, при расчете переходных процессов с помощью интеграла Дюамеля, или при построении ФЧХ по спектральному методу (см. примеры 3.6.4 и 3.6.6). Алгоритм построения графиков кусочно-непрерывных функций приведен ниже
3.3.1 Ввести имя функции, затем оператор присваивания 
.
3.3.2 Щелкнуть по кнопке «Add Line (Добавить строку программы) на панели «Программирование»» (см. рисунок 3.9), появится прямая линия и две строки, на каждой строке имеется место ввода (черный квадратик), в которые записываются аналитические выражения функции. Если число интервалов значений аргумента, для которых функция имеет разные выражения, больше двух, то по кнопке «Add Line» нужно щелкнуть два и более раз.
3.3.3 После аналитического выражения функции записывается оператор «if», который можно ввести с клавиатуры или с панели «Программирование»
3.3.4 После оператора «if» записывается интервал значений аргумента, для которого функция имеет соответствующее аналитическое выражение.
Дальнейшее построение графика такое же, как было описано выше (см. рисунок 3.10).
Рисунок 3.9 - Панель «Программирование»
Рисунок 3.10
- График кусочно-непрерывной функции 
3.4 Форматирование графиков
3.4.1 Для форматирования графика, нужно сделать двойной щелчок по полю графика, откроется окно форматирования, вверху которого расположены названия четырёх вкладок (см. рисунок 3.11).
3.4.2 X-Y Axes – отформатировать оси координат:
− Log Scale – представить численные значения на осях в логарифмической шкале. Если этот пункт не помечен, то численные значения наносятся в равномерной шкале.
− Grid Lines (линии сетки) – нанести сетку линий;
− Numbered (пронумеровать) – нанести численные значения для каждой линии сетки;
− Autoscale (автомасштаб) – автоматический выбор предельных численных значений на осях.
Рисунок 3.11 - Окно форматирования графика
(открыта вкладка X-Y Axes)
− Show Markers– нанести метки на графике. Если отметить «флажком» этот пункт подменю, на каждой оси появятся два места ввода, в которые можно вписать численные значения или одно число, или буквенное обозначение констант, а можно ничего не вписывать. На графике появятся горизонтальные и/или вертикальные пунктирные линии, соответствующие указанным значениям (см. рисунок 3.12);
− Auto Grid (автосетка) – автоматический выбор числа линий сетки. Если этот пункт подменю не отмечен, то можно задать нужное число линий сетки с помощью Number of Grids (см. рисунок 3.12, число линий сетки равно 4);
− Группа Axes Style (стиль осей) − задает стиль отображения координатных осей;
- Boxed (рамка) − оси в виде прямоугольника, ось абсцисс проведена по нижнему краю графика (см. рисунок 3.12);
- Crossed (визир) − оси в виде креста, ось абсцисс проведена через ноль ординаты;
- None − отсутствие осей;
- Equal Scales − устанавливает одинаковый масштаб по координатным осям.
Чтобы отформатировать оси координат, нужно щелкнуть мышью один раз по требуемому пункту подменю (поставить «птичку») и щелкнуть по кнопкам «Применить» и «ОК».
Рисунок 3.12 - Пример форматирования графика
3.4.3 Traces (линии графика) – позволяет форматировать графики функций, в этой вкладке представлены пункты (см. рисунок 3.13, 3.14):
− Legend Label ((метка легенды) – выбор графика функции;
− Symbol (символ) – выбор символа для отметки расчетных точек на графике. Список символов раскрывается в нижней части столбца Symbol: none - без отметки, x's - наклонный крестик, +'s - прямой крестик, box - квадрат, dmnd – ромб, o's – окружность;
− Line –установка типа линий графика. Список типа линий раскрывается в нижней части столбца Line: solid – сплошная линия, dot –точечная линия, dash –пунктирная линия, dadot – штрих-пунктирная линия;
− Color (цвет) – выбор цвета линий графика и базовых точек. В нижней части столбца Color раскрывается список цветов: red – красный, blu – синий; grn – зеленый, mag – сиреневый, cya – голубой, brn – коричневый, blk – черный, wht – белый;
− Type (тип) – установка типа графика. Список типа линий графика раскрывается в нижней части столбца Type: lines (линия) – построение графика линиями, points (точки) – построение графика точками, error (интервалы) – построение вертикальными черточками с оценкой интервала погрешностей, bar (столбец) – построение в виде столбцов гистограммы, step (ступенька) – построение графика ступенчатой линией, draw (протяжка) – построение графика протяжкой от точки до точки, stem (основа) – построение вертикальными черточками.
Рисунок 3.13 - Вкладка Traces
Рисунок 3.14 - Пример форматирования линий графиков
с помощью вкладки Traces
Для установки типа линий графика предпочтительнее использовать подпрограмму Line, при этом в подпрограмме Type должен быть установлен тип линии lines. Если использовать одновременно подпрограммы Line и Type, приоритет отдается подпрограмме Type .
− Weight (толщина) – установка толщины линий графика. В нижней части столбца Weight раскрывается список в виде цифр, позволяющий установить нужную толщину линии графика.
Чтобы отформатировать линии графика, нужно выбрать нужный параметр, щелкнуть мышью один раз по требуемому пункту и щелкнуть по кнопкам «Применить» и «ОК».
3.4.4 Labels (надписи) – позволяет вписать заголовок графика и названия аргумента и функции. В окне Title записывают текст заголовка, выбирают положение заголовка графика: вверху (отметить Above), или внизу (отметить Below) и отмечают «флажком» Show Title. Названия аргумента и функции (Axis Label) вписывают в окна X- Axis (название аргумента), Y- Axis (название функции) (см. рисунок 3.15).
Рисунок 3.15 - Пример применения вкладки Labels
3.4.5 Defaults – вернуться к виду графика, принятому по умолчанию (Change to default), или использовать по умолчанию для всех графиков данного документа (Use for default) сделанные изменения на графике (см. рисунок 3.16).
3.4.6 X-Y Trace (трассировка) – эта команда позволяет применить специальный графический курсор в виде двух пунктирных линий, пересекающих окно графика. Команду X-Y Trace выбирают в меню Format (Форматирование) подменю Graph (График, Трейс…), график должен быть выделен. При установке флажка Track Data Points (перемещение по точкам данных) графический курсор в виде двух пунктирных линий автоматически перемещается по кривой графика. Устанавливая курсор в любую точку кривой графика, можно определить её координату (см. рисунок 3.17).
Рисунок 3.16 - Вкладка Defaults
Рисунок 3.17 - Определение координаты точки кривой графика
3.5 Построение двумерных графиков функций, заданных таблично
При дискретном изменении аргумента, связь между аргументом и функцией задается в виде таблицы. Табличные значения функции могут быть получены как расчетным путем, так и экспериментально. Например, функция дискретного аргумента задана в виде таблицы 3.5.1. Для построения графиков функций, заданных таблично, аргумент и функция записываются в виде матриц-столбцов с N строками, для приведенного примера N=5.
Таблица 3.5.1 - Функция у(х) задана таблично.
|
х |
0 |
3 |
6 |
9 |
12 |
|
у |
0 |
8 |
5 |
7 |
20 |
Если диапазон изменений аргумента (ось абсцисс) и функции (ось ординат) не указывать, то предельные значения аргумента и функции определяются их минимальными и максимальными значениями. На полученном графике (см. рисунок 3.18,а) точки соединяются по умолчанию, отрезками прямой. Для построения графика без линейной интерполяции значений во вкладке Traces (линии графика) в пункте Type (установка типа графика) выбирают тип stem (построение вертикальными черточками) и в пункте Symbol (символ) выбирают символ для отметки расчетных точек на графике, например, +'s − прямой крестик (см. рисунок 3.18,б и пример 3.6.2)
Рисунок 3.18 - Построение графика функции, заданной таблично
3.6 Примеры построения графиков
Пример 3.6.1. Построение графиков токов и напряжений в цепи синусоидального тока.
В линейной электрической цепи при гармонических
воздействиях токи в ветвях и напряжения на любом участке цепи изменяются по
синусоидальному закону. Построим, графики тока 
и напряжения
, где ω=2πf, f=50Гц,
начальные фазы тока и напряжения заданы в градусах. Для правильного
построения графиков в MathСad после значений начальных фаз, заданных в
градусах, нужно напечатать deg
или перевести градусы в радианы. Выберем в качестве аргумента время t. Диапазон значений аргумента выберем
от 0 до 2Т, где Т=1/f=0,02с – период. Предельные значения
по оси ординат выберем немного больше амплитудных значений тока и напряжения
(см. рисунок 3.19). Можно выбрать в качестве аргумента ωt, диапазон значений аргумента от 0 до
4π – что соответствует двум периодам (см. рисунок 3.20).
Рисунок 3.19 - Графики синусоидальных тока и напряжения
(аргумент – время t)
Рисунок 3.20 - Графики синусоидальных тока и напряжения
(аргумент – ωt)
Пример 3.6.2. Построение графиков токов и напряжений в электрической цепи несинусоидального периодического тока.
В линейной электрической цепи с несинусоидальными периодическими
источниками питания токи в ветвях и напряжения на любом участке цепи также будут несинусоидальными периодическими функциями времени. Несинусоидальные периодические токи и напряжения могут быть представлены тригонометрическим рядом Фурье:
.
Построим график мгновенного несинусоидального периодического тока:
, 
= 0,2026 А – постоянная составляющая тока;
А − первая гармоника тока;
А – вторая гармоника тока.
Обязательно должны быть построены графики отдельных гармоник и график несинусоидального периодического тока, который получается суммированием графиков отдельных гармоник (см. пункт 3.2 Построение в одном шаблоне графиков нескольких функций). При построении графиков выберем в качестве аргумента ωt, диапазон значений аргумента от 0 до 4π. Предельные значения тока по оси ординат выберем немного больше максимального значения тока i(t). График тока каждой гармоники и суммарный график несинусоидального периодического тока отформатируем, используя вкладку Traces (линии графика), пункт Line –установка типа линий графика (см. 3.4.3 Traces и см. рисунок 3.21,а).
Рисунок 3.21,а - График несинусоидального периодического тока
Построим амплидутно-частотный и фазо-частотный спектры (см. пункт 3.5). Зависимость от частоты амплитудных значений гармонических составляющих несинусоидального периодического тока задана в виде таблицы 3.2, где основная частота принята равной 400 рад/с.
Таблица 3.2 - Амплидутно-частотный спектр несинусоидального тока.
|
ω рад/с |
0 |
400 |
2·400 |
|
Imk, А |
0,2026 |
0,504 |
0,147 |
Рисунок 3.21,б - Амплидутно-частотный спектр
Рисунок 3.21, в - Фазо-частотный спектр
Зависимость от частоты начальных фаз гармонических составляющих задана в виде таблицы 3.3.
Таблица 3.3 - Фазо-частотный спектр несинусоидального тока
|
ω рад/с |
0 |
400 |
2·400 |
|
φk, град. |
0 |
86,7 |
42,5 |
Графики амплидутно-частотного спектра и фазо-частотного спектра несинусоидального тока, построены в MathСad и отредактированы в Paint (см. рисунки 3.21, б, в).
Пример 3.6.3. Построение графиков переходных токов и напряжений.
Построим графики токов и напряжений в
переходном режиме в цепях второго порядка. Выражение свободной составляющей (тока
или напряжения) 
зависит от вида корней
характеристического уравнения:
для вещественных и
различных корней 
< 0 и 
< 0
,
для вещественных и равных
корней ==р
< 0
,
для комплексно-сопряжённых
корней 
(α – коэффициент затухания, ωСВ –
частота свободных колебаний)
.
а) Построение графиков переходных тока и напряжения в цепях второго порядка при постоянном источнике питания для случая, когда корни характеристического уравнения вещественные и различные:
−
переходное напряжение на емкости,
− принужденное
напряжение на емкости; 
− свободное
напряжение на емкости;
−
переходный ток в емкости.
При построении графиков диапазон значений аргумента выбираем от 0 до 5τmах, где τmах=1/500 с=0,002 с –максимальное значение постоянной времени цепи. На рисунке 3.22 показан график переходного тока, предельные значения ординаты выбраны больше максимальных значений тока.
На рисунке 3.23 показано построение в одном шаблоне графиков принужденного, свободного и переходного напряжения на емкости (см. пункт 3.2 Построение в одном шаблоне графиков нескольких функций), предельные значения ординаты выбраны больше максимальных значений напряжений. Графики напряжений и тока отформатированы с использованием вкладки Traces, .
Рисунок 3.22 - Переходный ток в емкости
Рисунок 3.23 - Переходное напряжение на емкости
б) Построение графиков переходных тока и напряжения в цепях второго порядка при постоянном источнике питания для случая, когда корни характеристического уравнения комплексно-сопряженные.
Рисунок 3.24 - Переходный ток в емкости
Рисунок 3.25 - Переходное напряжение на емкости
Ток 
и сводное напряжение 
на емкости изменяются
по гармоническому закону:
− переходный ток в емкости;
−
переходное напряжение на емкости;
− принужденное
напряжение на емкости;
−
свободное напряжение на емкости.
При построении графиков диапазон значений аргумента выбираем от 0 до 5/α, где α=1000 – коэффициент затухания. На рисунке 3.24 показан график переходного тока на емкости, на рисунке 3.25 показано построение графиков принужденного, свободного и переходного напряжения на емкости.
Пример 3.6.4. Интеграл Дюамеля. Построение графиков переходного тока и переходного напряжения.
Пусть электрическая цепь (см. рисунок 3.26),
параметры которой равны: 
подключается
к источнику напряжения 
с максимальным значениями UM=20 В длительностью tu=4мс
(см.рисунок 3.27).
Рисунок 3.26 - Электрическая схема Рисунок 3.27 - Напряжение источника
Ток 
и напряжение
на индуктивности 
были определены с помощью
интеграла Дюамеля, и представляют собой кусочно-непрерывные функции времени:
в
интервале 
;
=
в интервале 
.
в
интервале 
;
=
в интервале 
.
Рисунок 3.28 - График тока в индуктивности
Рисунок 3.29 - График напряжения на индуктивности
Построение в MathСad
графиков тока 
и напряжения показано на
рисунках 3.28 и 3.29. (см. пункт 3.3
Построение графиков кусочно-непрерывных функций).
Как видно из графика (см.
рисунок 3.28), ток в момент времени t=tu скачком не изменяется (согласно закону коммутации), в то время как напряжение источника в этот момент
времени уменьшается скачком от 
до 0. Как
видно из графика (см.
рисунок 3.29), напряжение в
момент времени t=tu изменяется
скачком. Диапазон значений аргумента
выбираем от 0 до 2∙tu.(здесь tu=0,004с). Предельные значения ординат принимаем
немногим больше максимальных (по абсолютной величине) значений,
соответственно, тока и напряжения .
Пример 3.6.5. Построение графиков амплитудно-частотных характеристик (АЧХ) и фазо-частотных характеристик (ФЧХ) передаточных функций электрической цепи.
Для
электрической цепи (см. рисунок 3.30) с параметрами
комплексная передаточная функция цепи по напряжению
, АЧХ 
и ФЧХ 
имеют вид:
АЧХ: 
ФЧХ: 
Рисунок 3.30 - Электрическая схема
На рисунках 3.31, 3.32 показаны графики
АЧХ и ФЧХ, построенные в MathCad.
Диапазон значений аргумента ω выбран от 0 до 4 ωГР (где
ωГР определено из условия
(ω/10000)=1). Диапазон значений ординаты для АЧХ выбран от 0 до 0.4, для ФЧХ – от 2
радиан (максимальное значение ФЧХ =
π/2 для частоты ω = 0) до 0. Для
выбора предельных значений ординаты при построении графика АЧХ определим
значения для частот ω = 0 и ω =
∞: 
,
.Для
выбора предельных значений ординаты при построении графика ФЧХ определим
значения для частоты ω = 0 и ω =
∞: 
,
.
Рисунок 3.31 - График АЧХ
Рисунок 3.32 - График ФЧХ
Пример 3.6.6 Спектральный метод. Построение графиков АЧХ и ФЧХ спектров непериодических входных воздействий
Построим графики АЧХ, ФЧХ спектров
непериодических входных воздействий 
в виде прямоугольного
видеоимпульса с амплитудой 
и длительностью
, t0=0.4мс (см. рисунки 3.33, 3.34, 3.35).
Рисунок 3.33 Рисунок 3.34 Рисунок 3.35
а) Спектр 
, АЧХ и ФЧХ для
видеоимпульса (см. рисунок 3.33) имеют вид:
, АЧХ: 
,
0 ,
если 
,
ФЧХ: 
π , если 
.
Построение графика АЧХ
показано на рисунке 3.36. Диапазон
значений аргумента выбран от ω = 0 до ω = 10π/tu (значение частоты ω = 10π/tu
соответствует значению аргумента
синуса 
). Диапазон значений ординаты выбран от =0 до > tuU.
Рисунок 3.36 - График АЧХ входного воздействия
Построение графика ФЧХ φ(ω) для входного воздействия показано на рисунке 3.37. Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ. Диапазон значений ординаты φ(ω) выбран от φ(ω)=0 до φ(ω)=4рад. Алгоритм построения графика ФЧХ φ(ω) такой же, как построение графика кусочно-непрерывной функции (пункт 3.3).
Рисунок 3.37- График ФЧХ входного воздействия φ(ω)
б) Спектр , АЧХ и ФЧХ для
видеоимпульса (см. рисунок 3.34) имеют вид:
,
АЧХ
,
 |
, если 
,
ФЧХ
+ π
, если 
.
График АЧХ показан на
рисунке 3.36, т.е. имеет такой же вид, как для входного воздействия (см.
рисунок 3.33).Построение графика ФЧХ φ(ω) входного воздействия показано на рисунке 3.38.
Рисунок 3.38 - График ФЧХ входного воздействия φ(ω)
Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ, от ω = 0 до ω = 10π/tu.
При построении графика ФЧХ желательно, чтобы угол φ(ω) не превышал π. В связи с этим рекомендуется применить функцию mod(x, y) − остаток от деления х на у, результат имеет тот же знак, что и х. Для случая построения графика ФЧХ: mod(φ(ω), π). Диапазон значений ординаты φ(ω) выбран от φ(ω)=0 до φ(ω)=− 4рад.
в) Спектр , АЧХ
и ФЧХ для видеоимпульса (см. рисунок 3.35)
имеют вид:
,
АЧХ
,
 |
, если ,
ФЧХ
+ π
, если 
.
Рисунок 3.39 - График ФЧХ входного воздействия φ(ω)
График АЧХ показан на
рисунке 3.36, т.е. имеет такой же вид, как для входного воздействия (см.
рисунок 3.33). Построение графика ФЧХ φ(ω)
входного воздействия показано на рисунке 3.39.
Пример 3.6.7 Спектральный метод. Построение графиков АЧХ и ФЧХ спектров реакции цепи.
а) б)
Рисунок 3.40 - Схемы электрической цепи
Построим графики АЧХ и ФЧХ для спектральной плотности
напряжения на индуктивности 
, если электрическая
цепь (см. рисунок 3.40), параметры которой 
подключена к источнику непериодического
напряжения u(t) в виде прямоугольного видеоимпульса с амплитудой 
и длительностью 
(см.
рисунок 3.34).
Спектральная плотность напряжения на индуктивности
определяется по формуле: 
, где 
− комплексная передаточная функция
цепи по напряжению (см. пример 3.6.5), АЧХ и ФЧХ которой равны: 
, 
− спектр
входного напряжения (см. пример 3.6.6), АЧХ и ФЧХ которого равны: 
,
, если 
+ π , если 
.
АЧХ напряжения на индуктивности определим как
произведение АЧХ комплексной передаточной функции
на
АЧХ входного напряжения 
:
ФЧХ напряжения
на индуктивности определим как сумму ФЧХ комплексной передаточной функции 
и ФЧХ входного напряжения 
:
, если 
,
+ π ,
если 
.
Построение
графика АЧХ 
показано на рисунке 3.41. Диапазон
значений аргумента (частоты ω) выбран такой же, как и при построении графика
АЧХ входного напряжения: от ω = 0 до ω = 10π/tu. Диапазон значений ординаты выбран от 0 до 0,0015 (максимальное
значение примерно равно 0,00117 В).
Рисунок 3.41- График АЧХ реакции цепи
Рисунок 3.42 - График ФЧХ реакции цепи 
Построение графика ФЧХ показано на рисунке 3.42. Диапазон значений аргумента (частоты ω) выбран такой же, как и при построении графика АЧХ входного напряжения: от ω = 0 до ω = 10π/tu. Диапазон значений ординаты φUL(ω) выбран от 2 рад до − 4рад.
3.7 Построение потенциальных и топографических диаграмм
Пример 3.7.1. Построение потенциальных диаграмм.
Построим
потенциальную диаграмму для электрической цепи постоянного тока (см. рисунок
3.43), параметры которой: Е1=60 В, Е2=20В, R1=50 Ом, R2 = 70Ом, R3=130Ом, R4=100Ом, R5=50Ом, R6=100Ом. Рассчитаем ток I. Выделим
каждый элемент цепи и примем потенциал одной из точек цепи равным нулю,
например, потенциал точки 8: 
. Рассчитаем
потенциалы точек цепи относительно точки 8, потенциал которой принят равным
нулю.
Рисунок 3.43 - Электрическая цепь
Потенциал в каждой точке электрической цепи
представим, как функцию суммы сопротивлений участка цепи от точки нулевого
потенциала до рассматриваемой точки: 
,
где 
Зависимочть потенциалов 
зададим
в виде таблицы 3.4.
Таблица 3.4 - Потенциалы точек электрической цепи
|
Точки цепи |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
RЭКВ,Ом |
0 |
0 |
50 |
120 |
250 |
250 |
350 |
400 |
500 |
|
φ,В |
0 |
60 |
56 |
50,4 |
40 |
20 |
12 |
8 |
0 |
Рисунок 3.44 - Потенциальная диаграмма
Для построения в MathCad потенциальной диаграммы потенциалы φ и суммарные сопротивления участка цепи Rэкв запишем в виде матриц-столбцов с 9 строками. На потенциальной диаграмме точки графика соединяются отрезками прямой (по умолчанию). Точки графика отмечаем, например, окружностями, для этого во вкладке Traces (линии графика) в пункте Symbol (символ) выбираем символ o's – окружность. Для отображения координатных осей в виде прямоугольника (ось абсцисс проведена по нижнему краю графика) во вкладке X-Y Axes, в группе Axes Style отмечаем Boxed(см. рисунок 3.44).
На рисунке 3.45. показана потенциальная диаграмма, отредактированная в Paint. На диаграмме проставлены номера точек схемы и записаны величины сопротивлений, в том порядке, что и при обходе схемы.
Рисунок 3.45 - Потенциальная диаграмма, отредактированная в Paint
Пример 3.7.2. Построение топографических диаграмм, совмещенных с векторными диаграммами токов.
Построим топографическую диаграмму, совмещенную с векторной диаграммой токов для электрической цепи (см. рисунок 3.46). В электрической цепи, параметры которой: R1=35Ом, R2=56Ом, R4=40Ом, XL1=26Ом, XL3=65Ом, XL4=20ОМ, ХС1=60Ом, XС2=40Ом, XС3=35Ом, действуют синусоидальные источники ЭДС:
и синусоидальный
источник тока: 
Для построения топографической диаграммы
выделяем каждый элемент схемы электрической цепи Принимаем потенциал точки 3
равным нулю:
и рассчитаем в MathCad
комплексные потенциалы остальных точек схемы (см. рисунок 3.47). Токи в ветвях
электрической цепи рассчитаны в разделе 2 данного пособия.
Рисунок 3.46 - Электрическая цепь
Рисунок 3.47- Расчет комплексных потенциалов в MathCad
Рисунок 3.48 - К построению топографической диаграммы, совмещенной с векторной диаграммой токов
Обозначим действительные части комплексных потенциалов через Х, мнимые – через У. При построение топографической диаграммы в MathCad действительные Х и мнимые У части комплексных потенциалов записываются в виде матриц-столбцов с N строками. Число строк N равно или больше числа потенциалов выделенных точек схемы, так как некоторые точки (узлы) могут повторяться несколько раз, например, при обходе параллельных ветвей. В рассматриваемой задаче потенциалы узлов 3 и 2 повторяются дважды (при расчете потенциалов в ветвях 2 и 4), следовательно, число строк в матрицах Х
и У будет равно 14 (см. рисунок 3.48). Для
построения векторной диаграммы токов, обозначим через Х1 действительные части
комплексных токов и через У1 мнимые части комплексных токов. Чтобы векторы
токов строились из начала системы координат, каждый ток определяется двумя
парами чисел: 0, 
и 0, 
,
где координаты: 0,0 – определяют начало вектора тока, а координаты , –
определяют его конец ( – действительная часть
комплексного тока, – мнимая часть комплексного
тока.
В Mathcad
действительные Х1 и мнимые У1 части
комплексных токов записываются в виде матриц-столбцов с 10 строками (см.
рисунок 3.48) для четырех токов в ветвях цепи и одного тока источника тока: 
.
Векторная диаграмма токов строится в одном шаблоне с топографической диаграммой, поэтому, чтобы векторы токов были соизмеримы с векторами, изображающими комплексные потенциалы, выбираем масштаб для векторов токов 1:50 (см. рисунок 3.48). После записи Х, Х1 иУ,У1 в виде матриц-столбцов, открываем шаблон двумерного графика (как было описано выше). В шаблоне графика вводим на оси абсцисс (ось действительных чисел) через запятую Х, Х1 и на оси ординат (ось мнимых чисел) вводим через запятую У, У1. Щелкаем мышью вне шаблона графика. Появляется топографическая диаграмма, совмещенная с векторной диаграммой токов (см. рисунок 3.48). Для построения диаграмм можно использовать функцию stack (см. рисунок 3.49).
Рисунок 3.49 - К построению топографической диаграммы, совмещенной с векторной диаграммой токов с помощью функции stack
Точки на топографической диаграмме отмечаем окружностями, для этого во вкладке Traces (линии графика) в пункте Symbol (символ) выбираем символ o's – окружность. Концы векторов токов отмечаем крестиком, для этого во вкладке Traces (линии графика) в пункте Symbol (символ) выбираем символ +'s - прямой крестик. Координатные оси отображаем в виде креста (ось абсцисс проведена через ноль ординаты), для этого во вкладке X-Y Axes, в группе Axes Style отмечаем Crossed. Увеличиваем размер, полученной диаграммы и форматируем, как было описано выше (см. рисунок 3.50).
Внимание! Масштабы по оси абсцисс и оси ординат должны быть одинаковые.
Рисунок 3.50 - Топографическая диаграмма, совмещенная с векторной диаграммой токов, построенная в MathCad
Полученную в MathCad топографическую диаграмму, совмещенную с векторной диаграммой токов нужно отредактировать в Paint. Отметить координатные оси: действительную (ось абсцисс) и мнимую (ось ординат). Обозначить точки на топографической диаграмме, соответствующие точкам на схеме. Проставить векторы напряжений на топографической диаграмме, при этом обратить внимание на направление векторов напряжений на диаграмме: векторы напряжений направлены относительно точек на топографической диаграмме противоположно положительным направлениям напряжений относительно соответствующих точек на схеме (см. рисунок 3.51).
Рисунок 3.51 - Топографическая диаграмма, совмещенная с векторной диаграммой токов, построенная в MathCad и отредактированная в Paint
4 Расчет переходных процессов классическим методом
Исходные данные:
Е=2000 В
С = 100 мкФ
R1=R2=100 Ом
L =1 Гн
Определить ток iR в переходном
режиме.
Рисунок 4.1
При расчете переходных процессов классическим методом ток в переходном режиме в ветви с активным сопротивлением можно представить:
iR = iRпр+ iRсв.
Принужденная составляющая тока iRпр =
=10А.
Для определения корней характеристического уравнения
воспользуемся методом входного сопротивления 
:
(4.1)
В среде MathСad присвоим параметрам цепи заданные в задаче числовые значения.
Выражение (4.1) приведем к виду рациональной дроби, числитель и знаменатель которой являются многочленами относительно p, с помощью оператора «collect», который находится на панели «Символика».
(4.2)
Для нахождения корней p1 и p2 характеристического уравнения приравняем выражения (4.2) к нулю и определим корни с помощью оператора «solve», который находится на панели «Символика» и применяется для решения уравнений в численном или символьном виде. Для ограничения количества значащих единиц следует ввести команду «float» и после запятой указать число значащих цифр, например 4. Чтобы появился результат необходимо щелкнуть левой кнопкой мыши по пустому месту.
Таким образом, корни характеристического уравнения комплексно-сопряженные: p1= –100 + j100 с-1, p2 = –100 – j100 с-1, где α=100 с-1, ωсв=100рад/с.
Для комплексно- сопряженных корней свободная составляющая искомого тока имеет следующий вид:
iRсв= Ае-αt sin(ωсвt + ψ) =Ае-100t sin(100t + ψ). (4.3)
Запишем уравнения искомого тока и его производной:
iR= 10 + Ае-100t sin(100t + ψ) (4.4)
= Ае-100t [-100sin(100t + ψ) +100cos(100t + ψ)].
Запишем систему (4.4) для момента времени t=0:
iR(0) = 10 + Аsinψ (4.5)
(0)
= –100 Аsinψ +100
Асos ψ.
Определим по законам коммутации независимые начальные условия iL(0) и uC(0):
iL(0) = iL(0-)
= 
= 20 А; uC(0) = uC(0-) = 
=2000
В.
Для определения постоянных интегрирования найдем
зависимые начальные условия iR(0) и (0) из законов Киргофа, записанных для момента времени t=0:
iR(0)R2 – uc(0)
=0 (4.6)
iL(0) – iR(0) – ic(0) = 0. (4.7)
Из уравнения (4.6) найдем iR(0)
=
= 20 A.
Из уравнения (4.7) найдем ic(0) = iL(0) – iR(0) = 0.
Перепишем уравнение (4.6) для произвольного момента времени:
iRR2 – 
=0.
Продифференцируем полученное выражение:
.
Перепишем последнее выражение для момента времени t = 0
и выразим 
:
, откуда 
.
Подставим в cистему (4.5) зависимые начальные условия:
20 = 10 + Аsinψ
(4.8)
0 = –100 Аsinψ +100 Асosψ.
Из
(4.8) определим Аsinψ = 10, Асosψ = 10, ψ = arctg
= 450, А = 14,1
Запишем выражение тока в переходном режиме:
iR= 10 + 14,1е-100t sin(100t + 450), А (4.9)
Для построения графика переходного тока iR в среде MathСad в
интервале времени от 0 до t = 5τ рассчитаем время окончания переходного
процесса при t = 5τ = 5
= 5
=0,01 c
. Таким образом, максимальное значение по
оси х равно 0,01с. Для определения наибольшего значения по оси у
рассчитаем значение iR(0) с помощью оператора «substitute» при t=0.
Этот оператор находится на панели «Символика» и применяется для решения
уравнений в численном или символьном виде при заданном значении переменной. Подробно
методика построения графиков приведена в разделе 3 данного пособия.
Рисунок 4.2
5 Расчет переходных процессов операторным методом
Исходные данные:
Е = 125 В
R1= 50 Ом
R2= 200 Ом
R4= 250 Ом
L = 0,01 Гн
С = 5 мкФ
Определить ток iL в переходном режиме.
Для составления эквивалентной операторной схемы определим независимые начальные условия iL(0) и uC(0) по законам коммутации:
iL(0) = iL(0-)
= 
= 0,25 А; uC(0) = uC(0-) = 
= 50
В.
Составим эквивалентную операторную схему:
Рисунок 5.2
Составим уравнения методом контурных токов относительно изображений контурных токов по схеме рисунок 5.2.
(5.1)
В среде MathCad решить систему уравнений (5.1) можно различными способами.
Способ 1. Набрать систему уравнений в шаблоне матрицы, с числом строк - 2 и числом столбцов - 1. Между левой и правой частями уравнений поставить логический знак равенства. Применить к системе уравнений, записанных в виде матрицы, операторы «solve», «explicit», «collect» которые находятся на панели «Символика» и используются для решения системы уравнений в символьном виде относительно заданной переменной.
Способ 2. Решить систему уравнений в матричной форме путем обращения матрицы коэффициентов. Где Z – квадратная матрица контурных сопротивлений; Ek – матрица-столбец контурных ЭДС; Iкк (p) – матрица-столбец контурных токов.
Таким образом:
. (5.2)
Для определения корней характеристического уравнения приравняем знаменатель выражения (5.2) к нулю.
Следовательно один корень р=0, остальные корни определяются из выражения
(5.3)
Решение квадратного уравнения (5.3) дает корни p1 = - 3000 +j4000 c-1;
p2 = - 3000 - j4000 c-1
Для определения оригинала используем следующий вид теоремы разложения:
, (5.4)
,
,
.
Подставив в полученные выражения p1 = - 3000 +j4000 c-1, получим:
.
Подставив рассчитанные значения в теорему разложения (5.4), получим:
(5.5)
Определение корней характеристического уравнения (5.3) и функций входящих в теорему разложения (5.4), (5.5) можно произвести в среде MathСad изложенными выше способами.
При построении графика в среде MathCad
рассчитаем время окончания переходного процесса t = 5τ = 5= 5
=0,0017
c для определения наибольшего значения по оси х.
Для определения порядка значений по оси у рассчитаем значения iL(0) и iLсв(0) с
помощью оператора «substitute» при t=0. Подробно методика построения графиков приведена в
разделе 3 данного пособия.
Рисунок 5.3
6 Расчет переходных процессов с помощью интеграла Дюамеля
На вход цепи (см. рисунок 6.1) с заданными параметрами R1= R3=40 Oм, R2= 20 Oм, L = 10 мГн, U = 20 В, tи = 4 мс подается импульс напряжения u(t) (см. рисунок 6.2). Определить ток i2(t) в переходном режиме.
Рисунок 6.1 Рисунок 6.2
Этап1. Для
определения переходной проводимости 
рассчитываем переходной
процесс при подключении цепи при нулевых начальных условиях i2(0)=0 к источнику единичного постоянного напряжения (см.
рисунок 6.3) и определяем ток i2(t).
Рисунок 6.3
Ток i2 в переходном режиме можно представить в виде i2= i2пр+ i2св.
Определим принужденное значение тока i2:
,
А.
, А.
Для записи свободной составляющей найдем корни характеристического уравнения, составленного для послекоммутационной схемы относительно ветви с индуктивностью:
Таким образом, 
При t=0: 0=0,0125Е+А, откуда, А=-0,0125Е, а значит
.
Следовательно, переходная проводимость 
равна:
Этап 2. Определение тока i2(t) в переходном режиме с помощью интеграла Дюамеля при подключении цепи на импульс напряжения u(t):
Рассчитаем i2(t) в интервале времени 
,
не включая скачка.
,
,
Проверить правильность расчета интеграла Дюамеля в среде MathCad в первом интервале можно с помощью операторов expand и collect.
Рассчитаем i2(t) в интервале времени 
.
Проверить правильность расчета интеграла Дюамеля в среде MathСad во втором интервале можно с помощью операторов expand и collect.
График i2(t) представляет собой кусочно-непрерывную функцию, заданную на первом интервале выражением (6.1) и на втором интервале выражением (6.2). График строится в интервале времени от 0 до 2tu. Для определения порядка значений по оси Y рассчитаем значения i2(tu) для обоих интервалов с помощью оператора «substitute» при t= tu= 0.004c, где i21(t)- значение тока i2(t) в первом интервале, i22(t)- значение тока i2(t) во втором интервале. Подробно методика построения графиков изложена в разделе 3 данного пособия.
Рисунок 6.4
Рисунок 6.5
7 Расчет переходных процессов спектральным методом
На вход цепи (см. рисунок 7.1) с заданными параметрами R1= R3=
=40Oм, R2= 20 Oм, L = 10 мГн, подается
импульс напряжения 
c U =
20 В, 
(см. рисунок 7.2). Определить uL(t) в переходном режиме.
Рисунок 7.1 Рисунок 7.2
Этап 1. Определение спектральной плотности входного сигнала.
Спектральную плотность входного сигнала можно определить с помощью прямого преобразования Фурье:
(7.1)
.
Проверить правильность расчета интеграла Фурье в среде Mathcad можно с помощью оператора в виде стрелки на панели «Вычисление», позволяющего произвести вычисление символически. В полученном выражении второе слагаемое стремится к нулю, поэтому полученный результат соответствует рассчитанному значению (7.1).
Амплитудно-частотная характеристика входного сигнала.
Фазо- частотная характеристика входного сигнала
Построение графиков АЧХ и ФЧХ спектральной плотности входного сигнала в среде MathСad приведено на рисунке 7.3. Подробно методика построения графиков приведена в разделе 3 данного пособия.
Рисунок 7.3
Этап 2. Определение комплексной передаточной функции для напряжения на индуктивности.
Определим спектральную плотность тока 
:
(7.2)
Спектральная плотность тока в ветви с индуктивностью:
. (7.3)
Определим спектральную плотность напряжения на
индуктивности 
:
. (7.4)
Комплексная передаточная функция для напряжения на индуктивности:
. (7.5)
Выражения (7.2) и (7.4) приведем в среде MathСad к
виду рациональной дроби, числитель и знаменатель которой являются многочленами
относительно 
, с помощью оператора «collect»,
который находится на панели «Символика».
Выделим АЧХ и ФЧХ комплексной передаточной функции:
. (7.6)
Построение графиков АЧХ и ФЧХ комплексной передаточной функции для напряжения на индуктивности в среде Mathcad приведено на рисунке 7.4. Подробно методика построения графиков приведена в разделе 3 данного пособия.
Рисунок 7.4
Этап 3. Определение напряжения на индуктивности в функции времени uL(t).
Запишем спектральную плотность напряжения на индуктивности:
. (7.7)
Заменим 
на 
.
(7.8)
Найдем корни характеристического уравнения 
, 
Для определения напряжения на индуктивности в функции времени используем следующий вид теоремы разложения:
, (7.9)
Запишем итоговое выражение напряжения на индуктивности:
(7.10)
Определение корней характеристического уравнения (7.8) и функций входящих в теорему разложения (7.9) можно произвести в среде MathСad изложенными выше способами. Результаты расчета приведены в прямоугольной рамке.
Построение графика напряжения на индуктивности в функции времени
в среде MathСad приведено 
на
рисунке 7.5. Для определения порядка значений по оси X рассчитаем и
наибольшее значение по оси X выбираем
равным наибольшему. Для определения порядка значений по оси Y
рассчитаем значения 
с помощью оператора «substitute» при t= 0.
Подробно методика построения графиков приведена в разделе 3 данного пособия.
Рисунок 7.5
Список литературы
1. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. – 544 с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.-М.: Высшая школа,1981. – 333 с.
3. Основы теории цепей. Учебник для вузов /Г.В.Зевеке и др.- М.: Энергоиздат, 1989. – 528 с.
4. Теория линейных электрических цепей. /Под редакцией И.Г.Кляцкина.-М.: Высшая школа, 1975.
5. Зернов И.В., Карпов В.Г. Теория радиотехнических цепей.-Л.: Энергия, 1972.
6. Шебес М.Р., Каблукова М.В. Задачник теории линейных электрических цепей: Учебное пособие для вузов.-М.: ВШ, 1990.-544 с.
7. Основы теории цепей: Учебник для вузов / В.П.Бакалов и др. -М.: 2000. – 592 с.
8. Попов В.П. Основы теории цепей: Учебник для вузов. - М., 2000. -576 с.
9. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. – т.1. – Санкт-Петербург: Питер, 2003.-463 с.
10. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. – т.2. – Санкт- Петербург: Питер, 2003.-576 с.
11. Жолдыбаева З.И., Зуслина Е.Х. Теория электрических цепей 1. Примеры расчета установившихся процессов в линейных электрических цепях. Учебное пособие. – Алматы: АИЭС, 2009.- 93 с.
12. Жолдыбаева З.И., Зуслина Е.Х. Теория электрических цепей 2. Примеры расчета установившихся и переходных процессов в линейных электрических цепях с сосредоточенными и распределенными параметрами. Учебное пособие. – Алматы: АИЭС, 2011.- 78 с.
13.Дьяконов В. MathCad 2000: учебный курс. -СПб.: Питер, 2001.- 592 с.
14. Кудрявцев Е.М. MathCad 2000 Pro. - М.: ДМК Пресс, 2001.- 576 с.
15. Гурский Д.А. Вычисления в MathCad.-Минск: Новое знание, 2003. 814 с.
16. Макаров Е. Г. MathСad. Учебный курс. - СПб.: Питер, 2009. 384 с.
Содержание
Введение 3
1 Расчет сложных разветвленных электрических цепей постоянного
тока 4
2 Расчет линейных электрических цепей синусоидального тока 15
3 Построение графиков функций в MathCad 25
4 Расчет переходных процессов классическим методом 63
5 Расчет переходных процессов операторным методом 67
6 Расчет переходных процессов с помощью интеграла Дюамеля 72
7 Расчет переходных процессов спектральным методом 77
Список литературы 83