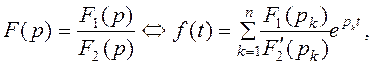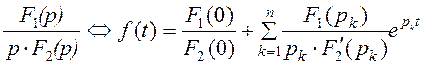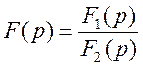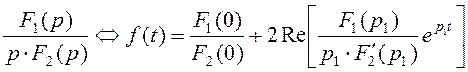МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
Е.Х.Зуслина
А.С.Баймаганов
С.Ю.Креслина
ЗАДАЧИ
ПОВЫШЕННОЙ СЛОЖНОСТИ ДЛЯ ОЛИМПИАД
ПО ТЕОРЕТИЧЕСКИМ ОСНОВАМ ЭЛЕКТРОТЕХНИКИ
И ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Учебное пособие
Алматы 2013
УДК 621.3.71:519.6(275.8)
ББК 31.2 Я73
З-95 Учебное пособие. Е.Х. Зуслина, А.С. Баймаганов, С.Ю. Креслина Задачи повышенной сложности для олимпиад по теоретическим основам электротехники и теории электрических цепей.
АУЭС. Алматы, 2013. – 64 с.
ISBN 978-601-7327-19-4
В пособии рассмотрены задачи повышенной трудности по расчету электрических цепей постоянного тока, расчету электрических цепей синусоидально тока, расчету электрических цепей несинусоидального тока и расчету переходных процессов в линейных электрических цепях. Пособие предназначено для студентов специальностей бакалавриата 5В071900, 5В070400, 5В070300, 5В074600, 5В060200, 5В071600, 5В100200.
Табл.1, ил.45, библиогр. - 12 назв.
ББК 31.2 Я73
РЕЦЕНЗЕНТЫ: КазАТК канд. техн. наук. доц. Б.Н. Хусаинов
АУЭС канд. техн. наук. доц. Л.М. Саламатина
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2012 г.
ISBN 978-601-7327-19-4
©НАО «Алматинский университет энергетики и связи», 2013г.
Введение
Дисциплины «Теория электрических цепей» и «Теоретические основы электротехники» являются базовыми курсами, на которые опираются профилирующие дисциплины всех специальностей АУЭС. Одним из значимых направлений деятельности кафедры «Теоретические основы электротехники» в процессе подготовки специалистов является работа с сильными, способными студентами. С этой целью кафедра ежегодно проводит университетскую Олимпиаду по ТЭЦ и ТОЭ для студентов 2-го курса. Олимпиада позволяет выявить наиболее талантливых учащихся и способствует повышению их интереса к изучению этих дисциплин.
Цель настоящего учебного пособия состоит в оказании помощи студентам при подготовке к олимпиаде по ТЭЦ и ТОЭ.
Как правило, конечной целью анализа электрических цепей является расчет мощностей её компонентов по заданным параметрам схемы. Мощность определяет материал, из которого изготавливается компонент, его габариты и стоимость. Также важно знать значения токов и напряжений элементов электрической цепи для расчета сечения проводников и свойств изоляционных материалов. И наоборот, целью синтеза электрических цепей является расчет параметров схемы по заданным значениям мощностей, токов и напряжений её компонентов. Именно этим целям и посвящены задачи, рассмотренные в настоящем учебном пособии.
Пособие включает задачи повышенной трудности по следующим разделам курсов ТЭЦ и ТОЭ: расчет электрических цепей постоянного тока, расчет электрических цепей синусоидально тока, расчет электрических цепей несинусоидального тока и расчет переходных процессов в линейных электрических цепях. Все задачи даны с подробными решениями, пояснениями, методическими указаниями, приведены основные положения теории и необходимые расчетные формулы.
1 Расчет электрических цепей постоянного тока
1.1 Основные теоретические положения
1.1.1 Методы эквивалентных преобразований.
Замена нескольких последовательно соединенных сопротивлений
одним эквивалентным: 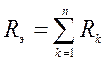 .
.
Напряжение при последовательном соединении распределяется прямо пропорционально этим сопротивлениям:

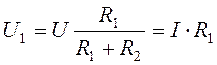 ,
, 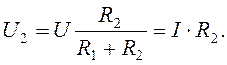
Замена нескольких параллельно соединенных сопротивлений
одним эквивалентным: 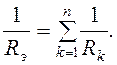 Для двух сопротивлений:
Для двух сопротивлений: 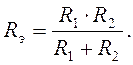
Токи в ветвях с параллельным соединением двух сопротивлений:


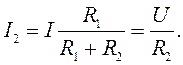
Формулы преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений и наоборот:
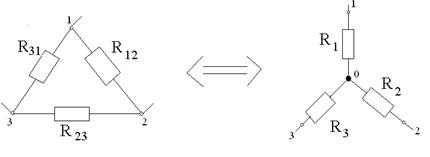
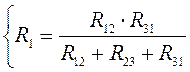 ;
;
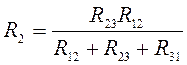 ;
;  ;
;
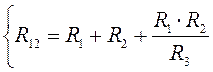 ;
;
 ;
; 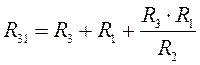 .
.
1.1.2 Методы расчёта разветвленных электрических цепей постоянного тока.
Законы Кирхгофа
Первый закон Кирхгофа: алгебраическая сумма токов в
узле электрической цепи равна нулю: 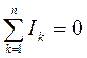 .
.
Второй закон Кирхгофа: алгебраическая сумма
напряжений на элементах любого замкнутого контура электрической цепи, исключая ЭДС,
равна алгебраической сумме ЭДС этого же контура:  . Напряжения на линейных
резисторах заменяют произведением
. Напряжения на линейных
резисторах заменяют произведением ![]() на основании закона Ома для участка цепи.
на основании закона Ома для участка цепи.
Для записи уравнений по второму закону Кирхгофа в систему уравнений выбирают независимые контуры, не содержащие источников тока.
Метод контурных токов
Уравнения по методу контурных токов записываются в виде:
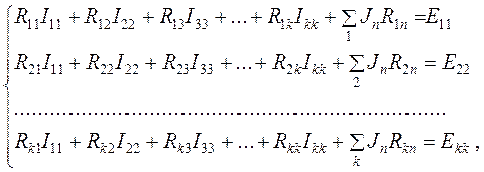
где ![]() – собственное сопротивление контура m,
равное сумме сопротивлений ветвей, входящих в контур m;
– собственное сопротивление контура m,
равное сумме сопротивлений ветвей, входящих в контур m;
![]() –
общее сопротивление контуров m и р, равное сумме сопротивлений
смежных ветвей контуров m и р;
–
общее сопротивление контуров m и р, равное сумме сопротивлений
смежных ветвей контуров m и р;
![]() –
напряжение на сопротивлении
–
напряжение на сопротивлении ![]() общей ветви контура р и контура
n , содержащего источник тока
общей ветви контура р и контура
n , содержащего источник тока ![]() ;
;
![]() –
алгебраическая сумма ЭДС контура р.
–
алгебраическая сумма ЭДС контура р.
Метод узловых потенциалов
Потенциал одного из узлов принимают равным нулю. Для определения потенциалов остальных узлов составляют систему уравнений:
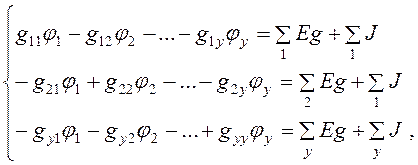
где ![]() – собственная узловая проводимость узла р,
равная сумме проводимостей ветвей, присоединенных к узлу р;
– собственная узловая проводимость узла р,
равная сумме проводимостей ветвей, присоединенных к узлу р;
![]() –
общая узловая проводимость узлов р и m, равная сумме проводимостей
ветвей, соединяющих узлы р и m;
–
общая узловая проводимость узлов р и m, равная сумме проводимостей
ветвей, соединяющих узлы р и m;
![]() –
алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу р
на проводимости этих ветвей;
–
алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу р
на проводимости этих ветвей;
![]() –
алгебраическая сумма токов источников тока, присоединённых к узлу р.
–
алгебраическая сумма токов источников тока, присоединённых к узлу р.
Если электрическая схема содержит ветвь с идеальным источником ЭДС Е и с сопротивлением, равным нулю, то при составлении уравнений по методу узловых потенциалов к нулю приравнивают потенциал одного из узлов, к которому присоединена данная ветвь. Тогда потенциал другого узла этой ветви будет равен +E или –E, в зависимости от направления ЭДС.
1.2 Примеры расчета линейных электрических цепей постоянного тока
Задача 1.2.1 В электрической цепи (см. рисунок 1.1) задано:
1)
![]()
![]() ;
;
2)
показания амперметров: ![]() ;
;
3)
мощность источников ЭДС ![]()
Требуется определить:
1) значения и направления токов в ветвях электрической цепи;
2) значения резисторов R1, R2, R3.

Рисунок 1.1 – Схема электрической цепи
Решение.
Определим направления токов I1, I3.
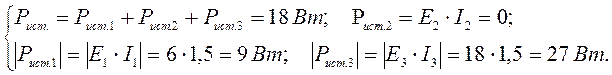
Ток I1 должен быть направлен противоположно направлению Е1, а ток I3 совпадать с направлением Е3, тогда
![]()
Преобразуем треугольник с одинаковыми сопротивлениями R4=R5 =R6 = R = 6Ом в эквивалентную звезду сопротивлений. Сопротивления лучей звезды
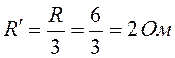 .
.
Получим эквивалентную схему, приведенную на рисунке 1.2.
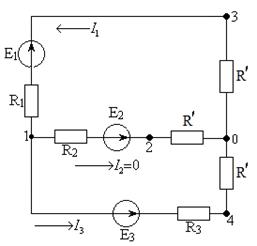
Рисунок 1.2 – Схема эквивалентной электрической цепи
Определим напряжение ![]() . Для простоты положим,
что
. Для простоты положим,
что ![]() . Тогда
. Тогда ![]() ,
, 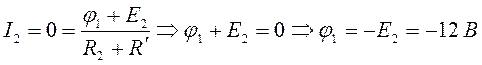 .
.
Это равенство выполняется при любом конечном значении R2
(при ![]() ).
).
Сопротивления R1 и R3 определяют из закона Ома для участка цепи:
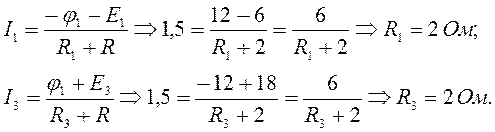
Определим потенциалы ![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Вернемся к исходной схеме и определим токи I4, I5, I6:
 и
направлен от узла 2. к. узлу 3, т.к.
и
направлен от узла 2. к. узлу 3, т.к. ![]() .
.
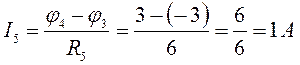 и
направлен от узла 4 к узлу 3
и
направлен от узла 4 к узлу 3 ![]() .
.
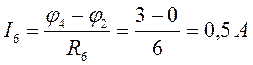 и
направлен от узла 4 к узлу 2
и
направлен от узла 4 к узлу 2 ![]() .
.
Задача 1.2.2 В
электрической цепи (см. рисунок 1.3) заданы значения всех сопротивлений: ![]() ;
; ![]() ;
; ![]() ;
; ![]() , также известно значение напряжения Uab=100В.
, также известно значение напряжения Uab=100В.
Требуется:
1) определить значения токов в ветвях электрической цепи;
2) проверить выполнение баланса мощностей источников и нагрузки.
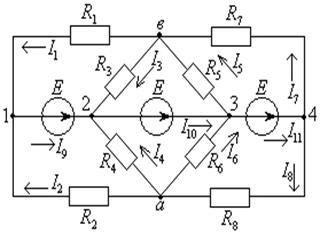
Рисунок 1.3 – Схема электрической цепи
Решение.
Примем φ1=0, тогда ![]() . Составим систему уравнений
методом узловых потенциалов для узлов a и b:
. Составим систему уравнений
методом узловых потенциалов для узлов a и b:
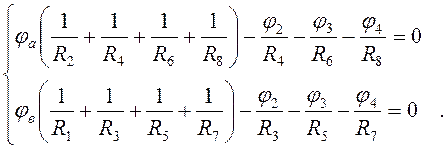 (1.1)
(1.1)
Подставим значения сопротивлений и потенциалов:
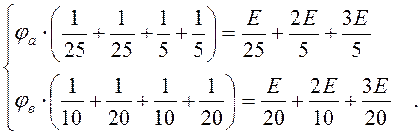 (1.2)
(1.2)
Упростим систему уравнений (1.2). Для этого умножим второе уравнение на 1,6 и вычтем его из первого, получим:
 (1.3)
(1.3)
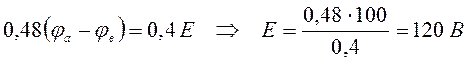 ,
где
,
где ![]() =Uab
=100В.
=Uab
=100В.
Найдем потенциалы узлов a и b, подставив в систему уравнений (1.3) найденное значение ЭДС Е =120В:
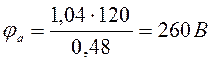 ,
, 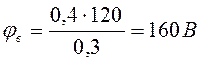 .
.
Потенциалы остальных узлов:
![]() .
.
Определим токи в ветвях схемы по закону Ома для участка цепи:

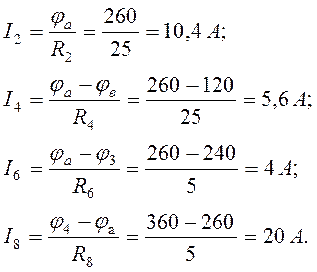
Токи в источниках ЭДС E определим из уравнений, составленных по первому закону Кирхгофа:
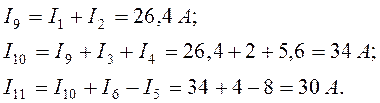
Проверим выполнение уравнения баланса мощностей источников и нагрузки:
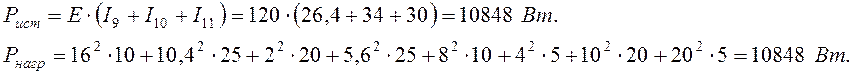
Задача 1.2.3 В электрической цепи (см. рисунок 1.4) заданы
значения всех сопротивлений и ЭДС: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Требуется:
1) определить значения токов в ветвях электрической цепи;
2) проверить выполнение баланса мощностей источников и нагрузки.
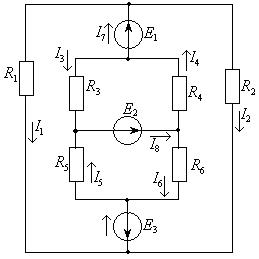
Рисунок 1.4 – Схема электрической цепи
Решение.
Преобразуем схему, заменив параллельно соединенные сопротивления одним сопротивлением, последовательно соединенные источники ЭДС одним:
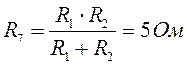 ,
, ![]() .
.
Получим эквивалентную схему, приведенную на рисунке 1.5.
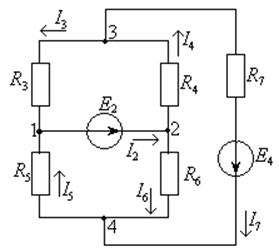
Рисунок 1.5 – Схема эквивалентной электрической цепи
Рассчитаем потенциалы узлов, используя метод узловых потенциалов:
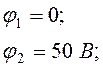

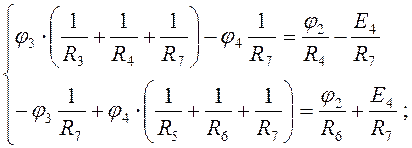
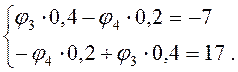
Определители системы уравнений:
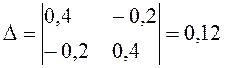 ;
;  ;
; 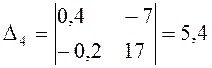 .
.
Потенциалы узлов φ3 и φ4:
 ;
; 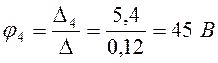 .
.
Токи в ветвях электрической цепи по закону Ома:
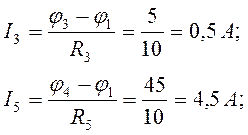
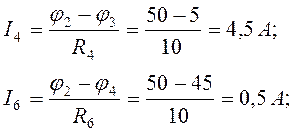
 .
.
Вернувшись к первоначальной схеме, определим оставшиеся токи:
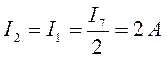 ;
; ![]() .
.
Проверим выполнение баланса мощностей источников и нагрузки:
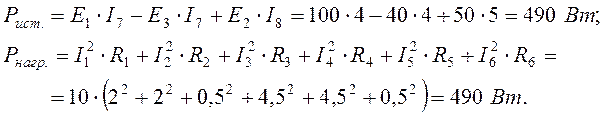
Задача 1.2.4 В электрической цепи (см. рисунок 1.6)
заданы значения резисторов ![]() и показания амперметров
и показания амперметров ![]() и
и ![]() .
.
Требуется определить:
1) значения сопротивления резистора R4 и ЭДС E;
2) значения токов в резисторах R2 и R3;
3) как изменить значение сопротивление резистора R4, чтобы амперметр A1 показал ток, равный 5А.

Рисунок 1.6 – Схема электрической цепи
Решение.
Заменим два параллельно соединенных сопротивления R2 и R3 одним эквивалентным:
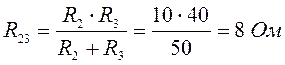 .
.
Определим сопротивление резистора R4, используя показания амперметров, первый закон Кирхгофа и закон Ома:
![]() ;
; ![]() ;
;
 .
.
Определим значение ЭДС из уравнения по второму закону Кирхгофа:
![]() .
.
Определим токи в резисторах R2 и R3 по закону Ома или по формуле разброса тока по двум параллельным ветвям:
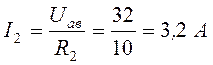 или
или
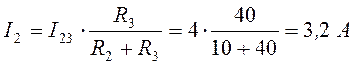 ;
;
 или
или
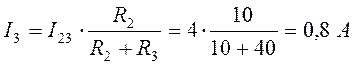 .
.
Определим эквивалентное входное сопротивление схемы, при котором амперметр A1 покажет ток 5А:
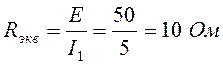 .
.
Выразим эквивалентное входное сопротивление схемы через R4:
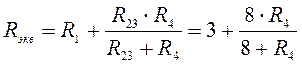 или
или 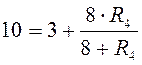 .
.
Рассчитаем значение сопротивления резистора R4:
![]() ,
, ![]() .
.
Задача 1.2.5 В электрической цепи постоянного тока, показанной на рисунке 1.7, заданы значения ЭДС и сопротивления резисторов:
![]()
![]()
Известны также мощности, потребляемые резисторами R1,
R3 и R4, соответственно ![]() и
и ![]() .
.
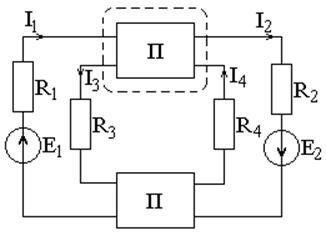
Рисунок 1.7 – Схема электрической цепи
Требуется найти мощность, потребляемую резистором R2, если известно, что в частях схемы, заключенных в прямоугольники, источников нет.
Решение.
По известным значениям мощностей и сопротивлений резисторов можно рассчитать токи в резисторах I1, I3 и I4:
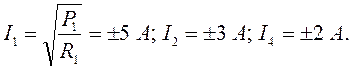
Далее запишем уравнение по первому закону Кирхгофа для показанного на рисунке 1.7 сечения схемы (при указанных направлениях токов):
![]() .
.
Из этого уравнения можно получить следующие возможные значения
тока I2:![]() .
.
Однако ![]() при всех значениях тока I2,
кроме значения I2 = 4A, т.е., только при этом значении
тока I2 выполняется баланс мощностей источников и нагрузки.
при всех значениях тока I2,
кроме значения I2 = 4A, т.е., только при этом значении
тока I2 выполняется баланс мощностей источников и нагрузки.
Таким образом, мощность потребляемая резистором R2:
![]() .
.
2 Расчет электрических цепей синусоидального тока
2.1 Основные теоретические положения
2.1.1 Расчет установившихся режимов линейных электрических цепей синусоидального тока.
Расчет установившихся режимов линейных электрических цепей синусоидального тока аналогичен расчету электрических цепей постоянного тока, с той лишь разницей, что все параметры цепи записывают в комплексной (символической) форме. Использование комплексных чисел для представления синусоидальных функций времени позволяет заменить дифференцирование умножением на jω, а интегрирование – делением на jω, то есть перейти от интегро-дифференциальных уравнений, составленных относительно мгновенных значений, к алгебраическим уравнениям, составленным относительно комплексных значений. Использование комплексных чисел позволило также ввести понятия индуктивного и емкостного реактивных сопротивлений, а следовательно и записать закон Ома для индуктивности и емкости аналогично как и для активного сопротивления.
Первый закон Кирхгофа: алгебраическая сумма
комплексов токов в узле равна нулю: 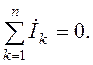
Второй закон Кирхгофа: алгебраическая сумма
комплексов падений напряжений на участках замкнутого контура равна
алгебраической сумме комплексов ЭДС этого же контура: 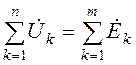 . Напряжения на линейных
элементах схемы заменяют произведением
. Напряжения на линейных
элементах схемы заменяют произведением ![]() на основании закона Ома для участка цепи,
где
на основании закона Ома для участка цепи,
где ![]() – полное
комплексное сопротивление ветви схемы.
– полное
комплексное сопротивление ветви схемы.
Комплексная мощность равна произведению комплекса действующих
значений напряжения на сопряженный комплекс действующего значения тока: ![]() .
. ![]() – активная мощность,
– активная мощность, ![]() – реактивная мощность.
– реактивная мощность.
2.1.2 Резонанс в электрических цепях.
Резонанс – это резкое увеличение амплитуды колебаний напряжения или тока. Различают резонанс напряжений, возникающий в последовательном колебательном LC-контуре, и резонанс токов – в параллельном LC-контуре.
Резонанс возникает в электрической цепи, содержащей индуктивность L и емкость C, при совпадении частоты вынужденных колебаний с частотой свободных колебаний ω0 LC-контура.
Основным признаком, что цепь находится в режиме резонанса, является совпадение по фазе входных напряжения и тока, то есть входное сопротивление или проводимость LC-контура при резонансе является чисто активным.
Резонансную частоту (частоту свободных колебаний ω0) удобно находить для последовательного колебательного LC-контура, приравняв к нулю реактивную составляющую входного сопротивления x=0, а для параллельного – реактивную составляющую входной проводимости b=0.
2.2 Примеры расчета электрических цепей синусоидального тока
Задача 2.2.1 В электрической цепи, схема которой представлена на рисунке 2.1, известны действующие значения: тока I=2A, входного напряжения Uвх=100В, напряжения на катушке индуктивности Uab=173В и напряжения на конденсаторе Ubc=100В.

Рисунок 2.1 – Схема электрической цепи
Требуется определить:
1) комплексные сопротивления катушки индуктивности Zкат. и конденсатора ZC;
2) построить векторную диаграмму напряжений;
3) рассчитать активную и реактивную мощности электрической цепи.
Решение.
Построим векторную диаграмму цепи, начиная с вектора тока, приняв его начальную фазу за ноль. Вектор напряжения на емкости Ubc=100В отстает по фазе от вектора тока на 90º. Вектор напряжения на реальной катушке индуктивности с потерями опережает вектор тока на угол φкат., меньший, чем 90º. Складывая векторы напряжений на емкости и катушке индуктивности, получим вектор входного напряжения. В полученном треугольнике известны все стороны – действующие значения напряжений. Определим углы треугольника (см. рисунок 2.3):
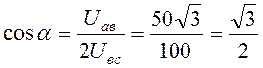 ;
;
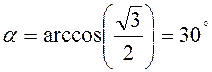 ;
;
![]() ;
;
![]() .
.

Рисунок 2.3 – Векторная диаграмма
Определим значения сопротивлений:
 ;
;
![]() ;
; 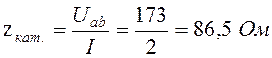 ;
;
![]() .
.
Рассчитываем мощности:
![]()
 ;
;
![]()
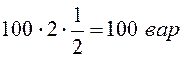 .
.
Задача 2.3.2 В цепи синусоидального тока, показанной на
рисунке 2.4, дано:![]()
![]()
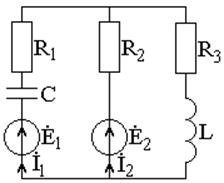
Рисунок 2.4 – Схема электрической цепи
Определить, каким должно быть соотношение амплитуд и сдвиг
фаз между напряжениями синусоидальных источников ![]() и
и ![]() , чтобы оба эти источника вырабатывали
только активную мощность?
, чтобы оба эти источника вырабатывали
только активную мощность?
Решение.
Источники будут вырабатывать только активную мощность, если их напряжения и токи совпадут по фазе. По методу узловых потенциалов:
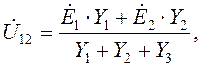
где  .
.
Токи ![]() и
и ![]() определяются по закону Ома для участка
цепи:
определяются по закону Ома для участка
цепи:
![]()
Учитывая, что эти токи должны совпадать по фазе,
соответственно, с ![]() и
и
![]() , можно записать:
, можно записать:
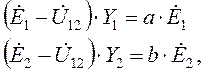
где a и b некоторые действительные числа.
Таким образом, требуемое условие будет выполнено, если
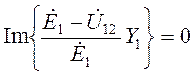 (2.1)
(2.1)
и
 . (2.2)
. (2.2)
Отсюда имеем
 и
и 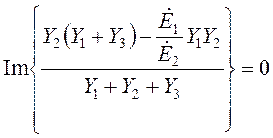 .
.
Обозначим 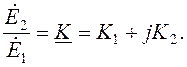 Тогда
Тогда 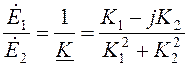 и после подстановки числовых значений
и после подстановки числовых значений ![]() получаем
получаем
![]() и
и
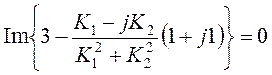 .
.
Отсюда имеем два уравнения
относительно ![]() и
и
![]() :
:
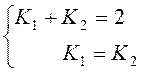
Тогда ![]()
Таким образом, соотношение амплитуд должно равняться ![]() и
и ![]() должна опережать
должна опережать ![]() по фазе на 45°.
по фазе на 45°.
Задача 2.2.3 В трехфазной цепи (см.
рисунок 2.5), соединенной треугольником, задано линейное напряжение и
сопротивления фаз ![]() ,
,
![]() .
.
Требуется определить:
1) фазные и линейные токи;
2) показания ваттметров;
3) активную мощность системы при обрыве линейного провода фазы «А».

Рисунок 2.5 – Схема трехфазной цепи
Решение.
Определяем комплексные фазные напряжения и токи. По найденным фазным токам определяем линейные токи.
Фазные напряжения: ![]() .
.
Фазные токи: ![]() ;
;
![]() ;
;
![]() .
.
Линейные токи: ![]() ;
;
![]() ;
;
![]() .
.
Определяем показания ваттметров:
![]() ;
;
![]() .
.
Строим векторную диаграмму в аварийном режиме при обрыве линейного провода фазы «А».

Рисунок 2.6 – Векторная диаграмма
Из диаграммы определяем напряжение:

Рассчитываем ток и активную мощность в фазе ab, так как только в ней есть активное сопротивление:
 ,
, ![]() .
.
Задача 2.2.4 В схеме, приведенной на рисунке 2.7, ЭДС
![]() ,
, ![]() и
и ![]() образуют симметричный
трехфазный источник напряжения прямой последовательности, а ЭДС
образуют симметричный
трехфазный источник напряжения прямой последовательности, а ЭДС ![]() ,
, ![]() и
и ![]() – симметричный источник обратной последовательности
(т.е.,
– симметричный источник обратной последовательности
(т.е., ![]() ,
, ![]() ).
).
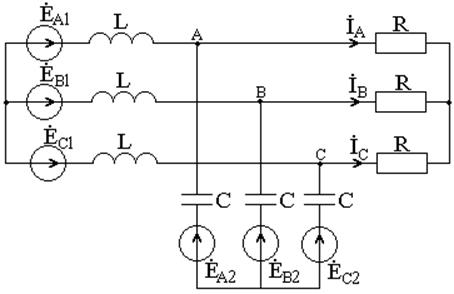
Рисунок 2.7 – Схема трехфазной цепи
Фазные напряжения и частота обоих источников одинаковые, но ![]() отстает по фазе от
отстает по фазе от ![]() на некоторый угол α. Модули всех сопротивлений равны между собой: XL=XC=R.
на некоторый угол α. Модули всех сопротивлений равны между собой: XL=XC=R.
Найдите, какое максимальное и какое минимальное линейное напряжение может быть получено на любой паре из точек A, B и C путем изменения угла сдвига фаз α, если фазное напряжение источников Uф равно 220В. Укажите, также, конкретные значения угла сдвига фаз α, при которых одно (любое) линейное напряжение имеет максимальное и минимальное значения.
Решение.
Общий режим цепи, получающийся в результате наложения двух симметричных режимов прямой и обратной последовательностей, конечно, будет несимметричным, т.е. при определенном значении угла сдвига фаз α модули линейных напряжений UAB, UBC и UCA вообще будут различными. Однако изменением угла сдвига фаз α можно добиться того, что максимальное значение поочередно принимают все три линейные напряжения. Благодаря симметрии всех потребителей эти максимальные (а также минимальные) значения линейных напряжений будут одинаковыми. Поэтому достаточно исследовать только одно линейное напряжение.
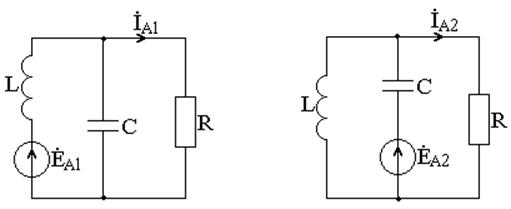
Рисунок 2.8 Рисунок 2.9
Ток фазы А в сопротивлении R можно найти наложением токов, полученных для схем на рисунках 2.8 и 2.9. Допустимо также объединение этих двух схем в одну, так как вследствие симметрии потребителей нулевая последовательность отсутствует. Следовательно, введение нулевого провода допустимо как в частных симметричных режимах, так и в общем режиме.
Из этих схем, с учетом того, что XL=XC=R, получим
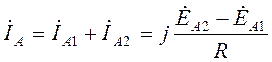 .
Тогда
.
Тогда  .
.
Отсюда можно выразить линейное напряжение ![]() :
:
![]() .
.
Для модуля напряжения ![]() имеем
имеем ![]() .
.
Далее, для строгого нахождения максимума и минимума UAB следовало бы
слагаемые представить в виде: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Затем выделить в
. Затем выделить в ![]() действительную и мнимую части и
возведением этих частей в квадрат выразить квадрат модуля
действительную и мнимую части и
возведением этих частей в квадрат выразить квадрат модуля ![]() . После этого дифференцированием
. После этого дифференцированием
![]() по α можно найти экстремальные значения. Однако все эти
операции получаются сравнительно громоздкими. Поэтому можно ограничиться более
простыми рассуждениями.
по α можно найти экстремальные значения. Однако все эти
операции получаются сравнительно громоздкими. Поэтому можно ограничиться более
простыми рассуждениями.
Представив ![]() в виде
в виде ![]() , видно, что слагаемые, заключенные в
скобки, представляют собой линейные напряжения источников, значения которых не
зависят от α и равны
, видно, что слагаемые, заключенные в
скобки, представляют собой линейные напряжения источников, значения которых не
зависят от α и равны ![]() .
.
Таким образом, путем изменения угла сдвига фаз α можно добиться того, чтобы эти напряжения находились
в противофазе или совпадали по фазе. В первом случае получим максимальное
значение линейного напряжения ![]() , а во втором минимальное
, а во втором минимальное ![]() . Как видно из топографических
диаграмм, приведенных на рисунках 2.10 и 2.11, в первом случае
. Как видно из топографических
диаграмм, приведенных на рисунках 2.10 и 2.11, в первом случае ![]() (см. рисунок 2.10), а
во втором
(см. рисунок 2.10), а
во втором ![]() (см.
рисунок 2.11).
(см.
рисунок 2.11).
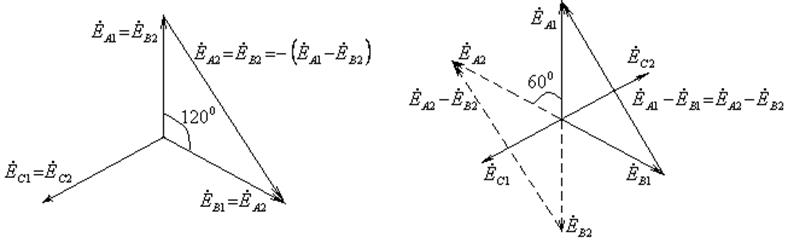 Рисунок 2.10 Рисунок
2.11
Рисунок 2.10 Рисунок
2.11
В результате получим: ![]() .
.
3 Расчет электрических цепей несинусоидального тока
3.1 Основные теоретические положения
Расчёт линейных электрических цепей с несинусоидальными периодическими источниками питания распадается на три этапа:
а) Разложение периодических несинусоидальных функций времени (ЭДС и токов источников тока) в тригонометрический ряд Фурье. Ряд Фурье представляет собой ортогональную многомерную систему координат:
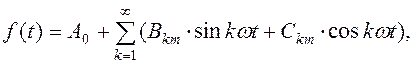
где A0 – постоянная составляющая, Bkm и Ckm – амплитуды синусной и косинусной гармонических составляющих:
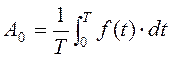 ,
,
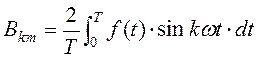 ,
, 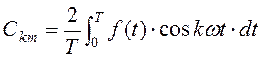 .
.
Первая гармоническая составляющая с циклической частотой ω (при k=1) и периодом T самой несинусоидальной функции называется основной гармоникой, а гармоники, начиная со второй и выше, – высшими гармоническими составляющими.
б) Применение принципа наложения и расчет токов и напряжений на элементах цепи для постоянной составляющей и для каждой из гармонических составляющих в отдельности. Расчет токов и напряжений для каждой гармонической составляющей проводят комплексным методом. При этом необходимо помнить, что индуктивное и емкостное сопротивления для различных гармоник изменяются. Индуктивное сопротивление с ростом частоты увеличивается, а емкостное уменьшается. Индуктивное и емкостное сопротивления k-той гармонической составляющей:
![]() ,
, 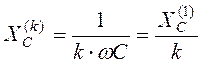 .
.
Недопустимо сложение комплексных токов и напряжений различных гармонических составляющих.
в) Получение итоговых результатов по результатам расчета для постоянной и отдельных гармонических составляющих. Результатами расчетов, как правило, являются мгновенные и действующие значения токов и напряжений, а также активная и полная мощности элементов электрической цепи.
Мгновенные значения токов и напряжений получают как сумму мгновенных значений постоянной и гармонических составляющих, например:
![]() .
.
Действующие значения токов и напряжений получают согласно тождеству Парсеваля (аналог теоремы Пифагора для многомерного ортогонального пространства):
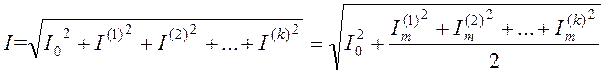 ,
,
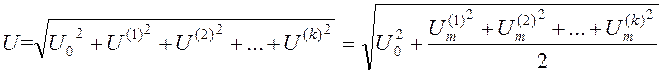 .
.
Активная мощность элемента электрической цепи равна сумме активных мощностей постоянной и гармонических составляющих
![]() , где
, где 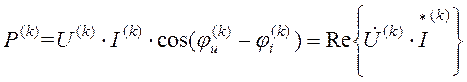
Полная мощность равна произведению действующих значений напряжения и тока элемента электрической цепи
![]() .
.
3.2 Примеры расчета электрических цепей с несинусоидальными ЭДС и токами
Задача 3.2.1 В электрической цепи (см. рисунок 3.1) заданы
мгновенные значения несинусоидальной ЭДС ![]() , значение источника
постоянной ЭДС E0=50В,
активное R=100Ом и реактивные сопротивления
для первой гармоники:
, значение источника
постоянной ЭДС E0=50В,
активное R=100Ом и реактивные сопротивления
для первой гармоники: ![]() ,
, ![]() ,
, ![]() .
.
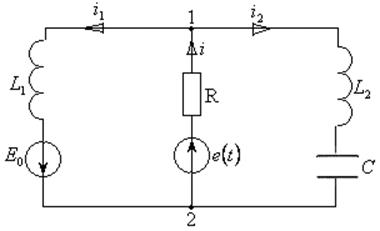
Рисунок 3.1 – Схема электрической цепи
Требуется определить: действующие и мгновенные значения токов в ветвях схемы, действующее и мгновенные значения напряжения на емкости.
Решение.
Расчёт постоянных составляющих токов и напряжения на емкости:
I20=0,
так как 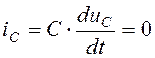 при
uC(t) = const;
при
uC(t) = const;
 ;
;
![]() ,
так как
,
так как ![]() и
и ![]() .
.
Расчёт составляющих токов и напряжения на емкости для первой гармоники:
![]() ;
;
комплексное сопротивление участка «1-2» цепи
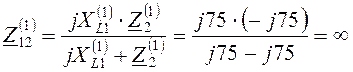 (резонанс
токов на 1-ой гармонике);
(резонанс
токов на 1-ой гармонике);
![]() ,
,
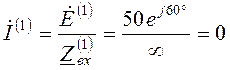 ;
;

Расчёт для второй гармоники:
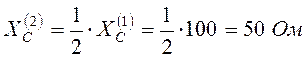 ;
;
![]() ;
;
![]() (резонанс напряжений на 2-ой
гармонике);
(резонанс напряжений на 2-ой
гармонике);
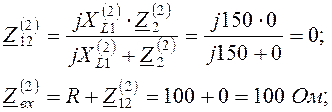
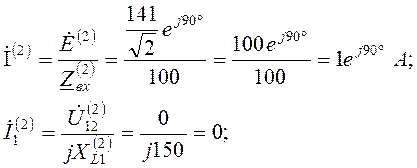
согласно первому закону Кирхгофа ![]() ;
;
![]() .
.
Расчёт действующих значений токов и напряжения на емкости:

Мгновенные значения токов и напряжения на конденсаторе uC(t):
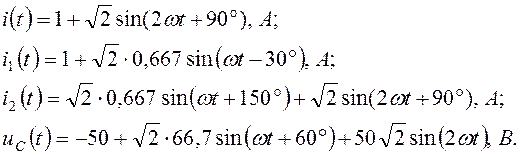
Задача 3.2.2 В электрической цепи (см. рисунок 3.2) задано:
![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
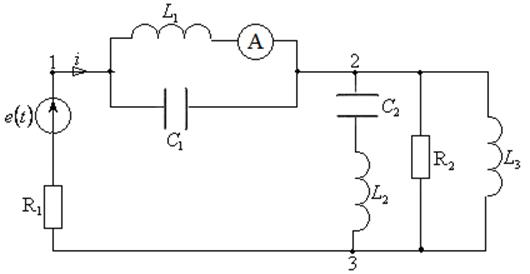
Рисунок 3.2 – Схема электрической цепи
Требуется:
1) определить емкости конденсаторов С1 и С2 такие, чтобы ток в резисторе R2 был равен нулю. Причем емкость конденсатора С1 должна быть меньше чем С2;
2) рассчитать показание амперметра электромагнитной системы (т.е. действующее значение тока в индуктивности L1);
3) рассчитать активную Pист., реактивную Qист., и полную Sист. мощности источника.
Решение.
1) Определим емкости С1 и С2.
На 1-ой гармонике должен быть резонанс напряжений в контуре L2C2, а на 2-ой гармонике – резонанс токов в контуре L1C1. Индуктивность L3 шунтирует резистор R2 на постоянном токе. В результате получим ток в резисторе R2, равный нулю.
Определим реактивные индуктивные сопротивления на 1-ой и 2-ой гармониках:
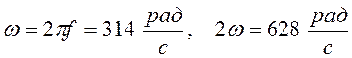 ;
;
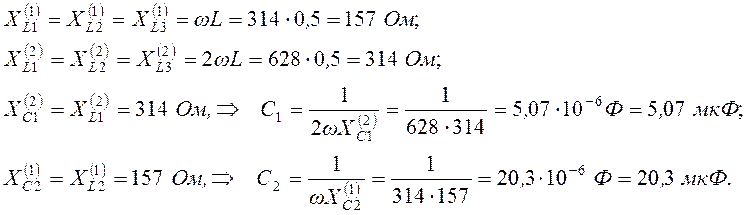
2)
Определим ток в индуктивности на всех гармониках ![]() :
:
Для постоянной составляющей:
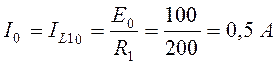 .
.
Для первой гармоники: ![]() так как
так как ![]() ;
;
 ;
;
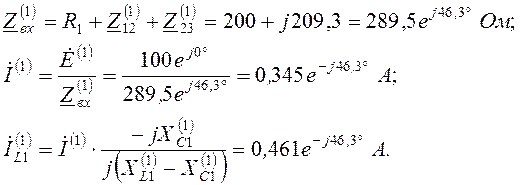
Для второй гармоники: ![]() , так как
, так как ![]() .
.
![]() ,
,
 .
.
Действующее значение тока в индуктивности ![]() :
:
![]()
![]() .
.
3) Рассчитаем мощности источника:
![]()
![]() ;
;

![]() ,
где
,
где
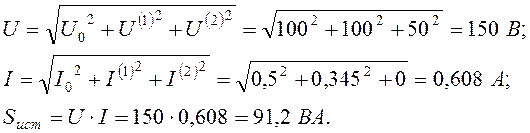
Задача 3.2.3 В электрической цепи (см. рисунок 3.3) задано:
![]() ;
;
![]()
 .
.
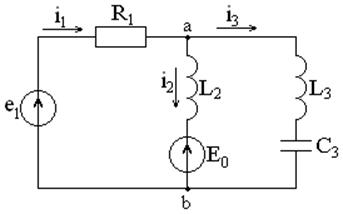
Рисунок 3.3 – Схема электрической цепи
Определить:
1) мгновенные и действующие значения токов i1, i2, i3 и напряжения на конденсаторе uc;
2) мощность, выделяемую в сопротивлении R1.
Решение.
Постоянные составляющие:
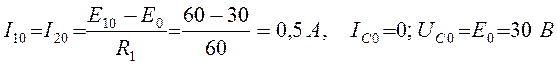 .
.
На основной и 2-ой гармониках цепь содержит один источник e1(t).
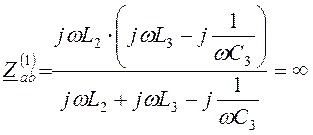 (резонанс
токов), тогда
(резонанс
токов), тогда ![]() .
.

Для 2-ой гармоники сопротивление третьей ветви равно нулю:
![]() (резонанс
напряжений),
(резонанс
напряжений),
тогда ![]() .
.
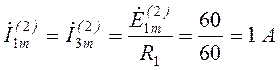 .
.
Находим мгновенные и действующие значения токов и напряжения на конденсаторе:
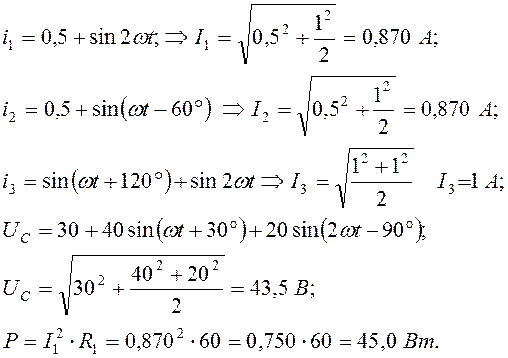
Задача 3.2.4 При подаче на вход некоторого пассивного
двухполюсника несинусоидального напряжения ![]() были измерены действующее значение
входного тока I = 5A, а также активная P = 40Вт и реактивная мощности Q = 30вар, потребляемые двухполюсником. После этого
эксперимент был повторен при действии другого входного напряжения, в котором
был сохранен прежний гармонический состав, а также амплитуды и начальные фазы
гармоник, но частота основной гармоники была удвоена по сравнению с первым
экспериментом. При этом оказалось, что действующее значение тока, активная и
реактивная мощности сохранили прежние значения.
были измерены действующее значение
входного тока I = 5A, а также активная P = 40Вт и реактивная мощности Q = 30вар, потребляемые двухполюсником. После этого
эксперимент был повторен при действии другого входного напряжения, в котором
был сохранен прежний гармонический состав, а также амплитуды и начальные фазы
гармоник, но частота основной гармоники была удвоена по сравнению с первым
экспериментом. При этом оказалось, что действующее значение тока, активная и
реактивная мощности сохранили прежние значения.
Требуется записать аналитические выражения мгновенных значений тока двухполюсника, как для первого, так и для второго экспериментов, если известно, что начальные фазы различных гармоник тока могут отличаться только на угол, не достигающий 90°. Что можно сказать о внутренней схеме двухполюсника для объяснения полученных результатов?
Решение.
В первом эксперименте ток может содержать первую и вторую гармоники: ![]() ,
,
а во втором – вторую и четвертую гармоники:
![]() .
.
При этом вторая гармоника одинакова в обоих случаях. Тогда можно составить выражения для активной и реактивной мощностей и действующего значения тока в обоих экспериментах:
![]() Вт; (3.1)
Вт; (3.1)
![]() вар; (3.2)
вар; (3.2)
![]() А2; (3.3)
А2; (3.3)
![]() Вт; (3.4)
Вт; (3.4)
![]() вар; (3.5)
вар; (3.5)
![]() А2. (3.6)
А2. (3.6)
Из уравнений (3.3) и (3.6) видно, что ![]() . Также из сравнения выражений
(3.1) с (3.4) и (3.2) с (3.5) видно, что
. Также из сравнения выражений
(3.1) с (3.4) и (3.2) с (3.5) видно, что ![]() .
.
Далее, используя выражения (3.1) и (3.2) (или (3.4) и
(3.5)), составим сумму ![]() откуда после сокращения на 10 получим:
откуда после сокращения на 10 получим:
![]() , или
, или
![]() .
.
Так как ![]() , то получим
, то получим ![]() .
.
Отсюда имеем три варианта: либо ![]() , либо
, либо ![]() , либо
, либо ![]() . В последнем случае
. В последнем случае ![]() , что противоречит условию
задачи о том, что сдвиг фаз не должен достигать 90°. Поэтому остаются только два
варианта:
, что противоречит условию
задачи о том, что сдвиг фаз не должен достигать 90°. Поэтому остаются только два
варианта: ![]() (в
этом случае также
(в
этом случае также ![]() ),
либо
),
либо ![]() .
.
Оба эти варианта удовлетворяют условию задачи, поэтому имеем два решения:
- в случае ![]() как для первого, так
и для второго экспериментов имеем
как для первого, так
и для второго экспериментов имеем
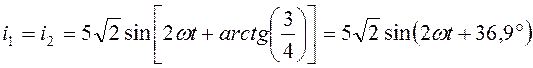 А,
А,
- в случае ![]() имеем для первого
эксперимента
имеем для первого
эксперимента
![]() А,
А,
- для второго эксперимента
![]() А.
А.
Полученный результат можно объяснить тем, что в первом случае схема двухполюсника содержит два последовательно соединенных параллельных LC-контура резонанса токов, настроенных на первую и четвертую гармоники, а во втором случае – один такой контур, настроенный на вторую гармонику.
Задача 3.2.5 В электрической цепи (см. рисунок 3.4) задано:
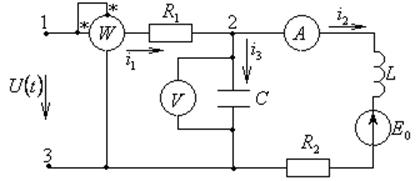
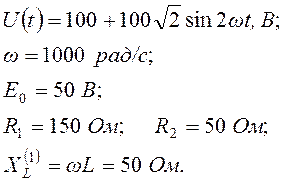
Рисунок 3.4 – Схема электрической цепи
Требуется определить:
1) емкость конденсатора, при которой цепь будет находиться в режиме резонанса на 2-ой гармонике;
2) показания приборов в этом режиме.
Решение.
Расчет постоянной составляющей.
![]() ,
так как в ветви находится конденсатор,
,
так как в ветви находится конденсатор,
 ,
,
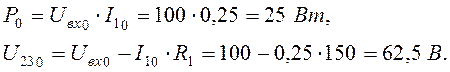
Расчет второй гармоники.
Приведем два варианта расчета емкости:
1-ый вариант.
Определим проводимости второй и третьей ветвей по условию резонанса Im{Y2+Y3}=0.
Запишем уравнение для проводимости второй ветви. Умножим дробь на сопряженное знаменателю выражение и выделим действительную и мнимую части. Рассчитываем значение емкости конденсатора.
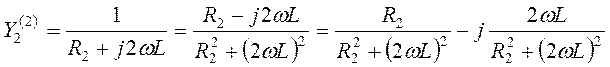 ;
;
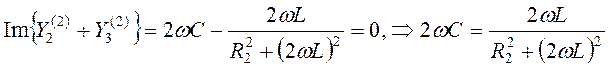 ;
;
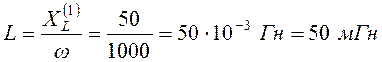 ;
;
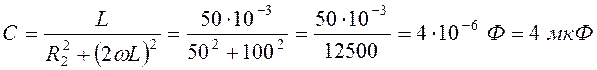 .
.
2-ой вариант.
Запишем эквивалентное сопротивление для исходной схемы. Преобразуем и выделим действительную и мнимую части.
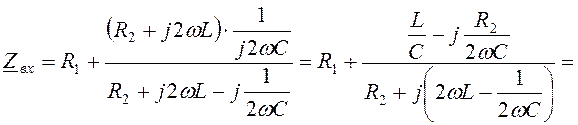
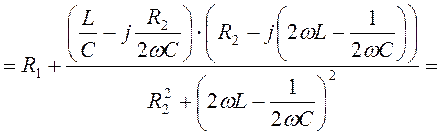
 .
.
По условию резонанса:
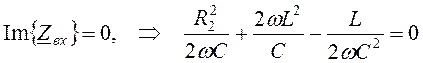 ,
,
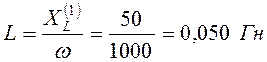 ;
;
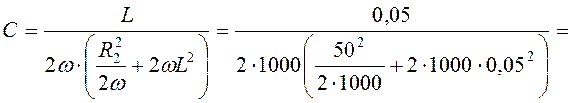
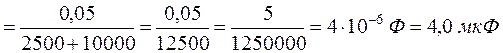 .
.
Для дальнейших расчетов схему удобно представить в преобразованном виде. Эквивалентная преобразованная схема приведена на рисунке 3.5.
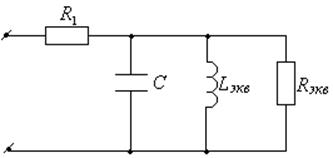
Рисунок 3.5 – Эквивалентная схема электрической цепи
Активные сопротивления эквивалентной схемы:
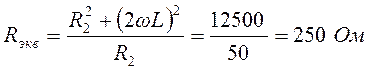 ,
, ![]()
Ток и активная мощность источника на 2-ой гармонике:
 .
.
Реактивная мощность источника равна нулю, так как на второй
гармонике схема находится в режиме резонанса (Im{Yвх}=0) ![]() .
.
Напряжение второй гармоники на участке 2-3 схемы:
![]() .
.
Токи во второй и третьей ветвях найдем по исходной схеме:
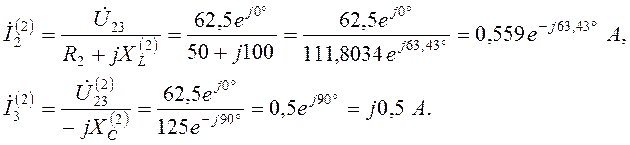
Активная мощность нагрузки на второй гармонике:
![]() .
.
Баланс активных мощностей источника и нагрузки на второй
гармонике выполняется: ![]() .
.
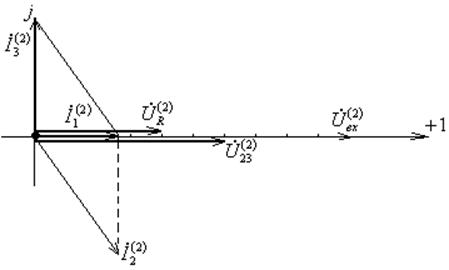
Рисунок 3.6 – Векторная диаграмма цепи на второй гармонике
Определим показания приборов.
Показание ваттметра:
![]()
Показание амперметра:

![]() .
.
Показание вольтметра:
![]() .
.
4 Расчет переходных процессов в линейных электрических цепях
4.1 Основные теоретические положения
Переходный процесс возникает в электрических цепях, при
различного рода воздействиях (подключении к цепи или отключении от цепи источников
электрической энергии, а также при скачкообразном изменении схемы цепи или
параметров входящих в нее элементов), которые называются коммутациями.
Коммутация осуществляется с помощью идеального ключа: сопротивление ключа в
разомкнутом положении равно ![]() , в замкнутом – 0.
, в замкнутом – 0.

Будем считать,
что коммутация происходит мгновенно ![]() . Начало отсчёта времени t = 0 совмещается с моментом коммутации.
. Начало отсчёта времени t = 0 совмещается с моментом коммутации.
Законы коммутации:
1) Ток в
индуктивности непосредственно после коммутации ![]() сохраняет значение, которое он имел до
коммутации при
сохраняет значение, которое он имел до
коммутации при ![]() :
:
![]()
2) Напряжение на
ёмкости непосредственно после коммутации ![]() сохраняет значение, которое оно имело до
коммутации при
сохраняет значение, которое оно имело до
коммутации при ![]() :
:
![]()
Начальные условия − значения токов и напряжений при t = 0.
Независимые начальные условия − это значения тока в
индуктивности ![]() и
напряжения на ёмкости
и
напряжения на ёмкости ![]() в момент коммутации t = 0, которые
определяются на основании законов коммутации путем расчета установившегося
режима в цепи до коммутации.
в момент коммутации t = 0, которые
определяются на основании законов коммутации путем расчета установившегося
режима в цепи до коммутации.
Зависимые начальные условия − это значения токов и
напряжений, а также их производных в момент коммутации t = 0, которые могут
изменяться скачком, например: ![]() и т.п. Они определяются по схеме,
образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.
и т.п. Они определяются по схеме,
образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.
В данном пособии рассматриваются два метода расчета переходных процессов в линейных электрических цепях: классический и операторный.
4.1.1 Классический метод расчета.
Порядок расчета переходных процессов классическим методом:
а) определяют независимые начальные условия ![]() и
и ![]() ;
;
б) записывают дифференциальные уравнения по законам Кирхгофа, искомую переменную (ток или напряжение) представляют в виде:
![]() ;
;
в) определяют принуждённую составляющую ![]() путём расчёта установившегося
режима в цепи после коммутации;
путём расчёта установившегося
режима в цепи после коммутации;
г) определяют свободную составляющую ![]() :
:
− составляют характеристическое уравнение любым методом, например, методом входного сопротивления, и вычисляют его корни;
− записывают свободную составляющую ![]() , выражение свободной составляющей
, выражение свободной составляющей
![]() зависит от
вида корней характеристического уравнения и для цепи второго порядка
зависит от
вида корней характеристического уравнения и для цепи второго порядка ![]() имеет вид:
имеет вид:
- при
действительных и различных корнях ![]() < 0 и
< 0 и ![]() < 0
< 0
![]() ;
;
- при
действительных и равных корнях ![]() =
=![]() =р < 0
=р < 0
![]() ;
;
-
при комплексно-сопряжённых корнях ![]() (α – коэффициент
затухания, ωсв – частота свободных колебаний)
(α – коэффициент
затухания, ωсв – частота свободных колебаний)
![]()
или
![]() .
.
− находят постоянные интегрирования, А1,
А2 или А, ψ.
Для цепи второго порядка постоянные интегрирования определяются по начальным
значениям искомой переменной и её первой производной ![]() .
.
Например, если корни характеристического уравнения действительные и различные:
![]() ,
, ![]() .
.
Если корни комплексно-сопряжённые:
![]() ,
, ![]() .
.
д) строят график ![]() .
.
4.1.2 Операторный метод расчета.
Порядок расчета переходных процессов операторным методом:
а) определяют независимые начальные условия: ![]() ;
;
б) составляют эквивалентную операторную схему для цепи после
коммутации. Ненулевые начальные условия ![]() учитываются введением внутренних
(расчетных) ЭДС (или источников тока): в ветвях с индуктивностью
вводится ЭДС
учитываются введением внутренних
(расчетных) ЭДС (или источников тока): в ветвях с индуктивностью
вводится ЭДС ![]() ,
в ветвях с емкостью вводится ЭДС
,
в ветвях с емкостью вводится ЭДС ![]() . Ниже приведены эквивалентные операторные
схемы замещения пассивных элементов:
. Ниже приведены эквивалентные операторные
схемы замещения пассивных элементов:
− резистивное сопротивление

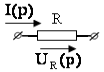
![]() ,
, ![]() ;
;
− индуктивность

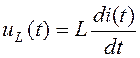 ,
, ![]()
− ёмкость

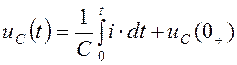 ,
, 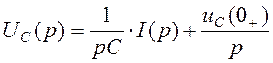 ;
;
в) рассчитывают по операторной схеме изображение искомой переменной (тока или напряжения) известными методами (законы Ома и Кирхгофа, МКТ, МУП, МЭГ и т.п.). Изображение имеет вид рациональной дроби:
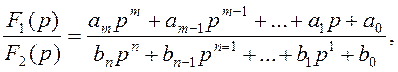
где m < n, ![]() – характеристическое
уравнение. Затем по изображению функции определяют ее оригинал – функцию
времени;
– характеристическое
уравнение. Затем по изображению функции определяют ее оригинал – функцию
времени;
г) оригинал определяют по теореме разложения (см. таблицу 4.1), по таблице оригиналов и изображений, с помощью обратного преобразования Лапласа.
Таблица 4.1 – Теорема разложения
|
Вид
корней характеристического уравнения |
Теорема разложения |
|
|
где |
|
знаменатель
имеет один нулевой корень: |
|
|
1.
характеристическое уравнение 2. |
1. 2. |
4.2 Примеры расчета переходных процессов в электрических цепях
Задача 4.2.1 В электрической цепи (см. рисунок 4.1), с параметрами:
![]() ,
,
![]() ,
, ![]()
до коммутации был установившийся режим,
создаваемый источником постоянной ЭДС ![]() . В момент
. В момент ![]() ключи
ключи ![]() одновременно замыкаются.
одновременно замыкаются.
Требуется определить: ток в ветви с ЭДС ![]() и построить его график.
и построить его график.
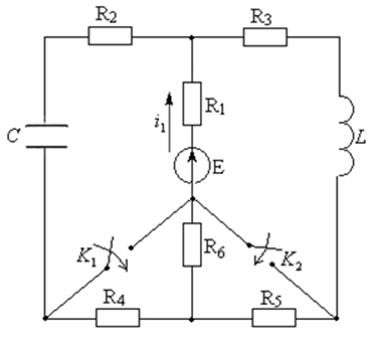
Рисунок 4.1 – Схема электрической цепи
Решение.
Классический метод расчета переходного процесса.
Определим независимые начальные условия (ННУ) ![]() .
.
Рассчитаем установившийся режим в цепи до коммутации.

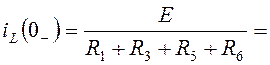
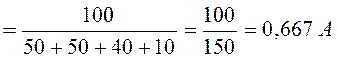 ,
,
![]() ,
,
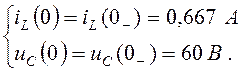 (4.1)
(4.1)
Запишем дифференциальные уравнения по законам Кирхгофа для цепи после коммутации:
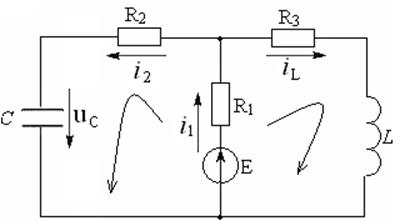
 (4.2)
(4.2)
Ток i1(t) представим в виде суммы принужденного и свободного токов:
![]() .
.
Определим принуждённый ток ![]() . Рассчитаем установившийся режим в цепи
после коммутации.
. Рассчитаем установившийся режим в цепи
после коммутации.
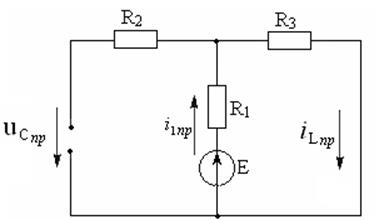
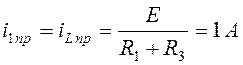 . (4.3)
. (4.3)
Определим свободный ток ![]() .
.
Получим характеристическое уравнение методом входного сопротивления:

Приравняем к нулю числитель:
![]() .
(4.4)
.
(4.4)
Подставим в уравнение (4.4) числовые значения:
![]() .
.
Определим корни характеристического уравнения:
![]() ,
,
![]() .
.
Корни характеристического уравнения вещественные и различные. Свободный ток запишем в виде:
![]() . (4.5)
. (4.5)
Для определения постоянных интегрирования А1, А2 запишем ток i1 и определим его производную:
![]() . (4.6)
. (4.6)
![]() .
.
Определим постоянные интегрирования А1, А2 по начальным значениям i1(0), i/1(0):
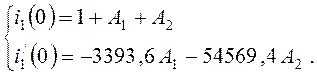 (4.7)
(4.7)
Найдём i1(0), i/1(0) из законов Кирхгофа, записанных для цепи после коммутации (4.2):
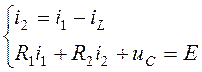 ;
;
![]() ;
;
![]() .
(4.8)
.
(4.8)
Рассчитаем i1(0):
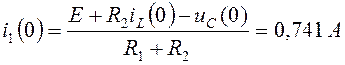 .
.
Продифференцируем выражение (4.8) и определим i/1:
![]() .
(4.9)
.
(4.9)
Запишем это уравнение для момента времени t=0:
![]() .
.
Из законов Кирхгофа, записанных для момента времени t=0, найдём iL/(0), uc/(0) и определим i/1(0):
 ;
;
 ;
;
![]() .
.
Подставим найденные числовые значения i1(0), i/1(0) в систему (4.7) и определим постоянные интегрирования:
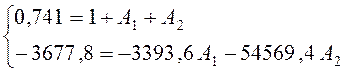 ;
;
А1 = − 0,348, А2 = 0,089.
Подставим найденные значения А1= – 0,348, А2=
0,089 в выражение (4.6) и получим переходный ток ![]() :
:
![]() .
.
Операторный метод расчета переходного процесса.
Независимые начальные условия определены в классическом методе и равны:
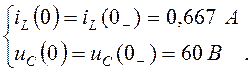
Нарисуем эквивалентную операторную схему для цепи после коммутации.
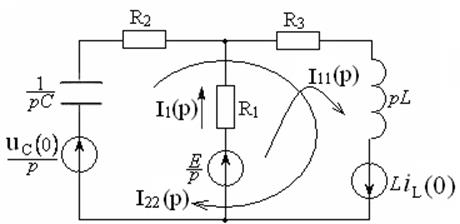
Рисунок 4.2 – Эквивалентная операторная схема
Определим изображение тока ![]() методом контурных токов:
методом контурных токов:
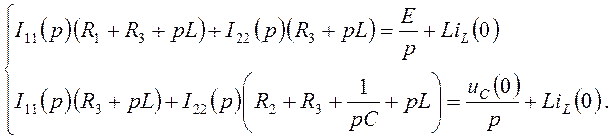 (4.10)
(4.10)
Решим систему уравнений (4.10), определим ![]() :
:
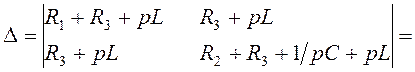
 ,
,
![]()
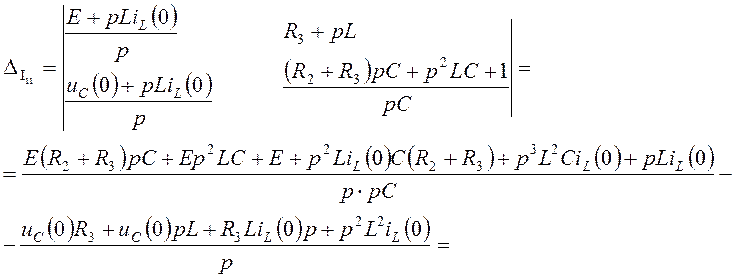
 .
.
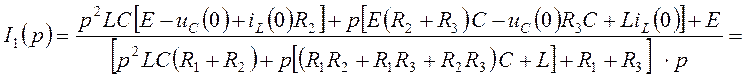
![]() , (4.11)
, (4.11)
где
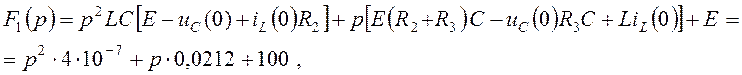
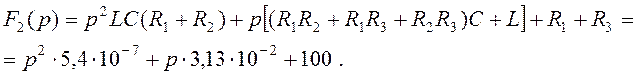
Определим корни характеристического уравнения ![]()
![]() ,
,
![]() .
.
Таким образом, корни знаменателя изображения тока ![]() равны:
равны:
p = 0, ![]() .
.
Ток i1(t) запишем по теореме разложения в виде:
 . (4.12)
. (4.12)
Рассчитаем:
![]() ;
;
![]()
![]()
![]()
![]()
Подставим рассчитанные значения в теорему разложения (4,12), получим переходный ток:
![]() .
.
На рисунке 4.3 показаны графики принужденного тока ![]() , свободного тока
, свободного тока ![]() и переходного тока
и переходного тока ![]() .
.
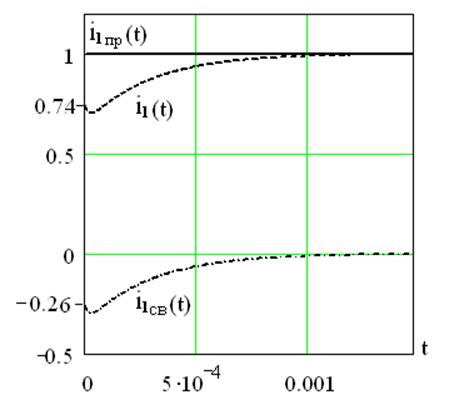
Рисунок 4.3 –
График тока ![]()
Задача 4.2.2. В электрической цепи (см. рисунок 4.4) с постоянным источником ЭДС Е = 60В в момент времени t = 0 одновременно ключ К1 замыкается, а ключ K2 размыкается. Параметры цепи: резисторы R1=30 Ом, R2=70Ом, R3=30 Ом, индуктивность L = 10 мГн, емкость C = 2 мкФ.
Требуется:
1) определить ток iL(t) после коммутации;
2) построить график тока iL(t).

Рисунок 4.4 – Схема электрической цепи
Решение.
Классический метод расчета переходного процесса.
Определим независимые начальные условия (ННУ): iL(0), uC(0). Рассчитаем установившийся режим в цепи до коммутации.
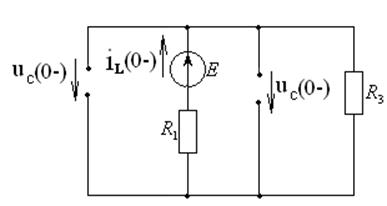
Рисунок 4.5 – Схема электрической цепи до коммутации
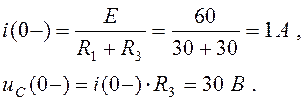 (4.13)
(4.13)
По законам коммутации:
 (4.14)
(4.14)
Запишем дифференциальные уравнения по законам Кирхгофа для цепи после коммутации. Сначала упростим схему:
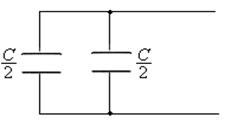
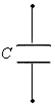
Схема цепи после коммутации представлена на рисунке 4.6.
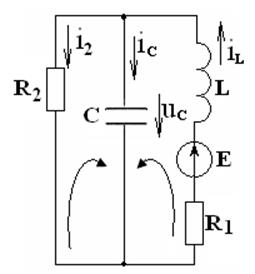
Рисунок 4.6 – Схема электрической цепи после коммутации
Дифференциальные уравнения по законам Кирхгофа для цепи после коммутации запишем в виде:
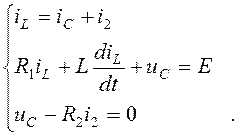 (4.15)
(4.15)
Ток iL(t) представим в виде суммы составляющих принужденного и свободного токов:
iL(t) = iLпр(t) + iLсв(t).
Определим составляющую принуждённого тока iLпр(t). Рассчитаем установившийся режим в цепи после коммутации.
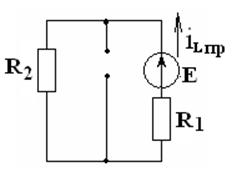
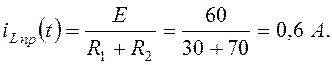 (4.16)
(4.16)
Определим составляющую свободного тока iLсв(t).
Получим характеристическое уравнение методом входного сопротивления:
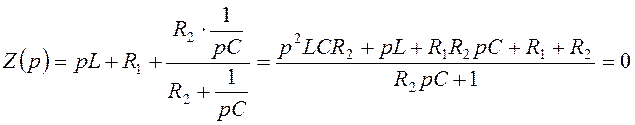 .
.
Приравняем к нулю числитель, подставим числовые значения и определим корни характеристического уравнения:
![]()
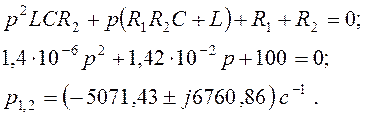 (4.17)
(4.17)
Корни характеристического уравнения комплексно-сопряженные. Составляющую свободного тока запишем в виде:
![]() .
.
Запишем переходный ток
![]() (4.18)
(4.18)
Для определения постоянных интегрирования А и ψ возьмем производную по времени t от тока iL(t):
![]() . (4.19)
. (4.19)
Запишем выражения (4.18) и (4.19) для момента времени t = 0:
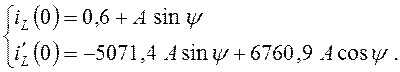 (4.20)
(4.20)
Значение производной ![]() найдем из второго уравнения системы
(4.15), записанного для момента времени t = 0:
найдем из второго уравнения системы
(4.15), записанного для момента времени t = 0:
 .
.
Подставим значения iL(0)=1А и ![]() = 0 в систему уравнений
(4.20), получим:
= 0 в систему уравнений
(4.20), получим:
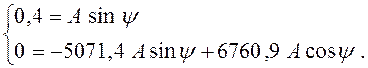 (4.21)
(4.21)
Подставим ![]() во второе уравнение системы (4.21):
во второе уравнение системы (4.21):
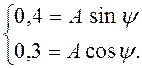 (4.22)
(4.22)
Поделим первое уравнение системы (4.22) на второе, получим:
![]() ,
,
![]() ;
;
постоянную интегрирования А определим по формуле:
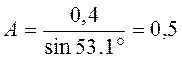 .
.
Подставим найденные значения в выражение (4.18) и получим переходный ток iL(t):
![]() .
.
Операторный метод расчета переходного процесса.
Независимые начальные условия определены в классическом
методе и равны: ![]() .
.
Нарисуем эквивалентную операторную схему для цепи после коммутации.
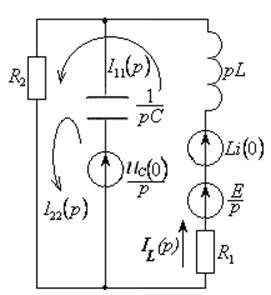
Рисунок 4.7 – Эквивалентная операторная схема
Определим изображение тока IL(p) методом контурных токов:
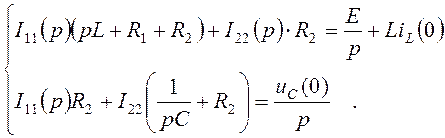 (4.23)
(4.23)
Решим систему уравнений (4.23) и найдем 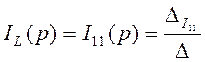 :
:

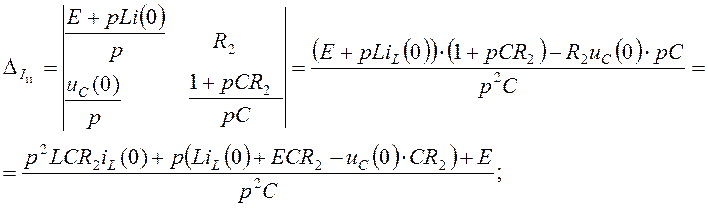
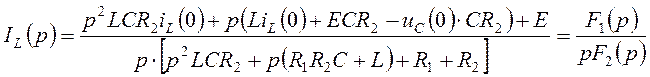 ,
(4.24)
,
(4.24)
где

![]() .
.
Определим корни характеристического
уравнения ![]()

Таким образом, корни знаменателя тока IL(p) равны:
![]() ,
,
![]() .
.
Ток iL(t) запишем по теореме разложения в виде:
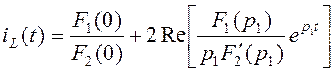 .
(4.25)
.
(4.25)
Рассчитаем:
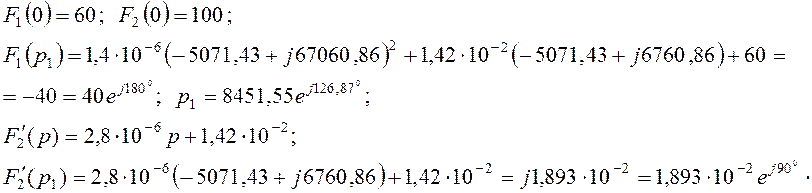
Подставим рассчитанные значения в выражение теоремы разложения (4.25), получим переходный ток iL(t):
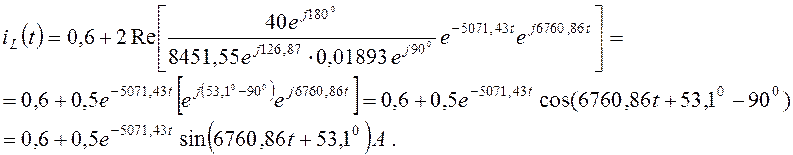
На рисунке 4.8 показаны графики составляющих принужденного iLпр(t) и свободного iLсв(t) токов, а также переходного тока iL(t).
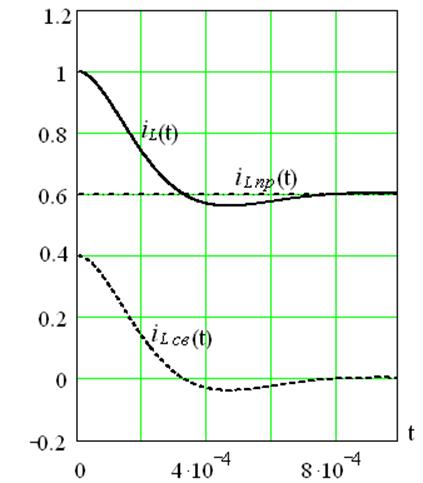
Рисунок 4.8 – Графики тока iL(t) и его составляющих
Задача 4.2.3. В электрической цепи (см. рисунок 4.9) в
момент времени ![]() ключ
К переключается с полюса 3 на полюс 1. Параметры цепи: постоянный
источник ЭДС
ключ
К переключается с полюса 3 на полюс 1. Параметры цепи: постоянный
источник ЭДС ![]() ,
сопротивления
,
сопротивления ![]() ,
индуктивность
,
индуктивность ![]() ,
конденсатор емкостью
,
конденсатор емкостью ![]() .
.
Требуется: определить: напряжение на емкости uC (t) после коммутации; построить график напряжения на емкости uC(t); определить токи во всех ветвях цепи после коммутации.
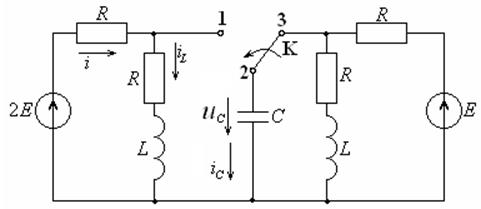
Рисунок 4.9 – Схема электрической цепи
Решение.
Классический метод расчета переходного процесса.
Определим независимые начальные условия (ННУ):![]() Рассчитаем
установившийся режим в цепи до коммутации.
Рассчитаем
установившийся режим в цепи до коммутации.

Рисунок 4.10 – Схемы для расчета ННУ
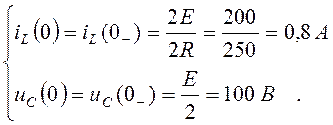 (4.26)
(4.26)
Уравнения по законам Кирхгофа для цепи после коммутации запишем в виде:
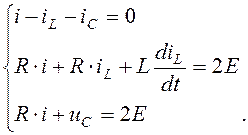 (4.27)
(4.27)
Переходное напряжение uC(t) запишем в виде
![]() .
.
Определим ![]() путем расчета установившегося режима в
цепи после коммутации.
путем расчета установившегося режима в
цепи после коммутации.
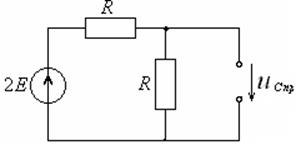
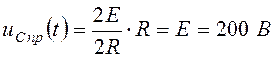 . (4.28)
. (4.28)
Определим свободную составляющую напряжения на ёмкости ![]() .
.
Составим характеристическое уравнение методом входного сопротивления:
 .
.
Приравняем к нулю числитель и получим характеристическое уравнение в виде:
![]() .
(4.29)
.
(4.29)
Подставим числовые значения и определим корни характеристического
уравнения: ![]() ;
;
![]() .
.
Корни характеристического уравнения вещественные и различные. Свободную составляющую напряжения запишем в виде:
![]() .
.
Для определения постоянных интегрирования А1,
А2 запишем напряжение uC(t) и определим его производную ![]() :
:
![]() ;
(4.30)
;
(4.30)
![]() .
.
Постоянные интегрирования А1, А2
определим по начальным значениям uC(0), ![]() :
:
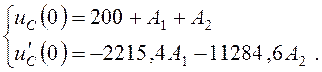 (4.31)
(4.31)
Начальное значение uC(0)=100В. Производная
![]() . Найдем iC(0)
из первого и третьего уравнений, записанных по законам Кирхгофа для цепи после
коммутации в начальный момент времени t = 0 (4.27):
. Найдем iC(0)
из первого и третьего уравнений, записанных по законам Кирхгофа для цепи после
коммутации в начальный момент времени t = 0 (4.27):
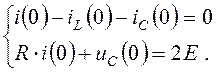 (4.32)
(4.32)
Из второго уравнения определим i(0), подставим в
первое уравнение и найдем ток iC(0), а затем ![]() :
:
 ;
;
![]() ;
;
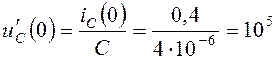 .
.
Подставим uC(0)=100В и ![]() в систему уравнений
(4.31) и определим постоянные интегрирования А1 и А2:
в систему уравнений
(4.31) и определим постоянные интегрирования А1 и А2:

![]() .
.
Подставим найденные значения А1, А2 в выражение (4.30) и получим переходное напряжение на конденсаторе uC(t):
![]() .
.
Определение токов во всех ветвях цепи после коммутации по найденному значению uC(t):
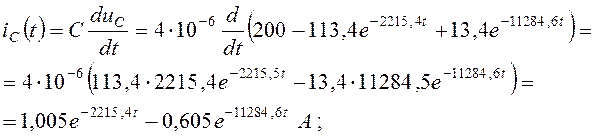
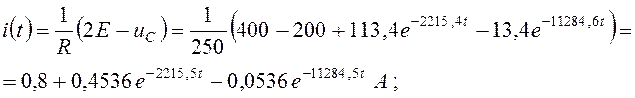
![]() . (4.33)
. (4.33)
Операторный метод расчета переходного процесса.
Независимые начальные условия определены в классическом
методе и равны: ![]() .
.
Нарисуем эквивалентную операторную схему для цепи после коммутации.

Рисунок 4.11 – Эквивалентная операторная схема
Изображение напряжения на конденсаторе найдем методом двух узлов:
 .
(4.34)
.
(4.34)
Преобразуем выражение (4.34), получим:
 .
(4.35)
.
(4.35)
Подставим числовые значения в выражение для изображения напряжения:
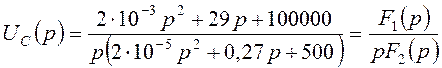 ,
,
где
![]() ,
, ![]() .
.
Определим корни характеристического
уравнения ![]() .
.
![]() .
.
Корни уравнения ![]() равны:
равны:
![]() .
.
Таким образом, корни знаменателя изображения напряжения UC
(p) равны: ![]() ,
, ![]() .
.
Так как знаменатель имеет нулевой корень и корни характеристического уравнения вещественные и различные, uC(t) запишем по теореме разложения в виде:
 .
(4.36)
.
(4.36)
Определим выражение производной ![]() и рассчитаем для p1
и p2:
и рассчитаем для p1
и p2:
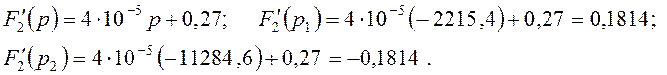
Рассчитаем остальные компоненты выражения (4.36):
![]()
![]() ;
;
![]() .
.
Подставим рассчитанные значения в выражение (4.36) и получим напряжение на конденсаторе uC(t):
![]() .
.

Рисунок 4.12 – Графики принужденного и свободного переходного напряжения uC(t)
Задача 4.2.4. В электрической цепи (см. рисунок 4.13) с источниками постоянной ЭДС: Е1=100В и Е2=50В, сопротивлениями: R1 = R3 = 40Ом, R2 = =R4 = 60Ом, R5 = R6 = 20Ом, индуктивностью L = 20 мГн, емкостью С = 2 мкФ: в момент времени t = 0 ключ К размыкается и в цепи происходит переходный процесс.
Определить: ток ![]() , напряжение
, напряжение ![]() после коммутации и построить графики
после коммутации и построить графики ![]() и
и ![]() .
.
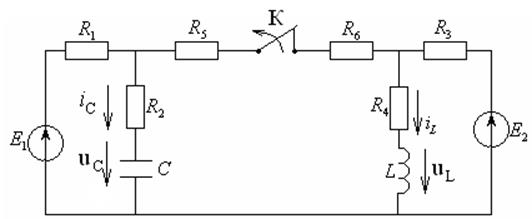
Рисунок 4.13 – Схема электрической цепи
Решение.
Переходный процесс в цепи рассчитаем классическим методом.
Определим независимые начальные условия: ![]() .
.
Независимые начальные условия определяются путем расчета установившегося режима в цепи до коммутации (см. рисунок 4.14).
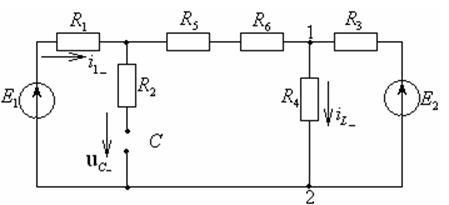
Рисунок 4.14 – Схема электрической цепи до коммутации
Найдем напряжение u12(0 –) по методу двух узлов:
 .
.
Токи рассчитаем по закону Ома:
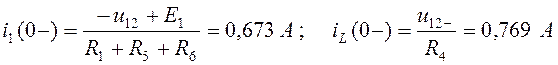 .
.
Напряжение на конденсаторе в цепи до коммутации равно:
![]() .
.
По законам коммутации:
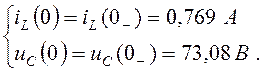 (4.37)
(4.37)
После размыкания ключа заданная электрическая цепь распадается на две независимые цепи первого порядка (см. рисунки 4.15 а и 4.15 б).
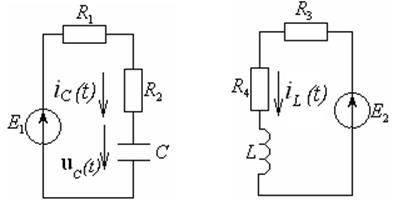
а) б)
Рисунок 4.15 – Электрические цепи после коммутации
Для нахождения емкостного тока iС(t)
рассчитаем переходный процесс в цепи (см. рисунок 4.15 а). Так как ток в
емкости равен  ,
рассчитаем переходное напряжение на емкости uC(t). Переходное напряжение на емкости представим в виде: uC(t) = uCпр(t)+uCсв(t).
,
рассчитаем переходное напряжение на емкости uC(t). Переходное напряжение на емкости представим в виде: uC(t) = uCпр(t)+uCсв(t).
Определим принужденное напряжение на емкости uCпр(t), путем расчета установившегося режима в цепи после коммутации (см. рисунок 4.16 а).
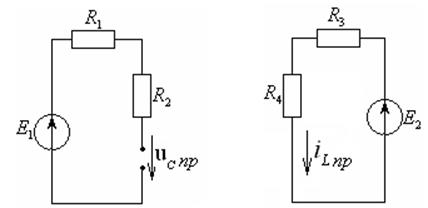
а) б)
Рисунок 4.16 – Эквивалентные схемы для расчета установившихся режимов после коммутации
Как видно из рисунка 4.16 а, ![]() .
.
Определим свободное напряжение на емкости uCсв. Характеристическое уравнение получим методом входного сопротивления. Входное сопротивление цепи (см. рисунок 4.15 а) имеет вид:
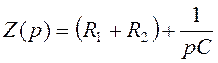 .
(4.38)
.
(4.38)
Приравняем Z(p) к нулю и определим корень характеристического уравнения Z(p) = 0:
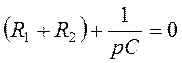 ;
;
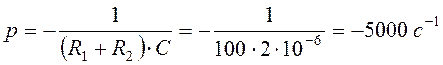 .
.![]()
Свободную составляющую uCсв(t) и результирующее переходное uC(t) напряжения на емкости запишем в виде:
![]() ,
, ![]() .
.
Найдем постоянную интегрирования А по начальному значению напряжения uC(0)=73,1 В:
73,1 = 100+А, отсюда определим А=73,1 – 100 = – 26,9 В.
Переходное напряжение на ёмкости равно:
![]() .
.
Определим ток в цепи:
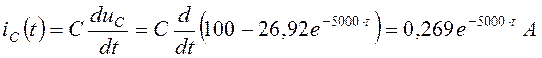 .
(4.39)
.
(4.39)
Как видно из выражения (4.39), принужденный ток в емкости
равен нулю и ![]() .
.
График тока ![]() приведен на рисунке 4.17.
приведен на рисунке 4.17.

Рисунок 4.17 – График переходного тока iC(t)
Для нахождения напряжения на индуктивности uL(t)
рассчитаем переходный процесс в цепи (см. рисунок 4.15 б). Так как напряжение
на индуктивности uL(t) равно 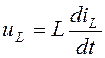 , рассчитаем ток в индуктивности
iL(t). Ток в индуктивности представим в виде: iL(t) = iLпр(t)+ iLсв(t).
, рассчитаем ток в индуктивности
iL(t). Ток в индуктивности представим в виде: iL(t) = iLпр(t)+ iLсв(t).
Определим принужденный ток в индуктивности iLпр(t), путем расчета установившегося режима в цепи после коммутации (см. рисунок 4.16 б).
Принуждённый ток в индуктивности равен:
 .
(4.40)
.
(4.40)
Определим свободную составляющую тока в индуктивности iLсв(t), для этого составим характеристическое уравнение методом входного сопротивления. Входное сопротивление цепи (см. рисунок 4.15 б) имеет вид:
![]() .
.
Приравняем Z(p) к нулю и определим корень характеристического уравнения:
![]() ,
откуда получим
,
откуда получим .
.
Свободную составляющую тока iLсв(t) и результирующий переходный ток в индуктивности iL(t) запишем в виде:
![]() .
(4.41)
.
(4.41)
Найдем постоянную интегрирования А по независимому начальному
значению тока в индуктивности iL(0 –)=0,769А из
уравнения составленного на основании закона коммутации ![]() :
:
0,5+А = 0,769, отсюда определим А = 0,769 – 0,5 =0,269А.
Переходный ток в индуктивности равен: ![]() .
.
Напряжение на индуктивности определим по формуле:
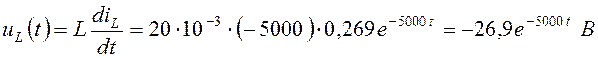 .
(4.42)
.
(4.42)
Как видно из выражения (4.42), принуждённая составляющая напряжения на индуктивности равна нулю и результирующее напряжение состоит только лишь из свободной составляющей uL(t) = uLсв(t).
График напряжения на индуктивности uL(t) приведен на рисунке 4.18.
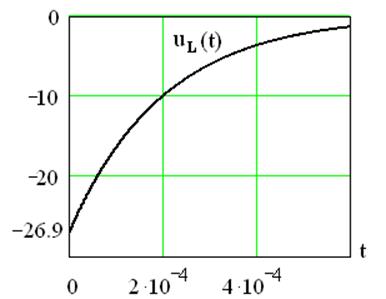
Рисунок 4.18 – График переходного напряжения uL(t)
Задача 4.2.5 Электрическая цепь (см. рисунок 4.19) содержит
два источника с одинаковыми постоянными ЭДС Е = 100В,
сопротивления ![]() и
и
![]() , индуктивности
, индуктивности
![]() и
и ![]() , ёмкости
, ёмкости ![]() и
и ![]() . В момент времени
. В момент времени ![]() ключи К1
и К2 одновременно размыкаются.
ключи К1
и К2 одновременно размыкаются.
Требуется:
1)
определить напряжения на конденсаторах ![]() и
и ![]() после размыкания ключей;
после размыкания ключей;
2)
определить токи в индуктивностях ![]() и
и ![]() после размыкания ключей;
после размыкания ключей;
3)
построить графики ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение.
Переходный процесс в цепи рассчитаем классическим методом.
Определим независимые начальные условия:
![]() и
и
![]() .
.
Независимые начальные условия определим путем расчета установившегося режима в цепи до коммутации (см. рисунок 4.20). Как видно из рисунка 4.20, независимые начальные условия равны:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.

Рисунок 4.19 – Схема электрической цепи

Рисунок 4.20 – Эквивалентная схема для расчета установившегося режима в цепи до коммутации
Схема электрической цепи после коммутации показана на рисунке 4.21.
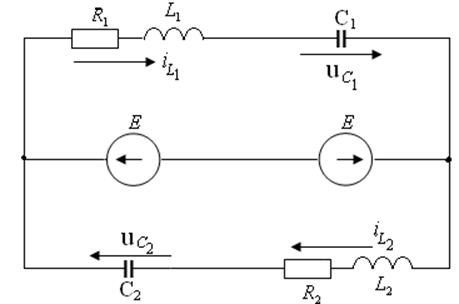
Рисунок 4.21 – Схема электрической цепи после коммутации
Напряжение между узлами электрической цепи (см. рисунок 4.21) равно нулю (Е − Е = 0), и электрическая цепь после коммутации распадается на две независимые цепи (см. рисунки 4.22 а и 4.22 б).
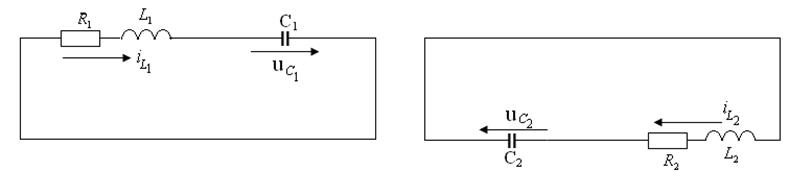
а) б)
Рисунок 4.22 –
Схемы для расчета ![]() ,
, ![]() ,
, ![]() ,
,
![]()
Рассчитаем переходной процесс в R1L1C1
– цепи (см. рисунок 4.22 а) и определим ![]() и
и
![]() .
.
Найдем сначала переходное напряжение ![]() :
: ![]() .
.
Принуждённая составляющая напряжения ![]() и переходное напряжение состоит
только из свободной составляющей:
и переходное напряжение состоит
только из свободной составляющей: ![]() . Для определения свободной
составляющей напряжения составим характеристическое уравнение методом входного
сопротивления и найдем его корни.
. Для определения свободной
составляющей напряжения составим характеристическое уравнение методом входного
сопротивления и найдем его корни.
Входное комплексное сопротивление цепи, где jω заменено
оператором p, ![]() приведем к общему знаменателю и приравняем
к нулю числитель, получим:
приведем к общему знаменателю и приравняем
к нулю числитель, получим:
![]() .
(4.43)
.
(4.43)
Корни характеристического уравнения (4.43) равны:
![]() .
.
Корни характеристического уравнения комплексно-сопряженные, свободное напряжение запишем в виде:
![]() .
(4.44)
.
(4.44)
Постоянные интегрирования А и ψ определим
по начальным значениям напряжения и его первой производной ![]() ,
, ![]() . Производная
. Производная ![]() имеет вид:
имеет вид:
![]() .
.
Запишем ![]() и
и ![]() :
:
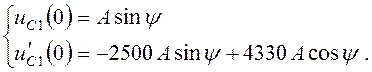 (4.45)
(4.45)
Начальное значение напряжения ![]() , так как
, так как ![]() , то
, то ![]() равно:
равно: 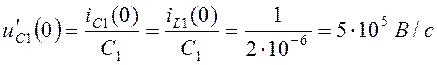 .
.
Подставим найденные значения ![]() ,
, ![]() в систему уравнений (4.45), получим:
в систему уравнений (4.45), получим:
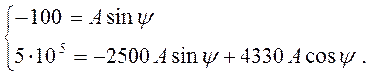 (4.46)
(4.46)
Решая систему уравнений (4.46), найдем постоянные интегрирования А и ψ:

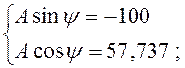 (4.47)
(4.47)
![]() ;
;
![]() .
.
Подставим найденные значения постоянных интегрирования в выражение (4.44) и получим переходное напряжение на конденсаторе:
![]() .
.
Ток в цепи ![]() определим по формуле:
определим по формуле:

![]() .
(4.48)
.
(4.48)
Чтобы сложить синусоидальные функции времени, применим комплексный метод расчета:
![]()
![]()
![]() ;
;
![]()
![]()
![]() ;
;
![]() .
.
Перейдем к мгновенным значениям:
![]() .
.
Таким образом, сумма двух синусоидальных функций равна:
![]() .
(4.49)
.
(4.49)
Подставим (4.49) в формулу (4.48) и получим выражение для
тока ![]() :
:
![]() .
(4.50)
.
(4.50)
Графики напряжения ![]() тока
тока ![]() представлены на рисунках 4.23 а и 4.23 б.
представлены на рисунках 4.23 а и 4.23 б.
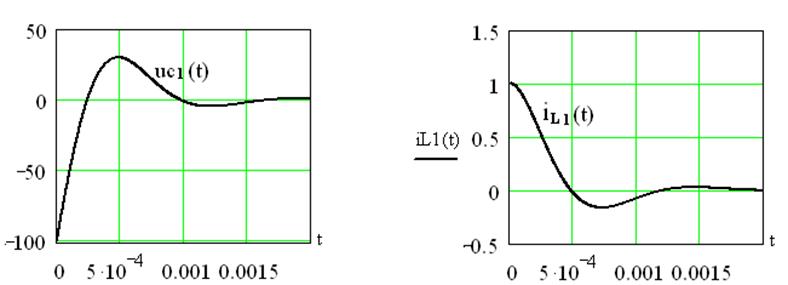
а) б)
Рисунок
4.23 – Графики напряжения ![]() и тока
и тока ![]()
Рассчитаем переходной процесс в R2L2C2
– цепи (см. рисунок 4.22 б) и определим ![]() ,
, ![]() .
.
Найдем сначала переходное напряжение ![]() :
:
![]() .
.
Принуждённая составляющая напряжения ![]() и переходное напряжение
включает только свободную составляющую:
и переходное напряжение
включает только свободную составляющую: ![]() .
.
Для определения свободной составляющей напряжения составим
характеристическое уравнение методом входного сопротивления и найдем его корни.
Комплексное сопротивление цепи (jω → p) ![]() приведем к общему знаменателю, приравняем
к нулю числитель, получим:
приведем к общему знаменателю, приравняем
к нулю числитель, получим:
![]() .
(4.51)
.
(4.51)
Корни характеристического уравнения (4.51) равны:
![]() .
.
Корни характеристического уравнения вещественные и различные, напряжение на емкости запишем в виде:
![]() .
(4.52)
.
(4.52)
Постоянные интегрирования определим по начальным значениям напряжения
и его первой производной ![]() ,
, ![]() . Производная
. Производная ![]() имеет вид:
имеет вид: ![]() .
.
Запишем ![]() и
и ![]() :
:
 (4.53)
(4.53)
Начальное значение напряжения ![]() , так как
, так как ![]() , то
, то ![]() равно
равно 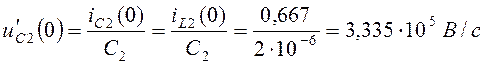 .
.
Подставим найденные
значения ![]() и
и ![]() в систему уравнений
(4.53), получим:
в систему уравнений
(4.53), получим:
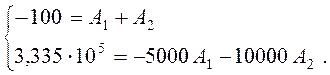 (4.54)
(4.54)
Решая систему уравнений (4.54), найдем постоянные интегрирования А1 и А2: А1 = −133,3 и А2 = 33,3.
Подставим найденные значения постоянных интегрирования в выражение (4.52) и получим переходное напряжение на емкости:
![]() .
.
Ток в цепи ![]() определим по формуле:
определим по формуле:
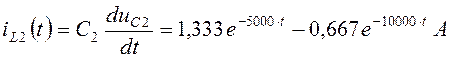 .
.
Графики напряжения ![]() и тока
и тока ![]() представлены на рисунках 4.24 а и 4.24
б.
представлены на рисунках 4.24 а и 4.24
б.
 а) б)
а) б)
Рисунок 4.24 – Графики напряжения ![]() и тока
и тока ![]()
1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. – 544 с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высшая школа,1981. – 333 с.
3. Основы теории цепей. Учебник для вузов/Г.В.Зевеке и др. – М.: Энергоиздат, 1989. – 528 с.
4. Теория линейных электрических цепей/Под редакцией И.Г.Кляцкина. – М.: Высшая школа, 1975.
5. Зернов И.В., Карпов В.Г. Теория радиотехнических цепей. – Л.: Энергия, 1972.
6. Шебес М.Р., Каблукова М.В. Задачник теории линейных электрических цепей: Учебное пособие для вузов. – М.: ВШ, 1990.-544 с.
7. Основы теории цепей: Учебник для вузов/В.П.Бакалов и др. – М.: 2000. – 592 с.
8. Попов В.П. Основы теории цепей: Учебник для вузов. – М., 2000. –576с.
9. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. – т.1. – Санкт-Петербург: Питер, 2003. – 463 с.
10. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. – т.2. – Санкт-Петербург: Питер, 2003. – 576 с.
11. Жолдыбаева З.И., Зуслина Е.Х. Теория электрических цепей 1. Примеры расчета установившихся процессов в линейных электрических цепях. Учебное пособие. – Алматы: АИЭС, 2009.- 93 с.
12. Жолдыбаева З.И., Зуслина Е.Х. Теория электрических цепей 2. Примеры расчета установившихся и переходных процессов в линейных электрических цепях с сосредоточенными и распределенными параметрами. Учебное пособие. – Алматы: АИЭС, 2011. – 78 с.
Содержание
Введение
1 Расчет электрических цепей постоянного тока
1.1 Основные теоретические положения
1.1.1 Методы эквивалентных преобразований
1.1.2 Методы расчёта разветвленных электрических цепей постоянного тока
1.2 Примеры расчета линейных электрических цепей постоянного тока
2 Расчет электрических цепей синусоидального тока
2.1 Основные теоретические положения
2.1.1 Расчет установившихся режимов линейных электрических цепей синусоидального тока
2.1.2 Резонанс в электрических цепях
2.2 Примеры расчета электрических цепей синусоидального тока
3 Расчет электрических цепей несинусоидального тока
3.1 Основные теоретические положения
3.2 Примеры расчета электрических цепей с несинусоидальными ЭДС и токами
4 Расчет переходных процессов в линейных электрических цепях
4.1 Основные теоретические положения
4.1.1 Классический метод расчета
4.1.2 Операторный метод расчета
4.2 Примеры расчета переходных процессов в электрических цепях
Список литературы