Алматинский институт энергетикии и свяхи

Кафедра теоретических основэлектротехники

 

 

ТЭЦ 1. Четырехполюсники. Линейные электрические цепи с несинусоидальными источниками.

Методические указания и задания к выполнению

расчетно-графических работ №3,4

для студентов очной формы обучения специальности 5В0719- Радиотехника, электроника и телекоммуникации

 

 

Алматы 2010

Составители: З.И.Жолдыбаева, Т.И.Коровченко. ТЭЦ1. Четырехполюсники. Линейные электрические цепи с несинусоидальными источниками. Методические указания и задания к выполнению расчетно-графических работ №3,4. – Алматы: АИЭС, 2010.- 18 с.

 Методические указания к расчетно-графическим работам №3,4 содержат общие положения к выполнению и оформлению  расчетно-графических работ, задания, схемы и параметры электрических цепей. Задания к   расчетно-графическим работам соответствуют рабочей  программе по ТЭЦ1.

 

Содержание

1. Общие положения по выполнению и оформлению расчетно-графических   работ  

2. Расчетно-графическая работа №3.  Расчет линейной электрической цепи   несинусоидального тока  

3. Расчетно-графическая работа №4. Расчет пассивных  четырехполюсников.  

4. Методические указания к выполнению расчетно-графических работ     

5. Список литературы                   

 

1 Общие положения по выполнению и оформлению расчетно - графических работ

1.1 Текст задания (условие задачи) должен быть переписан полностью, со всеми рисунками и числовыми значениями для своего варианта.

1.2 Расчетно-графическая работа должна быть написана только на одной стороне листа, при этом следует оставлять поля шириной не менее 4 см для замечаний преподавателя.

1.3 Расчеты должны сопровождаться пояснениями. Нельзя приводить только расчетные формулы и конечные результаты.

1.4 Расчетно-графические работы, в которых вычисления и пояснения приводятся крайне сокращенно, к защите не допускаются и возвращаются студентам на переработку.

1.5 Работа должна быть написана аккуратно, чернилами или шариковой ручкой (только синий и черный цвет).

1.6 В конце расчетно-графической работы должны быть указаны источники литературы и подпись выполнившего работу.

1.7 На титульном листе обязательно должны быть написаны фамилия, инициалы студента и номер зачетной книжки.

1.8 Рисунки, графики, схемы должны быть выполнены карандашом или черной пастой (тушью) с применением линейки и циркуля. Их не следует размещать среди текста. Они должны быть выполнены на отдельных листах миллиметровой или клетчатой бумаги.

1.9 На графиках обязательно указывать названия изображаемых величин, их единицы измерения. Масштабы подбирать так, чтобы было удобно пользоваться графиком или диаграммой. В соответствии с выбранными масштабами подписываются шкалы графиков и диаграмм.

1.10 Везде у параметров, имеющих определенные размерности, писать в окончательных результатах соответствующие единицы измерения. Все обозначения электрических величин должны соответствовать ГОСТу.

1.11 Расчетно-графическая работа должна быть сдана на проверку в срок, указанный преподавателем.В случае нарушения студентом срока  сдачи работы ему выдается дополнительное задание или другой вариант (по усмотрению преподавателя).

 

2  Расчетно-графическая работа №3.

Расчет линейных электрических цепей несинусоидального тока.

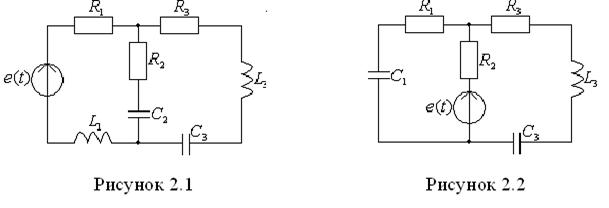
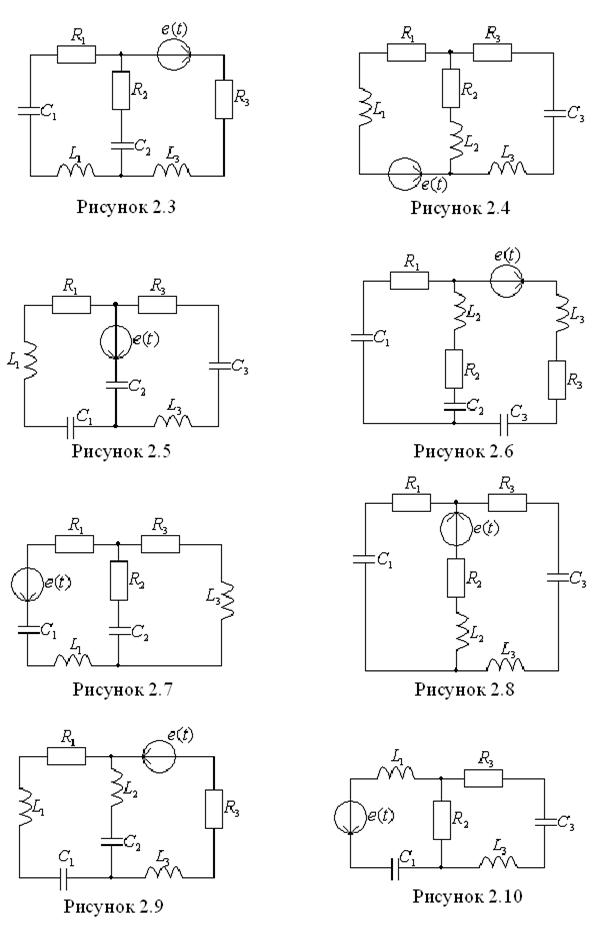
В цепи действует источник несинусоидальной периодической э.д.с. электрические схемы приведены на рисунках 2.1-2.10. Несинусоидальные периодические э.д.с. представлены на рисунках 2.11-2.16. Максимальные значения э.д.с., основная частота э.д.с. источника f, параметры элементов приведены в таблицах 2.1-2.3.

Требуется выполнить:

2.1 Определить гармонический состав несинусоидальной периодической э.д.с. и построить спектр амплитуд для трех гармоник.

2.2 Рассчитать мгновенные и действующие значения несинусоидальных токов по трем гармоникам во всех ветвях электрической цепи.

2.3 Рассчитать активную P, реактивную Q и полную S мощности, потребляемые электрической цепью.

2.4 Построить спектр амплитуд одного из токов и график мгновенных значений этого тока.

 2.5 Сделать анализ полученных результатов и сравнить графики несинусоидального тока и заданной э.д.с.

 

Таблица 2.1

Год поступления	Первая буква фамилии
Четный	АБВ	ГДЕ	ЖЗИ	КЛ	МН	ОПР	СТУ	ХФЦ	ЧШЩ	ЭЮЯ
Нечетный	ЭЮЯ	ЧШЩ	ХФЦ	СТУ	ОПР	МН	КЛ	ЖЗИ	ГДЕ	АБВ
№ схемы	2.1	2.2	2.3	2.4	2.5	2.6	2.7	2.8	2.9	2.10
Форма кривой э.д.с.	2.11	2.12	2.13	2.14	2.15	2.16	2.11	2.12	2.13	2.14
Em, B	45	50	40	35	30	25	20	55	40	60
f,кГц	1,5	0,8	1,2	2,0	0,6	2,5	0,5	1,5	2,0	2,5

  

Таблица 2.2

Год поступления	Предпоследняя цифра зачетной книжки
Четный	1	2	3	4	5	6	7	8	9	0
Нечетный	0	9	8	7	6	5	4	3	2	1
	50	40	60	70	100	45	50	80	100	75
	60	70	100	150	85	90	60	65	45	50
	100	60	50	40	30	80	65	50	80	40
	10	8	5	6	3,5	4	3	10	8	5
C1, мкФ	2,0	2,5	1,5	1,2	0,8	1,6	1,5	2,0	3,0	3,5

 

Таблица 2.3

Год поступления	Последняя цифра зачетной книжки
Четный	1	2	3	4	5	6	7	8	9	0
Нечетный	0	9	8	7	6	5	4	3	2	1
мГн	5,0	6,0	4,0	3,5	2,5	2,0	3,0	4,5	5,0	4,0
мГн	3,0	10	3,0	4,0	2,0	10	6,0	8,0	5,0	2,5
	1,5	2,0	1,0	2,5	1,6	3,0	2,0	3,0	4,0	0,5
	1,0	0,3	0,5	0,6	0,8	1,5	2,0	1,6	2,5	2,0

 

 

 

 

 

 

 

 

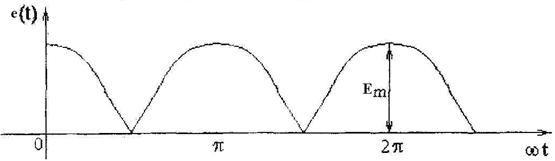
Рисунок 2.11

 

 

 

 

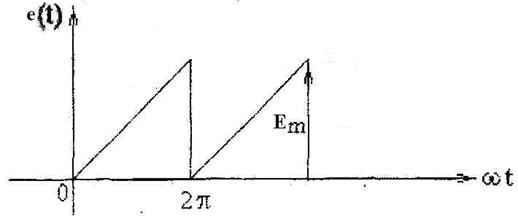
Рисунок 2.12

 

 

 

 

 

 

 

Рисунок 2.13

 

 

 

 

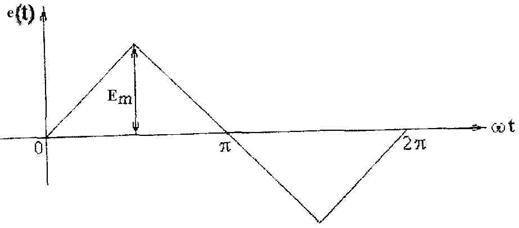
Рисунок 2.14

 

 

 

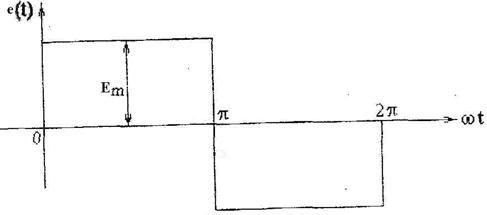
Рисунок 2.15

 

 

 

Рисунок 2.16

 

 

 3 Расчетно-графическая работа №4

Расчет пассивных четырехполюсников. Заданы схемы четырехполюсников (рисунки 3.1-3.10). Параметры элементов четырехполюсника приведены в таблицах 3.1-3.3.

Требуется выполнить:

3.1 Определить комплексные сопротивления четырехполюсника.

3.2 Определить А-параметры четырехполюсника, используя законы Кирхгофа и режимы холостого хода и короткого замыкания. Проверить выполнение соотношения А₁₁ А₂₂-А₁₂А₂₁=1.

3.3 Определить Z-, Y-,H – параметры четырехполюсника (согласно варианту).

3.4 Определить характеристичеcкие сопротивления Z_C1 и Z_C2 четырехполюсника, используя А-параметры и параметры холостого хода и короткого замыкания.

3.5 Определить характеристическую постоянную передачи Г_C, характеристическое ослабление A_C, фазовую постоянную B_C четырехполюсника, используя А-параметры и параметры холостого хода и короткого замыкания.

3.6 Определить комплексные передаточные функции нагруженного на сопротивление нагрузки Z_H четырехполюсника: H_U(jω); H_I(jω); H_Z(jω); H_Y(jω) и построить графики АЧХ и ФЧХ H_U(jω), вычислив параметры L и C четырехполюсника при частоте ω (см. таблицу 3.1).

 

Таблица 3.1

Год поступления	Первая буква фамилии
Четный	АБВ	ГДЕ	ЖЗИ	КЛ	МН	ОПР	СТУ	ХФЦ	ЧШЩ	ЭЮЯ
Нечетный	ЭЮЯ	ЧШЩ	ХФЦ	СТУ	ОПР	МН	КЛ	ЖЗИ	ГДЕ	АБВ
№ схемы	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8	3.9	3.10
ZH, Ом	50	60	40	45	55	30	80	50	60	70
ω, рад/с	1000	1500	1200	800	1300	2000	950	1400	1300	1100
Определить параметры	H	Z	Y	H	Z	Y	H	Z	Y	H

 

Таблица 3.2

Год поступления	Последняя цифра зачетной книжки
Четный	1	2	3	4	5	6	7	8	9	0
Нечетный	0	9	8	7	6	5	4	3	2	1
	20	30	35	40	45	15	25	50	20	30
	60	50	40	30	55	45	35	20	25	40
	15	25	20	65	30	40	18	10	15	20

 

Таблица 3.3

Год поступления	Предпоследняя цифра зачетной книжки
Четный	0	1	2	3	4	5	6	7	8	9
Нечетный	9	8	7	6	5	4	3	2	1	0
XL1	40	45	20	30	25	30	40	60	15	20
XL2	50	30	25	20	40	35	20	45	30	50
XL3	30	20	40	35	25	15	28	36	45	35
XC1	35	80	60	50	30	20	25	40	55	45
XC2	20	25	30	40	20	10	35	20	50	30
XC3	50	40	20	30	10	35	15	20	25	10

 

 

  

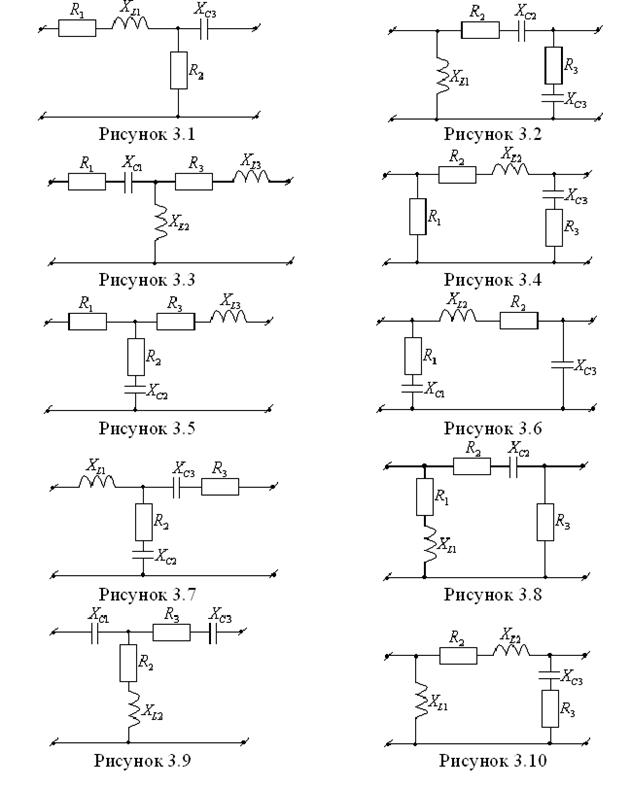
4. Методические указания к выполнению расчетно-графических работ.

4.1 Расчет электрических цепей с несинусоидальными источниками.

Периодическая негармоническая функция f(t), удовлетворяющая условиям Дирихле, может быть разложена в ряд Фурье.

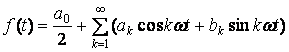
где ω=2π/T, a_k, b_k – коэффициенты ряда, определяемые уравнениями.

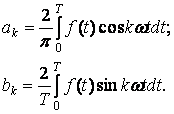
Величина 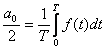-представляет среднее за период значение функции f(t) и называется постоянной составляющей или нулевая гармоника.

Ряд Фурье можно представить и в другой форме

                               *

где ,

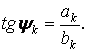
Выражение * следует понимать так, что периодическую функцию f(t) можно представить в виде суммы постоянной составляющей и гармонических колебаний с частотами kω, амплитудами c_k и начальными фазами ψ_k. Если на оси абсцисс отметить частоты гармонических составляющих kω и из этих точек восстановить перпендикуляры, длина которых равна c_k, то такой график представляет собой амплитудно- частотный спектр функции f(t). Аналогичный график, на котором показаны начальные фазы ψ_k, - фазо-частотный спектр функции f(t). Периодические функции f(t) имеют дискретные спектры.

Если периодическое несинусоидальное напряжение подключено к цепи, то расчет токов и напряжений на элементах цепи производится для каждой из гармоник отдельно символическим методом. При этом индуктивные и емкостные сопротивления для k-й гармоники равны , Расчет постоянной составляющей производится по методам расчета цепей постоянного тока, причем катушка для постоянного тока представляет собой короткозамкнутый участок, а ветвь с конденсатором – разомкнутый участок. Применив принцип наложения, мгновенное значение тока в ветви находят как сумму мгновенных значений составляющих токов

    

где I₀-постоянная составляющая тока ;

I_mk- амплитуда тока k-ой гармоники;

Ψ_ik-начальная фаза тока k-ой гармоники.

Действующее значение периодического несинусоидального тока I определяется действующими значениями его гармоник I_k

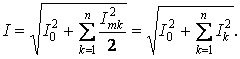
Аналогично определяется действующее значение напряжения

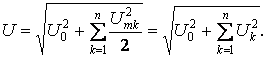
Активная мощность периодического негармонического сигнала – равна сумме активных мощностей отдельных гармоник

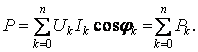
Аналогично определяется реактивная мощность

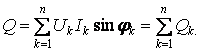
Полная мощность определяется как произведение действующих значений тока и напряжения

 .

 

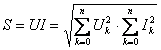4.2 Расчет пассивных четырехполюсников

 

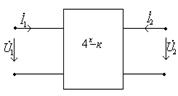Уравнения, связывающие входные и выходные токи и напряжения, называются уравнениями передачи четырехполюсника.

 

 

Существует шесть форм записи уравнений передачи четырехполюсника

Уравнения передачи в Z- параметрах

 

Уравнения передачи в Y- параметрах

 

 

Уравнения передачи в H- параметрах

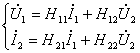
Уравнения передачи в A- параметрах

(токи и направлены слева направо –вариант прямой передачи сигнала)

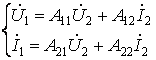
_{Уравнения передачи в B параметрах}

 

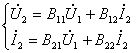
_{Уравнения передачи в F параметрах}

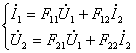
Параметры четырехполюсника можно определить различными способами:

1) составлением уравнений по законам Кирхгофа и представлением их в виде одной из форм уравнений передачи;

2) по значениям напряжений и токов в режимах холостого хода и короткого замыкания, например:

   ;

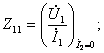
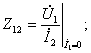
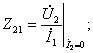
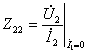3) разбивкой сложного четырехполюсника на более простые четырехполюсники, параметры которых известны.

Характеристические параметры четырехполюсника: характеристические сопротивления Z_C1  и Z_C2 и характеристическая постоянная передачи Г_С.

Характеристические параметры можно определить через А параметры

  

 .

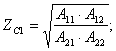
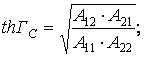
Характеристические параметры выражаются через параметры холостого хода и короткого замыкания

;

;

Постоянная передачи

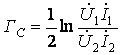(при согласованном включении четырехполюсника  

где А_С – характеристическая постоянная ослабления четырехполюсника (измеряется в Нр или дБ)

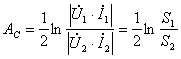
где S₁ и S₂ – полные мощности на входе и выходе четырехполюсника;

B_C – характеристическая постоянная фазы четырехполюсника (измеряется в рад или град).

Комплексные передаточные функции нагруженного четырехполюсника

 

 

 

 

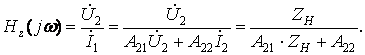
  Список литературы 

1.Бакалов В. П., Дмитриков В.Ф., Крук Б.Е. Основы теории цепей: Учебник для вузов. – М.: Радио и связь, 2000.-592с.

2.Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. - т.1. – Санкт-Петербург: Питер, 2003.

3.Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. - т.2. – Санкт-Петербург: Питер, 2003.

4.Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – М.: Энергоатомиздат, 1989.-528с.

5.Шебес М. Р., Каблукова М. В. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1990.-544с.

6. Жолдыбаева З.И., Зуслина Е.Х., Коровченко Т.И. Теория электрических цепей 1. Конспект лекций. – Алматы: АИЭС, 2007. – 79 с.

7. Жолдыбаева З.И., Коровченко Т.И. Теория электрических цепей. Учебное пособие. - Алматы: АИЭС, 2007. – 77 с.