АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ  

Кафедра теоретических основ электротехники

 

 

Теория электрических цепей 1,2

Переходные процессы в линейных электрических цепях

 

Программа, методические указания и задания к курсовой работе

для студентов специальности 050719 – Радиотехника,

электроника и телекоммуникации заочной формы обучения.

 

Алматы 2008

 

 СОСТАВИТЕЛЬ: Коровченко Т.И.

Теория электрических цепей 1,2. Программа, методические указания и задания к курсовой работе для студентов специальности  050719 – Радиотехника, электроника и телекоммуникации заочной формы обучения. – Алматы: АИЭС, 2008. – 14 с.

Приводится программа, методические указания и задания к курсовой работе по курсу «Теория электрических цепей 1,2» . Курсовая работа по теме  «Расчет переходных процессов в линейных электрических цепей» предназначена для студентов заочной формы обучения специальности 050719 - Радиотехника, электроника и телекоммуникации.

 

1 Программа курса ТЭЦ 1,2.

1.1 Объем курса ТЭЦ 1,2

Число кредитов-3

Всего-135 часов

Аудиторных занятий-30 часов,

в том числе:

лекций-6 часов,

практических занятий-14 часов,

лабораторных занятий-10 часов.

Занятия с элементами дистанционного обучения-21 час

Самостоятельная работа-90 часов

1.2 Цель и задачи дисциплины ТЭЦ 1,2

Цель дисциплины – изучение установившихся  процессов в линейных электрических цепях постоянного и однофазного синусоидального тока, резонансных режимов, переходных процессов, установившихся режимов в нелинейных  электрических цепях постоянного тока, в  линейных электрических цепях с распределенными параметрами. Этот курс, базирующийся на курсах физики и  высшей математики, содержит различные методы расчета электрических цепей постоянного, синусоидального и несинусоидального токов. Он имеет исключительное значение для формирования научного кругозора специалистов по радиотехнике, радиосвязи и телекоммуникационным системам и на нем основываются все радиотехнические дисциплины.

Задача дисциплины – подготовка студентов на  основе знаний качественных и количественных сторон процессов,  происходящих в различных электротехнических устройствах, для успешного и грамотного решения задач, которые ставят специальные радиотехнические дисциплины.

Пререквизиты дисциплины – изучению дисциплины предшествует освоение высшей  математики, физики, информатики.

Перечень смежных дисциплин: теория электрической связи, линии связи.

В результате изучения дисциплины студент должен освоить:

-           методы расчета установившихся  процессов в линейных электрических цепях;

-           резонансные режимы в электрических цепях;

-        расчет цепей при периодических несинусоидальных воздействиях;

-        четырехполюсники и электрические фильтры;

-        методы расчета  переходных процессов в линейных электрических цепях;

-   цепи с распределенными параметрами;

-        методы расчёта нелинейных цепей.

1.3 Содержание дисциплины

1.3.1 Цель и содержание курса «Теория электрических цепей 1,2». Основные задачи курса, его роль в подготовке специалиста.

1.3.2 Основные понятия, законы и методы расчета электрических цепей постоянного тока – 20 часов.

Элементы электрической цепи. Электрическая схема. Топология электрической цепи. Законы Ома и Кирхгофа. Преобразование электрических схем. Принцип наложения. Метод контурных токов. Метод узловых потенциалов. Метод двух узлов. Метод эквивалентного генератора. Баланс мощности.

Расчет электрических цепей с использованием компьютерных технологий.

1.3.3 Электрические цепи в режиме гармонических воздействий –30часов.

Способы представления гармонических колебаний. Гармонические колебания в резистивных, индуктивных и емкостных цепях. Гармонические колебания в цепи при последовательном и параллельном соединениях R,L,C элементов. Символический метод расчета цепей в разветвленных электрических цепях. Мощности в цепях синусоидального тока. Баланс мощностей в цепях при гармонических воздействиях. Топографические диаграммы. Трехфазные электрические цепи. Расчет трехфазных цепей. Мощности в трехфазных цепях. Компьютерное моделирование электрических цепей.

1.3.4 Резонанс в электрических цепях –10 часов.

Явление  резонанса и его значение в радиотехнике и электросвязи. Последовательный колебательный контур. Резонанс напряжений. Частотные характеристики последовательного контура. Полоса пропускания. Параллельный колебательный контур. Резонанс токов. Частотные характеристики параллельного контура.

1.3.5 Индуктивно связанные цепи – 6 часов.

Явление взаимной индукции. Последовательное и параллельное соединения индуктивно связанных элементов. Методы расчета индуктивно связанных цепей.

1.3.6 Цепи при периодических несинусоидальных воздействиях –6 часов.

Несинусоидальные воздействия. Разложение в ряд Фурье. Действующее, среднее значения и мощность периодического несинусоидального сигнала. Расчет цепей при периодических несинусоидальных воздействиях.

1.3.7 Четырехполюсники – 10 часов.

Общие положения и классификация. Уравнения передачи четырехполюсника. Параметры холостого хода и короткого замыкания четырехполюсника. Характеристические параметры четырехполюсников. Уравнения с гиперболическими  функциями.

1.3.8 Электрические фильтры – 8 часов.

Определение фильтров, их назначение и классификация. Низкочастотные, высокочастотные, полосовые, заграждающие фильтры.

1.3.9 Переходные процессы в электрических цепях –30 часов.

Переходный, установившийся, свободный режимы. Законы коммутации. Классический метод расчета переходных процессов в RL и RC цепях. Разряд емкости на RL цепь. Включение цепи RLC на постоянное напряжение. Переходные  процессы в разветвленных электрических цепях. Операторный метод расчета переходных процессов. Преобразование Лапласа и его свойства. Законы Ома и Кирхгофа в операторной форме.

Непериодическое воздействие. Преобразования Фурье и их свойства. Амплитудно-частотные и фазо-частотные характеристики. Применение спектрального метода для расчета переходных процессов.

Переходная характеристика. Интеграл Дюамеля. Импульсная характеристика цепи. Интеграл наложения.

1.3.10 Цепи с распределенными параметрами – 10 часов.

Общие положения. Уравнения передачи однородной линии. Падающие и отраженные волны. Вторичные параметры однородной линии. Входное сопротивление линии. Линия без потерь. Применение отрезков линии без потерь.

1.3.11 Нелинейные электрические цепи и методы их расчета –5 часов.

Нелинейные двухполюсники. Определение рабочих точек на характеристиках нелинейных двухполюсников. Методы расчета нелинейных цепей. Нелинейные цепи с источниками напряжения и тока.

1.4          Перечень практических занятий

1.4.1 Преобразование электрических цепей. Расчет цепей постоянного тока на основе законов Ома и Кирхгофа – 2 часа.

1.4.2 Расчет цепей постоянного тока методами контурных токов, узловых потенциалов и эквивалентного генератора. Построение потенциальной диаграммы цепи – 2 часа.

1.4.3 Расчет цепей с последовательным, параллельным и смешанным соединением элементов при гармоническом воздействии. Векторные и топографические диаграммы – 2 часа.

1.4.4  Расчет  разветвленных цепей при гармонических воздействиях символическим методом – 2 часа.

1.4.5 Расчет  резонанса напряжений и токов в колебательном контуре. Расчет цепей с взаимной индуктивностью – 1час.

1.4.6 Расчет цепей периодического несинусоидального тока.

Четырехполюсники –1час.

1.4.7 Расчет переходных процессов классическим, операторным и спектральным методами. –3 часа.

1.4.8 Расчет нелинейных электрических цепей. – 1час.

1.5 Перечень лабораторных работ

1.5.1  Исследование линейной электрической цепи постоянного тока –1 ч

1.5.2 Исследование разветвленной линейной электрической цепи однофазного синусоидального тока – 2 часа

1.5.3 Резонанс напряжений – 2 часа.

1.5.4 Исследование входных и передаточных частотных характеристик в цепях первого порядка – 2 часа

1.5.5 Исследование пассивных фильтров – 1 час

1.5.6 Исследование переходных процессов в цепях первого и второго порядков- 2 часа

1.6 Рекомендуемая литература

1.6.1 Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. – 544 с.

1.6.2 Основы теории цепей. Учебник для вузов /Г.В.Зевеке и др.-М.: Энергоиздат,1989.-528с.

1.6.3 Шебес М. Р., Каблукова М. В. Задачник теории линейных электрических цепей: Учебное пособие для вузов. – М.: ВШ, 1990. – 544 с.

1.6.4 Основы теории цепей: Учебник для вузов./ В. П. Бакалов и др. – М.: 2000. – 592 с.

1.6.5 Попов В.П. Основы теории цепей: Учебник для вузов. - М., 2000.-576с.

1.6.6 Кондратенко Л.Н., Коровченко Т.И. Теория электрических цепей. Программа, методические указания и контрольные задания (для студентов заочной формы обучения). – Алматы: АИЭС, 2003. – 28с.

1.6.7 Жолдыбаева З.И., Коровченко Т.И. Теория электрических цепей. Методические указания к выполнению лабораторных работ. Часть 1.- Алматы: АИЭС, 2004.- 27с.

1.6.8 Жолдыбаева З. И., Зуслина Е. Х., Коровченко Т. И. Теория электрических цепей 2. Конспект лекций. – Алматы: АИЭС, 2006. – 52 с.

1.6.9 Жолдыбаева З. И., Зуслина Е. Х., Коровченко Т. И. Теория электрических цепей 1. Конспект лекций. – Алматы: АИЭС, 2007. – 79 с.

1.6.10 Жолдыбаева З. И., Коровченко Т. И. Теория электрических цепей. Учебное пособие. – Алматы: АИЭС, 2007. – 77 с.

2 Методические указания к выполнению и оформлению курсовой работы

2.1 Методические указания к выполнению курсовой работы

Классический метод расчета переходных процессов в линейных электрических цепях второго порядка сводится к следующему:

а) определение независимых начальных условий – напряжения на конденсаторе UC (0) и тока в катушке индуктивности iL(0) в момент времени t=0. Так как в электрической цепи до коммутации действовал источник переменного синусоидального напряжения U(t)=Umsin(ωt+φu) (ключ находился в положении 1), то расчет установившихся значений UC(t) и  iL(t) до коммутации осуществляют комплексным методом. Сначала определяют комплексные амплитуды напряжения на конденсаторе  и тока в катушке, а затем переходят к их мгновенным значениям UC(t) и iL(t) и в полученные выражения подставляют t=0;

б) составление характеристического уравнения наиболее простым методом входного сопротивления. Для этого записывают формулу комплексного входного сопротивления для цепи после коммутации , в которой  заменяют на р и полученное выражение входного операторного сопротивления приравнивают нулю . После подстановки числовых значений параметров цепи рассчитывают корни характеристического уравнения – р1 ,р2  (цепь второго порядка);

в) определение искомого тока  (или напряжения ) в переходном режиме в виде суммы принужденной (установившейся) и свободной составляющих  или .

Принужденной режим цепи после коммутации (ключ находится в положении 2) обусловлен действием источника постоянного напряжения U0, поэтому принужденная составляющая тока  (или напряжения ) может быть найдена методами расчета цепей постоянного тока. Следует отметить, что сопротивление индуктивного элемента постоянному току равно  нулю, а емкостного элемента – бесконечности.

Выражение свободной составляющей тока  (или напряжения ) определяется видом корней характеристического уравнения . Если корни характеристического уравнения  и - различные и вещественные, то  имеет вид ,

где  и - постоянные интегрирования.

Если корни характеристического уравнения равны, т.е. , то  имеет вид .

В случае комплексно-сопряженных корней характеристического уравнения  ( – собственное затухание,  – частота свободных колебаний)  имеет вид ,

где  и  – постоянные интегрирования. В цепях второго порядка для определения постоянных интегрирования используют начальные условия, причем независимые начальные условия определяют из законов коммутации , , а зависимые начальные условия находят путем решения уравнений, составленных по законам Кирхгофа для цепи после коммутации при  t=0.

Расчет переходных процессов операторным методом сводится к следующему:

а) к составлению операторной  схемы замещения для цепи после коммутации с учетом начальных условий. При этом  функции времени ,,,, заменяются их операторными изображениями , ,  .  Сопротивления  реактивных  элементов заменяются их  операторными сопротивлениями.  Если по катушке индуктивности до коммутации  протекал ток , то эквивалентная  операторная схема  состоит  из операторного сопротивления  , последовательно с которым  включен  источник  напряжения с операторным  напряжением , направление  которого совпадает с направлением тока  в индуктивности до коммутации

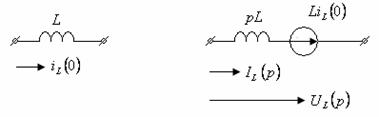
Изображение напряжения на катушке индуктивности определяется по формуле   .

 Если конденсатор до коммутации был заряжен до напряжения  , то эквивалентная операторная схема состоит из операторного сопротивления ,,,последовательно с которым включен источник напряжения с операторным напряжением , направление которого противоположно току.

 

Изображение напряжения на  конденсаторе определяется по формуле

определяется пображе.…..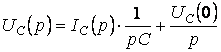

б) по операторной схеме замещения составляют уравнения по законам Кирхгофа (или по методу контурных  токов, методу узловых потенциалов) в операторной форме. В результате  решения полученных  уравнений находят изображения искомых  величин   (или  );

в) по найденному изображению  определяют оригинал  (или ) с помощью теоремы разложения. Если  изображение искомого тока или напряжения имеет вид рациональной дроби

,,

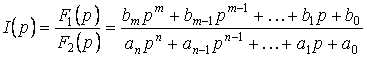причем

причем степень полинома   ниже степени полинома  (m<n), то оригинал определяется выражением

,,

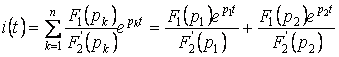где корни  и  уравнения  являются  вещественными. Если один из корней уравнения   равен нулю, т.е. , то оригинал находят по формуле

..

 

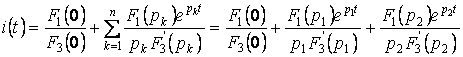Если корни  уравнения  комплексно- сопряженные, то оригинал находят по формуле

.

№

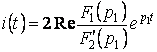2.2 Методические указания к оформлению курсовой работы

2.2.1 Курсовая работа должна быть выполнена в соответствии с фирменным стандартом «Работы учебные», АИЭС, 2002 г. и включать следующие разделы:

а) титульный лист;

б) содержание;

в) введение;

г) задание;

д) основная часть;

е) заключение;

ж) список литературы;

з) приложения.

2.2.2 Номер варианта курсовой работы определяется последней и предпоследней цифрами зачетной книжки и первой буквой фамилии студента.

2.2.3 Текст задания (условие задачи) должен быть переписан полностью со  всеми рисунками и числовами значениями для своего варианта.

2.2.4 Каждый этап курсовой работы должен быть озаглавлен.

2.2.5 Курсовая работа выполняется рукописным способом, а также с применением компьютерной печати (в программе Microsoft Word , шрифт высотой 14 пунктов с интервалом 1,0…1,5). Текст пишется на одной стороне листа белой бумаги формата А4. По всем четырем сторонам листа оставляются поля: левое – не менее 30мм, правое – не менее 10мм, верхнее и нижнее- 20мм.

2.2.6 Все листы курсовой работы должны иметь сквозную нумерацию, начиная с титульного листа, включая приложение. Номер листа пишется в правом верхнем углу без точки.

2.2.7 Расчеты должны сопровождаться пояснениями. Нельзя приводить только расчетные формулы и конечные результаты. Курсовые работы, в которых вычисления и пояснения приводятся сокращенно, к защите не допускаются и возвращаются студентам на доработку.

2.2.8 Рисунки, графики и схемы должны быть выполнены  аккуратно и пронумерованы. На графиках обязательно указываются названия изображаемых величин, их единицы измерения. Масштабы необходимо  подбирать так, чтобы было удобно пользоваться графиком или диаграммой. В соответствии с выбранным масштабом подписывают шкалы графиков и диаграмм.

2.2.9 У параметров, имеющих определенные размерности, писать в окончательных результатах соответствующие единицы измерения. Все обозначения электрических  величин должны соответствовать ГОСТу.

2.2.10 Во введении  обосновать необходимость изучения переходных процессов и методов их расчета.

2.2.11 В заключение провести анализ методов  расчета переходных процессов,  использованных в курсовой работе; сравнить результаты, полученные классическим и операторным методами

2.2.12 Курсовая работа засчитывается, если решения не содержат ошибок принципиального характера и если выполнены перечисленные требования.

2.2.13 Работа над курсовой работой помогает студентам проверить степень усвоения ими курса, вырабатывает навык четко и кратко излагать свои мысли.

2.2.14 По дисциплине «Теория электрических цепей 1,2» выполняется курсовая работа  «Переходные процессы в линейных электрических цепей». 

3. Задание к курсовой работе «Переходные процессы в линейных электрических цепях»

Цель задания: Освоение классического и операторного методов расчета переходных процессов в линейных электрических цепях, построение графиков мгновенных значений токов или напряжений в переходном режиме.

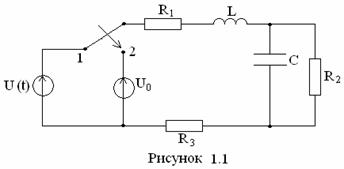
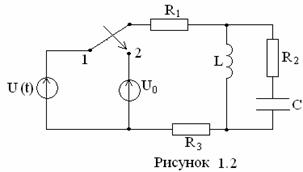
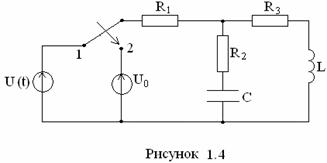
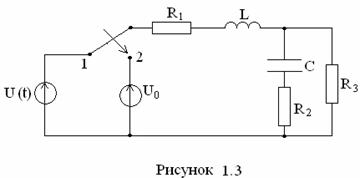
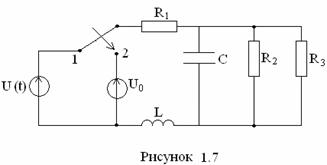
Содержание задания: Дана электрическая цепь (рис. 1.1 – 1.10), в которой в момент времени t = 0 происходит коммутация – цепь переключается от источника переменного синусоидального напряжения U(t)=Umsin(ωt+φu) к источнику  постоянного напряжения  (таблица 1.1). Параметры электрической цепи приведены в таблицах 1.2–1.3.

Требуется:

1. Определить закон изменения во времени тока в одной из ветвей или напряжения на каком-либо элементе после коммутации (таблица 1.3), решив задачу двумя методами: классическим и операторным.

2. Построить график изменения определяемой величины i(t) (или u(t)) в переходном режиме, используя программ  MathCAD или Excel.

Т а б л и ц а  1.1.

Год поступления

Первая буква фамилии

Четный

А Л

Ф

Б М

Ц

В Н

Ч

Г О

Ш

Д П

Щ

Е Р

Э

Ж С

Ю

З Т

Я

И У

К Х

Нечетный

К Ц

Э

ЧХ

Л

А Н

М

Б Ю

О

В П

Я

З Ф

Г Р

Ш

Е Т

Щ

Д С

И

У Ж

Um В

100

120

140

150

145

125

135

80

160

130

φu, град

30о

-45о

60о

-50о

40о

-60

120о

75о

-80о

-30о

f, кГц

0,8

1,0

0,65

1,2

1,5

0,85

1,3

2,0

1,8

1,6

Uо В

60

30

40

45

50

35

25

20

15

40

№ схемы

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10

 

 

Т а б л и ц а  1.2

Год поступления

Последняя цифра зачетной книжки

Четный

1

2

3

4

5

6

7

8

9

0

Нечетный

0

1

2

3

4

5

6

7

8

9

R1, Ом

70

65

120

30

35

25

40

45

50

60

R2, Ом

20

30

40

10

150

60

35

25

45

70

R3, Ом

60

50

30

120

100

150

250

35

60

80

 

Т а б л и ц а  1.3

Год поступления

Предпоследняя цифра зачетной книжки

Четный

1

2

3

4

5

6

7

8

9

0

Нечетный

0

1

2

3

4

5

6

7

8

9

L, мГн

15

8

20

25

30

35

40

45

50

10

C, мкФ

3

5

10

8

6

15

12

20

4

25

определить

il (t)

UL(t)

ic (t)

Uc(t)

iR1(t)

UR1(t)

iR2(t)

Uc(t)

ic (t)

il (t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Список литературы

1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. – 544 с.

2.Основы теории цепей. Учебник для вузов /Г.В. Зевеке и др.-М.: Энергоиздат,1989. – 528 с.

3. Шебес М. Р., Каблукова М. В. Задачник теории линейных электрических цепей: Учебное пособие для вузов. – М.: ВШ, 1990. – 544 с.

4 Основы теории цепей: Учебник для вузов./ В. П. Бакалов и др. – М.: 2000. – 592 с.

5. Попов В.П. Основы теории цепей: Учебник для вузов. - М.: 2000.-576с.

6. Кондратенко Л. Н., Коровченко Т.И. Теория электрических цепей. Программа, методические указания и контрольные задания (для студентов заочной формы обучения). – Алматы: АИЭС, 2003. – 28 с.

7. Жолдыбаева З. И., Коровченко Т.И. Теория электрических цепей. Методические указания к выполнению лабораторных работ. Часть 1.- Алматы: АИЭС, 2004. – 27 с.

8.Жолдыбаева З. И., Зуслина Е. Х., Коровченко Т.И. Теория электрических цепей 2. Конспект лекций – Алматы: АИЭС, 2006. – 52 с.

9. Жолдыбаева З. И., Зуслина Е.Х., Коровченко Т. И. Теория электрических цепей 1. Конспект лекций. – Алматы: АИЭС, 2007. – 79 с.

10.Жолдыбаева З. И., Коровченко Т. И. Теория электрических цепей. Учебное пособие. – Алматы: АИЭС, 2007. – 77 с.

 

Содержание

 

1 Программа курса ТЭЦ 1,2 ………………………………………………3

2 Методические указания к выполнению курсовой работы…………….6

3 Задание к курсовой работе………………………………………………10

4 Список литературы………………………………………………………14