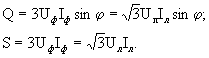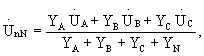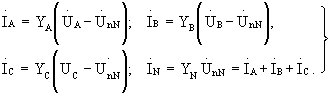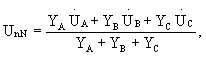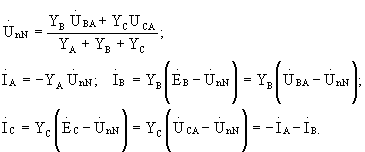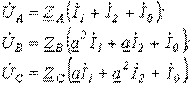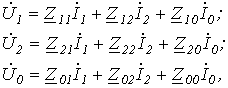АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра теоретических основ электротехники
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ 2
Конспект лекций
(для бакалавриата специальности 050718 – Электроэнергетика)
Алматы 2007
СОСТАВИТЕЛИ: В.И. Денисенко, С.Ю. Креслина. Теоретические основы электротехники 2. Конспект лекций (для студентов всех форм обучения специальности 050718 – Электроэнергетика). – Алматы: АИЭС, 2007.- 63 с.
Конспект лекции содержит 13 лекций по 4 разделам: трехфазные цепи, несинусоидальные токи, четырехполюсники, электрические фильтры.
Конспект лекций предназначен для студентов специальности 050718-Электроэнергетика.
Ил.48, библиограф.-5 назв.
Рецензент: канд. техн. наук, профессор кафедры ЭАПУ М.А.Мустафин
Печатается по плану издания Алматинского института энергетики и связи на 2007г.
Ó Алматинский институт энергетики и связи, 2007г.
Содержание
Введение……………………………………...…………………………..….4
1 Лекция 1………………….…………………...…………………………....5
2 Лекция 2……………………………………………………………….......10
3 Лекция 3…………………………………………………………………...15
4 Лекция 4………………………………………………………………...…19
5Лекция 5…………………………………………………………………....23
6 Лекция 6…………………………………………………………………...27
7 Лекция 7……………………………………………………………….......30
8 Лекция 8………………………………………………………………...…36
9 Лекция 9……………………………………………………………….......41
10 Лекция 10…………………………………………………………….......45
11 Лекция 11……………………………………………………………..….49
12 Лекция 12………………………………………………………………...53
13 Лекция 13…………………………………………………………….......56
Список литературы………………………………………………………...61
Введение
Дисциплина «Теоретические основы электротехники 2» является основным базовым обязательным курсом для подготовки бакалавров в области электроэнергетики. Назначение дисциплины заключается в изучении и описании как с качественной, так и с количественной стороны электромагнитных процессов и явлений, происходящих в различного рода электротехнических установках, представленных эквивалентными схемами замещения с помощью основных элементов электрических цепей.
Предлагаемый конспект лекций содержит 13 лекций по 4 разделам: трехфазные цепи, цепи несинусоидального тока, четырехполюсники, электрические фильтры.
В первом разделе рассмотрены основные понятия о трёхфазных источниках и трёхфазных цепях, расчёт симметричных и несимметричных режимов трёхфазных цепей, метод симметричных составляющих.
Во втором разделе рассмотрены основные понятия о несинусоидальных э.д.с., напряжениях и токах, максимальные, действующие и средние значения несинусоидальных периодических э.д.с., напряжений и токов, расчет цепей с несинусоидальными периодическими э.д.с. и токами, высшие гармоники в трехфазных цепях.
В третьем разделе приведены основные понятия, схемы и системы уравнений четырехполюсников.
В четвертом разделе рассмотрены основы теории к-фильтров, фильтры НЧ и ВЧ, полосовые и заграждающие k-фильтры.
Конспект лекций предназначен для студентов, обучающихся в бакалавриате по специальности 050718 – Электроэнергетика.
Трехфазные цепи
1 Лекция 1. Основные понятия о трехфазных цепях, симметричные режимы трехфазных цепей.
Цель лекции: Рассмотреть основные понятия о трехфазных цепях и способах их соединения, а также изучить методику расчета симметричных режимов трехфазных цепей.
1.1 Понятие о трёхфазных источниках питания и трёхфазных цепях
На рисунке 1.1 схематично показано устройство генератора переменного тока с тремя обмотками на статоре. Ради упрощения каждая обмотка показана состоящей только из двух проводов, заложенных в диаметрально противоположные пазы статора. Эти провода на заднем торце статора соединены друг с другом (соединения показаны пунктиром). На переднем торце статора они оканчиваются зажимами А, Х, В, У, С, Z, которые служат для подсоединения внешней цепи.
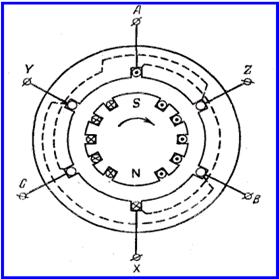
Рисунок 1.1
Наводимые в обмотках э.д.с. максимальны, когда ось полюсов ротора пересекает проводники статора. Для разных обмоток это происходит в различные моменты времени. Поэтому наводимые э.д.с. не совпадают по фазе.
Генераторы с несколькими обмотками, в которых наводятся э.д.с. одинаковой частоты, но сдвинутые относительно друг друга по фазе, называются многофазными генераторами.
Соответственно любые источники питания, имеющие несколько зажимов (полюсов), между которыми создаются напряжения одной и той же частоты, сдвинутые относительно друг друга по фазе, называются многофазными источниками питания. Совокупность электрических цепей с многофазными источниками питания называется многофазной системой электрических цепей. Отдельные ее части называются фазами, например, отдельные обмотки генератора называют фазными обмотками или, кратко, фазами генератора. Таким образом, в электротехнике термин “фаза” имеет два различных значения: он является понятием, характеризующим стадию периодического процесса и, с другой стороны, наименованием составной части многофазной системы электрических цепей.
По числу фаз многофазные источники питания и системы цепей подразделяются на двух-, трех-, четырехфазные и т. д. В соответствии с этой классификацией генератор с тремя обмотками (рисунок 1.1) - трехфазный, а цепи переменного тока, рассмотренные в предыдущих главах, можно назвать однофазными.
В электроэнергетике вследствие наибольшей экономичности и технического совершенства применяются почти исключительно трехфазные цепи. В установках, преобразующих переменный ток в постоянный, встречаются шести- и двенадцати фазные цепи. В автоматике и телемеханике применяются двухфазные цепи.
Крайним точкам фазных обмоток генераторов дают наименования “начало” и “конец”. В трехфазных генераторах “начала” обозначим первыми буквами латинского алфавита А, В и С, а “концы” - последними буквами Х, У и Z. При разметке руководствуются следующим условием: при одинаковых положительных направлениях э.д.с. во всех обмотках от “концов” к “началам” (или от “начал” к “концам”) э.д.с. должны быть сдвинуты по фазе друг относительно друга симметрично. Поясним сказанное на примере трехфазного генератора. Покажем, что разметка концов фазных обмоток на рисунке 1.1 удовлетворяет принятому условию, т.е. что э.д.с. в фазах А, В и С сдвинуты друг относительно друга симметрично на 1/3 периода. Выберем положительные направления э.д.с. во всех обмотках от концов к началам. В момент времени, соответствующий положению ротора, показанному на рисунке 1.1, э.д.с. в обмотке А максимальна и имеет направление, которое принято положительным, т.е. в этот момент э.д.с. в обмотке А достигает положительного максимума. Положительный максимум э.д.с. в обмотке В наступит позже, когда ротор повернется на 1/3 оборота. Так как один оборот ротора двухполюсного генератора соответствует одному периоду изменения э.д.с. в любой обмотке, то поворот ротора на 1/3 оборота соответствует 1/3 периода и, следовательно, э.д.с. в обмотке В отстает по фазе от э.д.с, в обмотке А на 1/3 периода. Рассуждая аналогично, можно убедиться, что э.д.с. в обмотке С отстает по фазе от э.д.с. в обмотке В также на 1/3 периода.
На рисунке 1.2 показаны векторная диаграмма и график мгновенных э.д.с. трехфазного генератора.
Порядок, в котором э.д.с. в фазных обмотках генератора проходят через одинаковые значения, например через положительные максимумы, называют последовательностью фаз или порядком чередования фаз. При указанном на рисунке 1.1 направлении вращения ротора получаем последовательность фаз АВС . Если изменить направление вращения ротора на противоположное, то последовательность фаз получится обратной. У генераторов роторы вращаются всегда в одном направлении, поэтому последовательность фаз никогда не изменяется и может быть раз навсегда установлена и обозначена.
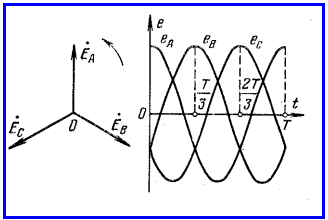
Рисунок 1.2
Ее обозначение связывают с наименованием фаз. Наименования устанавливаются первыми буквами латинского алфавита, причем таким образом, чтобы нормальный порядок букв (А, В и С) соответствовал последовательности фаз.
Рассмотренная совокупность э.д.с. в обмотках трехфазного генератора называется трехфазной системой э.д.с. Совокупности э.д.с. (напряжений, токов) в многофазных цепях называют многофазными системами э.д.с. (напряжений, токов). Эти системы называют симметричными, если все э.д.с. (напряжения, токи) равны по величине и если каждая э. д. с. (напряжение, ток) отстает по фазе от предыдущей э.д.с. (напряжения, тока) на один и тот же фазный угол, равный 2p/m, где m - число фаз.
На рисунке 1.3, а в качестве примера приведена векторная диаграмма симметричной системы э.д.с. шестифазного генератора.
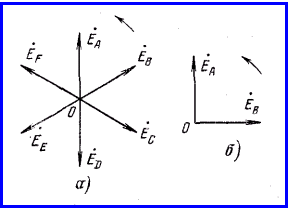
Рисунок 1.3
Двухфазные генераторы изготовляются таким образом, чтобы э.д.с. в одной из обмоток была сдвинута по фазе относительно э.д.с. другой обмотки на 1/4 периода. Векторная диаграмма системы э.д.с. двухфазного генератора приведена на рисунке 1.3, б, эта система э.д.с. несимметрична.
1.2 Соединения звездой и треугольником
Существуют два основных способа соединения обмоток генераторов, трансформаторов и приемников в трёхфазных цепях: соединение звездой и соединение треугольником. Например, соединение генератора и приемника звездой показано на рисунке 1.4, а соединение треугольником - на рисунке 1.5.
При соединении звездой (рисунок 1.4) все “концы” фазных обмоток генератора соединяют в одну общую точку. Общие точки обмоток генератора и ветвей звезды приемника называют
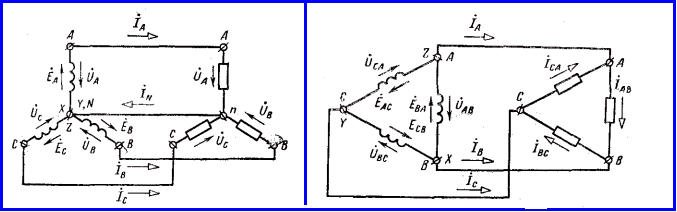
|
Рисунок 1.4 |
Рисунок 1.5 |
нейтральными или нулевыми точками, а соединяющий их провод - нейтральным или нулевым проводом. Остальные провода, соединяющие обмотки генератора с приемником, называют линейными.
При соединении треугольником (рисунок 1.5) фазные обмотки генератора
соединяются последовательно таким образом, чтобы “начало” одной обмотки
соединялось с “концом” другой обмотки. Общие точки каждой пары фазных обмоток
генератора и общие точки каждой пары ветвей приемника соединяются проводами,
носящими название линейных проводов. На первый взгляд может показаться, что
соединение обмоток генератора в треугольник равносильно короткому замыканию,
как это было бы при подобном соединении, например, гальванических элементов. На
самом деле, при симметричной системе э.д.с. сумма э.д.с., действующих в контуре
треугольника, в любой момент времени равна нулю. Убедиться в этом можно хотя бы
из рассмотрения векторной диаграммы и кривых мгновенных значений э.д.с. для
трехфазного генератора (рисунок 1.2).
Схемы соединения обмоток
источников питания и приемников не зависят друг от друга. В одной и той же цепи
могут быть источники питания и приемники с разными схемами соединений. Лучи
звезды или ветви треугольника приемника называют фазами приемника, а
сопротивления фаз приемника - фазными сопротивлениями. Электродвижущие силы,
наводимые в фазных обмотках генератора или трансформатора, напряжения на их
зажимах, напряжения на фазах приемниках и токи в них называют соответственно
фазными э.д.с., напряжениями и токами (Eф, Uф, Iф). Напряжения между линейными
проводами и токи в них называют линейными напряжениями и токами (Uл, Iл). При
соединении фаз звездой линейные токи равны фазным Iл = Iф. При соединении фаз треугольником
линейное напряжение между проводами, присоединенными к одной и той же фазе
приемника или источника питания, равно соответствующему фазному напряжению Uл =
Uф.
Положительные
направления токов во всех линейных проводах выберем одинаковыми от источника
питания к приемнику, а в нейтральном проводе - от нейтральной точки приемника к
нейтральной точке источника питания. Положительные направления э.д.с. и токов в
ветвях треугольника источника питания будем обычно выбирать в направлении АСВА,
а напряжений и токов в ветвях треугольника приемника - в направлении АВСА {рисунок
1.5).
Трёхфазную цепь и трёхфазный приемник называют симметричными, если комплексные сопротивления всех фаз одинаковы. В противном случае их называют несимметричными.
Если к симметричной трехфазной цепи приложена симметричная система напряжений, то получается симметричная система токов. Режим трёхфазной цепи, при котором трёхфазные системы напряжений и токов симметричны, называется симметричным режимом.
1.3 Симметричный режим трехфазной цепи
На рисунке 1.6 приведены топографическая диаграмма и векторная диаграмма токов при симметричном режиме для схемы по рисунку 1.4 и индуктивном характере нагрузки (j>0).
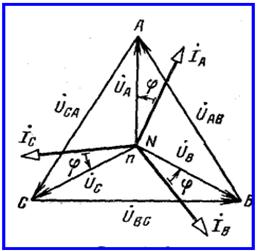
Рисунок 1.6
Ток в нейтральном проводе отсутствует: ![]()
Поэтому при симметричном приемнике нейтральный провод не применяют. Линейные напряжения определяются как разности фазных напряжений:
|
|
|
(1.1) |
Из равнобедренного треугольника АNB имеем:
|
|
|
(1.2) |
На рисунке 1.7 приведены векторные диаграммы напряжений и токов при симметричном режиме и j>0 для схемы рисунка 1.5.
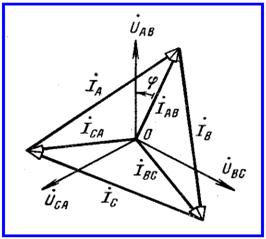
Рисунок 1.7
Линейные токи определяются как разности фазных токов:
|
|
|
(1-3) |
Причем
|
|
|
|
Активная мощность симметричного трехфазного приемника
|
|
|
|
Принимая во внимание, что при соединении ветвей приемника звездой
|
|
|
|
а при соединении ветвей приемника треугольником ![]() получим независимо от
вида соединения:
получим независимо от
вида соединения:
|
|
|
|
Следует помнить, что в этом выражении j - сдвиг по фазе между фазным напряжением и фазным током.
Аналогично для реактивной и полной мощностей симметричного трехфазного приемника имеем:
|
|
|
(1.6) (1.7) |
2 Лекция 2. Расчет симметричных и несимметричных режимов трехфазных цепей.
Цель лекции: Изучить методику расчета симметричных и несимметричных режимов трехфазных цепей со статической нагрузкой.
2.1 Расчет симметричных режимов трехфазных цепей
Для ознакомления с расчетами симметричных режимов рассмотрим порядок расчета
токов в симметричной цепи рисунке 2.1. Пусть напряжения на зажимах источника
питания симметричны и заданы и пусть известны сопротивления всех-элементов цепи
1, 2, 3 и 4. Для выполнения расчета проще всего преобразовать схему, заменив
соединения треугольниками источника питания и элементов 4 на
соединения звездами. Сопротивления фаз симметричной звезды в 3 раза меньше
сопротивлений фаз эквивалентного симметричного треугольника. Фазные напряжения
эквивалентного источника питания, соединенного звездой, в ![]() раз меньше заданных линейных
напряжений. Таким образом, получим схему, показанную на рисунке 2.2.
раз меньше заданных линейных
напряжений. Таким образом, получим схему, показанную на рисунке 2.2.
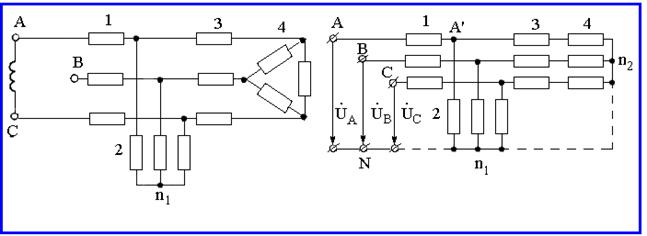
|
Рисунок 2.1 |
Рисунок 2.2 |
Все нейтральные точки в симметричном режиме имеют одинаковый потенциал. Поэтому, не нарушая режима схемы, соединим их проводом без сопротивления (показан пунктиром). Затем удалим из схемы две фазы, например В и С, и перейдем к схеме по рисунку 2.3. Это не изменит режима оставшейся фазы А.

Рисунок 2.3
Действительно, уравнения, составленные по законам Кирхгофа, для узла А' и для
контуров АА'n1N и А'n2n1А'
для схем, показанных на рисунках 2.2 и 2.3, одинаковы, а следовательно, токи и
напряжения в фазе А обеих схем также одинаковы. Токи в фазе А легко
рассчитывают по однофазной схеме (рисунок 2.3), например, методом ее
дальнейшего преобразования - заменой параллельного соединения
ветвей А'n2 и А'n1,
эквивалентным сопротивлением. Токи в фазах В и С по модулю такие же, что и в
фазе А. Токи в ветвях треугольника 4 в ![]()
![]() раз меньше токов в элементах 3 (в каждом
из элементов любой из групп ток сдвинут по фазе по отношению к токам в других
элементах той же группы на равные углы +
раз меньше токов в элементах 3 (в каждом
из элементов любой из групп ток сдвинут по фазе по отношению к токам в других
элементах той же группы на равные углы + ![]() или
или ![]() ).
).
Для расчета симметричных режимов в сложных разветвленных трехфазных цепях широко применяют моделирование соответствующих однофазных схем.
2.2 Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
При расчете симметричных режимов трехфазных цепей двигатели можно заменять эквивалентными схемами, состоящими из трех одинаковых сопротивлений, соединенных звездой или треугольником. Падения напряжения в фазах генератора могут учитываться как напряжения на трех одинаковых сопротивлениях.
Такие простые эквивалентные схемы для двигателей и такой простой учет падений напряжения в генераторах оказываются непригодными для расчета несимметричных режимов. Анализ процессов в трехфазных электрических машинах (двигателях и генераторах) при несимметричных режимах показывает, что для них справедливы более сложные эквивалентные схемы, не удовлетворяющие принципу взаимности. В настоящее время для расчета несимметричных режимов в трехфазных цепях с трехфазными двигателями почти исключительно пользуются специальным методом расчета - методом симметричных составляющих, который будет рассмотрен далее.
В этом параграфе ограничимся исследованием несимметричных режимов цепей при следующих двух условиях:
1) имеется только статическая нагрузка (нет электродвигателей);
2) падения напряжения в
генераторах не учитываются.
При двух указанных
ограничениях расчеты несимметричных режимов трехфазных цепей не содержат ничего
принципиально нового и могут выполняться любыми методами, известными из
предыдущих глав. Последующее содержание параграфа иллюстрирует это положение на
ряде частных примеров.
Пусть заданы несимметричные фазные напряжения UА, UВ и UС на зажимах несимметричного приемника (рисунок 2.4).
Определим токи. Заданные напряжения можно всегда приписать источникам э.д.с. (показаны пунктиром)
![]()
В схеме два узла, поэтому целесообразно применить для расчета метод узловых потенциалов.
Обозначая напряжение между нейтральными точками приемника и источника питания через UnN получаем:
|
|
|
(2.1) |
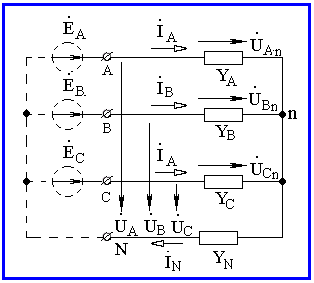
Рисунок 2.4
где YA , YB , YC , YN - проводимости ветвей;
|
|
|
(2.2) |
В предельном случае при ![]() имеем
имеем ![]() и, следовательно, напряжения на фазах приемника равны фазным напряжениям
источника питания. При этом условии ток в каждой фазе может быть подсчитан по
закону Ома независимо от токов остальных фаз.
и, следовательно, напряжения на фазах приемника равны фазным напряжениям
источника питания. При этом условии ток в каждой фазе может быть подсчитан по
закону Ома независимо от токов остальных фаз.
При отсутствии нейтрального провода расчет можно вести в таком же порядке. Изменится лишь выражение для напряжения UnN, поскольку YN = 0, а именно
|
|
|
(2.3) |
Однако обычно при отсутствии нейтрального провода бывают заданы не фазные, а линейные напряжения на зажимах цепи. Сумма линейных напряжений равна нулю, как сумма напряжений вдоль замкнутого контура, соединяющего зажимы А, В и С:
![]()
Учитывая эту связь, достаточно задать два линейных напряжения. Можно, например, их задать двумя источниками напряжения (рисунок 2.5) с э.д.с.
![]()
Тогда, принимая во внимание, что потенциалы точек N и А одинаковы, имеем:
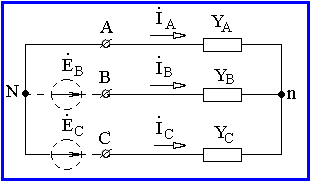
Рисунок 2.5
|
|
|
(2.4) |
Рассмотрим простейшую схему с несимметричным приемником; соединенным треугольником (рисунок 2.6). Если известны линейные напряжения между зажимами А', В', С', к которым присоединены сопротивления приемника, то задача определения токов элементарно проста. Ток в каждой ветви треугольника определяется по закону Ома, а затем находятся токи в проводах питающей линии.
Однако обычно бывают известны напряжения не на зажимах приемника, а на зажимах А, В, С источника питания, поэтому расчет несколько усложняется. Проще всего его провести, заменяя треугольник сопротивлений эквивалентной звездой. Тогда получается схема по рисунку 2.5 и токи в ней рассчитываются, как указано выше. По найденным токам определяются напряжения на зажимах треугольника в исходной схеме (рисунок 2.6) и затем токи в ветвях треугольника.
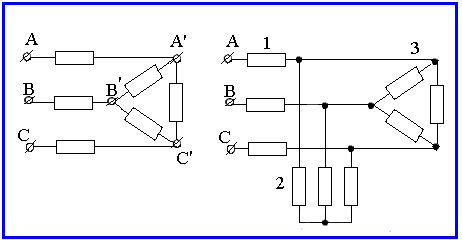
|
Рисунок 2.6 |
Рисунок 2.7 |
К преобразованию схемы следует прибегать и в случае цепи с несколькими приемниками, имеющими различные схемы соединений. Так, например, при расчете токов в цепи, представленной на рисунке 2.7, звезду 2 следует преобразовать в эквивалентный треугольник, ветви которого будут параллельны ветвям треугольника 3. После замены каждой пары параллельных ветвей треугольников одной ветвью получается рассмотренная выше схема (рисунок 2.6).
Заметим, что преобразование треугольника 3 в звезду не дало бы возможности продолжить упрощение схемы. Потенциалы нейтральных точек получившейся звезды и звезды 2 в общем случае различны и нейтральные точки этих звезд нельзя соединять друг с другом.
3 Лекция 3. Линейные и круговые диаграммы в трехфазных цепях, сравнение схем трехфазных цепей.
Цель лекции: Рассмотреть построение линейных и круговых диаграмм в трехфазных цепях, а также сравнить схемы трехфазных цепей, применяемых при питании однофазных приёмников.
3.1 Линейные и круговые диаграммы в трехфазных цепях
Пусть приемник соединен звездой (рисунок 2.5). Проводимости фаз
![]()
Фазные напряжения при заданных линейных напряжениях определяются на топографической диаграмме положением нейтральной точки, для определения положения которой обратимся к выражению (2-4).
Рассмотрим некоторые частные случаи.
Симметричный приемник при несимметричных линейных напряжениях. При
![]() вектор напряжения
вектор напряжения
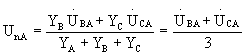
равен одной трети диагонали параллелограмма (рисунок 3.1). Отсюда следует, что нейтральной точке на топографической диаграмме соответствует центр тяжести треугольника линейных напряжений.
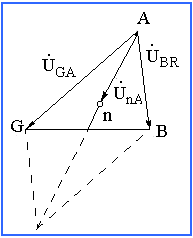
Рисунок 3.1
Приемник с однородными сопротивлениями фаз (YA=YB=YC), одно из которых изменяется.
При проводимости YA, изменяющейся от 0 до ¥ , получим:
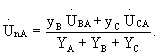
В этом выражении все величины постоянны, кроме уА. При изменении УА аргумент UnA остается неизменным, следовательно, направление вектора UnA сохраняется, а длина его изменяется. Конец вектора UnA описывает прямую линию (получается линейная диаграмма). Для построения этой прямой достаточно найти любые две точки, через которые она проходит. При УА= ¥ (ZA= 0) имеем UnA= 0 и точка n совпадает на топографической диаграмме с точкой А (рисунок 3.2).
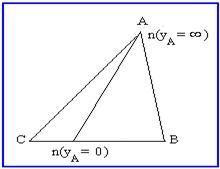
Рисунок 3.2
При уА = 0 (ZA= ¥ )получим IA= 0; IB= -I C .
Поэтому
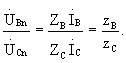
Отсюда видно, что UBn и UCn отличаются по фазе на 180о,
следовательно, точка n находится на отрезке, соединяющем точки В и С. Ее
положение на этом отрезке определяется отношением ZB/ZC
(на рисунке 3.2 положение точки n при УА = О показано для
случая, когда ZB/ZC= 2). Прямая, соединяющая точки
А и n (УА = О), представляет геометрическое место, описываемое
точкой n при изменении УА = О от 0 до
¥.
Приемник с неоднородными
сопротивлениями фаз , одно из которых изменяется.
Пусть yB =
yC = g , yA= ibC причем bC
изменяется от 0 до ¥.
Тогда
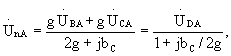
где
![]() Геометрическим местом, описываемым
точкой n при изменении bC, будет круговая
диаграмма. Выполним eе построение при симметричных линейных напряжениях.
Геометрическим местом, описываемым
точкой n при изменении bC, будет круговая
диаграмма. Выполним eе построение при симметричных линейных напряжениях.
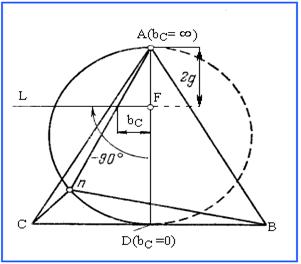
Рисунок 3.3
На топографической диаграмме (рисунок 3.3) эти напряжения представлены равносторонним треугольником АВС. Отложим хорду диаграммы UDA. Началом круговой диаграммы является точка А, она соответствует bC = ¥, при этом вектор UnA обращается в нуль. Конец хорды находится в точке D. Хорда АD соответствует вектору UnA при значении переменного параметра bC = 0 аналогично тому, как вектор Мo, представляет собой М при n = 0. Выбрав масштаб для проводимостей my отложим от начала хорды (точка А) по направлению к ее концу (точка D) отрезок AF, равный 2g, и затем из точки F под углом - y=-90o к хорде АD проведем линию изменяющегося параметра FL. Перпендикуляр, опущенный из начала диаграммы (из точки А) на линию изменяющегося параметра, совпадает с хордой и пересекается с перпендикуляром, восстановленным к середине хорды, в середине хорды. Таким образом, центр круговой диаграммы находится в середине хорды, которая в данном случае является диаметром. На топографической диаграмме показано положение точки n в частном случае, когда BC = g.
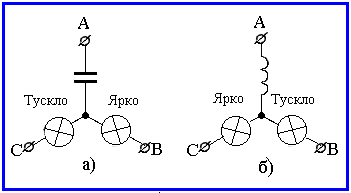
Рисунок 3.4
Напряжения UBn и UCn на одинаковых сопротивлениях в фазах В и C получаются неодинаковыми. Если в качестве сопротивлений взять лампы, то лампа в фазе В будет светить ярче, чем в фазе С. Поэтому две лампы и конденсатор, включенные по схеме рисунка 3.4, а, применяют как указатель последовательности фаз. Напряжение на лампе, которая светит ярко, опережает по фазе напряжение на лампе, которая светит тускло.
Можно вместо конденсатора включить катушку (рисунок 3.4, б). накал ламп будет также неодинаков. Однако в этом случае больший накал наблюдается у лампы, на которой напряжение отстает по фазе от напряжения на лампе, светящейся тускло. Показать это можно, заменив в фазе А (рисунок 2.5) переменную емкость переменной индуктивностью. Геометрическим местом потенциала точки n будет дуга окружности, показанная на диаграмме (рисунок 3.3 ) пунктиром.
3.2 Сопоставление схем трехфазных цепей, применяемых при питании однофазных приёмников.
В трехфазных цепях, питающих однофазные приемники (электросварочные аппараты, однофазные двигатели, электрические лампы и различные бытовые электроприборы), при изменении числа включенных приемников напряжение на их зажимах не должно по возможности изменяться, Это условие выполняется как при соединении приемников звездой с нейтральным проводом, так и при соединении их треугольником.
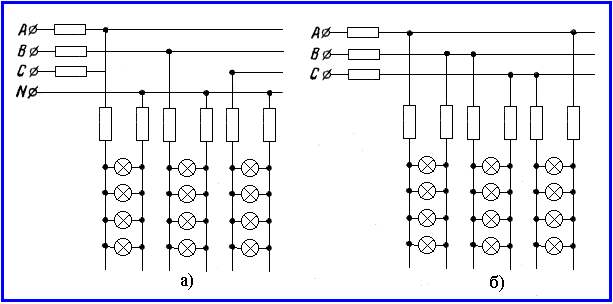
Рисунок 3.5
На рисунке 3.5 в качестве примера приведены соответствующие схемы включения электрических ламп. Если принять, что напряжения на зажимах источника питания (А, В, С и N) поддерживаются неизменными, и пренебречь падением напряжения в проводах, то в обеих схемах напряжения на лампах не отличаются от напряжений на зажимах источника питания и неизменны независимо от числа и мощности включенных в каждой группе ламп. Если оборвать нейтральный провод в схеме по рисунку 3.5,а, то между нейтральной точкой n приемника и нейтральной точкой N источника питания появится напряжение. Фазные напряжения на лампах будут зависеть от соотношения их сопротивлений во всех трех группах и будут изменяться при изменениях числа ламп, включенных в какой-либо группе. Поэтому соединение групп ламп звездой без нейтрального провода не применяется. При наличии нейтрального провода в случае перегорания предохранителя в одном из проводов магистральной линии, например в проводе А (рисунок 3.5, а), гаснут лампы, присоединенные только в этому проводу, остальные лампы имеют нормальный накал. В этом же случае в схеме треугольника (рисунок 3.8, б) под нормальным напряжением останется только одна группа ламп в ветви ВС. Две другие ветви треугольника окажутся соединенными последовательно, питаются эти ветви по-прежнему от магистральных проводов В и С. Лампы в этих ветвях треугольника будут иметь неполный накал. Напряжения между ветвями АВ и СА распределятся пропорционально их сопротивлениям. Чем больше включено ламп в одну из ветвей, например в АВ, тем ярче будут светить лампы в другой ветви СА (увеличение числа включенных ламп уменьшает сопротивление ветви).
Трехфазная цепь с нейтральным проводом обладает тем преимуществом, что может питать приемники, рассчитанные для работы при различных напряжениях. Приемники в такой цепи можно включать между линейными проводами на линейное напряжение и между линейными проводами и нейтральным проводом на фазное напряжение. На практике обычно встречаются низковольтные трехфазные цепи с нейтральными проводами и напряжениями:
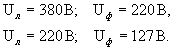
4 Лекция 4. Измерение активной мощности в трехфазных цепях, вращающее магнитное поле.
Цель лекции: Изучить схемы измерения активной мощности в трехфазных цепях и принцип получения вращающегося магнитного поля.
4.1 Измерение мощности в трехфазных цепях
Выясним, сколько ваттметров нужно включить для измерения активной мощности в трехфазной цепи при любом несимметричном режиме.
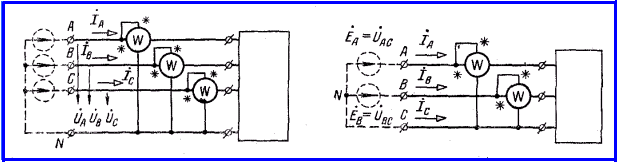
Рисунок 4.1 Рисунок 4.2
На рисунке 4.1 прямоугольником условно показана сколь угодно сложная цепь,
питаемая трехфазной линией с нейтральным проводом. Фазные напряжения на входе
линии с нейтральным проводом всегда можно приписать трем источникам напряжения
(показаны пунктиром). Из этого следует, что для измерения активной мощности в
трехфазной линии с нейтральным проводом нужно включить три ваттметра, как
показано на рисунке 4.1 (ваттметры измеряют активные мощности источников
напряжения).
В цепи без нейтрального
провода (рисунок 4.2) линейные напряжения на входных зажимах всегда можно
рассматривать получающимися от двух источников напряжения , например включенных
так, как показано пунктиром на рисунке 4.2. Следовательно, активная мощность
передачи энергии по линии без нейтрального провода может быть измерена двумя
ваттметрами. Следует иметь в виду, что возможны такие режимы работы цепи, при
которых стрелка того или иного ваттметра отклоняется в обратную сторону,
несмотря на правильное включение ваттметра в цепь. Тогда, чтобы сделать
отсчет по шкале, нужно изменить подключение обмотки напряжения или обмотки тока
соответствующего ваттметра на противоположное. Измеренную после этого
мощность следует считать отрицательной. Пример подобного случая приводится ниже.
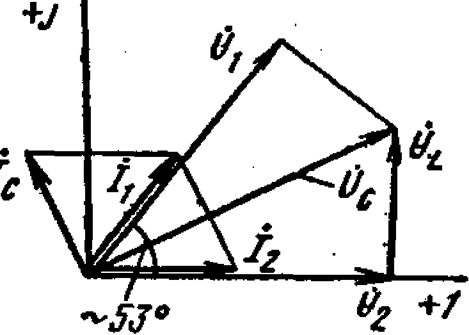
Выясним зависимость мощности, измеряемой каждым из ваттметров в схеме рисунку 4.2, от сдвига фаз между напряжениями и токами в частном случае симметричного режима. На рисунке 4.3 показана векторная диаграмма токов и напряжений. Линии, соединяющие центр тяжести треугольника напряжений с его вершинами, можно рассматривать как фазные напряжения эквивалентного приемника, соединенного звездой.
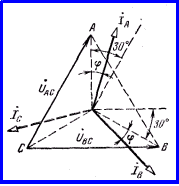
Рисунок 4.3
На основании схемы включения одноименных зажимов ваттметров и руководствуясь векторной диаграммой, можно записать:
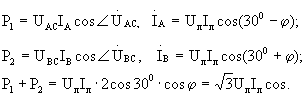
Как следует из этих выражений, показания ваттметров одинаковы только при j= 0. При j = 600 получаем Р2 = 0, а при j= - 600 имеем Р1 = 0. При j > 600 имеем Р2 < 0, а при j< - 600 получаем Р1< 0. При j= -+ 900 имеем Р2 =- Р1. Таким образом, при újú> 600 стрелка одного из ваттметров отклоняется в обратную сторону.
4.2 Вращающееся магнитное поле
Одним из основных преимуществ многофазных токов является возможность получения вращающихся магнитных полей, лежащих в основе принципа действия наиболее распространенных типов двигателей переменного тока. Вращающееся магнитное поле было получено физиком Г. Феррарисом в 1884 г., однако он пришел к ошибочному заключению о невыгодности его применения для создания электродвигателей.
В 1887 - 1888 гг. физик-инженер Н. Тесла сконструировал двухфазный асинхронный двигатель (наименование “асинхронный” будет пояснено в следующем параграфе), а в 1889 г. М. О. Доливо- Добровольский изобрел и построил трехфазный асинхронный двигатель. Н. Тесла в последующие годы вел работы по внедрению двухфазных двигателей, генераторов и электропередач в США.
Ознакомимся на простейшем примере с получением вращающегося магнитного поля посредством трехфазной системы токов.
Расположим три одинаковые катушки 1, 2 и 3 под углом 1200 друг относительно друга. На рисунке 4.4,а они показаны в поперечном разрезе.
Подключим катушки 1, 2 и 3 соответственно к фазам А, В и С источника питания таким образом, чтобы токи были симметричны ( рисунок 4.4, б) при показанных на рисунке 4.4,а положительных направлениях токов.
Рассмотрим схематические картины магнитного поля для различных моментов времени, следующих друг за другом
Пусть первый из рассматриваемых моментов времени соответствует совпадению линии времени с вектором I1. При этом i1>0, i2<0 и i3<0
Направления токов в катушках и схематическая картина магнитного поля показаны на рисунке 4.5, а, где пунктиром изображены две магнитные линии.
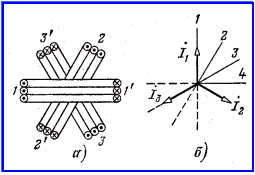
Рисунок 4.4
Для момента времени, соответствующего положению линии времени, отмеченному цифрой 2, i1>0 , i2 = 0 и i3<0 .
Направления - токов в катушках и схематическая картина поля даны на рисунке4.5, б. Далее на рисунке4.5, в и г показаны направления токов и схематические картины поля для моментов времени, соответствующих положениям линии времени 3 и 4. Сопоставление схематических картин магнитного поля, приведенных для различных, следующих друг за другом моментов времени, наглядно показывает вращение магнитного поля. Продолжив анализ, можно убедиться, что в течение одного периода переменного тока магнитное поле таких катушек совершает один полный оборот.
Направление вращения магнитного поля зависит исключительно от последовательности фаз токов в катушках. Если сохранить подключение катушки 1 к фазе А источника питания, катушку 2 подключить к фазе С, а катушку 3- к фазе В, то направление вращения поля изменится на противоположное.
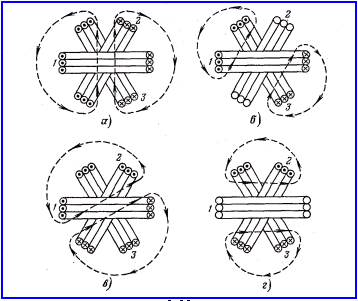
Рисунок 4.5
В этом можно убедиться, построив схематические картины магнитного поля для
различных моментов времени, аналогично тому, как это было показано выше.
Движущиеся в
пространстве магнитные поля, частным случаем которых является рассмотренный
пример, широко применяются в различных областях электротехники.
Для получения
движущегося магнитного поля нужно иметь минимум две пространственно смещенные
обмотки с несовпадающими по фазе токами.
4.3 Принципы действия асинхронного и синхронного двигателей
Поместим между неподвижными катушками (рисунок 4.6) в области вращающегося магнитного поля укрепленный на оси подвижный металлический барабан.
Если магнитное поле вращается по направлению движения часовой стрелки, то
барабан относительно поля вращается. в обратном направлении.
Принимая это во
внимание, по правилу правой руки найдем направление наведенных в барабане токов
(на рисунке 4.6 указаны крестиками и точками).
Затем, применяя правило
левой руки, убедимся, что взаимодействие этих токов с магнитным полем дает
силы, приводящие в движение барабан в том же направлении, в каком вращается
магнитное поле. Частота вращения барабана меньше частоты вращения магнитного
поля относительно катушек, так как при одинаковых угловых скоростях
прекратилось бы наведение токов в барабане и, следовательно, не было бы сил,
создающих вращающий момент.
Рассмотренное простейшее устройство поясняет принцип действия трехфазных асинхронных двигателей. Слово асинхронный заимствовано из греческого языка и означает неодновременный Этим словом подчеркивается различие в частотах вращающегося поля и ротора - подвижной части двигателя. Поместим между неподвижными катушками (рисунок 4.7) в области вращающегося магнитного поля укрепленный на оси подвижный электромагнит, питаемый постоянным током. На электромагнит действует вращающий момент, направление которого изменяется 2 раза за каждый оборот магнитного поля. Вследствие периодического изменения направления вращающегося момента и инерции подвижной системы электромагнит останется неподвижным. Однако, если его привести во вращение посредством какого -.либо приспособления с угловой скоростью, близкой к угловой скорости вращающегося поля, то он будет продолжать вращаться и достигнет частоты вращения, одинаковой с частотой вращения поля.
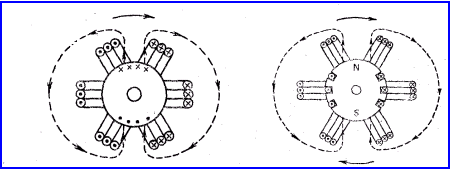
Рисунок 4.6 Рисунок 4.7
Рассмотренное устройство поясняет принцип действия трехфазных синхронных двигателей. Греческое слово синхронный означает одновременный. Этим словом подчеркивается одинаковая частота вращения вращающегося поля и ротора.
В электрических машинах для вращающегося магнитного поля создается магнитная цепь. Статор - неподвижная часть машины, выполняется в виде полого цилиндра, собранного из отдельных изолированных друг от друга стальных листов. Ротор - подвижная часть машины - в асинхронных двигателях выполняется в виде стального цилиндра, обычно также собранного из стальных листов с обмоткой, размещенной в пазах на его поверхности.
Лекция 5. Метод симметричных составляющих.
Цель лекции: Рассмотреть симметричные составляющие трёхфазной системы и их свойства.
5.1 Симметричные составляющие трехфазной системы величин
Метод симметричных составляющих относится к
специальным методам расчета трехфазных цепей и широко применяется для анализа
несимметричных режимов их работы, в том числе с динамической нагрузкой. В
основе метода лежит представление несимметричной трехфазной системы переменных
(ЭДС, токов, напряжений ) в виде суммы трех симметричных систем, которые
называют симметричными составляющими. Различают симметричные
составляющие прямой, обратной и нулевой последовательностей,
которые различаются порядком чередования фаз. Симметричную систему
прямой последовательности образуют ( рисунок 5.1,а) три одинаковых по модулю
вектора ![]() и
и ![]() со сдвигом друг по отношению к другу
на
со сдвигом друг по отношению к другу
на ![]() рад., причем
рад., причем ![]() отстает от
отстает от ![]() , а
, а ![]() - от
- от ![]() .
.
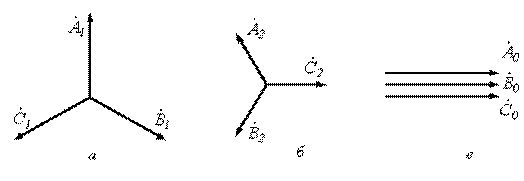
Рисунок 5.1
Введя оператор поворота ![]() , для симметричной системы прямой
последовательности можно записать
, для симметричной системы прямой
последовательности можно записать
![]() .
.
Симметричная система обратной
последовательности образована равными по модулю векторами ![]() и
и ![]() с относительным сдвигом по фазе на
с относительным сдвигом по фазе на ![]() рад., причем теперь
рад., причем теперь ![]() отстает от
отстает от ![]() , а
, а ![]() - от
- от ![]() ( рисунок 5.1,б). Для этой системы имеем
( рисунок 5.1,б). Для этой системы имеем![]() .
.
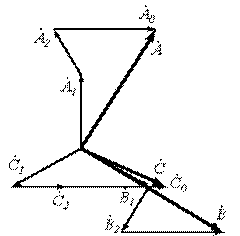
Рисунок 5.2
Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе ( рисунок 5.1,в):
![]() .
.
При сложении трех указанных систем векторов получается несимметричная система векторов ( рисунок 5.2).
Любая несимметричная система однозначно раскладывается на симметричные составляющие.
|
|
(5.1) |
|
|
(5.2) |
|
|
(5.3) |
Таким образом, получена система из трех уравнений
относительно трех неизвестных ![]() , которые, следовательно, определяются
однозначно. Для нахождения
, которые, следовательно, определяются
однозначно. Для нахождения ![]() сложим уравнения (5-1)…(5-3). Тогда, учитывая,
что
сложим уравнения (5-1)…(5-3). Тогда, учитывая,
что ![]() , получим
, получим
|
|
(5.4) |
Для нахождения ![]() умножим (5-2) на
умножим (5-2) на ![]() , а (5-3) – на
, а (5-3) – на ![]() , после чего полученные выражения сложим с (5-1).
В результате приходим к соотношению
, после чего полученные выражения сложим с (5-1).
В результате приходим к соотношению
|
|
(5.5) |
Для определения ![]() с соотношением (5.1) складываем уравнения (5.2)
и (5.3), предварительно умноженные соответственно на
с соотношением (5.1) складываем уравнения (5.2)
и (5.3), предварительно умноженные соответственно на ![]() и
и ![]() . В результате имеем:
. В результате имеем:
|
|
(5-6) |
Формулы (5-1)…(5-6) справедливы для любой системы
векторов ![]() , в том числе и
для симметричной. В последнем случае
, в том числе и
для симметричной. В последнем случае ![]() .
.
Помимо вычисления симметричные составляющие могут быть измерены с помощью специальных фильтров симметричных составляющих, используемых в устройствах релейной защиты и автоматики.
5.2 Свойства симметричных составляющих токов и напряжений различных последовательностей
Рассмотрим четырехпроводную систему на рисунке 5.3.
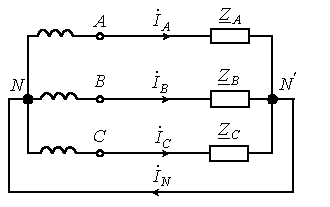
Рисунок 5.3
Для тока в нейтральном проводе имеем
![]() .
.
Тогда с учетом (4)
|
|
(5.7) |
т.е. ток в нейтральном проводе равен утроенному току нулевой последовательности.
Если нейтрального провода нет, то ![]() и соответственно нет составляющих тока
нулевой последовательности.
и соответственно нет составляющих тока
нулевой последовательности.
Поскольку сумма линейных напряжений равна нулю, то в соответствии с (5.4) линейные напряжения не содержат составляющих нулевой последовательности.
Рассмотрим трехпроводную несимметричную систему на рисунке 5. 4.
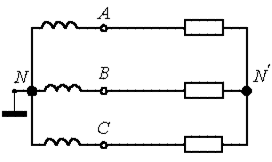
Рисунок 5.4
Здесь
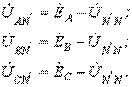
Тогда, просуммировав эти соотношения, для симметричных составляющих нулевой последовательности фазных напряжений можно записать
![]() .
.
Если система ЭДС генератора симметрична, то из последнего получаем
|
|
(5.8) |
Из (5.8) вытекает:
· в фазных напряжениях симметричного приемника отсутствуют симметричные составляющие нулевой последовательности;
· симметричные составляющие нулевой последовательности фазных напряжений несимметричного приемника определяются величиной напряжения смещения нейтрали;
· фазные напряжения несимметричных приемников, соединенных звездой, при питании от одного источника различаются только за счет симметричных составляющих нулевой последовательности; симметричные составляющие прямой и обратной последовательностей у них одинаковы, поскольку однозначно связаны с соответствующими симметричными составляющими линейных напряжений.
При соединении нагрузки в треугольник фазные токи ![]() и
и ![]() могут содержать симметричные составляющие
нулевой последовательности
могут содержать симметричные составляющие
нулевой последовательности ![]() . При этом
. При этом ![]() ( рисунок 5.5) циркулирует по контуру,
образованному фазами
( рисунок 5.5) циркулирует по контуру,
образованному фазами 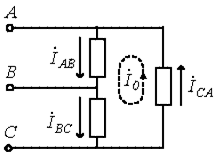 нагрузки.
нагрузки.
Рисунок 5.5
6 Лекция 6. Расчет симметричных трехфазных цепей методом симметричных составляющих.
Цель лекции: Показать применение симметричных составляющих напряжений и токов при расчёте симметричных трёхфазных цепей.
6.1 Сопротивления симметричной трехфазной цепи для токов различных последовательностей
Если к симметричной цепи приложена симметричная система фазных напряжений прямой (обратной или нулевой) последовательностей, то в ней возникает симметричная система токов прямой (обратной или нулевой) последовательности. При использовании метода симметричных составляющих на практике симметричные составляющие напряжений связаны с симметричными составляющими токов той же последовательности. Отношение симметричных составляющих фазных напряжений прямой (обратной или нулевой) последовательности к соответствующим симметричным составляющим токов называется комплексным сопротивлением прямой
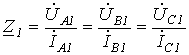 ,
,
обратной
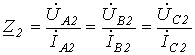
и нулевой
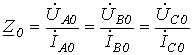
последовательностей.
Пусть имеем участок цепи на рисунке 6.1. Для фазы А этого участка можно записать

Рисунок 6.1
|
|
(6.1) |
Тогда для симметричных составляющих прямой и обратной
последовательностей с учетом, того, что ![]() , на основании (6.1) имеем
, на основании (6.1) имеем
![]() .
.
Отсюда комплексные сопротивления прямой и обратной последовательностей одинаковы и равны:
![]() .
.
Для симметричных составляющих нулевой
последовательности с учетом равенства ![]() соотношение (6.1) трансформируется в уравнение
соотношение (6.1) трансформируется в уравнение
![]() ,
,
откуда комплексное сопротивление нулевой последовательности
![]() .
.
В рассмотренном примере получено равенство сопротивлений прямой и обратной последовательностей. В общем случае эти сопротивления могут отличаться друг от друга. Наиболее типичный пример – различие сопротивлений вращающейся машины для токов прямой и обратной последовательностей за счет многократной разницы в скольжении ротора относительно вращающегося магнитного поля для этих последовательностей.
6.2 Применение метода симметричных составляющих для расчета симметричных цепей
Расчет цепей методом симметричных составляющих основывается на принципе наложения, ввиду чего метод применим только к линейным цепям. Согласно данному методу расчет осуществляется в отдельности для составляющих напряжений и токов различных последовательностей, причем в силу симметрии режимов работы цепи для них он проводится для одной фазы (фазы А). После этого в соответствии с (5.1)…(5.3) определяются реальные искомые величины. При расчете следует помнить, что, поскольку в симметричном режиме ток в нейтральном проводе равен нулю, сопротивление нейтрального провода никак ни влияет на симметричные составляющие токов прямой и обратной последовательностей. Наоборот, в схему замещения для нулевой последовательности на основании (5.7) вводится утроенное значение сопротивления в нейтральном проводе. С учетом вышесказанного исходной схеме на рисунке 6.2,а соответствуют расчетные однофазные цепи для прямой и обратной последовательностей (рисунок 6.2,б) и нулевой последовательности (рисунок 6.2,в).
![]()
![]()
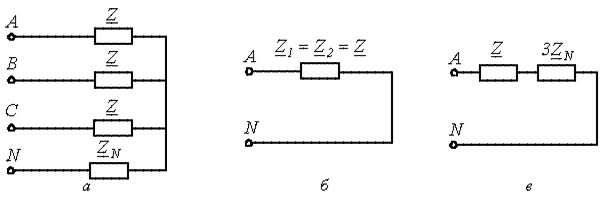
Рисунок 6.2
Существенно сложнее обстоит дело при несимметрии
сопротивлений по фазам. Пусть в цепи на рисунке 5.3 ![]() . Разложив токи на симметричные составляющие,
для данной цепи можно записать
. Разложив токи на симметричные составляющие,
для данной цепи можно записать
|
|
(6.2) |
В свою очередь
|
|
(6.3) |
Подставив в (6.3) значения соответствующих параметров из (6.2) после группировки членов получим
|
где |
(6.4) |
![]() ;
;

Из полученных соотношений видно, что если к несимметричной цепи приложена несимметричная система напряжений, то каждая из симметричных составляющих токов зависит от симметричных составляющих напряжений всех последовательностей. Поэтому, если бы трехфазная цепь на всех участках была несимметрична, рассматриваемый метод расчета не давал бы преимуществ. На практике система в основном является симметричной, а несимметрия обычно носит локальный характер. Это обстоятельство, как будет показано в следующей лекции, значительно упрощает анализ.
7 Лекция 7. Расчет несимметричных режимов трехфазных цепей методом симметричных составляющих.
Цель лекции: Показать применение метода симметричных составляющих при расчёте несимметричных режимов трёхфазных цепей.
7.1 Расчет симметричных составляющих токов и напряжений
В высоковольтных трехфазных цепях несимметричные режимы обычно возникают в аварийных условиях, чаще всего при несимметричных коротких замыканиях (замыканиях между фазами, замыкание одной или двух фаз на землю). Рассмотрим расчет несимметричных режимов на примере наиболее распространенного однофазного короткого замыкания.
Симметричная динамическая нагрузка подключена к симметричному трехфазному генератору с фазной э.д.с. Еф (рисунок 7.1). В цепи произошло короткое замыкание одной из фаз на землю (например, фазы С) на зажимах нагрузки.
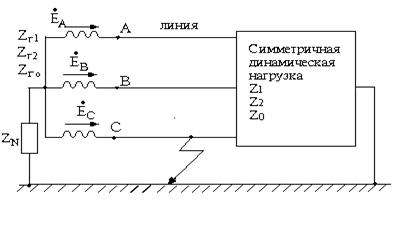 |
Рисунок 7.1
Для расчета несимметричного режима трехфазных цепей удобно пользоваться принципом компенсации, заменяя несимметричную нагрузку, которая возникает при коротком замыкании фазы на землю, источником напряжений, значения которых до окончания всего расчета остаются неизвестными. После такой замены вся цепь становится симметричной и для нее разноименные симметричные составляющие токов и напряжений не зависят друг от друга. Связи же между симметричными составляющими токов и напряжений различных последовательностей, обусловленных несимметрией, вводятся позднее.
Заменим несимметричную нагрузку, обусловленную
коротким замыканием фазы С (рисунок 7.1), тремя источниками неизвестных
напряжений ![]() .
Тогда получится симметричная схема, в которой помимо генератора с симметричной
трехфазной системой э.д.с. имеются источники несимметричных напряжений
.
Тогда получится симметричная схема, в которой помимо генератора с симметричной
трехфазной системой э.д.с. имеются источники несимметричных напряжений ![]() . Разложим напряжения
. Разложим напряжения ![]() на симметричные
составляющие прямой
на симметричные
составляющие прямой ![]() ,
обратной
,
обратной ![]() и
нулевой
и
нулевой ![]() последовательностей,
приняв фазу А за основную. Фазовый множитель а=еj120,
a2=e-j120.
последовательностей,
приняв фазу А за основную. Фазовый множитель а=еj120,
a2=e-j120.
 (7.1)
(7.1)
Тогда получим симметричную схему (рисунок 7.2), причем в ответвлении, где была несимметричная нагрузка, находятся источники трех симметричных систем напряжений прямой, обратной и нулевой последовательностей.
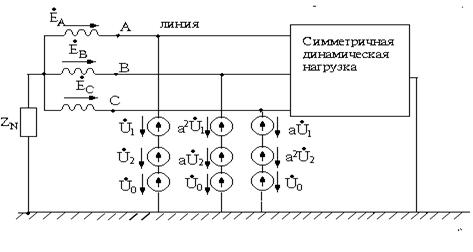 |
Рисунок 7.2
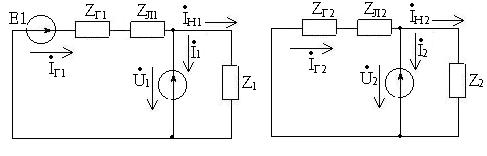 |
В симметричной цепи симметричная система напряжений какой-либо последовательности вызывает симметричную систему токов той же самой последовательности. Следовательно, можно составить три однофазные схемы для токов и напряжений различных последовательностей для фазы А. Эти схемы сокращенно назовем схемами прямой, обратной и нулевой последовательностей (рисунки 7.2, 7.3 и 7.4).
Рисунок 7.2 Рисунок 7.3
Сопротивление в нейтральном проводе ZN не оказывает влияния на симметричные составляющие токов прямой и обратной последовательностей, поэтому в схемах прямой и обратной последовательностей сопротивление ZN отсутствует. В схему нулевой последовательности вводится утроенное значение сопротивления ZN, т.к. ток в нейтральном проводе равен тройному значению составляющей тока нулевой последовательности, т.е.
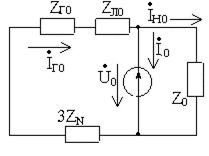 |
Рисунок 7.4
Для дальнейшего расчета целесообразно преобразовать
схемы отдельных последовательностей к простейшему виду, не затрагивая при этом
ветвей с источниками неизвестных напряжений ![]() .
.
В схеме прямой последовательности заменим ветви генератора и симметричной нагрузки эквивалентным генератором, э.д.с. которого определяется следующим выражением:
![]() (7.3),
(7.3),
где
![]() .
.
Эквивалентное сопротивление этого генератора равно:
![]() .
(7.4)
.
(7.4)
В схемах обратной и нулевой последовательностей объединяем ветви генератора и нагрузки:

Преобразованные схемы прямой, обратной и нулевой последовательностей представлены на рисунках 7.5, 7.6 и 7.7.
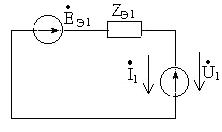
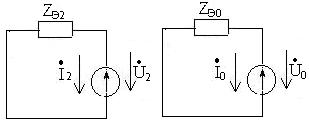
Рисунок 7.5 Рисунок 7.6 Рисунок 7.7
Для каждой из этих трех схем запишем уравнение по второму закону Кирхгофа:
 (7.5)
(7.5)
В этих трех уравнениях шесть неизвестных ![]() .
.
Дополнительные три уравнения, связывающие эти шесть неизвестных величин, составляются на основании заданной схемы несимметричной нагрузки. В нашем случае несимметрия обусловлена коротким замыканием фазы С на землю, поэтому схема несимметричной нагрузки имеет вид, представленный на рисунке 7.8.

Рисунок 7.8
Составим дополнительные уравнения для данной схемы:
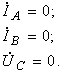 (7.6)
(7.6)
Раскладывая ![]() на симметричные составляющие, получим:
на симметричные составляющие, получим:
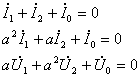 (7.7)
(7.7)
Объединяя уравнения (7.5) и (7.7), получим систему из шести уравнений с шестью неизвестными:
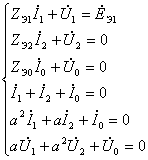 (7.8)
(7.8)
Покажем решение системы (7.8). Вычитая из четвертого уравнения пятое, получим:
![]() (7.9)
(7.9)
т.к. 1+а+а2=0 и, следовательно 1+а=-а2
Подставляя (7-9) в четвертое уравнение, получим:
![]() . (7.10)
. (7.10)
Умножая первое уравнение на а, второе на а2, и суммируя первые три уравнения системы (7-8) с учетом шестого уравнения этой системы, получим:
![]() или с учетом (7.9) и (7.10) получим
или с учетом (7.9) и (7.10) получим
![]() .
(7.11)
.
(7.11)
Симметричные составляющие напряжений в месте короткого замыкания на землю определяются из первых трех уравнений системы (7.8):
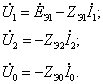
По схемам прямой, обратной и нулевой последовательностей (рисунки 7.3, 7.4, 7.5) рассчитываем симметричные составляющие токов генератора и нагрузки.
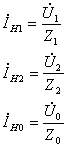
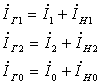
Симметричные составляющие напряжений на зажимах генератора находим по схемам
прямой, обратной и нулевой последовательностей (рисунки 7.3, 7.4, 7.5)
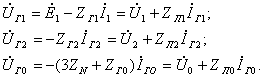
7.2 Расчет токов и напряжений на участках цепи
Фазные токи генератора
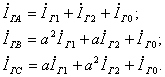
Фазные токи нагрузки:
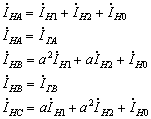
Ток короткого замыкания в фазе С
![]() .
.
Токи между фазами А , В и землей:
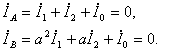
Фазные напряжения на зажимах генератора
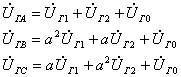
Напряжения в месте короткого замыкания

7.3 Расчет мощностей генератора
Активные мощности фаз
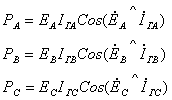
Активная мощность всей цепи
![]()
Реактивная мощность
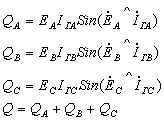
Полная мощность цепи
![]() .
.
НЕСИНУСОИДАЛЬНЫЕ ТОКИ
8 Лекция 8. Несинусоидальные э.д.с., напряжения и токи, разложение периодической несинусоидальной кривой в тригонометрический ряд.
Цель лекции: Рассмотреть основные понятия о несинусоидальных э.д.с., напряжениях и токах.
8.1 Несинусоидальные э.д.с., напряжения и токи
 На практике кривые э.д.с., напряжений и токов бывают обычно в большей
или меньшей степени отличны от постоянных или синусоидальных. Зависимость тока
или напряжения от времени может быть периодической, почти периодической и
непериодической.
На практике кривые э.д.с., напряжений и токов бывают обычно в большей
или меньшей степени отличны от постоянных или синусоидальных. Зависимость тока
или напряжения от времени может быть периодической, почти периодической и
непериодической.
На рисунке 8.1 показаны примеры кривых тока в цепи с насыщающимся реактором (рисунок 8.1, а) и в цепи
управляемого вентиля (рисунок 8.1, б). Рисунок 8.1
Генераторы периодических импульсов применяются в радиотехнике, автоматике, телемеханике, вычислительной технике, в автоматизированных системах управления. Форма импульсов может быть самой различной: пилообразной, ступенчатой и прямоугольной. При прохождении этих импульсов через различные электрические цепи их форма существенно изменяется.
На рисунке 8.1 кривые строго периодичны (период повторения Т) и представляют собой примеры несинусоидальных периодических токов.
При передаче, например,
радиотелеграфных и телефонных сигналов встречаются кривые тока, которые не
строго периодичны, но имеют периодически изменяющуюся огибающую с периодом ![]() и на малом интервале
времени могут считаться синусоидальными с периодом
и на малом интервале
времени могут считаться синусоидальными с периодом ![]() .
.
Кроме указанных типов несинусоидальных кривых часто приходится иметь дело с непериодическими кривыми, т.е. кривыми, у которых нет периода повторения. Эти кривые могут быть вполне определенными, как, например, при передаче одиночных импульсов, но могут быть и случайными, например, в случае шумов и помех.
8.2 Разложение периодической несинусоидальной кривой в тригонометрический ряд
Явления в линейных цепях при
периодических несинусоидальных сигналах проще всего поддаются исследованию,
если кривую разложить в тригонометрический ряд Эйлера – Фурье. Как
известно, всякая периодическая функция ![]() , удовлетворяющая условиям Дирихле, т.е.
имеющая на всяком конечном интервале конечное число разрывов первого рода и
конечное число максимумов и минимумов, может быть разложена в
тригонометрический ряд:
, удовлетворяющая условиям Дирихле, т.е.
имеющая на всяком конечном интервале конечное число разрывов первого рода и
конечное число максимумов и минимумов, может быть разложена в
тригонометрический ряд:
![]()
![]() (8.1)
(8.1)
где при k=0
![]()
![]()
Первый член ряда ![]() называется постоянной
составляющей или нулевой гармоникой, второй член
называется постоянной
составляющей или нулевой гармоникой, второй член ![]() - основной
синусоидой или первой гармоникой, а все остальные члены вида
- основной
синусоидой или первой гармоникой, а все остальные члены вида ![]() при
k>1 носят название высших
гармоник;
при
k>1 носят название высших
гармоник; ![]() - основная частота; Т – период
несинусоидальной периодической функции.
- основная частота; Т – период
несинусоидальной периодической функции.
Тригонометрический ряд после раскрытия синуса суммы для каждой из гармонических составляющих или, короче, гармоник, записывается и в иной форме:
![]()
![]()
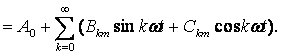 (8.2)
(8.2)
Здесь ![]()
![]()
Коэффициент ![]() ,
, ![]() и
и ![]() могут быть вычислены при помощи следующих
интегралов:
могут быть вычислены при помощи следующих
интегралов:
 (8.3)
(8.3)
Постоянная составляющая ![]() равна среднему
значению функции f(t) за ее
период
равна среднему
значению функции f(t) за ее
период ![]() .
.
Зная коэффициенты ряда (8.2), легко перейти к форме (8.1), подсчитывая
![]() и
и ![]() (8.4)
(8.4)
Вводя условно отрицательные
частоты, т.е. переходя к суммированию по
k от ![]() до
до ![]() , можно ряду (8.2) придать более
компактный вид (где по существу каждая гармоника, кроме нулевой, входит под
знак суммы дважды):
, можно ряду (8.2) придать более
компактный вид (где по существу каждая гармоника, кроме нулевой, входит под
знак суммы дважды):
![]() (8.2a)
(8.2a)
Постоянная составляющая в этом
выражении получается при k=0 , что
соответствует выражению (8.3), так как ![]()
Значительное число непериодических функций времени, с которыми приходится встречаться в электротехнике, удовлетворяет условию
![]() (8.5)
(8.5)
Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они раскладываются в ряд, который не содержит четных гармоник и постоянной составляющей:
![]()
![]() (8.6)
(8.6)
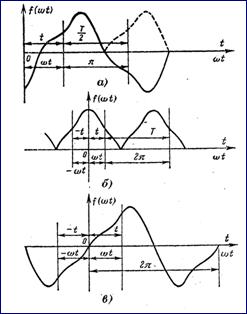 При выпрямлении переменного тока или напряжения
часто приходится встречаться с функциями, которые при соответствующем выборе
начала координат удовлетворяют условию (рисунок 8.2, б)
При выпрямлении переменного тока или напряжения
часто приходится встречаться с функциями, которые при соответствующем выборе
начала координат удовлетворяют условию (рисунок 8.2, б)
![]() (8.7)
(8.7)
Такие функции называются симметричными относительно оси ординат. В этом случае ряд не содержит синусов:
![]() (8.8)
(8.8)
В схемах умножения частоты встречаются функции, которые при выборе начала координат в точке нуля функции удовлетворяют условию (рисунок 8.2, в) Рисунок 8.2
![]() (8.9)
(8.9)
Такие функции называются симметричными oтносительно начало координат и раскладываются в ряд, не содержащий косинусов и постоянной составляющей:
![]() (8.10)
(8.10)
Если начало отсчета времени сдвигается,
то соответственно изменяется вид ряда, в котором амплитуды гармоник остаются
прежними, но изменяются их начальные фазы. Например, если перейти от функции
![]() ,
выражаемой рядом (12-1), к
,
выражаемой рядом (12-1), к ![]() т.е. сместиться начало отсчета времени на
т.е. сместиться начало отсчета времени на
![]() , то получим
ряд
, то получим
ряд
![]()
![]()
где ![]()
Совокупность гармонических составляющих несинусоидальной периодической функции называется ее дискретным частотным спектром.
Спектр можно характеризовать
некоторой зависимостью ![]() (спектр амплитуд) и
(спектр амплитуд) и ![]() (спектр фаз) от
частоты
(спектр фаз) от
частоты ![]() .
.
8.3 Максимальные, действующие и средние значения несинусоидальных периодических э.д.с., напряжений и токов.
Периодически изменяющаяся
несинусоидальная величина ![]() помимо своих гармонических составляющих
характеризуется тремя величинами:
помимо своих гармонических составляющих
характеризуется тремя величинами:
Максимальным значением за период
![]() , средним квадратичным за период или
действующим
значением
, средним квадратичным за период или
действующим
значением
 (8.11)
(8.11)
и средним по модулю значением
 , (8.12)
, (8.12)
Если кривая ![]() симметрична
относительно оси абсцисс и в течение половины периода функция
симметрична
относительно оси абсцисс и в течение половины периода функция
![]() ни
разу не изменяет знака, то среднее по модулю значение равно среднему значению
за половину периода:
ни
разу не изменяет знака, то среднее по модулю значение равно среднему значению
за половину периода:
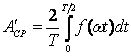 ,
(8.12, a)
,
(8.12, a)
причем в последнем выражении начало
отсчета времени должно быть выбрано так, чтобы
![]() . В
тех случаях, когда весь период функция ни разу не изменяет знака, среднее по
модулю значение равно постоянной составляющей
. В
тех случаях, когда весь период функция ни разу не изменяет знака, среднее по
модулю значение равно постоянной составляющей
![]() .
.
При несинусоидальных периодических процессах, как и при синусоидальных, обычно под значением э.д.с., тока или напряжения понимают действующее значение.
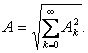 (8.13)
(8.13)
Таким образом, действующее значение периодической
несинусоидальной величины зависит только от действующих значений ее гармоник и
не зависит от их фаз ![]() .
.
Если, например, напряжение и состоит
из ряда гармоник ![]() ,
,
![]() ,
, ![]() и т.д., действующие
значения которых
и т.д., действующие
значения которых ![]() ,
,
![]() ,
, ![]() и т.д., то действующее
напряжение
и т.д., то действующее
напряжение
![]() .
(8.14)
.
(8.14)
Аналогично для тока
![]() . (8.15)
. (8.15)
8.4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых
При оценке несинусоидальных
периодических кривых в электроэнергетике, где кривые преимущественно
симметричны относительно оси абсцисс, пользуются коэффициентом формы кривой
![]() ,
коэффициентом амплитуды
,
коэффициентом амплитуды ![]() , коэффициентом искажения
, коэффициентом искажения
![]() .
.
Коэффициент формы определяется как отношение действующего к среднему по модулю значению:
![]() (8.16)
(8.16)
Для синусоиды ![]()
Коэффициент амплитуды равен отношению максимального к действующему значению:
![]() (8.17)
(8.17)
Для синусоиды ![]() .
.
Коэффициент искажения определяется как отношение действующего значения основной гармоники к действующему значению всей кривой:
![]() (8.18)
(8.18)
Для синусоиды ![]() .
.
В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник, который определяется как отношение действующего значения высших гармоник к действующему значению основной гармоники:
 (8.19)
(8.19)
При отсутствии постоянной составляющей  Для синусоиды
Для синусоиды ![]() .
.
9. Лекция 9. Расчет цепей с несинусоидальными периодическими э.д.с. и токами. Высшие гармоники в трехфазных цепях.
Цель лекции: усвоить расчет цепей с несинусоидальными периодическими э.д.с. и токами, высшие гармоники в трехфазных цепях
9.1 Расчет цепей с несинусоидальными периодическими э.д.с. и токами
Если в линейной цепи действует один или несколько источников несинусоидальных периодических э.д.с. или токов, то расчет такой цепи распадается на три этапа:
1.Разложение э.д.с. или токов источников на постоянную и несинусоидальные составляющие (получение дискретного спектра).
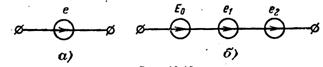 2. Применение принципа наложения и
расчет токов и напряжений в цепи для каждой из составляющих в отдельности.
2. Применение принципа наложения и
расчет токов и напряжений в цепи для каждой из составляющих в отдельности.
3. Совместное рассмотрение решений, Рисунок 9.1
полученных для каждой из составляющих.
Рассмотрим второй этап, представляющий собой основную часть расчета цепей с несинусоидальными э.д.с. и токами.
Если, например, несинусоидальная э.д.с. представлена в виде суммы постоянной и синусоидальных составляющих, то источник несинусоидальной э.д.с. можно рассматривать как последовательное соединение источника постоянной э.д.с. и источников синусоидальных э.д.с. с различными частотами. Так, если э.д.с. (рисунок 8.1, а)
![]() (9.1)
(9.1)
то действие источника такой э.д.с. аналогично действию трех последовательно соединенных источников э.д.с. (рисунок 8.1,б):
![]()
 (9.2)
(9.2)
Применяя принцип наложения и рассматривания действие каждой из составляющих э.д.с. в отдельности, можно найти составляющие токов во всех участках цепи.
Мгновенное значение тока в цепи
равно сумме мгновенных значений составляющих токов. Если, например, в
какой-либо ветви токи, создаваемые э.д.с. ![]() ,
, ![]() и
и ![]() , соответственно равны
, соответственно равны ![]() ,
, ![]() и
и ![]() , то общий ток
, то общий ток
![]() ,
(9.3)
,
(9.3)
Таким образом, расчет линейной цепи с несинусоидальными э.д.с. сводится к решению n задач с синусоидальными э.д.с., где n – число синусоидальных составляющих э.д.с. различных частот, и одной задачи с постоянным э.д.с.
При решении каждой из этих задач
необходимо учитывать, что для различных частот индуктивные и емкостные
сопротивления неодинаковы. Индуктивное сопротивление для ![]() й гармоники в
й гармоники в ![]() раз больше, а
емкостное, наоборот, в
раз больше, а
емкостное, наоборот, в ![]() раз меньше, чем для первой:
раз меньше, чем для первой:
![]()
![]() , (9.4)
, (9.4)
Чем больше ![]() , тем меньше по величине
реактивное сопротивление емкости для этой гармоники. Поэтому при напряжении,
близком к синусоидальному, ток в емкости может быть резко несинусоидальным
из-за высших гармоник. С увеличением порядка гармоники индуктивное
сопротивление для этой гармоники возрастает. Поэтому даже при резко
несинусоидальной кривой напряжения форма кривой тока через индуктивность
нередко приближается к синусоиде.
, тем меньше по величине
реактивное сопротивление емкости для этой гармоники. Поэтому при напряжении,
близком к синусоидальному, ток в емкости может быть резко несинусоидальным
из-за высших гармоник. С увеличением порядка гармоники индуктивное
сопротивление для этой гармоники возрастает. Поэтому даже при резко
несинусоидальной кривой напряжения форма кривой тока через индуктивность
нередко приближается к синусоиде.
При расчете каждой из гармоник можно пользоваться комплексным методом и строить векторные диаграммы для каждой из гармоник в отдельности. Однако недопустимо суммирование векторов и сложение комплексных напряжений и токов различных гармоник.
9.2 Мощность периодических несинусоидальных токов
Активная мощность периодического тока произвольной формы определяется как средняя мощность за период
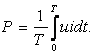 (9.5)
(9.5)
Если мгновенные значения напряжения и тока выразить в виде тригонометрических рядов, то получим:
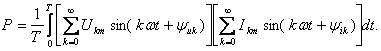
Так как среднее за период значение
произведения мгновенных значений синусоид различной частоты равно нулю и
тригонометрические ряды абсолютно сходятся при любых частотах ![]() , то
, то
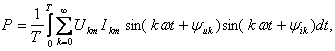
или после интегрирования
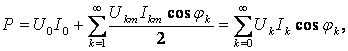 (9.6)
(9.6)
где ![]()
Из этого выражения следует очень важный
вывод, что средняя мощность несинусоидального тока равна сумме средних
мощностей отдельных гармоник (постоянная составляющая рассматривается как
нулевая гармоника с ![]() ):
):
![]() (9.7)
(9.7)
Кроме понятия активной мощности ![]() по аналогии с
синусоидальными токами вводится понятие полной мощности
по аналогии с
синусоидальными токами вводится понятие полной мощности ![]() , определяемой как произведение
действующих значений тока и напряжения:
, определяемой как произведение
действующих значений тока и напряжения:
![]() (9.8)
(9.8)
Активная мощность меньше полной;
исключение составляет только мощность в цепи, имеющей часто активное сопротивление,
когда ![]() , и,
следовательно,
, и,
следовательно, ![]() .
.
Отношение активной мощности к
полной называют коэффициентом мощности и иногда приравнивают косинусу
некоторого условного угла ![]() :
:
![]() .
(9.9)
.
(9.9)
Формально можно ввести понятие реактивной мощности, определяемой как сумма реактивных мощностей отдельных гармоник:
![]() . (9.10)
. (9.10)
Для несинусоидальных токов в отличие от синусоидальных квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей:
![]() (9.11)
(9.11)
9.3 Высшие гармоники в трехфазных цепях
В трехфазных цепях кривые
напряжения во второй и третьей фазах со сдвигом на треть периода обычно в
точности воспроизводят форму кривой напряжения в первой фазе. Так, например,
если напряжение ![]() в
фазе
в
фазе ![]() может
быть представлено некоторой функцией времени
может
быть представлено некоторой функцией времени ![]() то
то ![]()
![]()
где ![]() - период основной частоты.
- период основной частоты.
Рассмотрим гармонику порядка ![]() функции
функции ![]() во всех трех фазах. Пусть
во всех трех фазах. Пусть
![]()
Тогда, учитывая, что ![]() и подставляя вместо
и подставляя вместо ![]() соответственно
соответственно ![]() и
и ![]() , получаем:
, получаем:
![]()
![]()
Сравнивая полученные выражения для
различных значений ![]() ,
можно заметить, что напряжения гармоник порядка, кратного трем
,
можно заметить, что напряжения гармоник порядка, кратного трем ![]() где
где ![]() - любое целое число,
во всех фазах в любой момент времени имеют одно и то же направление. При
- любое целое число,
во всех фазах в любой момент времени имеют одно и то же направление. При ![]() гармоники трех фаз
образуют симметричную систему напряжений, последовательность которой совпадает
с последовательностью фаз первой гармоники. При
гармоники трех фаз
образуют симметричную систему напряжений, последовательность которой совпадает
с последовательностью фаз первой гармоники. При ![]() гармоники образуют симметричную систему
напряжений с последовательностью, обратной основной.
гармоники образуют симметричную систему
напряжений с последовательностью, обратной основной.
Таким образом, гармоники порядка 1,
4, 7, 10, 13 и т.д. образуют системы напряжений прямой
последовательности, гармоники 2, 5, 8, 11, 14 и т.д. образуют
системы напряжений обратной последовательности. Наконец, гармоники 3, 6,
9, 12 и т.д. образуют системы напряжений нулевой
последовательности. При наличии постоянной составляющей в напряжении
каждой из фаз она может рассматриваться как нулевая гармоника порядка, кратного
трем ![]() , т.е.
образующая нулевую последовательность.
, т.е.
образующая нулевую последовательность.
Рассмотрим различные схемы соединения трехфазных цепей.
Если фазы генератора соединены в звезду, то при несинусоидальном фазном напряжении линейные напряжения не содержит гармоник напряжений порядка, кратного трем, так как последние образуют системы нулевой последовательности.
Отсутствие гармоник порядка, кратного
трем, в линейных напряжениях приводит к тому, что отношение линейного
напряжения к фазному меньше ![]() . Действительно, фазное напряжение
. Действительно, фазное напряжение ![]() ,
,
а линейное напряжение ![]() .
.
Отсюда следует, что
![]() .
(9.12)
.
(9.12)
При симметричной нагрузке фазные токи основной частоты и все высшие гармоники, за исключением высших гармоника порядка, кратного трем, образуют системы прямой и обратной последовательности и дают в сумме нуль. Гармоники же порядка, кратного трем, образуют систему нулевой последовательности, т.е. имеют в любой момент времени одинаковые значения и направления. Поэтому ток в нейтральном проводе равен утроенной сумме токов гармоник нулевой последовательности:
![]() .
(9.13)
.
(9.13)
При отсутствии нейтрального провода токи в каждой из фаз не могут содержать высших гармоник порядка, кратного трем, так как в этой схеме сумма токов в любой момент времени должна равняться нулю, что не возможно при наличии высших гармоник порядка, кратного трем. Поэтому в приемнике нет напряжения от токов нулевой последовательности и между нейтральными точками генератора и симметричного приемника может появиться значительные напряжения, содержащее гармоники, кратное трем.
Если фазы генератора соединены треугольником, то при синусоидальном э.д.с. в фазах сумма э.д.с., действующих в замкнутом контуре генератора, не равна нулю, как при синусоидальных э.д.с., равна тройной сумме высших гармоник порядка кратного трем.
![]() .
(9.14)
.
(9.14)
Открытый треугольник с э.д.с., содержащие высшие гармоники, применяется как утроитель частоты.
Если фазы соединены в замкнутый треугольник, то э.д.с. гармоник порядка, кратного трем, вызывают внутренний ток в генераторе. Этот ток протекает в замкнутом треугольнике генератора даже и тогда, когда внешняя цепь генератора разомкнута. Составляющая фазной э.д.с., содержащая гармоники порядка, кратного трем, однако, не выявляется между зажимами фаз, так как она компенсируется падением напряжения на внутреннем сопротивлении фазы генератора. Фазное напряжение, равная в данном случае линейному,
![]() (9.15)
(9.15)
Поэтому во внешней цепи, подключенной к генератору, обмотки которого соединены треугольником, токи не содержат гармоник порядка, кратного трем.
Фазный ток генератора при симметричной нагрузке
![]() (9.16)
(9.16)
а линейный ток во внешней цепи
![]() (9.17)
(9.17)
ЧЕТЫРЕХПОЛЮСНИКИ .
10 Лекция 10. Основные понятия о четырехполюсниках.
Цель лекции: Рассмотреть основные понятия о четырехполюсниках , а также изложить методику вывода уравнений в А- форме.
10.1 Определение четырехполюсника.
Четырехполюсником называют электрическую схему, имеющую два входных и два выходных зажима. Трансформатор, линию передачи энергии, мостовую схему и т. п. можно рассматривать как четырехполюсники.
Принято изображать четырехполюсник в виде прямоугольника : выходящими из него концами (полюсами) тп и рд (рисунок 9.1,а). Если четырехполюсник содержит источники электрической энергии, та в прямоугольнике ставят букву А (активный); если буква А отсутствует, то это значит, что четырехполюсник пассивный.
Входной ток обозначают İ1, входное напряжение U1 ; ток и напряжение на выходе İ2 , и U2.
Четырехполюсник является передаточным звеном между источником питания и нагрузкой. К входным зажимам тп, как правило, присоединяют источник питания, к выходным зажимами—нагрузку.
Предполагается, что нагрузка четырехполюсника и напряжение на выходе при работе четырехполюсника в качестве связующего звена могут изменяться, но схема внутренних соединений четырехполюсника и значения сопротивлений в ней остаются неизменными.
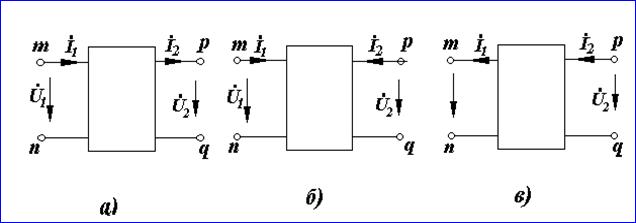 |
Рисунок 10.1
Четырехполюсник характеризуется двумя напряжениями U1 и U2 и двумя токами İ1 и İ2. Любые две величины из четырех можно определить через остальные. Так как число сочетаний из 4 по 2 равно 6, то возможны следующие 6 форм записи уравнений пассивного четырехполюсника:
А-форма:
![]() (10.1)
(10.1)
![]() ,
(10.2)
,
(10.2)
Y-форма ![]() (10.3)
(10.3)
![]() ,
(10.4)
,
(10.4)
Z-форма
![]() (10.5)
(10.5)
![]() ; (10.6)
; (10.6)
H-форма
![]() (10.7)
(10.7)
![]() ; (10.8)
; (10.8)
G-форма ![]() (10.9)
(10.9)
![]() ;
(10.10)
;
(10.10)
B-форма ![]() (10.11)
(10.11)
![]() ; (10.12)
; (10.12)
Обратим внимание на попарную инверсию Y- и Z-форм, A- и В-форм, H- и G-форм.
Исторически сложилось так, что для A-формы (ее будем считать основной) положительные направления для токов и напряжений соответствуют рисунок 10.1,a; для Y-, Z-, H-, G-форм— рисунок 10.1,б, В-форме—рисунок 10.1, в.
Обратим внимание на то, что ток İ2 на рисунке 10.1, б направлен противоположно направлению тока İ2 на рисунке 10.1, a.
На рисунке 10.1, в токи İ1 и İ2 изменили направление по сравнению с токами İ1 и İ2 на рисунке 10.1,а.
10.2 Вывод уравнений в A-форме.
Комплексные коэффициенты A, B,C,D в уравнениях (10.1) и (10.2) зависят от схемы внутренних соединений четырехполюсника, значений сопротивлений схемы и частоты. Для каждого четырехполюсника их можно определить расчетным или опытным путем. Для четырехполюсников, удовлетворяющих условию взаимности, коэффициенты связаны соотношением
АD-ВС=1 (10.13)
Выведем уравнения (9.1) и (9.2). С этой целью к
зажимам тп подключим источник э. д. с. ,
![]() а к
зажимам нагрузку pq-нагрузку
Z2 , (рисунок 10.2,
a).
а к
зажимам нагрузку pq-нагрузку
Z2 , (рисунок 10.2,
a).
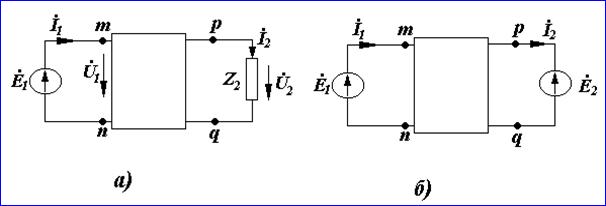
Рисунок 10.2
Напряжение на нагрузке ![]() , согласно теореме компенсации, заменим
нагрузку Z2
источником э. д. с. с э. д. с
, согласно теореме компенсации, заменим
нагрузку Z2
источником э. д. с. с э. д. с ![]() и направленной встречно току İ2
(рис. 10.2,6). Запишем выражения для токов İ1 и İ2,
выразив их через э. д. с. Ė1, Ė2 и
входные и взаимные проводимости ветвей
y11 ,y12,y21,y22
:
и направленной встречно току İ2
(рис. 10.2,6). Запишем выражения для токов İ1 и İ2,
выразив их через э. д. с. Ė1, Ė2 и
входные и взаимные проводимости ветвей
y11 ,y12,y21,y22
:
İ1= Ė1y11- Ė2y12; (10.14,а)
İ2= Ė1y21- Ė2y22; (10.14,б)
Если токи İ1 и İ2 рассматривать как контурные токи, то э. д. с. контуров, совпадающие с направлением контурных токов, войдут в уравнения, подобные уравнению, со знаком плюс, а э. д. с., не совпадающие с направлением соответствующих контурных токов—со знаком минус. Э. д. с. Ė1 направлена согласно с İ1 поэтому она вошла в уравнения (10.14,а) и (10.14,б) со знаком плюс; э. д. с. Ė2 направлена встречно İ2, поэтому она вошла в эти уравнения со знаком минус.
Для линейных четырехполюсников, не содержащих нелинейных элементов (для взаимных четырехполюсников), согласно принципу взаимности, у12=у21. Из (10.14,б) найдем
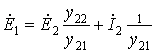 (10.14,в)
(10.14,в)
Подставив (9.14,в) в (9.14,а), получим
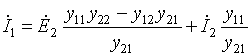 (10.14,г)
(10.14,г)
Обозначим:
А=y22/y21, В=1/y21, С=(у11у22 –у12 у21)/у21, D=y11/y21. (10.14,д)
В уравнениях (9.14,в) и (9.14,г) заменим Ė1
на ![]() и Ė2
, на
и Ė2
, на ![]() ,
и воспользовавшись обозначениями (9.14,д), получим уравнения в
A-форме:
,
и воспользовавшись обозначениями (9.14,д), получим уравнения в
A-форме:
![]() =A
=A![]() +B
İ2
;
+B
İ2
;
İ1=C![]() +D
İ2
;
+D
İ2
;
Проверим выполнение соотношения (10.13) для взаимного четырехполюсника:
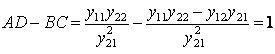
Четырехполюсник называют симметричным, если при перемене местами источника питания и нагрузки токи в источнике питания н нагрузке не изменяются. В симметричном четырехполюснике A=D. Уравнения (10.1) и (10.2) иногда записывают так:
![]() =A11
=A11![]() +A12İ2,,
(10.1'
)
+A12İ2,,
(10.1'
)
İ1=A21![]() +A22İ2,
(10.2
' )
+A22İ2,
(10.2
' )
где A11= A; A12=В; A21= С; А22=D.
Комплексные коэффициенты A, В, С, D, входящие в уравнения (10.1) и (10.2), можно определить по формулам (10.14,д), если схема внутренних соединений четырехполюсника и ее параметры известны, либо используя входные сопротивления четырехполюсника, полученные опытным или расчетным путем.
Комплексные входные сопротивления находят опытным путем с помощью ваттметра, амперметра и вольтметра по схеме, подобной схеме рисунка 10.1, а, с тем отличием, что вместо двухполюсника зажимами тп или рq (в зависимости от определяемого входного сопротивления) подключают испытуемый четырехполюсник.
Определим комплексное входное сопротивление четырехполюсника , при трех различных режимах его работы.
1. При питании со стороны зажимов тп и разомкнутой ветви рq (х. х. ветви рq). İ2 =0
![]() (10.15)
(10.15)
![]() 2. При питании со стороны зажимов тп и коротком
замыкании ветви рq (к. з. ветви рq).
U2=0
2. При питании со стороны зажимов тп и коротком
замыкании ветви рq (к. з. ветви рq).
U2=0
![]() (10.16)
(10.16)
3. При питании со стороны зажимов рq и коротком замыкании зажимов тп (U2,=0)
![]() (10.17)
(10.17)
Таким образом, для определения четырех неизвестных коэффициентов А, В, С, D располагаем четырьмя уравнениями:
АD -ВС=1,Z10 =А/С, Z1k =B/D,Z2k=B/A
Составим разность
![]() или
или
![]() (10.18)
(10.18)
Имеем
Z2k/Z1k=D/A (10.19)
Умножим (10.18) на (10.19):
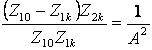
Отсюда
![]() (10.20)
(10.20)
Формула (9.20) позволяет определить коэффициент А; после этого коэффициент С находят из (10.15), в—из (10.17) и D—из (10.16).
Коэффициенты А и D имеют нулевую размерность, коэффициента B имеет размерность Ом, коэффициент С- См.
11 Лекция 11. Т и П –схемы замещения пассивного четырехполюсника. Характеристические (вторичные) параметры пассивных четырехполюсников.
Цель лекции: Дать сопоставления Т и П –схем замещения пассивного четырехполюсника. Определение коэффициентов одной формы уравнений через коэффициенты другой. Определение характеристических (вторичных) параметров пассивных четырехполюсников.
11.1 Т- и П-схемы замещения пассивного четырехполюсника .
Функция пассивного взаимного четырехполюсника как передаточного звена между источником питания и нагрузкой могут выполнять Т-схема (схема звезды рис. 11.1, а) или эквивалентная ей П-схема (схема треугольника рис. 11.1, б).
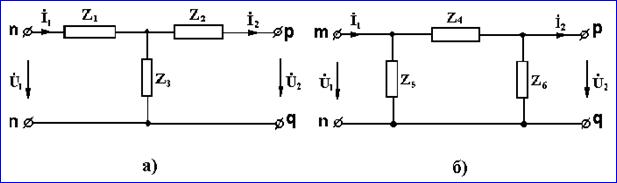
Рисунок. 11.1
Предполагается, что частота w фиксирована. Три сопротивления Т- или П-схемы подсчитывают с учетом того, что схема замещения должна обладать теми же коэффициентами A, B, C, D, что и заменяемый ею четырехполюсник.
Задача эта однозначна, так как, схема замещения содержит три элемента и четырехполюсник характеризуется тоже тремя параметрами (одна связь между А,В, С,D задана уравнением АD-ВС= 1).
Выразим напряжение U1 и ток İ1 Т-схемы (рисунок 10.1, а) через напряжение U2 и ток İ2.
 , (11. 1)
, (11. 1)
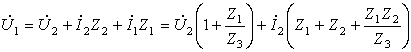 , (11. 2)
, (11. 2)
Сопоставим (11. 1) с (10.1) и (11.2) с (10.2).
Следовательно,
Z3=1/C;
![]() Z1=(A-1)/C;
(11. 3)
Z1=(A-1)/C;
(11. 3)
Z2=(D-1)/C;
Формулы (10. 3) позволяют найти сопротивления Z1, Z2, и Z3, (рис. 11.1, а) по коэффициентам четырехполюсника А, С, D. Аналогичные выкладки для П-схемы (рисунок 11.1,6) дают:
![]()
![]() B=Z4
;
B=Z4
; ![]()
![]() ;
(11. 4)
;
(11. 4)
Z4=B (11. 5)
Z5=B/(D-1) (11. 6)
Z6=B/(A-1) (11. 7)
Если четырехполюсник симметричный, то А=D и в Т-схеме замещения Z1=Z2, а в П-схеме Z5=Z6 .
11.2 Определение коэффициентов одной формы уравнений через коэффициенты другой.
Ту или иную форму записи уравнений применяют, исходя из соображений удобства. Так, в теории синтеза цепей используют обычно Y- или Z-форму записи. Параметры транзисторов для малых переменных составляющих дают в Y-, H- или Z-форме, так как в этих формах их удобнее определить практически. При нахождении связи между входными и выходными величинами различным образом соединенных четырехполюсников .
 |
Таблица 11.1
11.3 Характеристические сопротивления четырехполюсников.
В случае несимметричного четырехполюсника (A≠D) говорят о двух характеристических сопротивлениях ZC1 и ZC2, где ZC1 входное сопротивление со стороны зажимов тп,- когда нагрузка подключена к зажимам рq и равна ZC2, (рисунок 11.2, а);
 ,
(11.8)
,
(11.8)
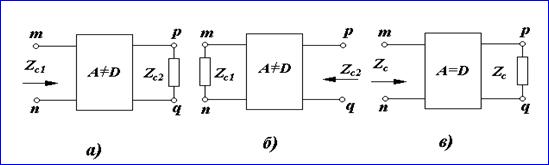
Рисунок 11.2
ZC2-входное
сопротивление со стороны зажимов рq, когда нагрузка
ZC2
подключена к зажимам тп (рисунок 11.2, б); при этом коэффициенты А и
D меняются местами: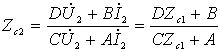 ; (11.9)
; (11.9)
Совместно решая (11.8) и (11.9), найдем:
![]()
![]() (11.10)
(11.10)
Учитывая, что A/С=Z10, B/D=Z2, В/А =, D/С = Z20, получим .
![]()
![]() (11.11)
(11.11)
Если четырехполюсник симметричен (А = D), то ZC1= ZC2= ZC , где ZC равно входному сопротивлению четырехполюсника, когда он нагружен на ZC (рисунок 11.2, в).
11.4 Постоянная передачи и единицы измерения затухания.
Для симметричного четырехполюсника, нагруженного на ZC,
![]()
![]() (11.12)
(11.12)
Комплексное
число ![]() полагают
равным еg, где
полагают
равным еg, где
g=а +jb=![]() - постоянная передачи. (11.13)
- постоянная передачи. (11.13)
Из формулы U1=U2eaejb İ1= İ2eaejb следует, что модуль U1 в еa раз больше модуля U2, а модуль İ1 в еa раз больше модуля İ2. По фазе U1 опережает U2, на угол b, ток İ1опережает İ2 также на угол b.
Величина а характеризует затухание четырехполюсника. Единицами измерения затухания являются неперы (Нп) и белы (Б). Неперы определены на основе натуральных логарифмов, а белы—на основе десятичных. Затухание в неперах
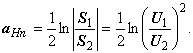 (11.14)
(11.14)
Если U1/U2=e, то затухание равно 1 Нп. Затухание в децибелах
аДБ =20lg ú U1/U2ú . (11.15)
Если U1 больше U2 , в 10 раз, то затухание равно 20 дБ, если U1/U2=100, то a =40 дБ.
Выразим неперы через
белы. Если
ú
S1/S2ú
=10, то
ú
U1/U2ú =![]() При этом
aНП=½ln10=1,15; аБ=lg10=1. Таким образом, 1 Б = 1.15 Нп, а 1 Нп=0,868 Б = 8,68
дБ.
При этом
aНП=½ln10=1,15; аБ=lg10=1. Таким образом, 1 Б = 1.15 Нп, а 1 Нп=0,868 Б = 8,68
дБ.
Для симметричного четырехполюсника A-форму уравнений (9.1) и (9.2) записывают иногда через гиперболические функции от аргумента g, полагая А=D=сhg, В=ZCshg, С =shg/ZC. При этом
AD-BC= сh2g- sh2g=1 и
![]() U1=chgU2+ZCshgİ2;
(11.16)
U1=chgU2+ZCshgİ2;
(11.16)

Убедимся в справедливости замены А на ch g :
![]()
![]()
![]()
форма записи через гиперболические функции используется, например, в теории фильтров.
ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
12 Лекция 12. Назначение и типы фильтров, основы теории фильтров.
Цель лекции: Изучить теорию фильтров и их назначение в электрических цепях.
12.1 Назначение и типы фильтров.
Под электрическими фильтрами понимают четырехполюсники, включаемые между источником питания и приемником (нагрузкой), назначение которых состоит в том, чтобы беспрепятственно—без затухания—пропускать к приемнику токи одних частот и задерживать, или пропускать, но с большим затуханием, токи других частот.
Диапазон частот, пропускаемых фильтром без затухания, называют полосой прозрачности; диапазон частот, пропускаемых с затуханием,—полосой затухания.
Электрические фильтры собирают обычно из индуктивных катушек и конденсаторов. Исключение составляют RС-фильтры. Фильтры используют главным образом в радиотехнике и технике связи, где применяются токи довольно высоких частот.
При высоких частотах индуктивные сопротивления wL индуктивных катушек во много раз больше их активных сопротивлений. Поэтому будем полагать, что активные сопротивления индуктивных катушек и активная проводимость конденсаторов равны нулю, т. е. фильтры составлены только из идеальных реактивных элементов.
Фильтры обычно собирают по симметричной Т- или -П-схеме .
При изучении фильтров будем пользоваться понятием о коэффициенте затухания и коэффициенте фазы .
Фильтры, в которых произведение продольного сопротивления на соответствующее поперечное сопротивление представляет собой некоторое постоянное для данного фильтра число (число k), не зависящее от частоты, принято называть k-фильтрами. Фильтры, в которых это произведение зависит от частоты, называют т-фильтрами.
Сопротивление нагрузки Zн, присоединяемое на выходе фильтра, должно быть согласовано с характеристическим сопротивлением фильтра ZC. В k-фильтрах ZC существенно изменяется в зависимости от частоты w, находящейся в полосе прозрачности. Это обстоятельство вызывает потребность изменять сопротивление нагрузки в функции от частоты (особенно при приближении к границе полосы прозрачности), что нежелательно. В m-фильтрах при определенных значениях коэффициента т, сопротивление ZC мало изменяется от частоты (в пределах полосы прозрачности) и потому нагрузка практически может быть одна и та же по величине для различных значений w, находящихся в этих пределах.
Качество фильтра тем выше, чем более резко выражены его фильтрующие свойства, т. е. чем более резко возрастает затухание в полосе затухания.
Фильтрующие свойства четырехполюсников физически обусловлены возникновением в них резонансных режимов — резонансов токов или резонансов напряжений.
12.2 Основы теории k-фильтров
Известно, что если нагрузка Zн согласована с характеристическим сопротивлением ZC четырехполюсника, то напряжение и ток в нагрузке İ2 связаны с напряжением U1 и током İ1 на входе четырехполюсника следующими соотношениями:
![]()
Множитель е-a определяет, во сколько раз модуль напряжения (тока) на выходе фильтра меньше модуля напряжения (тока) на входе фильтра.
Если а=0, то е-a=ео=1 и фильтр пропускает колебания без затухания. Таким образом, в полосе прозрачности а=0.
![]()
![]() В полосе затухания а>0. Множитель е-jb
, по модулю равный 1, свидетельствует о том, что напряжение и ток İ2;
отстают соответственно от и İ1 на угол
b.
В полосе затухания а>0. Множитель е-jb
, по модулю равный 1, свидетельствует о том, что напряжение и ток İ2;
отстают соответственно от и İ1 на угол
b.
Фильтрующие свойства четырехполюсника рассмотрим путем сравнения выражения для коэффициента А четырехполюсника с равным ему выражением гиперболического косинуса от аргумента a+jb:
A=сh(a+jb). (12.1)
Гиперболический косинус от суммы двух аргументов (с учетом того, что сhjb=сosb и shjb=jsinb) можно представить следующим образом:
сh (а + jb) = сh a соs b +jsh a sin b. (12.2)
Для любого фильтра, собранного по Т-схеме , А=1 + Z1/Z3.
Для фильтра, собранного по П-схеме , А = 1 + (Z4/Z5). Из каких бы реактивных сопротивлений ни был собран фильтр, отношение Z1/Z3, в Т-схеме и отношение Z4/Z5 в П-схеме всегда будет действительным (не мнимым и не комплексным) числом—отношение двух мнимых чисел всегда есть число действительное.
Следовательно, всегда будет действительным и коэффициент А. Но если коэффициент А действителен, то действительным должно быть и выражение равного ему сh(а+jb):
сh (а+jb)=ch а соs b+j sh a sin b=A.
Это выражение действительно, если
sh a sin b =0. (12.3)
При этом
ch a cos b =A. (12.4)
Уравнения (12.3) и (12.4) используют для определения границ полосы прозрачности и характера изменения угла b в зоне прозрачности, а также характера изменения коэффициента затухания а в полосе (полосах) затухания.
Равенство (12.3) для полосы прозрачности (a=0) удовлетворяется, так как sh a =sh 0=0. В силу того что сh 0=1, уравнение (12.4) для полосы прозрачности переходит в следующее:
cоsb=A. (12.5)
Круговой косинус (соs b) может изменяться в пределах от +1 до -1. Поэтому крайние значения коэффициента A [являющегося функцией частоты -А (w)] в полосе прозрачности равны ± 1, Полоса прозрачности в общем случае лежит в диапазоне частот от w1 до w2.
Значения w1 и w2 для фильтров НЧ и ВЧ определяют путем решения уравнений
A(w)=±1. (12.6)
Для полосовых и заграждающих фильтров w1 и w2 находят как корни уравнения А(w)=-1. Для них уравнение А(w)=1 дает, возможность определить так называемую резонансную частоту w0, находящуюся в интервале частот между w1 и w2.
Частоту, являющуюся граничной между полосой прозрачности и полосой затухания, называют частотой среза.
Характер изменения угла b в функции от w для зоны прозрачности определяют в соответствии с уравнением (12.5) следующим образом:
b = аrссоs A (w), (12.7)
Определим а и b для полосы затухания. В полосе затухания а > >0, Уравнение (12.3) удовлетворяется при условии
sin b=0, (12.8)
т. е. при
b=0, (12.9)
и (или) при
b=±p, (12.10)
Согласно уравнению (7.2), при b=0
сh а = А (w), (12.11)
а при b=±p сh а = - А (w). (12.12)
Уравнения (12.11) и (12.12) позволяют по значениям А как функции w найти сh а в полосе затухания, а по сh a найти а и,_таким образом, построить кривую а=ƒ(w). Из уравнений (12.9) и (12.10) следует, что в полосе затухания напряжение U2 выходе фильтра находится либо в фазе (при b=0). либо в противофазе (при b=±p) с напряжением U1 на входе фильтра.
В заключение необходимо отметить два важных положения.
1. С изменением частоты w меняются коэффициенты В и С четырехполюсника, поэтому изменяется и характеристическое сопротивление
![]()
Для того чтобы фильтр работал на согласованную нагрузку (только в этом случае справедлива изложенная здесь теория фильтров), при изменении частоты нужно менять и сопротивление нагрузки.
2. В полосе прозрачности характеристическое сопротивление фильтра всегда активное, а в полосе затухания — чисто реактивное (индуктивное или емкостное).
Если нагрузка фильтра не чисто активная или не согласована с характеристическим сопротивлением фильтра или если требуется учесть влияние активного сопротивления индуктивных катушек на работу фильтра (что существенно для низких частот), то, для построения зависимости U1/U2 = ƒ (w) и зависимости угла сдвига фаз между U1 и U2 в функции частоты можно воспользоваться, например, методом пропорциональных величин. Характеристическое сопротивление фильтра ZC берут равным внутреннему сопротивлению источника сигнала (генератора). При этом и генератор и фильтр работают в режиме согласования.
13 Лекция 13. К-фильтры НЧ и ВЧ ,полосовые и заграждающие k-фильтры
Цель лекции: Рассмотреть четыре типа фильтров и дать подробно их различие между собой .
13.1. k-фильтры НЧ и ВЧ, полосовые и заграждающие k-фильтры.
Фильтрами НЧ (ФНЧ} называют фильтры, пропускающие в нагрузку лишь низкие частоты: с w1 =0 до w2. Полоса их затухания находится в интервале от w2 до ∞.
Схемы двух ФНЧ приведены на рис. 13.1, а, б. Характер изменения коэффициента затухания а и коэффициента фазы b качественно иллюстрируют кривые рис. 13.1, в.
Под фильтрами ВЧ {ФВЧ} понимают фильтры, пропускающие в нагрузку лишь высокие частоты: с w1 до ∞. Полоса затухания их находится в интервале от 0. до w1.
Схемы двух ФВЧ приведены на рис. 13.2, а, б. Характер, изменения коэффициентов а и b для них иллюстрируется кривыми рис. 13.2, в.
![]() Рассмотрим вопрос об изменении величины характеристического
сопротивления ZC в полосе прозрачности для Т-фильтра НЧ (см. рис.
13.1, а) и для Т-фильтра ВЧ (рис. 13.2, а), а также для П-фильтров. С этой
целью в выражение подставим значения В и С .
Рассмотрим вопрос об изменении величины характеристического
сопротивления ZC в полосе прозрачности для Т-фильтра НЧ (см. рис.
13.1, а) и для Т-фильтра ВЧ (рис. 13.2, а), а также для П-фильтров. С этой
целью в выражение подставим значения В и С .
![]() Для Т-фильтра НЧ (см. рис.
13.1, а)
Для Т-фильтра НЧ (см. рис.
13.1, а)
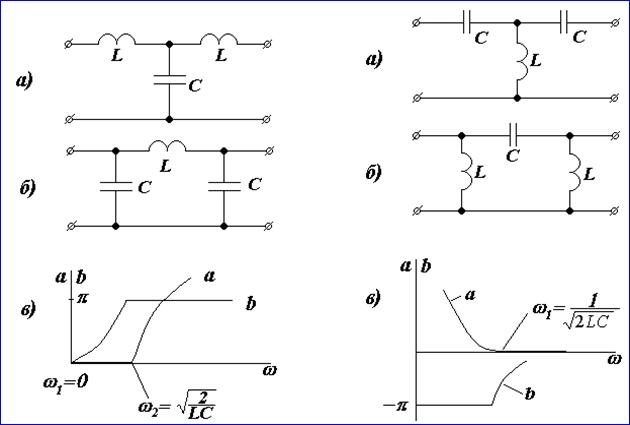
Рисунок 13.1 Рисунок 13.2
Для П-фильтра НЧ (см. рис. 13.1, б)
Для Т-фильтра ВЧ (рис. 13.2, а)
Для П-фильтра ВЧ (рис. 7.2, б)
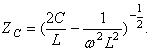 |
Если фильтр предназначен для работы на частотах, находящихся внутри полосы прозрачности данного фильтра и относительно далеко отстоящих от значения w, при котором ZC= 0, то сопротивление нагрузки ZН на выходе фильтров НЧ выбирают равным ZC, которое соответствует w=w1=0. Для Т-фильтра НЧ (см. рис. 13.1, а)
Для фильтров ВЧ обычно нагрузку согласовывают со значением ZC при w ®¥. Для Т-фильтра ВЧ (рис. 13.2, а). В полосе (полосах) затухания ZC оказывается чисто реактивным для всех типов k-фильтров.
Для того чтобы выяснить, индуктивный или емкостный характер имеет ZC в полосе затухания, следует определить характер входного сопротивления этого фильтра (фильтр всегда работает в режиме согласованной нагрузки) для предельного режима, а именно: для фильтров НЧ (рис. 13.1, а, б) при очень высокой частоте, а для фильтров ВЧ (рис. 13.2, а, б) при очень низкой частоте (теоретически при (w ®0.), считая выходные зажимы схем закороченными. Тот же результат будет получен, если считать их разомкнутыми. В результате определим, что в зоне затухания ZC имеет индуктивный характер для Т-фильтра НЧ (см. рис. 13.1, a) и П-фильтра ВЧ (рис. 13.2. б) и емкостный характер для П-фильтра НЧ (см. рис. 13.1, б) и Т-фильтра ВЧ (рис. 13.2, а).
Полосовые фильтры представляют собой фильтры, пропускающиев нагрузку лишь узкую полосу частот от w1 до w2.. Слева от w1и справа от находятся полосы пропускания .Схема простейшего полосового k-фильтра изображена на рис.13.3,а.Параметры схемы должны удовлетворять условию L1C1 =L2 C2.
Характер изменения a и b для полосового фильтра иллюстрируют кривые рис.13.3,а по заданным частотам ƒ1 и ƒ2 и сопротивлению нагрузки фильтра ZC при резонасной частоте ƒР=wР /2p :
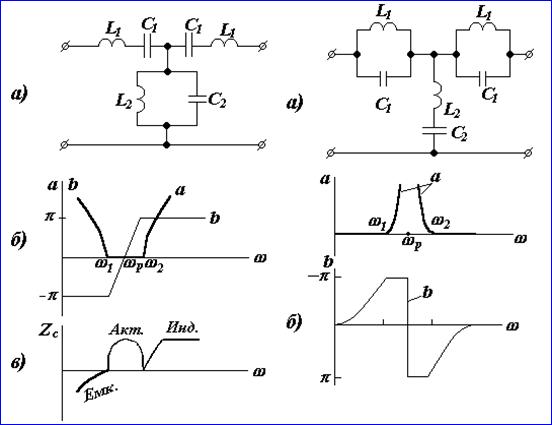 |
Рисунок 13.3 Рисунок 13.4

Под заграждающими фильтрами (рисунок 13.4, а) понимают фильтры, в которых полоса прозрачности как бы разрезана на две части полосой затухания (рис. 13.4, б). Слева от w1 и справа от w2 находятся две части полосы прозрачности.
В схеме простейшего заграждающего фильтра на рисунке 13.4, а L1C1=L2C2.
![]() Обозначим и
k=L1/L2
и
запишем формулы для определения
w1,2, а и
ZC фильтров рисунков 13.3. а и 13.4. а. Для рисунка
13.3, а
Обозначим и
k=L1/L2
и
запишем формулы для определения
w1,2, а и
ZC фильтров рисунков 13.3. а и 13.4. а. Для рисунка
13.3, а
 |
для рисунка 13.4 ,а
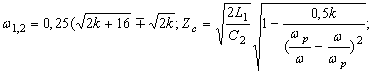 |
Для фильтра рис. 13.3, а в области частот от 0 до w1 ZC имеет емкостный характер, а в области частот от w2 до ¥—индуктивный. Для фильтра рис. 13.4. а в области частот от w1 до wP ZC имеет индуктивный характер, а в области от wP до w2 — емкостный.
13.2. RС-фильтры. Если сопротивление нагрузки фильтра очень велико (например, входное сопротивление лампового усилителя), то фильтр иногда выполняют из элементов R и С.
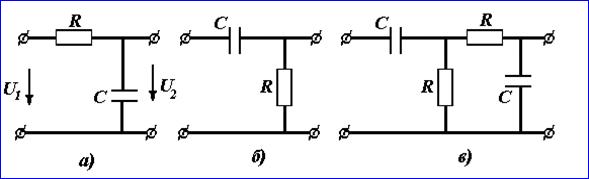 |
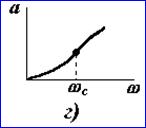 |
 |
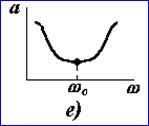 |
|||
|
Рисунок. 13.5
На рис. 13.5, а—в изображены схемы фильтров НЧ, ВЧ н полосового RС-фильтра, а на рис. 13.5, г-е— соответствующие им зависимости a=1n U1/U2=ƒ(w). Для всех RС-фильтров в рабочей зоне a≠ 0. Рабочая зона фильтра НЧ простирается от (w=0 до w=wC = 1/RС (принято условно) при а=0,343 Нп. Для фильтра ВЧ рабочая зона находится в диапазоне от w=wC = 1/RС при a=0,343 Нп до w=¥. В полосовом фильтре минимальное затухание имеет место при w = w0 = 1/RС.
Список литературы
1.К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л. Чечурин. Теоретические основы электротехники. – том 1. – СПб.: Питер, 2003.-463с.
2.Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. Основы теории цепей.- М.: Энергоатомиздат, 1989.-528с.
3.Л.А.Бессонов. Теоретические основы электротехники. – М.: Гардарики, 1999.-638с.
4.Г.В.Бакалов, В.Ф.Дмитриков, Б.Е.Крук. Основы теории цепей.- М.: Радио и связь, 2000.-592с.
5.Сборник задач по теоретическим основам электротехники/Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-543с.
Сводный план 2007 г., поз. 184