Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра теоретических основ электротехники

 

 

 

 

 

 

 

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ 2

Расчет трехфазных электрических цепей 

Методические указания и задания к расчетно-графическим работам №1,2,3

(для студентов специальности 5В081200 – Энергообеспечение сельского хозяйства)

 

 

 

 

 

Алматы 2011

 

СОСТАВИТЕЛИ: В.И. Денисенко, Р.М. Рахимова. ТОЭ2. Расчет трехфазных электрических цепей. Методические указания и задания к РГР №1,2,3 (для студентов специальности 5В081200 – Энергообеспечение сельского хозяйства). – Алматы: АУЭС, 2011 - 18 с.

 

 

Приводятся задания и методические указания к расчетно-графическим работам по курсу ТОЭ2 для тем: «Трехфазные цепи», «Цепи несинусоидального тока».

Расчетно-графические задания предназначены для студентов второго курса, обучающихся  в бакалавриате по специальности 5В081200 – Энергообеспечение сельского хозяйства.

Ил. 17, табл.9, библиогр. - 8 назв.  

 

Рецензент: канд. техн. наук, ст. преподователь К.А. Бакенов        

 

Печатается по плану издания НАО «Алматинского университета энергетики и связи» на 2011 г.

 

 

Ó НАО «Алматинский университет энергетики и связи», 2011г.

 

Содержание

 

1 Задание. Расчёт симметричных и несимметричных режимов в трехфазных цепях со статической нагрузкой                                                                              4

2 Задание. Расчёт несимметричных режимов трехфазных цепей методом симметричных составляющих                                                                                 7

3 Задание. Расчёт трехфазных  цепей с  несинусоидальными периодическими ЭДС                                                                                                                           10

Список литературы                                                                                                 17

 

1 Задание. Расчёт симметричных и несимметричных режимов в трёхфазных цепях со статической нагрузкой

 

К симметричному трёхфазному генератору с фазной ЭДС Еф через линию, сопротивление каждого провода которой Zпр, подключены два симметричных приёмника, соединённые звездой с фазными сопротивлениями Z1,  и треугольником, с фазными сопротивлениями Z2 (см. рисунок 1.1). Значения фазных ЭДС генератора и параметров цепи приведены в таблицах 1.1, 1.2, 1.3.

Выполнить следующее:

в соответствии с заданным вариантом рассчитать токи в линейных проводах и в фазах приёмников; фазные напряжения приёмников; активную, реактивную, полную мощности; построить векторные диаграммы для трёх режимов работы трёхфазной цепи:

1) симметричный режим;

2) обрыв одного из линейных проводов;


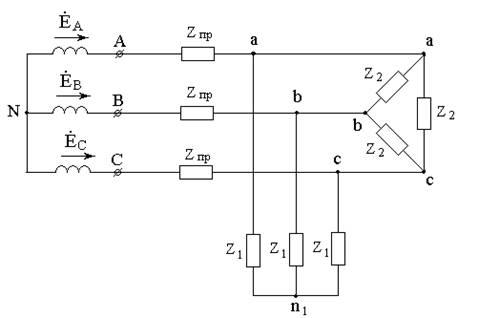3) обрыв одной из фаз приёмника.

 

Рисунок 1.1

 

 

Таблица1.1

Год

поступления

Первая буква фамилии

нечётный

АЯ

УЮ

Ф

КХ

БЛЦ

ВМЧ

ТЭИ

ЖСЗ

ДО

Щ

ЕПР

ГН

Ш

чётный

ФЕУ

ЦБХ

ГЧВ

ЩДШ

МЛК

ПОН

ЖСР

ТЗ

АИЭ

ЯЮ

Еф,В

120

220

380

127

220

120

60

100

200

180

 

Zпр, Ом

10+j4

12+j6

8+j5

20+j10

18+j9

7+j4

12+j8

10+j6

16+j9

15+j5

 

 

Таблица 1.2

Год

поступления

Последняя цифра зачётной книжки

нечётный

0

9

1

8

2

7

3

6

4

5

чётный

5

3

2

9

8

0

1

7

6

4

Z1, Ом

50- j20

60+ j30

70- j40

90+ j50

100- j60

100- j50

80- j100

60+ j80

70- j110

100+ j120

Обрыв линии

А

С

В

А

В

С

А

В

С

А

 

Таблица 1.3

Год

поступления

Предпоследняя цифра зачётной книжки

нечётный

1

0

9

8

3

4

5

6

2

7

чётный

7

2

6

5

4

1

0

9

8

3

Z2, Ом

100+ j80

80- j90

60+ j80

100- j50

40+ j90

30- j60

100- j120

120+ j70

80+ j40

90- j50

Обрыв фазы

 

аn1

ав

вc

вn1

ca

вc

сn1

вn1

aв

ca

 

Методические указания

 

Для расчёта симметричного режима трёхфазной цепи соединение приёмника треугольником с сопротивлениями Z2 заменяют на соединение эквивалентной звездой. Все нейтральные точки в симметричном режиме имеют одинаковый потенциал и их можно соединить проводом без сопротивления. Режим работы фазы А не изменится, если из полученной схемы удалить фазы В и С. В результате получим однофазную схему для расчёта токов в фазе А (рисунок 1.2, где - сопротивления эквивалентной звезды).


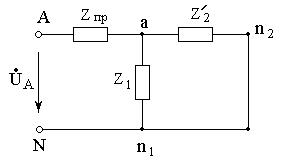Рисунок 1.2

 

Соответствующие токи в фазах В и С по модулю такие же, как и в фазе А и сдвинуты по фазе относительно токов в фазе А на угол ±1200.

Для расчёта несимметричных режимов трёхфазной цепи (обрыв в линии,  обрыв в одной из фаз  звезды или треугольника нагрузки) приёмник, соединённый звездой с сопротивлениями Z1, преобразовывают в эквивалентный треугольник, ветви которого параллельны ветвям треугольника приёмника с сопротивлениями Z2. Затем заменяют каждую пару параллельных ветвей треугольников одной ветвью, в результате получается схема с одним эквивалентным треугольником, который  заменяют эквивалентной звездой и рассчитывают методом двух узлов /Л1 7.1-7.3; Л2 10.1-10.9; Л3 6.1- 6.14; Л4 глава 6; Л7 3.1-3.2; Л8 1-4/.

 

 

2 Задание. Расчёт несимметричных режимов трехфазных цепей методом симметричных составляющих

 


Симметричная динамическая нагрузка подключена к симметричному трехфазному генератору с фазной ЭДС Еф (см. рисунок 2.1 и рисунок 2.2). Параметры генератора, линии и нагрузки приведены в таблицах 2.1, 2.2, 2.3. В трёхфазной цепи (см.рисунок 2.1) происходит  короткое замыкание одной из фаз на землю на зажимах нагрузки, а в трехфазной цепи (см. рисунок 2.2) происходит обрыв одного из линейных проводов. В соответствии с вариантом задания (см. таблица 2.1), используя метод симметричных составляющих, рассчитать токи и напряжения на всех участках цепи, определить активную, реактивную и полную мощности генератора.

Рисунок 2.1

 


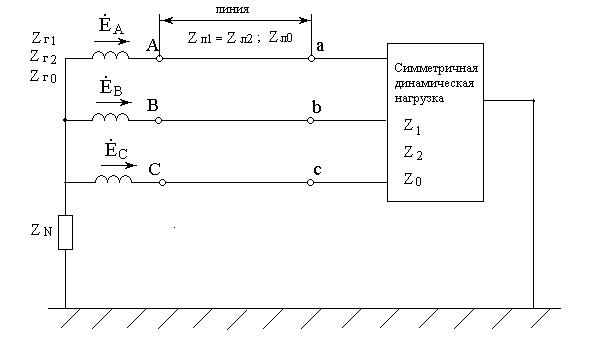Рисунок 2.2

 

Таблица 2.1

Год

поступления

Первая буква фамилии

нечётный

АНМ

БОЮ

ВПЯ

ГРШ

ДСИ

ЕТЩ

УЖ

ЗФ

ЧХЛ

КЦЭ

чётный

ЧХЛ

КЦЭ

АНМ

БОЮ

ВПЯ

ЗФ

ГРШ

ЕТЩ

ДСИ

УЖ

№ схемы

2.1

2.2

2.1

2.2

2.1

2.2

2.1

2.2

2.1

2.2

короткое

замыкание

фазы на землю

В

-

А

-

С

-

В

-

С

-

обрыв линии

-

А

-

С

-

В

-

С

-

В

Еф, В

380

400

220

127

250

200

350

450

500

300

Z0, Ом

¥

j0,5

¥

j0,7

¥

j0,4

¥

j0,8

¥

j0,9

 

 

Таблица 2.2

Год

поступления

Последняя цифра зачётной книжки

нечётный

8

2

9

1

7

3

6

4

5

0

чётный

0

8

5

2

4

9

6

1

3

7

Z1, Ом

4+ j3

5+ j4

4+ j6

6+ j3

5+ j5

3+ j5

6+ j5

5+ j6

3+ j4

4+ j5

Z2, Ом

0,3+ j0,4

0,4+ j0,6

0,3+ j0,7

0,5+ j0,7

0,6+ j0,9

0,6+ j1

0,4+ j0,8

0,25+ j0,7

0,35+ j0,8

0,45+ j1

ZЛ1= ZЛ2, Ом

j2,5

j4

j3,5

j3

j4,5

j3,2

j4,3

j4,7

j3,8

j5

ZЛ0, Ом

J11

j10

j9

j12

j14

j13

j16

j15

j7

j8

 

Таблица 2.3

Год

поступления

Предпоследняя цифра зачётной книжки

нечётный

7

1

6

2

5

3

4

8

9

0

чётный

9

1

0

7

8

6

4

2

5

3

ZГ1, Ом

0,25+ j2

0,2+ j1,5

0,3+ j2,5

0,33+ j2,8

0,4+ j2,3

0,22+ j1,8

0,38+ j2,2

0,23+ j1,4

0,45+ j3

0,28+ j1,7

ZГ2, Ом

j0,2

j0,18

j0,15

j0,25

j0,16

j0,14

j0,19

j0,23

j0,24

j0,17

ZГ0, Ом

j0,05

j0,08

j0,06

j0,09

j0,07

j0,1

j0,11

j0,12

j0,13

j0,14

ZN, Ом

j0,3

j0,2

j0,5

j0,6

j0,35

j0,25

j0,4

j0,55

j0,45

j0,15

 

Методические указания

 

Для расчётов несимметричных режимов трёхфазных цепей       методом симметричных составляющих используют принцип компенсации, заменяя несимметричную нагрузку (например, короткое замыкание одной из фаз на землю) или несимметричный участок в линии (например, обрыв одного из линейных проводов) источниками напряжений, значения которых до окончания всего расчёта остаются неизвестными. Заменив несимметричную нагрузку или несимметричный участок в линии тремя источниками с неизвестными напряжениями , получим симметричную трёхфазную цепь, которая содержит генератор с симметричной системой ЭДС и источник с несимметричными напряжениями .

Разложим  несимметричную систему напряжений  на симметричные составляющие , приняв фазу А за основную, и составим три независимые схемы прямой, обратной и нулевой последовательностей. Для этих схем записываются уравнения по второму закону Кирхгофа, в результате получаем три уравнения с шестью  неизвестными. Дополнительные три уравнения составляются на основании заданной схемы и параметров несимметричной нагрузки или несимметричного участка в линии. Решая полученную систему уравнений, определяют симметричные составляющие токов и напряжений, через которые рассчитываются токи и напряжения на всех участках цепи /Л1 7.4-7.5; Л2 11.1-11.7; Л3 6.20- 6.21; Л7 4.1-4.3; Л8 5-6/.

 

 

3 Задание. Расчет трехфазных цепей с несинусоидальными  периодическими ЭДС

 

К симметричному трехфазному генератору с несинусоидальными фазными ЭДС подключена симметричная нагрузка. Определить для схемы с нейтральным проводом:

- гармонический состав фазных ЭДС в фазах А, В, С;

- мгновенные значения токов в фазах А, В, С;

- мгновенное значение тока в нейтральном проводе;

- показания приборов;

- активную, реактивную, полную мощности.

Произвести аналогичный расчет при обрыве нейтрального провода  /Л1 8.1-8.5; Л2 12.1-12.10;  Л3 7.1-7.13;  Л4 глава 7;  Л7 5.1-5.4; Л8 8-9/.

Электрические схемы приведены на рисунках 3.1–3.10. Несинусоидальные кривые фазных ЭДС для фазы А представлены на рисунках 3.11–3.13. Параметры цепи приведены в таблицах 3.1 – 3.3. Основная частота фазных ЭДС генератора 

 

Таблица 3.1

Год

поступления

Последняя цифра зачетной книжки

Четный

№ схемы

1

3.1

2

3.2

3

3.3

4

3.4

5

3.5

6

3.6

7

3.7

8

3.8

9

3.9

0

3.10

Нечетный

№ схемы

9

3.1

7

3.2

5

3.3

3

3.4

1

3.5

8

3.6

6

3.7

4

3.8

0

3.9

2

3.10

20

15

10

22

13

12

8

14

16

9

-

-

50

90

-

-

40

60

-

45

35

-

-

45

65

-

-

55

25

45

40

30

60

50

-

-

-

-

70

90

-

-

-

-

-

80

90

95

-

85

-

20

25

-

80

30

40

35

45

70

-

-

-

-

-

100

50

80

-

-

60

70

50

40

50

-

-

-

60

-

 

 

 

         Таблица 3.2 

Год поступления

Предпоследняя цифра зачетной книжки

Четный

0

2

4

6

8

1

3

5

7

9

Нечетный

9

7

5

3

1

8

6

4

2

0

№ рисунка

3.11

3.12

3.13

3.11

3.12

3.13

3.11

3.12

3.13

3.11

 

         Таблица 3.3

Год поступления

Первая буква фамилии

Четный

АЛХ

БМЦ

ВНЧ

ГОШ

ДПЩ

ЕРЭ

ЖСЮ

ЗТЯ

ИУ

КФ

Нечетный

КФ

ИУ

ЗТЯ

ЖСЮ

ЕРЭ

ДПЩ

ГОШ

ВНЧ

БМЦ

АЛХ

3

5

2,5

2

5,5

1,5

4

6

3,5

4,5

220

270

100

360

127

120

60

110

380

200

 

 

Рисунок 3.1

 

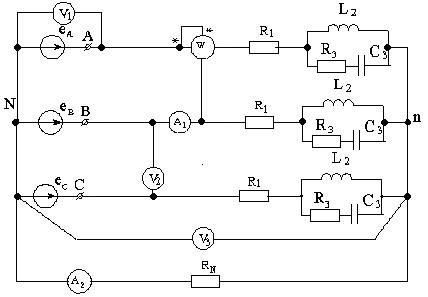
Рисунок 3.2

 

 

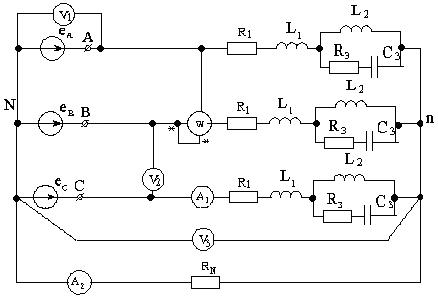
Рисунок 3.3

 

Рисунок 3.4

 

 

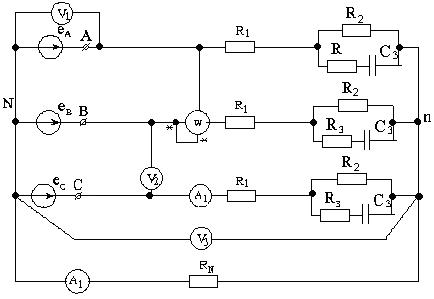
Рисунок 3.5

 

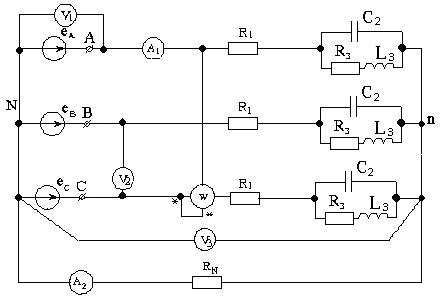
Рисунок 3.6

 

 

Рисунок 3.7

 

Рисунок 3.8

 

 

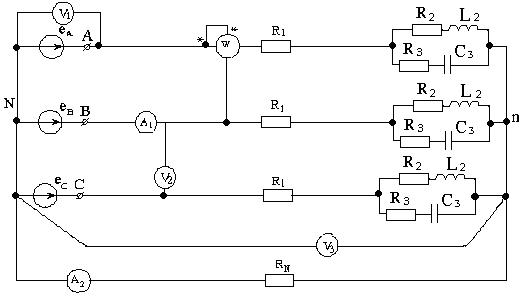
Рисунок 3.9

 

Рисунок 3.10

 

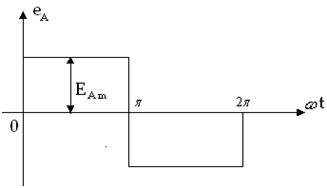
Рисунок 3.11

 

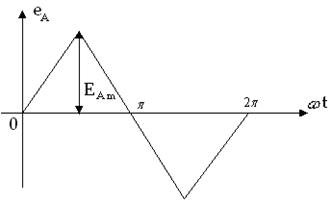
Рисунок 3.12

 

 

 

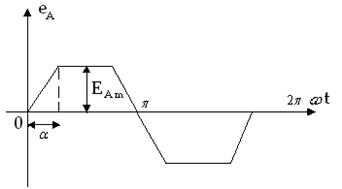
Рисунок 3.13

 

 

 

 

Список литературы

 

1 Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники. Том 1. – СПб.: Питер, 2009.- 512 с.

2 Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.- М.: Энергоатомиздат, 1989.-528 с.

3 Бессонов Л.А. Теоретические основы электротехники. – М.: Гардарики, 2006.- 701 с.

4 Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей.- М.: Высшая школа, 1990.- 544 с.

5 Бессонов Л.А. Сборник задач по теоретическим основам электротехники.-М.: Высшая школа, 2000.- 528 с.

6 Сборник задач  и упражнений по теоретическим основам электротехники/ Под ред. П.А.Ионкина.-М.: Энергоиздат, 1982.-768 с.

7 Денисенко В.И., Зуслина Е.Х. Теоретические основы электротехники: Учебное пособие.- Алматы.: АИЭС, 2000.- 83 с.

8 В.И.Денисенко, С.Ю.Креслина. Теоретические основы электротехники 2. Конспект лекций ( для студентов всех форм обучения специальности 050718 – Электроэнергетика).- Алматы: АИЭС, 2007.- 62 с.

 

Сводный план 2011 г., поз. 104