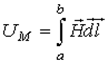Коммерциялық емес Акционерлік Қоғамы

АЛМАТЫ ЭНЕРГЕТИКАЛЫҚ ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ

Электротехниканың теориялық негіздері кафедрасы

 

 

Электротехниканың теориялық негіздері 2

Дәрістер жинағы

 (5В070200–Автоматтандыру және басқару мамандығының бакалавриат студенттеріне арналған)

 

 

Алматы 2012

Құрастырушылар: А.Т. Аршабекова, С.Ю. Креслина. Электротехниканың теориялық негіздері 2. Дәрістер жинағы (5В070200–Автоматтандыру және басқару мамандығының студенттеріне арналған). – Алматы: АЭжБУ, 2012.- 49 б.

 

Дәрістер жинағы ЭТН 2 пәні бойынша 11 дәрістен келесі негізгі бөлімдер бойынша құралған: «Сызықты электр тізбектеріндегі өтпелі кезеңдер», «Бейімделген параметрлі тізбектер», «Сызықты емес электрлі және магниттік тізбектер».

Дәрістер жинағы 5В070200–Автоматтандыру және басқару мамандығының студенттеріне арналған.

Сур.31, әдебиеттер-5 атау.

 

Пікір беруші: тех.ғыл.канд., профессор Копесбаев А.А. 

 

«Алматы энергетикалық және байланыс университеті» КЕАҚ 2012 ж. баспаға шығару жоспары бойынша орындалған.

 

Ó «Алматы энергетикалық және байланыс университеті » ҚЕАҚ, 2012 ж.

Мазмұны

 

Кіріспе                                                                                                                        4

1 бөлім. Сызықты электр тізбектеріндегі өтпелі кезеңдер                                    5

1 Дәріс.  Өтпелі кезеңдердің пайда болуы, коммутация заңдары, өтпелі кезеңдерді есептеудің классикалық әдісі                                                                5

2 Дәріс. Бір энергия жинақтауышы бар тізбектердегі өтпелі кезеңдерді Есептеу                                                                                                                     10

3 Дәріс. Екі энергия жинақтауышы бар тізбектердегі өтпелі кезеңдер             15

4 Дәріс 4.  Тармақталған тізбектердегі өтпелі үрдістерді есептеу, Дюамел интегралы                                                                                                  18

5 Дәріс. Өтпелі кезеңдерді есептеудің операторлық әдісі                                  21

6 Дәріс. Электрлік тізбектің спектральды анализ негіздері                               24

2 бөлім. Бейімделген параметрлері бар тізбектер                                               28

7 Дәріс. Ұзын желілердегі тоқтар мен кернеулер, біртекті ұзын желілердің теңдеулері (жалпы жағдай), біртекті желілердегі қалыптасқан синусоидалы режим                                                                         28

8 Дәріс. Әртүрлі жұмыс режиміндегі біртекті желілер, шығынсыз желілер    32

3 бөлім. Сызықты емес электрлі және магниттік тізбектер                                35

9 Дәріс. Сызықсыз тізбектер жайлы негізгі мағынасы, тұрақты токтың сызықсыз емес электрлік тізбектер әдістерінің анализі                         35

10 Дәріс. Магнит тізбегінің негізгі мағынасы мен заңдары                                41

11 Дәріс.  Магнит тізбегін есептеудің әдістері                                                     44

Әдебиеттер тізімі                                                                                                     49

  

Кіріспе 

«Электротехниканың теориялық негіздері 2» пәні автоматтандыру және басқару саласындағы бакалаврларды дайындау үшін негізгі базалы міндетті пән болып табылады. Пәннің негізгі тағайындалуы, электр тізбектерінің элементтері көмегімен құралған, баламалы алмастыру сұлбалармен келтірілетін, әртүрлі электротехникалық қондырғыларда өтетін электрмагниттік үрдістер мен құбылыстарды сапалы оқып білу мен сипаттау болып табылады.

Ұсынылып отырған дәрістер жинағы 11 дәрістен 3 бөлім бойынша құралған: «Сызықты электр тізбектеріндегі өтпелі кезеңдер», «Бейімделген параметрлі тізбектер», «Сызықты емес электрлі және магниттік тізбектер».

Бірінші бөлімде сызықты электр тізбектеріндегі өтпелі кезеңдерді есептеудің негізгі әдістері: классикалық, операторлық, жиіліктік, Дюамел интегралы қарастырылған.

Екінші бөлімде бейімделген параметрлі тізбектер жөнінде  негізгі ұғымдар, біртекті желідегі қалыптасқан режим, келісілген жүктемелі желінің және шығынсыз желінің теориялары қарастырылған.

Үшінші бөлімде сызықты емес тізбектер жөнінде негізгі ұғымдар және оларды есептеу әдістері, тұрақты және айнымалы токты сызықты емес электр тізбектерінің графикалық және аналитикалыық талдау әдістері, магниттік тізбектердің жалпы сиппаттамалары мен есептеу әдістері келтірілген.

 Дәрістер жинағы 5В070200 – Автоматтандыру және басқару мамандығы бойынша бакалавриатта оқитын студенттер үшін арналған.

 

1 бөлім. Сызықты электр тізбектеріндегі өтпелі кезеңдер

1 Дәріс.  Өтпелі кезеңдердің пайда болуы, коммутация заңдары, өтпелі кезеңдерді есептеудің классикалық әдісі

 

Дәрістің мақсаты: өтпелі кезеңдер жөнінде жалпы мәліметтер беру, сызықты электр тізбектеріндегі, оларды есептеудің классикалық әдісін меңгеру.

 

1.1           Өтпелі кезеңдердің пайда болуы, коммутация заңдары

 

Бұрынғы тақырыптарда, бейімделген параметрлі тізбектердегі қалыптасқан кезеңдер зерттелген, яғни бұндай тізбектерде, магниттік өріс, электр өрісі және жылудың бөлінуі, тізбектің жеке бөлімшелерінде бейімделген деп нақты дәлдікпен айтуға болатын, яғни параметрлерінің тізбекте нақты орны тағайындалған болатын.

Электротехника саласында қалыптасқан режимдерден өзге өтпелі режимдер немесе кезеңдер маңызды орын алады.

Өтпелі кезең – бір қалыптасқан режимнен, одан өзге қалыптасқан режимге алмасу үрдісі. Бұндай үрдістер коммутация кезінде, яғни электр тізбектерінің қосылуы немесе ажыратылуы кезінде  және тізбек параметрлерінің өзгеруі кезінде (мысалы жүктеменің өзгеруі) орын алады. Сұлбаларда бұл былай көрсетіледі                        ,                       .                         .      

Өтпелі кезеңдерді толығымен үш сатыға бөлуге болады.

1.                 Бастапқы қалыптасқан кезең.

2.                 Өтпелі кезең. Оның басталуы негізінде  есебінде қабылданады (кейбір жағдайларда коммутация алдындағы  уақытын және коммутациядан кейінгі   уақытын ажырата білу қажет).

3. Теория жүзінде уақытында келетін, ал тәжірибе жүзінде салыстырмалы қысқа уақыттан кейін келетін, соңғы қалыптасқан кезең. Бұл кезең қалыптасқан деп аталады.

Өтпелі кезең уақыты секундтар бөліктерімен есептеледі, алайда тоқ пен кернеу қалыптасқан режиммен салыстырғанда әлдеқайда үлкен мәндерге ие бола алады. Жалпы айтқанда жабдықтарды дұрыс таңдап алу үшін және қауіпсіздіктің сәйкесті шараларын қабылдау үшін, өтпелі кезеңдегі тоқтар мен кернеулерді дұрыс есептеп алу қажет.     

Тізбекпен байланысты магниттік және электр өрісінің энергиясы, әртүрлі қалыптасқан кезеңдер үшін әртүрлі болады. Оның соңғы өзгерісі үшін уақыт қажет. Сондықтан, егер тізбек магниттік өріс энергиясына ие болса (бұндай өріс тізбекте индуктивтілік орауышы бар болғанда үнемі пайда болады) немесе электрлі өріс энергиясына ие болса (тізбекте конденсатор бар болса) немесе екеуіне де ие болса – өтпелі үрдіс лезде жүріп өте алмайды, өйткені соңғы жағдай  мен элементтерінде элементтерінде шексіз жоғары қуаттар тудыратын еді, яғни бұның физикалық мағынасы жоқ. Магниттік өрістің энергиясы _м 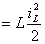. Бұның нәтижесінде 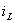тогы лезде өзгере алмайтыны және де өтпелі кезең кезінде өзінің өзгерісін, өтпелі кезеңге дейін ие болған мәннен бастайтыны шығады. Бұл жағдай коммутацияның бірінші заңы атымен белгілі  .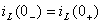

кернеуі  шамасына байланысты емес және сондықтан соңғы шамаға дейін лезде өзгере алады.

Электрлі өріс энергиясы . Яғни бұлжағдайда конденсатордағы кернеу лезде өзгере алмайды  – коммутацияның екінші заңы.  тоғы лезде өзгере алады.

Тізбекте тек 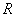болса, яғни электрлі де, магниттік те өріс болмаса, онда өтпелі үрдіс жүрмейді. Тоқ пен кернеу лезде, жаңа қалыптасқан мәндерге дейін өзгереді. Жалпы жағдайда электр тізбегі элементтерінің әртүрлі комбинацияларынан құралады, яғни өтпелі кезең орын алады. Оның ұзақтығы тоқ шамасына да, кернеу шамасына да тәуелді болмайды, ал тек тізбектің параметрлерімен ғана анықталады.

 

1.2           Өтпелі кезеңдерді есептеудің классикалық әдісі

 

Өтпелі кезеңдердің аналитикалық есептелуі, тұрақты коэффициенттері бар қарапайым сызықты дифференциалды теңдеулердің жалпы интегралдарын анықтауды ұйғарады. Өтпелі режимдегі электр тізбегінің тоқтары мен кернеулерінің сәйкестілігін сипаттайтын дифференциалды теңдеудің деңгейі, берілген тізбектегі электрлі немесе магниттік өріс энергиясының жиналу орындарының санымен анықталады. Конденсатордағы тоқ екені белгілі.  Дәл осы тоқ индуктивтілік орауышы бойымен өтетін болса, онда индуктивтіліктегі кернеу .

Жалпы жағдайда, тізбекте n энергия жиналу орны болатын болса, теңдеу келесі түрді қабылдайды:

 

….                                                   (1.1)

 

Оң бөлігі бар дифференциалды теңдеудің жалпы интегралы, осы теңдеудің жеке шешімінің және дәл сол теңдеудің оң бөлігісіз шешімінің суммасын, яғни теңдеудің жалпы шешуін көрсетеді.

Теңдеудің жалпы шешуі, тізбекпен байланысты электрлі және магниттік өрісте алғашқы уақыт мезетіндегі энергия қоры есебінен, тізбектегі сыртқы энергия көздерінің болмауы кезінде жүріп өтетін электрмагниттік үрдістерді физикалық анықтайды. Дегенмен шынайы тізбектерде энергияның сейілуі және оның жылу күйінде бөлініп шығуы үнемі орын алады.

Жалпы айтқанда, оң бөлігі жоқ сызықты дифференциалды теңдеулерден анықталатын тоқтар мен кернеулер, уақыт өту барысында нөлге қарай ұмтылады. Бұл құраушылар сыртқы энергия көздеріне тәуелді емес болады және сондықтан да еркін құраушылар деп аталады.

(1.1) теңдеуден анықталған, мысалы тоқтың еркін құраушысының жалпы түрі келесі болады:

 

 _ер. =  ,                                                                                       (1.2)

 

мұндағы – бастапқы шарттардан табылатын интегралдау тұрақтысы. Бастапқы шарттар деген, ол   кезіндегі лезде өзгере алмайтын шамалар, яғни  ;

– сипаттамалық теңдеудің түбірі.

(1.1) теңдеуіне қатысыты сипаттамалық теңдеу келесі түрді қабылдайды:

 

….                                                             (1.3)

 

Дифференциалды теңдеудің түбірлері саны, сол теңдеудің дәрежесіне  тең болады. Жалпы жағдайда түбірлер кешенді сандар болуы мүмкін, олардың нақты бөлігі әрдайым теріс таңбалы болады.

 

,

 

мұндағы экспонентаның сөну жылдамдығын сипаттайды және сөну коэффициенті деп аталады.  

Уақыт тұрақтысы .

Теңдеу түбірінің жорамал бөлігін , жеке тербелістердің бұрыштық жиілігі деп атайды

Теңдеудің жеке шешуі кезіндегі, яғни қалыптасқан режимдегі тоқ пен кернеудің мәнін береді. Бұл құраушысының сипаты мен шамасы сыртқы энергия көздерімен анықталады, сондықтан бұл құраушы еріксіз (қалыптасқан) деп аталады.

Мысалы (1.1) өрнегіндегі кернеу болса, онда еріксіз тоқ та  болады және уақытқа тәуелді болмайды. Сонда барлық туындылар нөлге теңеседі және  қалады. Тоқтың нәтижелі мәні теңдеудің жалпы және шеке шешулерінің соммасы ретінде анықталады: _{ер. к.}. анықталатын шама кернеу болса, онда  _ер.к. .

 Жалпы айтқанда, шешім беттесу әдісіне келтірілді: жеке шешімін анықтай отырып, тек сыртқы энергия көздері әрекет етеді деп ұйғарылады.  Еркін құраушысын анықтау кезінде, керісінше, сыртқы көздерді нөлге теңестіреді және де тізбекте энергияның жиналуымен бейімделген, тек ішкі әрекеттерді ескереді. Шынайы айтқанда, тек әрекеттік тоқтар мен кернеулер ғана бар екендігін, ал оларды еркін және еріксіз құраушыларға жіктеу, есептеуді жеңілдететін нұсқа екендігін ұмытпаған жөн

   

1.3. RL тізбегін тұрақты кернеуге қосу 

                                              

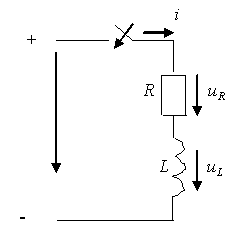
1.1    сурет - тізбегін тұрақты кернеуге қосу

 

Берілгені: , . Тізбектің  (1.1 суретті қара) қосылу уақытын деп алып, тоғын анықтау және оның уақытқа тәуелділік графигін тұрғызу.  

Тізбектің электрлі тепе теңдігінің дифференциалды теңдеуін құрастырамыз (дифференциалды түрдегі Кирхгофтың екінші заңы бойынша теңдеу)

 

             несесе _.                                                                       (1.4)

 

        екендігі белгілі                                                                 (1.5)

 

     (1.5) өрнегін (1.4) орнына қойсақ  ,                                         (1.6)

 Яғни  бірінші дәрежелі сызықты дифференциалды теңдеуге келдік.

       (1.6) өрнегінің жеке шешуін, яғни  шамасын анықтаймыз.

 

   . болғандықтан , , ал  (1.7)

      

Нәтижесінде, орауышта пайда болатын, тоқтың өзгеруіне  әсер ететін өзара индукция ЭҚК болмаса, тізбектегі кілттің тұйықталуының алғашқы сәтінен бастап жүріп өтетін, қалыптасқан кезеңнің тоғы шығады.  Теңдеудің жалпы шешуі, яғни _.

 

    .                                                                               (1.8)                                    

    

(1.8) өрнегін айнымалыларды бөлу арқылы шешейік: .   

       Интегралдап, өрнегіне келеміз. тұрақтысын, қандайда бір өзге  тұрақтысыныңретінде анықтауға болады, яғни  деп есептеуге болады.  Сонда:            

     ,

мұндағы  -  сипаттамалық теңдеуінің түбірі,  .     

 тұрақтысы бастапқы шарттардан анықталады: кезінде орауыштағы тоқ нөлге тең (коммутацияныың бірінші заңы бойынша), яғни  

 

.     

Осыдан    және     .                                        (1.9)

 

       Бұдан кейін  шамасын, толық шешуін келтірмей ақ,   өрнегін пайдаланып, жалпы түрінде келтіретін боламыз.  

        түбірі нақты болғандықтан, онда уақыт тұрақтысы.  Өлшем бірлігі  .   шамасын пайдаланып,  деуге  болады.   шамасының физикалық мағынасы:  кезінде   _ер.,  ал  _ер, сонымен   – еркін құраушы есе төмендейтін уақыт.

       Токтың әрекеттік мәні    

  

                               .                                   (1.10)

 

      1.2 суретінде графигі келтірілген: уақыт аралығында тоғы қалыптасқан кезеңнен 0,7%  ғана ерекшеленеді, яғни өтпелі үрдіс аяқталды деп айтуға болады.

           

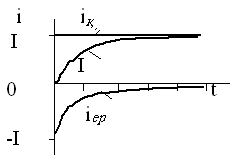
1.2 сурет - Өтпелі токтың уақытқа тәуелділік графигі

 

 

2 Дәріс. Бір энергия жинақтауышы бар тізбектердегі өтпелі кезеңдерді есептеу

   

Дәрістің мақсаты: қарапайым электр тізбектеріндегі өтпелі кезеңдерді есептеудің классикалық әдісін меңгеру.

 

       2.1 R,L элементтері бар тізбектерінің қысқа тұйықталуы

 

 

                                   
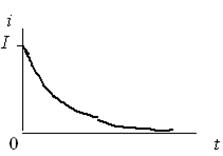
             2.1сурет -  элементтері                   2.2 сурет - Өтпелі токтың графигі

бар тізбектерінің қысқа тұйықталуы

 

        белгілі болсын.   анықтау қажет.

Дифференциалды түрдегі Кирхгофтың екінші заңы бойынша, тұйықталған контурдың теңдеуін құрайық:

 

                                          .                                           (2.1)  

 

Тоқтың қалыптасқан құраушысын анықтаймыз _қ (орауыштағы өтпелі кезең сыртқы кернеуге тәуелді емес болады). Осының салдарынан _ер.

       (2.1)  өрнегіндегі тоқтың еркін құраушысы _ер .     

Тізбектің сипаттамалық теңдеуі , яғни     

 Интегралдау тұрақтысын  бастапқы шарттардан анықтаймыз: 

  кезінде _ер..              

       2.2 суретінде   келтірілген.             (2.2)

            Энергияның шығынын тексерейік. Өтпелі кезеңнің басталуына дейін орауыштың магниттік өрісінде _м  энергия қоры болған. Өтпелі кезең уақыты барысында жылулыққа алмасқан энергия

 

 .

 

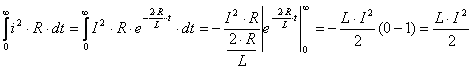Сонымен, магниттік өрістің барлық энергия қоры жылулық энергияға кедергісінде ауысты.

  

2.2 R,С тізбегін тұрақты кернеуге қосу

                                                          

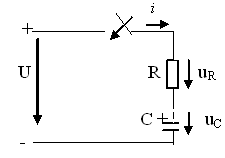
2.3 сурет -  тізбегін тұрақты кернеуге қосу

 

Тізбектегі конденсатор U₀ кернеуіне дейін зарядталған болатын деп есептейік. 2.3 суреттегі тізбек үшін, Кирхгофтың екінші заңы бойынша теңдеу келесі түрді қабылдайды:

 

                                         .                                                   (2.3) 

 

Тізбекте конденсатор бар болғандықтан, есептеуді энергия қорын анықтайтын шама кернеуі арқылы жүргізген дұрыс.

тоғын  арқылы  өрнектейік:    

 

                               .                                                               (2.4)

 

    (2.4)  өрнегін ескере отырып, тізбектің электрлі тепе теңдігінің теңдеуін келесі түрде жазайық:  

                                           

                                                ,                                                    (2.5)

мұндағы  _қ  ер.

     _қ  анықтайық:

.                                                                                                       (2.6)

 

     Бұл жердегі тоқ, конденсатор зарядталғанға дейін әрекет етіп тұрады.    

     (2.5)  теңдеуі бірінші реттік болғандықтан, онда кернеудің еркін құраушысы :

    _ер .                                                                                   (2.7)

 

       Тізбектің сипаттамалық теңдеуі , осыдан .

     

 Ом_.·Ф = Ом_.· Ом^.-1_.· с. = с.

 

         Интегралдау  тұрақтысын анықтайық:

    

                            .                                                        (2.8)

 

кезінде , осыдан  А = U₀ – U, нәтижесінде:

           _ер.  .                                                                                 (2.9)

 

 Ең соңғы нәтижесі: .                                            (2.10)

 

            болса                .

 

Конденсатордың зарядталған тоғы: .                (2.11)

 болса,  .                                                                                   (2.12)

      2.4 суретте  және  тәуелділіктерінің мысалдық түрі көрсетілген:  

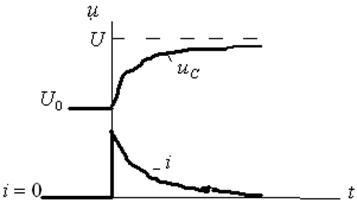
2.4 сурет - Ток пен кернеудің уақытқа тәуелді графиктері

 

                        

2.3 R,L тізбегін синусоидалы кернеуге қосу

                        

Бұндай өтпелі кезеңнің мысалына, өзекшенің аз қанығуы кезіндегі, трансформатордың бос жүріс режимінде қосылуын келтіруге болады.

Айнымалы тоқ тізбектеріндегі өтпелі кезеңдер, қай сәтте, кернеудің қандай лездік мәнінде тізбек қосылатынына қатты тәуелді болады. Сондықтан міндетті түрде, торап кернеуінің тек әрекеттік мәнін немесе амплитудасын ғана емес, ал тізбектің қосылу сәтіндегі бастапқы фазалы бұрышын да ескеру керек.

2.5 суреттегі тізбекті қарастырайық.

Берілген тізбек синусоидалы кернеуге қосылған делік, оның бастапқы фазасы  градусты, яғни  ) құрайды.                           

Бұл жерде де есптеу реті бұрынғыдағыдай болады, тек і_қ уақытқа тәуелді болады. 

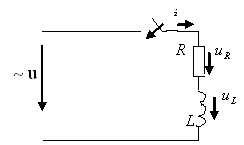
2.5 сурет -  тізбегін синусоидалы кернеуге қосу

 

Тізбектің электрлі тепе теңдігінің теңдеуін құрастырайық

 

                                            .                                                       (2.13)

 

Тоқтың еріксіз құраушысы _{еріксізқ.}, дегенмен қалыптасқаан режимде тоқ Ом заңіксіз құраушысы , дегенмен қалыптасқаан режимде тоқ Ом заңы бойынша анықталады

 

                                      _{еріксізқ} ,                                   (2.14)

 

мұндағы  ;

 

        .

 

Күрделі тізбектерде қалыптасқан режимнің тоғын кешенді түрде анықтап алған ыңғайлы, содан кейін İ_қ.  мәннен _қ. мәнге ауысқан ыңғайлы болады.

Тоқтың еркін құраушысыы  _ер ,                              (2.15)

мұндағы  , ал .

Жалпы тоқ  _пр.св .                                (2.16)

 кезінде  (коммутацияның бірінші заңы бойынша). Осыдан .

Соңында шығатыны  _ер ,                                     (2.17)

ал       .                                       (2.18)

 

(2.18) өрнектен, тоқ екі бөлімнен тұрақты амплитудаалы синусоидалы тоқтан және экспонента бойынша төмендейтін тұрақты тоқтан құралатыны көрініп тұр. Жалпы тоқтың шамасы бастапқы  бұрышына айтарлықтай тәуелді болады.  

  

 

 

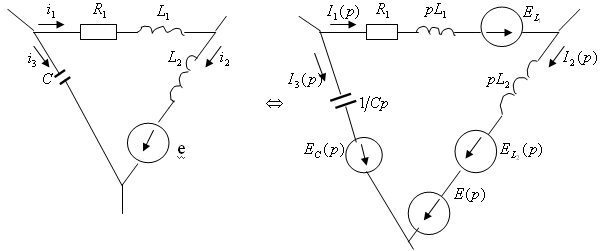
3 Дәріс. Екі энергия жинақтауышы бар тізбектердегі өтпелі кезеңдер  

 

Дәрістің мақсаты:  элементтерінің тізбектей жалғанған тізбектердегі және олардың тұрақты кернеуге жалғанған кездегі өтпелі кезеңдердің өтуі ерекшеліктерімен танысу.

 

        3.1 R,L,C тізбегіндегі өтпелі кезең

                                                           

 

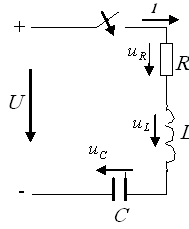
3.1 сурет -  тізбегін тұрақты кернеуге қосу

 

3.1 суреттегі тізбекте энергияның екі түрі магниттік өріс және электр өрісі энергиясының қоры сақталады. Яғни, тізбекте тоқ та, кернеу де лезде өзгермейді. Берілген тізбектің кез келген кернеуге  қосылуы кезіндегі ток  пен кернеуді  анықтайық. Тізбек қосылғанға дейін   болсын делік. Тізбектің электрлі тепе теңдігінің теңдеуі келесі түрді қабылдайды:

         

        .                                                                                     (3.1)

 

Сыйымдылығы бар тізбекті  арқылы есептеген оңай болғандықтан, (3.1) өрнегіндегі барлық шамаларды осы кернеу арқылы өрнектейік ; ; . Осы өрнектерді (3.1) қойып, екінші реттік сызықты дифференциалды теңдеуді аламыз:

         

.

 

 кезіндегі коэффициенттен құтылайық  

                                          ,                                      (3.2)

мұндағы _қер.

 

қ Ом заңы бойынша анықтайық. Қалыптасқан құраушы келтірілген кернеу түріне тәуелді болады. Егер  болса, онда _қ. болады. Егер   болса, онда қалыптасқан режимдегі тоқ та, кернеу де синусоидалы болып өзгереді. Бұл жағдайда есептеу кешенді түрде жүргізіледі, содан кейін уақыт функциясы тәрізді лездік мәндер анықталады.

u_Сер құраушысын анықтайық, бұл құраушы өтпелі кезеңнің ұзақтығы мен сипатын анықтайды.

 

   _.                                                                                         (3.3)  

                        

(3.3) теңдеуінің шешуі келесі болады:

                                              

                                                                                (3.4)

 

 сипаттамалық теңдеуінің түбірлері келесі түрде анықталады:

 .                                                                     (3.5)

       

Теңдеу түбірлерінің мәндері, тізбек параметрлерінің сәйкестіктеріне тәуелді болады. Үш жағдай болуы мүмкін:

 

а)   >     .

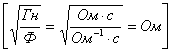Бұл шарттың орындалуы кезінде  болады және p₁, p₂  түбірлер, мәндері әртүрлі, теріс таңбалы нақты мәндер болып шығады.                          

Расында да,  деп белгілесек, мұндағы  –  мәнінен кіші нақты сан болса, онда  < 0; < 0.                  (3.5а)   

Абсолюттік шамасы бойынша | ₁ | < | ₂ |. Бұндай режим апериодтық деп аталады, өйткені ток пен кернеу, өзінің бағытын өзгертпей, қалыптасқан режимге қарай ұмтылады;

б) .   Бұл шарттың орындалуы кезінде және теңдеу түбірлері бұл жағдайда да нақты, теріс таңбалы сандар болады: . Бұл жағдайда     .                                                                  (3.6) 

Бұл режим критикалық деп аталады.

в)  < . Бұл жағдайда теңдеу түбірлері  мен , нақты бөлігі теріс таңбалы, кешенді-сыбайлас мәнді шамалар болады:

 

; ,                                                                      (3.7)

 

мұндағы    – сөну коэффициенті;

        = - меншікті тербелістердің бұрыштық жиілігі.

Бұндай режим периодтық немесе тербелмелі деп аталады. Бұл жерде орауыш пен конденсатор арасында көп мөлшердегі энергия алмасуы жүріп өтеді: энергия бірде магниттік өріске (тоқ өскен кезде), бірде электр өрісіне (конденсатордағы кернеу өскенде) ауысып құйылатындай болады.

Интегралдау тұрақтылары бастапқы шарттардан анықталады.

 

,                                                                        (3.8)

 

,                                                (3.9)

 

         кезінде:  ,

                       .                                             (3.10)

      

(3.10) теңдеулерінен  және  оңай анықталады.

 

4 Дәріс.  Тармақталған тізбектердегі өтпелі үрдістерді есептеу, Дюамел интегралы.

    

Дәрістің мақсаты: тармақталған тізбектердегі өтпелі кезеңдерді классикалық әдіспен және тізбектің кез келген кернеу көзіне қосылуы кезіндегі  есептеулерді меңгеру.

 

4.1 Тармақталған тізбектердегі өтпелі кезеңдерді классикалық әдіспен есептеу

 

Берілген есеп, тоқтар мен кернеулердің лездік мәндері үшін Кирхгоф заңдары бойынша құрастырылған теңдеулер көмегімен шешіледі, осы токтар мен кернеулер анықталуға тиіс.

Тармақталған тізбектер тармақтарындағы тоқтарды немесе кернеулерді есептеуді келесі реттілікпен жүргізген ыңғайлы болады:  

      -коммутациядан кейінгі токтың немесе кернеудің қалыптасқан құраушысын анықтаймыз (і_қ u_қ)

      - коммутациядан кейінгі режим үшін кірістік кедергінің Z(p)  (ЭҚК көзі бар тізбектер үшін) немесе кірістік өткізгіштіктің Y(p) (тоқ көзі бар тізбектер үшін) теңдеуін құрып, оны нөлге теңестіреміз. Бұл кезде реактивті кедергілер операторлы түрде келтірілу керек ( немесе );

           -   түрлендіруден кейін сипаттамалық теңдеуге келеміз, оған берілген параметрлердің мәндерін қойып, өтпелі шаманың еркін құраушысының  () түрін анықтайтын теңдеу түбірлерін  мен есептейміз. Теңдеу түбірлері теріс таңбалы < екі нақты сан шықса, онда еркін құраушыларды жазу үшін (3.4) теңдеуін пайдаланамыз, егер = болса - (3.6) өрнегін пайдаланамыз, егер түбірлер кешенді сыбайлас шамалар () болып шықса,

,                                                                             (4.1)

мұндағы  және  - интегралдау тұрақтылары;

 - тоқтың (кернеудің) теңдеуін жалпы түрде жазамыз:

= ;                                                            (4.2) 

 -  және  шамаларын есептеу үшін, тағы бір теңдеу қажет, ол үшін тоқтың (кернеудің) уақыт  бойынша бірінші туындысын аламыз. Сонда тұрақты ток тізбегі үшін:

;                                   (4.3)

 -  тоқ  (кернеу) және оның  туындысының теңдеулерін  кезі үшін жазамыз

,

                                   ;                                     (4.4)

 - коммутация заңдары және Кирхгоф теңдеулері бойынша,  кезіндегі коммутациядан кейінгі тізбек үшін бастапқы шарттарды анықтаймыз ,  , содан кейін (4.4) өрнектегі  және  интегралдау тұрақтыларын анықтаймыз;

-   және  мәндерін өрнегіне қойып, белгілі бір тармақтағы тоқтың  немесе кернеудің уақыт бойынша өзгеріс заңдылығын анықтаймыз.

 

       4.2 Электр тізбегін еркін пішінді кернеуге қосу

 

Кез келген тізбекті тұрақты кернеуге қосу кезінде, осы тізбектің өтпелі кезеңіндегі тоғын келесі түрде жазуға болады:

 

                                             ,                                              (4.14)

 

мұндағы  – тізбектің өтпелі өткізгіштігі. Бұл шама уақытқа және тізбек параметрлеріне тәуелді болады, тек кернеуге  тәуелді емес болады.

 = 1 В деп қабылдап, g(t) шамасы жөнінде сипаттауға болады. Яғни, шамасы, тізбектің 1 В кернеуге қосылған кездегі өтпелі кезең тоғына тең болады.

Әрбір берілген тізбек үшін, өтпелі өткізгіштікті не классикалық, не операторлық әдіспен есептеуге болады (кейінірек қарастырылады).  Мысалы тізбегін тұрақты кернеуге қосу кезінде (1.1суретті қараңыз), ток  тең болады. Яғни өткізгіштік  болады. Егер тізбек кернеуге  >0 уақыт мезетінде  қосылатын болса, онда тоқ  болатынын атап өткен жөн.                                          (4.15)

Бұл кездегі өтпелі кезеңнің басталу сәті болып табылады, ал бастапқы шарттар  үшін жазылады.

Тізбектің өтпелі өткізгіштігін біле отырып, тізбектің уақыт бойынша үздіксіз өзгеретін кез келген кернеу көзіне қосылуы кезіндегі тоғын анықтауға болатынын көрсетейік. Кернеу көзі  4.1 суретте көрсетілген пішінді болсын делік,  біле отырып, тоғын анықтау қажет болсын делік.

          

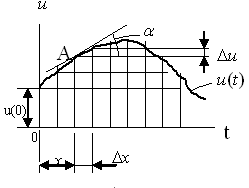
4.1 сурет - Еркін пішінді кернеу графигі

       

 Берілген кернеуді сатылы функцияға жуық алмастырамыз, оның сатылары теңдей уақыт аралықтары арқылы бірінен кейін бірі орналасады. Сонда  тоғын, t =0  уақыт сәтінде қосылатын кернеуінен келетін тоқ және «+» немесе «-» таңбалы бола алатын (тармақ төмендейтін болса),  арқылы бірінен кейін бірі қосылатын қарапайым  кернеулерден келетін тоқтардың қосындысынан тұрады деуге болады.

кернеуінен  келетін тоқ бөлігі  тең, ал қандай да бір  сәтінде қосылған кернеуден келетін тоқ бөлігі  болады.

 қисығына  нүктесінен жанама жүргізейік. Осы жанаманың абцисса осіне иілу бұрышының тангенісі, берілген нүктедегі  функциясының туындысына тең, яғни .  ескере отырып, кернеуінен келетін тоқ бөлігі келесі өрнекпен анықталады:

 

            .                                                            (4.16)

 

Шексіз төмен интегралдарға ауыса отырып, және де барлық тоқ бөліктерін қосып, келесі нәтижеге келеміз:

 

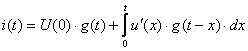                                           .                          (4.17)

(4.17) өрнегі  –Дюамель интегралы деп аталады.

Берілген интегралдан өзге, осы интергалдың тағы 5 түрін жазуға болады:

           ,    ,                                

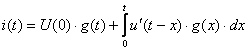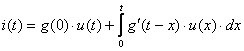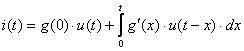
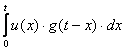             ,                .              (4.18)

 

Келтірілген интеграл түрлерінің барлығынан алғашқы төртеуі жиірек қолданылады, өйткені олардың қолданылуы қандай да бір есепті шешуді жеңілдетеді.

 

 

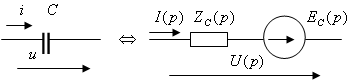
  5 Дәріс. Өтпелі кезеңдерді есептеудің операторлық әдісі

 

Дәрістің мақсаты: операторлық әдістің негіздерімен, операторлық бейнелерден уақыттық функцияларға өтумен танысу.

 

Маңызы – уақыт функциясын, оператор деп аталатын  кейбір кешендік айнымалы функциялармен алгебралық жолмен интегро-дифференциалдық теңдеулерге алмастыру болып табылады.

Берілген уақыт функциясы – түпнұсқа болып табылады. Айнымалыны ауыстыру нәтижесінде алынған функциясы – бейне болып табылады. Бұл функциялар бір-біріне тең емес. Сондықтан олардың арасында теңдік белгісі емес, сәйкестік белгісі қойылады.

Операторлық әдістің артықшылығы – алгебралық теңдеулер жүйесінің шешімі әлдеқайда дифференциалдық теңдеулер жүйесінің шешімінен жеңілдігінде.

Операторлық әдіспен есептеу келесі екі есептің шешіміне негізделеді:

-          берілген уақыттық функцияларды операторлыққа ауыстыру (яғни теңдеулердің алгебраизациясы);

-          операторлық функцияны уақыттыққа есептеу нәтижесінде есептеулерді ауыстыру.

Бірінші есеп Лаплас түрлендіру көмегімен есептелінеді.

.                                                      (5.1)

 

5.1 Өтпелі кезеңдер үшін электрлік тізбектің  негізгі элементтерінің есептеу сұлбалары.

 

Орынбасу элементтерінің параметрлері  болсын. Ток пен кернеудің операторлық бейнелері келесі түрде анықталады:

,   ,

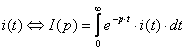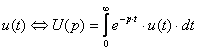ал олардың бастапқы мәндері және .

 активті кедергідегі тоқ пен кернеу Ом заңымен  байланысты. Операторлық түрде , яғни  (5.1 суретті қара).

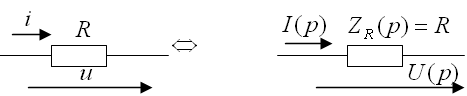
5.1 сурет - Активті кедергідегі кернеу және оның бейнесі

 

Идеалды индуктивтілік кезінде , ал операторлық түрде  (5.2 суретті қара).

 

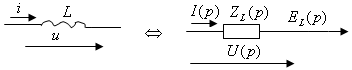
5.2 сурет - Индуктивтіліктегі кернеу және оның бейнесі

 

Осыдан операторлық сұлбада мен, тоқпен бағыты сәйкес келетін және нөлдік бастапқы шарттың нәтижесінде алынатын, ішкі ЭҚК бар.

Кондерсатордың тоғы . Оның операторлық бейнесі . Бірінші қосылғышты  түрінде қарастыруға болады (мұндағы ), ал екінші қосылғышты – конденсатордағы бастапқы кернеумен анықталатын ток түрінде қарастыруға болады (5.3суретті қара). .

 

5.3 сурет - Сыйымдылықтағы кернеу және оның бейнесі

 

5.2 Электрлік тізбектің операторлық түрдегі негізгі заңдары

 

Ом заңы. Ол тек ешқандай энергия көздері жоқ пассивті тізбекті қосқанда қолданылады, яғни нөлдік бастапқы шарттар кезінде (5.4 суретті қара).

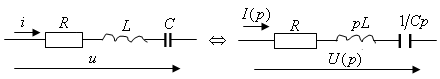
5.4 сурет - тізбегіндегі кернеу және оның бейнесі

 

 және  белгілі болсын. Онда , немесе                                     ,                                                (5.2) 

мұндағы .

 -ға ауыстырып, тізбектің  комплексті түрдегі кедергі формуласынан  оңай алуға болады.

 Кирхгофтың бірінші заңы.

    _. Жалпы жағдайда

                                                                                                                                                       (5.3)

 

Кирхгофтың екінші заңы.

 

 

5.5 сурет - Түйық контур және оның элементтерінің бейнелері

 

Кирхгофтың екінші заңы бойынша дифференциалды түрде теңдеу құрамыз .

Операторлық түрге көше отырып, келесі өрнекті аламыз:

,

мұндағы , , .

Жалпы жағдайда кез келген тұйық контур үшін:

                                     .                                                    (5.4)

Бұл жерде контурды айналып өту кезінде нөлдік бастапқы шарттар нәтижесінде алынатын ЭҚК те ескерілуі қажет.

Орынбасу операторлық сұлбаларын қалыптасқан режим кезінде тұрақты ток тізбектерін есептеу үшін белгілі кез келген тәсілмен есептеуге болады.

Берілген әдіспен тізбекті есептеудің тәртібі:

-    берілген есептік, яғни ЭҚК орнына олардың операторлық бейнелері көрсетілген, операторлық орынбасу сұлба тізбегін ауыстыру;

-    орынбасу сұлбасын кез келген белгілі әдістермен есептеу;

-    операторлық функциялардан түпнұсқаға өтерде тізбектің нақты тоқтары мен кернеулерін өтпелі режимде анықтау.

 

 

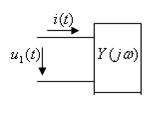
6 Дәріс. Электрлік тізбектің спектральды анализ негіздері

 

Дәрістің мақсаты: жиіліктік сипаттамалармен танысу, Фурье интегралын қолданып қарапайым тізбектердің өтпелі процесстерін есептеумен танысу.

 

6.1 Электрлік тізбектің жиіліктік сипаттамалары

 

Электрлік тізбектің кірісіне қандай да бір электрлік сигналмен әсер етсек, барлық элементтерде ток және кернеу түрінде реакция пайда болады. Сызықты электрлік тізбек үшін реакция спектрінің әсер ету реакциясына қатынасы тізбек пен жиілік параметрлерінің функциясы болып табылады. Егер реакция түрінде пассивті сызықты екіұштықтың (6.1 суретті қара) ток спектрін алсақ, онда бұл ток спектрінің қосымша кернеу спектріне қатынасы екіұштықтың жиіліктік сипаттамасын көрсетеді

                            ,                                          (6.1)

мұндағы - қосымша кернеудің жиіліктік спектрі. Ол  қосымша кернеудің белгілі функциясы бойынша тура Фурье түрлендіруінен анықталады

.

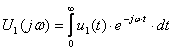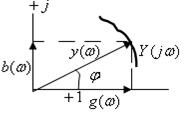
Электрлік тізбектің жиіліктік сипаттамасы жиіліктің кешенді функциясы түрінде көрсетіледі және кешенді жазықтықта, жиілігі артқан сайын модулі мен фазасы өзгеретін, вектор түрінде бейнеленуі мүмкін. Бұл вектор амплитуда-фазалық сипаттама деп аталын кейбір қисықты (6.2сурет) сипаттайды.

                                        

6.1 сурет - Пассивті сызықты екіұштық             6.2 сурет.- Вектор  амплитуда-    

                                                                                                 фазалық сипаттама

 

Екіұштықтар қасиеттерінің анализі кезінде амплитуда жиіліктік сипаттама және  фаза жиіліктік сипаттамамен бірге тағы олардың кешенді жазықтықтағы осьтер құраушыларын қарастыруға болады.

 векторының нақты сандар осіндегі проекциясы келесі нақты жиіліктік сипаттамасын береді:

                                    .                                              (6.2)

Осындай тәсілмен электрлік тізбектің жорамал жиіліктік сипаттамасы анықталады:

                                     .                                              (6.3)

Егер кез келген белгіленген  жиілігінің мәнін берсек, онда  және физикалық мағынасы анық бола бастайды. Бұл кезде кіріс кернеу мен тоқтың жиіліктік спектрі ішкі кернеу мен тоқ  жиіліктерінің кешенді амплитудаларына айналады, ал жиіліктік сипаттамасы тізбектің кешенді өткізгіштігі түрінде көрсетіледі

,

мұндағы - тізбектің активті кіріс өткізгіштігі;

-  жиілігі үшін электрлік тізбектің реактивті ішкі өткізгіштігі.

Осыдан тізбектің нақты жиіліктік сипаттамасы жиіліктің барлық диапазонында берілген толық ішкі өткізгіш кешенінің нақты бөлігін көрсетеді, ал жорамал жиіліктік сипаттамасы – жорамал бөлігін.

Қарапайым екіұштықтар және оларға сәйкес  жиіліктік сипаттамалары  6.3 суретте көрсетілген.

6.3 сурет - Қарапайым екіұштықтар және оларға сәйкес  жиіліктік сипаттамалары 

 

 тізбегінің кешенді өткізгіштігі:

.

Сәйкесінше ,   .

 тізбегінің кешенді өткізгіштігі:

.

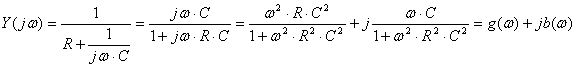  Мұнда ,       .

Күрделі пассивті сызықты тізбекте ішкі кернеу кірісіне реакция ретінде тек ішкі тоқты ғана емес, сонымен қатар сұлбаның кез келген тармағындағы ток пен кернеуді таңдауға болады.

Егер сұлбаның кез келген тармағын кедергі деп алсақ, онда сұлбаның қалған бөлігін  кіріс кернеуі және  шығыс кернеуі бар төртұштық түрінде көрсетуге болады.

Қарастырып отырған тармақтағы (төртұштықтың шығысында) кернеудің жиіліктік спектрінің қосымша кернеу жиіліктік спектріне қатынасы келесі түрдегі кешенді береліс функциясы болады:

 

 .                                                                               (6.4)

 

Жиіліктік сипаттама секілді кешенді беріліс функциясы амплитуда-жиілікітік  және фаза-жиіліктік сипаттама түрінде көрсетілуі мүмкін:

 

                                                                              (6.5)

 

немесе нақыт жиіліктік және жорамал жиіліктік сипаттама түрінде көрсетілуі мүмкін: .                                                (6.6)

 

6.2 Фурье интегралын қолданып тізбектегі өтпелі процесстерді есептеу

 

 кернеу көзіне электромагниттік қоры жоқ пассивті тізбекті қосқан кезде ( кезінде) жиіліктік әдіспен өтпелі процесстерді есептеуге болады. Бастапқы энергия қорымен, яғни нөлдік бастапқы шарттармен емес, тізбектерді осы әдіспен есептемейді. Бұдан басқа u(t) функциясы абсолютті интегралдануы керек, яғни .

Электрлік тізбектерін есептеу келесі тәртіппен орындалады:

-    тура Фурье түрлендіруінің көмегімен қосымша кернеудің спектрлік сипаттамасы анықталады ;

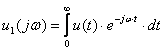-     комплексті беріліс функциясы немесе анықталатын шамаға қатысты есептелетін сұлбада жиіліктік сипаттамасы анықталады;

-    іздеп отырған шаманың спектральды сипаттамасы есептеледі. Бұл кезде барлық операциялар тізбектің қалыптасқан режиміндегідей символикалық әдіспен есептеледі

                             немесе .             (6.7)

Уақыттық функцияларға кері ауысу немесе тікелей кері Фурье түрлендіруі арқылы жүзеге асады

;   ,                      (6.8)

немесе Лаплас түрлендіруі кезіндегі операторлық әдісте қолданған секілді жіктеу теоремасы бойынша жүзеге асады

.                                                 (6.9)

Жіктеу теоремасында -ны  -ға ауыстыру керек.

 

2 бөлім. Бейімделген параметрлері бар тізбектер

 

7 Дәріс. Ұзын желілердегі тоқтар мен кернеулер, біртекті ұзын желілердің теңдеулері (жалпы жағдай), біртекті желілердегі қалыптасқан синусоидалы режим.

 

Дәрістің мақсаты: жалпы жағдайдағы ұзын желілердің теңдеулері мен негізгі мағынасымен, біртекті желілердегі қалыптасқан синусоидалы режиммен танысу.

 

7.1 Ұзын желілердегі тоқтар мен кернеулер, негізгі мағынасы

 

Алдында қарастырылып өткендей, әрбір тізбекте магниттік және электрлік өрісте жылуды жоғалтамыз, осыдан соларға қатысты  параметрлерге жеке орын беріледі. Реалды тізбектерде ток ағып жатқан кезде барлық өткізгіштерде жылу бөлінеді, магниттік және электрлік өрістер де тізбектің барлық бөлшектерімен байланысты. Тізбек бойымен энергияның таралуы шексіз жылдамдықпен жүзеге асатыны болжамданады. Бұл тек осы тізбекке энергия беретін, электрмагниттік толқындардың ұзақтығы ұзындығымен салыстырғанда әлдеқайда қысқа болатын, тізбектер үшін дұрыс.

Толқын ұзындығы деп бір период тербеліс ішінде электромагниттік толқын таралатын қашықтықты айтады .

f = 50 Гц кезінде  км. Тұрақты ток кезінде f = 0 және .

-мен өлшемдес шамалары бар тізбектерде, осы тізбектермен байланысты, электрлік және магниттік өрістерді тізбектің барлық бөліктерінде электромагниттік энергияның жылулыққа алмасуын ескеруге тура келеді. Мұндай тізбектер бейімделген параметрлері бар тізбектер деп аталады. Оларға радиотехникалық құрылғылар, байланыс жолдары, ұзындығы 100 км және одан асатын тарату желілері жатады. Бұндай тізбектер тағы ұзын желілер деп аталады, бірақ олар тек төменгі жиіліктер үшін ғана ұзын желілер болатынын ескеру қажет. Жоғарғы жиіліктер кезінде  метрмен өлшенеді (мысалы,  Гц кезінде м), осыдан бірнеше метрге жететін антенналар толқын ұзындығымен өлшемдес және ұзын желілер сияқты есептелуі керек.

Берілген ток пен кернеудің өзгерулері желінің элементарлы бөліктерге бөлінумен және әрбір бөлікте R активті кедергісі, L индуктивтілігі, ал өткізгіштер арасында – g активті өткізгіштік және С сыйымдылығының бар болуымен ескеріледі. Бұл желіні сипаттайтын параметрлерді оның барлық ұзындығының бойымен бейімделген. Осыдан аты – бейімделген параметрлері бар тізбектер деп аталады. Әрбір бөліктің ішінде желінің параметрлері топталған деп есептейді.

R, L, g және C желі бойымен біртекті бейімделген деп есептейміз. Мұндай желілер біртекті деп аталады. Әдетте желі 1 км ұзындыққа жататын параметрлермен сипатталады:

R₀  – тура және кері желі өткізгіштерінің активті кедергісі;

L₀ – тура және кері өткізгіштерден шыққан желінің индуктивтілігі;

       C₀ – өткізгіштердің арасындағы сыйымдылық;

       g₀ – өткізгіштер арасындағы ағуы.

 

7.2 біртекті желілердегі қалыптасқан синусоидалы режим

 

Бұл жерде желінің кез келген нүктесінде ток пен кернеу синусоидалы, бірақ ток пен кернеудің фазалары жалпы жағдайды әртүрлі.

Желінің жүктемелі соңынан  қашықтықта кейбір нүктеде орналасқан ток пен кернеу сәйкесінше тең болсын.

                ,

                       .                                                                    (7.1)

 

Синусоиданың лездік мәнінен комплексті бейнесіне өтуін мына түрде жазуға болады:

        ,  ,  , .      (7.2)

Алынған комплекстер уақыттан тәуелді емес. Осыдан, синусоидалы функцияларды сәйкес комплексті бейнелермен орын басып, бір ғана айнымалыдан -  қашықтығынан тәуелді шамалар үшін дифференциалды теңдеулерді аламыз, және есептеуді жеке туындыларсыз жүргізуге болады.

Теңдеу келесі символикалық түрде:

,

                                                 .                                         (7.3)

                                                 ;

                                                   ,                                                 (7.4)

 

мұндағы  - желінің бірлік ұзындығына желінің бойлық кедергісі;

 - желінің бірлік ұзындығына желінің көлденең кедергісі.

 және  желінің әртүрлі элементтеріне жататындықтан,  болады.

(7.4)-ны (7.3) қойып келесі өрнекті аламыз:

 

            ,               (7.5)                          .                              (7.6)

 

 бойынша (7.5) және (7.6)-ны қайтадан дифференциалдаймыз және шыққан айнымалыны бөлеміз:

 

                                              ,                                       (7.7)

                                               .                                       (7.8)

(7.8) теңдеуді шешеміз.

.

Осы теңдеудің жалпы шешімі:

                                      ,                                          (7.9)

 

мұндағы  мен  сипаттамалық теңдеудің түбірлері және  мен  интегралдаудың тұрақтылары жалпы жағдайда комплексті сандар болып табылады.

Біздің жағдайда сипаттамалық теңдеу келесі түрде болады

 

. Осыдан ,     .              (7.10)

 

 - толқынның таралу коэффициенті. Ол желінің 1км бойымен  кернеу мен  токтың өзгеруін сипаттайды. Алгебралық түрде комплекс мына түрде болады: ,

мұндағы  - 1км-ге толқынның өшу коэффициенті, ;

- 1км-ге фазаның өзгеру коэффициенті, .

(7.10) негізінде кернеу .                                        (7.11)

 

Токтың жалпы формуласын анықтау үшін (8.13)-ті (8.7)-ге қоямыз

 

                      .                                (7.12)

 

(7.12) келесі түрде жазамыз:

 

                                       ,                                                  (7.13)

мұндағы 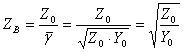  , 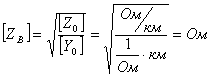 -           (7.14)

 

желінің толқындық немесе сипаттамалық кедергісі.

 

,

 

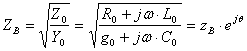мұндағы 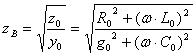;       (7.15)

Әуе желілері үшін = 300 – 600 Ом, кабельді үшін  50 Ом.

 және  интегралдау тұрақтылары келесі шекаралық шарттардан анықталады:

  ,  .                                                                                   (7.16)

 

,  ,

                          , .               (7.17)

 және  (7.11) пен (7.12) қойып, ток пен кернеуді анықтаймыз

, .   (7.18)

Осыдан ток пен кернеудің лездік мәндері:

,

   .     (7.19)

 

Гиперболалық функциялардағы ұзын желілердің теңдеуі

 

 кернеу мен  тогы бар мүшелерді топтастырып, (7.18) теңдеуін қайта жазамыз:

,

,

бірақ   ,  .                                                   (7.19)

(7.19) теңдеуін ескерсек, қалыптасқан синусоидалы режим кезінде ұзын желінің теңдеуі келесі түрде болады:

,

                                            .                                        (7.20)

Егер желінің кірісінде ток пен кернеуді табу керек болса, яғни , , онда бұл теңдеулерге  қою керек.

(7.20) – симметриялы пассивті төртұштықтың теңдеуі, тұрақтылары келесі мәнге тең:

,   ,       .

Кез келген симметриялы төртұштық сияқты желі Т-типті немесе П-типті симметриялы, параметрлерін төртұштықтың тұрақтылары арқылы анықтауға болатын, орынбасу сұлбаларымен оңай алмастырылуы мүмкін.

Кешенді аргументтен  гиперболалық функцияны анықтау бір қиындық туғызу мүмкін. Гиперболалық функцияны (7.21) формуладан анықтауға болады:

,

                ,        (7.21)

себебі ,  , немесе Эйлер формулалары бойынша:

                , .          (7.21а)

 

 

8 Дәріс. Әртүрлі жұмыс режиміндегі біртекті желілер, шығынсыз желілер

 

Дәрістің мақсаты: келісілген жүктемелі, бос жүріс, қысқа тұйықталу режимдерімен, шығынсыз желінің теңдеулерімен танысу.

 

8.1 Келісілген жүктемелі режим

 

Желінің шығысына қосылған қабылдағыштың кедергісі оның толқындық кедергісіне тең болсын .

Онда кернеу  және (8.20) теңдеу келесі түрде болады

                                               ,     ,                                    (8.1)

яғни өлшеулер қай жерде жүргізілмесін, желінің кез келген нүктесінде кернеу мен токтың қатынасы тұрақты болады

                                                .                                              (8.2)

Осыдан,  - желінің шығыс қысқыштары тұйықталғанда, желінің кіріс қысқыштарында дәл сондай  кедергісі бар болатын кедергі.

(8.20) теңдеуден  кезінде кедергіден ешқандай шағылысу жоқ . Желіде тек түсу толқындары анықталады.

Қарастырылып отырған режим келісілген жүктелмелі режим деп аталады. Себері бұл кезде желіде тек жалғыз толқын болады, осыдан  таралу коэффициентінің мағынасын нақтырақ анықтауға болады.

, яғни кернеудің модулі  заңы бойынша өзгереді.

Егер  болса, онда , ал өшу коэффициенті:

                                                                                                   (8.3)

 мен  векторларының арасындағы бұрыш  фаза өзгеру коэффициентіне тең:

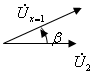
 - келісілен жүктеме кезінде x =1 ұзындықта ток пен кернеу векторларының бұрылу бұрышы.

Себебі  ток пен  кернеу желі бойымен бір заң бойынша өзгереді, осыдан кез келген нүктеде олардың арасындағы ығысу бұрышы бірдей және толқындық кедергінің  бұрышы тең болады. Сондықтан желінің сәйкесінше кірісі мен шығындағы қуаты келесі түрде анықталады:

                               ,

.

Таралу желісінің ПӘК .                                                     (8.4)

Желінің ПӘК жеке ток пен кернеуге қарағанда,  өшу коэффициентінен тәуелді екені (8.4) теңдеуден көрініп тұр.

 

8.2 Бос жүріс режимі (Z₂=∞)

 

Бос жүріс кезінде ток  және ұзын желінің теңдеуі келесі түрде болады:

                     , .                           (8.5)

Бос жүріс кезіндегі кіріс кедергі:

                                 .                                              (8.6)

 секілді  максимум мен минимумы бір-біріне қатысты толқын ұзындығының төртен бір бөлігіне ығысқан.

 

8.3 Қысқа тұйықталу режимі (Z₂=0)

 

Қысқа тұйықталу режимі кезінде кернеу  және желінің кез келген нүктесінде кернеу мен ток келесі түрде анықталады:

                , .                              (8.7)              

Қысқа тұйықталу кезіндегі желінің кіріс кедергісі:

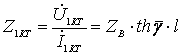                               .                                           (8.8)

Бос жүріс пен қысқа тұйықталудың берілгендері бойынша кіріс кедергі мен толқынның таралу коэффициентін анықтауға болатынын атап айтқан жөн. Себебі (8.6) және (8.8) формуладан:

 

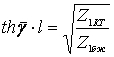                      ,.                                    (8.9)

 

3 бөлім. Сызықты емес электрлі және магниттік тізбектер

 

9 Дәріс. Сызықсыз тізбектер жайлы негізгі мағынасы, тұрақты токтың сызықсыз емес электрлік тізбектер әдістерінің анализі.

 

Дәрістің мақсаты: сызықсыз тізбектердің негізгі мағынасын және олардың есептеулерінің әдістерін қарастыру.

 

9.1 Сызықсыз элементтердің топталуы

 

Сызықсыз тізбектер деп құрамына жоқ дегенде бір сызықсыз элемент кіретін тізбекті айтады. Сызықсыз элементтер деп айнымалының (кернеу, ток, магниттік өріс, заряд, температура, жарықтық өріс) осы элементтерімен байланысты бағыттарынан және (немесе) шамаларынан тәуелді параметрлері бар элементтерді атайды. Сызықсыз элементтер қатаң аналитикалық өрнегі жоқ, эксперимент жүзінде анықталатын және кесте немесе сызба түрінде берілетін сызықсыз сипаттамалармен сипатталады. Сызықсыз элементтерді инерционды және инерционды емес деп бөлуге болады. Инерционды деп айнымалының өзгеру жылдамдығына байланысты сипаттамасы бар элементтерді айтады. Мұндай элементтерге айнымалының нақты мәндерінің арасындағы тәуелділікті анықтайтын статикалық сипаттамалар, айнымалының жорамал мәндерінің арасындағы байланысты орнататын, динамикалық сипаттамалардан ерекшеленеді. Инерционды емес деп айнымалының өзгеру жылдамдығына тәуелді емес сипаттамасы бар элементтерді айтады. Мұндай элементтерге статикалық және динамикалық сипаттамалары сәйкес келеді. Сипаттаманың түріне байланысты сызықсыз элементтерді симметриялық және симеттриялық емес сипаттамалар деп бөледі. Симметриялық деп оның шамасын анықтайтын бағытқа тәуелді емес, яғни координат жүйесінің басына қатысты симметриясы  бар сипаттаманы айтады. Симметриялық емес сипаттама үшін бұл шарт орындалмайды. Барлық сызықсыз элементтерді басқарылатын және басқарылмайтын деп бөлуге болады. Басқарылатын сызықсыз элементтер басқарылмайтынға қарағанда (әдетте үшполюстілер және көпполюстілер)  басқарылатын арналары болады. Бұл кезде кернеу, ток, жарықтық өрісті өзгерткенде, олардың негізгі сипаттамалары өзгереді.

 

9.2 Сызықсыз резисторлардың параметрлері

 

Сызықсыз резистордың жұмыс шартына және есептің түріне байланысты статикалық, дифференциалды және динамикалық кедергі деп бөледі. Егер сызықсыз элемент инерционды емес болса, онда ол берілген алғашқы екі параметрмен сипатталады.

Статикалық кедергі резисторлық элементтегі кернеудің өзі арқылы өтетін токтың қатынасы тең. Атап айтқанда 1 нүктесі үшін ВАС 9.1 суретте көрсетілген.

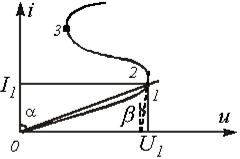
9.1 сурет - Сызықсыз резистордың ВАС

 

.

Дифференциалды кедергі кернеудің шексіз аз өсімшесінің сәйкес токтың өсімшесі қатынасына тең:

.

Басқарылмайтын сызықсыз резисторда әрқашан , ал  теріс мәндерді (11.1 суреттегі 2-3 бөлік ВАС) қабылдай алатынын атап айтқан жөн. Инернционды сызықсыз резистор жағдайында динамикалық ВАС анықталатын динамикалық кедергі  мағынасы еңгізіледі. Айнымалының өзгеру жылдамдығына байланысты тек шама ғана емес және де  таңбасы өзгереді.

 

9.3 Сызықсыз элементтердің тізбектей қосылған тізбектің графикалық есебі

 

Сызықсыз резисторларды тізбектей қосқан кезде ортақ аргумент ретінде тізбектей қосылған элементтерден өтетін ток алынады. Есеп келесі түрде жүзеге асады. Берілген жеке резисторларың  ВАС  декарт координат жүйесінде  тәуелділігі құрылады. Сосын кернеу осінде таңдалған масштабта тізбектің кірісіндегі берілген кернеуге сәйкес келетін нүкте алынады. Сол нүктеден  тәуелділігіне дейін қиылысатын перпендикуляр жүргізіледі.  қисығымен перпендикулярдың қиылысу нүктесінен токтар осіне вертикаль түсіріледі – берілген нүкте тізбектегі іздеп отырған токқа сәйкес келеді. Осы табылған мәнге сәйкес  тәуелділігін қолдана отырып жеке резистивті элементердегі  кернеуін анықтаймыз.

Берілген әдістің қолданыстың графикалық түрі 9.2 б суретте, 9.2 а суретте сәйкес тізбек көрсетілген.

 

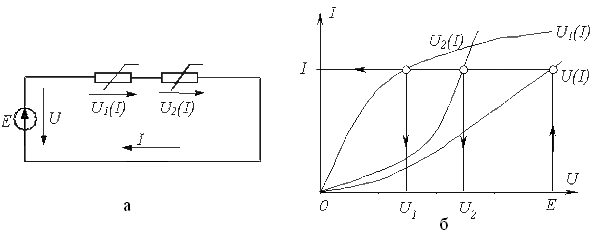
9.2 сурет - Сызықсыз элементтердің тізбектей жалғануы және оларды графикалық есептеу

 

Тізбектей қосылған екі резистивті элементі бар сызықсыз тізбек үшін графикалық шешімі басқа әдіспен де – қиылысу әдісімен жүзеге асуы мүмкін. Бұл жағдайда сызықсыз резисторлардың бірі, мысалы, 9.2а суреттегі  ВАС Е ЭҚК қорек көзінің ішкі кедергісі, ал басқасы – жүктемесі болып есептелінеді. Сонымен  теңдігі негізінде а нүктесі (9.3суретті қара), және  қисықтарының қиылысы, тізбектің жұмыс режимін анықтайды.  қисығы әртүрлі токтың мәндері үшін Е ЭҚК-нен  ВАС абсциссасын кеміту жолымен құрылады.  

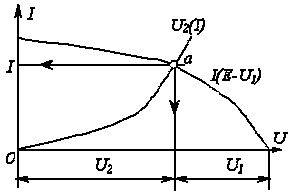
9.3 сурет - Графикалық есептеудің өзге түрі

 

 

 

9. 4  Резистивті элементтері параллель қосылған тізбек

 

Сызықсыз резисторларды параллель қосқан кезде ортақ аргумент ретінде параллель қосылған элементтерге қосылған кернеу алынады. Есептеу келесі түрде жүзеге асырылады. Жеке резисторлардың берілген  ВАС декарт координат жүйесінде  тәуелділігі құрылады. Сосын токтар осінде осінде таңдалған масштабта тізбектің кірісіндегі берілген токқа сәйкес келетін нүкте алынады. Сол нүктеден  тәуелділігіне дейін қиылысатын перпендикуляр жүргізіледі.  қисығымен перпендикулярдың қиылысу нүктесінен кернеу осіне вертикаль түсіріледі – берілген нүкте тізбектегі іздеп отырған кернеуге сәйкес келеді. Осы табылған мәнге сәйкес тәуелділігін қолдана отырып жеке резистивті элементердегі   тогын анықтаймыз.

Берілген әдістің қолданыстың графикалық түрі 11.4,б - суретте, 11.4,а - суретте сәйкес тізбек көрсетілген.

 

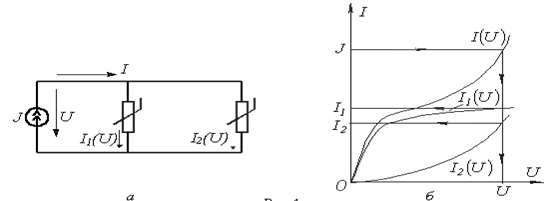
9.4 сурет - Сызықсыз элементтердің параллель жалғануы

және графикалық есептелуі

 

 

Резистивті элементтері тізбекті-параллель (аралас) қосылған тізбек

 

Мұндай тізбектердің есебі келесі түрде жүзеге асады. Берілген сұлба тізбектей қосылған резисторлардың тізбегі жүгінеді, жоғарыда көрсетілгендей элементтері параллель қосылған нәтижелі ВАС құрылады. Резистивті элементтері тізбектей қосылған шыққан сұлбаның есебі жүргізіледі, сосын соның негізінде берілген параллель тармақтағы токтар анықталады.

 

 

 

 

 

9.5 Екі түйіннің графикалық әдісі

 

Екі түйіні бар немесе соған келетін тізбектер үшін екі түйін әдісін қолдануға болады. Графикалық тәсілде әдістің жүзеге асуы келесі мағлұматта баяндалады. Барлық і-тармақтағы токтың   тәуелділікті графиктері ортақ шамалы функцияда – m және n түйіндерінің арасындағы  кернеуі құрылады. Әрбір берілген қисықтардан , оның басы і-тармақтағы  ЭҚК сәйкес келетін нүктеде тұратындай, кернеу осі бойымен өзіне параллель ығысады. Сосын осы нүктеде қалпына келген перпендикулярға қатысты айнадай шағылысады. Кай нүктеде графикалық түрде Кирхгофтың бірінші заңы   жүзеге асатыны анықталады. Сәйкес берілген нүктеде токтар есептің шешімі болып табылады.

 

9.6 Сызықсыз тізбектерді эквивалентті генератор әдісімен есептеу

 

Егер күрделі электрлік тізбекте сызықсыз резисторы бар бір тармақ бар болса, онда бұл тармақтағы токты активті екі екіұштықты теоремасы негізінде (эквивалентті генератор әдісі) анықтайды. Идеяның шешімі келесі тұжырымға негізделеді. Сызықсыз резисторы бар тармақ берілген тізбектен алынады, ал барлық қалғаны, яғни сызықты, сұлба активті екіұштық (АЕ) түрінде беріледі. АЕ теоремасы бойынша сызықты АЕ сұлбасын белгіленген тармақтың 1-2 қысқыштарына (9.5,а суретті қара) қатысты, ішкі кедергісі сызықты екіұштықтың ішкі кедергісіне тең және сызықсыз резисторы бар тұйықталған тармақ кезіндегі 1-2 қысқыштарындағы  кернеуге тең ЭҚК бар, эквивалентті генератор (9.5,б суретті қара) түрінде көрсетуге болады. Соңғы сұлба, мысалы, элементтері тізбектей қосылған тізбек түрінде графикалық әдіспен есептелінеді.

 

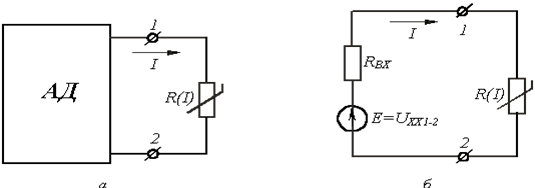
9.5 сурет - Сызықсыз элементті тізбекті эквивалентті генератормен алмастыру

 

Егер берілген тізбектің сызықты бөлігінде токты табу қажет болса, онда 9.5, б суреттегі сызықсыз сұлбаны есептеуден кейін орынбасу теоремасына сәйкес сызықсыз резистор ЭҚК немесе токпен алмасады. Содан кейін алынған сызықты тізбекті кез келген белгілі әдіспен есептеу анализі жүргізіледі.

 

9.7 Аналитикалық әдістер

 

Аналитикалық аппроксимация әдісі сызықсыз элементтің  сипаттамасын (немесе оның бөлігін) ортақ аналитикалық шамаға алмастыруға негізделген. Аналитикалық аппроксимацияның келесі түрлері қолданылады: дәрежелі көпмүшелікпен, трансцентдентті (экспотенциальды, гиперболалық, тригонометриялық) функциялармен (9.6 суретті қара). (а,b,c,…) коэффициенттерін таңдау аналитикалық шаманың сызықсыз сипаттаманың жұмыстық бөлігіне ең үлкен сәйкестігімен жүзеге асады. Бұл кезде аналитикалық қисық өтетін ең сипатты нүктелерін таңдалады. Нүктелердің саны аналитикалық шамадағы коэффициенттердің санына тең.

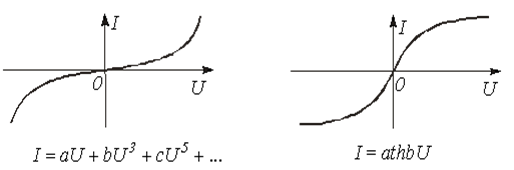                           9.6 Сурет

 

Бөлікті-сызықты аппроксимация әдісі сызықсыз элементтің сипаттамасын түзу сызықтардың бөліктері түрінде (9.7 суретті қара) көрсетуге негізделген. Соның нәтижесінде сызықсыз тізбек тұрақты коэффициенттері бар сызықты теңдеулермен (әрбір бөліктің шегінде) суреттелуі мүмкін.

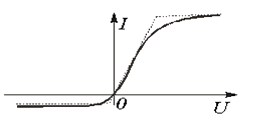
                                                  9.7 сурет

 

Тізбекте екі және одан көп сызықсыз резисторлар бар болса, онда әдістің жүзеге асуы қиынға түседі. Себебі, жалпы жағдайда, қисықтың қандай бөліктерінде жұмыстық нүктелер орналасатыны басынан белгілі.

Линеаризация әдісі бастапқы жағдайынан р жұмыстық нүктенің (9.8 суретті қара) аз ауытқулары кезінде сызықсыз тізбектің анализі үшін қолданылады.

9.8 сурет                                        9.9 сурет

 

Әдістің идеясы сызықсыз резисторды, берілген жұмыстық нүктеде дифференциалдыға тең, сызықты кедергіге немесе онымен тізбектей қосылған ЭҚК немесе параллель қосылған ток көзімен ауыстыру болып табылады. Сонымен линеаризационды ВАС-ға (9.8 суретті қара) сызықсыз резистордың (9.9 суретті қара) тізбектей қосылған орынбасу сұлбасы сәйкес келеді.

 

10 Дәріс. Магнит тізбегінің негізгі мағынасы мен заңдары

 

Дәрістің мақсаты: магнит тізбегінің негізгі сипаттамалары мен заңдарымен танысу.

 

10.1 Магнит тізбегін сипаттайтын негізгі шамалар

 

Магнит өрісінің концентрациясы және қалаған конфигурациясын беру үшін электротехникалық құрылғылардың жеке бөліктері ферромагнитті материалдардан орындалады. Бұл бөліктер магнитөткізгіштер немесе өзекшелер деп аталады. Магнит өрісі электротехникалық құрылғылардан өтетін токтардан, кейде – тұрақты магниттерден, құрылады. Ферромагниттік денелері бар және тізбек бойымен желінің магнит индукциясы тұйықталатын тұйықталатын тізбекті құраушы бар құрылғылар жиынтығы магнит тізбегі деп аталады.  Магнит өрісі 10.1 кестеде көрсетілген үш векторлы шамалармен сипатталады.

 

10.1 кесте

Атауы	Белгіленуі	Өлшем бірлігі	Анықтамасы
Магнит индукция векторы		Тл (тесла)	Ампер заңы бойынша магнит өрісінің токқа күштік қозғалысын сипаттайтын векторлық шама
Магниттенгендік векторв		А/м	Бірлік көлем заттың магнит моменті
Магнит өрісінің кернеулік векторы		А/м

 

Магнит тізбегін есептеуде қолданылатын негізгі скаляр шамалар 10.2 кестеде көрсетілген.

 

10.2 кесте

Атауы	Белгіленуі	Өлшем бірлігі	Анықтамасы
Магнит өрісі		Вб (вебер)	Магнитөткізгішінің  көлденең өткізгіші арқылы магнит индукциясының өріс векторы
Магнит қозғалғыш (магниттеу) күші МҚК (МК)		A	где - орамадағы ток,- ораманың орам саны
Магнит өрісі		А	Магнит өріс кернеулігінен сызықты интеграл

 

10.2 Ферромагниттік материалдардың сипаттамасы

 

Феррромагниттік материалдардың сипаттамасы магнит өріс кернеулігінен  магнит индукциясының тәуелділігімен сипатталады. Бұл кезде қисықтарды келесідей бөледі: бірмәнді  тәуелділіктерін көрсететін магниттеу және гистеризисті ілмектер – бір мағыналы емес  тәуелділіктер (10.1 суретті қара).

                                               10.1сурет - Гистерезис тұзағы

     Ферромагниттік материалды қайта магниттеу осы процесске шығындалатын энергиямен байланысты. Гистерезис ілмегінің ауданы қайта магниттеудің бір циклында ферромагнетиктің бірлік көлемінде бөлінетін энергияны сипаттайды. Осы шығындардың шамаларына қатысты және сәйкесінше гистерезис ілмегінің түріне қатысты ферромагнитті материалдарды магнитті жұмсақ және магнитті қатты деп бөледі. Бірінші түрі гистерезистің жіңішке ілмегіне және қатты көтерілетін магнитттеу қисығының негізіне қатысты сипатталады, ал екінші түрінде гистерезис ілмегінің үлкен ауданы және жай көтерілетін магниттеу қисығы бар. Магнитті жұмсақ материалдар (электротехникалық болаттар, темірникельді қоспалар, ферриттер) өзекшеде аз шығындарды анықтайды және айнымалы магнит өрісі (трансформаторлар, электр қозғалтқыштар) кезіндегі жұмыс істеуге арналған құрылғыларда қолданылады. Магнитті қатты материалдар (көміртекті болаттар, вольфрамды қоспалар) тұрақты магниттерді дайындау үшін қолданылады.

 

10.3 Магнит тізбектерінің негізгі заңдары

 

Магнит өрісінің үздіксіздік заңы (принципі): магнит индукция векторының өрісі тұйықталған бет арқылы нөлге тең

.

Толық ток заңы: еркін контур бойымен өтетін кернеулік векторының циркуляциясы осы контурды қамтитын токтардың алгебралық қосындысына тең

.

Магнит тізбегінің анализі кезінде ең алдымен олардың синтезі кезінде әдетте келесі жорамалдар қолданылады:

-    магнитөткізгіштің көлденең қимасының барлық нүктелерінде магниттік кернеулік, сәйкесінше магнит индукциясы бірдей

-    шашырау өрістері жоқ (магнитөткізгіштің кез келген тармақталмаған қимасынан өтетін магнит өрісі бірдей);

-    саңылаудың қимасы магнитөткізгіштің іргелес бөліктерінің қимасына тең. Бұл есептеу кезінде 10.3 кестеде көрсетілген магнит тізбектері үшін Кирхгоф және Ом заңдарын қолдануға мүмкіндік береді.

 

 

 

 

 

 

10.3 кесте

Заңның атауы	Заңның аналитикалық шамасы	Заңның тұжырымдамасы
Кирхгофтың бірінші заңы		Магнитөткізгіштің түйініндегі магнит өрістерінің алгебралық қосындысы нөлге тең
Кирхгофтың екінші заңы		Тұйықталған контур бойымен магнит кернеуінің алгебралық қосындысы контурдағы МҚК алгебралық қосындысына тең
Ом заңы	где	ұзындықты магнит өткізгішінің бөлігіндегі магнит кернеуінің құлауы магнит өрісінің және бөліктің магнит кедергісіне көбейтіндісіне тең

 

Тұжырымдалған магнит тізбегінің заңдары мен мағынасы 10.4 кестеде көрсетілген электрлік және магнит тізбегінің негізгі шамалары мен заңдары арасындағы формальды үйлестікті жүзеге асыруға мүмкіндік береді. 

 

10.4 кесте

Электрлік тізбек	Магнит тізбегі
Ток	Өріс
ЭҚК	МҚК (МК)
Электрлік кедергі	Магниттік кедергі
Электрлік кернеу	Магнит кернеуі
Кирхгофтың бірінші заңы:	Кирхгофтың бірінші заңы:
Кирхгофтың екінші заңы:	Кирхгофтың екінші заңы:
Ом заңы:	Ом заңы:

 

 

11 Дәріс.  Магнит тізбегін есептеудің әдістері

 

Дәрістің мақсаты: Магнит тізбегін есептеудің негізгі әдістерін меңгеру

 

Магнит тізбегінің сызықсыздығы,  ВАС аналогы болып табылатын және  ферромагнитті материалдың сипаттамасымен анықталатын,  тәуелділігінің сызықсыз сипаттамасымен анықталады. Тұрақты өріс кезіндегі магнит тізбегін есептеу кезінде әдетте магниттеудің негізгі қисығын қолданады. Практикада магнит тізбегін есептеуде екі типтік есеп кездеседі:  магнит өткізгіштіктің қандайда бір бөлігінде берілген магнит өрісін (берілген магнит индукциясының) құруға қажетті магниттік күштің шамасын анықтау есебі (синтездің есебі немесе «тура» есеп); берілген МК мәндері бойынша тізбектің жеке бөліктеріндегі өрісті (магнит индукциясын) анықтау есебі (анализ есебі немесе «кері» есеп). Екінші типті есептер әдетте қиынырақ және шешілуінде қиындық келтіретінін атап айтқан жөн. Жалпы жағдайда шешетін есептің типіне байланысты («тура» немесе «кері») есептің шешемі келесі әдістермен жүзеге асуы мүмкін: аналитикалық; графикалық; итерационды. Осы әдістердің біреуін қолданған кезде ең алдымен, егер орамадағы токтың бағыттары белгілі болса, сұлбада МК бағытын көрсету қажет немесе егер оларды анықтау қажет болса, оларды оң бағытпен алу қажет. Сосын магнит өрісінің оң бағыттары беріледі, содан кейін  эквивалентті орынбасу сұлбасын құруға және есептеуге кірісуге болады.

 

11.1 Есептеудің аналитикалық әдістері

 

Берілген әдістермен бірінші типті есептер – «тура» есептер шешіледі. Бұл кезде есептеу үшін бастапқы мәндер ретінде магнит тізбегінің негізгі геометриялық өлшемдері мен конфигурациясы берілген: ферромагнитті материалдың магниттеу қисығы (қисықтары) және магнит өрісі немесе магнтитөткізгішінің қандайда бір қимасындағы магнит индукциясы. Анықтау қажет: МК, орамадағы токты немесе орам санын.

 

11.1.1 Тармақталмаған магнит тізбегінің «тура» есебі

Берілген типті есептің шешімі келесі түрде жүзеге асады:

1) Орташа сызық белгіленеді (11.1 суреттегі пунктерленген сызық), сосын сол сызық магнитөткізгішті қимасы бірдей бөліктерге бөледі.

2) Барлық тізбек бойымен магнит өрісінің тұрақтылығынан әрбір і-бөлік үшін индукция мәні анықталады .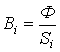

3) Магниттеу қисығы бойынша әрбір  мәні үшін ферромагниттік бөліктердегі  кернеулігі анықталады; саңылаудағы өріс кернеулігі келесі түрде анықталады: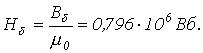  

4) Магнит тізбегі үшін Кирхгофтың екінші заңы бойынша контур бойымен магнит кернеуінің құлауын қосу жолымен іздеп отырған МК анықталады:

мұндағы  - саңылаудың ұзындығы

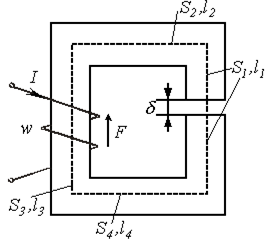
11.1 сурет - Тармақталмаған магниттік тізбек

 

11.1.2 Тармақталған магнит тізбегінің «тура» есебі

Тармақталған магнит тізбегін есептеу магнит тізбектері үшін Кирхгофтың бірінші және екінші заңдарын бірге қолдануға негізделген. Берілген типті есептің шешімі толығымен жоғарыда қарастырылған тармақталмаған тізбек үшін «тура» есептің шешілу алгоритіміне сәйкес келеді.

11.2 суреттегі магнит тізбегінің берілген геометриясы және ферромагнитті өзекшенің  сипаттамасы кезіндегі тармақталған магнит тізбегінің анализінің мысалы ретінде саңылауда  индукциясын құруға қажетті МК  анықтаймыз.

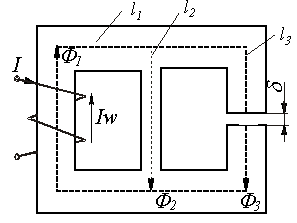
11.2 сурет - Тармақталған магнит тізбегі

 

Есептің шешілу алгоритмі келесідей:

1) Магнитөткізгіштің өзекшесінде магнит өрістерінің оң бағыттарын береміз (11.2 суретті қара).

2) Саңылауда  кернеулікті анықтаймыз және  тәуелділігі бойынша  - үшін мәні алынады.

3) Оң жақтағы контур үшін Кирхгофтың екінші заңын былай жазуға болады:  осыдан  және  тәуелділігі бойынша  анықтаймыз.

4) Кирхгофтың бірінші заңымен сәйкестігі . Онда және  тәуелділігі бойынша  анықтаймыз.

5) Кирхгофтың екінші заңымен сәйкестігінен іздеп отырған МК аламыз: .

 

11.2 Есептеудің графикалық әдістері

 

Графикалық әдістермен екінші типті есептер шығарылады – «кері» есептер. Бұл кезде есептеу үшін бастапқы мәндер ретінде магнит тізбегінің негізгі геометриялық өлшемдері мен конфигурациясы берілген: ферромагнитті материалдың магниттеу қисығы және де МК орама саны. Анықтау қажет: магнитөткізгіштің жеке бөліктеріндегі өріс мәндері (индукция). Берілген әдістер магнит тізбек бөліктерінің  вебер-амперлік сипаттамасын графикалық түде көрсетуге және сосын сәйкес графикалық құрылулар көмегімен Кирхгоф заңдары бойынша жазылған алгебралық теңдеулерді шешумен негізделген.

 

11.2.1 Тармақталмаған магнит тізбегі үшін «кері» есебі

Осындай типті есептің шешімі келесі түрде жүзеге асады:

1) «тура» есептің шешіміндей өрістің мәндері беріледі және олар үшін МК  анықталады. Бұл кезде, берілген МК шама бірнеше аз және бірнеше көп,  алу үшін мәндері біршама жақын екі өрісті таңдауға ұмтылу қажет.

2) алынған мәліметтерден магнит тізбегінің сипаттамасының бөлігі (берілген МК мәнінің жаңында) құрылады және сол арқылы берілген МК шамасына сәйкес келетін өріс анықталады. Саңылаулары бар тармақталмаған магнит тізбегін есептеу кезінде қиылысу әдісін қолданған ыңғайлы. Қиылысу әдісі кезінде іздеп отырған шешіміміз тізбектің сызықсыз бөлігінің сызықсыз вебер-амперлік сипаттамасының сызықты бөліктің сызықты сипаттамасымен қиылысу нүктесімен анықталады. Сызықты бөліктің сызықты сипаттамасы келесі теңдеудің негізінде құрылады:

мұндағы - саңылаудың магнит кедергісі.

 

 

11.2.2 Тармақталған магнит тізбегі үшін «кері» есебі

Магнит тізбегін эквивалентті электрлік орынбасу сұлбасымен ауыстыру (12.4 суретте 12.3 суреттегі магнит тізбегінің орынбасу сұлбасы көрсетілген) мұндай типті есептерді, сызықсыз электрлік тұрақты ток тізбектерінің анализіндегідей қолданылатын, барлық графикалық әдістер мен тәсілдерін қолдануға рұқсат береді.

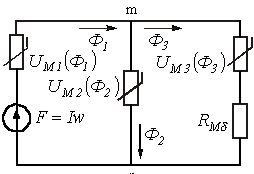
11.3 сурет - Тармақталған магнит тізбегінің есептік сұлбасы

 

Берілген әдіспен шешімнің идеясы қарастырылған сызықсыз резистивті тұрақты ток тізбектер үшін сияқты және келесіде тұжырымдалады:

1) магнит тізбегінің барлық і-тармағындағы өрістің  тәуелділігі ортақ шамалы функцияда – m және n түйіндерінің арасындағы  магнит кернеуі анықталады.

2) Кирхгофтың бірінші заңы  қандай нүктеде графикалық түрде жүзеге асатыны анықталады. Берілген нүктеге сәйкес келетін өрістер есепті шешімі болып табылады.

 

 

Јдебиеттер тізімі

 

1.К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. Теоретические основы электротехники. – том 2. – СПб.: Питер, 2003.-463 б.

2.Г.В.Зевеке, П.А. Ионкин, А.В. Нетушил, С.В.Страхов. Основы теории цепей.- М.: Энергоатомиздат, 1989.-528 б.

3.Л.А.Бессонов. Теоретические основы электротехники. – М.: Гардарики, 1999.-638 б.

4.Г.В. Бакалов, В.Ф. Дмитриков, Б.Е. Крук. Основы теории цепей.- М.: Радио и связь, 2000.-592 б.

5.Сборник задач по теоретическим основам электротехники/Л.Д. Бессонов, И.Г. Демидова, М.Е. Заруди и др.-М.: Высшая школа, 2003.-543 б.

 

Жиынтық жоспары 2012 ж., реті 291