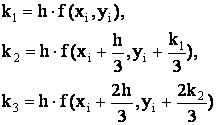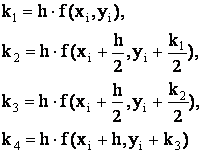НЕКОММЕРЧЕСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра информационных систем

 

 

 

ЧИСЛЕННЫЕ МЕТОДЫ 

Методические указания к выполнению

лабораторных работ

(для студентов всех форм обучения  специальности 5B060200 -Информатика)

 

 

 

Алматы 2012 

СОСТАВИТЕЛЬ: М.У. Зияханов. Численные методы. Методические указания к выполнению лабораторных работ (для студентов всех форм обучения  специальности 5B060200 -Информатика). – Алматы: АУЭС, 2012. – 45 с.

 

Методические указания по дисциплине «Численные методы» состоят из 7 лабораторных работ, охватывающие разделы алгебры, анализа, дифференциальных уравнений и  методы обработки экспериментальных данных. Методическое указания предназначены для приобретении практических навыков применения вычислительных методов при решений математических задач, разработка и создание алгоритма на языке программирования.

В каждой лабораторной работе излагаются необходимые теоретические сведения, которые подкрепляются конкретными примерами, а также предлагаются варианты заданий и контрольные вопросы.

Методические указания предназначены для студентов специальности 5В060200-«Информатика», весьма будет полезна и для студентов технических специальностей.

 

Ил.6, табл.12, библиогр. – 11 назв.

 

Рецензент: канд. тех. наук, доц. Ш.И. Имангалиев.

 

Печатается по дополнительному плану издания некоммерческого акционерного общества  «Алматинский университет энергетики и связи» на 2012 г.

 

 

ã НАО «Алматинский университет энергетики и связи», 2012 г

 

Дополнительный план 2012г., поз. 6  

 

Введение

5

Лабораторная работа № 1.  Решение алгебраических и трансцендентных уравнений

6

1.1      Теоретические сведения

6

1.1.1  Метод  деления пополам

6

1.1.2  Метод хорд

7

1.1.3  Метод касательных (Ньютона)

8

1.1.4  Метод простой итерации

9

1.2     Индивидуальные задания

10

1.3     Контрольные вопросы.

11

Лабораторная работа  № 2. Решение системы линейных алгебраических уравнений

12

2.1     Теоретические сведения

12

2.1.1  Алгоритм метода Гаусса

12

2.1.2  Итерационные методы Якоби и Зейделя.

14

2.2      Индивидуальные задания

16

2.3      Контрольные вопросы.

18

Лабораторная работа № 3. Интерполирование и приближение функций

19

3.1      Теоретические сведения

19

3.1.1  Интерполяционный  многочлен Лангранжа

20

3.1.2  Интерполяционный многочлен Ньютона

20

3.1.3   Метод наименьших квадратов

22

3.2      Индивидуальные задания

24

3.3      Контрольные вопросы.

25

Лабораторная работа №4. Методы численного интегрирования

26

4.1      Теоретические сведения

26

         4.1.1  Метод прямоугольников

26

4.1.2   Метод трапеций

26

4.1.3   Формула Симпсона

27

4.2       Индивидуальные задания

27

4.3       Контрольные вопросы.

28

Лабораторная работа №5. Решение задачи Коши для обыкновенных дифференциальных уравнений

29

5.1      Теоретические сведения

29

5.1.1   Метод Эйлера

29

5.1.2   Метод Рунге-Кутта

30

5.1.3   Решение задачи Коши для ОДУ второго порядка

31

5.2      Индивидуальные задания

32

5.3      Контрольные вопросы.

33

Лабораторная работа № 6. Методы приближенного решения краевых задач для обыкновенных дифференциальных уравнений

33

6.1    Теоретические сведения

33

6.1.1   Метод конечных разностей

34

6.1.2   Метод прогонки

35

6.1.3   Метод коллокаций

36

6.2      Индивидуальные задания

40

6.3      Контрольные вопросы.

41

Лабораторная работа № 7. Метод сеток для решения уравнения теплопроводности

41

7.1     Теоретические сведения

41

7.1.1  Явная схема

42

7.1.2   Неявная схема

42

7.2      Индивидуальные задания

43

7.3      Контрольные вопросы.

44

Список литературы

45

  

Введение

Рассматриваются различные типовые математические задачи, получаемые в процессе математического моделирования инженерных задач и задач автоматизированного управления. Для осуществления моделирования студент независимо от его специальности должен знать определённый минимальный набор алгоритмов вычислительной математики, а также владеть способами их программной реализации на персональном компьютере.

Изучение дисциплины «Численные методы» базируется на знаниях студентов, полученных при изучении физики, математики и информатики.

Целью лабораторного практикума является усвоение и закрепление теоретического материала, приобретение практических навыков приближенного решения математических задач с помощью соответствующих численных методов. Здесь приведены описания семи лабораторных работ, охватывающих все основные разделы изучаемого курса. Их можно выполнять на аудиторных занятиях и самостоятельно. Каждое описание содержит перечень необходимых теоретических материалов, даются примеры решения типовых задач, уделяется внимание проблеме поиска решения, обоснованию выбранного способа решения, алгоритм решения, контрольные вопросы, индивидуальные задания на группу до 24 человек и порядок выполнения работы.

Темы и задания соответствует типовой учебной программе и при их выполнении каждый шаг качественного характера следует подкреплять теоретическими положениями. Предполагается, что общее время на исследования, составление компьютерных программ (если они необходимы), вычисления и подготовку письменного отчета по работе не должно превышать 2 — 4 часов.

Требования к вычислительным средствам минимальны. Ручные расчеты можно выполнять на микрокалькуляторе, для автоматизации вычислений достаточно простейшей ПЭВМ с системой программирования Паскаль и др.

В работах, где основные расчеты организуются в программном режиме, по крайней мере один  шаг метода рекомендуется выполнить вручную. Это поможет лучше понять алгоритм вычислений, а затем описать его в виде компьютерной программы. В программах для итерационных процессов целесообразно предусмотреть вывод таблицы, отражающей результаты каждого шага процесса. Она явится хорошим наглядным материалом для анализа вычислений и беседы преподавателя с обучающимся.

В письменном отчете по лабораторной работе необходимо отразить следующее: тему работы и задание с учетом предложенного варианта, теоретические исследования (в краткой форме) и вычисления согласно порядку выполнения работы; программу для расчетов  и блок- схему (если она необходима); выводимую программой таблицу (если она предусмотрена); итоговые результаты в требуемой форме.

  

 

Лабораторная работа №1.

 

Решение алгебраических и трансцендентных уравнений

 

Цель работы – научить студентов  применять вычислительные методы для решения алгебраических и трансцендентных уравнений, часто встречающихся в инженерной практике.

 

1.1   Общие теоретические сведения

 

Во многих научных и инженерных задачах, например, в электродинамике при математическом моделировании электромагнитных волновых колебательных процессов в линиях передачи и резонаторах получают так называемое дисперсионное уравнение, возникает необходимость решения уравнений вида

 

                                                                                        (1.1)

 

 где функция определена и непрерывна на некотором интервале . Всякое значение , обращающее функцию  в нуль, т.е. такое, при котором , называется корнем уравнения, а процесс нахождения – решением уравнения (1.1).

Геометрически решение уравнения (1.1) состоит в нахождении точек пересечения графика функции  с осью ОХ.

Можно выделить два типа итерационных методов:

1) отделение корня, т.е. установление достаточно малого интервала (a,b), в котором содержится изолированный корень уравнения (1.1);

2) уточнение корня до заданной степени точности с помощью одного из итерационных методов.

 

1.1.1  Метод деления пополам

 

Метод половинного деления надежен и его практически удобно применять для грубого нахождения корня уравнения, так как с увеличением точности возрастает объем выполняемой работы из-за медленной сходимости итерационного процесса. Метод применяется, если непрерывна на отрезке и [a,b] и .

Суть метода заключается в следующем (рис.1.1). Допустим, что корень уравнения (1.1) отделен, т.е. найден промежуток , где имеется единственный корень. Теперь необходимо найти его приближенное значение с заданной точностью  

Алгоритм вычисления корня будет следующий:

а) определяется середина промежутка [a,b]: c=(a+b)/2;

б) проверяется условие, если это условие выполняется, то искомое решение найдено и выводится значение c;

в) если условие  не выполняется, то проверяется условие

;

если это выполняется, то b=c ,  в противном случае  a=c;

г) проверяется условие  если это условие выполняется, то процесс решения уравнения завершается и выводится значение c в качестве искомого решения; если это условие не выполняется, т.е. заданная точность не достигнута, то осуществляется переход к п. a) для продолжения вычислений.

Рис. 1.1. Метод половинного деления

 

1.1.2 Метод хорд

 

Пусть нужно найти корень уравнения  на отрезке [a,b], причем известно, что  непрерывна на [a,b] и   Кроме того, пусть и на отрезке [a,b] сохраняют свой знак. Заменим функцию  на отрезке [a,b] линейной функцией (рис.1.2), составив уравнение прямой, которая проходит через точки :

 

 

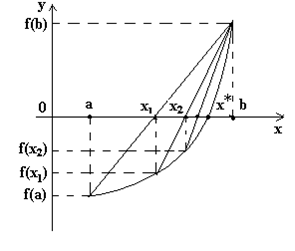
Рис. 1.2. Метод хорд

 

Учитывая  найдем первое приближенное значение корня   по формуле

Далее рассмотрим отрезки и выберем из них тот, на концах которого функция  имеет значения противоположных знаков. Те же вычисления выполним на выбранном отрезке и получим второе приближение к корню  и так до тех пор, пока не получим корень уравнения (1.1) с заданной степенью точности.

Алгоритм метода следующий. До начала итерационного процесса задаем точность ε, с которой нужно получить решение, и отрезок [a,b], содержащий корень. Затем:

а)  Вычисляем приближение к корню:

 

б) Проверяем выполнение неравенства , если оно выполняется, то  считаем решением, если же не выполняется, продолжаем вычисления.

с) Проверяем условие , и, если оно выполняется, полагаем , в противном случае  и повторяем вычисления с п.а.

 

1.1.3 Метод касательных (Ньютона)

 

Метод основан на замене  в точке начального приближения касательной, пересечение которой с осью Оx дает первое приближение , и т.д. Геометрическая интерпретация метода приведена на рис. 1.3.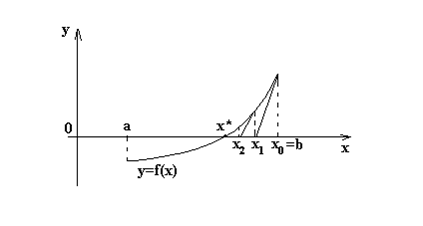

Рис. 1.3. Метод Ньютона

 

В общем случае очередное приближение  выражается через предыдущее приближение по формуле Ньютона:

 

                                                   (1.2)

Для завершения  вычислительного процесса должно быть задано условие, определяемое заданной точностью решения уравнения; оно имеет вид

 

                                                                                    (1.3)

    

При выборе начального приближения корня необходимо руководствоваться следующим правилом: за исходную точку следует выбирать тот конец отрезка [a,b], в котором знак функции совпадает со знаком второй производной. В ОДНОМ случае   и начальная точка , во втором   и в качестве начального приближения берем .

Алгоритм решения уравнения (1.1) методом касательных будет иметь следующий вид:

а) вводится в память компьютера значение первоначального приближения корня ;

б)  принимает значения ;

в) по формуле (1.2) определяется новое приближение корня;

г) проверяется условие (1.3); если оно выполняется, то вычислительный процесс завершается,  а если условие (1.3) не выполняется, то продолжается процесс вычисления п. в.;

 

1.1.4  Метод простой итерации

 

Заменим уравнение равносильным ему уравнением

 (1.4)

Выбрав начальное приближение  и подставив его в правую часть уравнения (1.4), получим  . Затем это значение снова подставим в правую часть уравнения (1.4) и найдем . Повторяя этот процесс, получаем числовую последовательность . При этом возможны два случая:

1) последовательность сходится, т.е. имеет предел и тогда этот предел будет корнем уравнения ;

2) последовательность расходится, т.е. не имеет предела или стремится к бесконечности.

Геометрическая интерпретация метода показана на рис. 1.5.

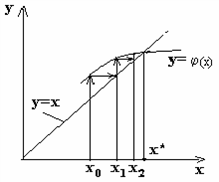
Рис. 1.5. Метод простой итерации

 

Метод сходится, если выполняется условие . Чем меньше, тем быстрее сходимость итерационного процесса. Практически метод простых итераций осуществляется так:

а) Преобразовать уравнение к виду (1.4) таким образом, чтобы .

б) Принять за начальное приближение любое число из отрезка [a,b].

в) Вычислять последовательность приближений по формуле

до тех пор, пока для двух последовательных приближений не будет выполнено неравенство  .   

           Пример1. Найти методом простой итерации на отрезке [1,2] корень уравнения

Решение. К виду  это уравнение можно преобразовать несколькими способами, например:

1. , т.е.

2. , т.е.

Проверим выполнение условия сходимости для [1,2]:

1) - условие не выполняется.

2) 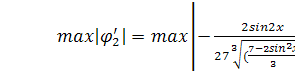 - условие выполняется, поэтому именно этот вариант следует использовать для организации итерационного процесса.                                    

1.2  Индивидуальные задания

 

Цель работы – найти все корни уравнения на отрезке [-10,10]. Варианты уравнений приведены в табл. 1.1. На первом этапе следует отделить корни. Для этого нужно вычислить значения функции на отрезке [-10,10] с шагом h = 0,5 и зафиксировать отрезки, на концах которых функция меняет свой знак. Для каждого варианта нужно построить график функции и таблицу ее значений на отрезке [-10,10] с шагом 0,5. После отделения корней следует уточнить корни одним из следующих методов с точностью ε = 0,001и построить блок-схему;

1) половинного деления,

2) хорд,

3) Ньютона,

4) простой итерации.

На каждой итерации в одну строку печатать   и ответить на контрольные вопросы.

Таблица 1.1

1

13

2

14

3

15

4

16

5

17

6

18

7

19

8

20

9

21

10

22

11

23

12

24

13

25

 

 

1.3  Контрольные вопросы.

 

1. Какие уравнения называются трансцендентными?

2. Какие вычислительные процессы считаются итерационными?

3. Для чего нужен первый этап - отделение корней?

4. Сформулируйте условия существования решения уравнения. Являются ли эти требования необходимыми и достаточными?

5. Почему монотонность функции является необходимым условием единственности для решения уравнения  ?

6. Что такое точность вычисления корня уравнения?

7. Можно ли использовать вышеприведенные программы для решения других уравнений?

8. Какие точные методы решения нелинейных уравнений вы знаете?

9. Что можно сказать о точности методов половинного деления, хорд, касательных и комбинированного? По каким параметрам их еще можно сравнить?

10. В соответствии с известной теоремой на отрезке [a, b] существует решение. Всегда ли его можно найти методом половинного деления, методом хорд, и т.п.?

 

Лабораторная работа  № 2.

 

Решение системы линейных алгебраических уравнений

 

Цель работы – научить студентов решать систему n - линейных алгебраических уравнений, к которым часто приводятся математические модели инженерных задач.

2.1 Теоретические сведения

 

Многие практические задачи механики, электротехники, автоматизированного управления и других часто приводят к системе линейных алгебраических уравнений, и решение её рассматривают как важное прикладное значение при разрешении различных проблем науки и техники. Общий вид такой системы может быть представлен так

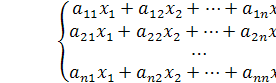                                          (2.1)         

где  заданные коэффициенты и свободные члены системы уравнений,  неизвестные величины, значения которых должны быть определены,

 

В настоящее время хорошо разработан арсенал численных методов решения линейных алгебраических уравнений на ЭВМ. Многообразие численных методов решения линейных алгебраических систем можно разделить на прямые (точные) и итерационные.

Примером прямого метода является метод Гаусса, метод Крамера, метод квадратного корня и другие.

К итерационным методам относятся: метод простой итерации, метод Зейделя, метод релаксации, градиентные методы и их модификации.

 

2.1.1 Алгоритм метода Гаусса

 

Компактная схема Гаусса. Компактная схема Гаусса дает экономный способ записи. Рассмотрим порядок составления схемы для системы (2.1). Все результаты вычислений будем записывать в одну таблицу (табл. 2.1).

Таблица 2.1

 

i

Свободные члены

I

1

2

3

 

1

II

2

 

3

 

 

 

1

III

4

 

 

IV

 

 

 

1

 

 

 

1

 

 

 

1

 

 

 

Порядок заполнения таблицы.

Прямой ход.

1) Записываем коэффициенты данной системы в трех строках и четырёх столбцах раздела I табл. 2.1.

2) Суммируем все коэффициенты по строке и записываем сумму в столбце ∑ (столбец контроля), например,  

3) Делим все числа, стоящие в первой строке, на  и результаты  записываем в четвертой строке раздела I.

4) Вычисляем  и делаем проверку. Если вычисления ведутся с постоянным числом знаков после запятой, то числа  и  не должны отличаться более чем на единицу последнего разряда. В противном случае следует проверить действия пункта 3).

5) По формулам  вычисляем коэффициенты  (i=2,3; j=2,3,4).

6) Делаем проверку. Сумма элементов каждой строки  не должна отличаться от  более чем на единицу последнего разряда. Результаты записываем в первые три строки раздела II.

7) Делим все элементы первой строки раздела II на  и результаты записываем в третьей строке раздела II.

8) Повторяем п. 5)-7).

Обратный ход.

9) Вычисляем

10) Для вычисления значений  используются лишь строки разделов I, II, содержащие единицы (отмеченные строки), начиная с последней.

11) Вычисляем  для чего используем элементы отмеченной строки раздела I:

 

2.1.2 Итерационные методы Якоби и Зейделя.

 

В методе Якоби итерации определяются следующим образом:

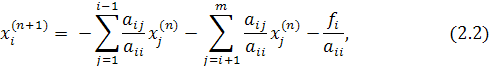
где

Начальные значения задаются произвольно. Окончание итераций определяется либо заданием максимального числа итераций , либо условием

где— заданное число.

Итерационный метод Зейделя имеет вид

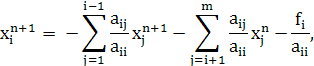
                                                              (2.3)

Чтобы понять, как находятся отсюда значения , i=1,2…,n запишем подробнее первые два уравнения системы (2.4):

 




                                            

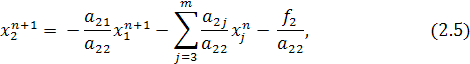
Условием сходимости итерационного процесса для систем линейных уравнений будет достаточно выполнения одного из следующих условий:

а)  в пространстве с метрикой

т.е. максимальная из сумм модулей коэффициентов при неизвестных в правой части системы (2.1), взятых по строкам, должна быть меньше единицы;

б)  в пространстве с метрикой

т.е. максимальная из сумм модулей коэффициентов при неизвестных в правой части системы (2.1), взятых по столбцам, должна быть меньше единицы;

в)  в пространстве с метрикой


т.е. сумма квадратов всех коэффициентов при неизвестных в правой части системы (2.1) должна быть меньше единицы.

Пример 1. Решить систему

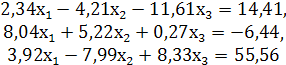
Методом простой итерации с точностью

Решение. Для обеспечения условия сходимости нужно получить систему вида (2.6) из системы (2.1) так, чтобы коэффициенты при неизвестных в правой части системы были существенно меньше единицы. Систему (2.1) с помощью равносильных преобразований надо привести к системе, у которой абсолютные величины коэффициентов, стоящих на главной диагонали, были больше абсолютных величин каждого из других коэффициентов при неизвестных в соответствующих уравнениях. Для этого первым уравнением возьмем второе, третьим- первое, а вторым – сумму первого с третьим:

Разделим теперь каждое уравнение на его диагональный коэффициент и выразим из каждого уравнения диагональное неизвестное:

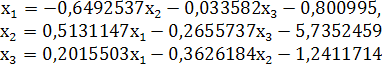
Теперь необходимо проверить одно из условий сходимости (2.6)-(2.8). Не выполнение одного из условий еще не означает, что метод итераций применить нельзя. Установим условие сходимости в пространстве с евклидовой метрикой  Имеем:

Итерационный процесс в евклидовом пространстве сходится, причем коэффициент сжатия  За начальное приближение можно взять точку (0;0;0).

Пример 2. Решить вышеприведенную систему методом Зейделя с точностью

Решение. Преимущество метода Зейделя перед методом простой итераций состоит в быстрой сходимости. Расчетные формулы итерационного процесса Зейделя будут иметь такой вид:

 

 

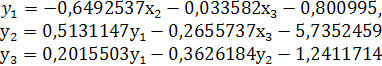
За начальное приближение можно взять столбец свободных членов (-0,8;-5,7;-1,2).

2.2  Индивидуальные задания

 

Цель работы – решить систему линейных уравнений (таб. 2.1) двумя способами, используя один из методов прямых и метода итерации:

1) метода Гаусса,

2) методы Якоби,

3) методы Зейделя.

         При применении итерационных методов преобразуйте систему к приведенному виду с выполнением условия сходимости итерационной последовательности.  Взяв в качестве начального приближения вектор свободных членов приведенной системы, найдите вручную первое приближение, затем определите его абсолютную погрешность и проверьте условие окончания итерационного процесса.

Таблица 2.1

№ варианта

Матрица коэффициентов системы А

Столбец свободных членов

I

II

III

 

1

13.14

-2.12

1.17

-2.12

6.3

-2.45

1.17

-2.45

4.6

 

1.27

2.13

3.14

2

7.31

0.42

0.54

0.66

0.42

-6.30

0.22

0.24

0.54

0.22

5.20

0.31

0.66

0.24

0.31

4.17

0.3

0.5

0.7

0.9

3

24.21

2.31

3.58

2.31

31.49

1.52

3.58

1.52

28.72

 

30.24

40.95

42.81

4

4.31

0.26

0.61

0.27

0.26

2.32

0.18

0.34

0.61

0.18

3.20

0.31

0.27

0.34

0.31

5.17

1.02

1.00

1.34

1.27

5

2.0

-0.45

1.6

-0.45

5

-2

1.6

-2

10

 

-3

1

0

6

10

2

1

2

10

3

1

3

10

 

12

13

14

7

5.1

1.5

1.0

1.5

8.5

0.5

1.0

0.5

10

 

10.83

9.20

17.20

8

3.1

1.5

1.0

1.5

2.5

0.5

1.0

0.5

10

 

10.83

9.20

17.20

9

-4.12

0.42

1.34

0.88

0.42

3.95

0.87

0.43

1.34

1.87

3.20

0.31

0.88

0.43

0.31

5.17

11.17

0.115

9.909

9.349

10

3.65

-2.27

0.18

-2.27

5.37

0.46

0.18

-0.46

2.16

 

2.25

0.93

1.33

11

3.23

0.42

1.24

0.88

0.42

4.06

0.87

0.43

1.24

1.87

4.30

0.35

0.88

0.43

0.35

6.28

1.17

0.11

7.90

8.34

12

7.6

05

-1.3

0.5

9.1

0.2

-1.3

0.2

5.8

 

1.9

9.7

-1.4

13

8.7

-2.2

-1.1

-0.7

-2.2

10

2.3

-0.7

-1.1

2.3

-5.1

2.8

-0.7

-0.7

2.8

7.9

1.1

-3.3

8.5

-1.7

14

2.23

-0.71

0.65

-0.71

-5.37

-1.46

0.65

-1.46

2.16

 

1.25

0.93

-0.87

15

5.23

0.14

0.30

0.40

0.14

7.32

0.22

0.24

0.30

0.22

-9.20

0.31

0.40

0.24

0.31

-4.17

1.02

1.00

1.34

1.27

16

5.8

0.3

-0.2

0.3

4.0

-0.7

-0.2

-0.7

-6.7

 

3.1

-1.7

1.1

17

3.88

3

2.67

3.78

2.79

2.37

3.45

2.39

1.96

 

10.41

8.36

7.62

18

2.53

3.95

2.78

2.36

4.11

2.43

1.98

3.66

1.94

 

12.66

21.97

13.93

19

2.69

2.73

2.93

2.47

2.39

2.52

2.07

1.92

2.02

 

19.37

19.43

20.80

20

4.07

2.84

4.99

3.79

2.44

4.50

3.37

1.95

3.97

 

40.77

27.68

49.37

21

3.19

4.43

3.40

2.89

4.02

2.92

1.48

3.53

2.40

 

33.91

47.21

32.92

22

2.95

5.11

4.38

2.58

4.62

3.82

2.16

4.14

3.30

 

44.16

46.68

65.34

23

2.93

3.47

4.78

2.55

2.98

4.22

2.14

2.50

3.70

 

46.41

54.78

75.81

24

3.74

4.02

4.18

3.36

3.51

3.61

2.94

3.04

3.09

 

63.26

67.51

70.03

 

2.3 Контрольные вопросы.

 

1. Какое условие является условием существования   единственного решения системы линейных алгебраических уравнений (2.1)?

2. Что такое прямые и итерационные методы.

3. От чего зависит точность данного метода ?

4. Назовите известные вам методы решения СЛАУ.

5. Чем точные методы отличаются от приближенных?

6.Что такое прямой и обратный ход в методе Гаусса?

7. Сравните достоинства и недостатки точных и приближенных методов.

8. Что такое матрица Якоби?

9. Исходная СЛАУ решается независимо двумя  методами – методом Якоби, методом Зейделя. Будут ли равны значения

а)  начального приближения (нулевой итерации);

б)  первой итерации?

 

 

Лабораторная работа № 3.

 

Интерполирование и приближение функций

 

Цель работы – изучение методов математико-статистической и компьютерной обработки результатов экспериментов, испытаний и статистических наблюдений, т.е. по значениям функции  в нескольких точках отрезка восстановить ее значения в остальных точках данного отрезка. Разумеется, такая постановка задачи допускает сколь угодно много решений.

 

3.1                     Теоретические сведения

 

Для установления закономерностей при изучении многих природных явлений проводятся эксперименты или осуществляют сбор статистических данных об объекте исследования.

Пусть функциональная зависимость задана таблицей 3.1.

Таблица 3.1

 

Обычно задача интерполирования формулируется так: найти многочлен  степени не выше n, значения которого в точках  совпадают со значениями данной функции, то есть .

Геометрически это означает, что нужно найти алгебраическую кривую вида

проходящую через заданную систему точек  (см. рис. 3.1). Многочлен  называется интерполяционным многочленом. Точки  называются узлами интерполяции.

 

 

 

 

 

 

 

 

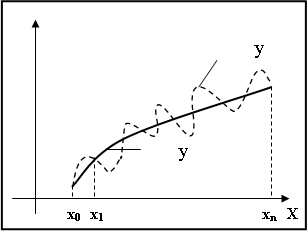Рис. 3.1. Интерполирование алгебраическим многочленом

 

3.1.1  Интерполяционный  многочлен Лангранжа

 

Интерполяционный многочлен Лагранжа:

 

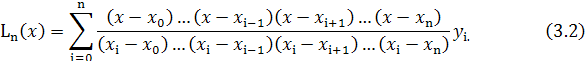
При n=1 мы имеем две точки, и формула Лагранжа представляет в этом случае уравнение прямой , проходящей через две заданные точки:

При n=2, получим уравнение параболы , проходящей через три точки:

 

Пример 1. Пользуясь интерполяционной формулой Лагранжа, составить уравнение прямой, проходящей через точки , если  

Решение. В данном случае многочлен Лагранжа примет вид

Уравнение искомой прямой есть

 

3.1.2    Интерполяционный многочлен Ньютона

 

Первый интерполяционный многочлен Ньютона

Первый интерполяционный многочлен Ньютона:

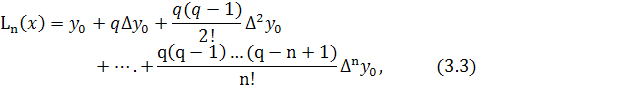
где

 

Многочлен (3.3) называется первым интерполяционным многочленом Ньютона .

При n=1 и n=2 из формулы (3.3) получаем частные случаи:

линейная интерполяция

квадратичная интерполяция

Пример 2. По данной таблице значений найти функцию

x

y

Δy

2,70

0,3704

-0,0028

2,72

0,3676

-0,0026

2,74

0,365

 

Решение. Используя формулу (3.6) при n=1получим

Второй интерполяционный многочлен Ньютона

 

Отличие второго интерполяционного многочлена Ньютона от (3.3), предусматривает поочередное подключение узлов в обратном порядке: сначала последний, потом предпоследний и т.д. и имеет вид:

 

+                            (3.4)

где

 

Ее также целесообразно использовать при значениях , т.е. в окрестности узла  для интерполирования назад (при q ∈ (-1, 0)) и экстраполирования вперед (при q > 0).

 

Пример 3. Используя таблицу значений функции y = sinx, требуется найти приближенные значения : а) sin 33; б) sin 41; в) sin 48; г) sin 54, записав предварительно соответствующие каждому случаю интерполяционные формулы.

 

 

x (в градусах)

x (в радианах)

y

Δy

Δy2

Δy3

30

0,5236

0,5000

 

 

 

 

 

 

 

 

 

 

 

 

0,0736

 

 

35

0,6109

0,5736

 

-0,0044

 

 

 

 

0,0692

 

-0,0005

40

0,6981

0,6428

 

-0,0049

 

 

 

 

0,0643

 

-0,0005

45

0,7854

0,7071

 

-0,0054

 

 

 

 

0,0589

 

-0,0003

50

0,8727

0,7660

 

-0,0057

 

 

 

 

0,0532

 

 

55

0,9599

0,8192

 

 

 

Решение. Составив таблицу разностей, видим, что третьи разности практически постоянны. Поэтому в формулах достаточно взять четыре члена.

а)  Для вычисления  имеем

По формуле первой интерполяционной формуле (3.3) и учитывая данные из таблицы, получим

б) Для вычисления , имеем точка  расположена в конце узла, поэтому для экстраполяции функции  здесь однозначно следует применить вторую  интерполяционную формулу Ньютона (3.4). Считая   записываем

формулу экстраполяции с учётом

 

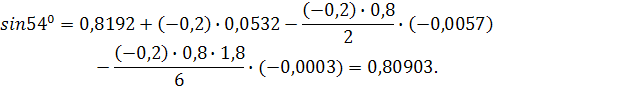
3.1.3    Метод наименьших квадратов

 

В дальнейшем  табличные данные из таблицы 3.1 называются статистическими (экспериментальными) и на основе этих данных должна быть получена функция, связывающая переменных  и :

                                       .

Для определения такой функции необходимо решить две задачи, называемые двумя основными задачами статистики:

- определение общего вида аппроксимирующей функции  может включать в себя неизвестные параметры, например, общий вид линейной функции  зависит от двух параметров, а общий вид квадратичной функции  - от трех параметров и т.д. ;

- определение конкретного вида функции, когда определены значения неизвестных параметров  и  или  

Первая задача решается феноменологическим методом, исходя из интуиции исследователя и заданной таблицы значений аргумента  и функции . Для решения второй задачи используется метод наименьших квадратов.

 

Суть метода наименьших квадратов

 

Рассмотрим метод нахождения параметров приближающей функции в общем виде  на примере приближающей функции с тремя параметрами:

                                                  ( 3.5)

Имеем   Сумма квадратов разностей соответствующих значений функций  будем иметь вид:

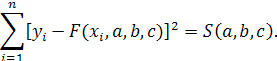
Задача  сводится к отысканию минимума.  Используем необходимое условие экстремума:

т.е.

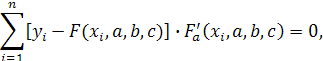
                       (3.6)

 

                                                        

Из системы линейных уравнений (3.6) определяются  коэффициенты a,b,c и получим конкретный вид искомой функции

Рассмотрим самый простой случай аппроксимации, когда в качестве  аппроксимирующей функции рассматривается линейная функция  . Этот случай называется линейной аппроксимацией. Тогда функция  имеет следующий вид

где  и   – неизвестные параметры, а условие минимума

После простых преобразований можно получить систему двух уравнений с двумя неизвестными  и   

                                        

Решая эту систему, можно получить значения неизвестных параметров  и   

где

 

3.2                   Индивидуальные задания

 

В заданий 1 по заданной таблице 3.2 значений функции составить формулу интерполяционного многочлена, вычислить значение функций, и начертите графики таблицы и найденного многочлена;

1)                формула Лангранжа,

2)                формула Ньтона,

3)                Метода наименьшего квадрата.

Построить график и отметить на нем узловые точки.

 В заданий 2 вычислить значение функции и построить график.

 

Таблица 3.2

 

Задание 1

Задание 2

№1

x

10.5

11

11.5

12

12.5

13

13.5

y

4

6

10

40

20

12

8

100

№2

x

12.5

13

13.5

14

14.5

15

15.5

7.8

y

5

15

40

25

8

4

1

№3

x

10

11

12

13

14

15

16

1200

y

8

10

60

12

5

3

2

№4

x

45

50

55

60

65

70

75

440

y

4

6

8

10

35

20

12

№5

x

11

11.5

12

12.5

13

13.5

14

5.2

y

5

10

30

25

15

10

5

№6

x

12

13

14

15

16

17

18

500

y

5

15

10

25

8

4

3

№7

x

30

32

34

36

38

40

42

5.8

y

5

15

40

25

8

4

3

№8

x

10

11

12

13

14

15

16

500

y

4

6

10

40

30

12

8

№9

X

13

14

15

16

17

18

19

400

Y

5

10

30

25

15

10

5

№10

x

25

30

35

40

45

50

55

330

y

6

7

13

11

22

20

16

№11

x

7

8

9

10

11

12

13

6.25

y

4

6

11

14

21

18

16

№12

x

5

10

15

20

25

30

35

170

y

4

10

9

23

8

5

2

№13

x

6

8

10

12

14

16

18

1.14

y

7

12

15

23

11

9

4

№14

x

7

8

9

10

11

12

13

900

y

5

8

11

20

17

9

2

№15

x

-5

-3

-1

1

3

5

7

830

y

7

10

14

24

16

8

3

№16

x

-4

-3

-2

-1

0

1

2

1.25

y

4

6

11

14

21

18

16

№17

x

5.5

10.5

15.5

20.5

25.5

30.5

35.5

2.4

y

4

10

9

23

8

5

2

№18

x

6.2

8.2

10.2

12.2

14.2

16.2

18.2

150

y

7

12

15

23

11

9

4

№19

x

7

8

9

10

11

12

13

3.56

y

-5

-8

-11

-20

-17

-9

-2

№20

x

5

7

9

11

13

15

17

1.25

y

-7

-10

-14

-24

-16

-8

-3

№21

2.0

2.3

2.5

2.7

2.9

3.1

3.3

3.5

400

 

5.8

6.1

6.3

6.6

7.4

7.6

7.8

8.0

№22

1.5

2

2.5

3

3.5

4

4.5

5

2.5

 

0

2.3

2.6

3.4

4.2

4.6

4.8

6

№23

1.5

2

2.5

3

3.5

4

4.5

5

1.17

 

0

-2.3

-2.6

-3.4

-4.2

-4.6

-4.8

-6

№24

x

10.5

11

11.5

12

12.5

13

13.5

2.35

 

y

-4

-6

-10

-40

-20

-12

-8

№25

x

12.5

13

13.5

14

14.5

15

15.5

350

 

y

-5

-15

-40

-25

-8

-4

-1

 

  

3.3 Контрольные вопросы.

 

1.В чем заключается задача интерполирования и аппроксимации?

2. В чем обоснованность приближения таблично заданной функции методом интерполирования.

3. Как обосновываются существование и единственность интерполяционного многочлена? Как связана его степень с количеством узлов интерполяции?

4. Запишите интерполяционные формулы Лагранжа и Ньютона.

5. Какие требования предъявляются а) к интерполяционным полиномам;
б) к аппроксимационным полиномам?

6. В чем заключается идея метода наименьших квадратов?

7. В каких случаях применяются формулы Ньютона для интерполирования
а) вперед, б) назад?

Лабораторная работа №4.

 

Методы численного интегрирования

 

Цель работы – изучение методов вычисления определенных интегралов на компьютере.

4.1   Теоретические сведения

 

Пусть на отрезке задана функция .  Разобьем отрезок с помощью точек на  элементарных отрезков  На каждом из этих отрезков возьмем произвольную точку  . Предел интегральной суммы при увеличении числа точек разбиения называется определенным интегралом от функции  на отрезке :

 

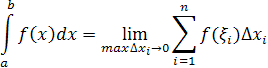
4.1.1    Метод прямоугольников

 

Формула прямоугольников для вычисления определенного интеграла

                     (4.1)

Алгоритм данного метода очень простой; требуется составить простой цикл для вычисления суммы.

Алгоритм вычисления будет следующий:

        а) ввод граничных условии a,b, количество итерации n;

        б) вычисление шага ,  присваиваем ;

в) начало цикла ;

        г) в цикле   ;

        е) вывод значения .

4.1.2   Метод трапеций

 

Следующим простейшим полиномом является линейная функция. Если выбрать ее совпадающей с  на концах частичного отрезка − то получим трапецию. Площадь ее принимается в качестве приближения к значению определенного интеграла и вычисляется по формуле трапеций (рис.4.1):

 

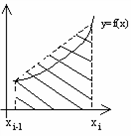
Рис.4.1. Метод трапеций

 

Для случая равномерного шага  формула трапеций для вычисления определенного интеграла

 

                     (4.2)

 

Алгоритм вычисления будет следующий:

        а) ввод граничных условии a,b, количество итерации n;

        б) вычисление шага ,  присваиваем ;

        в) вычисляем ;

г) начало цикла ;

        д) в цикле   ;

         е) вывод значения .

 

4.1.3   Формула Симпсона

 

Составная формула Симпсона или формула парабол:

.

                                                                                                               (4.3)

Формула Симпсона выглядит более громоздкой по сравнению с формулами прямоугольников и трапеций, но она значительно точнее их и может привести к требуемому результату при меньших .

Алгоритм вычисления будет следующий:

        а) ввод граничных условии a,b, количество итерации n;

        б) вычисление шага ,  присваиваем ;

        в) вычисляем ;

г) начало цикла ;

        д) в цикле: при четном  при нечетном  вычисляется , ;

         е) вывод значения .

 

4.2 Индивидуальные задания

 

 Решить определенный интеграл нижеперечисленными методами и построить блок-схему;

1)                     прямоугольника,

2)                     трапеции с помощью,

3)                     Симпсона.

Используя ручной расчёт или алгоритмический язык высокого уровня. Сделать сравнительный анализ используемых методов.

Вычислить   для заданного числа n разбиений отрезка [a,b] вышеперечисленными методами и построить график.

Таблица 4 - Индивидуальные задания

№

Подынтегральная функция

a

b

№

Подынтегральная функция

a

b

1

0

14

0

1

2

0

15

0

1

3

0

1

16

0

1

4

0

1

17

2

3

5

0

1

18

0,5

1,5

6

0

1

19

-1

1

7

0

20

1

2

8

0

21

0,2

1,2

9

22

-1

0

10

0

23

1,5

2,5

11

0

1

24

1

2

12

0

1

25

 

 

 

13

0

1

 

 

 

 

 

4.3 Контрольные вопросы.

 

1. Каковы преимущества численных методов интегрирования ?

2. Каковы недостатки численных методов интегрирования?

3. Какова точность вычисления определенного интеграла методом трапеций?

4. По Вашему мнению, какой из предложенных выше методов более точный ?

5. В каких случаях целесообразно применение численных методов интегрирования ?

 

Лабораторная работа №5.

 

Решение задачи Коши для обыкновенных дифференциальных уравнений

Цель работы – изучение численных методов решения обыкновенных дифференциальных уравнений, к которым приводятся инженерные задачи.

 

5.1 Теоретические сведения

 

Среди задач, с которыми приходится иметь дело в вычислительной практике, значительную часть составляют различные задачи, сводящиеся к решению обыкновенных дифференциальных уравнений. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей – законы Кирхгофа, в теории скоростей химических реакций – законы действия масс и т.д. Для простоты изложения методов решения задачи будем рассматривать случай одного обыкновенного дифференциального уравнения первого порядка.

Пусть на отрезке x0 £ x £ b требуется найти решение y(x) дифференциального уравнения

,                                                  (5.1)

 

удовлетворяющее при x = x0 начальному условию

                                                    (5.2)

Будем считать, что условия существования и единственности решения поставленной задачи Коши выполнены.

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация только об одной (предыдущей) точке, называются одношаговыми (задачи с начальными условиями или задачи Коши)  .

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация о нескольких (предыдущих) точках, называются многошаговыми (граничные задачи, когда дополнительные условия ставятся на концах рассматриваемого отрезка).

 

5.1.1   Метод Эйлера

 

Разностный способ. Рассматривая уравнение (5.1) в точке , с учетом (5.2) имеем равенство

Применяя к его левой части аппроксимацию производной правым разностным отношением первого порядка точности

Получаем

Общая расчетная формула метода Эйлера

с учётом начального условия (6.2), где

Алгоритм этих формул очень простой.

а) (начальные условия).

б) Вывод вычисленных значений  

в)  (вычисление значения искомой функции в новой точке)

г)  (переход к следующей точке).

д) Если  то осуществляется переход в п. б).

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага систематически возрастает.

 

5.1.2  Метод Рунге-Кутта

 

Существуют другие явные (т.е. значение явно вычисляется по k предыдущим значениям ) и одношаговые (k=1) методы. Наиболее распространенным из них является метод Рунге-Кутта. На его основе могут  быть построены разностные схемы разного порядка точности (таблица 5.1). Наиболее употребительной схемой метода Рунге-Кутта является схема 3.

Таблица 5.1.

№

Формула

вспомогательные переменные

порядок ошибки

1

2

3

 

 

Рассмотрим алгоритм метода Рунге – Кутта исходя из расчетных формул схема 3 (таблицы 5.1).

а) (начальные условия).

б) Вывод вычисленных значений

в) Вычислить

г)  (вычисление нового значения y).

д)  (переход к следующей точке).

е) Если  то осуществляется переход в п. б).

Метод Рунге-Кутта требует большого объема вычислений, однако обладает значительной точностью, что дает возможность проводить счет с большим шагом. Кроме того, важным преимуществом этого метода (например: перед методами Адамса и типа Адамса) является возможность применения «переменного шага», т.е. он допускает расчеты на неравномерных сетках.

 

5.1.3   Решение задачи Коши для ОДУ второго порядка

 

Рассмотрим задачу Коши для дифференциального уравнения второго порядка, разрешённого относительно второй производной:

                            (5.4)

С помощью замены уравнение (6.4) превратится в систему

                               (5.5)

 Аналогично дифференциальное уравнение n-го порядка сводится к

системе n-го порядка (n уравнений, каждое уравнение первого порядка ).

Решим данную систему методом Рунге-Кутта,  используя формулу схемы 3 из таблицы 5.1. Вычислим сначала восемь промежуточных коэффициентов ( четыре пары ):

 

 

После этого вычисляется  и   в новой точке по формулам :

 Для последнего  вычисляется только

 

5.2 Индивидуальные задания

 

 Решить дифференциальные уравнения нижеперечисленными методами и построить блок-схему;

1)         Эйлера,

2)         Рунге-Кутта используя таблицу 5.1, с приведенными схемами.

Используя ручной расчёт и алгоритмический язык высокого уровня. Сделать сравнительный анализ используемых методов.

Решить на отрезке [a,b] с шагом h задачу Коши для следующих дифференциальных уравнений и начертите ломаную Эйлера..

Таблица 5.2

№

Уравнение

a

b

h

y0

I

II

III

IV

V

VI

 

1

0

1

0.02

0.2

 

2

1

2

0.05

1

 

3

2

3

0.02

1

 

4

1

3

0.04

2

 

5

0

2

0.04

5

 

6

0

1

0.05

3

 

7

1

2

0.02

2

 

8

1

1.6

0.02

2

 

9

0.5

1

0.01

1

 

10

0

0.2

0.01

1

 

11

0

1

0.02

0.5

 

12

0

2

0.02

1

 

13

2

3

0.02

1

 

14

0

2

0.04

1

 

15

0

1

0.05

4

 

16

1

3

0,02

0

0

17

0,02

1

0

18

0

2

0.03

0

-2

19

0

2

0.04

0

0

20

0

3

0.03

2

1

21

1

3

0.02

e

3e

22

0

2

0.02

2+

1

23

0

2

0.02

3

0

24

0

2

0.02

1

2

25

0

2

0.02

1

1

  

5.3 Контрольные вопросы. 

1               Какие уравнения называются дифференциальными?

2. Сформулируйте задачу Коши для обыкновенных дифференциальных уравнений первого порядка.

3. Что является решением дифференциального уравнения: а) в высшей математике, б) в прикладной математике?

4. Какие методы решения дифференциальных уравнений называются одношаговыми, многошаговыми? Приведите примеры.

5. Сравните решения, полученные на первом, втором шаге методами Эйлера, Рунге-Кутта  (трудоемкость, погрешность…).

6. Как оценить погрешность применяемого метода? Как ее уменьшить?

7. Сравните одношаговые и многошаговые методы решения дифференциальных уравнений, указав достоинства и недостатки первых и вторых.

8. Можно ли использовать: а) многошаговые методы без одношаговых;
б) одношаговые методы без многошаговых?

 

 

Лабораторная работа № 6.

 

Методы приближенного решения краевых задач для обыкновенных дифференциальных уравнений

 

Цель работы – изучение  методов решений краевых задач для обыкновенных дифференциальных уравнений. Рассматривается несколько способов приближенного решения двухточечных линейных краевых задач для дифференциальных уравнений второго порядка.

6.1 Теоретические сведения

 

В инженерной практике и при решении многих задач механики, физики, теории колебаний и других часто возникает  необходимость решения краевой задачи для обыкновенных дифференциальных уравнений следующего вида

 

где – заданные, непрерывные и определенные в некотором промежутке  функции, а – независимая переменная,  – искомая функция. На границах промежутка заданы краевые условия:

при

 

где  – известные постоянные величины, j=0,1.

Если краевые условия (6.2) и (6.3) задаются:

1)     – условие называется условием первого рода,

2)     – условие называется условием второго рода,

3)     – условие называется условием третьего рода.

Требуется найти функцию  в промежутке  удовлетворяющую дифференциальному уравнению (6.1) и граничным условиям (6.2) и (6.3).

 

6.1.1  Метод конечных разностей

 

Идея метода конечных разностей (МКР) решения краевых задач весьма проста и видна уже из самого названия: вместо производных в дифференциальном уравнении используются их конечноразностные аппроксимации.

Введём на отрезке  сетку с шагом

 

На этой сетке определяются сеточные функции

отвечающие функциональным коэффициентам данного дифференциального уравнения (6.1). Считая у(х) точным решением данной краевой задачи (6.1)—(6.3), через

будем обозначать i-ю компоненту искомого каркаса приближенного решения  Значения производных аппроксимируем конечноразностными отношениями по симметричным формулам второго порядка точности

Тогда исходное дифференциальное уравнение (7.1) будет записано в виде дискретных формул относительно дискретных значений искомой функции  

 

После приведения подобных членов в (6.5) получаем стандартное трехточечное разностное уравнение второго порядка

 

 

где

при

Два недостающие уравнения системы (6.6) получаем из граничных условий (6.2) и (6.3),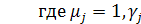

Формулы (6.6) представляют собой систему линейных алгебраических уравнений относительно неизвестных значений искомой функции в точках разбиения, причем эта система имеет особенность, ее основная матрица является трехдиагональной. Итак, вместо дифференциального уравнения (6.1) необходимо решить систему линейных алгебраических уравнений (6.6).

 

6.1.2   Метод прогонки

 

Особенность матрицы системы уравнений позволяет использовать метод прогонки, сущность которого заключается в следующем: решение системы (6.6) находят в виде следующей рекуррентной формулы

где  - неизвестные пока коэффициенты, называемые коэффициентами прогонки; они будут определены в дальнейшем. Из этой формулы, очевидно, следует следующая формула

Подставляя формулу (6.9) в систему уравнений (6.6), получим

 

 

Сравнение формул (6.10) и (6.8) позволяет получить формулы для вычисления коэффициентов прогонки

 

Эти формулы являются рекуррентными и для вычисления значений неизвестных коэффициентов прогонки необходимо вначале определить первоначальные коэффициенты, для чего используется граничное условие на левой границе рассматриваемого промежутка

,  

Вычисление значений коэффициентов прогонки по формулам (6.12) и (6.11) называется прямой прогонкой. После вычисления коэффициентов прогонки вычисляются значения искомой функции , для чего используется граничное условие на правой границе промежутка

и рекуррентная формула (6.8). Процесс вычисления значений искомой функции по формулам (6.13) и (6.8) называется обратной прогонкой.

Алгоритм решения краевой задачи уравнения (6.1)-(6.3) методом прогонки будет иметь следующий вид:

а) Ввод исходных данных .

б) Цикл для вычисления значений заданных функций  для

в) Цикл для вычисления коэффициентов системы уравнений (6.6)

г) Вычисление первоначальных коэффициентов прогонки по формулам (6.2).

д) Цикл для вычисления коэффициентов прогонки по формулам (6.11).

е) Определение значения искомой функции на правой границе по формуле (6.3).

ж) Цикл для вычисления значений искомой функции по формуле (6.8).

з) Вывод значений аргумента x и функции y.

 

6.1.3   Метод коллокаций

 

Для решения краевой задачи (6.1)-(6.3) зададим на отрезке  некоторую линейно независимую систему дважды непрерывно дифференцируемых функций   таких, что  удовлетворяет краевым условиям (6.2)-(6.3), т.е. , а остальные функции удовлетворяют однородным краевым условиям, т.е.

Заданная система функций  называется базисной.

Составим линейную комбинацию   базисных функций

С неизвестными пока коэффициентами  . В силу линейности операторов  функция при любых  удовлетворяет заданным краевым условиям (6.2)-(6.3).

Функция

называется невязкой. Чем ближе невязка нулю, то функция совпадает с решением краевой задачи, поэтому стараются подобрать параметры   так, чтобы невязка стала как можно меньше.

Приближённое решение краевой задачи (6.1)- (6.3) ищем в виде линейной комбинации базисных функций

 

Такая функция u удовлетворяет краевым условиям при любых . Подставляя функцию (6.16) в уравнение (6.1), получим некоторый остаточный член , не равный нулю, поскольку функция u не является точным решением уравнения (6.1). Таким образом, получается система алгебраических уравнений:

 

относительно неизвестных  . В более подробной записи имеет вид

 

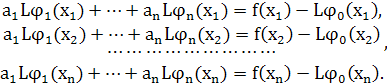
Если система однозначно разрешима, то найденные из нее коэффициенты   подставляются (6.16).  Число точек коллокаций должно согласовываться с количеством базисных функций. Чем больше используется базисных функций и, соответственно, точек коллокаций, тем точнее получается приближённое решение.

Алгоритм метода следующий:

1.    Выписать базисные функции

2.    Проверить выполнение нулевых краевых условий базисных функций.

3.    Записать приближенно-аналитическое решение краевой задачи в виде

4.    Записать все входящие в ДУ производные, продифференцировав решение  .

5.    Подставить полученные в п.3,4 выражения в ДУ.

6.    Записать функцию невязки  как разность левой и правой частей ДУ из п. 5.

7.    Выбрать внутри интервала, ограниченного краевыми точками, n штук ( по числу базисных функций) точек коллокаций.

8.    Записать условия равенства нулю функции невязки в точках коллокации- результат система алгебраических уравнений относительно неизвестных констант

9.    Вычислить константы

10.  Записаить окончательное приближенно-аналитическое решение краевой задачи.

11. Вычислить значение функции в точках коллокации.

Пример1. Методом коллокаций решить краевую задачу

на отрезке   при  

Решение. В качестве базисных функций выбираем полиномы . Функция  удовлетворяет неоднородным краевым условиям , а функции , — однородным краевым условиям . Точками коллокаций примем точки   Ограничимся тремя базисными функциями и положим приближенное решение уравнения равным

В результате невязка  будет равна

Подставляя координаты точек коллокаций  в выражение не-вязки, получим систему уравнений для определения коэффициентов  

Отсюда находим  и приближённое решение будет иметь вид

Пример2.Пусть дано дифференциальное уравнение второго порядка и его граничные условия, решить методом коллокаций

Решение.

На отрезке [a, b] выберем систему базисных функций

Проверим систему на ортогональность

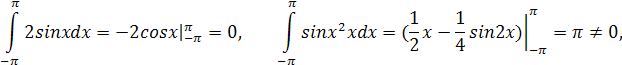
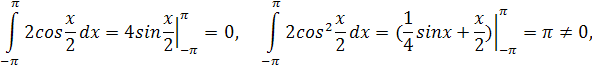
Выбранная система базисных функций является ортогональной и удовлетворяет условию выбора конечной системы базисных функций

Будем искать решение задачи в виде

1.    Рассмотрим решение задачи с двумя базисными функциями

Тогда решение

Составим невязку

 

На отрезке  выберем за точку коллокации 0.

Таким образом, решение задачи имеет вид

2.    Рассмотрим решение задачи с тремя базисными функциями

Тогда решение

Составим невязку

На отрезке  выберем две точки коллокации: 0 и . Составим систему уравнений

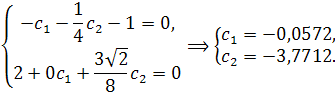
Таким образом, решение задачи (17)

 

6.2 Индивидуальные задания

 

 Решить дифференциальные уравнения нижеперечисленными методами и построить блок-схему;

1)         прогонки,

2)         коллокаций.

Используя ручной расчёт и алгоритмический язык высокого уровня. Сделать сравнительный анализ используемых методов.

Найти решения следующих дифференциальных уравнений при заданных граничных условиях:

 

Таблица 6

№

Уравнение

Граничные условия

h

1

0.01

2

0.01

3

0.01

4

0.01

5

0.01

6

0.01

7

0.01

8

0.01

9

0.01

10

y ¢¢ + x 2y ¢ + 2y  = 2x - 1

0.01

11

0.01

12

0.01

13

0.01

14

0.01

15

0.01

16

0.01

17

0.01

18

0.01

19

0.01

20

0.01

21

0.01

22

0.01

23

0.01

24

0.01

 

6.3 Контрольные вопросы.

 

1 Какая задача называется краевой?

2 Определите физическую сущность каждого члена уравнения (6.1), если оно описывает колебательное движение какого-либо объекта.

3 От какого параметра зависит точность метода ?

4 Почему производные искомой функции заменены формулами (6.4)?

5 Какая система алгебраических уравнений является системой с трехдиагональной матрицей ?

6 Почему процесс вычисления коэффициентов прогонки называется прямой прогонкой ?

7 Почему процесс вычисления значений искомой функции называется обратной прогонкой ?

 

Лабораторная работа № 7.

 

Метод сеток для решения уравнения теплопроводности

 

Цель работы – изучение одного из популярных методов – метод сеток для решения уравнений математической физики на примере задачи о теплопроводности.

7.1 Теоретические сведения

 

Рассмотрим решение дифференциального уравнения в частных производных параболического типа ( уравнение теплопроводности):

                                             (7.1)

для  и известных функциях

Геометрически область представляет собой «стакан», с трёх сторон которого значения функции заданы, а на верхней кромке ( при ) значения функции  не известны. Их вычисление и является целью рассматриваемых алгоритмов.

Наложим равномерную сетку на заданную прямоугольную область (стакан): по с маленьким шагом и по - с ещё меньшим шагом

Значение функции  будем обозначать

 

7.1.1   Явная схема

 

Пусть на некотором слое  известны все  (i=0,1,..,n). Попытаемся вычислить значения  во всех внутренних узлах (i=1,..,n-1) на  следующем слое. В граничных узлах нового слоя ( при i=0 и n) функция вычисляется по формулам .

Для внутренней точки  запишем конечно -разностные соотношения:


Подставим выражения (7.2)  в (7.1)  и выразим :

Эта формула носит название явная схема. Явная разностная схема называется условно устойчивой при ограничениях на  и  и удовлетворяет следующему условию:

Алгоритм нахождения решения такой системы (7.3) следует по слоям:

а) Решение на нулевом слое задано начальными условиями , ;

б) на  следующем слое находится по явной формуле ;

в) а значения  доопределяются из граничных условий, где  шаг по времени изменяется .

 

7.1.2   Неявная схема

 

Пусть на некотором слое  известны все  (i=0,1,..,n). Попытаемся вычислить значения  во всех внутренних узлах (i=1,..,n-1) на  следующем слое. В граничных узлах нового слоя ( при i=0 и n ) функция  вычисляется по формулам

Для внутренней точки ( i+1,j) запишем конечно –разностные соотношения:



Подставим выражения (7.4) в (7.1)) и в левой части полученного выражения с группируем значения  на новом j+1 слое (  для i=1,2,..,n:

 

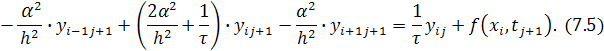
Решение (7.1) с помощью системы уравнений (7.5) носит название неявная схема. Решение получается более устойчивым по сравнению с явной схемой. Абсолютно устойчива при любом соотношении шага τ и h.

 

  Для фиксированного значения j система (7.5) имеет вид:

 

Здесь  и коэффициенты вычисляются по формулам:

 

Здесь для каждого шага по времени необходимо решить систему алгебраических уравнений с трехдиагональной матрицей. Такая система ранее (в предыдущей лабораторной работе №6) рассматривалась при решении краевой задачи для обыкновенных дифференциальных уравнений, для решения которой был использован метод прогонки.

Студенту рекомендуется самостоятельно составить алгоритм для данной расчетной схемы и разработать программу решения задачи.

                                

7.2 Индивидуальные задания

 

 Решить уравнение теплопроводности используя нижеперечисленные схемы и составить программу по указанным  блок-схемам рисунка (7.1) и (7.2);

1)         явная,

2)         неявная.

Сделать сравнительный анализ используемых схем.

Решить смешанную задачу для уравнения теплопроводности

                +f(x,t),                  где а =1,  f(x,t)= 0

с начальным условием            U(x,0) = j(x)

и граничными условиями      U(0,t) = y1(t),   U(L,t) = y2(t)

Таблица 7

№

j(x)

y1

y2

I

II

III

IV

1

0

2t + 1

2

2t

0

3

2t

2

4

t + 1

0

5

2t

0

6

-6t + 1

1,5

7

6t + 0,9

0,5

8

0,2

2(t – 0,2)

9

0,2

3(t + 0,2)

10

1

0,2t

11

0

2t

12

2t

1

13

5t+0,7

0,3

14

-5t

2

15

2

3t

16

0

2t + 1

17

2t

0

18

2t

2

19

t + 1

0

20

2t

0

21

-6t + 1

1,5

22

6t + 0,9

0,5

23

0,2

2(t – 0,2)

24

0,2

3(t + 0,2)

 

7.3   Контрольные вопросы.

 

1.  Какие уравнения называются уравнениями математической физики?

2. Назовите типы уравнений математической физики.

3. Какому типу относится уравнение теплопроводности?

4. Сравнительный анализ двух схем на устойчивость в зависимости от t и h, точность результата и количество итерации?

5. Почему формулу (7.5) называют неявной ?

6. В чем отличие конечно-разностного метода от метода сеток?

7. От какого параметра зависит точность метода сеток?

8. При выполнении какого условия явная расчетная схема устойчива?

9. Почему система (7.5) является системой с трехдиагональной матрицей ?

10. Почему формула (7.3) является явной ?

11. Назовите другие методы решения задач математической физики.