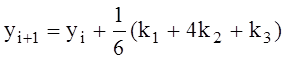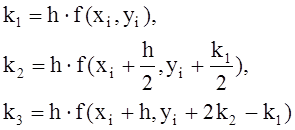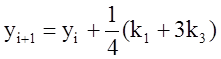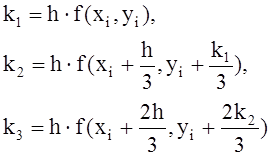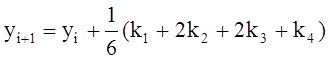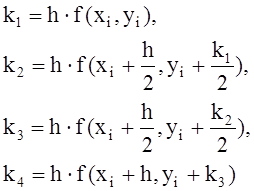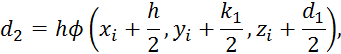Министерство образования и науки Республики Казахстан
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
М.У. Зияханов
Численные методы
Учебное пособие
Алматы 2013
|
УДК 519.6 (075.8) ББК 22.12я73 З-66 Численные методы: Учебное пособие/ М.У. Зияханов; АУЭС. Алматы, 2013. -84 с. ISBN 978-601-7436-04-9
|
|
В учебном пособии рассмотрены основные вопросы численных методов - решение алгебраических и трансцендентных уравнений, приближение функций, численное интегрирование, численные методы линейной алгебры, численные методы решения дифференциальных уравнений. В каждом разделе отражены основные понятия, законы и формулы, примеры решения типовых задач, уделено внимание проблеме поиска и обоснования выбранного способа решения.
Учебное пособие предназначено для студентов вузов, обучающихся по направлению «Информатика». Может быть полезна для студентов технических специальностей.
Ил. 9, табл. 12, схем 2, пример 31, библиогр. -9 назв.
ББК 22.12я73
Рецензенты: КазНПУ им. Абая, канд. физ.-мат., наук, доц. М.Ж. Бекпатшаев
АУЭС, канд. техн.наук, доц. А.Г. Ни.
Печатается по дополнительному плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013 г.
ISBN 978-601-7436-04-9
© НАО «Алматинский университет энергетики и связи», 2013 г.
Содержание
Введение
1 Погрешность решения задачи
1.1 Понятие погрешности
1.2 Действия над приближенными числами
1.3 Корректность
2 Решение алгебраических и трансцендентных уравнений
2.1 Метод деления пополам
2.2 Метод хорд
2.3 Метод секущих
2.4 Метод касательных (Ньютона)
2.5 Метод простой итерации
3 Решение систем нелинейных алгебраических и трансцендентных уравнений (НАТУ)
3.1 Метод Ньютона
3.2 Метод простой итерации
3.3 Метод Зейделя
4 Решение системы линейных алгебраических уравнений
4.1 Алгоритм метода Гаусса
4.2 Метод квадратных корней
4.3 Схема Халецского
4.4 Итерационные методы Якоби и Зейделя
5 Интерполирование и приближение функций
5.1 Интерполяционный многочлен Лангранжа
5.2 Интерполяционный многочлен Ньютона
5.2.1 Первый интерполяционный многочлен Ньютона
5.2.1 Второй интерполяционный многочлен Ньютона
5.3 Интерполяционные формулы Гаусса
5.3.1 Первая интерполяционная формула Гаусса
5.3.2 Вторая интерполяционная формула Гаусса
5.4 Интерполяционная формула Стирлинга
5.5 Интерполяционная формула Бесселя
5.6 Метод наименьших квадратов
6 Методы численного интегрирования
6.1 Метод прямоугольника
6.2 Метод трапеций
6.3 Формула Симпсона
7 Решение задачи Коши для обыкновенных дифференциальных уравнений
7.1 Метод Эйлера
7.2 Метод Рунге-Кутта
7.3 Метод Адамса
7.4 Приближенное решение задачи Коши для систем дифференциальных уравнений методом Рунге-Кутта
8 Решение краевых задач для обыкновенных дифференциальных уравнений
8.1 Сеточные методы
8.1.1 Метод конечных разностей
8.1.2 Метод прогонки
8.2 Приближенно-аналитические методы
8.2.1 Метод коллокаций
8.2.2 Метод наименьших квадратов
8.2.3 Метод Галеркина
Список литературы
Введение
Дисциплина «Численные методы» включена в план подготовки бакалавров, по специальности 5В060200 - «Информатика».
Математические модели процессов и явлений в различных областях науки и техники являются одним из основных способов получения новых знаний и технологических решений. В учебном пособии излагаются численные методы решения широкого круга математических задач, возникающих при исследовании физических и технических проблем. В целях лучшего понимания основные методы доведены до численных приложений - даны расчетные схемы и приведены числовые примеры с подробным ходом решения. Изложенные методы пригодны как для расчётов на ЭВМ, так и для ручных расчётов. В учебном пособии не предлагаются варианты заданий и контрольные вопросы для выполнения самостоятельных работ, так как они приведены в методическом указании к лабораторным работам по дисциплине «Численные методы», автор Зияханов М.У. Для полного понимания содержания материала от студента требуется минимальное знание алгебры, анализа и обыкновенных дифференциальных уравнений в объеме первого курса вузовского обучения.
1 Погрешность решения задачи
1.1 Понятие погрешности
Главная задача численных методов – фактическое нахождение решения с требуемой или, по крайней мере, оцениваемой точностью.
Отклонение истинного решения от приближенного называется погрешностью. Полная погрешность вычислений состоит из двух составляющих:
1) неустранимая погрешность;
2) устранимая погрешность.
Неустранимая погрешность обусловлена неточностью исходных данных и никаким образом не может быть уменьшена в процессе вычислений.
Устранимая погрешность состоит из двух составляющих:
а) погрешность аппроксимации (метода);
б) погрешность вычислений.
Эти составляющие могут быть уменьшены выбором более точных методов и увеличением разрядности вычислений.
Существуют четыре источника погрешностей, возникающих в результате численного решения задачи:
1) Математическая модель. Погрешность математической модели связана с ее приближенным описанием реального объекта. Погрешность матема-тической модели является неустранимой, в дальнейшем предполагается, что математическая модель фиксирована и ее погрешность учитываться не будет.
2) Исходные данные. Исходные данные обычно содержат погрешности, так как они либо неточно измерены, либо являются результатом решения некоторых вспомогательных задач. Во многих физических и технических задачах погрешность измерений составляет 1 – 10%. Погрешность исходных данных считается неустранимой и учитываться не будет.
3) Метод вычислений. Применяемые для решения задачи методы, как правило, являются приближенными. Погрешность метода необходимо определять для конкретного метода. Обычно ее можно оценить и проконтролировать. Следует выбирать погрешность метода так, чтобы она была не более чем на порядок меньше неустранимой погрешности.
4) Округление в вычислениях. Погрешность округления возникает из-за того, что вычисления производятся с конечным числом значащих цифр. Ок-ругление производят по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньше пяти, то содержимое сохраняемых разрядов не изменяется; в противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. При решении больших задач производятся миллиарды вычислений, но так как погрешности имеют разные знаки, то они частично взаимокомпенсируются.
Различают два вида погрешностей - абссолютную и относительную.
Абсолютной погрешностью числа ![]() называется величина
называется величина ![]() , удовлетворяющая
условию:
, удовлетворяющая
условию: ![]() (1.1)
(1.1)
где – ![]() точное
значение величины, а
точное
значение величины, а ![]() - её
приближенное значение. В этом случае говорят, что
- её
приближенное значение. В этом случае говорят, что ![]() определено
с точностью до
определено
с точностью до ![]() , т.е.
, т.е. ![]() .
.
Отношение абсолютной погрешности к абсолютному значению приближенной величины

называется относительной погрешностью ![]() .
Следовательно:
.
Следовательно:
![]()
Относительная погрешность чаще указывается в процентах. Точность результата лучше характеризует его относительная погрешность, которая показывает, какую часть самого числа составляет погрешность. Абсолютные и относительные погрешности числа принято округлять только в большую сторону, так как при округлениях границы неопределенности числа, как правило, увеличиваются. По этой причине вычисления ведут с одним – двумя запасными знаками.
Рассмотрим, как определяются верные значащие цифры чисел. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.
Например, числа 25,047 и -0,00250 имеют соответственно 5 и 3 значащих цифр.
Значащая цифра называется верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре. В противном случае цифра называется сомнительной.
Пример 1.1.
Для приближенного числа ![]() известна
абсолютная погрешность
известна
абсолютная погрешность ![]() . Требуется
определить его верные значащие цифры.
. Требуется
определить его верные значащие цифры.
Решение.
Проверим цифру 7. Половина единицы ее разряда: ![]()
Значит, она верная. Цифра 2: ![]() - тоже
верная. Верной будет и цифра 3:
- тоже
верная. Верной будет и цифра 3: ![]() , а вот
цифры 5 и 6 — сомнительные.
, а вот
цифры 5 и 6 — сомнительные.
Действительно, для 5: ![]() , т.е.
требуемое условие нарушено.
, т.е.
требуемое условие нарушено.
Если число имеет лишь верные цифры, его округленное значение имеет также лишь верные цифры. Приближенное значение числа, имеющего все верные цифры, может не совпадать с его точным значением. При вычислениях желательно сохранять такое количество значащих цифр, чтобы их число не превышало числа верных цифр более чем на две единицы.
1.1 Действия над приближенными числами
Сформулируем правила оценки предельных погрешностей при выполнении операций над приближенными числами. При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение.
При умножении или делении чисел друг на друга их относительные погрешности складываются. При возведении в степень приближенного числа относительная погрешность умножается на показатель степени.
Приведем формулы, определяющие погрешности арифметических операций.
1) При выполнении сложения:

2) При выполнении вычитания:

3) При выполении умножения:
![]()
4) При выполнении деления:
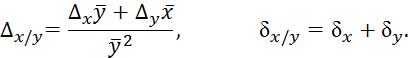
Пример 1.2. Определить, какое равенство точнее:
![]()
Решение.
1) Находим значения данных выражений с большим числом десятичных знаков:
![]()
![]()
2) Вычисляем предельные абсолютные погрешности
![]()
![]()
3) Вычисляем предельные относительные погрешности
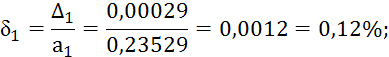
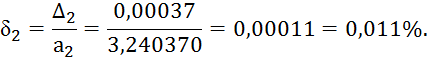
4) Т.к. ![]() , то
равенство
, то
равенство ![]() является
более точным.
является
более точным.
Пример 1.3. Вычислить и определить погрешности результата.
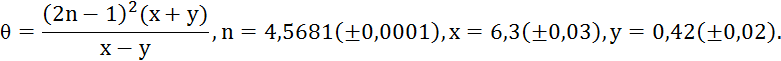
Решение.
1) Находим значения каждого действия с абсолютными погрешностями:
![]()
![]()
![]()
2) Вычисляем значение функции, и ее относительную погрешность:
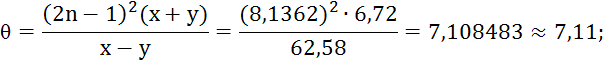
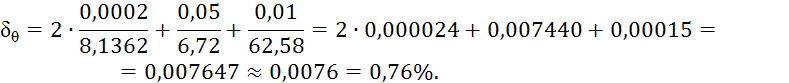
3) Зная относительную погрешность функции, определяем ее абсолютную погрешность:
![]()
Ответ: ![]()
Рассмотрим функцию ![]() Найдем
погрешность
Найдем
погрешность ![]() используя
выражение для полного дифференциала от z. Введем
приращение
используя
выражение для полного дифференциала от z. Введем
приращение ![]() :
: ![]() ,
, ![]() , а для
, а для ![]() :
:
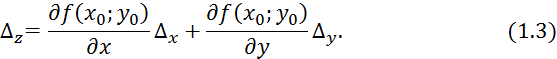
Тогда абсолютную погрешность z вычисления можно найти как:

После несложных преобразований получим выражение для ![]() :
:
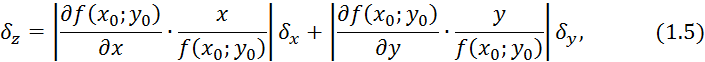
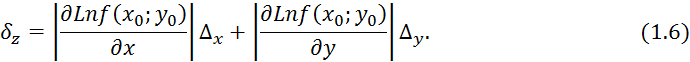
Пример 1.4. Пусть Z=X+Y.
Решение. Используя формулы (1.4) и (1.6), имеем:
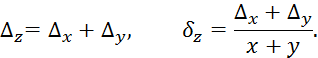
1.3 Корректность
Понятие корректности учитывает достаточно естественные требования, т. к. чтобы численно решать задачу, нужно быть уверенным, что ее решение существует. Столь же естественны требования единственности и устойчивости решения.
Решение задачи y* называется устойчивым по исходным данным x*, если оно зависит от исходных данных непрерывным образом. Это означает, что малому изменению исходных данных соответствует малое изменение решения. Строго говоря, для любого ε > 0 существует δ = δ (ε) > 0 такое, что всякому исходному данному x*, удовлетворяющему условию
|x – x*| < δ,
соответствует приближенное решение y*, для которого |y – y*| < ε.
Говорят, что задача поставлена корректно, если выполнены следующие три условия:
1) Решение существует при любых допустимых исходных данных.
2) Это решение единственно.
3) Это решение устойчиво по отношению к малым изменениям исходных данных.
Если хотя бы одно из этих условий не выполнено, задача называется некорректной.
2 Решение алгебраических и трансцендентных уравнений
Во многих научных и инженерных задачах, например, в электродинамике при математическом моделировании электромагнитных волновых колебательных процессов в линиях передачи и резонаторах получают так называемое дисперсионное уравнение, возникает необходимость решения уравнений вида:
![]() (2.1)
(2.1)
где функция ![]() определена
и непрерывна на некотором интервале
определена
и непрерывна на некотором интервале ![]() . Всякое
значение
. Всякое
значение ![]() ,
обращающее функцию
,
обращающее функцию ![]() в нуль,
т.е. такое, при котором
в нуль,
т.е. такое, при котором ![]() ,
называется корнем уравнения, а процесс нахождения – решением уравнения (2.1).
,
называется корнем уравнения, а процесс нахождения – решением уравнения (2.1).
Если функция ![]() представляет
собой многочлен относительно
представляет
собой многочлен относительно ![]() , то
уравнение (2.1) называется нелинейным алгебраическим (например,
, то
уравнение (2.1) называется нелинейным алгебраическим (например,![]() ); если же
в функцию
); если же
в функцию ![]() входят
элементарные (тригонометрические, логарифмические, показательные и др.) функции
– трансцендентным ( например,
входят
элементарные (тригонометрические, логарифмические, показательные и др.) функции
– трансцендентным ( например, ![]() ). С точки
зрения вычислительной математики они эквивалентны.
). С точки
зрения вычислительной математики они эквивалентны.
Геометрически решение уравнения (2.1) состоит в
нахождении точек пересечения графика функции: ![]() с осью ОХ.
с осью ОХ.
Методы решения нелинейных уравнений делятся на прямые и итерационные. Первые позволяют найти решение непосредственно с помощью формул и всегда обеспечивают получение точного решения (например, формула для решения квадратного уравнения). Однако они имеются лишь для ограниченного круга уравнений, поэтому на практике более широко используются методы второго типа - итерационные. В них задается процедура решения в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближенным, хотя может быть сколь угодно близким к точному. Кроме того, часто уравнения содержат коэффициенты, известные лишь приближенно, и, следовательно, сама задача о точном определении корней теряет смысл.
Можно выделить два типа итерационных методов:
1) Методы сужения интервала, содержащего корень
(например, методы половинного деления, золотого сечения). Здесь используется
только знак функции ![]() , а не ее
значения. Они являются относительно простыми, но имеют низкую скорость
сходимости.
, а не ее
значения. Они являются относительно простыми, но имеют низкую скорость
сходимости.
2) Методы аппроксимации, в которых функция ![]() заменяется
некоторой более простой функцией
заменяется
некоторой более простой функцией ![]() , для
которой и отыскивается корень (например, методы хорд, Ньютона). Используют
значения функции
, для
которой и отыскивается корень (например, методы хорд, Ньютона). Используют
значения функции![]() . Скорость
сходимости у них выше.
. Скорость
сходимости у них выше.
В общем случае задача решается в два этапа:
1) отделение корня, т.е. установление достаточно малого интервала (a,b), в котором содержится изолированный корень уравнения (2.1);
2) уточнение корня до заданной степени точности с помощью одного из итерационных методов.
Для отделения корней может быть использована теорема:
Если функция![]() непрерывна
на интервале и если
непрерывна
на интервале и если ![]() и
и ![]() имеют
противоположные знаки, т.е.
имеют
противоположные знаки, т.е. ![]() , то
, то ![]() имеет,
по крайней мере, один действительный корень на интервале (a,b). Если при этом
имеет,
по крайней мере, один действительный корень на интервале (a,b). Если при этом ![]() имеет
первую производную, не меняющую знак, то корень единственный.
имеет
первую производную, не меняющую знак, то корень единственный.
Рассмотрим пример, где требуется решить уравнение:
![]()
Задавая разные значения аргументу x, находят значения функции:
![]()
Например, при ![]() , при
, при ![]() , при
, при ![]() . Отсюда видно, что в промежутке
. Отсюда видно, что в промежутке ![]() заданное
уравнение может иметь решение. Для доказательства единственности этого решения
необходимо проверить монотонность функции
заданное
уравнение может иметь решение. Для доказательства единственности этого решения
необходимо проверить монотонность функции ![]() в данном
промежутке, она должна быть здесь монотонно возрастающей функцией, т.е. ее
первая производная должна быть положительной
в данном
промежутке, она должна быть здесь монотонно возрастающей функцией, т.е. ее
первая производная должна быть положительной ![]() . Убедимся
в этом, для этого определяем ее первую производную
. Убедимся
в этом, для этого определяем ее первую производную![]() , и здесь
легко можно показать, что она в промежутке
, и здесь
легко можно показать, что она в промежутке ![]() принимает
только положительные значения. Итак, выполняются оба условия единственности
корня уравнения (2.1) в данном промежутке.
принимает
только положительные значения. Итак, выполняются оба условия единственности
корня уравнения (2.1) в данном промежутке.
На втором этапе происходит уточнение корня с помощью
одного из итерационных методов, т.е. строится последовательность ![]() приближений
к решению, причем можно использовать один из двух критериев окончания итерационного
процесса:
приближений
к решению, причем можно использовать один из двух критериев окончания итерационного
процесса:
1) ![]() ,
,
2) ![]() .
.
Возможно их одновременное использование.
Важной характеристикой итерационных методов является
их порядок, характеризующий скорость сходимости, т.е. число итераций, за которое
достигается заданная точность. Обозначим через ![]() расстояние
между очередным приближением и точным решением. Очевидно, для сходимости метода
величина
расстояние
между очередным приближением и точным решением. Очевидно, для сходимости метода
величина ![]() должна быть
меньше, чем
должна быть
меньше, чем ![]() , т.е.
отношение
, т.е.
отношение 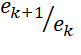 должно быть
меньше единицы. Чем меньше это отношение, тем выше скорость сходимости.
должно быть
меньше единицы. Чем меньше это отношение, тем выше скорость сходимости.
2.1 Метод деления пополам
Метод половинного деления надежен и его практически
удобно применять для грубого нахождения корня уравнения, так как с увеличением
точности возрастает объем выполняемой работы из-за медленной сходимости итерационного
процесса. Метод применяется, если ![]() непрерывна
на отрезке [a,b] и
непрерывна
на отрезке [a,b] и ![]() .
.
Суть метода заключается в следующем (см. рисунок 2.1).
Допустим, что корень уравнения (2.1) отделен, т.е. найден промежуток ![]() , где
имеется единственный корень. Теперь необходимо найти его приближенное значение
с заданной точностью
, где
имеется единственный корень. Теперь необходимо найти его приближенное значение
с заданной точностью ![]() Алгоритм вычисления корня будет следующий:
Алгоритм вычисления корня будет следующий:
а) определяется середина промежутка [a,b]: c=(a+b)/2;
б) проверяется условие![]() , если это
условие выполняется, то искомое решение найдено и выводится значение c;
, если это
условие выполняется, то искомое решение найдено и выводится значение c;
в) если условие ![]() не
выполняется, то проверяется условие
не
выполняется, то проверяется условие
![]() ;
;
если это выполняется, то b=c , в противном случае a=c;
г) проверяется условие ![]() если это
условие выполняется, то процесс решения уравнения завершается и выводится
значение c в качестве искомого решения; если это условие не
выполняется, т.е. заданная точность не достигнута, то осуществляется переход к
п. a) для продолжения вычислений.
если это
условие выполняется, то процесс решения уравнения завершается и выводится
значение c в качестве искомого решения; если это условие не
выполняется, т.е. заданная точность не достигнута, то осуществляется переход к
п. a) для продолжения вычислений.
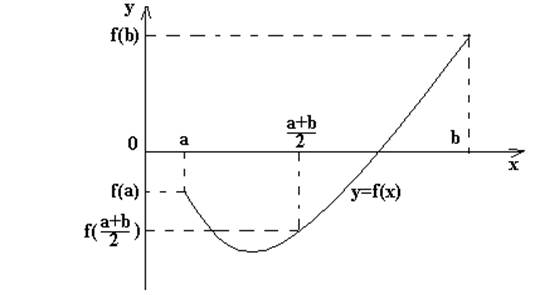

Рисунок 2.1 - Метод половинного деления
Пример 2.1. Методом деления пополам
решить уравнение ![]() с точностью
до 0,01.
с точностью
до 0,01.
Решение.
Интервал изоляции действительного корня определен выше, но можно определить,
графически построив графики функций ![]()
![]()
Разделив интервал ![]() пополам,
получим
пополам,
получим ![]() и вычислим
и вычислим ![]() Следовательно,
искомый корень находится в интервале
Следовательно,
искомый корень находится в интервале ![]() .
.
Примем ![]() В резуль- тате искомый корень находится в
интервале
В резуль- тате искомый корень находится в
интервале ![]()
Продолжая этот процесс, имеем:
![]() интервал
интервал ![]() ;
;
![]() интервал
интервал ![]() ;
;
![]() интервал
интервал ![]() ;
;
![]() интервал
интервал ![]() ;
;
![]() интервал
интервал ![]() ;
;
![]() интервал
интервал ![]() ;
;
![]() интервал
интервал ![]() ;
;
![]()
Таким образом, мы получили интервал ![]() . Отсюда видно,
что с точностью до 0, 01 искомый корень
. Отсюда видно,
что с точностью до 0, 01 искомый корень ![]() .
.
2.2 Метод хорд
В основе метода лежит линейная интерполяция функции по двум значениям, имеющим противоположные знаки. Метод хорд дает решение задачи для достаточно малых ε за меньшее число арифметических операций, чем метод половинного деления.
Пусть нужно найти корень уравнения ![]() на отрезке
[a,b], причем известно, что
на отрезке
[a,b], причем известно, что ![]() непрерывна
на [a,b] и
непрерывна
на [a,b] и ![]() Кроме
того, пусть
Кроме
того, пусть ![]() и
и ![]() на отрезке
[a,b] сохраняют свой знак. Заменим функцию
на отрезке
[a,b] сохраняют свой знак. Заменим функцию ![]() на отрезке
[a,b] линейной функцией (см. рисунок 2.2), составив уравнение прямой, которая
проходит через точки
на отрезке
[a,b] линейной функцией (см. рисунок 2.2), составив уравнение прямой, которая
проходит через точки ![]() :
:
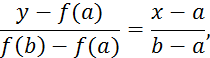
![]()
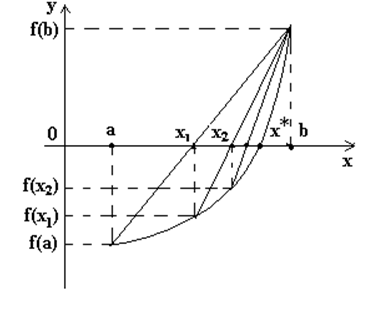
Рисунок 2.2 - Метод хорд
Учитывая ![]() найдем
первое приближенное значение корня
найдем
первое приближенное значение корня ![]() по формуле:
по формуле:
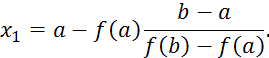
Далее рассмотрим отрезки ![]() и выберем
из них тот, на концах которого функция
и выберем
из них тот, на концах которого функция ![]() имеет
значения противоположных знаков. Те же вычисления выполним на выбранном отрезке
и получим второе приближение к корню
имеет
значения противоположных знаков. Те же вычисления выполним на выбранном отрезке
и получим второе приближение к корню ![]() и так до
тех пор, пока не получим корень уравнения (2.1) с заданной степенью точности.
и так до
тех пор, пока не получим корень уравнения (2.1) с заданной степенью точности.
Если ![]() - точный
корень уравнения
- точный
корень уравнения![]() ,
изолированный на отрезке [a, b], a
,
изолированный на отрезке [a, b], a ![]() —-приближенное
значение корня, найденное методом хорд, то оценка погрешности этого
приближенного значения такова:
—-приближенное
значение корня, найденное методом хорд, то оценка погрешности этого
приближенного значения такова:

Алгоритм метода следующий. До начала итерационного процесса задаем точность ε, с которой нужно получить решение, и отрезок [a,b], содержащий корень. Затем:
а) Вычисляем приближение к корню:
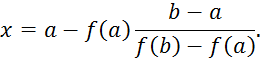
б) Проверяем выполнение неравенства ![]() , если оно
выполняется, то
, если оно
выполняется, то ![]() считаем решением, если же не выполняется, продолжаем вычисления.
считаем решением, если же не выполняется, продолжаем вычисления.
с) Проверяем условие ![]() , и, если
оно выполняется, полагаем
, и, если
оно выполняется, полагаем ![]() , в
противном случае
, в
противном случае ![]() и
повторяем вычисления с п.а.
и
повторяем вычисления с п.а.
Пример 2.2. Методом хорд решить
уравнение ![]() с точностью
до 0,01.
с точностью
до 0,01.
Решение. Из
предыдущего примера видно, что положительный корень заключен в промежутке ![]() . Найдем первое приближенное значение корня по формуле:
. Найдем первое приближенное значение корня по формуле:
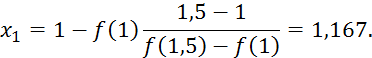
Так как ![]() ,
то применим метод хорд по промежутку
,
то применим метод хорд по промежутку ![]() :
:
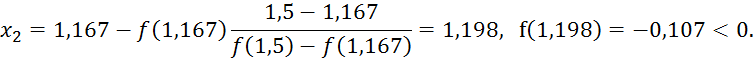
Найдем третье приближенное значение:
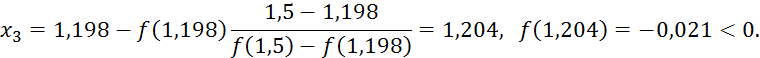
Найдем четвертое приближенное значение:
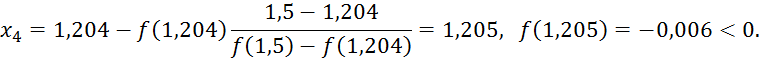
Следовательно, с точностью до 0,01 искомый корень равен 1,205.
2.3 Метод секущих
Метод реализуется алгоритмом метода хорд, только a и b
взяты с одной стороны от корня и не фиксируются. Геометрическая интерпретация
метода состоит в следующем (см. рисунок 2.3). Через точки проводим прямую (секущую)
до пересечения с осью Ох. Получаем точку ![]() и из нее
восстанавливаем перпендикуляр к оси Ох до пересечения с графиком функции
и из нее
восстанавливаем перпендикуляр к оси Ох до пересечения с графиком функции ![]() . Получим
точку
. Получим
точку ![]() . Через
точки
. Через
точки ![]() и
и ![]() проводим
секущую – получим точку
проводим
секущую – получим точку ![]() (пересечение
секущей с осью Ох) и т. д.
(пересечение
секущей с осью Ох) и т. д.
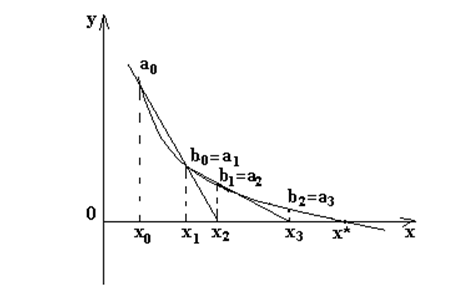
Рисунок 2.3 - Метод секущих
2.4 Метод касательных (Ньютона)
Метод основан на замене ![]() в точке
начального приближения касательной, пересечение которой с осью Оx дает первое
приближение
в точке
начального приближения касательной, пересечение которой с осью Оx дает первое
приближение ![]() , и т.д.
Геометрическая интерпретация метода приведена (см. рисунок 2.4). Приняв в
качестве начального приближения к корню
, и т.д.
Геометрическая интерпретация метода приведена (см. рисунок 2.4). Приняв в
качестве начального приближения к корню ![]() , некоторое
значение
, некоторое
значение ![]() восстанавливают
перпендикуляр из точки
восстанавливают
перпендикуляр из точки ![]() к оси Ох.
В точке его пересечения с графиком функции
к оси Ох.
В точке его пересечения с графиком функции![]() , для
которой отыскивается нуль, проводят касательную к кривой. Точка пересечения
касательной с осью Ох дает новое приближение
, для
которой отыскивается нуль, проводят касательную к кривой. Точка пересечения
касательной с осью Ох дает новое приближение ![]() к корню.
После этого процесс повторяют для точки
к корню.
После этого процесс повторяют для точки ![]() и т. д.
и т. д.
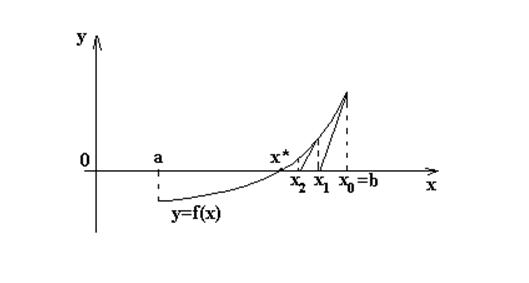
Рисунок 2.4 - Метод Ньютона
Уравнение касательной в точке ![]() - это
уравнение прямой, проходящей через заданную точку
- это
уравнение прямой, проходящей через заданную точку ![]() и имеющую
угловой коэффициент
и имеющую
угловой коэффициент ![]()
![]()
В точке ![]() пересечения
этой касательной с осью ОХ величина
пересечения
этой касательной с осью ОХ величина ![]() равняется
нулю:
равняется
нулю:
![]()
Отсюда получим значение ![]() :
:
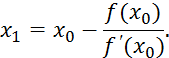
В общем случае очередное приближение ![]() выражается через предыдущее приближение
выражается через предыдущее приближение ![]() по формуле
Ньютона:
по формуле
Ньютона:
![]() (2.2)
(2.2)
Если будет задано первоначальное приближение корня, то
по формуле (2.2) могут быть найдены любые приближения искомого корня, следовательно,
можно получить бесконечный ряд чисел ![]() , i=1,2,3,
. . .. Если этот ряд сходится, то его предел должен быть истинным
значением искомого корня. Однако для достижения этого значения корня
необходимо выполнить бесконечное количество итераций. Поэтому для завершения
такого вычислительного процесса должно быть задано условие, определяемое
заданной точностью решения уравнения, оно имеет вид
, i=1,2,3,
. . .. Если этот ряд сходится, то его предел должен быть истинным
значением искомого корня. Однако для достижения этого значения корня
необходимо выполнить бесконечное количество итераций. Поэтому для завершения
такого вычислительного процесса должно быть задано условие, определяемое
заданной точностью решения уравнения, оно имеет вид
![]() (2.3)
(2.3)
При выборе начального приближения корня необходимо
руководствоваться следующим правилом: за исходную точку следует выбирать тот
конец отрезка [a,b], в котором знак функции совпадает со знаком
второй производной. В одном случае ![]() и
начальная точка
и
начальная точка ![]() , во втором
, во втором ![]() и в
качестве начального приближения берем
и в
качестве начального приближения берем ![]() .
.
Для оценки погрешности приближенного значения корня, найденного методом Ньютона, может быть использовано неравенство
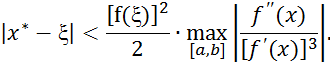
Алгоритм решения уравнения (2.1) методом касательных будет иметь следующий вид:
а) вводится в память компьютера значение
первоначального приближения корня ![]()
б) ![]() принимает
значения
принимает
значения ![]() ;
;
в) по формуле (2.2) определяется новое приближение корня;
г) проверяется условие (2.3); если оно выполняется, то вычислительный процесс завершается, а если условие (2.3) не выполняется, то продолжается процесс вычисления пункта в.
Пример 2.3. Применив дважды метод касательных, найти приближенное
значение действительного корня уравнения ![]() , изолированного
в промежутке [1; 1,5]. Приближенные значения
, изолированного
в промежутке [1; 1,5]. Приближенные значения ![]() и
и ![]() вычислить
с двумя знаками после запятой. Оценить погрешность приближенного значения
вычислить
с двумя знаками после запятой. Оценить погрешность приближенного значения ![]() .
.
Решение. Найдем первое приближенное значение корня по формуле:
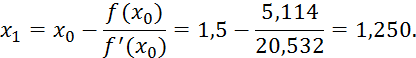
Определяем второе приближение:
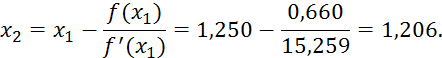
Оценим погрешность найденного приближенного значения корня:
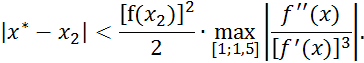
В интервале ![]() имеем
имеем
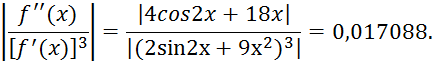
Наибольшего значения она достигает при ![]()

т.е. ![]() ; следовательно, в приближенном значении корня
1,206 все цифры верны.
; следовательно, в приближенном значении корня
1,206 все цифры верны.
2.5 Метод простой итерации
Заменим уравнение ![]() равносильным
ему уравнением
равносильным
ему уравнением
![]() (2.4)
(2.4)
Выбрав начальное приближение ![]() и
подставив его в правую часть уравнения (2.4), получим
и
подставив его в правую часть уравнения (2.4), получим ![]() . Затем это
значение снова подставим в правую часть уравнения (2.4) и найдем
. Затем это
значение снова подставим в правую часть уравнения (2.4) и найдем ![]() . Повторяя
этот процесс, получаем числовую последовательность
. Повторяя
этот процесс, получаем числовую последовательность ![]() . При этом
возможны два случая:
. При этом
возможны два случая:
1) последовательность ![]() сходится,
т.е. имеет предел и тогда этот предел будет корнем уравнения
сходится,
т.е. имеет предел и тогда этот предел будет корнем уравнения ![]() ;
;
2) последовательность ![]() расходится,
т.е. не имеет предела или стремится к бесконечности.
расходится,
т.е. не имеет предела или стремится к бесконечности.
Геометрическая интерпретация метода показана (см. рисунок 2.5).
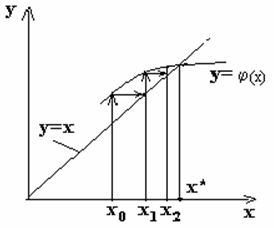
Рисунок 2.5 - Метод простой итерации
Метод сходится, если выполняется условие ![]() . Чем меньше,
тем быстрее сходимость итерационного процесса.
. Чем меньше,
тем быстрее сходимость итерационного процесса.
Для нахождения приближенного значения корня с
погрешностью, не превышающей ![]() ,
достаточно определить k так, чтобы выполнялось неравенство:
,
достаточно определить k так, чтобы выполнялось неравенство:

Практически метод простых итераций осуществляется так:
a)
Преобразовать уравнение ![]() к виду (2.4)
таким образом, чтобы
к виду (2.4)
таким образом, чтобы ![]() .
.
б) Принять за начальное приближение любое число из отрезка [a,b].
в) Вычислять последовательность приближений по формуле
![]()
до тех пор, пока для двух последовательных приближений
не будет выполнено неравенство ![]() .
.
Пример 2.4.
Найти методом простой итерации на отрезке [1,2] корень уравнения ![]()
Решение. К
виду ![]() это
уравнение можно преобразовать несколькими способами, например:
это
уравнение можно преобразовать несколькими способами, например:
1. ![]() , т.е.
, т.е. ![]()
2. 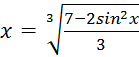 , т.е.
, т.е. 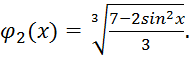
Проверим выполнение условия сходимости для [1,2]:
1) ![]() - условие
не выполняется.
- условие
не выполняется.
2) 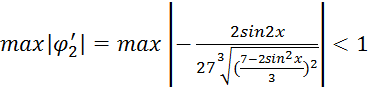 - условие
выполняется, поэтому именно этот вариант следует использовать для организации
итерационного процесса.
- условие
выполняется, поэтому именно этот вариант следует использовать для организации
итерационного процесса.
Найдем первое приближенное значение, приняв за
начальное значение ![]()
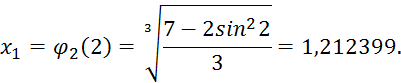
Найдем второе и последующие приближения:
![]()
![]()
Таким образом, искомый корень ![]()
3 Решение систем нелинейных алгебраических и трансцендентных уравнений (НАТУ)
Решением системы НАТУ
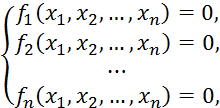 (3.1)
(3.1)
где – ![]() неизвестные;
неизвестные;
![]() – заданные
функции n переменных, называется совокупность чисел
– заданные
функции n переменных, называется совокупность чисел ![]() , которые,
будучи подставлены на место неизвестных
, которые,
будучи подставлены на место неизвестных ![]() , обращают
каждое уравнение в тождество.
, обращают
каждое уравнение в тождество.
Для систем НАТУ не существует каких-либо приемов грубого отделения корня. В некоторых случаях в результате составления таблиц данных функций или построения графиков с последующим определением координат точек пересечения можно получить приближенное значение корня. В большинстве практических случаев, когда решается серия систем, эта трудность отделения корней легко преодолима, так как решение предыдущей системы из этой серии является хорошим начальным приближением к решению очередной системы.
Для уточнения корней системы НАТУ применяются только итерационные, а не прямые методы. Чаще всего для решения систем НАТУ применяют метод Ньютона и его модификации.
3.1 Метод Ньютона
Разложим каждую функцию![]() системы
уравнений (3.1) в ряд Тейлора в окрестности точки
системы
уравнений (3.1) в ряд Тейлора в окрестности точки ![]() , тогда
, тогда
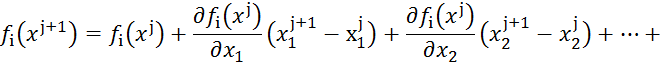

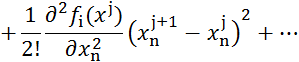
Если![]() близко к
близко к![]() , то можно
пренебречь членами второго и выше порядков, а если считать
, то можно
пренебречь членами второго и выше порядков, а если считать ![]() точным
решением, то можно записать:
точным
решением, то можно записать:
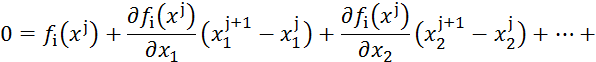
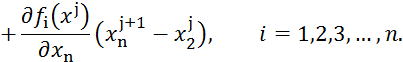
Или в матричном виде:
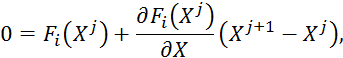
где
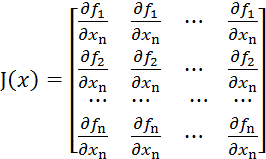 -матрица
Якоби (якобиан).
-матрица
Якоби (якобиан).
Тогда
![]()
Откуда
![]()
Это уравнение является n-мерным аналогом метода
касательных и в литературе часто называется методом Ньютона - Рафсона. Для
n-мерного метода Ньютона-Рафсона характерными являются те же проблемы сходимости,
что и для одномерного случая. Однако можно доказать, что если исходный (начальный)
вектор![]() близок к
близок к ![]() , то
n-мерный метод Ньютона-Рафсона будет всегда сходиться, причем скорость сходимости
будет квадратичной.
, то
n-мерный метод Ньютона-Рафсона будет всегда сходиться, причем скорость сходимости
будет квадратичной.
Пример 3.1. Решить систему:
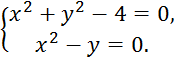
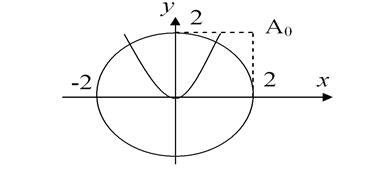
Решение. Начальное приближение выберем из рисунка:
Начнем вычисление корня с точки ![]() т.е.
т.е. ![]() Вычислим
частные производные, чтобы сформировать матрицу Якоби:
Вычислим
частные производные, чтобы сформировать матрицу Якоби:
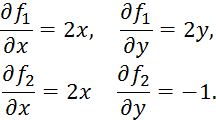
Поэтому
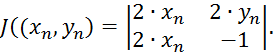
Для вычисления обратной матрицы второго порядка воспользуемся формулой:
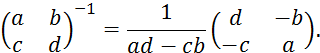
Для нашего случая:
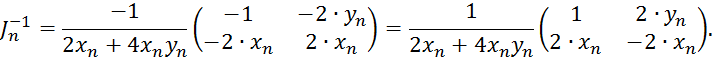
Подставляя в формулу (2.2), получим:
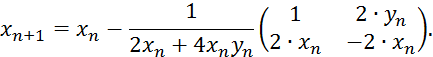
Выпишем окончательную формулу для совершения итераций при решении данного примера:
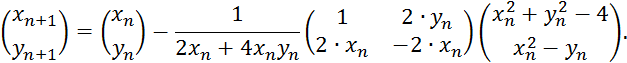
Если ![]() то
то

Сделаем вторую итерацию, вычислив ![]()
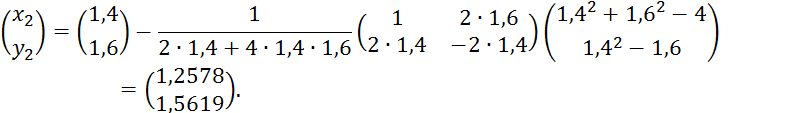
Процесс останавливаем, когда ![]() .
.
3.2 Метод простой итерации
Для применения этого метода систему НАТУ с помощью эквивалентных преобразований необходимо привести вначале к виду:
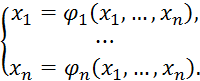
Затем следует задать начальное приближение ![]() и выполнить
итерацию по формулам:
и выполнить
итерацию по формулам:

Если ![]() , то
процесс заканчивается, иначе полученный вектор
, то
процесс заканчивается, иначе полученный вектор ![]() используется как исходный на второй итерации и т.д.
используется как исходный на второй итерации и т.д.
В общем случае итерации выполняются по формулам:
![]()
Преимуществом этого метода, по сравнению с методом Ньютона, является то, что здесь не требуется вычислять частные производные и решать СЛАУ. Однако низкая скорость сходимости (линейная) метода простой итерации является его серьезным недостатком и предпочтение обычно отдается методу Ньютона.
Пример 3.2. Возьмем тот же пример, что и в предыдущем параграфе:
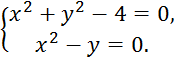
Решение. Преобразуем систему к виду:

За начальное приближение возьмем те же точки. Тогда
результатом первой итерации после подстановки ![]() и
и ![]() в правую
часть системы (3.3) станет точка
в правую
часть системы (3.3) станет точка ![]() ,
, ![]() . Теперь в
правую часть подставим
. Теперь в
правую часть подставим ![]() и
и ![]() и получим
и получим ![]() и
и ![]() и т.д.
и т.д.
3.3 Метод Зейделя
Метод Зейделя отличается от метода простой итерации
тем, что вычисленное новое значение компоненты ![]() тут же используется для вычисления нового значения
очередной компоненты
тут же используется для вычисления нового значения
очередной компоненты ![]() . В этом
методе итерации выполняются по формулам:
. В этом
методе итерации выполняются по формулам:
![]()
![]()
![]()
![]()
![]()
![]()
Как и в методе Ньютона, успех во многом зависит от выбора начальных значений неизвестных: они должны быть достаточно близки к точному решению. В противном случае итерационный процесс может расходиться. Множество точек n–мерного пространства, для которых итерационный процесс, использующий их в качестве начальных, сходится, называется областью сходимости метода. С увеличением числа уравнений системы область сходимости обычно уменьшается, поэтому при решении больших систем важным является опыт инженера при выборе начальной точки.
Условие сходимости ![]() и условие
прекращения итераций те же, что и в методе простых итераций.
и условие
прекращения итераций те же, что и в методе простых итераций.
Пример 3.3. Рассмотрим тот же пример, что и в предыдущем параграфе.
Решение. Итерации будут выполняться по формулам:
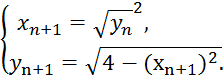
Метод Зейделя в данной задаче сходится быстрее метода простых итераций, но медленнее метода Ньютона.
4 Решение системы линейных алгебраических уравнений
Многие практические задачи механики, электротехники, автоматизированного управления и других часто приводят к системе линейных алгебраических уравнений, и решение её рассматривают как важное прикладное значение при разрешении различных проблем науки и техники. Общий вид такой системы может быть представлен так:
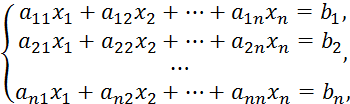 (4.1)
(4.1)
где ![]() заданные
коэффициенты и
заданные
коэффициенты и ![]() свободные
члены системы уравнений,
свободные
члены системы уравнений, ![]() неизвестные
величины, значения которых должны быть определены,
неизвестные
величины, значения которых должны быть определены, ![]()
В настоящее время хорошо разработан арсенал численных методов решения линейных алгебраических уравнений на ЭВМ. Многообразие численных методов решения линейных алгебраических систем можно разделить на прямые (точные) и итерационные.
В прямых (или точных) методах решение х системы (4.1) находится за конечное число арифметических действий. Примером прямого метода является метод Гаусса, метод Крамера, метод квадратного корня и другие. Отметим, что вследствие погрешностей округления при решении задач на ЭВМ прямые методы на самом деле не приводят к точному решению системы (4.1) и называть их точными можно, лишь отвлекаясь от погрешностей округления.
Итерационные методы (их называют также методами
последовательных приближений) состоят в том, что решение х системы
находится как предел при n ![]() последовательных
приближений
последовательных
приближений ![]() , где n —
номер итерации. Как правило, за конечное число итераций этот предел не достигается.
Обычно задается некоторое малое число
, где n —
номер итерации. Как правило, за конечное число итераций этот предел не достигается.
Обычно задается некоторое малое число ![]() >0 (точность) и вычисления проводятся до тех пор,
пока не будет выполнена оценка:
>0 (точность) и вычисления проводятся до тех пор,
пока не будет выполнена оценка:
|| ![]() ||<
||< ![]() .
.
К итерационным методам относятся: метод простой итерации, метод Зейделя, метод релаксации, градиентные методы и их модификации.
4.1 Алгоритм метода Гаусса
Подвергнем систему (4.1), называемую схемой единственного деления, следующему преобразованию.
Прямой ход состоит из n-1 шагов исключения.
1-й шаг. Целью
этого шага является исключение неизвестного ![]() из
уравнений с номерами
из
уравнений с номерами ![]() Предположим,
что коэффициент
Предположим,
что коэффициент ![]() Выполнение
условия
Выполнение
условия ![]() можно
добиться всегда путем перестановки уравнений системы. Будем называть его
главным элементом 1-го шага.
можно
добиться всегда путем перестановки уравнений системы. Будем называть его
главным элементом 1-го шага.
Найдем величины:
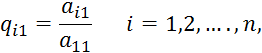
называемые множителями 1-го шага. Вычтем
последовательно из второго, третьего,…, n-го уравнений системы первое
уравнение, умноженное соответственно на ![]() Это позволит обратить в нуль коэффициенты
при
Это позволит обратить в нуль коэффициенты
при ![]() во всех уравнениях, кроме первого. В
результате получим эквивалентную систему
во всех уравнениях, кроме первого. В
результате получим эквивалентную систему

в которой ![]() и
и ![]() вычисляются по формулам
вычисляются по формулам
![]()
2-й шаг. Целью этого шага является исключение
неизвестного ![]() из уравнений с номерами
из уравнений с номерами ![]() Пусть
Пусть ![]() где
где ![]() коэффициент, называемый главным (или
ведущим) элементом 2-го шага. Вычислим множители 2-го шага
коэффициент, называемый главным (или
ведущим) элементом 2-го шага. Вычислим множители 2-го шага

и вычтем последовательно из третьего,
четвертого, …, n-го уравнения системы второе уравнение, умноженное
соответственно на ![]() В результате получим систему
В результате получим систему
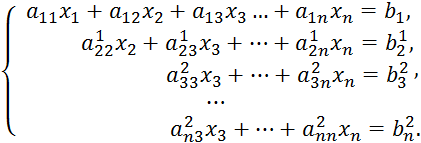
Здесь коэффициенты ![]() и
и ![]() вычисляются по формулам
вычисляются по формулам
![]()
Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.
k-й шаг. В предположении, что главный
(ведущий) элемент k-го шага ![]() отличен от нуля, вычислим множители k-го
шага
отличен от нуля, вычислим множители k-го
шага
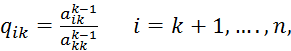 (4.2)
(4.2)
и вычтем последовательно из ![]() -го, …, n-го уравнений полученной
напредыдущем шаге системы k-e уравнение, умноженное соответственно на
-го, …, n-го уравнений полученной
напредыдущем шаге системы k-e уравнение, умноженное соответственно на ![]()
После (n - 1)-го шага исключения получим систему уравнений
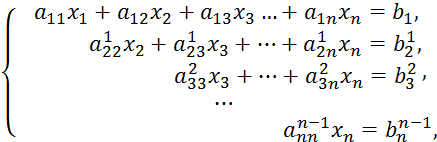
матрица A(n-1) которой
является верхней треугольной. Здесь коэффициенты ![]() и
и ![]() вычисляются по формулам:
вычисляются по формулам:
![]() (4.3)
(4.3)
На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы
находим ![]() . Подставляя найденное значение
. Подставляя найденное значение ![]() в предпоследнее уравнение, получим
в предпоследнее уравнение, получим ![]() . Осуществляя обратную подстановку,
далее последовательно находим
. Осуществляя обратную подстановку,
далее последовательно находим ![]()
![]()
Вычисления неизвестных здесь проводятся по формулам:

![]()
Заметим, что вычисление множителей, а также обратная
подстановка требуют деления на главные элементы ![]() . Поэтому, если один из главных элементов оказывается
равным нулю, то схема единственного деления не может быть реализована.
. Поэтому, если один из главных элементов оказывается
равным нулю, то схема единственного деления не может быть реализована.
Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
Компактная схема Гаусса. Компактная схема Гаусса дает экономный способ записи. Рассмотрим порядок составления схемы для системы (4.1). Все результаты вычислений будем записывать в одну таблицу (см. таблицу 4.1).
Таблица 4.1
|
|
i |
|
|
|
Свободные члены |
Σ |
|
I |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
II |
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
IIII |
4 |
|
|
|
|
|
|
IIV |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
Порядок заполнения таблицы.
Прямой ход.
1) Записываем коэффициенты данной системы в трех строках и четырёх столбцах раздела I (см. таблицу 4.1).
2) Суммируем все коэффициенты по строке и записываем
сумму в столбце ∑ (столбец контроля), например, ![]()
3) Делим все числа, стоящие в первой строке, на ![]() и результаты
и результаты ![]() записываем в четвертой строке раздела I.
записываем в четвертой строке раздела I.
4) Вычисляем ![]() и делаем проверку. Если вычисления ведутся с
постоянным числом знаков после запятой, то числа
и делаем проверку. Если вычисления ведутся с
постоянным числом знаков после запятой, то числа ![]() и
и ![]() не должны отличаться более чем на единицу последнего
разряда. В противном случае следует проверить действия пункта 3).
не должны отличаться более чем на единицу последнего
разряда. В противном случае следует проверить действия пункта 3).
5) По формулам ![]() вычисляем коэффициенты
вычисляем коэффициенты ![]() (i=2,3; j=2,3,4).
(i=2,3; j=2,3,4).
6) Делаем проверку. Сумма элементов каждой строки ![]() не должна отличаться от
не должна отличаться от ![]() более чем на единицу последнего разряда. Результаты
записываем в первые три строки раздела II.
более чем на единицу последнего разряда. Результаты
записываем в первые три строки раздела II.
7) Делим все элементы первой строки раздела II на
![]() и результаты записываем в третьей строке раздела II.
и результаты записываем в третьей строке раздела II.
8) Повторяем п. 5)-7).
Обратный ход.
9) Вычисляем ![]()
10) Для вычисления значений ![]() используются лишь строки разделов I, II, содержащие
единицы (отмеченные строки), начиная с последней.
используются лишь строки разделов I, II, содержащие
единицы (отмеченные строки), начиная с последней.
![]()
11) Вычисляем ![]() для чего используем элементы отмеченной строки
раздела I:
для чего используем элементы отмеченной строки
раздела I:
![]()
Пример 4.1. Решить систему методом Гаусса.
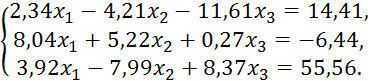
Решение. Используя компактную схему Гаусса и порядок заполнения таблицы (см. таблицу 4.2), решим данную систему.
Таблица 4.2
|
|
I |
|
|
|
Свободные члены |
Σ |
|
I |
1 |
2,34 |
-4,21 |
-11,61 |
14,41 |
0,93 |
|
2 |
8,04 |
5,22 |
0,27 |
-6,44 |
7,09 |
|
|
3 |
3,92 |
-7,99 |
8,37 |
55,56 |
59,86 |
|
|
|
1 |
-1,7991 |
-4,9615 |
6,1581 |
0,3974 |
|
|
II |
1 |
|
19,6848 |
40,1605 |
-55,9511 |
3,8949 |
|
2 |
|
-0,9375 |
27,8191 |
31,4202 |
58,3022 |
|
|
|
|
1 |
2,0402 |
-2,8424 |
0,1979 |
|
|
III |
1 |
|
|
29,7318 |
28,7555 |
58,4877 |
|
IV |
|
|
|
1 |
0,9672 |
1,9672 |
|
|
|
1 |
|
-4,8157 |
-3,8256 |
|
|
|
1 |
|
|
2,2930 |
3,2931 |
Разделом III заканчивается прямой ход. В столбце
свободных членов в первой строке раздела IV получено значение ![]() Для вычисления значения
Для вычисления значения ![]() и
и ![]() проделываются следующие вычисления:
проделываются следующие вычисления:
![]()
![]()
4.2 Метод квадратных корней
Метод квадратных корней разработан для решения линейных систем с эрмитовой или симметричной матрицей коэффициентов:
![]()
где ![]()
Симметричную матрицу можно представить в виде произведения двух транспонированных между собой треугольных матриц:
![]()
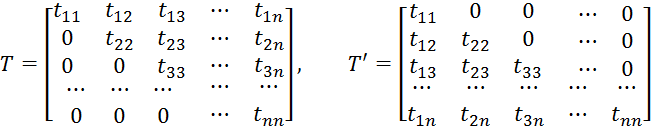
Перемножая матрицы T' и T, получим следующие уравнения:
![]()
![]() .
.
Последовательно находим:
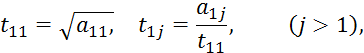
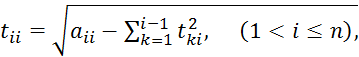 (4.6)
(4.6)
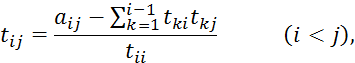
![]()
После подстановки в систему, последняя распадается на две системы с треугольными матрицами:

Запишем систему ![]() в развёрнутом виде:
в развёрнутом виде:
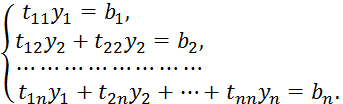
Отсюда последовательно находим:
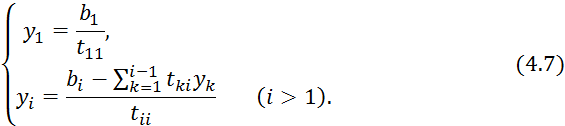
Решаем систему ![]() , записав её в развёрнутом виде:
, записав её в развёрнутом виде:
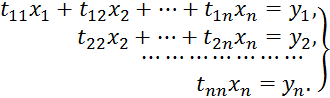
Решение имеет вид:
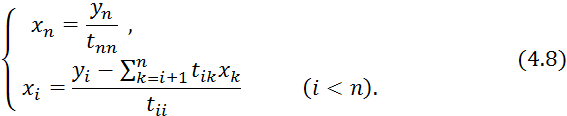
Прямым ходом с помощью формул вычисляются t[i,j] и y[i], обратным ходом по формуле находятся x[i].
Пример 4.2. Методом квадратных корней решить систему уравнений. Результаты вычислений будем записывать в одну таблицу (см. таблицу 4.3).
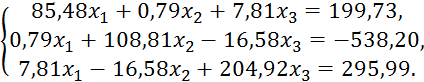
Таблица 4.3
|
iI |
|
|
|
|
|
|
|
|
|
293,831 |
|
|
|
|
|
|
|
|
|
|
-45,187 |
|
|
|
|
|
|
|
|
|
|
|
492,145
|
|
|
III |
|
|
|
|
|
9,24573 |
0,086158 |
0,845124 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IIII |
|
|
|
|
|
|
|
0,96718 |
|
|
Решение. Прямой ход.
1) В первый раздел (см. таблицу 4.3) записываем коэффициенты системы.
2) Суммируем коэффициенты по каждой строке и
результаты записываем в последнем столбце в качестве элементов ![]()
3) Находим ![]() . Для этого с помощью общих формул (4.6) напишем
формулы для вычислений
. Для этого с помощью общих формул (4.6) напишем
формулы для вычислений ![]() при n=3:
при n=3:
![]()
![]()
![]()

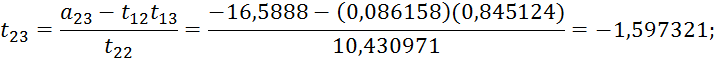
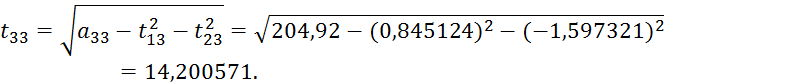
Результаты записываем в разделе II согласно схеме, указанной в левой части (см. таблицу 4.3).
4) Вычисляем элементы ![]() по формулам, аналогичным формулам (4.6):
по формулам, аналогичным формулам (4.6):
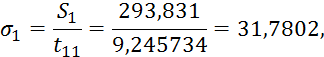

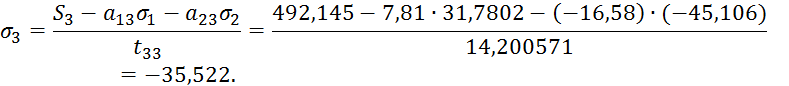
Обратный ход.
5) Находим ![]() . По формулам (4.7) последовательно будем
. По формулам (4.7) последовательно будем
иметь:

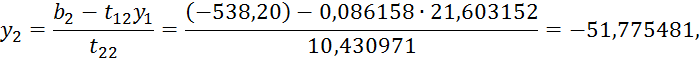


Значения ![]() ,- записываем в разделе II.
,- записываем в разделе II.
6) Находим ![]() .
.
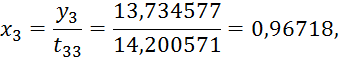


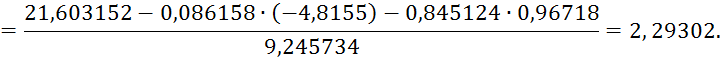
Результаты записываем в разделе III.
4.3 Схема Халецкого
Для удобства рассуждений систему линейных уравнений запишем в матричном виде
![]()
где ![]() квадратная матрица порядка n и
квадратная матрица порядка n и
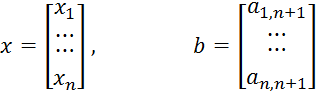
— векторы-столбцы. Представим матрицу А в виде
произведения нижней треугольной матрицы ![]() и верхней треугольной матрицы
и верхней треугольной матрицы ![]() с единичной диагональю, т. е.
с единичной диагональю, т. е.
![]() (4.9)
(4.9)
где
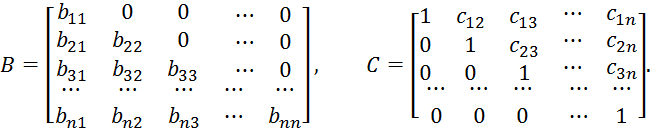
Тогда элементы ![]() определяются по формулам:
определяются по формулам:
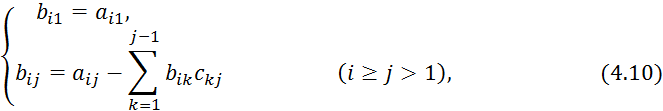 и
и

Отсюда искомый вектор ![]() может быть вычислен из цепи уравнений:
может быть вычислен из цепи уравнений:
![]() Так
как матрицы В и С—треугольные, то системы (4.12) легко решаются, а именно:
Так
как матрицы В и С—треугольные, то системы (4.12) легко решаются, а именно:
 и
и

Из формул (4.14) видно, что числа ![]() выгодно вычислять вместе с коэффициентами
выгодно вычислять вместе с коэффициентами ![]() . Этот метод получил название схемы Халецкого. В схеме
применяется обычный контроль с помощью сумм.
. Этот метод получил название схемы Халецкого. В схеме
применяется обычный контроль с помощью сумм.
Пример 4.3. Методом Халецкого решить систему уравнений.
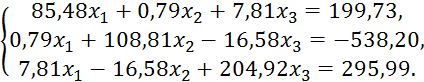
Результаты вычислений будем записывать в одну таблицу (см. таблицу 4.4). Схема Халецкого удобна для работы на клавишных вычислительных машинах, так как в этом случае операции «накопления» (4.10) и (4.11) можно проводить без записи промежуточных результатов.
Таблица 4.4
|
|
|
|
|
|
∑ |
|
|
|
|
∑ |
|
iI |
|
|
|
|
|
|
|
|
|
293,81 |
|
|
|
|
|
|
|
|
|
|
-445,18 |
|
|
|
|
|
|
|
|
|
|
|
492,14 |
|
|
III |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IIII |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Порядок заполнения таблицы.
1) В первый раздел таблицы 4.4 вписываем матрицу коэффициентов системы, ее свободные члены и контрольные суммы.
2) Элементы столбца ![]() из раздела I переносим в столбец
из раздела I переносим в столбец ![]() раздела II, так как
раздела II, так как ![]()
3) Вычисляем элементы первой строки раздела I на
элемент ![]() , в нашем случае на
, в нашем случае на ![]() .
.
Имеем:


![]() раздела II, начиная со второй строки.
Пользуясь формулами (4.10), определяем
раздела II, начиная со второй строки.
Пользуясь формулами (4.10), определяем ![]()
![]()
![]()
5) Заполняем вторую строку раздела II,
определяем ![]() для j=3,4,5 по формулам (4.11):
для j=3,4,5 по формулам (4.11):
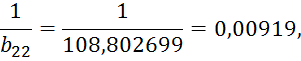
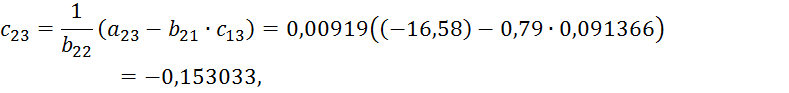
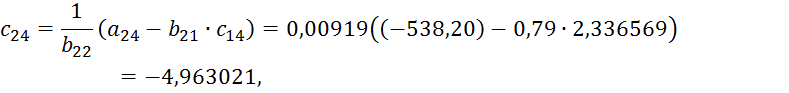
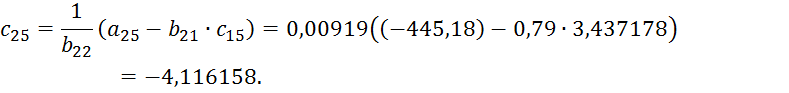
6) Заполняем столбец ![]() и третью строку раздела
II:
и третью строку раздела
II:
![]()
![]()
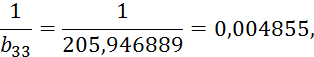
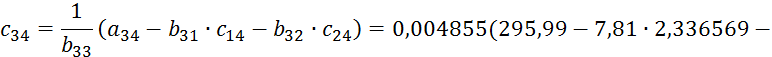
![]()
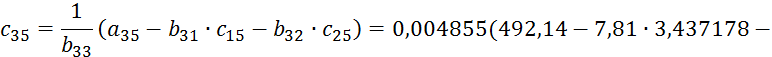
![]()
7) Определяем ![]() и
и ![]() (i=1,2,3) по формулам (4.13) и (4.14) и записываем в
раздел III:
(i=1,2,3) по формулам (4.13) и (4.14) и записываем в
раздел III:
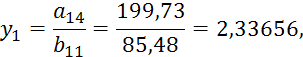
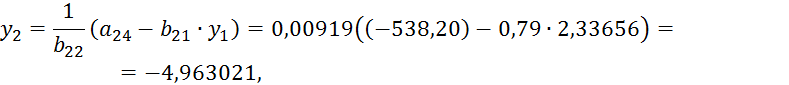
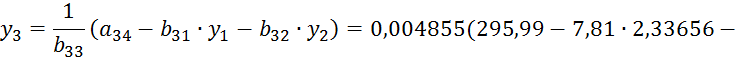
![]()
![]()
![]()
![]()
![]()
4.4 Итерационные методы Якоби и Зейделя
Перейдем к изучению итерационных методов решения систем линейных алгебраических уравнений. Рассмотрим сначала два примера итерационных методов. Для их построения предварительно преобразуем систему (4.1) к виду
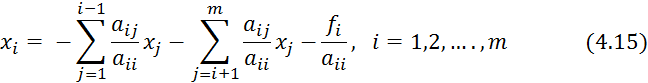
(при этом предполагается, что все ![]() отличны от нуля).
отличны от нуля).
Условимся, как обычно, считать значение суммы равным нулю, если верхний предел суммирования меньше нижнего. Так, уравнение (4.15) при i= 1 имеет вид:

В дальнейшем верхний индекс будет указывать номер итерации, например:
![]()
где ![]() итерация i-й компоненты вектора х.
итерация i-й компоненты вектора х.
В методе Якоби исходят из записи системы в виде (4.15), причем итерации определяются следующим образом:
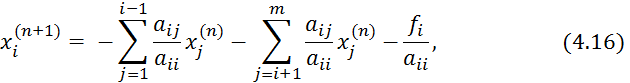
где ![]()
Начальные значения ![]() задаются произвольно. Окончание итераций определяется
либо заданием максимального числа итераций
задаются произвольно. Окончание итераций определяется
либо заданием максимального числа итераций ![]() , либо условием:
, либо условием:
![]()
где![]() — заданное число.
— заданное число.
Итерационный метод Зейделя имеет вид
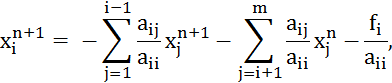
![]() (4.17)
(4.17)
Чтобы понять, как находятся отсюда значения ![]() , i=1,2…,n
запишем подробнее первые два уравнения системы (4.17):
, i=1,2…,n
запишем подробнее первые два уравнения системы (4.17):
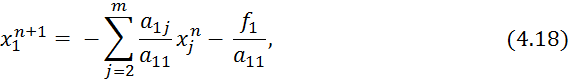
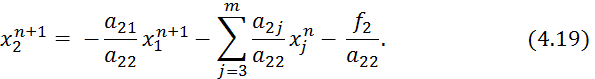
Первая компонента ![]() вектора
вектора ![]() находится из уравнения (4.17) явным образом, для ее
вычисления нужно знать вектор
находится из уравнения (4.17) явным образом, для ее
вычисления нужно знать вектор ![]() и значение
и значение ![]() . При нахождении
. При нахождении ![]() из уравнения (4.19) используются только что найденное
значение
из уравнения (4.19) используются только что найденное
значение ![]() и известные значения
и известные значения ![]() , j = 3, ..., m, с предыдущей итерации. Таким образом, компоненты
, j = 3, ..., m, с предыдущей итерации. Таким образом, компоненты ![]() вектора
вектора ![]() находятся из уравнения (4.18) последовательно,
начиная с i=1.
находятся из уравнения (4.18) последовательно,
начиная с i=1.
Условием сходимости итерационного процесса для систем линейных уравнений будет достаточно выполнения одного из следующих условий:
а) в пространстве с метрикой ![]()

т.е. максимальная из сумм модулей коэффициентов при неизвестных в правой части системы (4.1), взятых по строкам, должна быть меньше единицы;
б) в пространстве с метрикой ![]()

т.е. максимальная из сумм модулей коэффициентов при неизвестных в правой части системы (4.1), взятых по столбцам, должна быть меньше единицы;
в) в пространстве с метрикой ![]()
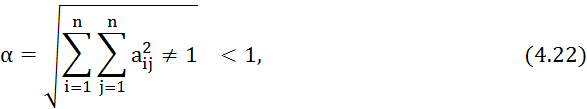 т.е.
сумма квадратов всех коэффициентов при неизвестных в правой части системы (4.1)
должна быть меньше единицы.
т.е.
сумма квадратов всех коэффициентов при неизвестных в правой части системы (4.1)
должна быть меньше единицы.
Пример 4.4. Решить систему
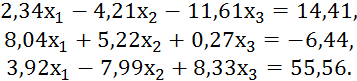
Методом простой итерации с точностью ![]()
Решение. Для обеспечения условия сходимости нужно получить систему вида (4.16) из системы (4.1) так, чтобы коэффициенты при неизвестных в правой части системы были существенно меньше единицы. Систему (4.1) с помощью равносильных преобразований надо привести к системе, у которой абсолютные величины коэффициентов, стоящих на главной диагонали, были больше абсолютных величин каждого из других коэффициентов при неизвестных в соответствующих уравнениях. Для этого первым уравнением возьмем второе, третьим- первое, а вторым – сумму первого с третьим:
 ,
,
Разделим теперь каждое уравнение на его диагональный коэффициент и выразим из каждого уравнения диагональное неизвестное:
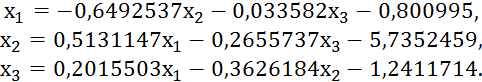
Теперь необходимо проверить одно из условий сходимости
(4.18)-(4.20). Не выполнение одного из условий еще не означает, что метод итераций
применить нельзя. Установим условие сходимости в пространстве с евклидовой
метрикой ![]() Имеем:
Имеем:
![]()
![]()
![]() 1.
1.
Итерационный процесс в евклидовом пространстве
сходится, причем коэффициент сжатия ![]() За начальное приближение можно взять точку (0;0;0).
За начальное приближение можно взять точку (0;0;0).
Пример 4.5. Решить систему

Методом Зейделя с точностью ![]() .
.
Решение.
Преимущество метода Зейделя перед методом простой итераций состоит в быстрой сходимости. Приведем данную систему к нормальному виду, облегчающую процесс преобразования. Запишем систему в матричном виде:
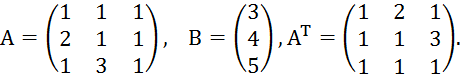
Умножим обе части системы на транспонированную матрицу, получим:
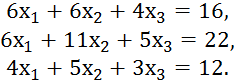
Данная нормальная система обладает рядом хороших свойств:
- Коэффициенты при неизвестных нормальной системы являются
симметрической (т.е. ![]()
- Все элементы главной диагонали нормальной системы
положительны (т.е. ![]()
Приведенная система, эквивалентная этой нормальной системе, будет выглядеть так:
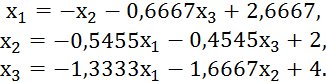
Расчетные формулы итерационного процесса Зейделя будут иметь такой вид:
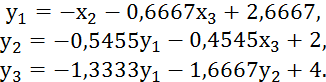
За начальное приближение можно взять столбец свободных членов (2,7;2;4).
5 Интерполирование и приближение функций
Для установления закономерностей при изучении многих природных явлений проводятся эксперименты или осуществляют сбор статистических данных об объекте исследования. Если набор экспериментальных данных получен со значительной погрешностью, то не имеет смысла использовать интерполяцию Лагранжа полиномами и сплайнами для обработки результатов. В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживает возможные выбросы за счёт погрешности эксперимента. Такую операцию называют аппроксимацией, полученную при этом функцию называют аппроксимирующей функцией, а ее график - аппроксимирующей линией. Пусть функциональная зависимость задана таблицей 5.1:
Таблица 5.1
|
|
|
|
|
|
|
|
|
|
|
|
Для функции ![]() , заданной таблицей (5.1), найти многочлен
, заданной таблицей (5.1), найти многочлен ![]() такой, что выполняется совокупность условий
интерполяции:
такой, что выполняется совокупность условий
интерполяции:
![]()
Найти многочлен ![]() — это значит, учитывая его каноническую форму:
— это значит, учитывая его каноническую форму:
![]()
Найти его n+1 коэффициенты ![]() .
.
Обычно задача
интерполирования формулируется так: найти многочлен ![]() степени не выше n, значения которого в точках
степени не выше n, значения которого в точках ![]() совпадают со значениями данной функции, то есть
совпадают со значениями данной функции, то есть ![]() .
.
Геометрически это означает, что нужно найти алгебраическую кривую вида:
![]()
проходящую через заданную систему точек ![]() (см. рисунок 5.1). Многочлен
(см. рисунок 5.1). Многочлен ![]() называется интерполяционным многочленом. Точки
называется интерполяционным многочленом. Точки ![]() называются узлами интерполяции.
называются узлами интерполяции.
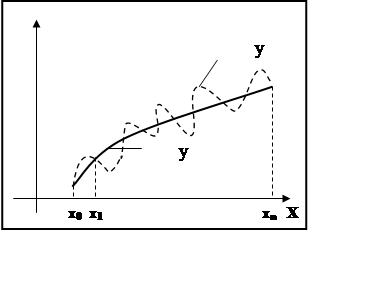
Рисунок 5.1 - Интерполирование алгебраическим многочленом
Для любой непрерывной функции f(x) сформулированная задача имеет единственное решение.
Действительно, для отыскания коэффициентов ![]() получаем систему линейных уравнений:
получаем систему линейных уравнений:
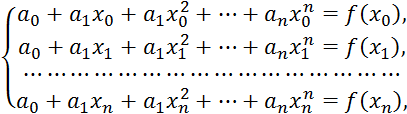
![]()
определитель которой (определитель Вандермонда)
отличен от нуля, если среди точек ![]() нет совпадающих.
нет совпадающих.
Решение системы (5.2) можно записать различным образом.
5.1 Интерполяционный многочлен Лангранжа
Пусть узлы ![]() расположены произвольным образом. Интерполяционный
многочлен будем искать в виде
расположены произвольным образом. Интерполяционный
многочлен будем искать в виде
![]()
![]()
Коэффициенты ![]() многочлена
многочлена ![]() подберем так, чтобы для него выполнялись условия (5.1).
подберем так, чтобы для него выполнялись условия (5.1).
При ![]() все слагаемые в (5.1), начиная со второго, равны нулю.
все слагаемые в (5.1), начиная со второго, равны нулю.
Следовательно, ![]() и потому
и потому

Действуя по аналогичной схеме при ![]() выводим:
выводим:
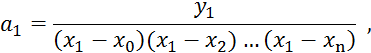
![]()
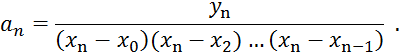
Подставив найденные коэффициенты в (5.3), получим общее выражение для интерполяционного многочлена Лагранжа:
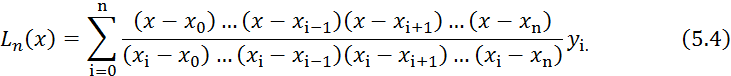
При n=1 мы имеем две точки, и формула Лагранжа представляет
в этом случае уравнение прямой ![]() , проходящей через две заданные точки:
, проходящей через две заданные точки:
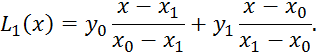
При n=2, получим уравнение параболы ![]() , проходящей через три точки:
, проходящей через три точки:
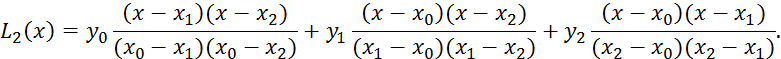
Для удобства вычисления лангранжевых коэффициентов может быть использована приведенная ниже схема 5.1:
Схема 5.1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим произведение элементов первой строки через ![]() , второй – через
, второй – через ![]() и т.д. Произведение элементов главной диагонали (в
схеме элементы подчеркнуты), очевидно, будет
и т.д. Произведение элементов главной диагонали (в
схеме элементы подчеркнуты), очевидно, будет ![]() .
.
Отсюда следует, что
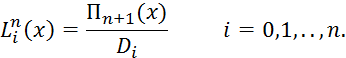
Следовательно
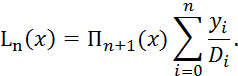
Пример 5.1.
Пользуясь интерполяционной формулой Лагранжа, составить уравнение прямой,
проходящей через точки ![]() , если
, если ![]()
Решение. В данном случае многочлен Лагранжа примет вид:
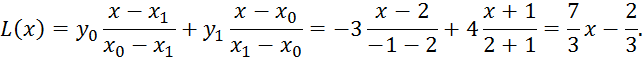
Уравнение искомой прямой есть ![]()
5.2 Интерполяционный многочлен Ньютона
5.2.1 Первый интерполяционный многочлен Ньютона.
Пусть функция ![]() задана на сетке равноотстоящих узлов:
задана на сетке равноотстоящих узлов: ![]() , где
, где ![]()
Будем искать интерполяционный многочлен n-й степени в виде:
![]()
![]()
Коэффициенты ![]() находим, исходя из условий (5.5).
находим, исходя из условий (5.5).
Пусть![]() . Тогда
. Тогда ![]() .
.
При ![]()

При ![]()
![]()
![]()
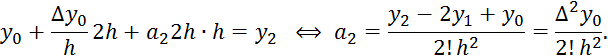
Аналогичным образом можно получить
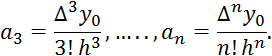
Для нескольких первых порядков разностей можно получить прямой подстановкой:
![]()
![]()
![]()
![]()
Можно описать одной рекуретной формулой, выражающий
конечную разность k- порядка![]() через разность k-1-го поряка:
через разность k-1-го поряка:
![]() , (5.6)
, (5.6)
где ![]()
Подметив закономерность в коэффициентах рассмотренных представлений конечных разностей, запишем общую формулу:
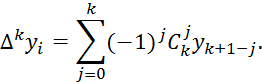
Подставим найденные значения ![]() в (5.5):
в (5.5):
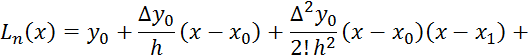
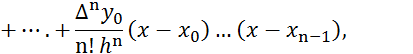
или запишем в более удобном виде

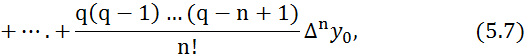
где
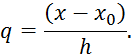
Многочлен (5.7) называется первым интерполяционным многочленом Ньютона .
При n=1 и n=2 из формулы (5.7) получаем частные случаи:
- линейная интерполяция
![]()
- квадратичная интерполяция
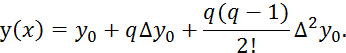
Пример 5.2. По данной таблице 5.2 значений найти функцию.
Таблица 5.2
|
y |
x |
Δy |
|
0,3704 |
2,70 |
-0,0028 |
|
0,3676 |
2,72 |
-0,0026 |
|
0,365 |
2,74 |
Решение. Используя формулу (5.7) при n=1, получим:
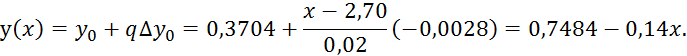
5.2.2 Второй интерполяционный многочлен Ньютона.
Для этого, в отличие от (5.5), форма интерполяционного
многочлена ![]() берется такой, которая предусматривает поочередное
подключение узлов в обратном порядке: сначала последний, потом предпоследний и
т.д.
берется такой, которая предусматривает поочередное
подключение узлов в обратном порядке: сначала последний, потом предпоследний и
т.д.
Коэффициенты ![]() этого многочлена находятся аналогично тому, как они
находились для многочлена (5.5), только здесь подстановка узловых точек вместо
этого многочлена находятся аналогично тому, как они
находились для многочлена (5.5), только здесь подстановка узловых точек вместо ![]() и рассмотрение интерполяционных равенств производится в обратном
порядке. Полагая
и рассмотрение интерполяционных равенств производится в обратном
порядке. Полагая ![]() имеем:
имеем:
![]()
![]() .
.
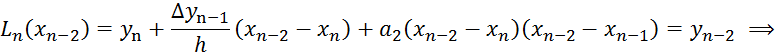
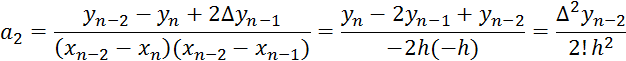
и т.д. В общем случае
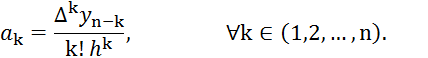
Таким образом, получаем второй интерполяционный многочлен Ньютона:
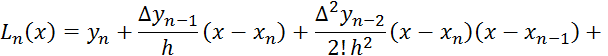
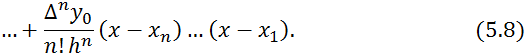
Положим в (5.8) ![]() иначе, введем новую переменную
иначе, введем новую переменную ![]() и преобразуем к ней входящие в (5.8) разности:
и преобразуем к ней входящие в (5.8) разности:
![]()
В результате приходим ко второй интерполяционной формуле Ньютона вида:
![]()
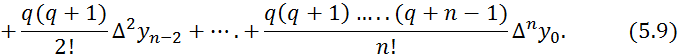
Ее также целесообразно использовать при значениях ![]() , т.е. в окрестности узла
, т.е. в окрестности узла ![]() для интерполирования назад (при q ∈ (-1, 0)) и экстраполирования вперед (при q > 0).
для интерполирования назад (при q ∈ (-1, 0)) и экстраполирования вперед (при q > 0).
5.3 Интерполяционные формулы Гаусса
5.3.1 Первая интерполяционная формула Гаусса.
Основным недостатком интерполяционных формул Ньютона
является то, что они используют лишь односторонние значения функции. На
практике часто оказывается полезным использовать формулы, в которых
присутствуют как последующие, так и предыдущие значения функции по отношению к
ее начальному значению ![]()
Рассмотрим![]() равноотстоящих узлов:
равноотстоящих узлов:
![]()
в которых заданы значения некоторой функции ![]()
Будем искать полином в виде
![]()
![]()
![]()
(5.10)
предполагающей постепенное подключение узлов ![]() ,: сначала при i = 0, затем
при i = 1, потом
при i = -1 и
т.д., т.е. с двух сторон от
,: сначала при i = 0, затем
при i = 1, потом
при i = -1 и
т.д., т.е. с двух сторон от ![]() .
.
Как и в предыдущих случаях, коэффициенты ![]() находим один за другим последовательной подстановкой
в L(x) и в интерполяционные
равенства
находим один за другим последовательной подстановкой
в L(x) и в интерполяционные
равенства ![]() , значений
, значений ![]()
Поступая по аналогии с выводом первой интерполяционной
формулы Ньютона, для коэффициентов ![]() получим следующие выражения:
получим следующие выражения:
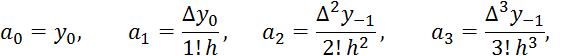
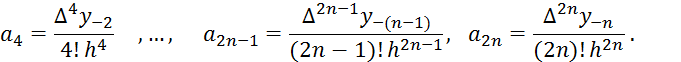
Введем новую переменную q=![]() и, выразив
через нее разности для всех
и, выразив
через нее разности для всех ![]() , ..., в результате подстановки этих разностей и выражений
коэффициентов в формулу (5.10), приходим к первой интерполяционной формуле
Гаусса
, ..., в результате подстановки этих разностей и выражений
коэффициентов в формулу (5.10), приходим к первой интерполяционной формуле
Гаусса
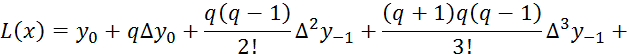
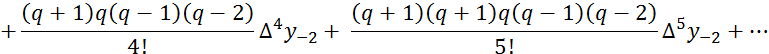
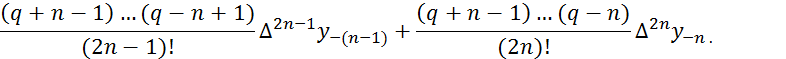
(5.11)
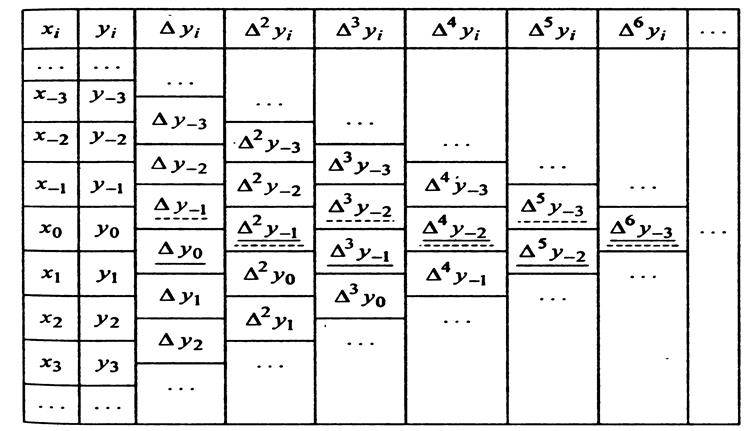
Записанные слагаемые легко дополнить следующими, если знать, что в этой формуле используются нижние центральные разности все возрастающих порядков, т.е. те, которые подчеркнуты в таблице 5.3 сплошной чертой.
Таблица центральных разностей
Таблица 5.3
5.3.2 Вторая интерполяционная формула Гаусса.
Совершенно аналогично, подключая узлы в другом порядке
(после ![]() ), сначала
предшествующий, затем последующий и т.д., т.е.
), сначала
предшествующий, затем последующий и т.д., т.е. ![]() удем искать полином в виде:
удем искать полином в виде:
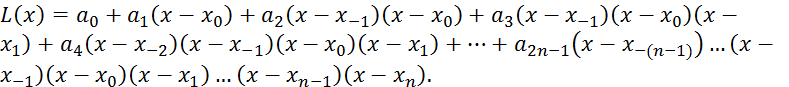
Проведя аналогичные выше выкладки, получим вторую интерполяционную формулу Гаусса (для интерполирования назад):

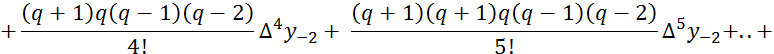
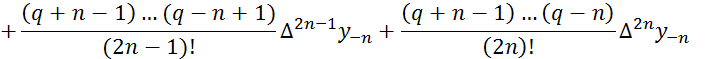
(5.12)
Формулы Гаусса применяются для интерполирования в
середине таблицы вблизи ![]() . При этом первая формула Гаусса (5.11) применяется
при
. При этом первая формула Гаусса (5.11) применяется
при ![]() , а вторая (5.12) – при
, а вторая (5.12) – при ![]() .
.
5.4 Интерполяционная формула Стирлинга
Среднее арифметическое первой (5.11) и второй (5.12) формул Гаусса дает интерполяционную формулу Стирлинга:
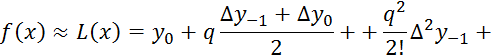
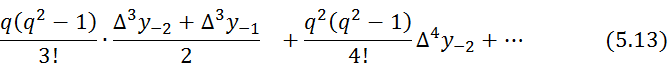
5.5 Интерполяционная формула Бесселя
Если же взять полусумму второго интерполяционного
многочлена Гаусса и такого же многочлена, но с нижними индексами, увеличенными
на единицу (т.е. с базовой точкой ![]() вместо
вместо ![]() ), тo придем к интерполяционной формуле Бесселя:
), тo придем к интерполяционной формуле Бесселя:
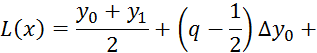
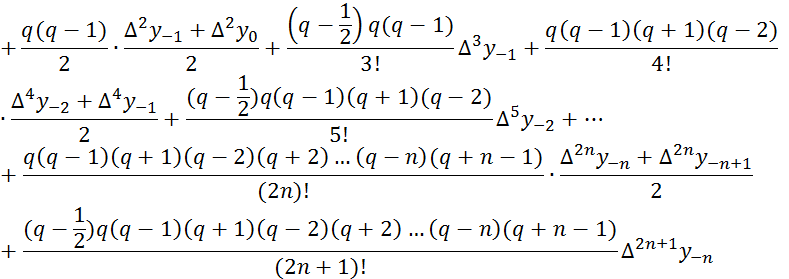
(5.14)
В последней формуле обращает на себя внимание тот
факт, что она сильно упростится, если в нее подставить значение ![]() , соответствующее значению аргумента
, соответствующее значению аргумента ![]()
Этот частный случай формулы Бесселя называют формулой интерполирования на середину:

(5.15)
Итак, если точка ![]() , в которой нужно найти приближенное значение таблично заданной функции
, в которой нужно найти приближенное значение таблично заданной функции
![]() , находится в начале или в конце таблицы, применяется
соответственно первая (5.7) или вторая (5.9) формулы Ньютона с таким выбором
базовой точки, чтобы значение
, находится в начале или в конце таблицы, применяется
соответственно первая (5.7) или вторая (5.9) формулы Ньютона с таким выбором
базовой точки, чтобы значение ![]() было как можно меньше. Если точка
было как можно меньше. Если точка ![]() находится в середине таблицы, то всегда можно зафиксировать точку
находится в середине таблицы, то всегда можно зафиксировать точку ![]() в таблице центральных разностей так, чтобы
в таблице центральных разностей так, чтобы ![]() либо было по модулю
либо было по модулю ![]() и тогда применять интерполяционную формулу Стирлинга (5.13),
либо, чтобы
и тогда применять интерполяционную формулу Стирлинга (5.13),
либо, чтобы ![]() использовать формулу
использовать формулу
Бесселя (5.15).
Пример 5.3. Используя таблицу значений функции y = sinx, требуется найти приближенные значения: а) sin 33; б) sin 41; в) sin 48; г) sin 54, записав предварительно соответствующие каждому случаю интерполяционные формулы.
Решение. Составив таблицу разностей таблица 5.4, видим,
Таблица 5.4
|
x (в градусах) |
x(в радианах) |
y |
Δy |
Δy2 |
Δy3 |
|
30 |
0,5236 |
0,5000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0736 |
|
|
|
35 |
0,6109 |
0,5736 |
|
-0,0044 |
|
|
|
|
|
0,0692 |
|
-0,0005 |
|
40 |
0,6981 |
0,6428 |
|
-0,0049 |
|
|
|
|
|
0,0643 |
|
-0,0005 |
|
45 |
0,7854 |
0,7071 |
|
-0,0054 |
|
|
|
|
|
0,0589 |
|
-0,0003 |
|
50 |
0,8727 |
0,7660 |
|
-0,0057 |
|
|
|
|
|
0,0532 |
|
|
|
55 |
0,9599 |
0,8192 |
|
|
|
что третьи разности практически постоянны. Поэтому в формулах достаточно взять четыре члена:
а) Для вычисления ![]() имеем
имеем

По формуле первой интерполяционной формуле (5.7) и, учитывая данные из таблицы, получим:
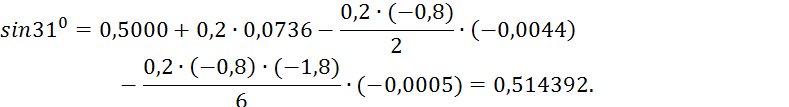
б) Для
вычисления ![]() имеем: точка
имеем: точка ![]() находится в средней части таблицы. Поэтому здесь
целесообразно применить формулу Стирлинга или Бесселя. Полагая здесь
находится в средней части таблицы. Поэтому здесь
целесообразно применить формулу Стирлинга или Бесселя. Полагая здесь ![]() и найдя
и найдя
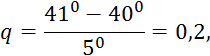
останавливаемся на формуле Стирлинга (5.13), которая в данном случае имеет вид:
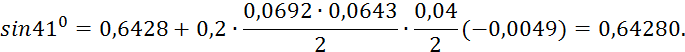
в) Для вычисления sin 48 также возможно применение центральных интерполяционных
формул. Положив ![]() и вычислив
и вычислив
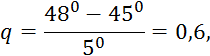
на основе (5.15) записываем интерполяционную формулу Бесселя:
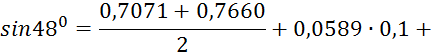
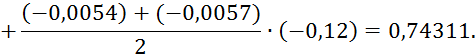
г) Для вычисления ![]() , имеем точка
, имеем точка ![]() расположена в конце узла, поэтому для экстраполяции
функции здесь однозначно следует применить вторую интерполяционную формулу
Ньютона (5.9). Считая
расположена в конце узла, поэтому для экстраполяции
функции здесь однозначно следует применить вторую интерполяционную формулу
Ньютона (5.9). Считая ![]() , записываем формулу экстраполяции с учётом
, записываем формулу экстраполяции с учётом
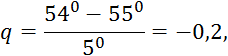
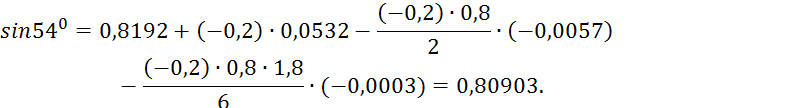
5.6 Метод наименьших квадратов
Можно, применить метод интерполяции: построить
интерполяционный многочлен (например, Лагранжа или Ньютона), значения которого
в точках ![]() будут
совпадать с соответствующими значениями
будут
совпадать с соответствующими значениями ![]() из таблицы 5.1. Однако совпадение значений в узлах
иногда может вовсе не означать совпадения характеров поведения исходной и
интерполирующей функции.
из таблицы 5.1. Однако совпадение значений в узлах
иногда может вовсе не означать совпадения характеров поведения исходной и
интерполирующей функции.
В
дальнейшем табличные данные из таблицы 5.1 называются статистическими (экспериментальными) и на
основе этих данных должна быть получена функция, связывающая
переменных ![]() и
и ![]() :
:
![]() .
.
Для определения такой функции необходимо решить две задачи, называемые двумя основными задачами статистики:
- определение общего вида аппроксимирующей функции, ![]() может
включать в себя неизвестные параметры, например:
может
включать в себя неизвестные параметры, например:

![]()

![]()
- определение неизвестных параметров ![]()
![]()
Первая задача решается феноменологическим методом,
исходя из интуиции исследователя и заданной таблицы значений аргумента ![]() и функции
и функции ![]() . Для
решения второй задачи используется метод наименьших квадратов.
. Для
решения второй задачи используется метод наименьших квадратов.
Суть метода наименьших квадратов
Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающей функции с тремя параметрами:
![]() ( 5.16)
( 5.16)
Имеем ![]() Сумма квадратов разностей соответствующих значений
функций
Сумма квадратов разностей соответствующих значений
функций ![]() будет иметь вид:
будет иметь вид:
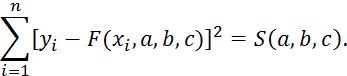
Задача сводится к отысканию минимума. Используем необходимое условие экстремума:
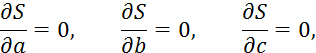
т.е.
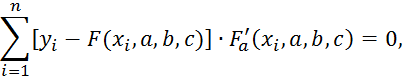
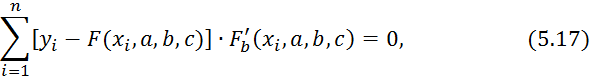
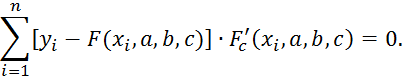
Из системы линейных уравнений (5.17) определяются
коэффициенты a,b,c и получим конкретный вид искомой функции ![]()
Естественно ожидать, что значения найденной функции ![]() в точках
в точках ![]() будут отличаться от табличных значений
будут отличаться от табличных значений ![]()
Значения разностей:
![]()
называются отклонениями измеренных значении ![]() от вычисленных по формуле (5.16).
от вычисленных по формуле (5.16).
Видно из примера, изменение количества параметров не приведет к искажению сущности метода, а выразится лишь в изменении количества уравнений в системе (5.17).
Рассмотрим самый простой случай аппроксимации, когда в
качестве аппроксимирующей функции рассматривается линейная функция ![]() . Этот случай называется линейной аппроксимацией.
Тогда функция
. Этот случай называется линейной аппроксимацией.
Тогда функция ![]() имеет
следующий вид:
имеет
следующий вид:
![]()
где ![]() и
и ![]() – неизвестные
параметры, а условие минимума:
– неизвестные
параметры, а условие минимума:
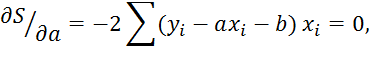
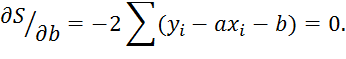
После простых преобразований можно получить систему
двух уравнений с двумя неизвестными ![]() и
и ![]() :
:
![]()
![]()
где ![]()
Решая эту систему, можно получить значения неизвестных
параметров ![]() и
и ![]()
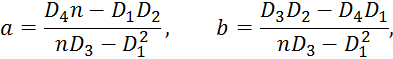
где
![]()
Пример 5.4. Рассмотрим построение и оценку экономико–математической модели среднесрочного прогноза спроса населения на электробытовые товары на основе данных динамики товарооборота за ряд лет (см. таблицу 5.5).
Таблица 5.5
|
Товарооборот |
1,8 |
4,3 |
4,3 |
6,4 |
5,7 |
7,5 |
7,8 |
9,2 |
? |
|
Время |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2030 |
Необходимо осуществить прогноз спроса на 2030 год, полагая, что тенденция изменения спроса за ряд предыдущих лет сохранится в будущем.
Решение.
Построим диаграмму рассеивания в корреляционном поле и сравним с имеющимся
графическими моделями математических форм связи. Для упрощения вычислительных
операций перейдем к новой системе координат ![]() (см. рисунок 5.2).
(см. рисунок 5.2).

Рисунок 5.2 – Диаграмма рассеивания
Определяем, что более всего подходит зависимость в виде параболы:
![]()
Задача сводится к отысканию её минимума, используем формулу (5.17) и после некоторых преобразований получим:
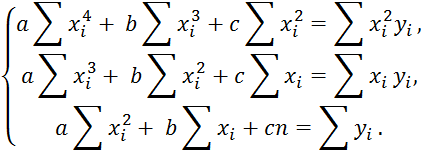
Для удобства проведения расчетов расположим результаты промежуточных вычислений с учетом последующего анализа в таблице 5.6.
Таблица 5.6
|
N |
|
|
|
|
|
|
|
|
|
1 |
1,8 |
2005 |
1 |
1 |
1 |
1 |
1,8 |
1,8 |
|
2 |
4,3 |
2006 |
2 |
4 |
8 |
16 |
17,2 |
8,6 |
|
3 |
4,3 |
2007 |
3 |
9 |
27 |
81 |
38,7 |
12,9 |
|
4 |
6,4 |
2008 |
4 |
16 |
64 |
256 |
102,4 |
25,6 |
|
5 |
5,7 |
2009 |
5 |
25 |
125 |
625 |
142,5 |
28,5 |
|
6 |
7,5 |
2010 |
6 |
36 |
216 |
1296 |
270 |
45 |
|
7 |
7,8 |
2011 |
7 |
49 |
343 |
2401 |
352,8 |
50,4 |
|
8 |
9,2 |
2012 |
8 |
64 |
512 |
4096 |
524,8 |
65,6 |
|
Σ |
47 |
- |
36 |
204 |
1296 |
8772 |
1543,6 |
250,6 |
Пользуясь: данными таблицы, систему нормальных уравнений перепишем в виде:
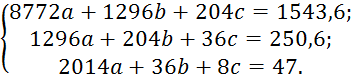
Решаем данную систему одним из методов решения систем алгебраических уравнений и находим значения коэффициентов:
![]()
На этом оснавании запишем экономико - математическую модель прогноза спроса населения на электробытовые товары:
![]()
Пользуясь полученной моделью, определим значения спроса населения:
![]()
6 Методы численного интегрирования
Пусть на отрезке ![]() задана функция
задана функция ![]() . Разобьем отрезок
. Разобьем отрезок ![]() с помощью точек
с помощью точек ![]() на
на ![]() элементарных отрезков
элементарных отрезков ![]() На каждом из этих отрезков возьмем произвольную точку
На каждом из этих отрезков возьмем произвольную точку
![]() . Предел интегральной суммы при увеличении числа точек
разбиения называется определенным интегралом от функции
. Предел интегральной суммы при увеличении числа точек
разбиения называется определенным интегралом от функции ![]() на отрезке
на отрезке ![]() :
:
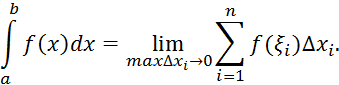
Геометрический смысл определенного интеграла
заключается в том, что он численно равен площади криволинейной трапеции,
ограниченной кривой ![]() , осью Ox и прямыми
, осью Ox и прямыми ![]() . Подынтегральная функция
. Подынтегральная функция ![]() может быть задана одним из трех следующих способов:
может быть задана одним из трех следующих способов:
1) Задается явная формула для ![]() .
.
2) Задана таблица значений ![]() на отрезке
на отрезке ![]() для некоторого фиксированного набора точек
для некоторого фиксированного набора точек ![]() .
.
В первом случае интеграл вычисляется с использованием
формулы Ньютона – Лейбница ![]() , где F(x)-первообразная. Однако во многих случаях
первообразная функция F (х) не может быть найдена с помощью элементарных
средств или является слишком сложной; вследствие этого вычисление
определенного интеграла может быть затруднительным или даже практически
невыполнимым. Во втором случае подынтегральная функция
, где F(x)-первообразная. Однако во многих случаях
первообразная функция F (х) не может быть найдена с помощью элементарных
средств или является слишком сложной; вследствие этого вычисление
определенного интеграла может быть затруднительным или даже практически
невыполнимым. Во втором случае подынтегральная функция ![]() задана
таблично, и тогда само понятие первообразной теряет смысл. Поэтому важное
значение имеют приближенные и в первую очередь численные методы вычисления
определенных интегралов.
задана
таблично, и тогда само понятие первообразной теряет смысл. Поэтому важное
значение имеют приближенные и в первую очередь численные методы вычисления
определенных интегралов.
Они основаны на аппроксимации ![]() некоторой другой функцией
некоторой другой функцией ![]() (чаще всего полиномом), интеграл от которой
вычисляется сравнительно просто:
(чаще всего полиномом), интеграл от которой
вычисляется сравнительно просто:
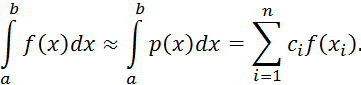
Это приближенное равенство называется квадратурной формулой. Разность
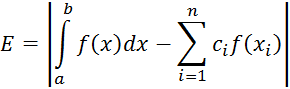
называется погрешностью квадратурной формулы.
К понятию определённого интеграла приводят самые разнообразные задачи: определение площади фигуры, объём тела вращения, длина дуги плоской кривой, отыскание работы переменной скорости и многие другие.
Основным недостатком численных методов является то,
что результат получается в виде приближенного числового значения. Точность этих
методов зависит от выбранного шага ![]() , чем меньше
шаг, тем точнее результат. Очевидно, что для достижения большой точности
необходимо производить большой объем вычислительной работы.
, чем меньше
шаг, тем точнее результат. Очевидно, что для достижения большой точности
необходимо производить большой объем вычислительной работы.
6.1 Метод прямоугольников
Разобьем отрезок ![]() на
на ![]() частичных отрезка с помощью точек
частичных отрезка с помощью точек ![]() и представим интеграл в виде суммы интегралов по этим
отрезкам:
и представим интеграл в виде суммы интегралов по этим
отрезкам:
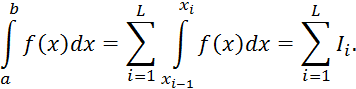
Аппроксимируем функцию ![]() на каждом частичном отрезке полиномом нулевой степени
(константой). Обозначим
на каждом частичном отрезке полиномом нулевой степени
(константой). Обозначим ![]() формула прямоугольников имеет вид
формула прямоугольников имеет вид ![]()
Суммируя эти значения интегралов на частичных отрезках, получим соответствующие составные формулы прямоугольников:
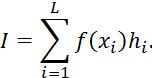
Формула прямоугольников для вычисления определенного интеграла
![]() (6.1)
(6.1)
Предельная абсолютная погрешность:

Алгоритм данного метода очень простой; требуется составить простой цикл для вычисления суммы.
Алгоритм вычисления будет следующий:
а) ввод граничных условии a,b, количество итерации n;
б) вычисление шага ![]() , присваиваем
, присваиваем ![]() ;
;
в) начало цикла ![]() ;
;
г) в цикле ![]() ;
;
е) вывод значения ![]() .
.
Пример 6.1. Найти ![]() по формуле прямоугольников, разбив интервал на 10
частей. Оценить погрешность.
по формуле прямоугольников, разбив интервал на 10
частей. Оценить погрешность.
Решение. При ![]() имеем
имеем ![]() Точками деления служат
Точками деления служат ![]() Найдем соответствующие значения подынтегральной
функции и запишем в таблице 6.1.
Найдем соответствующие значения подынтегральной
функции и запишем в таблице 6.1.
Таблица 6.1
|
x |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
|
y |
1 |
1,049 |
1,095 |
1,140 |
1,183 |
1,225 |
1,265 |
1,304 |
1,342 |
1,378 |
Используя формулу прямоугольников, получим:
I=0,1(1,000+1,049+1,095+1,140+1,183+1,225+1,265+1,304+1,342+1,378)≈1,20.
Оценим погрешность. В данном случае ![]() ) на отрезке [a,b] достигает наибольшего значения,
равного 0,5, при
) на отрезке [a,b] достигает наибольшего значения,
равного 0,5, при ![]() Таким образом,
Таким образом,
![]() Отсюда по формуле находим:
Отсюда по формуле находим:
![]() Следовательно,
Следовательно, ![]()
6.2 Метод трапеций
Следующим простейшим полиномом является линейная
функция. Если выбрать ее совпадающей с ![]() на
концах частичного отрезка
на
концах частичного отрезка ![]() то получим трапецию. Площадь ее принимается в
качестве приближения к значению определенного интеграла и вычисляется по формуле
трапеций (см. рисунок 6.1).
то получим трапецию. Площадь ее принимается в
качестве приближения к значению определенного интеграла и вычисляется по формуле
трапеций (см. рисунок 6.1).

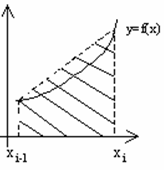
Рисунок 6.1 - Метод трапеций
Составная формула трапеций имеет вид:
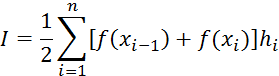
Для случая равномерного шага ![]() формула трапеций для вычисления определенного интеграла
формула трапеций для вычисления определенного интеграла
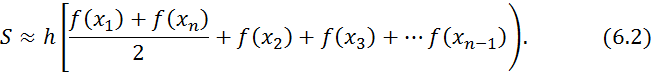
Предельная абсолютная погрешность

Алгоритм вычисления будет следующий:
а) ввод граничных условии a,b, количество итерации n;
б) вычисление шага ![]() , присваиваем
, присваиваем ![]() ;
;
в) вычисляем ![]() ;
;
г) начало цикла ![]() ;
;
д) в цикле ![]() ;
;
е) вывод значения ![]() .
.
Пример 6.2. Найти ![]() по формуле трапеций, разбив интервал на 10 частей.
Оценить погрешность.
по формуле трапеций, разбив интервал на 10 частей.
Оценить погрешность.
Решение. При тех же обозначениях, используя формулу трапеций, получим
I=0,1(![]() +1,049+1,095+1,140+1,183+1,225+1,265+1,304+1,342+1,378)≈1,218.
+1,049+1,095+1,140+1,183+1,225+1,265+1,304+1,342+1,378)≈1,218.
Далее. ![]() на отрезке [1,2]. Таким образом,
на отрезке [1,2]. Таким образом,
![]() Следовательно,
Следовательно, ![]()
6.3 Формула Симпсона
В качестве аппроксимирующего полинома
можно использовать полином второй степени. По трем точкам ![]() построим интерполяционный полином
Лагранжа :
построим интерполяционный полином
Лагранжа :
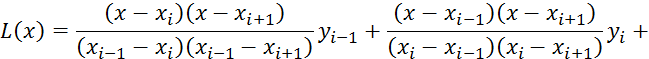

Для дальнейших преобразований введем
переменную ![]() с помощью равенства
с помощью равенства![]() и изменяя
и изменяя ![]() равным 0, 1, 2, получим значения
равным 0, 1, 2, получим значения ![]() , равные
, равные ![]() .
.
Выразим сплайн ![]() через новую переменную
через новую переменную ![]() :
:
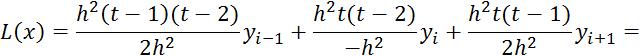
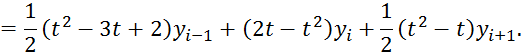
Учитывая, что ![]()
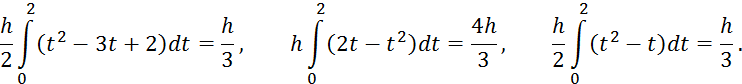
Площадь криволинейной трапеции
заменим площадью, ограниченной графиком ![]() . В этом случае:
. В этом случае:
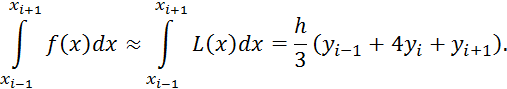
![]()
Полученная формула называется формулой Симпсона, или формулой парабол. Составная формула Симпсона:
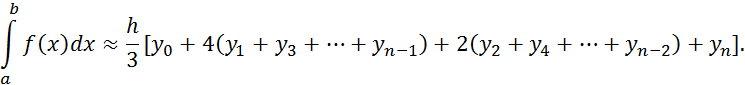
(6.3)
Формула Симпсона выглядит более
громоздкой по сравнению с формулами прямоугольников и трапеций, но она
значительно точнее их и может привести к требуемому результату при меньших ![]() .
.
Предельная абсолютная погрешность:
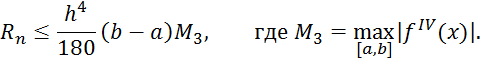
Алгоритм вычисления будет следующий:
а) ввод граничных условии a,b, количество итерации n;
б) вычисление шага ![]() , присваиваем
, присваиваем ![]() ;
;
в) вычисляем ![]() ;
;
г) начало цикла ![]() ;
;
д) в цикле: при четном ![]()
![]() при нечетном
при нечетном ![]() вычисляется
вычисляется ![]() ,
, ![]() ;
;
е) вывод значения ![]() .
.
7 Решение задачи Коши для обыкновенных дифференциальных уравнений
Среди задач, с которыми приходится иметь дело в вычислительной практике, значительную часть составляют различные задачи, сводящиеся к решению обыкновенных дифференциальных уравнений. Дифференциальное уравнение, полученное в результате исследования какого – либо реального явления или процесса, называют дифференциальной моделью этого явления или процесса. В процессе построения дифференциальных моделей важное, а подчас и первенствующее значение, имеет знание законов той области науки, с которой связана природа изучаемой задачи. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей – законы Кирхгофа, в теории скоростей химических реакций – законы действия масс и т.д. Обычно приходится прибегать к помощи приближенных методов решения подобных задач. В случае обыкновенных дифференциальных уравнений в зависимости от того, ставятся ли дополнительные условия в одной или нескольких точках отрезка изменения независимой переменной, задачи обычно подразделяются на одноточечные (задачи с начальными условиями или задачи Коши) и многоточечные. Среди многоточечных задач наиболее часто в прикладных вопросах встречаются так называемые граничные задачи, когда дополнительные условия ставятся на концах рассматриваемого отрезка.
В дальнейшем ограничимся рассмотрением численных методов решения задачи Коши. Для простоты изложения методов решения задачи будем рассматривать случай одного обыкновенного дифференциального уравнения первого порядка.
Пусть на отрезке x0 £ x £ b требуется найти решение y(x) дифференциального уравнения:
![]() , (7.1)
, (7.1)
удовлетворяющее при x = x0 начальному условию:
![]() (7.2)
(7.2)
Будем считать, что условия существования и единственности решения поставленной задачи Коши выполнены.
На практике найти общее либо частное решение задачи
Коши удается крайне редко, поэтому приходится решать эту задачу приближенно.
Отрезок ![]() накрывается сеткой (разбивается на интервалы) чаще
всего с постоянным шагом
накрывается сеткой (разбивается на интервалы) чаще
всего с постоянным шагом ![]() и по какому-то решающему правилу находится значение
и по какому-то решающему правилу находится значение ![]() ). Таким образом, в качестве решения задачи Коши
численными методами мы получаем таблицу, состоящую из двух векторов:
). Таким образом, в качестве решения задачи Коши
численными методами мы получаем таблицу, состоящую из двух векторов:
![]() – вектора аргументов и соответствующего ему вектора
функции
– вектора аргументов и соответствующего ему вектора
функции ![]() .
.
Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация только об одной (предыдущей) точке, называются одношаговыми.
Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация о нескольких (предыдущих) точках, называются многошаговыми.
В настоящее время существуют различные численные методы для решения задачи Коши (6.1) – (6.2). Ниже будут рассмотрены простые в применении методы – Эйлера, Рунге-Кутта, Адамса и Милна.
7.2 Метод Эйлера
Разностный способ. Рассматривая уравнение (7.1) в
точке ![]() , с учетом (7.2) имеем равенство:
, с учетом (7.2) имеем равенство:
![]()
Применяя к его левой части аппроксимацию производной правым разностным отношением первого порядка точности
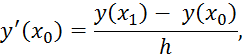
получаем
![]()
Общая расчетная формула метода Эйлера:
![]()
с учётом начального условия (7.2), где ![]()
Алгоритм этих формул очень простой.
а) ![]() (начальные условия).
(начальные условия).
б) Вывод вычисленных значений ![]()
в) ![]() (вычисление значения искомой функции в новой точке)
(вычисление значения искомой функции в новой точке)
г) ![]() (переход к следующей точке).
(переход к следующей точке).
д) Если ![]() то осуществляется переход в п. б).
то осуществляется переход в п. б).
Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага систематически возрастает.
Пример 7.1.
Используя метод Эйлера, найти значения функции ![]() , определяемой дифференциальным уравнением
, определяемой дифференциальным уравнением ![]() , при начальном условии
, при начальном условии ![]() шаг h=0,1. Ограничиться отысканием первых четырех значений
шаг h=0,1. Ограничиться отысканием первых четырех значений ![]() .
.
Решение.
Находим последовательные значения аргумента: ![]() Вычислим соответствующие значения искомой функции:
Вычислим соответствующие значения искомой функции:
![]()
![]()
![]()
![]()
Получаем таблицу
|
x |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
y |
1 |
1,1 |
1,18 |
1,25 |
1,31 |
7.2 Метод Рунге-Кутта
Существуют другие явные (т.е. значение ![]() явно вычисляется по k предыдущим
значениям
явно вычисляется по k предыдущим
значениям ![]() ) и одношаговые (k=1) методы.
Наиболее распространенным из них является метод Рунге-Кутта. На его основе
могут быть построены разностные схемы разного порядка точности (см. таблицу 7.1).
Наиболее употребительной схемой метода Рунге-Кутта является схема 3.
) и одношаговые (k=1) методы.
Наиболее распространенным из них является метод Рунге-Кутта. На его основе
могут быть построены разностные схемы разного порядка точности (см. таблицу 7.1).
Наиболее употребительной схемой метода Рунге-Кутта является схема 3.
Таблица 7.1.
|
№ |
Формула |
Вспомогательные переменные |
Порядок ошибки |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
Рассмотрим алгоритм метода Рунге – Кутта, исходя из расчетных формул схемы 3 (см. таблицу 7.1).
а) ![]() (начальные условия).
(начальные условия).
б) Вывод вычисленных значений ![]()
в) Вычислить ![]()
г) 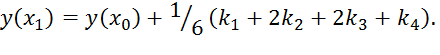 (вычисление нового значения y).
(вычисление нового значения y).
д) ![]() (переход к следующей точке).
(переход к следующей точке).
е) Если ![]() то осуществляется переход в п. б).
то осуществляется переход в п. б).
Метод Рунге-Кутта требует большого объема вычислений, однако обладает значительной точностью, что дает возможность проводить счет с большим шагом. Кроме того, важным преимуществом этого метода (например: перед методами Адамса и типа Адамса) является возможность применения «переменного шага», т.е. он допускает расчеты на неравномерных сетках.
Пример 7.2. Используя метод Рунге – Кутта, решить дифференциальное
уравнение ![]() на отрезке [0, 1] c начальным условием y(0) = 1.
Найти первые три точки, приняв шаг h = 0.05.
на отрезке [0, 1] c начальным условием y(0) = 1.
Найти первые три точки, приняв шаг h = 0.05.
Решение. Найдем числа
![]() 0,05;
0,05;
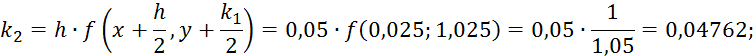
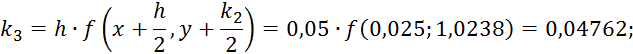
![]()
Отсюда
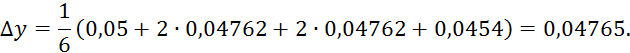
Таким образом, ![]() при
при ![]() Аналогично находим
Аналогично находим ![]() и т.д.
и т.д.
Для наглядности все полученные результаты сведем в таблицу 7.2.
Таблица 7.2
|
xi |
Метод Рунге-Кутта |
||||||
|
yi |
f(xi, yi) |
K1 |
K2 |
K3 |
K4 |
||
|
0 |
1 |
1 |
- |
- |
- |
- |
|
|
0.05 |
1.0477 |
0.9089 |
0.05 |
0.0477 |
0.0476 |
0.0454 |
|
|
0.1 |
1.0912 |
0.8321 |
0.0454 |
0.0435 |
0.0434 |
0.0416 |
|
|
0.15 |
1.1311 |
0.7658 |
0.0416 |
0.0399 |
0.0399 |
0.0383 |
|
7.3 Метод Адамса
В схемах Адамса, для вычисления следующего значения ![]() используется не только значение
используется не только значение ![]() , но и несколько предыдущих значений.
, но и несколько предыдущих значений.
Будем считать, что уже найдено несколько приближенных
значений ![]() решения
решения ![]() задачи (7.1)-(7.2) на равномерной сетке
задачи (7.1)-(7.2) на равномерной сетке ![]() и нужно получить правило для вычисления очередного
значения
и нужно получить правило для вычисления очередного
значения ![]() Для вывода таких правил используем интегро- интерполяционный
подход. А именно: проинтегрировав левую и правую части уравнения (7.1) по
промежутку
Для вывода таких правил используем интегро- интерполяционный
подход. А именно: проинтегрировав левую и правую части уравнения (7.1) по
промежутку ![]() в полученном равенстве:
в полученном равенстве:
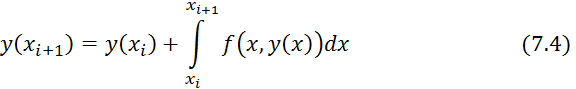
под интеграл вместо функции ![]() подставим интерполирующий ее многочлен
подставим интерполирующий ее многочлен ![]() . В дальнейшем дискретные приближенные значения
. В дальнейшем дискретные приближенные значения ![]() для краткости
для краткости ![]() , при
, при ![]()
При интерполировании назад из узла ![]() по второй интерполяционной формуле Ньютона (5.9) имеем:
по второй интерполяционной формуле Ньютона (5.9) имеем:
![]()
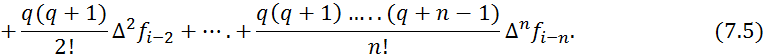
Подставка многочлена ![]() в равенство (7.4) приводит к формуле для вычисления
очередного значения
в равенство (7.4) приводит к формуле для вычисления
очередного значения ![]() вида:
вида:
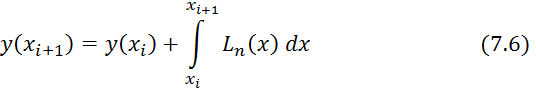
В результате применения к интегралу в (7.6) формулы Ньютона-Лейбница получаем многошаговый метод Адамса.
Сделаем в интеграле ![]() ) замену переменной
) замену переменной ![]() в соответствии с которой
в соответствии с которой
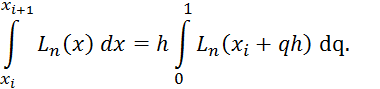
Тогда формула (7.4) может быть переписана в виде:
![]()
где
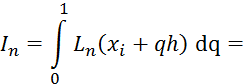

Таким образом, на основе (7.8) получается следующая конечно- разностная формула, определяющая экстраполяционный метод Адамса-Башфорта:
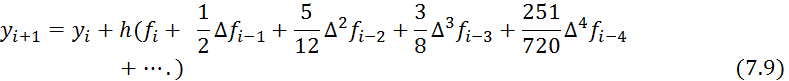
Рассмотрим простые частные случаи метода
Адамса-Башфорта (см. таблицу 7.3), соответствующие нескольким первым значениям
параметра к в формуле (7.7). При фиксировании ![]() в формуле (7.7) задается степень интерполяционного
многочлена (нулевая, первая, вторая и т.д.) и, соответственно, число слагаемых,
равное 1, 2, 3, ..., в правой части (7.8) или формулы (7.9)).
в формуле (7.7) задается степень интерполяционного
многочлена (нулевая, первая, вторая и т.д.) и, соответственно, число слагаемых,
равное 1, 2, 3, ..., в правой части (7.8) или формулы (7.9)).
Наиболее употребильной схемой метода Адамса является схема 4.
Таблица 7.3
|
№ |
Значение n |
Формула вычисления |
Ошибка точности |
|
1 |
n=0 |
|
|
|
2 |
n=1 |
|
|
|
3 |
n=2 |
|
|
|
4 |
n=3 |
|
|
Пример 7.3. Решить
дифференциальное уравнение 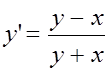 на отрезке [0, 1] c
начальным условием y(x=0) = 1.
Найти решение методом Адамса (с коррекцией) в точке x4, решение в трех первых точках найти методом Рунге-
Кутта, приняв шаг h = 0.05.
на отрезке [0, 1] c
начальным условием y(x=0) = 1.
Найти решение методом Адамса (с коррекцией) в точке x4, решение в трех первых точках найти методом Рунге-
Кутта, приняв шаг h = 0.05.
Решение. Значения функции в четырех первых точках возьмем из таблицы 7.2 (см. пример 7.2 в предыдущем разделе).
![]()
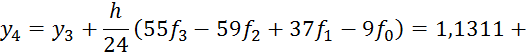
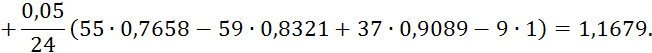
7.4 Приближенное решение задачи Коши для систем дифференциальных уравнений методом Рунге-Кутта
Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений.
Покажем это для случая систем двух уравнений вида:

Используя схему 3, формулы Рунге-Кутта запишем в следующем виде:
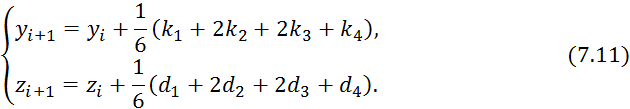
|
|
|
Если рассматривается задача Коши для обыкновенных дифференциаль-ных уравнений высшего порядка (7.1) - (7.2), то она приводится к системе дифференциальных уравнений обычном способом, понижением порядка уравнения.
Пусть необходимо решить задачу Коши для дифференциального уравнения второго порядка:
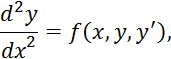
![]()
Введем вторую неизвестную функцию ![]() . Тогда сформулированная задача Коши заменяется
следующей:
. Тогда сформулированная задача Коши заменяется
следующей:

![]()
В заключение еще раз отметим особенность одношаговых методов, состоящую в том, что для получения решения в каждом новом расчетном узле достаточно иметь значение функции лишь в предыдущем узле. Это позволяет непосредственно вести счет, начиная с i=0 по известным начальным значениям. Кроме того, указанная особенность допускает изменение шага в любой точке в процессе счета, что позволяет строить численные алгоритмы с автоматическим выбором шага.
8 Решение краевых краевых задач для обыкновенных дифференциальных уравнений
8.1 Сеточные методы
В инженерной практике и при решении многих задач механики, физики, теории колебаний и других часто возникает необходимость решения краевой задачи для обыкновенных дифференциальных уравнений следующего вида:
![]()
где ![]() – заданные, непрерывные и определенные в некотором
промежутке
– заданные, непрерывные и определенные в некотором
промежутке ![]() функции, а
функции, а ![]() – независимая
переменная,
– независимая
переменная, ![]() – искомая функция. На границах промежутка
– искомая функция. На границах промежутка![]() заданы краевые условия:
заданы краевые условия:
![]()
![]()
где ![]() – известные
постоянные величины, j=0,1.
– известные
постоянные величины, j=0,1.
Если краевые условия (8.2) и (8.3) задаются:
1) ![]() – условие
называется условием первого рода,
– условие
называется условием первого рода,
2) ![]() – условие называется условием второго рода,
– условие называется условием второго рода,
3) ![]() – условие называется условием третьего рода.
– условие называется условием третьего рода.
Требуется найти функцию ![]() в промежутке
в промежутке ![]() удовлетворяющую дифференциальному уравнению (8.1) и
граничным условиям (8.2) и (8.3).
удовлетворяющую дифференциальному уравнению (8.1) и
граничным условиям (8.2) и (8.3).
Рассматривается несколько способов приближенного решения двухточечных линейных краевых задач для дифференциальных уравнений второго порядка. Сначала изучаются методы, позволяющие применить накопленный арсенал методов численного решения начальных задач. Далее на основе простейших аппроксимаций производных в узлах сетки строится удобный для автоматизированных вычислений метод конечных разностей получения каркасов решений и изучается его численная устойчивость.
Как известно, точное (аналитическое) решение краевых
задач вызывает еще большие трудности, чем решение задач Коши. Отсюда - повышенный
интерес, и большое разнообразие приближенных методов решения таких задач. По
типу представления результатов приближенного решения методы можно разделить на
две группы: приближенно-аналитические, дающие приближенное решение краевой
задачи на отрезке ![]() в виде некоторой конкретной функции, и собственно
численные или сеточные методы, дающие каркас приближенного решения на заданной
на
в виде некоторой конкретной функции, и собственно
численные или сеточные методы, дающие каркас приближенного решения на заданной
на ![]() сетке. По идейной основе приближенных методов их
можно классифицировать следующим образом:
сетке. По идейной основе приближенных методов их
можно классифицировать следующим образом:
1) методы сведения к задаче Коши (метод пристрелки, метод дифференциальной прогонки, метод редукции);
2) метод конечных разностей;
3) метод балансов или интегро-интерполяционный метод;
4) метод коллокации;
5) проекционные методы (моментов, Галёркина);
6) вариационные методы (наименьших квадратов, Ритца);
7) проекционно-разностные методы (метод конечных элементов);
8) методы сведения к интегральным уравнениям Фредгольма и др.
Ниже будут рассмотрены идеи и некоторые реализации методов 1, 2, 4, 5, 6 приведенного списка.
8.1.1 Метод конечных разностей.
Идея метода конечных разностей (МКР) решения краевых задач весьма проста и видна уже из самого названия: вместо производных в дифференциальном уравнении используются их конечноразностные аппроксимации.
Введём на отрезке ![]() сетку с шагом
сетку с шагом ![]()
![]()
На этой сетке определяются сеточные функции:
![]()
отвечающие функциональным коэффициентам данного дифференциального уравнения (8.1). Считая у(х) точным решением данной краевой задачи (8.1) - (8.3), через
![]()
будем
обозначать i-ю
компоненту искомого каркаса приближенного решения ![]() Значения производных аппроксимируем конечноразностными
отношениями по симметричным формулам второго порядка точности
Значения производных аппроксимируем конечноразностными
отношениями по симметричным формулам второго порядка точности
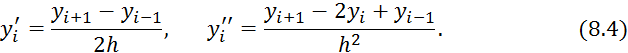
Тогда исходное дифференциальное уравнение (8.1) будет
записано в виде дискретных формул относительно дискретных значений искомой
функции ![]()

После приведения подобных членов в (8.5) получаем стандартное трехточечное разностное уравнение второго порядка:
![]()
где ![]()
при ![]()
Два недостающие
уравнения системы (8.6) получаем из граничных условий (8.2) и (8.3), 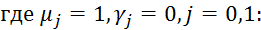
![]()
Формулы (8.6) представляют собой систему линейных алгебраических уравнений относительно неизвестных значений искомой функции в точках разбиения, причем эта система имеет особенность, ее основная матрица является трехдиагональной. Итак, вместо дифференциального уравнения (8.1) необходимо решить систему линейных алгебраических уравнений (8.6).
Пример 8.1. Методом конечных разностей найти решение краевой задачи
![]() ,
,
![]()
Решение. Заменяем уравнение системой конечно-разностных уравнений:
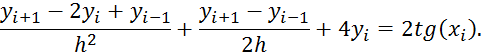
В результате приведение подобных членов получаем
![]()
Выберем шаг, равный 0,1. Тогда получим три внутренних узла
![]() Написав уравнение для каждого из этих узлов, получим
систему:
Написав уравнение для каждого из этих узлов, получим
систему:
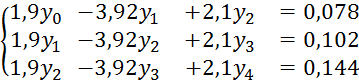
В граничных узлах имеем:
![]()
Используя эти значения, решаем систему и получаем:
![]()
8.1.2 Метод прогонки.
При применении метода конечных разностей к краевым задачам для дифференциальных уравнений второго порядка получается «трехчленная система» линейных алгебраических уравнений, каждое из которых содержит три соседних неизвестных. Для решения такой системы разработан специальный метод, получивший название метода прогонки.
Особенность матрицы системы уравнений позволяет использовать метод прогонки, сущность которого заключается в следующем: решение системы (8.6) находят в виде следующей рекуррентной формулы:
![]()
где ![]() -
неизвестные пока коэффициенты, называемые коэффициентами прогонки; они будут
определены в дальнейшем. Из этой формулы, очевидно, следует следующая формула:
-
неизвестные пока коэффициенты, называемые коэффициентами прогонки; они будут
определены в дальнейшем. Из этой формулы, очевидно, следует следующая формула:
![]()
Подставляя формулу (8.9) в систему уравнений (8.6), получим:
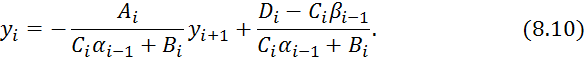
Сравнение формул (8.10) и (8.8) позволяет получить формулы для вычисления коэффициентов прогонки
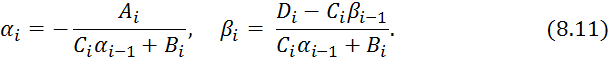
Эти формулы являются рекуррентными и для вычисления
значений неизвестных коэффициентов прогонки необходимо вначале определить первоначальные
коэффициенты, для чего используется граничное условие на левой границе
рассматриваемого промежутка ![]() :
:
![]() ,
, ![]()
Вычисление значений коэффициентов прогонки по формулам
(8.12) и (8.11) называется прямой прогонкой. После вычисления
коэффициентов прогонки вычисляются значения искомой функции ![]() , для чего
используется граничное условие на правой границе промежутка
, для чего
используется граничное условие на правой границе промежутка ![]() :
:
![]()
и рекуррентная формула (8.9). Процесс вычисления значений искомой функции по формулам (8.13) и (8.9) называется обратной прогонкой.
Алгоритм решения краевой задачи уравнения (8.1)-(8.3) методом прогонки будет иметь следующий вид:
а) Ввод исходных данных ![]() .
.
б) Цикл для вычисления значений заданных функций ![]() для
для
![]()
в) Цикл для вычисления коэффициентов системы уравнений
(8.6) ![]()
г) Вычисление первоначальных коэффициентов прогонки по формулам (8.12).
д) Цикл для вычисления коэффициентов прогонки по формулам (8.11).
е) Определение значения искомой функции на правой границе по формуле (8.13).
ж) Цикл для вычисления значений искомой функции по формуле (8.9).
к) Вывод значений аргумента x и функции y.
Пример 8.2. Методом прогонки найти приближенное решение уравнения
![]()
удовлетворяющее краевым условиям
![]()
Решение.
Примем ![]() и заменим уравнение и краевые условия системой конечно
– разостных уравнений
и заменим уравнение и краевые условия системой конечно
– разостных уравнений
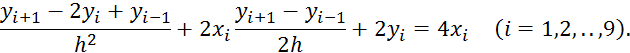
После приведения подобных членов получаем:
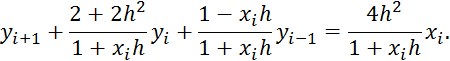
Таким образом, имеем:
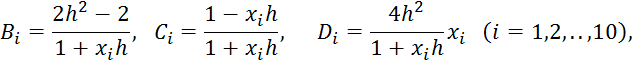
с учетом ![]() Учитывая формулу (8.12), имеем
Учитывая формулу (8.12), имеем ![]()
Таблица 8.1
|
i |
xi |
bi |
ci |
di |
|
|
yi |
|
0 |
0 |
-1,98 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0,1 |
-1,96 |
0,98 |
0,004 |
0,51 |
0,498 |
1,072 |
|
2 |
0,2 |
-1,941 |
0,961 |
0,008 |
0,689 |
0,324 |
1,126 |
|
3 |
0,3 |
-1,922 |
0,942 |
0,012 |
0,785 |
0,231 |
1,163 |
|
4 |
0,4 |
-1,904 |
0,923 |
0,015 |
0,848 |
0,168 |
1,187 |
|
5 |
0,5 |
-1,886 |
0,905 |
0,019 |
0,894 |
0,119 |
1,202 |
|
6 |
0,6 |
-1,868 |
0,887 |
0,023 |
0,93 |
0,077 |
1,212 |
|
7 |
0,7 |
-1,85 |
0,869 |
0,026 |
0,96 |
0,039 |
1,22 |
|
8 |
0,8 |
-1,833 |
0,852 |
0,03 |
0,985 |
0,003 |
1,231 |
|
9 |
0,9 |
-1,817 |
0,835 |
0,033 |
1,005 |
-0,03 |
1,247 |
|
10 |
1 |
1,27 |
Прямой ход. Записываем в таблице 8.1 числа ![]() и вычисляем значения
и вычисляем значения ![]() Затем по формулам (8.11) находим:
Затем по формулам (8.11) находим:
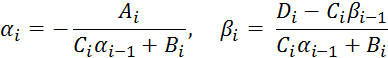
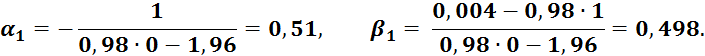
Записываем полученные числа в таблицу и приступаем к
последовательному вычислению ![]()
Обратный ход. Известно ![]() , определяем последовательно другие значения
, определяем последовательно другие значения ![]() используя формулу (8.9):
используя формулу (8.9):
![]()
![]() и т.д.
и т.д.
Покажем график значений ![]() на рисунке 8.1.
на рисунке 8.1.

Рисунок 8.1 – Зависимость значений y от x
8.2 Приближенно-аналитические методы
В настоящем параграфе мы рассмотрим вариационные методы решения краевых задач для обыкновенных дифференциальных уравнений, позволяющие получить приближенное решение краевой задачи в аналитической форме. Свое название эти методы получили потому, что их первое применение было связано с заменой краевой задачи для дифференциального уравнения некоторой вариационной задачей.
Для решения краевой задачи (8.1)-(8.3) зададим на
отрезке ![]() некоторую линейно независимую систему дважды
непрерывно дифференцируемых функций
некоторую линейно независимую систему дважды
непрерывно дифференцируемых функций ![]() таких, что удовлетворяет краевым условиям (8.2)-(8.3),
т.е.
таких, что удовлетворяет краевым условиям (8.2)-(8.3),
т.е. ![]() , а остальные функции удовлетворяют однородным краевым
условиям, т.е.
, а остальные функции удовлетворяют однородным краевым
условиям, т.е.![]()
Заданная система функций ![]() называется базисной.
называется базисной.
Составим линейную комбинацию базисных функций:
![]()
с
неизвестными пока коэффициентами ![]() . В силу линейности операторов
. В силу линейности операторов ![]()
![]() функция
функция ![]() при любых
при любых ![]() удовлетворяет заданным краевым условиям (8.2)-(8.3).
удовлетворяет заданным краевым условиям (8.2)-(8.3).
Действительно,
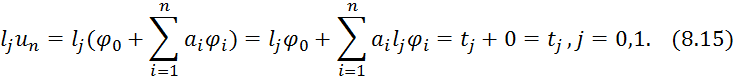
Функция
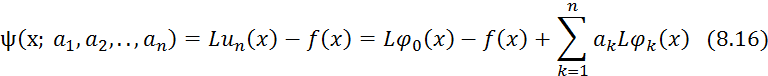
называется
невязкой. Невязка из (8.16) линейно зависит от параметров ![]() и является уклонением функции (8.14) от неизвестного
решения u(x) краевой задачи (8.1)-(8.3). Чем ближе невязка нулю, то функция
совпадает с решением краевой задачи, поэтому стараются подобрать параметры
и является уклонением функции (8.14) от неизвестного
решения u(x) краевой задачи (8.1)-(8.3). Чем ближе невязка нулю, то функция
совпадает с решением краевой задачи, поэтому стараются подобрать параметры ![]() так, чтобы невязка стала как можно меньше. Функцию (8.14)
при выбранных
так, чтобы невязка стала как можно меньше. Функцию (8.14)
при выбранных ![]() принимают за приближенное решение краевой задачи (8.1)-(8.3).
принимают за приближенное решение краевой задачи (8.1)-(8.3).
Приближённое решение краевой задачи (8.1)- (8.3) ищем в виде линейной комбинации базисных функций:
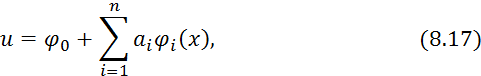
где определяемые на отрезке ![]() базисные функции
базисные функции ![]() (i =1,2,..,n) и дополнительная функция
(i =1,2,..,n) и дополнительная функция ![]() должны быть дважды дифференцируемыми и попарно
линейно независимыми. Кроме того, функция
должны быть дважды дифференцируемыми и попарно
линейно независимыми. Кроме того, функция ![]() должна удовлетворять данным краевым условиям (8.2), (8.3),
а функции
должна удовлетворять данным краевым условиям (8.2), (8.3),
а функции ![]() при i =1,2,..,n — соответствующим однородным краевым
условиям, т.е. должны выполняться равенства:
при i =1,2,..,n — соответствующим однородным краевым
условиям, т.е. должны выполняться равенства:

![]()
В таком случае функция ![]() , определяемая выражением (8.17), при любых значениях
коэффициентов
, определяемая выражением (8.17), при любых значениях
коэффициентов ![]() , гарантированно удовлетворяет краевым условиям (8.2),
(8.3). Действительно, например, в точке x=a
имеем:
, гарантированно удовлетворяет краевым условиям (8.2),
(8.3). Действительно, например, в точке x=a
имеем:
![]()
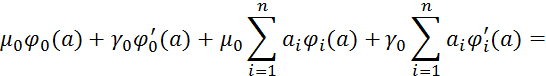
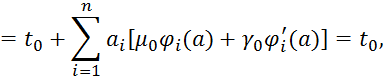
аналогично при x=b с помощью (8.3), (8.17) и (8.18) проверяется справедливость равенства
![]()
Успех решения краевой задачи (8.1) - (8.3) сильно
зависит от удачного выбора базисных функций ![]() ) в представлении приближенного решения (8.17). В
конкретных задачах выбор таких функций, по возможности, должен опираться на
априорные или эмпирические сведения о решении. В отсутствие таковых, т.е. в
рассматриваемом абстрактном случае, для смешанной краевой задачи (8.1) - (8.3),
можно предложить, например, следующий набор базисных функций.
) в представлении приближенного решения (8.17). В
конкретных задачах выбор таких функций, по возможности, должен опираться на
априорные или эмпирические сведения о решении. В отсутствие таковых, т.е. в
рассматриваемом абстрактном случае, для смешанной краевой задачи (8.1) - (8.3),
можно предложить, например, следующий набор базисных функций.
В качестве ![]() возьмем линейную функцию:
возьмем линейную функцию:
![]()
коэффициенты которой подберем так, чтобы она удовлетворяла неоднородным краевым условиям (8.2),(8.3), т.е. из линейной алгебраической системы:
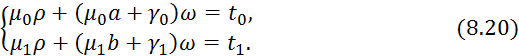
Функции ![]() при
при ![]() можно взять однопараметрическими вида
можно взять однопараметрическими вида
![]()
если в (8.2) ![]() , или вида
, или вида
![]()
в
самом общем случае. Очевидно, что при любых ![]() эти функции удовлетворяют первому из требуемых
равенств (8.18), если зафиксировать
эти функции удовлетворяют первому из требуемых
равенств (8.18), если зафиксировать
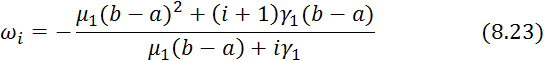
в выражении (8.21) и

в (8.22), то они будут подчиняться и второму из этих
равенств. Следовательно, можно рассчитывать, что с такими базисными функциями
при найденных методом коллокации (или каким- либо другим методом) коэффициентах
![]() , определенная посредством (8.17) функция u, будет удовлетворять краевым условиям и может служить
приближенным решением данной краевой задачи (8.1)-(8.3).
, определенная посредством (8.17) функция u, будет удовлетворять краевым условиям и может служить
приближенным решением данной краевой задачи (8.1)-(8.3).
Проблема формального выбора базисных функций ![]() значительно упрощается в случае, когда в задаче
(8.1)-(8.3) фигурируют однородные краевые условия первого рода, т.е. когда
значительно упрощается в случае, когда в задаче
(8.1)-(8.3) фигурируют однородные краевые условия первого рода, т.е. когда
![]()
В такой ситуации в выражении (8.17) не нужна функция ![]() , а в роли
, а в роли ![]() (
(![]() ) могут выступать, например, функции:
) могут выступать, например, функции:
![]()
или
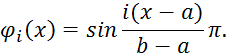
К этому случаю, т.е. к условиям (8.25), легко свести более общий случай неоднородных краевых условий первого рода:
![]()
С этой целью достаточно сделать линейную замену (линейный сдвиг)

Дважды дифференцируя эту функцию у и подставляя
результаты в уравнение (8.1), от задачи (8.1), (8.26) приходим к краевой задаче
с однородными краевыми условиями относительно новой переменной ![]() :
:
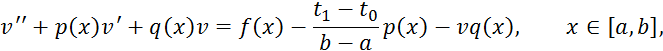
![]()
8.2.1 Метод коллокаций.
Рассмотрим решение методом коллокации линейного
дифференциального уравнения (8.1). Выбираем некоторую базисную систему линейно
независимых функций ![]() . При этом
. При этом ![]() удовлетворяет неоднородным, а остальные функции,
удовлетворяет неоднородным, а остальные функции, ![]() φi(x), удовлетворяют однородным
краевым условиям (8.2)-(8.3).
φi(x), удовлетворяют однородным
краевым условиям (8.2)-(8.3).
Приближённое решение краевой задачи (8.1)- (8.3) ищем в виде линейной комбинации базисных функций (8.17).
Такая функция u удовлетворяет краевым условиям
при любых ![]() . Подставляя функцию (8.17) в уравнение (8.1), получим
некоторый остаточный член
. Подставляя функцию (8.17) в уравнение (8.1), получим
некоторый остаточный член ![]() , не равный
нулю, поскольку функция u не является точным решением уравнения (8.1).
Если при выборе коэффициентов
, не равный
нулю, поскольку функция u не является точным решением уравнения (8.1).
Если при выборе коэффициентов ![]() будет выполнено условие
будет выполнено условие ![]() для всех
для всех ![]() ], то функция u(x) будет точным решением
уравнения (8.1).
], то функция u(x) будет точным решением
уравнения (8.1).
Однако так подобрать коэффициенты ![]() практически невозможно. Поэтому ограничиваются
требованием равенства нулю невязки в заданном множестве точек
практически невозможно. Поэтому ограничиваются
требованием равенства нулю невязки в заданном множестве точек ![]() на отрезке [a,b] — точки коллокаций. В этих точках
дифференциальное уравнение (8.1) будет удовлетворяться точно. Таким образом,
получается система алгебраических уравнений:
на отрезке [a,b] — точки коллокаций. В этих точках
дифференциальное уравнение (8.1) будет удовлетворяться точно. Таким образом,
получается система алгебраических уравнений:
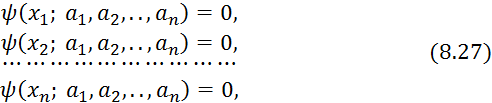
относительно
неизвестных ![]() . В более подробной записи имеет вид:
. В более подробной записи имеет вид:
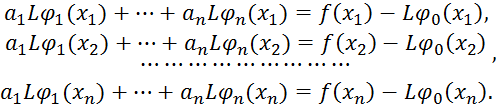
Если система однозначно разрешима, то найденные из нее
коэффициенты ![]() подставляются (8.17). Число точек коллокаций должно
согласовываться с количеством базисных функций. Чем больше используется базисных
функций и, соответственно, точек коллокаций, тем точнее получается приближённое
решение.
подставляются (8.17). Число точек коллокаций должно
согласовываться с количеством базисных функций. Чем больше используется базисных
функций и, соответственно, точек коллокаций, тем точнее получается приближённое
решение.
Алгоритм метода следующий:
1) Выписать базисные функции ![]()
2) Проверить выполнение нулевых краевых условий базисных функций.
3) Записать приближенно-аналитическое решение краевой
задачи в виде ![]()
4) Записать все входящие в ДУ производные,
продифференцировав решение ![]() .
.
5) Подставить полученные в п.3,4 выражения в ДУ.
6) Записать функцию невязки ![]() как разность левой и правой частей ДУ из п. 5.
как разность левой и правой частей ДУ из п. 5.
7) Выбрать внутри интервала, ограниченного краевыми точками, n штук ( по числу базисных функций) точек коллокаций.
8) Записать условия равенства нулю функции невязки в
точках коллокации- результат система алгебраических уравнений относительно неизвестных
констант ![]()
9) Вычислить константы ![]()
10) Записаить окончательное приближенно-аналитическое решение краевой задачи.
11) Вычислить значение функции ![]() в точках коллокации.
в точках коллокации.
Пример 8.3. Методом коллокаций решить краевую задачу
![]() на отрезке
на отрезке ![]() при
при ![]()
Решение. Составив систему (8.20) относительно коэффициентов ![]() и
и ![]() функции вида (8.19)
функции вида (8.19)
находим удовлетворяющую данным краевым условиям
линейную функцию ![]() Ограничиваясь одной базисной функцией
Ограничиваясь одной базисной функцией ![]() вида (8.21), по формуле (8.23) вычисляем коэффициент:
вида (8.21), по формуле (8.23) вычисляем коэффициент:
подстановка
которого в (8.21) при ![]() дает базисную функцию:
дает базисную функцию:
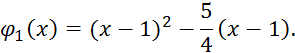
Возьмем в качестве узла коллокации середину рассматриваемого
Промежутка
- точку ![]() и потребуем, чтобы функция
и потребуем, чтобы функция
![]()
удовлетворяла в этой точке заданному дифференциальному уравнению.
Подставив в него
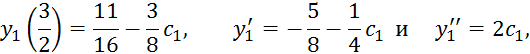 получаем
получаем
![]() .
.
Таким образом, простейшая коллокация с одним узлом приводит к приближению решения данной краевой задачи квадратичной функцией:
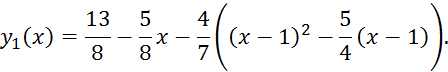
Пример 8.4. Методом коллокаций решить краевую задачу
![]() на отрезке
на отрезке ![]() при
при ![]()
Решение. В качестве базисных функций выбираем полиномы ![]() . Функция
. Функция ![]() удовлетворяет
неоднородным краевым условиям
удовлетворяет
неоднородным краевым условиям ![]() , а функции
, а функции ![]() , — однородным краевым условиям
, — однородным краевым условиям ![]() . Точками коллокаций примем точки
. Точками коллокаций примем точки 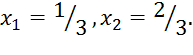 Ограничимся тремя базисными функциями и положим приближенное
решение уравнения равным
Ограничимся тремя базисными функциями и положим приближенное
решение уравнения равным
![]()
В результате невязка ![]() будет равна
будет равна
![]()
Подставляя координаты точек коллокаций 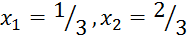 в выражение невязки, получим систему уравнений для
определения коэффициентов
в выражение невязки, получим систему уравнений для
определения коэффициентов ![]()
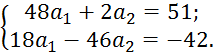
Отсюда находим: ![]() и приближённое решение будет иметь вид:
и приближённое решение будет иметь вид:
![]()
8.2.2 Метод наименьших квадратов.
Рассмотрим решение методом наименьших квадратов
линейного дифференциального уравнения (8.1). Выбираем некоторую базисную систему
линейно независимых функций ![]() . При этом
. При этом ![]() удовлетворяет неоднородным, а остальные функции,
удовлетворяет неоднородным, а остальные функции, ![]() φi(x), удовлетворяют однородным
краевым условиям (8.2)-(8.3). Приближённое решение ищется в виде:
φi(x), удовлетворяют однородным
краевым условиям (8.2)-(8.3). Приближённое решение ищется в виде:
![]()
Подставляя функцию u в дифференциальное уравнение (8.1), получаем невязку
![]() ,
,
которая на отрезке [a,b] должна быть минимальной по абсолютной величине.
Это требование выполняется при условии минимального значения интеграла от квадрата невязки:
![]() .
.
Для получения минимума интеграла S необходимо
приравнять к нулю частные производные S по коэффициентам ![]() , то есть
, то есть
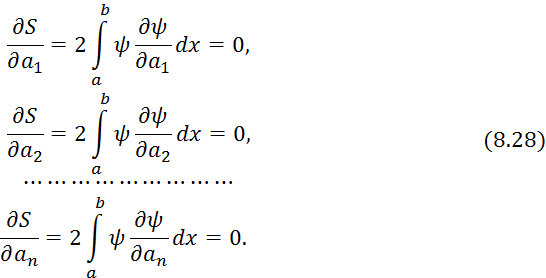
В результате получается система линейных
алгебраических уравнений относительно ![]() , откуда и определяются их значения.
, откуда и определяются их значения.
Пример 8.5. Методом коллокаций решить краевую задачу
![]() на отрезке
на отрезке ![]() при
при ![]()
Решение. Выбирая базисные функции в виде ![]()
![]() решение задачи ищем в виде:
решение задачи ищем в виде:
![]()
В результате невязка ![]() будет равна
будет равна
![]()
В этом случае интеграл от квадрата невязки будет иметь вид:
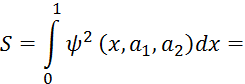
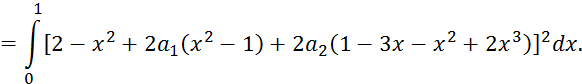
Для получения минимума интеграла S необходимо
приравнять к нулю частные производные S по коэффициентам ![]() , i = 1, 2, то есть
, i = 1, 2, то есть
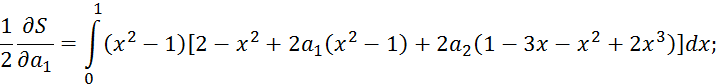
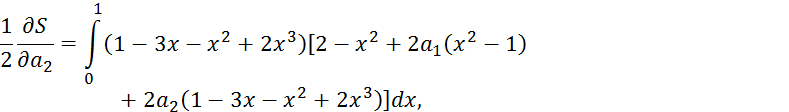
а после интегрирования получаем уравнения:

Отсюда находим: ![]() и приближённое решение будет иметь вид:
и приближённое решение будет иметь вид:
![]()
8.2.3 Метод Галеркина.
Алгоритм метода Галёркина также основан на выборе
базисной системы линейно независимых функций ![]() , из которых
, из которых ![]() удовлетворяет неоднородным краевым условиям, а
остальные функции
удовлетворяет неоднородным краевым условиям, а
остальные функции ![]() удовлетворяют однородным краевым условиям.
удовлетворяют однородным краевым условиям.
На основе этой базисной системы строится приближённое решение задачи в виде их линейной комбинации
![]()
В основе метода лежит требование ортогональности
базисных функций ![]() к невязке (8.16), т.е.
к невязке (8.16), т.е.

В результате получаем следующую систему линейных
алгебраических уравнений для коэффициентов ![]() Разрешая эту
систему, находим коэффициенты
Разрешая эту
систему, находим коэффициенты ![]() и
приближенное решение задачи u.
и
приближенное решение задачи u.
Пример 8.6. Методом Галеркина решить краевую задачу:
![]() на отрезке
на отрезке ![]() при
при ![]()
Решение. В качестве базисных функций выбираем полиномы ![]() . Функция
. Функция ![]() удовлетворяет
неоднородным краевым условиям
удовлетворяет
неоднородным краевым условиям ![]() , а функции
, а функции ![]() , — однородным краевым условиям
, — однородным краевым условиям ![]() . Ограничимся тремя базисными функциями и положим
приближенное решение уравнения равным
. Ограничимся тремя базисными функциями и положим
приближенное решение уравнения равным
![]()
В результате невязка ![]() будет равна
будет равна
![]()
Из условия ортогональности невязки к базисным функциям
получаем систему двух линейных уравнений для коэффициентов ![]() , i = 1, 2:
, i = 1, 2:
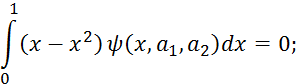
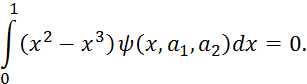
Подставляя в уравнение значения ![]() , после интегрирования получаем систему линейных
алгебраических уравнений:
, после интегрирования получаем систему линейных
алгебраических уравнений:
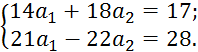
Отсюда находим: ![]() , и приближённое
решение будет иметь вид
, и приближённое
решение будет иметь вид
![]()
Пример 8.7. Пусть дано дифференциальное уравнение второго порядка и его граничные условия
![]()
![]() (8.29)
(8.29)
Решить методом Галеркина и коллокаций
Решение. Метод Галеркина.
На отрезке [a, b] выберем систему базисных функций:
![]()
Проверим систему на ортогональность
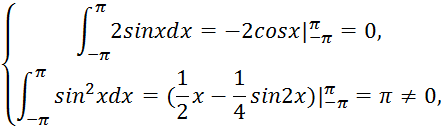
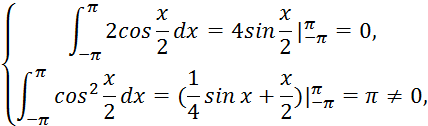

Выбранная система базисных функций является
ортогональной и удовлетворяет условию выбора конечной системы базисных функций ![]() на границах
на границах ![]() :
:
![]()
![]()
![]()
Решение краевой задачи (8.29) ищется в виде (8.17).
1) Рассмотрим решение задачи с двумя базисными функциями:
![]()
Тогда решение
![]()
Найдем невязку по формуле (8.16) для задачи (8.29) с двумя базисными функциями:
![]()
![]() выбирается таким образом, чтобы
выбирается таким образом, чтобы
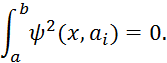
Так как ![]() ортогональна ко всем базисным функциям, то
ортогональна ко всем базисным функциям, то
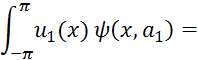
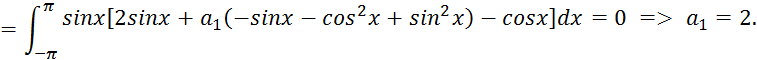
Тогда решение задачи (8.29):
![]()
2) Рассмотрим решение задачи с тремя базисными функциями:
![]() .
.
Тогда решение:
![]() Невязка
примет вид:
Невязка
примет вид:
![]()
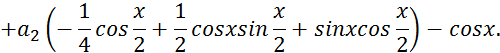
Из условия ортогональности невязки к базисным функциям
получаем систему двух линейных уравнений для коэффициентов ![]() , i = 1, 2:
, i = 1, 2:

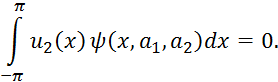
Коэффициенты ![]() и
и ![]() будем искать из системы:
будем искать из системы:
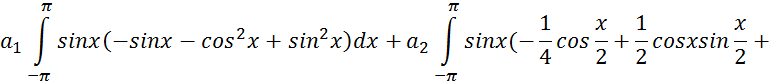
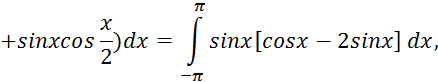
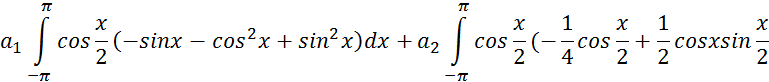

Решая данную систему, находим
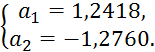
Тогда решение задачи (8.29):
![]()
Метод коллокации.
1) Рассмотрим решение задачи (8.29) с двумя базисными функциями
![]()
Тогда решение:
![]()
Составим невязку:
![]()
На отрезке [-π, π] выберем за точку коллокации 0.
![]()
Таким образом, решение задачи (8.29):
![]()
2) Рассмотрим решение задачи (8.29) с тремя базисными функциями:
![]() .
.
Тогда решение:
![]()
Составим невязку:
![]()
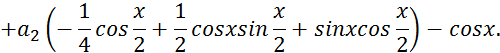
На отрезке ![]() выберем две точки коллокации: 0 и
выберем две точки коллокации: 0 и ![]() . Составим систему уравнений:
. Составим систему уравнений:
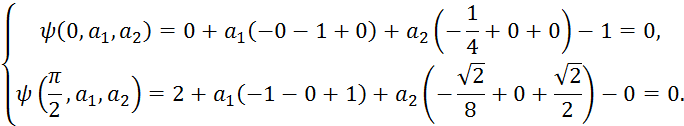
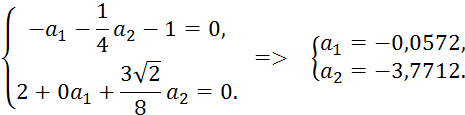
Таким образом, решение задачи (8.29):
![]()
Список литературы
1.Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Изд-во «Наука», 1972 .
2. Турчак Л.И. Основы численных методов: Учеб. пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 320 с.
3. Сливина Н.С. Лабораторный практикум по высшей математике: Учеб. пособие для втузов. –М.: Высш. шк. 1983. – 203 с.
4. Cамарский А.А., Гулин А.В. Математические модели в инженерных расчётах на ЭВМ. - М.: Наука, 1989. - 432 с.
5. Cамарский А.А. Теория разностных схем. – М.: Наука, 1977.
6. Марчук Г.И. Методы вычислительной математики. – М.: Наука, 1980.
7. Вержбицкий В.М. Основы численных методов: Учебник для вузов. – М.: Высш. шк., 2002.- 840 с.
8. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. - М.: Высшая школа, 2001.- 382 с.
9. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы.- М.: Лаборатория базовых знаний, 2002. – 632 с.