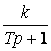Қазақстан Республикасының ғылым және білім министрлігі
«Алматы энергетика және байланыс университеті»
Комерциялық емес акционерлік қоғамы
Ш.И. Иманғалиев
Техникалық жүйелерді автоматтандыру
Оқу құралы
Алматы 2012
УДК 681.5.015
ББК 31.27- 05я73
И 48 Техникалық жүйелерді автоматтандыру
Оқу құралы/Ш.И. Иманғалиев
АЭжБУ. Алматы 2012. -123б.
ISBN 978-601-73-07-06-6
Өндірісті автоматтандыру проблемалары, негізгі түсініктері және жіктеулері қарастырылады. Өндіріс басқару объектісі түрінде бейнеленеді, қасиеттері анықталады, басқару жүйесінің құрылымы нақтыланады және оның типтік буындары мінезделеді. Жылу энергетика саласындағы қарапайым технологиялық объекттер түсіндіріледі және оларға қолданылатын басқару операциялары көрсетіледі. Сонымен бірге өндірістік объекттер мен басқару жүйесі элементтерін бейнелейтін математикалық модельдер (үздіксіз, дискретті) сарапталған. Оқу құралы 5В070200 – «Автоматтандыру және басқару», 5В070300 – «Ақпараттық жүйелер» мамандықтары бойынша оқитын студенттер мен магистранттарға арналған.
Кесте 2, Без.71, Библиогр.-10 атау.
ББК 31.27- 05я73
ПІКІР БЕРУШІ: ҚазҰТУ проффессор, техн. ғыл. канд., Жумағалиев Б.А. АЭжБУ доцент, техн. ғыл. канд., Джумагалиев Б.С.
Қазақстан Республикасының Білім және Ғылым министірлігінің 2011 жылғы баспа жоспары бойынша басылады.
ISBN 978-601-73-07-06-6
© Алматы энергетика және байланыс университеті, 2012ж.
Мазмұны
|
|
Кіріспе |
4 |
|
|
1 |
Өндірісті автоматтандыру мәселелері |
5 |
|
|
1.1 |
Негізгі мәселелер, түсініктер және жіктеулер |
5 |
|
|
1.2 |
Жүйенің құрылымы және элементтері |
8 |
|
|
1.3 |
Автоматтандырылған басқару жүйесі |
12 |
|
|
2 |
Өндірістік үрдістерді структуризациялау |
15 |
|
|
2.1 |
Өндірістік үрдістің басқару объектісі |
15 |
|
|
2.2 |
Басқарылатын технологиялық объекттердің қасиеттері |
20 |
|
|
2.3 |
Автоматты басқару жүйесінің типтік буындары |
24 |
|
|
2.4 |
Автоматты реттеуіштің қасиеттері |
55 |
|
|
3 |
Өндірістік үрдісті басқару |
59 |
|
|
3.1 |
Өндірістік үрдісті құрылымдау |
59 |
|
|
3.2 |
Үрдісті басқару операциялары |
65 |
|
|
3.3 |
Қарапайым технологиялық объекттер және олардың түрлері |
80 |
|
|
3.4 |
Қарапайым объекттердің сұлбалары және оның басқарулығын бағалау |
82 |
|
|
3.5 |
Қарапайым объекттерді басқару процедурасы |
90 |
|
|
4 |
Өндірістік үрдістің және басқару жүйесінің модельдері |
98 |
|
|
4.1 |
Үздіксіз өндірістік жүйенің моделі |
98 |
|
|
4.2 |
Дискретті өндірістік жүйенің моделі |
116 |
|
|
|
Әдебиеттер тізімі |
122 |
|
Кіріспе
Уақыт өткен сайын автоматтандыру ұғымы мен түсінігі кеңейе бастайды, оның ішіне кейбір ғылыми және техникалық дамуының жаңа жеке мәселелері кіргізіле басталды. Олар копьютерлеу, робаттау және басқа арнайы немесе салалық жаңа ұғымдар. Дегенмен оның мағынасы және негізгі міндеті өзгермей қалады – ол адамның керітартпалық еңбегін жеңілдету немесе одан босату босату.
Жылу энергетика саласы, технологиялық үрдістерді кеңінен механизациялаумен, жұмыс орталарының жоғары параметрмен, оны реттеудің дәлдігі талаптарымен, сонымен қатар өзіндік энергия көзімен ерекшеленеді. Сондықтан, осы ғылым мен техника саласына автоматты және автоматтандырылған басқару теориясының әдістері және жаңа техникалық құралдары қолданылады. Енді осы айтылғанға байланысты оның жалпы анықтамасын көрсеттік. Механизацияланған өндірісті автоматтандыру деп машиналарды, механизмдерді және қондырғыларды басқару, сонымен қатар арнайы құрылғылардың өлшеуіш құралдар, автоматты реттеуіштер және есептеу машиналары көмегімен олардың жұмыс істеуін бақылауды айтамыз. Ол адамның шектелген ойымен немесе онысызда жүзеге асырылады.
Сіздің назарларыңызға ұсынылған оқу құралы төрт бөлімнен тұрады. Бірінші бөлімде өдірісті автоматтандырудың негізгі мәселелері, түсініктері көрсетілген, сонымен бірге айтылған жүйелер жіктелген. Ал екінші бөлімде өндірістік үрдістердің құрылымы, басқару объектісі түрінде бейнеленді және оның негізгі қасиеттері талданған. Оны автоматтандыруға керекті типтік буындар мінезделген. Үшінші бөлімде жылу энергетика саласындағы қарапайым технологиялық объектер, оларды басқаруға керекті операциялар түсіндірілген. Оқу құралының соңғы бөлімінде өндірістік үрдісті және оны басқару жүйесінің екі түрлі математикалық модельдері берілген. Сонымен бірге бұл оқу құралының соңғы бөлімінде басқару жүйесінің негізгі элементтерін бейнелеуге керекті екі түрлі математикалық модельдер (үздіксіз, дискретті) сарапталған. Оларды түсіндіруге керекті қасиеттері және сандық мысалдары көрсетілген.
1 Өндірісті автоматтандыру мәселелері
1.1 Негізгі мәселелер, түсініктер және жіктеулер
Қазіргі қоғамның экономикалық дамуының түрлі кезеңдерінде, автоматтандыру өнеркәсіптік және әлеуметтік саланың ең негізгі мәселелерінің бірі болып қалады. Осы саладағы мәселе мен істерді түсіну үшін, алдымен оған керекті ғылыми техникалық жүйе туралы негізгі ұғымдар мен ұстанымдарды қарастыруымыз керек.
Автоматтандыру [1,3,9] – техникалық құралдарды, экономика – математикалық әдістерді және басқару жүйесін қолдану арқылы, адамды энергиялар, материалдар немесе ақпараттарды алу, өзгерту, беру және пайдалану үрдістеріне шектеулі немесе тікелей қатысуынан босату. Бұл анықтаманы нақтылай келсек, автоматтандырамыз: технологиялық, энергетикалық, көліктік және басқа өндірістік үрдістерді. Әр өнеркәсіптік өндірістің негізгі технологиялық немесе өндірістік үрдістер болып табылады. Ал біздің қарастыратын өндіріс саласы «жылуэнергетика» деп аталады.
Қазіргі жылу электр станциясында (ЖЭС), жылу және электрлік энергиясын өндіру мен үлестіруге байланысты көп еңбекті үрдістер негізінен механикаландырылған. Енді механикаландырылған өндірісті автоматтандыру деп машиналар, механизмдер жіне қондырғыларды басқаруды, сонымен қатар адамның шектеулі қатысуы немесе қатыспауы арқылы олардың жұмысын арнайы құрылғылар (өлшейтін аспаптар, автоматты реттеуіштер және есептеу машиналары) көмегімен бақылауды айтады.
Механикаландырылған технологияның үрдістері, жұмыс ортасы параметрлерінің жоғарғы деңгейі, оны реттеуіндегі дәлдік тараптары және өзінің энергия қайнар көзі сияқты ерекшеліктері бар жылуэнергетика саласын зерттеуге, автоматтандыруға керекті ғылыми және техника салалары: физика, химия, математика, жылуэнергетика, автоматика, жүйелік талдау, өлшеу, байланыс және есептеу техникалары. Жоғарыда айтылған ғылымдардың бізге керекті ең негізгісі автоматика болып табылады.
Автоматика (гректің αντοματυσ – «өздігінен әрекет ететін» сөзінен) – нәрсесі, адамның тікелей қатысуынсыз түрлі мақсатталған іс – әрекетті жүзеге асыруға арналған әдістер мен құралдардан ғылыми – техникалық сала. Бұл саланың ғылыми негізгі автоматты басқару жүйесі (АБЖ) теориясында көрсетілген. Онда АБЖ - құрылымы, математикалық модельдері, талдау және синтездеу әдіс – амалдары берілген. Енді, соңғы екі жалпылама анықтамаларын енгізейік.
Техникадағы басқару – жұмыс істеуіне қажетті алгоритмдеріне сәйкес, машиналардың, жүйелердің, үрдістердің күйін немесе параметрлерін мақсаттылықпен өзгертуді айтады. Техникалық құралдар өндірістік немесе технологиялық үрдістерді жүзеге асыру үшін қолданатындықтан, басқаруға екінші анықтамасын береміз. Технологиялық үрдістің ішкі күйінің керекті өзгеруін қамтамасыз ететін, ал қозғалатын объектерге – кеңістікте және уақытқа байланысты берілген траекториясымен қозғалатын әсерлер басқару атауының мағынасын білдіреді.
Жүйе – қаланып қойылған мақсаттарға жетуге арналған біріктірілген әр объекттер элементтердің жиынтығы.
Біздің жағдайда өндіріс немесе технологиялық үрдістерге керекті АТЖ болғандықтан, оның негізгі элементтері төмендегідей: машиналар, механизм және қондырғылар, өлшеуіш, байланыс, реттеуіш және есептеуіш құрылғылары мен жабдықтар.
Енді автоматтандырылған техникалық жүйенің (АТЖ) негізгі ұстанымдар қасиетіне және жалпы жіктемесіне тоқталайық. Басқару жүйесін жалпылама қарастырғанда ол екі негізгі элементтен тұрады: басқару объектісі мен басқару құралы. Мұндағы басқару объектісі деп технологиялық және өндірістік үрдісті іске асыратын қандайда болмасын агрегаттарды айтады. Ал басқару құралы, АБЖ басқаруды адамның тікелей қатысуынсыз жүзеге асыратын жалпы өндірістік немесе арнайы комплекстік құралдар болып табылады. Бұл жерде адамның міндетті қызметі автоматты қондырғының (жабдықтың) жұмысын бақылау, үрдісті басқару талабына сай жөндеу және күйге келтіру.
АБЖ-нің жалпы жіктелуі кейбір белгілеріне байланысты орындалады:
1. Басқару құралы мен объектісінің қосылу тәсіліне байланысты ажыратылған және тұйық жүйелер болып бөлінеді. Ажыратылған АБЖ-да басқару құралы объектіге оның күйін есепке алмай әсер етеді. Мұндай жүйелер қарапайым функцияларды орындауға қолданылады (қызмет, әрекет), мысалы жабдықты жүргізу, тоқтату немесе берілген уақыт интервалы (аралығы) арқылы реверсивтеу (қозғалыс бағытын өзгерту), технологиялық операцияларды бірізділік (жүйелік) тапсырыс түрінде орындау (программа – логикалық басқару).
Тұйық жүйе неғұрлым күрделі, бірақта жетілген жүйе болып есептеледі. Мұнда жұмыс істеу кезінде, басқару құралы объекттің қазіргі (нақтылы, фактілі) күйін ескереді, және оның негізінде объектіге керекті әсер дайындалып іске асырылады. Объект күйі туралы ақпарат кері байланыс арнасы арқылы жеткізіледі, әдетте ол бақылау – өлшеу аспабымен жүзеге асырылады. Осыдан кейін, басқарушы әсерлер тікелей байланыс арнасымен түрлі орындаушы құрылғыларына жеткізідеді.
2. Басқару үрдісіне жұмсалатын қосымша энергияның түріне байланысты, АБЖ электрлік (сонымен бірге электрондық), гидравликалық, пневматикалық және құрамдастырылған болып бөлінеді.
3. Буындар аралық әсер беру сипатына байланысты үздіксіз және периодты (мерзімді) әсерлер жүйелері болып кездеседі. Егер әсерлер алдын –ала тапсырылған уақыт интервалымен жіберілсе, оларды (бұл жүйені) импульстік деп атайды.
Тұйық сұлба түрінде құрастырылатын АБЖ-ның бөлек түрі автоматты реттеу (АРЖ) жүйесі болып келеді. Реттеу деп басқарудың жеке түрін айтады. Мұндағы объекттің шығысын (негізгі технологиялық параметр) тапсырылған (берілген) мәніне жақын ұстап тұрады немесе кейбір берілген заңдылықпен өзгертіледі.
АРЖ төмендегідей түрлері белгілі:
а) Айтылатын жүйеде, өндіріс техноллогиясына сәйкес, объекттің тапсырылған шығыс мәні қызметкермен қойылады. Тұрақтандыру жүйесі технологиялық талаптарға лайықты, оның келесі өзгеруіне дейін, объекттің шығысын тұрақты сақтайды.
б) Программалық реттеу жүйесі, талап етілген уақытқа байланысты заңдылық бойынша, объекттің шығысының тапсырыс мәнін өзгертеді.
в) Оптималды реттеу жүйесінде объекттің шығыс мәні алдын – ала тапсырылмайды. Онда, объекттің ерекшелігіне байланысты, тек жүйенің жұмыс үрдісі кезінде, объектке түрлі бағытта сыналатын әсерлердің бағытында оның шығысын. АБЖ құрамындағы басқару құралы автоматты реттеуіш түрін қабылдайды.
Функционалдық белгісі бойынша АБЖ ені үлкен классқа бөлуге болады – адаптивтік және адаптивтік емес. Соңғы жағдайда АБЖ қызмет істеу үрдісі кезінде басқарушы жабдықтың құрылымы мен параметрлері өзгермейді, немесе олар есептеу және жөнге салуда анықталған күйінде қалады. Бұл жүйені құрудың негізі деп, оның жұмыс істеуінің ішкі және сыртқы жағдайының өзгеру шамасы аз – кем болуын жорамалдау болып табылады. Егер жүйенің ішкі және сыртқы параметрлерінің өзгеру диапазоны өте үлкен болса, онда адаптивті емес жүйенің көмегімен оның қызметін қанағаттандыра алмаймыз. Бұл жағдайда басқару жүйесінің қасиетін өзгертетін үрдіс қолдануға тура келеді. Мұнда, жүйе қызметінің ішкі және сыртқы жағдайының өзгерген кезінде, оның реттеуішінің көрсеткіштері белгілі бір оптималдық мағынада таңдалып алынған соң өзгертіледі. Оны қарапайым сөзбен айтқанда, АБЖ пайда болған жағдайға бейімделінуі болып табылады.
Енді АБЖ сараптауды қысқа түрінде нақтыласақ, оны төмендегі түрінде көрсетуге болады.
қ1. Әсерлер принципі бойынша:
- ажыратылған (сыртқы әсерге байланысты);
- тұйық (ауытқуына байланысты);
- құрамдастырылған.
қ2. Басқару мақсаты бойынша:
- тұрақтандыру (тұрақты);
- программалық (берілген);
- қадағалаулық (еркінше);
- оптималдық (эксьремалды).
қ3. Басқару шамаларының санына байланысты:
- бір өлшемді;
- көп өлшемді.
қ4. Басқару тізбегіндегі сигналдар сипатына байланысты:
- үздіксіз (детерминирлік, стохастикалық);
- дискреттік (детерминирлік, стохастикалық).
қ5. Математикалық бейнелеуіне байланысты:
- сызықты;
- бейсызықты;
- айқын;
- айқын емес.
қ6. Параметрлер сипатына байланысты:
- стационарлық;
- стационарлық емес;
- жинақталған (топталған);
- бөлінген (үлестірілген).
1.2 Жүйенің құрылымы және элементтері
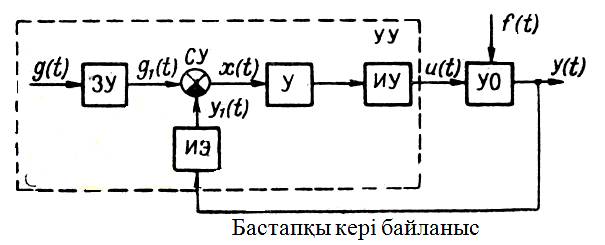
Енді типтік автоматты басқару жүйесінің құрылымын [7,8,10] қарастырайық. Ол 1 суретте көрсетілген
а)
 СҚ µ(t)
СҚ µ(t)
f(t) u(t)
g(t) g1(t) x(t) z(t)
z1(t)
б)
1 сурет - АБЖ типтік функционалдық сұлбасы
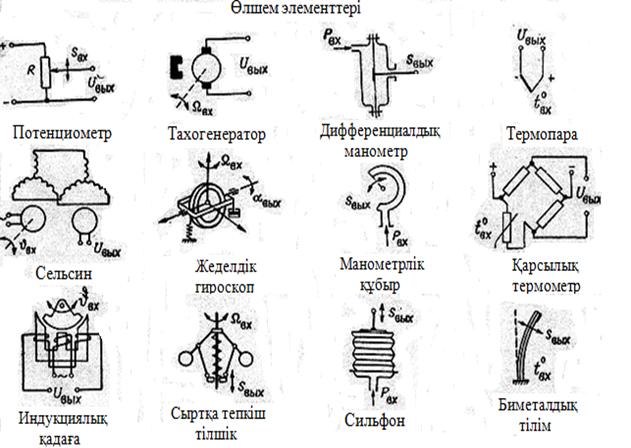
1. Өлшейтін қондырғы (элемент) басқару объектісінің (БО) шығысының нақты мәнін өлшейді және оны басқару қондырғысында қолдануға ыңғайлы күйге z1(t) түрлендіреді (2 суретті қара).
2 сурет
2. Тапсырма беруші қондырғы (ТҚ) басқару шамасының талап етілген мәнін анықтайтын тапсырма әсерін қалыптастырады, сонымен бірге оны z1(t) шамасымен бір мағыналық болуы үшін түрлендіреді. Себебі g1(t), z1(t) –мен салыстыруға ыңғайлы болуы қажет. Программалар немесе тапсырылған функционалдық тәуелділіктің тасымалдаушысы түрінде жұдырықты механизм, функционалдық потенциометр, магниттік және кинопленкалар қолданылады. Кейде, тапсырма беруші қондырғы өлшеу және салыстыру қондырғыларымен конструктірлік түрде біріктіріледі.
3. Салыстырмалы қондырғы (СҚ) кең тарамдық жағдайда x(t)= g1(t) - z1(t) айырмасы өлшенеді. Бұл x(t), басқару шамасы z(t)-ны, оның тапсырма мәнін g(t)-ден ауытқуына пропорционалды болады (3 суретті қара).
3 сурет
Басқару қондырғысы (БҚ) қателік x(t), басқару заңдылығы мен мақсатына байланысты басқару сигналын қалыптастырады. Басқару заңдылықтары туралы ақпарат кейінгі бөлімдерде жеткізіледі. Басқару қондырғысында жиі қолданылатын күшейткіштердің сұлбасы 4 суретте көрсетілген.
4 сурет
Орындаушы механизм (ОМ) басқарылатын объектіге басқару әсерін дайындайды және жібереді (5 суретті қара).

5 сурет
Сонымен бірге, басқару қондырғысының құрамына арнайы түзетуші (демпфирование іске асырушы) элементтер қосылады. Олар басқарудың сапасын жақсартады.
Енді өндрістік автоматты басқару (реттеу) жүйесінің функционалдық сұлбасымен таныстырасыз. Ол төменде көрсетілген
 f
f
z
z
ОМ – орындаушы механизм
РҚ(0) – реттеуші құрал (орган)
О – объект
Д – датчик (өлшеуіш тетік)
Р – реттеуіш
ҚА – қосымша аспап
Т – тапсырма беруші
КБ – кері байланыс
6 сурет
Онда объекттің шығыс мәні реттеуішке екі жолмен жіберіледі: 1-датчиктен, 2 - қосымша аспаптан. Ауқытқу деп объектіге сырттан әсер (бұл жүйеге байланысы жоқ) ететін қандайда болмасын факторды айтады. Оның әсерінен объекттің шығысы тапсырылған мәнінен ауытқиды. Автоматты реттеуіштің өндірістік үлгісінде оның құрамына салыстырушы элемент пен күшейткіш кіреді. Реттеуші орган объекттің шығысына жіберілетін реттеуіштің әсерін жүзеге асырады. Екеуінің ортасында орындаушы механизм орналасқан. Бұлардың екі түрі болады: а) электрлік (шығыс реттеуіші бар электрқозғалтқыш); б) гидро - немесе пневмоцилиндр, мұндағы поршень сұйықтың немесе сығылған ауа әсерінің көмегімен қозғалады (орнын ауыстырады).
1.3 Автоматтандырылған басқару жүйесі
Өндірістің қызметіне талдау жасау үшін оны кішігірім бөліктерге бөлу қажет. Ол түрлі иерархиялық белгілермен [1,9] жүзеге асырылады.
1. Уақыт иерархиясы. Басқарылатын объекттің күйі жөніндегі ақпараттың түсуінен басқару әсеріне дейінгі уақыт аралығын (интервалын) бұл иерархиянын белгісі деп қарастырамыз. Олар іс жүзіндегі (нақтылы) уақыт, 1 сағат, 1 ауысым, 1 күн, 1 декада, 1 ай, 1 квартал, 1 жыл.
2. Кеңістік иерархиясы. Басқарылатын объекттің орналасқан ауданы оның белгісі болып табылады. (Бірлескен өндіріс, өндіріс, цех, бөлімше).
3. Функционалдық иерархия. Ол жүйе элементтерінің функционалдық
бағыныштылығына байланысты жүзеге асырылады. (Президент, басты инженер, вице-президент, технология, экономика, техника және автоматика бөлімдері).
4. Ситуациялық иерархия. Ол өндірісте болатын жағдай тудыратын салдарына байланысты жасалады.
5. Информациялық иерархия. Басқаруға керек информацияның мәні оның (жауаптылығына) жаңартылуына және жеделділігіне байланысты іске асырылады.
Автоматтандырылған басқару жүйесін қолданудың төмендегідей өзгешеліктері бар. Олар: ақпараттың әдіс - амал (ақпаратты өңдеу), ықтималды әдіс (ішкі және сыртқы ықтимал ықпалды әсерді еске алу), жүйелік әдіс, адамды басқару контурына енгізу.
Қандайда болмасын үрдістерді басқару төрт түрге бөлінеді: автоматты, тікелей санды басқару, супервизорлы, адам – машиналы. Олардың бірінші түрін 1.2 параграфта толық түсіндірдік.
2. Тікелей санды басқарудың жалпы құрылымы
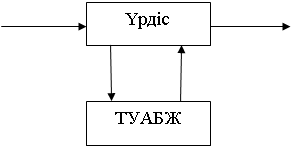 Кіріс
Шығыс
Кіріс
Шығыс
Өлшеу Басқару
7 сурет
3. Супервизорлы басқару.
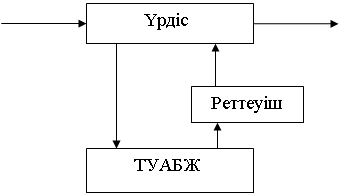 Кіріс Шығыс
Кіріс Шығыс
Басқару
Өлшеу
8 сурет
Реттеуішке тапсырма
4. Адам – машиналы басқару
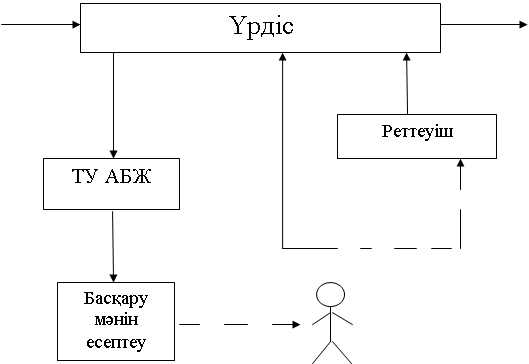 Кіріс Шығыс
Кіріс Шығыс
Басқару 1
Басқару 2 9 сурет
Реттеуішке тапсырм
ТУ АБЖ – дегеніміз адам мен машинадан тұратын басқару жүйесі. Бұл жүйе технологиялық объектіні қабылданған күштерге сәйкес оны оптималды басқару үшін ақпаратты жинау және өңдеуді қамтамасыз етеді.
ТУ АБЖ міндетті қызметі – басқару, ақпараттандыру және қосымша істер болып бөлінеді.
ТУ АБЖ құрамын, өз қызметін атқару үшін керекті төменде келтірілетін бөліктердің қарым – қатынасы түрінде қарастыруға болады. Олар:
1) Техникалық қамтамасыздандыру.
2) Ақпараттық қамтамасыздандыру.
3) Программалық қамтамасыздандыру.
4) Ұйымдастырулық қамтамасыздандыру.
5) Оперативтік қызметкерлер.
ТУ АБЖ сараптау.
1. Жүйенің өнеркәсіп құрылымындағы орналасқан деңгейіне байланысты.
а) Төменгі деңгейдегі ТУ АБЖ (технологиялық агрегат, участок).
б) Жоғарғы деңгейдегі ТУ АБЖ (цех, өндіріс).
в) Көп деңгейлі ТУ АБЖ.
2. Басқарылатын технологиялық үрдістің өту уақытына байланысты
а) Үздіксіз ТУ АБЖ.
б) Үздік ТУ АБЖ.
в) Үздіксіз - үздік ТУ АБЖ.
3. Басқарылатын технологиялық объекттің ақпарат қуаты (көлемі) шартына байланысты
а) ең кіші 10-40;
б) кіші 41-160;
в) орташа 161-650;
г) жоғары 651-2500;
д) үлкен 2501 және одан көп.
4. ТУ АБЖ жұмыс істеу түріне байланысты (қызмет)
а) ақпараттық;
б) локалды – автоматты;
в) кеңес беретін;
г) автоматты.
2 Өндірістік үрдістерді структуризациялау
2.1 Өндірістік үрдістің басқару объектісі
Кәсіпорынның ерекше элементтері [1,2,4]:
1) Еңбек заты - шығарылатын өнімнің құрамына кіретін материалдық объектер.
2) Еңбек әдісі немесе тәсілі - еңбек затын өңдеуге арналған станоктар, құрал-жабдықтар және орындары.
3) Кіріс қорын шығарылатын өнімге айналдыратын әрекет жиынын технологиялық үрдіс деп атайды.
Өндірістегі (фирмадағы) материалдық және экономикалық қарым - қатынастар жиынын өндірістік қарым - қатынастар деп атайды.
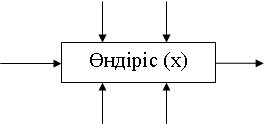 А В
А В
Qk Qш
У И
U Y
10 сурет - Басқару жүйесінің ірілендірілген құрылымы
Qk - еңбек затының құрылымы.
Qш - өңдеу арқылы пайда болатын еңбек өнімі.
А - шығын жиынтығы (электр энергиясы, бу, жұмыс күші және т. б. ).
В - қосымша компонеттер жиынтығы (қосымша бөлшектер, майлау материалдары және т. б. ).
Х - ішкі күйінің параметрлері.
Y - сыртқы әсерлер (брак, құралдар мен жұмыс күшінің жоғарлауы).
U - басқару әсерінің параметрлері.
Өндірісті басқару үрдісін үш негізгі деңгейге бөлуге болады:
1) Технологиялық үрдісті басқару деп оның ішкі күйі мен сыртқы әсеріне байланысты басқару заңдылығын оптимальді қолдануды айтады.
2) Еңбек әдісі және затын (нәрсесін), өндірістік қарым - қатынастарды басқару деп оларды тиімді пайдалануды айтады.
3) Объектті ұйымдастыру және экономикалық басқару дегеніміз оның тиімді критерийін оптимальдік мәніне жеткізу.
Өндірісті басқарудың түрлі құрылымдары бар: сызықты, функционалды, сызықты - сынықтылық, сызықты - функционалды, матрицалық.

11 сурет - Сызықты құрылым
Эл. - элемент
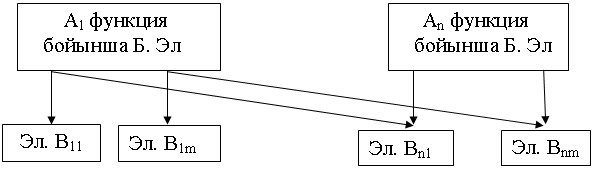
12 сурет - Функционалды құрылым
Б. Эл - басқарушы элемент
 |
. .
Сын. - сынықты Эл. –элемент
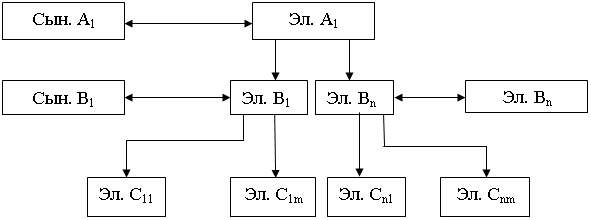
13 сурет - Сызықты-функционалды құрылым

Бас. - басшы, Эл. – элемент
14 сурет - Матрицалық құрылым
Енді нақты өндірістік объекттерді қарастырайық. Мұндағы реттелетін объекттің динамикалық қасиеттерін кейбір жағдайда сызықты дифференциалдық теңдеу арқылы арқылы көрсетуге болады. Ол объекттің кіріс және шығыс мәндерінің функционалдық тәуелділігін бейнелейді. Объекттің орнықты емес үрдісін анықтайтын дифференциалдық теңдеу оның физикалық заңдылықтар негізінде құрылады. Қарапайым объекттің (15 суретті қара) дифференциалдық теңдеуін мысал ретінде қарастырамыз.
Ыдысқа су Q1 мөлшерде (көлем өлшемі/сек) құйылды және Q2 мөлшерде жұмсалады (шығындалады). Енді белгілеу енгізейік:
∆h-деңгейдің тапсырылған мәнінен ауытқуы;
F - ыдыстың көлденең ауданы.
Объекттің тепе - теңдігі судың құйылу және ағып кету теңдігімен сипатталады.
![]() .
(2.1)
.
(2.1)
Сонымен бірге тапсырылған мәнінен ауытқуы (∆h) мен ыдысқа құйылған немесе жұмсалатын судың мөлшері өзергенде оның деңгейіде өзгереді.
Егер
![]() , (2.2)
, (2.2)
![]()
деп қабылданса, онда
![]() . (2.3)
. (2.3)
Қарастырылған мысалда, судың шығыны ыдыстың биіктігіне тәуелді
![]() . (2.4)
. (2.4)
Егер ∆h азғана болғанда, онда бірінші жуықтағанда мәні
![]() . (2.5)
. (2.5)
Мұндағы
![]() - тұрақты коэффициент.
- тұрақты коэффициент.
Осыны ескере отырып, (3) теңдеуді осылай жазуға болады
![]() . (2.6)
. (2.6)
Әрі қарай , көп таралған белгілеулерге
көшсек ![]() - уақыттың қазіргі
сәтіндегі реттелетін шаманың тапсырылған мәнінен
ауытқуы,
- уақыттың қазіргі
сәтіндегі реттелетін шаманың тапсырылған мәнінен
ауытқуы, ![]() –уақыттың
қазіргі сәтіндегі сұйықтықтың құйылуының
өзгеруі.
–уақыттың
қазіргі сәтіндегі сұйықтықтың құйылуының
өзгеруі.
Онда (2.6) теңдеуді төмендегі түрде көрсетуге болады
![]() .
(2.7)
.
(2.7)
Мұндағы
![]() – тұрақты уақыты (сек);
– тұрақты уақыты (сек);
![]() - объекттің
күшейту коэффициенті (реттелетін шаманың берілген әсерден
кейінгі орнықты ауытқуы бірге тең болады.
- объекттің
күшейту коэффициенті (реттелетін шаманың берілген әсерден
кейінгі орнықты ауытқуы бірге тең болады.
Қарапайым объекттің, дифференциалды теңдеу түріндегі басқаша жазылу формасы кейбір әдебиеттерде төмендегідей
![]() . (2.8)
. (2.8)
Мұндағы
![]() - объекттің өзін - өзі
туралау (түзету) коэффициенті
- объекттің өзін - өзі
туралау (түзету) коэффициенті
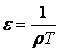 - екпін (ұмтылыс) жылдамдығы
(уақыттың бастапқы сәтінде, әсердің бірге
тең болған кезіндегі реттелетін шаманың өзгеру
жылдамдығы).
- екпін (ұмтылыс) жылдамдығы
(уақыттың бастапқы сәтінде, әсердің бірге
тең болған кезіндегі реттелетін шаманың өзгеру
жылдамдығы).
Дифференциалдық теңдеу көмегімен объекттің динамикалық қасиеттері тек біршама қарапайым объекттер болғанда ғана жүзеге асырылады.
Енді «қозғалтқыш – жұмыс машинасы» жүйесінің математикалық бейнесін қарастырайық.
Энергияның сақталу заңдылығына сәйкес бар болады
![]() ,
(2.9)
,
(2.9)
мұндағы,
кедергі күшін ![]() жеңіп шығу үшін
жұмсалатын қозғаушы күштің
жеңіп шығу үшін
жұмсалатын қозғаушы күштің ![]() жұмысы; қозғалыс
жылдамдығының өзгеруі оятатын (қоздыратын)
жүйенің кинетикалық энергиясының өзгеруі
жұмысы; қозғалыс
жылдамдығының өзгеруі оятатын (қоздыратын)
жүйенің кинетикалық энергиясының өзгеруі ![]() . Осы теңдеуді (2.9)
уақытқа байланысты дифференциалдағаннан кейін , қуаттардың
теңдеуін табамыз
. Осы теңдеуді (2.9)
уақытқа байланысты дифференциалдағаннан кейін , қуаттардың
теңдеуін табамыз
![]() ,
,
мұндағы ![]() - кедергі күшін
жеңу үшін жұмсалатын қуат.
- кедергі күшін
жеңу үшін жұмсалатын қуат.
![]() - жүйенің
кинетикалық энергия қорының өзгеруін бейнелейтін
динамикалық қуат.
- жүйенің
кинетикалық энергия қорының өзгеруін бейнелейтін
динамикалық қуат.
Ал айналатын денелер жүйесі үшін
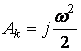 ,
,
мұндағы ![]() - қозғалтқыштың
айналу жиілігі. Ал инерция кезі (мезгілі, уақыты, моменті) мына
түрде болады
- қозғалтқыштың
айналу жиілігі. Ал инерция кезі (мезгілі, уақыты, моменті) мына
түрде болады

![]() - айналу
өсінен ri қашықтықтағы і-ші
дененің бөлігінің (кішкентай бөлшегінің ) массасы,
- айналу
өсінен ri қашықтықтағы і-ші
дененің бөлігінің (кішкентай бөлшегінің ) массасы,
 .
.
![]() -келтірілген инерция радиусы
-келтірілген инерция радиусы
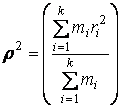 .
.
Егер инерция кезі (моменті) айналу бұрышы ![]() -ге
тәуелді болса, немесе
-ге
тәуелді болса, немесе ![]() сонымен бірге
уақытқа тәуелді болса, онда
сонымен бірге
уақытқа тәуелді болса, онда
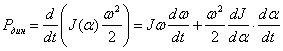 .
.
![]() ескере отырып және табылған
теңдеуді ω-ге
бөлсек, моменттердің баланс теңдеуін осылай жазуға
болады.
ескере отырып және табылған
теңдеуді ω-ге
бөлсек, моменттердің баланс теңдеуін осылай жазуға
болады.
![]() .
.
Егер ![]() , онда
, онда ![]() . Онда
(2.9) теңдеуді ескере отырып «қозғалтқыш - жұмыс
машинасы» жүйесінің қозғалу теңдеуін былай
жазуға болады
. Онда
(2.9) теңдеуді ескере отырып «қозғалтқыш - жұмыс
машинасы» жүйесінің қозғалу теңдеуін былай
жазуға болады
![]() (2.10)
(2.10)
Әрі қарай (2.10) теңдеуге кіретін айнымалылардың қандай факторларға тәуелділігін анықтау керек.
Қарастырған мысалда, қозғаушы момент ![]() машинаға түсетін
энергияға тәуелді немесе реттеуші органның қалпы
машинаға түсетін
энергияға тәуелді немесе реттеуші органның қалпы ![]() -ке және айналу жиілігі
-ке және айналу жиілігі ![]() -ге . Кедергі моменті
-ге . Кедергі моменті ![]() түрлі қосындылар
қатарынан тұрады: бір бөлігі тұрақты болуы
мүмкін (қажалу/үйкелу күші), келесісі -
түрлі қосындылар
қатарынан тұрады: бір бөлігі тұрақты болуы
мүмкін (қажалу/үйкелу күші), келесісі - ![]() -ге тәуелді («желдеткіш
әлеуеті/күші»), үшіншісі – өтетін жолдан, уақыттан
т. б. Енді Мд реттеуші органның қалпына және
айналу жиілігіне тәуелді (х, ω), ал кедергі моменті тек жиіліктен
деп ұйғарсақ. Онда қойылған шарттарға
байланысты (2.10) теңдеуді сызықты немесе бисызықты
түріне жатқызуға болады.
-ге тәуелді («желдеткіш
әлеуеті/күші»), үшіншісі – өтетін жолдан, уақыттан
т. б. Енді Мд реттеуші органның қалпына және
айналу жиілігіне тәуелді (х, ω), ал кедергі моменті тек жиіліктен
деп ұйғарсақ. Онда қойылған шарттарға
байланысты (2.10) теңдеуді сызықты немесе бисызықты
түріне жатқызуға болады.
2.2 Басқарылатын технологиялық объекттердің қасиеттері
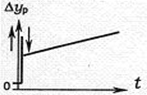
Энергетика объекттерінің көп кездесетін қасиеттерін оның екпін қисық сызығын тұрғызғанда байқауға болады (15 суретті қара).
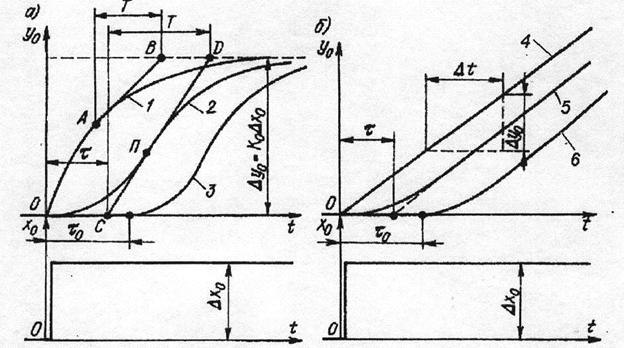
15 сурет
Мұндағы график түрінде көрсетілген қисық сызық, объекттің кірісіне to бастапқы уақыт сәтінде берілген ∆Хо сатылы әсерден кейінгі оның шығысы Уо өзгеруі көрсетілген. Объекттің кіріс әсер ретінде отын беру немесе ажыратқышты қосу т.б. қарастыра отырып үрдіс шығысының экспериментальді – хронометриялық өзгеруін өлшей аламыз. Осындай тәсілді объекттің құрамына кіретін бөлек буындардың себеп - салдар (нәтиже) байланысын анықтауға қолданылады.
16-сурет көп қолданылатын типтік объекттердің динамикалық параметрлері көрсетілген. Олар [4,6,10]:
К0 - статикалық объекттің беріліс коэффициенті;
Т - бірінші дәрежелі статикалық объекттің тұрақты уақыты;
τ0 - таза кешігу уақыты;
А1, А2 – коэффициенттер;
![]() - астатикалық
объекттің шартты беріліс коэффициенті;
- астатикалық
объекттің шартты беріліс коэффициенті;
![]() - астатикалық
объекттің шартты тұрақты уақыты;
- астатикалық
объекттің шартты тұрақты уақыты;
Т* - астатикалық объекттің «баяулату» тұрақты уақыты.
Қарапайым жағдайда дифференциалдық теңдеудің түрін екпін қисық сызығына байланысты визуалды бағаланады. Объект шығысы өз еркімен кейбір орнықты мәніне ұмтылуы оның сипатты статикалық қасиетін көрсетеді (16, а суретті қара).
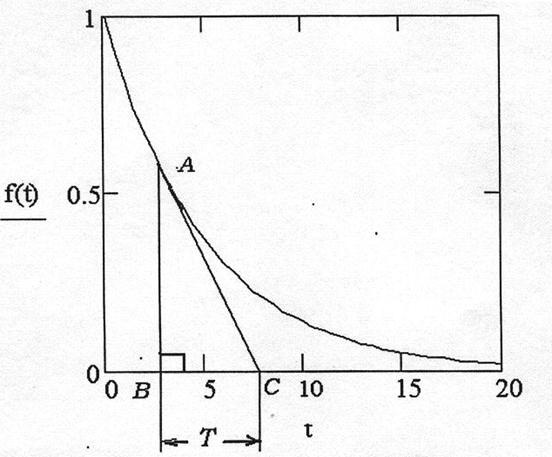
16 а сурет
Бұл қасиет астатикалық объектте болмайды (16, б суретті қара).
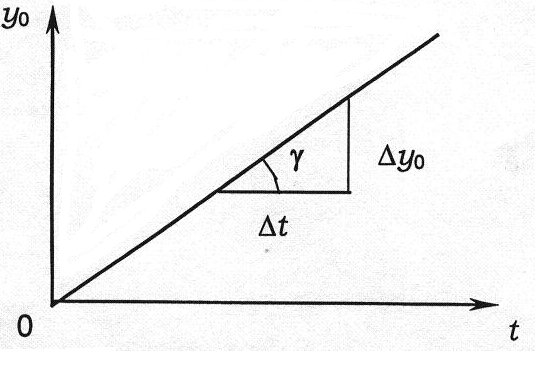
16 б сурет
Жоғарыда айтылған қасиеттері объектті бейнелейтін дифференциалдық теңдеулерден де көруге болады. Астатикалық объекттің формальді белгісі -математикалық модельде У0 мүшесінің болмауы.
Статикалық объекттердің орнықты күйіндегі беріліс коэффициенті шығыс және кірістің толық өзгеруі қатынасымен есептеледі
 . (2.11)
. (2.11)
Бірінші дәрежелі статикалық объекттің тұрақты уақыты өтпелі үрдіс кезіндегі оның шығысының өзгеру жылдамдығын сипаттайды.
Егер алдында қарастырған (16 суретті қара) 1 қисық сызықты алсақ, онда экспериментальді екпін қисық сызығы арқылы тұрақты уақытты анықтаудың графикалық амалын (тәсілін) көрсетуге болады. Ол үшін қисық сызық бойындағы қандай да болсын А нүктесін алып оған АВ жанамасын жүргіземіз. Енді А нүктесінен объекттің шығыс шамасының орнықты мәніне перпендикуляр тұрғызсақ, пайда болған АВ кесіндісі буынның тұрақты уақытына тең болады. Шынында, егер біз өзінің экспоненционалдық функциясын қарастырсақ
![]() . (2.12)
. (2.12)
Екпіннің қисық сызық формуласының негізгі
бөлігі деп, ![]() , ауқымында (өрісінде)
мысал келтірейік (18 сурет)
, ауқымында (өрісінде)
мысал келтірейік (18 сурет)
 . (2.13)
. (2.13)
Келесісі
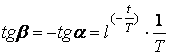 (2.14)
(2.14)
АВС ұшбұрыштың құрамындағы АВ
кестесі ![]() функциясының қазіргі
мәні (16 суретті қара). Осыдан А нүктенің еркінше
орнына байланысты
функциясының қазіргі
мәні (16 суретті қара). Осыдан А нүктенің еркінше
орнына байланысты
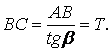 (2.15)
(2.15)
Жүйенің (буынның) тұрақты уақыты үлкен болған сайын, оның өтпелі үрдісі баяу өтеді. Бірінші дәрежелі статикалық объекттің өтпелі процессінің толық ұзақтығы (3. . . . . . . 5) Т.
Астатикалық объекттің дифференциалдық теңдеуін
де ![]() параметрі -шартталған
тұрақты уақыт деп аталады. Оның өлшемі аралас
болғандықтан, оған уақыт өлшемі және
объекттің кірісі мен шығысы өлшемдері кіреді. Кейде,
оған кері шама
параметрі -шартталған
тұрақты уақыт деп аталады. Оның өлшемі аралас
болғандықтан, оған уақыт өлшемі және
объекттің кірісі мен шығысы өлшемдері кіреді. Кейде,
оған кері шама ![]() - шартты беріліс коэффициенті
қолданылады. Өтпелі үрдістегі объекттің
шығысының өзгеру жылдамдығын
- шартты беріліс коэффициенті
қолданылады. Өтпелі үрдістегі объекттің
шығысының өзгеру жылдамдығын
![]() шамасы бейнелейді. Сонымен
бірге бұл жылдамдық объекттің кіріс мәніне
тәуелді болады. Салынған графикалық формада
көрсетілгендеі (16 сурет), объект шығысы (кіріс мәні аз
болғанда) жылдамдығының өсуі (үдеуі)
шамасы бейнелейді. Сонымен
бірге бұл жылдамдық объекттің кіріс мәніне
тәуелді болады. Салынған графикалық формада
көрсетілгендеі (16 сурет), объект шығысы (кіріс мәні аз
болғанда) жылдамдығының өсуі (үдеуі) ![]() және
және ![]() нақты мәнімен
анықталады.
нақты мәнімен
анықталады.
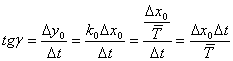 . (2.16)
. (2.16)
Екінші және одан да жоғары дәрежелі теңдеуі бар статикалық объекттерге келсек оның екпінінің қисық сызықты формасы S - түрінде болады. Бұл жағдайда экспериментальді екпін қисық сызығы арқылы дифференциалдық теңдеудің дәрежесі дәл анықталмайды. Дегенмен белгілі Симою интегралдық әдісі арқылы деп аталатын объектті идентификациялаудың есептеу әдісі (аудан әдісі) бар. Ұйымдастырылған эксперимент кезінде салынған екпін қисық сызығы дәлділігінің шектеулігі не байланысы үшінші дәрежелі жоғары дифференциалдық теңдеудің дәрежесінің анықталуы қиындатылады немесе анықталмауы мүмкін.
Энергетикалық объекттердің күрделігіне байланысты (бисызықты, бөлініп тұратын параметрлер), олар өтпелі кешігуі τn бар бірінші дәрежелі объекттер түрінде аппроксималанады (шамалас (жуық) суреттелу/көрсету). Статикалық объекттерге экспериментальды жолмен анықталған екпін қисық сызығында бүгілу нәтижесі табылады. Содан соң осы нүктеден өтетін және шығысын бастапқы мен соңғы мәнімен қиылысатын жанама жүргіземіз. Мұндағы ОС және ЕD кесінділері өтпелі кешігу τn мен тұрақты уақыт Т сәйкес келеді.
Екінші және одан да үлкен дәрежелі астатикалық объекттердің өтпелі кешігуінің анықталуы суретте көрсетілген (5 б қисық сызығы). Екінші дәрежелік диффренциалдық теңдеуі (Е) бар объекттің «бәсеңдететін/баяулайтын» Т* тұрақты τn шамасына дәл келеді.
Өтпелі үрдістің бастапқы кезеңін бейнелей түсіндіретін, сонымен қатар, күрделі астатикалық объекттің әр уақытта дәрежесі белгісіз болан кездегі аппроксималағанда да τn=T* тең деп алады. Егер объекттің коммуникациялық ұзындығына сәйкес, зат тек легінің қозғалыс уақытымен анықталатын таза кешігу τ0 болса, онда инженерлік есептерді шешуге шамалас (жуық) амалды қолданғанда жалпы кешігуі төмендегідей болады:
![]() . (2.17)
. (2.17)
2.3 Автоматты басқару жүйесінің типтік буындары
Осы заманғы АБЖ түрлі физикалық табиғаты, құрылымдық орындалуы, энергия қайнар көздері бар және т. б. элементтерден тұрады [2,4,7]. Соған қарамастан, осы элементтердің динамикалық қасиеттерін бір - біріне ұқсас дифференциалдық теңдеулермен бейнелеуге болады: позициялық, интегралдық, дифференциалдық.
Позициялық буындар
1 Инерциясыз буын.
Қозғалыс теңдеуі ![]() болатын
буынды инерциясыз буын деп атайды. Буынның беріліс функциясы
болатын
буынды инерциясыз буын деп атайды. Буынның беріліс функциясы
![]() . (2.18)
. (2.18)
Инерциясыз буынның мысалдары ретінде редуктор, кернеу бөлгіші, өлшегіш аспап бұрышы, инерциясыз күшейткішті және т. б қарастыруға болады (17 суретті қара).
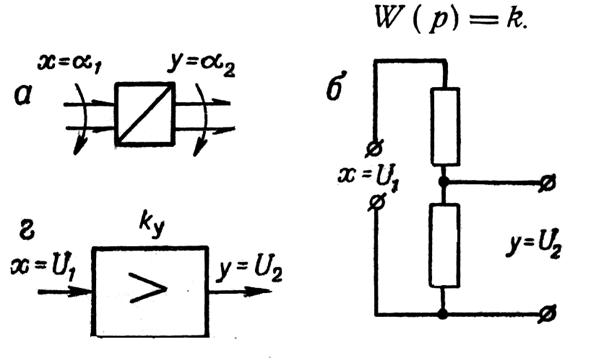
17 сурет
Кейбір автоматикалық жүйенің өлшеуіш элементтерінің (өлшегіш аспап бұрышының айырмасы, фотоэлектрлік датчик, магнитоэлектрлік өлшегіш аспап және т. б. инерциялық кешігу қасиеттері де кездеседі.
Инерциясыз буынның құрылымдық сұлбасы
|
![]()
![]()
Мұндағы инерциясыз буынның шығыс координаты кіріс координатын өзгеру заңдылығын беріліс коэффициенті К дәлдігімен қайталайды (17 суретті қара).
Инерциясыз буынның өтпелі функциясы
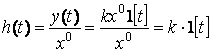 .
(2.19)
.
(2.19)
Буынның жиілік беріліс функциясы, амплитуда жиілік, логарифмдік амплитудалық және фазалық жиілік сипаттамалары төмендегі формулаларымен анықталады
![]()
![]() ,
,
![]() (2.20)
(2.20)
Буынның
амплитудалық жиілік сипаттамасы жиілік өсінен ![]() жоғары,
жоғары, ![]() төмен
өтеді, ал к=1болғанда жиілік өсімен беттеседі (17 суретті
қара).
төмен
өтеді, ал к=1болғанда жиілік өсімен беттеседі (17 суретті
қара).

18 сурет
Буынның логарифмдік жиілік сипаттамасы графигін қарастыра отырып, бұл буынның барлық жиіліктердегі тербелісті бірдей өткізеді деп айтуға болады.
Мұндағы
![]() нақты және жорамал
бөліктері.
нақты және жорамал
бөліктері.
![]()
![]() (2.21)
(2.21)
Буынның (2.19) формулаға сәйкес тұрғызылған амплитуда - фазалық жиіліктік сипаттамасы 18 суретте көрсетілген.
2 Бірінші дәрежелі аппериодикалық буын.
Қозғалысының дифференциалдық теңдеуі
![]() (2.22)
(2.22)
Болатын буынды бірінші дәрежелі аппериодикалық буын деп атайды. Бұл мұның операторлық формадағы жазылуы
![]() . (2.
23)
. (2.
23)
Буынның беріліс функциясы
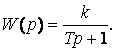
Кейде оны аппериодикалық буын немесе инерциялық буын деп атайды. Оның құрылымы 19 суретте көрсетілген
|
![]()
Аппериодикалық буындардың мысалдары ретінде тұрақты ток қозғалтқышы, екіфазалық асинхроннды қозғалтқыш, инерциялық кешігудегі ескеретін қүшейткіш, R, C мен R, L элементтері бар жылу қозғалтқышы.
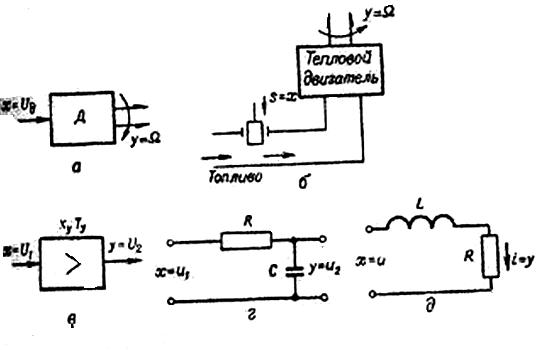
19 сурет
Буынның
өтпелі функиясын анықтау үшін, бастапқы шартты ескере
отырып ![]() және
және ![]() .
.
(2.20) дифференциалдық теңдеуін шешеміз
![]()
Өтпелі функция (19 сурет)
 (2.24)
(2.24)
Буынның тұрақты уақыты Т оның инерциялық кешігуін бейнелейді. Тұрақты уақыт Т неғұрлым көп болған сайын, кіріс пен шығыс координаталарының өзгеруін салыстырған анықталатын кешігу инерциясыда үлкен болады (19, б суретті қара).
Буынның кірісіне тұрақты сигнал берген кезде, ондағы өтпелі үрдіс өткеннен кейінгі буынның шығыс координатасы у кірісімен байланысы бұзылмайды:
![]() .
(2.25)
.
(2.25)
Мысалы, тұрақты ток электрқозғалтқышының айналу жылдамдығының орнықтылық мәні оған қосу сәтіндегі берілген кернеу шамасымен анықталады.
Жиілік (өтпелі) беріліс функциясы, буынның ЛАЖС, ЛФЖС төменгі формулаларымен анықталады:
 ,
,
 , (2.26)
, (2.26)
![]() .
.
ЛАЖС нүктелік графигін тұрғызу көп есептеуді талап етеді, сондықтан АБЖ есептеп зерттелгенде асимптатикалық ААЖС тұрғызылады. Енді кіші жиілік және үлкен жиілік асимптот ЛАЖС формулаларын табайық.
Жиілік
![]()
болғанда ![]()
формуласындағы ![]() қосындысын
бір санымен салыстырғанда ескермеуге болады.
қосындысын
бір санымен салыстырғанда ескермеуге болады.
Онда
![]() .
.
Бірінші дәрежелі апериодикалық буынның кіші жиілік
асимптоты жиілік осіне параллель және одан ![]() қашықтықта
орналасқан түзу болады. Егер жиілік
қашықтықта
орналасқан түзу болады. Егер жиілік ![]() болса
,
болса
,
![]() .
.
Ескереміз, жиілік осінің меже сызықтары/шәкілі
![]() сәйкес бірқалыпты
ораналасқан. Шығарылған формулаға байланысты ЛАЖС
жоғарғы жиілік асимптотасы – 20 дб/сек еңкеюі (иілуі) бар
тіке сызық болады. Жоғарғы жиілік асимптоттың жиілік
осімен қиылысу нүктесі табу үшін
сәйкес бірқалыпты
ораналасқан. Шығарылған формулаға байланысты ЛАЖС
жоғарғы жиілік асимптотасы – 20 дб/сек еңкеюі (иілуі) бар
тіке сызық болады. Жоғарғы жиілік асимптоттың жиілік
осімен қиылысу нүктесі табу үшін
![]() ,
,
![]() .
.
Табылған теңдеуден асимптоттың ості қиып өту жиілігін анықтаймыз.
![]() .
.
Буынның асимптотикалық ЛАЖС тұрғызуды былай
орындаған қиындық туғызбайды. Жиілік осінде
асимптотикалық ЛАЖС иілу нүктесін белгілейміз. Осы буынға ол
![]() , ол арқылы тік
жүргіземіз, оғн дейінгі сызық жиілік осіне параллель
жүргізіледі (болады). Ал оның оң жағындағы тік
сызық жиілік осінің
, ол арқылы тік
жүргіземіз, оғн дейінгі сызық жиілік осіне параллель
жүргізіледі (болады). Ал оның оң жағындағы тік
сызық жиілік осінің ![]() нүктесінен өтеді және оның – 20 дб/ден иілуі
болады. Нақтылы ЛАЖС асимптотикалыққа қарағанда
ең үлкен ауытқуы жиіліктің
нүктесінен өтеді және оның – 20 дб/ден иілуі
болады. Нақтылы ЛАЖС асимптотикалыққа қарағанда
ең үлкен ауытқуы жиіліктің ![]() маңында орын алады,
оның мәні
маңында орын алады,
оның мәні
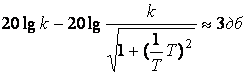 .
.
ЛФЖС буынның беріліс функциясы коэффициентіне тәуелді емес.
Түрлі тұрақты уақыттары Т1 және Т2
бар буындардың ЛФЖС-ның бұрылу жиілігі
![]() ,
, ![]() бола тұрсада
олардың түрлері өзгермейді (бірдей). Бірақ олар бір - біріне
жиілік осі бойында
бола тұрсада
олардың түрлері өзгермейді (бірдей). Бірақ олар бір - біріне
жиілік осі бойында ![]() шамасына
жылжытылған (20 суретті қара). Сондықтан ЛАЖС
тұрғызуға, тұрақты
шамасына
жылжытылған (20 суретті қара). Сондықтан ЛАЖС
тұрғызуға, тұрақты ![]() бар
буынға дайындалған шаблонды қолдану ыңғайлы
болады.
бар
буынға дайындалған шаблонды қолдану ыңғайлы
болады.
ЛАЖС және ЛФЖС графиктерінен көргендей, кіріс сигналы жиілігі өскенде буынның теріс фазалық жылжытуы өседі және буынның шығыс координатасының амплитудалық тербелісі азаяды. Бірінші дәрежелі апериодикалық буын кіші жиілік фильтрі деп аталады. Ол кіші жиілікті кіріс координатасы тербелісін жақсы өткізеді де, ал жоғарғы жиілікті тербелісті – жаман.
Буынның АФЖС, оның амплитуда жиілік сипаттамасымен
 (2.27)
(2.27)
және фазалық сипаттамасымен
![]() (2.28)
(2.28)
немесе нақты жиілік сипаттамасымен
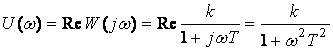 (2.29)
(2.29)
және жорамал жиілік сипаттамасы
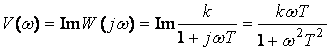 . (2.30)
. (2.30)
Графикалық тұрғызылады. Жалпылама буынның АФЖС жартылай шеңбер түрінде болады (20 суретті қара).
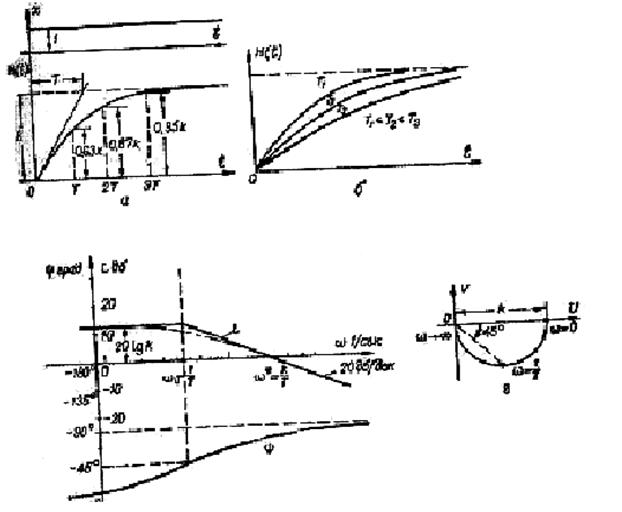
21 сурет
3 Екінші дәрежелі апериодикалық буын.
Қозғалыс дифференциалдық теңдеуі
 ,
, ![]() . (2.31)
. (2.31)
Болатын буынды екінші дәрежелі апериодикалық буын деп аталады. Ол операторлық түрде
![]() ,
, ![]() .
(2.32)
.
(2.32)
Буынның беріліс функциясы
 . (2.33)
. (2.33)

20 сурет
Құрылымдық сұлбада түрінде
көрсетілген 2 дәрежелі апериодикалық буынға мысал
әр суретте белгіленген. Осы буынның сипаттамалық
полиномының түбірі ![]() ,
, ![]() шарты
орындалғанда нақты болады. Оны басқаша бейнелеуге
мүмкіндік бар
шарты
орындалғанда нақты болады. Оны басқаша бейнелеуге
мүмкіндік бар
![]() , (2.34)
, (2.34)
мұндағы
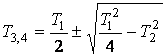 .
.
(2.34) формуласын ескере отырып, буынның беріліс функциясын төменде көрсетілген түрде жазуға болады
 (2.35)
(2.35)
немесе басқаша
 .
(2.36)
.
(2.36)
Екінші дәрежелі апериодикалық буынды, (2.35) пен (2.36) формуласына сәйкес тізбектеп немесе параллельді қосылған тұрақты уақыттары Т3 және Т4 екі бірінші дәрежелі апериодикалық буындар түрінде көрсете аламыз. Екінші дәрежелі апериодикалық буынның құрылымдық сұлбасын көргендей (22, в суретті қара)
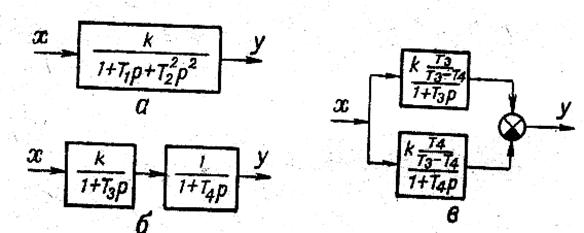
22 сурет
оның
өтпелі функциясын анықтау үшін өтпелі коэффициентті
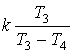 тұрақты
уақыты Т3 бірінші дәрежелі апериодикалық
буыннан, өтпелі коэффициенті
тұрақты
уақыты Т3 бірінші дәрежелі апериодикалық
буыннан, өтпелі коэффициенті ![]() мен тұрақты уақыты Т4 бірінші
дәрежелі апериодикалық буындардың өтпелі
функцияларының айырмасын табамыз:
мен тұрақты уақыты Т4 бірінші
дәрежелі апериодикалық буындардың өтпелі
функцияларының айырмасын табамыз:
 . (2.37)
. (2.37)
Буынның өтпелі функциясы ![]() графигі
23 а суретінде көрсетілген.
графигі
23 а суретінде көрсетілген.

23 а сурет
Буынның кірісіне сатылы тұрақты
![]() сигналын бергенде,
оның өтпелі үрдісі аяқталғаннан кейін буынның
шығыс координатасы кіріс координатасымен тәуелді
сигналын бергенде,
оның өтпелі үрдісі аяқталғаннан кейін буынның
шығыс координатасы кіріс координатасымен тәуелді
![]() .
(2.38)
.
(2.38)
Буынның жиілік өтпелі функция, ЛАЖС, ЛФЖС формулаларды көрсетілген
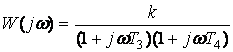 ,
(2.39)
,
(2.39)
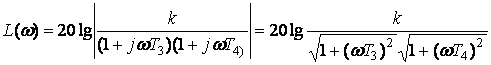 , (2.40)
, (2.40)
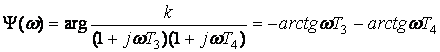 . (2.41)
. (2.41)
Енді асимптотикалық ЛАЖС формуласын шығарамыз. (2.40)
формуладағы жиілік мәні ![]() аймағында
орналасса, онда осы формуладағы
аймағында
орналасса, онда осы формуладағы ![]() және
және
![]() мүшелерін бірімен салыстыра отырып
ескермейміз. Онда
мүшелерін бірімен салыстыра отырып
ескермейміз. Онда
![]() .
(2.42)
.
(2.42)
Теңдеу (2.42) бейнелейтін тік сызық, жиілік осіне параллель
және одан ![]() қашықтықта
орналасқан (23 б сурет). Ал жиілігі
қашықтықта
орналасқан (23 б сурет). Ал жиілігі  аймақтағы
(2.40), бірмел салыстырғанда
аймақтағы
(2.40), бірмел салыстырғанда ![]() мүшесін
ескермейміз, сонда
мүшесін
ескермейміз, сонда
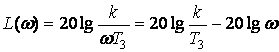 . (2.43)
. (2.43)
Теңдеу (2.43), иілуі - 20дб/дек және жиілік осін 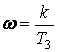 нүктесінде қиып өтетін тік
сызықтың теңдеуі болып есептеледі. Егер жиіліктің
нүктесінде қиып өтетін тік
сызықтың теңдеуі болып есептеледі. Егер жиіліктің 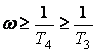 аймағын қарастырсақ,
аймағын қарастырсақ, ![]() және
және ![]() мүшелерімен
салыстырғанда бір санын ескермейміз. Бұл жағдайда
мүшелерімен
салыстырғанда бір санын ескермейміз. Бұл жағдайда
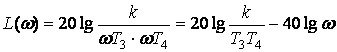 . (2.44)
. (2.44)
(2.44)
теңдеу, иілуі - 40дб/дек болатын және жиілік осін  нүктесінде қиып тік
сызық теңдеуі деп аталады. Асимптотикалық ЛАЖС
тұрғызылу принципі 23 б суретте анық көрсетілген. ЛАЖС
өскен сайын теріс фазалық қозғалу өседі
және амплитуда азаяды.
нүктесінде қиып тік
сызық теңдеуі деп аталады. Асимптотикалық ЛАЖС
тұрғызылу принципі 23 б суретте анық көрсетілген. ЛАЖС
өскен сайын теріс фазалық қозғалу өседі
және амплитуда азаяды.
Буынның АФЖС анықтауға керекті
![]() нақты
нақты
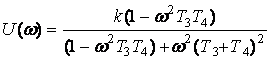
және жорамал
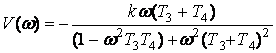 .
.
Оның амплитудалық жиілік
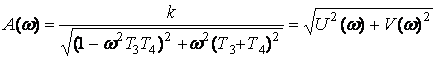 (2.45)
(2.45)
және фазалық жиілік
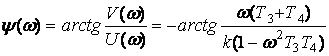 . (2.46)
. (2.46)
сипаттамалары осындай.
Екінші дәрежелі апериодикалық буын өз сипаттамасымен, тізбектеліп қосылған екі бірінші дәрежелі апериодикалық буындарға эквивалентт (22, б суретті қара). Ол шығыс тербелісінің қозғалуының үлкен болуы мен беріліс коэффициенті k және тұрақты уақыт Т буынмен салыстырғанда кіріс тербелісінің мықтап басылуымен түсіндіріледі. Буынның АФЖС түрі 23 в cуретінде көрсетілген.
4 Тербелмелі буын.
Қозғалыс дифференциалдық теңдеуі
 ,
, ![]() . (2.47)
. (2.47)
Немесе операторлық түрде
![]() ,
, ![]() . (2.48)
. (2.48)
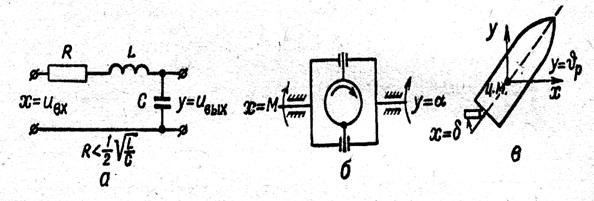
24 сурет
Буынның беріліс функциясы
 . (2.49)
. (2.49)
Есептеуге ыңғайлы болу үшін буынның беріліс функциясын көбінесе төмендегі түрде жазады
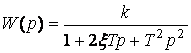 ,
(2.50)
,
(2.50)
мұндағы
T=T2, 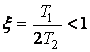 .
.
Тербелмелі буынның мысалы ретінде R,C,L тізбегі, созылғыштығын (серпінділігін) мен уйкелу жылдамдығын ескерілген механикалық керіліс, егер кіріс шамасы деп момент М, ал шығысы – бұрылыс бұрышы α демфирлігі ескерілген орнықты ракета қарастырылған (24 суретті қара).
Буынның сипаттамалық теңдеуінің түбірі
![]()
комплексті болып келеді
 ,
,
мұндағы
![]() ,
, 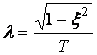 .
.
Буынның өтпелі функциясы
![]() .
.
Тербелме бейнесін қабылдайды.
Буынның өтпелі үрдісі оның тұрақты уақыты Т үлкейген және демпфирлік коэффициенті ξ кішірейген сайын ақырын (баяу) басылады.
Буынның асыра реттеу шамасы
![]() ,
,![]() .
.
Тек ξ демпфирлік коэффициент шамасына тәуелді. Сонымен бірге, буынның амплитуда жиіліктің сипаттамасының салыстырмалық шуы
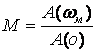 .
.
Мұндағы
![]() -
- ![]() максималдық
мән қабылдайтын жиілік, ξ тек демпфирлік коэффициентіне
тәуелді. Сондықтан буынның асыра реттеу шамасын М
шамасыменде анықтауға болады.
максималдық
мән қабылдайтын жиілік, ξ тек демпфирлік коэффициентіне
тәуелді. Сондықтан буынның асыра реттеу шамасын М
шамасыменде анықтауға болады.
Демпфирлік коэффициенттің ξ кіші мәндерінде ξ
< 0,5 тербелудің баяулау жиілігі ![]() .
.
Буынның кірісіне ![]() тұрақты сигналын енгізгенде, оның өтпелі
үрдісі өткеннен кейінгі шығыс координатасы кіріс
координатасымен қатаң байланысты
тұрақты сигналын енгізгенде, оның өтпелі
үрдісі өткеннен кейінгі шығыс координатасы кіріс
координатасымен қатаң байланысты
![]() .
.
Өтпелі беріліс функциясы, ЛАЖС және ЛАФС төмендегі формуламен есептеледі:
![]() ,
(2.51)
,
(2.51)
![]() , (2.52)
, (2.52)
 . (2.53)
. (2.53)
Буынның жиілік сипаттамасы 25 суретте көрсетілген.

25 сурет
Буынның ЛАЖС демпфирлеу коэффициенті шамасына өте күшті тәуелді. ξ ≥0,707 болған кезде функцияның түрі бірқалыпты азаюда болады, ал ξ<0,707 және жиілік жақындағанда оның резонанстық шыңы пайда болады.
Демпфирлеу коэффициенті ξ шамасы аз болған сайын, оның резонанс шыңы шамасы өседі.
![]() . (2.54)
. (2.54)
Буынның асимптотикалық ЛАЖС анықтау формуласы
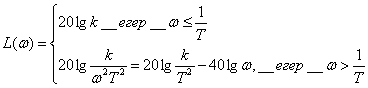 . (2.55)
. (2.55)
Буынның асимптотикалық ЛАЖС нақты ЛАЖС айырмасы бар.
Мысалы, ξ→0 кезде жиіліктің ![]() нүктесінде асимптотикалық ЛАЖС нақтысынан
ауытқу шамасы шексіздікке ұмтылады. Әдетте, ЛАЖС ЛФЖ Т=1с
және ξ түрлі мәндерінде дайындалған шаблондар
көмегімен тұрғызылады. Буынның АФЖС түрі 25 в суретте
көрсетілген. Жиілік ω өте кіші мән
қабылдағанда, ол жорамал осін жағалай созылған.
нүктесінде асимптотикалық ЛАЖС нақтысынан
ауытқу шамасы шексіздікке ұмтылады. Әдетте, ЛАЖС ЛФЖ Т=1с
және ξ түрлі мәндерінде дайындалған шаблондар
көмегімен тұрғызылады. Буынның АФЖС түрі 25 в суретте
көрсетілген. Жиілік ω өте кіші мән
қабылдағанда, ол жорамал осін жағалай созылған.
Буынның АФЖС анықтауға керекті W(jω) нақты
![]()
және жорамал
![]() .
.
Бұл буынның амплитудалық жиілік
![]()
және фазалық жиілік
![]()
сипаттамалары осындай.
5 Консервативті буын.
Консервативті буынның беріліс функциясының түрі
![]() .
(2.56)
.
(2.56)
Консервативті буынның мысалы ретінде демпфирленген тербелмелі буын, немесе оның демпфирлік коэффициенті ξ ескерілмесе. Техникалық түрдегі мысал деп демпфирлігі ескерілмеген статикалық орнықты қатты ракетаны алуға болады. Консервативті буын деп орнықтылықтың тербелмелі шекарасындағы буынды айтады. Оның өтпелі функциясын, тербелі буынның демпфирлік коэффициентін ξ=0 деп алғандағы жағдайды анықтаймыз.
![]() . (2.57)
. (2.57)
Бұл
өтпелі функция жиілігі ![]() басылмайтын
түрінде болады. Консервативті буынның шығыс координаты, кіріс
сигналы болмаған кезде де жиілігі гармониялық
заңдылықпен өзгеретінін атап өтуге болады. Оның
мәні
басылмайтын
түрінде болады. Консервативті буынның шығыс координаты, кіріс
сигналы болмаған кезде де жиілігі гармониялық
заңдылықпен өзгеретінін атап өтуге болады. Оның
мәні ![]() бастапқы
жағдайға тәуелді. Егер нольдік бастапқы жағдайы y(0)=0
болған кезде оның тербелісі болмайды.
бастапқы
жағдайға тәуелді. Егер нольдік бастапқы жағдайы y(0)=0
болған кезде оның тербелісі болмайды.
Жиілік беріліс функциясын, ЛАЖС және ЛФЖС анықтайтын формулалар
![]() ,
,
![]() , (2.58)
, (2.58)
 .
.
ЛАЖС мен ЛФЖС резонанс жиілік
![]() кезінде шығыс координатасы айырылады. Асимптотикалық ЛАЖС
түрі 26 суретте көрсетілген. Ондағы нақты ЛАЖС
түрі пунктирленіп сызылған.
кезінде шығыс координатасы айырылады. Асимптотикалық ЛАЖС
түрі 26 суретте көрсетілген. Ондағы нақты ЛАЖС
түрі пунктирленіп сызылған.
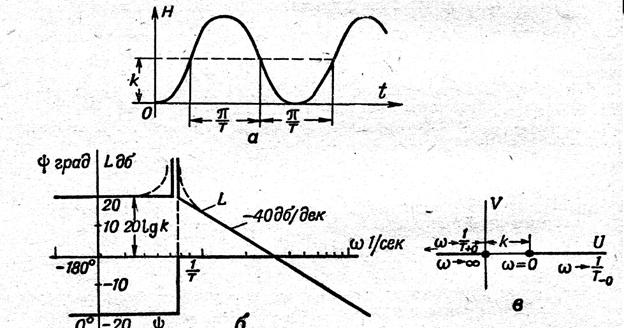
26 сурет
Буынның АФЖС анықтауға керекті W(jω) нақты
![]()
және жорамал
![]() .
.
Осы буынның амплитудалық жиілік
![]()
және фазалық жиілік
![]()
сипаттамалары осындай болады.
6 Тұрақты емес позициялық буын.
Беріліс функциялары төмендегідей тұрақты емес буындарды қарастырайық
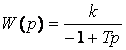 және
және  .
.
Беріліс функциясы
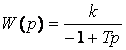 (2.59)
(2.59)
болатын буынды бірінші дәрежелі тұрақты емес апериодикалық буын деп атайды. Осы буынның мысалы ретінде өзін туралайтын жылу қозғалтқышы, аударып тастау кезіндегі тұрақты жүктемесі бар асинхрондық қозғалтқыш және т.б. қарастыруға болады.
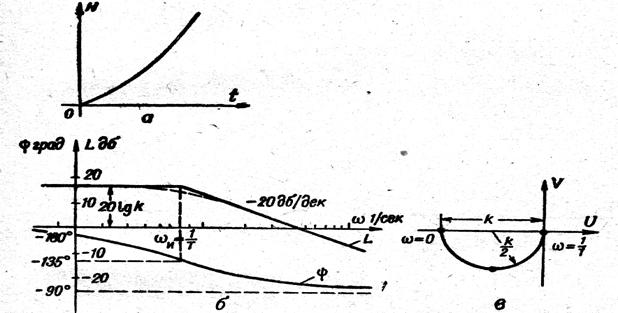
27 сурет
Буынның сипаттамалық теңдеуі
![]() .
.
Бір ғана оң түбірі болады
![]() .
.
Буынның өтпелі функциясы
![]() .
(2.60)
.
(2.60)
Ол ![]() бірқалыпты өсіп шексіздікке
ұмтылатын функция (27 суретті қара).
бірқалыпты өсіп шексіздікке
ұмтылатын функция (27 суретті қара).
Атап өтетін жайттың бірі болып, оның сыртқы
әсері болмаса да, егер ![]() буынның
шығыс координатасы
буынның
шығыс координатасы ![]() .
.
Буынның жиілік беріліс функциясы, ЛАЖС және АФЖС анықтайтын формулалар
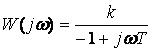 ,
,
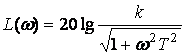 ,
,
![]() .
.
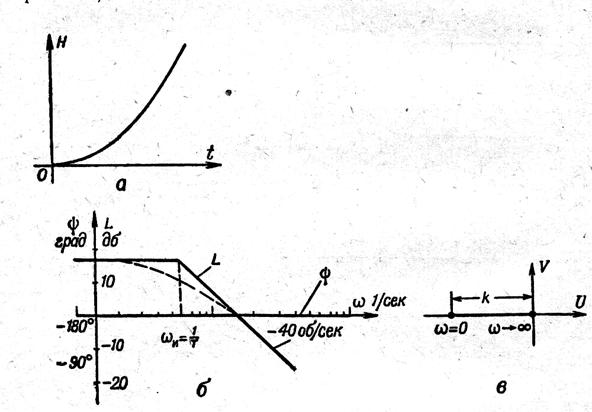
28 сурет
Тұрақты емес бірінші дәрежелі апериодикалық буынның ЛАЖС бірінші дәрежелі апериодикалық буынның осындай сипаттамасымен сәйкес келеді. Төмендегі 28 суретте осы буынның ЛАЖС, ЛФЖС және АФЖС көрсетілген.
Беріліс функциясы
 .
(2.61)
.
(2.61)
Буынға мысал ретінде статикалық тұрақты емес
қатты ракетаны айтуға болады. Бұл ракетаны тізбектеліп
қосылған беріліс функциясы 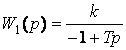 және беріліс функциясы
және беріліс функциясы  апериодикалық буын түрінде көрсетуге болады.
Буынның өтпелі функциясы уақыт өткен сайын өседі
және ұмтылады.
апериодикалық буын түрінде көрсетуге болады.
Буынның өтпелі функциясы уақыт өткен сайын өседі
және ұмтылады.
7 Таза кешігуі бар буын.
Теңдеуі түрі
![]() (2.62)
(2.62)
буынды, таза кешігуі бар буын деп атайды. Осы буын, кіріс сигналының формасын өзгерпейді, және уақыт осі бойында τ шамасын оңға қозғайды. Уақыт τ - таза кешігу уақыты (29 суретті қара).
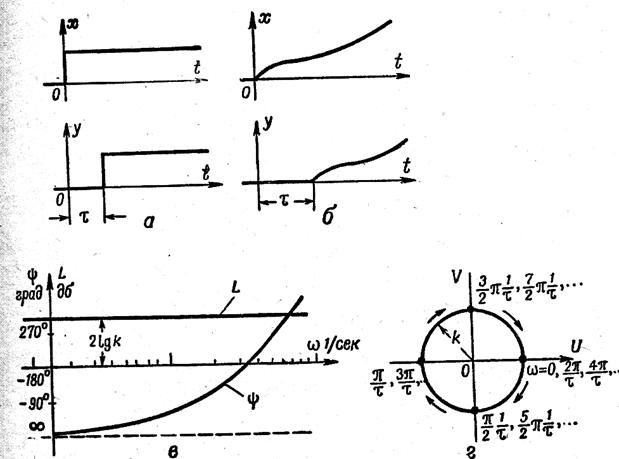
29 сурет
Осы буынға мысалдар ретінде радиобайланыс желісі (τ сигналдың таратқыштан қабылдағышқа жету уақыты). Құбыр жүргізушінің ұзындығы (τ құбыр жүргізушінің басынан аяғына дейінгі қысымның таралуы сұйық реактивті қозғалтқыштың жану камерасы (τ форсункаға отынды беру кезінен оның форсункада тұтану кезеңіне дейінгі уақыт) және т.б. (30 суретті қара).
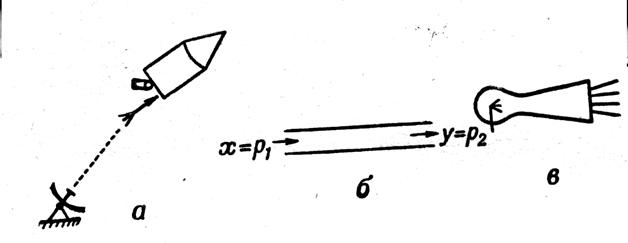 .
.
30 сурет
Теңдеу (2.60) операторлық түрде жазу үшін Тейлор қатарына жіктейміз:
 (2.63)
(2.63)
Енді операторлық түрде (2.63) жазамыз
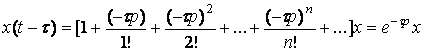 .
.
Теңдеулер (2.62) және (2.63) ескере отырып, оны операторлық түрде осылай жазамыз
![]() .
(2.64)
.
(2.64)
Кешігуі бар буынның беріліс функциясы
![]() .
(2.65)
.
(2.65)
Жиілік беріліс функциясын ЛАЖС және ЛФЖС анықтайтын формулалар:
![]() ,
,
![]() ,
,
![]() .
.
Буынның ЛАЖС және ЛФЖС 29 суретте көрсетілген.
Буынның шығысы тербелісінің амплитудасы жиілікке
тәуелді емес, ал шығыс тербелісінің фазасы кіріс тербелісінен
артта калады (кешігеді). Буынның АФЖС центрі координат басында
орналасқан және радиусы R=k шеңбер болады.
Жиіліктің ω 0-ден ∞ дейін өзгергенде, оның
нүктесі сағат тілі бағытында шеңбер бойымен
қозғалады. Буынның жиілік беріліс функциясы периоды
![]() ω жиілігіне
сәйкес периодикалық функция деп есептеледі. Сондықтан АФЖС
бейнелейтін нүктеге жиілік 0-ден ∞-дейін өзгергенде
көп рет шеңберді айналып өтеді.
ω жиілігіне
сәйкес периодикалық функция деп есептеледі. Сондықтан АФЖС
бейнелейтін нүктеге жиілік 0-ден ∞-дейін өзгергенде
көп рет шеңберді айналып өтеді.
8 Позициялық буындардың жалпы қасиеттері.
1. Тұрақты кіріс сигналы
![]() болғанда, өтпелі үрдіс
аяқталғандағы тұрақты позициялық
буындардың шығыс координатасы кірісімен қатаң
байланысты
болғанда, өтпелі үрдіс
аяқталғандағы тұрақты позициялық
буындардың шығыс координатасы кірісімен қатаң
байланысты
![]() .
(2.66)
.
(2.66)
Кешігу буынының АФЖС анықтауға керекті W(jω) анықталатын, оның нақты
![]()
және жорамал бөлігі
![]() .
.
Амплитуда жиілік
![]()
және фаза жиілік
![]() .
.
сипаттамалары.
Егер кіріс координатасы нольге тең болса, онда өтпелі үрдіс аяқталғаннан кейін оның шығыс координатасында нольге тең болады. Бұл айтылған ереже дұрыс консервативтік және тұрақсыз буындарға егер олар тұрақты автоматтық жүйе құрамына кірсе. Мысалы бұл құрылымдық сұлбасы 30 суретте көрсетілген жүйеге де дұрыс. Оған кері байланысы бар буынды топтастыру ережесін колданғанда:
 . (2.67)
. (2.67)
Егер k>1, бірлік кері байланысы бар орнықсыз бірінші
дәрежелік апериодикалық буын, беріліс коэффициенті ![]() және тұрақты
уақыты
және тұрақты
уақыты ![]() болатын орнықты бірінші
дәрежелік апериодикалық буынға эквивалентті.
болатын орнықты бірінші
дәрежелік апериодикалық буынға эквивалентті.
Кірісі
тұрақты сигнал ![]() болғанда,
оның өтпелі үрдісі аяқталғанда
болғанда,
оның өтпелі үрдісі аяқталғанда
![]() .
(2.68)
.
(2.68)
Орнықты емес буынның кіріс координатасының орнатылған мәні
![]() . (2.69)
. (2.69)
Формулалар (2.68) және (2.69) негізінде
![]() .
.
2. Буындар теріс фазалық жылжыту енгізеді.
Тек инерциясыз буын ғана олардың қатарына қосылмайды. Себебі, оның шығыс тербелісінің фазалық жылжытуы қандайда болмасын нольге тең.
3. Буындар жоғарғы жиіліктегі тербелісті жақсы өткізбейді. Жоғарғы жиілік аймағында, кіріс тербелісінің жиілігі өскен сайын оған сәйкес шығыс тербелісінің амплитудасы азаяды, ал ω→∞ кезде ол нольге ұмтылады.
Инерциясыз буын және таза кешігуі бар буынның шығыс тербелісінің амплитудасы жиілікке тәуелді емес болғандықтан, олардың жоғарыда айтылған ерекшеліктері болмайды.
Интегралдаушы буындар
1 Идеалды интегрирлеуші буын.
Буынның қозғалыс теңдеуі
 (2.70)
(2.70)
немесе
![]() (2.71)
(2.71)
немесе операторлық түрде
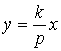 .
(2.72)
.
(2.72)
31 сурет
болатын буынды идеалды интегрирлеуші буын деп атайды.
Буынның беріліс функциясы
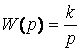 .
.
Интегрирлеуші буынның мысалы ретінде электрқозғалтқыш, гидроқозғалтқыш, интегрирленетін жетек (тетіктерді қозғалысқа келтіретін құрылғы) және т.б. (31 суретті қара).
Буынның өтпелі функциясы
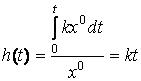 .
(2.73)
.
(2.73)
Тік сызық түрінде болады (32, а суретті қара)
Буынның кірісіне тұрақты сигнал
![]() бергенде оның
шығыс координатасы тұрақты жылдамдық
бергенде оның
шығыс координатасы тұрақты жылдамдық ![]() өзгереді.
Интегрирлеуші буынды еске сақтау элементі түрінде
қолдануға болады. Идеалды интегрирлеуші буын кіріс сигналын алып
тастаған кездегі шығыс координатасының мәнін
сақтап калады (32, б суретті қара).
өзгереді.
Интегрирлеуші буынды еске сақтау элементі түрінде
қолдануға болады. Идеалды интегрирлеуші буын кіріс сигналын алып
тастаған кездегі шығыс координатасының мәнін
сақтап калады (32, б суретті қара).
Буынның жиілік беріліс функциясы, ЛАЖС және ЛФЖС анықтайтын формулалар:
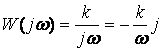 ,
(2.74)
,
(2.74)
![]() ,
,
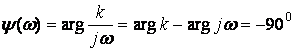 .
.
Буынның жиілік сипаттамалары 32, в және 32, г - суреттерінде бейнеленген.
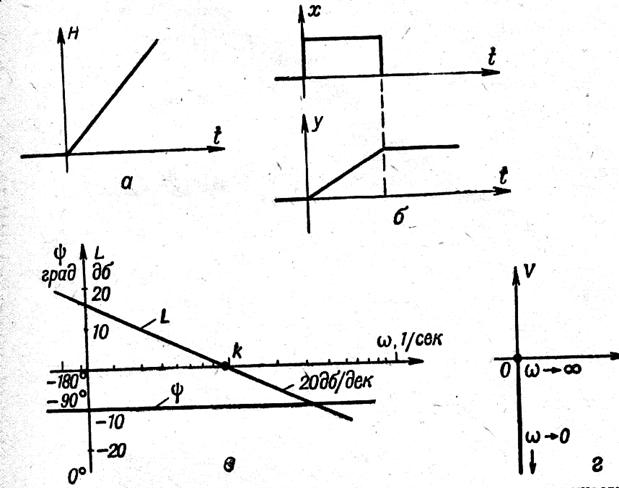
32 сурет
Буынның АФЖС элементтерді анықтауға керекті формулалар:
жиілік беріліс функциясының нақты
![]()
және жорамал
![]()
элементтері.
Буынның амплитуда жиілігі
![]()
фаза жиілік
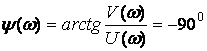
сипаттамалары.
1 Баяулатылған интегрирлеуші буын.
Беріліс функциясы
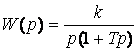
буынды баяулатылған интегрирлеуші буын деп атайды. Баяулатылған интегрирлеуші буын деп атайды. Баяулатылған интегрирлеуші буынның мысалы ретінде инерциялық кешігуі бар ескерілетін электрқозғалтқыш және гидроқозғалтқыш болады. Бұл буынды тізбектеліп қосылған бірінші дәрежелі апериодикалық буын мен идеалды интегрирлеуші буын түрінде бейнелеуге болады (33 суретті қара). Көрсетілген (33 суретті қара) буынның құрылымдық сұлбасына сәйкес, оның өтпелі функциясын анықтау үшін апериодикалық буынның өтпелі функциясын интегралдау жеткілікті:
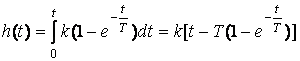 . (2.75)
. (2.75)
Буынның кірісіне тұрақты сигнал
![]() бергенде, оның
өтпелі үрдісі аяқталғаннан кейінгі шығыс
координатасының өзгеру жылдамдығы кіріс координатасымен
қатаң байланысты
бергенде, оның
өтпелі үрдісі аяқталғаннан кейінгі шығыс
координатасының өзгеру жылдамдығы кіріс координатасымен
қатаң байланысты
![]() .
(2.76)
.
(2.76)
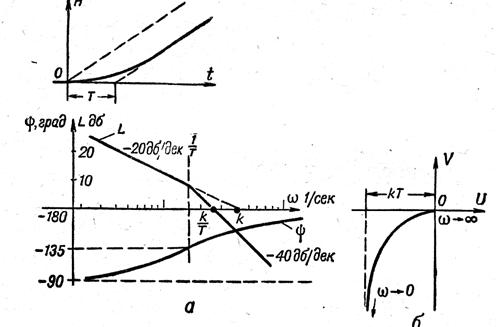
33 сурет
Мысалы, орнықты режим кезінде тұрақты ток қозғалтқышы роторының айналу жылдамдығы қозғалтқышқа қосылған кернеуге қатаң байланысты: козғалтқышқа косылған кернеу көп болған сайын, оның роторының айналу жылдамдығы да өседі.
Буынның жиілік беріліс функциясы, ЛАЖС және ЛФЖС анықталу формулалары:
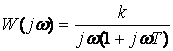 ,
,
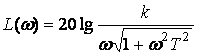 , (2.77)
, (2.77)
![]() .
.
Буынның Асимптотикалық ЛАЖС және ЛФЖС 36 - суретте көрсетілген. Буынның Асимптотикалық ЛАЖС оның L(ω) жуық (шамалас) формуласына байланысты тұрғызылады
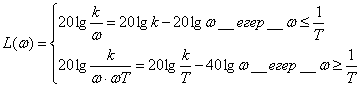 .
.
Кіші жиіліктегі ЛАЖС жиілік осін ω=k нүктесінде қиып өтеді. Кіріс тербелісінің жиілігін өсірген сайын шығыс тербелістің амплитудасы азаяды, ал теріс фазалық жылжуы өседі. Буынның АФЖС 35 - суретте көрсетілген. Буынның амплитудалық және фазалық жиілік сипаттамасын бейнелеуге керекті W(jω) элементтері
нақты
![]()
жорамал
 .
.
Амплитуда жиілік

фазалық жиілік
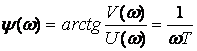
сипаттамалары.
2 Интегрирлеуші буындардың жалпы қасиеттері.
Интегрирлеуші буынның төменде көрсетілген қасиеттері бар:
1. Тұрақты кіріс сигналы бар
![]() болғанда оның өтпелі үрдісі
біткеннен кейінгі координатасы сызықтық заңдылықпен
өзгереді. Шығыс координатасы жылдамдығының
орнықты мәні кіріс координатасымен қатаң байланысты:
болғанда оның өтпелі үрдісі
біткеннен кейінгі координатасы сызықтық заңдылықпен
өзгереді. Шығыс координатасы жылдамдығының
орнықты мәні кіріс координатасымен қатаң байланысты:
![]() .
.
2. Буынның шығыс координатасы, егер кіріс сигналы нольге тең болғанның өзінде де нольге тең болмайды (33 сурет).
3. Буын теріс фазалық жылжыту жүзеге асырады.
4. Буын жоғарғы жиілік тербелісті жаман өткізеді.
Кіріс тербелісінің жиілігі өскенде оған сәйкес шығыс тербелісі азаяды, ал ол нольге ұмтылады.
Дифференциалданатын буындар
1 Идеалды дифференциалдаушы буын.
Буынның қозғалыс теңдеуі
![]() (2.78)
(2.78)
немесе операторлық түрде
![]() . (2.79)
. (2.79)
Болатын буынды идеалды дифференциалдық буын деп атайды.
Буынның беріліс функциясы
![]() .
(2.80)
.
(2.80)
Идеалды дифференциалдық буынның мысалы ретінде тахогенераторды айтуға болады (34 суретті қара).

34 сурет
Буынның өтпелі функциясы δ - функция немесе Дирак функциясы деп аталады (35, а суретті қара). Буынның кірісіне реалды секірме берген кезде шығыс координатасы импульс түрінде болады, ал оның шамасы кіріс сигналының жылдамдығының өсуімен анықталады. Өмірде кіріс координатасын кенет өзгертуге болмайды. Буынның жиілік беріліс функциясы, ЛАЖС және ЛФЖС анықтайтын формулалар:
![]() ;
(2.81)
;
(2.81)
![]() ;
;
![]() .
.
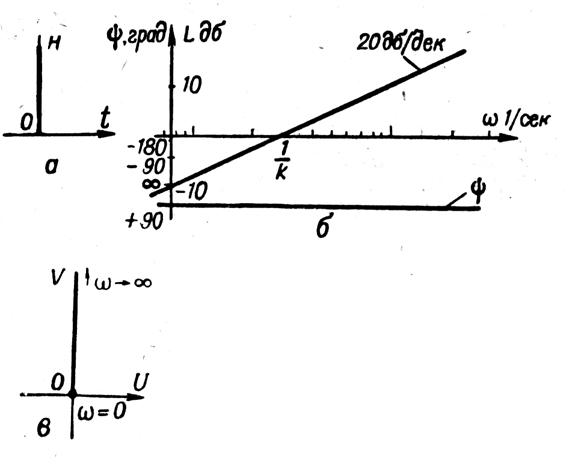
35 сурет
Идеалды дифференциалдық буынның ЛАЖС, ЛФЖС және АФЖС 35 б және 35 в суреттерінде көрсетілген. Кіріс тербелісінің жиілігін өсіргенде буынның шығыс тербелісінің амплитудасы өседі.
Позициялық және интеграциялық буындардан айырмашылығы, барлық жиілікте шығыс координатасы тербелісінің фазасы кіріс координатасы тербелісіне қарағанда озып кететін болады.
Буынның АФЖС W(jω) арқылы анықтауға керекті формулалар
нақты
![]()
жорамал ![]() бөлігі.
бөлігі.
Амплитуда жиілік ![]() .
.
Фаза
жиілік 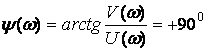 .
.
2 Баяулатылған дифференциалдық буын
Қозғалыс дифференциалдық теңдеуі
![]() (2.82)
(2.82)
немесе операторлық түрде
![]() .
.
Болатын буынды, баяулатылған дифференциалдық буын деп атайды.
Буынның беріліс функциясы
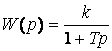 .
(2.83)
.
(2.83)
Дифференциалдық буынның мысалдары 36 суретте көрсетілген.
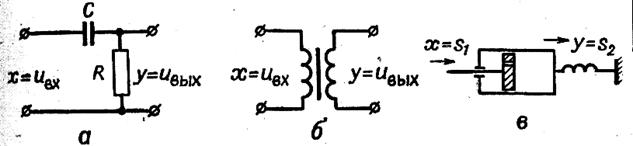
36 сурет
Дифференциалды R,C тізбектің беріліс функциясын мысал ретінде қарастырайық. Ом заңына сәйкес оның беріс функциясын анықтаймыз:
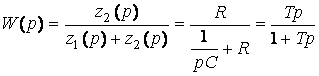 ,
,
мұндағы T=RC.
Буын (37 суретті қара) тізбектеп қосылған апериодикалық және идеалды дифференциалдық буындар түрінде бейнеленген. Осыған сәйкес буынның өтпелі функциясын табу үшін апериодикалық буынның өтпелі функциясын дифференциалдаймыз:
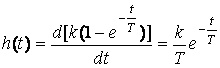 .
.
Егер t→∞ h(t) →0 (37, а суретті қара)
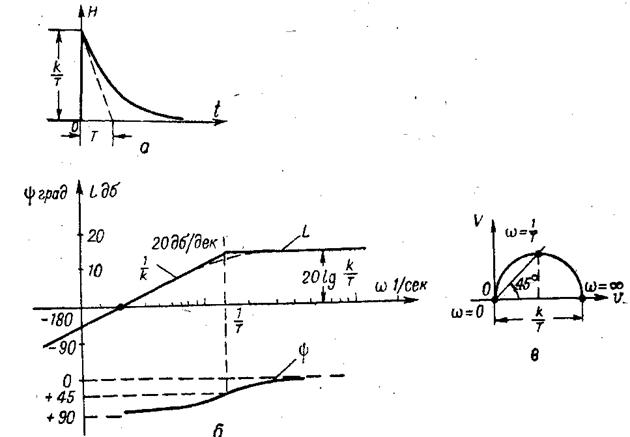
37 а сурет
Буынның кірісіне тұрақты сигнал бергенде оның өтпелі үрдісі өткеннен кейін шығыс координатасы нольге тең болады. Мысалы, егер дифференциалдаушы R,C тізбегінің кірісіне тұрақты кернеу беретін болсақ, уақыт өте бара конденсатор кіріс кернеу шамасына дейін зарядталады да оны шығысқа қарай өткізбейді.
Буынның жиілік беріліс функциясын, ЛАЖС және ЛФЖС анықтайтын формулалар:
 ;
;
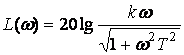 ;
(2.84)
;
(2.84)
![]() .
.
Буынның асимптотикалық ЛАЖС, ЛФЖС және АФЖС 37 - суретте көрсетілген. Буынның ЛАЖС L(ω)-нің шамалас формуларына байланысты тұрғызылады:
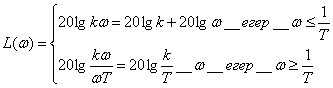 .
(2.85)
.
(2.85)
Жиілікті өсірген кезде шығыс тербеліс амплитудасының кіріс тербелісі амплитудасына қатынасы өседі, өзінің шегі шамасына ұмтылады. Шығыс тербелісінің фазасы кіріс фазасынан озады. Жиілік өскен сайын фазалық жылжыту кішірейеді.
Дифференциалдық буынның жалпы қасиеттері:
1) Қандайда болмасын тұрақты кіріс сигналы кезінде өтпелі үрдіс аяқталғаннан кейін буынның шығыс координатасы нольге тең болады.
2) Тұрақты жылдамдықпен өзгеретін кіріс сигналы кезінде, шығыс координатасының орнықты мәні кіріс координатасының жылдамдығының өзгеруімен қатаң байланысты
![]()
3) Буындар оң фазалық жылжыту іске асырады
4) Буындар төмен жиілікті тербелісті нашар «өткізеді». Кіріс тербелістің жиілігі төмендегенде оған сәйкес шығыс тербелісінің амплитудасы кішірейеді. Ал, кіріс тербелісінің жиілігі өскен сайын бұған сәйкес шығыс тербелісінің амплитудасы өседі. Буындар жоғарғы тербелістік екенін сездіреді.
Буынның сәйкес АФЖ сипаттамасын есептеуге керекті элементтер:
нақты
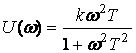
жорамал
![]() .
.
Амплитуда жиілік
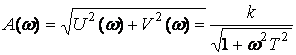
фазалық жиілік
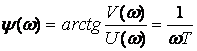
сипаттамалары.
2.4 Автоматты реттеуіштің қасиеттері
Қандайда реттеуіштің маңызды қасиеттері деп олардың реттеу алгоритмін атаймыз [1,6,9].
![]()
![]() (2.86)
(2.86)
Қарапайым реттеуіші алгоритм екіпозициялық деп аталады. Себебі ол реттеуіштің кіріс мәні тәуелді екі мүмкін жағдайы немесе орналасқан қалпының біреуін қабылдайды. Оның біреуі максималды ашылуына сәйкес келеді, мысалы отыққұбырының жапқышы немесе электр жылытушы қондырғысының электрқоректендіру тізбегіндегі контактті тұйықтау. Объектіге заттек немесе энергияны минималды беруі реттеуші органның басты жағдай болып есептеледі. Оның бөлектік түрі жапқышты толық жабу немесе контактті ажырату.
Электркедергі түрлі пештердің жұмыс кеңістігінің температурасы y0=θ реттейтін екіпозициялық алгоритмді төмендегі шартпен бейнелеуге болады
Егер θ< θтап болса, онда yp=yp max;
әйтпесе yp=yp min,
мұндағы θтап – температураның 0С пысырма мәні.
Конструкциялық тұрғыда екіпозициялық реттеуіш өте қарапайым болады. Ол қосымша өлшеуіш құрамына электрқосылғыш қондырғысы түрінде енгізіледі. Соған қарамай объекттің шығысы, бұл автореттеу тәсілі кезінде автотербеліс режимінде болады, айқындаса α ол тапсырыстан не төмен не жоғары мәнін қабылдайды. Мүмкіндік болса үшпозициялық реттеуіште қолданады, мұндағы реттеуіш органның үшінші позициясы объект шығысының орта мәніне сәйкес келеді. Дегенменде айтылған шешімдер реттеудің жоғарғы дәлдігін қамтамасыз етпейді. Түрлі түсті металл және қорытпа өндіретін керекті электрқыздырғыш қолданатын эффективті екіпозициялық қондырғыларды миксер деп атайды. Мұндағы, температура реттеуші өз жұмысында қоздырғышты толық сөндірудің орнына, температура тасырысынан үлкен болған кезде «үшбұрыш» - тан (380 В сызықты кернеу) «жұлдыз» - ға (220 В фазалық кернеу) ауыстыру. Электркедергі түрлі пеште кешігу және тұрақты уақытты үлестіргенде оның температурасы үшпозициялық реттеуіш қолданғанда жаман емес нәтижелер береді. Осы жағдайда температураның және екі мәні тапсырылады. Реттеу көрсетілген сұлбамен жүзеге асырылады:
1) Егер θ<θтап min онда ТҚ – «үшбұрыш».
2) Егер θтап min <θ<θтап max онда – «жұлдыз».
3) Егер θ>θтап max онда – «печті өшіру».
Бұл кезде температуның фактіге негізделген мәні, мысалы шақталық миксерде θтап max - θтап min аймағында анықталады. Екіпозициялық реттеуіштің ерекшелігі деп объем шығысының орташа факті негізделген мәнінің тапсырысына (орташа қателік) дәл келмеуін айтуға болады. Объект шығысы тербелісінің амплитудасы және орташа қателігі объект қасиетімен анықталады.
Қазіргі кезде үрдісті автореттеуге қолданылатын алгоритмдерді – сызықты алгоритмдер деп атайды. Үздіксіз әсері бар реттеуішке сәйкес келетін стандарттық сызықты реттеу алгоритмдерінің сипаттамасы 1 - кестеде берілген.
1 кесте
|
Реттегіш екпіннің сызығы
|
Қолдану облысы |
Құндылығы |
Кемдігі |
|
|
Көрінген нысандар |
Максималдық жылдамдығы |
Статикалық реттеу қателiгiнiң бар болуы |
|
|
Статикалық нысандар |
Статикалық нүктенің жоғары реттеулігі |
Астатикалық нысандарда қолдануға мүмкін емес |
|
|
Көрінген нысандар, соның ішінде маңызды таза кешіктірілімдерімен |
Реттеу дәлдігінің жоғарғы кезіндегі әмбебаптық қолдануы |
Құрылымның күрделiлiгi |
|
|
Көрінген нысандар |
Динамикалық реттеу дөлдігінің жоғарылатуы |
Статикалық қателіктерінің бар болуы. Тек қана аз инерциялық нысандарда тиімді |
|
|
Көрінген нысандар |
Динамикалық реттеу дөлдігінің жоғарылатуы |
Тек қана аз инерциялық нысандарда тиімді |
Идеалды П - реттеуіштің қасиеті, инерциясы жоқ (Т=0) статикалық объекттің қасиетіне ұқсас. Ал П - реттеуіш өзінің сипаттамасы бойынша, бірінші дәрежелі астатикалық объекттің қасиетін қайталайды. 1 кестеде көрсетілген бабына келтіру параметрі, оларды технологиялық үрдіс талабына сәйкес реттеуішті бабына келтіруге арналған. И - реттеуіштің жоғарғы дәлдігі, оның реттеуіші органының жылдамдық қозғалуымен түсіндіріледі:
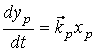 . (2.87)
. (2.87)
Оның әсері yp берілген тапсырманың орындалғанынша тынбайды.
Соңғы (2.87) формуласын мүшелеп интегрирлегенде реттеуші органның толық қозғалысын бағалай аламыз:
 . (2.88)
. (2.88)
Онда П - реттеуішінің әсерінен айырмашылығы бар. Бұл реттеуіш статикалық қателікті жояды.
Пропорционально - интегралды (ПИ) реттеуіш пропорционалды және интегралды реттеуіштердің құндылықтарын өзінде байланыстырады. Олар қандайда болмасын объектте қолданылады және тапсырманы орындаудың жоғарғы дәлдігін қамтамасыз етеді. ПИ - реттеуішінің η екпінінің қисық сызығына (38 суретті қара) қарап оның бабына келтіру (икемдеу) параметрінің мағынасын көріп түсінуге болды.
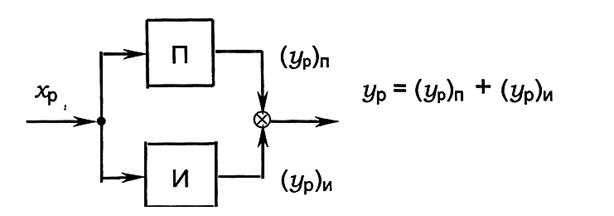
38 сурет
Мысалы оның интегралдық құрамдасын қарастырсақ, ол Ty екі еселенген уақыт деп аталады. Бұл уақыт ішінде реттеуші органның толық қозғалысы жалғыз пропорционал құрамдас реттеуіші іске асыратын (yp)П салыстырғанда Δyp екі еселенеді. ПИ-реттеу алгоритімінің бейнелеу түрі 1 кестеде көрсетілген.
 . (2.89)
. (2.89)
Мұндағы
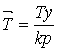 интегрирлеудің шартты
тұрақты уақыты
интегрирлеудің шартты
тұрақты уақыты
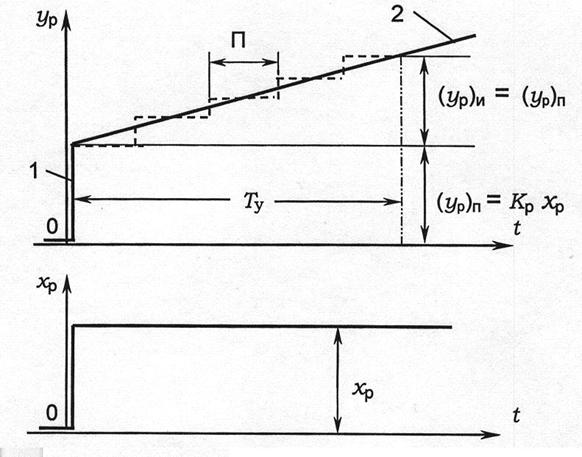
39 сурет
Автоматты реттеуіштердің өндірістік үлгілерінде тек үздіксіз ғана емес, сонымен бірге импульстік әсері бар режимдер кездеседі. Үздіксіз режимде әдетте реттеуіштің пропорционалдық құрамдасы жұмыс атқарады, себебі орындаушы механизмнің максималды мүмкін жылдамдығымен қамтамасыз ету талап етіледі. Импульстік режим кезінде, бірінен соң бірі П периодымен қосылатын орындаушы механизмнің талап етілген орташа жылдамдығын бабына келтіру үшін ыңғайлы. Осы жағдайда П шамасы бабына келтірудің қосымша параметрі болып есептеледі. Оны қолдану объекттің кешігуінің орнын толықтыруға орынды болып табылады.
Сызықты реттеуіштер құрамына, объектіге оның шығысының бірінші туындысына әсер ететін қосымша блок (дифференцирлеуші – Д) енгізуге мүмкіндік бар. Бұл xp сигналын сезінетін реттеуішпен салыстырғанда, ол объекттің шығысын тапсырылған мәніне тез жеткізуге жағдай туғызады. Нәтижесінде ПД және ПИД - реттеу жүзеге асырылады. Дегенмен олар аз инерциялық объекттерге қолдануға тиімді. Себебі ол объекттердің тұрақты уақыты аз, соған байланысты шығысының өзгеру жылдамдығы үлкен. Өтпелі үрдісті, буындарды және ашық пен тұйық автоматты басқару (реттеу) зерттеуге сандық модельдеу қолданылады. Бұл жүйені және буындарын модельдегенде үздіксіз және импульстік әсері бар түрлі сызықты реттеу алгоритмдері ішкі, сыртқы әсерлер мен тапсырманың өзгеруі ескеріледі.
3 Өндірістік үрдісті басқару
3.1 Өндірістік үрдісті құрылымдау
Өндірістік үрдісті жүйелік зерттеу.
Біздің қарастыратын өндірістік ұрдістердің (ӨҮ) түрлері [6,9]:
Түрлі дайын өнім шығаратын технологиялық немесе өндірістік үрдістер (мысалы мұнай мен химия өнімдері, қара және түсті металдар және т.б.).
Энергетикалық үрдістер – түрлі энергияларды өндіру, өндеу және таратып үлестіру.
Көлік үрдістері – жүк пен жолаушыларды кеңістік орнын ауыстыру.
Өнідірістік үрдістің әр - түрлілігіне қарамастан оны ғылыми зерттеуге және автоматтандыруға жүйелік тәсілдің жалпы принциптері қолданылады.
Жүйелік тәсілдердің негізінде, автоматтандырылған немесе автоматты басқарылатын өндірістік үрдісті зерттеу үшін олардың макро және микро құрылымы жасалады. Бірінші кезеңде автоматтандыру мамандары ӨҮ макроқұрылымын дайындайды. Мұндағы ӨҮ сыртқы технологиялық байланысы (ТБ) бар жүйенің жекеленбеген элементі түрінде қарастырылады («қара жәшік» макроблок). ӨҮ сыртқы ТБ түрлері:
1) Кіріс ТБ ӨҮ жүзеге асыруға керекті негізгі жұмыс ортасын, материал және энергиялар түрлерін беру.
2) Шығыс ТБ – ӨҮ жүзеге асырғанда шығарылған дайын өнім түрлері немесе энергия.
Сыртқы шығыс ТБ құрамына қоршаған ортаға әсер ететін ӨҮ қосымша өнімдер толқыны кіреді 40 сурет. ӨҮ макроқұрылымының мысалы.
Жылуэлектр станциясында (ЖЭС) электр энергиясын өндіретін ӨҮ мысал түрінде қарастырсақ:
x1 – негізгі суды беру (құбыр);
x2 – негізгі газ отыны (құбыр);
y1 – қолданушымен қосатын электр желісі;
y2 – атмосфераға жіберілетін толқыны.
Енді макроқұрылымды бейнелегеннен кейін оған макроталдау жасау керек:
- Кіріс және шығыс сыртқы ТБ
жұмыс ортасының дайын және қосымша
өнімдерінің аты, сонымен бірге өлшенетін басты технологиялық
көрсеткіштер
![]()
- Объекттің (ӨҮ) жалпы қорытынды моделін құру,немесе статикалық
y1=ƒ(x1,x2), y2=ƒ(x1)
динамикалық
![]()
түрде.
- Сыртқы
ТБ (![]() ) өлшенетін басты
технологиялық көрсеткіштерін пайдалана отырып ӨҮ
негізгі мақсаты оны басқарудың жалпы есептері мен
критерилерін қалыптастыру. Екінші кезеңде ӨҮ бейнелеуін
макроқұрылым түрінде қарастырамыз. Ол үшін:
) өлшенетін басты
технологиялық көрсеткіштерін пайдалана отырып ӨҮ
негізгі мақсаты оны басқарудың жалпы есептері мен
критерилерін қалыптастыру. Екінші кезеңде ӨҮ бейнелеуін
макроқұрылым түрінде қарастырамыз. Ол үшін:
- ӨҮ құрамдық технологиялық элементтерге бөлу, элементтер аралық ішкі ТБ орнату;
- Ішкі ТБ қозғалатын аралық жұмыс ортасы мен әр технологиялық элементтің аты мен көрсеткіштерін (параметрлерін) анықтау;
- Құрамдық элементтердің және ӨҮ нақтыматематикалық модельдерін құру;
- ӨҮ құрамдық эелементтерінің, оның негізгі мақсатын қамтамасыз ету үшін, қазіргі жағдайын көрсететін параметрлерді қолдана отырып жүзеге асыратын міндеттерін қалыптастыру. Макроқұрылымның қарапайым мысалы 1 – қосымшада көрсетілген.
Мұндағы 1-6 құрылымдық технологиялық элементтер, a,b,c,d,e – аралық жұмыс ортасы легінің ішкі ТБ.
Өндірістік үрдісті автоматты немесе автоматтандыру басқаруға дайындағанда оны иерархиядық бөлгені негізгі қолданылатын амалдардың бірі деп есептеу болады. ӨҮ бөліктік элементтері түрінде технология үрдістермен операцияларды қарастыруға болады. Алдымен ӨҮ жалпы анықтамасын берелік. Өндірістік үрдіс деп ТБ арқылы негізгі және аралық жұмыс байланысқан белгілі технологиялық үрдістер жиынтығын айтады. Оның ең басты мақсаты анықталған параметрлері мен көрсеткіштері бар негіз материалдар, жұмыс орталарынан дайын бұйымды (өнімді) және энергияны өндіру (алу) болып табылады.
Мысалы ЖЭС төмендегі негізгі ТҮ бөлуге болады:
- Табиғи суды химиялық өңдеу.
- Қатты отынды дайындау және жеткізу.
- Буды генерациялау (қыздырылған бу алу).
- Жылу айналдыру (бу энергиясын механикалық энергияға айналдыру).
- Электр энергиясын генерациялау.
Жүйелік тәсілге сүйене отырып технологиялық үрдісті (ТҮ) қарапайым технологиялық элементтердің жиынтығы ретінде қарастыруға болады. Өмірлік жағдайда бұл элементтерді технологиялық операция (ТО) деп түсінеді. Технологиялық операция деп жұмыс ортасы немесе материалдарға қандайда болмасын механикалық және физика - химиялық әсерлер арқылы бір материалды екіншісіне айналдыруды, ортаның қасиетін немесе сапалық көрсеткішін өзгертуді айтады.
Теплоэнергетикалық және басқа үрдістердің ТО мысалдары:
- негізгі және аралық жұмыс орталарын қондырғыға тасу, беру;
- қатты материалдарды фракциялау;
- түрлі жұмыстар ортасын және материалдарды анықталған температураға дейін қыздыру, суыту;
- сұйық және газ тәрізді орталарын сығу, кеңейту;
- жұмыс орталарын араластыру;
- жұмыс ортасын құрамдас компоненттерге бөлу;
- фильтрлеу;
- қарапайым химиялық реакция;
- жұмыс орталарын аралық шоғырлау.
Технологиялық үрдіс (ТҮ) шала деп бұйым немесе анықталған көрсеткіші бар жұмыс ортасын дайындау үшін қолданылатын тиісті ТО жиынтығын айтады. Мұндағы жұмыс оратсының материалдық легі ішкі ТБ көмегімен іске асырылады.
Қойылған мақсатқа жетуді қалау негізінде құрылған бір - бірімен байланыстағы әр - текті бөлшектердің (элементтердің) жиынтығын жүйе деп атайды (жүйе гректің system деген сөзі - бөліктерден құралған, тұтастық, қосылу).
Элемент (латынның стихия бастапқы заттек) күрделі тұтастың құрамдық бөлігі.
Әрі қарай ӨҮ тік және көлденең декомпозициялаймыз. Осы істелген жұмыстардың негізінде басқарудың деңгейлері пайда болады.
Жүйелік көзқарас принциптеріне сүйенсек, автоматты немесе автоматтандырылған басқаруды ұйымдастыруды төмендегідей қарастыруға болады:
ӨҮ – басқарудың жоғарғы үшінші иерархиялық деңгейінің объектісі.
ТҮ – басқарудың екінші иерархиялық деңгейінің объектісі.
ТО – басқарудың төменгі (бірінші) деңгейінің объектісі.
Ал, әр иерархиялық деңгейдегі объекттердің шығысы:
- жоғарғы деңнгейдің негізгі параметрлері, дайын өнімді бейнелейді;
- екінші деңгейдің аралық параметрлері, шала бұйым немесе аралық жұмыс ортасын бейнелейді;
- төменгі деңгейдің параметрлері, шикізат, материал және нақты жұмыс ортасын бейнелейді.
Өндірістік мекемелердегі ӨҮ көбіне ТҮ байланысты анықталады.
ТҮ өндірісі уақытқа байланысты өтуі бойынша: үздіксіз, дискретті және үздіксіз-дискретті болып бөлінеді. Үздіксіз үрдісті бейнелейтін белгілері:
- негізгі жұмыс ортасын беру және дайын өнім шығару үздіксіз үрдіс қарқынымен жүзеге асырылады;
- кіріс негізгі жұмыс арасы мен шығыс дайын өнім легтерінің өзгеруі, сонымен қатар өндіру үрдісі үздіксіз уақыт функцияларымен бейнеленеді.
- негізгі жұмыс ортасын өңдеу немесе энергияны өндіру технологияларында үздіксіз үрдіс үстемдік етеді.
- дайын өнімнің нақты параметрлері кезінде, үрдістің жұмыс істеуі ұзақ уақыт жалғасады;
Үздіксіз үрдістерге, бу генерациялау және басқада жылуэнергетика үрдістері, мұнай және табиғи газ өңдеу үрдістері, бірсыпыра металлургия үрдістері жатады.
Ал дискреттік үрдістер төмендегідей сипатталады:
- негізгі жұмыс ортасын, материалдарды беру және дайын өнім шығару бөлек мөлшермен жүзеге асырылады;
- негізгі жұмыс ортасы, өнім легтерінің және өңдеу үрідісінің өзгеруі дискреттік функциямен бейнеленеді.
Дискреттік үрдіске материалдарды өңдеу және дара бұйымдарды шығару ТҮ жатады. Мысалы, құрылыс материалдарын дайындау, ЖЭС көлік жабдықтарын қолдана отырып қатты отынмен қамтамасыз ету. Үздіксіз-дискретті үрдіс болғанда, олар екеуінің қасиеттерін үйлестіреді. Енді ТҮ үш түрі болғандықтан, оған керекті жиналатын, өңделетін және басқару сигналдарының екі түрі қолданылады:
- үздіксіз немесе аналогты түрдегі;
- дискретті түрдегі.
Түрлі өмірлік құрылымдардың ішінен жұмыс операцияларын орындайтын типтік микроқұрылымдарды бөлек көрсетуге болады.
Тізбектік микроқұрылым
Бұл құрылымның мысалы ретінде жұмыс ортасының негізгі параметрлерін өзгерту үшін біртипті немесе әр түрлі сатылы әсер түріндегі ТО қолдануды айтады (қыздыру, фильтрлеу және т.б.)
Қабысу микроқұрылымы
ӨҮ бұл түріндегі құрылымы деп түрлі негізгі жұмыс орталары немесе бұйымдардан өндірістің өнімін алуды айтады. Мысалы, ЖЭС түрлі отын фракцияларын жағу арқылы қыздырылған бу алу, машина жасау зауытындағы жинау үрдісі. Егер отын-ауа қоспасын дайындау үрдісін жану камерасына бергенге дейінгі жағдайы алдыңғы суретте көрсетілген. Бұл жерде екі түрлі отын және бастапқы мен екінші қайта ауа берілетін ТБ бар.
Тарқау микроқұрылымы
Осы микроқұрылым, мұнайды түрлі фракциялар немесе дайын өнімдерге бөлу негізінде мұнай өндеу өндірісінде қолданылады.
Реверсті үрдісі бар микроқұрылым
Егер өнім, қосымша өнім түзетуге немесе қайта қолданылуға қайтарылатын болса, ол үрдіс жоғарыда көрсетілген суреттей құрылымға ие болады. Мысалы, ЖЭС қоректендіру суын дайындауға жұмыс істеген будың конденсатын қайтару; қатты отынды жағуға керекті көміршауын дайындауда Сепарация ТО кейін көмірдің үлкен фракцияларын қайта ұнтақтау үрдісіне қайтару; өндірістік мұнайды судан және тұздан ажырату үрдісін тауарлық мұнайға сәйкес келмегенге дейін қайталау.
Автоматты немесе автоматтандырылған басқаруды ұйымдастыру және іске асыру үшін төмендегі графикалық құжаттардың тәжірибелік мағынасы зор: жабдық және тұрбақұбырлардың (ТБ) принциптік технологиялық сұлбасы;
Технологиялық жабдықтардың жұмыс сызбасы (конструкторлық құжаттың бірыңғай жүйесі)
Принципті технологиялық сұлба төмендегі қондырғылар түрін шартты графикалық бейнелейді:
- бөлек ТО орындайтын машина және механизм;
- қосымша ТО немесе ТҮ орындайтын қондырғылар немесе құрылма;
- бөлек ТЧ орындайтын машина, механизм және қондырғыдан тұратын агрегат.
Принципті технологиялық сұлба (ПТС) толық және жеңілдетілген болып бөлінеді.
Мұндағы толық ПТС макро және микро талдауға қолданғанда оқып түсінетіндер:
- сыртқы және ішкі ТБ, жұмыс орталарының аты, технологиялық параметрлердің өлшенетін орны, кіріс және шығыс легтерінің бөлінетін және қосылатын нүктелері, кіріс және шығыс ТБ шартпен анықталған орны;
- сыртқы ТБ арасындағы жабдықты көрсету, олар қайда жұмыс операциясын орындайды және басты мақсаты, оларға керекті ішкі ТБ, аралық жұмыс орталар легінің бөліну және қосылу нүктелері;
- жабдықтың орындайтын жұмыс операциясына сәйкес тік және көлденең декомпозициялау.
Өндірісті (технологиялық) үрдістерді сипаттайтын параметрлер құрамы олардың сандық және сапалық шамасы, сонымен бірге технологиялық жабдықтың техникалық пайдалану күйін бейнелейтін шамалар.
Негізгі жұмыс ортасы және дайын өнімнің легтерінің сандық шамалары:
- шығын лездегі мәнінің шамасы G(t) – т/сағ, мысалы будың, судың, сұйық және қатты отын, мұнай;
- көлемдік шығынның лездегі мәнінің шамасы Q(t) –м3/сағ, мысалы ауа, газ;
- генерацияланған электр қуатының лездегі мәнінің шамасы Nг(t) – Mвт (ЖЭС дайын өнімі, сыртқы ТБ);
- жіберілетін жылу энергиясының лездегі мәнінің шамасы Qж(t) – Гкал;
- момент шамасымен сипатталатын Mкр(t) - HM , механикалық энергияның лездегі мәнінің шамасы, мысалы жылу турбинасының жұмыс білігі және басқа жетекті машиналар.
Негізгі жұмыс орталары және дайын өнім легтерінің сапалық шамасы:
- қысым P(t), МПа (жылу энергиясы соған кіреді);
- температура T(t), 0C (“жылу энергиясы соған кіреді”);
- химиялық құрамы (дымқылдық (ылғалдық), сұйық ортаның тұзқұрамы, газ құрамы әр біреуі сәйкес өлшемінде;
- генерациялауға электр энергиясының кернеуі U(t), кВ;
- генерациялауға электр энергиясының жиілігі ω(t), Гц;
- жылу немесе электр энергиясын механикалыққа айналдырғанда айналу жылдамдығы n(t), айналым/мин;
ӨҮ жұмыс атқарған кезінде, аралық жұмыс ортасын жинауға арналған технологиялық операция деңгей H(t), м шамасымен сипатталады. Түрлі технологиялық критериі бар үрдістің жұмыс атқарғандағы, ӨҮ көрсеткіштерінің ең негізгісі болып – өнімділік аталады. Өнімділік дегеніміз белгілі уақыт бірлігі (сағат, күн, ай, квартал, жыл) кезінде өндірілген өнімнің жалпы саны.
Сонымен бірге кейбір қосымша көрсеткіштерде қолданылады:
- өнім бірлігіне негізгі жұмыс орталарының сыбағалы (салыстырмалы) шығыны;
- ТҮ әсерінің пайдалы коэффициенттері.
Мысалы, ЖЭС, Т аралық уақытындағы өнімділігі төмендегі формуламен бейнеленеді:
 ,
,
мұндағы Nг(t) электр қуатының қисық сызығы кВт * ч/күн немесе кВт * ч/жыл. Ал, жылу энергиясының мөлшері (жылы су легі)
![]() ,
,
мұндағы G – су желісі шығыны қазіргі шамасы; t1 және t2 – қолданушының кірісі мен шығысындағы температураның қазіргі мән; с – тұрақты коэффициент.
Жабдықтың техникалық немесе пайдалану күйін сипаттайтын параметрлерге: тұрба құрлары қабырғасы мен жабдықтар корпусының жылу ұлғайту шамасы, айналу механизмдерінің дірілдеу (тербелу) күйі, олардың подшибниктерінің температурасы және т.б. керекті сандық және сапалық, сонымен бірге жабдықтың пайдалану күйін сипаттайтын содан соң ӨҮ (ТҮ) көрсеткіштерін периодты есептеу автоматтандырылған үрдісті ақпаратпен қамтамасыздандырудың негізгі қызметтері (есептері) болып табылады.
ӨҮ (ТҮ) жұмыс операциялары көрсетілген тәсілдермен жүзеге асырылады:
- қолмен, сәйкестірілген адамның физикалық жұмыс күшінің қолданылуы;
- механикаландырылған, барлық жұмыс операциялары машина және механизмдермен орындалады;
- комбинацияланған, адам физикалық жұмыс күші машина және механизмдер сәйкестіріліп колданылады.
ӨҮ немесе ТҮ автоматтандыраудың бірінші шарты деп адамның физикалық жұмыс күші қолданылатын жұмыс операцияларын толық механизациялау болып табылады. Одан кейінгі шарттардың бірі, ол дайын өнімді шығаруға арнап құрастырған ӨҮ (ТҮ) дайындау және жүргізу процедурасы. Бұл процедураның өндірістік аты дайын өнім немесе энергияны алудың технологиялық режимі деп аталады.
Үрдістің түрлі кезеңдерін технологиялық режим регламенттайды:
- ӨҮ (ТҮ) бастапқы шарты, немесе үрдісті қосардың алдындағы (бастапқы кезең) негізгі жұмыс орналары сандық және сапалық параметрлерінің бастапқы мәні, жабдықтардың күйі;
- үрдісті жұмысқа қосу және сапалық параметрлерінің (қосу кезеңі және өнімнің тапсырылған параметрлер жиыны) номиналдық мәнді дайын өнім алу режиміне шығуды қамтамасыз ететін орындалатын ТО тізбегі мен олардың өту жағдайы;
- номиналдық өнімділікке жету үшін орындалатын ТО тізбегін қадағалау және номиналдық параметрлері бар дайын өнімді тұтынуға сәйкес оны реттеу (номиналдық режим кезеңі);
- үрдісті тоқтату күйіне нормальді аударуға керекті ТО тізбегін орындау (нормальді тоқтату кезеңі);
- дайын өнімнің сапалық параметрлерінің және технологиялық жабдықты техникалық немесе пайдаланулы күйін сипаттайтын параметрлердің кейін үрдісті авариялық жағдайдан тоқтау күйін аударуға қызмет жасайтын реттілік ТО орындалуы;
Технологиялық режимді жүргізу процедурасы үрдісті жүргізу ережесі, графиктер, таблицалар және т.б. түрінде дайындалады. Осы айтылған құжаттар үрдісті автоматты және автоматтандырылған басқару алгоритмдерін құруға керекті негізгі деректер болып есептеледі.
3.2 Үрдісті басқару операциялары
Үрдіске әсердің түрлері мен әдістері
Технологиялық және өндірістік үрдістерде технологиялық ережеге [1,6] (режимге) сәйкес дайын өнімді алуды қамтамасыз ететін мақсатталған, аяқталатын әсерлер жиынтығын басқару операциялары (БО) деп атайды. Ал басқару операцияларының жиынтығы басқару үрдісін (БҮ) құрайды. Басқару үрдісін жүзеге асыратын негізгі бағыттары:
- ТБ арқылы жұмыс ортасының легін сандық өзгерту;
- ТБ конфигурациясын өзгерту (үрдістік микроқұрылымына сәйкес жұмыс орталарының легін ажырату немесе қосу);
- Жұмыс операцияларының технологиялық құрамын өзгерту (құрам және технологиялық жабдықтың күйі) немесе үрдістің микроқұрылымын.
Өтетін ортаның физикалық қасиетіне байланысты ТБ қызметі төмендегідей сарапталады:
Гидравликалық, пневматикалық, газды, булы, қатты сусымалы материалдар және т.б. Сонымен бірге механикалық және электрлік энергияларды беру үшін оларға сәйкес механикалық және электрлік ТБ өмір сүреді. Сұйық және газ жұмыс орталарының ТБ түрінде түрлі конструкциясы құбырөткізгіш желілері қолданылады. Олар жұмыс ортасы параметрлеріне (Pr – жұмыс қысымы, Tr – жұмыс процедурасы) сай кестелік материалдар жасалады. Ал қатты сусымалы материалдардың ТБ ретінде түрлі конструкциялы конвейрлік желілер қолданылады, кейбірінде құбырөткізгіштер желісіде болуы мүмкін.
Сұйық және газдың орталарға арналған құбыр проводтарының негізгі техникалық сипаттамалары:
Dy – шартты диаметр, құбыр проводтың номиналдық ішкі диаметріне тең, мм (6 мм ден 2000 мм дейін);
ΔPТБ – ТБ-ға қысым деңгейінің айырмасы.
ΔРТБ=Р2-Р1, (3.1)
мұндағы Р1 – ТБ басындағы қысым, қайнар көзі объектісінің шығысындағы жұмыс ортасы, Р2 – ТБ аяғындағы қысым, қабылдағыш кірісіндегі жұмыс ортасы, ΔPТБ шамасы құбырөткізгіштің ұзындығы конфигурациясы және ішкі бетіне байланысты. Ол қазіргі желідегі қысыммен сипатталады. Ол желінің ұзындығынан, конфигурациясынан және құбырпроводтың ішкі бетіне байланысты. Мысалы, ТБ жұмыс ортасы арқылы шығынды G анықтаудың формуласы
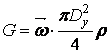 , (3.2)
, (3.2)
мұндағы
![]() ТБ арқылы
өтетін жұмыс ортасының жылдамдығы м/с; ρ - жұмыс
ортасының тығыздығы кг/м3.
ТБ арқылы
өтетін жұмыс ортасының жылдамдығы м/с; ρ - жұмыс
ортасының тығыздығы кг/м3.
Белгілі мақсатпен, сұйық және газ жұмыс ортасының ТБ белгілі телімінің легін мөлшерлеп (сандық) өзгерту үшін техникалық қондырғылар қойылады. Оны жүзеге асыратын бас қару органы төмендегі тәсілдер қолданылады:
- Дроссельді (өтпелі кесілген жер ауданының өзгеру шамасы s). Оны түрлі құбыр арматурасымен іске асырады [6], мұндағы
G=ƒ(s).
- Мөлшерлеу (түрлі сорғылар, компрессорлар және желдеткіштердің өнімділігін өзгерту [6,7]), мұндағы
G=ƒ(n).
n – жұмыс дөңгелегінің айналу жылдамдығы, об/мин G (Q – көпшілік шығын) жұмыс ортасының легінің мақсатталған өзгертуін S және n шамаларының уақыттың өзгеру формасына байланыс жүзеге асыратын техникалық құралдарды төмендегідей жіктеуге болады:
- үздіксіз әсер (үздіксіз форма);
- дискреттік әсер (сатылы немесе импульстік форма);
- үздіксіз - дискретті әсер (үздіксіз және дискреттік формалардың үйлесуі).
Үрдісті реттеуге үздіксіз әсерін қалыптастыруға арналған басқару органы және оның қасиеті
Басқару органдардың бұл түріне жататындар:
- сұйық және газды жұмыс орталарына арналған түрлі конструкциясы бар дроссельді реттеуіш құбырөткізгіш арматурасы;
- суық, ыстық ауа мен жану өнімдерінің легін жабдықтарда бағыттайтын, дөңгелек және тік бұрышты формалы дроссельді реттеуіш жабқыштар;
- электр энергиясын реттейтін электрлік және электрмеханикалық құралдар. Мысал ретінде жылыту элементтерін (күш беретін транзисторлар, күшейткіштер, айнымалы резисторлар, автотрансформаторлар және т.б.) қарастырамыз.
Автоматты басқару теориясына сәйкес, олардың қасиеті және бейнесі қарапайым күшейткіш буындай болады.
Дроссельді реттеуіш орган принциптік технологиялық және құрылымдық сұлбада осылай белгіленеді
мұндағы:
ƒв – объект-қайнар көзінен келетін жұмыс ортасының легі (ішкі ауытқу әсері);
U(G) – объект қабылдауға келетін жұмыс ортасының легі;
h* – механикалық үздіксіз үдемелі орын ауыстыру, мм - де. Жұмыс элементінің орнын өзгерткенде s шамасы өзгереді;
φ* – механикалық үздіксіз айналмалы орнын ауыстыру, градиенті.
Дроссельді реттеуіш органдардың негізгі конструктивті техникалық сипаттамалары:
- Dy – кіріс және шығыс келте құбырларының шартты өтпелі диаметрі, мм;
- Pr, Tr – жұмыс ортасының параметрлері;
- Kv – максималды өткізу мүмкіндігі, м3/сағ;
- Smax – өтпелі кесілген жердің максималдық ауданы, см2;
- Pmax – клапандағы қысымның максималды деңгей айырмасы;
- µ - шығын коэффициенті;
- Δh*(Δφ*) – жұмыс элементінің орын ауыстыру (бұрылу) диапазоны (өрісі).
Жоғарыда көрсетілген көрсеткіштерге байланысты, дроссельді реттеуіш орган арқылы өтетін пардың максималды көпшілік шығынның шамасы
![]() , (3.3)
, (3.3)
мұндағы ρ – жұмыс ортасының тығыздығы.
Дроссельді реттеу органы, басқару жүйесінің элементі ретінде төмендегі параметрлер мен тәуелділіктер арқылы сипатталады:
ΔG=Gmax-Gmin – реттеу диапазоны;
G=ƒ[h(φ)] – шығын сипаттамасы;
S=ƒ[h(φ)] – конструктивтік сипаттама.
Дроссельдік реттеу органының үрдіске тікелей физикалық әсерін беріліс коэффициенті шамасымен сипаттауға болады
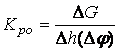 .
(3.4)
.
(3.4)
Дроссельді реттеу органының қосымша техникалық сипаттамасы ретінде керекті күш салу шамасын (айналмалы момент, Mv, H*M) қарастыруға болады. Ол күш, басқару органында орын ауыстыруды h(φ) қамтамасыз етеді. Реттеуші органдағы механикалық орын ауыстыру h(φ) түрлі үлгідегі және конструкциялық орындаушы механизмдермен жүзеге асырылады.
Үрдісті реттеуге дискретті әсерін қалыптастыруға арналған басқару органы және оның қасиеті
Бұл басқару органдарының түріне жататындар:
- Сұйық және газ орталарының легіне арналған дроссельді тиектеп қобылған арматура (ысырма, жапқыш, т.б.).
- Сұйық және газ орталары үшін өнімділігі реттелмейтін мөлшерлеуші органдар (сорғыштар, желдеткіштер, компрессорлар, олардың жұмыс дөңгелегінің айналу жылдамдығы реттелмейді, n=nном=const).
- Қатты сусымалы материалдарға арналған, өнімділігі реттелмейтін мөлшерлеуші органдар (тырналайтын, ленталы, шнектік коректендірушілер. Олардың жұмыс органдарының айналу жылдамдығы реттелмейді, n=nном=const).
АБЖ теориясы негізінде бұл басқару органы дискретті екілікті немесе екі орныққан орынды (позициялы) басқару жүйесінің элементі деп жіктеледі. Оның қабылдайтын екі күйін «0 немесе 1» деп бейнелейміз. Мұндағы «0» күйі, дроссельді тиектеліп қойылатын органдарда «Жабық» деген дискретті белгімен сипатталса, өнімділігі реттелмейтін мөлшерлеуші органдарда – «өшірілген» дискреттік белгі. Енді «1» күйі, дроссельді тиектеліп қосылған органдарда «Ашық», мөлшерлеуші органдарда «қосылған» белгілерімен сипатталады.
ТБ бар, осы түрдегі басқару органы екі күймен бейнеленеді:
«0» - байланысы жоқ, жұмыс ортасының шығыны G=0;
«1» - байланысы бар, жұмыс ортасының шығыны G=Gmax.
Дроссельді тиектеліп қойылатын органдардың принциптік технологиялық және құрылымдық сұлбасы ƒв және U(G) – объект-қайнар көзінен объект -қабылдаушыға келетін жұмыс ортасының легтері.
*h(φ) – механикалық дискретті үдемелі (айналмалы) орнын өзгерту. Ол тиектеліп қойылатын органдағы өтпелі кесілген жер ауданын өзгертетін әсер. Дроссельді тиектілік қобылатот арматураның конструктивті техникалық негізі сипаттамасы:
Дукл – кіріс және шығыс келте құбырларының шартты өтпелі диаметрі, мм;
Рr, Tr – жұмыс ортасының параметрлері;
![]() - ашық күйдегі
гидравликалық кедергі коэфициенті;
- ашық күйдегі
гидравликалық кедергі коэфициенті;
Мкр – үдемелі (айнамалы) орын ауыстыру (өзгерту) * h (![]() ) айнымалы моменті, Н*м.
) айнымалы моменті, Н*м.
Дроссельді
тиіктілік қоятын органдарды * h (![]() ) механикалық орнын ауыстыру (өзгерту) үшін
түрлі конструкциялы жетектер қолданылады.
) механикалық орнын ауыстыру (өзгерту) үшін
түрлі конструкциялы жетектер қолданылады.
Сұйық және газ жұмыс ортасына арналған, өнімділігі реттелмейтін мөлшерлеу органдарының принциптік және құрылымдық сұлбалары.


40 сурет
Мұндағы:
fв және U (G) объем - қайнар көзінен, объем – қабылдаушыға келетін жұмыс ортасының легтері.
*n – номиналдық айналу жылдамдығы об/мин-ғы.
Механикалық реверсивті емес әсер. Өндіріске керекті мөлшерлеу басқару органдарының аттары: сұйық жұмыс ортасына ө сорғы; газ тәрізді жұмыс ортасына – компрессор, желдеткіш.
Сорғыштар (желдеткіштердің) негізгі техникалық сипаттамалары:
Н – сорғышқа қысым, м.су бағаны (желдеткіш, мм. су бағаны) ;
Nном- жұмыс түбіндегі номиналды айнамалы жылдамдығы, об/мин;
N – жұмыс дөңгелегіне жеткізілетін қуат.
Айналымды механикаландыру *n жетектің көмегінен жүзеге асырылады. Онда көбіне айнымалы тоқты асинхронды электрқозғалтқыш қолданылады.
Үрдісті реттеуге үздіксіз – дискретті әсерін қалыптастыруға арналған басқару органы және оның қасиеті.
Осы басқару органдарының түріне жататындар:
- Сұйық және газ орталарына арналған, өнімділігі реттелетін мөлшерлеуші органдар (сорғылар, компрессорлар, желдеткіштер, жұмыс дөңгелегінің айналу жылдамдығы сорғылар, компрессорлар, желдеткіштер, жұмыс дөңгелегінің айналу жылдамдығы n - реттеледі).
- Қатты сусымалы материалдарға арналған, өнімділігі реттелетін мөлшерлеуші орган (қоректендіруші, мөлшерлеуші, тұрмыс органының айналу жылдамдығы n - реттеледі).
Өнімділігі реттелетін сорғы үшін төмендегідей тәуелдік бар:
![]()
![]() .
.
Басқару органы осы түрінің негізгі техникалық сипаттамасы деп төмендегі шамаларды айтуға болады:
∆G – өнімділікті реттеу диапазоны, ∆G= Gmax- Gmin;
∆n – айналу жылдамдығын реттеу диапазоны ∆n= nmax- nmin.
Cорғы (желдеткішті) қосқаннан кейінгі жұмыс күйіндегі, айналу жылдамдығының екінші мәні nmin үрдіске дискреттік әсердің шамасын анықтайды.
Реттелетін жетектің көмегімен айналдыру әсерін механикаландырады:
- Қоректену қайнар көзі ретелетін тұрақты тогты электрқозғалтқыш.
- Жиелік түрлендіргіштен қоректенетін синхронды айнымалы тогты электрқозғалтқыш.
- Бу және газ турбиналары.
ТБ басқару органдардың динамикалық сипаттамасы
АБЖ теориясы және жүйелік көзқарас
принциптеріне сүйене отырып, элементтердің кірісі h(t),
![]() немесе n(t),
шығысы G(t), немесе Q(t) болғандағы
қажеттілігін зерттейміз. Зерттелетін кіші жүйе екі элементтен
тұрады:
немесе n(t),
шығысы G(t), немесе Q(t) болғандағы
қажеттілігін зерттейміз. Зерттелетін кіші жүйе екі элементтен
тұрады:
- Басқару органы.
- Басқару органы орнатылған орыннан жұмыс ортасының мөлшерлік (сандық) параметрлері өлшенетін нүктеге дейінгі ТБ кесіндісі.
Соңғы
элементтің динамикалық қасиетін зерттеу үшін оның
кіріс U(t) – орындаушы механизмнің жетекті
қозғалтқыш тікелей берілетін әсер, ал шығыс - h(t),
![]() немесе n(t)
бейнеленген деп қарастырамыз. Жүйелік көзқараста, олар
басқару деңгейінің төменгісіндегі объект болып
есептелгендіктен:
немесе n(t)
бейнеленген деп қарастырамыз. Жүйелік көзқараста, олар
басқару деңгейінің төменгісіндегі объект болып
есептелгендіктен:
- Дроссельді
реттеуші орган болғанда – h*(![]() орын ауыстыру шамасы.
орын ауыстыру шамасы.
- Өнімділігі реттелетін дроссельді тиектелген орган және мөлшерлеуші орган болғанда – ол екі күйдің «0» немесе «1» біреуіне өтеуі.
- Өнімділігі реттелетін мөлшерлеуші орган болғанда - ∆n диапазонындағы айналу жылдамдығы шамасы.
Енді төменде келтірілген элементтердің бастапқы динамикалық қасиеттерін қарастырайық.
- Электрқозғалтқыштан немесе пневмо (гидро) жетектен тұратын жылдамдығы тұрақты орындаушы механизм (ЖТОМ).
- Дроссельді реттеуші (клапан) (қақпақша).
ТБ - ғы легті үздіксіз реттеу операциясын орындайтын басқару органы Н«А» шартты белгілейміз.
Бұл басқару органының принциптік технологиялық сұлбасы мен динамикалық сипаттамасының графикасы 41 суретте көрсетілген.
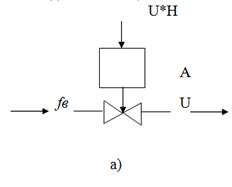
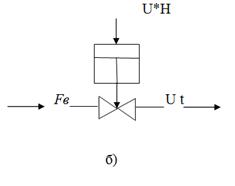
41 сурет
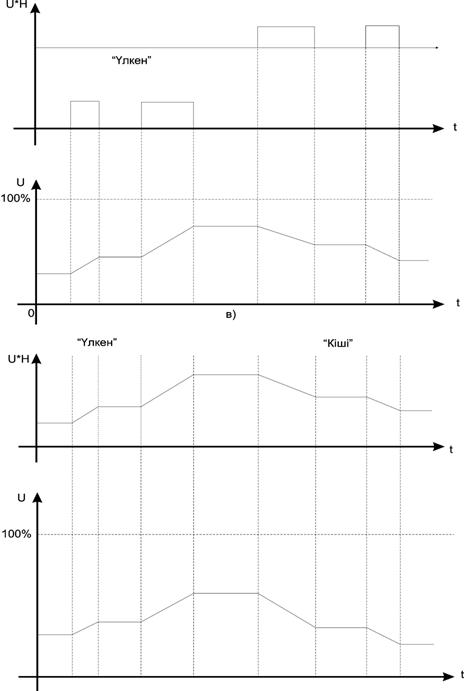 в
в
42 сурет
ТЖ ОМ бар «А» басқару органының кірісіндегі U*H105
Әсері екі каналды (әр канал бөлек техникалық құралмен қалыптастырады, мысалы күйме, қосып жүргізетін құрал) «үлкен» - «кіші»бұйрықтары болады. Әр каналдың бұйрығы айнымалы токтың кернеуі түріндегі енді модульденген импульстік сигналдар реттілігі болады. Мысалы үш фазалық қозғалтқыштың амплитудасы 380В. Шығыс сигналы орнының U% формасына қарап, ТЖОМ қасиеті интегралдың буындікі H дейміз. Ал пневмогидро жетекті әсері U*H бар «А» басқару органында бірканалды «үлкен - кіші» бұйрығы іске асырады. Ол жетек цилиндрінің ауданындағы күш арасының (сұйық немесе ауа) қысымы сигналын өзгертеді. Мұндағы қысым сигналы бір қондырғымен (қол пневматикалық органы) реттеледі. Бұл қондырғыдағы орындаушы механизм күшейіп кіші буын қасиетімен бейнеленеді(сипатталады). Себебі шығыс сигналының формасы, өзіне сәйкес беріліс коэфициенті бар кіріс сигналының формасының көшірмесі түрінде бейнеленген (пропорционалды ОМ). Орындаушы механизм конструкциясында (құрамында), дроссельді реттеу органдарының орнын ауыстыру үшін, оның қазіргі орнын U% қадағалауды қамтамасыз ететін аналогты датчик және шеткі екі орнын жөнінде сигнал беретін дискреттік қондырғылар (s1 - «жабық», s2 - «ашық») бар. Осы «А»106 басқару органының құрылымдық сұлбасы:
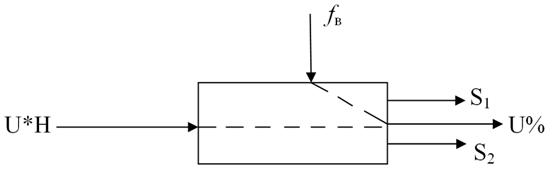
43 сурет
fв – жұмыс ортасының сыртқы әсері.
Енді дроссельді тиектелген орган және орындаушы механизмнен тұратын басқару органын «В» деп белгілейміз. Оның принциптік технологиялық сұлбасы 43 суретте келтірілген. Мұндағы а - ТЖОМ (жетек ішіне салынған) – электр қозғалтқышы бар, б - пневмогидро жетегімен, в - электромагнитті жетегімен.
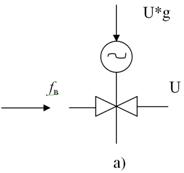
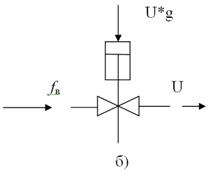
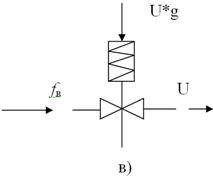


44 сурет
Электрқозғалтқышы бар ТЖОМ дроссельдік тиекті органды қозғау үшін екі каналды бұйрықпен U*g «ашу», «жабу» басқарылады. Бұл бұйрықтың жұмыс аралық уақыты Тсм (5-10с-тен 300с) болады. Егер S2 («ашық») немесе S1 («жабық») белгісі пайда болғанда бұйрық тоқтатылады.
Пневмо (гидро) және электромагнитті жетекші «В» басқару органдарының динамикалық сипаттамасы 44 суретте көрсетілген (д). Мұндағы U*g бірканалды бұйрық:
- пневмо – гидро жетекті қолданғанда, ол цилиндр қуысындағы дискретті қысым шамасы, «1» күйі «ашу» бұйрығы, ал «0» - «жабу».
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 - электромагнитті тиекті қолданғанда, ол номиналдық
шамадағы ток немесе кернеу дискреттік сигналы. «ашу» сигнал
бұйрығы бар, а «жабу» сигнал бұйрығы жоқ.
- электромагнитті тиекті қолданғанда, ол номиналдық
шамадағы ток немесе кернеу дискреттік сигналы. «ашу» сигнал
бұйрығы бар, а «жабу» сигнал бұйрығы жоқ.
U*g S1
S2
«В» басқару органының құрылымдық сұлбасы. Мұндағы S1 мен S2 «жабық» және «ашық» дискреттік сигналы (белгілері) белгілі орындаушы механизмдерінің қондырғыларымен қалыптысы. Пневмо – гидро және электромагнитті тиектің әсер уақыты Тсм = 0,5 – 1,0с электр тиекке қарағанда жылдам болады. Өтемділігі реттелмейтін электр тиегі бар сорғының технологиялық сұлбасы (а) және динамикалық сипаттамасы (б). 45 суретте көрсетілген.
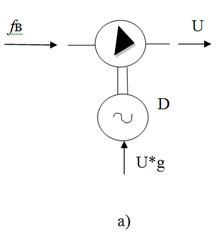
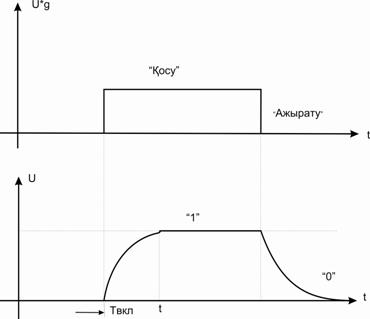
45 сурет - Басқарушы орган «D»
Мұндағы U*g бұйрығы амплитудасы 380В немесе 6кВ қоректендіруші кернеу түріндегі қозғалтқышқа берілетін дискреттік сигнал.
Бұл бұйрық бүкіл жұмыс аралық уақытында сақталады. Ал U% сигналы айналу жылдамдығының нөлдің бастапқы мәнінен номильдікке дейінгі өзгеруін сипаттайды («0» күйінен «1» күйіне өту уақыты Твкл). Осы басқару органында айналу жылдамдығы n өлшенбейтіндіктен S1 «ажыратылған» S2 «қосылған» дискреттік сигналды жүргізу (жіберу) қондырғысы (күш контактісі) қалыптастырады.
Енді 46 суретте реттелетін жетегі тұрақты токты электрқозғалтқышы тұратын сорғы (а) және бу немесе газды турбинасы бар сорғының (б) принципиалды технологиялық сұлбалары бейнеленген.
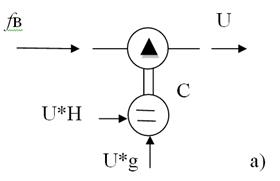

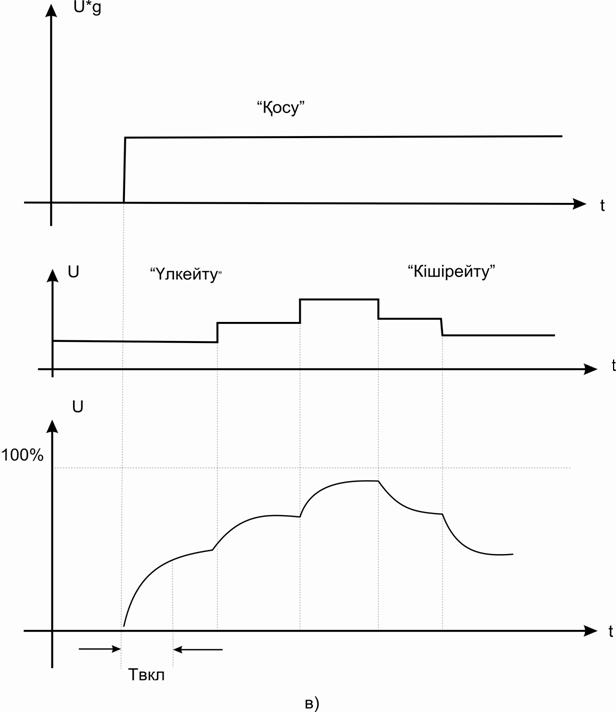
46 сурет
Бұл басқару органы екі түрлі бұйрық қолданады:
- U*g – n = nmin дейінгі екпінді қамтамасыз ету үшін «қосу» дискреттік бұйрығы.
- U*g - ∆ n реттеу диапазоны шегіндегі айналу санын реттеуге арналған «үлкейту - кішірейту» үздіксіз бұйрықтары.
Егер тұрақты тог қозғалтқышын қарастырсақ U*g қосудағы бастапқы қоздыру кернеуін қамтамасыз етеді, ал U*н – берілген диапазонда оны үздіксіз реттеуге арналған. Екі бұйрық бөлек қондырғылармен жүзеге асырылады. Басқару органы «С» динамикалық сипаттамасы 46 сурет (в) көрсетілген. Енді осы органның құрылымдық сұлбасын бейнелейік. Мұндағы n (t) – айналу жылдамдығы. S1 және S2 «қосу», «өшіру» белгілері.
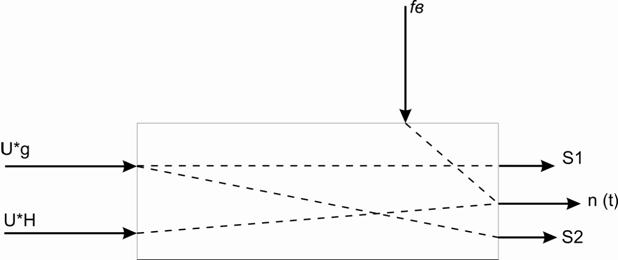
ТБ - ғы басқару органдарының қарапайым жүйесі
Енді шынайы «А», «В», «С», «Д» органдарының принципиалдық технологиялық сұлбаларынан тұратын қарапайым жүйені қарастырамыз. Бұл қондырғыларды бөліп шығаруға болады:
- жұмыс емес күйі (ТБ күйі «0»);
- жұмыс күйі (ТБ күйі «1»);
- жүйені жұмыс және жұмыс емес күйге кіргізу мен шағарудағы өтпелі күйі;
- тыйым салынған (авариялық) күй.
Төмендегі жүйені «S - A» символымен белгілейміз.
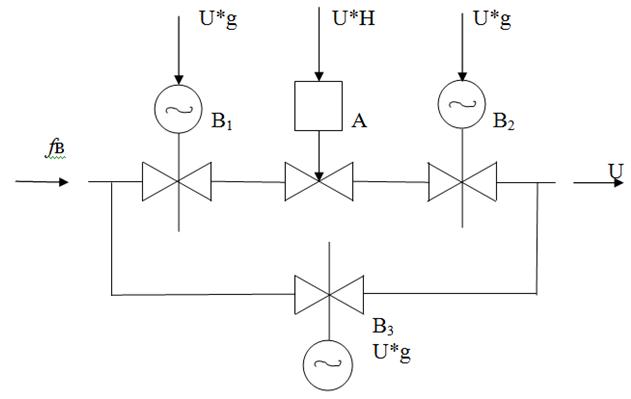
47 сурет
Бұл жүйе үш екіканалды дискреттік U*g бұйрықтары және бір екі каналды үздіксіз U*н бұйрықпен басқарылады. Жүйенің бастапқы күйі:
- В1, В2, В3 «0» күйімен сипатталады;
- А- U=0% мәні мен қосымша дискреттік белгісі «жабық» пен сипатталады;
- ТБ жалпы күйі «0».
Жүйедегі берілетін бұйрықтар процедурасын төмендегі реттілік түрінде
көрсетеміз;
- В3 → «1» (→күйдің өзгеруін бейнелейді);
- рұқсат етілген технологиялық В1 – «1», В2 – «1» бар болғанда, А белгіленген мәніне дейін ашылады;
- А белгіленген мәні дейін ашылғасын В3 → «0». Мұндағы В1 , В2 органдар, А органын оңдаған кезде екі жағынан жабуға да қолданылады. Жалпы «S -A» жүйесі, үрдіске үздіксіз – дискретті әсер береді. Енді «S – Б» қарапайым жүйесін қарастырайық. Оның сұлбасы 47 суретте көрсетілген.
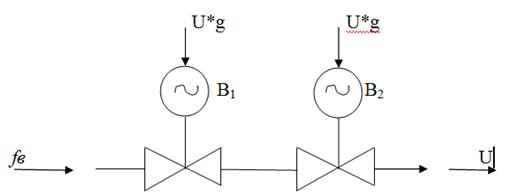
48 сурет
Бұл жүйе екі екіканалды U*g бұйрығын берумен басқарылады. Оны бастапқы күйі: В1 – «0», В2 – «0».
Жұмыс күйіне енгізу реттілігі
В1→ «1», В2→ «1».
Жүйе, жұмыс ортасы легін дискретті басқару операциясын іске асырады. Бұл жүйе түрлі технологиялық жағдайда қолданылады, мысалы ТБ жұмыс қысымы Pr >6,0мПа. Енді 49 және 50 суреттегі көрсетілген және «S – Б», «S – Г» деп белгіленген жүйе «соңғы агрегат» деп аталады. Осы жүйелер бір - бірінен кері байланыстағы клапанымен ғана ерекшеленеді.

49 сурет

50 сурет
Осы жүйені басқару екі дискретті екіканалды бұйрықтар В1,В2 және «Д» органныдағы жетекті қозғалтқыш берілетін U*g көмегімен жүзеге асырылады. Жүйенің жіберу алдындағы бастапқы күйі: В1, Д, В2 – «0».
Оны жұмыс күйіне шығарудың формальді емес процедурасы:
- В1 → «1»;
- В1 «1» белгісі болғанда, Д→ «1»;
- Д «1» белгісі болғанда, В2→ «1».
Бұл үш
белгінің «1» болуы «Сорғы агрегатының» жұмыс
күйінде екенін немесе ТБ «1» сипаттайды. Мұндағы ![]() белгісі қарама - қарсы
клапанды (бір бағытта ғана жіберілетін) бейнелейді.
белгісі қарама - қарсы
клапанды (бір бағытта ғана жіберілетін) бейнелейді.
3.3 Қарапайым технологиялық объекттер және олардың түрлері
Бірінші иерархиялық деңгейде қарапайым технологиялық объекттер [2,6] деп:
- Бөлек ТО орындайтын аппарат немесе машиналар.
- Кіріс немесе шығыс ТБ, оған олардың басқару органдарыда кіреді.
- ТО өтуін сипаттайтын негізгі технологиялық құрал - саймандар және басқада керекті параметрлер.
Қарапайым технологиялық объектті басқару процедурасы мен тәсілі төмендегі формаларға байланысты анықталады:
- қарастыратын қарапайым басқару объектті құрамына кіретін технологиялық үрдістің түрі (типі);
- ТО жүзеге асыру тәсілі (амалы);
- Хj (t) параметрінің өзгеру траектоиясына талап етілетін сипаттама. Ол дайын өнімді тұтынуға байланысты оның бастапқы түрінен, орнықты технологиялық режимдерге дейінгі үрдістің түрлі кезеңдерін қамтиды.
- басқару және ауытқу каналдарының әсерлері кезіндегі қарапайым технологиялық объекттің статикалық және динамикалық қасиеттері.
ТО орындау тәсілдеріне байланысты жабдықтар төмендегідей түрге бөлінеді:
- аппарат немесе машинаның бірініші түрі.
Ондағы Хj (t) параметрі бойынша орындалатын ТО, негізгі жұмыс ортасына объект – қайнар көзінен жеткізілген энергия көмегімен жүзеге асырылады;
- аппарат немесе машина екінші түрі.
Мұндағы Хj (t) параметрі бойынша орындалатын ТО, негізгі жұмыс ортасына сыртқы қайнар көзінен жеткізілген энергия арқылы жүзеге асырылады.
- аппарат немесе машинаның үшінші түрі.
Осындағы Хj (t) параметрі бойынша орындалатын ТО, екі немесе оданда көп негізгі жұмыс орталарының физико - химиялық әрекеттестік кезінде жүзеге асырылады.
Аппараттың бірінші түріне жататындар:
- сұйық және қатты жұмыс орталарын аралық қоректендіретін жабық сауыт (ыдыс). Мұндағы ТО (жұмыс ортасы деңгейінің шамасы) үздіксіз немесе периодты жүзеге асырылады;
- сұйық және қатты жұмыс орталарын механикалық фильтрлері (сүзгіштері). Фильтрлеу үздіксіз және периодты ТО (қысым айырмасы Р1 – Р2 немесе жұмыс ортасының көлемдік шығыны Q);
- сеператорлар (мұнай газ сеператоры, қатты бөлшектердің уақ және үлкен фракциялары үшін шаң ауаның легтің сеператоры). Ол ТО жаннат шығын шамасы немесе сеператорланған материалдар салмағымен сипаталады;
- бу немесе газ қысымын азайтатын редукциялық қондырғылар (Ғру – қондырғының өтпелі қиылысының ауданы, ТБ шығысының қысымы Р2);
- жұмыс ортасының түрлі энергиясы немесе қасиеттерін өзгертуші (түрлендіруші) (турбинаның Мкр айналу моменті, n – шығыс валының айналу жылдамдығы, тұрақты және айнымалы ток генераторлары, электрқуаты Nг, айнымалы тогтың W, кернеу шамасы U, жетег қозғалтқыштар).
Аппараттың екінші түріне жататындар:
- сұйық және газды жұмыс орталары үшін рекуперативтік жылу алмасу аппараттары (жылыту, салқындау, құбырлық жүйенің шығыс температурасы Т2);
- қатты жұмыс ортасы үшінмайдалайтын машиналар немесе диірмендер (шарлы барабандар немесе балғалы тангенсті диірмендер, N – жетек қозғалтқыштың қоректену электрлік қуаты, ∆Р – барабандағы қысым деңгейінің айырмасы);
- сұйық және газды жұмыс орталарын сығу (қысымды өсіру немесе азайту) операцияларын жүзеге асыратын сыртқы тепкіші сорғылар және желдеткіштер (аппарат шығысындағы жұмыс ортасының қысымы Р2).
Аппараттың үшінші түріне жататындар:
- екі жұмыс ортасының қысымы арқылы қозғалатын үздіксіз араластыру камерасы (g2=G1+G3, ТО өтуі Q2 немесе Т2 параметрлерімен сипатталады);
- активизаторы бар, үздіксіз немесе периодты әсерлі екі жұмыс ортасын араластыратын ыдыс (ТО Q2, Т2 сипатталады);
- екі жұмыс ортасының тікелей өзара әсерлесетін тарелкалық (табақшалық) контактор немесе абсорциялық бағана (бірінші төменнен жоғарыға, ал екіншісі жоғарыдан төмен қозғалады, олар өңделген жұмыс ортасының химиялық құрамымен сипатталады);
- жұмыс істеген будың негізгі конденсатын еркін оттегі бөлетін де аэрациялық бағана (табақшалық контактордың өңдеу үрдісіне ұқсас).
3.4 Қарапайым объекттердің сұлбалары және оның басқарулығын бағалау
Қарапайым объекттің макроқұрылымын сызып, оған жасалатын макроталдау қызметтері [2,3]:
- ТБ кіріс және шығыс құрамын, негізгі жұмыс орталары параметрлеінің атын, қосымша энергия қайнар көзін анықтау, сонымен бірге ТО сипаттайтын негізгі параметр Хj;
- аппарат жөніндегі деректерді қолдана отырып математикалық моделін құру, содан соң басқару объектісінің статикалық және динамикалық қасиеттерін бейнелеу;
- ТО негізгі мақсатын қамтамасыз ету үшін қарапайым объекттің басқару қызметіне формулировка беру.
Мысал (макросұлба – методикалық құрал).
Дегенмен ТО макроқұрылымы, объекттің басқару процедурасын толық суреттеуге мүмкіндігі жоқ. Сондықтан, ол үшін қарапайым объекттің микроқұрылымы жасақталады. Оның бейнесі 51 суретте көрсетілген.
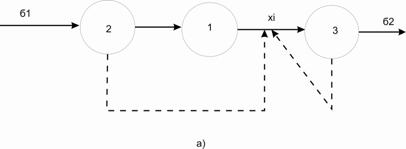

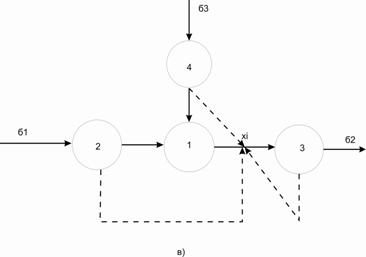
51 сурет
Бұл суреттегі: 1 - негізгі ТО, 1 - ші, 2 - ші, 3 - ші түрлі аппараттар xi параметрі бойынша орындалады; 2 - негізгі жұмыс ортасын беруге арналған қосымша ТО. Ол бөлек басқару органы немесе қарапайым жүйемен орындалады;
3 - өңделген өнімді тұтынушыға жеткізетін қосымша ТО. Ол бөлек басқару органы немесе қарапайым жүйемен орындалады; 4 - қосымша қайнар көзінен энергияны немесе екінші негізгі жұмыс ортасын жеткізетін ТО. Ол басқару органымен жүзеге асырылады;
![]() ,
,![]() ,
,![]() 3 - негізгі мен өнделген жұмыс
орталарын, қосымша энергия көздерін сипаттайын сандық
және саналық параметрлер жиынтығы.
3 - негізгі мен өнделген жұмыс
орталарын, қосымша энергия көздерін сипаттайын сандық
және саналық параметрлер жиынтығы.
Микроқұрылым негізгі және қосымша ТО басқа оның қарайтын объектерін бейнелейді:
-![]()
![]() параметрлеріне
әсерлердің қайнар көзі және олардың
бағыты;
параметрлеріне
әсерлердің қайнар көзі және олардың
бағыты;
-үрзісті дайындау немесе жүзеге асырудағы қосымша ТО орындау реттілігі;
-![]()
![]() параметрін
басқару әсерлерін тәсілдерін дайындаудың
мүмкіндік түрлері.
параметрін
басқару әсерлерін тәсілдерін дайындаудың
мүмкіндік түрлері.
Егер 51 суреттің (а) бөлігін мысал түрінде қарыстырау:
- өнделген жұмыс ортасын тұтынушы еркін пайдалнған кезде, негізігі жұмыс ортасын жіберуді өзгерту;
- негізгі жұмыс ортасы еркін жеткізілгенде, өнделген жұмыс ортасын пайдалануды өзгерту.
Микросұлба нақты мысал келтіру?
Әріқарай басқару объектісінің және қондырғылардың құрылымдық сұлбасынқұруға арналған негізгі белгілерді келтіреміз. Олар:
- Параметр
![]() (
(![]() ) өлшеу (E) ,
) өлшеу (E) , ![]() ХE өлшейтін параметрі.
ХE өлшейтін параметрі.
-
Басқару органдарының орнын (GE) және жай - күйін
![]() (GB,SB) өлшеу.
(GB,SB) өлшеу.
- Өлшенген параметрлер сигналдарын өзгерту(XT - үздіксіз, XS - дискретті).
- Жұмыс операцияларында өлшенетін параметрді (XI),басқару органдарының орның (GI) немесе жай - күйін (GBI,SBI) индикациялау.
- Жұмыс операцияларындағы параметрлердің қазіргі мәнін жазып тіркеу (R);
- ӨҮ, ТҮ көрсеткіш және параметрлерінің аутқу шамасын есептеу(Q).
- Параметрлердің (![]() )жоғарғы (H)
және төменгі (L) номиналдың мәнінен (
)жоғарғы (H)
және төменгі (L) номиналдың мәнінен (![]() AHL) ауытқуын (A)
ескертетін сигнал беру.
AHL) ауытқуын (A)
ескертетін сигнал беру.
- Параметрдің (![]() ) жоғарғы (H)
және төменгі (L) деңгейінен авариялық (Z) ауытқуы
(
) жоғарғы (H)
және төменгі (L) деңгейінен авариялық (Z) ауытқуы
(![]() ZHL) туралы сигнал беру.
ZHL) туралы сигнал беру.
- Бөлек «A», «B», «D», «C» басқару органдарымен а жаратылған түрде басқару(HS).
- «» тұйық түрінде басқару (GC,SC).
- ТБ күйін, конфигурациясын, құрылымдық құрамын немесе үрдістің құрымын өзгерту арқылы қарапайып басқару органдар жүйесін немесе тораптарды дискретті басқару (KS).
- «В» немесе «D» түрлі
басқару органы әсерінен,берілген жағдайдағы ТО -
ның өтіун бейнелейтін параметрлерді( ![]() S) К-позициялық реттеу.
S) К-позициялық реттеу.
- «А» немесе «С» түрлі
басқару органдары әсерімен, берілген жағдайдағы ТО – ның
өтуін бейнелейтін параметрлерді ТҮ параметрлерін реттеу (![]() C) үздіксіз реттеу.
C) үздіксіз реттеу.
- ТҮ басты мақсатын
бейнелейтін параметріне байланысты, ТО реттелетін параметрлерін үздіксіз
дәлдеп түзету (![]() C).
C).
- ӨҮ
(ӨҮ параметрлерін реттеу) мақсатын бейнелейтін параметрлеріне
байланысты, ТҮ реттелетін параметрлерін үздіксіз түзету (![]() C).
C).
- ӨҮ, ТҮ жұмыс операцияларының өтуін бейнелейтін параметр шамасы, төменгі немесе жоғарғы шектеу мәніне жеткен кезде шешім қабылдау және соған сәйкес басқару әсерін жасақтау.
- ӨҮ, ТҮ жұмыс операцияларының өтуін бейнелейтін параметр шамасы, төменгі немесе жоғарғы авариялық мәніне жеткен кезде шешім қабылдау және соған сәйкес басқару әсерін жасақтау.
Енді бірінші түрлі қондырғының
принциптік технологиялық сұлбасы (52 суретті қара) және
басқару объектісінің құрылымдық сұлбасы (53
суретті қара) көрсетілген. Бұл бірінші амалды әсер![]()
![]() параметрін
өзгерту үшін қалыптастырылады.
параметрін
өзгерту үшін қалыптастырылады.
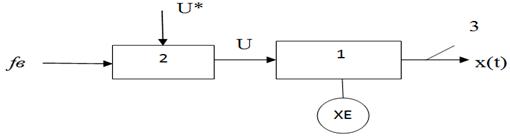
52 сурет - ТО – орындайтын қондырғының ПТС
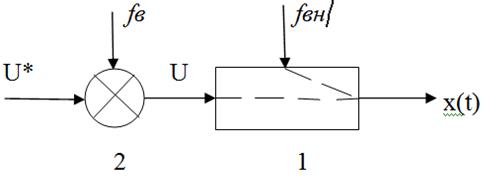
53 сурет
![]() параметріне байланысты,
қондырғының басқару объектісі түріндегі
құрылымдық сұлбасы.
параметріне байланысты,
қондырғының басқару объектісі түріндегі
құрылымдық сұлбасы.
Мұндағы: 1 – негізгі ТО орындайтын аппарат.
2 – кіріс ТБ (А, В, С немесе Д) еркін басқару органы.
3 – сыртқы ауытқу fвн қайнар көзі (шығыс ТБ).
АБТ
пәніне сүйене отырып басқару U және сыртқы
ауытқу fвн әсерлерінің ![]() параметріне өту каналдарын
көрсететін болсақ (54 суретті қара). Мұндағы Wu(p)
және Wf(p) екі каналдың беріс функциялары немесе
көрсетілген құрылымдық сұлбаның
математикалық модельдері.
параметріне өту каналдарын
көрсететін болсақ (54 суретті қара). Мұндағы Wu(p)
және Wf(p) екі каналдың беріс функциялары немесе
көрсетілген құрылымдық сұлбаның
математикалық модельдері.
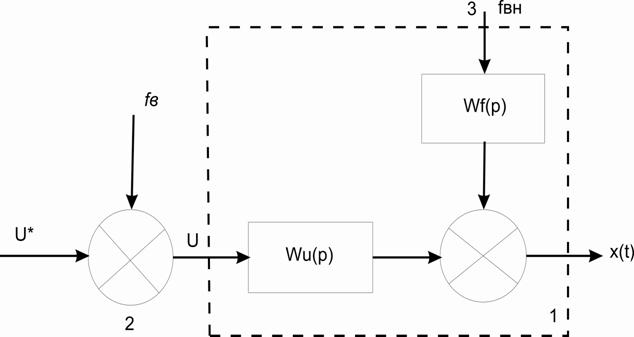
54 сурет
Бірінші түрлі технологиялық қондырғының математикалық моделінің құрылымдық сұлбасы (x(t) параметрлі басқару объектісі). Енді екінші және үшінші түрлі қондырғылардың микро құрылымдарына (51, б-в суреттерін қара) сүйене отырып, олардың құрылымдық сұлбаларын құрамыз.
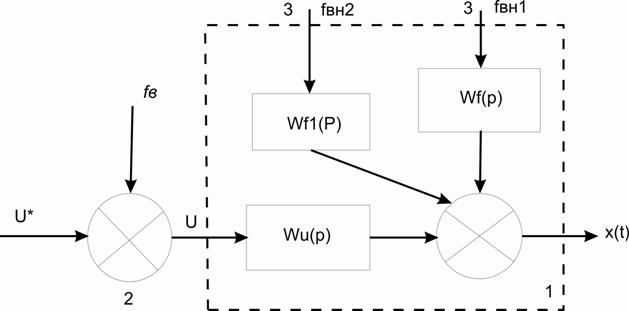
55 сурет
Екінші түрлі технологиялық қондырғының математикалық моделінің құрылымдық сұлбасы (55 суретті қара)
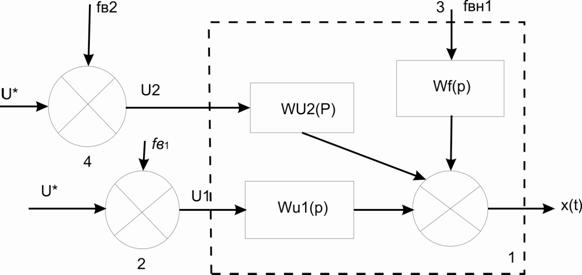
56 - сурет
Үшінші түрлі технологиялық қондырғының математикалық моделінің құрылымдық сұлбасы (56 суретті қара).
Қарапайым объекттердің басқаруын бағалау
Автоматты немесе автоматтандырылған басқарудың есебін қоюдың алдында қарапайым объектердің басқарулығын бағалаймыз. Мұндағы басқарулық деп U(t) және fвн(t) әсерлерінен кейінгі xi(t) қозғалу беталысын анықтауды айтады, оның салдарынан G1 (негізгі жұмыс ортасының шығыны) және G2 (өңделген жұмыс ортасының шығыны) материалдық балансының бұзылуы да кіреді.
Басқарулықты бағалаудың зерттелуі:
- Аналитикалаық әдістермен құрылған объекттердің математикалық моделдері басқару жүйесін жобалу үрдісі кезінде;
- нақтылы объектте, басқару жүйесін жөнге салу кезінде оның көрсеткіштері тәжірибелі түрде анықталады және түзетіледі.
Таңдап алынған, басқару әсерін қалыптастыратын әдіс үшін, xi(t) параметрі бойынша басқару объектісі түрінде қарастырылатын қондырғының (микрқұрылымдық) және құрылымдық сұлбаларының негізінде математикалық моделі құрылады. Бұл қондырғыны «қара жәшік» түрінде қарастырғанда, оның кірісіне шамасы ∆ U(t) және ∆ fвн(t) әсер беріледі. Сол кезде, xi(t) формасына байланысты екі түрге бөлінеді:
- статикалық инерциялық объект, ол τ – кешігу уақыты,
T – тұрақты уақыты, k – беріліс коэффициентімен сипатталады. (57, а суретті қара);
- астатикалық
инерциялық объект, бұл τ – кешігу уақыты, ![]() - екпін жылдамдығымен сипатталады
(57 суретті қара).
- екпін жылдамдығымен сипатталады
(57 суретті қара).
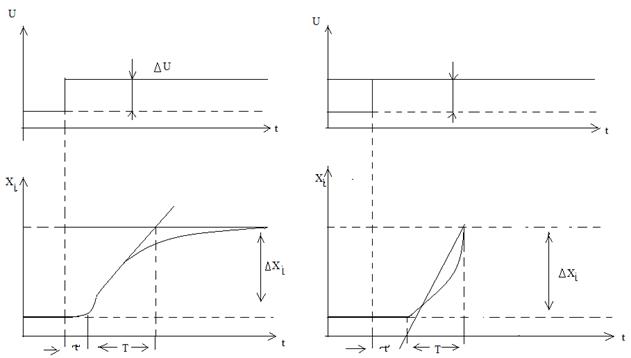
k=ΔXi/ΔU ε=ΔXi/ΔUT
a) б)
57 сурет - Статикалық (а) және астатикалық инерциялық (б) объекттердің динамикалық сипаттамасы
Бұл
объекттердің k, τ, T, ![]() коэффициенттерін
аппараттардың конструциялық сипаттамалары бойынша да табуға
болады. Статикалық инерциялық объекттің жеңілдетілген
беріліс функциясының бейнесі:
коэффициенттерін
аппараттардың конструциялық сипаттамалары бойынша да табуға
болады. Статикалық инерциялық объекттің жеңілдетілген
беріліс функциясының бейнесі:
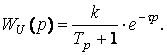 (3.5)
(3.5)
Оны, тізбектеп қосылған бірінші дәрежелі апериодикалы және транспорттық (көліктік) кешігу буындарының жиындар түрінде қарастыруға болады. Статикалық инерциялық объект қасиеті бар технологиялық қондырғылардағы өтетін ТО төмендегі жұмыс ортасы параметрлерімен сипатталады: шығын, қысым, температура, химиялық құрам, айналу жылдамдығы.
Астатикалық инерциялық объекттің жеңілдетілген беріліс функциясының түрі:
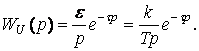 (3.6)
(3.6)
Мұндағы объект тізбектеп қосылған интегралдаушы және көліктік кету буындарымен бейнеленеді.
Жұмыс ортасын деңгейінің шамасына байланысты жинақтайтын қондырғыда астатикалық инерциялық объекттің қасиеттігі болады. Статикалық инерциялық обьекттің басқарулығын τ/T шамасымен жуық түрінде сипаттай аламыз. Айтылған τ/T шамасына байланысты статикалық инерциялық объекттерді төмендегі категорияларға бөлеміз (58 суретті қара).
Егер τ = 0 және T = 0 – инерциясыз (1).
Егер τ/T = 0
![]() 0,2 – аз инерциялы (2).
0,2 – аз инерциялы (2).
Егер
τ/T = 0,2 ![]() 1,5 – орта инерциялы (3).
1,5 – орта инерциялы (3).
Егер
τ/T ![]() 1,5 – жоғары
инерциялы (4).
1,5 – жоғары
инерциялы (4).

58 сурет - Статикалық инерциялық объекттердің түрлі категориялары
τ/T шамасының өсуімен статикалық инерциялық
объекттің басқарулығы нашарлайды және оператор технологтың
![]() – үздіксіз қолы
бос емес уақыты өседі. Қазіргі қолданылатын операцияны
автоматтандырылғанда, τ/T шамасы, алгоритм таңдауды
және АРЖ параметрлерін бабына келтіргенде ескеріледі. Астатикалық
инерциялық объекттің басқарулығына τ және Ԑ
шамаларымен анықталады. Ԑ кішірейуі және τ
өсуі
– үздіксіз қолы
бос емес уақыты өседі. Қазіргі қолданылатын операцияны
автоматтандырылғанда, τ/T шамасы, алгоритм таңдауды
және АРЖ параметрлерін бабына келтіргенде ескеріледі. Астатикалық
инерциялық объекттің басқарулығына τ және Ԑ
шамаларымен анықталады. Ԑ кішірейуі және τ
өсуі ![]() уақытының
өсуі әкеліп соқтырады, оның салдары қолмен
басқару кезінде басқарулықты нашарлатады. Басқару
объектісінің басқарулығын бағалауға көбіне
интегралдың критерийлер қолданылады. Сонымен бірге статикалық
инерциялық объекттің
уақытының
өсуі әкеліп соқтырады, оның салдары қолмен
басқару кезінде басқарулықты нашарлатады. Басқару
объектісінің басқарулығын бағалауға көбіне
интегралдың критерийлер қолданылады. Сонымен бірге статикалық
инерциялық объекттің ![]() =ƒ(U) немесе X=ƒ(
=ƒ(U) немесе X=ƒ(![]() ) тәуелдіктерін зерттеудің негізінде ∆U(∆
) тәуелдіктерін зерттеудің негізінде ∆U(∆![]() ) және
) және ![]() (
(![]() ) шамаларының жұмыс диапазонын анықтауға болады.
Ал сыртқы ауытқуды басудың негізгі деп ∆
) шамаларының жұмыс диапазонын анықтауға болады.
Ал сыртқы ауытқуды басудың негізгі деп ∆![]() -∆
-∆![]() ≥ 1 деген технологиялық шартты айта аламыз.
≥ 1 деген технологиялық шартты айта аламыз.
3.5 Қарапайым объекттерді басқару процедурасы
Қарапайым
объекттерді басқару ТҮ негізгі мақсатына сүйене отырып
оның түрлі кезендердегі ![]() (t)
траекториясы
анықтайды. Бұл үшін АБТні сәйкес, Xi параметрі бойынша
іске асырылатын ТО қамтамасыз ету үшін, қарапайым объектті
тоқтатылған күйден ретті түрде бір немесе бірнеше
аралық орнықты күйге көшіреміз, содан соң Xi
номиналдың мәніне жеткізу арқылы объектті жұмыс
күйіне шығарып өңделген жұмыс ортасын дайындауды
жүзеге асырамыз.
(t)
траекториясы
анықтайды. Бұл үшін АБТні сәйкес, Xi параметрі бойынша
іске асырылатын ТО қамтамасыз ету үшін, қарапайым объектті
тоқтатылған күйден ретті түрде бір немесе бірнеше
аралық орнықты күйге көшіреміз, содан соң Xi
номиналдың мәніне жеткізу арқылы объектті жұмыс
күйіне шығарып өңделген жұмыс ортасын дайындауды
жүзеге асырамыз.
Бұл қарапайым басқару объектісінің әр орнықты күйі төмендегіде сипатталады [2,6]:
- ТБ-тің кірісі мен шығысындағы В және Д түрлі басқару органдарының белгілі комбинациядан («0» және «1» жиыны) туратын күйі;
- дроссельді реттеу органының U% -ғы орны және өнімділігі реттелетін мөлшерлеуші органдардың n айналу жылдамдығының анықталған мәндері;
- негізгі жұмыс ортасы және қосымша энергия көздері параметрлерінің анықталған мәндері;
- аппараттың жұмыс күйін бейнелейтін параметрлердің анықталған мәні. Басқару объектісінің бір күйден екіншісіне өтуін көрнекті түрде көрсету үшін граф қолданылады.
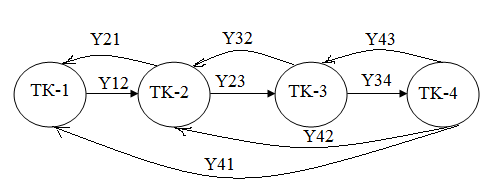
Мұндағы:
- Ү12, Ү23, Ү34 – объектті іске қосу үрдісі және Xi параметірінің тапсырылған траекториясы бойынша номиналдық мәніне жеткізу;
- Ү43, Ү32, Ү21 – объектті қалыпты тоқтату үрдісі және Xi парааметірінің мәнін бастапқы күйіне дейін төмендету;
- Ү42, Ү41- объектті тез немесе авариялық тоқтату үрдісі;
- осы басқару жүйесінің көрсетілген жағдайға жеткізгеннен кейін, ТҮ (ТО) басты мақсатына сәйкес - қарапайым басқару объектілерінің әр аралық және жұмыс күйлері үшін міндеттері қойылады, атқару процедуралары тұжырымдалады;
- басқару функцияларының негізгі құрамы және олардың автоматтандыру деңгейі анықталады.
Қарапайым объекттің сипаттамалары мен параметрлері
Басқару жүйесінің
басты мақсатына сәкес, БО жұмыс күйінде
Xi нақтылы
және ауытқу деңгейі
![]() беріледі
беріледі ![]() . Сонымен бірге, технологиялық ережелерге
сүйенсек,
Xi параметрінің жоғарғы
және төменгі шек мәніде анықталады (
. Сонымен бірге, технологиялық ережелерге
сүйенсек,
Xi параметрінің жоғарғы
және төменгі шек мәніде анықталады (![]()
Ximax=XiH+ΔXmax,
Ximin=XiH-ΔXmin . (3.6)
Ал, сонғы көрсеткіші түрінде технологиялық режим жұмыс кұйінде , Xi параметрлерінің төменгі жөне жоғарғы авариялық мәніде жеткізіледі:
![]() ,
,
![]() . (3.7)
. (3.7)
Технологиялық режимде Xi=f(G2) тәуелділігі туралы тапсырма беріледі. Ол дайын өнімді тұтану режиміне Xi параметрінің байланысын сипаттайды.
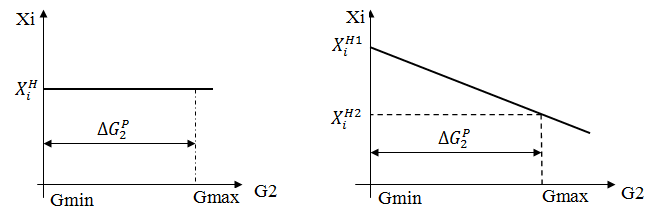
a) астатикалық б) статикалық
59 сурет - Жүктемелік сипаттама
Сонымен бірге, (![]() G2) түрлі сыртқы
әсер кезінде, объектің жұмыс күніндегі Xi параметрінің
тапсырма берілген мөнін ұстап тұруға талап
қойылды(сала бойынша):
G2) түрлі сыртқы
әсер кезінде, объектің жұмыс күніндегі Xi параметрінің
тапсырма берілген мөнін ұстап тұруға талап
қойылды(сала бойынша):
- Xi (t) бейнелейтін, өтпелі үрдістің бірінші амплитудасынан А1 ауытқуы рұқсат етілген үлкен мәнінен аспауы керек.
- Xi (t) бейнелейтін, өтпелі үрдістің V өшу деңгейінің(дәрежесінің) шамасы ψ немесе V кейін басқару коэффициенті ϕ.
Интегралдық критерийдің шектеулі - руқсат етілген шамасы
![]() .
.
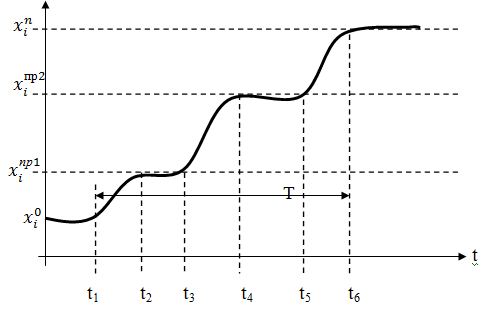
1)![]() ,
,
![]() - объекттің бірінші және
екінші аралық күйіндегі
Xi
мәні;
- объекттің бірінші және
екінші аралық күйіндегі
Xi
мәні;
2) t1 - операцияны іске қосуды бастау уақыты;
3) t0(T) - қондырғыны іске қосудың жалпы уақыты;
4)t1 –
t2 -
Xi
ді ![]() дан
дан
![]() ге көтеру уақыт интервалы ;
ге көтеру уақыт интервалы ;
5) t2 – t3 объекттің бірінші аралық күйінде болу ұзақтығы.
60 сурет
Қарапайым объектерді басқару міндеттері мен амалдары
Технологиялық аппараттардың бірінші түрі:
1) Материалдық балансты жұмыс күйінде сақтау (ұстап туру).
2) Технологиялық көрсеткішті орнықты күйінде ұстап туру(тұрақтандыру міндеті).
Үздіксіз ТҮ үшін, қойылған міндетті екі амалмен іске асыруға болады:
- Түйық Xi параметрін өлшеуге және түрлендіруге мүмкін болғанда.
- Ажыратылған Xi параметрін өлшеу және түрлендіру мүмкін емес немесе технологиялық мақсатқа лайықты емес болса.
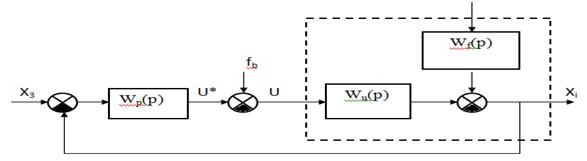
61 сурет - ХІ параметрін түйық АРЖ –нің құрылымдық сұлбасы
- ХІ - қысым, температура, шығыс ТБ-тық химиялық құрамы немесе аппаратурадағы жұмыс ортасының деңгейі;
- WР(р) - автоматты реттеуіштің беріліс функциясы;
- XI=f(G2) астатиқалық тәуелділік болғанда (жүктемелік сипаттама) ПН немесе ПИД реетеу заңдылықтары қолданылады;
- статиқалық тәуелсіздік болғанда П реттеу заңдылығы қолданылады;
- АРЖ, өңделген жұмыс ортасын тұтынуға тәуелсіз, негізгі жұмыс ортасын жіберу (жеткізіп беру) арқылы Хі нақтылы мәнін турақты ұстап тұрады;
- АРЖ, негізгі жұмыс ортасын жіберу (жеткізіп беру) еркін болған кезде, өңделген жұмыс ортасын тұтынушыға жіберу арқылы Хі нақтылы мәнін турақты ұстап тұрады.
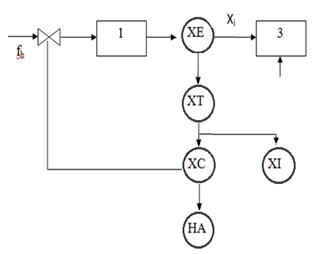
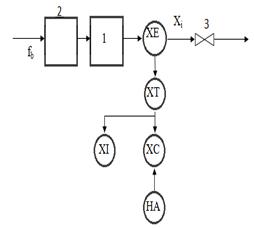
1- бірінші түрлі технологиялық аппарат;
2- дроссельді реттеуші жапқышы бар кіріс ТБ (еркін басқарушы органмен);
3- шығыс ТБ дағы А,В,С немесе Д түрлі еркін басқарушы орган (дросссельді реттеуші клапаны бар);
62 сурет
- ХЕ, ХТ, ХІ, ХС- Хі параметрін өлшеу, түрлендіру, индикациялау және үздіксіз реттеу операцияларын орындайтын локальдық техникалық жабдықтар;
- НА- тапсырманы қолмен енгізуді орындайтын техниқалық жабдық;
- негізгі жұмыс ортасын жіберуді өзгерту арқылы басқару әсерін құру;
- өңделген жұмыс ортасын жіберуді өзгерту арқылы басқару әсерін қалыптастыру;
Ажырату амалымен реттеу
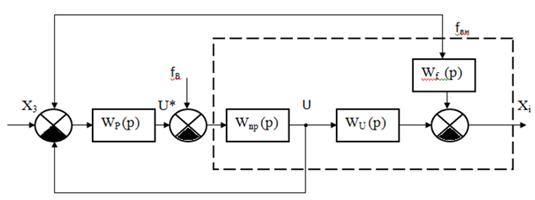
63 сурет
Төменде көрсетілген міндеттер варианттарымен, АРЖ жүзеге асыруға мүмкіндік бар:
- Xi=f(G2) тәуелділігі астатиқалық кезінде болғанда fвн(G2) шамасы туралы сигнал енгізбей Р1, Т1, немесе G1(Q1) параметрлері бойынша кіріс легі И-ды турақтандыруды жүзеге асыру;
- Хі=f(G2) тәуелділігі статитқалық болғанда, fвн(G2) шамасы туралы сигнал енгізіп, Р1, Т1, немесе G1(Q1) параметрлері бойынша кіріс легі И-ды тураұтандыруды жүзеге асыру;
- материалдық балансты тікелей қамтамасыз ету үшін, G-2 сыртқы ауытқу сигналын енгізу арқылы G1-ді тұрақтандыруды жүзеге асыру. Оны, G2 параметірінің өзгеруін, G1 параметірі арқылы автоматты қадағалауды іске асыру;
- Wпр(P) - аралық басқару объектісінің беріліс функциясы (негізгі жұмыс ортасырегінің И-ды бейнелейтін(сипаттайтын), реттеуші орган турған жерінен параметрді өлшейтін жабдық қойылған орнына өдейінгі құбыр бөлігі).
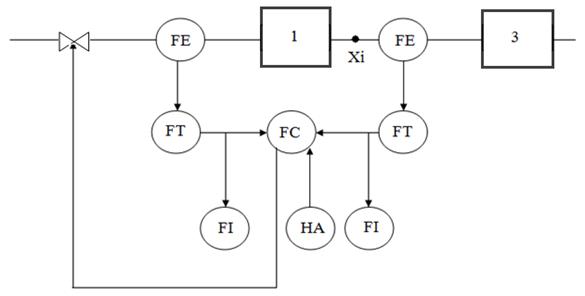
64 сурет
ТУ жоғарғы деңгейі параметрі мәніне немесе Хі параметірі сынама талдауының нәтижесіне (өңделген жұмыс отрасының химиялық қурамы)байланысты тапсырманы қолмен түзеу жүргізіледі.
FE, FT, FC, FI- өлшеу, өзгерту, үздіксіз реттеу және индикациялау функцияларын орындайтын локальдық техникалық жабтықтар.
Технологиялық аппараттардың екінші түрі
Басқарма мақсаттары:
1) Энергетикалық теңгерімнің сүйеуі (рекуперативтық жылу айырбастау аппараты)
![]() (*).
(*).
2) G1 жүйенің құбыр жүйесі арқылы шығыны.
3) c құбыр жүйенің жылу сыйымдылығы.
4) QT құбыр жүйе аппараттың жылулық энергия ағыны.
(*) формуласын өзгерте отыра жаңа формуланы шығара аламыз
![]() ,
,
Q1’ бастапқы жұмыс ортасынан берілетін жылу саны.
Xi(T1’) параметрінің тұрақтандыру мәселесі:
- Құбыр жүйенің жылуалмасу аппараттағы кірерінде тұрған, жылусақтаушыны аппараттың камерасына еркінше жіберіп және пайдаланып жатқан уақытта жылынып жатқан жұмыс ортасының мөлшерін өзгерту.
- Жылынып жатқан ортаны кіріс және шығыста еркінше қолданып жатқан уақытта аппараттық камерасындағы жылусақтаушының мөлшерін өзгерту.
- Жылынап жатқан ортаны кіріс және жылысақтаушыны еркінше жіберіп жатқан уақытта жылуалмасу аппараттың шығуындағы ортамен қолданылып жатқан мөлшерді өзгерту.
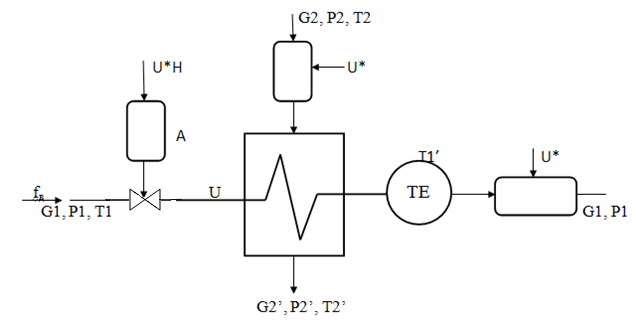
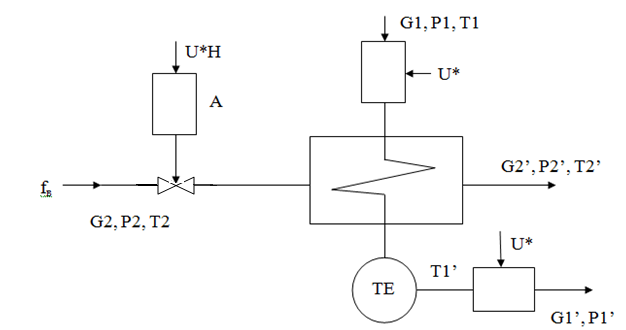
65 сурет
T1 параметрдің тұрақтандыру мәселесі тұйықталған және ашық салынған әдістермен іске асырыла алады.
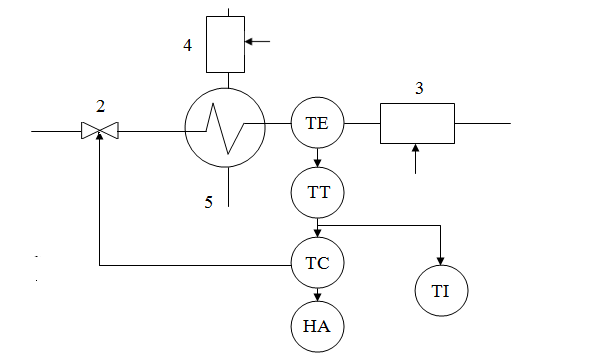
3 – қыздырылған жұмыс ортасының кез келген тұтынушы бағдарлаушы органы.
4 –жылусақтаушыны беретін кез келген тұтынушы бағдарлаушы органы.
5 – ТС –пайдаланылған жылусақтаушыға қарсылық білдіру үшін.
66 сурет - Үшінші турдің технологиялық аппараты
Басқару мақсаттары:
- ТО материалдық баланстың қолдауы
G1+k*G3 – G2=0 (**)
- G1, G3- бірінші және екінші бастапқы орталардың шығыны.
- G2 – алынған қоспаның шығыны.
- k - G3 және G1 арақатынас шығындарын анықтайтын коэффициент.
- (**)ТС шағыннан алған Q2 қоспасының химиялық құрамының қалыптасқан мәнін талап етеді
Q2=Q2H=const
АУ(P) мақсаттары (тұйықталған әдіс).
- Q2 нің G2 еркінімен пайдаланған кезінде G1 жіберуін өзгерту үшін өсер ететін тұрақтандыруы (ішкі бүлік).
- G3 параметрдің G1, белгілі арымқатынас коэффициенті бар параметрдің өзгеруін аңду.
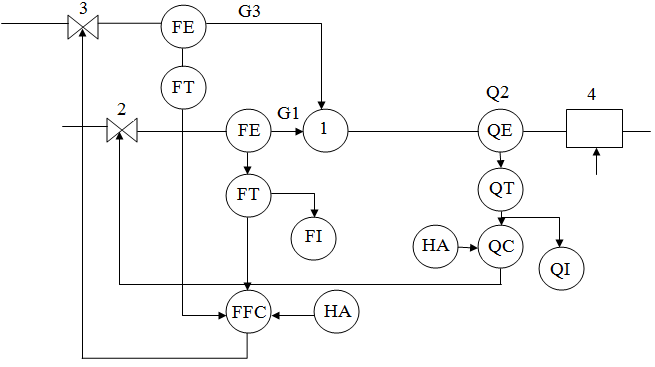
67 сурет
FFC - G3 (екінші параметр) параметрмен G1 G3тен жоғарғы иерархиялық деңгейдегі (бастаушы параметр) параметрдің мөлшер арасалмағын реттейтін жергілікті автоматтық құрылғы.
AҚ (алшақ салынған) мәселелері:
- G1дің мөлшерімен кіріс ағында еңгізіп түзететін сигналды шығыс ағынының G2 мөлшерімен тұрақтандыру;
- Алғашқы екінші жұмыс ортаның шығыс ағынын, арасалмақ коэффициенті бар G1 параметрдің өзгерістерін аңдуын қамтамасыз ететін G3 мөлшерімен тұрақтандыру.
4 Өндірістік үрдістің және басқару жүйесінің модельдері
4.1 Үздіксіз өндірістік жүйенің моделі
Сызықты жүйені сипаттаудың классикалық әдісі болып оның кірісі мен шығысының арасындағы байланысы дифференциалды [2,7,8] немесе айырымдық теңдеу көмегімен жазылған өрнек саналады. Дифференциалды теңдеулер үздіксіз жүйелерді сипаттау үшін қолданылады, ал айырымдық теңдеулер (разностные уравнения) – дискретті жүйелерді сипаттау үшін қолданылады. Үздіксіз жүйе дифференциалды теңдеулер жүйесімен сипаттала алатындықтан, теңдеулер жүйелерін талап етілген дифференциалды теңдеуге келтіру қарастырылады.
Бірінші ретті дифференциалдық теңдеуді (уақыт бойынша өзгеретін және тұрақты коэффициенттері бар) шешудің түпкілікті құрастырылған (детально разработанный) әдісі сипатталады. Ал жоғарғы ретті теңдеулерді шешудің жалпы әдісі тек стационарлы жүйелер үшін құрастырылған (детально разработан). Ал стационарлы емес жүйелердегі теңдеулерді талдау келесі параграфта қарастырылады. Бұнда тұрақты және айнымалы параметрлі дифференциалды теңдеулермен сипатталатын импульсті сипаттамаларды іздеудің әдістері қарастырылады.
Айырымдық теңдеулермен орындалатын операциялар дифференциалды теңдеулермен орындалатын операцияларға сәйкес ретпен түсіндіріледі. Қосымша ретінде тура және кері айырымдық операторлар жайлы параграф толықтырылған. Тараудың материалы сызықты жүйелерді қарастырумен шектелген. Бұнда тек қана шешу жолдарының аналитикалық әдістері келтіріледі. Бірақ практика жүзінде есептеу әдістерін қолдану дұрысырақ болар еді.
Үздіксіз жүйелерді дифференциалды теңдеулер түрінде көрсету.
Үздіксіз жүйелерді оның кірісі y(t) мен шығысы r(t) - ға қатысты дифференциалды теңдеу көмегімен жиі сипаттайды. Жалпы түрде теңдеу келесідей болады:
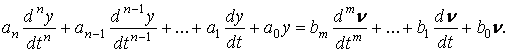 (4.1)
(4.1)
v(t) белгілі деп алсақ, теңдеудің оң жағын жиi ерiксiз көндiретiн функция F(t) деп көрсетуге болады,
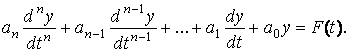 (4.2)
(4.2)
ai мен bi сызықты жүйелері үшін v немесе y функция болып табылмайды, бірақ t уақыттан тәуелді болуы мүмкін.
Тұрақты параметрлері бар сызықты жүйелер үшін бұл коэффициенттер тұрақты болуы қажет (68 суретті қара), мысалдары құрылған анықтамалардың мақұлдануы болып табылады.
Жүйенің дифференциалды теңдеуі алдын - ала берілуі мүмкін немесе жүйенің моделіне негізделіп табылуы тиіс. Соңғы жағдайда модель дифференциалды теңдеулер жүйесін береді. Дифферениалды теңдеулер жүйесін y(t) мен v(t)-ны байланыстыратын бір теңдеуге келтіру мысалда және келесі параграфта көрсетіледі.
Дифференциалдау операциясын бейнелейтін p операторы келесідей анықталады
![]() (4.3)
(4.3)
Егер с1 және с2 – тұрақты шамалар болса, онда
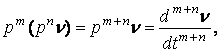
![]() (4.4)
(4.4)
![]() ,
,
мұндағы m мен n – теріс емес бүтін сандар. Ереже бойынша p операторын алгебралық сан ретінде қолдануға болады. Оның айрықша белгісі – ол келесі функциялармен коммутативті емес болып табылады
![]()
![]()
p операторының көмегімен (4.1) және (4.2) теңдеулері мына түрге келеді
![]() (4.5)
(4.5)
y пен v алдындағы жақша ішіндегі элементтердің өзі операторлар болып табылады. Коэффициенттері тұрақты болып келетін стационарлы жүйелер үшін соңғы өрнек символдық түрде келесідей жазылады
![]() (4.6)
(4.6)
Коэффициенттері уақыт функциялары болып табылатын (А және В уақыттан тәуелді операторлар), айнымалы параметрлері бар сызықты жүйелер үшін бұл келесі өрнекте есепке алынады
![]() (4.7)
(4.7)
А және В операторларының формальды анықтамасы соңғы үш өрнекті салыстырудан шығады.
Дифференциалдық теңдеулер жүйесін түрлендіру.
Үзіліссіз модель математикалық түрде дифференциалдық теңдеулер жүйесімен сипатталуы мүмкін. Теңдеулердің бір класы негізінен бөлек құраушыларды сипаттау үшін, ал екіншісі – осы құраушылардың арасындағы байланыстарды сипаттау үшін арналған. Модельді математикалық сипаттау кезінде теңдеудің аталған екі класы, әдетте, тәжірибелік тексерумен сәйкес келеді. Алынған теңдеулер жүйесі осы жүйенің кірісі мен шығысын байланыстыратын бір теңдеуге келтіруге болады. Бірақ мұндай түрлендіру әрқашан оңай болып табылмайды. Тұрақты коэффициенттері бар теңдеулер жүйесін шешу айнымалы коэффициенттері бар теңдеулер жүйесін шешуден оңай болғандықтан, бірінші кезекте алғашқысы қарастырылады.
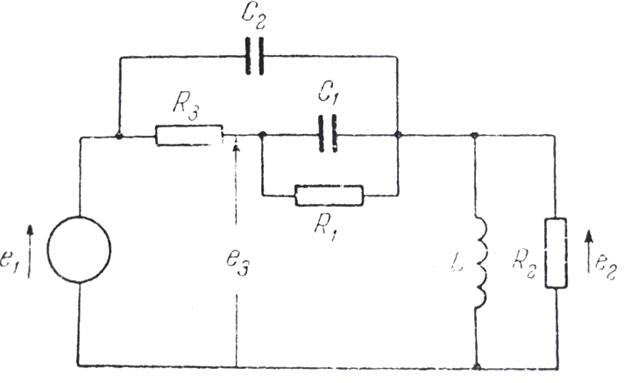
68 сурет
Мысал 68 суреттегі тізбек үшін шығысындағы кернеу е2 мен көздің кернеуі е1- ді байланыстыратын теңдеу жазайық
Сәйкесінше 3 - ші және 2 - ші түйіннен шығатын токтарды қоса отырып, келесіні аламыз
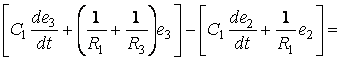
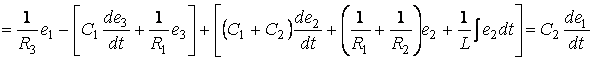 .
.
Интегралдан құтылу үшін екінші теңдеуді дифференциалдап, p=d/dt операторын енгізе отырып, теңдеуді келесі түрге келтіреміз
![]() .
.
Есепті қарапайымдау үшін барлық кедергілер,
сыйымдылықтар және индуктивтіктер сәйкесінше 1 Ом, 1 Фарада
және 1 Генриге тең етіп аламыз. Бірінші теңдеудің
әрбір мүшесіне ![]() операторын, ал екінші
теңдеудің әрбір мүшесіне p+2 операторларын
көбейтіп, олардың өзара қосамыз
операторын, ал екінші
теңдеудің әрбір мүшесіне p+2 операторларын
көбейтіп, олардың өзара қосамыз
![]() .
.
Құрамында ![]() бар өрнек жойылады.
бар өрнек жойылады.
![]()
![]()
ізделініп отырған нәтиже де осы.
Кез - келген тұрақты коэффициенттері бар екі дифференциалдық теңдеулер үшін берілген мысалдағы процедура орындалады. Егер L функциясы тек p болатын операторды білдірсе, онда теңдеулерді символдық түрде келесідей жазуға болады
![]()
![]() (4.8)
(4.8)
Бірінші теңдеуді ![]() - ге, ал екінші теңдеуді
- ге, ал екінші теңдеуді ![]() - ге көбейтіп, бірінен-бірін алып
тастаймыз.
- ге көбейтіп, бірінен-бірін алып
тастаймыз. ![]() болғандықтан
болғандықтан
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
Соңғы екі теңдеудің әрбіреуінің құрамында тек бір ғана тәуелсіз айнымалы бар.
Енді n дифференциалдық теңдеулер үшін жалпы жағдайды қарастырайық. Символдық түрде
![]() ,
,
![]() , (4.11)
, (4.11)
![]() ,
,
![]() операторлары тек қана p - дан тәуелді
болғандықтан, шешімді Крамер ережесін қолдану арқылы
көрсетуге болады
операторлары тек қана p - дан тәуелді
болғандықтан, шешімді Крамер ережесін қолдану арқылы
көрсетуге болады
![]() (4.12)
(4.12)
мұндағы ![]() – анықтауышпен анықталатын дифференциалдық оператор
– анықтауышпен анықталатын дифференциалдық оператор
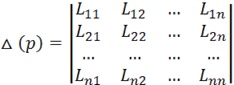 (4.13)
(4.13)
![]() – кі-ші
алгебралық толықтауыштпен, яғни
– кі-ші
алгебралық толықтауыштпен, яғни ![]() - ның к - ші
жол мен і-ші бағанды сызып тастағаннан пайда болған
анықтауыштың
- ның к - ші
жол мен і-ші бағанды сызып тастағаннан пайда болған
анықтауыштың ![]() -ге көбейтіндісі.
Айтылған материал тұрақты коэффициенттері бар
дифференциалдық теңдеулермен шектеледі. Айнымалы коэффициенттері
бар жүйелер үшін шығысы мен кірісін байланыстыратын
дифференциалдық теңдеу алу әлдеқайда
қиынырақ. Жүйе келесі теңдеулермен сипатталады деп
тұжырымдайық
-ге көбейтіндісі.
Айтылған материал тұрақты коэффициенттері бар
дифференциалдық теңдеулермен шектеледі. Айнымалы коэффициенттері
бар жүйелер үшін шығысы мен кірісін байланыстыратын
дифференциалдық теңдеу алу әлдеқайда
қиынырақ. Жүйе келесі теңдеулермен сипатталады деп
тұжырымдайық
![]()
![]()
y1-ді осы теңдеулерден табу үшін, біріншісін pt - ға, ал екіншісін tp - ға көбейтіп, бірінен - бірін алып көруге болады. Егер бұл орындалса, онда
![]()
![]()
Бірақ ![]() , ал
, ал ![]() =t(t
=t(t![]() . Бұдан
. Бұдан ![]() -ді айыру арқылы табуға болмайды.
-ді айыру арқылы табуға болмайды.
Параметрлері айнымалы болып келетін жүйелер үшін (4.9) және (4.10) теңдеулері орындалмайды, өйткені
![]()
(4.12) теңдеуі де осылай орындалмайды. Әдетте, жүйенің кірісі мен шығысын байланыстыратын өрнекті алу қолдан келсе де, (4.12) сияқты жалпы жағдайдағы қарапайым қолданатын формула жоқ. Дифференциалды теңдеулер жүйесін бір теңдеуге келтірудің қиындығын есепке алсақ, арнайы әдістерді қолдану жиі тиімді болып келеді. Осындай әдістердің бірі 5 - тарауда қарастырылады.
Сызықты дифференциалдық теңдеулердің негізгі қасиеттері.
n-ші ретті сызықты дифференциалды теңдеуді (4.5) түрінде жазуға болады:
![]() . (4.14)
. (4.14)
Осы параграфтағы барлық өрнектердің айнымалы параметрлі жүйелер үшін тұрақты параметрлі жүйелер үшін де орындалатынына байланысты, aл коэффициенттері жалпы жағдайда уақыт фунциясы болуы мүмкін. Егер соңғы теңдеудің оң жағы 0-ге тең болса, яғни
![]() (4.15)
(4.15)
онда бұндай теңдеуді біртекті деп атайды. (4.14) - теңдеуді сәйкесінше біртекті емес дифференциалды теңдеу деп атайды.
(4.15) - теңдеу n - нен артық емес сызықты тәуелді шешімі бола алады. Сызықты тәуелдсіздік ұғымы төртінші тарауда толығымен қарастырылады. Қысқаша, егер n объектінің кем дегенде біреуін басқалардың сызықты комбинация ретінде келтіруге болса, онда бұл сызықты тәуелді делінеді. Кері жағдайда объектілер тәуелсіз болып саналады. (4.15) - теңдеудің n шешімінің сызықты тәуелсіздігінің қажетті және жеткілікті шарты Вронский анықтауышының 0-ден өзгешелігі болып табылады. Егер y1, y2,…, yn – теңдеудің n шешімі болса, онда Вронский анықтауышы келесі түрде болады
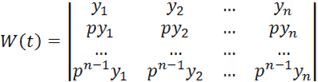 . (4.16)
. (4.16)
(4.15) - теңдеуінің жалпы шешімі келесідей болады
![]() , (4.17)
, (4.17)
мұндағы Кі – еркін тұрақтылар. Н индексі шешімінің біртекті теңдеуге сәйкес келетіндігін көрсетеді. Соңғы теңдеуден келесі тұжырым шығады: егер n тәуелсіз шешім белгілі болса, онда осы теңдеудің еркін шешімін n белгілі шешімнің сызықты комбинациясы түрінде келтіруге болады. Тұрақты параметрлері бар жүйелер үшін біртекті теңдеудің тәуелсіз шешімдерін табудың жалпы әдісі бар. Ал айнымалы параметрлі жүйелер үшін ондай әдіс жоқ.
Біртекті (4.14) - ші теңдеудің жалпы шешімі келесі түрге ие
![]() (4.18)
(4.18)
мұндағы yH - (4.17) - ң біртекті теңдеуге сәйкес шешімі, yР – (4.14)-теңдеуді қанағаттандыратын және, әдетте, дербес шешім деп атайтын еркін шешім (қандай жолмен алынғанынан тәуелсіз). yH –ді қосымша шешім деп те атайды. yР –ді табу үшін кез келген әдісті қолдануға болады. (даже метод «проб»). Мысалы, синусоидалы сигналдардың көзді электр тізбектері үшін айнымалы токты тізбектердегі бекітілген режимдер теориясын қолдануға болады (теория установившихся режимов). Келесі параграфта yH белгілі болғандағы yР – ны анықтау әдістері қарастырылады. yР –да еркін тұрақтылар болмағандықтан yH – дегідей y шешімінде n тұрақты болады. Оларды табу үшін бастапқы және шектік шарттарды білу қажет.
Бірінші ретті дифференицалдық теңдеулерді шешу.
Бірінші ретті сызықты дифференциалды теңдеу келесі түрде жазылады
![]() (4.19)
(4.19)
Ыңғайлылық үшін dy/dt алдындағы
коэффициентті бірге тең етіп аламыз. а коэффициенті жалпы жағдайда
уақыттан тәуелді болуы мүмкін. Берілген теңдеуді
интегралдаушы көбейткіш ![]() енгізу арқылы
шығарамыз. Теңдеудің екі жағына да осы көбейткішті
көбейтейік:
енгізу арқылы
шығарамыз. Теңдеудің екі жағына да осы көбейткішті
көбейтейік:
![]() . (4.20)
. (4.20)
Теңдеудің сол жағы
![]() –нің уақыт бойынша туындысы болып келеді, онда
–нің уақыт бойынша туындысы болып келеді, онда
![]() (4.21)
(4.21)
(4.21)-теңдеудің оң жағын интегралдау қиындық туғызғанымен, келтірілген әдіс a(t) коэффициентінің түрінен тәуелсіз шешудің қатаң процесдурасын ұсынады. Нәтиже екі құраушыдан да тұрады.
![]() – есептеу барысында интегралдау тұрақтысын жазып
отырудың қажеті жоқ.
– есептеу барысында интегралдау тұрақтысын жазып
отырудың қажеті жоқ.
4.19-мысал. dy/dt–ty=t теңдеуін шешу керек. Интегралдаушы
көбейткіш ![]() тең. Берілген теңдеуді осы көбейткішке
көбейтейік. Сонда
тең. Берілген теңдеуді осы көбейткішке
көбейтейік. Сонда

![]()
![]()
Айнымалыларды ажырату әдісі интегралдаушы көбейткішті қолдану әдісінен оңай болғанымен, бірінші ретті теңдеулер үшін жарамсыз болып қалады. Берілген мысалды оны қолдануға болмайды.
Тұрақты коэффициенттері бар дифференциалды теңдеулерді шешу
Сызықты стационарлы жүйелер сызықты дифференциалды теңдеулермен сипатталады. n-ретті біртекті және біртекті емес теңдеулер сәйкесінше (4.14) және (4.15) теңдеулермен беріледі. Мұндағы, ai – тұрақты коэффициенттер. Осы параграфта қарастырылатын әдістер кез-келген ретті теңдеу үшін орындалады.
Біртекті дифференциалды теңдеулер. n-ші ретті теңдеуді қарастырайық
![]() (4.22)
(4.22)
нәтиже y=ert деп ұйғарайық. Мұндағы, r – анықтама бойынша тұрақты шама. Онда
![]()
осы теңдеу t – кез-келген мәнінде орындалатындықтан,
![]() . (4.23)
. (4.23)
(4.23)-теңдеуді сипаттамалы теңдеу деп атайды. Оны (4.22)-теңдеуден тікелей жазуға да болады. (4.23)-нің сол жағында n-ші ретті полином тұр, сондықтан оның n түбірі бар. Онда (4.22) теңдеудің сәйкесінше шешімдері келесіге тең
![]()
Егер осы n - шешімдер сызықты тәуелді болса, онда біртекті дифференциалды теңдеудің жалпы шешімі келесідей болады
![]() . (4.24)
. (4.24)
Егер барлық ri түбірлері әр түрлі болса, онда (4.24)-тен
Вронский анықтауышы нөлден өзгеше екені шығады, ендеше n-
жеке шешімдері тәуелсіз болып келеді. Егер r1=r2, онда
![]() шешімдері де тәуелсіз. Егер, мысалы, r1 k-ға
бөлінсе, яғни r1=r2=…=rk, онда жалпы шешім келесідей жазылады
шешімдері де тәуелсіз. Егер, мысалы, r1 k-ға
бөлінсе, яғни r1=r2=…=rk, онда жалпы шешім келесідей жазылады
![]() (4.25)
(4.25)
Сонымен, ![]() -ді табу үшін n-ші ретті теңдеудің түбірлерін
ғана есептеу керек. Кейбір түбірлер комплексті түрде болуына
қарай, теңдеу шешімн басқа формада жазуға болады.
-ді табу үшін n-ші ретті теңдеудің түбірлерін
ғана есептеу керек. Кейбір түбірлер комплексті түрде болуына
қарай, теңдеу шешімн басқа формада жазуға болады.
(4.23)-теңдеу коэффициенттері нақты
болғандықтан, комплексті түбірлер комплексті байланысуы
керек. Егер түбірлердің біреуі r1=α+j![]() , мұндағы α және
, мұндағы α және ![]() -нақты шамалар, онда келесі түбірлердің біреуі r2=α–j
-нақты шамалар, онда келесі түбірлердің біреуі r2=α–j![]() -ға тең болуы керек.
-ға тең болуы керек.
Онда
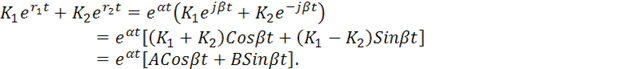
Нақты жүйеде аі – нақты сандар, ал yH – нақты уақыт функциясы. Сондықтан А және В еркін тұрақтылары да нақты сандар болуы керек. Ендеше К1 және К2 өз кезегінде комплексті байланысқан болуы керек. Бірдей жиіліктегі екі тригонометриялық өрнекті бір фазалық бұрышты өрнекке келтіруге болады. Оны келесі түрде жазуға болады
![]()
Біртекті емес дифференциалды теңдеулер. Белгісіз коэффициенттер әдісі. Келесі теңдеуді қарастырайық
![]() (4.26)
(4.26)
оның шешімі келесідей болады
![]() . (4.27)
. (4.27)
![]() F(t)=0 болғанда сәйкес біртекті теңдеуден
табылады.
F(t)=0 болғанда сәйкес біртекті теңдеуден
табылады. ![]() – дербес шешімін табудың 2 стандартты әдісі бар: белгісіз
коэффициенттер әдісі және параметрлерді вариациялау әдісі.
– дербес шешімін табудың 2 стандартты әдісі бар: белгісіз
коэффициенттер әдісі және параметрлерді вариациялау әдісі.
Белгісіз коэффициенттер әдісі F(t) функциясының
сызықты тәуелсіз туындылары шектеулі болғанда
қолданылады. F(t) t бүтін дәрежелі көпмүше немесе
экспоненциалды, синусоидалы, гиперболалы функцияның комбинациясы болуы
мүмкін. F(t) ![]() немесе
немесе ![]() тең болса, көрсетілген әдіс қолдануға
келмейді (егер шешімді үзіліссіз қатар ретінде іздемесе).
Әдіс негізіне y F(t) сызықты құраушылардың
комбинациясынан және олардың туындыларынан тұратыны кіреді;
және мұндағы әрбір элемент белгісіз коэффициентпен
кіреді. Осындай шешім (4.26) - теңдеуге қойылады. Белгісіз
коэффициенттер теңдеу t-ның барлық мәнінде
қанағаттанатындай етіп таңдалады. F(t) мүшесі
түрі бойынша біртекті теңдеудің шешімінің
құраушысымен дәл келсе, көрсетілген процедураның
түрі де өзгереді. Физикада бұл резонансқа сәйкес
келеді, яғни жүйе өзінің жиіліктерінің бірінде
қозады. Мысалы,
тең болса, көрсетілген әдіс қолдануға
келмейді (егер шешімді үзіліссіз қатар ретінде іздемесе).
Әдіс негізіне y F(t) сызықты құраушылардың
комбинациясынан және олардың туындыларынан тұратыны кіреді;
және мұндағы әрбір элемент белгісіз коэффициентпен
кіреді. Осындай шешім (4.26) - теңдеуге қойылады. Белгісіз
коэффициенттер теңдеу t-ның барлық мәнінде
қанағаттанатындай етіп таңдалады. F(t) мүшесі
түрі бойынша біртекті теңдеудің шешімінің
құраушысымен дәл келсе, көрсетілген процедураның
түрі де өзгереді. Физикада бұл резонансқа сәйкес
келеді, яғни жүйе өзінің жиіліктерінің бірінде
қозады. Мысалы,
![]()
теңдеуі үшін
![]() өрнегі А мен В таңдаудан тәуелсіз
өрнегі А мен В таңдаудан тәуелсіз ![]() болғанда қанағаттандырылмайды. Әрине,
көрсетілген типті возмущениемен шақырылған шешімнің
құраушысы возмущение жоқ кездегіден ақырынырақ
өшуі керек. Сондықтан шешімді келесі түрде іздеген жөн
болғанда қанағаттандырылмайды. Әрине,
көрсетілген типті возмущениемен шақырылған шешімнің
құраушысы возмущение жоқ кездегіден ақырынырақ
өшуі керек. Сондықтан шешімді келесі түрде іздеген жөн
![]()
Осы шешімді дифференциалды теңдеуге қоя отырып, оның А=1/2 және В=-1 тең болғанда қанағаттанатынын табамыз. Егер F(t) жеке мүшелері формасы бойынша yH мүшелерімен сәйкес келсе, онда шешу процедурасында анықталатын yP –дің сәйкес құраушыларына жалпы жағдайда t көбейтіледі. Осындай сұлба F(t) құрамында қосымша tn көбейткіші бар болса сақталады. Бірақ F(t)-ның қандай да бір мүшесі сипаттамалы теңдеудің түбіріне сәйкес келсе (мысалы, m-ші ретті түбір), онда yP -дің сәйкес мүшесін tm-ге көбейту керек.
4.22 мысал. Келесі теңдеудің жалпы шешімін табу керек
![]()
Сипаттамалы теңдеуі: ![]() ; осыдан r1=r2=1 және
; осыдан r1=r2=1 және ![]() Әдетте,
Әдетте, ![]() берілген мысалда сипаттамалы теңдеу екі бірдей түбірге ие,
-1; ендеше,
берілген мысалда сипаттамалы теңдеу екі бірдей түбірге ие,
-1; ендеше,
![]()
![]() - ны қайталап дифференциалдау қайтадан Ct
- ны қайталап дифференциалдау қайтадан Ct![]() және
және ![]() өрнектеріне келетінін байқаймыз, бұл өрнектер
өрнектеріне келетінін байқаймыз, бұл өрнектер ![]() дің шешімі болып табылмайды. Бұл келесідей
түсіндіріледі: бұл өрнектер сәйкес біртекті
теңдеудің шешімі болып табылады, сондықтан оларды
дифференциалды теңдеудің сол жағына қойған кезде
жойылып кетеді.
дің шешімі болып табылмайды. Бұл келесідей
түсіндіріледі: бұл өрнектер сәйкес біртекті
теңдеудің шешімі болып табылады, сондықтан оларды
дифференциалды теңдеудің сол жағына қойған кезде
жойылып кетеді. ![]() -ді қойып, жоғарыда айтылғандай келесіні аламыз
-ді қойып, жоғарыда айтылғандай келесіні аламыз
![]()
Бұдан, A=1/6, B=0, және соңғы түрі мынадай болады
![]()
Біртекті емес дифференциалды теңдеулер. Параметрлерді вариациалау. Белгісіз коэффициенттер әдісіне қарағанда yP-ді параметрлерді вариациялау арқылы табу әдісі F(t)-ның тәуелсіз туындылар саны шектеулі ма, жоқ па екеніне тәуелсіз қолданыла алады. Бірінші әдіске қарағанда ол тағы да (4.26) теңдеудегі ai коэффициенттері уақыттан тәуелді болса да, қолдануға келеді.
Параметрлерді вариациялау әдісі біртекті теңдеудің шешімдерінің құраушыларының негізінде дербес шешімді табу болып табылады. Оқырманға бұл әдіс белгісіз болуы мүмкіндігінен, алдымен бірінші ретті дифференциалды теңдеуді қарастырайық
![]() (4.28)
(4.28)
Келесі біртекті теңдеуді қанағаттандыратын шешім
![]() (4.29)
(4.29)
құрамында
![]() Дербес шешімді келесі түрде іздейміз
Дербес шешімді келесі түрде іздейміз
![]() (4.30)
(4.30)
Мұндағы барлық 3 функция да уақыт функциялары болып табылады. u-ды табу үшін (4.30) теңдеуді (4.28) теңдеуге қоямыз. Келесіні аламыз
![]()
мұндағы нүктелер t бойынша туындыны білдіреді. Түрлендірулерден кейін
![]()
Соңғы теңдеудегі жақша ішіндегі
көбейткіштер нөлге тең, себебі ![]() (4.29) - теңдеуді қанағаттандырады. Ендеше,
(4.29) - теңдеуді қанағаттандырады. Ендеше,
![]() (4.31)
(4.31)
4.23 мысал. Теңдеудің жалпы шешімін табу керек
![]()
Біртекті теңдеуінің шешімі
![]() яғни
яғни ![]()
![]() деп ұйғарып,
деп ұйғарып,
![]()
![]() және
және ![]() .
.
Жалпы шешімнің түрі келесідей болады
![]()
Енді екінші ретті дифференциалды теңдеуді қарастырайық:
![]() . (4.32)
. (4.32)
Келесі біртекті теңдеуді қанағаттандыратын шешім
![]() , (4.33)
, (4.33)
екі қосылғыштан тұрады:
![]() .
.
Дербес шешімді
![]() , (4.34)
, (4.34)
түрінде іздейміз. Мұндағы, u1 және u2 белгісіз уақыт функциялары болып табылады. u1 және u2-ні табу үшін екі шарт қажет. Біріншісі: (4.34) теңдеуі (4.32) теңдеуді қанағаттандыруы керек. Екіншісі: бұл шартты кез-келген ыңғайлы жолментаңдауға болады
![]()
![]() мен
мен ![]() үшін өрнектер келесі өрнекті қойсақ,
көлемі әлдейқайда азаяды
үшін өрнектер келесі өрнекті қойсақ,
көлемі әлдейқайда азаяды
![]() (4.35)
(4.35)
Сондықтан (4.35) теңдеуі екі қажетті шарттың біреуі болып табылады:
![]()
![]()
(4.32) теңдеуге қойғаннан келесіні аламыз
![]()
Түрлендіргеннен кейін
![]()
![]() мен
мен ![]() (4.33) теңдеуін қанағаттандыратындықтан,
(4.33) теңдеуін қанағаттандыратындықтан,
![]() (4.36)
(4.36)
u1 мен u2 үшін нақты формула алу үшін, (4.35) және (4.36) теңдеулерін бірге шешу керек. Сонда келесіні аламыз
![]()
![]() (4.37)
(4.37)
y1 мен y2 (4.33) теңдеуінің
сызықты тәуелсіз шешімдері болғандықтан, (4.16)-тен ![]() екені шығады. (4.37)-ның бөлімі нөлден
өзгеше болғандықтан, u1 мен u2 әрқашан
бар болады.
екені шығады. (4.37)-ның бөлімі нөлден
өзгеше болғандықтан, u1 мен u2 әрқашан
бар болады.
4.24 мысал. Теңдеудің жалпы шешімін табу керек
![]()
Біртекті теңдеуінің шешімі келесі түрде жазылады
![]()
Ендеше,
![]()
(4.37) теңдеу негізінде келесіні аламыз
![]()
![]()
Жалпы шешім келесі түрде болады
![]()
Шешімге әсер ететін интегралдар саны шектелген элементар функциялар түрінде өрнектеле алмайды. Оларды үзіліссіз қатарлар көмегімен көрсетуге болады. Бұлар белгілі функциялар: «интегралды синустар» мен «интегралды косинустар». Қорытынды үшін n-ші ретті (4.26) типті дифференциалды теңдеуді қарастырайық. Біртекті теңдеуінің шешімі мынадай түрде болады:
![]()
Дербес шешімін келесі түрде іздейміз
![]() (4.38)
(4.38)
мұндағы ui – t функциялары болып табылады. ui туындыларын келесі n теңдеудің біріккен шешімінен табамыз:
![]()
![]()
……………………………………….
![]()
мұндағы
нүктелер және жоғарғы индекстер t бойынша
туындыларды білдіреді. Алғашқы n-1 шарттары нәтижені
ыңғайлы формада алу мақсатымен еркін түрде
таңдалады. Соңғы теңдеу ![]() -дің шешімін (4.26) теңдеуге алдыңғы n-1 шартты
есепке ала отырып қойғаннан алынған. Жоғарыда
келтірілген теңдеулер жүйесі Крамер ережесі негізінде шешіледі
-дің шешімін (4.26) теңдеуге алдыңғы n-1 шартты
есепке ала отырып қойғаннан алынған. Жоғарыда
келтірілген теңдеулер жүйесі Крамер ережесі негізінде шешіледі
![]() (4.39)
(4.39)
мұндағы
W(t)=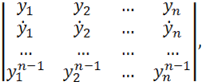 (4.40)
(4.40)
ал
![]() - алгебралық толықтауыш. (4.16) - тен егер y1, y2, …, yn –
біртекті дифференциалды теңдеудің тәуелсіз шешмідері болса, W(t)-
Вронский анықтауышы нөлден өзгеше екендігі шығады.
- алгебралық толықтауыш. (4.16) - тен егер y1, y2, …, yn –
біртекті дифференциалды теңдеудің тәуелсіз шешмідері болса, W(t)-
Вронский анықтауышы нөлден өзгеше екендігі шығады.
4.25 мысал. Теңдеудің жалпы шешімін табу керек
![]()
Біртекті теңдеудің шешімі мынаған тең:
![]()
W(t)=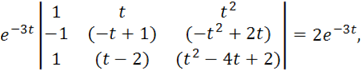
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Нәтижесінде жалпы шешімнің түрі келесідей болады
![]()
![]() -ді табудың екі стандартты әдісін салыстыра отырып,
белгісіз коэффициенттер әдісі оңайырақ екеніне көзіміз
жетті. Оның кемшілігі: возмущяющая функциялардың шектеулі классы
үшін ғана орындалады және параметрлері уақыт бойынша
өзгеретін жүйелер үшін қолдануға келмейді.
-ді табудың екі стандартты әдісін салыстыра отырып,
белгісіз коэффициенттер әдісі оңайырақ екеніне көзіміз
жетті. Оның кемшілігі: возмущяющая функциялардың шектеулі классы
үшін ғана орындалады және параметрлері уақыт бойынша
өзгеретін жүйелер үшін қолдануға келмейді.
Параметрлерді вариациялау әдісінде әрқашан
![]() белгілі болған кезде
белгілі болған кезде ![]() үшін нақты өрнек алуға болады. Шешім белгілі
функцияның интегралы түрінде беріледі, сондықтан
үшін нақты өрнек алуға болады. Шешім белгілі
функцияның интегралы түрінде беріледі, сондықтан ![]() -ді әдетте дербес интегралды шешім деп те атайды. Көптеген
жағдайларда интегралды есептеу қиынға әкеліп
соғады, сондықтан бұндай жерде сандық әдісті
қолданған жөн. Артықшылығы: бұл әдіс
кез-келген вынуждающие функцияларда орындалады және коэффициенттері
уақыт бойынша өзгеретін жүйелерде жалпылана алады.
-ді әдетте дербес интегралды шешім деп те атайды. Көптеген
жағдайларда интегралды есептеу қиынға әкеліп
соғады, сондықтан бұндай жерде сандық әдісті
қолданған жөн. Артықшылығы: бұл әдіс
кез-келген вынуждающие функцияларда орындалады және коэффициенттері
уақыт бойынша өзгеретін жүйелерде жалпылана алады.
![]() кірісі үшін дербес шешім. Коэффициенттері уақыт бойынша
өзгеретін жүйенің жалпы түрі теңдеуімен
сипатталады. А және В операторларын енгізе отырып, келесіні аламыз
кірісі үшін дербес шешім. Коэффициенттері уақыт бойынша
өзгеретін жүйенің жалпы түрі теңдеуімен
сипатталады. А және В операторларын енгізе отырып, келесіні аламыз
A(p)y(t)=B(p)υ(t). (4.41)
Егер ![]() онда дербес шешімнің түрі
онда дербес шешімнің түрі
![]()
мұндағы Н t-дан тәуелсіз. Осы өрнектерді дифференциалды теңдеуге қоя отырып, келесіні аламыз
![]()
![]()
екенін есепке алсақ, мұндағы В – дифференциалдық оператор р-ны s-ке ауыстырғаннан пайда болған функция, келесіні аламыз
![]() (4.42)
(4.42)
Бұдан H(s)-ті дифференциалды теңдеуден тікелей жазуға болады. Келесі өрнек те орындалады
![]() (4.43)
(4.43)
H(s)-ті әдетте жүйенің
беріліс функциясы деп атайды. ![]() -ға әсер ететін реакцияны оңай анықтау
мүмкіндігі еркін кіріс сигналды
-ға әсер ететін реакцияны оңай анықтау
мүмкіндігі еркін кіріс сигналды ![]() функциясы бойынша жіктеуге мүмкіндік береді. Терминологиясына
сай элементар функция – k(t,λ)=
функциясы бойынша жіктеуге мүмкіндік береді. Терминологиясына
сай элементар функция – k(t,λ)=![]() , ал осы элементар функцияға реакциясы келесідей болады K(t,λ)=H(λ)
, ал осы элементар функцияға реакциясы келесідей болады K(t,λ)=H(λ)![]() . Стационарлы электр тізбектері үшін H(s) беріліс функциясы
алдын-ала жазылып қойған дифференциалды теңдеуге
қарамай модель бойынша анықтала алады.
. Стационарлы электр тізбектері үшін H(s) беріліс функциясы
алдын-ала жазылып қойған дифференциалды теңдеуге
қарамай модель бойынша анықтала алады. ![]() болғанда, ток пен кернеу үшін дербес шешімнің
түрі
болғанда, ток пен кернеу үшін дербес шешімнің
түрі ![]() және
және ![]() 2-кестеде электр тізбегінің үш пассивті элементі
келтірілген.
2-кестеде электр тізбегінің үш пассивті элементі
келтірілген.
2 кесте

Келтірілген өрнектерді тізбек элементтерінің дифференциалды
теңдеуіне қоя отырып, кернеудің токқа қатынасын
анықтауға болады. Бұл қатынас импеданс деп аталады
және белгіленуі Z(s), уақыттан тәуелсіз болып келеді. Осындай
жолмен ![]() мен
мен ![]() арақатынасын тұрақты токты тізбек үшін
табуға болады.
арақатынасын тұрақты токты тізбек үшін
табуға болады.
4.26 мысал. 69 - суреттегі тізбек үшін дербес
![]() шешімді кіріс сигнал
шешімді кіріс сигнал ![]() тең болғанда анықтау:
тең болғанда анықтау:

Ендеше,
![]()
және
![]() болғанда, дербес шешім мынаған тең:
болғанда, дербес шешім мынаған тең:
![]()
(4.42) теңдеуді жүйенің кірісі мен шығысын байланыстыратын дифференциалды теңдеудің белгілі беріліс функциясын жазу үшін қолдануға болады. Жоғарыда келтірілген мысал үшін дифференциалды теңдеудің түрі келесідей болады:
![]()
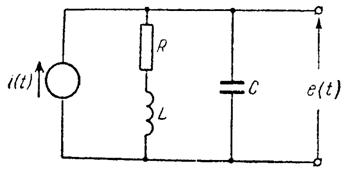
69 сурет
s айнымалыны әдетте комплексті жиілік
деп атайды. Айнымалы токты тізбектегі орнатылған режимдердегі анализ
кезінде 2 кестесінің өрнектері s=jw ауыстыруымен қолданылады. ![]() үшін дербес шешім келесі өрнектен анықталады:
үшін дербес шешім келесі өрнектен анықталады:
![]() (4.44)
(4.44)
Кіріс сигнал синусоидалы болған кезде дербес шешімді тікелей H(jw)-дан
анықтауға болады. ![]() және
және ![]() - ға реакция
- ға реакция ![]() тең болғандықтан,
тең болғандықтан, ![]() -ға реакция келесі түрде болады:
-ға реакция келесі түрде болады:
![]()
Егер H(jw) комплексті шамасы көрсеткіштік
![]() формада өрнектелсе, онда реакцияны былай жазуға болады
формада өрнектелсе, онда реакцияны былай жазуға болады
![]()
Жүйенің жиіліктік спектрі деп жиі аталатын H(jw) айнымалы токты тізбектердегі орнатылған режимдер теориясының негізін құрайды.
Еркін тұрақтыларды есептеу. Еркін тұрақтылар біртекті теңдеуді шешу кезінде бастапқы немесе шектік шарттар негізінде есептеледі. Көптеген жағдайларда жүйені сипаттайтын n-ретті дифференциалды теңдеуді шешу үшін, еркін тұрақтыларды анықтау кезінде y(t) мәндері және оның t=0+ кезіндегі n-1 туындылары қолданылады. 0+ символы t=0 уақыт мезетінен бастап тәуелді айнымалы мен оның туындыларының мәндері белгілі екендігін көрсетеді. Берілген шамалар t=0 уақыт моментіне жинақталған энергияға байланысты анықталады. Еркін тұрақтылар вынуждающая функциядан тәуелді және оларды yP табылмайынша, анықтау мүмкін емес.
4.27 мысал. 70 суретте жоғары жиілікті коррекциялы электронды күшейткіштің жеңілдетілген моделі көрсетілген. Сеткаға түсірілетін кернеу мынаған тең:
![]()
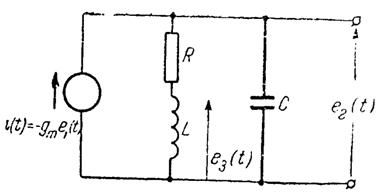
70 сурет
Қозбаған тізбек үшін e2(t) шығыс кернеуді табу керек. Кирхгоф заңына негізделіп тізбектің екі түйіні үшін теңдеу жазайық:
![]()
![]()
Екінші теңдеу интегралды алып тастағаннан кейін
дифференциалды теңдеуге түрленеді. Бірінші теңдеуді
![]() -ке қатысты жазып, оны екінші теңдеуге қоя отырып,
келесіні аламыз
-ке қатысты жазып, оны екінші теңдеуге қоя отырып,
келесіні аламыз
![]()
Күткеніміздей, басқа әдіспен біз 69 - суретке алынғандай теңдеу алдық. Сандық мәндерді қоя отырып, t уақытты микросекундта өрнектеп, келесіні аламыз
![]()
t>0 кезінде
![]()
Сипаттамалы теңдеуі:
![]()
Оның түбірлері
![]()
ендеше
![]() .
.
Дербес шешімді берілген дифференциалды теңдеудің анализінен немесе тұрақты токты тізбекте орнатылған режимдер теоремасы негізінде алуға болады
![]()
Жалпы шешімінің түрі келесідей t>0 болғанда
![]()
және тағы да t>0 болғанда
![]() .
.
K1 мен K2 e2 және t=0+ кезінде
de2/dt белгілі боғанда соңғы екі теңдеуден
анықталады. Есептің шарты бойынша, e2 кернеу және L
арқылы ток t<0 кезінде нөлге тең. Бұл шамалар бірден
өзгере алмайды (егер С арқылы ток импульсі, ал L
арқылы кернеу импульсі өтпесе), өйткені олар t=0+ уақыт
моментінде нөлге тең болып қалуы керек. de2/dt-ны
анықтау кезінде индуктивтік арқылы ток нөлге тең
болғандықтан, С арқылы өтетін ток мынаған
тең болуы керек: ![]()
![]() тең болғандықтан,
тең болғандықтан,
![]()
Ендеше, ![]()
![]()
![]()
Шешім келесідей болады:
![]()
Бірдей бастапқы шарттар. Көптеген шешуші жағдайларда бастапқы шарттар бірдей болып келеді. n-ретті дифференциалды теңдеу үшін (4.26) бірдей бастапқы шарттардың түрі келесідей болады
![]() (4.45)
(4.45)
Жалпы шешімді табу үшін алдында қолданған параметрлерді вариациялау әдісін жалпылауға болады. n=1 кезінде (4.30) және (4.31) теңдеулері келесі теңдеуге бірігеді:
![]() (4.46)
(4.46)
мұндағы
![]() - біртекті теңдеудің шешімі, ал z – фиктивті интегралдаушы
айнымалы. Жоғарғы шек алдында қарастырылған дербес
шешімге сәйкес келеді, ал төменгі шек біртекті
теңдеудің шешкенде беретін тұрақты.
- біртекті теңдеудің шешімі, ал z – фиктивті интегралдаушы
айнымалы. Жоғарғы шек алдында қарастырылған дербес
шешімге сәйкес келеді, ал төменгі шек біртекті
теңдеудің шешкенде беретін тұрақты. ![]() екенін ескертіп кетейік.
екенін ескертіп кетейік.
n=2 кезінде (4.34) пен (4.37) теңдеулері келесі теңдеуге бірігеді:
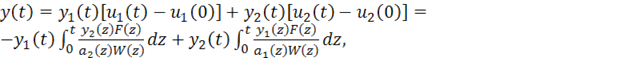 (4.47)
(4.47)
мұндағы
![]() мен
мен ![]() - біртекті теңдеудің шешімдері, ал W(t)-Вронский
анықтауышы,
- біртекті теңдеудің шешімдері, ал W(t)-Вронский
анықтауышы,
![]()
![]() екенін айта кетейік және
екенін айта кетейік және
![]()
Соңғы жақшадағы өрнек әрқашан
нөлге тең, сондықтан ![]()
Бастапқы шарттары бірдей n-ші ретті дифференциалды теңдеудің жалпы жағдайында (4.38) және (4.39) теңдеулерінен
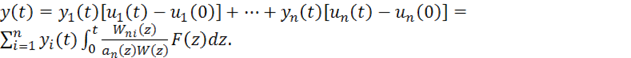 (4.48)
(4.48)
мұндағы W(t) және Wni(t) (4.40) теңдеуінен анықталады. Бұнда талқылау параметрлерді вариациялау әдісіне негізделетіндіктен, (4.45) және (4.48) теңдеулері параметрлері тұрақты да айнымалы жүйелер үшін де орындалады. Берілген теңдеулер стационарлы жүйелердің импульсті сипаттамасын табу кезінде қолданылады.
Дербес және қосымша шешімдердің физикалық мағынасы. Біртекті теңдеуді шешу (қосымша шешім) тек қана жүйенің қасиетінен тәуелді болып келеді, ал кірістегі әсерден тәуелсіз болады. Сипаттамалы теңдеу жүйенің параметрлерінен ғана тәуелді болып келеді, ал түбірлері қосымша шешімнің түрін анықтайды. Сыртқы көздер болмағанда (яғни жүйе алдын-ала жинақталған энергиядан қозса) қосымша шешім жалпы шешіммен сәйкес келеді. Сонымен, қосымша шешім сыртқы әсер болмағанда жүйенің күйін сипаттайды. Осыған байланысты қосымша шешімді еркін қозғалыс деп те атайды.
4.2 Дискретті өндірістік жүйенің моделі
Тура және кері айырым операторлары.
Соңғы айырымның теңдеуі дискретті айнымалылардың функцияларымен жұмыс істейді. y(k) функцияны білдіреді, мұндағы k бүтін мән қабылдайды.
Е жылжу операторын келесі түрде анықтаймыз [5,8,10]:
E[y(k)]=y(k+1). (4.49)
Осы оператордың кезекті қолданылуы :
![]() .
(4.50)
.
(4.50)
Немесе жалпы жағдайда,
![]() . (4.51)
. (4.51)
Кез келген бүтін және оң n үшін.
![]() айырым операторы келесі формуламен анықталады:
айырым операторы келесі формуламен анықталады:
![]() . (4.52)
. (4.52)
Осылайша соңғы теңдеуді келесі түрде жазуға болады:
![]() .
.
Мұнда ![]() және Е операторлары келесідей байланыста
және Е операторлары келесідей байланыста
![]() . (4.53)
. (4.53)
![]() функциясы
функциясы ![]() функциясының бірінші айырымы болып табылады.
функциясының бірінші айырымы болып табылады.
Жоғары реттің айырымы келесі формуламен анықталады:
![]()
![]()
немесе жалпы жағдайда,
![]() , (4.54)
, (4.54)
мұндағы
![]() биномиалды коэффициент. Соңғы теңдеу (4.51)
және (4.53) теңдеулерімен бірге келесі теңдеуді береді:
биномиалды коэффициент. Соңғы теңдеу (4.51)
және (4.53) теңдеулерімен бірге келесі теңдеуді береді:
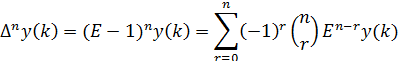
![]() және Е операторлары алгебраның қарапайым
заңына бағынады:
және Е операторлары алгебраның қарапайым
заңына бағынады:
![]() ,
,
![]() , (4.55)
, (4.55)
![]() ,
,
мұндағы
с- тұрақты өлшем, ал mменn- оң бүтін сандар. (4.55)
теңдеуі ![]() -ны Е-ге ауыстырғанда орындалады. Бұл операторлар
өзара коммутативті, бірақ жалпы жағдайда коммутативті емес:
-ны Е-ге ауыстырғанда орындалады. Бұл операторлар
өзара коммутативті, бірақ жалпы жағдайда коммутативті емес:
![]() .
.
Дискретті функцияларға арналған
![]() операторы p=d/dt дифференциалды операторының аналогы болып
табылады. Айтылғанды түсіну үшін
операторы p=d/dt дифференциалды операторының аналогы болып
табылады. Айтылғанды түсіну үшін ![]() үзіліссіз функциясын қарастырамыз, оның туындысы:
үзіліссіз функциясын қарастырамыз, оның туындысы:
![]() . (4.56)
. (4.56)
Егер функция t=nT (n=0,1,2, …) болатын дискретті сәтте қарастырылса, жылжу операторы және айырым операторы келесі түрде анықталады:
Ef(t)=f(t+T),
![]() (4.57)
(4.57)
Онда
![]() . (4.58)
. (4.58)
Немесе жалпы жағдайда,
![]() . (4.59)
. (4.59)
Осылайша бір-біріне ұқсас, бірақ бірдей емес айырым формулалары болады екен. Мысалы,
![]()
![]() . (4.60)
. (4.60)
m-ретті факториалды көпмүше келесі түрде анықталады:
![]() , (4.61)
, (4.61)
мұндағы
m - оң бүтін сан. ![]() m көпмүшеден тұрады. Айырым операторының
ережесін ескере отырып келесіні аламыз:
m көпмүшеден тұрады. Айырым операторының
ережесін ескере отырып келесіні аламыз:
![]() . (4.62)
. (4.62)
Дискретті функцияларда ![]() интегралды операторына аналогты оператор болады ма, егер мұнда:
интегралды операторына аналогты оператор болады ма, егер мұнда:
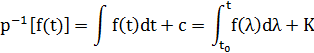 (4.63)
(4.63)
c және K -
интегралдау тұрақтысы. ![]() төменгі шегі тұрақты интегралдау бөлігін
қалыптастырады:
төменгі шегі тұрақты интегралдау бөлігін
қалыптастырады:
![]()
![]() . (4.64)
. (4.64)
(4.64) өрнегі келесі теңдіктің ортақ шешімі болып табылады:
![]() .
(4.65)
.
(4.65)
Сәйкесінше,
![]() . (4.66)
. (4.66)
Аналог бойынша ![]() кері айырым операторы (4.68) өрнегімен ортақ шешім болу
үшін
кері айырым операторы (4.68) өрнегімен ортақ шешім болу
үшін
![]() . (4.67)
. (4.67)
Төмендегі функцияның ортақ шешімі болу үшін
![]() . (4.68)
. (4.68)
Немесе сәйкесінше теңдікті қанағаттандыру үшін
![]() ,
(4.69)
,
(4.69)
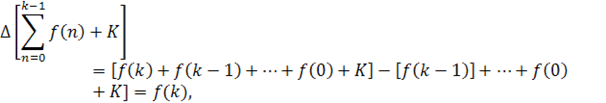
онда (4.68) және (4.69) теңдеулерін қанағаттандыратын кері айырым операторы төмендегідей түрде болады:
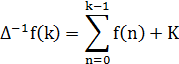 .
(4.70)
.
(4.70)
Кері операторды мына түрде жазсақ та болады:
![]() . (4.71)
. (4.71)
Мұнда
қосынды бекітілген айнымалы n арқылы жүзеге асырылады. (4.71)
теңдігінің төменгі шегі көрсетілмейді,
өйткені кез келген бекітілген f(0), f(1), f(2), мүшелерінің
санын (4.70) теңдеуіне К тұрақтысы арқылы біріктіруге
болады, яғни осыдан соң мұнда с тұрақтысы пайда
болады. (4.71) теңдеуінің төменгі шегіндегі еркіндік (4.63)
теңдеуінің ![]() тұрақты еркіндігінің аналогы болып табылады.
тұрақты еркіндігінің аналогы болып табылады.
Интегралды өте дәл есептеу үшін көп күш
қажет екендігі белгілі. Қосындының соңғы
мүшесін есептеуде ешқандай қиындық болмағандықтан,
![]() операторы үшін мұндай мәселе туындамайды.
Бірақ
операторы үшін мұндай мәселе туындамайды.
Бірақ ![]() үзіліссіз есептелуі үшін (4.71) теңдеуі негізінде
есептеу жалықтыратыны анық.
үзіліссіз есептелуі үшін (4.71) теңдеуі негізінде
есептеу жалықтыратыны анық. ![]() -ның үзіліссіз өсуі нәтижесінде қосынды
кезіндегі мүшелер саны да үзіліссіз өседі.
-ның үзіліссіз өсуі нәтижесінде қосынды
кезіндегі мүшелер саны да үзіліссіз өседі. ![]() -ны тұйық формада өрнектеуге ұмтылу керек.
-ны тұйық формада өрнектеуге ұмтылу керек.
Телескопикалық реттің қосындысы:
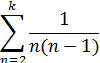
оңай табылады егер,
![]()
Бұдан шығатыны:
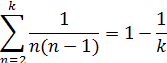 .
(4.72)
.
(4.72)
Кейбір өте қарапайым функциялардың қосындысы элементар функциялардың көмегімен тұйық формада болмайды.
Факториалдық көпмүшелік теңдеуді қолданғанда (4.62) теңдеу төмендегі түрге өзгереді:
![]() .
.
Немесе
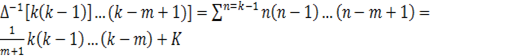 (4.73)
(4.73)
Дискретті жүйенің айырым теңделері түрінде берілуі
Дискретті жүйенің Y(k) шығысы мен v(k) кірісін біріктіретін айырым теңдеуінің жалпы түрі келесі теңдеумен беріледі:
![]() (4.74)
(4.74)
Немесе сәйкесінше,
[![]() ]y(k)=
]y(k)=![]() (4.75)
(4.75)
Көрсетілген екі теңдеудің кез-келгенін (4.49) мен (4.54) аралығындағы теңдеулердің негізінде алуға болады. Екінші теңдеу дифференциалды теңдеуінің аналогына жақын. Алайда біріншісін қолданған ыңғайлы.
![]() сызықиы жүйелері үшін y және v функция болып
табылмайды, бірақ олар
сызықиы жүйелері үшін y және v функция болып
табылмайды, бірақ олар ![]() -ға тәуелді. Тұрақты параметрлі
сызықтық жүйелер үшін бұл коэффициенттер
тұрақты өлшем болып табылады. Е жылжу операторын
қолдана отырып (4.74) теңдеуін келесі түрде жазуға
болады:
-ға тәуелді. Тұрақты параметрлі
сызықтық жүйелер үшін бұл коэффициенттер
тұрақты өлшем болып табылады. Е жылжу операторын
қолдана отырып (4.74) теңдеуін келесі түрде жазуға
болады:
(anEn+an-1En-1+…+a1E+a0)y(k)=(bmEm+…+b1E+b0)υ(k), (4.76)
v(k) кірісі белгілі болғандықтан, (4.74) теңдеуінің бірінші бөлігі F(k) функциясының мәжбүрлік теңдеуі ретінде көрсетіледі. Тұрақты параметрлі сызықтық жүйелер үшін соңғы теңдеу символдық түрде былай жазылады:
A(E)y(k)=B(E)υ(k)=F(k). (4.77)
Айырым теңдеулері дискретті айнымалы функциямен жұмыс істегенде қолданылады. Кіріс және шығыстың арасындағы байланыс t=kT теңдігі арқылы анықталады. Ол келесі айырым функциясы арқылы сипатталады:
![]()
мұндағы
![]() - бүтін сандар. Бұл теңдеуден шығатыны,
- бүтін сандар. Бұл теңдеуден шығатыны, ![]() кезінде шығыс өлшемі оның ескі мағынасы,
яғни t=kT-дан (k+n-1) арқылы және кірісінің
мағынасы t=kT-дан (k+m)T арқылы сипатталады. Бұл жүйе
үшін
кезінде шығыс өлшемі оның ескі мағынасы,
яғни t=kT-дан (k+n-1) арқылы және кірісінің
мағынасы t=kT-дан (k+m)T арқылы сипатталады. Бұл жүйе
үшін ![]() . Егер уақыт масштабын Т=1 болатындай етіп таңдайтын
болсақ, бұл теңдеу (4.74) теңдеуімен сәйкес
келеді.
. Егер уақыт масштабын Т=1 болатындай етіп таңдайтын
болсақ, бұл теңдеу (4.74) теңдеуімен сәйкес
келеді.
Мұндай теңдеулер басқа да жағдайлар да қолданылады. (4.76) және (4.77) теңдеулерінің оң жақ бөлігі кіріс өлшеміне тәуелді емес. Келесі екі мысалда айырылым теңдеулерінің әр түрлі жағдайларла қолданылуы көрсетіледі.
Мысал. 69 суретте Т-образды сұлба көрсетілген.

71сурет
Токтар К көрсеткішінің функциясы болып табылады.
Мұнда ![]() ны табу керек, k=0, 1, 2…,m. K-шы ұяшық үшін
теңдеу келесі түрде болады:
ны табу керек, k=0, 1, 2…,m. K-шы ұяшық үшін
теңдеу келесі түрде болады:
![]()
Бұл - екінші ретті айырым теңдеуі. Егер
![]() кедергісін С сыйымдылығымен алмастыратын болсақ,
теңдеу r-ші ұяшық үшін дифференциалды - айырым
теңдеуі болып табылады.
кедергісін С сыйымдылығымен алмастыратын болсақ,
теңдеу r-ші ұяшық үшін дифференциалды - айырым
теңдеуі болып табылады.
Сызықты айырым теңдеуінің негізгі қасиеттері.
n-ші ретті айырым теңдеуін келесі теңдеу арқылы өрнектеуге болады:
![]() . (4.78)
. (4.78)
Мұнда
![]() және
және ![]()
![]() ның барлық мәндері үшін анықталған.
Егер
ның барлық мәндері үшін анықталған.
Егер ![]() , болса, онда
, болса, онда ![]() ші ретті теңдеу аламыз. Дифференциалды теңдеуден айырмашылығы,
айырым теңдеуінің реті Е дәрежесінің
жоғарға және төменгі шектерінің айырымымен
анықталады.
ші ретті теңдеу аламыз. Дифференциалды теңдеуден айырмашылығы,
айырым теңдеуінің реті Е дәрежесінің
жоғарға және төменгі шектерінің айырымымен
анықталады. ![]() операторын қолданғанда, мысалы келесі теңдеуде:
операторын қолданғанда, мысалы келесі теңдеуде:
![]() (4.79)
(4.79)
Теңдеудің реті оның түріне тәуелді
болмауы мүмкін емес. Осылайша ![]() теңдеуі келесі теңдеуге эквивалентті:
теңдеуі келесі теңдеуге эквивалентті:
![]() .
.
(4.78) теңдеуді бірмүшелік емес айырым теңдеуі. Оның n-ші ретті бірмүшелік айырым теңдеуінен айырмашылығы келесі формуламен көрсетіледі:
![]() =0. (4.80)
=0. (4.80)
Айырым теңдеуін сонымен қатар рекурентті формула деп те атайды.
(4.78) теңдеуін келесі түрде жазуға болады:
![]()
(4.81)
y(0):y(n-1) өлшемдері белгілі болса,
![]() барлық
барлық ![]() аралығында жатады. Осылайша дифференциалды теңдеуден
айырмашылығы, айырым теңдеуі бойынша кез келген
аралығында жатады. Осылайша дифференциалды теңдеуден
айырмашылығы, айырым теңдеуі бойынша кез келген ![]() мәні үшін y(k)-ны анықтауға болады.
мәні үшін y(k)-ны анықтауға болады.
Әдетте (4.78) теңдеуінің шешімін тапқанда (4.81) теңдеуде көрсетілгендей итерациялық процестерді құрмаймыз.
n-ші ретті бірмүшелі дифференциалды теңдеудің n
сызықты тәуелсіз шешімдері бар. Егер
![]() болса, онда (4.80) тәуелсіз теңдеуін
болса, онда (4.80) тәуелсіз теңдеуін ![]() арқылы белгілеуге болады.Сызықты тәуелдінің
қажетті және жеткілікті шарты:
арқылы белгілеуге болады.Сызықты тәуелдінің
қажетті және жеткілікті шарты:
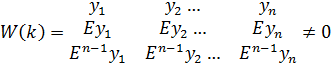 (4.82)
(4.82)
Жалпы түрде (4.80) теңдеудің жалпы шешімі келесідей түрде беріледі:
![]() , (4.83)
, (4.83)
мұндағы
![]() -
- ![]() ға тәуелді емес еркін тұрақтылар.
ға тәуелді емес еркін тұрақтылар.
Әдебиеттер тізімі
1. Плетнев Г.П. Автоматизация технологических процессов и производств в теплоэнергетике. – М.: Издательство МЭИ, 2005.
2. Стефани Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. М. – Л.: Государственное энергетическое издательсто, 1960.
3. Плетнев Г.П. Автоматическое регулирование и защита теплоэнергетических установок. – М.: Энергия, 1976.
4. Ротач В.Я. Расчет настройки промышленных систем регулирования. - М., Л.: Госэнерго издательство, 1961.
5. Ибраева Л.К., Хисаров Б.Д. Басқару объектерді модельдеу және идентификациялау. - Алматы, АЭжБУ, 2009.
6. Романчик А.Л., Рудакова Л.Н. Автоматизация технологических процесов ч. 1 и 2. - Алматы, АУЭС, 1999.
7. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – М.: Профессия, 2003.
8. Бекбаев А.Б., Сулеев Д., Хисаров Б.Д. Автоматты реттеу теориясы. – Алматы, 2005.
9. Бекбаев А.Б. Автоматика және өндірістік процесстерді автоматтандыру. – Алматы: Білім, 1995.
10. Сборник задач по теории автоматического регулирования и управления. Под. ред. В.А. Бесенерского – М.: Наука, 1978.