АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра инженерной графики и прикладной механики

ОСНОВЫ КОМПЬЮТЕРНОГО ЧЕРЧЕНИЯ И

3-D МОДЕЛИРОВАНИЯ

Конспект лекций

для студентов всех форм обучения специальностей

5B070200 – Автоматизация и управление,

5B070300 – Информационные системы,

5B071900 – Радиотехника, электроника и телекоммуникации,

5B070704 – Вычислительная техника и программное обеспечение

Алматы 2011

СОСТАВИТЕЛЬ: А.Д.Динасылов. Основы компьютерного черчения и 3-D моделирования. Конспект лекций для студентов всех форм обучения специальности 5B070200 – Автоматизация и управление, 5B070300 – Информационные системы, 5B071900 – Радиотехника, электроника и телекоммуникации, 5B070704 – Вычислительная техника и программное обеспечение. – Алматы: АУЭС, 2010. – 31 с.

Объем дисциплины «Основы компьютерного черчения и 3-D моделирования» составляет 90 часов (2 кредита), в том числе 8 часов лекций (теория построения чертежей и введение в 3D-моделирование), 16 часов практических занятий (практика построения чертежей), 16 часов лабораторных занятий (изучение элементов работы в компьютерной графической системе AutoCAD).

В конспекте кратко приводятся основные положения, излагаемые в лекционном курсе дисциплины «Основы компьютерного черчения и 3-D моделирования». В лекциях 1-3 излагаются основы теории построения чертежей: метод проецирования, комплексный чертеж точки, прямой и плоскости, способ замены плоскостей проекций и способ вращения вокруг проецирующей прямой, решение некоторых геометрических задач графическим способом. В лекции 4 даются общие понятия о поверхностях, а также излагаются начала 3-D моделирования в компьютерной графической системе AutoCAD.

Ил. 53, библиогр. - 9 назв.

Рецензент: канд техн. наук, проф. Яхъяев Э.А.

Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2010 г.

Содержание

Лекция 1. Метод проекций. Проекции точки и прямой	4
1.1 Центральное, параллельное и ортогональное проецирование	4
1.2 Проекции отрезка прямой линии	7
1.3 Точка на прямой	10
1.4 Следы прямой	10
1.5 Взаимное расположение двух прямых	11
Лекция 2. Проекции плоскости на чертеже	12
2.1 Способы задания плоскости на чертеже	12
2.2 Проекции плоскостей частного положения	13
2.3 Проекции плоских углов	16
2.4 Взаимное положение двух плоскостей	16
Лекция 3. Способы преобразования ортогональных проекций. Решение метрических и позиционных задач	17
3.1 Способ замены плоскостей проекций	17
3.2 Способ вращения вокруг оси, перпендикулярной к плоскости проекций	19
3.3 Классификация геометрических задач	21
3.4 Решение некоторых геометрических задач	22
Лекция 4. Общие понятия о поверхностях. Элементы 3-D моделирования в системе AutoCAD	24
4.1 Некоторые сведения о поверхностях	24
4.2 Общие понятия о 3-D моделировании в системе AutoCAD	26
4.3 Твердотельное моделирование	26
Список литературы	30

Лекция 1. Метод проекций. Проекции точки и прямой

Содержание лекции: цели, задачи и структура дисциплины; метод ортогонального проецирования; проекции точки и прямой линии.

Цели лекции: изучить метод ортогонального проецирования на две и три взаимно перпендикулярные плоскости, рассмотреть проецирование прямой.

Цель лекционного курса – дать теоретические основы построения изображений на чертежах. Базой для умения выполнять и читать чертежи, что необходимо как при проектировании изделий, так и при их изготовлении, эксплуатации и ремонте, является теория построения чертежей (ТПЧ). Изучение ТПЧ – наилучший способ развития пространственного воображения, без которого немыслимо инженерное творчество. Пространственное воображение позволяет мысленно представить форму и размеры предметов, их взаимное расположение в пространстве по чертежу, а также дает возможность представить еще не существующие изделия. Основной метод НГ – графический. Изучение теории необходимо сопровождать построением чертежей..

1.1 Центральное, параллельное и ортогональное проецирование

Рисунок 1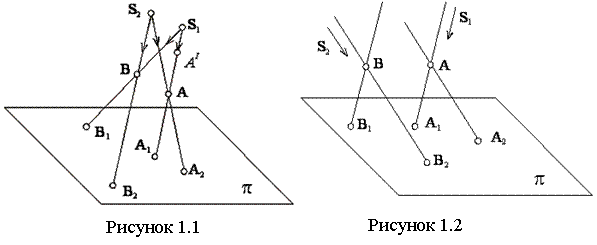

Пусть даны (см. рисунок 1.1) плоскость π (плоскость проекций) и вне ее точка S₁ (центр проецирования). Чтобы спроецировать точку А на плоскость π, через S₁ проводят прямую S₁A до ее пересечения с плоскостью π в точке А₁. Точка А₁- центральная проекция точки А, прямая S₁A₁ – проецирующий луч. Проекцией фигуры называют множество проекций всех ее точек.

Простейшими фигурами являются точки, прямые и плоскости, сложные фигуры состоят из множества точек, прямых и плоскостей.

Не изменяя положения π и взяв новый центр S₂, получаем новую проекцию точки А – точку А₂. Т.о., при заданных π и S несложно получить проекцию точки. Но, имея одну проекцию (например А₁), положение самой точки в пространстве нельзя определить, т.к. любая точка на S₁A₁ проецируется в одну и ту же точку А₁. Для решения нужно иметь две проекции (например А₁ и А₂).

Параллельное проецирование является частным случаем центрального проецирования, когда S=S_∞ (бесконечно удален от π). В этом случае проецирующие прямые параллельны между собой (см. рисунок 1.2). Параллельное проецирование полностью определяется положением плоскости (π) и направлением проецирования (S). Для определения положения точки в пространстве здесь также необходимо иметь две проекции, полученные при двух различных направлениях проецирования; положение точки определяется пересечением прямых, проведенных через А₁ и А₂ параллельно направлениям S₁ и S₂.

Свойства параллельных и центральных проекций:

а) каждая точка и линия в пространстве имеют единственную проекцию на заданную плоскость;

б) проекцией точки явлется точка;

в) прямая в общем случае проецируется на плоскость в виде прямой;

г) для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции точек провести прямую;

д) если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой прямой.

Для параллельных проекций, кроме перечисленного выше, справедливо:

е) если прямая параллельна направлению проецирования, то проекцией этой прямой является точка;

ж) отрезок прямой, параллельной плоскости проекций, проецируется на эту плоскость в натуральную величину.

Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, при котором направление проецирования S перпендикулярно плоскости проекции (см. рисунок 1.3).

Рисунок 1.3

Рисунок 1.4

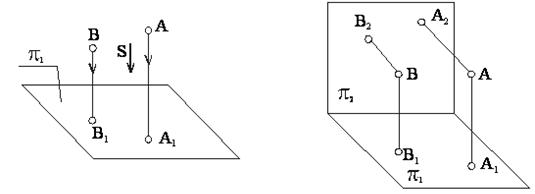
Здесь для определения положения точки в пространстве также необходимо иметь две параллельные проекции, полученные при двух направлениях проецирования. При ортогональном проецировании это проекции в двух взаимно перпендикулярных плоскостях π₁ и π₂(см. рисунок 1.4). В техническом черчении преимущественно применяется параллельное прямоугольное проецирование на 2 или 3 взаимно перпендикулярные плоскости.

Положение точки в пространстве двух взаимно перпендикулярных плоскостей, горизонтальной π₁ и фронтальной π₂,определяется ее проекциями А₁ и А₂ (см. рисунок 1.5). Плоскости π₁ и π₂делят пространство на квадранты.Линия пересечения плоскостей называется осью проекции Х.

Повернув плоскость π₁ вокруг оси проекции на 90º, получим одну плоскость чертежа. Проекции А₁ и А₂ расположатся на одном перпендикуляре к оси проекци – линии связи. В результате совмещения π₁ и π₂ получается эпюр Монжа или комплексный чертёж (см. рисунок 1.6).

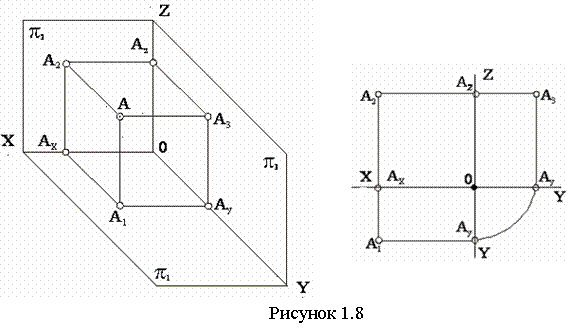Третья плоскость проекций π₃, перпендикулярная к π₁ и π₂, называется профильной плоскостью (см. рисунок 1.7). Помимо оси Х появляются оси проекций Y и Z. Буквой О обозначена точка пресечения плоскостей π₁, π₂, π₃.

Рисунок 1.7

Если мысленно разрезать плоскости по оси Y и повернуть π₁ вокруг оси Х на 90º, а π₃ – вокруг оси Z на 90º, то все три плоскости совместятся в одну плоскость чертежа (см. рисунок 1.8). Линии, связывающие проекции точки между собой, называются линиями связи.

Декартом была введена система прямоугольных координат, где плоскости π₁, π₂ и π₃ - плоскости координат, прямые, по которым они пересекаются - оси координат X, Y, Z, а точка пересечения осей координат - начало координат О. Плоскости координат делят пространство на 8 октантов. Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Координатами точки называются расстояния, отсекаемые линиями связи на осях координат. Расстояния ОА_х (см. рисунок 1.7) – абсцисса Х, ОА_у – ордината Y, ОА_z – аппликата Z.

1.2 Проекции отрезка прямой линии

Пусть даны проекции точек А и В (см. рисунок 1.9). Проведя через одноименные проекции этих точек прямые линии, получим проекции отрезка АВ – фронтальную (А₂В₂) и горизонтальную (А₁В₁).

В случае прямой общего положения точки А и В находятся на разных расстояниях от каждой из плоскостей π₁_, π₂, π₃, т.е. прямая АВ не параллельна ни одной из них и не перпендикулярна к ним. Здесь каждая из проекций меньше самого отрезка А₁В₁<АВ, А₂В₂<АВ, А₃В₃<АВ.

Прямая линия может занимать относительно плоскостей проекций особые (частные) положения. Прямая, параллельная одной из плоскостей проекций и не перпендинулярная двум другим, называется прямой уровня. Прямая, перпендикулярная одной из плоскостей проекций и, соответственно, параллельная двум другим, называется проецирующей.

Рассмотрим свойства проекций горизонтальной прямой уровня (обозначается буквой h) – это прямая, параллельная плоскости π₁ (см. рисунок 1.10). Здесь фронтальная проекция прямой параллельна оси проекций X, а горизонтальная проекция равна самому отрезку (А₂В₂║ОХ, А₁В₁=│АВ│).

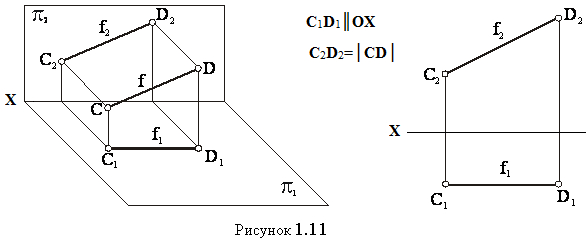
На рисунках 1.11 и 1.12 показаны проекции фронтальной f ║π₂) и профильной p║π₃ прямых уровня соответственно.

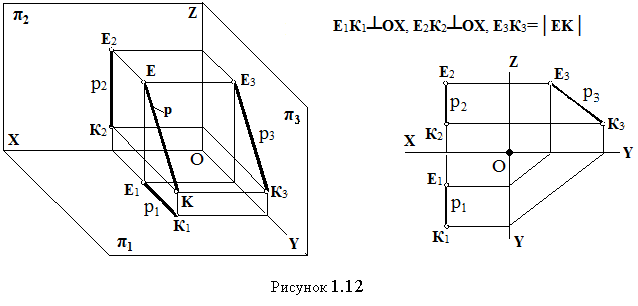Рассмотрим свойства проекций горизонтально-проецирующей прямой (см. рисунок 1.13). Здесь EK_┴ π₁, EK║π₁и EK║ π₁, проекция прямой на плоскость π₁ представляет собой точку (Е₁≡К₁), а проекции на плоскости π₂и π₃перпендикулярны осям ОХ и ОY соответственно (Е₂К_2┴ОХ, Е₃К_3┴ОY).

С₂≡D₂

С₁D₁^OX, C₃D₃^Z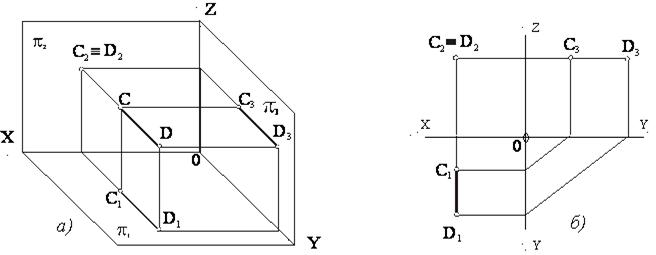

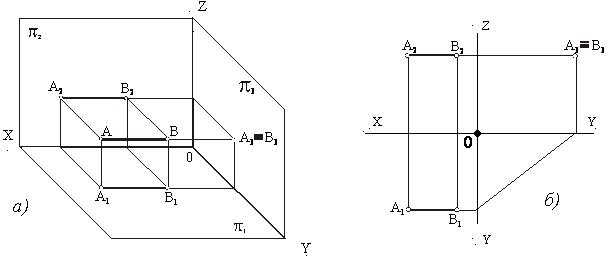
На рисунках 1.14 и 1.15 показаны проекции фронтально-проецирующей (CD^π₂) и профильно-проецирующей (AB^π₃) прямых соответственно.

А₃≡В₃А₁В₁║ОХ, А₂В₂║ОХ

Рисунок 1.14

Рисунок 1.15

1.3 Точка на прямой

Если точка принадлежит прямой, то проекции этой точки лежат на соответствующих проекциях этой прямой. При параллельном проецировании отношение отрезков прямой линии равно отношению их проекций (см. рисунок 1.16). Так как прямые АА₁, СС₁, ВВ₁ параллельны между собой, то, согласно теореме Фаллеса, .

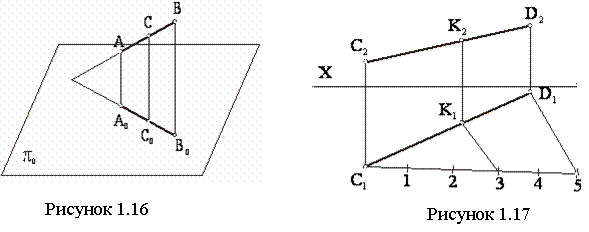
Этим свойством можно воспользоваться для деления отрезка прямой линии в заданном соотношении

Рисунок 1.17

(см. рисунок 1.17).

1.4 Следы прямой

Точки пересечения прямой с плоскостями проекций называются следами прямой (см. рисунок 1.18). Горизонтальная проекция горизонтального следа (точка М₁) совпадает с самим следом, а фронтальная проекция этого следа М₂ лежит на оси проекции Х. Фронтальная проекция фронтального следа N₂ совпадает со следом N, а горизонтальная его проекция N₁ лежит на той же оси проекции Х. Следовательно, чтобы найти горизонтальный след, надо продолжить фронтальную проекцию А₂В₂ до пересечения с осью Х и через точку М₂ провести перпендикуляр к оси Х до пересечения с продолжением горизонтальной проекции А₁В₁. Точка М≡М₁ – горизонтальный след прямой АВ. Аналогично находим фронтальный след N≡N₂.

Рисунок 1.18

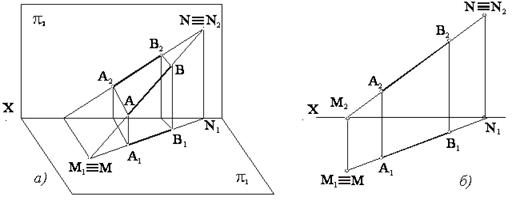
1.5 Взаимное расположение двух прямых

Две прямые в пространстве могут быть параллельными, пересекающимися или скрещивающимися.

Если две прямые в пространстве параллельны между собой, то их проекции на плоскости также параллельны между собой (см. рисунок 1.19). Обратное утверждение не всегда верно (сравни прямые С₀D₀ и CD на рисунке).

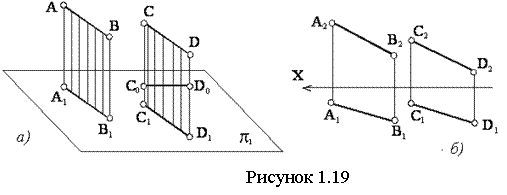
Если прямые пересекаются, то их одноименные проекции пересекаются между собой в точке, которая является проекцией точки пересечения этих прямых (см. рисунок 1.20).

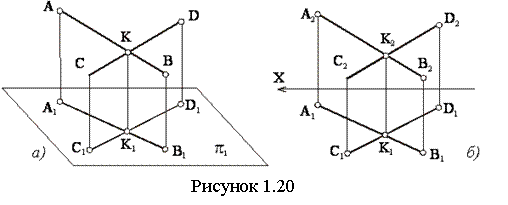
Скрещивающиеся прямые не пересекаются и не параллельны между собой (см. рисунок 1.21). Как видно на рисунке, точка с проекциями К₂ и К₁ принадлежит АВ, а точка с проекциями L₂ и L₁ принадлежит СD. Эти точки одинаково удалены от π₂, но расстояния их от π₁ различны: точка L расположена выше, чем точка К. Точки L и К - конкурирующие точки.

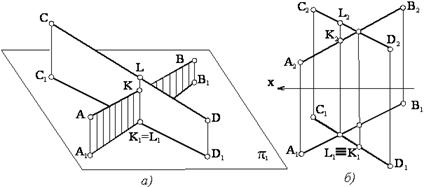
Лекция 2. Проекции плоскости на чертеже

Содержание лекции: способы задания проекций плоскости на чертеже; плоскости общего и частных положений; проекции плоских углов; проекции параллельных и пересекающихся плоскостей.

Цели лекции: изучить способы построения проекций плоскостей на чертеже и взамное расположение плоскостей.

2.1 Способы задания плоскости на чертеже

Плоскость на чертеже может быть задана:

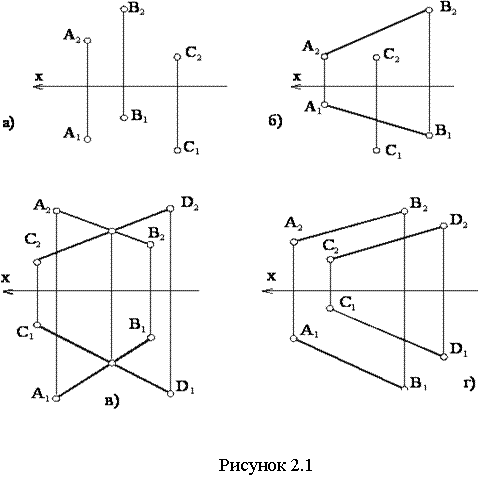
а) проекциями 3-х точек, не лежащих на 1-й прямой (см. рисунок 2.1,а);

б) проекциями прямой и точки, взятой вне прямой (см. рисунок 2.1,б);

в) проекциями двух пресекающихся прямых (см. рисунок 2.1,в);

г) проекциями двух параллельных прямых (см. рисунок 2.1,г);

д) проекциями любой плоской фигуры – треугольником, многоугольником, кругом и т.д. (см. рисунок 2.1,д);

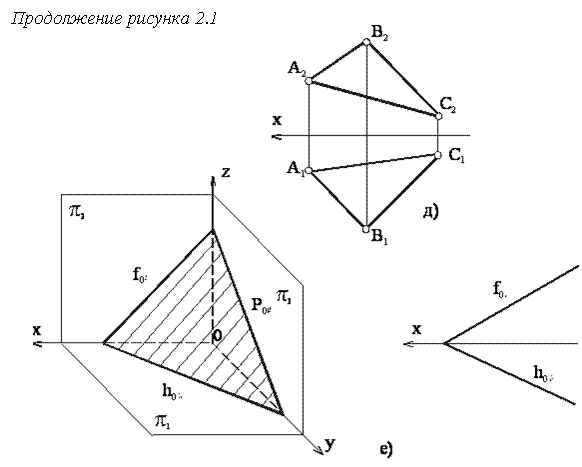
е) при помощи следов, под которыми понимают линии пересечения рассматриваемой плоскости с плоскостями проекций (см. рисунок 2.1,е).

2.2 Проекции плоскостей частного положения

Если плоскость не параллельна и не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения.

Плоскость, параллельная π₁, называется горизонтальной. Такая плоскость γ (АВС) показана рисунке 2.2. Фронтальная проекция этой фигуры представляет собой прямую, параллельную оси Х и совпадающую с фронтальным следом ƒ₀γ плоскости, а горизонтальная проекция γ₁(А₁В₁С₁) равна самой фигуре.

Плоскость, параллельная плоскости π₂, называется фронтальной (см. фигуру на рисунке 2.3). Её горизонтальная проекция представляет собой прямую линию, параллельную оси Х, а фронтальная проекция равна самой фигуре.

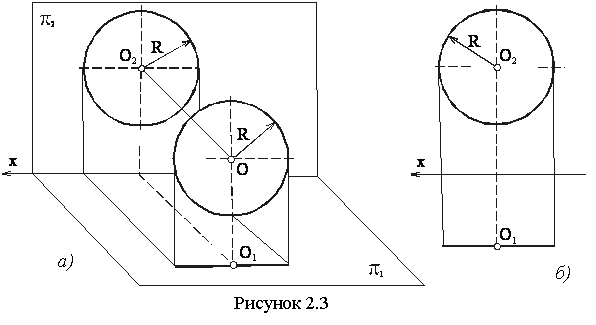
Плоскость, параллельную плоскости π₃, называют профильной плоскостью (см. рисунок 2.4).

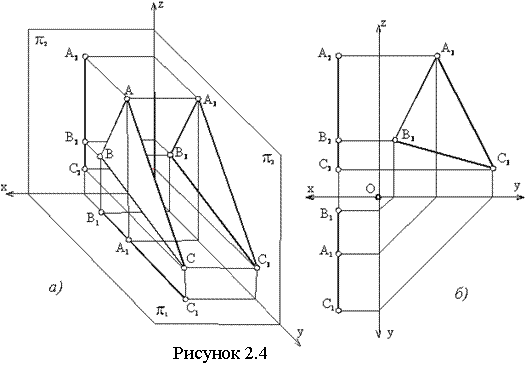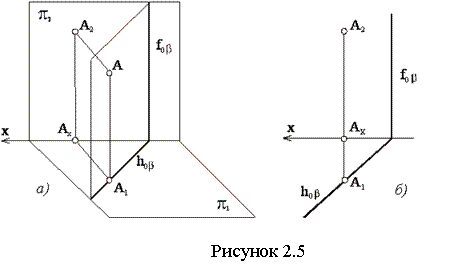
Плоскость, перпендикулярная π₁ (но не параллельная π₂ или π₃), называется горизонтально-проецирующей. На рисунке 2.5 горизонтально-проецирующая плоскость β задана следами. Фронтальный след такой плоскости ƒ_оβ перпендикулярен оси Х, а горизонтальный след h_оβ обладает собирательным свойством: горизонтальная проекция любой точки, линии или плоской фигуры, принадлежащей плоскости β, совпадает со следом h_оβ.

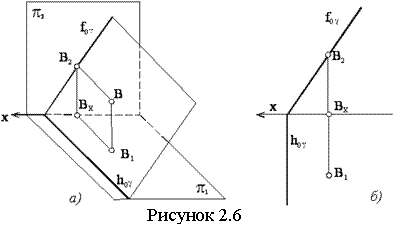
Плоскость, перпендикулярную плоскости π₂ (но не параллельную плоскости π₁ или π₃), называют фронтально-проецирующей (см. рисунок 2.6).

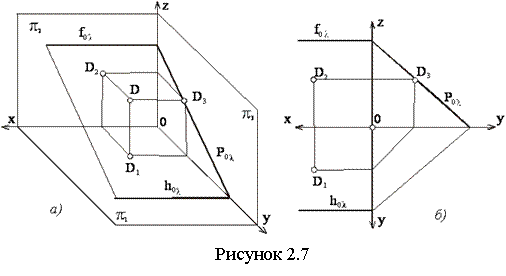
Плоскость, перпендикулярная плоскости π₃ (но не параллельная плоскости π₁или π₂), называется профильно-проецирующей (см. рисунок 2.7).

2.3 Проекции плоских углов

Если плоскость γ, в которой расположен некоторый угол АВС, перпендикулярна к плоскости проекции, то на эту плоскость угол проецируется в виде прямой линии (см. рисунок 2.8).

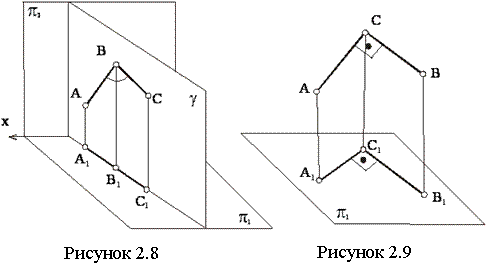Если плоскость прямого угла не перпендикулярна к плоскости проекции и хотя бы одна его сторона параллельна ей, то прямой угол проецируется на данную плоскость проекций в виде прямого угла (см. рисунок 2.9).

Рисунок 2.10

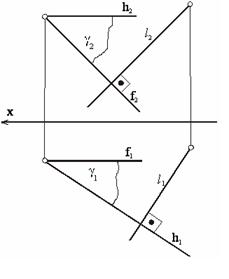Рассмотренные особенности проецирования прямого угла широко используются при решении задач. Например, две пересекающиеся между собой горизонталь h и фронталь ƒ будут составлять плоскость γ. Если из некоторой точки провести прямую ℓ (см. рисунок 34), перпендикулярную горизонтали и фронтали, то эта прямая будет перпендикулярна и плоскости γ.

2.4 Взаимное положение двух плоскостей

Две плоскости могут быть параллельными либо пересекающимися.

Если плоскости параллельны между собой, то в каждой из них можно построить две пересекающиеся прямые линии так, чтобы прямые одной плоскости соответственно были параллельны двум прямым другой плоскости.

На рисунке 2.11 плоскость β задана треугольником АВС, а плоскость γ – двумя пересекающимися прямыми m и n. Для того, чтобы плоскости β и γ были параллельны между собой, достаточно, чтобы m и n были параллельны, например, сторонам треугольника АВС: m║АВ, n║ВС. Прямые могут быть параллельны любым другим прямым, лежащим в плоскости β(АВС).

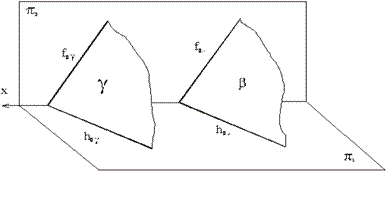Если плоскости заданы следами, то для параллельности плоскостей их следы должны быть параллельны между собой (см. рисунок 2.12), т.е. ƒ_0γ║ƒ_0β, h_0γ║h_0β.

Рисунок 2.11

Если следы плоскостей параллельны оси Х, то эти плоскости могут быть либо параллельными, либо пересекающимися. Для однозначного ответа нужно построить третий, профильный, след.

В лекции рассмаириваются вопросы, связанные с определением взаимного положения плоскости и прямой, плоскости и точки.

Лекция 3. Способы преобразования ортогональных проекций.

Решение метрических и позиционных задач

Содержание лекции: способ замены плоскостей проекций и способ вращения вокруг проецирующих прямых; понятия о метрических и позиционных задачах и методах их решения.

Цели лекции: рассмотреть понятия о способах преобразования ортогональных проекций, дать классификацию геометрических задач и рассмотреть решение некоторых из них.

Преобразование ортогональных проекций используется для приведения заданных на эпюре геометрических элементов в новое положение по отношению к плоскостям проекций, более удобное для решения конкретной задачи.

3.1 Способ замены плоскостей проекций

Способ заключается в том, что вводится дополнительная плоскость проекций и происходит переход к другой системе плоскостей проекций, при этом геометрические образы в пространстве сохраняют свое положение. При замене обязательно сохраняется взаимная перпендикулярность двух плоскостей проекций.

Пусть задана точка А и система двух плоскостей проекций p₁ и p₂ (см. рисунок 3.1). Введем плоскость p₄ ^ p₁ и не перпендикулярную p₂. Точка А₄– проекция точки А на p₄. Получаем две системы плоскостей проекций: основную p₁-p₂ и дополнительную p₁-p₄. При переходе от одной системы плоскостей проекций к другой аппликата Z₁ точки А и ее горизонтальная проекция А₁ остаются неизменными (инвариантными) для двух систем.

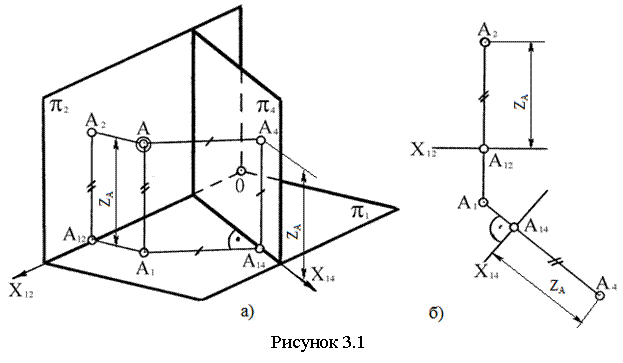
Рисунок 3.1 демонстрирует операцию перехода от одной системы плоскостей к другой на эпюре. Для того чтобы по заданной эпюре точки А (А₁, А₂) и новой оси проекций х₁₄построить проекцию этой точки на плоскости p₄ (А₄), необходимо:

1) из горизонтальной проекции точки А₁ опустить перпендикуляр на новую ось проекций х₁₄;

2) от точки А₁₄ на этом перпендикуляре отложить координату z точки А, т. е. А₁₄ А₄= А₁₂А₂= Z_A

Отметим, что нельзя менять обе плоскости проекций сразу. Новая плоскость проекций должна сохранять перпендикулярность к остающейся плоскости. Поэтому замену плоскостей можно производить только в последовательном порядке: сначала заменить одну плоскость, затем другую. Операцию можно повторять неоднократно, если это требуется для решения задачи.

Пример 3.1 - На рисунке 3.2 показано определение длины отрезка прямой АВ общего положения.

Для того, чтобы прямая общего положения АВ оказалась линией уровня, следует ввести новую плоскость p₄ (или p₅), которая была бы ей параллельна. На чертеже дополнительная плоскость p₄ перпендикулярна к плоскости p₁ и параллельна прямой АВ (ось Х₁₄ p₁/p₄ параллельна проекции А₁В₁), и тогда прямая АВ является фронталью в системе p₁-p₄. Через точки А₁ и В₁ проводим новые линии связи, перпендикулярные оси Х₁₄. Расстояние от оси Х₁₄ до А₄и В₄ равно расстояниям от А₂ и В₂ до оси Х₁₂. Образовавшейся системе плоскостей проекций p₁/p₄ прямая АВ (А₄В₄) является линией уровня, т.е. натуральной величиной отрезка АВ.

Аналогично можно прямую АВ преобразовать в горизонталь. Для этого оставим на месте p₂ и заменим p₁ на p₅, параллельную АВ и перпендикулярную к p₂. Теперь прямая АВ является линией уровня в системе p₂/p₅, и А₅В₅ является натуральной величиной АВ.

3.2 Способ вращения вокруг оси, перпендикулярной к плоскости проекций

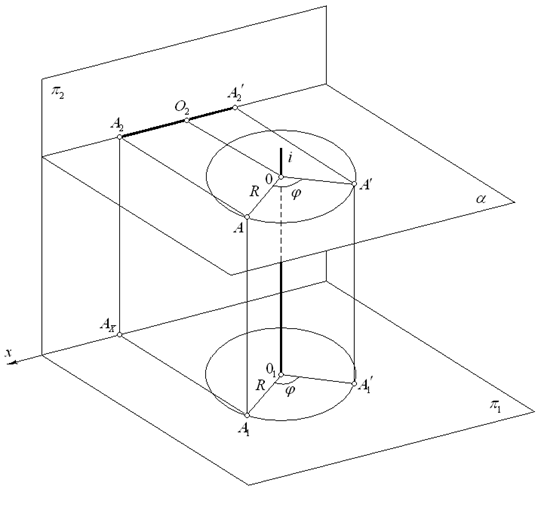Cпособ состоит в том, что заданную фигуру вращают вокруг оси, перпендикулярной к плоскости проекций с тем,чтобы привести ее в частное положение по отношению к не изменяющим своего положения плоскостям проекций.

Проследим, как будет изменяться положение точки А при ее вращении вокруг оси i , перпендикулярной p₁ (см. рисунок 3.3). Точка А перемещается по дуге окружности в плоскости a (a^i, и следовательно, a║p₁ ), поэтому эта окружность проецируется на плоскость p₁ без искажения, а на плоскость p₂ - в отрезок прямой, параллельной оси X. Таким образом, если точка А перемещается вокруг оси i по дуге окружности радиуса R на некоторый угол j, то она займет положение А¢. При этом горизонтальная проекция точки А₁повернется вокруг центра O₁на тот же угол j и займет положение А₁¢. Фронтальная проекция точки А₂ продвинется по прямой, параллельной оси X, и займет положение А₂¢.

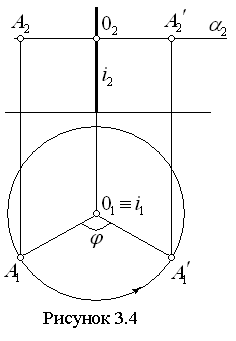На эпюре это будет выглядеть так, как показано на рисунке 3.4.

Аналогично можно выполнить вращение вокруг оси, перпендикулярной фронтальной плоскости p₂. Здесь фронтальная проекция точки перемещается по дуге окружности, а горизонтальная проекция - по прямой, параллельной оси X. Способ вращения геометрических фигур вокруг осей, перпендикулярных плоскостям проекций, широко используется при решении геометрических задач.

Пример 3.2 - На рисунке 3.5 показано определение длины отрезка прямой АВ способом вращения вокруг горизонтально-проецирующей оси i, проходящей через точку B.

При вращении точка В остается неподвижной, т.к. она лежит на оси вращения, при этом горизонтальная проекция точки А описывает окружность радиуса А₁В₁, а ее фронтальная проекция премещается параллельно оси X. Итак, поворачиваем проекцию А₁В₁ вокруг точки В₁до тех пор, пока она не не станет параллельной оси X (В₁А₁¢), при этом точка А₂ придет в положение А₂¢, и тогда отрезок В₂А₂¢ представляет собой натуральную величину отрезка АВ, а угол a - угол наклона прямой АВ к плоскости проекций p₁.

3.3 Классификация геометрических задач

Все задачи ТПЧ могут быть разделены на позиционные и метрические.

Позиционные задачи заключаются в определении принадлежности и в построении взаимных пересечений геометрических фигур.

Задачи на определение принадлежности одной геометрической фигуры другой могут быть подразделены на три вида:

а) принадлежность точки линии (АÎl);

б) принадлежность точки поверхности (АÎa); в) принадлежность линии поверхности (lÎa).

Задачи на построение пересечений геометрических фигур делятся на две группы:

а) пересечение линии с поверхностью (lÇa);

б) взаимное пересечение поверхностей (aÇb).

Метрическими задачами называются задачи, решение которых связано с определением на чертеже каких-либо метрических свойств фигур (длин участков линий, величин углов, площадей, объемов и т.п.).

Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства фигур, являются комплексными.

При параллельном (ортогональном) проецировании геометрические образы, произвольно расположенные в пространстве, проецируются на плоскости проекций с искажением. В этом случае искажаются проекции величин их линейных и угловых характеристик.

Определение неискаженных величин линейных и угловых характеристик фигур, произвольно расположенных в пространстве, по их проекциям и представляют собой класс метрических задач.

Многие метрические и комплексные задачи, которые встречаются в технике, решаются с помощью типовых приемов. Алгоритмы решения всех метрических задач опираются на два инварианта ортогонального проецирования:

а) теорему о проецировании прямого угла;

б) свойство любой плоской фигуры проецироваться без искажения (в конгруэнтную фигуру) на ту плоскость проекций, которая параллельна этой фигуре, т.е. (Ф Ì b) Ù (b êêp₁) Þ Ф₁ @ Ф.

Все метрические задачи могут быть отнесены к одной из трех групп:

а) задачи на определение расстояний от точки до другой точки, до прямой, до плоскости, до поверхности; от прямой до плоскости;

б) задачи на определение углов между:

- пересекающимися или скрещивающимися прямыми;

- прямой и плоскостью;

- плоскостями (определение величины двугранного угла);

в) определение величин плоских фигур.

3.4 Решение некоторых геометрических задач

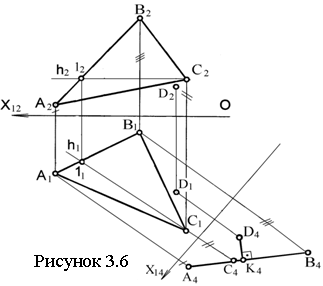Пример 3.3 – Определить расстояние от точки D до плоскости треугольника ABC (см. рисунок 3.6).

Решение. Воспользовавшись методом замены плоскостей проекций, переводим заданную плоскость общего положения в проецирующее положение, для чего проводим в плоскости горизонталь и вводим плоскость проекций π₄ перпендикулярно горизонтали.

Дано: a(АВС), D.

Требуется определить:

[D ∙ α (АВС)].

Алгоритм решения задачи (АРЗ):

1) һ Ì α (АВС)];

2) π ₄^ һ → Х₁₄ ^һ₁;

3) D₄, A₄, B₄,C₄;

4) D₄K₄ ^ A₄B₄;

5) D₄K₄ = [ D ∙ α].

Пример 3.4 – Определить кратчайшее расстояние между скрещивающимися прямыми (см. рисунок 3.7).

Решение. Переводим одну из прямых общего положения в проецирующее положение, для чего используем две замены плоскостей проекций; первой заменой переводим прямую DE в положение прямой уровня, а второй заменой переводим ее в проецирующее положение.

Дано: AB, DE.

Требуется определить:

[( [(AB)·(DE)],{(AB)-DE)}.

АРЗ:

1) p₄êêDE®x₁₄êêD₁E₁;

2) 2) A₄B₄, D₄E₄;

3) p₅^DE®x₄₅^D₄E₄;

4) D₅E₅, A₅B₅;

5) D₅C₅ ^ A₅B₅;

6) D₅C₅ = [(AB)·(DE)].

Рисунок 3.7

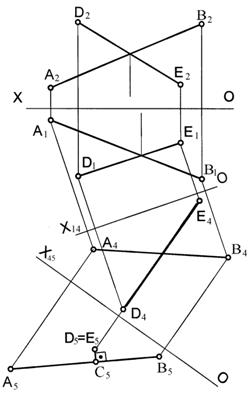
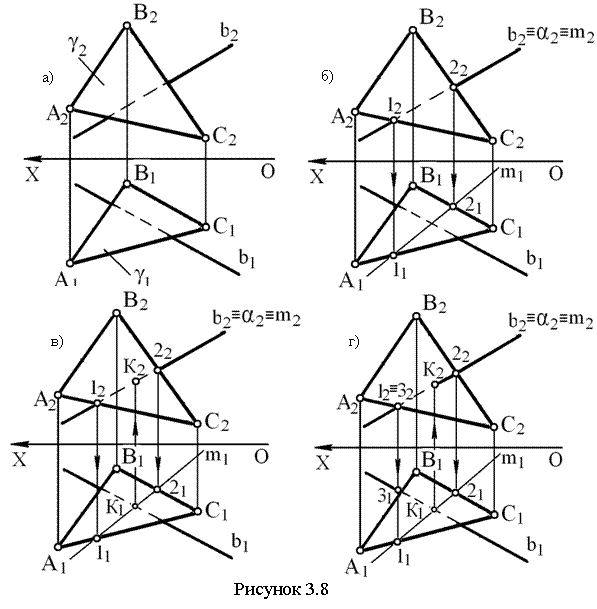
Пример 3.5 – Определить точку пересечения прямой с плоскостью (см. рисунок 3.8,а) и, считая плоскость непрозрачной, определить видимость прямой.

Дано: b, γ (АВС).

Требуется определить:

b∩γ (ABC).

АРЗ:

1) α ⊃b, α⊥π₂ → α₂ ≡ b₂;

2) 2) m = α∩γ, m₂ ≡ α₂≡ b₂;

3) 1₂ = m₂∩A₂C₂ ∧2₂= m₂ ∩ B₂C₂;

4) ↨ 1₁⊂A₁C₁∧2₁⊂B₁C₁;

5) m₁ = 1₁∪2₁;

6) K₁ = b₁∩m₁;

7) K₂⊂b₂;

8) K = b∩γ (ABC).

Лекция 4. Общие понятия о поверхностях. Элементы 3-D моделирования в системе AutoCAD

Содержание лекции: поверхности и их образование. Образование трехмерных объектов в системе AutoCAD. Построение моделей тел.

Цели лекции: дать общие понятия о поверхностях и их образовании, рассмотреть основы работы с трехмерными объектами в системе AutoCAD.

4.1 Некоторые сведения о поверхностях

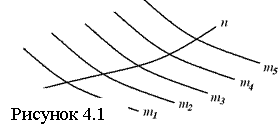
В ТПЧ поверхность (см. рисунок 4.1) рассматривают как множество последовательных положений движущейся линии (образующей) или другой поверхности в пространстве. Образующие могут быть прямыми и кривыми, последние – постоянными и переменными. Одна и та же поверхность нередко может быть образована движениями различных образующих. На чертеже показывают лишь некоторые положения образующей. Линию, пересечение с которой является обязательным условием движения образующей при образовании поверхности, называют направляющей (иногда используют линию, по которой движется точка, не лежащая на образующей). Из различных форм образующих, направляющих, а также закономерностей образования поверхности выбирают наиболее простые и удобные для изображения поверхности и для решения задач, связанных с ней.

Рассмотрим вкратце классификацию поверхностей, принятую в ТПЧ.

Поверхность, которая может быть образована движением прямой линии, называют линейчатой поверхностью (ЛП). ЛП, которая может быть развернута так, что всеми своими точками она совместится с плоскостью без разрывов и складок, называют развертываемой. К развертываемым поверхностям относятся такие ЛП, у которых смежные прямолинейные образующие параллельны либо пересекаются между собой, либо касательны к некоторой пространственной кривой. Остальные ЛП и все нелинейчатые поверхности - неразвертываемые. Развертываемые поверхности – многогранные, цилиндрические, конические и поверхности с ребром возврата (торсовые).

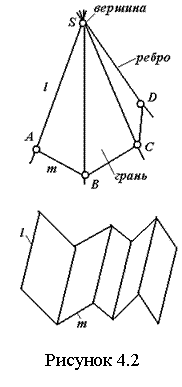
Многогранные (или гранные) поверхности образуются перемещением прямолинейной образующей по ломаной направляющей (см. рисунок 4.2). Если одна точка образующей неподвижна, то получается пирамидальная поверхность, если образующая параллельна заданному направлению – призматическая. Замкнутые гранные поверхности образуют многогранники. Грани – плоские многоугольники, ребра – линии пересечения граней, вершины – концы ребер (точки их пересечения). Пирамида – в основании многоугольник, остальные грани – треугольники с общей вершиной. Прямая пирамида – если вершина проецируется в центр основания. Правильная – если основание есть правильный многоугольник. Призма – две одинаковые грани в параллельных плоскостях, остальные – параллелограммы. Параллелепипед – если и основания параллелограммы. На чертеже многогранники изображаются проекциями вершин, ребер и граней. При построении изображений надо определять видимость ребер и граней.

У цилиндрической поверхности образующие всегда параллельны, направляющая - кривая линия. Частные случаи - прямой круговой цилиндр, наклонный круговой цилиндр. У конических поверхностей все прямолинейные образующие имеют общую неподвижную точку - вершину, направляющая - одна любая кривая линия. Частные случаи - прямой круговой конус, наклонный круговой конус. У поверхностей с ребром возврата прямолинейные образующие касательны к криволинейной направляющей.

Среди нелинейчатых поверхностей различают поверхности с постоянной и переменной образующей. Первые подразделяют на поверхности вращения с криволинейной образующей (сфера, тор, эллипсоид вращения и др.) и на циклические поверхности (поверхности изогнутых труб, пружин).

Каркасную поверхность задают некоторым множеством линий или точек поверхности. Обычно такие линии - плоские кривые, плоскости которых параллельны между собой. Два пересекающихся семейства линий каркаса образуют сетчатый каркас поверхности. Точки пересечения линий образуют точечный каркас поверхности (может быть задан координатами точек поверхности). Каркасные поверхности используют при конструировании корпусов турбин, баллонов электроннолучевых трубок (см. рисунок 4.3,а-в).

Тела с поверхностями вращения (ПВ) применяют во многих областях техники: баллон электронно-лучевой трубки, сосуд Дьюара и т.п. В зависимости от вида образующей ПВ могут быть линейчатыми, нелинейчатыми или состоять из частей таких поверхностей. ПВ - это поверхность, которая может быть получена путем вращения образующей вокруг неподвижной прямолинейной оси (см. рисунок 4.3,г), ось изображают штрихпунктирной линией. Вводят понятия параллелей и меридианов. Некоторые ПВ являются частными случаями других поверхностей. Так, можно говорить о цилиндре и о конусе вращения. Для них меридианами являются прямые. Они параллельны оси и равноудалены от нее для цилиндра или пересекают ось в одной и той же ее точке под одним и тем же углом к оси для конуса. Прямой круговой цилиндр и прямой круговой конус ограничены поверхностью вращения и плоскостями, перпендикулярными к оси. Меридиан цилиндра - прямоугольник, конуса - треугольник. Сфера является ограниченной поверхностью и может быть изображена на чертеже полностью. Экватор и меридианы сферы - равные между собой окружности. Тор получается при вращении окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр (различают открытый, закрытый и самопересекающийся тор).

В лекции рассматривается решение задач на определение положения точки, лежащей на поверхности прямого кругового цилиндра, прямого кругового конуса и сферы, на пересечение плоскости и прямой с этими поверхностями.

4.2 Общие понятия о 3-D моделировании в системе AutoCAD

Для создания 3-D объектов в CAD системах используют каркасное, поверхностное и твердотельное моделирование. В каркасной модели представляются только ребра объекта, грани не определены, модель является прозрачной, понятие объема отсутствует. В поверхностной модели определены ребра и грани. Модель является непрозрачной, она имеет объем, но массы не имеет (учитывает толщину стенок). Твердотельная модель (ТМ) позволяет описывать объект наиболее реалистично, она дает полную информацию о внешних гранях и ребрах объекта, а также описывает его внутреннюю структуру, модель имеет объем, массу. ТМ обеспечивает: просмотр из любой точки пространства, выполнение сечения модели, автоматизированное построение двухмерных чертежей, получение реалистичного изображения, добавление характеристик материала и внешнего освещения, решение физических задач.

4.3 Твердотельное моделирование

Алгоритм создания твердотельных моделей в AutoCAD основан на использовании трехмерных примитивов или двухмерных форм с последующим их превращением в трехмерные модели и на преобразовании трехмерных моделей с помощью команд редактирования тел.

Имеются следующие примитивы: Polysolid (Политела), Box (Параллелепипед), Wedge (Клин), Cone (Конус), Sphere (Сфера), Cylinder (Цилиндр), Pyramid (Пирамида), Torus (Тор).

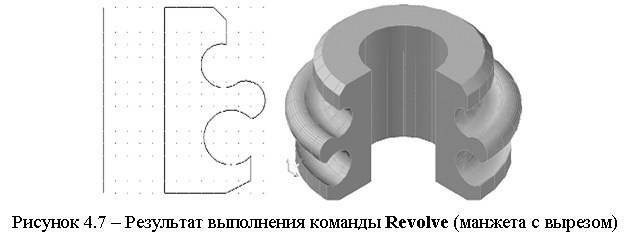
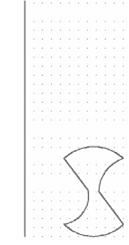
На рисунках 4.6 – 4.9 приведены результаты использования методов создания твердотельных моделей на основе двухмерных форм с использованием команд преобразования.

Рисунок 4.8 – Результаты выполнения команды Sweep

В AutoCAD имеется возможность построения твердотельной модели составного тела с использованием теоретико-множественных операций, представленных командами Union (Объединение), Subtract (Вычитание) и Intersect (Пересечение). На рисунках 4.10 - 4.12 показано построение модели плиты методом выдавливания с применением теоретико-множественных операций. Для этого сначала создаются двумерные контуры (см. рисунок 4.10). Затем эти контуры выдавливаются на нужную высоту (см. рисунок 4.11).

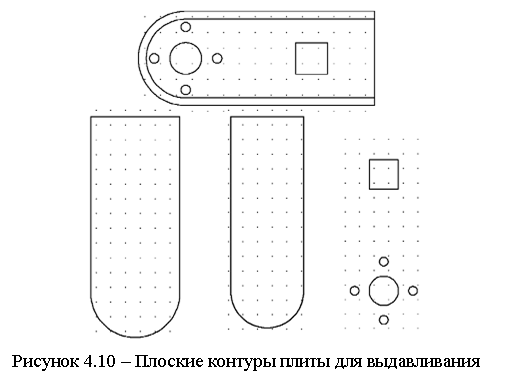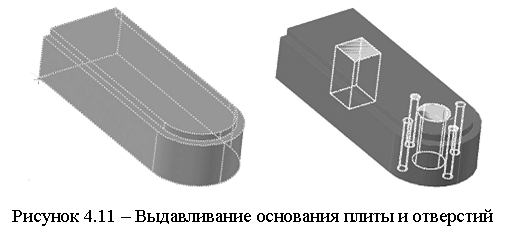
Далее выполняется объединение двух тел и вычитание из полученного тела отверстий. Результат построений в виде тонированной твердотельной модели плиты представлен на рисунке 4.12.

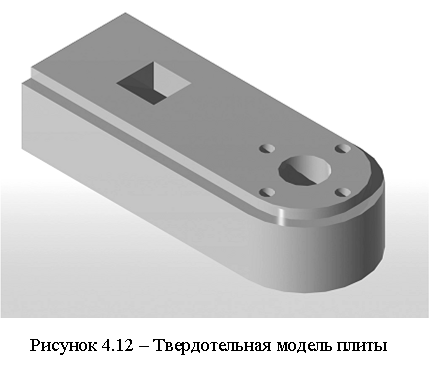Список литературы

1. Чекмарев А.А. Начертательная геометрия и черчение. – М.: Высшее образование , 2009. – 471 с.

2. Белякова Е.И., Зеленый П.В. Начертательная геометрия. – М.: Новое знание, 2010 – 247 с.

3. Королев Ю.А. Начертательная геометрия. – Спб.: Питер, 2010. - 256 с.

4. Романычева Э.Т., Соколова Т.Ю., Шандурина Г.Ф. Инженерная и компьютерная графика. – М.: ДМК Пресс, 2001. – 592 с.

5. Соколова Т.Ю. AutoCAD 2009. Учебный курс.- СПб.: Питер, 2008. – 576 с.

6. Жарков Н.В. AutoCAD 2009. Официальная русская версия.- СПб.: Наука и Техника, 2009. – 608 с.

7. Полещук Н.Н. Самоучитель AutoCAD 2011. – СПб.: БХВ-Петербург, 2010. – 544 с.

8. Мукашев М.Ш. Инженерная графика. Ч.1. Начертательная геометрия. – Алматы: АИЭС, 1999. – 180 с.

9. Динасылов А.Д. Инженерная и компьютерная графика. Введение в компьютерную графическую систему AutoCAD: Учебное пособие.- Алматы: АИЭС, 2003. – 104 с.

Сводный план 2010 г., поз. 293