МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
А.Д.Динасылов
К.С.Иванов
МЕХАНИКА.
Статика И кинематика: решение задач
Учебное пособие
Алматы 2013
УДК 621.01(075.8)
ББК 22.2я73
Д46. Механика. Статика и кинематика: Решение задач:
Учебное пособие /А.Д. Динасылов, К.С.Иванов;
Алматы: АУЭС, 2013. – 96 с.
Ил. 110, библиогр. - 13 назв.
ISBN 978-601-7098-77-3
Учебное пособие содержит примеры решения задач по разделам «Статика» и «Кинематика». Количество предлагаемых примеров ориентировано на усвоение студентами материала в соответствии с указанными разделами и для подготовки к различного вида контролю знаний, включая экзамен. В обоих разделах рассмотрению решения задач предшествует краткое изложение основных теоретических сведений.
Рассмотренные примеры расположены по мере возрастания их сложности, при этом они не выделены в отдельные подразделы по тематике, так как студенты должны сами ориентироваться в тематике задач.
Учебное пособие предназначено для студентов специальностей 5В074600 – Космическая техника и технологии, 5В071700 - Теплоэнергетика и может использоваться студентами других специальностей, изучающими дисциплину «Механика» или «Прикладная механика».
ББК 22.2я73
РЕЦЕНЗЕНТЫ: КазНТУ, д-р техн.наук, проф. С.Б. Косболов
АУЭС, канд.техн.наук, проф. А.А. Копесбаева.
ISBN 978-601-7098-77-3
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2012 г.
ã НАО «Алматинский университет энергетики и связи», 2013 г.
Содержание
|
|
c. |
|
1 Статика |
4 |
|
1.1 Сходящиеся системы сил |
5 |
|
1.2 Равновесие плоской системы сил |
7 |
|
1.3 Равновесие пространственной системы сил |
8 |
|
1.4 Центр тяжести |
9 |
|
1.5 Примеры решения задач статики |
10 |
|
2 Кинематика |
29 |
|
2.1 Основные понятия и задачи кинематики |
29 |
|
2.2 Задачи кинематики точки |
30 |
|
2.3 Задачи кинематики твердого тела |
33 |
|
2.4 Задачи на сложное движение точки |
42 |
|
2.5 Задачи на сложные движения твердого тела |
43 |
|
2.6 Примеры решения задач кинематики |
45 |
|
Список литературы |
95 |
1 Статика
Курс «Механика» в технических университетах может включать в себя либо только разделы теоретической механики, либо еще и отдельные разделы прикладной механики (сопротивления материалов, теории механизмов и машин, деталей машин и др.). Теоретическая механика (ТМ) традиционно делится на три части: статику, кинематику и динамику. В учебных планах ряда специальностей предусматривается также изучение раздела аналитической механики. В настоящем пособии рассмотрена методика решения задач, относящихся к статике и кинематике. Решение задач динамики и аналитической механики предполагается рассмотреть в отдельном пособии.
В разделе «Статика» изучают способы сложения сил и их разложения на составляющие, а также способы приведения к простейшему виду систем сил, приложенных к абсолютно твердому телу (АТТ) или к материальной точке (МТ). Системой сил (СС) называют совокупность сил, приложенных АТТ или к МТ. Главное место в статике занимает учение о равновесии систем сил.
Различают плоские и пространственные системы сил. В свою очередь, и те и другие делятся на системы сходящихся сил, системы параллельных сил и произвольные системы сил.
В данном разделе основное внимание уделено задачам на равновесие систем сил. Под равновесием твердого тела понимают состояние покоя тела по отношению к окружающим его телам. Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия самого тела. В покое твердое тело будет находиться лишь в том случае, если оно было в покое и до приложения к нему уравновешенной системы сил.
Наиболее общим методом решения задач статики на равновесие является аналитической метод. При использовании аналитического метода решения рекомендуется придерживаться следующего порядка. Прежде всего, надо ясно понять смысл задачи: установить, что задано и что требуется определить. Затем следует иллюстрировать задачу чертежом. После этого необходимо:
а) выявить объект (тело или точку), равновесие которого следует рассматривать; показать на чертеже активные силы, приложенные к объекту;
б) установить связи, наложенные на тело, освободить тело от связей и изобразить на чертеже реакции отброшенных связей;
в) проанализировать полученную систему сил (задаваемых и реакций) с точки зрения расположения их линий действия в пространстве, установив тем самым число уравнений равновесия;
г) выявив число неизвестных в задаче, установить ее статическую определимость;
д) выбрать оси координат и составить уравнения равновесия рассматриваемого тела под действием всех сил, в том числе и реакций связей;
е) решить эти уравнения относительно тех неизвестных, которые требуется определить по условиям задачи.
Уравнения равновесия лучше решать в общем виде. Найдя ответ в виде формулы, выражающей искомую величину через заданные, следует, не производя числовых расчетов, проверить правильность полученной величины с точки зрения размерности.
В большинстве задач статики нельзя заранее указать не только величину, но и направление той или иной реакции связи. В таких случаях неизвестную реакцию раскладывают на составляющие, направленные вдоль соответствующих осей координат, и вводят в уравнения равновесия в качестве неизвестных эти составляющие.
Если в результате решения уравнений величина какой-нибудь из составляющих окажется отрицательной, то это означает, что данная составляющая реакции в действительности направлена в сторону, противоположную положительному направлению оси. В тех случаях, когда истинное направление реакции не вызывает сомнения, лучше, не считаясь с принятым направлением оси, направлять реакцию в ту сторону, в которую она действует.
Если по условию задачи требуется определить действие тела на какую-нибудь связь (давление, натяжение нити, усилие в стержне и т.д.), то в уравнения равновесия следует вводить по-прежнему реакцию связи. Искомая сила будет равна по величине и противоположна по направлению этой реакции.
В статике приходится иногда решать задачи на
равновесие нескольких тел, каким-либо образом связанных между собой. В данном
случае для каждого тела в отдельности составляются уравнения равновесия с
учетом сил, с которыми действуют друг на друга тела, входящие в систему. Эти
силы попарно равны по величин![]() е и противоположны
по напрвлению. В некоторых случаях удобно рассматривать равновесие всей системы
связанных между собой тел как единого твердого тела (что возможно на основании
принципа затвердевания) и равновесие только некоторых из тел, входящих в
систему.
е и противоположны
по напрвлению. В некоторых случаях удобно рассматривать равновесие всей системы
связанных между собой тел как единого твердого тела (что возможно на основании
принципа затвердевания) и равновесие только некоторых из тел, входящих в
систему.
При отделении усилий в стержнях жесткой идеальной
конструкции рекомендуется пользоваться методом сечений, предполагая при этом,
что перерезанные стержни растянуты. Вследствие этого реакции таких стержней
будут направлены в сторону отброшенной части конструкции. Если в результате
решения задачи величина какой-нибудь из реакций окажется отрицательной, то это
означает, что![]() соответствующий стержень в действительности
сжат.
соответствующий стержень в действительности
сжат.
В настоящем учебном пособии для систем сходящихся сил, кроме задач на равновесие, рассматриваются задачи на определение равнодействующей силы. Напомним, что равнодействующей для рассматриваемой СС называют силу эквивалентную данной СС (не всякая СС имеет равнодействующую).
1.1 Сходящиеся системы сил
Система сил называется сходящейся,
если линии действия (ЛД) всех сил, входящих в систему, пересекаются в одной
точке. Сходящаяся система сил (ССС) всегда имеет равнодействующую, равную
векторной сумме всех сил системы, ![]() . Равнодействующая ССС равна
векторной сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения
ЛД слагаемых сил. Чтобы найти равнодействующую геометрическим способом, надо построить
в точке пересечений их ЛД силовой многоугольник на слагаемых силах; замыкающая
силового многоугольника и будет равнодействующей.
. Равнодействующая ССС равна
векторной сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения
ЛД слагаемых сил. Чтобы найти равнодействующую геометрическим способом, надо построить
в точке пересечений их ЛД силовой многоугольник на слагаемых силах; замыкающая
силового многоугольника и будет равнодействующей.
При решении задач аналитическим способом определяют проекции равнодействующей силы на декартовы оси координат
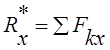 ,
, 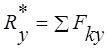 ,
, 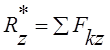 ,
(1.1)
,
(1.1)
ее модуль
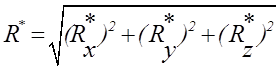 (1.2)
(1.2)
и ее направление по направляющим косинусам
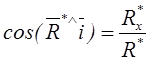 ,
, 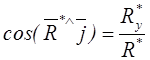 ,
, 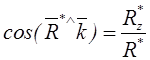 . (1.3)
. (1.3)
Для равновесия
ССС необходимо и достаточно, чтобы ее равнодействующая была равна нулю, т.е. ![]() или
или ![]() (условия
равновесия в векторном виде). Условия равновесия в геометрическом смысле состоят
в том, что должен быть замкнут силовой многоугольник, т.е. конец последнего вектора
должен совпасть с началом первого вектора. В аналитическом виде условия
равновесия выражаются в том, что должны равняться нулю суммы проекций на три
координатные оси всех сил, входящих в систему, т.е.
(условия
равновесия в векторном виде). Условия равновесия в геометрическом смысле состоят
в том, что должен быть замкнут силовой многоугольник, т.е. конец последнего вектора
должен совпасть с началом первого вектора. В аналитическом виде условия
равновесия выражаются в том, что должны равняться нулю суммы проекций на три
координатные оси всех сил, входящих в систему, т.е.
![]() ,
, ![]() ,
,
![]() . (1.4)
. (1.4)
Условия равновесия для плоской ССС имеют вид
![]() ,
, ![]() .
(1.5)
.
(1.5)
При решении задач оказывается полезной теорема о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, то эти силы лежат в одной плоскости и их ЛД пересекаются в одной точке.
Задачи на равновесие твердого тела под действием системы сходящихся сил можно решать геометрическим и аналитическим методами.
Первым методом удобно пользоваться лишь для плоской системы и особенно в трех случаях, когда общее число сил, действующих на тело, равно трем. При равновесии тела треугольник, построенный на этих силах, должен быть замкнутым.
Аналитическим методом можно пользоваться также и для пространственной системы сил при любом числе сил. При этом следует иметь в виду, что общее число неизвестных в задаче должно быть не больше трех для пространственной системы сходящихся сил и не больше двух для плоской системы сходящихся сил.
1.2 Равновесие плоской системы сил
Первая форма условий равновесия произвольной плоской СС: необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси и сумма алгебраических моментов сил относительно любого центра были равны нулю
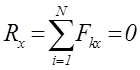 ,
, 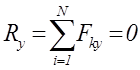 ,
, 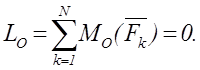 (1.6)
(1.6)
Вторая форма
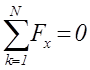 ,
, 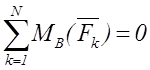 ,
, 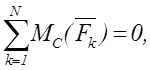 (1.7)
(1.7)
при
этом прямая ![]() не перпендикулярна
не перпендикулярна ![]() .
.
Третья форма
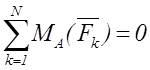 ,
, 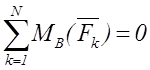 ,
, 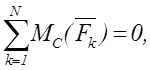 (1.8)
(1.8)
при этом А, В, С не лежат на одной прямой.
Для плоской системы параллельных сил
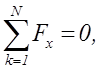 ,
, 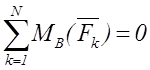 (1.9)
(1.9)
(ось Ox параллельна направлению сил) или
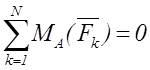 ,
, 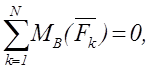 (1.10)
(1.10)
причем прямая, проходящая через А и В, не параллельна силам.
Для получения наиболее простых уравнений равновесия (если это не усложняет ход решения в остальном) следует одну из координатных осей проводить перпендикулярно возможно большему числу неизвестных сил, а за центр моментов брать точку, в которой пересекается возможно большее число неизвестных сил.
При вычислении момента силы иногда удобно раскладывать силу на составляющие и пользоваться теоремой Вариньона, согласно которой момент равнодействующей силы равен сумме моментов составляющих сил.
Если на тело наряду с силами действуют и пары, лежащие в плоскости сил, то при составлении уравнений равновесия в уравнения проекций пары не войдут, так как сумма проекций сил пары на любую ось равна нулю. В уравнениях же моментов к моментам сил алгебраически прибавятся моменты пар, поскольку сумма моментов сил пары относительно любого центра равна алгебраическому моменту пары.
Если на покоящееся тело наложены связи с трением, то к уравнениям равновесия с учетом сил трения следует добавить дополнительное условие
![]() (1.11)
(1.11)
где ![]() коэффициент
трения скольжения при покое;
коэффициент
трения скольжения при покое;
![]() величина нормальной
реакции.
величина нормальной
реакции.
При решении некоторых задач следует учитывать трение качения. Наибольшее значение момента трения качения определяется по формуле
![]() (1.12)
(1.12)
где δ - коэффициент трения качения;
N - модуль нормального давления.
1.2 Равновесие пространственной системы сил
Произвольная
СС, приложенных к телу, эквивалентна силе, равной главному вектору![]() , и паре сил с моментом, равным
главному моменту
, и паре сил с моментом, равным
главному моменту ![]() относительно какого-либо
центра О. Чтобы такая система находилась в равновесии, необходимо и
достаточно, чтобы были равны нулю
относительно какого-либо
центра О. Чтобы такая система находилась в равновесии, необходимо и
достаточно, чтобы были равны нулю ![]() и
и ![]() . Поэтому условия равновесия могут быть
представлены в векторной форме как
. Поэтому условия равновесия могут быть
представлены в векторной форме как
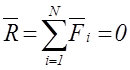 ,
(1.13)
,
(1.13)
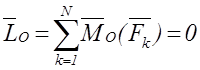 .
(1.14)
.
(1.14)
Эти условия эквивалентны аналитическим условиям равновесия в виде
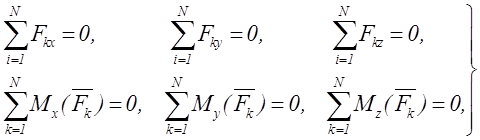 , (1.15)
, (1.15)
т.е. для равновесия произвольной пространственной СС, приложенных к АТТ, необходимо и достаточно, чтобы были равны нулю суммы проекций всех сил на три оси декартовой системы координат и суммы моментов всех сил относительно этих осей.
Условия равновесия для пространственной системы параллельных сил (ось z параллельна направлению действия сил) имеют вид
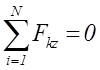 ,
, 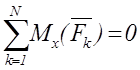 ,
, 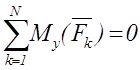 .
(1.16)
.
(1.16)
При решении пространственных задач следует иметь в виду, что могут встретиться такие частные случаи расположения сил, где некоторые из уравнений равновесия обращаются в тождества. Это произойдет, например, в случаях, когда все линии действия сил пересекают какую-либо одну ось, либо все силы перпендикулярны какой-либо оси, и в некоторых других случаях. Число неизвестных в таких задачах при их статической определенности будет менее шести.
Для нахождения момента силы относительно оси следует спроецировать силу на плоскость, перпендикулярную к оси, после чего найти алгебраический момент полученной проекции относительно точки пересечения оси и проведенной плоскости. Момент силы относительно оси считается положительным, если при наблюдении с положительного конца оси сила видна как стремящаяся повернуть тело против движения часовой стрелки.
Если сила параллельна оси или ее линия действия пересекает ось, то момент силы относительно оси равен нулю.
Значительно облегчает нахождение момента силы относительно оси применение теоремы Вариньона. Для применения этой теоремы силу, момент которой требуется определить, раскладывают на составляющие, одна из которых параллельна данной оси, а другие две (или одна) перпендикулярны. Нахождение моментов таких составляющих обычно не сложно.
Если сила задана аналитически (т.е. заданы ее проекции и координаты точки приложения), то для определения моментов силы относительно координатных осей пользуются формулами
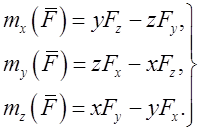 (1.17)
(1.17)
1.4 Центр тяжести
Координаты центра тяжести тела определяются по формулам
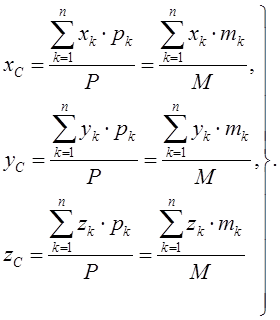 (1.18)
(1.18)
Суммы, стоящие в числителях, называют статическими моментами веса (массы) относительно плоскостей yOz, xOz, xOy соответственно.
Если тело однородно, то координаты его центра тяжести определяют по формулам
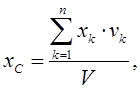
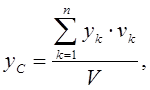
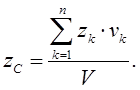 (1.19)
(1.19)
Координаты центра тяжести тонких однородных поверхностей (имеющих постоянный вес единицы площади) определяют по формулам
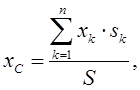
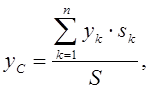
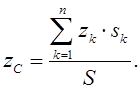 (1.20)
(1.20)
Координаты центра тяжести пластины (оси Ox, Oy расположены в плоскости пластины) будут
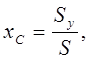 ;
; 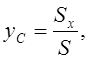 (1.21)
(1.21)
где 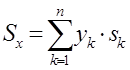 ,
, 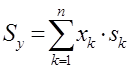 – статические моменты площади относительно
осей Ox и
Oy.
– статические моменты площади относительно
осей Ox и
Oy.
Аналогичные формулы применяют для определения координат центров тяжести тонких однородных стержней (имеющих постоянный вес единицы длины).
В формулах (1.19) и (1.20) vk, sk – объемы и площади тех частей, на которые разбивают имеющие сложную форму тела (поверхности), xk, yk , zk – центры тяжести этих частей.
При нахождении центра тяжести тела (фигуры) с отверстиями можно иметь применять формулы (1.18) - (1.20), считая веса, объемы или площади, соответствующие вырезанным частям, отрицательными. Для криволинейных тел (фигур), разбиваемых на бесконечно малые элементы, суммы в выражениях для статических моментов и масс (объемов, площадей) заменяют интегралами.
 1.5 Примеры решения задач статики
1.5 Примеры решения задач статики
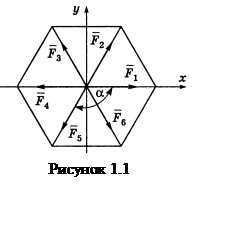
Пример 1.1 - В центре правильного шестиугольника приложены силы F1 = 1 Н, F2 =3 Н, F3 =5 Н, F4 = 7 Н, F5 =9 Н, F6 =11 Н, направленные к его вершинам (см. рисунок 1.1). Найти величину и направление равнодействующей и уравновешивающей сил.
Решение. Найдем
проекции равнодействующей сил ![]() на оси координат
на оси координат
![]()
![]()
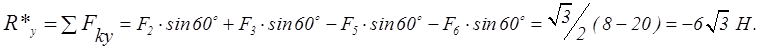 .
.
Тогда
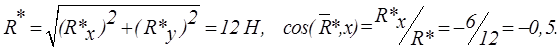
Так как
проекции равнодействующей на две координатные оси отрицательны и косинус угла
между ней и положительным направлением оси x равен -0,5, то заключаем,
что вектор ![]() направлен по вектору силы F5,
а вектор уравновешивающей силы
направлен по вектору силы F5,
а вектор уравновешивающей силы![]()
 Пример
1.2 - Требуется разложить силу в 8 кН на две силы, по 5 кН
каждая. Можно ли ту же силу разложить на две по 10 кН, 20 кН и т.д.?
Пример
1.2 - Требуется разложить силу в 8 кН на две силы, по 5 кН
каждая. Можно ли ту же силу разложить на две по 10 кН, 20 кН и т.д.?
Решение. Обозначим
силу, которую требуется разложить, через ![]() ,
две другие — соответственно
,
две другие — соответственно ![]() и
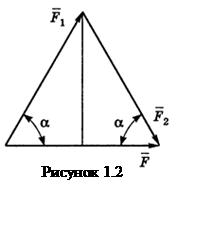
и ![]() . Изобразим на рисунке
1.2 силу F как
основание равнобедренного треугольника (т.к. F1=F2). Ввиду равенства углов
наклона F1 и F2 к основанию получим
. Изобразим на рисунке
1.2 силу F как
основание равнобедренного треугольника (т.к. F1=F2). Ввиду равенства углов
наклона F1 и F2 к основанию получим![]() , откуда
, откуда
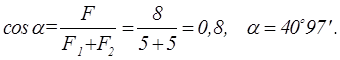
Аналогично можно решить задачу для F1 =10 Н, 20 Н и т.д., каждый раз определяя нужный угол. Это решение годится, когда не заданы направления разложения сил.
Пример 1.3 - Два трактора, идущих по берегам прямого канала с постоянной скоростью, тянут барку при помощи двух канатов. Силы натяжения канатов равны F1= 0,8 кН, F2= = 0,96 кН, угол между канатами равен α+β=60° (см. рисунок 1.3). Найти сопротивление воды Р, испытываемое баркой при ее движении, и углы α и β, которые должны составлять канаты с берегами канала, если барка движется параллельно берегам.
Решение. Изобразим на рисунке силы, действующие на барку. Так как барка движется с постоянной скоростью, то можно записать следующие уравнения равновесия:
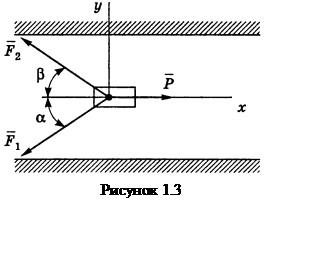
![]()
![]()
Из второго
уравнения следует 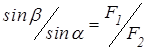 или (поскольку β=60-α)
или (поскольку β=60-α)
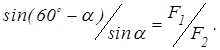
После преобразований получаем 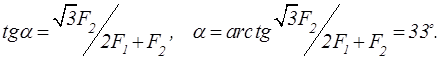
С учетом этого ![]() и из первого уравнения равновесия
и из первого уравнения равновесия ![]()
Пример 1.4 - Груз весом G = 2 кН (см. рисунок 1.4,а) удерживается краном, состоящим из двух невесомых стержней АВ и АС, прикрепленных в шарнирах В и С к вертикальной стене и составляющих с ней углы α1 = 60° и α2 = 40°. В точке А подвешен блок, через который перекинут грузовой трос, идущий к блоку в точке D и составляющий со стеной угол α3 = 60°. Весом троса и блока, а также размерами блока пренебречь. Определить усилия в стержнях.
Решение. Рассмотрим находящийся в равновесии груз (см. рисунок 1.4,б). На него действуют сила тяжести G и сила натяжения троса N1. Очевидно, что сила натяжения троса направлена вверх и по модулю равна весу груза N1 = G.
Если пренебречь трением на оси блока (см. рисунок 1.4,в), то силы натяжения ветвей его троса одинаковы N1 = N2.
Теперь рассмотрим мысленно вырезанный узел в точке А (или, что то же самое, блок с прилежащей к нему частью троса). На этот узел будут действовать силы натяжения ветвей троса N1 и N2 и реакции R1 и R2 стержней АВ и АС (см. рисунок 1.4,г). Реакции опорных стержней направлены, как известно, вдоль этих стержней. Направим их от узла А, считая стержни растянутыми. Составим уравнения равновесия в виде сумм проекций всех сил на оси x и у
![]()
![]()
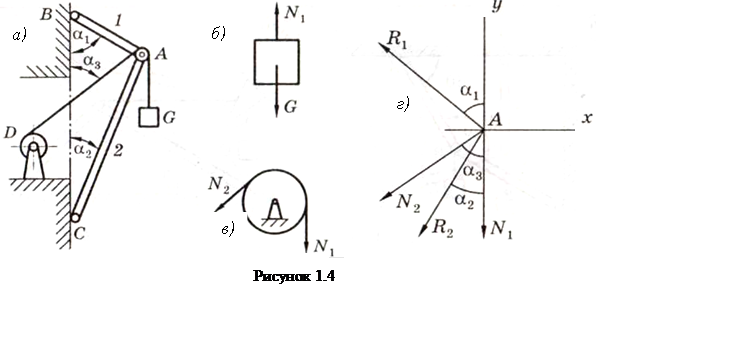 |
Решая эту систему уравнений и учитывая, что N1 = N2 = 2 кН, находим R1 = 0,611 кН, R2 = -3,52 кН. Знак «минус» у величины реакции R2 означает, что она имеет направление, противоположное принятому, т.е. стержень АС не растянут, а сжат.
 Пример
1.5 - Шар весом G подвешен на нити BC, составляющей с
вертикалью угол a, и опирается в точке A
на гладкую вертикальную стену (см. рисунок 1.5,а). Требуется определить
реакции стены N и нити T.
Пример
1.5 - Шар весом G подвешен на нити BC, составляющей с
вертикалью угол a, и опирается в точке A
на гладкую вертикальную стену (см. рисунок 1.5,а). Требуется определить
реакции стены N и нити T.
|
Используем геометрическое условие равновесия – построим силовой треугольник (см. рисунок 1.5,б), из которого получим
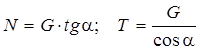 .
.
Решим эту же задачу с помощью аналитических условий равновесия. Проведем координатные оси Ax и Ay и составим два уравнения равновесия:
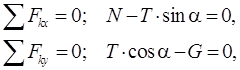
из которых получим
|
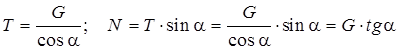 .
.
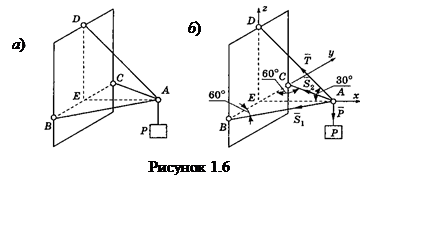 Пример 1.6
- Для конструкции на рисунке 1.6,а найти усилия S1
и S2 в стержнях АВ и ВС и усилие Т
в тросе AD, если дано, что
Пример 1.6
- Для конструкции на рисунке 1.6,а найти усилия S1
и S2 в стержнях АВ и ВС и усилие Т
в тросе AD, если дано, что ![]() Вес груза Р = 300 Н.
Плоскость ABС горизонтальная,
крепления стержней в точках A, В и C шарнирные.
Вес груза Р = 300 Н.
Плоскость ABС горизонтальная,
крепления стержней в точках A, В и C шарнирные.
Решение. На рисунке 1.6,б изображены система сил, приложенных к конструкции - это пространственная система сил, сходящихся в точке А. Для определения реакций проведем оси и составим уравнения равновесия :
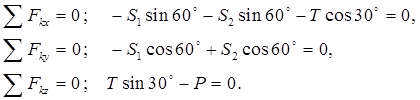
Решив систему уравнений, найдем T=600 Н; S1 = S2=-300 Н.
Можно сделать вывод, что стержни АВ и АС сжаты, трос AD растянут.
Пример 1.7 - На раму AB (см. рисунок 1.7,а) действуют сила F = 2 кН и пара сил, момент которой M = 1 кН×м. Определить реакции опор.
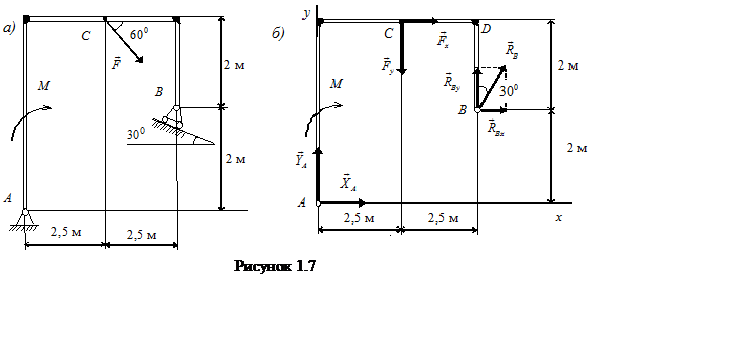 Решение.
Рассмотрим равновесие рамы AB, которую освободим от связей, заменив их
действие реакциями (см. рисунок 1.7,б):
Решение.
Рассмотрим равновесие рамы AB, которую освободим от связей, заменив их
действие реакциями (см. рисунок 1.7,б): ![]() –
составляющие реакции неподвижного цилиндрического шарнира A;
–
составляющие реакции неподвижного цилиндрического шарнира A; ![]() – реакция подвижного цилиндрического
шарнира B, направленная перпендикулярно опорной плоскости.
– реакция подвижного цилиндрического
шарнира B, направленная перпендикулярно опорной плоскости.
Разложим силы ![]() и
и ![]() на
составляющие, параллельные координатным осям:
на
составляющие, параллельные координатным осям:
![]() кН,
кН, ![]() кН,
кН,
![]() .
.
Пара сил задана величиной момента и направлением действия.
Для полученной плоской системы сил запишем три уравнения равновесия:
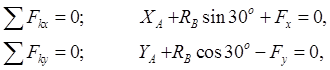
![]()
При составлении уравнений равновесия целесообразно координатные оси направить перпендикулярно неизвестным силам, а моменты сил вычислять относительно точек пересечения линий действия неизвестных сил, что обеспечит получение уравнений, содержащих минимальное число неизвестных. Из уравнений равновесия получим
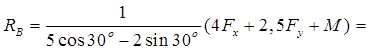
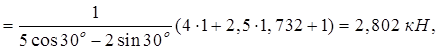
![]() кН,
кН,
![]() кН.
кН.
Отрицательные
значения реакций показывают, что действительные направления сил ![]() и
и![]() противоположны
первоначально выбранным.
противоположны
первоначально выбранным.
Для проверки правильности решения рассмотрим условие равновесия, не использованное при решении примера. Выберем точку D, относительно которой все найденные реакции имеют моменты, и вычислим сумму моментов всех сил относительно этой точки
![]()
![]() .
.
Условие равновесия выполнено.
Пример 1.8 - На консольную балку AB, показанную на рисунке 1.8,а, действуют сила Р= 1 кН, пара сил с моментом M = 3 кН×м, и равномерно распределенная нагрузка с интенсивностью q = 2 кН/м. Определить реакцию жесткой заделки А.
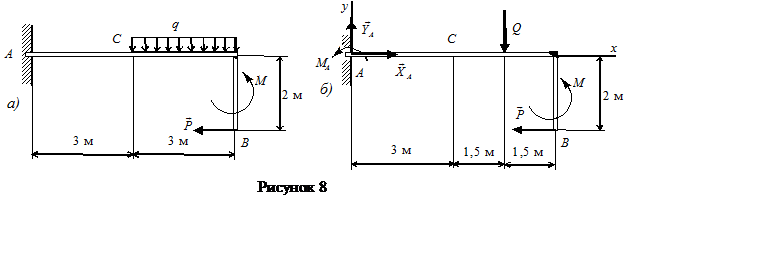
Решение.
Жесткая заделка препятствует перемещению точки А и повороту балки вокруг
этой точки. На закрепленный конец балки действует система реактивных сил,
которая приводится к силе, приложенной в точке А, и паре сил. Представим
силу составляющими ![]() ,
, ![]() , а
момент пары обозначим через
, а
момент пары обозначим через ![]() .
.
Освобождая
балку от связи, покажем три составляющие реакции жесткой заделки: ![]()
![]() ,
, ![]() (см. рисунок 1.8,б). Равномерно
распределенную нагрузку заменим ее равнодействующей, приложенной в середине
нагруженного участка,
(см. рисунок 1.8,б). Равномерно
распределенную нагрузку заменим ее равнодействующей, приложенной в середине
нагруженного участка, ![]() кН. Для
рассматриваемой плоской системы сил запишем три уравнения равновесия:
кН. Для
рассматриваемой плоской системы сил запишем три уравнения равновесия:
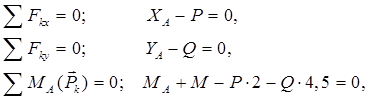
из которых получим
![]() = P = 1 кН,
= P = 1 кН, ![]() = 6 кН,
= 6 кН,
![]() = 2×1 + 4,5×6 - 3 = 26 кН×м.
= 2×1 + 4,5×6 - 3 = 26 кН×м.
Для проверки правильности решения вычислим сумму моментов всех действующих на балку сил относительно точки В
![]() .
.
Пример 1.9 - При сборке моста пришлось поднимать часть мостовой фермы ABC тремя канатами, расположенными, как указано на рисунке 1.9,а. Вес этой части фермы 42 кН, центр тяжести находится в точке D. Расстояния равны: AD = 4 м, DB = 2 м, BF= 1 м. Найти натяжения канатов, если прямая АС горизонтальна.
Решение. На рисунке 1.9,б показаны действующие силы и реакции связей.
Составим уравнения равновесия балки (для проекций сил на оси х и у и для моментов относительно точки Е):
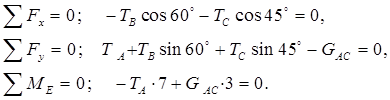
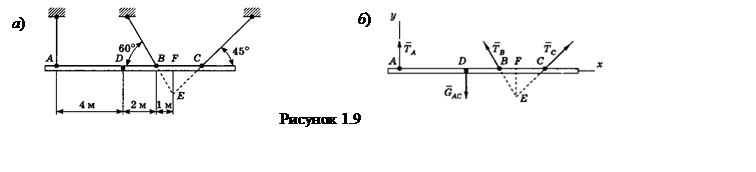
Решив систему, получим ТА =18 кН, ТВ = 17,57 кН, ТС= 12,43 кН.
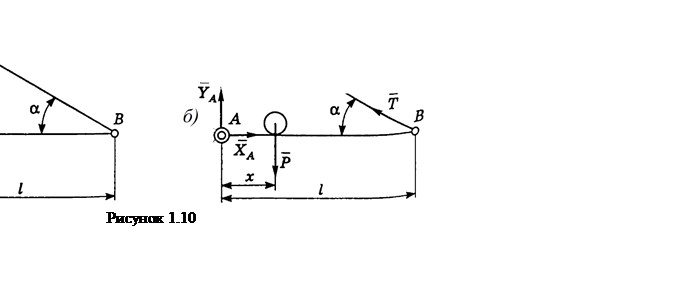
Пример 1.10 - Горизонтальная балка крана, длина которой равна l, у одного конца А укреплена шарнирно, а у другого конца В подвешена к стене посредством тяги ВС, угол наклона которой к горизонту равен α (см. рисунок 1.10,а). По балке может перемещаться груз Р, положение которого определяется переменным расстоянием х до шарнира А. Определить натяжение Т тяги ВС в зависимости от положения груза. Весом балки пренебречь.
Решение. Изобразим на рисунке 1.10,б действующие силы, при этом отбросим связи,
заменяя их действие реакциями связей. Составим уравнение
равновесия балки АВ для моментов сил относительно точки А: ![]() откуда
откуда ![]()
Пример 1.11 - Однородная балка AB весом P опирается на две гладкие наклонные плоскости CD и DE, находящиеся в вертикальной плоскости (см. рисунок 1.11,а); угол наклона первой из них к горизонту равен α, второй – (90°-α). Найти угол наклона балки к горизонту в положении равновесия θ и давления ее на опорные плоскости.
Решение. Покажем на силы, действующие на балку (см. рисунок 1.10,б). Составим уравнения равновесия в проекциях на оси х и у и для моментов относительно точки А:
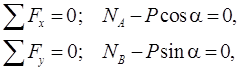
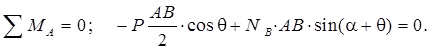
Отсюда![]()
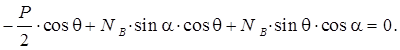
Преобразуем последнее выражение
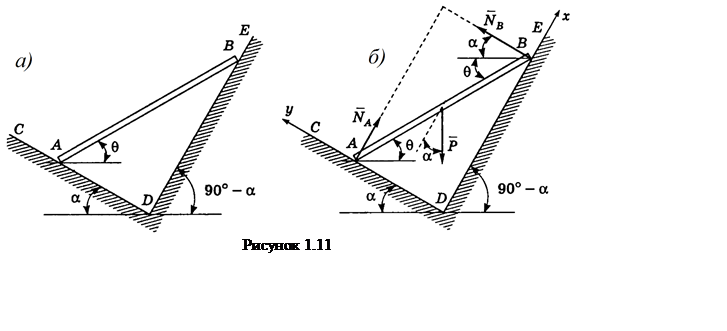
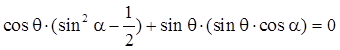 и окончательно
и окончательно ![]()
Пример
1.12 - Жесткая
рама закреплена в точке А с помощью неподвижного шарнира, а в точке В
шарнирной опорой на катках (см. рисунок 1.12,а). На раму действуют пара
сил с моментом М0 = 100 Н·м и две силы F1=10 H и F2=40
H; α = 60°; β = 30°,![]() м. Требуется определить опорные
реакции.
м. Требуется определить опорные
реакции.
Решение. Рассмотрим
равновесие рамы AB, которую освободим от связей, заменив их действие
реакциями (см. рисунок 1.12,б). Здесь![]() –
составляющие реакции неподвижного цилиндрического шарнира A;
–
составляющие реакции неподвижного цилиндрического шарнира A; ![]() – реакция подвижного цилиндрического
шарнира B, направленная перпендикулярно опорной плоскости.
– реакция подвижного цилиндрического
шарнира B, направленная перпендикулярно опорной плоскости.
Из условия, что рама находится в равновесии, следует следующая система уравнений
|
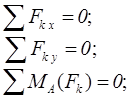
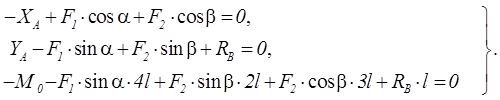
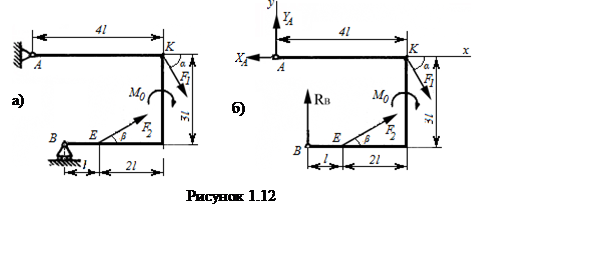
Из первого уравнения найдем
![]()
из третьего уравнения получаем
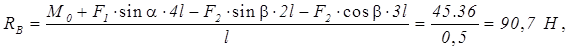
из второго уравнения найдем
![]()
Знак минус
указывает на противоположное направление силы по сравнению с тем, которое было
выбрано первоначально, т. е. сила ![]() направлена вниз.
направлена вниз.
Проверка: Составим уравнение моментов сил относительно точки В
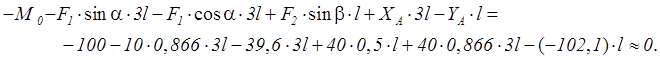
Пример 1.13 - Плоская рама, состоящая из двух изогнутых под прямым углом стержней, имеет две опоры - скользящую заделку в точке А и неподвижный шарнир в точке В. Части рамы соединены шарниром в точке С (см. рисунок 1.13,а). Размеры даны в метрах. К раме приложена горизонтальная сила Р=1 кН, вертикальная сила F=4 кН и момент М=3 кН∙м. Найти реакции опор.
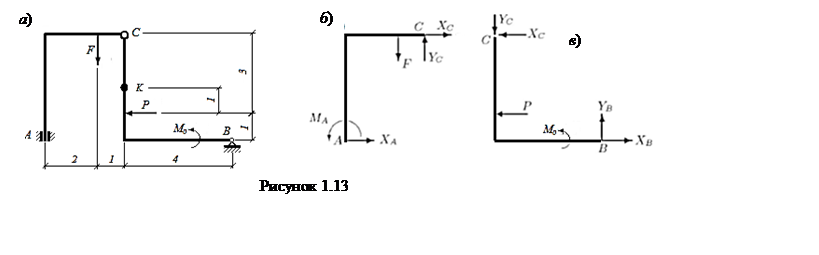
Решение. Эта задача – на равновесие составной конструкции. Скользящая заделка А имеет две неизвестные реакции: момент МА, препятствующий вращению, и горизонтальную силу ХА. Вертикальной реакции в точке А нет, т.е. стержень можно свободно вынуть из скользящей опоры. Действие неподвижного шарнира В заменяем горизонтальной реакцией ХВ и вертикальной YВ. Т.о., здесь на конструкцию наложено 4 связи. Для плоской системы сил число независимых уравнений равновесия 3. Если бы в точке С не было бы шарнира, то система была бы статически неразрешимой. Шарнир С снимает 1 связь (разрешает взаимный поворот двух частей конструкции).
Для решения задачи разобьем раму на две части по шарниру С. Отброшенные части заменим реакциями ХС, YС. На одну часть эти реакции действуют в одну сторону, на другую – в противоположную. Неизвестных сил стало 6, но и независимых уравнений можно составить 6, так как и конструкция в целом, и каждая из выделенных частей находятся в равновесии. Можно составить по 3 уравнения равновесия для каждой из частей либо 3 для одной из частей и 3 для конструкции в целом. Мы будем решать задачу первым способом.
Составим уравнения равновесия для левой части (см. рисунок 1.13,б)
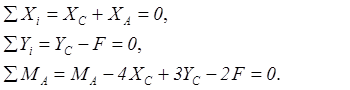
Составим уравнения равновесия для правой части рамы (см. рисунок 1.13,в)
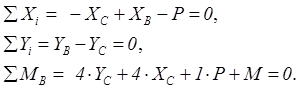
Решая полученную систему уравнений, найдем ХА=5 кН, YB=4 кН, MА=-24 кН∙м, ХВ=-4 кН, YС=4 кН, ХС=-5 кН.
Проверка. Составим уравнение равновесия в виде суммы моментов всех сил, действующих на раму, включая реакции опор, относительно какой-либо произвольной точки. Желательно, чтобы эта точка не лежала на линии действия реакции. Выберем точку К на посредине правой части рамы (см. рисунок 13,а). Внутренние реакции в сочленяющем шарнире С в уравнение не входят
∑MК= 4∙YВ-1∙Р+М+МА+2∙ХА+2∙ХВ+1∙F=4∙4-1∙1+3-24+2.5-2∙4+1∙4=0.
Проверка выполнена. Реакции найдены верно.
 Заметим, что если
разбить раму не по шарниру, а произвольно, то в месте разбиения к каждой из образовавшихся
частей, помимо двух взаимно перпендикулярных сил, надо будет приложить момент -
еще одну неизвестную реакцию. В результате в задаче будет 7 неизвестных и
прежние 6 уравнений. Так задача не может быть решена.
Заметим, что если
разбить раму не по шарниру, а произвольно, то в месте разбиения к каждой из образовавшихся
частей, помимо двух взаимно перпендикулярных сил, надо будет приложить момент -
еще одну неизвестную реакцию. В результате в задаче будет 7 неизвестных и
прежние 6 уравнений. Так задача не может быть решена.
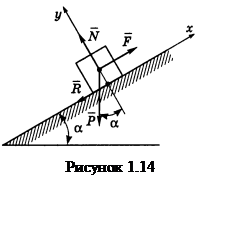
Пример
1.14 - Поезд поднимается по прямолинейному пути, имеющему уклон
0,008, с постоянной скоростью; вес поезда, не считая электровоза, 12 000 кН.
Какова сила тяги ![]() электровоза, если сопротивление
движению равно 0,005 давления поезда на рельсы?
электровоза, если сопротивление
движению равно 0,005 давления поезда на рельсы?
Решение. Покажем на рисунке 1.14 силы, действующей на поезд.
Так как поезд
движется прямолинейно и равномерно, то действующие на него силы взаимно
уравновешены. Запишем уравнение равновесия в проекциях на ось ![]()
![]() .
.
Тогда
![]() .
.
Так как угол ![]() мал, то sin
мал, то sin ![]() ,
поэтому
,
поэтому
![]() кH.
кH.
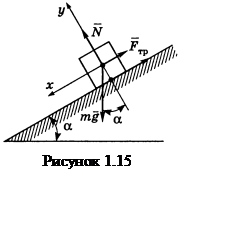 Пример 1.15
- Негладкой наклонной плоскости придан такой угол наклона к горизонту
Пример 1.15
- Негладкой наклонной плоскости придан такой угол наклона к горизонту![]() , что тяжелое тело, помещенное на эту
плоскость, спускается с той постоянной скоростью, которая ему сообщена в начале
движения. Определить коэффициент трения
, что тяжелое тело, помещенное на эту
плоскость, спускается с той постоянной скоростью, которая ему сообщена в начале
движения. Определить коэффициент трения ![]() .
.
Решение.
Так как тело совершает прямолинейное равномерное движение, то действующие на
него силы (см. рисунок 1.15) уравновешены. Запишем уравнения равновесия в
проекциях на оси ![]() и
и ![]()
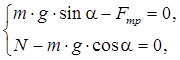 или
или 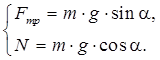
Следовательно, 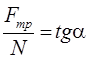 . А поскольку
. А поскольку ![]() ,
то
,
то ![]() .
.
Пример
1.16 - Найти угол естественного откоса земляного грунта, если
коэффициент трения для этого грунта ![]() . Углом
естественного откоса называется наибольший угол наклона откоса к горизонту, при
котором частица грунта, находящейся на откосе, остается в равновесии.
. Углом
естественного откоса называется наибольший угол наклона откоса к горизонту, при
котором частица грунта, находящейся на откосе, остается в равновесии.
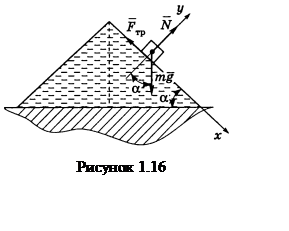 Решение. На
рисунке 1.16 показаны силы, действующие на частицу. Составим уравнения
равновесия в проекциях на оси
Решение. На
рисунке 1.16 показаны силы, действующие на частицу. Составим уравнения
равновесия в проекциях на оси ![]() и
и ![]()
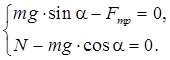
Поскольку
![]() ,
,
то из системы уравнений можно
получить соотношение ![]() . Следовательно,
. Следовательно, ![]() .
.
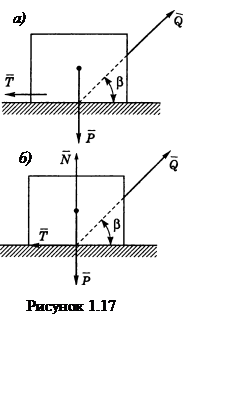 Пример 1.17
- Ящик весом
Пример 1.17
- Ящик весом ![]() стоит на шероховатой
горизонтальной плоскости с коэффициентом трения
стоит на шероховатой
горизонтальной плоскости с коэффициентом трения![]() .
Определить, под каким углом
.
Определить, под каким углом ![]() надо приложить
надо приложить ![]() и величину этой силы, при условии, что
надо сдвинуть ящик при наименьшей величине
и величину этой силы, при условии, что
надо сдвинуть ящик при наименьшей величине ![]() (см.
рисунок 1,17,а).
(см.
рисунок 1,17,а).
Решение. Составим
уравнения равновесия в проекциях сил на оси ![]() и
и ![]() (см. рисунок 1,17,б) и добавим
к ним соотношение, связывающее силу трения с нормальной реакцией
(см. рисунок 1,17,б) и добавим
к ним соотношение, связывающее силу трения с нормальной реакцией
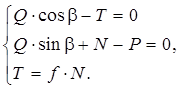
Из второго
уравнения системы имеем ![]() , тогда из третьего
, тогда из третьего![]() .
.
Следовательно, с учетом первого уравнения системы
![]()
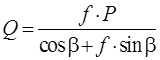 .
.
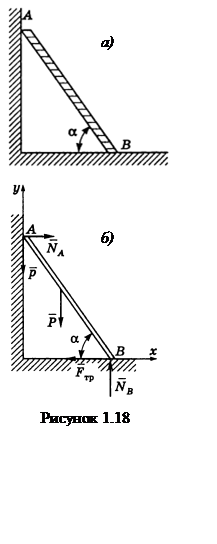
Величина ![]() принимает минимальное значение, когда
значение функции
принимает минимальное значение, когда
значение функции ![]() максимально. Исследуем на
экстремум
максимально. Исследуем на
экстремум
![]() Значит
Значит ![]() ,
когда
,
когда ![]() , т.е.
, т.е. ![]() .
.
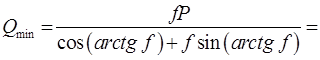
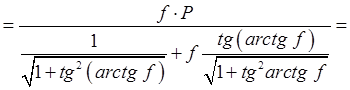
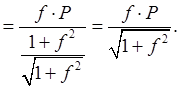
Пример
1.18 - Лестница ![]() весом Р
упирается в гладкую стену и опирается на горизонтальный негладкий пол (см.
рисунок 1,18,а). Коэффициент трения лестницы о пол равен
весом Р
упирается в гладкую стену и опирается на горизонтальный негладкий пол (см.
рисунок 1,18,а). Коэффициент трения лестницы о пол равен ![]() . Под каким углом
. Под каким углом ![]() к полу надо поставить, чтобы по ней
мог подняться доверху человек c весом p?
к полу надо поставить, чтобы по ней
мог подняться доверху человек c весом p?
Решение.
На основании рисунка 1,18,б запишем условие, связывающее силу трения и
давления в точке ![]()
![]() .
.
Обозначим длину лестницы l и составим уравнения равновесия лестницы (в проекциях на ось y и для моментов сил относительно точки A):
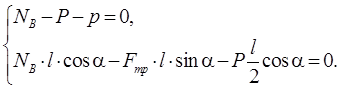
Из
первого уравнения имеем![]() Тогда из второго
Тогда из второго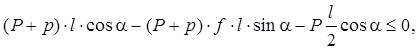 откуда
откуда 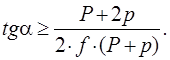
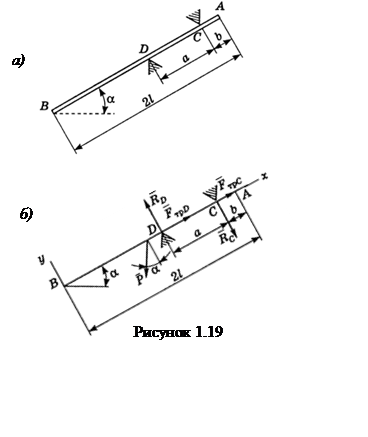 Пример 1.19
- Тяжелый однородный стержень
Пример 1.19
- Тяжелый однородный стержень ![]() лежит на двух опорах
C
и D, расстояние между которыми
лежит на двух опорах
C
и D, расстояние между которыми ![]() . Коэффициент трения стержня об опоры
равен f. Угол наклона стержня к горизонту равен
. Коэффициент трения стержня об опоры
равен f. Угол наклона стержня к горизонту равен ![]() . Какому условию должна удовлетворять
длина стержня
. Какому условию должна удовлетворять
длина стержня ![]() для того, что бы стержень
находился в равновесии, если толщиной его можно пренебречь?
для того, что бы стержень
находился в равновесии, если толщиной его можно пренебречь?
Решение. Для изображенных на рисунке сил, действующих на стержень, составим уравнения равновесия:
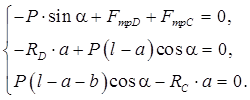
Из двух последних уравнений системы найдем реакции опор
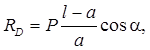
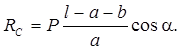
Рассмотрим
случай, когда ![]() т.е.
т.е. ![]() ,
или
,
или ![]() .
.
Подставив в
первое уравнение системы выражения для ![]() и
и ![]() и учитывая, что
и учитывая, что ![]() получим оценку
получим оценку
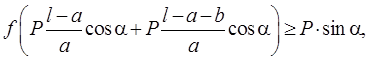
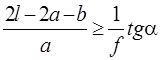 ,
,
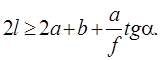
Если ![]() , то
, то 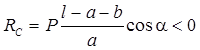 ,
следовательно,
,
следовательно, ![]() .
.
Однако при выполнении последнего неравенства и при заданном в условии расположении опоры C равновесие невозможно.
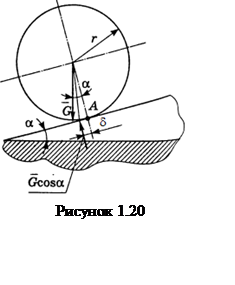 Итак, длина стержня
Итак, длина стержня ![]() должна удовлетворять условиям
должна удовлетворять условиям 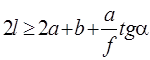 и
и
![]() Первое условие включает второе при
Первое условие включает второе при ![]() , где
, где ![]() угол
трения; если
угол
трения; если ![]() , то достаточно удовлетворить второму
условию; при
, то достаточно удовлетворить второму
условию; при ![]() равновесие при принятом на рисунке
расположении опоры
равновесие при принятом на рисунке
расположении опоры ![]() невозможно.
невозможно.
Пример
1.20 - Определить угол ![]() наклона
плоскости к горизонту, при котором ролик радиусом
наклона
плоскости к горизонту, при котором ролик радиусом ![]() мм
равномерно катится по плоскости. Материал трущихся тел – сталь, коэффициент
трения качения
мм
равномерно катится по плоскости. Материал трущихся тел – сталь, коэффициент
трения качения![]() мм. (Ввиду малости угла
мм. (Ввиду малости угла ![]() можно принять
можно принять ![]() .)
.)
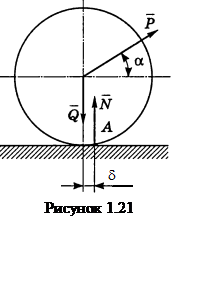 Решение. Покажем
на рисунке 1.20 силы, действующие на ролик. Составим уравнение моментов относительно
точки
Решение. Покажем
на рисунке 1.20 силы, действующие на ролик. Составим уравнение моментов относительно
точки ![]()
![]() ,
откуда находим
,
откуда находим ![]()
![]() .
.
Пример
1.21 - Определить силу ![]() ,
необходимую для равномерного качения цилиндрического катка диаметром
,
необходимую для равномерного качения цилиндрического катка диаметром ![]() см и весом
см и весом ![]() Н по
горизонтальной плоскости, если коэффициент трения качения
Н по
горизонтальной плоскости, если коэффициент трения качения ![]() см, а угол, составляемый силой
см, а угол, составляемый силой ![]() с горизонтальной плоскостью, равен
с горизонтальной плоскостью, равен ![]() .
.
Решение. Изобразим
на рисунке 1.21 силы, действующие на каток. Для определения искомой силы составим
уравнение моментов относительно точки ![]()
![]() . Отсюда найдем
. Отсюда найдем
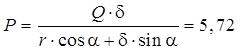 Н.
Н.
Пример 1.22 - На вал АВ ворота (см. рисунок 1.22,а) намотана веревка, поддерживающая груз Q. Радиус колеса С, насаженного на вал, в шесть раз больше радиуса вала r; другие размеры указаны на рисунке. Веревка, намотанная на окружность колеса и натягиваемая грузом Р весом 60 Н, сходит с колеса по касательной, наклоненной к горизонту под углом α = 30°. Определить вес груза Q, при котором ворот остается в равновесии, а также реакции подшипников А и В, пренебрегая весом вала и трением на блоке D.
|
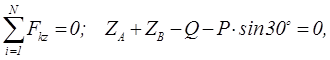
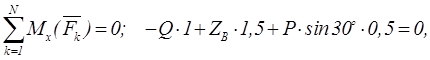
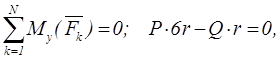
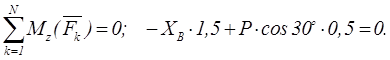
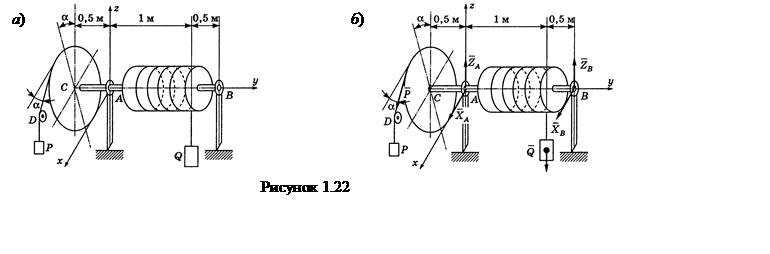
Решая систему, получим
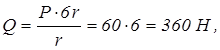
![]()
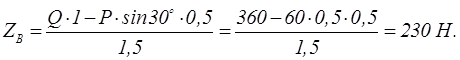
![]()
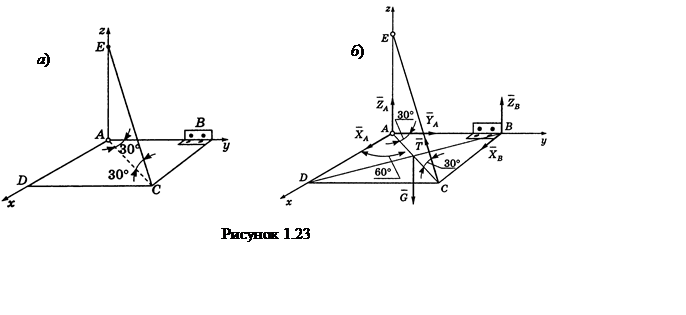
Пример 1.23 - Однородная прямоугольная рама весом 200 Н (см. рисунок 1.23,а) прикреплена к стене при помощи шарового
|
|
|
 |
|
|
|
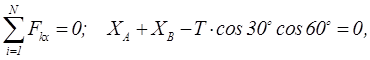
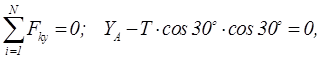
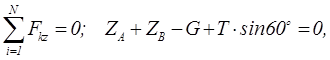
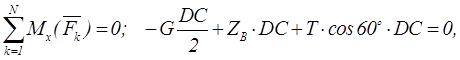
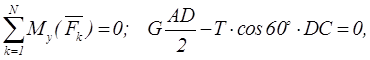
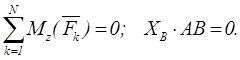
Решая систему, получим
![]()
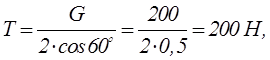
![]()
![]()
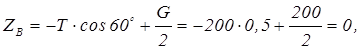
![]()
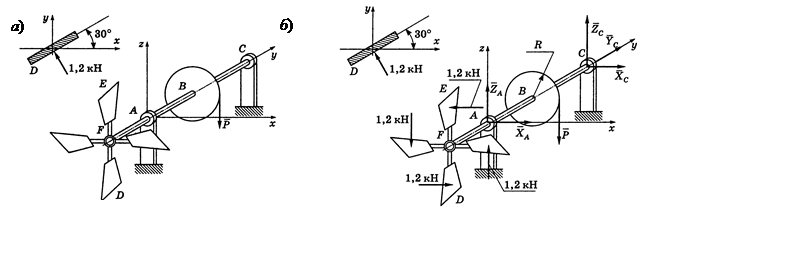
Пример 1.24 - Ветряной двигатель с горизонтальной осью АС имеет четыре симметрично расположенных крыла, плоскости которых составляют с вертикальной плоскостью, перпендикулярной оси АС, равные углы 30°. На расстоянии 2 м от оси к каждому крылу приложена нормально к его плоскости равнодействующая сил давления ветра, равная 1,2 кН (крыло D в проекции на плоскость ху изображено отдельно). Ось двигателя опирается в точке А на подшипник, в точке С - на подпятник и удерживается в покое вертикальным давлением Р на зубец колеса B, производимым шестерней, которая на рисунке не показана. Радиус колеса В равен 1,2 м; расстояния ВС =0,5 м, АВ = 1 м, AF= 0,5 м. Определить давление Р и реакции опор.
|
|
![]()
![]()
![]()
![]()
![]()
![]()
Решая систему, найдем
![]()
![]()
![]()
![]()
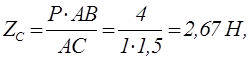
![]()
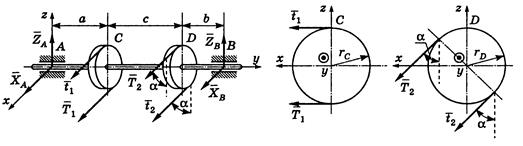
Пример 1.25 - Горизонтальный вал трансмиссии, несущий два шкива С и D ременной передачи, может вращаться в подшипниках А и В (см. рисунок 1.25,а). Радиусы шкивов: rc=20 см, rD =25 см; расстояния шкивов от подшипников: a=b=50 см; расстояние между шкивами с=100 см. Натяжения ветвей ремня, надетого на шкив С, горизонтальны и имеют величины Т1 и t1, причем Т1 =2t1 =5 кН, натяжения ветвей ремня, надетого на шкив D образуют с вертикалью угол α=30° и имеют величины Т2 и t2, причем Т2 = 2t2. Определить натяжения Т2 и t2 в условиях равновесия и реакции подшипников, вызванные натяжениями ремней.
|
|
|
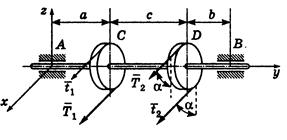
|
![]()
откуда после преобразований получим
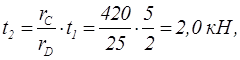
![]()
Запишем уравнение моментов сил относительно оси z
![]()
откуда найдем реакцию ХB
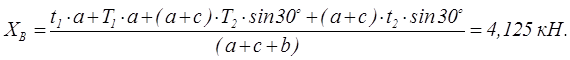
Составим уравнение равновесия сил в проекциях на ось х
![]()
откуда найдем,
![]()
Запишем уравнение моментов сил относительно оси х
![]()
тогда 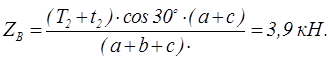
Составим уравнение равновесия в проекциях на ось z
![]()
откуда получим
![]()
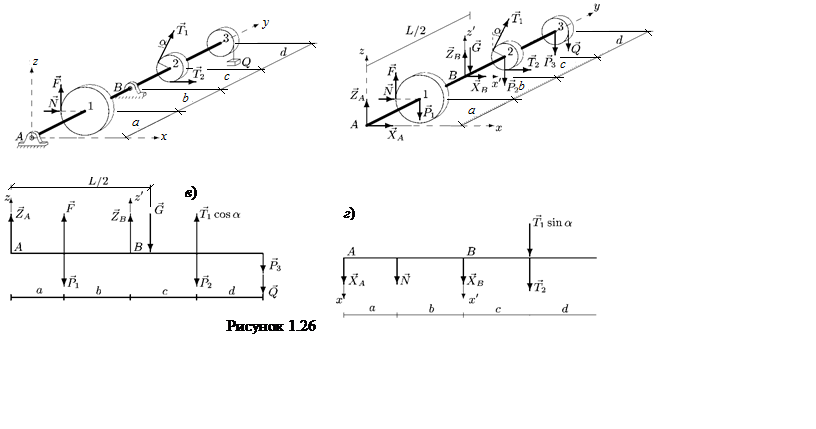
|
|
|
1. Действие цилиндрических опор А и В заменим реакциями ZA, ХА и ZB, ХB (см. рисунок 1.26,б). Вес вала G приложим в его центре. Вес груза изобразим вектором Q.
2. Для
определения силы давления запишем уравнение моментов относительно оси вала ![]()
Уравнение содержит одну неизвестную F. Линии действия остальных сил пересекают ось у и их моменты относительно оси вала равны нулю.
Из полученного уравнения находим
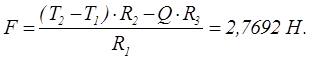
По условию N = F/0,1 = 27,692 Н.
3. Определяем вертикальные реакции шарнирных опор вала. Для этого составляем два уравнения моментов относительно горизонтальных осей, проходящих через шарниры А и В. Рассматриваем для удобства проекцию всех сил на плоскость zy (см. рисунок 1.26,в). Таким способом вычисление моментов относительно осей сводим к плоской задаче вычисления моментов относительно точек А и В.
Знаки моментов сил определяем как в задачах плоской статики: момент силы, стремящийся вращать тело вокруг моментной точки против часовой стрелки, считается положительным, по часовой стрелке - отрицательным. Моменты сил, перпендикулярных плоскости zy (и не изображенных на рисунке 1.26,в), относительно любой ее точки равны нулю.
Решая уравнения
![]()
![]()
![]()
![]()
получаем
![]()
![]()
4. Проверяем правильность нахождения вертикальных реакций, составляя уравнение равновесия в проекции на ось z (см. рисунок 1.26,в)
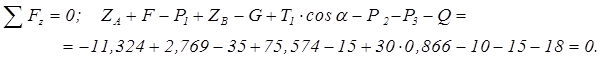
5. Определяем горизонтальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров. Рассматриваем горизонтальную проекцию силовой схемы (см. рисунок 1.26,г). Решая уравнения
![]()
![]()
получаем ХА = 25,1 Н, ХB= -124,792 Н.
6. Проверяем правильность нахождения горизонтальных реакций, составляя уравнение равновесия в проекции на ось х вдоль линии действия горизонтальных реакций
![]()
Реакции определены верно.
Пример
1.27 - Определить положение центра тяжести ![]() площади, ограниченной полуокружностью
площади, ограниченной полуокружностью ![]() радиусом
радиусом ![]() и
двумя прямыми равной длины
и
двумя прямыми равной длины ![]() и
и ![]() , причем
, причем ![]() (см.
рисунок 1.27,а).
(см.
рисунок 1.27,а).
Решение.
Проведем ось симметрии ![]() с началом в точке
с началом в точке ![]() (см. рисунок 1.27,б). Представленная
на рисунке фигура состоит из двух: 1 – полукруг
(см. рисунок 1.27,б). Представленная
на рисунке фигура состоит из двух: 1 – полукруг ![]() с
центром тяжести
с
центром тяжести ![]() ; 2 – треугольник
; 2 – треугольник ![]() с центром тяжести
с центром тяжести ![]() .
.
Обозначим через
![]() абсциссы точек
абсциссы точек ![]() и
через
и
через ![]() площади фигур 1 и 2. Найдем
площади фигур 1 и 2. Найдем
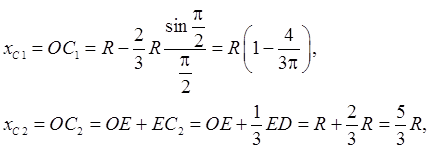
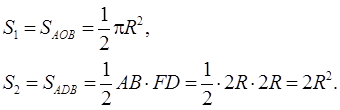
Подставляя
найденные соотношения в формулу 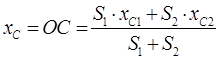 , получим
, получим
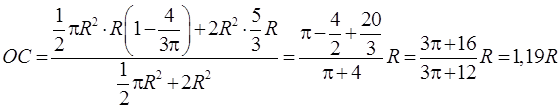 .
.
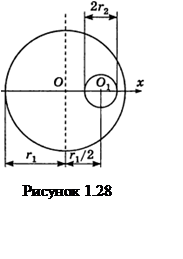
Пример
1.28 - Определить положение центра тяжести однородного диска с
круглым отверстием, предполагая радиус диска равным ![]() ,
радиус отверстия равным
,
радиус отверстия равным ![]() и центра этого
отверстия находящимся на расстоянии
и центра этого
отверстия находящимся на расстоянии ![]() от центра диска.
от центра диска.
Решение.
Введем систему координат с началом, совпадающим с центром диска ![]() (см. рисунок 1.28). Так как ось
(см. рисунок 1.28). Так как ось ![]() проходит и через центр отверстия, то
она является осью симметрии и, следовательно, центр тяжести будет располагаться
на этой оси. Обозначим диск без выреза фигурой 1 площадью
проходит и через центр отверстия, то
она является осью симметрии и, следовательно, центр тяжести будет располагаться
на этой оси. Обозначим диск без выреза фигурой 1 площадью ![]() и с центром тяжести
и с центром тяжести ![]() , отверстие – фигурой 2 площадью
, отверстие – фигурой 2 площадью ![]() и с центром тяжести
и с центром тяжести ![]() . Тогда получим
. Тогда получим
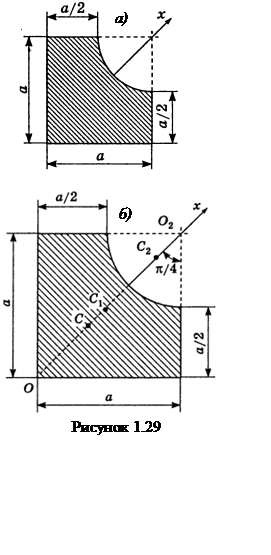
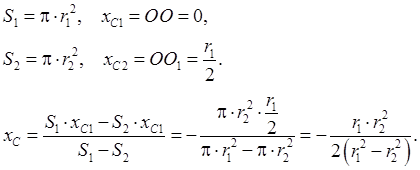
Пример 1.29 - Найти координаты центра тяжести фигуры, изображенной на рисунке 1.29,а.
Решение. Пусть
фигура 1 –квадрат без выреза; фигура 2 – вырез в четверть круга; а ![]() - соответственно площадь, центр
тяжести и координата центра тяжести фигуры
- соответственно площадь, центр
тяжести и координата центра тяжести фигуры ![]() -
аналогичные параметры фигуры 2, а центр тяжести
-
аналогичные параметры фигуры 2, а центр тяжести ![]() данной
фигуры имеет координату
данной
фигуры имеет координату ![]() (см. рисунок 1.29,б).
Тогда
(см. рисунок 1.29,б).
Тогда
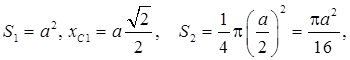
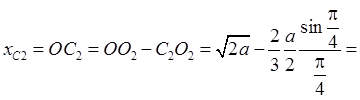
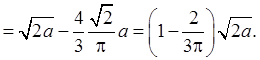
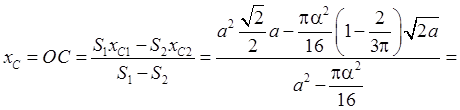
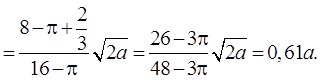
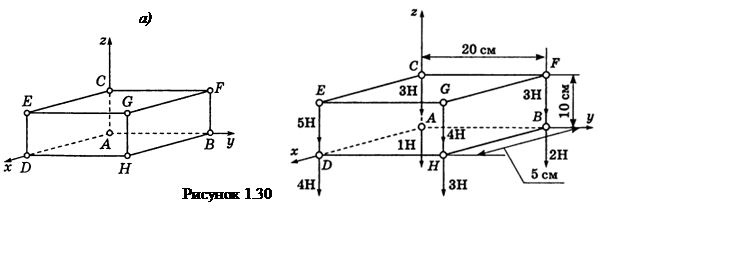
Пример
1.30 - Определить координаты центра тяжести системы грузов, расположенных
в вершинах прямоугольного параллелепипеда (см. рисунок 1.30,а), ребра
которого: ![]() см,
см, ![]() см,
см,
![]() см. Веса грузов в вершинах
см. Веса грузов в вершинах ![]() соответственно равны
соответственно равны ![]()
|
Тогда на основании рисунка 1.30,б получим
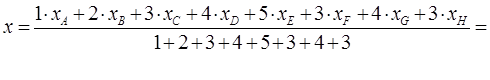
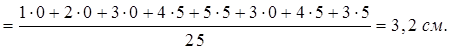
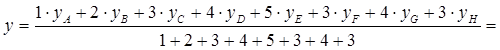
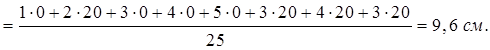
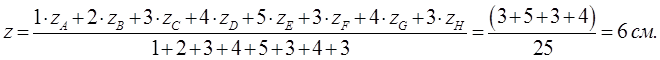
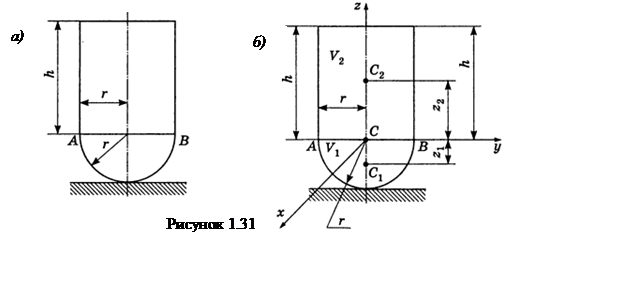
Пример
1.31 - Найти предельную высоту ![]() цилиндра,
при которой тело, состоящее из цилиндра и полушара
одинаковой плотности и одинакового радиуса
цилиндра,
при которой тело, состоящее из цилиндра и полушара
одинаковой плотности и одинакового радиуса ![]() (см.
рисунок 1.31,а), теряет устойчивость в положении равновесия, когда оно
опирается горизонтальную плоскость. (Центр тяжести всего тела должен совпадать
с центром полушара. Расстояние центра тяжести однородного полушара от его основание
равно
(см.
рисунок 1.31,а), теряет устойчивость в положении равновесия, когда оно
опирается горизонтальную плоскость. (Центр тяжести всего тела должен совпадать
с центром полушара. Расстояние центра тяжести однородного полушара от его основание
равно ![]() .)
.)
Решение. Потеря
устойчивости произойдет в том случае, если центр ![]() тяжести
тела окажется выше прямой
тяжести
тела окажется выше прямой ![]() (см. рисунок1.31,б).
В предельном случае центр тяжести совпадает с центром полушара. Тогда аппликату
центра тяжести тела находим как
(см. рисунок1.31,б).
В предельном случае центр тяжести совпадает с центром полушара. Тогда аппликату
центра тяжести тела находим как
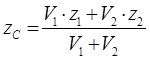 .
.
С учетом того,
что 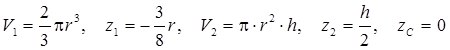 получим
получим
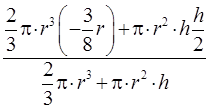 или
или 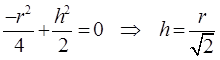 .
.
2 Кинематика
2.1 Основные понятия и задачи кинематики
Кинематика – раздел ТМ, в котором изучается МД материальных тел (их перемещение в пространстве с течением времени) без анализа условий, определяющих это движение. В качестве моделей материальных тел используются модели материальной точки (МТ) и механической системы (МС) или системы МТ. Однако, поскольку в кинематике понятие массы отсутствует, за материальную точку принимается геометрическая точка, а за МС – множество геометрических точек, в котором движение каждой точки зависит от положения и движения остальных его точек. Частным случаем такой системы является абсолютно твердое тело (АТТ) или просто твердое тело – множество геометрических точек, в котором расстояние между точками в любой момент времени остается неизменным.
Движение материальных тел в теоретической механике рассматривается относительно системы отсчета (СО). В СО входит тело отсчета и начало отсчета или связанная с телом отсчета система координатных осей. Телом отсчета называют тело, относительно которого изучается данное движение, а началом отсчета – некоторую точку тела отсчета.
В кинематике движение считается заданным, т.е. считаются известными функциями времени параметры, определяющие положение МС или какой-либо ее части относительно выбранной СО. По заданным законам движения отдельных точек или частей рассматриваемой МС определяются законы движения всей системы, других ее частей или точек, находятся их траектории, скорости и ускорения. Основными подразделами кинематики являются кинематика точки, кинематика твердого тела, сложное движение точки и сложное движение твердого тела.
2.2 Задачи кинематики точки
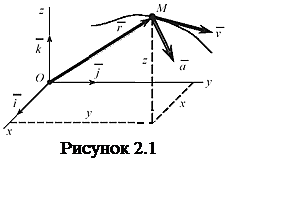
Движение МТ может быть задано векторным, координатным
или естественным способами. Векторный способ задания движения основан на задании
радиус–вектора ![]() точки, определяющего ее
положение относительно начала отсчета О, в виде функции времени (см. рисунок
2.1)
точки, определяющего ее
положение относительно начала отсчета О, в виде функции времени (см. рисунок
2.1)
![]() . (2.1)
. (2.1)
Кривую, описываемую в пространстве концом
радиус–вектора ![]() , называют траекторий точки. В
терминах векторной алгебры траектория точки – это годограф радиус–вектора точки
(вектор–функции
, называют траекторий точки. В
терминах векторной алгебры траектория точки – это годограф радиус–вектора точки
(вектор–функции ![]() скалярного аргумента t).
скалярного аргумента t).
При координатном способе задания движения вводится система координат, начало которой совмещается с началом отсчета О, и векторное уравнение (2.1) заменяется эквивалентной системой скалярных уравнений. Так, при использовании декартовой системы координат хОуz (см. рисунок 2.1) радиус–вектор точки представляется как
![]()
 где
где ![]() –
единичные вектора (орты) осей Ох, Оу, Оz;
–
единичные вектора (орты) осей Ох, Оу, Оz;
x,
y, z - координаты
точки (проекции ![]() на оси Ох, Оу, Оz).
на оси Ох, Оу, Оz).
Тогда уравнения движения (УД) точки записываются как
x = х(t); y = y(t); z = z(t). (2.2)
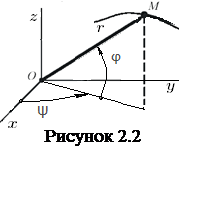
В сферических координатах (см. рисунок 2.2) УД точки имеют вид
r = r(t); φ = φ(t); y = y(t), (2.3)
где r – полярный радиус точки;
 φ, y - широта и
долгота точки.
φ, y - широта и
долгота точки.
Частным случаем уравнений (2.3) служат УД точки в полярных координатах
r = r(t); φ = φ(t). (2.4)
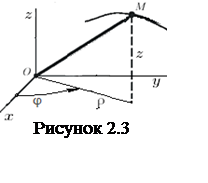
В цилиндрической системе координат для описания положения точки используют зависимости от времени радиуса r, угла φ и аппликаты z (см. рисунок 2.3)
r = r(t); φ = φ(t); z = z(t). (2.5)
Уравнения (2.2) – (2.5) можно рассматривать как уравнения траектории точки, представленные в параметрической форме (параметром служит время t). Исключая, например, из системы (2.4), параметр t, получим уравнение траектории точки в полярных координатах r = r(φ).
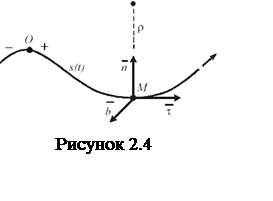 При задании движения естественным способом известными считаются
траектория точки и закон ее движения вдоль траектории, выражаемой зависимостью s
= s(t), где s
– дуга, которую описывает точка при движении вдоль траектории из начального положения
М0 в положение М (см. рисунок 2.4).
При задании движения естественным способом известными считаются
траектория точки и закон ее движения вдоль траектории, выражаемой зависимостью s
= s(t), где s
– дуга, которую описывает точка при движении вдоль траектории из начального положения
М0 в положение М (см. рисунок 2.4).
По известным уравнениям движения точки, записанным в
векторной или скалярной форме, можно найти ее скорость и ускорение. Вектор скорости
![]() характеризует
изменение радиус–вектора
характеризует
изменение радиус–вектора ![]() по величине и направлению, которое происходит при
движении точки вдоль траектории. При задании движения векторным способом вектор
скорости
по величине и направлению, которое происходит при
движении точки вдоль траектории. При задании движения векторным способом вектор
скорости ![]() определяется
равенством
определяется
равенством
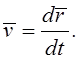 (2.6)
(2.6)
Вектор ![]() направлен по касательной к годографу радиус–вектора
направлен по касательной к годографу радиус–вектора ![]() (к
траектории точки) в сторону движения точки (см. рисунок 2.1).
(к
траектории точки) в сторону движения точки (см. рисунок 2.1).
 Вектор ускорения
Вектор ускорения ![]() , характеризующий изменение по величине и направлению
вектора скорости
, характеризующий изменение по величине и направлению
вектора скорости ![]() , определяется (см. рисунок. 2.5) как
, определяется (см. рисунок. 2.5) как
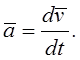
или с учетом (2.6) как
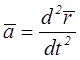
Если в некоторую точку О1 перенести
вектор скорости ![]() и
построить его годограф, то вектор ускорения
и
построить его годограф, то вектор ускорения ![]() будет направлен по касательной к годографу вектора
скорости
будет направлен по касательной к годографу вектора
скорости ![]() (см. рисунок 2.5).
(см. рисунок 2.5).
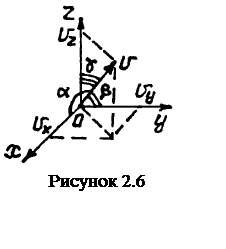 При
задании движения в декартовных координатах сначала находится проекции векторов
При
задании движения в декартовных координатах сначала находится проекции векторов ![]() и
и ![]() на оси
координат, затем подсчитываются их модули
на оси
координат, затем подсчитываются их модули
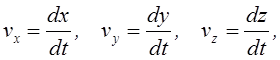
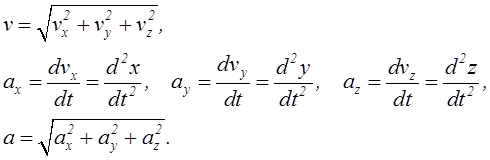
По полученным выражениям можно найти косинусы углов
α, β и γ (направляющие косинусы), которые составляет вектор ![]() (или
вектор
(или
вектор ![]() )
с осями координат Ох, Оу и Оz (см. рисунок
2.6)
)
с осями координат Ох, Оу и Оz (см. рисунок
2.6)
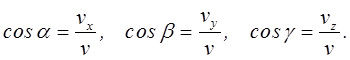
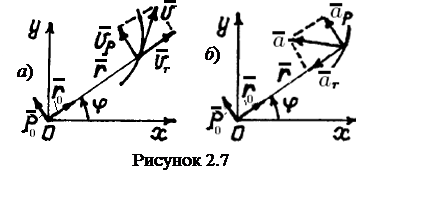 Если движение точки задано в полярных координатах,
вектора
Если движение точки задано в полярных координатах,
вектора ![]() и
и
![]() проецируются
на радиальное и трансверсальное (поперечное) направления, представляемые
единичными векторами
проецируются
на радиальное и трансверсальное (поперечное) направления, представляемые
единичными векторами ![]() и
и ![]() , приложенными в начале координат О. Радиальное
направление совпадает с направлением полярного радиуса, а трансверсальное образуется
поворотом вектора
, приложенными в начале координат О. Радиальное
направление совпадает с направлением полярного радиуса, а трансверсальное образуется
поворотом вектора ![]() на 90º против хода часовой стрелки (см. рисунок 2.7,а,б).
Проекции векторов
на 90º против хода часовой стрелки (см. рисунок 2.7,а,б).
Проекции векторов ![]() и
и ![]() на радиальное и трансверсальное направления определяются
равенствами
на радиальное и трансверсальное направления определяются
равенствами
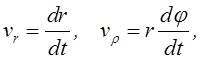
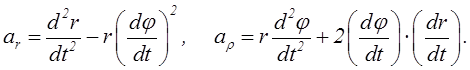
Так
как радиальное и трансверсальное направления взаимно перпендикулярны, то модули
векторов ![]() и
и
![]() подсчитывают
по формулам
подсчитывают
по формулам
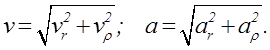
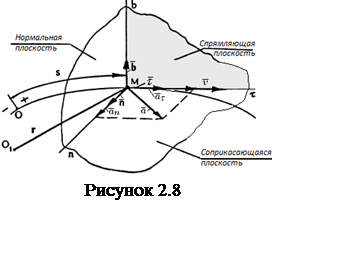 При
естественном способе задания движения для определения скорости и ускорения
вводится подвижная система координат с началом в движущейся точке и осями
естественного трехгранника: касательной t, нормальной n
и бинормальной b. Касательная ось направлена вдоль касательной к
траектории в данной точке в сторону возрастания координаты s,
нормальная ось – вдоль главной нормали к траектории к центру ее кривизны, а
бинормальная ось – перпендикулярно плоскости, образованной осями t и n (см. рисунок 2.8)так, чтобы вектора
При
естественном способе задания движения для определения скорости и ускорения
вводится подвижная система координат с началом в движущейся точке и осями
естественного трехгранника: касательной t, нормальной n
и бинормальной b. Касательная ось направлена вдоль касательной к
траектории в данной точке в сторону возрастания координаты s,
нормальная ось – вдоль главной нормали к траектории к центру ее кривизны, а
бинормальная ось – перпендикулярно плоскости, образованной осями t и n (см. рисунок 2.8)так, чтобы вектора ![]() ,
,![]() и
и ![]() образовывали правостороннюю систему
координат. Вектора
образовывали правостороннюю систему
координат. Вектора ![]() и
и ![]() представляются в виде
представляются в виде
![]()
где ![]() и
и ![]() – единичные вектора, определяющие
направления касательной и нормальной осей;
– единичные вектора, определяющие
направления касательной и нормальной осей;
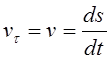 - проекция вектора
скорости точки на ось t
- проекция вектора
скорости точки на ось t
at, an – касательное и нормальное ускорения точки;
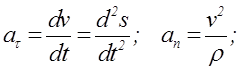
r - радиус кривизны траектории в данной точке.
Касательная составляющая ускорение (касательное или
тангенциальное ускорение) характеризует изменение скорости точки по величине, а
нормальная составляющая (нормальное ускорение) – по направлению. В прямолинейном
движении точки ее ускорение определяется только касательным ускорением at, а при движении точки по окружности с постоянной
скоростью v –
только нормальным ускорением an. Вектор ![]() направлен по касательной к траектории
в ту же сторону, что и вектор скорости
направлен по касательной к траектории
в ту же сторону, что и вектор скорости ![]() , или в
противоположную сторону, в зависимости от знака производной dv/dt. Вектор ускорения
, или в
противоположную сторону, в зависимости от знака производной dv/dt. Вектор ускорения ![]() всегда
направлен к центру кривизны (в сторону вогнутости) траектории точки. Так как
всегда
направлен к центру кривизны (в сторону вогнутости) траектории точки. Так как ![]() и
и ![]() взаимно
перпендикулярны, модуль вектора
взаимно
перпендикулярны, модуль вектора ![]() определяется как
определяется как
![]()
2.3 Задачи кинематики твердого тела
 Основными задачами кинематики АТТ являются разработка способов задания
его движения, изучение характеристик движения всего тела и отдельных его точек.
При изучении кинематики АТТ различают следующие виды движения: поступательное
движение, вращение вокруг неподвижной оси, плоское (или плоскопараллельное)
движение, вращение вокруг неподвижного центра и движение свободного твердого тела.
Для любого из этих видов движения справедлива следующая теорема, называемая
основной теоремой кинематики твердого тела: проекции скоростей двух точек
твердого тела на соединяющую их прямую в каждый момент времени равны. С помощью
этой теоремы можно определить скорость любой точки твердого тела по скоростям
трех его точек, не лежащих на одной прямой.
Основными задачами кинематики АТТ являются разработка способов задания
его движения, изучение характеристик движения всего тела и отдельных его точек.
При изучении кинематики АТТ различают следующие виды движения: поступательное
движение, вращение вокруг неподвижной оси, плоское (или плоскопараллельное)
движение, вращение вокруг неподвижного центра и движение свободного твердого тела.
Для любого из этих видов движения справедлива следующая теорема, называемая
основной теоремой кинематики твердого тела: проекции скоростей двух точек
твердого тела на соединяющую их прямую в каждый момент времени равны. С помощью
этой теоремы можно определить скорость любой точки твердого тела по скоростям
трех его точек, не лежащих на одной прямой.
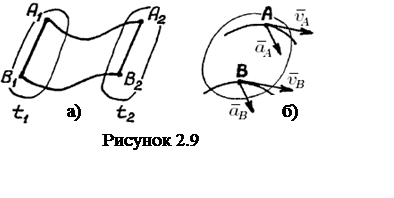
Поступательное движение твердого тела. Поступательным движением называется такое движение АТТ,
при котором прямая, соединяющая две любые точки тела в каждый момент времени
остается параллельной своему первоначальному положению (см. рисунок 2.9,а).
При поступательном движении твердого тела все его точки движутся по подобным
(конгруэнтным) траекториям с одинаковыми векторами скоростей и ускорений (![]()
![]() на рисунке 2.9,б). Поэтому
для задания движения и определения кинематических характеристик твердого тела,
совершающего поступательное движение, достаточно задать движение любой его
точки и определить ее кинематические характеристики.
на рисунке 2.9,б). Поэтому
для задания движения и определения кинематических характеристик твердого тела,
совершающего поступательное движение, достаточно задать движение любой его
точки и определить ее кинематические характеристики.
|
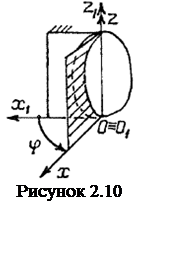
φ = φ(t),
где φ – двугранный угол между неподвижной относительно рассматриваемой СО плоскостью х1О1z1 и связанной с телом подвижной плоскостью хОz (см. рисунок 2.10).
Все точки тела описываются окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Вектор скорости любой точки твердого тела находится по формуле Эйлера
![]() (2.7)
(2.7)
где ![]() – радиус–вектор точки;
– радиус–вектор точки;
![]() -
вектор угловой скорости тела, направленный вдоль оси вращения и имеющий модуль,
который определяется производной
-
вектор угловой скорости тела, направленный вдоль оси вращения и имеющий модуль,
который определяется производной 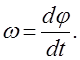
 За положительное направление вращения тела принимается направление,
которое наблюдатель, смотрящий с конца вектора
За положительное направление вращения тела принимается направление,
которое наблюдатель, смотрящий с конца вектора ![]() , видит противоположнным ходу часовой стрелки. Вектор
скорости
, видит противоположнным ходу часовой стрелки. Вектор
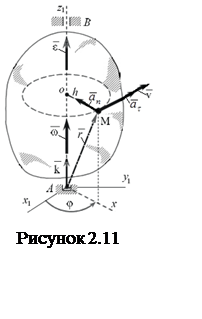
скорости ![]() направлен
по касательной к окружности радиуса h, которую
описывает точка вокруг оси вращения тела (см. рисунок 2.11). Модуль вектора
направлен
по касательной к окружности радиуса h, которую
описывает точка вокруг оси вращения тела (см. рисунок 2.11). Модуль вектора ![]() в
соответствии с формулой Эйлера подсчитывается как модуль векторного
произведения векторов
в
соответствии с формулой Эйлера подсчитывается как модуль векторного
произведения векторов ![]() и
и ![]() , т.е. v =w∙r∙sin(
, т.е. v =w∙r∙sin(![]() ) = w∙h.
) = w∙h.
Модуль вектора ![]() можно вычислить
по известным проекциям на оси системы координат хОуz вектора угловой
скорости тела wх, wу, wz и координатам
точки х, у, z. Представив правую часть (2.7) в виде
можно вычислить
по известным проекциям на оси системы координат хОуz вектора угловой
скорости тела wх, wу, wz и координатам
точки х, у, z. Представив правую часть (2.7) в виде
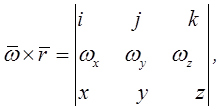
откуда получаем
vx = wy ∙z - wz ∙y, vy = wz∙ x - wx ∙z, vz = wx ∙y - wy ∙x,
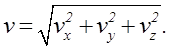
При определении вектора ускорения ![]() какой-либо
точки АТТ используем формулу Эйлера. Дифференцируя по времени равенство (2.7),
находим
какой-либо
точки АТТ используем формулу Эйлера. Дифференцируя по времени равенство (2.7),
находим
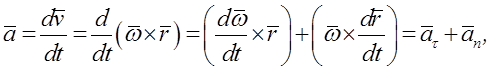
где ![]() – тангенциальная
и нормальная составляющие вектора
– тангенциальная
и нормальная составляющие вектора ![]() , равные
, равные
![]()
![]()
![]() – вектор
углового ускорения тела
– вектор
углового ускорения тела
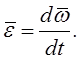
 Вектор углового ускорения
Вектор углового ускорения ![]() направлен
вдоль оси вращения тела в ту же сторону, что и вектор
направлен
вдоль оси вращения тела в ту же сторону, что и вектор ![]() , если
вращение тела ускоренное, или в обратную сторону, если вращение тела
замедленное. Поэтому тангенциальное ускорение
, если
вращение тела ускоренное, или в обратную сторону, если вращение тела
замедленное. Поэтому тангенциальное ускорение ![]() направлено по касательной к траектории точки в ту же
сторону, что и вектор
направлено по касательной к траектории точки в ту же
сторону, что и вектор ![]() , если вращение
тела ускоренное, или в обратную сторону, если вращение тела замедленное. Нормальное
ускорение
, если вращение
тела ускоренное, или в обратную сторону, если вращение тела замедленное. Нормальное
ускорение ![]() всегда
направлено по главной нормали к траектории точки, т.е. к оси вращения тела
вдоль радиуса описываемой точкой окружности (см. рисунок 2.11). Так как вектора
всегда
направлено по главной нормали к траектории точки, т.е. к оси вращения тела
вдоль радиуса описываемой точкой окружности (см. рисунок 2.11). Так как вектора
![]() и
и ![]() взаимно
перпендикулярны, модуль ускорения
взаимно
перпендикулярны, модуль ускорения ![]() находится как
находится как
![]()
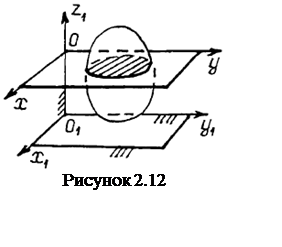
Плоскопараллельное движение твердого тела. Плоскопараллельным или плоским движением называют такое движение АТТ, при котором траектории всех точек тела расположены в плоскостях, параллельных некоторой неподвижной плоскости х1О1у1 (см. рисунок 2.12). При изучении плоского движения вместо движения всего тела рассматривают движение плоской фигуры – сечения тела плоскостью хОу, параллельной плоскости х1О1у1.
Движение плоской фигуры (плоское движение АТТ) задается как
xА = хА(t); yA = yA(t); φ = φ(t), (2.8)
где xА, yA – координаты некоторой точки (полюса) А плоской фигуры;
φ – угол поворота плоской фигуры (прямой, соединяющей полюс А с произвольной точкой В) относительно полюса А.
Согласно (2.8) движение плоской фигуры можно представить суммой двух движений: поступательного вместе с полюсом и вращательного вокруг полюса. Соответственно и скорость vB любой точки В плоской фигуры равна
![]() (2.9)
(2.9)
где ![]() – скорость полюса А;
– скорость полюса А;
![]() –
скорость точки В при вращении ее вокруг полюса А. При этом
условно предполагается, что через полюс А проходит ось вращения плоской
фигуры. Поэтому скорость
–
скорость точки В при вращении ее вокруг полюса А. При этом
условно предполагается, что через полюс А проходит ось вращения плоской
фигуры. Поэтому скорость ![]() , как и в случае вращения АТТ вокруг неподвижной оси,
определяется по формуле Эйлера
, как и в случае вращения АТТ вокруг неподвижной оси,
определяется по формуле Эйлера
![]()
где
![]() - вектор угловой скорости плоской фигуры;
- вектор угловой скорости плоской фигуры; ![]() –
радиус-вектор, определяющий положение точки В относительно полюса А.
–
радиус-вектор, определяющий положение точки В относительно полюса А.
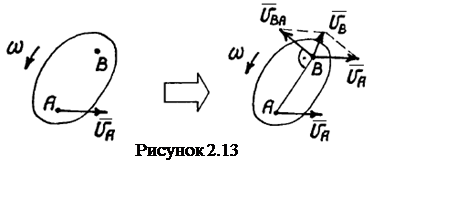 Равенство
(2.9) позволяет находить скорость
Равенство
(2.9) позволяет находить скорость ![]() любой точки В плоской фигуры, если известны угловая
скорость фигуры
любой точки В плоской фигуры, если известны угловая
скорость фигуры ![]() и
скорость
и
скорость ![]() какой-либо
другой ее точки А. Для этого в точку В переносится вектор
какой-либо
другой ее точки А. Для этого в точку В переносится вектор ![]() и
перпендикулярно радиусу АВ строится вектор
и
перпендикулярно радиусу АВ строится вектор ![]() с
учетом направления вращения плоской фигуры, которое определяет вектор
с
учетом направления вращения плоской фигуры, которое определяет вектор ![]() (см. рисунок 2.13). В результате геометрического сложения векторов
(см. рисунок 2.13). В результате геометрического сложения векторов ![]() и
и ![]() получается
искомый вектор
получается
искомый вектор ![]() .
.
Скорости точек плоской фигуры можно находить иначе, используя понятие мгновенного центра скоростей (МЦС). МЦС плоской фигуры – это такая точка Р, скорость которой в данный момент времени равна нулю. Точка Р может принадлежать плоской фигуре или лежать за ее пределами на плоскости хОу. Через точку Р в данный момент проходит мгновенная ось вращения твердого тела, перпендикулярная плоскости хОу. Поэтому согласно формуле Эйлера скорость любой точки А плоской фигуры описывается равенством
vA = w∙PA, (2.10)
 где РА – радиус окружности, которую описывает точка А
вокруг МЦС.
где РА – радиус окружности, которую описывает точка А
вокруг МЦС.
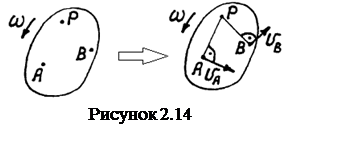
 Если
по условию задачи известны угловая скорость w плоской фигуры и
положение мгновенного центра скоростей Р, то для определения скорости
точки А (или любой другой точки В плоской фигуры) достаточно
соединить эту точку с центром Р, построить перпендикулярно радиусу РА
вектор
Если
по условию задачи известны угловая скорость w плоской фигуры и
положение мгновенного центра скоростей Р, то для определения скорости
точки А (или любой другой точки В плоской фигуры) достаточно
соединить эту точку с центром Р, построить перпендикулярно радиусу РА
вектор ![]() (для
точки В вектор
(для
точки В вектор ![]() перпендикулярно радиусу РВ) и с помощью формулы
(2.10) подсчитать его модуль (см. рисунок 2.14).
перпендикулярно радиусу РВ) и с помощью формулы
(2.10) подсчитать его модуль (см. рисунок 2.14).
При
решении обратной задачи, когда требуется найти положение мгновенного центра
скоростей Р и угловую скорость w плоской фигуры,
возможно следующие варианты. Допустим, что условием задачи заданы скорость ![]() в
какой-то одной точке А плоской фигуры и, по крайней мере, траектория движения
другой ее точки В. Для определения положения мгновенного центра Р
выполняется следующие построения. Через точку А проводится прямая MN,
перпендикулярная вектору
в
какой-то одной точке А плоской фигуры и, по крайней мере, траектория движения
другой ее точки В. Для определения положения мгновенного центра Р
выполняется следующие построения. Через точку А проводится прямая MN,
перпендикулярная вектору ![]() . Предположим, что точка В не принадлежит
прямой MN. Тогда через точку В перпендикулярно
касательной к ее траектории (вдоль которой направлен вектор
. Предположим, что точка В не принадлежит
прямой MN. Тогда через точку В перпендикулярно
касательной к ее траектории (вдоль которой направлен вектор ![]() скорости
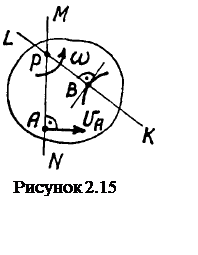
точки В), проводится прямая KL. Если прямые MN
и KL пересекаются, то в точке их пересечения находится
мгновенный центр скоростей Р (см. рисунок 2.15). Отрезки прямых РА
и РВ соответствует радиусам окружностей, которые описывают точки А
и В, вращаясь вокруг центра Р. Определяя расстояния РА, в
соответствии с формулой Эйлера находим угловую скорость плоской фигуры w
скорости
точки В), проводится прямая KL. Если прямые MN
и KL пересекаются, то в точке их пересечения находится
мгновенный центр скоростей Р (см. рисунок 2.15). Отрезки прямых РА
и РВ соответствует радиусам окружностей, которые описывают точки А
и В, вращаясь вокруг центра Р. Определяя расстояния РА, в
соответствии с формулой Эйлера находим угловую скорость плоской фигуры w
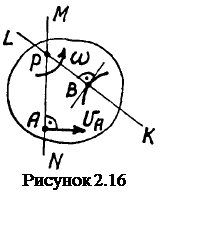
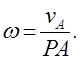 (2.11)
(2.11)
Если прямые MN и KL
оказываются параллельными, то это означает, что мгновенно центра скоростей в рассматриваемый
момент времени не существует (точка Р лежит в бесконечности). При этом
из (2.11) и (2.9) следует, что угловая скорость w плоской
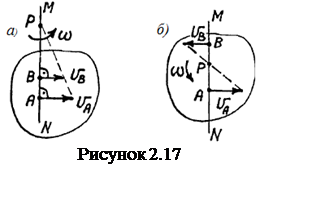
фигуры обращается в ноль, а скорость ![]() любой ее точки А становится равной скорости
любой ее точки А становится равной скорости ![]() любой
другой точки В (см. рисунок 2.16). Такое движение плоской фигуры
называется мгновенно-поступательным движением.
любой
другой точки В (см. рисунок 2.16). Такое движение плоской фигуры
называется мгновенно-поступательным движением.
 Теперь
предположим, что точка в расположена на прямой MN. В этом
случае для определения положения мгновенного центра скоростей Р и угловой
скорости w плоской фигуры необходимо знать модули и направления
скоростей точек А и В. Расстояния точек А и В до
мгновенного центра Р рассчитываются с помощью равенства (см. рисунок 2.17,а,б)
Теперь
предположим, что точка в расположена на прямой MN. В этом
случае для определения положения мгновенного центра скоростей Р и угловой
скорости w плоской фигуры необходимо знать модули и направления
скоростей точек А и В. Расстояния точек А и В до
мгновенного центра Р рассчитываются с помощью равенства (см. рисунок 2.17,а,б)
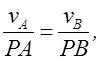
а угловая скорость w определяется выражением (2.11).
Ускорение
![]() любой
точки В плоской фигуры, как и ее скорость, можно представить суммой двух
слагаемых, характеризующих поступательное движение плоской фигуры вместе с полюсом
и вращательное движение вокруг полюса
любой
точки В плоской фигуры, как и ее скорость, можно представить суммой двух
слагаемых, характеризующих поступательное движение плоской фигуры вместе с полюсом
и вращательное движение вокруг полюса
![]() (2.12)
(2.12)
где ![]() – ускорение полюса А;
– ускорение полюса А;
![]() –
ускорение точки В при вращении ее вокруг полюса А;
–
ускорение точки В при вращении ее вокруг полюса А;
![]()
![]() ,
, ![]() – тангенциальная и нормальная составляющие вектора
– тангенциальная и нормальная составляющие вектора ![]() ,
,
![]()
![]()
![]() – вектор углового ускорения плоской фигуры.
– вектор углового ускорения плоской фигуры.
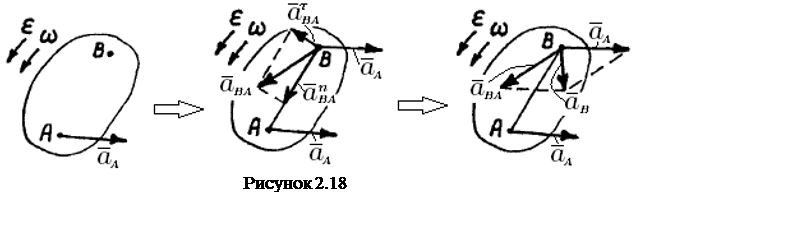 Как
видно, для определения ускорения
Как
видно, для определения ускорения ![]() с помощью формулы (2.12) необходимо знать ускорение
с помощью формулы (2.12) необходимо знать ускорение ![]() некоторой
точки А плоской фигуры, принимаемой за полюс, угловую скорость w и угловое ускорение ε плоской фигуры. Искомый вектор
некоторой
точки А плоской фигуры, принимаемой за полюс, угловую скорость w и угловое ускорение ε плоской фигуры. Искомый вектор ![]() получается
в результате геометрического сложения векторов
получается
в результате геометрического сложения векторов ![]() , который переносится в точку В, и составляющих
вектора
, который переносится в точку В, и составляющих
вектора ![]() .
Вектор
.
Вектор ![]() строится
перпендикулярно радиусу АВ в сторону, определяемую направлением
ускорения ε, а вектор
строится
перпендикулярно радиусу АВ в сторону, определяемую направлением
ускорения ε, а вектор ![]() – вдоль радиуса АВ к полюсу А (см. рисунок
2.18).
– вдоль радиуса АВ к полюсу А (см. рисунок
2.18).
Формула
(2.12) позволяет решать и обратную задачу, когда по заданным ускорениям ![]() и
и ![]() двух
точек плоской фигуры находится ее угловая скорость w и угловое ускорение ε. При этом используется взаимная
перпендикулярность векторов
двух
точек плоской фигуры находится ее угловая скорость w и угловое ускорение ε. При этом используется взаимная
перпендикулярность векторов ![]() и
и ![]() , которые
содержат угловую скорость и угловое ускорение в качестве сомножителей.
, которые
содержат угловую скорость и угловое ускорение в качестве сомножителей.
Ускорения точек плоской фигуры можно находить с помощью мгновенного центра ускорений (МЦУ). МЦУ плоской фигуры - это такая точка Q, ускорение которой в данный момент времени равно нулю. Как и МЦС, точка Q может принадлежать плоской фигуре или лежать за ее пределами на плоскости хОу. Причем, общем случае точки Р и Q не совпадают, т.е. скорость точки Q и ускорение точки Р отличны от нуля.
Из
формулы (2.12) следует, что если в качестве полюса выбрать МЦУ, то ускорение ![]() любой
точки В определяется суммой
любой
точки В определяется суммой
![]()
 Модули
векторов
Модули
векторов ![]() и
и
![]() выражаются
здесь равенствами
выражаются
здесь равенствами
![]() = ε∙ QВ,
= ε∙ QВ, ![]() = w2∙ QВ, (2.13)
= w2∙ QВ, (2.13)
а
вектор ![]() составляет
с направлением на МЦС (радиусом QВ на рисунке 2.19) угол α, тангенс которого
вычисляется по формуле
составляет
с направлением на МЦС (радиусом QВ на рисунке 2.19) угол α, тангенс которого
вычисляется по формуле
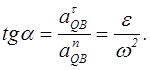 (2.14)
(2.14)
Как видно тангенс угла α зависит от значений угловой скорости w и углового ускорения ε, которые являются характеристиками движения плоской фигуры в целом. Поэтому вектор ускорения любой точки плоской фигуры составляет с отрезком, соединяющим эту точку с МЦУ, одинаковый угол α.
Для модуля вектора ![]() в соответствии с (2.13) можно записать
в соответствии с (2.13) можно записать
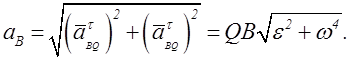 (2.15)
(2.15)
Аналогично определяется модуль вектора ускорения любой другой точки А плоской фигуры
![]() (2.16)
(2.16)
Из равенств (2.15), (2.16) находим
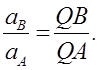 (2.17)
(2.17)
Т.о., модули ускорений точек плоской фигуры пропорциональны расстояниям этих точек до мгновенного центра ускорений Q.
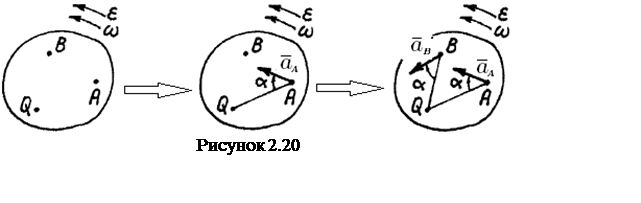
Формулы (2.14) – (2.17) позволяет решать следующие
задачи. Допустим, по известным значениям угловой скорости w, углового ускорения ε и заданному положению МЦУ (точка Q)
плоской фигуры требуется определить ускорение ![]() некоторой ее точки А. Для решения такой задачи
точку А соединяют с мгновенным центром Q и по
формуле (2.14) находят значение угла α. Под углом α к
радиусу QА,
отложенному в сторону, обратную знаку ускорения ε, строится искомый
вектор
некоторой ее точки А. Для решения такой задачи
точку А соединяют с мгновенным центром Q и по
формуле (2.14) находят значение угла α. Под углом α к
радиусу QА,
отложенному в сторону, обратную знаку ускорения ε, строится искомый
вектор ![]() (см. рисунок 2.20). Модуль вектора
(см. рисунок 2.20). Модуль вектора ![]() подсчитывают
с помощью равенства (2.16). Аналогичные построения выполняют при определении
ускорения
подсчитывают
с помощью равенства (2.16). Аналогичные построения выполняют при определении
ускорения ![]() любой
другой точки В плоской фигуры. Для вычисления модуля
любой
другой точки В плоской фигуры. Для вычисления модуля 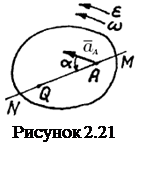 вектора
вектора ![]() удобно использовать равенство (2.17).
удобно использовать равенство (2.17).
Предположим теперь, что по значениям угловой скорости w плоской фигуры, ее углового ускорения ε и известному
ускорению ![]() какой-либо
точки А необходимо найти положение мгновенного центра ускорений Q.
Сначала по формуле (2.14) подсчитывается значение угла α. Затем
через точку А под углом α к вектору
какой-либо
точки А необходимо найти положение мгновенного центра ускорений Q.
Сначала по формуле (2.14) подсчитывается значение угла α. Затем
через точку А под углом α к вектору ![]() ,
отложенному в сторону, соответствующую направлению ускорения ε,
проводится прямая MN (см. рисунок 2.21.). На этой прямой на расстоянии
,
отложенному в сторону, соответствующую направлению ускорения ε,
проводится прямая MN (см. рисунок 2.21.). На этой прямой на расстоянии 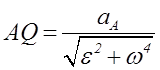 будет лежать мгновенный центр Q.
будет лежать мгновенный центр Q.
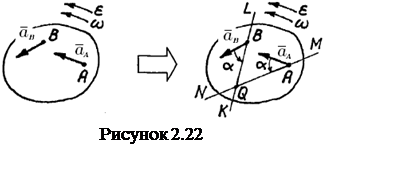 Если кроме угловой скорости w и углового
ускорения ε известны ускорения двух точек плоской фигуры
Если кроме угловой скорости w и углового
ускорения ε известны ускорения двух точек плоской фигуры ![]() и
и ![]() , то
мгновенный центр ускорений Q находится как точка пересечения прямых MN
и KL, проведенных через точки А и В,
соответственно, под углом α к векторам
, то
мгновенный центр ускорений Q находится как точка пересечения прямых MN
и KL, проведенных через точки А и В,
соответственно, под углом α к векторам ![]() и
и ![]() (см. рисунок 2.22). Значение угла α, как и в описанных
выше случаях, подсчитывается по формуле (2.14).
(см. рисунок 2.22). Значение угла α, как и в описанных
выше случаях, подсчитывается по формуле (2.14).
Вращение твердого тела вокруг неподвижного центра. Движение твердого тела называется вращением вокруг неподвижного центра (неподвижной точки), если одна из его точек в любой момент времени остается неподвижной. Для описания такого движения используется следующие зависимости
y = y(t); θ = θ(t); φ = φ(t), (2.18)
где y, θ, φ – углы Эйлера или углы прецессии, нутации и собственного вращения, соответственно.
Углы y, θ и φ определяют положение подвижной системы координат хОуz, связанной с вращающимся телом, относительно неподвижной системы х1О1у1z1. Угол прецессии y отсчитывается от оси О1х1 до линии узлов ОК (линии пересечения плоскостей х1О1у1 и хОу), угол собственного вращения φ – от линии узлов ОК до оси Ох (см. рисунок 2.23). Угол нутации θ определяется положение подвижной оси Оz относительно неподвижной О1z1.
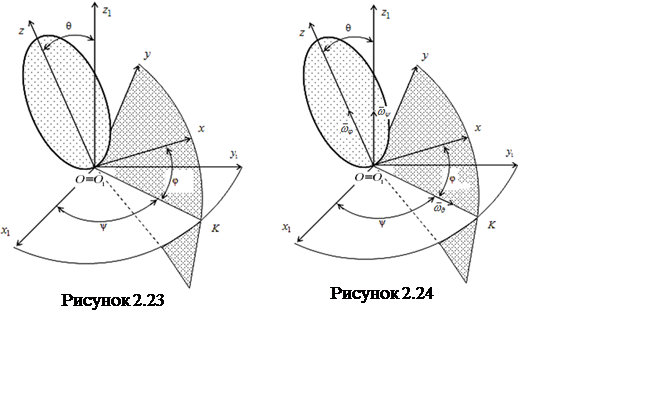 |
Согласно теореме Эйлера-Даламбера вращение твердого
тела вокруг неподвижного центра О можно рассматривать как непрерывную
последовательность бесконечно малых поворотов тела вокруг мгновенных осей
вращения, проходящих через точку О. Поворот тела вокруг мгновенной оси
происходит с мгновенной угловой скоростью ![]() , равной сумме (см. рисунок 2.24)
, равной сумме (см. рисунок 2.24)
![]() ,
(2.19)
,
(2.19)
где ![]() –
угловые скорости прецессии, нутации и собственного вращения, соответственно,
–
угловые скорости прецессии, нутации и собственного вращения, соответственно, 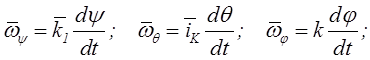
![]() – единичные вектора осей О1z1, Оz
и линии узлов.
– единичные вектора осей О1z1, Оz
и линии узлов.
Проецирование (2.19) на оси подвижной системы координат хОуz дает:
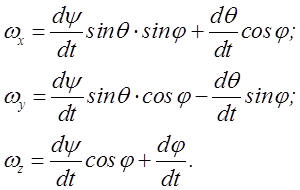 (2.20)
(2.20)
Уравнения (2.20), связывающие проекции вектора
мгновенной угловой скорости ![]() с зависимостями (2.18), называют кинематическими уравнениями
Эйлера.
с зависимостями (2.18), называют кинематическими уравнениями
Эйлера.
Скорость
![]() и
ускорение
и
ускорение ![]() любой
точки АТТ, вращающегося вокруг мгновенной оси с угловой скоростью
любой
точки АТТ, вращающегося вокруг мгновенной оси с угловой скоростью ![]() и
угловым ускорением
и
угловым ускорением ![]() , описываются теми же формулами, что и в случае
вращения АТТ вокруг неподвижной оси
, описываются теми же формулами, что и в случае
вращения АТТ вокруг неподвижной оси
![]()
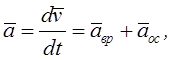 (21)
(21)
где ![]() – радиус–вектор точки;
– радиус–вектор точки;
![]() ,
, ![]() –
вращательная и осестремительная составляющие вектора
–
вращательная и осестремительная составляющие вектора ![]()
![]()
![]()
В отличие от случае вращения тела вокруг неподвижной
оси при вращении тела вокруг мгновенной оси вектор угловой скорости ![]() изменяется
и по модулю и по направлению. Поэтому характеризующий изменение вектора
изменяется
и по модулю и по направлению. Поэтому характеризующий изменение вектора ![]() вектор
углового ускорения
вектор
углового ускорения ![]() будет направлен по касательной к пространственной
кривой, которую описывает конец вектора
будет направлен по касательной к пространственной
кривой, которую описывает конец вектора ![]() (к
годографу вектора
(к
годографу вектора ![]() ), не совпадающей, как это было в случае вращения тела
вокруг неподвижной оси, с мгновенной осью вращения.
), не совпадающей, как это было в случае вращения тела
вокруг неподвижной оси, с мгновенной осью вращения.
Движение свободного твердого тела. Свободным твердым телом называется твердое тело, на перемещение которого не наложено никаких связей.
Движение свободного твердого тела, подобно плоскому движению, представляется суммой двух движений: поступательного вместе с полюсом и вращательного вокруг полюса. Но в отличие от плоского движения вращение вокруг полюса рассматривается здесь как вращение вокруг неподвижного центра. С учетом этой особенности скорости и ускорения точек свободного твердого тела определяется теми же формулами (2.9) и (2.12), которые приводились для плоского движения.
2.4 Задачи на сложное движение точки
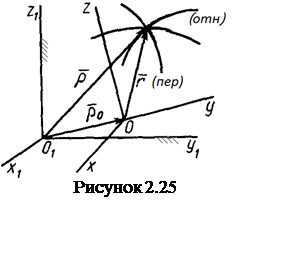 Движение точки М считается сложным, когда она одновременно
участвует в двух (или более) движениях: движении относительно подвижной системы
координатах хОуz и движении вместе с подвижной системой координат относительно
неподвижной х1О1у1z1 (см. рисунок 2.25). Движение
точки М относительно подвижной системы называется относительным движением,
движение точки М вместе с подвижной системой относительно неподвижной –
переносным движением, а движение точки М относительно неподвижной
системы – абсолютным движением.
Движение точки М считается сложным, когда она одновременно
участвует в двух (или более) движениях: движении относительно подвижной системы
координатах хОуz и движении вместе с подвижной системой координат относительно
неподвижной х1О1у1z1 (см. рисунок 2.25). Движение
точки М относительно подвижной системы называется относительным движением,
движение точки М вместе с подвижной системой относительно неподвижной –
переносным движением, а движение точки М относительно неподвижной
системы – абсолютным движением.
Скорости точки М в абсолютном, относительном и переносном движениях в соответствии с теоремой сложения скоростей связаны соотношением
![]()
где ![]() ,
, ![]() ,
, ![]() – абсолютная, относительная и переносная скорости
точки М.
– абсолютная, относительная и переносная скорости
точки М.
Абсолютное ускорение ![]() точки М согласно теореме сложения ускорений
(теореме Кориолиса) определяется суммой
точки М согласно теореме сложения ускорений
(теореме Кориолиса) определяется суммой
![]() ,
,
где ![]() ,
, ![]() – относительное и переносное ускорения точки М;
– относительное и переносное ускорения точки М;
![]() –
ускорение Кориолиса.
–
ускорение Кориолиса.
Относительное движение обычно задается естественным способом. Поэтому (см. раздел 2.2)
![]()
![]()
где ![]() ,
, ![]() – единичные вектора, направленные вдоль касательной и
нормали к траектории относительного движения точки М; vt - проекция вектора относительной скорости точки М
на направление касательной к траектории относительного движения точки М
– единичные вектора, направленные вдоль касательной и
нормали к траектории относительного движения точки М; vt - проекция вектора относительной скорости точки М
на направление касательной к траектории относительного движения точки М
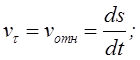
s
– дуга, которую описывает точка М в относительном движении вдоль
траектории; ![]() ,
, ![]() –
касательная и нормальная составляющие относительного ускорения точки М
–
касательная и нормальная составляющие относительного ускорения точки М
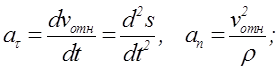
r - радиус кривизны траектории относительного движения точки М.
Переносное движение – это движение относительного
неподвижной системы координат той точки твердого тела, связанного с подвижной СО,
в которой в данный момент времени находится точка М. Поэтому модули и
направления векторов ![]() и
и ![]() находят по правилам, справедливым для соответствующего
вида движения твердого тела (см. раздел 2.3).
находят по правилам, справедливым для соответствующего
вида движения твердого тела (см. раздел 2.3).
Ускорение Кориолиса, характеризующее взаимное влияние относительного и переносного движений, определяется векторным произведением
![]() ,
,
где ![]() - вектор угловой скорости переносного движения.
- вектор угловой скорости переносного движения.
2.5 Задачи на сложные движения твердого тела
Движение твердого тела называется сложным, если его можно представить, как результат сложения двух (или более) движений: движения относительно подвижной системы координат хОуz (относительно движения) и движения вместе с подвижной системой координат относительно неподвижной х1О1у1z1 (переносного движения).
 Сложение поступательных движений. Так как при поступательном движении все точки АТТ
имеют подобные траектории, одинаковые скорости и ускорения, задачи кинематики
такого тела заменяются задачами кинематики точки (см. раздел 2.3). Поэтому,
когда относительное и переносное движения твердого тела является
поступательными, его абсолютное (сложное) движение будет также поступательным и
абсолютная скорость любой точки тела
Сложение поступательных движений. Так как при поступательном движении все точки АТТ
имеют подобные траектории, одинаковые скорости и ускорения, задачи кинематики
такого тела заменяются задачами кинематики точки (см. раздел 2.3). Поэтому,
когда относительное и переносное движения твердого тела является
поступательными, его абсолютное (сложное) движение будет также поступательным и
абсолютная скорость любой точки тела ![]() определяется теоремой сложения скоростей (см. раздел 2.4)
определяется теоремой сложения скоростей (см. раздел 2.4)
![]()
где ![]() ,
, ![]() –
скорости тела в относительном и переносном движениях.
–
скорости тела в относительном и переносном движениях.
Сложение вращательных движений вокруг пересекающихся
осей. Если твердое тело одновременно
вращается вокруг двух пересекающихся осей, то его абсолютным (сложным)
движением будет вращение с абсолютной угловой скоростью ![]() , равной
геометрической сумме угловых скоростей переносного
, равной
геометрической сумме угловых скоростей переносного ![]() и относительного вращений (см. рисунок 2.26)
и относительного вращений (см. рисунок 2.26)
![]()
Сложение вращательных движений вокруг параллельных
осей с угловыми скоростями, направленными в одну сторону. При одновременном вращении АТТ вокруг двух
параллельных осей с угловыми скоростями переносного ![]() и
относительного
и
относительного ![]() вращений,
направленными в одну сторону, его абсолютным (сложным) движением будет вращение
с абсолютной угловой скоростью
вращений,
направленными в одну сторону, его абсолютным (сложным) движением будет вращение
с абсолютной угловой скоростью ![]() , направленной в ту же сторону, и модулем, равным сумме
модулей угловых скоростей переносного и относительного вращений (см. рисунок
2.27)
, направленной в ту же сторону, и модулем, равным сумме
модулей угловых скоростей переносного и относительного вращений (см. рисунок
2.27)
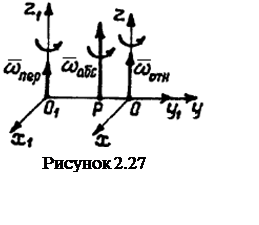 wабс = wпер + wотн.
wабс = wпер + wотн.
Вектор ![]() направлен вдоль мгновенной оси, которая делит внутренним
образом кратчайшее расстояние между осями переносного и относительного вращений
на части, обратно пропорциональные модулям угловых скоростей переносного и
относительного вращений
направлен вдоль мгновенной оси, которая делит внутренним
образом кратчайшее расстояние между осями переносного и относительного вращений
на части, обратно пропорциональные модулям угловых скоростей переносного и
относительного вращений
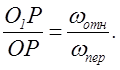
Сложение вращательных движений вокруг параллельных
осей с угловыми скоростями, направленными в разные стороны. При одновременном вращении АТТ вокруг двух
параллельных осей с угловыми скоростями переносного ![]() и
относительного
и
относительного ![]() вращений,
направленными в разные стороны, его абсолютным (сложным) движением будет
вращение с абсолютной угловой скоростью
вращений,
направленными в разные стороны, его абсолютным (сложным) движением будет
вращение с абсолютной угловой скоростью ![]() , направленной в сторону большей угловой скорости, и
модулем, равным разности модулей угловых скоростей переносного и относительного
вращений (см. рисунок 2.28)
, направленной в сторону большей угловой скорости, и
модулем, равным разности модулей угловых скоростей переносного и относительного
вращений (см. рисунок 2.28)
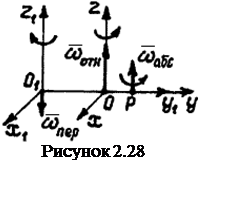 wабс = wпер + wотн.
wабс = wпер + wотн.
Вектор ![]() направлен вдоль мгновенной оси, которая делит внешним образом
кратчайшее расстояние между осями переносного и относительного вращений на
части, обратно пропорциональные модулям угловых скоростей переносного и относительного
вращений
направлен вдоль мгновенной оси, которая делит внешним образом
кратчайшее расстояние между осями переносного и относительного вращений на
части, обратно пропорциональные модулям угловых скоростей переносного и относительного
вращений
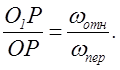
В случае, когда wпер = wотн, т.е. когда переносное и относительное вращения АТТ происходят с равными по модулю и противоположными по направлению угловыми скоростями, абсолютным (сложным) движением тела будет поступательное движение. Совокупность двух вращательных движений АТТ вокруг параллельных осей с угловыми скоростями, равными по модулю и противоположными по направлению, называют парой вращений.
2.6 Примеры решения задач кинематики
Пример 2.1 – Точка М движется в плоскости xOy согласно уравнениям x=2a∙cos2(k∙t/2), y=a∙sin(k∙t), где a и k – положительные постоянные. Определить уравнения движения точки в полярных координатах.
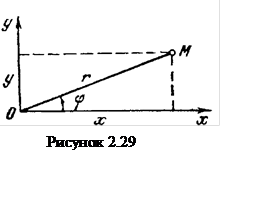 Решение. Для
решения задачи используем формулы, связывающие полярные координаты с
декартовыми (см. рисунок 2.29)
Решение. Для
решения задачи используем формулы, связывающие полярные координаты с
декартовыми (см. рисунок 2.29)
![]() . (1)
. (1)
Переписывая заданные уравнения движения в виде
![]() (2)
(2)
и сравнивая равенства (1) с уравнениями (2), получим уравнения движения точки в полярных координатах:
![]() .
.
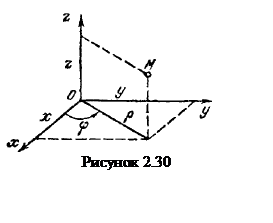 Пример 2.2
– Точка движется по винтовой линии x =a∙cos(k∙t), y =
a∙sin(k∙t), z = v∙t. Определить уравнения движения
точки в цилиндрических координатах.
Пример 2.2
– Точка движется по винтовой линии x =a∙cos(k∙t), y =
a∙sin(k∙t), z = v∙t. Определить уравнения движения
точки в цилиндрических координатах.
Решение. Для решения задачи используем формулы, связывающие цилиндрические координаты с декартовыми (см. рисунок 2.30)
![]() . (1)
. (1)
Сравнивая равенства (1) с заданными уравнениями движения, находим уравнения движения точки в цилиндрических координатах
![]()
Пример 2.3 – По данным уравнениям движения точки найти уравнения ее траектории в координатной форме и указать на рисунке направление движения.
|
а) x = 3t - 5, y = 4 - 2t. |
б) x = 2t, y = 8t2. |
|
в) x = 5 sin10t, y = 3 cos10t. |
г) x = 2 - 3 cos 5t, y = 4 sin 5t - 1. |
|
д) x = ch t = 1/2 (et + e-t), y = sh t = 1/2 (et - e-t). |
|
Решение. Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по уравнениям движения, заданным в виде
![]() (1)
(1)
записать уравнение траектории в координатной форме, достаточно из уравнений системы (1) исключить параметр t. Ниже приводится решение для всех случаев; в графическом виде найденные траектории показаны на рисунке 2.31.
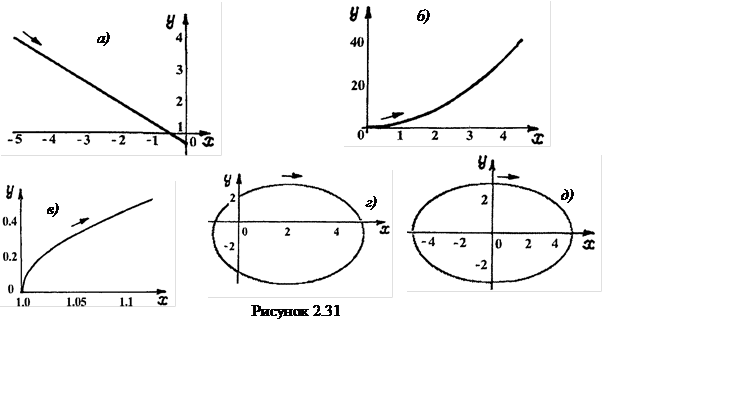
Из заданных в условии задачи уравнений, находим
а) 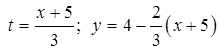 или
или ![]()
Координаты начальной точки определяем из уравнений движения при t =0: x =-5; y=4.
б) 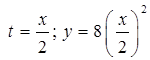 или
или
![]()
Координаты начальной точки определяем из уравнений движения при t=0: x= 0, y=0.
в) 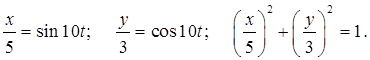
Полученное уравнение – уравнение эллипса с центром в начале координат и полуосями а = 5, b = 3. Координаты начальной точки определяем из уравнений движения при t = 0: x = 0, y = 3.
г) 
Полученное уравнение – уравнение эллипса с центром в точке х = 2, у = -1 и полуосями а = 3, b = 4. Координаты начальной точки определяем из уравнений движения при t = 0: x = -1, y = -1.
д) 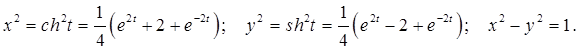
Полученное уравнение – уравнение равнобочной гиперболы. Координаты начальной точки определяем из уравнений движения при t = 0: x = 1, y = 0.
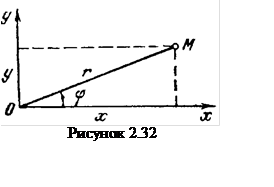 Пример 2.4
– Точка участвует одновременно в двух взаимно перпендикулярных затухающих
колебаниях, уравнения которых имеют вид x = A∙e-ht ∙cos(kt
+ ε), y = =A∙e-ht sin(kt + ε), где
A>0, h>0, k>0 и ε - некоторые постоянные.
Определить уравнения движения в полярных координатах и найти траекторию точки.
Пример 2.4
– Точка участвует одновременно в двух взаимно перпендикулярных затухающих
колебаниях, уравнения которых имеют вид x = A∙e-ht ∙cos(kt
+ ε), y = =A∙e-ht sin(kt + ε), где
A>0, h>0, k>0 и ε - некоторые постоянные.
Определить уравнения движения в полярных координатах и найти траекторию точки.
Решение. Для решения задачи используем формулы, связывающие полярные координаты с декартовыми (см. рисунок 2.32)
![]() (1)
(1)
Сравнивая равенства (1) с заданными уравнениями движения, находим уравнения движения точки в полярных координатах
![]() (2)
(2)
Уравнения (2) можно рассматривать как уравнения траектории точки, представленные в параметрической форме. Поэтому для записи уравнения траектории достаточно из системы (2) исключить параметр t
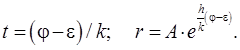
Полученное уравнение – уравнение логарифмической спирали.
Пример 2.5 – По заданным уравнениям движения точки найти уравнение ее траектории, а также указать закон движения точки по траектории, отсчитывая расстояние от начального положения точки.
|
а) x = 3t2, y = 4t2. |
б) x = 3 sin t, y = 3 cos t. |
|
в) x = a cos2 t, y = a sin2 t. |
г) x = 5 cos 5t2, y = 5 sin 5t2. |
Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движения
![]() (1)
(1)
Записать уравнение траектории в координатной форме, достаточно из уравнений системы (1) исключить параметр t. Для определения закона движения точки вдоль траектории используется известная формула для дифференциала плоской дуги ds
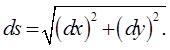 (2)
(2)
Из уравнений, заданных в условии задачи, находим
а) 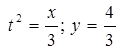 или
или ![]()
Полученное уравнение – уравнение прямой. Координаты начальной точки определяем из уравнений движения при t = 0: x = 0, y = 0. По формуле (2) вычисляем дифференциал дуги
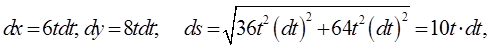
и записываем закон движения точки по траектории
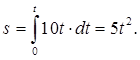
б) 
Полученное уравнение – уравнение окружности с центром в начале координат и радиусом R = 3. Координаты начальной точки определяем из уравнений движения при t = 0: x = =0, y = 3. По формуле (2) вычисляем дифференциал дуги
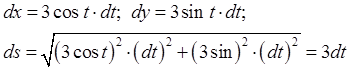
и записываем закон движения точки по траектории
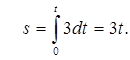
в) 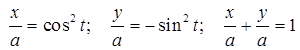 или
или ![]()
Полученное уравнение – уравнение отрезка прямой (0 ≤ х ≤ а). Координаты начальной точки определяем из уравнений движения при t = 0: x = 0, y = 0. По формуле (2) вычисляем дифференциал дуги
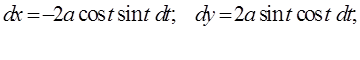
![]()
и записываем закон движения точки по траектории
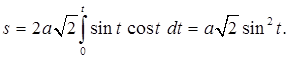
г) 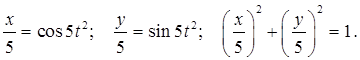
Полученное уравнение – уравнение окружности с радиусом R = 5 и центром в начале координат. Координаты начальной точки определяем из уравнений движения при t = 0: x = 5, y = 0. По формуле (2) вычисляем дифференциал дуги
![]()
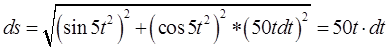
и записываем закон движения точки по траектории
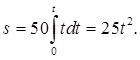
Пример 2.6 – Движение точки, описывающей фигуру Лиссажу, задается уравнениями x=3sint, y=2cos2t (t - в секундах). Найти уравнение траектории, вычертить ее и указать направление движения точки в различные моменты времени. Указать также ближайший после начала движения момент времени t1, когда траектория пересечет ось Ox.
Решение. Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движения записать уравнение траектории в координатной форме, достаточно из уравнений движения исключить параметр t. Используя известные формулы тригонометрии, находим из заданных уравнений движения
![]() или 4х2 + 9у = 18.
или 4х2 + 9у = 18.
Полученное уравнение – уравнение части параболы, ось которой совпадает с осью Оу (см. рисунок 2.33).
Координаты положение точки в различные моменты времени определяем из уравнений движения. При t = 0: х = 0, у = 2; при t = 0,5: х = 1,438, у = 1,08. Момент t1 при котором траектория движения точки пересекает ось Ох, находим из равенства у = 0
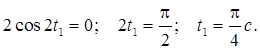
Пример 2.7 – Груз, поднятый на упругом канате, колеблется согласно уравнению x=a sin(kt+Зπ/2), где a - в сантиметрах, k - в рад/с. Определить амплитуду и круговую частоту колебаний груза, если период колебаний равен 0,4 с и в начальный момент x0=-4 см. Построить также кривую расстояний.
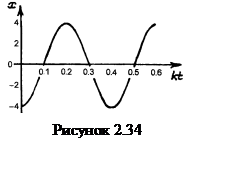 Решение. При t = 0 из уравнения колебаний находим амплитуду
колебаний
Решение. При t = 0 из уравнения колебаний находим амплитуду
колебаний
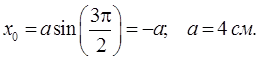
По известному периоду колебаний Т подсчитываем круговую частоту k
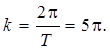
Кривая расстояний, т.е. зависимости х = х(kt), приведена на рисунке 2.34.
Пример 2.8 – Определить траекторию точки, совершающей одновременно два гармонических колебания равной частоты, но разных амплитуд и фаз, если колебания происходят по двум взаимно перпендикулярным осям: x=a sin(kt+α), y=b sin(kt+β).
Решение. Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движениям записать уравнение траектории в координатной форме, достаточно из уравнений движения исключить параметр t. Используя формулы тригонометрии, представим
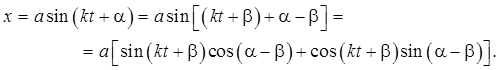
Учитывая, что
![]()
находим
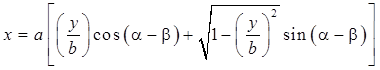
или
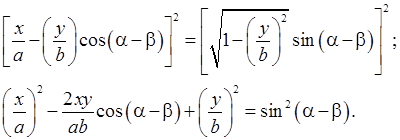
Полученное уравнение – уравнение эллипса с осями, повернутыми относительно осей системы координаты хОу.
Пример 2.9 – Найти уравнение траектории движения точки, получающегося при сложении взаимно перпендикулярных колебаний разной частоты:
1) x = a sin 2ωt, y = a sin ωt;
2) x = a cos 2ωt, y = a cos ωt.
Решение. Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движения записать уравнение траектории в координатной форме, достаточно из уравнений движения исключить параметр t. Используя известные формулы тригонометрии, находим
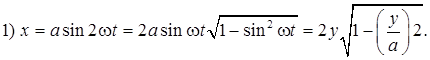
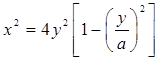 или
или ![]()
Полученное уравнение – уравнение фигуры Лиссажу, показанной на рисунке 2.35 при a=3, ω=1.
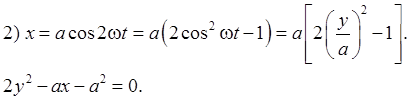
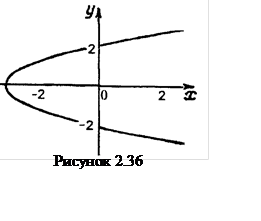 Полученное уравнение –
уравнение параболы, показанной на рисунке 2.36 при a=3,
ω=1.
Полученное уравнение –
уравнение параболы, показанной на рисунке 2.36 при a=3,
ω=1.
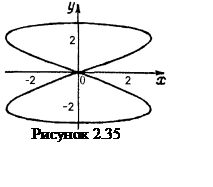
Пример 2.10 – Даны уравнения движения точки x = 2a cos2(kt/2), y = a sin kt, где a и k - положительные постоянные. Определить траекторию и закон движения точки по траектории, отсчитывая расстояние от начального положения точки.
Решение. Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движения записать уравнение траектории в координатной форме, достаточно из уравнений движения исключить параметр t. Используя известные формулы тригонометрии, находим
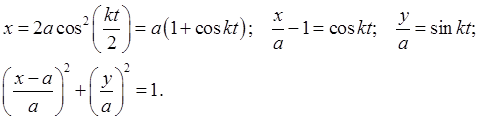
Полученное уравнение – уравнение окружности с радиусом а и центром, смещенным по оси абсцисс вправо на расстояние а. Координаты начальной точки определяем из уравнений движения при t = 0: x = 2a, y = 0.
При записи закона движения точки по траектории используем формулу для дифференциала плоской дуги ds
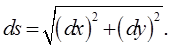
Из уравнений движения имеем
![]()
Следовательно,
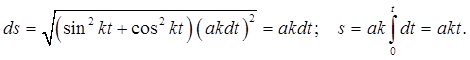
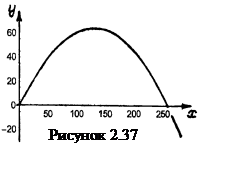 Пример 2.11
– Даны уравнения движения снаряда x = v0 cos α t, y = v0
sin α t - gt2/2, где v0 — начальная
скорость снаряда, α — угол между v0 и горизонтальной
осью x, g — ускорение силы тяжести. Определить траекторию движения
снаряда, высоту H, дальность L и время T полета снаряда.
Пример 2.11
– Даны уравнения движения снаряда x = v0 cos α t, y = v0
sin α t - gt2/2, где v0 — начальная
скорость снаряда, α — угол между v0 и горизонтальной
осью x, g — ускорение силы тяжести. Определить траекторию движения
снаряда, высоту H, дальность L и время T полета снаряда.
Решение. Уравнения движения снаряда можно рассматривать как уравнения его траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движения записать уравнение траектории в координатной форме, достаточно из уравнений движения исключить параметр t.
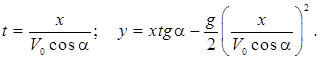
Полученное уравнение – уравнение параболы.
Время Т и дальность L полета найдем из уравнений движения при условии, что х = L, у = 0, когда t = Т
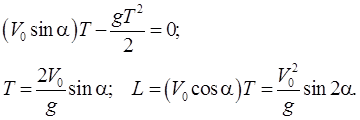
При определении
высоты полета снаряда Н учтем, что в высшей точке траектории снаряда 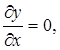 и из уравнения траектории получим
и из уравнения траектории получим
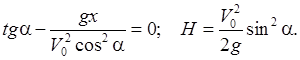
На рисунке 2.37 показана траектория снаряда, построенная при V0 = 50; g = 9,8; α = π/4.
Пример 2.12 – В условиях предыдущей задачи определить, при каком угле бросания α дальность полета L будет максимальной. Найти соответствующие высоту и время полета.
Решение. Решением предыдущей задачи для дальности полета L была получена следующая формула
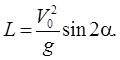 (1)
(1)
Эту формулу можно рассматривать как выражение функции L = L(α), экстремальное значение которой находится из равенства
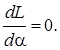 (2)
(2)
Подстановка выражения (1) и равенство (2) дает
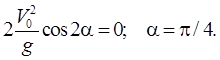
Т.е. при α = π / 4 функция L = L(α) достигает экстремального значения
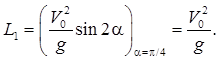
Это значение будет максимальным, если при α = π / 4 выполняется условие
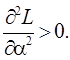 (3)
(3)
В данном случае
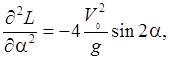
и условие (3) выполняется.
Из решения предыдущей задачи находим высоту Н1 и время Т1 полета, соответствующей максимальной дальности L1
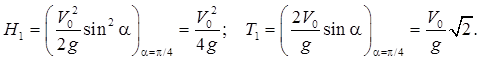
Пример 2.13 – Кривошип OA вращается с постоянной угловой скоростью ω=10 рад/с. Длина OA=AB=80 см. Найти уравнения движения и траекторию средней точки M шатуна, а также уравнение движения ползуна B, если в начальный момент ползун находился в крайнем правом положении; оси координат указаны на рисунке 2.38,а.
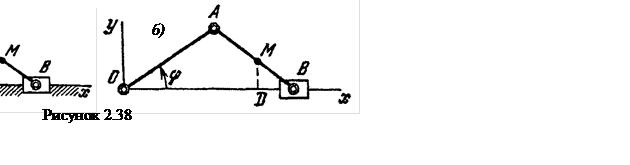
Решение. Уравнения движения точки М будем записывать в виде зависимостей хМ = х(t); yM = y (t), где хМ, yM – координаты точки М. Получаем (см. рисунок 2.38,б)
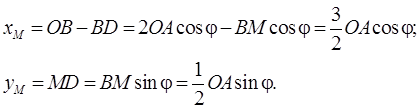
Учитывая, что φ = wt, и подставляя численные значения параметров, получим
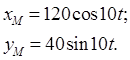 (1)
(1)
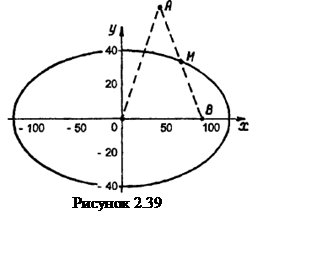 Уравнения движения точки
М можно рассматривать как уравнения ее траектории, представленные в
параметрической форме. Поэтому для того, чтобы записать уравнение траектории в
координатной форме, достаточно из уравнений (1) исключить параметр t. Находим
Уравнения движения точки
М можно рассматривать как уравнения ее траектории, представленные в
параметрической форме. Поэтому для того, чтобы записать уравнение траектории в
координатной форме, достаточно из уравнений (1) исключить параметр t. Находим
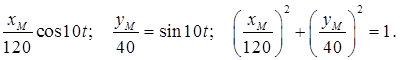
Полученное уравнение – уравнение эллипса с центром в начале координат и полуосями а = 120 см, b = 40 см (см. рисунок 2.39).
Ползун В движется вдоль оси Ох. Поэтому его движение описывается следующим уравнением
![]()
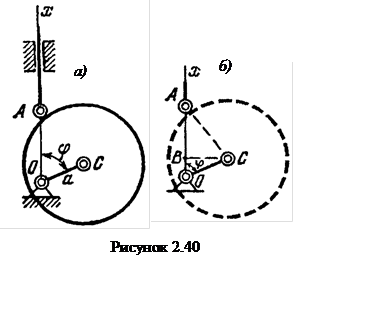 Пример 2.14
– Найти закон движения стержня (см. рисунок 2.40,а), если диаметр эксцентрика
d=2r, а ось вращения O находится от оси диска C на
расстоянии OC=a, ось Ox направлена по стержню, начало отсчета —
на оси вращения, a/r=λ.
Пример 2.14
– Найти закон движения стержня (см. рисунок 2.40,а), если диаметр эксцентрика
d=2r, а ось вращения O находится от оси диска C на
расстоянии OC=a, ось Ox направлена по стержню, начало отсчета —
на оси вращения, a/r=λ.
Решение. Стержень, установленный в направляющих, движется поступательно. Для того, чтобы найти закон его движения, достаточно записать уравнение движения любой его точки, например, точки А. Представим координату точки А суммой
![]() (1)
(1)
Из ∆ОВС и ∆АВС имеем (см. рисунок 2.40,б)
ОВ = ОС cos φ = a cosφ;
![]()
Подставим эти выражения в равенство (1), получим
![]()
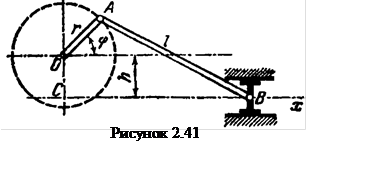 Пример 2.15
– Написать уравнение движения поршня нецентрального кривошипно-ползунного
механизма. Расстояние от оси вращения кривошипа до направляющей линейки h,
длина кривошипа r, длина шатуна l; ось Cx направлена по
направляющей ползуна (см. рисунок 2.41). Начало отсчета расстояний — в крайнем
правом положении ползуна; l/r=λ, h/r=k, φ=ω0t.
Пример 2.15
– Написать уравнение движения поршня нецентрального кривошипно-ползунного
механизма. Расстояние от оси вращения кривошипа до направляющей линейки h,
длина кривошипа r, длина шатуна l; ось Cx направлена по
направляющей ползуна (см. рисунок 2.41). Начало отсчета расстояний — в крайнем
правом положении ползуна; l/r=λ, h/r=k, φ=ω0t.
Решение. Когда точка В (поршень механизм) находится в ее крайнем правом положении кривошип ОА и шатун АВ образуют одну прямую (см. рисунок 2.42,а). Согласно условию задачи это положение точки В принимает за начало отсчета ее координаты хВ и последующее движение точки В происходит справа налево. Представим
![]() (1)
(1)
где хВ0, хВ1 – расстояние ВС при начальном и текущем положениях поршня (см. рисунок 2.42,а,б).
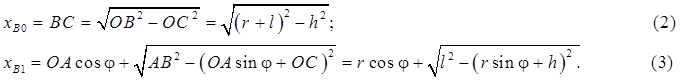
Подстановка выражений (2), (3) в равенство (1) дает
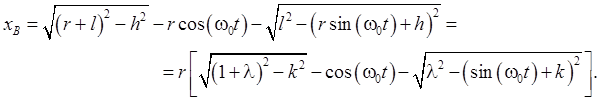
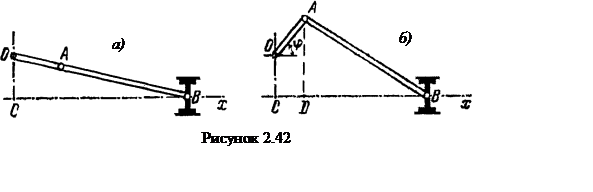 |
Пример 2.16 – Точка совершает гармонические колебания по закону x=a sin kt. Определить амплитуду a и круговую частоту k колебаний, если при x=x1 скорость v=v1, а при x=x2 скорость v=v2.
Решение. Сначала по заданному закону движения точки определяем ее скорость для любого момента времени
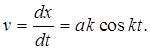
Затем находим значения скорости в моменты времени t1 и t2, когда х = х1 и х = х2
![]() (1)
(1)
При этом
![]() (2)
(2)
Из равенств (1), (2) записываем
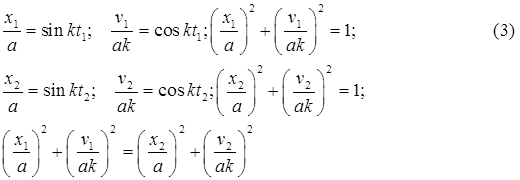
или
![]()
Отсюда
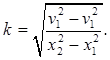
Для определения амплитуды колебаний а перепишем последнее из равенств (3) в виде
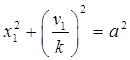
и используем полученное выражение для частоты k
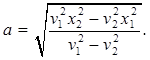
Пример 2.17 – Длина линейки эллипсографа AB=40 см, длина кривошипа OC=20 см, AC=CB (см. рисунок 2.43). Кривошип равномерно вращается вокруг оси O с угловой скоростью ω. Найти уравнения траектории и годографа скорости точки M линейки, лежащей на расстоянии AM=10 см от конца A.
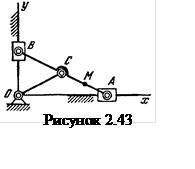 Решение. Прежде
всего составим уравнения движения точки М. Запишем выражения для
координат точки М
Решение. Прежде
всего составим уравнения движения точки М. Запишем выражения для
координат точки М
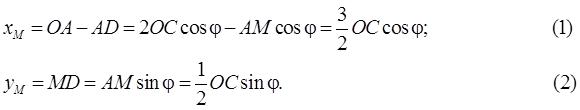
Кривошип вращается равномерно с угловой скоростью w, тогда после подстановки φ = wt равенства (1), (2) принимают вид уравнений движения точки М
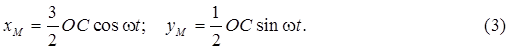
Уравнения (3) можно рассматривать как уравнения траектории, представленные в параметрической форме – координаты хМ и уМ выражены через параметр t. Исключая из уравнений (3) параметр t, находим
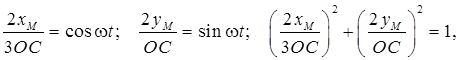
или после подстановки численных значений параметров эллипсографа
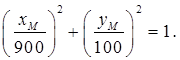
Уравнение траектории точки М, полученное путем исключения параметра t из уравнений (3), является уравнением годографа радиус-вектора точки М (см. рисунок 2.44,а).
Для записи
уравнения годографа скорости точки М используем тот же прием: составляем
выражения для проекций вектора скорости точки М, определяющие координаты
х1, у1 конца вектора ![]() (точки
М1 на рисунке 2.44,б), из которых затем исключаем
параметр t
(точки
М1 на рисунке 2.44,б), из которых затем исключаем
параметр t
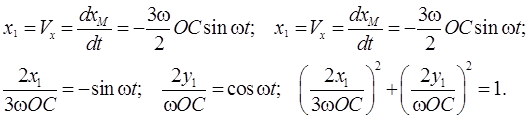
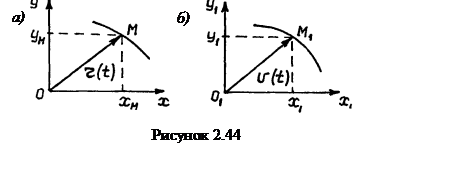 |
После подстановки численных значений параметров эллипсографа получаем
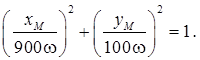
Пример
2.18 – Точка описывает фигуру Лиссажу согласно уравнениям
x = 2 cos t, y = 4 cos 2t (x, y - в сантиметрах, t —
в секундах). Определить величину и направление скорости точки, когда она
находится на оси Oy.
Решение. Для определения скорости точки сначала находим ее проекции vx и vу
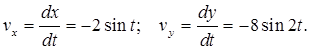 (1)
(1)
Если точка находится на оси Оу, то х = 0 и, следовательно, cost = 0. Отсюда вычисляем соответствующие моменты времени: t = π/2, 3 π/2, … Подстановка этих значений t в выражения (1) дает
![]()
Пример 2.19 – Кривошип OA вращается с постоянной угловой скоростью ω. Найти скорость середины M шатуна кривошипно-ползунного механизма и скорость ползуна B в зависимости от времени, если OA=AB=a (см. рисунок 2.38).
Решение. Составим уравнения движения точки М, представив ее координаты в виде
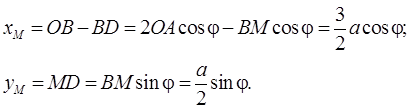
Учитывая, что φ = wt, записываем уравнения движения точки М
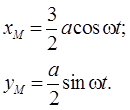
Затем определяем проекции скорости точки М и ее модуль
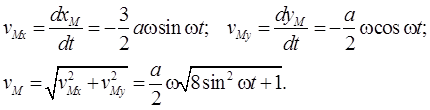
Ползун В совершает прямолинейное движение вдоль оси Ох, которое описывается уравнениями
![]()
Отсюда находим проекции и модуль скорости ползуна В
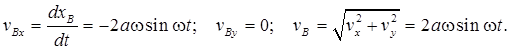
Пример 2.20 – Движение точки задано уравнениями x = v0t cos α0, y = v0t sin α0 – gt2/2,
причем ось Ox горизонтальна, ось Oy направлена по вертикали вверх, v0, g и α0<π/2 - величины постоянные. Найти: траекторию точки; координаты наивысшего ее положения; проекции скорости на координатные оси в тот момент, когда точка находится на оси Ox.
Решение. Уравнения движения точки можно рассматривать как уравнения ее траектории, представленные в параметрической форме. Поэтому, чтобы по заданным уравнениям движения записать уравнение траектории форме, достаточно из уравнений движения исключить параметр t. Тогда
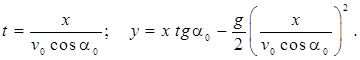
Полученное уравнение – уравнение параболы.
Для определения
координат наивысшего положения точки х1, у1
используем уравнение его траектории. Учитывая, что в этой точке траектории 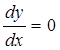 , находим
, находим
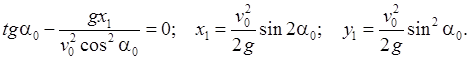
Проекции скорости для любого момента времени находим из уравнений движения
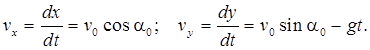 (1)
(1)
Момент времени t = t2, когда точка находится на оси Ох, определяем из уравнений движения, полагая у = 0
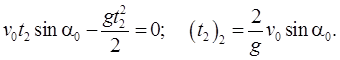
Подстановка полученного значения t2 в выражения (1) дает
![]()
Отметим, что координаты х1,у1 можно найти иначе, учитывая, что в верхней точке траектории vy = 0.
Пример 2.21 – Движение точки задано теми же уравнениями, что и в предыдущей задаче, причем v0=20 м/с, α0=60°, g=9,81 м/с2. Найти, с какой скоростью v1 должна выйти из начала координат в момент t=0 вторая точка для того, чтобы, двигаясь равномерно по оси Ox, она встретилась с первой точкой, и определить расстояние х1 до места встречи.
Решение. Так как движение второй точки происходит вдоль оси Ох, ее встреча с первой точки возможна, если уравнение движения второй точки имеет вид
![]()
Отсюда
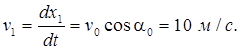
Первая точка пересекает ось Ох в момент t = t1, когда у = 0. Используем это условие для определения момента t1
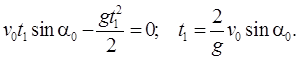
Подставив полученное выражение для t1 в уравнение движения второй точки, получим
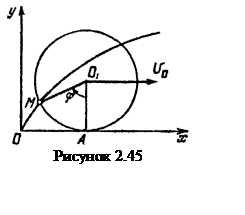
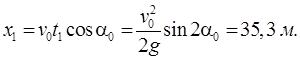
Пример 2.22 – Определить уравнения движения и траекторию точки обода колеса радиуса R=1 м автомобиля, если автомобиль движется по прямолинейному пути с постоянной скоростью 20 м/с. Принять, что колесо катится без скольжения; за начало координат взять начальное положение точки на пути, принятом за ось Ox.
Решение. Определим координаты точки М в момент времени, когда повернется на некоторый угол φ (см. рисунок 2.45)
![]() (1)
(1)
Так как автомобиль движется прямолинейно с постоянной скоростью, то
![]() (2)
(2)
Поскольку колесо катится по плоскости без скольжения, то через точку А касания колеса с плоскостью проходит мгновенная ось, вокруг которой в данный момент происходит вращение колеса с угловой скоростью ω, определяемой как
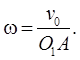 (3)
(3)
Учитывая, что ![]() и подставляя (2) и (3) в (1), получаем
и подставляя (2) и (3) в (1), получаем
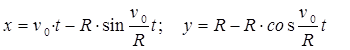
|
![]() (4)
(4)
Полученные уравнения (4) являются уравнениями циклоиды в параметрической форме.
Пример 2.23 - Заданы уравнения движения точки (х, у - в сантиметрах, t - в секундах)
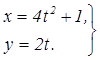 (1)
(1)
Определить траекторию точки и для момента времени t1 = 1 с найти положение точки на траектории, скорость и ускорение точки, касательную и нормальную составляющие ускорения, радиус кривизны в соответствующей точке траектории.
Решение.
1. Уравнения (1) можно рассматривать как уравнения траектории точки в параметрической форме, где параметром является время t. Чтобы найти уравнение траектории в координатной форме, исключим из (1) параметр t. В результате получим
x = y2+ 1 . (2)
Это - уравнение параболы с осью симметрии Ox (см. рисунок 2.46). Из (1) следует, что координаты x и y все время положительны, так как время t≥ 0. Значит, траекторией точки является верхняя ветвь параболы, показанная на рисунке 2.46 сплошной линией.
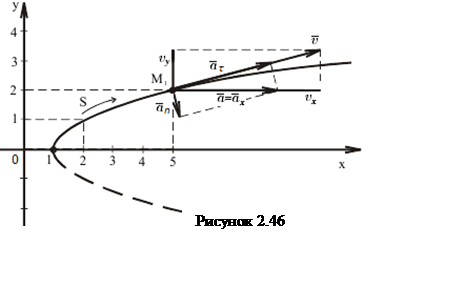 2.
Подставляя значение времени
t1=1с в (1), найдем положение точки
в указанный
момент времени
2.
Подставляя значение времени
t1=1с в (1), найдем положение точки
в указанный
момент времени
х1 = 5 см, у1 = 2 см (3)
и покажем его на траектории (точка M1 на рисунке 2.20).
3. Для определения скорости ![]() точки найдем проекции вектора скорости
на оси координат
точки найдем проекции вектора скорости
на оси координат
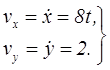 (4)
(4)
По найденным проекциям нетрудно найти модуль скорости и ее направление
![]() (5)
(5)
В момент времени t1 = 1 с
vx = 8 см/с, vy = 2 см/с, v = 8,124 см/с. (6)
На основании (6) строим в точке M1 траектории
вектор скорости ![]() как геометрическую сумму
составляющих
как геометрическую сумму
составляющих ![]() и
и ![]() где
где
![]() ,
, ![]() - орты осей x и y ). При этом вектор
- орты осей x и y ). При этом вектор ![]() должен быть направлен по
касательной к траектории точки (см. рисунок 2.20).
должен быть направлен по
касательной к траектории точки (см. рисунок 2.20).
4. Аналогично найдем ускорение ![]() точки по его проекциям на
координатные оси
точки по его проекциям на
координатные оси
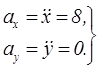 (7)
(7)
![]() (8)
(8)
Из (7) и (8) следует, что в данном случае проекции вектора ускорения на оси координат, а также его модуль не зависят от времени t, т.е. являются постоянными величинами. Для момента времени t1 = 1 с из (7) и (8) находим
![]()
![]() (9)
(9)
![]() (10)
(10)
По найденным значениям строим в точке M1 вектор скорости ![]() как
геометрическую сумму составляющих
как
геометрическую сумму составляющих![]() и
и ![]() В рассматриваемом случае
В рассматриваемом случае ![]() (см.
рисунок 2.20).
(см.
рисунок 2.20).
5. Определим касательную и нормальную составляющие ускорения точки. Касательная составляющая ускорения характеризует изменение вектора скорости по модулю, а нормальная - по направлению.
Модуль касательного ускорения точки ![]() можно найти
на основании формулы
можно найти
на основании формулы
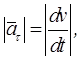 (11)
(11)
тогда с учетом (5) производную dv/dt можно представить в виде
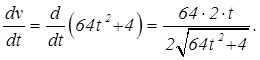 (12)
(12)
Для момента времени t1= 1 с на основании (12) с учетом (6) и (9) получим
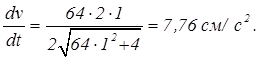 (13)
(13)
Т.о., модуль касательного ускорения точки в момент времени t1 = 1 с
![]() (14)
(14)
Знак "+" при dv/dt
показывает, что модуль скорости возрастает, т.е. движение точки является
ускоренным и направления векторов ![]() и
и ![]() совпадают (см. рисунок 2.20).
совпадают (см. рисунок 2.20).
Модуль нормального ускорения точки определим по формуле
![]() (15)
(15)
Для момента времени t1 = 1 с, учитывая (8) и (14), на основании (15) получим
![]() (16)
(16)
Нормальное ускорение точки направлено перпендикулярно касательному ускорению
в сторону вогнутости траектории (см. рисунок 2.20). Ускорение ![]() найдено как по составляющим
найдено как по составляющим ![]() так и по составляющим
так и по составляющим ![]() чем проверяется правильность проведенных
вычислений.
чем проверяется правильность проведенных
вычислений.
6. Радиус кривизны траектории ρ в рассматриваемой точке можно определить на основании формулы для нормального ускорения
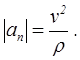 (17)
(17)
Тогда в точке M1 траектории, учитывая (6), (16) и (17), получим
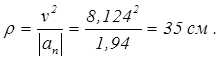
Пример 2.24 – Определить угловую скорость:
1) секундной стрелки часов;
2) минутной стрелки часов;
3) часовой стрелки часов;
4) вращения Земли вокруг своей оси, считая, что Земля делает один оборот за 24 часа;
5) паровой турбины Лаваля, варащающейся со суоростью 15000 об/мин.
Решение. Угловая скорость w, измеряемая в рад/с, связана с числом n оборотов в минуту равенством
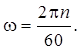
Используя это равенство, находим:
1) для секундной стрелки
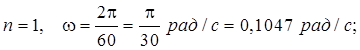
2) для минутной стрелки (один оборот в 1 час)
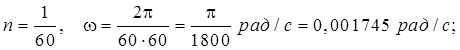
3) для часовой стрелки (один оборот за 12 часов)
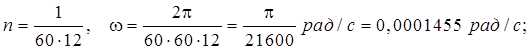
4) для вращения Земли (один оборот за 24 часа)
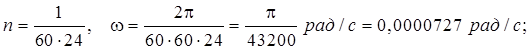
5) для паровой турбины Лаваля
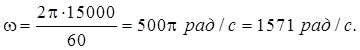
Пример 2.25 – Написать уравнение вращения диска паровой турбины при пуске в ход, если известно, что угол поворота пропорционален кубу времени и при t=3 с угловая скорость диска равна ω=27π рад/с.
Решение. Зависимость угла поворота диска φ от времени t имеет вид
![]()
где k – коэффициент пропорциональности.
Значение коэффициента k – определяем по известной угловой скорости w диска в момент t = 3 с
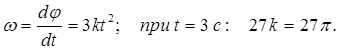
![]()
Следовательно, k = π, и при уравнение вращения диска паровой турбины применяем вид
![]()
Пример 2.26 - Маятник центробежного регулятора, вращающийся вокруг вертикальной оси AB, делает 120 об/мин. В начальный момент угол поворота был равен π/6 рад. Найти угол поворота и угловое перемещение маятника за время t=1/2 с.
Решение. При вращении маятника с постоянной угловой скоростью его угол поворота φ определяется зависимостью
![]() (1)
(1)
где φ0 – начальное значение угла поворота маятника.
В условии задачи скорость вращения маятника задана числом оборотом в минуту n, которое связано с угловой скорость w, измеряемой в рад/с, равенством
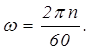 (2)
(2)
Подставляя численные значения в выражения (1), (2), находим
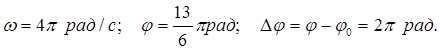
Пример 2.27 – Тело, начиная вращаться равноускоренно из состояния покоя, делает 3600 оборотов в первые 2 минуты. Определить угловое ускорение.
Решение. При вращении тела с постоянным угловым ускорением ε его угол поворота φ определяется зависимостью
![]()
где φ0, w0 – начальные значения угла поворота и угловой скорости тела.
Согласно условию задачи при t = 0: φ0 = w0 =0, а при t = 120 с φ = 3600 ∙ 2π = 7200 π рад. Следовательно,
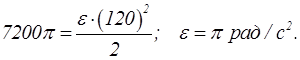
Пример 2.28 – Вал начинает вращаться равноускоренно из состояния покоя; в первые 5 с он совершает 12,5 оборота. Какова его угловая скорость по истечении этих 5 с?
Решение. При вращении вала с постоянным угловым ускорением ε его угол поворота φ и угловая скорость w определяются зависимостями
![]()
где φ0, w0 – начальные значения угла поворота и угловой скорости вала.
Согласно условию задачи при t = 0: φ0 = w0 =0, а спустя t = 5 с, φ = 12,5∙2π = 25π рад. Следовательно,
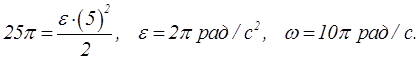
Пример 2.29 – Маховое колесо начинает вращаться из состояния покоя равноускоренно; через 10 мин после начала движения оно имеет угловую скорость, равную 4π рад/с. Сколько оборотов сделало колесо за эти 10 мин?
Решение. При вращении колеса с постоянным угловым ускорением ε его угол поворота φ и угловая скорость w определяются зависимостями
![]() (1)
(1)
где φ0, w0 – начальные значения угла поворота и угловой скорости колеса.
Полагая в равенствах (1) φ0 = w0 =0, w = 4 π; t = 10∙60 = 600 с, находим
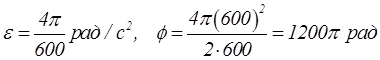
или в числах оборотов
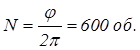
Пример 2.30 – Тело совершает колебания около неподвижной оси, угол поворота выражается уравнением φ = 20° sin ψ, где угол ψ выражен в угловых градусах зависимостью ψ=(2t)°, причем t берется в секундах. Определить угловую скорость тела в момент t=0, ближайшие моменты t1 и t2, в которые изменяется направление вращения, и период колебания T.
Решение. Переписав
уравнение движения тела в виде 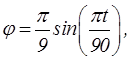 находим угловую
скорость тела ω
находим угловую
скорость тела ω
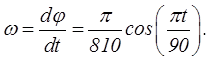 (1)
(1)
Отсюда: при t = 0, 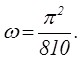
При определении моментов времени t1 и t2 учтем, что в моменты перемены направления вращения тела его угловая скорость обращается в нуль. Используя выражение (1), найдем
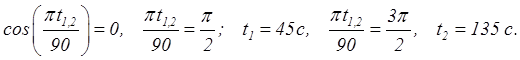
Моменты t1 и t2 разделяет половина периода Т (время размаха колебаний). Следовательно,
![]()
Отметим, что период колебаний Т можно определить иначе, переписав уравнение колебаний тела в общем для гармонический колебаний виде
![]()
где k - частота колебаний, связанная с периодом Т
известной формулой 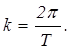
 Пример 2.31
– Часовой балансир совершает крутильные гармонические колебания с периодом T=1/2
с (см. рисунок 2.47). Наибольший угол отклонения точки обода балансира
от положения равновесия α=π/2 рад. Найти угловую скорость и
угловое ускорение баланса через 2 с после момента, когда балансир проходит
положение равновесия.
Пример 2.31
– Часовой балансир совершает крутильные гармонические колебания с периодом T=1/2
с (см. рисунок 2.47). Наибольший угол отклонения точки обода балансира
от положения равновесия α=π/2 рад. Найти угловую скорость и
угловое ускорение баланса через 2 с после момента, когда балансир проходит
положение равновесия.
Решение. Балансир совершает гармонические колебания, которые в общем виде описывается уравнением
![]()
где αm, k - амплитуда и частота колебаний.
В данном случае
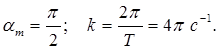
Тогда уравнение колебаний балансира принимает вид
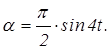
По известному уравнению колебаний находим угловую скорость w и угловое ускорение ε балансира
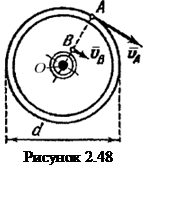
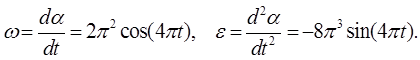
Отсюда при t = 2c
w = 2π2, ε = 0.
Пример 2.32 – Точка A шкива, лежащая на его ободе, движется со скоростью 50 см/с, а некоторая точка B, взятая на одном радиусе с точкой A, движется со скоростью 10 см/с; расстояние AB=20 см (см. рисунок 2.48). Определить угловую скорость ω и диаметр шкива.
Решение.Скорости точек А и В связывает с угловой скоростью шкива следующие выражения
![]() (1)
(1)
где ОА, ОВ – расстояния точек А и В до оси шкива.
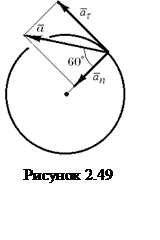 Представив
Представив ![]() можно
рассматривать равенства (1) как систему из двух уравнений с известными w и ОВ. Решая эту систему, находим
можно
рассматривать равенства (1) как систему из двух уравнений с известными w и ОВ. Решая эту систему, находим
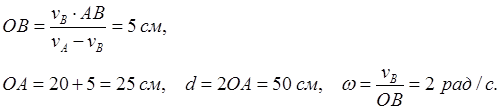
Пример 2.33
– Угол наклона полного ускорения точки обода махового колеса к радиусу
равен 60°. Касательное ускорение ее в данный момент ![]() м/с2.
Найти нормальное ускорение точки, отстоящей от оси вращения на расстоянии r=0,5
м. Радиус махового колеса R=1 м.
м/с2.
Найти нормальное ускорение точки, отстоящей от оси вращения на расстоянии r=0,5
м. Радиус махового колеса R=1 м.
Решение. Тангенциальное
![]() и нормальное
и нормальное![]() ускорения
являются взаимно перпендикулярными составляющими полного ускорения
ускорения
являются взаимно перпендикулярными составляющими полного ускорения![]() (см. рисунок 2.49). Поэтому для
точки обода колеса имеем
(см. рисунок 2.49). Поэтому для
точки обода колеса имеем
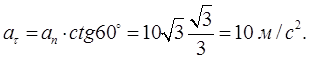
Используя формулу, определяющую нормальное ускорение точки обода колеса an = w2∙ R, находим угловую скорость колеса w
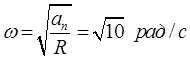
и нормальное ускорение точки колеса, отстоящей от оси вращения на расстоянии r = 0,5 м
an = w2∙ r = 10∙ 0,5 = 5 м/с2.
Пример 2.34 – Вал радиуса R=10 см приводится во вращение гирей P, привешенной к нему на нити (см. рисунок 2.50). Движение гири выражается уравнением x=100t2, где x — расстояние гири от места схода нити с поверхности вала, выраженное в сантиметрах, t — время в секундах. Определить угловую скорость ω и угловое ускорение ε вала, а также полное ускорение a точки на поверхности вала в момент t.
Решение. По заданному уравнению движения гири находим ее скорость vг и ускорение aг
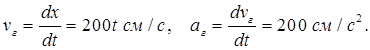
Скорость точки, лежащей на поверхности вала, равна скорости гири v=vг, а ускорение гири aг определяет тангенциальную составляющую полного ускорения точки aг = aτ. Учитывая это, определим
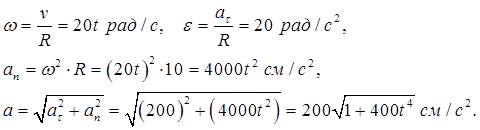
Пример 2.35 – Угловая скорость зубчатого колеса 1 диаметра D1=360 мм равна 10π/3 рад/с. Чему должен равняться диаметр зубчатого колеса 2, находящегося с колесом 1 во внутреннем зацеплении (см. рисунок 2.51), угловая скорость которого в три раза больше угловой скорости колеса 1?
Решение. Так как колеса находится в зацеплении, скорости из точек касания одинаковы
 v1
= v2, (1)
v1
= v2, (1)
причем
v1 = w1∙R1, v2 = w2∙R2, (2)
где w1, w2, R1, R2 – угловые скорости и радиусы колес.
Угловые скорости колес заданы условием задачи
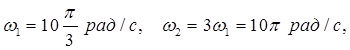
поэтому, используя равенства (1), (2), получим
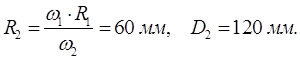
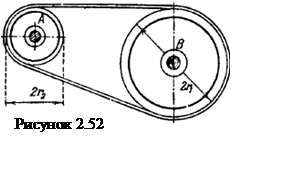 Пример 2.36
– Станок со шкивом A приводится в движение из состояния покоя бесконечным
ремнем от шкива B электромотора (см. рисунок 2.52). Радиусы шкивов: r1=75
см, r2=30 см. После пуска в ход электромотора его
угловое ускорение равно 0,4π рад/с2. Пренебрегая скольжением
ремня по шкивам, определить через сколько времени угловая скорость станка будет
равна 10π рад/с.
Пример 2.36
– Станок со шкивом A приводится в движение из состояния покоя бесконечным
ремнем от шкива B электромотора (см. рисунок 2.52). Радиусы шкивов: r1=75
см, r2=30 см. После пуска в ход электромотора его
угловое ускорение равно 0,4π рад/с2. Пренебрегая скольжением
ремня по шкивам, определить через сколько времени угловая скорость станка будет
равна 10π рад/с.
Решение. Учитывая,
что скорости точек, лежащих на поверхностях шкивов А и В,
одинаковы (шкивы соединены ремнем, проскальзыванием которого относительно
шкивов можно пренебречь), по известной угловой скорости ![]() шкива
А определим угловую скорость w1
шкива В
шкива
А определим угловую скорость w1
шкива В
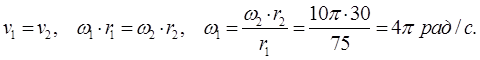 С другой стороны, так как
станок вращается с постоянным ускорением ε, его угловую скорость можно
подсчитать по формуле
С другой стороны, так как
станок вращается с постоянным ускорением ε, его угловую скорость можно
подсчитать по формуле
![]()
Отсюда
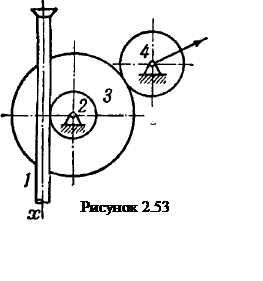
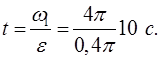
Пример 2.37 – В механизме стрелочного индикатора движение от рейки мерительного штифта 1 передается шестерне 2, на оси которой укреплено зубчатое колесо 3, сцепляющееся с шестерней 4, несущей стрелку (см. рисунок 2.53). Определить угловую скорость стрелки, если движение штифта задано уравнением x=a∙sink∙t и радиусы зубчатых колес соответственно равны r2, r3 и r4.
Решение. По заданному уравнению движения штифта определяем его скорость
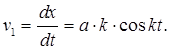
Рейка штифта находится в зацеплении с шестерней 2. Поэтому такую же скорость будет иметь точка, лежащая на поверхности шестерни 2
v2 = v1.
По известной скорости v2, находим угловую скорость шестерни 2
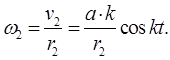 Так
как зубчатое колесо 3 укреплено на одной оси с колесам 2, их угловые скорости
одинаковы w3 = w2. По известной угловой скорости w3, находим скорость v3 точки касания шестерен 3 и 4, а
затем угловую скорость стрелки индикатора w4
Так
как зубчатое колесо 3 укреплено на одной оси с колесам 2, их угловые скорости
одинаковы w3 = w2. По известной угловой скорости w3, находим скорость v3 точки касания шестерен 3 и 4, а
затем угловую скорость стрелки индикатора w4
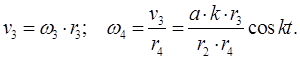
Пример 2.38 – Определить, через какой промежуток времени зубчатое коническое колесо O1 радиуса r1=10 см будет иметь угловую скорость, равную 144π рад/с, если оно приводится во вращение из состояния покоя таким же колесом O2 радиуса r2=15 см, вращающимся равноускоренно с угловым ускорением 4π рад/с 2(см. рисунок 2.54).
Решение. Так как колеса находятся в зацеплении, скорости их точек касания одинаковы
v2 = v1. (1)
Колеса вращаются вокруг неподвижных осей, поэтому (1) можно переписать в виде
w1∙ r1 = w2∙r2. (2)
Второе колеса начинает вращаться из состояния покоя с постоянным угловым ускорением ε2. Следовательно, для любого момента времени t
w2 = ε2∙t.
Выражая отсюда t и используя (2), находим
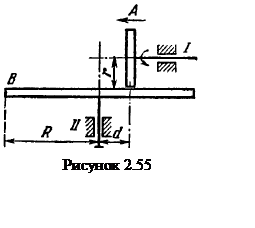
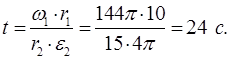
Пример 2.39 – Ведущий вал I фрикционной передачи (см. рисунок 2.55) вращается с угловой скоростью ω=20π рад/с и на ходу передвигается (направление указано стрелкой) так, что расстояние d меняется по закону d=(10-0,5t) см (t - в секундах). Даны радиусы фрикционных колес: r=5 см, R=15 см. Определить: 1) угловое ускорение вала II как функцию расстояния d; 2) ускорение точки на ободе колеса B в момент, когда d=r.
Решение. Так как колеса перекатываются одно по другому без проскальзывания, скорости их точек касания одинаковы
vА = vВ. (1)
Колеса вращаются вокруг неподвижных осей. Колеса вращаются вокруг неподвижных осей, поэтому (1) можно переписать в виде
![]()
Отсюда
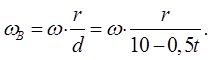
Находим угловое ускорение εВ вала II
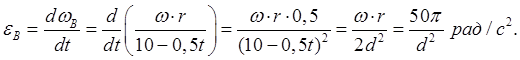
Ускорение точки на ободе колеса В подсчитаем по формулам для определения ускорений точек тела, вращающегося вокруг неподвижной оси
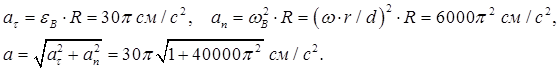
Пример 2.40 –
|
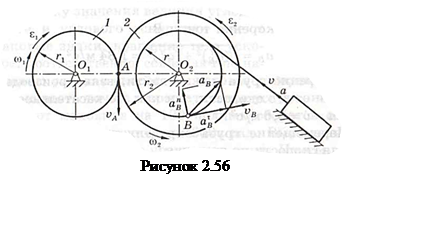 Решение. Найдем угловую скорость 𝜔1 колеса 1 из условия, что
оно вращается с угловым ускорением 𝜀1=const, учитывая, что
Решение. Найдем угловую скорость 𝜔1 колеса 1 из условия, что
оно вращается с угловым ускорением 𝜀1=const, учитывая, что 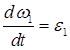 .
Интегрируя последнее уравнение по времени, получаем
.
Интегрируя последнее уравнение по времени, получаем![]() .
.
Постоянную интегрирования получаем из начального условия:
при t=0 𝜔1=0
(система находилась в покое), следовательно, ![]() .
.
Т.о., угловая скорость вала 1 определяется уравнением ![]() .
.
При t=1 c
получаем ![]() .
.
Шестерни 1 и 2 взаимодействуют без проскальзывания. Поэтому
скорости точек их касания (точка А) будут одинаковыми: ![]() .
.
|
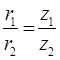 :
:
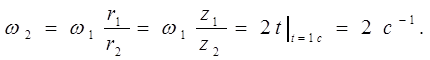
Угловое ускорение колеса 2 равно ![]() .
. ![]()
Так как трос нерастяжим и относительно барабана не проскальзывает, то скорость груза v будет равна скорости любой из точек на ободе барабана, в частности, скорости точки В:
![]()
Ускорение точки В равно векторной сумме касательного
(вращательного) и нормального (центростремительного) ускорений: ![]() .
.
Направление вращательного ускорения определяется
направлением углового ускорения 𝜀2,
а его модуль равен ![]() .
Центростремительное ускорение направлено к оси вращения вала 2 и равно по
модулю
.
Центростремительное ускорение направлено к оси вращения вала 2 и равно по
модулю ![]() .
.
Модуль ускорения точки В
![]()
Ускорение груза можно найти, взяв производную по времени от
его скорости, так как это касательное ускорение:![]()
Перемещение груза определяется интегрированием модуля скорости по времени:
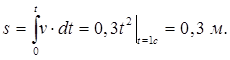
Пример 2.41 – Маховик радиусом R=0,5 м
вращается так, что его угловая скорость меняется в соответствии с равнением ![]() Для момента времени t=0,5 с после начала движения определить скорость
и ускорение точки на ободе маховика. Установить, за какое время маховик сделает
100 полных оборотов.
Для момента времени t=0,5 с после начала движения определить скорость
и ускорение точки на ободе маховика. Установить, за какое время маховик сделает
100 полных оборотов.
Решение. Для момента времени t=0,5
с получаем![]() , и скорость точки на ободе
маховика равна
, и скорость точки на ободе
маховика равна ![]() .
.
Угловое ускорение маховика
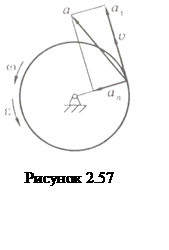
![]()
Ускорение точки на ободе маховика равно сумме двух составляющих
ускорений: ![]() ,
где
,
где ![]() и
и ![]() -касательное
(вращательное) и нормальное (центростремительное) ускорение точки.
-касательное
(вращательное) и нормальное (центростремительное) ускорение точки.
Учитывая, что вращательное ускорение равно по модулю ![]() ,
найдем
,
найдем ![]() ;
центростремительное ускорение
;
центростремительное ускорение ![]() .
.
Модуль полного ускорения точки
![]()
Направления скорости и ускорений показаны на рисунке 2.57.
Поскольку значения величин угловой скорости и углового ускорения имеют одинаковые знаки, вращение тела ускоренное. Соответственно, совпадают по направлению угловая скорость и угловое ускорение тела, а также скорость точки и вращательное ускорение.
Поворот маховика на 100 полных оборотов соответствует углу
его поворота 𝜑=200π
рад. Выражение для угла поворота найдем из уравнения ![]() .
Имеем
.
Имеем
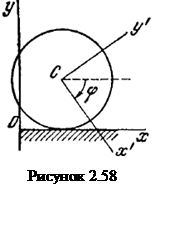
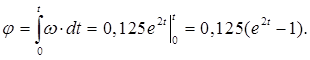
Т.о., 0,125(е2t-1)=200π, откуда находим t=4,26 с.
Пример 2.42 – Колесо радиуса R катится без скольжения по горизонтальной прямой (см. рисунок 2.58). Скорость центра C колеса постоянная и равна v. Определить уравнения движения колеса, если в начальный момент ось y' , жестко связанная с колесом, была вертикальна, а неподвижная ось y проходила в это время через центр C.
Решение. Колесо движется в вертикальной плоскости, совершая плоское движение, которое представляет сумму двух простейших движений: поступательного вместе с полюсом и вращательного вокруг полюса.
Поступательное движение колеса вместе с полюсом С описывается зависимостями вида
![]()
где хС, уС – координаты полюса С в осях неподвижной системы хОу.
Движение полюса С - равномерное и прямолинейное, поэтому xС = =v∙t, yC = R.
Вращательное движение колеса вокруг полюса С характеризует зависимость вида
φ = φ(t),
где φ – угол поворота колеса вокруг полюса С.
Так как колесо катится без скольжения, то дуга, которую опишет точка, лежащая на поверхности колеса, будет равна расстоянию хС, которое пройдет точка С. Следовательно,
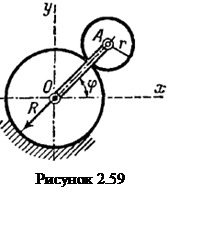
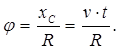
Т.о., движение колеса описывается системой уравнений
![]()
Пример 2.43 – Шестеренка радиуса r, катящаяся по неподвижной шестеренке радиуса R, приводится в движение кривошипом OA, вращающимся равноускоренно с угловым ускорением ε0 вокруг оси O неподвижной шестеренки (см. рисунок 2.59). Составить уравнения движения подвижной шестеренки, приняв за полюс ее центр A, если при t=0 угловая скорость кривошипа ω0=0 и начальный угол поворота φ0=0.
Решение. Шестеренка движется в вертикальной плоскости, совершая плоское движение, которое представляет сумму двух простейших движений: поступательного вместе с полюсом и вращательного вокруг полюса.
Поступательное движение шестеренки вместе с полюсом А описывается зависимостями вида
хА = хА(t), yA = yA(t),
где хА, yA – координаты полюса А в осях неподвижной системы хОу. В данном случае
хА = ОА∙cos φ = (R+r)∙cosφ; yA = OA∙sinφ = (R+r)∙sinφ.
Так как кривошип ОА вращается равноускоренно, его угол поворота φ определяется как
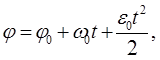
где ε0 – угловое ускорение кривошипа.
Согласно условию задачи φ0 = w0 = 0. Поэтому, равенство (1) принимает вид
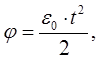
и уравнения движения полюса А принимают вид
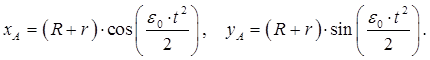
Вращательное движение шестеренки вокруг полюса А характеризует зависимость вида
φ1 = φ1(t),
где φ1 – угол поворота шестеренки вокруг полюса А.
Подвижная шестеренка не проскальзывает относительно неподвижной шестеренки, так как находится с ней в зацеплении. Поэтому дуга s1, которую опишет точка, расположенная на ободе подвижной шестеренки, будет равна дуге s, которую описывает центр шестеренки А. Учитывая, что точка А является общей для подвижной шестеренки и для кривошипа ОА, находим
![]()
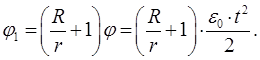
Т.о., движение подвижной шестеренки описывается системой уравнений

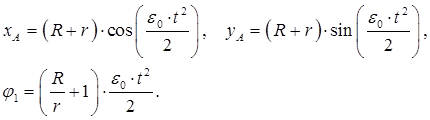
Пример 2.44 – Шестеренка радиуса r, катящаяся внутри неподвижной шестеренки радиуса R, приводится в движение кривошипом OA, вращающимся равномерно вокруг оси O неподвижной шестеренки с угловой скоростью ω0 (см. рисунок 2.60). При t=0 угол φ0=0. Составить уравнения движения подвижной шестеренки, приняв ее центр A за полюс.
Решение. Шестеренка движется в вертикальной плоскости, совершая плоское движение, которое представляет сумму двух простейших движений: поступательного вместе с полюсом и вращательного вокруг полюса.
Поступательное движение шестеренки вместе с полюсом А описывается зависимостями вида
хА = хА(t), yA = yA(t),
где хА, yA – координаты полюса А в осях неподвижной системы хОу. В данном случае
хА = ОА∙cos φ = (R-r)∙cosφ; yA = OA∙sinφ = (R-r)∙sinφ.
Так как кривошип ОА вращается равномерно и φ0=0, угол поворота φ определяется как
![]()
поэтому уравнения движения полюса А принимают вид
![]()
Вращательное движение шестеренки вокруг полюса А характеризует зависимость вида
φ1 = φ1(t),
где φ1 – угол поворота шестеренки вокруг полюса А.
Подвижная шестеренка не проскальзывает относительно неподвижной шестеренки, так как находится с ней в зацеплении. Поэтому дуга s1, которую опишет точка, расположенная на ободе подвижной шестеренки, будет равна дуге s, которую описывает центр шестеренки А. Учитывая, что точка А является общей для подвижной шестеренки и для кривошипа ОА, находим
![]()
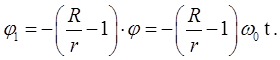
Итак, движение подвижной шестеренки описывается системой уравнений
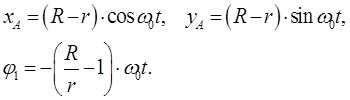
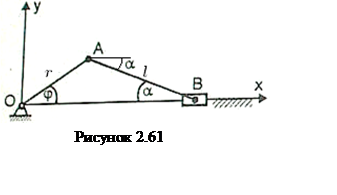 Пример 2.45
– Найти уравнения движения шатуна АВ, если кривошип вращается
равномерно; за полюс взять точку A на оси пальца кривошипа; r -
длина кривошипа, l - длина шатуна, ω0 - угловая скорость
кривошипа (см. рисунок 2.61). При t=0 угол α=0.
Пример 2.45
– Найти уравнения движения шатуна АВ, если кривошип вращается
равномерно; за полюс взять точку A на оси пальца кривошипа; r -
длина кривошипа, l - длина шатуна, ω0 - угловая скорость
кривошипа (см. рисунок 2.61). При t=0 угол α=0.
Решение.
Так как кривошип вращается равномерно, то угол поворота кривошипа выражается
как ![]()
Запишем выражения для координат полюса А
![]()
Из треугольника OAB по теореме синусов имеем
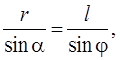 откуда
откуда 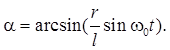
Т.о., движение подвижной шатуна АВ описывается системой уравнений
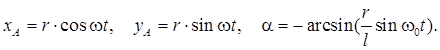
Пример 2.46 – Колесо катится по наклонной плоскости, образующей угол 30° с горизонтом. Центр O колеса движется по закону xO=10t2 см, где x - ось, направленная параллельно наклонной плоскости (см. рисунок 2.62,а). К центру O колеса подвешен стержень OA=36 см, качающийся вокруг горизонтальной оси O, перпендикулярной плоскости рисунка, по закону φ=(π/3)∙sin(πt/6) рад. Найти скорость конца A стержня AO в момент времени t=1 с.
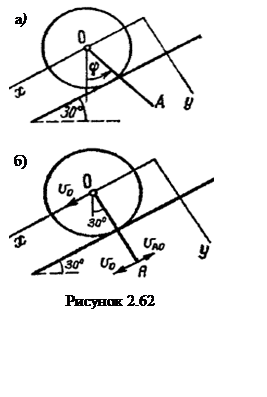 Решение. Стержень
ОА совершает плоское движение в вертикальной плоскости. В соответствии с
общей формулой плоского поля скоростей вектор
Решение. Стержень
ОА совершает плоское движение в вертикальной плоскости. В соответствии с
общей формулой плоского поля скоростей вектор ![]() скорости
точки А стержня можно представить суммой
скорости
точки А стержня можно представить суммой
![]()
где ![]() - вектор скорости
полюса (точки О);
- вектор скорости
полюса (точки О);
![]() - вектор скорости вращения точки
А вокруг полюса О,
- вектор скорости вращения точки
А вокруг полюса О,
![]()
где – ![]() вектор
угловой скорости стержня.
вектор
угловой скорости стержня.
В данном случае
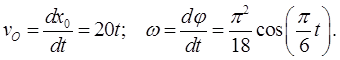
При t = 1 c;
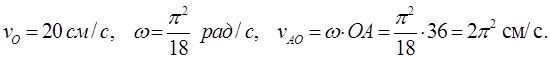
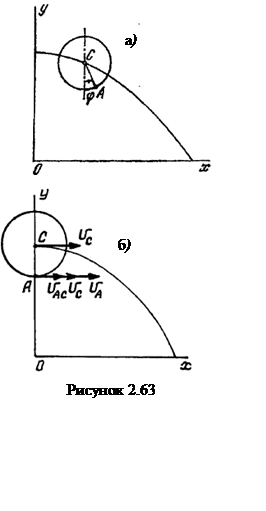 Определим взаимное расположение
векторов
Определим взаимное расположение
векторов ![]() и
и ![]() . Скорость полюса
. Скорость полюса ![]() , характеризующая прямолинейное
движение центра колеса О, направлена вдоль оси х вниз. Скорость
, характеризующая прямолинейное
движение центра колеса О, направлена вдоль оси х вниз. Скорость
![]() , характеризующая вращательное
движение точки А вокруг полюса О, направлена перпендикулярно
радиусу ОА вверх (с учетом направления вращения стержня, указанного
стрелкой на рисунке 2.62,а). Так как при t
= 1 с стержень ОА расположен перпендикулярно оси
, характеризующая вращательное
движение точки А вокруг полюса О, направлена перпендикулярно
радиусу ОА вверх (с учетом направления вращения стержня, указанного
стрелкой на рисунке 2.62,а). Так как при t
= 1 с стержень ОА расположен перпендикулярно оси 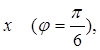 вектора
вектора ![]() и
и ![]() оказываются направленными по
одной прямой в разные стороны (см. рисунок 2.62,б). Следовательно,
оказываются направленными по
одной прямой в разные стороны (см. рисунок 2.62,б). Следовательно,
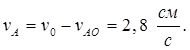
Пример 2.47 – При движении диска радиуса r=20 см в вертикальной плоскости xy его центр C движется согласно уравнениям xC=10t м, yC=(100-4,9t2) м. При этом диск вращается вокруг горизонтальной оси C, перпендикулярной плоскости диска, с постоянной угловой скоростью ω=π/2 рад/с. Определить в момент времени t=0 скорость точки A, лежащей на ободе диска. Положение точки A на диске определяется углом φ=ωt, отсчитываемым от вертикали против хода часовой стрелки (см. рисунок 2.63,а).
Решение. В
соответствии с общей формулой плоского поля скоростей вектор ![]() скорости точки А диска
можно представить суммой
скорости точки А диска
можно представить суммой
![]()
где ![]() – вектор
скорости полюса (точки С);
– вектор
скорости полюса (точки С); ![]() - вектор
скорости вращения точки А вокруг полюса С
- вектор
скорости вращения точки А вокруг полюса С
![]()
В данном случае
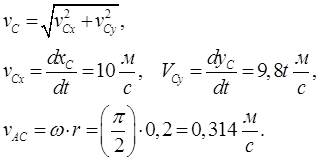
При t=0: 𝜑=0; vCy=0; vC=vCx=10м/с.
Вектора ![]() и
и ![]() оказываются
направленными по одной прямой, параллельной оси х, вправо (см. рисунок 2.63,б).
Следовательно, и вектор
оказываются
направленными по одной прямой, параллельной оси х, вправо (см. рисунок 2.63,б).
Следовательно, и вектор ![]() будет направлен по той же
прямой, а его модуль – определяться скалярной суммой
будет направлен по той же
прямой, а его модуль – определяться скалярной суммой
![]()
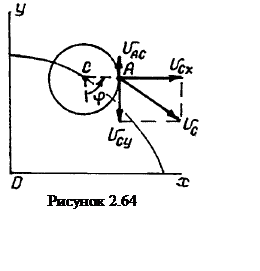 Пример 2.48 –
Сохранив условие предыдущей задачи, определить скорость точки A в момент
времени t=1 с.
Пример 2.48 –
Сохранив условие предыдущей задачи, определить скорость точки A в момент
времени t=1 с.
Решение.Используя полученные при решении предыдущей задачи выражения, находим при t=1 c (см. рисунок 2.64)
𝜑=π/2; vCx=10 м/с; vCy=-9,8 м/с.
Вектор ![]() направлен
параллельно оси y вверх. Поэтому
направлен
параллельно оси y вверх. Поэтому
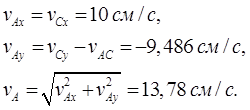
Пример 2.49 – Два одинаковых диска радиуса r каждый соединены цилиндрическим шарниром A (см. рисунок 2.65,а). Диск I вращается вокруг неподвижной горизонтальной оси O по закону φ=φ(t). Диск II вращается вокруг горизонтальной оси A согласно уравнению ψ=ψ(t). Оси O и A перпендикулярны плоскости рисунка. Углы φ и ψ отсчитываются от вертикали против хода часовой стрелки. Найти скорость центра C диска II.
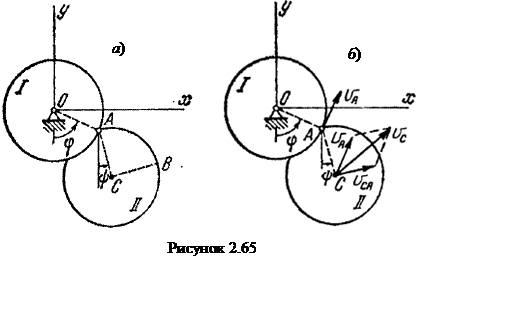 |
Решение. В
соответствии с общей формулой плоского поля скоростей скорость ![]() точки С диска II можно представить суммой
точки С диска II можно представить суммой
![]() (1)
(1)
где ![]() - вектор скорости полюса (точки
А);
- вектор скорости полюса (точки
А);
![]() - вектор скорости вращения
точки С вокруг полюса А,
- вектор скорости вращения
точки С вокруг полюса А,
![]()
![]() - вектор угловой скорости
вращения диска II,
- вектор угловой скорости
вращения диска II,
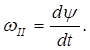
Согласно условию задачи диск I вращается вокруг неподвижной оси. Поэтому скорость точки А, принадлежащей диску I, определяется по формуле
![]()
где wI - угловая скорость вращения диска I,
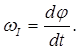
Вектор ![]() перпендикулярен
радиусу ОА и имеет следующие проекции на оси Ох, Оy (см. рисунок 2.65,б)
перпендикулярен
радиусу ОА и имеет следующие проекции на оси Ох, Оy (см. рисунок 2.65,б)
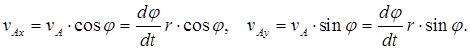
Вектор ![]() перпендикулярен радиусу CА окружности, которую описывает точка С
при вращении вокруг полюса А, и имеет следующие проекции на оси Ох, Оy
перпендикулярен радиусу CА окружности, которую описывает точка С
при вращении вокруг полюса А, и имеет следующие проекции на оси Ох, Оy
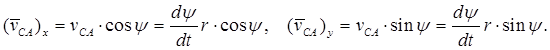
Т.о., согласно равенству (1) скорость точки С представляется следующими выражениями
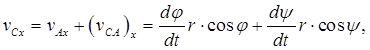

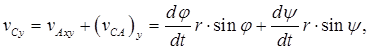
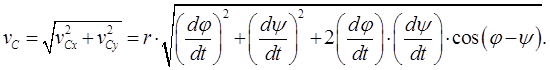
Пример 2.50 – Точильный станок (см. рисунок 2.66) приводится в движение педалью OA=24 см, которая колеблется около оси O по закону φ=(π/6)sin(πt/2) рад (угол φ отсчитывается от горизонтали). Точильный камень K вращается вокруг оси O1 с помощью стержня AB. Оси O и O1 перпендикулярны плоскости рисунка. Найти скорость точки D, лежащей на ободе точильного камня K радиуса R=2BO1, при t=0, если в этот момент OA и O1B расположены горизонтально.
Решение. Рассмотрим последовательно движение трех звеньев точильного станка: педали ОА, стержня АВ и точильного камня К.
Педаль ОА вращается вокруг неподвижной оси О. По заданному закону движения находим угловую скорость w0 педали и скорость точки А
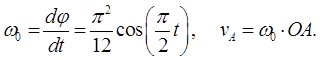
Вектор ![]() направлен перпендикулярно
радиусу ОА (см. рисунок 2.67,а).
направлен перпендикулярно
радиусу ОА (см. рисунок 2.67,а).
При t=0: 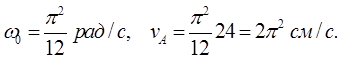
Точка А является общей для
педали ОА и для стержня АВ. Другая точка стержня принадлежит и
стержню и точильному камню К, который вращается вокруг неподвижной оси О1.
Поэтому вектор ![]() скорости точки В камня
будет направлен перпендикулярно радиусу О1В. Движение стержня
АВ в общем случае является плоским. Однако, в рассматриваемый момент
времени согласно условию задачи радиусы окружностей, которые описывают точки А
и В при вращении вокруг осей О и О1,
оказываются параллельными. Поэтому параллельными будут и вектора
скорости точки В камня
будет направлен перпендикулярно радиусу О1В. Движение стержня
АВ в общем случае является плоским. Однако, в рассматриваемый момент
времени согласно условию задачи радиусы окружностей, которые описывают точки А
и В при вращении вокруг осей О и О1,
оказываются параллельными. Поэтому параллельными будут и вектора![]() и
и ![]() скоростей
этих точек (см. рисунок 2.67,б). Так как вектора
скоростей
этих точек (см. рисунок 2.67,б). Так как вектора ![]() и
и
![]() не перпендикулярны
стержню АВ, его плоское движение вырождается в мгновенно-поступательное
движение, при котором скорости всех точек стержня становятся равными и по
величине и направлению. Т.о., vB
= vА=
не перпендикулярны
стержню АВ, его плоское движение вырождается в мгновенно-поступательное
движение, при котором скорости всех точек стержня становятся равными и по
величине и направлению. Т.о., vB
= vА=![]() .
.
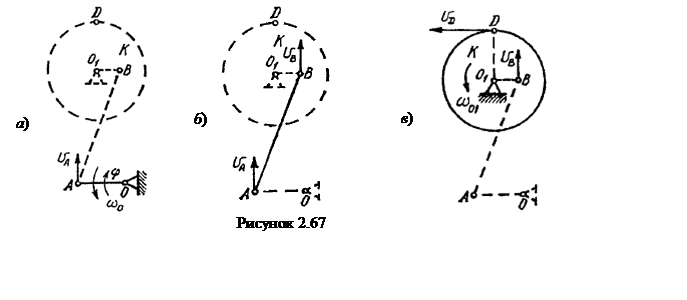 |
Полагая теперь, что точка В принадлежит точильному камню К, определяем угловую скорость камня w0 и скорость точки D (см. рисунок 2.67,в)
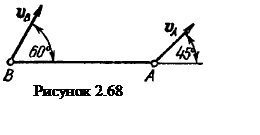
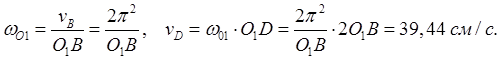
Пример 2.51
– Стержень AB длиной 0,5 м движется в плоскости рисунка.
Скорость ![]() (vA=2
м/с) образует угол 45° с осью x, совмещенной со стержнем (см. рисунок
2.68). Скорость
(vA=2
м/с) образует угол 45° с осью x, совмещенной со стержнем (см. рисунок
2.68). Скорость ![]() точки B образует
угол 60° с осью x. Найти модуль скорости точки B и угловую
скорость стержня.
точки B образует
угол 60° с осью x. Найти модуль скорости точки B и угловую
скорость стержня.
Решение. Для определения модуля скорости точки В используем основную теорему поля скоростей твердого тела, согласно которой
![]()
Отсюда
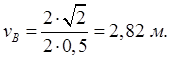
Чтобы найти
угловую скорость стержня w, построим
МЦС стержня АВ. МЦС - это такая точка P,
вокруг которой в данный момент времени вращаются все точки стержня АВ.
Точки А и В движутся по окружностям вокруг центра P со скоростями, вектора которых ![]() и
и
![]() перпендикулярны радиусам
AN и BN.
Чтобы найти МЦС стержня из точек проводим перпендикуляры к векторам
перпендикулярны радиусам
AN и BN.
Чтобы найти МЦС стержня из точек проводим перпендикуляры к векторам ![]() и
и ![]() до их
пересечения в точке N (см. рисунок 2.69). Учитывая,
что
до их
пересечения в точке N (см. рисунок 2.69). Учитывая,
что
![]()
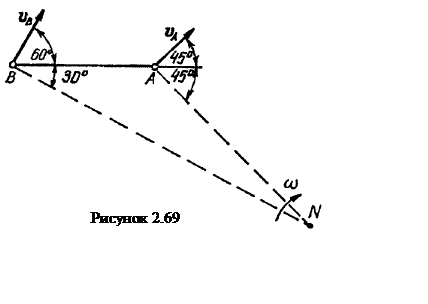 расстояние точки А до центра
N находим по
теореме синусов
расстояние точки А до центра
N находим по
теореме синусов
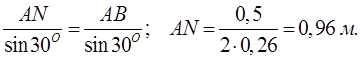
По известным значениям скорости точки А и радиуса AN подсчитываем значение угловой скорости стержня
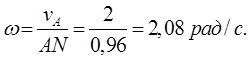
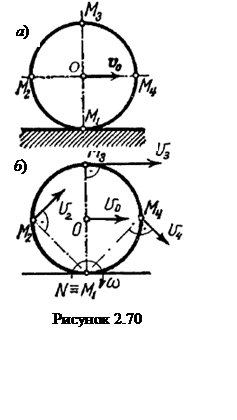 Пример 2.52 –
Колесо радиуса R=0,5 м катится без скольжения по прямолинейному
участку пути (см. рисунок 2.70,а); скорость центра его постоянна и равна
v0=10 м/с. Найти скорости концов M1, M2,
M3 и M4 вертикального и горизонтального диаметров
колеса. Определить его угловую скорость.
Пример 2.52 –
Колесо радиуса R=0,5 м катится без скольжения по прямолинейному
участку пути (см. рисунок 2.70,а); скорость центра его постоянна и равна
v0=10 м/с. Найти скорости концов M1, M2,
M3 и M4 вертикального и горизонтального диаметров
колеса. Определить его угловую скорость.
Решение. Колесо совершает плоское движение. Скорости точек М1, М2, М3 и М4 найдем с помощью МЦС колеса. В рассматриваемой задаче положение МЦС известно заранее: так как колесо катится без скольжения по неподвижному основанию, то скорость V1 точки М1 колеса, касающейся в данный момент времени основания, равна нулю. Т.е. МЦС колеса N совпадает с точкой М1 (см. рисунок 2.70,б). По заданной скорости точки О определим угловую скорость вращения колеса вокруг центра N
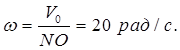
Учитывая, что точки М2, М3 и М4 описывают окружности вокруг центра N со скоростями, вектора которых V2, V3, и V4 перпендикулярны радиусам этих окружностей NM2, NM3 и NM4, находим
![]()
![]()
Пример 2.53 – Подвижный блок 1 и неподвижный блок 2 соединены нерастяжимой нитью (см. рисунок 2.71,а). Груз K, прикрепленный к концу этой нити, опускается по вертикали вниз по закону x=2t2 м. Определить скорости точек C, D, B и E, лежащих на ободе подвижного блока, в момент t=1 с в положении, указанном на рисунке, если радиус подвижного блока 1 равен 0,2 м, а CD⊥BE. Найти также угловую скорость блока 1.
Решение. По заданному закону движения определим скорость vк груза К
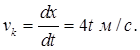 (1)
(1)
Скорость точки D, общей для нити и подвижного блока I, направлена вдоль нити и, так как нить считается и нерастяжимой, имеет модуль, равный модулю скорости груза К
vD = vK. \ (2)
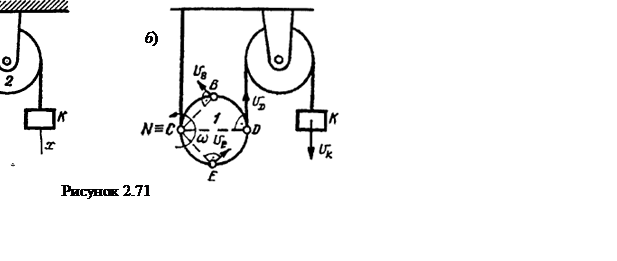 Блок 1 совершает плоское
движение (в плоскости рисунка). Угловую скорость w
блока и скорости его точек С, В и Е определим с помощью МЦС. В
рассматриваемый задаче предполагается, что блок 1 катится без скольжения по
неподвижной части нити АС и, следовательно, скорость VС точки С блока,
соприкасающейся с этой частью нити, равна нулю. Этим в условии задается положение
МЦС блока: точка N совпадает с точкой С.
Блок 1 совершает плоское
движение (в плоскости рисунка). Угловую скорость w
блока и скорости его точек С, В и Е определим с помощью МЦС. В
рассматриваемый задаче предполагается, что блок 1 катится без скольжения по
неподвижной части нити АС и, следовательно, скорость VС точки С блока,
соприкасающейся с этой частью нити, равна нулю. Этим в условии задается положение
МЦС блока: точка N совпадает с точкой С.
Т.о., для блока
1 известны скорость точки D и положение МЦС - точка N. Точки D,
B и Е описывают окружности вокруг центра N со скоростями, вектора
которых![]() перпендикулярны радиусам ND, NB и NE соответствующих окружностей (см. рисунок 2.71,б).
Определив угловую скорость вращения блока 1 относительно МЦС, найдем значения
скоростей точек при t=1c
перпендикулярны радиусам ND, NB и NE соответствующих окружностей (см. рисунок 2.71,б).
Определив угловую скорость вращения блока 1 относительно МЦС, найдем значения
скоростей точек при t=1c
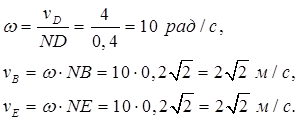
Ранее было найдено, что vD = vK =4 м/с.
Пример 2.54 – Колесо радиуса r=1 м катится без скольжения ускоренно по прямолинейному рельсу, имея в данный момент времени скорость центра v0=1 м/с и ускорение центра а0=1 м/с2 (см. рисунок 2.72,а). Определить угловую скорость и угловое ускорение колеса, скорости и ускорения точек его обода М1, М2, М3 и М4, а также установить положение МЦС и МЦУ колеса.
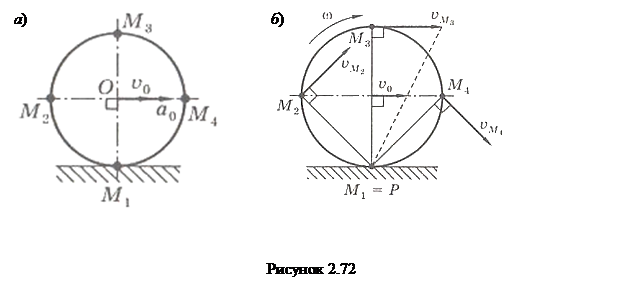 |
Решение.
1. Определение скоростей. У колеса, катящегося без
скольжения по неподвижной поверхности, МЦС (точка Р) находится в точке касания
с этой поверхностью (см. рисунок 2.72,б). В данном случае это точка ![]() .
.
Скорости точек плоской фигуры пропорциональны расстояниям от
этих точек до МЦС: ![]() , где ω - угловая скорость тела. Применяем эту формулу к точке О:
, где ω - угловая скорость тела. Применяем эту формулу к точке О:
![]() откуда
откуда ![]()
Для точек М2 и М3 расстояния до точки Р одинаковы, поэтому одинаковы и модули скоростей этих точек:
![]()
Скорость точки М3 определяется
как ![]() Направления скоростей
перпендикулярны отрезкам, соединяющим точки с МЦС.
Направления скоростей
перпендикулярны отрезкам, соединяющим точки с МЦС.
Для вычисления скоростей можно было использовать также и
теорему о сложении скоростей, выбрав в качестве полюса центр колеса:![]() где
где ![]() Скорость
Скорость
![]() перпендикулярна отрезку МО и
направлена по ходу вращения.
перпендикулярна отрезку МО и
направлена по ходу вращения.
Можно было также использовать следствие из этой теоремы о равенстве проекций скоростей точек на ось, проходящую через эти точки.
2. Определение ускорений. Вычислим сначала угловое ускорение колеса, формально дифференцируя выражение угловой скорости
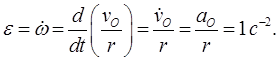
Здесь использован тот факт, что движение центра колеса
прямолинейное и, следовательно, касательное ускорение точки ![]() совпадает с полным ускорением.
совпадает с полным ускорением.
Для вычисления ускорений точек колеса применим теорему о
сложении ускорений: ![]() выбрав в качестве полюса
центр колеса. Вращательное ускорение точки относительно полюса
выбрав в качестве полюса
центр колеса. Вращательное ускорение точки относительно полюса ![]() и направлено перпендикулярно отрезку МО
по ходу углового ускорения, а центростремительное
и направлено перпендикулярно отрезку МО
по ходу углового ускорения, а центростремительное ![]() всегда
направлено от точки к полюсу.
всегда
направлено от точки к полюсу.
Тогда для точек М1 М2 М3
и М4 получим ![]() Направления
их показаны на рисунке 2.73,а.
Направления
их показаны на рисунке 2.73,а.
Складывая в каждой точке три вектора, модули которых равны
по 1 м/с2, получаем ![]()
3. Определение положения МЦУ. Найти положение МЦУ (точки Q, ускорение которой равно нулю) можно на основании известных положений:
а) все ускорения составляют один и тот же угол β с направлениями из этих точек на МЦУ, при этом
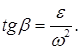
В данном случае tg β=1 и β=450. Повернув каждое ускорение на угол β по ходу углового ускорения, на пересечении лучей получим точку Q (см. рисунок 2.47,б). Т.о., МЦУ колеса для принятых исходных данных оказывается на середине отрезка М1М4;
б) ускорения точек пропорциональны расстояниям от этих точек до МЦУ:
![]()
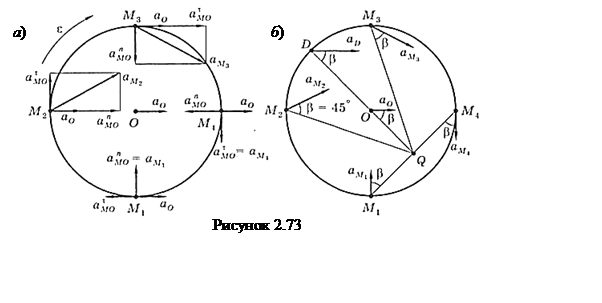
В силу одинаковости расстояний до МЦУ в данном случае
оказываются равны между собой модули ускорений ![]() , а
также
, а
также![]() . Из всех точек колеса самое большое
ускорение будет иметь точка D (см. рисунок 2.47,б):
. Из всех точек колеса самое большое
ускорение будет иметь точка D (см. рисунок 2.47,б):
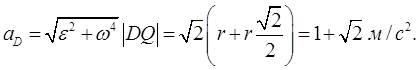
Пример 2.55 – Кривошип ОА длиной 0,2 м
вращается равномерно с угловой скоростью ![]() и
приводит в движение шатун АВ длиной 1 м. Ползун В движется
по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также
скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно
перпендикулярны и образуют с вертикалью угол 450 (см. рисунок 2.74,а).
и
приводит в движение шатун АВ длиной 1 м. Ползун В движется
по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также
скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно
перпендикулярны и образуют с вертикалью угол 450 (см. рисунок 2.74,а).
Решение.
1. Определение скоростей. Вычислим скорость точки А как точки вращающегося кривошипа
![]()
Она направлена перпендикулярно ОА (см. рисунок 2.74,б).
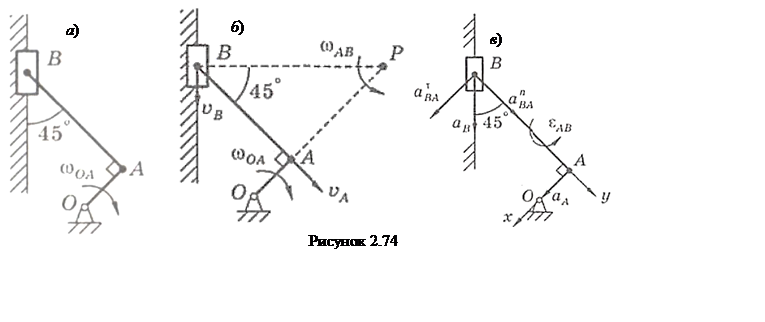
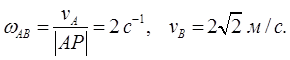
Скорость ползуна ![]() направлена по
направляющей вертикально.
направлена по
направляющей вертикально.
Для шатуна АВ, совершающего плоское движение, известны направления скоростей двух точек А и В. Восставляя перпендикуляры к векторам этих скоростей, находим точку Р их пересечения - МЦС шатуна.
Используя известную формулу для скоростей
точек при плоском движении, получаем ![]()
Из треугольника АВР имеем ![]() и
тогда
и
тогда
2. Определение ускорений. Вычислим сначала ускорение точки А
как точки кривошипа: ![]() .
.
Здесь тангенциальное ускорение ![]() , так как
, так как ![]() , поскольку
, поскольку ![]() .
Тогда полное точки А равно нормальному ускорению
.
Тогда полное точки А равно нормальному ускорению
![]()
и направлено к оси вращения – точке О (см. рисунок 2.74,в).
Для вычисления ускорения точки В воспользуемся теоремой о сложении ускорений, взяв точку А в качестве полюса:, тогда
![]() (
(![]() )
)
Центростремительное ускорение точки В в относительном
вращении вокруг точки А по модулю равно ![]() , и
направлено от точки В к полюсу – точке А.
, и
направлено от точки В к полюсу – точке А.
Модуль тангенциального ускорения ![]() определяется
по формуле
определяется
по формуле ![]() и
пока не может быть вычислен, поскольку неизвестна величина углового ускорения
и
пока не может быть вычислен, поскольку неизвестна величина углового ускорения ![]() .
Направление вектора
.
Направление вектора ![]() также
не может быть определено однозначно, так как неизвестно направление углового
ускорения, т.е. неизвестно, ускоренным или замедленным является поворот шатуна.
Примем пока этот поворот ускоренным, тогда направление
также
не может быть определено однозначно, так как неизвестно направление углового
ускорения, т.е. неизвестно, ускоренным или замедленным является поворот шатуна.
Примем пока этот поворот ускоренным, тогда направление ![]() совпадает
с направлением
совпадает
с направлением ![]() , а
вектор
, а
вектор ![]() направим
перпендикулярно отрезку ВА по ходу углового ускорения.
направим
перпендикулярно отрезку ВА по ходу углового ускорения.
Вектор ускорения точки В направлен по вертикальной
прямолинейной направляющей. Будем пока считать движение ползуна ускоренным и
направим ускорение ![]() в
ту же сторону, что и скорость
в
ту же сторону, что и скорость ![]() (см.
рисунок 2.74,в).
(см.
рисунок 2.74,в).
Теперь в равенстве (![]() )
все ускорения имеют определенное направление, и мы можем записать это уравнение
в проекциях на выбранные оси. Имеем в проекциях на оси x и y соответственно
)
все ускорения имеют определенное направление, и мы можем записать это уравнение
в проекциях на выбранные оси. Имеем в проекциях на оси x и y соответственно
![]()
![]()
Из последнего уравнения получаем ![]() тогда из первого
тогда из первого 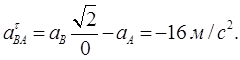 Отсюда следует, что
Отсюда следует, что 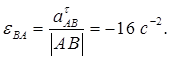
Отрицательные знаки у величин ![]() и
и ![]() показывают,
что их истинные направления противоположны принятым.
показывают,
что их истинные направления противоположны принятым.
Пример 2.56 – Для планетарного механизма, кинематическая схема которого показана на рисунке 2.75, определить скорости и ускорения точек A и B, если R1= 0,6 м, R2= 0,4 м, ωOA = 1 с-1, εOA = 1 с-2, α = 60°.
Решение: Последовательно рассмотрим движения каждого из двух подвижных звеньев планетарного механизма. При этом нужно начинать со звена, угловая скорость и угловое ускорение которого заданы. Т.о., начнем исследование кинематики механизма с кривошипа OA.
1. Кривошип OA совершает вращательное движение вокруг неподвижной оси, проходящей через точку О перпендикулярно плоскости рисунка. Определим скорость и ускорение точки А кривошипа, которая одновременно принадлежит и шестерне II.
Абсолютная величина скорости точки А определяется по формуле
vA = ωOA ∙│OA│ = ωOA∙ (R1 + R2 ). (1)
Для заданного положения механизма
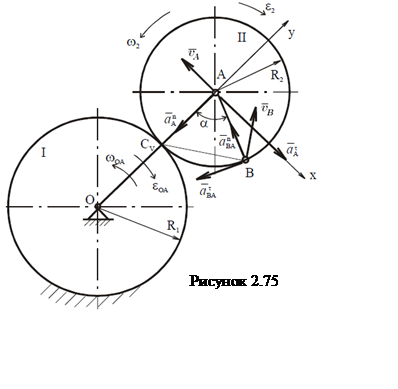 vA = 1∙ (0,6 + 0,4)
=1 м/с . (2)
vA = 1∙ (0,6 + 0,4)
=1 м/с . (2)
Вектор скорости ![]() направлен
перпендикулярно радиусу вращения ОА в направлении вращения, указанном на
рисунке 2.75 дуговой
стрелкой ωOA.
направлен
перпендикулярно радиусу вращения ОА в направлении вращения, указанном на
рисунке 2.75 дуговой
стрелкой ωOA.
Ускорение точки А представим в виде суммы касательной и нормальной составляющих
![]() (3)
(3)
Величины нормального и касательного ускорений определяются соответственно по формулам:
![]() (4)
(4)
![]() (5)
(5)
Для заданного положения механизма
![]() (6)
(6)
![]() (7)
(7)
При этом нормальное ускорение точки А направлено по радиусу окружности, описываемой точкой к центру этой окружности - к точке О. Касательное ускорение направлено по касательной к этой окружности (перпендикулярно OA) в сторону, указанную дуговой стрелкой εOA. Это объясняется тем, что при замедленном вращении (по условию задачи кривошип ОА вращается замедленно) касательное ускорение направлено в сторону, противоположную направлению вращения, указанному дуговой стрелкой ωOA. В то же время при замедленном вращении угловое ускорение направляется также в сторону, противоположную направлению угловой скорости.
Величина ускорения точки А в соответствии с соотношением (3) и с учетом (6) и (7) для заданного положения механизма определится как
![]()
2. Шестерня II совершает плоскопараллельное (плоское) движение. Учитывая, что шестерня II катится без скольжения по неподвижной шестерне I, мгновенный центр скоростей (точка Сv) подвижной шестерни будет находиться в точке соприкосновения двух шестерен (см. рисунок 2.75).
Для заданного положения планетарного механизма выше определена скорость центра шестерни II (точка А). Зная величину скорости одной из точек и положение мгновенного центра скоростей подвижной шестерни, можно определить величину ее мгновенной угловой скорости по формуле
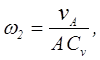 (8)
(8)
где расстояние ACv=R2.
Подставляя значение ACv=R2 и (1) в (7), получаем
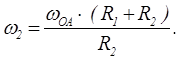 (9)
(9)
Для заданного положения механизма
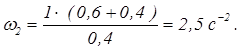 (10)
(10)
Направление мгновенного вращения шестерни II вокруг мгновенного центра скоростей (точки Cv), определяемое направлением скорости точки, условно показано на рисунке 2.75 дуговой стрелкой ω2 .
Шестерня II в указанном положении движется замедленно. Это следует из сопоставления
направлений векторов ![]() и
и ![]() (они направлены в противоположные стороны).
Следовательно, угловое ускорение ε2 шестерни II направлено в
сторону, противоположную направлению угловой скорости ω2, что
условно показано на рисунке 2.75 дуговой стрелкой ε2.
(они направлены в противоположные стороны).
Следовательно, угловое ускорение ε2 шестерни II направлено в
сторону, противоположную направлению угловой скорости ω2, что
условно показано на рисунке 2.75 дуговой стрелкой ε2.
Величину углового ускорения ε2 определим по формуле
![]() (11)
(11)
Учитывая (8), на основании (11) получим
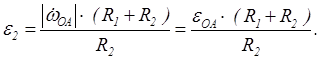 (12)
(12)
где εOA - величина углового ускорения кривошипа ОА.
Для заданного положения механизма
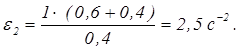 (13)
(13)
Таким образом для некоторого момента времени найдены положение мгновенного центра скоростей, угловая скорость, угловое ускорение подвижной шестерни II, а также ускорение точки А. Это позволяет найти скорость и ускорение любой точки шестерни.
Прежде всего определим абсолютную величину скорости точки B как
vB = ω2 ∙ BCv , (14)
где BCv - расстояние от точки В до мгновенного центра скоростей.
Расстояние BCv определим из треугольника ABCv . Этот треугольник равносторонний и, следовательно,
BCv = R2= 0,4 м . (15)
Для заданного положения механизма, учитывая (10) и (15), на основании (14) получим
vB= 2,5 . 0,4 =1 м/с . (16)
Вектор скорости ![]() направлен
перпендикулярно прямой BCv.
направлен
перпендикулярно прямой BCv.
Ускорение точки B можно найти на основании теоремы об ускорениях точек плоской фигуры, приняв точку A за полюс
![]() (17)
(17)
где ![]() и
и ![]() соответственно
нормальное и касательное ускорения точки B при относительном
вращательном движении шестерни II вокруг полюса А.
соответственно
нормальное и касательное ускорения точки B при относительном
вращательном движении шестерни II вокруг полюса А.
Учитывая (3), формулу (17) представим в виде
![]() (18)
(18)
Величины нормального и касательного ускорений точки B при относительном вращательном движении шестерни II вокруг полюса A определяются по формулам
![]() (19)
(19)
![]() (20)
(20)
Для заданного положения механизма на основании (19) и (20) с учетом (10) и (13) получим
![]() (21)
(21)
![]() (22)
(22)
Нормальное ускорение ![]() направлено вдоль ВА к
центру относительного вращения (к полюсу А), а касательное
направлено вдоль ВА к
центру относительного вращения (к полюсу А), а касательное ![]() направлено перпендикулярно
прямой АВ в сторону, указанную дуговой стрелкой ε2.
направлено перпендикулярно
прямой АВ в сторону, указанную дуговой стрелкой ε2.
Т.о., найдены модули четырех векторов ускорений, стоящих в правой части векторного равенства (18), и показаны их направления для точки В на рисунке 2.49. Найдем ускорение точки В как геометрическую сумму четырех показанных в точке ускорений аналитическим способом. Для этого спроецируем вектора, стоящие в правой и левой части равенства (18), на две оси координат x, y (см. рисунок 2.75)
![]() (23)
(23)
![]() (24)
(24)
Учитывая (6), (7), (21) и (22), на основании (23) и (24) найдем для заданного положения механизма проекции ускорения точки В на оси x, y
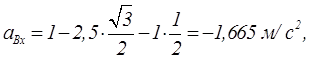
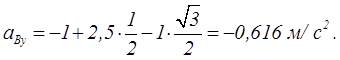
Проекции вектора ускорения ![]() (лежащего в плоскости xy
) на две оси координат полностью определяют его модуль и направление. Итак,
величина
(лежащего в плоскости xy
) на две оси координат полностью определяют его модуль и направление. Итак,
величина
![]()
Пример 2.57 - Для дифференциального механизма, кинематическая схема которого показана на рисунке 2.76, определить скорости и ускорения точек A и B, если R1= 0,2 м, R2= 0,1 м, ωOA = 2 с-1, εOA = 2 с-2, ω1 = 1 с-1, ε1=1 с-2, α = 90°.
Решение. Рассмотрим последовательно движение каждого из трех звеньев дифференциального механизма, начиная с одного из ведущих звеньев, т.е. начиная со звена, для которого заданы угловая скорость и угловое ускорение.
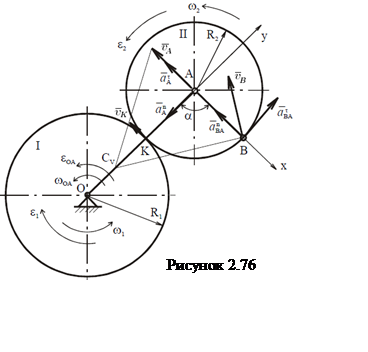 1.
Кривошип ОА совершает вращательное движение вокруг неподвижной оси, проходящей
через точку O перпендикулярно плоскости рисунка. Определим скорость и
ускорение точки A кривошипа, принадлежащей одновременно шестерне II.
1.
Кривошип ОА совершает вращательное движение вокруг неподвижной оси, проходящей
через точку O перпендикулярно плоскости рисунка. Определим скорость и
ускорение точки A кривошипа, принадлежащей одновременно шестерне II.
Величину скорости точки А определяем по формуле
vA = ωOA ∙│OA│ = ωOA∙ (R1 + R2 ). (1)
Для заданного положения механизма
vA = 2∙ (0,1 + 0,2) = 0,6 м/с . (2)
Вектор скорости ![]() направлен
перпендикулярно радиусу вращения ОА в направлении вращения, указанном на
рисунке 2.50 дуговой стрелкой ωOA.
направлен
перпендикулярно радиусу вращения ОА в направлении вращения, указанном на
рисунке 2.50 дуговой стрелкой ωOA.
Ускорение точки А представим в виде суммы касательной и нормальной составляющих
![]() (3)
(3)
Величины нормального и касательного ускорений определяются по формулам:
![]() (4)
(4)
![]() (5)
(5)
Для заданного положения механизма
![]() (6)
(6)
![]() (7)
(7)
Нормальное ускорение точки А направлено по радиусу окружности, описываемой точкой к центру окружности О. Касательное ускорение направлено по касательной к этой окружности (перпендикулярно OA) в сторону, указанную дуговой стрелкой εOA.
Величина ускорения точки А в соответствии с соотношением (3) и с учетом (6) и (7) для заданного положения механизма определится как
![]()
2. Шестерня I совершает вращательное движение вокруг той же оси, что и кривошип ОА. Определим величину скорости точки K касания двух шестерен
vK= ω1∙R1. (8)
Для заданного положения механизма
vK= 1∙0,2=0,2 м/c. (9)
Вектор ![]() направлен
перпендикулярно радиусу вращения R1 в направлении вращения
шестерни I, указанном на рисунке дуговой стрелкой ω1.
направлен
перпендикулярно радиусу вращения R1 в направлении вращения
шестерни I, указанном на рисунке дуговой стрелкой ω1.
3. Шестерня II совершает плоскопараллельное движение. Для момента времени, соответствующего заданному положению механизма, выше определены скорости двух точек этой шестерни (точек A и K), а также ускорение точки А. Это позволяет определить скорость и ускорение любой точки шестерни II.
Прежде всего, необходимо найти положение мгновенного центра скоростей
(точку Cv) шестерни II. Так
как скорости точек A и K параллельны друг другу и при этом линия AK
перпендикулярна скоростям ![]() и
и
![]() , то МЦС находится
в точке пересечения прямых, проведенных через начала и концы векторов скоростей
(см. рисунок 2.50). Здесь учтено, на основании сравнения (2) и (9), что vA> vK.
, то МЦС находится
в точке пересечения прямых, проведенных через начала и концы векторов скоростей
(см. рисунок 2.50). Здесь учтено, на основании сравнения (2) и (9), что vA> vK.
Величина угловой скорости шестерни II может быть определена из соотношения
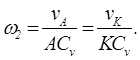 (10)
(10)
Из свойств пропорции получим
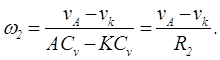 (11)
(11)
Подставляя (1) и (8) в (11), получим
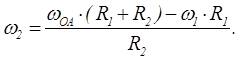 (12)
(12)
Для заданного положения механизма
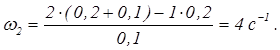 (13)
(13)
Направление вращения шестерни II вокруг мгновенного центра скоростей (точки Cv), определяемое направлением скоростей точек A и K, условно показано на рисунке дуговой стрелкой ω2.
Алгебраическую величину углового ускорения шестерни II определим на основании формулы
![]() (14)
(14)
Учитывая (12), из (14) получим
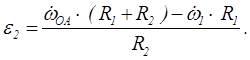 (15)
(15)
По условию задачи кривошип OA вращается
ускоренно. Это значит, что абсолютная величина угловой скорости кривошипа ωOA возрастает. В этом случае ![]() , т.е.
, т.е.
![]() (16)
(16)
где ![]() - заданная абсолютная величина
углового ускорения кривошипа.
- заданная абсолютная величина
углового ускорения кривошипа.
Шестерня I вращается замедленно. При этом
абсолютная величина угловой скорости шестерни I убывает
и, следовательно,![]() Т.о.,
Т.о.,
![]() (17)
(17)
где ![]() - заданная величина углового
ускорения шестерни I.
- заданная величина углового
ускорения шестерни I.
В результате подстановки (16) и (17) в (15) найдем
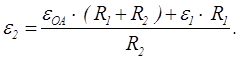
Для заданного положения механизма
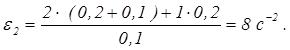 (18)
(18)
Так как знаки ω2 и ε2 совпадают, шестерня II вращается ускоренно. Направление ε2 покажем на рисунке дуговой стрелкой в ту же сторону, что ω2.
На основании (1), (10) и (12) нетрудно найти расстояние ACv
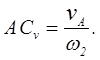
Для заданного положения механизма, учитывая (2) и (13), получим
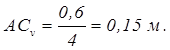
Величину скорости vB точки B можно найти по формуле
vB=ω2∙BCv, (19)
где
![]() (20)
(20)
Учитывая (13) и (20) на основании (19) найдем величину скорости точки B для заданного положения механизма
vB=4∙0,18 = 0,72 м/с.
Вектор скорости ![]() направлен
перпендикулярно прямой BCv в
сторону вращения шестерни II, указанную дуговой стрелкой ω2.
направлен
перпендикулярно прямой BCv в
сторону вращения шестерни II, указанную дуговой стрелкой ω2.
Ускорение точки B можно найти на основании теоремы об ускорениях точек плоской фигуры, приняв точку A за полюс
![]() (21)
(21)
где ![]() и
и ![]() соответственно
нормальное и касательное ускорения точки B при относительном
вращательном движении шестерни II вокруг полюса А.
соответственно
нормальное и касательное ускорения точки B при относительном
вращательном движении шестерни II вокруг полюса А.
С учетом (3) формула (21) принимает вид
![]() (22)
(22)
Величины нормального и касательного ускорений точки B при относительном вращательном движении шестерни II вокруг полюса A определяются по формулам
![]() (23)
(23)
![]() (24)
(24)
Для заданного положения механизма на основании (23) и (24) с учетом (13) и (18) получим
![]() (25)
(25)
![]() (26)
(26)
Нормальное ускорение ![]() направлено вдоль ВА к
центру относительного вращения (к полюсу А), а касательное
направлено вдоль ВА к
центру относительного вращения (к полюсу А), а касательное ![]() направлено перпендикулярно
прямой АВ в сторону, указанную дуговой стрелкой ε2.
направлено перпендикулярно
прямой АВ в сторону, указанную дуговой стрелкой ε2.
Таким образом для точки В найдены модули четырех векторов ускорений, стоящих в правой части векторного равенства (22), и показаны их направления на рисунке 2.50. Найдем ускорение точки В как геометрическую сумму четырех показанных в точке ускорений аналитическим способом. Для этого спроецируем вектора, стоящие в правой и левой части равенства (22), на две оси координат x, y (см. рисунок 2.76)
![]() (23)
(23)
![]() (24)
(24)
Проекции вектора ускорения ![]() (лежащего в
плоскости xy ) на две оси координат полностью определяют его модуль и
направление. Тогда модуль полного ускорения
(лежащего в
плоскости xy ) на две оси координат полностью определяют его модуль и
направление. Тогда модуль полного ускорения
![]()
Пример 2.58 - Дано: схема механизма в заданном положении (см. рисунок 2.77,а): φ = =30°; ОА = 30 см; АВ = 70 см; ВС = 35 см; CD = 40 см; l = 90 см ; ω0=π/6 с-1. Определить:
1) скорости точек А, В, С, D механизма и угловые скорости всех его звеньев при помощи мгновенных центров скоростей;
2) скорости этих же точек методом проекций на прямую, соединяющую точки;
3) ускорения точек А, В, C, а также угловое ускорение звена АВ (аналитическим способом).
Решение. Построим механизм в выбранном масштабе ml = 1:10 (см. рисунок 2.77,а).
При исследовании кинематики плоского механизма будем рассматривать последовательно движение каждого звена механизма, начиная с ведущего звена, угловая скорость которого задана.
1) Определение скоростей точек и угловых скоростей звеньев механизма с помощью мгновенных центров скоростей.
1.1) Звено ОА совершает вращательное движение вокруг неподвижного центра O. Определим скорость точки А кривошипа, которая одновременно принадлежит и звену АВ. Величина скорости точки А определяется по формуле
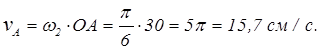
Вектор скорости ![]() направлен
перпендикулярно радиусу вращения ОА в направлении вращения, указанном на
рисунке 2.77,а дуговой стрелкой ω0.
направлен
перпендикулярно радиусу вращения ОА в направлении вращения, указанном на
рисунке 2.77,а дуговой стрелкой ω0.
1.2) Звено АВ совершает плоскопараллельное (плоское) движение.
Выше найдена скорость точки А этого звена и известна линия действия
скорости точки В (![]() -
вдоль прямой OВ). Мгновенный центр
скоростей звена АВ (точка Сv1)
находится на пересечении перпендикуляров, восставленных в точках А и В
к векторам их скоростей
-
вдоль прямой OВ). Мгновенный центр
скоростей звена АВ (точка Сv1)
находится на пересечении перпендикуляров, восставленных в точках А и В
к векторам их скоростей ![]() и
и
![]()
Точка С принадлежит звену АВ. Соединим точку С с
мгновенным центром скоростей Сv1.
Вектор скорости ![]() точки
С направлен перпендикулярно к прямой CСv1.
точки
С направлен перпендикулярно к прямой CСv1.
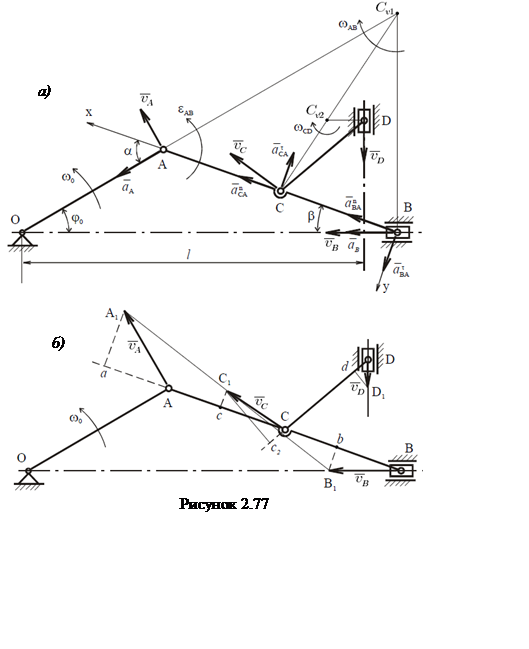 |
Для звена CD мгновенный центр скоростей определяем аналогично.
Известна линия действия скорости точки С (![]() )
и линия действия скорости в точке D (по вертикали). Восставим
перпендикуляр в точке D к вертикали до пересечения с прямой CСv1 в точке Сv2. Точка Сv2 и есть мгновенный центр
скоростей звена СD.
)
и линия действия скорости в точке D (по вертикали). Восставим
перпендикуляр в точке D к вертикали до пересечения с прямой CСv1 в точке Сv2. Точка Сv2 и есть мгновенный центр
скоростей звена СD.
Измеряем расстояния от точек А, В, С и D до соответствующих мгновенных центров скоростей
|АСv1| = 8 см, |ВСv1| = 6 см, |ССv1| = 6,1 см, |CСv2| = 3 см, |DСv2| = 1,4 см.
Учитывая масштаб ml, получаем
АСv1 = 80 см, ВСv1 = 60 см, ССv1 = 61 см, CСv2 = 30 см, DСv2 = 14 см.
Скорости точек плоской фигуры пропорциональны расстояниям до мгновенных центров скоростей. Для звена АВ имеем
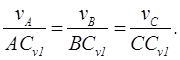
Отсюда находим
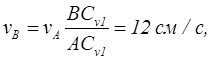
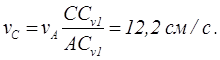
Аналогично для звена CD получим
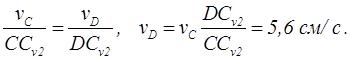
1.3) Определим величины угловых скоростей звеньев механизма. Скорость любой точки звена равна произведению угловой скорости этого звена на расстояние от точки до мгновенного центра скоростей
![]()
Отсюда
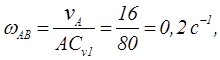
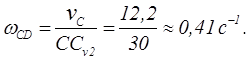
Из рисунка 2.51,а следует, что вращения звеньев AB и CD вокруг мгновенных центров скоростей происходят по часовой стрелке.
2) Определение скоростей этих же точек методом проекций на прямую, соединяющую точки.
Для определения скоростей точек методом проекций вновь строим механизм в заданном масштабе ml = 1:10 на рисунке 2.77,б. С помощью теоремы о проекциях скоростей двух точек плоской фигуры на прямую, их соединяющую, и теоремы о геометрическом месте концов векторов скоростей точек прямой, определяем скорости точек В, C и D.
На рисунке 2.77,б находим проекцию вектора скорости ![]() , который построен в
масштабе (mv=1:4 см∙с-1/см), на
прямую АВ. Откладываем от точки В отрезок Aa = Bb вдоль
прямой АВ. Восставляем в точке b перпендикуляр к прямой АВ
до пересечения с прямой OВ, по которой направлен вектор скорости и
, который построен в
масштабе (mv=1:4 см∙с-1/см), на
прямую АВ. Откладываем от точки В отрезок Aa = Bb вдоль
прямой АВ. Восставляем в точке b перпендикуляр к прямой АВ
до пересечения с прямой OВ, по которой направлен вектор скорости и ![]() в точке В. Соединяем
концы векторов скоростей точек А и B прямой A1B1.
От точки C вдоль прямой АВ откладываем отрезок Cc = Aa и
восставляем из точки с перпендикуляр до пересечения с прямой A1B1
в точке С1. Отрезок СC1 определяет вектор
скорости и
в точке В. Соединяем
концы векторов скоростей точек А и B прямой A1B1.
От точки C вдоль прямой АВ откладываем отрезок Cc = Aa и
восставляем из точки с перпендикуляр до пересечения с прямой A1B1
в точке С1. Отрезок СC1 определяет вектор
скорости и ![]() в точке С.
в точке С.
Скорость точки D определяем аналогично. Находим проекцию скорости ![]() на прямую СD.
Откладываем от точки D отрезок Dd = Cc2. Восставляем
перпендикуляр из точки d до пересечения в точке D1 с
вертикалью, по которой направлен вектор скорости
на прямую СD.
Откладываем от точки D отрезок Dd = Cc2. Восставляем
перпендикуляр из точки d до пересечения в точке D1 с
вертикалью, по которой направлен вектор скорости ![]() в точке D. Отрезок DD1
изображает вектор скорости
в точке D. Отрезок DD1
изображает вектор скорости![]() .
.
Измеряя длины отрезков ВВ1, СC1, и DD1 и, учитывая масштаб скорости mv , найдем величины скоростей в точках В, С и D
vB = 12 см/c, vC = 12,2 см/с, vD = 5,6 см/с.
3) Определение ускорений точек А, В и С, а также углового ускорения εAB звена АВ аналитическим способом.
Так как кривошип OA вращается равномерно, ускорение точки A направлено к центру О и равно
![]()
Для определения ускорения точки В звена AВ воспользуемся теоремой об ускорениях точек плоской фигуры. Считая точку A полюсом, запишем
![]() (1)
(1)
Нормальное ускорение точки В во вращательном движении вокруг полюса A направлено от точки В к точке A вдоль AВ и равно
![]()
Что касается ускорений ![]() точки В и
точки В и![]() то известны только линии действия этих векторов:
то известны только линии действия этих векторов: ![]() - по прямой OВ
вдоль направляющих ползуна,
- по прямой OВ
вдоль направляющих ползуна, ![]() - перпендикулярно AВ.
Зададимся произвольно их направлениями по указанным линиям (см. рисунок 2.77,б
). Эти ускорения определим, проецируя векторное равенство (1) на оси координат.
Знак в ответе показывает, соответствует ли истинное направление вектора
расчетному.
- перпендикулярно AВ.
Зададимся произвольно их направлениями по указанным линиям (см. рисунок 2.77,б
). Эти ускорения определим, проецируя векторное равенство (1) на оси координат.
Знак в ответе показывает, соответствует ли истинное направление вектора
расчетному.
Выбрав направления осей x и y, как показано на рисунке 2.77,б, получим
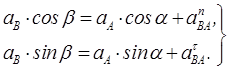 (2)
(2)
Углы α и β измеряем на рисунке 2.77,б с помощью транспортира. Из (2) получим
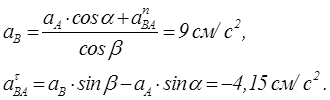
Поскольку ![]() отрицательно, то направление
вектора противоположно выбранному на рисунке 2.77,б.
отрицательно, то направление
вектора противоположно выбранному на рисунке 2.77,б.
Угловое ускорение шатуна АВ с учетом того, что здесь ![]() - алгебраическая величина,
определяется по формуле
- алгебраическая величина,
определяется по формуле
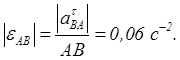
Направление ускорения ![]() относительно
полюса А определяет направление углового ускорения
относительно
полюса А определяет направление углового ускорения![]() , которое показано на рисунке 2.51,б
дуговой стрелкой.
, которое показано на рисунке 2.51,б
дуговой стрелкой.
Для определения ускорения точки С примем за полюс точку А и в соответствии с теоремой об ускорениях точек плоской фигуры запишем равенство
![]()
Направление вектора ускорения ![]() точки С заранее
неизвестно.
точки С заранее
неизвестно.
Нормальное и тангенциальное ускорения точки С во вращательном движении вокруг полюса А
![]()
![]()
Вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() и направлен соответственно угловому
ускорению
и направлен соответственно угловому
ускорению ![]() .
.
Ускорение точки С находим способом проекций
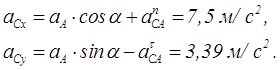
Найдем величину вектора ускорения точки C по формуле
![]()
Пример 2.59 - Тело D движется поступательно вдоль оси х так, что координата некоторой его точки меняется как xD=t3+t2, м (см. рисунок 2.78,а).
По жёлобу ОА, который представляет собой дугу
окружности радиуса R=20 м, движется
точка М так, что длина дуги ОМ=s=5π∙t2, м. Для момента времени t=1 с определить абсолютную скорость ![]() и абсолютное ускорение
и абсолютное ускорение ![]() точки М.
точки М.
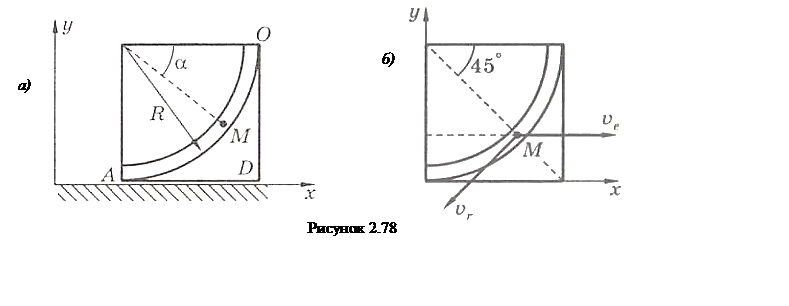 Решение.
Решение.
1. Определение ![]() . Согласно теореме о
сложении скоростей, абсолютная скорость равна векторной сумме относительной и
переносной скоростей,
. Согласно теореме о
сложении скоростей, абсолютная скорость равна векторной сумме относительной и
переносной скоростей, ![]()
Относительную скорость точки (скорость по отношению к телу D) находим, вычисляя ее алгебраическое значение как
производную от дуговой координаты по времени: ![]() и
при t=1 с получаем
и
при t=1 с получаем ![]()
Чтобы определить направление этой скорости, следует установить, где находится точка М в данный момент времени.
Вычисляя длину дуги![]() ,
определяем значение угла α:
,
определяем значение угла α: ![]() -
точка М находится в середине дуги ОА (см. рисунок 2.78,б).
-
точка М находится в середине дуги ОА (см. рисунок 2.78,б).
Скорость ![]() точки направлена по
касательной к ее траектории (окружности) в сторону увеличения длины дуги
(дуговой координаты), так как алгебраическое значение скорости положительно.
точки направлена по
касательной к ее траектории (окружности) в сторону увеличения длины дуги
(дуговой координаты), так как алгебраическое значение скорости положительно.
Переносной скоростью по определению будет скорость той точки тела D, с которой в данный момент времени совпадает точка М.
В имеющемся случае поступательного движения тела скорости всех его точек одинаковы (это скорость тела D), и тогда, поскольку движение прямолинейное, переносную скорость можно найти как производную от координаты, т.е.
![]()
и
при t=1 с получаем![]() .
Направлена она по оси х, так как
.
Направлена она по оси х, так как![]() .
.
Складывать вектора ![]() и
и ![]() удобнее всего с помощью
проекций. Проецируя равенство
удобнее всего с помощью
проекций. Проецируя равенство ![]() на оси (см. рисунок 2.78,б),
получаем
на оси (см. рисунок 2.78,б),
получаем
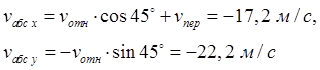
и
окончательно ![]()
2. Определение![]() . Согласно теореме
Кориолиса, абсолютное ускорение равно векторной сумме относительного,
переносного и кориолисова ускорений,
. Согласно теореме
Кориолиса, абсолютное ускорение равно векторной сумме относительного,
переносного и кориолисова ускорений,
![]()
В данном случае кориолисова ускорения ![]() не будет, так как переносное движение
поступательное и его угловая скорость
не будет, так как переносное движение
поступательное и его угловая скорость![]()
Относительное ускорение ![]() в
общем случае складывается из касательного и нормального ускорений, т.е.
в
общем случае складывается из касательного и нормального ускорений, т.е. ![]()
Касательное относительное ускорение ![]() вычисляем
через производную от алгебраического значения скорости:
вычисляем
через производную от алгебраического значения скорости: ![]() Ускорение
Ускорение
![]() направлено туда же, куда и скорость
направлено туда же, куда и скорость ![]() , так как знаки их алгебраических
значений совпадают (ускоренное движение).
, так как знаки их алгебраических
значений совпадают (ускоренное движение).
Нормальное относительное ускорение ![]() находим
через скорость и радиус кривизны траектории как
находим
через скорость и радиус кривизны траектории как
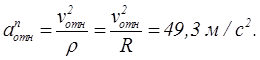
Оно направлено к центру окружности желоба (см. рисунок 5.22,б).
Переносное ускорение (поскольку движение тела D поступательное и прямолинейное) ищем, дифференцируя найденную ранее переносную скорость
![]()
и
при t=1 с имеем![]() Это
ускорение совпадает по направлению
Это
ускорение совпадает по направлению ![]() .
Проецируя на оси уравнение
.
Проецируя на оси уравнение ![]() , получим проекции вектора абсолютного
ускорения как
, получим проекции вектора абсолютного
ускорения как
![]()
![]()
Окончательно
![]()
Пример 2.60 - Тело D
вращается в плоскости рисунка (см. рисунок 2.79,а) вокруг оси О1
так, что его угол поворота равен ![]()
По жёлобу ОА движется точка М так, что алгебраическое значение длины дуги равно
![]()
Желоб
является окружностью радиусом R=20 см, расстояние ![]() Для момента времени t=1 с определить абсолютную скорость
Для момента времени t=1 с определить абсолютную скорость![]() и абсолютное ускорение
и абсолютное ускорение ![]() точки М.
точки М.
Решение.
1. Определение ![]() . По теореме о
сложении скоростей имеем
. По теореме о
сложении скоростей имеем ![]() .
.
Относительную скорость точки (скорость по отношению к телу D) находим, вычисляя ее алгебраическое значение как
производную от дуговой координаты по времени: ![]()
![]() Чтобы найти
направление этой скорости, установим, где находится точка М. При t=1 с, находим ОМ=20
Чтобы найти
направление этой скорости, установим, где находится точка М. При t=1 с, находим ОМ=20![]() см и устанавливаем,
что длина дуги составляет половину длины окружности, т.е. точка М
находится в точке А желоба (см. рисунок 2.79,б).
см и устанавливаем,
что длина дуги составляет половину длины окружности, т.е. точка М
находится в точке А желоба (см. рисунок 2.79,б).
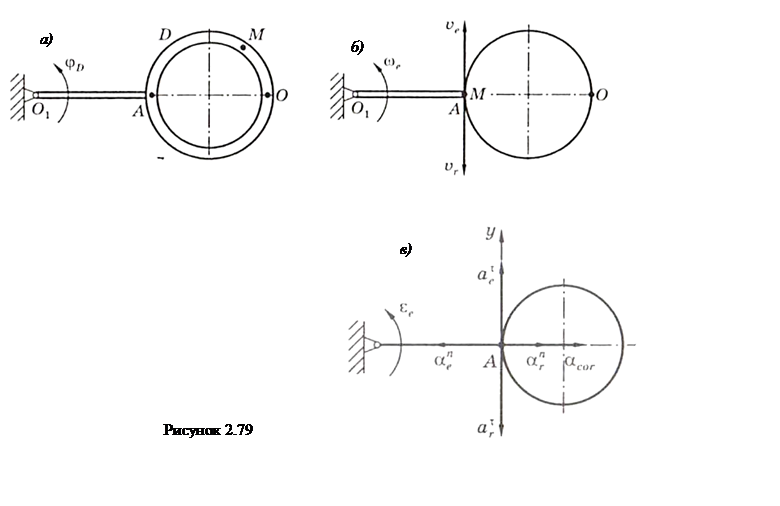 |
Скорость ![]() точки направлена по
касательной к ее траектории в сторону увеличения дуговой координаты, так как
алгебраическое значение скорости положительно.
точки направлена по
касательной к ее траектории в сторону увеличения дуговой координаты, так как
алгебраическое значение скорости положительно.
Переносной скоростью по определению будет скорость той точки вращающегося тела D, с которой совпадает точка М, т.е. скорость точки А:
![]()
где алгебраическое
значение угловой скорости переносного движения равно![]()
То
есть, при t=1 с получаем ![]() и
и ![]() Алгебраическое значение угловой
скорости положительно, следовательно, вращение происходит по направлению угла
поворота. Переносная скорость направлена перпендикулярно отрезку О1А
по ходу вращения.
Алгебраическое значение угловой
скорости положительно, следовательно, вращение происходит по направлению угла
поворота. Переносная скорость направлена перпендикулярно отрезку О1А
по ходу вращения.
Поскольку вектора ![]() и
и ![]() направлены противоположно, то
модуль абсолютной скорости равен
направлены противоположно, то
модуль абсолютной скорости равен ![]()
2. Определение ![]() . По теореме
Кориолиса
. По теореме
Кориолиса ![]() или
или
![]() (
(![]() )
)
Вычислим и покажем на рисунке все пять ускорений (см. рисунок 2.79,в)
Относительное касательное ускорение вычисляем через его алгебраическое значение:
![]()
Ускорение ![]() направлено туда же,
куда и скорость
направлено туда же,
куда и скорость ![]() , так как знаки их алгебраических
значений совпадают (ускоренное движение):
, так как знаки их алгебраических
значений совпадают (ускоренное движение): ![]()
Относительное нормальное ускорение направлено к центру
желоба и равно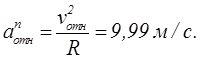
Переносное ускорение в данном случае – это ускорение точки А тела D.
Так как алгебраическое значение углового ускорения равно его модулю
![]() то переносное вращательное ускорение
равно
то переносное вращательное ускорение
равно
![]()
Оно направлено перпендикулярно О1А по ходу
углового ускорения, и поскольку алгебраические значения угловой скорости и
углового ускорения совпадают по знаку (ускоренное вращение), следовательно,![]() совпадает по направлению с
совпадает по направлению с ![]() .
.
Переносное центростремительное ускорение направлено к оси О1 и равно
![]()
Кориолисово ускорение![]() и
его модуль равен
и
его модуль равен
![]()
Так как вектор угловой скорости тела лежит на оси вращения,
то в данном случае он перпендикулярен плоскости чертежа и угол между ним и
вектором относительной скорости равен 900. Тогда ![]() .
.
Направление кориолисова ускорения может быть найдено или по
общему правилу для векторного произведения, или по специальному правилу
Жуковского. В нашем случае достаточно повернуть скорость ![]() на 900 по ходу вращения
тела.
на 900 по ходу вращения
тела.
Сложение векторов произведем с помощью проекций.
Спроецировав равенство (![]() ) на оси, получим
) на оси, получим
![]()
![]()
![]() ;
;
![]() и
окончательно
и
окончательно![]()
Пример 2.61
- Диск радиуса R = 0,5 м вращается вокруг своего вертикального
диаметра OB (см. рисунок 2.80) по закону ![]() (φ
измеряется в радианах, t – в секундах; положительное направление
отсчета угла φ показано на рисунке дуговой стрелкой). По ободу
диска движется точка M по закону
(φ
измеряется в радианах, t – в секундах; положительное направление
отсчета угла φ показано на рисунке дуговой стрелкой). По ободу
диска движется точка M по закону 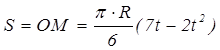 , где S измеряется в метрах; положительное и отрицательное
направления отсчета дуговых координат S от точки O указаны
знаками плюс (+) и минус (-) соответственно). Определить абсолютную
скорость и абсолютное ускорение точки M в момент времени t1=1
с.
, где S измеряется в метрах; положительное и отрицательное
направления отсчета дуговых координат S от точки O указаны
знаками плюс (+) и минус (-) соответственно). Определить абсолютную
скорость и абсолютное ускорение точки M в момент времени t1=1
с.
Решение. Для определенности свяжем жестко с диском систему координат O1xyz (координатная плоскость Oyz совмещена с плоскостью диска). Движение точки М рассматриваем как сложное. Вращение диска (подвижной системы координат O1xyz) вокруг вертикальной неподвижной оси O3z считаем переносным. При этом движение точки М по ободу диска будет относительным. Рассмотрим более полно эти движения.
1. Закон переносного вращательного движения задан уравнением
![]() (1)
(1)
Определим угловую скорость и угловое ускорение переносного вращения как алгебраические величины
![]()
![]()
При t1=1 c
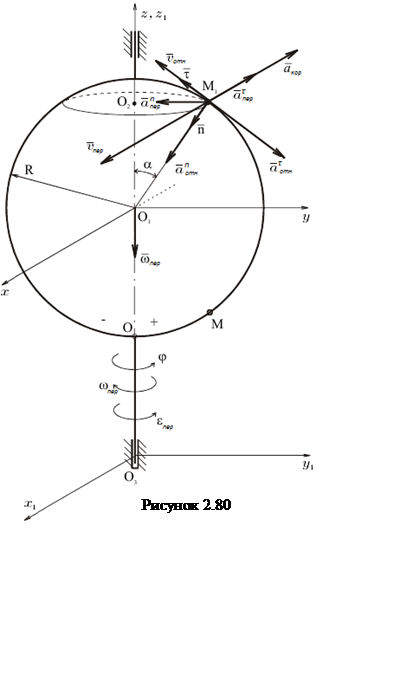
![]()
![]() (2)
(2)
Знак угловой скорости определяет направление вращения тела вокруг неподвижной оси. В рассматриваемом случае ω<О. Это означает, что вращение в момент времени t1= 1 с происходит в направлении убывания угла φ (т.е. в отрицательном направлении отсчета φ). Путем сопоставления знаков угловой скорости и углового ускорения можно установить характер вращательного движения, т.е. является оно ускоренным или замедленным. В рассматриваемом случае знаки угловой скорости и углового ускорения разные ω<0, ε>0). Это показывает, что в момент времени t1=1с абсолютная величина угловой скорости убывает, т.е. вращение диска является замедленным. На рисунке 2.54 ω и ε показаны дуговыми стрелками.
2. Относительное движение точки M задано естественным способом
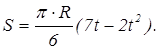 (3)
(3)
Сначала установим положение точки M на дуге окружности в момент времени t1 =1 с. Подставляя в уравнение (3) t1=1 с, получим
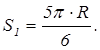 (4)
(4)
Центральный угол, соответствующий дуге окружности (4), определится по формуле
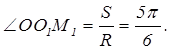
Из рисунка 2.80 следует, что
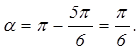
В положении M1 точки покажем орты двух естественных
осей ![]() и
и ![]() (
(![]() направим по касательной к
окружности радиуса R в сторону возрастания дуговой координаты S,
а
направим по касательной к
окружности радиуса R в сторону возрастания дуговой координаты S,
а ![]() по главной нормали к центру
окружности O).
по главной нормали к центру
окружности O).
3. Найдем абсолютную скорость точки М по формуле
![]()
где ![]() и
и ![]() соответственно переносная и относительная скорости точки.
соответственно переносная и относительная скорости точки.
Для определения переносной скорости точки в момент времени t1=1 с нужно мысленно остановить относительное движение точки в положении M1 и определить ее скорость как точки, жестко связанной с подвижной системой координат, т.е. с диском. Диск, как было указано выше, совершает вращательное движение вокруг неподвижной оси O1. В силу этого величина переносной скорости определится по формуле
![]() (6)
(6)
где h - расстояние от точки M1 до оси вращения.
Из прямоугольного треугольника O1M1O2 (см. рисунок 2.80)
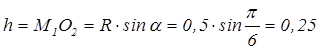 м. (7)
м. (7)
Т.о., на основании (6) с учетом (2) и (7) величина переносной скорости точки М в момент времени t1=1 с будет
![]() =0,25 м/с. (8)
=0,25 м/с. (8)
Вектор ![]() направлен перпендикулярно плоскости
диска (значит параллельнооси O1x)
в направлении вращения, указанном дуговой стрелкой ωe.
направлен перпендикулярно плоскости
диска (значит параллельнооси O1x)
в направлении вращения, указанном дуговой стрелкой ωe.
Для определения относительной скорости ![]() точки M1
нужно мысленно остановить переносное движение (вращение диска) и найти скорость
точки при ее движении по окружности радиуса R по закону (3). Проекция
вектора
точки M1
нужно мысленно остановить переносное движение (вращение диска) и найти скорость
точки при ее движении по окружности радиуса R по закону (3). Проекция
вектора![]() на направление орта
на направление орта ![]() определяется как
определяется как
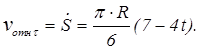 (8)
(8)
В момент времени t1=1 с
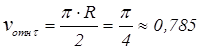 м/с.
(10)
м/с.
(10)
Так как вектора ![]() и
и ![]() взаимно перпендикулярны (вектор
взаимно перпендикулярны (вектор![]() расположен в плоскости O1yz, а вектор
расположен в плоскости O1yz, а вектор ![]() параллелен оси O1x), величину абсолютной скорости можно определить по
теореме Пифагора. При t1=1 с
параллелен оси O1x), величину абсолютной скорости можно определить по
теореме Пифагора. При t1=1 с
![]()
4. Определим абсолютное ускорение точки M.
В рассматриваемом случае переносное движение не является поступательным. В силу этого найдем абсолютное ускорение точки на основании теоремы Кориолиса по формуле
![]() ,
(13)
,
(13)
где ![]() ,
, ![]() ,
, ![]() - переносное, относительное и кориолисово ускорения точки.
- переносное, относительное и кориолисово ускорения точки.
При определении абсолютного ускорения
целесообразно разложить ![]() и
и ![]() на
нормальную и касательную составляющие, при этом соотношение (13) примет вид
на
нормальную и касательную составляющие, при этом соотношение (13) примет вид
![]() (14)
(14)
Для определения переносного ускорения точки в момент времени t1=1 с, как и при определении переносной скорости, мысленно остановим относительное движение и определим ускорение точки M1 как точки, неизменно связанной с диском (с подвижной системой координат). При вращательном движении диска вокруг неподвижной оси O3z1 величины нормального и касательного ускорения точки М1 диска определяются как
![]() (15)
(15)
![]() (16)
(16)
Вектор ![]() направлен по радиусу окружности, описываемой точкой М1
диска, к центру этой окружности - точке O2 (
направлен по радиусу окружности, описываемой точкой М1
диска, к центру этой окружности - точке O2 (![]() параллелен
оси O1y).
параллелен
оси O1y).
Ускорение ![]() направлено по касательной к этой окружности, т.е. перпендикулярно
направлено по касательной к этой окружности, т.е. перпендикулярно![]() (
(![]() параллелен
оси O1x). Так как диск в момент времени t1=1 с вращается замедленно, то вектора
параллелен
оси O1x). Так как диск в момент времени t1=1 с вращается замедленно, то вектора ![]() и
и ![]() направлены
в противоположные стороны, т.е. направление вектора
направлены
в противоположные стороны, т.е. направление вектора ![]() определяется
направлением углового ускорения
определяется
направлением углового ускорения![]() , которое показано на рисунке 2.80 дуговой стрелкой.
, которое показано на рисунке 2.80 дуговой стрелкой.
При естественным способе задания относительного
движения проекции относительного ускорения точки на естественные оси,
положительные направления которых определяются ортами ![]() и
и ![]() , можно найти по формулам
, можно найти по формулам
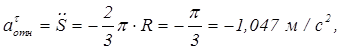 (17)
(17)
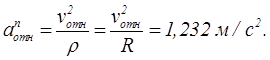 (18)
(18)
Отрицательный знак проекции ![]() указывает,
что вектор
указывает,
что вектор ![]() направлен
в сторону, противоположную орту
направлен
в сторону, противоположную орту![]() . Нормальное ускорение всегда направлено в сторону орта
. Нормальное ускорение всегда направлено в сторону орта![]() , т.е.
по главной нормали к центру кривизны траектории точки. Таким образом, в
рассматриваемом случае
, т.е.
по главной нормали к центру кривизны траектории точки. Таким образом, в
рассматриваемом случае ![]() направлен
к центру O1, окружности радиуса R, являющейся
траекторией относительного движения точки. Величины относительного касательного
направлен
к центру O1, окружности радиуса R, являющейся
траекторией относительного движения точки. Величины относительного касательного![]() и
относительного нормального
и
относительного нормального ![]() ускорений согласно (17) и (18) будут равны
ускорений согласно (17) и (18) будут равны
![]() (19)
(19)
![]() (20)
(20)
Ускорение Кориолиса определяется по формуле
![]() (21)
(21)
Вектор угловой скорости переносного вращения ![]() направлен
по оси вращения в ту сторону, откуда вращение наблюдается против хода часовой
стрелки (см. рисунок 2.80). В момент времени t1=1 с, учитывая (2),
направлен
по оси вращения в ту сторону, откуда вращение наблюдается против хода часовой
стрелки (см. рисунок 2.80). В момент времени t1=1 с, учитывая (2),
![]() (22)
(22)
Модуль ускорения Кориолиса на основании свойств векторного произведения равен
![]() (23)
(23)
Из (23) с учетом (22) и (11) получим
![]() (24)
(24)
Ускорения Кориолиса направлено перпендикулярно
плоскости, проходящей через вектора и ![]() (вектор
(вектор ![]() при этом нужно перевести в точку M1) в
сторону, откуда кратчайшее совмещение
при этом нужно перевести в точку M1) в
сторону, откуда кратчайшее совмещение ![]() с
с ![]() видно
против хода часовой стрелки. Так как вектора
видно
против хода часовой стрелки. Так как вектора ![]() и
и ![]() расположены
в плоскости O1yz, то
расположены
в плоскости O1yz, то ![]() направлено параллельно оси O1x в
сторону, противоположную оси O1x.
направлено параллельно оси O1x в
сторону, противоположную оси O1x.
Направление ускорения Кориолиса можно найти
другим способом, применив правило Н.Е.Жуковского, заключающееся в следующем.
Прежде всего, нужно найти проекцию вектора ![]() на плоскость, перпендикулярную оси вращения (на плоскость O1yz).
В данном случае эта проекция направлена также, как вектор
на плоскость, перпендикулярную оси вращения (на плоскость O1yz).
В данном случае эта проекция направлена также, как вектор![]() . Затем необходимо повернуть найденную
проекцию в направлении вращения, указанному дуговой стрелкой
. Затем необходимо повернуть найденную
проекцию в направлении вращения, указанному дуговой стрелкой![]() , на
угол π/2. Полученное в результате поворота направление проекции относительной
скорости будет соответствовать направлению
, на
угол π/2. Полученное в результате поворота направление проекции относительной
скорости будет соответствовать направлению![]() .
.
Для определения абсолютного ускорения найдем
его проекции на оси координат x, y, z. Согласно (14) проекция
абсолютного ускорения на любую ось равна алгебраической сумме проекций
ускорений![]() на ту же ось. Проекции этих ускорений на оси координат
легко найти из рисунка. Таким образом, для момента времени t1=1 с:
на ту же ось. Проекции этих ускорений на оси координат
легко найти из рисунка. Таким образом, для момента времени t1=1 с:
![]()
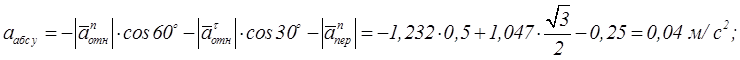
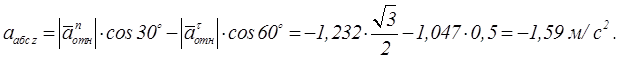
По трем проекциям абсолютного ускорения нетрудно найти его модуль и направление. Модуль абсолютного ускорения
![]()
Список литературы
1. Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 1990.
2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Учебник: в 2-х т. - М.: Наука, 2002.
3. Мещерский И.В. Сборник задач по теоретической механике. Учеб. пособие. - СПб.: Лань, 2005.
4. Тарг С.М. Краткий курс теоретической механики. Учебник. - М.: Наука, 2002.
5. Яблонский А.А. Курс теоретической механики. Учебник: в 2-х т. - М.: Высшая школа, 2002.
6. Сборник заданий для курсовых работ по теоретической механике. Учеб. пособие /Под ред. А.А.Яблонского. - М.: Высшая школа, 1985.
7. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Учеб. пособие: в 2-х частях. - М.: Наука, 1984.
8. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Учеб. пособие: в 2-х т. - М.: Наука, 1983.
9. Сборник задач по теоретической механике. Учеб. пособие./Под ред. К.С.Колесникова. - М.: Высшая школа, 1983.
10. Сборник коротких задач по теоретической механике: Учеб. пособие./Под ред. О.Э. Кепе. - М.: Высшая школа, 1989.
11. Аркуша А.И. Техническая механика. Руководство к решению задач по теоретической механике. - М.: Высш. шк., 2002.
12. Теоретическая механика. Статика. Практикум: учебное пособие /В.А.Акимов и др.; под общ. ред. проф. А.В. Чигарева. — Минск: Новое знание; М.: ЦУПЛ, 2010.
13. Динасылов А.Д. Механика. Конспект лекций для студентов специальности 5B074600 – Космическая техника и технологии. – Алматы: АУЭС, 2013.
Алмас Даменович Динасылов,
Константин Самсонович Иванов
МЕХАНИКА.
Статика И кинематика: решение задач
Учебное пособие
Редактор Т.С.Курманбаева
Св. тем. план 2012 г., поз. 55
Сдано в набор . .13 г.
Формат 60х84 1/16
Типографская бумага №2
Учебно-изд.листов – 6,0. Тираж 100 экз. Заказ . Цена 600 тенге.
Подписано к печати . . 2013 г.
Копировально-множительное бюро
некоммерческого акционерного общества
«Алматинский университет энергетики и связи»
050013, Алматы, ул. Байтурсынова, 126