Коммерциялық
емес акционерлік қоғам
АЛМАТЫ
ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Инженерлік
графика және қолданбалы механика кафедрасы
МЕХАНИКА
5В074600 – Ғарыштық техника
және технологиялар
мамандығы студенттеріне арналған дәріс
жинағы
Алматы 2013
ҚҰРАСТЫРҒАНДАР: Тойбаев С.Н., Дінасылов А.Д. Механика: 5В074600 - Ғарыштық техника және технологиялар мамандығы студенттеріне арналған дәріс конспектілері.-Алматы: АЭжБУ, 2013.–61 б.
Дәріс коспектілері 5В074600 - Ғарыштық техника және технологиялар мамандығының студенттері үшін оқылатын дәрістер курсының «Механика» пәні бойынша негізгі теориялық материалдарын қамтиды. Конспектіде статика, кинематика, механикалық жүйе динамикасы, сонымен қатар аналитикалық механика негіздері және космостық қозғалыстың теориясы қарастырылады.
Дәріс көлеміне шектеу қойылғандықтан, кейбір жағдайлардың қорытындысы шығарылмаған және материалды оқып үйрену үшін келтірілген мысалдар саны жеткіліксіз, сондықтан студенттер пәнді оқып үйренгенде коспектінің соңында көрсетілген тізімдегі қосымша әдебиеттерді пайдаланады.
Дәріс коспектілерін «Механика» немесе «Қолданбалы механика» пәндерін оқитын басқа мамандықтардың студенттері де пайдалануға болады.
Без. - 37, әдеб. көрсеткіші – 11 атау.
Пікір беруші: техн. ғыл. канд. Тулбаев А.А.
«Алматы энергетика және байланыс университеті» коммерциялық емес акционерлік қоғамының 2013 жылғы жоспары бойынша басылады.
© «Алматы энергетика және байланыс университетінің» КЕАҚ, 2013 ж.
Мазмұны
|
1 дәріс. Кіріспе. Статиканың нeгізгі ұғымдары мeн аксиомалары. Тоғысатын күштер жүйесі |
4 |
|
2 дәріс. Нүктеге және оське қатысты күш моменттері. Күштер жұбы. Күштер жүйесін берілген центрге келтіру |
7 |
|
3 дәріс. Күштер жүйесінің тепе-теңдігі. Үйкеліс. Ауырлық центрі |
11 |
|
4 дәріс. Нүкте кинематикасы және қатты дененің қарапайым қозғалыстары |
14 |
|
5 дәріс. Қатты дененің жазық параллель қозғалысы. Нүктенің күрделі қозғалысы |
18 |
|
6 дәріс. Қатты дененің қозғалмайтын нүктені айнала қозғалысы. Еркін қатты дененің жалпы жағдайдағы қозғалысы |
23 |
|
7 дәріс. Қатты дененің күрделі қозғалысы |
27 |
|
8 дәріс. Нүкте динамикасы. Нүкте динамикасының жалпы теоремалары |
32 |
|
9 дәріс. Нүктенің түзу сызықты тербелмелі қозғалысы |
37 |
|
10 дәріс. Қатты дене және механикалық жүйе динамикасының негіздері. Механикалық жүйе динамикасының теоремалары |
43 4 |
|
11 дәріс. Аналитикалық механиканың элементтері |
48 |
|
12 дәріс. Айнымалы массалы нүкте қозғалысы. Циолковский есебі |
54 |
|
Әдебиеттер тізімі |
60 |
1 дәріс. Кіріспе. Статика аксиомалары. Статиканың негізгі ұғымдары мен аксиомалары. Тоғысатын күштер жүйесі
Дәрістің мазмұны: механика техниканың теориялық базасы ретінде; кіріспе ұғымдар және статиканың аксиомалары; тоғысқан күштер жүйелері және олардың тепе-теңдігінің шарттары.
Дәрістің мақсаты: механиканың рөлін анықтау, статиканың негізгі ұғымдарын және аксиомаларын тұжырымдау, тоғысатын күштер жүйесін қарапайымдату және оның тепе-теңдік шарттарын қарастыру.
«Механика» - бакалаврларды жалпы техникалық дайындау негізіндегі пән. Механика машина жасау саласының теориялық негізі болып келеді, ол машиналар, механизмдер, аспаптардың сенімділігін, жобалау сапасын және дұрыс қолдануын арттыруда үлкен рөлді атқарады.
Механика (М) – материялық денелер механикалық қозғалысының (МҚ) жалпы заңдары туралы ғылым. МҚ - денелердің кеңістіктегі салыстырмалы орналасуының уақыт өтуімен өзгеруі. МҚ дербес жағдайы – денелердің тепе-теңдігі, бұл олардың тек тыныштық қалпы емес, бірқалыпты түзу сызықты қозғалысы да. Механикада денелердің өзара механикалық әрекеттесуі қарастырылады, яғни нәтижесінде денелер қозғалысының өзгеруі. М статика, кинематика және динамика бөлімдерінен тұрады. Статикада күштер жүйелерін түрлендіру әдістері және олардың тепе-теңдігінің шарттары зерттеледі. Денелердің қозғалысы кинематикада күштер ескерілмей қарастырылады, динамикада күштер ескеріліп, қарастырылады.
1.1 Статиканың негізгі ұғымдары мен аксиомалары. Үш күш туралы теорема
М зерттеу объектілері ретінде денелердің модельдері алынады, олар материялық нүкте (МН), МН жүейсі және абсолют қатты дене (АҚД).
МН деп өлшемдерін ескермеуге болатын, массасы нүктеде жинақталады деп есептелетін денені айтамыз. МН жүйесі деп орналасуы мен қозғалыстары өзара байланысудағы МН жиынтығын айтамыз. АҚД - кез келген нүктелері арасындағы қашықтықтары өзгермейтін дене. Шынында барлық денелер күштер әсерінен өз өлшемдерін және формасын өзгертеді (дефомацияланады). Көбінесе сол деформациялар аз болғандықтан, денені абсолют қатты дене деп деформацияларды есепке алмауға болады.
Дененің тепе-теңдік немесе
қозғалыс қалпы оның басқа денелермен өзара
механикалық әрекеттенуіне тәуелді, осының өлшемі -
күш. Күш – вектор, ол сан шамасымен, бағытымен және
түсу нүктесімен сипатталады. Графикалық түрде күш
бағытталған түзудің кесіндісімен көрсетіледі.
Күш бағыты бойындағы түзу күштің әсер
ету сызығы (ӘС) деп аталады. Күшті, мысалы ![]() деп белгілейміз, сонда
деп белгілейміз, сонда ![]() оның
модулі. Қатты денеге немесе нүктеге түсетін күштер
жиынтығы күштер жүйесі (КЖ) деп аталады. Оны
оның
модулі. Қатты денеге немесе нүктеге түсетін күштер
жиынтығы күштер жүйесі (КЖ) деп аталады. Оны ![]() деп
белгілейміз.
деп
белгілейміз.
Егер қатты денеге әсер ететін КЖ-н
дененің тыныштық немесе қозғалыс қалпын
өзгертпей, басқа КЖ-не ауыстыруға болса, олар баламалы
күштер жүйелері деп аталады ![]() ~
~![]() . Егер берілген КЖ бір ғана күшке баламалы
болса, сол күш қарастырылудағы КЖ-нің деп аталады. Оны
. Егер берілген КЖ бір ғана күшке баламалы
болса, сол күш қарастырылудағы КЖ-нің деп аталады. Оны ![]() * деп белгілесек, сонда
* деп белгілесек, сонда ![]() *~
*~![]() . Кез
келген КЖ-нде тең әсерлісі бола бермейді. КЖ денеге түскенде,
ол дененің тыныштық немесе қозғалыс қалпын
өзгертпейтін болса, КЖ теңгерілген деп аталады. Теңгерілген
КЖ-нің әсері нөлге баламалы, яғни
. Кез
келген КЖ-нде тең әсерлісі бола бермейді. КЖ денеге түскенде,
ол дененің тыныштық немесе қозғалыс қалпын
өзгертпейтін болса, КЖ теңгерілген деп аталады. Теңгерілген
КЖ-нің әсері нөлге баламалы, яғни ![]() ~0.
Егер күшті
КЖ-не қосқанда,
ол сонымен бірге нөлге баламалы жаңа
КЖ-н құрса,
күшті
КЖ-н теңгеретін
күш
деп атайды. Дененің бір
нүктесіне түсетін күш қадалған күш деп
аталады.
~0.
Егер күшті
КЖ-не қосқанда,
ол сонымен бірге нөлге баламалы жаңа
КЖ-н құрса,
күшті
КЖ-н теңгеретін
күш
деп атайды. Дененің бір
нүктесіне түсетін күш қадалған күш деп
аталады.
Статика төмендегі 6 аксиомаға негізделеді:
1) Денеге түсетін екі күш
тепе-теңдікте болу үшін олардың шамалары тең болуы
және күштер өздерінің
түсу нүктелері арқылы өтетін түзу бойымен
қарама-қарсы бағытталуы қажетті де жеткілікті: F1
= F2, бірақ ![]() .
.
2) Күштер жүйесінің қатты денеге әсерін өзгертпей, соған теңгерілген КЖ-н қосуға немесе алып тастауға болады. Салдары: АҚД-ге түсетін күштің әсерін өзгертпей, оны ӘС бойымен дененің кез келген нүктесіне көшіруге болады, яғни күш - жылжымалы вектор.
3) Бір нүктеге түсетін екі күштің тең
әсерлісі сол күштер қабырғалары болатын
параллелограмның диагоналі ретінде анықталады, ![]() .
.
4) Екі дене бір-біріне шамалары тең
және бір түзу бойымен қарама-қарсы
бағытталған күштермен әсер етеді: F21
= F12, ![]() .
.
5-аксиоманың алдында бірнеше ұғымды енгіземіз. Егер дененің кеңістікте кез келген орын ауыстыруы мүмкін болса, ол еркін дене деп, керісінше - еркін емес деп аталады. Дене қозғалысының еркіндігін шектейтін шарттар байланыстар деп аталады. Дене түскен күштер әсерінен байланыс кедергілік жасап тұрған орын ауыстыруды орындауға тырысып, оған күш түсіреді. Біржолы байланыс та денеге модулі тап сондай, қарама-қарсы бағытталған байланыстың реакциясы деп аталатын күшті түсіреді. Реакциялардан басқа күштерді актив (пәрменді) күштер деп атаймыз. Байланыс реакциясының актив күштерден айырмашылығы – оның шамасы актив күштерге тәуелді және алдын ала белгісіз. Реакцияның бағыты - байланыс дененің қозғалысына кедергілік жасайтын бағытқа қарама-қарсы. Кейбір байланыстардың (тіректердің) реакцияларын қарастырайық:
а) тегіс бет (үйкеліс ескерілмейді) дененің бет үстінде жылжуына кедергілік жасамайды, ол тек қана бетке тік бағытпен қозғалуға кедергілік жасайды. Сондықтан оның реакциясы жанасып тұрған денелердің беттеріне ортақ нормаль бойымен бағытталады және жанасу нүктесіне түседі;
б) икемді жіп (шынжыр); реакция жіп (шынжыр) бойымен бағытталады;
в) цилиндрлік топса (подшипник) немесе жылжымайтын топсалы тұғыр. Тесіктерінен өтетін білікпен қосылған екі дене топсалы қосылысты құрайды. Біліктің осьтік сызығы топсаның осі деп аталады. Дене топса осіне перпендикуляр бағытта орын ауыстыра алмайды, бірақ ол оське қатысты айнала алады. Сондықтан реакциясы топса осіне перпендикуляр жазықтықта кез келген бағытталуы мүмкін. Әдетте оны екі құраушы күшке жіктейді;
г) каток түріндегі тірек немесе жылжымалы топсалы тұғыр. Үйкеліс күші ескерілмесе, реакция домалау бетінің нормалі бойымен бағытталады;
д) сфералық топса және өкшелік. Мұндай байланыс дененің бір нүктесі ешқандай орын ауыстыру ала алмайтындай қылып бекітеді, ал сол нүктеге қатысты дене кеңістікте кез келген бағытта айналуы мүмкін. Реакция бекітілген нүкте арқылы өтеді, оны үш құраушы күшке жіктейді;
е) екі шетінде топсалармен бекітілген, салмағы ескерілмейтін сырық. Реакциялар топсалардың центрлерінен өтетін түзу бойымен бағытталады.
5) Еркін емес денені, байланыстарды алып тастап және олардың әсерін реакциялармен ауыстырып, еркін дене ретінде қарастыруға болады.
6) Қатаю аксиомасы. Деформацияланатын дененің КЖ-нің әсерінен болған тепе-теңдік қалпы, оған қосымша байланыстарды орнатса, тіпті денені қатайған (абсолют қатты) дене ретінде қарастырса да, өзгермейді.
Үш күш туралы теорема: егер дене бір жазықтықта орналасқан үш параллель емес күш әсерінен тепе-теңдік қалпында болса, онда сол күштердің әсер ету сызықтары бір нүктеде қиылысады.
1.2 Тоғысатын күштер жүйесі
Күштер жүйеcі (КЖ) келесі түрлерде болуы мүмкін: тоғысатын, параллель және кез келген. Тоғысатын күштер жүйесі деп күштердің әсер ету сызықтары (ӘС) бір нүктеде қиылысатын КЖ-н атайды. Параллель деп ӘС өзара параллель КЖ-н атайды. Кез келген деп ӘС қиылыспайтын және параллель емес КЖ-сі аталады. Аталған күштер жүйелері жазық және кеңістік болуы мүмкін. Егер барлық күштердің ӘС бір жазықтықта жатса, КЖ жазық деп, керісінше жағдайда кеңістік деп аталады.
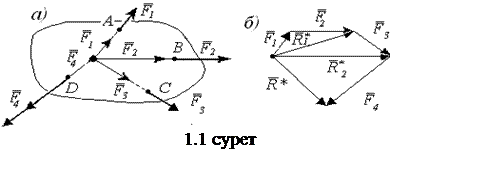 Денеге А, В, С, D нүктелерінде түсірілген
әсер ету сызықтары О нүктесінде қиылысатын
Денеге А, В, С, D нүктелерінде түсірілген
әсер ету сызықтары О нүктесінде қиылысатын ![]() күштерін
қарастырайық (1.1,а-суретті қараңыз). Күштерді
олардың ӘС бойымен О нүктеге көшіріп, оларды
тізбектеп күштер үшбұрышы ережесімен қосамыз (1.1,б-суретті
қараңыз). Алдымен
күштерін
қарастырайық (1.1,а-суретті қараңыз). Күштерді
олардың ӘС бойымен О нүктеге көшіріп, оларды
тізбектеп күштер үшбұрышы ережесімен қосамыз (1.1,б-суретті
қараңыз). Алдымен ![]() ,
, ![]() күштерінің тең
әсерлі
күштерінің тең
әсерлі ![]() күшін, сонан соң
күшін, сонан соң ![]() ,
, ![]() күштерінің тең әсерлі
күштерінің тең әсерлі ![]() күшін, сөйтіп т.б.
табамыз. Сонда:
күшін, сөйтіп т.б.
табамыз. Сонда: ![]() ,
, ![]() ,
, ![]() . Күштер саны n болса,
онда
. Күштер саны n болса,
онда
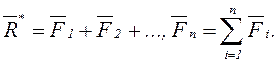 (1.1)
(1.1)
![]() күшін былай
да табуға болады: алдымен
күшін былай
да табуға болады: алдымен ![]() векторын тұрғызып,
оның ұшынан
векторын тұрғызып,
оның ұшынан ![]() векторын, содан кейін
векторын, содан кейін ![]() векторының ұшынан
векторының ұшынан ![]() векторын
және сөйтіп т.б. тұрғызамыз. Сонда
векторын
және сөйтіп т.б. тұрғызамыз. Сонда ![]() күші бірінші вектордың
басын соңғы вектордың ұшымен қосады. Сонымен,
тоғысатын КЖ-нің тең әсерлісін геометриялық
тәсілімен табу үшін, күштердің қиылысу
нүктесінде күш көпбұрышын тұрғызу керек;
күші бірінші вектордың
басын соңғы вектордың ұшымен қосады. Сонымен,
тоғысатын КЖ-нің тең әсерлісін геометриялық
тәсілімен табу үшін, күштердің қиылысу
нүктесінде күш көпбұрышын тұрғызу керек; ![]() оның тұйықтаушысы болып келеді.
оның тұйықтаушысы болып келеді.
Тоғысатын КЖ-нің тең әсерлі күшін аналитикалық тәсілмен анықталуын қарастырайық. Ол үшін (1.1) теңдеуін декарт координаттар жүйесінің осьтеріне проекциялап, тең әсерлі күшінің проекцияларын анықтаймыз:
![]() ,
, 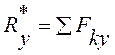 ,
,
![]() . (1.2)
. (1.2)
Тең әсерлі күшінің модулі мен бағыты келесі формулалармен табылады:
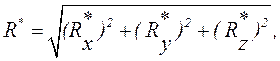 (1.3)
(1.3)
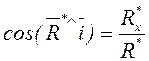 ,
,  ,
, 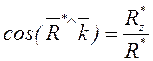 . (1.4)
. (1.4)
Тоғысатын КЖ тепе-теңдікте болуы
үшін ![]() , яғни
, яғни ![]() болуы
керек (тепе-теңдік шартының векторлық түрдегі жазылуы).
Геометриялық түрде: күш көпбұрышы
тұйықталу керек. Аналитикалық түрде: барлық
күштердің үш оське проекцияларының қосындылары
нөлге тең болуы,
болуы
керек (тепе-теңдік шартының векторлық түрдегі жазылуы).
Геометриялық түрде: күш көпбұрышы
тұйықталу керек. Аналитикалық түрде: барлық
күштердің үш оське проекцияларының қосындылары
нөлге тең болуы,
![]() ,
, ![]() ,
, ![]() .
(1.5)
.
(1.5)
Тоғысатын жазық КЖ үшін
![]() ,
, ![]() .
(1.6)
.
(1.6)
2 дәріс. Күштің нүктеге және оське қатысты моменті. Күштер жұбы. Күштер жүйесін берілген центрге келтіру
Дәрістің мазмұны: күштің нүктеге және оське қатысты моменті; күштер жұбы, күштер жұбының қасиеттері, күштер жүйесін центрге келтіру.
Дәрістің мақсаты: күштің нүктеге және оське қатысты моментінің қасиеттерін, күштер жұбының қасиеттерін, күштер жұптары жүйесін қарапайымдатуды және оның тепе-теңдік шарттарын, кез келген күштер жүйесін қарапайым түрге келтіруін зерттеу.
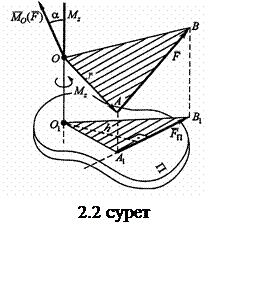
2.1 Күштің нүктеге қатысты және оське қатысты моменті
![]() күшінің
О нүктесіне қатысты моменті деп (2.1-суретті
қараңыз) О нүктесінде түсетін және
төмендегі формуламен анықталатын
күшінің
О нүктесіне қатысты моменті деп (2.1-суретті
қараңыз) О нүктесінде түсетін және
төмендегі формуламен анықталатын ![]() векторы аталады:
векторы аталады:
![]() (2.1)
(2.1)
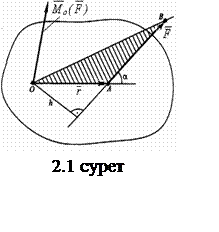 мұндағы
мұндағы ![]() - О нүктесінен
- О нүктесінен ![]() күші
түсетін А нүктесіне жүргізілген радиус-вектор.
күші
түсетін А нүктесіне жүргізілген радиус-вектор.
![]() векторының модулі күштің F модулі мен О
нүктесінен күштің әсер ету сызығына дейін
ең қысқа қашықтығының, яғни
күштің О нүктесіне қатысты иінінің
көбейтіндісіне тең.
векторының модулі күштің F модулі мен О
нүктесінен күштің әсер ету сызығына дейін
ең қысқа қашықтығының, яғни
күштің О нүктесіне қатысты иінінің
көбейтіндісіне тең.
![]() =F∙h. (2.2)
=F∙h. (2.2)
![]() моменті
моменті ![]() күшінің
О нүктесіне қатысты айналдыру әсерін сипаттайды.
күшінің
О нүктесіне қатысты айналдыру әсерін сипаттайды. ![]() радиус-векторын О
нүктесінен
радиус-векторын О
нүктесінен ![]() күшінің ӘС-нда жатқан кез
келген нүктесіне жүргізуге болады. Егер О нүктесі
күштің әсер ету сызығында жатса, онда күштің
О нүктесіне қатысты моменті нолге тең болады (иіні
нөлге тең)
күшінің ӘС-нда жатқан кез
келген нүктесіне жүргізуге болады. Егер О нүктесі
күштің әсер ету сызығында жатса, онда күштің
О нүктесіне қатысты моменті нолге тең болады (иіні
нөлге тең) ![]() күштер жүйесі үшін
күштер жүйесі үшін
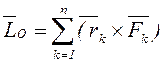 , (2.3)
, (2.3)
векторы күштер жүйесінің О нүктесіне қатысты бас моменті деп аталады.
 Жазық күштер жүйесі үшін
күштің нүктеге қатысты алгебралық моментін қолданған
ыңғайлы, өйткені бұл жағдайда барлық
күштердің векторлық моменттері бір-біріне параллель болады.
Күштің нүктеге қатысты алгебралық моменті деп
күш модулінің күш иініне көбейтіндісі аталады.
Жазық күштер жүйесі үшін
күштің нүктеге қатысты алгебралық моментін қолданған
ыңғайлы, өйткені бұл жағдайда барлық
күштердің векторлық моменттері бір-біріне параллель болады.
Күштің нүктеге қатысты алгебралық моменті деп
күш модулінің күш иініне көбейтіндісі аталады.
![]() . (2.4)
. (2.4)
Күш денені сағат тілінің қозғалысына қарсы бағытта айналдыруға тырысса, алгебралық момент оң таңбамен, керісінше теріс таңбамен алынады.
![]() күшінің оське қатысты моменті деп оның осьте
жатқан кез келген нүктеге қатысты векторлық
моментінің сол оське проекциясы аталады, яғни
күшінің оське қатысты моменті деп оның осьте
жатқан кез келген нүктеге қатысты векторлық
моментінің сол оське проекциясы аталады, яғни
![]() . (2.5)
. (2.5)
Басқаша: ![]() күшінің
оське қатысты моменті - күштің оське перпендикуляр жазықтыққа
түсірілген проекциясының (2.2-суретті қараңыз)
жазықтық пен осьтің қиылысу нүктесіне
қатысты алгебралық моменті
күшінің
оське қатысты моменті - күштің оське перпендикуляр жазықтыққа
түсірілген проекциясының (2.2-суретті қараңыз)
жазықтық пен осьтің қиылысу нүктесіне
қатысты алгебралық моменті
![]() . (2.6)
. (2.6)
Күштің оське қатысты моменті
күш пен ось бір жазықтықта орналасса, нөлге тең. Күштің
координат жүйесінің басына қатысты ![]() моменті (2.1) формуласына сай мына
формуламен анықталады:
моменті (2.1) формуласына сай мына
формуламен анықталады:
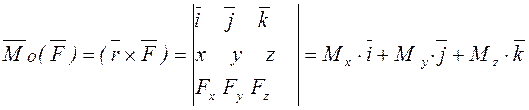 .
.
2.2 Параллель күштерді қосу
АҚД-ге түскен екі параллель және бір жаққа бағытталған күштің тең әсерлісінің модулі күштер модульдерінің қосындысына тең, бағыты күштерге параллель және бағыттас. Тең әсерлінің ӘС-ғы берілген күштердің ӘС арасындағы түзуді күштер модульдеріне кері пропорционал бөліктерге іш жағынан бөліп өтеді. Керісінше, кез келген күшті екі параллель және сол күшке бағыттас күшке жіктеуге болады.
Өзара тең емес, параллель және қарсы бағытталған екі күштің тең әсерлісінің модулі күштер модульдерінің айырмашылығына тең және бағыты үлкен күштің бағытымен бірдей болады. Тең әсерлінің ӘС-ғы үлкен күштің ӘС сыртынан, күштердің ӘС арасындағы түзу сызықты кесіндіні күштер модульдеріне кері пропорционал бөліктерге сыртқы жағынан бөліп өтеді.
2.3 Күштер жұбы. Күштер жұбының моменті
 АҚД-ге түсетін күштер жұбы деп
модульдері тең, параллель, бір-біріне қарсы бағытталған
және бір түзуде жатпайтын екі күштің жүйесін
атаймыз (2.3-суретті қараңыз). Күштердің
қосындысы нөлге тең, бірақ күштер жұбы
теңгерілмейді. Күштердің ӘС арасындағы ең
қысқа қашықтық жұптың иіні d
деп, ал күштер орналасқан жазықтық жұптың
әсер ету жазықтығы деп аталады. Денеге түсетін бірнеше
жұптың жиынтығы күштер жұптарының
жүйесі деп аталады. Жұп тең әсерлі күшке
келтірілмейді. Жұптың денеге әсері жұптың
әсер ету жазықтығына перпендикуляр
АҚД-ге түсетін күштер жұбы деп
модульдері тең, параллель, бір-біріне қарсы бағытталған
және бір түзуде жатпайтын екі күштің жүйесін
атаймыз (2.3-суретті қараңыз). Күштердің
қосындысы нөлге тең, бірақ күштер жұбы
теңгерілмейді. Күштердің ӘС арасындағы ең
қысқа қашықтық жұптың иіні d
деп, ал күштер орналасқан жазықтық жұптың
әсер ету жазықтығы деп аталады. Денеге түсетін бірнеше
жұптың жиынтығы күштер жұптарының
жүйесі деп аталады. Жұп тең әсерлі күшке
келтірілмейді. Жұптың денеге әсері жұптың
әсер ету жазықтығына перпендикуляр ![]() векторлық
моментімен сипатталады, бұл вектордың шамасы F∙d тең,
және вектордың ұшынан қарағанда, жұп денені
сағат тіліне қарсы айналдыруға тырысатын болып
көрінеді. Күштер жұбын оның әсер ету
жазықтығында және параллель жазықтыққа,
күш модулі мен жұп иінін өзгертіп, бірақ жұп
модулі мен оның денені айналдыруға тырысатын бағытын
сақтап, көшіруге болады, яғни күштер
жұбының векторлық моменті – еркін вектор.
векторлық
моментімен сипатталады, бұл вектордың шамасы F∙d тең,
және вектордың ұшынан қарағанда, жұп денені
сағат тіліне қарсы айналдыруға тырысатын болып
көрінеді. Күштер жұбын оның әсер ету
жазықтығында және параллель жазықтыққа,
күш модулі мен жұп иінін өзгертіп, бірақ жұп
модулі мен оның денені айналдыруға тырысатын бағытын
сақтап, көшіруге болады, яғни күштер
жұбының векторлық моменті – еркін вектор.
Векторлық моменттері бірдей екі күштер жұбы баламалы болады.
Егер күштер жұптары бір жазықтықта орналасса, олардың моменттерін алгебралық шамалар ретінде қарастыруға болады. Жұп денені сағат тіліне қарсы айналдыруға тырысса, оның моменті оң, керісінше теріс болып саналады. Сонда күштер жұптарының жазық жүйесі үшін
![]() (2.7)
(2.7)
Жұптарды қосу туралы теорема: күштер
жұптарының жүйесі векторлық моменті барлық
жұптардың векторлық моменттерінің қосындысына
тең бір жұпқа баламалы, яғни 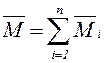 және жұптар жүйесінің тепе-теңдік шарты
және жұптар жүйесінің тепе-теңдік шарты
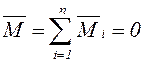 . (2.8)
. (2.8)
2.4 Күштерді параллель көшіру туралы теорема
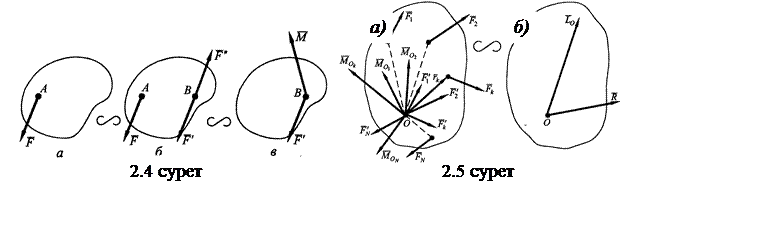 АҚД-ге түсетін күшті, оның
денеге әсерін өзгертпей, дененің кез келген басқа
нүктесіне, күштер жұбын қосып, өзіне параллель
көшіруге болады (2.4-суретті қараңыз); жұптың
моменті күштің сол нүктеге қатысты моментіне тең.
АҚД-ге түсетін күшті, оның
денеге әсерін өзгертпей, дененің кез келген басқа
нүктесіне, күштер жұбын қосып, өзіне параллель
көшіруге болады (2.4-суретті қараңыз); жұптың
моменті күштің сол нүктеге қатысты моментіне тең.
2.5 Күштер жүйесін берілген центрге келтіру
АҚД-ге әсер ететін кез келген КЖ-н бір центрге келтіруге болады, сонда күштер жүйсі келтіру центріне түсетін жүйенің бас векторына тең бір күш пен моменті жүйенің сол центрге қатысты бас моментіне тең бір жұпқа ауыстырылады (2.5-суретті қараңыз); мұндағы
 (2.9)
(2.9)
 . (2.10)
. (2.10)
![]() шамасы келтіру
центрінің таңдалуына тәуелсіз, ал
шамасы келтіру
центрінің таңдалуына тәуелсіз, ал ![]() –
тәуелді.
–
тәуелді.
АҚД-ге әсер ететін екі КЖ, олардың бас векторлары және бір нүктеге қатысты бас моменттері бірдей болғанда, баламалы.
Вариньон теоремасы: егер КЖ-нің тең әсерлі күші болса, оның кез келген нүктеге немесе оське қатысты моменті жүйенің барлық күштерінің сол нүктеге немесе оське қатысты моменттерінің қосындысына тең.
3 дәріс. Күштер жүйелерінің тепе-теңдігі. Үйкеліс. Ауырлық центрі
Дәрістің мазмұны: күштер жүйелерінің тепе-теңдік шарттары, сырғанау үйкелісі мен домалау үйкелісі, қатты денелердің ауырлық центрі.
Дәрістің мақсаты: кеңістік және жазық күштер жүйелерінің тепе-теңдік шарттарын анықтау, үйкеліс болғанда есептерді шешудің ерешеліктерін қарастыру, дененің ауырлық центрін анықтауды үйрену.
3.1 Денеге түсірілген күштер жүйесінің тепе-теңдік шарттары
Кез келген КЖ тепе-теңдікте болу үшін мына теңдеулердің орындалуы қажетті де жеткілікті:
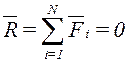 ,
, 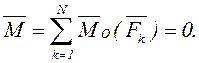 (3.1)
(3.1)
Бұл шарттар келесі тепе-теңдіктің аналитикалық шарттарына баламалы:
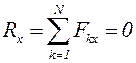 ,
,  ,
, 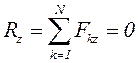 ,
,
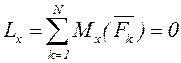 ,
, 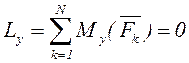 ,
, 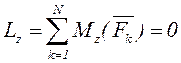 , (3.2)
, (3.2)
яғни АҚД-ге әсер ететін кез келген КЖ-нің тепе-теңдігі үшін барлық күштердің декарт координаттар жүйесінің үш осіне проекцияларының қосындылары және сол осьтерге қатысты барлық күштер моменттерінің қосындылары нөлге тең болуы қажетті де жеткілікті.
Кеңістік параллель КЖ үшін (Oz осі күштермен бағыттас)
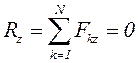 ,
, 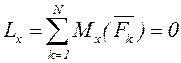 ,
, 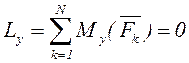 . (3.3)
. (3.3)
Кез келген жазық КЖ-сі үшін: күштердің екі координат осіне проекцияларының қосындылары және кез келген центрге қатысты күштердің алгебралық моменттерінің қосындысы нөлге тең болуы қажетті де жеткілікті.
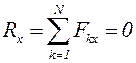 ,
,  ,
, 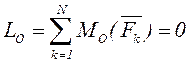 .
(3.4)
.
(3.4)
Екінші түрі:
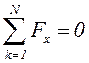 ,
, 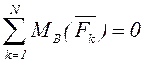 ,
,  , (3.5)
, (3.5)
мұнда ![]() түзуі
түзуі ![]() осіне перпендикуляр емес болу керек.
осіне перпендикуляр емес болу керек.
Үшінші түрі:
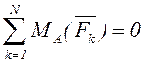 ,
, 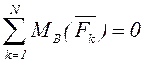 ,
,  , (3.6)
, (3.6)
мұнда А, В, С бір түзудің бойында жатпау керек.
Жазық параллель күштер жүйесі үшін тепе-теңдік шарттары
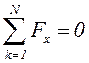 ,
, 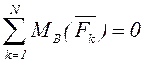 ,
(3.7)
,
(3.7)
мұнда Ox осі күштерге перпендикуляр болмау керек; немесе
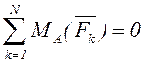 ,
, 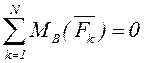 ,
(3.8)
,
(3.8)
мұнда А мен В нүктелерінен өтетін түзу күштерге параллель болмау керек.
3.2 Денелер жүйесінің тепе-теңдігі. Статикалық түрде анықталатын және статикалық түрде анықталмайтын жүйелер
Денелер жүйесінің бөліктерін қосатын байланыстар ішкі байланыстар деп аталады. Егер сыртқы байланыстарды күштерге ауыстырса, тепе-теңдік шарттары оларды анықтау үшін жеткіліксіз болады. Есептерді шешу әдістері:
а) қосымша тепе-теңдік шарттарын құрады, мысалы, ішкі топсаға қатысты моменттерінің қосындысы түрінде;
б) конструкцияны, оның ішкі байланыстарын күштерге ауыстырып, бөліктерге ойша жіктейді де әр бөлігі үшін тепе-теңдік теңдеулерін құрайды.
Егер байланыстар реакцияларының белгісіз құраушыларының саны тәуелсіз тепе-теңдік теңдеулерінің санына тең болса, қарастырылатын жүйе статикалық түрде анықталатын, одан артық болса статикалық түрде анықталмайтын жүйе (САЖ) деп аталады. САЖ жүйелердегі реакцияларды АҚД үшін қолданатын әдістермен табу мүмкін емес. Мұндай есептерді шешу үшін денелердің деформациялануын есепке алу керек.
3.3 Сырғанау үйкелісі. Тегіс емес беттің реакциясы
Сырғанау үйкелісінің Кулон – Амонтон заңдары:
1) Бір денені басқа дененің үстінде жылжытуға
тырысқан жағдайда олардың жанасу жазықтығында ![]() үйкеліс
күші пайда болады, оның модулі 0≤F≤ Fmax
. Денеге түсірілген үйкеліс күші күш түскен
нүктесінің мүмкіндік жылдамдығына
қарама-қарсы болады.
үйкеліс
күші пайда болады, оның модулі 0≤F≤ Fmax
. Денеге түсірілген үйкеліс күші күш түскен
нүктесінің мүмкіндік жылдамдығына
қарама-қарсы болады.
2) Максимальды үйкеліс күші f үйкеліс коэффициенті мен N нормаль қысым күшінің көбейтіндісіне тең
Fmax=f∙N. (3.9)
f - жанасатын денелердің материалдары мен беттерінің қалпына (кедір-бұдырлығына, температурасына, ылғалдылығына және т.б.) тәуелді, ол тәжірибе арқылы анықталады. Мәндері: ағаш пен ағаш - 0,4-0,7; метал мен метал - 0,15-0,25; болат пен мұз - 0,027.
Тыныштық үйкелісі мен сырғанау үйкелісі айыра танылады. Тыныштық үйкелісінің коэффициенті Fmax үйкеліс күші арқылы анықталады. Әдетте ол сырғанау үйкелісінің коэффициентінен артық. Сырғанау жылдамдығының өсуімен сырғанау үйкелісінің коэффициенті басында шамалы азаяды, содан кейін айтарлықтай өзгермейді.
3) Максимальды үйкеліс күші жанасатын беттердің ауданына тәуелсіз.
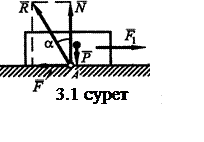 Тегіс емес беттің реакциясы екі
құраушы арқылы анықталады, олар
Тегіс емес беттің реакциясы екі
құраушы арқылы анықталады, олар ![]() (модулі
нормаль қысым күшіне тең) және
(модулі
нормаль қысым күшіне тең) және ![]() үйкеліс күші (3.1-суретті
қараңыз). Толық
үйкеліс күші (3.1-суретті
қараңыз). Толық ![]() реакциясы нормаль бағыттан α бұрышына
ауытқиды (tg α = F/N).
реакциясы нормаль бағыттан α бұрышына
ауытқиды (tg α = F/N).
Горизонталь тегіс беттің үстінде тұрған
денеге ауырлық күштен басқа сыртқы күш
түспесе, онда F = 0, толық реакция R = N және ол
тіреуіш бетіне перпендикуляр болады. Денеге шамасы аз ![]() күшін түсіріп, біз оны
қозғалтуға тырыссақ, қозғалыс бола
қалмайды, өйткені
күшін түсіріп, біз оны
қозғалтуға тырыссақ, қозғалыс бола
қалмайды, өйткені ![]() үйкеліс күші пайда
болады және F<Fmax.
үйкеліс күші пайда
болады және F<Fmax. ![]() күші
артқан сайын
күші
артқан сайын ![]() үйкеліс күші де артады. F1 = Fmax
болғанда тепе-теңдіктің шеткі қалпы орын алады, сонда
толық реакция
үйкеліс күші де артады. F1 = Fmax
болғанда тепе-теңдіктің шеткі қалпы орын алады, сонда
толық реакция ![]() вертикальдан үйкеліс
бұрышы деп аталатын αmax бұрышына
ауытқиды. Оны φ арқылы белгілеп, мынаны анықтаймыз:
вертикальдан үйкеліс
бұрышы деп аталатын αmax бұрышына
ауытқиды. Оны φ арқылы белгілеп, мынаны анықтаймыз:
tg φ= Fmax/N=f . (3.10)
Идеалды емес байланыстың реакциясының бағыты үйкеліс бұрышымен шеттеледі. Әдетте үйкеліс күші ескерілуімен денелер тепе-теңдігінің шеткі (үйкеліс күші максималды болғандағы) қалпы қарастырылады.
3.4 Домалау кезіндегі байланыстың реакциясы
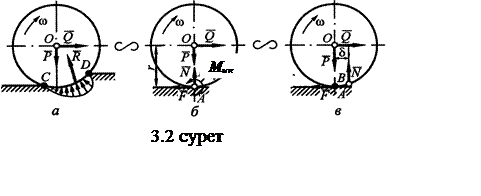 3.2,а-суретте домалау кезінде цилиндр тіреуші
бетке жаншылып, онымен домалау бағыты жағына ығысқан СD
доғасымен кескінделетін бетпен әрекеттескені көрсетілген.
3.2,а-суретте домалау кезінде цилиндр тіреуші
бетке жаншылып, онымен домалау бағыты жағына ығысқан СD
доғасымен кескінделетін бетпен әрекеттескені көрсетілген.
Тіреуші беттің ![]() толық
реакциясы беттің деформациясынан туындаған таралған
күштердің қосындысы ретінде цилиндрдің домалауына
кедергі жасайды. Бір дененің басқа дененің бетінде домалау
кезінде пайда болатын кедергі домалау үйкелісі деп аталады. Инженерлік
есептеулер жүргізуде керегі - домалауға кедергі моменті (3.2,б-суретті
қараңыз). Құбылыстың сұлбасын
жасағанда, домалау деформацияланбайтын бетінде қарастырылады, ал
толық
реакциясы беттің деформациясынан туындаған таралған
күштердің қосындысы ретінде цилиндрдің домалауына
кедергі жасайды. Бір дененің басқа дененің бетінде домалау
кезінде пайда болатын кедергі домалау үйкелісі деп аталады. Инженерлік
есептеулер жүргізуде керегі - домалауға кедергі моменті (3.2,б-суретті
қараңыз). Құбылыстың сұлбасын
жасағанда, домалау деформацияланбайтын бетінде қарастырылады, ал ![]() толық реакциясы А нүктеcінен δ
шамасына ауытқыған В нүктесіне түсетін екі
құраушы күш арқылы көрсетіледі (3.2,в-суретті
қараңыз).
толық реакциясы А нүктеcінен δ
шамасына ауытқыған В нүктесіне түсетін екі
құраушы күш арқылы көрсетіледі (3.2,в-суретті
қараңыз). ![]() күші –
сырғанау үйкеліс күші, ал
күші –
сырғанау үйкеліс күші, ал ![]() -
нормаль реакциясы. Онда
-
нормаль реакциясы. Онда
N = P, F = Q, Qmax∙r = δ∙N. (3.11)
δ∙N = (Мкед)max көбейтіндісі домалауға кедергі моменті деп аталады. Q күші аз болса, N күшінің ауытқуы да аз болады; Q өсуімен ауытқу артады. Qmax болғанда цилиндр тепе-теңдіктің шеткі қалпына жетеді, сонда N вертикаль диаметрден домалау үйкелісінің коэффициенті деп аталатын, δ шеткі қашықтығында өтеді. δ коэффициенті жанасатын денелер материалдардың қасиеттеріне және беттерінің қалпына тәуелді, ол тәжірибелік түрде анықталады (рельс үстімен домалаған дөңгелек δ = 0,005 см, шарикті подшипникте δ = 0,001 см).
3.5 Қатты дененің ауырлық центрі
Дененің А1, A2
нүктелерінде
түсетін екі параллель ![]() және
және ![]() күшті қарастырайық (3.3-суретті
қараңыз).
күшті қарастырайық (3.3-суретті
қараңыз). ![]() тең
әсерлісінің әсер ету сызығы қосылатын
күштерге параллель және A1A2 түзуінде
жатқан С нүктесінен өтеді. С
нүктесінің орнын Вариньон теоремасын қолданып
анықтай аламыз, онда
тең
әсерлісінің әсер ету сызығы қосылатын
күштерге параллель және A1A2 түзуінде
жатқан С нүктесінен өтеді. С
нүктесінің орнын Вариньон теоремасын қолданып
анықтай аламыз, онда
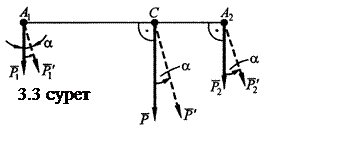
![]() . (3.12)
. (3.12)
![]() ,
, ![]() күштерін А1, А2
нүктелерінің айналасында бірдей α бұрышына бұрғанда,
тең әсерлі күші де сол бағытта α бұрышына бұрылады және
дәл сол С нүктесіне түседі. С
нүктесі параллель күштердің центрі деп аталады. Кез келген
күштер саны үшін де осылай болады.
күштерін А1, А2
нүктелерінің айналасында бірдей α бұрышына бұрғанда,
тең әсерлі күші де сол бағытта α бұрышына бұрылады және
дәл сол С нүктесіне түседі. С
нүктесі параллель күштердің центрі деп аталады. Кез келген
күштер саны үшін де осылай болады.
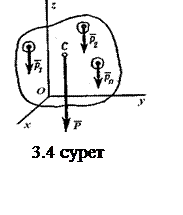 Дене бөлшектеріне түсетін
Дене бөлшектеріне түсетін ![]() ,
, ![]() ,…,
,…, ![]() ауырлық күштерінің тең
әсерлісін
ауырлық күштерінің тең
әсерлісін ![]() деп белгілейік (3.4-суретті
қараңыз). Оның модулі дененің салмағы деп аталады
және келесідей анықталады:
деп белгілейік (3.4-суретті
қараңыз). Оның модулі дененің салмағы деп аталады
және келесідей анықталады:
![]() . (3.13)
. (3.13)
С нүктесі ![]() параллель ауырлық
күштерінің центрі болып келеді, ол дененің ауырлық
центрі деп аталады. Сонымен, АҚД-нің ауырлық центрі – денемен
өзгеріссіз байланысқан дененің кеңістікте кез келген
орналасуында дене бөлшектеріне түсетін ауырлық
күштерінің тең әсерлі күшінің ӘС
өтетін нүкте; оның координаттары
параллель ауырлық
күштерінің центрі болып келеді, ол дененің ауырлық
центрі деп аталады. Сонымен, АҚД-нің ауырлық центрі – денемен
өзгеріссіз байланысқан дененің кеңістікте кез келген
орналасуында дене бөлшектеріне түсетін ауырлық
күштерінің тең әсерлі күшінің ӘС
өтетін нүкте; оның координаттары
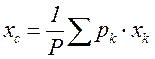 ,
, 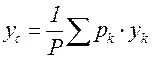 ,
, 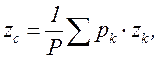 (3.14)
(3.14)
мұндағы ![]() ,
, ![]() ,
, ![]() –
– ![]() ауырлық
күштері түсетін нүктелердің координаттары.
ауырлық
күштері түсетін нүктелердің координаттары.
4 дәріс. Нүкте кинематикасы және дененің қарапайым қозғалыстары
Дәрістің мазмұны: кинематиканың кіріспе ұғымдары, нүкте кинематикасы, траектория, нүктенің жылдамдығы мен үдеуі; қатты дененің ілгерілемелі, айналмалы және жазық параллель қозғалыстары.
Дәрістің мақсаты: нүкте қозғалысының және қатты дененің қарапайым қозғалыстарының кинематикалық сипаттамаларын қарастыру.
4.1 Кинематикаға кіріспе. Нүкте қозғалысының берілу тәсілдері
Дененің қозғалысы ретінде оның санақ жүйесіне (СЖ) қатысты кеңістікте орналасуының уақыт өтуімен өзгеруін түсінеді. СЖ басқа денелерден және осылармен байланысқан координат жүйесінен тұрады. Денелердің қозғалысы кеңістікте уақыт өтуімен орындалады. Кеңістік үш өлшемді Евклид кеңістігі деп қарастырылады. Кинематика есептерінде t уақыты аргумент болып алынады. Басқа айнымалылардың барлығы (арақашықтар, жылдамдықтар және т.б.) t -ның функциялары ретінде қарастырылады. Уақыт бір бастапқы мезгілден есептеледі.
Есептерді шешу үшін дененің (нүктенің) қозғалысы кинематикалық түрде берілу керек, яғни дененің (нүктенің) кез келген уақыт мезгілінде берілген СЖ-не қатысты орналасуы берілу керек. Қозғалысты зерттеу оның берілу тәсілдерін анықтаудан басталады. Кинематиканың мақсаты – нүктенің (дененің) қозғалыс заңын біле отырып, барлық кинематикалық шамаларды табу әдістерін анықтау.
Қозғалыстағы нүкте берілген СЖ-не қатысты жасайтын сызық нүктенің траекториясы деп аталады (түзу және қисық сызықты қозғалыс).
Нүктенің қозғалысы үш тәсілдің біреуімен берілуі мүмкін.
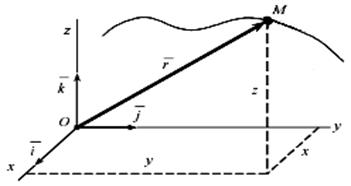
1. Векторлық тәсіл. Нүктенің орны оның радиус-векторымен (4.1-суретті қараңыз) анықталады.
![]() .
(4.1)
.
(4.1)
2. Координаттық тәсіл. Нүктенің орнын оның координаттарымен анықталады.
![]() .
(4.2)
.
(4.2)
|
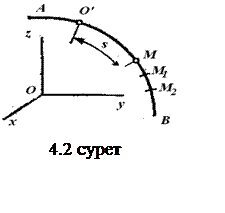
3. Табиғи тәсіл. Нүктенің траекториясы (4.2-суретті қараңыз), траекториясындағы санақ басы мен санақ бағыты және келесі түрде қозғалыс заңы беріледі:
![]() . (4.3)
. (4.3)
4.2 Нүктенің жылдамдығы мен үдеуі
Нүктенің
жылдамдығы ![]() векторының t аргументі
бойынша бірінші ретті туындысына тең екендігі дәлелденеді
векторының t аргументі
бойынша бірінші ретті туындысына тең екендігі дәлелденеді
![]() . (4.4)
. (4.4)
Нүктенің үдеуі жылдамдық векторының уақыт бойынша бірінші ретті туындысына, яғни нүктенің радиус-векторының екінші ретті туындысына тең.
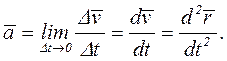 (4.5)
(4.5)

 |
Қозғалыс координаттық тәсілмен берілген жағдайдағы нүктенің жылдамдығы мен үдеуін анықтау үшін келесі теореманы қолданамыз: вектордың туындысының қозғалмайтын өске проекциясы вектордың сол оське проекциясының туындысына тең.
Сонда жылдамдықтың проекциялары үшін келесі орын алады:
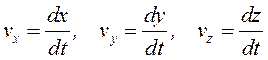 (4.6)
(4.6)
немесе:
![]() . (4.7)
. (4.7)
Үдеудің проекциялары үшін келесі болады:
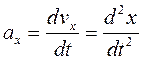 ,
, 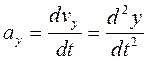 ,
,
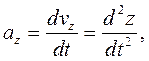 (4.8)
(4.8)
немесе:
![]() , (4.9)
, (4.9)
яғни үдеудің координаттар осьтеріне проекциялары жылдамдықтың сәйкес проекцияларының уақыт бойынша бірінші ретті туындыларына немесе кординаттардың екінші ретті туындыларына тең.
Қозғалыс табиғи тәсілмен берілген жағдайда нүктенің жылдамдығы мен үдеуі олардың Мtnb табиғи үшжақтықтың осьтеріне проекциялары арқылы табады. Осьтердің бағыттары:
- Мt - s санағының оң бағытына сәйкес траекторияға жанама бойынша;
- Мn бас нормалі – траекториямен жанасу жазықтығында траекторияның ойыс жағына жүргізілген нормалі бойынша;
- Mb бинормалі – алдынғы екі оське перпендикуляр бойынша, олармен оң өстер жүйесін құрайтын болып, бағытталады.
Нүктенің жылдамдығын анықтаймыз:
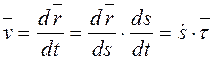 . (4.10)
. (4.10)
Жылдамдықтың нүкте траекториясының жанамасына проекциясы:
![]() . (4.11)
. (4.11)
Осыдан ![]() және жылдамдықтың модулі
және жылдамдықтың модулі ![]()
Нүктенің үдеуі үшін:
 . (4.12)
. (4.12)
Мұнда 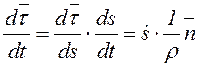 (ρ –
қарастырылатын орнында нүктенің траекториясының
қисықтық радиусы), сонда:
(ρ –
қарастырылатын орнында нүктенің траекториясының
қисықтық радиусы), сонда:
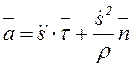 , (4.13)
, (4.13)
яғни үдеу векторы жанама және нормаль құраушыларының қосындысына тең:
![]() . (4.14)
. (4.14)
![]() векторы жанасу
жазықтығында, яғни Mtn жазықтығында
жатады. (4.13) теңдігін Мt, Мn және
Mb осьтеріне проекциялап, келесіге келеміз:
векторы жанасу
жазықтығында, яғни Mtn жазықтығында
жатады. (4.13) теңдігін Мt, Мn және
Mb осьтеріне проекциялап, келесіге келеміз:
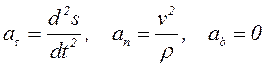 . (4.15)
. (4.15)
4.3 Қатты дененің ілгерілемелі қозғалысы және тұрақты ось төңірегіндегі айналмалы қозғалысы
 АҚД-нің
ілгерілемелі қозғалысы деп денеде жүргізілген кез келген
түзу өзіне параллель болып қала беретін
қозғалысты айтады, сонда дене нүктелерінің
траекториялары кез келген сызық болулары мүмкін. Келесі теорема орын
алады: ілгерілемелі қозғалыста дене нүктелері бірдей
траекторияларды сызады және әр уақыт мезгілінде модульдері
мен бағыттары бірдей жылдамдықтар мен үдеулерге ие болады. Яғни,
АҚД-нің кинематикасы нүктенің кинематикасына
келтіріледі.
АҚД-нің
ілгерілемелі қозғалысы деп денеде жүргізілген кез келген
түзу өзіне параллель болып қала беретін
қозғалысты айтады, сонда дене нүктелерінің
траекториялары кез келген сызық болулары мүмкін. Келесі теорема орын
алады: ілгерілемелі қозғалыста дене нүктелері бірдей
траекторияларды сызады және әр уақыт мезгілінде модульдері
мен бағыттары бірдей жылдамдықтар мен үдеулерге ие болады. Яғни,
АҚД-нің кинематикасы нүктенің кинематикасына
келтіріледі.
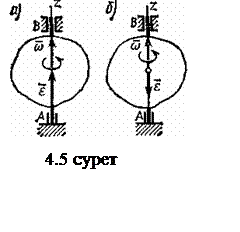
АҚД-нің тұрақты (қозғалмайтын) ось төңірегінде айналғанда, оның осьте жатқан нүктелері қозғалмайды (4.5-суреттегі АВ). Ось арқылы екі жазықтық жүргізейік – қозғалмайтын және денемен байланысқан қозғалатын. Олардың арасындағы екі жақтық j бұрышы (дененің бұрылу бұрышы) айналу осінің оң бағыты жағынан қарағанда сағат тіліне қарсы болып көрінгенде, оң болып есептеледі. Қозғалыс заңы:
j = j (t). (4.16)
Бұрыштық жылдамдық j бұрышының уақыт өтуімен өзгеруін сипаттайды:
w = dj/dt,
яғни ![]() . (4.17)
. (4.17)
Дененің
бұрыштық жылдамдығын ![]() векторымен кескіндеуге болады.
векторымен кескіндеуге болады.
Бұрыштық үдеу ω-ның уақыт өтуімен өзгеруін сипаттайды:
e = dw/dt = d2
j/dt2, яғни
![]() . (4.18)
. (4.18)
Қозғалыс кезінде w=const болса, айналу бірқалыпты деп аталады. (4.17) формуласын интегралдап, айналу заңын анықтаймыз:
![]() . (4.19)
. (4.19)
Бірқалыпты
айналу кезінде ![]() болса, онда:
болса, онда:
![]() . (4.20)
. (4.20)
 Қозғалыс
кезінде бұрыштық үдеу тұрақты болса (e=const), айналу бірқалыпты айнымалы деп
аталады, оның заңы келесі түрде жазылады:
Қозғалыс
кезінде бұрыштық үдеу тұрақты болса (e=const), айналу бірқалыпты айнымалы деп
аталады, оның заңы келесі түрде жазылады:
![]() . (4.21)
. (4.21)
w мен e таңбалары бірдей болса, айналу – бірқалыпты үдемелі, әртүрлі болса, бірқалыпты кемімелі болады.
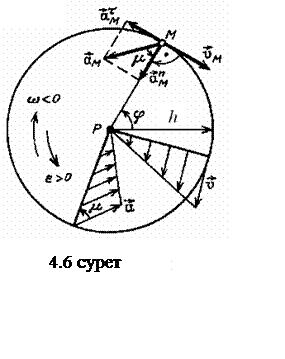
Айналатын дене нүктелерінің жылдамдықтары мен үдеулерін анықтаймыз (4.6-суретті қараңыз).
Айналу кезінде М нүктесі радиусы h тең, жазықтығы айналу осіне перпендикуляр және P центрі осьте жататын шеңберді кескіндейді. dt уақыт ішінде дене dφ бұрышына бұрылады, М нүктесі ds = h∙dφ орын ауыстыру жасайды. Сонда:
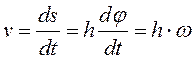 . (4.22)
. (4.22)
Нүктенің үдеулерін анықтаймыз:
 . (4.23)
. (4.23)
![]() үдеуі траекторияға жанама
бағытталады (үдемелі айналу кезінде айналу бағытына
сәйкес және кемімелі айналу кезінде айналу бағытына
қарсы),
үдеуі траекторияға жанама
бағытталады (үдемелі айналу кезінде айналу бағытына
сәйкес және кемімелі айналу кезінде айналу бағытына
қарсы), ![]() үдеуі
әрқашан МP радиусы бойымен оське қарай бағытталады.
Нүктенің толық үдеуі:
үдеуі
әрқашан МP радиусы бойымен оське қарай бағытталады.
Нүктенің толық үдеуі:
![]() , (4.24)
, (4.24)
m бұрышы (4.6-суретті қараңыз) келесі тәуелдік арқылы анықталады:
![]() . (4.25)
. (4.25)
![]() және
және ![]() векторлары
үшін келесі формулаларды шығаруға болады:
векторлары
үшін келесі формулаларды шығаруға болады:
![]() ,
(4.26)
,
(4.26)
![]() . (4.27)
. (4.27)
5 дәріс. Қатты дененің жазық параллель қозғалысы. Нүктенің күрделі қозғалысы
Дәрістің мазмұны: дененің жазық параллель қозғалысының кинематикасы; нүктенің күрделі қозғалысы.
Дәрістің мақсаты: жазық параллель қозғалысының және нүктенің күрделі қозғалысының кинематикалық сипаттамаларын оқып үйрену.
5.1 Жазық параллель қозғалыстың теңдеулері және оны ілгерілемелі мен айналмалы қозғалыстарға жіктеу. Дене нүктелерінің жыдамдығы
АҚД-нің жазық параллель немесе жазық қозғалысы деп дененің барлық нүктелері бір қозғалмайтын жазықтыққа параллель жазықтарда орын ауыстыратын қозғалысты атайды (5.1-суретті қараңыз).
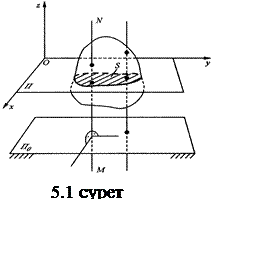
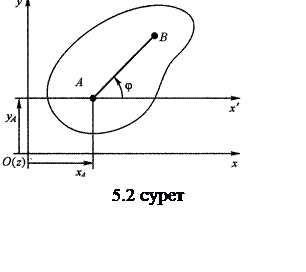
Дене қозғалысын зерттеу үшін оның S қимасының Оху жазықтығында қозғалысын зерттеуге жеткілікті. S фигурасының орны АВ кесіндісінің орналасуымен анықталады (5.2-суретті қараңыз). Қозғалыс заңын білу үшін келесі тәуелдіктерді білу қажет.
![]() . (5.1)
. (5.1)
Жазық
қозғалысты полюспен бірдей ілгерілемелі қозғалысы және
полюс төңірегіндегі айналмалы қозғалысының
қосындысы ретінде қарастыруға болады. Енді жазық фигура
нүктелерінің жылдамдықтарын және үдеулерін
анықтайық. Кез келген B нүктесінің орны ![]() радиус-векторымен анықталады (5.3-суретті
қараңыз), олай болса:
радиус-векторымен анықталады (5.3-суретті
қараңыз), олай болса:
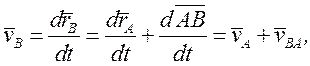 (5.2)
(5.2)
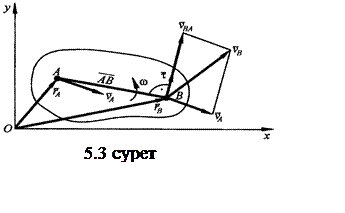
![]() (5.3)
(5.3)
мұндағы w - фигураның бұрыштық жылдамдығы.
Кез келген қозғалыстағы АҚД нүктелерінің жылдамдықтарын анықтағанда келесі теореманы қолдануға болады: дененің екі нүктесінің жылдамдықтарының оларды қосатын түзуге проекциялары тең.
5.2 Жазық фигура нүктелерінің жылдамдықтарын жылдамдықтардың лездік центрін қолданумен анықтау
Жылдамдықтардың лездік центрін (ЖЛЦ) деп жылдамдығы қарастырылатын уақыт мезетінде нөлге тең жазық фигураның нүктесі аталады.
 t уақыт
мезгілінде жазық фигураның А және В
нүктелері бір-біріне параллель емес
t уақыт
мезгілінде жазық фигураның А және В
нүктелері бір-біріне параллель емес ![]() және
және
![]() жылдамдықтарына ие болсын (5.4-суретті
қараңыз). Сонда
жылдамдықтарына ие болсын (5.4-суретті
қараңыз). Сонда ![]() векторына жүргізілген Аа
және
векторына жүргізілген Аа
және ![]() векторына жүргізілген Вb
перпендикулярларының қиылысу Р нүктесі
жылдамдықтардың лездік центрі болады, өйткені
векторына жүргізілген Вb
перпендикулярларының қиылысу Р нүктесі
жылдамдықтардың лездік центрі болады, өйткені ![]() = 0. Егер t уақыт
мезгілінде Р нүктесін полюс ретінде алса, онда (5.2) формуласы
бойынша А нүктенің жылдамдығы былай табылады
= 0. Егер t уақыт
мезгілінде Р нүктесін полюс ретінде алса, онда (5.2) формуласы
бойынша А нүктенің жылдамдығы былай табылады ![]() . Сонымен, қарастырылатын уақыт
мезгілінде фигура нүктелерінің жылдамдықтары фигура
қозғалысы ЖЛЦ төңірегіндегі айналмалы
қозғалыс болғандай анықталады. Сонда:
. Сонымен, қарастырылатын уақыт
мезгілінде фигура нүктелерінің жылдамдықтары фигура
қозғалысы ЖЛЦ төңірегіндегі айналмалы
қозғалыс болғандай анықталады. Сонда:
![]() ,
, ![]() .
(5.4)
.
(5.4)
(5.4) теңдігінен келесі шығады:
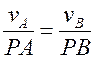 , (5.5)
, (5.5)
яғни жазық фигура нүктелерінің жылдамдықтары олардың ЖЛЦ-не дейінгі қашықтықтарына пропорционал. Осыдан қорытындылар:
а)
ЖЛЦ-нің орнын анықтау үшін жазық фигураның кез
келген екі А, В нүктелерінің ![]() ,
,
![]() жылдамдықтарының бағыттарын білген
жеткілікті; ЖЛЦ А және В нүктелерінен олардың
жылдамдықтарына тұрғызылған перпендикуляр-лардың
қиылысу нүктесінде орналасады;
жылдамдықтарының бағыттарын білген
жеткілікті; ЖЛЦ А және В нүктелерінен олардың
жылдамдықтарына тұрғызылған перпендикуляр-лардың
қиылысу нүктесінде орналасады;
б)
жазық фигураның кез келген нүктесінің жылдамдығын
анықтау үшін фигураның бір А нүктесінің
жылдамдығының модулі мен бағытын және оның
басқа В нүктесінің жылдамдығының
бағытын білген жеткілікті. Сонда А және В
нүктелерінен ![]() мен
мен ![]() бағыттарына
перпендикулярлар тұрғызып, ЖЛЦ-н табамыз және
бағыттарына
перпендикулярлар тұрғызып, ЖЛЦ-н табамыз және ![]() бағытымен фигураның айналу
бағытын анықтаймыз. Содан кейін
бағытымен фигураның айналу
бағытын анықтаймыз. Содан кейін ![]() белгілі
болғандықтан, (5.5) бойынша жазық фигураның кез келген М
нүктесінің
белгілі
болғандықтан, (5.5) бойынша жазық фигураның кез келген М
нүктесінің ![]() жылдамдығын таба
аламыз. Сонда
жылдамдығын таба
аламыз. Сонда ![]() векторы РМ-ға
перпендикуляр фигураның айналу бағытына сәйкес
бағытталады;
векторы РМ-ға
перпендикуляр фигураның айналу бағытына сәйкес
бағытталады;
в) кез келген уақыт мезетінде жазық фигураның w бұрыштық жылдамдығы фигура нүктесінің жылдамдығы мен оның ЖЛЦ-не дейінгі қашықтығының қатынасына тең:
 . (5.6)
. (5.6)
5.3 Жазық фигура нүктелерінің үдеулерін анықтау
Жазық фигураның кез келген B нүктесінің үдеуі ілгерілемелі және айналмалы қозғалыстарындағы үдеулердің қосындысына тең.
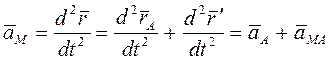 . (5.7)
. (5.7)
Есетерді шешу кезінде (5.7) теңдікті келесі түрде жазған ыңғайлы:
![]() . (5.8)
. (5.8)
5.4 Нүктенің күрделі қозғалысы. Жылдамдықтарды және үдеулерді қосу туралы теоремалар
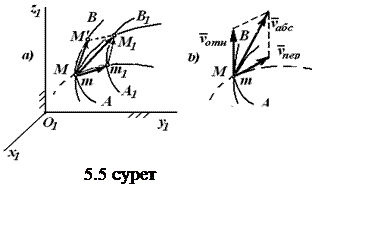 Есептерді шешу
кезінде нүктенің қозғалысын екі СЖ қатысты
қарастырған қолайлы болады, олардың біреуі негізгі
болып саналады (шартты қозғалмайтын), екіншісі – біріншісіне
қатысты қозғалады. М нүктесінің
қозғалатын Oxyz СЖ-не қатысты қозғалысын
қарастырайық және осы Oxyz СЖ-сі
қозғалмайтын О1х1у1z1
СЖ-не қатысты қозғалыста болсын (5.5-суретті
қараңыз). Келесі анықтамаларды енгіземіз:
Есептерді шешу
кезінде нүктенің қозғалысын екі СЖ қатысты
қарастырған қолайлы болады, олардың біреуі негізгі
болып саналады (шартты қозғалмайтын), екіншісі – біріншісіне
қатысты қозғалады. М нүктесінің
қозғалатын Oxyz СЖ-не қатысты қозғалысын
қарастырайық және осы Oxyz СЖ-сі
қозғалмайтын О1х1у1z1
СЖ-не қатысты қозғалыста болсын (5.5-суретті
қараңыз). Келесі анықтамаларды енгіземіз:
а) М нүктесінің қозғалатын СЖ-не қатысты (Oxyz осьтеріне қатысты) қозғалысы салыстырмалы қозғалыс деп аталады;
б)
қозғалмайтын О1х1у1z1
СЖ-не қатысты Oxyz СЖ-нің қозғалысы М
нүктесі үшін тасымал қозғалыс болады. Охуz осьтерімен
өзгеріссіз байланысқан, қарастырылатын уақыт мезетінде қозғалатын
М нүктесімен түйісетін m нүктесінің
жылдамдығы М нүктесінің сол уақыт мезгіліндегі
тасымал жылдамдығы (![]() ), ал m нүктенің
үдеуі - М нүктесінің
), ал m нүктенің
үдеуі - М нүктесінің ![]() тасымал
үдеуі деп аталады. Сонда
тасымал
үдеуі деп аталады. Сонда
![]() ,
, ![]() ; (5.9)
; (5.9)
в) М нүктесінің қозғалмайтын О1х1у1z1 СЖ-не қатысты қозғалысы абсолют немесе күрделі қозғалыс деп аталады.
М
нүктесінің күрделі қозғалысын
қарастырайық. Нүкте Dt=t1-t уақыт
аралығында АВ траекториясы бойымен ![]() векторымен анықталатын салыстырмалы қозғалысын
жасайтын болсын (5.6,а-суретті қараңыз). АВ
қисығы қозғалатын Oxyz осьтерімен бірге
қозғалып, сол уақыт аралығында жаңа A1B1
орнына келеді. Біржолы АВ қисығының t
уақыт мезгілінде М нүктесімен түйісетін m
нүктесі
векторымен анықталатын салыстырмалы қозғалысын
жасайтын болсын (5.6,а-суретті қараңыз). АВ
қисығы қозғалатын Oxyz осьтерімен бірге
қозғалып, сол уақыт аралығында жаңа A1B1
орнына келеді. Біржолы АВ қисығының t
уақыт мезгілінде М нүктесімен түйісетін m
нүктесі ![]() тасымал орын ауыстыруын
жасайды. Нәтижесінде М нүктесі М1 орнына
келіп, Dt уақыт
ішінде абсолют
тасымал орын ауыстыруын
жасайды. Нәтижесінде М нүктесі М1 орнына
келіп, Dt уақыт
ішінде абсолют ![]() орын ауыстыруын жасайды.
Векторлық Мm1М1 үшбұрышынан
келесі шығады:
орын ауыстыруын жасайды.
Векторлық Мm1М1 үшбұрышынан
келесі шығады:
![]() .
.
Осы
теңдіктің екі жағын Dt-ға
бөліп, оны нөлге ұмтылдырып, шектерді
қарастырғанда, келесіге келеміз ![]() .
Нәтижесінде келесі шығады:
.
Нәтижесінде келесі шығады:
![]() . (5.10)
. (5.10)
![]() векторлары сәйкес
траекторияларына жанама бағытталады (5.6,б-суретті
қараңыз). Сонымен, жылдамдықтарды қосу теоремасын
дәлелдедік: күрделі қозғалыста нүктенің
абсолют жылдамдығы оның салыстырмалы және тасымал
жылдамдықтарының векторлық қосындысына тең. Егер
векторлары сәйкес
траекторияларына жанама бағытталады (5.6,б-суретті
қараңыз). Сонымен, жылдамдықтарды қосу теоремасын
дәлелдедік: күрделі қозғалыста нүктенің
абсолют жылдамдығы оның салыстырмалы және тасымал
жылдамдықтарының векторлық қосындысына тең. Егер ![]() мен
мен ![]() арасындағы бұрышы a болса, онда абсолют жылдамдығының модулі.
арасындағы бұрышы a болса, онда абсолют жылдамдығының модулі.
![]() . (5.11)
. (5.11)
Салыстырмалы, тасымал және абсолют үдеулердің арасындағы тәуелдікті табайық. (5.10) теңдігінен келесі шығады:
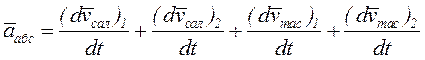 . (5.12)
. (5.12)
Мұнда ![]() мен
мен ![]() векторларының
салыстырмалы қозғалыстағы өзгерістері 1 индексімен
белгіленген, тасымал қозғалыстағы өзгерістері – 2
индексімен.
векторларының
салыстырмалы қозғалыстағы өзгерістері 1 индексімен
белгіленген, тасымал қозғалыстағы өзгерістері – 2
индексімен.
Анықтама бойынша салыстырмалы үдеу салыстырмалы жылдамдықтың тек қана салыстырмалы қозғалыста болатын өзгерісін сипаттайды, сонда Охуz осьтерінің қозғалысы, яғни тасымал қозғалысы, есепке алынбайды. Сондықтан:
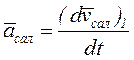 . (5.13)
. (5.13)
Тасымал
үдеу тасымал жылдамдықтың тек қана тасымал
қозғалыстағы өзгерісін сипаттайды, өйткені ![]() , мұндағы m - Охуz
осьтерімен өзгеріссіз байланысқан нүкте, ол тек қана
сол осьтермен қозғалғанда, яғни тасымал
қозғалыста үдеуге ие болады. Сондықтан:
, мұндағы m - Охуz
осьтерімен өзгеріссіз байланысқан нүкте, ол тек қана
сол осьтермен қозғалғанда, яғни тасымал
қозғалыста үдеуге ие болады. Сондықтан:
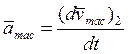 . (5.14)
. (5.14)
Нәтижесінде (5.12) теңдігінен келесі шығады:
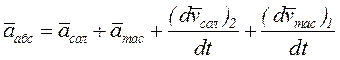 . (5.15)
. (5.15)
Келесі белгіні енгізейік:
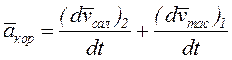 . (5.16)
. (5.16)
Салыстырмалы
жылдамдықтың тасымал қозғалыстағы өзгерісін
және тасымал жылдамдықтың салыстырмалы
қозғалыстағы өзгерісін сипаттайтын ![]() шамасы нүктенің
бұрынды немесе Кориолис үдеуі деп аталады. Нәтижесінде (5.15)
теңдік келесі түрде жазылады:
шамасы нүктенің
бұрынды немесе Кориолис үдеуі деп аталады. Нәтижесінде (5.15)
теңдік келесі түрде жазылады:
![]() . (5.17)
. (5.17)
(5.17) формуласы үдеулерді қосу Кориолис теоремасын өрнектейді: нүктенің күрделі қозғалысында оның абсолют үдеуі үш үдеулерінің, яғни салыстырмалы, тасымал және кориолис үдеулерінің векторлық қосындысына тең.
Кориолис үдеуі келесі фомуламен анықталатыны дәлелденеді:
![]() . (5.18)
. (5.18)
![]() мен
мен ![]() тапқан кезде олар да бірнеше
құраушылардың қосындысы болуы мүмкін екенін
есепке алу керек.
тапқан кезде олар да бірнеше
құраушылардың қосындысы болуы мүмкін екенін
есепке алу керек.
Тасымал қозғалыс ілгерілемелі болатын
дербес жағдайында ![]() =0, сонда
үдеулерді қосу теоремасы қарапайымдалады.
=0, сонда
үдеулерді қосу теоремасы қарапайымдалады.
![]() . (5.19)
. (5.19)
6 дәріс. Қатты дененің қозғалмайтын нүктені айнала қозғалысы. Еркін қатты дененің жалпы жағдайдағы қозғалысы
Дәрістің мазмұны: бір нүктесі қозғалмайтын дененің қозғалысы, еркін қатты дененің жалпы жағдайдағы қозғалысы.
Дәрістің мақсаты: қатты дененің сфералық қозғалысы және жалпы жағдайдағы қозғалысы кинематикасын оқып үйрену.
6.1 Бір нүктесі қозғалмайтын дененің қозғалысы
 Бір нүктесі қозғалмайтын
дененің қозғалысын айналмалы немесе сфералық дене деп
атау қабылданған. Қозғалмайтын жүйе
Бір нүктесі қозғалмайтын
дененің қозғалысын айналмалы немесе сфералық дене деп
атау қабылданған. Қозғалмайтын жүйе ![]() және қарастырылып отырған денеге
қатаң бекітілген жүйе
және қарастырылып отырған денеге
қатаң бекітілген жүйе ![]() .
Бұл координаттар жүйелерінің бастары болып дененің
қозғалмайтын
.
Бұл координаттар жүйелерінің бастары болып дененің
қозғалмайтын ![]() нүктесі қабылданған
(6.1 суретті қараңыз).
нүктесі қабылданған
(6.1 суретті қараңыз).
![]() Қатты
дененің әр уақыт мезетінде сәйкес орнын,
қозғалмайтын жүйенің орнымен салыстыра
қарасақ, онда бұл дененің орны қозғалмалы
жүйенің орнымен толық анықталады. Ал
қозғалмалы жүйенің қозғалмайтын
жүйеге қатысты орны белгілі бір бұрыштармен анықталады.
Ондай бұрыштардың саны тоғыз. Бұл бұрыштардың
үшеуі ғана тәуелсіз бұрыштар, ал қалған
алтауын осы тәуелсіз бұрыштар арқылы өрнектеу
арқылы табуға болады. Бірақ, алты бұрыштарды тәуелсіз
бұрыштар арқылы анықтау, әдетте, көп
қиындық келтіреді, сондықтан, қозғалмайтын бір
ғана нүктесі бар қатты дененің орнын анықтау
үшін, көп жағдайда, ерекше бұрыштар қолданылады.
Бұл бұрыштардың саны үшеу және олар Эйлер
бұрыштары деп аталады.
Қатты
дененің әр уақыт мезетінде сәйкес орнын,
қозғалмайтын жүйенің орнымен салыстыра
қарасақ, онда бұл дененің орны қозғалмалы
жүйенің орнымен толық анықталады. Ал
қозғалмалы жүйенің қозғалмайтын
жүйеге қатысты орны белгілі бір бұрыштармен анықталады.
Ондай бұрыштардың саны тоғыз. Бұл бұрыштардың
үшеуі ғана тәуелсіз бұрыштар, ал қалған
алтауын осы тәуелсіз бұрыштар арқылы өрнектеу
арқылы табуға болады. Бірақ, алты бұрыштарды тәуелсіз
бұрыштар арқылы анықтау, әдетте, көп
қиындық келтіреді, сондықтан, қозғалмайтын бір
ғана нүктесі бар қатты дененің орнын анықтау
үшін, көп жағдайда, ерекше бұрыштар қолданылады.
Бұл бұрыштардың саны үшеу және олар Эйлер
бұрыштары деп аталады.
Қозғалмалы жазықтықтың ![]() қозғалмайтын
жазықтықпен
қозғалмайтын
жазықтықпен ![]() қиылысу нүктесін
қиылысу нүктесін ![]() әрпімен белгілейміз (6.1-суретті
қараңыз). Суретте көрсетілген
әрпімен белгілейміз (6.1-суретті
қараңыз). Суретте көрсетілген ![]() сызығы
түйіндер сызығы деп аталады. Егер
сызығы
түйіндер сызығы деп аталады. Егер ![]() осі
осі
![]() осіне кіші бұрышпен сағат
тілінің айналуына қарсы бағытпен бұрылса, онда
осіне кіші бұрышпен сағат
тілінің айналуына қарсы бағытпен бұрылса, онда ![]() сызығының бағыты
оң деп есептеледі.
сызығының бағыты
оң деп есептеледі.
Эйлер бұрыштары:
![]() - прецессия бұрышы,
- прецессия бұрышы, ![]() жазықтығында жатады,
түйіндер сызығы
жазықтығында жатады,
түйіндер сызығы ![]() және
және ![]() осінің
арасындағы бұрыш;
осінің
арасындағы бұрыш;
![]() - таза айналу бұрышы немесе меншіктік
айналу бұрышы,
- таза айналу бұрышы немесе меншіктік
айналу бұрышы, ![]() жазықтығында
жатады, түйіндер сызығы
жазықтығында
жатады, түйіндер сызығы ![]() және
және ![]() осінің арасындағы
бұрыш;
осінің арасындағы
бұрыш;
![]() - нутация бұрышы,
- нутация бұрышы, ![]() жазықтығында жатады,
жазықтығында жатады, ![]() және
және ![]() осьтерінің арасындағы
бұрыш.
осьтерінің арасындағы
бұрыш.
Аталған тоғыз бұрыштар Эйлер бұрыштары арқылы өрнектеліп, қатты дененің сфералық қозғалысын зерттеуді жеңілдетеді. Бір нүктесі қозғалмайтын қатты дене қозғалыста болған кезде Эйлер бұрыштары өзгеріп отырады.
Егер қатты дененің сфералық қозғалысының төмендегі теңдеулері (қатты дененің сфералық қозғалысының теңдеулері)
![]() (6.1)
(6.1)
берілсе, онда әр уақыт мезетінде сәйкес Эйлер бұрыштарын табуға болады, демек, дененің қозғалмайтын жүйеге қатысты орнын анықтауға болады.
Эйлер-Даламбердің теоремасы «Қозғалмайтын нүктесі бар кез келген дененің қарапайым орын ауыстыруы дегеніміз, осы қозғалмайтын нүкте арқылы өтетін айналымның кейбір лездік айналу осі төңірегінде қарапайым бұрылысы болатынын білдіреді» деп тұжырымдайды. Лездік айналу осі осы уақыт мезетінде ғана қозғалыссыз болады және кез келген басқа уақыт мезетінде бұл басқа ось болып кетеді. Лездік айналу осі дененің қозғалмайтын нүктесі арқылы өтіп, оның шеткі жоғарғы қабаты мен құрастырылған қабатын қозғалысы барысында сипаттайды.
Дененің қозғалысын сипаттау
үшін бұрыштық жылдамдық векторы енгізіледі. Бұрыштық
жылдамдық векторы ![]() лездік айналу осінде орналасқан
және оның төбесінен айналуы сағат тілі жүрісіне
қарсы бағытталған.
лездік айналу осінде орналасқан
және оның төбесінен айналуы сағат тілі жүрісіне
қарсы бағытталған.
Қатты дененің лездік бұрыштық
жылдамдығын, айналу қозғалысы секілді, вектор ретінде
көрсетеміз. Вектор, айналу қозғалысы секілді, лездік айналу
осінің бойында жатады, ал оның бағытын денеге
қараған кезде, ол сағат тіліне қарсы бағытта
қозғалатын жаққа қарай бағыттаймыз.
Бұрыштық жылдамдық векторын дененің
қозғалмайтын нүктесіне түсірген ұтымды болады.
Дененің лездік бұрыштық жылдамдығын ![]() символымен белгілейміз. Дененің
сфералық қозғалысы кезінде
символымен белгілейміз. Дененің
сфералық қозғалысы кезінде ![]() шамасы,
жалпылама алғанда, модулі мен бағыты өзгереді. Сонымен сфералық
қозғалыстағы дененің лездік бұрыштық
үдеуі деп
шамасы,
жалпылама алғанда, модулі мен бағыты өзгереді. Сонымен сфералық
қозғалыстағы дененің лездік бұрыштық
үдеуі деп ![]() шамасының модулі мен
бағытының өзгеруін сипаттайтын шаманы, яғни:
шамасының модулі мен
бағытының өзгеруін сипаттайтын шаманы, яғни:
 (6.2)
(6.2)
Векторлар ![]() және
және ![]() бір осьтің бойымен
бағытталмайды. Лездік бұрыштық жылдамдық векторы
бір осьтің бойымен
бағытталмайды. Лездік бұрыштық жылдамдық векторы ![]() лездік айналу осінің бойымен
бағытталады, ал
лездік айналу осінің бойымен
бағытталады, ал ![]() векторы бұрыштық
үдеуі осі деп аталатын остің бойымен бағытталады.
векторы бұрыштық
үдеуі осі деп аталатын остің бойымен бағытталады.
Лездік бұрыштық жылдамдық пен лездік бұрыштық үдеу, бір ғана қозғалмайтын нүктесі бар қатты дененің кинематикалық күйін сипаттайтын, негізгі шамалар болып табылады.
Бұрыштық жылдамдық өзгерісін ұзындығы және бағыты бойынша бұрыштық үдеу көрсетеді, сондықтан бұрыштық үдеу және бұрыштық жылдамдық коллинеарлы емес. Нүктенің жылдамдық векторы сияқты, бұрыштық жылдамдық векторының соңын сипаттайтын траекторияға бұрыштық үдеу жанама бойымен бағытталған.
Дене нүктесінің үдеуі мен жылдамдығы мынадай формуламен анықталады:
![]() , (6.3)
, (6.3)
6.1 мысал. - Қозғалмалы
конустың Ox осі қозғалмайтын Oz1 осіне
қатысты тұрақты ![]() бұрыштық
жылдамдықпен айнала қозғалады (6.2-суретті
қараңыз). Осы қозғалмалы конус қозғалмайтын
конустың бүйір бетімен сырғанамай домалайды. P, A,
B нүктелерінің жылдамдықтарын және
қозғалмалы конустың бұрыштық жылдамдығын,
сонымен қатар
бұрыштық
жылдамдықпен айнала қозғалады (6.2-суретті
қараңыз). Осы қозғалмалы конус қозғалмайтын
конустың бүйір бетімен сырғанамай домалайды. P, A,
B нүктелерінің жылдамдықтарын және
қозғалмалы конустың бұрыштық жылдамдығын,
сонымен қатар ![]() , OA = 50 см, α= 30° болғанда В нүктесінің үдеуін
анықтау керек.
, OA = 50 см, α= 30° болғанда В нүктесінің үдеуін
анықтау керек.
Шешуі: Ең алдымен дене айналысының лездік осін орналастырып алайық. Қозғалмайтын конус бетімен қозғалмалы конус сырғанамай қозғалатын болғандықтан, P нүктесін қосқанда, осы уақыт мезетінде қозғалмалы конустың барлық нүктелері қозғалмайтын конус нүктелерімен сәйкес келеді. Бұл нүктелердің жылдамдықтары нөлге тең. Бұдан шығатын қорытынды, біріншіден, дененің лездік айналу осі осы уақыт мезетінде OP түзуінде орналасқан, екіншіден, P нүктесінің жылдамдығы нөлге тең.
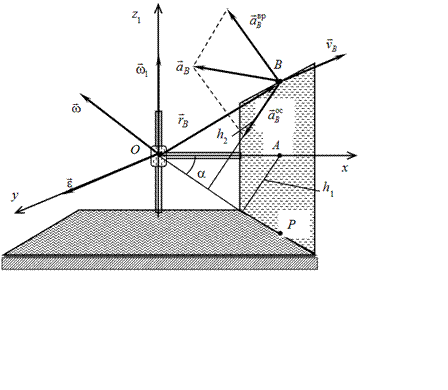 Ox осінде жатқан А нүктесінің жылдамдығы
Ox осінде жатқан А нүктесінің жылдамдығы ![]() .
.
А нүктесінен лездік айналу осіне дейінгі ара қашықтық h1-ді белгілеу арқылы дененің бұрыштық жылдамдығын табамыз:
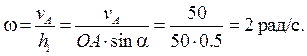 Ары қарай B нүктесінің
жылдамдығын анықтаймыз:
Ары қарай B нүктесінің
жылдамдығын анықтаймыз:
![]() В нүктесінің
үдеуін анықтаймыз.
В нүктесінің
үдеуін анықтаймыз. ![]() векторы
қозғалмайтын Oz1 осінің
төңірегінде айналады, оның бұрыштық
жылдамдығы
векторы
қозғалмайтын Oz1 осінің
төңірегінде айналады, оның бұрыштық
жылдамдығы ![]() модулі бойынша
тұрақты болғандықтан
модулі бойынша
тұрақты болғандықтан ![]() векторының
модулі де тұрақты.
векторының
модулі де тұрақты.
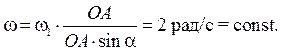
Осыған
байланысты, оның уақыт бойынша алынған туындысын, яғни ![]() векторын, мына формула бойынша
анықтаймыз
векторын, мына формула бойынша
анықтаймыз ![]() . Бұл вектор y
осі бойымен бағытталып,
. Бұл вектор y
осі бойымен бағытталып, ![]() және
және ![]() векторлары орналасқан
жазықтыққа перпендикуляр. Оның модулі
векторлары орналасқан
жазықтыққа перпендикуляр. Оның модулі  .
.
В нүктесінің радиус-векторын қозғалмайтын нүкте арқылы жүргіземіз және оның үдеуінің құраушы векторларын анықтаймыз:
![]() ;
;
![]() ;
;
![]() .
.
Косинустар
теоремасы бойынша ![]() и
и ![]() векторларының
арасындағы бұрышы 120°-қа тең, нүкте
үдеуінің модулін табамыз:
векторларының
арасындағы бұрышы 120°-қа тең, нүкте
үдеуінің модулін табамыз:
![]()
Айналмалы үдеу векторы жылдамдық векторымен бір түзудің бойында жатпайды.
6.1 Еркін қатты дененің қозғалысы
Еркін қатты дененің кеңістіктегі
орнын анықтау үшін екі координаттар жүйесін алайық: ![]() қозғалмайтын жүйесі
және қозғалыстағы денеге бекітілген
қозғалмалы жүйесі
қозғалмайтын жүйесі
және қозғалыстағы денеге бекітілген
қозғалмалы жүйесі ![]() . Сонымен
қоса, тағы бір
. Сонымен
қоса, тағы бір ![]() жүйесін
аламыз, бұл жүйенің басы екінші жүйенің басымен
бір нүктеде, яғни
жүйесін
аламыз, бұл жүйенің басы екінші жүйенің басымен
бір нүктеде, яғни ![]() нүктесінде
болады, ал осьтері қозғалмайтын жүйенің осьтеріне
параллель орналасқан (6.3-суретті қараңыз).
нүктесінде
болады, ал осьтері қозғалмайтын жүйенің осьтеріне
параллель орналасқан (6.3-суретті қараңыз).
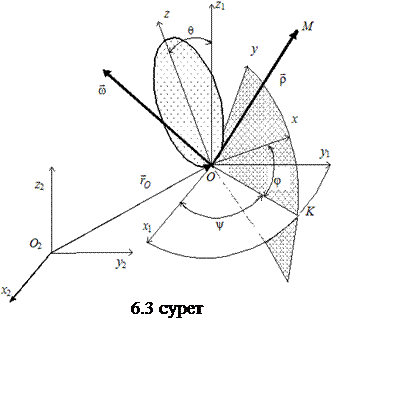 Дененің қозғалмайтын координаттар
жүйесіне қатысты кеңістіктегі орны, қозғалмалы
жүйенің
Дененің қозғалмайтын координаттар
жүйесіне қатысты кеңістіктегі орны, қозғалмалы
жүйенің ![]() кеңістіктегі орнымен
толығымен анықталады. Бұл қозғалмалы
жүйенің, қозғалмайтын жүйеге қатысты орны,
координаттар жүйесінің басы
кеңістіктегі орнымен
толығымен анықталады. Бұл қозғалмалы
жүйенің, қозғалмайтын жүйеге қатысты орны,
координаттар жүйесінің басы ![]() нүктесімен
және
нүктесімен
және ![]() осьтерінің
осьтерінің ![]() жүйесіне қатысты орнымен
анықталады.
жүйесіне қатысты орнымен
анықталады.
Бұл кезде ![]() нүктесінің
қозғалмайтын жүйеге қатысты орны оның
нүктесінің
қозғалмайтын жүйеге қатысты орны оның ![]() координаттарымен, ал
координаттарымен, ал ![]() жүйесінің
жүйесінің ![]() жүйесіне қатысты орны
Эйлер бұрыштарымен анықталады.
жүйесіне қатысты орны
Эйлер бұрыштарымен анықталады.
Дене еркін қозғалыста болған кезде,
оның ![]() қозғалмайтын жүйеге
қатысты кеңістіктегі орнын анықтайтын алты шамалардың
барлығы да өзгереді.
қозғалмайтын жүйеге
қатысты кеңістіктегі орнын анықтайтын алты шамалардың
барлығы да өзгереді.
Дененің қозғалысы белгілі болу үшін, аталған алты шамалардың барлығы да, уақытқа тәуелді функциясы ретінде берілу керек, демек:
![]()
![]() (6.4)
(6.4)
Бұл теңдеулер, еркін қатты дене қозғалысының теңдеулері деп аталады. Сонымен, еркін қатты дененің еркіндік дәрежесі – алтау.
Алғашқы үш тәуелділіктер ілгерілемелі қозғалысқа, ал екінші үш тәуелділіктер – сфералық қозғалысқа сәйкес келеді.
Сфералық қозғалыс қазіргі жағдайда О полюсі арқылы өтетін лездік айналу осінің төңірегіндегі қарапайым бұрылыстар сериясында берілуі мүмкін болғандықтан, дененің кез келген нүктесінің жылдамдығы мен үдеуі сәйкесінше ілгерілемелі қозғалыстың жылдамдығы мен үдеуінің, сонымен қатар полюске қатысты қозғалыстағы нүктенің жылдамдығы мен үдеуінің геометриялық жиынтығына тең болады. Еркін қатты дене қозғалысының жылдамдығы мен үдеуін анықтау үшін мынадай формуланы жазамыз:
![]() . (6.5)
. (6.5)
Мұнда ![]() және
және ![]() – дененің М
нүктесінің жылдамдығы мен үдеуі;
– дененің М
нүктесінің жылдамдығы мен үдеуі; ![]() және
және ![]() – О
полюсінің жылдамдығы мен үдеуі;
– О
полюсінің жылдамдығы мен үдеуі; ![]() –
дененің бұрыштық жылдамдығы.
–
дененің бұрыштық жылдамдығы. ![]() қозғалмалы
координат жүйесіндегі М нүктесінің радиус-векторы
қозғалмалы
координат жүйесіндегі М нүктесінің радиус-векторы ![]() .
.
7 дәріс Қатты дененің күрделі қозғалысы
Дәрістің мазмұны: АҚД-нің күрделі қозғалысы; ілгерілемелі, айналмалы қозғалыстарды қосу, айналмалы және ілгерілемелі қозғалыстар.
Дәрістің мақсаты: ілгермелі қозғалыстарды, параллель осьтерді айналуындағы лездік айналуларын, өзара қиылысатын осьтерді айналуындағы лездік айналуларын қосуды, лездік ілгермелі және айналу қозғалыстарын қосудың жекеленген түрлерін қарастыру.
7.1 Ілгермелі қозғалыстарды қосу
Қатты дене уақыт мезетінде ілгермелі
қозғалыстың екі түрімен (салыстырмалы және
тасымал) қозғалыста болсын (7.1-суретті қараңыз). ![]() есептеу жүйесіне қатысты
есептеу жүйесіне қатысты ![]() жылдамдығымен, ал
қозғалмайтын
жылдамдығымен, ал
қозғалмайтын
![]() жүйесіне қатысты
жүйесіне қатысты ![]() жылдамдығымен
қозғалыста болсын. Ілгермелі қозғалыс кезінде дене
нүктелерінің жылдамдықтары өзара тең
(геометриялық тұрғыдан) болатындықтан, осы
дененің нүктелерінің салыстырмалы және тасымал
жылдамдықтары да геометриялық теңдікте болады. Сондықтан,
жылдамдықтарды қосу теоремасы негізінде – дене
нүктелерінің абсолют жылдамдықтары сәйкес векторлар
жылдамдығымен
қозғалыста болсын. Ілгермелі қозғалыс кезінде дене
нүктелерінің жылдамдықтары өзара тең
(геометриялық тұрғыдан) болатындықтан, осы
дененің нүктелерінің салыстырмалы және тасымал
жылдамдықтары да геометриялық теңдікте болады. Сондықтан,
жылдамдықтарды қосу теоремасы негізінде – дене
нүктелерінің абсолют жылдамдықтары сәйкес векторлар ![]() арқылы
тұрғызылған параллелограмның диогоналына тең
болады:
арқылы
тұрғызылған параллелограмның диогоналына тең
болады:
![]() .
(7.1)
.
(7.1)

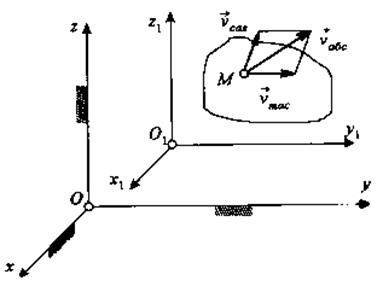 Сонымен, егер қатты дененің екі ілгермелі
қозғалысын қоссақ, онда дененің абсолют
қозғалысы да ілгермелі қозғалыс болады, ал оның
жылдамдығы осы қозғалыстың құраушы
қозғалыстарының геометриялық қосындысына
тең болады. Егер қатты дене уақыт мезетінде бірнеше ілгермелі
қозғалыста болса, онда дененің абсолют қозғалысы да
ілгермелі қозғалыс болады, ал оның жылдамдығы осы
барлық қозғалыстардың құраушы
қозғалыстарының геометриялық жиынына тең болады,
яғни
Сонымен, егер қатты дененің екі ілгермелі
қозғалысын қоссақ, онда дененің абсолют
қозғалысы да ілгермелі қозғалыс болады, ал оның
жылдамдығы осы қозғалыстың құраушы
қозғалыстарының геометриялық қосындысына
тең болады. Егер қатты дене уақыт мезетінде бірнеше ілгермелі
қозғалыста болса, онда дененің абсолют қозғалысы да
ілгермелі қозғалыс болады, ал оның жылдамдығы осы
барлық қозғалыстардың құраушы
қозғалыстарының геометриялық жиынына тең болады,
яғни
![]() (7.2)
(7.2)
7.2 Қатты дененің параллель осьтерді айналуындағы лездік айналуларын қосу
Егер қатты дене параллель осьтерді айнала қозғалысы кезінде, бір уақытта, айналудың екі түріне қатысса, онда оның барлық нүктелері айналу осіне перпендикуляр жазықтықта қозғалады, яғни, дененің абсолют қозғалысы жазық қозғалыс болып табылады. Мұндай қозғалыстардың үш түрі болады.
Олар:
1) айналудың құраушылары бір жаққа бағытталған;
2) айналудың құраушылары әр жаққа бағытталған, ал айналудың бұрыштық жылдамдықтарының модульдері бір-біріне тең болмайды;
3) айналудың құраушылары әр жаққа бағытталған, ал айналудың бұрыштық жылдамдықтарының модульдері өзара тең. Қозғалыстардың аталған түрлерін жеке-жеке қарастырайық.
1. Айналудың құраушылары бір жаққа бағытталған.
Қатты дене ![]() осін
айнала қозғалсын, ал бұл осьтің өзі
қозғалмайтын
осін
айнала қозғалсын, ал бұл осьтің өзі
қозғалмайтын ![]() осін айнала
қозғалсын (7.2-суретті қараңыз). Бұл кезде
дененің
осін айнала
қозғалсын (7.2-суретті қараңыз). Бұл кезде
дененің ![]() осін айнала
қозғалуы салыстырмалы қозғалыс болады, ал дененің
осы осьпен бірге
осін айнала
қозғалуы салыстырмалы қозғалыс болады, ал дененің
осы осьпен бірге ![]() осін айнала
қозғалуы – тасымал қозғалысы болып табылады.
осін айнала
қозғалуы – тасымал қозғалысы болып табылады.
Қатты дененің осы
қозғалыстардағы бұрыштық жылдамдықтарын ![]() және
және ![]() символдарымен
белгілейік.
символдарымен
белгілейік.
 Қарастырылып отырған денені айналу осіне
перпендикуляр
Қарастырылып отырған денені айналу осіне
перпендикуляр ![]() жазықтығымен
екіге бөлеміз. Қиылған жердегі жазықтықтың
түрі
жазықтығымен
екіге бөлеміз. Қиылған жердегі жазықтықтың
түрі ![]() фигурасымен көрсетілген. Осы
жазықтық
фигурасымен көрсетілген. Осы
жазықтық ![]() қозғалысы
дененің жалпы қозғалысын анықтайды.
қозғалысы
дененің жалпы қозғалысын анықтайды.
![]() Суретте
көрсетілген
Суретте
көрсетілген ![]() және
және ![]() нүктелері
нүктелері ![]() жазықтығындағы
айналу осьтерінің іздері болып табылады. Уақыт мезетінде
жазықтығындағы
айналу осьтерінің іздері болып табылады. Уақыт мезетінде ![]() фигурасының лездік жылдамдық
центрі болатыны белгілі. Сонымен қатар, фигураның кез келген
нүктесінің абсолют жылдамдығы салыстырмалы және тасымал
жылдамдықтарынан тұратынын ескерсек, онда бұл
жылдамдықтардың өзара тең және
қарама-қарсы бағытталатыны белгілі. Ал
фигурасының лездік жылдамдық
центрі болатыны белгілі. Сонымен қатар, фигураның кез келген
нүктесінің абсолют жылдамдығы салыстырмалы және тасымал
жылдамдықтарынан тұратынын ескерсек, онда бұл
жылдамдықтардың өзара тең және
қарама-қарсы бағытталатыны белгілі. Ал ![]() фигурасының лездік жылдамдық
центрі
фигурасының лездік жылдамдық
центрі ![]() және
және ![]() нүктелерінің
араларында жататын болғандықтан, ол нүктені
нүктелерінің
араларында жататын болғандықтан, ол нүктені ![]() нүктесімен белгілейміз де, лездік
жылдамдық центрі дейміз. Бұл кезде салыстырмалы
жылдамдықтың модулі тасымал жылдамдығының модуліне
тең болады, яғни
нүктесімен белгілейміз де, лездік
жылдамдық центрі дейміз. Бұл кезде салыстырмалы
жылдамдықтың модулі тасымал жылдамдығының модуліне
тең болады, яғни ![]() . Ал келесі
шамалар:
. Ал келесі
шамалар: ![]() ,
, ![]() бұрыннан
белгілі болғандықтан:
бұрыннан
белгілі болғандықтан:
 .
(7.3)
.
(7.3)
Фигураның абсолют бұрыштық
жылдамдығын табу үшін, ![]() нүктесін
қарастырайық. Бұл нүкте салыстырмалы қозғалысқа
қатыспайды, сондықтан:
нүктесін
қарастырайық. Бұл нүкте салыстырмалы қозғалысқа
қатыспайды, сондықтан:
![]() .
.
Бірақ ![]() және
және
![]() болғандықтан (7.3)-ші
формуланы пайдаланып, келесі өрнекті аламыз:
болғандықтан (7.3)-ші
формуланы пайдаланып, келесі өрнекті аламыз:
![]() .
(7.4)
.
(7.4)
Енді дененің қозғалысына келетін
болсақ, оның осы мезеттегі абсолют қозғалысын лездік жылдамдық
центрі арқылы өтетін және айналуды құрайтын осьтерге
параллель ![]() лездік осін айналу
қозғалысы ретінде қабылдаймыз. Сонымен, қатты
дененің параллель осьтерді айналуындағы бір бағыттағы
екі лездік айналысын қосқанда дененің абсолют
қозғалысы пайда болады. Дененің абсолют бұрыштық
жылдамдығының модулі және құрама айналулардың
бұрыштық жылдамдықтарының жиыны бір-біріне тең
болады.
лездік осін айналу
қозғалысы ретінде қабылдаймыз. Сонымен, қатты
дененің параллель осьтерді айналуындағы бір бағыттағы
екі лездік айналысын қосқанда дененің абсолют
қозғалысы пайда болады. Дененің абсолют бұрыштық
жылдамдығының модулі және құрама айналулардың
бұрыштық жылдамдықтарының жиыны бір-біріне тең
болады.
Лездік ось ![]() дененің
сыртында жатуы да мүмкін. Сонымен қатар, ол екі цилиндрлік беттер
жасай отырып, кеңістіктегі орнын үнемі өзгертіп отырады.
дененің
сыртында жатуы да мүмкін. Сонымен қатар, ол екі цилиндрлік беттер
жасай отырып, кеңістіктегі орнын үнемі өзгертіп отырады.
2. Айналудың құраушылары әр жаққа бағытталған, ал айналудың бұрыштық жылдамдықтарының модульдері бір-біріне тең болмайды.
Қатты дене ![]() осін
айнала қозғалсын, ал оның салыстырмалы бұрыштық
жылдамдығы
осін
айнала қозғалсын, ал оның салыстырмалы бұрыштық
жылдамдығы ![]() болсын, сонымен қатар,
ось осы айналу осімен бірге
болсын, сонымен қатар,
ось осы айналу осімен бірге ![]() осін айнала
қозғалсын (7.3-суретті қараңыз), ал оның
бұл кездегі тасымал бұрыштық жылдамдығы
осін айнала
қозғалсын (7.3-суретті қараңыз), ал оның
бұл кездегі тасымал бұрыштық жылдамдығы ![]() болсын. Айналу бағыттары
әртүрлі және
болсын. Айналу бағыттары
әртүрлі және ![]() .
.
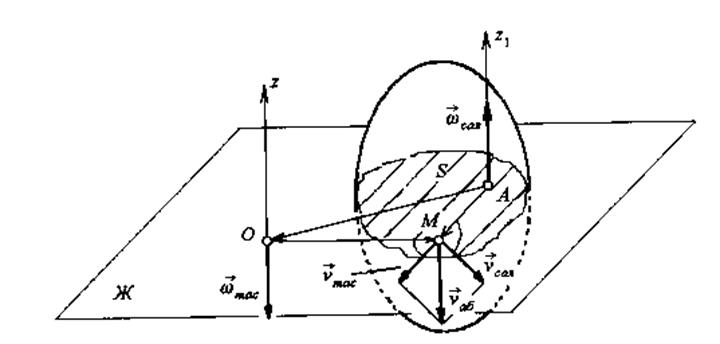
![]() Жоғарыдағы
ойымызды жалғастыра отырып, дененің осы мезеттегі абсолют
қозғалысы лездік
Жоғарыдағы
ойымызды жалғастыра отырып, дененің осы мезеттегі абсолют
қозғалысы лездік ![]() осін айнала
қозғалысы болып табылады.
осін айнала
қозғалысы болып табылады.
Қарастырылып отырған жағдайда лездік
ось ![]() және
және ![]() осьтерінің
сырт жағында жатады. Дененің абсолют бұрыштық
жылдамдығы өзінің модулі бойынша, айналуды
құраушы бұрыштық жылдамдықтардың
модульдерінің айырмасына тең болады, яғни:
осьтерінің
сырт жағында жатады. Дененің абсолют бұрыштық
жылдамдығы өзінің модулі бойынша, айналуды
құраушы бұрыштық жылдамдықтардың
модульдерінің айырмасына тең болады, яғни:
![]() .
(7.5)
.
(7.5)
Сонымен, қатты дененің параллель осьтерді айналуындағы әр бағыттағы, бұрыштық жылдамдықтарының модульдері әртүрлі екі лездік айналысын қосқанда дененің абсолют қозғалысы пайда болады. Дененің абсолют бұрыштық жылдамдығының модулі, айналуды құрайтын бұрыштық жылдамдықтардың айырмасына тең болады.
Бұл кезде де лездік осьтер екі цилиндрлік беттер жасай отырып, кеңістіктегі орнын үнемі өзгертіп отырады.
3. Айналудың құраушылары әр жаққа бағытталған, ал айналудың бұрыштық жылдамдықтарының модульдері өзара тең.
 Қатты дене
Қатты дене ![]() осін айнала қозғалсын, ал оның
салыстырмалы бұрыштық жылдамдығы
осін айнала қозғалсын, ал оның
салыстырмалы бұрыштық жылдамдығы ![]() болсын,
сонымен қатар, ол осы айналу осімен бірге
болсын,
сонымен қатар, ол осы айналу осімен бірге ![]() осін
айнала қозғалсын (7.4-суретті қараңыз), ал оның
бұл кездегі тасымал бұрыштық жылдамдығы
осін
айнала қозғалсын (7.4-суретті қараңыз), ал оның
бұл кездегі тасымал бұрыштық жылдамдығы ![]() болсын. Айналу бағыттары
әртүрлі және
болсын. Айналу бағыттары
әртүрлі және ![]() .
.
 Қатты
дененің параллель осьтердегі модульдері өзара тең,
бірақ қарама-қарсы бағытталған
бұрыштық жылдамдықтармен айнала
қозғалысындағы екі лездік айналудың осындай
жиынтығы лездік айналудың жұбы деп аталады.
Қатты
дененің параллель осьтердегі модульдері өзара тең,
бірақ қарама-қарсы бағытталған
бұрыштық жылдамдықтармен айнала
қозғалысындағы екі лездік айналудың осындай
жиынтығы лездік айналудың жұбы деп аталады.
Қарастырып отырған денені айналу осіне
перпендикуляр ![]() жазықтығымен
екіге бөліп, қиылған жердегі
жазықтығымен
екіге бөліп, қиылған жердегі ![]() жазықтығының
айналуын қарастырайық (7.4-суретті қараңыз).
жазықтығының
айналуын қарастырайық (7.4-суретті қараңыз).
Осы ![]() жазықтығының
кез келген
жазықтығының
кез келген ![]() нүктесінің салыстырмалы
қозғалысы
нүктесінің салыстырмалы
қозғалысы ![]() шамасына тең
және тасымал қозғалысы
шамасына тең
және тасымал қозғалысы ![]() болғандықтан,
оның абсолют қозғалысы
болғандықтан,
оның абсолют қозғалысы
![]() .
.
Бұл өрнектегі ![]() шамасын
шамасын
![]() арқылы алмастырып,
арқылы алмастырып, ![]() екенін ескеріп, келесі формуланы
аламыз:
екенін ескеріп, келесі формуланы
аламыз:
![]() .
.
Бұл өрнектегі ![]() және
және
![]() шамалары
шамалары ![]() нүктесінің
нүктесінің
![]() жазықтығының қай
жерінде орналасқанына тәуелді болмағандықтан, осы
жазықтықтың барлық нүктелерінің
жылдамдықтары бірдей деп қорытынды жасауға болады. Ал мұндай
жағдай тек дененің лездік ілгермелі қозғалысына
тән екені белгілі.
жазықтығының қай
жерінде орналасқанына тәуелді болмағандықтан, осы
жазықтықтың барлық нүктелерінің
жылдамдықтары бірдей деп қорытынды жасауға болады. Ал мұндай
жағдай тек дененің лездік ілгермелі қозғалысына
тән екені белгілі.
Сонымен, модульдері өзара тең және
параллель, бірақ қарама-қарсы бағытталған екі
бұрыштық жылдамдықтардың жұбы деп, ал ![]() векторы – бұрыштық
жылдамдықтар жұбының моменті деп аталады, яғни:
векторы – бұрыштық
жылдамдықтар жұбының моменті деп аталады, яғни:
![]() (7.6)
(7.6)
Егер қозғалыстың барлық уақытында бұрыштық жылдамдықтардың жұбы бар болса, онда мұндай қозғалыс үздіксіз (перманентті) ілгермелі қозғалыс болып табылады.
7.3 Қатты дененің өзара қиылысатын осьтерді айналуындағы лездік айналуларын қосу
Қатты дененің өзара қиылысатын екі осьтерді бір кезде айналуындағы құрама қозғалысын қарастырайық. Мұндай қозғалыстың мысалы ретінде 7.5 - суретте көрсетілген механизмнің жұмысын келтіруге болады. Бұл суреттегі конус тәріздес 2-ші тісті доңғалақ (шестерня) қозғалмайды, ал 1-ші тісті доңғалақ қозғалыста (теңселу) болады.
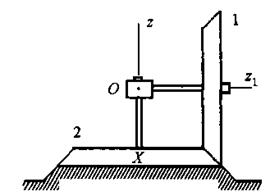
![]() Қатты
дене уақыттың осы сәтінде
Қатты
дене уақыттың осы сәтінде ![]() осін
айнала қозғалсын, ал оның салыстырмалы бұрыштық
жылдамдығы
осін
айнала қозғалсын, ал оның салыстырмалы бұрыштық
жылдамдығы ![]() болсын, сонымен қоса,
ол осы айналу осімен бірге қозғалмайтын
болсын, сонымен қоса,
ол осы айналу осімен бірге қозғалмайтын ![]() осін
айнала қозғалсын (7.5-сурет), ал оның бұл кездегі
тасымал бұрыштық жылдамдығы
осін
айнала қозғалсын (7.5-сурет), ал оның бұл кездегі
тасымал бұрыштық жылдамдығы ![]() болсын.
Айналудың салыстырмалы және тасымал осьтерінде жатқан
болсын.
Айналудың салыстырмалы және тасымал осьтерінде жатқан ![]() нүктесі қозғалмайтын
нүкте, сондықтан дененің абсолют қозғалысы, осы
қозғалмайтын
нүктесі қозғалмайтын
нүкте, сондықтан дененің абсолют қозғалысы, осы
қозғалмайтын ![]() нүктесін
айнала қозғалатын сфералық қозғалыс болып
табылады, сонымен қатар, дененің осы сәттегі
қозғалысы – қозғалмайтын нүкте арқылы
өтетін лездік осьті айналу қозғалысы болып табылады.
нүктесін
айнала қозғалатын сфералық қозғалыс болып
табылады, сонымен қатар, дененің осы сәттегі
қозғалысы – қозғалмайтын нүкте арқылы
өтетін лездік осьті айналу қозғалысы болып табылады.
7.4 Қатты дененің лездік ілгермелі және айналу қозғалыстарын қосудың жекеленген түрлері
Қатты дененің күрделі қозғалысы лездік ілгерлемелі қозғалысынан және айналу қозғалысынан тұруы мүмкін. Мысал ретінде вертолеттің пропеллерінің қозғалысын келтіруге болады.
Күрделі қозғалыстың үш түрін айыруға болады:
- ілгерлемелі қозғалыстың жылдамдығы айналу осіне перпендикуляр;
- ілгерлемелі қозғалыстың жылдамдығы айналу осіне параллель;
- ілгерлемелі қозғалыстың жылдамдығы айналу осімен сүйір немесе доғал бұрыш жасайды.
8 дәріс. Нүкте динамикасы
Дәрістің мазмұны: кіріспе ұғымдары мен аксиомалар; нүкте қозғалысының дифференциалдық теңдеулері және жалпы теоремалары.
Дәрістің мақсаты: динамиканың ұғымдары мен нүкте қозғалысының дифференциалдық теңдеулерін қарастыру, нүкте динамикасының жалпы теоремаларын қолдану.
8.1 Динамика аксиомалары
Динамикада материялық денлердің, олардың инерциясын есепке алуымен күштер әсерінен пайда болатын қозғалысы қарастырылады. Инерция - материялық дененің өзінің қозғалыс немесе тыныштық қалпын күштер түспеген кезде сақтап қалу қасиеті. Ілгерілемелі қозғалыстағы дене инерциясының өлшемі - дененің массасы m.
Нүкте динамикасы төмендегі 4 аксиомаға негізделеді:
1) Күштер түспейтін материялық нүкте (МН), оған күштер түсіп, қалпын өзгерткенге дейін тыныштықта немесе бірқалыпты түзу сызықты қозғалыста болады. Күштер болмағандағы нүктенің қозғалысы инерциялық қозғалыс деп аталады. Инерция заңы орындалатын СЖ инерциялық СЖ деп аталады.
2) МН-нің үдеуі оған түсетін күшке пропорционал және сол күшпен бағыттас. Динамиканың негізгі теңдеуі:
![]() . (8.1)
. (8.1)
3) Екі МН бір-біріне модульдері тең және нүктелерді қосатын түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді.
4) Әр күш бөлек түскенде МН алатын үдеулердің векторлық қосындысы барлық күштер біржолы түскенде алатын үдеуіне тең:
![]() (8.2)
(8.2)
(8.2) теңдеуінің орнына (8.1)
теңдеуін, ![]() күші ретінде тең
әсерлі күшті алып, қолдануға болады.
күші ретінде тең
әсерлі күшті алып, қолдануға болады.
Ауырлық күш әсерінен денелер бірдей ![]() үдеуіне ие болады, ол
ауырлық күш үдеуі немесе еркін түсу үдеуі деп
аталады. Егер МН-ге тек қана
үдеуіне ие болады, ол
ауырлық күш үдеуі немесе еркін түсу үдеуі деп
аталады. Егер МН-ге тек қана ![]() ауырлық
күші түсетін болса, онда (6.1) бойынша:
ауырлық
күші түсетін болса, онда (6.1) бойынша:
![]() .
(8.3)
.
(8.3)
Дененің орналасуына және оған түсетін күштерге тәуелсіз, ал дененің салмағы дене орнының географикалық еніне және оның Жер орталығына дейінгі қашықтығына тәуелді.
8.2 Материялық нүкте қозғалысының дифференциалдық теңдеулері
МН {![]() } күштер
жүйесінің әсерінен (күштер арасына реакциялар да бар) Оxyz
инерциялық СЖ-не қатысты қозғалатын болсын. (8.2)
теңдеуін декарт координат осьтеріне немесе табиғи осьтерге
проекциялап, қозғалысының дифференциалдық
теңдеулерін (ҚДТ) аламыз:
} күштер
жүйесінің әсерінен (күштер арасына реакциялар да бар) Оxyz
инерциялық СЖ-не қатысты қозғалатын болсын. (8.2)
теңдеуін декарт координат осьтеріне немесе табиғи осьтерге
проекциялап, қозғалысының дифференциалдық
теңдеулерін (ҚДТ) аламыз:
![]() (8.4)
(8.4)
Немесе:
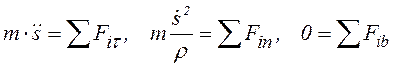 .
(8.5)
.
(8.5)
ҚДТ нүкте динамикасының екі негізгі есебін шешу үшін қолданылады:
а) нүкте қозғалысы бойынша оған түсетін күшті анықтау;
б) нүктеге түсетін күштер бойынша оның қозғалысын анықтау.
8.3 Материялық нүктенің салыстырмалы қозғалысы
Динамика заңдары тек инерциялық СЖ-нде
орындалады. МН-нің кейбір СЖ-не қатысты қозғалысын
қарастырайық және осы СЖ басқа инерциялық СЖ-не
қатысты еркінше қозғалатын болсын. P нүктесі {![]() } күштер әсерінен
қозғалатын болсын. Инерциялық СЖ-нде динамиканың негізгі
(8.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17)
формуласымен табылады:
} күштер әсерінен
қозғалатын болсын. Инерциялық СЖ-нде динамиканың негізгі
(8.2) теңдеуі орындалады. Нүктенің абсолют үдеуі (5.17)
формуласымен табылады:
![]() (8.6)
(8.6)
(6.6) теңдігін (6.2) теңдігіне қойып, түрлендіреміз.
![]() (8.7)
(8.7)
Келесі белгілеулерді қабылдаймыз:
![]() (8.8)
(8.8)
![]() (8.9)
(8.9)
![]() және
және ![]() тасымал және кориолис инерция
күштері деп аталады.
тасымал және кориолис инерция
күштері деп аталады.
(8.7) теңдігін келесі түрде жазуға болады:
![]() (8.10)
(8.10)
(8.10) - теңдеуі МН-нің салыстырмалы қозғалысы динамикасының негізгі теңдеуі.
МН-нің салыстырмалы қозғалысы негізгі теңдеуінің дербес жағдайлары:
а) ілгерілемелі тасымал қозғалыс кезінде:
![]()
![]() (8.11)
(8.11)
б) түзу сызықты бірқалыпты тасымал қозғалыс кезінде:
![]() (8.12)
(8.12)
Мұнда (8.12) мен (8.2) бірдей болады,
өйткені ![]() . Сондықтан бұл СЖ
инерциялық болады. Механикалық тәжірибелер арқылы СЖ
тыныштықта екенін немесе ілгерілемелі бірқалыпты және
түзу сызықты қозғалыста екенін анықтау
мүмкін емес (Галилейдің салыстырмалылық принципі);
. Сондықтан бұл СЖ
инерциялық болады. Механикалық тәжірибелер арқылы СЖ
тыныштықта екенін немесе ілгерілемелі бірқалыпты және
түзу сызықты қозғалыста екенін анықтау
мүмкін емес (Галилейдің салыстырмалылық принципі);
в) салыстырмалы тыныштық қалпында:
![]() (8.13)
(8.13)
Бұл МН-нің салыстырмалы тепе-теңдігінің теңдеуі.
8.4 Нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема
Динамиканың көптеген есептерін шешу кезінде ҚДТ-н интегралдаудың орнына динамиканың жалпы теоремаларын қолданған тиімділеу болады.
Нүктенің
қозғалыс мөлшерінің өзгеруі туралы теоремасын
қарастырайық. МН-нің қозғалыс мөлшері деп ![]() шаманы айтады. Күштің элементар импульсі деп
шаманы айтады. Күштің элементар импульсі деп ![]() шаманы айтады.
шаманы айтады. ![]() күшінің шекті t1
уақыт ішіндегі
күшінің шекті t1
уақыт ішіндегі ![]() импульсі
импульсі 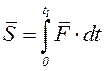 . Импульстің модулі мен
бағытын проекциялар арқылы табуға болады:
. Импульстің модулі мен
бағытын проекциялар арқылы табуға болады:
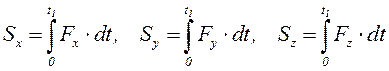 .
(8.14)
.
(8.14)
Динамиканың негізгі теңдеуін келесі түрде жазуға болады:
 . (8.15)
. (8.15)
Бұл дифференциалдық түрдегі нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема: нүктенің қозғалыс мөлшерінің уақыт бойынша туындысы нүктеге түсетін күштердің векторлық қосындысына тең. Шекті түрдегі сол теорема: нүктенің қозғалыс мөлшерінің кейбір уақыт аралығында өзгеруі оған түсетін күштердің сол уақыт аралықтағы импульстерінің векторлық қосындысына тең:
![]() .
(8.16)
.
(8.16)
Есептерді шешу кезінде әдетте теңдеулердің проекциялары қолданылады.
8.5 Нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теорема
МН-нің қозғалыс мөлшерінің О центріне қатысты моменті деп келесі шаманы айтады
![]() (8.17)
(8.17)
мұндағы ![]() - қозғалыстағы
нүктенің О центрінен жүргізілген радиус-векторы.
- қозғалыстағы
нүктенің О центрінен жүргізілген радиус-векторы.
Сонда ![]() векторы
векторы ![]() және О
центрі арқылы өтетін жазықтыққа перпендикуляр
бағытталады, aл модулі
және О
центрі арқылы өтетін жазықтыққа перпендикуляр
бағытталады, aл модулі ![]() .
.
Нүктенің
қозғалыс мөлшерінің О центрінен өтетін Оz
осіне қатысты моменті ![]() векторының сол оське проекциясына тең:
векторының сол оське проекциясына тең:
![]() .
(8.18)
.
(8.18)
мұндағы g -![]() векторы мен Оz осі
арасындағы бұрыш.
векторы мен Оz осі
арасындағы бұрыш.
Теорема: нүктенің қозғалыс мөлшерінің кейбір қозғалмайтын центрге қатысты алынған моментінің уақыт бойынша туындысы әсер ететін күштің сол центрге қатысты векторлық моментіне тең:
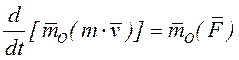 . (8.19)
. (8.19)
Оське қатысты моменттер теоремасы:
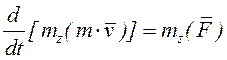 . (8.20)
. (8.20)
(8.19)
теңдеуінен ![]() болса,
болса, ![]() болатыны шығады.
болатыны шығады.
8.6 Күштің жұмысы. Күштің қуаты. Нүктенің кинетикалық энергиясының өзгеруі туралы теорема
М
нүктесіне түсетін ![]() күшінің
(8.1-суретті қараңыз) элементар жұмысы келесі:
күшінің
(8.1-суретті қараңыз) элементар жұмысы келесі:
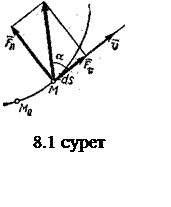 dW = Ft ∙ds, (8.21)
dW = Ft ∙ds, (8.21)
мұндағы Ft - ![]() күшінің
М нүктесінің траекториясына нүктенің орын
ауыстыру бағытымен жүргізілген Мt жанамасына
проекциясы;
күшінің
М нүктесінің траекториясына нүктенің орын
ауыстыру бағытымен жүргізілген Мt жанамасына
проекциясы;
ds - нүктенің элементар орын ауыстыруының модулі.
ds=|d![]() |
болғандықтан (мұндағы d
|
болғандықтан (мұндағы d![]() -
нүктенің элементар орын ауыстыру векторы), (8.21) теңдігін
келесі түрде жазуға болады
-
нүктенің элементар орын ауыстыру векторы), (8.21) теңдігін
келесі түрде жазуға болады
dW= ![]() . (8.23)
. (8.23)
Сонымен, күштің элементар жұмысы - күштің оның түсу нүктесінің орын ауыстыру векторына скаляр көбейтіндісіне тең.
Күштің шекті M0M1 орын ауыстыруындағы (8.1-суретті қараңыз) жұмысы
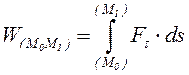 ,
(8.24)
,
(8.24)
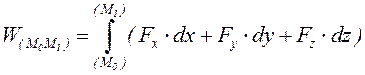 . (8.25)
. (8.25)
Күштің қуаты - күштің уақыт бірлігінде жасайтын жұмысына тең шама.
![]() , (8.26)
, (8.26)
яғни қуат күштің жанама құраушысының жылдамдыққа көбейтіндісіне тең.
Нүктенің
кинетикалық энергиясы (КЭ) деп ![]() тең скаляр
шаманы айтады. Теорема: нүкте КЭ-нің оның кейбір орын
ауыстыру кезіндегі өзгерісі нүктеге түсетін барлық
күштердің сол орын ауыстырудағы жұмыстарының
алгебралық қосындысына тең:
тең скаляр
шаманы айтады. Теорема: нүкте КЭ-нің оның кейбір орын
ауыстыру кезіндегі өзгерісі нүктеге түсетін барлық
күштердің сол орын ауыстырудағы жұмыстарының
алгебралық қосындысына тең:
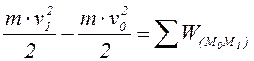 . (8.27)
. (8.27)
8.7 Нүкте үшін Даламбер принципі
Массасы m
материялық нүктеге актив күштер (тең әсерлісі ![]() деп белгіленген) және
байланыстың
деп белгіленген) және
байланыстың ![]() реакциясы түсетін
болсын. Осы күштер әсерінен нүкте инерциялық СЖ-не
қатысты кейбір
реакциясы түсетін
болсын. Осы күштер әсерінен нүкте инерциялық СЖ-не
қатысты кейбір ![]() үдеуімен
қозғалады.
үдеуімен
қозғалады.
Келесі нүктенің инерция күші деп аталатын шаманы енгіземіз.
![]() . (8.28)
. (8.28)
Сонда, егер кез келген уақыт мезгілінде нүктеге түсетін актив және реакция күштеріне инерция күшін қосса, алынған күштер жүйесі теңгеріледі, яғни:
![]() .
(8.29)
.
(8.29)
Бұл МН үшін Даламбер принципін өрнектейді.
9 дәріс. Материалық нүктенің түзу сызықты тербелістері
Дәрістің мазмұны: материалық нүктенің еркін гармоникалық тербелісі, өшпелі тербелістері, кедергі болмағандағы еріксіз тербелістер, еріксіз тербелістері кезіндегі кедергілерді ескеру.
Дәрістің мақсаттары: қозғалыстың дифференциалдық теңдеуін құру және олардың түзу сызықты тербелістер мысалында интегралдауының әдістемесін үйрену.
9.1 МН еркін гармоникалық тербелісі
Массасы ![]() нүктенің
түзу сызықты қозғалысын қарастырайық.
Нүктеге қозғалмайтын
нүктенің
түзу сызықты қозғалысын қарастырайық.
Нүктеге қозғалмайтын ![]() центріне
тарту күші
центріне
тарту күші ![]() әсер етсін, ал
бұл күш центрден қашықтыққа пропорционал
болсын (9.1-суретті қараңыз):
әсер етсін, ал
бұл күш центрден қашықтыққа пропорционал
болсын (9.1-суретті қараңыз):
![]()
Бұл өрнектегі ![]() -
қатаңдық коэффициенті деп аталатын,
пропорционалдықтың оң коэффициенті.
-
қатаңдық коэффициенті деп аталатын,
пропорционалдықтың оң коэффициенті.
![]()
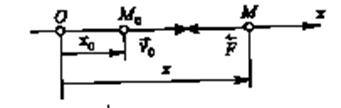 Егер
Егер ![]() нүктесі
нүктесі ![]() центрінде жатса, онда ол
тепе-теңдік күйде болады, өйткені бұл кезде
центрінде жатса, онда ол
тепе-теңдік күйде болады, өйткені бұл кезде ![]() . Ал енді, нүкте
тепе-теңдік күйден шығарылса, онда
. Ал енді, нүкте
тепе-теңдік күйден шығарылса, онда ![]() күші
нүктені бұрынғы күйіне қайтып әкелуге
тырысады, яғни тепе-теңдік күйді қалыптастыруға
тырысады. Осы күш бірінші дәрежелі ауытқуға
пропорционал болса, онда оны сызықтық қалпына келтіруші
күш деп атайды. Бұл күштің түп негізі
әртүрлі болуы мүмкін, бірақ көпшілік
жағдайда, оған – Гук заңына бағынышты серпімділік
күштері негіз болатыны белгілі.
күші
нүктені бұрынғы күйіне қайтып әкелуге
тырысады, яғни тепе-теңдік күйді қалыптастыруға
тырысады. Осы күш бірінші дәрежелі ауытқуға
пропорционал болса, онда оны сызықтық қалпына келтіруші
күш деп атайды. Бұл күштің түп негізі
әртүрлі болуы мүмкін, бірақ көпшілік
жағдайда, оған – Гук заңына бағынышты серпімділік
күштері негіз болатыны белгілі.
Нүктенің қозғалыс заңын
анықтау үшін, қозғалыстың дифференциялдық
теңдеуін құрып, содан кейін оны интегралдаймыз. Координата ![]() центріне оң жақта болса
центріне оң жақта болса ![]() , онда күш сол жаққа
бағытталады; егер
, онда күш сол жаққа
бағытталады; егер ![]() нүктесі
нүктесі ![]() центрінен сол жақта болса
центрінен сол жақта болса ![]() , онда күш оң
жаққа бағытталады. Сондықтан күштің
, онда күш оң
жаққа бағытталады. Сондықтан күштің ![]() осіне проекциясы әр
уақытта
осіне проекциясы әр
уақытта ![]() теңдеуімен
анықталады және нүкте қозғалысының дифференциалдық
теңдеуі келесідей жазылады:
теңдеуімен
анықталады және нүкте қозғалысының дифференциалдық
теңдеуі келесідей жазылады:
![]() .
.
Теңдіктің екі жағын ![]() -ге бөліп, келесі белгілеуді
қабылдаймыз:
-ге бөліп, келесі белгілеуді
қабылдаймыз:
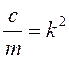 .
(9.1)
.
(9.1)
Осыдан кейін келесі дифференциалдық теңдеуді аламыз:
![]() .
(9.2)
.
(9.2)
Осы теңдеу нүктенің еркін гармоникалық тербелісінің дифференциалдық теңдеуі болып табылады.
Енді қозғалыстың бастапқы шарттарын тұжырымдайық:
- алғашқы сәтте нүкте ![]() орнында болсын,
орнында болсын,
- жылдамдығының ![]() осіне
проекциясы, яғни
осіне
проекциясы, яғни ![]() ,
, ![]() және
және
![]() .
.
(9.2)-ші теңдеу (![]() ) коэффициенті
тұрақты, біртекті сызықтық теңдеу
болғандықтан, оны шешу үшін сипаттайтын теңдеуін
құрып, оның түбірлерін табу керек. Сипаттайтын
теңдеу:
) коэффициенті
тұрақты, біртекті сызықтық теңдеу
болғандықтан, оны шешу үшін сипаттайтын теңдеуін
құрып, оның түбірлерін табу керек. Сипаттайтын
теңдеу: ![]() , ал түбірлері
, ал түбірлері ![]() және
және ![]() ,
бұл теңдіктердегі
,
бұл теңдіктердегі ![]() . Сонымен, (13)-ші
теңдеудің шешуі:
. Сонымен, (13)-ші
теңдеудің шешуі:
![]() .
(9.3)
.
(9.3)
Интегралдаудың тұрақтылары бастапқы шарттардан табылады.
Шарт бойынша: егер ![]() болса, онда
болса, онда ![]() . Бұл шартты қолдану үшін, алдымен (9.3)-теңдеуді
дифференциалдаймыз, яғни:
. Бұл шартты қолдану үшін, алдымен (9.3)-теңдеуді
дифференциалдаймыз, яғни:
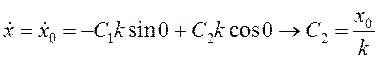 .
.
Онда: 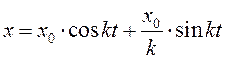 .
(9.4)
.
(9.4)
Нүкте қозғалысының сипаттамаларын айқын көрсету үшін, (9.3)-ші формуланы басқаша өрнектейік. Ол үшін, интегралдаудың тұрақтыларын келесі тұрақтылармен алмастырайық:
![]() .
.
Осы шамаларды (9.3)-ші формулаға қойсақ:
![]() .
(9.5)
.
(9.5)
Алынған (9.3)-ші және (9.5)-ші формулалар нүктенің еркін гармоникалық тербелістерінің теңдеулері деп аталады. Оның ішінде, (9.5)-ші формуланы – тербеліс теңдеуінің амплитудалық түрі (формасы) деп атайды.
Соңғы формуладағы:
тұрақты шама ![]() тербелістің амплитудасы деп
аталады, бұл шама нүктенің тепе-теңдік орнынан ең
үлкен ауытқуын көрсетеді; тұрақты шама
тербелістің амплитудасы деп
аталады, бұл шама нүктенің тепе-теңдік орнынан ең
үлкен ауытқуын көрсетеді; тұрақты шама ![]() тербелістің бастапқы
фазасы деп, ал
тербелістің бастапқы
фазасы деп, ал ![]() шамасы тербеліс фазасы деп
аталады.
шамасы тербеліс фазасы деп
аталады.
9.2 Нүктенің өшпелі тербелістері
Еркін тербеліске сызықтық заңдылықпен өзгеретін кедергі күшінің әсерін қарастырамыз.
Қозғалыстағы нүктеге әсер ететін күштер (9.2-суретті қараңыз):
- сызықтық қалпына келтіруші
күш - ![]() ,
,
- нүкте жылдамдығының бірінші
дәрежесіне пропорционал кедергі күші - ![]() .
.
![]()
 Бұл теңдіктегі
Бұл теңдіктегі ![]() -кедергі
коэффициенті деп аталатын тұтқыр ортаның кедергісін
сипаттайтын тұрақты шама.
-кедергі
коэффициенті деп аталатын тұтқыр ортаның кедергісін
сипаттайтын тұрақты шама.
Кез келген уақыттағы ![]() нүктесінің орны
9.2-суретте көрсетілген. Координат басы ретінде нүктенің
тепе-теңдік күйде болатын
нүктесінің орны
9.2-суретте көрсетілген. Координат басы ретінде нүктенің
тепе-теңдік күйде болатын ![]() нүктесі
қабылданған.
нүктесі
қабылданған.
Нүкте қозғалысының дифференциалдық теңдеуі:
![]() ,
,
мұндағы ![]() ,
, ![]() теңдігімен анықталады.
Онда:
теңдігімен анықталады.
Онда:
![]() немесе
немесе 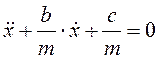 .
.
Теңдеудегі тұрақты шамаларды төмендегінше белгілейік:
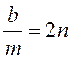 ,
, 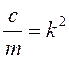 .
(9.6)
.
(9.6)
Осы тұрақтылықтарды теңдеуге қойып, коэффициентері тұрақты болатын біртекті, сызықтық дифференциалдық теңдеуін аламыз:
![]() (9.7)
(9.7)
Мұны шешу үшін оның сипаттайтын теңдеуін құрып, түбірлерін табамыз:
![]() .
(9.8)
.
(9.8)
Алынған шешімге байланысты, үш түрлі жағдай болу мүмкін:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() . Коэффициент
. Коэффициент ![]() (бұл коэффициент демфирлік
коэффициент деп аталады – немісше
(бұл коэффициент демфирлік
коэффициент деп аталады – немісше ![]() , яғни
«өшу») тербеліс болатын ортаның кедергісінің дәрежесін
көрсететін болғандықтан, бірінші жағдайды-аз кедергілі
жағдай , екінші-көп кедергілі жағдай, ал
үшінші-дағдарыс кедергілі жағдайы деп атаймыз.
, яғни
«өшу») тербеліс болатын ортаның кедергісінің дәрежесін
көрсететін болғандықтан, бірінші жағдайды-аз кедергілі
жағдай , екінші-көп кедергілі жағдай, ал
үшінші-дағдарыс кедергілі жағдайы деп атаймыз.
Тәжірибеде жиі кездесетін бірінші жағдайды
қарастырайық. Бұл жағдайда ![]() болғандықтан,
сипаттайтын теңдеуінің түбірлері комплекстік сан болады.
Оларды келесі түрде жазайық:
болғандықтан,
сипаттайтын теңдеуінің түбірлері комплекстік сан болады.
Оларды келесі түрде жазайық:
![]() ,
(9.9)
,
(9.9)
![]() (9.10)
(9.10)
(9.9)-ші формуладағы ![]() .
.
(9.7) дифференциалдық теңдеудің қарастырылып отырған жағдай үшін шешімі:
![]() (9.11)
(9.11)
Тұрақтыларды басқаша өрнектейік:
![]() ,
, ![]() (9.12)
(9.12)
Алынған өрнектерді теңдеуге қойып, амплитуда түріндегі шешім аламыз:
![]() (9.13)
(9.13)
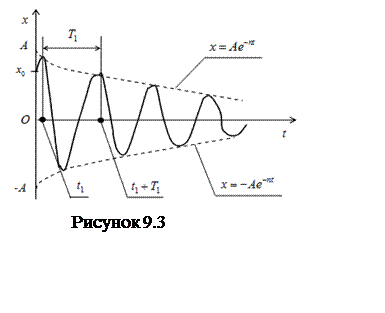 Ал,
Ал, ![]() және
және ![]() өрнектеріндегі
өрнектеріндегі ![]() көбейткіші, бұл
шамалардың уақытқа байланысты азаятынын көрсетеді.
Мұндай тербелістер өшпелі (өшетін) тербелістер деп аталады.
Өшпелі тербелістің графигі 9.3-суретте көрсетілген. Суреттен
көрініп тұрғандай, өшпелі тербелістің графигі
басқа екі графиктің арасында жатыр. Ол графиктердің
теңдеулері
көбейткіші, бұл
шамалардың уақытқа байланысты азаятынын көрсетеді.
Мұндай тербелістер өшпелі (өшетін) тербелістер деп аталады.
Өшпелі тербелістің графигі 9.3-суретте көрсетілген. Суреттен
көрініп тұрғандай, өшпелі тербелістің графигі
басқа екі графиктің арасында жатыр. Ол графиктердің
теңдеулері ![]() және
және ![]() .
.
Тербелістегі нүкте, белгілі бір
тұрақты уақыт аралығында, өзінің
тепе-теңдік күйінен оңға және солға
ауытқып отырады. Бұл ауытқулардың ең үлкен
шамалары ![]() бір-біріне тең болмайды
және осы ауытқулардың бір бағыттағы ең
үлкен шамаларының ара-қашықтығы өшпелі
тербелістердің периоды (9.3-суретті қара) деп аталады.
бір-біріне тең болмайды
және осы ауытқулардың бір бағыттағы ең
үлкен шамаларының ара-қашықтығы өшпелі
тербелістердің периоды (9.3-суретті қара) деп аталады.
Тепе-теңдік күйінен ауытқудың ![]() сәтіндегі фаза
сәтіндегі фаза ![]() шамасына тең болса, ал
шамасына тең болса, ал ![]() сәтіндегі фазаның одан
айырмашылығы
сәтіндегі фазаның одан
айырмашылығы ![]() -ге тең болады,
яғни
-ге тең болады,
яғни ![]() . Осы теңдіктен:
. Осы теңдіктен:
 немесе
немесе  (9.14)
(9.14)
Өшпелі тербелістің периоды, еркін
тербелістің периодынан көп болатыны (9.11)-ші формуладан
көрініп тұр. Өйткені, ![]() , ал
бұл қатынас, физикалық тұрғыдан
қарағанда, кедергінің әсерімен негізделеді. Сонымен
қатар, егер ортаның кедергісі аз болса, онда (30)-шы
формуладағы
, ал
бұл қатынас, физикалық тұрғыдан
қарағанда, кедергінің әсерімен негізделеді. Сонымен
қатар, егер ортаның кедергісі аз болса, онда (30)-шы
формуладағы ![]() шамасын ескермей,
шамасын ескермей, ![]() деп қарастыруға болады,
яғни кедергі аз болса, онда ол нүкте тербелісінің периодына
әсер етпейді.
деп қарастыруға болады,
яғни кедергі аз болса, онда ол нүкте тербелісінің периодына
әсер етпейді.
Бірақ, өшпелі тербеліс кезінде
тепе-теңдік өрісінен ең үлкен ![]() ауытқудың
шамасы бірталай азаяды. Аауытқудың шамасын кеміту үшін тербелістің
декременті
ауытқудың
шамасы бірталай азаяды. Аауытқудың шамасын кеміту үшін тербелістің
декременті ![]() (
(![]() -латынша
«кему») қабылданады.
-латынша
«кему») қабылданады.
9.3 Нүктенің кедергі болмағандағы еріксіз (амалсыз) тербелістері
Нүктенің тербелісін тудыру үшін, оны орнықты тепе-теңдік күйінен шығарғаннан кейін, оған қалпына келтіруші күш әсер етіп тұру керек.
Егер нүктені орнықты тепе-теңдік күйінен шығарған өзгермелі күш, одан әрі, қозғалыс кезінде де әсер ете берсе, онда осы күштің және қалпына келтіруші күштің әсерінен, нүкте амалсыз тербелісте болады. Бұған мысал ретінде темір жол көпірін келтіруге болады: рельстердің қосылған жерлеріне дөңгелектердің соққысы көпірдің тербелісін тудырады.
Жоғарыда айтып кеткендей, еріксіз тербелістерді күшті ауытқытқыш күштері деп атағанбыз. Бұл күштер уақытқа байланысты әртүрлі заңдылықпен өзгеріп отырады. Біз бұл күштің қарапайым және тәжірибеде жиі кездесетін түрін зерттейміз, яғни тербеліс болатын түзуге бұл күштің проекциясы синус заңдылығымен өзгеретін түрін зерттейміз. Ол заңдылық:
![]() (9.15)
(9.15)
мұндағы:
![]() - ауытқытқыштық
күштің ең үлкен (максимальді) шамасы;
- ауытқытқыштық
күштің ең үлкен (максимальді) шамасы;
![]() - аталған
күштің бұрыштық жиілігі;
- аталған
күштің бұрыштық жиілігі;
![]() - осы
күштің бастапқы фазасы.
- осы
күштің бастапқы фазасы.
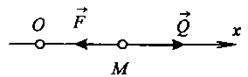
![]() Екі
күштің әсерінен туындайтын нүкте қозғалысын
қарастырамыз. Ол күштер:
Екі
күштің әсерінен туындайтын нүкте қозғалысын
қарастырамыз. Ол күштер:
а) сызықтық қалпына келтіруші күш;
б) гармоникалық ауытқыштық күш. Әзірше кедергі күшін ескермейміз.
Егер ауытқыштық күші болмаса, онда
координата басы ![]() -нүктенің
тепе-теңдік күйінің орны болып табылады (9.4-суретті
қараңыз).
-нүктенің
тепе-теңдік күйінің орны болып табылады (9.4-суретті
қараңыз).
Бұл кезде ![]() немесе
немесе
![]() . (9.16)
. (9.16)
Бұл формуладағы:
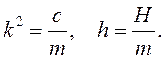 (9.17)
(9.17)
(9.16)-шы теңдеудің шешімін ![]() түрінде қарастырамыз.
Бұл жердегі
түрінде қарастырамыз.
Бұл жердегі ![]() -сәйкес
теңдеудің жалпы шешімі,
-сәйкес
теңдеудің жалпы шешімі, ![]() -сәйкес
теңдеудің дербес шешімі. Біртекті
-сәйкес
теңдеудің дербес шешімі. Біртекті ![]() теңдеуінің
шешімі бізге белгілі.
теңдеуінің
шешімі бізге белгілі.
Дербес шешімінің екі түрін қарастырамыз.
1. ![]() Бұл
жағдайда дербес шешім (9.16)-шы теңдеудің оң
жағының түрінде табылады, яғни:
Бұл
жағдайда дербес шешім (9.16)-шы теңдеудің оң
жағының түрінде табылады, яғни:
![]()
мұндағы ![]() -
тұрақты шама, оның шамасы
-
тұрақты шама, оның шамасы 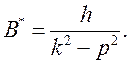 Онда:
Онда:
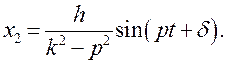 (9.18)
(9.18)
Сонымен, дифференциалдық теңдеудің жалпы шешімі:
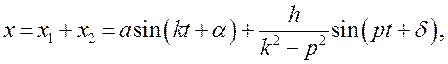 (9.19)
(9.19)
немесе
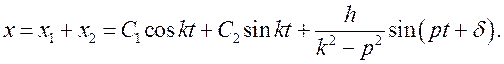 (9.20)
(9.20)
Қорытынды: екі күштің, яғни
сызықтық қалпына келтіруші күшпен гармоникалық
ауытқыштық күштің ![]() әсерінен
нүкте күрделі тербеліс қозғалысында болады (кедергі
күші ескерілмеген). Бұл қозғалыс – екі
гармоникалық қозғалыстың жиынынан тұрады,
олардың бұрыштық жиіліктері:
әсерінен
нүкте күрделі тербеліс қозғалысында болады (кедергі
күші ескерілмеген). Бұл қозғалыс – екі
гармоникалық қозғалыстың жиынынан тұрады,
олардың бұрыштық жиіліктері: ![]() және
және
![]() .
.
Бірінші тербелістерді - ![]() -
әдетте, меншікті тербелістер деп атайды, ал екінші тербелістерді -
-
әдетте, меншікті тербелістер деп атайды, ал екінші тербелістерді - 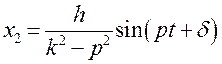 - таза еріксіз тербелістер деп атайды.
- таза еріксіз тербелістер деп атайды.
2. Енді бұрыштық жиілік ![]() бұрыштық жиілік
бұрыштық жиілік ![]() бір-бірімен тең, яғни
бір-бірімен тең, яғни ![]() жағдайын қарастырамыз.
Бұл кезде резонанс құбылысы пайда болады.
жағдайын қарастырамыз.
Бұл кезде резонанс құбылысы пайда болады.
9.4 Резонанс құбылысы
(9.16)-шы теңдеудің дербес шешімін келесі түрде аламыз:
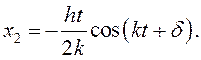 (9.21)
(9.21)
Бұл формуланы, 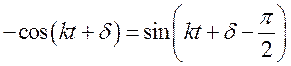 екенін
ескеріп, келесі түрде жазамыз:
екенін
ескеріп, келесі түрде жазамыз:
 (9.22)
(9.22)
Енді (9.16)-шы дифференциалдық теңдеудің толық шешімін келтірейік:
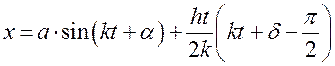 .
(9.23)
.
(9.23)
Резонанс кезіндегі таза амалсыз тербелісті
қарастырайық. Резонанс кезінде, амалсыз тербеліс
ауытқыштық күшінен фазасы бойынша ![]() шамасына
қалып қоятынын (9.22)-ші формуладан көруге болады.
Синустың өзгермелі коэффициентінің модулінің шамасы –
резонанс кезіндегі амалсыз тербелістің амплитудасы болып саналады,
яғни:
шамасына
қалып қоятынын (9.22)-ші формуладан көруге болады.
Синустың өзгермелі коэффициентінің модулінің шамасы –
резонанс кезіндегі амалсыз тербелістің амплитудасы болып саналады,
яғни:
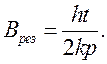 (9.24)
(9.24)
Келтірілген формула (9.24) бойынша, резонанс кезінде амплитуда уақытқа пропорционал және шексіз өседі, бірақ тербеліс кезінде, әр уақытта да, кедергі туындайтын болғандықтан, амплитуда үлкен болғанымен, ол шексіз өспейді. Амплитуданың резонанс кезінде қарқындап өсуі көптеген қиындықтар тудырады.
Мысалы, ғимараттардың, көпірлердің, мотордың, машиналардың және тағы басқалардың қирауына (істен шығуына) алып келіп соғады. Сондықтан, резонанс құбылысына техникада көп көңіл бөлу керектігі туындайды.

![]()
Еріксіз тербелістің резонанс кезіндегі графигін
тұрғызайық (9.5-суретті қараңыз). Алдымен, екі
шектеу түзулерін жүргіземіз, олардың теңдеулері 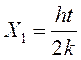 және
және 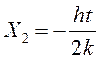 .
Бұл кезде
.
Бұл кезде ![]() болғандықтан, 9.21-ші
формуланың негізінде, резонанс кезіндегі амалсыз тербелістің
графигі, тұрғызылған екі түзулердің арасында
жатады, яғни:
болғандықтан, 9.21-ші
формуланың негізінде, резонанс кезіндегі амалсыз тербелістің
графигі, тұрғызылған екі түзулердің арасында
жатады, яғни:
![]() .
.
10 дәріс. Жүйе және қатты дене динамикасының негіздері. Механика жүйе динамикасының теоремалары
Дәрістің мазмұны: механикалық жүйе, оның массасы, массалар центрі және инерция моменттері; жүйе қозғалысының дифференциалдық теңдеулері; жүйе динамикасының жалпы теоремалары және Даламбер принципі.
Дәрістің мақсаты: жүйенің динамикалық сипаттамаларын, қозғалыстың дифференциалдық теңдеулерін, негізгі динамика теоремаларын зерттеу.
10.1 Механикалық жүйе. Масса, массалар центрі және инерция моменттері
Механикалық
жүйе (МЖ) деп өзара әрекеттесетін МН-лердің немесе денелердің
жиынтығы аталады. Материалдық дене оны құрайтын
бөлшектердің МЖ-сі болып келеді. Жүйенің
нүктелеріне қарастырылып отырған жүйеге кірмейтін
денелерден түсетін ![]() , k= 1,2 …,n
күштері сыртқы күштер деп аталады. Ішкі күштер деп
жүйе нүктелері бір-біріне түсіретін
, k= 1,2 …,n
күштері сыртқы күштер деп аталады. Ішкі күштер деп
жүйе нүктелері бір-біріне түсіретін ![]() ,
k= 1,2 …,m күштері аталады. Ішкі күштер жүйесінің
бас векторы мен бас моменті нөлге тең, бірақ жалпы
жағдайда олар теңгерілмейді, өйткені олардың
әсерінен жүйе нүктелерінің орын ауыстырулары болуы
мүмкін (АҚД үшін теңгеріледі).
,
k= 1,2 …,m күштері аталады. Ішкі күштер жүйесінің
бас векторы мен бас моменті нөлге тең, бірақ жалпы
жағдайда олар теңгерілмейді, өйткені олардың
әсерінен жүйе нүктелерінің орын ауыстырулары болуы
мүмкін (АҚД үшін теңгеріледі).
Жүйе массасы деп жүйе нүктелері массаларының қосындысын атайды.
M=Σmk. (10.1)
Жүйенің массалар центрінің (ЖМЦ) орны келесідей анықталады:
 , (10.2)
, (10.2)
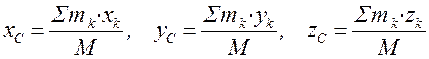 .
(10.3)
.
(10.3)
Дене үшін келесі болады 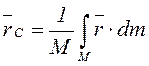 , (10.4)
, (10.4)
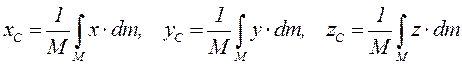 .
(10.5)
.
(10.5)
Біртекті гравитациялық өрісте массалар мен ауырлық центрлері түйіседі.
МЖ-нің оське және нүктеге қатысты инерция моменттері келесі шамалар:
Jl=Σmk∙hk2, (10.6)
JO=Σmk∙rk2, (10.7)
мұндағы hk мен rk – дененің массасы mk нүктесінің l осіне дейінгі және O нүктесіне дейінгі қашықтықтары.
Қатты дене үшін оське және нүктеге қатысты инерция моменттері:
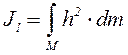 , (10.8)
, (10.8)
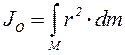 . (10.9)
. (10.9)
Декарт осьтеріне және координаттар басына қатысты инерция моменттері:
Jx=Σmk∙(yk2+zk2), Jy=Σmk∙(xk2+zk2), Jz=Σmk∙( xk2+yk2), (10.10)
JO=Σmk∙rk2= Σmk∙( xk2+yk2+zk2). (10.11)
Координаттық жазықтықтарға қатысты инерция моменттері келесіге тең:
Jxy=Σmk∙ zk2, Jyz=Σmk∙xk2, Jxz=Σmk∙yk2. (10.12)
Келесі тәуелдіктер орын алатынын дәлелдеуге болады:
2JO= Jx+ Jy+ Jz, (10.13)
JO= Jxy+ Jyz+ Jxz. (10.14)
Дене үшін инерция моменттері келесі интегралдармен анықталады:
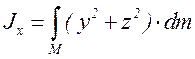 ,
, 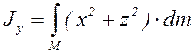 ,
, 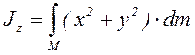 .
(10.15)
.
(10.15)
Гюйгенс-Штейнер теоремасы: жүйенің кейбір z осіне қатысты Jz инерция моменті сол оське параллель, массалар центрінен өтетін zC осіне қатысты жүйенің JzC инерция моментінің және жүйенің M массасының осьтердің d арақашықтығының квадратына көбейтіндісінің қосындысына тең.
![]() . (10.16)
. (10.16)
Параллель осьтер жиынтығы арасында массалар центрінен өтетін оське қатысты инерция моменті ең кіші болады.
10.2 Жүйе қозғалысының дифференциалдық теңдеулері. Жүйенің массалар центрі қозғалысы туралы теорема
МЖ-ге кіретін нүктелер үшін қозғалыстарының дифференциалдық теңдеулерін (ҚДТ) векторлық түрде жазуға болады
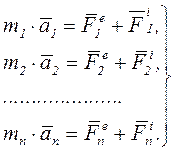 (10.17)
(10.17)
(10.17) осьтерге проекциялап, оське проекциялары түріндегі ҚДТ-н аламыз. Жүйе үшін динамиканың негізгі есебінің толық шешуі ҚДТ-н интегралдап, жүйенің әр нүктесінің қозғалыс теңдеулерін және байланыстардың реакцияларын анықтаудан тұрады. Бұны аналитикалық түрде тек дербес жағдайда ғана орындауға болады. Бірақ көптеген есептерді шешкенде жүйе қозғалысын жалпы анықтайтын кейбір сипаттамаларын табу жеткілікті болады. (10.17) теңдеулерін қосып, келесіні аламыз:
![]() .
(10.18)
.
(10.18)
(10.2) формуласын есепке алып, келесіге келеміз:
![]() .
(10.19)
.
(10.19)
Бұл ЖМЦ қозғалысы туралы теорема: ЖМЦ массасы жүйенің массасына тең және оған жүйенің барлық сыртқы күштері түсетін МН секілді қозғалады. (10.19) теңдігін координаттық осьтерге проекциялап, массалар центрі қозғалысының декарт координат жүйесі осьтеріне проекцияларындағы дифференциалдық теңдеулерін табуға болады. (10.19) теңдігінен ілгерілемелі қозғалыстағы денені массасы дененің массасына тең МН секілді қарастыруға болатыны шығады. Қалған жағдайларда денені МН секілді тек дене қозғалысының айналмалы бөлігін ескермеуге болса ғана қарастыруға болады. МЖ-нің массалар центрі қозғалысының заңын анықтаған кезде белгісіз ішкі күштерді қарастырмауға болады. Теореманың салдары (ЖМЦ қозғалысының сақталу заңы): ішкі күштер ЖМЦ қозғалысын өзгертпейді.
10.3 Жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема
Жүйенің қозғалыс мөлшері (ЖҚМ) деп келесі шаманы атайды.
![]() . (10.20)
. (10.20)
Мынаны көрсетуге болады:
![]() ,
(10.21)
,
(10.21)
яғни ЖҚМ жүйе массасының оның
массалар центрінің жылдамдығына көбейтіндісіне тең.
Егер жүйе қозғалысында оның массалар центрі
қозғалмай тұрса, онда ЖҚМ нөлге тең
(мысалы, дененің массалар центрінен өтетін тұрақты осьті
айналатын дене). Егер дене қозғалысы күрделі болса,
ЖҚМ-ң шамасы дененің массалар центрі
төңірегіндегі айналмалы қозғалысына тәуелсіз
(домалайтын дөңгелек үшін айналуына тәуелсіз ![]() ).
).
Дифференциалдық түрдегі ЖҚМ-нің өзгеруі туралы теоремасы: ЖҚМ-нің уақыт бойынша туындысы жүйенің барлық сыртқы күштерінің векторлық қосындысына тең.
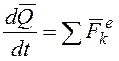 . (10.22)
. (10.22)
Интегралдық түрде: ЖҚМ-нің кейбір уақыт аралығында өзгерісі жүйеге түсетін сыртқы күштердің сол уақыт аралығындағы импульстерінің векторлық қосындысына тең.
![]() .
(10.23)
.
(10.23)
Салдары (ЖҚМ-нің сақталу заңы): ішкі күштер ЖҚМ-н өзгертпейді, сондықтан есептерді шешу кезінде ішкі күштерді қарастырмауға болады.
10.4 Қозғалыс мөлшерлерінің бас моментінің өзгеруі туралы теорема
Берілген О центріне
қатысты жүйенің қозғалыс
мөлшерлерінің бас моменті (ЖҚМБМ) немесе кинетикалық
моменті деп жүйенің барлық нүктелерінің
қозғалыс мөлшерлерінің сол центрге қатысты
моменттерінің векторлық қосындысына тең ![]() шамасы аталады.
шамасы аталады.
![]() .
(10.24)
.
(10.24)
Дәл солай координаттық осьтерге қатысты қарастырамыз.
![]() ,
, ![]() ,
, ![]() . (10.25)
. (10.25)
ЖҚМБМ-нің өзгеруі туралы теорема (моменттер теоремасы): кейбір қозғалмайтын центрге қатысты ЖҚМБМ-нің уақыт бойынша туындысы жүйенің барлық күштерінің сол центрге қатысты моменттерінің қосындысына тең.
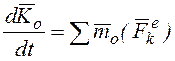 .
(10.26)
.
(10.26)
Қозғалмайтын осьтерге проекциялап, проекциялардағы теореманы аламыз.
Теорема дененің айналмалы қозғалысын және жүйенің жалпы жағдайда қозғалысын зерттеу үшін қолданылады, өйткені жалпы жағдайдағы қозғалыс ілгерілемелі және айналмалы қозғалыстардан тұрады. Егер полюс ретінде массалар центрі алынса, онда қозғалыстың ілгерілемелі бөлігін массалар центрі қозғалысы туралы теоремасын, ал айналмалы бөлігін моменттер теоремасын қолданумен зерттеуге болады. Сонда алдын ала белгісіз ішкі күштер қарастырылмайды.
Денемен бірге ілгерілемелі қозғалатын координаттар жүйесі үшін оның центріне қатысты моменттер теоремасы орын алады. Сонда теореманың түрі қозғалмайтын центрге қатысты теоремасымен бірдей болады. Сондай жүйенің осьтерге де қатысты моменттері үшін осыған ұқсас теңдеулер шығады.
Теореманың салдары (ЖҚМБМ-нің сақталу заңы): ішкі күштер ЖҚМБМ-ін өзгертпейді. Сонда жүйе өзгермейтін жүйе болса, ол тұрақты бұрыштық жылдамдықпен айналады, ал өзгеретін болса, онда ішкі (немесе сыртқы) күштер әсерінен жүйе нүктелерінің осьтен қашықтығы өзгеруі мүмкін, ал одан жүйенің бұрыштық жылдамдығының өзгерісі болады.
10.5 Жүйенің кинетикалық энергиясының өзгеруі туралы теорема
Жүйенің кинетикалық энергиясы (КЭ) деп келесі скаляр шаманы атайды.
![]() .
(10.27)
.
(10.27)
КЭ жүйенің ілгерілемелі де, айналмалы да
қозғалыстарын сипаттайды. Т шамасының ![]() мен
мен ![]() шамаларынан
айырмашылығы КЭ
әрқашан оң скаляр шама болып келеді, оның
өзгеруіне сыртқы да ішкі де кұштер әсерін тігізеді.
шамаларынан
айырмашылығы КЭ
әрқашан оң скаляр шама болып келеді, оның
өзгеруіне сыртқы да ішкі де кұштер әсерін тігізеді.
Дененің ілгерілемелі, айналмалы және жазық қозғалыстағы КЭ-сы.
![]() , (10.28)
, (10.28)
![]() , (10.29)
, (10.29)
![]() .
(10.30)
.
(10.30)
Дифференциалдық түрдегі жүйенің КЭ-сы өзгеруі туралы теорема.
![]() .
(10.31)
.
(10.31)
Интегралдық түрдегі теорема: жүйенің КЭ-сы кейбір орын ауыстыру кезіндегі өзгерісі жүйеге түсірілген барлық сыртқы және ішкі күштердің сол орын ауыстырудағы жұмыстарының қосындысына тең:
![]() .
(10.32)
.
(10.32)
10.6 Жүйе үшін Даламбер принципі
МЖ-нің нүктелеріне түсетін инерция
күштерін ![]() бас векторы мен
бас векторы мен ![]() бас моментіне келтіруге болады (O
нүктесі – қозғалмайтын келтіру центрі). Сонда қозғалыстағы
жүйені, оған әсер ететін күштерге
бас моментіне келтіруге болады (O
нүктесі – қозғалмайтын келтіру центрі). Сонда қозғалыстағы
жүйені, оған әсер ететін күштерге ![]() мен
мен ![]() қосып, тыныштықтағы
жүйе ретінде қарастыруға болады. Жүйенің кез
келген қозғалысында
қосып, тыныштықтағы
жүйе ретінде қарастыруға болады. Жүйенің кез
келген қозғалысында ![]() екенін дәлелдеуге болады Егер
АҚД оның Oxy материялық симметриялығы
жазықтығында жазық параллель қозғалысын жасайтын
болса, онда оның инерция күштерін С қозғалатын
массалар центріне келтіруге болады. Сонда Cz өсі – дененің
бас инерция осі болады. Сол оське қатысты инерция моментін
екенін дәлелдеуге болады Егер
АҚД оның Oxy материялық симметриялығы
жазықтығында жазық параллель қозғалысын жасайтын
болса, онда оның инерция күштерін С қозғалатын
массалар центріне келтіруге болады. Сонда Cz өсі – дененің
бас инерция осі болады. Сол оське қатысты инерция моментін ![]() арқылы және
бұрыштық үдеуін ε арқылы белгілеп,
арқылы және
бұрыштық үдеуін ε арқылы белгілеп, ![]() болатынын дәлелдеуге болады.
болатынын дәлелдеуге болады.
10.7 Айналмалы қозғалыстағы дене динамикасының негізгі теңдеуі
Қозғалмайтын оське қатысты айналу қозғалысын жасайтын дене үшін кеселіні аламыз:
![]() (10.33)
(10.33)
мұндағы Iz – дененің айналу өсіне қатысты инерция моменті;
ε – дененің бұрыштық үдеуі;
Mz – сырқы күштердің оське қатысты мементтерінің қосындысы.
11 дәріс. Аналитикалық механиканың элементтері
Дәрістің мазмұны: байланыстар және олардың классификациясы, жалпылама орын ауыстыру және жалпылама күштер, динамиканың жалпы теңдеуі, Лагранждың 2-текті теңдеуі, виртуальды орын ауыстыру принципі.
Дәрістің мақсаты: аналитикалық механиканың негізгі түсініктері және әдістемелерін оқып үйрену.
Динамиканың негізгі теоремалары МЖ динамикасының көпшілік есептерін шешуге мүмкіндік береді, бірақ кейбір жағдайларда теореманың қайсысын қолданған дұрыс екенін алдынала болжау мүмкін емес. МЖ қозғалысының дифференциальдық теңдеулерін құруда аналитикалық механика жалпы әдістемелік нұсқау береді.
11.1 Байланыстар және олардың классификциясы
Еркін емес МЖ нүктесінің координатасы мен жылдамдығына қойылған шектеу байланыс деп аталады. Еркін емес МЖ нүктесінің координатасы мен жылдамдығын қанағаттандыратын теңдеу байланыс теңдеуі деп аталады
 11.1
мысал – 11.1-суретте көрсетілген екі
нүкте ұзындығы l-ге тең созылмайтын
сырықпен байланысқан. Байланыс теңдеуі мынадай болады:
11.1
мысал – 11.1-суретте көрсетілген екі
нүкте ұзындығы l-ге тең созылмайтын
сырықпен байланысқан. Байланыс теңдеуі мынадай болады:
![]() , (11.1)
, (11.1)
мұндағы
![]() – нүктенің декарттық
координаттары.
– нүктенің декарттық
координаттары.
11.2 мысал – Мұздың бетінде
қозғалатын конкиді қарастырамыз. Пышағы мұзбен
бір А нүктесінде жанасады делік (11.2-суретті
қараңыз). Конкидің орнын үш ![]() координаттар арқылы
көрсетеміз. А нүктесі пышаққа перпендикуляр
бағытта сырғанамайды деп есептейміз, онда оның
жылдамдығы пышағының бойымен бағыттас болады,
шындығында
координаттар арқылы
көрсетеміз. А нүктесі пышаққа перпендикуляр
бағытта сырғанамайды деп есептейміз, онда оның
жылдамдығы пышағының бойымен бағыттас болады,
шындығында 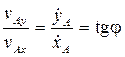 , осыдан келесі байланыс
теңдеуін аламыз:
, осыдан келесі байланыс
теңдеуін аламыз:
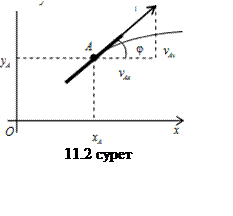
![]() . (11.2)
. (11.2)
Егер баланыс теңдеуіне уақыт тура кіретін болса, онда байланыс стационарлы емес, керісінше жағдайда - стационарлы деп аталады.
Егер байланыс, МЖ нүктелерінің координаттары байланыстардың шекті теңдеумен өрнектелсе, онда мұндай байланыс голономды деп аталады.
Егер байланыс интегралданатын дифференциалды теңдеумен өрнектелсе, онда байланыс голономды, ал интегралданбайтын дифференциалды теңдеумен өрнектелсе, онда байланыс голономды емес болып табылады.
Егер байланыс тек теңдеумен өрнектелетін болса, онда ол ұстайтын байланыс, ал байланыс теңдеуімен қоса теңсіздікпенде өрнектелетін болса, онда ұстамайтын байланыс деп аталады.
Келешекте тек голономды ұстайтын байланысты қарастырамыз.
11.2 Виртуалды орын ауыстырулар
МЖ нүктесінің, уақыт мезетіндегі орнынан, шексіз жақын орынға уақыттың сол сәтінде, МЖ байланыстары бөгет болмайтын кез келген элементар орын ауыстыруы нүктенің виртуалды орын ауыстыруы деп аталады.
Стационар емес голономды байланысқа бағынатын МЖ-ні қарастыралық:
f(x, y, z, t) = 0. (11.3)
Теңдеуді дифференциалдап, содан кейін вариациаласақ алатынымыз:
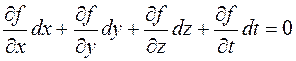 , (11.4)
, (11.4)
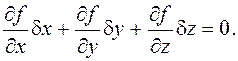 (11.5)
(11.5)
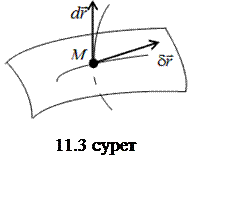 Бұл теңдеулерден нақты орын
ауыстыру
Бұл теңдеулерден нақты орын
ауыстыру ![]() және
және ![]() әр
түрлі теңдеулерді қанағаттандыратынын көреміз,
сондықтан нақты орын ауыстыру, виртуалды орын ауыстырулардың
ешқайсысымен дәл келмейді. МЖ-нің виртуалды орын ауыстыруы
деп, осы жүйенің барлық нүктелерінінің виртуалды
орын ауыстыруларының жиынтығы болып табылатыны есте болуы керек.
әр
түрлі теңдеулерді қанағаттандыратынын көреміз,
сондықтан нақты орын ауыстыру, виртуалды орын ауыстырулардың
ешқайсысымен дәл келмейді. МЖ-нің виртуалды орын ауыстыруы
деп, осы жүйенің барлық нүктелерінінің виртуалды
орын ауыстыруларының жиынтығы болып табылатыны есте болуы керек.
Түсінікті болу үшін мына бір мысалды қарастыралық. Еркін емес нүктені қарастыралық. Нүкте қозғалмайтын бетте тұрақты түрде жататын болсын. Уақыттың бір мезетінде, қарастырылып отырған нүктенің орны М болсын. Бұл орын радиус-векторымен анықталады, ал нүкте осы орнынан өзі жатқан кез келген көрші орынға ауыса алады.
Сәйкес виртуалды орын ауыстыру, берілген жазықтыққа жанама жазықтықта жататыны көрінеді. Нағыз орын ауыстыру виртуалды орын ауыстырулардың біреуімен дәл келеді, өйткені бет стационар байланысты іске асырып тұр.
Осыдан кейін, виртуалды жұмыс ұғымы
керек болатындықтан, олардың анықтамасын береміз. Сонымен,
нүктеге түсірілген ![]() күшінің,
өзі әсер етіп тұрған нүктенің виртуалды
орын
күшінің,
өзі әсер етіп тұрған нүктенің виртуалды
орын ![]() ауыстыруында сәйкес жасайтын элементар жұмысы,
оның осы мезеттегі виртуалды жұмысы деп аталады. Бұл
жұмысты
ауыстыруында сәйкес жасайтын элементар жұмысы,
оның осы мезеттегі виртуалды жұмысы деп аталады. Бұл
жұмысты ![]() арқылы белгілесек:
арқылы белгілесек:
![]() .
(11.6)
.
(11.6)
МЖ нүктелеріне түсірілген күштер
жүйесінің ![]() , виртуалды орын
, виртуалды орын ![]() ауыстыруларына сәйкес жасайтын
элементар жұмыстарының қосындысы, олардың осы мезеттегі
виртуалды жұмысы деп аталады, яғни:
ауыстыруларына сәйкес жасайтын
элементар жұмыстарының қосындысы, олардың осы мезеттегі
виртуалды жұмысы деп аталады, яғни:
![]() .
(11.7)
.
(11.7)
11.3 Жүйенің еркіндік дәреже саны және жалпылама координаттары
МЖ-нің виртуалды орын ауыстыруы деп байланыстар босататын оның нүктелерінің кез келген виртуалды орын ауыстыру жиынтығын айтамыз. Жүйенің әр түрлі сан алуан көптеген орын ауыстыруы болады, олардың ішінен өз ара тәуелсіз орын ауыстыруды таңдап алынады, сол арқылы кез келген виртуалды орын ауыстыруы өрнектеледі. МЖ-нің өз ара тәуелсіз орын ауыстыру саны оның еркіндік дәреже саны деп аталады. (ЕДС).
d голономды байланысқа бағынатын N материалық нүктелер жүйесін қарастырамыз. Жүйенің орны нүктелерінің 3N декарттық координаттарымен анықталады, оның ішінде s = 3N – d тәуелсіз болады. Голономды жүйе үшін тәуелсіз координаттар саны ЕДС-мен сәйкес келеді.
МЖ орнын жалпылама координаттар деп аталатын кез келген өзара тәуелсіз параметрлер арқылы бір мәнді анықтауға болады.
11.3 мысал – Иінтіректі-бұлғақты механизмнің орны (11.4-суретті қараңыз) O, A, B нүктелерімен анықталады.
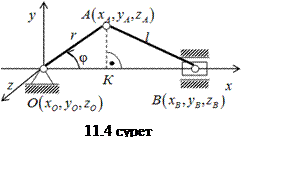 Байланыстардың
теңдеулерін жазамыз:
Байланыстардың
теңдеулерін жазамыз:
![]()
![]()
![]() .
.
Мұндағы байланыстардың саны d = 8, нүктелердің саны N = 3 және жүйенің ЕДС s = 3N– d = 1. Жалпылама координат ретінде φ бұрышын қабылдаймыз, онда:
![]()
![]() .
.
Яғни жалпылама координат φ бұрышы жүйенің орнын бірмәнді анықтайды.
11.4 Еркін емес МЖ динамикасының негізгі есебі. Идеал байланыстар
МЖ нүктелеріне түсірілген күштер
актив күштер ![]() және байланыстың
реация күштері
және байланыстың
реация күштері ![]() болып бөлінеді. Алдын
ала белгісіз реакция күштерінен айырмашылығы, актив күштер МЖ
орнына, жылдамдығына және уақытқа тәуелді функция
арқылы беріледі:
болып бөлінеді. Алдын
ала белгісіз реакция күштерінен айырмашылығы, актив күштер МЖ
орнына, жылдамдығына және уақытқа тәуелді функция
арқылы беріледі:
![]() .
.
Жүйе ҚДТ-ін жазамыз:
![]() . (11.7)
. (11.7)
Еркін емес МЖ динамикасының негізгі есебі: актив күштер және нүктелерінің бастапқы орындары, жылдамдықтары байланыстарымен тығыз байланыста берілген жүйе қозғалысын анықтау.
Мұнда 6N белгісіздер:
![]() нүктелердің
3N координаттары және
нүктелердің
3N координаттары және ![]() байланыс реакция күштерінің проекциялары;
байланыс реакция күштерінің проекциялары;
Белгісіз шамаларды байланыстыратын скалярлық қатынастардың саны 3N + d;
3N (11.7) теңдеулері және d байланыс теңдеулері. Барлық байланыстарды идеал деп санап, алуға болатын 6N – (3N + d) = 3N – d = s қатынас болуы қажет.
Байланыс идеалды деп аталады, сол жағдайда егер оның кез келген орнында жүйенің кез келген виртуалды орын ауыстырғанда байланыс реакция күштері жұмыстарының қосындысы нөлге тең болса:
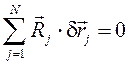 или
или 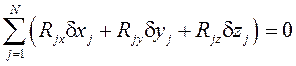 . (11.8)
. (11.8)
3N вариация ![]() координаттарының
ішінде 3N – d = s тәуелсіз. (11.8) теңдеуінде 3N
– s = d тәуелді вариациаларды тәуелсіздер
арқылы өрнектеп және тәуелсіз вриациалардың
коэффициенттерін нөлге теңестіріп, қажетті s қатынасты
аламыз.
координаттарының
ішінде 3N – d = s тәуелсіз. (11.8) теңдеуінде 3N
– s = d тәуелді вариациаларды тәуелсіздер
арқылы өрнектеп және тәуелсіз вриациалардың
коэффициенттерін нөлге теңестіріп, қажетті s қатынасты
аламыз.
Идеал байланыстың мысалына бетінде
қозғалатын МН-ні және қозғалмайтын жылтыр бетті
келтіруге болады. Мұнда бетке нормаль бойымен реакция күші
бағытталады, ал кез келген виртуалды орын ауыстыру векторы бетке М нүктесі
арқылы жүргізілген жанама жазықтығында жатады,
скалярлық көбейтіндісі ![]()
Жылтыр бет идеал болады сонда тек сонда, егер ол қозғалатын немесе деформациаланатын болса.
Идеалды байланысқа үйкеліс болмайтын топса, деформациаланбайтын салмақсыз сырық, АҚД ішкі байланыстары т.б. жатады. Үйкеліс күшін есепке алмайтын жағдайда, үйкеліс күшінің нормаль құраушысын актив күш қатарына жатқызуға болады. Ары қарай барлық байланыстарды идеалды деп есептейміз.
11.5 Жалпылама күш
Орны ![]() . берілуімен
біртекті анықталатын МЖ-ні қарастырамыз. Нүктенің радиус-векторын
. берілуімен
біртекті анықталатын МЖ-ні қарастырамыз. Нүктенің радиус-векторын
![]() және t арқылы
өрнектейміз:
және t арқылы
өрнектейміз:
![]() (11.9)
(11.9)
және вариацианың радиус-векторын анықтаймыз:
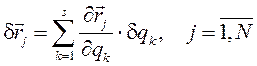 . (11.10)
. (11.10)
Қандай да ![]() -
де барлық актив күштердің жұмыстарының
қосындысын анықтаймыз:
-
де барлық актив күштердің жұмыстарының
қосындысын анықтаймыз:
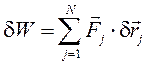 . (11.11)
. (11.11)
(11.11) и (11.10) формулаларынан қосындының ретін өзгерте отырып, алатынымыз:
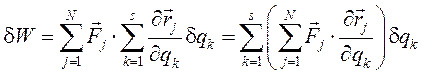 . (11.12)
. (11.12)
Белгілеулер енгіземіз:
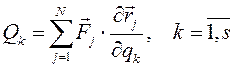 , (11.13)
, (11.13)
Онда (11.12) теңдігі келесі түрде жазылады:
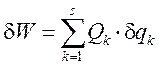 .
(11.14)
.
(11.14)
![]() -ның
алдындағы коэффициентіне тең
-ның
алдындағы коэффициентіне тең ![]() шаманы
жүйе актив күштерінің виртуалды жұмыстарының
шаманы
жүйе актив күштерінің виртуалды жұмыстарының ![]() жалпылама координаттарына сәйкес
жалпылама күштері деп атайды. Жалпылама күштеді анықтау
үшін, жүйеге тек қана бір жалпылама координаты
өзгеретін виртуалды орын ауыстыру беріледі. Сәйкес жалпылама
күшке актив күш жұмыстарының қосындысы
есептеледі:
жалпылама координаттарына сәйкес
жалпылама күштері деп атайды. Жалпылама күштеді анықтау
үшін, жүйеге тек қана бір жалпылама координаты
өзгеретін виртуалды орын ауыстыру беріледі. Сәйкес жалпылама
күшке актив күш жұмыстарының қосындысы
есептеледі:
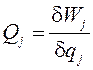 .
(11.15)
.
(11.15)
11.6 Динамиканың жалпы теңдеулері
Келешекте орны ![]() арқылы
анықталатын, мінсіз және голономды байланыстарымен N
нүктелерден тұратын МЖ-ні қарастырамыз. Жүйенің
әр нүктесі үшін келесі теңдеуді жазуға болады:
арқылы
анықталатын, мінсіз және голономды байланыстарымен N
нүктелерден тұратын МЖ-ні қарастырамыз. Жүйенің
әр нүктесі үшін келесі теңдеуді жазуға болады:
![]() немесе
немесе ![]() . (11.16)
. (11.16)
Жүйеге уақыт мезетін белгілеп алып
және радиус-векторы ![]() өсімшесін
алатын виртуалды орын ауыстыру береміз. (11.16)-дің әр
теңдеуін
өсімшесін
алатын виртуалды орын ауыстыру береміз. (11.16)-дің әр
теңдеуін ![]() -ге скалярлы көбейтіп
және алынған көбейтінділерді қосамыз:
-ге скалярлы көбейтіп
және алынған көбейтінділерді қосамыз:
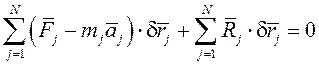 . (11.17)
. (11.17)
Байланыс мінсіз болғандықтан соңғы қосынды нөлге тең, онда:
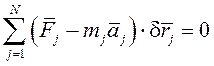 .
(11.18)
.
(11.18)
Мұндағы ![]() – j-ы
МН-нің инерция күші,
– j-ы
МН-нің инерция күші, ![]()
![]() – актив және инерция күштерінің жұмыстары, онда
(11.18)-ді келесіше жаза аламыз:
– актив және инерция күштерінің жұмыстары, онда
(11.18)-ді келесіше жаза аламыз:
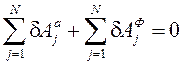 . (11.19)
. (11.19)
Бұл динамиканың жалпы теңдеуі (ДЖТ): мінсіз байланыстағы жүйенің қозғалысы кезінде кез келген виртуальды орын ауыстыруында кез келген уақыт мезетінде актив және инерция күштерінің жұмыстарының қосындысы нөлге тең. ДЖТ-і мінсіз байланыстар құрамына кірмейтін ДЖТ-ін алуға мүмкіндік береді. Ол кез келген ЕДС-ғы жүйе үшін пайдалануға болады. Жүйенің ЕДС-ы үлкен болғанда Лагранждың 2-текті теңдеулерін пайдаланған ыңғайлы болады.
11.7 Лагранждың 2-текті теңдеулері
Лагранждың 2-текті теңдеулерін қорытып шығару қарастырылады:
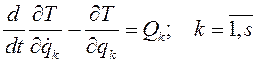 . (11.20)
. (11.20)
Дифференциалдаудан кейін осы теңдеулердің
сол жағына t, ![]() ,
, ![]() және
және ![]() шамалары
кіреді. Жалпылама
шамалары
кіреді. Жалпылама ![]() күші t,
күші t, ![]() ,
, ![]() параметрлеріне
тәуелді болады. Яғни Лагранждың теңдеулері 2-ретті
дифференциалдық теңдеулердің s жүйесін
құрайды және барлық жүйенің реті 2s-ке
тең. Бұл жүйе дифференциалдық теңдеулерінің
ең кіші мүмкіндік реті.
параметрлеріне
тәуелді болады. Яғни Лагранждың теңдеулері 2-ретті
дифференциалдық теңдеулердің s жүйесін
құрайды және барлық жүйенің реті 2s-ке
тең. Бұл жүйе дифференциалдық теңдеулерінің
ең кіші мүмкіндік реті.
(11.20)-ны интегралдап МЖ қозғалысын
толық анықтайтын ![]()
![]() тәуелділігін алуға мүмкіндік береді. Сонымен
қатар МЖ еркін емес болғанда мінсіз байланыс реакция күшін
анықтауға болады. (11.9)-ға
тәуелділігін алуға мүмкіндік береді. Сонымен
қатар МЖ еркін емес болғанда мінсіз байланыс реакция күшін
анықтауға болады. (11.9)-ға ![]() тәуелділігін
қойып
тәуелділігін
қойып ![]() тәуелділігін аламыз, оларды
дифференциалдау арқылы барлық нүктелердің
жылдамдықтарын және үдеулерін анықтаймыз. Ары
қарай (11.16)-дан алатынымыз:
тәуелділігін аламыз, оларды
дифференциалдау арқылы барлық нүктелердің
жылдамдықтарын және үдеулерін анықтаймыз. Ары
қарай (11.16)-дан алатынымыз:
![]() . (11.21)
. (11.21)
11.8 Виртуалды орын ауыстыру принципі
МЖ-нің қажетті де жеткілікті шарттарын виртуалды орын ауыстыру қағидасы ұйымдастырады: мінсіз, голономды, стационарлы және ұстап тұратын байланыстарға бағынатын қандай да бір жүйенің орны, тепе-теңдік орны болуы үшін жүйенің барлық нүктелерінің бастапқы жылдамдықтары нөлге тең болуы және берілген орнынан оның кез келген виртуалды орнын ауыстырғанда барлық актив күштер жұмыстарының қосындысы нөлге тең болуы қажетті де жеткілікті, яғни:
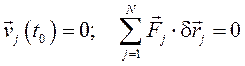 . (11.22)
. (11.22)
12 дәріс Айнымалы массалы МН қозғалысы. Циолковский есебі
Дәрістің мазмұны: айнымалы массалы МН қозғалысының диференциальдық теңдеуі, Мещерскийдің теңдеуі, Циолковскийдің 1–ші және 2-есебі.
Дәрістің мақсаты: космостық қозғалыс теориясының элементін оқып үйрену.
Космостық ракета ұшқан кезінде жану өнімдерін бөліп шығару барысында және керексіз бөліктерін бөліп шығарғанда, оның массасы өзгереді. Дәрісте МН массасының өзгеруіне байланысты негізгі мәселе қарастырылады.
12.1 Айнымалы массалы МН қозғалысының дифференциалдық теңдеуі
Айнымалы массалы нүкте ҚДТ-ін, күштердің байланыссыз заңдылығын және ЖҚМ өзгеруі туралы теореманы пайдаланып аламыз. Мұнда нүктеге түсірілген күштен басқа нүктеден бөлініп шыққан d'M бөлшектен туындайтын күш әсер етеді.
dt уақыт өсімшесінде ![]() жылдамдығының жалпы өзгеруі тұрақты
масса үшін
жылдамдығының жалпы өзгеруі тұрақты
масса үшін ![]() күшінің әсерінде
күшінің әсерінде ![]() жылдамдығының өзгеруінен
және
жылдамдығының өзгеруінен
және ![]() күші болмағандағы нүктенің массасы
өзгергенде туындайтын
күші болмағандағы нүктенің массасы
өзгергенде туындайтын ![]() жылдамдығы өзгеріcінің
қосындысы болып табылады. Айнымалы
массасы М нүктені қарастырайық.
жылдамдығы өзгеріcінің
қосындысы болып табылады. Айнымалы
массасы М нүктені қарастырайық. ![]() күшінің әсерінде dt
уақыт өсімшесінде массасы тұрақты нүктенің
жылдамдығы келесі шамаға өзгереді:
күшінің әсерінде dt
уақыт өсімшесінде массасы тұрақты нүктенің
жылдамдығы келесі шамаға өзгереді:
![]() (12.1)
(12.1)
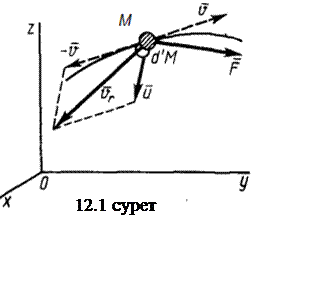 dt
уақыт аралығында
dt
уақыт аралығында ![]() күшінің әсері болмағанда оның
массасының өзгеруінен болатын нүктенің
күшінің әсері болмағанда оның
массасының өзгеруінен болатын нүктенің ![]() жылдамдығының өзгеруі
массасы тұрақты механикалық жүйенің
қозғалыс мөлшерінің өзгеруі туралы теорема
арқылы анықталады.
жылдамдығының өзгеруі
массасы тұрақты механикалық жүйенің
қозғалыс мөлшерінің өзгеруі туралы теорема
арқылы анықталады.
МЖ айнымалы масса нүктелерінен кұрастырылғандықтан және одан бөлінетін бөлшектер сыртқы күштің әсеріне тәуелсіз, онда оның қозғалыс мөлшері тұрақты шама болады. Бөлінетін бөлшектермен бірге нүктелердің өз ара әсерлерінің ішкі күштері өзгермейді. ЖҚМ сақталу заңынан алатынымыз:
![]() (12.2)
(12.2)
dt уақыт өсімшесінде айнымалы массалы нүкте мен одан d'M
массасымен бөлініп шығатын бөлшектердің тек өзара әсерлерін есепке аламыз,
нүктеге және алдын ала бөлініп шыққан
бөлшекке әсерін ескермейміз (12.1 суретті қараңыз). Oxyz
координатар жүйесіне қатысты қозғалатын t уақыт
мезетінде массасы M(t) бір ғана нүктені қарастыратын
болғандықтан ![]() -ны аламыз.
-ны аламыз.
t + dt уақыт мезетінде сол Oxyz координаттар
жүйесіне қатысты жылдамдығы ![]() болатын массасы (M - d'M) нүкте
және жылдамдығы
болатын массасы (M - d'M) нүкте
және жылдамдығы ![]() массасы d'M бөлініп шыққан бөлшектер
бар болады. t + dt
уақыт мезетінде олардың қозғалыс мөлшерін
анықтаймыз:
массасы d'M бөлініп шыққан бөлшектер
бар болады. t + dt
уақыт мезетінде олардың қозғалыс мөлшерін
анықтаймыз:
![]()
![]() екенін
ескере отырып (12.2) теңдігін ауыстыра отырып, алатынымыз:
екенін
ескере отырып (12.2) теңдігін ауыстыра отырып, алатынымыз:
![]() .
.
d'M >0 болғанда немесе, dМ таңбасы енгізіп (онда dM<0), алатынымыз:
![]() (12.3)
(12.3)
(12.1) и (12.2) теңдіктерін немесе ![]() ескеріп
жалпы жылдамдықтың өзгеруін келесі түрде жазамыз:
ескеріп
жалпы жылдамдықтың өзгеруін келесі түрде жазамыз:
![]()
Ауыстырулардан кейін Мещерскийдің (1897 г.) ҚДТ-ін аламыз:
![]() (12.4)
(12.4)
Егер Oxyz координаттар жүесіне
қатысты ілгерілемелі қозғалатын қозғалмалы
координаттар жүйесімен айнымалы массалы нүктені
байланыстырсақ, онда массасы dM бөлініп шыққан
бөлшектің абсолют ![]() жылдамдығы жылдамдықтарды қосу теоремасы бойынша
төмендегідей түрде жазылады
жылдамдығы жылдамдықтарды қосу теоремасы бойынша
төмендегідей түрде жазылады ![]()
Мұндағы ![]() және
және ![]() бөлініп шыққан бөлшектің
салыстырмалы жылдамдығы.
бөлініп шыққан бөлшектің
салыстырмалы жылдамдығы.
(12.4) теңдігіне ![]() шамасын
қойып алатынымыз:
шамасын
қойып алатынымыз:
 (12.5)
(12.5)
Егер 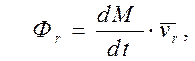 деген белгілеу енгізсек, онда (12.5) теңдігі
келесі түрде жазылады:
деген белгілеу енгізсек, онда (12.5) теңдігі
келесі түрде жазылады:
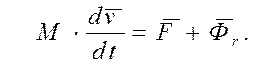 (12.6)
(12.6)
![]() шамасы реактив күш деп аталады, ал dM/dt
массаның өзгеру жылдамдығы болып табылады. Ол бірлік
уақытта нүкте массасының өзгеруін сипаттайды, мысалы 1
секундта. Сондықтан реактивті күш нүктенің
секундтағы өзгеруін айнымалы массалы нүктеден бөлініп
шыққан бөлшектің салыстырмалы жылдамдығына
көбейткенге тең.
шамасы реактив күш деп аталады, ал dM/dt
массаның өзгеру жылдамдығы болып табылады. Ол бірлік
уақытта нүкте массасының өзгеруін сипаттайды, мысалы 1
секундта. Сондықтан реактивті күш нүктенің
секундтағы өзгеруін айнымалы массалы нүктеден бөлініп
шыққан бөлшектің салыстырмалы жылдамдығына
көбейткенге тең.
Нүктенің массасы кеміген жағдайда
уақыт өзгеруіне байланысты dM/dt шамасы теріс,
көбейетін болса – оң болады. Нүктенің массасы одан
бөлшек бөлініп шығатын болғандықтан реактивті
күш ![]() бөлініп шыққан бөлшектің
бөлініп шыққан бөлшектің ![]() салыстырмалы жылдамдығының
бағытына қарсы, ал нүкте массасы көбейгенде dM/dt
шамасы нөлден үлкен және реактивті күш
салыстырмалы жылдамдығының
бағытына қарсы, ал нүкте массасы көбейгенде dM/dt
шамасы нөлден үлкен және реактивті күш ![]() салыстырмалы
салыстырмалы ![]() жылдамдықтың бағытымен
бағытталады. Реактивті қозғалтқыш dM/dt
массасының өзгеру жылдамдығы теріс және массаның
секундтағы жоғалуына тең болады, ал
қозғалтқыштың қалдық шығатын
тесігінен шығатын газдың
жылдамдықтың бағытымен
бағытталады. Реактивті қозғалтқыш dM/dt
массасының өзгеру жылдамдығы теріс және массаның
секундтағы жоғалуына тең болады, ал
қозғалтқыштың қалдық шығатын
тесігінен шығатын газдың ![]() жылдамдығы болады. Реактивті күш қалдық
шығатын тесігінен шығатын газдың жылдамдығына
қарсы бағытталған тарту күші болып табылады.
жылдамдығы болады. Реактивті күш қалдық
шығатын тесігінен шығатын газдың жылдамдығына
қарсы бағытталған тарту күші болып табылады.
(12.6) теңдігін тік бұрышты координаттар жүйесіне проекциалап келесі теңдіктерді аламыз:
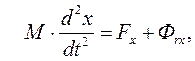
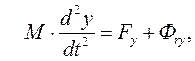
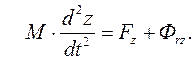 (12.7)
(12.7)
Айнымалы массалы МН қозғалысының диференциалдық теңдеуін материалық нүкте және айнымалы массалы жүйе үшін жалпы теоремалардан қорытып шығаруға болады.
12.2 Циолковскидің екі есебі
Цилковскидің бірінші есебі. Тек қана бір реактивті
күштің әсерінде «еркін кеңістікте» айнымалы массалы
нүкте түзу сызықты қозғалыста болсын делік.
Бөлініп шыққан бөлшектің салыстырмалы ![]() жылдамдығы
тұрақты және айнымалы массалы нүкте
қозғалысының
жылдамдығы
тұрақты және айнымалы массалы нүкте
қозғалысының ![]() жылдамдығы бағытына
қарама-қарсы бағытталған деп санаймыз (12.2-суретті
қараңыз). (12.5) теңдігін
Ох осіне проекциалап алатынымыз:
жылдамдығы бағытына
қарама-қарсы бағытталған деп санаймыз (12.2-суретті
қараңыз). (12.5) теңдігін
Ох осіне проекциалап алатынымыз:
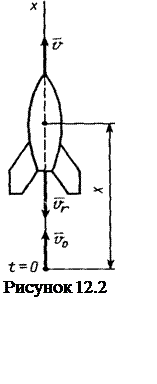
![]()
Айнымалыларды ажыратып және интегралдап алатынымыз:
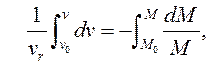
мұндағы v0 және M0 – бастапқы жылдамдығы (реактивті күш бағытымен бағытталған) және сәйкес бастапқы массасы.
Интегралдап, алатынымыз:
![]() (12.8)
(12.8)
Нүктенің (ракетаның) массасы тек жанбаған бөлігінің Мр массасынан тұратын және сұйықтың массасын m арқылы белгілеп, жаныстың соңын сипаттайтын шаманы (12.8)-ге қойып, жанып болғанан кейінгі v1 жылдамдығы үшін алатынымыз:
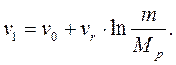
Циолковский Z = m/Mp санын енгізіп, Циолковскидің формуласын аламыз:
![]() (12.9)
(12.9)
Осыдан, v1 жылдамдығы массалардың өзгеруіне тәуелсіз болатынын көреміз.
Жанып болғаннан кейінгі жылдамдығын көбейтуді, реактивтік қозғалтқыш сопласынан шығатын газдың жылдамдығын көбейту арқылы, немесе көпсатылы ракетаның лақтырылатын Z санын көбейту арқылы іске асыруға болады.
Нүкте қозғалысының теңдеуін анықтау үшін (12.8)-ден алатынымыз:
![]()
немесе, х = 0 t = 0 бастапқы уақыт мезетінде, х = 0 болатынын ескеріп, интегралдау амалын орындап, алатынымыз:
![]() (12.10)
(12.10)
Массаның түзу сызықты өзгеру заңдылығы үшін келесі теңдікті жазуға болады:
М = М0∙(1-α∙t), (12.11)
мұндағы α = const – көлемдік салмақ, М0 – бастапқы уақыт мезетіндегі массасы.
Масса өзгерісінің көрсеткіштік өзгеру заңдылығы үшін мынадай тәуелділік ұйымдастырамыз:
М = М0∙e α∙t. (12.12)
(12.11)-і массаның түзу сызықты өзгеру заңдылығы үшін (12.10)-ды интегралдау амалын орындап, келесі қозғалыс теңдеуін аламыз:
![]() (12.13)
(12.13)
(12.12)-ге сәйкес масса өзгерісінің көрсеткіштік өзгеру заңдылығы үшін:
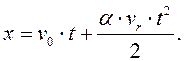 (12.14)
(12.14)
Атап өтуге болады, (12.11)-і массаның сызықтық өзгеру заңдылығы үшін, егер vr = const болса, онда (-dM/dt) = α∙M0 = const, Фr =(-dM/dt)∙vr= α∙M0∙vr = const болады.
Көрсеткіштік заңдылық үшін секундтық массаның жойылуы және реактивті күш айнымалы болып табылады, ал нүктеге түсірілген реактивтік Фr күші әсерінде болатын айнымалы массалы нүктенің үдеуі тұрақты болады, яғни:
аr= Фr/M= α∙vr = const.
Циолковскидің екінші есебі. Егер айнымалы массалы нүкте (ракета) жерге жақын тік сызық бойымен қозғалса, онда g=const және ауаның кедергісін ескермей, сонымен қатар Циолковскидің бірінші есебінің барлық жуықтауларын ескере отырып, келесі нүкте ҚДТ-ін аламыз:
![]()
Интегралдау амалын пайдаланып, алатынымыз:
![]()
Егер нүктенің орнын бастапқы орнынан бастайтын болсақ, онда х үшін массаның сызықтық заңдылық кезінде алатынымыз:
 (12.15)
(12.15)
Масса өзгерісінің көрсеткіштік заңдылығы үшін алатынымыз:
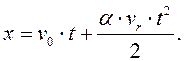 (12.16)
(12.16)
Әдебиеттер тізімі
1. Жолдасбеков Ө.А., Сағитов М.Н. Теориялық механика. – Алматы: Ғылым, 2002.
2. Тойбаев С.Н. Теориялық механика: Оқу құралы. – «Бастау», 2006.
3. Нұғыман А.М. Теориялық механика негіздері. – Семей: Шәкәрім атындағы СМУ, 2002.
4. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: Учебник в 2-х т. – М.: Наука, 2002.
5. Мещерский И.В. Сборник задач по теоретической механике: Учеб. пособие. – СПб.: Изд-во «Лань», 2005.
6. Никитин Н.Н. Курс теоретической механики: Учебник. – М.: Высшая школа, 1990.
7. Тарг С.М. Краткий курс теоретической механики: Учебник. – М.: Наука, 2002.
8. Яблонский А.А. Курс теоретической механики: Учебник: в 2-х т. – М.: Высшая школа, 2002.
9. Сборник заданий для курсовых работ по теоретической механике. Учебное пособие./Под ред. А.А.Яблонского. – М.: Высшая школа, 1985.
10. Механика: Есептеу-графикалық жұмыстарды орындауға әдістемелік нұсқаулар және тапсырмалар (5В074600–Ғарыштық техника және технология студенттеріне арналған). – Алматы, 2012.
11. Механика. 5В074600 – Ғарыштық техника және технологиялар мамандығы cтуденттері үшін өзіндік жұмыстарын орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. – Алматы, 2012.
2013 ж. жиынтық жоспары, реті 316
Тойбаев Серікбай Несіпбекұлы
Дінасылов Алмас Дәменұлы
МЕХАНИКА
5В074600 – Ғарыштық техника және технологиялар
мамандығы студенттеріне арналған дәріс
коспектілері
Редакторы Советова З.С.
Стандарттау бойынша маман Молдабекова Н.Қ.
2013 ж. басуға қол қойылды
Пішіні 60х84 1/16
Тиражы 50 дана.
№ 1 типографиялық қағаз
Көлемі 3,8 оқу-бас. ә.
Тапсырыс . Бағасы 380т.
«Алматы энергетика және байланыс
университеті»
коммерциалық емес акционерлік
қоғамының
көшірмелі - көбейткіш бюросы
050013, Алматы, Байтұрсынұлы
көщесі, 126