Коммерциялық емес акционерлік қоғам
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Инженерлік графика және қолданбалы механика кафедрасы
МЕХАНИКА
5В074600 – Ғарыштық техника және технологиялар мамандығы cтуденттері үшін өзіндік жұмыстарын орындауға арналған әдістемелік нұсқаулар мен тапсырмалар
Алматы 2012
ҚҰРАСТЫРУШЫ: С.Н. Тойбаев. Механика. 5В074600 – Ғарыштық техника және технологиялар мамандығы cтуденттері үшін өзіндік жұмыстарын орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. - Алматы: АЭжБУ, 2012. – 56 б.
«Механика» пәні жоғары оқу орындарында оқитын 5В074600 – Ғарыштық техника және технологиялар студенттері үшін міндетті болып табылады. Әдістемелік нұсқауда көрсетілген мамандық студенттеріне өзіндік жұмыстарды орындауға арналған әдістемелік нұсқаулар және тапсырмалар берілген. Қажетті оқулықтар тізімі берілген.
Без. - 39, әдебиет – 9 атау.
Пікір беруші: техн. ғыл. канд., профессор Дінасылов А.Д.
«Алматы энергетика және байланыс университетінің» ҚЕАҚ 2012 жылғы жоспары бойынша басылады.
© «Алматы энергетика және байланыс университеті» ҚЕАҚ, 2012 ж
.
Мазмұны
|
Статика 1 Жинақталатын күштер жүйесі |
4 4 |
|
2 Нүктеге қатысты күш моменті |
7 |
|
3 Жазықтықтағы кез келген күштер жүйесі |
8 |
|
4 Кеңістіктегі кез келген күштер жүйесі |
9 |
|
5 Үйкеліс күші. Ауырлық центрді анықтау |
10 |
|
Кинематика 6 Нүкте қозғалысының берілу тәсілдері. Нүкте қозғалысының теңдеуі және траекториясы |
12 12 |
|
7 Қозғалысы координаттық және табиғи тәсілдермен берілген нүктенің жылдамдығын және үдеуін анықтау. Жанама және нормаль құраушы үдеулері |
13 |
|
8 Дененің ілгерілемелі және айналмалы қозғалысы |
16 |
|
9 Қатты дененің жазық параллель қозғаласы. Жазық параллель қозғалыстағы қатты дене нүктелерінің жылдамдықтары және үдеулері |
18 |
|
10 Нүктенің күрделі қозғалысы. Абсолют жылдамдық және абсолют үдеу |
22 |
|
Динамика 11 Динамиканың негізгі екі есебі. Материялық нүкте қозғалысының дифференциалдық теңдеулерін интегралдау |
26 26 |
|
12 Материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема |
31 |
|
13 Жұмыс. Материялық нүктенің кинетикалық энергиясының өзгеруі туралы теорема. Қатты дене және жүйе динамикасы. Механикалық жүйе. Жүйенің массасы |
34 |
|
14 Механикалық жүйенің массалар центрі туралы теорема. Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема |
38 |
|
15 Механикалық жүйенің кинетикалық моменті туралы теорема. Айналмалы қозғалыстағы дененің дифференциалдық теңдеуі. Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема |
43 |
|
Әдебиеттер тізімі |
56 |
Статика
1 Жинақталатын күштер жүйесі
1.1 Жазықтықтағы жинақталатын күштер жүйесі
1.1-мысал. Салмағы ![]() біртекті цилиндр көлденең жазықтықтың
бетінде жатыр. Әсер етуші сызығы ауырлық центрі арқылы
өтетін
біртекті цилиндр көлденең жазықтықтың
бетінде жатыр. Әсер етуші сызығы ауырлық центрі арқылы
өтетін ![]() вертикаль күш цилиндрді үстінен
қысады (1.1 суретті қара).
вертикаль күш цилиндрді үстінен
қысады (1.1 суретті қара).
Цилиндрдің көлденең жазықтықты қысатын күшін табу керек.
 |
Шешуі: 1) Цилиндрге бір түзудің
бойында түсірілген ![]() салмақ күшін және
салмақ күшін және
![]() қысатын күшті көрсетеміз.
қысатын күшті көрсетеміз.
2) Денені байланыстан босатамыз, оның
әсерін реакция күшімен ауыстырамыз. Реакция күші
![]() жазықтыққа перпендикуляр жоғары
бағытталады.
жазықтыққа перпендикуляр жоғары
бағытталады.
3) Осы күштердің геометриялық тепе-теңдік шартын жазамыз
![]() .
.
Күштерді параллель оське проекциялап, алатынымыз
![]() немесе
немесе
![]() .
.
1.2-мысал. Салмағы
![]() ға тең жүк, суретте
көрсетілгендей, С нүктесіне ілінген. А, В
және С нүктелерінде сырықтар топсалармен бекітілген. АС
және ВС сырықтарының реакция күштерін табу керек
(1.2 суретті қара).
ға тең жүк, суретте
көрсетілгендей, С нүктесіне ілінген. А, В
және С нүктелерінде сырықтар топсалармен бекітілген. АС
және ВС сырықтарының реакция күштерін табу керек
(1.2 суретті қара).
Берілгені:
![]() .
.
Анықтау
керек: ![]() .
.
Шешуі: 1) Нүкте деп аталатын С денесінің тепе-теңдігін қарастырамыз.
2) С
нүктесіне түсірілген актив күш ![]() .
.
3) С
нүктесін байланыстардан босатамыз. АС, ВС сырықтары
![]() дағы
байланыстар. Бұлардың реакция күштерін
дағы
байланыстар. Бұлардың реакция күштерін ![]() деп
белгілейміз.
деп
белгілейміз. ![]() күшінің әсерінен АС сырығы созылады,
сондықтан оның реакция күші АС бойымен С-дан А
нүктесіне қарай бағытталады. ВС сырығы
күшінің әсерінен АС сырығы созылады,
сондықтан оның реакция күші АС бойымен С-дан А
нүктесіне қарай бағытталады. ВС сырығы ![]() күшінің
әсерінен сығылады, сондықтан оның реакция күші ВС
бойымен В-дан С нүктесіне қарай бағытталады (1.2
суретті қара).
күшінің
әсерінен сығылады, сондықтан оның реакция күші ВС
бойымен В-дан С нүктесіне қарай бағытталады (1.2
суретті қара).
Сонымен, С
нүктесі ![]() күштерінің
әсерінен тепе-теңдікте тұрған нүкте болып
табылады.
күштерінің
әсерінен тепе-теңдікте тұрған нүкте болып
табылады.
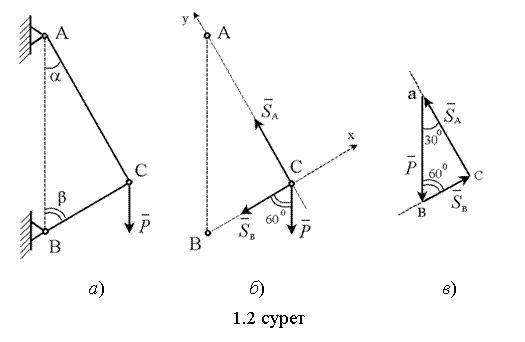 |
4) Бұл есеп
геометриялық әдіс арқылы тез шешіледі. Күштер
үшбұрышын құрамыз. Үшбұрышты
құру белгілі ![]() күшінен басталады. Кез
келген бір
күшінен басталады. Кез
келген бір ![]() нүктесінен бастап берілген масштабта алынған,
нүктесінен бастап берілген масштабта алынған, ![]() күшіне
тең, яғни параллель (ав) кесіндісін саламыз (1.2, в суретті
қара). Кесіндінің бір ұшы а арқылы екі реакция
күштерінің бірінің (мысалы
күшіне
тең, яғни параллель (ав) кесіндісін саламыз (1.2, в суретті
қара). Кесіндінің бір ұшы а арқылы екі реакция
күштерінің бірінің (мысалы ![]() реакция
күшінің) бағытына параллель түзу жүргізіп,
оның екінші ұшы в арқылы қалған реакция
күші (бізде
реакция
күшінің) бағытына параллель түзу жүргізіп,
оның екінші ұшы в арқылы қалған реакция
күші (бізде ![]() ) бағытына параллель (вс)
түзуін жүргіземіз. Сонда осы екі түзудің
қиылысқан нүктесі, күштердің авс
үшбұрышының үшінші төбесін береді.
) бағытына параллель (вс)
түзуін жүргіземіз. Сонда осы екі түзудің
қиылысқан нүктесі, күштердің авс
үшбұрышының үшінші төбесін береді.
Осыдан кейін,
![]() күштерінің
модульдерін анықтау үшін авс үшбұрышынан оның белгісіз
қабырғаларын табу керек.
күштерінің
модульдерін анықтау үшін авс үшбұрышынан оның белгісіз
қабырғаларын табу керек.
Күштер үшбұрышының (ав) қабырғасы белгілі. Оның бұрыштарын анықтағаннан кейін, синустар теоремасына сүйене отырып, мына қатынастарды жазамыз
![]()
Осы өрнектен
 ,
, ![]() .
.
Қарастырылған
мысалды проекция әдісімен, яғни аналитикалық әдіспен
шешеміз. Координаттар жүйесінің бас нүктесін С
топсасына орналастырамыз. ![]() осін ВС бойымен
оң жаққа, ал
осін ВС бойымен
оң жаққа, ал ![]() осін АС бойымен
жоғары бағыттаймыз.
осін АС бойымен
жоғары бағыттаймыз.
С нүктесіне түсірілген күштер жүйесінің тепе-теңдігін өрнектейтін теңдеулерді жазамыз
![]() ,
, ![]() .
.
Бұл құрылған екі теңдеулер жүйесін шешу арқылы белгісіз күштерді табамыз
![]() ,
, ![]() .
.
(![]() таңбасы
таңбасы
![]() күшінің
бағыты, суретте көрсетілген бағытына қарама-қарсы
бағытталатынын көрсетеді, яғни ВС сырығы
сығылады.
күшінің
бағыты, суретте көрсетілген бағытына қарама-қарсы
бағытталатынын көрсетеді, яғни ВС сырығы
сығылады.
Өзіндік жұмыс тапсырма есептері
№№ 2.6, 2.7, 2.8, 2.9, 2.15, 2.18, 2.19, 2.21, 2.23, 2.24, [1].
1.2 Кеңістіктегі жинақталатын күштер жүйесі
1.3-мысал. Салмағы
![]() ға тең жүк, 1.3 суретте көрсетілгендей, А нүктесіне
ілінген. С, В нүктелерінде сырықтар АВ және АС
топсалармен, ал
ға тең жүк, 1.3 суретте көрсетілгендей, А нүктесіне
ілінген. С, В нүктелерінде сырықтар АВ және АС
топсалармен, ал ![]() нүктесіне сым арқанмен бекітілген.
Сырықтардың реакция күштерін (
нүктесіне сым арқанмен бекітілген.
Сырықтардың реакция күштерін (![]() ) және сым арқанның керілу
күшін (
) және сым арқанның керілу
күшін (![]() ) табу керек (1.3 суретті қара).
) табу керек (1.3 суретті қара).
Берілгені: ![]()
Шешуі: 1) Нүкте деп алуға болатын, А денесінің тепе-теңдігін қарастырамыз.
2) А нүктесіне түсірілген
актив күш ![]() .
.
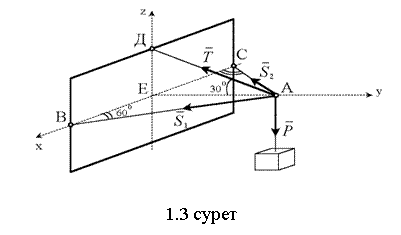 |
3) А нүктесін байланыстардан
босатамыз. АВ, АС сырықтары және
![]() сым арқаны А-дағы байланыстар. Бұлардың
реакция күштерін
сым арқаны А-дағы байланыстар. Бұлардың
реакция күштерін ![]() деп белгілейміз. Егер бір нүктеге
жинақталатын күштер жүйесі кеңістікте орналасқан
күштер жүйесі болса, онда есеп шығарудың
аналитикалық тәсілін пайдалану тиімді. А нүктесіне
түсірілген күштер жүйесінің тепе-теңдігін
өрнектейтін теңдеулерді жазамыз
деп белгілейміз. Егер бір нүктеге
жинақталатын күштер жүйесі кеңістікте орналасқан
күштер жүйесі болса, онда есеп шығарудың
аналитикалық тәсілін пайдалану тиімді. А нүктесіне
түсірілген күштер жүйесінің тепе-теңдігін
өрнектейтін теңдеулерді жазамыз
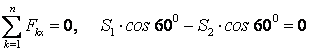 ,
,
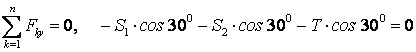 ,
,
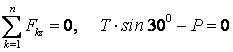 .
.
Бұл
құрылған үш теңдеулер жүйесін шешу
арқылы белгісіз күштерді табамыз: Т = 6000 Н, S1
= S2 = –3000 Н. ![]() және
және ![]() күштері
теріс таңбалы болып шықты. Сондықтан олар суретте біз
көрсеткен бағытқа қарама-қарсы бағытталуы
тиіс, яғни сырықтар АВ және АС сығылады.
күштері
теріс таңбалы болып шықты. Сондықтан олар суретте біз
көрсеткен бағытқа қарама-қарсы бағытталуы
тиіс, яғни сырықтар АВ және АС сығылады.
Өзіндік жұмыс тапсырма есептері
№№ 6.1, 6.2, 6.3, 6.4, 6.5, 6.6, 6.7, 6.8, 6.9, 6.10, [1].
2 Нүктеге қатысты күш моменті
2.1-мысал. Ұзындығы
![]() және салмағы
және салмағы
![]() біртекті арқалық
қалыңдығы
біртекті арқалық
қалыңдығы ![]() қабырғаға А және В
нүктелерінде тірелетіндей болып енгізіліп қойылған.
Арқалықтың соңына салмағы 4 Н жүк
қабырғаға А және В
нүктелерінде тірелетіндей болып енгізіліп қойылған.
Арқалықтың соңына салмағы 4 Н жүк
![]() ілінген. А және В нүктелеріндегі реакция
күштерін табу керек (2.1 суретті қара).
ілінген. А және В нүктелеріндегі реакция
күштерін табу керек (2.1 суретті қара).
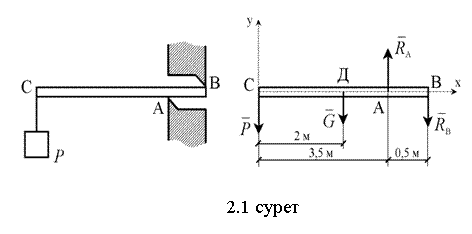 |
Шешуі: 1) СВ арқалығының тепе-теңдігін қарастырамыз.
2) СВ-ға
әсер етуші актив күштер векторларын суретте көрсетеміз. Актив
күштер болып табылатындар: ![]() .
.
3) СВ
арқалығын байланыстардан босатамыз. А және В
тіректерінің ![]() және
және ![]() реакция
күштері арқалыққа перпендикуляр бағытталады.
реакция
күштері арқалыққа перпендикуляр бағытталады.
Түсірілген күштер жүйесінің тепе-теңдігін өрнектейтін теңдеулерді жазамыз
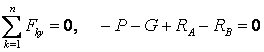 ,
,
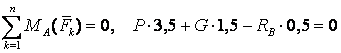 .
.
4) Бұл құрылған екі теңдеулерді шешу арқылы белгісіз күштерді табамыз
![]() ,
, ![]() .
.
Өзіндік жұмыс тапсырма есептері
№№ 3.6, 3.7, 3.8, 3.9, 3.12, 3.13, 3.14, 3.15, 3.16, 3.17, [1].
3 Жазықтықтағы кез келген күштер жүйесі
3.1-мысал. Екі қадалған күштердің және бірқалыпты таралған күштердің әсеріндегі арқалықтың А және В тіректері реакция күштерін табу керек. Бірқалыпты таралған күштердің қарқындылығы, түсірілген күштердің шамалары және өлшем бірліктері суретте көрсетілген (3.1-суретті қара).
Шешуі: 1) АВ
арқалығының тепе-теңдігін қарастырамыз.
Арқалыққа түсірілген актив күштер:
![]() .
.
2) Бірқалыпты таралған
күштердің қарқындылық күштің шамасын
табу үшін, ұзындықтың бір өлшеміне келетін
![]() ді ұзындыққа көбейтеміз
ді ұзындыққа көбейтеміз
![]() .
.
3) Арқалықты байланыстан
босатамыз. Ол үшін А және В топсаларын алып тастап,
олардың орнына ![]() ,
, ![]() , және
, және
![]() реакция күштерін түсіреміз.
реакция күштерін түсіреміз.
4) Алынған жазық күштер жүйесінің тепе-теңдігін өрнектейтін үш теңдеулер жүйесін жазамыз
 |
 ,
,

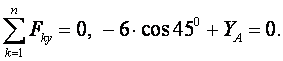
5) Бұл құрылған үш теңдеулер жүйесін шешу арқылы белгісіз күштерді табамыз
![]() .
.
Өзіндік жұмыс тапсырма есептері
№№ 4.19, 4.21, 4.22, 4.25, 4.26, 4.27, 4.28, 4.29, 4.30, 4.31, [1].
4 Кеңістіктегі кез келген күштер жүйесі
4.1-мысал. 4.1 суретте
сұлбасы бейнеленгендей, ![]() жүкті жұмысшы
шығырдың (ворот) көмегімен ұстап тұр;
барабанның радиусы
жүкті жұмысшы
шығырдың (ворот) көмегімен ұстап тұр;
барабанның радиусы ![]() , саптың
ұзындығы
, саптың
ұзындығы ![]() ,
, ![]() . Сап АК
көлденең болғандағы, сапқа түсірілген
қысым
. Сап АК
көлденең болғандағы, сапқа түсірілген
қысым ![]() күшін және А және В тіректердің
осьтеріне түсіретін қысым күштерін табу керек.
күшін және А және В тіректердің
осьтеріне түсіретін қысым күштерін табу керек. ![]() күші
вертикаль бағытталған.
күші
вертикаль бағытталған.
Шешуі: белгісіз күштерді табу үшін шығырдың тепе-теңдігін қарастырамыз. Шығырға түсірілген күштер:
- шамасы ![]() ге тең арқанның тартылыс күші
ге тең арқанның тартылыс күші
![]() ;
;
- актив күш ![]() және цилиндрлік топсалардың реакция күштері
және цилиндрлік топсалардың реакция күштері
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Күштердің кеңістік жүйесінің тепе-теңдігін өрнектейтін теңдеулер жүйесін жазамыз
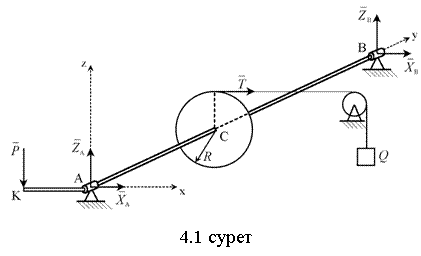 |
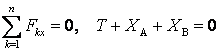 ,
,
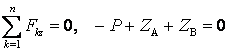 ,
,
 ,
,
 ,
,
![]() .
.
Құрылған бес теңдеулер жүйесін шешу арқылы белгісіз күштерді табамыз
Р = 100 Н, ХА = 400 Н, ZА = – 100 Н, ХВ = – 400 Н, ZВ = 0.
Өзіндік жұмыс тапсырма есептері
№№ 8.5, 8.7, 8.8, 8.12, 8.13, 8.14, 8.15, 8.16, 8.17, 8.24, [1].
5 Үйкеліс күші. Ауырлық центрді анықтау
5.1-мысал. Саты АВ вертикаль
қабырғаға сүйеп қойылған (5.1 суретті
қара). Саты мен қабырға және еденнің
арасындағы үйкеліс коэффициеттері
![]() және
және ![]() . Сатының адаммен бірге салмақ
күші
. Сатының адаммен бірге салмақ
күші ![]() , сатыны
, сатыны
![]() қатынасына бөлетін С нүктесіне
түсірілген. Сатының тепе-теңдік жағдайында, саты мен
қабырға арасындағы
қатынасына бөлетін С нүктесіне
түсірілген. Сатының тепе-теңдік жағдайында, саты мен
қабырға арасындағы ![]() бұрыштың ең үлкен
мәнін, сонымен қатар қабырға және еденнің
нормаль құраушы реакция күштерін табу керек.
бұрыштың ең үлкен
мәнін, сонымен қатар қабырға және еденнің
нормаль құраушы реакция күштерін табу керек.
Шешуі: сатыға әсер етуші бір
ғана актив күш бар. Ол сатының салмақ күші
![]() , оны суретте көрсетеміз. Сатыны байланыстардан босатамыз. Еден
мен қабырғаның сатыға жасайтын әсерлерін
, оны суретте көрсетеміз. Сатыны байланыстардан босатамыз. Еден
мен қабырғаның сатыға жасайтын әсерлерін
![]() нормаль қысым және
нормаль қысым және
![]() үйкеліс күштерімен ауыстырамыз. Үйкеліс
күшінің шекті шамасында бұрыш
үйкеліс күштерімен ауыстырамыз. Үйкеліс
күшінің шекті шамасында бұрыш
![]() болады, сондықтан
болады, сондықтан
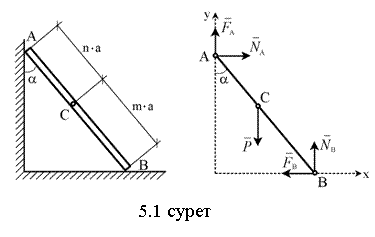 |
![]() ,
, ![]() .
.
Күштердің жазық жүйесінің тепе-теңдігін өрнектейтін теңдеулерін екі проекциялық, бір нүктеге қатысты момент теңдеулері түрінде жазамыз
![]() ,
,
![]() ,
,
 .
.
Құрылған бес теңдеулер жүйесін шешу арқылы белгісіз күштерді табамыз
 ,
, 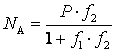 ,
,  .
.
5.2-мысал. Радиусы ![]() болатын
болатын
![]() дөңгелек сегмент ауданының
ауырлық центрі С-ны табу керек.
дөңгелек сегмент ауданының
ауырлық центрі С-ны табу керек. ![]() (5.2 суретті қара).
(5.2 суретті қара).
Шешуі: ауырлық центрі
![]() симметрия осінің бойында жатыр. Берілген сегмент
симметрия осінің бойында жатыр. Берілген сегмент
![]() ауданын ойша
ауданын ойша
![]() сектор ауданына дейін толықтырамыз. Сонда
берілген аудан орнына сектор ауданы мен ауданы теріс таңбалы
сектор ауданына дейін толықтырамыз. Сонда
берілген аудан орнына сектор ауданы мен ауданы теріс таңбалы
![]() шығады.
шығады.
Координаттар осьтерінің бас нүктесі ретінде О-ны аламыз да, остерді суреттегідей бағыттаймыз. Есеп шартына сай топтау әдісінен шығатын өрнек, мынадай түрде жазылады
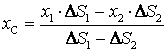 .
.

Өрнектегі белгісіз шамалар:
![]() сектор ауданы
сектор ауданы![]()
![]() үшбұрышының ауданы
үшбұрышының ауданы![]()
![]() сектор ауданының ауырлық центрінің абсциссасы
сектор ауданының ауырлық центрінің абсциссасы![]()
![]() үшбұрышы ауданының ауырлық центрінің
абсциссасы.
үшбұрышы ауданының ауырлық центрінің
абсциссасы.
Осыларды есептейік
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Осы шамаларды негізгі өрнекке қойсақ алатынымыз
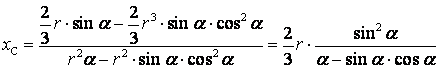 .
.
![]() және
және ![]() болғанда
болғанда
![]() .
.
Өзіндік жұмыс тапсырма есептері
№№ 9.4, 9.5, 9.6, 9.7, 9.8, 9.9, 9.10, 9.11, 9.12, 9.13, [1].
Кинематика
6 Нүкте қозғалысының берілу тәсілдері. Нүкте қозғалысының теңдеуі және траекториясы
6.1-мысал. Нүкте қозғалысының берілген ![]() теңдеулерінен
оның траекториясының теңдеуін анықтау, сонымен
қатар нүктенің бастапқы орнынан саналатын
қашықтығын траектория бойында нүкте
қозғалысының заңдылығы арқылы көрсету
қажет.
теңдеулерінен
оның траекториясының теңдеуін анықтау, сонымен
қатар нүктенің бастапқы орнынан саналатын
қашықтығын траектория бойында нүкте
қозғалысының заңдылығы арқылы көрсету
қажет.
Шешуі: теңдеулердің екі жағын квадраттап және оларды мүшелерін қоссақ, алатынымыз
![]() немесе
немесе ![]() .
.
Сонымен, траекториясы-центрі бас
нүктесінде болатын радиусы 3 бірлікті ұзындықтағы
шеңбер (6.1 суретті қара). Траектория бойында қозғалыс
заңдылығын анықтаймыз. ![]() және
және
![]() координаттарынан t бойынша туынды таба отырып, алатынымыз
координаттарынан t бойынша туынды таба отырып, алатынымыз

![]() .
.
Осы мәндерді төмендегі теңдікке қойып
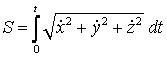 ,
(1)
,
(1)
мынадай заңдылықты аламыз
 немесе
немесе ![]() .
(2)
.
(2)
(2)-теңдеу траектория бойында
нүкте қозғалысының заңдылығын береді. (1)-теңдеуден,
егер ![]() болғанда
болғанда ![]() , яғни нүкте
, яғни нүкте ![]() орнында
болатындығын, ал егер
орнында
болатындығын, ал егер ![]() өсіп бастаса,
оң таңбаны қабылдап
өсіп бастаса,
оң таңбаны қабылдап ![]() те өсетінін, ал
те өсетінін, ал ![]() кемитінін
көреміз.
кемитінін
көреміз.
Өзіндік жұмыс тапсырма есептері
№№ 10.2(1,2), 10.4(1,2) [1].
7 Қозғалысы координаттық және табиғи тәсілдермен берілген нүктенің жылдамдығын және үдеуін анықтау. Жанама және нормаль құраушы үдеулері
7.1 Қозғалысы координаттық тәсілмен берілген нүктенің жылдамдығын анықтау
7.1.1-мысал. Қосиін ОА
тұрақты ![]() бұрыштық жылдамдықпен айнала
қозғалады және
бұрыштық жылдамдықпен айнала
қозғалады және
![]() . Қосиін-бұлғақты механизм
бұлғағының ортасында орналасқан М нүктесінің
және жылжыма В-ның жылдамдықтарын табу керек.
. Қосиін-бұлғақты механизм
бұлғағының ортасында орналасқан М нүктесінің
және жылжыма В-ның жылдамдықтарын табу керек.
Шешуі: М және В нүктелерінің қозғалыс теңдеулері берілмеген, сондықтан, оларды құру қажет. Механизмді кез келген орнында кескіндейміз. Координаттар осьтері 7.1 суретте көрсетілген. М және А нүктелерінен осьтерге МД, МЕ және АК перпендикуляр түзулерді тұрғызамыз. Онда алатынымыз
![]()
![]()
![]()
 |
![]() мәндерін
ескере отырып, M және B нүктелерінің
қозғалыс теңдеулерін құрамыз
мәндерін
ескере отырып, M және B нүктелерінің
қозғалыс теңдеулерін құрамыз
![]()
![]()
![]()
M және B нүктелерінің жылдамдықтарын анықтаймыз
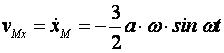 ,
, 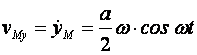 ,
,
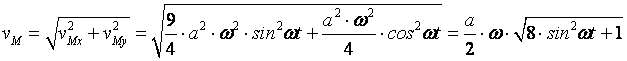 ,
,
![]() .
.
7.2 Қозғалысы координаттық тәсілмен берілген нүктенің үдеуін анықтау
7.2.1-мысал. Дизельдің
қосиін жұдырықшасының қозғалысы
![]() теңдеулерімен
берілген. Жұдырықша жылдамдығын, жанама және нормаль
құраушы үдеулерін табу керек.
теңдеулерімен
берілген. Жұдырықша жылдамдығын, жанама және нормаль
құраушы үдеулерін табу керек.
Шешуі: нүкте жылдамдығының осьтерге проекцияларын анықтаймыз
![]() ,
, ![]() .
.
Жылдамдық модулі мынадай өрнекпен анықталады
![]() см/с.
см/с.
Жанама құраушы үдеуі жылдамдықтың жанама оске проекциясынан уақыт бойынша алынған бірінші туындысына тең
![]() см/с2.
см/с2.
Жылдамдықтың сәйкес остердегі проекцияларынан уақыт бойынша бірінші туындыларын есептей отырып, үдеудің координаттар остерінде проекцияларын анықтаймыз
![]() ,
,
![]() .
.
Үдеу модулі мынадай өрнектермен анықталады
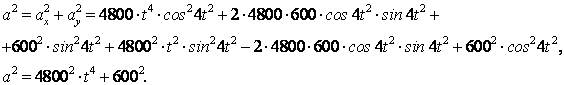
Толық үдеу мен жанама және нормаль құраушыларының арасында мынадай байланыс бар
![]() .
.
Онда
![]() .
.
Осыдан
![]() см/с2.
см/с2.
7.3 Нүктенің бірқалыпты және бірқалыпты айнымалы қозғалысы
7.3.1-мысал. Пойыз радиусы ![]() шеңбер доғасы бойымен кемімелі
қозғалыс жасайды және
шеңбер доғасы бойымен кемімелі
қозғалыс жасайды және ![]() жол
жүргенде, бастапқы жылдамдығы
жол
жүргенде, бастапқы жылдамдығы ![]() , ал соңғы жылдамдығы
, ал соңғы жылдамдығы ![]() (7.2 суретті қара). Пойыздың бастапқы және
соңғы доға ұзындығындағы толық
үдеулерін, сонымен қатар осы доғаның
ұзындығын жүріп өтетін уақытын анықтау
қажет.
(7.2 суретті қара). Пойыздың бастапқы және
соңғы доға ұзындығындағы толық
үдеулерін, сонымен қатар осы доғаның
ұзындығын жүріп өтетін уақытын анықтау
қажет.
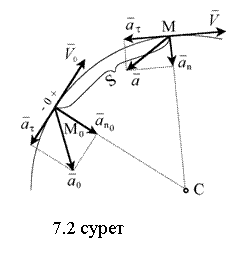
Шешуі: пойыздың бір
нүктесінің қозғалысын қарастырамыз, мысалы
ауырлық центрінің. Доғалық координаттың О
нүктесін М нүктесінің бас нүктесі ретінде
және қозғалыстың бағытын оң бағыт
ретінде қабылдаймыз. (7.2 суретті қара). Онда
![]() .
.
Нүктенің кемімелі қозғалысы үшін, қозғалыс теңдеуі төмендегі өрнекпен анықталады
![]() , (1)
, (1)
![]() .
(2)
.
(2)
Есептің берілгені бойынша:
- қозғалатын
![]() нүктесінің
соңғы қозғалыс аралығы, аралықтың
ұзындығына тең, яғни
нүктесінің
соңғы қозғалыс аралығы, аралықтың
ұзындығына тең, яғни ![]() ;
;
- аралықтың бас
нүктесінде жылдамдығы ![]() , ал аралықтың
соңғы нүктесінде жылдамдығы
, ал аралықтың
соңғы нүктесінде жылдамдығы ![]() ;
;
- шеңбердің барлық
нүктелерінде оның радиусы ![]() .
.
(1) және (2)-теңдіктен табатынымыз
![]() ,
, ![]() .
.
Алынған теңдеулер жүйесін шеше отырып, қозғалыс уақытын және жанама құраушы үдеуін анықтаймыз
 ,
, 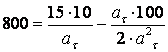 ,
, ![]() ,
,
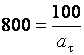 ,
, ![]() .
.
Нүктенің бастапқы аралықта нормаль құраушы үдеуі
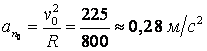 ,
,
ал соңғы аралықта
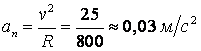 .
.
Толық үдеудің бастапқы және соңғы аралықта шамасы
![]() ,
,
![]() .
.
Өзіндік жұмыс тапсырма есептері
№№ 10.2, 10.12, 11.3, 11.5, 12.1, 12.2, 12.3, 12.7, 12.8, 12.10, [1].
8 Дененің ілгерілемелі және айналмалы қозғалысы
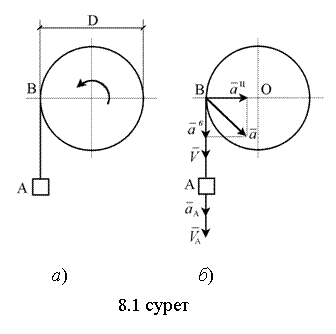
8.1-мысал. Атанаққа
оралған жіпке ілінген жүк A, атанақты айналмалы қозғалысқа
келтіре отырып, тыныштық қалпынан бірқалыпты үдемелі
төменгі бағытта қозғалады. Атанақ бірінші 3 сек
арлығында 9 айналыс жасайды. Атанақтың диаметрі
![]() .
.
Атанақ бетіндегі нүктенің 5 сек уақыт мезгіліндегі жылдамдығын және үдеуін табу керек (8.1 суретті қара).
Шешуі: атанақтың бірқалыпты айнымалы айналмалы қозғалыс теңдеуін жазамыз
![]() .
(1)
.
(1)
Бұрыштық жылдамдықтың айналу осіндегі проекциясы айналу бұрышы (1)-ден уақыт бойынша алынған туындыға тең
![]() .
.
Бастапқы мәндері:
![]() . Осы
шарттарды ескере отырып (1) және (2) - теңдеулерді мынадай
түрде жазамыз
. Осы
шарттарды ескере отырып (1) және (2) - теңдеулерді мынадай
түрде жазамыз
 |
![]() .
(2)
.
(2)
![]() ,
(3)
,
(3)
![]() . (4)
. (4)
![]() уақыт мезгілін де
уақыт мезгілін де ![]() айналыс
болғандықтан, (3) – теңдеуден бұрыштық үдеу
айналыс
болғандықтан, (3) – теңдеуден бұрыштық үдеу
![]() ді табамыз
ді табамыз
![]() .
.
(4)–теңдеуден
![]() мезгіліндегі
атанақтың бұрыштық жылдамдығы
мезгіліндегі
атанақтың бұрыштық жылдамдығы ![]() -ны
табамыз
-ны
табамыз
![]() .
.
Атанақтың бетіндегі B нүктесінің (8.1, б суретті қара) сызықтық жылдамдығын, жанама және нормаль құраушы үдеулерін осы уақыт мезетінде анықтаймыз
![]() м/с,
м/с,
![]() м/с2,
м/с2,
![]() м/с2.
м/с2.
Атанақтың бетіндегі нүктенің толық үдеуінің модулі
![]() м/с2.
м/с2.
Жүктің жылдамдығы атанақтың бетіндегі нүктенің сызықтық жылдамдығына тең
![]() м/с.
м/с.
Жүктің үдеуі атанақтың бетіндегі нүктенің жанама құраушы үдеуіне тең
![]() м/с2.
м/с2.
8.2-мысал. Радиусы
![]() тістегеріш
1-ге отырғызылған радиусы
тістегеріш
1-ге отырғызылған радиусы ![]() білікті (валды) жүк В
айналмалы қозғалысқа келтіреді. Жүк тыныштық
қалпынан қозғалып бастайды және тұрақты
білікті (валды) жүк В
айналмалы қозғалысқа келтіреді. Жүк тыныштық
қалпынан қозғалып бастайды және тұрақты ![]() үдеумен
қозғалады. Тістегеріш 1-мен іліністе болатын радиусы
үдеумен
қозғалады. Тістегеріш 1-мен іліністе болатын радиусы ![]() тістегеріш
2-нің қозғалыс заңдылығын табу керек (8.2 суретті
қара).
тістегеріш
2-нің қозғалыс заңдылығын табу керек (8.2 суретті
қара).
Шешуі: жүк В (8.2 суретті
қара) бастапқы жылдамдықсыз тұрақты
![]() үдеумен
қозғалып бастайды, сондықтан кез келген уақыт мезетінде
үдеумен
қозғалып бастайды, сондықтан кез келген уақыт мезетінде
![]() болады.
болады.
Біліктің бетіндегі нүкте
жылдамдығы осы жылдамдыққа және
![]() ге
тең. Сондықтан
ге
тең. Сондықтан
![]() ,
, ![]() .
.
Осы өрнектен
![]() ні
табамыз. Іліністегі нүкте С-ның сызықтық
жылдамдығы екі тістегерішке ортақ
ні
табамыз. Іліністегі нүкте С-ның сызықтық
жылдамдығы екі тістегерішке ортақ
![]() , осыдан
, осыдан
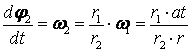 .
.
Осы теңдіктің екі
жағында ![]() -ға көбейтіп,
мынадай теңдік аламыз
-ға көбейтіп,
мынадай теңдік аламыз

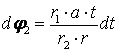 .
.
Теңдіктің солжағын
0-ден ![]() ге, ал оң жағын 0-ден
ге, ал оң жағын 0-ден ![]() ға дейінгі шектерде
интегралдай отырып, тістегеріш 2-нің бірқалыпты айнымалы айналмалы
қозғалыс заңдылығын табамыз
ға дейінгі шектерде
интегралдай отырып, тістегеріш 2-нің бірқалыпты айнымалы айналмалы
қозғалыс заңдылығын табамыз
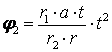 .
.
Өзіндік жұмыс тапсырма есептері
№№ 13.2, 13.3, 13.4, 13.5, 13.14, 13.18, 14.1, 14.3, 14.4, 14.5, [1].
9 Қатты дененің жазық параллель қозғаласы. Жазық параллель қозғалыстағы қатты дене нүктелерінің жылдамдықтары және үдеулері
9.1-мысал.
Қосиін-бұлғақты
механизмде қосиіннің айналу центрі жылжыма В-ның көлденең
траекториясынан а қашықтықта орналасқан.
Қосиіннің бұрылу бұрышы ![]() заңдылығымен
өзгереді, мұндағы
заңдылығымен
өзгереді, мұндағы ![]() тұрақты
коэффициент. Қосиіннің ұзындығы
тұрақты
коэффициент. Қосиіннің ұзындығы ![]() , ал
бұлғақтың ұзындығы
, ал
бұлғақтың ұзындығы ![]() .
.
Бұлғақ AB-ның жазық параллель қозғалыс теңдеулерін анықтау керек.
Шешуі: бас нүктесі O болатын қозғалмайтын xOy координаттар жүйесін жүргіземіз (9.1 суретті қара). Бас нүктесі А болатын қозғалмалы x1Ay1 координаттар жүйесін таңдап аламыз. Сонымен, қосиіннің A нүктесі полюс болады.
Полюстің қозғалыс теңдеулерін жазамыз
![]()
Бұлғақтың бұрылу бұрышы
мен уақыт арасындағы байланысы болатын үшінші теңдеуді табу
үшін, AB кесіндісін y осіне проекциялаймыз. x1
және x осьтерінің арасындағы
бұрышты ![]() арқылы
белгілеп, мынадай теңдік аламыз
арқылы
белгілеп, мынадай теңдік аламыз
![]() ,
,
немесе,
![]() ,
, ![]() ,
, ![]() болғандықтан
болғандықтан

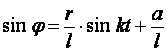 .
.
Бұлғақ AB-ның жазық параллель қозғалыс теңдеулері мынадай болады
![]() ,
, ![]() ,
, 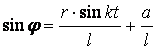 .
.
9.2-мысал. Радиусы
![]() түзу
рельс бойымен сырғанамай дөңгелеп қозғалады
және оның центрінің жылдамдығы тұрақты
түзу
рельс бойымен сырғанамай дөңгелеп қозғалады
және оның центрінің жылдамдығы тұрақты ![]() .
.
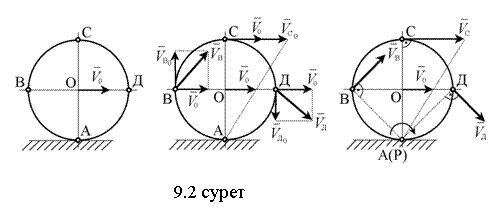
Дөңгелектің көлденең және вертикаль диаметрлерінің соңғы A, B, C, D нүктелерінің жылдамдықтарын және дөңгелектің бұрыштық жылдамдығын анықтау керек.
Шешуі: І-тәсіл (жылдамдықтардың таралу формулаларын пайдалану).
Полюс ретінде О центрін
қабылдаймыз (9.2 суретті қара).
Онда дөңгелектің кез келген нүктесінің
жылдамдығы полюс жылдамдығы мен полюсті айнала қозғалыс
жылдамдығының геометриялық қосындысына тең,
мысалы ![]() .
Дөңгелек сырғанамай дөңгелеп
қозғалатын болғандықтан дөңгелек пен
рельстің жанасушы А нүктесінің жылдамдығы
.
Дөңгелек сырғанамай дөңгелеп
қозғалатын болғандықтан дөңгелек пен
рельстің жанасушы А нүктесінің жылдамдығы
 |
нөлге тең VА=0, яғни
А нүктесі лездік жылдамдық центрі болып табылады. Бұл нүктеде полюсті айнала қозғалыс
жылдамдығы ![]() мен
полюс жылдамдығы
мен
полюс жылдамдығы ![]() ның шамалары тең, ал бағыттары қарама-қарсы, яғни
ның шамалары тең, ал бағыттары қарама-қарсы, яғни ![]() . A, B, C
және D нүктелерінен полюске дейінгі
ара қашықтықтары тең. Сондықтан,
нүктелердің полюсті айнала қозғалыс жылдамдықтары
өз-ара тең, яғни
. A, B, C
және D нүктелерінен полюске дейінгі
ара қашықтықтары тең. Сондықтан,
нүктелердің полюсті айнала қозғалыс жылдамдықтары
өз-ара тең, яғни
![]() .
.
Әрбір
нүктеден полюс жылдамдығы ![]() ны және
дөңгелектің радиусына перпендикуляр полюсті айнала
қозғалыс жылдамдығын тұрғызып алатынымыз
ны және
дөңгелектің радиусына перпендикуляр полюсті айнала
қозғалыс жылдамдығын тұрғызып алатынымыз
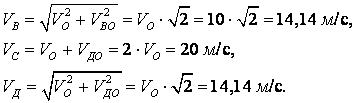
Бұрыштық жылдамдығы
 .
.
ІІ-тәсіл (жылдамдықтар лездік центрін пайдалану).
Дөңгелектің жылдамдықтар лездік центрі A–ны полюс ретінде қабылдаймыз. Онда дөңгелектің барлық нүктелерінің жылдамдықтары лездік жылдамдық центрін айнала қозғалыс жылдамдықтары болады. Барлық нүктелердің жылдамдықтарының шамалары мынадай қатынастармен анықталады
![]()
![]() ,
,
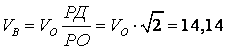 м/c,
м/c,
![]() м/c.
м/c.
мұндағы
PB = PД = ![]() .
.
Бұрыштық жылдамдығы мынадай қатынаспен анықталады
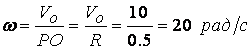 .
.
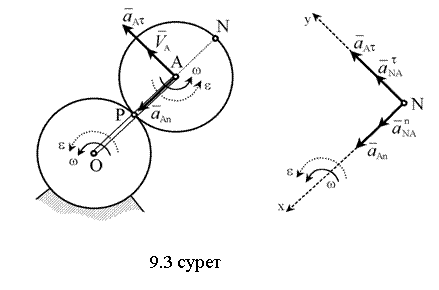
9.3-мысал. Радиусы
![]() тістегерішті
радиусы сондай қозғалмайтын тістегеріштің осі О-ға
қатысты айнала қозғалатын қосиін ОА
қозғалысқа келтіреді. Қосиін
тістегерішті
радиусы сондай қозғалмайтын тістегеріштің осі О-ға
қатысты айнала қозғалатын қосиін ОА
қозғалысқа келтіреді. Қосиін ![]() бұрыштық
жылдамдықпен айнала қозғалады және бұрыштық
жылдамдығы
бұрыштық
жылдамдықпен айнала қозғалады және бұрыштық
жылдамдығы ![]() . 2-тістегеріштің
. 2-тістегеріштің ![]() нүктесінің
үдеуін анықтау керек (9.3 суретті қара).
нүктесінің
үдеуін анықтау керек (9.3 суретті қара).
Шешуі: 1)
![]() және
және ![]() -ны
анықтаймыз. Есепті шешу үшін 2-тістегеріштің
қозғалысын қарастырамыз. Есептің берілгені бойынша
тістегеріштің А нүктесінің
-ны
анықтаймыз. Есепті шешу үшін 2-тістегеріштің
қозғалысын қарастырамыз. Есептің берілгені бойынша
тістегеріштің А нүктесінің ![]() жылдамдығын
және
жылдамдығын
және ![]() үдеуін есептеу жеңіл және осы нүктені полюс
ретінде қабылдаймыз
үдеуін есептеу жеңіл және осы нүктені полюс
ретінде қабылдаймыз
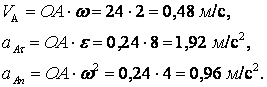
![]() ,
, ![]() ,
, ![]() векторларының бағыттары 9.3 суретте көрсетілген.
векторларының бағыттары 9.3 суретте көрсетілген.
2) Тістегеріш 2-нің
бұрыштық жылдамдығы ![]() анықтаймыз.
Тістегеріштің жанасу P нүктесі ЛЖЦ болады,
сондықтан
анықтаймыз.
Тістегеріштің жанасу P нүктесі ЛЖЦ болады,
сондықтан
![]() ,
, 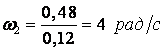 .
.
![]() ның бағытын
(тістегеріштің айналу бағытын)
ның бағытын
(тістегеріштің айналу бағытын) ![]() анықтайды.
анықтайды.
3) Тістегеріш 2-нің
бұрыштық үдеуі ![]() ні анықтаймыз. AP
= R шамасы барлық уақытта тұрақты,
сондықтан
ні анықтаймыз. AP
= R шамасы барлық уақытта тұрақты,
сондықтан
![]() ,
, 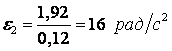 .
(1)
.
(1)
 |
4) Нүкте N-нің үдеуін мынадай формуламен анықтаймыз
![]() .
(2)
.
(2)
Бұл үшін
![]() және
және
![]() шамаларын анықтаймыз. Біздің жағдайда
шамаларын анықтаймыз. Біздің жағдайда
![]() және
және ![]() ,
,
![]() .
.
Суретте (9.3 суретті қара)
![]() ,
, ![]() ,
, ![]() ,
, ![]() векторларының
бағыттарын көрсетеміз.
векторларының
бағыттарын көрсетеміз.
5)
![]() ді есептейміз. Nx
және Ny осьтерін жүргіземіз,
ді есептейміз. Nx
және Ny осьтерін жүргіземіз, ![]() ді осы осьтерге
проекциялары арқылы анықтаймыз
ді осы осьтерге
проекциялары арқылы анықтаймыз
![]() ,
,
![]() .
.
Осыдан
![]() .
.
Өзіндік жұмыс тапсырма есептері
№№ 15.2, 16.2, 16.3, 16.4, 16,9, 16.24, 16.29, 18.1, 18.2, 18.15, [1].
10 Нүктенің күрделі қозғалысы. Абсолют жылдамдық және абсолют үдеу
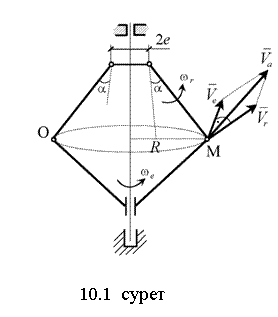
10.1-мысал.
Тік (вертикаль) осьті ![]() бұрыштық жылдамдықпен
айнала қозғалатын центрден тепкіш Уатт реттегішінің шарлары,
машина күшінің өзгеруіне байланысты осы осьтен
алшақтайды және қарастыратын орнында бұрыштық
жылдамдығы
бұрыштық жылдамдықпен
айнала қозғалатын центрден тепкіш Уатт реттегішінің шарлары,
машина күшінің өзгеруіне байланысты осы осьтен
алшақтайды және қарастыратын орнында бұрыштық
жылдамдығы ![]() .
.
Берілгені:
![]() ,
, ![]()
![]() .
.
Қарастыратын уақыт мезгілінде реттегіш шарларының абсолют жылдамдығын табу керек (10.1 суретті қара).
 |
Шешуі: қозғалмалы
санақ жүйесін реттегіштің осьті айнала қозғалатын
бөлшектерімен байланыстырамыз. Шарлардың тасымал
қозғалысы, олардың ![]() бұрыштық
жылдамдықпен тік осьті айнала қозғалысы, ал салыстырмалы
қозғалысы, шарлардың сырықтарымен бірге олардың
бұрыштық
жылдамдықпен тік осьті айнала қозғалысы, ал салыстырмалы
қозғалысы, шарлардың сырықтарымен бірге олардың ![]() бұрыштық
жылдамдықпен ілінетін осьті айнала қозғалыста болады.
бұрыштық
жылдамдықпен ілінетін осьті айнала қозғалыста болады.
Әрбір шардың
центрінің тасымал қозғалыс траекториясы, центрі реттегіш осінің
бойында жататын көлденең шеңбер болады. Салыстырмалы
қозғалыс траекториясы, центрі сырық ілінетін осьтің бойында
болатын және реттегіштің жазықтығында жататын радиусы
![]() ге
тең шеңбер доғасы.
ге
тең шеңбер доғасы.
Тасымал қозғалыс шеңберінің радиусы
![]() .
.
Шар центрінің абсолют жылдамдығы тасымал және салыстырмалы жылдамдықтардың геометриялық қосындысына тең (10.1 суретті қара)
![]() ,
,
![]() ,
, ![]() сәйкес траекторияларына жанама
бойымен бағытталады, ал шамалары
сәйкес траекторияларына жанама
бойымен бағытталады, ал шамалары
![]() .
.
Жылдамдықтар
![]() және
және ![]() өзара перпендикуляр, сондықтан,
өзара перпендикуляр, сондықтан, ![]() векторының
шамасы мынаған тең
векторының
шамасы мынаған тең
![]() .
.
10.2-мысал. Радиусы ![]() шар (10.2 суретті қара)
шар (10.2 суретті қара)
![]() диаметрін
диаметрін
![]() (есептеудiң оң бағыты суретте доғалы
стрелкамен көрсетiлген) заңдылығымен айнала
қозғалады. Үлкен шеңбер («меридианмен)
(есептеудiң оң бағыты суретте доғалы
стрелкамен көрсетiлген) заңдылығымен айнала
қозғалады. Үлкен шеңбер («меридианмен)
![]() бойымен
бойымен
![]() нүктесі
нүктесі
![]() (
(![]() -тің оң бағыты
-тің оң бағыты
![]() -дан
-дан
![]() -ға қарай есептеледі) заңдылығымен
қозғалады.
-ға қарай есептеледі) заңдылығымен
қозғалады.
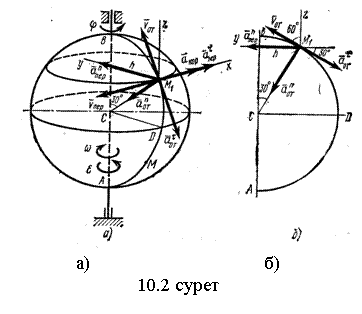 |
Берілгені: ![]() ,
,
![]()
![]() (
(![]() радианмен,
радианмен,
![]() метрмен,
метрмен,
![]() секундпен өлшенеді). Табу қажеті:
секундпен өлшенеді). Табу қажеті:
![]() . мезетінде
. мезетінде
![]() және
және
![]() .
.
Шешуі: ![]() доғаның бойымен қозғалысын
салыстырмалы (
доғаның бойымен қозғалысын
салыстырмалы (![]() нүктенің салыстырмалы траекториясы), ал
шардың айналмалы қозғалысын
нүктенің салыстырмалы траекториясы), ал
шардың айналмалы қозғалысын![]() тасымал қозғалыс деп есептеп,
нүкте
тасымал қозғалыс деп есептеп,
нүкте ![]() -нің қозғалысын күрделі қозғалыс
ретінде қарастырамыз. Онда нүктенің
-нің қозғалысын күрделі қозғалыс
ретінде қарастырамыз. Онда нүктенің
![]() абсолюттік жылдамдығы және
абсолюттік жылдамдығы және
![]() абсолюттік үдеуі төмендегі өрнектермен
анықталады
абсолюттік үдеуі төмендегі өрнектермен
анықталады
![]() , (1)
, (1)
мұндағы,
![]() .
.
Салыстырмалы және тасымал қозғалыстардың сипаттамаларын анықтаймыз.
1) Салыстырмалы қозғалыс. Бұл қозғалыс төмендегі заңдылықпен мүмкін болады
![]() . (2)
. (2)
Бірішіден, ![]() уақыт мезетінде
уақыт мезетінде
![]() доғаның бойында
доғаның бойында
![]() нүктесі қайсы аралықта болатынын белгілейміз.
нүктесі қайсы аралықта болатынын белгілейміз.
![]() уақыт мезетінде (2)-теңдеуден алатынымыз
уақыт мезетінде (2)-теңдеуден алатынымыз
![]() .
.
онда
![]() , немесе
, немесе
![]() °.
°.
Анықталған бұрышқа
сәйкес 10.2-суретте нүктенің орнын көрсетеміз (![]() нүктесі).
нүктесі).
Енді ![]() мәндерін табамыз
мәндерін табамыз

 ,
,
мұндағы
![]() салыстырмалы траекторияның
қисықтық радиусы, яғни
салыстырмалы траекторияның
қисықтық радиусы, яғни
![]() доғасы.
доғасы. ![]() болатынын ескере отырып,
болатынын ескере отырып,
![]() . уақыт үшін алатынымыз
. уақыт үшін алатынымыз
![]() ,
,
![]() ,
,
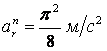 . (3)
. (3)
Таңбалары ![]() векторы
векторы
![]() аралықты есептеудің оң
бағытымен, ал
аралықты есептеудің оң
бағытымен, ал ![]() кері бағытта,
кері бағытта,
![]() векторы
векторы ![]() доғасының С орталығына
бағытталатынын көрсетеді. Барлық осы векторларды 10-суретте
көрсетеміз. Көрнекі болу үшін 10 б-суретте
доғасының С орталығына
бағытталатынын көрсетеді. Барлық осы векторларды 10-суретте
көрсетеміз. Көрнекі болу үшін 10 б-суретте
![]() доғасы чертеж жазықтығымен беттестірілген.
доғасы чертеж жазықтығымен беттестірілген.
2) Тасымал қозғалыс. Бұл қозғалыс төмендегі заңдылықпен мүмкін болады (айналмалы)
![]() .
.
Тасымал айналмалы қозғалыстың
![]() бұрыштық жылдамдығын және
бұрыштық жылдамдығын және
![]() бұрыштық үдеуін анықтаймыз
бұрыштық үдеуін анықтаймыз
![]() .
.
![]() мезетінде
мезетінде
![]() . (4)
. (4)
Таңбасы уақыт мезеті
![]() болғанда,
болғанда,
![]() -нің бағыты
-нің бағыты
![]() бұрылу бұышының оң
есептеу бағытымен, ал
бұрылу бұышының оң
есептеу бағытымен, ал ![]() -ның бағыты оған қарсы
бағытталатынын көрсетеді. 10.2 а-суретте сәйкес
доғалық стрелкамен көрсетеміз.
-ның бағыты оған қарсы
бағытталатынын көрсетеді. 10.2 а-суретте сәйкес
доғалық стрелкамен көрсетеміз.
Нүктенің тасымал ![]() жылдамдығын және
жылдамдығын және
![]() тасымал үдеуін анықтау үшін,
алдымен нүкте
тасымал үдеуін анықтау үшін,
алдымен нүкте ![]() ден айналу осіне дейінгі
ден айналу осіне дейінгі
![]() қашықтықты тауып аламыз, ол
қашықтықты тауып аламыз, ол
![]() . Онда
. Онда
![]() уақыт мезетінде (4) – теңдікті ескере
отырып, алатынымыз
уақыт мезетінде (4) – теңдікті ескере
отырып, алатынымыз
![]() ,
,
![]() ,
,
![]() . (5)
. (5)
![]() және
және ![]() бағыттарын ескере отырып
бағыттарын ескере отырып
![]() ,
,
![]() , бағытарын және
, бағытарын және
![]() векторын (оське қарай бағытталған)
10 а–суретте көрсетеміз.
векторын (оське қарай бағытталған)
10 а–суретте көрсетеміз.
3) Кориолис үдеуі. ![]() векторы мен айналу осінің (
векторы мен айналу осінің (![]() векторының) арасындағы бұрыш 60°
болғандықтан
векторының) арасындағы бұрыш 60°
болғандықтан ![]() уақыт мезетінде [(3) және
(4)–теңдікті қара]
уақыт мезетінде [(3) және
(4)–теңдікті қара]
![]() . (6)
. (6)
![]() векторын айналу осіне перпендикуляр жазықтыққа
проекциялап және жазықтықтағы осы проекциясын
векторын айналу осіне перпендикуляр жазықтыққа
проекциялап және жазықтықтағы осы проекциясын
![]() бағытымен, яғни сағат тілі бағытымен 90°-қа
бұрып
бағытымен, яғни сағат тілі бағытымен 90°-қа
бұрып ![]() бағытын анықтаймыз. Басқаша
бағытын анықтаймыз. Басқаша
![]() ескеріп
ескеріп
![]() бағытын анықтауға болады. 10 а–суретте
бағытын анықтауға болады. 10 а–суретте
![]() векторының бағытын көрсетеміз.
векторының бағытын көрсетеміз.
Енді
![]() және
және
![]() шамаларын есептеуге болады.
шамаларын есептеуге болады.
4) Абсолюттік жылдамдық ![]() -ны анықтау.
-ны анықтау.
![]() , ал
, ал
![]() және
және
![]() векторлары өзара перпендикуляр болғандықтан,
векторлары өзара перпендикуляр болғандықтан,
![]() мезетінде
мезетінде
 .
.
5) Абсолют үдеу ![]() -ны анықтау. Үдеулерді қосу
теоремасы негізінде
-ны анықтау. Үдеулерді қосу
теоремасы негізінде
![]() . (7)
. (7)
Абсолют үдеу ![]() -ны анықтау үшін
-ны анықтау үшін
![]() координаттар жүйесін жүргіземіз (10.2 б суретті
қара) және
координаттар жүйесін жүргіземіз (10.2 б суретті
қара) және ![]() векторының кординаттар осьтеріне проекцияларын
есептейміз.
векторының кординаттар осьтеріне проекцияларын
есептейміз. ![]() және
және ![]() векторлары
векторлары
![]() осінің бойында, ал
осінің бойында, ал
![]() ,
,
![]() және
және
![]() векторлары
векторлары
![]() доға жазықтығында
орналасқанын ескереміз, яғни
доға жазықтығында
орналасқанын ескереміз, яғни ![]() жазықтығында (10 суретті қара). (3),
(5), (6) теңдіктерін ескере отырып (7) - теңдіктің екі
жағын да координаттар осьтеріне проекциялап,
жазықтығында (10 суретті қара). (3),
(5), (6) теңдіктерін ескере отырып (7) - теңдіктің екі
жағын да координаттар осьтеріне проекциялап,
![]() уақыт мезетінде алатынымыз
уақыт мезетінде алатынымыз
![]() .
.
![]() .
.
![]()
Осыдан ![]() уақыт мезетінде абсолют үдеу
уақыт мезетінде абсолют үдеу
![]() ның шамасын табамыз
ның шамасын табамыз
![]() .
.
Жауабы: ![]() болғанда,
болғанда,
![]() ,
, ![]()
Өзіндік жұмыс тапсырма есептері
№№ 21.3, 22.1, 22.3, 22.15, 22.17, 23.14, 23.18, 23.19, 23.27, 23.29, [1].
Динамика
11 Динамиканың негізгі екі есебі. Материялық нүкте қозғалысының дифференциалдық теңдеулерін интегралдау
11.1-мысал.
Салмағы ![]() жүк
жатқан көлденең (горизонталь) платформа
жүк
жатқан көлденең (горизонталь) платформа ![]() үдеумен
вертикаль төмен қозғалады (11.1 суретті қара). Олар
бірге қозғалғанда жүктің платформаға
түсіретін қысым күшін табу керек.
үдеумен
вертикаль төмен қозғалады (11.1 суретті қара). Олар
бірге қозғалғанда жүктің платформаға
түсіретін қысым күшін табу керек.
Шешуі: жүкке бір ғана
актив күші түсірілген – оның салмағы
![]() .
Байланыстардан босату аксиомасын пайдаланып, ойша платформаны алып тастаймыз
да, оның әсерін вертикаль жоғары бағытталған
.
Байланыстардан босату аксиомасын пайдаланып, ойша платформаны алып тастаймыз
да, оның әсерін вертикаль жоғары бағытталған ![]() реакция
күшімен ауыстырамыз.
реакция
күшімен ауыстырамыз.
x–осін қозғалысқа бағыттас төмен қарай тік (вертикаль) бағыттаймыз (11.1 суретті қара). Жүктің негізгі теңдеуі мына түрде жазылады
![]() ,
,
осы теңдеуден:
![]() .
.
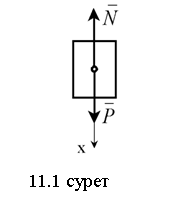 |
Яғни жүктің
платформаға түсіретін қысым күші де
![]() -ға
тең болады.
-ға
тең болады.
11.2-мысал.
Массасы ![]() материалық нүктенің
қозғалысы мынадай теңдеулермен анықталады
материалық нүктенің
қозғалысы мынадай теңдеулермен анықталады ![]() (см).
(см).
Нүктеге әсер етуші күштің проекцияларының нүкте координаттарына тәуелділігін анықтау керек.
Шешуі: алдымен нүкте үдеуінің проекцияларын табамыз. Ол үшін есептің шартында берілген қозғалыс теңдеулерінен уақыт бойынша екі рет туынды аламыз
![]() .
.
Нүкте қозғалысының дифференциалдық теңдеулерін пайдалану арқылы күштің координаттар осьтеріндегі проекцияларын табамыз
![]() .
.
Сан мәндерін орындарына қойып, нүктеге әсер етуші күштің проекцияларының нүкте координаттарына тәуелділігін анықтаймыз
![]() .
.
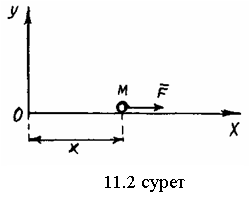
11.3-мысал. Массасы ![]() ге тең, бойында электрдің е заряды бар
материялық нүкте кернеуі
ге тең, бойында электрдің е заряды бар
материялық нүкте кернеуі ![]() болатын біртекті электр өрісінде
орналасқан. Мұндағы А және k берілген тұрақты
шамалар. Электр өрісінде материялық нүктеге
болатын біртекті электр өрісінде
орналасқан. Мұндағы А және k берілген тұрақты
шамалар. Электр өрісінде материялық нүктеге
![]() бағыты
бағыты
![]() кернеуіне қарай бағытталған
күш әсер етеді. Нүктенің бастапқы орнын
координаттардың бас нүктесі ретінде қабылдап, оның
қозғалысын анықтау керек. Салмақ күшінің
әсерін ескермей, бастапқы жылдамдығын нөлге тең
деп санау керек (11.2 суретті қара).
кернеуіне қарай бағытталған
күш әсер етеді. Нүктенің бастапқы орнын
координаттардың бас нүктесі ретінде қабылдап, оның
қозғалысын анықтау керек. Салмақ күшінің
әсерін ескермей, бастапқы жылдамдығын нөлге тең
деп санау керек (11.2 суретті қара).
 |
Шешуі: материялық нүктеге
әсер етуші бір ғана күш бар, ол
![]() . Нүкте қозғалысы – түзу сызықты
қозғалыс. Бойымен нүкте қозғалатын түзуді
. Нүкте қозғалысы – түзу сызықты
қозғалыс. Бойымен нүкте қозғалатын түзуді
![]() осі ретінде қабылдаймыз. Нүкте қозғалысын
сипаттайтын дифференциалдық теңдеу біреу ғана
осі ретінде қабылдаймыз. Нүкте қозғалысын
сипаттайтын дифференциалдық теңдеу біреу ғана
![]()
Осы дифференциалдық теңдеудің айнымалы шамаларын ажыратып жазамыз
![]()
Теңдеу бір рет интегралданғаннан кейін мына түрге келеді
![]() .
.
![]() ді табу үшін бастапқы мәндер
ді табу үшін бастапқы мәндер
![]()
![]() шамаларын жоғарыдағы
шамаларын жоғарыдағы
![]() өрнегіне қоямыз. Сонда
өрнегіне қоямыз. Сонда
![]()
Алдыңғы теңдікке ![]() мәнін қойып оны
қайта жазуға болады
мәнін қойып оны
қайта жазуға болады
![]()
Соңғы теңдеуден
 ,
,
мұндағы тұрақты
![]() -нің нөлге тең екендігін ,
-нің нөлге тең екендігін ,
![]() болғанда
болғанда
![]() болатын бастапқы шартынанан анықтаймыз.
болатын бастапқы шартынанан анықтаймыз.
Сонымен, М нүктенің қозғалыс заңдылығы мынадай өрнекпен беріледі
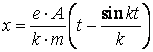 .
.
11.4-мысал. Массасы ![]() ге тең нүкте М үйкеліссіз көлбеу
жазықтық пен кедергілі ортада қозғалсын. Ортаның
кедергі күші жылдамдықтың бірінші дәрежесіне
пропорционал болсын
ге тең нүкте М үйкеліссіз көлбеу
жазықтық пен кедергілі ортада қозғалсын. Ортаның
кедергі күші жылдамдықтың бірінші дәрежесіне
пропорционал болсын ![]() мұндағы k тұрақты шама
(11.3 суретті қара). Нүктенің қозғалыс
заңдылығын анықтау керек.
мұндағы k тұрақты шама
(11.3 суретті қара). Нүктенің қозғалыс
заңдылығын анықтау керек.
Шешуі:
![]() осін келбеу
жазықтық бойымен бағыттайық. Нүктенің
қозғалыс теңдеуі
осін келбеу
жазықтық бойымен бағыттайық. Нүктенің
қозғалыс теңдеуі
![]()
![]() (
(![]() )
)
(![]() ) теңдеуіндегі
) теңдеуіндегі
![]() және
және ![]() айнымалыларды ажыратып жазамыз
айнымалыларды ажыратып жазамыз
 (б)
(б)
(б)-теңдеуді бір рет интегралдап мынадай теңдеу аламыз
![]() (в)
(в)
![]() болғанда,
болғанда, ![]() (г)
(г)
Бұл бастапқы мәндерді (в) теңдеуіне қойсақ
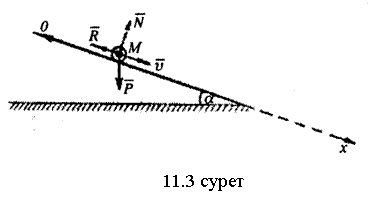
![]()
Олай болса (в) теңдеуі мына түрде қайта жазылады
![]()
Осыдан
![]() (ж)
(ж)
(ж) теңдеуді тағы бір рет интегралдап мынаны аламыз
![]() (к)
(к)
(г)-дегі бастапқы шарттарды пайдалана отырып (з) теңдеуінен Сә тұрақтысын табамыз
![]()
Осыны ескеріп (з) теңдеуін қайта жазамыз
![]() (и)
(и)
Сөйтіп, нүктенің кедергілі ортада көлбеу жазықтықпен қозғалысының заңын (и) теңдеуі түрінде анықтадық. Орта кедергісінің нүктеге әсері k тұрақты кедергі коэффициентімен сипатталады.
11.5-мысал. Салмағы
![]() -ға
тең дененің бағыты көкжиекпен a бұрышын жасайтын
бастапқы жылдамдығы
-ға
тең дененің бағыты көкжиекпен a бұрышын жасайтын
бастапқы жылдамдығы ![]() берілген. Бұдан
әрі қарай дене тек салмақ күші және ауа кедергісі
берілген. Бұдан
әрі қарай дене тек салмақ күші және ауа кедергісі
![]() -дің әсерінен ғана қозғалады. Ауа
кедергісін дене жылдамдығының бірінші дәрежесіне пропорционал
деп есептеп (
-дің әсерінен ғана қозғалады. Ауа
кедергісін дене жылдамдығының бірінші дәрежесіне пропорционал
деп есептеп (![]() ), оның қозғалыс теңдеулерін табу керек (11.4 суретті
қара).
), оның қозғалыс теңдеулерін табу керек (11.4 суретті
қара).
Шешуі: координаттардың
бас нүктесі ретінде нүктенің алғашқы орнын
қабылдап, ![]() осін көлденең
бағыттаймыз. Нүктенің кез келген бір орнын қарастырып,
оған сол уақыт cәтінде әсер ететін күштерді
көрсетейік. Нүкте қозғалысының негізгі
теңдеуі
осін көлденең
бағыттаймыз. Нүктенің кез келген бір орнын қарастырып,
оған сол уақыт cәтінде әсер ететін күштерді
көрсетейік. Нүкте қозғалысының негізгі
теңдеуі
![]() немесе
немесе ![]() .
.
Бұл
теңдеулерді ![]() осьтеріне проекциялаймыз
осьтеріне проекциялаймыз

![]() .
.
Теңдеулердің
екі жақтарын ![]() массасына бөліп,
оларды қайта жазамыз
массасына бөліп,
оларды қайта жазамыз
![]() .
(а)
.
(а)
Екі теңдеу
де коэффициенттері тұрақты, сызықтық теңдеулер
болып табылады. Сызықтық теңдеулерді интегралдаудың
жалпы теориясы бойынша ![]() деп белгілеп, (а)
жүйесіндегі бірінші теңдеудің сипаттаушы теңдеуін
жазамыз
деп белгілеп, (а)
жүйесіндегі бірінші теңдеудің сипаттаушы теңдеуін
жазамыз
![]()
Бұл сипаттаушы
теңдеудің түбірлері ![]()
![]() болғандықтан (а)
жүйесіндегі бірінші теңдеудің жалпы шешімі мына түрде
анықталады
болғандықтан (а)
жүйесіндегі бірінші теңдеудің жалпы шешімі мына түрде
анықталады
![]() ,
,
мұндағы
![]() және
және
![]() - интегралдау тұрақтылары. Енді
- интегралдау тұрақтылары. Енді ![]()
![]() бастапқы
шамаларды пайдалансақ,
бастапқы
шамаларды пайдалансақ, ![]() және
және ![]() арасындағы
тәуелділікті беретін екі теңдеу аламыз
арасындағы
тәуелділікті беретін екі теңдеу аламыз
![]()
![]() .
.
Осы жүйеден

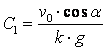 .
.
Сондықтан да (а) жүйесінің бірінші теңдеуінің интегралы мынадай
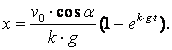
(а) жүйесіндегі екінші теңдеудің жалпы шешімі
![]() ,
,
мұндағы
![]() біртекті
дифференциалдық теңдеудің жалпы шешімі, ал
біртекті
дифференциалдық теңдеудің жалпы шешімі, ал ![]() біртекті
емес дифференциалдық теңдеудің дербес шешімі. Дербес шешім
біртекті
емес дифференциалдық теңдеудің дербес шешімі. Дербес шешім ![]() -ні таңдау
әдісін қолдану арқылы табамыз
-ні таңдау
әдісін қолдану арқылы табамыз
![]()
Ал ![]() -ді сипаттаушы теңдеу
арқылы, жоғарыда
-ді сипаттаушы теңдеу
арқылы, жоғарыда ![]() -ті табуға қолданылған
әдіспен анықтаймыз
-ті табуға қолданылған
әдіспен анықтаймыз
![]()
Сөйтіп, (а) жүйесіндегі екінші дифференциалдық теңдеудің жалпы шешімі мынадай
![]() .
.
Енді
![]() интегралдау
тұрақтыларын табу қалды. Ол үшін бастапқы
шарттарды пайдаланамыз:
интегралдау
тұрақтыларын табу қалды. Ол үшін бастапқы
шарттарды пайдаланамыз: ![]() болғанда
болғанда ![]() болады.
Осы шамаларды
болады.
Осы шамаларды ![]() өрнегіне және
өрнегіне және ![]() өрнегіне
қойсақ
өрнегіне
қойсақ
![]()
![]() ,
,
теңдеулерін аламыз. Бұлардан

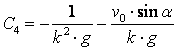 .
.
Сөйтіп, екінші біртекті емес дифференциалдық теңдеудің шешімін таптық
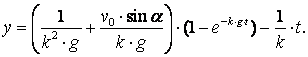
Нүктенің қозғалысын анықтайтын кинематикалық теңдеулерді қатарлап жазамыз

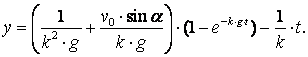
Өзіндік жұмыс тапсырма есептері
№№ 27.1, 27.2, 27.3, 27.4, 27.7, 27.8, 27.30, 27.40, 27.42, 27.43, [1].
12 Материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема
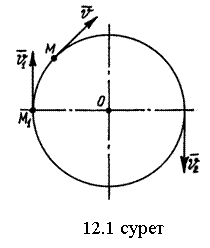
12.1-мысал. Материялық нүкте М
шеңбер бойымен бірқалыпты қозғалады (12.1 суретті
қара). Нүктенің массасы ![]() және оның жылдамдығы
және оның жылдамдығы
![]() . Нүкте жарты шеңбер жол жүріп,
. Нүкте жарты шеңбер жол жүріп,
![]() орнынан
орнынан
![]() орнына орын ауыстырған уақыт
аралығындағы нүктеге түсірілген күштің
орнына орын ауыстырған уақыт
аралығындағы нүктеге түсірілген күштің
![]() импульсін анықтау керек.
импульсін анықтау керек.
 |
Шешуі: материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманы пайдаланамыз
![]() ,
,
мұндағы
![]() және
және
![]() сәйкес
сәйкес
![]() және
және
![]() нүктелерінің жылдамдық векторлары.
нүктелерінің жылдамдық векторлары.
Есептің берілгені бойынша
![]() , яғни
, яғни
![]() ,
,
импульс
![]() -тің бағыты
-тің бағыты
![]() -нің бағытымен бағыттас, ал
оның шамасы
-нің бағытымен бағыттас, ал
оның шамасы
![]() .
.
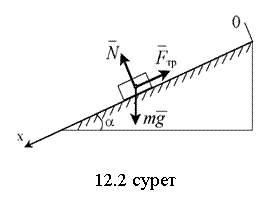
12.2-мысал. Горизонтпен
![]() бұрышын
жасайтын тегіс емес көлбеу жазықтық бетімен салмақты дене
төмен тқозғалады. Дененің
бұрышын
жасайтын тегіс емес көлбеу жазықтық бетімен салмақты дене
төмен тқозғалады. Дененің ![]() жолды
қанша уақыт ішінде жүріп өтетінін анықтау керек.
Көлбеу жазықтықтың үйкеліс коэффициенті
жолды
қанша уақыт ішінде жүріп өтетінін анықтау керек.
Көлбеу жазықтықтың үйкеліс коэффициенті ![]() , көлбеу бұрышы
, көлбеу бұрышы ![]() , дененің
бастапқы жылдамдығы
, дененің
бастапқы жылдамдығы ![]() (12.2 суретті қара).
(12.2 суретті қара).
Шешуі: есептің шартына сай сурет салып аламыз (12.2 суретті қара). Координаттар остерінің бірін көлбеу жазықтық бетімен бағыттаймыз.
Есептің шартында уақыт сұралғандықтан, есепті шешуге қозғалыс мөлшерінің өзгеруі туралы теореманы қолданған жөн
 |
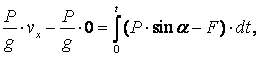
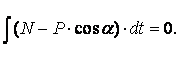 (а)
(а)
Біз (а)
жүйесін құрарда М нүктесіне әсер етуші
![]() күштерін
алдымен
күштерін
алдымен ![]() осіне, одан кейін
осіне, одан кейін ![]() осіне проекцияладық.
(а) жүйесіндегі екінші теңдеуден
осіне проекцияладық.
(а) жүйесіндегі екінші теңдеуден
![]()
![]()
(а) жүйесіндегі бірінші теңдеуден
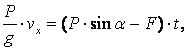
мұндағы F нормаль қысымға пропорционал үйкеліс күші
![]()
Сондықтан да
![]()
Соңғы теңдеудің екі жағын да P-ға қысқартып және айнымалыларын бөлектеп жазу арқылы мынадай теңдікті аламыз
![]()
Бұл теңдеудің сол жағын 0-ден l-ге дейін, ал оң жағын 0-ден Т-ға дейін интегралдаймыз
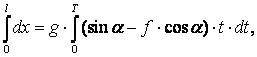
![]()
Соңғы теңдеуден керекті уақыт Т-ны табамыз
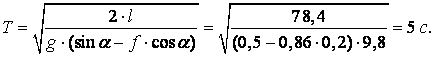
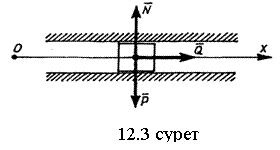
12.3-мысал. Салмағы
![]() -ға тең дене (12.3 суретті қара)
-ға тең дене (12.3 суретті қара)
![]() күшінің әсерінде көлденең бағыттаушы
бойымен қозғалады, оның бағыттаушыға параллель
күшінің әсерінде көлденең бағыттаушы
бойымен қозғалады, оның бағыттаушыға параллель
![]() осіне проекциясы мынадай заңдылықпен өзгереді:
осіне проекциясы мынадай заңдылықпен өзгереді:
![]() мұндағы
мұндағы ![]() және
және
![]() - тұрақты шамалар. Үйкеліс
күшін есепке алмаймыз.
- тұрақты шамалар. Үйкеліс
күшін есепке алмаймыз. ![]() уақыт мезетінде дене жылдамдығын
анықтау керек.
уақыт мезетінде дене жылдамдығын
анықтау керек.
 |
Шешуі: дененің қозғалысы ілгерілемелі қозғалыс, сондықтан оны материялық нүкте ретінде қарастырамыз.
Денеге салмақ ![]() күші, бағыттаушының реакциясы
күші, бағыттаушының реакциясы
![]() және
және
![]() , күші әсер етеді. Салмақ
, күші әсер етеді. Салмақ
![]() және
және
![]() реакция күштері теңгеріледі. Яғни
реакция күштері теңгеріледі. Яғни
![]() күші
күші
![]() күшіне тең.
күшіне тең.
Материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманы пайдаланамыз
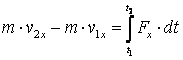 , (а)
, (а)
мұндағы
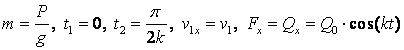 .
.
Сондықтан ![]() теңдеуін мына түрде жазамыз
теңдеуін мына түрде жазамыз
 , немесе
, немесе
![]()
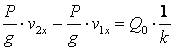 .
.
Осыдан ![]() уақыт мезгілінде дене жылдамдығының
уақыт мезгілінде дене жылдамдығының
![]() осіне проекциясын анықтаймыз
осіне проекциясын анықтаймыз
![]() .
.
Өзіндік жұмыс тапсырма есептері
№№ 28.1, 28.2, 28.3, 28.4, 28.5, 28.6, 28.7, 28.8, 28.9, 28.10, [1].
13 Жұмыс. Материялық нүктенің кинетикалық энергиясының өзгеруі туралы теорема. Қатты дене және жүйе динамикасы. Механикалық жүйе. Жүйенің массасы
13.1 Жұмыс. Материялық нүктенің кинетикалық энергиясының өзгеруі туралы теорема
13.1-мысал. Салмағы
![]() жүкті
горизонтпен 30°
бұрыш құратын көлбеу жазықтықтың
бойымен
жүкті
горизонтпен 30°
бұрыш құратын көлбеу жазықтықтың
бойымен ![]() биіктікке көтеру үшін жұмсалатын ең аз
жұмысты анықтау қажет. Үйкеліс коэффициенті 0,5-ке
тең (3.15 сурет
биіктікке көтеру үшін жұмсалатын ең аз
жұмысты анықтау қажет. Үйкеліс коэффициенті 0,5-ке
тең (3.15 сурет![]() ті қара).
ті қара).
Шешуі: жүкке түсірілген күштер:
- салмақ күші![]() ;
;
- үйкеліс күші –
![]() ;
;
- көлбеу
жазықтықтың нормаль реакция күші![]() . Көлбеу жазықтыққа параллель, бас
нүктесі қозғалыс басталатын нүкте болатын жоғары
бағытта x осін бағыттаймыз.
. Көлбеу жазықтыққа параллель, бас
нүктесі қозғалыс басталатын нүкте болатын жоғары
бағытта x осін бағыттаймыз.
Жүкті жоғары көтеруге жұмсалатын жұмыс, түсірілген күштердің жұмыстарының қосындысына тең
![]()
Салмақ күшінің жұмысы теріс шамаға тең, себебі жүк жер бетінен жоғары көтеріледі
![]() .
.
Үйкеліс күшінің жұмысын мынадай формула арқылы анықтаймыз
![]() .
.
![]()
![]()
![]()
 x
x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 s
s
![]()
![]()
![]() h
h
![]()
![]() a
a
O
a
![]()
13.1 сурет
Егер жүк
![]() биіктікке
көтерілетін болса
биіктікке
көтерілетін болса  , онда
, онда
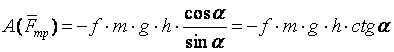 .
.
Орын ауыстыру бағытына
перпендикуляр болғандықтан, нормаль реакция
![]() -нің
жұмысы нөлге тең, яғни
-нің
жұмысы нөлге тең, яғни ![]() .
.
Сонымен, жүкке түсірілген күштер жұмыстарының қосындысы
![]()
![]() .
.
Модулін қабылдаймыз
![]() .
.
13.2-мысал. Шахта лифтісі
![]() жылдамдықпен
төмен қарай қозғалады. Лифтінің массасы
жылдамдықпен
төмен қарай қозғалады. Лифтінің массасы ![]() . Егер
лифтіні ұстап тұратын арқан үзілетін болса, онда
лифтіні
. Егер
лифтіні ұстап тұратын арқан үзілетін болса, онда
лифтіні ![]() жолда тоқтату үшін, сақтандырушы парашют лифті мен
шахтаның арасында қандай шамада үйкеліс күшін пайда
болдыруы қажет? Үйкеліс күшін тұрақты деп
санаймыз.
жолда тоқтату үшін, сақтандырушы парашют лифті мен
шахтаның арасында қандай шамада үйкеліс күшін пайда
болдыруы қажет? Үйкеліс күшін тұрақты деп
санаймыз.
Шешуі: материалық
нүктеге түсірілген ![]() салмақ күшін
және
салмақ күшін
және ![]() күшін көрсетеміз (13.2 суретті қара). Материалық
нүктенің кинетикалық энергиясының өзгеруі туралы
теореманы пайдаланамыз
күшін көрсетеміз (13.2 суретті қара). Материалық
нүктенің кинетикалық энергиясының өзгеруі туралы
теореманы пайдаланамыз
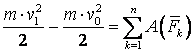 .
.
Материалық нүктеге
түсірілген күштердің ![]() орын ауыстыруында
жұмысын есептейміз
орын ауыстыруында
жұмысын есептейміз
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() s
s
![]()
x
13.2 сурет
Материалық нүкте төмен қарай қозғалатын болғандықтан, салмақ күшінің жұмысы оң шама болады
![]() .
.
Үйкеліс күшінің жұмысы теріс шамаға тең, себебі үйкеліс күші мен орын ауыстыру бағыттары қарама-қарсы
![]()
Соңғы уақыт
мезгілінде лифтінің тоқтайтынын есепке ала отырып,
![]() ,
кинетикалық энергияның өзгеруі туралы теоремаға
қоямыз
,
кинетикалық энергияның өзгеруі туралы теоремаға
қоямыз
 .
.
Осыдан
 ,
,
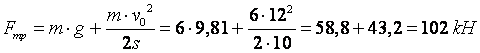 .
.
Өзіндік жұмыс тапсырма есептері
№№ 30.1, 30.2, 30.3, 30.4, 30.5, 30.6, 30.7, 30.8, 30.9, 30.10, [1].
13.2 Қатты дене және механикалық жүйе динамикасы. Жүйе массасы. Материялық жүйенің массалар центрі, қатты дененің инерция моменттері
13.2.1-мысал.
Салмақтары ![]() муфталар A және B-дан,
салмағы
муфталар A және B-дан,
салмағы ![]() иінтректен және
салмағы
иінтректен және
салмағы ![]() AB сызғышынан
құрастырылған эллипсограф механизмінің
массалар центрінің траекториясын анықтау керек.
AB сызғышынан
құрастырылған эллипсограф механизмінің
массалар центрінің траекториясын анықтау керек.
Берілгені:
![]() . Сызғыш
және иінтірек тіртекті, ал муфтаны нүкте массалы деп есептеу керек.
. Сызғыш
және иінтірек тіртекті, ал муфтаны нүкте массалы деп есептеу керек.
Шешуі: координаттар осьтерін
қабылдаймыз (13.3 суретті қара). Жүйенің массалар
центрі C* -ның орнын анықтау үшін оның
![]() координаттарын
мынадай өрнектермен анықтау керек
координаттарын
мынадай өрнектермен анықтау керек
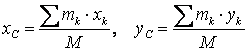 ,
,
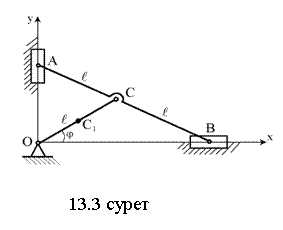 |
ғни қарастырылып отырған жүйенің құрамында төрт дене бар болғандықтан: А и В муфталары, ОС иінтірегі және АВ сызғышы, онда
 ,
,  .
.
Суреттен көретініміз
![]() (т. А),
(т. А), ![]() (т. В),
(т. В),
![]() (т. С1),
(т. С1), ![]() (т. С),
(т. С),
![]() .
.
Онда
 ,
,
 .
.
Массалар центрі траекториясын анықтау үшін осы теңдеулерден уақытты аластаймыз. Ол үшін осы теңдеулердің екі жағын да квадраттап оларды қосамыз
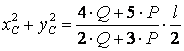 .
.
Сонымен, массалар центрінің
траекториясы центрі О нүктесі және радиусы
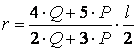 -ге
тең шеңбер болады.
-ге
тең шеңбер болады.
13.2.2-мысал. Радиусы
![]() , ал биіктігі
, ал биіктігі ![]() цилиндрдің осіне
перпедикуляр және цилиндрдің массалар
центрінен
цилиндрдің осіне
перпедикуляр және цилиндрдің массалар
центрінен ![]() қашықтықтағы C нүктесі
арқылы өтетін z осіне қатысты тұтас біртекті цилиндрдің
инерция радиусын есептеу қажет.
қашықтықтағы C нүктесі
арқылы өтетін z осіне қатысты тұтас біртекті цилиндрдің
инерция радиусын есептеу қажет.
Шешуі: цилиндрдің массалар
центрі арқылы ![]() осіне параллель
осіне параллель ![]() осін
жүргіземіз. Цилиндрдің осіне перпендикуляр және массалар
центрі арқылы өтетін оське қатысты инерция моменті (таблицалы
түрде) мынадай өрнекпен анықталатыны белгілі
осін
жүргіземіз. Цилиндрдің осіне перпендикуляр және массалар
центрі арқылы өтетін оське қатысты инерция моменті (таблицалы
түрде) мынадай өрнекпен анықталатыны белгілі
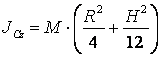 .
.
Гюйгенс теоремасы бойынша:
![]() , мұндағы
, мұндағы ![]() .
.
Анықтайтынымыз
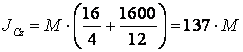 ,
,
![]() .
.
Инерция моментімен инерция радиусының арасындағы байланыс мынадай өрнекпен анықталады
![]() .
.
Осыдан z осіне қатысты цилиндрдің инерция радиусын анықтаймыз
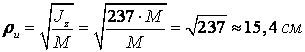 .
.
Өзіндік жұмыс тапсырма есептері
№№ 35.1, 35.2, 35.3, 35.4, 35.5, 35.6, 35.10, 35.17, 35.19, 35.20, [1].
14 Механикалық жүйенің массалар центрі туралы теорема. Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема
14.1 Механикалық жүйенің массалар центрі туралы теорема
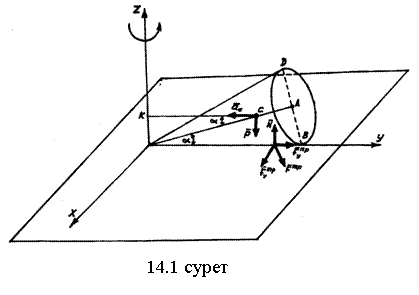 14.1.1-есеп.
Біртекті конус көлденең жазықтықтың бетінде дөңгелеп
қозғалады (14.1 суретті қара). Конустың
14.1.1-есеп.
Біртекті конус көлденең жазықтықтың бетінде дөңгелеп
қозғалады (14.1 суретті қара). Конустың
![]() төбесі қозғалмайды, ал оның биіктігі
төбесі қозғалмайды, ал оның биіктігі
![]() вертикаль
вертикаль
![]() осін бірқалыпты
осін бірқалыпты
![]() жиілікпен айнала қозғалады.
жиілікпен айнала қозғалады.
Конустың салмағы
![]() , ал биіктігі
, ал биіктігі
![]() . Конустың биіктігі мен жасаушысының
арасындағы бұрыш
. Конустың биіктігі мен жасаушысының
арасындағы бұрыш
![]() . Жазықтық пен конустың
арсындағы үйкеліс күшін анықтау керек.
. Жазықтық пен конустың
арсындағы үйкеліс күшін анықтау керек.
Шешуі. Конустың массалар центрінің
қозғалысын қарастырамыз. Конус біртекті
болғандықтан, оның ауырлық центрі
![]() биіктігі
биіктігі
![]() -ның бойында орналасқан және
-ның бойында орналасқан және
![]() . Есептің берілгені бойынша ауырлық центрінің
. Есептің берілгені бойынша ауырлық центрінің
![]() үдеуі
үдеуі
![]() осіне қарай, осы оське перпендикуляр
осіне қарай, осы оське перпендикуляр
![]() бойымен бағытталады.
бойымен бағытталады.
![]() үдеудің шамасы
үдеудің шамасы
![]() ,
,
мұндағы
![]() конус биіктігі
конус биіктігі
![]() -ның
-ның
![]() осін айнала қозғалысының
бұрыштық жылдамдығы.
осін айнала қозғалысының
бұрыштық жылдамдығы.
![]() ,
,
![]() теңдіктерін ескере отырып, мына теңдікті аламыз
теңдіктерін ескере отырып, мына теңдікті аламыз
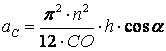 .
.
Конусқа түсірілген сыртқы күштер:
- салмақ күші
![]() , жазықтықтың нормаль реакциясы
, жазықтықтың нормаль реакциясы
![]() және үйкеліс күші
және үйкеліс күші
![]() және
және ![]() және
және ![]() күштері
күштері ![]() осіне параллель;
осіне параллель;
- ![]() күшінің әсер ету сызығы
жазықтықта жатыр.
күшінің әсер ету сызығы
жазықтықта жатыр.
Массалар центрінің қозғалысы туралы теореманы пайдаланып, мынадай векторлық теңдеуді құрамыз
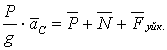
Теңдіктің екі жағын координаттар осьтеріне проекциялаймыз
![]()
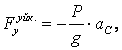
![]()
Осыдан
![]()
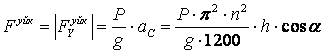 .
.
![]() , ал
, ал
![]() болғандықтан үйкеліс күші
болғандықтан үйкеліс күші
![]() жасаушы бойымен
жасаушы бойымен
![]() төбесіне қарай бағытталады.
төбесіне қарай бағытталады.
14.1.2-есеп. Паром палубасындағы жүк жүкшығыр бойымен тұмсығынан құйрығына қарай қозғалады (14.2 суретті қара).
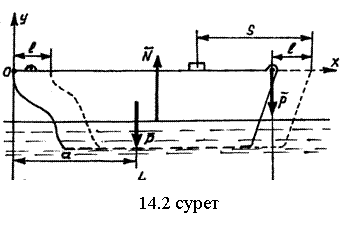 |
Жүктің және паромның
салмақтары![]() және
және
![]() . Егер жүк полубаның бойымен
. Егер жүк полубаның бойымен
![]() аралыққа орын ауыстыратын болса, онда паром қандай
аралыққа орын ауыстырады?
аралыққа орын ауыстыратын болса, онда паром қандай
аралыққа орын ауыстырады?
Шешуі: паром және жүкті бір жүйе ретінде қарастырамыз. Бұл жүйеге келесі сыртқы күштер түсірілген:
- паромның салмағы
![]() ;
;
- жүктің салмағы
![]() ;
;
- гидростатикалық су қысымы
![]() . Барлық сыртқы күштердің горизонталь
. Барлық сыртқы күштердің горизонталь
![]() осіне проекциялары нөлге тең болғандықтан,
массалар центрі жылдамдығының сақталу заңы бойынша
осіне проекциялары нөлге тең болғандықтан,
массалар центрі жылдамдығының сақталу заңы бойынша
![]() .
.
Бастапқы уақыт мезгілінде жүйе тыныштықта болады, сондықтан
![]() .
.
Осыдан
![]() .
.
Яғни қарастырып отырған жүйенің массалар центрі өзінің орнын өзгеріссіз сақтайды. Координаттың бас нүктесі ретінде жүйе қозғалып бастағанға дейінгі паромның құйрығындағы нүкте О-ны қабылдаймыз. Онда, жүйенің бастапқы және соңғы орын ауыстыруларының массалар центрі асциссалары үшін келесі теңдіктер сәйкес келеді
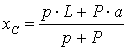 ,
,
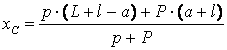 ,
,
мұндағы ![]() паромның ұзындығы;
паромның ұзындығы;
![]() паромның ауырлық центрінен, құйрығы
арқылы жүргізілген вертикаль түзуге дейінгі ара
қашықтық;
паромның ауырлық центрінен, құйрығы
арқылы жүргізілген вертикаль түзуге дейінгі ара
қашықтық;
![]() анықталатын паромның орын ауыстыру аралығы.
анықталатын паромның орын ауыстыру аралығы.
Алдыңғы теңдіктердің оң жақтарын теңестіреміз
![]() .
.
Осыдан
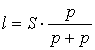 .
.
Орын ауыстыру ![]() шамасы паромның өлшеміне
және ауырлық центрінің орнына байланыссыз екенін
көреміз.
шамасы паромның өлшеміне
және ауырлық центрінің орнына байланыссыз екенін
көреміз.
Сұрақ. Паром қайсы бағытта қозғалады?
Жауап.
![]() 0 болғандықтан паром оңға орын ауыстырады (14.2
суретті қара). Егер
0 болғандықтан паром оңға орын ауыстырады (14.2
суретті қара). Егер ![]() <0 болса, онда паром қарама-қарсы
бағытта қозғалған болар еді.
<0 болса, онда паром қарама-қарсы
бағытта қозғалған болар еді.
Өзіндік жұмыс тапсырма есептері
№№ 35.1, 35.2, 35.3, 35.4, 35.5, 35.6, 35.10, 35.17, 35.19, 35.20, [1].
14.2 Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема
14.2.1-есеп. Вертикаль
жазықтыққа қатысты симметриялы
![]() каналы бойымен сұйық
каналы бойымен сұйық ![]() жылдамдықпен ағады (14.3 суретті
қара).
жылдамдықпен ағады (14.3 суретті
қара).
Каналдың көлденең
қимасы тұрақты және ![]() -қа тең. Сұйықтың
түйіршігінің жылдамдық векторы каналға кірерде горизонтпен
-қа тең. Сұйықтың
түйіршігінің жылдамдық векторы каналға кірерде горизонтпен
![]() , ал каналдан шығарда горизонтпен
, ал каналдан шығарда горизонтпен
![]() бұрыш жасайды.
бұрыш жасайды.
Сұйықтың канал қабырғасына түсіретін қысым күшінің көлденең құраушысын анықтау керек.
Шешуі: мәселені шешу үшін,
жүйенің қозғалыс мөлшерінің өзгеруі туралы
теореманы пайдаланамыз. Механикалық жүйе ретінде каналдың
қабырғаларымен, ![]() және
және
![]() қималарымен шектелген,
қималарымен шектелген,
![]() уақыт сәтіндегі көлемді толтыратын сұйық
түйіршіктерінің жүйесін қарастырамыз.
уақыт сәтіндегі көлемді толтыратын сұйық
түйіршіктерінің жүйесін қарастырамыз.
Қандай да ![]() уақыт аралығында
сұйық түйіршіктері орын ауыстырады және
уақыт аралығында
сұйық түйіршіктері орын ауыстырады және
![]() көлемді толтырады. Механикалық жүйенің
қозғалыс мөлшері
көлемді толтырады. Механикалық жүйенің
қозғалыс мөлшері ![]() уақыт мезгілінде
уақыт мезгілінде
![]() , ал
, ал ![]() уақыт мезгілінде
уақыт мезгілінде
![]() болады. Айырмасы
болады. Айырмасы
![]() ,
,
 |
![]() уақыт аралығындағы жүйе қозғалыс
мөлшерінің өсімшесіне тең.
уақыт аралығындағы жүйе қозғалыс
мөлшерінің өсімшесіне тең.
Қозғалыс мөлшері
![]() ,
,
![]() және
және
![]() көлемдерді толтыратын сұйық
түйіршіктерінің
көлемдерді толтыратын сұйық
түйіршіктерінің ![]() және
және
![]() қозғалыс мөлшерінің
қосындысына тең, яғни
қозғалыс мөлшерінің
қосындысына тең, яғни
![]() .
.
Дәл осы сияқты,
![]() көлемді толтыратын сұйық түйіршіктерінің
қозғалыс мөлшерін
көлемді толтыратын сұйық түйіршіктерінің
қозғалыс мөлшерін ![]() деп белгілейміз, онда
деп белгілейміз, онда
![]() .
.
Сұйықтың каналмен біркелкі
қозғалысында ![]() уақыт аралығында қозғалыс
мөлшері
уақыт аралығында қозғалыс
мөлшері ![]() өзгермейді
өзгермейді
![]() , немесе
, немесе
![]()
![]() (
(![]()
мұндағы
![]() және
және
![]() сұйық түйіршіктерінің
сұйық түйіршіктерінің
![]() және
және
![]() қималарындағы сәйкес
жылдамдықтары;
қималарындағы сәйкес
жылдамдықтары; ![]() және
және
![]() -
-![]() және
және
![]() көлемдердегі сұйықтың
массалары.
көлемдердегі сұйықтың
массалары.
Есептің берілгені бойынша каналдың көлденең қималары тұрақты, сондықтан
![]() .
.
Сұйықтың
тығыздығын ![]() , ал
, ал
![]() уақыт аралығында сұйық
түйіршіктерінің орын ауыстыруын
уақыт аралығында сұйық
түйіршіктерінің орын ауыстыруын ![]() деп белгілейміз.
деп белгілейміз.
Каналдың кез келген екі қимасы арқылы бір уақыт мезгілінде бірдей сұйық ағып өтеді, сондықтан
![]() .
.
![]() теңдігін көлденең
теңдігін көлденең
![]() осіне проекциялаймыз
осіне проекциялаймыз
![]() .
.
Теңдіктің екі жағын
![]() -ға бөліп, туындының анықтамасын
пайдалансақ, алатынымыз
-ға бөліп, туындының анықтамасын
пайдалансақ, алатынымыз
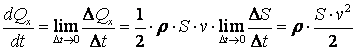 . (
. (![]()
Теорема бойынша
![]() ,
,
![]()
мұндағы
![]() жүйеге түсірілген сыртқы
күштердің негізгі векторының
жүйеге түсірілген сыртқы
күштердің негізгі векторының
![]() осіне проекциясы.
осіне проекциясы.
![]() және
және
![]() теңдіктерінің оң жақтарын
теңестіру арқылы алатынымыз
теңдіктерінің оң жақтарын
теңестіру арқылы алатынымыз
![]() .
.
Судың тығыздығы
![]() . Онда
. Онда
![]() .
.
14.2.2-есеп. Массалары
![]() және
және
![]() екі шар көлденең жазықтықтың
бетінде дөңгелеп қозғалады (14.4 суретті қара).
Шарлар біртекті және олардың диаметрлері тең. Шарлардың
жылдамдықтары
екі шар көлденең жазықтықтың
бетінде дөңгелеп қозғалады (14.4 суретті қара).
Шарлар біртекті және олардың диаметрлері тең. Шарлардың
жылдамдықтары ![]() және
және
![]() .
.
Шарлардың соқтығысынан
соң 1-шар центрінің жылдамдығы
![]() -ке тең болады, ал оның
бағыты өзгермейді.
-ке тең болады, ал оның
бағыты өзгермейді.
Соқтығыстан соң
![]() -шар центрі қандай жылдамдықпен қозғалатынын
анықтау керек. Шарлар мен жазықтықтың арасындағы
үйкеліс есепке алынбайды.
-шар центрі қандай жылдамдықпен қозғалатынын
анықтау керек. Шарлар мен жазықтықтың арасындағы
үйкеліс есепке алынбайды.
Шешуі: шарларды жүйе ретінде
қарастырамыз. Бұл жүйе үшін, соқтығыс
кезіндегі шарлардың өзара әсер күштері ішкі
күштер болады. Сыртқы күштердің
![]() осіне проекциялары нөлге тең, яғни,
жүйенің қозғалыс мөлшерінің сақталу
заңы бойынша:
осіне проекциялары нөлге тең, яғни,
жүйенің қозғалыс мөлшерінің сақталу
заңы бойынша:
![]()
![]() немесе
немесе
![]() ,
,
мұндағы
![]() және
және
![]() соқтығысқа дейінгі
және соқтығыстан кейінгі жүйе қозғалыс
мөлшерінің
соқтығысқа дейінгі
және соқтығыстан кейінгі жүйе қозғалыс
мөлшерінің ![]() осіне проекциялары.
осіне проекциялары.
![]() және
және
![]() -шарлар центрлерінің жылдамдықтарын
-шарлар центрлерінің жылдамдықтарын
![]() және
және
![]() деп белгілейміз. Сонда
деп белгілейміз. Сонда
![]() ,
,
![]() .
.
![]() және
және
![]() теңдіктерін ескере отырып, алдыңғы
екі теңдіктің екі жағын теңестіреміз
теңдіктерін ескере отырып, алдыңғы
екі теңдіктің екі жағын теңестіреміз
![]() .
.
Осыдан
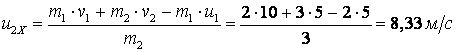 .
.
 |
![]() болғандықтан
болғандықтан
![]() -шар қозғалысының
бағыты өзгермейді.
-шар қозғалысының
бағыты өзгермейді.
Өзіндік жұмыс тапсырма есептері
№№ 36.1, 36.2, 36.3, 36.4, 36.5, 36.7, 36.8, 36.9, 36.10, [1].
15 Механикалық жүйенің кинетикалық моментінің өзгеруі туралы теорема. Айналмалы қозғалыстағы дененің дифференциалдық теңдеуі. Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема
15.1 Механикалық жүйенің кинетикалық моментінің өзгеруі туралы теорема. Айналмалы қозғалыстағы дененің дифференциалдық теңдеуі
15.1.1-есеп. Көлденең
![]() осьті айнала қозғалатын радиусы
осьті айнала қозғалатын радиусы
![]() салмағы
салмағы
![]() -ге тең шкивке трос оралған. Тростың
соңына салмағы
-ге тең шкивке трос оралған. Тростың
соңына салмағы ![]() -ға тең жүк ілінген. Шкивке
тұрақты айналдырушы момент түсірілген (15.1 суретті
қара).
-ға тең жүк ілінген. Шкивке
тұрақты айналдырушы момент түсірілген (15.1 суретті
қара).
Көтерілетін жүктің
![]() үдеуін табу керек.
үдеуін табу керек.
Шешуі: жүктің
![]() жылдамдығына тең, шкивтің бетіндегі кез келген
нүктенің жылдамдығын
жылдамдығына тең, шкивтің бетіндегі кез келген
нүктенің жылдамдығын ![]() деп белгілеп, жүк және шкивтен
құрылған механикалық жүйенің
деп белгілеп, жүк және шкивтен
құрылған механикалық жүйенің
![]() осіне қатысты кинетикалық моментін анықтаймыз:
осіне қатысты кинетикалық моментін анықтаймыз:
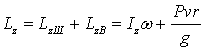 ,
,
мұндағы: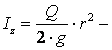 шкивтің
шкивтің
![]() осіне қатысты инерция моменті;
осіне қатысты инерция моменті;
![]() шкивтің бұрыштық жылдамдығы;
шкивтің бұрыштық жылдамдығы;
 жүктің
жүктің
![]() осіне қатысты қозғалыс мөлшер
моменті.
осіне қатысты қозғалыс мөлшер
моменті.
Мәндерін орындарына қоямыз
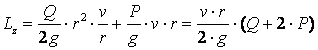 .
.
Жүйеге түсірілген сыртқы
күштердің ![]() осіне қатысты негізгі моменті мына түрде
анықталады
осіне қатысты негізгі моменті мына түрде
анықталады
![]() .
.
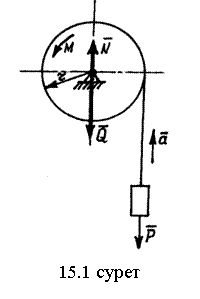 |
Механикалық жүйенің оське қатысты кинетикалық моментінің өзгеруі туралы теореманы пайдаланамыз
![]() ,
,
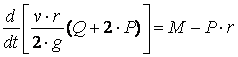 ,
,
 ,
,
мұндағы ![]() сондықтан
сондықтан
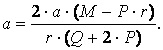
15.1.2-есеп. Радиусы
![]() және
салмағы
және
салмағы ![]() біртекті диск болатын көлденең
платформа, дискінің
біртекті диск болатын көлденең
платформа, дискінің ![]() центрі арқылы
өтетін вертикаль
центрі арқылы
өтетін вертикаль ![]() осін айнала
қозғалады (15.2 суретті қара). Платформаның үстінде
осін айнала
қозғалады (15.2 суретті қара). Платформаның үстінде
![]() осінен
осінен ![]() қашықтықта
салмағы Р арба орналасқан. Платформаның
қашықтықта
салмағы Р арба орналасқан. Платформаның ![]() бұрыштық
жылдамдығын келесі берілгендер бойынша анықтау керек:
бұрыштық
жылдамдығын келесі берілгендер бойынша анықтау керек:
а) платформаның
бетінде арба радиусы ![]() шеңбер бойымен
сағат тіліне қарама-қарсы тұрақты салыстырмалы
жылдамдықпен қозғалғанда (бастапқы уақыт
мезгілінде платформа және арба тыныштықта болады);
шеңбер бойымен
сағат тіліне қарама-қарсы тұрақты салыстырмалы
жылдамдықпен қозғалғанда (бастапқы уақыт
мезгілінде платформа және арба тыныштықта болады);
б)
арбаның қозғалу шарты өзгермейді; платформа
бастапқы уақыт мезгілінде сағат тіліне
қарама-қарсы бағытта тұрақты ![]() бұрыштық
жылдамдықпен айнала қозғалады (бастапқы уақыт
мезгілінде арба платформамен бірге қозғалады);
бұрыштық
жылдамдықпен айнала қозғалады (бастапқы уақыт
мезгілінде арба платформамен бірге қозғалады);
в)
арбаның қозғалу шарты өзгермейді; платформа
бастапқы уақыт мезгілінде сағат тіліне
қарама-қарсы бағытта тұрақты ![]() бұрыштық
жылдамдықпен айнала қозғалады (бастапқы уақыт
мезгілінде арба платформамен бірге қозғалады);
бұрыштық
жылдамдықпен айнала қозғалады (бастапқы уақыт
мезгілінде арба платформамен бірге қозғалады);
г) арбаның
қозғалу шарты өзгермейді, бастапқы уақыт
мезгілінде платформа және арба тыныштықта болады, ![]() осін
айнала қозғалғанда пайда болатын шамасы тұрақты
үйкеліс моменті
осін
айнала қозғалғанда пайда болатын шамасы тұрақты
үйкеліс моменті ![]() әсер етеді.
әсер етеді.
Арбаны материалық нүкте ретінде қарастыру қажет.
Шешуі: «а» жағдайы. “платформа-арба” жүйесінің қозғалысын қарастырамыз. Жүйеге келесі сыртқы күштер түсірілген:
- платформаның салмақ күші;
- арбаның салмақ күші
![]() ;
;
- байланыстардың реакция
күштері ![]() және
және ![]()
![]() осіне
қатысты барлық күштердің моменттері нөлге
тең, себебі күштер
осіне
қатысты барлық күштердің моменттері нөлге
тең, себебі күштер ![]() және
және ![]() .
.
 |
![]() осіне параллель, ал
күштер
осіне параллель, ал
күштер ![]() және
және ![]() оны қиып
өтеді. Есептің берілгені бойынша тіректегі үйкеліс моменттері
нөлге тең.
оны қиып
өтеді. Есептің берілгені бойынша тіректегі үйкеліс моменттері
нөлге тең.
Сонымен, жүйеге түсірілген
сыртқы күштердің ![]() осіне қатысты
негізгі моменті нөлге тең
осіне қатысты
негізгі моменті нөлге тең
![]() .
.
Жүйенің
![]() осіне
қатысты кинетикалық моментінің сақталуы туралы шарты
бойынша
осіне
қатысты кинетикалық моментінің сақталуы туралы шарты
бойынша
![]()
Бастапқы уақыт мезгілінде платформа және арба тыныштықта болғандықтан, кинетикалық моменттің бастапқы шамасы нөлге тең
![]()
Сондықтан
![]() .
.
Жүйенің
![]() осіне
қатысты кинетикалық моменті платформаның және
арбаның сол оске қатысты кинетикалық моменттерінің
қосындысына тең
осіне
қатысты кинетикалық моменті платформаның және
арбаның сол оске қатысты кинетикалық моменттерінің
қосындысына тең
 ,
,
мұндағы
 платформаның
платформаның ![]() осіне қатысты
инерция моменті, ал
осіне қатысты
инерция моменті, ал ![]() арбаның абсолют
жылдамдығы. Арба күрделі қозғалыс жасайды, платформамен
бірге айналмалы тасымал қозғалыста, платформаға қатысты
салыстырмалы қозғалыста болады. Жылдамдықтарды
қосу туралы теорема бойынша
арбаның абсолют
жылдамдығы. Арба күрделі қозғалыс жасайды, платформамен
бірге айналмалы тасымал қозғалыста, платформаға қатысты
салыстырмалы қозғалыста болады. Жылдамдықтарды
қосу туралы теорема бойынша
![]()
Арбаның тасымал қозғалыстағы
жылдамдығының модулі ![]() -ге тең және
-ге тең және ![]() радиусына
перпендикуляр сағат тіліне қарама-қарсы платформаның
айналу бағытымен бағытталады. Арбаның салыстырмалы
жылдамдығы
радиусына
перпендикуляр сағат тіліне қарама-қарсы платформаның
айналу бағытымен бағытталады. Арбаның салыстырмалы
жылдамдығы ![]() шамасымен
берілген және салыстырмалы қозғалысының траекториясы
болатын радиусы
шамасымен
берілген және салыстырмалы қозғалысының траекториясы
болатын радиусы ![]() шеңберге
жанама бойымен сағат тіліне қарама-қарсы
бағытталған. Сондықтан
шеңберге
жанама бойымен сағат тіліне қарама-қарсы
бағытталған. Сондықтан
![]() .
.
![]() ,
, ![]() мәндерін
кинетикалық момент өрнегіне қойып және оның
сақталу заңын ескере отырып алатынымыз
мәндерін
кинетикалық момент өрнегіне қойып және оның
сақталу заңын ескере отырып алатынымыз
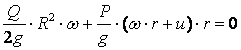 .
.
Осы теңдеуді шеше отырып
платформаның бұрыштық жылдамдығы
![]() -ны
табамыз
-ны
табамыз
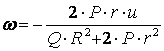 .
.
«б» жағдайы. Бұл
жағдайда мынадай кинетикалық моменттің
![]() осіне
қатысты шарты орындалады
осіне
қатысты шарты орындалады ![]() , күштер
сұлбасы өзгермейді, бірақ бастапқы кинетикалық
момент келесі шамаға тең болады
, күштер
сұлбасы өзгермейді, бірақ бастапқы кинетикалық
момент келесі шамаға тең болады
 .
.
![]() жағдайындағы
айтылғандарды ескере отырып алатынымыз
жағдайындағы
айтылғандарды ескере отырып алатынымыз


 .
.
Сонымен, арба қозғалып бастағаннан
кейін платформаның бұрыштық жылдамдығы өзгереді.
Егер ![]() болса,
онда
болса,
онда ![]() және
платформа сағат тіліне қарсы бағытта айнала
қозғалады. Егер
және
платформа сағат тіліне қарсы бағытта айнала
қозғалады. Егер 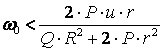 болса, онда
болса, онда ![]() және платформа
сағат тілімен бағыттас бағытта айнала қозғалады.
және платформа
сағат тілімен бағыттас бағытта айнала қозғалады.
«в» жағдайы. Бұл
жағдайда мынадай кинетикалық моменттің
![]() осіне
қатысты шарты орындалады
осіне
қатысты шарты орындалады ![]() бірақ бастапқы
кинетикалық момент келесі шамаға тең болады
бірақ бастапқы
кинетикалық момент келесі шамаға тең болады
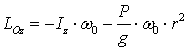 .
.
Сондықтан
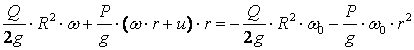 ,
,
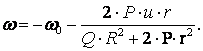
Сонымен, арба қозғалып бастағанда платформаның бұрыштық жылдамдығы көбейеді және платформа сағат тілімен бағыттас бағытта айнала қозғалады.
«г» жағдайы. Егер қарастыратын жағдайға кинетикалық моменттің сақталу шартын пайдалансақ, онда жүйеге түсірілген сыртқы күштердің негізгі моменті, оське қатысты тұрақты үйкеліс моментіне тең болады.
Арбаның платформаға қатысты қозғалыс бағыты сағат тіліне қарсы бағытта және платформа сағат тіліне қарсы бағытта бұрыштық жылдамдықпен айналған жағдайын қарастырайық. Онда оське қатысты үйкеліс моменті теріс болады, яғни
![]() ,
,
және
![]() .
.
Бастапқы уақыт мезгілінде
платформа және арба тыныштықта болғандықтан,
![]() . Сондықтан
. Сондықтан
![]()
![]() жағдайындағы
айтылғандарды және
жағдайындағы
айтылғандарды және ![]() ,
, ![]() бағыттарын ескере отырып
алатынымыз
бағыттарын ескере отырып
алатынымыз

осыдан

Сонымен, платформа ![]() жағдайдағыдай, сағат
тіліне қарсы емес, алдын ала қабылдағандай сағат
тілімен бағыттас айналады. Сондықтан,
жағдайдағыдай, сағат
тіліне қарсы емес, алдын ала қабылдағандай сағат
тілімен бағыттас айналады. Сондықтан, ![]() үйкеліс моментінің модулі
оң болады, яғни теңдіктің оң
жағындағы екінші мүшенің таңбасын
өзгертеміз
үйкеліс моментінің модулі
оң болады, яғни теңдіктің оң
жағындағы екінші мүшенің таңбасын
өзгертеміз
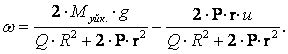
Алынған қорытындыға талдау
жүгізетін болсақ, онда платформа уақытқа бірмәнді
кемімелі бұрыштық жылдамдықпен айналатынын және келесі
уақыт мезгілінде 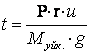 тоқтайтынын көреміз.
тоқтайтынын көреміз.
15.1.3-есеп. Салмағы
![]() , радиусы
, радиусы
![]() шкивті айналмалы қозғалысқа
келтіретін белдіктің тартылыс күштері
шкивті айналмалы қозғалысқа
келтіретін белдіктің тартылыс күштері
![]() және
және
![]() (15.3 суретті қара).
(15.3 суретті қара).
Бұрыштық жылдамдығы
![]() тұрақты болатын шкивке түсірілген
тұрақты болатын шкивке түсірілген ![]() кедергі моментін анықтау керек. Шкив біртекті
дөңгелек диск.
кедергі моментін анықтау керек. Шкив біртекті
дөңгелек диск.
Шешуі: шкивтің
![]() осін айнала қозғалысының дифференциалдық
теңдеуін құрамыз
осін айнала қозғалысының дифференциалдық
теңдеуін құрамыз
 |
![]() ,
,
мұндағы  шкивтің
айналу осіне қатысты инерция моменті.
шкивтің
айналу осіне қатысты инерция моменті.
Осыдан, белгісіз кедергі моментін анықтаймыз
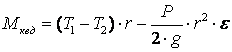 .
.
15.4-есеп.
Тегершіктің бетіндегі нүктенің ![]() жылдамдығына
пропорционал, тежеуші момент
жылдамдығына
пропорционал, тежеуші момент ![]() пайда
болатын, тегершікті тез тоқтату үшін электрлік тежеуші
қолданылады
пайда
болатын, тегершікті тез тоқтату үшін электрлік тежеуші
қолданылады ![]() , мұндағы
, мұндағы ![]() тұрақты
коэффициент. Подшипникте пайда болатын үйкеліс күш моменті
тұрақты
коэффициент. Подшипникте пайда болатын үйкеліс күш моменті ![]() тұрақты
деп есептеуге болады; тегершіктің диаметрі
тұрақты
деп есептеуге болады; тегершіктің диаметрі ![]() , оның
айналу осіне қатысты инерция моменті
, оның
айналу осіне қатысты инерция моменті ![]() . Тегершіктің
бастапқы бұрыштық жылдамдығы
. Тегершіктің
бастапқы бұрыштық жылдамдығы ![]() .
.
Тегершіктің қанша
![]() уақыт
аралығында тоқтайтынын анықтау керек.
уақыт
аралығында тоқтайтынын анықтау керек.
Шешуі: тегершіктің ості айнала қозғалысының дифференциалдық теңдеуін құрамыз
![]() ,
,
немесе
![]() ,
,
мұндағы
![]() .
.
Айнымалыларды айыра отырып, алатынымыз
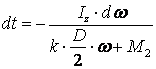 .
.
0-ден Т-ға және ![]() ден
ден ![]() ге дейінгі шектерде
интегралдаймыз
ге дейінгі шектерде
интегралдаймыз
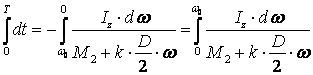 ,
,
 .
.
Өзіндік жұмыс тапсырма есептері
№№ 37.1, 37.2, 37.3, 35.4, 37.5, 37.6, 37.7, 37.8, 37.9, 37.10, [1].
15.2 Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема
15.2.1-есеп. Салмағы
![]() пойыз өрге қарай түзу сызықты, ілгерілемелі
қозғалады;
пойыз өрге қарай түзу сызықты, ілгерілемелі
қозғалады; ![]() . Оның қозғалысына кедергі
күші пойыздың салмағының
. Оның қозғалысына кедергі
күші пойыздың салмағының
![]() -ның
-ның
![]() -ын құрайды. 750 м жол жүргенде жылдамдығы 18-ден 36
-ын құрайды. 750 м жол жүргенде жылдамдығы 18-ден 36
![]() -қа өзгереді (15.4 суретті қара).
-қа өзгереді (15.4 суретті қара).
Локомотивтің тұрақты тарту күшін анықтау керек.
Шешуі: пойыздың ілгерілемелі
қозғалысын материалық нүктенің
қозғалысы ретінде қарастырып, ![]() орын
ауыстыруында нүктенің кинетикалық энергиясының
өзгеруі туралы теореманы пайдаланамыз. Осы орын ауыстыруда пойыздың
жылдамдығы
орын
ауыстыруында нүктенің кинетикалық энергиясының
өзгеруі туралы теореманы пайдаланамыз. Осы орын ауыстыруда пойыздың
жылдамдығы ![]() -тан
-тан ![]() -қа
өседі.
-қа
өседі.
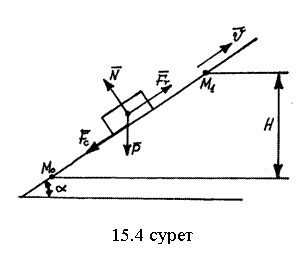 |
Пойызға әсер ететін
күштер: локомотивтің тарту күші ![]() ,
пойыздың салмақ күші
,
пойыздың салмақ күші ![]() ,
рельстің нормаль реакция күші
,
рельстің нормаль реакция күші ![]() және
қозғалысына кедергі күші
және
қозғалысына кедергі күші ![]()
![]() , ал
, ал ![]() .
.
![]() тарту
күшінің
тарту
күшінің ![]() орын
ауыстырғандағы жұмысы мынаған тең
орын
ауыстырғандағы жұмысы мынаған тең
![]() .
.
Пойыздың
![]() салмақ
күшінің жұмысы, вертикаль
салмақ
күшінің жұмысы, вертикаль ![]() орын
ауыстыруына байланысты және мынаған тең
орын
ауыстыруына байланысты және мынаған тең
![]() ,
,
мұндағы
![]() -бұрышы
өте аз болғандықтан
-бұрышы
өте аз болғандықтан ![]() және
және
![]() .
.
![]() жылдамдығына
перпендикуляр, рельстің реакция
жылдамдығына
перпендикуляр, рельстің реакция ![]() күшінің
жұмысы нөлге тең.
күшінің
жұмысы нөлге тең.
Кедергі
![]() күшінің
күшінің
![]() орын
ауыстырғандағы жұмысы мынаған тең
орын
ауыстырғандағы жұмысы мынаған тең
![]() .
.
Пойыздың
![]() массасының
шамасын және барлық күштер жұмыстарының шамаларын
анықтаймыз
массасының
шамасын және барлық күштер жұмыстарының шамаларын
анықтаймыз
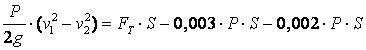 .
.
Локомотивтің тарту күшінің шамасын табамыз
![]()
15.2.2-есеп. Электр
қозғаушының роторы ![]() бұрыштық
жылдамдықпен айнала қозғалады. Ұзындығы
бұрыштық
жылдамдықпен айнала қозғалады. Ұзындығы ![]() иінтірек
АВ негізі С тежеушіден және диаметрі
иінтірек
АВ негізі С тежеушіден және диаметрі ![]() тежеуші
дискіден тұратын, тежеуші негіз оны қосқаннан кейін
жұмыс істеп бастайды (15.5 суретті қара). Диск мен негіздің
арасындағы үйкеліс коэффициенті
тежеуші
дискіден тұратын, тежеуші негіз оны қосқаннан кейін
жұмыс істеп бастайды (15.5 суретті қара). Диск мен негіздің
арасындағы үйкеліс коэффициенті ![]() , ара
қашықтық
, ара
қашықтық ![]() . Иінтірек соңына
. Иінтірек соңына ![]() күш
түсірілген. Қозғаушының валымен айналатын
бөлшектерінің салмағы
күш
түсірілген. Қозғаушының валымен айналатын
бөлшектерінің салмағы ![]() , ал айналу өсіне
қатысты радиус инерциясы
, ал айналу өсіне
қатысты радиус инерциясы ![]() . Негіз С-ның
өлшемі, иінтіректің салмағы және тіректегі
үйкеліс есепке алынбайды.
. Негіз С-ның
өлшемі, иінтіректің салмағы және тіректегі
үйкеліс есепке алынбайды.
Қозғаушының қанша айналыс жасап тоқтайтынын анықтау керек.
Шешуі: механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теореманы пайдаланамыз
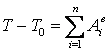 .
.
Соңғы кинетикалық энергия ![]() , ал бастапқы
кинетикалық энергия
, ал бастапқы
кинетикалық энергия
![]() .
.
Қозғаушының валына
түсірілген күштердің ішінде тек үйкеліс күші
![]() жұмыс
жасайды. Ол мынаған тең
жұмыс
жасайды. Ол мынаған тең
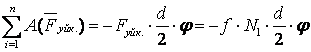 .
.
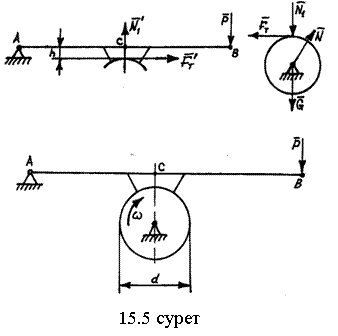
Иінтіректің
![]() реакция
күшін анықтау үшін, айналу
реакция
күшін анықтау үшін, айналу ![]() осіне қатысты,
тежеуші иінтірекке түсірілген күштердің моменттер
теңдеуін құрамыз
осіне қатысты,
тежеуші иінтірекке түсірілген күштердің моменттер
теңдеуін құрамыз
![]() ,
,
![]()
мұндағы
![]() тежеуші
негіздің биіктігі.
тежеуші
негіздің биіктігі.
Әсер және қарсы әсер заңы бойынша
![]() .
.
Егер тежеуші негіздің биіктігін
есепке алмасақ ![]() , онда
, онда ![]() -теңдеуінен алатынымыз
-теңдеуінен алатынымыз
![]() .
.
Әсер және қарсы әсер заңы бойынша
![]() .
.
Онда
![]() ,
,
мұндағы
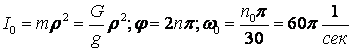 .
.
Алдыңғы теңдікті мынадай түрге келтіреміз
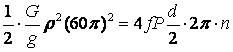 .
.
Осыдан
 айн.
айн.
15.2.3-есеп. Егер автомобильдің
моторын сөндірген уақыт мезгілінде жылдамдығы
![]() -ға
тең болса, онда түзу жолдың бойында қанша
-ға
тең болса, онда түзу жолдың бойында қанша ![]() жол
жүріп тоқтайды? Жүргізуші және жолаушыларды бірге
есептегенде автомобильдің кузовының салмағы
жол
жүріп тоқтайды? Жүргізуші және жолаушыларды бірге
есептегенде автомобильдің кузовының салмағы ![]() ,
төрт дөңгелектерінің әрбіреуінің
салмағы
,
төрт дөңгелектерінің әрбіреуінің
салмағы ![]() , массалар центрі
арқылы өтетін оське қатысты радиус инерциясы
, массалар центрі
арқылы өтетін оське қатысты радиус инерциясы ![]() ,
дөңгелектің радиусы
,
дөңгелектің радиусы ![]() , домалау үйкеліс
коэффициенті
, домалау үйкеліс
коэффициенті ![]() . Дөңгелек сырғанамай дөңгелейді.
Ауаның кедергі күшін және кузовтың вертикаль орын ауыстыруын
есепке алмаймыз (15.6 суретті қара).
. Дөңгелек сырғанамай дөңгелейді.
Ауаның кедергі күшін және кузовтың вертикаль орын ауыстыруын
есепке алмаймыз (15.6 суретті қара).
Шешуі: “Жүргізуші және жолаушылармен бірге автомобильді” өзгермейтін механикалық жүйе ретінде қарастырамыз. Ішкі үйкелісті есепке алмасақ, онда барлық ішкі күштердің жұмыстарының қосындысы нөлге тең.
Сондықтан
 .
.
![]()
Соңғы кинетикалық энергия ![]() , яғни
, яғни
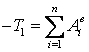 ,
, ![]()
ал бастапқы кинетикалық энергия
![]() ,
,
Мұндағы;
- 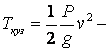 автомобильдің
ілгерілемелі қозғалысының кинетикалық энергиясы;
автомобильдің
ілгерілемелі қозғалысының кинетикалық энергиясы;
-
 дөңгелектің
жазық параллель қоз-ғалысының кинетикалық
энергиясы;
дөңгелектің
жазық параллель қоз-ғалысының кинетикалық
энергиясы;
-
![]() дөңгелектің
массалар центрінің жылдамдығы;
дөңгелектің
массалар центрінің жылдамдығы;
- 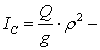 дөңгелектің
массалар центрі
дөңгелектің
массалар центрі ![]()
![]() арқылы өтетін оське
қатысты инерция моменті.
арқылы өтетін оське
қатысты инерция моменті.
Дөңгелектің
жылдамдықтар лездік центрі дөңгелек пен жолдың жанасу
нүктесінде орналасқан. Сонда ![]() және
және
![]() .
.
![]() мәндерін
мәндерін ![]() өрнегіне
қоямыз
өрнегіне
қоямыз
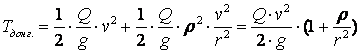 .
.
Сонымен жүйенің кинетикалық энергиясы бастапқы орнында
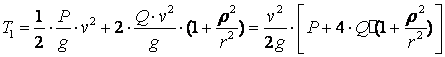 .
.
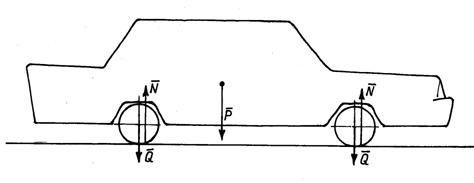 |
15.6 сурет
Жүйеге түсірілген сыртқы
күштер: салмақ күштері ![]() және
және ![]() ,
жолдың нормальдық реакциясы
,
жолдың нормальдық реакциясы ![]() , дөңгелек пен
жолдың арасындағы үйкеліс күші
, дөңгелек пен
жолдың арасындағы үйкеліс күші ![]() .
.
Жүйеге түсірілген барлық
сыртқы күштердің ![]() орын
ауыстырғандағы жұмыстарының қосындысы мынадай
өрнекпен анықталады
орын
ауыстырғандағы жұмыстарының қосындысы мынадай
өрнекпен анықталады
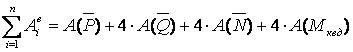 ,
, ![]() .
.
Есептің шарты бойынша, кузов пен
доңғалақ вертикаль орын ауыстырмайды және
![]() .
.
![]()
![]() болғандықтан
болғандықтан ![]() үйкеліс
күші доңғалақ пен жолдың түйісетін
нүктесіне, яғни
үйкеліс
күші доңғалақ пен жолдың түйісетін
нүктесіне, яғни ![]() жылдамдықтар лездік
центріне түсірілген деп қарастырылады. Осы үйкеліс
күшінің қуаты нөлге тең
жылдамдықтар лездік
центріне түсірілген деп қарастырылады. Осы үйкеліс
күшінің қуаты нөлге тең
![]() немесе
немесе ![]() .
.
Сонымен, үйкеліс күшінің
ақырғы ![]() орын ауыстыруында, қуаттан
уақыт бойынша алынған интегралына тең жұмысы да
нөлге тең
орын ауыстыруында, қуаттан
уақыт бойынша алынған интегралына тең жұмысы да
нөлге тең
![]() .
.
Дөңгелектердің
![]() жұмыстарының
қосындысын анықтау үшін, радиустары, домалау үйкеліс
коэффициенттері және жүктемелері барлық төрт дөңгелектер
үшін бірдей болатынын есепке аламыз, сондықтан осы
жұмыстардың қосындысын бір дөңгелекке келтіреміз.
Нормаль қысым күші мынадай өрнек арқылы
анықталады
жұмыстарының
қосындысын анықтау үшін, радиустары, домалау үйкеліс
коэффициенттері және жүктемелері барлық төрт дөңгелектер
үшін бірдей болатынын есепке аламыз, сондықтан осы
жұмыстардың қосындысын бір дөңгелекке келтіреміз.
Нормаль қысым күші мынадай өрнек арқылы
анықталады
![]() .
.
Онда
![]() .
.
Элементарлық жұмысы
![]() ,
,
мұндағы:
-
![]() жылдамдықтар лездік
центрі
жылдамдықтар лездік
центрі ![]() -ға қатысты элементарлық бұрылу бұрышы
-ға қатысты элементарлық бұрылу бұрышы ![]() болғандықтан
болғандықтан
![]() және
және ![]()
![]() ;
;
-
![]() бұрылу бұрышы
мен домалау үйкеліс қос күш моментінің бағыттары
қарама-қарсы болғандықтан, жұмысы теріс болады.
бұрылу бұрышы
мен домалау үйкеліс қос күш моментінің бағыттары
қарама-қарсы болғандықтан, жұмысы теріс болады.
![]() толық орын
ауыстыруында домалау үйкеліс қос күш моменті
жұмыстарының қосындысын есептеу үшін,
толық орын
ауыстыруында домалау үйкеліс қос күш моменті
жұмыстарының қосындысын есептеу үшін, ![]() мәнінен
мәнінен
![]() -ден
-ден ![]() -ке дейігі шектерінде интеграл аламыз
-ке дейігі шектерінде интеграл аламыз
![]() .
.
Сонымен
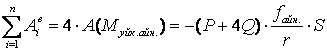 .
.
![]() және
және ![]() мәндерін
(**) теңдеуіне қойып
мәндерін
(**) теңдеуіне қойып ![]() -ке қатысты шешеміз
-ке қатысты шешеміз
 .
.
Сан мәндерін
![]()
![]() орындарына қоя
отырып, алатынымыз
орындарына қоя
отырып, алатынымыз

Өзіндік жұмыс тапсырма есептері
№№ 38.1, 38.2, 38.3, 38.4, 38.5, 38.6, 38.7, 38.8, 38.9, 38.10, [1].
Әдебиеттер тізімі
1. Жолдасбеков Ө.А., Сағитов М.Н. Теориялық механика. – Алматы: Ғылым, 2002.
2. Тойбаев С.Н. Теориялық механика. Оқу құралы. – «Бастау», 2006.
3. Нұғыман А.М. Теориялық механика негіздері. – Семей: Шәкәрім атындағы СМУ, 2002.
4. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Учебник: в 2-х т. – М.: Наука, 2002.
5. Мещерский И.В. Сборник задач по теоретической механике. Учеб. пособие. – СПб.: Изд-во «Лань», 2005.
6. Никитин Н.Н. Курс теоретической механики. Учебник. – М.: Высшая школа, 1990.
7. Тарг С.М. Краткий курс теоретической механики. Учебник. – М.: Наука, 2002.
8. Яблонский А.А. Курс теоретической механики. Учебник: в 2-х т. – М.: Высшая школа, 2002.
9. Сборник заданий для курсовых работ по теоретической механике. Учебное пособие./Под ред. А.А.Яблонского. – М.: Высшая школа, 1985.
2012ж. жиынтық жоспары, реті. 245