Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра компьютерных технологий
ОСНОВЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
Методические указания к выполнению лабораторных работ для студентов
всех форм обучения специальности 5В070300 – Информационные системы
Алматы 2011
СОСТАВИТЕЛИ: Мусатаева Г.Т., Конуспаева А.Т., Байжанова Д.О. Основы компьютерного моделирования. Методические указания к выполнению лабораторных работ для студентов всех форм обучения специальности 5В070300 – Информационные системы. - Алматы: АУЭС, 2011. - 39 с.
Методические указания составлены в соответствии с требованиями квалификационной характеристики специалиста, Государственных стандартов, типовой программы курса. Они составлены с учетом активизации процесса изучения основ курса, закреплению лекционного курса и являются подготовкой к проведению лабораторных работ.
Методические указания предназначены для студентов всех форм обучения специальности 5В070300 – Информационные системы.
Библиография – 7 названий.
Рецензент: канд. физ.-мат. наук, доцент Б. М. Шайхин.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.
© НАО «Алматинский университет энергетики и связи», 2011 г.
1 Лабораторная работа. Моделирование динамики производственных процессов
Цель работы: познакомиться с методикой нахождения математической зависимости между совокупностями данных (регрессионный анализ), и её практическим применением на примере оценки деятельности предприятия. Познакомиться с методикой моделирования производственных функций, основанного на многовариантных данных наблюдений. Расширить понимание применения метода регрессионного и дисперсионного анализа.
Постановка задачи
Любой производственный процесс представляет собой технологию (набор технологий) для «переработки» ресурсов в готовую продукцию. Ресурсы (от фр. ressources — средства, запасы, источники средств). Приобретение ресурсов связано с затратами. Применительно к реальному производству под затратами можно понимать: расход денежных средств на приобретение сырья, оплата труда персоналу, налоговые отчисления и т. д.
Одна из задач данного курса преследует своей целью определение доли каждого из видов затрат в готовой продукции. Результатом моделирования является производственная функция, устанавливающая влияние каждого из видов производственных затрат на выпуск готовой продукции.
При моделировании, как и в прошлой работе, используется регрессионный метод ( от лат. regressio — движение назад ), суть которого заключается в том, что делается попытка математического описания реального явления по его результатам или проявлениям.
Уравнение искомой функции имеет вид:
Y = a0 + a1x1 + a2x2 +×××+ anxn,
где Y — стоимость готовой продукции,
a0 — денежное выражение постоянно присутствующих, не изменяющихся затрат (начальный капитал, земельный налог, амортизационные отчисления и т. д.)
a1××× an — денежное выражение единицы соответствующего вида затрат x1××× xn.
В результате решения задачи должны быть получены числовые значения коэффициентов a0××× an. Процесс моделирования базируется на исходных данных, полученных в результате нескольких наблюдений за производственным процессом.
Пример решения задачи
Чтобы решение сделать более наглядным, разобьём его на этапы:
1) Сбор исходной информации.
2) Преобразование таблицы исходной информации в аргументную матрицу.
3) Преобразования аргументной матрицы с целью получения системы уравнений (системы нормальных уравнений).
4) Решение системы нормальных уравнений и получение формулы производственной функции.
5) Определение погрешностей моделирования и пригодности полученной производственной функции.
1) Сбор исходной информации
|
п/п |
x1 |
x2 |
Y |
|
1 |
14 |
8 |
260 |
|
2 |
4.8 |
30 |
311.2 |
|
3 |
4.9 |
26 |
280.5 |
|
4 |
5 |
20 |
234 |
|
5 |
5.5 |
16 |
209 |
|
6 |
6 |
10.5 |
172 |
|
7 |
7.5 |
8.3 |
175.4 |
|
8 |
8 |
4.4 |
151.2 |
Предположим, некоторое производство перерабатывает x1 и x2 (единиц) исходных материалов в неделю, в результате чего, выпускается готовой продукции на сумму Y. Произведя восемь замеров x1, x2 и Y в разное время (например, с промежутком в одну неделю), получим исходную таблицу данных для построения производственной функции (модели).
2) Создание аргументной матрицы
Согласно общему виду уравнения производственной функции
a0 + a1x1 + a2x2 = Y
преобразуем таблицу исходных данных в матрицу. В результате получим следующее:
|
1 |
14 |
8 |
260 |
|
1 |
4.8 |
30 |
311.2 |
|
1 |
4.9 |
26 |
280.5 |
|
1 |
5 |
20 |
234 |
|
1 |
5.5 |
16 |
209 |
|
1 |
6 |
10.5 |
172 |
|
1 |
7.5 |
8.3 |
175.4 |
|
1 |
8 |
4.4 |
151.2 |
№1
Отбросив четвёртый столбец получим аргументную матрицу исходных данных:
|
1 |
14 |
8 |
|
1 |
4.8 |
30 |
|
1 |
4.9 |
26 |
|
1 |
5 |
20 |
|
1 |
5.5 |
16 |
|
1 |
6 |
10.5 |
|
1 |
7.5 |
8.3 |
|
1 |
8 |
4.4 |
№2
3) Получение системы нормальных уравнений
Для нахождения коэффициентов a0××× a2 требуется решить систему трёх уравнений. Коэффициенты интересующих нас уравнений можно получить путём перемножения двух полученных матриц. Однако, вторую матрицу перед умножением нужно транспонировать (поменять местами строки и столбцы). Итак, транспонируем аргументную матрицу. В результате получим:
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
14 |
4.8 |
4.9 |
5 |
5.5 |
6 |
7.5 |
8 |
|
8 |
30 |
26 |
20 |
16 |
10.5 |
8.3 |
4.4 |
№3
Две матрицы могут быть перемножены если у них «внутренние» размерности одинаковые (т. е. число строк первой матрицы равно числу столбцов второй). Результатом произведения является матрица, размеры которой совпадают с «внешними» размерами матриц-множителей (число столбцов — как у первой, число строк — как у второй). В нашем случае, результатом перемножения двух матриц является матрица из четырёх столбцов и трёх строк. Для нахождения элемента результирующей матрицы, находящегося в строке i и столбце j нужно умножить каждый элемент первой матрицы, находящийся в строке i на соответствующий элемент второй матрицы, находящийся в столбце j, и полученные значения произведений сложить.
В результате вычислений получим результирующую матрицу:
|
8 |
55,7 |
123,2 |
1793,3 |
|
55,7 |
454,5 |
731,85 |
12384,8 |
|
123,2 |
731,85 |
2494,5 |
30660,1 |
№4
Элементы матрицы представляют собой коэффициенты системы трёх уравнений. Система имеет вид:
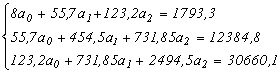
4) Решение системы нормальных уравнений
Систему уравнений можно решить любым способом (подстановкой, методом Жордана-Гаусса и т. д.). Каждый из способов имеет свои достоинства и недостатки, заключающиеся либо в чрезмерной громоздкости, либо в потери точности вычислений. При использовании ЭВМ, когда громоздкость вычислений не играет заметной роли, систему можно решить методом «обратной матрицы». При расчёте «вручную» можно воспользоваться довольно простым, но не очень точным методом «исключения переменных». Разделим почленно каждое из уравнений на коэффициент при a0. Получим:
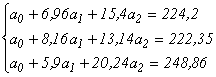
Вычтем почленно из первого уравнения второе, а затем третье с целью получения системы из двух уравнений с двумя неизвестными.
Аналогично, разделив первое уравнение на -1.2, второе на 1.06, и вычтя из первого уравнения второе получим:
![]() , откуда
, откуда ![]() .
.
Подставляя a2 в любое из двух уравнений системы найдём a1 , после чего, произведя подстановку значений a1 и a2 в систему из трёх уравнений найдём значение a0. В результате вычислений найдём:
![]()
![]() .
.
С учётом найденных значений коэффициентов уравнение производственной функции примет вид:
Y=8,32+13,45x1+7,9x2.
5) Определение погрешностей моделирования
Используя метод дисперсионного анализа (от лат. dispersus — рассыпанный, рассеянный), следует выяснить пригодность полученной модели.
В качестве критериев, оценивающих качество модели воспользуемся четырьмя показателями: абсолютной погрешностью (SОст), коэффициентом детерминации (D), индексом корреляции (I), критерием Фишера (FРасч).
Найдём среднюю
фактически произведённую продукцию : 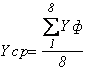 ;
; ![]() .
.
Для удобства дальнейших расчётов заполним таблицу:
|
N |
Yф |
Yт |
(Yф - Yср)2 |
(Yт - Yср)2 |
(Yф - Yт) |
(Yф - Yт)2 |
|
1 |
260 |
260.14 |
1284,3 |
1294,7 |
-0.14 |
0.02 |
|
2 |
311.2 |
310,9 |
7575,5 |
7520,9 |
0,3 |
0,09 |
|
3 |
280.5 |
280.5 |
3173.9 |
3173,9 |
0 |
0 |
|
4 |
234 |
234.2 |
96,8 |
101,7 |
-0,2 |
0.06 |
|
5 |
209 |
209.2 |
229,9 |
222,5 |
-0.2 |
0.06 |
|
6 |
172 |
172.3 |
2720,9 |
2685,3 |
-0.3 |
0.11 |
|
7 |
175.4 |
175.1 |
2377,8 |
2409,9 |
0.3 |
0,11 |
|
8 |
151.2 |
150.9 |
5323,5 |
5373,1 |
0,3 |
0,11 |
|
Сумма: |
22782.7 |
22782,1 |
0.06 |
0,56 |
||
Совокупность исходных данных Yф имеет 8 степеней свободы (n=8); совокупность расчётных данных Yт имеет 3 степени свободы (v=3); совокупность Yср имеет 1 степень свободы.
Следовательно, совокупность (Yф - Yср) имеет 7 степеней свободы; (Yт - Yср) имеет 2 степени свободы; (Yф - Yт) имеет 5 степеней свободы.
Теперь можно определить дисперсии:
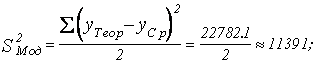
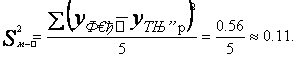
Абсолютная погрешность
составит: ![]()
Коэффициент
детерминации: 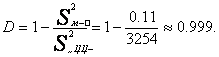
Индекс корреляции: ![]()
Критерий Фишера: 
Вывод: Качество модели приемлемое т. к. индекс корреляции больше 0,7 и расчётный критерий Фишера больше табличного для данного случая (FТаб = 5,8).
Краткие указания к выполнению работы
Запустите Microsoft Excel и в одну из верхних ячеек листа появившейся книги внесите номер варианта полученного задания и название лабораторной работы.
Создание аргументной матрицы
Решение задачи нужно начать с создания матрицы исходных данных (матрица №1). После этого создайте массив аргументной матрицы (матрица №2).
Получение системы нормальных уравнений
Создайте массив, представляющий собой транспонированную аргументную матрицу (матрица №3), используя функцию ТРАНСП.
Используя функцию МУМНОЖ, умножьте полученную транспонированную матрицу на матрицу исходных данных (№1), в результате чего вы получите массив, состоящий из коэффициентов нормальных уравнений системы ( матрица №4).
Решение системы нормальных уравнений
Итак, получили массив коэффициентов нормальных уравнений системы. Правый столбец полученного массива представляет собой столбец результатов уравнений. Как говорилось выше, систему нужно решать методом «обратной матрицы». Для этого разделите полученный массив на две части: массив аргументов и массив результатов. Следует помнить, что полученный массив аргументов должен получиться «квадратным» (число строк равно числу столбцов), иначе нахождение обратной матрицы будет невозможным. Используя функцию МОБР, создайте массив, представляющий собой обратную матрицу от матрицы аргументов нормальных уравнений.
Используя функцию МУМНОЖ, умножьте полученную обратную матрицу на матрицу результатов нормальных уравнений системы. В результате умножения получится массив, состоящий из одного столбца и содержащий искомые коэффициенты уравнения производственной функции: a0 ,a1 ,...,an . Производственная функция получена!
Определение погрешностей моделирования
Основной частью данного этапа является создание таблицы (см. выше).
Для вычисления значений столбцов (Yф - Yср)2 и (Yт - Yср)2 требуется среднее арифметическое значение фактических Y. Поэтому, перед тем, как создавать таблицу, удобно в отдельной ячейке вычислить Yср, воспользовавшись функцией СРЗНАЧ.
Для нахождения сумм значений столбцов (Yф-Yср)2, (Yт-Yср)2 и (Yф-Yт)2 удобно воспользоваться кнопкой «Автосуммирование» на стандартной панели инструментов.
При определении
дисперсий ![]() следует
помнить, что совокупность исходных данных Yф имеет n случайных степеней
свободы (по числу наблюдений), совокупность расчётных данных Yт имеет v степеней свободы (по
числу постоянных коэффициентов формулы производственной функции a0 ,a1 ,...), совокупность Yср имеет 1 степень свободы.
следует
помнить, что совокупность исходных данных Yф имеет n случайных степеней
свободы (по числу наблюдений), совокупность расчётных данных Yт имеет v степеней свободы (по
числу постоянных коэффициентов формулы производственной функции a0 ,a1 ,...), совокупность Yср имеет 1 степень свободы.
Значение табличного
критерия Фишера определяется по соответствующей таблице на основании степеней
свободы числителя ![]() ,
и знаменателя
,
и знаменателя ![]() .
Числа степеней свободы числителей расположены в столбцах таблицы, а числа
степеней свободы знаменателей — в строках. На пересечении соответствующей
строки и столбца находится числовое значение табличного критерия Фишера для
данного случая.
.
Числа степеней свободы числителей расположены в столбцах таблицы, а числа
степеней свободы знаменателей — в строках. На пересечении соответствующей
строки и столбца находится числовое значение табличного критерия Фишера для
данного случая.
Каждый шаг решения задачи должен сопровождаться исчерпывающими комментариями. Отчёт о выполнении лабораторной работы печатается на бумаге и сохраняется в виде файла *.XLS .
Контрольные вопросы
1) В чём суть регрессионного метода моделирования?
2) Какой практический смысл имеют коэффициенты a1××× an, какую размерность они имеют?
3) Какой практический смысл имеют переменные x1××× xn, какую размерность они имеют?
4) Как решить систему уравнений методом «обратной матрицы» средствами Microsoft Excel.
5) Как определить качество модели на основании индекса корреляции, критерия Фишера?
2 Лабораторная работа. Моделирование производственных функций
Цель работы: познакомиться с методикой построения математической модели, описывающей развитие процесса во времени (тренда). Познакомиться с особенностями прогнозирования будущего состояния системы.
Применить полученные знания в решении задачи. Научиться решать системы уравнений методом «обратной матрицы» с использованием Microsoft Excel.
Постановка задачи
Деятельность любого предприятия можно характеризовать результатами его работы. Причём, в качестве критерия оценки можно выбрать практически любой производственный показатель (тоннаж выпускаемой продукции, оборот средств, количество обслуживаемых клиентов и т. д.) Наблюдая за изменением, выбранного для наблюдения параметра, можно сделать общую оценку тенденции развития предприятия. Более того, установив связь между моментами времени наблюдений и динамикой изменения выбранного параметра, можно прогнозировать состояние предприятия в будущем.
Выяснение общей тенденции (тренда) развития предприятия предполагает построение математической модели на основе наблюдений за выбранным производственным показателем. Совокупность наблюдений (уровней), зависящая от времени получила название временного ряда. Наблюдения должны производиться через равные промежутки времени. Следует отметить, что при построении данной модели не предполагается учёта внутрипроизводственных экономических параметров, деятельность предприятия изучается как бы извне.
Искомая математическая модель описывается формулой параболического тренда второй степени:
Y=a0+a1×t+a2×t2 .
В результате решения задачи должны быть получены числовые значения коэффициентов a0, a1, a2. Процесс моделирования базируется на временном ряде, полученном в результате наблюдений за производственным процессом.
После того, как будет построена данная математическая модель, возникает возможность математического прогнозирования состояния исследуемого параметра на несколько шагов вперёд.
Пример математической модели, может быть применён для любого реального процесса, имеющего тенденцию. Понятно, что моделирование абсолютно случайного процесса — невозможно.
Пример решения задачи
Чтобы решение сделать более наглядным, разобьём его на этапы:
1) Сбор исходной информации.
2) Преобразование таблицы исходной информации с целью получения системы уравнений (системы нормальных уравнений).
3) Решение системы нормальных уравнений и получение формулы искомого тренда.
4) Определение погрешностей моделирования и пригодности полученной модели.
5) Построение графиков изменения наблюдаемого параметра на основе формулы полученной модели (теоретические значения) и фактических значений с целью их визуального сравнения.
6) Использование полученной модели для прогнозирования состояния исследуемого производственного показателя на будущее.
1) Сбор исходной информации
Предположим, некоторое предприятие выпускает Yф тонн продукции в месяц. На основании наблюдений в течение десяти месяцев, ежемесячно фиксируя объём выпускаемой продукции, была сформирована таблица.
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Yф |
3,2 |
5 |
6 |
8,5 |
10 |
11 |
13 |
14 |
14,5 |
16 |
2) Получение системы нормальных уравнений
Для того, чтобы найти неизвестные коэффициенты формулы тренда a0, a1, a2 нужно составить и решить систему уравнений.
3) Решение системы нормальных уравнений
Систему уравнений можно решить любым способом (подстановкой, методом Жордана-Гаусса и т.д.). Каждый из способов имеет свои достоинства и недостатки, заключающиеся либо в чрезмерной громоздкости, либо в потери точности вычислений. При использовании ЭВМ, когда громоздкость вычислений не играет заметной роли, систему можно решить методом «обратной матрицы». При расчёте «вручную» можно воспользоваться довольно простым, но не очень точным методом «исключения переменных».
Итак, решив систему уравнений, находим искомые коэффициенты тренда:
a0=1.055
a1=2.027
a2=-0.054.
С учётом полученных значений коэффициентов, уравнение тренда будет иметь вид: Y=1.055+2.027×t-0.054×t2.
4) Определение погрешностей моделирования
Используя метод дисперсионного анализа (от лат. Dispersus - рассыпанный, рассеянный) следует выяснить пригодность полученной модели.
В качестве критериев, оценивающих качество модели воспользуемся четырьмя показателями: абсолютной погрешностью (SОст), коэффициентом детерминации (D), индексом корреляции (I), критерием Фишера (FРасч).
Найдём среднюю фактически
произведённую продукцию: 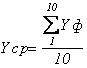 ;Yср= 10.12.
;Yср= 10.12.
Для удобства дальнейших расчётов заполним таблицу:
|
t |
Yф |
Yт |
(Yф - Yср)2 |
(Yт - Yср)2 |
(Yф - Yт) |
(Yф - Yт)2 |
|
1 |
3,2 |
3,028 |
47,886 |
50,293 |
0,171 |
0,029 |
|
2 |
5 |
4,893 |
26,214 |
27,321 |
0,106 |
0,011 |
|
3 |
6 |
6,649 |
16,974 |
12,044 |
-0,649 |
0,421 |
|
4 |
8,5 |
8,297 |
2,624 |
3,320 |
0,202 |
0,040 |
|
5 |
10 |
9,837 |
0,014 |
0,079 |
0,162 |
0,026 |
|
6 |
11 |
11,269 |
0,774 |
1,320 |
-0,269 |
0,072 |
|
7 |
13 |
12,592 |
8,294 |
6,112 |
0,407 |
0,166 |
|
8 |
14 |
13,807 |
15,054 |
13,594 |
0,192 |
0,037 |
|
9 |
14,5 |
14,913 |
19,184 |
22,978 |
-0,413 |
0,171 |
|
10 |
16 |
15,911 |
34,574 |
33,54516 |
0,088 |
0,007 |
|
Сумма: |
171,596 |
170,611 |
0 |
0,984 |
||
Совокупность исходных данных Yф имеет 10 степеней свободы (n=10) - по числу наблюдений; совокупность расчётных данных Yт имеет 3 степени свободы (v=3) — по числу коэффициентов в формуле модели; совокупность Yср имеет 1 степень свободы. Следовательно, совокупность (Yф - Yср) имеет 9 степеней свободы, (Yт - Yср) имеет 2 степени свободы, (Yф - Yт) имеет 7 степеней свободы. Теперь можно определить дисперсии:
![]() .
.
![]() .
.
Абсолютная погрешность составит:
Коэффициент детерминации: ![]()
Индекс корреляции: ![]()
Критерий Фишера: ![]()
Вывод: Качество модели приемлемое т.к. индекс корреляции больше 0,7 и расчётный критерий Фишера больше табличного для данного случая (Fтаб= 4,7).
5) Построение графиков
По оси абсцисс откладываются номера наблюдений t (1,2...10), а по оси ординат — фактические и теоретические значения наблюдаемого параметра. Таким образом, расположив на одном чертеже два графика, можно визуально проконтролировать качество полученной модели.
6) Прогнозирование
Для того, чтобы предсказать состояние исследуемого параметра на 11 и 12 месяце развития процесса производства, нужно вычислить числовое значение Yпр по полученному уравнению тренда Y=1.055+2.027×t-0.054×t2.
При t=11 Y=1.055+2.027×11-0.054×112»16.8.
При t=12 Y=1.055+2.027×12-0.054×122»17.6.
Однако, данные значения предсказанных величин нельзя принимать за «чистую монету». Дело в том, что уравнение тренда, используемое при прогнозировании, построено на основании дискретных данных, имеющих определённую дисперсию (отклонения от строгого математического закона). Поэтому, данное уравнение описывает динамику процесса, в большей или меньшей степени, приближённо. Следовательно, предсказываемое состояние изучаемого параметра должно характеризоваться не конкретным числом, а неким числовым диапазоном (интервалом прогноза).
Каково числовое значение интервала прогноза? Здесь возможны два варианта.
1) Если значение наблюдений больше 30, то считается, что случайные отклонения имеют нормальное распределение. В качестве вероятностной оценки разброса отклонений Yф от Yпр в экономике, чаще всего, принимают уровень значимости a=0,05 (или доверительную вероятность g=0,95). Согласно закона нормального распределения вероятности 0,95 соответствует отклонение 2×Sост. Значит, можно ожидать, что в дальнейшем, значение исследуемого параметра будет находиться в диапазоне Yпр=Y±2×Sост.
2) Если число наблюдений меньше 30, то «ширина» интервала прогноза зависит от их числа и определяется по таблице Стьюдента (ga). В данном случае число наблюдений равно 10, поэтому интервал прогноза, обеспеченный вероятностью 0,95 определяется величиной 2,23×Sост (т. к. ga =2,23). С учётом этого, результаты прогнозирования можно записать в виде:
При t=11 Yпр=1.055+2.027×11-1.054×112± 2,23×0,375,
15,96 £ Yпр £ 17,63.
При t=12 Yпр=1.055+2.027×12-1.054×122± 2,23×0,375,
16,74 £ Yпр £ 18,42.
Кроме того, могут возникнуть неучтённые при моделировании факторы, влияющие на тенденцию процесса, а следовательно, на увеличение дисперсии. Поэтому, чем долгосрочнее прогноз, тем интервал предсказываемых значений шире, что неизбежно приводит к потере точности прогнозирования. Для учёта ухудшения прогнозирования вводится дополнительный коэффициент k.
Выполняя вычисления, находим k: при i=1, k»1,45; при i=2, k»1,6.
Таким образом, окончательное прогнозирование параметра:
При t=11 Yпр=1.055+2.027×11-1.054×112± 2,23×0,375×1,45,
15,59 £ Yпр £ 18,01.
При t=12 Yпр=1.055+2.027×12-1.054×122± 2,23×0,375×1,6,
16,24 £ Yпр £ 18,92.
Краткие указания к выполнению работы
Запустите Microsoft Excel и в одну из верхних ячеек листа появившейся книги внесите номер варианта полученного задания и название лабораторной работы.
Ввод исходных данных
Исходные данные разместите в виде горизонтальной таблицы, в правом столбце которой, вычислите значения сумм t и Yф (эти числа используются далее по решению). Например:
|
|
|
|
|
|
|
|
|
|
|
|
Сумма |
|
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
55 |
|
Yф |
3,2 |
5 |
6 |
8,5 |
10 |
11 |
13 |
14 |
14,5 |
16 |
101,2 |
Получение системы нормальных уравнений
Вычисление слагаемых уравнений системы оформите в виде таблицы, в правом столбце которой, вычислите значения соответствующих сумм. Например:
|
|
|
|
|
|
|
|
|
|
|
|
Сумма |
|
t2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
385 |
|
t3 |
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
3025 |
|
t4 |
1 |
16 |
81 |
256 |
625 |
1296 |
2401 |
4096 |
6561 |
10000 |
25333 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yф×t |
3,2 |
10 |
18 |
34 |
50 |
66 |
91 |
112 |
130,5 |
160 |
674,7 |
|
Yф×t2 |
3,2 |
20 |
54 |
136 |
250 |
396 |
637 |
896 |
1174,5 |
1600 |
5166,7 |
Диапазоны ячеек, образующих строки, следует получать с использованием формул массива (CTRL+SHIFT+ENTER).
Используя полученные числовые данные, сформируйте систему нормальных уравнений. На листе Excel она будет иметь примерно такой вид:
|
10 |
55 |
385 |
|
101,2 |
|
55 |
385 |
3025 |
|
674,7 |
|
385 |
3025 |
25333 |
|
5166,7 |
.
Решение системы нормальных уравнений
Итак, получили массив коэффициентов нормальных уравнений системы. Правый столбец полученного массива представляет собой столбец результатов уравнений. Как говорилось выше, систему нужно решать методом «обратной матрицы». Для этого разделите полученный массив на две части: массив аргументов и массив результатов. Следует помнить, что полученный массив аргументов должен получиться «квадратным» (в данном случае - 3´3), иначе нахождение обратной матрицы будет невозможным. Используя функцию МОБР, создайте массив, представляющий собой обратную матрицу от матрицы аргументов нормальных уравнений.
Используя функцию МУМНОЖ, умножьте полученную обратную матрицу на матрицу результатов нормальных уравнений системы. В результате умножения получится массив, состоящий из одного столбца и содержащий искомые коэффициенты уравнения искомого тренда: a0, a1, a2. Уравнение модели получено!
Определение погрешностей моделирования
Основной частью данного этапа является создание таблицы (см. выше).
Для вычисления значений столбцов (Yф - Yср)2 и (Yт - Yср)2 требуется среднее арифметическое значение фактических Y. Поэтому, перед тем, как создавать таблицу, удобно в отдельной ячейке вычислить Yср, воспользовавшись функцией СРЗНАЧ.
Для нахождения сумм значений столбцов (Yф - Yср)2, (Yт - Yср)2 и (Yф - Yт)2 удобно воспользоваться кнопкой «Автосуммирование» на стандартной панели инструментов.
При определении
дисперсий ![]() следует
помнить, что совокупность исходных данных Yф имеет n случайных степеней свободы
(по числу наблюдений), совокупность расчётных данных Yт имеет 3 степени свободы
(по числу постоянных коэффициентов формулы тренда a0, a1, a2), совокупность Yср имеет 1 степень свободы.
следует
помнить, что совокупность исходных данных Yф имеет n случайных степеней свободы
(по числу наблюдений), совокупность расчётных данных Yт имеет 3 степени свободы
(по числу постоянных коэффициентов формулы тренда a0, a1, a2), совокупность Yср имеет 1 степень свободы.
Значение табличного
критерия Фишера определяется по соответствующей таблице на основании степеней
свободы числителя ![]() ,
и знаменателя
,
и знаменателя ![]() .
Числа степеней свободы числителей расположены в столбцах таблицы, а числа
степеней свободы знаменателей - в строках. На пересечении соответствующей
строки и столбца находится числовое значение табличного критерия Фишера для
данного случая.
.
Числа степеней свободы числителей расположены в столбцах таблицы, а числа
степеней свободы знаменателей - в строках. На пересечении соответствующей
строки и столбца находится числовое значение табличного критерия Фишера для
данного случая.
Построение графиков
Построение графиков выполняется посредством кнопки «Мастер диаграмм» стандартной панели инструментов. В качестве диапазонов исходных данных, удерживая клавишу CTRL, укажите один за другим столбцы последней таблицы Yф и Yт вместе с заголовками. Когда чертёж будет готов, то заголовки столбцов отобразятся в легенде.
Прогнозирование
Самое сложное на этом
этапе работы — правильно составить формулу расчёта коэффициента учёта ухудшения
прогнозирования. Её следует составлять непосредственно через строку формул.
Элементы ![]() и
и ![]() этой формулы вами уже
найдены в таблице формирования системы нормальных уравнений, что немного
облегчает задачу.
этой формулы вами уже
найдены в таблице формирования системы нормальных уравнений, что немного
облегчает задачу.
Контрольные вопросы
1) Какие виды процессов можно моделировать? Назовите несколько примеров моделируемых процессов.
2) В каком виде даётся информация для моделирования процесса?
3) Как осуществляется прогнозирование? Почему нельзя абсолютно точно предсказать состояние исследуемого параметра?
4) Почему точность прогнозирования тем хуже, чем долгосрочнее прогноз?
3 Лабораторная работа. Определение парных коэффициентов корреляции
В силу того, что на основании парных коэффициентов корреляции основывается обоснованный выбор исходных данных для моделирования производственной функции (см. предыдущую работу), их нужно определять перед моделированием. Но, руководствуясь соображениями методики преподавания, рассмотрим задачу определения парных коэффициентов корреляции после задачи на моделирование производственных функций.
Цель работы: познакомиться с экономическим смыслом парных коэффициентов корреляции. Освоить математический инструментарий их нахождения. Исследовать результаты наблюдений на предмет их пригодности для моделирования производственной функции.
Постановка задачи
В реальном производстве размеры затрат x1×××xn всегда, некоторым образом, связаны друг с другом. Например, увеличение потребления сырья неизбежно влечёт за собой увеличение транспортных расходов, затрат на хранение и т. д. Если изменение одного вида затрат влечёт за собой пропорциональное (или близкое к пропорциональному) изменение других затрат, то моделирование производственной функции становится невозможным (или, по крайней мере, весьма затруднительным).
Вспомните общий вид производственной функции:
Y = a0 + a1x1 + a2x2 +××× +anxn,,
где Y — стоимость готовой продукции;
a0 — денежное выражение постоянно присутствующих, не изменяющихся затрат;
a1 ××× an — денежное выражение единицы соответствующего вида затрат x1 ××× xn.
Легко увидеть, что производственная функция определяет влияние любого из видов затрат x1 ××× xn на выпуск готовой продукции Y. В случае пропорционального изменения одного вида затрат в зависимости от другого выяснить влияние каждого из них на выпуск готовой продукции становится невозможным.
В алгебраической интерпретации затраты x1 ××× xn можно рассматривать как многомерные векторы. Поэтому, случай пропорциональности их составляющих называется коллинеарностью исходных факторов x1 ××× xn (в случае, близком к пропорциональности говорят о мультиколлинеарности).
Перед моделированием производственной функции полезно проверить совокупность исходных факторов x1 ×××xn на отсутствие коллинеарности (мультиколлинеарности). Это достигается нахождением парных коэффициентов корреляции (от лат. Correlatio — соотношение, взаимозависимость), которые показывают уровень взаимосвязи исходных факторов друг с другом и уровень влияния исходных факторов на результат y. Парные коэффициенты корреляции, устанавливающие связь между любым из исходных факторов x1×××xn и результатом Y, позволяют установить значимость данного исходного фактора. Исходный фактор, для которого парный коэффициент корреляции по отношению к Y слишком мал, следует исключить из процесса моделирования. Говорят, что уровень значимости данного исходного фактора пренебрежимо мал. Парные коэффициенты корреляции принято обозначать буквой r.
Задача корреляции заключается в обоснованном выборе исходных производственных факторов. Выбор производится по двум критериям: недопустимость мультиколлинеарности исходных факторов и выяснение их значимости. Мультиколлинеарность наступает при парном коэффициенте корреляции более чем 0,85, а уровень значимости принят равным 0,05.
Пример решения задачи
1) Сбор исходной информации
Допустим, в результате наблюдений за процессом была получена исходная информация с целью нахождения производственной функции. Перед моделированием следует проверить параметры x1, x2, x3 на мультиколлинеарность и выявить уровень их значимости для Y.
|
N п/п |
x1 |
x2 |
x3 |
Y |
|
1 |
2 |
7 |
5 |
45 |
|
2 |
18 |
6 |
26 |
80 |
|
3 |
14 |
17 |
31 |
134 |
|
4 |
15 |
16 |
33 |
190 |
|
5 |
6 |
17 |
14 |
170 |
2) Создание матрицы отклонений от среднего
Найдём среднее арифметическое значение каждого столбца:
x1ср= 11; x2ср =12,6; x3ср=21,8; yср=123,8.
Отнимая от каждого элемента столбца соответствующее среднее значение, получим матрицу отклонений от среднего:
|
N п/п |
x1 - x1ср |
x2 - x2ср |
x3 - x3ср |
Y - Yср |
|
1 |
-9 |
-5,6 |
-16,8 |
-78,8 |
|
2 |
7 |
-6,6 |
4,2 |
-43,8 |
|
3 |
3 |
4,4 |
9,2 |
10,2 |
|
4 |
4 |
3,4 |
11,2 |
66,2 |
|
5 |
-5 |
4,4 |
-7,8 |
46,2 |
Согласно вышесказанному, каждый из четырёх столбцов полученной матрицы можно рассматривать как многомерный вектор. В связи с этим, все дальнейшие действия по определению парных коэффициентов корреляции r можно рассматривать как нахождение косинусов углов между любыми двумя векторами.
Немного геометрии: например, даны два вектора: A(a1;a2 ) и B(b1;b2 ). Косинус угла между ними равен результату от деления скалярного произведения данных векторов на произведение их модулей. Вычисления заметно упростятся, если векторы будут заранее приведены к векторам, с единичным модулем (векторы будут нормированы). В этом случае, знаменатель дроби будет равен 1 и Cosj будет равен скалярному произведению векторов.
3) Нормирование матрицы отклонений
Найдём модули всех четырёх векторов по формулам:
![]()
![]()
![]()
![]()
В результате расчётов получим:
![]()
![]()
![]()
![]()
Разделив каждый элемент столбца матрицы отклонений на соответствующее значение модуля, получим нормированную матрицу отклонений. В геометрической интерпретации каждый из четырёх столбцов представляет собой многомерный вектор, «длина» которого равна 1. Поэтому, в обозначениях столбцов полученной матрицы нормированных отклонений будем использовать индекс 0.
4) Вычисление парных коэффициентов корреляции
Согласно вышесказанному, вычисление парных коэффициентов корреляции сводится к скалярному произведению пар полученных нормированных векторов.
|
N п/п |
x01 |
x02 |
x03 |
y0 |
|
1 |
-0,67 |
-0,50 |
-0,70 |
-0,65 |
|
2 |
0,52 |
-0,59 |
0,18 |
-0,36 |
|
3 |
0,22 |
0,39 |
0,39 |
0,08 |
|
4 |
0,30 |
0,30 |
0,47 |
0,55 |
|
5 |
-0,37 |
0,39 |
-0,33 |
0,38 |
![]()
![]()
![]()
![]()
![]()
На основании полученных значений парных коэффициентов корреляции, можно сделать вывод:
- по признаку значимости ни одним из параметров нельзя пренебречь т. к. 0,29>0.05; 0.89>0.05; 0.56>0.05;
- но между параметрами x1 и x3 наблюдается мультиколлинеарность т. к. 0,91>0,85. При моделировании влияние каждого из этих параметров, в отдельности, будет определить достаточно сложно, поэтому один из них должен быть удалён из процесса моделирования, либо параметры x1 и x3 должны быть объединены в один.
Краткие указания к выполнению работы
Запустите Microsoft Excel и в одну из верхних ячеек листа появившейся книги внесите номер варианта полученного задания и название лабораторной работы.
Создание матрицы отклонений от среднего
Среднее арифметическое каждого из столбцов матрицы исходных данных можно найти, используя функцию СРЗНАЧ.
Нормирование матрицы отклонений
Для определения модуля каждого из векторов отклонений удобно воспользоваться функциями СУММКВ (сумма квадратов) и КОРЕНЬ.
Вычисление парных коэффициентов корреляции
Этот этап сводится к попарному скалярному умножению векторов. Умножение сразу всех векторов можно сделать, умножив нормированную матрицу отклонений на транспонированную. Произведите транспонирование нормированной матрицы отклонений, используя функцию ТРАНСП. Используя функцию МУМНОЖ, перемножьте матрицы. Результатом будет являться матрица, содержащая все парные коэффициенты корреляции. Понятно, что диагональ полученной матрицы будет заполнена единицами. Нетрудно понять, что косинус угла между совпадающими векторами равен 1.
|
|
x01 |
x02 |
x03 |
y0 |
|
x01 |
1 |
0,06 |
0,91 |
0,29 |
|
x02 |
0,06 |
1 |
0,41 |
0,89 |
|
x03 |
0,91 |
0,41 |
1 |
0,56 |
|
y0 |
0,29 |
0,89 |
0,56 |
1 |
Если в качестве транспонируемой матрицы взять не всю нормированную матрицу отклонений, а только её аргументную часть, то результат от умножения матриц можно получить в виде:
|
|
x01 |
x02 |
x03 |
y0 |
|
x01 |
1 |
0,06 |
0,91 |
0,29 |
|
x02 |
0,06 |
1 |
0,41 |
0,89 |
|
x03 |
0,91 |
0,41 |
1 |
0,56 |
На основании полученных значений парных коэффициентов корреляции необходимо сделать вывод о пригодности выбранных производственных факторов для моделирования.
Примечание
Парные коэффициенты корреляции можно найти посредством встроенной функции Microsoft Excel КОРРЕЛ(массив1; массив 2) из категории статистических. Исходные данные «массив 1» и «массив 2» должны представлять из себя совокупности исследуемых данных, внесённых в диапазоны ячеек. Можете проверить правильность решения задачи, решив её с использованием данной встроенной функции.
Каждый шаг решения задачи должен сопровождаться комментариями. Отчёт о выполнении лабораторной работы печатается на бумаге и сохраняется в виде файла *.XLS.
Контрольные вопросы
1) Почему перед моделированием производственной функции следует найти парные коэффициенты корреляции между совокупностями исходных данных?
2) Каков экономический смысл парных коэффициентов корреляции?
3) В чём заключается геометрическая интерпретация парных коэффициентов корреляции?
4) Решение задачи показало, что парный коэффициент корреляции между совокупностями каких-либо параметров x больше чем 0,85. Что это значит? Как поступить?
5) Какая встроенная функция Microsoft Excel предназначена для нахождения парных коэффициентов корреляции? Каков синтаксис её оформления?
4 Лабораторная работа. Планирование эксперимента
Цель работы: познакомиться с методикой планирования эксперимента. Построить математическую модель технологического процесса по данным, являющимися результатом активного эксперимента.
Постановка задачи
Исходные данные для моделирования производственной функции являются результатом наблюдения за реальным процессом. Сбор данных таким способом иногда называют пассивным экспериментом. Ведь исследователь не может повлиять на протекающий процесс. Роль исследователя сводится лишь к констатации параметров процесса на текущем этапе наблюдения и их фиксированию.
При исследовании эффективности тех или иных производственных технологий (например в химической промышленности) часто возникает необходимость выявления влияния каждого из технологических параметров на объёмы выхода и качества получаемой продукции. Классическим примером можно считать технологии производства, зависящие от температуры, давления и продолжительности проведения реакций. Понятно, что для выявления влияния этих технологических параметров на выход продукции следует провести несколько опытов с различными соотношениями температура-давление-время. Исследователь может заранее задавать соотношения данных технологических параметров и наблюдать за изменениями выхода продукции от опыта к опыту. В этом случае исследователь уже выступает не просто в роли наблюдателя, а в роли «конструктора» эксперимента, полностью контролируя процесс сбора экспериментальной информации. Сбор информации, при котором исследователь целенаправленно задаёт значения входным параметрам, принято называть активным экспериментом.
Главный вопрос при проведении любого активного эксперимента можно сформулировать так: каким наименьшим количеством опытов можно ограничиться и какое соотношение технологических параметров следует установить в каждом из опытов, чтобы полученные экспериментальные данные были наиболее объективными и пригодными для математического моделирования процесса.
Реализация всех возможных комбинаций факторов возможна при, так называемом, полном факторном эксперименте, количество опытов которого определяется по формуле:
N = nk ,
где k — число факторов;
n — количество уровней их значений.
Например, изучается влияние на выход продукта (Y) трёх факторов: температуры (x1), в диапазоне от 100 до 200 °C, давления (x2) от 2×105 до 6×105 Па и времени проведения реакции (x3) от 10 до 20 мин. Если экспериментатор выберет всего два уровня значений параметров (максимальный и минимальный) то количество опытов в полном факторном эксперименте составит:
N = 23 = 8.
Пригодность исходных данных для моделирования производственной функции определяется вычислением парных коэффициентов корреляции между их массивами. Причём, чем меньше значения парных коэффициентов корреляции между массивами факторов (x1-xn), тем лучше. При проведении активных экспериментов есть возможность сделать массивы значений факторов «ортогональными», т. е. свести значения соответствующих парных коэффициентов корреляции к нулю. В геометрической интерпретации это означает, что многомерный вектор Y можно разложить на составляющие, которыми являются многомерные векторы x1-xn по взаимно перпендикулярным осям. Такое планирование эксперимента обеспечивает максимальную объективность исходных данных и приводит к упрощению решения задачи по построению математической модели.
Проведя восемь необходимых опытов и фиксируя уровни выхода продукции (Y), можно составить таблицу результатов полного факторного эксперимента по рассматриваемому технологическому процессу.
|
Номер опыта |
Температура, °С (x1) |
Давление, Па (x2) |
Время, мин (x3) |
Выход продукции (Y) |
|
1 |
100 |
2×105 |
10 |
2 |
|
2 |
200 |
2×105 |
10 |
6 |
|
3 |
100 |
6×105 |
10 |
4 |
|
4 |
200 |
6×105 |
10 |
8 |
|
5 |
100 |
2×105 |
20 |
10 |
|
6 |
200 |
2×105 |
20 |
18 |
|
7 |
100 |
6×105 |
20 |
8 |
|
8 |
200 |
6×105 |
20 |
12 |
Обратите внимание на порядок чередования значений факторов, обеспечивающий нулевые значения парных коэффициентов корреляции между их массивами.
Пример решения задачи
1) Безразмерный масштаб факторов
Выбор конкретных уровней значений каждого из факторов предоставляет ещё одну возможность в упрощении решения задачи: перевод значений в относительные безразмерные единицы с диапазоном изменения от -1 до +1. Например, минимальному уровню температуры (100 °С) будет соответствовать -1, а максимальному (200 °С) — +1.
Таким образом, таблица исходных данных в безразмерном масштабе будет выглядеть так:
|
Номер опыта |
Температура (x1) |
Давление (x2) |
Время (x3) |
Выход продукции (Y) |
|
1 |
-1 |
-1 |
-1 |
2 |
|
2 |
1 |
-1 |
-1 |
6 |
|
3 |
-1 |
1 |
-1 |
4 |
|
4 |
1 |
1 |
-1 |
8 |
|
5 |
-1 |
-1 |
1 |
10 |
|
6 |
1 |
-1 |
1 |
18 |
|
7 |
-1 |
1 |
1 |
8 |
|
8 |
1 |
1 |
1 |
12 |
2) Искусственное увеличение числа факторов
Таблицу наблюдений можно расширить, добавив ещё четыре фактора, полученных «искусственно». Эти дополнительные столбцы можно получить посредством почленного перемножения массивов, полученных экспериментальным путём. Введение в уравнение математической модели, в качестве слагаемых, произведений факторов придаёт ей «кубическую гибкость», а значит, повышает точность описания процесса.
С учётом ввода в моделирование искусственно полученных факторов, уравнение модели можно записать в виде:
Y = a0 + a1x1 + a2x2 +a3x3+a12x1x2+a13x1x3+ a23x2x3 +a123x1x2x3.
А таблица исходных данных в безразмерном масштабе примет вид:
|
N |
x1 |
x2 |
x3 |
x1×x2 |
x1×x3 |
x2×x3 |
x1×x2×x3 |
Y |
|
1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
2 |
|
2 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
6 |
|
3 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
4 |
|
4 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
8 |
|
5 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
10 |
|
6 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
18 |
|
7 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
8 |
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
3) Проверка факторов на отсутствие взаимозависимости
Далее, следует убедиться в том, что значения парных коэффициентов корреляции между массивами факторов имеют нулевые значения.
rx1x2=0; rx1x3=0; rx1 x1x2=0; rx1 x1x3=0; rx1 x2x3=0; rx1 x1x2x3=0;
rx2x3=0; rx2 x1x2=0; rx2 x1x3=0; rx2 x2x3=0; rx2 x1x2x3=0;
rx3 x1x2=0; rx3 x1x3=0; rx3 x2x3=0; rx3 x1x2x3=0;
rx1x2 x1x3=0; rx1x2 x2x3=0; rx1x2 x1x2x3=0;
rx1x3 x2x3=0; rx1x3 x1x2x3=0;
rx2x3 x1x2x3=0.
Таким образом, для семи массивов факторов определяется двадцать один парный коэффициент корреляции.
4) Создание аргументной матрицы
Согласно общему виду уравнения математической модели
a0 + a1x1 + a2x2 +a3x3+a12x1x2+a13x1x3+ a23x2x3 +a123x1x2x3 = Y
преобразуем таблицу исходных данных в матрицу, добавив столбец фиктивной переменной. В результате получим следующее:
|
1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
-1 |
2 |
|
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
6 |
|
1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
4 |
|
1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
-1 |
8 |
|
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
10 |
|
1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
18 |
|
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
-1 |
8 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
5) Вычисление коэффициентов уравнения модели
Коэффициенты a0, a1 , a2 , a3, a12 , a13 , a23 и a123 находятся как средние арифметические значения почленных произведений массива Y и соответствующего массива x.
Аналогично вычисляются значения других коэффициентов модели:
a1=2.5, a2=-0.5, a3=3.5, a12=-0.5, a13=0.5, a23=-1.5, a123=-0.5.
Таким образом, уравнение модели получено и имеет вид:
Y= 8.5 +2.5x1 - 0.5x2 +3.5x3 - 0.5x1x2+0.5x1x3 -1.5x2x3 - 0,5x1x2x3.
Краткие указания к выполнению работы
После оформления заголовка лабораторной работы сформируйте таблицу исходных данных в соответствии с полученным вариантом задания.
Следующим шагом является создание расширенной таблицы исходных данных в безразмерном масштабе. Столбцы x1x2, x1x3, x2x3 и x1x2x3 удобно получать с использованием формул массива.
Убедитесь в корректности исходных данных, вычислив все необходимые парные коэффициенты корреляции с использованием функции КОРРЕЛ.
Для вычисления коэффициентов модели используйте функцию СРЗНАЧ.
После того, как модель будет построена, выполните проверку, вычислив массив Yт и сравнив его с Yф.
Контрольные вопросы
1) Чем отличается активный эксперимент от наблюдения за изучаемым процессом?
2) В чём заключается планирование эксперимента и какую цель оно преследует?
3) Что такое расширенная таблица исходных данных в безразмерном масштабе?
4) Зачем в формулу математической модели вводят «искусственные» факторы?
5) Как вычисляются коэффициенты математической модели, рассмотренной на этом занятии?
6) Как проверить правильность решения данной задачи?
5 Лабораторная работа. Моделирование простейших случайных потоков
Цель работы: получить представление о параметрах, характеризующих временные ряды случайных событий. Познакомиться с методикой выявления временных рядов, временные интервалы которых распределены по экспоненциальному закону.
Расширить познания о возможностях программного приложения Microsoft Excel в статистических расчётах. Исследовать случайный временной ряд, предложенный в качестве упражнения. Используя возможности Microsoft Excel, произвести имитацию случайных событий, создав ряд с экспоненциальным законом распределения временных интервалов.
Постановка задачи
Система услуг является основной и главной частью экономики. В ней реализуется взаимодействие встречно заинтересованных потоков: обслуживаемый поток (поток заявок) и обслуживающий поток (поток услуг). Оба потока являются случайными, и поэтому, неизбежно либо с одной, либо с другой стороны образуются очереди. Возникает проблема максимально гармоничного сопряжения потока заявок с потоком услуг, с целью уменьшения потери времени на ожидание с той и другой стороны. Решение проблемы сводится к производственной оценке времени как остродефицитного ресурса, для чего необходимо установить временные параметры обоих потоков.
Классическим (и самым распространённым) является
случай, в котором потоки заявок и услуг являются случайными, и временные
интервалы между событиями распределены по экспоненциальному закону. Поток
характеризуется средним интервалом времени между событиями: 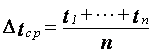 (час), где n — количество временных
интервалов t и плотностью потока
(час), где n — количество временных
интервалов t и плотностью потока 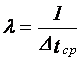 (событий в час).
(событий в час).
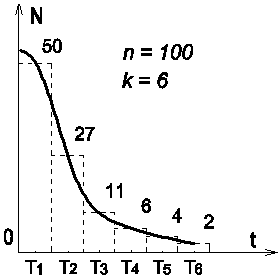
На рисунке изображён график экспоненциального закона распределения временных интервалов для ста наблюдений. Промежуток времени, в котором находятся временные интервалы разделён на шесть частичных интервалов (k = 6). Хорошо видно, что в совокупности наблюдений преобладают короткие интервалы (максимальное число наблюдений (50) попадает в частичный интервал N 1). С увеличением длительности интервалов их число быстро уменьшается (в частичный интервал N 6 попало всего два наблюдаемых временных интервала).
Экспоненциальный закон распределения описывается формулой:
![]() ,
,
где Ni — частота ( количество временных интервалов;
попадающих в i-й частичный интервал);
n — общее число наблюдений;
DT — ширина частичного интервала (час);
l — плотность потока (событий в час);
Ti — среднее значение i-го частичного интервала (час).
Реальный поток подвержен влиянию внешних дестабилизирующих факторов. Поэтому, прежде чем использовать его для моделирования системы массового обслуживания (СМО) необходимо выяснить, можно ли считать случайными отклонения интервалов времени от экспоненциального распределения, или они носят неслучайный характер. Если отклонения носят неслучайный характер, то данный поток не может быть использован при моделировании СМО, другими словами, временные интервалы между событиями распределены не по экспоненциальному закону.
Пример решения задачи
1) Исходные данные
Имеется совокупность наблюдений временных интервалов между событиями:
|
N |
t (час) |
N |
t (час) |
N |
t (час) |
|
1 |
0,027 |
11 |
0,018 |
21 |
0,09 |
|
2 |
0,128 |
12 |
0,348 |
22 |
0,08 |
|
3 |
0,068 |
13 |
0,157 |
23 |
0,223 |
|
4 |
0,032 |
14 |
0,043 |
24 |
0,51 |
|
5 |
0,037 |
15 |
0,402 |
25 |
0,105 |
|
6 |
0,085 |
16 |
0,213 |
26 |
0,12 |
|
7 |
0,035 |
17 |
0,107 |
27 |
0,36 |
|
8 |
0,077 |
18 |
0,213 |
28 |
0,285 |
|
9 |
0,123 |
19 |
0,118 |
29 |
0,042 |
|
10 |
0,008 |
20 |
0,025 |
30 |
0,123 |
Требуется выяснить, можно ли данную совокупность наблюдений рассматривать как совокупность, в которой временные интервалы распределены по экспоненциальному закону.
2) Определение параметров совокупности наблюдений
Среднее значение временных интервалов: 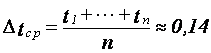 (часа).
(часа).
Плотность потока: 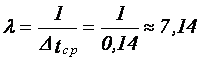 (событий в час).
(событий в час).
Найдём минимальный и максимальный временной интервал:
tMIN = 0,008, tMAX = 0,51.
Ориентировочно количество частичных интервалов можно определить по формуле Стерджесса: k = 1+ 3,32 lg n = 1 + 3,32 lg 30 » 5,9.
В данном случае, удобно взять количество частичных интервалов равное шести, при этом ширина частичного интервала равна 0,1 часа. Распределив временные интервалы совокупности наблюдений по частичным интервалам получим, таблицу фактических частот распределения.
|
Таблица частот распределения |
|
|
Частичный интервал |
Фактическая частота |
|
0,1 |
14 |
|
0,2 |
8 |
|
0,3 |
4 |
|
0,4 |
2 |
|
0,5 |
1 |
|
0,6 |
1 |
3) Моделирование теоретических частот распределения
|
Частичный интервал |
T |
Теоретическая частота |
|
0,1 |
0,05 |
14,988 |
|
0,2 |
0,15 |
7,339 |
|
0,3 |
0,25 |
3,594 |
|
0,4 |
0,35 |
1,760 |
|
0,5 |
0,45 |
0,862 |
|
0,6 |
0,55 |
0,422 |
Нужно выяснить какие частоты распределения будет иметь теоретическая совокупность временных интервалов с аналогичными параметрами. (n = 30; l = 7,14; DT = 0,1).
Найдём среднее значение каждого i-го частичного интервала
(Ti) и, воспользовавшись
формулой экспоненциального закона распределения ![]() , моделируем теоретические частоты.
, моделируем теоретические частоты.
4) Сравнение фактической и теоретической частоты распределения
Теперь нужно сравнить фактические частоты распределения с теоретическими. Для этого используют критерия Пирсона (c 2 Пирсона).
В результате вычислений получиться: c2 » 1. Расчётный c 2 Пирсона должен быть меньше табличного. Если таблицы с критическими значениями c 2 Пирсона нет под рукой, можно проверить выполнение условия Романовского. Условие Романовского заключается в следующем:
 ,
,
где k — количество частичных интервалов.
В данном случае значение левой части неравенства примерно равно 1,06.
Вывод: Так как условие Романовского выполняется, то отклонения от экспоненциального закона в распределении временных интервалов фактической совокупности носят случайный характер. Следовательно, совокупность фактических временных интервалов можно считать экспоненциальной.
Указания к выполнению работы
Исходные данные
1. Запустите Microsoft Excel и в одну из верхних ячеек листа появившейся книги внесите номер варианта полученного задания и название лабораторной работы.
2. Исходные данные оформите в виде единого столбца.
Параметры совокупности наблюдений
1) Используя функцию СРЗНАЧ из категории статистических, вычислите Dtср.
2) Найдите плотность потока ![]() .
.
3) Используя функции МАКС и МИН из категории статистических, найдите максимальный и минимальный временной интервал.
4) На основании максимального и минимального значений временных интервалов выберите необходимое количество и ширину частичных интервалов. Удобно, если ширина частичного интервала будет выбрана равной 0,1 ( 0,05, 0,2 ) часа. Оформите выбранные значения частичных интервалов в виде столбца.
5) Группировку исходных данных по выбранным частичным интервалам (в Microsoft Excel принят термин «Карманы») удобнее всего сделать, воспользовавшись алгоритмом «Гистограмма». Для этого во всплывающем меню «Сервис» выберите пункт «Анализ данных...» и из списка алгоритмов выберите «Гистограмма». Появится окно, примерный вид которого изображён на рисунке.
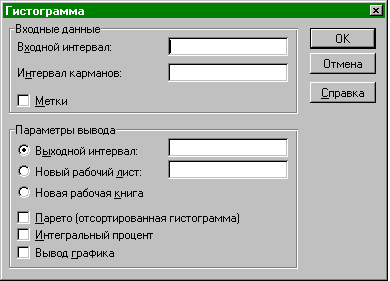
В рамке «Входные данные» в окно ввода «Входной интервал» внесите ссылку на столбец исходных данных, а в окно «Интервал карманов» — на столбец выбранных частичных интервалов.
В рамке «Параметры вывода» установите точечный переключатель в положение «Выходной интервал», а в соответствующем окне установите ссылку на ячейку, в которой будет расположен левый верхний угол будущего отчёта алгоритма «Гистограмма». Больше никаких установок делать не нужно (см. рисунок).
После нажатия на текстовую кнопку «Ok» будет выведен отчёт в виде таблицы из двух столбцов: «Карман» и «Частота». В строке «Ещё» указано количество наблюдений не попавших в последний частичный интервал. Если число и ширина частичных интервалов вами было выбрано верно, то в строке «Ещё» должен быть ноль.
Сравнение фактической и теоретической частоты распределения
1) Для наглядности и удобства дальнейших расчётов нужно создать таблицу. Её можно создать на основе таблицы отчёта алгоритма «Гистограмма». В добавленный столбец «Середина» внесите средние значения соответствующих карманов. Столбцы «Частота фактическая» и «Частота теоретическая» лучше расположить рядом.
Воспользовавшись формулой ![]() , заполните столбец «Частота
теоретическая». Это удобно сделать, посредством создания формулы массива.
Для возведения числа е в степень используйте функцию EXP из категории
математических.
, заполните столбец «Частота
теоретическая». Это удобно сделать, посредством создания формулы массива.
Для возведения числа е в степень используйте функцию EXP из категории
математических.
|
Карман |
Середина |
Частота фактическая |
Частота теоретическая |
|
0,1 |
0,05 |
14 |
|
|
0,2 |
0,15 |
8 |
|
|
0,3 |
0,25 |
4 |
|
|
0,4 |
0,35 |
2 |
|
|
0,5 |
0,45 |
1 |
|
|
0,6 |
0,55 |
1 |
|
2) Ниже полученной таблицы вычислите значение критерия Пирсона и условия Романовского.
Критерий Пирсона можно легко найти, воспользовавшись функцией ПИРСОН из категории статистических. В окне вызванной функции ПИРСОН нужно указать ссылки на массивы фактической и теоретической частоты распределения.
Условие
Романовского вычисляется по формуле: 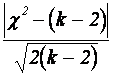 , где c 2 — полученный критерий Пирсона. Для составления
этой формулы потребуется функция ABS (модуль) и КОРЕНЬ из категории математических.
, где c 2 — полученный критерий Пирсона. Для составления
этой формулы потребуется функция ABS (модуль) и КОРЕНЬ из категории математических.
3) После того, как будет проверено условие Романовского, следует построить диаграммы фактической и теоретической частот распределения. Это позволит наглядно оценить отклонения фактической совокупности временных интервалов от экспоненциального закона распределения.
Нажмите на кнопку «Мастер диаграмм» стандартной панели инструментов. В качестве диапазонов исходных данных, удерживая клавишу CTRL, укажите один за другим столбцы «Частота фактическая» и «Частота теоретическая» вместе с заголовками. Когда диаграмма будет готова, то заголовки столбцов отобразятся в легенде диаграммы. Следующим шагом укажите тип диаграммы — гистограмму. Озаглавьте будущую диаграмму «Частоты распределения», а в качестве названия оси Х наберите: «Частичные интервалы».
4) Сформулируйте и запишите вывод о проделанной работе.
Каждый шаг решения задачи должен сопровождаться комментариями. Отчёт о выполнении лабораторной работы печатается на бумаге и сохраняется в виде файла *.XLS.
Дополнительное задание
На другом листе файла лабораторной работы, сгенерировать 100 временных интервалов, выраженных в минутах, распределённых по экспоненциальному закону. Плотность потока l = 6 (событий в час). Выбрать ширину и количество частичных интервалов (карманов), воспользовавшись алгоритмом «Диаграмма», сгруппировать и построить гистограмму частот распределения.
Для генерации случайных экспоненциально
распределённых временных интервалов нужно воспользоваться формулой: 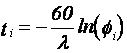 , где fi — случайные числа от
нуля до единицы, генерируемые функцией СЛЧИС. Ещё потребуется функция LN (натуральный логарифм)
из категории математических.
, где fi — случайные числа от
нуля до единицы, генерируемые функцией СЛЧИС. Ещё потребуется функция LN (натуральный логарифм)
из категории математических.
Чтобы предотвратить автоматическую генерацию случайных чисел, следует установить режим пересчёта документа вручную («Сервис» ® «Параметры» ® закладка «Вычисления»).
Контрольные вопросы
1) Почему перед решением задачи массового обслуживания следует выяснить, можно ли считать исследуемый временной ряд экспоненциальным?
2) Какими параметрами характеризуется временной ряд случайных событий?
3) На основании чего можно сделать вывод о том, что отклонения от экспоненциального закона в распределении временных интервалов фактической совокупности носят случайный характер?
6 Лабораторная работа. Разомкнутая система массового обслуживания
Цель работы: получить представление о замкнутых и разомкнутых системах массового обслуживания и принципах их функционирования. Познакомиться с параметрами, описывающими системы массового обслуживания и методикой их математического описания.
Применяя полученные знания, решить задачу, обосновав выбор одной из трёх систем массового обслуживания.
Краткие теоретические сведения
Наука, занимающаяся изучением систем массового обслуживания (СМО) называется теорией массового обслуживания (ТМО). Основным её направлением является минимизация потерь времени в СМО при встрече двух случайных потоков: потока заявок (требований) и потока услуг. Функционирование систем массового обслуживания впервые начало изучаться при организации работы телефонных сетей. Затем научные подходы ТМО были применены к планированию военных операций. В настоящее время изучение функционирования систем массового обслуживания охватывает очень широкий их спектр и является одним из важнейших вопросов экономики.
В зависимости от характера входящего потока заявок, СМО принято разделять на два типа: разомкнутые (СМОР) и замкнутые (СМОЗ). В СМОР поток состоит из требований на одноразовое обслуживание. Классическими примерами СМОР являются предприятия сферы быта и услуг. А в СМОЗ поток требований циклический.
Рассмотрим схему функционирования разомкнутой СМО подробнее.
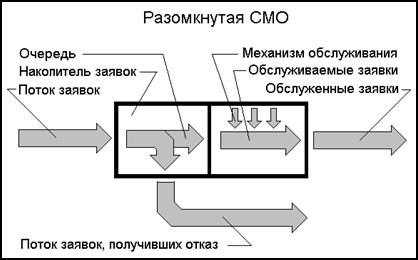
В системе массового обслуживания встречаются два взаимодействующих друг с другом случайных потока. Первый - поток заявок на обработку, имеющий среднюю плотность l (заявок/час). Второй – поток, обслуживающих аппаратов (каналов обслуживания) со средней производительностью m (заявок/час) каждый. Будем считать, что все каналы имеют одинаковую производительность. Перед поступлением заявок на обслуживание они проходят накопитель, в котором образуется очередь если все каналы системы в данный момент заняты. Размер накопителя обозначим M, а количество обслуживающих аппаратов — N. Функционирование СМОР, в основном, зависит от данных четырёх параметров. Это можно записать так: СМОР(l, m, M, N).
В том случае, если размер очереди сравнялся с размером накопителя, то вновь поступающие заявки получают отказ в обслуживании.
В классическом варианте моделирования СМО предполагается обязательное выполнение следующих требований:
1) Заявка не получившая отказ, а значит, попавшая в очередь накопителя, не может самопроизвольно его покинуть;
2) Входящий случайный поток должен иметь экспоненциальное распределение временных интервалов;
3) Время обслуживания заявок должно подчиняться экспоненциальному или нормальному распределению.
Под действием двух встречающихся потоков система в каждый конкретный момент времени может находиться в одном из своих состояний. Количество состояний СМО определяется по формуле M+N+1. Если эти состояния считать случайными событиями (ведь они формируются случайными потоками), то можно говорить о вероятности пребывания СМО в каком-либо из них в исследуемом промежутке времени (рабочий день, смена и т. д.).
Пример решения задачи
В качестве конкретной СМО рассмотрим парикмахерскую. Предположим, что параметры данной СМО следующие:
- парикмахерская обслуживает поток клиентов со средней плотностью l=8 (заявок/час);
- в парикмахерской работают три мастера (N=3);
- средняя производительность каждого мастера составляет m=2 (заявок/час);
- зал ожидания имеет три места (M=3).
1) Возможные состояния системы
Прежде всего нужно выяснить сколько состояний может иметь данная система. Перечислим их:
S0 — состояние, при котором в парикмахерской нет клиентов, все мастера свободны;
S1 — обслуживается один клиент, двое из трёх мастеров свободны, зал ожидания пуст;
S2 — обслуживаются два клиента, два мастера заняты, зал ожидания пуст;
S3 — обслуживаются три клиента, все мастера заняты, зал ожидания пуст;
S4 — в парикмахерской четыре клиента: трое из них обслуживаются, четвёртый ожидает своей очереди в зале ожидания;
S5 — в парикмахерской пять клиентов, все мастера заняты, два клиента ожидают очереди;
S6 — в парикмахерской шесть клиентов, все мастера и все места в зале ожидания заняты.
Седьмой клиент, видя занятость всех мастеров и отсутствие свободных мест в зале ожидания, покидает парикмахерскую необслуженным, т. е. получает отказ системы. Других состояний кроме этих семи система иметь не может. Как отмечалось выше, их количество вычисляется по формуле M+N+1. Таким образом, 3+3+1=7.
В процессе работы СМО наблюдается её переход от одного соседнего состояния к другому. Под действием потока заявок система загружается, переходя от состояния к состоянию в направлении S0®S6. С другой стороны, система стремится саморазгрузиться (S6®S0) потоком выполняемых ею услуг, т. е. усилиями мастеров.
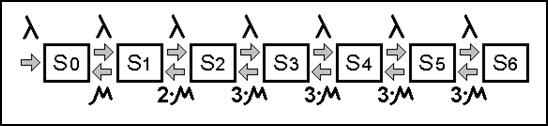
Следует обратить особое внимание на то, что на разных переходах разгрузка системы характеризуется различной её производительностью. Так, например, на переходе S1-S0 работает один мастер и производительность системы равна m. А на переходах S3-S2, S4-S3, S5-S4, S6-S5 система работает с максимальной производительностью 3×m (работают все три мастера). Каждый из переходов характеризуется коэффициентом использования обслуживающей системы R, который определяется как частное плотности потока заявок и производительности. Найдём числовые значения коэффициента использования обслуживающей системы на каждом из переходов.
![]()
![]() .
.
2) Вероятности состояний
Выше было сказано, что пребывание СМО в данный период времени в одном из состояний — событие случайное. В силу того, что в рассматриваемом примере, СМО имеет полную комбинацию возможных состояний из семи, сумма вероятностей нахождения системы в каждом из них равна единице. Запишем это высказывание в виде формулы: P0+P1+P2+P3+P4+P5+P6=1. Здесь P0-P6 - вероятности пребывания системы в состояниях S0-S6 соответственно.
Вероятность свободного состояния СМО можно найти по формуле:
![]() ,
,
где n — индексный номер максимально загруженного состояния СМО (в данном случае n=6).
Следовательно, число слагаемых знаменателя (включая 1) равно количеству состояний исследуемой СМО. Подставив числовые значения, найдём P0 для данного примера.
Вероятность каждого последующего состояния можно определить по формуле:
![]() .
.
Подставив числовое значение вероятности P0 и соответствующего коэффициента использования системы, получим вероятность пребывания СМО в состоянии S1.
P1 = P0 × R1,0 = 0.0122 × 4 = 0.0488.
Аналогично вычисляем вероятности других состояний.
P2 = P1 × R2,1 = 0.0488 × 2 = 0.097;
P3 = P2 × R3,2 = 0.097 × 1.33 » 0.13;
P4 = P3 × R4,3 = 0.13 × 1.33 » 0.173;
P5 = P4 × R5,4 = 0.173 × 1.33 » 0.23;
P6 = P5 × R6,5 = 0.23 × 1.33 » 0.307.
Выше было сказано, что полная комбинация состояний состоит из S0-S6. Поэтому сумма соответствующих вероятностей P0-P6 должна быть равна 1. На данном этапе решения задачи следует обязательно сделать эту проверку.
3) Характеристики СМО
Следующим этапом исследования является определение характеристик функционирования СМО, на основании которых делается вывод о её пригодности в обслуживании данного потока заявок.
Средняя длина очереди заявок определяется как среднее число требований в накопителе по формуле TM=M0×P0+M1 ×P1+...+Mn ×Pn, где Mn — количество занятых мест в накопителе в каждом из состояний S0-Sn. Таким образом, для данной задачи имеем:
TM=0×0.0122+0×0.0488+0×0.097+0×0.13+1×0.173+2×0.23+3×0.307»1.56.
Вероятность отказа очередному клиенту PОТК определяется как вероятность максимально загруженного состояния системы, при котором в накопителе нет мест ожидания. В нашем случае PОТК= P6 » 0.307.
Относительная пропускная способность ОПС=1- PОТК=1-0,307=0,693.
Абсолютный отказ (заявок/час) определяется как произведение плотности потока заявок и вероятности отказа. АО = l × PОТК = 8× 0.307» 2.46.
Абсолютная пропускная способность (заявок/час) находится как произведение плотности потока заявок и ОПС. АПС = l×ОПС = 8× 0,693 » 5,54.
Среднее время ожидания в накопителе (час) находится по формуле:
WM = TM / АПС = 1,56 / 5,54 » 0,28.
Среднее время нахождения заявки в СМО (час)
WS = WM + 1 / m = 0.28 + 1 / 2 » 0.78.
Средняя длина очереди мастеров TN = N0×P0+N1×P1+...+Nn×Pn,
где Nn — число свободных мастеров в каждом из состояний S0-Sn. В нашем случае:
TN= 3×0.0122+2×0.0488+1×0.097+0×0.13+0×0.173+0×0.23+0×0.307» 0.232.
Среднее число занятых мастеров ZN = N - TN = 3 - 0.232 » 2.77. Понятно, что среднее число занятых мастеров равно среднему числу обслуживаемых заявок.
Среднее суммарное число заявок в СМО определяется как сумма средней длины очереди заявок в накопителе и среднего числа обслуживаемых заявок.
TS = TM + ZN = 1.56 + 2.77 » 4.33.
Краткие указания к выполнению работы
Вам предстоит, на основании полученных числовых значений, описанных выше параметров, выбрать одну из трёх описанных в задании систем массового обслуживания. Выполнив алгоритм решения для исследования первой из них, воспользуйтесь буфером обмена и скопируйте решение на два других листа документа Excel. Полученные копии решений вы сможете использовать для исследования двух оставшихся СМО.
При составлении алгоритма решения следует очень внимательно следить за тем, чтобы все последующие действия опирались только на данные ячеек, где выполнялись предыдущие. Это обеспечит алгоритму решения целостность, а значит, его пригодность для безошибочного расчёта характеристик двух других систем.
Примерный вариант оформления задачи представлен на рисунке. После ввода исходных данных сразу же найдите число возможных состояний вашей СМО. Именно это число станет отправной точкой в решении.
Коэффициенты использования системы оформите в виде отдельной таблицы. При составлении их формул будьте внимательны: каждый переход характеризуется своим числом работающих мастеров.
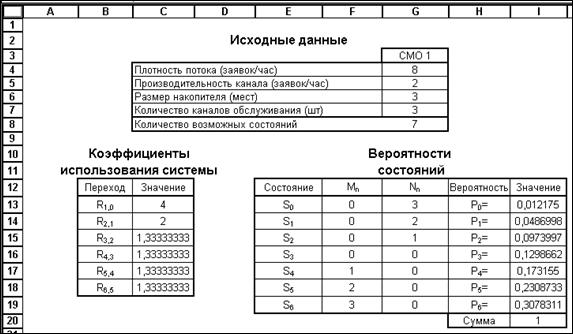
Вычисление вероятностей состояний
Параметры, характеризующие каждое из состояний системы удобно оформить в виде таблицы (в данном случае, диапазон ячеек E12:I19). В столбцы Mn и Nn внесите количество занятых мест в накопителе и число незанятых мастеров в каждом из состояний S0-Sn соответственно.
Самое главное на данном этапе решения — правильно вычислить вероятность свободного состояния системы P0. Для составления этой формулы следует воспользоваться функцией ПРОИЗВЕД из категории математических. Она позволяет вычислить произведение значений указанного диапазона ячеек. Лишний раз обратите внимание, что число слагаемых знаменателя (включая 1) равно количеству состояний СМО. В данном случае, в ячейку I13 внесена формула:
=1/(1+C13+ПРОИЗВЕД(C13:C14)+ПРОИЗВЕД(C13:C15)+ПРОИЗВЕД(C13:C16)+ПРОИЗВЕД(C13:C17)+ПРОИЗВЕД(C13:C18)).
После этого, одну за другой, вычислите остальные вероятности состояний. Правильность решения на этом этапе нужно обязательно проверить, найдя сумму всех вероятностей, которая должна быть равна 1 (ячейка I20).
Вычисление характеристик СМО
Вычисление десяти необходимых характеристик СМО не связана ни с какими трудностями, поэтому эта часть документа на рисунке не показана. При вычислении средней длины очереди заявок TM и средней очереди мастеров TN удобно воспользоваться знакомой вам по прошлым работам функцией СУММПРОИЗВ.
В качестве критериев выбора одной из трёх предложенных СМО используйте точку зрения предполагаемого клиента. Выбор парикмахерской не составит для вас большого труда, если вы представите себя её посетителем.
Контрольные вопросы
1) На какие два основные вида делятся системы массового обслуживания? Кратко характеризовать каждый из них. Какова, в общем случае, структура СМО? Привести примеры СМО.
2) Какими параметрами характеризуется любая СМО? Выполнение каких требований предполагается при её моделировании?
3) Чем характеризуется каждое из состояний системы? Как определить число состояний?
4) Какой величиной характеризуется каждый из переходов? Как её найти?
5) Что показывает вероятность состояния? Почему сумма вероятностей состояний должна быть равна единице?
6) Кратко характеризовать и объяснить каждую из приведённых десяти характеристик СМО.
1) Г. Вагнер. Основы исследования операций. Т.1. - М.: Мир, 1972. - 335 с.
2) Павлов А.А., Гриша С.Н., Основы системного анализа и проектирования. - Киев: Высш. шк., 1991. - 367 с.
3) Бахвалов Н.С. Численные методы. - М.: Наука, 1973. - 630 с.
4) Фурунджиев Р.И. и др. Применение математических методов и ЭВМ. Практикум: Учеб. пособие для вузов. - Минск: Высш. шк.,1988. - 991с.: илл.
5) Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. Учеб. пособие для вузов. - М.: Высш. шк., 1989. - 367 с.: илл.
6) Банди Б., Основы линейного программирования, пер. с англ. – М.: Радио и связь, 1989.-176 с.: илл.
7) Полак Э. Численные методы оптимизации. Единичный подход. Пер. с англ. Ф.Н. Ерешко. Под ред. И.А. Вателя. – М.: Мир, 1974, 376 c. с черт.
Содержание
|
1 Лабораторная работа. Моделирование динамики производственных процессов |
3 |
|
2 Лабораторная работа. Моделирование производственных функций |
9 |
|
3 Лабораторная работа. Определение парных коэффициентов корреляции |
16 |
|
4 Лабораторная работа. Планирование эксперимента |
21 |
|
5 Лабораторная работа. Моделирование простейших случайных потоков |
25 |
|
6 Лабораторная работа. Разомкнутая система массового обслуживания |
32 |
|
Список литературы |
39 |
Сводный план 2011 г. поз. 260