Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра компьютерных технологий

 

 

 

ОСНОВЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ 

Конспект лекций для студентов всех форм обучения специальности

5В070300 – Информационные системы

 

 

Алматы 2011 

СОСТАВИТЕЛИ: Мусатаева Г.Т., Конуспаева А.Т., Байжанова Д.О. Основы компьютерного моделирования. Конспект лекций для студентов всех форм обучения специальности 5В070300 – Информационные системы. -  Алматы: АУЭС, 2011. - 58 с. 

 

Конспект лекций разработаны в соответствии с требованиями  квалификационной характеристики специалиста, Государственных стандартов, типовой программы курса. Они составлены с учетом активизации процесса изучения основ курса и являются подготовкой к проведению лабораторных работ.

Конспект лекций предназначены для студентов всех форм обучения специальности 5В070300 – Информационные системы.

Библиография – 7 названий. 

 

Рецензент: канд. физ.-мат. наук, доцент Б. М. Шайхин.

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.

 

© НАО «Алматинский университет энергетики и связи», 2011 г.

  

1 Лекция. Основные понятия компьютерного моделирования. Сложные системы. Характеристики сложных систем. Задачи компьютерного моделирования сложных систем

 

В современном обществе системные представления уже достигли такого уровня, что мысль о полезности и важности системного подхода к решению возникающих в практике проблем вышла за рамки специальных научных истин и стала привычной, общепринятой. Не только ученые, но и инженеры, педагоги, организаторы производства, деятели культуры обнаружили системность собственной деятельности и стараются осуществлять свою работу осознанно системно. Широко распространилось понимание, что наши успехи связаны с тем, насколько системно мы подходим к решению проблем, а наши неудачи вызваны отступлениями от системности. Было бы неверным считать, что "мышление стало системным" только недавно. Мышление системно всегда и другим быть не может. Системность - это не такое качество, которым можно обладать или не обладать. Однако системность имеет разные уровни. Сигналом о недостаточной системности существующей деятельности является появление проблемы; разрешение возникшей проблемы осуществляется путем перехода на новый, более высокий уровень системности в нашей деятельности. Поэтому системность не столько состояние, сколько процесс.

Понятие организационной системы

Что же понимается под организационной системой? Прежде всего - это система с социальным и экономическим интересом, имеющая цель существования и обладающая ресурсами для построения, исходя из цели существования структуры и отношений, необходимых для получения некоторого результата, который обычно называют конечным продуктом. Основным признаком организационной системы является ее субъективизм, т.е. присутствие в ней субъекта, имеющего интерес и цель. Системообразующим признаком, несомненно, является цель существования системы, но изначально, еще до формирования системы, необходимо, чтобы в среде ее обитания появились проблема и интерес. Именно после осознания этого субъектами актуальной среды, т.е. среды, активно связанной с проблемой, начинают преобразовываться либо разрушаться существовавшие организации. В случае, если достигнуто то или иное соглашение по поводу реализации проявленного интереса, а также решен вопрос доступа к ресурсам, начинается процесс осознания цели и формирования организационной системы [1].

Итак, организационная система - это множество структурно и функционально определенных и, как правило, активных элементов, которые характеризуются общностью цели, являющейся информационным образом конечного продукта, ради которого система существует.

Определенная цель - главное для существования организационной системы. В этом ее, с одной стороны, неискоренимый субъективизм, с другой - отражение объективных процессов. Цель - это концентрированное выражение идеологии существования системы, она должна описывать "нормативы и стандарты" конечного продукта жизнедеятельности системы. Уже потом, на основе определенной цели, строится стратегия и тактика управления системой, формируется структура системы, распределяются ресурсы и строятся алгоритмы функционирования элементов.

Организационная система возникает и функционирует в актуальной среде, которую мы договорились, в соответствии с предметом рассматриваемых явлений, называть обществом или общественно-экономическим процессом. Очевидно, что общество также можно рассматривать как организационную систему, цели которой носят более общий характер и описывают продукт жизнедеятельности более сложной и объемной системы. Будем называть такие цели "интересами общества".

При определении цели организационной системы имеют место два начала - объективное и субъективное. Объективное начало цели определяется проблемной ситуацией, возникающей в обществе. Существование проблемы порождает необходимость системообразующей деятельности. Для того чтобы цель была сформулирована и начала образовываться система, необходим некоторый субъект организационно-экономической среды, который выявляет, формулирует проблему и, в конечном счете, определяет цель.

Выявление и описание проблемной ситуации - это одна из наиболее, сложных и ответственных процедур в общественно-экономических процессах. Возникновение проблемных ситуаций есть следствие диалектического характера развития систем, происходящего через преодоление противоречий. Противоречия являются внутренней причиной всякого движения и прогресса. В рассматриваемых процессах движущей силой такого рода, прежде всего, является противоречие между растущими потребностями людей и возможностью их удовлетворения Неудовлетворенные потребности, которые, как правило, изначально носят объективный характер, в конечном счете, получают субъективное выражение в оценке параметров существующего положения и осознания необходимости их изменения. Возможности удовлетворения потребностей ограничиваются множеством объективных и субъективных факторов: существующими системами, методами управления, уровнем научно-технологического развития, ресурсным обеспечением, природой и допустимым уровнем воздействия на нее и т.п. Выявление и формулировка проблемы - это творческий процесс. В качестве средств, повышающих качество выявления проблемы, можно рекомендовать разнообразные методы прогнозирования и планирования. Противоречия в общественно-экономических процессах разрешаются через целенаправленную деятельность субъектов и служат постоянной движущей силой общественного развития. Противоречие на определенной стадии своего развития создает проблемную ситуацию, разрешение которой является системообразующим фактором. Можно утверждать, что каждая проблемная ситуация в своей эволюции объективно проходит несколько стадий развития. Обычно выделяют три стадии: скрытое развитие, явное развитие и превращение проблемы в постоянно действующий неблагоприятный фактор. Задачами цивилизованного разрешения проблемных ситуаций являются выявление и разрешение проблем на ранних стадиях развития.

Определение целей в организационных системах является специфическим, субъективным процессом, однако то, насколько при этом учтена объективная реальность и цели более высокого уровня, определяет надежность и жизнеспособность создаваемых организационных систем. Цивилизованное общество должно делегировать для создания и управления организациями людей, четко представляющих его интересы. Для общества не имеют смысла поддержка и стимулирование таких субъектов, которые стремятся реализовать стратегии, не соответствующие его интересам. Механизмом регулирования этих процессов являются системы контроля и стимулирования, ориентирующие субъектов на реализацию интересов общества. Однако при этом необходимо учитывать, что активность субъектов сложно описать, поэтому организационные системы относятся к классу сложных систем. Ограничения выражаются интересами общества и явно отражены в законодательных и нормативных актах, целевых установках и планах, определяющих общественно-экономические процессы. Реально эти ограничения позволяют определить следующее:

- рациональное использование основных и оборотных фондов системы (оборудования, производственных площадей, ресурсов, сырья и продукции, производимых другими системами и т.п.);

- рациональное потребление природных ресурсов (воды, воздуха, полезных ископаемых и т.п.);

- рациональное использование труда субъектов системы, т.е. рациональное использование их рабочей силы.

Подведем некоторые итоги, касающиеся определения организационной системы. Можно сделать вывод, что определить организационную систему можно, рассматривая основные этапы деятельности по ее синтезу и анализу.

Такая деятельность обычно называется системной деятельностью или системным подходом. Эта деятельность позволяет определить средства разрешения проблемных ситуаций и ответить на следующие вопросы: "что?", "как?", "кто?", "при каких условиях?", "чем?".

Другими словами, следует осознать проблемную ситуацию, определить цели ее ликвидации, для реализации целей построить соответствующую организационную структуру, определить ограничения функционирования системы, процедуру планирования деятельности и систему стимулирования элементов организации, при этом для обеспечения согласованности и согласия должны быть учтены и рационально использованы ресурсы общества.

Теоретическую базу для формирования подходов к решению перечисленных задач дает системный анализ. В разделе 1.4 дано изложение основных понятий этого инструмента исследования систем, содержащихся в книге Ф.И. Перегудова и Ф.П. Тарасенко [2].

Техническими средствами для этого служат компьютерные технологии. Их совершенствование и использование для самых разнообразных нужд, создание алгоритмов и программных систем для ЭВМ приобрели исключительно важное значение. Настолько важное, что все связанное с использованием ЭВМ стали выделять в отдельную область науки и техники, названную информатикой.

Но не менее важная сторона процесса кибернетизации связана с изучением самих систем, созданием методов организации и управления сложными системами, развитием системных представлений, системных теорий.

 

2 Лекция. Принцип системного подхода в моделировании. Классификация видов моделирования. Аналитические и имитационные модели

 

В настоящее время существуют 3 системных понятия:

- теория систем;
- системный подход;
- системный анализ.

Термин «теория систем» введен Берталанфи в 30 гг. Фундаментальные работы принадлежат русскому ученому А. А. Богданову. Этой проблематикой занимались ИИ Шмальгаузен, ВН Беклемишев. Математическая теория систем разработана М.Массаровичем, Д. Марко, И. Такахарой (“Теория иерархических многоуровневых систем”).

Термин «системный подход» определяет способ исследования явлений, их взаимосвязь с другими явлениями. Инструментом системного подхода является системный анализ, который базируется на теории систем.

Термин «системный анализ» определяет такой способ изучения сложных объектов, при котором рассматриваются их части (подсистемы и элементы) с целью выяснения влияния связей элементов и подсистем на свойства объекта в целом.

Это прямая задача анализа. Обратная задача заключается в выборе элементов и подборе связей для получения объекта с требуемыми свойствами (синтез).

Цель анализа - определить, возможно, полное множество ситуаций, пребывание в которых существенно влияет на качество функционирования управляемой системы.

Задачи целевого анализа

1) Выделение количественных показателей для главных и основных показателей.

2) Древовидная детализация главной и основных целей по элементам организации с выделением количественных показателей.

3) Установление диапазонов значений для количественных показателей элементов целевой компоненты СУ.

4) Описание алгоритмов взаимосвязи отдельных целевых показателей.

Задачи информационного анализа

1) Описание документов и сообщений, представляющих собой информационный инструментарий управления.

2) Описание процедур получения значений показателей и документов.

3) Описание структуры документов и их элементов, показателей, отношений, объектов.

Задачи ситуационного анализа

1) Многоуровневая классификация состояний управляемого процесса в пространстве производственных показателей, в том числе целевых. При этом выделяются ситуации множества состояний, для которых технология управления является общей в части ее исполнения и информационных документов.

2) Установление соответствия ситуаций - информационный элемент для увязки экономических элементов потерь с элементами издержек управления.

3) Динамическая характеристика ситуаций, показывающая возможную частоту их возникновения и, т.о., частоту опроса параметров модели ситуации с целью ее идентификации.

4) Экономическая характеристика ситуаций в виде описания в пространстве целевых показателей системных потерь, которые будут наблюдаться в случае отказа от контроля ситуации.

5) Описание алгоритмических моделей ситуаций для использования их в качестве элементов организационной компоненты систем управления.

Задачи организационно-функционального анализа

1) Описание организационной структуры системы управления и ее элементов -линейчатых, функциональных и целевых подразделений.

2) Прикрепление ситуаций к подразделениям для сопровождения моделей ситуаций и принятия решений о действиях в данных ситуациях .

3) Описание прикрепления отдельных процедур подготовки и обработки данных к подразделениям и исполнениям.

4) Выработка вариантов рекомендаций по изменению состава подразделений.

Задачи информационно-стоимостного анализа

1) Определение количественных характеристик размеров информационной базы.

2) Определение издержек, связанных с поддержанием информационных инструментов управления.

3) Оценка потребностей в технических средствах поддержки информационной модели и оценка загрузки этих средств.

Вопросы анализа и синтеза систем

Анализ, как метод исследования, изначально органически присущий человеческому мышлению, имеет колоссальное значение в науке и практике. Математический анализ, исследования элементарных частиц, анатомия, организация конвейерной технологии - все это (и не только это) служит иллюстрацией эффективности анализа. Успехи аналитического метода привели к тому, что сами понятия "анализ" и "научное исследование" стали восприниматься как синонимы. Идеалом, высшей формой познания, стала считаться причинно-следственная закономерность, при которой причина является необходимым и достаточным условием осуществления следствия.

Однако многие исследователи обращали внимание на то, что роль синтеза не сводится только к "сборке деталей", полученных при анализе.

Среди специалистов по системной деятельности особенно настойчиво эту мысль подчеркивает Р. Акофф [1]. Он отмечает, что результатом анализа является определение структуры, понимание того, как система работает, но не понимание того, почему и зачем она это делает: "Синтетическое мышление требует объяснить поведение системы. Оно существенно отличается от анализа. На последнем шаге анализа знания о частях агрегируются в знание о целом... Синтетическое мышление открывает не структуру, а функцию, оно открывает, почему система работает так, а не то, как она делает это".

Таким образом, анализ и синтез дополняют друг друга. Системное мышление совмещает оба указанных метода. Как бы то ни было, и при аналитическом, и при синтетическом подходах наступает момент, когда необходимо разложить целое на части, либо объединить части в целое. Эти операции называют соответственно декомпозицией и агрегированием.

В случае декомпозиции задача распадается на подзадачи, система - на подсистемы, цели - на подцели и т.д. При необходимости этот процесс повторяется, что неизбежно приводит к иерархическим структурам. Необходимо отметить, что решение этих задач для сложных систем плохо формализовано, поэтому операцию декомпозиции обычно выполняют эксперты. Качество построенных экспертами иерархий зависит как от их компетентности в данной области знаний, так и от применяемой методики декомпозиции. Задачей системного подхода является переход от чисто эвристического, интуитивного подхода к более осознанному, алгоритмическому выполнению декомпозиции. Основанием такой декомпозиции являются модели рассматриваемой системы.

Для декомпозиции системы, прежде всего, используются модели «черного ящика», состава, структуры, конструкции (структурно-функциональные схемы). Однако выбор формальной модели лишь подсказывает, какого типа должна быть модель-основание для анализа. Можно сказать, что формальную модель следует наполнить содержанием, для того чтобы она стала основанием для декомпозиции. Критерием качества использования модели является критерий полноты анализа, поэтому полнота формальной модели должна быть предметом особого внимания. Одна из важных задач системного анализа состоит в накоплении наборов полных формальных моделей. Этому процессу есть хорошая аналогия в теории искусственного интеллекта: понятие фрейма - декларативного представления данных для описания некоторой стандартной ситуации. Можно сказать, что одной из важнейших задач системного анализа является формирование формальных фреймов для анализа различных систем. Приведем несколько примеров.

Например, схему входов организационной системы можно моделировать набором требований, предъявляемых к исследуемой системе следующими объектами: самой исследуемой системой, вышестоящими системами, существенной для исследуемой системы средой обитания, нижестоящими системами или объектами управления. Такая модель-фрейм является достаточно полной, к ней нечего добавить (перечислено все, что воздействует на систему), а изъятие любого элемента лишит ее полноты [2].

Следующей моделью, относящейся к организационным системам, является модель жизненного цикла системы. Фрейм жизненного цикла организационной системы управления отражает взаимосвязь основных функций управления: целевыявление и прогнозирование деятельности, планирование, организация исполнения и оперативное управление, контроль, учет и анализ.

Жизненный цикл производственной системы включает следующие элементы: выявление потребности, подготовка производства, испытание средств и объекта производства, производство, организация реализации объекта производства, сопровождение и модернизация средств и объекта производства, организация ликвидации отходов и объектов производства.

Полнота формальной модели является необходимым, но не достаточным условием декомпозиции. В конечном счете, все зависит от полноты содержательной модели, которая строится "по образу" формальной модели, но не тождественна ей. Фрейм лишь привлекает внимание эксперт к необходимости рассмотреть, что именно в реальной системе соответствует каждому из элементов и какие из них должны быть включены в| содержательную модель.

Очевидно, что вопрос достаточной степени детализации содержательных моделей, в отличие от фреймовых, окончательно решить невозможно. Чтобы сохранить полноту и возможность расширения содержательной модели, часто используют логическое замыкание перечня ее элементов компонентой "все остальное". Эта компонента постоянно напоминает эксперту, что он, возможно, не учел что-то важное.

Таковы некоторые аспекты того, каким образом осуществляется акт разложения целого на части. Возникает вопрос, можно ли дать рекомендации по всему многоступенчатому процессу декомпозиции - от первого уровня до последнего? Попытки положительного ответа на данный вопрос имеются в существующих процедурах построения иерархий и деревьев цели систем.

В определенном смысле противоположной декомпозиции является операция агрегирования, т.е. объединения элементов и понятий в единое целое. Результат операции агрегирования обычно называют агрегатом. Объединенные в агрегат, взаимодействующие элементы образуют систему, которая обладает не только внешней целостностью - обособленностью от среды, но и внутренней целостностью - природным единством. Если внешняя целостность отображается моделью "черного ящика", внутренняя целостность связана со структурой системы. Наиболее яркое проявление внутренней целостности системы состоит в том, что свойства системы не являются только суммой свойств ее составных частей. Система есть нечто большее, система в целом обладает такими свойствами, которых нет ни у одной из ее частей, взятой в отдельности. Модель структуры подчеркивает, главным образом, связанность элементов. Структурное взаимодействие дает то что при объединении частей в целое возникает нечто качественное новое, такое, чего не было и не могло быть без этого объединения.

Для проектирования организационной системы или совершенствования, связанного с определением ее структуры и технологии функционирования, требуется использование не только приведенных язык внешнего описания, но и следующих языков внутреннего описания:

- языка описания иерархии и структуры взаимодействия для представления распределения власти;

- языка описания структуры функционирования для описания распределения ответственности;

- языка описания информационных и материальных потоков для описания технологической структуры функционирования;

- языка описания планирования, контроля, учета, анализа, регулирования стимулирования для описания технологии функционирования.

Приведенные примеры показывают, что конфигуратор являет моделью описания систем в "системе координат" того пространства, которое позволяет моделировать достижение некоторой цели. Если цель меняется, меняются пространство описания, "его координаты", а значит, конфигуратор. Хотя здесь и использовано понятие координатной систем? следует, конечно, понимать , что конфигуратор - это содержательная модель адекватность, которая может быть достижима для простых систем. Для сложных систем критерием достижимости языков описания уровней, конфигуратора может быть один - практика их применения.

Весьма частой является ситуация, которая требует агрегативного описания системы. Она состоит в том, что объекты, с которыми приходит иметь дело, слишком многообразны, а используемые для их описания конфигураторы имеют большую размерность, что приводит "необозримым" объемам данных. В данном случае на первый план выступает уменьшение размерности описаний за счет их структурирования: агрегат объединяет части в нечто целое.

 

3 Лекция. Этапы компьютерного моделирования. Принципы построения моделирующих алгоритмов. Общая структура моделирующих алгоритмов

 

Функциональные (динамические) модели систем используют глубокую формализацию. Рассматривая выход y (t) системы (это может быть вектор) как ее реакцию на управляемые u ( t ) и неуправляемые v ( t ) входы x ( t ) = { u ( t ), v ( t )} (см. рисунок 3.1), его на уровне модели "черного ящика" можно выразить как совокупность двух процессов: Хт= ( x ( t )) и YT -{y(t)}, teT .

Чаще y ( t ) необходимо считать результатом некоторого преобразования Ф процесса x(t), т.е. y ( t )=Ф( x ( t )).

Рисунок 3.1 - Процессы системы на уровне «черного ящика»

 

Такое соответствие между входом и выходом можно описать тем или иным способом. Какой именно способ - зависит от того, что нам известно, и в какой форме можно использовать эти знания.

Например, иногда бывает известно, что система мгновенно преобразует вход в выход, т.е. что у (t) является функцией только x (t) в тот же момент времени. Для таких безынерционных систем остается найти аналитическую функцию, выражающую зависимость у - Ф(х). Даже в такой достаточно простой постановке задача имеет совсем непростые варианты, которые зависят от того, что известно о функции Ф (в параметризованном случае Ф принадлежит семейству функций, известных с точностью до параметров; параметризованном - вид функции Ф неизвестен), и от наличия или отсутствия некоторых общих сведений о ее свойствах (непрерывности гладкости, монотонности, симметричности и т.п.). Дополнительные варианты (и дополнительные трудности) возникают, если входы или выходы наблюдаются с помехами или искажениями. При этом разные предположения о природе этих помех приводят к принципиально отличающимся решениям задачи (например, в случае, когда вероятностное распределение помехи известно точно, известно с точностью до числовых параметров или неизвестно совсем).

С другой стороны, класс, системы, которые можно считать безынерционными, весьма узки. Необходимо строить математические модели систем, выход которых определяется не только значением входа в данный момент времени, но и теми значениями, которые были на входе в предыдущие моменты. Более того, в самой системе с течением времени как под влиянием входных воздействий, так и независимо от них могут происходить изменения, что также следует отражать в модели.

В последующих разделах второй главы даны элементарные понятия построения аналитических зависимостей.

f(x) = f(x.)+f'(x.)(x-x.)+(1/2)(ξ)(x-x.),

где ξ - некоторая точка отрезка с концами x. и x. Поэтому в предположении двукратной дифференцируемости функции f на X условием ее выпуклости является неравенство

f' ( x )≥0.

Аналогичные рассуждения можно провести и для многомерного случая. При этом условие заменяется требованием положительной полуопределенности матрицы вторых производных f "( x ).

При описании допустимого множества, на котором ищется минимум функции f, помимо ее области задания X, обычно вводятся те или иные ограничения. Например, в рассматриваемых на рисунке 3.1 случаях такими ограничениями на всей вещественной оси -?<х<+? могут быть неравенства х ≥ а и х ≤ b , которые можно записать в единообразном виде:

В дальнейшем для ограничений, которых может быть несколько (например, m ), будем пользоваться универсальным обозначением

g i ( x ) ≤ 0, i = 1,2,..., m .

В случае g 1 ( x )= a - x и g 2 ( x ) = x - b . Для широкого класса задач при заданном множестве X с ограничениями удобно пользоваться формулой

D = { x € X : g i ( x ) ≤ 0, i = 1,2,..., m }.

Здесь через D обозначено допустимое множество. Заметим, что выпуклость множества D можно гарантировать, если все функции g - выпуклые. Задача о поиске

min { f ,( x ) : x € D } (4.7)

называется задачей выпуклого программирования.

Входные, выходные данные, переменные состояния. Модель структуры системы

Для достижения ряда практических целей достаточно модели "черного ящика" или модели состава. Однако, очевидно, что есть вопросы, решить которые с помощью этих моделей нельзя. Чтобы получить велосипед недостаточно иметь "ящик" со всеми отдельными его деталями. Необходимо еще правильно соединить все детали между собой, т. е., установить между элементами определенные связи - отношения. Совокупность необходимых и достаточных для достижения цели отношений между элементами называется структурой системы.

Бесконечность природы проявляется и в том, что между реальными объектами, вовлеченными в систему, имеется большое (может быть, бесчисленное) количество отношений. Однако когда мы рассматриваем некоторую совокупность объектов как систему, то из всех отношений важными, т.е. существенными для достижения цели, являются лишь некоторые. Точнее, в модель структуры (т.е. в список отношений) мы включаем только конечное число связей, которые, по нашему мнению, существенны по отношению к рассматриваемой цели. Например, при расчете механизма обычно не учитываются силы взаимного притяжения его деталей, хотя, согласно закону всемирного тяготения, такие силы объективно существуют. Зато вес деталей (т.е. сила их притяжения к земле) учитывается обязательно.

Отношения между элементами могут быть самыми разнообразными. Однако можно попытаться их классифицировать и перечислить. Трудность состоит в том, что мы знаем не все реально существующие отношения и вообще неизвестно, является ли конечным их число. Интересное исследование было проведено с естественными языками. Выделение языковых конструкций, выражающих отношения (типа: находиться на (под, около,...), быть причиной, быть подобным, быть одновременно, состоять из, двигаться к (от, вокруг,...) и т.п.), привело к выводу, что в большинстве языков число выражаемых отношений примерно одинаково (около 200).

Модели структуры часто представляют в виде структурных схем. В структурной схеме указываются все элементы системы, все связи между элементами внутри системы и связи определенных элементов с окружающей средой (входы и выходы системы).

Пример

С целью построения математической модели используем задачу “о двух картошках”.

 Фирма по производству пищевых полуфабрикатов выпускает из картофеля:

- продукт 1 - картофельные дольки;

- продукт 2 - картофельные кубики;

- продукт 3 - картофельные хлопья.

Каждый продукт получается путем соответствующей переработки и подлежит определенной упаковке. Картофель направляется на соответствующую линию после предварительной сортировки.

Фирма закупает картофель у 2-х поставщиков, причем выход продуктов 1, 2, 3 из 1 тонны картофеля поставщика 1 и 2 различный (см. таблицу).

 

 

Какое количество картофеля необходимо закупить у поставщика 1, 2 для получения максимальной прибыли.

Относительная прибыль получается как разность между полной выручкой с продукции, полученной из 1 тонны картофеля, и стоимостью 1 тонны картофеля. Другие виды расходов не рассматриваются для простоты. Сюда могут входить:

- затраты на транспортировку сырья или продукции;

- затраты на обслуживание оборудования;

- оплата труда и т. д.

Если принять Р₁- количество картофеля, закупленного у поставщика 1; Р₂- количество картофеля, закупленного у поставщика 2; тогда в соответствии с условиями таблицы значения Р₁ и Р₂ должны подчиняться условиям :

0,2Р₁ + 0,3Р₂ =< 1,8 для продукта 1;

0,2Р₁ + 0,1Р₂ =< 1,2 для продукта 2;

0,3Р₁ + 0,3Р₂ =< 2,4 для продукта 3.

При этом Р₁ >= 0; Р₂ >=0, исходя из физического смысла задачи.

Задача оптимизации сводится к таким Р₁ и Р₂ , которые обеспечат максимальную прибыль, то есть:

5Р₁ + 6Р₂ = max (3)

Описание (1), (2), (3) является математической моделью анализа задачи “о двух картошках”.

Для описания линейной статической оптимизационной модели необходимо и достаточно

- описание целевой функции;

- описание основных условий ограничения;

- описание дополнительных условий ограничения.

 

4 Лекция. Аналитико-имитационный аппарат компьютерного моделирования. Метод Монте-Карло

 

Выпуклой называется функция f, определенная на выпуклом множестве X которая при любых α (0,1) и х', х" X удовлетворяет неравенству

_.

Если выпуклая функция f непрерывна и дифференцируема, то для любых выполняется дифференциальное неравенство

_.                                                                                                             (4.1.1)

Здесь в правой части стоит скалярное произведение векторов и . Наоборот, если дифференцируемая функция f при любых удовлетворяет неравенству (4.1.1), то это выпуклая функция.

Геометрически неравенство (4.1.1) означает следующее. Построим график функции f и в точке графика проведем к нему касательную гиперплоскость. Тогда для каждого правая часть неравенства (4.1.1) совпадает с соответствующей ординатой касательной гиперплоскости, т. е. график выпуклой функции расположен выше (точнее, не ниже) касательной гиперплоскости.

Для рассматриваемого одномерного случая неравенство (1) принимает вид

_.                                                                                                              (4.1.2)

В правой части неравенства (1) и соответственно (2) присутствуют два члена разложения функции f пo формуле Тейлора в окрестности точки . Заметим, что для дважды дифференцируемой функции можно написать представление

_,

где - некоторая точка отрезка с концами и Поэтому в предположении двукратной дифференцируемой функции f на X условием ее выпуклости является неравенство

_.                                                                                            (4.2)

Аналогичные рассуждения можно провести и для многомерного случая. При этом условие (4.2) заменяется требованием положительной полуопределенности матрицы вторых производных f"(x).

При описании допустимого множества, на котором ищется минимум функции f, помимо ее области задания X, обычно вводятся те или иные ограничения. Например, в случаях такими ограничениями на всей вещественной оси  могут быть неравенства и , которые можно записать в единообразном виде:

и _.                                                                                                                                  (4.3)

В дальнейшем для ограничений, которых может быть несколько (например, m), будем пользоваться универсальным обозначением:

_.                                                                                                                                                (4.4)

В случае (3) и . Для широкого класса задач при заданном множестве X с ограничениями (5) удобно пользоваться формулой

Здесь через D обозначено допустимое множество. Заметим, что выпуклость множества D можно гарантировать, если все функции - выпуклые. Задача о поиске  называется задачей выпуклого программирования.

Условия экстремума

Необходимое условие экстремума. Рассмотрим вначале задачу безусловной минимизации, но будем теперь считать, что f (x) — скалярная функция векторного аргумента размерности n, т. е. X = Еn. Если х^~ - точка её безусловного локального экстремума, то в x^~j будет достигаться экстремум функции f(x^~1, x^~2,...,x^~j-1,x^j,x^~j+1,...,x^~n) по одной переменной х^j, которая получается из функции f(x), если зафиксировать все переменные, кроме x^j, положив хⁱ=х^~i для i≠j. Для функции же одной переменной f(x^~1,...,x^~j-1,x^j,x^~j+1,...,x^~n) необходимым условием экстремума является равенство нулю соответствующей частной производной. Проведя это рассуждение для всех j=l,...,n, приходим к следующей теореме.

Теорема 4.1. Для того чтобы в точке х функция f(x¹,...,хⁿ⁾ имела безусловный локальный экстремум, необходимо, чтобы все ее частные производные обращались в х^~ в нуль:

                                                                           (4.5)

 

Условие стационарности мы будем записывать еще в одной из следующих эквивалентных форм:

 

 

где f()= f'() – п - мерный вектор с компонентами который принято называть градиентом функции f (х) в точке .

Справедливо и обратное утверждение, так как из последнего равенства, в силу произвольности независимых приращений dxⁱ, i = l,...n, следует, что все частные производные в точке равны нулю:

 

 

Условия (4.5) образуют систему п уравнений для определения п компонент вектора х. Эти уравнения могут иметь различную природу и допускать любое количество решений, в частности, не иметь ни одного. Как и выше, точки х, являющиеся решениями системы уравнений (4.5), будем называть стационарными, а условие (4.5) - необходимым условием экстремума.

Достаточные условия. После того как решение х системы уравнений (4.5) будет найдено, необходимо еще определить характер стационарной точки х. Для этого нужно исследовать поведение функции f (x) в окрестности стационарной точки х. Снова воспользуемся разложением функции f(х) в ряд Тейлора, предполагая ее дважды непрерывно дифференцируемой по всем переменным х',...,х". Тогда получим

                                            (4.6)

где ξⁱ = xⁱ – xⁱ.

Здесь через  обозначили элементы матрицы вторых производных функции f(x) в стационарной точке х, а через ||ξ|| — какую-нибудь норму вектора ξ, например, . Далее матрицу вторых производных мы будем обозначать так:

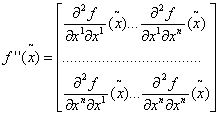.                                                             (4.7)

Напомним, что квадратичная форма называется неотрицательно определенной в точке х, если

                                                                                     (4.8)

и положительно-определенной, если

                                                                                     (4.9)

для любых векторов .

Соответственно, симметричная матрица вторых производных f"(x) называется неотрицательно-определенной в точке  если выполнено (4.8), и положительно определенной, если выполнено (4.9). Неположительно-определенным и отрицательно-определенным квадратичным формам и матрицам соответствуют противоположные знаки в неравенствах (4.8), (4.9).

Таким образом, с учетом разложения (4.6) приходим к следующей формулировке условий второго порядка экстремальности функции

Теорема 4.2. Для того чтобы дважды непрерывно дифференцируемая функция n переменных f (х) имела в стационарной точке х безусловный локальный минимум (максимум), достаточно, чтобы матрица ее вторых производных была положительно- (отрицательно-) определенной.

Проверка знако-определенности матриц может быть осуществлена, например, с помощью критерия Сильвестра. Согласно этому критерию необходимым и достаточным условием положительной определенности квадратичной формы (x,Ax), где A = {aij}- симметричная n*n матрица, является выполнение n неравенств:

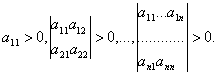
Необходимыми достаточным условием отрицательной определенности квадратичной формы (х, Ах) является выполнение цепочки следующих n неравенств:

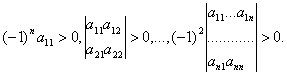
Если квадратичная форма не меняет знака, но обращается в нуль, то для определения характера стационарной точки требуется исследование производных более высокого порядка.

 

5 Лекция. Случайные числа и принцип их моделирования. Метод усечения. Конгруэнтный метод. Метод суммирования

 

Рассмотрим теперь задачу на относительный экстремум. Решение задачи об отыскании экстремумов функции n переменных f(x) на всем пространстве Е_n может быть сведено с помощью необходимых условий к решению системы уравнений, в результате чего определяются стационарные точки функции f(x). Оказывается, что аналогичное сведение возможно и для задачи отыскания экстремумов функции f (x) при наличии ограничений типа равенств . Условия принято еще называть уравнениями связи.

Уточним, что именно мы будем понимать под решением задачи на относительный экстремум. Точку х, удовлетворяющую условиям, договоримся назвать допустимой.

Определение 4.1. Допустимая точка доставляет относительный цокольный минимум функции f(x), если можно указать такое число ε > 0, что для всех x, удовлетворяющих уравнениям связи и условию

имеет место неравенство

Метод Лагранжа состоит из следующих этапов:

1) Составляется функция n + m переменных, которая называется Функцией Лагранжа:

                                                                                                                    (5.1)

где λ= λ ₁,..., λ _m - произвольные множители.

2) Вычисляются и приравниваются нулю ее частные производные no x и λ:

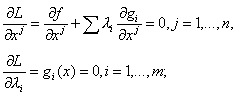                                                                                                       (5.2)

3) Решается система (5.2) n + m уравнений относительно n + m неизвестных x¹,...,xⁿ, λ₁,..., λ_m.

Система уравнений (5.2) представляет собой необходимые условия первого порядка в задаче на относительный экстремум, а ее решения ¹,...,ⁿ принято называть условно-стационарными точками.

Необходимые условия экстремума не определяют характера стационарной точки. Вопрос о наличии в ней относительного экстремума и о выяснении его типа может быть решен с помощью разложений функций f(x), g_i(x) в ряд Тейлора.

Пусть пара {, λ}- решение уравнений (5.2). Попробуем понять, чем определяются соотношения между значениями функции f(x) в точке и в близких к ней допустимых точках вида +ξ. Точки +ξ должны теперь удовлетворять уравнениям связи. Заменим при этом приращение функции f(x) приращением функции Лагранжа (5.1) с множителями Тогда получим

(5.3)

причем первое слагаемое правой части равно нулю, т. е.

                                                                (5.4)

Так как анализируемые смещения ξ из точки не должны нарушать условий связи (5.1), разложение функции g(x) в ряд Тейлора в окрестности приводит к равенству

Отсюда, пренебрегая вторым слагаемым, в линейном приближении имеем

                                                                                                                (5.5)

Это уравнение при каждом к определяет касательную в точке  гиперплоскость к поверхности ограничения g_k(x)=0, а необходимое условие экстремума второго порядка в задаче на относительный экстремум и достаточное условие однозначно связаны со знакоопределенностью квадратичной формы

              

для векторов, удовлетворяющих равенствам (5.5).

По аналогии с теоремой 4.2 заключаем, что для того, чтобы условно-стационарная точка  реализовала локальный относительный минимум, достаточно, чтобы квадратичная форма была положительно-определенной и отрицательно определенной для максимума.

 

6 Лекция. Анализ последовательности случайных чисел. Критерии качества последовательностей случайных чисел. Метод возмущения

 

Постановка задачи

Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку , что .

Стратегия поиска

Метод относится к пассивным стратегиям. Задается начальный интервал неопределенности L₀ = [a₀,b₀] и количество вычислений функции N. Вычисления производятся в N равноотстоящих друг от друга точках (при этом интервал L₀) делится на N +1 равных интервалов). Путем сравнения величин f(x_i), i=1,…N находится точка x_k , в котором значение функции наименьшее. Искомая точка минимума х* считается заключенной в интервале [x_k-1 , x_k+1].

Алгоритм

Шаг 1. Задать начальный интервал неопределенности L₀ = [a₀ , b₀] , N - количество вычислений функции.

Шаг 2. Вычислить точки , равноотстоящие друг от друга.

Шаг 3. Вычислить значения функции в N найденных точках: x_i, i=1,…N.

Шаг 4. Среди точек x_i, i=1,…N, найти такую, в которой функция при­нимает наименьшее значение:

_.

Шаг 5. Точка минимума х* принадлежит интервалу:

на котором в качестве приближенного решения может быть выбрана точка

.

Сходимость

Для метода равномерного поиска характеристика относительного умень­шения начального интервала неопределенности находится по формуле

, где N - количество вычислений функции.

Метод деления интервала пополам

Постановка задачи

Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку , что .

Стратегия поиска

Метод относится к последовательным стратегиям и позволяет исключить из дальнейшего рассмотрения на каждой итерации в точности половинку текущего интервала неопределенности. Задается начальный интервал неопределенности, а алгоритм уменьшения интервала, являясь, как и в общем слу­чае гарантирующим, основан на анализе величин функции в трех точках, равномерно распределенных на текущем интервале (делящих его на че­тыре равные части). Условия окончания процесса поиска стандартные: поиск за­канчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.

Алгоритм

Шаг 1. Задать начальный интервал неопределенности и l > 0 - требуемую точность.

Шаг 2. Положить k = 0.

Шаг 3. Вычислить среднюю точку , , _.

Шаг 4. Вычислить точки: , и , . Заметим, что точки , , делят интервал на четыре равные части.

Шаг 5. Сравнить значения и :

а) если < , исключить интервал положив = , . Средней точкой нового интервала становится точка := (см. рисунок 6.1, а). Перейти к шагу 7;

б) если , перейти к шагу 6.

Шаг 6. Сравнить с :

а) если < , исключить интервал , положив =, . Средней точкой нового интервала становится точка : = (см. рисунок 6.1, б). Перейти к шагу 7;

б) если , исключить интервалы , положив , = . Средней точкой нового интервала останется : = (см. рисунок 6.1, в).

Шаг 7. Вычислить и проверить условие окончания:

а) если , процесс поиска завершается и . В качестве приближенного решения можно взять середину последнего интервала: ;

б) если то положить k=k + l и перейти к шагу 4.

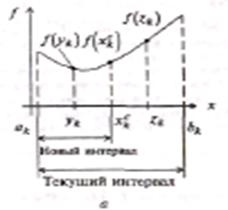
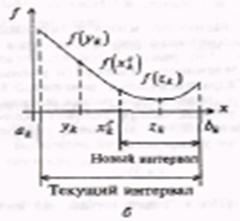
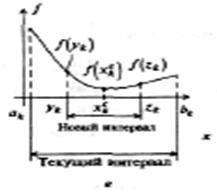
Рисунок 6.1

 

Сходимость

Для метода деления интервала пополам характеристика относительного уменьшения начального интервала неопределенности находится по формуле

 ,

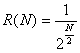где N – количество вычислений функции.

Замечания

1) Средняя точка последовательно получаемых интервалов всегда совпадает с одной из трех пробных точек, найденных на предыдущей итерации. Следовательно, на каждой итерации требуются два новых вычисления функции.

2) Если задана величина R(N), то требуемое для достижения желаемой точности количество вычислений функции находится как наименьшее целое, удовлетворяющее условию .

3) Текущие интервалы имеют четные номера , , ,…, где индекс указывает на сделанное количество вычислений функции.

 

7 Лекция. Моделирование случайных событий. Моделирование простых событий. Моделирование полной группы событий. Моделирование сложных событий

 

Постановка задачи

Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку , что .

Стратегия поиска

Метод относится к последовательным стратегиям. Задается начальный ин­тервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. Для их нахождения текущий ин­тервал неопределенности делится пополам и в обе стороны от середины откла­дывается по , где - малое положительное число. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего ин­тервала неопределенности оказывается меньше установленной величины.

Алгоритм

Шаг 1. Задать начальный интервал неопределенности , > 0 - малое число, l > 0 - точность.

Шаг 2. Положить k = 0.

Шаг 3. Вычислить , f{y_k), , f(_Zk).

Шаг 4. Сравнить f(y_k) с f(_Zk):

а) если f{y_k) <, f(z_k), положить a_k+l = a_k,, b_k+1, =b_k (см. рисунок 5.6, а) и перейти к шагу 5;

б) если f{y_t)> f(z_k), положить а_к+1 =у_к, b_k+1, =b_k (см. рисунок 5.6, б).

Шаг 5. Вычислить и проверить условие окончания:

а) если , процесс поиска завершается и .В качестве приближенного решения можно взять середину последнего интервала: ;

б) если положить k = k+1 и перейти к шагу 3.

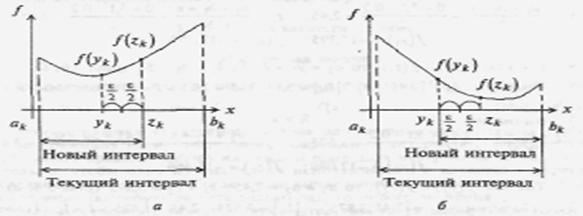
Рисунок 7.1

 

Сходимость

Для метода дихотомии характеристика относительного уменьшения начального интервала неопределенности находится по формуле 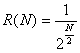, где N - количество вычислений функции.

Замечания

1) Текущие интервалы имеют четные номера , , ,…, где индекс указывает на сделанное количество вычислений функции, как и в методе деления интервала пополам.

2) Эффективность методов дихотомии и деления интервала пополам при малых можно считать одинаковой.

Метод золотого сечения

Постановка задачи

Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку , что .

Для построения конкретного метода одномерной минимизации, работаю­щего по принципу последовательного сокращения интервала неопределенности, следует задать правило выбора на каждом шаге двух внутренних точек. Конечно, желательно, чтобы одна из них всегда использовалась в качестве внутренней и для следующего интервала. Тогда число вычислений функции сократится вдвое и одна итерация потребует расчета только одного нового значения функции. В ме­тоде золотого сечения в качестве двух внутренних точек выбираются точки золо­того сечения.

Определение. Точка производит "золотое сечение" отрезка, если отноше­ние длины всего отрезка к большей части равно отношению большей части к меньшей.

На отрезке [,] имеются две симметричные относительно его концов точки и :

.

Кроме того, точка у₀ производит золотое сечение отрезка [,], а точка - отрезка [,] (см. рисунок 7.2).

Рисунок 7.2

Cтратегия поиска

Метод относится к последовательным стратегиям. Задается начальный ин­тервал неопределенности и требуемая точность. Алгоритм уменьшения интер­вала опирается на анализ значений функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда с учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.

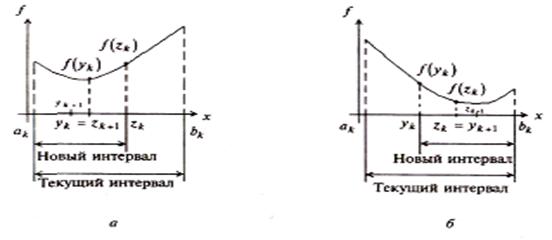
Рисунок 7.3

 

Алгоритм

Шаг 1. Задать начальный интервал неопределенности и l > 0 - требуемую точность.

Шаг 2. Положить k = 0.

Шаг 3. Вычислить ; , .

Шаг 4. Вычислить f{y_k), f(_Zk).

Шаг 5. Сравнить f{y_k) и f(_Zk):

а) если , то положить , и ,  (см. рисунок 7.3, а). Перейти к шагу 6;

б) если , положить , и , (см. рисунок 7.3, б).

Шаг 6. Вычислить и проверить условия окончания:

а) если , процесс поиска завершается и . В качестве приближенного решения можно взять середину последнего интервала: ;

б) если , положить k = k + i и перейти к шагу 4.

 

8 Лекция. Моделирование непрерывных случайных величин. Классификация методов моделирования непрерывных случайных величин

 

Как известно из курсов анализа, градиент скалярной функции f(x) в некоторой точке хk направлен в сторону наискорейшего возрастания функции и ортогонален линии уровня (поверхности постоянного значения функции f(x), проходящей через точку хk). Вектор, противоположный градиенту f'(хk), антиградиент, направлен в сторону наискорейшего убывания функции f(x). Выбирая в качестве направления спуска pk антиградиент функции f(x) в точке хk, мы приходим к итерационному процессу вида

                                                        (8.1)

В координатной форме этот процесс записывается следующим образом:

                                                             (8.2)

Все итерационные процессы, в которых направление движения на каждом шаге совпадает с антиградиентом (градиентом) функции, называются градиентными методами и отличаются друг от друга способами выбора шага -k, но наиболее распространены два - метод с дроблением шага и метод наискорейшего спуска.

Градиентные методы с дроблением шага

Рассмотрим процесс (8.1). Первая проблема, с которой мы сталкиваемся при его реализации, - это выбор шага αk. Достаточно малый шаг αk обеспечит убывание функции, т. е. выполнение неравенства

                                                                       (8.3)

но может привести к неприемлемо большому количеству итераций, необходимых для достижения точки минимума.

С другой стороны, слишком большой шаг может вызвать неожиданный рост функции (невыполнение условия (8.3)) либо привести к колебаниям около точки минимума.

В методе градиентного спуска с дроблением шага величина - k выбирается так, чтобы было выполнено следующее неравенство:

,                                                 (8.4)

где 0 <-ε< 1 — произвольно выбранная постоянная (одна и та же для всех итераций). Очевидно, что требование (8.3) на выбор шага более жесткое, чем условие (8.4), но имеет тот же смысл: функция должна убывать от итерации к итерации. Процесс (8.1) с выбором шага, удовлетворяющего неравенству (8.4). протекает следующим образом.

Выбираем число α > 0, одно и то же для всех итераций. На k-й итерации проверяем выполнение неравенства (8.4) при α k = α. Если оно выполнено, полагаем α k = α и переходим к следующей итерации. Если нет, то шаг ее, дробят, например, пополам αk=α/2 и вновь проверяют (8.4).

Метод наискорейшего спуска

Можно, конечно, выбрать некоторую постоянную для всех итераций величину шага, обеспечивающую убывание функции f(x) от итерации к итерации. Однако, обычно, шаг при этом оказывается очень малым, что приводит к необходимости проводить большое количество итераций для достижения точки минимума. Поэтому методы спуска с переменным шагом являются более экономными. Процесс, на каждой итерации которого шаг - к выбирается из условия минимума функции f(x) в направлении движения, т. е.

                                                   (8.5)

называется методом наискорейшего спуска. В этом варианте градиентного спуска на каждой итерации требуется решать задачу одномерной минимизации (8.5). Разумеется, этот способ выбора αk сложнее, чем рассмотренные в предыдущем пункте.

Градиентные методы

Метод проекции градиента (метод Розена[ Rozen J.B.]) применяется в за­дачах поиска условного экстремума с ограничениями типа равенств и неравенств

Применение метода в задаче с ограничениями типа равенств.

Постановка задачи

Найти минимум дифференцируемой функции при ограничениях , j = 1….m т.е. такую точку , что .

где функции , j = 1….m являются дифференцируемыми функциями х.

Стратегия поиска

Стратегия поиска решения задачи методом проекции градиента со­стоит в построении последовательности точек , вычисляемых по правилу:

,

где есть вектор, вычисляемый для каждого значения k . Прирашение определяется из условия проекции вектора на аппроксимирующую плоскость, задаваемую уравнением,  которая аппроксимирует в точке , k = 0,1,…, поверхность Г, задаваемую уравнениями , j = 1….m. Здесь A_k - матрица размера вида

,

a - вектор столбец, .

На рисунке 8.1 в точке построена аппроксимирующая прямая для задачи .

Ее уравнение , так как ;

 и, следователь­но, .

Вектор определяется по формуле , где называется градиентной составляющей приращения; она равна

и обладает следующим свойством: градиентная составляющая приращения в линейном приближении не меняет вектор невязки условий связи. Это означает, что под действием градиентной составляющей точка движется параллельно или по плоскости  (см. рисунок 8.1). Составляющая называется ком­пенсационной составляющей приращения и равна . Эта со­ставляющая обладает, в линейном приближении, свойством компенсировать век­тор невязки условий связи на величину . Под действием составляющей осуществляется проекция точки на плоскость  (см. рисунок 8.1).

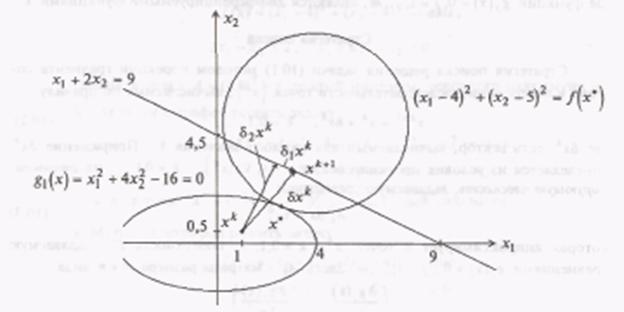
Рисунок 8.1

 

Величина шага может выбираться как из условия убывания f{x) при переходе из точки в точку , так и из условия

_.                                                        (8.6)

Задача (8.6) может решаться либо с использованием необходимых и доста­точных условий минимума: применяемых непосредственно к функции или к аппроксимирующим ее полиномам, либо с использованием численных методов.

Расчет заканчивается в точке , в которой , где - заданное число. В полученной точке требуется обязательная проверка выполнения достаточных условий минимума функции в задаче, Точное равенство свидетельствует о точном выполнении необходимых условий экстремума, при этом вектор множителей Лагранжа определяется по формуле _.

Знание приближения вектора , определяемого вышеописанной формулой , позволит осуществить проверку достаточных условий в точке .

Замечание. Если в задаче ограничения линейны, т.е. име­ют вид , то матрица А постоянна. Это означает, что в силу свойства компенсационной составляющей она вычисляется единст­венный раз в точке . При этом начальная точка попадает в область допустимых решений за одну итерацию. Дальнейший процесс построения последова­тельности {} связан с вычислением составляющей _.

Алгоритм

Шаг 1. Задать ,, число итераций М.

Шаг 2. Положить k = 0.

Шаг 3. Проверить выполнение условия k > М :

а) если неравенство выполнено, то расчет окончен Вычислить , прове­рить необходимые и достаточные условия минимума и оценить результат;

б) если неравенство не выполнено, то перейти к шагу 4.

Шаг 4. Вычислить матрицу

_.

Шаг 5. Вычислить _.

Шаг 6. Вычислить _.

Шаг 7.Вычислить _.

Шаг 8. Вычислить _.

Шаг 9. Вычислить _.

Шаг 10. Проверить выполнение условий и :

а) если и , то расчет окончен. Перейти к вычислению и проверке достаточных условий минимума;

б) если и , то положить и перейти к шагу 11;

в) если и , то положить и перейти к шагу 13;

г) если и , перейти к шагу 11.

Шаг 11. Получить точку _.

Шаг 12. Определить из условия .

Шаг 13. Вычислить . Положить k = k +1 и перей­ти к шагу 3.

Замечание: Если ограничения в задаче линейны, то при k > 1 на шаге 3 переходим к шагу 8. На шаге 10 следует положить = 0.

 

9 Лекция. Метод обратной функции. Метод исключения Дж.Неймана. Метод предельных теорем. Метод композиции. Моделирование специальных непрерывных распределений

 

Задача линейного программирования состоит в нахождении максимума или минимума линейной функции при конечном числе линейных ограничений. Эта задача возникает во многих прило­жениях. Она же обычно является составной частью методов опти­мизации в нелинейном случае при поэтапной линеаризации зада­чи. Для задачи линейного программирования принято несколько канонических форм записи. Для многих практических задач усло­вие хi >0 (i = 1,2,...,n) является естественным, поэтому широко распространена следующая форма:

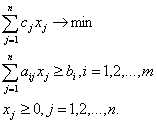                                                                          (9.1)

В дальнейшем изложении будем считать, что условия неотрицательности включены в общий список неравенств. Введя в рассмотрение векторы b = (b1,..,bm)^T c = (c1,...,cn)^T и х = (х1, х2,...,хn)^T и матрицу A = (аij) (i = l,2,...,m; j=l,2,...,n) задачу можно переписать в виде:

min{(c,x):Ax>b}                                                                                (9.2)

В нашем случае f(x) = (c,x), gi(x) = bi -(Ax)i, i = l,2,...,m. Поэтому функция Лагранжа для поставленной задачи линейного программирования принимает вид

                                                         (9.3)

или, если ввести вектор множителей Лагранжа λ = (λ1, λ2,..., λn)^T, то

.                                         (9.4)

Функция φ(λ) в наших условиях имеет вид

.

Поэтому, в силу произвольности х конечное значение функция φ может принимать лишь при λ, удовлетворяющих системе линейных уравнений

с-А^T λ = 0

или

.                                                                         (9.5)

Таким образом, двойственной для задачи (9.1) оказывается следующая задача линейного программирования:

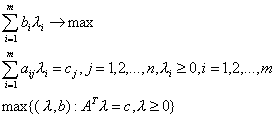
Рассмотрим теперь вопросы о численном решении.

Схема решения задачи планирования производства симплекс-методом

Одним из основных методов решения задач линейного прог­раммирования является симплекс-метод, с помощью которого ищется оптимальное базисное решение.

Пусть решается задача минимизации функции

                                                                                                                                                      (9.6)

при ограничениях

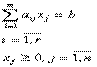_.                                                                                                                                               (9.7)

Выбрав некоторый базис, например, для определенности (х₁, х₂,...,х_r), можно преобразовать задачу (9.6), (9.7) к виду:

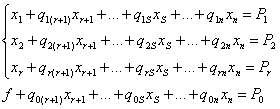                                                                                   (9.8)

Из коэффициентов уравнений системы и выражения (9.8), которое также записано в виде линейного уравнения с правой частью, составим таблицу 9.1, которая называется симплекс-таблицей.

 

Таблица 9.1 -Симплекс-таблица

 

Каждому базису соответствует своя симплекс-таблица. Отметим, что без учета последней строки столбцы коэффициентов при базисных неизвестных образуют единичную матрицу, а последний столбец дает нам значения базисных переменных. Элемент же Р₀ представляет собой значение целевой функции в базисном решении. Симплекс-таблицу удобно использовать для анализа и оценки соответствующего ей базиса.

Если в последнем столбце симплекс-таблицы нет отрицательных элементов, кроме, может быть, последнего

                                                                                                                                                    (9.9)

то соответствующий этой симплекс-таблице базис допустим. Критерий оптимальности базиса для задачи минимизации формулируется следующим образом. Если в последней строке симплекс-таблицы нет положительных элементов, кроме, может быть, последнего:

                                                                                                                                         (9.10)

то соответствующий базис оптимален.

Действительно, последней строке симплекс-таблицы соответствует выражение (9.8), из которого можно получить соотношение

f=P₀-[q_0(r+1)+...+q_0nx_n].                                                                       (9.11)

В любом решении значения свободных переменных не могут быть отрицательными. Если для некоторого решения хотя бы одно q_0s положительно, то имеется возможность уменьшить значение f за счет роста соответствующего x_s. В случае, если выполняется соотношение (9.10), возможности уменьшить функцию S ниже зафиксированного значения Р₀ нет. Сформулируем теперь критерий отсутствия оптимального решения.

Если в симплекс-таблице имеется столбец, последний элемент которого положителен, а все остальные элементы неположительные, то соответствующая задача линейного программирования не имеет оптимального решения. Заметим, что такой столбец может быть только столбцом коэффициентов при свободных переменных. Формально критерий записывается следующим образом: если имеется такое значение S (r+l≤S≤n), что

                                                                                                                              (9.12)

то      f_min=-∞.                                                                                              (9.3)

Эти условия означают, что область допустимых решений системы (9.7) не ограничена. Действительно, рассмотрим решение, в котором все свободные переменные, кроме x_s, равны нулю. В таком решении значения базисных переменных в силу (9.7) определяются по формулам:

_,                                                                                                                                 (9.4)

а значение целевой функции

f=P₀-q_0sx_s.                                                                                          (9.5)

В силу (9.12) значение целевой может при росте x_s уменьшаться беспредельно, в то же время значения остальных переменных остаются в допустимой области.

Рассмотрим теперь процесс перехода от некоторого фиксированного базиса (x₁, х₂,..., х_r) к новому базису. Такой переход необходим в случае, если не выполнены критерии оптимальности базисного решения. В этом случае в симплекс-таблице имеется столбец, соответствующий некоторому свободному переменному, в котором последний элемент положителен. Пусть этот столбец соответствует переменному х_s

q_0s>0.                                                                                                 (9.16)

Пусть, кроме того, в s -ом столбце имеются и другие положительные элементы. Среди них выбираем тот, который стоит в строке j соответствующей следующему соотношению:

_.                                                                                                                                             (9.17)

Такой элемент q_is при высказанных предложениях всегда существует. Его называют разрешающим элементом. Столбец и отроку симплекс-таблицы, на пересечении которых находится разрешающий элемент, называют, соответственно, разрешающим столбцом и разрешающей строкой.

Сформулируем правило преобразования симплекс-таблицы с помощью разрешающего элемента:

1) Все элементы разрешающего столбца, кроме разрешающего элемента, заменяются нулями:

_.                                                                                                                            (9.18)

Здесь и далее штрихом отмечены новые значения элементов, полу­чающиеся после преобразования.

2) Все элементы разрешающей строки получаются делением на разрешающий элемент

_.                                                                                                                                     (9.19)

3) Все остальные элементы симплекс-таблицы преобразуются по так называемому правилу прямоугольника

_.                                                                                                        (9.20)

Заметим, что элементы столбцов, соответствующих переменным, вхо­дящим в старый и новый базис, при этом остаются неизменными и их просто надо переписать в прежнем виде.

4) Элементы последнего столбца преобразуются по формулам:

_,                                                                                                                                                            (9.21)

_,                                                                                                                   (9.22)

_.                                                                                                                                             (9.23)

Отметим, что допустимость старого базиса и условие (9.17) обеспечивают допустимость нового базиса. Действительно, очевидно, что ≥0. Кроме того, рассматривая (9.21) при двух возможных предположениях, получаем:

а) если q_ls≤0, тогда

б) q_ls > 0,тогда с учетом (9.17).

_.

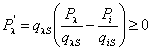Условие (9.6) и допустимость старого базиса обеспечивают невозрастание базисного значения целевой функции. Действительно, , следовательно, из (9.10) следует, что ≤ Р₀. Необходимо отметить, что разрешающий элемент в данной симплекс-таблице может быть не единственный. В этом случае для преобразования симплекс-таблицы можно выбрать любой из них.

С учетом изложенного выше можно описать следующий метод решения основной задачи линейного программирования, называемый симплекс-методом.

Шаг 1. Отыскиваем какое-нибудь допустимое базисное решение. Обычно здесь используется специфика решаемой задачи. Формируем первую симплекс-таблицу, соответствующую выбранному базису.

Шаг 2. Анализируем полученный базис на оптимальность. Если среди элементов последней строки нет положительных элементов, кроме, может быть, последнего, то решение задачи найдено, все данные о нем содержатся в последнем столбце симплекс-таблицы. Если среди элементов последней строки есть положительные, то рассматриваются два исхода:

а) если хотя бы над одним из положительных элементов последней отроки в столбце нет других положительных элементов, то задача не имеет решения;

б) в противном случае, переходим к третьему шагу.

Шаг 3. Выбираем разрешающий элемент и преобразуем симплекс-таблицу по приведенному выше правилу преобразования. Затем переходим к выполнению шага 2.

Симплекс-метод за конечное число шагов приводит к решению задачи, либо позволяет убедиться в его отсутствии.

 

10 Лекция. Моделирования дискретных случайных величин. Основной метод моделирования дискретных случайных величин. Моделирование геометрического закона распределения. Моделирование закона распределения Пуассона

 

Одной из наиболее распространенных задач линейного программирования является транспортная задача, состоящая в отыскании оптимального плана перевозов грузов от поставщиков к потребителям.

В общем случае модель транспортной задачи имеет следующий вид. Имеется m поставщиков , n потребителей однородной продукции, a_j - количество продукции; производимое i-м поставщиком; b_j - количество продукции, необходимое В_j; C_ij - тариф перевозки (стоимость перевозки единицы продукта) из А_i в B_j.

Необходимо определить план перевозок {Х_ij} , для которого

                                                                                                                             (10.1)

                                                                                                                              (10.2)

                                                                                                                                                (10.3)

                                                                                                                         (10.4)

Различают 2 вида моделей транспортной задачи: закрытую транспортную задачу, когда объемы производства равны объемам потребления:

                                                                                                                                                  (10.5)

открытую транспортную задачу, когда равенство (10.5) не выполняется.

Практически, все методы решения транспортной задачи используют так называемую матрицу перевозок (см. таблица 10.1), которая является наглядным изображением плана перевозок.

В этой таблице вначале формируют первый опорный план для транспортной задачи, а затем производят его улучшение. Существует несколько способов формирования начального опорного плана. Здесь рассматривается метод минимального элемента. Сущность этого метода заключается в том, что опорный план строится последовательно за n+m-1 шагов. На каждом шаге заполняется клетка соответствующая пути перевозок с наименьшим тарифом С_ij. Описание действий на первом шаге выглядит следующим образом. Находим минимальный тариф

.

Определяем допустимую величину перевозок из А_ij в B_ij

X_ij^* = min{ a_i, b_j }.

В случае, если a_i>b_j, т.е. х^*_ij=b_j, закрываем для дальнейшего рассмотрения j-ый столбец матрицы перевозок, а величину a_i, корректируем:

a_i = а_i – b_j

В случае, если a_i < b_j, т.е. х^*_ij = а_i, закрываем для дальнейшего рассмотрения i-ую строку, а величину b_j, корректируем:

b_j = b_j – a_i.

Последующие шаги выполняются аналогично первому, без учета закры­тых строк и столбцов.

 

Таблица 10.1 - Матрица перевозок

 

Алгоритм Хичкока

Предположим, что уже построено дополнительное базисное решение, в котором некоторые из переменных Xij отличны от 0, а остальные переменные небазисные и, следовательно, равны 0.

Если Ui и Vj - симплекс - множители для ограничений, соответствующих i-й строке и j-му столбцу в этом базисе, то после умножения i-й строки на Ui, j-го столбца на Vj и прибавления стоимости C получим:

.

Коэффициенты при Xij равны Сij-Ui-Vj, так как Xij входят всего в два ограничения, соответствующих i-той строке и j-му столбцу. Если это уравнение является канонической формой целевой функции, соответствующей базису, то коэффициенты при базисных переменных равны 0.

Таким образом для базисных переменных справедливо соотношение : Cij-Ui-Vj=0.

Следовательно, можно определить Ui и Vj. Имеется m неизвестных Ui и n неизвестных Vj. Поскольку m+n-1 базисных переменных, получаем систему из m+n-1 уравнений и m+n неизвестных. Решая, находим Ui и Vj. Проверим, оптимально ли это решение. Если Cij - коэффициент при Xij в канонической форме целевой функции, то следует, что Cij=Cij -Ui-Vj.

Для базисных переменных Cij=0. Для небазисных отрицательное значение указывает на то, что переменная Xij должна быть включена в базис, что приводит к уменьшению целевой функции. Cij вычисляется для небазисных переменных. Если для небазисных переменных Cij положительны, значит получится оптимальное решение. Значение стоимости можно задать уравнением:

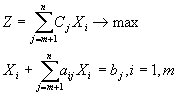
Xij>=0, j=1,n , bj>=0, i=1,m или в матричной форме

z=Cx max

EX1+AX2=B

X1>=0, B>=0

где Х1 - вектор-столбец базисных переменных из m-компонентов; Х2 - вектор-столбец небазисных переменных из (n-m)-компонентов; С=(0;...;0; С m+1 ;...; С n ) - вектор коэффициентов целевой функции приведенной к небазисным переменным, т.е. компоненты этого вектора могут быть использованы в качестве оценок оптимальности; А - матрица коэффициентов небазисных переменых размером m(m-n); Е - единичная m-матрица.

В тех случаях, когда модель содержит m уравнений, для построения пробных решений используется m переменных, принимающих некоторые положительные значения при нулевых значениях остальных переменных.

Алгоритм решения задачи методом Хичкока

1) Ввод начальных значений m, n, Xij, Cij, Ai, Bj.

2) Вычислить базисное допустимое решение по принципу: "Самая дешевая продукция реализуется первой".

3) Вычислить коэффициенты Ui, Vj для базисного допустимого решения.

4) Найти Cij для небазисных переменных.

5) Если все Cij>=0, то переходим к следующему этапу, иначе к пункту 3.

6) Вычислить оптимальное решение.

7) Вывод оптимального решения.

 

11 Лекция. Моделирование многомерных случайных величин. Метод последовательного моделирования. Обобщенный метод исключения Дж. Неймана. Метод моментов

 

В соответствии с поведением объектов, модели можно классифицировать следующим образом:

Линейные. Это такие модели, в которых целевая функция и условия ограничения выражаются линейными зависимостями.

Линейные модели могут быть статическими и динамическими.

Статические модели описывают объект вне временного интервала (управляющие переменные не изменяются во времени). Линейная статическая модель, как правило, описывается системой линейных алгебраических уравнений.

Динамические модели описывают объект, критерии которого изменяются во времени. Описываются такие модели системой дифференциальных уравнений.

Линейные модели дают возможность проводить глубокий и эффективный анализ коммерческой или производственной системы, результаты которого в сочетании с опытом специалистов позволяют добиться максимального успеха.

Нелинейные модели описывают объекты с нелинейным характером изменения управляющих переменных. Могут описываться системой интегральных уравнений или методами имитационного моделирования (как совокупность критериев, изменяющихся случайным образом).

Нелинейные модели могут быть как статическими, так и динамическими.

Сетевые модели

Сетевые модели представляют собой частный случай моделей линейного программирования. Они относятся к задачам распределения продукции. Имеют экономический смысл для промышленных фирм, которые располагают несколькими предприятиями и хранят запасы продукции в различных пунктах.

Сетевым моделям присуща особенность математических характеристик, которая позволяет выделить их в отдельную группу для изучения. Сетевым моделям присуща специфическая терминология и набор понятий, принятые для описания.

Определения

Сеть (или линейный граф) состоит из множества узлов и множества дуг, соединяющих различные пары узлов. На каждой дуге задано направление связи. Такая сеть называется ориентированной .

Для описания ориентированной сети узлы ее нумеруются числами натурального ряда 1,2,...,р. Дуги нумеруются парой (i, j), где i - номер узла, из которого выходит дуга; j - номер узла, в который входит дуга.

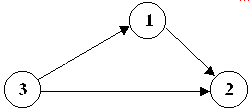
Объект перемещения по дуге (i, j) называется единичным потоком.

Если все узлы сети можно разбить на два подмножества G 1 и G 2 , то такие сети называются двудольными. В двудольной сети все узлы i принадлежат подмножеству G 1 ; все узлы j - подмножеству G 2 .

Сети, в которых поток, выходящий из узла i в узел j остается единичным, могут быть описаны матрицей (или таблицей) инциденций узлы-дуги. Каждый узел отображается строкой матрицы. Каждая дуга - столбцом. Направление потока указывает коэффициент 1 в строке, соответствующей узлу i, и коэффициент -1 в строке, соответствующей узлу j.

Последовательность дуг соединяющая узлы i и j называется путем между узлами .

Если i =j , то путь называется контуром.

Сеть называется связной , если существует хотя бы один путь между любой парой узлов.

Если все дуги пути ориентированы так, что единичный поток может пройти по этому пути, такой путь называется ориентированной цепью .

Ориентированная цепь, которая начинается и заканчивается в одном узле, называется ориентированным циклом.

Если сеть не содержит ни одного ориентированного цикла, она называется ациклической.

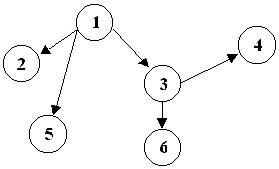
Частным случаем сети является связная сеть, которая содержит р узлов и р-1 дуг. Такая сеть называется деревом и не содержит контуров.

Общая постановка задачи

Для характеристики сетей в прикладных задачах оптимизации фигурируют следующие характеристики:

1) U ij - пропускная способность дуги (i, j); (как правило U ij і 0).

2) T k - чистый поток из узла “k”.

Если T k і 0, то из узла k должно выходить на T k единиц потока больше, чем входит в него.

Если T k <0, то из узла k должно выходить на T k единиц потока меньше, чем входит в него.

Если T k =0, то поток, входящий в узел k равен потоку, выходящему из него. Рационально принять

                                  (11.1)

1) C ij - стоимость доставки единичного потока по дуге (i,j). Для любого ориентированного цикла S C ij і 0.

2) X ij - величина потока по дуге (i,j) в течение заданного периода.

Общую задачу оптимизации можно сформулировать как задачу минимизации

                                                                                          (11.2)

при ограничениях

.                                                               (11.3)

0 Ј X ij Ј U ij для всех i и j                                                               (11.4)

(11.2) - целевая функция; (11.3) - уравнения сохранения потока или уравнения материального баланса.

Обобщенная сетевая задача

Для сетевой задачи условия несколько изменяются, если единичный поток заменить на A ij і 0. При A ij > 1 происходит усиление потока; при A ij < 1- уменьшение . Матрица инициаций узлы - дуги изменится путем замены -1 на -A ij .

Модель обобщенной сетевой задачи можно описать следующим образом:

минимизировать                                                                        (11.5)

при ограничениях                                                         (11.6)

.                                                                        (11.7)

X ij і 0 для всех i и j                                                                           (11.8)

S i - производственная мощность i- ого узла.

D j - потребительная мощность j- ого узла.

Матрицу инициаций обобщенной сетевой задачи можно представить следующим образом:

 

		x 11 x 12 ... x 1n	x 21 x 22 ... x 2n	...	x 11 x 12 ...x 1n
поставщики	1 2 .. .. m	1 1 ... 1	1 1 ... 1	...	1 1 ... 1	Ј S 1 Ј S 2 .. .. Ј S m
потребители	1 2 .. .. n	-А 11 -А 12 .. .. -А 1n	-А 21 -А 22 .. .. -А 2n	...	-A m1 -A m2 .. .. -A mn	Ј -D 1 Ј -D 2 .. .. Ј -D n
		C 11 C 12 ... C 1n	C 11 C 12 ... C 1n	...	C m1 C m2 ...C mn	min

12 Лекция. Моделирование случайных процессов. Моделирование нестационарных случайных процессов. Моделирование стационарных случайных процессов. Моделирование марковских процессов

 

Оптимизационные модели, для практической реализации которых необходимо полностью детерминированное представление всех исходных данных, составляют класс линейных. К такими моделями относятся линейные и модели управления запасами, календарного планирования и замены оборудования. Но существует также и другой класс моделей, именуемый стохастическими (или вероятностными), которые в значительно большей степени приспособлены для анализа задач, связанных с оптимизацией так называемой пропускной способности. В этих моделях используются данные предыдущих наблюдений (или измерений), позволяющие описать вероятностный характер поступления «заявок» на обслуживание и, следовательно, заострить внимание на элементах неопределённости, свойственных задачам такого типа. В зависимости от математической структуры модели для получения численных решений задач стохастического характера могут использоваться алгоритмы линейного и нелинейного программирования, методы динамического программирования, а в тех случаях, когда ни один из перечисленных способов не приводит к успеху, возможно применение так называемого имитационного моделирования.

Далее будут рассмотрены хорошо структурированные модели, позволяющие разобраться в подробностях метода стохастического программирования. Один исключительно важный класс вероятностных моделей связан с задачей управления запасами в условиях, когда спрос на продукцию заранее не известен.

Стохастические модели управления запасами

Рассматриваются конкретные классы задач организационного управления, при решении которых оказалось целесообразным использовать методы исследования операций. К этим задачам относятся:

- управление запасами;

- системы массового обслуживания.

При этом математические модели и алгоритмы строятся применительно к условиям, характерным для этих вполне конкретных задач, а получаемые в результате решения, как правило, представляют собой не просто плановые «ориентиры», а определяют оптимальную стратегию «поведения» в реальной обстановке. Также следует помнить, что наиболее распространенные приложения моделей управления запасами относятся к сфере промышленного производства и оптовой торговли, хотя сложившиеся ранее традиции начинают быстро изменяться. Встречаются, в частности, научно обоснован ные системы управления запасами, используемые на крупных промышленных предприятиях в связи с регулированием процедур складирования сотен, а порой даже тысяч различных видов сырья, полуфабрикатов и готовой продукции. В такого рода системах принятие всех управляющих решений относительно пополнения запасов возлагается, как правило, на очень ограниченное число людей.

Простота операционной модели

Модели управления запасами относятся к числу весьма редко встречающихся операционных моделей, для которых результирующие оптимальные решения могут быть реализованы в режиме быстрой смены ситуаций (когда, например, условия меняются ежедневно). Это объясняется тем, что применительно к управлению запасами суть оптимального решения состоит в том, чтобы сформулировать два следующих правила:

1) Правило, позволяющее определить, когда (т.е. при наличии каких условий) запасы подлежат пополнению.

2) Правило, позволяющее определить объём пополнения запасов.

Другими словами, эта стратегия дает возможность рассчитывать время и объем каждого очередного пополнения запасов, т. е. основ­ные параметры управляющего решения. Независимо от степени сложности математической модели и алгоритма решения задачи, с помощью которых отыскивается такого рода стратегия, ее форму­лировку в виде правил указанного выше типа всегда легко интерпре­тировать. В ряде случаев формирующие стратегию правила задаются в виде таблиц, и от руководителя требуется лишь простановка зна­чений различного рода показателей, таких, как стоимость единицы складируемой продукции или средний уровень спроса.

Существует три вида стохастических моделей управления запасами:

- статическая модель;

- динамическая модель;

- статическая и динамическая модели в комплексе.

 

13 Лекция. Моделирование потоков событий. Свойства потоков событий. Моделирование простейшего потока. Моделирование потоков Эрланга. Моделирование потоков Пальма, Моделирование неординарных потоков случайных событий

 

Принятие решений в условиях незнания

В этой лекции рассматриваются задачи принятия решения n 0 управлению сложными системами в условиях неопределенности, вызванной незнанием. Такие ситуации очень часто называет "играми против природы". В этих играх, с одной стороны, выступает активный участник (управляющий субъект). Субъект принимает решения по управлению системой, воздействуя на контролируемые факторы. С другой стороны, на систему воздействует природа. В отличие от субъекта, который знает, чего он хочет природа пассивна, ее действия - это просто возможные состояния. И хотя бытует мнение, что природа всегда так подбирает свое состояние, чтобы максимально навредить Человеку, это, конечно, не так. Еще Эйнштейн сказал, что "Господь бог изощрен, но не злонамерен".

Будем предполагать, что множество вариантов решений субъекта по управлению системой конечно

A = { α1, α2, α3, … , αm }.

Множество состояний природы также будем предполагать конечным

B = { β1, β2, β3, … , βn }.

Если субъект принимает решение  αi , а природа в этот момент находится в состоянии  βj , то получится некоторый исход vij . Перебирая все возможные комбинации (αi , βj ) получим матрицу исходов размера m x n .

Заметим, что vij - это не числа, а элементы некоторого абстрактного множества исходов.

Пример 1. ("Реализация нефтепродуктов"). "Все основные положения этого раздела будем иллюстрировать на одном простом примере. Представим себе следующую ситуацию. У субъекта, занимающегося коммерцией, имеется один миллион тенге. У него же имеется автозаправочная станция, и ему хотелось бы вложить свои деньги в организацию розничной продажи бензина и дизельного топлива. На оптовом рынке бензин можно закупить по цене 20000 тенге за тонну, а дизельное топливо по цене 10000 тенге за тонну.

Исходя из возможностей складирования и других факторов, определяемых технологией розничной продажи, субъект рассматривает три альтернативы оптовой закупки нефтепродуктов:

1) α1 - на все деньги купить 50 тонн бензина;

2) α2 - закупить 25 тонн бензина и 50 тонн дизельного топлива;

3) α3 - закупить 100 тонн дизельного топлива.

Природа, в качестве которой в данном случае выступает рынок, формирует розничные цены на нефтепродукты. Пусть возможны два крайних случая:

1) β1 - цена на бензин 30 тенге за литр, цена на дизтопливо 12 тенге за литр;

2) β2 - цена на бензин 20 тенге за литр, цена на дизтопливо 17 тенге за литр.

Матрица исходов имеет размер 3 * 2, в ее клетках следует записать ощущения, которые получает субъект в результате реализации соответствующих комбинаций αi , βj

 

Таблица 13.1 - Матрица исходов

 

Исходы можно описать следующим образом:

1) v 11 — прекрасная сделка, так как на рынке высока цена на бензин, которого закуплено максимально возможное количество, кстати, можно подсчитать и прибыль от данной операции, в случае, если рассматриваемая ситуация реализуется:

(50/0.8)*30000 - 1000000 ≈ 0.9 млн. тенге;

2) v 21 - конечно, прибыль будет, но не в таком объеме, если бы закупить один бензин:

((25/0.8)*30000 + (50/0.85)*12000) - 1000000 ≈ 0.6млн. тенге;

3) v 31 - имеет место неправильный выбор, более выгодно было бы закупить бензин:

(100/0.85)*12000- 1000000 ≈ 0.4 млн. тенге;

4) v 12 - абсолютно неверный выбор: надо было закупать Дизтопливо:

(50/0.8)*20000 - 1000000 ≈ 0.3 млн. тенге;

5) v 22 - прибыль есть, но не в таком объеме, если бы закупить только дизтопливо:

((25/0.8)*20000 + (50/0.85)*17000) - 1000000 ≈ 0.6 млн. тенге;

6) v 32 - прекрасная сделка, так как на рынке высока цена на Дизельное топливо, которого закуплено максимально возможное количество:

(100/0.85)*17000 - 1000000 ≈ 1 млн. тенге.

Отметим, что здесь плотность бензина принята 0.8 г/см³, а плотность дизельного топлива 0.85 г/см³. Расчеты весьма приближенно оценивают возникающую ситуацию, так как, во-первых, цены на рынке нельзя предсказать достоверно, во-вторых, плотность топлива зависит от погодных условий. Тем не менее, расчеты прибыли приведены для того, чтобы показать, что ощущения субъекта имеют под собой вполне определенный прагматический смысл.

Итак, матрица исходов построена. Теперь задача субъекта заключается в том, чтобы выбрать такое решение а*, которое было бы в некотором смысле наилучшим. При этом, конечно, предполагается, что субъекту совершенно неизвестно, в каком состоянии будет находиться природа (т.е. какой из двух приведенных вариантов рыночной конъюнктуры будет иметь место). Это предположение, возможно, покажется слишком сильным - ведь всегда можно узнать существующие цены и прогноз их изменения. Однако пока сознательно оставляем такие возможности без внимания, так как в дальнейшем проведение экспериментов будет рассматриваться особо.

В то время как природа безразлична к исходам, которые получаются в процессе деятельности, этого нельзя сказать" о субъекте. Сознательный, целенаправленный выбор решения предполагает, что на множестве исходов существует субъективное отношение порядка. Если субъекта спросить: "Какой из исходов - vi или vj Вам предпочтительнее (полезнее)?", он почти всегда сможет сказать, какой именно. Сложнее бывает ответить на вопрос: "Во сколько раз vi лучше vj ?", хотя приведенные расчеты показывают принципиальную возможность количественной оценки. В большинстве случаев такие расчеты проводить не имеет смысла, так как они весьма условны. Тем не менее количественная мера полезности исходов необходима. Д. Нейман и О. Моргенштерн [6] создали теорию полезности, которая позволяет решить задачу оценки субъектом полезности, исходов задачи выбора.

Основная задача количественной теории полезности может быть сформулирована следующим образом: имеется к произвольных исходов v1, v2 , ..., vk нужно построить функцию Q (V) (функцию полезности), отображающую множество исходов на множество действительных чисел с привычными порядком и метрикой. Задача эта очень непростая, ведь требуется найти универсальную единицу измерения экономических, этических, психологических и прочих последствий исходов. Построить строгую аксиоматическую теорию полезности, удалось, используя понятие субъективной вероятности [6]. Надо сказать, что затем появились и другие методики количественного измерения полезности. В настоящее время можно говорить о самостоятельном научном направлении, занимающемся этим вопросом, - "квалиметрии".

Рассмотрим в несколько упрощенном виде подход Неймана-Моргенштерна.

Пусть задано множество исходов

v1 , v2 , v3 ,…, vk.

Рассмотрим на этом множестве отношение предпочтительности. Будем cчитать, что vi, предпочтительнее или равноценно vj (обозначаем vi ≥ vj ), если субъекту с его точки зрения, vi кажется не менее полезным, чем vj .

Теория Неймана-Моргенштерна основана на нескольких аксиомах.

Аксиома 1 (транзитивность)

Отношение предпочтительности имеет место для любых двух исходов из заданного множества, и это отношение транзитивно. Следствие. Все исходы можно упорядочить по убыванию предпочтительности: v1 ≥ v2 ≥ v3 … ≥ vn.

Аксиома 2 (непрерывность)

Эта аксиома имеет основополагающее значение для теории. Предположим, что множество исходов упорядочено, vi - самый лучший, vk - самый худший, a vi ( vj ≥ vi ≥ vk ) - некоторый промежуточный исход. Далее предположим, что мы организовали изображаемую беспроигрышную лотерею, в которой всего два выигрыша: vi : вероятностью и vk с вероятностью 1-й. Обозначим эту лотерею

.

После этого зададим субъекту вопрос, что он предпочитает - получить просто исход vi или принять участие в лотерее с двумя выигрышами, один из которых явно лучше vi , а другой явно хуже?

К примеру, спросим, что ему больше нравится - получить безусловно 5-и лет в кино или участвовать в лотерее, в которой лучший выигрыш – автомобиль, а худший "выигрыш" - штраф 1000 тенге. Вероятнее всего, субъект не даст сразу ответа, а поинтересуется, каковы вероятности выигрыша автомобиля и, соответственно, проигрыша 1000 тенге. Если Вы скажете, что в данной лотерее выигрыш машины происходит с вероятностью 0.99999, а потеря денег с дополнительной вероятностью 0.00001, то субъект, «конечно, предпочтет лотерею. Ну а если вероятности поменять местами, то лучше от лотереи отказаться и предпочесть билет в кино.

Можно предполагать, что если плавно изменять вероятность, то найдется такая "точка равновесия", в которой участие в лотерее и безусловное получение билета станут равноценными.

Аксиома непрерывности утверждает, следующее:

для всякого исхода vi найдется такое число vi что исход vi эквивалентен Лотерее

.

Заметим, что u i не есть вероятность в объективном смысле этого понятия, скорее, это - субъективный вероятностный вес исхода vi , в шкале vi , vk ).

Аксиома 3 (монотонность)

V i,j v i ≥ v j <=> u i ≥ u j

То есть vi предпочтительнее или равноценен vj тогда и только тогда когда соответствующая ему субъективная вероятность не менее чем у vj

Эта аксиома в сочетании с двумя предыдущими, дает основание принять в качестве полезности каждого исхода vi, соответствующую ему субъективную вероятность ui , т. е.

Q(v i ) = u i.

 

14 Лекция. Идентификация случайных закономерностей. Идентификация числовых характеристик выборки. Идентификация функций распределения непрерывных случайных величин. Идентификация законов распределения дискретных случайных величин. Оценка результатов идентификации

 

Экспертные методы выбора

При исследовании сложных систем возникают проблемы, выходящие за пределы формальных математических постановок задач. В таком случае прибегают к услугам экспертов, т.е. лиц, чьи суждения и интуиция могут уменьшить сложность проблемы. В следующем лекции мы подробнее рассмотрим работу экспертов - системных аналитиков.

Обсудим вопросы привлечения экспертов к решению конкретной и частной задачи системного анализа - задачи выбора. Правда, в этой частной задаче имеются и некоторые общие черты экспертных методов (например, подходы к оценке компетентности экспертов, к интерпретации даваемых ими результатов и пр.).

Основная идея экспертных методов состоит в том, чтобы использовать интеллект людей, их способность искать и находить решение слабо формализованных задач. Однако особенность интеллектуальной деятельности людей состоит в том, что она во многом зависит от внешних и внутренних условий. Поэтому в методиках организации экспертных оценок специальное внимание уделяется созданию благоприятных условий и нейтрализации факторов, неблагоприятно влияющих на работу экспертов.

Факторы, влияющие на работу эксперта

Очень важную роль играют факторы психологического характера. Прежде всего, эксперты должны быть освобождены от ответственности за использование результата экспертизы. Дело не только в том, что лицо, принимающее решения, не хочет или не должно возлагать ответ­ственность на других, но и в том, что сама ответственность накладывает психологические ограничения на характер выбора, а этого на стадии оценки альтернатив желательно избежать. Однако это еще не все. При­ходится также учитывать, что оценка, даваемая экспертом, может зави­сеть от межличностных отношений с другими экспертами и иногда даже от того, известна ли его оценка другим лицам. На ход экспертизы могут повлиять и личная заинтересованность эксперта, т.е. его необъектив­ность, и другие личностные качества (самолюбивость, конформизм, сила характера и пр.). С другой стороны, обычно сложность проблемы выходит за рамки возможностей одного человека. Было бы неразумно не использовать тот очевидный факт, что коллективная деятельность открывает дополнительные возможности для взаимного стимулирования.

Поскольку взаимодействие между экспертами может, как стимули­ровать, так и подавлять их деятельность, в разных случаях используют методики экспертиз, имеющие различные степень и характер взаимного влияния экспертов друг на друга: анонимные и открытые опросы и анке­тирование, совещания (комитеты, коллегии, комиссии, штабы), дис­куссии (консилиумы, суды, ученые советы), деловые игры, мозговой штурм и т.д. Рассмотрим наиболее типичные процедуры экспертного выбора.

Методы обработки мнений экспертов

Простейший вариант состоит в следующем. Экспертам раздают анкеты с просьбой оценить предлагаемые альтернативы. Заполненные анкеты собирают, обрабатывают и полученную информацию в некото­ром обобщенном виде передают лицу, принимающему решение. На практике возникает ряд вопросов, от ответа на которые зависит, какой именно способ обработки экспертных мнений следует применить в дан­ном конкретном случае.

Сложнее обстоит дело, когда альтернативы нельзя оценить сразу одним числом и экспертам предлагается дать оценки отдельно по каж­дому показателю. Например, оценка качества промышленного изделия складывается из оценок признаков социальных (уровень потребности), функциональных (степень соответствия назначения), экономических, эстетических, эргономических и др. Следующее уточнение вводят в случае неоднородности группы экспертов. Естественно придать различные (а не одинаковые, равные 1/n) веса мнениям экспертов, имеющих разную квалификацию. Опреде­ление коэффициента компетентности i-го эксперта можно поручить самим экспертам.

В тех случаях, когда эксперты лишь упорядочивают альтернативы, т.е. используют только порядковую шкалу, возможность арифмети­ческих операций отпадает. Тогда переходят к обработке либо относительных частот предпочтений данной альтернативы, либо рангов; иногда используют "медианную" альтернативу или расстояния между ранжированиями.

Более глубокие сведения о сравниваемых альтернативах можно получить, изучая "тонкую структуру" суждений экспертов. Дело в том, что оценки экспертов "разбросаны" в пространстве критериев или упорядочений неравномерно, и чаше всего можно выделить несколько кластеров, т.е. кучно расположенных оценок, можно обнаружить и "выбросы", т.е. оценки, далеко отстоящие от кластеров.

Значительный интерес представляет выяснение общего между близкими оценками и различий между отдаленными оценками. Это выполняют уже в ходе уточняющих опросов, в других терминах. Например, при сравнении качества промыш­ленных изделий выяснилось, что кластеры связаны с такими отсутствовавшими в исходной анкете признаками, как различная жест­кость правил приемки для различных альтернатив, технологические раз­личия между моделями изделий и т.д. Возможен и более детальный анализ расхождений экспертов во мнениях.

Создание операционной модели информационной системы. Алгоритмы решения сетевых задач

Основные положения. Симплексный метод решения транспортной задачи.Классическая транспортная задача формулируется как минимизация

                                                                                         (14.1)

при ограничениях:

, i=1… m (поставки),                                                                   (14.2)

^, j=1… n (спрос),                                                               (14.3)

x_ij і 0 для всех i, j.                                                                              (14.4)

S_i, D_j - неотрицательные целые числа, удовлетворяющие условию.

(общие поставки=общему спросу).                              (14.5)

Из соотношений (14.2), (14.3), (14.5) очевидно, что модель содержит избыточные ограничения: если любые n+m-1 ограничений (14.2) удовлетворяются также. (Можно доказать, умножив каждое ограничение (3) на -1 и сложив любые n+m-1 с использованием условия (14.5). Получится уравнение, тождественное оставшемуся ограничению).

Следовательно, любое из уравнений (14.2) или (14.3) можно опустить без ущерба. В итоге получим модель из m+n-1 независимых ограничений.

В любое базисное решение необходимо включить m+n-1 переменную.Тогда двойственная задача линейного программирования запишется :максимизировать

                                                                                  (14.6)

при ограничениях

v_i + w_j Ј c_ij для всех (i, j),                                                                 (14.7)

где v_i и w_j не ограничены по знаку.

Следствие теоремы двойственности и теоремы дополняющей нежесткости заключается в том, что если х^*_ij при всех (i, j) удовлетворяют условию (14.2), (14.3), (14.4), а v_i^* и w_j^* удовлетворяют условию (14.7), если х^*_ij (v_i^* + w_j^*- с_ij)=0 при всех (i, j), то набор х^*_ij является оптимальным решением задачи (14.1) - (14.4).

На основе этих следствий разработаны алгоритмы решения сетевых задач. Общей идеей является то, что на каждой итерации для пробных значений х_ij, v_i, w_j всегда выполняется 2 из 3-х условий:

1) допустимость исходной задачи. Она формулируется соотношениями ограничения (14.2) - (14.4);

2) допустимость двойственной задачи (формулируется соотношением (14.7);

3) условия дополнительной нежесткости.

 

15 Лекция. Моделирование систем массового обслуживания. Моделирование одноканальных систем массового обслуживания. Моделирование систем массового обслуживания с ненадежными элементами. Моделирование систем массового обслуживания с относительным приоритетом. Компьютерное моделирование экономико-организационных систем. Компьютерное моделирование типовой экономической цепочки «Поставщик - склад - потребитель». Моделирование системы распределения ресурсов

 

В симплексном алгоритме на каждой итерации выполняются условия (1) и (3). Вычислительная процедура заканчивается, как только выполнится условие (2).    Применительно к транспортной задаче в симплексном алгоритме реализуется последовательность шагов:

Шаг 1. Выбирается m+n-1 маршрутов (дуг), являющихся допустимым базисным решением.

Шаг 2. Проверяется возможность улучшения решения заменой одной из базисных переменных. Если результат положительный, то переход к шагу 3, иначе - прекращение вычислений.

Шаг 3. Определяется, какой маршрут исключается из базиса, когда в него введена новая переменная (в шаге 2).

Шаг 4. Изменяются потоки остальных базисных маршрутов. Переход к шагу 2.Предположим, что модель приведена к виду классической транспортной задачи: Минимизировать

при ограничениях, заданных матрицей ограничений

Допустим, что имеется допустимое базисное решение, содержащее m+n-1 маршрут. Если единичный поток направляется по небазисному маршруту, то для сохранения допустимости по соответствующей строке и столбцу матрицы ограничений необходимо снять 1 с базисного маршрута. Эти изменения приведут к изменению потоков по всем базисным переменным. Окончательные изменения можно оценить по общему изменению затрат, обусловленному добавлением единичного потока по небазисному маршруту и соответственно изменением потоков базисных маршрутов. Если результат улучшает значение целевой функции, и новый маршрут вводится в решение, то схема изменений указывает сколько единиц потока можно направить по этому новому маршруту, и какая базисная переменная при этом обратится в "0".

 

	Столбец					Поставки
строка		1	2	...	n
	1	с11 х11	с12 х12	... ...	c1n x1n	S1
	2	c21 x21	c22 x22	... ...	c2n x2n	S2
	...	... ...	... ...	... ...	... ...	...
	m	cm1 xm1	cm2 xm2	... ...	cmn xmn	Sm
cпрос		D1	D2	...	Dn

 

Процедура сводится к решению m+n-1 уравнений ограничения двойственной задачи, соответствующих текущему базису

v_i + w_j = c_ij для каждой базисной х_ij                                                           (15.1)

и затем определить значения

v_i + w_j - c_ij для небазисной х_ij .                                                                   (15.2)

Величины, входящие в (15.2) соответствуют коэффициентам строки "0" симплекс-матрицы. Если значение выражения (15.2) > 0, то х_ij необходимо ввести в базис.

Если все значения выражения (15.2) Ј 0 и решение является допустимым как для прямой, так и для двойственной задачи, то текущее базисное решение является оптимальным.

Пример реализации

Рассмотрим транспортную задачу со следующими условиями ограничения.

 

		Столбец				Поставки
		1	2	3	4
строка	1	2	3	11	7	6
	2	1	0	6	1	1
	3	5	8	15	9	10
cпрос		7	5	3	2

 

На основании данного ранее описания симплексного алгоритма реализации транспортной задачи необходимо выполнить следующее: Итерация 1

Шаг 1.

Выбрать n + m - 1 маршрут

m=3; n=4;  m+n-1=6.

Распределение поставки по самым дешевым маршрутам в первых двух строках, а в третьей дополним их до полного удовлетворения спроса.

 

Матрица ограничений примет вид:

		Столбец				Поставки
		1	2	3	4
строка	1	2 6	3	11	7	6
	2	1	0 1	6	1	1
	3	5 1	8 4	15 3	9 2	10
cпрос		7	5	3	2

 

Общие затраты = 2*6 + 0*1 + 5*1 + 8*4 + 15*3 + 9*2 = 12 + 0 + 5 + 32 + 45 + 18 = 112.

Шаг 2.

Проверить возможность улучшения значения целевой функции за счет введения в базис новой переменной

 

		Столбец				Поставки
		1	2	3	4
строка	1	2 6 -1	3 +1	11	7	6
	2	1	0 1	6	1	1
	3	5 1 + 1	8 4 - 1	15 3	9 2	10
cпрос		7	5	3	2

 

Оценка маршрута = е уменьшение затрат - е увеличение затрат = (2 + 8) -(3+5) = 2.

Аналогично необходимо проверить влияние на изменение целевой функции всех небазисных маршрутов. Процедуру можно ускорить, если перейти к оценке переменных двойственной задачи, и сравнивать различия между левыми и правыми частями двойственных ограничений, соответствующих небазисным маршрутам.

Применив систему линейных равенств к исходному решению, получим систему соотношений для базисных маршрутов двойственной задачи:

v₁ + w₁ = 2 маршрут (1, 1);

v₂+ w₂= 0 маршрут (2, 2)4

v₃+  w₁ = 5  маршрут (3, 1);

v₃ +  w₂= 8 маршрут (3, 2);                                                               (15.3)

v₃ + w₃ = 15 маршрут (3, 3);

v₃ + w₄ = 9 маршрут (3, 4).

Запись (15.3) - 6 уравнений с 7 неизвестными. Для решения необходимо выбрать одну переменную. Дать ей произвольное значение. Возьмем v₃ = 0. (Причиной появления лишней переменной является избыточность уравнений ограничения m + n). Присвоение v₃ произвольного значения эквивалентно вычеркиванию строки 3 с целью избавления от избыточности.

При v₃ = 0:

w₄ = 9 - v₃  = 9;

w₃ = 15 - v₃ = 15w₂ = 8 - v₃  = 8 w₁ = 5 - v₃  = 5;                                 (15.4)

v₂ = 0 - w₂ = -8;

v₁ = 2 - w₁ -3.

Описание структуры для последовательного отыскания значений переменных называется триангуляцией.

Исключив из (15.4) v₃, мы получим систему из m уравнений с m неизвестными треугольной структуры.

Если переменной v₃ присвоить значение, отличное от "0", то каждая переменная v_i увеличится, а w_j уменьшится на эту величину. Таким образом, значения v_i + w_j и v_i + w_j - с_ij останутся без изменения.

На основании теоремы о двойственности свойствами треугольной структуры обладает система уравнений, определяющих значения базисных переменных х_ij

х₁₁= 6 ,                            (строка 1);

х₂₂ = 1,                           (строка 2);

х₁₁ + х₃₁ = 7,                   (столбец 1);                                                          (15.5)

х₂₂ + х₃₂ = 5,                   (столбец 2);

х₃₃ = 3,                           (столбец 3);

х₃₄ = 2,                           (столбец 4).

Если система (10) имеет структуру верхнего треугольника, то система (12) имеет структуру нижнего треугольника, так как строка коэффициентов k-того уравнения в (12) является столбцом коэффициентов k-той переменной в (10).Система (12) разрешается следующим образом:

х₁₁ = 6х₂₂ = 1х₃₁ = 7 - 6 = 1х₃₂ = 5 - 1 = 4х₃₃ = 3;

х₃₄ = 2.

Оценку каждого маршрута, не входящего в базис, можно определить по формуле v_i + w_j - c_ij.

Используя значения двойственных переменных можно найти следующие результаты:

-3 + 8 - 3 = 2 маршрут (1, 2);

-3 + 15 - 11 = 1 маршрут  (1, 3);

-3 + 9 - 7 = -1 маршрут (1, 4);

-8 + 5 - 1 = -4 маршрут (2, 1);

(13)-8 + 15 - 6 = 1 маршрут (2, 3);

-8 + 9 - 1 = 0 маршрут (2, 4).

Положительные числа указывают на возможность уменьшения целевой функции (Это маршруты (1, 2), (1, 3), (2, 3)). Из трех возможных маршрутов необходимо выбрать (1, 2), так как он имеет наибольшую оценку (это эквивалент симплекс-критерия 1).

Шаг 3.

Определим величину потока по маршруту (1, 2). Схему изменений мы определили выше (уменьшим потоки по маршрутам (1, 1) и (3, 2). Текущие значения этих потоков соответственно равны 6 и 4. Следовательно, увеличение потока по маршруту (1, 2) возможно до 4, вследствие чего маршрут (3, 2) исключается.

 

	столбец				поставка
строка	2	4			6
		1			1
	5		3	2	10
спрос	7	5	3	2

 

Общие затраты = общие затраты предыдущего решения - общая экономия = 112 - 2*4 = 104 (эквивалент симплекс- критерия II) Шаг 4. Вносятся изменения в маршруты, что дает второе пробное базисное решение при котором целевая функция = 104. Итерация 2 начинается с шага 2. Проверка полученного решения на оптимальность или возможность улучшения.

Двойственные соотношения в новом базисе:

v₁+w₁ = 2 маршрут (1, 1);

v₂+ w₂ = 0 маршрут (2, 2);

v1 +w₂ = 3 маршрут (1, 2);

v₃+w₁= 5 маршрут (3, 1)          ;                                                                  (15.6)

v₃+w₃ = 15 маршрут (3, 3);

v₃+ w₄= 9 маршрут (3, 4).

При v₃ = 0

w₄ = 9;

w₃ = 15;

w₁ = 5;

v₁ = 2 - w₁ = -3;                                                                                 (15.7)

w₂ = 3 - v₁ = 6;

v₂ = 0 - w₂ = -6.

Оценки маршрутов можно записать:

-3 + 15 - 11 = 1 маршрут (1, 3);

-3 + 9 - 7  = -1 маршрут (1, 4);

-6 + 5 - 1 = -2 маршрут (2, 1);

(16)-6 + 15 - 6 = 3 маршрут (2, 3);

-6 + 9 - 1 =2  маршрут  (2, 4);

0 + 6 - 8 = -2 маршрут (3, 2).

В новое решение введем маршрут (2, 3)

Схема изменений примет вид:

 

	столбец				Поставки
строка	2-1	4+1			6
		1-1	+1		1
	5+1		3-1	2	10
Спрос	7	5	3	2

 

Общие затраты = 104 - 1*3 = 101 Все маршруты, кроме одного изменились. Может быть случай, когда изменяются все базисные маршруты.Маршрут (2, 2) выводится из базиса, так как общее изменение потока = 1.

Данные таблицы можно считать потоками третьего пробного базиса.

v₁+v₃+w₂  = 3маршрут (1, 2);

v₁+ w₁ = 2 маршрут (1, 1);

v₂  +  w₃= 6маршрут (2, 3);                                                               (15.8)

v₃+ w₃ = 15 маршрут (3, 3);

v₃ + w₁= 5 маршрут (3, 1);

w₄ = 9 маршрут (3, 4).

При v₃ = 0:

w₁ = 5;

w₃ = 15;

w₄ = 9;

v₂ = 6 - 15 = -9;                                                                                  (15.9)

v₁ = 2 - 5 = -3;

w₂ = 3 + 3 = 6.

Оценки маршрутов:

-3 + 15 - 11 = +1,            маршрут (1, 3);

-3 + 9 - 7 = -1,                маршрут (1, 4);

-9 + 5 - 1 = -5,                маршрут  (2, 1);

-9 + 9 - 1 = -1,                маршрут  (2, 4);

0 + 6 - 15 = -9,                маршрут (3, 2).

Итерация 3

Включаем маршрут (1, 3) в базис

 

		Столбец				Поставки
		1	2	3	4
Строка	1		5	1		6
	2			1		1
	3	7		1	2	10
спрос		7	5	3	2

 

Общие затраты = 101 - 1*1 = 100.

Заключения по симплексному методу

Теорема о треугольном свойстве. Оптимальность. Целочисленность. Полнота и область применимости алгоритма. Сходимость.

При реализации симплексного алгоритма применительно к сетевым моделям мы ссылались на теорему о треугольном свойстве, суть которой заключается в следующем:    Исключив любое из уравнений в избыточной системе ограничений, мы получим, что каждый базис обладает треугольным свойством. Следовательно, для последовательного определения значений любого множества базисных переменных достаточно операций сложения и вычитания.

Применительно к сетевым моделям в методе постоянно использовалось треугольное свойство системы линейных уравнений.

Оптимальность

При реализации симплексного алгоритма процедуры направлены на последовательное улучшение значения целевой функции вплоть до достижения оптимального решения. В любом решении все поставки Si распределяются по маршрутам i-той строки, причем в строке каждое Cij можно уменьшить на одну и ту же величину, и это не повлияет на оптимальное решение.

Аналогичную процедуру можно выполнить над Cij в каждом j-том столбце. Допустим, что для каждой i-той строки v_i =const . Допустим , что в целевом функции значения Сij заменены значениями Cij - (v_i + w_j). Модель с исходными коэффициентами Сij и модель с новыми коэффициентами имеют одно оптимальное решение.

При завершении симплекс-процедуры выполняется условие

Cij - (v_i + w_j) >=0 для всех (i, j),                                                          (15.10)

так как Сij, v_i , w_j - элементы окончательной таблицы оценок.

Минимальное значение новой целевой функции >= 0, так как все коэффициенты целевой функции знакоположительные.

Так как для базисных маршрутов выражение (15.10) выполняется как равенство, то в окончательное решение входят только те маршруты, в которых коэффициенты затрат равны “0”. Следовательно, улучшить решение невозможно.

Если для некоторого небазисного маршрута имеется оценка Cij = 0, то можно найти новое оптимальное решение, введя этот маршрут в базис.

Целочисленность

Как отмечалось ранее, дополнительное ограничение

x_ij = 0, 1, 2, ... для всех (i, j)                                                                (15.11)

на оптимальное значение целевой функции не влияет.    Применительно к транспортной задаче алгоритм строится на поиске только таких решений, которые удовлетворяют условию (15.11).    Рассуждения основаны на следующих положениях:

1) поскольку модель имеет конечное оптимальное решение, существует оптимальное базисное решение.каждый базис имеет треугольную структуру;

2) каждый коэффициент матрицы транспортной задачи равен 1 или -1.

Таким образом, при определении базисных x_ij используются только операции сложения и вычитания.

Полнота и область применимости

Если на шаге 2 более чем 1 маршрут имеет максимальную оценку, то можно выбрать любой из них.    Если на шаге 3 более чем 1 поток становится равным “0” при введении в базис нового маршрута, то новый базис называется вырожденным. В новом базисе должны остаться все маршруты с нулевыми потоками, кроме одного.

Симплексный метод применим к любым сетевым моделям, которые можно привести к виду транспортных. Причем, условие Сij> 0 не является обязательным.

Сходимость

Оптимальному решению таким образом должно соответствовать конечное значение целевой функции. Если решение улучшается на каждой итерации, то метод должен сходиться так как значение целевой функции должно уменьшаться по крайней мере на 1. В случае вырожденного базиса значение целевой функции может быть неизменным на нескольких итерациях. В этом случае существует опасность зацикливания. Исключить вырожденность можно путем введения небольших возмущений в поставки и спрос.

Если принять новые поставки равными nSi для i = 1, 2, ... m-1 и nSm + n,

а новые потребности nDj + 1 при j =1, 2, ... n, то значение целевой функции будет изменяться на каждой итерации.

Окончательный результат подвергается обратному преобразованию в исходные единицы x_ij / n с последующим округлением.

При этом выполняются все ограничения по поставкам и спросу. При этом решение остается оптимальным.

Сеть общего вида

Свойствами треугольной структуры и существованием целочисленного оптимального решения обладают модели, соответствующие задачам:

                                                                                (15.12)

при ограничениях

, k=1, 2, ... p                                                (15.13)

(15.13) - уравнение баланса в узлах сети.

Xij >= 0 для всех (i, j) принадлежащих сети,                                    (15.14)

где                                                                                                  (15.15)

и каждая Tk – целочисленная.

В данной модели имеется избыточность в ограничениях, которую можно убрать, исключив одно из уравнений. Каждый базис из (P-1) уравнения обладает свойствами треугольной структуры. А так как все коэффициенты в (15.13) имеют значения +1, -1, то соответствующее решение будет целочисленным.

Двойственная задача этой задачи формулируется:

                                                                                          (15.16)

при ограничениях

, для всех (i, j) принадлежащих сети                                (15.17)

где каждая y_k не ограничена по знаку.

Можно последовательно найти значения соответствующих двойственных переменных при условии, что известно любое базисное решение. Набор из Р-1 базисной переменной обозначает исключение одной из дуг сети, что соответствует древовидной структуре.

Суть применения симплексного алгоритма к такой структуре в выборе перспективной дуги, которая разрушает структуру дерева, образуя контур. Далее, максимально возможный поток направляется по этой дуге, изменяя потоки по остальным дугам контура. Такое перераспределение потока приводит к исключению одной из дуг контура, в результате чего восстанавливается древовидная структура.

 

 

Список литературы

 

1)     Г. Вагнер. Основы исследования операций. Т. 1. - М.: Мир, 1972. - 335 с.

2)     Павлов А.А., Гриша С.Н., Основы системного анализа и проектирования. - Киев: Высш. шк., 1991. - 367 с.

3)     Бахвалов Н.С. Численные методы. - М.: Наука, 1973. - 630 с.

4)     Фурунджиев Р.И. и др. Применение математических методов и ЭВМ. Практикум: Учеб. пособие для вузов. - Минск: Высш. шк.,1988. - 991с.: илл.

5)     Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. Учеб. пособие для вузов. - М.: Высш. шк., 1989. - 367 с.: илл.

6)     Банди Б., Основы линейного программирования., пер. с англ.-М.: Радио и связь, 1989.-176 с.: илл.

7)     Полак Э. Численные методы оптимизации. Единичный подход. Пер. с англ. Ф.Н. Ерешко. Под ред. И.А. Вателя. – М.: Мир, 1974, 376 c. с черт.

 

Содержание

 

1 Лекция. Роль системных представлений в человеческой деятельности	3
2 Лекция. Теория систем, системный подход, системный анализ	6
3 Лекция. Понятие математической модели	10
4 Лекция. Выпуклые функции	14
5 Лекция. Относительный экстремум. Метод множителей Лагранжа. Поисковые методы 0-го порядка. Метод равномерного поиска	18
6 Лекция. Поисковые методы 0-го порядка. Метод равномерного поиска	20
7 Лекция. Метод дихотомии	22
8 Лекция. Общая схема градиентного спуска	25
9 Лекция. Линейное программирование	30
10 Лекция. Транспортная задача	34
11 Лекция. Линейные и нелинейные модели	37
12 Лекция. Стохастические модели	40
13 Лекция. Модели принятия решений в условиях неопределенности	42
14 Лекция. Неформальные процедуры принятия решений	46
15 Лекция. Симплексный метод решения транспортной задачи	49
Список литературы	57

 

Сводный план 2011 г. поз. 385