Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра компьютерных технологий
МОДЕЛИ И МЕТОДЫ ТЕОРИИ УПРАВЛЕНИЯ
Методические указания к выполнению лабораторных работ
для студентов специальности
5В070400 – Вычислительная техника и программное обеспечение
Алматы, 2013
СОСТАВИТЕЛИ: З.К. Куралбаев и Е.А. Зуева. Модели и методы теории управления. Методические указания к выполнению лабораторных работ для студентов специальности 5В070400 – Вычислительная техника и программное обеспечение. – Алматы: АУЭС, 2013. – 34 с.
Методические указания содержат указания по подготовке к проведению четырех лабораторных работ по изучению методов и моделей теории управления в оптимизационной математике, критериев принятия оптимальных решений, возникающих в процессах моделирования и управления систем.
В данных указаниях приведены описания каждой лабораторной работы, дана методика проведения и ход выполнения, оговорен перечень рекомендуемой литературы и контрольные вопросы в конце каждой темы.
Выполнение лабораторных работ определяет фундаментальную основу профессионального образования курсу «Модели и методы теории управления». Предметом изучения дисциплины «Модели и методы теории управления» является освоение основных методов оптимизационной математики и критерии выбора оптимального решения в системах различной степени сложности и назначения.
Илл. 16, табл. 15, библиогр. - 3 назв.
Рецензент: старший преподаватель кафедры ТКС Шахматова Г. А.
Печатается по плану издания некоммерческого акционерного общества “Алматинский университет энергетики и связи” на 2012г.
© НАО “Алматинский университет энергетики и связи”, 2013 г.
Введение
Данное методическое указание представляет сборник лабораторных работ, ориентированных на специфику методов вычислений в задачах оптимизационной математики для студентов специальности 5В070400 - «Вычислительная техника и программное обеспечение».
Изучение дисциплины предполагает приобретение студентами опыта в построении и изучении математических моделей путем анализа полученных численных результатов.
Методические указания охватывают основные темы курса. Главное внимание уделяется построению математических моделей с использованием программы Excel 2003 (так как в ней содержится оптимизационный компонент «Поиск решений»). Материал по каждой работе включает в себя цель, задания, методические указания для выполнения, варианты, предлагаемые для самостоятельного выполнения и контрольные вопросы для самостоятельной подготовки.
Этапы выполнения работ: проработка теоретической части, повторение реализации решения задачи-примера в Excel 2003, выбор своего варианта задания, выполнение заданий, ответы на контрольные вопросы, создание отчета и его защита у преподавателя.
Темы лабораторных работ: решение систем линейных алгебраических уравнений методом Жордана-Гаусса; симплекс-метод; метод потенциалов для решения транспортной задачи; метод Гомори для решения задач целочисленного программирования.
Выбор варианта заданий студенту по каждой лабораторной работе определяет преподаватель.
Выполнение каждой работы должно завершаться оформлением отчета. Отчет о проделанной работе должен содержать:
- титульный лист;
- цель и задание работы;
- краткие итоги теоретической подготовки (ответы на контрольные вопросы);
- результаты проделанной работы (набранные и обработанные тексты, графики, диаграммы, рисунки и другие объекты);
- выводы своими словами по работе (что получилось, обсуждение метода, анализ полученных итогов деятельности студента и т.д.).
Выполнение практических заданий дает возможность выработки навыков и знаний у студентов.
В список литературы включены книги, рекомендуемые студентам для дополнительного изучения.
1 Лабораторная работа №1. Решение систем линейных алгебраических уравнений методом Жордана-Гаусса
Цели работы: изучение основ оптимизационного анализа; приобретение навыков программирования типичных экономических задач.
1.1 Методические указания к выполнению работы
Система m линейных уравнений с n неизвестными выглядит так:
 (1)
(1)
Решение (1) -
совокупность n чисел а1, а2,
..., аn таких, что при подстановке вместо неизвестных
каждое уравнение обращается в тождество. Системе уравнений сопоставим матрицу А из
коэффициентов и расширенную матрицу ![]() , полученную присоединением к матрице столбца свободных
членов:
, полученную присоединением к матрице столбца свободных
членов:
A = 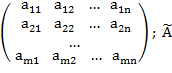 =
= 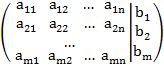 .
.
Над строками расширенной
матрицы ![]() можно осуществлять преобразования:
можно осуществлять преобразования:
- перестановка любых уравнений (строк) между собой;
- умножение/деление всех коэффициентов строки на число;
- вычеркивание полной нулевой строки.
По методу Жордана-Гаусса, в левой части матрицы нужно получить по диагонали единицы, остальные – нули. Общее решение можно записать:
x1= b'1 - a'1 r+1xr+1 -…- a'1nxn,
x2= b'2 - a'2 r+1xr+1 -…- a'2nxn,
…
xr = b'r - a'r r+1xr+1 -…- a'r nxn.
Придавая каждой из
стоящих в правых частях равенств переменных xr+1,xr+2, …, xn произвольные значения,
получаются частные решения. Если определитель матрицы отличен от нуля, r - количество переменных, m – количество ненулевых
строк, то (r-m) переменные называются свободными.
Базисным решением системы уравнений называется частное решение, в котором свободные
переменные имеют нулевые значения. Каждому разбиению на основные и свободные
переменные соответствует одно базисное решение, а количество способов разбиения
не превышает ![]() . Если все компоненты базисного решения неотрицательны, то
такое решение называется опорным. Ниже приведены решения трех задач для случаев:
задача 1 – r=m; задача 2 – r-m=1; задача 3 – r-m=2.
. Если все компоненты базисного решения неотрицательны, то
такое решение называется опорным. Ниже приведены решения трех задач для случаев:
задача 1 – r=m; задача 2 – r-m=1; задача 3 – r-m=2.
Задача 1. Решить методом
Жордана-Гаусса:  .
.
Решение. Составляем расширенную матрицу, в качестве направляющего элемента - элемент а(0)11=1. Преобразуем первый столбец в единичный: к второй и третьей прибавляем первую строку, соответственно умноженную на (-2) и (-4). В третьей матрице выбираем направляющий элемент а(1)22=-3. Так как а(1)22≠ 1, то делим вторую строку на (-3); далее умножаем вторую строку на 1 и 3 и складываем соответственно с первой и третьей строками. Для четвертой матрицы выбираем направляющий элемент а(2)33= - 2. Так как а(2)33≠1, то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку на (-4/3) и (-2/3) и складываем соответственно с первой и второй строками.
![]()
![]()
![]()
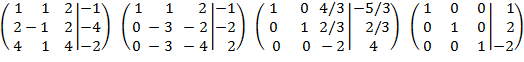 ,
,
откуда x1=1, x2=2, x3=-2.
Делаем проверку, подставляя найденные значения вместо x1, x2, x3 в левую часть исходной задачи 1, в результате получаются соответствующие правые части: проверка верна. Ответ: {1; 2; -2}.
Задача 2. Решить методом Жордана-Гаусса: 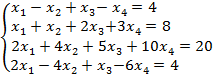 .
.
Решение. Составляем расширенную матрицу:
![]()
![]()
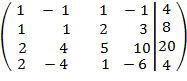
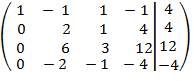
![]()
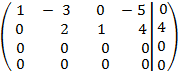 эквивалентно:
эквивалентно:
![]() .
.
Общее решение
имеет вид: ![]()
Найдем базисные решения. Для этого полагаем x2=0, x4=0, тогда x1=0, x3=4. Базисное решение имеет вид: (0; 0; 4; 0).
Получим другое базисное
решение: в качестве свободных примем x3 и x4. Выразим x1 и x2 через x3 и x4: ![]() . Тогда
базисное решение примет вид: {6; 2; 0; 0}. Делается проверка.
. Тогда
базисное решение примет вид: {6; 2; 0; 0}. Делается проверка.
Задача
3. Решить методом Жордана-Гаусса: 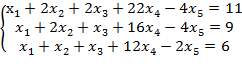 .
.
Решение. Составляем и преобразуем расширенную матрицу. Для второй матрицы в качестве направляющего выбираем элемент а(0)11=1, преобразуем первый столбец в единичный: ко второй и третьей строкам прибавляем первую строку, умноженную на (-1). Для третьей матрицы выбираем направляющий а(1)32=-1, умножаем третью строку на (-1), преобразуем второй столбец в единичный: к первой строке прибавляем третью строку, умноженную на (-2). Для четвертой строки выбираем направляющий элемент а(2)22=-1, так как а(2)22≠1, то умножаем вторую строку на (-1), преобразуем третий столбец в единичный: вторую строку складываем с третьей.
![]()
![]()
![]()
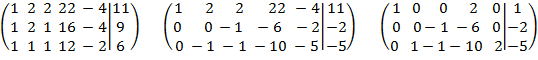
![]()
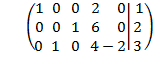 эквивалентно:
эквивалентно:
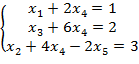 .
.
Общее
решение имеет вид: 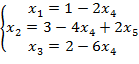 .
.
Переменные x1, x2, x3 являются базисными, частное решение получается из общего путем придания конкретных значений свободным переменным. Если свободные x4 и x5 положить равными нулю, то получим первое базисное решение x1=1, x2=3, x3=2, x4=0, x5=0, то есть {1; 3; 2; 0; 0).
Общее число базисных
решений не более чем ![]() =
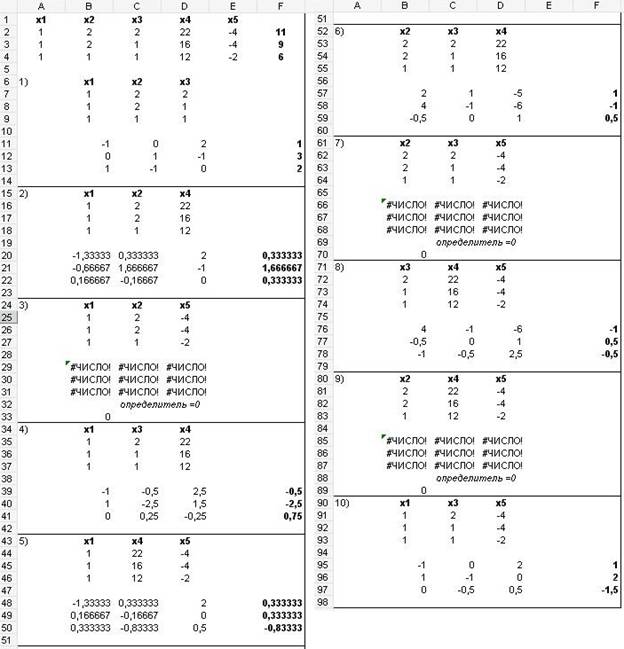
= ![]() (в таблице 1 даны все 10 возможных решений-комбинаций).
(в таблице 1 даны все 10 возможных решений-комбинаций).
Решение с помощью Excel 2003. Общее число групп определяется функцией ЧИСЛКОМБ. Числовые аргументы усекаются до целых; если любой из аргументов не число, то ЧИСЛКОМБ возвращает значение ошибки «#ИМЯ?»; если число<0 или число_выбранных<0 или число<число_выбранных, то функция ЧИСЛКОМБ возвращает ошибку «#ЧИСЛО!»; комбинация - любое множество объектов безотносительно к их порядку. На рисунке 1 показано использование функции.
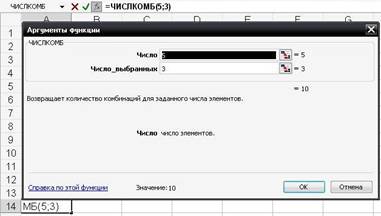
Рисунок 1 - Число сочетаний из 5 по 3 равно 10
В задаче 3 число базисных решений равно 7, так как три группы переменных: третья, седьмая и девятая не могут быть базисными, потому что определитель матрицы коэффициентов при них равен нулю (см. таблицу 1).
Рассмотрим по шагам получение всех базисных решений с помощью Excel, начиная с первого x1, x2, x3.
1. Матрица коэффициентов
при x1, x2, x3 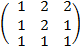 находится
в ячейках B7:D9, выделен диапазон для размещения обратной матрицы B11:D13,
введена формула для вычислений (см. рисунок 2).
находится
в ячейках B7:D9, выделен диапазон для размещения обратной матрицы B11:D13,
введена формула для вычислений (см. рисунок 2).
2. В диапазон следует
нажать клавиши CTRL+SHIFT+ENTER. В диапазоне B11:D13 размещена обратная матрица
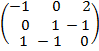 (см. рисунок 3).
(см. рисунок 3).
3. Надо умножить полученную
обратную матрицу на вектор-столбец свободных членов ![]() . На рисунке 4 показан выделенный диапазон для результата
умножения и введена функция. Затем в диапазоне также следует нажать клавиши
CTRL+ SHIFT+ENTER. В диапазоне F11:F13 получено первое базисное решение x1=1,
x2=2, x3=2, x4=0, x5=0 (см.
рисунок 5).
. На рисунке 4 показан выделенный диапазон для результата
умножения и введена функция. Затем в диапазоне также следует нажать клавиши
CTRL+ SHIFT+ENTER. В диапазоне F11:F13 получено первое базисное решение x1=1,
x2=2, x3=2, x4=0, x5=0 (см.
рисунок 5).
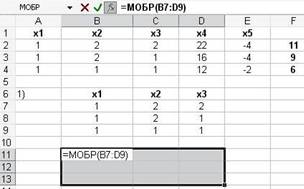
Рисунок 2 - Выделен диапазон для размещения обратной матрицы в ячейках B11:D13 и введена формула для вычислений
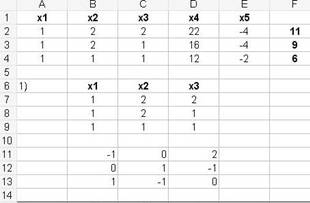
Рисунок 3 - В диапазоне B11:D13 размещена обратная матрица
Для получения второго базисного решения для переменных x1, x2, x4 выполняем указанную последовательность действий (см. рисунок 6). Второе базисное решение имеет вид: (0.333, 1.667, 0, 0.333, 0).
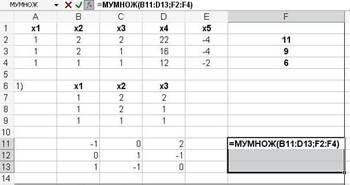
Рисунок 4 - Умножение обратной матрицы на столбец свободных членов
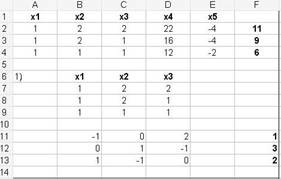
Рисунок 5 - В диапазоне F11:F13 получено решение на первом шаге
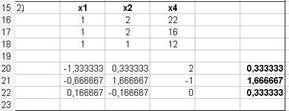
Рисунок 6 - Второе базисное решение
Для третьей группы переменных x1, x2, x5 нельзя найти базисное решение, потому что определитель равен нулю (см. рисунок 7).
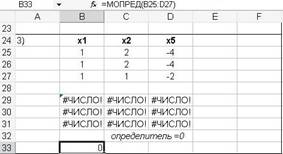
Рисунок 7 - В ячейке B33 результат выполнения функции МОПРЕД – определитель равен нулю
В таблице 1 содержатся промежуточные таблицы и результаты вычислений по всем 10 группам переменных, то есть результат решения задачи 3. Столбец F содержит базисные решения.
Т а б л и ц а 1 – Таблицы решения задачи 3
1.2 Задания
Решить методом Жордана-Гаусса систему уравнений (часть 1 – решить вручную; 2 – решение в Excel: выписать все возможные базисные решения).

Вариант 2:
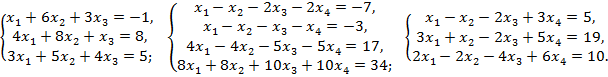
Вариант 3:
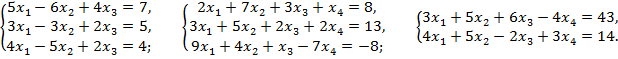
Вариант 4:
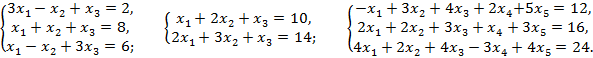
Вариант 5:
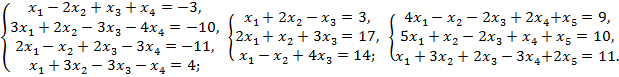
Вариант 6:

Вариант 7:
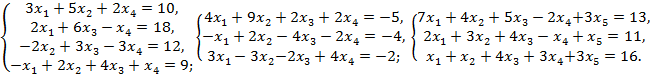
Вариант 8:
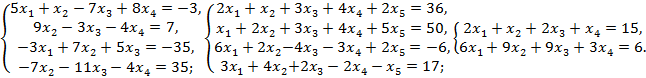
Вариант 9:
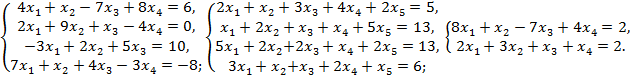
Вариант 10:
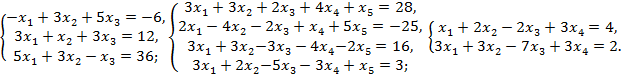
1.3 Контрольные вопросы
1. Что означает понятие «совместная система?
2. Поясните суть метода Жордана-Гаусса.
3. Назовите и поясните альтернативные
методы решения системы линейных уравнений.
2 Лабораторная работа №2. Симплекс-метод
Цели работы: приобретение знаний и навыков решения типовой задачи линейного программирования с помощью симплекс-метода; выработать умение формулировать математическую модель экономической задачи и реализацию решения ее на компьютере.
2.1 Методические указания к выполнению работы
Для решения задач линейного программирования существуют специальные методы, но есть общий метод решения - симплекс-метод - отыскание какого-нибудь допустимого решения и последовательного перехода от найденного допустимого решения к новому допустимому решению, для которого функция изменяется в нужном направлении.
К задачам, решаемым симплекс-методом, относятся такие задачи, как «Определение наилучшего состава смеси», «Задача об оптимальном плане выпуска продукции», «Оптимизация межотраслевых потоков», «Задача о выборе производственной программы», «Транспортная задача», «Задача размещения», «Задача о питании», «Модель Неймана расширяющейся экономики» и другие. Во всех таких задачах требуется найти максимум или минимум линейной функции при условии, что её переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные уравнения, так и линейные неравенства. Эти задачи сводятся с помощью определенных математических приемов к одной и той же задаче, которая называется основной (канонической) задачей линейного программирования:
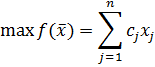
при ограничениях

Суть метода. Все неизвестные произвольно подразделяют на базисные и свободные, число базисных переменных определяется числом линейно-независимых уравнений, остальные – свободны, им придают любые значения и подставляют в систему. Любому набору свободных неизвестных можно придать бесчисленное множество произвольных значений, дающих бесчисленное множество решений. Если все свободные приравнять к нулю, то решение будет состоять из значений базисных неизвестных. Такое решение называется базисным. Среди базисных решений системы можно найти оптимальное, а в некоторых случаях и несколько оптимальных решений, но все они обеспечат экстремум целевой функции. Если найти какой-либо базисный план, а затем улучшить его, то получится оптимальное решение.
Задача 4. Фирма производит изделия двух видов A1 и A2 с помощью последовательной обработки каждой из них в трех цехах. Данные в таблице 2.
Т а б л и ц а 2 – Исходные данные задачи 4
|
Названия цехов |
Нормы затрат времени на 1 изделие, час/сут. |
Объем ресурсов, час/сут. |
|
|
Изделие А1 |
Изделие А2 |
||
|
|
|
|
|
|
B1 |
0,1 |
0,2 |
12 |
|
B2 |
0,2 |
0,1 |
10 |
|
B3 |
0,3 |
0,3 |
21 |
|
Прибыль на 1 изделие, у.е. |
65 |
80 |
- |
Определить количества xj, j=1,2, изделий Aj, которые необходимо изготовить для достижения максимальной прибыли F(x)=65x1+80x2, то есть найти оптимальный план суточного выпуска изделий А1 и А2. Это типичная задача производственного планирования. Х1 и x2 не произвольны, так как есть ограничения на суточное время работы в цехах. Эти ограничения:
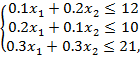 (2)
(2)
x1 и x2 не отрицательны: x1≥0; x2≥0. Требуется найти такое неотрицательное решение x1, x2, при котором целевая F(x) принимает максимальное значение.
а) графический метод построения.
Так как переменные x1 и x2 неотрицательны, то множество точек (x1, x2), являющихся возможными решениями задачи, лежит в первом квадранте плоскости х1▪х2 (см. рисунок 8). Если в первом неравенстве системы заменить знак «≤» на знак «=», то получим уравнение прямой линии 0,1·х1+0,2·х2=12. Эта прямая (прямая 1) делит плоскость х1▪х2 на две полуплоскости, для одной выполнено 0,1·х1+0,2·х2>12, для другой - 0,1·х1+0,2·х2<12. Подстановкой (0,0) в левую часть убеждаемся, что начало координат лежит в полуплоскости, удовлетворяющей требуемому ограничению 0,1·х1+0,2·х2≤12, допустимой для этого ограничения является полуплоскость, содержащая (0,0). Определим полуплоскости для других ограничений системы (прямые 2 и 3). В результате многоугольник ОАВСД - область допустимых решений (см. рисунок 8).
Любая точка (x1, x2), лежащая в этом многоугольнике, определяет количество изделий А1 и А2, обеспечивающих необходимые суточные затраты времени в цехах В1, В2 и В3. Из множества этих точек надо выбрать такую, в которой целевая функция F достигает своего максимального значения.
Для некоторого
фиксированного значения F* линейная функция F=65·x1+80·x2
представляет собой прямую линию. Задаваясь различными значениями F*
(например, 0, 1, 2 и т.д.), получим семейство параллельных прямых – линий
уровня функции F. Увеличению значений F соответствует перемещение
указанной прямой параллельно самой себе вверх по направлению вектора ![]() =
=![]() . Из
рисунка 8 видно, что максимальное значение функции F на допустимом множестве
точек OABCD соответствует прямой, проходящей через точку В пересечения прямых
0,1·х1+0,2·х2=12 и 0,3·x1+0,3·x2=21.
Координаты точки В: х1=20, х2=50 дают оптимальное
решение исходной задачи, при этом Fmax = 65·20+80·50=5300.
. Из
рисунка 8 видно, что максимальное значение функции F на допустимом множестве
точек OABCD соответствует прямой, проходящей через точку В пересечения прямых
0,1·х1+0,2·х2=12 и 0,3·x1+0,3·x2=21.
Координаты точки В: х1=20, х2=50 дают оптимальное
решение исходной задачи, при этом Fmax = 65·20+80·50=5300.

Рисунок 8 – Графическое решение задачи 4
Таким образом, фирме в сутки необходимо изготовить 20 изделий А1 и 50 изделий А2, чтобы получить наибольшую прибыль 5300 у.е. Если бы фирма изготавливала только изделие А1, то пришлось бы изготавливать 50 штук, при этом получив наибольшую прибыль F=50·65=3250 у.е., а при изготовлении только изделия А2 – 60 штук, что дало бы F=80·60=4800 у.е. прибыли.
б) графическое решение с помощью Excel 2003.
1. Задаем название столбцов: в А1 - «х1», В1 – «прямая 1», С1 – «прямая 2», D1 - «прямая 3», Е1 – «линия уровня F=0».
2. В столбце А, начиная с ячейки А2 таблицы Excel, задаем последовательность значений переменной х1 как арифметическую прогрессию с первым членом, равным нулю, разностью 5 и предельным значением 130 и значением по столбцам через пункт меню «Правка»-«Заполнить»-«Прогрессия». Получившийся диапазон значений: А2:А28.
3. В ячейки В2, С2, D2 вводим формулы (в системе (2) вместо знаков неравенств используем знак «=» и находим значения переменной х2 в каждом из трех уравнений) В2=(12-0,1*A2)/0,2; С2=(10-0,2*A2)/0,1; D2=(21-0,3*A2)/0,3 и распространим их значения на остальные ячейки вниз до 28 строки включительно. Вводим в ячейку Е2 формулу =-65*A2/80 (которая получается из выражения для целевой функции при F=0) и распространяем значения функции также вниз до Е28 включительно. Значения в этом столбце позволяют построить линии уровня F=0.
4. Выделяем диапазон А1:Е28, задаем команду «Вставка/Диаграмма», в открывшемся окне Мастера диаграмм выбираем Тип «Точечная»; Вид «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров», нажимаем 2 раза «Далее» и получаем диаграмму.
5. Форматируем построенную диаграмму.
Устанавливаем курсор мыши на числа оси Y (ось Y), вызываем контекстное меню, в котором выбираем «Формат оси». В открывшемся диалоговом окне выбираем вкладку «Шкала», в которой в пункте «Шкала по оси Y (значений)» указываем опции:
- минимальное значение: -10;
- максимальное значение: 110;
- цена основных делений: 20;
- цена промежуточных делений: 10;
- ось Х (значений) пересекает в значении: 0.
Затем устанавливаем курсор мыши на ось Х так, чтобы ниже ее появилась надпись Ось Х (категорий) и щелкаем правой кнопкой мыши. Появляется контекстное меню, в которой выбираем «Формат оси». В открывшемся диалоговом окне выбираем вкладку «Шкала», в которой в пункте «Шкала по оси Х (категорий)» указываем опции:
- минимальное значение: 0;
- максимальное значение: 150;
- цена основных делений: 50;
- цена промежуточных делений: 10;
- ось Y (значений) пересекает в значении: 0.
Во вкладке «Вид» задаем более толстую толщину сплошной осевой линии.
В диалоговом окне «Параметры диаграммы» задаем названия диаграммы, осей, а также указываем оси, линии сетки, легенду. В результате таблица данных и график принимают вид, указанный на рисунке 9.
Точка пересечения прямых 1 и 3 является точкой выхода линий уровня из многоугольника допустимых решений (наивысшая точка пересечений) и имеет координаты (20; 50). Эта точка является точкой максимума целевой функции F. Значение функции в этой точке можно найти, задав формулу =65*20+80*50=5300.
в) составление симплекс-таблиц.
Запишем задачу в канонической форме:
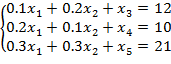 , (3)
, (3)
- 65·x1 - 80·x2 = -F → min (4)
где х3≥0, х4≥0, х5≥0 являются дополнительными переменными.
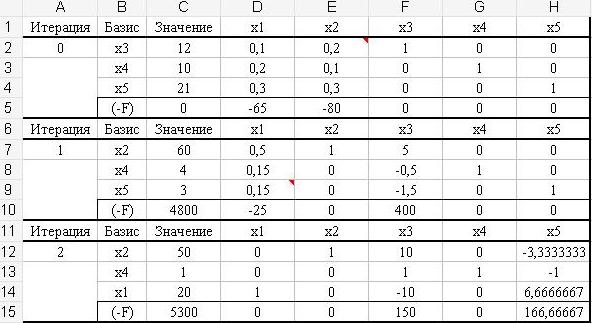
Составляем в Excel симплекс-таблицы (см. таблицу 3). Первая расположена в блоке A1:H5. Так как все коэффициенты bi в (3) положительны, а коэффициенты при дополнительных переменных х3, х4 и х5 равны +1, то возьмем некоторый набор х1=х2=0, х3=12, х4=10 и х5=21, образующий начальное базисное допустимое решение. Эти значения указаны в столбце С таблицы 3. Коэффициенты при неизвестных хi i=1, 2, 3, 4, 5 введены в ячейки блока D2:H4, а коэффициенты целевой функции (-F) - в строку 5.
Рисунок 9 – Графическое решение задачи в Excel
Т а б л и ц а 3 – Симплекс-таблицы
Поскольку функция цели (-F)
в (4) выражена через небазисные переменные х1 и х2,
а коэффициенты при х1 и х2 отрицательны, то
любое изменение неотрицательных переменных приводит к убыванию (-F). Для
простоты будем увеличивать переменную с большим по модулю коэффициентом, то
есть х2. Однако такое увеличение х2 будет
сопровождаться изменением переменных х3 и х4,
так как они связаны соотношениями (3). Значит х2 не может
увеличиваться неограниченно. Из первого равенства системы (3) х3=0
при х2=12/0,2=60, из второго х4=0 при х4=0
при х2=10/0,1=100, а из третьего х5=0 при х2=21/0,3=70.
Так как х3, х4 и х5 неотрицательны,
то мы не можем увеличивать х2 до значения более, чем до 60, то
есть ![]() .
.
Значит, положительный наибольший элемент диапазона D2:H2 находится в ячейке Е2, и столбец Е - разрешающий столбец. Наименьшее отношение положительных свободных членов ограничений (3) к положительным элементам этого столбца соответствует элементу ячейки Е2, который и будет разрешающим элементом таблицы. Он обозначен в правом верхнем углу ячейки треугольником.
Разделив первое ограничение на коэффициент 0,2 при х2, получим 0,5·х1+х2+5·х3=60. Предварительно умножив это преобразованное ограничение на соответствующие коэффициенты при х2 во 2-м, 3-м равенствах систем (3) и (4) и вычтя его из этих равенств, исключим переменную х2 отовсюду, кроме первого, куда она входит с коэффициентом 1:
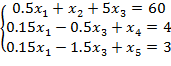 (5)
(5)
- 25·x1+ 400·x3 = -F +4800.
Коэффициенты системы (5) вычисляются в ячейках блока A6:H10, составляющей вторую симплекс-таблицу (см. рисунок 9). При этом в ячейку C7 введена следующая формула =C$2/$E$2 (напомним, Е2 – наибольший положительный элемент предыдущей таблицы). Формулу из С7 копируем в ячейки D7:H7 этой же строки.
В ячейку С8 записываем =C3-C$2/$E$2*$E3 (или =C3-C$7*$E3). Формулу копируем в ячейки блока C8:H9.
Система уравнений (5) является канонической формой исходной задачи, но уже для базиса х2, х4 и х5. Теперь эти переменные х2, х4 и х5 составляют базисное допустимое решение, а переменные х1 и х3 стали небазисными.
Отметим, что дальнейшего
уменьшения функции (-F) можно добиться только за счет увеличения х1,
поскольку коэффициент при х1 в выражении для функции цели в (5)
отрицательный. Найдем пределы изменения х1 из условия
неотрицательности х2, х4 и х5.
Из первого уравнения (5) следует, что х2=0 при х1=60/0,5=120,
из второго уравнения (5) х4=0 при х1=4/0,15=26,7,
из третьего уравнения (5) х5=0 при х1=3/0,15=20.
Следовательно, переменную х1 нельзя увеличивать более, чем до 20,
т.е. ![]() .
.
Положительный наибольший элемент D9:H9 находится в ячейке D9, столбец D – разрешающий. Наименьшее отношение положительных свободных членов ограничений (5) к положительным элементам этого столбца соответствует элементу D9, который и будет разрешающим элементом таблицы, обозначен в правом углу треугольником.
Третье ограничение (5) делим на коэффициент х1, равный 0.15 и умножив полученное на соответствующие коэффициенты при х1, исключим переменную х1 из первого, второго ограничений и выражения для целевой функции (-F): получим каноническую форму исходной задачи, но в базисе х2, х4 и х1.
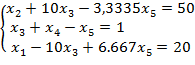 (6)
(6)
150·x3+ 166.667·x5 = -F +5300.
Коэффициенты системы (6) вычисляются в ячейках блока A11:H15, составляющей третью симплекс-таблицу. Начинаем с третьей строчки так как наибольший положительный элемент был именно в этой строке. При этом в ячейку C14 вводим формулу =C$9/$D$9, далее которую копируем в ячейки D14:H14. В ячейку С12 записываем =C7-C$9/$D$9*$D7, далее ее копируем в остальные ячейки блока C12:H13. В ячейку C15 введена формула =C10-C$9/$D$9*$D10 и скопирована в ячейки D15:H15 этой же строки. Переменные х2, х4 и х1 для этой формы составляют базисное допустимое решение. Отметим, что теперь увеличение любой из небазисных переменных х3 и х5 в выражении для целевой функции (6) приводит к увеличению (-F), поскольку коэффициенты при этих переменных положительны. Следовательно, дальнейшее убывание (-F) невозможно, и минимум функции (-F), равный 5300, найден. Он достигается при базисном допустимом решении х1=20, х2=50, х3=0, х4=1, х5=0.
Процесс этих вычислений можно интерпретировать геометрически. Последовательность канонических форм исходной задачи соответствует постепенному переходу из точки O в точку В - точку минимума функции (-F) (4), через вершины O–A–B многоугольника допустимых решений (см. рисунок 9).
Если же в уравнениях (3), (4) в качестве базисной выбрать х1, то переход в точку минимума совершился бы по цепочке вершин O–D–C–B, по более длинному пути. Описание получения канонических форм представляет собой итерационный процесс. Номера итераций указаны в столбце А таблицы 3.
г) решение задачи с помощью встроенных функций Excel 2003.
Для решения оптимизационных задач в табличном процессоре Excel 2003 используется пункт «Поиск решения» в меню «Сервис» на панели инструментов. Если этого пункта нет, то необходимо установить соответствующую надстройку. Для этого в меню «Сервис» нужно выбрать пункт «Надстройки» и в диалоговом окне установить флажок слева от надписи «Поиск решения». В меню «Сервис» появится пункт «Поиск решения». В соответствии с данными таблицы 2 составим в Excel таблицу 4.
Т а б л и ц а 4 – Таблица данных
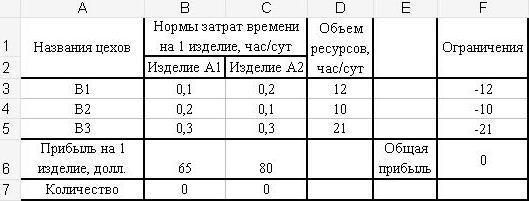
Числа в ячейках столбца «Ограничения» подсчитаны с помощью формул. Формула =СУММПРОИЗВ(В3:С3;$B$7:$C$7)-D3 введена в ячейку F3 и продолжена в ячейках F4:F5 таблицы. Эта формула также скопирована в F6, но без вычитаемого D6. Выделим ячейку F6 с целевой функцией и вызовем «Сервис»-«Поиск решения». В диалоговом окне указываем «Установить целевую ячейку:» $F$6, «Равной:» максимальному значению, «Изменяя ячейки:» $B$7:$C$7, «Ограничения: (Добавить)» $F$3:$F$5<=0. Так как все ограничения имеют одинаковые знаки «<=», то здесь они введены блоком (в «Ограничениях их необходимо вписать тремя отдельными строками»). Количества xj, j=1, 2 изделий являются целыми числами, поэтому необходимо наложить еще ограничение: $B$7:$C$7=целое (целочисленная оптимизация). В «Параметры» установим флажки «Линейная модель» и «Неотрицательные значения», запустим «Выполнить». Поиск решения даст результат: х1=20; х2=50. Целевая функция равна Fmax=5300. Этот результат поиска максимума F совпадает с результатами, полученными в пунктах (а-в) с помощью построения графиков и составления симплекс-таблиц в Excel.
Задача 5. Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающихся составом и стоимостью. Данные о сплавах приведены в таблице 5. Полученный сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12,8 кг. Определить количества xj, j=1, 2 сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье.
Т а б л и ц а 5 – Исходные данные задачи 5
|
Компоненты сплава |
Содержание компонентов, % |
|
|
сплав № 1 |
сплав № 2 |
|
|
|
|
|
|
Медь |
10 |
10 |
|
Олово |
10 |
30 |
|
Цинк |
80 |
60 |
|
Стоимость 1 кг, у.е. |
5 |
4 |
Эта задача математически формулируется следующим образом: требуется найти минимум функции F=5·x1+4·x2, (7)
при ограничениях 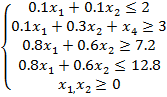 . (8)
. (8)
Неравенства описывают ограничения, накладываемые на количество того или иного металла в полученном сплаве.
а) графический метод построения.
На рисунке 10 линии – это неравенства (8), обозначены цифрами 1, 2, 3, 4.
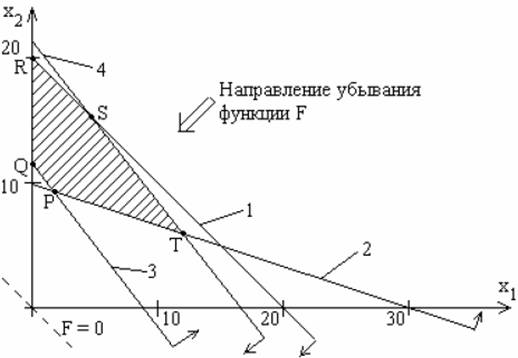
Рисунок 10 – Графическое решение задачи 5
Допустимой областью
является пятиугольник PQRST. Целевая функция F (7) убывает в направлении
вектора -![]() =
=![]() Минимальное значение этой функции достигается в точке Р с
координатами х1=2, х2=9,333 и равно 47,333.
Точка Р, являющаяся оптимальным решением
задачи (7),
(8), есть вершина допустимой области PQRST.
Минимальное значение этой функции достигается в точке Р с
координатами х1=2, х2=9,333 и равно 47,333.
Точка Р, являющаяся оптимальным решением
задачи (7),
(8), есть вершина допустимой области PQRST.
б) графическое решение с помощью Microsoft Excel.
Проводится аналогично как при решении задачи 4.
в) составление симплекс-таблиц.
Проводится аналогично как при решении задачи 4.
г) решение задачи с помощью встроенных функций Excel.
В соответствии с данными задачи 5 составим в Excel таблицу 6.
Т а б л и ц а 6 – Исходные данные задачи 5 в Excel
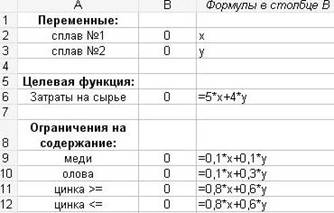
В таблице 6 ячейкам В2 и В3 присвоены имена х и у соответственно с помощью команд «Вставка»-«Имя … Присвоить». В ячейки В2 и В3 занесены нулевые значения. В ячейки В6,В9-В12 введены формулы, указанные в таблице 6 справа от соответствующих ячеек.
Выделим ячейку B6 с формулой для целевой функции и вызовем «Сервис»-«Поиск решения». В диалоговом окне укажем: «Установить целевую ячейку:» $B$6, «Равной:» минимальному значению, «Изменяя ячейки:» $B$2:$B$3, «Ограничения:» $B$9<= 2; $B$10 >=3; $B$11 >=7,2; $B$12 <=12,8 (см. рисунок 11). В окне «Параметры» установим флажки «Линейная модель» и «Неотрицательные значения». Запустим «Выполнить». Поиск решения вернет результат: х=2; y=9,333333333. Целевая функция равна Fmin=47,33333333. Этот результат поиска минимума функции F совпадает с результатом, полученным с помощью графиков (см. рисунок 10). Точка с найденными координатами (2; 9.333333333) находится на пересечении прямых 2 и 3, соответствующих второму и третьему ограничениям (8).
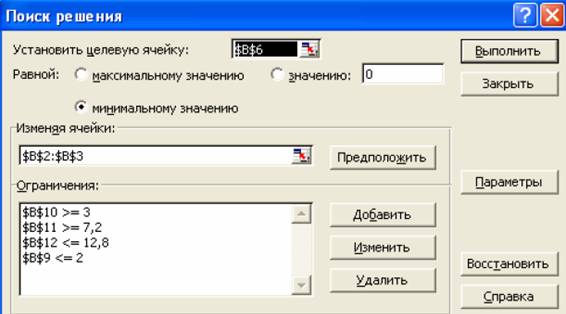
Рисунок 11 – Установка условий при подборе параметра поиска решения
2.2; Задания
Решить нижеприведенные задания по вариантам:
а) графическим методом;
б) графически с помощью Microsoft Excel;
в) составлением симплекс-таблиц;
г) с помощью встроенных функций Excel.
Полученные результаты сравнить.
Задание 1. Оптимальный план суточного выпуска строительных изделий.
Процесс изготовления строительных изделий двух видов состоит в последовательной обработке каждого из них в трех цехах. Пусть aij - время обработки каждого изделия вида j в цехе i, чаc/cут; i=1,2,3; j=1,2;
bi - время работы цеха i, час/сут;
cj - прибыль от реализации одного изделия вида j, у.е.;
xj – количество изделий вида j, шт.
Составить такой план суточного выпуска изделий, чтобы прибыль от их производства была максимальной. Исходные данные по вариантам взять в таблице 7.
Т а б л и ц а 7 – Исходные данные для задания 1 по вариантам
|
вариант |
a11 |
a12 |
a21 |
a22 |
a31 |
a32 |
b1 |
b2 |
b3 |
c1 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,1 |
1,0 |
0,6 |
0,1 |
0,5 |
0,4 |
12 |
10 |
21 |
65 |
80 |
|
2 |
0,2 |
0,9 |
0,5 |
0,6 |
0,6 |
0,5 |
13 |
11 |
20 |
70 |
85 |
|
3 |
0,3 |
0,8 |
0,7 |
0,2 |
0,7 |
0,6 |
14 |
12 |
19 |
75 |
90 |
|
4 |
0,4 |
0,7 |
0,4 |
0,7 |
0,8 |
0,7 |
15 |
13 |
18 |
80 |
95 |
|
5 |
0,5 |
0,6 |
0,8 |
0,3 |
0,9 |
0,8 |
16 |
14 |
17 |
85 |
100 |
|
6 |
0,6 |
0,5 |
0,3 |
0,8 |
1,0 |
0,9 |
17 |
15 |
16 |
90 |
75 |
|
7 |
0,7 |
0,4 |
0,9 |
0,4 |
0,1 |
1,0 |
18 |
16 |
15 |
60 |
70 |
|
8 |
0,8 |
0,3 |
0,2 |
0,9 |
0,2 |
0,3 |
19 |
17 |
14 |
55 |
65 |
|
9 |
0,9 |
0,2 |
1,0 |
0,5 |
0,3 |
0,2 |
20 |
18 |
13 |
50 |
60 |
|
10 |
1,0 |
0,1 |
0,1 |
1,0 |
0,4 |
0,1 |
21 |
19 |
12 |
45 |
55 |
Задание 2. Задача об оптимальном составе смеси.
Для приготовления b0
кг смеси с заданными свойствами используются вещества Аj,
j=1,2,3. В xj кг вещества Аj содержится
aijxj кг химического элемента Bi,
i=1,2. Содержание элемента Bi в смеси должно заключаться
в пределах от ![]()
![]() кг. Стоимость 1кг вещества Aj составляет cj
у.е.
кг. Стоимость 1кг вещества Aj составляет cj
у.е.
Требуется определить такой состав для приготовления смеси, при котором общая стоимость израсходованных веществ была бы минимальной. Исходные данные по вариантам взять в таблице 8.
Т а б л и ц а 8 – Исходные данные для задания 2 по вариантам
|
вар. |
a11 |
a12 |
a13 |
a21 |
a22 |
a23 |
|
|
|
|
b0 |
c1 |
c2 |
c3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,1 |
1,0 |
0,6 |
0,1 |
0,5 |
0,4 |
3,2 |
5,0 |
7,0 |
5,2 |
15 |
5 |
14 |
5 |
|
2 |
0,2 |
0,9 |
0,5 |
0,6 |
0,6 |
0,5 |
3,4 |
4,8 |
6,8 |
5,4 |
20 |
6 |
13 |
14 |
|
3 |
0,3 |
0,8 |
0,7 |
0,2 |
0,7 |
0,6 |
3,6 |
4,6 |
6,6 |
5,6 |
25 |
7 |
12 |
6 |
|
4 |
0,4 |
0,7 |
0,4 |
0,7 |
0,8 |
0,7 |
3,8 |
4,4 |
6,4 |
5,8 |
30 |
8 |
11 |
13 |
|
5 |
0,5 |
0,6 |
0,8 |
0,3 |
0,9 |
0,8 |
4,0 |
4,2 |
6,2 |
6,1 |
35 |
9 |
10 |
7 |
|
6 |
0,6 |
0,5 |
0,3 |
0,8 |
1,0 |
0,9 |
4,2 |
4,0 |
6,0 |
6,2 |
40 |
10 |
9 |
12 |
|
7 |
0,7 |
0,4 |
0,9 |
0,4 |
0,1 |
1,0 |
4,4 |
3,8 |
5,8 |
6,4 |
45 |
11 |
8 |
8 |
|
8 |
0,8 |
0,3 |
0,2 |
0,9 |
0,2 |
0,3 |
4,6 |
3,6 |
5,6 |
6,6 |
50 |
12 |
7 |
11 |
|
9 |
0,9 |
0,2 |
1,0 |
0,5 |
0,3 |
0,2 |
4,8 |
3,4 |
5,4 |
6,8 |
55 |
13 |
6 |
9 |
|
10 |
1,0 |
0,1 |
0,1 |
1,0 |
0,4 |
0,1 |
5,0 |
3,2 |
5,2 |
7,0 |
60 |
14 |
5 |
10 |
1. В чем состоит суть симплекс-метода, опишите алгоритм построения симплекс-таблиц.
2. Какие задачи можно отнести к задачам, решаемым с помощью симплекс-метода?
3. Что означает «базисное допустимое решение», «базисные переменные»?
4.
Что
такое «целевая функция» и по какому принципу осуществляется выбор разрешающего
элемента в симплекс-таблицах?
3 Лабораторная работа №3. Метод потенциалов для решения транспортной задачи
Цели работы: изучение постановки классической транспортной задачи; реализация решения на компьютере.
3.1 Методические указания к выполнению работы
Транспортная задача – это задача об оптимальном плане перевозок продуктов из пунктов отправления в пункты потребления. Разработка оптимальных схем потоков позволяет снизить затраты на перевозки. Когда суммарный объем предложений не равен общему объему спроса задача называется несбалансированной. Выделяют два критерия: стоимости (минимум затрат на перевозку) или расстояний; времени (минимум времени).
Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей ее можно решить проще (для задач малой размерности). Разработано много алгоритмов решения транспортной задачи: распределительный метод, метод потенциалов, дельта-метод, венгерский метод, метод дифференциальных рент, различные сетевые методы и т. д.
Задача заключается в отыскании плана перевозок продукции с m складов к n, который потребовал бы минимальных затрат. Если потребитель j получает единицу продукции (по прямой дороге) со склада i, то возникают издержки рij. Предполагается, что транспортные расходы пропорциональны перевозимому количеству продукции, т.е. перевозка k единиц продукции вызывает расходы k▪рij. Далее предполагается, что

где
bi - количество продукции на складе i;
aj – потребность потребителя j;
xij -количество продукции со склада i потребителю j.
Надо решить задачу:
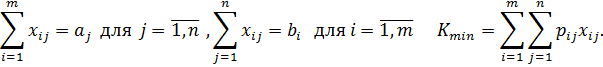
![]()
Найти план перевозок, чтобы затраты по перевозкам были минимальными.
Задача 6. Дана транспортная задача с тремя поставщиками и пятью потребителями. Переписав данные в виде таблицы, получим (см. таблицу 9):
Т а б л и ц а 9 – Исходные данные задачи 6

Решение с помощью Microsoft Excel 2003.
В ячейки заносится матрица цен и ограничения по столбцам и строкам, F11 "=СУММПРОИЗВ(B7:F9;B2:F4)", вычисляющая произведение элементов массивов и суммирующая затем получившиеся значения (см. рисунок 12).
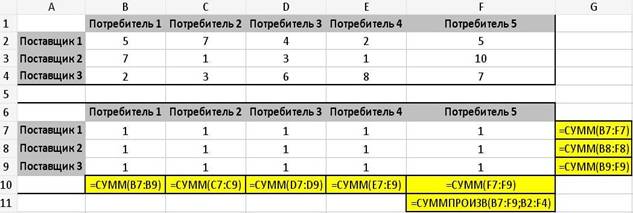
Рисунок 12 – Значения и функции в ячейках таблицы
Выделив (B7:F7), вызываем «Формат ячеек» и в вкладке "Число" выставляем число десятичных знаков равным нулю; ставим курсор на F11 и вызываем «Сервис»-«Поиск решений» с параметрами: «Установить целевую ячейку» $F$11, «Равной:» min значению, «Изменяя ячейки:» $B$7:$F$9, «Ограничения:» добавить $B$7:$F$9>= 0, $B$10=100, $C$10=130, $D$10=80, $E$10=190, $F$10=100, $G$7=200, $G$8=175, $G$9= 225. Нажимаем "Выполнить" (см. рисунок 13). Из F11 видим, что минимальные затраты составляют: 1610 ед. А в ячейках (B7:F9) был получен план грузоперевозок.
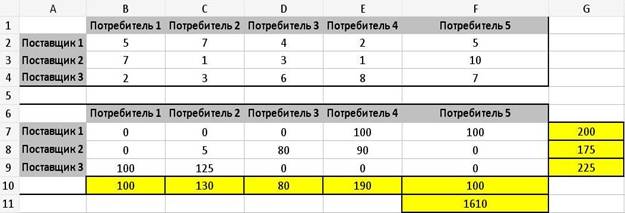
Рисунок 13 – Конечный результат решения задачи
3.2 Задания
Решить транспортную задачу по вариантам из таблицы 10.
Т а б л и ц а 10 – Исходные данные заданий по вариантам

3.3 Контрольные вопросы
1. По каким критериям можно оптимизировать решение?
2. Опишите алгоритм решения методом потенциалов.
3. Какие методы еще есть дл
решения транспортной задачи? В чем их специфика?
4 Лабораторная работа №4. Метод Гомори для решения задач целочисленного программирования
Цели работы: изучение класса задач целочисленного программирования; ознакомление с особенностями задач и приемов их решения; приобретение способности реализовать решение на ПК.
4.1 Методические указания к выполнению работы
Часть задач может иметь решения только в целых числах, например, число турбин, судов, животных может быть только целым числом. Такие задачи решаются методами целочисленного программирования. Общая постановка задач линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.
Методы целочисленной оптимизации делятся на три основные группы: а) методы отсечения; б) комбинаторные методы; в) приближённые методы.
Методы отсечения используют оптимальные решения, найденные для задач линейного программирования. Сужая область допустимых планов до целочисленных границ, т. е. отсекая нецелочисленные допустимые планы, методами отсечения получают решения задач целочисленного программирования.
Комбинаторные методы достигают решений задач целочисленного программирования, рассматривая возможные варианты целочисленных ограничений для задачи оптимизации.
Приближённые методы опираются на приближённые методы нахождения экстремумов функций нескольких переменных и используют различные способы округления полученных нецелочисленных решений до целых значений. Особенно удобно применять приближённые методы в случае решения задачи целочисленного программирования относительно двух переменных.
Метод Гомори относится к методам отсечения.
Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план) Х=(х1, х2,…, хn), при котором линейная функция
![]() (10)
(10)
принимает максимальное значение при ограничениях:
![]() (11)
(11)
![]() (12)
(12)
Сначала находится оптимальное решение задачи симплекс-методом. Если полученное решение целочисленное, то цель достигнута. Если же оптимальное решение не является целочисленным, то в условия задачи вводится дополнительное ограничение, которое отсекает от области допустимых решений полученное нецелочисленное решение и не отсекает от нее ни одной точки с целочисленными координатами. Далее симплекс-методом решается расширенная задача: находится ее опорное и оптимальное решение. Если новое решение не будет целочисленным, то вводится еще одно дополнительное ограничение. Процесс построения дополнительных ограничений и решения задачи симплекс-методом продолжается до тех пор, пока не будет найдено оптимальное целочисленное решение или не будет установлено, что его не существует.
Таким образом, необходимо найти сначала опорное решение расширенной задачи, а потом оптимальное. Признаком отсутствия целочисленного решения задачи линейной оптимизации является то, что в строке с дробным свободным членом все остальные элементы целые. В дополнительном ограничении, построенном по этой строке, дробное число будет только в столбце свободных членов, а остальные дробные части будут равны нулю.
Алгоритм.
1. Симплексным методом решается задача (10)-(12) без учета условия целочисленности переменных. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования.
2. Если среди компонент оптимального решения есть нецелые, то выбирают компоненту с наибольшей целой частью и по соответствующему уравнению системы ограничений формируется правильное отсечение и любое допустимое решение целочисленной задачи должно удовлетворять неравенству:
![]() (13)
(13)
3. Неравенство (13) введением дополнительной неотрицательной целочисленной переменной преобразовывают в равносильное уравнение
![]() (14)
(14)
и включают его в систему ограничений (11).
4. Полученную расширенную задачу надо решить симплексным методом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (10)-(13) решена. В противном случае возвратиться к пункту 2.
Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден.
Решение задачи целочисленного программирования в Excel 2003.
Задачи целочисленного программирования решаются так же, как и общие задачи линейного программирования, только лишь при решении задач целочисленного программирования необходимо добавить указание на то, то разыскиваемые оптимальные значения переменных могут принимать только целые значения. В окне «Добавление ограничения» («Изменение ограничения») надо выбрать в списке, расположенном посередине, значение "цел" (см. рисунок 14).
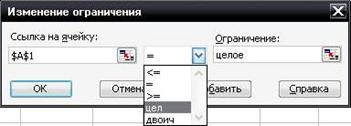
Рисунок 14 – Выбор функции для указания целых значений аргумента
Задача 7. Методом Гомори найти
решение задачи целочисленного программирования, состоящей в определении
максимального значения функции![]() при условии
при условии

x1, x2 ≥0, x1, x2 – целые.
а) решение задачи с помощью таблиц.
Выравнивая неравенства с помощью вспомогательных переменных x3, x4 получаем задачу линейного программирования в каноническом виде:
![]()

x1, x2 ≥0, x1, x2 – целые.
Решаем задачу линейного программирования симплексным методом, используя поэтапный переход от одного базиса к другому. Ход решения задачи и полученное оптимальное решение в смысле задачи линейного программирования представлены в таблице 11.
Т а б л и ц а 11 – Ход решения задачи
|
Базис xбаз |
Свободные члены уравнений |
Неизвестные в задаче программирования |
Оценка элемента строки δ1 |
|||
|
x1 |
x2 |
x3 |
x4 |
|||
|
|
|
|
|
|
|
|
|
x3 |
|
3 |
|
1 |
0 |
|
|
x4 |
10 |
2 |
5 |
0 |
1 |
2 |
|
Δj |
F=0 |
-5 |
-11 |
0 |
0 |
- |
|
x2 |
21/16 |
3/4 |
1 |
1/4 |
0 |
|
|
x4 |
|
|
0 |
|
1 |
|
|
Δj |
|
|
0 |
|
0 |
|
В найденном оптимальном
плане значение х2 равно дробному числу, найдем дробную
часть и дробные части всех элементов строки, содержащей переменную х2,
а именно: ![]()
Для найденных значений
дробных частей неравенство Гомори: ![]() . Выравниваем
неравенство Гомори с помощью новой вспомогательной переменной х5,
переносим свободный член уравнения в правую часть и получаем новое ограничение:
. Выравниваем
неравенство Гомори с помощью новой вспомогательной переменной х5,
переносим свободный член уравнения в правую часть и получаем новое ограничение:
![]() Добавляем в таблицу строку, содержащую новое ограничение и
столбец, с новой переменной и продолжаем решать задачу двойственным симплексным
методом, так как теперь в таблице записан псевдоплан (см. таблицу 12).
Добавляем в таблицу строку, содержащую новое ограничение и
столбец, с новой переменной и продолжаем решать задачу двойственным симплексным
методом, так как теперь в таблице записан псевдоплан (см. таблицу 12).
Т а б л и ц а 12 – Ход решения задачи
Базис xбаз |
Свободные члены уравнений |
Неизвестные в задаче программирования |
Оценка элемента строки δ1 |
||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
|||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
1 |
|
0 |
0 |
|
|
x4 |
|
|
0 |
|
1 |
0 |
|
|
x5 |
|
|
0 |
|
0 |
0 |
← |
|
Δj |
|
|
0 |
|
0 |
1 |
|
|
x2 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
x4 |
25/6 |
0 |
0 |
-2/3 |
1 |
-7/3 |
|
|
x1 |
5/12 |
1 |
0 |
1/3 |
0 |
-4/3 |
|
|
Δj |
|
0 |
0 |
|
0 |
|
|
Полученное оптимальное решение расширенной задачи содержит нецелое значение переменной х1, поэтому находим для этой строки дробные части всех нецелых чисел, а именно:
![]()
и новое неравенство Гомори имеет вид:
![]()
Добавляем его к решаемой задаче, выравниваем с помощью вспомогательной переменной х6 и решаем расширенную задачу (см. таблицу 13).
Т а б л и ц а 13 – Расширенная таблица
Базис xбаз |
Свободные члены уравнений |
Неизвестные в задаче программирования |
|||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
||
|
|
|
|
|
|
|
|
|
|
x2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
x4 |
|
0 |
0 |
|
1 |
|
0 |
|
x1 |
|
1 |
0 |
|
0 |
|
0 |
|
x6 |
|
0 |
0 |
|
0 |
|
|
|
Δj |
|
0 |
0 |
|
0 |
|
0 |
|
x2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
x4 |
5 |
0 |
0 |
0 |
1 |
-1 |
-2 |
|
x1 |
0 |
1 |
0 |
0 |
0 |
-2 |
1 |
|
x3 |
5/4 |
0 |
0 |
1 |
0 |
2 |
-3 |
|
Δj |
11 |
0 |
0 |
0 |
0 |
1 |
5 |
Оптимальное решение задачи целочисленного программирования Fmax=11 при х = (0; 1).
б) решение задачи с помощью встроенных функций Excel.
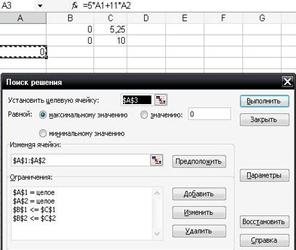
Заносим значения функции, как показано в таблице 14. Для решения используем «Поиск решения» меню «Сервис», «Установить целевую ячейку:» указываем $А$4; «Равной:» максимальному значению; «Изменяя ячейки:» - диапазон изменения $A$1:$A$2. Для приведения в рабочее состояние математической программы поиска оптимального решения заданной задачи необходимо установить ограничения, учитываемые при её решении: нажимаем на кнопку «Добавить», расположенную справа от поля «Ограничения» - появляется окно ограничений. Для добавления первого ограничения (3x1+4x2 ≤21/4) в поле «Ссылка на ячейку» указываем В1, а в списке, расположенном посередине, выбираем знак "<=" и в поле «Ограничение» указываем ячейку С1. После этого нажимаем на кнопку «Добавить». Аналогично добавляем оставшееся ограничения задачи 2x1+5x2 ≤10. Помня о том, что x1, x2 – целые числа, добавляем еще 2 условия (см. рисунок 14): «Ссылка на ячейку:» $A$1 = целое; $A$2 = целое. Добавив условие, закрываем окно, нажав на кнопку «Отмена». Окно «Поиск решения» примет вид, показанный на рисунке 15а.
Т а б л и ц а 14 – Формулы для расчета данных в Excel

а) б)
Рисунок 15 – Вид окна «Поиска решения»
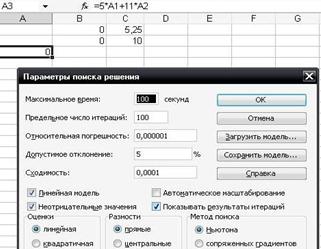
При нажатии на кнопку «Параметры» появится окно «Параметры поиска решения», если есть необходимость в знании промежуточных результатов при поиске оптимального решения, нужно отметить пункт «Показывать результаты итераций» в открывшемся окне (см. рисунок 15б).
В Excel в качестве методов поиска решения задачи предлагаются метод Ньютона и метод сопряженных градиентов. Для решения задач линейного программирования обычно используется метод Ньютона. Предельное число итераций, относительная погрешность и допустимое отклонение выбираются соответствующими той задаче, оптимальное решение которой находится. Максимальное время назначается по опыту решения аналогичных задач на используемом компьютере. Показанные установки в окне «Параметры поиска решения» (см. рисунок 15б), как правило, оказываются достаточными для получения оптимального решения задач линейного и целочисленного программирования. В этом окне отмечаем галочкой пункты «Линейная модель» и «Неотрицательные значения» (по условию нашей задачи x1 и x2 – положительные числа). Нажимаем на кнопку «ОК», после чего вновь появляется окно «Поиск решения», и уже в этом окне нажимаем на кнопку «Выполнить». Параметры в окне должны выбираться реальные, соответствующие заданным числовым характеристикам конкретной задачи. Увлечение большим числом итераций и малыми значениями относительной погрешности в производственных задачах может привести к необоснованному увеличению времени поиска решения. На экран выводится окно «Результаты поиска решения» (см. рисунок 16).
Нажатием на кнопку «ОК» закрываем окно. После этого в ячейках, отведённых для записи решения задачи, появляются числа (см. рисунок 17).
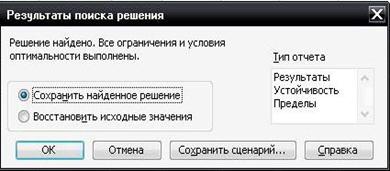
Рисунок 16 – Вид окна параметров «Поиска решения»
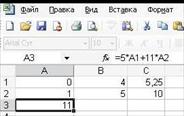
Рисунок 17 – Решение задачи 7
В ячейке А3 находим значение целевой функции F(х), соответствующее найденному решению. В ячейках А1 и А2 указаны соответствующие значения переменных x1, x2. Для задачи 7 оптимальное решение имеет следующий вид: F=11, x1=0, x2=1, что совпадает с решением, полученным в предыдущем пункте решения (а).
4.2 Задания
Методом Гомори найти решение задачи целочисленного программирования, состоящей в определении максимального значения функции. Целевая функция и неравенства заданы в таблице 15. В задачах x1, x2 ≥0. Найти оптимальный план максимального значения функции.
Т а б л и ц а 15 – формулы для расчета данных в Excel
|
Вариант |
F(x) |
Ограничения |
||
|
1 |
2 |
3 |
||
|
|
|
|
|
|
|
1 |
x1 + x2 |
3x1 + 3x2 ≤ 15 |
3x1 + x2 ≤ 12 |
x1 - x2 ≥ 1 |
|
2 |
2x1 + x2 |
4x1 + 5x2 ≤ 20 |
3x1 - 3x2 ≤ 13 |
x1 + 2x2 ≥ 2 |
|
3 |
4x1 - x2 |
4x1 - x2 ≥ 9 |
4x1 + 3x2 ≤ 26 |
x1 + 7x2 ≤ 7 |
|
4 |
x1 + x2 |
4x1 + 3x2 ≤ 25 |
4x1 + x2 ≤ 16 |
x1 + x2 ≥ 2 |
|
5 |
6x1 - x2 |
3x1 + x2 ≤ 9 |
6x1 - x2 ≤ 13 |
2x1 + 3x2 ≤ 18 |
|
6 |
8x1 - x2 |
x1 + 7x2 ≤ 7 |
4x1 - x2 ≤ 10 |
10x1 + 5x2 ≥ 10 |
|
7 |
6x1 - x2 |
3x1 - 7x2 ≤ 14 |
3x1 + 7x2 ≤ 21 |
x1 + 2x2 ≥ 3 |
|
8 |
10x1 - x2 |
5x1 - 5x2 ≥ 25 |
4x1 + 8x2 ≤ 36 |
4x1 + 3x2 ≤ 26 |
|
9 |
6x1 + 2x2 |
9x1 - 9x2 ≥ 18 |
2x1 + 4x2 ≤ 18 |
4x1 - x2 ≥ 9 |
|
10 |
9x1 - x2 |
4x1 - x2 ≥ 4 |
2x1 - 3x2 ≤ 12 |
x1 + x2 ≤ 8 |
4.3 Контрольные вопросы
1. Какие есть методы решения задач целочисленного программирования?
2. В чем суть метода Гомори?
3. Какие решения при применении метода Гомори могут быть потеряны?
Список литературы
1. Куралбаев З.К. Модели и методы управления. Учебное пособие. – АУЭС, Алматы, 2011. – 125 с.
2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. – 319 с.
3. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели. – СПб.: Лань, 2000.
Содержание
|
Введение |
3 |
|
1 Лабораторная работа №1. Решение систем линейных алгебраических уравнений методом Жордана-Гаусса |
4 |
|
2 Лабораторная работа №2. Симплекс-метод |
11 |
|
3 Лабораторная работа №3. Метод потенциалов для решения транспортной задачи |
23 |
|
4 Лабораторная работа №4. Метод Гомори для решения задач целочисленного программирования |
26 |
|
Список литературы |
34 |
Сводный план 2012г., поз. 230