Некоммерческое акционерное общество

Алматинский институт энергетики и связи 

Кафедра автоматической электросвязи 

 

 

Часть 2

Сети связи 

Методические указания к выполнению лабораторных работ

для студентов всех форм обучения специальности 

050719 − Радиотехника, электроника и телекоммуникации

  

 

Алматы 2009

Составила: Г.П. Данилина. Теория телетрафика и сети связи. Часть 2. Сети связи. Методические указания к лабораторным работам для студентов всех форм обучения специальности 050719 − Радиотехника, электроника и телекоммуникации. − Алматы: АИЭС, 2009. −      с. 

Методические указания к лабораторным работам содержат теоретическое обоснование и алгоритмы решения задач построения и эксплуатации сетей связи.  

Введение

 

В настоящее время при проектировании и управлении сетями телекоммуникации решаются два типа задач – задачи анализа и синтеза. К первому типу относятся задачи, в которых известна структура сети и требуется определить ее экономические или технологические характеристики, например, стоимость сети, пропускную способность, нагрузку.

В задачах синтеза считаются известными потоки, необходимо определить структуру сети, местоположение узлов, величину пучков каналов.

К задачам оптимизации относятся такие, в которых определяются параметры, обеспечивающие экстремальное качество сети (минимум стоимости, максимум производительности, наилучшее качество обслуживания и др.) при заданных потоках и объеме оборудования.

В общем случае комплексное решение задачи очень сложно, она решается поэтапно, с введением ряда упрощений.

1 Лабораторная работа № 1 Решение задач районирования

 

Для некоторого относительно обособленного района и заданного на нем распределения абонентов и местоположения АТС определить привязку абонентов к АТС таким образом, чтобы критерий оптимальности достигал минимального значения при некоторых технологических ограничениях.

 

1.1 Цель работы

 

Изучать методы решения задачи районирования, т.е. привязки абонентов к АТС таким образом, чтобы затраты на построение сети (или длина сети) были минимальными при выполнении технологических ограничений.

 

1.2 Подготовка к выполнению работы

 

Изучить [2,3,5] и настоящее методическое указание. Примем расстояния прокладки кабеля по ортогональным трассам от абонентов до АТС. Район разбивается на элементарные квадраты со стороной , каждому участку (i,j) ставится в соответствие некоторое число аij, равное количеству телефонных аппаратов, иными словами, район интерпретируется двумерной таблицей, в каждой клетке которой размещается число аij - число телефонных аппаратов.

 

1.3 Теоретическая часть

 

Расстояние между клеткой (i,j) и клеткой (k,l) определится по формуле (1.1):

,                                                                                     (1.1)

где  – размер дискреты.

 

 

1

2

3

…

m

1

a11

a12

 

 

a1m

2

 

 

 

 

 

.

.

.

0

 

 

 

 

n

an1

an2

 

 

anm

 

Известными считаются число АТС, их координаты и емкости.
Задача состоит в определении привязки абонентов к АТС таким образом, чтобы длина ортогональных линий  была минимальной, а количество присоединенных абонентов к каждой АТС не превышало ее емкости.

1.3.1 Алгоритм решения

Шаг 1. Определяются расстояния  от каждой клетки (i,j) до АТС1 и расстояния до АТС2 .

Шаг 2. Строятся две матрицы  и  следующим образом:

если , то , ;

если , то , .

Алгоритм построения матриц закончен, если i=n, j=m.

Шаг 3. Определить сумму ТА в каждой из матриц  и  и сравнить с мощностью станций. Если 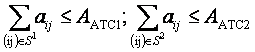, то решение задачи закончено – определена привязка абонентов к АТС с кратчайшими длинами путей и выполнены ограничения по емкости станций. В противном случае – Шаг 4.

Шаг 4. Поскольку емкости станций выбирались предварительно, то перегрузка одной означает недогрузку другой. Поэтому в Шаге 4 выбираются граничные клетки (чаще это клетки ) и производится перекрепление их к другой АТС.

 

1.3.2 Рассмотрим небольшой пример

Задана матрица нагрузок, координаты АТС и их мощность А1 и А2, размер дискрет .

 

     i

j

1

2

3

4

5

6

7

1

2

6

5

4

1

4

2

2

3

2

6

4

11

3

4

3

6

10

7

11

3

2

0

4

0

3

6

4

8

11

4

 

АТС1=(3.2)           А1=65         =10

АТС2=(2.6)           А1=66

 

Шаг 1. Подсчитать расстояния от каждой дискреты до АТС1 и АТС2 по формуле (1.1), сформировать матрицы  и

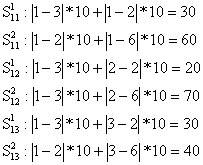
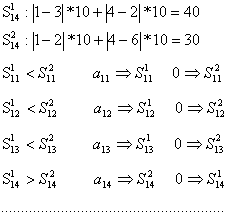
Аналогично получим все элементы матриц  и . Это означает, что произведено районирование матрицы А.

 

i

j

1

2

3

4

5

6

7

1

2

6

5

0

0

0

0

2

3

2

6

0

0

0

0

3

6

10

7

11

0

0

0

4

0

3

6

4

0

0

0

 

 

 

 

 

 

 

i

j

1

2

3

4

5

6

7

1

0

0

0

3

1

4

2

2

0

0

0

4

11

3

4

3

0

0

0

0

3

2

0

4

0

0

0

0

8

11

4

 

 

 

  

 

1.4 Содержание работы

 

Изучить указанную литературу, рассмотреть в [3] случаи трех АТС (может быть и больше). Разработать блок-схему и программу решения задачи. Найти общую сумму абонентов, разделить на 2, определив допустимую емкость станции. Вариант матрицы определяется по последней цифре зачетной книжки.

 

1.5 Контрольные вопросы

 

1.5.1 По какому критерию решается задача районирования?

1.5.2 Как определяется расстояние между двумя точками плоскости?

 

1.6 Указания к составлению отчета

 

1.6.1 Постановка задачи.

1.6.2 Исходная информация.

1.6.3 Блок-схема программа.

1.6.4 Листинг программы.

1.6.5 Распечатка таблиц районирования.

 

1.7 Исходная информация

 

0)

 

6

9

12

15

17

21

25

8

7

10

11

23

0

0

4

0

5

15

0

11

7

6

0

3

4

0

17

12

8

3

2

8

10

12

11

13

15

15

13

0

3

4

 

 

А:

  

 

1)

 

2

7

8

2

6

5

4

3

7

8

4

3

6

0

5

7

11

4

2

9

8

1

3

5

0

0

17

0

0

4

5

8

7

1

10

6

9

10

11

3

6

0

0

4

15

11

7

1

3

5

7

0

0

4

2

1

3

7

11

10

 

 

          А:

  

 

2)

 

15

12

17

2

11

8

21

25

23

14

15

17

15

14

12

4

9

7

11

21

31

4

13

11

4

1

2

3

5

7

3

2

1

4

2

8

19

22

17

15

4

6

 

 

          А:

 

 

 

3)

  

2

6

9

12

8

3

7

11

3

8

3

7

4

5

4

2

10

0

0

0

4

8

3

7

15

11

8

10

4

3

7

4

4

2

3

6

5

4

8

9

1

0

0

3

4

2

7

5

 

5)

 

3

0

11

9

7

2

5

6

2

8

9

4

5

6

5

0

7

2

5

13

4

7

10

11

14

12

7

6

5

10

18

15

12

11

22

3

4

7

9

1

7

8

7

4

1

11

12

10

1

0

0

1

2

4

3

7

 

 

          А:

 

 

  

6)

 

0

3

5

2

4

12

10

11

9

15

10

9

4

3

8

7

10

11

7

4

1

2

9

10

12

9

4

2

14

13

11

12

12

9

7

11

4

6

4

3

 

 

          А:

  

7)

 

8

3

5

3

4

7

9

6

7

7

8

4

2

2

4

13

5

8

9

11

13

7

6

11

15

21

6

10

10

8

12

4

3

2

1

4

10

 

16

11

7

8

13

14

20

12

11

 

 

А:

 

 

 

 

8)

 

10

14

2

2

12

7

2

7

8

9

9

3

12

7

8

12

4

4

2

8

10

12

4

6

6

13

12

7

0

5

11

11

6

5

3

11

21

6

6

16

4

0

4

1

2

2

5

11

7

 

 

А:

 

  

 

9)

 

7

24

1

5

6

11

1

3

4

5

6

7

8

13

2

14

7

4

0

25

21

4

5

6

5

7

9

20

11

9

7

11

11

9

16

16

12

11

13

7

12

0

7

3

0

12

8

13

14

 

 

А:

 

 

 2 Лабораторная работа №2. Нахождение кратчайшего пути

 

В телекоммуникациях задачу нахождения путей определенного качества часто называют задачей маршрутизации. Под качеством при этом понимают минимальное расстояние между узлами ai и aj, или минимальную стоимость, или максимальную надежность. Существует огромное количество методов решения. В настоящей работе рассмотрим один из них – метод Флойда (R. W. Floyd).

 

 2.1 Цель работы

 

Изучить методы построения минимальной длины.

 

2.2. Подготовка к выполнению работы

 

Изучить [2, 5, 6] и настоящее методическое указание. Определить исходную информацию, соответствующую варианту.

 

2.3 Алгоритм решения

 

Этот алгоритм позволяет найти кратчайшие пути между любыми двумя вершинами графа.

Исходными данными для алгоритма является матрица весов дуг . Диагональные элементы равны 0. Если дуга из  в  отсутствует, то . Над матрицей весов выполняется n итераций, в результате последовательно получаются матрицы . После k-й итерации элемент  матрицы  показывает длину кратчайшего из тех путей, ведущих из вершины  в вершину , что проходит только через вершины с номерами, не большими, чем k.

На k-й итерации к элементам матрицы  применяется  треугольный оператор:

 

                                                                      (2.1)

 

Для вычисления проводится сравнение величины  (это длина пути от  к  без участия вершин, номера которых равны или больше k) с величиной  (т.е. длина пути от  к  плюс длина пути от  к ). Если путь через k-ю вершину ближе, то элемент  изменяет свое значение.

Чтобы потом восстановить номера вершин, составляющих кратчайший путь от  к , надо использовать вспомогательную матрицу , которую сначала необходимо инициализировать нулями, а затем на каждой итерации k, если оказалось, что , записывать на место  номер k вершины, путь через которую оказался ближе.

Итак, алгоритм Флойда заключается в следующем:

а) инициализируем матрицу А(0) значениями длин дуг; диагональным элементам присваиваем нулевые значения. Инициализируем нулями матрицу путей Р(0). Полагаем k=1.

б) рассматриваем возможность применения треугольного оператора ко всем элементам матрицы А(k-1), т.е. если верно неравенство

то выполняем следующие действия:

1)     заменяем в матрице А(k-1) элемент  на сумму ;

2)     в матрице Р(k-1) элемент  заменяем на k;

в) после рассмотрения всех элементов матрицы А(k-1) в результате выполнения пункта б) получаем матрицы А(k )и P(k). Если k=n, то конец, иначе полагаем k=k+1 и переходим к началу п. б).

 

2.3.1 Пример

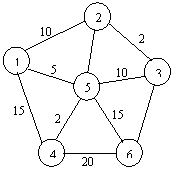
Рассмотрим пример. Граф и матрица длин приведены на рисунке 2.1.

 

         

 

 

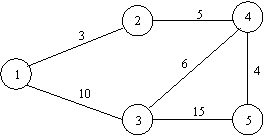
Рисунок 2.1 – Граф и матрица длин

 

Выполняя пункт б) алгоритма Флойда, выделяем в матрице весов первую строку и первый столбец и пытаемся применить треугольный оператор ко всем элементам матрицы, т.е. проверяем, не является ли какой-либо путь короче, если идти через вершину . Видим, что улучшить можно только значения а23 и а32. Заменяем а23 на а21+ а13=3+10=13 и устанавливаем р23=1; аналогично заменяем а32 на а31+ а12=10+3=13 и устанавливаем р32=1. Получаем

 

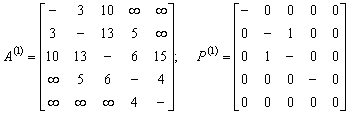
Полагаем k=2, выделяем вторую строку и второй столбец матрицы А(1). Треугольный оператор применяется к элементам а14, а41. Новые матрицы весов и путей:

 

 

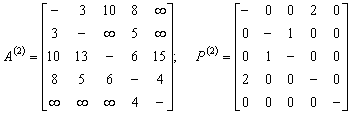
Полагаем k=3, выделяем третью строку и третий столбец матрицы А(2). Треугольный оператор применяется к элементам а15 и а25. Новые матрицы весов и путей:

 

 

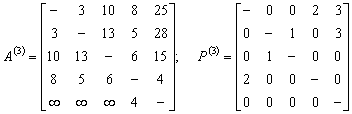
Полагаем k=4, выделяем четвертую строку и четвертый столбец матрицы А(3). Треугольный оператор применяется к элементам а23, а32, а51, а25, а52, а35, а53. Новые матрицы весов и путей:

 

 

Полагаем k=5, выделяем пятую строку и пятый столбец матрицы А(4). Треугольный оператор не применим ни к одному элементу, поэтому обе матрицы остаются без изменений, т.к. , то вычисления закончены.

По матрице кратчайших путей An можно узнать длину кратчайшего пути из любой вершины. Например, d15=12, чтобы восстановить сам ближайший путь, надо воспользоваться матрицей Р4, например, если нас интересует маршрут из  в , находим, что Р15=4, значит, кратчайший маршрут проходит через вершину . Ту же процедуру повторяем для каждого сегмента полученного пути . Так, для перехода  имеем Р14=2, а для перехода  = Р45=0, для перехода  имеем Р12=0, следовательно, кратчайший путь – .

 

2.4 Контрольные вопросы

 

2.4.1 Критерии маршрутизации.

2.4.2 Является ли метод Флойда итерационным? Критерий окончания расчетов.

2.4.3 Какой оператор лежит в основе алгоритма?

 

2.5 Указания к составлению отчета

 

1. Постановка задачи

4. Листинг программы

2. Исходная информация

5. Матрица Аn и Pn

3. Блок-схема программы

6. Кратчайший путь

 

2.6 Исходная информация

 


а)                                                       б)

  

 

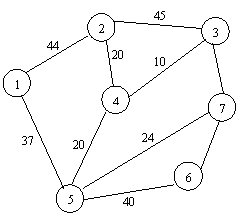
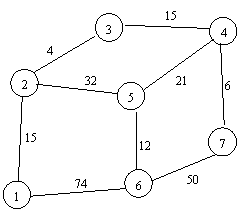         в)                                                     г)

 

 

 

 

 

 

 

 

 

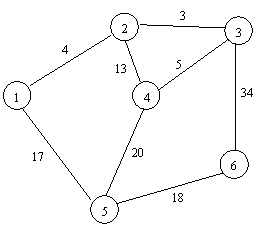д)                                                        

 

 

 

 

 

 

 

 

n

0

1

2

3

4

5

6

7

8

9

 

3 Лабораторная работа №3 Расчет нагрузки на обходных направлениях

 

Возможность построения на сети нескольких путей между двумя пунктами повышает надежность сети, вероятность установления соединения, улучшает использование каналов.

Одной из задач этой области исследования является задача расчета нагрузки на обходном направлении.

 

3.1 Постановка задачи

 

Пусть между двумя пунктами I и J существует телефонная нагрузка А. Число каналов, соединяющих пункты I и J, равно . В случаях, когда нагрузка превышает пропускную способность линий, избыточная нагрузка, сбрасывается на обходное направление через пункт S.

 

 

 

 

 

В случае, если обходного пути (или нескольких путей) нет или их пропускная способность недостаточна, излишняя нагрузка сбрасывается, теряется. Потери определяют качество связи. Задача заключается в определении числа каналов на обходном направлении сети, обеспечивающее заданное качество связи, т.е. величину потерь р0.

Задан фрагмент иерархической сети с транзитным узлом S, приведенный на рисунке 3.1. На обходное направление, отмеченное двойной линией, поступают избыточные потоки с направлений 1,2,...К. Нагрузка, не обслуженная каналами обходного направления, теряется. Все пучки каналов полнодоступные.

3.1.1 Цель работы.

Изучить методы расчета нагрузки на обходных направлениях.

3.1.2 Подготовка к выполнению работы.

Изучить [2, 3] и настоящее методическое указание. Определить исходную информацию, соответствующую варианту.

 

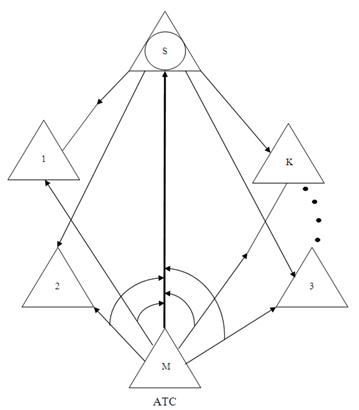
Рисунок 3.1 - Фрагмент иерархической сети с обходным направлением (М, S)

 

3.2 Теоретическая часть

 

Вероятность потерь определяется по формуле Эрланга

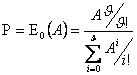                                                                                 (3.1)

где A – поступающая нагрузка, Эрл;

 – число каналов линии.

Коэффициент рассеяния и дисперсия избыточной нагрузки определяются по формулам

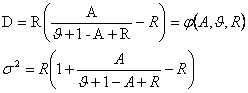             .                                             (3.2)

 

Фрагмент иерархической сети с K направлениями

 

Aj, Jj, j =1,2,…K

где Aj — величина поступающего потока;

Jj  – число линий.

Весь избыточный поток поступает на обходное направление.

Определить количество линий Jоб  на обходном направлении таким, чтобы потери не превышали р0.

Алгоритм решения задачи можно представить последовательностью

шагов:

а) для  каждого направления j  с  избыточным потоком  вычислить математическое ожидание избыточной нагрузки Rj, по формуле

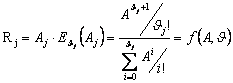;                                                             (3.3)

б) определить коэффициент рассеяния избыточной нагрузки на направлении j

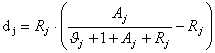;                                                                 (3.4)

 

в) определить нагрузку на обходное направление, коэффициент
рассеяния

; ;                                                                                (3.5)

г) вычислить нагрузку, поступающую на обходное направление и необходимое количество линий.

,                                                                         (3.6)

.                                                                    (3.7)

д) определить Jо6. так, чтобы

.                                                                                          (3.8)

  

3.3 Иллюстративный пример

 

Даны нагрузка Аj, и количество каналов Jj  по трем направлениям:

 

Аj

15

8.5

15

Jj

13

10

13

 

Поступающие потоки Aj - пуассоновские. Определить избыточную нагрузку на каждом направлении Rj, коэффициент рассеяния dj, сформировать поток обходного направления и определить число каналов обходного направления так, чтобы вероятность потерь на нем не превышала р0 (например,  р0 =0,01).

По формуле 3.3 определим избыточные потоки

 

R1 =15E13(15) = 15·0,263 = 3,95

R2 = 8,5 ·E10(8,5) = 8,5·0,145 = 1,232

R3 = 3,95

.

 

По формуле 3.4 подсчитаем коэффициент рассеяния

 

d1 =4,48; d2 =1,29; d3=4,48; D = 10,25.

 

По формуле 3.6 определяем

 

.

По формуле 3.7 определяем количество каналов на обходном направлении.

 

.

 

По формуле 3.8 определяем роб

 

Роб = E18(26.5), больше чем роб > р0.

 

Необходимо организовать цикл расчета (рисунок 3.2) по первой формуле Эрланга, увеличивая значения Jоб  – на единицу до тех пор, пока потери не будут удовлетворять условию рi  р0.

Для рассматриваемого примера Jоб  = 37 каналам. 

 

 

 

 

 

 

 

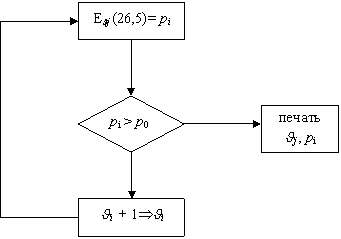Рисунок 3.2 – Алгоритм расчета количества линий,
              удовлетворяющих pi  p0

3.4 Контрольные вопросы

 

1.       Каков закон распределения потока на обходном направлении?

2.       Что такое избыточный поток? Чем характеризуется?

3.       Чем определяется качество связи? Как улучшается?

 

3.5 Указания к составлению отчета

 

1.       Постановка задачи.

2.       Исходная информация.

3.       Блок схема программы.

4.       Листинг программы.

5.       Результаты решения.

 

3.6 Исходная информация

 

По таблице 3.1 определяем обходные направления (схему) в зависимости от последней цифры зачетки.

 

Т а б л и ц а 3.1

 

0

1

2

3

4

5

6

7

8

9

Комбинация направлений

1,2,3

2,3

3,4,1

2,4,5

1,2,5

2,3,5

1,4,5

3,4,5

1,3,5

4,5,2

 

Значение нагрузки Ai и числа каналов Ji приведены в таблице 3.2, где
i –последняя цифра зачетной книжки, а m – порядковый номер фамилии студента в журнале. 

 

Т а б л и ц а 3.2

 

A1, J1

A2, J2

A3, J3

A4, J4

A5, J5

m1 = 1,2,3,4,5

12,4;14

8,3;10

10,6;11

7,3;8

5,7;7

m2 = 6,7,8,9,10

5,4;7

3,5;4

2,7;3

1,87;2

0,97;1

m3 = 11,12,13,14,15

2,4;3

10,3;12

4,8;6

5,4;7

3,4;4

m4 = 16,17,18,19,20

5,8;6

0,8;1

3,1;4

5,1;6

1,7;2

m5 = 21,22,23,24,25

0,8;1

1,5;2

0,7;1

4,2;5

2,4;3

m6 = 26,27,28,29,30

8,4;9

7,7;8

0,9;1

2,2;3

4,2;5

 

 

Список литературы 

1.      Дурнев В.Г., Зеневич Б. И. и др. Электросвязь. Введение в специальность. – М.: Радио и связь, 1988.

2.      Давыдов Г. Б., Рогинский В. Н., Толчан А. Я. Сети электросвязи. – М.: Связь, 1977.

3.      Теория сетей электросвязи. Под ред. В. Н. Рогинского – М.: Радио и связь, 1981.

4.      Зайончковский Е.А. и др. Автоматическая междугородная телефонная сеть связи. – М.: Радио и связь, 1984.

5.      Берж К. Теория графов и ее применения. – М.: Иностранная литература, 1962.

6.      Шварц М. Сети ЭВМ. Анализ и проектирование. – М.: Радио и связь, 1981.

  

Содержание

 

Введение

3

1. Лабораторная работа №1. Решение задачи районирования

4

2. Лабораторная работа №2. Построение кратчайшего пути
методом Флойда

9

3. Лабораторная работа №3. Расчет нагрузки на обходных направлении

13

4. Список литературы

19