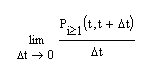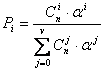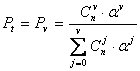Некоммерческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра автоматической электросвязи
ТЕОРИЯ ТЕЛЕТРАФИКА
Конспекты лекций
(для студентов специальности 050719 – Радиотехника, электроника и телекоммуникации)
Алматы 2007
СОСТАВИТЕЛЬ: К. Х. Туманбаева. Теория телетрафика. Конспекты лекций для студентов специальности 050719 – Радиотехника, электроника и телекоммуникации. - Алматы: АИЭС, 2007.- 36 с.
Изложены конспекты восьми лекций по дисциплине «Теория телетрафика». В них представлены основы теории обслуживания сообщений в системах коммутации и сетях связи. Излагаются методы прогнозирования нагрузки, расчета качества обслуживания в телекоммуникационных системах. Представлены приближенные инженерные методы расчета.
Ил.8, , библиогр.- 5 назв.
Рецензент: канд.техн.наук, проф. Г.С.Казиева.
Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2007 г.
© НАО «Алматинский институт энергетики и связи», 2007 г.
Введение
Целью преподавания дисциплины «Теория телетрафика» является подготовка студентов, владеющих основными принципами построения математических моделей обслуживания потоков сообщений, необходимых для решения задач оптимального проектирования систем коммутации и сетей связи и их квалифицированного обслуживания.
Изучив основные методы теории телетрафика, студент сможет рассчитать характеристики качества обслуживания в телекоммуникационных системах, управлять основными параметрами качества обслуживания реальных сетей и систем и измерять их, а также предложить оптимальные с точки зрения качества обслуживания технические решения при проектировании новых сетей и систем.
Задачами преподавания дисциплины являются овладение студентами методов прогнозирования нагрузки, расчета качества обслуживания в коммутационных системах с потерями и с ожиданием, методов анализа различных моделей потоков вызовов.
Учебным планом для данной дисциплины отводится 2 кредита, всего 90 часов, из них для аудиторных занятий - 42, для самостоятельной работы – 48 час.
|
Курс |
Семестр |
Аудит. занятия |
Лекции |
Практ. занятия |
Лаборат. работы |
Расчетно- графич. работы |
Экзамен |
|
4 |
7 |
42 |
17 |
8 |
17 |
2 |
7 |
Лекция 1. Цели и основные задачи теории телетрафика
Цель лекции: ознакомление студентов с целью и задачами дисциплины, с основной моделью обслуживания потоков сообщений, исследуемой в теории телетрафика, с основными терминами теории, свойствами и характеристиками потоков вызовов.
Содержание:
а) цели и задачи дисциплины;
б) основные понятия теории телетрафика;
в) свойства и характеристики потоков вызовов.
Основы теории были заложены в трудах датского математика, сотрудника Копенгагенской телефонной компании А.К.Эрланга. Труды были опубликованы в 1908-1918 гг. Новая научная дисциплина называлась теорией телетрафика, предметом её изучения стали процессы обслуживания системами распределения информации поступающих потоков сообщений и их численных характеристик. К системам распределения информации относятся: сети связи, коммутационная станция, коммутационный узел и их отдельные части, обслуживающие поступающие сообщения.
Результаты, полученные А.К. Эрлангом, послужили базой теории массового обслуживания, известной вам из курса «Моделирование систем телекоммуникаций». В настоящее время теория массового обслуживания, помимо инфокоммуникаций, эффективно используется для решения задач торговли, транспорта и других сфер экономической деятельности.
Основная математическая модель процесса обслуживания, исследуемая в теории телетрафика содержит следующие компоненты: поток поступающих сообщений, систему обслуживания, дисциплину и характеристики качества обслуживания.
Под дисциплиной обслуживания поступающих сообщений понимают способ обслуживания (без потерь сообщений, с явными потерями, с ожиданием, повторением, комбинированием), порядок обслуживания (в порядке очередности, в случайном порядке, с приоритетом), способ искания свободных выходов (упорядоченный или случайный).
К характеристикам качества обслуживания поступающего потока сообщений относятся: вероятность потери сообщения, среднее время обслуживания сообщения, среднее время ожидания начала обслуживания, пропускная способность системы обслуживания и другие.
Основной задачей теории телетрафика является задача анализа, а именно задача определения характеристик качества обслуживания в зависимости от свойств и параметров поступающего потока вызовов, системы и дисциплины обслуживания. Наряду с этой задачей решается и обратная – нахождение параметров системы обслуживания в зависимости от параметров и свойств потока вызовов и качества обслуживания.
К основным направлениям теории относятся разработка методов построения оптимальных структур коммутационных схем, методов расчета пропускной способности, задачи по оптимизации структуры сети связи и расчету показателей качества обслуживания.
Нормирование и оптимальное распределение по участкам сети и этапам соединения показателей качества обслуживания – еще один класс задач теории телетрафика.
Математический аппарат теории телетрафика базируется на теории вероятностей, комбинаторике и математической статистике.
Познакомимся с основными терминами теории.
Сообщение – это форма представления информации, имеющая признаки начала и конца, и предназначенная для передачи через сеть связи или систему коммутации.
Сообщением могут быть телефонный разговор, телеграмма, факсимильная передача, теле-радио передача, компьютерный файл. Сообщение характеризуется объемом, занимаемого канала, временем передачи, адресами источника и приёмника, формой представления информации (аналоговая, цифровая).
Вызов - это требование источника на установление соединения, поступившее в сеть связи или коммутационную систему с целью передачи или обслуживания сообщения.
Вызов характеризуется только моментом своего поступления. Источником вызова могут быть телефоны, телеграфы, факсимильные аппараты или компьютер, они же могут быть и приёмниками. Вызовы подразделяются на несколько видов:
обслуженный – получивший соединение, при этом получивший соединение с требуемым приемником называется полностью обслуженным, а вызов, получивший соединение на некотором участке сети, называется частично обслуженным;
успешный – окончившийся передачей сообщения приемнику;
потерянный – получивший отказ в обслуживании;
задержанный – ожидающий начала установления соединения, ждущий в очереди;
первичный – первый для данного сообщения вызов;
повторный – поступивший в сеть связи через случайный или детерминированный промежуток времени, после того как предыдущий был потерян.
Занятие – это любое использование прибора, линии, устройства с целью установления соединения независимо от того закончилось оно передачей сообщения или нет. Характеризуется моментом занятия и длительностью.
Освобождение – возвращение прибора, линии, устройства в исходное, нерабочее состояние. Характеризуется моментом наступления.
Множество последовательных моментов поступления вызовов образует поток вызовов.
Поток вызовов называется детерминированным (неслучайным), если эта последовательность моментов заранее предопределена. Если данная последовательность является случайной, то поток вызовов называется случайным.
Детерминированные потоки редко встречаются на практике. Примером детерминированных потоков могут служить потоки моментов начала и окончания передач программ радио – и телевещания, поток сеансов связи с искусственными космическими спутниками. В сетях связи в основном имеют место случайные потоки вызовов.
Для задания случайных потоков используется
вероятностные законы распределения следующих случайных величин: моментов
поступления вызовов ![]() , промежутков между соседними вызовами (zk) и
числа поступающих вызовов в промежутке [0, t].
, промежутков между соседними вызовами (zk) и
числа поступающих вызовов в промежутке [0, t].
Случайные потоки вызовов классифицируются в зависимости от наличия или отсутствия следующих трех свойств: стационарности, последействия и ординарности.
Стационарность означает, что с течением времени вероятностные характеристики потока не меняются, иначе говоря, для стационарного потока вероятность поступления i вызовов за промежуток времени t зависит только от длины этого промежутка и не зависит от расположения его на оси времени.
Это значит, что для стационарного потока вероятность поступления некоторого числа вызовов за какой-то промежуток времени зависит от длины этого промежутка и не зависит от его начала. В противном случае поток является нестационарным. Интенсивность потоков вызовов на телефонных сетях резко колеблется в зависимости от времени суток, количество вызовов за единицу времени в дневные и вечерние часы достигает максимальной величины, а в ночные часы уменьшается. Это означает, что поток вызовов, поступающий в течение суток, являются нестационарным. Но внутри ограниченного отрезка суток, например часа, нестационарность телефонного потока вызовов малоощутима, что позволяет для практических задач полагать его стационарным.
Ординарность означает невозможность группового поступления вызовов, то есть вероятность поступления двух и более вызовов за любой бесконечно малый промежуток есть величина бесконечно малая. В сетях связи потоки вызовов ординарны.
Примером ординарного потока является поток вызовов, поступающий на АТС от абонентской группы любой ёмкости. Потоки телефонных вызовов к абонентам диспетчерской или конференц - связи, потоки телеграмм являются неординарными.
Последействие означает зависимость вероятностных характеристик вызовов от предыдущих событий.
Примером потока без последствия может служить поток телефонных вызовов, поступающих от большой группы источников. Действительно, лишь небольшая часть абонентской группы одновременно участвует в телефонных соединениях. Поэтому вероятность поступления, какого – либо числа вызовов от большой группы источников на любом отрезке времени практически не зависит от процесса поступления вызовов до начала данного отрезка.
Поток вызовов являются с потоком с последствием, если вероятность поступления того или иного числа вызовов за некоторый промежуток времени зависит от процесса поступления вызовов до начала этого промежутка.
К основным характеристикам потока вызовов следует отнести ведущую функцию потока, его параметр и интенсивность.
Ведущая функция
![]()
![]() случайного
потока есть математическое ожидание числа вызовов в промежутке [0,t). Функция
случайного
потока есть математическое ожидание числа вызовов в промежутке [0,t). Функция ![]() - неотрицательная, неубывающая.
- неотрицательная, неубывающая.
Под параметром потока l (t) в момент времени t понимается предел отношения вероятности поступления не менее одного вызова в промежутке [t,t+Dt] к длине этого промежутка Dt при Dt ®0:
|
|
λ(t) =
Согласно определению стационарного потока, вероятность поступления определённого числа вызовов за некоторый промежуток времени одна и та же, не зависит от месторасположения на оси времени этого промежутка. Следовательно, и плотность вероятности поступления вызовов стационарного потока, то есть его параметр l(t) есть величина постоянная, не зависящая от момента t, то есть l(t) = l .
Параметр потока l(t) характеризует не поток вызовов, а поток вызывающих моментов, и эта характеристика относится не ко всему отрезку [0,t], а лишь к фиксированному моменту t.
Интенсивность стационарного потока μ есть математическое ожидание числа вызовов, поступающих в единицу времени.
Для ординарных потоков μ=λ=const
Лекция 2. Потоки вызовов
Цель лекции: ознакомление студентов с основными видами потоков вызовов, применяемых в теории телетрафика.
Содержание:
а) простейший поток вызовов;
б) свойства и характеристики простейшего потока;
в) нестационарный пуассоновский поток;
г) примитивный поток.
Стационарный, ординарный поток без последействия называется простейшим.
Задается простейший поток семейством вероятностей ![]() (t)
поступления i вызовов в промежутке t
(t)
поступления i вызовов в промежутке t
Вероятность ![]() (t) вычисляется по формуле
(t) вычисляется по формуле
![]() (t)=
(t)= ![]() (2.1)
(2.1)
где λ- параметр потока, постоянная величина, поскольку поток стационарный.
λ=μ, поскольку поток ординарный
Формула (2.1) называется формулой Пуассона или распределением Пуассона.
Рассмотрим формулу (2.1). Вычислим отношение двух
соседних вероятностей.![]()
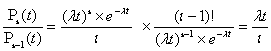
При i≤λt→![]() (t)<
(t)<![]() (t), а при i>λt→
(t), а при i>λt→![]() (t)>
(t)>![]() (t).
Следовательно, с ростом Iiвероятность Pi(t)
растет, пока i ≤ λt и начинает уменьшаться
при i>λt.
(t).
Следовательно, с ростом Iiвероятность Pi(t)
растет, пока i ≤ λt и начинает уменьшаться
при i>λt.
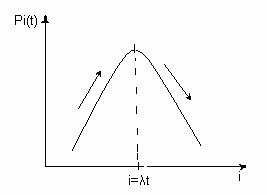
Рисунок 2.1
Функция ![]() (t) при целом значении λt максимума достигает в
2-х точках, при i=λt, i=λt-1, а при дробном значении в одной точке i =
[λt].
(t) при целом значении λt максимума достигает в
2-х точках, при i=λt, i=λt-1, а при дробном значении в одной точке i =
[λt].
При решении λt практических задач используют значения вероятности поступления не менее i вызовов за промежуток t
Р≥i (t)=![]() (t)
(t)
Значения вероятностей Р≥i (t) для некоторых величин х=λt и i приведены таблично в приложениях учебников [1,2]. Используя данные таблицы, далее можно вычислить вероятность поступления не более i вызовов за промежуток t и вероятность поступления i вызовов за данный промежуток.
P≤i(t) = 1 - P≥i (t) и Pi(t) = P≥i (t) - P≥i+1(t) (2.2)
Пример. Рассчитать вероятности поступления 5, не менее 5, и не более 5 вызовов за промежуток времени t=180 секунд, если λ=160 вызовов в час.
![]() (t),
(t), ![]() (t),
(t), ![]() (t)-?
(t)-?
Вычисляем
λt=![]()
С помощью таблицы [1,2]
находим ![]() (t)=0,9004,
(t)=0,9004, ![]() (t)=0,8088.
(t)=0,8088.
Тогда по формуле (2.2)
![]() (t)=1-0,8088=0,1912,
(t)=1-0,8088=0,1912,
![]() (t)=0,9004-0,8088=0,0916.
(t)=0,9004-0,8088=0,0916.
Простейший поток можно задать еще следующим способом: функцией распределения промежутка между соседними вызовами z
![]()
F(t)=P(z<t)=1-P(z>t)
Вероятность P(z>t) равносильна вероятности того, что внутри промежутка длиной t не поступит ни одного вызова.
![]() F(t)=P(z>t)=1-
F(t)=P(z>t)=1-![]() (t)=1-
(t)=1-![]() (2.3)
(2.3)
Закон распределения (2.3) называется показательным, а λ его параметром.
Рассмотрим свойства и характеристики простейшего
потока. Математическое ожидание величины промежутка между соседними вызовами z ,
равна Mz=1/λ. Дисперсия данной величины равна 1/![]() ,
следовательно,
,
следовательно,
среднеквадратическое отклонение σz= 1/λ, то есть имеет место равенство
Mz = σz= 1/λ.
Совпадение этих величин используют для проверки того, что случайная величина z распределяется по показательному закону.
Математическое ожидание числа вызовов i за промежуток времени t равно λt, дисперсия числа вызовов за промежуток t равна также λt, то есть
Mi = Di = λt.
Cовпадение этих величин используют на практике при проверке соответствия реального потока простейшему.
При объединении нескольких независимых простейших потоков образуется также простейший поток с параметром, равным сумме параметров входных потоков
λ = λ1 + λ2 + ... + λn
При разъединении поступающего простейшего потока с параметром λ на n направлений образуются n простейших потоков.
Перечисленные свойства и характеристики простейшего потока широко используются при расчетах станционного оборудования и сетей связи.
Модель простейшего потока получила наибольшее по отношению ко всем другим моделям распространение в теории телетрафика.
Рассмотрим коротко другие виды потоков вызовов.
Нестационарный пуассоновский поток - это ординарный поток без последействия, для которого в любой момент времени t существует конечный параметр λ(t).
Различают потоки с переменным и случайным параметрами. В первом случае λ(t)- известна, во-втором - λ(t)- случайная функция.
Рассмотрим λ(t) с переменным параметром, в этом случае λ(t) может быть непрерывной или ступенчатой. В последнем случае функция меняет свое значение скачками в заранее известные или случайные моменты времени t1, t2, … tn.
Модель пуассоновского потока с переменным параметром выглядит следующим образом
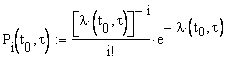
где Pi(t0,τ) - вероятность поступления i вызовов в промежутке (t0, t0 + τ);
λ(t0,τ) - математическое ожидание числа вызовов, поступивших в промежутке (t0, t0 + τ);
![]() -средняя интенсивность
потока вызовов в промежутке τ.
-средняя интенсивность
потока вызовов в промежутке τ.
Данная модель позволяет достаточно хорошо описать реальный нестационарный поток вызовов, например, поступление вызовов на телефонную станцию в течение суток.
Примитивным потоком называется ординарный поток, параметр которого λi, прямо пропорционален числу свободных источников Ni, в состоянии обслуживаемой системы i
λi=αNi=α(N-i)
где α – параметр потока вызовов от одного свободного источника;
N – общее число источников;
i – число занятых источников.
Математической моделью примитивного потока является распределение Бернулли
![]()
где ![]() –
число поступивших вызовов;
–
число поступивших вызовов;
![]() – общее количество источников;
– общее количество источников;
![]() – нагрузка, поступающая от одного источника (
– нагрузка, поступающая от одного источника (![]() ,
, ![]() – интенсивность потока от
одного источника);
– интенсивность потока от
одного источника);
![]() - вероятность поступления к вызовов.
- вероятность поступления к вызовов.
При вычислении ![]() удобно использова рекуррентную
формуллу Бернулли
удобно использова рекуррентную
формуллу Бернулли
![]() .
.
В модели потока учитывается, что вызовы могут поступать только от свободных источников. Наибольшее значение параметр потока принимает тогда, когда все источники свободны, и наименьшее, когда i достигает максимума.
Данная модель потока вызовов применяется, когда число источников не очень большое, когда N >300-500 поток превращается в простейший.
Лекция 3. Нагрузка
Цель лекции: ознакомление студентов с важным понятием, характеризующим функционирование системы коммутации, нагрузкой, единицами измерения интенсивности нагрузки, основными видами нагрузки, с методом расчета интенсивности абонентской нагрузки.
Содержание
а) определение нагрузки, интенсивности нагрузки, единицы измерения;
б) виды нагрузки;
в) факторы, влияющие на изменение нагрузки;
г) расчет интенсивности поступающей нагрузки.
Нагрузка, а точнее обслуживаемая в момент времени t нагрузка, есть число одновременно обслуживаемых вызовов или, что то же самое число занятых входов, выходов, линий и приборов в этот момент времени.
Поскольку нагрузка - величина случайная, то при расчетах используют её математическое ожидание.
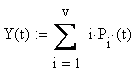
где Pi (t) - вероятность занятия i линий из v возможных в момент времени t.
При постоянной вероятности Pi в пределах некоторого промежутка времени величина Y(t) будет также постоянной.
Математическое ожидание нагрузки называется интенсивностью нагрузки. Нагрузка и ее интенсивность измеряется в Эрлангах (Эрл.).
Интенсивность нагрузка 2.5 Эрл. означает, что либо число занятых линий за рассматриваемый промежуток времени в среднем равна 2,5, либо в среднем за рассматриваемый промежуток занято 2,5 линий.
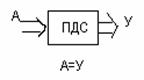
Существует три основных вида нагрузки : поступающая, обслуженная и потерянная.
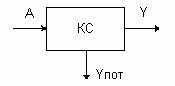
Рисунок 3.1
На рисунке 3.1 А – поступающая нагрузка, У- обслуженная нагрузка и
![]() - потерянная нагрузка.
- потерянная нагрузка.
Поступающую нагрузку А можно только прогнозировать, обслуженную нагрузку У можно измерить, а потерянную можно определить как разность между поступившей и обслуженной
![]() =А-У
=А-У
При
измерениях интенсивности нагрузки, ее определяют как среднее число занятых
линий в пучке за промежуток времени (![]() ).
).
На интенсивность нагрузки влияют следующие факторы: структурный состав абонентов (доля квартирного, народнохозяйственного и административного секторов), ритм местной жизни (начало и конец рабочего лня), время суток, день недели, число месяца, месяц года.

Рисунок 3.2
На рисунке 3.2 приведено приблизительное суточное распределение интенсивности нагрузки для двух секторов абонентов.
При исследовании суточного распределения нагрузки выделяют промежуток длиной в 1 час, когда нагрузка достигает своего максимального значения. Этот час называют часом наибольшей нагрузки (ЧНН).
Кроме того, выделяют промежуток длиной в 3 часа, когда нагрузка достигает своего наибольшего значения. Его называют периодом наибольшей нагрузки (ПНН).
Степень концентрации нагрузки в ЧНН и ПНН оценивается с помощью соответствующих коэффициентов концентрации.
Коэффициент концентрации в
ЧНН: 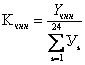 ,
где
,
где ![]()
![]() ,
,![]()
Коэффициент концентрации в
ПНН: 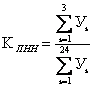
Чем меньше коэффициент концентрации, тем равномерней загружено коммутационное оборудование, тем меньше его объема требуется для выполнения одной и той же работы.
Расчет интенсивности поступающей нагрузки.
Расчет интенсивности поступающей нагрузки производят по следующей формуле:
![]() (3.1)
(3.1)
где А - величина поступающей нагрузки, (эрл.);
![]() -
число абонентов i-ой категории;
-
число абонентов i-ой категории;
n - число категории абонентов;
![]() -
число вызовов в ЧНН, поступающих от одного абонента i-категории;
-
число вызовов в ЧНН, поступающих от одного абонента i-категории;
ti - средняя длительность одного занятия для i-категории.
При
проектировании АТС значения ![]() и
и![]() определяются конкретно для каждого телефонного района
с помощью статистических наблюдений.
определяются конкретно для каждого телефонного района
с помощью статистических наблюдений.
При расчете рассматриваются следующие основные категории абонентов:
- абоненты квартирного сектора;
- абоненты народнохозяйственного сектора;
- абоненты таксофонов;
- абоненты от соседних линий, учрежденных АТС.
Теперь рассмотрим как определяется величина ti . Для этого определим
виды занятий.
Занятия бывают успешные и неуспешные. К успешным относятся занятия окончившиеся разговором.
Причинами неуспешных занятий являются:
а) занятость вызываемого абонента;
б) отсутствие ответа вызываемого абонента;
в) ошибки при наборе номера абонента;
г) технические причины.
При расчете нагрузки примем следующие доли различных занятий:
![]() -доля занятий окончившихся разговором
(0,4÷0,5);
-доля занятий окончившихся разговором
(0,4÷0,5);
![]() - доля занятий, не окончившихся разговором из-за
занятости вызываемого абонента (0,15÷0,3);
- доля занятий, не окончившихся разговором из-за
занятости вызываемого абонента (0,15÷0,3);
![]() - доля неуспешных занятий из-за неправильного набора
(0,1÷0,03);
- доля неуспешных занятий из-за неправильного набора
(0,1÷0,03);
![]() - доля неуспешных занятий из-за не ответа
(0,1÷0,2);
- доля неуспешных занятий из-за не ответа
(0,1÷0,2);
![]() - доля неуспешных занятий по техническим причинам
(0,01÷0,02).
- доля неуспешных занятий по техническим причинам
(0,01÷0,02).
При
этом сумма всех принятых значений перечисленных величин должна быть равна
единице, ![]() .
.
Обозначим
через ![]() ,
,![]() средние
длительности соответствующих занятий, определим их значения.
средние
длительности соответствующих занятий, определим их значения.
Длительность успешного занятия
![]()
где ![]() -
длительность ответа станции (≈3с.);
-
длительность ответа станции (≈3с.);
![]() -
длительность установления соединения (1.5m+2.5c),
где m – число
цифр в номере;
-
длительность установления соединения (1.5m+2.5c),
где m – число
цифр в номере;
![]() -сигнал
вызова с≈7с;
-сигнал
вызова с≈7с;
Т - продолжительность разговора (для каждой категории своя);
![]() -
отбой (1с, О с) .
-
отбой (1с, О с) .
Длительность занятия когда абонент занят.
![]()
где ![]() - продолжительность сигнала занято (≈5с).
- продолжительность сигнала занято (≈5с).
Средняя длительность, когда нет ответа
![]()
где ![]() - средняя длительность, когда нет ответа (≈30с.).
- средняя длительность, когда нет ответа (≈30с.).
Средняя длительность неуспешного занятия из-за ошибки при наборе номера составляет приблизительно 7с.
Средняя длительность неспешного занятия по техническим причинам составляет приблизительно также 7с.
Теперь рассчитывается общая средняя длительность одного занятия по формуле:
![]()
Данная величина рассчитывается для каждой категории отдельно.
Полученные значения ti подставляются в формулу (3.1). Получаем значение, поступившей нагрузки в эрлангах.
На практике применяют упрощенной метод расчета нагрузки, в котором определяют среднюю длительность занятия по формуле
t = αpptp
где α - коэффициент непроизводительного занятия коммутационной системы, определяется из диаграммы при известных Т и pp [1].
Лекция 4. Методы расчета однозвенной полнодоступной коммутационной системы с явными потерями
Цель лекции: ознакомление студентов с марковскими процессами, с уравнением Колмогорова – Чепмена, с выводом первой формулы Эрланга для расчета однозвенной полнодоступной КС с явными потерями.
Содержание
а) марковский процесс, уравнение Колмогорова – Чепмена;
б) характеристики качества обслуживания полнодоступной системы с явными потерями;
б) вывод первой формулы Эрланга;
Рассмотрим коммутационную систему (КС)
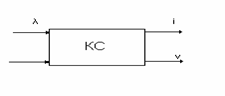
Число занятых линий x из v в момент времени t является случайной величиной.
Обозначим через {x} – состояние системы, когда занято x линий из v. При поступлении вызова (занятии линии) или окончании его обслуживания (освобождение линии) система переходит из одного состояния в другое. Причем, если система находилась в состоянии {x}, то перейти может в одно из следующих состояний: {x - 1}, {x}, {x + 1}. Но при этом состояние в будущем зависит только от настоящего и не зависит от прошлого. Такие случайные процессы называются марковскими, в честь выдающегося русского математика А.А.Маркова.
Пусть за промежуток времени τ система могла перейти из состояния k в состояние i с вероятностью pki (τ). Вероятность того, что система в момент времени t – τ находилась в состоянии k, обозначим через Pk (t – τ).
Тогда система уравнений для вероятностей состояний имеет вид:
Pi (t) = ∑ Pk (t – τ) * pki (τ), i = 1,2, …, v (4.1)
где Pi (t) – вероятность нахождения системы состоянии i в момент времени t. Суммирование в (4.1) производится по всем возможным состояниям системы.
Уравнение (4.1) носит название уравнения Колмогорова – Чепмена и является основным при анализе систем массового обслуживания.
Уравнение Колмогорова – Чепмена относится к классу рекуррентных соотношений, позволяющих вычислить вероятность состояний Марковского случайного процесса на любом шаге (этапе) при наличии информации на предшествующем этапе. Существует много способов решения данной системы уравнений. Далее мы будем рассматривать так называемые установившиеся режимы, когда вероятность не зависит от времени.
Рассмотрим однозвенную полнодоступную коммутационную систему (ПД КС) с явными потерями.
Полнодоступной коммутационной системой называется система, в которой каждому входу доступен любой свободный выход
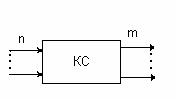
Системой с явными потерями мы называем систему, в которой вызов, получивший отказ в обслуживании теряется. Следовательно, в такой системе нет очереди.
Характеристиками качества обслуживания, QoS (Quality of Service), для системы с явными потерями служат следующие показатели:
а) вероятность потери вызова, поступившего в некотором промежутке времени, равная отношению средних интенсивностей потоков потерянных и поступивших вызовов в этом промежутке;
б) вероятность потери по времени в некотором промежутке, равная вероятности занятости в этом промежутке всех доступных источнику соединительных путей в требуемом направлении;
в) вероятность потери по нагрузке в некотором промежутке времени, равная отношению интенсивностей потерянной и поступившей нагрузок в этом промежутке времени;
Постановка задачи. Пусть на ПД КС с v выходами поступает простейший поток вызовов с параметром λ. Время обслуживания одного вызова случайная величина, распределенная по показательномуу закону со среднем значением, принятым за единицу времени (h = 1 у.е.в.). Дисциплина обслуживания – с явными потерями.
В символике Кендалла описываемая система может быть представлена как M/M/v/L. Задача впервые поставлена и решена Эрлангом.
Необходимо определить вероятности потери вызова, потери по времени и потери по нагрузке: Pв , Pt и Pн .
Пусть {x} – состояние системы, когда занято x линий из v, а P(x) – вероятность пребывания системы в состоянии x.
 |
Рисунок 4.1
На рисунке 4.1 представлена цепь Маркова. В рассматриваемом случае, λ1 = λ2 = . . . = λn = λ поскольку поток простейший и для него λ – const. Параметр μi - параметр освобождений, μi = х.
Тогда уравнение (4.1) в условиях статистического равновесия примет вид
λP(х-1)=хP(х) (4.2)
Интенсивность перехода в более высокое состояние, умноженное на вероятность пребывания системы в данном состоянии равна интенсивности перехода в более низкое состояние, умноженное на вероятность пребывания системы в данном состоянии.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
---------------------------------------------------
![]() ;
;
---------------------------------------------------
![]() ;
;
__________________________________
![]() . Прибавим Р(0) к
обеим частям.
. Прибавим Р(0) к
обеим частям.
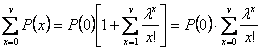
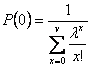
![]()
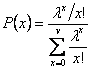 – первое распределение Эрланга.
– первое распределение Эрланга.
При решении практических задач ![]() (
(![]() ), где
), где ![]() – поступающая нагрузка.
– поступающая нагрузка.
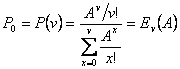 – первая формула Эрланга, в некоторых источниках её называют В – формулой
Эрланга.
– первая формула Эрланга, в некоторых источниках её называют В – формулой
Эрланга.
С помощью данной формулы при известных значениях поступающей нагрузки А и числа линий v можно вычислить вероятность потери поступающего вызова.
Данная формула табулирована. Для вычисления Ev(A) при больших значениях v используют рекуррентную формулу.
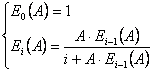 .
.
Итак, с помощью первой формулы Эрланга можно вычислить характеристики качества обслуживания полнодоступной системы с явными потерями, когда на неё поступает простейший поток вызовов. Среди перечисленных ниже характеристик главной является вероятность потери поступившего вызова:
а) вероятность потери по времени
Pt = Ev (A);
б) вероятность потери вызова
Pв = Ev (A);
в) вероятность потери по нагрузке
Pн = Ev (A);
г) пропускная способность определяется следующим образом (значение У табулировано)
У = А – Упот = А – А* Ev (A) = А(1 - Ev (A));
д) пропускная способность отдельных выходов при случайном занятии
![]() ,
,
при упорядоченном занятии
![]() .
.
Лекция 5. Обслуживание примитивного потока полнодоступной системой с явными потерями.
Цель лекции: ознакомление с методами расчета характеристик качества обслуживания полнодоступной системы с явными потерями, когда поступающий поток является примитивным и с методами расчета полнодоступной системы с ожиданием.
Содержание:
а) обслуживание примитивного потока;
б) формула Энгсета, характеристики качества обслуживания;
в) вторая формула Эрланга, характеристики качества обслуживания;
г) модели Кроммелина и Бёрке.
Постановка задачи. На полнодоступную систему с явными потерями поступает прмитивный поток вызовов. Время обслуживания вызовов распределено по показательному закону. Необходимо определить характеристики качества обслуживания вызовов, а именно вероятность потери вызова Рв , вероятность потери по времени Pt и вероятность потери по нагрузке Рн .
Параметр примитивного потока определяется по формуле
λк=α*(n-k) (5.1)
где λк - параметр примитивного потока;
α – интенсивность потока от одного источника;
n – общее число источников;
к – число занятых источников.
Рассмотрев цепь Маркова, аналогично решению задачи в предыдущей лекции, определим вероятность занятия линий
|
|
|
(5.2) |
Подставив в формулу (5.2) значение λк из формулы (5.1).Получим
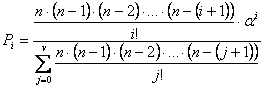 ;
;
Учитывая, что
![]() ;
;
преобразуем формулу к виду
|
|
(5.3) |
|
|
(5.4) |
Характеристики качества обслуживания QoS (Quality of Service) примитивного потока полнодоступной системой с явными потерями вычисляются по следующим формулам:
а) вероятность потери вызова по времени
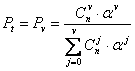 ;
;
б) вероятность потери поступившего вызова
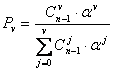
Значение ![]() можно определить по таблице:
можно определить по таблице: ![]() . Всегда имеет место
. Всегда имеет место ![]()
![]()
![]() ;
;
в) вероятность потери по нагрузке:
![]() ;
;
г) пропускная способность системы:
![]() , где
, где ![]() ;
;
д) интенсивность поступающей нагрузки
![]() ;
;
е) интенсивность потенциальной нагрузки
![]() .
.
Полнодоступная система с ожиданием.
Постановка задачи. На полнодоступную систему с ожиданием поступает простейший поток вызовов с параметрами λ. Длительность обслуживания распределена по показательному закону
![]() ,
,
где ![]() =
=![]() -
среднее время обслуживания.
-
среднее время обслуживания.
Если в момент поступления вызова все линии заняты, то вызов становится в очередь и ждет своего обслуживания. Вызовы из очереди выбираются в порядке поступления. В символике Кендалла имеем систему
M / M / v / r=∞ / FF.
Требуется определить вероятность ожидания поступившего вызова в очереди, математические ожидания длительности ожидания и длины очереди.
Задача в таком виде впервые была поставлена и решена Эрлангом. В задаче, поставленной Эрлангом, число мест ожидания r=∞.
Решение поставленной задачи позволяет оценить характеристики качества обслуживания полнодоступной системы с ожиданием:
а) вероятность ожидания в очереди для поступившего вызова
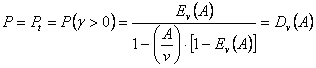 (5.5)
(5.5)
где где А – поступающая нагрузка, а (5.5) называется второй формулой Эрланга;
б) математическое ожидание длительности пребывания в очереди
![]() ;
; ![]()
в) математическое ожидание длины очереди
![]() .
.
Обслуживание вызовов простейшего потока при постоянной длительности занятия.
В полнодоступной системе с ожиданием величина поступающей нагрузки равна обслуженной, поскольку считается, что в этом случае потерянной нагрузки нет.
 |
Пусть {i} – состояние системы в момент времени t, v - число выходов в системе.
Если i <= v, то все вызовы находятся в обслуживании.
Усли i>v, то v-вызовов находятся в обслуживании, а r=i-v – ждут в очереди.
Известны три способа выбора вызова из очереди:
а) FIFO – упорядоченный выбор;
б) RANDOM – выбор из очереди является случайным;
в) LIFO – вызов поступивший последним обслуживается первым.
Модель Кроммелина.
На полнодоступную систему с ожиданием поступает простейший поток вызовов, время обслуживания одного вызова постоянно и равно h. Число мест ожидания r=∞. Способ выбора из очереди FIFO. В символике Кендалла -
M / D / v / r=∞ / FF.
Определить вероятность ожидания вызова в очереди, более чем допустимое время. Решение было найдено Кроммелином.
В инженерной практике при решении подобных задач используют диаграммы Кроммелина, которые отражают зависимость между условным временем t* и вероятностью ожидания сверх допустимого времени P(t*>γ*). При решении подобных задач необходимо определить η=А/v – интенсивность нагрузки поступающую на одну линию. Затем определяется t*=tд/h – где
tд – допустимое время ожидания.
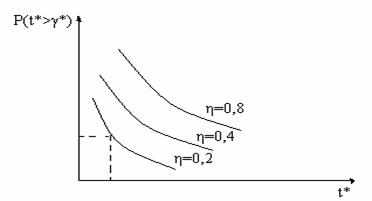 |
Рисунок 5.1
Модель Бёрке.
На полнодоступную систему с ожиданием поступает простейший поток вызовов, число линий на выходе v=1. Время обслуживания одного вызова постоянно и равно h. Число мест ожидания r=∞. Способ выбора из очереди RANDOM.
Определить вероятность ожидания вызова в очереди более чем допустимое время. Задача поставлена и решена Бёрке.
Результаты, полученные Бёрке, также представлены в виде диаграммы [1,2].
Модель системы с ожиданием при случайной длительности обслуживания, распределенной по показательному закону (модель Эрланга), достаточно хорошо описывает работу устройств разговорного тракта, если на них поступает простейший поток вызовов, которые обслуживаются с ожиданием.
Модель Берке соответствует условиям работы одного управляющего устройства, например, маркера координатной АТС.
Если вызовы обслуживаются несколькими управляющими устройствами, то используется модель Кроммелина.
Лекция 6. Неполнодоступные системы
Цель лекции: ознакомление студентов с неполнодоступными системами, с алгоритмом построения оптимальной схемы неполнодоступного включения и с методами их расчета.
Содержание:
а) структура неполнодоступных систем;
б) типы неполнодоступных схем;
в) цилиндр и матрица связности;
г) алгоритм построения оптимальной схемы;
д) методы расчета неполнодоступных схем.
Неполнодоступное включение линий – это простой экономичный способ объединения мелких полнодоступных пучков в один крупный неполнодоступный, позволяющий повысить использование линий.
Наибольшее распространение способ получил в электромеханических АТС. В настоящее время принципы неполнодоступного включения нашли применение в системах мобильной радиосвязи при динамическом распределении каналов между сотами. Поэтому метод актуален и сегодня, возможно будет использовании и в будущих системах телекоммуникаций.
Неполнодоступная коммутационная система состоит из g - нагрузочных групп, каждая из которых является полнодоступной системой из n-входов и D-выходов, и схемы неполнодоступного включения v линий.
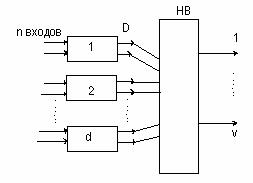
Рисунок 6.1
В такой коммутационной системе каждому из n входов доступны не все, а лишь D линий из V. Параметр D называется доступностью схемы.
Построить схему неполнодоступного включения означает определенным образом подключить v линий к D*g –выходам. При заданных параметрах g,D,V можно построить множество схем НД-го включения.
Необходимым условием для построения схемы НВ является неравенство: D<V<D*g.
Важной характеристикой схемы НВ включения является коэффициент уплотнения: γ=g*D/V, который показывает сколько в среднем выходов различных групп подключено к одной линии.
Неполнодоступные схемы бывают трех типов:
а) ступенчатая;
б) равномерная;
в) идеально – симметричная.
На практике чаще применяются первые две.
Ступенчатая схема - число выходов нагрузочных групп, обслуживаемых одной линией, различно и монотонно увеличивается с ростом номера выхода.
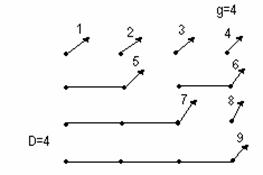 |
Равномерная схема - чсло выходов нагрузочных групп, обслуживаемых одной линией одинаково. Пропускная способность равномерной схемы выше, чем у ступенчатой.
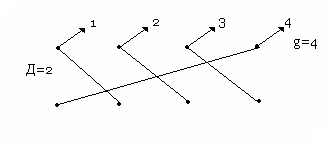 |
В неполнодоступных схемах используют три типа включения линий: прямое, перехваченное и со сдвигом.
При прямом включении объединяются одноименные выходы соседних нагрузочных групп
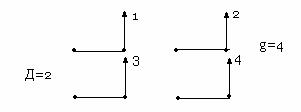 |
При перехваченном включении выходы каждой нагрузочной группы соединяются по возможности с одноименными выходами остальных нагрузочных групп.
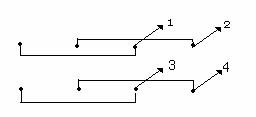 |
При включении со сдвигом выходы одной группы соединяются с разноименными выходами других групп. Сдвиг может быть с перехватом и без. Сдвиг с перехватом называется циклической схемой.
Цилиндр
Циклическая схема называется цилиндром, если выполняется условие V=g.
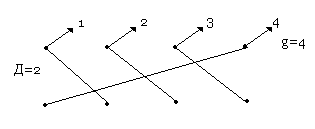 |
При этом коэффициент уплотнения равен γ=g* D /V= D .
Цилиндр – это элементарная, равномерная схема для которой V=g (число выходов совпадает с числом нагрузочных групп) Число D для цилиндра называется шагом, шаг указывает сколько групп подключено к одной линии.
Кроме размера, называемого шагом каждый цилиндр характеризуется наклоном.
|
|
Наклон =1
|
|
Наклон =2
Оптимальные неполнодоступные схемы.
Как было отмечено раньше, для любых g ,V и D можно построить несколько схем неполнодоступного включения. Но из них нужно выбрать оптимальную. То есть такую, которая обеспечит максимальную пропускную способность. Для проверки оптимальности схем используется матрица связности.
Матрица связности - это квадратная матрица порядка g
(число нагрузочных групп). Элементами главной диагонали матрицы являются числа
D - доступность. Элемент ![]() матрицы
равен числу связи между
матрицы
равен числу связи между ![]() и j нагрузочной группой. Очевидно, что
и j нагрузочной группой. Очевидно, что ![]() =
=![]() .
Матрица симметрична относительно главной диагонали.
.
Матрица симметрична относительно главной диагонали.
Пример. Даны пять нагрузочных групп, D =4, v=8.
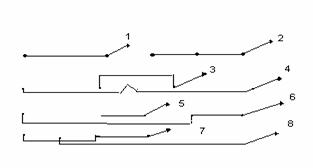
![]()
![]()
 Построим
матрицу связности.
Построим
матрицу связности.
Матрица связности является оптимальной, если для любых ее двух элементов, кроме элементов главной диагонали выполняется условие
![]() (6.1)
(6.1)
а также для любых bi = ∑ aij , i # j, выполняется
![]() <1
(6.2)
<1
(6.2)
В рассмотренном примере условие (6.2) не выполняется , поэтому матрица связности не является оптимальной.
Лекция 7. Алгоритм построения оптимальной схемы неполнодоступного включения и методы расчета.
Цель лекции: ознакомление студентов с алгоритмом построения схемы неполнодоступного включения (НВ) и с методами её расчета.
Содержание:
а) алгоритм построения оптимальной схемы неполнодоступного включения;
б) расчет схемы (НВ) с помощью третьей формулы Эрланга;
в) приближенные методы расчета схемы (НВ).
г) двухзвенные системы.
Алгоритм построения оптимальной схемы неполнодоступного включения.
Исходные данные: V, g и Д.
1) Определить шаг цилиндра, используемого в схеме:![]() ,
где
,
где ![]() -
целая часть. В схеме будут использованы r и (r+1)
- шаговые цилиндры.
-
целая часть. В схеме будут использованы r и (r+1)
- шаговые цилиндры.
2) Определить общее число цилиндров в
схеме: ![]() .
.
3) Определить число r-шаговых
цилиндров в схеме: ![]() .
.
4) Определить число (r+1)- шаговых
цилиндров: ![]()
5) Определить наклон цилиндра, его можно определить с помощью таблиц приложения учебника [1]. Необходимо подобрать такую последовательность цилиндров, чтобы матрица связности была оптимальна.
Методы расчета неполнодоступных схем.
Постановка задачи. Пусть на неполнодоступную систему поступает поток с параметрам λ. Требуется определить вероятность потери вызова.
Допустить, что число входов нагрузочной группы больше числа выходов, т.е. n>Д.
Введём следующие обозначения.
Пусть {x} – состояние системы, когда занято х линий из V.
P(x) – вероятность пребывания системы в состоянии х.
Когда х=Д или х>Д появляются потери.
Обозначим
через Тз=![]() -
коэффициент блокировки. Если х = Д , то заблокирована одна нагрузочная группа
-
коэффициент блокировки. Если х = Д , то заблокирована одна нагрузочная группа
Тз= ![]() =
1
=
1
Обозначим через Т(х)=Тз/g – вероятность того, что вызов поступит на блокированную группу.
Обозначаем через μ(х)= 1-Т(х) - вероятность того, что вызов поступит на неблокированную группу.
Построив цепь Маркова, составим уравнение статистического равновесия. Решение уравнения получим в виде

Полученное уравнение носит название третьего распределения Эрланга.
Вероятность потери легко определяется для идеально-симметричных систем (ИСС).
Идеально-симметричным
называется такое равномерное, неполнодоступное включение при котором каждой
нагрузочной группе доступна своя, отличная от других комбинация из Д линий, а
общее число нагрузочных групп g=![]() .
.
Общая вероятность потери вызова в неполнодоступной системе равна:
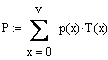
Если х<Д, то Т(х)=0 (ни одна из групп не будет заблокирована)
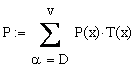
|


ИСС не получили практического применения, поскольку для их построения необходимо очень большое число нагрузочных групп. Однако, результаты их расчёта используются для оценки потерь в реальных системах неполнодоступного включения. ИСС используются в теоретических расчётах.
Приближенные методы расчёта неполнодоступных схем:
1) Упрощенная формула Эрланга
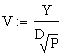
где V – число линий;
У – интенсивность обслуженной нагрузки;
D – доступность;
Р – вероятность потери.
2) Формула О’Делла
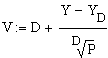
где V – число линий;
У – интенсивность обслуживания нагрузки;
D – доступность;
Р – вероятность потери;
УD – нагрузка, обслуженная полнодоступным пучком из D линий (определяется таблично).
3) Формула Пальма-Якобеуса
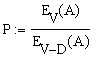
где EV (A) - первая формула Эрланга;
А – поступающая нагрузка;
Р - вероятность потери;
4) Модифицированная формула Пальма-Якобеуса.
Вместо поступающей нагрузки А берётся значение фиктивной поступающей нагрузки Аф, причём берется значение фиктивной нагрузки (Аф<А), удовлетворяющее равенству:
Аф=У/(1-Еv(Аф))
где У – обслуженная нагрузка.
Найденное Аф подставляется в формулу Пальма-Якобеуса
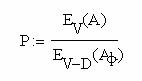 |
5) Инженерный метод: V=α*A+β , где
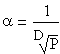 ,
, 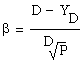
Двухзвенные коммутационные системы
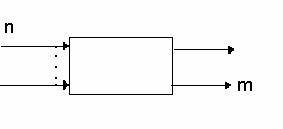 До сих пор
мы рассматривали полнодоступные и неполнодоступные однозвенные системы.
Перейдем к рассмотрению многозвенных систем. Одним из элементов многозвенной
системы является коммутатор. Он представляет собой элементарную полнодоступную
систему.
До сих пор
мы рассматривали полнодоступные и неполнодоступные однозвенные системы.
Перейдем к рассмотрению многозвенных систем. Одним из элементов многозвенной
системы является коммутатор. Он представляет собой элементарную полнодоступную
систему.
Обслуживание, поступающего на вход вызова заключается в подключении этого входа к свободному выходу в одной точки коммутации.
Рассмотрим структуру двухзвенной коммутационной системы
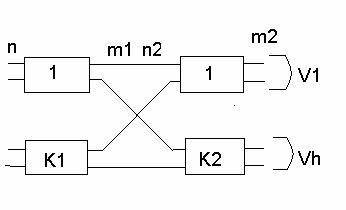
Введем следующие обозначения:
ni - число входов в коммутаторе i –го звена;
mi - число выходов в коммутаторе i–го звена;
Ki- число коммутаторов в i–м звене;
h- число направлений;
Vh - число выходов в h-м направлений;
qr - среднее число выходов в коммутаторе последнего звена, подключенных к r-му направлению.
Справедливы следующие соотношения
![]() -
число входов;
-
число входов;
![]() -
число выходов;
-
число выходов;
![]() - число промежуточных линий;
- число промежуточных линий;
![]() -
связность между звеньями;
-
связность между звеньями;
В двухзвенной коммутационной системе для установления соединения входа с выходом, требуется 2 точки коммутации и одна промежуточная линия. Таким образом соединительный путь содержит два звеньевых элемента - промежуточную линию и выход. Коммутационные схемы, содержащие два и более звеньев в соединительном пути, называются звеньевыми.
Лекция 8. Методы расчета двухзвенных и многозвенных систем.
Цель лекции: ознакомление студентов с основными методами расчета двухзвенных и многозвенных систем.
Содержание:
а) комбинаторный метод расчета двухзвенных систем;
б) метод эффективной доступности;
в) методы расчета многозвенных схем.
Комбинаторный метод расчета двухзвенных систем.
Метод разработан шведским ученым Якобеусом. Он предполагал, что потери вызова в двухзвенной схеме возникают в трех случаях:
а) если заняты все промежуточные линии, которые могут быть использованы для поступившего вызова;
б) если заняты все выходы в требуемом направлении;
в) когда возникают неудачные комбинации свободных промежуточных линий и свободных выходов.
Пусть вызов поступил на вход первого коммутатора, когда i промежуточных линий из m заняты. Если же выходы требуемого направления, соответствующие m-i линиям заняты, то появятся потери.
Обозначим
через ![]() -
вероятность занятия i промежуточных линий, принадлежащих одному коммутатору
первого звена. Вероятность занятия m-i выходов
обозначим через
-
вероятность занятия i промежуточных линий, принадлежащих одному коммутатору
первого звена. Вероятность занятия m-i выходов
обозначим через ![]() . Тогда
. Тогда
![]() (8.1)
(8.1)
Данная формула справедлива при выполнении следующих условий:
а)
события описываемое вероятностями ![]() и
и ![]() являются независимыми.
являются независимыми.
б) занятие промежуточных линий и свободных выходов является случайным и равновероятным.
Когда число источников вызовов является неограниченным, то поступающий поток считается простейшим, и искомые вероятности определяются как:
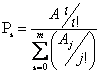 ,
,
![]() .
.
![]() Метод эффективной доступности.
Метод эффективной доступности.
Рассмотрим двухзвенную схему (рисунок 7.1). В первом звене k коммутаторов в каждом из них n входов и m выходов. В коммутаторе второго звена q выходов. Данная система является полнодоступной, так как любому входу доступен любой свободный выход, но в такой схеме в соединении точек коммутации участвют также промежуточные линии, которые могут быть заняты. Поэтому по сравнению с однозвенной полнодоступной системой расчёт вероятности потерь усложняется. Поскольку система прибывает в большом числе состояний. В настоящее время существует много приближенных методов расчёта двухзвенных схем. Рассмотри один из них.
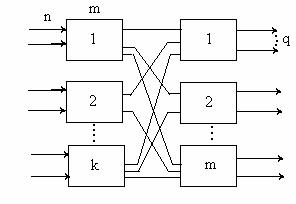
Рисунок 8.1
Метод эффективной доступности основан на понятии переменной доступности. В рассматриваемой схеме, если все промежуточные линии свободны, то каждому входу доступен любой выход. В этом случае
Dmax=m*q
При наличии i-занятых промежуточных линий доступность уменьшается на i*q
Di=m*q-i*q=(m-i)*q
Теперь определим минимальную доступность, когда n ≤ m
Dmin=m*q-(n-1)*q=(m-n+1)*q (8.2)
Таким образом,
Dmin ≤ Di ≤ Dmax
После этого рассматриваем двухзвенную систему как однозвенную неполнодоступную. Доступность такой системы назовём эффективной доступностью Dэ. Математически доказано, что Dэ < Ď, где Ď – математическое ожидание величины доступности, тогда имеем
Dmin < Dэ < Ď или
Dэ = Dmin + Θ*(Ď-Dmin) (8.3)
где Θ – коэффициент определяемый в зависимости от потерь из-за внутренних блокировок.
Ď=q*(m-Ym) (8.4)
где Ym – интенсивность нагрузки, обслуженной m промежуточными линиями.
Вычислив значения Dmin по формуле (8.2) и Ď по формуле (8.4), и подставив в формулу (8.3) полученные значения, получим эффективную доступность Dэ .
После этого расчёт вероятности потерь можно вести по приближенным формулам для неполнодоступных однозвенных схем, таких как метод О’Делла, Пальма - Якобеуса, инженерный и другие. В этих формулах вместо D нужно брать величину Dэ.
Многозвенные схемы.
Многозвенные коммутационные системы образуются за счет соединения ряда "строительных блоков".
Расчет показателей качества обслуживания для многозвенных систем – очень сложная задача. Существует (в дополнение к имитационному моделированию) ряд аналитических методов анализа соответствующих моделей. Выбор метода зависит от свойств используемых звеньевых систем (в частности, выполнения функций "сжатия" или "расширения").
Многозвенные системы могут рассматриваться как сети массового обслуживания (СеМО). Анализ СеМО – одна из самых сложных задач теории телетрафика. В АТС электромеханического типа используется алгоритм обслуживания вызовов с явными потерями. Поэтому необходимо рассматривать СеМО без возможности ожидания. Чаще рассматриваются СеМО с ожиданием. Они служат хорошими моделями для современных систем коммутации.
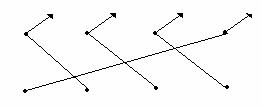
Один из способов анализа многозвенных схем – построение вероятностных графов. На шестом рисунке показаны возможные вероятностные графы для трехзвенной схемы.

Рисунок 8.2
Структура каждого графа отображает возможные пути установления соединений. Если для каждого ребра графа определить вероятность успешного установления пути, то между точками "А" и "В" можно определить возможные потери. Установим для графа, показанного в левой части шестого рисунка, такие условия:
![]() – вероятность успешного создания пути
между точками "А" и "2-1";
– вероятность успешного создания пути
между точками "А" и "2-1";
![]() – вероятность успешного создания пути
между точками "А" и "2-2";
– вероятность успешного создания пути
между точками "А" и "2-2";
![]() – вероятность успешного создания пути
между точками "2-1" и "3";
– вероятность успешного создания пути
между точками "2-1" и "3";
![]() – вероятность успешного создания пути
между точками "2-2" и "3";
– вероятность успешного создания пути
между точками "2-2" и "3";
![]() – вероятность успешного создания пути
между точками "3" и "В".
– вероятность успешного создания пути
между точками "3" и "В".
Вероятность успешного установления пути между точками
"А" и "3" – ![]() может быть определена по такой формуле:
может быть определена по такой формуле:
![]() .
.
Тогда искомая вероятность потери вызова между точками
"А" и "В" – ![]() рассчитывается следующим образом:
рассчитывается следующим образом:
![]() .
.
Эта вероятность равна единице при таких условиях: нет
путей между точками "3" и "В" (это эквивалентно ![]() ), нет путей между
точками "А" и "2-1", а также между точками "2-2"
и "3" (это равнозначно совпадению событий
), нет путей между
точками "А" и "2-1", а также между точками "2-2"
и "3" (это равнозначно совпадению событий ![]() ). Очевидно, что для
рассматриваемой модели наиболее важна доступность пути между точками
"3" и "В".
). Очевидно, что для
рассматриваемой модели наиболее важна доступность пути между точками
"3" и "В".
Также существуют такие методы расчета многозвенных схем, как КЛИГС и ЦИРБ [1,2].
Задачами теории телетрафика также являются способы распределения нагрузки, нормирование потерь на различных ступенях искания, измерения параметров нагрузки и потерь. С ними студентам необходимо знакомиться самостоятельно [1,2,3,4,5].
В заключении необходимо отметить, что в теории телетрафика появляются новые направления и методы. Характерными особенностями задач теории телетрафика, появившихся в связи с использованием новых технологий, является необходимость многоуровневого рассмотрения задач.
Развитие теории телетрафика можно рассматривать с различных позиций. Эволюция теории телетрафика связана с изменением принципов построения инфокоммуникационной системы. Основными движущими силами, стимулировавшими изменения этих принципов, можно считать:
а) интенсивное развитие новых видов коммуникаций, среди которых следует выделить сети мобильной связи и Internet;
б) изменение методов передачи и коммутации, обусловленное переходом на IP технологию.
Список литературы
1. Корнышев Ю.Н., Пшеничников А.П., Харкевич А.Д. Теория телетрафика. - М.: Радио и связь, 1996.
2. Крылов В,В., Самохвалова С.С. Теория телетрафика и её приложения. – СПб, 2005.
3. Корнышев Ю.Н., Фань Г.Л. Теория распределения информации - М.: Радио и связь, 1988.
4. Лагутин В.С., Степанов С.Н. Телетрафик мультисервисных сетей связи. - М.: Радио и связь, 2000.
5. Теория телетрафика. Методические указания к выполнению расчетно – графических работ. / Туманбаева К.Х. – АИЭС, 2007
Содержание
Лекция 1. Цели и основные задачи теории телетрафика ………………………..
Лекция 2. Потоки вызовов ………………………………………………………...
Лекция 3. Нагрузка ……………………………………………………………….
Лекция 4. Методы расчета однозвенной полнодоступной коммутационной системы с явными потерями …
Лекция 5. Обслуживание примитивного потока полнодоступной системой с явными потерями ……………
Лекция 6. Неполнодоступные системы ………… …………………………….
Лекция 7. Алгоритм построения оптимальной схемы неполнодоступного включения и методы расчета ……
Лекция 8. Методы расчетов двухзвенных и многозвенных систем …………..
Сводный план 2007 г., поз.196
Кумысай Хасеновна Туманбаева
ТЕОРИЯ ТЕЛЕТРАФИКА
Конспект лекций для студентов специальности 050719 – Радиотехника, электроника и телекоммуникации
Редактор Т.С. Курманбаева
Специалист по стандартизации Н.М. Голева
Подписано в печать __ . __. ___ Формат 60х84 1/16
Тираж ___ экз. Бумага типографская №1
Объем уч. – изд. л. Заказ __ . Цена _____