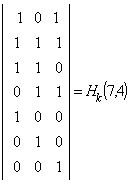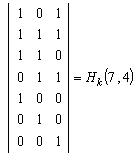МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН

 

Алматинский институт энергетики и связи

 

 

Кафедра автоматической электросвязи

 

 

 

 

 

 

 

А.Д. Джангозин, К.С. Чежимбаева

 

ПОМЕХОУСТОЙЧИВЫЕ ЦИКЛИЧЕСКИЕ КОДЫ

Учебное пособие

 

 

 

 

 

 

 

 

Алматы 2006

 

 

 

УДК 621.37:378 (075.8)

ББК 32.84 я 7

Д 40

Джангозин А.Д., Чежимбаева К.С.

 Помехоустойчивые циклические коды: Учебное пособие – Алматы: АИЭС, 2006.- 78с. 

 

 

 

В пособии даётся классификация разновидностей, характеристик и параметров корректирующих кодов, изложены принципы построения, формирования и обработки помехоустойчивых циклических кодов, их определение, свойства и эффективность, а также реализация кодирующих и декодирующих устройств этих кодов на базе  линейных переключательных схем. Приводятся примеры применения циклических кодов и линейных переключательных схем в радиотехнических системах при выполнении  курсовых  проектов. А также дан перечень рекомендуемой литературы.

Пособие предназначено для студентов всех форм обучения специальностей 380140 – Сети связи и системы коммутации и 380240 – Многоканальные телекоммуникационные системы.

 

Ил.21, табл.17, библиогр.- 20назв.

 

 

Рецензент: канд. техн. наук, доцент кафедры АТМ, КазНТУ, Бейсембаев А.А., канд. техн. наук, доцент АИЭС  Туманбаева К.Х.

 

 

 

 

 

Печатается по дополнительному плану издания министерство Образование и Науки Республики Казахстан  на 2006 г.

 

 

ISBN 9965-708-47-9

 

 

               

     

 

 ãАлматинский институт энергетики и связи, 2006г.

 

Введение

 

Динамичный переход нашей технологической цивилизации на цифровые системы обработки и передачи информации создает много проблем при проектировании современных систем информатики и телекоммуникации

В настоящее время, в связи с многократно возросшими объёмами передаваемой и сохраняемой информации, ужесточились требования к её достоверности. Одним из самых перспективных методов решения этой проблемы является помехоустойчивые кодирование на основе корректирующих кодов. В последнее время коды, исправляющие ошибки, нашли применение во многих системах передачи и хранения информации. Наиболее известные из них – это сотовые системы связи,  различные системы спутниковой телефонной связи, накопители информации на магнитных дисках, система звукозаписи на компакт - дисках и др. Во всех вышеприведенных примерах систем с помехозащищённой обработкой информации используются наиболее простые и эффективные циклические корректирующие коды, которые, наряду с простотой кодирования и декодирования, отличаются достаточно большой корректирующей способностью.

 

1 Классификация корректирующих кодов

 

Все корректирующие коды можно разделить на два класса: блочные и не­прерывные.

Блочные коды — коды, в которых каждому сообщению (или элементу) сопос­тавляется блок из n символов (кодовый вектор длиной n). Операции кодирования и декодирования в каждом блоке производятся отдельно.

Непрерывные коды представляют собой непрерывную последовательность символов, не подразделяемую на блоки. Такие коды называются также рекуррент­ными, цепными, свёрточными, конволюционными. Процессы кодирования и декоди­рования осуществляются непрерывно. Передаваемая последовательность образуется путем размещения в определённом порядке проверочных символов между инфор­мационными символами исходной последовательности.

Как блочные, так и непрерывные коды делятся на разделимые и нераз­делимые.

Разделимые коды предусматривают возможность чёткого разграничения ин­формационных и проверочных символов.

Неразделимые коды не предусматривают такой возможности и к ним от­носятся, например, коды с постоянным весом (КПВ).

Разделимые коды делятся, в свою очередь, на систематические (линейные или групповые) и несистематические (нелинейные).

Систематические коды характеризуются тем, что сумма по модулю 2 двух разрешённых кодовых комбинаций кодов этого класса снова даёт разрешённую ко­довую комбинацию.

Кроме того, в систематических кодах информационные символы, как прави­ло, не изменяются при кодировании и занимают определённые заранее заданные места. Проверочные символы вычисляются как линейная комбинация информаци­онных, откуда и возникло другое наименование этих кодов — линейные. Для сис­тематических кодов принимается обозначение [n, k] - код, где k — число информа­ционных символов в кодовой комбинации, n — общее число символов в коде.

Несистематические коды не обладают отмеченными выше свойствами и применяются значительно реже, чем систематические, в частности, в несиммет­ричных каналах связи. К этому классу кодов относятся такие, например, коды, как КПВ, итеративные, комбинационные и антифединговые [3].

Циклические коды составляют большую группу наиболее широко используемых на практике линейных, систематических кодов. Их основное свойство, давшее им назва­ние, состоит в том, что каждый вектор, получаемый из исходного кодового вектора пу­тём циклической перестановки его символов, также является разрешённым кодовым вектором. Принято описывать циклические коды (ЦК) при помощи порождающих по­линомов степени , где  -  число проверочных символов в кодовом слове. В связи с этим ЦК относятся к разновидности полиномиальных кодов.

Операции кодирования и декодирования ЦК сводятся к известным процедурам умножения и деления полиномов. Для двоичных кодов эти операции легко реализуются технически с помощью линейных переключательных схем (ЛПС), при этом получаются относительно простые схемы кодеков, в чём состоит одно из практических достоинств ЦК.

Коды Файра могут исправлять пакет ошибок длиной  и обнаруживать пакет ошибок длиной.[заметим, что в кодах Файра понятие кодового расстояния d не используется] 

Среди циклических кодов особое место занимает класс кодов, предложенных Боузом и Чоудхури и независимо от них Хоквингемом. Коды Боуза—Чоудхури-Хоквингема получили сокращённое наименование БЧХ- коды.

БЧХ- коды являются обобщением кодов Хемминга на случай исправления не­скольких независимых ошибок (q_и >1). Частными случаями БЧХ- кодов являются коды Файра, предназначенные для обнаружения и исправления серийных ошибок ("пачек" ошибок), код Голея - код, исправляющий одиночные, двойные и тройные ошибки (d_min=7), коды Рида-Соломона (РС- коды), у которых символами кода являются много­разрядные двоичные числа.

 

 

1.1            Полиномиальное определение циклических кодов и операции

                     с ними

 

 

Циклические коды являются частным случаем систематических, линейных [n, k]-кодов. Название ЦК получили из-за своего основного свойства: циклическая переста­новка символов разрешённой кодовой комбинации даёт также разрешённую кодовую комбинацию. При циклической перестановке символы кодового слова перемещаются слева направо на одну позицию, причем крайний справа символ переносится на место крайнего левого.

Если, например, А₁ - 101100, то разрешённой кодовой комбинацией будет и А₂ - 010110, полученная циклической перестановкой. Отметим, что перестановка про­изводится вместе с проверочными символами, и по правилам линейных кодов сумма по модулю 2 двух разрешённых кодовых комбинаций даёт также очередную разрешён­ную кодовую комбинацию.

Описание ЦК связано с представлением кодовых комбинаций в виде полино­мов (многочленов) фиктивной переменной "X". Для примера переведём кодовое слово А₁ = 101100 в полиномиальный вид

 

i	6	5	4	3	2	1
код	1	0	1	1	0	0

 

При этом А₁ (Х) = 1 X⁵ + 0  X⁴ + 1  X³ + 1  X² + 0 X¹ + 0 Х° = X⁵ + X³ + X².

 

Действия с кодовыми векторами, представленными в виде полиномов, произ­водятся по правилам арифметики по модулю 2, в которой вычитание равносильно сложению. Так, из равенства Хⁿ -1 =0 получаем Хⁿ =1. Прибавив к левой и правой час­тям по единице, имеем Хⁿ + 1=11=0. Таким образом, вместо двучлена Хⁿ -1 можно ввести бином Хⁿ +1 или 1 + Хⁿ, из чего следует, что Х^k Х^k = Х^k (1  1) = 0 и при по­следующих операциях с полиномами необходимо вычёркивать пары фиктивных пе­ременных X с одинаковыми степенями.

Приведём далее порядок суммирования (вычитания), умножения и деления по­линомов с учётом того, что операция суммирования осуществляется по модулю 2. В примерах используем вышеприведённые кодовые комбинации А₁(Х) = X⁵ + X³+ X²  и  А₂(Х) = X⁴ + Х²+ X.

Суммирование (вычитание):

 

А₁ +А₂ = А₁ - А₂= X⁵ + X⁴+ X³ +Х²+ Х²+ Х = Х⁵+Х⁴+ Х³+ X

 

или

  

 

А₁                101100

          

А₂           010110

                

                111010 = Х⁵+Х⁴+ Х³+ X

 

Умножение:

А₁ хА₂  = (Х⁵+ Х³+ Х²)(Х⁴+ Х²+X)= Х⁹+Х⁷ + Х⁶ +Х⁷+ Х⁵+Х⁴ + Х⁶+ Х⁴+Х³ = Х⁹+Х⁵+ Х³=1000101000

 

Деление:

 

   X⁵ + X³ + X²      X⁴ + X² + X

-                            X

   X⁵ + Х³+ Х²

 

     0     0      0     - остаток при делении   = 0.

 

Из последнего примера следует, что при циклическом сдвиге вправо на один раз­ряд необходимо исходную кодовую комбинацию поделить на X, а умножение на X экви­валентно сдвигу влево на один символ.

На основании того, что будет сказано далее о ЦК, нельзя установить теоретиче­ски те или иные свойства этих кодов, ряд приводимых ниже результатов придётся принять без соответствующих доказательств на веру. Однако, рассмотрев приведённые далее примеры, можно понять и освоить специфику и идеологию формирования и об­работки ЦК.

 

1.2            Порождающие полиномы циклических кодов

 

Формирование разрешённых кодовых комбинаций ЦК В₁(X) основано на пред­варительном выборе так называемого порождающего (образующего) полинома G(Х), который обладает важным отличительным признаком: все комбинации В₁(X) делятся на порождающий полином G(Х) без остатка, т. е.

 

= А_i(Х)    (при остатке  R(Х) = 0),                                             (1.1)

где А_i(Х)    — информативный полином (кодовая комбинация первичного кода, преоб­разуемого в корректирующий ЦК).

Поскольку, как отмечалось выше, ЦК относятся к классу блочных разделимых ко­дов, у которых при общем числе символов n число информационных символов в А_i(Х) равно k, то степень порождающего полинома определяет число проверочных симво­лов   r =n - k.

Из этого свойства следует сравнительно простой способ формирования разре­шённых кодовых комбинаций ЦК — умножение комбинаций информационного кода А_i(Х) на порождающий полином

 

В_i(Х).                                                                          (1.2)

 

В теории циклических кодов доказывается, что порождающими могут быть толь­ко такие полиномы, которые являются делителями двучлена (бинома) Хⁿ +1

 

 = Н(Х)    (при остатке R(Х) = 0).                                                (1.3)

 

Возможные порождающие полиномы, найденные с помощью ЭВМ, све­дены в обширные таблицы. Так, в [6] приведены таблицы G(Х) с записью полино­мов в восьмеричной системе счисления (при mod 8). В этом случае весовые коэффи­циенты k_i представляют три двоичных знака в соответствии со следующим кодом

 

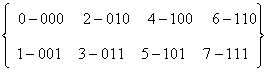  .                                                       (1.4)

Двоичные символы являются весовыми коэффициентами порождающих полиномов, коэффициенты восьмеричной системы счисления расположены слева от них с учётом того, что 0k_i7 (при mod 8). Например, 3425 обозначает много­член 10-й степени. В двоичной записи числу 3425 (mod 8) эквивалентно число 011100010101, и соответствующий многочлен равен X¹⁰ + X⁹ + X⁸ + X⁴ + X² + 1. Как видно из этого примера, восьмеричная система счисления для записи многочле­нов выбрана, в частности, из соображений экономии длины записи (бумаги) в три раза при больших объёмах табулированных значений, что подчёркивает извест­ный недостаток двоичной системы счисления.

Некоторые из порождающих полиномов приведены в таблице 1.

Следует отметить, что с увеличением максимальной степени порождающих полиномов г резко увеличивается их количество. Так, при r=3 имеется всего два полинома, а при r = 10 их уже несколько десятков.

Первый порождающий полином минимальной степени r=1, удовлетворяющий условию (1.3), формирует код с проверкой на чётность при двух информативных символах и одном проверочном, обеспечивающем обнаружение однократной ошибки, поскольку минимальное кодовое расстояние d_min=2. В общем случае ко­эффициент избыточности КПЧ минимален

                                                                                                     (1.5)

а относительная скорость кода - максимальна и равна

                                                                                              (1.6)

 

В связи с этим КПЧ иногда называют быстрым кодом.

 

Таблица 1 – Некоторые порождающие полиномы

r-степень полинома	Порождающий полином	Запись поли­нома по mod 2	Запись поли­нома по mod 8	n	k	Примечание
1	Х+1	11	3	3	2	Код с проверкой на чётность (КПЧ)
2	Х2+X+1	111	7	3	1	Код с повторением
3	Х3+Х2+1 Х3+Х+1	1101 1011	13    15	7 7	4 4	Классический код Хемминга
4	Х4+Х3+1 Х4+Х+1 Х4+Х2+X+1 Х4+Х3+Х2+1	11001 10011 10111 11101	31    23    27    35	15 15 7 7	11 11 3 3	Классический код  Хемминга  Коды Файра - Абрамсона
5	Х5+Х2+1 Х5+Х3+1 …..	100101 101001	45    51	31 31	26 26	Классический код  Хемминга
6	….. Х6+Х5+Х4+ +Х3+Х2+ Х1 +1 ….. ….	1111111	177	7	1	Код с повторением

 

Второй порождающий полином степени r =2, являющийся «партнёром» пер­вого   =  при разложении бинома с n = 3, определяет код с повторением единственного информативного символа к =1 ("0" или "1").

Отметим, что ЦК принадлежат к классу линейных кодов, у которых кодовые комбинации "000 ... 00" и "111... 11 " являются разрешёнными.

У кода с повторением возможности обнаружения и исправления ошибок без­граничны, поскольку число повторений l [1] определяет минимальное кодовое рас­стояние

                                           d_min=l.                                                              (1.7)

В общем случае коэффициент избыточности кодов с повторением кодовых комбинаций является максимально возможным:

и при увеличении l приближается к 1, а скорость (1.6) – минимальна

                                              .                                                 (1.8)

Таким образом, коды с проверкой на чётность и коды с повторением - до не­которой степени антиподы. Первый код очень быстр (всего один дополнительный символ), но зачастую "легкомыслен". Возможности второго кода с повторением по исправлению ошибок теоретически безграничны, но он крайне "медлителен" [7].

Следующие порождающие полиномы в таблице 1 со степенью r = 3 позволяют сформировать набор классических корректирующих кодов Хемминга (7, 4). Коды Хемминга также принадлежат к классу ЦК, однако при этом группа проверочных символов кода получается сразу "в целом" при делении информативной кодовой группы на порождающий полином, а не "поэлементно". Отметим, что два варианта, порождающих полиномов кода Хемминга (7,4), с записью по модулю 2 в виде 1101 и 1011 представляют собой так называемые двойственные многочлены (по­линомы).

Двойственные многочлены определяются следующим образом: если задан по­лином в виде

h(Х) = h₀ +h₁(Х) + h₂Х² + ... + h_r Х^r,

то двойственным к нему полиномом является

                              = h₀ Х^r +h₁ Х^r-1 +…+h,                                        (1.9)

т. е. весовые коэффициенты исходного полинома, зачитываемые слева направо, стано­вятся весовыми коэффициентами двойственного полинома при считывании их справа налево. Говоря образно, набор весовых коэффициентов "вывёртывается наизнанку".

Обратим внимание на то, что в полных таблицах, порождающих ЦК полиномов, двойственные полиномы, как правило, не приводятся [6].

Наряду с тем, что порождающие полиномы кода Хемминга (7,4) являются двой­ственными друг другу, они также являются неприводимыми.

Неприводимые полиномы не делятся ни на какой другой полином степени меньше r, поэтому их называют ещё неразложимыми, простыми и примитивными.

Далее в таблице 1 при значениях r = 4 и 5 попадают следующие классические ко­ды Хемминга (15, 11) и (31, 26). Порождающие их полиномы также являются двойст­венными друг к другу и неприводимыми. Напомним, что к классическим кодам Хемминга относятся коды, у которых n = 2^r-1, а k= 2^r-1-r [3], с минимальным кодовым расстоя­нием d_min⁼3, позволяющим исправлять однократные ошибки и обнаруживать двойные.

       При значениях r = 4 в таблице 1 попадают двойственные порождающие многочлены кода Абрамсона (7, 3), являющиеся частным случаем кодов Файра, порождающие поли­номы для которых имеют вид

 

                                         ,                                      (1.10)

где р(Х) - неприводимый полином.

Коды Абрамсона совпадают с кодами Файра, если положить с = 1. Число прове­рочных символов r = 4 определяет общее число символов в коде (значность кода), по­скольку для этих кодов n = 2 ^r-1- 1. Эти коды исправляют все одиночные и смежные двойные ошибки (т.е. серии длиной 2). Помещённые в таблице 1 коды Абрамсона (7,3) яв­ляются первыми циклическими кодами, исправляющими серийные ошибки (пакеты ошибок). В этом применении ЦК оказываются особенно эффективными. Обратим внимание на то, что при с =1 в (1.10) порождающими полиномами р(Х) являются двой­ственные полиномы X³ + Х²+ 1 и X³ + Х+ 1, образующие код Хемминга (7,4) при r = 3.

Серийные ошибки возникают в результате воздействия в канале передачи сооб­щений помех импульсного характера, длительность которых больше длительности од­ного символа. При этих условиях ошибки уже не независимы, а возникают пачками, об­щая длительность которых соответствует длительности помехи.

В заключение на основании данных таблице 1 приведём все возможные порождаю­щие полиномы для кодовых комбинаций с числом символов n = 7.

В соответствии со свойством (1.3) порождающих полиномов  бином X⁷ +1 рас­кладывается на три неприводимых полинома

 

,               (1.11)

 

каждый из которых является порождающим для следующих кодов

-   код с проверкой на чётность, КПЧ (7, 6);

- первый вариант кода Хемминга (7,4);

- двойственный (X) второй вариант кода Хемминга.

Кроме того, различные вариации произведений G_1,2,3(Х) дают возможность полу­чить остальные порождающие полиномы:

- код Абрамсона (7,3);

-двойственный  ;

- код с повторением (7,1).

Таким образом, для постоянного заданного значения п все возможные порож­дающие полиномы ЦК размещаются между кодами с проверкой на чётность (n, n-1) (r =1) и кодами с повторением (n, 1) (r =n -1), которые правомерно и называют "кодами антиподами".

При выборе применяемых в системах связи корректирующих кодов необходимо позаботиться о том, чтобы, во-первых, избыточность кода была минимальной, т. е. от­носительная скорость кода или эффективность кода была максимальной, а, во-вторых, техника кодирования и декодирования была по возможности проста.

 

1.3 Принципы формирования и обработки разрешённых кодовых комбинаций циклических кодов

 

На основании материалов предыдущего раздела можно дать следующее опреде­ление циклических кодов.

Циклические коды (ЦК) составляют множество многочленов В_i(Х) степени n-1 и менее (до r =n - k, где r - число проверочных символов), кратных порождающему (обра­зующему) полиному G(Х) степени r, который, в свою очередь, должен быть делителем бинома Xⁿ + 1, т. е. остаток после деления бинома на G(Х) должен равняться нулю.

Учитывая, что ЦК принадлежат к классу линейных, групповых кодов, сформулиру­ем ряд основных свойств, им присущих:

а) сумма разрешённых кодовых комбинаций ЦК образует разрешённую кодовую комбинацию

 

                                 В_i(Х)В_j(Х)= В_k(Х);                                               (1.12)

 

б) поскольку к числу разрешённых кодовых комбинаций ЦК относится нулевая комбинация 000...00, то минимальное кодовое расстояние d_min для ЦК определяется минимальным весом разрешённой кодовой комбинации

 

                                          D_min =W_min.                                                     (1.13)

 

в) циклический код не обнаруживает только такие искажённые помехами кодовые комбинации, которые приводят к появлению на стороне приёма других разрешённых комбинаций этого кода из набора N_о;

г) значения проверочных элементов r =n - k для ЦК могут определяться путем суммирования по модулю 2 ряда определённых информационных символов кодовой комбинации А_i(Х). Например, для кода Хемминга (7,4) с порождающим полиномом G(Х)=Х³+Х+1 алгоритм получения проверочных символов будет следующим [3]

r₁ = i₁ i₂i₃;

r₂ = i₂ i₃i₄ ;                                                                                        (1.14)

r₃ = i₁ i₂i₄.

 

Эта процедура свидетельствует о возможности "поэлементного" получения проверочной группы для каждой кодовой комбинации А_i(Х). В соответствии с (1.14) могут строиться кодирующие устройства для ЦК [3];

д) как было показано на примере в подразделе 1.1, умножение полинома на X при­водит к сдвигу членов полинома на один разряд влево, а при умножении на Х^r соответ­ственно, на г разрядов влево с заменой r младших разрядов полинома "нулями". Умно­жение полинома на X свидетельствует о том, что при этой процедуре X является "опера­тором сдвига". Деление полинома на X приводит к соответствующему сдвигу членов по­линома вправо с уменьшением показателей членов на 1. Процедура сдвига позволяет  исходной кодовой комбинации А_i(Х) после домножения её на Х^r дописать справа г про­верочных символов;

е) поскольку   разрешённые   кодовые   слова   ЦК   В_i(Х)   без   остатка   делятся на порождающий полином G(Х) с получением итога в виде информационной комбинации A_i(Х) (1.1), то имеется возможность формировать В_i(Х) на стороне передачи (кодирующее устройство) простым методом умножения (1.2).

Два последних свойства ЦК позволяют осуществить построение кодеров ЦК двумя методами: методом умножения и методом деления полиномов. Рассмотрим достоинства и недостатки этих методов с учётом вариантов построения декодеров ЦК, соответствую­щих этим методам.

Метод умножения позволяет при формировании разрешённых кодовых комбина­ций по алгоритму (1.2) использовать любой порождающий полином, лишь бы его макси­мальная степень была равна числу необходимых проверочных символов r.

Однако этот метод обладает двумя существенными недостатками.

Во-первых, при формировании ЦК методом умножения в полученной комбинации В_i(Х) в явном виде не содержатся информационные символы. Код получается неразде­лимым с "перетасованными" информативными и проверочными символами, что затруд­няет его декодирование, так как это приводит к необходимости применять метод макси­мального правдоподобия в декодирующем устройстве (ДУ).

Метод максимального правдоподобия (ММП) предполагает при исправлении ошибок принимаемую кодовую комбинацию отождествлять с той разрешённой, к которой принятая находится ближе всего. При таком непосредственном способе декодирования в памяти запоминающего устройства (ЗУ) декодера необходимо хранить все разрешённые кодовые комбинации N_о, что требует на стороне приёма больших объёмов ЗУ и большого времени обработки при декодировании. Эти обстоятельства являются вторым недостат­ком метода умножения при кодировании ЦК.

Исследования показывают [5-8], что хороший циклический корректирующий код с кратностью исправляемых ошибок g_u5 при относительной скорости кода В_k > 0,5, т. е. коэффициенте избыточности k < 0,5, должен иметь число информационных символов k > 40 . Это значение и приводит к техническим трудностям при процедуре декодирова­ния по ММП, сводящейся к сравнению принятой кодовой комбинации со всеми Nо раз­решёнными.

Для примера определим время декодирования Т_дк принятой кодовой комбина­ции, если число информационных символов в ней k= 40 и для сравнения использует­ся ЭВМ со скоростью 10⁷ операций в секунду. Будем полагать, что для сравнения при­нятой кодовой комбинации с одной из разрешённых достаточно одной операции на ЭВМ. Тогда для проведения

N_о = 2^k = 2⁴⁰ сравнений потребуется время декодирования

 

Т_дк     .   

Как видно из примера, задача декодирования простым перебором и сравнением непосильна даже для современных ЭВМ.

В соответствии с этим основным направлением в теории кодирования является поиск таких кодов и алгоритмов их формирования и обработки, для которых не требуется хранение в ЗУ разрешённых кодовых комбинаций. Эти задачи решаются, в частности, при построении кодеров на основе деления полиномов, а при декодировании — на ос­нове синдромного метода декодирования (СМД).

Метод деления полиномов позволяет представить разрешённые к передаче кодовые комбинации в виде разделённых информационных A_i(Х) и проверочных R_i(Х) символов, т. е. получить блочный код.

Поскольку число проверочных символов равно r, то для компактной их записи в последние младшие разряды кодового слова надо предварительно к A_i(Х) справа при­писать r "нулей", что эквивалентно умножению A_i(Х) на оператор сдвига Х^r (свой­ство (д) ЦК).

На практике предпочитают использование метода деления полиномов при по­строении кодеков, поскольку при этом имеется возможность представить кодовую комбинацию в виде разделённых информационных и проверочных символов

                             В_i(Х)= A_i(Х)Х^r +R_i(Х) ,                                               (1.15)

 

где R_i(Х)  — остаток от деления A_i(Х) Х^r /G(Х).

В алгоритме (1.15) можно выделить три этапа формирования разрешённых ко­довых комбинаций в кодирующем устройстве:

а)    к   комбинации   первичного   кода   A_i(Х) дописывается   справа   г   нулей, что эквивалентно умножению A_i(Х) на Х^r;

б)     произведение     делится    на    соответствующий    порождающий полином G(Х) и определяется остаток R_i(Х), степень которого не превышает r -1, этот ос­таток и даёт группу проверочных символов;

в) вычисленный остаток присоединяется справа к .

Пример 1. Рассмотрим процедуру кодирования по алгоритму (1.15): для кодо­вой комбинации А=1001 сформировать кодовую комбинацию циклического кода (7,4).

В заданном ЦК n=7, k = 4, r = 3 и из таблицы 1.1 выберем порождающий полином G(Х) = X³ + X + 1 (код Хемминга). Выполним три необходимые операции для получения кодовой комбинации ЦК согласно алгоритму (1.15)

 ~ X³ + 1 , (знак " ~ " - тильда - означает соответствие).

а)   = (Х³ + 1) Х³ = Х⁶+Х³ ~ 1001000, (n=7);

 

б)  A_i(Х) Х^r /G(Х) =   X⁶       + X³         X³ + X + 1

                                   +                     X³ + X

                                    X⁶ + X⁴ + X³    

                                            X⁴

                                    +

                                          X ⁴ + Х²+ X

 

                                                  Х²+Х      – остаток Р_i(Х)= Х²+Х  ~110;                                

 

в) В_i(Х) = A_i(Х) Х^r +R_i(Х)= 1001110-итоговая комбинация ЦК.

 

Синдромный метод декодирования (СМД) предполагает в ДУ принятую кодовую комбинацию поделить на порождающий полином. Если принятая комбинация являет­ся разрешённой, т. е. не искажена помехами в канале связи, то остаток от деления бу­дет нулевым. Ненулевой остаток свидетельствует о наличии в принятой кодовой ком­бинации ошибок, остаток от деления и называется синдромом.

Термин "синдром" заимствован из медицинской практики (от греч. вместе бе­гущий) и означает сочетание (комплекс) симптомов болезни, характерное для опреде­лённого заболевания. В теории кодирования синдром, который также называют опознавателем ошибки, обозначает совокупность признаков, характерных для определённой ошибки. Для исправления ошибки на стороне приёма необходимо знать не только факт её существования, но и её местонахождение, которое определяется по установленно­му виду вектора ошибки z(Х).

После передачи по каналу с помехами принимается кодовое слово

                                    В_i(Х) =В_i(Х) + z(Х),                                             (1.16)

где В_i(Х) - передаваемая кодовая комбинация; z(Х) — полином (вектор) ошибки, имеющий степень от 1 до n -1.

При декодировании принятое кодовое слово делится на G(Х)

                                       ,                                           (1.17)

где остаток от деления S_i(X) и является синдромом.

Если при делении получается нулевой остаток S_i (Х) = 0, то выносится решение об отсутствии ошибки z(Х) = 0. Если остаток (синдром) ненулевой S_i(Х)0, то выносится решение о наличии ошибки и определяется шумовой вектор (полином) z(Х), а затем -передаваемое кодовое слово, поскольку из (1.16) следует

                                       В_i(Х) = В_i(Х) +z(Х).                                          (1.18)

Всякому ненулевому синдрому соответствует определённое расположение (кон­фигурация) ошибок. Взаимосвязь между видом синдрома и местоположением оши­бочного символа находится довольно просто. Достаточно в любую разрешённую кодо­вую комбинацию ввести ошибку и выполнить деление на G(Х). Полученный остаток (1.17) - синдром и будет указывать на ошибку в этом символе.

В качестве примера для ЦК Хемминга (7,4), позволяющего исправлять одно­кратную ошибку при d_min= 3 (таблица 1), взаимосвязь между синдромом и ошибочным символом для двух возможных порождающих полиномов кода (7,4) приведена в таблице 2. Пользуясь этой таблицей, можно найти местоположение ошибки и исправить её.

Для параметров рассмотренного ранее примера 1, где была показана процедура кодирования кодовой комбинации A_i = 1001 при использовании порождающего полинома G(Х) = X³ + X +1 для кода Хемминга (7,4), исправляющего однократную ошибку, приве­дём в примере 2 процедуру декодирования принятой с помехой кодовой комбинации.

Пример 2. Принятая кодовая комбинация ЦК (7,4) имеет вид В_i'(Х)=1011110. Определить и исправить ошибку в В_i(X), если она имеется.

Выполним три необходимые операции, проводимые при декодировании:

 

Таблица 2

Номер символа  комбинации со  старшего разряда	Ошибочный сим­вол полинома комбинации	Синдром для порождающего полинома G(Х)=X3 +Х+1	Синдром для порождающего полинома G(Х)= X3 + X2 +1	Шумовой вектор z(Х)
7 6 5 4 3 2 1	X6 X5 X4 X3 X2 X1 X0	cм. 1.29	см. 1.29	1000000 0100000 0010000 0001000 0000100 0000010 0000001
	Нет ошибки	000	000	0000000

 

а) в соответствии с алгоритмом (1.17) производим деление

 

B_i(X)/ G(Х) = X⁶ + X⁴ + X³+X² +X    X³+X +1   

                      X⁶ + X⁴ + Х³                              X³

                                              

                                              Х² + Х    -    остаток  R(Х) = Х² + Х~110,

 

отметим, что совпадение остатков в примере 1 и 2 — чисто случайное, в примере 1 остаток являлся проверочной группой кода, а в примере 2 - синдромом;

б)  по полученному синдрому 110 в  соответствующем опознавателе синдрома (де­шифраторе   синдрома,   локаторе   ошибки)   определяем   вид   шумового   вектора z(Х)    0010000 (таблица 2);

в)  воспользовавшись     алгоритмом     (1.18),     исправляем     принятую  кодовую комбинацию В_i' (X) и получаем переданную комбинацию В_i(X):

В_i (X) = В_i (X) + z(Х) =   1011110

                                         +

                                         0010000

 

                                         1001110 - исправленная комбинация на выходе ДУ с инвертированием неверно принятого символа.

Число проверочных символов r =n - k определяет число исправляемых ошибок. Значение r должно быть достаточным для получения необходимого числа синдро­мов (опознавателей ошибок). Так, для исправления всех одиночных (однократных) ошибок необходимо = n +1 синдромов, так как шумовой вектор может принимать сле­дующие n значений:

000...01, 000...10,..., 001...00, 010...00, 100...00,

кроме того, необходим один синдром для определения факта безошибочного приёма ко­довой комбинации Sо = 000...00. Таким образом, для двоичных кодов при необходимо­сти исправления всех однократных ошибок требуется выполнение соотношения

= 2^n-k = 2^r = n+1 ,                                                                              (1.19)

поскольку синдром формируется на месте г проверочных разрядов кода.

Плотноупакованные коды – такое название получили коды, у которых соблюдаются точное равенство в (1.19) числа необходимых синдромов для исправления ошибок заданной кратности. Вследствие уникальности таких кодов плотноупакованные коды называют также "совершенными" или "оптимальными". К таким кодам относятся коды Хемминга, которые при минимальном кодовом расстоянии d_min =3 обеспечивают  исправление всех однократных ошибок, поскольку у классических кодов Хемминга число символов n= 2^r-1 удовлетворяет условию (1.19).

В общем случае при необходимости исправления всех независимых ошибок кратности до q_и включительно требуемое число синдромов определяется выражением

 

                                     ,                   (1.20)

где - число сочетаний из n по  I, причем , так как 0!=1.

С учетом (1.19) и (1.20), можно получить выражение для оценки числа проверочных символов r при необходимости исправления q_и – кратных ошибок в принятых кодовых комбинациях

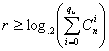                                                 .                                        (1.21)

Занимаясь поиском плотноупакованных кодов ("код без потерь"), М. Голей заметил ( опубликовано  в1949 году), что

 

                                     , 

а это означало, что может существовать плотноупакованный двоичный (23,12) код, удовлетворяющий условию (1.20), исправляющий все кодовые комбинации с тремя или менее ошибками. Он показал, что такой код действительно существует, и в дальнейшем этот код получил его имя.

Код Голея относится к классу ЦК с порождающими двойственными (дуальными) полиномами (4.9)

                             G(Х) = Х¹¹+Х¹⁰+Х⁶ +Х⁵+Х⁴+Х²+1;                          (1.22)

                             (Х) = Х¹¹+Х⁹+Х⁷ +Х⁶+Х⁵+Х+1.

Простыми вычислением проверяется, что

,

в связи с чем в качестве порождающего полинома ЦК Голея (23,12) можно использовать как G(Х), так и  (Х).

Код Голея, гарантированно исправляющий ошибки с кратностью не менее трех включительно, обладает минимальным кодовым расстоянием d_min=2q_u+1=7, что, как правило, указывается в маркировке кода (23,12,7). Добавление к этому коду общей проверки на четность по всем позициям увеличивает на единицу как общую длину кода, так и минимальное кодовое расстояние d_min=8.

Расширенный код Голея, имеющий маркировку (24,12,8), состоит из 12 информационных символов и 12 проверочных, т.е. представляет собой код, обладающий скоростью ½ и избыточностью, также равной ½.

Обратим  внимание на то, что плотноупакованные коды Хемминга и Голея – циклические, которые принадлежат классу двоичных линейных кодов. Общим для линейных двоичных кодов является наличие в качестве разрешенного нулевого кодового слова 000…00, что приводит к тому, что минимальный вес w_min ненулевого разрешенного кодового слова равен минимальному кодовому расстоянию d_min (1.13).

В общем случае вес кодовых комбинаций может принимать различные значения, и совокупность чисел кодовых комбинаций с постоянным весом N_w определяют как распределение весов кода или как спектр весов кода. Распределение весов в коде Голея (23,12,7) следующее

;  ;  ;  ,

а в расширенном коде Голея –

; ;  .                                                  (1.23)

 

Кодовые слова с весом 12,8 и 16,  выделенные из кода (24,12,8), образуют КПВ максимальной мощности.

К сожалению, кроме кодов Хемминга (d_min=3, q_и=1) и кода Голея (23, 12, 7), пока не найдено других совершенных, плотноупакованных кодов, число синдромов у которых точно соответствует требуемому значению для гарантированного исправления ошибок заданной кратности.

 

1.3.1     Построение порождающих и проверочных матриц

           циклических кодов

 

Наряду с полиномиальным способом задания кода, структуру построения кода можно определить с помощью матричного представления. При этом в ряде случаев проще реализуется построение кодирующих и декодирующих устройств ЦК.

Рассмотрим варианты формирования и обработки ЦК, заданных в виде порож­дающих и проверочных матриц, на конкретном примере ЦК Хемминга (7,4), восполь­зовавшись выражением (1.11), в котором определены двойственные (дуальные) поро­ждающие полиномы кода

Х⁷+1 = (X +1)  (Х³+Х+1)  (Х³+Х²+1),

что соответствует кодам (7, 6); (7, 4); (7, 4).

Пример 3. Задан ЦК (7,4) дуальными порождающими полиномами

G(7,4) = Х³+Х+1   и    (7,4) = X³ +Х²+1.

Составить порождающие матрицы для формирования разрешённых кодовых комбинаций и проверочные матрицы для получения синдромов.

Первой строкой в матрице записывается порождающий полином (в двоичном представлении) с доумножением его на оператор сдвига Х^r для резервирования места под запись r = 3 проверочных символов. Следующие

 k -1 строк матриц получаются путём последовательного циклического сдвига базового кодового слова матрицы G и  на од­ну позицию вправо, поскольку при этом по определению ЦК также получаются разре­шённые к передаче кодовые комбинации

 

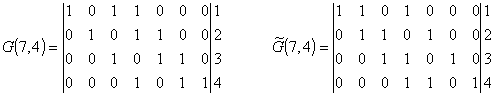                 (1.24)

 

Однако в таком виде эти порождающие матрицы размерностью k х n (n столбцов, k строк) могут образовать только неразделимый ЦК, т. е. код, у которого не определены жёстко места информационных и проверочных элементов. Для построения порождаю­щей матрицы, формирующей разделимый блочный код, необходимо матрицу преобра­зовать к каноническому виду путём простых линейных операций над строками.

С учётом свойства ЦК (1.12) каноническую форму матрицы можно получить пу­тём сложения ряда разрешённых кодовых комбинаций. Каноническая матрица должна в левой части порождающей ЦК матрицы содержать единичную диагональную квад­ратную подматрицу порядка"k" для получения в итоге блочного ЦК. С этой целью для получения первой строки канонической матрицы G_k(7,4) необходимо сложить по моду­лю 2 строки с номерами 1, 3 и 4 матрицы G(7, 4), а для матрицы (7,4); —строки с номерами 1, 2 и 3 матрицы (7,4). В этом случае в матрицах (1.24) в первых строках ос­таются "1" только на первых позициях, а остальные "k-1" символов заменяются "0", что и соответствует первым строкам единичных подматриц порядка "k". Нормирование по­следующих трёх строк канонических матриц производится путём соответствующего суммирования строк матриц (1.24).

В итоге имеем следующий вид дуальных канонических матриц

 

 

       

 

 

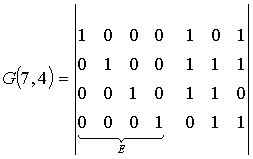
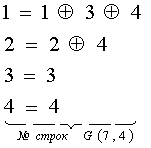
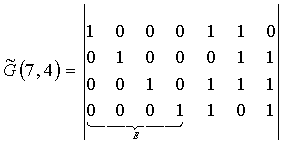
                      (1.25)              

 

Процесс кодирования первичных кодов на стороне источника сообщений сводится к умножению информационных посылок, представленных в виде векто­ров (Х),  на соответствующую порождающую каноническую матрицу

 

                                       .                                             (1.26)

      

Эта процедура позволяет получить блочные коды Хемминга "в целом", т, е. получить проверочную группу символов r₁, r₂, r₃ сразу после выполнения операции (1.26). Наряду с этим, имеется возможность формировать символы проверочной группы поэлементно, где 3 проверочных символов задавались следующими равенствами проверки на чётность

r₁ = i₁ i₂i₃;               r₁ = i₁ i₃i₄;

r₂ = i₂ i₃i₄;                r₂ = i₁ i₂i₃;                                                  (1.27)                                                     

          r₃ = i₁ i₂i₄;                r₃ = i₂ i₃i₄.                   

                                                  

Обратим внимание на то, что алгоритм (1.27) просто получается из рассмотрения порождающих коды Хемминга матриц (1.25), в которых проверочные подматрицы, содер­жащие 3 столбца (r-1, r₂, rз), имеют символы" 1" в тех строках, номера которых совпадают с маркировкой информационных символов i      в равенствах (1.27) ((1.14)).

При матричном варианте обработки принятых кодов на стороне получателя сообщений для получения синдрома необходимо принятую, возможно искажён­ную в канале, кодовую комбинацию  умножить на проверочную матрицу Н(Х)

                                          =-Н(Х).                                             (1.28)

Процедура построения проверочной матрицы Н достаточно подробно рас­смотрена в [3]. Заметим, что матрица Н с размерностью n х r может быть полу­чена из порождающей матрицы канонического вида (1.25) путём дополнения про­верочной подматрицы единичной матрицей размерности r х r, что даёт следую­щий вид дуальных проверочных матриц

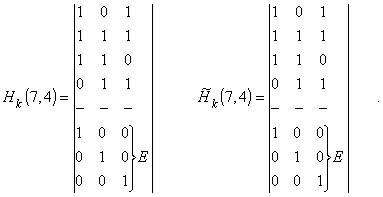                               (1.29)

По определённому с помощью полученного синдрома (1.28) соответству­ющему шумовому вектору исправляются ошибки (1.18).

Интересно отметить, что в таблице 2, в которой рассмотрена связь между син­дромом и шумовым вектором для кода (7,4), колонки с синдромами дуальных по­рождающих полиномов полностью совпадают с (1.29).

В ЦК Хемминга (n , k) все проверочные r = n - k разряды размещаются в конце кодовой комбинации и, как отмечалось, формируются «в целом». При по­элементном получении проверочных символов (1.27) целесообразно, чтобы каж­дый синдром представлял собой двоичное число, указывающее на номер разря­да, в котором произошла ошибка. Коды, в которых синдромы (опознаватели) со­ответствуют указанному принципу, и предложил впервые Хемминг. В этом случае для кода (7, 4) проверочные символы r₁,, r₂, r₃ (таблица 2) размещаются на первой, второй и четвертой позициях кодовой комбинации, отсчитываемых справа налево. Такое построение кодов упрощает декодирующее устройство на стороне получа­теля сообщений.

1.4 Укороченные циклические коды

 

Поскольку ЦК порождаются делителями бинома Хⁿ +1 (1.3), то для большей части значений n и k имеется относительно мало кодов, удовлетворяющих всем свойствам, присущим ЦК (подраздел 1.3). Поэтому естественно попытаться найти среди линейных кодов такие, которые хотя и не являются в действительности циклическими, обладают похожей математической структурой и столь же легко реализуются.

При разработке систем передачи информаций, работающих с дискретными сигналами в предположении необходимости исправления (обнаружения) ошибок, число информативных символов k_Σ выбирают, как правило, таким, чтобы оно было кратным длине первичного кода k₁

, где

а значение где число проверочных символов должно удовлетворять заданному значению кратности обнаруживаемых и исправляемых ошибок. В частности, ЭВМ обычно обмениваются машинными словами в виде байтов, состоящих из восьми символов (k1=8).

При этом n_Σ и k_S часто не совпадают с табулированными в [6] ЦК. В этом случае по таблице [6] находят ЦК, который соответствует обоснованному значению r = n-k для классического, табулированного ЦК, а затем уменьшают n и k_S до n - ℓ и k_S = k - ℓ, получая укороченный ЦК.

Укороченные циклические коды (УЦК) получают из полных ЦК, используя для передачи информаций только кодовые комбинаций полного кода, содержащие слева ℓ нулей. Это дает возможность построить УЦК (n - ℓ, k - ℓ) путем исключения первых ℓ столбцов и ℓ строк из порождающей матрицы (1.24). Полученный код не будет строго циклическим, так как циклический сдвиг не всегда будет приводить к получению очередной разрешённой кодовой комбинации. Поэтому укороченные (усечённые) ЦК часто называют псевдоциклическими или квазициклическими.

Укороченные ЦК сохраняют основные свойства классических ЦК

(подраздел 1.3), к числу которых относятся следующие:

а) УЦК образуются делителями бинома Хⁿ +1, порождающими полиномами G(X), такими же, как у полных ЦК;

б) УЦК относятся к классу линейных (групповых) кодов, для которых сумма разрешённых кодовых комбинаций УЦК также являются разрешённой кодовой комбинацией (4.12);

в) УЦК обладает таким же минимальным (конструктивным) кодовым расстоянием, как у исходного ЦК, и таким же числом проверочных символов (4.21), но не может быть плотноупакованным;

г) УЦК исправляет такое же число ошибок, что и ЦК, т.е. имеет такую же кратность обнаруживаемых и исправляемых ошибок;

д) при построении кодеков УЦК используются те же схемы, что и для классических ЦК, при условии, что каждому усечённому коду спереди приписывается ℓ нулей.

Специфику построения УЦК рассмотрим на следующем примере

 

Пример 4. Передаче подлежит сообщение, закодированное стандартным кодом МТК-2 с числом информационных символов k=2. Обеспечить у получателя сообщений исправление однократной ошибки в кодовом слове.

Однократная ошибка исправляется при минимальном кодовом расстоянии dmin=3, этому значению удовлетворяют коды Хемминга (7,4), (15,11), (31,26)...(таблица 1). Код (7,4) с числом информационных символов k=4 не удовлетворяет условию примера при необходимости передачи k=5. Этому условию удовлетворяет следующий по порядку код Хемминга (15,11), если из общего числа символов n=15 и числа информативных символов k=11 вычесть одно и то же число е=6 (исключение первых e столбцов и е строк порождающей код матрицы с размерностью k x n), получаем УЦК (9,5), удовлетворяющий условию примера k=5, dmin=3,с числом проверочных символов r=4.

Для опорного ЦК (15,11) бином Хn+1 раскладывается на следующие неприводимые полиномы

 

,

 из которых для построения кода r=4 можно выбрать любой из трёх последних. Выберем в качестве порождающего полинома G(X) = X4+X+1 и на основе матрицы этого ЦК (15,11) покажем, как осуществляется отсечка

 

(1.30)

 

 

 

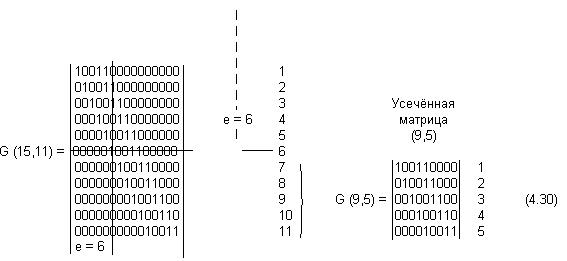
Приведём усечённую матрицу G(9,5) к каноническому виду путём соответствующего суммирования строк по аналогии с проводимыми преобразованиями с матрицами (1.24) и (1.25) и получим соответствующие равенства проверки на чётность при поэлементном формировании усечённого кода (9,5) (см. (1.27) в качестве аналога

(1.31)

    

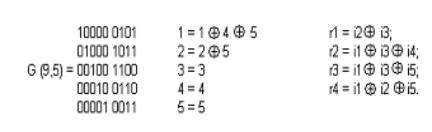
(1.31)

Таким образом, УЦК (9,5) полностью удовлетворяет условиям примера 4.

 

1.5 Структурный состав линейных переключательных схем

 

Цикличность перестановок при формировании разрешенных кодовых комбинаций ЦК лежит в основе техники построения кодирующих устройств (КУ) и декодирующих устройств (ДУ) циклических кодов. Эта техника применяет сдвигающие регистры (СР) в виде триггерных цепочек с теми или иными обратными связями. Такие СР называют также многотактными линейными переключателями схемами (ЛПС) и линейными кодовыми фильтрами Хаффмана, который первым начал изучение ЛПС с точки зрения линейных фильтров. Кстати, Д.Хаффман является и автором принципа, состоящего в том, что «две точки зрения лучше, чем одна», получившего широкое применение в настоящее компромиссное время.

При построении ЛПС используется 3 вида элементарных устройств:

а) сумматор, имеющий, как правило, два входа и один выход, причем для двоичных кодов суммирование осуществляется по модулю 2;

б) ЗУ, имеющее один вход и один выход и представляющее собой одну тригерную ячейку (один разряд) СР;

в) устройство умножения на постоянную величину, имеющее один вход и один выход. Эти устройства изображаются на схемах так, как показано на рисунке 1.  

Рисунок 1

 

Линейными переключательными схемами с конечным числом состояний называются любые схемы, содержащие конечное число сумматоров, устройств памяти и устройств умножения на константу, соединённых любым допустимым способом.

В бинарном случае сумматор (равно как и вычитатель) представляет собой логический элемент «исключающее ИЛИ», а устройство памяти является устройством задержки (D-триггером). Устройства задержки, включенные последовательно, составляют СР, в ячейках которого выходной символ совпадает с входным символом в предшествующий момент времени. К СР подводится шина сдвига, с помощью которой тактовыми пульсами (ТИ) осуществляется продвижение по разрядам СР записанной кодовой информации. Как правило, шина сдвига не показывается на схемах с изображениями ЛПС.

При формировании и обработке двоичных ЦК введение в схему ЛПС умножителя на константу, равную 1, эквивалентно введению дополнительного соединения, а умножитель на константу, равную 0, соответствует отсутствию такого соединения.

Предполагается, что на вход СР, входящего в состав ЛПС, кодовая комбинация подается последовательно, с периодичностью, равной периоду следования ТИ в шине сдвига. Аналогично, последовательно во времени появляются кодовые символы на выходе СР. когда входом или выходом является многочлен, представляющий при двоичной обработке набор «1» и «0», то на входном или на выходном конце СР появляются только коэффициенты («1» или «0»), начиная с коэффициентов высших порядков. Это обуславливается тем, что при делении у делителя сначала должны быть обработаны коэффициенты высших порядков.

В последующих разрядах описываются схемы, используемые для умножения и деления любых многочленов на некоторый фиксированный, в частности, порождающий полином.

 

1.6 Умножение полиномов на базе ЛПС

 

Cхема, изображенная на рисунке 2, используется для умножения любого полинома на входе

          .

На фиксированный полином, в частности, порождающий:

        

предполагается, что первоначально все разряды СР содержат нули, а на вход коэффициенты полинома А(Х) поступают, начиная с коэффициентов высших порядков (со старших разрядов), после чего следует r нулей.

Первый вариант ЛПС для умножения полиномов

 

 

 

 

 

 

 

 

 

 

	выход

 

 

 

 

 

 

 

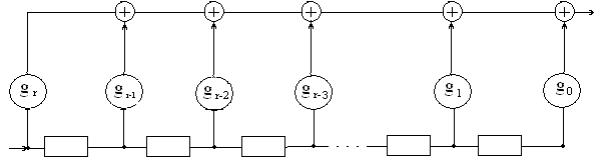
вход

 

 

 

Рисунок 2

 

Произведение полиномов

        

.                                     (1.32)

 

Когда на входе ЛПС появляется первый (старший) коэффициент полинома А(Х), то он умножится в первом устройстве умножения на g_r и появится на выходе уже как результат перемножения а_кg_r, проследовав «транзитом» через все схемы суммирования по модулю 2. Кроме того, а_к запишется в первом разряде СР, а все остальные разряды СР будут содержать нули. Спустя единицу времени, с появлением в шины сдвига второго ТИ на входе появится а_к-1, который перемножится с g_r  и сложится в первой схеме суммирования по модулю 2 с а_кg_r-1, сформировав на выходе сумму а_к-1g_r+a_kg_r-1;

т.е.   второй коэффициент произведения А(Х)G(X). Дальнейшие операции производятся аналогичным образом. После r+k сдвигов СР полностью обнуляется и на выходе появляются значения a₀g₀, равные первому коэффициенту произведения (1.32), так что произведение на выходе ЛПС последовательно получается в полном составе.

Второй вариант умножения полиномов показан на рисунке3.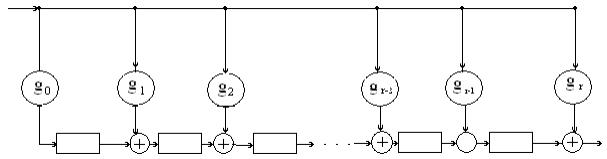

	вход
			выход

 

                                                                                                            

Рисунок 3

 

Коэффициенты произведения формируются непосредственно в СР после того, как первый символ подаётся на вход, на выходе появляется последний коэффициент (1.32) а_кg_r, а разряды СР содержат только нули. После одного сдвига ячейки СР содержат элементы a_kg_0,, a_kg₁, … , a_kg_r-1, а вход равен a_k-1. При этом выход СР равен a_kg_r-1 + a_k-1g_r, т.е. равен второму коэффициенту (1.32), после появления среднего ТИ в шине сдвига (не показана на рисунке 2 и 3) на выходе появляется третий коэффициент (1.32), дальнейшие операции проводятся аналогичным образом.

Схемы умножения могут иметь более чем один вход, если добавить к ЛПС, изображенной на рисунке 3, вторую шину с цепочкой устройств умножения, связанных с соответствующими схемами суммирования по модулю 2, тогда схема будет реализовывать процедуру суммирования произведений двух пар полиномов, причем ЗУ в виде СР будет только одно.

         

.                                                             (1.33) 

 

Пример 5. Составить две схемы кодирующих устройств ЦК Хемминга (7,4) на базе двух рассмотренных вариантов ЛПС для умножения полиномов (рисунок 4). В качестве порождающего полинома использовать полином

 (примеры 1 и 3).

выход

.g3=1

.g2=0

.g=1

.g2=0

.g3=1

 

вход

выход

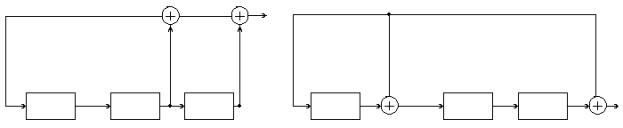Рисунок 4

 

Напомним (подраздел 1.3), что применение в кодерах метода умножения приводит, к сожалению, к формированию неразделимых ЦК.

 

1.7 Деление полиномов на базе ЛПС

 

Схема для деления полинома  на полином  представлена на рисунке 5. Динамическое ЗУ в виде СР вначале должно содержать все нули. Для деления полиномов СР охвачен обратной связью, т.е. выход СР соединяется со входом.  Для подчеркивания противоположного направления шины обратной связи коэффициент умножителя обозначается как g_r^-1, однако для двоичных кодов результат умножения и деления на единицу одинаков, поэтому указанное обозначение в дальнейшем использоваться не будет.

Первый вариант ЛПС для деления полиномов.

 

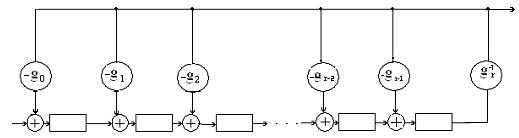
			выход
	вход

 

 

 

 

 

 

Рисунок 5

 

Для первых r – сдвигов, т.е. до тех пор, пока первый входной символ не достигнет конца РС, выход принимает значения, равные «0». После этого на выходе появляется первый нулевой выход, который равен a_kg_r^-1 – первому коэффициенту частного. Для каждого коэффициента частного g_j необходимо вычесть из делимого полином G(X). Это вычитание производится с помощью обратной связи. После k сдвигов на выходе появится частное от деления, а остаток от деления будет находиться в РС.

Работу схемы легче всего понять с помощью примеров построения КУ и ДКУ на базе ЛПС.

Второй вариант ЛПС с делением на генераторный полином.

 

 

 

 

 

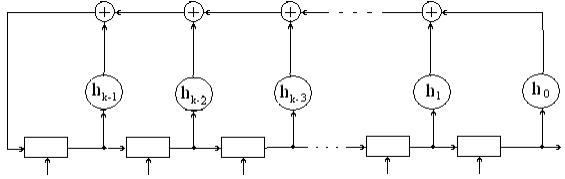
Bi(X)

выход

.а0

.а1

.а2

.аk-2

.аk-1

 

 

 

 

 

 

Рисунок 6

 

При построении КУ ЦК, а также генераторов различных кодов последовательностей, в частности, последовательностей максимальной длины (М – последовательностей), применяется в ряде случаев так называемый генераторный полином . Этот полином называют также проверочным, если он получается при делении бинома  на порождающий полином G(X

                                            .                                              (1.34)

При использовании этой схемы в качестве КУ ЦК исходную кодовую комбинацию А(Х) параллельно, одновременно записывают в k разрядов СР.

С первым тактом на выход будет выдан коэффициент b_n-1 = a_k-1, произойдет сдвиг в право в СР, и в освободившуюся ячейку памяти будет записано вычисленное значение проверочного бита . Со вторым тактом на выход будет считан коэффициент b_n-2 = a_k-2, произойдет сдвиг, и в освободившуюся первую ячейку СР запишется второй проверочный бит    , через n-k тактов будут вычислены все n-k проверочных символов  и записаны в СР. После к тактов, т.е. после вывода на выход всех информационных символов, станут выводиться проверочные символы в том же порядке, в каком они вычислялись. На выходе получается блочный код. После к тактов процесс кодирования одной комбинации А_i(Х) заканчивается, и СР принимает исходное состояние. Для кодирования следующей комбинации необходимо стереть А_i(Х), ввести в СР новую А_j(Х) и повторит ь цикл из n тактов.

Рассмотрим более конкретную работу этой схемы на примере использования её в качестве КУ с привязкой начальных к данным предыдущих примеров 1,2 и 3.

Пример 6. Построить схему КУ, обеспечивающего кодирование ЦК Хемминга (7,4) с порождающим полиномом  путем вычисления блока проверочных символов «в целом», используя проверочный полином Н(Х). Проследить по тактам процесс кодирования и состояния элементов схемы при кодировании исходной комбинации 1001~ .

Построение схемы КУ определяется проверочным полиномом (1.34)

.

Так как к=4, то число разрядов СР равно четырем. По виду проверочного полинома определяем, что  .

Схема КУ для условий примера приведена на рисунке 7, состояние ячеек СР и выхода схемы по тактам – в таблице  4.

В исходном положении в триггерные ячейки СР записываются информационные символы  ~1001, учитывая наличие обратной связи в СР с выхода на вход, суммирование по модулю 2 выходов ячеек Х¹, Х² и Х³ даст символ записи в ячейку Х⁰. После первого сдвига в Х⁰ будет записан символ проверочной группы r₁, который при последующих сдвигах продефилирует на выход СР. Из таблицы 4 видно, что после n=7 тактов на выходе образуется комбинация 0111001 (старшим разрядом вперед), такая

же, как в примерах 1 и 2.

 

 

 

 

 

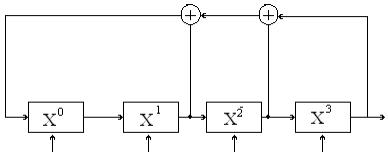
		h4=1		h3=0		h1=1		h0=1
										выход Bi(X)

 

 

 

 

                                                              A_i(X)

 

Рисунок 7

 

                   Таблица 4

Номер такта	Состояние ячеек				выход
	Х0	Х1	Х2	Х3
А(Х)	1	0	0	1	--
1 2 3 4 5 6 7	1 1 0 1 0 0 1	1 1 1 0 1 0 0	0 1 1 1 0 1 0	0 0 1 1 1 0 1	1 0 0 1 1 1 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При этом триггерные ячейки СР принимают исходное значение 1001, при необходимости возможно повторение процедуры кодирования этой же кодовой комбинации А(Х) путем подачи очередных, следующих n=7 тактов. Таким образом, этот способ кодирования так же, как и первый вариант схемы для деления полиномов, обеспечивает получение кодовой комбинации разделимого, блочного ЦК. Кроме того, подобная  ЛПС может быть

 

 

использована для генерации определенной кодовой комбинации, в частности, М – последовательности.

Рассмотрение вариантов построения ЛПС, выполняющих операции умножения и деления полиномов, с целью использования в кодеках УК, позволяет сделать следующие выводы:

а) в КУ ЦК процедура умножения полиномов приводит к получению неразделимых кодов, что усложняет их последующее декодирование. Поэтому операция умножения редко используется в устройствах формирования и обработки ЦК;

б) при делении на порождающий полином G(X) код на выходе КУ получается разделимым и СР содержит r разрядов. Так как в большинстве случаев используется ЦК, у которых число проверочных символов r существенно меньше числа информационных (r<k), то СР в этом случае будет иметь меньшее число разрядов, чем при делении на генераторный полином;

в) при делении в КУ исходной кодовой комбинации на генераторный многочлен ЦК также получается разделимым, но в СР требуется использовать не r, а k разрядов, которых как правило больше.

Применение этого способа более целесообразно в тех случаях, когда одна и так же кодовая комбинация передаётся по каналу связи многократно, например, при передаче формата сообщения с аварийных буев в системах поиска и спасения терпящих бедствие объектов.

Линейные переключательные схемы широко применяются как при формировании и обработке ЦК, так и при генерировании кодированных последовательностей, в частности, М – последовательностей. Рассмотрим ряд характерных примеров применения ЛПС в технике связи. 

 

1.8 Циклические коды, обнаруживающие и исправляющие

      пакеты ошибок (коды Файра)

 

Под пакетом ошибок длиной b понимают такой вид комбинации помехи, в которой между крайними разрядами, пораженными помехами, содержится b - 2 разряда. Например, при b = 5 комбинации помехи, т. е. пакет ошибок, могут иметь следующий вид: 10001 (поражены только два крайних символа), 11111 (поражены все символы), 10111, 11101, 11011 (не поражен лишь один символ), 10011, 11001, 10101 (пора­жены три символа). При любом варианте непременным условием пакета данной длины является поражение крайних символов.

Коды Файра могут исправлять пакет ошибок длиной b_s и обнаруживать пакет ошибок длиной b_r [заметим, что в кодах Файра понятие кодо­вого расстояния d, а следовательно, и уравнение d = r+s+1  не используются].

Образующий многочлен кода Файра Р(Х)_ф определяется из выражения

                                                                    (1.35)

где Р(Х) — неприводимый многочлен степени .

Из принципа построения кода следует, что

                                                                                                     (1.36)
                                                                                                   (1.37)

При    этом    с    не    должно    делиться    нацело    на    число    е,    где

                                                                                                   (1.38)

Неприводимый многочлен Р(Х) выбирают из таблицы 5, согласно урав­нению (1.33), но так, чтобы удовлетворялось условие (1.38). Длина слова п равна наименьшему общему кратному чисел с и е, так как только в этом случае многочлен Хⁿ + 1 делится на Р(Х)_Ф без остатка [при п'<.п никакой многочлен Х^n’+1  не делится на Р(Х)_Ф]

 

                                       .                                                 (1.39)

Число контрольных символов

                                                                                                        (1.40)

 

Таблица 5 - Неприводимые многочлены и их эквиваленты

P()=X+1311 P(X2)=X2 +X+17111 P(X3)=X3 +X+1111011 P(X3)=X3 + X2+1131101 P(X4)=X4 +X+11910011 P(X4)=X4 + X3+12511001 P(X4)=X4 + X3+ X2 +X+1 311111 P(X5)=X5 + X2+137100101 P(X5)=X5 + X3+141101001

P(X5)=X5 + X3+ X2 +X+147101111 P(X5)=X5 + X4+ X2 +X+155110111 P(X5)=X5 + X4+ X3 +X+159111011 P(X5)=X5 + X4+ X3 + X2+161111101 P(X6)=X6 + X+1671000011 P(X7)=X7 + X3 +113710001001 P(X8)=X8 + X4+ X3 + X2+1 285100011101 P(X9)=X9 + X4+110411000010001 P(X10)=X10 + X3 +1205710000001001

 

Для кода Файра приведем два примера.

Пример 7. Согласно статистическим характеристикам помех, b_s = 5 и b_r = 6. По этим данным требуется построить код Файра.

На основании (1.36) и (1.37)

.

 По таблице 5 находим неприводимый многочлен пятой степени

                                        Р(Х)= Х⁵ + Х²+ 1.

Согласно    (1.35),    образующий   многочлен

Р(Х)_Ф = (Х⁵ + Х²+ 1)( Х¹⁰ +1)==X¹⁵ + X¹²+ X¹⁰+ X⁵+ X²+1.

 

Согласно (1.38), е = 2⁵ — 1 = 31. Поэтому длина кода n = НОК(31,10)=310. Из (1.40) число контрольных и проверочных  символов

k=n-m=310-15=295;

m = 10 + 5= 15, т. е. в данном случае оно равно степени образующего многочлена. В итоге получаем код (310, 295).Избыточность такого кода, если учитывать его исправляющую способность, невелика: И=m/n= 15/310 = 0,048

Представляет интерес сравнение избыточности кода той же длины при исправлении того же числа ошибок, но не сгруппированных в пакет, т. е. рассеянных по всей длине слова. Если воспользоваться для этой цели кодами БЧХ и близким значением n=127, то при s=4 можно по изложен­ной методике подсчитать, что число контрольных символов m=28, т.е. получен код (127,99). Избыточность такого кода И = 28/127 = 0,22, т.е. значительно выше, чем у кода Файра. Это очевидно: исправить четыре ошибки, находящиеся в одном месте, проще, чем ошибки, рассредоточен­ные по всей длине комбинации.

Заметим, что существует следующее правило: если циклический код рассчитан на обнаружение независимых ошибок, он может обнаружить также пакет ошибок длиной т.

При делении кодовой комбинации G(X)=1000000…………..000  на образующий полином вида 1001010000100101 получаем остаток 100101000010010.

Пример 8. Согласно статистическим характеристикам помех, b_s =4 и b_r = 5. По этим данным требуется построить код Файра.

Исправить пакет b_s=4—значит исправить одну из следующих комбинаций ошибок, пораженных помехами: 1111, 1101, 1011 и 1001. В то же время этот код может обнаружить одну из комбинаций в пять символов, рассмотренных ранее (10001, 11111 и т. д.).

На основании (1.36) и (1.37) с≥8 и l≥4. По таблицам 5 находим неприводимый многочлен четвертой степени  Р(Х)= Х⁴ + Х+ 1.

Согласно    (1.35),    образующий   многочлен будет   равен

Р(Х)_Ф = (Х⁴ + Х+ 1)( Х⁸ +1)=X¹² + X⁹+ X⁸ + X⁴+ X+1.

Согласно (1.38), е = 2⁴ - 1 = 15. Поэтому длина кода n= НОК (15,8) =120. Из (1.40) число контрольных проверочных символов

k=n-m=120-12=108;

 m = 8 + 4= 12, т. е. в данном случае оно равно степени образующего многочлена. В итоге получаем код (120, 108) Избыточность такого кода, если учитывать его исправляющую способность, невелика: И— 12/120 = 0,1

Представляет интерес сравнение избыточности кода той же длины при исправлении того же числа ошибок, но не сгруппированных в пакет, т. е. рассеянных по всей длине слова. Если воспользоваться для этой цели кодами БЧХ и близким значением n=127, то при s=4 можно по изложен­ной методике подсчитать, что число контрольных символов m=28, т.е. получен код (127,99). Избыточность такого кода И = 28/127 = 0,22, т.е. значительно выше, чем у кода Файра. Это очевидно: исправить четыре ошибки, находящиеся в одном месте, проще, чем ошибки, рассредоточен­ные по всей длине комбинации.

Заметим, что существует следующее правило: если циклический код рассчитан на обнаружение независимых ошибок, он может обнаружить также пакет ошибок длиной т.

При делении кодовой комбинации G(X)=1000000…………..000 на образующий полином вида 11001000011001 получаем остаток 110010001100.

 

1.9 Декодирование кодов Файра

 

Рассмотрев код, исправ­ляющий единичные и двойные смежные ошибки, мы установили необходимость двух схем в детекторе оши­бок, настроенных на два выделенных синдрома. При большом числе выделенных синдромов, как это имеет место, например, в случае кодов, исправляющих пакеты ошибок значительной длины, такой подход неприемлем, так как декодирующее устройство оказывается чрезвы­чайно сложным.

В связи с этим разработаны коды, в схемах декоди­рования которых детектор ошибки автоматически наст­раивается на нужный выделенный синдром. Осуществля­ется это за счет схемы деления на второй соответствую­щим образом подобранный многочлен. Образующий многочлен таких кодов, следовательно, представляет со­бой произведение двух многочленов

 

                                                                      (1.41)

 

В качестве примера рассмотрим класс кодов Файра с образующим многочленом

                                                                     (1.42)

 

где р(х)— неприводимый многочлен степени m ³ b, принадлежащий показателю степени е = 2^m - 1;

      b - длина корректируемого пакета ошибок.

Поступающую из канала связи кодовую комбинацию h{x) представляем суммой по модулю два, неискаженной комбинации кода f{x) и вектора, соответствующего пачке ошибок В(х)

 

                                                                              (1.43)

 

где  - характеризует положение пачки ошибок В(х) в векторе ошибки. Вектор f(x) делится на каждый из много­членов g₁(х) и g₂(x) без остатка. Поэтому процесс декоди­рования можно анализировать, ограничиваясь вектором x^jВ(х). Отметим, что при выбранном нами соотношении числа разрядов в пакете ошибок и степени образующего многочлена т = b совокупность различных исправляемых пакетов ошибок является одновременно совокупностью остатков, получаемых при делении  на р(х).  В качестве остатка на n-м такте (выделенного синдрома) при паке­те ошибок в старших разрядах h(x) желательно иметь сам многочлен ошибки.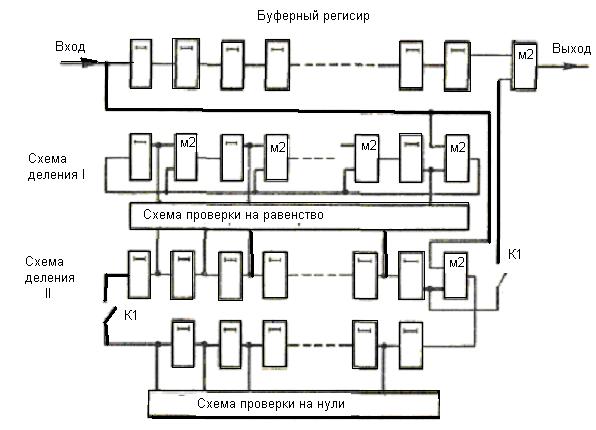

 

Рисунок 8

 

Тогда на следующих тактах, вы­водя его в узел коррекции синхронно с последователь­ностью h(x) из буферного регистра, легко исправить искаженные символы.

Остаток на n-м  такте мы получим только в том слу­чае, если будем использовать схему, обеспечивающую деление с первого такта и требующую домножения h(x) на х^m.

Для случая поступления кодовых комбинаций, разне­сенных во времени, схема декодирующего устройства для кодов Файра представлена на рисунке 8.

При поступлении h(x) в схему деления I [на много­член р(х)] в ней начинается закономерное чередование остатков. В(х), являющийся одним из остатков, появля­ется в первый раз на (2^m - 1)-м такте. Следовательно, для того чтобы он появился на n-м такте, общее число разрядов должно быть кратно 2^m - 1.

В процессе деления h(x) на многочлен х^2b-1+1, при­надлежащий показателю (2b - 1), образуется (2b - 1) остатков. Вектор типа В(х)х^b-1 является одним из остат­ков. Он возникает впервые на (2b - 1)-м такте, и затем его появление циклически повторяется с периодом (2b - I) тактов.

Если мы желаем выставить этот остаток в детек­торе ошибки, т. е. получить его также на n-м такте, то п должно быть кратно (2b - 1). Чтобы детектор ошибки не сработал раньше, числа 2^m-1 и 2b - 1 должны быть взаимно простыми, а n — наименьшим кратным этих чисел.

Равенство остатков В(х) в регистрах двух схем деле­ния, а также равенство нулю остальных (b—1) разрядов в схеме деления II (на многочлен х^2b-1 + 1) являются условиями возможности исправления обнаруженного пакета ошибок и устанавливаются схемным путем.

После фиксации условий, допускающих исправление пакета, ключ К₁ замыкается, а ключ K₂ размыкается. На схему коррекции (сумматор по модулю два) одно­временно начинают выводиться символы В(х) как с бу­ферного регистра, так и со схемы деления II. При этом пакет ошибок В(х) в векторе h(x) устраняется.

В общем случае, когда В(х) начинается не со старше­го разряда, а с j-го, для обеспечения равенства остатков, полученных на n-ы такте, нужно проводить последо­вательные домножения их на х с приведением по моду­лю р(х) в одной схеме и по модулю (х^2b-1 + 1) - в дру­гой.

Если пачка начинается с j-го разряда, то необходимо сделать дополнительно (n — j) тактов, прежде чем остат­ки в регистрах сравняются, причем с учетом домножения h(x) на x^mj может принимать значения от 1 до n.

За (n - /) дополнительных сдвигов содержимое бу­ферного регистра сместится, и ошибочные символы снова окажутся непосредственно перед схемой коррекции.

Если за время вывода h(x) из буферного регистра условия возможности проведения коррекции не были выполнены, то обнаружена неисправимая ошибка.

Пример 9 -  Рассмотреть  процесс  исправления  пакетов  ошибок кодом Файра с образующим многочленом

                                                                          (1.42)

Код может исправлять пакеты ошибок, состоящие из трех символов (где b=b_s = 3). Длина кодовой комбинации равна n = (2^b - 1)(2b -1) = (2³ -1) (23-1)=35. Предположим, что в трех старших разрядах нулевой кодовой комбинации возникла пачка ошибок типа В(х) = 101.

При делении В(х) на g₁(x) = х³ + х² + 1 остаток В(х) будет появ­ляться в регистре с периодом 7 тактов. Действительно,

 

 

 

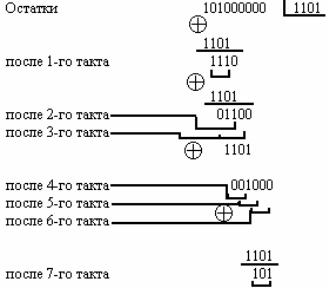
Чередование остатков B(x) x^b-1 при делений B(x) на g₂ (x) = x⁵ +1 происходит с периодом 5 тактов:

 

 

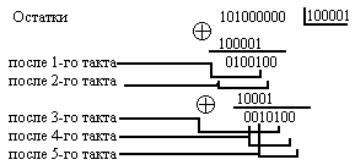
Условия возможности исправления пакета ошибок выполняются на 35-ом такте. За последующие три такта при выводе кодовой комбинации из буферного регистра на схему коррекции пачка ошибок устраняется.

Пример 10.Образующий многочлен таких кодов представляет собой произведение двух многочленов

 g(x)= g₁(x) g₂(x)= Р_ф(х)

 Р_ф(х) = (х⁵+х²+1)(х¹⁰+1)                               

 g₁(x) = (х⁵+х²+1) = 100101

 g₂(x)= = (х¹⁰+1) = 10000000001

Длина кодовой комбинации

n=(2^b-1)  (2b-1)=(2⁵-1)(2*5-1)=279

Предположим, что при делении В(х)  на g₂(х) остаток В(х) будет появляться в регистре с периодом 9 тактов.

 

 

 

 

 

Таблица 6 – Остатки от деления В(х) на g₁(х)  и  g₂(х).

Номер такта	Остаток в регистре схемы деления g2(x)	Остаток в регистре схемы деления g1(x)
1 2 . . . 9 . . . 31 . . . 279	0100000001 1100000001 . . . 1010000000 . . . . . . . 1010000000	01101 11111 11010 . . . . . . 10100 . . . 10100

 

Условия возможности исправления пакета ошибок выполняются на 279-ом такте. За последующие три такта при выводе кодовой комбинации из буферного регистра на схему коррекции пачка ошибок устраняется.

 

1.10 Циклические коды Боуза -Чоудхури -Хоквингема

 

Коды Боуза - Чоудхури - Хоквингема (БЧХ) представляют собой обширный класс кодов, способных исправлять несколько ошибок и занимающих заметное место в тео­рии и практике кодирования. Интерес к кодам БЧХ определяется по меньшей мере тремя следующими обстоятельствами:

а)   среди   кодов  БЧХ  при   небольших  длинах  существуют  хорошие  (но,  как правило, не лучшие из известных) коды;

б)  известны относительно простые и конструктивные методы их кодирования и декодирования;

в)  полное понимание построения кодов   БЧХ является наилучшей отправной точкой для изучения многих других классов кодов.

Коды БЧХ независимо открыли Хоквингем (1959) и Боуз и Рой-Чоудхури (1960), которые доказали ряд теорем, устанавливающих существование таких ЦК, у которых минимизируется число проверочных символов, а также указывающих пути нахождения порождающих полиномов для этих кодов.

Корректирующие свойства ЦК могут быть определены на основании следую­щей теоремы: для любых значений m и g_u существует ЦК длиной n = 2^m-1, исправ­ляющий все ошибки кратности g_u и менее (g_u <m) и содержащий не более n -k < g_u проверочных символов. Так, например, при n = 15, m= 4 и различных g_u число прове­рочных символов будет равно: g_u =1, n - k = m g_u = 4*1= 4; g_u = 2, mg_u = 4*2 = 8; g_u = 3, m g_u = 4*3 = 12. Соответствующие коды (n, к) будут (15,11), (15,7), (15,3). Напомним, что минимальное кодовое расстояние d_min=2g_u+1, и применительно к ЦК оно чаще называ­ется конструктивным расстоянием. Если величины g_u или d выбрать слишком больши­ми, то получившийся в результате код будет тривиальным — в нём будет лишь один ли­бо (при r > n) ни одного информационного символа.

В таблице 7 даны параметры и порождающие полиномы некоторых кодов БЧХ. По­линомы приведены в восьмеричной форме записи, старшая степень расположена слева.

Например, коду (15,7) соответствуют двоичное представление 111010001 и мно­гочлен G(Х) = X⁸ + X⁷ + X⁶ + X⁴ +1. Подробные таблицы порождающих полиномов  цик­лических кодов БЧХ приведены в [6].

 

Таблица 7

m	n	k	r	gu	G(X)-mod 8	m		k	R	gu	G(X)-mod 8
3 4   5       6	7 15   31       63	4 11 7 26 21 16 11 57 51 45 39 36	3 4 8 5 10 15 20 6 12 18 24 27	1 1 2 1 2 3 5 1 2 3 4 5	13 23 721 45 3551 107657 5423325 103 12471 1701317 166623567 1033500423	7         8	127         225	120 113 106 99 92 247 239 231 223   215	7 14 21 28 35 8 16 24 32   40	1 2 3 4 5 1 2 3 4   5	211 41567 11554743 3447023271 624730022327 435 267543 156720665 75626641375   23157564726421

 

Коды БЧХ с длиной 2^m -1 называют примитивными кодами БЧХ. К ним, в част­ности, относятся классические коды Хемминга, исправляющие однократные ошибки. К кодам БЧХ относятся также коды, длина n которых является делителем 2^m -1. Напри­мер, код Голея (23, 12, 7) (подраздел 1.3) также принадлежит классу кодов БЧХ, поскольку при m = 11 примитивный код БЧХ имеет длину n=2¹¹ -1 = 2047, причём это зна­чение без остатка делится на длину кода Голея n = 23 (2047 : 23 = 89), который отно­сится к непримитивным БЧХ- кодам [5, 6].

Как отмечалось выше, все примитивные коды БЧХ обладают конструктивным расстоянием d_min =2 +1. Расстояние можно увеличить до 2 + 2. Для этого нужно основ­ной порождающий полином БЧХ - кода домножить на бином Х+1, т.е. G₁(Х) = (Х+1) х G_БЧХ(Х), что повлечёт за собой прибавление к коду одного проверочного символа, обеспечивающего проверку на чётность всех символов кода БЧХ. Таким образом полу­чается расширенный код БЧХ.

Адекватно можно получить укороченный (усечённый) БЧХ - код, следуя алгорит­му, изложенному в подразделе 1.4.

Коды Рида—Соломона (РС) являются важным и широко используемым подмно­жеством кодов БЧХ. Двоичный код Рида—Соломона получится, если взять основание ко­да q=2^s. Это означает, что каждый символ кода заменяется s - значной двоичной после­довательностью. Если исходный код с основанием q исправляет ошибки кратности <, то полученный из него двоичный код имеет 2s проверочных символов (по 2 на каж­дый блок из символов) из общего числа n =s -(2^s - 1). Код может исправлять серийные ошибки (пакеты ошибок) длиной ≤b = s * ( -1 )+1 .

Коды  РС, наряду с кодами Файра (1.10), являются наиболее подходящими для ис­правления серийных ошибок, а также в каскадных системах кодирования в качестве внешних кодов.

Построение кодеров и декодеров ЦК основывается на применении ЛПС, содер­жащих сдвигающие регистры. Как отмечает Р. Блейхут [5], ЛПС «были сразу использова­ны большинством исследователей и вошли в литературу без всяких фанфар».

 

1.6.1 Циклические коды с d³5. Эти коды, разработанные Боузом, Чоудхури и Хоквинхемом (сокращенно коды БЧХ), позволяют обнаруживать и ис­правлять любое число ошибок. Заданными при кодировании является число ошибок s, которое следует исправить, и общее число символов, по­сылаемых в линию, т. е. длина слова п. Числа информационных симво­лов к и контрольных символов т, а также состав контрольных символов подлежат определению.

Методика кодирования такова:

а) коды БЧХ для исправления ошибок.

1. Выбор длины слова. При кодировании по методу БЧХ нель­зя выбирать произвольную длину слова n. Первым ограничением является то, что слово может иметь только нечетное число символов. Однако даже при этом не все нечетные числа могут составлять длину слова. Здесь могут быть два случая:

1) по заданному n находят такое число h, чтобы удов­летворялось равенство 2^h - 1=п. Например, при n = 7 h = 3, при n=15 h = 4, при n = 31 h =5, при n=63 h =6 и т. д.;

2) находят такое число h, чтобы удовлетворялось равенство

(2^h-1)/g=n,                                                                                      (1.45)

где h>0— целое число, a g - нечетное положительное число, при делении на которое n получается целым нечетным числом.

Разлагая 2ⁿ - 1  на сомножители, получаем следующие числа n и g:

7=2³-1=7                               255=2⁸-1=17x5x3

15=2⁴-1=5x3                           511=2⁹-1=73x7

31=2⁵-1=31                             1023=2¹⁰-1=31x11x3

63 = 2⁶-1=7x3x3=21x3             2047=2¹¹-1=89x23
        127 = 2⁷ -1=127                               4095=2¹²-1=3x3x5x7x13

Так, из четвертой строки следует, что при h = 6 длина слова может быть равна не только 63 (первый случай), но и 21   (q=3).

2. Определение кодового расстояния. Кодовое расстояние определяют, согласно d = 2s+l.

3. Определение образующего многочлена Р(Х).

Образующий многочлен есть наименьшее общее кратное (НОК) так называемых минимальных многочленов М(X) до порядка 2s-1 включительно, причем образующий многочлен  составляется из произведения некоторого числа нечетных минимальных многочленов

 

P(X)=HOK[M₁ (X) M₃ (X)… M_2S-1 (X)]…                                                      (1.46)

 

Минимальные многочлены являются простыми неприводимыми много­членами, метод определения которых дается в [26]. Заметим, что если среди минимальных многочленов окажутся два одинаковых, то один из них исключается.

4. Определение числа минимальных многочленов L.

Из уравнения (1.46) следует, что порядок минимальных многочленов определяется как 2S - 1. Если учесть, что этот образующий многочлен состоит  только   из   нечетных   минимальных   многочленов,

то  числа их определяется просто. Например, если s = 3, то 2s — 1 =5. Это значит, что в уравнении (1.46) будут записаны минимальные

многочлены  М₁(Х), М₃(Х) и М₅(х), т.е L=3. Если s = 8, то 2s-1 =15, и в уравнении будут использованы  минимальные многочлены M₁(Х),

M₃ (Х), M₅(Х), M₇(Х), M₉(Х), M₁₁(Х), M₁₃(Х), M₁₅(Х), т.е. L=8. Таким образом, число минимальных многочленов равно числу исправляемых ошибок

                                                     L=s                                              (1.47)

 

5. Определение старшей степени l минимального многочлена. Степень l есть такое наименьшее целое число, при котором 2^l-1 нацело

делится на n  или  ng, т.е. n=2^l-1 или 2^l-1=2^l-1.
Отсюда следует, что

l = h.                                                                                                    (1.48)

6. Выбор минимальных многочленов. После того как
определены число минимальных многочленов L и степень старшего много­члена l, многочлены выписывают из таблицы 8. При этом НОК

может быть составлено не только из многочленов старшей степени l.

Это, в частности, касается многочленов четвертой и шестой степеней.

 7. Определение степени β образующего многочлена Р^b(Х). Степень образующего многочлена зависит от НОК и не
превышает произведения ls или lL, так как L=s. После нахождения всех минимальных  многочленов  образующий  многочлен  находят по уравне­нию (1.46).

 

Таблица 8

Номер М(Х)	Минимальные многочлены различных степеней, записанные в виде кодовых комбинации
	2	3	4	5	6	7	8	9
M1(Х) M3(Х) M5(Х) M7(Х) M9(Х) M11(Х) M13(Х)	111	1011 1101	10011 11111     111 11001	100101 111101 110111 101111 110111 111011	1000011 1010111 1100111 1001001      1101 1101101	10001001 10001111 10011101 11110111 10111111 11010101 10000011	100011101 101110111 111110011 101101001 110111101 111100111 100101011	1000010001 1001011001 1100110001 1010011001 1100010011 1000101101 1001110111

 

8. Определение числа контрольных символов. Так как число контрольных символов m  равно степени образующего многочлена, то в коде длины n.

 

                                                 b = m £ ls.                                            (1.49)

 

9. Определение числа информационных символов. Его производят обычным порядком из равенства k=n-m. Даль­нейшие этапы кодирования аналогичны рассмотренным для циклических кодов c d < 4, т. е. находят дополнительную матрицу, составляют образую­щую матрицу, по которой рассчитывают все кодовые комбинации;

б) коды БЧХ для обнаружения ошибок. Их строят следующим образом. Если необходимо образовать код с обнаружением четного  числа ошибок, то по заданному числу r согласно d=r+1, т.е. r=d-1 и d=2s+1, т.е. s=(d-1)/2, находят значения d и s. Дальнейшее кодирование выполняют, как и ранее. Если требуется обнаружить нечетное число ошибок, то находят ближайшее меньшее целое число s и кодирование производят так же, как и в предыдущем случае, с той лишь разницей, что найденный согласно (1.46) образующий многочлен дополнительно умножают на двучлен (Х+1). Например, требуется построить код БЧХ, обнаруживающий семь ошибок при n=15. Находим, что d=8, а ближайшее меньшее значение s=3. Далее определяем многочлен Р(Х)  и умножаем его на двучлен (Х+1), Таким образом построен код БЧХ .

Пример 11. Даны следующие параметры: s=2, n= 31.

Методика кодирования:

а) определим кодовое расстояние

d=2s+1=22+1=5.

Для исправления s_и.ош.2 необходимо иметь d₀2 s_и.ош+1, длина кодовой комбинации должна удовлетворять условию:

 

 

(2^h-1)/g=n,

где h>0— целое число, a g - нечетное положительное число, при делении на которое n получается целым нечетным числом;

б) определение минимального количества многочленов

L=S, значит L=2;

в) определение старшей степени l минимального многочлена

n=2^l-1, 31=2^l-1, l=5,

зная l, выбираем из таблицы 8 минимальные многочлены:

M₁=x⁵+x²+1,

M₃=x⁵+x⁴+ x³⁺ x² +1;

г) определение образующего многочлена Р(Х)

P(Х)=HOK[M₁(Х),M₃(Х),…,M_2s-1(x)],

P(Х)=M₁(Х)M₃(Х).

Минимальные многочлены являются простыми непроводимыми многочленами, метод определения которых дается в [ 26].

Заметим что, если среди минимальных многочленов окажутся два одинаковых, то один из них исключается.

Р(Х)= Х¹⁰+Х⁹+ Х⁸ + Х⁶ + Х⁵ + Х³ + 1;

д) определение степени β образующего многочлена Р^b(Х)  

b = 10;

е) определение числа контрольных символов. Так как число контрольных символов m  равно степени образующего многочлена, то в коде длины n.

b = m £ ls, m=10;

ж) определение числа информационных символов. Его производят обычным порядком из равенства k=n-m=31-10=21.

Получаем код БЧХ (31,21) с s=2.

При делении кодовой комбинации

 G(X)Х^r=1000000000000000000000000000000 на образующий полином вида Р(Х)=11101101001 получаем остаток R(X)=1010010011.

 

Пример 12. Кодирование кода БЧХ (с обнаружением).

12.1 Расчет параметров кодирующего устройства

Для построения структурной схемы кодирующего устройства кода БЧХ необходимо рассчитать следующие параметры:

 

Исходные данные:

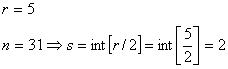
Решение :

а) определение кодового расстояния.

d= r+1=5+1=6;

б) определение минимального количества многочленов

L=S,

L=2;

в) определение старшей степени l минимального многочлена

n=2^l-1, 31=2^l-1, l=5

Зная l, выбираем из таблицы 8 минимальные многочлены:

M₁=x⁵+x²+1,

M₃=x⁵+x⁴+ x³⁺ x² +1;

г) определение образующего многочлена Р(Х):

P(Х)=HOK[M₁(Х),M₃(Х),…,M_2s-1(x)]

P(Х)=M₁(Х)M₃(Х).

Если необходимо образовать код обнаружением четного числа ошибок, кодирование выполняют, как ранее. Если обнаруживать нечетное число ошибок, то находят ближайшее число [s], лишь образующий полином умножается на (Х+1).

Р(Х)= (Х¹⁰+Х⁹+ Х⁸ + Х⁶ + Х⁵ + Х³ + Х + 1)+(Х+1)= Х¹¹+ Х⁸ + Х⁷ + Х⁵ + Х⁴ +Х³ + Х + 1;

д) определение степени β образующего многочлена Р^b(Х). Степень образующего многочлена зависит от НОК и не
превышает произведения ls или lL, так как L=s.

b = 11;

е) определение числа контрольных символов. Так как число контрольных символов m  равно степени образующего многочлена, то в коде длины n

 

b = m £ ls, m = 11;

ж) определение числа информационных символов

k=n-m=31-11=20.

Получим код БЧХ [31;20].

 

1.11 Декодирование циклических кодов БЧХ с обнаружением и исправлением нескольких ошибок

 

1.11.1 Рассмотрим схемную реализацию декодирования комбинации 100000011101000, искаженной двумя ошибками и принявшей вид 111000011101000. Декодер состоит (рисунок 9) из делителя, выполненного для деления на многочлен Р(Х)=  Х⁸ + Х⁷ + Х⁶ + Х⁴  + 10  и запоминающего устройства, представляющего собой регистр с сумматором символов k. Комбинация поступает одновременно на делитель и запоминающее устройство, начиная со старшего разряда. Искаженные символы в комбинации отмечены точками. В начале ключ К₁ замкнут, а ключ К₂  разомкнут.  В таблице 9 показан процесс деления, начиная с такта 8, так как в первые семь тактов происходит заполнение делителя и обратная связь не проявляется. В такте 15 синдром (остаток от деления) оказывается записанным в ячейках регистра (01001110). Однако его вес W=4 больше числа исправляемых ошибок s, поэтому делитель делает еще один шаг (такт первый), в процессе которого снова осуществляется деление на многочлен Р(Х). Синдром 10011100 опять имеет вес W=4. Только после третьего такта W=2=s. В этот момент ключ К₁ размыкается, а ключ К₂  замыкается, и синдром с делителя начинает поступать на сумматор запоминающего устройства, у которого ключ К₃ замкнут, а ключ К₄ разомкнут. Это устройство в такте 15 первого этапа полностью заполнилось. А на втором этапе его работы начался циклический сдвиг записанной информации (таблица 10). Так, в такте 1 единица из ячейки Х⁶ информационных символов переместилась в ячейку Х⁰ контрольных символов m. В такте 2 эта единица передвинулась в ячейку Х¹, а её место в ячейке заняла следующая единица и т.д. Первые шесть нулей синдрома не влияют на работу запоминающего устройства. Лишь в тактах 10 и 11 две единицы синдрома, складываясь по модулю 2 с двумя ошибочными единицами символов k (обозначены точками), «уничтожают» их, т.е. исправляют ошибки. Регистр ЗУ продолжает переключаться до окончания второго цикла (этапа) его работы.  После такта 15 ключи К₂ и К₃  размыкаются, а ключи К₁ и К₄ замыкаются: начинается считывание исправленной комбинации и одновременная запись новой.

Таким образом, декодирование состоит из двух этапов. На первом этапе осуществляется нахождение остатка и запись кодовой комбинации, на втором – её исправление и расстановка символов k и  m на свои места.

 

 

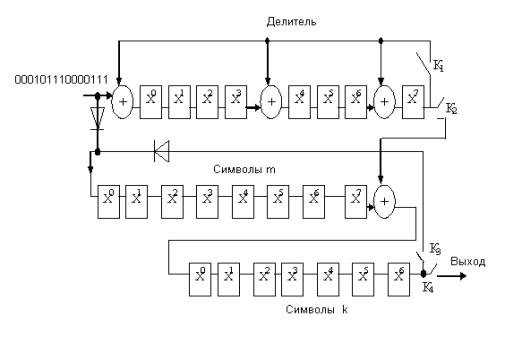
Рисунок 10

 

 

 

 

 

 

Таблица 9

Номер такта	Делимое	Состояние ячеек делителя								Вес остатка
		X0	X1	X2	X3	X4	X5	X6	X7
VIII	1	1	0	0	0	0	i	i	1
IX	1	0	1	0	0	1	0	0	0
X	1	1	0	1	0	0	1	0	0
XI	0	0	1	0	1	0	0	1	0
XII	1	1	0	1	0	1	0	0	1
XIII	0	1	1	0	1	1	1	1	1
XIV	0	1	1	1	0	0	1	0	0
XV	0	0	1	1	1	0	0	1	0	4
I		0	0	1	1	1	0	0	1	4
II		1	0	0	1	0	1	1	1	5
III		1	1	0	0	0	0	0	0	2

 

Таблица 10 – Работа ЗУ

Номер такта	Символы m									Символы k
	X0	X1	X2	X3	X4	X5	X6	X7		X0	X1	X2	X3	X4	X5	X6
XV	0	0	0	1	0	1	1	1		0	0	0	0	i	i	1
I	1	0	0	0	1	0	1	1		1	0	0	0	0	i	i
II	i	1	0	0	0	1	0	1		1	1	0	0	0	0	i
III	i	i	1	0	0	0	1	0		1	1	1	0	0	0	0
	a   Cиндром 11000000
IV	0	i	i	1	0	0	0	1		0	1	1	1	0	0	0
V	0	0	i	i	1	0	0	0		1	0	1	1	1	0	0
VI	0	0	0	i	i	1	0	0		0	1	0	1	1	1	0
VII	0	0	0	0	i	i	1	0		0	0	1	0	1	1	1
VIII	1	0	0	0	0	i	i	1		0	0	0	1	0	1	1
1IX	1	1	0	0	0	0	i	i		1	0	0	0	1	0	1
X	1	1	1	0	0	0	0	i		0	1	0	0	0	1	0
XI	0	1	1	1	0	0	0	0		0	0	1	0	0	0	1
XII	1	0	1	1	1	0	0	0		0	0	0	1	0	0	0
XIII	0	1	0	1	1	1	0	0		0	0	0	0	1	0	0
XIV	0	0	1	0	1	1	1	0		0	0	0	0	0	1	0
XV	0	0	0	1	0	1	1	1		0	0	0	0	0	0	1

 

1.11.2 Рассмотрим процесс исправления единичной ошибки при использований кода (7,4) с образующим многочленом  и применений в декодирующем устройстве схем деления за n и  k тактов.

 Определим опознаватели ошибок и выделенный синдром для случая использования схемы деления за n тактов:

 

 

Детектор ошибки, обеспечивающий формирование на выходе сигнала только в случае появления в схеме деления остатка 110, можно реализовать посредством двух логических элементов НЕ и одного логического элемента ИЛИ – НЕ.

На рисунке 11 приведена схема соответствующего декодирующего устройства. В таблице 11 представлен процесс исправления ошибки для случая, когда кодовая комбинация 1001011 (таблица 11) поступила на вход декодирующего устройства с искаженным символом в 4-м разряде (1000011).

После n (в данном случае 7) тактов в схему деления II переписывается

 

 

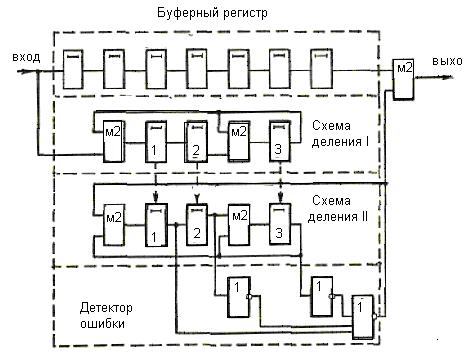
Рисунок 11

 

 

 

Таблица 11

Номер такта	Вход	Состояние ячеек схем деления			Выход после коррекций
		1	2	3
1	1	1	0	0
2	0	0	1	0
3	0	0	0	0
4	0	1	0	1
5	0	1	1	1
6	1	0	1	0
7	1	1	0	1
					Переписывается в схему деления II
8	0	1	1	1	1
9	0	1	1	0	01
10	0	0	1	1	001
11	0	0	0	0	1001
12	0	0	0	0	01001
13	0	0	0	0	1101001
14	0	0	0	0	.

 

опознаватель ошибки 101. На каждом  последующем такте, на выходе буферного регистра появляется неискаженный символ корректируемой кодовой комбинации, а в схеме деления II - новый остаток. Выделенный синдром появится в схеме деления на 10-м такте, когда искаженный символ займет крайнюю правую ячейку регистра. На следующем такте он попадает в корректирующий сумматор и будет там исправлен импульсом, поступающим с выхода детектора ошибки. Этот же импульс по цепи обратной связи приводит ячейки схемы деления II в нулевое состояние (корректирует выделенный синдром).

При использований схемы деления за k тактов соответствие между векторами ошибок и остатками на n-м такте иное.

 

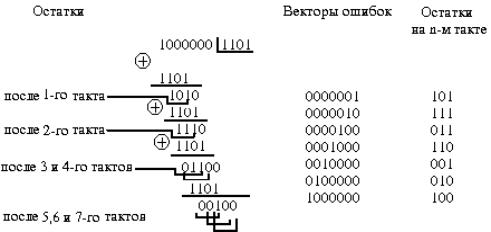
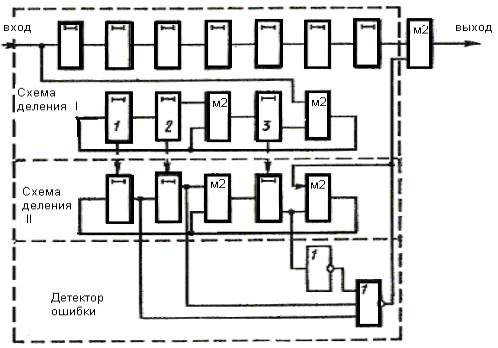
Рисунок 12

 

Детектор для выделенного синдрома 100 можно построить из одного логического элемента НЕ и одного элемента ИЛИ – НЕ.

На рисунке 6.20 представлена схема декодирующего устройства для этого случая.

Таблица 12 позволяет проследить по тактам процесс исправления ошибки в кодовой комбинации 1000011 (искажен символ в 4-ом разряде).

Таблица 12

Номер такта	Вход	Состояние ячеек схем деления			Выход после коррекций
		1	2	3
1	1	1	0	1
2	0	1	1	1
3	0	1	1	0
4	0	0	1	1
5	0	1	0	0
6	1	1	1	1
7	1	0	1	1
					Переписывается в схему деления II
8	0	1	0	0	1
9	0	0	1	0	01
10	0	0	0	1	001
11	0	0	0	0	1001
12	0	0	0		01001
13	0	0	0	0	101001
14	0	0	0	0	1101001

Сравнение показывает, что использование в декодирующем устройстве схемы деления за k тактов предпочтительно, так как выделенный синдром в этом случае при любом объеме кода содержит единицу в старшем и нули во всех остальных разрядах, что приводит к более простому детектору ошибки.

 

1.12 Код Хэмминга

 

На практике широко используется код Хэмминга. Код Хэмминга предназначен для исправления ошибок и имеет кодовое расстояние d₀=3. Покажем на примере (7,4) кода, используя, можно обеспечить исправление одиночных ошибок. Кодовые комбинации (7,4) кода в общем случае имеют вид а = (а₁, а₂, а₃, а₄, b₁, b₂, b₃). Правила формирования проверочных элементов должны быть такими, чтобы в результате проверок на четность числа единиц в группах информационных элементов можно было указать на порядковый номер искаженного элемента. Для этого каждый информационный элемент должен участвовать, как минимум, в двух проверках из трех (r=3). Например, для кода (7,4) можно записать

 

                           а₁ а₂ а₁ b₁=0;

                           а₂ а₃ а₄ b₂=0;                                                    (1.50)

                              а₁ а₂ а₄ b₃=0.

 

Возможны и другие варианты выбора групп проверочных элементов. Если все уравнения (1.50) удовлетворяются, это свидетельствует об отсутствии ошибок в принимаемой комбинации либо о наличии необнаруживаемой ошибки. Невыполнение первого и третьего уравнений свидетельствует об ошибочном приеме а₁ всех трех уравнении  а₂, первого и второго - а₃, второго и третьего его – а₄.

Результат проверок на четность удобно записывать в виде r- разрядного двоичного проверочного числа, называемого синдромом. Например, при искажении элемента а₄ синдром S=011, а при отсутствии ошибок S=000. Очевидно, что в общем случае число различных синдромов 2^r должно быть меньше всех вариантов ошибок.

На рисунке 13 и 14 приведены схемы кодирующего и декодирующего устройств (7,4) кода Хэмминга. Единичные элементы комбинации первичного кода, поступающие из кодера оконечного устройства в параллельный код, записываются в ячейки 1 – 4 регистра. Одновременно группы информационных элементов поступают на три сумматора по модулю 2, с помощью которых формируются проверочные элементы  b₁, b₂ и b₃, записываемые в ячейке 5 – 7 регистра. Под воздействием продвигающих импульсов на выходе регистра формируется в последовательном коде комбинация избыточного кода.

Комбинация, поступающая из канала, записывается в течение семи тактов в регистр 1, (рисунок 14), после чего с помощью сумматоров по

модулю 2 проверяется на четность число единиц в группах элементов в соответствии с (1.50). Если синдром, поступающий от сумматоров на вход дешифратора, отличен от нуля, то на одном из выходов дешифратора появляется сигнал 1, который записывается в ячейку регистра 2, порядковый номер которого соответствует порядковому номеру искаженного элемента. Далее под воздействием тактовых импульсов искаженный разряд в регистре 1 и единица в регистре 2 продвигаются параллельно и одновременно появляются на выходах регистров. В устройстве исправления ошибок (УИО), функцию которого выполняет также сумматор по модулю 2, искаженный элемент заменяется противоположным.

 

                                                                            Регистр 1

Вых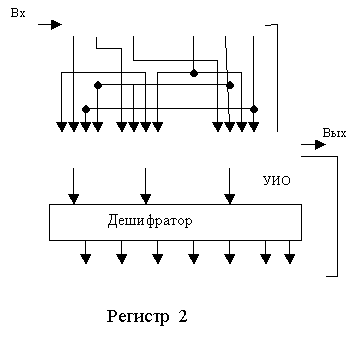

     Регистр             

7

6

5

4

3

2

1

7

6

5

4

3

2

1

    

 

                                                                      

      b₁

                                                                         

  b₂

   

    b₃

7

6

5

4

3

2

1

            а₄     а₃    а₂    а₁                                                                                                                       

 

Рисунок 14 – Декодирующее                       устройство кода Хэмминга

УИО

               Комбинация

              первичного кода

 

Рисунок 13 – Кодирующее                       устройство кода Хэмминга

 

 

 

 

 

 

1.13 Применение кода Рида – Соломона

 

Выше мы рассматривали основные двоичные коды, исправляющие ошибки, очевиден недостаток этих кодов – малая загруженность линии связи. Действительно, через линию связи проходит только два сигнала: сигнал "0" и сигнал "1", в то время как возможности линии допускают гораздо меньшую дискретность и большее количество дискретных уровней.

Наличие ошибок, обусловленных помехами в каналах передачи, а так- же физическими повреждениями носителей в каналах хранения, требует введения избыточности в информацию, подлежащей  передаче и хранению. Помехоустойчивая обработка двоичной информации кодов с основанием  позволяет получить достаточно простые реализации кодирующих и декодирующих устройств при высокой исправляющей и обнаруживающей способностях, как в отношении независимых, так и корректированных ошибок. К ним относятся линейные блоковые коды с основанием .

Общая характеристика и способы кодирования

Если каждому из недвоичных векторов длиной "а" сопоставить один из символов недвоичного алфавита, то вместо двоичной последовательности длиной k·a можно рассматривать эквивалентную двоичную последовательность длиной "k". Помеха устойчивости обработки такой информации возможна с помощью различных кодов с основанием k =.

В случае линейных блоковых кодов (n, k) преобразование исходного информационного вектора  длиной k в кодовый вектор , длиной n > k осуществляется с помощью линейной операции

,               (1.51)

где  -  строки порождающей матрицы G размерностью k и n, являющимися базисными векторами кода. Эти векторы должны быть линейно независимыми, чтобы любая их сумма не была базисным вектором

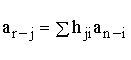                                         , ,                               (1.52)

коэффициенты  составляют матрицу  размерностью , так что .

С учетом соотношений (1.51) выражения для  можно записать в канонической форме

                                                           ,                                (1.53)

где  - единичная матрица размерностью . Кроме того, матрица R входит в состав проверочной матрицы H, которая в канонической форме соответствует соотношению (1.52) и имеет вид:

                                                           ,                                   (1.54)

где  - единичная матрица размерностью .

Кодовые векторы (кодовые слова) A составляют нулевое пространство матрицы H, так как

                                     ,                                                            (1.55)

коэффициенты  так же является символами рассматриваемого недвоичного алфавита объемом, , которым соответствуют двоичные векторы длиной "а" или многочлены фиктивной переменной x с двоичными коэффициентами. Например, вектору (010111) соответствует многочлен .

Сложение недвоичного алфавита. Операция сложения символов недвоичного алфавита выполняется путем поразрядного (по модулю два) сложения соответствующих векторов. Например,

(1011) + (0110) = (1101).

Все k символы недвоичного алфавита образует мультипликативную группу, включающую в себя нулевой элемент 0, которому соответствует вектор (00...0), единичный элемент, которому соответствует вектор (00...010), а также все целые положительные степени  до k-2 включительно.

Кроме того, на всю мультипликативную группу накладывается требование цикличности

.

Перемножение недвоичного алфавита.

Перемножение элементов группы для сохранения длины эквивалентных векторов выполняется как перемножение соответствующих многочленов по модулю некоторого многочлена F(x) степени а, т.е. . Для  многочлены даны в таблице 12. То есть  правило перемножения необходимы для того, чтобы разрядность кода не переполнялась, так как

,

то, деление на  эквивалентно умножению  .

Для построения мультипликативной группы рассмотрим пример.

Построим мультипликативную группу для , .

Операция по модулю F(x) означает, что , следовательно, элементу  соответствует многочлен  и вектор (11), значения отдельных элементов (символов недвоичного алфавита) представлены в таблице 13.

 

 

 

 

 

 

Таблица 12 – Многочлены F(x) для

	F(x) в виде многочлена	F(x) в виде числа
2		111
3		1011
4		10011
5		100101
6		1000011
7		10000011
8		100001111
9		1000010001
10		10000001001

 

Расстояния Хемминга между векторами определяется как число различий в отдельных элементах. Например, расстояние между векторами  и  равно двум. Минимальное расстояние Хемминга по всему множеству кодовых векторов называется кодовым расстоянием d. С помощью такого кода может быть гарантировано, исправлено t ошибок и восстановлено y стираний, если d>2t+y.

 

Таблица 13 – Значение отдельных элементов недвоичного алфавита

Элементы группы	Элементы многочленов	Элементы векторов
0	-	00
1	1	01
		10
		11

 

Прохождение вектора  (кода) через канал может быть представлено как

                                                      ,                                       (1.56)

где  - вектор на выходе канала, причем

.

Существуют различные способы декодирования полученных из канала векторов ** (по минимуму расстояние, мажоритарное, синдромное декодирование). Наиболее распространенный способ синдромного декодирования, основанный на вычислении синдромов **, являющихся векторами длинны r

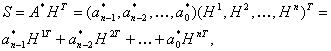                             (1.57)

где  - векторы столбцы матрицы H.                                                                                                                                                                                                                                                                                                                                                                                                                       .                                     (1.58)

Значение синдрома S зависит от вектора ошибок и вида проверочной матрицы. означает, что векторы  и  кодовые (т.е. информация получена без ошибок).  означает, что из канала получен некодовый вектор, т.е. информация получена с ошибкой. В этом случае можно ограничиться обнаружением d – 1 ошибки, и принятый вектор просто отбросить (декодирование с обнаружением ошибок). Ошибки можно исправить, если каждому их образцу будет однозначно соответствовать свой вид синдрома. Так,  если ошибочно принят один из символов , то , и чтобы эти синдромы были различными для каждого образца ошибок, необходимо различие всех  для  и . Таким образом, общее число синдромов  должно быть достаточным для исправления любого из  образцов ошибок на любой из n – позиции, полученных  из канала вектора им для выявления факта ошибок

                                              .                                       (1.59)

Отсюда максимальная длина кода для гарантированного исправления одной ошибки .

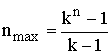                                             .                                           (1.60)

Рассмотрим пример.

Для   и  максимальная длина кода , следовательно, можно построить (5,3) линейный код для гарантированного исправления одной ошибки. Проверочная матрица  должна иметь размерность . В качестве первого столбца произвольно выберем

,

поэтому

,   ,

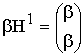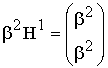так как , , то произвольно выбираем 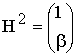, тогда 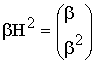, 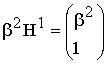. Далее поскольку , , , то выберем произвольно 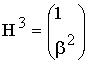 и далее возьмем  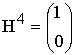и , и проверочная матрица будет иметь каноническую форму.

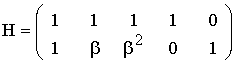                                             ,                 (1.61)

где

.

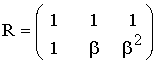Пусть , тогда  получим выражение

,

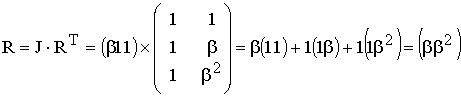и

.

Вообще для   и проверочная матрица имеет вид

.

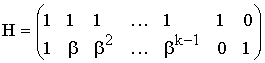Кодирующие преобразователи.

Кодовый вектор  может быть переведен в двоичную форму.

.

Преобразуем матрицу в двоичную форму с учетом выше рассмотренных результатов

,

,

,

,

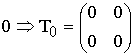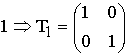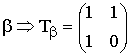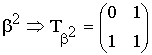где  - это матрица размерностью .

Проверочная и порождающая матрицы будут иметь вид.

 

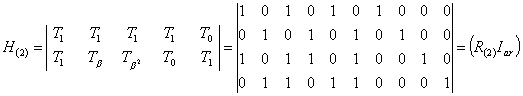
Порождающая матрица

.

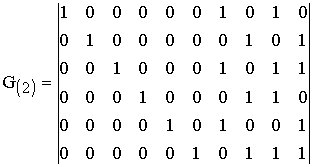Информационному вектору  соответствует двоичный вектор . Кодовый вектор в двоичной форме можно получить как

,

что соответствует  и совпадает с результатом примера два.

Декодирующие преобразователи с исправлением ошибок.

Наиболее простые алгоритмы разработаны для исправления одиночной ошибки с помощью линейных кодов с основанием k=2^a  и с d=3. Можно, например, предусмотреть выполнение следующих операций:

-       вычислить ;

-       если S=0, то получателю выдать вектор ;

-       если , то для   вычислить ;

-                  так как значение j, при котором , в случае одной ошибки соответствует ее образцу , произвести коррекцию: ;

-                  выдать получателю скорректированный информационный вектор: .

Пример.

Для (5,3) кода, декодируем вектор, принятый из канала .

В соответствии с рассмотренным алгоритмом:

1 ;

2 , ,  ;

3 ;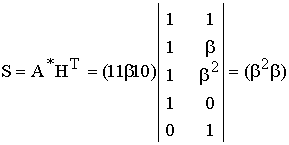

4  e_n-3=e₂=b ², a^*_n-3=a^*₂=b, ;

5  , .

Для исправления одиночных ошибок с помощью кодов с двумя проверочными символами, имеющими проверочные матрицы вида:

,

не обязательно хранить в памяти матрицу H.

 

1.14 Общая характеристика кодов Рида - Соломона

 

Кодами Рида - Соломона называют циклические коды у которых основание равно не двум, как обычно, а некоторому числу .

, .

Таким образом, число символов алфавита также будет равно 2^а, что дает возможность в "а" раз повысить скорость прохождения информации через линии связи, потому что вместо двоичных последовательностей длиной , мы будем иметь последовательность длиной . Алфавитом кода является мультипликативная группа, в которой существует элемент "0", элемент "1" и примитивный элемент b, а также все целые положительные степени b от двух до k-2 включительно.

В такой группе обязательно должны определяться сложения и умножения.

Сложение элементов мультипликативной группы осуществляется как сложение соответствующих им двоичных векторов или многочленов с фиктивной переменной по модулю два.

Все k символы недвоичного алфавита образуют мультипликативную группу, включающую в себя нулевой элемент 0, которому соответствует вектор (00...0), единичный элемент цифрой 1, которому соответствует (элемент) вектор(00...01), примитивный элемент b, которому соответствует вектор (00...10), а также все целые положительные степени b до k-2 включительно.

Группа является циклической, так что .

Длина кода Рида - Соломона равна , порождаемая многочленом

,

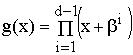где  d- кодовое расстояние (нечетное), а b - примитивный элемент мультипликативной группы, объединяющий все k символы недвоичного алфавита.

Очевидно, что

,

является корнями g(x), т.е. .

Как для любого циклического кода, число контрольных символов равно степени порождающего много члена

.

Число информационных символов . Коды Рида - Соломона обладают всеми свойствами линейных кодов, следовательно, можно построить порождающие и проверочные матрицы. Их находят путем деления единицы с нулями на выбранный многочлен  и выписывания всех промежуточных остатков. При этом должны быть соблюдены условия:

- число остатков должно быть равно числу информационных символов k;

-для проверочной матрицы пригодны лишь остатки весом W, не меньшим числа обнаруживаемых ошибок r, т.е. не меньшим двух.

 

1.15 Выбор числа символов и образующего многочлена

 

Рассмотрим такой пример, что на некотором объекте существует система телемеханики с линиями связи, в которых дискретность уравнения равна восьми, при этом необходимо, чтобы была возможность обнаружить двойные и исправлять одиночные ошибки, т.е. кодовое расстояние должно быть не менее трех

                                                         .

С другой стороны, для того, что бы работать с восьмиуровневой системой информации; необходимо чтобы

, т.е. ,

тогда

.

Следующий этап построения кода является нахождение символов недвоичного алфавита, для  из таблицы 3 .1 находим

.

Итак, первым элементом группы должен быть ноль, т.е. (000). Второй элемент-единица, т.е. (001). Третий элемент - . Четвертый элемент - . Пятый элемент синтезируется из условия

,

так как

,

,

,

.

После нахождения элементов алфавита сведем их в таблицу 14.

Теперь необходимо построить многочлен, пользуясь формулой порождающего многочлена

.

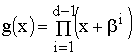Итак,

.

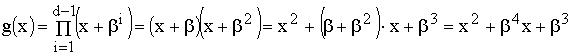Таким образом

.

После нахождения  можно приступить к кодированию.

 

Таблица 14 – Недвоичный алфавит Рида – Соломона

Символ	Многочлен	Вектор
0	-	000
1	1	001
b		010
		100
		011
		110
		111
		101

 

1.16  Кодирование кодов Рида - Соломона

 

Как было указано ранее, для аппаратной реализации наиболее удобен способ кодирования, в котором получаются разделимые  коды (кодирования, деления на порождающий многочлен) т.е. исходную комбинацию умножить на , а затем прибавить к полученной комбинации остаток от деления.

.

То есть  делим на . В нижерассматриваемом примере будет показано осуществление аппаратного кодирования.

Пример.

Пусть дана исходная комбинация 10000. Умножим на  и получим комбинацию 1000000.

Теперь эту комбинацию делим на порождающий многочлен, и мы найдем контрольные символы

,

,

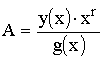получим

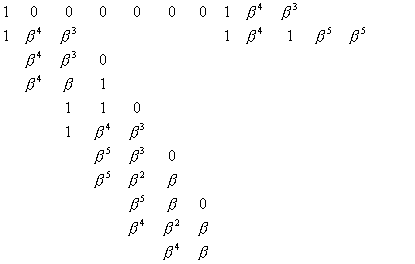
Таким образом, мы нашли контрольные символы: , и тогда вся комбинация примет вид

.

Отсюда легко получить

,

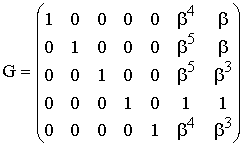например, для

,

.

 

 

 

 

 

1.17 Декодирование

 

Декодирование кодов Рида - Соломона производится аналогично декодированию циклических кодов, то есть принятая комбинация делится на образующий многочлен .

Если остаток от деления отсутствует, то это означает, что в принятом коде ошибки нет (т.е. не искажен). Для вышеприведенного примера эта будет выглядеть таким образом

Исправление ошибки происходит следующим образом.

Многочлен , принятый из линии связи, делится на  - образующий многочлен, при этом к  с каждым шагом дописывается . При получении остатка вида , , где  - это номер позиции, где произошла ошибка, а  - вид ошибки. Ее можно исправить

.

В примере, приведенном ниже, мы можем наглядно удостовериться, каким образом это происходит.

Предположим, что  в выше построенной комбинации произошла одна ошибка в четвертом символе, т.е. вместо  была принята комбинация .

Осуществим деление полученной комбинации на порождающий многочлен

,

.

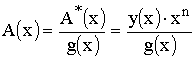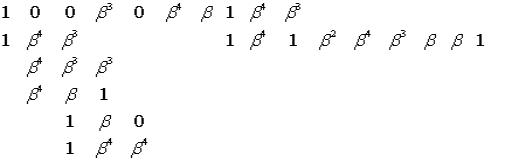
Отсюда видно, что ошибка произошла, в четвертом символе исходный символ был "0", так как . Если остаток содержит более двух символов, то это говорит о том, что произошло больше одной ошибки, значит исправление невозможно.

 

1.18 Понятие о сверточном кодировании

 

Кодирование и декодирование сверточных кодов осуществляется непрерывно, без деления информационной последовательности на блоки. Сверточные коды являются частным случай непрерывных (рекуррентных) кодов. В основу их построения положен принцип формирования проверочных разрядов путем суммирования по модулю 2 каждого информационного разряда с некоторым разрядом наоборот предыдущих разрядов. Примеры простейших сверточных кодеров приведены на рисунке 15 (а). Входящая информационная последовательность u₁, u₂, u₃,…., u_t поступает в регистр многотактного фильтра (N=3), некоторые из ячеек которого  связаны с двумя сумматорами по модулю 2.На контакт 1 коммутатора К подан информационный символ, на контакты 2 и 3 – проверочные символы. После поступления каждого информационного символа коммутатор осуществляет считывание трех символов (информационного и двух проверочных) и передает их в канал. Поскольку в рассматриваемом случае в канал подается как информационный, так и проверочные символы, то выходная кодовая последовательность является систематической. Однако выход с первой ячейки на контакт 1 может отсутствовать или на этот контакт могут быть поданы и выходы других ячеек, в результате чего код будет несистематическим. В общем случае сверточный кодер имеет вид, представленный на рисунке 15 (б). Считывание выходных символов коммутатором осуществляется после каждого поступления l  информационных символов, где l = 1, 2,…, причем l кратно N, т.е. N/ l= n.

Для задания сверточного кода достаточно указать длину регистра, и какие его ячейки связаны с каждом из сумматоров по модулю 2. Число сумматоров в схеме на рисунке 15 (б)  m=3, так как для упрощения на рисунке не показан сумматор, включенный между ячейкой и контактом 1 коммутатора. Связи i-сумматора описываются i-порождающей последовательностью

g_{i =} g_i1, g_i2,….., g_in,

 

где g_ij =1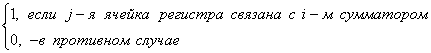

 

 

 

 

 

 

 

 

 

 

 

 

 

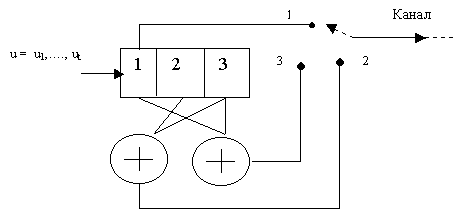
а)

 

 

 

 

 

 

 

 

 

 

 

 

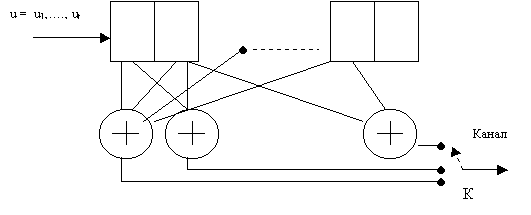
б)

 

Рисунок 15 – Пример структуры схемы сверточного кодера

 

Матрица , i= 1, 2,….., N называется порождающей матрицей. Например, для кодера рисунка 15 (а)  N=3, m=3 g_i1=101, g_i2= 010, g_i3 = 011, следовательно, g_i = 101010011. Выходной сигнал i-го символа u_t равен

 

где u_t=0 при .

 

Важным параметром сверточного кода является кодовое ограничение . Длина кодового ограничения в теории сверточных кодов играет роль, аналогичную длине блока в теории блочных кодов. В случае l=1,  т.е. N=n, . Кодовое ограничение представляет число кодовых символов, порождаемых кодером в промежутке времени между поступлением в него данного информационного символа и выводом его в канал. В примере

(рисунок 15 а)  .

Удобным аппаратом для рассмотрения кодирования и декодирования сверточных кодов является кодовое дерево. На рисунке 16 изображен пример кодового дерева для сверточного кодера (рисунок 15 (а)).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

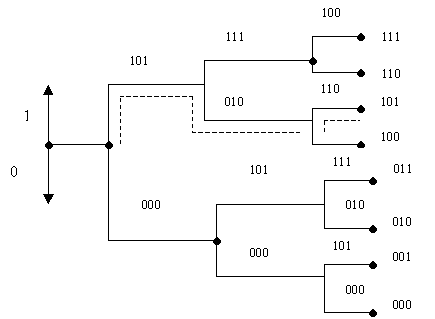
Рисунок 16 – Кодовое дерево

 

Точками обозначены узлы кодового дерева, соответствующие определенной информационной последовательности на входе кодера. Начальный (крайний слева) узел соответствует моменту до начала поступления информации. Отрезки между двумя соседними узлами называются ребрами. Совокупность нескольких последовательных ребер называется ветвью. Для определения узла, соответствующего некоторой определенной информационной последовательности, двигаются из начального узла по кодовому дереву, делая шаг вниз при поступлении информационного символа 0 и шаг вверх при поступлении информационного символа 1. Вдоль ребер написаны кодовые символы на выходе кодера, генерируемые при переходе от данного узла к соседнему, справа. Пунктиром показана ветвь, соответствующая входящей информационной последовательности 101.

Рассмотрим в качестве примера работу кодера (рисунок 15 (а)) при поступлении на его вход информационной последовательности 101. Предположим, что к моменту поступления кодовой последовательности все ячейки регистра находились в состоянии 0. Тогда после записи единицы в первую ячейку на выходе кодера будет считана кодовая комбинация 101

(вторую строку в таблице 15). Затем в первую ячейку регистра записывается второй символ информационной последовательности (нуль), а ее первый символ переписывается во вторую ячейку, в результате чего в канал будет передана кодовая комбинация 010. После записи в первую ячейку регистра третьего информационного символа (единицы) в канал будет передана кодовая комбинация 110. После поступления на вход кодера информационного символа подаются N нулей (в рассматриваемом примере N=3), в результате чего в канал передаются еще три группы символов: 010, 011, 000, а регистр возвращается в первоначальное положение.

Таким образом, информационная последовательность 101, состоящая из L=3 символов, в результате сверточного кодирования превращается в кодовую комбинацию 101010110010011000, состоящую из . Обычно информационная последовательность состоит из большого числа символов, так что L>>N, поэтому число символов в выходной последовательности превышает их число во входной в m раз. Несмотря на большую избыточность, сверточные коды находят распространение благодаря хорошим корректирующим свойствам.

 

Таблица 15

Номер пункта	Содержимое ячейки			Содержимое сумматора			Примечания
	1	2	3	1	2	3
1	0	0	0	0	0	0	Исходное состояние
2 3 4	1 0 1	0 1 0	0 0 1	1 0 1	0 1 1	0 0 0	Ввод в регистр 101
5 6 7	0 0 0	1 0 0	0 1 0	0 0 0	1 1 0	0 1 0	Ввод в регистр 000

 

Процедура декодирования сверточных кодов аналогична процедуре кодирования, и ее удобно рассматривать с помощью кодового дерева, рисунок 16. Поступающая на вход декодера последовательность анализируется по группам из m=3 элемента. Сначала m первых элементов подаются на два входных дешифратора, первый из которых выделяет комбинацию 101, а второй – комбинацию 000. В зависимости от того, какая из комбинаций поступила в m первых элементов, открывается путь А одной из пар дешифраторов, выделяющих m вторых элементов, значения которых определяются кодовым деревом до тех пор, пока сигнал не появится на одном из 2^N=8 выходов декодера. Такая процедура декодирования получила название последовательного декодирования.

Описанный процесс происходит таким образом, когда в принимаемой последовательности отсутствуют ошибки. Например, при передаче информационной последовательности 101 в дискретный канал, как выше было показано, поступает последовательность 101010110, которая при отсутствии ошибок в соответствии с кодовым деревом (рисунок 16 (пунктир)) правильно декодируется в 101. При наличии ошибок декодирование окажется  неэффективным так как              отдельные группы принятой кодовой последовательности не будут совпадать с ребрами кодового дерева.

Возенкрафтом предложена вероятностная процедура декодирования, заключающаяся в выборе при декодировании такой кодовой комбинации, которая отличается от принятой последовательности в наименьшем  числе разрядов. В таком случае если принятая последовательность (вернее, ее отдельная группа из m элементов) не совпадает ни с одним ребром, выходящим из данного узла, то декодер следует сначала по ребру у каждого числа совпадающих символов больше. Очевидно, что при числе ошибок в группе из m элементов, большем, чем m/2, такой декодер сначала проследует к неправильному А узлу. Однако маловероятно, чтобы, сделав такую ошибку, декодер нашел в этом неправильном узле ребро, хорошо согласующееся со следующей группой m принятых символов.

Рассмотрим, например, кодовое дерево (рисунок 17), соответствующее декодеру N=4, m=5, изображенному на рисунке 18.

При передаче информационной последовательности х=1010 на выходе кодера получим у = 11111, 01010, 11000, 01001.Предположим, что вектор ошибки в канале е = 00010, 01101, 00000, 00000, тогда на вход декодера поступит последовательность γ = 11101, 00111, 11000, 01001. В этом случае,

как показано на рисунке 17 сплошной линией, декодер из начального А узла  следует сначала по правильному пути к узлу В, а из него – по неправильному пути к узлу С (пунктир), так как 00111 отличается от 10101 в двух разрядах, а от 01010 – в трех. Но из ребер, выходящих из узла С, не совпадает с 11000 столько же разрядов (два или три), сколько у правильного пути (в узел Д), что дает основание декодеру обнаружить ошибочный поворот и вернуться в узел В для исправления ошибки.

Алгоритм Возенкрафта аналогичен последовательности действий водителя автомобиля, который,  сделав неправильный поворот на развилке дорог, быстро обнаруживает ошибку, возвращается на развилку и требует новую дорогу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

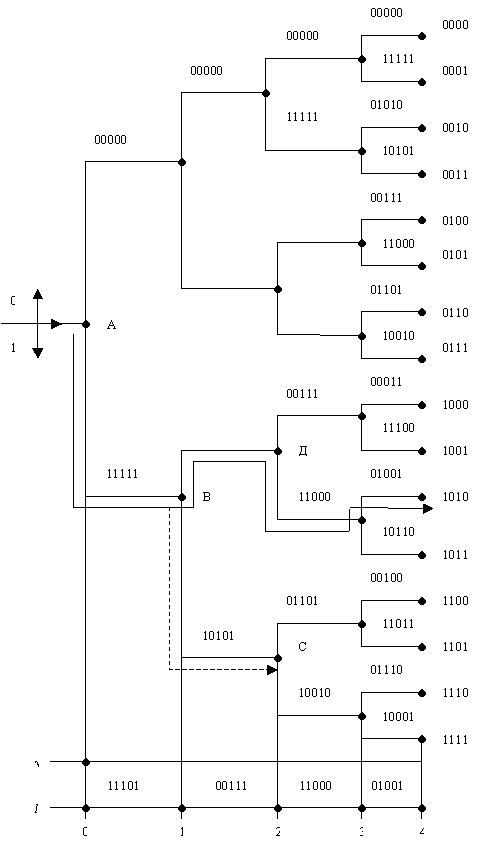
Рисунок 17 – Кодовое дерево для декодера

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 18 - Схемы  сверхточных кодера и декодера

 

Рассмотрим в качестве примера работу декодера (рисунок 18) при поступлении на его вход последовательности Г, которая записывается в буфер входа, откуда группами по пять элементов переписывается в регистр 1, одновременно в Х-регистр от генератора Г подается случайная последовательность нулей и единиц, и в регистр 2 записывается гипотетическая последовательность у*. Затем производится вычисление расстояния  Хемминга между принятой и гипотетической последовательностями d(l)=γy*. Пусть в первый разряд регистра Х от Г записана единица, тогда на первом ребре d(l)=111011111=1.

Так как декодер выбирает путь по принципу d<m/2-путь правильный, d>m/2-путь неправильный , то в рассматриваемом примере (m=5, d=1) в узле а путь выбран правильно, в первом разряде Х-регистра фиксируется единица. После этого в регистр 1 записывается группа символов 00111, а в регистр 2 поступает вторая гипотетическая комбинация. Предположим, что при этом в первый разряд Х-регистра от Г поступила единица, тогда d(2)=0011110101=2. Если же в первый разряд Х-регистра был записан нуль, то d^/ (2)= 0011101010=3

Поскольку 2<5/2<3, то декодер в узле  принимает неправильное решение и идет в узел С. Для обнаружения факта  принятие неправильного решения декодер по мере движения вдоль кодового дерева вычисляет текущее значение d(l) и в каждом узле сравнивает d(l) с исключающей функцией критерия k(l). Если d(l) превышает k(l), то пробный путь отбрасывается как маловероятный и декодер возвращается на ближайшее неисследованное ребро, для которого d(l) < k(l), и снова движется вперед, пока удовлетворяется это условие. Для простоты реализации декодера в качестве k(l) выбирают прямую линию. При больших l доля искаженных сигналов в дискретном симметричном канале приблизительно равна  переходной вероятности канала p, поэтому если y*l соответствует правильному пути, то,  естественно,  ожидать,  что d(l) будет колебаться около прямой, коэффициент наклона которой равен рm (I на рисунке 19). Если те y*l соответствует неправильному пути  из начального узла (l=0), то d(l) будет колебаться около прямой с наклоном  m/2 (II на рисунке 19). Исходя из вышеизложенного,  Возенкрафт предлагает в качестве d(l) принять прямую с коэффициентом наклона p’m, где p<p’<0.5, не проходящую через путь при l=0, т.к. начальные символы могут быть тоже искажены (III на рисунке 19). На этом рисунке показаны примеры  личные графики  значений d(l) для правильного (IV на рисунке 19) и неправильного (V на рисунке 19) путей.

Алгоритм последовательного декодирования Возенкрафт был усовершенствован Фано, который ввел вместо d(l) так называемое переношенное расстояние t(l) =d(l)-p’ml, где l- количество ребер, на которое декодер углубился в кодовом дереве, и назвал соответствующие критерии порогами. Эти пороги принимают вид горизонтальных прямых, отстоящих друг от друга на расстоянии D (на рисунке 20).

Если  y*(l) соответствует правильному пути, то t(l) обычно близко к отрицательной величине (p-p’)ml и уменьшается с ростом  l. Если y*(l) соответствует правильному пути,  то t(l),  как правило,  близко к (1/2-p’)ml и увеличивается с ростом l (I на рисунке 20) при безошибочном декодировании поведение t(l) будет характеризовываться  с неуклонным следованием вниз от исходного нулевого порога (II на рисунке 20). Если же  в начале возникли ошибки, то их действие на каком-либо участке вызывает увеличение t(l) и принятый на данном этапе текущий порог iD, где i=1,2,…, в следующем  узле нарушается (III на рисунке 20).

Если y*(l) соответствует правильному пути, то t(l) обычно близко к отрицательной величине (р-p’)ml и уменьшается с ростом l. Если y*(l) соответствует неправильному пути, то t(l), как правило,   близко к (1/2- p’)ml и увеличивается с ростом l (I на рисунке 20). При бесконечном декодировании поведение t(l) будет характеризовываться неуклонным следованием вниз от исходного нулевого порога (II на рисунке 20). Если же в канале возникли ошибки, то их действие на каком – либо участке вызывает увеличение t(l), и принятый на данном этапе текущий порог i∆, где i=1,2,…., в следующем узле нарушается (III на рисунке 20).Это свидетельствует о том, что декодер может находиться на неверном пути и следуя заложенным в алгоритме указаниям, “возвращаться” на один узел назад. Проверяем возможные варианты  путей из этого узла.

Если этот путь отыскивается,  декодер следует по тому пути, но в случае, если варианты пути требуют увеличения порога, декодер возвращается к  первоначальному варианту, считая его правильным, и начинает дальнейшее движение- поиск по кодовому дереву. Рассмотрим пример (рисунок 21): первая кодовая комбинация или первый исследуемый узел обозначаются единицей. Для этого узла текущий порог равен D. Вторая поступившая комбинация ошибочна в трех элементах. Из первого узла возможны два пути – узел 2-2’. Так как узел 2’ не превышает текущего порога. Декодер направляется в узел 2’. Но следующие поступившие комбинации превышают сразу два порога, поэтому декодер, согласно алгоритму,  возвращается в узел 1. Исследуем узел 2. Из узла 2 возникает благоприятный путь в узел 3 и т.п. Таким образом, декодер благополучно исправляет вторую искаженную кодовую комбинацию.                

 

 

 

 

 

 

 

 

 

 

 

 

 

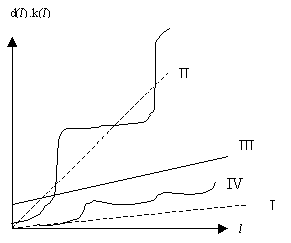
Рисунок 19 – К выбору критерия исключения

 

 

 

 

 

 

 

 

 

 

 

 

 

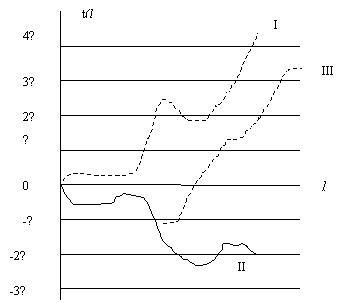
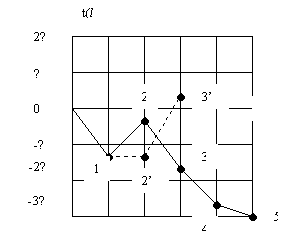
Рисунок 21 – Пример поиска по

                                                                                         алгоритму Фано

 

Рисунок 20 – К пояснению                                   Алгоритма Фано

          

 

1.19 Программная реализация «Сверточного кодера»

 

 

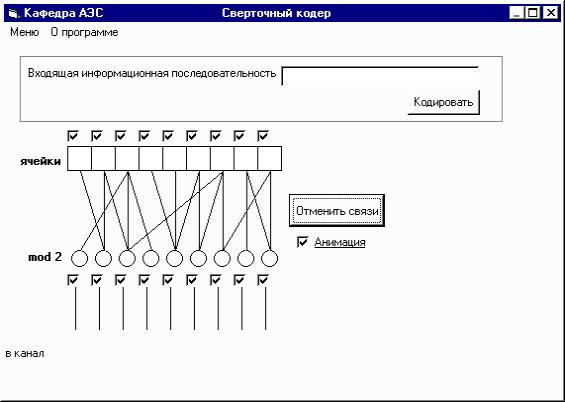
При создании программы была использована программа Visual Basic 6.0

В программе использованы следующие объекты

 

Таблица 16

Объект	Описание
	Данный объект предназначен для ввода бинарной (двоичной «0», «1») информации
	Кнопка кодировать, при нажатии выполняется функция кодирования
	Объекты Check1 предназначены для выбора ячеек
	Объекты Check2 предназначены для выбора сумматоров
	Данная кнопка предназначена для отмены связей между ячейками и сумматорами
	Объект Animation(Check) используется для показа анимации выводимого сигнала с сумматоров
	Объект Kanal(Label) используется для вывода закодированного сигнала

 

 

 

 

 

 

 

 

 

 

 

В программе содержатся следующие функции и процедуры:

 

Таблица 17

Процедуры	Описание
Sub Check1_Click(Index As Integer)	Выбор ячеек   кодера
Sub Check2_Click(Index As Integer)	Выбор сумматоров mod 2 кодера
Sub Command1_Click()	Отменить связи между кодерами и сумматорами
Sub Command2_Click()	Непосредственное кодирование входного сигнала,  действие кнопки кодировать
Sub Image1_Click(Index As Integer)	Создает связь между ячейкой и сумматором
Sub Image2_Click(Index As Integer)	Создает связь между сумматором и ячейкой
Sub Form_Load()	Загрузка начальных параметров
Sub mnuExit_Click()	Меню выход
Sub mnuKoder_Click()	Меню кодировать
Sub mnuName_Click()	Меню о программе
Sub Timer1_Timer()	Включение таймера анимации
Sub Migalka(k As Integer)	Непосредственная анимация

 

Ниже приводится листинг программы