Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра Автоматическая электросвязь
МОДЕЛИРОВАНИЕ В ТЕЛЕКОММУНИКАЦИЯХ
Конспект лекций для магистрантов специальности
6M071900 – Радиотехника, электроника и телекоммуникации
Алматы 2013
Составитель: Лещинская Э.М. Моделирование в телекоммуникациях. Конспект лекций для магистрантов специальности 6М071900 – Радио- техника, электроника и телекоммуникации. - Алматы: АУЭС, 2013. – 65с.
В конспекте лекций по дисциплине «Моделирование в телекоммуникациях» излагаются математические методы и модели, применяемые для исследования и построения систем связи. Конспект лекций предназначен для магистрантов специальности 6М071900 – Радиотехника, электроника и телекоммуникации.
Ил. 3, табл.3, библиогр.- 13 назв.
Рецензент: доцент Башкиров М.В.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013г.
© НАО «Алматинский университет энергетики и связи», 2013 г.
Введение
«Моделирование в телекоммуникациях» - теоретический курс для магистрантов специальности 6М071900 – Радиотехника, электроника и телекоммуникации.
Целью курса является ознакомление магистрантов с основными понятиями моделирования систем, методами построения математических моделей, описывающих работу объектов телекоммуникаций, разработкой алгоритмов их реализации; методами статистического анализа показателей работы систем телекоммуникаций.
Задачами преподавания дисциплины является овладение основными принципами моделирования систем, статистическими методами сбора, обработки и анализа данных, методикой построения и анализа моделей, применяемых в телекоммуникациях.
Изучение курса, помимо лекционных и практических занятий, предполагает выполнение расчетно-графических работ с применением компьютера и проведение самостоятельных работ с целью углубления общих знаний теории.
В результате изучения курса магистрант должен знать наиболее практически ценные математические методы и модели, применяемые в отрасли связи, уметь сформулировать словесную формулировку задачи в соответствии с поставленными целями, преобразовать словесную постановку задачи в математическую модель, выбрать метод решения поставленной задачи, решить задачу наиболее эффективным методом.
Лекция 1. Основные понятия теории моделирования систем
Цель лекции: ознакомление студентов с общими вопросами теории
моделирования систем.
Содержание:
а) модель и моделирование;
б) система и комплекс, свойства систем;
в) эффективность систем;
г) анализ и синтез систем.
Модель - физический или абстрактный объект, адекватно отображающий исследуемую систему.
Моделирование - замещение одного исходного объекта другим объектом, называемым моделью и проведение экспериментов с моделью с целью получения информации о системе путем исследования свойств модели.
Объектами моделирования в технике являются системы и протекающие в них процессы. В частности, в телекоммуникациях объектами моделирования являются средства связи, комплексы, системы и сети. При этом, наибольший интерес представляют конструктивные модели, допускающие не только фиксацию свойств (как в произведениях искусств), но и исследование свойств систем (процессов), а также решение задач проектирования систем с заданными свойствами.
Моделирование предоставляет возможность исследования таких объектов, прямой эксперимент с которыми:
1) трудно выполним;
2) экономически невыгоден;
3) вообще невозможен.
Система (от греч. systema - целое, составленное из частей; соединение) - совокупность взаимосвязанных элементов, объединенных в одно целое для достижения некоторой цели, определяемой назначением системы.
Элемент - минимальный неделимый объект, рассматриваемый как единое целое.
Сложная (большая) система характеризуется большим числом входящих в его состав элементов и связей между ними.
Комплекс - совокупность взаимосвязанных систем.
Структура системы задается перечнем элементов, входящих в состав системы, и связей между ними.
Способы описания структуры системы:
а) графический - в форме:
1) графа, в котором вершины соответствуют элементам системы, а дуги - связям между ними;
2) схем, широко используемых в инженерных приложениях, в которых элементы обозначаются в виде специальных символов;
б) аналитический - путем задания количества типов элементов, числа элементов каждого типа и матрицы связей (инцидентности), определяющей взаимосвязь элементов.
Функция системы - правило достижения поставленной цели, описывающее поведение системы и направленное на получение результатов, предписанных назначением системы.
Способы задания функции системы:
а) алгоритмический - словесное описание в виде последователь- ности шагов, которые должна выполнять система для достижения поставленной цели;
б) аналитический - в виде математических зависимостей в терминах некоторого математического аппарата: теории множеств, теории случайных процессов, теории дифференциального или интегрального исчисления и т.п.;
в) графический - в виде временных диаграмм или графических зависимостей;
г) табличный - в виде различных таблиц, отражающих основные функциональные зависимости, например, в виде таблиц булевых функций, Способы описания функции системы:
д) автоматных таблиц функций переходов и выходов и т.п.
Организация системы - способ достижения поставленной цели за счет выбора определенной структуры и функции системы. В соответствии с этим различают структурную и функциональную организацию системы.
Функциональная организация определяется способом порождения функций системы, достаточных для достижения поставленной цели.
Структурная организация определяется набором элементов и способом их соединения в структуру, обеспечивающую возможность реализации возлагаемых на систему функций.
Любым сложным системам присущи фундаментальные свойства, требующие применения системного подхода при их исследовании методами математического моделирования.
Такими свойствами являются:
1) целостность, означающая, что система рассматривается как единое целое, состоящее из взаимодействующих элементов, возможно неоднородных, но одновременно совместимых;
2) связность - наличие существенных устойчивых связей между элементами и/или их свойствами;
3)
организованность
- наличие
определенной структурной и функциональной организации,
обеспечивающей снижение энтропии
(степени
неопределенности) системы по сравнению с энтропией
системообразующих факторов,
определяющих возможность создания
системы.
4) интегративность - наличие качеств, присущих системе в целом, но не свойственных ни одному из ее элементов в отдельности. Таким образом, можно сделать следующие важные выводы:
– система не есть простая совокупности элементов;
– расчленяя систему на отдельные части и изучая каждую из них в отдельности, нельзя познать все свойства системы в целом.
В общем случае моделирование направлено на решение задач:
-анализа, связанных с оценкой эффективности систем, задаваемой в виде совокупности показателей эффективности;
-синтеза, направленных на построение оптимальных систем в соответствии с выбранным критерием эффективности.
Эффективность - степень соответствия системы своему назначению. Эффективность систем обычно оценивается набором показателей эффективности.
Показатель эффективности (качества) - мера одного свойства системы.
Показатель эффективности всегда имеет количественный смысл.
Критерий эффективности - мера эффективности системы, обобщающая все свойства системы в одной оценке - значении критерия эффективности. Если при увеличении эффективности значение критерия возрастает, то критерий называется прямым, если же значение критерия уменьшается, то критерий называется инверсным.
Критерий эффективности служит для выбора из всех возможных вариантов структурно-функциональной организации системы наилучшего (оптимального) варианта.
Оптимальная система - система, которой соответствует максимальное (минимальное) значение прямого (инверсного) критерия эффективности из всех возможных вариантов построения системы, удовлетворяющих заданным требованиям.
Анализ - процесс определения свойств, присущих системе.
Синтез - процесс порождения функций и структур, удовлетворяющих требованиям, предъявляемым к эффективности системы.
Параметры описывают первичные свойства системы и являются исходными данными при решении задач анализа;
Характеристики описывают вторичные свойства
системы и
определяются в процессе
решения задач анализа как функция параметров.
Множество параметров технических систем можно разделить на:
- внутренние, описывающие структурно-функциональную организацию системы, к которым относятся:
1) структурные параметры, описывающие состав и структуру системы;
2) функциональные параметры, описывающие режим функционирования системы.
- внешние, описывающие взаимодействие системы с внешней по отношению к ней средой, к которым относятся:
1) нагрузочные параметры, описывающие входное воздействие на систему, например частоту и объем используемых ресурсов системы;
2) параметры внешней (окружающей) среды, описывающие обычно неуправляемое воздействие внешней среды на систему.
Параметры могут быть:
а) детерминированными или случайными;
б) управляемыми или неуправляемыми.
Характеристики системы делятся на:
а) глобальные, описывающие эффективность системы в целом;
б) локальные, описывающие качество функционирования отдельных элементов или частей (подсистем) системы.
Тогда закон функционирования системы можно представить в следующем виде:
Н(У) = fc(S,F,Y,X,t),
где fc - функция, функционал, логические условия, алгоритм, таблица или словесное описание, определяющее правило (закон) преобразования входных величин (параметров) в выходные величины (характеристики);
Н(У) - вектор характеристик, зависящий от текущего момента времени t.
S – структурные параметры;
F – функциональные параметры;
Y – нагрузочные параметры;
X – параметры внешней среды.
Процесс - последовательная смена состояний системы во времени.
Состояние системы задается совокупностью значений переменных, описывающих это состояние. Система совершает переход из одного состояния в другое, если описывающие ее переменные изменяются от значений, задающих одно состояние, на значения, которые определяют другое состояние. Причина, вызывающая переход из состояния в состояние, называется событием.
Классификация систем и процессов выполняется в зависимости от конкретных признаков, в качестве которых будем использовать:
а) способ изменения значений величин,
описывающих состояния
системы
или процесса;
б) характер протекающих в системе процессов;
в) режим функционирования системы (режим процесса).
Лекция 2 Построение математических моделей
Цель лекции: ознакомление студентов с основными задачами и методами создания моделей в телекоммуникации.
Содержание:
а) основные требования к модели;
б) классификация моделей;
в) этапы создания модели;
г) методы моделирования.
Ко всем разрабатываемым моделям предъявляются два противоречивых требования:
– простота модели;
– адекватность исследуемой системе.
Требование простоты модели обусловлено необходимостью построения модели, которая может быть рассчитана доступными методами. Построение сложной модели может привести к невозможности получения конечного результата имеющимися средствами в приемлемые сроки и с требуемой точностью.
Степень сложности (простоты) модели определяется уровнем ее детализации, зависящим от принятых предположений и допущений: чем их больше, тем ниже уровень детализации и, следовательно, проще модель и, в то же время, менее адекватна исследуемой системе.
Адекватность – соответствие модели оригиналу, характеризуемое степенью близости свойств модели свойствам исследуемой системы.
Модели могут быть классифицированы в зависимости от:
1) характера функционирования исследуемой системы:
детерминированные, функционирование которых описывается детерминированными величинами, стохастические или вероятностные, функционирование которых описывается случайными величинами;
2) характера протекающих в исследуемой системе процессов:
непрерывные, в которых процессы протекают непрерывно во времени и дискретные, в которых процессы меняют свое состояние скачкообразно в дискретные моменты времени;
3) степени достоверности исходных данных об исследуемой системе:
а) с априорно известными параметрами;
б) с неизвестными параметрами;
4) режима функционирования системы:
а) стационарные, в которых характеристики не меняются со временем;
б) нестационарные, в которых характеристики изменяются со временем;
5) назначения:
а) статические или структурные, отображающие состав и структуру системы;
б) динамические или функциональные, отображающие функциони- рование системы во времени;
в) структурно-функциональные, отображающие структурные и функциональные особенности организации исследуемой системы;
6) способа представления (описания) и реализации:
а) концептуальные или содержательные,
представляющие собой
описание (в простейшем
случае словесное) наиболее существенных
особенностей структурно-функциональной организации исследуемой
системы;
б) физические или материальные - модели, эквивалентные или подобные оригиналу (макеты) или процесс функционирования которых такой же, как у оригинала и имеет ту же или другую физическую природу;
в) математические или абстрактные, представляющие собой формализованное описание системы с помощью абстрактного языка, в частности с помощью математических соотношений, отражающих процесс функционирования системы;
г) программные (алгоритмические, компьютерные) - программы для ЭВМ, позволяющие наглядно представить исследуемый объект посредством имитации или графического отображения математических зависимостей, описывающих искомый объект.
Соответственно различают физическое, математическое и компьютерное моделирование.
Моделирование, как процесс исследования сложных систем, в общем случае предполагает решение следующих взаимосвязанных задач:
1) разработка модели;
2) анализ характеристик системы;
3) синтез системы;
4) детальный анализ синтезированной системы.
Разработка модели состоит в выборе конкретного математического аппарата, в терминах которого формулируется модель, и построении модели или совокупности моделей исследуемой системы, отображающих возможные варианты структурно-функциональной организации системы. В процессе разработки модели необходимо определить состав и перечень параметров и характеристик модели в терминах выбранного математического аппарата, и установить их взаимосвязь с параметрами и характеристиками исследуемой системы, то есть выполнить параметризацию модели.
Анализ характеристик системы с использованием разработанной модели заключается в выявлении свойств и закономерностей, присущих процессам, протекающим в системах с различной организацией, и выработке рекомендаций для решения основной задачи системного проектирования - задачи синтеза.
Синтез системы заключается в определении параметров системы, удовлетворяющих заданным требованиям к характеристикам системы.
В зависимости от целей можно выделить следующие частные задачи (этапы) синтеза:
1) структурный синтез, состоящий в выборе способа структурной организации системы, в рамках которой могут быть удовлетворены требования технического задания;
2) функциональный синтез, состоящий в выборе режима (способа) функционирования системы;
3) нагрузочный синтез, состоящий в определении требований к параметрам нагрузки, обеспечивающим функционирование системы с заданным качеством.
При исследовании технических систем с дискретным характером функционирования наиболее широкое применение получили следующие методы математического моделирования:
1) аналитические (аппарат теории вероятностей, теории массового обслуживания, теории случайных процессов, методы оптимизации);
2) численные (применение методов численного анализа для получения конечных результатов в числовой форме);
3) статистические или имитационные (исследования на ЭВМ, базирующиеся на методе статистических испытаний и предполагающие применение специальных программных средств и языков моделирования: GPSS , SIMULA, ИМСС и др.).
4) комбинированные.
Аналитические методы состоят в построении математической модели в виде математических символов и отношений.
Численные методы основываются на построении конечной последовательности действий над числами. Применение численных методов сводится к замене математических операций и отношений соответствующими операциями над числами. Результатом применения численных методов являются таблицы и графики зависимостей, раскрывающих свойства объекта.
Статистические методы применяют в тех случаях, когда анализ математической модели даже численными методами может оказаться нерезультативным из-за чрезмерной трудоемкости или неустойчивости алгоритмов в отношении погрешностей аппроксимации и округления. Строится имитационная модель, в которой процессы, протекающие в системе, описываются как последовательности операций над числами, представляющими значения входов и выходов соответствующих элементов.
При построении имитационных моделей широко используется метод статистических испытаний (метод Монте-Карло). Процедура построения и анализа имитационных моделей методом статистических испытаний называется статистическим моделированием. Статистическое моделирование представляет собой процесс получения статистических данных о свойствах моделируемой системы.
Комбинированные методы представляют собой комбинацию выше перечисленных методов.
Математический аппарат исследования операций.
Линейное программирование – раздел математики, позволяющий найти экстремальное значение линейной функции многих переменных, если ограничения, связывающие эти переменные, тоже линейны. К задачам линейного программирования приводит анализ широкого круга технико-экономических процессов, где возникает необходимость поиска оптимального решения.
Нелинейное программирование – задача ставится примерно также как и в линейном программировании, но функции (целевая и ограничения) не предполагаются линейными.
Динамическое программирование – особый математический аппарат, при котором для отыскания оптимального управления планируемая операция разбивается на ряд «шагов» или «этапов» и планирование идет от этапа к этапу. На каждом этапе выбор управления осуществляется с учетом интересов операции в целом.
Теория массового обслуживания - прикладная область теории случайных процессов. Изучает вероятностные модели систем обслуживания, в которых заявки на обслуживание поступают в случайные моменты времени и в случайном количестве. В тех случаях, когда следует обеспечить такую скорость обслуживания, при которой время ожидания остается ниже некоторого установленного уровня, теория массового обслуживания позволяет определить необходимые для этого меры и рассчитать соответствующие затраты.
Теория управления запасами. Анализ моделей управления запасами сводится к установлению последовательности процедур снабжения и управления запасов, при которой обеспечиваются минимальные суммарные затраты, связанные с транспортировкой и хранением продукции, а также из-за неудовлетворенного спроса.
Теория игр - теория математических моделей принятия оптимальных решений в условиях конфликта и неопределенности. При этом в качестве конфликта можно рассматривать любые разногласия участников моделируемого процесса.
Теория графов. Решаются многие сетевые задачи, имеющие актуальное значение при организации связи: задачи о максимальном потоке, о кратчайшей связывающей сети, построения кольцевого маршрута и т.д.
Лекция 3. Методы сбора и систематизации статистической информации
Цель лекции: ознакомление студентов с основными методами сбора и систематизации статистической информации.
Содержание:
а) методы сбора и источники статистической информации;
б) систематизация статистических данных;
в) ряды распределения.
Построение математической модели сопровождается сбором необходимых сведений об объекте моделирования. Для того чтобы эти сведения были полными и достоверными, необходимо производить сбор данных в соответствии с правилами, разработанными статистической наукой.
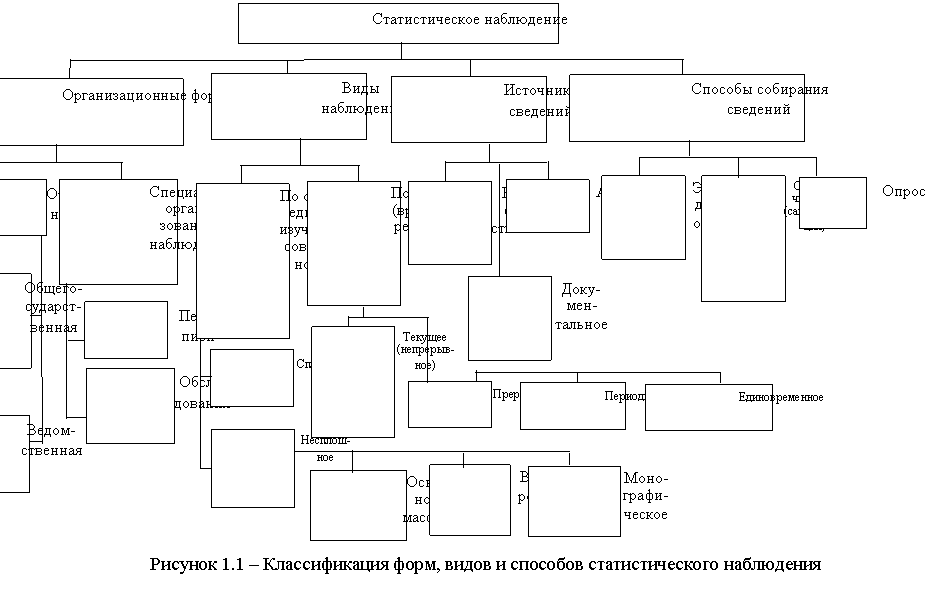
Сбор данных об исследуемой совокупности путем регистрации заранее намеченных существенных признаков с целью получения обобщающих характеристик называется в статистике статистическим наблюдением.
Основные формы, виды и способы статистического наблюдения представлены на рисунке 1.1.
Отчетность – это такая форма статистического наблюдения, при которой предприятия в определенные сроки в установленном виде предоставляют в статистические органы необходимые сведения. Это основной источник данных. В том случае, если отчетность не содержит необходимых сведений, проводят специально организованное наблюдение или эксперимент.
Сплошное наблюдение, при котором обследованию подлежат все единицы изучаемой совокупности.
Несплошное наблюдение, при котором обследуется часть совокупности, отобранная определенным способом.
Выборочное наблюдение - наблюдение, основанное на принципе случайного отбора тех единиц совокупности, которые будут подвержены исследованию.
Монографическое наблюдение – представляет собой детальное глубокое изучение отдельных единиц совокупности, имеющих существенные различия по сравнению со всеми единицами.
Непосредственное наблюдение – вид наблюдения, при котором необходимые сведения получают путем подсчета и измерения единиц совокупности.
Экспедиционный способ наблюдения заключается в том, что специально привлеченные и обученные работники посещают каждую единицу наблюдения и собирают сведения.
Статистическое наблюдение проводится по программе, где указываются цель и задачи наблюдения; определяется объект и единица наблюдения; разрабатываются формуляр и инструкция; определяются организационные вопросы: время наблюдения и место наблюдения.
Объект наблюдения – это та совокупность, о которой должны быть собраны сведения. Выделение объекта наблюдения связано с определением границ совокупности в пространстве, во времени и по материальной сущности.
Единица наблюдения – составной элемент объекта наблюдения, который является носителем признаков, подлежащих регистрации.
При наблюдении заполняется статистический бланк, называемый формуляром. Формуляр заполняется на основании инструкции.
Время наблюдения предусматривает срок наблюдения – это время, в течение которого осуществляется регистрация сведений и критический момент – момент времени, по состоянию на который проводится регистрация собираемых сведений.
Орган наблюдения – перечень конкретных исполнителей, осуществляющих подготовку и проведение наблюдения и несущих ответственность за эту работу.
Место наблюдения – это пункт, где проводится регистрация наблюдаемых фактов, и заполняются формуляры наблюдения.
Точность статистического наблюдения – степень соответствия значения какого-либо признака, найденного посредством наблюдения, действительному его значению.
При сборе статистических сведений возможны ошибки при заполнении формуляров, подразделяемые на случайные и систематические. Систематические ошибки имеют тенденциозный характер и бывают преднамеренными и непреднамеренными.
Устранить ошибки наблюдения возможно проведением логического или арифметического контроля собранных данных.
Статистическая сводка – представляет собой обобщение (систематизацию) статистического материала, полученного в ходе наблюдения с помощью итоговых подсчетов, выполняемых по определенной системе.
Группировкой называется расчленение единиц изучаемой совокупности на однородные группы по определенным существенным признакам.
Виды группировок:
Типологическая группировка – это расчленение однородной совокупности на однородные группы и выявление на этой основе экономических типов явлений.
Структурная группировка – предназначена для изучения состава однородной совокупности по какому-либо варьирующему признаку.
Аналитическая группировка – группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками. Особенностью аналитической группировки является то, что единицы группируются по факторному признаку и каждая выделенная группа характеризуется средними величинами результативного признака.
Под факторным признаком понимается признак-причина, под воздействием которого изменяется результативный признак – признак следствие.
В основе группировки могут быть количественные и качественные признаки.
При построении группировки по качественному признаку производится лишь подсчет единиц совокупности, имеющих значение группировочного признака. Данная группировка принимает вид атрибутивного ряда распределения.
Группировка по дискретному признаку проводится аналогично группировке по качественному признаку, с образованием дискретного вариационного ряда распределения. В случае непрерывного признака образуется интервальный вариационный ряд распределения.
При построении интервальной группировки определяется число групп и величина интервала.
Число групп (n) может быть определено логическим (задается исследователем), механическим способом (получается механически с учетом заданной величины интервала) или аналитическим способом с помощью формулы Стерджесса
n=1+3,32 lgN,
где N – число единиц совокупности.
Величина интервала (i) в случае равномерного ряда распределения (i = const) определяется по формуле
![]()
где x max, x min – соответственно максимальное и минимальное значения признаков совокупности. Интервалы группировок могут быть закрытыми и открытыми.
Закрытыми называются интервалы, у которых имеются нижняя и верхняя границы. Открытые – это те интервалы, у которых указана только одна граница: верхняя – у первого; нижняя - у последнего.
Для группировки единиц совокупности, характеризуемых несколькими признаками, используется метод кластерного анализа. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких признаков, можно представить как точку в пространстве этих признаков, значения которых рассматриваются как координаты в многомерном пространстве. Основным критерием группировки (кластеризации) является то, что различия между группами (кластерами) должны быть более существенным, чем между единицами, отнесенными к одной группе.
Лекция 4. Анализ статистических данных с использованием средних величин и показателей вариации.
Цель лекции: ознакомление студентов с методами расчета статистических показателей, используемых в моделировании для анализа собранных данных.
Содержание:
а) виды средних величин;
б) показатели вариации;
в) методы расчета дисперсии.
Средняя величина является обобщающей характеристикой изучаемой совокупности, показывающей типичный уровень варьирующего признака в расчете на единицу совокупности. Средние величины относятся к двум классам: степенные и структурные средние.
Среди степенных средних в статистическом анализе наибольшее применение нашли:
1) Средняя арифметическая простая
![]()
где
![]() – средняя
арифметическая; хi – отдельные варианты признака; n –
количество групп.
– средняя
арифметическая; хi – отдельные варианты признака; n –
количество групп.
Средняя арифметическая простая используется в том случае, если у всех группировочных признаков равны между собой частоты признака.
1) Средняя арифметическая взвешенная – используется, если частоты признака не равны между собой
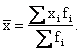
2) Средняя гармоническая взвешенная используется при отсутствии данных о частотах признака (F = x·f) или вариантах признака (х)
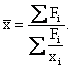
3) Средняя гармоническая простая используется в том случае, если у всех вариантов признака равны между собой объемы признака (F=const)
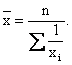
4) Средняя квадратическая (![]() )
)
простая ![]()
взвешенная 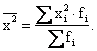
5) Средняя геометрическая (![]() )
)
простая ![]()
взвешенная
![]()
К структурным средним, наиболее часто используемым статистикой, относят моду и медиану.
Мода (Мо) – это значение признака, наиболее часто встречающегося в данном ряду. В дискретном ряду распределения моду определяют по наибольшей частоте.
В интервальном ряду распределения мода определяются по формуле
![]()
где
![]() - нижняя
граница модального интервала;
- нижняя
граница модального интервала; ![]() - величина модального интервала;
- величина модального интервала; ![]() - частота модального
интервала;
- частота модального
интервала; ![]() -
частота интервала, предшествующего модальному;
-
частота интервала, предшествующего модальному; ![]() - частота интервала, следующего за
модальным. Модальный интервал выбирается по максимальной частоте в исследуемом
ряду распределения.
- частота интервала, следующего за
модальным. Модальный интервал выбирается по максимальной частоте в исследуемом
ряду распределения.
Медиана (Ме) – это значение признака, которое приходится на середину ранжированного ряда распределения.
Ранжированный ряд распределения представлен значениями всех признаков в порядке возрастания. Порядковый номер признака в ранжированном ряду распределения определяется по сумме накопленных частот (кумулятивным частотам). В дискретном ряду распределения медиана определяется исходя из условий:
Если в вариационном ряду ![]() случаев (нечетное число), то значение
признака у случая
случаев (нечетное число), то значение
признака у случая ![]() будет
медианным, т.е.
будет
медианным, т.е.
![]() .
.
Если в вариационном ряду ![]() случаев (четное число), то медиана равна
средней арифметической из двух серединных значений
случаев (четное число), то медиана равна
средней арифметической из двух серединных значений
![]()
В интервальному ряду распределения медиана определяется по формуле

где
![]() - начало
медианного интервала;
- начало
медианного интервала; ![]() - величина медианного интервала;
- величина медианного интервала; ![]() - сумма накопленных частот до медианного
интервала;
- сумма накопленных частот до медианного
интервала; ![]() -
частота медианного интервала.
-
частота медианного интервала.
Медианный интервал определяется по кумулятивным частотам, где впервые сумма частот превысит половину всех частот. Выбор вида средней для характеристики совокупности производится в зависимости от особенностей изучаемого явления и от цели определения средней.
Средние величины, характеризуя вариационный ряд одним числом, не учитывают степень вариации признака. Для ее измерения используют показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации (R)
![]() .
.
Среднее линейное отклонение (Д) представляет собой среднюю арифметическую из абсолютных значений отклонений вариантов от средней.
Рассчитывают:
простое 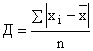 ,
,
взвешенное 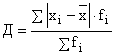 .
.
Дисперсия
(![]() ) наиболее часто используемый показатель
вариации, показывает среднюю площадь отклонений вариантов признака от средней
величины.
) наиболее часто используемый показатель
вариации, показывает среднюю площадь отклонений вариантов признака от средней
величины.
простая ![]() ,
,
взвешенная 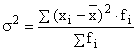 .
.
Преобразовав указанные формулы определения дисперсии, можно получить упрощенный вариант формулы (дисперсия методом моментов)
![]() .
.
Среднее квадратическое отклонение (![]() ) определяется как квадратный корень из
дисперсии
) определяется как квадратный корень из
дисперсии ![]() .
.
Для сравнения степени вариации признака в разных совокупностях используется коэффициент вариации (ν):
![]() .
.
Коэффициент вариации может также использоваться для характеристики степени однородности исследуемой совокупности. Вариация признака определяется не только для количественных, но и для качественных признаков, представленных альтернативным признаком:
Дисперсия альтернативного признака равна
![]() ,
,
где p – доля единиц совокупности обладающих изучаемым признаком; g – доля единиц совокупности, не обладающих изучаемым признаком. p+g=1.
Внутригрупповая
дисперсия (![]() )
показывает вариацию результативного признака в каждой группе, выделенной по
факторному признаку:
)
показывает вариацию результативного признака в каждой группе, выделенной по
факторному признаку:
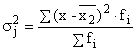 ,
,
где
х – варианты результативного признака; ![]() - среднее значение признака по группе
факторного признака;
- среднее значение признака по группе
факторного признака; ![]() -
частота признака в каждой группе.
-
частота признака в каждой группе.
Межгрупповая
дисперсия (![]() ) показывает вариацию групповых
средних (
) показывает вариацию групповых
средних (![]() ) от
средней по всей совокупности (
) от
средней по всей совокупности (![]() ):
):
![]() ,
,
где
![]() - количество
единиц в каждой группе.
- количество
единиц в каждой группе.
Общая дисперсия
(![]() ) показывает
вариацию во всей совокупности без учета выделения групп по факторному признаку:
) показывает
вариацию во всей совокупности без учета выделения групп по факторному признаку:
![]() .
.
Между общей дисперсией (![]() ), средней из групповых (
), средней из групповых (![]() ) и межгрупповой
дисперсией (
) и межгрупповой
дисперсией (![]() ),
существует взаимосвязь, называемая «правило сложения дисперсий»:
),
существует взаимосвязь, называемая «правило сложения дисперсий»:
![]() ,
,
![]() .
.
С использованием указанных дисперсий можно определить влияние факторного (группировочного) признака на вариацию результативного.
Оценка влияния основывается на расчете коэффициента детерминации или эмпирического корреляционного отношения (η):
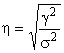 .
.
Если η>0,5 это свидетельствует о влиянии факторного признака на вариацию результативного признака.
Лекция 5. Парная регрессия и корреляция
Цель лекции: изучение методов построения статистической регрессионной модели связи.
Содержание:
а) функциональные и стохастические зависимости;
б) основы корреляционно-регрессионного анализа;
в) построение статистической регрессионной модели связи
между факторным признаком х и результирующим признаком у.
При моделировании достаточно часто возникает необходимость в построении статистических моделей, позволяющих выявить взаимосвязь между явлениями или процессами.
Различают два вида связей – функциональные и стохастические. Функциональной называется зависимость, при которой одному значению факторного признака строго соответствует единственное значение результативного признака.
Стохастическая зависимость характеризуется тем, что результативный признак не полностью определяется факторным признаком, его влияние проявляется в среднем при достаточно большом числе наблюдений. Наиболее часто для исследования стохастических зависимостей используют метод корреляции.
Первая задача корреляции заключается в математическом выражении изменения результативного признака в связи с изменением одного или несколько факторных признаков. Данная задача решается определением уравнения (модели) регрессии и носит название регрессионного анализа. Вторая задача состоит в определении различных показателей тесноты связи и называется корреляционным анализом.
Регрессионный анализ включает в себя этапы:
1) Логический анализ – разделение коррелирующих признаков на факторные и результативный.
2) Определение типа зависимости. Корреляционная зависимость называется парной, если она имеет место между двумя признаками (факторным и результативным) и множественной (многофакторной) – между тремя и более связанными между собой признаками.
Парная зависимость называется линейной, если
может быть описана уравнением прямой линии ![]() и нелинейной, описываемой
уравнением:
и нелинейной, описываемой
уравнением:
гиперболы ![]() ;
;
параболы ![]() и т.д.
и т.д.
Определить тип уравнения зависимости можно, исследуя зависимость графически, построением корреляционного поля или эмпирической линии регрессии.
При построении корреляционного поля в системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – результативного. Каждое пересечение линий, проводимых через эти оси, обозначается точкой.
При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем теснее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связей.
Эмпирическая линия регрессии строится в системе координат, где на оси абсцисс откладывается значение факторного признака, а на оси ординат рассчитанное среднее для данного факторного признака значение результативного.
3) Определение параметров уравнения регрессии.
Оценка параметров уравнения регрессии (а0, а1, а2 и т.д.) осуществляется методом наименьших квадратов на основе системы нормальных уравнений.
Для нахождения параметров линейной парной регрессии (![]() ) система нормальных
уравнений имеет вид:
) система нормальных
уравнений имеет вид:
![]()
Для гиперболы ![]()
![]()
В уравнениях регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков, а коэффициент регрессии а1 показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу собственного измерения.
Для оценки тесноты связи в статистическом анализе используют показатели:
эмпирического корреляционного отношения (ηэ)
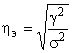 ,
,
где
![]() -
межгрупповая вариация результативного признака;
-
межгрупповая вариация результативного признака; ![]() - общая вариация результативного
признака.
- общая вариация результативного
признака.
Наличие взаимосвязей между результативным и факторным признаком имеет при η ≥ 0,5.
Универсальным показателем тесноты связи является показатель теоретического корреляционного отношения или индекс корреляции (ηm)
 ,
,
где
![]() -
рассчитанные (теоретические) значения результативного признака.
-
рассчитанные (теоретические) значения результативного признака.
Показатель теоретического корреляционного отношения может использоваться для оценки тесноты связи не только в парных, но и многофакторных зависимостях.
Для оценки тесноты связи прямолинейной зависимости используется линейный коэффициент корреляции (r)
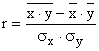 или
или
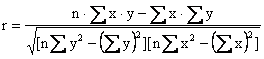 .
.
Линейный коэффициент корреляции может изменяться от -1 до +1. Чем ближе значение r по абсолютной величине к единице, тем теснее связь. Если r>0, то связь между факторным и результативным признаками прямо пропорциональная, если r<0, то обратно пропорциональная.
Построим статистическую регрессионную модели связи между факторным признаком х и результирующим признаком у.
Пусть имеется n выборочных статистических данных:
|
x |
x1 |
x2 |
… |
xn |
|
y |
y1 |
y2 |
|
yn |
Уравнение
линейной связи между факторами x
и y имеет
вид:
![]() .
.
Для
определения коэффициентов ![]() применим формулы:
применим формулы:
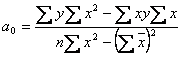 ,
,
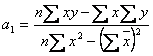 .
.
Зная ![]() по
уравнению
по
уравнению ![]() можно
определить теоретические значения
можно
определить теоретические значения ![]() для каждого x из выборки.
для каждого x из выборки.
Определим остаточную дисперсию, возникающую за счёт
отклонений теоретических значений ![]() от исходных значений y.
от исходных значений y.
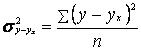 ,
,
Для
определения значимости коэффициентов ![]() используется критерий Стьюдента.
используется критерий Стьюдента.
Вычислим значения:
![]() .
.
Зададим
уровень значимости ![]() и
число степеней свободы k=n-2.
и
число степеней свободы k=n-2.
По таблицам распределения Стьюдента находим ![]() .
.
Если ![]() , то
коэффициент
, то
коэффициент ![]() значим.
Если
значим.
Если ![]() , то
коэффициент
, то
коэффициент ![]() значим.
значим.
Вычислим индекс корреляции (теоретическое корреляционное отношение):
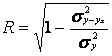 .
.
Для
определения значимости индекса корреляции R используется критерий Фишера:
![]() .
.
Зададим уровень значимости ![]() и степени свободы
и степени свободы ![]() =1,
=1, ![]() =n-2.
=n-2.
По таблицам распределения Фишера находим ![]() .
.
Если ![]() , то
индекс корреляции признаётся существенным.
, то
индекс корреляции признаётся существенным.
Индекс детерминации ![]() означает долю факторного признака в
общей дисперсии.
означает долю факторного признака в
общей дисперсии.
По величине индекса корреляции R на основании
шкалы Чеддока можно сделать вывод об адекватности модели статистическим
данным.
Вычислим среднюю ошибку аппроксимации по формуле:
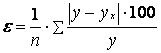 .
.
В случае линейной связи вычисляется линейный коэффициент
корреляции:
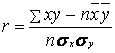 .
.
Для оценки значимости линейного коэффициента корреляции
используется критерий Стьюдента:
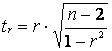 .
.
Зададим уровень значимости ![]() и число степеней свободы n -2.
и число степеней свободы n -2.
По таблицам распределения Стьюдента находим ![]() . Если
. Если ![]() , то линейный коэффициент
корреляции признаётся существенным.
, то линейный коэффициент
корреляции признаётся существенным.
Лекция 6. Множественная регрессия и корреляция
Цель лекции: изучение принципов построения моделей множественной регрессии.
Содержание:
а) назначение и смысл параметров модели множественной регрессии;
б) этапы построения модели;
в) нахождение коэффициентов модели и оценка их статистической значимости;
г) оценка качества модели.
Суть регрессионного анализа: построение математической модели и определение ее статистической надежности. Вид множественной линейной модели регрессионного анализа:
Y = b0 + b1xi1 + ... + bjxij + ... + bkxik + ei ,
где ei - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.
Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной.
Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т.е. является нормативным коэффициентом.
Рекомендуется, чтобы число наблюдаемых значений (объем выборки) превышало число независимых факторов не менее чем в три раза.
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии b0, b1,..., bk. По имеющимся статистическим данным для переменных Xi и Y необходимо:
– получить наилучшие оценки неизвестных параметров b0, b1,..., bk;
– проверить статистические гипотезы о параметрах модели;
– проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).
Построение моделей множественной регрессии состоит из следующих этапов:
1) выбор формы связи (уравнения регрессии);
2) определение параметров выбранного уравнения;
3) анализ качества уравнения и проверка адекватности уравнения эмпирическим данным, совершенствование уравнения.
Рассмотрим модель множественной регрессии с двумя переменными вида:
Y = b0 +b1х1 + b2х2.
Найти неизвестные b0, b1, b2 можно, решив систему трех линейных уравнений с тремя неизвестными b0,b1,b2, полученными методом наименьших квадратов:
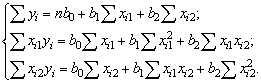
Для решения системы можно воспользоваться формулами
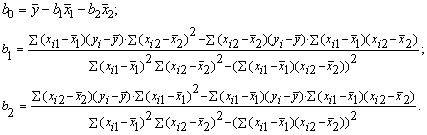
Выборочные дисперсии эмпирических коэффициентов множественной регрессии можно определить следующим образом:
![]()
Здесь z'jj - j-тый диагональный элемент матрицы Z-1 =(XTX)-1.
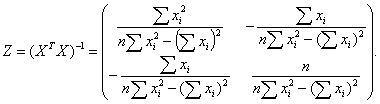
При этом:
![]()
![]()
где m - количество
объясняющих переменных модели.
В частности, для уравнения множественной регрессии
Y = b0 + b1X1 + b2X2
с двумя объясняющими переменными используются следующие формулы:
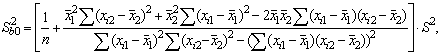
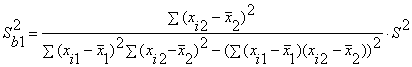
или
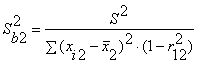
![]() ,
,![]() ,
,![]() .
.
Здесь r12 - выборочный коэффициент корреляции между объясняющими переменными X1 и X2;
Sbj - стандартная ошибка коэффициента регрессии;
S
- стандартная ошибка множественной регрессии (несмещенная оценка).
По аналогии с парной регрессией после определения точечных оценок bj
коэффициентов βj (j=1,2,…,m) теоретического уравнения множественной
регрессии могут быть рассчитаны интервальные оценки указанных коэффициентов.
Доверительный интервал, накрывающий с надежностью (1-α) неизвестное значение параметра βj, определяется как
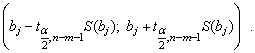
Проверка статистической значимости коэффициентов уравнения множественной регрессии.
Статистическая значимость коэффициентов множественной регрессии с m объясняющими переменными проверяется на основе t-статистики:
![]()
![]() имеющей в данном случае распределение Стьюдента с числом степеней
свободы v = n- m-1. При требуемом уровне значимости наблюдаемое значение
t-статистики сравнивается с критической точкой распределения Стьюдента.
имеющей в данном случае распределение Стьюдента с числом степеней
свободы v = n- m-1. При требуемом уровне значимости наблюдаемое значение
t-статистики сравнивается с критической точкой распределения Стьюдента.
В случае, если ![]() , то статистическая значимость соответствующего
коэффициента множественной регрессии подтверждается. Если же установлен факт не
значимости коэффициента bj, то рекомендуется исключить из уравнения
переменную Xj.
, то статистическая значимость соответствующего
коэффициента множественной регрессии подтверждается. Если же установлен факт не
значимости коэффициента bj, то рекомендуется исключить из уравнения
переменную Xj.
Проверка общего качества уравнения множественной регрессии.
Для этой цели, как и в случае парной регрессии, используется коэффициент детерминации R2:
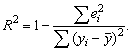
Справедливо соотношение
0<=R2<=1. Чем ближе этот коэффициент к единице, тем больше
уравнение множественной регрессии объясняет поведениеY.
Для множественной регрессии коэффициент детерминации является
неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей
переменной никогда не уменьшает значение R2, так как каждая
последующая переменная может лишь дополнить, но никак не сократить информацию,
объясняющую поведение зависимой переменной.
Иногда при расчете коэффициента детерминации для получения несмещенных оценок в
числителе и знаменателе вычитаемой из единицы дроби делается поправка на число
степеней свободы, т.е. вводится так называемый скорректированный (исправленный)
коэффициент детерминации:
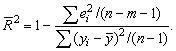
Соотношение может быть представлено в следующем виде:
![]()
![]() для m>1. С ростом значения
m скорректированный коэффициент детерминации растет медленнее, чем
обычный. Очевидно, что
для m>1. С ростом значения
m скорректированный коэффициент детерминации растет медленнее, чем
обычный. Очевидно, что ![]() только
при R2 = 1.
только
при R2 = 1. ![]() может
принимать отрицательные значения.
может
принимать отрицательные значения.
Доказано, что ![]() увеличивается
при добавлении новой объясняющей переменной тогда и только тогда, когда
t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в
модель новых объясняющих переменных осуществляется до тех пор, пока растет
скорректированный коэффициент детерминации. Рекомендуется после проверки общего
качества уравнения регрессии провести анализ его статистической значимости. Для
этого используется F-статистика:
увеличивается
при добавлении новой объясняющей переменной тогда и только тогда, когда
t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в
модель новых объясняющих переменных осуществляется до тех пор, пока растет
скорректированный коэффициент детерминации. Рекомендуется после проверки общего
качества уравнения регрессии провести анализ его статистической значимости. Для
этого используется F-статистика:
![]() .
.
Показатели F и R2 равны или не равны нулю одновременно. Если F=0, то R2=0, следовательно, величина Y линейно не зависит от X1,X2,…,Xm. Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из требуемого уровня значимости α и чисел степеней свободы v1 = m и
v2 = n - m - 1, определяется на основе распределения Фишера. Если F>Fкр, то R2 статистически значим.
Лекция 7. Моделирование одномерных временных рядов
Цель лекции: ознакомление студентов с методами моделирования временных рядов.
Содержание:
а) интервальные и моментные временные ряды;
б) аналитические показатели ряда динамики;
в) аддитивная и мультипликативная модели временных рядов;
г) автокорреляция уровней временного ряда.
В работе многих организаций связи возникает необходимость анализа изменения процессов и явлений во времени. В частности, актуальной и важной является проблема анализа и прогнозирования трафика в различных телекоммуникационных сетях, которая может быть успешно решена методами математического моделирования временных рядов.
Временным рядом (рядом динамики, динамическим рядом) называется упорядоченная во времени последовательность численных показателей
{(yi,ti), i=1,2,...,n}, характеризующих уровни развития изучаемого явления в последовательные моменты или периоды времени.
Величины yi называются уровнями ряда, а ti – временными метками (моменты или интервалы наблюдения). В зависимости от способа выражения уровней (у) ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
Динамические ряды могут быть интервальными, если характеристика явления дается за определенный промежуток времени (час, день, месяц, год и т.п.) и моментными, если составляющие его показатели оцениваются на определенный момент времени рассматриваемого периода.
В зависимости от расстояния между уровнями, ряды динамики подразделяются на равномерные (представлены всеми последующими периодами) и неравномерные. Чаще рассматриваются временные ряды с равными интервалами между наблюдениями, в качестве значений ti берутся порядковые номера наблюдений и временной ряд представляется в виде последовательности y1, y2 ,..., yn , где n – количество наблюдений
Средний уровень ряда определяется:
1) в моментном ряду (равномерном) по формуле средней хронологической простой
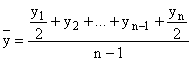 ;
;
2) в моментном (неравномерном ряду) по формуле средней хронологической взвешенной:
![]() ;
;
3) в интервальном равномерном
![]() ;
;
в интервальном неравномерном
![]() .
.
Аналитические показатели ряда динамики представляют собой результат сравнений двух уровней ряда динамики. Сравнение может осуществляться базисным (каждый последующий уровень сравнивается с первым, принятым за базу) и цепным способами (каждый последующий уровень сравнивается с предыдущим).
Абсолютный прирост показывает на сколько абсолютных единиц один уровень ряда динамики больше или меньше другого:
1) абсолютный прирост базисный ![]() ;
;
2) абсолютный прирост цепной ![]() .
.
Средний абсолютный прирост определяется только для
цепных показателей (![]() )
)
![]() .
.
Темп роста – показывает, во сколько раз один уровень ряда динамики больше или меньше другого.
Темп роста базисный ![]() .
.
Темп роста цепной ![]() .
.
Средний темп роста (![]() )
)
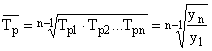 .
.
Темп прироста показывает, на сколько процентов один уровень больше или меньше другого уровня.
Темп прироста базисный ![]() .
.
Темп прироста цепной ![]() .
.
Средний темп прироста ![]() .
.
Абсолютное значение одного процента прироста (А) представляет собой отношение абсолютного прироста
к темпу прироста и определяется по формуле ![]() .
.
Абсолютное значение одного процента прироста определяется только для цепных приростов. Среднее абсолютное значение одного процента прироста не рассчитывается.
Целью исследования временного ряда является выявление закономерностей в изменении уровней ряда и построении его модели в целях прогнозирования и исследования взаимосвязей между явлениями.
При исследовании временного ряда его обычно представляют в виде совокупности трех составляющих:
– долговременной тенденции (Т), т. е. устойчивого увеличения или уменьшения значений уровней ряда (тренда);
– периодических колебаний (S);
– случайных колебаний (E).
На рисунке 7.1 показан график временного ряда, на котором прослеживаются все три составляющие.
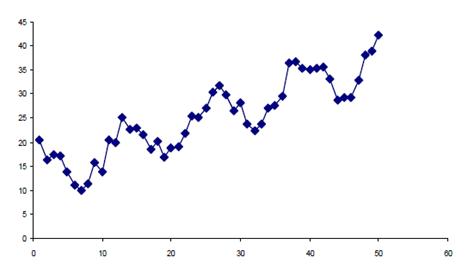
Рисунок 7.1 – Временной ряд
Различным образом объединяя эти компоненты, можно получить различные модели временного ряда (Y):
– аддитивную
Yt = Tt + St + Et;
– мультипликативную
Yt = Tt ·St · Et;
– смешанную
Yt = Tt · St + Et.
Периодические колебания принято подразделять на сезонные и циклические.
Основная задача исследования временного ряда заключается в выявлении и придании количественного выражения составляющим его отдельным компонентам.
Как правило, наличие той или иной составляющей можно определить с помощью визуального анализа графика временного ряда (рисунок 7.1).
Перед построением модели исходные данные проверяются на сопоставимость (применение одинаковой методики получения или расчета данных), однородность (отсутствие случайных выбросов), устойчивость (наличие закономерности в изменении уровней ряда) и достаточность (число наблюдений должно в 7–10 превосходить число параметров модели).
Важной особенностью временных рядов по сравнению с данными наблюдений, относящихся к одному периоду времени, является, как правило, наличие связи между последовательными уровнями ряда, вызванное действием каких-либо долговременных причин, что приводит к наличию таких составляющих ряда, как долговременная тенденция и периодическая составляющая.
Корреляционная зависимость между последовательными уровнями временного ряда называется автокорреляцией уровней временного ряда.
Степень тесноты автокорреляционной связи между уровнями ряда может быть определена с помощью коэффициентов автокорреляции, т. е. коэффициентов линейной корреляции между уровнями исходного временного ряда и уровнями ряда, сдвинутыми на несколько шагов назад во времени.
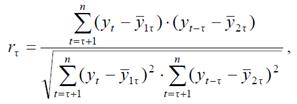
где τ – величина сдвига, называемая лагом, определяет порядок коэффициента автокорреляции,
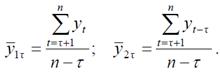
Функцию r(τ) = rτ называют автокорреляционной функцией временного ряда, а ее график – коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты.
Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию.
Если наиболее высоким оказался коэффициент автокорреляции порядка т, то ряд содержит циклические колебания с периодичностью в т моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, то ряд не содержит тенденции и циклических колебаний.
Лекция 8. (продолжение лекции 7)
Цель лекции: ознакомление студентов с методами моделирования временных рядов.
Содержание:
а) моделирование тенденции временного ряда;
б) сглаживание временного ряда по методу скользящей средней;
в) метод аналитического выравнивания;
г) оценка адекватности и точности модели;
д) моделирование периодических колебаний.
Моделирование тенденции временного ряда является важнейшей классической задачей анализа временных рядов. Решение этой задачи начинается, как правило, с проверки наличия тенденции и формулирования предложений о характере долговременной тенденции, после чего уже строится модель тенденции как функции времени.
Для диагностирования наличия тенденции наиболее широко применяются метод сравнения средних и метод Фостера-Стюарта.
Сглаживание временного ряда по методу скользящей средней заключается в последовательном расчете средних уровней из заданного числа по порядку уровней ряда, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Каждое звено скользящей средней – это уровень за соответствующий период, который относится к середине выбранного периода, если число уровней скольжения нечетное. Например, для ряда динамики, представленного уровнями у1, у2, у3, у4, у5 скольжение 3-х уровневой средней будет иметь вид:
![]() ;
; ![]() ;
; ![]() .
.
Нахождение скользящей средней по четному числу уровней несколько сложнее, так как средняя может быть отнесена к середине между двумя периодами, находящимися в середине интервала сглаживания.
Чтобы ликвидировать такой сдвиг, применяют способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенному периоду.
![]() ;
; ![]() .
.
Центрированием получаем ![]() .
.
При использовании скользящей средней с длиной активного участка g = 2p+1 первые и последние р уровней ряда сгладить нельзя, их значения теряются. Очевидно, что потеря значений последних точек является существенным недостатком, т. к. для исследователя последние «свежие» данные обладают наибольшей информационной ценностью.
Отметим, что важным свойством процедуры сглаживания является полное устранение периодических колебаний из временного ряда, если длина интервала сглаживания берется равной или кратной периоду колебаний. Это обстоятельство используется при выделении периодической составляющей временного ряда.
Аналитическим выравниванием временного ряда называют нахождение аналитической функции ŷ = f(t), характеризующей основную тенденцию изменения уровней ряда с течением времени. Сама функция f(t) носит название кривой роста. При аналитическим выравнивании исходят из предположения, что аддитивная модель временного ряда может быть представлена как сумма двух компонент
y(t) = f(t) + εt,
где εt – случайная компонента с нулевой средней и постоянной дисперсией выражает ошибку модели из-за действия случайных факторов.
Чаще всего в качестве кривой роста применяются следующие функции:
- линейная yt = a0 + a1t ;
- парабола второго и более высоких порядков
yt = a0 + a1 t1 + a2t2 + ...+ ak tk;
- гиперболическая yt =a0 + a1/ t;
- экспонента ![]() ;
;
- степенная ![]() ;
;
- логистическая кривая 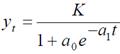 .
.
Построение таких функций ничем не отличается от построения уравнений парной регрессии (линейной или нелинейной) с учетом того, что в качестве зависимой переменной используются фактические уровни временного ряда yt, а в качестве независимой переменной моменты времени t = 1,2, ..., n. Для определения вида тенденции (аналитической зависимости) применяются такие методы, как
– качественный анализ изучаемого процесса;
– построение и визуальный анализ графика зависимости уровней ряда от времени;
– расчет и анализ показателей динамики временного ряда (абсолютные приросты, темпы роста и др.);
– анализ автокорреляционной функции исходного и преобразованного временного ряда.
Проверка адекватности модели основывается на анализе ряда остатков
et = yt - yˆt . (i = 1, 2, …, n)
Модель считается адекватной, если остатки:
- являются случайными;
- распределены по нормальному закону;
- имеют равное нулю среднее значение e = 0;
- независимы между собой.
1) Проверка случайности остатков заключается в установлении факта отсутствия или наличия тенденции остатков. Для этой цели может использоваться критерий серий.
2) Нормальность распределения остатков считается установленной (приближенно) если одновременно выполняются следующие неравенства:

где А – выборочная характеристика асимметрии, δA, δэ – среднеквадратические ошибки выборочных характеристик асимметрии и эксцесса, определяемые соотношениями
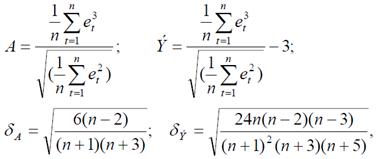
3) Проверка равенства нулю среднего значения ряда остатков e = 0 осуществляется с помощью критерия Стьюдента. Гипотеза о равенстве нулю e = 0 отвергается, если выполняется условие
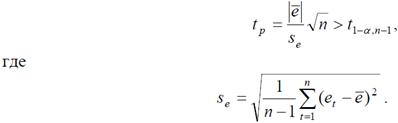
4) Под независимостью ряда остатков понимается отсутствие в нем автокорреляции, т. е. отсутствует зависимость каждого значения ряда от предыдущих значений. Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут коррелировать между собой.
Для проверки ряда остатков на отсутствие автокорреляции уровней остатков используется критерий Дарбина-Уотсона. Этот критерий основан на расчете величины
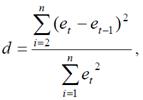
представляющей собой отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Оценка точности модели тенденции заключается в оценке близости модельных значений тенденции к фактическим уровням ряда и осуществляется с помощью вычисления таких показателей, как:
- дисперсия остатков σ2 остò ;
-
средняя ошибка аппроксимации  ;
;
- коэффициент детерминации R2.
Моделирование периодических колебаний.
Простейший прием выделения периодической компоненты основан на использовании сглаживания временного ряда по методу простой скользящей средней. Предварительно следует определиться с видом модели временного ряда – аддитивной или мультипликативной. Это можно сделать на основе анализа графика временного ряда. Если амплитуда периодических колебаний примерно постоянна, то следует выбрать аддитивную модель
Y = T + S + E,
в которой амплитуда колебаний периодической компоненты предполагается постоянной, не зависящей от времени. Если амплитуда периодических колебаний возрастает с ростом уровней ряда, то следует выбрать мультипликативную модель временного ряда
Y = T · S · E.
Выделение периодической компоненты основывается на том, что если исходный временной ряд содержит периодическую компоненту с периодом g, то сглаженный по методу простой скользящей средней временной с интервалом сглаживания g такой компоненты уже не содержит. Таким образом, в случае аддитивной модели периодическая компонента выделяется путем нахождения разности между соответствующими уровнями исходного и сглаженного ряда.
В случае мультипликативной модели периодическая компонента выделяется путем нахождения отношения между соответствующими уровнями исходного и сглаженного ряда. Затем вычисляется средние значения, соответствующие наблюдениям внутри одного периода колебаний.
При моделировании сезонных колебаний нашли широкое применение метод включения в модель фиктивных переменных и метод гармонического анализа.
Лекция 9. Прогнозирование уровней временного ряда
Цель лекции: ознакомление студентов с методами прогнозирования временных рядов.
Содержание:
а) прогнозирование уровней временного ряда на основе кривых роста;
б) адаптивное прогнозирование;
в) использование экспоненциальной средней для краткосрочного прогнозирования;
г) адаптивные полиномиальные модели.
Прогнозирование уровней ряда на основе кривых роста.
Построенная модель тенденции (кривая роста) может использоваться для прогнозирования. Кривая роста позволяет получить выровненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.
Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы:
1) на основе качественного анализа выбор одной или нескольких кривых, форма которых соответствует характеру изменения временного ряда;
2) оценка параметров выбранных кривых;
3) оценка точности и проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой роста;
4) расчет точечного (по формуле (9.1)) и интервального прогнозов.
Чтобы по имеющемуся временному ряду y1, y2 ,..., yn осуществить прогноз на L шагов вперед, необходимо в построенную модель тенденции (кривую роста) ŷ = f(t) подставить значение аргумента, соответствующее интервалу прогноза
ŷn(+L) = f(tn+L). (9.1)
Полученное значение ŷn(+L) называется точечным прогнозом.
Следующим этапом является определение доверительного интервала прогноза, т. е. пределов, в которых лежит точечное значение уровня явления с заданной вероятностью (степенью уверенности). Эта процедура называется вычислением интервального прогноза. Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции тенденции по кривым роста, может быть вызвано:
1) субъективной ошибочностью выбора вида кривой;
2) погрешностью оценивания параметров кривых;
3) погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени. Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза.
Доверительный интервал для линейной тенденции вычисляется по формуле
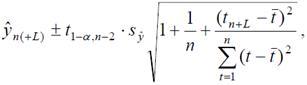 (9.2)
(9.2)
где n – длина временного ряда; L – период упреждения (прогнозирования); ŷn(+L) – точечный прогноз на момент n+L; t1-α , n-2 – значение t-статистики Стьюдента при уровне значимости α и числе степеней свободы n–2; syˆ – средняя квадратическая ошибка оценки прогнозируемого показателя
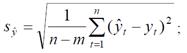
m – число параметров модели кривой роста (для линейной модели m =2).
Для линейной модели формулу (9.2) можно записать следующим образом
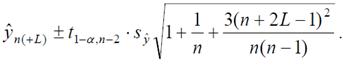
Ширина доверительного интервала зависит от уровня значимости, периода упреждения, среднего квадратического отклонения временного ряда от тренда и степени полинома.
Адаптивные модели прогнозирования.
При анализе временных рядов часто более важной бывает текущая тенденция (тенденция в данный момент времени, определяемая несколькими последними наблюдениями), а не тенденция, сложившая на длительном интервале времени. Соответственно, наиболее ценной является информация последнего периода. Исходя из этого в последнее время важное значение получили, так называемые, адаптивные методы прогнозирования.
Адаптивными называются методы прогнозирования, позволяющие строить самокорректирующиеся (самонастраивающиеся) математические модели, которые способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда.
Особенностями адаптивных методов прогнозирования является:
– способность учитывать информационную ценность уровней временного ряда (с помощью системы весов, придаваемых этим уровням);
– использование рекуррентных процедур уточнения параметров модели по мере поступления новых данных наблюдений и тем самым адаптация модели применительно к новым условиям развития явления.
Благодаря указанным свойствам адаптивные методы особенно удачно используются при краткосрочном прогнозировании (при прогнозировании на один или несколько шагов вперед).
Адаптивные методы, как правило, основаны на использовании процедуры экспоненциального сглаживания.
Для экспоненциального сглаживания временного ряда используется рекуррентная формула
![]() (9.3)
(9.3)
где St – значение экспоненциальной средней в момент t; уt – значение временного ряда в момент t; α – параметр сглаживания, α = const, 0< α < l;
β = 1 – α . Совокупность значений St образует сглаженный временной ряд.
Соотношение (9.3) позволяет выразить экспоненциальную среднюю St через предшествующие значения уровней временного ряда уt. При n → ∞
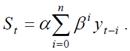
Таким образом, величина St оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда αβ i убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от «возраста» наблюдений).
Например, при α = 0,4 вес текущего наблюдения уt будет равен α = 0,4, вес предыдущего уровня уt–1 будет соответствовать α ·β = 0,4·0,6 = 0,24; для уровня уt–2 вес составит α ·β2 = 0,144; для yt–3 – α ·β3 = 0,0864 и т. д.
Таким образом, с одной стороны, желательно увеличивать вес более свежих наблюдений, что может быть достигнуто повышением α (согласно (9.3), с другой стороны, для сглаживания случайных отклонений величину α нужно уменьшить. Выбор параметра сглаживания α с учетом этих двух противоречивых требований составляет задачу оптимизации модели.
В качестве начального значения S0 используется среднее арифметическое значение из всех имеющихся уровней временного ряда или из какой-то их части. Вес, приписываемый этому значению, уменьшается по экспоненциальной зависимости по мере удаления от первого уровня. Поэтому для длинных временных рядов влияние неудачного выбора S0 погашается.
Использование экспоненциальной средней для краткосрочного прогнозирования.
При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда имеет вид
yt = α1,t + et, (9.4)
где α1,t – варьирующий во времени средний уровень ряда, et – случайные отклонения с нулевым математическим ожиданием и дисперсией σ2.
Прогнозная модель определяется соотношением
yˆτ (t) = αˆ1,t, (9.5)
где ŷτ(t) – прогноз, сделанный в момент t на τ единиц времени (шагов) вперед; αˆ1,t – оценка α1,t.
Величина параметра модели αˆ1,t принимается равной экспоненциальной средней St в момент t:

Прогнозирование предполагает следующую последовательность действий:
– на основании исходного временного ряда y1, y2, …, yn вычисление по формуле (9.3) сглаженных уровней ряда S1, S2, …, Sn;
– вычисление αˆ1,n = Sn;
– осуществление прогноза на τ шагов вперед yˆτ (n) = αˆ1,n.
Перегруппировав члены выражение (9.3) можно записать по-другому:
St = St-1 + α (yt - St-1 ) .
Если величину (yt - St-1) рассматривать как погрешность прогноза, то новый прогноз St получается как результат корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.
Адаптивные полиномиальные модели.
Для временных рядов, имеющих ярко выраженную тенденцию, целесообразно использовать модели линейного роста, в которых процедуре экспоненциального сглаживания подвергаются оценки коэффициентов адаптивной модели. В этих моделях прогноз может быть получен с помощью следующего выражения:
![]()
где αˆ1,t и αˆ2,t – текущие оценки коэффициентов; τ – время упреждения прогноза.
Наиболее часто применяются следующие три модели данного типа, отличающиеся рекуррентными выражениями для пересчета текущих оценок коэффициентов (параметры адаптации или параметры экспоненциального сглаживания 0 < α1, α2, α3, β < 1):
– двухпараметрическая модель Ч. Хольта

– однопараметрическая модель Р. Брауна
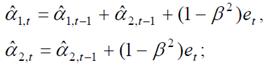
– трехпараметрическая модель Дж. Бокса и Г. Дженкинса
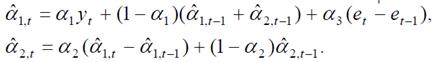
Начальные значения коэффициентов αˆ1,t и αˆ2,t принимаются равными коэффициентам уравнения регрессии, построенного по начальным уровням ряда. et = yt – ŷ1(t–1) – ошибка прогноза.
Лекция 10. Основы математического программирования. Постановка задачи линейного программирования
Цель лекции: ознакомление студентов с основными понятиями и направлениями математического программирования
Содержание:
а) понятие математического программирования;
б) основные направления математического программирования;
в) целевая функция, ограничения, критерий оптимальности;
г) математические постановки задач, приводящие к моделям линейного программирования
Математическое программирование - это раздел теории оптимизации, занимающийся изучением и решением задач минимизации (максимизации) функции нескольких переменных на подмножестве конечномерного векторного пространства, которое задано в виде системы уравнений или неравенств. Методы математического программирования представляют собой класс моделей, применяемых для формализации задач планирования целенаправленной деятельности, предусматривающих распределение ограниченного количества ресурсов разных видов.
Модели программирования относятся к категории детерминированных моделей. Термин программирование понимается как поиск наилучших планов.
Математическое программирование подразделяется на линейное, целочисленное, нелинейное, динамическое программирование.
Одним из направлений математического программирования является линейное программирование, в котором ярко проявляются специфические трудности нахождения экстремума на границе допустимой области переменных. В отличие от линейного программирования теория экстремальных задач, в которой целевая функция и/или функции, задающие ограничения, не линейны, называется нелинейным программированием
Класс задач оптимизации, в которых область определения переменных состоит из отдельных изолированных точек, составляет предмет изучения дискретного программирования.
Широкий класс нелинейных и дискретных задач может решаться с использованием идеи рекуррентного подхода (методов типа математической индукции), являющихся основой динамического программирования, идея которого первоначально была предложена Р. Беллманом.
Для решения задач оптимизации со случайными параметрами разработано стохастическое программирование.
Развиты также методы решения задач оптимизации, в которых переменная принимает только два значения «истинно» - «ложно» или «да» — «нет». Такие методы относят к булевому программированию.
Методы математического программирования находят свое применение в самых различных областях техники и экономики.
Анализ постановки и решения задачи математического программирования позволяет выявить следующие особенности:
1) введение понятий целевая функция и ограничения и ориентация на их формирование является фактически некоторыми средствами постановки задачи;
2) при использовании методов математического программирования появляется возможность объединения в единой модели разнородных критериев (разных размерностей, предельных значений), что очень важно при отображении реальных проектных и производственных ситуаций;
3) модель математического программирования допускает выход на границу области определения переменных;
4) изучение методов решения задач математического программирования позволяет получить представление о пошаговом алгоритме получения результата моделирования.
Математические постановки задач, приводящие к моделям линейного программирования
Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем и систем связи, в управлении промышленными предприятиями, при составлении проектов сложных систем. Данные задачи имеют единую постановку: найти значения переменных x1, …, xn, доставляющие оптимум заданной линейной формы F(x)=c1x1 + c2x2+… + cnxn при выполнении системы ограничений, представляющих собой также линейные формы.
Постановка задачи линейного программирования.
Линейное программирование – раздел теории оптимизации, посвященный решению экстремальных задач, в которых целевая функция и ограничения линейны. Родоначальником линейного программирования считают Л.В. Канторовича, который в 30-е годы XX века предложил метод решения оптимизационных задач. Л.В. Канторович разработал метод разрешающих множителей для решения задачи линейного программирования. В последующем, в 50-е гг. XX в. независимо от Канторовича метод решения задачи линейного программирования (так называемый симплекс-метод) был развит американским математиком Дж. Данцигом, который в 1951 г. и ввел термин «линейное программирование».
Слово «программирование» объясняется тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, предприятия. Слово «линейное» отражает линейную зависимость между переменными.
Приведем простейший пример задачи линейного программирования.
Предположим, что в трех цехах (Ц1, Ц2, ЦЗ) изготавливается два вида изделий И1 и И2. Известна загрузка каждого цеха аi (оцениваемая в данном случае в процентах) при изготовлении каждого из изделий и прибыль (или цена реализуемой продукции в тенге) сi от реализации изделий. Требуется определить, сколько изделий каждого вида следует производить при возможно более полной загрузке цехов, чтобы получить за рассматриваемый плановый период максимальную прибыль или максимальный объем реализуемой продукции.
Такую ситуацию удобно отобразить в таблице, которая подсказывает характерную для задач математического программирования форму представления задачи, т. е. целевую функцию (в данном случае определяющую максимизацию прибыли или объема реализуемой продукции)
![]()
и ряд ограничений (в данном случае диктуемых возможностями цехов, т.е. их предельной 100%-ной загрузкой)
5 х1 + 4х2 ≤ 100;
1.6 х1+ 17.4 х2 ≤ 100;
2.9 х1 + 5.8 х2 ≤ 100.
Таблица 10.1- Исходные данные
|
Изделие |
Цех (участок) |
Цена |
||
|
|
Ц1 |
Ц2 |
ЦЗ |
Изделия |
|
И1 |
5% |
1.6% |
2.9% |
240 тенге |
|
И2 |
4% |
17.4% |
5.8% |
320 тенге |
|
Максимальная загрузка |
100% |
100% |
100% |
|
Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования. Графическое решение задачи приведено на рисунке 10.1.
Ограничения здесь задают область допустимых решений в форме (заштрихованного) четырехугольника, а семейство (пунктирных) прямых, представляет собой линии уровня целевой функции F .
Существует два крайних положения линии уровня, когда она «касается» допустимого множества. Этим двум положениям в данном случае соответствуют две точки «касания» - начало координат (0, 0) и точка (9, 13). Первая из этих точек - точка минимума, а вторая - максимума данной функции F вида (1) на допустимом множестве (2).
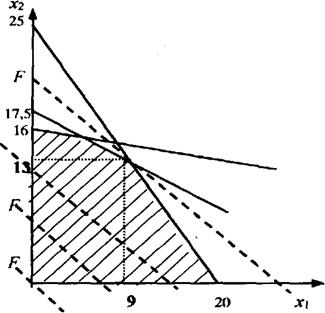
Рисунок 10.1 – Графическое решение ЗЛП
Постановка данной задачи выглядит следующим образом. Имеется множество переменных X = (x1, х2,..., хn). Целевая функция линейно зависит от управляемых параметров:
![]()
Имеются ограничения, которые представляют собой линейные формы;
![]()
![]()
Задача линейного программирования формулируется так: определить максимум линейной формы
F(x1,…,xn )=max(c1x1+…+cnxn)
при условии, что точка (х1, х2,..., хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств:
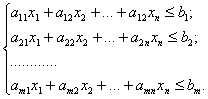
Любое множество значений (х1*, х2*,..., хn*), которое удовлетворяет системе неравенств задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство:
c1х1o+ c2 х2o+..+ cn хno ≥ c1х1+ c2 х2+..+ cn хn
для всего множества значений x1, х2,..., хn, то значение х1o..хno является оптимальным решением задачи линейного программирования.
Лекция 11. Содержательные постановки задач линейного программирования. Методы решения задач линейного программирования
Цель лекции: ознакомление студентов с задачами распределения ресурсов и методами решения задач линейного программирования
Содержание:
а) задачи распределения ресурсов;
б) математическая формулировка задачи об оптимальном использовании ресурсов;
в) численные методы математического программирования.
Во второй половине XX в. при решении практических задач стали находить широкое применение математические методы. Они стали использоваться при перспективном и текущем планировании научно-исследовательских работ, проектировании различных объектов, управлении технологическими и производственными процессами, прогнозировании развития социальных и производственных систем, оптимизации маршрутов перевозки грузов. Особенно часто к математическим методам прибегают при решении задач оптимизации функционирования производственных систем, при распределении материальных и трудовых ресурсов и страховых запасов, при выборе местоположения предприятий, исследовании и оценке безопасности функционирования объектов повышенного риска. Постановки перечисленных задач носят оптимизационный характер, где в качестве критериев эффективности применяются различные целевые функции. Рассмотрим некоторые постановки задач, являющиеся типовыми задачами системных исследований.
Задачи распределения ресурсов.
Задачи распределения ресурсов возникают, когда существует определенный набор работ или операций, которые необходимо выполнить, а имеющихся в наличии ресурсов для выполнения каждой из них наилучшим образом не хватает. Способы распределения ограниченных ресурсов при выполнении различных операций в системе управления могут быть различными. Для того чтобы решить задачу распределения ресурсов, необходимо сформулировать некоторую систему предпочтений или решающее правило. Такое правило принятия решений по определению объема ресурсов, которые, целесообразно выделить для каждого процесса, обычно разрабатывается с учетом оптимизации некоторой целевой функции при ограничениях на объем имеющихся ресурсов и временные характеристики.
В зависимости от условий задачи распределения ресурсов делятся на три класса.
1) Заданы и работы, и ресурсы. Требуется распределить ресурсы между работами таким образом, чтобы максимизировать некоторую меру эффективности (скажем, прибыль) или минимизировать ожидаемые затраты (издержки производства). Например, предприятию установлено производственное задание в рамках оговоренного срока. Известны мощности предприятия. При изготовлении продукции изделия проходят обработку на разных станках. Естественным является ограничение — одновременно на одном станке может обрабатываться только одна единица продукции. Мощности предприятия ограниченны и не позволяют для каждого изделия использовать наилучшую технологию. Требуется выбрать такие способы производства для каждой единицы продукции, чтобы выполнить задание с минимальными затратами.
2) Заданы только наличные ресурсы. Требуется определить, какой состав работ можно выполнить с учетом этих ресурсов, чтобы обеспечить максимум некоторой меры эффективности. Приведем пример. Имеется предприятие с определенными производственными мощностями. Требуется произвести планирование ассортимента и объема выпуска продукции, которые позволили бы максимизировать доход предприятия.
3) Заданы только работы. Необходимо определить, какие ресурсы требуются для того, чтобы минимизировать суммарные издержки. Например, составлено расписание движения автобусов пригородного и междугороднего сообщения на летний период времени. Требуется определить необходимое количество водителей, кондукторов, контролеров и прочего обслуживающего персонала, чтобы выполнить план перевозок с минимальными эксплуатационными затратами.
Математическая формулировка задачи об оптимальном использовании ресурсов.
Для изготовления n видов продукции используется m видов ресурсов.
Обозначим через xj число единиц j-го вида продукции (j=1,…,n), запланированной к производству,
bi- запас i-го ресурса (i=1,…,m),
aij -число единиц ресурса i, затрачиваемого на изготовление единицы продукции j-го вида (aij- технологические коэффициенты),
cj- выручка от реализации единицы продукции j-го вида (или цена продукции j-го вида).
Тогда математическая модель задачи об использовании ресурсов в общей постановке примет следующий вид.
Найти такой план X=(x1, …, xn) выпуска продукции, который удовлетворял бы системе ограничений:
![]()
и при котором целевая функция достигала бы своего максимального значения
![]()
Одной из достаточно часто встречающихся задач системного анализа является транспортная задача линейного программирования. Постановке и решению этой задачи посвящена лекция 13.
Численные методы математического программирования.
Численные методы математического программирования – раздел вычислительной математики, связанный с отысканием решения задач математического программирования в тех случаях, когда затруднено получение строго математического решения. Численные методы оптимизации, численный вычислительный эксперимент считаются важным разделом системного анализа.
Численные методы представляют собой последовательность однотипных шагов, итераций.
Выделяют конечные и бесконечные численные методы.
Конечные методы позволяют получать решение за конечное (но обычно заранее неизвестное) число шагов. К ним относят:
а) симплекс-метод (с полной симплексной таблицей, с использованием обратной матрицы, с мультипликативным представлением обратной матрицы);
б) двойственный симплекс-метод;
в) метод последовательного сокращения невязок (комбинация обычного и двойственного симплекс-метода);
г) метод наискорейшего спуска;
д) метод сопряженных градиентов для минимизации квадратичной функции;
е) методы условной минимизации, основанные на теореме Куна-Такера.
Область применения конечных методов ограничена линейным программированием и квадратичным программированием.
Бесконечные методы основаны на построении последовательности все более точных приближений к решению. При этом, прекращая процесс на том или ином шаге итераций, можно получить решение с заданной точностью.
К этой группе методов относят:
1) метод Брауна-Робинсона, основанный на связи между парой задач линейного программирования (исходной и двойственной) и матричной игрой, т.е. на применении при решении задач математического программирования методов теории игр;
2) метод штрафных функций или метод штрафов, базирующийся на использовании функций штрафов.
Поскольку конечные и бесконечные методы математического программирования обладают общими достоинствами и недостатками, вводят классификацию методов по видам итераций.
При этом выделяют 4 вида итераций:
1) методы возможных направлений.
Строится последовательность хk, к = 0,1,..., так, что каждое хk удовлетворяет всем ограничениям задачи. Вблизи очередного приближения хk минимизируемая функция и ограничения (существенные для хk) аппроксимируются более простыми (как правило, линеными или квадратичными). Решая получающуюся вспомогательную задачу линейного или квадратичного программирования, находят возможное (т.е. не выходящее за пределы области допустимых решений) направление, являющееся одновременно и направлением убывания функции. Сдвиг по этому направлению приводит к новой точке хk+1 .
Примерами могут служить симплексный метод в линейном программировании и метод проекции градиента и условного градиента, метод возможных направлений Зойтендейка в нелинейном программировании;
2) методы, в которых последовательные приближения хk не удовлетворяют ограничениям, и в процессе итераций невязка в выполнении ограничений сводится к нулю.
При этом обычно используются те же приемы и аппроксимации и решения вспомогательных задач, что и в 1-й группе.
К этой группе относят двойственный симплекс-метод в линейном программировании, метод отсечения в выпуклом программировании, при этом точка хk отсекается путем добавления нового линейного ограничения;
3) итерационный процесс ведется не только по исходным, но и по двойственным переменным (множителям Лагранжа, оптимальным оценкам).
Одна итерация метода заключается в решении задачи о выборе оптимального варианта при заданных ценах на ресурсы (без учета их ограниченности) и в последующем пересчете цен в зависимости от степени нарушения ограничений на ресурсы.
К этой группе относится градиентный метод Эрроу-Гурвица-Удзавы;
4) методы, основанные на учете ограничений с помощью штрафов.
Штрафы включаются в минимизируемую функцию. При этом получается последовательность задач на безусловный минимум, каждая из которых может решаться с помощью различных методов. Задачи могут решаться с помощью градиентного метода, метода сопряженных градиентов, метода Ньютона и т. д.
К численным методам относят также методы решения задач специального вида: транспортные (Транспортная задача), блочные (Блочное программирование).
В современных условиях при применении компьютерных технологий число методов расширяется. В частности, разрабатываются методы, основанные на использовании кусочно-линейной аппроксимации, комбинаторных алгоритмов, разработке непрерывных вариантов дискретных методов, строится непрерывная траектория х(t), задаваемая дифференциальными уравнениями.
Лекция 12. Решение задач линейного программирования симплекс-методом
Цель лекции: ознакомление студентов с алгоритмом симплексного метода.
Содержание:
а) идея метода;
б) определение первоначального допустимого базисного решения задачи;
в) правило перехода к лучшему решению;
г) критерий проверки оптимальности найденного решения.
В основе симплекс-метода лежит идея поиска базисного решения с последующим переходом от одного базиса к другому таким образом, чтобы целевая функция при этом все время увеличивалась, если речь идет о задаче максимизации. Для начала работы требуется, чтобы заданная система ограничений выражалась равенствами, причем в этой системе ограничений должны быть выделены базисные неизвестные. Решение задачи при помощи симплекс-метода распадается на ряд шагов. На каждом шаге от данного базиса Б переходят к другому, новому базису Б1 с таким расчетом, чтобы значение функции f(x) не уменьшалось, т. е. fБ’≥fБ. Для перехода к новому базису из старого базиса удаляется одна из переменных и вместо нее вводится другая из числа свободных. После конечного числа шагов находится некоторый базис Б(k) , для которого fБ(k) есть искомый максимум для линейной функции f, а соответствующее базисное решение является оптимальным, либо выясняется, что задача не имеет решения.
Пусть мы имеем задачу линейного программирования.
Целевая функция вида:
![]()
и ограничения
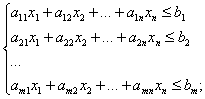
![]() ,
, ![]() .
.
Обозначим свободные коэффициенты ограничений aj0=bj. Приведем матрицу ограничений к каноническому виду:
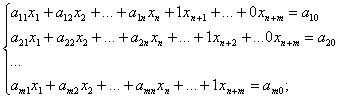 (12.1)
(12.1)
Приведем записанную систему к виду, где выделены базисные переменные.
Введем условные обозначения:
x1, x2 , ... , xr - базисные переменные;
xr+1, xr+2 , ... , xn - свободные переменные.
Будем применять метод полного исключения к расширенной матрице ограничений. Выбираем направляющий элемент aij на данной итерации. В результате преобразования Гаусса получим новые значения коэффициентов:
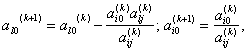 (12.2)
(12.2)
Если l≠I, l=1,2,…,m.
Выясним условия, при которых новое
базисное решение будет допустимым, т.е. ![]() для всех l.
для всех l.
По предположению, al0≥0,
тогда ![]()
Если ![]() то очевидно,
то очевидно, ![]() , так как
, так как ![]() ,
, ![]()
Если ![]() то
то 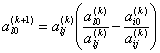 будет больше нуля при всех значениях l=1,2,…,m тогда и
только тогда, когда
будет больше нуля при всех значениях l=1,2,…,m тогда и
только тогда, когда 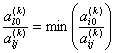 при условии
при условии ![]()
Преобразование Гаусса называется симплексным преобразованием, если направляющий элемент определяют по следующим правилам:
1) направляющий столбец выбирают из условия, что в нем имеется хотя бы один положительный элемент;
2) направляющую строку выбирают так, чтобы отношения аi0 / aij были минимальными при условии, что aij>0.
Задачи линейного программирования, решаемые с помощью симплекс-метода, основываются на представлении решения в табличной форме. Рассмотрим последовательность действий при решении задачи линейного программирования.
По последней системе ограничений и целевой функции в каноническом виде построим симплекс-таблицу.
Все дальнейшие преобразования связаны с изменением содержания этой таблицы. Нижняя строка элементов аок, к = 0,…, т+п называется индексной. Элементы индексной строки вычисляются следующим образом:
![]()
означает номер соответствующей строки.
Таблица 12.1- Симплекс-таблица
|
С |
|
|
С1 |
С2 |
С3 |
… |
Сj |
… |
Cn |
0 |
… |
0 |
|
|
Bx |
A0 |
A1 |
A2 |
A3 |
… |
Aj |
… |
An |
An+1 |
… |
An+m |
|
cn+1 |
xn+1 |
a10 |
a11 |
a12 |
a13 |
… |
a1j |
… |
a1n |
1 |
… |
0 |
|
cn+2 |
xn+1 |
a20 |
a21 |
a22 |
a23 |
… |
a2j |
… |
a2n |
0 |
… |
0 |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
cn+i |
xn+i |
ai0 |
ai1 |
ai2 |
ai3 |
… |
aij |
… |
ain |
0 |
… |
0 |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
cn+m |
xn+m |
am0 |
am1 |
am2 |
am3 |
… |
amj |
… |
amn |
0 |
… |
1 |
|
|
|
a00 |
a01 |
a02 |
a03 |
… |
a0j |
… |
a0n |
a0m+1 |
… |
a0m+n |
Поскольку на первом шаге заполнения таблицы все элементы сn+i равны нулю, то элементам индексной строки присваиваются значения соответствующих элементов целевой функции данного столбца, взятые с обратным знаком, т.е. аok= -Ск. Последняя строка таблицы служит для определения направляющего столбца.
Элемент а00 равен
значению целевой функции, которое вычисляется по формуле ![]() - номер базисной
переменной (индексация идет по строкам таблицы).
- номер базисной
переменной (индексация идет по строкам таблицы).
В столбце Вх записываются базисные переменные, на первом шаге в качестве базисных выбирают фиктивные переменные {хп+к }, к =1,…,т. В дальнейшем фиктивные переменные необходимо вывести из базиса.
В столбец С записываются коэффициенты при хп+к, на первом шаге значения этих коэффициентов равны нулю.
Для перехода от базиса фиктивных переменных к базису реальных переменных применяют следующие правила:
1) в качестве направляющего столбца выбирают столбец Аj для которого выполняется условие
a0J = min{aoi), l = l,…, п+т при а0l < 0,
т.е. выбирается минимальный элемент, при условии, что этот элемент отрицательный;
2) выбирают направляющую
строку, для чего каждый элемент столбца свободных членов делится на
соответствующий элемент направляющего столбца. Элемент столбца свободных
членов находится в одной строке с элементом направляющего столбца ![]() . Из всех возможных соотношений выбирается минимальное
. Из всех возможных соотношений выбирается минимальное 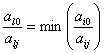 при условии, что arj > 0, 1 < r
< т.
при условии, что arj > 0, 1 < r
< т.
Применяя сформулированные правила, определяем направляющий элемент. Далее выполняется шаг симплексных преобразований.
Переменная, которая соответствует направляющему столбцу, вводится в базис, а переменная, соответствующая направляющей строке, выводится из базиса. При этом для переменной, вводимой в базис, изменяется соответствующее значение коэффициента целевой функции. Вместо коэффициента сn+i соответствующего старой базисной переменной, в таблице записывается значение коэффициента целевой функции при переменной, вводимой в базис.
Если направляющий элемент аij , то переход от данной таблицы к следующей осуществляется с использованием следующих правил:
1) для всех элементов направляющей строки
![]()
где к - номер шага (к = 1,
2,...); i - номер направляющей строки; j - номер направляющего столбца; ![]() £ = 0, т.е.
все элементы направляющей строки делим на направляющий элемент, в итоге
направляющий элемент стал равным единице;
£ = 0, т.е.
все элементы направляющей строки делим на направляющий элемент, в итоге
направляющий элемент стал равным единице;![]()
2) в направляющем столбце
необходимо получить ![]() ,
для всех
,
для всех ![]() ,
r≠i, при
,
r≠i, при
![]() , т.е. в
направляющем столбце должны быть все нули кроме направляющего элемента, который
равен единице.
, т.е. в
направляющем столбце должны быть все нули кроме направляющего элемента, который
равен единице.
Для всех остальных элементов, включая индексную строку, производим вычисления
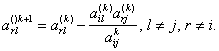 (12.3)
(12.3)
Симплексные преобразования повторяют до тех пор, пока не реализуется один из двух возможных исходов:
а) все a0i ≥ 0 - это условие оптимальности базиса последней табицы;
б) найдется такой элемент a0j< 0, при котором все элементы столбца аrj < 0, - это признак неограниченности целевой функции на множестве допустимых решений.
Лекция 13. Транспортные задачи линейного программирования
Цель лекции: ознакомление студентов с постановкой и методами решения транспортных задач линейного программирования.
Содержание:
а) постановка задачи;
б) методы составления начального опорного плана;
в) понятие потенциала и цикла;
г) методы отыскания оптимального решения транспортной задачи.
Транспортная задача является одной из наиболее распространенных специальных задач линейного программирования. Под названием "транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Наиболее часто встречаются следующие задачи, относящиеся к транспортным:
1) прикрепление потребителей ресурса к производителям;
2) привязка пунктов отправления к пунктам назначения;
3) взаимная привязка грузопотоков прямого и обратного направлений;
4) отдельные задачи оптимальной загрузки промышленного оборудо вания;
5) оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.
Рассмотрим математическую модель
прикрепления пунктов отправления к пунктам назначения. Имеются m
пунктов отправления груза и объемы отправления по каждому пункту a1,
a2 ,...,am . Известна потребность в грузах
b1, b2 ,...,bn по
каждому из n пунктов назначения. Задана матрица стоимостей
доставки по каждому варианту cij , ![]()
![]() . Необходимо рассчитать оптимальный план
перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го
пункта отправления (от поставщика) в каждый j-ый пункт назначения
(до потребителя) xij с минимальными транспортными
издержками.
. Необходимо рассчитать оптимальный план
перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го
пункта отправления (от поставщика) в каждый j-ый пункт назначения
(до потребителя) xij с минимальными транспортными
издержками.
В общем виде исходные данные представлены в таблице 13.1.
Таблица 13.1 – Распределительная таблица

Транспортная задача называется закрытой,
если объем отправляемых грузов ![]() .равен суммарному объему потребности
в грузах по пунктам назначения
.равен суммарному объему потребности
в грузах по пунктам назначения ![]() Если такого равенства нет, задачу
называют открытой.
Если такого равенства нет, задачу
называют открытой.
Все грузы из i-х пунктов должны быть отправлены, т.е.:
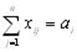 ,
,![]() (13.1)
(13.1)
Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:
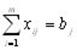 ,
,
![]() (13.2)
(13.2)
Суммарные объемы отправления должны
равняться суммарным объемам назначения). Должно выполняться условие
неотрицательности переменных: ![]() ,
, ![]() ,
, ![]() . Перевозки необходимо осуществить с
минимальными транспортными издержками (функция цели):
. Перевозки необходимо осуществить с
минимальными транспортными издержками (функция цели):
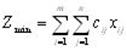 (13.3)
(13.3)
Вместо матрицы стоимостей перевозок (cij ) могут задаваться матрицы расстояний. Уравнение баланса является обязательным условием решения транспортной задачи. Поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. Транспортным задачам присущи следующие особенности: распределению подлежат однородные ресурсы; условия задачи описываются только уравнениями; все переменные выражаются в одинаковых единицах измерения; во всех уравнениях коэффициенты при неизвестных равны единице; каждая неизвестная встречается только в двух уравнениях системы ограничений.
Опорный план является допустимым решением транспортной задачи и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов.
Методы составления начального опорного плана.
Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля.
Диагональный метод, или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки неизвестного x11 и заканчивается в клетке неизвестного xmn , т. е. идет как бы по диагонали таблицы перевозок.
Метод наименьшей стоимости. При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф.
Метод Фогеля. В распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность. В строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в расчет не принимаются. На каждом этапе загружается только одна клетка.
Для перехода от одного базиса к другому при решении транспортной задачи используются так называемые циклы. Циклом пересчета в таблице перевозок называется последовательность неизвестных, удовлетворяющая следующим условиям:
1) Одно из неизвестных последовательности свободное, а все остальные базисные.
2) Каждые два соседних в последовательности неизвестных лежат либо в одном столбце, либо в одной строке.
3) Три последовательных неизвестных не могут находиться в одном столбце или в одной строке.
4) Если, начиная с какого-либо неизвестного, мы будем последовательно переходить от одного к следующему за ним неизвестному то, через несколько шагов мы вернемся к исходному неизвестному.
Если каждые два соседних неизвестных цикла соединить отрезком прямой, то будет получено геометрическое изображение цикла – замкнутая ломаная из чередующихся горизонтальных и вертикальных звеньев, одна из вершин которой находится в свободной клетке, а остальные - в базисных клетках.
Можно доказать, что для любой свободной клетки таблицы существует один и только один цикл, содержащий свободное неизвестное из этой клетки. Снабдим вершины цикла поочередно знаками "+" и "–", приписав вершине в свободной клетке знак "+". В вершинах со знаком "+" число x прибавим к прежнему значению неизвестного, находящегося в этой вершине, а в вершинах со знаком "–" это число x вычтем из прежнего значения неизвестного, находящегося в этой вершине.
Если в качестве x выбрать наименьшее из чисел, стоящих в вершинах, снабженных знаком " – " , то, по крайней мере, одно из прежних базисных неизвестных примет значение нуль, и мы можем перевести его в число свободных неизвестных, сделав вместо него базисным то неизвестное, которое было свободным. Описанное выше преобразование таблицы перевозок называется пересчетом по циклу.
Припишем каждой базе Ai, , некоторое число ui, и каждому потребителю Bj некоторое число vj :
![]() ,
,
так что
ui, + vj = cij , (13.4)
где cij – тарифы, соответствующие клеткам, заполненным базисными неизвестными. Эти числа ui, и vj называются потенциалами.
Для базисных клеток сумма потенциалов строки и столбца, в которых находится эта клетка, равна тарифу, соответствующему этой клетке; если же клетка для неизвестного xpq свободная, то сумму потенциалов
![]() (13.5)
(13.5)
называют косвенным тарифом этой клетки. Следовательно, алгебраическая сумма тарифов для свободной клетки xpq равна разности ее настоящего (“истинного”) и косвенного тарифов:
![]() (13.6)
(13.6)
Потенциалы можно найти из системы равенств (13.4), рассматривая их как систему (m + n - 1) уравнений с m+n неизвестными.
Критерий оптимальности базисного решения транспортной задачи: если для некоторого базисного плана перевозок алгебраические суммы тарифов по циклам для всех свободных клеток неотрицательны, то этот план оптимальный. Имея некоторое базисное решение, вычисляют алгебраические суммы тарифов для всех свободных клеток. Если критерий оптимальности выполнен, то данное решение является оптимальным; если же имеются клетки с отрицательными алгебраическими суммами тарифов, то переходят к новому базису, производя пересчет по циклу, соответствующему одной из таких клеток. Для нового решения также проверяют выполнимость критерия оптимальности и в случае необходимости снова совершают пересчет по циклу для одной из клеток с отрицательной алгебраической суммой тарифов и т. д.
Методы отыскания оптимального решения транспортной задачи.
1) Распределительный метод. При этом методе для каждой пустой клетки строят цикл и для каждого цикла непосредственно вычисляют алгебраическую сумму тарифов.
2) Метод потенциалов. При этом методе предварительно находят потенциалы баз и потребителей, а затем вычисляют для каждой пустой клетки алгебраическую сумму тарифов с помощью потенциалов.
Лекция 14. Задачи дискретного программирования
Цель лекции: ознакомление студентов с постановкой и методами решения задач дискретного программирования.
Содержание:
а) постановка задачи дискретного программирования;
б) математические модели задач дискретного программирования;
в) метод ветвей и границ для задачи целочисленного программирования.
Постановка задачи дискретного программирования. Многие задачи системного анализа описываются математическими моделями дискретного программирования. Рассмотрим общую задачу максимизации.
Найти ![]()
![]()
![]() при условиях
при условиях
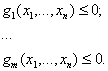
![]() (14.1)
(14.1)
где D - некоторое множество.
Если множество D является конечным или счетным, то условие (14.1) - это условие дискретности, и данная задача является задачей дискретного программирования (ЗДП).
Если вводится ограничение х; - целые числа (j=l,2,..., n), то приходят к задачам целочисленного программирования (ЦП), которое является частным случаем дискретного программирования.
В задачах дискретного программирования область допустимых решений является невыпуклой и несвязной. Поэтому отыскание решения таких задач сопряжено со значительными трудностями. В частности, невозможно применение стандартных приемов, используемых при замене дискретной задачи ее непрерывным аналогом, состоящих в дальнейшем округлении найденного решения до ближайшего целочисленного. Например, рассмотрим следующую ЗЛП: найти max (x1-3x2 +3х3) при условиях
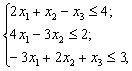
где х1, х2, х3 ≥ 0, xj - целые числа (j = 1,2,3).
Игнорируя условие целочисленности, находим оптимальный план симплекс-методом:
x1опт=0,5, x2опт=0, x3опт=4,5.
Проверка показывает, что никакое округление компонент этого плана не дает допустимого решения, удовлетворяющего ограничениям этой задачи. Искомое целочисленное решение задачи x1опт =2, x2опт=0, x3опт=5.
Таким образом, для решения задачи дискретного программирования (ЗДП) необходимы специальные методы. Методы решения ЗДП по принципу подхода к проблеме делят на три группы: 1) методы отсечения или отсекающих плоскостей; 2) метод ветвей и границ; 3) методы случайного поиска и эвристические методы.
Математические модели задач дискретного программирования.
По структуре математической модели задачи дискретного программирования разделяют на следующие классы:
1) задачи с неделимостями;
2) экстремальные комбинаторные задачи;
3) задачи на несвязных и на невыпуклых плоскостях;
4) задачи с разрывными целевыми функциями.
Рассмотрим некоторых из них.
Задачи с неделимостями. Математические модели задач с неделимостями основаны на требовании целочисленности переменных {xi}, вытекающем из физических условий практических задач.
К таким задачам относится задача об определении оптимальной структуры производственной программы, где {х1, х2,..., хп} - объемы выпуска продукции.
Эта задача заключается в отыскании
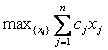 (14.2)
(14.2)
при ![]() ,
(14.3)
,
(14.3)
![]() целые при
целые при ![]() (14.4)
(14.4)
Задача о ранце. Рассмотрим постановку данной задачи. Турист готовится к длительному переходу в горах. В рюкзаке он может нести груз, масса которого не более W. Этот груз может включать в себя п типов предметов, каждый предмет типа j, массой wj , j= 1,2,..., n. Для каждого типа предмета турист определяет его ценность Ej во время перехода. Задача заключается в определении количества предметов каждого типа, которые он должен положить в рюкзак, чтобы суммарная ценность снаряжения была максимальной.
Обозначим через хj количество предметов j-го типа в рюкзаке.
Тогда математическая модель задачи такова:
![]() (14.5)
(14.5)
при ограничениях
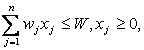 xj - целое, j=
1,2,..., n. (14.6)
xj - целое, j=
1,2,..., n. (14.6)
Экстремальные комбинаторные задачи. В данных задачах необходимо найти экстремум некоторой целевой функции, заданной на конечном множестве, элементами которого служат перестановки из n символов (объектов).
Одной из наиболее простых задач этого класса является задача о назначениях: найти такую перестановку (р1,р2,..., рn) из чисел 1,2,3,...,n,
при которой обеспечен ![]() по всем перестановкам.
по всем перестановкам.
Вводим переменные:
Хij = 1, если i-й механизм предназначен для j-ой работы;
хij = 0 — в противном случае.
Очевидно, что должно выполняться условие
![]() (14.7)
(14.7)
Данные ограничения означают,
что один механизм может быть предназначен для выполнения только одной работы.
Тогда задача будет состоять в определении таких чисел {хij}, при которых достигается минимум функционала ![]() при ограничениях
(14.7).
при ограничениях
(14.7).
Задача о коммивояжере. Имеется (n + 1) город. Задана матрица
С = ||cij || расстояний между городами. Выезжая из исходного города Aij , коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город Аij. Требуется определить, в каком порядке следует объезжать города, чтобы суммарное пройденное расстояние было минимально.
Введем переменные: хij = 1, если коммивояжер переезжает из населенного пункта Аi в Аj; хij - 0 - в противном случае.
Математическая модель задачи имеет следующий вид: найти
![]() (14.8)
(14.8)
при условиях
![]() (j=1,2,…n); (14.9)
(j=1,2,…n); (14.9)
![]() (j=1,2,…n); (14.10)
(j=1,2,…n); (14.10)
![]() (14.11)
(14.11)
где ui, uj - произвольные целые и неотрицательные числа.
Условие (14.9) означает, что коммивояжер выезжает из каждого города один раз, а условие (14.10) - что он въезжает один раз в каждый город.
Метод ветвей и границ для задачи целочисленного программирования.
Рассмотрим целочисленную задачу ЛП:
минимизировать
![]() (14.12)
(14.12)
при условиях
![]() (14.13)
(14.13)
![]() (14.14)
(14.14)
![]() - целые числа. (14.15)
- целые числа. (14.15)
Процесс поиска оптимального
решения начинают с решения непрерывной задачи ЛП. Если полученный при этом
оптимальный план ![]() не
удовлетворяет условию (14.15), то значение целевой функции
не
удовлетворяет условию (14.15), то значение целевой функции ![]() дает нижнюю оценку для
искомого решения, т.е.
дает нижнюю оценку для
искомого решения, т.е.![]() .
.
Пусть некоторая переменная хi0 (1 ≤ i0 ≤ т) не получила в плане ![]() целочисленного решения.
В целочисленном плане значение хi0 следует либо уменьшить, по крайней мере до [хi0], либо
увеличить, по крайней мере до [хi0]+ 1.
целочисленного решения.
В целочисленном плане значение хi0 следует либо уменьшить, по крайней мере до [хi0], либо
увеличить, по крайней мере до [хi0]+ 1.
Если границы изменения хi0 заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи ЛП. Эти задачи состоят в максимизации и минимизации хi0 при условиях (14.13) и (14.14).
Теперь для каждого фиксированного целочисленного значения хi0 в найденном отрезке [хi0min, хi0max] находят min z, решая задачу ЛП с ограничениями (14.13), (14.14) и с дополнительным ограничением хi0≤ki0..
Таким образом, все указанные
выше возможности можно представить в виде некоторого дерева, в котором вершина
0 отвечает плану ![]() ,
а каждая из соединенных с ней вершин отвечает оптимальному плану следующей
задачи: минимизировать z при
условиях (14.13), (14.14) и дополнительном условии, что переменной хi0 дано значение хi0 ≤ кi0, где кio - целое
число. Каждой из таких вершин приписывают оценку, которая равна min z при
указанных выше ограничениях. Очевидно,
,
а каждая из соединенных с ней вершин отвечает оптимальному плану следующей
задачи: минимизировать z при
условиях (14.13), (14.14) и дополнительном условии, что переменной хi0 дано значение хi0 ≤ кi0, где кio - целое
число. Каждой из таких вершин приписывают оценку, которая равна min z при
указанных выше ограничениях. Очевидно, ![]() , для всех k.
, для всех k.
Если оптимальные планы
полученных задач удовлетворяют условиям целочисленности, то план с минимальной
оценкой ![]() и
будет оптимальным планом исходной задачи. В противном случае возникает
необходимость в продолжении ветвления. При этом каждый раз для очередного ветвления
выбирают вершину с наименьшей оценкой.
и
будет оптимальным планом исходной задачи. В противном случае возникает
необходимость в продолжении ветвления. При этом каждый раз для очередного ветвления
выбирают вершину с наименьшей оценкой.
Процесс продолжают до тех пор, пока продолжение ветвления становится невозможным. Каждая конечная вершина отвечает некоторому допустимому целочисленному плану. Вершина с минимальной оценкой дает оптимальный план.
Лекция 15. Динамическое программирование
Цель лекции: ознакомление студентов с понятием и методами решения задач динамического программирования
Содержание:
а) понятие динамического программирования;
б) принцип оптимальности Беллмана;
в) дискретная модель динамического программирования;
Динамическое программирование - раздел теории оптимизации, посвященный исследованию и решению экстремальных задач специального вида, в которых целевая функция (целевой функционал) имеет вид суммы слагаемых (соответственно - интеграла). В основе метода динамического программирования лежит идея разбиения исходной задачи на последовательный ряд более простых задач. Основной областью приложения динамического программирования являются многошаговые процессы, т.е. процессы, протекающие во времени (дискретном или непрерывном).
Метод динамического программирования достаточно прост. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.
Главным рабочим инструментом динамического программирования является метод рекуррентных соотношений, в основе которого лежит необходимое условие оптимальности, выражаемое обычно в виде так называемого принципа оптимальности и уравнения Беллмана (по имени американского математика Р. Беллмана).
Принцип оптимальности Беллмана утверждает, что оптимальный процесс (т.е. оптимальное управление и соответствующая ему оптимальная траектория) для всего периода управления обладает тем свойством, что любая его часть, рассматриваемая на промежутке времени, входящем в исходный промежуток, также представляет собой оптимальный процесс для этого частичного промежутка времени. Иными словами, любая часть оптимального процесса необходимо является оптимальным процессом.
Основные особенности дискретной модели динамического программирования состоят в следующем:
1) задача оптимизации интерпретируется как многошаговый процесс управления;
2) целевая функция равна сумме целевых функций для каждого шага;
3) выбор управлений хк на к-м шаге определяется только состоянием системы Sk-1на предыдущем шаге и не зависит от состояния системы на более ранних этапах управления;
4) состояние Sk на к-м шаге зависит только от предшествующего состояния Sk-1, и управления xk, принимаемого на данном шаге, т.е.
Sk=fk(Sk-1, xk) . (15.1)
Схематически модель динамического программирования иллюстрирует следующая схема:
![]() (15.2)
(15.2)
Число этапов n, как правило, считается фиксированным, однако в некоторых задачах n может быть неограниченным, что соответствует задаче с бесконечным горизонтом управления.
Следует иметь в виду, что принцип Беллмана справедлив только для задач, для которых целевые функции можно описать в виде аддитивных функций от траектории, т. е. для процессов с определенной структурой зависимости управлений.
Это означает, что критерий оптимальности (целевая функция) F имеет вид
![]() (15.3)
(15.3)
где числовая функция φk оценивает качество управленческого решения на к-м шаге.
Оптимальное управление удовлетворяет следующему принципу оптимальности Беллмана: предположим, что, осуществляя управление, уже выбрана последовательность оптимальных управлений x1, x2, ... , xp, на первых р шагах, которой соответствует последовательность состояний (т.е. траектория) S1, S2, ... , Sp. Требуется завершить процесс, т.е. выбрать xp+1.,..., хn (а значит и Sp+1,,... , Sn). Тогда, если завершающая часть процесса не будет максимизировать функцию
![]() (15.4)
(15.4)
то и весь процесс
управления не будет оптимальным. В частности, при р = п - 1
получаем
требование максимизации функции ![]() , зависящей от переменной хn.
, зависящей от переменной хn.
На основе принципа оптимальности Беллмана строится система рекуррентных соотношений (уравнения Беллмана):
![]() (15.5)
(15.5)
где /, - заданная векторная функция соответствующих переменных, к = п,n-1,...,1, которым должен удовлетворять оптимальный процесс.
Максимум в правой части
равенства (2) берется по всем управлениям х, допустимым на шаге к. Тем самым, при вычислении ![]() на каждом шаге
приходится решать семейство задач максимизации функции переменной
х, зависящих от состояния Sk-1 на предыдущем (k-1)-м шаге. При этом
величина
на каждом шаге
приходится решать семейство задач максимизации функции переменной
х, зависящих от состояния Sk-1 на предыдущем (k-1)-м шаге. При этом
величина ![]() есть
оптимальное значение критерия оптимальности.
есть
оптимальное значение критерия оптимальности.
Вычисление оптимального процесса на основе уравнений Беллмана (15.2) в каждом конкретном случае может оказаться непростой задачей, требующей навыка и изобретательности.
Модели динамического программирования применяются при распределении дефицитных капитальных вложений между предприятиями, при составлении календарных планов текущего и капитального ремонта оборудования и его замены и т.д.
Возможности применения метода динамического программирования ограничиваются рядом недостатков этого метода. Первая трудность, которая характеризует его применение, возникает при формировании задачи оптимизации исследуемого процесса. Затем, в отличие от линейного программирования, где имеется универсальный алгоритм решения задач – симплекс-метод - в динамическом программировании отсутствует общий алгоритм, пригодный для всех задач. Динамическое программирование дает лишь общее направление решения конкретной задачи, и потому в каждом отдельном случае требуется находить наиболее подходящий метод оптимизации. Исследование динамического программирования встречает некоторые трудности и при решении задач высокой размерности, которая определяется не только количеством переменных состояния и уравнения, но и частотой их варьирования. Эффективное применение динамического программирования предполагает необходимость использования современных компьютерных технологий.
Классические задачи динамического программирования.
2) Задача последовательного принятия решения
3) Задача об использовании рабочей силы
5) Задача о ранце: из неограниченного множества предметов со весе. свойствами «стоимость» и «вес» требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при ограниченном суммарном
6) Алгоритм Флойда-Уоршелла: найти кратчайшие расстояния между всеми вершинами взвешенного ориентированного графа.
Список литературы
- Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высшая школа, 1998.
- Шелухин О.И., Тенякшев А.М., Осин А.В. Моделирование информационных систем.-М.: Радиотехника, 2005.
- Алиев Т.И. Основы моделирования дискретных систем.- СПб.: СПбГУ ИТМО, 2009-363 с.
- Туманбаева К.Х. Моделирование систем телекоммуникаций /Учебное пособие – Алматы, АИЭС, 2007.
- Кузовкова Т.А. Статистика связи.- М.: Радио и связь. 2003.
- Четыркин Е.М. Статистические методы прогнозирования.- М.: Статистика, 1977.
- Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Моисейкина Л.Г., Рыбакова Е.С. Теория статистики. – М.: Московская финансово-промышленная академия, 2004 – 198 с.
- Лещинская Э.М., Калиева С.А. Применение пакета GPSS при моделировании систем телекоммуникаций /Учебное пособие – Алматы, АИЭС, 2010.
- Банди Б. Основы линейного программирования. - М.: «Радио и связь», 1989 – 176 с.
- Лукашин, Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов : учеб. пособие / Ю.П. Лукашин. – М.: Финансы и статистика, 2003.
- Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование: Учебник. – М.: Финансы и статистика, 2001.
- Акулич И.Л. Математическое программирование в примерах и задачах.- М. Высш.школа, 1986.
- Гребенников А.В., Крюков Ю.А. Прогнозирование значений трафика данных с использованием временных рядов. Эл. журнал «Системный анализ в науке и образовании», 2011, №3.
Содержание
|
Введение |
3 |
|
Лекция 1. Основные понятия теории моделирования систем |
4 |
|
Лекция 2. Построение математических моделей |
8 |
|
Лекция 3. Методы сбора и систематизации статистической информации |
12 |
|
Лекция 4. Анализ статистических данных с использованием средних величин и показателей вариации |
16 |
|
Лекция 5. Парная регрессия и корреляция |
20 |
|
Лекция 6. Множественная регрессия и корреляция |
24 |
|
Лекция 7. Моделирование одномерных временных рядов |
28 |
|
Лекция 8. (продолжение лекции 7) |
32 |
|
Лекция 9. Прогнозирование уровней временного ряда |
36 |
|
Лекция 10. Основы математического программирования. Постановка задачи линейного программирования |
40 |
|
Лекция 11. Основы математического программирования. Постановка задачи линейного программирования |
44 |
|
Лекция 12. Решение задач линейного программирования симплекс-методом |
48 |
|
Лекция 13. Транспортные задачи линейного программирования |
52 |
|
Лекция 14. Задачи дискретного программирования |
56 |
|
Лекция 15. Динамическое программирование |
60 |
|
Список литературы |
63 |
Сводный план 2013 г., поз. 265