Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра «Электроника»

ОСНОВЫ АВТОМАТИКИ

Методические указания на выполнение расчетно-графических работ

для студентов специальности «5В071600 – Приборостроение»

Алматы 2013

СОСТАВИТЕЛИ: Б.С.Байкенов. Основы автоматики. Методические указания на выполнение расчетно-графических работ для студентов специальности «5В071600 – Приборостроение». – Алматы: АУЭС, 2013. – 14 с.

Методические указания предназначены для приобретения практических навыков студентом использования основных законов управления и методов построения систем автоматического управления и средств, необходимых для их реализации.

В методических указаниях изложены методы преобразования структурных схем, определение передаточных функций систем со сложным соединением звеньев, а также систем управления с учетом влияния внешних воздействий.

Методическая разработка составлена в целях закрепления лекционного материала и предназначена для студентов специальности «5В071600 –Приборостроение».

Ил. 25, табл. 1, библиогр. – 5 назв.

Рецензент: старший преп. кафедры ТКС Г.А. Шахматова

Печатается по плану издания Некоммерческого акционерного общества “Алматинский университет энергетики и связи” на 2013 г.

Св. план 2013 г., поз.163

Введение

Дисциплина «Основы автоматики» является вводной в специальность, позволяющей студенту ознакомится с целями, задачами и этапами разработки информационно-измерительных и управляющих автоматических систем.

Основной целью методических указаний является закрепление теоретических знаний и приобретение студентами практических навыков для решения задач по упрощению структурных схем систем со сложным соединением звеньев, определению передаточных функций систем с последовательным и параллельным соединением звеньев, а также передаточных функций одноконтурных и многоконтурных систем.

Кроме того, в методических указаниях приведены простые примеры построения автоматических устройств, дающих представление студенту о выбранной специальности.

РГР№1 связана с изучением методов расчета передаточных функций систем со сложным соединением звеньев.

РГР№2 посвящена изучению методов расчета передаточных функций систем с перекрещивающимися связями.

Методические указания разработаны в строгом соответствии с требованиями Государственного стандарта образования для бакалавриата по специальности «5В071600 –Приборостроение».

1 Расчетно-графическая работа №1. Системы со сложным соединением звеньев

Задача 1.1

Определить передаточные функции систем с последовательным и параллельным соединением звеньев, а также передаточные функции одноконтурных и многоконтурных систем.

Руководство к выполнению

Передаточная функция (ПФ) эквивалентного звена, последовательно соединенных звеньев, равна произведению передаточных функций этих звеньев

(1.1)

где W_i – передаточные функции последовательно соединенных звеньев.

ПФ эквивалентного звена, параллельно соединенных звеньев, равна сумме ПФ этих звеньев

(1.2)

где W_i – передаточные функции параллельно соединенных звеньев.

Рассмотрим структурную схему разомкнутой системы со сложным соединением звеньев и определим ее передаточную функцию.

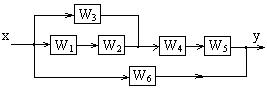
Рисунок 1.1 – Структурная схема разомкнутой системы

Пользуясь формулами (1.1) и (1.2), последовательно, по шагам, производим преобразование схемы:

W₁₂ = W₁ W₂ – последовательное соединение;

W₁₃ = W₃ + W₁₂ = W₃ + W₁ W₂ – параллельное соединение;

W₄₅ = W₄ W₅ - последовательное соединение;

W₁₅ = W₁₃ W₄₅ = (W₃ + W₁ W₂) ∙ W₄ W₅ - последовательное соединение;

W₀ = W₁₅ + W₆ = (W₃ + W₁ W₂) ∙ W₄ W₅ + W₆ - параллельное соединение.

ПФ замкнутой системы (контура) равна отношению передаточных функций между входом и выходом (разомкнутая система) к сумме: единица плюс произведение ПФ разомкнутой системы на ПФ обратной связи.

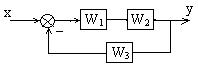
Рисунок 1.2 – Структурная схема замкнутой системы

По определению передаточная функция замкнутой системы будет равна:

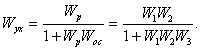(1.3)

В многоконтурной структурной схеме ПФ эквивалентного звена замкнутого контура можно заменить одним звеном.

Рассмотрим трехконтурную замкнутую систему с одним входом х и определим ее передаточную функцию.

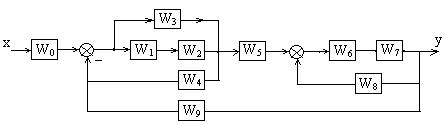
Рисунок 1.3 – Структурная схема трехконтурной системы

В двух контурах, лежащих между входом и выходом, необходимо заменить последовательно-параллельные соединения звеньев эквивалентными.

W₁₃ = W₁ W₂ + W₃; W₆₇ = W₆ W₇. (1.4)

Тогда структурная схема системы примет вид:

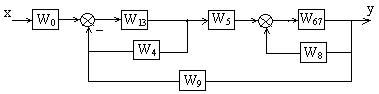
Рисунок 1.4 – Схема без последовательно-параллельных соединений звеньев

Передаточные функции внутренних контуров будут равны

(1.5)

В ПФ второго контура W₆₈ в знаменателе минус, т.к. обратная связь положительная. Если эти два контура заменить эквивалентными звеньями, то структурная схема будет одноконтурной.

Рисунок 1.5 – Одноконтурная структурная схема системы

Последний контур заменяется эквивалентным звеном с ПФ:

(1.6)

Тогда получим только два последовательно соединенных звена W₀ и W_19.

ПФ системы будет равна произведению ПФ последовательно соединенных звеньев.

W_yx = W₀ W₁₉ . (1.7)

Передаточные функции систем с двумя входами определяются обычным способом, как и для систем с одним входом, но при этом полагают, что сигнал другого входа равен нулю.

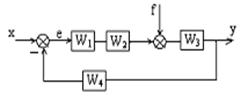
Рисунок 1.6 – Структурная схема системы с двумя входами

Найдем ПФ системы относительно входа х, полагая f = 0,

(1.8)

Определим ПФ системы относительно f, полагая х = 0,

(1.9)

Общая ПФ системы будет равна сумме ПФ отдельных входов:

(1.10)

В следящих системах выходом является сигнал рассогласования е, который должен быть равным нулю, т.е. система должна повторять входной сигнал. Например, привод антенны радара, следящий за воздушной целью.

Тогда ПФ следящей системы относительно входа х, при f = 0, будет равна

(1.11)

Для лучшего восприятия схемы со стороны входа f схему можно представить как

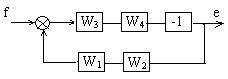
Рисунок 1.7 – Структурная схема со стороны возмущающего воздействия f

Левый сумматор схемы (рисунок 1.6) имеет отрицательный вход (отрицательная обратная связь) и отсутствие задающего сигнала х, поэтому его можно представить как инвертор с ПФ W = -1.

Тогда ПФ следящей системы относительно возмущающего воздействия будет равна:

(1.12)

ПФ системы относительно обоих входов будет равна:

(1.13)

1.2 Задание

Варианты задания соответствуют порядковому номеру студента в журнале. Для первой половины номеров нужно выполнить 1,3,5 пункты, а для второй - 2,4,6.

1. Определить передаточную функцию системы.

Рисунок 1.8 – Структурная схема разомкнутой системы

2. По заданным ПФ системы необходимо построить структурную схему:

а) [(W₁ + W₂) W₃ + W₄ W₅] (W₆ + W₇) + W₈ ;

б) [(W₁ W₂ + W₃ W₄)(W₅ + W₆)] (W₇ + W₈) W₉ ;

в) [W₁ (W₂ + W₃ W₄)] [W₅ + W₆] W₇ + W₈ W₉.

3. Определить ПФ многоконтурной системы.

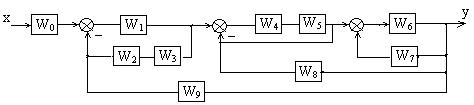
Рисунок 1.9 – Пятиконтурная схема системы

4. Определить ПФ четырехконтурной системы.

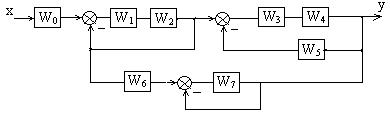
Рисунок 1.10 – Четырехконтурная схема системы

5. Определить ПФ системы относительно задающего сигнала х и возмущающего воздействия f по структурной схеме (см. рисунок 1.11).

6. Определить ПФ следящей системы относительно задающего сигнала х, возмущающего воздействия f и выхода е по структурной схеме.

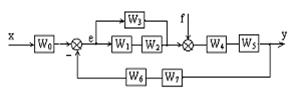
Рисунок 1.11 – Структурная схема системы

2 Расчетно-графическая работа №2. Системы с перекрещивающи-мися связями

Задача 2.1

Определить ПФ систем с перекрещивающимися связями.

Руководство к выполнению

Сумматор – устройство, соединяющее провода с выхода звеньев, а узлы –место соединения проводов, от которого они идут на вход звеньев.

Перенос сумматора может быть в двух случаях: по ходу сигнала и против.

1) По ходу сигнала – во входные цепи сумматора добавляется звено с передаточной функцией, через которое осуществляется перенос.

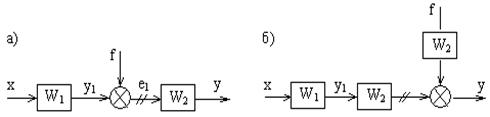
а) до переноса и б) после.

Рисунок 2.1 – Перенос сумматора по ходу сигнала

2) Против хода сигнала – к одной из входных цепей сумматора добавляется звено с обратной передаточной функцией W^-1, через которое осуществляется перенос.

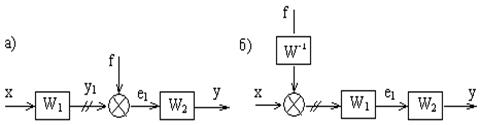
а) до переноса; б) после.

Рисунок 2.2 – Перенос сумматора против хода сигнала

Неэквивалентные участки сумматора отмечены двумя черточками – это участки линии связи, имеющие противоположное подключение. Например, провод, соединяющий выход сумматора с входом звена до переноса, после переноса будет соединять выход звена, через которое осуществлен перенос, с входом сумматора, т.е. наоборот (см. рисунок 1.13).

Перенос узла также может быть в двух случаях: по ходу и против хода сигнала.

1) По ходу сигнала – в выходные цепи узла добавляется звено с обратной передаточной функцией W^-1 , через которое осуществляется перенос.

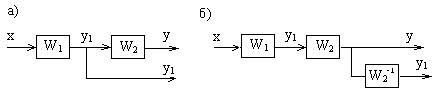
а) схема до переноса; б) после.

Рисунок 2.3 – Перенос узла по ходу сигнала

2) Против хода сигнала – в выходные цепи узла добавляют звено с ПФ, через которое произвели перенос узла.

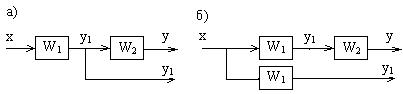
а) схема до переноса; б) после.

Рисунок 2.4 – Перенос узла против хода сигнала

В структурных схемах узлы, а также сумматоры можно переставлять между собой местами.

Рисунок 2.5 – Перестановка мест узлов и сумматоров

Если осуществляется перенос узла через сумматор, то тогда в схеме добавляется сумматор, но с одним отрицательным входом (вычитатель).

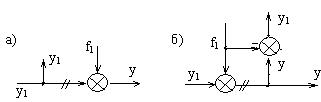
а) до переноса и б) после.

Рисунок 2.6 – Перенос узла через сумматор по ходу сигнала

Если перенос узла через сумматор осуществляется против хода сигнала, то в схеме добавляется суммирующее звено.

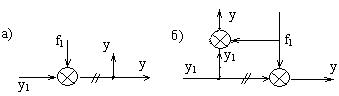
а) до переноса; б) после.

Рисунок 2.7 – Перенос узла через сумматор против хода сигнала

Замкнутую систему называют многоконтурной, если при ее размыкании получается цепь, содержащая параллельные или обратные связи (ОС), т.е. она помимо главной обратной связи содержит местные обратные связи или параллельные связи.

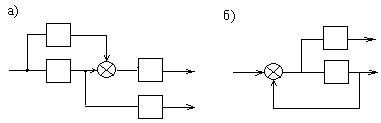
а) с параллельными цепями; б) с ОС.

Рисунок 2.8 – Структурные схемы систем

Для вычисления ПФ многоконтурной системы необходимо с помощью перестановки или переноса узлов и сумматоров освободиться от перекрывающихся связей. Перекрывающиеся связи – это цепи, в которых контур ОС или параллельной связи охватывает участок цепи другой ОС или параллельной связи.

Рассмотрим пример определения ПФ трехконтурной системы с перекрывающимися связями по входам х и f, а также выходам у и е.

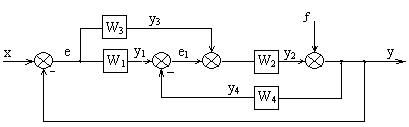
Рисунок 2.9 – Структурная схема многоконтурной системы

В начале необходимо избавиться от перекрещивающихся связей (перехлест ОС у₃ и у₄; вынести из контура сигнал воздействия f) путем переноса и перестановки узлов и сумматоров многоконтурной системы (рисунок 2.10).

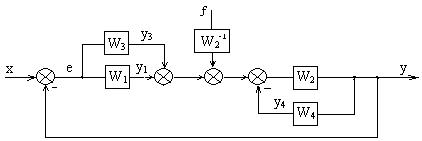
Рисунок 2.10 – Структурная схема трехконтурной системы без перекрещивающихся связей

Далее первый контур, образованный параллельными звеньями W₁и W₃, заменяется эквивалентным звеном W₁₃, а второй контур с звеном W₂ , охваченное ОС звеном W₄, заменяется эквивалентной ПФ замкнутой системы с отрицательной обратной связью (ООС) W_24.

W₁₃ = W₁ + W₃ ; (2.1)

Получим эквивалентную одноконтурную систему, имеющую вид:

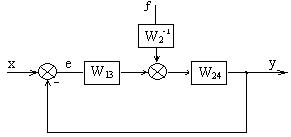
Рисунок 2.11 – Структурная схема эквивалентной одноконтурной системы

При вычислении ПФ по входу х полагаем, что возмущающее воздействие f = 0. Передаточные функции системы по входу х относительно выходов у и е имеют вид:

(2.2)

При вычислении ПФ по входу f полагаем, что задающий сигнал х = 0. При этом сравнивающее звено (сумматор) становится инвертирующим звеном с ПФ равной W = -1. Инвертирующее звено в замкнутый контур можно не вводить, если второй сумматор преобразовать в сравнивающее звено (один вход отрицательный). Тогда структурную схему можно представить как

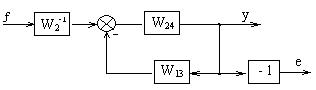
Рисунок 2.12 – Структурная эквивалентная схема по входу f

Передаточные функции системы по входу f относительно выходов у и е имеют вид:

(2.3)

САУ с одной (на выходе) управляемой или регулируемой величиной называют одномерными. Следовательно, рассматриваемая система является многоконтурной одномерной системой. Одномерная система с двумя входными величинами (задающий сигнал х и возмущающее воздействие f) описывается дифференциальным уравнением:

(2.4)

В операторном виде дифференциальное уравнение системы можно выразить через передаточную функцию как

(2.5)

По найденному выходному сигналу у(р) по формуле (2.5) можно перейти к уравнению (2.4), т.е. перейти из комплексной области р в область t.

Например, пусть W₁ = k₁ ; W₂ = k₂/(p + 1); W₃ = k₃/p; W₄ = k₄ системы, представленной на рисунке 2.10.

Тогда передаточные функции относительно двух входов х , f и выхода у будут равны:

(2.6)

где

Поэтому уравнение примет вид:

(2.7)

Умножив левую часть уравнения у(р) на знаменатель ПФ и заменив р = d/dt, получим уравнение, имеющее вид:

(2.8)

2.1 Задание

Варианты задания соответствуют порядковому номеру студента в журнале. Для первой половины номеров нужно выполнить 1-й пункт, а для второй - 2.

Дано: W₁ = k₁; W₄ = k₄; W₅ = k₅.

k₁ = 1; k₂ = 2; k₃ =0,5; k₄ = 0,5; k₅ = 2.

1. Осуществить преобразование структурной двухконтурной системы и найти передаточную функцию.

Рисунок 2.13 – Двухконтурная разомкнутая система

2. Определить передаточную функцию замкнутой системы (рисунок 2.14) относительно обоих входов х и f, а также общую передаточную функцию относительно выхода. Показать дифференциальное уравнение замкнутой системы в действительных переменных t.

Рисунок 2.14 – Двухконтурная замкнутая система

Список литературы

1. Анхимюк В.Л. Теория автоматического управления. – Мн.: Дизайн ПРО, 2002. – 352 с.

2. Воронов А.А. Теория автоматического управления: В 2-х ч. - Ч.1 Линейные системы. - М.: Высшая школа, 1986. – 423 с.

3. Олсон Г. Цифровые системы автоматизации и управления. – СПб.: Невский диалект, 2001. – 540 с.

4. Терехов В.М. Системы управления электроприводов. – М.: Изд. центр «Академия», 2006. – 304 с.

5. Фрайден Дж. Современные датчики. Справочник. - М.: Техносфера, 2005. - 592 с.

Содержание

Введение	3
1 РГР №1.	3
2 РГР №2.	7
Список литературы	13