ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ
Алматы энергетика және байланыс институтының
О.З.Рутгайзер, Б.М.Шайхин
РАДИОАВТОМАТИКА
Оқу құралы
Алматы 2008
Оқу құралында радиоавтоматиканың дискреттік және цифрлық жүйелері бойынша негізгі теориялық және практикалық материал келтірілген, микроконтроллерді тұйық жүйелерде қолдану сұрақтары қарастырылған.
Мазмұны
Кіріспе............................................................................................................................. 4
1 Пәннің оқылу шеңберінен шықпай шешілетін мәселелер...................................... 5
2 Дискрет жүйелердің математикалық бейнеленуі.................................................... .7
2.1 Кванттау процесін бейнелеу.............................................................................. 7
2.2 Импульстік теоpема...........................................................................................11
2.3 Айырымдық теңдеулер..................................................................................... 12
2.4 Z- түрлендіру......................................................................................................14
2.5 Z-түрлендірудің теоремалары...........................................................................16
2.6 Кері Z-түрлендіру...............................................................................................18
2.7 Импульстік беріліс функциясы.........................................................................20
2.8 Реттілігі ноль бекіткіш.......................................................................................23
2.9 Дискрет жүйе буындарының тізбекті қосылуы...............................................26
2.10 Тұйық импульсті жүйелер...............................................................................27
3 Дискрет жүйелерді уақыттық және жиіліктік аймақта талдау.............................28
3.1 Орнықтылықты уақыттық аймақта талдау......................................................28
3.2 Орнықтылықтың алгебралық критерийі..........................................................30
3.3 Уақыттық аймақта импульсті жүйе сапасының анализі.................................33
3.4 Орныққан қатенің анализі.................................................................................35
3.5 Өтпелі процесс бойынша жүйе сапасының анализі........................................40
3.6 Жиіліктік сипаттамалардың пайдаланылуы мен жүйе сапасының анализі..43
3.7 Қашықтық бойынша нысанаға автоматты ілесе жүруі бар импульсті радиоқашықтық өлшегішінің анализі........................................................................ 51
4 Микропроцессорлар басқару жүйелерінде............................................................ 56
4.1 Жалпы мазмұны .......................................................................................... 56
4.2 Алдын ала сүзгілеу.............................................................................................60
4.3 Бергіштердің істен шығуымен байланысты қателер.......................................61
4.4 Микропроцессорлық басқару жүйелеріндегі кешігу......................................61
4.5 Сандық аспектілер............................................................................................. 63
4.6 Сызықсыз атқарушы механизмдер................................................................. 65
Әдебиеттер тізімі......................................................................................................... 67
![]() Кіріспе
Кіріспе
Автоматтық құрылғылар радиоқондырғылардың негізгі элементтеріне жатады. Бұл құрылғылардың көмегімен радиотехникалық қондырғының негізгі параметрлерінің тұрақтандырылуы; объектілер координаттарын автоматты анықтау, радиотехникалық информацияны өңдеу; құрамына радиоқондырғы кіретін басқару жүйесі үшін командаларды өндіру және тағы басқа осы сияқты мәселелер шешімін табады. Қазіргі уақытта радиоқондырғылар жиі күрделі автоматтық басқару жүйелерінің (АБЖ) құрамына кіреді. Бұл жағдай радиоқондырғылардың жұмыс істеуінің дәлдігі мен тез әрекеттілігіне (шапшаңдығына) қойылатын талаптар деңгейін көтереді.
Автоматтық басқару жүйелердің (АБЖ) құрамында кілт немесе микроконтроллерлер болады. Бұл жағдайда сигналдың квантталуы шарасыз процесс болып табылады да, үзіліссіз сигнал деңгейлері әртүрлі реттілікпен немесе ұзақтығы әртүрлі импульстермен немесе сандар тізбегімен ауыстырылады (алмастырылады). Құрамында цифрлық есептеу машинасы (ЦЕМ) болатын жүйелерде соңғылар: 1) реттегіштің; 2) реттегіштің және салыстыру құрылғысының; 3)түзетуші құрылғының немесе объектінің өзінің ролін атқаруы мүмкін.
Уақыт бойынша сигналдардың дискреттелуі жүйені дискретті етеді, ал деңгей бойынша кванттау – сызықты емес етеді. Процестердің екеуі де әдістемелік қателіктерімен қабаттасып жүреді. Дискретті және цифрлық жүйелердің артықшылықтары белгілі: жоғары дәлдік пен бөгеуілден қорғанушылық, жоғары сенімділік, ығудың (дрейфтің) жоқ болуы, аналогтық реттегіштермен салыстырғанда бейімделгіштігінің үлкен болуы. Үзіліссіз жүйені талдау нәтижелерін импульсті немесе цифрлық жүйелерге механикалық түрде көшіру орнықтылықтың жойылуы, шектік циклдердің пайда болуы және т.б. осындай қажетсіз салдарға келтіруі мүмкін. Осымен байланысты үзіліссіз процестерді дискретті түрде басқару – кванттау жиілігінің таңдалуын, орнықтылықтың талдануын, микроконтроллер параметрлерінің және түйіндесу құрылғыларының параметрлерінің есепке алынуын шешуді талап етеді. Осы мәселелер оқу құралында қарастырылады.
1 Пәннің оқылу шеңберінен шықпай шешілетін мәселелер
Радиотехникалық жүйелерде информация үзілімі хабарларды импульстік модуляция түрлері әртүрлі: амплитудалық (АИМ), уақыттық (УИМ),
ендік-импульстік (ЕИМ), кода-импульстік (КИМ) радиосигналдар арқылы таратқанда бірінші кезекте пайда болады. Пайдалы информацияның үзілімі ұйымдастырылған бөгеуілдердің кейбір түрлерінің радиожүйеге әсерінің нәтижесінде де болуы мүмкін.
Зерттеу мәселелерін (міндеттерін) дискреттік жүйелердің ерекше мысалы болып табылатын қозғалмалы объектілерінің қашықтық бойынша автоматтық ілесе жүру жүйесінің (ҚАІЖ) мысалы негізінде қарастырайық.
Нысанға дейінгі қашықтық D радиолокациялық станция (РЛС) антеннасының импульс шығару және оны қабылдау мезеттерінің уақыт аралығына пропорционал (1.1-суретті қара).
![]()
мұндағы t2 - шағылысқан импульстің қабылдану мезеті;
t1 - импульстің сәулелену мезеті;
с – радиотолқындардың таралу жылдамдығы.
Бұл өрнекке сәйкес белгілі сұлбалармен (схемалармен) жеткілікті дәл орындалатын уақыт санауын t1 мезетте бастау керек. Келесі міндет – t2 мезетті де, дәл айқындап алу. Бұл жерде қиын жағдайлар пайда болады. Ұзақтығы 1 мкс импульс уақыт жаймасында ұзын бойлығы 150м аумағын алады да, бұл пішіні (формасы) әртүрлі бөгеуілдермен бұрмаланатын импульстің келу мезеті дәлсіз айқындалу себебінен қашықтықты өлшеудің сәйкесті қателігінің болуы мүмкіндігін тудырады. Қашықтықты санау дәлдігін жоғарылату үшін импульс ұзақтығын кемітуге болады, бірақ онда РЛС-тің қабылдау құрылғысының өткізу жолағын кеңейту керек, ал бұл оның сезгіштігінің кемуіне ұшыратады. Әрбір бейнесигналды бөлу әдісі, импульс ұзақтығын кемітпей жоғары санау дәлдігін алуға мүмкіндік береді. Мұндай әдіс импульстің энергетикалық орта жерінен біршама тұратын шағылысқан сигнал орнын салыстыруға негізделген. Екі жартылай стробтар түрінде өндірілетін тіректік импульс шағылысқан сигналмен беттестіріледі және оң жақтағы жартылай стробқа тура келетін сигналдың интегралдық кернеулерін салыстырады. Салыстыру уақыттық дискриминатормен орындалады. ҚАІЖ-нің функционалдық сұлбасы 1.1-суретте келтірілген, ал 1.2-суретте дискриминатор жұмысының уақыттық диаграммалары келтірілген.
Дегенмен, қашықтық бойынша автоматтық ілесе жүрудің (ҚАІЖ) қатесі тек объектіден шағылысқан импульстің келу уақытын өлшеу дәлдігімен ғана емес, ізіне түсіп отырған объектінің қозғалу сипаттамаларымен, автоматтық жүйенің күшейту коэффициентімен, оның жиіліктік қасиеттерімен, квантталу периодымен, яғни РЛС-тің зондтаушы импульстерінің өкшелей жүру периодымен де анықталады. Ажыратылған жүйенің күшейту коэффициентін жоғарылату және жалғасып жүретін зондтаушы импульстер периодын кеміту есесінен ҚАІЖ дәлдігін арттыруға ынталану динамикалық қатенің өсуіне, орнықсыз процестерге келтіруі мүмкін. Бұл жүйеде микропроцессордың қолданылуы және оның көмегімен түрлі мәселелерді шешу: өлшеу, сүзгілеу, деректерді енгізуді іске асыру операцияларының орындалу уақыты бойынша елеулі кідірулерге және орнықсыз процестердің пайда болуына келтіруі мүмкін.
Мұндай жүйелерді зерттеу үшін цифрлық жүйелердің арнайы теориясы қажет болғандықтан, бұл жүйенің жұмысы сызықты стационар жүйелер теориясының шеңберінен шықпай толығымен түсіндірілуі мүмкін емес.
 |
а)
 |
1.1 Сурет – ҚАІЖ-нің функционалдық сұлбасы
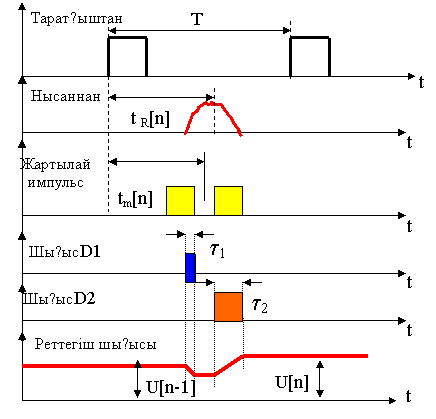
1.2 Сурет – Дискpиминатоp жұмысының уақыттық диаграммалары
2 Дискрет жүйелердің математикалық бейнеленуі
2.1 Квантталу процесін бейнелеу
Квантталу операциясын аналогтық немесе үзіліссіз сигналдың модуляцияланған импульсті немесе цифрлық сигналға түрлендіру деп қарастыруға болады. Модуляцияның көп тараған түрі амплитудалы-импульстік модуляция (АИМ) болып табылады.
2.1-суретте таңдамасы ақырлы уақытты периодты кванттаушының құрылымдық сұлбасы көрсетілген. Периоды Т болатын тасымалдаушы генератор құрамына импульсті элемент ИЭ (кілт) кіретіндіктен, амплитудасы үзіліссіз x (t) хабарға сәйкесті x (t) импульсті t уақытқа қалыптастырады. Осындай кванттаушының сұлбасы 2.2-суретте келтірілген.
АИМ түрлерінің бірнешеуі бар. АИМ-нің бірінші түрінде ИЭ шығысындағы импульстердің амплитудасы импульс ұзақтығы ішінде x (t) үзіліссіз сигналдың өзгерулерін қайталайды. Осындай АИМ болатын сигнал 2.3-суретте келтірілген.

2.1 Сурет – Амплитудалы-импульстік 2.2 Сурет – Кванттаушының
модулятор кванттаушы ретінде сұлбасы
2.3.-суреттен импульсті элемент ИЭ екі параметрлермен, тұйықталу Т периодымен және тұйықталу t ұзақтығымен сипатталатыны көрініп тұр. Модуляция түрінің басқасында ИЭ шығысындағы импульстің амплитудасы уақыт бойы тұрақты және импульстің бастапқы мезетіндегі x(t) сигнал мәніне тәуелді болады. Модуляцияның осындай АИМ түрі 2.4-суретте келтірілген.
Жоғарыда келтірілген амплитудалы-импульстік модулятордың көзқарас жүйесі (концепциясы) кванттау операциясын математикалық талдау үшін пайдалы екен. Амплитудалы-импульстік модуляция процесімен сипатталатын кванттаушы сызықты құрылғы болып табылады.
Алайда ақырлы енді импульстердің есепке алынуы жеткілікті күрделі болуы мүмкін. Егер кванттаушының импульстер ұзақтығы нөл немесе таңдама уақыты нөл болса, онда кванттаушының математикалық бейнеленуі оңайлатылып ықшамдалуы мүмкін. Бұл жағдайда шығыс сигнал үзіліссіз сигналдың лездік мәндерімен анықталады да, бірлік ауданды импульстер тізбегін қарастыру мүмкіндігі болады. Бұл жағдайда импульсті элемент идеал импульсті элемент (ИИЭ) деп аталады, ал оның шығыс сигналы решеткалық функция деп аталады. Идеал кванттаушының сигналдары 2.6-суретте, ал кванттаушының өзі 2.5-суретте келтірілген.
 |
|
2.3 Сурет – Бірінші тектік АИМ 2.4 Сурет – Екінші тектік АИМ
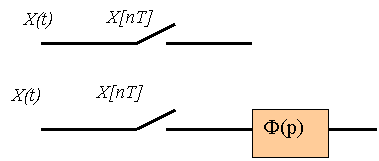
а)
б)
2.5 Сурет – Кванттаушылар:
а - идеалды;
б – Ф(р) - қалыптастырғышы бар идеалды
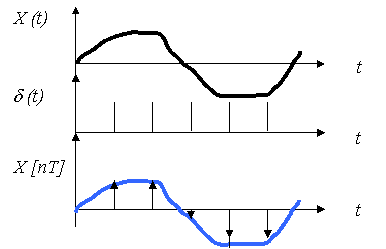
Т 2Т 3Т 4Т 5Т
2.6 Сурет – Идеал кванттаушы сигналдары
Идеал импульсті элементтен екінші тектік АИМ болатын импульсті элементке көшу үшін қалыптастырушы Ф(p) элементті қосымша қосу керек. Бұл - импульстерді берілген пішіні (формасы) болатын импульстерге түрлендіруші сызықты стационар буын. Осындай қалыптастырғышы болатын импульсті элементтің сұлбасы 2.5 б-суретте келтірілген.
АИМ-ді орындайтын импульсті элемент сызықты буын болып табылады. Импульсті модуляция әдістерінің басқаларында ИЭ (импульсті элемент) сызықты емес буын болып табылады. Мысалы ЕИМ кезінде импульстер ұзақтығы сигнал шамасына тәуелді болғанда, x (t) сигналдарға қатысты суперпозиция принципі орындалмайды.
Жоғарыда айтылғанды есепке алғанда дискретті тұйықталған жүйе 2.7-суретте көрсетілген түрде келтірілуі мүмкін.
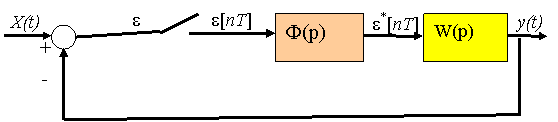 |
2.7 Сурет –Тұйықталған дискретті жүйе
Дискретті жүйенің қалыптастырушы элементі де параметрлері тұрақты сызықты буын болып табылады, сондықтан оны үзіліссіз бөлікке жатқызып, келтірілген үзіліссіз бөлікті (КҮБ) алуға болады.
Импульсті сигнал жоғары жиілікті құраушылардан тұрады, себебі кванттаушыны гармоникалар генераторы ретінде қарастыруға болады.
Импульстерінің
екі ақырлы кванттаушы үшін кіріс және шығыс
сигналдарының амплитудалық спектрлері 2.8-суретте келтірілген.
Бұл суреттен көрінетіндей, шығысы негізгі
құраушысынан және бір-бірінен ![]() s кванттау жиілігіне
тең қашықтықта орналасатын барлық
аударылған құраушыларынан тұратын гармоникалар
генераторы ретінде кванттаушыны елестетуге болады.
s кванттау жиілігіне
тең қашықтықта орналасатын барлық
аударылған құраушыларынан тұратын гармоникалар
генераторы ретінде кванттаушыны елестетуге болады.
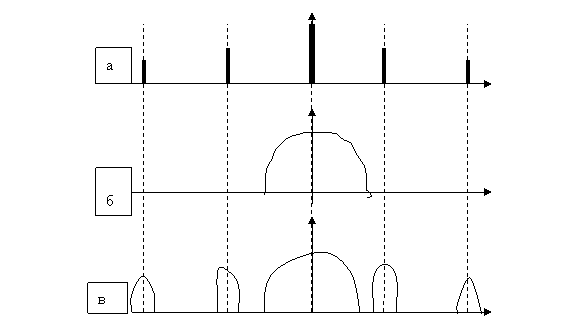
2.8 Сурет – Ені ақырлы импульстер болатын кванттаушы үшін кіріс және шығыс сигналдарының амплитудалық спектрлері:
а – бірлік импульстер тізбегінің спектрі; б – үзіліссіз кіріс сигналының спектрі; в – кванттаушының шығыс сигналының спектрі
Жиіліктердің негізгі жолағы үзіліссіз кіріс сигналындағы барлық ақпаратты береді. Осы ақпаратта, жиіліктердің бүйірлік жолақтарында қайталанады.
2.8
в – суретте көрсетілген ![]() үшін жиіліктік спектр кванттау
жиілігі х
(t)
– сигналдың жоғарғы жиіліктік (ЖЖ)
құраушысын екі еседен тым артық асып түскен шартта
алынған. Бұл спектрдің ЖЖ құраушысы
жүйенің үзіліссіз бөлігімен сүзгіленуі тиіс. Сигнал
y(t)-нің толық сүзгіленбеу себебінен қосымша
қателер пайда болуы мүмкін.
үшін жиіліктік спектр кванттау
жиілігі х
(t)
– сигналдың жоғарғы жиіліктік (ЖЖ)
құраушысын екі еседен тым артық асып түскен шартта
алынған. Бұл спектрдің ЖЖ құраушысы
жүйенің үзіліссіз бөлігімен сүзгіленуі тиіс. Сигнал
y(t)-нің толық сүзгіленбеу себебінен қосымша
қателер пайда болуы мүмкін.
2.2 Импульстік теоpема
Автоматтық жүйеде кванттауды пайдаланғанда келесі сұрақты қоюға тура келеді: кванттау жиілігіне қойылатын шектеулер қандай? Кез келген нақты кванттаушының ақырлы максималь түрлендіру жиілігі болуы тиіс болғанмен, теория жүзінде кванттау жиілігінің жоғарғы шегі жоқ.
Қызық болып табылатыны – кванттау жиілігінің төменгі шегі. Бұл жағдайда интуициялық түсініктісі келесі. Егер үзілісссіз сигнал уақыт бойынша тез өзгерсе, онда, оны тым төменгі жиілікпен кванттай отырып, таңдау мезеттері аралығындағы сигнал туралы маңызды информацияны жоғалтып алуға болады, яғни алғашқы сигналды дискретті таңдамалардағы информация бойынша қалпына келтіру мүмкін болмай қалады. Сигналды қалпына келтіру мүмкін болу үшін
2.8-суретте келтірілген амплитудалық спектрлерден кванттаудың ең төменгі жиілігі 2ωс екен деген қорытындыға келуге болады. Бұл жердегі ωс – сигнал спектріндегі ең жоғарғы жиілік. Формалды түрде бұл тезис импульстік теорема ретінде белгілі. Теореманың тұжырымы келесі: егер сигналдың ωс [рад/с] шамасынан жоғары жиіліктері жоқ болса, ол аралығы Т=(0,5*2π/ωс) дискретті уақыт мезеттерінде өлшенген өзінің мәндерімен толық сипатталады. Дегенмен, кванттау жиілігінің таңдап алынуына нақты түрде тұйық жүйелер орнықтылығының талаптары және сигналдың квантталуын теориялық минимумнан жоғарырақ жиілікпен орындалуы тиіс ете алатын басқа да талаптар ықпал етеді. Оның үстіне спектрі шектелген сигналдар байланыс немесе басқару жүйелерінде физикалық түрде болмайды. Нақты дүниедегі физикалық сигналдардың бәрі жиіліктердің кең ауқымын бүркейтін гармоникалардан тұрады. Бірақ жоғарғы жиіліктік (ЖЖ) құраушылар амплитудаларының едәуір бәсеңдеуі салдарынан сигнал спектрі шектелген болады деп болжанады. Сондықтан тәжірибе жүзінде бұл факторлар идеал төменгі жиіліктік (ТЖ) сүзгінің жүзеге аспайтындығымен үйлесе (тіркесте) үзіліссіз сигналдың дискреттік таңдамалары бойынша оның дәлме-дәл жаңғыртуын импульстік теорема орындалғанның өзінде де мүмкін емес етеді. Сонымен бірге ажыратылған жүйедегі синусоидалы сигналды қалпына келтіру кезінде мүмкін болатын қателерді де ескеру керек.
2.1 Кесте – Сигналды кванттау және қалпына келтіру кезіндегі салыстырмалы қателер
|
Кезе ң аралығындағы квантталудың саны |
Салыстырмалы қате |
|
2 5 10 20 50 100 200 500
|
1,5 0,6 0,3 0,15 0,06 0,03 0,015 0,006 |
2.3 Айырымдық теңдеулер
Импульстік жүйенің құрылымдық сұлбасында импульстік элементтің бар болуы кез келген импульстік жүйенің тек дискретті бірдей қашықтықтағы уақыт мезеттерінде ғана сыртқы үзіліссіз әсерге жауап беруіне келтіреді. Сондықтан импульстік жүйелерді талдағанда сыртқы әсерді сипаттайтын үзіліссіз х(t) функцияны сәйкесті х [nT] решеткалық функциямен, яғни тек дискретті
бір-бірінен бірдей қашықтықтардағы тәуелсіз t – айнымалының мәндерінде ғана мәндері өзгеретін функциямен ауыстыруға болады. Бұл мәндердің арасында решеткалық функция 0-ге тең. Егер t=nT болса, решеткалық функция үзіліссізден алынады. Жиі тәуелсіз айнымалының дискретті мәндер арасындағы қашықтықты 1-ге тең деп санаған ыңғайлы. Ол үшін өлшемсіз t=t/T айнымалыны енгізейік, онда келесіні аламыз
f(t)=f(nT)=f(t)=f(n) . (2.1)
Мысал 2.1. f(t)=e –αt болсын. Решеткалық функция үшін өрнек жазу керек. (2.1) - өрнекті пайдаланып келесіні аламыз
f[nT]=e –α nt , f[n]=e –α n . (2.2)
Үзіліссіз жүйелерде функцияның өзгеру жылдамдығы бірінші туындымен анықталады, осыған ұқсас дискретті жүйелер үшін решеткалық функцияның өзгеру жылдамдығы бірінші ∆ f[n] айырыммен анықталады.
∆f[n]=f[n] - f[n-1] . (2.3)
Осыған ұқсас решеткалық функцияның өзгеру үдеуін сипаттайтын екінші айырым да табылуы мүмкін.
![]() (2.4)
(2.4)
Жалпы жағдайда “k”-сыншы айырым үшін өрнек келесі болады:
![]() . (2.5)
. (2.5)
Решеткалық y[n] функция және оның айырымдары арасындағы қатынас ақырғы айырымдардағы теңдеуді немесе айырымдық теңдеуді анықтайды:
![]() (2.6)
(2.6)
Айырымдық теңдеулер дифференциалдық теңдеулердің шешілуін бағдарламалауда пайдаланылуы мүмкін.
Мысал 2.2. Инерциялық буынның шығысындағы өтпелі процестің айырымдық теңдеуін құру керек, егер инерциялық буынның беріліс функциясы келесі болса, онда
![]() .
.
Келесі дифференциалдық теңдеуді аламыз
![]() .
.
Дифференциалдарды ақырғы айырымдармен ауыстырып келесіге келеміз
![]() .
.
Бұл өрнекті түрлендіріп, алатынымыз
![]() ,
,
 ,
,
![]() .
.
2.4 Z- түрлендіру
Z-түрлендіру дискретті жүйелерді талдау және жобалау үшін жетілдірілген маңызды математикалық әдіс болып табылады. Уақыттың үзіліссіз функциясы Лаплас бойынша кескінделумен ауыстырылуы мүмкін екені белгілі
 (2.7)
(2.7)
Егер уақыттың ∆t=T ақырлы аралығын алып, ағымдық уақытты t=nT түрінде, бұл жердегі n=0,1,2,3,... деп берсек, онда соңғы өрнектегі интеграл келесі түрде берілуі мүмкін:
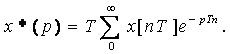 (2.8)
(2.8)
Р-комплекс айнымалыны жаңа Z-комплекс айнымалыға ауыстыруды жүргізейік. Ауыстыруды келесі түрде орындайық
e pT= z. (2.9)
Соңғы (2.9) теңдеуді Р-ға қатысты шешіп, алатынымыз келесі
p=(1/T) ln z. (2.10)
Онда (2.8) - өрнекті келесі түрде беруге болады
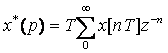 .
. ![]() (2.11)
(2.11)
Өрнектің оң жақ бөлігінің екінші көбейткіші f(t) функцияның Z-түрлендірілуі деп аталып жүр.
![]() (2.12)
(2.12)
Кейде ұқсас формуланың символдық жазылуы қолданылады
X (z) = Z[x(nT)]. (2.13)
Өрнек (2.12), шын мәнісінде, уақыттың дискретті функциясының Т шамасына бөлінген Лаплас түрлендіруі болып табылады. Жалпы алғанда Лаплас түрлендіруі бар болатын кез келген f(t) функция үшін де Z-түрлендіру бар болады.
Өрнек (2.13) f(t) функцияның Z-түрлендіруін тапқанда пайдаланылады. Алайда, бұл өрнектің қолайсыздығы – оның ақырсыз қатар болуында.
Анықтамалықтар мен оқулықтарда табуға болатын кейбір жиі кездесетін функциялар үшін Z-түрлендірулердің табылу жолдарын келесі мысалдар көрсетеді.
Мысал 2.3. Бірлік баспалдақты x(t)=1(t) функцияның Z-түрлендіруін табайық
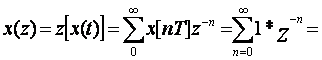
![]() .
(2.14)
.
(2.14)
Прогрессияның еселігі
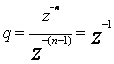 .
.
Қатар мүшелерінің қосындысы
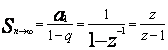
мұндағы a1 –қатардың бірініші мүшесі.
Демек
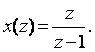
Егер (2.14) - қатардың сол және оң жақтардың z -1 шамасына көбейтіп, содан кейін осы пайда болған өрнекті (2.14) - қатардан алып тастасақ (азайтсақ), қатар қосындысын анықтау процедурасын ықшамдауға болады. Расында да,
![]() -
-
![]()
![]() ,
,
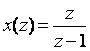 .
.
Мысал 2.4. Сызықты x(t)=t*1(t) функция үшін Z-түрлендіруін табайық. (2.12)-өрнекті пайдаланып табатынымыз келесі:
![]()
![]() (2.15)
(2.15)
Қатарды ықшамды түрде беру үшін (2.15)-өрнектің екі жағын z -1 шамасына көбейтеміз
![]()
(2.15)-өрнекті соңғы өрнекке азайтып алатынымыз келесі
![]() .
(2.16)
.
(2.16)
Соңғы (2.16)-өрнекті (2.14)-қатарымен салыстыратын болсақ, (2.16)-өрнектің жақшаларының ішіндегісі (2.14)-қатарына сәйкесті, сондықтан келесі өрнекті жаза аламыз
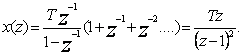
2.5. Z-түрлендірудің теоремалары
Z-бейнелеудің пайдаланылуы жиі Z-түрлендірудің теоремаларын қолданумен белгіленіп қойылуы мүмкін. Бұл теоремаларды дәлелсіз келтірейік.
1.Қосындылау және азайту. Егер f1(t) және f2(t) функциялардың Z-түрлендірулері бар болса, онда
![]() . (2.17)
. (2.17)
2.Тұрақтыға көбейту. Егер F(Z) f(t)-функциясының Z-түрлендірілуі болса, онда
![]() (2.18)
(2.18)
мұндағы a -тұрақты.
3.Уақыт аймағы бойынша ығысу. Егер f(t)-функцияның Z-түрлендірілуі F(Z) болса, онда
![]() .
(2.19)
.
(2.19)
Мысал 2.5. Бірлік баспалдақты функцияны кванттаудың бір Т периодына кідірткендегі Z-түрлендіруін табайық. Уақыт аймағы бойынша ығысу теоремасын (2.19) - өрнекті пайдаланып табатынымыз келесі
![]() .
.
4. Түпнұсқаны экспонентке көбейту туралы (бейнелер аймағындағы ығысу) теорема. Егер f(t)-функцияның Z-түрлендірілуі F(Z) болса, онда
![]() . (2.20)
. (2.20)
5. Бастапқы мән туралы теорема. Егер f(t)-функцияның Z-түрлендірілуі F(Z) болса және егер келесі limz=∞ F(Z) – шек бар болса, онда
![]() (2.21)
(2.21)
Теоремадан t=0 кезіндегі f(t) дискретті сигналдың мәні Z= ∞ кезіндегі F(Z) мәнімен анықталады деген қорытынды келіп шығады.
6. Ақырлы мән туралы теорема. Егер f(t)-функцияның Z-түрлендірілуі бар болса, сонымен бірге, егер (1-Z-1 ) F(Z)-функцияның /Z/=1 – бірлік радиусты шеңберде немесе оның сыртында полюстері жоқ болса, онда
![]() (2.22)
(2.22)
Мысал 2.6. Ақырлы мән туралы теореманы пайдаланып, берілген Z-түрлендіру үшін f[nT] функцияның ақырлы мәнін анықтау келесі өрнекпен беріледі
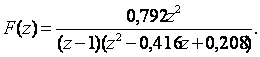
Бұл функцияның орнықтылығын тексерейік
![]()
Бөлімнің түбірлерін анықтайық, яғни беріліс функцияның полюстерін анықтайық. Зерттелініп отырған функцияның бірлік шеңберде полюстері жоқ болғандықтан, жүйе орнықты. Демек, келесі өрнекті жаза аламыз
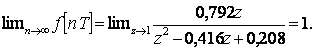
7. Дифференциалдау теоремасы. f(t,a)-функцияның Z-түрлендірілуі F(z,a) болсын делік, ал а-бұл жерде тәуелсіз айнымалы немесе тұрақты, онда
![]() .
(2.23)
.
(2.23)
2.6 Кері Z-түрлендіру
Лаплас түрлендіруі және оның кері түрлендіруі бірмәнді болып табылады. Z-түрлендіру үшін кері Z-түрлендіру бірмәнді болып табылмайды. F(z)-функцияның кері Z-түрлендіруінің қисынды нәтижесі, тек t=nT-кванттау мезеттерінде ғана f(t)-функцияға тең f(nT) функциясы болып табылады.
Бірлік импульстер тізбегіне сәйкесті және келесіге тең z / (z-1) бірлік баспалдақты функция үшін кері Z-түрлендіру мәндері t=0,Т,2Т, ... мезеттерде бірге тең кез келген функция бола алтындығын 2.9.-суреттен көруге болады. Кері Z-түрлендірудің бірмәнді еместігі осы әдістің шектеуінің бірі болып табылады.
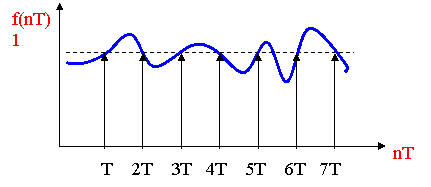 |
2.9 Сурет – Кері Z-түрлендірудің бірмәнді еместігі
Кері Z-түрлендірудің белгіленуі келесі
![]() (2.24)
(2.24)
Кері Z-түрлендіру жай бөлшектерге жіктеу әдісімен анықталуы мүмкін. Бұл әдіс Лаплас түрлендіруіндегі жай бөлшектерге жіктеу әдісіне жақын. Үзіліссіз жүйелерді талдағанда F(p) функцияның кері Лаплас түрлендіруін келесі түрде жіктеп табуға болады
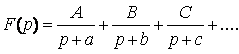 (2.25)
(2.25)
мұндағы а,в и с - F(p) функцияның теріс полюстері (бұл жерде жай полюстер жағдайы болжанып отыр);
А,В,С – осы полюстердегі F(p) функцияның қалындылары. Онда F(p) функцияның кері Лаплас түрлендіруі келесі болып анықталады
![]() (2.26)
(2.26)
Z-бейнелеу үшін F(z) функцияны (2.25) өрнектегі түрде берудің қажеті жоқ, себебі A/z+a түріндегі өрнектер үшін Z-түрлендірулер кестесінде кері Z-түрлендіру жоқ. Сонымен бірге 2.2-кестеден Az/(z-e -at ) функцияның кері Z-түрлендіруі Ae –ant мәніне тең. Демек, F(z)/z функцияны жай бөлшектерге жіктеген ыңғайлы. Жіктегеннен кейін F(z) функцияны алу үшін F(z)/z функция үшін өрнектің екі бөлігін де z-ке көбейтеді.
Егер F(z) функцияның f(nT) деген кері Z-түрлендіруі табылған болса, онда F(z) функцияның кері Z-түрлендіруі келесі түрде анықталады
![]() (2.27)
(2.27)
Мысал 2.8. Келесі Z-түрлендіру берілген
![]() (2.28)
(2.28)
мұндағы а - тұрақты оң сан; Т - кванттау периоды. F(z) деген функцияның кері Z-түрлендіруін табыңыз.
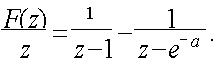
F(z)/z функциясының жай бөлшектерге жіктелуі келесіні береді
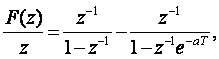

Демек
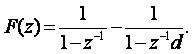
F(z) функцияның кері Z-түрлендіру мәні кванттау мезетінде
![]()
уақыт функциясы ретінде анықталатындай болып, 2.2.-кестеден табыла алынады.
2.7 Импульстік беріліс функциясы
Осыған дейін дискретті жүйелердің қарастырылуы дискретті сигналдардың қасиеттерін зерттеуге және математикалық сипаттауға келтірілетін. Енді сызықты жүйенің кірісіне дискретті сигнал түсірілгендегі жағдайды талдайық. Кірісіне x(t)-үзіліссіз сигнал келіп түскен сызықты ажыратылған жүйе үшін (2.10 а–суретті қара) кіріс-шығыс арақатынасы келесі беріліс функциямен сипатталады
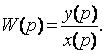
Енді осы жүйенің кірісіне квантталған сигналды 2.10 б – суретте көрсетілгендей түсіретін болсақ, онда беріліс функцияны келесі жолмен алуға болады
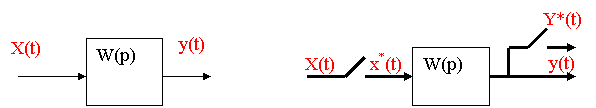 |
а б
2.10 Сурет – Үзіліссіз (a) және дискpетті (б) кіріс сигналдары болатын сызықты жүйе
Буынның y(t) шығыс сигналы W(p) буынның сүзгілеу қасиетінің нәтижесінде үзіліссіз болып табылады. Импульстік жүйенің шығыс сигналын ыңғайлы бөліп шығару үшін кілттің тұйықталу мезеттеріне сәйкесті дискретті (үзікті) уақыт мезеттерінде S пен синхронды жұмыс істейтін жалған кілттен кейінгі y*(t) жалған шығыс сигналды қарастырайық. Буынның кірісіне t=0 мезетінде бірлік импульс түсірілсін делік және импульстер қалыптастырғышы жоқ деп болжайық. Бұл жағдайда кіріс және шығыс сигналды келесі түрде келтіруге болады
![]()
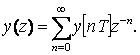 (2.29)
(2.29)
Бұдан басқа үзіліссіз жүйенің шығыс сигналын g(t) импульсті өтпелі функциямен сипаттауға болады
![]() (2.30)
(2.30)
бұл жердегі g(t) – үзіліссіз бөліктің зілдеме функциясы. Келесі t=nT алмастыруды қойып, алатынымыз
![]() (2.31)
(2.31)
Соңғы (2.31) - өрнекті (2.29) - өрнек ішіне қойып, алатынымыз
 (2.32)
(2.32)
Егер m=n – l немесе n=m + l айнымалыны енгізсек, онда алатынымыз
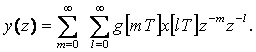 (2.33)
(2.33)
Бұл жерде зілдеме функцияның Z-бейнесі келесіге тең
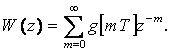 (2.34)
(2.34)
(2.34) - өрнек сызықты жүйенің импульстік беріліс функциясы болып табылады. Шығыс сигнал үшін келесі өрнекті жазуға болады
![]() (2.35)
(2.35)
Демек, импульстер қалыптастырғышы жоқ кезде дискретті беріліс функцияны анықтау үшін орындалатын тәртіп (процедура) келесі болуы тиіс:
1. Үзіліссіз буынның немесе жүйенің дағдылы беріліс функциясын алу.
2. g(t) – импульстік беріліс функцияны (зілдеме функциясын) анықтау.
3. g[nT] – зілдеме функцияның решеткалық функциясын анықтау.
4. Z-түрлендіру қатарын қосындылау нәтижесінде дискретті беріліс функцияны алу.
Мысал 2.9. Беріліс функциясы келесіге тең
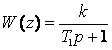 буынның
дискретті беріліс функциясын анықтау.
буынның
дискретті беріліс функциясын анықтау.
Мұнда инерциялық буынның зілдеме функциясын анықтаймыз
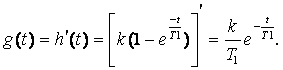
Келесі қадамда g[nT] решеткалық функцияны анықтаймыз
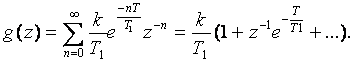
Содан кейін беріліс функцияны анықтаймыз
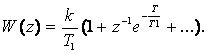 (2.36)
(2.36)
(2.36)- өрнектің екі бөлігін z-1 e-T/T1 шамасына көбейтіп алып тастасақ, келесі дискретті беріліс функцияны аламыз
 (2.37)
(2.37)
2.8 Реттілігі нөл бекіткіш
Жоғарыдағы жағдайдан айырмашылығы импульстік элементтен кейінгі импульстер тізбегі келіп түсетін импульстер мәндеріне тәуелді nT мезетінде амплитудасы өзгеретін баспалдақты сигналдарға қалыптастырушы элементпен түрлендіріледі. Осындай түрлендіруші элемент реттілігі нөл бекіткіш (РНБ) деп аталады. Бекіткіштің бұл түрі таңдау және сақтау құрылғыда бекіту операциясын модельдеу үшін қолданыла алады. Бұл жағдайда
![]() (2.38)
(2.38)
(2.38)- өрнек кіріс және шығыс сигналдары 2.11-суретте келтірілген, РНБ-нің (реттілігі нөл бекіткіштің) импульстік өтпелі функциясын анықтайды.
 |
2.11 Сурет – Импульсті әрекетке реттілігі нөл бекіткіштің (РНБ-нің) жауабы
Реттілігі нөл бекіткіштің (РНБ-нің) шығыс сигналы үзіліссіз сигналдың баспалдақты жуықтамасы екенін және кванттау жиілігін өсіру бұл жуықтаманың дәлдігін арттыруға келтіретінін атап кетейік. РНБ шығысындағы сигналды h(t) және h(t-T) сигналдардың екеуімен модельдеуге болады (2.11-суретті қара). Жоғарыдағы 2.11-суреттен импульсті әрекетке РНБ-нің жауабын көруге болады да, оны келесі түрде жазуға болады
![]() (2.39)
(2.39)
мұндағы h(t) – бірлік баспалдақты функция.
Олай болса, (2.39)- өрнекке сүйеніп, РНБ-нің беріліс функциясын келесі түрде жаза аламыз
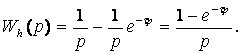 (2.40)
(2.40)
Демек, W(p) Z-түрлендіруі келесі болып шығады
 (2.41)
(2.41)
Бұл нәтиже ақиқат, себебі кванттау периоды кезінде РНБ дискретті сигналды тұрақты етіп ұстайды. Бірақ практика жүзінде жағдайлардың көбінде реттілігі нөл бекіткіштен кейін жүйенің үзіліссіз бөлігі болады (2.12-суретті қара). Бұл жағдайда жүйенің шығыс сигналының Z-түрлендіруі келесі
![]() (2.42)
(2.42)
Бұл жерде,
![]()
 |
2.12 Сурет – Реттілік нөл бекіткіші (РНБ) бар жүйе
РНБ-ның (2.40) өрнектегі беріліс функциясын соңғы өрнекке қойып алатынымыз келесі
 (2.43)
(2.43)
Сонымен, РНБ-сі бар ажыратылған дискретті жүйенің беріліс функциясын іздеу [ W(p) ]-беріліс функцияның ажыратылған үзіліссіз бөлігін табуға, одан кейін Z-түрлендіруге көшіп, алынған нәтижені [ ( z-1)/z] шамаға көбейтуге саяды.
Мысал 2.9. РНБ-сі бар ажыратылған дискретті жүйенің үзіліссіз бөлігінің беріліс функциясы W(p)=k/p болғандағы беріліс функциясын анықтау.
Жүйенің үзіліссіз бөлігінің өтпелі функциясын анықтаймыз
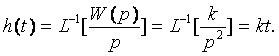
Содан кейін h[z] өтпелі функция сигналының Z-түрлендіруін анықтаймыз. Сызықты өсетін сигнал үшін нәтиже 2.4-мысалда алынған болатын. Сондықтан, бұл мысалдың соңғы нәтижесін пайдаланып, алатынымыз келесі
![]()
Алынған нәтижені (z-1)/z шамасына көбейтеміз де, келесіні аламыз:
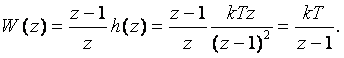
Ұқсас әдіспен қарапайым жүйелердің басқа өтпелі функциялары үшін Z-түрлендіруді алуға болады. Есептеулерді ықшамдау үшін 2.2-кестені пайдалануға болады.
Мысал 2.10. РНБ-сі бар ажыратылған дискретті жүйенің беріліс функциясын 2.2-кестені пайдаланып анықтаймыз.
Жоғарыдағы (2.43)- өрнекке сүйеніп, егер W(p) келесі түрде берілген болса
![]()
деп алып, W1(Z) беріліс функцияны табамыз
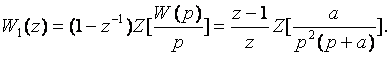
2.2-кестеден ![]() – Z-түрлендіруді
тауып, оны (z-1)/z шамасына көбейтіп, келесіні табамыз
– Z-түрлендіруді
тауып, оны (z-1)/z шамасына көбейтіп, келесіні табамыз
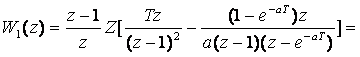
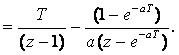
2.9 Дискрет жүйе буындарының тізбекті қосылуы
2.2 Кесте – Кейбір үзіліссіз буындардың Z-түрлендіруі
|
Лаплас түрлендіруі |
Z-түрлендіру |
|
1/р 1 /p2 1 /p3 1/(p+a) 1/( p+a)2 a/p (p+a) a/p2(p+a) |
z / z-1 Tz / (z-1)2 T2z(z+1) /2(z-1)3 z/ (z-e-aT) Tz e-aT /(z-e-aT)2 (1- e-aT )z /(z-1)(z-e-aT) Tz / (z-1)2 - (1- e-aT )z / a(z-1)(z-e-aT)
|
Буындары тізбекті қосылған дискрет жүйені қарастырғанда бүкіл жүйенің беріліс функциясын анықтау мәселесіне келген жөн. Төмендегі 2.13-суретте W1(p) және W2(p) буындары тізбекті қосылған дискрет жүйе көрсетілген. Буындардың екеуі S1-кванттаушыға ұқсас және онымен синхрондалған S2-кванттаушымен бөлінген.

|
|
2.13 Сурет – Кванттаушымен бөлінген дискрет жүйе буындарының тізбекті қосылуы
Бүкіл жүйенің импульсті беріліс функциясы келесі жолмен анықталады. W1(p) және W2(p) буындардың шығысындағы сигналдар келесі:
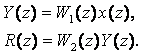
Сонымен, R(z)-нәтижелік сигнал келесі
![]() (2.44)
(2.44)
Демек, кванттаушымен бөлінген екі сызықты буындардың импульсті беріліс функциясы осы буындардың импульсті беріліс функцияларының көбейтіндісіне тең.
Келесі 2.14-суретте көрсетілгендей екі буын тізбекті қосылғанмен, кванттаушымен бөлінбеген болса, бүкіл жүйенің импульсті беріліс функциясы келесі түрде жазылуы тиіс
![]() (2.45)
(2.45)
Жалпы жағдайда келесі түрде де жазылатынын белгілеп кетейік
![]()
Сонымен, алдымен нәтижелік жүйенің беріліс функциясын табу керек (буындардың беріліс функцияларын көбейту жолымен), тек содан кейін ғана нәтижелік жүйенің Z-түрлендіруін анықтауға болады.
 |
2.14 Сурет – Кірісінде кванттаушысы болатын буындардың қосылуы
2.10 Тұйық импульсті жүйелер
Төмендегі 2.15-суретте келтірілген басқарудың импульсті жүйесін қарастырайық.
X(p)
Y(p) 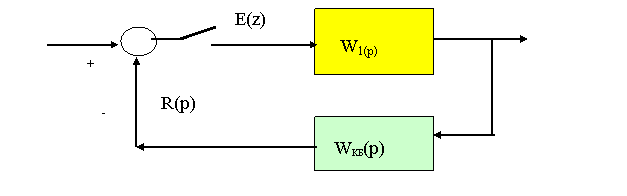
2.15 Сурет – Тұйық импульсті жүйе
Ажыратылған жүйе буындарының беріліс функциялары белгілі деп болжайық. Онда үзіліссіз жүйелердің ұқсастығына қарай қарастырып, тұйықталған импульсті жүйенің беріліс функциясын аламыз

(2.46)
(2.46)-шы өрнекті түрлендіріп келесі өрнекті аламыз
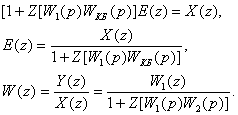 (2.47)
(2.47)
3 Дискрет жүйелерді уақыттық және жиіліктік аймақта талдау
Басқару жүйенің жұмыс қабілеттілігін анықтағанда импульсті жүйенің орнықтылығын талдау маңызды болады. Үзілссіз жүйелердегідей тек орнықты импульсті жүйе ғана оған жүктелген қызметті (функцияларды) орындау үшін пайдаланылуы мүмкін. Орнықтылықтың жалпы белгілері импульстік жүйелер жағдайында да дұрыс болып қала бергенмен, яғни орнықты жүйеде шектелген кіріс сигналдарға шектелген шығыс сигналдары сәйкесті болуы тиіс, алайда импульсті элементтердің бар болуы орнықтылықты талдау кезінде қосымша күрделіліктерді береді.
3.1 Орнықтылықты уақыттық аймақта талдау
Үзіліссіз жүйелердегідей импульстік жүйенің айырымдық теңдеуінің жалпы шешімін оң жақтағы бөлігі болатын теңдеудің жеке шешімі және оң жақ бөлігі теңдеудің жалпы шешімі түрінде келтіруге болады
![]() (3.1)
(3.1)
Xв [nT] құраушы жүйенің мәжбүр қозғалысын, ал Xо[nT] – өтпелі қозғалысын сипаттайды. Жүйе қозғалысының орнықтылығы туралы біртекті теңдеу шешімінен анықталатын Xо[nT] құраушы бойынша жорамалдауға болады. Үзіліссіз басқару жүйелерінің жобалануы жиі жүйенің беріліс функциясының нөлдері мен полюстерінің Р-жазықтықта орналасуын талдауға негізделген. Егер тұйықталған жүйенің беріліс функциясының барлық полюстері, яғни сипаттаушы теңдеудің түбірлері сол жақтағы «Р»-түбірлердің жартыжазықтығында жатса, онда жүйе орнықты. Орнықтылықтың шекарасы жорамал ось болып табылады (3.1-суретті қара). Осыған ұқсас Z-түрлендірудің беріліс функциясының полюстері мен нөлдері жүйенің тұйықталу мезеттеріндегі жауабын анықтайды. Тұйықталған импульстік жүйе үшін Z-кескіндегі теңдеу сипаттаушы теңдеуді алуға мүмкіндік береді де, егер оның Z1, Z2,....,Zn түбірлері нақты болса, онда сипаттаушы теңдеудің шешімін келесі түрде жазуға болады
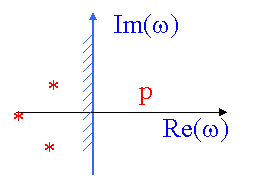 |
3.1 Сурет – Орнықты жүйе үшін Р жазықтықтағы түбірлер
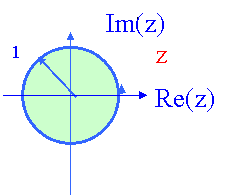 |
3.2 Сурет – Z – жазықтығының бетіндегі орнықтылық шекарасын бейнелеу
![]() (3.2)
(3.2)
мұндағы C1 ,С2 ,.....Сm – бастапқы шарттардан анықталатын тұрақты коэффициенттер.
Егер
![]() немесе
немесе ![]() болып, сигнал X0 нөлге
ұмтылса, яғни
болып, сигнал X0 нөлге
ұмтылса, яғни
![]() (3.3)
(3.3)
жүйе орнықты болады.
Бұл соңғы теңдеудің шарттарын орындау үшін (3.2)-өрнектегі әрбір қосылғыш келесі теңсіздікті қанағаттандыруы тиіс
![]() (3.4)
(3.4)
өз кезегінде, бұл шарт егер барлық Z1 , Z2 ,.., Zm түбірлер модульдері бойынша бірден аспаса ғана орындалады.
Демек, импульсті жүйенің қажетті және жеткілікті орнықтылық шарты келесі теңсіздіктің орындалуы болып табылады
/Zm/<1. (3.5)
Соңғы теңсіздікті Р-комплекс айнымалыны Z=е pT комплекс айнымалыға немесе Р-жазықтықты Z- түбірлердің комплекс жазықтығына түрлендіруді орындап, графикпен түсіндіруге болады.
Комплекс айнымалының P=jw мәнін (2.9)-теңдеуге қойып, келесіні жаза аламыз: Z=ejwT айнымалы w 0-ден 2π/Т шамасына дейін өзгергенде айнымалы z бірлік радиусты шеңберді Z- жазықтық бетінде салады. W-ның шамасын одан әрі өзгерткенде (2π/Т-ден 4π/Т шамасына дейін), айнымалы W шеңберді қайталап салады. Демек, түбірлер орналасуының орнықты және орнықты емес аймақтарының шекарасы болып табылатын Р жазықтықтағы жорамал осьтің кесіндісі 3.2-суретте көрсетілгендей центрі координаталар басында болатын бірлік шеңбермен Z-жазықтық бетінде бейнеленеді.
Егер жүйенің түбірі комплексті-түйіндескен, яғни p1 = - c+ jw болса, онда
Z=epT =e -cT *e –jwT.
Бұл жағдайда Р-түбірлер жазықтығында
түбірдің нақты бөлігінің артуымен Р1
түбірдің орны орнықтылық шекарасынан алыстайды,
яғни жүйе орнықтырақ бола бастайды, онда ![]() ақырсыздыққа
ұмтылуымен
ақырсыздыққа
ұмтылуымен ![]() нөлге
ұмтылады. Сол жақтағы Р жартыжазықтыққа Z түбірлер
жазықтығында бірлік радиусты дөңгелектің ішкі
беті сәйкесті болады. Ал, Р жазықтықтың оң
жақ жартысындағы нүктелер болса, олар Z
жазықтықтағы бірлік дөңгелектің
сыртқы аймағында бейнеленеді.
нөлге
ұмтылады. Сол жақтағы Р жартыжазықтыққа Z түбірлер
жазықтығында бірлік радиусты дөңгелектің ішкі
беті сәйкесті болады. Ал, Р жазықтықтың оң
жақ жартысындағы нүктелер болса, олар Z
жазықтықтағы бірлік дөңгелектің
сыртқы аймағында бейнеленеді.
Тұйық жүйеде өтпелі процестің өшуі неғұрлым үлкен болса, соғұрлым бұл жүйедегі орнықтылық қоры үлкен болатыны түсінікті. Төмендегі 3.3-суретте екі түбірлер үшін тең өшу сызықтары келтірілген. Сипаттаушы теңдеу түбірлерінің бірлік радиусты шеңберге салыстырмалы орналасуы бойынша сызықты импульсті жүйенің орнықтылығын анықтау ыңғайсыз және күрделі болады (мысалы, сипаттаушы теңдеудің реті жоғары болғанда). Бұл жағдайда орнықтылық критерийлерімен пайдаланып қалуға болады. Орнықтылық критерийлері сипаттаушы теңдеудің түбірлерін есептеуден бастайды да, / Z / < 1 түбірлердің негізгі теңсіздігінен шығатын қатыстарды орнықтылықты анықтау үшін табады.
3.2 Орнықтылықтың алгебралық критерийі
Сипаттаушы өрнектің түбірлерін зерттеу үшін Гурвиц критерийін
қолдану әдісін қарастырайық.

![]()
3.3 Сурет - Z-жазықтықтағы тұрақты өшу сызықтары
Алдын ала Z-кескінде сипаттаушы көпмүшені жазайық
![]() (3.6)
(3.6)
Гурвиц критерийі сипаттаушы көпмүше түбірлерінің Z-комплекс айнымалының жарамал өсіне салыстырмалы орналасуын бағалауға мүмкіндік береді. Ал, теңдеулердің Z-кескіндегі орнықтылығын анықтау үшін түбірлердің бірлік радиусты шеңберге салыстырмалы орналасуын анықтау талап етіледі. Демек, Z=(1+W)/(1-W)-шеңбердің түрлендіруін бірлік шеңбер жорамал өсіне айналатындай, ал бірлік дөңгелектің іші сол жақ жарты жазықтыққа бейнеленетіндей етіп орындау керек. Мұндай бейнелеу келесі бисызықтық түрлендірумен орындалады.
Z=(1+w)/ (1-w). (3.7)
Жоғарыдағы (3.6)- өрнектің айнымалысын ауыстырып келесіге келеміз
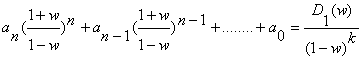 (3.8)
(3.8)
бұл жерде D(w)- жаңа w-айнымалыдан
"n" дәрежелі көпмүше болып табылады да, келесіге
тең болып шығады ![]()
![]() (3.9)
(3.9)
D(w)-көпмүшенің түбірлері теріс нақты түбірлер болу үшін Гурвиц анықтауыштарының бәрі оң болғаны қажетті және жеткілікті.
Мысал 3.1. Зерттелініп отырған жүйе екінші ретті,
яғни n=2 болсын делік. Бисызықты түрлендіруді
пайдаланып, жүйенің орнықтылығын зерттеу қажет.
Соңғы (3.9)- өрнекті ескеріп, n=2
болғандағы сипаттаушы теңдеуді келесі түрде жаза аламыз ![]()
![]()
![]()
![]()
Демек
![]() ,
,
![]() ,
,
![]() .
.
Егер D(w)- көпмүшенің
коэфициенттері оң болса, яғни ![]() ,
, ![]() ,
,![]() болса, онда екінші ретті жүйе үшін Гурвиц
анықтауыштары оң болады. Егер
болса, онда екінші ретті жүйе үшін Гурвиц
анықтауыштары оң болады. Егер ![]() ,
,![]() болса, жүйе орнықты болады.
болса, жүйе орнықты болады.
 Мысал 3.2 Құрылымдық
сұлбасы 3.4-суретте келтірілген реттілігі нөл бекіткіші болатын
тұйық жүйенің орнықтылығын
қарастырайық.
Мысал 3.2 Құрылымдық
сұлбасы 3.4-суретте келтірілген реттілігі нөл бекіткіші болатын
тұйық жүйенің орнықтылығын
қарастырайық.
3.4 Сурет - Басқару жүйенің құрылымдық сұлбасы
Тұйық жүйенің беріліс функциясы үшін келесі өрнекті жазуға болады
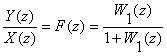
Демек, орнықтылықты зерттеу үшін W1(z)- функциясын табу қажет. Алдағы 2- бөлімдегі (2.43)-өрнекке сүйеніп және 2.2-кестені пайдаланып, келесіні аламыз:
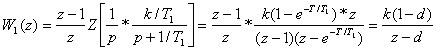 . (3.10)
. (3.10)
Жүйенің сипаттаушы теңдеуі келесі
![]() . (3.11)
. (3.11)
Бұл 3.11-теңдеу бірінші ретті болғандықтан ïZï<1- бөлгіш алымы үшін жүйе орнықты болады. Кванттаудың әртүрлі Т-периодтарында орнықтылық шекарада болатын жүйенің "k" мәнін анықтайық. Бұл жағдайда
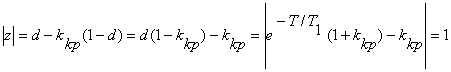 .
.
![]() деп болжап,
деп болжап,![]() шаманы қатарға жіктеп және
бұл қатардың бірінші екі мүшелерімен шектеліп,
табатынымыз келесі
шаманы қатарға жіктеп және
бұл қатардың бірінші екі мүшелерімен шектеліп,
табатынымыз келесі
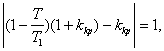

Егер
![]() болса, онда бұл
шарт орындалады. Соңғы өрнектен Т/Т1=0,1
болғанда kкр=19. Егер кванттау периодын өзгертсек, онда Т/Т1=0,2
болғанда "k"-ның мәні келесіге kкр=9 тең
болып шығады. Күшейту коэффициенті тұрақты
болғанда кванттау периоды неғұрлым үлкен болса,
жүйені орнықсыз ету ықтималдығы соғұрлым
үлкен болады.
болса, онда бұл
шарт орындалады. Соңғы өрнектен Т/Т1=0,1
болғанда kкр=19. Егер кванттау периодын өзгертсек, онда Т/Т1=0,2
болғанда "k"-ның мәні келесіге kкр=9 тең
болып шығады. Күшейту коэффициенті тұрақты
болғанда кванттау периоды неғұрлым үлкен болса,
жүйені орнықсыз ету ықтималдығы соғұрлым
үлкен болады.
Сонымен, үзіліссіз жүйеден айырмашылықта импульсті жүйенің тіпті бірінші реттісінің өзі орнықсыз болуы мүмкін. Жүйенің орнықтылық қоры кванттаудың Т-периодының шамасына тәуелді.
3.3 Уақыттық аймақта импульсті жүйе сапасының анализі
Егер орнықтылықты талдаудың кезеңі импульсті жүйенің жұмыс істеу қабілеттілігі туралы қорытынды берсе, онда сапаны талдау нәтижесінде импульстік жүйелердегі басқару процестерінің нақты көрсеткіштері мен сипаттамалары айқындалады. Цифрлық басқару жүйелердің шығыс айнымалылары әдетте үзіліссіз t аргументтің функциясы болғандықтан, жүйе сапасын уақыттық аймақта бағалау қажет. Бірақ Z-түрлендіруді пайдаланғанда шығыс айнымалылар тек дискреттеу мезеттерінде ғана өлшенеді. Мұндай дискретті көрсетілім дәлме-дәл болуы да, болмауы да мүмкін – бәрі кванттау периодына тәуелді, басқа сөзбен айтқанда, y(t)-шығыс айнымалының y*(t)-дискретті сигналмен айтарлықтай айырмашылығы болуы мүмкін.
Үзіліссіз жүйелердің анализіндегідей, уақыттық аймақтағы импульсті жүйенің тәртібі қайта реттеу, өтпелі процестің өсу уақыты мен аяқталу уақыты, өшу, тербелістердің өзіндік жиілігі сияқты аталым-терминдермен сипатталынуы мүмкін. Уақыттық аймақтағы басқарушы цифрлық жүйенің сапасы жиі, оның кірісіне бірлік сатылы функция түрінде тест сигналын түсіру жолымен анықталады. Жүйенің бірлік сатылы әсерге жауабы үзіліссіз жүйелердегідей өтпелі функция деп аталады.
Төмендегі 3.5-суретте басқарушы цифрлық жүйенің типтік өтпелі функциясы көрсетілген.

3.5 Сурет – Басқарушы цифрлық жүйенің типтік өтпелі функциясы tmax –бірінші max жету уақыты, tөтп-өтпелі процесс уақыты
3.3.1 P және Z жазықтықтардағы түбірлер орналасуы мен уақыттық сипаттама арасындағы байланыс
Сипаттаушы теңдеу түбірлерінің Р-жазықтықтағы орналасуы мен өтпелі функция арасындағы байланыс үзіліссіз жүйелер үшін белгілі. Мысалы, сол жақтағы Р-жартыжазықтықта орналасқан комплексті-түйіндескен түбірлер экспоненциалды өшетін тербелмелі процестерді береді; нақты осьтің теріс бөлігіндегі түбірлер бірсарынды (монотонды) өшетін процестерге сәйкесті болады; жорамал ось бойында орналасатын жорамал түйіндес түбірлер өшпейтін гармоникалық тербелістердің пайда болуына келтіреді. Р жазықтықтың оң жақ жартысындағы түбірлер алшақталатын процестерге сәйкесті.
|
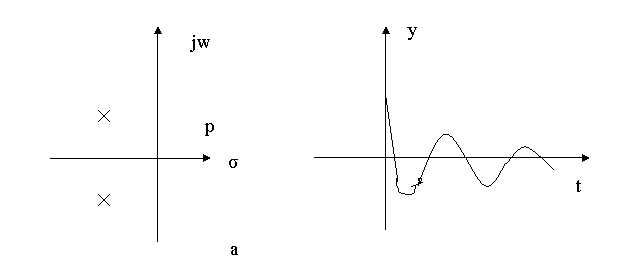
3.6 Сурет – Үзіліссіз жүйенің полюстері (а) және еркін қозғалыс (б)
Жоғарыда біз Р және Z жазықтықтар арасындағы байланысты тапқанмен, цифрлық жүйелердегі кванттау операциясы ерекше көңіл талап ететін эффекттерді береді. Мысалы, егер, импульстік теорема орындалмаса, онда кванттау нәтижесіндегі полюстердің ығысу эффектісі жүйе жауабының бұрмалануына келтіруі мүмкін. Жоғарыдағы 3.6 а-суретте екінші ретті үзіліссіз жүйенің беріліс функциясының полюстері көрсетілген, ал 3.6 б-суретте осы жүйенің еркін қозғалысы келтірілген.
Келесі 3.8-суретте бірінші және екінші ретті жүйенің P және Z жазықтықтардағы түбірлердің орналасу мысалдары және оларға сәйкесті болатын уақыттық сипаттамалары келтірілген.
3.3.2 Импульстік жүйелер сапасын бағалаулар
Сапаны бағалаулар тікелей және жанама болып бөлінеді. Тікелей бағалаулар өтпелі процестің қисығы бойынша, ал жанама бағалаулар – есептеу жолымен анықталады. Орныққан режимдегі жүйенің дәлдігі қателер коэффициенттерінің көмегімен бағалануы мүмкін.
3.4 Орныққан қатенің анализі
Басқару жүйенің қателік сигналы эталон болып табылатын кіріс сигналдың және шығыс айнымалының арасындағы айырым ретінде анықталады. Цифрлық басқару жүйелерінің орныққан қатесін талдау үшін 3.7-суретте келтірілген құрылымдық схеманы пайдалануға болады. Бұл жағдайда e(t)-қателік сигнал келесі болады
e(t)=x(t) - g(t). (3.12)
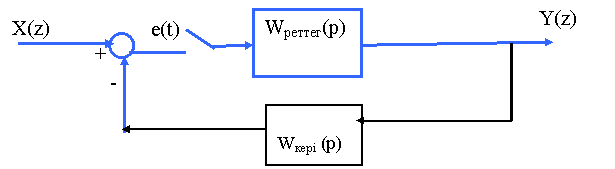 |
3.7 Сурет – Цифpлық басқару жүйесі
Цифрлық жүйе үшін e (t) сигналын пайдаланады. Орныққан қате, яғни тұйықталу мезеттерде өтпелі процесс аяқталғаннан кейін қате келесі өрнекпен беріледі
![]() (3.13)
(3.13)
Z-түрлендіруді және (2.22) өрнекпен берілген ақырлы мән туралы теореманы пайдаланып, келесіге келеміз
![]() (3.14)
(3.14)
Соңғы
жазғанымыз ![]() функция / Z / = 1 бірлік
шеңбер ішінде немесе оның сыртында полюстерге иеленбейтін шарт
орындалғанда әділ болатынын ескертейік.
функция / Z / = 1 бірлік
шеңбер ішінде немесе оның сыртында полюстерге иеленбейтін шарт
орындалғанда әділ болатынын ескертейік.
Сызықты үзіліссіз басқару жүйелерінің теориясынан орныққан қате жүйеге түсірілген эталондық әсер түріне және жүйенің параметрлеріне тәуелді цифрлық басқару жүйелерінде де пайдалануға болатын жүйе сапалығымен сипатталады.
Алдағы 3.7-суретте көрсетілген жүйе үшін қателік сигналының Z-түрлендіруін келесі түрде беруге болады
 (3.15)
(3.15)
Осы соңғы өрнекті (3.14)-ке қойып, алатынымыз келесі
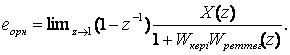 (3.16)
(3.16)
Соңғы (3.16)-өрнек орныққан қате X(z) эталон кіріс сигналына да, WкеріWреттег(z) ажыратылған контурдың беріліс функциясына да тәуелді екенін көрсетеді. Кіріс сигналдардың келесі сызықты функция, сатылы және параболалы функция сияқты негізгі түрлерін қарастырайық.
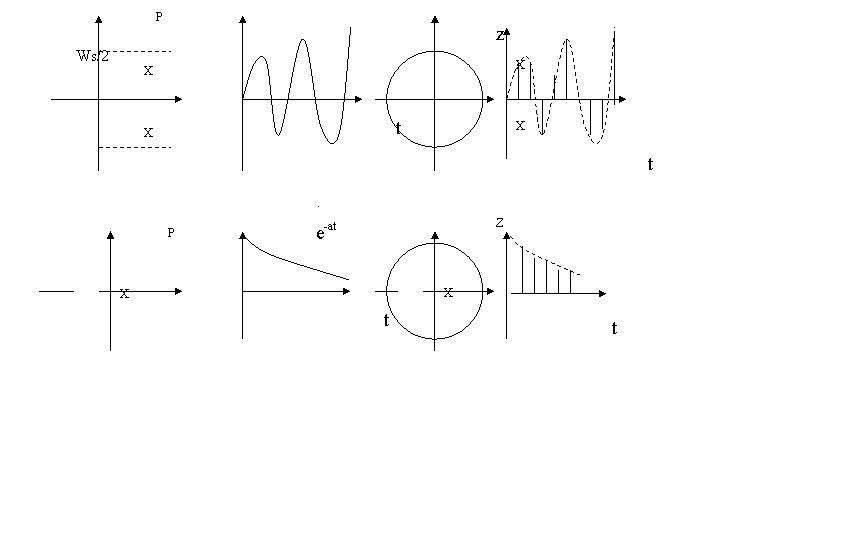
3.8 Сурет – Уақыттық сипаттамаларға сәйкесті түбірлердің Р және Z – жазықтықтардағы орналасуы
3.4.1 Сатылы кіріс сигналындағы орныққан қате
Алдағы 3.7-суретте көрсетілген цифрлық басқару жүйенің кіріс сигналы, шамасы X-сатылы функция болсын делік. Бұл жағдайда X(t) функцияның Z-түрлендіруі келесі
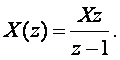 (3.17)
(3.17)
(3.17)- өрнекті (3.16)-ға қойып алатынымыз
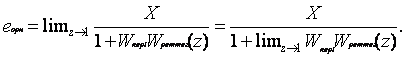 (3.18)
(3.18)
мұндағы
 (3.19)
(3.19)
Орналасуы бойынша сапалылықты келесі өрнекпен анықтайық
![]() (3.20)
(3.20)
Онда (3.18) өрнек келесі түрге айналады
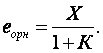 (3.21)
(3.21)
(3.21)-өрнектен жүйенің орныққан қатесі бойынша сапалылыққа кері пропорционал екені көрініп тұр. Сонымен, сатылы кіріс функция кезінде орныққан қате нөлге тең болу үшін жүйенің “К”- орналасуы бойынша сапалылығы ақырсыз болуы тиіс. Сапалылық “К”, шынында, статика күйіндегі ажыратылған жүйенің күшейту коэффициенті болып табылады. Орналасу бойынша сапалылық “К” тек қана сатылы функция кезінде мағыналы екеніне ерекше көңіл аудару керек.
3.4.2.1 Сызықты кіріс сигналындағы орныққан қате
Цифрлық басқару жүйенің кіріс сигналы X(t)- сызықты кіріс функциясы үшін Z-түрлендіру келесіге тең
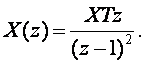 (3.22)
(3.22)
(3.22)-өрнекті (3.16)-өрнекке қойып алатынымыз
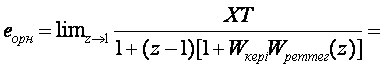
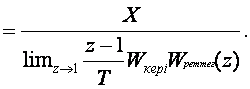 (3.23)
(3.23)
Жылдамдық бойынша сапалылықты келесі өрнекпен анықтайық
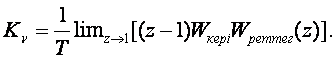 (3.24)
(3.24)
сонда (3.23)-өрнек келесі түрге келеді
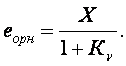 (3.25)
(3.25)
(3.25)-өрнек келесіні көрсетеді: сызықты кіріс сигналы кезінде орныққан қате жүйенің жылдамдығы бойынша сапалылыққа кері пропорционал. Егер Kν жылдамдық бойынша сапалылық ақырсыздыққа тең болса, орныққан қате нөлге тең болады. Жылдамдық бойынша сапалылық Kν тек кіріс сигнал сызықты функция кезінде ғана мағыналы екенін ескерген жөн.
3.4.3 Параболалық x(t)=at/2 кіріс функциясындағы орныққан қате
Z-түрлендірудің түрі келесі
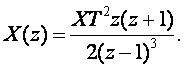 (3.26)
(3.26)
(3.16)-өрнекке сәйкес тұйықталу кездеріндегі (мезеттеріндегі) орныққан қатені келесі түрде анықтауға болады
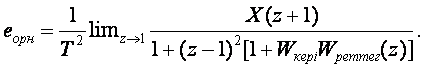 (3.27)
(3.27)
немесе
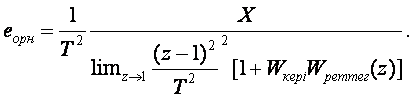 (3.28)
(3.28)
Үдеу бойынша сапалылықты келесі өрнекпен анықтайық
![]() (3.29)
(3.29)
Онда (3.28)-өрнек келесі түрге келеді
![]() (3.30)
(3.30)
Осының алдындағы жағдайларға ұқсас үдеу бойынша сапалылық тек қана параболалық функцияларға қатысты болады.
Сонымен, өтпелі функцияға және жүйенің орнықтылығына кванттау ықпалы жағымсыз екені, бірақ цифрлық басқару жүйесінің орныққан қатесі кванттау периодына тәуелсіз екені (Kν мен Kа үшін тәуелділіктерде Т-айнымалы (кванттау периоды) (3.23), (3.28) өрнектерді ашқанда қысқарады) жоғарыда көрсетілген.
3.5 Өтпелі процесс бойынша жүйе сапасының анализі
Импульсті жүйенің кірісіне сатылы функцияны түсіргенде оның шығысында болатын өтпелі процесті құрайық.
Решеткалық уақыт функцияның белгілі Z-түрлендіруі бойынша t=nT нүктелерде f[nt] мәндерін анықтау үшін ең кең таралған үш әдістердің біреуін қолданады. Бұл әдістер келесі:
- Z-дәрежелері бойынша f(z) үшін ақырсыз қатарды анықтау;
- элементар бөлшектерге f(z) функцияны жіктеу;
- кері түрлендірудің интегралын зерттеу.
Дәрежелік қатарға жіктеу әдісін нақтырақ қарастырайық. Өткен бөлімдегі (2.24)-өрнектен F(z) функцияның кері Z-түрлендіруі Z-дәрежелері бойынша ақырсыз қатарға жіктеу арқылы анықталуы мүмкін. Төмендегі қатарды (2.12) өрнекке сүйеніп алуға болады
Y(z) =y(0) z0 +y(1T)z-1 +y(2T)z-2+ y(3T)z-3+..+y(nT)z-n. 3.31)
Демек, қатардың коэффициенттері кванттау мезеттеріндегі f(t) функцияның мәндеріне сәйкесті болады.
Мысал 3.3. Алдағы 3.7-суретте келтірілген цифрлық басқару жүйедегі өтпелі процесті анықтау керек делік. Ал Z-бейнедегі тұйықталған жүйенің беріліс функциясының түрі келесі:
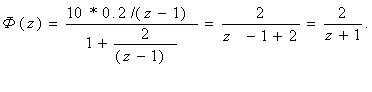
Сатылы кіріс сигналдың Z-бейнесі келесі
X(z) =z/(z-1),
Y(z) шығыс сигналдың Z-бейнесі келесі
Y(z) =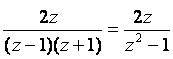
Бұл соңғы өрнектің алымын бөліміне бөлу Y(z) үшін ақырсыз дәрежелік қатарды береді
Y(z) = Y(0)*z0 +Y(T)*z-1 + Y(2T)*z-2 + Y(3T)*z-3 + Y(4T)*z-4. (3.32)
![]() 2z
z2 - 1
2z
z2 - 1
![]() 2z - 2z -1
2z - 2z -1
![]() 0
+ 2z -1 + 0z -2 +2z -3 +0z - 4
+2z -5..
0
+ 2z -1 + 0z -2 +2z -3 +0z - 4
+2z -5..
0 + 2z -1
2z -1 - 2z -3
0 + 2 z -3
2z -3 - 2z -5
2z -5
(3.31)-өрнектің коэффициенттерін және дәрежелері бірдей Z үшін бөлінділерді салыстырып алатынымыз
![]()

3.9 Сурет - Жүйедегі өтпелі процесс
Алынған мәндерге сәйкесті 3.9-суретте y[nT] үшін тұйық жүйедегі өтпелі процесс келтірілген. Шынында да жүйенің сипаттаушы теңдеуінің түбірі 1-ге тең болғандықтан, жүйе орнықтылықтың шекарасында болатынын 3.9-суреттен көруге болады.
Мысал 3.4. Өткен бөлімдегі 3.9-суретте келтірілген жүйедегі өтпелі процесті анықтау керек делік. Бұл тұйық жүйенің Z-бейнедегі беріліс функциясының түрі келесі

Бұл тұйық жүйенің сипаттаушы теңдеуі бірінші ретті болады да, оның түбірі 0,5-ке тең. Демек, жүйе орнықты болуы тиіс.
Сатылы кіріс сигналдың Z-бейнесі келесі
x(z) =z/(z-1).
Y(z) шығыс сигналының Z-кескіні
Y(z) =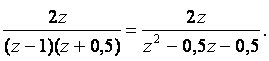
Осы өрнектің алымын бөлімге бөлгенде Y(z) үшін ақырсыз дәрежелік қатарды аламыз:
Y(z) = Y(0)*z0 +Y(T)*z-1 + Y(2T)*z-2 + Y(3T)*z-3 + Y(4T)*z-4. (3.32)
![]() 2z
z2 – 0,5z - 0,5
2z
z2 – 0,5z - 0,5
![]() 2z -1- z -1
2z -1- z -1
![]() 0 + 2z -1 + 1z -2 +1,5z -3 +1,25z -4
+1,375z-5
0 + 2z -1 + 1z -2 +1,5z -3 +1,25z -4
+1,375z-5
1 + z -1
1 - 0,5z -1 – 0,5z -2
1,5z -1 + 0,5 z -2
1,5z -1 - 0,75z -2 - 0,75z -3
![]() 1,25 z -2 +
0,75z -3
1,25 z -2 +
0,75z -3
(3.31)-қатардың коэффициенттерін және дәрежелері бірдей Z үшін бөлінділерді салыстырып алатынымыз
![]()
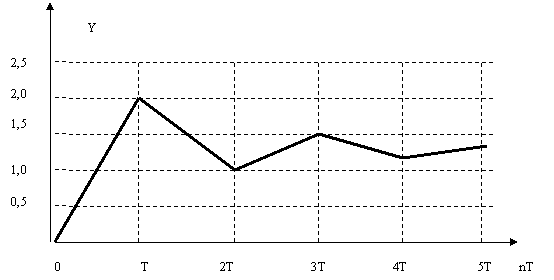
3.10 Сурет – Орнықты жүйедегі өтпелі процесс (мысал 3.4)
Алынған мәндерге сәйкесті 3.10-суретте Y[nT] үшін тұйық жүйедегі өтпелі процесс келтірілген. Шынында да жүйенің сипаттаушы теңдеуінің түбірі 1-ден кем (0,5-ке тең) болғандықтан, жүйе орнықты болатынын 3.10-суреттен көруге болады.
3.6 Жиіліктік сипаттамалардың пайдаланылуы мен жүйе сапасының анализі
Алдыңғы бөлімдерде цифрлық басқару жүйелердің уақыттық сипаттамасы Z-жазықтықта беріліс функциясының нөлдерінің және полюстерінің орналасуы бойынша бағаланған болатын. Бұл әдістің кемшіліктері жоқ емес. Мысал ретінде келесі жағдайды атап кетейік.
Максимал қайта реттеудің және өтпелі функцияның максимал уақытының нөлдер мен полюстердің орналасуына тәуелділігін тек екінші ретті жүйелер үшін ғана оңай табуға болады.
Жиіліктік аймақта тәжірибе жүзінде күрделілігі кез келген сызықты стационар жүйелерге қолданыла алатын анализ бен синтездің графикалық және графо-аналитикалық әдістерінің айтарлықтай көбі бар. Үзіліссіз жүйелер үшін мүлтіксіз жетілдірілген бұл әдістердің бәрі цифрлық басқару жүйелеріне де кеңінен таратылуы мүмкін.
Жиіліктік әдістің мәні келесі: сызықты стационар жүйенің сапасы туралы оның гармоникалық сигналдарға қатысын орнығу жауабы бойынша жориды. Жиіліктік сипаттамаларды пайдаланып, жүйенің уақыттық сипаттамаларын болжауға немесе салуға болады. Лаплас түрлендіруінен жиіліктік сипаттамаларға өту p=jw алмастыру жолымен орындалатыны белгілі; осыған ұқсас z-айнымалы аймағында z=ejw алмастыру орындалады. Бірақ, цифрлық басқару жүйелерінің бірқатар арнайы ерекшеліктері бар. Сондықтан оларды талдағанда жиіліктік әдістерге ерекше көңіл аударылуы тиіс. Мысалы, сызықты үзіліссіз жүйенің гармоникалық кіріс сигналға жауабы дәл сол жиілікте болады, ал тек сызықты емес жүйелерде ғана гармоникалар пайда болуы мүмкін. Керісінше, сызықты цифрлық жүйелерде кванттаушы гармоникалар генераторы сияқты әрекет етеді. Осы себептен жиіліктік аймақта цифрлық басқару жүйелерін зерттеудегі негізгі қолайсыздық – осы жоғарғы жиілікті гармоникалар жиіліктік сипаттамаларды салуды (тұрғызуды) қиындатады.
Цифрлық басқару жүйелердің жиіліктік аймақта зерттелуін Найквист годографын немесе логарифмдік жиіліктік сипаттамаларын пайдаланып орындауға болады.
1. Найквист годографын W(z) беріліс функциясы үшін салып және оның (-1, j0) қатысты орналасуын зерттеп, тұйық жүйенің орнықтылығы туралы қорытынды жасауға болады.
2. Логарифмдік амплитуда-жиіліктік сипаттама (ЛАЖС) деп отырғанымыз амплитуданың децибелмен графикалық берілуі және ажыратылған жүйенің беріліс функциясының фазалық бұрышының ω жиілікке тәуелділігі болып табылады. Бұл сипаттамаларды тұйық жүйенің орнықтылығын талдау үшін пайдалануға болады.
3.6.1 Бисызықты түрлендіру әдісі
Цифрлық басқару жүйелерінің жиіліктік сипаттамаларын салу үшін бисызықты түрлендіруді пайдалануға болады.
 (3.33)
(3.33)
Бұл қатынастан
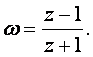 (3.34)
(3.34)
(3.34)-өрнектегі Z=e jωT = cosωT +jsinωT мәнін қойып алатынымыз

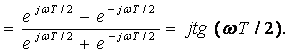 (3.35)
(3.35)
Сонымен, Z-жазықтықтағы бірлік шеңбер комплексті W-жазықтықтың сол жақ жартысына сәйкес, ал жорамал осьтің оң бағыты жиіліктердің 0 < ω < ωs ауқымына сәйкес.
Комплексті ω-айнымалының түрі келесі болсын делік
![]() (3.36)
(3.36)
Онда (3.35) өрнектен келесі қатысқа келе аламыз
![]() (3.37)
(3.37)
Бұл қатынас ω жиілік пен λ-салыстырмалы псевдожиілік арасындағы байланысты береді. Егер ωT/2 шамалары кіші болса
![]()
![]() (3.38)
(3.38)
деп санауға болады. Сондықтан бұл соңғы шарт орындалғанда псевдожиіліктің ωT/2 шамасын жай жиілікпен ауыстыруға болады. Ол үшін кванттау периодының абсолют псевдожиілігі қарастырылуға енгізіледі. (3.38)-өрнектен алатынымыз
![]()
![]() (3.39)
(3.39)
Демек,
![]() болады да, ω-жиілікпен
болады да, ω-жиілікпен
![]() -
псевдожиілік араларындағы байланысты табамыз. Жоғарыдағы
(3.35)- өрнекті ескеріп, келесіні табамыз:
-
псевдожиілік араларындағы байланысты табамыз. Жоғарыдағы
(3.35)- өрнекті ескеріп, келесіні табамыз:
![]() (3.40)
(3.40)
3.6.2 Логарифмдік амплитуда-жиіліктік сипаттамалар (ЛАЖС)
Алғашқы көз тастағанда бисызықтық түрлендіру ешбір артықшылықтар бермейді. Бірақ бисызықтық түрлендіру көмегімен беріліс функция ЛАЖС-ты салу үшін тәжірибе жүзінде қиыншылыққа ұрынбайтындай түрге келтіріледі. ЛАЖС-тың салынуын нақтылы мысалдан көрейік.
Мысал 3.4. Ажыратылған цифрлық жүйенің үзіліссіз бөлігінің беріліс функциясы келесі болсын делік
![]() (3.41)
(3.41)
Жүйеде реттілігі нөл бекіткіш (РНБ) бар. Бекіткіші бар кілт үзіліссіз бөлік алдында орналастырылған. ЛАЖС және фазожиіліктік (ФЖС) сипаттамаларын салу керек. Беріліс функцияны келесі түрге келтірейік
![]() (3.42)
(3.42)
Өткен 2.9-бөлімдегі 2.2-кестеден W1 (p) мен W2 (p) үшін Z-түрлендіруді табайық

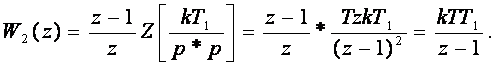 (3.43)
(3.43)
Келесі W(ω)=W1 (ω) + W2 (ω) беріліс функциясы соңғы (3.43)-өрнекке (3.34)- қатынасты қою жолымен табылады

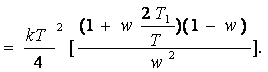 (3.44)
(3.44)
ω жиілік пен ![]() - псевдожиілік арасындағы
байланысты беретін (3.39)- өрнекті пайдаланып, келесі жиіліктік беріліс
функциясын аламыз
- псевдожиілік арасындағы
байланысты беретін (3.39)- өрнекті пайдаланып, келесі жиіліктік беріліс
функциясын аламыз
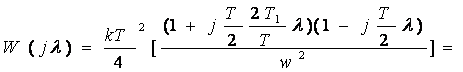
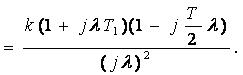 (3.45)
(3.45)
Жиіліктік беріліс функциясының модулі
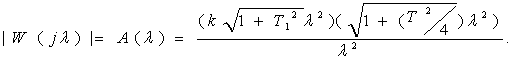 (3.46)
(3.46)
Фазажиіліктік сипаттама
![]() (3.47)
(3.47)
Жоғарыдағы өрнектер бойынша және үзіліссіз жүйелер үшін пайдаланылатын ережелер бойынша асимптоталық ЛАЖС пен ЛФЖС сипаттамаларын (3.11-сурет) тұрғызайық.
Жиіліктік
беріліс функциясының (3.45) өрнегінің алымына кіретін
және минимал емес фазалық буын болып табылатын ![]() - мүшенің
амплитудалық сипаттамасы тездетуші буынмен дәлдеседі. Бұл
жағдайда осы буынның ЛАЖС сипаттамасы λ псевдожиілік
шамасы кіші кезде көлбеулігі нөл болатын асимптотаны, ал λ
шамасы үлкен кезде көлбеулігі +20дБ/дек болатын түзу
сызықты құрады. Бұл екі сызықтар
- мүшенің
амплитудалық сипаттамасы тездетуші буынмен дәлдеседі. Бұл
жағдайда осы буынның ЛАЖС сипаттамасы λ псевдожиілік
шамасы кіші кезде көлбеулігі нөл болатын асимптотаны, ал λ
шамасы үлкен кезде көлбеулігі +20дБ/дек болатын түзу
сызықты құрады. Бұл екі сызықтар ![]() =2/Т шамасына тең болғанда
қиылысады. Бұл буынның фазажиіліктік сипаттамасы
инерциялық буынның сипаттамасымен дәлдеседі де,
=2/Т шамасына тең болғанда
қиылысады. Бұл буынның фазажиіліктік сипаттамасы
инерциялық буынның сипаттамасымен дәлдеседі де, ![]() =2/Т жиілікте 45o шамасына
фазалық ығысуды береді. Жоғарыда қарастырылған
мысалдың (3.41)- өрнегіне сәйкесті цифрлық
жүйенің сызықты үзіліссіз бөлігінің беріліс
функциясын және цифрлық жүйенің дәл сол
үзіліссіз бөлігінің (3.45)-өрнекке сәйкесті псевдожиілік
үшін беріліс функциясын салыстырған пайдалы. Бұл
өрнектерден олар, егер ω=λ деп есептелсе,
=2/Т жиілікте 45o шамасына
фазалық ығысуды береді. Жоғарыда қарастырылған
мысалдың (3.41)- өрнегіне сәйкесті цифрлық
жүйенің сызықты үзіліссіз бөлігінің беріліс
функциясын және цифрлық жүйенің дәл сол
үзіліссіз бөлігінің (3.45)-өрнекке сәйкесті псевдожиілік
үшін беріліс функциясын салыстырған пайдалы. Бұл
өрнектерден олар, егер ω=λ деп есептелсе, ![]() көбейтіндіге
дейін дәлдесетіні көрініп тұр.
көбейтіндіге
дейін дәлдесетіні көрініп тұр.
Сонымен,
төменгі жиіліктер аймағында цифрлық жүйенің
сипаттамалары үзіліссіз бөліктің жиіліктік сипаттамаларымен
дәлдеседі. Осыдан ![]() =2/Т жиіліктен
кем жиіліктер аймағында цифрлық жүйелер үшін ЛАЖС мен
ЛФЖС сипаттамаларының салыну ретін ұсынуға болады. (Бұл
жиілік информацияны дискреттеумен байланысты.)
=2/Т жиіліктен
кем жиіліктер аймағында цифрлық жүйелер үшін ЛАЖС мен
ЛФЖС сипаттамаларының салыну ретін ұсынуға болады. (Бұл
жиілік информацияны дискреттеумен байланысты.)
Сызықты цифрлық жүйенің беріліс функциясын алу реті келесі:
а) ажыратылған цифрлық жүйенің үзіліссіз бөлігінің W(p) беріліс функциясын табамыз;
б) W жиілікті ![]() псевдожиілікке ауыстырып,
псевдожиілікке көшеміз де, табылған өрнекті
псевдожиілікке ауыстырып,
псевдожиілікке көшеміз де, табылған өрнекті![]() шамасына
көбейтеміз.
шамасына
көбейтеміз.
Осындай жолмен алынған ЛАЖС пен ЛФЖС сипаттамалар шамасы 2/Т жиіліктен кем жиіліктер үшін дұрыс (жөн).
3.6.3 Жоғары жиіліктер аймағында ЛАЖС сипаттамаларын тұрғызу ерекшеліктері
Логарифмдік сипаттамалардың жоғарғы жиіліктік аймақтағы салыну ерекшеліктерін қарастырайық. Бұл аймақта келесі теңсіздік ωT>2 орындалғанда ЛАЖС-тың үзіліссіз бөлігі 3.12-суретте келтірілгендей бірнеше нұсқа болуы мүмкін. Штрих түріндегі сызық жоғарғы жиіліктік және төменгі жиіліктік аймақтарды бөліп тұр. Төмендегі 3.12-суреттегі сипаттамалар 2/Т-жиілікте ЛАЖС сипаттамалар көлбеулігімен ерекшеленеді. Бұл ЛАЖС-терді келесі өрнектердің біреуімен жуықтауға болады.
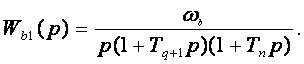 (3.48)
(3.48)
Бұл жерде T ,...,Тn – жиіліктері 2/T шамасынан үлкен жиіліктерді түйіндестіруші уақыт тұрақтылары;
Wв-ЛАЖС-тың жоғарғы жиіліктік бөлігінің бірінші асимптотасының децибелі нөл осімен қиылысу жиілігімен анықталатын жоғарғы жиіліктік бөліктің беріліс коэффициенті (кездейсоқ оқиғада ωқиық-қиық жиілігімен дәлдесуі мүмкін, (3.12 а-суретті қара)). Екінші жағдайда 3.12 б-суретті қара.
 (3.49)
(3.49)
Z-түрлендірулер
кестесінің деректері негізінде және![]() псевдожиіліктің алмастыруын
пайдаланып келесі өрнекті жаза аламыз
псевдожиіліктің алмастыруын
пайдаланып келесі өрнекті жаза аламыз
![]()
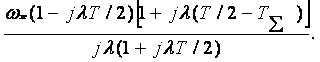 (3.50)
(3.50)
Мұндағы  .
.
Бұл өрнек ЛАЖС сипаттаманы салу үшін пайдаланылуы мүмкін және модулі келесі болады
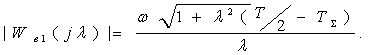 (3.51)
(3.51)
Сонымен,
жоғарғы жиіліктік «құйырықты»
салғанда Т - кіші уақыт
тұрақтыларының қосындысын және (1-![]() қосымша
көбейткішті де есепке алуға тура келеді.
қосымша
көбейткішті де есепке алуға тура келеді.
ЛАЖС сипаттаманың екінші нұсқасы үшін (3.12 б-суретті қара) келесіні аламыз
![]()
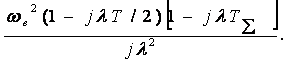 (3.52)
(3.52)
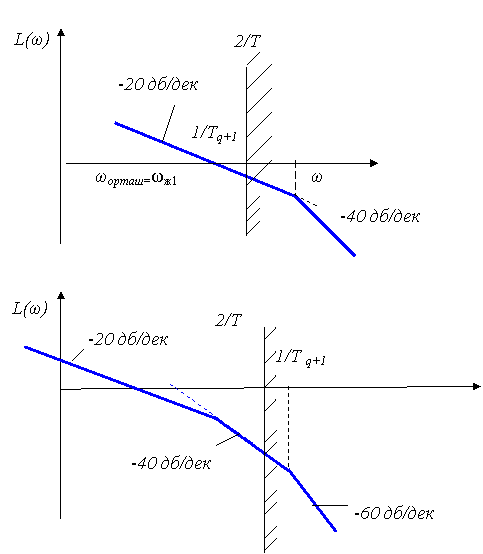
3.12 Сурет - Жоғарғы жиіліктік аймақтағы сипаттамалар
Өрнектер
(3.51) және (3.52) ЛАЖС пен ЛФЖС сипаттамаларын салу үшін
пайдаланылуы тиіс. Төменгі жиіліктік және жоғарғы
жиіліктік сипаттамалардың түйіндесуі жиіліктің шамасы ![]() =2/Т кезінде болады,
мысалы, жоғарғы жиілікті есепке алғандағы 3.12
б-суреттегі ЛАЖС-тің өзгеруі 3.13-суретте пунктирмен
көрсетілген.
=2/Т кезінде болады,
мысалы, жоғарғы жиілікті есепке алғандағы 3.12
б-суреттегі ЛАЖС-тің өзгеруі 3.13-суретте пунктирмен
көрсетілген.
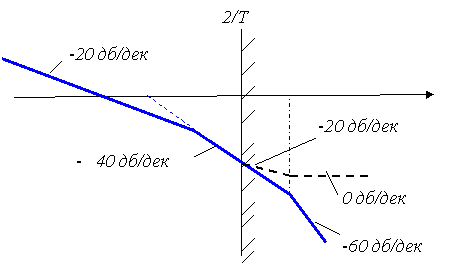
3.13 Сурет - Жоғары жиілікті аймақтағы дискреттеуді есепке алу
3.6.4 Модуль және фаза бойынша орнықтылық қоры
Басқару
жүйелерінің салыстырмалы орнықтылығын бағалау
үшін модуль бойынша және фаза бойынша қор сияқты
көрсеткіштерді пайдаланады. Цифрлық басқару жүйелеріне
үйлестіре бұл көрсеткіштердің мағынасы
үзіліссіз жүйелер үшін сияқты. Мысал ретінде
3.11-суретті пайдаланып, амплитудалық және фазалық сипаттамалардың
0 дБ және -1800 өткел нүктелерін
сәйкесті түрде белгілейік. Онда децибелмен алынған модуль
бойынша қор, фаза мәні -1800 болатын жиіліктегі 0
дБ деңгейдің және L(![]() ) амплитудалық
сипаттама арасындағы кесіндіге тең. Фаза бойынша қор
) амплитудалық
сипаттама арасындағы кесіндіге тең. Фаза бойынша қор ![]() қиық қиық
жиілігіндегі
-1800 деңгей және фазалық сипаттама
арасындағы айырым ретінде өлшенеді. Егер фаза бойынша қор
теріс болса, онда жүйе орнықсыз болып шығады. Егер
ажыратылған жүйенің беріліс функциясының полюстері мен
нөлдері бірлік шеңбердің сыртында болмаса, онда модуль бойынша
теріс қор да, жүйенің орнықсыз екенін дәлелдейді.
қиық қиық
жиілігіндегі
-1800 деңгей және фазалық сипаттама
арасындағы айырым ретінде өлшенеді. Егер фаза бойынша қор
теріс болса, онда жүйе орнықсыз болып шығады. Егер
ажыратылған жүйенің беріліс функциясының полюстері мен
нөлдері бірлік шеңбердің сыртында болмаса, онда модуль бойынша
теріс қор да, жүйенің орнықсыз екенін дәлелдейді.
3.7 Қашықтық бойынша нысанға автоматты ілесе жүруі бар импульсті радиоқашықтық өлшегішінің анализі
Импульстік жүйелердің талқыланған талдау әдісін әрекет қағидасы бұрын қарастырылған радиоқашықтық өлшегішінің сұлбасына қолданайық. Қашықтық өлшегіш екі режімде жұмыс істейді: іздеу режімі және ілеспе режімінде. Іздеу режімінде нысанның ізделуі және қармалуы орындалады. Ілеспе режімінде қашықтық өлегіші ажыратылған импульсті жүйе болып табылады. Бірінші бөлімдегі 1.2-суретте келтірілген дискриминатор жұмысының уақыттық диаграммаларына сәйкесті жүйеде ұзақтықтары әртүрлі
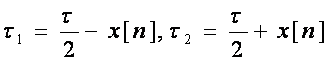
мұндағы x[n]-ілеспе қате. Жүйеде
таңбалары әртүрлі бұл екі импульс қосылады.
Қосындыланған сигнал «τ» 3.14-суретте келтірілген (бұл жерде ![]() τ1 -теріс, ал τ 2-
оң импульстер).
τ1 -теріс, ал τ 2-
оң импульстер).
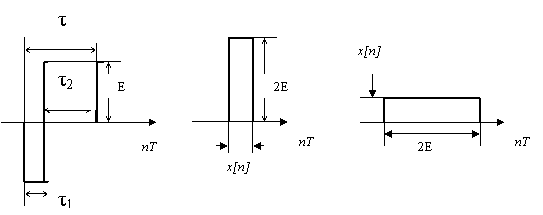
а б в
3.14 Сурет – Қашықтық өлшегіштің импульсінің түрленуі
3.14, а-суреттен берілген жүйенің импульсті элементі x[n] қатені биполярлық импульстер тізбегіне айналдыратыны көрініп тұр. Тізбектің мұндай түрі ендік-импульстік модуляция (ЕИМ) ретінде қарастырыла алады. Модуляцияның осындай түрінде басқару жүйесі сызықты емес ретінде қарастырылуы тиіс, ал бұл жағдай анализді айтарлықтай қиындатады. Белгілі бір жағдайларда бұл жүйені сызықты ретінде қарастыруға болатынын көрсетуге болады, бірақ ол үшін оны амплитудалық модуляция орын алатындай жүйе ретінде қарастыруға мүмкіндік беретін түрлендірулер керек.
Егер сигнал (3.14,а-суретті қара) мүлтіксіз интегратор кірісіне түсірілсе, онда оның шығысында τ1 мен τ2 айырымына пропорционал сигналды аламыз. Сонымен бірге интегратордың шығысында дәл осындай айырымды, 3.14,б-суретте келтірілген сигналды кіріске түсіріп те алуға болады. Сірә, интегратордың шығысында шамасы бойынша осындай сигналды, егер оның кірісіне ауданы бойынша 3.14,б-суреттегі сигналмен бірдей сигналды түсірсе де алуға болады (3.14,в-суретті қара). Олай болғанда соңғы сигнал x[n] қатемен амплитуда бойынша модуляцияланады да, демек, жоғарыда көрсетілген шарттарда жүйе амплитудалық модуляцияланатын жүйе ретінде қарастырылады. Онда қашықтық өлшегіштің (1.1-суретті қара) құрылымдық сұлбасын 3.15-суреттегі түрде қарастыруға болады.
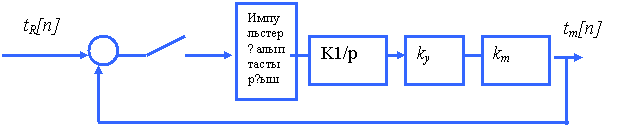
3.15 Сурет - Ілеспе режіміндегі бір интеграторы бар радиоқашықтық өлшегіштің жуық құрылымдық схемасы
Бұл схемада уақыттық дискриминатор импульстерді 3.14, в-суретке сәйкесті түрде өндіретін қалыптастырушы элементпен және мүлтіксіз интегратормен ауыстырылған, ал ky және km арқылы күшейткіштің күшейту коэффициенті және уақыттық модулятордың пропорционалдық коэффициенті сәйкесті белгіленген. Импульстер аралығы Е-шамасымен анықталатындықтан (3.14,в-суретті қара), импульстердің салыстырмалы ұзақтығын γ =1 деп санайық та, демек, қалыптастырушы элемент реттілігі нөл бекіткіш (РНБ) болып саналады.
Ажыратылған жүйенің үзіліссіз бөлігінің беріліс функциясын табайық.
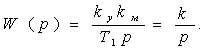 (3.53)
(3.53)
Беріліс функцияның Z-түрлендіруі келесі
![]() (3.54)
(3.54)
Тұйық жүйенің Z-кескіндегі беріліс функциясын анықтайық
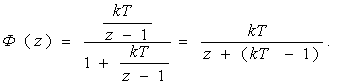 (3.55)
(3.55)
(3.55)- өрнектен егер | Z | < 1 болса, жүйе орнықты болатыны, демек, kТ<2 екені көрініп тұр. Сонымен, күшейтудің сындық коэффициенті келесі болып шығады kсын=2/Т. Қашықтық өлшегіштің жиіліктік сипаттамаларын да салайық. Ол үшін 3.6. 2-бөлімде ұсынылған әдісті пайдаланайық. Олай болғанда беріліс функциясының W-жазықтықтағы кескінін аламыз.
W(ω)= k (1-jTl/2)/ l. (3.56)
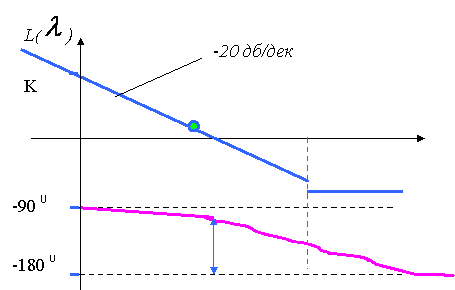
Қашықтық өлшегіштің логарифмдік амплитуда-жиіліктік сипаттамасы (ЛАЖС) және ЛФЖС төменде 3.16-суретте келтірілген.
Бұл суреттен kсын=2/Т шамасында жүйе орнықсыз екені (себебі коэффициент мәні осындайда амплитуда бойынша қор нөлге тең) көрініп тұр. Егер kТ<2 болса, онда жүйедегі өтпелі процесс тербелмелі, ал егер kТ<1 болса, онда жүйедегі өтпелі процесс экспоненциалдық болып табылады.
![]()
![]()
![]()
3.16 Сурет - Қашықтық өлшегіштің ЛАЖС-ы және ЛФЖС-ы
3.7.1 Нысананың түрлі қозғалу заңдарындағы қатенің өзгерулері
(3.54) өрнекті пайдаланып, қате бойынша тұйық жүйенің беріліс функциясын анықтайық:
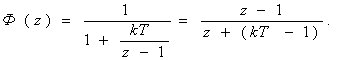 (3.57)
(3.57)
3.7.1.1 Нысана қозғалмайды. Келесі болжау орындалсын делік: nT=0 – уақыт мезетіне дейін x[nT]=0, яғни қате жоқ деп болжансын. Содан кейін нысана өзінің орнын ∆R шамасына секіріспен өзгертті де, қозғалмай тұрып қалды. Осы ∆R-қашықтыққа сәйкесті уақыттық ығысу келесі
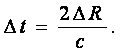 (3.58)
(3.58)
Мұнда с=3*108м/с –жарық жылдамдығы. Егер тұйық жүйенің беріліс функциясын анықтайтын (3.57) өрнекте сапалылықтың (3.20) өрнегіне сәйкесті Z=1деп алсақ, жүйенің орныққан күйдегі қатесін табамыз. Сонымен ФX(z)=0 екенін табамыз, яғни бұндай ұйытқу үшін қате нөлге тең.
3.7.1.2 Нысана тұрақты жылдамдықпен қозғалып келеді. Бұл жағдайда нысанадан шағылысқан импульстің t уақыттық ығысуы келесі өрнектен анықталына алады
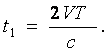 (3.59)
(3.59)
Мұндағы V- нысана жылдамдығы; Т- таратқыш импульстерінің арасындағы период.
Жылдамдық бойынша сапалылықты беретін (3.24) өрнекке сәйкесті жүйенің сапалылығын анықтаймыз
![]() (3.60)
(3.60)
Демек, нысана тұрақты жылдамдықпен қозғалғанда жүйедегі қате, (3.57) өрнекті есепке алғанда, келесі шамамен анықталады
![]() (3.61)
(3.61)
Қашықтық өлшегіш (3.59) өрнекке сәйкесті, яғни шағылысқан импульстің уақыттық ығысуына тәуелді нысананы қатемен қадағалап байқайды. Нысананың қозғалу жылдамдығы неғұрлым үлкен болса, қате соғұрлым үлкен, ал таратқыштың зондтаушы импульстері арасындағы қашықтық неғұрлым кіші болса, қате де соғұрлым кіші болады.
Кейбір мөлшерлік қатыстарды анықтайық. Экспонентамен анықталатын жүйедегі өтпелі процесс үшін келесі kТ<1 шарт орындалуы тиіс те, бұл жағдайда k = 1/Т деп алайық. Сондықтан белгілі бір өтпелі процесс кезіндегі келесі минимал орныққан қатені табамыз (жоғарыдағы айтылғанды ескеріп).
 (3.62)
(3.62)
Соңғы (3.62) өрнектен жүйенің қатесі Т-дискреттеу периодымен анықталатыны көрініп тұр, бірақ импульстер аралығын кеміту қашықтық өлшегішінің талап етіліп отырған жұмыс істеу қашықтығымен шектеледі.
Нысанаға ілесе жүрудің талап етіліп отырған қашықтығы 1000 км деп болжайық. Бұл жағдайда зондтаушы импульстің қайтып келу уақыты (3.58) келесі:
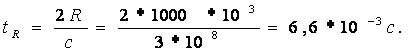 (3.63)
(3.63)
Зондтаушы импульстер аралығының уақыты tR шамасынан үлкен болуы тиіс, мысалы, Т=100*10-3 с болуы мүмкін. Бұл жағдайда нысананың жылдамдығы V= 1000км/сағ болғанда жүйенің минималь қатесі келесіге тең
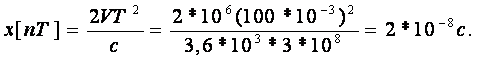 (3.64)
(3.64)
4 Микропроцессорлар басқару жүйелерінде
Өткен бөлімдерде цифрлық басқару жүйелерінің математикалық талдау негіздері қарастырылды. Барлық жағдайларда кванттау периодын таңдау цифрлық басқару жүйенің не орнықтылығымен, немесе оның сапасының жалпы көрсеткіштерімен анықталады. Цифрлық реттегіштің параметрлері олардың физикалық іске асуы және жүйенің сапасы көзқарасынан аналитикалық таңдап алынады. Дегенмен, аналогтық немесе дискреттік жүйелерде болмайтын элементтермен және дискретті процестермен анықталатын физикалық шектеулер цифрлық басқару жүйелеріне тән. Мысалы, цифрлық басқару жүйелерінде кванттау периоды таймермен беріледі де, процессордың арифметикалық операцияларды және инструкцияларды орындау жылдамдығына тәуелді болады. Егер есептеуіш құрылғы ретінде микропроцессор қолданылса, онда программаның орындалу жылдамдығы салыстырмалы баяу. Демек, цифрлық басқару жүйесінің аппараттық жасауы кванттау жиілігіне шектеу қояды. Цифрлық басқару жүйені жобалағанда тағы бір басқа шектеу – сөздің ақырлы ұзындығы деген бар. Бұл, процессор ішінде сандардың бәрі іске асырылуы мүмкін емес екенін көрсетеді. Мысалы, 8 биттен тұратын сөз тек 28 =256 шешу деңгейлерін қамтамасыз ететіні белгілі. Демек, мәндері 0,995; 1,316 болатын сандар сөзінің ұзындығы 8 бит болатын микропроцессорда дәлме-дәл іске асырыла алмайды.
4.1 Жалпы мазмұндама
4.1.1 ЭЕМ негізінде цифрлық реттегіштердің орындалуы. Цифрлық реттегіштің беріліс функциясы ЭЕМ программасы түрінде іске асырылуы мүмкін. Программалаудың үш негізгі әдісі белгілі: тікелей, тізбекті және параллель.
ЭЕМ ерекше арифметикалық операцияларды: қосу, көбейту, азайту, жадтау, ығысу және т.б орындауға қабілетті. Сонда да кейбір микро-ЭЕМ тікелей екі санды көбейте алмайды.
4.1.1.1 Тікелей программалау. Цифрлық реттегіштің физикалық жүзеге асырыла алатын дискретті беріліс функциясы келесі түрде жазыла алады:
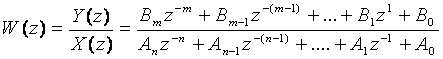 (4.1)
(4.1)
мұндағы ![]() , «m» және «n» – оң
сандар, X(z), Y (z) – реттегіштің кіріс және
шығыс сигналдарының сәйкесті Z-түрлендірулері.
, «m» және «n» – оң
сандар, X(z), Y (z) – реттегіштің кіріс және
шығыс сигналдарының сәйкесті Z-түрлендірулері.
Белгіленуі Wp(z) – тікелей программалауға көшу үшін соңғы (4.1) өрнек ішінде айқастырылған көбейтуді орындап кері Z-түрлендіруді алайық:
![]()
![]() (4.2)
(4.2)
Бұл теңдеудің Y (t) функцияға қатысты шешімі келесіні береді
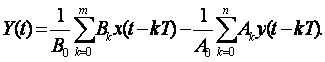 (4.3)
(4.3)
Бұл өрнек Y(t) шығыс сигналдың мәні осы және өткен шығыс сигналдың мәндеріне тәуелді екенін көрсетеді. (4.3) формула бойынша есептеулер программасын құру үшін екі математикалық операциялар қажет. Бірінші операция – бұл деректерді жинақтау. ЭЕМ жады ішінде кіріс және шығыс сигналдардың болып өткен дискретті мәндері жинақталады. Екінші операцияға келесі арифметикалық амалдар енеді: тұрақты сандарға көбейту, қосу және азайту.
Айталық
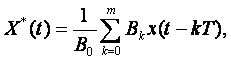
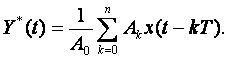 (4.4)
(4.4)
Онда (4.3) өрнек келесі түрге келеді
Y(t)=X*(t)- Y*(t). (4.5)
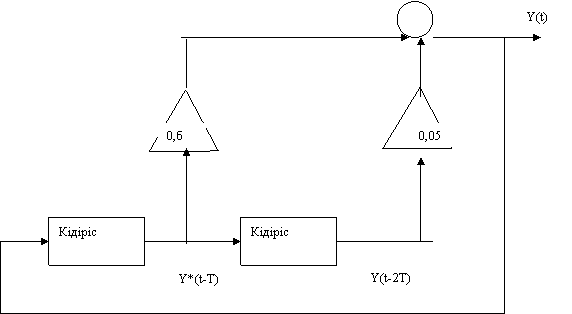 |
ет - Ьеріліс функцияның тікелей программалануы
(4.4) және (4.5)- өрнектердің тікелей программалануы мысал үшін 4.1-суретте құрылымдық сұлба түрінде бейнеленген. Детектордың жинақталуы кідіріс элементтерімен ескеріледі.
Мысал 4.1. Цифрлық реттегіштің келесі беріліс функциясын қарастырайық:
![]() (4.6)
(4.6)
Бұл беріліс функциясының физикалық жүзеге асырыла алатындығы айқын. Соңғы (4.6) өрнекте айқастырылған көбейтуді орындап, келесіні аламыз
![]() (4.7)
(4.7)
Бұд теңдеудің екі бөлігінен де кері Z-түрлендіруді алайық
![]() (4.8)
(4.8)
Мұндағы Т - кванттау периоды. Тікелей программалаудың құрылымдық сұлбасы 4.1-суретте көрсетілген.
4.1.1 Цифрлық жүйелердің машиналық іске асырылуы
Цифрлық ПИ-реттегішті іске асыру үшін пайдаланылатын МП-жүйенің құрылымдық сұлбасы 4.2-суретте көрсетілген. Кванттаудың келесі мезетін анықтау үшін бұл сұлбада әрбір Т секунд сайын импульс өндіретін программалық таймер қолданылған. Бұл импульс екі мақсат үшін пайдаланылады. Біріншіден, импульс МП-нің үзілім құрына келіп түседі де, бұл жұмыс программасының тоқтауына және үзілім программасының орындалуына келтіреді.
Екіншіден, таймерден келетін уақыт импульсі АЦТ-ні басқару құрына түседі де, бұл кезде y(t) объекттің шығыс координатасының лездік мәні квантталады және бекітіледі. Содан кейін АЦТ бұл y(kT) мәнді екілік кодтың N разрядтарына түрлендіреді. Бұл процесс үшін ақырлы уақыт талап етіледі. Демек, АЦТ деректер дайындығының құры арқылы дискретті деректер түрлендіріліп болғаны туралы МП-ге хабарлауы тиіс. Бұл кезде МП жұмысының екінші үзілімі орын алады да, y(kT) мәндердің шығарылуы орындалады және ол (МП) басқарудың келесі мәнін есептеуге кіріседі. Басқарушы сигналдың бұл жаңа мәні есептелінгеннен кейін МП басқару сигналын шығару үшін таймерден келесі үзілімді күтеді.

4.2 Сурет – ПИ – реттегіштің іске асырылуының құрылымдық схемасы
ҚК- қуат күшейткіші,
ТСҚ- таңдау-сақтау құрылғысы.
Тапсырма беруші үшін жарамды басқару жүйесін алу үшін келесі маңызды сұрақтарды үлкен ұқыптылықпен зерттеу қажет
- іске асырудың сандық аспекттері;
- бергіштер;
- атқару механизмдері;
- пpогpаммалау.
4.2 Алдын ала сүзгілеу
Басқару жүйені іске асырғанда есептеу машинасының қоршаған ортамен өзара әрекетіне қатал назардың аударылуы маңызды. Осыған байланысты микро-ЭЕМ-нің бергішпен инерфейсінің ұйымдастырылуын қарастырайық.
Егер бергіштің шығысындағы сигнал жиіліктері басқару жүйенің қиық жиілігінен жоғары периодты құраушысынан тұрса, онда ерекше күрделіліктер пайда болады. Үзіліссіз жүйеде мұндай қатыс жиі жүйе арқылы өткенде периодты құраушының елеулі бәсеңдеуіне үміттенуге мүмкіндік беретін. Цифрлық жүйелерде мұндай периодты сигналдың бары күрделіліктердің пайда болуына келтіреді.
Бергіштерден сигналды АЦТ кірісіне қосарда, алдымен сигналдардың алдын ала сүзгіленуін өткізген дұрыс. Алдын ала сүзгілеудің пайдалалығын келесі мысалдар көмегімен көрсетуге болады (4.3-суретті қара).
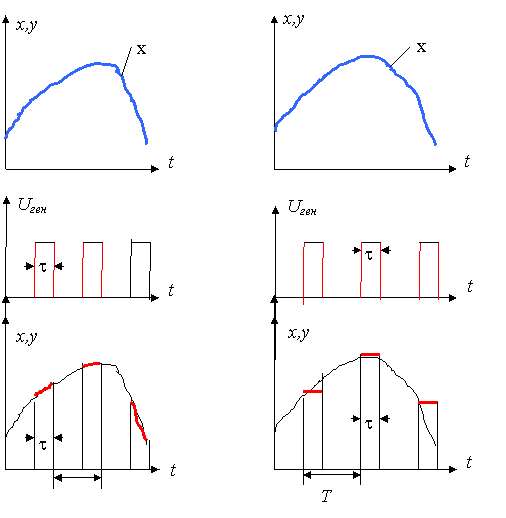
Үзіліссіз сигнал синусоидалық ұйытқының (fb=0,9 Гц) тіктөртбұрышты толқынмен қабаттасуынан алынған болсын делік (4.3,а-суретті қара). Бұл сигнал қиық жиілігі Wқиық=0,5 Гц тұйық жүйеде орын алады. Бұл жүйеде кванттау жиілігі fкв=1 Гц пайдаланылады делік.
 |
а) в)
б)
4.3 Сурет – Жиілікті жұту эффектісі
Алдын ала 4.3, в-суретті қарастырайық. Бұл суретте периодты сигнал және квантталған сигналды сипаттайтын нүктелер келтірілген. Бұл суреттен кванттаудан кейін жиілігі fкв - fв = 0,1 Гц болатын жаңа периодты сигнал пайда болатыны көрініп тұр. Демек, 4.3, б-суретте көрсетілгендей, кванттаудан кейін қосындыланған сигнал ішінде, жүйемен басылуы тиіс f=0,9 Гц жиілік орнына, тұйық жүйемен күшейтіле алатын 10с периодпен сигнал пайда болды. Төменгі жиілікті тербелістердің пайда болу эффектісінен құтылу үшін алғашқы аналогты сүзгіні пайдалану керек. Бұл сүзгі қиық жиілігінен жиілігі жоғары периодты ұйытқуларды басу үшін керек. Сүзгінің Wв жиіліктік жолағы Т-кванттау периодына кері пропорционал. Шамамен бұл байланыстың түрі келесі: WвT=0,5÷1.
Реттеу жүйесін есептегенде осы алғашқы сүзгінің динамикалық қасиеттерін есепке алу міндетті түрде орындалуы тиіс екенін, ал кванттау жиілігі өзгергенде сүзгі параметрлерін де өзгерту керек екенін ескертейік.
4.3 Бергіштердің істен шығуымен байланысты қателер
Шуылдардың (периодты тербелістердің) себебінен болатын қателерден басқа, өлшенген сигналдарда басқаруды есептеу процедурасында да қателер болуы мүмкін. Бұл қателердің көздері ретінде, мысалы, бергіштер және түрлендіргіштер болуы мүмкін. Осындай қателер әдетте үлкен шашылумен және кіші ықтималдықпен сипатталады. Басқару жүйелерін компьютермен іске асырғанда мұндай қателерді шығарып тастау үшін айтарлықтай тиімді тәсілдер бар.
Сенімділікті талап ететін жүйелерде жоғары дәрежелі сенімділікке бергіштерді қосарлаумен жетеді. Бұл тәсілде сигналдар айырымы берілген табалдырықтық саннан асып түскенде апаттық сигнал беретін логикалық сұлбаға екі бергіштер қосылады. Сонымен, қос бергіштерді не қисынды сигналды, немесе оның істен шығуы туралы хабарлаушы сигналды беретін бір бергіш ретінде қарастыруға болады. Үш бергіштер де пайдаланылуы мүмкін. Онда өлшеніліп отырған мән екіден кем емес бергіштердің көрсетімдері дәлдессе ғана дұрыс деп саналады.
Микропроцессорлық басқаруды пайдаланғанда түрлі аппараттық және программалық қателерді тіркеу мүмкіндіктері бар. Мысалы, АЦ-түрлендіргішке бекітілген кернеулер көздеріне жалғанған бірнеше қосымша арналардың қосылуы автотестілеуге және үлгілеуге жол ашады. ЦА- және АЦ- түрлендіргіштерді байланыстырып, ЦА – түрлендіргішті автоматты түрде тестілеуге болады.
4.4 Микропроцессорлық басқару жүйелеріндегі кешігу
Нақтылы уақытта ақпаратты өңдеуді талап етпейтін жағдайлардың көбінде есептеу операцияларының жылдамдығы айтарлықтай мән атқармайды. Дегенмен, басқару жүйесі үшін нақтылы уақыт режимі қажет деп саналады да, ақпаратты өңдеумен байланысты уақыттық кідірістер жүйенің сипаттамаларына айтарлықтай ықпал тигізуі мүмкін.
Кідірістердің жүйеге ықпалын аналитикалық түрде зерттеу үшін ең алдымен олардың ұзақтығын анықтаған маңызды. Бұл жағдайда уақыттық кідірістермен байланысты екі сұрақ туады: біріншіден, егер процессор ішіндегі санау жылдамдығы баяу болса, басқару алгоритмінің ұйғарған барлық қажетті есептеулерін орындау үшін жеткілікті бола ма, екіншіден, уақыттық кідіріс тұйық жүйенің орнықтылығына қалай ықпал етеді?
Микропроцессордың есептеу процедурасымен байланысты уақыттық кідірістер, кез келген қолданбалы есептер дестесінен шақырып алына алатын бағыныңқы программаларды есепке алып, басқару заңын іске асыратын программаны талдаудан анықталуы мүмкін. Микропроцессордың нақты инструкцияны орындау уақыты осы инструкцияны орындау кезінде микропроцессор өтуі тиіс машиналық күйлердің жалпы санына тура пропорционал. Мысалы, "Intel 8080" микропроцессоры үшін әрбір күй 500 нс, яғни бір секундта процессор 2 млн. күйлер арқылы өтеді. Осындай жылдамдық өте жоғары болып көрініуі мүмкін, бірақ қарапайым программаны орындағанның өзінде мыңдаған машиналық күйлер керек болып қалуы мүмкін.
Нақты инструкцияларды орындау үшін қажет машиналық күйлердің мөлшері туралы ақпарат микропроцессорды пайдалану бойынша анықтамалықтарда табылуы мүмкін.
Мысал ретінде төменде "Intel 8080" микропроцессордың түрлі есептеу процедураларын орындау кезіндегі әдеттегі уқыт шығындары келтірілген. Бұл мысал жылжымалы үтірмен сандардың қосындылануы және көбейтілуі айтарлықтай уақыт талап ететінін көрсетеді.
Орындалу уақыты, мкс
Жылжымалы үтірмен
сандардың қосындылануы 18,5 - 202.5
Жылжымалы үтірмен
сандардың көбейтілуі 63.5 - 446
Жылжымалы үтірмен
сандардың бекітілген
үтірлі түрін түрлендіру 25 - 109
Төмендегі 4.4-суретте "Intel 8080" микропроцессорында АЦТ бағыныңқы программаның орындалуын іске асыратын программаның үзіндісі келтірілген.
|
Орындалу уақыты, мкс |
|
|
|
CALL CURT |
|
АЦТ қосалқы программа
|
|
2,5 |
MOV H,B |
|
|
3,5 |
MUI L,OH |
|
|
8 |
SHLD X1 |
Х1-ді жадыға жүктеу
|
|
2,5 |
MOV H,C |
|
|
8 |
SHLD X2 |
Х2-ні жадыға жүктеу |
|
8 |
LDHL KP |
|
|
2,5 |
MOV B,H |
|
|
2,5 |
MOV C,L |
|
|
8 |
LDHL X1 |
|
|
2 |
XCHG |
|
|
47,5 мкс |
|
|
4.4 Сурет – Микропроцессор үшін бағыныңқы программа
Бағыныңқы программа мәтінінің сол жағынан әрбір инструкцияны орындауға қажет уақыт көрсетілген. Жалпы кідіріс уақыты 47,5 мкс болып тұр. Жалпы жағдайда программаларды орындағанда уақыттық кідіріс кездейсоқ шама болып табылады да, кіріс деректердің жинағына тәуелді екеніне ерекше көңіл аудару керек. Кіріс деректердің басқа жинағы инструкциялар жиынтығын өзгертуі мүмкін.
Жалпы жағдайда үтірі бекітілген формада берілген сандармен амалдар орындағанда қажет болатын процессорлық уақыт азырақ, сондықтан, цифрлық реттегішті тәжірибе жүзінде іске асырғанда сандардың осындай түрде берілуі басқалардан гөрі артығырақ қолданылады. Мысалы, үтірі бекітілген формадағы сандарды қосудың типтік уақыты 2 мкс болады.
Сөйтіп, уақыттық кідірістер жұмысшы программаның орындалуымен анықталады. Цифрлық реттегішті құрғанда бұл кідірістерді елемеуге болмайды. Уақыттық кідірістер тұйық жүйелердің сипаттамаларына қолайсыз ықпал ететіні жақсы белгілі, сондықтан олар цифрлық басқару жүйелерін жобалау кезінде еске алынуы тиіс.
4.5 Сандық аспектілер
Автоматтық басқару жүйелерін іске асыру кезінде сандық өзгешелігі жағынан бірқатар сұрақтар туады: түрлендіргіштердің қателігі қандай болуы тиіс; есептеулер қандай дәлдікпен орындалуы тиіс. Бұл сұрақтарға жауап беру үшін басқарудың сапасына және тұйық жүйенің орнықтылығына осындай шектеулердің ықпал жасау өзгешелігін түсіну керек. Бұл сұрақтарға жауап бергенде өрескел бағалаулармен шектелуге болады.
4.5.1 Сөздің ақырлы ұзындығының ықпалы. Қателердің негізгі көздері келесі:
- АЦ-түрлендіргіштегі дискреттеу;
- операцияларды орындағандағы дөңгелектеу және толып кету;
- ЦА-түрлендіргіштердегі дискреттеу.
АЦ-түрлендіргіштердің әдеттегі түрлерінің дәлдігі 8, 10, 12 және 14 белгілер болады. Бұл (максимал шамадан пайызбен алғанда) 0,4; 0,1; 0,0025; 0,006 айыруға сәйкесті. ЦА-түрлендіргіштердің де дәлдігі шектелген; әдеттегі мәні 10 разрядқа тең болады.
АЦТ разрядтарының санын көбейтіп есептеулер дәлдігін арттыруға болады, бірақ бұл әрекет ақпаратты өңдеу уақытын кешігу уақыты ретінде қарастыруға болады. Түрлендірудің ақырлы уақыты АЦТ үшін жиілік бойынша кіріс сигналдың жоғарғы шекарасын, демек, тұйық жүйенің өткізу жолағын шектейді. Кіріс сигналдың жиілігін арттыру түрлендіру дәлдігінің пайдаланылып отырған разрядтар санына тура келмеуіне келтіруі мүмкін.
4.1 Кесте – АЦТ кірісіндегі сигналдың максималь жиілігі (рад/с)
|
Түрлендіру уақыты |
Сөздің ұзындығы, бит
|
|||||
|
4 |
6 |
8 |
10 |
12 |
16 |
|
|
10-3 |
125 |
31 |
7,8 |
1,9 |
0,48 |
0,03 |
|
10-5 |
12500 |
3100 |
78 |
195 |
48,8 |
3,0 |
|
10-6 |
125000 |
31000 |
7800 |
1950 |
48,8 |
30,0 |
ЭЕМ ішіндегі сандар түрлі тәсілдермен беріліуі мүмкін, ең жиі пайдаланылатындары келесілер: үтірі бекітілген дара және екі еселік дәлдікпен; үтірі жылжымалы дара дәлдікпен. Жалпы айтқанда, дөңгелектеу және сандарды шектелген разрядтар мөлшерімен беру біршама аз қателер тудырса, түрлендіргіштердің толып кетуі апатты салдарға келтіруі мүмкін. Сондықтан ең алдымен сөздің талап етіліп отырған ұзындығын түрлендірілетін айнымалының мәнімен келістіру керек.
4.5.2 Деңгей бойынша кванттау эффектілері. Деңгей бойынша кванттау сатыларының мөлшері (саны) жүйелердің динамикалық қасиеттеріне айтарлықтай ықпал етеді. Олардың саны жеткіліксіз болғанда дискреттер арасында периодты ауыстырып қосу режимдері пайда болып тұруы мүмкін (автотербелістер).
Аналогты-цифрлық түрлендіргіш деңгей бойынша түрлендіруді орындайды. Кванттаушының қатесі разрядтардың санына тәуелді де, ал кванттаушының өзі сызықты емес құрылғы болып табылады. Осыған байланысты цифрлық басқару жүйедегі кванттау эффектерінің аналитикалық талдануы айтарлықтай күрделі. Сонымен бірге тұйық жүйелердегі деңгей бойынша кванттау жалпы жағдайда орныққан қатенің және өшпейтін тербелістердің (автотербелістердің) пайда болуына келтіруі мүмкін екенін де ескеру керек. Қарапайым мысалдармен осы жағдайды көрсетейік. Екі тұйық цифрлық жүйелерді қарастырайық (4.5-суретті қара).
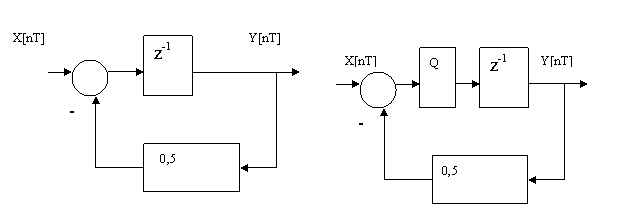
а б
4.5 Сурет – Цифрлық жүйелер а) кванттаушысыз және б) Q-кванттаушымен
4.5,а-суретте кванттаушының эффектін елемейміз, ал 4.5,б-суретте деңгей бойынша квантаушыны ескереміз. Енді 4.5-суретке сәйкесті тұйық жүйенің беріліс функциясын анықтаймыз
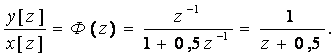 (4.9)
(4.9)
(4.9)-өрнектен жүйе орнықты екені көрініп тұр, демек, t кезіндегі Х[0] бастапқы мәнмен байланысты өтпелі процесс нөлге ұмтылады.
4.5,б- суреттегі жүйе үшін сөздің ұзындығы 4 бит болсын деп болжайық, онда деңгей бойынша кванттау қадамы g=2=0,0625. Оң таңбалы сигналдар үшін кванттаушының сипаттамалары келесі жолмен есептеледі
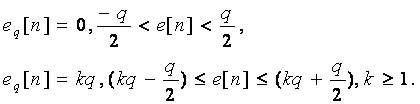
4.2-кестеде X(n)=0 және y[0]=0,58 болған кездегі y[n]-шығыс сигналдың мәндері келтірілген (нәтижелер дербес ЭЕМ-ді қолданып, модельдеу әдісімен табылған).
Тәжірибе жүзінде орныққан қате де, автотербелістер де ұнамсыз болып табылады да, сондықтан оларды мүмкіндігінше минималь етуге тырысады. Автотербелістердің аналитикалық есептелуін арнайы есептеу әдістерін пайдаланып орындауға болады.
4.2-кестеден жүйенің шығысында амплитудасы +g және преиоды 2-ге тең тербелістер орнығатынын көруге болады.
4.2 Кесте – Есептеу нәтижелері
|
n |
y[n] |
e[n] |
eg[n] |
|
0 |
0,58000 |
-0,2900 |
-0,31250 |
|
1 |
-0,31250 |
0,15625 |
0,18750 |
|
2 |
0,18750 |
-0,09375 |
-0,12500 |
|
3 |
-0,12500 |
0,06250 |
0,06250 |
|
4 |
0,06250 |
-0,03125 |
-0,06250 |
|
5 |
-0,06250 |
0,03125 |
0,06250 |
|
6 |
0,06250 |
-0,03125 |
-0,06250 |
|
7 |
-0,06250 |
0,03125 |
0,06250 |
4.5.3 Дискреттеудің сызықты анализі. Дөңгелектеудің және дискреттеудің ықпалын идеясы нақты операцияларды, олардың идеал модельдеріне ауыстыру және аддитив ұйытқуларды қосу әдістеріне негізделген сызықты анализ көмегімен бағалауға болады (4.6-суретті қара). Төмендегі 4.6-суретте кванттаудың және дөңгелектеудің сызықты модельдері келтірілген. Егер деңгей бойынша кванттау сатыларының саны көп болса, онда оның ықпалын ескермейді. Бұл жүйені сызықты етеді де, импульсті жүйелердің математикалық аппаратын пайдалануға рұқсат береді.
Опеpация Белгіленуі Сызықты
модель
|
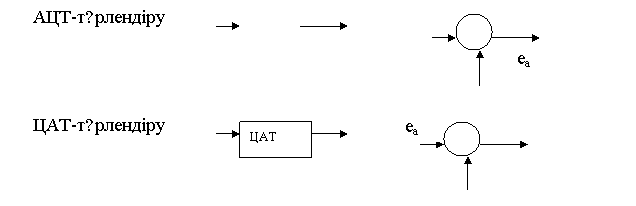
4.6 Сурет – Кванттаудың сызықты модельдері
Дөңгелектеудің және дискреттеудің сызықты модельдерінің көмегімен олардың ықпалын бағалау есебін қандай да бір сызықты жүйенің анықталған немесе стохастикалық кіріс сигналға жауабын есептеуге келтіруге болады. Сызықты модельдер егжей-тегжейлі есептеулерсіз сапалық бағалауларды алуға мүмкіндік береді. Дегенмен, сызықты модель дискреттеумен қоздырылатын барлық эффектілерді, мысалы, автотербелістерді ескермейтінін ұмытпау керек.
4.6 Сызықсыз атқарушы механизмдер
Жоғарыда баяндалған пікірлер процесті сызықты модельмен сипаттауға мүмкін деген болжауға сүйенген, мысалы, буынның шындыққа негізделген сипаттамасының сызықтандырылуын пайдалануы мүмкін. Бірақ, жиі келесі жағдай болып қалады. Жүйедегі буын айтралықтай сызықты емес делік, мысалы, ол атқарушы құрылғы болуы мүмкін. Осындай сызықты еместік қанығуы бар механизм болуы мүмкін. Егер осындай сызықты еместікке назар аударылмаса, онда айтарлықтай күрделендірулер пайда болуы мүмкін. Бұл кедергілерді жоюдың түрлі әдістері бар. Егер, мысалы, сызықты еместіктің шығысындағы сигнал өлшеніле алатын болса, онда сызықты емес объекттің сызықты моделін пайдаланып, қанығу мезетін әрдайым анықтауға болады. Егер сызықты еместіктің шығысында сигналды өлшеп алуға жолы түспесе, онда енді объекттің сызықты емес моделін пайдаланып, сигналдың қанығу аумағына түсу мезетін де бағалауға болады.
Әдебиеттер тізімі
1. Рутгайзер О.З. Радиоавтоматика: Учебное пособие.- Алматы: АЭИ, 1992. -76с.
2. Куо Б. Теория и проектирование цифровых систем управления. - М.: Машиностроение, 1986. -448с.
3. Коновалов Г.Ф. Радиоавтоматика. –М.: Высшая школа,1990. -335с.
4. Рутгайзер О.З., Шайхин Б.М. Микропроцессорлар автоматты басқару жүйелерінде: Оқу құралы. – Алматы: АЭжБИ, 1997. -54б.