МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Алматинский институт энергетики и связи
Е.Ж.Айтхожаева
Цифровые устройства и микропроцессоры.
Цифровые устройства
Учебное пособие
Алматы 2006
В учебном пособии излагаются
арифметические и логические основы цифровых устройств (ЦУ) и микропроцессоров;
фундаментальные алгоритмы арифметической обработки чисел; основные понятия
теории микропрограммных ЦУ; методы
синтеза ЦУ.
Основной целью учебного пособия является
закрепление теоретических знаний, формирование умений и выработка навыков по
выполнению основных арифметических операций и разработке
граф-схем алгоритмов арифметических операций в двоичной системе счисления, решению
задач абстрактного и структурного синтеза микропрограммных ЦУ. В учебном
пособии рассматривается теоретический материал, приводятся примеры применения теоретического
материала, контрольные вопросы подготовки студентов к занятиям по каждой теме,
список литературы.
Учебное
пособие предназначено для студентов, обучающихся по специальностям направления
050704 - Вычислительная техника и программное обеспечение.
Содержание
|
Введение……………………………………………………………………... |
4 |
|
1 Представление числовой
информации в цифровых устройствах……… |
4 |
|
2 Алгебраическое сложение в двоичной системе счисления с использованием прямого, обратного и дополнительного кодов вцифровых устройствах.…………………………… |
11 |
3 Умножение чисел в
двоичной системе счисления …………...................
|
17
|
|
4. Деление чисел в
двоичной системе счисления…………………............. |
24 |
|
5 Комбинационные
схемы………………………………………………….. |
30 |
|
6 Цифровые устройства
с памятью………………………….……............... |
35 |
|
7 Стандартные
элементы памяти – триггеры……………………………… |
44 |
|
8 Микропрограммные
устройства………………………………………….. |
49 |
|
9 Интерпретационный
метод синтеза МПУ……………………………….. |
53 |
|
Список литературы………………………………………………….............. |
58 |
Введение
Цифровым устройством
(ЦУ) называется устройство, служащее для преобразования дискретной информации,
представленной в виде цифр. Математической моделью цифрового устройства является
цифровой автомат. Чаще всего в цифровых устройствах используется стандартный
двоичный алфавит (0 или 1).
Цифровые устройства
преобразовывают дискретную информацию, представленную в виде слов. При этом в
ЦУ используются сигналы – материально- энергетическая форма представления
информации.
Двоичная цифра в ЦУ
отображается состоянием составляющих его элементов, а при передаче информации
от элемента к элементу - электрическими сигналами в линиях связи. Состояние
элементов определяется уровнем напряжения или тока на выходе элемента, либо
наличием или отсутствием электрического импульса, либо фазой или частотой
электрических колебаний. При этом одно из состояний элемента принимается за
единицу, другое за нуль.
Среди цифровых устройств
можно выделить ЦУ без памяти (комбинационные схемы) и ЦУ с памятью.
Комбинационные схемы являются более простыми устройствами, представляются в
виде совокупности связанных между собой определенных элементов схем, все
сигналы имеют конкретное значение (0 или 1). ЦУ с памятью состоят из двух
частей: комбинационной схемы и памяти.
Цифровые устройства,
предназначенные для выполнения каких либо операций (например, микропроцессор),
являются цифровыми операционными устройствами (ЦОУ). Цифровое операционное
устройство состоит из управляющей части (управляющий автомат) и операционной
части (операционный автомат).
1 Представление
числовой информации в цифровых устройствах
Перевод чисел из одной системы счисления в другую. При переводе
чисел из одной системы счисления в другую могут использоваться различные
способы перевода чисел. Наиболее
простой способ перевода основан на применении таблиц эквивалентов.
Перевод чисел по
таблице эквивалентов используется только в том случае, если основания систем
счисления q и h связаны соотношением q=hk,
где k
- целое число. Перевод чисел осуществляется заменой
каждой цифры (символа) исходной системы
счисления на ее эквивалент в новой системе счисления по таблице эквивалентов.
Причем каждой цифре в q-й системе счисления соответствует эквивалент в h–й системе, занимающий k-позиций.
В таблице 1
представлена таблица эквивалентов для q=8,
h=2. В таблице 2 представлена таблица
эквивалентов для q=16, h=2.
Таблица 1 Таблица 2
|
q=8 |
h =2 |
|
q =16 |
h=2 |
|
0 |
000 |
|
0 |
0000 |
|
1 |
001 |
|
1 |
0001 |
|
2 |
010 |
|
2 |
0010 |
|
3 |
011 |
|
3 |
0011 |
|
4 |
100 |
|
4 |
0100 |
|
5 |
101 |
|
5 |
0101 |
|
6 |
110 |
|
6 |
0110 |
|
7 |
111 |
|
7 |
0111 |
|
|
|
|
8 |
1000 |
|
|
|
|
9 |
1001 |
|
|
|
|
A |
1010 |
|
|
|
|
B |
1011 |
|
|
|
|
C |
1100 |
|
|
|
|
D |
1101 |
|
|
|
|
E |
1110 |
|
|
|
|
F |
1111 |
Пример - Перевести двоичное число Х2=101011,11001 в
шестнадцатеричную систему счисления.
Решение: исходное число
условно разбивается на тетрады, начиная от запятой вправо и влево. Затем каждая
тетрада заменяется на восьмеричный эквивалент в соответствии с таблицей
эквивалентов.
Х
2= 0010 1011, 1100 1000
Х
16= 2 B, C 8 .
Ответ: Х 16=2B,C8.
При невыполнении
условия q=hk применяется
другой способ перевода, основанный на делении
целой и умножении дробной части числа
на основание q новой системы
счисления.
Для перевода целой
части числа необходимо целую часть числа и получающиеся от деления частные
последовательно делить на основание новой системы счисления q до тех пор, пока очередное частное не
будет меньше q. Последнее частное и
остатки, записанные в новой системе счисления в последовательности обратного
получения, дадут целую часть числа в новой системе счисления.
Особенность способа
деления на основание заключается в том, что все вычисления выполняются в
исходной системе счисления, в этой
же системе получаются и цифры искомого числа. Способ деления на основание можно
рекомендовать при переводе чисел из десятичной системы в систему с любым
основанием.
Пример - Перевести
десятичное число Х10=99 в двоичную систему счисления (q=2).
Решение:
_99|2___
98 _49 |2__
1 48
_24 |2__
1 24 _12 |2_
0 12 _6 |2
0 6 _3 |2
0 2 1<q .
1
Ответ: Х2=1100011.
Для перевода дробной
части числа необходимо дробную часть числа, а также дробные части получающихся
произведений, последовательно умножать
на основание новой системы счисления. Целые части получающихся произведений,
записанные в новой системе счисления, дадут искомую дробную часть числа.
Процесс умножения выполняется до получения необходимого количества разрядов
результата.
Пример - Перевести
десятичную дробь Х10=0,735 в двоичную систему счисления (q=2).
Решение: 0,735
x 2
1,470
x 2
0,940
x 2
1,880
x 2
1,760 .
Ответ: Х2=0,1011.
Для перевода чисел в десятичную систему счисления из любой другой
системы счисления удобно использовать способ полиномиальный перевода,
основанный на том, что для позиционных систем счисления смешанное число Х= хn
хn-1…х0 ,хn … хn можно представить
в виде полинома
Х = хnhn + хn-1hn-1 +…+ х0h0
+ х-1h-1 +…+ х-m h-m, где h
- основание системы счисления, хi - коэффициент, представляющий собой цифру системы счисления с
основанием h (хi ![]() h-1).
h-1).
Пример - Перевести двоичное число Х2=100111,011
в десятичную систему счисления.
Решение:
Х10=1´25 + 0´24 + 0´23 + 1´22 + 1´21 + 1´20 + 0´2-1 + 0´2-2 +
0´2-3 = 71,375.
Ответ: Х10=71,375.
Кодирование чисел. Для упрощения выполнения
операций алгебраического сложения числа представляются в прямых, обратных или
дополнительных кодах. Все числа в прямом коде (п.к.) представляются в виде: знак числа . число. При этом знак «+» кодируется как 0, «-» кодируется как 1:
G= + 0, г1,
г2, …,гn = 0. г1,
г2, …,гn
G= - 0, г1,
г2, …,гn = 1. г1, г2, …,гn
Пример - Представить числа А
и B в прямом коде: А=+0.10010, B=-0.11011.
Решение: Ап.к
=0.10010 п.к. и Вп.к
=1.11011 п.к..
Прямой, обратный (о.к.) и дополнительный коды (д.к.) двоичных
положительных чисел одинаковы и равны самому числу:
(G+)п.к.=
(G+)о.к.= (G+)д.к.
Пример - Представить
положительное число А в прямом коде: А =+0.010111.
Решение: Ап.к. = Ао.к.= Ад.к.=0.010111.
Для получения обратного кода отрицательного числа знаковому разряду
присваивается «1», а в цифровой части единицы заменяются на нули, нули – на единицы:
(G-)o.к=1.д1,
д2, …,дn, , где дi=0, если гi=1
дi=1, если гi=0
Для получения дополнительного кода отрицательного числа необходимо к младшему разряду обратного кода числа
прибавить единицу:
(G-)д.к.=
1. о1, о2, …,оn =1+ 0. о1, о2,
…,оn , где 0. о1, о2, …,оn - дополнение
модуля числа до единицы в целой части ( 1- |0. г1, г2,
…,гn|)
(G-)о.к.
- (G-) = 1. д1, д2, …,дn - (-0. г1,
г2, …,гn )= 1.11…1=2-2-n
(G-)о.к.= G- +2-2-n
(G-)д.к.
- (G-)=1+(1-|0. г1, г2, …,гn|) –
(-0. г1, г2, …,гn ) = 2
(G-)д.к.=G-+2
(G-)дк=(G-)о.к.+2-n
Пример - Представить число
А=-0.101011 в прямом,
обратном и дополнительном кодах.
Решение: Ап.к. =1.101011, Ао.к..=1.010100,
Ад.к. =1.010101.
Представление чисел в форме с фиксированной и
плавающей запятой. Для выполнения
операций над числовыми данными в ЦУ используются специальные формы записи
чисел: естественная и нормальная.
При естественной форме
записи число записывается в естественном виде 1750; 14,85; 0,003572 и т.д. Для
удобства обработки чисел в разрядной сетке машины положение запятой всегда
жестко фиксировано и называется представлением чисел с фиксированной запятой
(или точкой, т.к. запятую в ЭВМ принято изображать точкой).
Для фиксированной
запятой, когда в п-разрядной сетке размещается смешанное двоичное
число Х, которое имеет к-разрядов в
целой и т-разрядов в дробной части, наименьшее значащее число (без учета
знака) будет: |Xмин|=00...0, 00...0012=2-т. Наибольшее значащее число: |Xмакс|=11...111,11...1112=
2к -2-т
Таким образом, диапазон
представимости для двоичных смешанных чисел Х получается равным 2-т
![]() |X|
|X|![]() 2к
-2-т
2к
-2-т
Из этой формулы можно
найти диапазон представимости для двух граничных случаев дробных и целых чисел.
Практически в ЭВМ
сейчас применяется для фиксированной запятой представление чисел в виде целых.
При нормальной форме
запись одного и того же числа может принимать разный вид:
1750=175*10¢=1,75*103=0,175*103 и т.д.
В общем виде эту запись
можно представить как X=MxqP, где Мх мантисса
числа, Р - порядок (целое число), q- параметр представления, совпадающий с
основанием системы счисления мантиссы. Поскольку параметр q- величина
постоянная для конкретной машины, то в разрядной сетке машины он не
записывается. Число Х представляется в машине условно, как Х=МхРх,
где q-1£½Mx½<1. Такая мантисса называется нормальной, а число
нормализованным. Так как в этой форме представления запятая в числе не жестко
фиксирована, то оно также называется представлением числа с плавающей запятой
(точкой).
В машинах, в которых
q=2, для нормализованного числа мантисса имеет вид: 0,х0х1х2...хп
. Так как целая часть мантиссы всегда меньше 1, то целая часть и запятая,
отделяющая целую часть от дробной части, не указывается.
Используются две формы
машинного представления числа (без основания, целой части и запятой):
|
знак числа |
Мантисса (Мх) |
знак порядка |
Порядок (Рх) |
или
|
знак числа |
знак порядка |
Порядок (Рх) |
Мантисса (Мх) |
Мантисса, имеющая вид
0,1… называется нормализованной, 0,0… - ненормализованной. В цифровых устройствах
при представлении чисел с плавающей запятой используется нормализованная
мантисса, так как при этом достигается большая точность представления числа.
Если в результате вычислений получается ненормализованная мантисса, то она
подвергается нормализации путем сдвига влево с соответствующим изменением
порядка результата.
Следует отметить, что порядок числа Рх
имеет смысл указателя истинного положения запятой. Если мантисса Мх
есть двоичное число, то умножение такого числа на 2Рх соответствует
перемещению запятой на Рх двоичных позиций правее (при Рх>0) или на Рх
позиций левее (при Рх<0)
относительно ее положения в мантиссе. В последнем случае между истинной и
машинной запятой в исходном числе имеется Рх нулей.
Диапазон чисел,
однозначно представимых в разрядной сетке, определяется неравенством: Xmin
£½X½£ Xmax , где Xmin и Xmax наименьшее
и наибольшее значение числа с учетом формы его представления. Диапазон
представимых чисел, заданных в форме с плавающей запятой, подсчитывается в зависимости
от диапазона представления мантиссы Мх, порядка Рх и
параметра q.
Представление
чисел в форме с плавающей запятой по
сравнению с запятой фиксированной расширяет диапазон представимых чисел. Важным
преимуществом чисел с плавающей запятой является также сохранение при
выполнении операций наибольшего количества значащих цифр вследствие
нормальности их форм. Поэтому представление чисел в машине с плавающей запятой
более точно.
Однако, несмотря на
большие преимущества, представление чисел в форме с плавающей запятой
применяется не во всех ЭВМ. Это объясняется сложностью реализации алгоритмов
операций: одновременно необходимо выполнить действия над двумя числами - мантиссой и порядком.
Контрольные вопросы
1. В чем заключается полиномиальное представление числа, приведите
пример.
2. Что такое система счисления?
3. Какая система счисления называется позиционной?
4. Назовите способы перевода чисел из одной системы счисления в другую.
5..Сформулируйте правила получения прямых,
обратных и дополнительных кодов положительных и отрицательных чисел.
2 Алгебраическое
сложение в двоичной системе счисления с использованием прямого, обратного и
дополнительного кодов в цифровых устройствах
Алгебраическое сложение в двоичной системе
счисления. Операция алгебраического
сложения и вычитания в ЦА осуществляется в обратном или дополнительном кодах.
Использование этих кодов позволяет заменить определение разности вычислением
суммы.
При алгебраическом сложении двух двоичных чисел с использованием
обратного кода положительные слагаемые представляются в прямом коде,
отрицательные
- в обратном и производится арифметическое суммирование этих кодов,
включая и знаковые разряды. При возникновении переноса из разряда знака единица
переноса прибавляется к младшему разряду суммы кодов (циклический перенос). В
результате получается сумма в прямом коде, если сумма положительна, или в
обратном коде, если сумма отрицательна:
а) G>0, Q>0: S=(G)п.к.+ (Q)п.к.;
б) G<0, Q<0: S= (G-)о.к.+
(Q-)о.к.= (G-) + 2 - 2-n
+ (Q-) + 2- 2-n= (G-+Q-) +(2-2-n)+
(2-2-n) = (S-о.к.);
в) G>0, Q<0: S=(G+)п.к.+(Q-)о.к.=(G+)
+ (Q-) + 2-2-n =[(G+) + (Q-)] + 2-2-n = S + 2-2-n:
1) если S<0: S- +2-2-n= (S-)о.к.;
2) если S>0: S+ +2-2-n=(S+)п.к. .
Пример - Сложить два
числа (А+В>0) с разными знаками в обратном коде: А=+0.1001, В= -0.0101.
Решение: число А
представляется в прямом коде, число В
представляется в обратном коде и производится их сложение.
[A] о.к =[A] п.к = 0.1001
[B] о.к = + 1.1010
10.0011
С учетом циклического
переноса:
[A] п.к +[B]
о.к =0.0100=[А+B] о.к =[А+B] п.к .
Ответ: А+В=+0.0100.
При алгебраическом сложении двух чисел с использованием дополнительных кодов,
положительные слагаемые представляются в прямом коде, отрицательные
- в дополнительном и производится арифметическое
суммирование, включая разряды знаков, которые при этом рассматриваются как
разряды целых единиц. При возникновении переноса из разряда знака единица
переноса отбрасывается. В результате получается сумма в прямом коде, если сумма
положительна, и в дополнительном коде, если сумма отрицательна:
а) G>0, Q>0: S= S=(G)п.к.+ (Q)п.к.;
б) G<0, Q<0: S= (G-)д.к.+ (Q-)д.к.=
(G-) + 2 + (Q-) + 2 = [G- + Q-
+ 2] +2 = (S-)д.к. + 2;
в) G>0, Q<0: S=(G+)п.к.+ (Q-)д.к. =
(G+) + (Q-)+ 2= (G+ + Q-) +2 = S +
2:
1) если S<0: S- + 2 =S-д.к.;
2) если S>0: S+ +2 =Sп.к. .
Пример - Сложить два
числа (А+В>0) с разными знаками
А=+0,1001, В=-0,0101 в дополнительном коде.
Решение: число А
представляется в прямом коде, число В
представляется в дополнительном коде и выполняется их сложение.
[A] д.к. =[A] п.к = 0.1001
[B]
д.к. = +1.1011
10.0100
[A] п.к + [В] д.к. =0.0100=[A+ В]
д.к.=[A+В] п.к .
Ответ: А+В=+0.0100.
При решении задачи на
ЭВМ возможны два вида выхода результатов за пределы диапазона представления.
В первом виде числа по абсолютной величине
становятся меньше наименьшего значащего
числа, которое можно записать в разрядную сетку: A<Amax, а
во втором случае они могут стать больше наибольшего представимого числа:
½A½>Amin.
В первом случае
получают число, состоящее из одних нулей (машинный нуль). Во втором случае
происходит переполнение разрядной сетки. Различают два вида переполнения:
положительное, когда A>+Amax и отрицательное, когда A<-Amax.
Поскольку различить
правильный и ошибочный машинный нуль невозможно, то полученные нули в разрядной
сетке для чисел с фиксированной запятой обычно не считаются ошибочными. Однако
при работе с плавающей запятой получение мантиссы равной нулю, при порядке не
равном нулю, считается ошибкой.
Для ликвидации
переполнения вводятся соответствующие масштабные множители.
Возникновение
переполнения разрядной сетки при представлении чисел в форме с плавающей
запятой возможно как для порядков, так и для мантисс.
Переполнение порядков
является истинным переполнением - признаком того, что полученное число или
больше наибольшего представимого числа (положительное переполнение порядков)
или меньше наименьшего представимого числа (отрицательное переполнение
порядков).
Что касается
переполнения мантисс, то от него можно избавиться, сдвинув мантиссу вправо на
один разряд. Так как при этом число уменьшается, то для компенсации этого уменьшения
необходимо увеличить порядок на одну единицу.
При сложении чисел с одинаковыми знаками
может возникнуть переполнение. Полученный результат при этом превосходит по
абсолютной величине максимально допустимое значение для данного формата чисел. В
ЦА случаи переполнения обнаруживаются специальной схемой. При обнаружении
переполнения вырабатывается сигнал прерывания.
Для того, чтобы
обнаружить переполнение разрядной сетки иногда под знак изображаемого числа
отводятся два разряда («+» кодируется как 00, «-» кодируется как 11). Такое
изображение числа называется модифицированным. С учетом представления чисел в
модифицированном коде сигнал переполнения вырабатывается при появлении в
знаковых разрядах кодовых комбинаций 01 или 10. При этом 01-признак переполнения в положительной области чисел, 10
- в отрицательной области
чисел.
Алгебраическое сложение
чисел с плавающей запятой выполняется в соответствии с формулой Z=A+B , где A=MAQPA, B=MBQPB , Z=MZQPZ . При выполнении операции необходимо при равенстве порядков
выполнить сложение мантисс:
MzQPZ = MAQPA ± MBQPB=
QPA=PB (MA +MB).
Если PA![]() PB,
необходимо выполнить уравнивание порядков. Процедура уравнивания порядков
заключается в том, что меньший порядок увеличивается до значения большего с
одновременной компенсацией изменения величины числа путем уменьшения мантиссы.
Чтобы уменьшить мантиссу необходимо сдвинуть ее вправо.
PB,
необходимо выполнить уравнивание порядков. Процедура уравнивания порядков
заключается в том, что меньший порядок увеличивается до значения большего с
одновременной компенсацией изменения величины числа путем уменьшения мантиссы.
Чтобы уменьшить мантиссу необходимо сдвинуть ее вправо.
Для
уравнивания порядков выполняется определение их разности
DP=PA-PB. Модуль |DP| указывает на сколько двоичных
разрядов необходимо сдвинуть вправо мантиссу. Если
DP>0 , то сдвигается мантисса MA, в
противном случае сдвигается мантисса MB.
После
уравнивания порядков обычным способом, как для чисел с фиксированной запятой,
вычисляется алгебраическая сумма мантисс, а в качестве порядка результата
берется больший порядок одного из чисел (при равенстве PA=PB любой из порядков).
Полученное
число MzQPZ является окончательным результатом, если мантисса MZ
имеет нормальную форму. Если форма отличается от нормальной, то
завершающая процедура операции- нормализация мантиссы.
При
нарушении нормальной формы вида |MZ|<Q-1 мантисса
результата увеличивается последовательным сдвигом влево до ликвидации этого
нарушения. Это действие сопровождается согласованным уменьшением порядка
результата: сдвигу влево на один двоичный разряд мантиссы соответствует
уменьшение на одну единицу порядка.
Если
применяются модифицированные коды, то признаком переполнения (нарушения
нормализации влево) служит появление разных цифр (01 или 10) в знаковых
разрядах. Оно устраняется сдвигом мантиссы результата вправо на один разряд при
Q=2 и увеличением порядка результата на единицу. При увеличении порядка может
возникнуть переполнение порядка. В этом случае вырабатывается сигнал прерывания.
Пример
- Пусть требуется сложить два двоичных числа А и В, записанные в формате
{1,4,5} (первый двоичный разряд
- знак числа, следующие четыре двоичных разряда
- порядок со знаком P, последние пять двоичных разрядов
- модуль мантиссы M):
|
[А] пр= |
0 |
1 |
100 |
10110 |
знак числа А знак порядка PА PА MA
[В] пр
= |
1 |
0 |
011 |
11010 |
знак числа В знак порядка PВ PВ MB
Решение:
а)
уравниваются порядки слагаемых, для чего из порядка PA вычитается порядок PВ.
Вычитание производится в дополнительном коде.
В этом
случае PA п.к. = 1.100
PB д.к.= +0.101
![]() PA +PB =
0.001
PA +PB =
0.001
Поскольку
DP>0 , то сдвигается вправо на один разряд мантисса [МВ]п.к. =1.11010. После сдвига [ М’В]п.к. =1.01101;
б)
складываются мантиссы с использованием дополнительного кода
[MA]п.к.= 0.10110
[M’B]д.к.= +1.10011
![]() [MZ] п.к =
0.01001 (нарушение
нормализации вправо);
[MZ] п.к =
0.01001 (нарушение
нормализации вправо);
в)
выполняется нормализация - мантисса MZ сдвигается на один разряд
влево и из значения порядка суммы вычитается единица. Нормализованный результат
+ 0,1001*22.
Сумматоры прямого, обратного и дополнительного
кодов двоичных чисел.
Для сложения
двоичных чисел в цифровых устройствах применяются параллельные сумматоры
прямого, обратного и дополнительного кодов, которые строятся на основе
одноразрядных сумматоров. Одноразрядный сумматор – это схема,
предназначенная для сложения одного
i-го разряда двоичных чисел с учетом переноса из предыдущего младшего разряда
(складываются три двоичные цифры). Схема, предназначенная для сложения двух
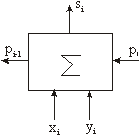
двоичных цифр, называется полусумматором. Условное обозначение одноразрядного
сумматора представлено на рисунке 1, таблица 3 представляет табличное задание
функционирования работы одноразрядного сумматора.
X = x1 x2 …
+ Y = y1
y2…
S
= s1 s2 …
Рисунок 1 – Условное
обозначение одноразрядного сумматора
Стандартное изображение
полного одноразрядного сумматора на функциональных схемах представлено на
рисунке 2. На рисунке 3 представлено стандартное изображение полусумматора.
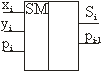
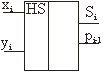
Рисунок 2 – Полный
сумматор Рисунок 3 - Полусумматор
Таблица 3
|
xi |
yi |
pi |
si |
pi-1 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
На основе
одноразрядного сумматора можно построить
последовательный сумматор, предназначенный для сложения n-разрядных двоичных
чисел (см. рисунок 4), сложение чисел в котором осуществляется
поразрядно, начиная с младших разрядов. На каждом шаге сложения осуществляется
сложение в одном разряде и получают значение соответствующего разряда суммы и
перенос в следующий старший разряд, сложение в котором будет выполняться на
следующем шаге сложения.
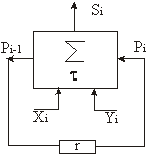 t
- задержка на один шаг сложения
t
- задержка на один шаг сложения
Тсл=
nt (время сложения)
Рисунок 4 – Последовательный
сумматор
В последовательном
сумматоре для выполнения сложения n-разрядных двоичных чисел необходим один
одноразрядный сумматор, требуемое время сложения Тсл=
nt.
В современных цифровых
устройствах в основном используются более быстродействующие параллельные n-разрядные сумматоры, для построения которых
необходимо иметь n одноразрядных
сумматоров, последовательно соединенных между собой (см. рисунок 4).
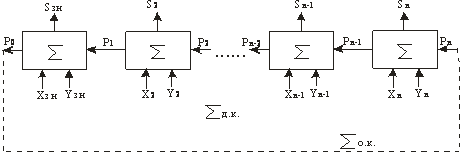
Рисунок 4 -
Параллельный n-разрядный сумматор
Контрольные
вопросы
1. Дайте определение
модифицированного кода, цель его использования
2. Сформулируйте правила выполнения операции алгебраического сложения с
использованием обратных и дополнительных кодов, приведите пример, используя
модифицированный код.
3. Сформулируйте правила выполнения операции сложения для чисел с фиксированной запятой.
4. Сформулируйте правила
выполнения операции сложения для чисел с плавающей
запятой.
5. Какие существуют типы сумматоров, что
они собой представляют?
3 Умножение чисел в двоичной системе счисления
Умножение чисел с
произвольным сочетанием знаков удобно выполнять, если сомножители заданы в
прямом коде. В этом случае независимо от знаков сомножителей модуль
произведения определяется перемножением модуля множимого на все разряды
множителя и последующего сложения получения частичных произведений, а знак
произведения определяется как сумма по модулю 2 знаков обоих сомножителей.
Умножение чисел можно
производить, начиная с младших разрядов либо со старших разрядов множителя. В
процессе умножения можно сдвигать либо сумму частичных произведений (СЧП), либо
множимое. Комбинируя эти возможности получают четыре основных метода умножения.
Первый вариант -
умножение младшими разрядами вперед множителя со сдвигом СЧП вправо при
неподвижном множимом.
Второй вариант -
умножение младшими разрядами вперед множителя со сдвигом множимого влево при
неподвижной СЧП.
Третий вариант -
умножение старшими разрядами вперед множителя со сдвигом СЧП влево при
неподвижном множимом.
Четвертый вариант -
умножение старшими разрядами вперед множителя со сдвигом вправо множимого и
неподвижной СЧП.
Ниже приведены
структуры операционного устройства для
умножения младшими разрядами вперед (рис.5) и старшими разрядами вперед (рис.6)
со сдвигом суммы.
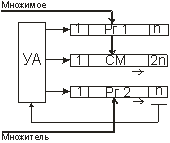
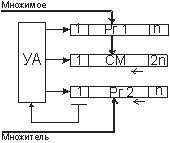
Рисунок 5 - Умножение Рисунок 6 -
Умножение
младшими разрядами
вперед старшими разрядами вперед
При умножении младшими
разрядами вперед, если очередной разряд множителя равен 1, то множимое
прибавляется к накопленной промежуточной сумме частичных произведений.
Полученная очередная сумма сдвигается на один разряд вправо (или множимое на
один разряд влево) и осуществляется переход к анализу следующего разряда
множителя. Если следующий анализируемый разряд множителя равен 0, то суммирование
множимого к промежуточной сумме частичных произведений не производится, а
осуществляется только сдвиг на один разряд вправо суммы частичных произведений
(или сдвиг множимого на разряд влево). Знак произведения определяется как сумма
по модулю два знаков сомножителей.
Умножение старшими
разрядами вперед выполняется аналогично, только изменяется направление сдвигов.
Анализ вариантов
умножения показывает, что по аппаратным затратам умножения со сдвигом СЧП более
экономично, чем умножение со сдвигом множимого: в первом случае суммарная
разрядность всех регистров и СМ - 4n, во втором - 5n.
Умножение на
n-разрядный множитель выполняется за время Ty=n(tсд+р1tсл), где р1-
вероятность появления единицы в анализируемом разряде множителя (р1=0,5).
tсл - время сложения на сумматоре,
tсд -время
сдвига СЧП или множимого. Но при умножении со сдвигом множимого сдвиг множимого
в Рг2 и сложение в СМ можно совместить во времени, т.к. сдвиг осуществляется
намного быстрее, чем сложение. В этом случае Ty=n(р0tсд+р1tсл), где р0
- вероятность появления нуля в анализируемом разряде множителя (р0=0,5).
Таким образом, умножение со сдвигом множимого экономичнее по времени.
Пример - Умножить числа
А=-6 и В=+5 в прямом
двоичном коде (младшими разрядами вперед со сдвигом суммы).
Решение: A=1.110п.к. , B=0.101п.к.
Знак произведения 3HZ=3H
A![]() 3H
B=1
3H
B=1![]() 0=1.
0=1.
Исходная СЧП 000000 Множитель
101
+110 .
1-я СЧП 110 000
Сдвинутая 1-я СЧП 011
000
Сдвинутая 2-я СЧП 001
100
+110
![]() 3-я СЧП 111 100
3-я СЧП 111 100
Сдвинутая 3-я СЧП
011 110
Ответ: [A* B] п.к. =1.011 110.
При умножении чисел с
плавающей запятой исходят из того, что произведение двух чисел A=MAQPA и
B=MBQPB
равно:
Z=MZQPZ = MA * MB * QPA +PB.
Отсюда видно, что
порядок произведения Pz равен
сумме порядков сомножителей Pz =PA+PB, а
мантисса произведения Mz равна произведению мантисс
сомножителей Mz =MA*MB.
Перемножение мантисс
выполняется аналогично умножению чисел, представленных в естественной форме с
фиксированной точкой. Порядок произведения определяется путем алгебраического
суммирования порядков сомножителей. В общем случае операция умножения чисел с плавающей
запятой состоит из следующих этапов:
- определяется знак
произведения путем сложения по модулю 2 знаковых разрядов
мантисс сомножителей;
- определяется порядок
произведения путем сложения порядков множимого и множителя;
- выполняется умножение мантисс одним из
известных методов;
- производится нормализация результата.
Методы ускорения операций умножения. На выполнение операции умножения приходится примерно
70% времени выполнения операций в ЭВМ. Поэтому в настоящее время разработано и
используется достаточно много методов ускорения умножения. Ниже рассматриваются
наиболее распространенные.
Умножение с анализом
нескольких разрядов множителя. Одним
из методов ускорения умножения является сокращение шагов умножения за счет
анализа на каждом шаге нескольких (q) разрядов множителя: умножение с анализом
двух разрядов множителя, трех разрядов множителя и т.д. Каждая группа разрядов
расшифровывается независимо друг от друга, как обычное двоичное слово. Считая
множитель условно целым, получают при расшифровке одно из чисел 0, 1, 2,..., 2q
-1 и в качестве очередного слагаемого, в этом случае, используется сдвинутое
необходимым образом, относительно текущей суммы частичных произведений одно из
2q кратных множимого А: 0, 1А, 2А, 3А,..., (2q-1)А. Те кратные кА, для которых
к - четно, можно получить простым сдвигом А на к/2 разрядов влево, а для
нечетных к кратные множимого кА формируются путем выполнения операции
суммирования (к-1)А+А, где (к-1) - четно.
Кратные множимого кА
формируются в начале умножения с использованием одного и того же сумматора, что
приводит к дополнительным временным затратам, и хранятся в дополнительном блоке
регистров, который вводят в состав АУ. Можно уменьшить необходимое количество
кратных кА, что приведет к уменьшению временных затрат и блока регистров, а в
случае q=2 надобность в предварительном получении кА вообще отпадает. Для этого
при расшифровке очередной группы из q-разрядов множителя учитывается
дополнительно разряд соседней группы. Если в двоичном коде множителя имеется
подряд несколько единиц начиная с к-го разряда по m-ый разряд (к и m-веса разрядов), то эту группу единиц
можно представить как ![]() .
Тогда
.
Тогда ![]() (0111110 = 1000000-000010
(0111110 = 1000000-000010 ![]() =1000010), т.е. осуществляется переход к системе с
цифрами 1,0,-1. Это позволяет вместо
умножения на несколько единиц, следующих друг за другом в множителе, выполнять
умножение всего на две единицы 1 и -1 (одно сложение и одно вычитание), что
порождает два варианта умножения:
=1000010), т.е. осуществляется переход к системе с
цифрами 1,0,-1. Это позволяет вместо
умножения на несколько единиц, следующих друг за другом в множителе, выполнять
умножение всего на две единицы 1 и -1 (одно сложение и одно вычитание), что
порождает два варианта умножения:
а) если в группе одна
единица находится между двумя нулями (00100), то m+1=k+1 и 2m+1-2к=2
к+1 -2 к =2 к, что приводит к необходимости
прибавления множимого с учетом веса того разряда множителя, в котором находится
единица;
б) если в группе
разрядов один нуль находится между двумя единицами (1101...), то вес разряда, в
котором находится нуль равен к и
тогда -2 к+1 -2 к =-2 к, что приводит к
необходимости вычитания множимого с учетом веса разряда множителя, в котором
находится нуль. Исходя из изложенного выше видно, что сложение и вычитание
множимого при умножении на к-ый разряд выполняется лишь в том случае, когда в
множителе происходит смена цифр (с нуля на единицу или с единицы на нуль). Для
определения знака арифметического действия надо знать цифру последующего
разряда, чтобы определить, разделяет ли анализируемая цифра группу нулей (или
группу единиц) или начинает собой последовательность единиц (или
последовательность нулей). При расшифровке группы разрядов с учетом
дополнительного разряда соседней группы и появляется возможность совместного рассмотрения
предыдущего разряда, анализируемого разряда и последующего разряда. При таком методе расшифровки группы
разрядов старший разряд соседней младшей группы рассматривается как
дополнительный младший разряд. В процессе умножения он будет участвовать в
расшифровке группы разрядов дважды: один раз как старший разряд этой группы,
второй - как дополнительный разряд соседней старшей группы.
Известен и другой
вариант умножения с анализом нескольких разрядов и учетом дополнительного
разряда из предыдущей группы разрядов. В этом варианте дополнительный разряд
формируется в процессе расшифровки предыдущей группы разрядов в виде переноса в
последующую группу разрядов. Перенос может равняться нулю или единице и
образуется при переходе в систему с цифрами 1,0,-1. Умножение на два разряда
множителя (q=2) с учетом переноса из предыдущей пары разрядов с младших
разрядов множителя со сдвигом суммы и переходом к системе с цифрами 1,0,-1
описано ниже. Значения разрядов группы двух младших разрядов множителя могут
быть 00, 01, 10, 11. При значении пары разрядов 00 множимое не суммируется с
сумой частичного произведения, а производится простой сдвиг на два разряда
вправо СЧП. В случае пары 10 к СЧП прибавляется одинарное множимое и СЧП
сдвигается вправо на два разряда. Если значение анализируемой группы разрядов
11, то комбинация рассматривается как 11=100-001=10-1, что означает запоминание
единицы переноса в следующий такт и вычитание на данном такте множимого из СЧП
с последующим сдвигом полученного СЧП на два разряда вправо.
При умножении этим методом
единицу переноса запоминают в триггере коррекции /ТГК/, который будет входить в
состав соответствующих арифметических устройств и учитывают при анализе
следующей группы (пары) разрядов множителя. При ТГК=1, если следующая 00, то
она рассматривается как 01, если 01, то - как 10, если 10, то - как 11 (и
запоминание в ТГК единицы) и, наконец, если 11, то - как 00 (и в триггере ТГК
запоминается единица).
Пример -
Найти произведение двух чисел А=-0.100101 и В=-0.100011, используя ускоренный метод умножения с анализом двух разрядов множителя.
Решение: [А] п.к.=11,100101, [В] п.к. =11,100011
При умножении под знак отводится два разряда из-за возможной его потери
при сдвиге СЧП влево.
[-А]п.к.=00,100101, [В]д.к.
=11,011101,
[А]д.к.=11,011011, [2А]д.к.=10,110110.
Множимое: 11,011011
Множитель: 11,011101
Исходная СЧП
00,000000000000 01
+ 11,011011 [А]д.к.
ПерваяСЧП 11,011011000000
Сдвинутая на 2 разряда
1-я СЧП 11,110110110000 11,
ТГК=1
+ 00,100101 [-А]п.к.
Вторая СЧП
00,011011110000
Сдвинутая на 2 разряда
2-я СЧП 00,000110111100 01+1=10
+10,110110 [2А]д.к.
Третья СЧП 10,111100111100
Сдвинутая на 2 разряда
3-я СЧП 11,101111001111 11
+00,100101 [-А]п.к.
4-я СЧП 00,010100001111
Ответ: [А*В]пр =0,010100001111.
Изложенные
выше принципы ускорения умножения
реализованы в различных методах ускорения умножения, которые широко применяются
в современных ЦУ.
Контрольные
вопросы
1. Перечислите
методы умножения чисел в двоичной системе счисления и сформулируйте правила
выполнения операции умножения для каждого метода (умножение чисел с
фиксированной запятой).
2. Приведите сравнительные характеристики четырех вариантов умножения.
3. Назовите методы ускорения операции умножения, сформулируйте правила использования
данных методов.
4. Сформулируйте правила выполнения операции умножения чисел с плавающей
запятой.
5. Приведите структуры операционного автомата для умножения
младшими разрядами вперед и старшими разрядами вперед со сдвигом множимого.
4 Деление чисел в двоичной системе счисления
При делении по заданному делимому А и делителю В определяется частное Z
= А/В. Очевидно, что В≠0, так как деление на нуль не имеет смысла.
Вследствие того, что в
цифровой машине наиболее часто применяется такое представление числа, когда оно
меньше единицы, то на делимое, делитель и частное накладываются дополнительные
ограничения: |A|<1, |В|<1, |Z| < 1.
Из последнего
неравенства следует, что во избежание переполнения должно выполняться
неравенство | A |<| В |.
Если результат деления
из-за соотношений величин делимого и делителя получается больше единицы, то
операция не выполняется. При этом вырабатывается сигнал «Переполнение» или «Ошибка». При делении
чисел в прямых кодах в операции участвуют модули делимого и делителя. Знак
частного (как и при умножении) определяется как сумма по модулю 2 знаков
делимого и делителя, а модуль частного – как частное от деления модуля делимого
на модуль делителя.
Процесс деления состоит
из последовательности операций вычитания делителя из делимого, а затем из
образующихся остатков, предварительно сдвинутых на каждом шаге деления влево на
один разряд. Если очередной остаток положительный, то в разряд частного
записывается единица, если остаток отрицательный – нуль. При вычитании
используются дополнительный или обратный коды делителя. Процесс вычитания
повторяется, количество повторений определяется разрядностью частного.
В зависимости от того,
какие действия производятся после получения очередного отрицательного остатка
для определения следующего значения разряда частного, различают методы деления
с восстановлением и без восстановления остатков.
При первом методе
предыдущий остаток восстанавливается путем суммирования модуля делителя |В|
к отрицательному остатку Ri, т.е. (Ri + |В|). Для
получения очередного разряда частного восстановленный остаток сдвигается на
один разряд влево (т.е. удваивается) и из него вычитается делитель 2· (Ri +|В|) – |В|.
При втором методе
отрицательный остаток сдвигается на один разряд влево и к нему прибавляется
делитель 2Ri + |В|, т.к. 2 (Ri +|В|)
- |В|= 2Ri + |В|.
При выполнении операции
деления результат получается одинаковым, если сдвигать остатки деления влево
при неподвижном делителе, либо сдвигать делитель вправо при неподвижном остатке
от деления. Таким образом, возможны четыре варианта выполнения операции
деления: деление с восстановлением (без восстановления) остатков со сдвигом
делителя вправо при неподвижном остатке от деления; деление с восстановлением
(без восстановления) остатков со сдвигом остатков влево при неподвижном
делителе.
Алгоритм деления
двоичных чисел без восстановления остатков сводится к выполнению следующих
действий:
а) проверяется на нуль
делитель и, если он равен нулю, формируется признак переполнения разрядной
сетки и завершается выполнение операции;
б) определяется знак
частного;
в) вычитается из
делимого делитель: если результат (остаток)
R0 ≥ 0, то операция завершается (происходит
переполнение разрядной сетки);
г) делитель двигается
вправо на один разряд или полученный остаток Ri удваивается путем сдвига его влево на один
разряд;
д) если Ri
< 0 , то в частное записывается 0 и делитель прибавляется к остатку, а если
Ri > 0, то очередная цифра частного равна 1 и делитель вычитается
из остатка;
е) пункты 4 и 5
повторяются до получения (п + 1)-й цифры частного;
ж) частное округляется
и ему присваивается знак.
Ниже приведена структура
операционного устройства для деления чисел с восстановлением и без восстановления остатков (рис.7) со
сдвигом остатков.
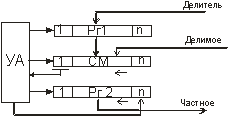
Рисунок 7 – Деление
чисел со сдвигом остатка
Анализ вариантов схем деления
показывает, что деление со сдвигом остатков по аппаратурным затратам является более экономичным, по сравнению с
делением со сдвигом делителя: общая разрядность регистров и СМ в первом
варианте равна приблизительно 5п, во втором - 3п . Время выполнения операции деления со сдвигом
суммы: Tg = (n+1)(
tсл +
tсд ), где (п+1) - разрядность частного вместе со знаком ,
tсд - время сдвига суммы в СМ ,
tсл - время, необходимое для суммирования (вычитания) делителя к остатку. При оценке времени деления со сдвигом
делителя
tсл можно пренебречь , так как
tсд
<
tсл и сдвиг делителя в Рг 1 можно
совместить во времени с выполнением операции суммирования (вычитания) в СМ.
Тогда Tg = (n+1)
tсл . Таким образом, деление со сдвигом делителя менее экономичен по аппаратурным
затратам, но является более быстродействующим.
Пример - Разделить без восстановления
остатков делимое А= +0,1001 на делитель
В =-0,1011.
Решение: | A | = 0.1001, | B | = 0.1011.
Знак частного: 0
Å 1=1.
| A |
= 0.1001 Пояснения
+
1.0101
[-|В|]д.к. (пробное вычитание)
В псевдознаковый
разряд 1.1110
остаток R0
< 0
частного
записывается 0 1.1100 сдвиг R0 влево
+ 0.1011
[+|В|] (суммирование делителя)
В 1-й старший
разряд 0.0111 остаток R1
> 0
частного записывается
1 0.1110 сдвиг R1 влево
+
1.0101 [-|В|]д.к. (вычитание делителя)
Во 2-й разряд 0.0011 остаток R2
> 0
частного записывается
1 0.0110 сдвиг R2 влево
+ 1.0101
[-|В|]д.к. (
вычитание делителя)
В 3-й разряд 1.1011
остаток R3
< 0
частного записывается
0 1.0110
сдвиг R3 влево
+ 0.1011
[+|В|] (суммирование делителя)
В 4-й разряд
0.0001 остаток R4
> 0.
частного записывается
1
Ответ:
[А : В]п.к.
= 1.1101 .
Деление чисел с плавающей
запятой (точкой) выполняется по
следующим соотношениям:
Z=A/B=MAQPA / MBQPB = (MA / MB )QPA
-PB.
Отсюда видно, что при
делении чисел с плавающей запятой порядки вычитаются (РА – РВ),
а мантиссы делятся (MZ = MA / MB).
Разность порядков
определяется как РZ = РА
+(– РВ) и выполняется аналогично алгебраическому сложению
чисел, представленных в естественной форме с фиксированной точкой. Деление
мантисс выполняется аналогично делению чисел, представленных в естественной
форме с фиксированной точкой.
В общем случае операция
деления чисел с плавающей запятой состоит из следующих этапов:
а) определяется знак частного
путем сложения по модулю 2 знаковых
разрядов мантисс чисел;
б) определяется порядок
частного путем вычитания из порядка делимого порядка делителя;
в) производится деление
модулей мантисс одним из известных методов;
г) производится
нормализация результата путем сдвига ненормализованной мантиссы частного и
изменения полученного порядка частного.
Ускорение операции
деления. Методы ускорения операции
деления можно разбить на две группы: формирование нескольких цифр частного на
каждом шаге деления, выполнение операции деления через умножение или с
использованием другой процедуры.
Одновременное
определение нескольких цифр частного.
В основе методов этой группы лежит следующая идея. Если на каком-то шаге
деления получен остаток Ri , либо достаточно малый, либо достаточно близкий
делителю В по абсолютной величине, то можно определить сразу несколько цифр
частного. В случае малости остатка Ri ( к нулевых старших разрядов)
при делителе, равном 0,1… в частное можно записать сразу к нулей,
сдвинуть остаток на к разрядов влево,
вычесть делитель и продолжать деление дальше.
Если же остаток и
делитель имеют к одинаковых старших
цифр (близки по абсолютной величине),
то в частное можно записать сразу к единиц,
без сдвига остатка произвести вычитание из него делителя, затем сдвинуть
полученный результат влево на к
разрядов, прибавить делитель и продолжать деление дальше.
Ускорение наблюдается
только в указанных выше двух случаях.
Развитием изложенной
выше идеи является метод одновременного определения двух цифр частного: остаток
сдвигается сразу на два разряда и из сдвинутого остатка вычитается делитель.
Вычитание производится до тех пор, пока не получится отрицательный остаток, что
является признаком окончания шага деления. Если при первом вычитании сразу
получился отрицательный остаток, то в частное записывается 00. Если отрицательный остаток получился после
второго вычитания, то в частное записывается 01, после третьего вычитания в
частное записывается 10 и после четвертого 11.
Алгоритм прост по
логике, но требует для одновременной проверки всех четырех условий
значительного усложнения арифметического устройства путем введения: цепей сдвига для передачи делителя В и 2В прямым
и инверсным кодом, регистра для формирования и хранения утроенного делителя 3В,
цепей для передачи 3В прямым и инверсным кодом, трех сумматоров.
Этот алгоритм можно
упростить, если каждую пару цифр частного определять, исходя из анализа
нескольких старших разрядов делителя В
и сдвинутого остатка 22
·Ri-1. При этом, если старшие разряды остатка 22 ·Ri-1 совпадают со старшими разрядами делителя В,
то предполагается, что 22·Ri-1 принадлежит к области с наибольшим значением пары цифр частного и
исходя из этого находится остаток Ri. Но здесь возможно получение
отрицательного остатка Ri . Это означает, что получена величина
остатка, уменьшенного на В и удовлетворяющего условию: - В ≤ Ri' = Ri - В
< 0. Чтобы не восстанавливать Ri'
< 0 , на следующем шаге производится коррекция остатка следующим образом:
если раньше проверялось условие кВ
≤ 22 ·Ri-1 < ( к+1)В, где
к = 0 , 1 , 2 , 3, то теперь должно проверяться эквивалентное ему
условие ( к-4)В ≤
22 ·(Ri-1 – В) < ( к-3 )В, т.к. (- В),
уменьшающий величину остатка, после сдвига остатка влево на 2 разряда
увеличится в 4 раза (- 4В) и при
проверке условий эту составляющую надо учитывать.
Пример
- Найти
Z = А : В по методу
одновременного определения двух цифр частного при А = +0,10001111 и В = -0,1011.
Решение: [A]n.к. =
0.10001111 , [B]n.к. =
1.1011 ,
| B | =
0.1011, | A | = 0.100001111, [-| B |]д.к.
= 1.0101.
Знак частного: 0
Å 1=1.
Выполняется деление модуля делимого на модуль
делителя, под знак отводится три разряда из-за возможности его потери при
сдвиге остатка влево на два разряда.
000.10001111
| A | (R0 )
010.00111100
сдвинутый влево R0
+ 101.1111 [-| 3B |]д.к.
000.00101100 R1
> 0
000.10110000 сдвинутый влево R1
+ 111.0101 [-| B |]д.к.
000.00000000 R2 = 0
Первый раз выполняется операция (22 ·R0 –3В), т.к.
старшие разряды (второй и третий) остатка 22 ·R0 совпадают со старшими разрядами делителя В,
что дает возможность предполагать максимальную определяемую пару цифр
частного 11. Второй раз выполняется
операция (22 ·R1 – В), т.к. старшие разряды остатка 22
·R1 нулевые, а старший
разряд В равен единице, что дает возможность предполагать пару цифр
частного 00 или 01.
Ответ: [A : В]n.к.
= 1.1101.
Контрольные
вопросы
1. Перечислите
методы деления чисел в двоичной системе счисления.
2. Сформулируйте правила выполнения операции деления для каждого метода (деление
чисел с фиксированной запятой).
3. Приведите сравнительную характеристику четырех вариантов деления.
4. Назовите методы ускорения операции деления, сформулируйте правила
использования данных методов.
5. Сформулируйте правила выполнения операции деления чисел с плавающей
запятой.
5 Комбинационные схемы
Любое устройство можно
рассматривать в виде, имеющем п-входов и m-выходов. При m=1
устройство является одновыходной схемой, в противном случае
- многовыходной.
На вход устройства поступают
входные слова, составленные из символов входного алфавита Х={х1, х2,
... , хп }, на выходе
- выходные слова, составленные из символов выходного
алфавита У={у1,
у2, ... , уm } . При n-входах и m- выходах
длина входного слова
- n, длина выходного слова
- т. Общее число различных входных и выходных сигналов конечно в виду
конечности алфавитов и конечности входных и выходных слов.
Если работа устройства
в момент времени
ti полностью определяется входным
словом, поступившим в момент времени
ti, то устройство называется
комбинационной схемой или конечным автоматом без памяти.
Конечные автоматы без
памяти являются наиболее простыми логическими устройствами (выходное слово
определяется только входным словом) и работа их описывается булевскими
выражениями. Поэтому можно сказать, что булевы функции являются математическими
моделями комбинационных схем.
При этом моделью
одновыходной схемы является булевское уравнение у= f(х1, х2,
... , хп ), а моделью многовыходной схемы является система
булевских уравнений
у1 =
f1(х1, х2,..., хi,..., хп );
. . . . . . . . . . . . . . . . . . .
уj =
fj(х1, х2, ... , хi,..., хп
);
. . . . . . . . . . . . . . .
. . . .
уm =fm(х1, х2, ... , хi,..., хп
).
При проектировании комбинационных
схем приходится решать задачи их синтеза и анализа.
Синтез комбинационных схем. Этапы синтеза комбинационных схем:
а) по физическому
описанию составляется математическое описание (система булевских уравнений);
б) по математическому описанию составляют функциональную схему,
предварительно решая задачу минимизации;
в) по функциональной
схеме составляют принципиальную схему.
Математическая модель
комбинационной схемы – это представление ФАЛ в виде совершенной дизъюнктивной
нормальной формы (СДНФ): дизъюнкции конъюнкций переменных по наборам, на
которых выходная функция равна единице. Составляется для каждого набора
конъюнктивный терм (минитерм), связывающий переменные x1, x2,
... , xn
, представленные в прямой или инверсной форме, знаком конъюнкции. Терм
должен обращаться в единицу только на одном наборе, а на остальных наборах
- в нуль. Для этого те переменные, которые в указанном
наборе равны нулю, берутся со знаком инверсии, остальные
- без знака инверсии.
Если
ai
- значение переменной xi в
наборе, то в общем виде можно записать
 , где
, где ![]() , если
ai = 0 и
, если
ai = 0 и ![]() если
ai = 1.
если
ai = 1.
В случае наличия
нескольких наборов, на которых логическая функция обращается в единицу, необходимо
составить такие конъюнкции для каждого набора, которые объединяются знаком
дизъюнкции. В результате получается логическое выражение
- аналитическое представление булевой функции в виде
СДНФ
![]() ,
,
где ![]() - указание, что дизъюнкция берется только по тем
наборам, на которых функция принимает значение единицы.
- указание, что дизъюнкция берется только по тем
наборам, на которых функция принимает значение единицы.
Решая задачу
минимизации СДНФ, решают задачу получения минимальной комбинационной схемы. Для
получения кратчайшей или минимальной аналитической записи к СДНФ применяют
правила склеивания и поглощения.
Терм называется
элементарным, если в нем каждая переменная встречается не более одного раза.
Количество переменных, образующих терм, называется его рангом r. Два элементарных терма одинакового
ранга называются соседними, если они являются функциями одних и тех же
переменных и отличаются только знаком отрицания (инверсии) одной из переменных.
Правило склеивания для конъюнктивных термов. Дизъюнкцию двух соседних минитермов ранга r можно заменить элементарным минитермом ранга
r-1, являющимся общей частью
исходных термов (например, у = х1
х2 ![]() 3
Ú х1
х2 х3 = х1 х2).
3
Ú х1
х2 х3 = х1 х2).
Правило поглощения для конъюнктивных термов. Дизъюнкцию двух элементарных минитермов разных
рангов, из которых один является общей частью другого, можно заменить
минитермом, имеющим меньший ранг (например, у = х1 х2
х3
Ú х1
х2 = х1 х2).
Правила склеивания и
поглощения основываются на свойствах элементарных функций.
Пример - Получить МДНФ функции f( х1 , х2 , х3
) , если она принимает значение единицы на наборах 001 , 100 , 101 , 111.
Записывается СДНФ функции и преобразовывается
f ( х1 , х2 , х3 ) = ![]()
![]()
![]() х1 х2 х3
=
х1 х2 х3
= ![]() 2х3
Ú х1
2х3
Ú х1![]() 2
Ú х1х3 .
2
Ú х1х3 .
При анализе
комбинационных схем решается задача, обратная задаче синтеза, т.е. по имеющейся комбинационной схеме
необходимо составить ее математическую модель.
Логические элементы. Решая задачу синтеза комбинационной схемы, решают задачу реализации
булевых функций. Основой для реализации булевых функций являются логические
элементы. В настоящее время созданы логические элементы, которые реализуют все
основные элементарные функции алгебры логики. Функция дизъюнкции реализуется
элементом ИЛИ, функция конъюнкции
- элементом И, функция инверсии
- элементом НЕ, функция Шеффера
- элементом И-НЕ, функция Вебба
- элементом ИЛИ-НЕ. Булевы переменные и функции представляют собой
значения сигналов входов и выходов логических элементов. Существуют элементы,
выполняющие сложные логические функции. Например, элемент И-ИЛИ-НЕ реализует функцию ![]() На рисунке 8 представлены основные
логические элементы:
На рисунке 8 представлены основные
логические элементы:
а) элемент ИЛИ
(дизъюнктор);
б) элемент И
(конъюнктор);
в) элемент НЕ
(инвертор);
г) элемент И-НЕ;
д) элемент ИЛИ-НЕ.
а) б) в)



г) д)


Рисунок 8 - Основные
логические элементы
Отдельные логические элементы можно соединять в схемы. Соединенные
согласно булевскому выражению, они являются логической схемой (переключательной
схемой), в которой выход полностью определен значениями сигналов на входе, т.е. комбинационной схемой. При синтезе
комбинационных схем необходимо иметь функционально полный набор логических
элементов. Набор логических элементов является функционально полным, если он
реализует функционально полную систему ФАЛ.
Под системой логических элементов D
понимается некоторое множество логических элементов, реализующих элементарные
булевы операции на основе физических явлений. При этом подразумевается, что
число различных типов элементов из D ограничено, но не ограничено число
элементов каждого типа. Система элементов D характеризуется конечным набором
логических операций, определяющих типы элементов (базис системы), коэффициентом
объединения по входу I, коэффициентом разветвления по выходу U и
задержкой сигнала на элементе
Dt.
Если в качестве системы
булевых функций, реализуемой логическими элементами, выбраны {Ú,
Ù,
ù}, то говорят, что реализован булев базис.
Проектирование схем в булевом базисе осуществляется наиболее просто, т.к.
методы минимизации в основном ориентированы на булев базис. Если в системе
логических элементов реализованы функции Шеффера, Пирса (И-НЕ, ИЛИ-НЕ), то говорят, что реализован одноэлементный базис
(универсальный).
Существуют также
системы логических элементов, реализующие смешанный базис. В случае не булевых
базисов обычно схема описывается математически в булевом базисе, минимизируется
в нем, а затем осуществляется переход к заданному базису.
Пример - Ниже будет
рассмотрен пример синтеза одноразрядного сумматора. Одноразрядный
комбинационный сумматор представляет собой схему с тремя входами и двумя
выходами. Три входа для приема i-го разряда исходных чисел (ai и bi)
и сигнала переноса из соседнего младшего разряда сумматора в данный разряд (pi-1).
На двух выходах одноразрядного сумматора формируются i-ый разряд суммы (Si)
и сигнал переноса в соседний старший разряд (Pi). Булевы функции Si
и Pi можно задать таблично в виде таблицы истинности (см.
таблицу 4). По данной таблице с учетом
наборов переменных, на которых функции Si и Pi принимают значения равное 1,
составляем совершенные дизъюнктивные нормальные формы (СДНФ) и минимизируем их.
![]() ,
,
![]()
По
полученным уравнениям строится
логическая схема в базисе И, ИЛИ, НЕ.
Таблица
4
|
аi |
bi |
p1 |
pi-1 |
Si |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |

Рисунок 9 - Схема полного одноразрядного сумматора в
базисе И, ИЛИ, НЕ
Контрольные вопросы
1. Дайте определение
логического элемента.
2. Приведите обозначения
основных логических элементов.
3. Дайте определение
комбинационной схемы.
4. Что собой
представляют модели комбинационных схем?
5. В чем заключаются
задачи анализа и синтеза комбинационных схем?
6 Цифровые устройства с памятью
В большинстве случаев
работа цифрового устройства в момент ti
определяется не только входным словом в момент времени ti, но
и зависит также от входных слов, поступивших в предыдущие моменты времени.
Такое цифровое устройство является автоматом с памятью (часто называют просто
конечный автомат). Конечные автоматы изучаются в теории автоматов.
Качественно новый этап в проектировании цифровых устройств начался с развитием
теории автоматов. Общая теория автоматов делится на абстрактную и структурную
теории автоматов.
Абстрактный автомат. Абстрактная теория автоматов не рассматривает
структуру автомата, его входных и выходных сигналов. Состояния автомата,
входные и выходные сигналы обозначаются буквами алфавита.
Для
абстрактного конечного автомата определены конечные алфавиты: входной алфавит
X={x1, x2,…, xF}, выходной алфавит Y={y1,
y2,…, yG} и алфавит состояний A={a1, a2,…,
aM}. Число входных сигналов конечно и они рассматриваются как
причина перехода из одного состояния в другое a(t-1)®a(t). Число выходных сигналов конечно и каждому
отличному от нуля моменту автоматного времени соответствует выходной сигнал
y(t). Выходной сигнал y(t) может появиться во времени только после входного
сигнала x(t), соответствующего этому же моменту времени, в момент перехода из
состояния a(t-1) в a(t) или после перехода. В первом случае y(t) однозначно определяется парой a(t-1) и x(t). Во
втором случае y(t) определяется только a(t). Для любого данного автомата всегда
имеет место одна из двух возможностей. Поэтому различают автоматы 1 рода
(автоматы Мили) и 2 рода (автоматы Мура). Абстрактные автоматы являются
математическими моделями реальных физических устройств и задаются в виде
совокупности шестёрки объектов: конечного множества X входных сигналов (входной
алфавит); конечного множества Y выходных сигналов (выходной алфавит); множества
A, называемого множеством состояний автомата; a0ÎA (начальное состояние автомата) и двух функций:
d(a,x) и
l(a,x), задающих однозначные
отображения множества пар (a,x), где aÎA и xÎX, во множества A и Y. Функция
d(a,x) называется функцией переходов автомата, а функция
l(a,x) – функцией выходов. Если автомат задан функцией
выходов, то это автомат 1 рода (Мили), сдвинутой функцией выходов – 2 рода
(Мура).
Для
автомата 1-го рода a(t) =
d (a (t-1), x(t)); y(t) =
l (a (t-1), x(t)).
Для автомата 2-го рода a(t) =
d (a
(t-1), x(t)); y(t)=
l (a(t), x(t)) =
l (a(t)).
Для
задания автоматов могут использоваться два типа языков: начальные и стандартные
(автоматные языки). В стандартных языках задания автоматов функции выходов и
перехода задаются в явном виде. В начальных языках эти функции в явном виде не
задаются и поэтому они называются языками описания цифровых автоматов.
В качестве стандартных
языков задания автоматов используются таблицы переходов и выходов, матрицы
переходов, таблицы включений, диаграммы переходов и т.д. Наиболее
распространёнными являются табличный способ задания с помощью таблиц переходов
и выходов и графический способ задания в виде графа.
При табличном способе
задания автомата Мили описание работы автомата задаётся таблицей переходов и
выходов, в которых строки обозначаются входными сигналами xf (f=1,2,…,F), а столбцы –
состояниями am (m=1,2,…,M). На пересечении f-й строки и m-го столбца
в таблице переходов записывается функция переходов d(am,xf)=as, в таблице выходов
- функция выходов
l(am,xf)=yg (g=1,2,…,G). Для задания автомата Мили необходимо задать ещё
начальное условие a0 О A (обычно a0=a1).
Для задания автоматов Мура удобно
пользоваться одной отмеченной таблицей
переходов, в которой каждому столбцу, помимо состояния приписывается ещё и
выходной сигнал, соответствующий этому состоянию.
При
графическом способе задания автоматов, описание работы автомата задаётся в виде
ориентированного связного графа, вершины которого соответствуют состояниям
автомата, а дуги – переходам между
ними. Две вершины am и as графа автомата связаны между
собой дугой, направленной от am к as, если в автомате
имеется переход от состояния am к состоянию as, т.е. если
d (am, xf) = as при некотором xf О
X. Дуге (am,as) графа автомата Мили приписывается входной
сигнал xf и выходной сигнал yg, если он определён, в
противном случае ставится прочерк. Граф автомата Мура отличается от графа автомата Мили тем, что выходной сигнал yg
приписан вершине графа.
Существуют
неполностью определенные автоматы (частичные), в которых функции переходов и
выходов заданы не для всех пар (a,x).
Автоматы реализуют
отображения входных слов в выходные слова. Два абстрактных автомата с
одинаковыми входными и выходными алфавитами называются эквивалентными,
если они реализуют одинаковые алфавитные отображения X в Y (X®Y). Из этого
определения видно, что автомат Мура и автомат Мили могут быть эквивалентны,
если удовлетворяются условия, указанные в определении эквивалентных автоматов.
Переход от автомата Мура к эквивалентному автомату Мили и от автомата Мили к
эквивалентному автомату Мура называется взаимной транспозицией автоматов.
Транспозиция автоматов
Мили в автоматы Мура, как правило, приводит к увеличению числа состояний
автоматов, в то время как транспозиция автоматов Мура в автоматы Мили не
увеличивает число состояний автоматов.
Существование
эквивалентных автоматов делает возможным решение задачи минимизации внутренних
состояний автомата. В основе алгоритма минимизации полностью определённых
автоматов Мили лежит идея разбиения всех состояний исходного абстрактного
автомата на попарно непересекающиеся классы эквивалентных состояний и замене
каждого класса эквивалентности одним состоянием. Получающийся минимальный
автомат будет иметь столько внутренних состояний, на сколько классов
эквивалентности разбиваются состояния исходного автомата. В один класс
эквивалентности объединяются эквивалентные (неразличимые) состояния. Состояния
am и as являются эквивалентными (am ғ as), если реакция
автомата в состоянии am совпадает с реакцией в состоянии as
на всевозможные входные слова. В этом случае можно считать одно из этих
состояний избыточным, т.к. состояние am можно заменить на состояние
as или наоборот, а реакция автомата на всевозможные входные слова не
изменится. Более слабой эквивалентностью является k
- эквивалентность. Состояния am и as k
- эквивалентны, если
реакция автомата в состоянии am совпадает с реакцией автомата в
состоянии as на всевозможные входные слова длины k.
Для определения
эквивалентности состояний необходимо начать с определения слабой
эквивалентности: 1–эквивалентности, 2–эквивалентности и т. д.
Два состояния
абстрактного автомата являются 1 – эквивалентными в том случае, если автомат,
находясь в любом из них, при подаче всякого входного сигнала выдаёт один и тот
же выходной сигнал. Объединение всех 1 – эквивалентных состояний образует 1
- класс эквивалентности. Разбиение на классы 1
- эквивалентных состояний будет в дальнейшем
обозначаться
p1.
Два 1
- эквивалентных состояния называются 2
- эквивалентными, если они переводятся любым входным
сигналом также в 1
- эквивалентные состояния. Объединение всех 2
- эквивалентных состояний образуют 2
- класс эквивалентности. Разбиение на классы 2
- эквивалентных состояний обозначается
p2.
Эти определения можно
распространить до k–эквивалентных состояний и до k
- классов эквивалентности (разбиение
pk). Признаком достижения разбиения на классы
эквивалентных состояний является выполнение условия, которое формулируется
теоремой, доказываемой в курсе высшей алгебры: если для некоторого k разбиение состояний автомата на
(k+1)
- классы эквивалентности
совпадает с разбиением на k
- классы эквивалентности, то оно является разбиением и на классы
эквивалентных состояний. Существенным является тот факт, что разбиение
множества состояний автомата на классы эквивалентных состояний может быть
получено за конечное число шагов.
Структурный автомат.
Структурная теория автоматов занимается
изучением структурных автоматов. Структурный автомат является дальнейшей
детализацией абстрактного автомата. В структурном автомате учитывается
структура входных и выходных сигналов, а также самого устройства.
При синтезе
структурного автомата необходимо выполнить переход от абстрактного автомата к
структурному автомату. При этом решаются две основные задачи: кодирование
входного X и выходного Y алфавитов, алфавита состояний A; определение системы
логических функций возбуждения Ur и выходов Wn, которая
является математической моделью комбинационной схемы автомата.
Для абстрактного
автомата задаётся входной алфавит X={x1, x2, … , xF}
и выходной алфавит Y={y1, y2, … , yG}, а также
алфавит состояний A={a1, a2,
… , aM}.
Каждый входной сигнал xf
ОX кодируется вектором (ef1,
… efp, … , efP), где efpО{0,1}, P і ]log2F[. Каждый
выходной сигнал ygОY
кодируется вектором (eg1, egn,, …, egN), где egnО{0,1}, N і ]log2G[. Каждое
состояние amОA кодируется
вектором (em1,
emr,… , emR), где emr О{0,1}, R і ]log2M[.
Удобно
структурный автомат представить в виде двух частей: памяти и комбинационной
схемы (см. рисунок 10), где T1,T2,…,TR - элементарные автоматы памяти
(хранение состояний), V1,V2,…,VR - сигналы обратной связи (информация о
состояниях), U1,U2,…,UN – сигналы для
переключения автомата из одного состояния в другое (функции возбуждения памяти).

Рисунок 10 - Структурный автомат в общем виде
На
этапе структурного синтеза автоматов предварительно выбираются элементарные автоматы,
из которых строится по заданному абстрактному автомату структурный автомат. При
этом используют два типа элементарных автоматов: автоматы с памятью
- элементы памяти и автоматы без
памяти
-
логические элементы. Элементарными автоматами называются автоматы, которые
заданы в одном и том же структурном алфавите. Наиболее распространённым структурным алфавитом является в настоящее
время двоичный алфавит.
Методы структурного синтеза автоматов теоретически
обосновываются теоремой о структурной полноте: всякая система элементарных
автоматов, содержащая автомат Мура, обладающий полнотой, и какую-либо
функционально полную систему логических элементов, является структурно полной.
При наличии структурно полной системы задача синтеза структурного автомата может
быть сведена к задаче синтеза комбинационной схемы.
Автомат Мура обладает полнотой, если он обладает
полнотой переходов и выходов. Полнота
переходов автомата Мура означает, что для любой пары состояний (bm,bs)
найдётся входной сигнал qf, который переведёт автомат из состояния bm
в состояние bs, т.е. в каждом столбце должны встречаться все
состояния автомата. Полнота выходов автомата Мура означает, что каждое
состояние отмечено своим, отличным от других, выходным сигналом di.
В таком случае число выходных сигналов равно числу состояний автомата Мура.
Следовательно, в автомате Мура с полной системой выходов можно отождествить
состояние автомата с его выходными сигналами. В связи с этим для состояний и
выходных сигналов в дальнейшем будут использоваться одни и те же обозначения,
т.е. отмеченная таблица переходов в автоматах Мура с полной системой выходов
превращается в таблицу переходов.
Противогоночное кодирование. Одной из задач
структурного синтеза автомата является задача кодирования состояний. При кодировании
различным состояниям автомата ставятся в соответствие различные двоичные коды.
Переход автомата из одного состояния в другое осуществляется за счёт изменения
состояний элементов памяти – триггеров.
При переключении элементов памяти возможно
возникновение состязаний из-за различия во времени их срабатывания.
Возникновению состязаний способствуют также различные задержки сигналов
возбуждения, поступающих на входы элементов памяти по логическим цепям, имеющим
неодинаковую длину. Если при переходе автомата из одного состояния в другое
несколько элементов памяти меняют своё состояние, то между ними начинаются состязания. Запоминающий
элемент, который изменит своё состояние раньше, чем другие элементы памяти,
может через цепь обратной связи изменить сигналы на входах некоторых
запоминающих элементов до того, как участвующие в состязании элементы изменят
своё состояние. Это может привести к переходу, непредусмотренному графом
автомата. Переходя из состояния am в состояние as под воздействием
входного сигнала xf автомат может оказаться в некотором
промежуточном состоянии ak, которое определяется тем, какой элемент
памяти выиграл состязание. Если автомат из состояния ak под
действием того же входного сигнала xf перейдёт в состояние as,
то состязания являются некритическими (допустимыми). Если же в этом автомате
есть переход под воздействием входного сигнала xf из состояния ak
в состояние al (al № as), то автомат может перейти в состояние al,
а не в as. Правильность работы автомата будет нарушена, поэтому
такие состязания называются критическими или гонками.
Существуют различные способы ликвидации
гонок в автоматах, в том числе и применение специальных методов кодирования.
Наиболее распространённым методом противогоночного
кодирования является соседнее кодирование, когда любые два состояния, связанные
дугой на графе, кодируются наборами, отличающимися только одной переменной. При
этом исключается возможность состязаний между элементами памяти, т.к. при
каждом переходе из состояния в состояние переключается один элемент памяти. Но
соседнее кодирование состояний возможно лишь при выполнении следующих условий:
- в графе автомата отсутствуют циклы с нечётным числом вершин;
- два соседних состояния второго порядка не имеют больше двух
состояний, лежащих между ними (состояниями второго порядка называются два
состояния, путь между которыми состоит из двух дуг).
При невыполнении этих условий соседнее кодирование
невозможно и можно применить противогоночное кодирование с развязыванием пар
переходов.
Если (a,b) и (g,d) – две пары двоичных кодов длины R, то они называются
развязанными, когда r-й разряд кода (1 Ә
r Ә R) принимает одно значение в паре (a,b) и противоположное
в паре (g,d). В противном случае пары двоичных
кодов называются связанными.
Алгоритм противогоночного кодирования с
развязыванием пар переходов предусматривает просмотр всех пар состояний,
связанных дугой перехода: (am,as), (ak,al)
и т.д. Если для этих пар имеется хотя бы один общий входной сигнал xf,
осуществляющий эти переходы, то разрядам кодов этих состояний (a,b) и
(g,d) присваиваются такие значения, чтобы пары
кодов состояний были развязанными хотя бы по одной переменной.
Такой подход к кодированию исключает гонки в
автомате, т.к. известна следующая теорема: в автомате, состояния которого
закодированы двоичными кодами конечной длины, гонки отсутствуют тогда, когда
для любых двух переходов (am,as)
и (ak,al) (as,al),
проходящих под действием одного и того же входного сигнала, соответствующие
пары кодов состояний развязаны.
Различные варианты кодирования состояний
автомата приводят к различным выражениям функций возбуждения памяти и функций
выхода, что приводит к изменению сложности комбинационной схемы.
Взаимодействие автомата с внешней средой. Существует
несколько моделей взаимодействия автомата с внешней средой: синхронная, асинхронная и согласованная.
В случае асинхронной модели автомат
взаимодействует с внешней средой только через входные сигналы z1,z1,…,zL,
поступающие из внешней среды, и выходные сигналы W1,W2,…,WN,
поступающие во внешнюю среду. Такая схема может функционировать, если все её состояния устойчивые. Состояние
as называется устойчивым, если для любого входного воздействия xfОX, такого, что функция
переходов d(am,xf)= as,
имеет место равенство d(as,xf)=as.
В асинхронном автомате все состояния устойчивые.
В синхронном автомате помимо входов z1,z1,…,zL
и выходов W1,W2,…,WN существует дополнительный
внешний вход p, по которому поступают синхроимпульсы СИ от генератора
синхроимпульсов (ГСИ) через равные промежутки
времени. Синхроимпульсы позволяют организовать переключение синхронного
автомата из одного состояния в другое через интервалы времени, равные периоду
следования СИ. В момент прихода СИ р=1 и p=0 при его отсутствии. Происходит
тактирование входных сигналов автомата импульсами p определённой длительности.
Переход из одного состояния в другое может происходить лишь при p=1. При этом
необходимо, чтобы длительность сигнала p (tp) была меньше самого
короткого пути прохождения тактированного сигнала обратной связи по
комбинационной схеме, что позволяет избежать явление гонок в автомате.
Потактная работа автомата может
осуществляться как путём непосредственного тактирования входных сигналов, так и
использованием элементов памяти (триггеров) с дополнительными синхровходами, на
которые и осуществляется подача СИ с ГСИ. В последнем случае осуществляется
тактирование функций возбуждения. Время между двумя соседними СИ называется
тактом работы автомата. Он определяется временем, необходимым для переключения
элементов памяти состояний (TП), временем на дешифрирование
состояний (ТД) и максимальным временем формирования выходных функций
или функций возбуждения (TВ).
Для автомата Мили такт работы Т=ТП+ТД+ТВ,
т.к. формирование функций возбуждения и функций выхода происходит параллельно.
Для автомата Мура такт работы Т= ТП+ТД+ТВ+ТВЫХ,
т.к. формирование выходных функций (ТВЫХ) происходит после
переключения элементов памяти, которое осуществляется при наличии сигналов со
схем формирования функций возбуждения ТВ.
В согласованной модели взаимодействия
автомата и внешней среды помимо входов z1,z1,…,zL
и выходов W1,W2,…,WN существует дополнительный
внешний вход G и дополнительный внешний выход R.
При сигнале G=1 входные сигналы z1,z1,…,zL
и могут быть считаны схемой автомата, т.е. сигналом G осуществляется своего
рода тактирование входных сигналов. Автомат реагирует на входные сигналы только
при G=1 (можно провести аналогии с сигналом p в синхронном автомате).
Выходные сигналы W1,W2,…,WN
могут быть считаны внешней средой лишь при наличии сигнала R=1.
Сигналы G=1 и R=1
должны поступать поочерёдно, т.к. после считывания автоматом из внешней среды
входных сигналов z1,z1,…,zL (G=1) им будут
выработаны выходные сигналы W1,W2,…,WN,
которые должны быть считаны внешней средой (R=1).
Из рассматриваемых
трёх моделей автомата наиболее надёжной является согласованная модель, наиболее
быстродействующей – асинхронная модель.
Контрольные вопросы
1. Дайте определение
конечного автомата.
2. Дайте определение
абстрактного автомата.
3. Перечислите объекты,
с помощью которых задается абстрактный автомат.
4. Задачи синтеза
структурного автомата.
5. Приведите общую
схему структурного автомата (в виде памяти и комбинационной схемы).
7 Стандартные элементы памяти – триггеры
При синтезе структурного автомата элементы
памяти обычно выбираются из некоторого набора типов стандартных элементов
памяти. Это упрощает синтез структурного автомата и его физическую реализацию.
Наиболее часто в качестве элементов памяти используются различные триггеры:
D-триггер, T-триггер, RS- триггер, JK-триггер.
Триггеры представляют собой
автоматы Мура, которые имеют два внутренних состояния, одно из которых
кодируется цифрой 1, другое – 0. Каждому внутреннему состоянию соответствует
свой выходной сигнал. Триггеры обладают полной системой переходов и выходов.
Так как у триггеров алфавит состояний совпадает с выходным алфавитом, то в
дальнейшем состояния и выходные сигналы триггеров в момент времени t будут
обозначаться Q(t). Обычно триггеры имеют два выхода: Q и инверсный ему ![]() .
.
Для описания функционирования триггеров
используются таблицы переходов и характеристические уравнения, задающие
зависимость Q(t+1) от Q(t) и входных сигналов. При использовании триггеров в качестве
элементов памяти структурного автомата необходимо составить для них таблицы
входов, представляющие собой функции входов (возбуждений): какой входной сигнал
должен быть подан на входы триггера, чтобы перевести его из одного состояния в
другое.
D-триггер (элемент задержки) имеет один
вход и два выхода. Он осуществляет задержку поступающего на его вход сигнала на
один такт. Условное обозначение D-триггера представлено на рисунке 11. На рисунке 12 представлены таблица
переходов и таблица входов D-триггера.

Рисунок 11 – Условное обозначение D-триггера
Таблица переходов Таблица входов
|
|
D(t) |
Q(t+1) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Рисунок
12 – Таблица переходов и таблица входов
D-триггера
Как видно из таблицы переходов состояние, в которое
переходит D-триггер, совпадает с его выходным сигналом. Характеристическая
функция D-триггера: ![]() .
.
T-триггер (триггер со счётным
входом) имеет один вход и два выхода. С
приходом входного сигнала, равного единице, T-триггер меняет своё состояние на
противоположное. Условное обозначение
T-триггера приведено на рисунке
13. На рисунке 14 представлены таблица переходов и таблица входов
T-триггера.

Рисунок 13 – Условное
обозначение T-триггера
Таблица переходов Таблица входов
|
|
T(t) |
Q(t+1) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
|
1 |
0 |
1 |
Рисунок 14 – Таблица переходов и таблица входов T-триггера
Характеристическая функция T-триггера:
![]() .
.
RS-триггер (триггер с раздельными
входами) имеет два входа (R – нулевой, S – единичный) и два выхода. Условное
обозначение RS-триггера приведено на рисунке 15. При поступлении
единицы на нулевой R–вход триггера, триггер переходит в состояние 1.
Одновременное поступление единицы на R – вход и S – вход (11) запрещено. На рисунке 16 представлена
таблица переходов и таблица входов RS-триггера.

Рисунок 15 – Условное
обозначение RS-триггера
Таблица переходов Таблица входов
|
|
R(t) S(t) |
Q(t+1) |
|
0 |
00Ú10 |
0 |
|
0 |
01 |
1 |
|
1 |
10 |
0 |
|
1 |
00Ú01 |
1 |
Рисунок 16 – Таблица переходов и таблица входов RS-триггера
Характеристическая функция RS-триггера:
![]() JK-триггер
(универсальный триггер) имеет два входа (J-единичный вход, K-нулевой вход) и два выхода. Условное
обозначение JK-триггера приведено на рисунке
17. При J=K=1 универсальный триггер работает
как триггер со счётным входом, при остальных входных комбинациях он работает
как RS-триггер. На рисунке 18 представлена таблица переходов и таблица входов RS-триггера.
JK-триггер
(универсальный триггер) имеет два входа (J-единичный вход, K-нулевой вход) и два выхода. Условное
обозначение JK-триггера приведено на рисунке
17. При J=K=1 универсальный триггер работает
как триггер со счётным входом, при остальных входных комбинациях он работает
как RS-триггер. На рисунке 18 представлена таблица переходов и таблица входов RS-триггера.

Рисунок 17 - Условное
обозначение JK-триггера
Таблица переходов Таблица входов
|
|
J(t) K(t) |
Q(t+1) |
|
0 |
00Ú01 |
0 |
|
0 |
10Ú11 |
1 |
|
1 |
01Ú11 |
0 |
|
1 |
00Ú10 |
1 |
Рисунок 18 – Таблица переходов и таблица входов JK -триггера
Характеристическая функция JK-триггера:
![]() .
.
DV-триггер имеет два входа
(D,V) и два выхода. Условное обозначение DV-триггера приведено на рисунке
5. При
V=1 триггер работает как элемент задержки, при V=0 триггер сохраняет текущее
состояние.

Рисунок 19 – Условное
обозначение DV-триггера
Таблица переходов Таблица
входов
|
|
D(t) V(t) |
Q(t+1) |
|
0 |
00Ú01Ú10 |
0 |
|
0 |
11 |
1 |
|
1 |
01 |
0 |
|
1 |
00Ú10Ú11 |
1 |
Рисунок 20 – Таблица переходов и таблица входов DV-триггера
При схемной реализации автоматов
используются триггеры с более сложной
организацией. Например, уже перечисленные триггеры, но имеющие дополнительно
синхровход C (синхронные триггеры). С помощью синхровходов осуществляется
синхронизация работы устройства. Входные сигналы проходят на вход триггера лишь
тогда, когда на синхровход C поступает сигнал C=1.
При синтезе структурного автомата на
D-триггерах таблица входов совпадает с таблицей переходов и выражения функций
возбуждения памяти составляются по таблице переходов автомата. Чем реже будут
встречаться единицы в таблице переходов, тем минимальнее будут выражения
функций возбуждения памяти и, следовательно, комбинационная схема автомата.
Поэтому при использовании D-триггеров в
качестве элементов памяти автомата можно применять следующий алгоритм
кодирования состояний:
а) состояние as, в которое
существует больше всего переходов, кодируется кодом 00…00;
б) следующие состояния, в которые существует
также большое количество переходов, кодируются кодами, содержащими одну
единицу: 00…01, 00…10,…01…00, 10…00;
в) для кодирования оставшихся состояний
сначала используют все двоичные коды, содержащие по две единицы, затем по три единицы
и т. д. До тех пор, пока не будут закодированы все состояния.
Таким образом, чем чаще встречается
состояние am в таблице переходов, тем меньше единиц должно быть в
его коде.
Для упрощения
выходных функций аналогичный подход можно применить и для кодирования выходных
сигналов yg: чем чаще встречается выходной сигнал yg в
таблице выходов, тем меньше единиц должен содержать его код. Это приводит к
минимизации той части комбинационной схемы автомата, которая формирует выходные
сигналы: ![]()
В том случае, когда таблица переходов не
совпадает с таблицей входов, описанный выше алгоритм кодирования не даёт
желаемого результата. Используются другие подходы к кодированию состояний.
Например, при использовании в качестве элементов памяти T-, RS-, JK- триггеров необходимо
кодировать состояния таким образом, чтобы суммарное число изменений состояний
элементов памяти на всех переходах состояний было минимальным, что можно
достичь используя соседнее кодирование.
Контрольные вопросы
1. Назовите стандартные
элементы памяти, приведите их обозначения.
2. Опишите работу RS,
JK- триггеров (таблицы переходов).
3. Опишите работу D, T
- триггеров (таблицы переходов).
4. Сформулируйте
алгоритм кодирования состояний при использовании в качестве элементов памяти D-триггеров.
5. Сформулируйте
алгоритм кодирования состояний при использовании в качестве элементов памяти T-, RS-, JK- триггеров.
8 Микропрограммные
устройства
При проектировании
любых цифровых устройств, в том числе и микропроцессоров, широко применяется
концепция микропрограммирования.
Концепция микропрограммирования предполагает, что преобразование
информации выполняется некоторым операционным устройством и включает следующие основные положения:
а) любое преобразование
информации рассматривается как сложное действие, которое разделяется на
последовательность элементарных действий над словами информации;
б) преобразование
описывается алгоритмом (микропрограммой) в терминах элементарных операторов,
называемых микрооперациями (МО), и элементарных предикатов, называемых
логическими условиями (ЛУ);
в) микропрограмма (МП)
определяет порядок выполнения МО и проверки ЛУ;
г) логические условия
принимают значения 1 (истина) или 0 (ложь) в зависимости от значений слов,
преобразуемых микрооперациями, и управляют порядком следования МО;
д) на основе МП
определяются структура и порядок функционирования устройства во времени.
Цифровые устройства,
построенные на основе МП называются
микропрограммными устройствами (МПУ).
В функциональном и
структурном отношении МПУ разделяется на две части: операционный автомат (ОА) и
управляющий автомат (УА). УА генерирует последовательность управляющих
сигналов, предписанную МП, и соответствующими значениями логических условий. ОА
служит для выполнения элементарных действий над словами информации, которые
определены этой последовательностью управляющих сигналов.
Функция ОА определяется
множеством входных слов D (данные), множеством выходных слов R (результаты),
множеством внутренних слов S, используемых для представления промежуточных
результатов, множеством МО Y={y1,y2,…,yN},
множеством ЛУ X={x1,x2,…,xL}. Функция ОА
задана, если заданы множества D, R, S, Y, X.
Словам
информации в ОА ставятся в соответствие регистры, разрядность которых совпадает
с разрядностью соответствующих слов. Любая МО yj выполняется над
словами информации (или их полями) и изменяет состояние регистров. Выполнение
микроопераций обеспечивается соответствующими комбинационными схемами ОА.
Микрооперация, определяющая элементарное действие, записывается в виде левой
части, знака присваивания (:=) и правой части. В правой части указываются
идентификаторы слов, которые являются операндами, в левой части – идентификатор
слова
- результата.
Для выполнения
преобразований над словами информации в ОА используются микрооперации
установки, передачи, инвертирования, сдвига, счёта, сложения, бинарные
логические, комбинированные. Ниже даны определения и приведены примеры
указанных МО.
МО установки
обеспечивают присвоение слову или его полю значения константы (например,
СМ:=0).
МО инвертирования
обеспечивают изменение значения слова или его поля на инверсное (например, ![]() ).
).
МО передачи выполняют
присваивание слову или его полю значения другого слова или поля слова
(например, Рг1:=Рг2, Рг2 (3ё15):=СМ(1ё13)).
МО сдвига служат для
изменения положения разрядов слова (поля) по отношению к начальному путём
перемещения каждого разряда на k-позиций влево или вправо (например, Рг1:=L(k)Рг1
- левый сдвиг содержимого Рг1, СМ:=R(k)СМ
- правый сдвиг содержимого СМ).
МО счёта обеспечивают
изменение значения слова на единицу (например, Сч:=Сч+1).
МО сложения служат для
присваивания слову значения суммы слагаемых (например, СМ:=Рг1+СМ).
Бинарные логические МО
присваивают слову или полю слова значение, получаемое поразрядным применением
логических операций (Ъ, Щ, Е) к соответствующим разрядам слагаемых (например, СМ(0ё1):=СМ(0ё1) Е Рг(0ё1)).
Комбинированные МО
содержат в себе несколько действий, присущих МО разного типа (например, СМ:=L(1)Рг1+Рг2).
Логические условия
вычисляются в операционном автомате в зависимости от значений слов (полей
слов), преобразуемых микрооперациями, и подаются в управляющий автомат в
качестве осведомительных сигналов xiОX.
Если несколько микроопераций (yt1, y t2,…, ytn)
реализуются в ОА одновременно, то они образуют микрокоманду Yt={yt1,
yt2,…, ytn}. Одновременно в ОА могут выполняться те МО,
которые структурно и функционально совместимы. МО называются структурно
совместимыми, если структура ОА допускает их параллельное выполнение.
Функциональная совместимость МО имеет место в том случае, когда результаты
выполнения микроопераций не зависят от последовательности их выполнения.
Функция
УА определяется структурой микропрограммы, функциональные операторы которой {y1,
y2,…, yN}=Y, а предикаты – {x1, x2,…,
x L}=X. Управляющие сигналы
yj, поступающие из УА в ОА и инициирующие МО, отождествляются
с МО yjÎY. Осведомительные сигналы xi, поступающие
из ОА в УА, отождествляются с ЛУ xiÎX. Функция УА задана, если задана микропрограмма с
множеством микроопераций Y и множеством логических условий X. УА, построенный
по микропрограмме, называется микропрограммным автоматом.
Для описания
микропрограмм могут использоваться начальные языки описания автоматов при условии
описания алгоритма функционирования автомата в терминах микроопераций и
логических условий.
Начальные языки
описания автоматов задают алгоритм их функционирования. Алгоритм
функционирования автомата задаётся в виде отображения входных последовательностей
в выходные последовательности, т.е. отображения множества слов во входном
алфавите X в множество слов в выходном алфавите Y.
Одним из
распространённых начальных языков описания автоматов является язык операторных
схем алгоритмов (ОСА). В настоящее время язык ОСА существует в трёх
модификациях: логические схемы алгоритмов (ЛСА), матричные схемы алгоритмов
(МСА), графические схемы алгоритмов (ГСА).
ГСА наиболее наглядны и
представляют собой графическую запись алгоритма. ГСА – ориентированный связный
граф, содержащий вершины четырёх типов: одну начальную, одну конечную,
операторные и условные вершины. ГСА удовлетворяет следующим требованиям:
а)
имеет одну начальную вершину с одним выходом и без входа;
б)
имеет одну конечную вершину с одним входом и без выхода;
в) содержит операторные вершины с одним входом
и одним выходом;
г) содержит условные вершины с одним входом и
двумя выходами;
д) вершины соединяются с помощью дуг,
направленных от выхода к входу (каждый выход соединяется с одним входом и любой
вход соединен, по крайней мере, с одним выходом);
е) один из выходов условной вершины может
соединяться с её входом, что недопустимо для операторной вершины;
ж) для любой вершины ГСА существует, по крайней
мере, один путь в конечную вершину;
з) в каждой условной вершине записывается xiÎX;
и) в каждой операторной вершине записывается
один или несколько yjÎY.
При использовании ГСА
для задания микропрограммы, X представляет собой множество логических условий
(x1, x2,…,xL), a Y-множество микроопераций (y1, y 2,…yN).
При составлении
микропрограммы в операторных вершинах ГСА записывается содержательное
обозначение микроопераций yjÎY в виде операторов присваивания, а в условных
вершинах – логические условия xiÎX в виде логических выражений. Функционально и структурно
совместимые МО записываются в одной операторной вершине и образуют микрокоманду
Yt. Такая ГСА называется содержательной.
Перечень микроопераций
и логических условий, входящих в содержательную ГСА, является исходной
информацией для синтеза операционного автомата МПУ.
В процессе
проектирования МПУ от содержательной ГСА переходят к кодированной ГСА, путём
выполнения кодирования микроопераций некоторыми символами yjÎY, логических условий
- символами xiÎX. В кодированной ГСА в операторных вершинах записываются
символы из множества Y, в условных
- символы из множества X.
Кодированные ГСА
являются исходной информацией для синтеза УА с жёсткой логикой или
программируемой логикой.
Контрольные вопросы
1..Дайте определение микрооперации, приведите
классификацию микроопераций.
2. Дайте определение
микрокоманды.
3. Дайте определение
МПА.
4. Назовите начальные
языки описания МПА.
5..Дайте определение ГСА (графические схемы
алгоритмов), сформулируйте требования, которым должны удовлетворять ГСА.
9 Интерпретационный метод
синтеза МПУ
Синтез управляющего
автомата осуществляется по кодированной ГСА. В результате получают УА,
вырабатывающий управляющие сигналы Y={y1, y2,…,yN},
порядок следования которых зависит от микропрограммы и значения логических
условий X={x1, x2, …, xL}. УА с жёсткой
логикой строится на базе использования логических элементов и элементов памяти.
Изменить алгоритм его работы нельзя, не изменяя соединений между элементами.
Интерпретация МП конечным автоматом с памятью
получила название интерпретационного метода синтеза УА. В интерпретационном
методе синтеза выделяют этап абстрактного
синтеза и этап структурного синтеза автомата.
Абстрактный синтез автомата. В интерпретационном методе синтеза к этапу абстрактного синтеза автомата
относится:
а) получение отмеченной
ГСА;
б) определение путей
перехода;
в) построение графа
автомата;
г) кодирование
состояний;
д) построение функции
выхода yjÎY;
е) построение функций
возбуждения с учётом выбранного элемента памяти;
ж) совместную
минимизацию функций возбуждения и функций выхода и построение схемы
структурного автомата.
Существуют некоторые
особенности выполнения интерпретационного метода синтеза, связанные с выбранной
моделью автомата (Мили или Мура).
Получение отмеченной ГСА при синтезе автомата
Мили осуществляется следующим образом:
а) вход вершины, следующей за начальной и
вход конечной вершины отмечаются символом a0;
б) входы всех вершин, следующих за
операторными, отмечаются символами a1, a2,…, aM;
в) входы отмечаемых вершин отмечаются
разными символами, за исключением конечной вершины, и не более одного раза.
Пути перехода определяются между двумя соседними отметками am
и as(amÎA, asÎA). Путь перехода от отметки am к отметке as
в направлении ориентации дуг ГСА может включать как условные (x1m, x2m,…,xrm),
так и операторную (yt) вершины.
Получение отмеченной ГСА при синтезе
автомата Мура отличается тем, что:
а) начальная и конечная вершины отмечаются
символом a0;
б) все операторные вершины отмечаются
символами a1, a2,…, aM.
Число используемых символов определяет алфавит состояний A={a0, a1,…, aM}
синтезируемого автомата.
На
рисунке 21 и 22 представлены отмеченные ГСА для автомата Мили и для автомата
Мура.


Рисунок 21 – Отмеченная
ГСА Рисунок 22 – Отмеченная ГСА
(автомат Мили) (автомат Мура)
Ниже представлены
прямые таблицы переходов для автомата Мили (таблица 5) и автомата Мура (таблица
2).
Таблица
5 Таблица 6
|
am |
as |
x(am,
as) |
Y(am, as) |
|
am |
as (Y) |
x(am, as) |
|
a0 |
a1 |
1 |
y1 , y2 |
|
a0 |
a1(y1,y2) |
1 |
|
a1 |
a2 |
x1 |
y2 , y3 |
|
a1 |
a2 (y2,y3) |
x1 |
|
a1 |
a0 |
|
- |
|
a1 |
a1(y1,y2) |
|
|
a2 |
a3 |
x2 |
y4 |
|
a2 |
a3 (y4) |
x2 |
|
a2 |
a3 |
|
- |
|
a2 |
а4(y5) |
|
|
a3 |
a0 |
1 |
y5 |
|
а4 |
a0 (y5) |
1 |
Структурный синтез автомата. При синтезе структурного МПА необходимо выполнить переход
от абстрактного автомата к структурному автомату. При этом решаются две
основные задачи: кодирование алфавита состояний A; определение системы
логических функций возбуждения Ur и выходов yjÎY, которая является математической моделью
комбинационной схемы автомата.
В интерпретационном
методе синтеза к этапу структурного
синтеза автомата относится:
а) кодирование состояний;
б) построение функции выхода yjÎY;
в) построение функций возбуждения с учётом
выбранного элемента памяти;
г) совместную минимизацию функций
возбуждения и функций выхода и построение функциональной схемы структурного
автомата.
При кодировании различным состояниям
автомата ставятся в соответствие различные двоичные коды. Переход автомата из
одного состояния в другое осуществляется за счёт изменения состояний элементов
памяти – триггеров. В качестве элементов памяти используются различные
триггеры: D-триггер, T-триггер, RS-триггер, JK-триггер. Комбинационная схема
автомата строится на основе функционально полной системы логических элементов.
Для получения минимальной комбинационной
схемы автомата используются специальные алгоритмы кодирования в зависимости от
типа элементов памяти.
При использовании D-триггеров в качестве
элементов памяти автомата, необходимо состояние as, в которое
существует больше всего переходов, закодировать кодом, в котором отсутствуют
единицы - кодом 00…00.
Следующие состояния, в которые существует
также большое количество переходов, кодируются кодами, содержащими одну
единицу: 00…01, 00…10,…01…00, 10…00.
Для кодирования оставшихся состояний
используют сначала все коды, содержащие две единицы (из R компонент), затем три
единицы и т. д. (до тех пор, пока не будут закодированы все состояния).
При использовании в качестве элементов
памяти T-, RS-, JK- триггеров необходимо кодировать состояния таким образом,
чтобы суммарное число изменений состояний элементов памяти на всех переходах
состояний было минимальным.
Контрольные вопросы
1..Что
собой представляет содержательная ГСА, кодированная ГСА?
2. Назовите этапы синтеза абстрактного
МПА.
3. Сформулируйте правило получения
отмеченной ГСА для автомата Мили, Мура.
4. Назовите этапы синтеза структурного
МПА.
5. Сформулируйте правила кодирования
состояний при использовании D-триггеров,
T-, RS-, JK- триггеров.
Cписок литературы
1. Савельев А.Я.
Основы информатики: Учебник/ - М.: МГТУ им.И.Э.Баумана, 2001.- 328 с.
2. Самофалов К.Г. и др. Прикладная теория цифровых автоматов. - Киев: Высшая школа, 1987. – 456 с.
3. Айтхожаева Е.Ж. Прикладная теория цифровых автоматов. -
Алматы: Издательство КазПТИ, 1993.- 103 с.
4. Лысиков Б.Г. Арифметические и
логические основы цифровых автоматов. – Минск: Высшая школа, 1980. – 336 с.
5. Миллер Р. Теория переключательных схем,
т.1–П. – М.: Наука, 1971. – 414 с.
6. Глушков В.М. Синтез цифровых автоматов.
- М.: Физматгиз, 1962. – 476 с.
7. Баранов С.И. Синтез
микропрограммных автоматов. – Л.:
Энергия, 1979.-216 с.
8. Айтхожаева Е.Ж., Петрищенко С.Н., Проектирование
управляющего автомата. Методические указания и задание на курсовую работу для
студентов всех форм обучения специальностей 370340. – Алматы: ПМЛ, АИЭС, 2005.-16 с.