АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ  И СВЯЗИ

                     

                                                                                              

 

 

Кафедра инженерной графики и прикладной  механики

 

 

 

 

ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ  ГРАФИКА

МЕТРИЧЕСКИЕ ЗАДАЧИ

ЧАСТЬ 2

Методические указания к выполнению

семестровой работы

(для студентов всех форм обучения специальностей

050717 – Теплоэнергетика, 050718 – Электроэнергетика,

050719 – Радиотехника, электроника и телекоммуникации)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алматы 2006

СОСТАВИТЕЛИ: А.Д. Динасылов, Э.А. Яхъяев, А.Б.Досаева.

Инженерная и компьютерная графика. Метрические задачи. Часть 2. Методические указания к выполнению семестровой работы  (для студентов всех форм обучения специальностей 050717 – Теплоэнергетика, 050718 – Электроэнергетика, 050719 – Радиотехника, электроника и телекоммуникации).- Алматы: АИЭС, 2006. - 30 с.: ил.

 

 

В указаниях рассматривается методика и решение задач на тему «Метрические задачи» раздела «Теория построения чертежей», даны графические способы решения метрических задач по определению величин углов и натуральной величины плоских фигур.

Индивидуальные задания для самостоятельных работ студентов по разделу «Теория построения чертежей» приведены в 1 части методических указаний.

 Методические указания предназначены для студентов, обучающихся по всем специальностям бакалавриата и изучающих дисциплину «Инженерная и компьютерная графика», и могут оказаться полезными при подготовке к экзамену.

Ил. 15, библиогр.- 12 назв.

 

 

 

 

Рецензент: канд. техн. наук, доцент Мукашев М. Ш.

 

 

 

 

 

 

Печатается по плану издания Алматинского института энергетики и связи   на 2006 г.

 

                                 ©   Алматинский институт энергетики и связи, 2006 г.

 

 

Содержание

 

Введение                                                                                                                          4

1   Определение величины углов                                                                                   6

1.1   Построение взаимно перпендикулярных прямых, прямой и плоскости, плоскостей                                                                                                             6

1.2   Угол между двумя пересекающимися прямыми                                     12

1.3   Угол между двумя скрещивающимися прямыми                                    15

1.4   Угол между прямой и плоскостью                                                            17

1.5   Угол между двумя плоскостями                                                                21       

2   Определение величин плоских фигур                                                                    24

Список литературы                                                                                                       29

 

 

 

         Введение

 

Метрическими задачами называются задачи, решение которых связано с определением на чертеже каких-либо метрических свойств образов. К метрическим свойствам относят длины участков линий, величины углов, площадей, объемов и т.п.

Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства геометрических образов, называют комплексными.

При параллельном (ортогональном) проецировании геометрические образы, произвольно расположенные в пространстве, проецируются на плоскости проекций с искажением. В этом случае искажаются проекции величин их линейных и угловых характеристик.

Определение неискаженных величин линейных и угловых характеристик геометрических образов, произвольно расположенных в пространстве, по их проекциям и представляют собой класс метрических задач, который мы рассмотрим в настоящих методических указаниях.

Многие метрические и комплексные задачи, которые встречаются в технике, являются типовыми и решаются с помощью типовых приемов, которые необходимо понять и  запомнить. Знание этих приемов и умение применить их на практике позволяют овладеть аппаратом начертательной геометрии, с помощью которого задачи можно решать легко и быстро.

Алгоритмы решения всех метрических задач опираются на два инварианта ортогонального проецирования:

 

а) теорему (прямую и обратную) о проецировании прямого угла. Напомним ее. Если одна сторона прямого угла параллельна плоскости проекции, а вторая ей не перпендикулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой  угол.

 

                                                                                                          

(ABC = 90 ⁰) Ù ([BC] // p₁ , [BA] ^ p ₁) Þ A^’B^’C’ = 90 ⁰;

 

б) свойство любой плоской фигуры проецироваться без искажения (в конгруэнтную фигуру) на ту плоскость проекций, которая параллельна  этой фигуре, т.е. (Ф Ì b) Ù (b // p₁) Þ Ф’ @ Ф.

          Все многообразие метрических задач может быть подразделено на три группы:

а) включает в себя определение расстояний:

- от точки до другой точки;

- от точки до прямой;

- от точки до плоскости;

- от точки до поверхности;

- от прямой до плоскости;

б) включает в себя определение углов между:

           - пересекающимися прямыми;

           - скрещивающимися прямыми;

           - прямой и плоскостью;

           - плоскостями (определение величины двугранного угла);

          в) определение величин плоских фигур.

         Для решения этих задач необходимо  изучить типовые приемы решения задач методами  начертательной геометрии.

 Первый этап – сосредоточиться и осмыслить постановку задачи.

 Что дано? Что требуется?  Какие условия ставятся и возможно ли им удовлетворить?

  Второй этап – поиск связи между исходными данными и искомыми.

 Здесь составляется план решения задачи. 

Третий этап – реализация плана; здесь необходим контроль правильности решения и точности графических построений.

Завершающий этап – анализ решения задачи.

Рассмотрим решение некоторых метрических задач, связанных с определением величин углов и натуральной величины плоских фигур.

 

1    Определение величины углов

 

     К этому классу метрических задач относятся задачи на определение величины углов между двумя прямыми линиями, прямой линией и плоскостью, двумя плоскостями.

Отметим ряд свойств ортогональных проекций плоских углов:

а) если стороны угла не параллельны плоскости проекции, то угол проецируется на эту плоскость с искажением;  

б) если хотя бы одна сторона тупого, прямого или острого угла параллельна плоскости проекции, то проекцией угла на эту плоскость будет угол с тем же названием, что и сам угол (тупой, прямой, острый);

в) если обе стороны любого угла параллельны плоскости проекций, то на эту плоскость проекций угол  проецируется без искажения;

г) если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве;

д) если проекция некоторого угла, у которого одна сторона параллельна плоскости проекции, равна прямому углу, то и проецируемый угол также прямой.

Следствие д имеет важное значение. Базируясь на нем, можно просто с минимальным числом геометрических построений решать на эпюре Монжа  задачи по построению:

а) прямых линий, перпендикулярных друг к другу;

б) прямой линии, перпендикулярной к плоскости;

в) взаимно перпендикулярных плоскостей.

 

 

 

1.1  Построение взаимно перпендикулярных прямых, прямой и плоскости,  плоскостей

      

          Особый интерес с точки зрения решения задач начертательной геометрии представляет перпендикулярные прямые. Из инвариантного свойства (в) следует, что любой угол (в том числе и прямой) между двумя пересекающимися прямыми проецируется без искажения, если обе стороны этого угла параллельны плоско-сти проекций.

Прямой угол по инвариантному свойству 2 проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций.        

Рассмотрим некоторые метрические задачи, связанные с определением величин углов.

1. Через точку А провести прямую  , пересекающую горизонталь  h под прямым углом (рисунок 1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 1

 

Так как одна из сторон  (h) прямого угла параллельна плоскости p₁, то на эту плоскость прямой угол спроецируется без искажения. Поэтому через горизонтальную проекцию А₁ точки А проводим горизонтальную проекцию

  ₁ ^ h₁. Отмечаем точку К₁ =  ₁ ∩ h₁. Находим К₂ (К₂ Î h₂). Точки А₂ и К₂ определяют  прямую   линию    ₂.

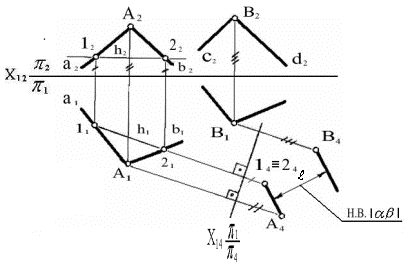
2. Через точку А провести прямую линию,     пересекающую прямую ВС, под углом 90ғ (рисунок 2).

  

 

                                                              

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

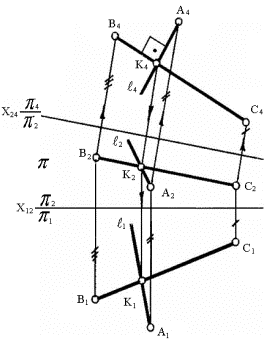
Рисунок 2

 

Так как отрезок ВС занимает произвольное положение по отношению к плоскостям проекций, поэтому вначале данный отрезок необходимо перевести в положение, параллельное какой - либо плоскости проекции. На рисунке 2 отрезок [ВС] переведен в положение, параллельное плоскости p₄. Это сделано с помощью способа замены плоскостей проекций путем замены плоскости p₁ →  p₄,            т.е. p₁ ^ p₂ → p₄ ^ p₂; p₄ ¤¤  ВС;  Х₂₄  ¤¤  В₂С₂. В результате такой замены в новой системе p₂/p₄ [ВС] определяет горизонтальную прямую, через точку А₄ проводим         ₄ ^ В₄С₄. Отмечаем точку К₄ =   ₄ ∩ В₄С₄. Находим проекции точки К (К₂ Î В₂С₂  и К₁ Î В₁С₁). Точки К₂ и К₁ совместно с А₂ и А₁ определяют проекции прямой линии   .

3. Из точки А Î б (АВС) требуется провести перпендикуляр к плоскости б (рисунок 3).

Из курса стереометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна хотя бы к двум пересекающимся прямым, принадлежащим этой плоскости.                   

Если в плоскости взять непроизвольные пересекающиеся прямые, а её горизонталь и фронталь, то для того, чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости,  а фронтальная проекция – к фронтальной проекции фронтали той же плоскости:

^ h,    ^ f,  h ∩ f,  h Ì б,  f Ì б Þ    ^ б.

 

При этом прямые углы между прямой l и прямыми h и f  на соответствующие плоскости проекций спроецируются без искажения:

    ₁ ^ h₁,     ₂ ^ f₂.  

На рисунке 3  показаны прямые линии, перпендикулярные плоскостям, заданным различными способами:

 

б (АВС),  в (d  ¤¤  e),  д (h_од  ∩  f _од).

 

 

Для того чтобы определить направление проекций перпендикуляра    (рисунок 3, а), проводим проекции горизонтали и фронтали плоскости б (АВС). Через точку А проводим горизонтальА1 и фронталь А2. Горизонтальная проекция искомого перпендикуляра   ₁ проходит через точку А₁ перпендикулярно к А₁1₁ (h₁), а фронтальная проекция      ₂  - через А₂ перпендикулярно А₂2₂ (f₂).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

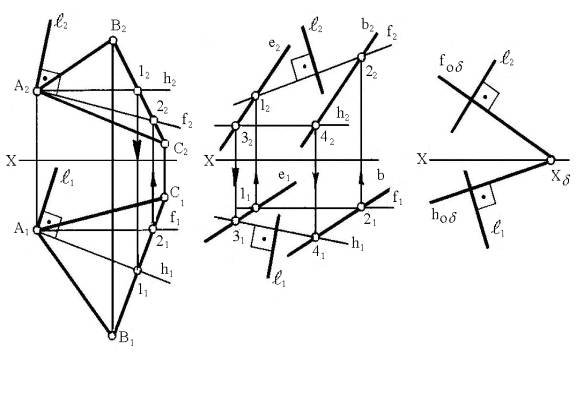
                                                a)                                                     б)                                             в)

 

 

 

 

 

 

 

 

 

 

Рисунок 3

₁^ h₁,     ₂ ^ f₂,  h ∩ f ,  h Ì А ВС,  f  Ì АВС Þ     ^ (АВС).

   ₁  ^ h₁,     ₂ ^ f₂,  h ∩ f , h Ì в (d  ¤¤  e), f  Ì в (d  ¤¤  e) Þ     ^ в

(рисунок 3, б).

Если плоскость задана следами (рисунок 3, в), то горизонталью и фронталью плоскости являются ее пересекающиеся следы. Следовательно, прямая     перпендикулярна плоскости д, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости h_од  и  f _од:     ₁ ^ h_од,             ₂ ^  f _од Þ    ^ д.

4. Через данную прямую АВ провести плоскость в, перпендикулярную плоскости б (DEF).  Плоскости б  и  в  перпендикулярны, если одна плоскость проходит через перпендикуляр к другой плоскости:     ^ в,:     Ì б Þ б ^ в.                  

На рисунке 4 изображена прямая , перпендикулярная плоскости треугольника  б (DEF) (  ₁ ^ h₁,   ₂ ^ ѓ₂), следовательно, любая плоскость, проходящая через прямую    ,  будет перпендикулярна плоскости  б (DEF) (на рисунке изображена плоскость треугольника АВС, заданная отрезком  ВС прямой     и произвольной точкой А).

                       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

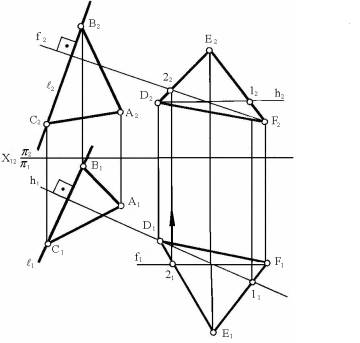
Рисунок 4

Для определения направления проекций перпендикуляра к плоскости б находим горизонтальную проекцию горизонтали (h₁) и фронтальную проекцию фронтали (f₂);  из проекции произвольной точки  В, принадлежащей прямой АВ,     проводим проекции перпендикуляра     ₁ ^ h₁ и     ₂ ^ f₂. 

Плоскость в (    ∩ АВ) ^ б (DEF), так как в Π    ^ б:

 

а)  h (D₁) Î б (DEF);  h₂ Î D₂;  h₂ ^ D₂D₁;  h₂ ∩ E₂F₂ = 1₂;  1₂1₁ ¤¤ D₁D₂;

 

1₂1₁ ∩ E₁F₁ = 1₁;  D₁ È 1₁ = h₁;

 

б)  f (F2) Î б (DEF);  f₁ Π F₁;  f₁ ^ D₁D₂;  f₁ ∩ D₁E₁ = 2₁;  2₁2₂  ¤¤  D₁D₂;

 

2₁2₂ ∩ D₂E₂ = 2₂;   F₂  È 2₂ = f ₂;

     в)    ₁ ^ h₁;    ₂ ^ f₂;

г)  в Π    ^ б  т.е. в  ^ б.

Через прямую     можно провести множество плоскостей перпендикулярно к заданной плоскости б, а через заданную прямую (АВ) – только одну.

 

1.2  Угол между двумя пересекающимися прямыми

 

Если обе стороны плоского угла параллельны плоскости проекций, то угол проецируется на эту плоскость без искажения. Поэтому задачу определения величины плоского угла можно свести к построению его проекции на той плоскости проекций, которой параллельны обе его стороны.

Наиболее рациональным способом определения величины угла является вращение его плоскости вокруг линии уровня (вокруг горизонтали или фронтали) до положения, параллельного соответствующей плоскости проекций.

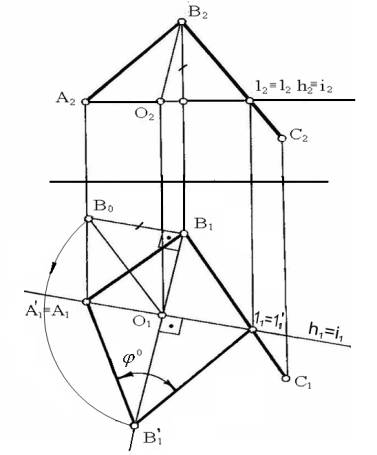
Пример определения величины плоского угла АВС способом вращения вокруг линии уровня (горизонтали) показан на рисунке 5.

 

 

    

 

 

 

 

 

 

 

Рисунок 5

 

Через точку А (А₁ А₂) проведена горизонталь h (h₁, h₂), принадлежащая плоскости угла АВС, и принята за ось вращения i. Вокруг этой оси выполнен поворот треугольника АВ1 до положения, параллельного горизонтальной плоскости проекций p₁ (А₁В’₁1₁ ¤¤ p₁). Точки  А и 1 расположены на оси вращения, поэтому в процессе вращения своего положения в пространстве не меняют, а  точка В перемещается в пространстве по окружности, горизонтальная проекция точки В будет перемещаться по прямой О₁В₁ ^ А₁1_1. Чтобы найти новую горизонтальную проекцию B’₁ точки В, определим натуральную величину радиуса вращения ОВ. Радиус вращения точки определен способом построения прямоугольного треугольника В₀В₁0₁. Радиус вращения точки В проецируется на p₁ без искажения    R = 0₁B’₁.

После поворота плоскость треугольника заняла положение, параллельное плоскости проекций  p₁ (А₁В’₁1₁ ¤¤ p₁), следовательно, на  эту плоскость угол АВ1 проецируется без искажения. ÐА₁В’₁1₁ = Ð АВ1= АВС= ц°.

Построения выполнены в следующем порядке:

а) проведена  плоскость вращения точки В - горизонтально-проекцирующая  плоскость д, перпендикулярная к горизонтали (т.е. к оси вращения);

б) отмечен центр вращения точки В в пересечении горизонтали с пл. д (точка 0₁,  0₂) и указаны проекции оси вращения (0₁В₁ и 0₂В₂₎;

в) определена натуральная величина радиуса вращения (её выражает гипотенуза 0₁В₀ треугольника 0₁В₁В₀);

г) проведена дуга окружности радиуса 0₁В₀ и на пл.  д найдена точка          В′₁ - горизонтальная проекция вершины угла  после его поворота вокруг горизонтали до совмещения с плоскостью,  построен угол ц = ÐА₁ В′₁1₁,  равный искомому.      

На рисунке 6 данная задача решена при помощи способа перемены плоскостей проекций – двукратной замены плоскостей проекций.

Сначала плоскость угла АВС преобразуется в проецирующую  АВС ^ p₄ (Х₁₄ ^ h₁), а затем выбирается новая плоскость проекций p₅, параллельная плоскости угла АВС (p₅  ¤¤ АВС, Х₄₅   ¤¤  С₄А₄В₄). На эту плоскость проекций  (p₅) угол АВС проецируется без искажения ÐА₅В₅С₅ =  ÐАВС = цғ.

 

 

 

 

 

 

 

 

 

 

 

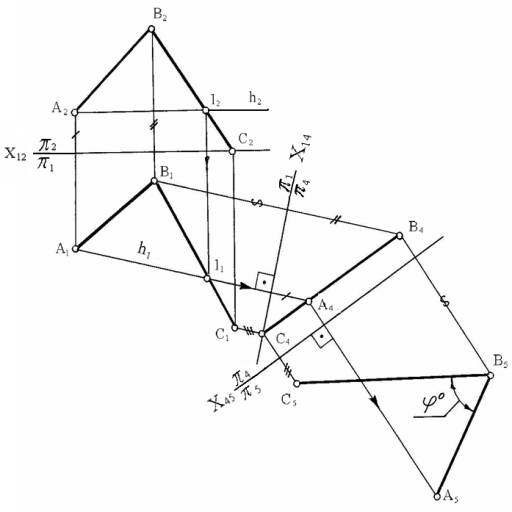
Рисунок 6

 

1.3 Угол между двумя скрещивающимися прямыми

 

Угол между двумя скрещивающимися прямыми определяется величиной угла между двумя пересекающимися прямыми, проведенными из произвольной точки пространства параллельно данным скрещивающимся прямым.

На рисунке 7 показан пример решения такой задачи. Сначала выбирается произвольная точка К (К₁, К₂).  Затем через эту точку проводятся две прямые с  и  d, параллельные двум заданным скрещивающимися прямыми а и b (с₁ ¤¤  a₁,   

 c₂  ¤¤ a₂,  d₁  ¤¤ b₁, d₂ ¤¤  b₂).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

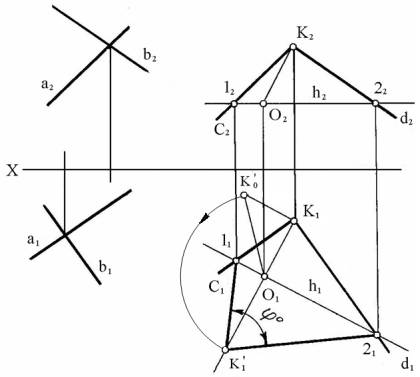
Рисунок 7

 

 

Угол между пересекающимися прямыми линиями c и d (точка К – точка их пересечения) определяется любым известным способом преобразования ортогональных проекций. На рисунке 7 показано определение этого угла способом вращения вокруг горизонтали.

 

1.4  Угол между прямой и плоскостью

 

Углом между прямой  а и  плоскостью p’ называется угол j° между этой прямой и ее ортогональной проекцией на данную плоскость (т. е. угол АВА’, рисунок 8): Ð(а, p’) = Ð( а, а’) = ÐАВА’ = j°,где а¢ и  А’ - соответственно ортогональные проекции прямой а точки А на  плоскость p¢.

 

 

 

 

 

                                                 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    

Рисунок 8

 

Из приведенного определения следует, что величину угла j можно найти следующим образом:

а) на  прямой   а берем любую точку А(А Ë p^’) и проводим через нее прямую    ,  перпендикулярную к заданной плоскости p^’. AA^’ ^ p^’, A Î a;

     б) находим точку А’:  А’ =    ∩  p^’;

в) находим точку В:  В = а ∩  p^’;

г) строим отрезок ВА¢;

д) определяем истинный вид угла АВА¢ (ц).

Решение этой задачи можно упростить, если определять не угол между прямой и плоскостью (ц°), а угол между этой прямой и перпендикуляром из произвольной точки  прямой на плоскость, т. е. ш: ц + ш = 90°, ц = 90° - ш; сторонами угла ц являются прямые а и     (   ^p^’).

На рисунке 9 и 10 показано определение угла ш° между прямой FG и   плоскостью б, заданной плоской фигурой  АВС (рисунок 9) и следами    (рису-нок 10).

Из произвольной точки (рисунок 9) D (D₁, D₂), принадлежащей прямой FG, опущен перпендикуляр DE на заданную плоскость (АВС) :  D₁E₁ ^ Һ₁, D₂E₂ ^  Һ₂.

Угол ш°  между двумя пересекающимися прямыми FG  и DE определен вращением вокруг горизонтали. Угол ц° между прямой FG и заданной плоскостью б (АВС) определяется как дополняющий до 90°  угол ш°                  (ш° + ц° = 90°). Данный способ более прост, если не требуется строить проекции угла  ц.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 9

          На рисунке 10 дан пример определения угла ц°,  образованного прямой   и плоскостью б = (h ∩ f). Из произвольной точки D, принадлежащей прямой    , ,

опущен  перпендикуляр DЕ на заданную плоскость: D₁Е₁ ^ h_об, D₂Е₂ ^ f_об. Угол ш° между двумя пересекающимися прямыми     и  DЕ определен способом двукратной замены плоскостей проекций. Угол ц° между прямой       и плоскостью б определяется как дополняющий до 90°    угол ш°  (ш°  + ц°  =  90°). 

 

 

 

 

 

 

 

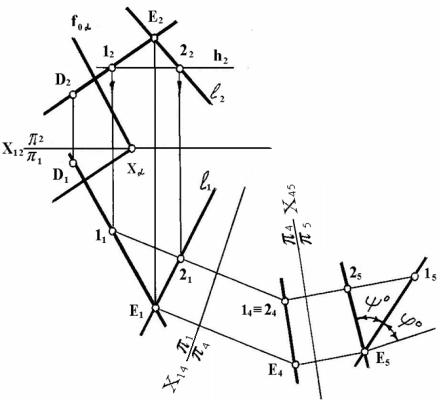
Рисунок 10

 

 

1.5 Угол между двумя плоскостями

 

          Две плоскости, пересекаясь между собой, образуют четыре попарно равных двугранных угла. Каждый из них измеряется линейным углом, который получается при пересечении этих плоскостей третьей плоскостью, перпендикулярной к линии их пересечения. Истинную величину этого угла можно определить несколькими способами.

На рисунке 11 показан пример определения двугранного угла между плоскостью б, заданной  следами, и плоскостью в плоской фигурой ABC.

Из произвольной точки пространства K опущены перпендикуляры  K3 и K4 на заданные плоскости б и в:  

 

K₁ 3₁ ^ Һ_oб,   K₂ 3₂  ^  f_oб ;

 

  K₁ 4₁ ^ Һ₁,    K₂ 4₂  ^  f₂.

 

Плоский угол ц° = Ð3K4 между этими перпендикулярами определен способом  двукратной замены плоскостей проекций. Сначала плоскость угла  3K4 преобразуется в проецирующую (p₄ ^ 3K4, Х₁₄ ^  Һ¢₁), а затем выбирается новая плоскость проекций p₅, параллельная плоскости угла 3K4 (p₅  ¤ ¤ 3K4,                  Х₄₅   ¤ ¤  3₄K₄4₄).

На новую плоскость проекции p₅ угол j ° спроецируется без искажения      3₅К₅4 ₅ = 3К4 = j °.

Угол j °  получился острым (j ° <  90°), значит, он равен линейному углу  Y °,  измеряющему двугранный угол между заданными плоскостями a и b.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

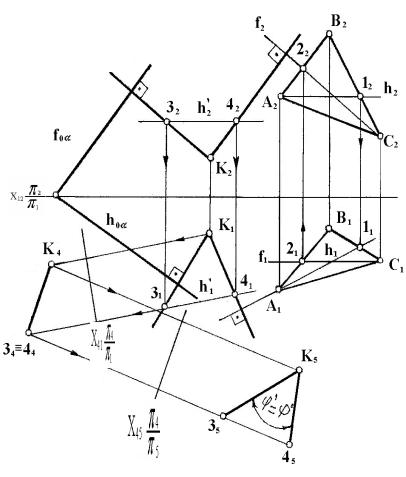
Рисунок 11

 

Задача на определение двугранного угла несколько облегчается, если задано ребро этого угла MN (рисунок 12). Для определения линейного угла j°, измеряющего двугранный угол, в этом случае достаточно расположить его так, чтобы ребро MN оказалось перпендикулярным плоскости проекций. На рисун - ке 12 эта задача решена двукратной заменой плоскости проекций.

 

 

 

 

 

 

 

 

 

 

 

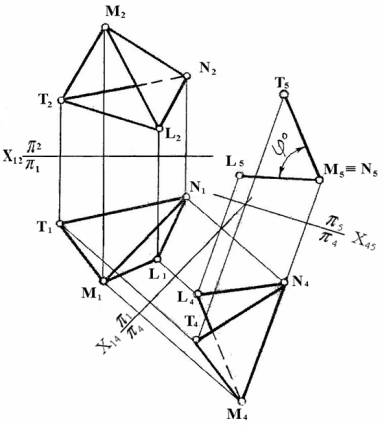
Рисунок 12

 

Сначала выбирается плоскость p₄ параллельная ребру MN (p₄  ¤¤  MN ,  X₁₄  ¤¤  M₁ N₁), а затем плоскость p₅, перпендикулярную ребру MN (p₅ ^ MN ,     X₄₅ ^ M₄N₄).

На новую плоскость проекции (p₅) ребро MN cпроекцируется в виде точки M₅  ≡ N₅, грани MNT и MNL – отрезками прямых, а линейный угол ц ° – в натуральную величину.

 

         2   Определение величин плоских фигур

 

К этому классу метрических задач относятся задачи на определение вели -чин плоских фигур, произвольно расположенных в пространстве. Плоские фигу -ры, произвольно расположенные в пространстве, проецируются на плоскости

проекций с искажениями. Определив величины этих плоских фигур по их проекциям, мы можем измерить любые их линейные и угловые характеристики: длины сторон, углы между сторонами, расстояния от вершин до сторон и т. п..

         Для определения величин плоских фигур применяют различные методы преобразования ортогональных проекций: плоскопараллельное перемещение, вращение вокруг линий уровня и замена плоскостей проекций.

На рисунке 13 определена натуральная величина треугольника АВС, лежащего в плоскости общего положения.

Вначале произведем плоскопараллельное движение треугольника относительно горизонтальной плоскости проекций (p₁), расположив его во фронтально-проецирующее положение В’₂, А’₂, С’₂. Для этого в плоскости треугольника проведем  горизонталь  Һ и построим новую горизонтальную

 

 

 

 

 

 

 

 

 

 

 

 

 

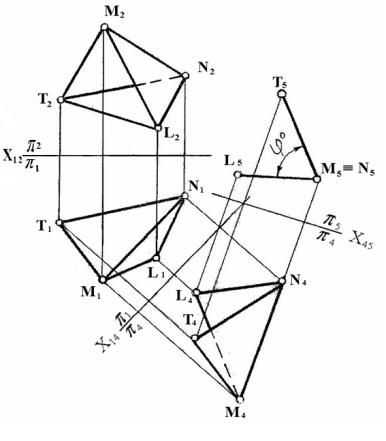
Рисунок 13

проекцию А’₁В’₁С’₁ треугольника так, чтобы горизонтальная проекция  Һ₁ горизонтали стала перпендикулярной к фронтальной плоскости проекций (p₂). Фронтальные проекции  А₂В₂С₂ вершин треугольника будут перемещаться по горизонтальным прямым, которые являются проекциями плоскостей движения этих точек. Их новые положения  А’₂, В’₂, С’₂ можно найти в пересечении этих прямых с вертикальными линиями связи. Фронтальная проекция  (А’₂, В’₂, С’₂) треугольника представляет собой отрезок прямой.

Вторым плоскопараллельным движением, уже относительно фронтальной плоскости проекций (p₂), переместим треугольник в положение, параллельное горизонтальной плоскости проекций (p₁). Для этого фронтальную проекцию А^”₂, В^”₂, С^”₂  треугольника расположим горизонтально (А^”₂, В^”₂, С^”₂  ¤¤  p₁). Гори -зонтальные проекции A₁^”B₁^”C₁^” точек найдем в пересечении прямых, являющихся проекциями плоскостей движения точек A^’₁, B^’₁, C^’₁ c вертикальными линиями связи, проведенными из точек A^”₂, B^”₂, C^”₂ . Полученная горизонтальная проекция A₁^”B₁^”C₁^” треугольника АВС и выражает натуральную величину.

Рассмотрим, как можно определить натуральную величину треугольника АВС способом вращения вокруг линии уровня (рисунок 14). Метод вращения вокруг линий уровня дает возможность плоскость общего положения одним вращением совместить с плоскостью уровня и, следовательно, сразу получить натуральную величину плоской фигуры, лежащей в заданной плоскости.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

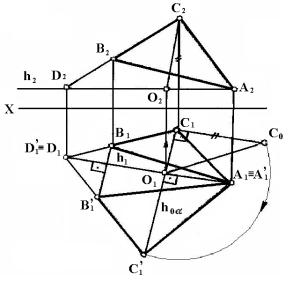
Рисунок 14

В качестве оси вращения на рисунке 14 взята горизонталь AD. Точка А расположенная на оси вращения, при вращении останется на месте. Следовательно, для изображения горизонтальной проекции треугольника АВС после поворота необходимо найти положение проекций двух других его вершин (В и С). При вращении треугольника АВС вокруг его горизонтали AD (AD Ì АВС, AD ¤¤ p₁). Точки D и A не меняют своего положения в процессе вращения треугольника (D ≡ D₁ , А ≡ А₁ ), так как они принадлежат оси вращения Һ (D Î Һ, A Π Һ), а горизонтальные проекции точек В и С перемещаются по прямым, перпендикулярным Һ₁ (В₁ В^’₁ ^ Һ₁ , С₁ С^’₁ ^  Һ₁).

На рисунке 15 показано вращение точки С вокруг горизонтальной оси Һ. Через горизонтальную проекцию точки С (С₁) проводится горизонтальный след плоскости вращения (Һ_oб ^  Һ₁), и находится центр вращения 0 (0₁, 0₂). Затем определяется величина радиуса вращения R = 0₁С₀ (как гипотенуза треугольника, катетами которого являются горизонтальная проекция радиуса вращения  R = 0₁ С₁ и разность координат Z точек А и С). Радиус вращения R  откладывается от центра вращения 0₁ на прямой Һ_oб  (0₁С^’₁ = R = 0₁С₀), и определяется положение точки после поворота С₁ (С^’₁). Положение точки В^’₁ можно найти, не определяя радиуса вращения точки В: как точку пересечения двух прямых, из которых одна является перпендикуляром  (горизонтальная проекция плоскости вращения точки В),  проведенным из точки В₁ к прямой А₁D₁, а другая проходит

через найденную точку С^’₁ и точку D₁ (горизонтальную проекцию точки D₁, принадлежащей стороне ВС и расположенной на оси вращения).

     Проекция А^’₁В^’₁С^’₁ представляет натуральную величину треугольника АВС, так как после поворота плоскость треугольника стала параллельной плоскости p₁. Проекция треугольника на фронтальной плоскости проекций p₂ обратится в отрезок прямой, совпадающей с Һ₂. Так как эта проекция не нужна для решения данной задачи, она на рисунке 14 не показана.

Если требуется повернуть плоскую фигуру до положения, параллельного плоскости p₂, за ось вращения надо выбирать фронталь (все остальные построения аналогичны).

 На рисунке 15 дан пример построения натуральной величины плоской фигуры способом замены плоскостей проекций. В системе плоскостей проекций p₂ / p₁ задан треугольник АВС  (А₁В₁С₁ , А₂ В₂ С₂). Для определения натуральной величины необходимо заменить плоскости проекций дважды.

 

 

 

 

 

 

 

 

 

 

 

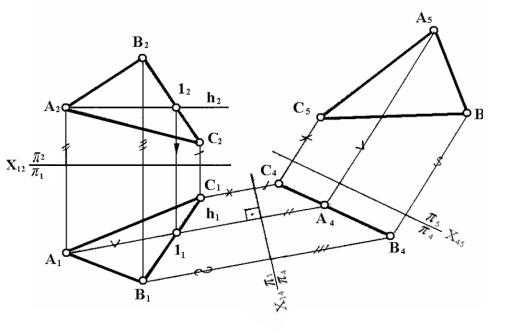
Рисунок 15

 

     Первая замена плоскостей проекций.
         Проводим новую плоскость p₄ перпендикулярно плоскости треугольника АВС (p₄  ^ АВС, p₄  ^ p₁). В плоскости АВС зададим горизонталь Һ и выберем новую фронтальную плоскость проекций  p₄  ^ Һ. Новая ось Х₁₄ ^  Һ₁.Тогда в системе p₁ / p₄  плоскость АВС станет проецирующей и ее проекция на p₄  -        А₄С₄В₄ обратится в прямую линию.

При второй замене вместо горизонтальной плоскости p₁ вводим новую горизонтальную плоскость p₅ ¤¤ АВС. При этом новая ось Х₄₅ ¤¤ А₄С₄В₄. Через точки А₄, С₄, В₄ проводим перпендикулярно оси Х₄₅ линии связи, на которых откладываем от этой оси расстояния, равные расстояниям точек А₁, В₁, С₁  до оси Х₁₄. Новая проекция А₅ В₅ С₅ выражает натуральную величину заданной фигуры АВС (А₅В₅С₅ = АВС).

 

 

 

 

Список литературы

 

1.      Виноградов В. Н., Ройтман И. А. Сборник задач и методические указания по начертательной геометрии. – М.: Просвещение, 1972 .

2.       Гордон В. О., Семенцов – Огиевский М. А. Курс начертательной геометрии:  Учебное пособие / Под. ред.  Иванова Ю. Б. –  М.: Наука, 1988.          – 288 с.

3.      Гордон В. О., Иванов Ю. Б., Солнцева Т. Е. Сборник задач по курсу начертательной геометрии. Учебное пособие для вузов. – 6 – е изд., перераб.

- М.: Наука. Гл. ред. физ. – мат. лит., 1989. – 320 с. - JSBN  5 – 02 – 013926 – 2.

4.      Лаптев О. В., Числив П. А. Задачник по начертательной геометрии. – М., 1999.

5.      Павлова А. А. Начертательная геометрия. Учебник для студентов высших учебных заведений. – М.: ООО “ Издательство Астрель “:  ООО “ Издательство АСТ “, 2001. – 304 с.: ил.

6.      Стрижаков А. В., Мартиросов А. Л., Кубарев А. Е. Начертательная геометрия / Серия “ Высшее образование“ – Ростов Н/Д: Феникс, 2004. – 320 с.

7.      Тарасов Б. Ф., Дудкина Л. А., Немолотов С. О. Начертательная геометрия. – СПб.: Издательство “ Лань “, 2001. – 256 с.: ил.

8.      Мукашев М. Ш. Инженерная графика. Часть 1. Начертательная геометрия. Лекции и методические указания по выполнению самостоятельных работ. – Алматы, 1999. – 180 с.

9.      Мукашев М. Ш., Дуйсенов С. А., Калиев Б. З. Инженерлік және машиналық графика, 1 – бөлім. Сызба геометрия. Оқу құралы. АЭжБИ. Алматы, 2004. – 8б.

10.  Яхъяев Э.А. Техническое черчение (для учащихся колледжа): Учебное пособие. АИЭС. Алматы, 2005. -  103 с.: ил.

11. Фролов С. А. Начертательная геометрия: Учебное пособие для втузов. – М.: Машиностроение, 1983.

12. Фролов С. А. Сборник задач по начертательной геометрии. – М.: Машиностроение, 1986.

 

 

 

Сводный план 2006  г. Поз 103

 

 

Алмаз Даменович Динасылов

Эркин Алимджанович Яхъяев

Айгуль Борибековна Досаева

 

ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА

МЕТРИЧЕСКИЕ ЗАДАЧИ

ЧАСТЬ 2

 

Методические указания к выполнению

семестровой работы

(для студентов всех форм обучения специальностей

050717 – Теплоэнергетика, 050718 – Электроэнергетика,

050719 – Радиотехника, электроника и телекоммуникации)

 

 

 

 

Редактор Ж.М. Сыздыкова

 

Подписано в печать…………                         Бумага типографская № 2

Тираж 350 экз.                                                 Заказ…………

Формат 60 ´ 40    1/16                                     Цена…………

Объем -………уч. изд. л.

 

 

 

 

Копировально-множительное бюро

Алматинского интитута энергетики и связи

050013 , Алматы  ул. Байтурсунова 126