Алматинский институт энергетики и связи

Кафедра инженерной графики и прикладной механики»

Инженерная и компьютерная графика.

Позиционные задачи

Методические указания к выполнению

семестровой работы

(для студентов всех форм обучения специальностей

050702 – Автоматизация и управление, 050704 – Вычислительная

техника и программное обеспечение, 050717 – Теплоэнергетика,

050718 – Электроэнергетика, 050719 – Радиотехника, электроника и телекоммуникации)

Алматы 2006

СОСТАВИТЕЛИ: А.Д. Динасылов, Э.А. Яхъяев, А.Б. Досаева. Инженерная и компьютерная графика. Позиционные задачи. Методические указания к выполнению семестровой работы (для студентов всех форм обучения специальностей 050702 – Автоматизация и управление, 050704 – Вычислительная техника и программное обеспечение, 050717 – Теплоэнергетика, 050718 – Электроэнергетика, 050719 – Радиотехника, электроника и телекоммуникации). - Алматы: АИЭС, 2006 – 29 с., ил.

В указаниях рассматривается методика и решение задач на тему «Позиционные задачи» раздела «Теория построения чертежей», даны графические способы решения позиционных задач на взаимное положение и взаимопринадлежность рассматриваемых геометрических образов.

Указания предназначены для студентов по специальностям бакалавриата, изучающих дисциплину «Инженерная и компьютерная графика», и могут оказаться полезными при подготовке к экзамену.

Ил. 20, библиогр.- 12 назв.

Рецензент: канд. техн. наук, доцент Мукашев М. Ш.

Печатается по плану издания Алматинского института энергетики и связи на 2006 г.

Содержание

Введение 4

1 Основные понятия о позиционных задачах 5

2 Взаимное положение точки и прямой 5

3 Прямая и точка в плоскости 7

4 Взаимное положение плоскостей 13

4.1 Плоскости параллельные 13

4.2 Пересекающиеся плоскости 15

Приложение А. Комплект задач 25

Список литературы 27

Введение

Фундаментальные дисциплины закладывают базу научно-технического развития страны; классическими представителями этих наук являются графические дисциплины – начертательная геометрия и черчение. Они составляют фундамент политехнического образования.

В связи с развитием электроники и машиностроения не только инженер и техник, но и рабочий должен владеть интернациональным и выразительным языком техники – чертежом. Чертеж выполняют на базе законов начертательной геометрии.

Начертательная геометрия позволяет просто и наглядно решать графическими методами многие важные теоретические и практические задачи. Она даёт теорию методов графического моделирования, необходимую для современного уровня технического творчества, для обучения и преподавания цикла технических дисциплин.

В последнее время в связи с широким использованием ЭВМ и машинной графики в различных отраслях знаний значительно расширилась практика применения их в начертательной геометрии.

С изучением начертательной геометрии приходит умение изображать всевозможные сочетания геометрических форм на плоскости, решать позиционные и метрические задачи, производить исследования геометрических образов по их изображениям.

В практике проектирования и эксплуатации машин и механизмов широко применяются графические методы расчета. Они наиболее наглядны и часто значительно проще и доступнее аналитических, что помогает более обоснованно принимать технические решения. В наше время графические методы решения сложных технических задач на проекционных чертежах нашли широкое применение.

Широкий круг геометрических задач в начертательной геометрии подразделяются на позиционные и метрические.

В настоящих методических указаниях рассмотрены позиционные задачи, в которых требуется установить взаимное положение и взаимопринадлежность рассматриваемых геометрических образов. Рассмотрим основные позиционные задачи на простейших геометрических образах (точка, прямая, плоскость), являющихся базовыми при исследовании и конструировании сложных технических форм.

1 Основные понятия о позиционных задачах

Все задачи начертательной геометрии условно могут быть разделены на позиционные и метрические.

Позиционные задачи заключаются в определении принадлежности и в построении взаимных пересечений геометрических фигур.

Задачи на определение принадлежности одной геометрической фигуры другой могут быть подразделены на три вида:

а) принадлежность точки линии (А h);

б) принадлежность точки поверхности (А d );

в) принадлежность линии поверхности (d ).

Задачи на построение пересечений геометрических фигур делятся на две группы:

а) пересечение линии с поверхностью ( g );

б) взаимное пересечение поверхностей (g b).

Рассмотрим задачи на взаимную принадлежность одних геометрических элементов другим, на пересечение – построение точки пересечение прямой и плоскости, двух прямых, линии пересечения двух плоскостей. В решении позиционных задач не учитывается метрические свойства фигур.

2 Взаимное положение точки и прямой линии

Точка и прямая линия в пространстве могут быть различно расположены относительно друг друга и плоскостей проекций. На рисунке 1 приведены примеры, когда точка лежит над прямой линией (точка С), под прямой (точка Д), за прямой (точка Е) и принадлежит прямой (точка F).

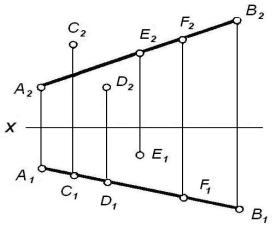
Рисунок 1

Если точка в пространстве принадлежит прямой, то её проекции принадлежат соответствующим проекциям этой прямой. Например, точка F принадлежит прямой АВ. Её фронтальная проекция F₂ принадлежит фронтальной проекции А₂В₂ прямой АВ, горизонтальная F₁ – горизонтальной проекции А₁В₁ (F₂d А₂В₂, F₁ d А₁В₁). Если бы хотя бы одна проекция точки не принадлежит соответствующей проекции прямой, то эта точка не принадлежит прямой.

Из инвариантного свойства 4 (если точка F делит отрезок в отношении m/n, то и проекция этой точки делит в таком же отношении проекцию этого отрезка) следует, что проекции точки F (F₁, F₂), принадлежащей отрезку АВ, делят соответствующие проекции отрезка в том же отношении, в каком точка F делит отрезок АВ, т.е.

АF/FВ = m/n => А₁F₁/F₁В₁ = А₂F₂ /F₂В₂ = m/n

На рисунке 2 показан пример деления отрезка в отношении АС/СВ=3/2.

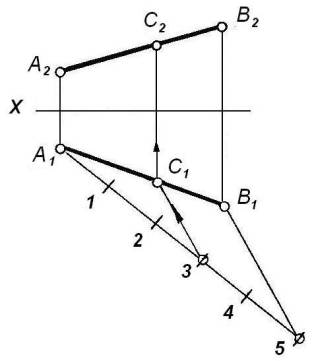
Рисунок 2

Из произвольной точки концов отрезка АВ (например, из точки А₁) проводим произвольную прямую линию и откладываем на ней пять равных между собой отрезков. Точку 5 соединяем с точкой В₁. Через точку 3 проводим прямую, параллельную прямой 5 - В₁, до пересечения с А₁В₁ в точке С₁ . По точке С₁ строим проекцию С₂. В точке С отрезок АВ разделен в отношении 3:2, считая от точки А.

3 Прямая и точка в плоскости

Существуют два признака принадлежности прямой плоскости:

а) если две точки прямой принадлежат плоскости;

б) если прямая имеет с плоскостью одну общую точку и при этом параллельна какой-нибудь прямой, лежащей в этой плоскости.

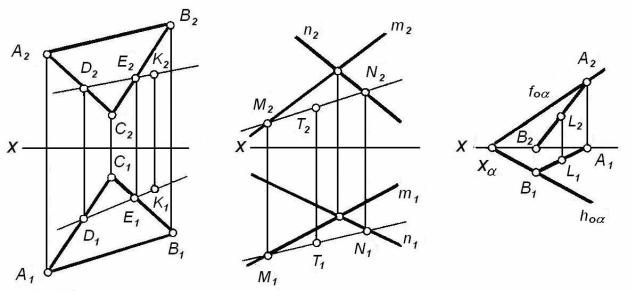
На рисунке 3 показаны прямые линии DE и MN, принадлежащие разным плоскостям. Прямая DE принадлежит плоской фигуре (АВС), так как она проходит через точки D и E, расположенные на сторонах этой плоской фигуры (D d AB, E d BC, то DE d (ABC)).

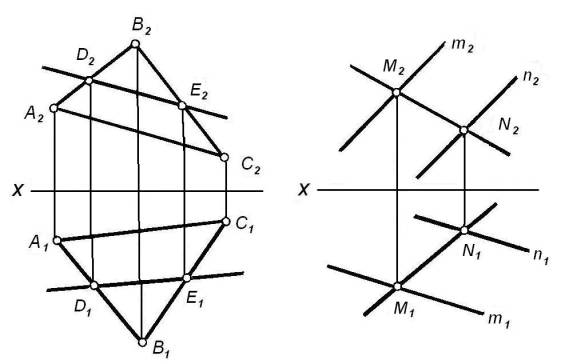
Рисунок 3

Прямая MN принадлежит плоскости b, заданной параллельными прямыми m и n, так как она проходит через точки M и N, расположенные на этих прямых.

Прямая линия АВ (рисунок 4) принадлежит плоскости , заданной следами, так как она проходит через точки А и В, расположенные на следах этой плоскости h_о и f_о.

Точки А и В являются следами этой прямой, поэтому прямая АВ принадлежит плоскости (h_оg f_о), так как её следы принадлежат одновременно следам плоскости (справедливо и обратное утверждение: если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости):

АВ d <=> В h h_о, А h f_о_.

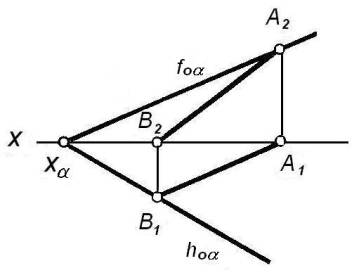
Рисунок 4

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.

На рисунке 5 показаны точки К, T и L, принадлежащие соответственно плоской фигуре (АВС) и плоскостям, заданным пересекающимися прямыми b (m gn) и следами (h g f):

K d DE, DE d (ABC) => K h (ABC);

T d MN, MN d b (m g n) => T h b (m g n);

L d AB, AB d (h g f) => L h (h g f).

Рисунок 5

Пример. Дана плоскость (ABC) и точка D (рисунок 6). Определить, лежит ли точка D в плоскости (ABC).

Рисунок 6

Решение. Через горизонтальные (фронтальные) проекции точки и любой точки, принадлежащей заданной плоскости (ABC) (например, точки А), проведем горизонтальную проекцию А₁Е₁ прямой АЕ (фронтальную проекцию А₂Е₂ прямой АЕ) и найдем фронтальную проекцию А₂Е₂ (горизонтальную проекцию А₁Е₁). Если D₂d А₂Е₂, (D₁d А₁Е₁), то D d (ABC).

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, принадлежащей плоскости. Чтобы изобразить такую прямую, надо в плоскости задать прямую и параллельно ей провести требуемую прямую.

Пример. Через точку А (рисунок 7) необходимо провести прямую АВ, параллельную плоскости , заданной треугольником DEK.

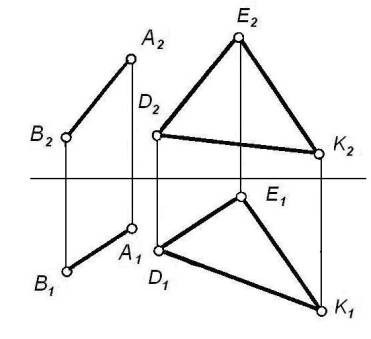
Рисунок 7

Для этого через горизонтальную проекцию А₁ точки А проведем горизонтальную проекцию А₁В₁ искомой прямой параллельно горизонтальной проекции любой прямой, лежащей в плоскости (DEK), например, прямой DE (А₁В₁ o D₁E₁). Через фронтальную проекцию А₂ точки А параллельно D₂E₂ проводим фронтальную проекцию А₂В₂ искомой прямой АВ (А₂В₂ o D₂E₂). Прямая линия АВ параллельна плоскости , заданной треугольником DEK.

Через данную точку можно провести бесчисленное множество прямых линий, параллельных заданной плоскости.

Если прямая пересекает плоскость, то она имеет с этой плоскостью только одну общую точку.

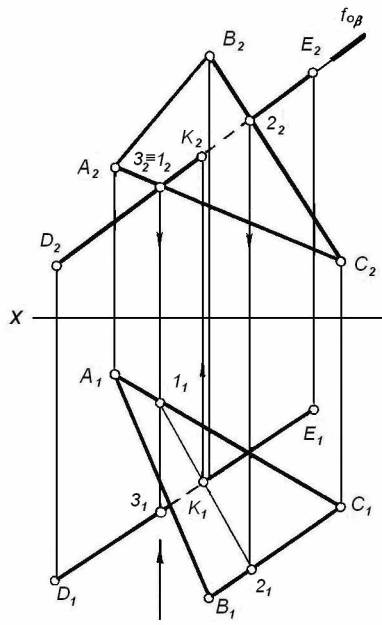
Пусть даны прямая DE и плоскость (ABC) (рисунок 8), необходимо построить точку К пересечения прямой DE с плоскостью (ABC).

Рисунок 8

Для нахождения точки К выполним следующие построения:

а) через прямую DE проведем вспомогательную, например, фронтально-проецирующую плоскость b. Её след f_о_b совпадает с фронтальной проекцией D₂E₂ заданной прямой DE;

б) находим линию 12 пересечения двух плоскостей: данной (АВС) и вспомогательной b. Эта линия соединит точки 1 и 2 пересечения прямых АС и ВС с плоскостью b. Фронтальные проекции 1₂ и 2₂будут лежать на следе f_о_b_, а горизонтальные проекции 1₁ и 2₁ должны быть найдены на А₁С₁ и В₁С₁ соответственно. Таким образом, прямая линия 12 = b g (ABC);

в) находим точку К пересечения двух прямых: данной DE и полученной 12. Горизонтальная проекция этой точки К₁ = D₁E₁g 1₁2₁, а фронтальная К₂ d D₂E₂.

Теперь необходимо определить видимость прямой DE относительно плоскости, заданной треугольником (АВС). На фронтальной проекции в точке 1₂ пересекаются проекции D₂E₂ и А₂С₂. Так как прямые DE и АС в пространстве скрещиваются, то в указанную точку (1₂) проецируются две конкурирующие точки, одна из них (1) принадлежит АС, а другая (3) принадлежит прямой DE. Обе эти точки лежат на одной фронтально-проецирующей прямой. Видимой будет та из них, которая ближе к наблюдателю и, следовательно, дальше от ₂. По проекции на ₁ ясно, что ближе к наблюдателю (и дальше от ₂) расположена точка 3₁, принадлежащая прямой DE, следовательно, D₂K₂- видимая. В точке К прямая DE пересекает плоскость (АВС), и поэтому на участке K₂E₂ проекция прямой становится невидимой. Аналогично определяется видимость проекции D₁E₁ на ₁.

Нахождение точки пересечения прямой с плоскостью значительно упрощается, если эта плоскость является проецирующей. На рисунке 9 дана фронтально-проецирующая плоскость , заданная её фронтальным следом f_о_, и отрезок прямой АВ. Для отыскания проекции точки К₁=А₁В₁g находим точку К₂= А₂В₂g f_о. Полученная точка будет фронтальной проекцией искомой точки, а её горизонтальная проекция К₁ располагается на А₁В₁.

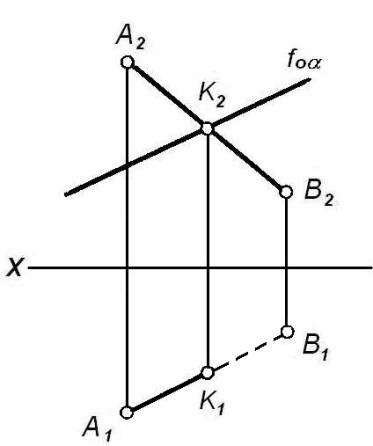
Рисунок 9

4 Взаимное положение плоскостей

Рассмотрим два случая взаимного положения плоскостей: плоскости параллельные и пересекающиеся.

4.1 Плоскости параллельные

Плоскости параллельны, если в одной из них возможно провести две пересекающиеся прямые, соответственно параллельные двум пересекающимся прямым второй плоскости.

Например, через точку D (рисунок 10) провести плоскость b, параллельную плоскости (АВС).

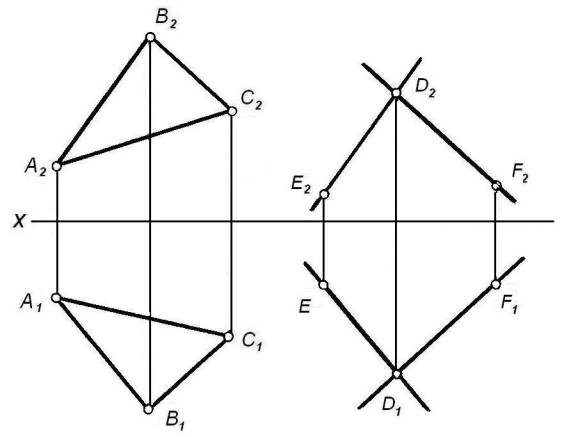
Рисунок 10

Через точку D следует построить прямые, соответственно параллельные двум пересекающимся прямым плоскости (АВС): DE o АВ (D₁E₁o А₁В₁, D₂E₂o А₂В₂ ) и DF o BC (D₁F₁ o B₁C₁, D₂F₂ o B₂C₂). Пересекающиеся прямые DE и DF определяют плоскость b, которая параллельна плоскости . Горизонтали и фронтали параллельных плоскостей соответственно параллельны.

Плоскости, заданные следами, будут параллельны, если следы одной плоскости параллельны, одноименны следам другой плоскости. На чертеже у этих плоскостей соответственно параллельны фронтальные проекции f_о и f_о_b, фронтальных следов и горизонтальные проекции h_о и h_о_b горизонтальных следов (рисунок 11).

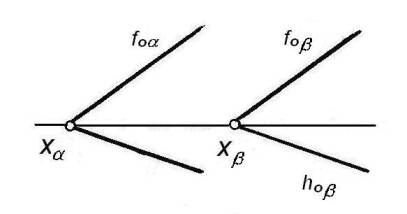
Рисунок 11

4.2 Пересекающиеся плоскости

Если две плоскости не параллельны друг другу, то они пересекаются по прямой линии, поэтому определяется положением двух принадлежащих ей точек.

Рассмотрим несколько случаев пересекающихся плоскостей:

а) две горизонтально-проецирующие плоскости и b пересекаются по прямой , перпендикулярной ₁ (рисунок 12). Горизонтальной проекцией этой линии пересечения является точка ₁ = h_оg h_о_b, а фронтальной – прямая X;

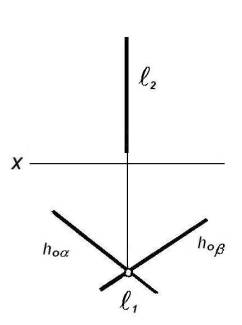
Рисунок 12

б) горизонтально-проецирующая плоскость и фронтально-проецирующая плоскость b пересекаются по прямой (рисунок 13). Горизонтальная проекция ₁этой прямой совпадает с горизонтальным следом h_о, а фронтальная проекция ₂ совпадает с фронтальным следом f_о_b;

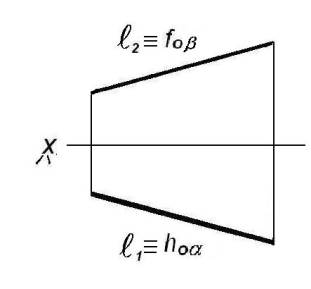
Рисунок 13

в) построение линии пересечения плоскости общего положения(АВgВС) с фронтально-проецирующей плоскостью b показано на рисунке 14.

Находим точки 1₂ =А₂В₂ g f₀_b и 2₂= А₂С₂ g f₀_b. Прямая 1₂2₂ – фронтальная проекция линии пересечения. Через 1₂ и 2₂ проводим линии связи и находим точки 1₁ и 2₁. Прямая 1₁2₁ – горизонтальная проекция прямой 12 = gb .

Если одна из плоскостей проецирующая, одна проекция линии их пересечения определяется без вспомогательных построений. Она совпадает с той проекцией проецирующей плоскости, которая представляет собой линию.

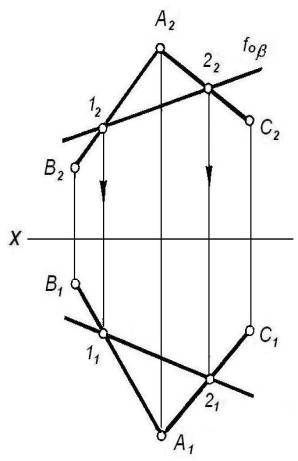
Рисунок 14

На рисунке 15 плоскости и b заданы следами.

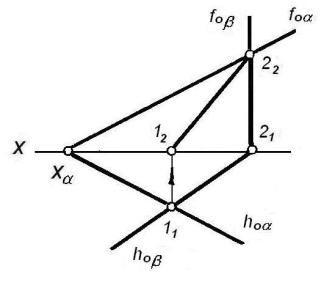
Рисунок 15

Плоскость β горизонтально-проецирующая, поэтому горизонтальная проекция 1₁2₁ линии пересечения плоскостей совпадает с горизонтальным следом этой плоскости: 1₁2₁ = h_о_b. Чтобы найти фронтальную проекцию линии пересечения, будем рассматривать её как прямую, лежащую в плоскости . Точка 2₂ d f_о_, так как точка 2₁d X. Точка 1₂ d X, так как 1₁ d h_о. Соединив прямой точки 1₂ и 2₂, получим фронтальную проекцию линии пересечений заданных плоскостей (12 = g b).

Построение линии пересечения плоскостей общего положения, заданных следами, показано на рисунке 16. Точка 2 инцидентна следам обоих плоскостей, следовательно, инцидентна линии их пересечения. Точно также точка 1 инцидентна этой линии. Соединим (на эпюре) одноименные проекции точек 1 и 2, получим проекции линий пересечения плоскостей a и β.

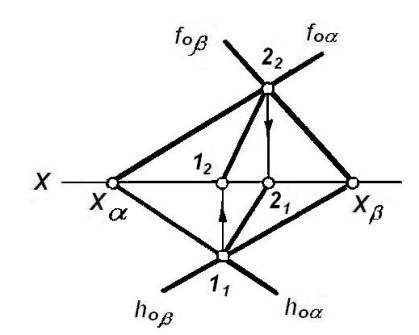
Рисунок 16

Если какие-либо одноименные следы плоскостей не пересекаются в пределах чертежах (рисунок 17), можно рассечь обе заданные плоскости и b вспомогательной горизонтальной или фронтальной плоскостью. Построив линии пересечения плоскостей заданных и вспомогательной, определим общую для заданных плоскостей точку. В качестве вспомогательных плоскостей взяты произвольные две горизонтальные плоскости y и j (y o₁, f₀_y o X и j o₁, o f₀_j₎

Горизонтали плоскостей пересекаются в точках M и N соответственно (f₀_y g = 1, f₀_y g b = 2, f₀_j g = 3, f₀_j g b = 4). Соединив одноименные проекции точек M и N, получим проекции линии пересечения плоскостей.

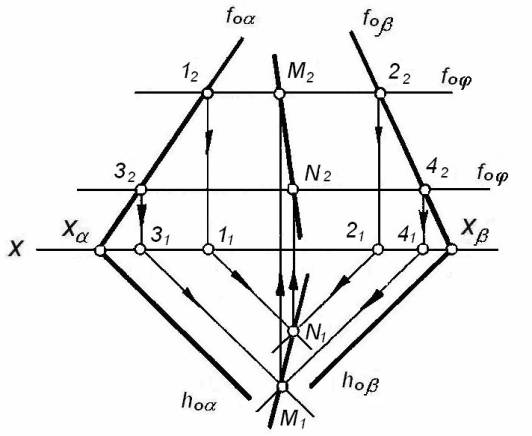
Рисунок 17

На рисунке 18 изображены плоскости и b, горизонтальные следы которых параллельны, фронтальные пересекаются в точке К.

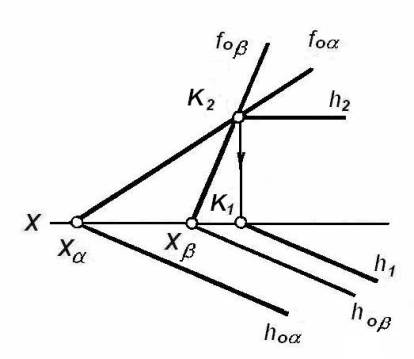
Рисунок 18

Точка пересечения горизонтальных следов – несобственная; чтобы соединить её с точкой К₁ необходимо через К₁ провести прямую, параллельную следам плоскостей. Такая линия является горизонтальной проекцией горизонтали обеих плоскостей. Её фронтальная проекция параллельна оси X.

Рассмотрим, как построить линию пересечения двух плоскостей общего положения (АВС) и b (DEK), и установим видимость этих треугольников относительно плоскостей проекций (рисунок 19).

Рассечем заданные плоскости (АВС) и b (DEK) вспомогательной горизонтальной плоскостью y (f₀_y), проходящей, например, через точку А. Определив линии пересечения А2 и 13 этой плоскости с заданными плоскостями, отметим общую точку М (вначале её горизонтальную проекцию М₁), проводим линию связи и находим точку М₂.

Рисунок 19

Проведем горизонтально-проецирующую плоскость j (h₀_j) через сторону АС треугольника АВС. Горизонтальная проекция стороны АС (А₁С₁) лежит на горизонтальной проекции плоскости j, сама же плоскость пересекается с плоскостью треугольника по прямой линии АС. Определив линию пересечения 45 плоскостей j и b (DEK), отметим точку N (АС g 45 = N). Линия пересечения (АВС) и b (DEK) проходит через точку M и N.

Для определения видимости воспользуемся конкурирующими точками скрещивающихся прямых. Возьмём, например, точки 4 d DF и 6 d АС. Их горизонтальные проекции расположены в пересечении горизонтальных проекций названных прямых (D₁F₁ g А₁С₁ = 4₁ 6₁).

Найдя фронтальные проекции точек 4 и 6 (4₂ и 6₂), устанавливаем, что точка 6 при направлении проецирования, перпендикулярном ₁, расположена ближе к наблюдателю, следовательно, она видима. Видимой будет и прилегающая к точке 6 часть отрезка АС (до точки пересечения N₁ с плоскостью DEF). О видимости отрезка АВ можно судить, рассмотрев конкурирующие в месте кажущегося пересечения прямых DF и АВ или EF и АВ при том же направлении проецирования.

Для определения видимости при направлении проецирования, перпендикуляром ₂, рассмотрим конкурирующие точки 7 d EF и 8 d ВС. Построив горизонтальные проекции этих точек, устанавливаем, что точка 8 d ВС расположена ближе к наблюдателю, чем точка 7 d EF. Следовательно, спереди виден отрезок ВС, а отрезок от точки Е до точки пересечения прямой с плоскостью АВС (М) виден. Рассуждая аналогично, устанавливаем, что отрезок DE оказывается видимым, отрезок же DF – частично закрытым треугольником АВС.

Рассмотрим построение линии пересечения двух плоскостей общего положения (рисунок 20), плоскости, заданной двумя прямыми АВ и ВС ( = (АВ g ВС)), и плоскости b, заданный двумя параллельными прямыми а и b (b = (a o b)).

Чтобы построить линию пересечению двух плоскостей, необходимо найти две точки, принадлежащие одновременно обеим плоскостям, и соединить их.

Для определения положения точек М и N, принадлежащих линии пересечения плоскостей и b, возьмём две вспомогательные горизонтальные плоскости y и j, пересекающие каждую из заданных плоскостей по горизонтали 12 и 34. Эти прямые, расположенные в плоскости, в пересечении определяют первую точку – М, принадлежащую линии пересечения плоскостей и b.

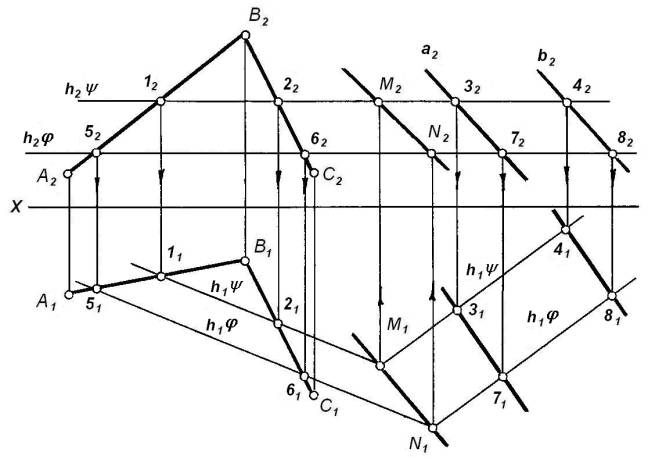
Рисунок 20

Взяв плоскость j, получим в ее пересечении с плоскостями и b горизонтали 56 и 78. Эти прямые, расположенные в плоскости j, в пересечении определяют вторую точку, общую для плоскостей и b,– точку N.

Построив горизонтальные проекции M₁ и N₁точек, найдем на фронтальных проекциях h₂_y и h₂_j плоскостей y и j фронтальные проекции M₂ и N₂ точек M и N. Здесь MN (M₁N₁, M₂N₂) – отрезок искомой линии пересечения плоскостей и b.

При построении линии пересечения плоскостей и b следует иметь в виду, что вспомогательные секущие плоскости y и j взаимно параллельны. Поэтому, построив проекцию прямых 1₁2₁ и 3₁4₁, для построения проекции 5₁6₁ и 7₁8₁ прямых достаточно взять только по одной точке, принадлежащей каждой из этих прямых (например, точки 6₁ и 7₁), так как прямая 5₁6₁ параллельна прямой 1₁2₁, а прямая 7₁8₁ параллельно прямой 3₁4₁.

Рассмотренный пример часто называют общим способом построения линии пересечения двух плоскостей.

Приложение А

Комплект задач

Задача №1

По заданным координатам построить две проекции точек АВСDЕК.

Задача № 2

Построить горизонтальную проекцию точки F и провести прямую l, проходящую через точку F(70; Y; 40) и параллельную плоскости α(AB || DN).

Задача №3

Построить перпендикуляр к плоскости β(АВ ∩ АD) и отложить на нем отрезок АК равный 40 мм.

Задача №4

Построить точку пересечения прямой DК с плоскостью α(ABС) и определить ее видимость на проекциях.

Задача №5

Построить проекции линии пересечения плоскостей α(ABС) и β(DЕК).

Задача №6

Определить натуральную величину отрезка АВ различными способами.

Задача №7

Определить расстояние от точки D до плоскости α(ABС).

Задача №8

Определить расстояние между скрещивающимися прямыми АВ и DЕ.

Задача №9

Построить точки пересечения прямой АВ со следующими поверхностями:

а) с конусом, радиус основания которого 30мм, высота 50мм, а ось вращения проходит через середину отрезка АВ;

б) с пирамидой СDЕК.

Задача №10

Определить натуральную величину сечения пирамиды АВСЕ горизонтально-проецирующей плоскостью γ, проходящей через середину ребра АВ и параллельно ребру ВС.

Список литературы

1. Виноградов В. Н., Ройтман И. А. Сборник задач и методические указания по начертательной геометрии. – М.: Просвещение, 1972.

2. Гордон В. О., Семенцов – Огиевский М. А. Курс начертательной геометрии: Учебное пособие / Под. ред. Иванова Ю. Б. – М.: Наука, 1988. – 288 с.

3. Гордон В. О., Иванов Ю. Б., Солнцева Т. Е. Сборник задач по курсу начертательной геометрии: Учебное пособие для Вузов. – 6 – е изд., перераб.

- М.: Наука. Гл. ред. физ. – мат. лит., 1989. – 320 с. - JSBN 5 – 02 – 013926 – 2.

4. Лаптев О. В., Числив П. А. Задачник по начертательной геометрии. – М., 1999.

5. Павлова А. А. Начертательная геометрия. Учебник для студентов высших учебных заведений. – М.: ООО “ Издательство Астрель “: ООО “ Издательство АСТ “, 2001. – 304 с.: ил.

6. Стрижаков А. В., Мартиросов А. Л., Кубарев А. Е. Начертательная геометрия / Серия “ Высшее образование “. – Ростов Н/Д: Феникс, 2004. – 320 с.

7. Тарасов Б. Ф., Дудкина Л. А., Немолотов С. О. Начертательная геометрия. – СПб.: Издательство “ Лань “, 2001. – 256 с.: ил.

8. Мукашев М. Ш. Инженерная графика. Часть 1. Начертательная геометрия. Лекции и методические указания по выполнению самостоятельных работ. – Алматы, 1999. – 180 с.

9. Мукашев М. Ш., Дуйсенов С. А., Калиев Б. З. Инженерлік және машиналық графика 1 – болім. Сизба геометрия. Оқу қуралы. АЭ ж БИ. -Алматы, 2004. – 8б.

10. Яхъяев Э.А. Техническое черчение (для учащихся колледжа): Учебное пособие. - Алматы, АИЭС: 2005. - 103 с., ил.

11. Фролов С. А. Начертательная геометрия: Учебное пособие для ВТУЗов. – М.: Машиностроение, 1983.

12. Фролов С. А. Сборник задач по начертательной геометрии. – М.: Машиностроение, 1986.

Сводный план 2006 г., поз.

Алмас Даменович Динасылов

Эркин Алимджанович Яхъяев

Айгуль Борибековна Досаева

Инженерная и компьютерная графика

Позиционные задачи

Методические указания к выполнению семестровой работы

(для студентов всех форм обучения специальностей 050717 - Электроэнергетика, 050718 –Теплоэнергетика, 050719- Радиотехника, электроника и телекоммуникации

Редактор Л.Т. Сластихина

Подписано в печать Бумага типографская № 2

Тираж 350 экз Заказ ……..

Формат 60х40 1/16 Цена 70 тг.

Объем - 2,0 уч.-изд. л.

Копировально-множительное бюро

Алматинского института энергетики и связи

050013, Алматы, ул. Байтурсынова, 126