Некоммерческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра инженерной графики и прикладной механики
ПРИКЛАДНАЯ МЕХАНИКА
Конспект лекций
для студентов всех форм обучения специальности 050717 – Теплоэнергетика

Алматы 2008
СОСТАВИТЕЛЬ: А.Д.Динасылов, Р.К.Койлыбаева. Прикладная механика. Конспект лекций для студентов всех форм обучения специальности 050717 – Теплоэнергетика. – Алматы: АИЭС, 2008. – 80 с.
Приводится основной теоретический материал дисциплины «Прикладная механика», излагаемый в лекционном курсе для студентов специальности 050717 – Теплоэнергетика. В лекциях 1-7 излагаются основы статики, кинематики и динамики механических систем. В лекциях 8-9 рассматриваются некоторые вопросы теории механизмов и машин. В лекциях 10-16 рассматриваются основы расчетов элементов конструкций на прочность и жесткость.
Ряд положений приводится без выводов ввиду ограниченности объема конспекта, количество примеров недостаточно для полного усвоения материала, поэтому предполагается, что при изучении дисциплины студенты будут пользоваться дополнительной литературой, список которой приведен в конце конспекта.
Конспект лекций
может использоваться студентами других специальностей, изучающих дисциплину «Прикладная механика» или «Механика».
Содержание
|
Лекция 1. Вводные понятия. Аксиомы статики. Сходящиеся силы |
6 |
|
1.1 Основные понятия статики |
6 |
|
1.2 Аксиомы статики. Теорема о трех силах |
7 |
|
1.3 Система сходящихся сил |
9 |
|
Лекция 2. Момент силы относительно точки и оси. Пара сил. Приведение системы сил к заданному центру |
10 |
|
2.1 Момент силы относительно точки и относительно оси |
10 |
|
2.2 Сложение параллельных сил |
12 |
|
2.3 Пара сил. Момент пары сил |
12 |
|
2.4 Теорема о параллельном переносе силы |
13 |
|
2.5 Приведение системы сил к заданному центру |
13 |
|
Лекция 3. Условия равновесия систем сил. Трение. Центр тяжести |
14 |
|
3.1 Условия равновесия системы сил |
14 |
|
3.2 Равновесие системы тел |
15 |
|
3.3 Статически определимые и статически неопределимые системы |
15 |
|
3.4 Трение скольжения. Реакция шероховатой поверхности |
16 |
|
3.5 Реакция связи при качении |
17 |
|
3.6 Центр тяжести твердого тела |
17 |
|
Лекция 4. Кинематика точки и простейших движений тела |
18 |
|
4.1 Введение в кинематику |
18 |
|
4.2 Способы задания движения точки |
19 |
|
4.3 Скорость и ускорение точки при векторном способе задания движения |
19 |
|
4.4 Скорость и ускорение точки при координатном способе задания движения |
20 |
|
4.5 Скорость и ускорение точки при естественном способе задания движения |
21 |
|
4.6 Поступательное движение твердого тела |
21 |
|
4.7 Вращательное движение твердого тела вокруг неподвижной оси |
22 |
|
Лекция 5. Плоскопараллельное движение твердого тела. Сложное движение точки |
23 |
|
5.1 Уравнения плоскопараллельного движения |
23 |
|
5.2 Определение скоростей точек плоской фигуры |
24 |
|
5.3 Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей |
24 |
|
5.4 Определение ускорений точек плоской фигуры |
25 |
|
5.5 Сложное движение точки. Относительное, переносное и абсолютное движения |
25 |
|
5.6 Теорема о сложении скоростей |
26 |
|
5.7 Теорема Кориолиса о сложении ускорений |
27 |
|
Лекция 6. Динамика точки |
28 |
|
6.1 Аксиомы динамики |
28 |
|
6.2 Дифференциальные уравнения движения материальной точки |
29 |
|
6.3 Относительное движение материальной точки |
29 |
|
6.4. Теорема об изменении количества движения точки |
30 |
|
6.5 Теорема об изменении момента количества движения точки |
31 |
|
6.6 Работа силы. Мощность силы. Теорема об изменении кинетической энергии точки |
31 |
|
6.7 Принцип Даламбера для точки |
32 |
|
Лекция 7. Основы динамики системы и твердого тела |
32 |
|
7.1 Механическая система. Масса, центр масс и моменты инерции |
32 |
|
7.2 Дифференциальные уравнения движения системы. Теорема о движении центра масс системы |
34 |
|
7.3 Теорема об изменении количества движения системы |
34 |
|
7.4 Теорема об изменении главного момента количеств движения |
35 |
|
7.5 Теорема об изменении кинетической энергии системы |
36 |
|
7.6 Принцип Даламбера для системы |
36 |
|
Лекция 8. Основные понятия теории механизмов и машин. Структурный анализ механизмов |
37 |
|
8.1 Основные понятия. Структурные элементы механизмов |
37 |
|
8.2 Основные виды механизмов |
39 |
|
8.3 Структурные формулы кинематических цепей и механизмов |
41 |
|
8.4 Понятия о структурном анализе и синтезе механизмов |
42 |
|
Лекция 9. Кинематический и кинетостатический анализ плоских рычажных механизмов |
43 |
|
9.1 Общие сведения и виды плоских рычажных механизмов |
43 |
|
9.2 Кинематический анализ механизмов |
43 |
|
9.3 Кинетостатический анализ механизмов |
45 |
|
Лекция 10. Введение в сопротивление материалов. Задачи и методы сопротивления материалов |
49 |
|
10.1 Задачи сопротивления материалов. Расчетная схема |
49 |
|
10.2 Метод сечений. Внутренние силовые факторы в поперечном сечении стержня |
50 |
|
10.3 Понятия о напряжениях, перемещениях и деформациях |
51 |
|
10.4 Закон Гука. Принципы независимости действия сил и Сен-Венана |
53 |
|
10.5 Общие принципы расчета элементов конструкции |
53 |
|
Лекция 11. Растяжение и сжатие стрежней |
53 |
|
11.1 Продольная сила и нормальные напряжения |
54 |
|
11.2 Удлинения стержня и закон Гука |
55 |
|
11.3 Статически неопределимые системы при растяжении-сжатии |
56 |
|
11.4 Напряженное и деформированное состояния при растяжении |
57 |
|
Лекция 12. Механические свойства материалов при растяжении и сжатии |
|
|
12.1 Диаграммы растяжения |
59 |
|
12. 2 Особенности испытаний на сжатие |
61 |
|
12.3 Влияние температуры и времени на свойства материалов |
61 |
|
Лекция 13. Расчеты на прочность при растяжении-сжатии. Концентрация напряжений |
62 |
|
13.1 Условие прочности при растяжении-сжатии. Три вида задач |
62 |
|
13.2 Концентрация напряжений |
64 |
|
Лекция 14. Чистый сдвиг. Кручение стержня круглого поперечного сечения |
65 |
|
14.1 Напряжения и деформации при чистом сдвиге |
65 |
|
14.2 Кручение стержня с круглым поперечным сечением |
66 |
|
Лекция 15. Геометрические характеристики поперечных сечений. Внутренние силовые факторы при изгибе |
69 |
|
15.1 Статические моменты и центр тяжести плоской фигуры |
69 |
|
15.2 Моменты инерции сечения |
70 |
|
15.3 Главные оси и главные моменты инерции |
71 |
|
15.4 Изгиб. Внутренние силовые факторы при изгибе |
72 |
|
15.5 Дифференциальные зависимости между изгибающим моментом и поперечной силой |
73 |
|
Лекция 16. Напряжения и расчеты на прочность при изгибе. Сложное сопротивление |
74 |
|
16.1 Напряжения при чистом изгибе |
74 |
|
16.2 Напряжения и расчеты на прочность при поперечном изгибе |
76 |
|
16.3 Косой изгиб и внецентренное растяжение-сжатие |
77 |
|
16.4 Изгиб с кручением |
78 |
|
Список литературы |
79 |
Лекция 1. Вводные понятия. Аксиомы статики. Сходящиеся силы
Содержание лекции: прикладная механика, как теоретическая база техники; вводные понятия и аксиомы статики, системы сходящихся сил и условия их равновесия.
Цели лекции: определить роль прикладной механики в подготовке бакалавров, сформулировать вводные понятия и аксиомы статики, рассмотреть упрощение и условия равновесия системы сходящихся сил.
«Прикладная механика» - дисциплина, лежащая в основе общетехнической подготовки бакалавров для отраслей энергетики. Прикладная механика является теоретической базой машиностроения и играет большую роль в повышении надежности, качества проектирования и правильной эксплуатации машин, механизмов, приборов в энергетике. Дисциплина включает в себя взаимосвязанные разделы теоретической механики, теории механизмов и машин, деталей машин и сопротивления материалов.
Теоретическая механика (ТМ) есть наука об общих законах механического движения (МД) и равновесия материальных тел. Под МД понимается изменение относительного положения материальных тел в пространстве с течением времени. Наблюдать и изучать МД материальных тел можно по отношению к другим материальным телам, с которыми связывают систему координатных осей, называемую системой отсчета. Частным случаем МД является равновесие материальных тел, под которым надо понимать не только состояние покоя, но и состояние равномерного прямолинейного движения. В механике изучаются механические взаимодействия тел, т.е. взаимодействия, в результате которых происходит изменение движения тел или изменение их размеров и формы (деформация).
ТМ принято делить на статику, кинематику и динамику. Статикой называют раздел ТМ, в котором изучаются методы преобразования системы сил, а также устанавливаются условия их равновесия. В кинематике изучается движение тел без учета действующих на них сил. В динамике изучается движение материальных тел с учетом действующих на них сил.
1.1 Основные понятия статики
Объектами изучения ТМ являются модели материальных тел, а именно, материальная точка (МТ), система МТ и абсолютно твердое тело (АТТ).
МТ называют материальное тело, размерами которого в рассматриваемых условиях можно пренебречь, считая, что масса тела сосредоточена в точке. Системой МТ называются совокупность МТ, положения и движения которых взаимосвязаны между собой (например, механизм). АТТ называют тело, в котором расстояния между любыми точками остаются неизменными. Все реальные тела в результате воздействий в определенной мере изменяют свои размеры и форму (деформируются). Эти деформации зачастую малы, и при решении ряда задач ими можно пренебречь, считая тело абсолютно твердым.
Состояние равновесия или движения тела зависит от
характера его механических взаимодействий с другими телами, мерой которых
является сила. Сила - вектор, характеризующийся численной величиной,
направлением и точкой приложения. Графически сила изображается направленным
отрезком прямой. Прямая, вдоль которой направлена сила, называется ее линией
действия (ЛД). Силу будем обозначать прописной буквой латинского алфавита с
надчеркиванием, например ![]() , тогда F=
, тогда F=
![]() -
модуль силы. Совокупность сил, действующих на какое-либо твердое тело или
точку, называют системой сил. Обозначать ее будем
-
модуль силы. Совокупность сил, действующих на какое-либо твердое тело или
точку, называют системой сил. Обозначать ее будем ![]() .
.
Если систему сил (СС), действующих на твердое тело,
можно заменить другой СС, не изменяя при этом состояния покоя или движения
тела, то эти СС называют эквивалентными ![]() ~
~![]() .
.
Если данной СС эквивалентна одна сила, то эта сила называется
равнодействующей для рассматриваемой СС. Если обозначить ее как ![]() *, то
*, то ![]() *~
*~![]() . Не каждая СС имеет
равнодействующую.
. Не каждая СС имеет
равнодействующую.
СС называют уравновешенной, если она, будучи
приложенной к телу, не изменяет его состояния покоя или движения. Действие
уравновешенной СС эквивалентно нулю, т.е. ![]() ~0.
Силой, уравновешивающей СС, называют силу, которая,
будучи присоединенной к этой СС, составит вместе с ней новую СС, эквивалентную нулю.
~0.
Силой, уравновешивающей СС, называют силу, которая,
будучи присоединенной к этой СС, составит вместе с ней новую СС, эквивалентную нулю.
Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на часть точек данного объема или данной части поверхности тела, называются распределенными.
1.2 Аксиомы статики
В основе статики лежит ряд аксиом.
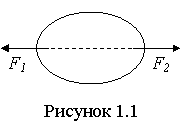
1. Аксиома равновесия системы двух сил. Для равновесия двух сил, приложенных к телу,
необходимо и достаточно, чтобы эти силы были равны по величине и направлены
вдоль прямой, соединяющей их точки приложения, в противоположные стороны: F1
= F2, но
![]() (рисунок 1.1).
(рисунок 1.1).

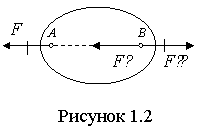

2. Аксиома добавления и отбрасывания уравновешенной СС. Не изменяя действия системы сил на твердое тело, можно к этой системе прибавить или отнять от нее уравновешенную СС. Следствие: не изменяя действия силы на АТТ, ее можно переносить в любую точку тела вдоль ее ЛД (рисунок 1.2), т.е. сила – скользящий вектор.
3. Аксиома параллелограмма сил. Равнодействующая двух сил, приложенных в одной точке
под углом друг к другу, определяется диагональю параллелограмма, построенного
на этих силах как на сторонах (рисунок 1.3), т.е. ![]() .
.
4. Аксиома взаимодействия. Силы, с которыми действуют
друг на друга два тела, всегда равны по величине и направлены вдоль одной
прямой в противоположные стороны: F21 = F12,
![]() .
.
Прежде чем сформулировать 5-ю аксиому, введем несколько понятий.
Если тело может получать любые перемещения в пространстве, то оно называется свободным. Если же некоторые перемещения для тела невозможны, то тело называется несвободным. Условия, ограничивающие свободу движения тела, называются связями. Связи осуществляются при помощи материальных тел, твердых или гибких. Тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, действует на нее с некоторой силой. Одновременно связь действует на тело с такой же по модулю, но противоположно направленной силой, называемой реакцией связи. Силы, не являющиеся реакциями, будем называть активными. Реакция связи отличается от активных сил тем, что ее численная величина зависит от активных сил и наперед неизвестна. Направление реакции противоположно направлению, по которому связь препятствует движению тела. Рассмотрим, как направлены реакции некоторых видов связей (опор):
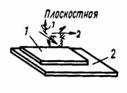
а) гладкая поверхность (трением можно пренебречь) не препятствует скольжению по ней тела, а препятствует только его движению по нормали к поверхности. Поэтому ее реакция направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке;
б) гибкая нить или цепь. Здесь реакция направлена вдоль нити или цепи;
в) цилиндрический шарнир (подшипник) или шарнирно-неподвижная опора. Два тела, соединенные валом, проходящим через отверстия в этих телах, образуют шарнирное соединение. Осевая линия вала называется осью шарнира. Тело не может перемещаться по направлению, перпендикулярному к оси шарнира, но может поворачиваться вокруг оси. Поэтому реакция может иметь любое направление в плоскости, перпендикулярной оси шарнира. Обычно ее раскладывают на две составляющие;
г) опора типа катка или шарнирно-подвижная опора. Если пренебречь трением, то реакция направлена по нормали к поверхности качения;
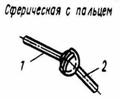
д) сферический шарнир и подпятник. Этот вид связи закрепляет какую-либо точку тела так, что она не может совершать никаких перемещений в пространстве, при этом тело может как угодно поворачиваться вокруг этой точки. Реакция проходит через закрепленную точку, а направление ее заранее неизвестно, поэтому реакцию разлагают на три составляющие;
е) невесомый стержень, закрепленный с двух сторон шарнирами. На стержень действуют только две силы, приложенные в центрах шарниров. Стержень находится в равновесии, поэтому эти силы (реакции) должны быть направлены вдоль прямой, проходящей через центры шарниров.
Для несвободного тела имеет место следующая аксиома.
5. Аксиома связей. Несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями.
6. Аксиома затвердевания. Равновесие изменяемого (деформируемого) тела, находящегося под действием данной СС, не нарушится, если наложить на него дополнительные связи вплоть до того, что рассматривать тело, как затвердевшее (абсолютно твердое).
Теорема о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Доказательство: Пусть тело находится в равновесии под
действием трех сил:
![]() . Так как они не параллельны и лежат в одной
плоскости, то линии действия двух сил
. Так как они не параллельны и лежат в одной
плоскости, то линии действия двух сил ![]() пересекаются и их можно сначала перенести в точку
пересечения, а затем заменить равнодействующей
пересекаются и их можно сначала перенести в точку
пересечения, а затем заменить равнодействующей ![]() . Тогда
. Тогда
![]() уравновешивает силу
уравновешивает силу
![]() , а это значит, что их линии действия совпадают, то
есть линии действия всех трех сил пересекаются в одной точке.
, а это значит, что их линии действия совпадают, то
есть линии действия всех трех сил пересекаются в одной точке.
1.3 Система сходящихся сил
Различают следующие типы систем сил (СС): система сходящихся сил, система параллельных сил, произвольная СС. СС сил называется сходящейся, если линии действия (ЛД) всех сил системы пересекаются в одной точке. СС называется параллельной, если ЛД сил параллельны между собой. Произвольной называется такая СС, ЛД которых не параллельны и не пересекаются в одной точке. Все указанные СС могут быть как плоскими, так и пространственными. СС называется плоской, если ЛД всех сил лежат в одной плоскости; в противном случае СС пространственная.
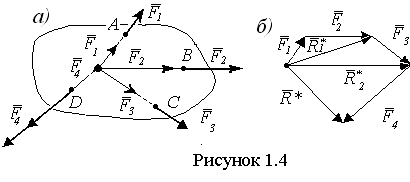
Пусть к телу в
точках А, В, С,
D приложены силы ![]() , ЛД
которых пересекаются в точке О (рисунок 1.4 а). Перенесем силы вдоль их ЛД
в точку О и будем последовательно складывать силы по правилу силового
треугольника (рисунок 1.4 б). Сначала найдем равнодействующую
, ЛД
которых пересекаются в точке О (рисунок 1.4 а). Перенесем силы вдоль их ЛД
в точку О и будем последовательно складывать силы по правилу силового
треугольника (рисунок 1.4 б). Сначала найдем равнодействующую ![]() сил
сил ![]() и
и ![]() , затем
, затем ![]() сил
сил
![]() и
и ![]() и
т.д. Получим следующее:
и
т.д. Получим следующее: ![]() ,
, ![]() ,
, ![]() =
=![]() . Если сил n, то
. Если сил n, то
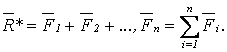 (1.1)
(1.1)
![]() можно определить
также, отложив вектор
можно определить
также, отложив вектор ![]() и приложив к его концу
вектор
и приложив к его концу
вектор ![]() , затем к концу
, затем к концу ![]() -
вектор
-
вектор ![]() , и т.д. Равнодействующая
, и т.д. Равнодействующая ![]() соединяет начало первого вектора с
концом последнего. Т.о., равнодействующая системы сходящихся сил равна векторной
сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения ЛД слагаемых
сил. Чтобы найти равнодействующую геометрическим способом, надо построить в
точке пересечения их ЛД силовой многоугольник на слагаемых силах; замыкающая
силового многоугольника будет равнодействующей.
соединяет начало первого вектора с
концом последнего. Т.о., равнодействующая системы сходящихся сил равна векторной
сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения ЛД слагаемых
сил. Чтобы найти равнодействующую геометрическим способом, надо построить в
точке пересечения их ЛД силовой многоугольник на слагаемых силах; замыкающая
силового многоугольника будет равнодействующей.
Рассмотрим аналитический способ определения равнодействующей системы сходящихся сил. Спроецируем векторное равенство (1.1) на оси прямоугольных координат и найдем проекции равнодействующей
![]() ,
, ![]() ,
,
![]() .
(1.2)
.
(1.2)
Модуль равнодействующей силы определяется, как
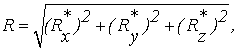 (1.3)
(1.3)
а направление - по трем направляющим косинусам
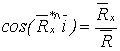 ,
, 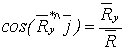 ,
,  . (1.4)
. (1.4)
Для равновесия системы
сходящихся сил необходимо и достаточно, чтобы ее равнодействующая была равна
нулю, т.е., ![]() или
или
![]() (условия равновесия в векторном виде). Условия
равновесия в геометрическом смысле выражаются в том, что силовой многоугольник
должен быть замкнут, т.е., конец последнего вектора должен совпасть с началом
первого вектора. В аналитическом виде они выражаются в том, что
должны равняться нулю суммы проекций на три координатные оси всех сил, входящих
в систему,
(условия равновесия в векторном виде). Условия
равновесия в геометрическом смысле выражаются в том, что силовой многоугольник
должен быть замкнут, т.е., конец последнего вектора должен совпасть с началом
первого вектора. В аналитическом виде они выражаются в том, что
должны равняться нулю суммы проекций на три координатные оси всех сил, входящих
в систему,
![]() ,
,
![]() ,
,
![]() .
(1.5)
.
(1.5)
Условия равновесия для плоской системы сходящихся сил
![]() ,
,
![]() . (1.6)
. (1.6)
Лекция 2. Момент силы относительно точки и оси. Пара сил. Приведение системы сил к заданному центру
Содержание лекции: момент силы относительно точки и оси; пара сил, свойства пар сил, приведение системы сил к центру.
Цели лекции: изучить свойства момента силы относительно точки и оси, свойства пары сил, упрощение и условия равновесия системы пар сил, упрощение произвольной системы сил.
2.1 Момент силы относительно точки и относительно оси
Моментом силы
![]() относительно точки О (рисунок 2.1) называется
вектор
относительно точки О (рисунок 2.1) называется
вектор ![]() , приложенный в точке О перпендикулярно
плоскости треугольника ОАВ и равный
, приложенный в точке О перпендикулярно
плоскости треугольника ОАВ и равный
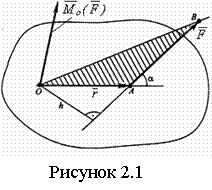
![]() (2.1)
(2.1)
где
![]() - радиус-вектор, проведенный из точки О в точку А
приложения силы
- радиус-вектор, проведенный из точки О в точку А
приложения силы ![]() .
.
Модуль вектора
![]() равен произведению модуля силы F на расстояние
h от точки О до линии действия силы, которое называется плечом силы
относительно точки О, т. е.
равен произведению модуля силы F на расстояние
h от точки О до линии действия силы, которое называется плечом силы
относительно точки О, т. е.
![]() =F∙h. (2.2)
=F∙h. (2.2)
Момент ![]() характеризует вращательное
действие силы
характеризует вращательное
действие силы ![]() относительно
точки О. Радиус-вектор
относительно
точки О. Радиус-вектор ![]() может быть проведен
из точки О не только в точку А, но и в любую другую точку,
лежащую на линии действия силы
может быть проведен
из точки О не только в точку А, но и в любую другую точку,
лежащую на линии действия силы ![]() . Момент силы относительно точки равен нулю, когда
линия действия силы проходит через эту точку.
. Момент силы относительно точки равен нулю, когда
линия действия силы проходит через эту точку.
Для системы сил
![]() вектор
вектор
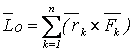 , (2.3)
, (2.3)
равный сумме моментов всех этих сил относительно точки О, называется главным моментом системы сил относительно точки О.
В случае плоской системы сил удобно вместо векторного момента силы относительно точки использовать понятие алгебраического момента силы относительно точки, т.к. в этом случае векторные моменты всех сил параллельны друг другу. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы
![]() .
(2.4)
.
(2.4)
Знак «плюс» берется, если сила стремится вращать тело относительно точки против часовой стрелки, «минус» – если по часовой стрелке.
Моментом силы ![]() относительно оси называется проекция векторного
момента этой силы, взятого относительно любой точки оси, на эту ось, т. е.
относительно оси называется проекция векторного
момента этой силы, взятого относительно любой точки оси, на эту ось, т. е.
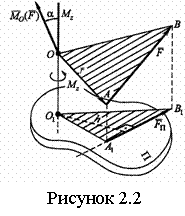
![]() . (2.5)
. (2.5)
Проекция на ось момента силы
![]() ,
взятого относительно какой-либо точки О этой оси Oz, не
зависит от положения точки на оси.
,
взятого относительно какой-либо точки О этой оси Oz, не
зависит от положения точки на оси.
Иначе: момент силы
![]() относительно оси - это алгебраический момент
проекции этой силы на плоскость, перпендикулярную оси, взятый относительно
точки пересечения оси с плоскостью (рисунок 2.2)
относительно оси - это алгебраический момент
проекции этой силы на плоскость, перпендикулярную оси, взятый относительно
точки пересечения оси с плоскостью (рисунок 2.2)
![]() .
(2.6)
.
(2.6)
Момент силы относительно оси равен нулю, если сила и
ось находятся в одной плоскости. Момент силы относительно начала
координат ![]() равен по (2.1)
равен по (2.1)
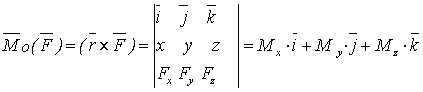 ,
,
откуда получим моменты силы относительно осей координат
![]() ,
,
![]() ,
, ![]() .
(2.7)
.
(2.7)
2.2 Сложение параллельных сил
Две приложенные к АТТ и направленные в одну сторону параллельные силы имеют равнодействующую, параллельную им, равную по модулю сумме их модулей и направленную в ту же сторону. Линия действия (ЛД) равнодействующей расположена между ЛД заданных сил и делит внутренним образом отрезок прямой между ЛД этих сил на части, обратно пропорциональные модулям сил. Обратно, любую силу можно разложить на две параллельные силы, направленные в ту же сторону.
 Две неравные параллельные силы, направленные в противоположные
стороны имеют равнодействующую, равную по модулю разности модулей сил,
параллельную им и направленную в сторону большей силы. ЛД равнодействующей
расположена за ЛД большей из них и делит внешним образом отрезок прямой между ЛД
заданных сил на части, обратно пропорциональные модулям сил.
Две неравные параллельные силы, направленные в противоположные
стороны имеют равнодействующую, равную по модулю разности модулей сил,
параллельную им и направленную в сторону большей силы. ЛД равнодействующей
расположена за ЛД большей из них и делит внешним образом отрезок прямой между ЛД
заданных сил на части, обратно пропорциональные модулям сил.
2.3 Пара сил. Момент пары сил
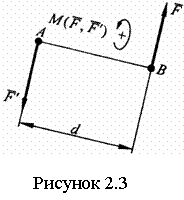
Парой сил, приложенной к АТТ, называют систему двух
равных по модулю параллельных сил, направленных в противоположные стороны и не
лежащих на одной прямой (рисунок 2.3). Сумма сил пары равна нулю, но пара сил
не уравновешена. Кратчайшее расстояние между ЛД сил пары называют плечом пары,
а плоскость, в которой лежат силы пары - плоскостью действия пары. Совокупность
нескольких пар сил, действующих на тело, называется системой пар сил. Пара не
приводится к равнодействующей. Действие пары на тело характеризуется моментом
M![]() , равным ±F∙d, а также положением плоскости
действия пары в пространстве и направлением, в котором пара стремится вращать
тело, т.о., момент пары сил есть вектор.
, равным ±F∙d, а также положением плоскости
действия пары в пространстве и направлением, в котором пара стремится вращать
тело, т.о., момент пары сил есть вектор.
Векторный момент пары сил - это вектор
![]() , перпендикулярный
плоскости действия пары и направленный в ту сторону, откуда видно, что пара
стремится повернуть тело против часовой стрелки, и численно равный произведению
модуля одной из сил пары на ее плечо. Пару сил можно переносить куда угодно в
плоскости и в параллельную плоскость, изменяя модуль силы и плечо пары, но,
сохраняя при этом неизменными модуль момента пары и направление, в котором она
стремится вращать твердое тело, т.е. векторный момент пары сил есть свободный
вектор.
, перпендикулярный
плоскости действия пары и направленный в ту сторону, откуда видно, что пара
стремится повернуть тело против часовой стрелки, и численно равный произведению
модуля одной из сил пары на ее плечо. Пару сил можно переносить куда угодно в
плоскости и в параллельную плоскость, изменяя модуль силы и плечо пары, но,
сохраняя при этом неизменными модуль момента пары и направление, в котором она
стремится вращать твердое тело, т.е. векторный момент пары сил есть свободный
вектор.
Две пары сил, имеющие одинаковые векторные моменты, эквивалентны независимо от того, где каждая из них расположена (в одной плоскости или в параллельных плоскостях) и чему равны модули сил и плечи пар.
Если пары расположены в одной плоскости, то их векторные моменты направлены перпендикулярно этой плоскости в ту или иную сторону в зависимости от направления, в котором пара стремится вращать тело. В этом случае моменты пар можно различать по модулю и знаку, рассматривая их как алгебраические величины. Момент пары считают положительным, если пара стремится вращать тело против часовой стрелки, и отрицательным при противоположном направлении. Тогда для плоской системы пар сил
![]() (2.8)
(2.8)
и  .
(2.9)
.
(2.9)
Теорема о сложении пар сил. Совокупность пар сил,
действующих на тело, эквивалентна одной паре сил с векторным моментом, равным
сумме векторных моментов всех пар сил, 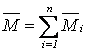 . Тогда условия равновесия системы пар сил, действующих
на твердое тело, имеют вид
. Тогда условия равновесия системы пар сил, действующих
на твердое тело, имеют вид
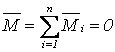 .
(2.10)
.
(2.10)
2.4 Теорема о параллельном переносе силы
Силу, приложенную к твердому телу, можно, не изменяя ее действия, перенести параллельно самой себе в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (рисунок 2.4).
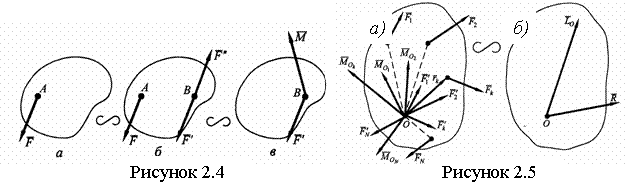 2.5 Приведение системы сил к заданному центру
2.5 Приведение системы сил к заданному центру
Произвольную систему сил, действующих на АТТ, можно привести к какому-либо центру, заменив все действующие силы одной силой, равной главному вектору системы сил, приложенному в этом центре, и одной парой сил с моментом, равным главному моменту системы сил относительно того же центра (рисунок 2.5)
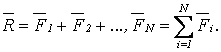 (2.11)
(2.11)
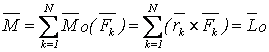 .
(2.12)
.
(2.12)
При этом ![]() не зависит от
выбора центра приведения, а
не зависит от
выбора центра приведения, а ![]() – зависит.
– зависит.
Две системы сил, приложенных к АТТ, эквивалентны, если они имеют одинаковые главные векторы и главные моменты относительно одного и того же центра.
Сформулируем теорему Вариньона: если система сил имеет равнодействующую, то момент равнодействующей относительно любой точки или оси равен сумме моментов всех сил системы относительно той же точки или оси.
Лекция 3. Условия равновесия систем сил. Трение. Центр тяжести
Содержание лекции: условия равновесия систем сил; трение скольжения и качения; центр тяжести твердых тел.
Цели лекции: изучить условия равновесия пространственных и плоских систем сил, рассмотреть особенности решения задач при наличии трения, научиться определять центры тяжести тел.
3.1 Условия равновесия системы сил
Произвольная СС, приложенных к телу, эквивалентна одной
силе, равной главному вектору ![]() , и одной паре сил с
моментом, равным главному моменту
, и одной паре сил с
моментом, равным главному моменту ![]() относительно какого-либо центра О. Чтобы такая
система находилась в равновесии, необходимо и достаточно равенство нулю
относительно какого-либо центра О. Чтобы такая
система находилась в равновесии, необходимо и достаточно равенство нулю ![]() и
и ![]() . Поэтому условия равновесия могут быть представлены в
векторной форме как
. Поэтому условия равновесия могут быть представлены в
векторной форме как
 ,
(3.1)
,
(3.1)
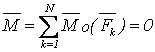 .
(3.2)
.
(3.2)
Эти условия эквивалентны аналитическим условиям равновесия в виде
![]()
 ,
, 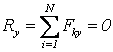 ,
,
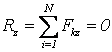 ,
,
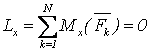 ,
,
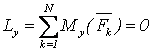 ,
, 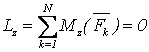 , (3.3)
, (3.3)
т.е., для равновесия произвольной СС, приложенных к АТТ, необходимо и достаточно равенства нулю сумм проекций всех сил на оси декартовой системы координат и сумм моментов всех сил относительно этих осей.
Условия равновесия для пространственной системы параллельных сил (ось Oz параллельна направлению действия сил) имеют вид
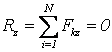 ,
, 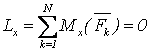 ,
,
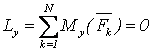 .
(3.4)
.
(3.4)
Первая форма условий равновесия произвольной плоской СС: необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси и сумма алгебраических моментов сил относительно любого центра были равны нулю
 ,
, 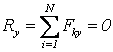 ,
, 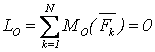 .
(3.5)
.
(3.5)
Вторая форма
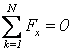 ,
,
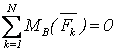 ,
, 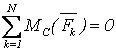 (3.6)
(3.6)
при
этом ![]() не перпендикулярна
не перпендикулярна ![]() .
.
Третья форма
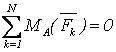 ,
,
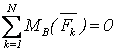 ,
,
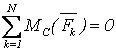 (3.7)
(3.7)
при этом А, В, С не лежат на одной прямой.
Условия равновесия для плоской системы параллельных сил имеют вид
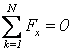 ,
,
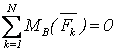 (3.8)
(3.8)
(при этом ось Ox не должны быть перпендикулярной направлению сил) или
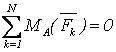 ,
,
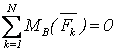 (3.9)
(3.9)
причем прямая, проходящая через А и В, не параллельна силам.
 3.2
Равновесие системы тел
3.2
Равновесие системы тел
Связи, соединяющие части системы тел, называют внутренними. Если внешние связи заменить силами, то условий равновесия недостаточно для их определения. Методы решения задач:
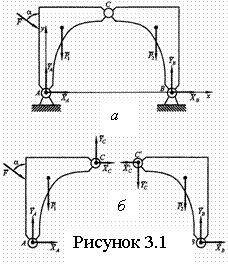
а) пользуясь свойствами внутренних связей, составляют дополнительные условия равновесия. Так, для системы на рисунке 3.1 а, четвертым уравнением будет равенство нулю суммы моментов относительно шарнира С всех сил, приложенных к какую-либо одной из ее половин;
б) мысленно расчленяют конструкцию на отдельные части, заменяя внутренние связи силами (рисунок 3.1 б). Для каждой половины имеем по три независимых условия равновесия, из которых находим шесть неизвестных.
3.3 Статически определимые и статически неопределимые системы
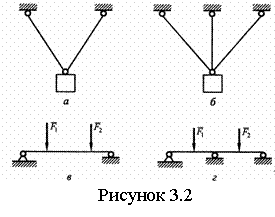
Если число неизвестных составляющих реакций связей равно числу независимых уравнений равновесия (рисунок 3.2 а, в), то рассматриваемую систему называют статически определимой, если больше - статически неопределимой (рисунок 3.2 б, г). Определить реакции в статически неопределимых системах методами, изложенными в этом разделе для АТТ, невозможно. Для решения таких задач необходимо учитывать деформируемость тел и дополнительно составлять уравнения деформаций.
 3.4
Трение скольжения. Реакция шероховатой поверхности
3.4
Трение скольжения. Реакция шероховатой поверхности
Законы трения скольжения (Кулона – Амонтона):
1. При стремлении сдвинуть одно тело относительно
другого в плоскости их соприкосновения возникает сила трения ![]() , модуль
которой может принимать любые значения в интервале 0≤F≤
Fmax. Сила трения приложена к телу и направлена в сторону, противоположную
возможному направлению скорости точки приложения силы.
, модуль
которой может принимать любые значения в интервале 0≤F≤
Fmax. Сила трения приложена к телу и направлена в сторону, противоположную
возможному направлению скорости точки приложения силы.
 2. Максимальная сила трения равна произведению коэффициента
трения f на силу нормального давления N
2. Максимальная сила трения равна произведению коэффициента
трения f на силу нормального давления N
Fmax=f∙N. (3.10)
Коэффициент трения - безразмерная величина, зависящая от материалов и состояния поверхностей соприкасающихся тел (шероховатость, температура, влажность и т. п.); определяется опытным путем. Значения f: дерево по дереву 0,4-0,7; металл по металлу 0,15-0,25; сталь по льду 0,027.
Различают коэффициенты трения покоя и трения скольжения. Коэффициент трения покоя определяется по максимальной силе трения Fmax, соответствующей предельному состоянию равновесия, когда малейшее увеличение внешних сил вызывает движение. Обычно он больше коэффициента трения скольжения. С увеличением скорости скольжения значение последнего сначала незначительно уменьшается, а затем остается практически неизменным.
3. Максимальная сила трения в довольно широких пределах не зависит от площади соприкасающихся поверхностей.
Реакцию шероховатой поверхности представляют в виде
двух составляющих: нормальной реакции ![]() (равна
по модулю силе нормального давления) и перпендикулярной ей силы трения
(равна
по модулю силе нормального давления) и перпендикулярной ей силы трения ![]() (рисунок 3.3). Полная реакция
(рисунок 3.3). Полная реакция ![]() отклонена от нормали на некоторый угол α
(tg α = F/N).
отклонена от нормали на некоторый угол α
(tg α = F/N).
Если тело лежит на горизонтальной шероховатой
поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то
F = 0, а полная реакция R = N и перпендикулярна опорной
поверхности. Приложив к телу силу ![]() , мы стремимся
вызвать его движение, но оно не происходит, так как возникает сила трения
, мы стремимся
вызвать его движение, но оно не происходит, так как возникает сила трения ![]() , причем F≤ Fmax. С
увеличением силы
, причем F≤ Fmax. С
увеличением силы ![]() будет возрастать и сила
будет возрастать и сила ![]() . При F1 = Fmax
наступит предельное состояние равновесия, при котором полная реакция
. При F1 = Fmax
наступит предельное состояние равновесия, при котором полная реакция ![]() отклонится от вертикали на угол
αmax, называемый
углом трения. Обозначив его через φ, находим, что тангенс угла
трения равняется коэффициенту трения
отклонится от вертикали на угол
αmax, называемый
углом трения. Обозначив его через φ, находим, что тангенс угла
трения равняется коэффициенту трения
tg φ= Fmax/N=f . (3.11)
Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения. Равновесие тел с учетом сил трения скольжения рассматривают обычно для предельного состояния, когда сила трения достигает максимального значения. Реакция неидеальной связи представляется двумя составляющими: нормальной реакцией N и максимальной силой трения Fmax.
3.5 Реакция связи при качении
На рисунке 3.4 а показано, что при качении цилиндр вдавливается в опорную плоскость и контактирует с ней по некоторой поверхности, которая образует дугу СD, сдвинутую в направлении качения.
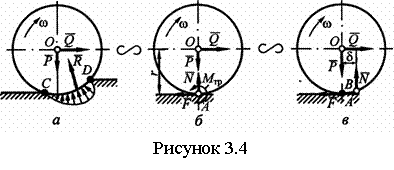 Полная реакция
Полная реакция ![]() опорной
поверхности на цилиндр как сумма системы распределенных сил, вызванных деформацией
поверхности, препятствует качению цилиндра. Это сопротивление, возникающее
при качении одного тела по поверхности другого, называют трением качения. В инженерных расчетах нас интересует момент
сопротивления качению (рисунок 3.4 б). Схематизируя явление,
рассматривают качение по недеформируемой поверхности, а полную реакцию
опорной
поверхности на цилиндр как сумма системы распределенных сил, вызванных деформацией
поверхности, препятствует качению цилиндра. Это сопротивление, возникающее
при качении одного тела по поверхности другого, называют трением качения. В инженерных расчетах нас интересует момент
сопротивления качению (рисунок 3.4 б). Схематизируя явление,
рассматривают качение по недеформируемой поверхности, а полную реакцию ![]() представляют в виде двух составляющих,
приложенных в точке В, смещенной от точки А в сторону возможного
качения на некоторую величину δ (рисунок 3.4 в). Сила
представляют в виде двух составляющих,
приложенных в точке В, смещенной от точки А в сторону возможного
качения на некоторую величину δ (рисунок 3.4 в). Сила ![]() - сила трения скольжения, а сила
- сила трения скольжения, а сила ![]() - нормальная реакция. Из условий
равновесия имеем
- нормальная реакция. Из условий
равновесия имеем
N = P, F = Q, Qmax∙r = δ∙N. (3.12)
Произведение δ∙N = (Мтр)max называется моментом сопротивления качению, или моментом трения качения. Если сила Q мала, то смещение силы N от вертикального диаметра цилиндра также мало; с увеличением Q это смещение возрастает. При Qmax цилиндр достигнет предельного состояния равновесия, и нормальная реакция N будет отстоять от вертикального диаметра на предельном расстоянии δ, которое называется коэффициентом трения качения. Коэффициент δ зависит от свойств материалов и состояния поверхностей соприкасающихся тел, определяют его опытным путем. Так, при качении колеса по рельсу δ = 0,005 см, в шариковом подшипнике δ = 0,001 см.
3.6 Центр тяжести твердого тела
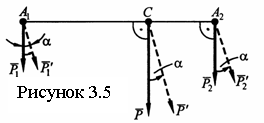
Рассмотрим две параллельные силы ![]() и
и
![]() , приложенные к телу в точках А1
и
A2 (рисунок 3.5). Равнодействующая
, приложенные к телу в точках А1
и
A2 (рисунок 3.5). Равнодействующая ![]() , ее линия действия
параллельна слагаемым
силам и проходит через некоторую
точку С, лежащую на прямой
A1
A2,.
Положение точки С найдем
с помощью
теоремы Вариньона
, ее линия действия
параллельна слагаемым
силам и проходит через некоторую
точку С, лежащую на прямой
A1
A2,.
Положение точки С найдем
с помощью
теоремы Вариньона ![]() , откуда
, откуда
![]() . (3.13)
. (3.13)
Повернув силы
![]() и
и
![]() на один и тот же угол
α вокруг точек А1, А2,
придем к выводу, что и равнодействующая повернется в ту же сторону на
угол α и будет приложена в
той же точке С,
называемой центром параллельных сил. Аналогично -
для любого числа сил.
на один и тот же угол
α вокруг точек А1, А2,
придем к выводу, что и равнодействующая повернется в ту же сторону на
угол α и будет приложена в
той же точке С,
называемой центром параллельных сил. Аналогично -
для любого числа сил.
Равнодействующую сил тяжести ![]() ,
, ![]() ,…,
,…, ![]() ,
приложенных к частицам данного тела, обозначим
,
приложенных к частицам данного тела, обозначим ![]() (рисунок
3.6). Модуль этой силы называется весом тела и определяется равенством
(рисунок
3.6). Модуль этой силы называется весом тела и определяется равенством

![]() . (3.14)
. (3.14)
Точка С является центром параллельных сил тяжести ![]() и называется центром тяжести тела.. Т.о.,
центр тяжести АТТ - неизменно связанная с телом точка, через которую проходит ЛД
равнодействующей сил тяжести, приложенных к частицам данного тела, при любом
положении тела в пространстве. Координаты центра тяжести определяются формулами
и называется центром тяжести тела.. Т.о.,
центр тяжести АТТ - неизменно связанная с телом точка, через которую проходит ЛД
равнодействующей сил тяжести, приложенных к частицам данного тела, при любом
положении тела в пространстве. Координаты центра тяжести определяются формулами
![]() ,
, ![]() ,
, ![]() (3.15)
(3.15)
где ![]() ,
, ![]() ,
, ![]() – координаты точек приложения сил
тяжести
– координаты точек приложения сил
тяжести ![]() .
.
Лекция 4. Кинематика точки и простейших движений тела
Содержание лекции: вводные понятия кинематики, кинематика точки, траектория, скорость, ускорение точки; поступательное и вращательное движение твердого тела.
Цели лекции: изучить кинематические параметры движения точки и простейших движений твердого тела.
4.1 Введение в кинематику
Кинематика - раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности и действующих на них сил. Под движением понимают изменение с течением времени положения данного тела в пространстве по отношению к другим телам, образующим вместе с системой координат систему отсчета (СО), выбор которой в кинематике произволен.
Движение тел совершается в пространстве с течением времени. Пространство рассматривают как трехмерное евклидово пространство. Время считается. протекающим одинаково во всех рассматриваемых СО. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматривают как функции от t. Отсчет времени ведется от некоторого начального момента.
 Для решения задач
кинематики надо, чтобы изучаемое движение тела
(точки) было кинематически задано, что означает задать положение этого тела (точки) относительно данной
СО в любой момент времени. Изучение движения начинается с установления
способов задания движения.
Основная
задача кинематики - зная закон движения точки (тела), установить методы
определения всех кинематических величин, характеризующих данное движение.
Для решения задач
кинематики надо, чтобы изучаемое движение тела
(точки) было кинематически задано, что означает задать положение этого тела (точки) относительно данной
СО в любой момент времени. Изучение движения начинается с установления
способов задания движения.
Основная
задача кинематики - зная закон движения точки (тела), установить методы
определения всех кинематических величин, характеризующих данное движение.
Непрерывная линия, которую описывает движущаяся точка относительно данной СО, называют траекторией точки. Если траекторией является прямая, движение точки называют прямолинейным, а если кривая - криволинейным.
4.2 Способы задания движения точки
Движение точки может быть задано одним из трех способов.
1.
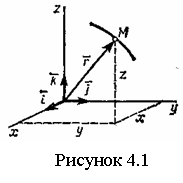
Векторный способ. Пусть точка М движется по отношению к некоторой системе
отсчета Oxyz. Положение точки в любой момент времени можно определить,
задав ее радиус-вектор ![]() (рисунок 4.1) как функцию от
времени
t
(рисунок 4.1) как функцию от
времени
t
![]() . (4.1)
. (4.1)
Это и есть закон движения точки в векторной форме.
 2.
Координатный способ. Положение
точки можно непосредственно определять
ее координатами, изменяющимися при движении с течением времени
2.
Координатный способ. Положение
точки можно непосредственно определять
ее координатами, изменяющимися при движении с течением времени
![]() . (4.2)
. (4.2)
Это - закон движения точки в прямоугольных декартовых координатах.
3. Естественный способ. Задать движение точки естественным способом – это задать (рисунок 4.2) ее траекторию, начало отсчета на траектории с указанием направлений отсчета и закон движения в виде
![]() . (4.3)
. (4.3)
4.3 Скорость и ускорение точки при векторном способе задания
движения
Одной из
основных кинематических характеристик движения точки является ее скорость.
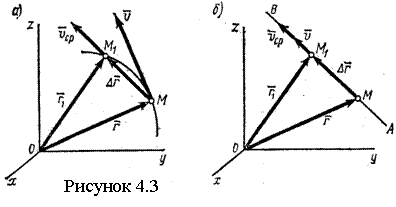
Пусть в момент времени t точка находится в положении М определяемом
радиусом-вектором ![]() , а в момент t1
приходит в положение М1, определяемое вектором
, а в момент t1
приходит в положение М1, определяемое вектором ![]() (рисунок 4.3). Тогда перемещение точки
за промежуток времени
(рисунок 4.3). Тогда перемещение точки
за промежуток времени ![]() определяется вектором
перемещения точки
определяется вектором
перемещения точки ![]() . На треугольнике ОММ1
видно, что
. На треугольнике ОММ1
видно, что ![]() ; следовательно,
; следовательно, ![]() . Отношение вектора перемещения точки к
соответствующему промежутку времени дает векторную величину, называемую средней
по модулю и направлению скоростью точки за промежуток времени
Dt,
. Отношение вектора перемещения точки к
соответствующему промежутку времени дает векторную величину, называемую средней
по модулю и направлению скоростью точки за промежуток времени
Dt,
![]() . Скоростью точки в данный момент
времени t называется величина
. Скоростью точки в данный момент
времени t называется величина ![]() , так что
скорость есть первая производная от вектора
, так что
скорость есть первая производная от вектора ![]() по
аргументу t
по
аргументу t
![]() . (4.4)
. (4.4)
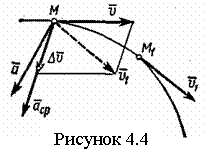
Ускорением
точки называется векторная величина, характеризующая изменение с течением
времени модуля и направления скорости точки. Пусть в некоторый момент времени t
точка находится в положении М и имеет скорость ![]() , а в момент t1
приходит в положение
M1 и имеет скорость
, а в момент t1
приходит в положение
M1 и имеет скорость
![]() (рисунок 4.4). Тогда
за промежуток времени
(рисунок 4.4). Тогда
за промежуток времени
![]() скорость точки получает приращение
скорость точки получает приращение ![]() ,
всегда направленное в сторону вогнутости траектории. Отношение
,
всегда направленное в сторону вогнутости траектории. Отношение
![]() к
Dt определяет
среднее ускорение точки
за
промежуток времени
к
Dt определяет
среднее ускорение точки
за
промежуток времени
![]() .
Ускорением
точки в данный момент времени
t
называют векторную
величину, к которой стремится
.
Ускорением
точки в данный момент времени
t
называют векторную
величину, к которой стремится
![]() при стремлении промежутка времени
Dt
к нулю
при стремлении промежутка времени
Dt
к нулю
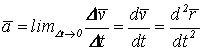 . (4.5)
. (4.5)
Т.о., вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
4.4 Скорость и ускорение точки при координатном способе задания движения
Используем следующую теорему: проекция производной от вектора на ось, неподвижную в данной СО, равна производной от проекции дифференцируемого вектора на ту же ось.
Тогда для проекций скорости имеем
![]() (4.6)
(4.6)
или ![]() . (4.7)
. (4.7)
Т.о., проекции скорости точки на координатные оси равны первым производным от проекций соответствующих координат точки по времени.
Для проекций ускорения имеем
 ,
, 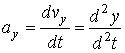 ,
, 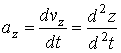 (4.8)
(4.8)
или ![]() , (4.9)
, (4.9)
т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.
4.5 Скорость и ускорение точки при естественном способе задания движения
Здесь ![]() и
и ![]() определяют
по их проекциям на оси естественного трехгранника Мtnb, имеющие начало в
точке М и движущиеся вместе с нею. Направления осей:
Мt - по касательной к
траектории в сторону положительного отсчета s; главная нормаль
Мn
- по нормали к
траектории, лежащей в соприкасающейся плоскости, и направленной в сторону
вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так,
чтобы она образовывала с ними правую систему осей.
определяют
по их проекциям на оси естественного трехгранника Мtnb, имеющие начало в
точке М и движущиеся вместе с нею. Направления осей:
Мt - по касательной к
траектории в сторону положительного отсчета s; главная нормаль
Мn
- по нормали к
траектории, лежащей в соприкасающейся плоскости, и направленной в сторону
вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так,
чтобы она образовывала с ними правую систему осей.
Определим скорость точки
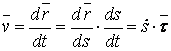 . (4.10)
. (4.10)
Проекция скорости точки на касательную к ее траектории
![]() .
(4.11)
.
(4.11)
Очевидно,
что ![]() и модуль
скорости
и модуль
скорости ![]() .
.
Для ускорения точки имеем
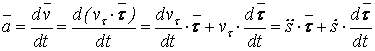 .
(4.12)
.
(4.12)
Т.к.
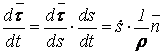 (ρ
– радиус кривизны траектории точки в рассматриваемом положении), то
(ρ
– радиус кривизны траектории точки в рассматриваемом положении), то
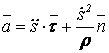 ,
(4.13)
,
(4.13)
т.е., ускорение равно сумме касательной и нормальной составляющих
![]() .
(4.14)
.
(4.14)
Вектор
![]() лежит в соприкасающейся плоскости, т. е. в
плоскости Mtn. Проецируя обе части
равенства (4.13) на оси Мt,
Мn и
Mb, получим
лежит в соприкасающейся плоскости, т. е. в
плоскости Mtn. Проецируя обе части
равенства (4.13) на оси Мt,
Мn и
Mb, получим
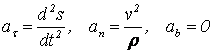 . (4.15)
. (4.15)
4.6 Поступательное движение твердого тела
Поступательным называется такое движение АТТ, при котором любая прямая, проведенная в теле, перемещается, оставаясь параллельной себе, при этом траектории его точек могут быть любыми кривыми. Справедлива теорема: при поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Кинематика АТТ в этом случае сводится к кинематике точки.
 4.7 Вращательное
движение твердого тела вокруг неподвижной оси
4.7 Вращательное
движение твердого тела вокруг неподвижной оси
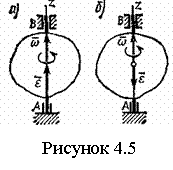
При вращении АТТ вокруг неподвижной оси, его точки, лежащие на оси, остаются неподвижными (АВ на рисунке 4.5). Через ось проведем две плоскости - неподвижную и подвижную, связанную с телом. Двугранный угол j между ними называют углом поворота тела и считают положительным, когда он отсчитывается от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Закон вращения АТТ вокруг неподвижной оси – это зависимость
 j =
j (t).
(4.16)
j =
j (t).
(4.16)
Угловая скорость характеризует изменение j
w =
dj/dt или ![]() . (4.17)
. (4.17)
Угловую
скорость тела можно изобразить в виде вектора ![]() с
модулем, равным |w|, и направленного вдоль оси вращения тела в
ту сторону, откуда вращение видно происходящим против хода часовой стрелки.
с
модулем, равным |w|, и направленного вдоль оси вращения тела в
ту сторону, откуда вращение видно происходящим против хода часовой стрелки.
Угловое
ускорение характеризует изменение ![]() с течением времени
с течением времени
e =
dw/dt =
d2
j/dt2 или ![]() .
(4.18)
.
(4.18)
Если во все время движения
w=const, то вращение называют
равномерным. Из формулы (4.17), интегрируя, найдем его закон ![]() . (4.19)
. (4.19)
При равномерном
вращении, если ![]() , то
, то ![]() .
(4.20)
.
(4.20)
Если угловое ускорение тела во все время движения остается постоянным (e=const), то вращение называется равнопеременным, закон которого имеет вид
![]() . (4.21)
. (4.21)
Если w и e имеют одинаковые знаки, вращение - равноускоренное, если разные — равнозамедленное.
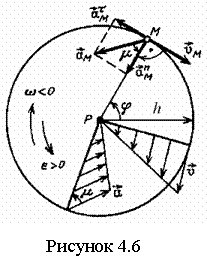
Определим скорости и ускорения точек вращающегося тела (рисунок 4.6).
При вращении точка М описывает окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр P лежит на оси. За время dt тело поворачивается на угол dj, точка М совершает перемещение ds = h∙ dj. Тогда
![]() . (4.21)
. (4.21)
Ускорения точки найдем как
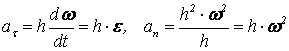 . (4.22)
. (4.22)
Ускорение
![]() направлено по касательной к траектории
(в сторону движения при ускоренном вращении и в обратную сторону при
замедленном), ускорение
направлено по касательной к траектории
(в сторону движения при ускоренном вращении и в обратную сторону при
замедленном), ускорение ![]() всегда направлено
по радиусу МP к оси. Полное ускорение точки равно
всегда направлено
по радиусу МP к оси. Полное ускорение точки равно
![]() , (4.23)
, (4.23)
а угол m (рисунок 4.6) определяется через зависимость
![]() .
(4.24)
.
(4.24)
Для
векторов ![]() и
и ![]() можно
получить формулы
можно
получить формулы
![]() ,
(4.25)
,
(4.25)
![]() . (4.26)
. (4.26)
Лекция 5. Плоскопараллельное движение твердого тела. Сложное движение точки
Содержание лекции: кинематика плоскопараллельного движения тела; сложное движение точки.
Цели лекции: изучить кинематические параметры плоскопараллельного движения тела и сложного движения точки.
5.1 Уравнения плоскопараллельного движения
 Плоскопараллельным или плоским движением АТТ называют
движение, при котором все точки тела движутся в плоскостях, параллельных некоторой
неподвижной плоскости (рисунок 5.1).
Плоскопараллельным или плоским движением АТТ называют
движение, при котором все точки тела движутся в плоскостях, параллельных некоторой
неподвижной плоскости (рисунок 5.1).
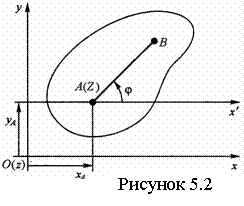
Для изучения движения тела достаточно изучить, как движется в плоскости Оху сечение S тела. Положение фигуры S в плоскости Оху определяется положением отрезка АВ (рисунок 5.2.). Зная координаты хА, уА точки А (полюса) и угол j, можно определить положение отрезка АВ. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости
![]() .
(5.1)
.
(5.1)
Уравнения (5.1) называют уравнениями плоского движения АТТ. Первые два из них определяют движение, которое фигура совершала бы при j=соnst - это поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при хА =const, уА =const, т. е. когда полюс А неподвижен; это вращение фигуры вокруг полюса А. Т.о., плоское движение можно рассматривать как слагающееся из поступательного движения вместе с полюсом, и вращательного движения вокруг полюса.
5.2 Определение скоростей точек плоской фигуры
Пусть
поступательная составляющая движения характеризуется скоростью ![]() . Положение любой точки
B фигуры определяется
по отношению к осям Оху радиусом-вектором
. Положение любой точки
B фигуры определяется
по отношению к осям Оху радиусом-вектором ![]() (рисунок
5.3). Тогда
(рисунок
5.3). Тогда
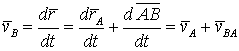 . (5.2)
. (5.2)
При этом
скорость ![]() , которую точка
B получает при
вращении фигуры вокруг полюса А, будет равна
, которую точка
B получает при
вращении фигуры вокруг полюса А, будет равна
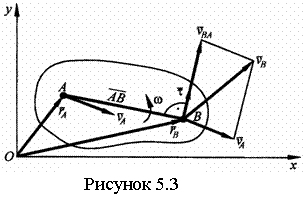
![]() (5.3)
(5.3)
где w - угловая скорость фигуры.
При определении скоростей точек АТТ оказывается полезной следующая теорема (справедлива для произвольного движения): проекции скоростей двух точек тела на соединяющую их прямую равны.
5.3 Определение скоростей точек плоской фигуры с помощью
мгновенного центра скоростей
Другой метод определения скоростей точек плоской фигуры основан на понятии о мгновенном центре скоростей (МЦС) - это точка плоской фигуры, скорость которой в данный момент времени равна нулю.
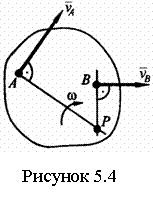 Пусть в момент
времени t точки А и В плоской фигуры имеют скорости
Пусть в момент
времени t точки А и В плоской фигуры имеют скорости ![]() и
и ![]() , не
параллельные друг другу (рисунок 5.4). Тогда точка Р, лежащая на пересечении
перпендикуляров Аа к вектору
, не
параллельные друг другу (рисунок 5.4). Тогда точка Р, лежащая на пересечении
перпендикуляров Аа к вектору ![]() и
Вb к вектору
и
Вb к вектору ![]() , и будет мгновенным центром скоростей,
так как
, и будет мгновенным центром скоростей,
так как ![]() = 0.
= 0.
Если теперь в момент времени t взять точку Р за полюс, то по формуле (5.2) скорость точки А будет
![]() .
.
Т.о., скорости точек фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг МЦС. При этом
![]() ,
, ![]() .
(5.4)
.
(5.4)
Из равенства (5.4) следует, что
![]()
![]() , (5.5)
, (5.5)
т.е., скорости точек плоской фигуры пропорциональны их расстояниям от МЦС.
Полученные результаты приводят к следующим выводам:
а) для
определения МЦС достаточно знать только направления ![]() и
и
![]() каких-либо двух точек А и В
плоской фигуры; МЦС находится в точке пересечения перпендикуляров, восставленных
из точек А и В к скоростям этих точек;
каких-либо двух точек А и В
плоской фигуры; МЦС находится в точке пересечения перпендикуляров, восставленных
из точек А и В к скоростям этих точек;
б) для
определения скорости любой точки плоской фигуры достаточно знать модуль и направление
скорости какой-нибудь одной точки А фигуры и направление скорости другой
ее точки В. Тогда, восстановив из точек А и В
перпендикуляры к ![]() и
и ![]() ,
найдем МЦС и по направлению
,
найдем МЦС и по направлению ![]() определим направление
поворота фигуры. После этого, зная
определим направление
поворота фигуры. После этого, зная ![]() , найдем по (5.5)
скорость
, найдем по (5.5)
скорость ![]() любой точки М плоской фигуры.
Направлен вектор
любой точки М плоской фигуры.
Направлен вектор ![]() перпендикулярно РМ в
сторону поворота фигуры;
перпендикулярно РМ в
сторону поворота фигуры;
в) угловая скорость w плоской фигуры равна в каждый момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от МЦС
![]() .
(5.6)
.
(5.6)
5.4 Определение ускорений точек плоской фигуры
Ускорение
любой точки М плоской фигуры складывается из ускорений, которые точка
получает при поступательном и вращательном движениях этой фигуры. Положение
точки М по отношению к осям Оху определяется радиусом-вектором ![]() , где
, где ![]() = AM.
Тогда
= AM.
Тогда
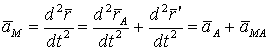 . (5.7)
. (5.7)
Т.о., ускорение
любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь
другой точки А, принятой за полюс, и ускорения, которое точка М
получает при вращении фигуры вокруг этого полюса. При решении задач удобно
вектор ![]() заменять его касательной (
заменять его касательной (![]() ) и нормальной (
) и нормальной (![]() )
составляющими и представить равенство (5.7) в виде
)
составляющими и представить равенство (5.7) в виде
![]() .
(5.8)
.
(5.8)
5.5 Сложное движение точки. Относительное, переносное и абсолютное движения
При решении
задач оказывается целесообразным рассматривать движение точки по отношению к
двум СО, из которых одна считается основной (условно неподвижной), а другая -
движущейся по отношению к первой. Движение, совершаемое при этом точкой,
называют сложным. Рассмотрим точку М, движущуюся по
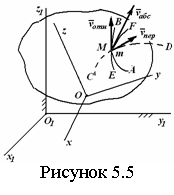 отношению к подвижной
СО Oxyz, которая, в свою очередь, движется относительно неподвижной СО
О1х1у1z1 (рисунок 5.5). Введем
определения:
отношению к подвижной
СО Oxyz, которая, в свою очередь, движется относительно неподвижной СО
О1х1у1z1 (рисунок 5.5). Введем
определения:
а) движение, совершаемое точкой М по отношению к подвижной СО (к осям Oxyz), называется относительным движением;
б) движение,
совершаемое подвижной СО Oxyz по отношению к неподвижной системе
О1х1у1z1, является для точки М
переносным движением. Скорость неизменно связанной с подвижными осями
Охуz точки
m, с которой в данный
момент времени совпадает движущаяся точка М, называется переносной
скоростью точки М в этот момент времени (![]() ), а
ускорение этой точки
m
- переносным ускорением
), а
ускорение этой точки
m
- переносным ускорением
![]() точки М. Тогда
точки М. Тогда
![]() ,
, ![]() ;
(5.9)
;
(5.9)
в) движение, совершаемое точкой по отношению к неподвижной системе отсчета О1х1у1z1, называется абсолютным или сложным.
5.6 Теорема о сложении скоростей
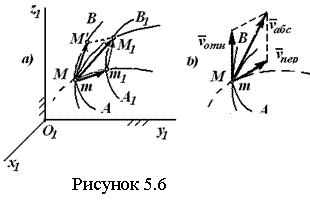 Рассмотрим сложное
движение точки М. Пусть она совершает за промежуток времени
Dt=t1-t относительное
перемещение вдоль траектории АВ, определяемое вектором
Рассмотрим сложное
движение точки М. Пусть она совершает за промежуток времени
Dt=t1-t относительное
перемещение вдоль траектории АВ, определяемое вектором ![]() (рисунок 5.6 а). Сама кривая АВ,
двигаясь вместе с подвижными осями Oxyz, перейдет за тот же промежуток
времени в какое-то новое положение A1B1.
Одновременно точка m кривой АВ, с которой в момент времени t
совпадает точка М, совершит переносное перемещение
(рисунок 5.6 а). Сама кривая АВ,
двигаясь вместе с подвижными осями Oxyz, перейдет за тот же промежуток
времени в какое-то новое положение A1B1.
Одновременно точка m кривой АВ, с которой в момент времени t
совпадает точка М, совершит переносное перемещение ![]() . В результате точка М придет в
положение М1 и совершит за время
Dt абсолютное
перемещение
. В результате точка М придет в
положение М1 и совершит за время
Dt абсолютное
перемещение ![]() . Из векторного треугольника Мm1М1
имеем
. Из векторного треугольника Мm1М1
имеем
![]() .
.
Деля обе
части этого равенства на
Dt и переходя к пределу, получим ![]() . В результате находим, что
. В результате находим, что
![]() . (5.10)
. (5.10)
Направлены
![]() по касательным к соответствующим
траекториям (рисунок 5.6 б). Т.о., доказана теорема о сложении скоростей:
при сложном движении абсолютная скорость точки равна геометрической сумме
относительной и переносной скоростей. Если угол между
по касательным к соответствующим
траекториям (рисунок 5.6 б). Т.о., доказана теорема о сложении скоростей:
при сложном движении абсолютная скорость точки равна геометрической сумме
относительной и переносной скоростей. Если угол между
![]() и
и
![]() равен
a, то по модуль скорости
равен
a, то по модуль скорости
![]() . (5.11)
. (5.11)
5.7 Теорема Кориолиса о сложении ускорений
Найдем зависимость между относительным, переносным и абсолютным ускорениями точки. Из равенства (5.10) получим
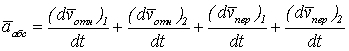 . (5.12)
. (5.12)
Здесь
изменения, которые векторы
![]() и
и
![]() получают при
относительном движении, отмечены индексом 1, а при переносном движении -
индексом 2.
получают при
относительном движении, отмечены индексом 1, а при переносном движении -
индексом 2.
Но, по определению, относительное ускорение характеризует изменение относительной скорости только при относительном движении; движение осей Охуz, т. е. переносное движение при этом во внимание не принимается. Поэтому
![]() . (5.13)
. (5.13)
В свою
очередь, переносное ускорение характеризует изменение переносной скорости
только при переносном движении, так как ![]() ,
где
m - точка, неизменно связанная с осями
Охуz и, следовательно,
получающая ускорение только при движении вместе с этими осями, т. е. при
переносном движении. Поэтому
,
где
m - точка, неизменно связанная с осями
Охуz и, следовательно,
получающая ускорение только при движении вместе с этими осями, т. е. при
переносном движении. Поэтому
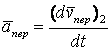 .
(5.14)
.
(5.14)
В результате из равенства (5.12) получим
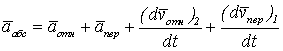 . (5.15)
. (5.15)
Введем обозначение
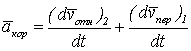 .
(5.16)
.
(5.16)
Величина
![]() , характеризующая изменение
относительной скорости точки при переносном движении и переносной скорости
точки при ее относительном движении, называется поворотным, или кориолисовым,
ускорением точки. В результате равенство (5.15) примет вид
, характеризующая изменение
относительной скорости точки при переносном движении и переносной скорости
точки при ее относительном движении, называется поворотным, или кориолисовым,
ускорением точки. В результате равенство (5.15) примет вид
![]() . (5.17)
. (5.17)
Формула (5.17) выражает следующую теорему Кориолиса о сложении ускорений: при сложном движении ускорение точки равно геометрической сумме трех ускорений, относительного, переносного и поворотного (кориолисова).
Доказывается, что вектор ускорения Кориолиса определяется как
![]() .
(5.18)
.
(5.18)
При нахождении ![]() и
и ![]() нужно учитывать, что каждый из них
может являться суммой нескольких составляющих, например, касательного и нормального
ускорений.
нужно учитывать, что каждый из них
может являться суммой нескольких составляющих, например, касательного и нормального
ускорений.
В частном случае, когда переносное движение является
поступательным движением, ![]() =0, и теорема о
сложении ускорений упрощается
=0, и теорема о
сложении ускорений упрощается
![]() . (5.19)
. (5.19)
Лекция 6. Динамика точки
Содержание лекции: вводные понятия и аксиомы динамики точки; дифференциальные уравнения движения; общие теоремы динамики точки.
Цели лекции: изучить понятия динамики, дифференциальные уравнения движения точки, научиться применять общие теоремы динамики точки для определения характеристик движения точки.
6.1 Аксиомы динамики
Динамикой называют раздел механики, в котором рассматривается движение материальных тел под действием приложенных к ним сил с учетом инерции. Инерцией называется свойство материального тела сохранять состояние движения или покоя при отсутствии действующих на тело сил. Физическую величину, зависящую от количества вещества и являющуюся мерой инерции тела в поступательном движении, называется массой тела m.
Основой динамики точки являются 4 аксиомы, изложенные ниже.
1-я аксиома (закон инерции): материальная точка (МТ), к которой не приложены силы, находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к ней силы не изменяют этого состояния. Движение МТ при отсутствии сил называют инерциальным. Систему отсчета (СО), в которой действует закон инерции, называют инерциальной СО. В большинстве задач СО, связанная с Землей, считается инерциальной.
2-я аксиома (основной закон динамики): ускорение МТ пропорционально приложенной к ней силе и направлено так же, как сила. Основное уравнение
![]() .
(6.1)
.
(6.1)
3-я аксиома (закон о действии и противодействии): две МТ действуют друг на друга с равными по модулям силами, которые лежат на соединяющей эти точки прямой и направлены в противоположные стороны.
4-я аксиома (закон независимости действия сил): геометрическая сумма ускорений, которые сообщаются МТ отдельно каждой приложенной к ней силой, равна ускорению, которое МТ получит под действием на нее всех сил.
![]() (6.2)
(6.2)
Вместо (6.2) можно пользоваться уравнением (6.1),
понимая под силой ![]() равнодействующую.
равнодействующую.
Под действием на тело силы тяжести у тела возникает
одно и то же ускорение ![]() , которое называют
ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена
только сила тяжести
, которое называют
ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена
только сила тяжести ![]() , то по (6.1)
, то по (6.1)
![]() .
(6.2)
.
(6.2)
Масса тела не зависит от его местонахождения и от сил, приложенных к телу, а вес тела меняется с изменением ускорения силы тяжести в зависимости от географической широты места и расстояния от центра Земли.
6.2 Дифференциальные уравнения движения материальной точки
Рассмотрим движение МТ под действием сил {![]() } относительно инерциальной СО
Оxyz,
считая, что среди сил имеются реакции связей.
} относительно инерциальной СО
Оxyz,
считая, что среди сил имеются реакции связей.
Проецируя уравнение (6.2) на естественные оси, получаем естественные дифференциальные уравнения движения (ДУД)
 ; (6.3)
; (6.3)
проецируя на декартовы оси, получаем ДУД точки в декартовых координатах
![]() (6.4)
(6.4)
ДУД применяются к решению двух основных задач динамики МТ:
1-я основная задача: по движению точки найти приложенную к ней силу. Здесь нужно продифференцировать уравнения движения МТ и результаты подставить в (6.3) или (6.4), откуда определяется приложенная к точке сила;
2-я основная задача: по силам, приложенным к точке, найти ее движение. Решая эту задачу, нужно в общем случае найти вторые интегралы дифференциальных уравнений (6.3) или (6.4). В частных случаях возможно интегрирование ДУД точки, применяя метод разделения переменных.
6.3 Относительное движение материальной точки
Законы динамики справедливы только в инерциальной СО.
Рассмотрим движение МТ относительно СО, которая движется произвольно
относительно инерциальной СО. Рассмотрим движение точки
P
под действием сил {![]() }. В инерциальной СО справедливо
основное уравнение динамики (6.2). Абсолютное ускорение точки можно найти по
формуле (5.17)
}. В инерциальной СО справедливо
основное уравнение динамики (6.2). Абсолютное ускорение точки можно найти по
формуле (5.17)
![]() (6.5)
(6.5)
Подставим (6.5) в равенство (6.4) и преобразуем его
![]() (6.6)
(6.6)
Примем обозначения
![]() (6.7)
(6.7)
и
![]() (6.8)
(6.8)
Векторы
![]() и
и
![]() называют
соответственно переносной и кориолисовой силами инерции.
называют
соответственно переносной и кориолисовой силами инерции.
Равенство (6.6) можно записать в виде
![]() (6.9)
(6.9)
Уравнение (6.9) называют основным уравнением динамики относительного движения МТ. Уравнения относительного движения МТ составляются также, как в случае абсолютного движения, если к числу действующих сил добавить переносную и кориолисову силы инерции. Наблюдатель, который находится в движущейся неинерциальной системе отсчета, воспринимает переносную и кориолисову силы инерции, как реально существующие силы. Но это неверно, так как в неинерциальной СО законы механики Ньютона не действуют, и рассматривать явления с точки зрения предыдущих аксиом нельзя.
Частные случаи основного уравнения относительного движения МТ:
а) при поступательном переносном движении
![]()
![]() (6.10)
(6.10)
б) при прямолинейном и равномерном переносном движении
![]() (6.11)
(6.11)
Уравнения (6.11) и (6.2) совпадают, так как
![]() .
Следовательно, данная система отсчета инерциальна. Механическими опытами
невозможно установить, неподвижна ли система отсчета, или она движется
поступательно, равномерно и прямолинейно (принцип относительности Галилея);
.
Следовательно, данная система отсчета инерциальна. Механическими опытами
невозможно установить, неподвижна ли система отсчета, или она движется
поступательно, равномерно и прямолинейно (принцип относительности Галилея);
в) в относительном состоянии покоя
![]() (6.12)
(6.12)
Это уравнение относительного равновесия МТ.
6.4. Теорема об изменении количества движения точки
При решении многих задач динамики вместо интегрирования ДУД оказывается более эффективным использование т.н. общих теорем динамики.
Рассмотрим
теорему об изменении количества движения точки. Количеством движения МТ
называют величину ![]() , равную произведению массы
точки на ее скорость. Вектор
, равную произведению массы
точки на ее скорость. Вектор ![]() направлен по касательной
к траектории точки.
направлен по касательной
к траектории точки.
Элементарным импульсом силы называют величину
![]() (6.13)
(6.13)
равную произведению
силы на элементарный промежуток времени. Направлен импульс вдоль линии действия силы.
Импульс ![]() силы
силы ![]() за
конечное время
t1
за
конечное время
t1
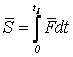 . (6.14)
. (6.14)
Модуль и направление импульса можно вычислить по его проекциям
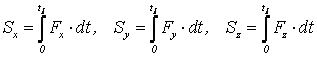 . (6.15)
. (6.15)
Основной закон динамики можно представить в виде
![]() .
(6.16)
.
(6.16)
Это теорема об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Та же теорема в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за этот промежуток времени
![]() . (6.17)
. (6.17)
При решении задач обычно пользуются уравнениями в проекциях.
6.5 Теорема об изменении момента количества движения точки
Моментом
количества движения точки относительно некоторого центра О называется
векторная величина ![]() , определяемая равенством
, определяемая равенством
![]() (6.18)
(6.18)
где ![]() — радиус-вектор движущейся точки,
проведенный из центра О.
— радиус-вектор движущейся точки,
проведенный из центра О.
При этом
вектор ![]() направлен перпендикулярно плоскости,
проходящей через
направлен перпендикулярно плоскости,
проходящей через ![]() и центр О, a
и центр О, a ![]() .
.
Момент
количества движения точки относительно какой-нибудь оси Оz, проходящей
через центр О, равен проекции вектора ![]() на
эту ось
на
эту ось
![]() (6.19)
(6.19)
где
g — угол между
вектором ![]() и осью Оz.
и осью Оz.
Теорема: производная по времени от момента количества движения точки, взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра
![]() .
(6.20)
.
(6.20)
Теорема моментов относительно оси
![]() . (6.21)
. (6.21)
Из
уравнения (6.20) следует, что если ![]() , то
, то ![]() .
.
6.6 Работа силы. Мощность силы. Теорема об изменении кинетической энергии точки
Элементарной
работой силы ![]() , приложенной в точке М (рисунок
6.1), называют скалярную величину
, приложенной в точке М (рисунок
6.1), называют скалярную величину
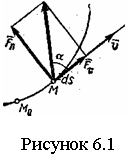 dW =
Ft
∙ds
(6.22)
dW =
Ft
∙ds
(6.22)
где
Ft — проекция силы ![]() на касательную
Мt к траектории точки М,
направленную в сторону перемещения точки;
на касательную
Мt к траектории точки М,
направленную в сторону перемещения точки;
ds — модуль элементарного перемещения точки М.
Т.к. ds
= |d![]() | (здесь
d
| (здесь
d![]() - вектор
элементарного перемещения точки), то равенство (6.22) можно представить в виде
- вектор
элементарного перемещения точки), то равенство (6.22) можно представить в виде
dW=
![]() . (6.23)
. (6.23)
Т.е., элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения.
Работа силы на конечном перемещении M0M1 (рисунок 6.1) определяется как
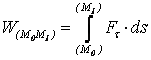 , (6.24)
, (6.24)
 . ( 6.25)
. ( 6.25)
Мощностью называют величину, равную работе, совершаемой силой в единицу времени. Если работа совершается равномерно, то мощность P = W/t1 (здесь t1 - время, течение которого произведена работа W). В общем случае
![]() , (6.26)
, (6.26)
т.е., мощность равна произведению касательной составляющей силы на скорость.
Кинетической
энергией (КЭ) точки называют скалярную величину ![]() . Теорема: изменение КЭ точки
при некотором ее перемещении равно алгебраической сумме работ всех действующих
на точку сил на том же перемещении.
. Теорема: изменение КЭ точки
при некотором ее перемещении равно алгебраической сумме работ всех действующих
на точку сил на том же перемещении.
![]() . (6.26)
. (6.26)
6.7 Принцип Даламбера для точки
Пусть на
МТ с массой
m действует система активных сил, равнодействующую
которых обозначим ![]() , и реакция связи
, и реакция связи ![]() . Под действием этих сил точка будет
двигаться по отношению к инерциальной СО с некоторым ускорением
. Под действием этих сил точка будет
двигаться по отношению к инерциальной СО с некоторым ускорением ![]() .
.
Введем в рассмотрение величину
![]() ,
(6.27)
,
(6.27)
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки. Тогда оказывается, что если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной, т. е.
![]() .
(6.28)
.
(6.28)
Это положение выражает принцип Даламбера для МТ.
Лекция 7. Основы динамики системы и твердого тела
Содержание лекции: механическая система, ее масса, центр масс и моменты инерции; дифференциальные уравнения движения системы; общие теоремы динамики и принцип Даламбера для системы.
Цели лекции: изучить динамические характеристики системы, диффе-ренциальные уравнения движения, основные теоремы динамики для системы.
7.1 Механическая система. Масса, центр масс и моменты инерции
Механической системой (МС) называют совокупность
взаимодействующих МТ или тел. Материальное тело является МС составляющих его частиц. МС, движение
точек которой не ограничено связями, называется системой свободных материальных
точек. Внешними силами ![]() ,
k=
1,2 …,n называют
силы, c которыми
на точки системы действуют тела, не принадлежащие к этой системе. Внутренними
силами называют силы
,
k=
1,2 …,n называют
силы, c которыми
на точки системы действуют тела, не принадлежащие к этой системе. Внутренними
силами называют силы ![]() ,
k= 1,2 …,m,
c которыми
взаимодействуют точки системы. Можно показать, главный вектор и главный момент системы системы внутренних сил равны нулю. Отсюда не вытекает, что
внутренние силы уравновешиваются в общем случае, т.к. они могут вызывать
перемещения точек системы (уравновешиваются в АТТ).
,
k= 1,2 …,m,
c которыми
взаимодействуют точки системы. Можно показать, главный вектор и главный момент системы системы внутренних сил равны нулю. Отсюда не вытекает, что
внутренние силы уравновешиваются в общем случае, т.к. они могут вызывать
перемещения точек системы (уравновешиваются в АТТ).
Массой системы называют сумму масс частиц системы
M=Σmk. (7.1)
Положение центра масс системы (т. С) определяется по формулам
![]() ,
(7.2)
,
(7.2)
![]() .
(7.3)
.
(7.3)
Для тела имеем
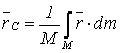 ,
(7.4)
,
(7.4)
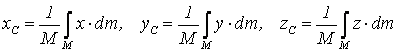 .
(7.5)
.
(7.5)
В однородном поле силы тяжести центры масс и тяжести совпадают.
Моментами инерции МС относительно оси и точки называют величины
Jl=Σmk∙hk2. (7.6)
JO=Σmk∙rk2 (7.7)
где hk и rk – расстояние точки тела с массой mk от оси l и точки O.
Для твердого тела момент инерции относительно оси и точки
![]() , (7.8)
, (7.8)
![]() .
(7.9)
.
(7.9)
Моменты инерции относительно декартовых осей и начала координат
Jx=Σmk∙(yk2+zk2), Jy=Σmk∙(xk2+zk2), Jz=Σmk∙( xk2+yk2), (7.10)
JO=Σmk∙rk2= Σmk∙∙( xk2+yk2+zk2). (7.11)
Моменты инерции относительно координатных плоскостей равны
Jxy=Σmk∙ zk2, Jyz=Σmk∙xk2, Jxz=Σmk∙yk2. (7.12)
Имеются зависимости 2JO= Jx+ Jy+ Jz, (7.13)
JO= Jxy+ Jyz+ Jxz. (7.14)
Для тела моменты инерции определяются интегралами по массе
![]() ,
, ![]() ,
, ![]() .
(7.15)
.
(7.15)
Теорема Гюйгенса-Штейнера: момент инерции системы Jz относительно какой-либо оси z равен сумме момента инерции системы JzC относительно параллельной ей оси zC, проходящей через центр масс, и произведения массы системы M на квадрат расстояния между осями d
![]() . (7.16)
. (7.16)
Среди семейства параллельных осей момент инерции относительно оси, проходящей через центр масс - наименьший.
7.2 Дифференциальные уравнения движения системы. Теорема о движении центра масс системы
Для точек, входящих в МС, можно записать дифференциальные уравнения движения (ДУД) системы в векторной форме
 (7.17)
(7.17)
Проецируя (7.17) на оси, получим ДУД в проекциях оси. Полное решение основной задачи динамики для системы состоит в том, чтобы проинтегрировать ДУД и определить закон движения каждой точки системы и реакции связей. Выполнить это аналитически удается лишь в частных случаях, когда число точек мало, иначе приходится интегрировать уравнения численно. Однако при решении многих задач бывает достаточным найти некоторые характеристики, определяющие движение системы в целом. Сложив почленно уравнения (7.17), получим
![]() . (7.18)
. (7.18)
С учетом формулы (7.2) можно получить соотношение
![]() . (7.19)
. (7.19)
Это теорема о движении центра масс системы: центр масс системы движется как МТ, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Проецируя обе части равенства (7.19) на координатные оси, можно получить ДУД центра масс в проекциях на оси декартовой системы координат.
Из (7.19) следует, что поступательно движущееся тело можно рассматривать как МТ с массой, равной массе тела. В остальных случаях тело можно рассматривать как МТ, когда допустимо не принимать во внимание вращательную часть движения тела. При определении закона движения центра масс МС можно исключать из рассмотрения все неизвестные внутренние силы.
Следствие из теоремы (закон сохранения движения центра масс системы): внутренние силы не изменяют движение центра масс системы.
7.3 Теорема об изменении количества движения системы
Количеством движения системы (КДС) называют величину
![]() .
(7.20)
.
(7.20)
Можно показать, что
![]() ,
(7.21)
,
(7.21)
т. е.
КДС равно произведению массы всей системы на скорость ее центра масс. Если система
движется так, что центр масс остается неподвижным, то КДС равно нулю (например,
в случае тела, вращающегося вокруг неподвижной оси, проходящей через его центр
масс). Если же движение тела является сложным, то величина КДС не зависит от
его вращательного движения вокруг центра масс (для катящегося колеса ![]() независимо от вращения).
независимо от вращения).
Теорема об изменении КДС в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил
![]() .
(7.22)
.
(7.22)
В интегральной форме: изменение КДС за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени
![]() .
(7.24)
.
(7.24)
Следствие (закон сохранения КДС): внутренние силы не могут изменить КДС, и при решении задач внутренние силы можно не рассматривать.
7.4 Теорема об изменении главного момента количеств движения
Главным
моментом количеств движения системы (ГМКДС)
или кинетическим моментом относительно данного центра
О
называется величина ![]() , равная геометрической сумме
моментов количеств движения всех точек системы относительно этого центра
, равная геометрической сумме
моментов количеств движения всех точек системы относительно этого центра
![]() .
(7.25)
.
(7.25)
Аналогично имеем относительно координатных осей
![]() ,
, ![]() ,
,
![]() . (7.26)
. (7.26)
Теорема об изменении ГМКДС (теорема моментов): производная по времени от ГМКДС относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра
![]() . (7.27)
. (7.27)
Проецируя на неподвижные оси 0хyz, получим теорему в проекциях.
Теорема применяется для изучения вращательного движения тела, а также движения системы в общем случае, т.к. последнее слагается из поступательного и вращательного движения. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изучена с помощью теоремы о движении центра масс, а вращательная - с помощью теоремы моментов. При этом из рассмотрения исключаются наперед неизвестные внутренние силы.
Для системы координат, движущейся поступательно вместе с телом, справедлива теорема моментов относительно его центра масс. Она имеет тот же вид, что и относительно неподвижного центра. Для моментов относительно осей такой системы также получаются схожие уравнения.
Следствие из теоремы (закон сохранения ГМКДС): внутренние силы не изменяют ГМКДС. При этом если система неизменяема, то она вращается с постоянной угловой скоростью, а если изменяема, то под действием внутренних (или внешних) сил расстояния отдельных ее точек от оси могут изменяться, что вызовет изменение угловой скорости.
7.5 Теорема об изменении кинетической энергии системы
Кинетической энергией (КЭ) системы называют скалярную величину
![]() . (7.28)
. (7.28)
КЭ является
характеристикой и поступательного, и вращательного движений системы. Отличие Т
от ![]() и
и ![]() состоит
в том, что КЭ является скалярной существенно положительной величиной,
не зависящей от направлений движения частей МС, и не характеризует их изменение.
Внутренние силы действуют на части системы по взаимно противоположным направлениям,
поэтому они не изменяют векторные величины
состоит
в том, что КЭ является скалярной существенно положительной величиной,
не зависящей от направлений движения частей МС, и не характеризует их изменение.
Внутренние силы действуют на части системы по взаимно противоположным направлениям,
поэтому они не изменяют векторные величины ![]() и
и ![]() . Но если под действием внутренних сил
будут изменяться модули скоростей точек системы, то при этом будет изменяться и
величина Т. Т.о., T отличается
от величин
. Но если под действием внутренних сил
будут изменяться модули скоростей точек системы, то при этом будет изменяться и
величина Т. Т.о., T отличается
от величин ![]() и
и
![]() еще и тем, что на ее изменение влияет
действие и внешних, и внутренних сил. КЭ тела в частных случаях движения:
еще и тем, что на ее изменение влияет
действие и внешних, и внутренних сил. КЭ тела в частных случаях движения:
а) при поступательном движении
![]() ,
(7.29)
,
(7.29)
б) при вращательном движении
![]() ,
(7.30)
,
(7.30)
в) при плоскопараллельном движении
![]() . (7.31)
. (7.31)
Теорема об изменении КЭ сиcтемы в дифференциальной форме
![]() .
(7.32)
.
(7.32)
В интегральной форме: изменение КЭ системы при некотором перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.
![]() .
(7.33)
.
(7.33)
7.6 Принцип Даламбера для системы
Силы инерции, действующие на точки МС, можно привести
к главному вектору ![]() и главному моменту
и главному моменту ![]() (точка
O – неподвижный
центр приведения). Формулировка
принципа Даламбера для МС: систему, находящуюся в движении, можно рассматривать
как находящуюся в состоянии равновесия, включая в число
(точка
O – неподвижный
центр приведения). Формулировка
принципа Даламбера для МС: систему, находящуюся в движении, можно рассматривать
как находящуюся в состоянии равновесия, включая в число
![]() и
и ![]() .
Можно
доказать, что при любом движении системы
.
Можно
доказать, что при любом движении системы ![]() равен
взятому со знаком «минус» произведению массы системы на ускорение центра масс
равен
взятому со знаком «минус» произведению массы системы на ускорение центра масс ![]() . Для АТТ, совершающего плоскопараллельное
движение в плоскости материальной симметрии тела
Oxy, силы
инерции могут быть приведены к подвижному центру масс С. Тогда ось Cz
- главная центральная ось инерции тела. Обозначая через
. Для АТТ, совершающего плоскопараллельное
движение в плоскости материальной симметрии тела
Oxy, силы
инерции могут быть приведены к подвижному центру масс С. Тогда ось Cz
- главная центральная ось инерции тела. Обозначая через ![]() момент инерции относительно этой оси и
через ε – угловое ускорение, можно доказать, что
момент инерции относительно этой оси и
через ε – угловое ускорение, можно доказать, что ![]() .
.
Лекция 8. Основные понятия теории механизмов и машин. Структурный анализ механизмов
Содержание лекции: задачи теории механизмов и машин, основные понятия, структурный анализ механизмов
Цели лекции: определить круг задач, решаемых методами теории механизмов и машин, изучить основные понятия ТММ.
8.1 Основные понятия. Структурные элементы механизмов
В технике используются различные машины – устройства для преобразования энергии и совершения полезной работы. Они подразделяются на машины-двигатели (электро-, гидродвигатели, ДВС и др.) и машины-орудия (выполняют технологические или транспортные операции). Механизм - это часть машины, состоящая из взаимосвязанных тел, предназначенных для преобразования движения одного или нескольких тел в требуемые движения других тел. Механизм осуществляет передачу энергии или движения (как правило, с преобразованием сил и характеристик закона движения) от источника к рабочим органам машины, а также преобразование и регулирование механического движения. Если в преобразовании участвуют как твердые, так и жидкие или газообразные тела, то механизм называют соответственно гидравлическим или пневматическим. Изучением движения и работы механизмов занимается теория механизмов и машин (ТММ).
Любой механизм состоит из звеньев и кинематических пар (КП). Звено – это часть механизма, движущаяся как единое целое. Звено может быть простым (состоящим из одной детали) или сложным (составным). Звенья различают по конструктивным признакам (вал, поршень и т.д.), по деформативности (жесткое и гибкое звено), по характеру движения. Звено, совершающее полнооборотное вращение вокруг неподвижной оси, называют кривошипом; при неполнооборотном вращении - коромыслом; звено, движущееся возвратно-поступательно, - ползуном и т. д. Формирование механизма осуществляется с помощью КП (таблица 8.1) - соединений (сопряжений) двух звеньев, допускающих их относительное движение.
Конструктивно любая КП представляет собой подвижное сопряжение соединительных частей звеньев, в котором «силовой поток» от одного звена к другому передается за счет геометрического или силового замыкания.
КП передают нагрузку и движение и часто определяют работоспособность и надежность механизма и машины в целом. По характеру соприкосновения элементов КП подразделяют на низшие (контактируют по поверхности) и высшие (контактируют по линиям или в точках). Отметим, что под нагрузкой высшие КП также соприкасаются по поверхностям, но их размеры пре
|
Т а б л и ц а 8.1 |
|||
|
Класс пары |
Число условий связи |
Название пары, рисунок |
Условное обозначение |
|
|
|
|
|
|
|
|
|
|
|
І |
1 |
|
|
|
ІІ |
2 |
|
|
|
ІІІ |
3 |
|
|
|
ІІІ |
3 |
|
|
|
IV |
4 |
|
|
|
IV |
4 |
|
|
|
V |
5 |
|
|
|
V |
5 |
|
|
|
V |
5 |
|
|
небрежимо малы в сравнении с поверхностью сопрягаемой части звена. Поэтому высшие пары имеют меньшие потери на трение и более компактны, но последние обладают большей нагрузочной способностью.
По числу наложенных условий связи S или степеней подвижности Н относительных движений звеньев КП делят на классы (И. И. Артоболевский). Свободное тело в пространстве имеет 6 степеней подвижности, и Н=6-S. При S=6 КП становится жестким соединением (звеном), а при S=0 КП не существует, и два звена движутся независимо друг от друга. При S=1 КП имеют 5 степеней подвижности (пятиподвижные), при S=2 - 4 степени подвижности (четырехподвижные) и т. д.
В таблице 8.1 даны примеры КП и их условные обозначения. Наиболее распространены КП 5-го класса (одноподвижные) - поступательная, вращательная и винтовая; в винтовой паре между поступательным перемещением l и углом поворота j есть зависимость l=p∙j/(2p), где p - шаг резьбы.
Возможны и другие классификации пар (например, по характеру движения, по расположению в пространстве и др.).
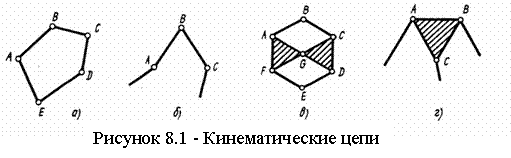 Систему звеньев, соединенных с помощью КП (рисунок 8.1),
называют кинематической цепью (КЦ). Различают замкнутые и незамкнутые КЦ. В
замкнутой КЦ каждое звено входит не менее чем в две КП, в незамкнутой (открытой)
цепи имеются звенья, входящие лишь в одну КП. Т.о., механизм - это КЦ, в которой
при заданном движении одного или нескольких звеньев относительно любого из них
все остальные звенья движутся определенным образом. Звено, относительно
которого оцениваются параметры движения (перемещения, скорости), называют стойкой.
В качестве стойки чаще берут неподвижное звено (в транспортных машинах стойкой
считают раму). В КЦ различают входное и выходное звенья (может быть по нескольку).
Входным называют звено, которому сообщается движение от двигателя, выходным -
звено, реализующее движение, для выполнения которого предназначен механизм. КЦ
подразделяется также на плоские и пространственные, на простые и сложные.
Простой называют КЦ, у которой каждое звено входит в соединение с другим звеном
с помощью одной или двух КП. В противном случае цепь называют сложной.
Систему звеньев, соединенных с помощью КП (рисунок 8.1),
называют кинематической цепью (КЦ). Различают замкнутые и незамкнутые КЦ. В
замкнутой КЦ каждое звено входит не менее чем в две КП, в незамкнутой (открытой)
цепи имеются звенья, входящие лишь в одну КП. Т.о., механизм - это КЦ, в которой
при заданном движении одного или нескольких звеньев относительно любого из них
все остальные звенья движутся определенным образом. Звено, относительно
которого оцениваются параметры движения (перемещения, скорости), называют стойкой.
В качестве стойки чаще берут неподвижное звено (в транспортных машинах стойкой
считают раму). В КЦ различают входное и выходное звенья (может быть по нескольку).
Входным называют звено, которому сообщается движение от двигателя, выходным -
звено, реализующее движение, для выполнения которого предназначен механизм. КЦ
подразделяется также на плоские и пространственные, на простые и сложные.
Простой называют КЦ, у которой каждое звено входит в соединение с другим звеном
с помощью одной или двух КП. В противном случае цепь называют сложной.
Строение механизма определяет его основные характеристики (виды движений, число степеней подвижности и др.). Отсюда - задачи структурного анализа механизмов: а) определение количества свобод движения механизмов в зависимости от геометрических форм сопряжений звеньев и их количества; б) разделение механизма на структурные группы; в) обеспечение заданных траекторий движения точек звеньев. Для структурного анализа используют структурную схему - простейшую расчетную модель механизма, описывающую принцип его действия. Механизм изображают с помощью условных обозначений звеньев (обозначают цифрами, размеры не указывают) и КП (обозначают буквами). Неподвижное звено отмечают штриховкой.
8.2 Основные виды механизмов
Исходя из кинематических, конструктивных и функциональных свойств, механизмы подразделяют на различные виды.
Примеры – на рисунках 8.2 – 8.8 приведены примеры основных видов механизмов.
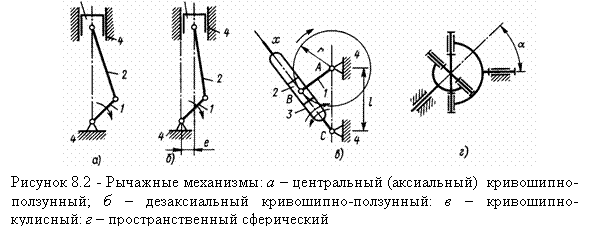
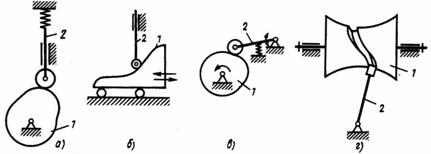
|
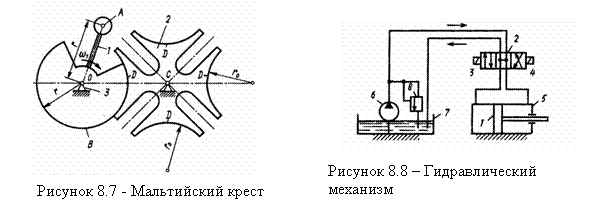 |
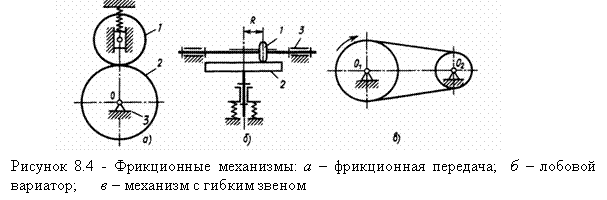
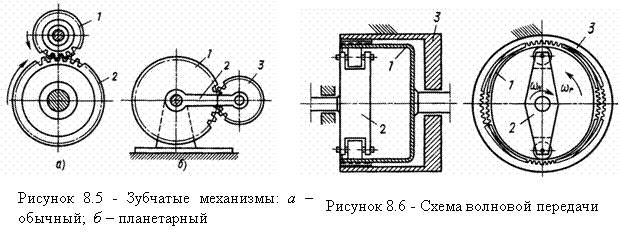
8.3 Структурные формулы кинематических цепей и механизмов
Структурные формулы связывают число степеней свободы КЦ механизма H с числом звеньев, а также с числом и видом его КП.
Если число степеней свободы механизма H совпадает с числом обобщенных координат, то разность между общим числом координат, определяющих положение всех звеньев механизма, и числом независимых уравнений, связывающих эти координаты, дает H.
Каждое отдельно взятое звено имеет 6 степеней подвижности в пространстве, и для k звеньев общее число степеней подвижности (ЧСП) будет 6k. Соединение звеньев в КП накладывает связи на относительное движение звеньев. Эти ограничения зависят от класса КП, т. е. числа условий связи. Если число КП каждого класса обозначить через рn, где индекс n - номер ее класса, то в общем случае в КЦ будет р1 пар 1-го класса, р2 пар 2-го класса и т.д. Следовательно, из 6k степеней подвижности, которыми обладают свободные звенья, следует исключить степени подвижности, запрещенные в КП. Тогда ЧСП пространственной КЦ будет
H = 6k - 5р5 - 4р4 - 3р3 - 2р2 - р1. (8.1)
Если одно из звеньев КЦ неподвижно (стойка), то степень подвижности КЦ (ЧСП относительно звена, принятого за неподвижное) будет
W = 6n - 5р5 - 4р4 - 3р3 - 2р2 - р1. (8.2)
Если звенья механизма движутся в одной плоскости (или параллельных плоскостях), то получаем плоский механизм, и структурная формула (8.2) принимает вид (П.Л.Чебышев, 1869 г.)
W = 3n - 2р5 - р4. (8.3)
Структурные формулы (8.2) и (8.3) получены из предположения, что все уравнения связи независимы. В некоторых механизмах в общее число наложенных связей может войти q избыточных (повторных) связей. Тогда формулы (2.2) и (2.3) принимают вид
W = 6n - 5р5 - 4р4 - 3р3 - 2р2 – р1+q, (8.4)
W = 3n - 2р5 - р4 1+q. (8.5)
При q=0 механизм представляет собой статически определимую систему, и сборка его происходит без деформации звеньев (самоустанавливающийся механизм), а при q>0 - статически неопределимую систему. Сборка и движение такого механизма происходят при деформировании его звеньев, т.к. размеры звеньев невозможно изготовить с абсолютной точностью.
8.4 Понятия о структурном анализе и синтезе механизмов
Под структурным анализом механизма понимается определение количества звеньев и КП, классификация КП, определение степени подвижности механизма, а также установление класса и порядка механизма.
Структурным синтезом называется проектирование структурной схемы механизма, состоящей из неподвижного и подвижных звеньев и КП.
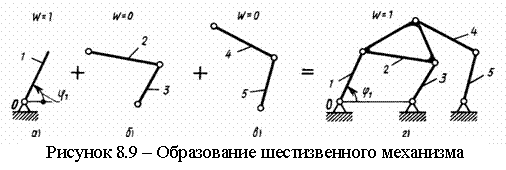
Для нахождения структурной схемы используется метод
присоединения т.н. структурных групп Ассура к ведущему звену или основному механизму.
Рисунок 8.9 - Пример образования плоскостного 6-тизвенного механизма
Группой Ассура называют КЦ, которая при
присоединении ее элементами внешних пар к стойке получает нулевую степень подвижности.
Структурные формулы групп Ассура получаются из формулы (8.3): W=3n — 2p5,
откуда p5 = 3n/2, где
n - число подвижных звеньев. Отсюда следует,
что число КП 5-го класса в группе - обязательно четное число. На рисунке 8.9 приведен
пример
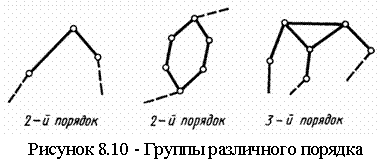 присоединения двух 2-хповодковых групп
к ведущему звену.
присоединения двух 2-хповодковых групп
к ведущему звену.
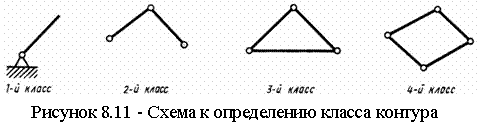 Класс и порядок механизма определяются по той группе,
которая имеет наивысший класс и входит в состав механизма. Порядок группы
определяется числом элементов, которыми группа присоединяется к основному
механизму (рисунок 8.10). Класс группы определяется классом наивысшего по
классу контура, входящего в его состав. Класс контура определяется количеством
КП, в которые входят его звенья (рисунок 8.11). Номер класса группы равен
числу КП, входящих в замкнутый контур, образованный внутренними КП, за исключением
двухповодковой группы, которая условно относится ко второму классу.
Класс и порядок механизма определяются по той группе,
которая имеет наивысший класс и входит в состав механизма. Порядок группы
определяется числом элементов, которыми группа присоединяется к основному
механизму (рисунок 8.10). Класс группы определяется классом наивысшего по
классу контура, входящего в его состав. Класс контура определяется количеством
КП, в которые входят его звенья (рисунок 8.11). Номер класса группы равен
числу КП, входящих в замкнутый контур, образованный внутренними КП, за исключением
двухповодковой группы, которая условно относится ко второму классу.
Класс и порядок механизма зависят от того, какое звено является ведущим. Принцип наслоения групп распространяется на механизмы, звенья которых являются твердыми телами.
Лекция 9. Кинематический и кинетостатический анализ плоских рычажных механизмов
Содержание лекции: кинематический и кинетостатический анализ плоских рычажных механизмов графоаналитическим методом.
Цели лекции: изучить приемы анализа кинематики плоских рычажных механизмов и реакций в кинематических парах механизмов графоаналитическим методом.
9.1 Общие сведения и виды плоских рычажных механизмов
Среди рычажных механизмов наиболее распространены плоские четырехзвенные механизмы. Они могут иметь четыре шарнира (шарнирные четырехзвенники), три шарнира и одну поступательную пару или два шарнира и две поступательные пары.
В зависимости от соотношений длин звеньев (правило Грасгофа) шарнирные четырехзвенники, показанные на рисунках 9.1 а, б, в, называют кривошипно-коромысловым, двухкривошипным или двухкоромысловым механизмом. Механизмы на рисунках 9.1 г, д, е, ж называют кривошипно-ползунным нецентральным, с качающимся цилиндром, центральным, с качающейся кулисой механизмом соответственно, на рисунке 9.1 и - синусным механизмом.
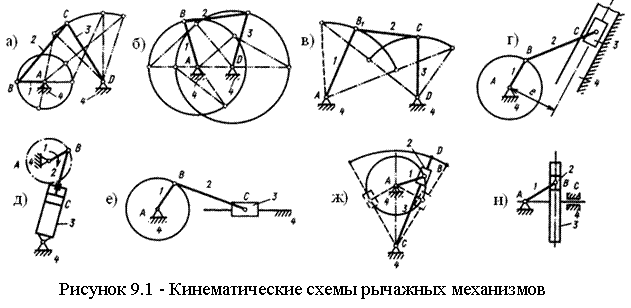
9.2 Кинематический анализ механизмов
Задачи кинематического анализа (КА) механизма состоят в определении параметров движения его звеньев (перемещений, скоростей и ускорений) по заданному закону движения входного (ведущего) звена. Из анализа положений звеньев и траекторий их точек можно определить правильность действия механизма и соответствие траекторий точек рабочего органа технологическому процессу, а также найти пространство, требуемое для размещения механизма. Скорости (угловые и линейные) звеньев используют для определения кинетической энергии механизма при решении задач динамики и для оценки условий рабочего процесса в машине. По ускорениям (угловым и линейным) находят инерционные нагрузки на звенья, которые используют для оценки прочности звеньев.
КА выполняют по кинематической схеме, которая содержит размеры звеньев. Для выполнения КА используют аналитические, графические и экспериментальные методы. Ниже рассматривается только графический метод, который, хотя и имеет низкую точность, обладает наглядностью. В графическом методе КА механизмов выполняют построение планов положений, скоростей и ускорений в соответствующих масштабах.
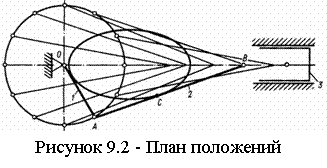 Планом положений
механизма называется
графическое изображение взаимного расположения звеньев, соответствующее выбранным
моментам
времени.
С помощью плана можно наглядно проследить за движением
его звеньев и точек. Рассмотрим в
качестве
примера кривошипно-шатунный механизм (рисунок 9.2), где 1 — кривошип, 2 — шатун, 3 — ползун. Положение т.С на шатуне определяется
длинами отрезков АС и СВ. Для построения траектории точек А, В и С необходимо
построить ряд последовательных положений механизма. Плавная линия, проведенная через
все одноименные точки,
будет искомой
траекторией точки звена.
Планом положений
механизма называется
графическое изображение взаимного расположения звеньев, соответствующее выбранным
моментам
времени.
С помощью плана можно наглядно проследить за движением
его звеньев и точек. Рассмотрим в
качестве
примера кривошипно-шатунный механизм (рисунок 9.2), где 1 — кривошип, 2 — шатун, 3 — ползун. Положение т.С на шатуне определяется
длинами отрезков АС и СВ. Для построения траектории точек А, В и С необходимо
построить ряд последовательных положений механизма. Плавная линия, проведенная через
все одноименные точки,
будет искомой
траекторией точки звена.
Положение звена, из которого начинается отсчет его движения в одном направлении, называют начальным или крайним. Положение, в котором кривошип 1 и шатун 2 располагаются на одной прямой, называют мертвым.
Построение планов скоростей и ускорений основано на графическом решении векторных уравнений движения. Для их построения должна быть известна его кинематическая схема и задан закон движения ведущего звена.
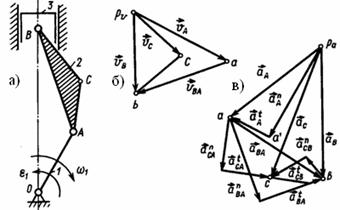 Пример 9.1 – Определить линейные
скорости и ускорения точек А, В, С, а также угловую
скорость и угловое ускорение звена 3 для заданного положения кривошипно-ползунного
механизма (рисунок 9.3 а),
если известны угловые скорость w1 и ускорение точек e1
ведущего звена.
Пример 9.1 – Определить линейные
скорости и ускорения точек А, В, С, а также угловую
скорость и угловое ускорение звена 3 для заданного положения кривошипно-ползунного
механизма (рисунок 9.3 а),
если известны угловые скорость w1 и ускорение точек e1
ведущего звена.
![]() Построение плана скоростей начинают с определения скорости т.А
кривошипа по формуле
Построение плана скоростей начинают с определения скорости т.А
кривошипа по формуле ![]() . Вектор скорости
. Вектор скорости
![]() направлен
перпендикулярно кривошипу ОА в направлении его вращения
направлен
перпендикулярно кривошипу ОА в направлении его вращения ![]() .
.
Рассматривая
т.В, принадлежащую
звену 2, в
относительном движении
вокруг т.А., найдем ее скорость как
векторную сумму скоростей переносного и
относительного движений ![]() . Здесь
. Здесь ![]() известна и по величине, и по направлению, а два слагаемых справа
известны лишь по направлению,
известна и по величине, и по направлению, а два слагаемых справа
известны лишь по направлению, ![]() ⃦
⃦![]() и
и ![]() . Для определения неизвестных значений этих векторов строим план
скоростей в выбранном масштабе
. Для определения неизвестных значений этих векторов строим план
скоростей в выбранном масштабе ![]() . Из произвольного полюса
. Из произвольного полюса ![]() (рисунок 9.3 б) проводим вектор
(рисунок 9.3 б) проводим вектор ![]() , перпендикулярный кривошипу ОА, соответствующий на плане
скоростей абсолютной скорости
, перпендикулярный кривошипу ОА, соответствующий на плане
скоростей абсолютной скорости ![]() . Из конца вектора
. Из конца вектора ![]() (точка а) проводим линию в направлении относительной скорости
(точка а) проводим линию в направлении относительной скорости ![]() , перпендикулярную АВ, а из полюса
, перпендикулярную АВ, а из полюса ![]() — линию в направлении скорости
— линию в направлении скорости ![]() , параллельную ОВ. На пересечении этих линий находим точку b.
Вектор
, параллельную ОВ. На пересечении этих линий находим точку b.
Вектор ![]() изображает скорость
изображает скорость ![]() точки В, а вектор
точки В, а вектор ![]() — скорость
— скорость ![]() . Значения действительных скоростей находим по формулам
. Значения действительных скоростей находим по формулам ![]() и
и ![]() .
.
Определить скорость т. С шатуна можно с помощью теоремы подобия для скоростей. Согласно теореме отрезки прямых линий, соединяющие точки на схеме звена механизма, и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные и одинаково расположенные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90°.
Вектор
![]() скорости т.С находим построением на отрезке ab треугольника abc, подобного треугольнику ABC, повернутому на 90°. Для этого из
точки а плана скоростей проводим
линию, перпендикулярную АС, а
через точку b — перпендикулярную ВС. На пересечении этих линий находим точку С. Значение скорости
в этой точке вычисляем по формуле
скорости т.С находим построением на отрезке ab треугольника abc, подобного треугольнику ABC, повернутому на 90°. Для этого из
точки а плана скоростей проводим
линию, перпендикулярную АС, а
через точку b — перпендикулярную ВС. На пересечении этих линий находим точку С. Значение скорости
в этой точке вычисляем по формуле ![]() . Угловая скорость шатуна
. Угловая скорость шатуна ![]() . Направление
. Направление ![]() находим по вектору скорости
находим по вектору скорости ![]() .
.
Построение
плана ускорений начинается с построения абсолютного ускорения
т.А кривошипа, равного векторной сумме
нормальной ![]() и тангенциальной
и тангенциальной ![]() составляющих
составляющих ![]() . Выбрав масштаб плана ускорений
. Выбрав масштаб плана ускорений ![]() , из произвольной
полюса
, из произвольной
полюса ![]() (рисунок 9.3 в) откладываем ускорение
(рисунок 9.3 в) откладываем ускорение ![]() в виде вектора
в виде вектора ![]() , а из т. а' проводим вектор ускорения
, а из т. а' проводим вектор ускорения ![]() (вектор
(вектор ![]() ), направление которого определено направлением углового ускорения e1. Соединяя полюс
), направление которого определено направлением углового ускорения e1. Соединяя полюс ![]() с т. а, находим полное ускорение точки А (отрезок
с т. а, находим полное ускорение точки А (отрезок ![]() )
) ![]() . Ускорение т.В находим из уравнения
. Ускорение т.В находим из уравнения ![]() . Значение нормальной
составляющей относительного ускорения определяется по формуле
. Значение нормальной
составляющей относительного ускорения определяется по формуле ![]() . Вектор
. Вектор ![]() направлен по АВ к центру вращения (т.А) и откладывается
из точки а плана. Направление тангенциальной
составляющей вектора
направлен по АВ к центру вращения (т.А) и откладывается
из точки а плана. Направление тангенциальной
составляющей вектора ![]() проводим
через конец вектора
проводим
через конец вектора ![]() перпендикулярно
ему. Направление абсолютного ускорения точки В
известно (
перпендикулярно
ему. Направление абсолютного ускорения точки В
известно (![]() ⃦
⃦![]() ) и соответствующая линия проходит через полюс
) и соответствующая линия проходит через полюс ![]() . Пересечение
этих двух линий определит положение точки b на плане, а следовательно, величину ускорения
. Пересечение
этих двух линий определит положение точки b на плане, а следовательно, величину ускорения ![]() . Вектор
. Вектор ![]() изображает
полное относительное ускорение
изображает
полное относительное ускорение ![]() . Угловое
ускорение звена шатуна
. Угловое
ускорение звена шатуна ![]() . Перенося вектор
ускорения
. Перенося вектор
ускорения ![]() в т.В и рассматривая движение т.В относительно т.А,
находим направление
в т.В и рассматривая движение т.В относительно т.А,
находим направление ![]() .
.
Ускорение
![]() определяется из векторных
уравнений
определяется из векторных
уравнений ![]() и
и ![]() . Здесь
. Здесь ![]() и
и ![]() , а также
, а также ![]() и
и ![]() . Отсюда определяем положение т. c на плане ускорений, и окончательно определяем
. Отсюда определяем положение т. c на плане ускорений, и окончательно определяем ![]() .
.
9.3 Кинетостатический анализ механизмов
Основной задачей кинетостатического анализа (КСА) является определение реакций связей (реакций в КП) по известным массам и моментам инерции звеньев, внешним силам и моментам, действующим на звенья, а также законам их движения. КСА проводят для ряда положений механизма, чтобы определить закон изменения реакций за цикл. По результатам расчета находят уравновешивающие силы (моменты), которые нужно приложить к ведущим звеньям для удержания механизма в заданном положении либо движущие силы (моменты) для обеспечения требуемого движения звеньев, силы и моменты сил трения в КП, кпд механизма. КСА механизма позволяет определить оптимальную конструкцию звеньев путем расчета их на прочность, жесткость, вибростойкость, износоустойчивость при проектировании, выполнить расчет опор и направляющих на долговечность, выбрать мощность двигателя, решить вопросы регулирования механизма, уравновешивания движущих масс, расчета фундамента машины.
![]()
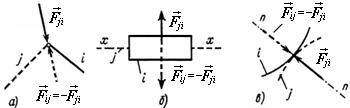 В ТММ силы подразделяют на движущие силы и силы сопротивления
или моменты этих сил. К движущим силам Fд или моментам Мд
относят такие, которые обеспечивают движение механизма. Вектора движущих сил совпадают
с векторами скоростей точек их приложения или составляют с ними острые углы. Работа
движущих сил
Wд>0. Силы сопротивления Fc
или моменты этих сил Мс делятся на силы полезных или технологических
сопротивлений Fпс и силы вредных (пассивных) сопротивлений Fвс.
Вектора Fпс противоположны векторам скоростей точек их
приложения на звеньях механизма или составляют с ними тупые углы, и их работа
Wпс<0. К Fвс относят
силы трения в КП, силы аэродинамических сопротивлений и др. На преодоление этих
сил затрачивается дополнительная работа, так что работа сил суммарных
сопротивлений
Wс =
Wпс +
Wвс. Отметим, что деление сил на движущие и силы
сопротивления достаточно условно (силы тяжести при подъеме и опускании; силы
трения между шкивом и ремнем).
В ТММ силы подразделяют на движущие силы и силы сопротивления
или моменты этих сил. К движущим силам Fд или моментам Мд
относят такие, которые обеспечивают движение механизма. Вектора движущих сил совпадают
с векторами скоростей точек их приложения или составляют с ними острые углы. Работа
движущих сил
Wд>0. Силы сопротивления Fc
или моменты этих сил Мс делятся на силы полезных или технологических
сопротивлений Fпс и силы вредных (пассивных) сопротивлений Fвс.
Вектора Fпс противоположны векторам скоростей точек их
приложения на звеньях механизма или составляют с ними тупые углы, и их работа
Wпс<0. К Fвс относят
силы трения в КП, силы аэродинамических сопротивлений и др. На преодоление этих
сил затрачивается дополнительная работа, так что работа сил суммарных
сопротивлений
Wс =
Wпс +
Wвс. Отметим, что деление сил на движущие и силы
сопротивления достаточно условно (силы тяжести при подъеме и опускании; силы
трения между шкивом и ремнем).
При движении звеньев с ускорением возникают
силы инерции, приводящиеся к главному вектору ![]() и главному моменту
и главному моменту
![]() . Здесь m - масса звена,
. Здесь m - масса звена,
![]() - ускорение центра масс звена (принимается из плана ускорений),
- ускорение центра масс звена (принимается из плана ускорений),
![]() - угловое ускорение звена,
- угловое ускорение звена,
![]() - момент инерции масс звена относительно оси, проходящей через
центр масс перпендикулярно плоскости движения звена. Направления этих сил и
моментов противоположны направлениям соответствующих ускорений, а их работа за
цикл равна нулю.
- момент инерции масс звена относительно оси, проходящей через
центр масс перпендикулярно плоскости движения звена. Направления этих сил и
моментов противоположны направлениям соответствующих ускорений, а их работа за
цикл равна нулю.
Реакция ![]() в КП - это усилие, с которым звено j воздействует на звено
i в месте их соприкосновения (
в КП - это усилие, с которым звено j воздействует на звено
i в месте их соприкосновения (![]() ). Если рассматривать механизм в целом, то реакции в КП взаимно
уравновешиваются (внутренние силы). При рассмотрении отдельного звена реакции
отброшенных связей становятся внешними силами. Во вращательной КП известна
точка приложения реакции (рисунок 9.4 а) и неизвестны направление и
значение реакции. В поступательной КП известно направление реакции (
). Если рассматривать механизм в целом, то реакции в КП взаимно
уравновешиваются (внутренние силы). При рассмотрении отдельного звена реакции
отброшенных связей становятся внешними силами. Во вращательной КП известна
точка приложения реакции (рисунок 9.4 а) и неизвестны направление и
значение реакции. В поступательной КП известно направление реакции (![]() ) и неизвестны точка приложения реакции и ее величина (рисунок 9.4
б). В высшей КП плоского механизма известны точка приложения реакции и
ее направление, но неизвестно числовое значение (рисунок 9.4 в).
) и неизвестны точка приложения реакции и ее величина (рисунок 9.4
б). В высшей КП плоского механизма известны точка приложения реакции и
ее направление, но неизвестно числовое значение (рисунок 9.4 в).
При проектировании механизма КСА выполняется в два этапа. На первом этапе задаются законом движения ведущего звена, массами и моментами инерции звеньев и определяют реакции в КП без учета сил трения. Используя эти результаты, определяют силы трения, и на втором этапе с их учетом определяют истинные реакции в КП.
КСА основан на использовании принципа
д'Аламбера. Уравнения кинетостатики удобно составлять для групп Ассура, т.к.
они являются статически определимыми системами (при отсутствии избыточных
связей). При проведении КСА механизм условно расчленяют на группы Ассура,
начиная от ведущего звена. В основе декомпозиции лежит следующий принцип: не
нарушая движения или покоя системы, можно отбрасывать отдельные связи и прикладывать
к системе соответствующие силы реакции. Это приводит к уравнениям равновесия для
группы звеньев в виде одного векторного соотношения 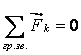 и одного
скалярного соотношения
и одного
скалярного соотношения
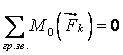 . Здесь суммирование выполняется
по всем звеньям, входящим в группу, и по всем силам, включая реакции отброшенных
связей.
. Здесь суммирование выполняется
по всем звеньям, входящим в группу, и по всем силам, включая реакции отброшенных
связей.
Силовой расчет начинается с последней, т. е. наиболее удаленной от ведущего звена группы, и кончается расчетом ведущего звена.
В зависимости от того, какое звено механизма принято за ведущее, структурный его состав может быть различным.
В общем случае силовой расчет начинается с той группы, которая имеет в качестве неизвестных сил только реакции. Обычно это будет та структурная группа, к которой приложена или движущая сила, или сила полезного сопротивления. Затем следует перейти к соседней группе. В конце расчета останется структурная группа, к которой будет приложена уравновешивающая сила или уравновешивающий момент. При расчете последней группы находят как уравновешивающую силу, так и оставшуюся реакцию. Как правило, эта группа содержит неподвижное звено; тогда реакции и уравновешивающую силу (или момент) находят, рассматривая равновесие подвижного звена группы, называемого крайним звеном.
Пример 9.2 –
Рассмотрим, как выполняется КСА для двухповодковой группы второго класса
первого вида, схема которой приведена на рисунке 9.5 а. На звенья 2
и 3 действуют известные силы и моменты. В точках В и D прикладываем
неизвестные реакции ![]() и
и ![]() отброшенных звеньев 1 и 4 на оставшиеся 2
и 3, условно направляя их вверх. Уравнение равновесия группы имеет вид
отброшенных звеньев 1 и 4 на оставшиеся 2
и 3, условно направляя их вверх. Уравнение равновесия группы имеет вид ![]() . Разложим
вектора реакций на составляющие по направлениям звеньев (нормальные) и перпендикулярно
им (тангенциальные). Тогда уравнение равновесия примет вид
. Разложим
вектора реакций на составляющие по направлениям звеньев (нормальные) и перпендикулярно
им (тангенциальные). Тогда уравнение равновесия примет вид![]() . Составляющие
. Составляющие
![]() и
и ![]() определяют
из условия равновесия звеньев 2 и 3 в виде уравнения моментов для
каждого из звеньев относительно точки С. Для звена 2
определяют
из условия равновесия звеньев 2 и 3 в виде уравнения моментов для
каждого из звеньев относительно точки С. Для звена 2 ![]() откуда
откуда ![]() Для
звена 3
Для
звена 3
![]() откуда
откуда ![]()
![]()
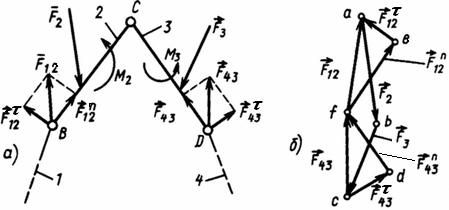 Составляющие
реакций
Составляющие
реакций ![]() и
и ![]() и полные
реакции
и полные
реакции ![]() и
и ![]() определяем
из плана сил (рисунок 9.5 б), построенного на основе уравнения
равновесия в виде векторной суммы сил. Из начала плана сил (т. а) в
выбранном масштабе mF проводим
вектор
определяем
из плана сил (рисунок 9.5 б), построенного на основе уравнения
равновесия в виде векторной суммы сил. Из начала плана сил (т. а) в
выбранном масштабе mF проводим
вектор ![]() и
из его конца - вектор
и
из его конца - вектор ![]() . Из начала вектора
. Из начала вектора ![]() и из конца вектора
и из конца вектора ![]() проводим найденные выше силы
проводим найденные выше силы ![]() и
и ![]() . Из т. d и е проводим
линии в направлении сил
. Из т. d и е проводим
линии в направлении сил ![]() и
и ![]() . Точка пересечения этих двух линий f
определит числовые значения и направления сил
. Точка пересечения этих двух линий f
определит числовые значения и направления сил ![]() ,
,![]() ,
, ![]() и
и ![]() .
Полная реакция во внутреннем шарнире С двухповодковой группы
определяется из условий равновесия сил, действующих на звено 2 или 3
в виде
.
Полная реакция во внутреннем шарнире С двухповодковой группы
определяется из условий равновесия сил, действующих на звено 2 или 3
в виде ![]() или
или ![]() Соединяя
точки b и f, можно найти реакции
Соединяя
точки b и f, можно найти реакции ![]() (не показано).
(не показано).
Рассмотрим расчет ведущего звена механизма. Это звено входит со стойкой во вращательную или поступательную пару пятого класса. Для того чтобы ведущее звено находилось в равновесии, необходимо дополнительно ввести уравновешивающую силу Fур или уравновешивающий момент Мур, которые бы уравновесили все силы и моменты, приложенные к ведущему звену. Направление Fур и Мур принимаются противоположно направлению вращения ведущего звена. Если найденные в результате расчета значения Fур и Мур оказываются отрицательными, это означает, что в действительности направление силы (момента) совпадает с направлением вращения, т.е. сила (момент), которую нужно приложить к звену, является движущей силой (моментом).
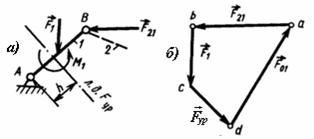 Пример 9.3 –
Определить уравновешивающую силу для ведущего звена, изображенного на рисунке
9.6 а. Ведущее звено соединено со стойкой вращательной парой. Пусть к
ведущему звену приложена уравновешивающая сила, линией действия которой
задаемся. Для определения Fур составляем
уравнение моментов относительно точки А для звена
Пример 9.3 –
Определить уравновешивающую силу для ведущего звена, изображенного на рисунке
9.6 а. Ведущее звено соединено со стойкой вращательной парой. Пусть к
ведущему звену приложена уравновешивающая сила, линией действия которой
задаемся. Для определения Fур составляем
уравнение моментов относительно точки А для звена
![]()
![]() откуда
откуда
![]() или
или
![]()
Реакция ![]() определяется из плана сил, который строится согласно
уравнению
определяется из плана сил, который строится согласно
уравнению ![]() (рисунок 9.6 б).
(рисунок 9.6 б).
Силу ![]() можно найти, не проводя КСА, с
использованием следующей теоремы Н. Е. Жуковского: если векторы всех сил,
приложенных к различным точкам звеньев и уравновешенных на механизме,
перенести параллельно самим себе в одноименные точки повернутого на 90° плана
скоростей, приняв фигуру плана за жесткий рычаг, то сумма моментов всех
указанных сил относительно полюса плана будет равна нулю.
можно найти, не проводя КСА, с
использованием следующей теоремы Н. Е. Жуковского: если векторы всех сил,
приложенных к различным точкам звеньев и уравновешенных на механизме,
перенести параллельно самим себе в одноименные точки повернутого на 90° плана
скоростей, приняв фигуру плана за жесткий рычаг, то сумма моментов всех
указанных сил относительно полюса плана будет равна нулю.
Лекция 10. Введение в сопротивление материалов. Задачи и методы сопротивления материалов
Содержание лекции: задачи сопротивления материалов, расчетная схема, допущения, внутренние силовые факторы, метод сечений, понятия о напряжениях, перемещениях, деформациях и о методах расчета.
Цели лекции: определить круг задач, решаемых методами сопротивления материалов, изучить основные понятия.
10.1 Задачи сопротивления материалов. Расчетная схема
Различные сооружения, машины, аппараты и приборы помимо других качеств должны обладать прочностью и жесткостью. Прочностью – это способность твердых тел воспринимать действие сил без разрушения. Жесткость – способность твердых тел воспринимать действие сил без существенного изменения размеров и формы (без значительных деформаций). Для обеспечения прочности и жесткости элементы (детали) конструкций должны быть изготовлены из подходящего материала и иметь необходимые размеры. Сопротивление материалов (СМ) – наука о прочности и жесткости элементов конструкций. Основные положения СМ опираются на законы и теоремы статики, но в СМ наиболее существенным является свойство деформируемости тел. Цель СМ – дать простые приемы расчета типичных элементов конструкций. В СМ используются приближенные методы, основанные на приемлемых гипотезах.
Решение начинается с выбора расчетной модели или расчетной схемы (РС) – это описание объекта, освобожденное от несущественных факторов. В зависимости от требуемой точности и рассматриваемой стороны явления для одного объекта можно использовать несколько РС. С другой стороны, к одной и той же РС может быть сведен ряд объектов.
Выбор РС начинается со схематизации свойств материала. Принято рассматривать все материалы, независимо от их микроструктуры, как однородную сплошную среду, что позволяет использовать аппарат анализа бесконечно малых. Сплошная среда наделяется свойствами реального материала. Так, все твердые тела в определенной степени обладают свойством упругости, т.е. способностью восстанавливать свои первоначальные размеры и форму после снятия внешних сил, вызвавших их изменение. В большинстве задач среда считается абсолютно упругой. Когда отступление от абсолютной упругости становится существенным, то сплошную среду наделяют другими свойствами. Обычно в СМ среда рассматривается как изотропная.
Вводятся упрощения и в геометрию объекта; в СМ она
приводится к схеме стержня или оболочки. Стержень – это тело, одно из измерений
которого (длина) намного больше двух других. Оболочка – тело, у которого одно
из измерений (толщина) намного меньше двух других. Геометрически стержень может быть образован путем перемещения плоской фигуры (рисунок 10.1) вдоль некоторой кривой - оси стержня. Плоская фигура, имеющая центр
 тяжести на оси и
нормальная к ней, называется его поперечным сечением. Стержень может быть
прямолинейным или
криволинейным, иметь постоянное или переменное сечение вдоль оси.
Ниже рассматривается расчет только стержней и
стержневых систем.
тяжести на оси и
нормальная к ней, называется его поперечным сечением. Стержень может быть
прямолинейным или
криволинейным, иметь постоянное или переменное сечение вдоль оси.
Ниже рассматривается расчет только стержней и
стержневых систем.
Упрощения вводятся и в системе сил. Так, вводится понятие сосредоточенной силы. В СМ различают внешние и внутренние силы. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на конструкцию заменяется силами, которые относят к внешним силам. Эти силы подразделяют на объемные (силы тяжести, инерции, магнитного притяжения и др.) и поверхностные (силы контактного взаимодействия с окружающими телами). В число внешних сил включают не только заданные (активные) силы, но и реакции связей, дополняющие систему сил до равновесной. Равновесную систему сил, включающую в себя активные и реактивные силы, называют нагрузкой. Величина и характер распределения внешних сил зависят от того, где проходит граница между объектом и окружающими телами. Различают силы статические (медленно изменяющиеся во времени, не вызывающие существенных сил инерции), динамические (быстро изменяющиеся во времени, вызывающие силы инерции, которые надо учитывать в расчетах; динамические силы могут быть ударными, внезапно приложенными и вибрационными), повторно-переменные (силы, действие которых периодически и многократно повторяются). Силы, характеризующие взаимодействие между частями самого объекта, относят к внутренним силам. При этом внутренние силы возникают не только между отдельными частями объекта, но и между всеми смежными частицами объекта при его нагружении. Обычно считают, что если объект не нагружен внешними силами, то внутренних сил в нем нет.
10.2 Метод сечений. Внутренние силовые факторы в поперечных сечениях стержня
Пусть к стержню (рисунок 10.2 а) приложена нагрузка
{F1,
F2, …,
Fn}.
Внутренние силы, возникающие
в стержне, выявляются, если рассечь
его мысленно на две части, например, сечением А (метод сечений). Т.к. связи между частями стержня устранены, необходимо действие одной части на другую заменить системой внутренних сил {FА}
в сечении
(рисунок 10.2 б).
В разных
сечениях
возникают, в общем случае, различные внутренние
силы. Система сил, возникающих
в плоскости А', обратна по знаку системе сил в плоскости А". Внутренние силы распределяются некоторым сложным образом по сечению. При этом условия равновесия для правой
и левой частей стержня должны удовлетворяться
по отдельности. Главный вектор и главный
момент внутренних сил в сечении А могут быть
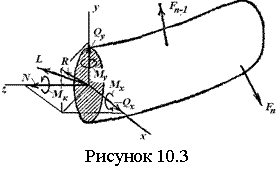 определены из условий равновесия любой из частей.
определены из условий равновесия любой из частей.
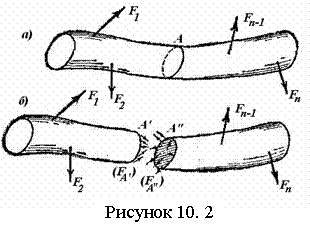 Из уравнений равновесия можно определить не
закон распределения
внутренних сил, а только их статические эквиваленты (при условии, что внешние силы заданы). Приведем систему внутренних сил к центру тяжести сечения. В результате получим главный вектор
Из уравнений равновесия можно определить не
закон распределения
внутренних сил, а только их статические эквиваленты (при условии, что внешние силы заданы). Приведем систему внутренних сил к центру тяжести сечения. В результате получим главный вектор ![]() и
главный момент
и
главный момент ![]() (рисунок 10.3).
Выберем систему координат, направив ось
z
по
нормали к сечению, а
оси х и у расположим в его плоскости.
Спроецировав
(рисунок 10.3).
Выберем систему координат, направив ось
z
по
нормали к сечению, а
оси х и у расположим в его плоскости.
Спроецировав
![]() и
и ![]() на оси, получаем 6 составляющих: три силы и три момента,
которые называют внутренними силовыми факторами (ВСФ) в сечении стержня.
Составляющую
N
называют нормальной или
продольной силой, силы
Qx
и
Qy
- поперечными силами,
момент Мк - крутящим моментом, а моменты Мх
и Му - изгибающими моментами
относительно осей х и у.
При известных внешних силах все
ВСФ определяются из 6
уравнений равновесия,
составляемых для
отсеченной части.
на оси, получаем 6 составляющих: три силы и три момента,
которые называют внутренними силовыми факторами (ВСФ) в сечении стержня.
Составляющую
N
называют нормальной или
продольной силой, силы
Qx
и
Qy
- поперечными силами,
момент Мк - крутящим моментом, а моменты Мх
и Му - изгибающими моментами
относительно осей х и у.
При известных внешних силах все
ВСФ определяются из 6
уравнений равновесия,
составляемых для
отсеченной части.
Соответственно ВСФ классифицируют виды нагружения (растяжение, сжатие, кручение, изгиб и др.). Для определения вида нагружения, необходимо воспользоваться методом сечений и выявить, какие ВСФ возникают в его сечениях. Результаты представляют в виде графиков (эпюр).
10.3 Понятия о напряжениях, перемещениях и деформациях
Чтобы характеризовать распределение внутренних сил по сечению, вводят понятие напряжения. Вектором полного напряжение в точке К в сечении S называют величину
![]() (10.1)
(10.1)
где ![]() - элементарная площадка в окрестности
точки
K;
- элементарная площадка в окрестности
точки
K;
![]() - равнодействующая
внутренних сил, приходящихся на площадку.
- равнодействующая
внутренних сил, приходящихся на площадку.
 Напряжение есть
внутренняя сила, приходящаяся на единицу площади (измеряют в паскалях). Напряжение р
может быть разложено
на 3 составляющие: по нормали к сечению (нормальное напряжение
s)
и по двум осям
в плоскости сечения(
касательные
напряжения
t). Если через т. К провести другую секущую площадку, напряжение
будет, вообще говоря, другим. Совокупность напряжений для всего множества
площадок, проходящих
через точку, образует напряженное
состояние в точке (определяется 6-ю числовыми величинами).
Напряжение есть
внутренняя сила, приходящаяся на единицу площади (измеряют в паскалях). Напряжение р
может быть разложено
на 3 составляющие: по нормали к сечению (нормальное напряжение
s)
и по двум осям
в плоскости сечения(
касательные
напряжения
t). Если через т. К провести другую секущую площадку, напряжение
будет, вообще говоря, другим. Совокупность напряжений для всего множества
площадок, проходящих
через точку, образует напряженное
состояние в точке (определяется 6-ю числовыми величинами).
Под действием внешних сил все тела изменяют свои размеры и форму (деформируются). Это существенно влияет на распределение в теле внутренних сил, хотя эти изменения, как правило, незначительны. При деформировании точки тела меняют свое положение в пространстве. Вектор, имеющий начало в точке недеформированного тела, а конец в той же точке деформированного тела, называется вектором линейного перемещения точки. Вводят также понятие углового перемещения: отрезок прямой между двумя близкими точками до и после деформирования поворачивается в пространстве на некоторый угол, который также характеризуется вектором.
Если на систему наложены связи, достаточные для того, чтобы запретить ее перемещение в пространстве как жесткого целого, то систему называют кинематически неизменяемой. Именно такие системы и рассматриваются, как правило, в СМ. В противном случае рассматривается только часть перемещений, обусловленная деформациями. Тогда для большинства систем перемещения любой точки являются малыми по сравнению с размерами тела. Поэтому согласно принципу начальных размеров при составлении уравнений статики не учитывают изменение размеров (имеются исключения).
Чтобы характеризовать интенсивность изменения размеров и формы тела, рассмотрим тело до и после деформирования (рисунок 10.4). Величину
![]() (10.2)
(10.2)
называют линейной деформацией или просто деформацией в точке А по направлению АВ (порядок 10-3). В той же точке в другом направлении деформация, вообще говоря, будет другой. В направлении осей х, у и z имеем eх, eу и ez.
Рассмотрим прямой угол, образованный в теле двумя отрезками OD и ОС (рисунок 10.4). После нагружения тела внешними силами этот угол изменится и примет значение C'O'D'. Величину
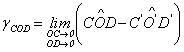 (10.3)
(10.3)
называют угловой деформацией или углом сдвига в точке О в плоскости COD.
В координатных плоскостях углы сдвига обозначают через gуz, gzx и gху.
10.4 Закон Гука. Принципы независимости действия сил и Сен-Венана
В большинстве случаев перемещения в некоторых пределах пропорциональны действующим силам (Гук, 1660 г.). Здесь коэффициент пропорциональности зависит как от физических свойств материала, так и от геометрии системы. В современной трактовке закон Гука определяет линейную зависимость между напряжением и деформацией, и тогда коэффициенты пропорциональности являются константами материала. Линейная же зависимость между перемещениями и силами получается как следствие. Зависимость сохраняется и при возрастании, и при убывании сил и отражает упругие свойства системы.
Можно доказать, что системы, для которых выполняется закон Гука, подчиняются принципу суперпозиции (принципу независимости действия сил), в соответствии с которым перемещения и внутренние силы в упругом теле, не зависят от порядка приложения внешних сил. Если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий от каждой силы.
При решении задач СМ используется принцип Сен-Венана. Предполагается, что если к телу приложена самоуравновешивающаяся система сил, то напряжения и деформации быстро убывают при удалении от места приложения нагрузки. Согласно этому принципу способ приложения нагрузки влияет только на деформацию тела в малом объеме, примыкающем к месту приложения нагрузки, и не влияет на деформацию тела вдали от точек ее приложения.
10.5 Общие принципы расчета элементов конструкции
Чтобы получить ответ на вопрос, удовлетворяет ли конструкция требованиям прочности, жесткости, надежности, необходимо, прежде всего, выбрать метод расчета. Наиболее распространенным методом расчета на прочность является расчет по напряжениям: считается, что критерием надежности конструкции является напряжение (напряженное состояние) в точке. При этом на основании анализа конструкции выявляются наибольшие (расчетные) напряжения. Эти напряжения сопоставляются с предельным значением для данного материала, полученным на основе предварительных лабораторных испытаний. Из сопоставления делается заключение о прочности конструкции.
Если необходимо добиться наименьших изменений формы конструкции, производится расчет по допускаемым перемещениям (расчет на жесткость). Это не исключает одновременной проверки системы на прочность по напряжениям. Существуют другие методы, связанные с качественно отличными явлениями, такими, как устойчивость, эффект повторных нагрузок, динамическое воздействие и др. Вопрос же о степени надежности конструкции в конкретных условиях изучается в курсах деталей машин, динамики прочности турбомашин, аппаратов и процессов химического производства и т. д.
Лекция 11. Растяжение и сжатие стержней
Содержание лекции: нормальная сила, напряжения и деформации, перемещения, потенциальная энергия деформации, напряженное и деформированное состояния при растяжении (сжатии).
Цели лекции: изучить механику растянутых (сжатых) стержней.
11.1 Продольная сила и нормальные напряжения
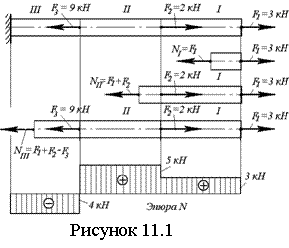 Растяжение - вид нагружения стержня, при
котором в его поперечных сечениях возникает только нормальная сила
N, а все
остальные ВСФ равны нулю. При растяжении направление
N совпадает с
направлением внешней нормали к рассматриваемому сечению. Сжатие формально
отличается от растяжения только направлением
N, хотя имеются и
существенные отличия (сжатие длинных стержней сопровождается изгибом, характер
разрушения при растяжении и сжатии различен). Обычно растяжение или сжатие
возникает при нагружении стержня осевыми силами. Эпюру
N строят с
использованием метода сечений, при этом
N
равна сумме
проекций на продольную ось всех сил, расположенных по одну сторону от
рассматриваемого сечения
Растяжение - вид нагружения стержня, при
котором в его поперечных сечениях возникает только нормальная сила
N, а все
остальные ВСФ равны нулю. При растяжении направление
N совпадает с
направлением внешней нормали к рассматриваемому сечению. Сжатие формально
отличается от растяжения только направлением
N, хотя имеются и
существенные отличия (сжатие длинных стержней сопровождается изгибом, характер
разрушения при растяжении и сжатии различен). Обычно растяжение или сжатие
возникает при нагружении стержня осевыми силами. Эпюру
N строят с
использованием метода сечений, при этом
N
равна сумме
проекций на продольную ось всех сил, расположенных по одну сторону от
рассматриваемого сечения
N = ∑Fiz. (11.1)
Растягивающую силу N считают положительной, сжимающую – отрицательной. Тогда проекция внешней силы в (11.1) должна браться со знаком «+», если сила направлена от сечения, и со знаком «-», если направлена к сечению. На рисунке 11.1 показан пример построения эпюры N.
N есть равнодействующая внутренних нормальных сил в поперечном сечении, и она связана с напряжениями этом сечении зависимостью
![]() (11.2)
(11.2)
 где σ – нормальное напряжение в
произвольной точке сечения, принадлежащей малой площадке
dA;
где σ – нормальное напряжение в
произвольной точке сечения, принадлежащей малой площадке
dA;
A – площадь поперечного сечения .
Для нахождения напряжений σ в каждой точке сечения нужно знать закон их распределения по сечению. Рассмотрим стержень постоянного поперечного сечения, изготовленный из однородного материала и нагруженный приложенными по концам растягивающими силами F (рисунок 11.2). До нагружения проведем на его боковой поверхности линии, перпендикулярные оси. Опыт показывает, при нагружении эти линии остаются прямыми и перпендикулярными оси. Это позволяет считать, что поперечные сечения стержня, плоские до нагружения, остаются плоскими и при действии нагрузки (гипотеза плоских сечений). Т.к. одинаковым удлинениям соответствуют одинаковые напряжения, то напряжения во всех точках поперечного сечения одинаковы, так что
![]() откуда
откуда ![]() (11.3)
(11.3)
Нормальное напряжение считается положительным при растяжении и отрицательным при сжатии. В рассматриваемом примере имеем однородное напряженное состояние – во всех точках стержня напряженное состояние одно и то же. Если стержень имеет переменное сечение (рисунок 11.3), то при таком же нагружении напряженное состояние не будет однородным.
11.2 Удлинения стержня и закон Гука
Размеры растянутого стержня меняются в зависимости от приложенных сил. Так, стержень на рисунке 11.2 удлиняется на величину ∆l, называемую абсолютным (полным) удлинением стержня. Т.к. здесь имеет место однородное напряженное состояние, то и линейная деформация (т.н. относительное удлинение) во всех точках одинакова и равна
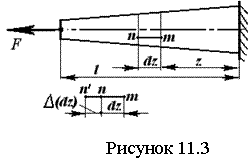
![]() .
(11.4)
.
(11.4)
В случае неоднородного напряженного состояния (рисунок 11.3)
![]() . (11.5)
. (11.5)
В пределах малых ε для большинства материалов справедлив закон Гука (линейная зависимость между σ и ε)
σ=Е∙ε (11.6)
где E – модуль Юнга (модуль упругости I рода).
Модуль Юнга определяется экспериментально; в таблице 11.1 приведены значения E для некоторых материалов.
Т а б л и ц а 11.1
|
Материал |
сталь |
медь |
латунь |
алюминий и алюминиево- магниевые сплавы |
дерево вдоль волокон |
|
Е∙105, МПа |
1,9-2,0 |
1,2 |
1,0-1,2 |
0,7-0,8 |
0,08-0,12 |
Из (11.5) с учетом (11.3) и (11.4), получим после интегрирования
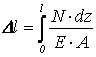 .
(11.7)
.
(11.7)
Для стержня, имеющего постоянное сечение и нагруженного по концам силами F, имеем N=F=const, и абсолютное удлинение равно
![]() .
(11.8)
.
(11.8)
Здесь E∙А - жесткость стержня при растяжении-сжатии.
Если наряду с упругими деформациями нужно учитывать температурные деформации, то суммарная деформация определяется, как
![]() (11.9)
(11.9)
где α – коэффициент температурного расширения материала;
∆t – приращение температуры.
При медленном (статическом) нагружении стержня работа внешних сил полностью преобразуется в потенциальную энергию деформации U, которая при справедливости закона Гука записывается как
![]() .
(11.10)
.
(11.10)
В случае стержня постоянного сечения, изготовленного из однородного материала и нагруженного силами по концам, имеем
![]() .
(11.11)
.
(11.11)
11.3 Статически неопределимые системы при растяжении-сжатии
На рисунке 11.5 а показан кронштейн, состоящий из двух стержней. Продольные силы в стержнях можно определить с использованием способа вырезания узлов, записав уравнения равновесия в виде сумм проекций сил на 2 координатные оси, откуда несложно найти N1 и N2. Если в конструкцию добавить еще один стержень (рисунок 11.5 б), то она будет более прочной и жесткой, но определить усилия N1 , N2 и N3 только из уравнений статики уже не удастся: неизвестных 3, а уравнений статики по-прежнему 2 (имеем 1 раз статически неопределимую систему). Система на рисунке 11.5 в 2 раза статически неопределима. Степенью статической неопределимости (СНН) называют разность между числом связей и числом независимых уравнений статики. Определение всех неизвестных сил (раскрытие статической неопределенности) возможно при использовании дополнительных уравнений (уравнений перемещений).
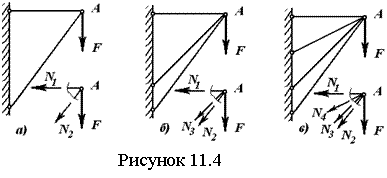 Пример 11.1- На рисунке 11.5 а показан
стержень, защемленный по обоим концам и нагруженный силой
F; требуется
определить реакции RA и
RB.
Пример 11.1- На рисунке 11.5 а показан
стержень, защемленный по обоим концам и нагруженный силой
F; требуется
определить реакции RA и
RB.
Решение. Здесь можно составить только одно уравнение равновесия
![]() (11.12)
(11.12)
Для
определения RA и
RB необходимо составить еще одно уравнение (СНН=1). Для 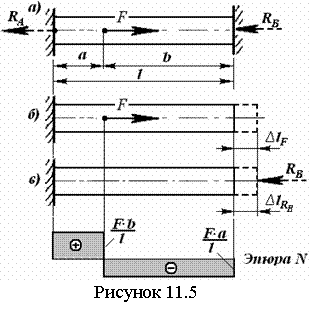 этого отбросим заделку справа и заменим ее влияние на
стержень реакцией RB. Теперь предположим, что действует только сила
F,
а силы RB
нет. Под действием F деформируется только левый участок стержня длиной а,
в результате чего сечение, где приложена сила, перемещается вправо на
∆lF=F∙a/(E∙A).
Правый
участок стержня длиной b при этом не деформируется, а перемещается вправо, как
жесткое тело, на такую же величину ∆lF.
Предположим теперь, что действует только сила
RB,
а силы F нет. Под действием
RB
деформируется весь стержень, в результате правый конец стержня перемещается влево
на ∆lRB=F∙l/(E∙A). В действительности правый конец стержня, будучи заделанным,
не получает перемещения. Т.е., перемещение его вправо, вызванное силой
F,
должно быть равно перемещению влево, вызванному силой
RB,
этого отбросим заделку справа и заменим ее влияние на
стержень реакцией RB. Теперь предположим, что действует только сила
F,
а силы RB
нет. Под действием F деформируется только левый участок стержня длиной а,
в результате чего сечение, где приложена сила, перемещается вправо на
∆lF=F∙a/(E∙A).
Правый
участок стержня длиной b при этом не деформируется, а перемещается вправо, как
жесткое тело, на такую же величину ∆lF.
Предположим теперь, что действует только сила
RB,
а силы F нет. Под действием
RB
деформируется весь стержень, в результате правый конец стержня перемещается влево
на ∆lRB=F∙l/(E∙A). В действительности правый конец стержня, будучи заделанным,
не получает перемещения. Т.е., перемещение его вправо, вызванное силой
F,
должно быть равно перемещению влево, вызванному силой
RB,
∆lF - ∆lRB = 0 (11.13)
или
![]() . (11.14)
. (11.14)
Из (11.14) и (11.12) определяем RA и RB. Далее построение эпюры N, определение напряжений, деформаций, перемещений производится так же, как в статически определимой задаче.
В элементах статически определимых систем ВСФ и напряжения возникают только от действия внешней нагрузки, а в элементах статически неопределимых систем усилия могут возникать и при отсутствии внешней нагрузки, например, в результате изменения температуры, смещения опорных закреплений, неточности изготовления отдельных элементов конструкции.
11.4 Напряженное и деформированное состояния при растяжении
Рассмотрим напряжения в наклонных сечениях стержня, составляющих угол α с поперечным сечением (рисунок 11.6 а). Если площадь поперечного сечения равна A, то площадь наклонного сечения равна A/cosα.
На рисунке 11.6 б видно, что p∙Aα = F и F=σ∙A, поэтому
р = F/ Aα = σ∙cosα. (11.15)

Разложим р на составляющие σα и τα (рисунок 11.6 в). Получаем
σα= р∙cosα = σ∙cos2α, (11.16)
τα= р∙sinα
= ![]() σ∙cos2α. (11.17)
σ∙cos2α. (11.17)
Отсюда имеем:
а) при α=0 (в поперечных сечениях) σα= σ, τα=0;
б) при α=90ْ (в продольных сечениях) σα= 0, τα=0, т.е., продольные слои не имеют силового взаимодействия;
в) при α=45ْ напряжение τ имеет наибольшее значение τmax= σ/2;
г) для сечений с углом α и (α+90ْ) абсолютная величина τ одна и та же; это закон парности касательных напряжений, который выполняется всегда.
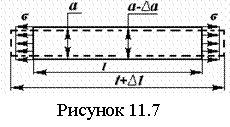 Рассмотрим деформации при
растяжении. Опыт показывает, что в определенных пределах продольное удлинение стержня (рисунок 11.7)
сопровождается пропорциональным поперечным сужением. Поперечная деформация ε´=∆а/а
и
Рассмотрим деформации при
растяжении. Опыт показывает, что в определенных пределах продольное удлинение стержня (рисунок 11.7)
сопровождается пропорциональным поперечным сужением. Поперечная деформация ε´=∆а/а
и
ε´=- µ∙ε (11.18)
где µ - коэффициент поперечной деформации (Пуассона); значения µ для металлов лежат в пределах 0,25… 0,35.
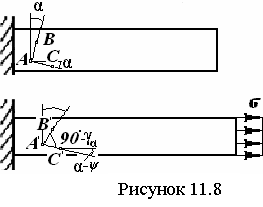 В
стержне возникают также угловые деформации γα (рисунок 11.8).
Можно доказать, что угол сдвига γα
пропорционален
напряжению τα на соответствующей площадке. Это - закон Гука для
сдвига
В
стержне возникают также угловые деформации γα (рисунок 11.8).
Можно доказать, что угол сдвига γα
пропорционален
напряжению τα на соответствующей площадке. Это - закон Гука для
сдвига
τ=G∙∙γ (11.18)
где G – модуль сдвига или модуль упругости II рода.
Между параметрами упругости материала Е, G и µ имеется взаимосвязь
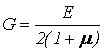 .
.
Лекция 12. Механические свойства материалов при растяжении и сжатии
Содержание лекции: назначение испытаний, диаграммы растяжения и сжатия, характеристики прочности и пластичности материалов, наклеп, влияние температуры и времени на свойства, ползучесть.
Цели лекции: ознакомиться с методикой проведения испытаний материалов на растяжение и сжатие, изучить основные механические характеристики материалов.
Для изучения свойств материалов и установления значений предельных напряжений проводят испытания образцов материала вплоть до разрушения. Испытания производят при статической, ударной и циклической нагрузках на растяжение, сжатие, кручение и изгиб (реже на сложное сопротивление). Т.к. результаты испытаний зависят от формы образца, скорости его деформирования, температуры при испытании и т. д., то эксперимент ведут в стандартных условиях на специальных машинах.
12.1 Диаграммы растяжения
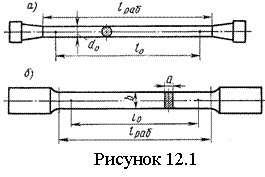 Наиболее распространены испытания на растяжение
статической нагрузкой, т.к. они наиболее просты и дают возможность судить о
поведении материала при других видах деформации.
Наиболее распространены испытания на растяжение
статической нагрузкой, т.к. они наиболее просты и дают возможность судить о
поведении материала при других видах деформации.
Для испытаний применяют цилиндрические и плоские образцы (рисунок 12.1). Обычно цилиндрические образцы имеют размеры d0=20 мм и l0=10d0 или l0=5d0.
При испытании записывается диаграмма зависимости между растягивающей силой F и удлинением образца Δl. Для возможности сравнения результатов по образцам различных размеров, диаграмму F-Δl рассматривают и как диаграмму σ-ε. Это не совсем верно, поскольку подразумевается, что σ=F/A0 и ε=∆l/l0 (A0, l0 –первоначальная площадь поперечного сечения образца и первоначальная длина образца). Т.к. истинные σ и ε должны определяться через текущие значения A и l, то такую диаграмму в координатах σ и ε называют условной диаграммой растяжения.
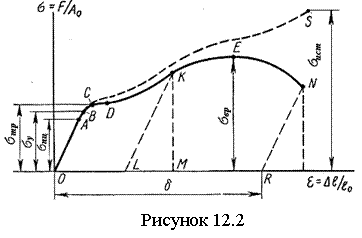 На рисунке 12.2 сплошной линией показана условная
диаграмма растяжения малоуглеродистой стали. На участке ОА до некоторого
напряжения σпц, называемого пределом пропорциональности,
ε растет пропорционально σ, т.е. выполняется закон Гука
(для стали СтЗ σпц≈ 200 МПа). Дальше
диаграмма становится криволинейной, до величины σу, называемой
пределом упругости, материал еще сохраняет упругие свойства. Разница между σпц
и σу невелика (для СтЗ σу≈ 210
МПа), и на практике их не различают.
На рисунке 12.2 сплошной линией показана условная
диаграмма растяжения малоуглеродистой стали. На участке ОА до некоторого
напряжения σпц, называемого пределом пропорциональности,
ε растет пропорционально σ, т.е. выполняется закон Гука
(для стали СтЗ σпц≈ 200 МПа). Дальше
диаграмма становится криволинейной, до величины σу, называемой
пределом упругости, материал еще сохраняет упругие свойства. Разница между σпц
и σу невелика (для СтЗ σу≈ 210
МПа), и на практике их не различают.
При дальнейшем увеличении нагрузки наступает момент (т.С), когда деформации начинают расти без увеличения нагрузки. Горизонтальный участок СD называется площадкой текучести, соответствующее напряжение - пределом текучести σтр (240…400 МПа для СтЗ).
Далее диаграмма поднимается вверх, материал вновь приобретает способность сопротивляться растяжению. В т.Е достигается наибольшее условное напряжение, называемое пределом прочности или временным сопротивлением σвр (для СтЗ σвр=400…500 МПа). На образце появляется резкое местное сужение, т.н. шейка (рисунок 12.3 б). Площадь сечения образца в шейке быстро уменьшается и, как следствие, падает усилие и σ. Разрыв образца происходит по наименьшему сечению. Предел прочности не есть напряжение, при котором происходит разрушение образца. Если относить растягивающую силу не к A0, а к площади шейки, то напряжение в шейке перед разрывом σист (в т.N) существенно больше, чем σвр.
 Кроме указанных характеристик прочности материала, при
испытании определяют также относительное остаточное удлинение при разрыве δ,
являющееся характеристикой пластичности материала
Кроме указанных характеристик прочности материала, при
испытании определяют также относительное остаточное удлинение при разрыве δ,
являющееся характеристикой пластичности материала
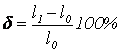 (12.1)
(12.1)
где l0 – первоначальная расчетная длина образца;
l1– расчетная длина образца после разрыва.
Для СтЗ δ ≥24%, у высокопрочных сталей δ=(7…10)%. Это удлинение является усредненным, истинное удлинение возникает в месте разрыва.
Для изучения значительных пластических деформаций необходимо знать истинную диаграмму растяжения (кривая OCS на рисунке 12.2).
Рассмотренная диаграмма растяжения является характерной для т.н. пластичных материалов, т. е. материалов, способных получать значительные остаточные деформации без разрушения. К весьма пластичным материалам относятся медь, алюминий, латунь, малоуглеродистая сталь и др., к менее пластичным - дуралюмин и бронза, к слабо пластичным – большинство легированных сталей. Ряд пластичных материалов при растяжении дает диаграмму без площадки текучести; для них устанавливается т.н. условный предел текучести – это напряжение, которому соответствует определенная величина остаточной деформации. Условному пределу текучести σ0,2 соответствует остаточная деформация 0,2%.
Противоположным свойству пластичности является
хрупкость. Для хрупких материалов величина δ не превышает 2-5%. К
хрупким материалам относятся чугун, инструментальная сталь, камень, бетон,
стекло, и др. Отметим, что деление материалов на пластичные и хрупкие является
условным, т.к. в зависимости от условий испытания (скорости нагружения,
температуры) и вида напряженного состояния хрупкие материалы способны вести
себя как пластичные, а пластичные – как хрупкие. Так, чугунный образец при всестороннем
сжатии ведет себя как пластичный материал.
Cтальной же образец
с 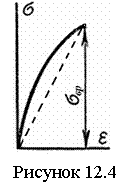 выточкой разрушится при сравнительно небольших δ.
выточкой разрушится при сравнительно небольших δ.
Диаграмма растяжении образцов из хрупких материалов (рисунок 12.4) имеет ряд особенностей. Здесь отклонение от закона Гука начинается очень рано. Разрыв наступает внезапно при очень малых деформациях, без шейки. При испытании определяют только предел прочности σвр. При расчетах отклонение от закона Гука для хрупких материалов не учитывают, заменяя криволинейную диаграмму прямолинейной. Заметное влияние на σвр оказывают размеры образца, что оценивают масштабным коэффициентом.
Вернемся к диаграмме на рисунке 12.2. Оказывается, что если при нагружении образца не был превышен σу, то при разгружении деформации полностью исчезнут, и при повторном нагружении образец будет себя вести так же, как при первом. Если же он был нагружен до напряжения, бóльшего σу, например до т. К, то разгрузка пойдет по прямой КL, параллельной ОА. Упругая часть деформации (отрезок LM) исчезнет, пластическая (отрезок OL) останется. Если образец нагружать снова, то диаграмма пойдет по прямой LK до точки K, а далее по линии KEN до разрыва. Удлинение при разрыве LR меньше, чем ОR. Т.о., при повторных нагружениях образца, предварительно растянутого до возникновения в нем напряжений, бóльших σу, предел пропорциональности повышается до того уровня, которого достигли напряжения при предшествующей нагрузке. Это т.н. закон разгрузки и повторного нагружения, и явление называют наклепом.
12. 2 Особенности испытаний на сжатие
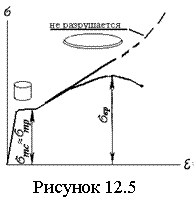 Используют образцы в форме кубиков или невысоких цилиндров (h≤ 3d)
- иначе может возникнуть изгиб. Применение очень коротких образцов также
нежелательно: силы трения на торцах значительно искажают картину.
Используют образцы в форме кубиков или невысоких цилиндров (h≤ 3d)
- иначе может возникнуть изгиб. Применение очень коротких образцов также
нежелательно: силы трения на торцах значительно искажают картину.
Вид диаграммы сжатия хрупких материалов такой же, как диаграммы растяжения. По диаграмме определяют σвс и δ, при этом σвс обычно больше σвр.
На рисунке 12.5 показана типичная диаграмма сжатия пластичного материала. Вначале она идет так же, как и диаграмма растяжения, а затем круто вверх – образец сплющивается и не разрушается. Пределы текучести при растяжении и сжатии для пластичных сталей практически одинаковы.
12.3 Влияние температуры и времени на свойства материалов
Изучение влияние температуры tº и фактора времени t на свойства материалов представляет собой очень сложную задачу, поэтому рассматриваются частные задачи.
На рисунке 12.6 показаны зависимости модуля упругости Е, предела текучести σтр, временного сопротивления σвр и удлинения при разрыве δ от tº для малоуглеродистой стали. В интервале tº 0…300ºС модуль упругости незначительно уменьшается. Более существенно изменяются σвр и δ, причем имеет место охрупчивание – удлинение при разрыве уменьшается. При дальнейшем увеличении tº пластические свойства стали восстанавливаются, а прочностные интенсивно снижаются. Охрупчивание при повышенных tº характерно для малоуглеродистых сталей. Легированные стали и цветные сплавы показывают монотонное возрастание δ и снижение σвр и σтр.
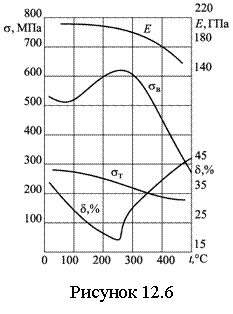 При повышенных
tº (для органических материалов и при низких
tº) напряжения и деформации в нагруженной детали изменяются
во времени – это т.н. ползучесть.
При повышенных
tº (для органических материалов и при низких
tº) напряжения и деформации в нагруженной детали изменяются
во времени – это т.н. ползучесть.
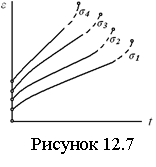 Частным проявлением ползучести является последействие
- рост необратимых деформаций при постоянном напряжении. Пример: увеличение
размеров дисков и лопаток паровой или газовой турбины под влиянием центробежных
сил и высокой tº. Другим
частным проявлением свойств ползучести является релаксация – самопроизвольное
изменение во времени напряжений при неизменной деформации, как например,
ослабление затяжки болтов соединений, работающих в условиях высоких
tº.
Частным проявлением ползучести является последействие
- рост необратимых деформаций при постоянном напряжении. Пример: увеличение
размеров дисков и лопаток паровой или газовой турбины под влиянием центробежных
сил и высокой tº. Другим
частным проявлением свойств ползучести является релаксация – самопроизвольное
изменение во времени напряжений при неизменной деформации, как например,
ослабление затяжки болтов соединений, работающих в условиях высоких
tº.
Основные характеристики материала в условиях ползучести:
а) предел длительной прочности – это отношение нагрузки, при которой происходит разрушение растянутого образца через заданный промежуток времени, к первоначальной площади сечения;
б) предел ползучести – напряжение, при котором пластическая деформация за заданный промежуток времени достигает заданной величины.
Лекция 13. Расчеты на прочность при растяжении-сжатии. Концентрация напряжений
Содержание лекции: допускаемые напряжения, запас прочности, условие прочности при растяжении-сжатии, концентрация напряжений.
Цели лекции: изучить методику расчетов на прочность при растяжении-сжатии
13.1 Условие прочности при растяжении-сжатии. Три вида задач
Рассмотрим вопрос о том, как использовать полученные в результате испытаний на растяжение и сжатие механические характеристики материалов в расчетах элементов конструкций на прочность.
Наиболее распространенным является метод расчета на прочность по напряжениям. Согласно этому методу расчет ведется по наибольшему напряжению, возникающему в конструкции, которое не должно превышать предельной для материала величины, σmax<σпред, при этом необходимо предусмотреть некоторый запас прочности, так что должно выполняться условие прочности
σmax≤[σ]. (13.1)
Здесь [σ] – допускаемое напряжение, которое определяется как некоторая часть от предельного напряжения,
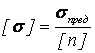 (13.2)
(13.2)
где [n] – нормативное значение запаса прочности, назначаемое в зависимости от степени ответственности конструкции, точности расчетной схемы, опыта проектирования и условий работы конструкции. При этом [n] всегда >1,0 и его значения для различных элементов конструкций приводятся в нормативных документах.
В качестве σпред для элементов конструкций, изготовленных из пластичных материалов обычно принимают σтр (для испытывающих растяжение) или σтс (для испытывающих растяжение) для того, чтобы избежать образования заметных остаточных деформаций в конструкции. Для хрупких, а в некоторых случаях и для умеренно пластичных материалов качестве σпред принимают σвр или σвс при растяжении или сжатии соответственно.
Другая форма условия прочности по этому же методу
n≥[n] (13.3)
где n – фактический (расчетный) запас прочности, определяемый как n=σпред/ σmax.
Т.о., при растяжении-сжатии условие прочности (13.1) принимает вид
![]() .
(13.4)
.
(13.4)
Пользуясь этим условием, можно решать:
а) задачи проверочного расчета. Здесь по заданным нагрузке и размерам поперечного сечения стержня определяют фактические напряжения и сравнивают их с допускаемыми, т.е., непосредственно проверяют выполнение условия (13.4). Перенапряжение недопустимо с точки зрения обеспечения прочности, а недонапряжение ведет к перерасходу материала;
б) задачи проектного расчета. По известным нагрузке и допускаемому напряжению определяют размеры поперечных сечений стержней, требуемые по условию прочности
![]() ;
(13.5)
;
(13.5)
в) задачи определения предельной грузоподъемности (несущей способности). Здесь по заданным размерам поперечного сечения стержня и известному допускаемому напряжению определяют допускаемую продольную силу
![]() ,
(13.5)
,
(13.5)
после чего, установив связь между продольной силой и нагрузкой (с помощью уравнений статики), можно определить допускаемую нагрузку.
Следует иметь в виду, что сжатые стержни, кроме расчета на прочность, должны также рассчитываться на устойчивость, т.к. при определенном значении сжимающей силы может произойти выпучивание (потеря устойчивости) стержня.
Отметим также, что критерий прочности, принятый в методе допускаемых напряжений (напряжения в точке), не всегда характеризует условие наступления разрушения конструкции. В ряде случаев за такой критерий правильнее принимать предельную нагрузку, которую может выдержать система, не разрушаясь и не изменяя существенно свою форму.
Пример 13.1 - Для чугунного стержня (рисунок 10.1) с площадью сечения А=4 см2 проверить условие прочности при допускаемом напряжении на растяжение [σр] = 30 МПа и допускаемом напряжении на сжатие [σс] = 100 МПа.
Решение. На левом участке стержень испытывает сжатие, на двух других – растяжение. Cечение стержня постоянно, продольная сила N на среднем участке по модулю больше, чем на двух других, причем здесь имеем растяжение, а [σр] больше [σс], поэтому оказывается достаточным проверить условие прочности для среднего участка. Имеем σ=N/A=5∙103/4∙102=12,5 МПа<[σр] = 30 МПа, поэтому условие прочности для стержня в целом выполняется.
13.2 Концентрация напряжений
Расчет стержней переменного сечения производится так же, как и стрежней постоянного сечения. Предполагается, что в поперечных сечениях возникают только равномерно распределенные нормальные напряжения, а продольные сечения свободны от напряжений.
В тех случаях, когда сечение стержня меняется резко (около выточек, галтелей, отверстий и т.д.), распределение напряжений не соответствует простому растяжению (рисунок 13.1). Отступление от закона равномерного распределения напряжений, соответствующего простому растяжению, вблизи мест резкого изменения поперечного сечения называется концентрацией напряжений. Концентрация напряжений проявляется в следующем:
а) σ в поперечных сечениях распределяются неравномерно, причем наибольшего значения они достигают у мест изменения сечения;
б) в поперечных и продольных сечениях имеют место как σ, так и τ.
Для определения закона распределения напряжений в концентраторах используют методы теории упругости или экспериментальные методы, при этом обычно определяют теоретический коэффициент концентрации напряжений α=σmax/σ0, показывающий, во сколько раз наибольшее напряжение в сечении σmax превышает номинальное напряжение σ0=F/Aнетто. Значения α приводятся в справочниках (он зависит только от геометрии концентратора).
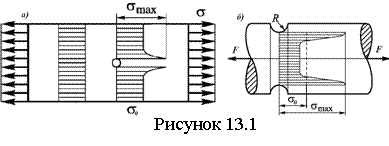 Знание α оказывается недостаточным для
расчета детали на прочность. Если бы материал вплоть до разрушения следовал бы
закону Гука, тогда прочность снижалась бы в α раз; на практике –
меньше чем α раз. Поэтому экспериментально определяют эффективный коэффициент
концентрации напряжений, показывающий, во сколько раз предел прочности образца
с концентратором меньше, чем предел прочности образца без концентратора,
kσ =
σв/σвк.
Отметим, что при расчете на прочность стержней из пластичного материала, находящихся
под действием статических нагрузок, концентрацию напряжений не принимают во
внимание, т.е. считают, что kσ =1, и
условие прочности записывают, как
Знание α оказывается недостаточным для
расчета детали на прочность. Если бы материал вплоть до разрушения следовал бы
закону Гука, тогда прочность снижалась бы в α раз; на практике –
меньше чем α раз. Поэтому экспериментально определяют эффективный коэффициент
концентрации напряжений, показывающий, во сколько раз предел прочности образца
с концентратором меньше, чем предел прочности образца без концентратора,
kσ =
σв/σвк.
Отметим, что при расчете на прочность стержней из пластичного материала, находящихся
под действием статических нагрузок, концентрацию напряжений не принимают во
внимание, т.е. считают, что kσ =1, и
условие прочности записывают, как ![]() . Это объясняется
тем, что для пластичного материала исчерпание несущей способности наступает
тогда, когда напряжения во всех точках сечения равны
σт
. При
постепенном увеличении силы F после достижения максимальными напряжениями величины
σт
напряжения вблизи отверстия не могут возрастать до тех пор, пока не пройдена
площадка текучести, а продольные волокна не могут удлиняться как в свободном
состоянии, т.к. они стеснены. С увеличением
нагрузки должна увеличиваться и продольная сила – это происходит за счет роста
напряжений в волокнах, где σ <
σт, при этом зона текучести растет до тех пор, пока
везде не будет σ=σт – наступает
общая текучесть. Т.е., картина предельного состояния имеет такой же вид, как и
в случае отсутствия концентрации напряжений.
. Это объясняется
тем, что для пластичного материала исчерпание несущей способности наступает
тогда, когда напряжения во всех точках сечения равны
σт
. При
постепенном увеличении силы F после достижения максимальными напряжениями величины
σт
напряжения вблизи отверстия не могут возрастать до тех пор, пока не пройдена
площадка текучести, а продольные волокна не могут удлиняться как в свободном
состоянии, т.к. они стеснены. С увеличением
нагрузки должна увеличиваться и продольная сила – это происходит за счет роста
напряжений в волокнах, где σ <
σт, при этом зона текучести растет до тех пор, пока
везде не будет σ=σт – наступает
общая текучесть. Т.е., картина предельного состояния имеет такой же вид, как и
в случае отсутствия концентрации напряжений.
В случае хрупких материалов концентрация напряжений существенно снижает прочность деталей (пример – разрезка стекла, когда бороздка, оставленная стеклорезом, играет роль концентратора).
Лекция 14. Чистый сдвиг. Кручение стержня круглого поперечного сечения
Содержание лекции: - чистый сдвиг, крутящий момент, напряжения и деформации при кручении, расчеты на прочность и жесткость.
Цели лекции: изучить особенности чистого сдвига и механику кручения стержней круглого и кольцевого поперечного сечения, получить формулы для расчетов на прочность и жесткость.
14.1 Напряжения и деформации при чистом сдвиге
Чистый сдвиг – это напряжен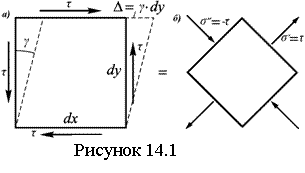 ное состояние, при котором на гранях выделенного из тела элемента
возникают только касательные напряжения
t
(рисунок 14.1 а). Однородный чистый сдвиг
имеет место при кручении тонкостенной трубки (рисунок 14.2).
ное состояние, при котором на гранях выделенного из тела элемента
возникают только касательные напряжения
t
(рисунок 14.1 а). Однородный чистый сдвиг
имеет место при кручении тонкостенной трубки (рисунок 14.2).
Можно доказать, что если из элемента, находящегося в условиях чистого сдвига, вырезать элемент с гранями, наклоненными под углами в 45º к исходным граням, то на них касательных напряжений не будет, а будут иметь место только нормальные напряжения (рисунок 14.1 б). При этом на одной паре противоположных граней напряжения являются растягивающими (σ’=t), на другой – сжимающими (σ”=t).
Как отмечалось ранее, касательные напряжения t связаны с угловой деформацией γ законом Гука
t=G∙γ. (14.1)
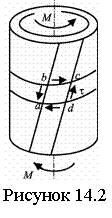 Можно
доказать, что при чистом сдвиге стороны элемента не изменяют своей длины при
деформировании, изменение объема также равно нулю.
Можно
доказать, что при чистом сдвиге стороны элемента не изменяют своей длины при
деформировании, изменение объема также равно нулю.
Аналогично испытаниям материала на растяжение и сжатие, проводят испытание на чистый сдвиг. Для этого используют тонкостенные трубки, закручиваемые моментами. В результате получают условную диаграмму сдвига в координатах t и γ, которая имеет сходство с диаграммой растяжения, при этом для пластичных металлов предел текучести tт=(0,5…0,55)σт.
Напряженное состояние, близкое к чистому сдвигу, возникает в заклепках, болтах (устанавливаемых без зазора), шпонках, шлицах, сварных швах.
14.2 Кручение стержня с круглым поперечным сечением
Под кручением понимается такой вид нагружения стержня, при котором в его поперечных сечениях возникает только крутящий момент Мкр, а остальные ВСФ равны нулю. Кручение обычно возникает при нагружении стержня парами сил (скручивающими моментами), плоскости действия которых перпендикулярны продольной оси стержня. Эпюру крутящего момента строят с использованием метода сечений, при этом Мкр равен сумме моментов относительно продольной оси стержня всех пар сил, расположенных по одну сторону от рассматриваемого сечения
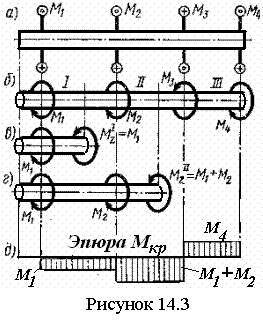 Мкр = ∑Mi.
(14.2)
Мкр = ∑Mi.
(14.2)
Правило знаков: если наблюдатель со стороны внешней нормали к сечению видит момент Мкр направленным против часовой стрелке, то он считается положительным, иначе - отрицательным. Внешние моменты в (14.2) должны браться с противоположным правилом. На рисунке 14.3 показан пример построения эпюры Мкр.
При расчете стержня (вала) обычно требуется определить напряжения и угловые перемещения в зависимости от величин внешних моментов. Методами СМ можно получить решение только для стрежня кругового или кольцевого поперечного сечения (будем рассматривать только этот случай) и для тонкостенных стержней.
В случае кручения стержня с круговым поперечным сечением будем считать, что каждое поперечное сечение стержня поворачивается в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских сечений).
 Рассмотрим стержень с круговым поперечным сечением,
нагруженный по концам моментами M (рисунок 14.4 а). В его поперечных сечениях
возникает постоянный крутящий момент Мкр=M. Двумя поперечными
сечениями, выделим из стержня элемент длиной dz, а из него свою очередь
двумя цилиндрическими поверхностями с радиусами
r и
(r + dr) –элементарное
кольцо, показанное на рисунке 14.4 в. В результате кручения правое
торцевое сечение кольца повернется на угол dj. При этом образующая
цилиндра АВ повернется на угол g и займет положение
АВ ¢. Дуга
BВ ¢ равна с одной стороны,
r ∙dj, а с другой
стороны - g ∙dz. Следовательно,
Рассмотрим стержень с круговым поперечным сечением,
нагруженный по концам моментами M (рисунок 14.4 а). В его поперечных сечениях
возникает постоянный крутящий момент Мкр=M. Двумя поперечными
сечениями, выделим из стержня элемент длиной dz, а из него свою очередь
двумя цилиндрическими поверхностями с радиусами
r и
(r + dr) –элементарное
кольцо, показанное на рисунке 14.4 в. В результате кручения правое
торцевое сечение кольца повернется на угол dj. При этом образующая
цилиндра АВ повернется на угол g и займет положение
АВ ¢. Дуга
BВ ¢ равна с одной стороны,
r ∙dj, а с другой
стороны - g ∙dz. Следовательно,
![]() .
(14.3)
.
(14.3)
Угол g представляет собой угол сдвига цилиндрической поверхности под действием касательных напряжений t. Величину
![]() (14.4)
(14.4)
называют относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.
Из рассмотрения (14.3) и (14.4) получим
g = r∙θ. (14.5)
По закону Гука для сдвига
τ=G ∙r∙θ (14.6)
где t - касательные напряжения в поперечном сечении стержня. Парные им напряжения возникают в продольных плоскостях (рисунок 14.4 г).
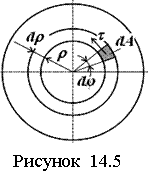 Очевидна (рисунок 14.5) зависимость
Очевидна (рисунок 14.5) зависимость ![]() . С учетом (14.6) получаем
. С учетом (14.6) получаем ![]() . Интеграл представляет
собой чисто геометрическую характеристику и называется полярным моментом
инерции сечения
. Интеграл представляет
собой чисто геометрическую характеристику и называется полярным моментом
инерции сечения
![]() .
(14.7)
.
(14.7)
Т.о., получаем ![]() или
или
 .
(14.8)
.
(14.8)
Величину ![]() называют
жесткостью стержня при кручении.
называют
жесткостью стержня при кручении.
Из (14.8), с учетом (14.4) получим
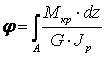 . (14.9)
. (14.9)
Если Мкр и ![]() по длине стержня постоянны, то из
(14.9) найдем
по длине стержня постоянны, то из
(14.9) найдем
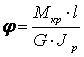 . (14.10)
. (14.10)
Подставляя (14.8) в (14.6) получим выражение для напряжений
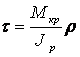 . (14.11)
. (14.11)
Т.о., касательные напряжения распределены вдоль радиуса по линейному закону и имеют максимальное значение в точках, наиболее удаленных от центра. При этом
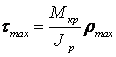 или
или 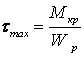 . (14.12)
. (14.12)
Величина
![]() (14.13)
(14.13)
называется полярным моментом сопротивления поперечного сечения стержня. Формулы (2.10), (2.12) справедливы для кругового и кольцевого сечений.
Полярный момент инерции для круглого сечения найдем из (14.7), учитывая, что элементарная площадь пояска dA=2π∙ρ∙dρ (рисунок 14.4). Имеем
 или
или
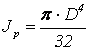 . (14.14)
. (14.14)
Полярный момент сопротивления для круглого сечения
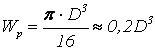 . (14.15)
. (14.15)
Для кольцевого сечения (с наружным D и внутренним d диаметрами) имеем
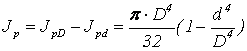 . (14.16)
. (14.16)
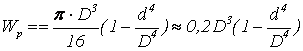 . (14.17)
. (14.17)
Условие прочности и условие жесткости при кручении имеют вид
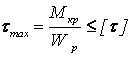 ,
(14.18)
,
(14.18)
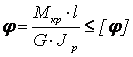 или
или 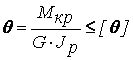 (14.19)
(14.19)
где [τ], [φ], [θ] – допускаемое касательное напряжение, допускаемый полный и допускаемый относительный углы закручивания соответственно.
Пример 14.1 - Для стального стержня кругового сечения (рисунок 14.3) требуется подобрать диаметр из условия прочности при [τ] = 100 МПа, M1=2 кН∙м, M2=3 кН∙м, M3=9 кН∙м, M4=4 кН∙м. Для найденного значения диаметра проверить условие жесткости, если [θ]=3 град/м, модуль сдвига для стали G=8∙104 МПа.
Решение. Т.к. поперечное сечение стержня постоянно, опасными будут сечения на втором слева участке, где крутящий момент максимален, Mкр2 = 5 кН∙м.
Из условия прочности (14.18) находим ![]() м. Округляя в большую сторону,
выбираем окончательно D = 65 мм.
м. Округляя в большую сторону,
выбираем окончательно D = 65 мм.
Определяем момент инерции поперечного
сечения
Jp=π∙D4/32=1,785∙10-5 м3. Проверяем условие жесткости ![]() =2,01
град/м < [θ]=3 град/м, т.е. условие жесткости выполняется.
=2,01
град/м < [θ]=3 град/м, т.е. условие жесткости выполняется.
Лекция 15. Геометрические характеристики поперечных сечений. Внутренние силовые факторы при изгибе
Содержание лекции: статические моменты, центр тяжести, моменты инерции, главные оси и главные моменты инерции плоских фигур; внутренние силовые факторы при изгибе.
Цели лекции: изучить геометрические характеристики поперечных сечений стержня, используемые в теории изгиба стержней; изучить особенности построения эпюр изгибающих моментов и поперечных сил.
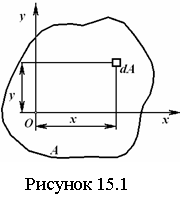 15.1 Статические моменты и центр тяжести плоской
фигуры
15.1 Статические моменты и центр тяжести плоской
фигуры
Рассмотрим некоторую плоскую фигуру в системе координат x, y (рисунок 15.1). Интегралы
![]() ,
, ![]() ( 15.1)
( 15.1)
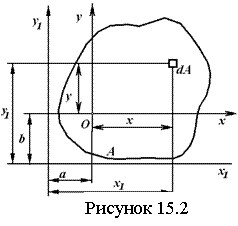 называются
статическими моментами фигуры относительно оси x и оси y
соответственно.
называются
статическими моментами фигуры относительно оси x и оси y
соответственно.
Выясним, как изменяются статические моменты сечения при параллельном переносе координатных осей (рисунок 15.2). Очевидно, что x = x1 - a; y = y1 - b.
Тогда
![]() ,
,
![]() .
.
Величины
а и b можно подобрать (причем единственным образом) так, чтобы
статические моменты ![]() и
и ![]() были
равны нулю. Ось, относительно которой статический момент равен нулю, называется
центральной. Точка пересеченияцентральных осей называется центром тяжести
сечения.
были
равны нулю. Ось, относительно которой статический момент равен нулю, называется
центральной. Точка пересеченияцентральных осей называется центром тяжести
сечения.
В системе координат (x1, y1) координаты центра тяжести равны
![]() ,
, ![]() . (15.2)
. (15.2)
Отметим, что статический момент составного сечения равен сумме статических моментов составляющих областей.
15.2 Моменты инерции сечения
Возвращаясь к рисунку 15.1, рассмотрим три интеграла
![]() , (15.3)
, (15.3)
![]() , (15.4)
, (15.4)
![]() . (15.5)
. (15.5)
Первые два интеграла называются осевыми моментами инерции относительно осей x и y соответственно, третий - центробежным моментом инерции сечения относительно осей x, y. Осевые моменты всегда положительны, центробежный может быть как положительным, так и отрицательным.
При параллельном переносе координатных осей (рисунок 15.2) моменты инерции изменяются в соответствии с формулами
![]() ,
(15.6)
,
(15.6)
![]() ,
(15.7)
,
(15.7)
![]() . (15.8)
. (15.8)
Если x1 и y1 - центральные,
то ![]() и
и
![]() ,
( 15.9)
,
( 15.9)
![]() ,
(15.10)
,
(15.10)
![]() .
(15.11)
.
(15.11)
Т.о., при параллельном переносе осей в случае, когда одна из осей – центральная, осевые моменты инерции изменяются на величину, равную произведению площади на квадрат расстояния между осями. При этом в семействе параллельных осей момент инерции относительно центральной оси минимален.
Пример 15.1 - Определить осевые моменты инерции прямоугольника относительно осей x1, y1 и x, y (рисунок 15.3).
Решение. В качестве элементарной площадки dA возьмем полоску шириной b и высотой dy. Тогда
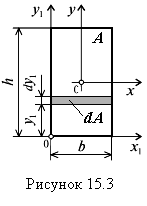
![]()
![]() .
.
По формуле (15.9)
получаем ![]() . (15.12)
. (15.12)
Аналогично получаем ![]() ,
, ![]() .
Центробежный момент инерции
.
Центробежный момент инерции ![]() ввиду того, что
оси x и y являются
осями симметрии, а относительно осей x1 и y1 равен
ввиду того, что
оси x и y являются
осями симметрии, а относительно осей x1 и y1 равен![]() .
.
Отметим, что моменты инерции составного сечения равны суммам моментов инерции составляющих областей.
15.3 Главные оси и главные моменты инерции
Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. Из рисунка 15.4 легко установить, что
u = y∙ sin a + x ∙ cos a; v = y∙ cos a - x∙ sin a . (15.13)
Из выражений
![]() ,
, ![]() ,
, ![]()
с учетом (15.13) после несложных преобразований получим

![]() , (15.14)
, (15.14)
![]() , (15.15)
, (15.15)
![]() .
(15.16)
.
(15.16)
Складывая первые два уравнения, получаем
![]() (15.17)
(15.17)
Т.о., сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей при повороте осей постоянна и равна полярному моменту инерции плоской фигуры.
С помощью (15.17) несложно определить осевой момент
инерции кругового сечения относительно диаметра. Т.к.
![]() ввиду
симметрии, то
ввиду
симметрии, то
![]() (15.18)
(15.18)
Т.к. с изменением угла
a
значения
![]() и
и ![]() . изменяются, а их
сумма остается постоянной, то существует такое значение
a=a0,
при
котором один из моментов
. изменяются, а их
сумма остается постоянной, то существует такое значение
a=a0,
при
котором один из моментов
![]() или
или ![]() достигает своего максимального
значения, другой – минимального. Значение
a0 найдем, исследуя на экстремум
достигает своего максимального
значения, другой – минимального. Значение
a0 найдем, исследуя на экстремум
![]() или
или ![]() . Найдем
. Найдем
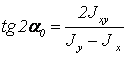 . (15.19)
. (15.19)
Оказывается, что при
a=a0
одновременно
центробежный момент инерции
![]() обращается
в нуль. Оси, относительно которых центробежный момент инерции равен нулю, а
осевые моменты инерции принимают экстремальные значения, называются главными
осями инерции. Осевые моменты инерции относительно главных осей называются
главными моментами инерции. Они определяются с использованием (15.14), (15.15)
и (15.19) как
обращается
в нуль. Оси, относительно которых центробежный момент инерции равен нулю, а
осевые моменты инерции принимают экстремальные значения, называются главными
осями инерции. Осевые моменты инерции относительно главных осей называются
главными моментами инерции. Они определяются с использованием (15.14), (15.15)
и (15.19) как
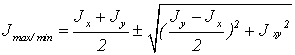 .
(15.20)
.
(15.20)
Радиусом инерции плоской фигуры относительно какой-либо оси l называют величину, определяемую как
![]() .
(15.21)
.
(15.21)
15.4 Изгиб. Внутренние силовые факторы при изгибе
Изгибом называют такой вид нагружения стержня, при котором в его поперечных сечениях возникает изгибающий момент M. Если при этом все остальные ВСФ равны нулю, то имеем чистый изгиб. Чаще наряду с M возникает поперечная сила Q, и тогда имеем поперечный изгиб.
При решении задач изгиба важно уметь строить эпюры в.с.ф. Для этого используют метод сечений. Будем рассматривать изгиб стержня с горизонтальной в недеформированном состоянии осью, при котором все активные силы лежат в вертикальной плоскости (yz).
Поперечная сила в каком-либо сечении балки равна сумме проекций на вертикальную ось всех внешних сил, действующих по одну сторону от сечения (приложенных к части стержня, отсеченной рассматриваемым сечением)
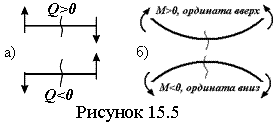
![]() .
(15.22)
.
(15.22)
Правило знаков для поперечной силы: если проекция равнодействующей внешних сил, лежащих слева от сечения (рисунок 15.5), направлена снизу вверх, то Q положительна, в противоположном случае отрицательна. Для правой части – наоборот.
Изгибающий момент равен сумме моментов относительно поперечной оси рассматриваемого сечения всех внешних сил, действующих по одну сторону от сечения (приложенных к отсеченной части стержня)
![]() .
(15.23)
.
(15.23)
Правило знаков для изгибающего момента: эпюру M строят на сжатом волокне, т.е., ординату M откладывают в сторону вогнутости упругой линии стержня (рисунок 15.5 б). Если какая-либо сила (или пара сил) стремится изогнуть стержень относительно рассматриваемого сечения выпуклостью вниз, то ее момент в (15.23) следует брать со знаком «плюс», в противоположном случае – со знаком «минус».
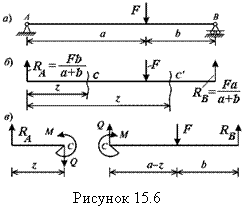 Пример
15.2 - Рассмотрим построение эпюр для стержня, приведенного на
рисунке 15.6 а). Решение задачи начинаем с определения полной системы
внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями
(рисунок 15.5 б).
Пример
15.2 - Рассмотрим построение эпюр для стержня, приведенного на
рисунке 15.6 а). Решение задачи начинаем с определения полной системы
внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями
(рисунок 15.5 б).
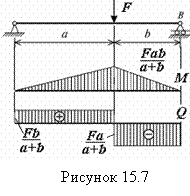 Из условий равновесия
определяем реакции в опорах
Из условий равновесия
определяем реакции в опорах ![]() ,
, ![]() .
.
Сечением С на расстоянии z от левой опоры мысленно разделим стержень на две части, заменив действие отброшенной части силой Q и моментом M. По формулам (15.22) и (15.23) найдем
![]() ,
, ![]() .
.
Для участка справа имеем
![]() ,
, ![]() .
.
На рисунке 15.7 приведены эпюры, построенные по полученным выражениям для двух участков- первого (0 £ z £ a) и второго (a £ z £ a + b).
15.5 Дифференциальные зависимости между изгибающим моментом и поперечной силой
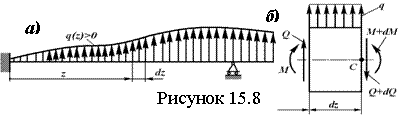 Рассмотрим стержень (рисунок 15.8 а),
нагруженный распределенной нагрузкой
q(z). Показанное направление
q считаем
положительным. Составляя уравнения равновесия для элемента
dz,
вырезанного из стержня (рисунок 15.8 б) и отбрасывая величины высшего
порядка малости, получаем дифференциальные зависимости Журавского между
интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом
Рассмотрим стержень (рисунок 15.8 а),
нагруженный распределенной нагрузкой
q(z). Показанное направление
q считаем
положительным. Составляя уравнения равновесия для элемента
dz,
вырезанного из стержня (рисунок 15.8 б) и отбрасывая величины высшего
порядка малости, получаем дифференциальные зависимости Журавского между
интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом
![]() ,
, ![]() ,
, 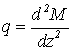 . (15.24)
. (15.24)
Из (15.24), в частности, следует, что при q = const функция Q линейная, а функция M - квадратичная. Если на каких-то участках бруса распределенная нагрузка отсутствует (q = 0), то Q = const, а M - линейная функция от z.
В сечениях, где приложена сосредоточенная сила, эпюра Q претерпевает скачок на величину внешней силы. И, наконец, в тех сечениях, где Q принимает нулевое значение и меняет знак, функция Mx достигает экстремальных значений. В сечениях, где приложен внешний момент, эпюра M претерпевает скачок на величину внешнего момента.
Лекция 16. Напряжения и расчеты на прочность при изгибе. Сложное сопротивление
Содержание лекции: напряжения и расчеты на прочность при чистом и поперечном изгибе; косой изгиб, внецентренное растяжение (сжатие), изгиб с кручением.
Цели лекции: сформулировать условия прочности при изгибе; рассмотреть расчеты на прочность при сложном сопротивлении.
16.1 Напряжения при чистом изгибе
 При чистом изгибе имеем
Q=0,
M=const. Под действием
M стержень изгибается. В случае однородного стержня изменение
кривизны всех участков одинаково. При этом справедлива гипотеза плоских
сечений: поперечные сечения стержня, плоские и перпендикулярные недеформированной
оси стержня до нагружения, остаются плоскими и перпендикулярными
деформированной оси стержня после нагружения. Тогда деформации при чистом
изгибе можно рассматривать как результат поворота поперечных сечений друг относительно
друга (рисунок 16.1). Рассмотрим два сечения, расположенных на расстоянии
dz
друг от друга.
В результате поворота правого сечения относительно левого на угол
dθ верхние
слои удлинятся, нижние укоротятся. Существует слой, в котором удлинения отсутствуют
– это нейтральный слой CD. Между радиусом кривизны нейтрального слоя ρ,
углом dθ и длиной
dz
существует зависимость dz=
ρ∙dθ. Деформация произвольно взятого отрезка
AB длиной
dz равна
При чистом изгибе имеем
Q=0,
M=const. Под действием
M стержень изгибается. В случае однородного стержня изменение
кривизны всех участков одинаково. При этом справедлива гипотеза плоских
сечений: поперечные сечения стержня, плоские и перпендикулярные недеформированной
оси стержня до нагружения, остаются плоскими и перпендикулярными
деформированной оси стержня после нагружения. Тогда деформации при чистом
изгибе можно рассматривать как результат поворота поперечных сечений друг относительно
друга (рисунок 16.1). Рассмотрим два сечения, расположенных на расстоянии
dz
друг от друга.
В результате поворота правого сечения относительно левого на угол
dθ верхние
слои удлинятся, нижние укоротятся. Существует слой, в котором удлинения отсутствуют
– это нейтральный слой CD. Между радиусом кривизны нейтрального слоя ρ,
углом dθ и длиной
dz
существует зависимость dz=
ρ∙dθ. Деформация произвольно взятого отрезка
AB длиной
dz равна
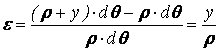 .
(16.1)
.
(16.1)
Согласно закону Гука
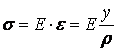 .
(16.2)
.
(16.2)
Т.о., при чистом изгибе напряжения распределяются в поперечном сечении по линейному закону. Нейтральная линия (НЛ) – это геометрическое место точек, в которых σ=0; очевидно, она перпендикулярна плоскости кривизны изогнутого стержня.
Т.к.
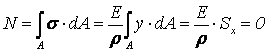 при
чистом изгибе, то
при
чистом изгибе, то ![]() , т.е. НЛ проходит через
центр тяжести поперечного сечения. Мы рассматриваем частный случай изгиба, при
котором изогнутая ось стержня лежит в плоскости действия момента
M
. Тогда
, т.е. НЛ проходит через
центр тяжести поперечного сечения. Мы рассматриваем частный случай изгиба, при
котором изогнутая ось стержня лежит в плоскости действия момента
M
. Тогда
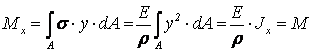 ,
(16.3)
,
(16.3)
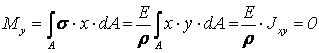 . (16.4)
. (16.4)
Из
(16.4) следует, что ![]() , т.е., изменение кривизны
стержня в плоскости M имеет место тогда, когда плоскость
M
проходит через одну из главных осей инерции сечения. Такой изгиб называется
прямым в отличие от косого, при котором плоскость
M и плоскость
кривизны стержня не совпадают.
, т.е., изменение кривизны
стержня в плоскости M имеет место тогда, когда плоскость
M
проходит через одну из главных осей инерции сечения. Такой изгиб называется
прямым в отличие от косого, при котором плоскость
M и плоскость
кривизны стержня не совпадают.
Из (16.3) получаем выражение для кривизны стержня
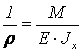 .
(16.5)
.
(16.5)
Здесь
![]() - момент инерции сечения относительно
главной центральной оси, перпендикулярной плоскости изгибающего момента.
Величина
- момент инерции сечения относительно
главной центральной оси, перпендикулярной плоскости изгибающего момента.
Величина ![]() называется жесткостью стержня при
изгибе.
называется жесткостью стержня при
изгибе.
Подставляя (16.5) в (16.2), получаем выражение для напряжения σ
 .
(16.6)
.
(16.6)
Максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии
 , (16.7)
, (16.7)
где
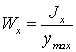 - момент сопротивления сечения
изгибу.
- момент сопротивления сечения
изгибу.
Условие прочности при чистом изгибе имеет вид
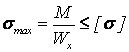 ,
(16.8)
,
(16.8)
где ![]() - допускаемое
напряжение.
- допускаемое
напряжение.
Отметим, что в случае материала стержня, неодинаково
сопротивляющегося растяжению и сжатию, бывает необходимым выполнять расчет на
прочность как по максимальным растягивающим, так и по максимальным сжимающим
напряжениям. Наиболее экономичными являются такие формы поперечных сечений, для
которых при одинаковой площади получаются наибольшие значения ![]() - это, например, стандартные прокатные
профили типа двутавров, швеллеров (рисунок 16.2) и др.
- это, например, стандартные прокатные
профили типа двутавров, швеллеров (рисунок 16.2) и др.
16.2 Напряжения и расчеты на прочность при поперечном изгибе
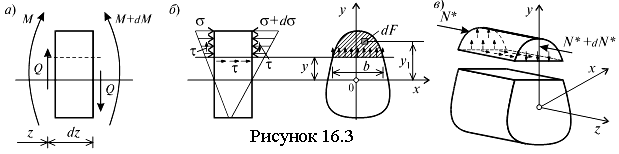 При поперечном изгибе
Q≠0,
M=vary, в поперечных сечениях стержней возникают не только
нормальные напряжения σ, но и касательные τ. Возникновение
τ сопровождается появлением угловых деформаций γ, и
т.к. τ распределены γ по сечению неравномерно, поперечные
сечения стержня не остаются плоскими. Однако на значениях σ не
сказывается заметным образом, и формулы (16.5) и (16.6) можно считать справедливыми
с достаточной точностью.
При поперечном изгибе
Q≠0,
M=vary, в поперечных сечениях стержней возникают не только
нормальные напряжения σ, но и касательные τ. Возникновение
τ сопровождается появлением угловых деформаций γ, и
т.к. τ распределены γ по сечению неравномерно, поперечные
сечения стержня не остаются плоскими. Однако на значениях σ не
сказывается заметным образом, и формулы (16.5) и (16.6) можно считать справедливыми
с достаточной точностью.
Считая, что по ширине b напряжения τ в поперечном сечении распределены равномерно, удобно их определить через парные им напряжения в продольном сечении, расположенном на расстоянии y от НЛ (рисунок 16.3). Записывая уравнения равновесия для отсеченной продольным сечением части элемента длиной dz, получаем формулу Журавского для касательных напряжений
 (16.9)
(16.9)
где ![]() - статический
момент относительно оси x части
площади, расположенной выше продольного сечения.
- статический
момент относительно оси x части
площади, расположенной выше продольного сечения.
В большинстве случаев τ не сказываются на прочности стержней (исключая тонкостенные и короткие стержни). Тогда для стержней постоянного поперечного сечения, изготовленных из материала, одинаково работающего на растяжение и сжатие, условие прочности при поперечном изгибе имеет вид
 (16.10)
(16.10)
Пример 16.1 – Требуется проверить прочность балки прямоугольного сечения по условию (16.9), если F= 4 кН, l=1.2 м, b= 40 мм, h= 60 мм, [σ]= 160 МПа. Проанализировать влияние касательных напряжений на прочность балки.
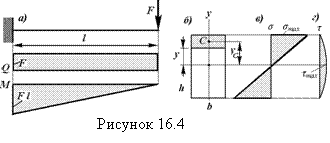 Решение.
Построим эпюры поперечных сил и изгибающих моментов. Поперечная сила постоянна
по длине балки, а изгибающий момент имеет наибольшее по модулю значение в
заделке (опасное сечение)
Решение.
Построим эпюры поперечных сил и изгибающих моментов. Поперечная сила постоянна
по длине балки, а изгибающий момент имеет наибольшее по модулю значение в
заделке (опасное сечение) ![]() =F∙l=4.8 кН∙м.
Момент сопротивления изгибу Wx =b∙h2/6=2.4∙104
мм3. Проверяем условие прочности
=F∙l=4.8 кН∙м.
Момент сопротивления изгибу Wx =b∙h2/6=2.4∙104
мм3. Проверяем условие прочности
![]() МПа>[σ]=200
МПа – условие прочности не выполняется.
МПа>[σ]=200
МПа – условие прочности не выполняется.
Оценим влияние
τ на прочность балки. Эпюра
распределения σ по поперечному сечению показана на рисунке 16.4 в,
в опасном сечении ![]() . Определим напряжения τ. Имеем
. Определим напряжения τ. Имеем ![]() .
Касательные напряжения по (16.10) равны
.
Касательные напряжения по (16.10) равны ![]() ,
эпюра показана на рисунке 16.4 г. Наибольших значений τ
достигают в точках на НЛ, где
,
эпюра показана на рисунке 16.4 г. Наибольших значений τ
достигают в точках на НЛ, где ![]() , а σ
нулевые. В наиболее удаленных от НЛ точках, где σ максимальны, напряжения
τ нулевые. При этом отношение
, а σ
нулевые. В наиболее удаленных от НЛ точках, где σ максимальны, напряжения
τ нулевые. При этом отношение ![]()
![]() =4l/h, т.е. для длинной
балки касательные напряжения пренебрежимо малы.
=4l/h, т.е. для длинной
балки касательные напряжения пренебрежимо малы.
16.3 Косой изгиб и внецентренное растяжение-сжатие
 При косом изгибе плоскость изгибающего момента
не совпадает ни с одной из главных осей поперечного сечения (рисунок 16.5).
Косой изгиб удобно рассматривать как одновременный изгиб стержня относительно
главных осей x и y. Для этого общий вектор изгибающего момента М
раскладывают на составляющие
Mx = M×sina и My = M×cosa . Нормальное
напряжение в точке, имеющей координаты x и y, определяется как
При косом изгибе плоскость изгибающего момента
не совпадает ни с одной из главных осей поперечного сечения (рисунок 16.5).
Косой изгиб удобно рассматривать как одновременный изгиб стержня относительно
главных осей x и y. Для этого общий вектор изгибающего момента М
раскладывают на составляющие
Mx = M×sina и My = M×cosa . Нормальное
напряжение в точке, имеющей координаты x и y, определяется как
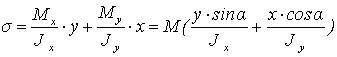 .
(16.11)
.
(16.11)
Напряжения пропорциональны расстоянию точки от нейтральной линии (НЛ), уравнение НЛ имеет вид
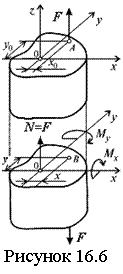
 .
(16.12)
.
(16.12)
При косом изгибе НЛ не перпендикулярна плоскости действия изгибающего момента, т.к. Jx≠Jy, т.е., стержень «предпочитает» изгибаться не в плоскости изгибающего момента, а в некоторой другой плоскости, где жесткость на изгиб меньше.
При внецентренном растяжении (сжатии) равнодействующая внешних сил F не совпадает с осью стержня, как при простом растяжении, а смещена относительно оси z и параллельна ей (рисунок 16.6). При этом в поперечных сечениях стержня возникает нормальная сила N= F и изгибающие моменты Mx = F×y0 и My = F×x0 (здесь x0 , y0 – координаты точки А приложения силы F). Нормальное напряжение s в произвольной точке В с координатами x, y равно
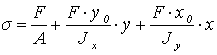 . (16.13)
. (16.13)
Напряжения пропорциональны расстоянию точки от нейтральной линии (НЛ), уравнение которой имеет вид
 или
или 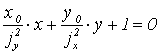 . (16.14)
. (16.14)
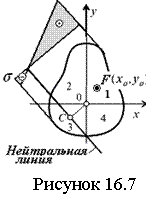 Расстояние от начала координат до НЛ (рисунок
16.7) равно
Расстояние от начала координат до НЛ (рисунок
16.7) равно
 . (16.15)
. (16.15)
При совместном действии изгиба и растяжения (или сжатия), используя, как и выше, принцип независимости действия сил, находят суммарные нормальные напряжения в поперечных сечениях стержня и расчет на прочность во всех этих случаях выполняют по суммарному напряжению.
16.4 Изгиб с кручением
Будем рассматривать стержни кругового поперечного сечения, испытывающие одновременное действие изгиба и кручения. В поперечных сечениях стержня возникают нормальные напряжения, связанные с изгибающим моментом, и касательные напряжения, связанные с крутящим моментом (касательными напряжениями от действия поперечных сил пренебрегаем).
Наибольшие напряжения возникают в точках A и B (рисунок 16.8 а)
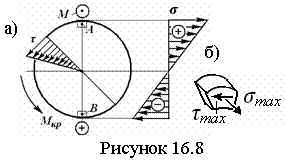
![]() ,
,
![]() , (16.16)
, (16.16)
при этом имеем частный случай сложного напряженного состояния - т.н. упрощенное плоское напряженное состояние, показанное на рисунке 16.8 б.
Для возможности суждения о прочности материала в условиях сложного напряженного состояния вводят понятие эквивалентного напряжения – это такое напряжение, которое следует создать в растянутом образце с тем, чтобы оно было равноопасным (имело одинаковый запас прочности) с оцениваемым напряженным состоянием.
В рассматриваемом случае эквивалентное напряжение по 3-й и 4-й теориям прочности определяются по формулам
![]() ,
, ![]() . (16.17)
. (16.17)
Подставляя сюда (16.17) и учитывая, что для круглого сечения Wp=2 Wкр, получаем условия прочности для стержней круглого поперечного сечения, испытывающих одновременное действие изгиба с кручением
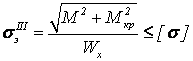 ,
, 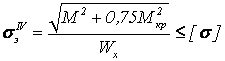 . (16.18)
. (16.18)
Список литературы
1. Курс теоретической механики: Учебник для вузов / В. И. Дронг, B. В. Дубинин, М. М. Ильин и др.; Под общ. ред. К. С. Колесникова. - М.: Изд-во МГТУ им. Н. Э. Баумана, 2005. - 736 с.
2. Никитин Н.Н. Курс теоретической механики: Учебник для машиностр. и приборостроит. спец. вузов - М.: Высш. шк., 1990. - 607 с.
3. Тарг С.М. Краткий курс теоретической механики: Учебник для студентов технических вузов - М.: Высш. шк., 2007. – 416 с.
4. Кирсанов М. Н. Решебник. Теоретическая механика /Под ред. А. И. Кириллова. - М.: ФИЗМАТЛИТ, 2002. - 384 с.
5. Зозуля В.В., Мартыненко А.В., Лукин А.Н. Теоретическая механика. – Харьков: Изд-во Нац. ун-та внутр. дел, 2004. - 244 с.
6. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. - М.: Высш. шк., 2003. – 352 с.
7. Феодосьев В.И. Сопротивление материалов: Учебник для вузов. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2000. – 592 с.
8. Степин П.А. Сопротивление материалов: Учебник для немашиностроит. спец. вузов. – М.: Высш. шк., 1989. – 367 с.
9. Зозуля В.В., Мартыненко А.В., Лукин А.Н. Механика материалов. – Харьков: Изд-во Нац. ун-та внутр. дел, 2001, 404 с.
10. Горшков А. Г., Трошин В. Н., Шалашилин В. И. Сопротивление материалов: Учеб. пособие. - М.: ФИЗМАТЛИТ, 2005. - 544 с.
11. Агамиров Л.В. Сопротивление материалов: Краткий курс. Для студентов вузов. – М.: ООО «Издательство Астрель», 2003. – 256 с.
12. Олофинская В.П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий. – М.: Форум: Инфра-М, 2007. - 349 с.
13. Дунаев П.Ф., Леликов О.П. Детали машин: Курсовое проектирование: Учеб. пособие. – 2-е изд. – М.: Высш. шк., 1990. – 399 с.
14. Иосилевич Г.Б., Строганов Г.Б., Маслов Г.М. Прикладная механика. - М.: Высш.шк.,1989. – 352 с.
15. Прикладная механика. Методические указания и задания к выполнению расчетно-графических работ (для студентов всех форм обучения специальностей 050702 - Автоматизация и управление, 050717 – Теплоэнергетика) – Алматы: АИЭС, 2006. – 38 с.
16. Буланов Э.А. Решение задач по сопротивлению материалов. – М.: Высш. шк., 1994. – 206 с.