Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра радиотехники
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Конспект лекций
(для студентов всех форм обучения специальности
5B071900 – Радиотехника, электроника и телекоммуникации)
Алматы 2012
Сводный план 2011 г., поз. №349
Составители: Т.А.Павлова, Б.Р.Накисбекова. Теория электрической связи. Конспект лекций (для студентов всех форм обучения специальности 5В071900 - Радиотехника, электроника и телекоммуникации). – Алматы: АУЭС, 2011.- 84 с.
Данная разработка предназначена для студентов всех форм обучения специальности 5В071900 – Радиотехника, электроника и телекоммуникации.
В конспекте лекций рассматриваются описания систем связи, основные характеристики электрических сигналов, каналов связи и используемой аппаратуры, а также теоретические основы теории связи, в полной мере охватываются все вопросы, которые должен знать студент после изучения технологий электрической связи.
Ил.57, библиогр. - 20 назв.
Рецензент: канд. техн. наук, профессор Медеуов У.И.
Печатается по плану издания некоммерческого акционерного общества «Алматинскй университет энергетики и связи» на 2011 г.
Ó НАО «Алматинский университет энергетики и связи», 2012г.
Введение
Настоящий конспект лекций предназначен для студентов всех форм обучения специальности 5В071900 – Радиотехника, электроника и телекоммуникации, обучающихся по курсу «Теория электрической связи».
Излагаются основные закономерности и методы передачи сообщений по каналам связи. Рассматриваются способы математического представления сообщений, сигналов и помех, методы формирования и преобразования сигналов в системах (каналах) электрической связи, вопросы помехоустойчивости и пропускной способности систем электросвязи, методы экономного и помехоустойчивого кодирования, оптимального приема сообщений, принципы многоканальной передачи, основы цифровой обработки сигналов.
Лекция 1. Общие сведения о системах электросвязи
Содержание лекции:
- понятия: информация, сообщения, сигналы. Системы, каналы и сети связи. Основные характеристики системы связи. Структурная схема простейшей одноканальной системы связи.
Цель лекции:
- выработка критериев классификации, а также установление определенной терминологии.
Под информацией понимают совокупность сведений, данных о каких-либо событиях, явлениях или предметах. В отличие от материального и энергетического ресурсов, информационный ресурс не уменьшается при потреблении, накапливается со временем, сравнительно легко и просто с помощью технических средств обрабатывается, хранится и передаётся на значительные расстояния.
Для передачи или хранения информации используют различные знаки (символы), позволяющие выразить (представить) её в некоторой форме. Совокупность знаков, отображающих ту или иную информацию, называют сообщением.
Передача сообщений (а, следовательно, и информации) на расстояние осуществляется с помощью какого-либо материального носителя (бумаги, магнитной ленты и т.д.) или физического процесса (звуковых или электромагнитных волн, тока и т.д.). Физический процесс, отображающий (несущий) передаваемое сообщение, называется сигналом. Сигналы формируются путём изменения тех или иных параметров физического носителя в соответствии с передаваемым сообщением. Этот процесс (изменения параметров носителя) принято называть модуляцией.
Сигнал передаёт (развёртывает) сообщение во времени. Следовательно, он всегда является функцией времени, даже если сообщение (например, неподвижное изображение) таковым не является. Если сигнал представляет собой функцию x(f), принимающую только определённые дискретные значения х (например, 1 и 0), то его называют дискретным или дискретным по уровню (амплитуде). Точно так же и сообщение, принимающее только некоторые определённые уровни, называют дискретным, Если же сигнал (или сообщение) может принимать любые уровни в некотором интервале, то они называются непрерывными или аналоговыми.
В некоторых случаях сообщение или сигнал задают не на всей оси времени, а в определённые моменты t. Такие сообщения (сигналы) называют дискретными по времени в отличие от непрерывных по времени, заданных на всей оси t. Например, речь является сообщением непрерывным как по уровню, так и по времени, а датчик температуры, выдающий её значения через каждые 5 мин, служит источником сообщений, непрерывных по величине, но дискретных по времени. На рисунке 1.1 наглядно проиллюстрированы различные виды сигналов: а) непрерывный сигнал; б) дискретный по времени сигнал; в) сигнал, квантованный по уровню; г) цифровой сигнал. Сигнал с конечным числом дискретных уровней часто называют цифровым, поскольку уровни можно пронумеровать числами с конечным числом разрядов.
Сообщение с помощью специальных устройств (датчиков) обычно преобразуется в электрическую величину b(f) — первичный сигнал. При передаче речи такое преобразование выполняет микрофон, при передаче изображения — телевизионная камера. В большинстве случаев первичный сигнал является низкочастотным колебанием, которое отображает передаваемое сообщение.
В некоторых случаях первичный сигнал непосредственно передают по линии. Так поступают, например, при обычной городской телефонной связи. Для передачи на большие расстояния (по кабелю или радиоканалу) первичный сигнал преобразуют в высокочастотный.

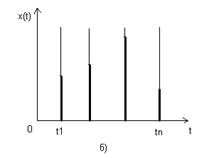
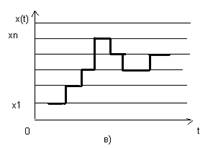
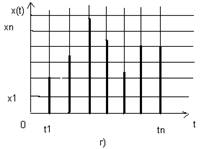
Рисунок 1.1 - Виды сигналов
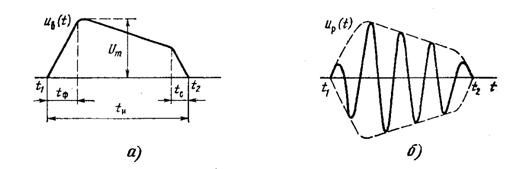
Рисунок 1.2 - Импульсные сигналы
Импульсными сигналами являются сигналы, отличные от нуля в течение ограниченного времени. Эти сигналы существуют лишь в пределах конечного отрезка (tl, t2). При этом различают видеоимпульсы (см. рисунок 1.2 а) и радиоимпульсы (см. рисунок 1.2 б). Если Uв(t)—видеоимпульс, то соответствующий ему радиоимпульс Uр(t) = Uв(t) cоs(wt+jo) (частота w и начальная фаза jo могут быть произвольными). В радиоимпульсе uB(t) называется огибающей, а функция cos(wt+jo) —заполнением. Параметрами видеоимпульса принято считать его амплитуду Um, длительность tи, длительность фронта tф, длиmельность спада tc. Происхождение терминa «видеоимпульс» связано с тем, что впервые такие импульсы начали применять для описания сигналов в телевидении.
Если бы передаваемое сообщение было детерминированным, т.е. заранее известным с полной достоверностью, то передача его не имела бы смысла. Такое детерминированное сообщение не содержит информации. Поэтому сообщения следует рассматривать как случайные события (или случайные величины, случайные функции). Детерминированный сигнал не может быть носителем информации. Его можно использовать лишь для испытаний системы связи или отдельных её элементов.

Рисунок 1.3 - Временная диаграмма тока через микрофон
Параметрами сигнала являются: длительность Т, его динамический диапазон D и ширина спектра F. Всякий сигнал, рассматриваемый как временной процесс, имеет начало и конец. Поэтому длительность сигнала Т является естественным его параметром, определяющим интервал времени, в пределах которого сигнал существует.
Динамический диапазон - это отношение наибольшей мгновенной мощности сигнала к той наименьшей мощности, которую необходимо отличать от нуля при заданном качестве передачи. Он выражается обычно в децибелах. Динамический диапазон речи диктора, например, равен 25...30 дБ, небольшого вокального ансамбля 45...65 дБ, симфонического оркестра 70...95 дБ. Во избежание перегрузок канала в радиовещании динамический диапазон часто сокращают до 35...45 дБ.
Ширина спектра сигнала F – интервал частот, в пределах которого сосредоточены основные спектральные составляющие сигнала. Ширина спектра различных сигналов неодинакова. Так, речевой сигнал, передаваемый по телефонным каналам, занимает спектр 300 – 3400 Гц, музыкальный – спектр 20 – 16000 Гц, телеграфный 0 – 200 Гц, а телевизионный – 50 Гц – 6,5 МГц.
Введем более общую и наглядную характеристику – объем сигнала
Vc = Tc Fc Dc (1.1)
Объём сигнала Vc даёт общее представление о возможностях данного множества сигналов как переносчиков сообщений. Чем больше объём сигнала, тем больше информации можно "вложить" в этот объём и тем труднее передать такой сигнал по каналу связи с требуемым качеством.
На рисунке 1.4 изображена структурная схема простейшей одноканальной системы связи. Рассмотрим назначение отдельных элементов этой схемы. Источником сообщений и получателем в одних системах связи может быть человек, в других - различного рода устройства (автомат, вычислительная машина и т.д.). Устройство, преобразующее сообщение в сигнал, называют передающим, а устройство, преобразующее принятый сигнал в сообщение - приёмным. С помощью первичного преобразователя в передающем устройстве сообщение а, которое может иметь любую физическую природу (изображение, звуковое колебание и т.п.), преобразуется в первичный электрический сигнал b(t). В телефонии, например, эта операция сводится к превращению акустических колебаний в пропорционально изменяющееся электрическое напряжение на выходе микрофона. В передатчике первичный сигнал b(t} (обычно низкочастотный) превращается во вторичный (высокочастотный) сигнал и(t), пригодный для передачи по используемому каналу. Это осуществляется посредством модуляции.
Линией связи называется физическая среда и совокупность аппаратных средств, используемых для передачи сигналов от передатчика к приёмнику. В системах электрической связи — это, прежде всего кабель или волновод, в

Рисунок 1.4 - Структурная схема простейшей одноканальной системы связи
системах радиосвязи — область пространства, в котором распространяются электромагнитные волны от передатчика к приёмнику. При передаче канальный сигнал u(t) может искажаться, и на него могут накладываться помехи n(t). Приёмное устройство обрабатывает принятое колебание z(t) = s(t) + n(t), представляющее собой сумму пришедшего искажённого сигнала s(t) и помехи n(t), и восстанавливает по нему сообщение а, которое с некоторой погрешностью отображает переданное сообщение а. Совокупность технических средств для передачи сообщений от источника к потребителю называется системой связи. Этими средствами являются передающее устройство, линия связи и приёмное устройство. Внедрение высокоэффективных ЭВМ привело к необходимости быстрого развития систем передачи данных, обеспечивающих обмен информацией между вычислительными средствами и объектами автоматизированных систем управления.
Лекция 2. Кодирование и модуляция. Помехи и искажения
Содержание лекции:
- основные характеристики канала связи. Преобразование дискретного сообщения в сигнал. Аддитивные и мультипликативные помехи. Искажения.
Цель лекции:
- выработка критериев кодирования и модуляции, а также вычисление отклика физической системы на известное входное воздействие.
Каналом связи называется совокупность средств, обеспечивающих передачу сигнала. Канал связи можно характеризовать так же, как и сигнал, тремя параметрами: временем Tк, в течение которого по каналу возможна передача, динамическим диапазоном Dк и полосой пропускания канала Fк. Под динамическим диапазоном канала понимают отношение допустимой мощности передаваемого сигнала к мощности неизбежно присутствующей в канале помехи, выраженное в децибелах.
Обобщённой характеристикой канала является его ёмкость (объём)
Vк = Tк Fк Dк. (2.1)
Необходимым условием неискаженной передачи по каналу сигналов с объемом Vс, очевидно, должно быть
Vc < Vk. (2.2)
При этом условиях объём сигнала полностью "вписывается" в объем канала.
Система связи называется многоканальной, если она обеспечивает передачу нескольких сообщений по одной общей линии связи. Структурная схема простейшей многоканальной системы связи изображена на рисунке 1.3. Для разделения сигналов на приёмном конце, очевидно, необходимо, чтобы они различались между собой по некоторому признаку. В практике многоканальной связи преимущественно применяют частотный и временной способы разделения.

Рисунок 2.1 - Структурная схема простейшей многоканальной системы передачи
Преобразование дискретного сообщения в сигнал обычно осуществляется в виде двух операций — кодирования и модуляции. Кодирование представляет собой преобразование сообщения в последовательность кодовых символов, а модуляция — преобразование этих символов в сигналы, пригодные для передачи по каналу. С помощью кодирования и модуляции источник сообщений согласуется с каналом.
При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определённая совокупность кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, отображающих дискретные сообщения, образует код. Правило кодирования может быть выражено кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом, а их количество т — основанием кода. В общем случае при основании кода т правила кодирования К элементов сообщения сводятся к правилам записи К различных чисел в т-ичной системе счисления. Число разрядов п, образующих кодовую комбинацию, называется разрядностью кода или длиной кодовой комбинации. В зависимости от системы счисления, используемой при кодировании, различают двоичные и т-ичные (недвоичные) коды.
Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Устройства, осуществляющие кодирование и декодирование, называют соответственно кодером и декодером. Как правило, это логические устройства. На рисунке 2.2 изображена структурная схема системы передачи дискретных сообщений, а на рисунке 2.3 поясняется процесс преобразования дискретного сообщения в сигнал.
В современных системах передачи дискретных сообщений принято различать две группы относительно самостоятельных устройств: кодеки и модемы. Кодеком называются устройства, преобразующие сообщение в код (кодер) и код в сообщение (декодер), а модемом — устройства, преобразующие код в сигнал (модулятор) и сигнал в код (демодулятор). Канальные устройства (полосовые усилители передатчика и приёмника, корректоры и т.п.) вместе с линией связи образуют непрерывный канал, а последний вместе с модемом – дискретный канал. Непрерывный канал обозначен на рисунке 1.4 и 2.1 блоком "линия связи".

Рисунок 2.2 - Структурная схема системы передачи дискретных
сообщений
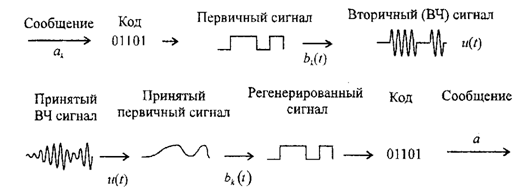
Рисунок 2.3 - Процесс преобразования дискретного сообщения в сигнал и сигнала в дискретное сообщение
Общий принцип модуляции состоит в
изменении одного или нескольких параметров несущего колебания
(переносчика)
f (t,![]() , ...) в соответствии с передаваемым сообщением. Так,
если в качестве переносчика выбрано гармоническое колебание
, ...) в соответствии с передаваемым сообщением. Так,
если в качестве переносчика выбрано гармоническое колебание ![]() то можно образовать
три вида модуляции: амплитудную (AM), частотную
(ЧМ) и фазовую (ФМ).
то можно образовать
три вида модуляции: амплитудную (AM), частотную
(ЧМ) и фазовую (ФМ).
Если переносчиком является периодическая
последовательность импульсов ![]() , то при заданной форме импульсов
v(/)
можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную
(АИМ), широтно-импульсную (ШИМ), время-импульсную (ВИМ, ФИМ)
и частотно-импульсную (ЧИМ). Применение радиоимпульсов позволяет получить ещё
два вида модуляции: по частоте и по фазе высокочастотного заполнения.
Длительность посылки первичного сигнала
bц(t) при
дискретной передаче определяет скорость передачи посылок (техническую
скорость или скорость модуляции). Измеряется техническая скорость в Бодах.
Один Бод - это скорость, при которой за 1 с передаётся одна посылка. Если
длительность посылки Т выражена в секундах, то скорость модуляции v =
1/ Т в Бодах.
, то при заданной форме импульсов
v(/)
можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную
(АИМ), широтно-импульсную (ШИМ), время-импульсную (ВИМ, ФИМ)
и частотно-импульсную (ЧИМ). Применение радиоимпульсов позволяет получить ещё
два вида модуляции: по частоте и по фазе высокочастотного заполнения.
Длительность посылки первичного сигнала
bц(t) при
дискретной передаче определяет скорость передачи посылок (техническую
скорость или скорость модуляции). Измеряется техническая скорость в Бодах.
Один Бод - это скорость, при которой за 1 с передаётся одна посылка. Если
длительность посылки Т выражена в секундах, то скорость модуляции v =
1/ Т в Бодах.
По характеру воздействия на сигнал различают аддитивные и мультипликативные помехи. Аддитивной является помеха, мгновенные значения которой складываются с мгновенными значениями сигнала. Мешающее воздействие аддитивной помехи определяется суммированием с полезным сигналом.
Мультипликативной называется помеха, мгновенные значения которой перемножаются с мгновенными значениями сигнала. Мешающее действие мультипликативных помех проявляется в виде изменения параметров полезного сигнала, в основном амплитуды. Мультипликативные помехи непосредственно связаны с процессом прохождения сигнала в среде распространения и поэтому ощущаются только при наличии сигнала в системе связи. Например : телефонная или радиотрансляционная линия с плохими контактами, интерференционные замирания сигнала при приеме на декаметровых волнах.
В реальных каналах электросвязи обычно имеет место не одна, а совокупность помех.

Рисунок 2.4 - Формы сигналов при двоичном коде для различных видов дискретной модуляции
Под искажениями понимают такие изменения формы сигнала, которые обусловлены известными свойствами цепей и устройств, по которым проходит сигнал. Главная причина искажений сигнала— переходные процессы в линии связи, цепях передатчика и приемника. При этом различают искажения: линейные, возникавшие в линейных цепях; нелинейные, возникающие в нелинейных цепях. В общем случае искажения отрицательно сказываются на качестве воспроизведения сообщений и не должны превышать установленных значений (норм). При известных характеристиках канала связи форму сигнала на его выходе всегда можно рассчитать. А дальше изменение формы сигнала можно скомпенсировать корректирующими цепями. Другое дело помехи — они заранее неизвестны поэму не могут быть устранены полностью.
Борьба с помехами — основная задача теории и техники связи. Любые теоретические и технические решения о выполнении кодера и декодера, передатчика и приемника системы связи должны приниматься с учетом того, что в линии связи имеются помехи.
При всем многообразии методов борьбы с помехами их можно свести к трем направлениям:
1) Подавление помех в месте их возникновения. Это достаточно эффективное и широко применяемое мероприятие, но не всегда приемлемо. Ведь существуют источники помех, на которые воздействовать нельзя (грозовые разряды, шумы Солнца и др.).
2)Уменьшение помех на путях их проникновения в приемник. Следует отметить, что помехи обычно воздействуют на сигнал в среде распространения. Поэтому как проводные, так и радиолинии строятся так, чтобы обеспечить заданный уровень помех.
3)Ослабление влияния помех на принимаемое сообщение в приемнике, демодуляторе, декодере. Именно это направление борьбы с помехами является предметом изучения в теории электросвязи.
Лекция 3. Математические модели сообщений и сигналов. Спектральные представления сигналов
Содержание лекции:
- теория ортогональных сигналов. Ортогональные сигналы и обобщенные ряды Фурье. Примеры ортонормированных базисов. Периодические сигналы и ряды Фурье. Ряд Фурье. Спектральная диаграмма периодического сигнала. Комплексная форма ряда Фурье.
Цель лекции:
- возможность представлять сигналы посредством обобщенных рядов Фурье. Найти спектральное разложение периодического сигнала
Два сигнала и и v называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю
(u,v)=
![]() u(t)v{t)dt=0. (3.1)
u(t)v{t)dt=0. (3.1)
Пусть H— гильбертово пространство сигналов с конечным
значением энергии (линейное пространство со скалярным произведением, полное в
том смысле, что оно содержит в себе все предельные точки любых сходящихся
последовательностей векторов из этого пространства). Эти сигналы
определены на отрезке времени [t1,
t2], конечном или бесконечном. Предположим, что на этом
же отрезке задана бесконечная система функций {![]() },
ортогональных друг другу и обладающих единичными нормами
},
ортогональных друг другу и обладающих единичными нормами
![]() (ui,uj) = 1, если
i=j (3.2)
(ui,uj) = 1, если
i=j (3.2)
0, если
i![]() j.
j.
Говорят, что при этом в пространстве
сигналов задан ортонормированный базис. Разложим произвольный сигнал
s(t)![]() H
в ряд
H
в ряд
s(t)= ![]() .
(3.3)
.
(3.3)
Представление (3.3) называется обобщенным рядом Фурье сигнала s(t) в выбранном базисе. Коэффициенты данного ряда находят следующим образом. Возьмем базисную функцию иk произвольным номером k, умножим на нее обе части равенства (1.27) и затем проинтегрируем результаты по времени
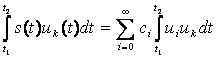 .
(3.4)
.
(3.4)
Ввиду ортонормированности базиса в правой части равенства (3.4) останется только член суммы с номером i = k, поэтому
 . (3.5)
. (3.5)
Теперь есть возможность характеризовать сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье сk.
Ортонормированная система гармонических функций. На отрезке [0,Т] система тригонометрических функций с кратными частотами, дополненная постоянным сигналом образует ортонормированный базис.
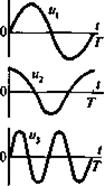
 (3.6)
(3.6)
Ортонормированная система функций Уолша. В последнее время под влиянием методов обработки дискретных сигналов большое внимание уделяют ортонормированной системе функций Уолша, которые на отрезке своего существования [-Т/2, Т/2] принимают лишь значения ±1.
Введем безразмерное время ![]() и будем обозначать k-ю
функцию Уолша, как это принято, символом wal (k,
и будем обозначать k-ю
функцию Уолша, как это принято, символом wal (k,![]() ). Идею построения этой
системы легко усмотреть из рисунка 3.1, на котором изображены графики
нескольких первых функций Уолша. Очевидна нормированность функций Уолша при любом
значении k: ||wal (k,
). Идею построения этой
системы легко усмотреть из рисунка 3.1, на котором изображены графики
нескольких первых функций Уолша. Очевидна нормированность функций Уолша при любом
значении k: ||wal (k, ![]() )||2=
)||2=![]()

Рисунок 3.1 - Графики нескольких первых функций Уолша
Ортогональность этих функций следует из принципа их построения и может быть проверена непосредственно.
Разложение сигнала с конечной энергией, заданного на отрезке времени [-Т/2,Т/2], в обобщенный ряд Фурье по функциям Уолша имеет вид
s(t)=
![]() . (3.7)
. (3.7)
Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов для радиотехники обусловлено рядом причин:
а) гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями;
б) техника генерирования гармонических сигналов относительно проста.
Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение этого сигнала. Отдельные гармонические компоненты сигнала образуют его спектр.
Математической моделью процесса, повторяющегося во времени, является периодический сигнал s(t) со следующим свойством:
s (t) = s (t ± пТ), п = 1, 2, ... (3.8)
Здесь T - период сигнала.
В электросвязи наибольшее применение находят одиночные импульсы или их периодическая последовательность, форма которых приближается к прямоугольной. Для периодической последовательности импульсов, кроме перечисленных выше параметров, вводится понятие скважности, определяемой как отношение периода к длительности импульса: S=Tltи.
Зададим на отрезке времени [-T/2, T/2] ортонормированный базис (3.6).
Любая функция um из этого базиса удовлетворяет условию периодичности (3.8). Поэтому, выполнив ортогональное разложение сигнала s (t) в этом базисе, т. е. вычислив коэффициенты Cm=(s,um), получим спектральное разложение
![]() (3.9)
(3.9)
справедливое на всей бесконечности оси времени.
Ряд вида (3.9) называется рядом Фурье данного сигнала. Введем основную частоту ω1=2π/T последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения, запишем ряд Фурье для периодического сигнала
![]() (3.10)
(3.10)
с коэффициентами
![]() ,
,
![]() ,
(3.11)
,
(3.11)
![]() .
.
Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами ωn = nω1 (n = 1, 2, 3, ...), кратными основной частоте последовательности. Каждую гармонику можно описать ее амплитудой An и начальной фазой φn. Для этого коэффициенты ряда Фурье следует записать в виде
an=Ancosφn, bn=Ansinφn так, что
An=![]() ,
tgφn=bn/an.
,
tgφn=bn/an.
Подставив эти выражения в (3.10), получим другую, эквивалентную форму ряда Фурье
![]() .
(3.12)
.
(3.12)
Спектральная диаграмма периодического сигнала - графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают: а) амплитудные и б) фазовые спектральные диаграммы (см. рисунок 3.2). Здесь по горизонтальной оси в некотором масштабе отложены частоты гармоник, а по вертикальной оси представлены их амплитуды и начальные фазы.

Рисунок 3.2 - Спектральные диаграммы некоторого периодического сигнала
Спектральное разложение
периодического сигнала можно выполнить, используя систему базисных функций,
состоящую из экспонент с мнимыми показателями 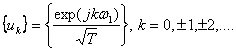 (3.13)
(3.13)
Легко видеть, что функции этой системы периодичны с периодом Т и ортонормированы на отрезке времени [-Т/2, Т/2], так как

Ряд Фурье произвольного периодического сигнала в данном случае принимает вид
![]() (3.14)
(3.14)
![]() . (3.15)
. (3.15)
Выражение (3.14) представляет собой ряд Фурье в комплексной форме.
Лекция 4. Динамическое представление сигналов. Дискретизация сигналов во времени
Содержание лекции:
- принцип динамического представления. Представление непрерывной функции дискретной последовательностью отсчётов её мгновенных значений. Спектральная трактовка дискретизации. Теорема отсчётов. Восстановление непрерывной функции по отсчётам.
Цель лекции:
- установить возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром, исходя из отсчетных значений (выборок), взятых через равные промежутки времени.
Способ получения моделей сигналов состоит в следующем. Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Если теперь устремить к нулю длительность отдельных элементарных сигналов, то, естественно, в пределе будет получено точное представление исходного сигнала. Будем называть этот способ описания сигналов динамическим представлением, подчеркивая этим развивающийся во времени характер процесса.
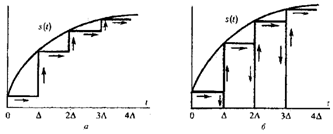
Широкое применение нашли два способа
динамического представления. Согласно первому из них, в качестве элементарных
сигналов используются ступенчатые функции, возникающие через равные промежутки
времени ![]() (см.
рисунок 4.1 а). Высота каждой ступеньки равна приращению сигнала на интервале
времени
(см.
рисунок 4.1 а). Высота каждой ступеньки равна приращению сигнала на интервале
времени ![]() .
.
При втором способе элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее (см. рисунок 4.1б).

Рассмотрим свойства элементарного сигнала, используемого для динамического представления по первому способу.
![]()
Если функция описывает процесс перехода некоторого физического объекта из «нулевого» в «единичное» состояние. Математическая модель предельного сигнала получила название функции включения или функции Хевисайда.
![]() 0,
t<0,
0,
t<0,
![]() ½,
t=0, (4.1)
½,
t=0, (4.1)
1, t>0.
В теоретической радиотехнике функции включения широко используются для описания разрывных, в частности, импульсных сигналов.
s(t) =s0
![]() (t)+
(t)+
![]() (4.2)
(4.2)
Переходя ко второму способу динамического представления сигнала, когда элементами разложения служат короткие импульсы, следует ввести новое важное понятие.
Рассмотрим импульсный сигнал прямоугольной формы, заданный следующим образом
![]() . (4.3)
. (4.3)
При любом выборе параметра ![]() площадь этого импульса
равна единице
площадь этого импульса
равна единице
![]()
Пусть теперь величина ![]() стремится к нулю. Импульс,
сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна
неограниченно возрастать. Предел последовательности таких функций при
стремится к нулю. Импульс,
сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна
неограниченно возрастать. Предел последовательности таких функций при ![]()
![]() 0 носит название дельта-функции, или
функции Дирака:
0 носит название дельта-функции, или
функции Дирака: ![]() (4.4)
(4.4)
Дельта-функция — интересный математический объект. Будучи равной нулю всюду, за исключением точки t = 0 (принято говорить, что она сосредоточена в этой точке), дельта-функция тем не менее обладает единичным интегралом:
![]() . (4.5)
. (4.5)
Вернемся к задаче описания аналогового сигнала суммой примыкающих друг к другу прямоугольных импульсов (см. рисунок 4.1,б).
![]() . (4.6)
. (4.6)
Итак, если непрерывную функцию умножить на
дельта-функцию и произведение проинтегрировать по времени, то результат будет
равен значению непрерывной функции в той точке, где сосредоточен ![]() -импульс. Принято говорить,
что в этом состоит фильтрующее свойство дельта-функции.
-импульс. Принято говорить,
что в этом состоит фильтрующее свойство дельта-функции.
Для точного представления произвольной
непрерывной функции Рисунок 6.1. ![]() на конечном интервале времени
на конечном интервале времени
![]() необходимо
располагать данными о мгновенных значениях (отсчётах) этой функции во всех
точках интервала, т.е. непрерывным множеством отсчётов, отстоящих друг от друга
на бесконечно малые интервалы. Некоторое приближённое представление о функции
необходимо
располагать данными о мгновенных значениях (отсчётах) этой функции во всех
точках интервала, т.е. непрерывным множеством отсчётов, отстоящих друг от друга
на бесконечно малые интервалы. Некоторое приближённое представление о функции
![]() можно
составить по её отображению в виде дискретной последовательности импульсов,
имеющих на интервалах
можно
составить по её отображению в виде дискретной последовательности импульсов,
имеющих на интервалах ![]() значения
значения
![]() , называемых отсчётами.
, называемых отсчётами.
Операция замены непрерывной функции
последовательностью отсчётов её мгновенных значений называется дискретизацией.
В качестве простейшей физической модели дискретизации рассмотрим коммутационное
устройство (см.
 рисунок 4.2 а).
рисунок 4.2 а).
![]()
![]()
С помощью
ключа Кл обеспечивается периодическое с частотой дискретизации
![]() подключение
к источнику непрерывного сигнала
подключение
к источнику непрерывного сигнала ![]() (см.
рисунок 4.2 б) на время
(см.
рисунок 4.2 б) на время ![]() , т.е. производится замена непрерывной функции
, т.е. производится замена непрерывной функции![]() последовательностью
последовательностью![]() на
интервалах
на
интервалах ![]() (см. рисунок 4.2 в).
(см. рисунок 4.2 в).
Дискретный сигнал ![]()
В спектральной области произведению
функций времени соответствует свёртка их спектров. Пусть спектр функции
![]() финитен
и имеет вид, представленный на рисунке 4.3 а, где
финитен
и имеет вид, представленный на рисунке 4.3 а, где
![]() -
верхняя (граничная) частота. Спектр периодической последовательности импульсов
дискретизации является линейчатым (см. рисунок 4.3 б); частота дискретизации
определяется интервалом дискретизации
-
верхняя (граничная) частота. Спектр периодической последовательности импульсов
дискретизации является линейчатым (см. рисунок 4.3 б); частота дискретизации
определяется интервалом дискретизации
![]() . Спектры дискретизированного сигнала представлены для
случаев, когда
. Спектры дискретизированного сигнала представлены для
случаев, когда ![]() (см. рисунок 4.3 в),
(см. рисунок 4.3 в),![]() (см. рисунок 4.3 г) и
(см. рисунок 4.3 г) и
![]() (см.
рисунок 4.3 д). Для неискажённого воспроизведения функции
x(t) по последовательности отсчётов посредством
идеального фильтра низких частот необходимо выбирать частоту дискретизации так,
чтобы спектральные компоненты свёртки
(см.
рисунок 4.3 д). Для неискажённого воспроизведения функции
x(t) по последовательности отсчётов посредством
идеального фильтра низких частот необходимо выбирать частоту дискретизации так,
чтобы спектральные компоненты свёртки
![]() с каждой и
дискретных составляющих периодической функции
с каждой и
дискретных составляющих периодической функции
![]() располагались в не перекрывающихся областях (см.
рисунок 4.3). Этому соответствуют значения
располагались в не перекрывающихся областях (см.
рисунок 4.3). Этому соответствуют значения
![]() . При
. При
![]() спектральные
области перекрываются, в полосу частот
спектральные
области перекрываются, в полосу частот
![]() дискретизируемого сигнала попадут спектральные
компоненты смежных областей и возникнут искажения при восстановлении
функции по отсчётам. Для точного воспроизведения непрерывной функции с ограниченным
(финитным) спектром достаточно располагать значениями функции
(отсчётами) лишь в отдельных точках. Модели сигналов с ограниченным спектром
часто используются в технике связи.
дискретизируемого сигнала попадут спектральные
компоненты смежных областей и возникнут искажения при восстановлении
функции по отсчётам. Для точного воспроизведения непрерывной функции с ограниченным
(финитным) спектром достаточно располагать значениями функции
(отсчётами) лишь в отдельных точках. Модели сигналов с ограниченным спектром
часто используются в технике связи.
Теорема отсчётов
Котельникова: непрерывная функция ![]() , не содержащая частот
выше граничной
, не содержащая частот
выше граничной ![]() , полностью определяется
отсчётами мгновенных значений
, полностью определяется
отсчётами мгновенных значений ![]() в точках, отстоящих друг от друга на
интервалы
в точках, отстоящих друг от друга на
интервалы ![]() . Интервал
. Интервал ![]() называется
интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию
называется
интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию
![]() в
виде ряда
в
виде ряда
![]() .
(4.7)
.
(4.7)
Из сопоставления ряда (4.7) с общим видом обобщённого ряда Фурье в пространстве Гильберта следует, что элементарными базисными функциями в разложении Котельникова являются отсчетные функции.
![]() .
(4.8)
.
(4.8)
где постоянная ![]() вводится
с учетом нормировки функций (4.8).
вводится
с учетом нормировки функций (4.8).
Процедура восстановления непрерывной функции
![]() по
отсчётам её мгновенных значений
по
отсчётам её мгновенных значений ![]() вытекает непосредственно из (4.7): нужно перемножить
значения отсчётов
вытекает непосредственно из (4.7): нужно перемножить
значения отсчётов ![]() на соответствующие отсчётные функции (4.8) и
просуммировать полученные произведения. Эти операции иллюстрирует рисунок 4.4.
Спектральная трактовка процесса восстановления
на соответствующие отсчётные функции (4.8) и
просуммировать полученные произведения. Эти операции иллюстрирует рисунок 4.4.
Спектральная трактовка процесса восстановления
![]() следует из рисунка 4.3. Для полного восстановления
необходимо просуммировать бесконечное множество членов ряда (4.7). Однако если
функция с ограниченным спектром
следует из рисунка 4.3. Для полного восстановления
необходимо просуммировать бесконечное множество членов ряда (4.7). Однако если
функция с ограниченным спектром ![]() рассматривается на конечном интервале Т (см.
рисунок 4.4, а), то точное разложение (6.1) можно заменить следующим
приближённым разложением
рассматривается на конечном интервале Т (см.
рисунок 4.4, а), то точное разложение (6.1) можно заменить следующим
приближённым разложением
![]() .
(4.9)
.
(4.9)
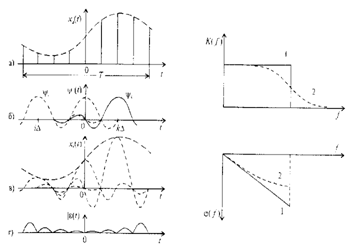
Конечное число отсчётов п, определяющее![]() , равно (
, равно (![]() ),
), ![]() . Параметр
. Параметр ![]() , играющий важную роль в
ТЭС, называют базой сигнала.
, играющий важную роль в
ТЭС, называют базой сигнала.
![]()
![]()
![]()
Лекция 5. Амплитудная модуляция
Содержание лекции:
- амплитудно-модулированные колебания. Амплитудный модулятор.
Цель лекции:
- изучение простейших видов модулированных сигналов. Получение амплитудно-модулированных сигналов.
Амплитудная модуляция состоит в пропорциональном первичному сигналу
x(t) изменении амплитуды переносчика ![]() .
.
В простейшем случае гармонического сигнала
![]() амплитуда
амплитуда
![]() (5.1)
(5.1)
В результате имеем АМ колебание
![]() . (5.2)
. (5.2)
|
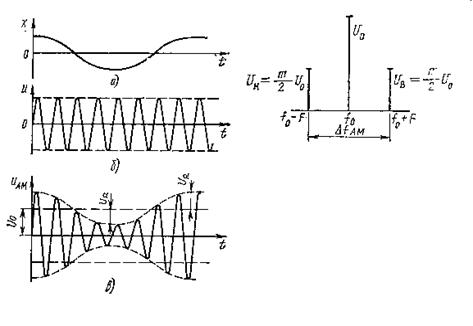
Рисунок 5.1
На рисунке 5.1 изображены графики
колебаний ![]() .
Огибающая АМ колебания соответствует выражению (5.1) Максимальное отклонение амплитуды
.
Огибающая АМ колебания соответствует выражению (5.1) Максимальное отклонение амплитуды
![]() от
от ![]() представляет амплитуду
огибающей
представляет амплитуду
огибающей ![]() ;
согласно (5.1)
;
согласно (5.1) ![]() .
Отношение амплитуды огибающей к амплитуде несущего (немодулированного),
колебания называется коэффициентом модуляции
.
Отношение амплитуды огибающей к амплитуде несущего (немодулированного),
колебания называется коэффициентом модуляции
![]() . (5.3)
. (5.3)
Обычно ![]() . Коэффициент модуляции, выраженный
в процентах, т. е. М =
m
·100%, называют глубиной модуляции.
Коэффициент модуляции пропорционален амплитуде модулирующего сигнала.
. Коэффициент модуляции, выраженный
в процентах, т. е. М =
m
·100%, называют глубиной модуляции.
Коэффициент модуляции пропорционален амплитуде модулирующего сигнала.
Используя (5.3), выражение (5.2) записывают в виде
![]() . (5.4)
. (5.4)
Для определения спектра АМ колебания раскроем скобки в выражении (5.4)
![]() . (5.5)
. (5.5)
Согласно (7.5) АМ колебание является суммой трех
высокочастотных гармонических колебаний близких частот (поскольку ![]() или
или ![]() ):
):
а) колебания несущей частоты f0 с амплитудой U0;
б) колебания верхней боковой частоты
f0+F
с амплитудой ![]() ;
;
в) колебания нижней боковой частоты
f0-F с такой же
амплитудой ![]() .
.
Спектр АМ колебания (5.5) приведен на рисунке 5.2. Ширина спектра равна удвоенной частоте модуляции: ∆fAM=2F. Амплитуда несущего колебания при модуляции не изменяется; амплитуды колебании боковых частот (верхней и нижней) пропорциональны глубине модуляции, т. е. амплитуде Х модулирующего сигнала. При m=1 амплитуды колебаний боковых частот достигают половины несущей (0,5U0).
 Первичный сигнал x(t) характеризуется амплитудой Х и частотой модуляции
W. В
модулированном колебании информация о первичном сигнале содержится в боковых частотах:
в амплитудах
Первичный сигнал x(t) характеризуется амплитудой Х и частотой модуляции
W. В
модулированном колебании информация о первичном сигнале содержится в боковых частотах:
в амплитудах ![]() ,
пропорциональных амплитуде X, и в расстоянии боковых частот от несущей,
равном Ω. Несущее колебание никакой информации не содержит, и в процессе
модуляции оно не меняется. Поэтому можно ограничиться передачей только боковых
полос, что и реализуется в системах связи на двух боковых полосах (ДБП) без несущей.
Более того, поскольку каждая боковая полоса содержит полную информацию о первичном
сигнале, можно обойтись передачей только одной боковой полосы (ОБП). Модуляция,
в результате которой получаются колебания одной боковой полосы, называется однополосной
(ОМ). Очевидными достоинствами систем связи ДБП и ОБП являются возможности
использования всей мощности передатчика на передачу только боковых полос (двух
или одной) сигнала, что позволяет повысить дальность и надежность связи. При однополосной
модуляции, кроме того, вдвое уменьшается ширина спектра модулированного
колебания, что позволяет соответственно увеличить число сигналов, передаваемых
по линии связи в заданной полосе частот.
,
пропорциональных амплитуде X, и в расстоянии боковых частот от несущей,
равном Ω. Несущее колебание никакой информации не содержит, и в процессе
модуляции оно не меняется. Поэтому можно ограничиться передачей только боковых
полос, что и реализуется в системах связи на двух боковых полосах (ДБП) без несущей.
Более того, поскольку каждая боковая полоса содержит полную информацию о первичном
сигнале, можно обойтись передачей только одной боковой полосы (ОБП). Модуляция,
в результате которой получаются колебания одной боковой полосы, называется однополосной
(ОМ). Очевидными достоинствами систем связи ДБП и ОБП являются возможности
использования всей мощности передатчика на передачу только боковых полос (двух
или одной) сигнала, что позволяет повысить дальность и надежность связи. При однополосной
модуляции, кроме того, вдвое уменьшается ширина спектра модулированного
колебания, что позволяет соответственно увеличить число сигналов, передаваемых
по линии связи в заданной полосе частот.
![]()
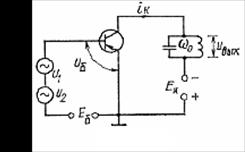
На практике в качестве нелинейных элементов модуляторов используются транзисторы. Модулируемое высокочастотное напряжение подают во входную цепь нелинейного элемента. Модулирующий же сигнал вводят в цепи различных электродов: в цепь базы или коллектора (соответственно базовая или коллекторная модуляция). Рассмотрим схему базовой модуляции на транзисторе (см. рисунок 5.3).
Напряжение на базе содержит, кроме смещения Еб, определяющего положение рабочей точки, колебания низкой и высокой частот
![]() . (5.6)
. (5.6)
Здесь u1 =
U1
cos ω0t
–
высокочастотное напряжение; u2 =
U2
cos Ωt – модулирующее
низкочастотное напряжение. На рисунке 7.4
a-в по характеристике
прибора iк=Ф(uб) методом проекций
построена зависимость iк от времени.
Коллекторный ток представляет последовательность импульсов, отличающихся друг
от друга высотой Imax и углом отсечки θ. Если разложить каждый из этих импульсов тока в
ряд Фурье за период высокой частоты 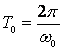 , получим постоянную составляющую и
гармоники высокой частоты.
, получим постоянную составляющую и
гармоники высокой частоты.
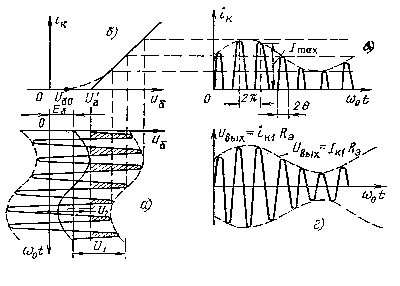
Напряжение на контуре, настроенном на частоту ω0, создается только первой гармоникой ik1=Ik1cos ω0t: uвых=ik1Rэ=Ik1 Rэcos ω0t.Изменение высоты и ширины импульсов тока во времени приводит к изменению амплитуды Iк1 с низкой частотой Ω. Поэтому выходное напряжение получается модулированным по амплитуде (см. рисунок 5.4 г). Режим работы модулятора, определяемый величинами Eб, U1 и U2, нельзя выбирать таким, чтобы все мгновенные значения находились в пределах линейного участка характеристики транзистора, так как в этом случае коллекторный ток будет иметь такую же форму, что и uб, амплитуда высокочастотной составляющей тока ik1 будет постоянной, а потому напряжение на выходе окажется немодулированным. При осуществлении модуляции могут возникать искажения огибающей AM колебания. Оценка величины искажений и выбор режима работы, обеспечивающего их отсутствие, по характеристике прямой передачи ik1(uб) практически невозможны. Для решения этой задачи целесообразен иной подход к рассмотрению работы модулятора. Напряжение uб можно рассматривать как сумму высокочастотного колебания u1 и напряжения смещения uб(t)= Eб+ u2(t), медленно изменяющегося с низкой частотой, а модуляцию как следствие изменения смещения, приводящего к изменению импульсов тока и их первой гармоники. Так как амплитуда выходного напряжения пропорциональна Iк1, для получения неискаженной модуляции требуется, чтобы амплитуда Iк1 изменялась пропорционально изменению напряжения смещения. Зависимость Iк1 от Eб при постоянной амплитуде U1 называется статической модуляционной характеристикой. Она может быть рассчитана по статической характеристике прибора (см. рисунок 5.5 а): при неизменной амплитуде U1 и различных смещениях Eб, с помощью одного из методов спектрального анализа определяем амплитуду Iк1 и строим зависимость Iк1 (Eб) (см. рисунок 5.5 б), которая и является статической модуляционной характеристикой.
Рисунок 5.5
Отметим некоторые ее особенности. При смещении, равном напряжению запирания U’б, получаются импульсы тока ik с углом отсечки θ=900, а потому Iк1≠0. Амплитуда Iк1 уменьшится до нуля, когда смещение достигнет величины E’б= U’б−U1. Если при изменении смещения колебание и1 не выходит за пределы линейного участка статической характеристики транзистора, амплитуда Iк1 не меняется. Обычно в средней части статической модуляционной характеристики имеется линейный участок MN. Для получения неискаженной модуляции с наибольшей глубиной m нужно выбирать рабочую точку A на середине этого участка (смещение Eб0) и использовать низкочастотный модулирующий сигнал с такой амплитудой U2, при которой работа происходит в пределах участка MN. В этом случае изменение Iк1 во времени (жирная линия на графике Iк1 (t)) не отличается от модулирующего сигнала, т. е. имеет место неискаженная модуляция. Если взять большую амплитуду U2, при которой в процессе работы будут использоваться нелинейные участки модуляционной характеристики, огибающие Iк1 и Uвых окажутся искаженными и притом тем сильнее, чем больше U2.Для построения зависимости iк1(t) и аналогичного графика Uвых(t) достаточно симметрично ниже оси абсцисс провести вторую огибающую и промежуток между огибающими заполнить колебаниями частоты ω0 (см. рисунок 5.5в). Коэффициент модуляции в соответствии с обозначениями рисунка 5.5 может быть подсчитан по статической модуляционной характеристике как m=∆ Iк1/ Iк1ср.
Лекция 6. Угловая модуляция
Содержание лекции:
- колебания при угловой модуляции. Спектры при угловой модуляции.
Цель лекции:
- изучение простейших видов модулированных сигналов.
Фазовая модуляция
заключается
в пропорциональном первичному сигналу x(t) изменении фазы φ переносчика
![]()
![]() , (6.1)
, (6.1)
где а — коэффициент пропорциональности. Амплитуда колебания при фазовой модуляции не изменяется, поэтому аналитическое выражение ФМ колебания
![]() .
(6.2)
.
(6.2)
Если модуляция осуществляется гармоническим сигналом x(t) =Xsin Ωt, то мгновенная фаза
![]() . (6.3)
. (6.3)
 Первые два слагаемых (8.3) определяют
фазу немодулированного колебания, третье — изменение фазы колебания в
результате модуляции.
Первые два слагаемых (8.3) определяют
фазу немодулированного колебания, третье — изменение фазы колебания в
результате модуляции.
![]()
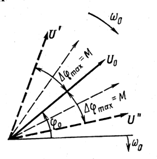
Фазомодулированное колебание наглядно характеризуется векторной диаграммой на рисунке 8.1, построенной на плоскости, вращающейся по часовой стрелке с угловой частотой w0. Немодулированному колебанию соответствует неподвижный вектор U0. Фазовая модуляция заключается в периодическом с частотой Ω повороте вектора U относительно U0 на угол ∆φ(t)=aXsinΩt. Крайние положения вектора U обозначены U’ и U’’. Максимальное отклонение фазы модулированного колебания от фазы немодулированного колебания
M=∆φmax=aX (6.4)
называется индексом модуляции. Индекс модуляции М пропорционален амплитуде Х модулирующего сигнала. Он в такой же степени характеризует ФМ колебание, как коэффициент модуляции т — AM колебание.
Используя (6.4), перепишем ФМ колебание (6.2) как
![]() .
(6.5)
.
(6.5)
Мгновенная частота ФМ колебания
![]() . (6.6)
. (6.6)
Таким образом, ФМ колебание в разные
моменты времени имеет различные мгновенные частоты, отличающиеся от частоты
несущего колебания ![]() на
величину
на
величину ![]() ,
что позволяет рассматривать ФМ колебание как модулированное по частоте.
,
что позволяет рассматривать ФМ колебание как модулированное по частоте.
Наибольшее отклонение частоты ω от ω0 называется девиацией частоты ∆ωД. Согласно (6.6)
∆ωд =MΩ или ∆fД =MF. (6.7)
Частотная модуляция заключается в пропорциональном первичному сигналу x(t) изменении мгновенной частоты переносчика
ω=ω0+ax(t), (6.8)
где а — коэффициент пропорциональности.
Мгновенная фаза ЧМ колебания: 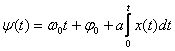 .
.
Аналитическое выражение ЧМ колебания с
учетом постоянства амплитуды можно записать в виде:
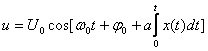 . (6.9)
. (6.9)
В простейшем случае модуляции
гармоническим колебанием ![]() мгновенная частота
мгновенная частота
![]() , где
, где
![]() —
девиация частоты, т. е. максимальное
ее отклонение от несущей частоты ω0, вызванное модуляцией.
Аналитическое выражение этого ЧМ колебания согласно (6.9)
—
девиация частоты, т. е. максимальное
ее отклонение от несущей частоты ω0, вызванное модуляцией.
Аналитическое выражение этого ЧМ колебания согласно (6.9)
![]() .
.
Слагаемое ![]() характеризует изменение фазы, получающееся при ЧМ.
Это позволяет рассматривать ЧМ колебание как ФМ колебание с индексом модуляции
характеризует изменение фазы, получающееся при ЧМ.
Это позволяет рассматривать ЧМ колебание как ФМ колебание с индексом модуляции
![]() ,
(6.10)
,
(6.10)
и записать его аналогично (8.9)
![]() . (6.11)
. (6.11)
Из сказанного следует, что ФМ и ЧМ колебания имеют много общего. Так колебание вида (8.11) может быть результатом как ФМ, так и ЧМ гармоническим первичным сигналом. Кроме того, ФМ и ЧМ характеризуются одними и теми же параметрами (индексом модуляции М и девиацией частоты ∆fД), связанными между собой одинаковыми соотношениями: (6.7) и (6.10).
 Наряду с отмеченным сходством частотной
и фазовой модуляции между ними имеется и существенное отличие, связанное с
различным характером зависимости величин М и ∆fД от частоты F первичного
сигнала:
Наряду с отмеченным сходством частотной
и фазовой модуляции между ними имеется и существенное отличие, связанное с
различным характером зависимости величин М и ∆fД от частоты F первичного
сигнала:
- при ФМ индекс модуляции не зависит от частоты F, а девиация частоты согласно (1.23) пропорциональна F;
|
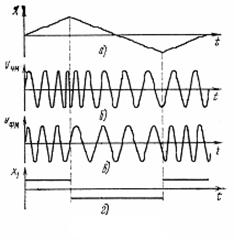
Различие между частотной и фазовой
модуляцией особенно заметно, когда модуляция производится сложным сигналом,
содержащим большое число компонент с разными частотами. Для иллюстрации
сказанного на рисунках 6.2 б,в построены графики ЧМ и ФМ колебаний,
соответствующие сигналу x(t)
треугольной формы (см. рисунок 6.2 а). При ЧМ увеличение
x(t) сопровождается возрастанием
w и наоборот.
При ФМ ∆φ(t) =
ax (t),
a ω=
ω0+adx/dt.
Поэтому на
участках, где dx/dt>0,
мгновенная частота ω больше несущей на величину ![]() ; на участках с
dx/dt< 0
частота
ФМ колебания меньше ω0 на величину ∆ω.
Таким образом, ФМ сигналом x(t) треугольной
формы совпадает с ЧМ сигналом x1(t) (см. рисунок 8.2 г) прямоугольной формы. И вообще любое-колебание с угловой модуляцией может быть получено как в результате ФМ
первичным сигналом x(t), так и ЧМ
первичным сигналом х1(t)=dx/dt.
К
сказанному следует добавить, что частотная и фазовая модуляция различаются
также способами их осуществления.
; на участках с
dx/dt< 0
частота
ФМ колебания меньше ω0 на величину ∆ω.
Таким образом, ФМ сигналом x(t) треугольной
формы совпадает с ЧМ сигналом x1(t) (см. рисунок 8.2 г) прямоугольной формы. И вообще любое-колебание с угловой модуляцией может быть получено как в результате ФМ
первичным сигналом x(t), так и ЧМ
первичным сигналом х1(t)=dx/dt.
К
сказанному следует добавить, что частотная и фазовая модуляция различаются
также способами их осуществления.
Исходным для определения спектров колебаний при гармонической угловой модуляции является выражение (6.11). Примем для упрощения выражений φ0=0 и перепишем (6.11) в виде
![]() .
(6.12)
.
(6.12)
Выражение (6.12) представляет сумму двух квадратурных колебаний частоты ω0, из которых каждое модулировано по амплитуде частотой Ω. Угловую модуляцию принято подразделять на узкополосную (М<0,5 рад) и широкополосную (M>0,5рад). Наибольшее распространение в технике связи имеет широкополосная ЧМ с М>>1. Начнем с определения спектра узкополосной угловой модуляции. Полагая M << l, имеем
![]() ,
(6.13)
,
(6.13)
а потому
![]() . (6.14)
. (6.14)
Таким образом, спектр узкополосных сигналов угловой модуляции аналогичен спектру простейшего AM колебания, показанному на рисунке 5.2. Он содержит компоненты несущей частоты ω0 и двух боковых частот ω0+Ω и ω0−Ω. Параметром, определяющим амплитуды боковых частот, здесь является индекс модуляции М. Ширина спектра узкополосной угловой модуляции такая же, как и при AM: она равна удвоенной частоте модуляции. Несмотря на идентичность спектров, рассматриваемое колебание отличается от AM колебания, что является следствием различия в знаках (т. е. в сдвиге фаз на 180°) компонент нижней боковой частоты в выражениях (6.14) и (5.5). Это означает возможность преобразования AM колебания в узкополосное ФМ колебание поворотом фазы одной из боковых частот на 180°.
При широкополосной угловой модуляции
M
>> 1 выражения (5.5) и (6.14)
несправедливы. Приходится спектр колебаний определять непосредственно из
(6.12). Выражения ![]() и
и
![]() являются
периодическими функциями частоты, а потому они могут быть разложены в ряды Фурье.
Первая из этих функций является четной, вторая—нечетной.
являются
периодическими функциями частоты, а потому они могут быть разложены в ряды Фурье.
Первая из этих функций является четной, вторая—нечетной.
![]()
![]()
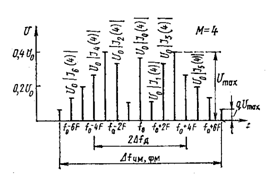
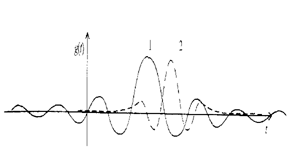
где Jn(M) — функция Бесселя первого рода п-го порядка от аргумента М. Таким образом, спектр ЧМ и ФМ колебаний, модулированных гармоническим сигналом, оказывается дискретным, симметричным относительно ω0 и содержащим бесконечное число боковых частота вида ω0±nΩ с амплитудами An=U0Jn(M). Для М=4 он построен на рисунке 6.3. При ограничении спектра необходимо учитывать влияние двух противоречивых факторов: в более узкой полосе частот ослабляется влияние помех, но одновременно увеличиваются искажения сигнала из-за отсутствия опускаемых составляющих. На практике выбирают компромиссное решение. Отличие ширины спектра сигналов гармонической угловой модуляции от интервала частот 2∆fд, в пределах которого происходит изменение мгновенной частоты сигнала:
а) теоретическая ширина спектра ∆fчм, фм=∞;
 б)
практическое ее значение при М<<1 оказывается
∆fчм, фм=2F>>2∆fд, а при
M>>1
∆fчм, фм
несколько превышает 2∆fд и лишь приближенно считается равной ей (8.17). Рассмотрим
влияние параметров модулирующего сигнала
x(t)=XcosΩt на спектры ФМ и ЧМ колебаний, используя (8.17). При
изменении амплитуды Х модулирующего сигнала спектры ФМ и ЧМ колебаний изменяются
одинаково. При возрастании Х происходит пропорциональное увеличение индекса
модуляции, спектры расширяются за счет увеличения числа спектральных компонент.
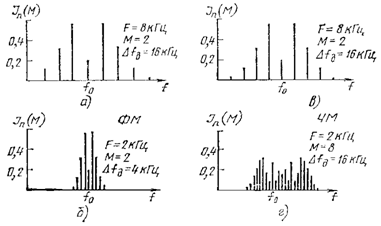
Изменение частоты F модулирующего колебания по-разному влияет на
изменение спектров ФМ и ЧМ колебаний. При ФМ изменение
F
не влияет на величину индекса модуляции, а следовательно,
и на число спектральных составляющих (см. рисунки 6.4 а, б).
б)
практическое ее значение при М<<1 оказывается
∆fчм, фм=2F>>2∆fд, а при
M>>1
∆fчм, фм
несколько превышает 2∆fд и лишь приближенно считается равной ей (8.17). Рассмотрим
влияние параметров модулирующего сигнала
x(t)=XcosΩt на спектры ФМ и ЧМ колебаний, используя (8.17). При
изменении амплитуды Х модулирующего сигнала спектры ФМ и ЧМ колебаний изменяются
одинаково. При возрастании Х происходит пропорциональное увеличение индекса
модуляции, спектры расширяются за счет увеличения числа спектральных компонент.
Изменение частоты F модулирующего колебания по-разному влияет на
изменение спектров ФМ и ЧМ колебаний. При ФМ изменение
F
не влияет на величину индекса модуляции, а следовательно,
и на число спектральных составляющих (см. рисунки 6.4 а, б).
![]() При ЧМ с
уменьшением F индекс модуляции увеличивается, что приводит к увеличению
числа спектральных компонент (см. рисунки 6.4 в, г). В итоге ширина спектра ЧМ
колебания от частоты почти не зависит, а при ФМ изменяется пропорционально F.
При ЧМ с
уменьшением F индекс модуляции увеличивается, что приводит к увеличению
числа спектральных компонент (см. рисунки 6.4 в, г). В итоге ширина спектра ЧМ
колебания от частоты почти не зависит, а при ФМ изменяется пропорционально F.
Лекция 7. Частотная модуляция. Фазовая модуляция. Импульсная модуляция. Общие сведения о детектировании
Содержание лекции:
- частотный и фазовый модуляторы. Импульсная модуляция. Общие сведения о детектировании.
Цель лекции:
- Получение часто-модулированных и фазо-модулированных сигналов. Изучение импульсно-модулированных сигналов.
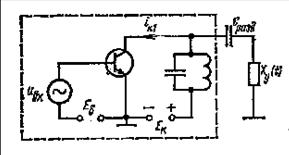
Для получения частотной модуляции нужно, чтобы частота колебаний автогенератора изменялась под действием первичного сигнала uΩ. На рисунке 7.1 приведена схема автогенератора (обведена пунктирной линией),
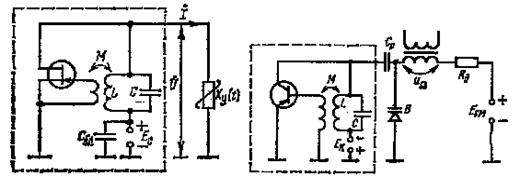
Рисунок 7.1
вырабатывающего синусоидальное напряжение u=Ucosωt с частотой ω, приблизительно равной резонансной частоте контура ω0. Следовательно, изменение частоты генерируемых колебаний может быть достигнуто изменением емкости или индуктивности контура. Для осуществления частотной модуляции параллельно контуру генератора подключают параметрический элемент—реактивное управляемое сопротивление Xy(t), величина которого изменяется под воздействием модулирующего сигнала: Xy(t)=Φ(uΩ).
В рассмотренных случаях изменение частоты колебаний происходит пропорционально изменениям емкости или индуктивности. Если емкость или индуктивность изменяются пропорционально первичному сигналу и притом в небольших пределах, изменение частоты также пропорционально uΩ, т. е. частотная модуляция будет неискаженной.
В качестве управляемого сопротивления в транзисторных генераторах обычно используют варикапы, подключаемые к генератору, как показано на рисунке 7.1. На варикап В подается смещение Eсм и модулирующее напряжение uΩ. Остальные элементы на рисунке 7.1 имеют вспомогательное значение: емкость Cp большей величины разделяют цепи питания генератора и варикапа по постоянному току, позволяя в каждой из них установить нужные напряжения; добавочное сопротивление RД величиной порядка сотен килоом включается для того, чтобы источник смещения и вторичная обмотка трансформатора не шунтировали контур генератора.
Следовательно, емкость варикапа изменяется с частотой Ω и ее гармоник; кроме того, изменяется и ее среднее значение.
Если емкость контура состоит только из емкости варикапа (С0=Св0), то модуляционная характеристика автогенератора с варикапом - зависимости отклонения частоты генератора от изменения напряжения ∆u на варикапе. Поскольку эта зависимость нелинейная, ЧМ, возникающая при воздействии низкочастотного модулирующего напряжения, должна сопровождаться искажениями (изменением частоты генерации с частотами 2Ω, 3Ω, ...) и сдвигом средней частоты. Увеличение девиации частоты сопровождается увеличением искажений и сдвига средней частоты.
Для осуществления фазовой модуляции (ФМ) нужно иметь устройство, на выходе которого фаза колебаний изменяется пропорционально модулирующему сигналу. Для этого можно использовать те же самые управляемые реактивные сопротивления Xy(t). Однако подключать их нужно к контуру усилителя, а не генератора, как это имело место в случае ЧМ. Такая схема показана на рисунке 7.2.
![]()
![]() Будем считать, что
напряжение на входе усилителя uвх=UBXcosω1t,
и
первая гармоника тока ik1 синфазна
с напряжением uвх.
Изменение резонансной частоты контура с помощью реактивного управляемого
сопротивления Xy вызывает
изменение амплитуды и фазы напряжения на контуре. Их величины при заданном токе
ik1 определяются
по частотной и фазовой характеристикам контура. Частота же колебаний в стационарном
режиме при любой настройке контура равна частоте ω1 входного
сигнала.
Будем считать, что
напряжение на входе усилителя uвх=UBXcosω1t,
и
первая гармоника тока ik1 синфазна
с напряжением uвх.
Изменение резонансной частоты контура с помощью реактивного управляемого
сопротивления Xy вызывает
изменение амплитуды и фазы напряжения на контуре. Их величины при заданном токе
ik1 определяются
по частотной и фазовой характеристикам контура. Частота же колебаний в стационарном
режиме при любой настройке контура равна частоте ω1 входного
сигнала.
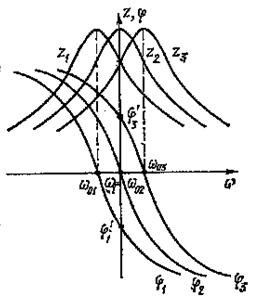
На рисунке 7.3 построены
частотные Z(ω) и фазовые ф(ω) характеристики контура
для трех значений резонансной частоты ω01<ω1;
ω02=ω1 и ω03>ω1.
На рисунке 7.4 для этих же трех случаев построены векторные диаграммы. При любой
настройке контура сдвиг фаз напряжения на контуре ![]() по отношению к току
по отношению к току
![]() определяется ординатой фазовой характеристики на
частоте ω1, а эквивалентное сопротивление — ординатой частотной
характеристики на частоте ω1. Если резонансная частота контура
медленно изменяется под действием управляющего сигнала от ω01
до ω03 и обратно, фаза выходного напряжения (напряжения на
контуре) меняется между φ΄1 и φ΄3, т.
е. имеет место ФМ напряжения на контуре. Одновременно в результате изменения
эквивалентного сопротивления контура для частоты ω1 возникает
паразитная AM.
определяется ординатой фазовой характеристики на
частоте ω1, а эквивалентное сопротивление — ординатой частотной
характеристики на частоте ω1. Если резонансная частота контура
медленно изменяется под действием управляющего сигнала от ω01
до ω03 и обратно, фаза выходного напряжения (напряжения на
контуре) меняется между φ΄1 и φ΄3, т.
е. имеет место ФМ напряжения на контуре. Одновременно в результате изменения
эквивалентного сопротивления контура для частоты ω1 возникает
паразитная AM.

Рисунок 7.4
Уравнение фазовой характеристики контура с добротностью Q для небольших расстроек ∆ω имеет вид
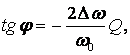 (7.1)
(7.1)
где ∆ω= ω1−ω0.
 Если ∆ω изменяется пропорционально модулирующему
сигналу uΩ, то неискаженная ФМ имеет место, когда изменение
φ пропорционально ∆ω, т.е.
на линейном участке фазовой характеристики (7.1), где
tgφ=φ.
Это справедливо лишь для небольших
индексов модуляции, не превышающих 20—30°.
Если ∆ω изменяется пропорционально модулирующему
сигналу uΩ, то неискаженная ФМ имеет место, когда изменение
φ пропорционально ∆ω, т.е.
на линейном участке фазовой характеристики (7.1), где
tgφ=φ.
Это справедливо лишь для небольших
индексов модуляции, не превышающих 20—30°.
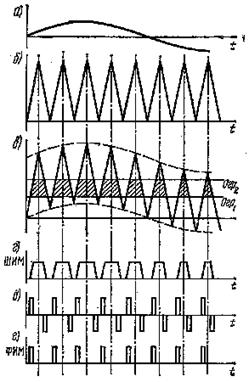
Обратимся к способам формирования ИМ колебаний (см. рисунок 7.5). Первичная АИМ может осуществляться теми же методами, что и AM. Так, можно использовать схему базовой модуляции (см. рисунок 5.3), вводя вместо напряжения u1 последовательность импульсов и применяя в качестве нагрузки резистор вместо контура.
![]() Простейший
способ формирования ШИМ и ФИМ, имеющих более широкое распространение,
поясняется графиками рис. 7.5. Если сложить модулирующее напряжение (а)
с периодической последовательностью треугольных импульсов (б) и их сумму
(в) пропустить через двусторонний ограничитель, на выходе последнего
получим трапецеидальные импульсы ШИМ (г). Крутизна фронтов импульсов
зависит от соотношения амплитуды и ширины импульсов. Если пропустить полученный
сигнал (г) через дифференцирующее устройство (д), а затем через
ограничитель по минимуму с нулевым уровнем
ограничения, получим сигнал ФИМ (е),
сдвиг импульсов которого
относительно центров треугольных импульсов (б) окажется пропорциональным
модулирующему сигналу. Импульсные модуляторы выполняются на транзисторах и
диодах.
Простейший
способ формирования ШИМ и ФИМ, имеющих более широкое распространение,
поясняется графиками рис. 7.5. Если сложить модулирующее напряжение (а)
с периодической последовательностью треугольных импульсов (б) и их сумму
(в) пропустить через двусторонний ограничитель, на выходе последнего
получим трапецеидальные импульсы ШИМ (г). Крутизна фронтов импульсов
зависит от соотношения амплитуды и ширины импульсов. Если пропустить полученный
сигнал (г) через дифференцирующее устройство (д), а затем через
ограничитель по минимуму с нулевым уровнем
ограничения, получим сигнал ФИМ (е),
сдвиг импульсов которого
относительно центров треугольных импульсов (б) окажется пропорциональным
модулирующему сигналу. Импульсные модуляторы выполняются на транзисторах и
диодах.
Детектирование представляет собой процесс, обратный модуляции. При модуляции один из параметров высокочастотного переносчика изменяется пропорционально первичному сигналу. Детектирование заключается в восстановлении того первичного сигнала, которым производилась модуляция. Детектирование считается неискаженным, если напряжение на выходе детектора повторяет закон изменения параметра модулированного колебания (амплитуды в случае AM, частоты в случае ЧМ, фазы в случае ФМ).
Поскольку в спектре модулированного колебания содержатся только высокочастотные компоненты (несущая и боковые частоты), а результатом детектирования является получение низкочастотных колебаний, линейные цепи для детектирования непригодны. В большинстве случаев детекторы являются устройствами нелинейными, реже — параметрическими.
На рисунке 7.6 приведена обобщенная схема детектора, состоящая из двух элементов: а) нелинейного (НП) или параметрического (ПП) преобразователя, в выходном токе которого при воздействии на вход гармонического напряжения uBX=Ucos(ωt+φ) появляется постоянная составляющая I΄0, б) фильтра нижних частот ФНЧ, предотвращающего прохождение на выход детектора высокочастотных составляющих. Требование к преобразователям заключается в том, что величина I΄0 должна зависеть:
¾ в детекторе AM сигналов от U;
¾ в детекторе ЧМ сигналов от ω;
¾ в детекторе ФМ сигналов от φ.

Рисунок 7.6
При подаче на вход модулированного колебания, один из параметров которого меняется с низкой частотой, постоянная составляющая тока I΄0 на выходе соответствующего детектора также будет изменяться с низкой частотой, и это колебание после ФНЧ выделится на выходе детектора. Для неискаженного детектирования необходимо, чтобы компонента тока I΄0 изменялась пропорционально модулируемому параметру (U, ω или φ). В связи с этим важнейшими характеристиками детекторов являются характеристики детектирования, под которыми подразумеваются зависимости I΄0 от U в амплитудных, от ω в частотных и от φ в фазовых детекторах.
Лекция 8. Детектирование АМ и ЧМ-колебаний в нелинейных цепях
Содержание лекции:
- амплитудный и частотный демодуляторы.
Цель лекции:
- изучение процессов детектирования амплитудно-модулированных и часто-модулированных и сигналов.
На рисунке 8.1а—в показано графическое определение тока, протекающего через диод при воздействии на него AM напряжения
![]() (8.1)
(8.1)
![]()

Поскольку диод обладает односторонней проводимостью, ток i имеет характер импульсов длительностью в половину периода частоты ω, амплитуда которых изменяется при изменении огибающей входного напряжения. В получившейся последовательности импульсов тока содержится уже и низкочастотная составляющая частоты Ω. Действительно, импульсы тока i различаются главным образом амплитудой I. Зависимость i(t) можно рассматривать как результат модуляции импульсов тока, записанных в виде ряда Фурье I0+I1cosω0t+I2cos2ω0t+… , колебанием низкой частоты Ω
![]() (8.2)
(8.2)
 Таким образом, ток i содержит
постоянную составляющую и компоненты высокой частоты ω и ее гармоник,
каждая из которых модулирована низкочастотным сигналом.
Таким образом, ток i содержит
постоянную составляющую и компоненты высокой частоты ω и ее гармоник,
каждая из которых модулирована низкочастотным сигналом.
На рисунке 8.3в штрихпунктирная линия изображает зависимость постоянной составляющей тока от времени I΄0(t), определяемой как среднее значение тока i за период высокой частоты ω:
![]()
![]() (8.3)
(8.3)
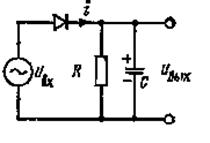
Для выделения низкочастотного сигнала последовательно с нелинейным элементом включают такую цепь RC (см. рисунок 8.2), чтобы
![]() (8.4)
(8.4)
Здесь емкость С выполняет роль ФНЧ: в силу (8.4) высокочастотные компоненты тока напряжения на выходе почти не создают. Для того чтобы низкочастотные компоненты тока создавали большое выходное напряжение, сопротивление R должно быть достаточно большим и притом 1/ΩC>>R с тем, чтобы для низких частот сопротивление нагрузочной цепи ZH≈R. Объединяя эти неравенства, получаем условия, определяющие выбор емкости С:
![]() (8.5)
(8.5)
График uвыx(t) рисунке 8.1г показывает форму выходного напряжения.
![]()
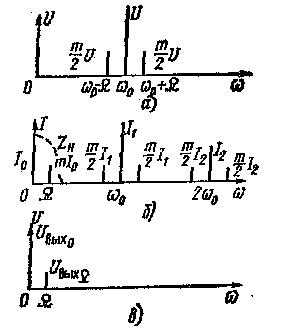 На рисунках 8.3а и б представлены спектры напряжения
(8.1) и тока (8.2). Пунктирная линия на рисунке 8.3б изображает зависимость
ZH(ω) при условии (8.5). Перемножая амплитуды спектральных компонент
на соответствующие величины ZH, получаем спектр выходного напряжения (см. рисунок 8.3в).
На рисунках 8.3а и б представлены спектры напряжения
(8.1) и тока (8.2). Пунктирная линия на рисунке 8.3б изображает зависимость
ZH(ω) при условии (8.5). Перемножая амплитуды спектральных компонент
на соответствующие величины ZH, получаем спектр выходного напряжения (см. рисунок 8.3в).
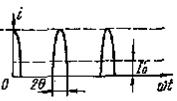
Переходя к более подробному рассмотрению процесса детектирования, отметим, что сопротивление нагрузки R обычно выбирается настолько большим, что учет его влияния на ток i оказывается необходимым. Пусть на детектор в схеме (см. рисунок 8.2) действует синусоидальное напряжение частоты ω0=2π/T0
![]() (8.6)
(8.6)
![]()

 Напряжение на диоде
u=uвх+U0.
Вследствие наличия цепочки
RC,
оно отличается от напряжения (8.6) на величину
постоянного смещения U0=-I΄0R .На рисунке 8.4 показано определение тока с учетом
влияния U0 для кусочно-линейной
аппроксимации характеристики диода. При больших
R
диод работает с небольшими углами отсечки θ, т.
е. ток через диод протекает только в течение небольшой части периода, соответствующей
заштрихованной части входного сигнала. Так как сопротивление открытого диода
мало, в это время происходит быстрый заряд конденсатора С, сопровождающийся
возрастанием напряжения uс
на нем. Когда uвх
оказывается меньшим
uс
диод запирается,
входное напряжение перестает влиять на процессы в
RС-цепи, конденсатор
С разряжается через большое сопротивление
R.
Согласно (8.5) постоянная времени разряда τраз=RC>>T0/2π или τраз>>T0. Поэтому за
ту часть периода Т0, пока конденсатор разряжается, напряжение
uс
уменьшается
незначительно. Характер изменения по времени
uвх,
uвых=uc
и тока
i,
протекающего через диод, показан на рисунке 8.5. Пренебрегая пульсацией
напряжения uвых, будем
в дальнейшем считать его при воздействии сигнала (8.6) постоянным и равным
U0
(штрих-пунктирная на рисунке 8.5).
Напряжение на диоде
u=uвх+U0.
Вследствие наличия цепочки
RC,
оно отличается от напряжения (8.6) на величину
постоянного смещения U0=-I΄0R .На рисунке 8.4 показано определение тока с учетом
влияния U0 для кусочно-линейной
аппроксимации характеристики диода. При больших
R
диод работает с небольшими углами отсечки θ, т.
е. ток через диод протекает только в течение небольшой части периода, соответствующей
заштрихованной части входного сигнала. Так как сопротивление открытого диода
мало, в это время происходит быстрый заряд конденсатора С, сопровождающийся
возрастанием напряжения uс
на нем. Когда uвх
оказывается меньшим
uс
диод запирается,
входное напряжение перестает влиять на процессы в
RС-цепи, конденсатор
С разряжается через большое сопротивление
R.
Согласно (8.5) постоянная времени разряда τраз=RC>>T0/2π или τраз>>T0. Поэтому за
ту часть периода Т0, пока конденсатор разряжается, напряжение
uс
уменьшается
незначительно. Характер изменения по времени
uвх,
uвых=uc
и тока
i,
протекающего через диод, показан на рисунке 8.5. Пренебрегая пульсацией
напряжения uвых, будем
в дальнейшем считать его при воздействии сигнала (8.6) постоянным и равным
U0
(штрих-пунктирная на рисунке 8.5).![]()
 Это позволяет записать
напряжение на диоде как u=Ucosω0t−I΄0R.
Это позволяет записать
напряжение на диоде как u=Ucosω0t−I΄0R.
Данный детектор обладает линейной характеристикой детектирования, и детектирование в нем происходит без искажений. Детектор с линейной характеристикой детектирования называется линейным детектором. Диодный детектор является линейным в случае достаточно больших амплитуд входного сигнала, когда пригодна кусочно-линейная аппроксимация его характеристики. При этом следует помнить, что линейный детектор является устройством нелинейным, работающим с отсечкой тока. Из-за нелинейности характеристики детектирования изменение амплитуды входного сигнала вызывает непропорциональное изменение постоянной составляющей тока детектора, поэтому низкочастотные колебания на выходе детектора искажаются по сравнению с огибающей AM колебания.
Диодные детекторы обычно бывают квадратичными при амплитудах входных сигналов U≤0,1÷0,2 В и линейными при U>0,5÷1 В. Чтобы избежать искажений, следует принимаемый AM сигнал усилить до детектора настолько, чтобы его амплитуда была достаточно большой.
На выходе детектора ЧМ колебаний должно получаться напряжение, пропорциональное отклонение частоты колебаний от среднего значения. Существуют две группы методов решения этой задачи:
1) ЧМ сигнал преобразуется в AM или ФМ сигнал и затем детектируется амплитудным или фазовым детектором;
2)
 ЧМ сигнал преобразуется в последовательность коротких
импульсов той же частоты, создающих постоянное напряжение, пропорциональное
числу импульсов в единицу времени.
ЧМ сигнал преобразуется в последовательность коротких
импульсов той же частоты, создающих постоянное напряжение, пропорциональное
числу импульсов в единицу времени.
![]() Рассмотрим работу детектора, основанного на преобразовании
ЧМ в AM с помощью расстроенного колебательного контура
(см. рисунок 8.6). Пусть через контур, настроенный на частоту ωP,
протекает ЧМ ток iЧМ
с постоянной амплитудой I
и меняющейся частотой ω(t)=ω0+∆ω(t).На рисунке 8.7 приведены
частотная характеристика контура ZЭ(ω) и зависимость ω(t). Если частота ω(t) изменяется достаточно медленно, можно в любой момент
определять амплитуду напряжения на контуре
UK
как
произведение амплитуды тока I на величину сопротивления
ZЭ(ω)
для данной мгновенной частоты UK(ω)=IZЭ(ω).
Рассмотрим работу детектора, основанного на преобразовании
ЧМ в AM с помощью расстроенного колебательного контура
(см. рисунок 8.6). Пусть через контур, настроенный на частоту ωP,
протекает ЧМ ток iЧМ
с постоянной амплитудой I
и меняющейся частотой ω(t)=ω0+∆ω(t).На рисунке 8.7 приведены
частотная характеристика контура ZЭ(ω) и зависимость ω(t). Если частота ω(t) изменяется достаточно медленно, можно в любой момент
определять амплитуду напряжения на контуре
UK
как
произведение амплитуды тока I на величину сопротивления
ZЭ(ω)
для данной мгновенной частоты UK(ω)=IZЭ(ω).
![]()
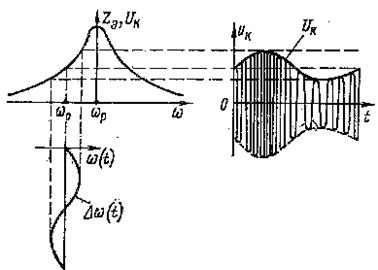
Амплитуда UK будет изменяться приблизительно пропорционально ∆ω(t), если несколько расстроить контур относительно несущей частоты сигнала ω0, как показано на рисунке 8.7. Определяем UK(t) на рисунке 8.7 методом проекций. Если нанести симметрично вторую огибающую (пунктир) и высокочастотное заполнение, получим форму напряжения uK(t). Последнее оказывается модулированным одновременно и по амплитуде и по частоте, причем закон изменения UK(t) примерно такой же, что и ∆ω(t). Для получения низкочастотного сигнала uвых достаточно uK(t) подать на линейный амплитудный детектор как показано на рисунке 8.6. Недостаток схемы заключается в появлении искажений вследствие нелинейности скатов частотной характеристики контура.
В рассмотренной схеме детектора как и в детекторах, основанных на преобразовании ЧМ в ФМ, выходное напряжение зависит не только от величины отклонения частоты ∆ω, но также и от амплитуды входного ЧМ сигнала. Последняя же может меняться, например, из-за воздействия помех, что приводит к искажениям uвых. Для предотвращения этого ЧМ сигнал перед частотным детектором пропускают через ограничитель амплитуды.
Наличие индуктивностей в рассмотренных частотных детекторах первой группы затрудняет их реализацию средствами микроэлектроники. Поэтому все большее распространение получают методы детектирования второй группы. Процессы в них сходны с показанными на рисунке 7.5: ЧМ колебание подвергается двустороннему ограничению, дифференцированию и ограничению по минимуму, в результате чего получается последовательность коротких однополярных импульсов (рисунок 8.1в) с частотой ω(t), пропускаемых затем через интегрирующее устройство. Выходное напряжение последнего пропорционально среднему значению этой последовательности за некоторый отрезок времени, т. е. ω(t).
Лекция 9. Потенциальные возможности дискретных каналов связи
Содержание лекции:
- основной понятийный аппарат теории информации. Поток ошибок в реальных каналах.
Цель лекции:
- сформулировать исходные понятия: частное количество информации, энтропия источника, количество информации, передаваемой по каналу связи (взаимная информация).
Пусть дискретный источник сообщений выдал некоторую последовательность символов а. Дадим формальное определение частного количества информации i(a), содержащейся в этом сообщении, исходя из следующих естественных требований:
а) количество информации i(d) должно быть аддитивной функцией, т.е. для пары взаимно независимых сообщений а1, а2 оно должно равняться сумме количества информации в каждом из них, т.е. i( а1, а2) = i(а1) + i(а2);
б) количество информации, содержащейся в достоверном сообщении (имеющем вероятность Р(а) = 1), равно нулю;
в) количество информации должно зависеть только от вероятности переданного сообщения, т.е. i(d) =f(P(a));
г) количество информации должно быть непрерывной функцией от Р(а).
Можно показать, что единственная функция, удовлетворяющая всем этим условиям, имеет вид
i(a)=-logP(a)≥0. (9.1)
Основание логарифма в (9.1) может быть выбрано произвольным, что влияет лишь на единицу измерения количества информации. Если в качестве основания выбрано 2, то информация измеряется в двоичных единицах или в битах, а если е (как в натуральных логарифмах), то информация будет измеряться в натуральных единицах или в нотах. Из соотношения (6.8) видно, что количество информации, содержащейся в сообщении, тем больше, чем меньше вероятность его появления, причём, количество информации, содержащейся в сообщении о "невозможном" событии, равно бесконечности.
Энтропия источника сообщений. Для того, чтобы получить исчерпывающую информационную характеристику источника сообщений, который, вообще говоря, может выдавать последовательности неограниченной длины, нужно вычислить предел среднего количества информации i(a[n]), отнесённый к одному символу последовательности. Полученная величина, обозначенная через H(А), называется энтропией источника сообщений, т.е. если источник не обладает памятью, то, используя свойство логарифмической функции, легко показать, что его энтропия будет
![]() ,
(9.2)
,
(9.2)
где
P(ai),
i=0,1,...,K-1, — вероятности выдачи источником символов
ai![]() A, причём они не зависят от номера элемента
последовательности, так как источник является стационарным. Прежде чем пояснить
наглядный смысл нового понятия энтропии, опишем её основные свойства:
A, причём они не зависят от номера элемента
последовательности, так как источник является стационарным. Прежде чем пояснить
наглядный смысл нового понятия энтропии, опишем её основные свойства:
а) H(А) ≥ 0, причём H(А) = 0 тогда и только тогда, когда одна из последовательностей имеет единичную вероятность, а все остальные — нулевую. (Это свойство очевидно из определения энтропии);
б) для любого стационарного источника сообщений
![]() . (9.3)
. (9.3)
Поскольку выражение в правой части (9.3) - это энтропия источника без памяти, то данное свойство означает, что память уменьшает энтропию источника;
в) для любого стационарного источника сообщений
![]() , (9.4)
, (9.4)
причём, равенство имеет место тогда, и только тогда, когда источник не имеет памяти и все его символы равновероятны.
Воспользовавшись свойствами 1-3, можно наглядно пояснить смысл понятия энтропии — это средняя информативность источника на один символ, определяющая "неожиданность" или "непредсказуемость" выдаваемых им сообщений. Полностью детерминированный источник, выдающий лишь одну, заранее известную последовательность, обладает нулевой информативностью. Наоборот, наиболее "хаотический" источник, выдающий взаимно независимые и равновероятные символы, обладает максимальной информативностью. Энтропия источника сообщений тесно связана с понятием его избыточности, которое формально определяется следующим образом
![]() (9.5)
(9.5)
Как видно из выражения (9.5), чем больше энтропия источника, тем меньше его избыточность и наоборот.
Если источник сообщений имеет
фиксированную скорость ![]() симв/с, то определим производительность
источника H’(А) как энтропию в единицу времени,
(секунду)
симв/с, то определим производительность
источника H’(А) как энтропию в единицу времени,
(секунду)
H’(A)=υиH(A). (9.6).
Количество информации, передаваемой по каналу связи (взаимная информация). Определим условную энтропию H(Х|У) входа канала Х при известном выходе Y как МО
![]() ,
(9.7)
,
(9.7)
где верхний индекс п в квадратных скобках означает длину входных и выходных последовательностей.
В частном случае канала без памяти легко получить из (9.8)
![]() .
(9.9)
.
(9.9)
Условная энтропия обладает следующими свойствами:
а) H(Х|У)≥ 0. (Доказывается по определению H(Х|У));
б) если вход и выход канала связаны взаимно однозначно, т.е.
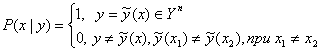
то H(Х/Y) = 0 (Это свойство очевидно);
в) H(Х|У) ≤ (X); (9.10)
г) H(Х|У) = H(Х), (9.11)
тогда, и только тогда, когда Р(х|у) = Р(х)
при всех ![]() ,
, ![]() , т.е. когда х и
у взаимно независимы. Приведённые выше свойства позволяют наглядно пояснить
смысл понятия условной энтропии Н(Х Y). Это средняя информация, теряемая
с каждым символом в канале связи из-за помех.
, т.е. когда х и
у взаимно независимы. Приведённые выше свойства позволяют наглядно пояснить
смысл понятия условной энтропии Н(Х Y). Это средняя информация, теряемая
с каждым символом в канале связи из-за помех.
Определим количество информации, передаваемой по каналу связи I(X,Y), или взаимную информацию между выходом Y и входом Х как разность между количеством информации, поступающей на вход (которое, как мы знаем, равно энтропии входа H(Х)), и количеством информации, потерянным в канале связи (которое, как мы только что выяснили, равно условной энтропии H(Х|Y)).
I(X,Y) = H(Х) - H(Х Y). (9.12)
Эта величина обладает следующими свойствами:
а) I(X,Y) = I(Y,X) = H(Y) - H(Y|Х);
б) I(X,Y) ≥ 0
(Следует непосредственно из свойства 3 условной энтропии);
в) I(X,Y) =
0, тогда и только тогда, когда вход и выход канала статистически независимы,
т.е. Р(у|х) = р(у) при всех х ![]() Х",
y
Х",
y![]() Y".
(Следует непосредственно из свойства 4 условной энтропии).
Y".
(Следует непосредственно из свойства 4 условной энтропии).
Определение взаимной информации иллюстрируется рисунком 9.1.
Если для канала связи задана скорость передачи υк [симв/с], то аналогично определению производительности источника можно определить скорость передачи информации по каналу связи I(X,Y)
I’(X,Y) = υк I(Х,Y) [бит/с]. (9.13)
Определим пропускную способность С дискретного канала связи с помехами как максимум количества информации I(X,Y) по всевозможным распределениям р(x) входа канала, т.е.
![]() и
и ![]() , (9.14)
, (9.14)
где ![]() — длительность передаваемого единичного элемента. Из
определения видно, что пропускная способность канала связи зависит только от
свойств самого канала, т.е. входного и выходного алфавитов X,
Y
и заданного на них условного распределения вероятностей р(у|х), х
— длительность передаваемого единичного элемента. Из
определения видно, что пропускная способность канала связи зависит только от
свойств самого канала, т.е. входного и выходного алфавитов X,
Y
и заданного на них условного распределения вероятностей р(у|х), х ![]() Х", у
Х", у
![]() Y", и не
зависит от того источника, который подключён ко входу канала.
Y", и не
зависит от того источника, который подключён ко входу канала.

Рисунок 9.1 - Иллюстрация передачи информации по каналу с помехами
В реальных условиях прием двоичных символов всегда происходит с ошибками. Это означает, что вместо символа «1» принимается символ «О» и наоборот. Ошибки могут возникать из-за импульсных помех, действующих в канале связи; изменения за время передачи характеристик канала: снижения уровня передачи, нестабильности амплитудно- и фазо-частотных характеристик канала; кратковременных перерывов; ремонтно-профилактических работ на линии во время сеанса связи. Часть указанных причин носит эксплуатационный характер и в принципе может быть устранена такими мерами как повышение качественных показателей аппаратуры связи и особенно коммутационной техники.
Улучшению качества канала связи, особенно на линиях большой протяженности, способствует включение таких устройств как фазовые корректоры, регенеративные ретрансляторы и т. д. Несмотря на подобные меры, при работе по современному дискретному каналу вероятность ошибки (на единичный элемент) будет не меньше 10-3-10-4, однако при передаче данных допускается, чтобы Pош не превышало 10-6. Появление ошибок обычно носит случайный характер и, как правило, является следствием совокупности мешающих факторов, часть которых может быть вообще неизвестна. Поэтому целесообразно исследовать свойства потока ошибок математическим аппаратом теории случайных процессов. Имея такие модели, можно выбирать соответствующие меры повышения помехоустойчивости.
Критерий качества, пригодный для всех дискретных каналов, заключается в нормировании вероятности ошибки для данного вида сообщений. Так, вероятность ошибки при передаче данных - не более 10-6 (на единичный элемент). Методы повышения верности можно разбить на две группы. К первой группе относятся методы увеличения помехоустойчивости приема единичных элементов, связанные с выбором уровня сигнала, отношения сигнал/помеха, ширины полосы канала, статистикой ошибок в канале связи и т. п. Ко второй группе относятся методы обнаружения и исправления ошибок, основанные на искусственном введении избыточности в передаваемое сообщение.
Лекция 10. Методы повышения верности передачи дискретной информации
Содержание лекции:
- избыточность сигналов дискретной информации. Принципы помехоустойчивого кодирования. Кодовое расстояние. Число обнаруживаемых и исправляемых ошибок.
Цель лекции:
- рассмотреть методы повышения верности передачи и надежности систем ПДИ.
Понятие «избыточность»
определяется средним количеством информации, содержащемся в передаваемом
сообщении. При двоичном кодировании в условиях равновероятности передаваемых
двоичных символов «О» и «1» каждый единичный элемент содержит максимальное
количество информации: ![]() бит, где
R = 2 — основание кода. Если же единичные элементы
поступают в канал с разными вероятностями, то один единичный элемент переносит
меньшее количество информации. В этом случае говорят, что в сигнале есть
избыточность. Ее можно оценить как отношение
бит, где
R = 2 — основание кода. Если же единичные элементы
поступают в канал с разными вероятностями, то один единичный элемент переносит
меньшее количество информации. В этом случае говорят, что в сигнале есть
избыточность. Ее можно оценить как отношение ![]() . Поскольку пропускная способность
определяется в виде (9.14), то систему передачи надо строить так, чтобы
. Поскольку пропускная способность
определяется в виде (9.14), то систему передачи надо строить так, чтобы
![]() было максимальным, т. е. требовать, чтобы среднее
количество информации
было максимальным, т. е. требовать, чтобы среднее
количество информации ![]() было равно
Iтах
(1 бит для двоичного кода).
было равно
Iтах
(1 бит для двоичного кода).
При отсутствии
избыточности, когда любая комбинация двоичных символов представляет собой
передаваемое сообщение, обнаружить ошибки в принятой кодовой комбинации
невозможно. Чтобы обнаружить ошибку и даже определить место ошибочно принятого
единичного элемента, необходимо увеличить объем сигнала, представляющего кодовую
комбинацию. Увеличить избыточность передаваемого сигнала можно по-разному. Так
как объем сигнала расчитывается по (1.2), то его увеличение возможно за счет
увеличения Dк (Рк),
![]() и Т.
Практические возможности увеличения избыточности за счет мощности и ширины
спектра сигнала в системах передачи дискретной информации по стандартным каналам
резко ограничены. Поэтому основное развитие получили методы повышения верности
приёма, основанные на увеличении времени передачи. Эти методы реализуются системами
без обратной связи и системами с обратной связью. В системах без обратной
связи (однонаправленных системах) для повышения
верности
приема используются следующие основные способы:
и Т.
Практические возможности увеличения избыточности за счет мощности и ширины
спектра сигнала в системах передачи дискретной информации по стандартным каналам
резко ограничены. Поэтому основное развитие получили методы повышения верности
приёма, основанные на увеличении времени передачи. Эти методы реализуются системами
без обратной связи и системами с обратной связью. В системах без обратной
связи (однонаправленных системах) для повышения
верности
приема используются следующие основные способы:
1) помехоустойчивое кодирование, т. е. использование кодов, исправляющих ошибки;
2) многократная передача кодовых комбинаций;
3) одновременная передача кодовой комбинации по нескольким параллельно работающим каналам.
Наиболее эффективно избыточность используется при применении помехоустойчивых кодов для исправления ошибок. При этом в кодовые комбинации вводится постоянная, заранее рассчитанная избыточность (дополнительные элементы, сформированные по известным правилам). Повысить верность передачи без существенного снижения пропускной способности можно, вводя переменную избыточность в сообщение в зависимости от состояния канала. Такие системы являются адаптивными, т. е. приспосабливающимися к условиям канала. Для их построения нужно уметь оценивать на приеме статистику ошибок в канале и передавать эти данные на передающую станцию. Таким образом, необходимо иметь дополнительный обратный канал от приемника к передающей станции, и поэтому вся система связи оказывается системой с обратной связью.
В обычном равномерном
непомехоустойчивом коде число разрядов в кодовых комбинациях определяется
числом сообщений и основанием кода n=
log2K.
Любая из n кодовых
комбинаций представляет собой какой-то знак алфавита. Если в процессе передачи
такой кодовой комбинации произойдет одна ошибка, то принятая кодовая
комбинация будет интерпретироваться приемником как кодовая комбинация,
соответствующая другому знаку. Таким образом, возникающие в кодовых комбинациях
ошибки обнаружить невозможно, поскольку нельзя отличить ошибочную комбинацию от
безошибочной. Все n
кодовые
комбинации разрешены, и возникающие ошибки просто переводят одну разрешенную
комбинацию в другую, также разрешенную. Обнаружить ошибку в данном случае
может только получатель, прочтя принятое текстовое сообщение. За счет огромной
языковой и смысловой избыточности текста можно легко восстановить переданное
сообщение. Коды, у которых все кодовые комбинации разрешены к передаче,
называются простыми или равнодоступными. Очевидно, что при
передаче цифровой информации восстановление ошибочно принятых цифр невозможно.
Цифровая информация избыточностью не обладает. Ясно, что текстовое сообщение,
принятое с ошибками, верно восстанавливается только за счет содержащейся в нем
избыточности. В этом состоит идея помехоустойчивого кодирования: в
передаваемую кодовую комбинацию необходимо внести по определенным
«грамматическим» правилам избыточность (признаки разрешенной комбинации).
Правила внесения избыточности, т. е. признаки, должны быть известны не только
на передаче, но и на приеме. Если на приемной стороне эти признаки в кодовой
комбинации не обнаруживаются, то считается, что произошла ошибка (или ошибки).
В противном случае (при наличии признаков) считается, что кодовая комбинация
принята правильно (является разрешенной).
Внесение
избыточности при использовании
корректирующих (помехоустойчивых) кодов
обязательно связано с увеличением п — числа разрядов (длины) кодовой комбинации.
Таким образом, все множество ![]() комбинаций можно разбить на два подмножества:
подмножество разрешенных комбинаций, т. е. обладающих определенными признаками,
и подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного тем, что в канал передаются не все
кодовые комбинации N0,
которые можно сформировать из имеющегося числа
разрядов п—
N0, а
только их часть N,
которая
составляет подмножество разрешенных комбинаций:
комбинаций можно разбить на два подмножества:
подмножество разрешенных комбинаций, т. е. обладающих определенными признаками,
и подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного тем, что в канал передаются не все
кодовые комбинации N0,
которые можно сформировать из имеющегося числа
разрядов п—
N0, а
только их часть N,
которая
составляет подмножество разрешенных комбинаций:
N<N0. (10.1)
Если в результате искажений переданная кодовая комбинация переходит в подмножество запрещенных кодовых комбинаций, то ошибка будет обнаружена. Однако если совокупность ошибок в данной кодовой комбинации превращает ее в какую-либо другую разрешенную, то в этом случае ошибки не могут быть обнаружены. Поскольку любая из N разрешенных комбинаций может превратиться в любую из N0 возможных, то общее число таких случаев равно N*N0. Очевидно, что число случаев, в которых ошибки обнаруживаются, равно N(N0—N), где N0—N— число запрещенных комбинаций. Тогда доля обнаруживаемых ошибочных комбинаций составит
![]()
(10.2) (6.2)
![]()
 Аналогичное рассуждение можно провести и для случая
исправления ошибок, если рассматривать код, исправляющий ошибки. При использовании
этого кода нужно произвести разбиение множества
Аналогичное рассуждение можно провести и для случая
исправления ошибок, если рассматривать код, исправляющий ошибки. При использовании
этого кода нужно произвести разбиение множества ![]() (j=1,2,…,
N0—N) всех запрещенных комбинаций на N непересекающихся
подмножеств {Мк}. Каждое из подмножеств {Мк} приписывается
одной из передаваемых кодовых комбинаций Ак. Способ приема
состоит в том, что если принята комбинация
(j=1,2,…,
N0—N) всех запрещенных комбинаций на N непересекающихся
подмножеств {Мк}. Каждое из подмножеств {Мк} приписывается
одной из передаваемых кодовых комбинаций Ак. Способ приема
состоит в том, что если принята комбинация ![]() *,то считается, что передана Ак,
т. е. если принятая кодовая комбинация осталась в том же подмножестве, что
и переданная, то принимается решение о приеме комбинации Ак. Сказанное
можно проиллюстрировать рисунке 10.1, где приняты следующие обозначения: А1...Ап —
множество разрешенных (передаваемых) комбинаций;
*,то считается, что передана Ак,
т. е. если принятая кодовая комбинация осталась в том же подмножестве, что
и переданная, то принимается решение о приеме комбинации Ак. Сказанное
можно проиллюстрировать рисунке 10.1, где приняты следующие обозначения: А1...Ап —
множество разрешенных (передаваемых) комбинаций; ![]() — множество всех возможных запрещенных
комбинаций, в которые в результате различных ошибок могут перейти комбинации {Ак},
М1, М2 ..., МN—
подмножества, на которые разбиты запрещенные комбинации.
— множество всех возможных запрещенных
комбинаций, в которые в результате различных ошибок могут перейти комбинации {Ак},
М1, М2 ..., МN—
подмножества, на которые разбиты запрещенные комбинации.
Способ приема состоит
в том, что если принимается кодовая комбинация (В1, В2
или В3, принадлежащая подмножеству
M1,
то считается, что передавалась комбинация A1
(показано на рисунке стрелками). Если действительно комбинация В1
(или В2, В3) образовалась из А1,
то ошибка исправлена. Если принятая кодовая комбинация переходит в другое
подмножество М2, то декодер примет ошибочное решение о
передаче комбинации А2. Очевидно, что каким бы образом не
разбивалось множество ![]() на
подмножества {Мк}, ошибка всегда исправляется в
N0—N
случаях.
на
подмножества {Мк}, ошибка всегда исправляется в
N0—N
случаях.
Общее число переходов комбинаций АN
в комбинации ![]() равно
N(N0—N) , а
это
есть число всех обнаруживаемых ошибочных
комбинаций.
равно
N(N0—N) , а
это
есть число всех обнаруживаемых ошибочных
комбинаций.
Для того, чтобы можно было обнаруживать и исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от неразрешенной. Если ошибки действуют независимым образом (как случайные независимые события), то вероятность преобразования одной кодовой комбинации в другую будет тем меньше, чем большим числом разрядов они различаются. Если интерпретировать кодовые комбинации как точки в пространстве, то отличие выражается в расстоянии между ними. Количество разрядов, которыми отличаются две кодовые комбинации, можно принять за расстояние между ними. Для определения этого расстояния нужно сложить две кодовые комбинации по модулю 2 и подсчитать число единиц в полученной сумме. Обозначим кодовое расстояние через d. У простого кода
dmin=d0=1. (10.3)
Рассмотрим, чему равно d0 помехоустойчивого кода. При d0>2 код способен обнаруживать и исправлять ошибки. При d0=1 такой возможности нет.
Нужное кодовое расстояние устанавливается введением определенного количества дополнительных разрядов в кодовую комбинацию. Обозначим число (кратность) обнаруживаемых ошибок через to, а число исправляемых ошибок — через tu. Ошибка не обнаруживается, если одна разрешенная комбинация переходит в другую разрешенную. Для обеспечения возможности обнаружения всех ошибок кратностью до t0 ,кодовое расстояние определяется неравенством
d0![]() t0+1. (10.4)
t0+1. (10.4)
![]()
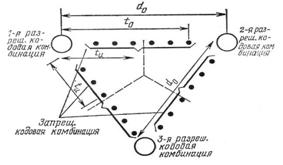 Это соотношение иллюстрируется рисунком 10.2. Переход
от одной точки к другой на рисунке 10.2 соответствует искажению одного
разряда.
Это соотношение иллюстрируется рисунком 10.2. Переход
от одной точки к другой на рисунке 10.2 соответствует искажению одного
разряда.
Для обеспечения возможности исправления всех ошибок кратности до tи включительно кодовое расстояние
d0![]() 2tИ+1. (10.5)
2tИ+1. (10.5)
Чтобы код обнаруживал ошибки
кратностью to и исправлял ошибки кратностью
tи, кодовое расстояние должно быть равно
d0![]() t0+tИ+1. (10.6)
t0+tИ+1. (10.6)
Очевидно, что количество дополнительных разрядов r связано с кодовым расстоянием do. Кодовое расстояние будет тем большим, чем больше избыточность кода и чем равномернее распределены расстояния между разрешенными кодовыми комбинациями. Формула для кода с d0=3
r![]() log2(n+1). (10.7)
log2(n+1). (10.7)
Лекция 11. Классификация помехоустойчивых кодов. Циклические коды
Содержание лекции:
- классификация помехоустойчивых кодов. Циклические коды. Обнаружение ошибок при циклическом кодировании. Определение места ошибки. Выбор образующего полинома.
Цель лекции:
- получить знания основ помехоустойчивого кодирования.
![]()
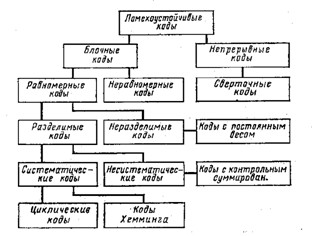 Помехоустойчивые коды (см. рисунок 11.1) делятся на
блочные и непрерывные. К блочным относятся коды, в которых каждому сообщению
соответствует блок из п символов (разрядов) или блоки с разным числом символов.
Непрерывные коды, к которым относятся рекуррентные (называемые также сверточными),
представляют собой непрерывные последовательности единичных элементов, не
разделенные на блоки. В таких кодах избыточные разряды помещаются в
определенном порядке между информационными. В разделимых кодах элементы информационной
и проверочной частей кодовой комбинации всегда стоят на определенных местах. В
неразделимых кодах деление на информационные и проверочные разряды
отсутствует. К таким кодам относится код с постоянным весом. Код называется
линейным, если любая разрешенная кодовая комбинация может быть получена в
результате линейной операции над набором
k ненулевых линейно-независимых кодовых комбинаций. В
систематических кодах проверочные элементы формируются линейным преобразованием
информационных.
Помехоустойчивые коды (см. рисунок 11.1) делятся на
блочные и непрерывные. К блочным относятся коды, в которых каждому сообщению
соответствует блок из п символов (разрядов) или блоки с разным числом символов.
Непрерывные коды, к которым относятся рекуррентные (называемые также сверточными),
представляют собой непрерывные последовательности единичных элементов, не
разделенные на блоки. В таких кодах избыточные разряды помещаются в
определенном порядке между информационными. В разделимых кодах элементы информационной
и проверочной частей кодовой комбинации всегда стоят на определенных местах. В
неразделимых кодах деление на информационные и проверочные разряды
отсутствует. К таким кодам относится код с постоянным весом. Код называется
линейным, если любая разрешенная кодовая комбинация может быть получена в
результате линейной операции над набором
k ненулевых линейно-независимых кодовых комбинаций. В
систематических кодах проверочные элементы формируются линейным преобразованием
информационных.
Циклические коды относятся к классу линейных систематических кодов и обладают всеми их свойствами. Удобно рассматривать кодовые комбинации циклического кода не в виде последовательности нулей и единиц, а в виде полинома некоторой степени. Любое число в любой системе счисления можно представить в общем виде как
![]() ,
(11.1)
,
(11.1)
где х — основание системы счисления; ai - цифры данной системы счисления; п-1, п-2,... — показатель степени, в которую возводится основание, и одновременно порядковые номера, которые занимают разряды, начиная от старшего, кончая нулевым. Для двоичной системы х=2, а ai либо «0», либо «1».
Очевидно, что при записи кодовой
комбинации в виде многочлена единица в 1-м разряде записывается членом ![]() , а нуль вообще
не записывается. Представление кодовых многочленов позволяет установить
однозначное соответствие между ними и свести действия над комбинациями к
действию над многочленами. Так, сложение двоичных многочленов сводится к
сложению по модулю 2 коэффициентов при равных степенях переменной
x.
Например,
, а нуль вообще
не записывается. Представление кодовых многочленов позволяет установить
однозначное соответствие между ними и свести действия над комбинациями к
действию над многочленами. Так, сложение двоичных многочленов сводится к
сложению по модулю 2 коэффициентов при равных степенях переменной
x.
Например,
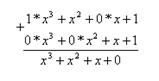
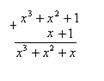
![]() ,
,
Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2.
Например, ![]()
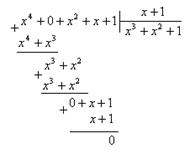 |
Деление также осуществляется, как обычное деление многочленов; при этом операция вычитания заменяется операцией сложения по модулю 2*:
Коды названы
циклическими потому, что циклический сдвиг аn-2,
аn-3,…,
а2,
а1, а0, аn-1
разрешенной комбинации
аn-1,
аn-2,…,
а2,
а1, а0
также является разрешенной комбинацией. Такая циклическая перестановка при
использовании представления в виде полиномов появляется в результате умножения
данного полинома на х. Если ![]() , то
, то ![]() Чтобы степень многочлена не превышала
n-1, член
Чтобы степень многочлена не превышала
n-1, член ![]() заменяется единицей, поэтому
заменяется единицей, поэтому
![]()
Например, имеем
кодовую комбинацию ![]() Сдвинем
ее на один разряд. Получим
Сдвинем
ее на один разряд. Получим
![]()
![]()
Очевидно, что
![]()
Теория построения циклических кодов базируется на разделах высшей алгебры, изучающей свойства двоичных многочленов. Особую роль в этой теории играют так называемые неприводимые многочлены, т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней. Такой многочлен делится только на самого себя и на единицу. Из высшей алгебры известно, что на неприводимый многочлен делится без остатка двучлен хп+1. В теории кодирования неприводимые многочлены называются образующими полиномами, поскольку они «образуют» разрешенные кодовые комбинации.
Идея построения
циклического кода сводится к тому, что полином, представляющий информационную
часть кодовой комбинации, нужно преобразовать в полином степени не более п—1,
который без остатка делится на образующий полином Р(х). Существенно
при этом, что степень последнего соответствует числу разрядов проверочной
части кодовой комбинации. В циклических кодах проверочная часть получается
сразу, т. е. используется алгоритм ![]() . Тогда все разрешенные комбинации
циклического кода, представленные в виде полиномов, будут обладать одним
признаком: делимостью без остатка на образующий полином Р(х). Построение
разрешенной кодовой комбинации сводится к следующему:
. Тогда все разрешенные комбинации
циклического кода, представленные в виде полиномов, будут обладать одним
признаком: делимостью без остатка на образующий полином Р(х). Построение
разрешенной кодовой комбинации сводится к следующему:
1) Представляем информационную часть кодовой комбинации длиной k в виде полинома Q(х).
2) Умножаем Q(х) на одночлен хr и получаем Q(х)хr, т. е. производим сдвиг k-разрядной кодовой комбинации на г разрядов.
3) Делим многочлен Q(х)хr на образующий полином Р(х), степень которого равна r.
В результате умножения Q(х) на хr степень каждого одночлена, входящего в Q(х), повышается на r. При делении произведения хrQ(х) на образующий полином степени r получается частное С(х) такой же степени, что и Q(х). Результаты этих операций можно представить в виде
![]()
где R(х) — остаток от деления Q(х)хr на Р(х). Поскольку С(х) имеет такую же степень, что и Q(х), то С(х) представляет собой кодовую комбинацию того же k-разрядного кода. Степень остатка не может быть, очевидно, больше степени образующего полинома, т. е. его наивысшая степень равна r—1. Следовательно, наибольшее число разрядов остатка не превышает r. Умножив обе части (6.18) на Р(х), получим
F(х) = С(х)Р(х) = Q (х)хr+R(х) (11.2)
(знак вычитания заменяется знаком сложения по модулю 2). Очевидно, что F(х) делится на Р(х) без остатка. Полином F(х) представляет собой разрешенную кодовую комбинацию циклического кода. Из (11.2) следует, что разрешенную кодовую комбинацию циклического кода можно получить умножением кодовой комбинации Q(х) простого кода на одночлен хr и добавлением к этому произведению остатка R(х), полученного в результате деления произведения на образующий полином Р(х).
Обнаружение ошибок
при циклическом кодировании сводится
к делению принятой кодовой комбинации на тот же образующий полином, который использовался
при кодировании (вид его, разумеется, должен быть известен на приеме). Если
ошибок в принятой кодовой комбинации нет (или они такие, что данную передаваемую
кодовую комбинацию превращают в другую разрешенную), то деление на образующий
полином произведется без остатка. Если при делении получится остаток, то это и
свидетельствует о наличии ошибки. Остаток от деления в циклических кодах
играет роль синдрома. Остаток от деления — синдром циклического кода, не равный
нулю, — свидетельствует о наличии ошибки. В кодах с образующим
полиномом степени г остаток представляется в виде полинома, степень которого
меньше r. Это означает, что количество различных ненулевых
остатков может быть равным ![]() . Номер разряда, в котором произошла
ошибка, однозначно связан с видом получающегося при этом ненулевого остатка.
Это позволяет по виду синдрома (остатка) определить место ошибки. Таким образом,
для исправления ошибок необходимо обеспечить условие, при котором
количество различных ненулевых остатков будет равно количеству элементов п (при
исправлении одной, ошибки) или числу комбинаций из п по
tи,
где tи —
количество ошибок, исправляемых кодом. Следует подчеркнуть, что не все неприводимые
многочлены позволяют формировать 2r—1
различных остатков. Это присуще только определенному классу многочленов,
которые именуются «примитивными». Так,
. Номер разряда, в котором произошла
ошибка, однозначно связан с видом получающегося при этом ненулевого остатка.
Это позволяет по виду синдрома (остатка) определить место ошибки. Таким образом,
для исправления ошибок необходимо обеспечить условие, при котором
количество различных ненулевых остатков будет равно количеству элементов п (при
исправлении одной, ошибки) или числу комбинаций из п по
tи,
где tи —
количество ошибок, исправляемых кодом. Следует подчеркнуть, что не все неприводимые
многочлены позволяют формировать 2r—1
различных остатков. Это присуще только определенному классу многочленов,
которые именуются «примитивными». Так, ![]() удовлетворяет указанному
требованию, а
удовлетворяет указанному
требованию, а![]() —
нет, т. е.
—
нет, т. е. ![]() —примитивный многочлен. Исходя из приведенных соображений, в качестве
образующих многочленов используют примитивные многочлены. Их признаком является
наличие остатка, равного единице только для х° и хп, где
п — количество элементов в кодовой комбинации. Между
n и
r для
таких полиномов имеется зависимость 2r=п—1. Здесь п — максимальное количество
элементов, при котором число различающихся ненулевых остатков равно п—1.
Поэтому в таблицах образующих полиномов указываются только примитивные
полиномы.
—примитивный многочлен. Исходя из приведенных соображений, в качестве
образующих многочленов используют примитивные многочлены. Их признаком является
наличие остатка, равного единице только для х° и хп, где
п — количество элементов в кодовой комбинации. Между
n и
r для
таких полиномов имеется зависимость 2r=п—1. Здесь п — максимальное количество
элементов, при котором число различающихся ненулевых остатков равно п—1.
Поэтому в таблицах образующих полиномов указываются только примитивные
полиномы.
Для определения
места ошибки в циклическом коде существует несколько методов, основанных
на анализе синдрома Р(х). Принятую кодовую комбинацию
F'(х)
можно представить в виде ![]() , где Е (х) —многочлен
ошибки. Остаток от деления принятой кодовой комбинации
F'п(х)
на Р(х) равен остатку от
деления на Р(х) кодовой комбинации ошибки Еп(х), если
Fп(х) =
F'п(х)
, где Е (х) —многочлен
ошибки. Остаток от деления принятой кодовой комбинации
F'п(х)
на Р(х) равен остатку от
деления на Р(х) кодовой комбинации ошибки Еп(х), если
Fп(х) =
F'п(х)![]() Еп(х).
Это условие справедливо, если код способен исправлять
количество ошибок tи, равное
или меньшее веса комбинации Еп(0,1). На основе этого
свойства можно заключить, что синдром не зависит от переданной кодовой комбинации,
а определяется лишь наличием ошибок. Указанное свойство можно использовать для
определения ошибочно принятого элемента. Предположим, что ошибка произошла в
старшем разряде переданной кодовой комбинации
a1. В этом случае
R1(х) -
есть
остаток от деления принятой комбинации
Fп(х)
на Р(х).
Такой же остаток R1
(х) получается, если разделить на Р(х)
комбинацию ошибки, т. е. многочлен хп-1. Но
такой же остаток получится при ошибке в разряде а2, если
F/п(х)
умножить
на х. То же будет и при ошибке в разряде а3, если
Fп(х)
умножить на х2, и т. д.
Еп(х).
Это условие справедливо, если код способен исправлять
количество ошибок tи, равное
или меньшее веса комбинации Еп(0,1). На основе этого
свойства можно заключить, что синдром не зависит от переданной кодовой комбинации,
а определяется лишь наличием ошибок. Указанное свойство можно использовать для
определения ошибочно принятого элемента. Предположим, что ошибка произошла в
старшем разряде переданной кодовой комбинации
a1. В этом случае
R1(х) -
есть
остаток от деления принятой комбинации
Fп(х)
на Р(х).
Такой же остаток R1
(х) получается, если разделить на Р(х)
комбинацию ошибки, т. е. многочлен хп-1. Но
такой же остаток получится при ошибке в разряде а2, если
F/п(х)
умножить
на х. То же будет и при ошибке в разряде а3, если
Fп(х)
умножить на х2, и т. д.
Лекция 12. Спектральный анализ непериодических сигналов. Преобразование Фурье. Спектральные плотности неинтегрируемых сигналов. Энергетические спектры сигналов
Содержание лекции:
- периодическое продолжение импульса. Понятие спектральной плотности сигнала. Обратное преобразование Фурье. Условие существования спектральной плотности сигнала. Связь между длительностью импульса и шириной его спектра. Обобщенная формула Рэлея. Взаимная спектральная плотность сигналов. Энергетический спектр. Корреляционный анализ сигналов. Сравнение сигналов, сдвинутых во времени.
Цель лекции:
- получить спектральные характеристики непериодических (импульсных) сигналов методом обобщения рядов Фурье. Определить требования к ширине полосы пропускания радиотехнического устройства. Представить сигналы посредством их спектральных плотностей. Использовать энергетический спектр для получения различных инженерных оценок. Понять, как возникает потребность в сигналах со специально выбранными свойствами.
Пусть s (t) - одиночный импульсный сигнал конечной длительности. Дополнив его мысленно такими же сигналами, периодически следующими через некоторый интервал времени T, получим изученную ранее периодическую последовательность Sпер (t), которая может быть представлена в виде комплексного ряда Фурье
![]() (12.1) с
коэффициентами
(12.1) с
коэффициентами  .
(12.2)
.
(12.2)
Для того, чтобы вернуться к одиночному импульсному сигналу, устремим к бесконечности период повторения Т. При этом очевидно:
а) частоты соседних гармоник nω1 и (n + l)ω1 окажутся сколь угодно близкими, так что в формулах (12.1) и (12.2) дискретную переменную nω1 можно заменить непрерывной переменной ω — текущей частотой;
б) амплитудные коэффициенты Сn станут неограниченными малыми из-за наличия величины Т в знаменателе формулы (12.2).
Наша задача состоит теперь в нахождении предельного вида формулы (12.1) при T→∞.
Рассмотрим малый интервал частот
Δω, образующий окрестность некоторого выбранного значения частоты
ω0. В пределах этого интервала будет содержаться
N=Δω/ω1=
ΔωT/(2π) отдельных
пар спектральных составляющих, частоты которых отличаются сколь угодно мало.
Поэтому составляющие можно складывать так, как будто все они имеют одну и ту
же частоту и характеризуются одинаковыми комплексными амплитудами
![]()
В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащихся внутри интервала Δω
![]() .
(12.3)
.
(12.3)
Функция  (12.4)
(12.4)
носит название спектральной плотности сигнала s (t). Формула (12.4) осуществляет преобразование Фурье данного сигнала.
Решим обратную задачу спектральной теории сигналов: найдем сигнал по его спектральной плотности, которую будем считать заданной.
![]() .
.
Поскольку в пределе частотные интервалы между соседними гармониками неограниченно сокращаются, последнюю сумму следует заменить интегралом
![]() . (12.5)
. (12.5)
Эта важная формула называется обратным преобразованием Фурье для сигнала s(t).
Сформулируем окончательно фундаментальный результат: сигнал s(t) и его спектральная плотность S(ω) взаимно однозначно связаны прямым и обратным преобразованиями Фурье
![]() ,
(12.6)
,
(12.6)
![]() .
.
Спектральное представление сигналов открывает прямой путь к анализу прохождения сигналов через широкий класс радиотехнических цепей, устройств и систем.
Сигналу s(t) можно сопоставить его спектральную плотность s(ω) в том случае, если этот сигнал абсолютно интегрируем, т. е. существует интеграл
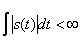 .
.
Подобное условие значительно сужает класс допустимых сигналов. Так, в указанном классическом смысле невозможно говорить о спектральной плотности гармонического сигнала и (t) =Umcosω0t , существующего на всей бесконечной оси времени.
Важный вывод: чем меньше длительность импульса, тем шире его спектр.
Под шириной спектра понимают частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например, изменяется в пределах от |S|max, до 0.1|S|max.
Произведение ширины
спектра импульса на его длительность есть постоянное число, зависящее только от
формы импульса и, как правило, имеющее порядок единицы: ![]() Чем короче длительность
импульса, тем шире должна быть полоса пропускания соответствующего усилителя.
Короткие импульсные помехи имеют широкий спектр и поэтому могут ухудшать условия
радиоприема в значительной полосе частот.
Чем короче длительность
импульса, тем шире должна быть полоса пропускания соответствующего усилителя.
Короткие импульсные помехи имеют широкий спектр и поэтому могут ухудшать условия
радиоприема в значительной полосе частот.
Математические модели многих сигналов, широко применяемых в радиотехнике, не удовлетворяют условию абсолютной интегрируемости, поэтому метод преобразований Фурье в обычном виде к ним неприменим. Однако можно говорить о спектральных плотностях таких сигналов, если допустить, что эти плотности описываются обобщенными функциями.
Пусть два сигнала и(t) и v(t), в общем случае комплексно-значные, определены своими обратными преобразованиями Фурье.
Найдем скалярное произведение этих сигналов, выразив один из них, например v(t), через его спектральную плотность

Полученное соотношение представляет собой обобщенную формулу Рэлея. Легко запоминающаяся трактовка этой формулы такова: скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей. Если сигналы тождественно совпадают, то скалярное произведение становится равным энергии
![]() .
(12.7)
.
(12.7)
Назовем взаимным энергетическим спектром вещественных сигналов u(t) и v(t) функцию
![]() ,
(12.8)
,
(12.8)
такую, что
![]() .
(4.9)
.
(4.9)
Нетрудно заметить, что Re Wuv(ω)—четная, а Im Wuv(ω)—нечетная функция частоты. Вклад в интеграл (12.9) дает только вещественная часть, поэтому
![]() . (12.10)
. (12.10)
Последняя формула дает возможность проанализировать «тонкую структуру» взаимосвязи сигналов.
Более того, обобщенная формула Рэлея, представленная в виде (12.10), указывает на принципиальный путь, позволяющий уменьшить степень связи между двумя сигналами, добившись в пределе их ортогональности. Для этого один из сигналов необходимо подвергнуть обработке в особой физической системе, называемой частотным фильтром. К этому фильтру предъявляется требование: не пропускать на выход спектральные составляющие, находящиеся в пределах частотного интервала, где вещественная часть взаимного энергетического спектра велика. Частотная зависимость коэффициента передачи такого ортогонализирующего фильтра будет обладать резко выраженным минимумом в пределах указанной области частот.
Спектральное представление энергии сигнала легко получить из обобщенной формулы Рэлея, если в ней сигналы и(t) и v(t) считать одинаковыми. Формула (12.8), выражающая спектральную плотность энергии, приобретает вид
![]() . (12.11)
. (12.11)
Величина Wu(ω) носит название спектральной плотности энергии сигнала и(t), или, короче, его энергетического спектра. Формула (3.2) при этом запишется так
![]() .
(12.12)
.
(12.12)
Соотношение (4.12) известно как формула Рэлея (в узком смысле), которая констатирует следующее: энергия любого сигнала есть результат суммирования вкладов от различных интервалов частотной оси.
Изучая сигнал с помощью его энергетического спектра, мы неизбежно теряем информацию, которая заключена в фазовом спектре сигнала, поскольку в соответствии с формулой (4.11) энергетический спектр есть квадрат модуля спектральной плотности и не зависит от ее фазы.
Обратимся к упрощенной идее работы импульсного радиолокатора, предназначенного для измерения дальности до цели. Здесь информация об объекте измерения заложена в величине τ — задержке по времени между зондирующим и принятым сигналами. Формы зондирующего и(t) и принятого и(t-τ) сигналов одинаковы при любых задержках. Структурная схема устройства обработки радиолокационных сигналов, предназначенного для измерения дальности, может выглядеть так, как это изображено на рисунке 12.1.
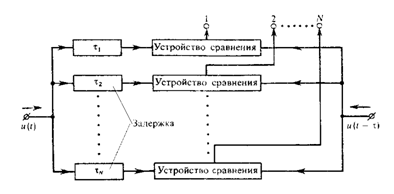
Рисунок 12.1 - Устройство для измерения времени задержки сигналов
Лекция 13. Принципы корреляционного анализа. Случайные процессы и их основные характеристики
Содержание лекции:
- автокорреляционная функция сигнала. Связь между энергетическим спектром сигнала и его автокорреляционной функцией. Взаимокорреляционная функция двух сигналов. Некоторые свойства взаимокорреляционной функции. Связь ВКФ с взаимной спектральной плотностью. Понятие случайного процесса. Плотность вероятности и интегральная функция распределения (ИФР).
Цель лекции:
- показать связь между АКФ и энергетическим спектром сигнала. Ввести характеристику совокупности двух сигналов — их взаимокорреляционную функцию (ВКФ). Изучить явления при передаче сообщений в условиях, когда детерминированное описание сигналов принципиально невозможно и на смену ему приходит вероятностное (статистическое) описание. Описать свойства случайных сигналов, изучая совокупности случайных многомерных величин.
Для количественного определения степени отличия сигнала и(t) и его смещенной во времени копии u(t-τ) принято вводить автокорреляционную функцию (АКФ) сигнала u(t), равную скалярному произведению сигнала и копии
![]() .
(13.1)
.
(13.1)
В дальнейшем будем предполагать, что исследуемый сигнал имеет локализованный во времени импульсный характер, так что интеграл вида (13.1) заведомо существует.
К числу простейших свойств АКФ можно отнести ее четность
Bu(τ)=Bu(-τ). (13.2)
Наконец, важное свойство автокорреляционной функции состоит в следующем: при любом значении временного сдвига т модуль АКФ не превосходит энергии сигнала
![]() . (13.3)
. (13.3)
Итак, АКФ представляется симметричной кривой с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала и(t) автокорреляционная функция может иметь как монотонно убывающий, так и колеблющийся характер.
Действительно, в соответствии с формулой (13.1) АКФ есть скалярное произведение: Bu(τ)=(u, uτ). Здесь символом uτ обозначена смещенная во времени копия сигнала и (t-τ).
Обратившись к обобщенной формуле Рэлея, можно записать равенство
![]() .
.
Спектральная плотность смещенного во
времени сигнала ![]() ,
откуда
,
откуда ![]() .
.
Таким образом, приходим к результату
![]() .
(13.4)
.
(13.4)
Квадрат модуля спектральной плотности, как известно, представляет собой энергетический спектр сигнала. Итак, энергетический спектр и автокорреляционная функция связаны преобразованием Фурье
![]() . (13.5)
. (13.5)
Имеется и обратное соотношение
![]() . (13.6)
. (13.6)
Эти результаты принципиально важны по двум причинам. Во-первых, оказывается возможным оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала.
Во-вторых, формулы (13.4) и (13.6) указывают путь экспериментального определения энергетического спектра. Часто удобнее вначале получить автокорреляционную функцию, а затем, используя преобразование Фурье, найти энергетический спектр сигнала.
Обобщая формулу (13.1), назовем взаимокорреляционной функцией двух вещественных сигналов и(t) и v(t) скалярное произведение вида
![]() (13.7)
(13.7)
Если в формуле (5.7) заменить переменную интегрирования, введя
х = t-τ, так что dt=dx, то, очевидно, возможна и такая запись
![]() .
(13.8)
.
(13.8)
Поэтому
![]() . (13.9)
. (13.9)
В отличие от автокорреляционной функции
одиночного сигнала, ВКФ, описывающая свойства системы двух
неодинаковых сигналов, не является четной функцией аргумента τ: ![]() .
.
Если рассматриваемые сигналы имеют
конечные энергии, то их взаимокорреляционная функция ограничена. Это
утверждение следует из неравенства Коши — Буняковского: ![]() , откуда
, откуда
![]() , (13.10)
, (13.10)
так как сдвиг сигнала во времени не влияет на значение его нормы.
Следует обратить внимание на то, что при τ=0 значения ВКФ вовсе не обязаны достигать максимума.
Выразим ВКФ двух сигналов через их спектральные характеристики. На основании обобщенной формулы Рэлея
![]() .
.
Имея в виду, что величина ![]() есть взаимный
энергетический спектр сигналов и(t) и
v(t),
определенный в бесконечном интервале частот -∞<ω<∞,
приходим к выводу: взаимокорреляционная функция и взаимный энергетический
спектр двух сигналов связаны парой преобразований Фурье.
есть взаимный
энергетический спектр сигналов и(t) и
v(t),
определенный в бесконечном интервале частот -∞<ω<∞,
приходим к выводу: взаимокорреляционная функция и взаимный энергетический
спектр двух сигналов связаны парой преобразований Фурье.
В основе большинства методов исследования общей теории связи лежит представление о процессе передачи сообщения как некоторого случайного процесса, развивающегося (чаще всего) во времени. Словом случайный подчеркивается то обстоятельство, что предопределить заранее точное протекание процесса невозможно. По определению, случайный процесс Х(t)—это особого вида функция, характеризующаяся тем, что в любой момент времени t принимаемые ею значения являются случайными величинами. Типичным примером случайного процесса может служить напряжение Z(Q) = s(t) + N(t) на входе приёмника. Наблюдая напряжение в данный момент, мы не можем с полной определённостью предсказать, каково будет его значение в последующие моменты времени. Это объясняется тем, что параметры формируемого передатчиком канального сигнала s(t) (амплитуда, частота, фаза) изменяются случайным образом в соответствии с передаваемым сообщением a(t). Кроме того, в процессе передачи сигнал подвергается воздействию различных аддитивных помех N(t), имеющих случайный характер, например, в виде электрических разрядов в атмосфере, помех от электрического транспорта, помех от других радиостанций и т.д. Случайность процесса X(t) проявляется в том, что вид наблюдаемой функции случайным образом меняется от одного наблюдения к другому. Однако получаемая в результате каждого отдельного опыта функция х(t) не случайна, её называют реализацией случайной функции. Случайный процесс представляет собой бесконечную совокупность таких реализации, образующих статистический ансамбль. На рисунке 5.1 показаны четыре реализации случайного процесса. Если на графике множества реализации случайной функции Х(t) (см. рисунок 13.1) выбрать момент (сечение) t1, то множество {х(r)(t1)} значений реализации в этот момент образует случайную величину X. Значения этой случайной величины заранее неизвестны. Но можно установить некоторые закономерности, по которым можно судить о том, что в данном сечении случайная величина с вероятностью Р будет принимать значение в определённых пределах [x, x+∆x].
Для непрерывных процессов X(t) распределение вероятностей в заданном сечении t1 характеризуется одномерной плотностью вероятностей (ПВ)
![]() ,
,
выражающей отношение вероятности того, что случайная
величина X(t) примет
значения в интервале ![]() ,
к величине интервала ∆х На рисунке 13.2, а изображён типовой
график одномерной ПВ.
,
к величине интервала ∆х На рисунке 13.2, а изображён типовой
график одномерной ПВ.
Вероятность того, что случайная величина
X
примет значение в интервале (x1;x2) определяется
выражением ![]() .
.

Рисунок 13.1 - Задание случайного процесса через совокупность его реализаций Рисунок 13.2 - Типовой график (а) одномерной ПВ и (б) одномерной ИФР
Другой важной характеристикой случайных
величин Х является ИФР F(x), определяемая как вероятность того, что случайная
величина X не превзойдёт некоторого значения х ![]() .
.
ИФР имеет следующие свойства:
а)F(-∞)=0;
б) F(∞)=1;
в) F(x) — неубывающая функция, т.е. F (x2) ≥ F (x1) при х2 > x1;
г) P[x1≤X≤x2]=F(x2)- F(x1)
График ИФР F{x) приведён на рисунке 13.2, б.
В прикладных задачах часто предполагают, что ИФР являются дифференцируемыми функциями и определяют w(x) как производную от ИФР:
![]() .
.
Для более полного описания случайного процесса нужно располагать его n-мерной плотностью вероятности w(x1, x2,…, xn; t1,t2,…, tn) или n-мерной ИФР F(x1, x2,…, xn; t1,t2,…, tn), выражающих свойства случайного процесса в произвольных сечениях t1,t2,…, tn. Для полного описания непрерывного во времени СП приходится п→∞ .
Моменты, которые наблюдаются в сечениях процессов, зависят от временных аргументов, они получили название моментных функций. Для статистической радиотехники наибольшее значение имеют три моментные функции низших порядков, называемые математическим ожиданием, дисперсией и функцией корреляции.
Лекция 14. Случайные процессы и их основные характеристики. Общие сведения о каналах связи. Преобразование сигналов в линейных каналах связи
Содержание лекции:
- случайные стационарные процессы. Спектральная плотность мощности случайного процесса. Функция корреляции случайного процесса с ограниченным спектром. Общие сведения о каналах связи. Воздействие детерминированных сигналов на линейные стационарные системы. Системные операторы. Стационарные и нестационарные системы. Линейные и нелинейные системы. Импульсные характеристики линейных стационарных систем. Интеграл Дюамеля.
Цель лекции:
- описать сигналы, которые отображают развивающиеся во времени случайные явления, изучив теорию случайных процессов. Показать, что между" корреляционными и спектральными свойствами случайных сигналов существует глубокая и тесная связь. Провести классификацию каналов связи.
Случайными стационарными процессами принято называть случайные процессы, статистические характеристики которых одинаковы во всех сечениях.
Если ограничить требования тем, чтобы
математическое ожидание т и дисперсия σ2 процесса не
зависели от времени, а функция корреляции зависела лишь от разности ![]() , т.е.
, т.е. ![]() , то подобный случайный
процесс будет стационарен в широком смысле. Как следует из определения,
функция корреляции случайного стационарного процесса является четной.
, то подобный случайный
процесс будет стационарен в широком смысле. Как следует из определения,
функция корреляции случайного стационарного процесса является четной.
![]() .
.
Кроме того, абсолютные значения этой функции при любых τ не превышают ее значения при τ=0
![]() . (14.1)
. (14.1)
Для описания случайных процессов наряду с корреляционными функциями B(τ) широко используются спектральные характеристики, в частности, спектральная плотность мощности G(f). Между B(τ) и G(f) существует пара преобразований Фурье. Для случайных стационарных процессов эти соотношения строго установлены А.Я. Хинчиным и Н. Винером.
Дисперсию (среднюю мощность) СП можно
найти путём интегрирования C(f) по частоте
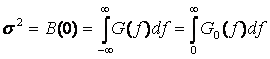 ,
,
где G0(f) - СПМ, определённая на положительных частотах. Методом равновеликого прямоугольника (или по иному критерию) можно найти не только интервал корреляции СП ("ширину" B(τ)), но и эффективную ширину его спектра Fэ ("ширину" G0(f)). Произведение этих параметров удовлетворяет условию τкор Fэ.~К , где К — константа, имеющая порядок единицы.
Случайный процесс, характеризуемый СПМ G0(f)=N0, равномерной на всех частотах (см. рисунок 14.1 а), называют белым шумом (по аналогии с белым светом в оптике). Если спектр G0(f) ограничен сверху частотой FB (см. рисунок 14.1, б), то процесс называется квазибелым шумом. Его дисперсия σ2 == B(0) = N0FB. Найдём ФК квазибелого шума:
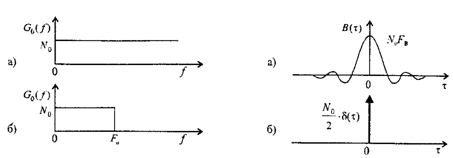
 |
 .
(14.2)
.
(14.2)
Полученная ФК отображена на рисунке 14.2 а. Обратим внимание на то, что при значениях, кратных 1/2FB, значения B(τ) проходят через нуль. Это означает, что сечения процесса, разделённые интервалом k/2FB (k — целое число), не коррелированны между собой. Если беспредельно увеличивать граничную частоту FB, то от квазибелого шума придём к абсолютно случайному процессу (белому шуму), у которого два несовпадающих сечения не коррелированны; КФ белого шума выражается δ-функцией (см. рисунок 14.2 б)
![]() .
(14.3)
.
(14.3)
Результат (14.3) следует из (14.2), если воспользоваться определением δ-функции. Белый шум является математической идеализацией реального процесса, так как средняя мощность (B(0)), необходимая для создания такого процесса, оказывается бесконечно большой. Примером помехи типа белого шума является тепловой шум резисторов, имеющий практически равномерную спектральную плотность на частотах вплоть до 6∙1012 Гц.
Классификация каналов связи возможна с использованием различных признаков. В зависимости от назначения систем каналы связи делят на телеграфные, фототелеграфные, телефонные, звукового вещания, передачи данных, телевизионные, телеметрические, смешанные и т.п.
В зависимости от распространения сигналов между пунктами связи в свободном пространстве или по направляющим линиям выделяют каналы радио (в частности, космические каналы) и проводной связи (воздушные, кабельные, волоконно-оптические линии связи, волноводные СВЧ тракты и т.п.)
В зависимости от характера связи между сигналами на входе и выходе канала различают каналы (звенья, цепи) линейные и нелинейные.
Различают каналы чисто временные (с сосредоточенными параметрами), в которых сигналы на входе и выходе описываются функциями одного скалярного параметра (времени t), и пространственно-временные каналы (с распределёнными параметрами), в которых сигналы на входе и (или) выходе описываются пространственными координатами (х, у, z). Такие сигналы называют полями.
Более существенна классификация каналов электрической связи по диапазону используемых ими частот. В настоящее время в радиосвязи применяют частоты примерно от 3-103 до 3-1012 Гц. Благодаря созданию и широкому внедрению квантовых генераторов (лазеров), освоен и диапазон световых волн (оптический диапазон). Практически в оптико-волоконных линиях связи используются частоты порядка 1014 Гц (длины волн 1,55; 1,35; 0,85 мкм). Для современного этапа развития техники связи характерна тенденция к переходу на всё более высокие частоты.

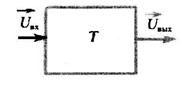 Радиотехническое устройство независимо от своего назначения
и уровня сложности представляет собой систему, т. е. совокупность
физических объектов, между которыми существуют определенные взаимодействия. В
структуре системы можно выделить вход, на который подается исходный сигнал,
и выход, откуда снимается преобразованный сигнал. Если интересуются лишь
связью между сигналами на входе и выходе и не описывают внутренние процессы в
системе, то говорят, что система представляет собой «черный ящик». Как входной
сигнал uвх(t),
так и выходной сигнал uвых(t),
называемый также откликом или выходной реакцией системы, описываются
одиночными функциями времени или в виде т-мерного вектора
Радиотехническое устройство независимо от своего назначения
и уровня сложности представляет собой систему, т. е. совокупность
физических объектов, между которыми существуют определенные взаимодействия. В
структуре системы можно выделить вход, на который подается исходный сигнал,
и выход, откуда снимается преобразованный сигнал. Если интересуются лишь
связью между сигналами на входе и выходе и не описывают внутренние процессы в
системе, то говорят, что система представляет собой «черный ящик». Как входной
сигнал uвх(t),
так и выходной сигнал uвых(t),
называемый также откликом или выходной реакцией системы, описываются
одиночными функциями времени или в виде т-мерного вектора ![]() ,а выходной сигнал
— в виде n-мерного вектора
,а выходной сигнал
— в виде n-мерного вектора ![]() .
.
Классификацию систем проводят на основании существенных свойств их математических моделей. Принято говорить, что система стационарна, если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал. Если Т — оператор стационарной системы, то
![]() (14.4)
(14.4)
при любом значении t0. Стационарные системы называют также системами с постоянными во времени параметрами.
Если же свойства системы не инвариантны относительно выбора начала отсчета времени, то такую систему называют нестационарной (системой с переменными во времени параметрами или параметрической системой).
Важнейший принцип классификаций, систем основан на том, что различные системы по-разному ведут себя при подаче на вход суммы нескольких сигналов. Если оператор системы таков, что справедливы равенства
![]() , (14.5)
, (14.5)
где ![]() — произвольное число, то данная
система называется линейной. Условия (14.5) выражают фундаментальный принцип
суперпозиции. Если эти условия не выполняются, то говорят, что система
является нелинейной.
— произвольное число, то данная
система называется линейной. Условия (14.5) выражают фундаментальный принцип
суперпозиции. Если эти условия не выполняются, то говорят, что система
является нелинейной.
Путь анализа прохождения детерминированных сигналов через линейные цепи основан на временном или частотном представлении свойств сигналов и систем.
Пусть некоторая линейная стационарная
система описывается оператором Т. Для простоты будем полагать, что входной и
выходной сигналы одномерны. По определению, импульсной характеристикой системы
называется функция h(t),
являющаяся откликом системы на входной сигнал ![]() (t). Это означает, что функция
h(t) удовлетворяет
уравнению
(t). Это означает, что функция
h(t) удовлетворяет
уравнению
![]() . (14.6)
. (14.6)
Поскольку система стационарна, аналогичное уравнение будет и в случае, если входное воздействие смещено во времени на производную величину t0:
![]() . (14.7)
. (14.7)
Следует ясно представить себе, что импульсная характеристика так же, как и порождающая ее дельта-функция, есть результат разумной идеализации. С физической точки зрения импульсная характеристика приближенно отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом системы, например, периодом ее собственных колебаний.
Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении детерминированного сигнала через такую систему
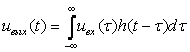 . (14.8)
. (14.8)
Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля.
Каков бы ни был конкретный вид импульсной характеристики физически осуществимой системы, всегда должен выполняться важнейший принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может возникнуть до момента появления импульса на входе. Отсюда вытекает ограничение на вид допустимых импульсных характеристик
h (t)=0 при t<0. (14.9)
Для физически реализуемой системы верхний предел в формуле интеграла Дюамеля может быть заменен на текущее значение времени
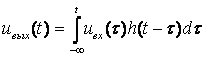 . (14.10)
. (14.10)
Лекция 15. Преобразование сигналов в линейных и нелинейных каналах связи
Содержание лекции:
- переходные и частотные характеристики линейных стационарных систем. Условие физической реализуемости. Спектральный метод. Преобразование случайных сигналов в детерминированных линейных каналах. Воздействие стационарных случайных сигналов на безынерционные нелинейные цепи. Прохождение случайных сигналов с широким спектром через узкополосные цепи.
Цель лекции:
- Систематическое решение задач о прохождении разнообразных сигналов через линейные системы. Показать применение спектрального подхода как к задаче нахождения реакции системы, так и к проблеме числовой оценки выходного сигнала. Исследовать ту связь между статистическими характеристиками процессов X(t) и Y(t), которая может быть найдена на основе математической модели системы.
Физически реализуемая система должна быть, кроме того, устойчивой. Это означает, что ее импульсная характеристика должна удовлетворять условию абсолютной интегрируемости
 .
(15.1)
.
(15.1)
Пусть на входе линейной стационарной
системы действует сигнал, изображаемый функцией Хевисайда ![]() . Выходную реакцию
. Выходную реакцию
![]() (15.2)
(15.2)
принято называть переходной характеристикой системы.
Поскольку система стационарна, переходная
характеристика инвариантна относительно временного сдвига
![]() .
.
Переходная характеристика физически
реализуемой системы отлична от нуля лишь при ![]() , в то время, как g (t) = 0 при
t
< 0.
, в то время, как g (t) = 0 при
t
< 0.
Между импульсной и переходной характеристиками имеется тесная связь. Действительно, так как δ(t)=dσ/dt, то на основании (14.6)
 .
(15.3)
.
(15.3)
Покажем, что комплексный сигнал uвх(t) = exp (jωt) при любом значении частоты ω есть собственная функция cтaциoнaрнoгo оператора. Для этого воспользуемся интегралом Дюамеля вида (14.8) и вычислим
 .
(15.4)
.
(15.4)
Отсюда видно, что собственным значением системного оператора является комплексное число
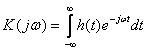 , (15.5)
, (15.5)
называемое частотным коэффициентом передачи системы.
Формула (15.5) устанавливает принципиально важный факт — частотный коэффициент передачи и импульсная характеристика линейной стационарной системы связаны между собой преобразованием Фурье. Поэтому всегда, зная функцию K(jω), можно определить импульсную характеристику
![]() . (15.6)
. (15.6)
Важнейшее положение теории линейных стационарных систем - любую такую систему можно рассматривать либо во временной области с помощью ее импульсной или переходной характеристик, либо в частотной области, задавая частотный коэффициент передачи. Оба подхода равноценны, и выбор одного из них диктуется удобствами получения исходных данных о системе и простотой вычислений.
Часто пользуются представлением частотного коэффициента передачи в показательной форме
![]() .
(15.7)
.
(15.7)
Обе входящие сюда вещественные функции
носят специальные названия: ![]() — амплитудно-частотная характеристика
(АЧХ), φK(ω) - фазочастотная характеристика (ФЧХ)
системы.
— амплитудно-частотная характеристика
(АЧХ), φK(ω) - фазочастотная характеристика (ФЧХ)
системы.
Далеко не каждая функция К (jω) может являться частотным коэффициентом передачи физически реализуемой системы. Простейшее ограничение связано с тем, что импульсная характеристика h(t) такой системы обязана быть вещественной
K(jω)=K*(-jω). (15.8)
В соответствии с формулой (10.13) модуль частотного коэффициента передачи (АЧХ) есть четная, а фазовый угол (ФЧХ) — нечетная функция частоты.
Каким должен быть частотный коэффициент передачи для того, чтобы выполнялись условия физической реализуемости (14.9) и (15.1). Приведем без доказательства окончательный результат, известный под названием критерия Пэли — Винера: частотный коэффициент передачи физически реализуемой системы должен быть таким, чтобы существовал интеграл
![]() . (15.9)
. (15.9)
Спектральный метод анализа прохождения радиотехнических сигналов через линейные стационарные системы - целый комплекс математических приемов, в основе которых лежит использование свойств частотного коэффициента передачи системы.
![]() .
(15.10)
.
(15.10)
Это основная формула спектрального метода, свидетельствующая о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и выходе:
![]() .
(15.11)
.
(15.11)
Исследование преобразований случайных процессов при их прохождении через линейные динамические системы (как с регулярными, так и со случайно меняющимися параметрами) связано с решением задач двух типов: определение корреляционной функции (спектральной плотности мощности) отклика Y(t) на выходе системы, заданной своими характеристиками, по данной корреляционной функции (или спектральной плотности мощности) входного воздействия X(t) определение многомерного распределения вероятностей отклика У(t) на выходе системы по многомерному распределению входного воздействия X(t).
В стационарной детерминированной линейной системе с
финитной, т.е. ограниченной во времени пределами 0...![]() ИХ
g(t) отклик
ИХ
g(t) отклик
![]() . (15.12)
. (15.12)
Шаг дискретизации ![]() можно выбрать равным интервалу
корреляции входного процесса 1/Fx. Допустим, что
входной процесс центрирован
можно выбрать равным интервалу
корреляции входного процесса 1/Fx. Допустим, что
входной процесс центрирован ![]() (t)=0,
тогда центрирован и выходной процесс. Узкая полоса
пропускания
(t)=0,
тогда центрирован и выходной процесс. Узкая полоса
пропускания ![]() означает,
что длительность импульсной характеристики τ велика по сравнению с
означает,
что длительность импульсной характеристики τ велика по сравнению с ![]() . Сечение выходного
процесса Y(t) в любой момент
времени t определяется согласно (15.12) N слагаемыми
суммы. В эту сумму входит много некоррелированных между собой сечений процесса
X(t).
Распределение вероятностей такой суммы согласно центральной предельной теореме
теории вероятности близко к гауссовскому (тем ближе, чем больше
N, определяемое отношением
Fx/∆F). В предельном случае, если на вход канала воздействует
белый шум, у которого ширина спектра бесконечна (не совпадающие во времени
отсчёты не коррелированы), а канал имеет ограниченную полосу пропускания, то N
. Сечение выходного
процесса Y(t) в любой момент
времени t определяется согласно (15.12) N слагаемыми
суммы. В эту сумму входит много некоррелированных между собой сечений процесса
X(t).
Распределение вероятностей такой суммы согласно центральной предельной теореме
теории вероятности близко к гауссовскому (тем ближе, чем больше
N, определяемое отношением
Fx/∆F). В предельном случае, если на вход канала воздействует
белый шум, у которого ширина спектра бесконечна (не совпадающие во времени
отсчёты не коррелированы), а канал имеет ограниченную полосу пропускания, то N![]() и выходной процесс
будет строго гауссовским. Отмеченное свойство линейного канала сохраняется и
при изменении параметров канала.
и выходной процесс
будет строго гауссовским. Отмеченное свойство линейного канала сохраняется и
при изменении параметров канала.
ФК выходного стационарного процесса
Y(t)![]() .
.
Предположим, что на входе безынерционной нелинейной системы присутствует случайный сигнал x(t), являющийся одной из реализаций стационарного случайного процесса X(t). Выходной сигнал y(t) связан с входным воздействием зависимостью вида y{t)=f[x{t)]; ансамбль реализаций y{t) задает стационарный случайный процесс Y(t), Ставится задача найти связь между статистическими характеристиками процессов X(t) и Y(t). При этом возможны два частных подхода:
1) По известной и-мерной плотности вероятности входного случайного процесса рвх(х1, х2,...,хn; tl , t2,...,tn) ищут аналогичную функцию рвых(y1, y2,...,yn; tl , t2,...,tn)определяющую выходной сигнал.
2) Исследование проводят в рамках корреляционной теории — ищут математическое ожидание ту и функцию корреляции Ry(t) выходного случайного процесса. Наряду с функцией корреляции интерес может представлять спектральная плотность мощности Wy(w) выходного сигнала.
Если x1, x2, ..-, хn — случайные значения, наблюдаемые на входе в моменты времени t1, t2,...,tn соответственно, то, учитывая безынерционный характер преобразования, имеем на выходе в те же моменты времени
y1=f(x1), y2=f(x2),…, yn=f(xn). (15.13)
Применив обратную функцию x=g(y), получим
x1=g(y1), х2 =g(y2),.., хn =g(yn). (15.14)
Тогда многомерная плотность вероятности на выходе
рвых(y1, y2,...,yn = рвх[g(y1), g(y2),.., g(yn)]½D½, (15.15)
где D — якобиан преобразования функции (15.13).
Формула (15.15) решает поставленную задачу в самом общем виде.
Простейшая статистическая характеристика стационарного случайного процесса — его среднее значение, получающееся путем усреднения по ансамблю реализаций. Чтобы вычислить среднее значение сигнала после нелинейного безынерционного преобразования, нужно располагать одномерной плотностью вероятности pвых(y). На основании принципа усреднения
my = (15.16)
Спектр колебаний на выходе нелинейного преобразователя разбивается на бесконечную сумму составляющих, каждая из которых отображает индивидуальный узкополосный случайный процесс. Максимумы спектральных плотностей мощности этих составляющих наблюдаются на частотах nwо. Помимо этого в спектре выходного сигнала возникает низкочастотная составляющая в окрестности нулевой частоты, которую можно рассматривать как результат амплитудного детектирования входного сигнала. При различных видах характеристики нелинейного элемента можно ожидать появления тех или иных гармоник центральной частоты входного случайного колебания.
Часто приходится рассматривать воздействие на линейные частотно-избирательные цепи широкополосных случайных сигналов, образованных, например, хаотической последовательностью коротких импульсов. В этом случае если эффективная ширина спектра входного случайного процесса значительно превышает ширину полосы пропускания системы, то реальный случайный процесс можно заменить эквивалентным ему белым шумом с односторонним спектром мощности N0 = Nx (f0), где f0 ~ некоторая точка в пределах полосы пропускания.
Лекция 16. Модель дискретно-непрерывного канала. Критерии качества и правила приема дискретных сообщений. Теория помехоустойчивости систем передачи дискретных сообщений
Содержание лекции:
- модель дискретно-непрерывного канала. Критерий Котельникова. Оптимальные алгоритмы приема при полностью известных сигналах (когерентный прием).
Цель лекции:
- дать математическое описание канала. Синтезировать оптимальный демодулятор.
Дискретно-непрерывный канал с независимыми символами
bi, на входе и непрерывным сигналом
z(t) на выходе описывается априорными вероятностями
входных символов P(bi) и переходными (условными)
плотностями w[z|
bi] принимаемой
реализации z{t) (на заданном
интервале Т) при условии передачи символа
bi. Эту плотность называют функцией
правдоподобия. Вместо функций правдоподобия дискретно-непрерывный канал
можно описать апостериорными вероятностями Р(bi|z) передачи
символа bi; при фиксации на приёме колебания
z(t). Согласно формуле Байеса
![]() ,
,
где
плотность принимаемого колебания ![]() , (16.1)
, (16.1)
где P(bi) — априорная вероятность передачи символа bi (т.е. та вероятность, которая имеет место до наблюдения и анализа, и определяемая статистикой источника сообщения и правилом кодирования).
Рассмотрим сначала широко распространённый критерий Котельникова или критерий идеального наблюдателя, согласно которому качество демодулятора оценивают безусловной (средней) вероятностью правильного приёма символа.
Пусть на вход демодулятора в течение
отрезка [0, T] приходит некоторый
элемент сигнала z(t).
Предположим, что демодулятор принимает при этом решение, что передан символ
bi,
т.е. выдаёт оценку ![]() . Вероятность того, что это решение
правильно, очевидно, равна условной вероятности
P(bi|z(t)) того, что действительно передавался символ
bi, при условии
прихода реализации элемента сигнала z(t). Её называют
апостериорной вероятностью символа
bi (т.е. вероятностью, определённой после опыта,
заключающегося в наблюдении и анализе сигнала
z(t)).
. Вероятность того, что это решение
правильно, очевидно, равна условной вероятности
P(bi|z(t)) того, что действительно передавался символ
bi, при условии
прихода реализации элемента сигнала z(t). Её называют
апостериорной вероятностью символа
bi (т.е. вероятностью, определённой после опыта,
заключающегося в наблюдении и анализе сигнала
z(t)).
Другими словами, критерий идеального
наблюдателя обеспечивается решающей схемой, построенной по правилу максимума
апостериорной вероятности — решение ![]() , принимается в том случае, если
выполняется система из т - неравенств
, принимается в том случае, если
выполняется система из т - неравенств
![]() .
(16.2)
.
(16.2)
Для двоичной системы сигналов упомянутое правило сводится к проверке неравенства
P(1|z) > P(0|z). (16.3)
При выполнении неравенства (16.3) регистрируется символ 1, в противном случае — 0.
Подставив (16.1) в (16.2) и учитывая, что w(z) — безусловная плотность вероятности, не являющаяся функцией i, можно записать правило решения по критерию идеального наблюдателя в следующей форме
![]()
Приёмник, реализующий этот алгоритм , называют приёмником Котельникова. Для двоичной системы правило сводится к проверке неравенства
![]() (16.4)
(16.4)
при выполнении которого регистрируется символ 1, а при невыполнении — 0.
Для построения решающей схемы по правилу критерия идеального наблюдателя необходимо знать априорные вероятности символов P(bi), а также свойства модулятора и канала, определяющие условные плотности w(z|bi),j - функции правдоподобия.
Критерий Котельникова можно записать
иначе. Решение о том, что передавался символ
bi
должно приниматься, если для всех j≠
i
выполняются т — 1 неравенств ![]() .
(16.5)
.
(16.5)
Отношение в левой части этого неравенства называется отношением правдоподобия двух гипотез: о том, что передавался символ bi, и о том, что передавался символ bj. Его обозначают Λij,.
В случае, когда все т символов передаются равновероятно, т.е. P(bi) = 1/m, правило (16.5) упрощается
Λij>1,
i![]() .
(16.6)
.
(16.6)
Иногда вводят в рассмотрение помимо т
гипотез о передаче символов ![]() ещё дополнительную ("шумовую")
гипотезу о том, что никакой сигнал не передавался, т.е.
z(t) ==
n(t) — чистая помеха. Отношение правдоподобия
ещё дополнительную ("шумовую")
гипотезу о том, что никакой сигнал не передавался, т.е.
z(t) ==
n(t) — чистая помеха. Отношение правдоподобия ![]() обычно обозначают
просто Λi. Тогда правило (16.6) можно записать так
обычно обозначают
просто Λi. Тогда правило (16.6) можно записать так
Λi > Λj при всех j ≠ i. (16.7)
Такое правило максимума правдоподобия реализует критерий идеального наблюдателя при том условии, что все символы передаются равновероятно.
Для двоичной системы правило (16.7) сводится к проверке неравенства
Λ1>Λ0. (16.8)
В технике связи преимущественно применяют правило максимального правдоподобия (16.7), (16.8). В том случае, когда все символы передаются равновероятно, правило максимального правдоподобия реализует критерий идеального наблюдателя. Однако очень часто это правило решения применяют и при неизвестных или известных, но не одинаковых априорных вероятностях символов. Конечно, оно не обеспечивает в этих случаях максимума вероятности правильного приёма. Изменив решающую схему на схему, построенную по правилу максимальной апостериорной вероятности (16.3), реализующему критерий идеального наблюдателя, можно было бы уменьшить вероятность ошибок. При этом, очевидно, пришлось бы сократить области приёма маловероятных и расширить области высоковероятных символов. В результате редко передаваемые символы принимались бы менее надёжно, нежели часто передаваемые. Но редкие символы несут больше информации, чем частые. Поэтому переход от правила максимального правдоподобия к правилу максимальной апостериорной вероятности, хотя и уменьшает безусловную вероятность ошибки, может привести к увеличению потери информации при демодуляции.
Предположим, что все искажения в канале строго детерминированы и случайным является только гауссовский аддитивный шум n(t), который вначале полагаем белым, со спектральной плотностью n0. Это значит, что при передаче символа bi (i=0,1,…,m-1) принимаемое колебание можно описать моделью:
z(t)=si(t)+n(t), 0 ≤ t ≤ T, (16.9)
где все si(t)= γf(t-τ-kT,bk(i)) = γui(t-τ) известны.
Определим в этих условиях алгоритм работы оптимального (т.е. основанного на правиле максимального правдоподобия) демодулятора, анализирующего сигнал на тактовом интервале О...T. Для этого необходимо найти отношения правдоподобия для всех т возможных сигналов относительно нулевой гипотезы (z(t)= n(t)). Задача затрудняется тем, что ширина спектра сигнала бесконечна (поскольку он финитный), а поэтому пространство сигналов бесконечномерное L2(T). Для таких сигналов (или бесконечномерных векторов) не существуют плотности вероятностей. Однако существуют n-мерные плотности вероятностей для любых п сечений сигнала.
Заменим вначале белый шум квазибелым, имеющим ту же одностороннюю спектральную плотность мощности n0, но только в некоторой полосе частот F= п/2Т, где n>>1. Рассмотрим дополнительную гипотезу, т.е. будем считать, что z(t) - стационарный шум с нулевым МО. Возьмём на тактовом интервале п равноотстоящих сечений через Δt=1/2F=T/n. Отсчёты Z1,...,Zn в этих сечениях для квазибелого гауссовского шума независимы. При гипотезе, что передавался символ bi, согласно (16.9) n(t)=z(t)-si(t).
Вернёмся к исходной задаче для белого шума. Для этого будем расширять полосу F, тогда число сечений п стремится к бесконечности, а Δt — к нулю. Правило приёма сводится к проверке системы неравенств
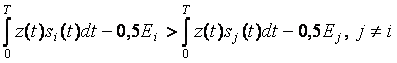 ,
(16.10)
,
(16.10)
где  — энергия ожидаемого сигнала
Si(t). Выражение
(16.10) определяет те операции (алгоритм приёма), которые должен
совершать оптимальный приёмник над входным колебанием. Для двоичной системы
алгоритм (16.10) сводится к проверке одного неравенства
— энергия ожидаемого сигнала
Si(t). Выражение
(16.10) определяет те операции (алгоритм приёма), которые должен
совершать оптимальный приёмник над входным колебанием. Для двоичной системы
алгоритм (16.10) сводится к проверке одного неравенства
 (16.11)
(16.11)
При выполнении неравенства (16.11) регистрируется символ "1", в противном случае "0".
 Устройство, непосредственно
вычисляющее скалярное произведение (или корреляционный интеграл)
Устройство, непосредственно
вычисляющее скалярное произведение (или корреляционный интеграл) 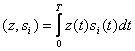 , (16.12)
, (16.12)
называют активным фильтром или коррелятором, поэтому приёмник, реализующий алгоритм (16.10), называют корреляционным.
![]() На рисунке
16.1 показана структурная схема приёмного устройства, работающего в
На рисунке
16.1 показана структурная схема приёмного устройства, работающего в
Если сигналы ui(t) выбраны таким образом, что все их реализации (а следовательно, и все реализации si(t)) имеют одинаковые энергии (Ei = const), алгоритм приёма (16.10) (и соответственно его реализация) упрощается (отпадает необходимость в вычитающих устройствах) и принимает вид
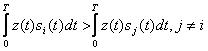 . (16.13)
. (16.13)
Из (16.13) видно, что правило решения не изменится, если сигнал z(t), поступающий на вход демодулятора, умножить на любое число. Поэтому система, в которой все реализации сигнала имеют равную энергию, отличается тем, что оптимальный алгоритм приёма в ней не требует знания "масштаба" приходящего сигнала или, другими словами, знания коэффициента передачи γ канала. Эта особенность обусловила широкое распространение систем сигналов с равной энергией, что важно для каналов с замираниями, в которых коэффициент передачи флуктуирует. Заметим, что для двоичной системы неравенство (13.11) можно представить в более простом виде
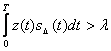 , (16.14)
, (16.14)
где sΔ(t)=s1(t)-s0(t) — разностный сигнал;
λ = 0,5(E1-E0) — пороговый уровень.
Лекция 17. Оптимальный приемник с согласованным фильтром
Содержание лекции:
- реализация оптимального алгоритма приема при полностью известных сигналах (когерентный прием) на СФ.
Цель лекции:
-синтезировать оптимальный демодулятор.
Скалярное произведение (16.12) можно
вычислить не только с помощью активного фильтра (коррелятора), описанного в
предыдущем параграфе, но и с помощью описанного линейного фильтра с постоянными
параметрами. Если на вход фильтра подать принимаемый сигнал
z(t), то напряжение на выходе фильтра в момент времени 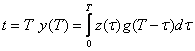 , где
g(τ)
— импульсная характеристика фильтра. Выберем её такой, чтобы в момент
t
= Т получить значение у(T), равное скалярному произведению (16.12). Это будет
выполнено при следующем согласовании g(T-τ)
= si(τ) или
g(t)
= si(T-τ).
(17.1)
, где
g(τ)
— импульсная характеристика фильтра. Выберем её такой, чтобы в момент
t
= Т получить значение у(T), равное скалярному произведению (16.12). Это будет
выполнено при следующем согласовании g(T-τ)
= si(τ) или
g(t)
= si(T-τ).
(17.1)
В более общем случае согласованным фильтром для сигнала s(t) называют линейный пассивный фильтр с постоянными параметрами и ИХ
g(t)=as(t0-t), (17.2)
где а, t0 — постоянные. Функция g(t) является зеркальным отображением s(t) относительно оси, проведённой через точку t0/2 (см. рисунок 14.1). Для физической реализуемости фильтра необходимо и достаточно, чтобы g(t) = 0 при t < 0. В частности, для финитного сигнала s(t), поступающего на вход фильтра в момент t = 0 и заканчивающегося в момент Т, условие физической реализуемости согласованного фильтра заведомо выполняется, как видно из рисунка 17.1, если постоянная t0 (момент отсчёта) удовлетворяет условию
t0-T ≥ 0 или t0 ≥ T. (17.3)
Передаточная функция (частотная характеристика) согласованного фильтра с ИХ (14.2) определяется преобразованием Фурье
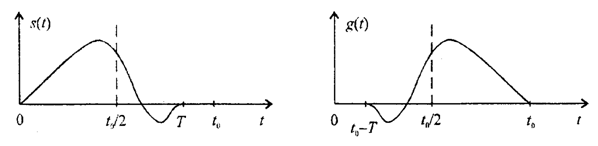
Рисунок 17.1 - Сигнал S(t) и импульсная характеристика g(t) линейного фильтра, согласованного с этим сигналом
![]() , (17.4)
, (17.4)
где ![]() —
функция, комплексно-сопряжённая со спектральной плотностью сигнала
s(t). Следовательно, с точностью до коэффициента а
АЧХ согласованного фильтра определяется амплитудным спектром сигнала
s(t) (т.е. фильтр лучше передаёт те частоты, которые дают
больший вклад в энергию сигнала), а его фазо-частотная характеристика (без
учёта слагаемого — ωt0 определяемого задержкой
to) обратна по знаку фазовому
спектру сигнала s(f). Благодаря
этому в момент tо все
составляющие спектра принимаемого сигнала складываются в фазе и дают
максимальный отклик.
—
функция, комплексно-сопряжённая со спектральной плотностью сигнала
s(t). Следовательно, с точностью до коэффициента а
АЧХ согласованного фильтра определяется амплитудным спектром сигнала
s(t) (т.е. фильтр лучше передаёт те частоты, которые дают
больший вклад в энергию сигнала), а его фазо-частотная характеристика (без
учёта слагаемого — ωt0 определяемого задержкой
to) обратна по знаку фазовому
спектру сигнала s(f). Благодаря
этому в момент tо все
составляющие спектра принимаемого сигнала складываются в фазе и дают
максимальный отклик.
Согласно формуле (17.1) в момент времени T напряжение на выходе согласованного фильтра пропорционально сигналу на выходе интегратора активного фильтра в схеме рис. 16.1. Поэтому демодулятор, реализующий алгоритм (16.11), может быть выполнен и на базе согласованных фильтров. Структурная схема такого демодулятора для двоичной системы показана на рисунке 17.2, где СФ, — фильтр, согласованный с сигналом Si(f).
Отклик согласованного фильтра на финитный сигнал длительностью Т, поданный ко входу в момент времени 0, существует лишь на финитном интервале протяжённостью 2T. Действительно, если на вход фильтра подан сигнал, с которым он согласован, то сигнальная составляющая на выходе согласованного фильтра
 , (17.5)
, (17.5)
где Bs{tQ — t} — ФК сигнала s(t) при аргументе t0—t. Для финитного сигнала она определена на интервале (0,2T) и имеет максимум в точке t = t0 == Т. Подчеркнём, что формы полезного сигнала на входе и выходе согласованного фильтра, как правило, существенно отличаются друг от друга. Задачей согласованного фильтра является не восстановление формы сигнала, искажённой шумом, а получение одного отсчёта, по которому можно судить о присутствии или отсутствии на входе фильтра сигнала известной формы.

Рисунок 17.2 - Оптимальный демодулятор на основе согласованных фильтров
Произвольный линейный стационарный фильтр с импульсной характеристикой g(t) даёт на своём выходе в момент времени t0≥. Т значение отношения пиковой мощности сигнала к дисперсии шума
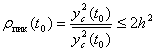 , (17.6)
, (17.6)
где 2h2 ~ значение ![]() согласованного фильтра
(h2=E/N0 — отношение энергии
сигнала длительности Т к спектральной плотности шума на положительных
частотах).
согласованного фильтра
(h2=E/N0 — отношение энергии
сигнала длительности Т к спектральной плотности шума на положительных
частотах).
Рассмотрим возможности реализации согласованных фильтров. Согласованный фильтр для финитного сигнала произвольного вида s(t) можно в принципе построить на основе неискажающей длинной линии, обеспечивающей задержку сигнала на время Т, с бесконечной плотностью отводов. Практически можно брать отводы в дискретных точках с разносом Δ == 0,5/F, где F - эффективная ширина спектра сигнала.
Действительно, с помощью схемы, показанной на рисунке 14.3, можно с заданной точностью синтезировать любой сигнал s(t), представленный усечённым рядом Котельникова
![]() ,
,
где ak=s(kΔ); Δ=1/(2F); F— ширина спектра сигнала.
Как следует такой сигнал можно получить на
выходе идеального ФНЧ с полосой пропускания F, подавая на его вход
последовательность δ-импульсов с весами ![]() через интервалы времени Δ. Это
осуществляется с известным приближением в схеме рисунка 17.3. Если на вход
линии в начальный момент подаётся один короткий импульс, аппроксимирующий
δ -функцию, то с отводов снимаются такие же импульсы, разнесённые на интервалы
Δ, которые, пройдя через взвешивающие блоки
ak, поступают поочередно на вход ФНЧ. Взвешивающие блоки
содержат аттенюаторы или усилители с коэффициентом усиления
через интервалы времени Δ. Это
осуществляется с известным приближением в схеме рисунка 17.3. Если на вход
линии в начальный момент подаётся один короткий импульс, аппроксимирующий
δ -функцию, то с отводов снимаются такие же импульсы, разнесённые на интервалы
Δ, которые, пройдя через взвешивающие блоки
ak, поступают поочередно на вход ФНЧ. Взвешивающие блоки
содержат аттенюаторы или усилители с коэффициентом усиления ![]() , а также при отрицательных
, а также при отрицательных ![]() — инверторы.
— инверторы.
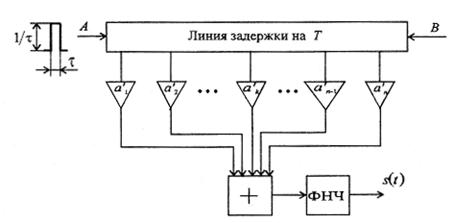
Рисунок 17.3 - Реализация фильтра, согласованного с произвольным непрерывным сигналом на основе линии задержки с отводами и блоками
взвешивания
Схема рисунка 17.3 представляет собой линейный фильтр, называемый трансверсальным, с импульсной реакцией s(t). Легко видеть, что если входной импульс подать не в точку А, а в точку В, то будет синтезирован сигнал, представляющий зеркальное отображение s(t). Поэтому та же схема со входом в точке В оказывается фильтром, согласованным с s(t).
При активном фильтре достаточно потребовать, чтобы неточность взятия отсчёта была мала по сравнению с тактовым интервалом, а при согласованном фильтре — по сравнению с периодом высокочастотного заполнения радиоимпульса (так называемый когерентный отсчёт). Трудность обеспечения когерентного отсчёта в согласованном фильтре вполне соизмерима с трудностью реализации когерентных опорных генераторов в активном фильтре.
Отметим одно важное обстоятельство, свойственное согласованному фильтру. Пусть на его вход поступает колебание z(t) (см. рисунок 17.4 а), а фильтр согласован с финитным сигналом s(t). Тогда сигнал на его выходе в момент времени t
 . (17.7)
. (17.7)
На выходе фильтра, согласованного с сопряжённым сигналом s(t), колебание z(t) даёт отклик (см. рисунок 17.4 б)
 . (17.8)
. (17.8)
Сигналы (17.7) и (17.8) сопряжены по Гильберту с точностью до знака. Огибающая на выходе фильтра, согласованного с сигналом s(t) (или s(t)),
![]() . (17.9)
. (17.9)
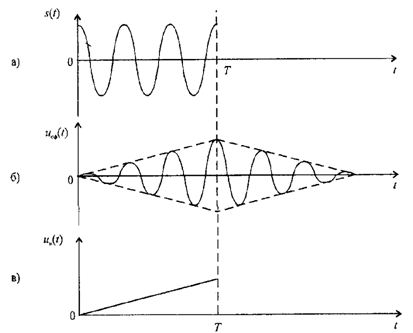
Рисунок 17.4 - Сигналы на выходе согласованного фильтра и корреляционной схемы при подаче на вход прямоугольного радиоимпульса
Лекция 18. Помехоустойчивость оптимального когерентного приема. Теоремы Шеннона
Содержание лекции:
- помехоустойчивость оптимального когерентного приема. Теоремы Шеннона.
Цель лекции:
- определить потенциальную помехоустойчивость для двоичной системы с аддитивным БГШ в канале, когда при приёме точно известны оба ожидаемых сигнала: s1(t) и s0(t), полагая, что априорные вероятности этих сигналов одинаковы.
Приходящий сигнал z(t) является случайным, так как, во-первых, заранее не известна реализация передаваемого сигнала, во-вторых, он содержит случайную помеху N(t)
В этом случае согласно (5.26) алгоритм оптимального приёма
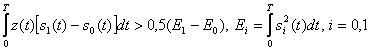 .
(18.1)
.
(18.1)
При выполнении неравенства (18.1) оптимальный приёмник регистрирует символ 1, соответствующий сигналу s1(t), в противном случае — символ 0, соответствующий сигналу S0(t). Если действительно передаётся символ 1, то z(t) = s1(t) + N(t). При этом вероятность ошибки определяется вероятностью того, что неравенство (18.1) не выполнено, т.е. вероятностью выполнения обратного неравенства.
Если N(t) - нормальный белый стационарный шум с нулевым средним и односторонней спектральной плотностью мощности n0, то вероятность ошибки через Q-функцию можно записать в виде
 . (18.2)
. (18.2)
Функция 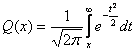 табулирована и называется дополнительной
функцией ошибок. При заданной интенсивности помехи
nq
потенциальная помехоустойчивость двоичной системы
зависит только от так называемой эквивалентной энергии сигналов
табулирована и называется дополнительной
функцией ошибок. При заданной интенсивности помехи
nq
потенциальная помехоустойчивость двоичной системы
зависит только от так называемой эквивалентной энергии сигналов
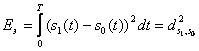 , (18.3)
, (18.3)
которая равна квадрату расстояния между сигнальными точками в пространстве Гильберта. Помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов независимо от формы используемых сигналов. Последние, в частности, могут быть как простыми (отрезками синусоиды с малой базой), так и сложными (шумоподобными, с большой базой).
На рисунке 18.1 в двумерном пространстве
показаны точки сигналов для двоичной системы: рисунок 18.1 а -
AM
при s0(t)=0,
 ; рисунок
18.1 б — ЧМ с ортогональными сигналами
; рисунок
18.1 б — ЧМ с ортогональными сигналами  ,
, 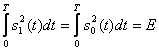 ; рисунок 18.1 в — ФМ с противоположными
сигналами s1(t)=-s0(t).
; рисунок 18.1 в — ФМ с противоположными
сигналами s1(t)=-s0(t).
Из рисунка видно, что по сравнению с двоичной AM для двоичной ЧМ

Рисунок 18.1 - К определению эквивалентной энергии двоичных систем AM, ЧМ, ФМ
эквивалентная энергия сигнала Eэ=||s1- s0||2 в 2 раза больше, а для двоичной ФМ - в 4 раза больше.
Соотношение (18.3) позволяет осуществлять оптимальный выбор сигналов s1(t) и S0 (t) или соответственно u1(t) и У0(t), обеспечивающих максимально возможную помехоустойчивость при заданной энергии сигналов Е.
Интеграл 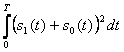 принимает только неотрицательные значения,
поэтому его минимум равен нулю и достигается при условии
s1(t)=-s0(t), в двоичном канале с постоянными параметрами и
аддитивным БГШ оптимальной оказывается система с противоположными сигналами.
Этому условию удовлетворяют, например, двуполярные импульсы, сигналы двоичной
фазовой модуляции (ФМ), если разность фаз сигналов Δφ=π
и.т.п.
принимает только неотрицательные значения,
поэтому его минимум равен нулю и достигается при условии
s1(t)=-s0(t), в двоичном канале с постоянными параметрами и
аддитивным БГШ оптимальной оказывается система с противоположными сигналами.
Этому условию удовлетворяют, например, двуполярные импульсы, сигналы двоичной
фазовой модуляции (ФМ), если разность фаз сигналов Δφ=π
и.т.п.
Для всех таких систем Еэ = 4Е и вероятность ошибки
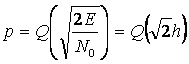 , (18.4)
, (18.4)
где ![]() отношение энергии сигнала на входе
демодулятора к спектральной плотности мощности флуктуационной помехи.
отношение энергии сигнала на входе
демодулятора к спектральной плотности мощности флуктуационной помехи.
Для системы с ортогональными сигналами
равной энергии (например, при известных условиях для системы двоичной ЧМ),
когда 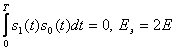 и
минимальная вероятность ошибки
и
минимальная вероятность ошибки
p = Q(h). (18.5)
Сравнивая (18.5) и (18.4), приходим к выводу, что переход от системы с ортогональными сигналами к системе с оптимальными (противоположными) сигналами позволяет в рассматриваемом канале обеспечить неизменное качество связи (вероятность ошибки) при понижении средней мощности передатчика в 2 раза, т.е. даёт энергетический выигрыш в 2 раза (или на 3 дБ). Этот вывод следует также из рисунка 18.1.
В двоичной системе с пассивной паузой,
полагая s0(t)=0 и  , получаем для минимальной
вероятности ошибки
, получаем для минимальной
вероятности ошибки
 .
(18.6)
.
(18.6)
Отсюда видно, что при переходе от системы AM к системе ЧМ энергетический выигрыш по максимальной мощности равен 2, а при переходе к системе ФМ - 4. Если же сравнение вести не по пиковой, а по средней мощности, то переход от AM к ЧМ не даёт энергетического выигрыша, поскольку при ЧМ средняя мощность равна максимальной, а при AM - вдвое меньше максимальной (если s1 и s0 передаются с одинаковой вероятностью).
Система ФМ, как и другие системы с противоположными сигналами, обеспечивает максимальную для двоичной системы потенциальную помехоустойчивость. Однако реализация демодулятора для когерентного приёма ФМ встречает определённые трудности. При построении демодулятора с активным фильтром возникает проблема поддержания равенства фаз опорного генератора и приходящего сигнала. Если пытаться строить его на основе согласованного фильтра (см. рисунок 17.2), то возникает не менее трудная задача взятия когерентного отсчёта. Возникает так называемое явление обратной работы, вследствие которого практическое внедрение системы с двоичной фазовой модуляцией оказалось затруднительным.
Эффективный метод устранения этого явления был найден путём перехода к относительным методам модуляции, предложенным Н.Т. Петровичем. Они сводятся к модуляции информационного параметра передаваемой посылки элемента сигнала относительно того же параметра предшествующей посылки. При относительной фазовой манипуляции (ОФМ) сообщение содержится не в абсолютном значении фазы элемента сигнала, а в разности фаз двух соседних элементов, при этом символ 1 передаётся повторением той реализации сигнала, которая имела место в качестве предыдущего элемента, а символ 0 — реализацией с обратной фазой, либо наоборот.
Сигналы ОФМ могут приниматься различными методами. Рассмотрим квазикогерентный приём сигналов ОФМ (называемый методом сравнения полярностей).
Определим вероятность ошибки в системе ОФМ при учёте флуктуационной помехи в канале при когерентном приёме. Очевидно, что ошибочная регистрация символа при приёме методом сравнения полярностей возможна в результате одного из двух несовместных событий:
а) знак данного элемента принят ошибочно, а знак предыдущего - верно;
б) знак данного элемента принят верно, а знак предыдущего - ошибочно.
Каждое из этих событий имеет вероятность
pФМ(1-pФМ)- Таким образом, в
нормальных условиях эксплуатации, когда требуется
pФМ<<1,
pОФМ=2
pФМ=2Q[![]() ].
].
Таким образом, "платой" за устранение обратной работы является удвоение вероятности ошибки, обусловленной шумом в канале.
Очевидно, что при рассматриваемом методе приёма сигналов ОФМ образующийся дискретный канал является марковским. Вероятность ошибки в нём зависит от того, правильно или ошибочно приняты предыдущие символы. Подавляющее большинство ошибок группируется по две.
Для систем равновероятных ортогональных сигналов равной энергии канал симметричен, и можно оценить вероятность ошибки простым неравенством
![]() . (18.7)
. (18.7)
Теорема 1. О кодировании источника.
Существует способ кодирования, при котором средняя длина последовательности канальных символов п , приходящаяся на один символ источника сообщений,
![]() . (18.8)
. (18.8)
Не существует способа кодирования, при котором ![]() меньше, чем
меньше, чем
![]()
Теорема 2. Основная теорема Шеннона.
Если производительность источника H¢(A) меньше пропускной способности С¢ в единицу времени дискретного канала с помехами, то при любом d > 0 существует способ кодирования и декодирования источника и канала, при котором сообщения передаются получателю с вероятностью ошибки меньшей, чем d, и в среднем без растущих задержек во времени. Если H¢(A) > С¢, то такого способа кодирования не существует.
Не всегда следует использовать как канальное кодирование, так и кодирование источника. Последнее для достижения заметного эффекта может оказаться нереализуемо сложным.
Лекция 19. Преобразование сигналов в каналах связи. Аддитивные помехи в канале
Содержание лекции:
- прохождение сигналов через случайные каналы связи. Флуктуационные помехи. Сосредоточенные по спектру помехи. Импульсные помехи. Шумы приемных антенн.
Цель лекции:
- рассмотреть в общих чертах характерные преобразования сигнала в случайных линейных каналах (цепях). Познакомиться с физическими явлениями, которые порождают флуктуации напряжения и тока в радиотехнических цепях.
В простейшем случае случайное преобразование сигнала сводится к суммированию сигнала с независимым от него случайным процессом, называемым аддитивной помехой или аддитивным шумом. В более сложных каналах к этому добавляются случайные изменения параметров канала, в результате которых даже в отсутствие аддитивных помех принимаемый сигнал не определяется однозначно передаваемым.
В самом общем виде линейную систему (или линейный
канал) можно описать случайной ИХ G(t,![]() ), представляющей
случайную функцию двух аргументов: t
(момента наблюдения реакции) и
t (времени, прошедшего с момента подачи
d-импульса на вход цепи). Такова, например, ИХ любой
линейной системы, параметры которой подвергаются воздействию случайных внешних
влияний, например, температуры, давления, влажности и т.д. Случайный линейный
канал можно характеризовать также случайной передаточной функцией переменных
), представляющей
случайную функцию двух аргументов: t
(момента наблюдения реакции) и
t (времени, прошедшего с момента подачи
d-импульса на вход цепи). Такова, например, ИХ любой
линейной системы, параметры которой подвергаются воздействию случайных внешних
влияний, например, температуры, давления, влажности и т.д. Случайный линейный
канал можно характеризовать также случайной передаточной функцией переменных ![]() и
t
и
t
![]() . (19.1)
. (19.1)
Функция корреляции процесса Y(t) на выходе случайного канала с характеристикой (4.41) при подаче на вход стационарного процесса X(t) определяется выражением
![]() , (19.2)
, (19.2)
где ![]() - системная характеристика
случайного канала.
- системная характеристика
случайного канала.
Остановимся подробнее на моделях, с которыми чаще всего приходится встречаться. Модель для случайного входного воздействия X(t)
![]() , (19.3)
, (19.3)
где параметры t и (или) g флуктуируют. Обычно такие флуктуации в проводных линиях связи вызываются изменениями внешних условий и происходят чрезвычайно медленно и в очень не больших относительных пределах. В радиоканалах при многолучевом распространении волн, в гидроакустических каналах и других флуктуации выражены более заметно.
Более сложный случай имеет место, когда сигнал проходит по параллельным путям от входа канала к его выходу (рисунок 19.1), так что на выходе каждого пути сигнал имеет вид
![]() ,
,
где ![]() фазовый сдвиг в канале,
a
фазовый сдвиг в канале,
a
![]() (t) — процесс,
сопряжённый с X(t)
по
Гильберту, но значения
(t) — процесс,
сопряжённый с X(t)
по
Гильберту, но значения ![]() и
и ![]() для разных путей различны и к тому же в небольших
пределах флуктуируют. Такого рода многопутевое распространение сигнала
характерно для большинства радио-, гидроакустических и некоторых других каналов
(в том числе проводных).
для разных путей различны и к тому же в небольших
пределах флуктуируют. Такого рода многопутевое распространение сигнала
характерно для большинства радио-, гидроакустических и некоторых других каналов
(в том числе проводных).

 Энергия волны распространяется обычно в неоднородной
среде и испытывает отражение от различных неоднородностей. Эти неоднородности
могут быть распределены внутри относительно небольшого отражающего (рассеивающего)
объёма. В этом случае разности хода (разности значений
Энергия волны распространяется обычно в неоднородной
среде и испытывает отражение от различных неоднородностей. Эти неоднородности
могут быть распределены внутри относительно небольшого отражающего (рассеивающего)
объёма. В этом случае разности хода (разности значений ![]() ) для отдельных путей невелики.
Если по такому каналу направить очень короткий импульс, то и на его выходе
импульс будет довольно коротким. Такой канал принято называть однолучевым.
Наличие разных путей ("подлучей") не вызывает в этом случае
существенного рассеяния (растяжения) сигнала во времени, но приводит к
возникновению явления замираний, которое заключается в более или менее быстрых
случайных изменениях передаточной функции канала (мультипликативная помеха).
) для отдельных путей невелики.
Если по такому каналу направить очень короткий импульс, то и на его выходе
импульс будет довольно коротким. Такой канал принято называть однолучевым.
Наличие разных путей ("подлучей") не вызывает в этом случае
существенного рассеяния (растяжения) сигнала во времени, но приводит к
возникновению явления замираний, которое заключается в более или менее быстрых
случайных изменениях передаточной функции канала (мультипликативная помеха).
Если по однолучевому каналу с замираниями
передаётся относительно узкополосный сигнал, а среднеквадратическое отклонение
запаздывания ![]() в
отдельных подлучах удовлетворяет условию
в
отдельных подлучах удовлетворяет условию
![]() , (19.4)
, (19.4)
где Fc - ширина
спектра сигнала, то изменения начальных фаз на разных частотах ![]() в спектре сигнала,
равные
в спектре сигнала,
равные ![]() , почти
одинаковы. При этом все составляющие спектра сигнала замирают
"дружно", т.е. их амплитуды и фазы изменяются одинаково. Такие замирания
называются общими или гладкими. Если же условие (19.4) не выполнено, то
в разных областях спектра сигнала процессы замираний не совпадают (селективные
по частоте замирания). При этом наблюдаются существенные изменения формы
сигнала, что характерно для многолучевых каналов радиосвязи (приходящие в точку
приёма сигналы образованы отражением от сильно разнесённых в пространстве
рассеивающих объёмов).
, почти
одинаковы. При этом все составляющие спектра сигнала замирают
"дружно", т.е. их амплитуды и фазы изменяются одинаково. Такие замирания
называются общими или гладкими. Если же условие (19.4) не выполнено, то
в разных областях спектра сигнала процессы замираний не совпадают (селективные
по частоте замирания). При этом наблюдаются существенные изменения формы
сигнала, что характерно для многолучевых каналов радиосвязи (приходящие в точку
приёма сигналы образованы отражением от сильно разнесённых в пространстве
рассеивающих объёмов).
В каналах связи аддитивные помехи
вызываются различными причинами и могут принимать различные формы,
индивидуальные реализации которых трудно учесть. Именно эти помехи чаще
вызывают необратимые преобразования передаваемых сигналов. Аддитивные помехи
по их электрической и статистической структуре разделяют на три основных
класса: флуктуационные (распределённые по частоте и времени), сосредоточенные
по частоте (квазигармонические) и сосредоточенные во времени (импульсные). С
физической точки зрения аддитивные флуктуационные помехи порождаются в
системах связи различного рода флуктуациями, т.е. случайными отклонениями тех
или иных физических величин (параметров) от их средних значений. Так,
источником шума в электрических цепях могут быть флуктуации тока, обусловленные
дискретной природой носителей заряда (электронов, ионов). Дискретная природа
электрического тока проявляется в полупроводниковых приборах в виде дробового
эффекта (при заданном режиме питания схем случайно меняется число
создаваемых носителей заряда). Если учесть, что ![]() , то удельная дисперсия флуктуационного
тока (А2/Гц), приходящаяся на полосу частот в 1 Гц,
, то удельная дисперсия флуктуационного
тока (А2/Гц), приходящаяся на полосу частот в 1 Гц,
N0=2eI0. (19.5)
Это соотношение получило в радиотехнике название формулы Шотки. Согласно ей, эквивалентная шумовая схема электронного прибора содержит в себе источник тока, создающий белый шум со спектральной плотностью N0.
Дробовой шум электронных приборов имеет постоянный спектр мощности вплоть до частот в несколько сотен мегагерц, а затем начинает уменьшаться с ростом частоты.
Наиболее распространённой причиной шума в аппаратуре связи являются флуктуации, обусловленные тепловым движением. Одной из главных причин возникновения шума являются флуктуации объемной плотности электрического заряда в проводящих телах (резисторах) из-за хаотического теплового движения носителей заряда. Случайное тепловое движение носителей заряда в любом проводнике вызывает случайную разность потенциалов (напряжения) на его концах. Среднее значение такого напряжения равно нулю, а переменная составляющая проявляется как шум. Тепловой шум на входе приёмника представляет собой случайный гауссовский процесс с нулевым средним и спектральной плотностью мощности - Формула Найквиста
No = 2Wo = 4kTR. (19.6)
Специфическим для полупроводниковых приборов является шум, называемый фликер-шумом, который возникает в результате разного рода поверхностных явлений. Его спектральная плотность в широком диапазоне частот подчиняется гиперболическому закону (она пропорциональна 1/f ). Обычно на частотах выше 10 кГц фликер-шумами пренебрегают. Космические помехи в системах радиосвязи, вызванные радиоизлучением солнца и других космических объектов – это флуктуационные шумы. Источником шума в радиотехническом устройстве может быть приемная антенна, на выходе которой возникает случайное напряжение под воздействием хаотических флуктуации электромагнитного поля. Поскольку на выходе антенны, малой по сравнению с длиной волны, возникает напряжение и = El. У естественных помех земного происхождения подавляющая часть мощности этого шума сосредоточена на частотах ниже 30 МГц.
К сосредоточенным по спектру аддитивным помехам принято относить сигналы посторонних радиостанций, преднамеренные помехи, излучения генераторов высокой частоты различного назначения (промышленных, медицинских) и т.п. В общем случае это модулированные колебания, т.е. квазигармонические колебания с изменяющимися параметрами. В одних случаях эти колебания являются непрерывными (например, сигналы вещательных и телевизионных радиостанций), в других - они носят импульсный характер (сигналы радиотелеграфных станций и систем передачи данных). Ширина спектра сосредоточенной помехи в большинстве случаев не превышает полосы пропускания приёмника, а в некоторых случаях она намного уже этой полосы. В диапазоне коротких волн сосредоточенные по спектру помехи являются основными, определяющими качество связи, и считаются случайными колебаниями с флуктуациями фаз и амплитуд (замираниями), распределение которых такое же, как у полезных сигналов.
К импульсным (сосредоточенным во времени) аддитивным помехам принято относить помехи в виде одиночных импульсов, следующих один за другим через такие большие промежутки времени, что переходные явления в приёмнике от одного импульса успевают практически затухнуть к моменту прихода следующего импульса. К таким помехам относят многие виды атмосферных и индустриальных помех. Заметим, что "флуктуационная помеха" и "импульсная помеха" являются понятиями относительными. В зависимости от частоты следования импульсов одна и та же помеха может воздействовать как импульсная на приёмник с широкой полосой пропускания и как флуктуационная на приёмник с относительной узкой полосой пропускания. На практике импульсные помехи приходится рассматривать как случайный, относительно широкополосный (тем шире, чем короче импульсы помехи) процесс, состоящий из отдельных редких, случайно распределённых во времени и по амплитуде импульсов. Вероятностные свойства таких помех описываются распределением вероятностей амплитуд импульсов и распределением временных интервалов между этими импульсами с помощью модели Пуассона (11.8). Обозначим символом v среднее число электронов, прибывающих на анод за 1 с. Вероятность прибытия на анод ровно п электронов
![]() .
(19.7)
.
(19.7)
Для этого закона характерно наличие существенных значений в области больших амплитуд, что соответствует реальной модели импульсной помехи. Это медленные (суточные, сезонные) флуктуации амплитуд радиосигналов, обусловленные поглощениями сигнала в среде распространения.
Лекция 20. Прием сигналов с неопределенной фазой (некогерентный прием). Потенциальные возможности дискретных каналов связи. Свойство эргодичности
Содержание лекции:
- прием сигналов с неопределенной фазой (некогерентный прием). Основной понятийный аппарат теории информации. Вектор ошибок.
Цель лекции:
- синтезировать оптимальный демодулятор. Сформулировать исходные понятия.
Многие каналы можно описать моделью (19.3) с флуктуирующей фазой. Нередко фаза флуктуирует довольно быстро, и точную её оценку получить не удаётся. Кроме того, оценка фазы требует иногда применения сложных устройств. Поэтому даже в тех случаях, когда принципиально можно оценить начальную фазу приходящего сигнала, порой от этого отказываются и используют алгоритм, построенный в предположении, что начальная фаза приходящего сигнала не известна и может принимать любое значение на интервале (0, 2π). Такой метод приёма называется некогерентным.
Для вывода правила оптимального некогерентного приёма будем исходить из логарифма отношения правдоподобия lnΛi для сигнала si(t), которое при точно известной начальной фазе выражается формулой
![]() .
.
Используя представление для сигнала,
![]() ,
,
где γ — известный коэффициент передачи канала, а θ - случайный сдвиг в канале, формулу для lnΛi можно (после устремления Δt→0) записать так
 .
(20.1)
.
(20.1)
Здесь lnΛi является случайной величиной, принимающей различные
значения при различных θ. Правило максимума правдоподобия в такой ситуации
заключается в выборе такого решения, для которого математическое ожидание
Λi будет наибольшим. При нахождении ![]() заметим, что второй интеграл в
правой части (20.1) от θ не зависит и равен энергии
EПi сигнала
ui(t) на входе канала (на передатчике). Это ясно из того,
что подынтегральной функцией является квадрат сигнала
Ui(t),
сдвинутого по фазе на θ, что, как известно, не влияет на его энергию.
Таким образом, учитывая, что
заметим, что второй интеграл в
правой части (20.1) от θ не зависит и равен энергии
EПi сигнала
ui(t) на входе канала (на передатчике). Это ясно из того,
что подынтегральной функцией является квадрат сигнала
Ui(t),
сдвинутого по фазе на θ, что, как известно, не влияет на его энергию.
Таким образом, учитывая, что ![]() , получаем с введением обозначений
, получаем с введением обозначений
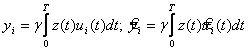 ,
,
![]() и
и 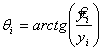 , (20.2)
, (20.2)
 - модифицированная функция Бесселя нулевого порядка.
- модифицированная функция Бесселя нулевого порядка.
Вместо того чтобы сравнивать отношения правдоподобия, можно сравнить их логарифмы, что приводит к следующему правилу (алгоритму) оптимального некогерентного приёма для двоичной системы сигналов
 . (20.3)
. (20.3)
При выполнении этого неравенства регистрируется 1, в противном случае - 0.
 Величины yi
и
Величины yi
и ![]() можно
получить в момент отсчёта Т на выходе активного фильтра с опорными
сигналами, равными соответственно ui(t) и
можно
получить в момент отсчёта Т на выходе активного фильтра с опорными
сигналами, равными соответственно ui(t) и ![]() . С учётом сказанного, понятно построение
на основе активных фильтров схемы, называемой квадратурной и реализующей
алгоритм (20.3) (см. рисунок 20.1). Здесь Г0, Г1
-соответственно генераторы опорных сигналов
u0(t),
u1(t);
φ
—фазовращатель всех сигнальных компонент на –π/2 (преобразователь Гильберта);
БОМ - блок определения модуля вектора Vi=| уi,+j
. С учётом сказанного, понятно построение
на основе активных фильтров схемы, называемой квадратурной и реализующей
алгоритм (20.3) (см. рисунок 20.1). Здесь Г0, Г1
-соответственно генераторы опорных сигналов
u0(t),
u1(t);
φ
—фазовращатель всех сигнальных компонент на –π/2 (преобразователь Гильберта);
БОМ - блок определения модуля вектора Vi=| уi,+j![]() |, по
ортогональным компонентам; НУ - нелинейные безынерционные устройства с характеристикой
|, по
ортогональным компонентам; НУ - нелинейные безынерционные устройства с характеристикой

 Подчеркнём, что величины
Vi не зависят от начальной фазы сигналов
ui(t)
и, как
видно из (20.2), пропорциональны огибающей (в моменты отсчёта, кратные
T) на выходе фильтра, согласованного с сигналом
ui(t). Таким
образом, алгоритм (20.3) можно реализовать и на базе согласованных фильтров,
как показано на рисунке 20.2.
Подчеркнём, что величины
Vi не зависят от начальной фазы сигналов
ui(t)
и, как
видно из (20.2), пропорциональны огибающей (в моменты отсчёта, кратные
T) на выходе фильтра, согласованного с сигналом
ui(t). Таким
образом, алгоритм (20.3) можно реализовать и на базе согласованных фильтров,
как показано на рисунке 20.2.
Для двоичной системы с пассивной паузой, полагая, что символ 0 передаётся сигналом u0(t) = 0, правило можно записать в виде
V1>λ, (20.4)
где пороговый уровень ![]() ,
,
а функция x = f(y) обратна функции у = lпI0(х). При выполнении неравенства (20.4) (превышение V1 над порогом) регистрируется символ 1, в противном случае — символ 0.
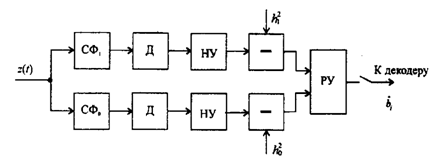
Рисунок 20.2 - Квадратурная схема реализации оптимального приема дискретных сообщений при неопределенной фазе сигнала
Введём ещё одно полезное определение.
Будем называть вектором ошибок поразрядную разность (разумеется, по
модулю т) между принятым и переданным векторами. В общем случае для
любых входных и выходных сигналов последовательностей п кодовых символов
должна быть указана вероятность того, что при подаче на вход канала
любой заданной последовательности В[n] кодовых символов на выходе появится некоторая реализация
случайной последовательности ![]() . Кодовые символы обозначим числами от 0 до
m-1, где т различных символов (основание кода),
что позволит производить над ними арифметические операции. При этом все п - последовательности
(векторы), число которых равно mn, образуют п
— мерное конечное векторное пространство, если "сложение"
понимать как поразрядное суммирование по модулю т и аналогично
определить умножение на скаляр.
. Кодовые символы обозначим числами от 0 до
m-1, где т различных символов (основание кода),
что позволит производить над ними арифметические операции. При этом все п - последовательности
(векторы), число которых равно mn, образуют п
— мерное конечное векторное пространство, если "сложение"
понимать как поразрядное суммирование по модулю т и аналогично
определить умножение на скаляр.
Это значит, что прохождение дискретного
сигнала через канал можно рассматривать как сложение входного вектора с
вектором ошибки. Вектор ошибки играет в дискретном канале примерно ту же роль,
что и помеха в непрерывном канале. Таким образом, для любой модели дискретного
канала можно записать, пользуясь сложением в векторном пространстве (поразрядным,
по модулю m) ![]() , где
, где ![]() и
и ![]() — случайные последовательности из п
символов на входе и выходе канала;
— случайные последовательности из п
символов на входе и выходе канала; ![]() — случайный вектор ошибки, который в общем
случае зависит от
— случайный вектор ошибки, который в общем
случае зависит от ![]() .
Различные модели отличаются распределением вероятностей вектора
.
Различные модели отличаются распределением вероятностей вектора ![]() . Смысл вектора ошибки
особенно прост в случае двоичных каналов (т = 2), когда его компоненты
принимают значения 0 и 1. Всякая единица в векторе ошибок означает, что в соответствующем
месте передаваемой последовательности символ принят ошибочно, а всякий нуль
означает безошибочный приём символа. Число ненулевых символов в векторе ошибок
называется его весом. Образно говоря, модем, осуществляющий переход от
непрерывного канала к дискретному, преобразует помехи и искажения непрерывного
канала в поток ошибок.
. Смысл вектора ошибки
особенно прост в случае двоичных каналов (т = 2), когда его компоненты
принимают значения 0 и 1. Всякая единица в векторе ошибок означает, что в соответствующем
месте передаваемой последовательности символ принят ошибочно, а всякий нуль
означает безошибочный приём символа. Число ненулевых символов в векторе ошибок
называется его весом. Образно говоря, модем, осуществляющий переход от
непрерывного канала к дискретному, преобразует помехи и искажения непрерывного
канала в поток ошибок.
Случайный стационарный процесс называют эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени. Операция усреднения выполняется над единственной реализацией х(t), длительность Т которой теоретически может быть сколь угодно велика. Обозначая усреднение по времени угловыми скобками, запишем математическое ожидание случайного эргодического процесса
 , (20.5)
, (20.5)
которое равно постоянной составляющей выбранной реализации.
Дисперсия подобного процесса
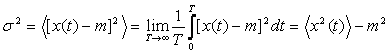 . (20.6)
. (20.6)
Поскольку величина <x2> представляет собой среднюю мощность реализации, а величина m2 — мощность постоянной составляющей, дисперсия имеет наглядный смысл мощности флуктуационной составляющей эргодического процесса. Аналогично находят функцию корреляции
 (20.7)
(20.7)
Случайный процесс эргодичен, если выполнено условие Слуцкого
 . (20.8)
. (20.8)
Интервал корреляции
 . (20.9)
. (20.9)
Определение интервала корреляции согласно (20.9) называют методом равновеликого прямоугольника: интервал корреляции равен основанию прямоугольника с высотой, равной 1, площадь которого равна площади под кривой |R(τ)| при τ≥0 (см. рисунок 9.1).

Рисунок 20.3 - Определение интервала корреляции методом равновеликого прямоугольника
Список литературы
1. Андреев В.С. Теория нелинейных электрических цепей. – М.: Связь, 1972.
2. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2003.
3. Баскаков С.И. Лекции по Теории цепей. – М.: МЭИ, РОСВУЗНАУКА, 1991.
4. Цифровые фильтры в электросвязи и радиотехники. Под ред. Л. М. Гольденберга. - М.: «Радио и связь», 1982.
5. Цифровые фильтры и их применение. Под. ред. Н. Н. Слепова. – М.: Энергоатомиздат, 1983.
6. Теория электрической связи. Под ред. Д.Д. Кловского. - М.: «Радио и связь», 1999.
7. Скляр Б. Цифровая связь. - М., С-П., К., 2003.
8. Панфилов И.П., Дырда В.Е. Теория электрической связи. - М.: «Радио и связь», 1991.
Содержание
|
|
|
|
Введение |
3 |
|
Лекция 1. Общие сведения о системах электросвязи |
4 |
|
Лекция 2. Кодирование и модуляция. Помехи и искажения |
8 |
|
Лекция 3. Математические модели сообщений и сигналов. Спектральные представления сигналов |
12 |
|
Лекция 4. Динамическое представление сигналов. Дискретизация сигналов во времени |
16 |
|
Лекция 5. Амплитудная модуляция |
20 |
|
Лекция 6. Угловая модуляция |
24 |
|
Лекция 7. Частотная модуляция. Фазовая модуляция. Импульсная модуляция. Общие сведения о детектировании |
28 |
|
Лекция 8. Детектирование АМ и ЧМ-колебаний в нелинейных цепях |
32 |
|
Лекция 9. Потенциальные возможности дискретных каналов связи |
36 |
|
Лекция 10. Методы повышения верности передачи дискретной информации |
40 |
|
Лекция 11. Классификация помехоустойчивых кодов. Циклические коды |
44 |
|
Лекция 12. Спектральный анализ непериодических сигналов. Преобразование Фурье. Спектральные плотности неинтегрируемых сигналов. Энергетические спектры сигналов |
48 |
|
Лекция 13. Принципы корреляционного анализа. Случайные процессы и их основные характеристики |
52 |
|
Лекция 14. Случайные процессы и их основные характеристики. Общие сведения о каналах связи. Преобразование сигналов в линейных каналах связи |
56 |
|
Лекция 15. Преобразование сигналов в линейных и нелинейных каналах связи |
60 |
|
Лекция 16. Модель дискретно-непрерывного канала. Критерии качества и правила приема дискретных сообщений. Теория помехоустойчивости систем передачи дискретных сообщений |
64 |
|
Лекция 17. Оптимальный приемник с согласованным фильтром |
68 |
|
Лекция 18. Помехоустойчивость оптимального когерентного приема. Теоремы Шеннона Лекция 19. Прием сигналов с неопределенной фазой (некогерентный прием). Потенциальные возможности дискретных каналов связи. Свойство эргодичности Лекция 20. Преобразование сигналов в каналах связи. Аддитивные помехи в канале Список литературы |
72 76 80 84 |