Некоммерческое акционерное общество

Алматинский университет энергетики и связи

 Кафедра  радиотехники

 

 

 

 

ТЕОРИЯ ПЕРЕДАЧИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

 Конспект лекций

для студентов всех форм обучения специальности 

5В071900 – Радиотехника, электроника и телекоммуникации

 

 

 

Алматы 2011 

СОСТАВИТЕЛИ: Куликов А.А., Хорош А.Х. Теория передачи электромагнитных волн. Конспект лекций для студентов всех форм обучения специальности 5В071900 – «Радиотехника, электроника и телекоммуникации». – Алматы: АУЭС, 2011. –  58 с.

 

Конспект лекций предназначен для студентов специальности 5В071900 – «Радиотехника, электроника и телекоммуникации» всех форм обучения.

В конспекте лекций по курсу «Теория передачи электромагнитных волн» рассматриваются основные принципы распространения электромагнитных волн в различных средах, основные типы волноводов предназначенных для передачи электромагнитных волн, приведен обзор основных элементов волноводных трактов, а также рассмотрены вопросы согласование элементов волноводных трактов.

Табл. –  2, ил. – 56, библиогр. –  8 назв.

 

Рецензент: канд. техн. наук, проф. С.В. Коньшин

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на  2009 г.

 

 

Ó НАО «Алматинский университет энергетики и связи», 2011 г.

 

Содержание

 

Лекция №1. Общие положения теории электромагнитного поля. Основные законы электродинамики Лекция №2.  Плоские электромагнитные волны. Поляризация волн Лекция №3. Падение плоских электромагнитных волн на границу раздела двух сред Лекция №4. Падение плоской электромагнитной волны на границу раздела с немагнитной хорошо проводящей средой. Линии передачи Лекция №5. Прямоугольный металлический волновод Лекция №6. Волны высших типов в прямоугольном волноводе. Поверхностные токи. Энергетические характеристики Лекция №7. Круглый металлический волновод Лекция №8. Коаксиальный волновод Лекция №9. Полосковые линии передачи и диэлектрический волновод Лекция №10. Распространение ЭМВ в линиях конечной длины Лекция №11. Потери в линиях передачи электромагнитной энергии.  Свободные колебания в объемных резонаторах Лекция №12. Согласование линий передачи Список литературы

4  8   12  17   21 25  29 33 37  42 46  52 57

 

 

Лекция №1. Общие положения теории электромагнитного поля. Основные законы электродинамики

 

В курсе «Теория передачи электромагнитных волн» рассматривается классическая нерелятивистская электродинамика. Это частная версия теории электромагнетизма, в которой основные понятия - напряженности полей, заряды и токи - не выводятся из чего-либо, а постулируются. Кроме того, методы, которые мы будем использовать, справедливы в условиях, когда скорости движущихся тел много меньше скорости света.

Согласно основным положениям макроскопической электродинамики электромагнитное поле (ЭМП) в каждой точке, в каждый момент времени определяется четырьмя величинами:  - вектор напряженности электрического поля, В/м; - вектор электрического смещения, Кл/м²; - вектор напряженности магнитного поля, А/м;  - вектор магнитной индукции, Тл. Кроме этих четырех векторов в уравнениях электромагнитного поля присутствуют еще две величины: плотность свободного электрического заряда  (А/м²) и плотность электрического тока (тока проводимости) (Кл/м³), они характеризуют источники поля - заряды и токи.

Если нет макроскопических перемещений вещества, то плотность тока и плотность заряда связаны уравнением непрерывности:

 ,                                                                                           (1.1)

выражающим тот факт, что ток проводимости обусловлен движением свободных зарядов.  - сила действующая на заряд q.

Векторное поленеобходимо для описания электрического поля в материальной среде (например, в диэлектрике) - поле электрического смещения. Магнитное поле в отличие от электрического поля взаимодействует с движущимися заряженными частицами и описывается вектором магнитной индукции .

В результате движения в электромагнитном поле на заряд q действует Сила Лоренца:  . Первое слагаемое обусловлено электрическим полем, второе – магнитным.

- характеризует силу тока через единичную площадку перпендикулярную вектору скорости заряженных частиц.

q - объемная плотность заряда в объеме V.

 Векторы ЭМП и величины j и r зависят от 3-х пространственных координат и времени t. Они связаны между собой системой уравнений Максвелла:

,                                                                                         (1.2)

,                                                                                                    (1.3)

,                                                                                                (1.4)

.                                                                                                     (1.5)

Уравнение (1.2) называют обычно первым, а (1.4) - вторым уравнениями Максвелла Дж. Кларка. (1873  - трактат об электричестве и магнетизме).

Все 4 уравнения - обобщение опытных данных.

Уравнение (1.2)  - дифференциальная формулировка закона полного тока и гипотезы Максвелла о токе смещения.

Уравнение (1.3) - закон Гаусса.

(1.4) - закон электромагнитной индукции (Фарадей).

(1.5) - закон неразрывности магнитных силовых линий.

Система уравнений (1.2)-(1.5) справедлива для электромагнитных полей в любых средах, но их недостаточно для решения конкретных задач (неизвестных больше чем уравнений). (1.3) и (1.5) - практически скалярные уравнения. В систему следует включить уравнения, учитывающие влияние среды на протекающие в ней электромагнитные явления, называемые материальными уравнениями (1.6)-(1.8):

                                                                                                     (1.6)

                                                                                                    (1.7)

                                                                                                     (1.8)

Величиной - абсолютной диэлектрической проницаемостью - характеризуют свойства диэлектриков (веществ, не проводящих электрический ток) неполярных и полярных:

.

Где ε₀ – электрическая постоянная (ε₀=10^-9/36π  Ф/м),

– относительная  диэлектрическая проницаемость (безразмерная величина) (вакуум, воздух 1; полиэтилен = 2,25; пресная вода  81).

Свойства магнетиков характеризуют магнитная проницаемость или абсолютная магнитная проницаемость:

.

Где =4*10^-7 Гн/м – магнитная постоянная.

Величина  может быть меньше 1 и много больше.

У диамагнетиков - уменьшающих поле - <1 (как правило, близко к единице). К ним относится большинство веществ.

У парамагнетиков, увеличивающих магнитное поле, -  незначительно больше 1. (кислоты, азот некоторые металлы и т.д.)

Особый класс веществ - ферромагнетики. У них .

σ (См/м) - удельная проводимость (серебро – 6.1*10⁷, медь – 5.7*10⁷).

Уравнение (1.8) называют законом Ома в дифференциальной форме.

Уравнения (1.6)-(1.8) охватывают электромагнитные свойства достаточно большого числа сред, но многие свойства реальных веществ не учитывают, т.е. соотношения прямой пропорциональности между  и ,  и  - в линейных средах могут нарушаться.

В диэлектрике нелинейная зависимость наблюдается каждый раз, когда  становится очень высокой и возникает электрический пробой.

Нелинейные свойства в обычных условиях проявляют сегнетодиэлектрики.

Особый интерес представляют материальные среды, в которых векторы  и  - неколлинеарные. В этом случае свойства среды зависят от направления распространения ЭМВ через нее - анизотропные среды (ферриты, ионосфера и т.д.)

Для описания их свойств используют тензорную форму  и , например, в декартовой системе координат:

.

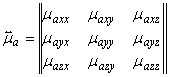Все прочие можно считать изотропными средами.

Процесс измерения любого поля - в сущности, извлечение некоторой энергии из поля, т.е. необходимо определить, как связана энергия поля с величинами, характеризующими поле.

Согласно макроскопической теории поля электромагнитная энергия распределена в пространстве, занятом полем, с некоторой объемной плотностью таким образом, что электромагнитная энергия, содержащаяся в объеме V, выражается в виде объемного интеграла:

.                                                                                      (1.9)

W - полный запас энергии ЭМП внутри объема V в фиксированный момент времени (измеряется в Дж).

Изменяться во времени эта энергия может за счет двух процессов:

1) Она может внутри данного объема превращаться другие, неэлектромагнитные формы энергии (тепловая, химическая, кинетическая ускоренных частиц...) или возникать из неэлектромагнитных  форм.

2) Эта энергия, оставаясь электромагнитной, может вытекать из данного объема (или втекать в него) через поверхность S, ограничивающую данный объем.

Первый процесс характеризуется мощностью потерь Р_ПОТ.

Второй - мощностью излучения S.

,                                                                                       (1.10)

,                                                                                               (1.11)

где

                                                                                                  (1.12)

вектор плотности потока мощности электромагнитного поля  - вектор Пойнтинга (1884 - английский ученый)

Величины Р_ПОТ и S могут быть положительными и отрицательными (отрицательность Р_ПОТ - идет превращение других видов энергии в электромагнитную; отрицательность S показывает, что в данный объем поступает энергия из внешнего пространства). Выражения (1.11)-(1.12) справедливы для любых сред.

Величина объемной плотности электромагнитной энергии

 .

Мощности тепловых потерь

,

где ρ – объемная плотность мощности тепловых потерь

.

Теорема Остроградского-Гаусса:

токи и заряды являются источниками ЭМП, а также сами возникают под действием поля. На практике приходится учитывать также токи и заряды, которые вызываются внешними источниками и практически не зависят от возбужденного ими электромагнитного поля.

Такие токи принято называть "сторонними" и векторное поле плотности сторонних токов  следует ввести, как заранее заданную функцию в уравнения Максвелла, а также в уравнение Умова-Пойнтинга:

,

где .

Соотношение Умова-Пойнтинга представляет собой математическую формулировку закона сохранения энергии для электромагнитного поля

Так как в большинстве практических задач материальные среды можно считать линейными, то в них будет справедлив принцип суперпозиций  ЭМП: если  частные решения уравнений Максвелла, то решением будет и сумма вида .

Решение уравнений можно значительно упростить, если исключить временную переменную.

Для упрощения уравнений Максвелла вводится величина

                                                                                           (1.13)

называемой комплексной диэлектрической проницаемостью данного вещества, которая учитывает и проводящие и поляризационные свойства.

 

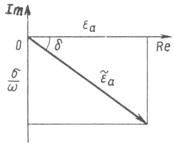
Рисунок 1.1 – Угол диэлектрических потерь

Действительная часть - интенсивность процесса поляризации, мнимая - плотность токов проводимости (потери) (см. рисунок 1.1).

В комплексной плоскости (см. рисунок 1.1)  - угол диэлектрических потерь (в справочниках обычно приводят tg):

.

На частотах СВЧ диапазона для хороших диэлектриков   tg=10^-5¸10^-4, если tg>10^-3 - диэлектрик принято считать плохим.

При анализе гармонических полей удобней использовать комплексный вектор Пойнтинга:

.                                                                                               (1.14)

Действительная его часть равна плотности потока мощности усредненной за период (действительный  вектор, который определяет направление переноса энергии):

.

Если комплексный вектор Пойнтинга чисто мнимый, то процесс не переносит мощности (перенос реактивной мощности).

 

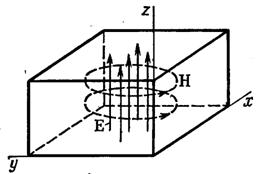
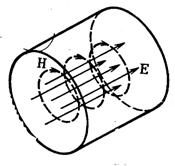
Лекция №2.  Плоские электромагнитные волны. Поляризация волн

 

Рассмотрим бесконечное трехмерное пространство, в котором отсутствуют свободные заряды r=0 и с заданными электродинамическими параметрами , одинаковыми во всех точках. Гармонически изменяющийся электромагнитный процесс будет описываться системой уравнений Максвелла. Из уравнений (1.2)-(1.5), путем математических преобразований, выводится уравнения Гельмгольца:   

.                                                                                     (2.1)

Уравнение (2.1) – однородное дифференциальное уравнение второго порядка. Для простоты решения введем параметр:

                                                                                               (2.2)

и будем считать, что: . Кроме того,  зависит только от координаты z, то есть: . Тогда решение уравнения (2.1) будет:

,                                                                           (2.3)

где  и  корни уравнения (2.2). Распишем их:

,

.

Отсюда: , и выражение (2.3) запишется в виде:

.                                                                           (2.4)

Выражение (2.4) – однородная плоская волна. Первое слагаемое – волна, распространяющаяся в сторону уменьшения z. Второе – в сторону увеличения. Отсюда величина g – коэффициент  распространения.

Плоской называют волну, распространяющуюся вдоль какой-либо координаты и неизменную в каждый фиксированный момент времени в плоскости перпендикулярной этой координате:

.

Параметр b играет роль «пространственной» частоты процесса – коэффициент фазы (1/м). Её период: , где l - длина волны.

Поверхность, удовлетворяющая условию:  называется волновой фронт (фазовый фронт, поверхность равных фаз), перемещающийся вдоль оси z с фазовой скоростью:

.

Величина a – коэффициент  ослабления плоской волны в среде (1/м).

В расчетах чаще используют погонное затухание:

  дБ/м.

Используя второе уравнение Максвелла, найдем Н и подставим величину g:

.

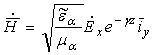Некоторые выводы:

–  в однородной плоской волне векторы Е и Н перпендикулярны;

–  и Е и Н перпендикулярны оси распространения – поперечная волна;

– комплексные амплитуды векторов Е и Н в любой точке пространства связаны коэффициентом пропорциональности Zc.

Zc - характеристическое (волновое) сопротивление:

.                                                                  

Волновое сопротивление Zc характеризует среду и, в общем случае, не связано с тепловыми потерями.

Определим плотность потока мощности плоской ЭМВ:

,

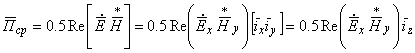или с учетом Zс:

.        

Рассмотрим, как изменятся приведенные выше соотношения, если среда распространения – вакуум: .

Коэффициент распространения:  чисто мнимый (потерь нет). Коэффициент фазы ,  тогда  фазовая скорость   не зависит от частоты.

Отсюда Z₀ – действительное, и равно  Ом. Векторы Е и Н колеблются в фазе. Отметим, что для атмосферного воздуха это тоже справедливо.

В среде без потерь, но с e>1, m>1:

;   

.         

На практике в СВЧ - диапазоне используют, как правило, диэлектрик с малыми потерями и m » 1. Для расчета основных характеристик плоских ЭМВ в этом случае используются следующие выражения:

,

.

Если tgs<<1, то есть, в случае малых потерь, , а a – прямо пропорционален w и s:

.       

Характеристическое сопротивление в этом случае:

.               

Так как Zс – комплексная величина, то векторы Е и Н колеблются не синфазно и угол сдвига фаз приблизительно равен s/2.

В хорошо проводящих средах, даже при постоянстве m_а, абсолютная диэлектрическая проницаемость  является функцией частоты: , то есть наблюдается частотная дисперсия.

Говорят, что на заданной частоте w материальная среда является хорошо проводящей (металлоподобной),  если:

s¤w>>e_а,                                                                                                     (2.5)

то есть плотность токов проводимости значительно превышает плотность токов смещения и поляризационных токов.

Как следствие на низких частотах неидеальные диэлектрики и полупроводники становятся металлоподобными (сухая почва при частоте f=1МГц ведет себя как хорошо проводящая среда). Но даже на самых высоких частотах радиодиапазона неравенство (2.5) выполняется для металлов с большим запасом.

В хорошо проводящей среде можно приближенно считать:

.

Тогда .

Используя выражение,  перейдем к a и b:

.            

Обе величины сильно зависят от w, дисперсия ярко выражена:

;

.

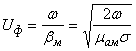Характеристическое сопротивление:

.       

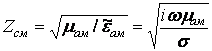Величина  означает, что в проводнике вектор Н сдвинут по фазе относительно вектора Е на 45°.

Если a ¹ 0, то амплитуда плоской ЭМВ изменяется вдоль координаты распространения Z по закону .

Расстояние, на котором амплитуда уменьшается в е раз, называют глубиной проникновения или толщиной поверхностного слоя (d):

;  

.

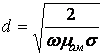На СВЧ диапазоне глубина проникновения очень мала. Для меди на 10ГГц d = 0,6 мкм, это позволяет использовать тонкие (10-20 мкм) слои хороших проводников для уменьшения потерь.

Частотная дисперсия характерна также для плазмы (ионизированный газ), для нее:

;

;

.

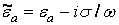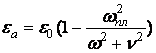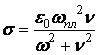Где n – частота столкновений электронов с нейтральными молекулами,

w_пл – собственная (плазменная) частота, при которой при n = 0, e_а = 0.

,

где Ne – электронная концентрация.

Если потери отсутствуют, то фазовая скорость выражается:

.

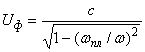Скорость переноса информации (скорость перемещения в пространстве энергии, или медленной огибающей, или группы волн):

,

Эта формула справедлива для узкополосных сигналов (можно применять для радиоимпульсов и т.д.). Такая частотная зависимость приводит к расплыванию (увеличению длительности) импульсов.

Рассмотрим поляризацию волн. Полагаем, что вектор Е имеет две составляющие,  и . Найдем положение кривой, которая служит геометрическим местом концов вектора Е суммарного процесса. Перепишем составляющие в виде: , . Возводим их в квадрат и складываем:

 .

Это уравнение эллипса, а про волну говорят, что это эллиптически поляризованная волна (см. рисунок 2.1).

 

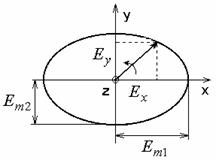
Рисунок 2.1 – Эллиптически поляризованная волна

 

В этом случае вектор Е вращается против часовой стрелки, если смотреть с конца i_z – лево поляризованная волна.

Частные случаи:

– Равна нулю одна из составляющих или сдвиг фаз между ними равен нулю. Тогда конец вектора Е перемещается вдоль линии произвольно, в общем случае, ориентированной относительно системы координат. Волна – линейно поляризованная.

– Равны амплитуды Е_m1 = Е_m2, а сдвиг фаз - 90°. Тогда кривая окружность, волну называют волной с круговой поляризацией.

Легко заметить, что суперпозиция двух волн с линейными поляризациями, сдвинутых по фазе и пространственно на 90°, дают эллиптически поляризованную волну, две волны с круговыми поляризациями и противоположными направлениями вращения, в результате суперпозиции дают волну линейно поляризованную.

 

Лекция №3. Падение плоских электромагнитных волн на границу раздела двух сред

 

Граничные условия – соотношения, показывающие связь между значениями векторов ЭМП в разных средах, у поверхности раздела называют граничными условиями.

Полная система граничных условий состоит из четырех формул:

;                                                                                           (3.1)

;                                                                                                   (3.2)

;                                                                                                   (3.3)

.                                                                                         (3.4)

Формула (3.1) показывает, что нормальная компонента вектора D претерпевает скачек на величинуповерхностного заряда .  На самом деле поверхностных зарядов не бывает, толщина слоя конечна и D меняется постепенно. Но математическая модель  удобнее.

Если свободные заряды на границе раздела сред отсутствуют , то для вектора Е:

 .

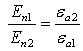Нормальная компонента вектора Е претерпевает разрыв.

Формула (3.2) показывает, что тангенсальная составляющая вектора Е, непрерывна при переходе через границу раздела двух сред.

Для вектора B нормальные составляющие непрерывны (3.3), а тангенсальные составляющие вектора Н претерпевает скачек на величину плотность поверхностного тока  (3.4), направленного ортогонально вектору  (или его составляющей).

На поверхности раздела с идеальным проводником , внутри которого поле отсутствует, согласно уравнению Максвелла будут справедливы следующие граничные условия:

;

;

;

.

Рассмотрим падение плоских электромагнитных волн на границу раздела двух сред. Границу раздела будем полагать бесконечно протяженной. Плоскость, проходящая через нормаль к границе раздела параллельно направлению распространения, называют плоскостью падения.

Если вектор Е перпендикулярен этой плоскости, то волна – нормально поляризованная, если параллелен, волна – параллельно поляризованная.

Любую другую ориентацию вектора Е следует рассматривать как суперпозицию .

 Падение волны с нормальной поляризацией на границу раздела двух сред изображено на рисунке 3.1.

 

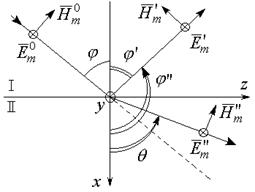
Рисунок 3.1 – Падение волны с нормальной поляризацией на границу раздела двух сред

 

Амплитуды напряженностей электрического и магнитного поля падающей, отраженной и преломленной волны определяются выражениями:

;

;

;

;

;

.

Падающая волна под углом j частично (или полностью) отражается от границы раздела сред под углом j” и частично (или полностью) проходит во вторую среду под углом θ. Амплитуды напряженности электрического поля отраженной и преломленной волны обозначены в этих выражениях как некоторые величины А и В соответственно. Можно считать, что ориентация векторов  относительно направления распространения не меняется.

Волновое сопротивление первой среды:

.

Волновое сопротивление второй среды:

.

Из граничных условий следует равенство тангенсальных составляющих: . Граничные условия должны выполняться при любых z. Это возможно только, если зависимость от z для всех трех векторов напряженности электрического поля одинаковы. Отсюда вытекают два закона:

–  угол падения равен углу отражения

;                          

– и закон Снелля

,       

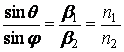где n - показатель преломления среды

.

Из закона сохранения энергии определим постоянные А и В на границе раздела (А и В амплитуды отражённой и преломлённой волн соответственно):

А = RЕ°;

В = ТЕ°,

где R - коэффициент отражения, T - коэффициент преломления (коэффициенты Френеля).

В случае нормальной поляризации:

1+R_^=T_^;  

1-R_^=Т_^.

Модуль R характеризует соотношение между амплитудами падающей и отражённой волны, а аргумент - сдвиг фаз между этими полями:

R_^ =;

T_^ =.

Вывод при параллельной поляризации аналогичен, получаем: 

R_{| |}=;

T_|| =.

При нормальном падении ЭМВ, когда j = 0, плоскость падения становится неопределённой и различие поляризаций пропадает:

R_^= - R_||=;

T_^= T_|| =.

Знак ’’минус’’ за счёт того, что R_^ и T_^ коэффициенты по электрическому полю, R_êê и T_êê – по магнитному.

Для обычных диэлектриков существует угол падения, при котором падающая волна целиком проходит во вторую среду называемый – Угол Брюстера. Это возможно в следующих случаях:

– необходимо, чтобы R_^ и R_êê равнялись 0 для любого угла падения j, что для реального диэлектрика означает , т.е. электромагнитные свойства вещества неотличимы от свойств вакуума, если он – первая среда, или (m/e = 1):  Z_С2 = Z_С1;

– для параллельной поляризации, когда :

;

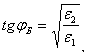– для нормальной поляризации, когда :

.

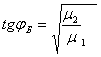От границы раздела обычных диэлектриков волна с нормальной поляризацией отражается всегда.

Волна с эллиптической поляризацией отражается от границы всегда.

Отметим условия, при которых вещество полностью отражает падающие на него электромагнитные волны:

– если  при конечном значении m, то коэффициенты отражения стремятся к предельным значениям: R_êê = - 1;  R_^ = 1. К этому предельному случаю очень близко подходят металлы, у них e имеет большую мнимую часть. Металлы – почти идеальные зеркала для электромагнитных волн.

– вещества, у которых при конечной значение e, величина магнитной проницаемости m была бы весьма велика, то для них: R_êê=1; R_^= -1. Например,÷Rç стремится к 1 для критической плазмы (e £ 0);

– в случае, когда волна распространяется из оптически плотной среды в менее плотную оптическую среду (n₂<n₁):

.

Коэффициент отражения от системы из n слоёв описывается следующим выражением:

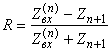
где

.

 - входной импеданс системы, причём, если угол падения не равен нулю, то следует использовать:

ç ;

ç.

при перпендикулярной и параллельной поляризациях соответственно. Углы j рассчитывают исходя из законов Снелля.

Частные случаи:

– Полуволновой слой, когда

Входной импеданс: .

Коэффициент отражения:

,

то есть полуволновой слой не оказывает никакого действия на падающую волну. В частности, если Z₁ = Z₃ , то отражение отсутствует (можно использовать как фильтр частот и направлений).

– Четвертьволновой просветляющий слой, когда

 

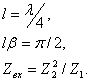
Коэффициент отражения будет равен нулю, если сопротивление: , среднегеометрическое. Используют при согласовании.

С учётом всего вышесказанного изобразим зависимость R и T от j на границе раздела (качественно) (см. рисунок 3.2).

 

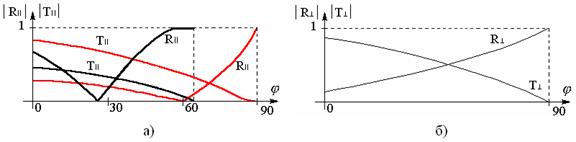
Рисунок 3.2 – Зависимости коэффициента отражения и коэффициента преломления от угла падения: а) для параллельной поляризации;

б) для нормальной поляризации

 

Зависимость от толщины слоя носит осциллирующий характер, причём если в слое есть потери, то амплитуда осцилляций стремится к постоянной величине – дальняя граница перестаёт оказывать влияние (волны затухают, не доходя до неё).

 

Лекция №4. Падение плоской электромагнитной волны на границу раздела с немагнитной хорошо проводящей средой. Линии передачи

 

Рассмотрим падение плоской электромагнитной волны из воздуха под углом j на границу раздела с немагнитной хорошо проводящей средой. Такая материальная среда имеет комплексный показатель преломления

.

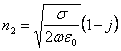По закону Снелля,

,

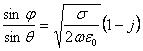откуда видно, что в хорошо проводящей среде преломленная волна распространяется под комплексным углом и поэтому является неоднородной плоской волной (см. рисунок 4.1а).

 

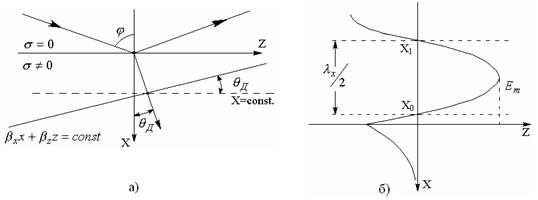
Рисунок 4.1 – Падение плоской электромагнитной волны на границу раздела сред между воздухом и металлом: а) образование неоднородной плоской волны; б) образование стоячей волны

 

У неоднородной плоской волны поверхности равной амплитуды и поверхности равной фазы не совпадают. Поверхность равной амплитуды перпендикулярна оси х, т.е. на рисунке 4.1,а показана как х=const. Поверхности равной фазы соответствует плоскость .

Во второй среде направление распространения волны образует угол q_Д с осью x. q_Д - истинный (действительный) угол:

.

Волна расположена перпендикулярно поверхностям равных фаз.

Учитывая, что для металлов:

,

тогда   То есть при любом угле падения j на поверхность хорошо проводящей среды преломлённая волна распространяется практически вдоль нормали к границе раздела.

Плоскости равных фаз и амплитуд практически совпадают – волна однородная. Волна – поперечная, причём Е и Н сдвинуты по фазе на  .

Так как амплитуда быстро убывает по экспоненте из-за большого затухания (см. рисунок 4.1,б), то поле есть практически в тонком поверхностном слое (явление поверхностного эффекта), причём во второй среде есть продольная составляющая.

По закону Ома:  J = dE, весь ток сосредоточен возле поверхности. Эффективное сечение меньше геометрического, а активное сопротивление на ВЧ может быть во много раз больше, чем по постоянному току (проводник можно выполнить в виде трубы), т.е. полагают, что ток течёт в виде бесконечно тонкого слоя.

,

где Z_СМ – поверхностное сопротивление проводника, d – глубина проникновения.

В первой среде ЭМП имеет структуру плоской волны, распространяющейся вдоль поверхности раздела (вдоль z) – направленная волна. Поверхности равных фаз – плоскости, перпендикулярные z. Амплитуды E и H зависят от x и от j. Поверхности равных амплитуд – плоскости, перпендикулярные x (см. рисунок 4.1,б).

Эта волна – неоднородная плоская волна, у которой есть продольная составляющая H_z (для волны с параллельной поляризацией – E_z).

Фазовая скорость:

 ,

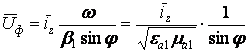то есть  больше , но меньше . Причём, чем больше j, тем меньше . Длина волны вдоль z:

.

Изменение Е и Н вдоль оси x имеет характер стоячей волны в первой среде (см. рисунок б):

.

Поперечные составляющие изменяются в фазе, а продольная сдвинута на 90°, в результате комплексный вектор Пойнтинга.

В среднем энергия распространяется только вдоль оси z, а в перпендикулярном по отношению к z направлении – только реактивный поток энергии. Это дает возможность создать направленную передачу ЭМВ, т.е. линии передач и другие устройства сверхвысоких частот (УСВЧ).

Классифицировать УСВЧ будем по функциям (см. таблица 4.1), которые они выполняют в линии передачи, независимо от того, для какой цели выполняется та или иная функция.

Линии передачи принято классифицировать по типу направляемых волн.

Типы волн:

1) поперечные или волны Т-типа – отсутствуют составляющие E и Н, направленные вдоль направления распространения энергии (T-transfers (поперечные)) Т-(ТЕМ);

2) электрические (Е- типа) Е-(ТМ);

3) магнитные (Н-типа) Н-(ТЕ);

4) смешанные (HE- типа) или гибридные.

Кроме того, все линии передачи делят на два больших класса:

1) закрытого типа – вся энергия сосредоточенна в пространстве, ограниченном металлической  оболочкой от внешней среды;

2) открытого типа - поле, строго говоря, распределено во всем пространстве (подавляющая часть вблизи), поэтому параметры этих линий подвержены влиянию окружающей среды (метеоусловия, расположенные вблизи объекты и т.д.)

 

Т а б л и ц а 4.1 – Классификация устройств СВЧ

Наименование класса устройств	Функциональные признаки
1. Отрезки регулярных линий передач	Направленная передача ЭМЭ
2. Соединительные устройства	Соединения отрезков регулярных линий, элементов или узлов
а) Неподвижные и подвижные сочленения
б) Уголки и изгибы
в) Трансформаторы и фильтры типов волн
г) Вращающиеся сочленения
3. Делители мощности	Разделение энергии, передаваемой в одном канале, на несколько каналов или сложение энергии из нескольких каналов в одном
4. Переключающие устройства (коммутаторы)	Временные соединения различных каналов
5. Развязывающие устройства	Понижение уровня мощности, проходящей из одного канала в другой, или полная развязка между каналами
а) Аттенюаторы
б) Направленные ответвители
в) Циркуляторы
г) Вентили
6.Поляризационные преобразователи	Преобразование поляризации проходящих волн
7. Фазирующие устройства	Поддержание или изменение фазы или разности фаз колебаний в линии
а) Фазовращатели
б) Секции дифференциального Фазового сдвига
8. Мостовые (гибридные) соединения	Сложение, вычитание и калиброванное разделение мощности ЭМВ в четырех канальном соединении
а) Двойные Т-образные
б) Щелевые
в) Кольцевые
г) Шлейфовые
9. Защитные устройства	Предохранение нагрузки или узла от чрезмерной мощности
10. Согласующие устройства	Согласование тракта в целом его отдельных элементов и узлов для получения заданного коэффициента отражения
11. Симметрирующие устройства	Переход от несимметричной линии или узла к симметричной линии или узлу.

 

Так как линии передачи состоят из линейных сред то для упрощения их анализа удобно представить поперечные проекции поля ,, и  через продольные проекции поля  и .

Введем два параметра:

1) продольное волновое число .

2) поперечное волновое число  т.е. .

Особенность направляемых волн: комплексная амплитуда каждой из шести проекций векторов Е и Н зависит от пространственных координат по закону:

.

Начальную фазу волны всегда можно подобрать так, чтобы - была действительной. Сторонние источники отсутствуют, и поле описывается уравнениями Максвелла. Путем несложных преобразований получаем связь между продольными и поперечными составляющими поля:

;

;

;

 .

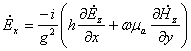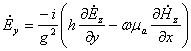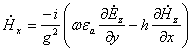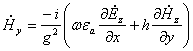Аналогично в любой другой системе координат.

Итак, достаточно найти лишь две функции для любой направляющей системы, а остальные проекции  определяют через них .

 

Лекция №5. Прямоугольный металлический волновод

 

Прямоугольный металлический волновод – это полая металлическая идеально проводящая () труба с поперечным сечением прямоугольной формы (см. рисунок 5.1).

 

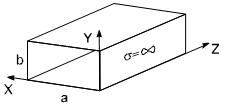
Рисунок 5.1  – Прямоугольный металлический волновод

 

Полагаем, что волновод заполнен средой с параметрами (воздух) . Внутри волновода на всем протяжении оси могут существовать волны типа – H:

Для этих волн характерно .

Функция  является решением уравнения Гельмгольца:

,

где   – поперечное волновое число.

 При решении уравнения Гельмгольца следует учитывать граничные условия (тангенциальная составляющая Е на металле обращается в 0):

     при y = 0, y = b;

     при x = 0, x = а.

Решая уравнение Гельмгольца, получаем:

.

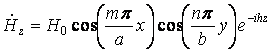Решения отличные от нуля возможны только при условии:

,

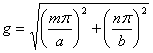где m и n – любые целые положительные числа не равные нулю одновременно (иначе силовые линии магнитного поля Н - незамкнуты и нарушается четвертое уравнение Максвелла).

Каждому значению g, (собственное значение) соответствует одно из множества решений уравнений Максвелла, которое в данном случае называют волной , где m и n – индексы волны данного типа. Физически они означают количества стоячих полуволн, возникающих внутри волновода вдоль координатных осей x и y соответственно.

Используя формулы перехода ( ), получаем выражения для остальных проекций . В результате структура ЭМП волны типа  описывается формулами:

    ;

   

   

   

    ; .

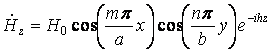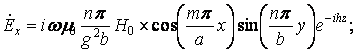
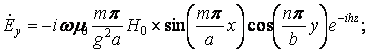
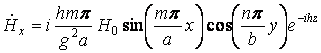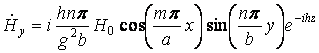Приведенная система формул содержит исчерпывающую информацию об электромагнитном поле волн типа . Картина поля периодична вдоль оси z; пространственным периодом служит длина волны в волноводе:

    .                                                                                                      (5.1)

Продольное волновое число  определяет рабочую область волновода. Если рабочая длина волны  мала настолько, что , то h-действительна, и электромагнитное колебание распространяется в виде бегущей волны постоянной амплитуды. Если увеличить  так, что , то вместо бегущих волн в волноводе могут существовать лишь не распространяющиеся колебания, амплитуда которых уменьшается по экспоненте вдоль z, а фаза во всех поперечных сечениях постоянна – волновод работает в режиме отсечки. Пограничный случай возникает на такой рабочей частоте, когда:  .

При этом h = 0 , , а длину волны генератора называют критической:

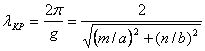.                                                                      (5.2)

Используя выражения (5.1) можно получить зависимости  от

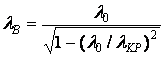 ,                                                                              (5.3)

которая называется дисперсионной характеристикой волновода. Эта характеристика найдена лишь при условии, что зависимость от z определяется exp(-ihz), и в предположении существования режима отсечки, тогда эта зависимость относится к волне любого типа в полом металлическом волноводе с любым сечением.

Изобразим дисперсионную характеристику (см. рисунок 5.2). До  область прозрачности т.к. .

     

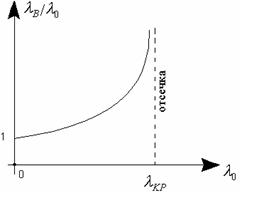
Рисунок 5.2 – Дисперсионная характеристика волновода

 

На этом участке фазовая и групповая скорость определяется выражениями:

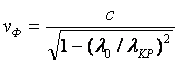;                                                                           (5.4)

.                                                                             (5.5)

При этом фазовая скорость всегда больше скорости света, а групповая скорость всегда меньше скорости света. Их произведение  на любой частоте.

Волна .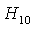

Подставив в формулу (5.2) индексы волны m = 1 и n = 0, получим критическую длину волны для волны :

.

Подставив эти индексы волны в выражения для составляющих поля волны , получим формулы описывающие структуру ЭМП волны :

    ;

    ;

    ;

    .

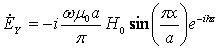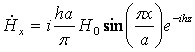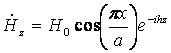Построим зависимости составляющих поля волны типа , нормировав их на максимальные значения (см. рисунок 5.3).

 Для наглядного представления пространственной структуры поля построим картину силовых линий электрического и магнитного полей (см. рисунок 5.4). В поперечном сечении - стоячая волна и эта картина смещается вдоль z с фазовой скоростью.

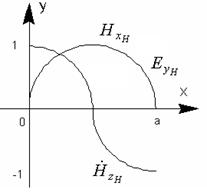
Рисунок 5.3 – Нормированные зависимости составляющих поля волны типа

 

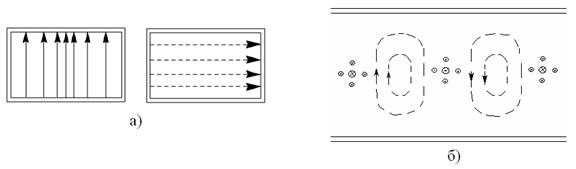
Рисунок 5.4 – Пространственная структура поля силовых линий электрического и магнитного полей: а) вид спереди; б) вид сверху

 

Для Е - концентрация в центре максимальна, а на боковых стенках – 0. Силовые линии для Н должны быть замкнуты, и зависимость от у – отсутствует. Максимумы  и  сдвинуты в пространстве по фазе на 90 ( и  совпадают). Через каждые полдлины волны направление меняется.

Т.к. Е - имеет только одну составляющую – , то вектор Е – линейно поляризован. Что касается  - в общем случае – вектор эллиптически поляризован, причем при X = 0 , а/2 , а – линейно поляризован, а при условии   вектор Н поляризован по кругу (всегда сдвинуты по фазе на 90). Это условие выполняется при  и . Эти точки расположены симметрично относительно центра (примерно а/4 от боковой стенки). 

Вектор Пойнтинга, как следует из выражений для составляющих поля, имеет две составляющие -, но в среднем поле распространяется только вдоль оси z:

   

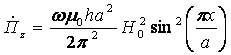
т.е. максимум энергии приходится на середину волновода.

 

Лекция №6. Волны высших типов в прямоугольном волноводе. Поверхностные токи. Энергетические характеристики

 

Построим диаграмму типов волн в прямоугольном волноводе. Из формулы (5.2) следует, что чем больше m и n, тем меньше  (см. рисунок 6.1).

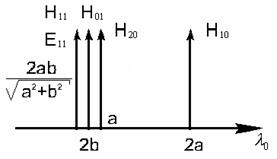
Рисунок 6.1 – Диаграмма типов волн в прямоугольном волноводе

 

На диаграмме четко разделены 3 характерные области:

1) область отсечки – -распространяющихся типов волн не существует;

2) одномодовый режим – в пределах этой области распространяется только волна типа ;

3) область многоволновости – помимо  (основной тип) по волноводу могут распространяться волны высших типов (их наличие не обязательно, но возможно – зависит от способа возбуждения и т.д.). Чем выше тип колебания, тем меньше его  отличается от предыдущей.

Теоретически волновод работает в одно-волновом режиме в двукратной полосе частот –  реально диапазон гораздо уже. При  повышается вероятность возбуждения высших типов. При  резко возрастают омические потери в стенках волновода (при  волны есть и при  для волны ).

Практически рекомендуемый диапазон:

1,05а.         

Реально волноводы используют в диапазоне 50см – 1мм (в диапазоне 6см – 1мм повсеместно). Весь этот диапазон перекрывают волноводы стандартных сечений, например, 3,6х1,8 мм, 7,2х3,4 мм, 23х10 мм, 72х34 мм, соответственно для 4мм, 8 мм, 3 см, 10 см диапазона длин волн. Их размеры задаются ГОСТом (справочник по волноводной технике). Условное графическое обозначение на схемах (см. рисунок 6.2).

 

Рисунок 6.2 – Условное графическое обозначение прямоугольного волновода

 

Волновод предпочтительнее использовать в одномодовом режиме поскольку:

1) поперечные габариты волновода оказываются минимальными;

2) структура поля волны низшего типа устойчива по отношению к введению внутрь волновода каких-либо неоднородностей (возникшие на неоднородности высшие типы – затухнут на расстоянии порядка  от неоднородности);

3) необходимость обеспечения эффективной работы оконечных устройств;

4) неравномерность АЧХ волновода в многомодовом режиме (за счет интерференции волн разных типов с различными  – вплоть до исчезновения поля на определенных частотах) (см. рисунок 6.3).

Характеристическое сопротивление волновода – отношение модулей поперечных составляющих векторов Е и Н:

.

Для всех волн Н-типа:

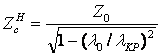.                                                                                (6.1)

 

Рисунок 6.3 – АЧХ волновода в различных режимах: 1 – одномодовый       режим; 2 – многомодовый режим

 

 

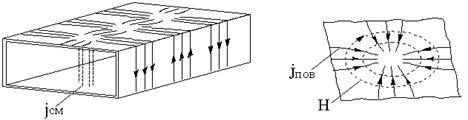
Рисунок 6.4 – Распределение токов на стенках волновода

 

Рассмотренной структуре поля волнам типа  соответствуют распределения токов на стенках волновода (см. рисунок 6.4). При построении учитываем что:, т.е. семейство линий    перпендикулярно силовым линиям магнитного поля. То есть они сдвинуты на 90 (). Линии полного тока замкнуты ( замыкается через ): .

Связь волновода с окружающим пространством происходит через щели, прорезанные в его стенках. Щель – прямоугольное отверстие, длина которого много больше ширины (см. рисунок 6.5). Если щель перерезает линии поверхностного электрического тока, то ток, протекающий к кромке, будет создавать избыток «+» зарядов. На противоположной кромке «-». Так как направление протекания тока меняется через каждые пол периода, то щель будет работать как излучатель (или наоборот).

 

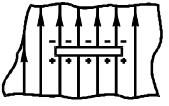
Рисунок 6.5 – Щель на стенке волновода

 

Щель эффективно излучает, если она перерезает линии поверхностного тока. Если щель прорезать наискосок, то получается комбинация продольной и поперечной составляющих электрического поля.

Построим картину поля для волн  более высоких типов. Для волн типа  картину для  следует повторить вдоль оси X (широкая стенка m раз),  например, волна (см. рисунок 6.6).

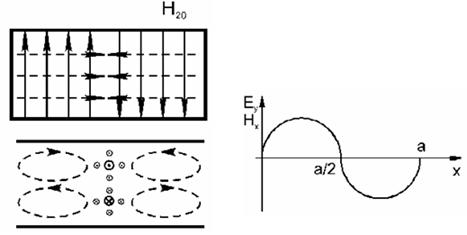
Рисунок 6.6 – Картина поля волны типа

 

Качественно картинка не изменится, если рассматривать волны типа , только вся структура развернется на 90 градусов.

Для волны типа  картинка поля представлена на рисунке 6.7а. Картина любого типа  может быть получена повторением картины  m – раз вдоль широкой стенки волновода и n – раз вдоль узкой.

Структуру электромагнитного поля волны типа  () рассматривать так подробно не будем. Методика вывода – как для , только граничные условия  при X=0, X=а. При Y=0, Y=b (краевая задача Дирихле). В результате получаем:

.

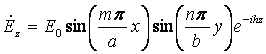Для получения ненулевого решения индексы m и n должны быть отличными от нуля. Простейший тип волны Е. Силовые линии магнитного поля образуют кольца в поперечной плоскости, а линии Е должны подходить к металлу по нормали, имеют вид скобок (см. рисунок 6.6б). Принцип получения картин для  из  как для  из .

Критическая длина волны  и ,  – определяется по тем же формулам, что и для волны Н-типа (они справедливы для всех полых волноводов). Характеристическое сопротивление волн типа :

.                                                                                 (6.2)

 

Рисунок 6.6 – Картина поля волн: а – ; б –

 

Мощность, переносимая по прямоугольному волноводу волной  определяется  формулой:

 .      

Если вместо  подставить напряжённость электрического поля пробоя сухого атмосферного воздуха , можно вычислить предельную допустимую мощность. Если работать на центральной частоте диапазона   , то с учетом трехкратного запаса прочности . Для повышения прочности используют инертные газы, газ под давлением, откачивание газа.

 

Лекция №7. Круглый металлический волновод

 

Круглый металлический волновод – это труба круглого сечения радиусом r=a из идеально проводящего металла бесконечно протяженная вдоль оси z (см. рисунок 7.1). Среда внутри – вакуум.

 

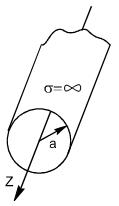
Рисунок 7.1 – Круглый металлический волновод

 

Для получения математического решения используем цилиндрическую систему координат (в дальнейшем ЦСК). При исследовании волн Н-типа следует исходить из уравнений Гельмгольца:

.

Воспользуемся выражением оператора Лапласа в ЦСК, получаем:

.                                                            (7.1)

Электрический вектор имеет касательную составляющую, которая должна обращаться в ноль на металле  (составляющая  отлична от нуля). Тогда граничное условие принимает вид:

 при r = a.

Используя метод разделения переменных, преобразуем выражения (7.1) к виду:

.                                                                       (7.2)

В математике уравнение (7.2) хорошо изучено – Уравнение Бесселя. В этом уравнение m=0, 1, 2, … – целые числа, являющиеся одним из индексов волны Н – типа.

При решении уравнения (7.2) необходимо учесть, что поле принимает конечное значение в любой точке поперечного сечения волновода, получаем:

,                                                                 (7.3)

где  - функция Бесселя (см. рисунок 7.2) или цилиндрическая функция первого рода порядка m. Роль функций Бесселя такая же, как sin и cos в декартовой системе координат, но вид значительно отличается от вида sin и cos. Функция Бесселя непериодическая, и её амплитуда уменьшается с ростом аргумента.

 

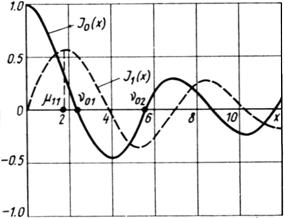
Рисунок 7.2 – Графики функции Бесселя

 

Найдем из граничных условий поперечное волновое число g:

 будет равно 0 при r = a, если   при r = a.

Количество корней этого уравнения неограниченно, корни обозначают , тогда:

,                                 

и выражение (7.3) приобретает вид

 .          

Номер корня n – второй индекс волны.

Физический смысл индексов:

m – число вариаций поля по угловой координате φ,

n – характеризует изменение поля по координате r.

Каждой паре m и n соответствует оригинальная картина поля в волноводе причем  (иначе или ). Критическая длина:

.

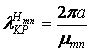Наименьшему корню производной функции Бесселя соответствует низший тип волны , тогда . Структура поля получается путем  деформации основной волны прямоугольного волновода (см. рисунок 7.3).

Правила, которые мы использовали при построении картин поля высших типов волн в прямоугольном волноводе, для круглого волновода не применимы.

 определяются выражениями (5.3), (5.4), (5.5), (6.1), (6.2).

 

Рисунок 7.3 – Структура поля волны Н₁₁ в круглом волноводе

 

Вывод выражений для волн Е типа аналогичен, но т.к. граничные условия для них  при r = a, то

,

где  корень уравнения .

Низшей среди волн Е типа будет волна  для нее , . Таблицы для  и  приведены в справочниках.

Выражение для продольной составляющей поля волн Е типа:

.

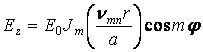Индекс m = 0 означает, что картина по  - симметрична, например, волна (см. рисунок 7.4).

 

Рисунок 7.4 – Структура поля волны  в круглом волноводе

 

определяется по (6.2).

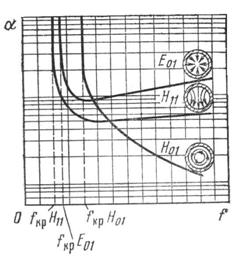
Диаграмма типов волн в круглом волноводе изображена на рисунке 7.5.

Волновод работает в одномодовом режиме (волна типа ) при , т.е. коэффициент  перекрытия - 1,3, а реально еще меньше.

 

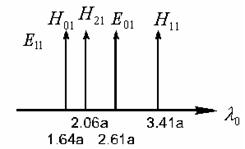
Рисунок 7.5 – Диаграмма типов волн в круглом волноводе

 

Из-за явления поляризационной неустойчивости волны типа  он в основном используется в виде коротких отрезков. Зато наличие симметричных типов (m=0) практически весьма ценно для создания вращающихся сочленений. Для этой цели обычно используют волны типов  (см. рисунки 7.4 и 7.6).

 

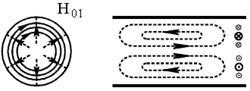
Рисунок 7.6 Структура поля волны  в круглом волноводе

 

Для волны  величина предельно допустимой мощности не намного превосходит допустимую мощность для прямоугольного волновода (отсутствие граней), а поляризация – линейная:

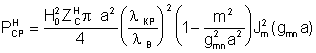.                                              (7.4)

Выражение (7.4) справедливо для любой волны Н типа, когда m1.

Если возбудить две волны  , ортогональные друг другу и сдвинутые по фазе на 90 градусов, то получим волну  с круговой поляризацией с допустимой напряженностью поля в каждой точке, но с удвоенной мощностью.

У волны Н_0n типа в круглом волноводе поверхностный ток имеет только азимутальную составляющую, и с ростом частоты потери стремятся к нулю. 

Условное графическое обозначение круглого волновода на схемах представлено на рисунке 7.7.

Рисунок 7.7 – Условное графическое обозначение круглого волновода

 

Напоследок мы отметим, что в результате дисперсии будет наблюдаться расплывание импульса из-за разницы в групповых скоростях (V_гр) для различных составляющих спектра, как в круглом волноводе, так и в прямоугольном.

Чем уже полоса сигнала, чем меньше расстояние и чем слабее зависимость затухания от частоты, тем меньше искажается комплексная огибающая. Затухание наряду с ослаблением приводит к изменению формы спектра, в частности смещение эффективной несущей в сторону тех частот, где затухание меньше. Сигнал, который при этом воспринимается, обусловлен частью спектра вблизи эффективной несущей.

 

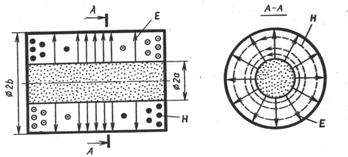
Лекция №8. Коаксиальный волновод

 

Коаксиальный волновод - это два соосных металлических цилиндра (см. рисунок 8.1), разделенных диэлектриком.

 

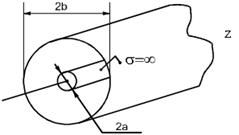
Рисунок 8.1 – Коаксиальный волновод

 

Общее для волн Т-типа . Такое возможно, если волна распространяется вдоль направляющей системы без отражений, то есть для любой составляющей решение имеет вид:

.

Коэффициент фазы и продольное волновое число при этом совпадают:

.

Для волн Т-типа (всегда имеется в виду низший тип волны):

,

т.е. волновод должен пропускать колебания любых частот вплоть до постоянного тока. Для этого в волноводе с волной Т-типа должны быть минимум два проводника разделенных слоем диэлектрика.

Волновой фронт перемещается со скоростью:

.

Волны Т-типа не имеют дисперсии.

В однородной материальной среде без зарядов третье уравнение Максвелла  будет всегда выполняться, если принять:

,

где  - вспомогательная функция, называемая скалярным электрическим потенциалом. Знак «-» выбран, чтобы вектор Е начинался на  «+» и заканчивался на «-» зарядах (принято в электротехнике).

Подставляем: .

Для коаксиальной линии (в дальнейшем КЛ) удобнее использовать ЦСК. Из-за полной симметрии волновода  двумерное уравнение Лапласа принимает вид:

 или .

Находим  с учетом граничных условий: потенциал наружного проводника равный нулю (заземлён), а внутренний равен U.

Получаем:

.

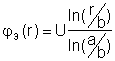Амплитуду вектора Е определим как:

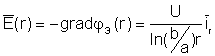,                                                                    (8.1)

то есть составляющая поля Е имеет только r-ю составляющую и для комплексной амплитуды (диэлектрик без потерь):

.

Для определения Н используем второе уравнение Максвелла:

 ,

,

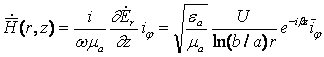т.е. Н имеет только азимутальную составляющую.

Токи на металле имеют только z составляющую и разное направление на внутренней и внешней трубе, причем их амплитуды равны:

.

Для коаксиальной линии в отличие от полых волноводов удобно ввести волновое сопротивление:

.     

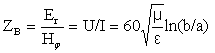Волновое сопротивление Z_В не связано с потерями энергии - это только коэффициент пропорциональности между Е и Н.

Зная Е и Н определим мощность переносимую вдоль оси волновода:

.

Структура поля в коаксиальном волноводе представлена на рисунке 8.2.

 

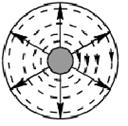
Рисунок 8.2 – Структура поля волны Т типа в коаксиальном волноводе

 

Чтобы определить высшие типы волн в коаксиальном волноводе надо решать уравнения аналогичные тем, которые решались для круглого волновода.

Как показал анализ, первым высшим типом в коаксиальной линии является, при любом внешнем радиусе b, волна близкая по структуре к волне в круглом волноводе типа  (см. рисунок 8.3).

 

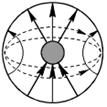
Рисунок 8.3 Структура поля волны  типа в коаксиальном волноводе

 

Соответственно определяется  как для круглого волновода, при условии a<<b:

.

Если внутренний радиус a стремится к внешнему радиусу b (), то структура напоминает волну типа  в прямоугольном волноводе, свернутом в кольцо, и определяется выражением:

.

 

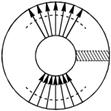
Рисунок 8.4 – Структура поля волны  типа в коаксиальном волноводе

 

Диапазон одномодовой работы (имеется в виду  - в среде заполняющей коаксиальный волновод):

.       

Имеется несколько особенностей использования коаксиального волновода.

Максимальная напряженность электрического поля, как следует из (8.1), имеет место у поверхности центрального проводника и определяется как:

,

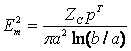т.е. при заданной мощности есть оптимальное соотношение между a и b, при котором E_m - минимальна (передача максимально допустимой мощности).

Полагая b = const, дифференцируя по a и приравнивая к нулю (нахождение экстремума) определяем: ln b/a=0.5, этому соотношению соответствует:  Ом, а соответствующее ему значение мощности:  кВт, (а - в метрах), т.к.  .

Из условия одноволновости максимальный радиус центрального проводника и

 кВт,

 - в метрах.

 Для прямоугольного волновода  кВт.

Аналогично определяется оптимальное соотношение между a и b, при котором минимальная разность потенциалов между проводниками, получим: ln b/a =1, что соответствует:

Ом.

Международная электрическая комиссия рекомендует выбирать для передачи большой мощности сопротивление при Ом.

Обычно используют гибкие коаксиальные линии - кабели их внутренний проводник делают сплошным, сплетенным из проволочек или трубчатым.

Материал - обычно медь или латунь для прочности биметаллический (стальная проволока покрытая медью).

Внешний проводник - либо труба (жесткая), либо в виде оплетки из проволоки или ленты (гибкая).

Изолирующая часть на СВЧ выполняется обычно из фторопласта-4, полиэтилена и т.д., при этом она может быть не сплошной, а из шайб.

Использование диэлектрического заполнения приводит к тому, что  резко уменьшается:

а) за счет теплового пробоя;

б) в небольших промежутках между диэлектриком и проводником есть воздух (всегда), в нем Е в  раз больше, чем в диэлектрике и

.

Как правило, коаксиальный волновод используют для передачи небольших мощностей (до сотен Вт) в диапазоне от f=0 до 10 ГГц (из-за возникновения высших типов волн). Стандартные варианты волнового сопротивления Z_В для различных конструкций 50, 75, 100, 150, 200 Ом.

 

Лекция №9. Полосковые линии передачи и диэлектрический волновод

 

В полосковых линиях передач часто в качестве подложек используют диэлектрик на основе оксида алюминия - поликор (), лейкосапфир (), кроме того, любые диэлектрики с низкими потерями (7..16 иногда до 10000-керамика).

Как видно из таблицы 9.1, где показаны сравнительные конструкции полосковых линий (в дальнейшем ПЛ), они относятся к направляющим системам открытого типа. Наличие нескольких изолированных проводников означает, что fкр=0, т.е. волна в ПЛ должна соответствовать волне Т-типа.

Строгий анализ достаточно сложный, но качественно структуру можно получить, деформируя коаксиальную линию (см. рисунок 9.1,а).

 

Рисунок 9.1 – Структура поля волны в полосковой линии:

 а) Т типа;  б) типа Н₂₀

 

 

Т а б л и ц а 9.1 – Сравнение конструкций полосковых линий

Сравнение конструкций полосковых линий (а - достоинства, б - недостатки)
Симметричная волновая линия: а) малые габариты; б) относительно большие потери и масса.	Высокодобротная линия: а) низкие потери, высокое волновое сопротивление; б) требует крепления, сравнительно большие габариты.
Несимметричная полосковая линия (2...3): а) малые габариты и масса; б)большие потери, отсутствие экрана.	Микрополосковая линия (): а) малые габариты и масса; б) сравнительно большие потери, нет экрана.
Щелевая линия: а) наличие эллиптической поляризации, простая конструкция, высокое сопротивление; б) большие потери, нет экрана.	Копланарная линия: а) наличие эллиптической поляризации, простая конструкция, высокое сопротивление; б) большие потери, нет экрана.
Линия с подвешенной подложкой: а) низкие потери, малый разброс параметров, высокое сопротивление; б) требует крепление, сравнительно большие габариты.

 

Из-за неоднородности по сечению диэлектрического заполнения ЭМП имеет все 6 составляющих, а, следовательно,  зависит от частоты , т.е. дисперсия тем заметнее, чем больше e. Но при условии, что a>>b, c>>b, c>>a, практически вся энергия сосредоточена внутри ПЛ и продольными составляющими можно пренебречь – волна квази - Т типа.

Первый высший тип волны в ПЛ Н₂₀, представлен на рисунке 9.1,б, на длине немного превышающей размер а, укладывается одна полуволна электрического поля ЭМВ, т.е. .

Волновое сопротивление в симметричной ПЛ:

,

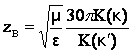где К(к) - полные эллиптические интегралы первого рода, ,  .

Для несимметричной ПЛ:

.

Обе формулы получены в предположении, что толщина центрального проводника много меньше b. Волновое сопротивление несимметричной ПЛ несколько больше симметричной при одинаковом соотношении a/b.

В ПЛ можно передавать мощности того же порядка, что и в коаксиальной линии. Для увеличения электрической прочности края центрального проводника закругляют.

Диэлектрические волноводы – это одно из наиболее перспективных направлений развития линий передачи электромагнитных сигналов в настоящее время  (в основном в виде  волоконного световода).

Диэлектрический волновод – это бесконечно длинный диэлектрический цилиндр радиуса а, выполненный из диэлектрика с параметрами ε_а, μ₀ (среда-1), расположенный в среде с параметрами ε₀, μ₀ (среда-2).

Продольные составляющие волновых уравнений в цилиндрической системе координат запишутся в виде: 

;

;

где

;

.

Общее решение первого уравнения - линейная комбинация функций Бесселя и Неймана, однако, напряженность в любой точке внутри диэлектрического цилиндра (в том числе и в точке, где r=0) должна быть конечной. Вне цилиндра, где структура должна соответствовать структуре поверхностной волны, амплитуды полей должны убывать по экспоненте при удалении от границы раздела. Этому требованию удовлетворяют функции Ханкеля второго рода от чисто мнимого аргумента.

При решении необходимо учесть, что продольное число h одинаково и в первой и во второй среде, а также что на границе раздела двух диэлектриков r=a, тангенсальные составляющие ЭМП должны быть непрерывны. Получаем трансцендентное уравнение:

  

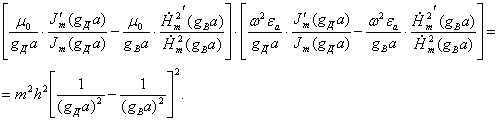
Это уравнение служит для определения неизвестного коэффициента h (численно или графически).

Детальный анализ позволяет заключить следующее:

1) В диэлектрическом волноводе может существовать бесконечно большое число различных типов волн, имеющих различный характер изменения поля по координатам  r, .

2) В диэлектрическом волноводе невозможно раздельное существование несимметричных волн Е и Н. Оба этих типа образуют единую смешанную волну и распространяются совместно.

Симметричные волны  могут существовать в диэлектрическом волноводе независимо друг от друга.

3) Каждый тип волны имеет свою критическую частоту, которая находится из условия:

 .

Низшим типом волны является волна (см. рисунок 9.2). Эта волна не имеет критической  частоты, т.е. может распространяться вдоль диэлектрического стержня на всех частотах и при любом диаметре стержня.

4) Величина фазовой скорости волны в диэлектрическом волноводе лежит между величиной фазовой  скорости  волны Т-типа, распространяющейся в среде окружающей волновод, и величиной  этой волны в среде с параметрами ε_а, μ₀.

 

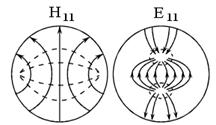
Рисунок 9.2 – Структура поля волны типа в диэлектрическом волноводе

                                                      

5) Энергия волны распространяется внутри и вне диэлектрического стержня. Чем больше радиус стержня по сравнению с длиной волны ЭМ колебания и чем больше соотношение ε_а/ε₀, тем большая часть энергии распространяется внутри диэлектрического стержня. При приближении  энергия внутри стержня стремится к нулю.

У волны  энергия внутри стержня стремится к нулю при .

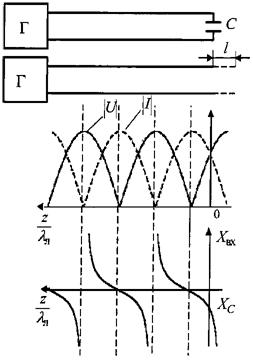
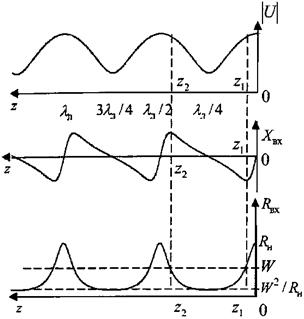
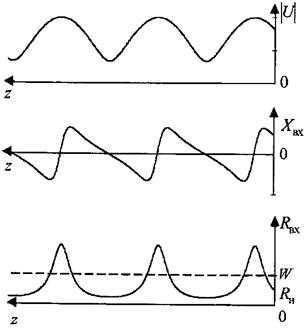
На практике диэлектрические волноводы используются в УКВ диапазоне в качестве элементов  конструкции антенн и в более коротковолновом диапазоне как линии передачи.

Для возбуждения волн в диэлектрическом стержне можно использовать схему, изображенную на рисунке 9.3. Скосы служат для уменьшения отражения.

 

Рисунок 9.3 – Схема возбуждения диэлектрического стержня

 

Линии передачи (световоды) представляют собой тонкую (несколько микрометров) нить из особо чистого кварца или искусственного полимера. Погонные потери в такой линии не более 5 дБ/км (у некоторых затухание не более 0,1 дБ/км.). Для сравнения, в прямоугольном волноводе на частоте 10ГГц  затухания примерно 0.02 дБ/м.

Несущая частота в оптическом диапазоне очень высока и полоса пропускания очень широкая - скорость передачи информации до тысяч Мбит/с.

На практике используют световоды с различной геометрией поперечного сечения и различными профилями показателя преломления (1-ступенчатый, 2-градиентный, реальные профили изрезаны (чисто технологически)).

 

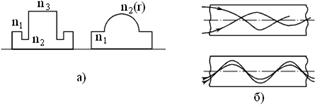
Рисунок 9.4 – Профили показателя преломления в световодах (а) и распространение волн в них (б)

 

Наиболее оптимальный закон для градиентного - параболический: 

,

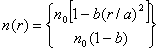первая формула при , вторая при .

При таком законе все меридиональные лучи лежат в плоскостях содержащих ось z, входящие в волокно в одной точке под разными углами, пересекают ось волновода в одной и той же точке, то же самое относительно параллельно входящих лучах в разных точках (см. рисунок 9.4,б):

Т.е. различные моды имеют одинаковое время распространения - отсутствует межмодовая дисперсия. Моды - сигналы входящие под разными углами.

На самом деле есть не только меридиональные лучи, но и косые (винтовые) и т.д. - для них дисперсия есть.

Лекция №10. Распространение ЭМВ в линиях конечной длины

 

Обрыв линии передачи, подключение нагрузки и т. п. – эквивалентно изменению граничных условий.

На конце линии образуется новая структура поля, отвечающая новым граничным условиям. Это изменение трактуют как появление в линии, кроме основной (падающей) волны, волны, распространяющейся от конца к началу (отраженной), причем, если линия работает в одномодовом режиме, то структура отраженной волны не отличается от падающей волны.

Коэффициент отражения в любом  сечении линии:

   .

Наличие отраженной волны приводит к изменению входного сопротивления отрезка линии. Рассмотрим несколько частных случаев:

1) Холостой ход  Zн=¥ (режим стоячих волн).

Используем интегральные характеристики U и I, но можно использовать и универсальные – дифференциальные характеристики E и H.

Чтобы не учитывать высшие типы волн, следует  рассматривать поле в линии на расстоянии нескольких длин волн в линии.

Эпюры напряжения, тока и сопротивления в линии с холостым ходом представлены на рисунке 10.1, входное сопротивление линии в режиме холостого хода описывается формулой

.

2) Короткое замыкание Zн=0 (режим стоячих волн). Отличается только сдвигом кривых для U и I на l/4 (см. рисунок 10.2). Входное сопротивление линии в режиме короткого замыкания описывается формулой

 

Рисунок 10.1 – Эпюры напряжения, тока и сопротивления в линии с холостым ходом	Рисунок 10.2 – Эпюры напряжения, тока и сопротивления в короткозамкнутой линии

3. Произвольная реактивная нагрузка.

При реактивной нагрузке, активная мощность в ней выделяется и модуль /R/=1. Задачу проще всего решать, заменяя сосредоточенную C (см. рисунок 10.3) или L (см. рисунок 10.4) на отрезок линии, т.е:

 ,

замена на отрезок с холостым ходом или

ctg hl=-X_L/Zв ,

замена на отрезок с коротким замыканием .

 

Рисунок 10.3 – Эпюры напряжения, тока и сопротивления в линии с емкостной нагрузкой	Рисунок 10.4 – Эпюры напряжения, тока и сопротивления в линии с индуктивной нагрузкой

 

Рисунок 10.5 – Эпюры напряжения в линии с активной нагрузкой

 

 

4) Чисто активная нагрузка (Zн=Rн).

Возможны два случая активной нагрузки: 

1. Rн>Zв,   КБВ=Zв/Rн.

2. Rн<Zв,  КБВ=Rн/Zв.

В обоих случаях режим работы линии – смешанный (см. рисунок 10.5).

Амплитуда отраженной волны меньше падающей (часть энергии потребляется нагрузкой). Эпюры напряжения и входного сопротивления в линии, нагруженной на активное сопротивление, показаны на рисунке 10.6.

 

Рисунок 10.6 – Эпюры напряжения и входного сопротивления в линии, нагруженной на активное сопротивление	Рисунок 10.7 – Эпюры напряжения и входного сопротивления в линии, нагруженной на комплексное сопротивление

 

5)  Согласованный режим (Rн=Zв=W).

КБВ=1, R=0,  .  При этом отношение Е к Н в любом сечении – постоянно. Фаза меняется по линейному закону.

Режим наиболее желательный (бегущая волна), Zвх не зависит от частоты и Zвх=Zв=W.

Теоретически полное согласование возможно, но на практике обычно КБВ»0,9¸0,95 и, следовательно, входное сопротивление – комплексная величина. Если рассмотреть эпюры напряжения и входного сопротивления в линии в согласованном режиме, то чем КБВ ближе к единице, тем меньше разница между максимальным и минимальным значением величин, изображенных на рисунке 10.6, т.е. графики приближаются к прямой линии.

6) КОМПЛЕКСНАЯ НАГРУЗКА.

В этом случае имеет место режим смешанных волн, отличие от  графиков, изображенных на рисунке 10.6, в дополнительном фазовом сдвиге на нагрузке, рисунок 10.7.

КБВ рассчитывают  по формуле:

,

где   .

А расстояние от нагрузки до ближайшего максимума равно l:

 .

7) Линия с потерями.

За счет потерь амплитуда уменьшается при удалении от генератора, рисунок 10.8:

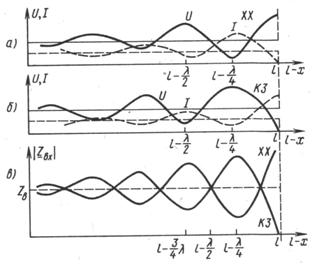
Рисунок 10.8 – Эпюры: а) напряжения, тока в линии с потерями в режиме холостого хода; б) напряжения, тока в линии с потерями в режиме короткого замыкания; в) входного сопротивления в линии с потерями в режимах холостого хода и короткого замыкания

 

Важной характеристикой линии является её КПД. КПД – отношение активной мощности Р_Н, выделяемой в нагрузке к активной мощности, подводимой к входу линии:

h=Р_Н/Р.

Если в линии режим бегущей волны (R_Н=Z_В), то Е и Н связаны через сопротивление линии и

h=е^-2az»1-2az.

Если нагрузка не согласована, надо учитывать отражение:

.

После подставки:

h=е^-2az(1-R²).

Из рисунка 10.9 видно, там, где потери малы, h для различных КБВ почти совпадают (az<0,1).

В диапазоне КВ особой степени согласования не надо и допустимы значения КБВ≥0,3 ¸0,5. В диапазоне СВЧ  КБВ³0,8¸0,9.

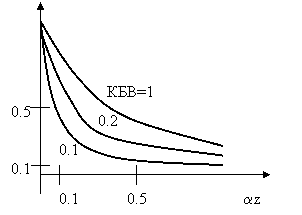
Рисунок 10.9 – Зависимость КПД линии от длины при различных значениях КБВ

 

Лекция №11. Потери в линиях передачи электромагнитной энергии.  Свободные колебания в объемных резонаторах

 

Источники потерь:

1) конечное значение проводимости металла (есть составляющая Е касательная к металлу, а следовательно, существует средний за период поток мощности, направленный в глубь металла);

2) небольшие токи проводимости в диэлектрике, заполняющем волновод (как правило, небольшие потери по сравнению с потерями в металле);

3) потери на излучение в  окружающее пространство (если линия спроектирована без ошибок, эти потери не велики).

Для учета потерь следует предположить, что продольное волноводное число – комплексная величина:

,

,

где погонное затухание линии передачи, выраженное в Нп/м. В технике чаще пользуются величиной выраженной  в дБ/м.

,

причем  .

В любом фиксированном сечении произвольной линии средняя мощность, переносимая волной Р₀ – в точке z = 0:

.

Если известны частота сигнала, проводимость стенок и структура поля в волноводе, то погонное затухание определяется формулой:

 .               

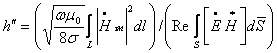Для коаксиального волновода получаем:

.      

 

Рисунок 10.1 – К определению погонного затухания Т-волны в коаксиальном волноводе

 

В прямоугольном волноводе с воздушным заполнением для основного типа волны Н₁₀:

.

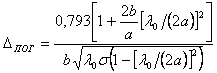В круглом волноводе для основного типа волны Н₁₁:

.

 

Рисунок 10.2 – Зависимость затухания от частоты для круглого волновода	Рисунок 10.3 – График затухания в полосковой линии

 

Из графиков для круглого волновода (см. рисунок 10.2) видно, что диапазон одномодовой работы и диапазон минимального затухания не совпадают. При частоте приближающейся к  потери растут за счет уменьшения толщины поверхностного слоя (повышения сопротивления). В прямоугольном волноводе графики выглядят аналогично. Однако для круглого волновода есть исключения волны типа H_om, для этих волн потери неограниченно убывают при увеличении частоты (объясняется это тем, что есть только азимутальные составляющие тока, которые убывают по амплитуде с ростом частоты). При этом существенный выигрыш можно получить при отношении , тогда получаемое затухание 12 дБ/км. Ограничение для других типов волн делают в виде колец или спирали, наносят на металл поглощающую пленку и т.д.

С точки зрения затухания полосковая линия подобна коаксиальной линии. В случае сплошного диэлектрического заполнения затухание в полосковой линии соизмеримо с коаксиальной линией, диаметр внешней оплетки которой равен 2b. Главное отличие от коаксиальной линии в том, что здесь нет оптимального с точки зрения потерь соотношения между размерами проводников (см. рисунок 10.3).

Выбор типа линии и размеров поперечного сечения ведется исходя из заданного значения КПД, максимальной пропускаемой мощности Р_ДОП, работы на единственном типе колебания (одномодовый режим), в заданном диапазоне частот f_MAX-f_MIN, при минимуме вносимых искажений. Линия должна обладать необходимой степенью экранировки (ЭМС), и разумеются конструктивно – экономические факторы (габариты, вес, стоимость и т.д.).

Свободные колебания в объемных резонаторах.

Объемным резонатором называется часть пространства, ограниченная металлической стенкой. В таком объёме могут происходить ЭМ колебания, поэтому на СВЧ он имеет свойства колебательного контура с высокой добротностью:

.

Т.к. резонаторы используют как элементы сложных устройств, соединяемых различными линиями передачи, то обычно их выполняют в виде закороченных  отрезков линий передач, соответственно резонаторы могут быть открытого и закрытого типа.

Из уравнений Максвелла следует выражение для частоты ЭМ колебаний:

         

 То есть резонансная частота зависит от структуры поля в резонаторе, его формы и размера. Причём таких частот может быть бесконечное число.  Колебание, резонансная частота которого минимальна, называется низшим. Могут существовать вырожденные волны.

Добротность резонаторов определяется формулой:  .

Общие потери в резонаторе:

ΔW=ΔW_мет + ΔW_д +ΔW_∑ +ΔW_вн,

где ΔW_вн – энергия, отдаваемая во внешние устройства, ΔW_мет – энергия потерь на металле, ΔW_∑ - энергия, теряемая за счет воздействия радиации, ΔW_д – энергия, теряемая в диэлектрике.

Если нет у резонатора внешнего устройства, которому он отдает энергию, то добротность ненагруженного  резонатора называется – собственной  добротностью:

 

и

.

Энергия потерь в металлических оболочках определяется: 

и

.

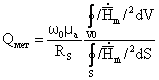  Структуры полей определяются числом вариаций не только по поперечным координатам, но и по продольной координате. При этом чтобы различать типы волн используют третий индекс: Н_mnp,  E_mnp,  T_p,  HЕ_mnp. Р – число стоячих полуволн вдоль продольной оси, при этом для  Е  , для остальных .

Например, в прямоугольном резонаторе один из основных типов Н₁₀₁ (см. рисунок 10.4), причём эта структура не отличается от структуры Е₁₁₀, эти два колебания – вырожденные.

 

Рисунок 10.4 – Волна типа Н101 в прямоугольном резонаторе	Рисунок 10.5 – Волна типа Е010 в цилиндрическом резонаторе

 

Резонансная длина волны в прямоугольном резонаторе для волн Е и Н

,

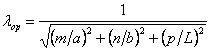добротность этого колебания (с учетом металла):

.

На практике добротность в сантиметровом диапазоне достигает нескольких десятков тысяч.

В цилиндрическом резонаторе резонансная длина волны:

, 

.

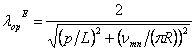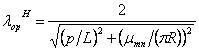Наиболее часто на практике используют Е₀₁₀,Н₁₁₁,Н₀₁₁. Особенность колебания Е₀₁₀ состоит в том, что резонансная длина волны не зависит от L, поэтому можно делать малогабаритные резонаторы, его добротность

.

 Использование колебания Н₀₁₁ обусловлено тем, что у этого колебания очень малые потери, что соответствует добротности сотни тысяч (реально несколько меньше), например, при . Что позволяет использовать его в качестве высокочастотного волномера.

 

 

У коаксиального резонатора (см. рисунок 10.6):

,

.

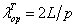Для уменьшения геометрической длины коаксиального резонатора между центральным проводником и короткозамкнутой пластиной оставляют зазор. Ширина зазора выбирается меньше четверти длины волны, чтобы концентрация Е в зазоре была максимальна. Резонансной будет частота, на которой  и определяется из равенства:

,

где Z_B-волновое сопротивление коаксиальной линии.

Добротность у такого резонатора меньше, чем у обычного резонатора.

Когда требуется взаимодействие электромагнитного колебания с электронным потоком, используется тороидальный квазистационарный резонатор (рисунок 10.7) или магниронный резонатор (рисунок 10.8).

Характерная особенность квазистационарных резонаторов – четко выраженное разделение электрических и магнитных полей. Это позволяет рассматривать такие резонаторы как колебательные контуры с сосредоточенными параметрами: .

 

Рисунок 10.8 – Магнитронный резонатор	Рисунок 10.9 – Резонатор бегущей волны

 

Для тороидального квазистационарного резонатора:

,

.

Для ячейки магнитронного резонатора:

.

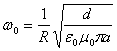Существуют резонаторы (рисунок 10.9), в которых явление резонанса имеет место в режиме бегущей волны (свёрнутая в кольцо линия передачи её длина должна быть кратна числу ).

Добротность нагруженного резонатора на практике проще определить из формулы: .

Время затухания колебаний: t (за это время энергия уменьшится в 100 раз).

  

Лекция №12. Согласование линий передачи

 

Согласование состоит в полной или частичной компенсации отраженной волны. Независимо от характера и типа согласующего устройства (СУ), а также полосы частот, где оно обеспечено, схема согласования имеет вид изображенный на рисунке 12.1.

 

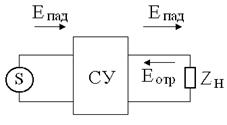
Рисунок 12.1 – Схема согласования

 

Назначение СУ - устранить отраженную волну.

Существует два метода согласования:

1) Поглощение отраженной волны в СУ. При этом падающая волна проходит без потерь (или с малыми потерями).

2) Создают в линии еще одну волну, амплитуда которой равна по величине амплитуде волны, отраженной от нагрузки и сдвинута по фазе на 180⁰.

В основе первого метода лежит использование мостовых схем или независимых устройств. Эти устройства поглощают отраженную волну независимо от вида нагрузки и, так как эти устройства широкополосны, то решается проблема широкополосного согласования произвольных нагрузок. Недостаток – относительно большие потери падающей волны и полная потеря энергии отраженной волны – низкий КПД.

СУ второго типа это, как правило, набор реактивных элементов практически не вносящих потери, эти устройства многократно, переотражая отраженную волну, обеспечивают ее поглощение нагрузкой (т.е. СУ надо помещать как можно ближе к нагрузке, чтобы избежать потери в линии). Недостаток – ограниченная полоса пропускания – тем уже, чем жестче требования к КСВ. Ограничений по полосе нет, только если сопротивление нагрузки чисто активное.

Узкополосное согласование.

Режим бегущей волны создается только на одной фиксированной частоте.

Методика:

1) Проводимость нагрузки:  Y_Н=G_Н+iB_Н , где  G_Н¹0, с помощью отрезка линии длиной l трансформируют в  Y₁=G_В1+iB₁ , активная часть равна волновой проводимости линии.

2) Реактивная часть проводимости Y₁ компенсируется включением равной по величине и обратной по знаку проводимости.

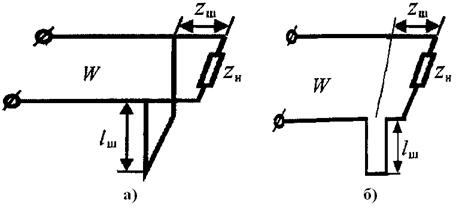
Рисунок 12.2 – Включение шлейфа: а) параллельное; б) последовательное

 

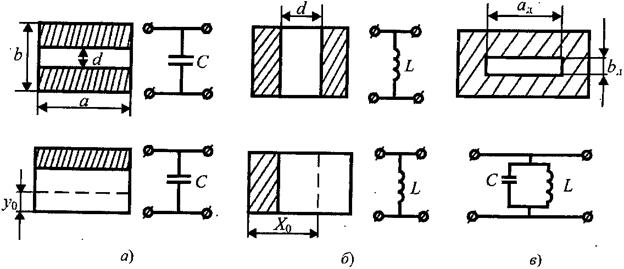
Рисунок 12.3 – Диафрагмы: а) емкостная; б) индуктивная;

 в) резонансная

 

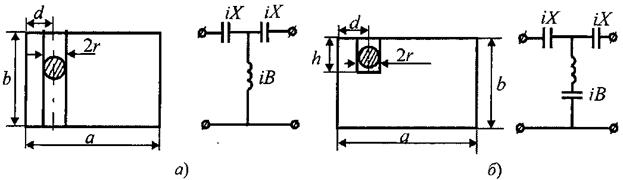
Рисунок 12.4 – Штыри: а) индуктивный; б) резонансный

 

Узкополосное согласование в линиях с волнами Т–типа чаще всего выполнятся с помощью шлейфов (см. рисунок 12.2), который имеет реактивное сопротивление. В полых волноводах вместо шлейфа могут использоваться диафрагмы (см. рисунок 12.3) или штыри (см. рисунок 12.4).

Место включения шлейфа выбирается так, чтобы Z_BX в месте разрыва активное и равно Z_B.

Если использовать реактивные элементы нежелательно, то применяют четвертьволновой трансформатор:  L_тр=l_Bтр/4. Место включения трансформатора выбирают так, чтобы оно приходилось или в узел или в пучность напряжённости электрического поля, т.е. было чисто активным (см. рисунок 12.5).

Чтобы согласование было идеальным, надо в минимуме: , в максимуме  .

Если Z_Н – чисто активное, то трансформатор можно подключать прямо к нагрузке.

КБВ (КСВ) имеется в виду тот, что был до согласования.

 

Рисунок 12.5 – Эпюры напряжений в линии: а) с комплексной нагрузкой; б) с комплексной нагрузкой и трансформатором W_тр>W_л; в) с комплексной нагрузкой и трансформатором W_тр<W_л

 

Широкополосное согласование.

Если согласование надо обеспечить в полосе >10% или при использовании сигналов с широким спектром, надо применять другие методики. Следует добиваться, чтобы рассогласование в заданной полосе не превышало установленной величины.

Основные принципы:

1) частотные компенсаторы;

2) ступенчатые трансформаторы;

3) неоднородные линии (плавные переходы).

Принцип частотной компенсации состоит во взаимной компенсации частотных изменений сопротивления нагрузки и согласующих элементов (см. рисунок 12.6). Подбирается необходимый закон частотного изменения сопротивления согласующих элементов и реализуется подбором длины и W шлейфов, и трансформаторов   -В_Н+В_ШЛ.

Наклон кривой В_ШЛ подобран примерно равным наклону кривой В_Н с обратным законом в пределах большей части полосы частот. В результате суммарная проводимость (реактивная) уменьшается и меньше меняется с частотой. Наклон кривой В_ШЛ прямо пропорционален длине шлейфа и обратно пропорционален его волновому сопротивлению W_ШЛ.

 

Рисунок 12.6 – Частотная компенсация: а) схема включения;

б) зависимость активной проводимости нагрузки от частоты; в) зависимости реактивных проводимостей нагрузки, шлейфа и их суммы от частоты

 

 - среднее значение тангенса угла наклона кривой В_шл.

f_р – резонансная частота.

,   где  n = 1,2,3…

Подбирая W и n можно регулировать ширину полосы рабочих частот.

Чем больше n, тем выше добротность контура и  полоса рабочих частот уже, чем больше W, тем полоса рабочих частот шире.

Рассмотренная схема обеспечивает компенсацию реактивности, а если надо компенсировать активную часть, придется использовать трансформатор. 

 

Рисунок 12.7 – Переходы: а) ступенчатый трансформатор; б) экспоненциальный трансформатор

 

Ступенчатые трансформаторы используют для согласования линии с активной нагрузкой или с нагрузкой с небольшим реактивным сопротивлением. Ступенчатые трансформаторы представляют собой каскадное соединение n отрезков линии (ступенек), имеющих различные сопротивления W (см. рисунок 12.7,а).

Число ступенек, их длина и волновые сопротивления зависят от выбора вида полинома и неравномерности АЧХ в полосе пропускания.

Наиболее часто используют трансформаторы с Чебышевской и с максимально плоской частотной характеристикой.

Строгий расчет известен только для n≤4, в остальных случаях – приближенный. В справочной литературе есть таблицы готовых величин для расчета разных типов трансформаторов.

Плавные переходы практически предельный случай ступенчатых переходов (см. рисунок 12.7,б).

W₂=W₀·exp(bl),

где  W₂ – сопротивление, включенное на конце линии,  b – постоянная характеризующая степень изменения параметров вдоль линии.

Сравнение ступенчатых и плавных переходов:

а) при равных условиях длина ступенчатого перехода заметно короче;

б) полоса пропускания плавного перехода заметно шире (в сторону ВЧ);

в) при высоких требованиях к электрической прочности, плавный  переход предпочтительнее. 

 

Список литературы 

1. Пименов Ю.В. и др. Техническая электродинамика. - М.:Связь, 2000.

2. Петров Б.М. и др. Электродинамика и распространение радиоволн: Учебник для вузов - М.: Горячая линия - Телеком, 2003.

3. Баскаков С.И. Электродинамика и распространение радиоволн. – М.: Высш.школа, 1992.

4. Электродинамика и распространение радиоволн. Сборник задач. Под. ред. Баскакова С.И. – М.: Высш.школа, 1981.

5. Фальковский О.И. Техническая электродинамика. – М.: Связь,1978.

6. Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. - М.: Наука, 1989.

7. Федоров Н.Н. Основы электродинамики. - М.: Высшая школа, 1980.

8. Унгер Г.Г. Оптическая связь. - М.: Связь, 1979. 

 

 Сводный план 2009 г., поз. 203