АЛМАТИНСКИЙ ИНСТИТУТ
ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра телекоммуникационных
систем
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Программа,
методические указания и
контрольные задания
для
студентов специальности
050719 – Радиотехника, электроника и
телекоммуникации
заочной
(дистанционной) формы обучения
Алматы 2006
СОСТАВИТЕЛЬ: Л. И. Сарженко. Теория электрической
связи. Программа, методические указания и контрольные задания
(для студентов специальности 050719 – Радиотехника, электроника и
телекоммуникации заочной (дистанционной) формы обучения). – Алматы: АИЭС, 2006
-40 с.
Данная
разработка предназначена для студентов заочной (дистанционной) формы
обучения специальности 050719 –
Радиотехника, электроника и телекоммуникации.
В
методических указаниях к изучению курса приводятся программа дисциплины с
контрольными вопросами по разделам, задания и исходные данные для вариантов
контрольной работы, методические указания по выполнению контрольной работы,
требования к ее содержанию и оформлению, список рекомендуемой литературы.
Ил. 4, табл. 11, библиогр
-12 назв.
Рецензент: канд. техн. наук, доц. С.В. Коньшин
Печатается по дополнительному плану издания
Алматинского института энергетики и связи
на 2006г.
©
Алматинский институт энергетики и связи, 2006г.
Введение
Курс
«Теория электрической связи» является обязательным предметом для студентов
высших учебных заведений и включается в учебные планы в качестве базовой
дисциплины.
Цель курса -
изучение основных закономерностей передачи информации в телекоммуникационных
системах. Кроме того, студентов необходимо ознакомить с основными концепциями,
моделями и принципами построения телекоммуникационных систем и сетей,
современными тенденциями их развития и стандартами в области телекоммуникаций.
Задачи
курса - в результате изучения дисциплины у студентов должны сформироваться
знания, навыки и умения, позволяющие самостоятельно проводить математический
анализ физических процессов в аналоговых и цифровых устройствах формирования,
преобразования и обработки сигналов, оценивать реальные и предельные
возможности пропускной способности и помехоустойчивости телекоммуникационных
систем.
В курсе
ТЭС принят единый методологический подход к анализу и синтезу современных
телекоммуникационных систем и устройств на основе вероятностных моделей
сообщений, сигналов, помех и каналов в системах связи. В свою очередь теоретической
базой курса ТЭС являются основные сведения из дисциплин естественно-научного и
профессионального циклов: математики, информатики, физики, дискретной
математики, теории вероятностей и математической статистики, основ теории
цепей, электроники, основ схемотехники. Предусмотренные программой ТЭС знания
являются не только базой для последующего изучения специальных дисциплин
базового и профилирующего циклов, но имеют также самостоятельное значение для
формирования дипломированных специалистов направлений телекоммуникации.
В рамках
учебного плана в 4 кредита из 180 часов, выделенных на изучение дисциплины ТЭС,
аудиторные занятия составляют 46 часов (лекции – 20 час, практические занятия –
12 час, лабораторные занятия – 14 час). Занятия с элементами дистанционного
обучения-22часа.
Оставшиеся 112 часов выделены на самостоятельные занятия студентов.
Предусмотрено выполнение и защита 1 контрольной, 1 курсовой, лабораторных работ
и сдача экзамена по курсу.
Таким
образом, работа студента по изучению курса складывается главным образом из
самостоятельной работы над литературой, рекомендуемой в методических указаниях,
а также из усвоения материала на лекциях и практических занятиях. Существенную
помощь в изучении дисциплины оказывают студенту лабораторные занятия и
самостоятельное выполнение контрольной
и курсовой работ, в том числе и под
руководством преподавателя.
В
программе дисциплины «Теория электрической связи» приводится литература, рекомендуемая для изучения разделов курса. Для
каждого раздела приводятся данные по основной литературе и той дополнительной
литературе, где вопросы раздела изложены более полно и ясно или изложение этого
вопроса отсутствует в основной литературе. В списке литературы приведен
перечень дополнительных учебников, которые помогут в изучении вопросов
дисциплины, если отсутствуют основные учебники из списка литературы.
Для
самопроверки усвоения учебного материала в каждом разделе приведены контрольные
вопросы, ответы на которые помогут в усвоении материала.
Если у
студента при изучении курса возникли затруднения (неясности по изучаемому
материалу, по решению задач контрольной и курсовой работ), он может обратиться
на кафедру телекоммуникационных систем АИЭС для получения письменной или устной
консультации, в том числе с использованием электронных технологий.
Студент
допускается к экзамену только после выполнения и защиты всех лабораторных работ
(получение допуска по лабораторным работам), защиты контрольной и курсовой работ.
Защита
контрольной и курсовой работ проводится
до экзамена в назначенное преподавателем время. Без защищенных контрольной и
курсовой работ студент к экзамену не
допускается.
Перед экзаменом проводится тестирование. Студент, набравший проходной балл, допускается к экзамену.
В
экзаменационных билетах содержатся два теоретических вопроса и задача, типа
сокращенных и упрощенных задач
контрольного задания, или задач, решаемых на практических занятиях и
приведенных в задачниках [3,7]. Поэтому на решение задач по каждому разделу
курса следует обратить особое внимание. Студентам настоятельно рекомендуется
при изучении курса решать или разбирать решение задач по каждому разделу. Эти
задачи содержатся в литературе [3,7], также в качестве примеров в каждом
разделе учебников [1,2,4,6,8,9,10].
На
экзамене по ТЭС может быть проведен устный опрос по курсовой или контрольной
работам. Студенты должны быть готовы дать ответ по выполненным в контрольной
или курсовой работах заданиям.
Алматинский
институт энергетики и связи просит студентов бережно относиться к методической
литературе, выпускаемой институтом.
1
Программа курса «Теория электрической связи»
1.1 Введение (1 час, лекция
0,5 час.)
Цель
и содержание курса « Теория электрической связи». Основные задачи курса, роль в
подготовке специалиста. Понятия и определения.
1.2 Общие
сведения о системах электросвязи (11 час, лекция 1,5 час.)
Информация,
сообщения, сигналы. Сообщения, их источники и получатели. Сигнал как носитель
сообщения. Сообщение и информация. Случайный характер сообщений и сигналов.
Основные параметры сигналов: длительность, ширина спектра и динамический
диапазон. Примеры: речевые (телефонные), вещательные, телевизионные,
телеграфные сигналы, сигналы передачи данных.
Классификация телекоммуникационных систем по
назначению, способу действия и технической реализации.
Система
связи и канал связи. Структурная схема системы связи.
Дискретные
и непрерывные каналы, их основные характеристики. Диапазон частот
электромагнитных колебаний, используемых в системах передачи информации.
Многоканальные системы передачи. Понятие о системах связи.
Помехи и
искажения в каналах. Аддитивные и мультипликативные помехи. Классификация помех
по физическим свойствам и происхождению. Кодирование
и модуляция, равномерные и неравномерные коды, корректирующие коды. Модуляция
как операция преобразования сообщения в сигнал. Структурная схема системы
передачи дискретных сообщений, модем и кодек. Передача непрерывных сообщений.
Демодуляция и декодирование. Решающее устройство. Понятие о методах обработки
сигнала в демодуляторе.
Дискретизация
и кодирование непрерывных сообщений.
Квантование
по уровню. Принцип импульсно – кодовой модуляции.
Основные
характеристики систем передачи информации: помехоустойчивость и скорость
передачи. Пропускная способность и системы передачи информации [1, с. 10–25; 2,
с. 5–23; 8, с. 8-20].
1.2.1 Контрольные вопросы
1.2.1.
1 Что такое информация, сообщение,
сигнал? Что общего и в чем отличие между этими понятиями?
1.2.1.2 В
чем заключается преобразование сообщения в сигнал? Что такое первичный,
вторичный сигнал?
1.2.1.3 Что понимают под линией, каналом, системой
связи?
1.2.1.4 Что понимают под помехами и
шумами в канале связи?
1.2.1.5 Перечислите известные вам источники помех. В
чем существенное
отличие
помех от искажений?
1.2.1.6 В
чем отличие аддитивных и мультипликативных помех? Приведите примеры тех и
других помех в радио- и проводных каналах. Объясните причины их возникновения.
1.2.1.7 Какие устройства обязательно входят в
систему электросвязи? Почему?
1.2.1.8 Какие основные показатели
характеризуют систему связи? От чего зависят эти показатели?
1.2.1.9 Какая разница между дискретными и
непрерывными сообщениями?
1.2.1.10 В чем отличие между дискретной и
непрерывной модуляцией?
1.3 Математические
модели сообщений, сигналов и помех (20 час, лекция 4 час.)
Классификация
сообщений, сигналов и помех. Детерминированные и случайные процессы, их
математические модели. Прямые и косвенные модели процессов. Представление
сообщений и сигналов в различных метрических и топологических пространствах.
Разложение
функций в ортогональные ряды по базисным функциям пространства сигналов.
Основные соотношения между элементами функциональных линейных пространств.
Обобщенный ряд Фурье.
Спектральное и временное представление
сигналов. Теорема Котельникова. Разложение аналогового сигнала в базисе Уолша.
Представление цифровых сигналов векторами пространства Хемминга.
Характеристики
случайных процессов (СП). Стационарные и нестационарные СП. Эргодическое
свойство стационарных СП. Особенности нестационарных процессов.
Функции
корреляции и их свойства. Гауссовский СП. Спектр плотности мощности и его связь
с функцией корреляции. Функция корреляции “белого” шума с ограниченным
спектром. Эффективная ширина спектра.
Описание
дифференциальными (разностными) уравнениями.
Комплексное
и квазигармоническое представление узкополосных СП. Преобразование Гильберта,
комплексный сигнал. Статические характеристики огибающей и фазы узкополосного
СП. Корреляционная функция узкополосного СП
[1, с. 29–73; 5, с.16–67; 6, с. 38–87; 8, с.–23–51, с. 119-131; 9, с.
74-103].
1.3.1 Контрольные
вопросы
1.3.1.1
Какие сигналы можно разложить в ряде Фурье?
1.3.1.2 Что такое спектр сигнала? Нарисуйте спектр
гармонического сигнала.
1.3.1.3
Что называется математической моделью электрического сигнала?
Для чего
необходимо знать математическую модель сигнала?
1.3.1.4
Как принято определять длительность
и ширину спектра реального сигнала? Какова связь между длительностью
импульса и шириной его спектра.
1.3.1.5 Как связаны между собой спектральные плотности
видеоимпульса и радиоимпульса?
1.3.1.6 Чему
равен максимальный интервал
дискретизации речевого и
телевизионного сигналов, если верхнюю частоту в спектре сигналов принять
равными 4к Гц и 6,5 МГц?
1.3.1.7
Реакцией какой электрической цепи определяется
функция отсчетов Котельникова при воздействии на вход бесконечно короткого
импульса?
1.3.1.8
Поясните физический смысл математического ожидания и дисперсии. Какой
физический смысл имеют математическое ожидание и дисперсия стационарного
процесса, имеющего размерность тока или напряжения?
1.3.1.9
Что такое “белый шум”, “квазибелый шум”?
1.3.1.10
Что такое реализация случайного процесса, и каким числом реализаций может характеризоваться случайный процесс?
1.3.1.11 Что
называется сечением случайного процесса?
1.3.1.12
Какой случайный процесс называют стационарным в широком (узком) смысле и каковы
свойства его корреляционной функции?
1.3.1.13 Что
такое случайный процесс с
δ-корреляцией? Какова характерная особенность спектра
δ-импульса?
1.3.1.14 Какими параметрами определяется двумерная
плотность
вероятности
нормального стационарного процесса?
1.3.1.15 Какой физический смысл имеет энергетический
спектр стационарного случайного процесса и какова его размерность?
1.3.1.16 Как определяется ширина энергетического
спектра по методу эквивалентного прямоугольника?
1.3.1.17 Какими соотношениями связаны корреляционная
функция и энергетический спектр стационарного случайного процесса?
1.3.1.18
Какая связь существует между шириной энергетического спектра и интервалом
корреляции для случайных процессов?
1.3.1.19
Как геометрически можно представить сигналы и помехи в различных точках системы
связи?
1.3.1.20
В чем заключается проблема согласования сигнала с каналом по их физическим
характеристикам?
1.4 Методы формирования и преобразования
сигналов (20 час, лекция 4 час.)
Модуляция
и детектирование. Преобразование колебаний в нелинейных цепях. Линейное
усиление. Нелинейное резонансное усиление гармонических колебаний. Преобразование
частоты.
Формирование
и детектирование сигналов амплитудной модуляции (АМ). АМ с подавленной несущей
(АМ-ПН), однополосная модуляция (ОМ). Временное, спектральное и векторное
представление АМ колебаний. Формирование
модулированных сигналов в нелинейных цепях. Анализ модуляционных характеристик
на ЭВМ. Схемы модуляторов. Принцип когерентного и некогерентного
детектирования. Использование параметрических и нелинейных элементов для
детектирования. Схемы детекторов сигналов АМ, АМ-ПН, ОМ. Анализ характеристик
детекторов на ЭВМ.
Формирование
и детектирование сигналов угловой модуляции. Свойства и характеристики сигналов
угловой модуляции в частотной и временной областях для детерминированных и
случайных моделей сообщений. Узкополосная и широкополосная угловая модуляция,
различие в спектрах ЧМ и ФМ сигналов. Методы формирования ЧМ и ФМ сигналов.
Принципы детектирования сигналов угловой модуляции в нелинейных цепях. Схемы
фазовых и частотных детекторов.
Формирование
и детектирование сигналов, модулированных дискретными сообщениями. Понятие
синхронизации и принципы ее обеспечения в системах электросвязи.
Помехоустойчивость
приема при использовании неоптимальных детекторов. Анализ помехоустойчивости
диодного детектора АМ сигналов,
выходное отношение сигнал-помеха и его зависимость от параметров модуляции
сигнала и помехи. Помехоустойчивость когерентного детектирования.
Помехоустойчивость ЧМ, явление порога при ЧМ.
Модуляция
и детектирование импульсного переносчика. Методы амплитудно-импульсной
модуляции. Спектры импульсно-модулированных колебаний при детерминированной и
случайной сообщений [1, с. 82–124; 4, с. 72–106; 6, с. 92–114; 8, с. 56–72; 9,
с. 107-129].
1.4.1
Контрольные вопросы
1.4.1.1 Для каких целей используется модуляция в
системах связи?
1.4.1.2
Перечислите основные параметры АМ, ЧМ и ФМ сигналов. Какие ограничения
накладываются на их значения?
1.4.1.3
Какое свойство функций Бесселя позволяет считать спектр сигналов с угловой
модуляции ограниченным?
4. 1.4.1.4
Как рассчитать ширину спектров АМ, ЧМ и ФМ сигналов?
1.4.1.5 Как
изменится ширина спектров однотональных АМ, ЧМ и ФМ сигналов, если
частоту модулирующего сигнала увеличить вдвое? Если амплитуду модулирующего
сигнала увеличить вдвое? Почему?
6.1.4.1.6 Какова причина искажений модулированных
сигналов, наблюдаемых при
перемодуляции?
1.4.1.7 В каком соотношении обычно находятся между
собой частоаты
несущего и модулирующего колебаний?
1.4.1.8 Чем принципиально отличаются осциллограммы
сигналов с балансной амплитудной модуляцией и обычных АМ сигналов?
9.1.4.1.9 В чем заключаются сходство и различия между
сигналами с ЧМ и ФМ?
10.1.4.1.10 Как связаны между собой частота модуляции,
индекс и девиация частоты при ЧМ и
ФМ?
11.1.4.1.11 Как следует выбирать индекс угловой модуляции, чтобы в спектре модулированного сигнала
отсутствовала несущая составляющая?
1.4.1.12 В чем заключается явление “обратной работы” в
системах с ДФМ? В чем особенность ДОФМ и каковы ее достоинства и недостатки?
13.1.4.1.13 От каких параметров импульсной несущей
зависит ширина спектра импульсных видов модуляции?
1.4.1.14 Что такое двойная модуляция, для чего она
используется?
1.4.1.15 АМ колебание описывается формулой: u(t)=130[1+1+0,25*cos(102t+300)+0,75*cos(3*10 2 t+45 0)]*cos(10 5 t+60 0). Изобразите спектральную диаграмму этого сигнала,
вычислите амплитуды и начальные фазы всех спектральных составляющих. Постройте
векторную диаграмму этого сигнала для момента времени t=0.
1.4.1.16 По спектральной фазовой диаграмме АМ сигнала
вычислите начальные фазы каждой из составляющих модулирующего колебания.
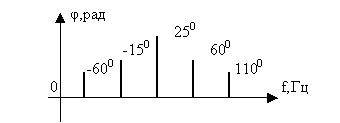

1.4.1.17 ЧМ сигнал с амплитудой 2.7В имеет мгновенную частоту,
изменяющуюся во времени по закону: ω(t)=10 9 [1+10 -4 cos(2*10 3 t)]. Найдите индекс модуляции и
запишите математическую модель этого сигнала.
1.4.1.18 Однотональный
ФМ сигнал имеет частоту модуляции
Ω=10 4 рад/с. При какой девиации
частоты в спектре
этого сигнала будут
отсутствовать составляющие на
частотах ω 0 ± Ω
?
1.4.1.19 Определите
индекс модуляции ЧМ
сигнала, промодулированного низкой частотой F=7 кГц. Несущая частота fо=180
МГц, максимальное значение частоты fmax=182,5 МГц.
1.4.1.20 Постройте спектральную диаграмму ФМ сигнала с
амплитудой 3В и девиацией фазы Δ
φ д =3 рад. Несущую и модулирующую частоты взять из11 задачи в вопросе
1.4.1.19.
1.5
Математические модели каналов связи (6 час, лекция 1час.)
Преобразование
сигналов в каналах электросвязи.
Классификация
каналов электросвязи. Прохождение случайных сигналов через детерминированные
линейные и нелинейные системы. Случайные линейные каналы и их характеристики,
особенности проводных и радиоканалов, замирания сигналов. Флуктуационные,
сосредоточенные и импульсные помехи, их вероятностные характеристики.
Модели
непрерывных каналов. Идеальный канал без помех, канал с аддитивным гауссовым
шумом. Канал с неопределенной фазой сигнала, однолучевой канал с замираниями.
Канал с межсимвольной интерференцией и аддитивным шумом.
Модели
дискретного канала. Симметричный канал без памяти, канал со стиранием.
Дискретные каналы с памятью. Марковский канал.
Уравнения
состояния. Марковские модели каналов. Уравнение состояния и наблюдения в
скалярной и векторной форме. Моделирование каналов на основе метода переменных
состояний [1, с. 124-162; 2, с. 70-95].
1.5.1.Контрольные вопросы
1.5.1.1
По каким признакам можно
классифицировать каналы связи?
1.5.1.2 Какие каналы
называются непрерывными, дискретными и дискретно – непрерывными?
1.5.1.3 Что понимают под
каналом с межсимвольной интерференцией, чем определяется память этого канала?
1.5.1.4 Как связаны между
собой импульсная и передаточная характеристики линейной системы?
1.5.1.5 Какие изменения
претерпевает сигнал при прохождении по каналу, если не учитывать аддитивного шума?
Что понимается под искажением сигнала?
1.5.1.6 Чем вызваны
нелинейные искажения сигналов в каналах связи и как можно ослабить их влияние?
1.5.1.7 Что понимается под
аддитивной флуктуационной, аддитивной гармонической (сосредоточенной по
спектру), аддитивной импульсной помехами? Каковы причины их появления в каналах
связи и каковы меры по борьбе с ними?
1.5.1.8 В модели дискретного
симметричного канала без памяти вероятность
ошибочного приема единичного
элемента (символа) р-10-3. Найдите вероятность ошибочного приема
семиразрядной (n=7) кодовой комбинации
(Р≥1,n), вероятность наличия в
семиразрядной кодовой комбинации ошибки кратности не меньше t=1,2,3,9.
1.5.1.9 То же для канала
модели Прутова для р=10-3,α=0
и α=0,5.
1.5.1.10 Какие два типа
задач в основном решаются при рассмотрении прохождения случайных воздействий
через канал связи и его звенья?
1.6 Теория помехоустойчивости систем передачи дискретных сообщений
(96 час, лекция 1 час.)
Постановка
задачи об оптимальном демодуляторе (приемнике) дискретных сообщений. Критерии
качества и правила приема дискретных сообщений. Критерий максимума средней
вероятности правильного приема. Решающая схема, построенная по правилу
максимума апостериорной вероятности. Отношение правдоподобия.
Оптимальный
прием в дискретно-непрерывном канале без искажений при наличии аддитивного
белого шума. Синтез алгоритмов и схем оптимальных приемников (корреляционный
приемник, согласованный фильтр). Цифровые методы обработки сигналов в
приемниках. Неоптимальные методы приема дискретных сообщений.
Потенциальная помехоустойчивость при точно
известном множестве сигналов. Вероятность ошибки приема для двоичной сигналов
системы при белом гауссовом шуме. Сравнительная оценка помехоустойчивости АМ,
ЧМ, ФМ сигналов. Относительная фазовая
модуляция. Вероятность ошибки при многопозиционных сигналах.
Алгоритм оптимального приема в каналах с МСИ.
Помехоустойчивость в канале с МСИ. Процессор Витерби.
Оптимальный прием при неопределенной фазе и
амплитуде сигнала. Сравнение потенциальной помехоустойчивости когерентного и
некогерентного приема.
Прием дискретных сообщений в условиях
флуктуации фаз и амплитуд сигналов. Разнесенный прием. Способы разнесенного
приема.
Прием дискретных сообщений в каналах с
сосредоточенными по спектру и импульсными помехами [1, с. 165-214; 2, с.
159-201; 8, с. 258-267].
1.6.1
Контрольные вопросы:
1.6.1.1 Какое приемное устройство (решающую схему)
называют
оптимальной?
1.6.1.2 Что понимают под алгоритмом работы приемника (решающей
схемой)?
1.6.1.3 На сколько непересекающихся областей принятия решения
следует разбить пространство принимаемых сигналов при передаче двоичных
символов и использовании стирания?
1.6.1.4 Поясните смысл оптимального разбиения пространства
принимаемых сигналов при передаче дискретных сообщений.
1.6.1.5 Поясните смысл критерия идеального наблюдателя
(Котельникова) при передаче дискретных сообщений.
1.6.1.6 Как можно геометрически интерпретировать алгоритм
оптимального приема по правилу максимального правдоподобия при точно известном
сигнале и гауссовском белом шуме в канале?
1.6.1.7 Какую импульсную переходную характеристику и комплексный коэффициент передачи имеет линейный
фильтр, согласованный при белом гауссовском шуме с сигналом s(t)?
1.6.1.8 Какую форму имеет сигнальная составляющая на выходе
согласованного фильтра при финитных входных воздействиях? Похожа ли она на
форму переданного сигнала?
1.6.1.9 Как строится схема оптимального приема дискретных
сообщений при точно известном сигнале и белом гауссовском шуме в канале,
реализованная на базе согласованных фильтров?
1.6.1.10 Как в принципе
можно построить согласованный фильтр для сигналов произвольного вида?
1.6.1.11 Что понимают под потенциальной помехоустойчивостью
системы связи?
1.6.1.12 В чем заключается явление «обратной работы», наблюдаемое
в системах ФМ?
1.6.1.13 Почему в системах ОФМ можно успешно бороться с явлением
«обратной работы»?
1.6.1.14 Какой схемой осуществляется оптимальный когерентный прием
сигналов ОФМ и как определяется вероятность ошибочного приема в этой схеме при
учете флуктуационного шума в канале?
1.6.1.15 Как можно записать алгоритм оптимального некогерентного
приема дискретных сообщений при неопределенной фазе сигнала?
1.6.1.16 Поясните реализацию алгоритма оптимального некогерентного
приема при неопределенной фазе сигнала на корреляционной технике и
согласованных фильтрах.
1.6.1.17 В какой мере упрощается алгоритм и схемная реализация
оптимального приема при определенной фазе сигнала для систем с активной паузой?
1.6.1.18 Какой формулой определяется минимальная вероятность
ошибки для двоичной системы с активной паузой, ортогональной в усиленном
смысле, при неопределенной фазе сигнала и флуктуационном шуме?
1.6.1.19 Как определяется вероятность ошибки при оптимальном
приеме сигнала ОФМ и неопределенной фазе?
1.6.1.20 Поясните возможности повышения качества систем связи
(особенно в каналах с замиранием) за счет разнесенного приема.
1.7 Основы теории информации (6 час, лекция 1 час.)
Количественная мера информации дискретного источника.
Энтропия как мера неопределенности сообщений, основные свойства энтропии.
Собственная информация источника. Энтропия источника без памяти при
равновероятном и неравновероятном выборе символов. Избыточность и
производительность источника.
Взаимная информация – количество информации на выходе
дискретного канала относительно его входа. Свойства взаимной информации.
Надежность канала и энтропия шума. Скорость передачи
информации по дискретному каналу.
Теорема кодирования Шеннона для дискретных каналов
связи [1, с. 220-255; 2, с. 101-124; 8, с. 295-304].
1.7.1 Контрольные
вопросы
1.7.1.1 Чем
определяется количество информации, заключенное в конкретном сообщении?
1.7.1.2 Почему мера
количества информации должна логарифмически зависеть от вероятности сообщения?
1.7.1.3 Чему равна
энтропия источника дискретных сообщений при равновероятных и независимых
сообщениях? Как она изменится при увеличении объема алфавита?
1.7.1.4 Напишите
выражение для энтропии источника при объеме алфавита L и неравных вероятностях элементарных сообщений,
полагая, что сообщения выбираются независимо друг от друга.
1.7.1.5 Что
называется избыточностью алфавита источника?
1.7.1.6 Определить
избыточность алфавита двоичного источника, выдающего сообщения «0» и «1»
независимо с вероятностями р (0)=0,1;
р (1)=0,9.
1.7.1.7 Сколько
можно составить различных последовательностей из 32 русских букв длиной в 100
букв?
1.7.1.8 Чему равна
энтропия источника непрерывных сообщений? Можно ли точно передать непрерывное
сообщение по каналу с конечной пропускной способностью?
1.7.1.9 Чем
отличается дифференциальная энтропия от обычной энтропии?
1.7.1.10 Дайте
определение пропускной способности канала связи.
1.7.1.11 В каких
случаях важно знать пропускную способность канала связи?
1.7.1.12 Чему равна
пропускная способность канала связи, составленного из последовательного
соединения нескольких каналов с различными пропускными способностями? А при
параллельном соединении?
1.7.1.13 Сравните
пропускные способности двух дискретных каналов без помех, если в первом канале
основание кода m1=2. а во втором канале m2=8 и
количество символов, передаваемых в секунду, в первом канале v1=10, а во
втором канале v2=40.
1.7.1.14 Сравнить
пропускные способности тех же каналов, если в них появилась помеха, вызывающая
в обоих каналах ошибки с вероятностью р=0,5. Оба канала при этом симметричны.
1.7.1.15 Как
изменится пропускная способность канала с аддитивным нормальным белым шумом при
расширении полосы пропускания канала?
1.7.1.16 Для
передачи радиовещательных программ в системе многоканальной связи обычно
объединяют несколько телефонных каналов. Почему нельзя для этого
воспользоваться одним телефонным каналом?
1.8 Помехоустойчивое кодирование (18 час, лекция
3час.)
Блочные корректирующие коды. Обнаружение и исправление
ошибок. Систематические линейные коды. Декодирование линейных кодов. Коды
Хемминга. Циклические коды. Декодирование при обнаружении и исправлении ошибок.
Мажоритарное декодирование. Матричное представление циклических кодов.
Предельные возможности помехоустойчивого кодирования. Системы с информационной
и решающей обратной связью. Помехоустойчивость систем с обратной связью.
Эффективность систем с ОС в каналах с переменными параметрами [1, с. 257-305; 2, с. 131-1554;
8,с.307-315].
1.8.1 Контрольные вопросы
1.8.1.1 По каким
признакам можно классифицировать коды?
1.8.1.2
Какая разница между экономным и помехоустойчивым кодированием?
1.8.1.3 В чем заключается метод укрупнения алфавита
источника? Зачем это используется?
1.8.1.4 Почему
короткие помехоустойчивые коды не обеспечивают большой эффективности?
1.8.1.5 Какой код является корректирующим?
1.8.1.6 Перечислить
параметры корректирующих кодов и пояснить их смысл.
1.8.1.7 Для чего используются проверочные символы в
кодовых комбинациях корректирующего кода?
1.8.1.8 Может ли
один и тот же помехоустойчивый код использоваться в системе с обнаружением и в
системе с исправлением ошибок?
1.8.1.9 Что такое
синдром кода? Как он вычисляется для циклических кодов и как используется при
декодировании?
1.8.1.10 Пояснить
процесс обнаружения ошибок в кодах с постоянным весом, с проверкой на четность,
циклических.
1.8.1.11 В чем идея мажоритарного декодирования
избыточных кодов?
1.8.1.12 Какие коды называют рекуррентными или
цепными?
1.8.1.13 Чем
объяснить малую эффективность избыточного кодирования кодом (7,4) при медленных
замираниях в канале и большую эффективность этого кода в условиях быстрых
замираний?
1.9
Принципы многоканальной связи и распределения информации (12 час, лекция 2
час.)
Основные
положения теории разделения сигналов в
системах многоканальной связи. Системы передачи с линейно-независимыми
сигналами.
Условия разделимости сигналов, определитель Грамма. Геометрическая трактовка разделения
сигналов.
Частотное,
временное и фазовые разделения сигналов. Структурные схемы многоканальных систем. ЧРК, ВРК, ФРК, особенности формирования
групповых сигналов и построения разделяющих устройств.
Разделение сигналов по форме. Структурная
схема разделения линейно независимых сигналов. Примеры использования в качестве переносчиков функций Уолша, полиномов
Лежандра, Чебышева, Лагерра.
Комбинационное
разделение сигналов. Разделение сигналов по уровню, многочастотные и
многофазовые сигналы. Многопозиционные сигналы с амплитудно-фазовой модуляцией.
Комбинационное уплотнение на основе представления группового сигнала блочным
нелинейным несистематическим кодом.
Система
передачи с многостанционным доступом. Принцип многостанционного доступа к общему тракту передачи на основе
ЧРК, ВРК, разделения сигналов по форме. Примеры псевдослучайных (шумоподобных) сигналов: последовательности
Баркера, ЛРП, ШПС на основе частотно-временных матриц. Принцип статистического
уплотнения. Пропускная способность систем многоканальной связи. Влияние
взаимных помех на пропускную способность канала.
Принципы
распределения информации. Основные
положения теории массового обслуживания. Сеть распределения информации и ее
элементы. Структура систем распределения информации. Многоуровневая архитектура
связи и протоколы [1, с. 348-377; 2, с. 257-278].
1.9.1 Контрольные вопросы
1.9.1.1 Сформулируйте основные преимущества многоканальной передачи
и поясните
общую структурную схему многоканальной системы передачи.
1.9.1.2 Каким
требованиям должны удовлетворять канальные сигналы при формировании группового сигнала системы
многоканальной передачи?
1.9.1.3 Какие устройства обязательно должны входить
в систему передачи с ЧРК, с ВРК?
1.9.1.4 Каковы преимущества и недостатки
однополосной модуляции (ОБП) по
сравнению с обычной АМ в системах передачи с ЧРК?
1.9.1.5 В чем основные
преимущества и какие недостатки имеют цифровые методы передачи непрерывных сигналов?
1.9.1.6 Какие операции производят с аналоговым
сигналом для преобразования его в цифровой?
1.9.1.7 В
чем необходимость квантования отсчетов в ЦСП?
1.9.1.8 Поясните принцип действия аналого-цифрового и
цифро-аналогового преобразователей для различных видов цифровой модуляции.
1.9.1.9 Что такое
линейные коды в ЦСП? Для чего они необходимы?.
1.9.1.10 Поясните суть кодового разделения сигналов.
Приведите обобщенную структурную схему
системы передачи с кодовым разделением сигналов. Приведите обобщенную
структурную схему передачи с кодовым разделением сигналов.
1.10 Анализ эффективности и оптимизация систем связи
(12 час, лекция 2 час.)
Методологические
принципы системного анализа. Иерархичность структуры СПИ. Принцип декомпозиции
и агрегирования. Моделирование СПИ с помощью ЭВМ. Математическая формулировка
задачи оптимизации. Показатели частотной, энергетической и информационной
эффективности.
Эффективность
аналоговых и цифровых систем при различных видах модуляции. Эффективность
многоканальных систем. Выбор сигналов и помехоустойчивость кодов. Компенсация
помех и искажений в канале. Сокращение избыточности, сжатие данных. Перспективы
развития телекоммуникационной техники на основе современных информационных
технологий, системы мультимедиа [1, с. 400-4274 2, с. 282-297].
1.10.1 Контрольные вопросы
1.10.1.1
Как определяются показатели информационной, энергетической и частотной
эффективности систем связи?
1.10.1.2
Какими методами можно осуществить обмен показателей эффективности β на
γ и γ на β?
1.10.1.3
Как изменится энергетическая эффективность системы передачи дискретных
сообщений при уменьшении требуемой вероятности ошибки р? Уменьшится она или
увеличится? Покажите это на примере двоичного канала.
1.10.1.4 Поясните сущность и сравните между собой
известные способы повышения эффективности систем передачи непрерывных
сообщений.
1.10.1.5 На основе выражений для расстояния между сигналами определите энергетический
выигрыш симплексных сигналов по сравнению с ортогональными.
1.10.1.6 На какой основе могут быть построены системы,
в которых достигается повышение как
энергетической, так и частотной эффективности?
1.10.1.7 Какие факторы в реальных системах приводят к
снижению эффективности по сравнению с предельной?
2 Содержание аудиторных занятий
2.1 Содержание лекций
Лекция 1 (2 час.)
Структурные схемы и основные характеристики систем электросвязи. Понятие
сигнала, его основные характеристики. Многоканальные системы передачи. Помехи и
искажения в каналах. Классификация помех. Общие понятия кодирования -
декодирования, модуляции – демодуляции.
Основные характеристики детерминированных сигналов, их математические
модели. Энергия сигнала [1, с. 10-27;
2,с.10-23; 6,с. 11-27; 8,с. 8-29].
Лекция 2 (2 час.) Периодические сигналы и ряды Фурье.
Спектральная диаграмма периодического сигнала.
Спектральный анализ непериодических сигналов.
Преобразование Фурье и его основные свойства. Разложение функций в ряд
Котельникова. Дискретизация по теореме Котельникова. Теорема Котельникова.
Спектральное пояснение теоремы Котельникова
[1, с.29-36; 2, с.64-69; 4, с. 20-27; 6, с. 38-55, 119-127; 8, с.
29-42].
Лекция 3 (2 час.) Корреляционный анализ сигналов.
Автокорреляционная функция дискретного сигнала. Взаимно корреляционная функция
двух сигналов. Случайные процессы и их основные характеристики. Гауссовский
СП. Спектр плотности мощности и его связь с функцией корреляции. Функция
корреляции “белого” шума с ограниченным спектром. Эффективная ширина спектра
[1, с. 49-60; 6, с. 77-87; 9, с. 77-87].
Лекция 4
(2 час.) Формирование сигналов
амплитудной модуляцией (АМ). АМ с подавленной несущей (АМ-ПН), однополосная
модуляция (ОМ). Временное, спектральное и векторное представление АМ колебаний. Схемы модуляторов [1, с. 88-96;
6, с. 92-100; 8, с. 56-64; 9, с. 92-100].
Лекция 5
(2 час.) Формирование сигналов угловой
модуляции. Свойства и характеристики сигналов угловой модуляции в частотной и
временной областях. Детектирование.
Использование параметрических и нелинейных элементов для детектирования.
Схемы детекторов сигналов АМ, АМ-ПН, ОМ.
Принципы детектирования сигналов угловой модуляции в нелинейных цепях.
Схемы фазовых и частотных детекторов [1, с. 96-112; 4, с. 100-114; 8, с. 64-72;
9, с. 115-139].
Лекция
6 (2 часа) Преобразование сигналов в каналах электросвязи.
Классификация
каналов электросвязи. Прохождение случайных сигналов через детерминированные
линейные и нелинейные системы. Модели непрерывных каналов. Модели дискретного
канала. Постановка задачи об оптимальном демодуляторе (приемнике) дискретных
сообщений. Критерии качества и правила приема дискретных сообщений [1, с.
126-130, 149-157, 165-169; 2, с. 70-89, 159-174].
Лекция 7
(2 час.) Основные информационные характеристики источников дискретных
сообщений. Скорость передачи информации и пропускная способность непрерывного
канала, канала с шумами. Теорема кодирования Шеннона [1, с. 220-246; 2, с.
101-114].
Лекция 8
(2 час.) Основные принципы помехоустойчивого кодирования. Коды Хэмминга,
циклические, сверточные, каскадные коды. Образующие и проверочные матрицы
кодов, матрицы синдромов [8, с. 307-315; 10, с. 99-124].
Лекция 9
(2 час.) Техническая реализация помехоустойчивого кодирования: построение
кодеров и декодеров. Эффективность избыточного кодирования [10, с. 124-129].
Лекция 10
(2 час.) Принципы многоканальной связи.
Пропускная способность систем многоканальной связи. Система передачи с
многостанционным доступом. Частотное, временное и фазовые разделения сигналов.
ЧРК, ВРК, ФРК, особенности формирования групповых сигналов и построения разделяющих
устройств [1, с. 349-377; 2, с. 257-278].
2.2 Примерный
перечень тем практических занятий
2.2.1 Системы
связи и способы передачи сообщений.
2.2.2
Сообщения, сигналы, помехи.
2.2.3 Каналы
связи.
2.2.4 Основы
теории передачи информации.
2.2.5 Основы
теории помехоустойчивого кодирования.
2.2.6 Прием
дискретных сообщений.
2.2.7 Прием
непрерывных сообщений.
2.2.8 Цифровые
методы передачи непрерывных сообщений.
2.2.9 Теория
многоканальной передачи сообщений.
2.2.10 Методы повышения эффективности систем передачи
сообщений.
2.2.11 Спектральные представления сигналов.
2.2.12 Сигналы с ограниченным спектром.
2.2.13 Динамическое представление сигналов.
2.2.14 Геометрические методы в теории сигналов.
2.2.15 Спектральное представление непериодических
сигналов.
2.2.16 Энергетический спектр сигнала.
Автокорреляционная функция сигнала.
2.2.17 Сигналы с амплитудной модуляцией.
2.2.18 Сигналы с угловой модуляцией.
2.2.19 Теорема Котельникова.
2.2.20 Узкополосные сигналы.
2.2.21 Спектральный метод анализа линейных систем.
2.2.22 Операторный метод анализа линейных систем.
2.2.23 Низкочастотный эквивалент
частотно-избирательной цепи.
2.2.24 Детектирование АМ, ФМ, ЧМ сигналов.
2.2.25 Характеристики случайных величин.
2.2.26 Корреляционный анализ случайных сигналов.
2.2.27 Случайные узкополосные сигналы.
Прохождение
случайных сигналов через линейные системы.
2.3 Примерный
перечень тем лабораторных занятий
2.3.1
Преобразование формы и
спектра сигнала безынерционным нелинейным элементом.
2.3.2 Преобразование частоты.
2.3.3
Амплитудная модуляция.
2.3.4
Детектирование амплитудно-модулированных колебаний.
2.3.5
Частотная модуляция и детектирование.
2.3.6 Код
Хэмминга.
2.3.7 Теорема
Котельникова.
2.3.8
Случайные процессы.
2.3.9
Прохождение цифрового сигнала по радиоканалу.
2.3.10 Исследование однополосной модуляции (ОМ).
2.4
Примерный перечень тем
курсовых работ
2.4.1
Прохождение суммы
сигнала и шума через линейное устройство.
2.4.2
Прохождение суммы
сигнала и шума через нелинейное (например: радиоприемное) устройство.
2.4.3
Разложение периодических
сигналов в ряд Фурье.
2.4.4
Спектральная плотность
сигналов.
2.4.5
Автокорреляционная и
взаимная корреляционная функции. Энергия сигнала.
2.4.6
Модулированные
колебания.
2.4.7
Аналитический сигнал.
2.4.8
Анализ воздействия
сигналов на линейные системы.
2.4.9
Анализ воздействия
сигналов на нелинейные системы.
2.4.10 Генерирование гармонических колебаний.
2.4.11 Цепи с
переменными параметрами.
2.4.12 Построение квазиоптимальной по критерию
минимума вероятности ошибки системы связи.
Студенты выполняют курсовую работу на одну из предложенных тем.
В деканате ФЗО ПС имеются методические указания и
задание на курсовую работу по теории электросвязи со списком рекомендуемой
литературы.
3 Контрольное задание и методическое указание к нему
Прежде чем приступить к выполнению контрольного
задания, ознакомьтесь с порядком выбора варианта и требованиями по выполнению,
оформлению контрольной работы.
3.1 Требования к выполнению контрольной работы.
В соответствии с учебным планом студенты выполняют по
курсу ТЭС одну контрольную работу.
Выполнение контрольной работы поможет студенту глубже освоить наиболее важные
разделы курса, получить навыки в решении задач, встречающихся в инженерной
практике.
Решение каждой задачи следует начать с изучения
относящегося к теме задания теоретического материала. Это может быть проведено
по учебной литературе, приведенной в методических указаниях к решению задачи.
Выполнять задания нужно вдумчиво, четко представляя ход решения, умея
обосновать полученный результат. Выполненная работа сдается на проверку
(рецензенту) преподавателю кафедры «Телекоммуникационные системы». После
проверки, если работа не допущена к защите, она возвращается на доработку.
Студент должен или переделать ее, или исправить все отмеченные ошибки и
выполнить все указания рецензента в соответствии с его замечаниями, а затем
работа вновь отдается на рецензию. Все исправления и дополнения, сделанные по
указаниям рецензента, помещаются на чистой стороне листа в том месте, где
обнаружены ошибки или заданы вопросы.
Проверенная работа должна быть защищена. После допуска
к защите, студент защищает ее в назначенное преподавателем время. Для успешной защиты необходимо: внести
исправления по замечаниям рецензента, ответить письменно или устно (в
зависимости от требований рецензента) на поставленные вопросы, уметь полностью
объяснить ход решения задач, обосновать правильность использования расчетных
формул, смысл входящих в них символов.
Во время защиты контрольной работы каждый студент должен быть готов дать
пояснения по существу решения задач контрольной работы, четко представлять ход
решения, уметь обосновать полученный результат.
Следует помнить, что контрольная работа, выполненная
небрежно, не полностью или не по своему варианту, не рецензируется и
возвращается студенту на переоформление, доработку или переделку по своему
варианту.
3.2
Требования к оформлению контрольной работы
3.2.1 Контрольная работа выполняется в простой
ученической тетради в клетку или на листах белой бумаги формата А4. Она должна
быть аккуратно оформлена, текст разборчиво написан или напечатан (компьютерный
набор) на одной стороне листа. Другая сторона листа предназначена для внесения
студентом исправлений и дополнений по результатам рецензии.
3.2.2 Титульный лист контрольной работы оформляется в
соответствии с правилами оформления контрольных работ и включает название
дисциплины, ФИО студента, номер группы и номер зачетной книжки.
3.2.3 В начале
каждой задачи приводится условие задачи и исходные данные для своего варианта.
3.2.4 Страницы
текста, рисунки, таблицы и формулы нумеруются. Все вычисления приводят
достаточно полно, чтобы можно было проверить их правильность, сопровождают
необходимыми пояснениями.
3.2.5
Расчетные формулы записывают в общем виде с расшифровкой буквенных
обозначений и указанием размерностей. Все числовые значения необходимо затем
подставлять только в основных единицах.
3.2.6 В конце
контрольной работы приводится список использованной студентом в работе
литературы. В тексте работы должны быть краткие пояснения решения задачи, а
также ссылка на использованную литературу при приведении формул, схем,
теоретического материала.
3.2.7 Студент
подписывает свою работу с указанием даты выполнения.
Внимание,
контрольные работы, выполненные без соблюдения выше- перечисленных требований,
возвращаются на доработку.
3.3 Контрольная работа
Выбор
варианта
Студенты
выполняют в контрольной работе четыре задачи из семи. Номера выполняемых задач
определяются по первой букве фамилии студента согласно таблице 1.
Таблица 1
|
Первая буква фамилии |
А,Е,Л |
Б,Ж,М |
В,З,Н |
Г,И,О |
Д,К,П |
|
Номера выполняемых задач |
1,2,4,5 |
1,2,3,6 |
1,2,4,6 |
1,2,3,5 |
1,2,4,7 |
|
Первая буква фамилии |
Р,Х,Ы |
С,Ц,Э |
Ч,Ю |
У,Ш,Я |
Т,Ф,Щ |
|
Номера выполняемых задач |
1,2,3,7 |
1,2,4,7 |
1,2,3,5 |
1,2,4,5 |
1,2,3,6 |
Номер варианта соответствует двум последним цифрам
(предпоследней и последней) номера зачетной книжки.
Например, если номер зачетной книжки 953103, то номер варианта будет 03.
Задача 1
На вход
линейного элемента (электрического фильтра) подается периодический
сигнал.
Требуется:
а) разложить в
ряд Фурье (в тригонометрической форме) сигнал на входе фильтрующей цепи,
определить постоянную составляющую и коэффициенты первых пяти гармоник, не
равных нулю;
б) записать мгновенные значения напряжений на входе;
в) изобразить дискретный спектр входного сигнала;
г) построить график входного напряжения или тока по
пяти гармоникам и постоянной составляющей;
д) начиная со второй по пятую гармоники, расчет
произвести на ЭВМ. Исходные данные к задаче приведены в таблице 2 и рисунке 1.
Таблица 2
|
Последняя цифра зачетной
книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
U1, мВ |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
|
Предпоследняя цифра
зачетной книжки |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Форма сигнала- рисунок 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
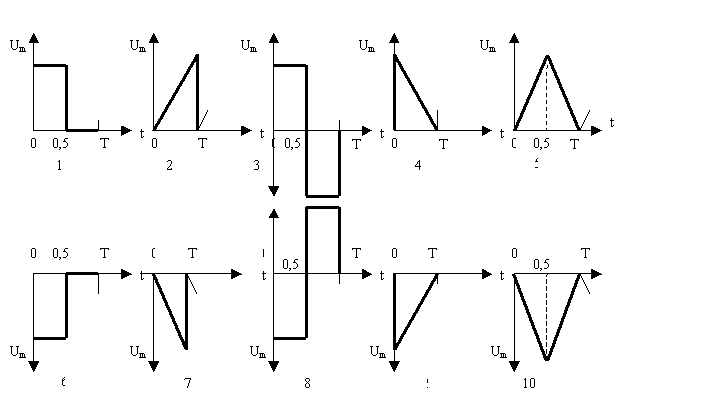

Рисунок 1
Методические указания к задаче 1
С материалом по спектральному представлению сигналов
можно ознакомиться в [4, с. 20–27; 6,
с. 38–43].
Рассмотрим задачу на примере сигнала, изображенного на
рисунке 2.
Последовательность треугольных униполярных импульсов –
функция четная относительно оси ординат, поэтому
U(t)= ![]() ∑an cos nω1t;
∑an cos nω1t;
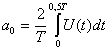 ;
;
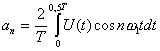 .
.![]()


Рисунок 2
Cоставим уравнение сигнала на участке 0≤t≤0,5 Т:
t=0; U(t)=10 мВ;
t=0,5Т; U(t)=0;
Следовательно:
![]() а0=
а0=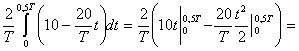
![]() ;
;
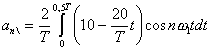 =
=
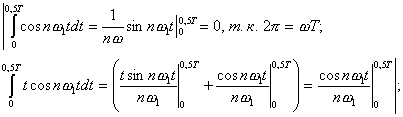
![]() ;
;
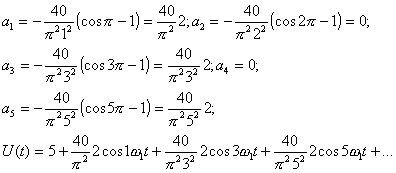
Построение спектрограммы тригонометрического ряда
Фурье – [4, рисунок 2 .4 (б); 8, рисунок 2.6].
Задача 2
Прямоугольный импульс длительностью τи
представляется рядом Котельникова. При этом возникают перепады длительностью
τф, определяемые в процентах от длительности импульса.
Требуется:
а)
определить число отсчетов N, необходимое
для представления импульса рядом Котельникова;
б)
длительность перепадов восстановленного импульса τф, при
условии, чтобы она не превышала n% от τи;
в)
объяснить, почему форма восстановленного импульса отличается от формы исходного
импульса.
Исходные данные к задаче приведены в таблице3.
Таблица 3
|
Последняя цифра зачетной книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
n% |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
3 |
|
Предпоследняя цифра
зачетной книжки |
9 |
8 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
τи, мс |
1,0 |
1,5 |
2,5 |
0,5 |
3,0 |
2,5 |
4,0 |
3,5 |
5,5 |
4,5 |
Методические указания к задаче 2
С материалом по представлению сигналов с ограниченной
полосой частот рядом Котельникова можно ознакомиться в [4, с.59 – 64; 8, с.122
– 125; 10, с.36 - 42].
Следует уяснить, что при представлении сигнала рядом
Котельникова коэффициенты разложения u(kΔt) равны мгновенным значениям непрерывного сигнала u(t) в моменты kΔt и они называются отсчетами сигнала.
На
рисунке 3 изображены:
а) прямоугольный импульс длительностью τи;
b)
последовательность отсчетов, взятых из прямоугольного импульса с интервалом
дискретизации Δt;
c)
соответствующие этим отсчетам базисные
функции 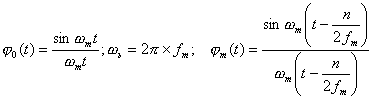
и их сумма, т. е. восстановленный импульс.
Задержка этих функций во времени обусловлена
инерционностью специального формирующего фильтра. При учете задержки график
восстановленного сигнала имеет перепады τф , отсчитываемый
между точками a и b, с и d. Практически
τф≈1,5Δt. При
этом предполагается, что положение точки а совпадает с истинным моментом
скачка.
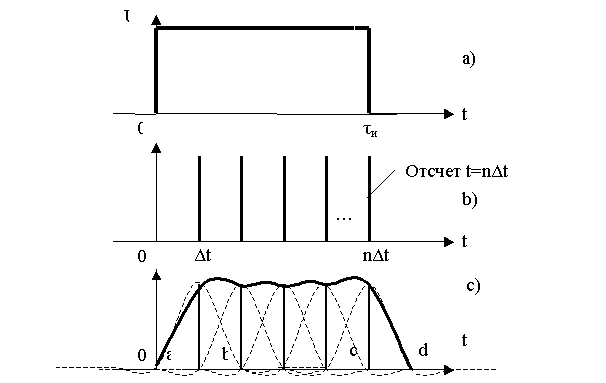

Рисунок 3
Рассмотрим случай, когда τи=3,5мс,
длительность перепадов не превышает n = 2%
от τи.
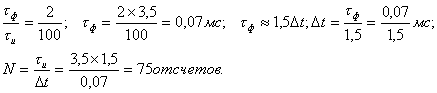
Задача 3
Заданы: несущее колебание
![]() ;
;
модулирующий
сигнал
![]()
где
U0 - амплитуда
несущего колебания, В;
ω0 -
частота несущего колебания, рад;
φ - начальная фаза несущего
колебания, рад;
S0 -
амплитуда модулирующего колебания, В;
Ώ –
частота модулирующего колебания, рад;
Ψ –
начальная фаза модулирующего колебания, рад.
Требуется:
а)
в соответствии с вариантом записать аналитическое выражение
амплитудно–модулированного колебания с коэффициентом модуляции М; частотно –
модулированного колебания с девиацией частоты ωд; фазо–
модулированное колебание с индексом модуляции m;
б)
построить амплитудно–частотный и фазочастотный спектры АМ, ЧМ и ФМ колебаний;
в) изобразить качественно графики несущего,
модулирующего и модулированного АМ, ЧМ и ФМ колебаний (временные диаграммы).
Исходные данные к задаче приведены в таблице 4 и
таблице5
Таблица
4
|
Предпоследняя цифра номера зачетной книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
U0,
В |
3,4 |
1,2 |
2,6 |
1,5 |
0,8 |
0,7 |
0,4 |
1,2 |
0,2 |
3,2 |
|
f0 , МГц |
8,1 |
2,0 |
3,0 |
3,6 |
4,2 |
5,1 |
6,2 |
7,1 |
4,1 |
2,2 |
|
φ0 , рад |
π/10 |
π/4 |
4/3 |
π/5 |
π/6 |
π/18 |
π/12 |
π/18 |
π/9 |
π/7 |
|
S0 , В |
1.3 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,1 |
1,2 |
|
F, кГц |
1,8 |
0,4 |
0,6 |
0,8 |
1,2 |
2,4 |
4,2 |
2,6 |
3,2 |
3,6 |
|
Ψ, рад |
0 |
π/10 |
π/9 |
π/8 |
π/7 |
π/6 |
π/5 |
π/4 |
π/3 |
π/2 |
Таблица 5
|
Последняя цифра номера зачетной книжки |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
ωд,, кГц |
2,6 |
1,25 |
2,4 |
4,0 |
7,2 |
1,65 |
3,6 |
3,4 |
5,2 |
9,6 |
|
m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
2 |
3 |
5 |
|
Глубина модуляции k, % |
50 |
30 |
40 |
60 |
70 |
80 |
45 |
65 |
75 |
85 |
Методические указания к задаче 3
С материалом по амплитудной (АМ), угловой (ЧМ и ФМ)
модуляциями можно ознакомиться в литературе [4; с. 72–109; 8; с. 56-70; 9; с.107-129].
Следует уяснить, что в гармоническом несущем колебании
![]()
можно
изменять пропорционально модулирующему колебанию
![]() ,
,
однозначно
связанному с передаваемым сообщением,
амплитуду ![]() ;
;
начальную фазу ![]() ;
;
частоту ![]() .
.
В соответствии с этим получим амплитудно –
модулированное (АМ), фазомодулированное (ФМ) и частотно – модулированное (ЧМ)
колебания.
Полная фаза АМК -
![]() ;
;
ФМК - ![]() ;
;
ЧМК - 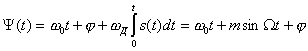 ;
;
Аналитические выражения для мгновенных значений
тонально - модулированных колебаний в общем случае имеют вид
АМК ![]() ,
,
где ![]() ;
;
ФМК ![]() ,
,
где ![]() ;
;
ЧМК ![]() ,
,
где m=ωД//Ω.
В развернутом виде, удобном для построения
спектрограмм модулированных колебаний, выражения для мгновенных значений
тональных модулированных колебаний преобразуем к виду
АМК
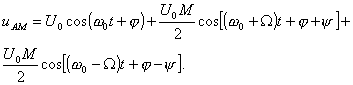
Так как ![]()
в
равной степени соответствует ЧМК и ФМК, для построения выражения в развернутом
виде для колебаний с угловой модуляцией воспользуемся соотношениями из теории
Бесселевых функций и получим
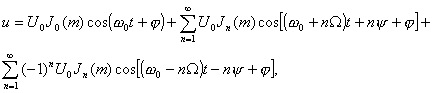
где
Jn(m) – функции
Бесселя первого рода n – го порядка с
индексом m в качестве аргумента. Значения
функций Бесселя приведены в таблице приложения. Учитываем, что:
- для нечетных n J-n(m)= - Jn(m);
- для четных n
J-n(m)=Jn(m).
Задача 4
Вольт – амперная характеристика (ВАХ) биполярного
транзистора амплитудного модулятора аппроксимирована выражением
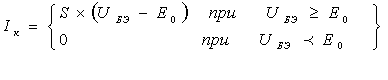 ,
,
где Iк – ток коллектора транзистора, мА;
UБЭ –
напряжение на базе транзистора, В;
S- крутизна характеристики (ВАХ), мА/В;
E0 –
напряжение отсечки, В.
Требуется:
а) объяснить назначение модуляции несущего сигнала и
кратко описать различные виды аналоговой модуляции;
б) изобразить упрощенную схему
транзисторного амплитудного модулятора, описать принцип его работы и назначение
элементов схемы;
в)
дать определение статической модуляционной характеристики (СМХ), рассчитать и построить СМХ при заданных S, Е0 и значении амплитуды несущего
высокочастотного (ВЧ) сигнала Um
–таблица 4.1.;
г) с помощью СМХ определить
оптимальное напряжение смещения Ебопт и допустимую величину
амплитуды UΩmax
модулирующего сигнала uмод(t)= UΩcosΩt, соответствующие неискаженной модуляции
(Ω=2πF);
д)
рассчитать коэффициент модуляции М для выбранного режима и построить
спектральную и векторную диаграммы однотонального АМ сигнала, записать
математическое выражение этого сигнала.
Исходные
данные к задаче приведены в таблице 6.
Таблица
6
|
Предпоследняя цифра номера зачетной книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
S, мА/В |
10 0 |
95 |
110 |
85 |
120 |
75 |
115 |
90 |
105 |
80 |
|
Последняя цифра номера зачетной книжки |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
f0, кГц |
300 |
350 |
400 |
450 |
500 |
550 |
600 |
650 |
700 |
750 |
|
E0, В |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,35 |
0,45 |
0,5 |
0,6 |
0,5 |
|
Um, В |
0,4 |
0,5 |
0,6 |
0,7 |
0,7 |
0,4 |
0,5 |
0,6 |
0,7 |
0,6 |
|
F, кГц |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
5,0 |
4 |
3,0 |
Методические указания к задаче 4
С материалом по амплитудной (АМ), угловой (ЧМ и ФМ)
модуляциями можно ознакомиться в литературе [4, с. 72–109; 8, с.64-70; 9, с.
115-122]. С материалом по амплитудным
модуляторам можно ознакомиться в литературе [4, с. 255–257; 6, с. 291–293; 19, с. 291-294].
Под СМХ понимается зависимость амплитуды первой
гармоники тока коллектора Iк1 транзистора от постоянного напряжения смещения на
безе Uбэ, при
постоянной амплитуде напряжения несущего колебания.
Расчет СМХ следует производить для пяти – семи
значений напряжения смещения на
интервале от (Е0 - Um) до (Е0 + Um), и в пределах которого угол отсечки изменяется от 00
до 1800 (от 0 до π рад). Для значений Uбэ и заданных Е0 и Um определяется угол отсечки Ө [6, с. 280;
9, с. 293].
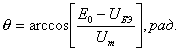
С помощью Ө определяется значение амплитуды
первой гармоники тока коллектора Iк1 [6, пример 11.2; 9,
пример 4.4]
![]() ,
,
где γ1(Ө)
– коэффициент Берга. Формулы расчета коэффициентов Берга (Приложение Б).
Для
исключения нелинейных искажений необходимо использовать только линейный участок
модуляционной характеристики в диапазоне токов Iкmin…Iкmax.
Оптимальное напряжение смещения Uбэоп лежит на середине линейного участка СМХ, а допустимая
величина амплитуды модулирующего напряжения UΩmax выбирается так, чтобы напряжение на базе транзистора
не выходило за пределы линейного участка СМХ.
Коэффициент модуляции определяется по СМХ для
выбранного режима по формуле
![]() ,
,
где Iкmax и Iкmin – максимальное и минимальное значения тока Iк1 по СМХ
для U БЭmax и U БЭvin.
Задача 5
Вольт-амперная характеристика (ВАХ) диода линейного
диодного детектора аппроксимирована отрезками двух прямых линий
![]()
где I – ток диода;
S– крутизна вольт – амперной характеристики (ВАХ);
U– напряжение на диоде.
АМ сигнал с однотональной модуляцией, аналитически
записанный как
![]() ,
,
где Um -
амплитуда несущего сигнала, В;
М - коэффициент модуляции;
F– частота модулирующего колебания, Гц;
f0–частота
несущего сигнала, Гц,
подан
на вход детектора.
Требуется:
а)
пояснить назначение детектирования модулированных колебаний;
б)
изобразить схему линейного диодного детектора, описать принцип его работы и
назначение элементов, входящих в схему детектора;
в)
рассчитать сопротивление нагрузки Rн для получения заданного коэффициента детектирования КД;
г)
выбрать значение емкости нагрузки детектора СН при заданных f0 и F;
д)
рассчитать и построить спектры напряжений на входе и выходе детектора.
Исходные данные к задаче приведены в таблице 7.
Таблица 7
|
Последняя цифра номера
зачетной книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
S. мА/В |
35 |
40 |
45 |
50 |
55 |
60 |
35 |
40 |
45 |
50 |
|
М |
0,7 |
0,8 |
0,9 |
0,75 |
0,85 |
0,65 |
0,75 |
0,85 |
0,8 |
0,85 |
|
F, кГц |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
5,0 |
4,5 |
3,0 |
|
Предпоследняя цифра номера зачетной книжки |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Um, В |
1,1 |
1,0 |
1,2 |
1,3 |
1,5 |
1,4 |
1,7 |
1,4 |
1,5 |
,1,3 |
|
f0, кГц |
300 |
350 |
400 |
450 |
500 |
550 |
600 |
650 |
700 |
750 |
|
КД |
0,65 |
0,75 |
0,7 |
0,8 |
0,85 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
Методические указания к задаче 5
С материалом по детектированию можно ознакомиться в
литературе[4, с. 239–247; 6, с. 297–299; 9, с.299-301].
Линейный режим детектирования – это режим больших
амплитуд с кусочно–линейной аппроксимацией ВАХ.
Чтобы цепь реальной нагрузки любого детектора
эффективно отфильтровывала полезный модулирующий сигнал и подавляла паразитные
высокочастотные составляющие, необходимо выполнение двух неравенств
1/(ΩCН)>>RН; 1/(ω0CH)<<
RН.
Определяем CH, удовлетворяющее этим неравенствам.
Вторым условием хорошей работы детектора необходимо,
чтобы сопротивление нагрузки RН значительно превышало сопротивление диода в его прямой
проводимости, т.е., чтобы S RН>>1.
Коэффициент передачи детектора
КД=cos Ө; tgӨ - Ө=π/(SRH),
где
Ө - угол отсечки в радианах.
Определяем RН, удовлетворяющее этим выражениям.
Амплитуды входного и выходного напряжений связаны соотношением
![]() .
.
Постоянная составляющая тока амплитудного детектора
![]() .
.
Поэтому среднее значение выходного напряжения
![]()
где
γо – коэффициент Берга, его нахождение – методические указания
к задаче 4.
Аналитическая запись НЧ и ВЧ сигналов, а также АМК в
виде, удобном для построения спектрограмм –
методические указания к задаче 3.
Задача 6
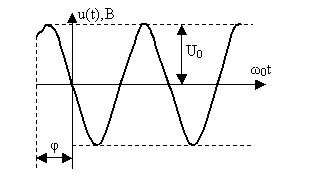
Задан стационарный случайный процесс
![]()
где U0 – амплитуда, В и
![]() частота представляют собой детерминированные величины, а
частота представляют собой детерминированные величины, а
φ - случайная величина;
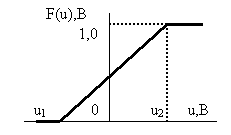
графически
задана функция распределения F(u) стационарного случайного процесса.
Требуется:
а)
определить корреляционную функцию случайного процесса;
б)
определить плотность вероятности и изобразить примерный вид реализации этого
процесса.
Исходные данные к задаче приведены в таблицах 8 и 9.
Таблица 8
|
Последняя цифра номера зачетной книжки |
Случайный процесс |
U0, В |
f0,кГц |
|
0 |
|
1,4 |
300 |
|
1 |
2,1 |
400 |
|
|
2 |
2,5 |
350 |
|
|
3 |
2,8 |
440 |
|
|
4 |
3,0 |
380 |
|
|
5 |
3,2 |
260 |
|
|
6 |
3,4 |
320 |
|
|
7 |
3,5 |
280 |
|
|
8 |
3,6 |
420 |
|
|
9 |
3,8 |
450 |
Таблица 9
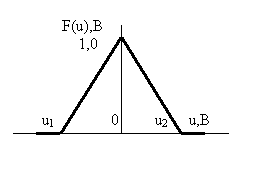
|
Последняя цифра номера зачетной книжки |
График функции распределения |
Предпоследняя цифра номера зачетной книжки |
X1 |
X2 |
|
0 |
|
9 |
-3 |
4 |
|
1 |
8 |
-5 |
3 |
|
|
2 |
7 |
-2 |
6 |
|
|
3 |
6 |
-4 |
8 |
|
|
4 |
5 |
-4 |
4 |
|
|
5 |
|
4 |
-3 |
4 |
|
6 |
3 |
-5 |
3 |
|
|
7 |
2 |
-2 |
6 |
|
|
8 |
1 |
-4 |
8 |
|
|
9 |
0 |
-4 |
4 |
Методические
указания к задаче 6
С материалом по основным характеристикам случайных
процессов можно ознакомиться в литературе [4, с. 109–142: 6, с. 142–163; 9,
с.151-162].
Одной из основных характеристик случайной величины U(t1) является интегральная функция распределения F(u):
![]() 0≤F(u)≤1,
0≤F(u)≤1,
Р – символ, характеризующий вероятность события.
Для непрерывной во времени случайной величины удобно
пользоваться одномерной плотностью распределения вероятности (плотностью вероятности)
![]() удовлетворяющей
условию нормировки:
удовлетворяющей
условию нормировки:
![]()
В практических расчетах находят:
математическое
ожидание
![]()
представляет
среднее значение случайного процесса в текущий момент времени t;
дисперсию
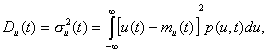
характеризует
разброс мгновенных значений реализаций случайного процесса относительно его
среднего значения. Физический смысл величины среднеквадратического отклонения –
действующее значение случайного напряжения на единичном сопротивлении, а
дисперсия – мощность переменной составляющей случайного процесса.
Функция корреляции представляет собой меру связи между
сечениями случайного процесса, взятыми в моменты времени t1 и t2.
![]() .
.
При t1=t2, т.е. при совмещении сечений случайного процесса,
функция корреляции численно равна дисперсии
![]() .
.
Расчет корреляционной функции гармонического сигнала –
[9, пример 2.4].
Рассмотрим пример решения задачи.
Пусть функция распределения F(u) представлена
прямой, проходящей через две точки с координатами (u1 , F(u1)) и (u2 , F(u2))
![]() .
.
При u1=
-4, F(u)1=0, u2=5, F(u)2=1
получаем ![]() .
.
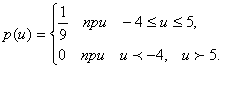
Условие нормировки выполняется
![]() .
.
График плотности распределения и одна из реализаций
случайного процесса - рисунок 4.
Функцию корреляции рекомендуется рассчитать двумя
методами и сравнить результаты.
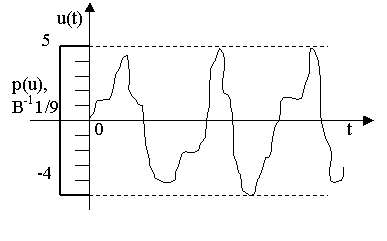

Рисунок 4.
Задача 7
Задана кодовая комбинация простого первичного кода
Q(0,1)
Требуется:
а) закодировать ее помехоустойчивым циклическим кодом,
исправляющим однократную ошибку (tиспр.=1);
б) проверить правильность построения кодовой
комбинации циклического кода F(0,1);
в) составить таблицу синдромов циклического кода;
г) проверить, будет ли исправлена однократная ошибка в
i – м разряде кодовой комбинации циклического кода;
д) построить структурную схему кодера циклического
кода.
Исходные данные к задаче приведены в таблице10.
Таблица 10
|
Последняя
цифра зачетной
книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Первая
половина кодовой комбинации |
10 |
11 |
10 |
01 |
10 |
11 |
01 |
01 |
11 |
10 |
|
Предпоследняя
цифра зачетной
книжки |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Вторая
половина кодовой комбинации |
11 |
10 |
01 |
11 |
00 |
11 |
10 |
10 |
11 |
01 |
|
Номер
ошибочного разряда i |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
2 |
3 |
4 |
Методические указания к задаче 7
С материалом по корректирующим кодам можно
ознакомиться в литературе [1 , с.273 – 282; 8, с. 307–319; 10, с.110–118,
123–124, 127-129].
Циклические коды относятся к классу линейных
систематических кодов. Кодовые комбинации циклического кода удобно
рассматривать в виде полинома некоторой степени
![]() ,
,
где
x – основание системы счисления;
ai – цифры данной системы счисления;
n – 1, n – 2,… -
показатель степени, в которую возводится основание, и одновременно порядковые
номера.
Минимальное кодовое расстояние связано с количеством
исправляемых ошибок зависимостью
![]() .
.
Следует помнить, что только для кода с d0 = 3
известно точное соотношение для определения количества проверочных символов r: (6.9) [12],где n=k+r. Здесь k – длина
кодовой комбинации простого кода (количество информационных символов), n – общая длина корректирующего кода. Это соотношение
можно представить в виде:
![]() .
.
Подбором определяется значение r, удовлетворяющее этому соотношению.
Величина r
является также показателем степени образующего полинома, который можно выбрать
из таблицы 18.1 [8, с. 316] или из таблицы 6.2 [10, с. 114].
Пункт 1 задания следует выполнять в
последовательности.
Определить d0, затем r и n, выбрать образующий полином и составить кодовую
комбинацию циклического кода. Кодирование можно проводить как в алгебраическом,
так и в цифровом виде. Кодирование циклическим кодом рассмотрено в примерах
18.5 [8] и 6.3 [10] .
Правильность построения кодовой комбинации проверяется
делением составленной комбинации на образующий полином. Если при делении
получится ненулевой остаток, это говорит о неверном кодировании, т. е.
полученная кодовая комбинация относится к запрещенным комбинациям этого кода.
Получение нулевого остатка (деление без остатка) говорит о верном кодировании,
т. е. кодовая комбинация является разрешенной.
Построение производящей матрицы циклического кода
рассмотрено в примере 6.9. [10].
Построение проверочной матрицы из производящей - материал [10, с. 121-122].
Построение матрицы синдромов производится
транспонированием проверочной матрицы. В таблице 18.2. [8] приведена
взаимосвязь между синдромом и искаженным символом циклического кода.
Проверка возможности исправления ошибки заключается во
введении ошибки в заданный разряд кодовой комбинации, делении полученной
комбинации на образующий полином, нахождении остатка и в определении соответствия полученного остатка
(синдрома) синдрому кода при ошибке в этом разряде.
Схему кодера выполнять по типу (рисунок 6.9) в [10] .
Описание принципа построения кодирующего устройства циклического кода приведено
в [10, с.127-129]. Следует помнить, что
число ячеек сдвигающего регистра и регистра задержек выбирается равным степени
образующего полинома, а число сумматоров – на единицу меньше веса образующего
полинома. Сумматоры по модулю два включаются перед ячейками, которые стоят на
позициях единиц в образующем полиноме, за исключением старшего разряда.
Например, если образующий полином P(x)= x3+x2+1, что соответствует P(0,1)=1101, тогда регистр сдвига должен иметь 3 ячейки
(образующий полином 3-й степени), в него включаются два сумматора (так как вес
образующего полинома W=3), сумматоры
включаются перед первой и третьей ячейками.
Список литературы
Основная литература
1. Теория
электрической связи: Учебник для вузов/ Зюко А.Г., Кловский Д.Д., Коржик В.И.,
Назаров М.В. - М.: Радио и связь, 1999.
Дополнительная
литература
2. Зюко
А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. - М.:
Радио и связь, 1986.
3. Кловский
Д.Д., Шилкин В.А. Теория электрической связи. Сб. задач и упражнений: Учебное
пособие для вузов. - М.: Радио и связь, 1990.
4. Гоноровский
И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986.
5. Кловский Д.
Д.Теория передачи сигналов. – М.: Радио и связь, 1973.
6. Баскаков
С.И. Радиотехнические цепи и сигналы. -
М.: Высшая школа, 2000.
7. Баскаков
С.И. Радиотехнические цепи и сигналы. Руководство к решению задач. – М.: Высшая
школа, 2002.
8. Панфилов
И. П., Дырда В. Е. Теория электрической связи. – М.: Радио и связь,1991.
9. Нефедов
В.И. Основы радиоэлектроники и связи. – М.: Высшая школа, 2002.
10. Емельянов Г. А., Шварцман В. О. Передача
дискретной информации. – М.: Радио и связь,1982.
11. Справочник
по специальным функциям с формулами, графиками и математическими таблицами /
Под ред. М. Абрамовица и И. Стиган. – М.: Наука,1979.
12. Прудников
А.П. и др. Интегралы и ряды. Элементарные функции. – М.: Наука, 1981.
Приложение А
Тригонометрические формулы преобразования (А1)
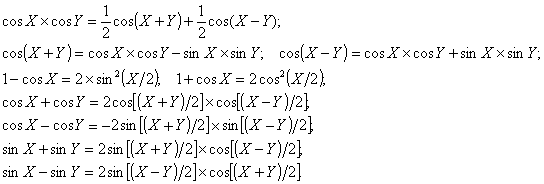
Формулы расчета коэффициентов Берга
(А2)
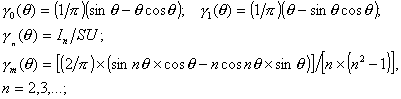
Формулы расчета различных интегралов
(А3)
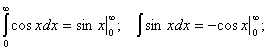
Интегрирование по частям ![]() ;
;
Пример-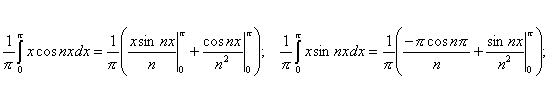
Интегрирование методом замены переменной 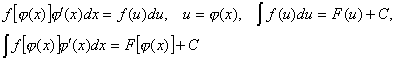
Приложение Б
Таблицы функций Бесселя первого рода для больших
индексов модуляции
Таблица Б 1
|
n |
Jn(1) |
Jn(2) |
Jn(3) |
Jn(4) |
Jn(5) |
Jn(6) |
Jn(7) |
|
0 |
0,765 |
0,224 |
-0,260 |
-0,397 |
-0,178 |
0,150 |
0,300 |
|
1 |
0,440 |
0,577 |
0,339 |
-0,066 |
-0,328 |
-0,277 |
-0,005 |
|
2 |
0,115 |
0,353 |
0,486 |
0,364 |
0,047 |
-0,243 |
-0,301 |
|
3 |
0,020 |
0,129 |
0,309 |
0,430 |
0,365 |
0,115 |
-0,168 |
|
4 |
0,003 |
0,034 |
0,132 |
0,281 |
0,391 |
0,358 |
0,158 |
|
5 |
|
0,007 |
0,043 |
0,132 |
0,261 |
0,362 |
0,348 |
|
6 |
|
0,001 |
0,011 |
0,049 |
0,131 |
0,246 |
0,339 |
|
7 |
|
|
0,003 |
0,015 |
0,053 |
0,130 |
0,234 |
|
8 |
|
|
|
0,004 |
0,018 |
0,057 |
0,128 |
|
9 |
|
|
|
|
0,006 |
0,021 |
0,059 |
|
10 |
|
|
|
|
0,001 |
0,007 |
0,024 |
|
11 |
|
|
|
|
|
0,002 |
0,008 |
|
12 |
|
|
|
|
|
|
0,003 |
Примечания-
1 Значения функций Бесселя, равные нулю, означают не
абсолютное их равенство нулю, а очень малую величину, которой можно пренебречь.
2 Отрицательные значения функций Бесселя говорят о
начальной фазе этих составляющих, равных 1800 (π радиан).
Содержание
Введение……………………………………………………… .... 3
1
Программа курса Теория электрической связи …………….. 5
2
Содержание установочных занятий……………………………
16
2.1 Содержание лекций……………………………………. 16
2.2 Примерный перечень тем
практических занятий……. 18
2.3 Примерный перечень тем лабораторных занятий…… 18
2.4
Примерный перечень тем курсовых работ……………
19
3
Контрольное задание и методическое указание к нему…….. 19
3.1 Требования к
выполнению контрольной работы…… 19
3.2 Требования к оформлению контрольной работы…… 20
3.3 Контрольная работа……………………………………. 21
Список литературы………………………………………………. 37
Приложение
А.……………………………………………………. 38
Приложение
Б……………………………………………………. 39
Св. План 2006г., поз. 196
Людмила Ивановна Сарженко
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Программа,
методические указания и
контрольные задания
(для
студентов специальности
050719 –
Радиотехника, электроника и телекоммуникации заочной (дистанционной) формы
обучения )
Редактор Ж. М. Сыздыкова
Специалист по стандартизации Н. М. Голева
Подписано в печать Формат 60х84
Тираж 250 экз. Бумага типографская №1
Объем 2,5
уч.-изд. л.
Заказ № Цена тенге.
Копировально – множительное
бюро
Алматинского института
энергетики и связи
050013, Алматы, Байтурсынова, 126