Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра телекоммуникационных систем

  

 

ЗАЩИТА ИНФОРМАЦИИ В ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМАХ

Методические указания к выполнению курсовой  работы

для студентов  специальности

5В071900 - Радиотехника, электроника и телекоммуникации

 

 

 Алматы 2013

 

СОСТАВИТЕЛИ: А.С. Байкенов, Е.А. Шкрыгунова. Защита информации  в телекоммуникационных системах.  Методические указания  к  выполнению  курсовой работы для студентов   специальности 5В071900 – Радиотехника, электроника и телекоммуникации – Алматы; АУЭС, 2012 –   23с. 

 

Методические указания содержат общие положения по выполнению курсовой  работы. Приводится рекомендуемая литература.

Ил. 3 , табл.10 , библиогр.- 3  назв. 

 

Рецензент: канд. техн. наук, проф. К.Х. Туманбаева. 

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.

© НАО “Алматинский университет энергетики и связи”, 2013 г.

Содержание

 

Введение	4
Задание  № 1	5
Задание 1.1	5
Методические указания к решению задания 1.1	5
Задание 1.2	9
Задание № 2	13
Задание 2.1	13
Методические указания к решению задания 2.1	13
Задание 2.2	16
Методические указания к решению задания 2.2	16
Задание 2.3	19
Методические указания к заданию 2.3	20
Список литературы	22

 

Введение

 

Целью курсовой работы является ознакомление студентов с математической основой построения систем защиты информации в телекоммуникационных системах - методами криптографии. Курсовая работа направлена на формирование у студентов систематизированного  представления о принципах, методах и средствах реализации защиты данных.

Курсовая работа посвящена изучению систем шифрования с закрытым ключом. Задание №1 посвящено шифрованию с закрытым ключом. Рассматривается алгоритм  RSA, а также предлагаются расчеты  по электронной подписи с использованием  хеш-функции.

Задание №2 посвящено асимметричному шифрованию или шифрованию с открытым ключом. Рассматриваются алгоритмы   Диффи–Хелмана, Шамира и Эль-Гамаля.

 

Исследование симметричных и ассиметричных методов шифрования

 

Целью курсовой работы является ознакомление студентов с математической основой построения систем защиты информации в телекоммуникационных системах - методами криптографии.

 

Задание  № 1

 

Задание  1.1. Несимметричное шифрование – дешифрование

 

Зашифровать информацию по методу RSA для последующей передачи.

Сгенерировать секретный ключ с предложенными двумя вариантами и с использованием расширенного алгоритма Эвклида.

Вариант задания определяется последними цифрами номера студенче-ского билета. По номеру i (предпоследняя цифра) студент выбирает сообщение для зашифровывания, по j – требуемые для реализации этого алгоритма числа р и q.

 

Таблица 1.1 - Исходные данные:

I	0	1	2	3	4
Сообщение	Принтер	Интеграл	Минус	Модуль	Плюс
J	0	1	2	3	4
p q	7.11	5.17	3.11	11.19	13.17

 

Продолжение таблицы 1.1

I	5	6	7	8	9
Сообщение	Число	Дробь	Корень	Остаток	Степень
J	5	6	7	8	9
p q	7.17	5.11	7.13	11.17	5.13

 

Методические указания к решению задания 1.1

 

Одним из наиболее распространенных методов несимметричного шифрования - дешифрования является метод шифрования с открытым ключом, в котором используется алгоритм RSA.

Несмотря на довольно большое число различных СОК (система с открытым ключом), наиболее популярна – криптосистема RSA, разработанная в 1977 году и получившая название в честь ее создателей: Рона Ривеста, Ади Шамира и Леонарда Эйдельмана.

Они воспользовались тем фактом, что нахождение больших простых чисел в вычислительном отношении осуществляется легко, но разложение на множители произведения двух таких чисел практически невыполнимо. Доказано (теорема Рабина), что раскрытие шифра RSA эквивалентно такому разложению. Поэтому для любой длины ключа можно дать нижнюю оценку числа операций для раскрытия шифра, а с учетом производительности современных компьютеров оценить и необходимое на это время.

Возможность, гарантированно оценить защищенность алгоритма RSA стала одной из причин популярности этой СОК на фоне десятков других схем. Поэтому алгоритм RSA используется в банковских компьютерных сетях, особенно для работы с удаленными клиентами (обслуживание кредитных карточек).

Рассмотрим математические результаты, положенные в основу этого алгоритма.

Теорема 1. (Малая теорема Ферма.)

Если р – простое число, то

                                               x^p-1 = 1(mod p)                                           (1)

для любого х, простого относительно р, и

                                                x^p = x(mod p)                                            (2)

для любого х.

Доказательство. Достаточно доказать справедливость уравнений (1) и (2) для x^p. Проведем доказательство методом индукции.  

Очевидно, что уравнение (3) выполняется при х=0 и 1.

Далее

x^p = (x –1 + 1)^p = C(p,j)(x –1)^j = (x –1)^p + 1(mod 2),

так как C(р,j)=0(mod р) при 0<j<р.

С учетом этого неравенства и предложений метода доказательства по индукции, теорема доказана.

 

Определение. Функцией Эйлера φ(n) называется число положительных целых, меньших n и простых относительно n.

 

Таблица 1.2 - Исходные данные:

N	2	3	4	5	6	7	8	9	10	11	12
φ(n)	1	2	2	3	2	6	4	6	4	10	4

 

Теорема 2. Если n = рq, (р и q – отличные друг от друга простые числа), то

φ(n)=(р-1)(q-1).

Теорема 3. Если n = рq, (р и q - отличные друг от друга простые числа)  и х – простое относительно р и q, то

x^φ(n) = 1(mod n).

Следствие. Если n = рq, (р и q - отличные друг от друга простые числа) и е простое относительно (n), то отображение

E_в,n : xx^в(mod n)

является взаимно однозначным на Z_n.

Очевиден и тот факт, что если е – простое относительно f(n), то существует целое d, такое, что

                                             ed ≡ 1 (mod φ(n)).                                        (3)

На этих математических фактах и основан популярный алгоритм RSA.

Пусть n = рq, где р и q – различные простые числа. Если e и d удовлетворяют уравнению, то отображения Еe,n и Еd,n являются инверсиями на Zn. Как Еe,n, так и Еd,n легко рассчитываются, когда известны e, d, р, q.

Если известны e и n, но р и q неизвестны, то Еe,n представляет собой одностороннюю функцию; нахождение Еd,n по заданному n равносильно разложению n. Если р и q – достаточно большие простые, то разложение n практически неосуществимо. Это и заложено в основу системы шифрования RSA.

Шифросистема RSA.

Система RSA в настоящее время является наиболее распространенной системой шифрования с открытым ключом.

Пусть n = pq – целое число, представляемое в виде произведения двух больших простых чисел p, q. Числа e и d, определяющие алгоритмы шифрования и расшифрования соответственно, должны отвечать условию

                                              ed ≡ (mod φ(n)),                                          (1)

где φ(n) = (p-1)(q-1) – значение функции Эйлера от числа n.

Пусть k = (n,p,q,e,d) – выбранный ключ, состоящий из открытого ключа k1 = (n,e) и секретного ключа k2 = (n,p,q,d).

Пусть M – блок открытого текста и C – соответствующий блок шифрованного текста. Тогда правила шифрования и расшифрования определяются формулами:

                    С = E_k (M) =M^e (mod n),        D_k(C) = C^d (mod n).                (2)

Заметим, что в соответствии с (2)  D_k(C) = M.

При нахождении значений e и d, удовлетворяющих условию (1), значение e обычно задают таким образом, чтобы оно было взаимнопростым с φ(n), а значение d определяют из уравнения

                                               φ(n)x + ed = 1.                                           (3)

В общем случае уравнение (3) имеет вид ax + by = c (здесь a = φ(n), b = e, y = d) и называется Диафантовым уравнением.

Решение этого уравнения

                                   y = (–1)^μ · a_μ-1 · x = (–1)^μ+1 · b _μ-1                                                  (4)

можно получить с помощью разложения отношения a/b в цепную дробь:

 

,

 

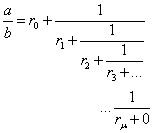где μ – порядок цепной дроби, т.е. индекс коэффициента дроби, у которого остаток равен нулю,

            

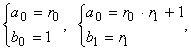
                         (5)

а для всех членов, начиная с третьего справедливо

       

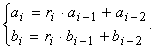
                              (6)

 

Таким образом, для решения уравнения (3) необходимо представить отношение a/b в виде цепной дроби, определить при этом значения r₀, r₁…r_μ и μ. Потом в соответствии с (4) – (6) определяются значения a_i, b_i, а также x и y.

 

Пример.

Зашифруем аббревиатуру RSA, используя p = 17, q = 31. Для этого вычислим n = pq = 527 и μ(n) = (p-1)(q-1) = 480. Выберем далее в качестве e число, взаимно простое с μ(n), например, e = 7. С помощью цепных дробей найдем целые числа x и y, удовлетворяющие соотношению μ(n)x + ey = 1. Запишем 480x + 7y = 1

 

Следовательно,

μ = 3, a₀ = 68, b₀ = 1, a₁ = 69, a₂ = 1·69 + 68 = 137, b₂ = 1·1 + 1 = 2.

Таким образом, x = –2, y = –137.

Поскольку

–137 (mod 480) = 343, то d = 343.

Проверка

7 · 343 = 2401 = 1(mod 480).

Теперь представим данное сообщение в виде последовательности чисел, содержащихся в интервале 0…526. Для этого буквы R, S и A закодируем пятимерными двоичными векторами, воспользовавшись двоичной записью их порядковых номеров в алфавите:

         R = 18 = (10010), S = 19 (10011), A = 1 (00001).

Тогда RSA = (100101001100001). Укладываясь в заданный интервал 0…526, получаем следующее представление:

RSA = (100101001), (100001) = (M₁ = 297, M₂ = 33).

Далее последовательно шифруем M₁ и M₂:

C₁ = E_k (M₁) = M₁^в = 297⁷ (mod 527) = 474.

При этом мы воспользовались тем, что

 

 

 

т.е. 297⁷ = ((297²)³297)(mod 527) = ((200³(mod 527)297)mod 527),

C₂ = E_k(M₂) = M₂^в = 33⁷(mod 527) = 407.

В итоге получаем шифротекст: С₁ = 474, С₂ = 407.

При расшифровании нужно выполнить следующую последовательность действий. Во-первых, вычислить

D_k (C₁) = C₁^d = 33⁷ (mod 527) = 474³⁴³ (mod 527).

Отметим, что при возведении в степень, удобно воспользоваться тем, что 343 = 256 + 64 + 16 + 4 + 2 + 1. На основании этого представления получаем:

474²(mod 527) = 174,      474⁴(mod 527) = 237,  

474⁸(mod 527) = 307,      474¹⁶(mod 527) = 443,  

474³²(mod 527) = 205,    474⁶⁴(mod 527) = 392,  

474¹²⁸(mod 527) = 307,   474²⁵⁶(mod 527) = 443,  

в силу чего

474³⁴³(mod 527) = (443×392×443×237×174×474)(mod 527) = 297,  

Аналогично

407³⁴³(mod 527) = 33.  

Возвращаясь к буквенной записи, получаем после расшифрования RSA.

Произвести генерацию закрытого ключа используя расширенный алгоритм Эвклида, подробно описанный в алгоритме Шамира п.2.2.

        

Задание 1.2. Хеширование и цифровая подпись документов

 

Используя данные задания 1.1, получить хеш – код m для сообщения М при помощи хеш – функции Н, взятой из рекомендаций МККТТ Х.509. Вектор инициализации Н₀ выбрать равным нулю.

Вычислить цифровую подпись методом RSA под электронным документом М, используя рассчитанный хеш – код m и секретный ключ d.

Представить схему цифровой подписи с подробным описанием ее функционирования.

Хеш – функцию МККТТ Х.509 запишем следующим образом:

H_i=[(H_i-1 Å M_i)²] (mod n), где i=l,n, H₀ – вектор инициализации, М_i =М₁,М₂,М₃…,М_n - длина блока.

Все блоки делят пополам и к каждой половине прибавляют равноценное количество единиц. С преобразованными таким образом блоками производят интеграционные действия.

 

Пример.

Необходимо получить хеш – код сообщения ПРЕДЕЛ при помощи хеш функции Х.509 с параметрами p=3, q=11.

Порядок вычисления хеш – кода:

а) получить значение модуля: n=pq= 3×11=33;

б)представить сообщение в виде номеров букв русского алфавита в десятичном и двоичном видах:

         П                 Р            Е               Д                Е               Л

         16                17             6                 5                  6                12

00010000, 00010001, 00000110, 00000101, 00000110, 00001100:

в) Разбить байт пополам, добавив в начало полубайта единицы, и получить хешируемые блоки М_i:

 

Таблица 1.3 - Исходные данные:

 

г) Выполнить интеративные шаги:

Первая интерация

М1	11110001
Å
Н0=0	00000000
Н0 Å М1	11110001=24110
[(H0Å M1)2] (mod 33)	2412 mod 33 = 10
Н1	1010=00001010

 

Вторая интерация

М2	11110000
Å
Н1	00001010
Н1 Å М2	11111010=25010
[(H1Å M2)2] (mod 33)	2502 mod 33 = 19
Н1	00010011

 

Третья интерация

М3	11110001
Å
Н2	00010011
Н2 Å М3	11100010=22610
[(H2Å M3)2] (mod 33)	2262 mod 33 = 28
Н3	00011100

 

Четвертая интерация

М4	11110001
Å
Н3	00011100
Н3 Å М4	11101101=23710
[(H3Å M4)2] (mod 33)	2372 mod 33 = 6
Н4	00000110

 

Пятая интерация

М5	11110000
Å
Н4	00000110
Н4 Å М5	11110110=24610
[(H4Å M5)2] (mod 33)	2462 mod 33 = 15
Н5	00001111

 

Шестая интерация

М6	11110110
Å
Н5	00001111
Н5 Å М6	11111001=24910
[(H5Å M6)2] (mod 33)	2492 mod 33 =18
Н6	00010010

 

Седьмая интерация

М7	11110000
Å
Н6	00010010
Н6 Å М7	11100010 = 22610
[(H6Å M7)2] (mod 33)	2262 mod 33 = 28
Н7	00011100

 

Восьмая интерация

М8	11110101
Å
Н7	00011100
Н7 Å М8	11101001= 233
[(H7Å M8)2] (mod 33)	2332 mod 33 = 2
Н8	00000010

 

 

Девятая интерация

М9	11110000
Å
Н8	00000010
Н8 Å М9	11110010 = 24210
[(H8Å M9)2] (mod 33)	2422 mod 33 = 11
Н9	00001011

 

Десятая интерация

М10	11110110
Å
Н9	00001011
Н9 Å М10	11111101 = 253
[(H9Å M10)2] (mod 33)	2532 mod 33 = 22
Н10	00010110

 

Одиннадцатая интерация

М11	11110000
Å
Н10	00010110
Н10 Å М11	11100110 =23010
[(H10ÅM11)2] (mod 33)	2302 mod 33 = 32
Н11	00100000

 

Двенадцатая интерация

М12	11111100
Å
Н11	00100000
Н11 Å М12	11011100 = 22010
[(H11ÅM12)2] (mod 33)	2202 mod 33 = 22
Н12	00010110

 

Таким образом, исходное сообщение ПРЕДЕЛ имеет хеш – код m=22.

Для вычисления цифровой подписи используем следующую формулу:

S=m^d (mod n) = 22³ mod 33 = 22.

Пара (M, S) передается получателю как электронный документ М, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа d.

Получив пару (M, S), получатель вычисляет хеш – код сообщения М двумя способами:

1) Восстанавливает хеш – код m’, применяя криптографическое преобразование подписи S с использованием открытого ключа e:

 

m’=S^e (mod n) =22⁷ mod 33 = 22.

 

2) Находит результат хеширования принятого сообщения с помощью той же хеш – функции: m=H(M) =22.

При равенстве вычисленных значений m’ и m получатель признает пару (M, S) подлинной.

 

Контрольные вопросы

 

1. Изложите принципиальную схему организации секретной связи с использованием системы шифрования с открытым ключом.

2. Изложите принципиальную схему организации обмена документами, заверенными цифровой подписью.

3. Перечислите основные требования, предъявляемые к хеш-функции, пригодной для использования при вычислении цифровой подписи документа.

 4. Каким образом с помощью криптосистемы RSA можно организовать передачу шифрованных сообщений, подлинность которых подтверждена цифровой подписью? Приведите примеры.

 

Задание  №2

 

Задание  2.1. Система с открытым ключом Диффи-Хелмана

 

Сгенерировать секретные ключи для пяти абонентов по методу  Диффи-Хеллмана (DH). Для этого взять значение секретного ключа x из таблицы 1. Соответствующие значения открытого ключа вычислить и результаты внести в таблицу.  Вариант задания определяется по номеру i (предпоследняя цифра) и j (последняя цифра зачетной книжки) – требуемая для реализации этого алгоритма число x .

Число j – начальный номер для второго абонента при выборе числа x. Для выбора x для связи с пятью абонентами необходимо по циклической процедуре выбрать x по последней цифре зачетки. Например, цифры в зачетной книжке (15). Выбираем для первого абонента x=11, т.к. i =1. Для второго по второй цифре x =29, т.к. j= 5. Для третьего по формуле (j +1)=i выбираем x= 31, т.к. j =6. Для четвертого выбираем x = 37, j =7. Для пятого выбираем x = 39, т.к. j=8.  Если, например, последняя цифра (27)  больше пяти - пусть j =7, то выбираем x =  31,37, 39,41, 7.

Рекомендуемые значения p = 30803, g = 2.

 

Таблица 2.1 -  Исходные данные:

I	0	1	2	3	4
X	7	11	13	17	19

 

I	5	6	7	8	9
x	29	31	37	39	41

 

Методические указания к решению задания 2.1

 

Первая система с открытым ключом — система Диффи-Хеллмана.

Эта криптосистема была открыта в середине 70-х годов американ­скими учеными Диффи (Whitfield Diffie) и Хеллманом (Martin Hell-man) и привела к настоящей революции в криптографии и ее практи­ческих применениях. Это первая система, которая позволяла защи­щать информацию без использования секретных ключей, передавае­мых по защищенным каналам. Для того чтобы продемонстрировать одну из схем применения таких систем, рассмотрим сеть связи с N пользователями, где N — большое число. Пусть мы хотим органи­зовать секретную связь для каждой пары из них. Если мы будем использовать обычную систему распределения секретных ключей, то каждая пара абонентов должна быть снабжена своим секретным ключом, т.е. всего потребуется  ключей.

Если абонентов 100, то требуется 5000 ключей, если же абонен­тов 10⁴ , то ключей должно быть 5∙10⁷. Мы видим, что при большом числе абонентов система снабжения их секретными ключами стано­вится очень громоздкой и дорогостоящей.

Диффи и Хеллман решили эту проблему за счет открытого рас­пространения и вычисления ключей. Перейдем к описанию предло­женной ими системы.

Пусть строится система связи для абонентов А,В,С,... .

У каж­дого абонента есть своя секретная и открытая информация. Для  организации этой системы выбирается большое простое число р и некоторое число g, 1 < g < р — 1 такое, что все числа из множе­ства {1, 2, ∙ ∙ ∙ , р — 1} могут быть представлены как различные сте­пени g mod p (известны различные подходы для нахождения таких чисел g, один из них будет представлен ниже). Числа р и g известны всем абонентам.

Абоненты выбирают большие числа X_a,X_b,X_c, которые хра­нят в секрете (обычно такой выбор рекомендуется проводить случай­но, используя датчики случайных чисел). Каждый абонент вычис­ляет соответствующее число Y, которое открыто передается другим абонентам,

Y_А = g^Xa mod р ,

Y_B = g^Xb mod р..                                                                                             (1)

Yс = g^Xc mod р.

В результате получаем следующую таблицу.

 

Таблица 2.2 - Ключи пользователей в системе Диффи-Хеллмана

Абонент	Секретное число	Открытый ключ	Закрытый ключ
A B C	XA XB XC	YA YB YC	ZAB, ZAC ZBA, ZBC ZCA, ZCB

 

Допустим, абонент А решил организовать сеанс связи с В, при этом обоим абонентам доступна открытая информация из таблицы 2. Абонент А сообщает В по открытому каналу, что он хочет передать ему сообщение. Затем абонент А вычисляет величину

Z_AB = (Y_B)^ХА modp.                                               (2)

Никто другой, кроме А, этого сделать не может, так как число Х_А секретно.

В свою очередь, абонент В вычисляет число

Z_BA = (Y_A)^XBmodp.                                               (3)

На рисунке 1 представлена схема обмена ключами в системе Диффи-Хеллмана.

Остановимся теперь на упомянутой выше задаче выбора числа р. При произвольно заданном g она может оказаться трудной зада­чей, связанной с разложением на простые множители числа g - 1. Дело в том, что для обеспечения высокой стойкости рассмотренной системы число g - 1 должно обязательно содержать большой простой множитель. Поэтому часто рекомендуют использовать следующий подход.

Число р выбирается таким, чтобы выполнялось равенство

р=2q+1 (где q- также простое число)

и были справедливы неравенства

1 < g < р - 1    и    g^q mod р 1.

Для того чтобы система была устойчива к криптоанализу, необходимо выбирать число р очень большим.

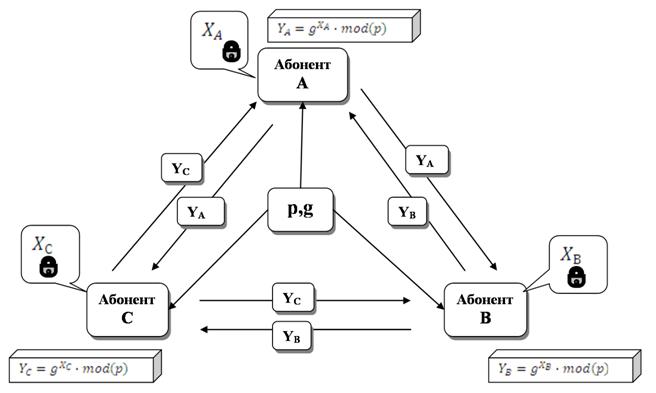
Рисунок 1 - схема обмена ключами в системе Диффи-Хеллмана

 

Пример.

Пусть g = 43. Выберем пара­метр p. Попробуем взять q=17 401.

Соответственно р=2*17 401+1=34 803. Проверим: 43¹⁷⁴⁰¹ mod 34 803 = 17 746. Необходимые условия выполняются, значит, такое р подходит. Итак, мы выбрали параметры р = 34 803, g = 43. Теперь каждый або­нент выбирает секретное число и вычисляет соответствующее ему открытое число. Пусть выбраны Х_A = 7, Х_B = 13. Вычисляем Y_A = 43⁷ mod 34 803 = 11 689, Y_B = 43¹³ mod 34 803 = 14 479. Пусть А и В реши­ли сформировать общий секретный ключ. Для этого А вычисляет Z_AB = 14479⁷ mod 34 803=6 415, а В вычисляет Z_BA = 11 689¹³ mod 34 803 = 6 415. Теперь они имеют общий ключ 6 415, который не передавался по кана­лу связи.

 

Контрольные вопросы

1. Какими преимуществами перед другими алгоритмами с закрытым ключом обладает система Диффи-Хеллмана?

2. Дайте краткую характеристику системы Диффи-Хеллмана.

3. Объясните, почему число р, необходимое при вычислении секретных ключей, следует выбирать большим?

 

Задание  2.2. Шифрование по алгоритму Шамира

 

Зашифровать сообщение по алгоритму Шамира для трех абонентов,  взяв значение сообщения m и значение p из таблицы 2.3. По номеру i (предпоследняя цифра) студент выбирает сообщение для зашифровывания, по j – требуемые для реализации этого алгоритма число р.  Выбор данных для других абонентов произвести циклически согласно процедуре (I + 1) и (G + 1). Например, последние цифры номера зачетной книжки – (26). Выбираем для трех абонентов (сообщение, p) -  (16,49), (18,51), (20,53).

 

Таблица 2.3 – Исходные данные

I	0	1	2	3	4
Сообщение	12	14	16	18	20
G	0	1	2	3	4
p	29	31	37	41	43

 

I	5	6	7	8	9
Сообщение	22	24	26	28	30
G	5	6	7	8	9
p	47	49	51	53	57

 

Методические указания к заданию 2.2

 

Этот шифр, предложенный Шамиром (Adi Shamir), был первым, позволяющим организовать обмен секретными сообщениями по от­крытой линии связи для лиц, которые не имеют никаких защищен­ных каналов и секретных ключей и, возможно, никогда не видели друг друга. (Напомним, что система Диффи-Хеллмана позволяет сформировать только секретное слово, а передача сообщения потре­бует использования некоторого шифра, где это слово будет исполь­зоваться как ключ.)

Перейдем к описанию системы. Пусть есть два абонента А и В, соединенные линией связи. А хочет передать сообщение m абоненту B так, чтобы никто не узнал его содержание. А выбирает случай­ное большое простое число р и открыто передает его В. Затем А выбирает два числа  с_{А и} d_A , такие, что

с_Аd_A mod (р - 1) = 1.                                          (2.1)

Эти числа А держит в секрете и передавать не будет. В тоже вы­бирает два секретных числа с_в и d_в, такие, что

                                                    с_вd_в mod (p - 1) = 1.                                         (2.2)

После этого А передает свое сообщение m, используя трехсту­пенчатый протокол. Если m < р (m рассматривается как число), то сообщение т передается сразу , если же m  р, то сообще­ние представляется в виде m₁, m₂,..., m_t, где все m_i < р, и затем передаются последовательно m₁, m₂,..., m_t. При этом для кодиро­вания каждого m_i лучше выбирать случайно новые пары (c_A,d_A) и (c_B,d_B) — в противном случае надежность системы понижается. В настоящее время такой шифр, как правило, используется для пере­дачи чисел, например, секретных ключей, значения которых меньше р. Таким образом, мы будем рассматривать только случай m < р.

Описание протокола.

Шаг 1.  А вычисляет число

х₁ =m^СА modp,                                       (2.3)

где m — исходное сообщение, и пересылает х₁ к В.

Шаг 2.   В, получив х₁, вычисляет число

х₂ = х₁^CB mod p.                                       (2.4)

и передает х₂ к А.

Шаг 3.  А вычисляет число

х₃ = х₂^dA mod p.                                       (2.5)

и передает его В.

Шаг 4.   В, получив х₃, вычисляет число

                                               Х₄ = x₃^dB mod p.                                      (2.6)

Схема обмена ключами по алгоритму Шамира представлена на рисунке 2.     

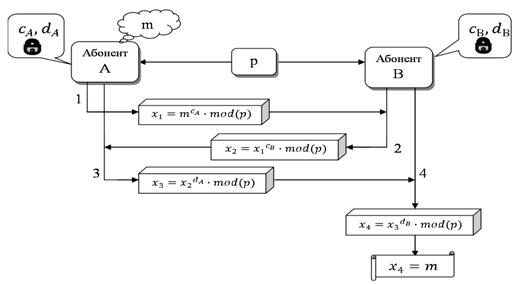
Рисунок 2 - схема обмена ключами в системе Шамира

 

Утверждение (свойства протокола Шамира):

1)   х₄ = m, т.е. в результате реализации протокола от А к В действительно передается исходное сообщение;

2)   злоумышленник не может узнать, какое сообщение было пе­редано.

Доказательство. Вначале заметим, что любое целое число е  0 может быть представлено в виде е = k(р — 1)+r, где r = е mod (p - 1). Поэтому на основании теоремы Ферма

 

.   (2.7)

 

Справедливость первого пункта утверждения вытекает из следую­щей цепочки равенств:

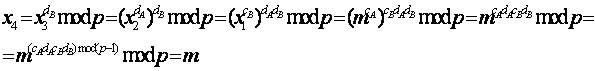          (предпоследнее равенство следует из (2.7), а последнее выполняется в силу (2.1) и (2.2)).

 

           Доказательство второго пункта утверждения основано на пред­положении, что для злоумышленника, пытающегося определить m, не существует стратегии более эффективной, чем следующая. Вначале он вычисляет C_B из (2.4), затем находит d_B и, наконец, вычисляет Х₄ = m по (2.6). Но для осуществления этой стратегии злоумышленник должен решить задачу дискретного логарифмирования (2.4), что практически невозможно при больших р.           

Опишем метод нахождения пар c_A,d_A и с_B,d_B, удовлетворяющих (2.1) и (2.2). Достаточно описать только действия для абонента А, так как действия для В совершенно аналогичны. Число с_A выбираем случайно так, чтобы оно было взаимно простым с р-1 (по­иск целесообразно вести среди нечетных чисел, так как р - 1 четно), Затем вычисляем d_A с помощью обобщенного алгоритма Евклида.

 

Пример.

 Пусть А хочет передать В сообщение m = 10. А выбирает р = 23, с_А = 7 (gcd(7,22) = 1) и вычисляет d_A = 19. Аналогично, В выбирает параметры c_B = 5 (взаимно простое с 22) и d_B = 9.

Переходим к протоколу Шамира.

Шаг 1. x₁ = 10⁷ mod 23 = 14.

Шаг 2. х₂ = 14⁵ mod 23 = 15.

ШагЗ.  x₃= 15¹⁹ mod 23 = 19.

Шаг 4. х₄ = 19⁹ mod 23 = 10.

Таким образом, В получил передаваемое сообщение m = 10.      

 

 

Контрольные вопросы

1. Дайте краткую характеристику системы шифрования по алгоритму Шамира.

2. Сколько пересылок между двумя абонентами необходимо совершить для передачи одного сообщения в данном алгоритме?

3. Какими преимуществами перед другими алгоритмами шифрования обладает система Шамира?

 

Задание  2.3. Шифрование по алгоритму Эль-Гамаля

 

По таблице 2.4 выбрать сообщение m и секретный ключ x  и провести шифрование по методу Эль-Гамаля для пяти абонентов. Вариант задания определяется последними цифрами номера студенческого билета. По номеру i (предпоследняя цифра) студент выбирает сообщение для зашифровывания, по j (последняя цифра) – требуемые для реализации этого алгоритма  секретный ключ x. Исходные данные для других четырех секретных ключей x выбираются циклически по процедуре (i+1) и (j+1). Например, последние цифры 24. Выбираем для пяти абонентов- (сообщение, x) - (9,37), (11,43), (13,47), (3,51), (15,29). Результаты заносятся в таблицу по схеме «абонент – секретный ключ – открытый ключ». Аналогично таблице 2.5. Рекомендуемые значения для p = 30803, g = 2.

Таблица 2.4 - Исходные данные

I	0	1	2	3	4
Сообщение	5	7	9	11	13
G	0	1	2	3	4
X	29	11	13	7	19

 

I	5	6	7	8	9
Сообщение	3	15	11	15	13
G	5	6	7	8	9
X	31	37	43	47	51

 

Методические указания к заданию 2.3

 

Пусть имеются абоненты А, В, С, ..., которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищен­ных каналов связи. Шифр, предло­женный Эль-Гамалем (Tahcr ElGamal), решает эту задачу, используя, в отличие от шифра Шамира, только одну пересылку со­общения. Фактически здесь используется схема Диффи-Хеллмана, чтобы сформировать общий секретный ключ для двух абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ. Для каждого следующего со­общения секретный ключ вычисляется заново. Перейдем к точному описанию метода.

Для всей группы абонентов выбираются некоторое большое про­стое число р и число g, такие, что различные степени g суть раз­личные числа по модулю р. Числа р и g передаются абонентам в открытом виде (они могут использоваться всеми або­нентами сети).

Затем каждый абонент группы выбирает свое секретное число c_i, 1 < с_i < р - 1 и вычисляет соответствующее ему открытое число d_i,

d_i=g^cimodp.                                                  (3.1)

Результат представлен в таблице 2.5.

Необходимо выбрать числа p и g так, чтобы они отвечали следующим требованиям:

g^q mod p 1,

где p=2q+1.

Таблица 2.5- Ключи пользователей в системе Эль-Гамаля

Абонент	Секретный ключ	Открытый ключ
А	сА	dA
В	сВ	dB
С	сD	dC

 

Покажем теперь, как А передает сообщение абоненту В. Бу­дем предполагать, как и при описании шифра Шамира, что сообще­ние представлено в виде числа m < р.

Схема обмена ключами по алгоритму Эль-Гамаля представлена на рисунке 3.       

 

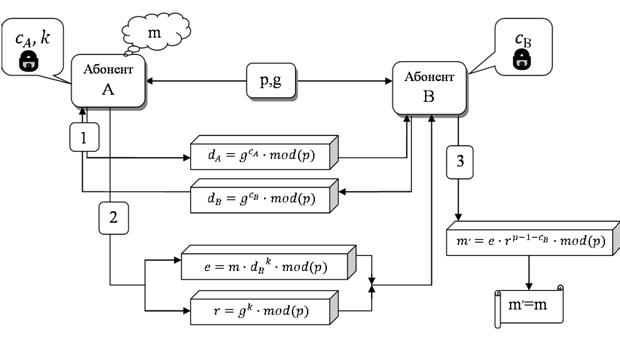  Рисунок 3 - схема обмена ключами в системе Эль-Гамаля

 

Шаг 1. А формирует случайное число к, 1  к  р-2, вычисляет числа

r = g^k mod p,                                                                                                         (3.2)                                                                                                                        e = m d_B^k mod p                                                                                                  (3.3)

и передает пару чисел (r, е) абоненту В.

Шаг 2.  В, получив (r,е), вычисляет

m' = е r^p-1-c_Bmod р.                                                                                 (3.4)

Ясно,  что по аналогичной схеме могут передавать сообщения все абоненты в сети. Заметим, что любой абонент, знающий открытый ключ абонента В, может посылать ему сообщения, зашифрованные с помощью открытого ключа d_B. Но только абонент В, и никто другой, может расшифровать эти сообщения, используя известный только ему секретный ключ с_В. Отметим также, что объем шифра в два раза превышает объем сообщения, но требуется только одна передача данных (при условии, что таблица с открытыми ключами заранее известна всем абонентам).

 

 

Контрольные вопросы

1. Дайте краткую характеристику системы шифрования по алгоритму Эль-Гамаля.

2. Сколько секретных ключей генерируется для пересылки, например, трех сообщений между абонентами А и В?

3. Какими основными преимуществами обладает эта система перед другими?

 

 Список литературы

 

1.Романец Ю. В. Защита информации в компьютерных системах и сетях. /Под ред. В.Ф. Шаньгина. – М.: Радио и связь 1999

2.Петраков А.В. Основы практической защиты информации. 2-е издание Учебн. Пособие. – М.: Радио и связь, 200 с.

3. Рябко Б. Я., Фионов А.Н. Криптографические методы защиты информации. –М.: Горячая линия- Телеком, 2005.

 

Сводный план 2012 г., поз. 165