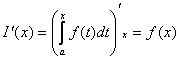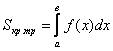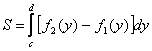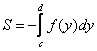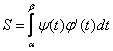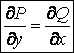АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Математика 2
Конспект лекций
(для студентов всех форм обучения всех специальностей)
Бакалавриат
Алматы 2008
СОСТАВИТЕЛЬ: Дулэпо В.М., Ким Л.Н. Математика 2. Конспект лекций (для студентов всех форм обучения всех специальностей). Бакалавриат - Алматы: АИЭС, 2008.- с.
Настоящее учебное пособие содержит краткий конспект 14 лекций по основным разделам курса высшей математики, вошедших в раздел Математика 2 ("Теория функций многих переменных", "Интегральное исчисление") и соответствует учебному плану бакалавриата всех специальностей второго семестра очного обучения Алматинского института энергетики и связи.
Предназначено для студентов высших технических учебных заведений.
Содержание
Предисловие ………………………………………………..……………… 3
Функции многих переменных
1.1 Лекция 1. Функции многих переменных………………………..
1.2 Лекция 2. Функции многих переменных (продолжение)………
Интегральное исчисление
1.3 Лекция 3. Неопределённый интеграл……………………………
1.4 Лекция 4. Интегрирование рациональных дробей……………..
1.5
Лекция 5. Интегрирование тригонометрических и
иррациональных выражений…………………………
1.6 Лекция 6. Определённый интеграл………………………………
1.7 Лекция 7. Формула Ньютона-Лейбница…………………………
1.8 Лекция 8. Применение определённых интегралов. Несобственные интегралы ………
1.9 Лекция 9. Двойные интегралы …………………………………..
1.10 Лекция 10. Тройные интегралы …………………………………..
1.11 Лекция 11. Криволинейные интегралы …………………………
1.12 Лекция 12. Вычисление КИ-2. Независимость от пути ……….
1.13 Лекция 13. Формула Ньютона-Лейбница для КИ-2. Поверхностные интегралы …
1.14 Лекция 14. Формулы Остроградского и Стокса ……………….
Список литературы ..……………..…………………….……………..…….
Лекция 1. Функции многих переменных
В науке и технике часто приходится встречаться с одновременным изменением нескольких переменных.
Примеры. 1) ![]() .
.
2)
![]()
3)
![]()
В дальнейшем будем в основном рассматривать функции двух переменных.
Этому есть две причины. Во-первых, принципиального различия между двумя и большим количеством переменных нет, увеличение числа переменных лишь ведёт к громоздкости выкладок. Во-вторых, функции двух переменных допускают наглядную геометрическую иллюстрацию.
Пусть дано пространство R2 - множество упорядоченных пар чисел (х,у). Геометрически - множество точек плоскости (х,у).
Если существует
правило или закон, по которому каждой паре (х,у) соответствует определенное
число z, то говорят, что
z называется
функцией двух переменных х и у и этот факт обозначается
z =
f(x,
y)
или z =
f(P), где
P(x ,y).
R2 называется областью определения (задания, существования) функции.
Множество чисел z называется областью изменения (значений) функции.
Обозначение частных значений функции в конкретной точке:
![]()
Примеры. ![]() - значение функции в
любой точке,
- значение функции в
любой точке,
![]() - значение в точке
Р(1, у).
- значение в точке
Р(1, у).
Основные способы задания функции: аналитический (формульный) и табличный.
Виды аналитического способа: явный и неявный.
Примеры. ![]() - явное задание
функции z(x,y),
- явное задание
функции z(x,y),
![]() - неявное
задание функции z(x,y).
- неявное
задание функции z(x,y).
Аналогично
выше приведённому задаются функции трёх и более переменных:
![]()
Геометрическое изображение функции двух переменных
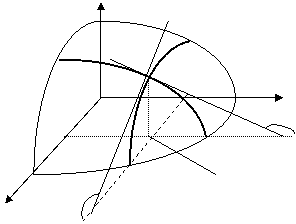
Рассмотрим z = f(x, y), определённую в G. В каждой точке (х,у) восстановим перпендикуляр длиной z. Конец перпендикуляра в пространстве имеет координаты (x,y,z = f(x,y)) (см. рис.).
Сплошному перемещению
точки Р будет соответствовать сплошное перемещение точки
Q,
которая опишет некоторую поверхность. Эта поверхность и будет геометрическим
изображением функции z =
f(x,
y).
Замечание. Функцию трёх и более переменных геометрически изобразить невозможно.

Предел функции
Одновременное
стремление аргументов х,у к своим предельным значениям х0,у0
будем обозначать ![]() ,
где Р(х,у), Р0(х0,у0).
,
где Р(х,у), Р0(х0,у0).
Число А называется пределом функции
f(P)
при ![]() , если
, если ![]() , такое, что из
неравенства
, такое, что из
неравенства ![]() следует
неравенство
следует
неравенство ![]() .
.
Обозначение:
![]()
Примечание. При кажущейся полной аналогии понятий предела функции одной и нескольких переменных существует глубокое различие между ними. В случае функции одной переменной для существования предела в точке необходимо и достаточно равенства пределов справа и слева от предельной точки х0. В то время как для функций двух переменных стремление к предельной точке Р может происходить по бесконечному числу направлений, и поэтому требование существования предела для такой функции жестче по сравнению с функцией одной переменной.
Примеры. 1) Найти ![]() .
.
Пусть стремление к
предельной точке (0; 0) происходит по прямой ![]() . Тогда
. Тогда
![]()
Предел не существует, так как он зависит от значения к.
2) Найти  .
.
По прямой ![]() предел один и тот же
предел один и тот же ![]() .
.
По кривой ![]()
 . Следовательно,
исходный предел не существует.
. Следовательно,
исходный предел не существует.
Непрерывность функции
Функция f(P) называется непрерывной в точке Р0, если:
1) f(P) определена в точке Р и некоторой её окрестности;
2) f(P) имеет предел в точке Р0;
3)
![]()
Точка Р0 называется точкой разрыва функции f(P), если она принадлежит области определения функции и для неё не выполняется хотя бы одно из условий 2)-3).
Точки разрыва могут образовывать линии или поверхности разрыва.
Частные производные
Рассмотрим функцию z =f(x,y). Полагая у = у0 = сonst, получим функцию одной переменной z =f(x,y0).
 Производная от функции многих переменных по одной из
них в
Производная от функции многих переменных по одной из
них в
предположении постоянства остальных аргументов называется частной
производной этой функции по соответствующей переменной:
![]()
![]()
Производная по х равна скорости
изменения функции вдоль оси Ох и также
равна тангенсу угла наклона касательной
в соответствующем направлении.
Замечание. Отыскание
частных
производных производится по тем же
формулам и правилам,
что и случае функции одной переменной.
Пример. ![]()
Дифференциал функции
![]() - частное приращение функции в
точке (х, у) по
х.
- частное приращение функции в
точке (х, у) по
х.
![]() - частное приращение функции в
точке (х, у) по у.
- частное приращение функции в
точке (х, у) по у.
Если ![]() , то на основании теории функции
одной переменной:
, то на основании теории функции
одной переменной:
![]() и (аналогично)
и (аналогично) ![]() .
.
Выражение ![]() (главная часть
приращения) называется частным дифференциалом функции
z
= f (x,y) по переменной х и обозначается
(главная часть
приращения) называется частным дифференциалом функции
z
= f (x,y) по переменной х и обозначается ![]() .
.
Так же: ![]() - частный дифференциал по
переменной у. С учётом введённых обозначений:
- частный дифференциал по
переменной у. С учётом введённых обозначений: ![]() и
и ![]() .
.
![]() - полное приращение функции
z в
точке (х,у);
- полное приращение функции
z в
точке (х,у); ![]() -
его краткая запись.
-
его краткая запись.
Полное приращение можно записать в виде:
![]()
![]() . Первое
выражение – частное приращение функции
. Первое
выражение – частное приращение функции
по х, второе – по у. Следовательно,
![]() . Выражение
. Выражение
![]() (главная
часть полного приращения) называется полным дифференциалом
функции в точке.
(главная
часть полного приращения) называется полным дифференциалом
функции в точке. ![]()
Производная сложной функции
Пусть
![]() , причем
, причем ![]() , то есть
z
- сложная функция. Тогда
, то есть
z
- сложная функция. Тогда

Приведённые формулы обобщаются на случай любого числа независимых переменных:
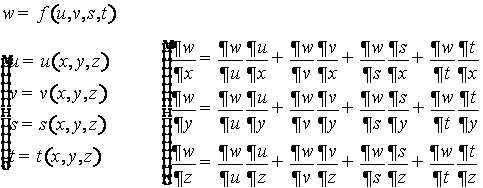
Пример. 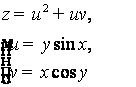

Лекция 2
Функции многих переменных (продолжение)
Производная от неявно заданной функции
В
выражении ![]() функция
функция
![]() задана
неявно. Не всякое уравнение
задана
неявно. Не всякое уравнение ![]() определяет
определяет ![]() . Например, уравнение
. Например, уравнение ![]() не определяет никакой функции
z,
так как не существует ни одной тройки чисел, удовлетворяющих этому уравнению.
не определяет никакой функции
z,
так как не существует ни одной тройки чисел, удовлетворяющих этому уравнению.
Если
условия теоремы выполнены, то существует однозначная ![]() и левая часть уравнения
и левая часть уравнения ![]() является сложной
функцией. По соответствующему правилу дифференцирования получим:
является сложной
функцией. По соответствующему правилу дифференцирования получим:
![]()
![]()
![]()
Пример.
![]()

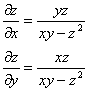
Уравнения касательной плоскости и нормали
Случай 1. Пусть поверхность задана уравнением ![]() . Запишем уравнение касательной прямой
(параллельной плоскости Охz, см. рис. на с.) как прямой, проходящей через данную
точку в данном направлении с учётом постоянства величины у:
. Запишем уравнение касательной прямой
(параллельной плоскости Охz, см. рис. на с.) как прямой, проходящей через данную
точку в данном направлении с учётом постоянства величины у:
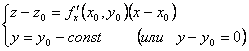 (1)
(1)
Вторая касательная прямая (параллельная Оуz):
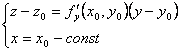 (2)
(2)
Запишем
уравнение (касательной) плоскости, проходящей через точку ![]() с нормальным вектором
с нормальным вектором ![]() :
:
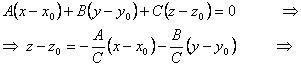
![]() (3)
(3)
Касательные прямые принадлежат этой плоскости, поэтому они должны удовлетворять последнему уравнению. Подставим (1) в (3):
![]()
Аналогично:
![]() .
.
Окончательно:
![]() - уравнение касательной плоскости, проведенной в точке
- уравнение касательной плоскости, проведенной в точке ![]() .
.
Случай 2. Пусть поверхность задана уравнением ![]() и пусть существует
и пусть существует ![]() . Тогда (см.
производную неявной функции) :
. Тогда (см.
производную неявной функции) :
![]() .
.
Уравнение касательной плоскости примет вид:
![]() или
или
![]() (
(
![]() в
точке
в
точке ![]() ).
).
Замечание. Последнее
уравнение имеет смысл и тогда, когда ![]() .Это означает, что
.Это означает, что
касательная плоскость в данной точке параллельна оси
Oz.
< Прямая, перпендикулярная к касательной
плоскости в точке касания,
называется нормалью к поверхности в данной точке.
![]() - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку ![]() в направлении вектора
в направлении вектора ![]() . В качестве
. В качестве ![]() можно взять вектор (
можно взять вектор (![]() )
- нормальный вектор касательной плоскости. Тогда:
)
- нормальный вектор касательной плоскости. Тогда:
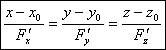 - уравнение нормали в случае неявного задания поверхности (
- уравнение нормали в случае неявного задания поверхности (
![]() вычислены
в точке
вычислены
в точке ![]() ).
).
 - уравнение нормали в случае явного задания поверхности.
- уравнение нормали в случае явного задания поверхности.
Частные производные высших порядков
Если ![]() имеет непрерывные
частные производные, то они снова являются функциями переменных х,у и в
случае их дифференцируемости в нужной точке можно снова вычислять частные
производные:
имеет непрерывные
частные производные, то они снова являются функциями переменных х,у и в
случае их дифференцируемости в нужной точке можно снова вычислять частные
производные:
![]() - частная производная второго порядка.
- частная производная второго порядка.
![]() .
.
![]() - смешанная частная производная второго порядка. Аналогично
вводятся
- смешанная частная производная второго порядка. Аналогично
вводятся ![]() и
так далее.
и
так далее.
Пример. ![]()
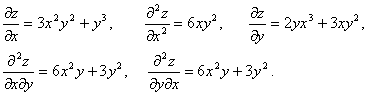
Замечание. Равенство смешанных производных не случайно. Об этом свидетельствует
следующая теорема.
Теорема.
Если функция ![]() и
её частные производные
и
её частные производные ![]() определены
определены
и непрерывны в точке и в некоторой её окрестности, то в этой точке
![]() (без доказательства).
(без доказательства).
Экстремум функции нескольких переменных
< Точка Р0 называется точкой
максимума функции ![]() , если в
, если в
некоторой окрестности этой точки выполняется неравенство
|
0(х0,у0) |
![]() .
.
Аналогично определяется точка минимума. Общее название - точка экстремума.
Теорема (необходимый признак экстремума).
Если функция ![]() дифференцируема
дифференцируема
в точке Р0 и достигает в ней экстремума,
то все её частные производные первого
порядка в этой точке равны нулю.
· (Для функции двух переменных).
Возьмем функцию ![]() и положим
и положим ![]() . Тогда получим функцию
одной переменной
. Тогда получим функцию
одной переменной ![]() с
экстремумом в точке х0. По необходимому признаку экстремума функции
одной переменной имеем
с
экстремумом в точке х0. По необходимому признаку экстремума функции
одной переменной имеем ![]() . Аналогично
. Аналогично ![]() .
¶
.
¶
Точка Р0 называется стационарной точкой данной функции.
Пример. ![]() . Найти стационарные точки.
. Найти стационарные точки.
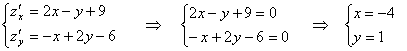
Примечание. Всякая экстремальная точка дифференцируемой функции
будет и
стационарной точкой. Однако не всякая стационарная точка является
экстремальной.
Пример. ![]() . Точка Р0(0,0)
- стационарная, но
z = 0 не является
. Точка Р0(0,0)
- стационарная, но
z = 0 не является
экстремумом.
Замечание. Экстремум функции может быть в точках не дифференцируемости функции.
Пример. ![]() . В точке (0,0) функция
z
имеет минимум, однако её частные
. В точке (0,0) функция
z
имеет минимум, однако её частные
производные в этой точке не существуют.
Теорема (достаточный признак экстремума функции).
Пусть Р0
- стационарная точка, причём в этой точке и её
окрестности ![]()
имеет непрерывные частные производные до третьего порядка включительно.
Обозначим:
![]()
1) Если
в стационарной точке Р0 ![]() то функция
то функция ![]() в этой точке имеет экстремум: максимум
при A < 0 и минимум при
A > 0.
в этой точке имеет экстремум: максимум
при A < 0 и минимум при
A > 0.
2) Если
в точке Р0 ![]() то функция
то функция ![]() в этой точке экстремума не имеет.
в этой точке экстремума не имеет.
3)
Если ![]() то вопрос о наличии экстремума
остается открытым.
то вопрос о наличии экстремума
остается открытым.
(Без доказательства).
Пример. Найти экстремумы функции
![]() .
.
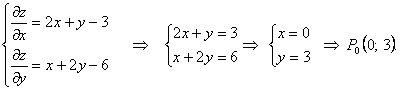
![]() 2 > 0,
B = 1, C = 2.
2 > 0,
B = 1, C = 2. ![]() , поэтому
, поэтому ![]()
Условный экстремум
< Экстремум функции, найденный при условии, что изменение её
аргументов ограничено некоторыми дополнительными уравнениями
(условиями), называется условным экстремумом.
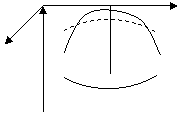
Пример. Найти экстремум функции ![]() при условии, что
при условии, что ![]() .
.
|
М
|
![]() - полусфера.
- полусфера.
![]() - секущая
плоскость.
- секущая
плоскость.
![]() , тогда
, тогда
![]() - функция одной переменной.
К ней применимо соответствующее правило поиска экстремума:
- функция одной переменной.
К ней применимо соответствующее правило поиска экстремума:
![]() ,
, ![]() - стационарная точка.
- стационарная точка.
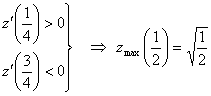 .
.
На рисунке: точка М - абсолютный максимум функции,
точка М1 - условный максимум.
Задача. Из куска проволоки длиной
l
сделать каркас прямоугольного параллелепипеда
с
наибольшим объёмом.
![]() - объём.
- объём.
![]() - периметр
- периметр ![]() .
.
![]() - функция двух переменных.
- функция двух переменных.
 .
.
При найденных
x,
y,
H
объём параллелепипеда может быть максимальным или минимальным. Но очевидно,
что ![]() при
H =
0, поэтому V будет максимальным при найденных размерах каркаса.
при
H =
0, поэтому V будет максимальным при найденных размерах каркаса.
Наибольшие и наименьшие значения функции в области
Пусть ![]() определена и непрерывна
в замкнутой ограниченной области. Тогда она имеет в этой области
определена и непрерывна
в замкнутой ограниченной области. Тогда она имеет в этой области ![]() и
и ![]() . Если они находятся внутри
области, то совпадают с экстремумами и находятся выше указанным способом.
. Если они находятся внутри
области, то совпадают с экстремумами и находятся выше указанным способом.
Если ![]() и
и ![]() достигаются на границе области,
заданной уравнением
достигаются на границе области,
заданной уравнением ![]() ,
то для их нахождения нужно решить задачу на отыскание наибольших и наименьших
значений функции при условии
,
то для их нахождения нужно решить задачу на отыскание наибольших и наименьших
значений функции при условии ![]() .
.
|
В(5)
О 1 А(5) |
Пример 1. Найти наибольшие
и наименьшие значения функции ![]() в треугольнике
в треугольнике ![]() .
.
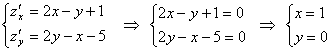
![]() - экстремум
внутри области.
- экстремум
внутри области.
На границе ОА: ![]() - к этой функции
одной переменной применяем соответствующие правила нахождения
- к этой функции
одной переменной применяем соответствующие правила нахождения ![]() и
и ![]() на отрезке [0, 5].
на отрезке [0, 5].
![]()
![]() ,
,
![]()
На границе АB:
![]() . Вдоль АВ функция имеет вид
. Вдоль АВ функция имеет вид ![]() на отрезке [0, 5].
на отрезке [0, 5].
![]()
![]() ,
,
![]()
На границе ОВ: х = 0, ![]() на [0, 5].
на [0, 5].
![]()
![]()
![]()
Сравнивая между собой выделенные значения, получим результат:
![]()
![]() .
.
Пример 2. Найти наибольшие и
наименьшие значения функции ![]() в
в
круге ![]() .
.
![]() внутри области.
внутри области.
На границе перейдём к полярным координатам:

![]() при к =
0;2.
при к =
0;2.
![]() при
к = 1;3.
при
к = 1;3.
интегральное исчисление
- Первообразная
- Существование первообразной
- Неопределенный интеграл
- Свойства интегралов
Лекция 1. Неопределенный интеграл
В разделе
«Дифференциальное исчисление» мы рассматривали (главную) задачу нахождения производной
по известной функции: дана ![]() , найти
, найти ![]() .
.
Раздел
«Интегральное исчисление» рассматривает обратную задачу нахождения самой
функции по ее известной производной: дана ![]() , найти
, найти ![]() .
.
|
Определение. Пусть в некоторой области определены функции f(x) и F(x), и пусть F’(x) = f(x). Тогда f(x) называется производной F(x), а F(x) – первообразной f(x). |
Примеры 1. f(x) = 3x2 ÞF(x) = x3, т.к. F’(x) = 3x2.
2. f(x) = -sin x ÞF(x) = cos x, т.к. (cos x)’ = -sin x.
Итак, F(x) = x2
– первообразная для f(x) = 2x. Но F1(x)
= x2 + 3 – тоже первообразная, и вообще F(x) = x2
+ C – первообразная, т.к. F’(x) = 2x. Т.о. если ![]() имеет первообразную
имеет первообразную ![]() , то первообразных
имеется бесчисленное множество:
, то первообразных
имеется бесчисленное множество: ![]() .
.
Всякая ли функция имеет первообразную? Нет не всякая.
|
Теорема. Если |
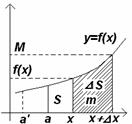 Геометрическое
обоснование:
Геометрическое
обоснование:
Рассмотрим график непрерывной
функции ![]() . Этот
график (непрерывность важна!) имеет связь с
. Этот
график (непрерывность важна!) имеет связь с ![]() –площадью фигуры, ограниченной
–площадью фигуры, ограниченной ![]() , отрезком [a;x] и прямыми
, отрезком [a;x] и прямыми ![]() ,
, ![]() . Меняя
. Меняя ![]() , меняется и
, меняется и ![]() , следовательно,
, следовательно, ![]() – функция от
– функция от ![]() . Найдем математическую
связь между
. Найдем математическую
связь между ![]() и
и
![]() . Вначале
найдем
. Вначале
найдем ![]() . Для
этого пусть
. Для
этого пусть ![]() получит
приращение
получит
приращение ![]() , тогда
, тогда ![]() получит
приращение
получит
приращение ![]() . Из чертежа:
. Из чертежа:
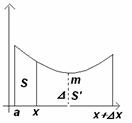 m·Dx<DS<m·Dx Þ
m·Dx<DS<m·Dx Þ ![]() .
Устремим
.
Устремим ![]() ,
тогда
,
тогда ![]() ,
, ![]() Þ
Þ ![]()
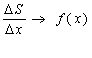 , т.е. для непрерывной функции
, т.е. для непрерывной функции ![]() существует функция
площади
существует функция
площади ![]() ,
которая является первообразной по отношению к
,
которая является первообразной по отношению к ![]() . В этом и заключается связь между
. В этом и заключается связь между ![]() и
и ![]() .
.
Геометрически
тоже легко видеть, что первообразных для ![]() – бесчисленное множество. Взяв за начало
точку a’, получим новую функцию – площадь фигуры с
основанием
– бесчисленное множество. Взяв за начало
точку a’, получим новую функцию – площадь фигуры с
основанием ![]() ,
которая отличается от
,
которая отличается от ![]() на
постоянную величину. Следовательно:
на
постоянную величину. Следовательно:
|
Теорема. Две
первообразные от |
|
Определение. Если Примечание. Множитель |
Здесь ![]() – подынтегральная функция,
– подынтегральная функция,
![]() – подынтегральное выражение,
– подынтегральное выражение,
![]() – переменная интегрирования,
– переменная интегрирования,
![]() - знак интеграла.
- знак интеграла.
Нахождение первообразной для данной функции называется интегрированием этой функции.
|
Пояснение: выражение
«неопределенный интеграл» объясняется тем, что константа |
 Правильность найденной
первообразной всегда может быть проверена дифференцированием результата.
Правильность найденной
первообразной всегда может быть проверена дифференцированием результата.
Геометрически
интервал – множество функций ![]() – представляет собой совокупность кривых,
полученных сдвигом по оси
– представляет собой совокупность кривых,
полученных сдвигом по оси ![]() параллельно самим себе.
параллельно самим себе.
Свойства неопределенного интеграла
Из определения следует:
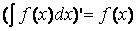 .
.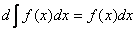 .
.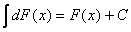 .
(Проверяется взятием дифференциалов от обеих частей)
.
(Проверяется взятием дифференциалов от обеих частей)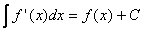 .
(Следует из определения)
.
(Следует из определения)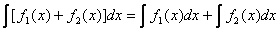 .
(Доказывается взятием производных от обеих частей)
.
(Доказывается взятием производных от обеих частей)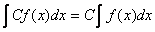
Таблица интегралов
Таблица интегралов получается исходя из таблицы производных.

Далее рассмотрим основные способы вычисления интегралов.
1. Непосредственное интегрирование
2. Внесение функции под знак дифференциала
Для функции y = f(x) известна формула: dy = y¢dx.
Использование этой формулы слева направо можно назвать вынесением функции из-под знака дифференциала, справа налево - внесением функции (интегрирование) под знак дифференциала:
dy = y¢ dx .
![]() - вынесение (дифференцирование),
- вынесение (дифференцирование),
![]() - внесение (интегрирование)
.
- внесение (интегрирование)
.
Примеры

Способ внесения позволяет значительное число интегралов сразу сделать табличными.
Примеры
![]()
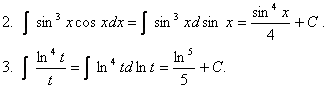
3. Интегрирование путем замены переменной
Замена переменной производится с помощью подстановок двух видов.
§
Если подынтегральная функция такова, что её можно
представить в виде ![]() ,
то применяют подстановку
,
то применяют подстановку ![]() и тогда
и тогда ![]()
Примечание. Этот случай замены представляет собой способ внесения функции под знак дифференциала с записью подстановки.
§
Во втором случае подбирают подстановку ![]() ( j(t) - монотонная,
непрерывно дифференцируемая функция) таким образом, чтобы новый
интеграл стал табличным, либо путь его нахождения был ясен. Общая
формула при такой подстановке:
( j(t) - монотонная,
непрерывно дифференцируемая функция) таким образом, чтобы новый
интеграл стал табличным, либо путь его нахождения был ясен. Общая
формула при такой подстановке: ![]()
Пример
Интегрирование по частям основано на
применении формулы![]()
![]() где
где
![]() -
непрерывно дифференцируемые функции. Данный способ применяют при
нахождении следующих типов интегралов:
-
непрерывно дифференцируемые функции. Данный способ применяют при
нахождении следующих типов интегралов:
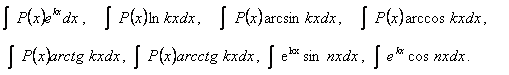
Пример

Лекция 4. Интегрирование рациональных дробей, тригонометрических и иррациональных выражений
5. Интегрирование выражений, содержащих квадратный трехчлен
·
Интегралы видов ![]() ,
,  и др. с помощью выделения
полного квадрата сводятся к табличным:
и др. с помощью выделения
полного квадрата сводятся к табличным:

Пример.
![]()
Интегралы
более общих видов ![]() и
и
![]()
после выделения в
числителе производной 2ах +
b
квадратного трёхчлена можно представить в виде суммы двух
интегралов, один из которых имеет вид ![]() а другой есть интеграл вида (1).
а другой есть интеграл вида (1).
(см. предыдущий пункт).
Пример. ![]() .
.
Интегрирование простейших дробей
Простейших дробей всего четыре вида:
1.
![]() 2.
2.
![]() (m –
целое, >1) 3.
(m –
целое, >1) 3. ![]() (квадратный трехчлен не имеет действительных корней). 4.
(квадратный трехчлен не имеет действительных корней). 4.![]() (n-целое,>1).
(n-целое,>1).
Интегрирование:
1. ![]() .
.
2. ![]() .
.
3. ![]() - см. раздел об интегрирование
квадратного трехчлена.
- см. раздел об интегрирование
квадратного трехчлена.
4. ![]() - см. раздел об интегрирование
квадратного трехчлена.
- см. раздел об интегрирование
квадратного трехчлена.
5. ![]() . Первое слагаемое вычисляется
методом внесения функции под знак дифференциала (предыдущий раздел), а второе
сводится к виду
. Первое слагаемое вычисляется
методом внесения функции под знак дифференциала (предыдущий раздел), а второе
сводится к виду ![]() и
методом по частям степень знаменателя понижается на единицу:
и
методом по частям степень знаменателя понижается на единицу: 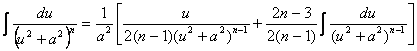 . Продолжая этот
процесс, придем к табличному интегралу
. Продолжая этот
процесс, придем к табличному интегралу ![]() .
.
Дополнение: Многочлены n-ной степени
1. Многочлены n-ой степени.
2. Теорема Безу.
3. Основная теорема.
4. Разложение многочлена на множители во множестве комплексных и действительных чисел.
5. Представление рациональной дроби в виде суммы простейших дробей.
6. Интегрирование рациональных дробей.
Определение. Многочленом n-ой степени называется функция вида
|
|
![]() где
где![]() –
const.,
z – переменная. Считается, что
–
const.,
z – переменная. Считается, что
![]()
![]() .
.
Определение. Если ![]() , то а называется корнем или нулем
многочлена.
, то а называется корнем или нулем
многочлена.
Пусть![]() – любая
константа. Представим z в виде
– любая
константа. Представим z в виде ![]() .Тогда
.Тогда ![]() = [возводим в
степень и приводим подобные члены] =
= [возводим в
степень и приводим подобные члены] = ![]() (2)
(2)
(2) называется разложением многочлена по степеням (z-z0).
![]()
![]() Для того, чтобы
Для того, чтобы ![]() была корнем, необходимо и достаточно,
чтобы
была корнем, необходимо и достаточно,
чтобы![]() . Если
. Если ![]() , то
, то ![]() можно записать в виде:
можно записать в виде:![]()
![]() , (3)
, (3)
где![]() – многочлен (n-1)-ой
степени. Обратно, если
– многочлен (n-1)-ой
степени. Обратно, если ![]() можно представить в виде (3), (т.е.
можно представить в виде (3), (т.е. ![]() можно разделить на
можно разделить на ![]() без остатка), то
без остатка), то ![]() есть корень
есть корень![]() . Тем самым доказана теорема
Безу:
. Тем самым доказана теорема
Безу:
|
Для того, чтобы многочлен |
ÿ
Пусть ![]() - корень
- корень![]() . Тогда справедлива
формула (3). Если при этом
. Тогда справедлива
формула (3). Если при этом ![]() , то на основании теоремы Безу многочлен
, то на основании теоремы Безу многочлен
![]() не
делится на
не
делится на ![]() и,
значит,
и,
значит, ![]() не делится на
не делится на![]() . В этом случае
. В этом случае ![]() называется простым корнем
многочлена
называется простым корнем
многочлена![]() .
.
ÿ
Если теперь ![]() = 0, то по теореме Безу
= 0, то по теореме Безу
![]() делится
на
делится
на ![]() ,a
,a
![]()
ÿ
делится на![]() , т.е.
, т.е.![]() . Если при этом
. Если при этом ![]() не делится на
не делится на ![]() , то
, то ![]() называется
корнем
называется
корнем ![]() кратности
2.
кратности
2.
В
общем случае:![]() ,
,
![]() Þ
Þ ![]() – корень кратности
s.
– корень кратности
s.
Всякий ли многочлен обладает корнями? Если нет, то множество К нуждалось бы в дальнейшем расширении.
|
Всякий многочлен n-ой степени имеет хотя бы один корень (в общем случае комплексный). |
Основная теорема
теории многочленов.
(без доказательства)
Следствие. Многочлен n-ой степени имеет n комплексных корней (с учетом
кратности): ![]() ,
где
,
где
![]() .
.
ÿ
![]() =
êпо основной теореме
ê=
=
êпо основной теореме
ê= ![]() =
ê
=
ê![]() - тоже многочлен
ê
- тоже многочлен
ê
=![]()
![]() появился потому, что
старший член после раскрытия скобок
появился потому, что
старший член после раскрытия скобок
должен
быть равен ![]() .
Среди
.
Среди ![]() могут
быть одинаковые. Отсюда следует доказываемая формула (нестрогое доказательство)
#
могут
быть одинаковые. Отсюда следует доказываемая формула (нестрогое доказательство)
#
Пример. Разложить на множители ![]() .
.
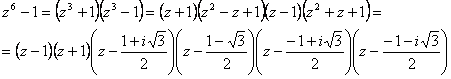
Примечание.
Если нужно разложение только с действительными корнями, то
следует остановиться на предпоследнем выражении.
В общем случае многочлен с действительными коэффицентами может быть
представлен в виде ![]() (¨)
(¨)
Все константы – действительные.
Рациональные дроби
ÿ
Отношение двух многочленов ![]() называется
рациональной дробью (функцией).
называется
рациональной дробью (функцией).
ÿ Дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе.
Неправильную дробь всегда можно представить в виде целой части и правильной дроби, поэтому рациональную дробь всегда можно считать правильной.
Пример.
![]()
Теорема. Если знаменатель рациональной дроби разложен на множители по формуле (¨), то дробь можно представить в виде:
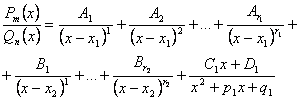
ПРИМЕЧАНИЯ. 1) Каждая скобка в знаменателе доводится до степени, равной кратности соответствующего корня.
2) Аi, Bi, Ci, Di,… - постоянные, но пока неопределенные (неизвестные) коэффициенты.
Пример. Разложить на простейшие дроби:
![]() A=1, B=2, C=D=1.
A=1, B=2, C=D=1.
Схема интегрирования рациональных дробей
Из двух последних пунктов следует, что ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ СВОДИТСЯ К ИНТЕГРИРОВАНИЮ ПРОСТЕЙШИХ ДРОБЕЙ. При этом можно руководствоваться следующей схемой:
1) Если рациональная дробь неправильная, то выделяется целая часть и правильная дробь.
2) Знаменатель правильной дроби разлагается на множители по формуле (¨).
3) Правильная дробь разлагается на множители по формуле простейших дробей (см. пункт о рациональных дробях) с неопределенными коэффициентами.
4) Вычисляются неопределенные коэффициенты (2 способа).
5) Интеграл от рациональной дроби заменяется суммой интегралов от целой части и простейших дробей.
6) Интегрируется целая и дробная части.
Пример.
![]()
Лекция 5. Интегрирование некоторых тригонометрических и иррациональных функций
Интегрирование тригонометрических функций
1. ![]() Вычисление интегралов такого типа
проводится с помощью универсальной тригонометрической подстановки
Вычисление интегралов такого типа
проводится с помощью универсальной тригонометрической подстановки ![]() . При этом:
. При этом:
а)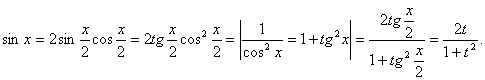
b)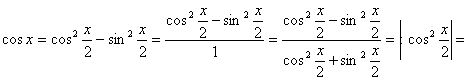
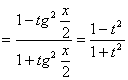 c)
c)![]() ,
,
![]()
Таким образом, интеграл (1)
сводится к интегралу от рациональной дроби 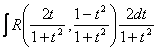 (смотри предыдущую лекцию).
(смотри предыдущую лекцию).
Пример.
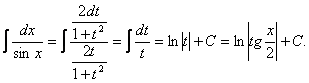
2. ![]() Универсальная тригонометрическая
подстановка часто приводит к громоздким вычислениям. Для интегралов
рассматриваемого типа применяются более простые подстановки:
Универсальная тригонометрическая
подстановка часто приводит к громоздким вычислениям. Для интегралов
рассматриваемого типа применяются более простые подстановки:
1)![]() -если
-если ![]() нечетное.
нечетное.
2)![]() -если
-если ![]() четное.
четное.
3 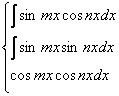 Применяются формулы
Применяются формулы
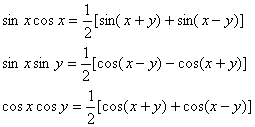
Интегрирование некоторых иррациональных выражений
1. Интегралы вида ![]()
![]() ,
, ![]() приводятся к табличным интегралам с
помощью соответствующих тригонометрических подстановок:
приводятся к табличным интегралам с
помощью соответствующих тригонометрических подстановок:
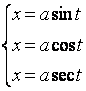
Пример .

2. ![]() - интеграл от дифференциального бинома.
Такие интегралы выражаются через элементарные функции только в трех случаях:
- интеграл от дифференциального бинома.
Такие интегралы выражаются через элементарные функции только в трех случаях:
1) ![]() - целое число, тогда данный
интеграл сводится к интегралу от рациональной функции с помощью подстановки
- целое число, тогда данный
интеграл сводится к интегралу от рациональной функции с помощью подстановки ![]() , где
, где ![]() - наименьшее общее
кратное знаменателей дробей
- наименьшее общее
кратное знаменателей дробей ![]() и
и ![]() .
.
2) ![]() - целое число, в данном случае
интеграл рационализуется с помощью подстановки
- целое число, в данном случае
интеграл рационализуется с помощью подстановки ![]() , где
, где ![]() знаменатель числа
знаменатель числа ![]() .
.
3) ![]() -целое число, в этом случае
применяется подстановка
-целое число, в этом случае
применяется подстановка ![]() , где
, где ![]() -знаменатель дроби
-знаменатель дроби ![]() .
.
Примеры. 1)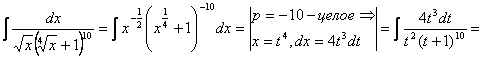

2)
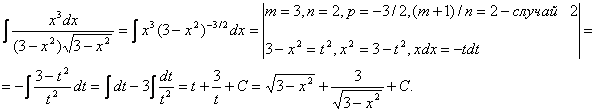
3)
О неберущихся интегралах
Всякая непрерывная на интервале функция имеет первообразную. Однако не всегда эта первообразная выражается через известные нам элементарные функции. Таковы, например, интегралы
1) ![]() 2)
2)
![]() 3)
3) ![]() 4)
4) ![]() и др.
и др.
Такие интегралы называются неберущимися (в элементарных функциях).
Список способов вычисления интегралов.
- Непосредственное интегрирование.
- Внесение функции под знак дифференциала.
- Замена переменной.
- Интегрирование по частям.
- Интегрирование выражений, содержащих квадратный трехчлен.
- Интегрирование простейших дробей.
- Интегрирование рациональных дробей.
- Интегрирование некоторых тригонометрических выражений.
- Интегрирование некоторых иррациональных выражений.
Лекция 6. Определенный интеграл.
 Задачи, приводящие к понятию определенного интеграла
Задачи, приводящие к понятию определенного интеграла
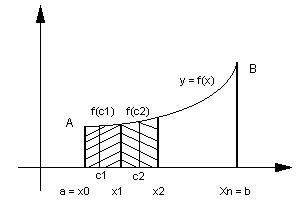
Задача о площади криволинейной трапеции
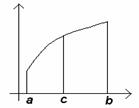
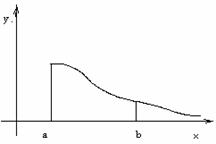
Пусть задана непрерывная функция y = f(x) на интервале [a;b]. Она определяет криволинейную трапецию.
Для вычисления Sтр разобьем [a;b] на n элементарных отрезков точками a = x0,x1,x2,…,xn = b. Эти точки разобьют большую трапецию на n элементарных.
На каждом элементарном отрезке [x1;xi+1] выберем произвольную точку c1 и построим соответствующие прямоугольники с высотами f(ci).
Площадь одной маленькой трапеции приблизительно равна площади соответствующего прямоугольника, а вся:
![]() где
где
![]()
Или ![]() (1)
(1)
Равенство
(1) тем точнее, чем меньше ![]() - наибольший из диаметров разбиения.
- наибольший из диаметров разбиения.
ПРИМЕЧАНИЕ. Так как площади фигур измеряются в квадратных мм, м, км и т.д., то необходимо дать определение площади криволинейной фигуры.
k Площадь
S криволинейной трапеции называется предел суммы площадей
Sn прямоугольников при ![]()
![]() (2)
(2)
Таким образом вычисление площади криволинейной трапеции приводит к вычислению предела (2)
Задача о пройденном пути
Пусть задан закон движения какой-либо точки уравнением s = f(t). Тогда f(t) равна скорости движения точки. В физике часто решают обратную задачу: дана скорость v = v(t) прямолинейно движущейся точки и требуется найти путь, пройденный точкой от момента t = a до t = b.
Разобьем [a;b] точками
t0,t1,…,tn
на n
малых отрезков времени. Выберем на каждом отрезке произвольную точку
ci и приближенно будем считать скорость на отрезке постоянной
и равной v(ci). Так как движение на элементарном отрезке будет
равномерным, то путь, пройденный точкой за элементарный отрезок времени, составляет
v(ci)(ti-ti-1), а
путь за весь [a;b] будет равен ![]() Это равенство тем точнее, чем меньше
Это равенство тем точнее, чем меньше
![]()
По определение, путем называется ![]() (3)
(3)
Таким образом, вычисления пути приводит к вычислению предела (3).
Вывод: в рассмотренных задачах применен одинаковый метод решения. Этот метод используется во многих задачах науки и практики. Поэтому изучим выражение (2) без конкретного его содержания, но иногда привлекая его к для лучшего понимания.
Определенный интеграл
Пусть задана непрерывная f(x) на [a;b]. Выполним следующие действия:
1. Разобьем [a;b] на n частей точками x0<x1<…<xn.
2. Выберем на каждой части [xi-1;xi] по одной точке ci и вычислим в ней значение f(ci).
3.
Умножим f(ci) на длину
xi –
xi-1 и
сложим все произведения; сумма вида ![]() называется интегральной суммой (Римана)
для f(x) по заданному разбиению отрезка [a;b].
называется интегральной суммой (Римана)
для f(x) по заданному разбиению отрезка [a;b].
4.
Увеличим число точек разбиения и
найдем ![]()
ПРИМЕЧАНИЕ. Указанный предел настолько важен, что получил собственное имя:
Определение.
Предел интегральной суммы ![]() (если он существует) называется
определенным интегралом (по Риману) от функции
f(x) по
отрезку [a;b].
(если он существует) называется
определенным интегралом (по Риману) от функции
f(x) по
отрезку [a;b].
Обозначение: 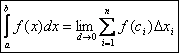 (5)
(5)
Если предел $, то функция f(x) называется интегрируемой на [a;b].
f(x) – подынтегральная функция;
f(x)dx – подынтегральное выражение;
a,b – нижний и верхний пределы интегрирования.
ПРИМЕЧАНИЯ.
1. Очевидно, что предел не зависит ни от способа разбиения интервала [a;b], ни от выбора точек ci.
2. Неопределенный интеграл – функция, определенный - число!
3.
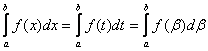 и т.д.
и т.д.
Какие функции являются интегрируемыми? (от каких функция можно вычислять определенный интеграл?)
ТЕОРЕМА. Непрерывная на [a;b] функция f(x) интегрируема на этом отрезке
(без доказательства)
На основании определения процедура вычисления интеграла является громоздкой. Желательно получить более простой метод вычисления.
Геометрический и механический смысл определенного
интеграла
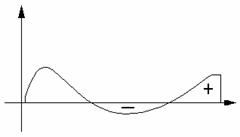
Из результата задачи о вычислении площади следует геометрический смысл:
Определенный интеграл от функции f(x) по отрезку [a;b] равен площади криволинейной трапеции.
Из результата задачи о пройденном пути следует механический смысл определенного интеграла:
Определенный интеграл от скорости по отрезку времени равен пути, пройденному точкой от момента t = a до t = b.
Основные свойства определенного интеграла
Рассматриваемые в свойствах функции предполагаются интегрируемыми.
1) 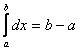
Доказательство:  #
#
2)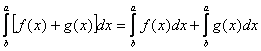
Доказательство:
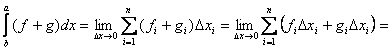
![]() |после
перегруппировки
|после
перегруппировки![]() =
=
![]()
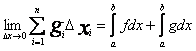 #
#
3)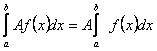 .
.
4)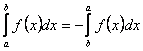 .
.
Пояснение для доказательства:
![]()
 В этом случае
В этом случае ![]() , т.е.
, т.е. ![]() в интегральной сумме. #
в интегральной сумме. #
5)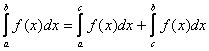
Примечание. Свойство справедливо и тогда, когда точка находится
вне ![]() .
.
6)Если подынтегральная функция не меняет знака, то интеграл есть число того же знака, что и функция.
Доказательство: Пусть
![]() Тогда в
Тогда в![]() все слагаемые неотрицательные
а предел неотрицательной величины неотрицателен.
все слагаемые неотрицательные
а предел неотрицательной величины неотрицателен.
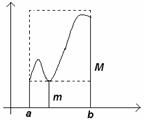
7)
(Об оценке интеграла). Если ![]() на
на ![]() , то
, то
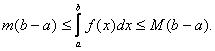
Рассмотрим две функции: ![]() и
и ![]() .
.
![]() |по свойству 6|
|по свойству 6|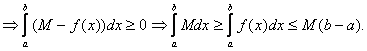
 Аналогично
Аналогично
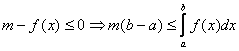
8) (Об интегрирование неравенств).
Если ![]() и
и ![]() , то
, то 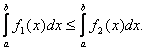
1*
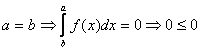
2* ![]() , т.к. все
, т.к. все
![]()
Переходя к пределу при ![]() , получим доказываемое
свойство.
, получим доказываемое
свойство.
Вывод: неравенства можно почленно интегрировать.
9)
(О среднем значении). Если ![]() интегрируема
на
интегрируема
на ![]() и
и 
![]()
![]() , то
, то ![]() такая точка
такая точка ![]() , для которой
, для которой 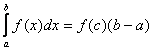 -(1*)
-(1*)
Доказательство: 1)
Если ![]() , то 1*
очевидно
, то 1*
очевидно
2)
Если ![]() -
переменная, то
-
переменная, то ![]()
![]() | по свойству 7
|
| по свойству 7
|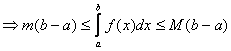 :
:
![]()
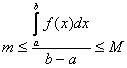 . Т.к.
. Т.к. ![]() - непрерывна, то она
принимает все значения между
- непрерывна, то она
принимает все значения между ![]() и
и ![]() , в том числе в некоторой точке
, в том числе в некоторой точке ![]() и значение
и значение 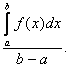 Следовательно,
Следовательно, - (2*) #
- (2*) #
![]() в
формулах 1* и 2* называется средним значением функции
в
формулах 1* и 2* называется средним значением функции ![]() на отрезке
на отрезке ![]() .
.
Лекция 7. Производная от интеграла с переменным верхним пределом. Формула Ньютона-Лейбница
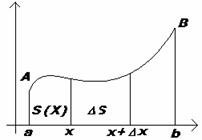 Пусть
Пусть ![]() непрерывна на
непрерывна на ![]() . Рассмотрим интеграл
. Рассмотрим интеграл ![]() :
: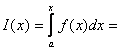 | или для большего удобства |
| или для большего удобства | 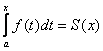 - площадь
криволинейной трапеции. Если изменяется верхний предел
- площадь
криволинейной трапеции. Если изменяется верхний предел ![]() , то
, то ![]() есть функция от
есть функция от ![]() . Поэтому
. Поэтому 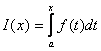 называют интегралом
с переменным верхним пределом.
называют интегралом
с переменным верхним пределом.
ТЕОРЕМА (о производной от интеграла с переменным верхним пределом).
|
Производная от определенного
интеграла, рассматриваемого как функция его верхнего предела, равна значению
его подынтегральной функции в точке дифференцирования: |
Доказательство: ![]() ;
;
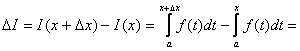 | согласно свойству |
| согласно свойству |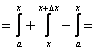
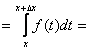 | по теореме о среднем |
| по теореме о среднем |![]() ,
,
![]()
![]() |
если
|
если ![]() , то
, то ![]() и
и ![]() |
|![]()
![]() .
.
ПРИМЕЧАНИЯ.
1)Т.к. ![]() , то
, то ![]() является первообразной
для
является первообразной
для ![]() , т.е.
, т.е. 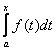 является первообразной
для
является первообразной
для ![]() .
.
2)
Известно, что![]() ,
где
,
где ![]() -какая-либо
первообразная для
-какая-либо
первообразная для
![]() . Т.к.
. Т.к. 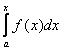 -первообразная для
-первообразная для ![]() , то она находится среди
всех первообразных
, то она находится среди
всех первообразных ![]() ,
т.е.
,
т.е. 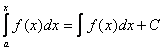 .
.
Формула Ньютона-Лейбница
- Формула Ньютона-Лейбница;
- Интегрирование по частям;
- Замена переменной в определенном интеграле;
- Определенный интеграл от четной и нечетной функции.
ТЕОРЕМА. (основная теорема интегрального исчисления)
Если F(x) – первообразная для f(x) на [a;b], то
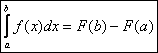 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница.
· Из
предыдущей теоремы, 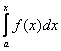 -
первообразная для f(x). Значит,
она находится среди всех первообразных F(x) + C (см. определение неопределенного
интеграла):
-
первообразная для f(x). Значит,
она находится среди всех первообразных F(x) + C (см. определение неопределенного
интеграла): 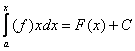 (1)
(1)
Положим в (1) х = а и x = b.
Тогда: х =
а Þ 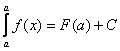 Þ
Þ
![]() Þ
Þ ![]()
x = b Þ  Þ
Þ 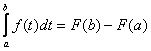 .
.
Так как 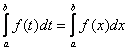 , то
, то  #
#
Сокращенная
запись: 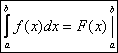 ,
, ![]() - знак двойной
подстановки пределов a и
b.
- знак двойной
подстановки пределов a и
b.
ПРИМЕРЫ. Вычислить интеграл.
1) ![]() 2)
2) 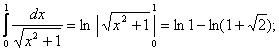 3)
3) 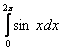 ; 4)
; 4) ![]()
5) Найти
среднее значение функции y = sin x
на [0;p], 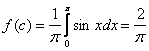 ;
;
6) ![]() 7)
7)
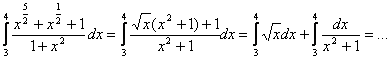
Интегрирование по частям в определенном интеграле
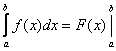 - формула Ньютона-Лейбница. Следовательно,
- формула Ньютона-Лейбница. Следовательно,
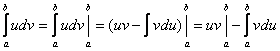 Þ
Þ
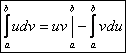
Пример. Вычислить
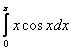
Замена переменной в определенном интеграле
Пусть в 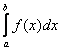 (
(![]() непрерывна на [a,b]). Требуется ввести новую переменную
t, которая связана со старой соотношением
непрерывна на [a,b]). Требуется ввести новую переменную
t, которая связана со старой соотношением ![]() , причем
, причем ![]() ,
, ![]() ,
, ![]() - непрерывна на [a,b].
- непрерывна на [a,b].
Если f(t) имеет первообразную F(t), то ![]() (1)
(1)
![]()
По формуле ![]() (Ньютона-Лейбница) вычислим
интеграл:
(Ньютона-Лейбница) вычислим
интеграл:
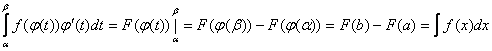
Итак, 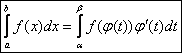 (2)
(2)
Примечание. Возвращаться в определенном интеграле к первоначальной переменной нет необходимости, так как пределы интегрирования изменяются в соответствии с подстановкой.
Примеры
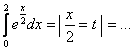
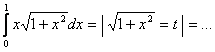
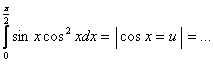
Определенный интеграл от четной и нечетной
функции по интервалу [-a,a]
Рассмотрим 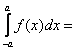 | по свойству 4 |
| по свойству 4 | 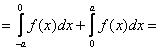 ç в первом интеграле замена x
= -t, при x = -a t = a, второй интеграл x = 0 t = 0 без изменения ç
ç в первом интеграле замена x
= -t, при x = -a t = a, второй интеграл x = 0 t = 0 без изменения ç
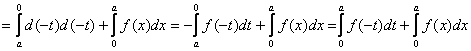 =
=
= | в первом
интеграле заменим t = x
| 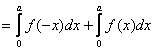 .
.
1.
Если f(x) – четная, то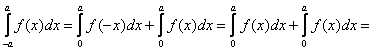
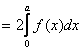
2.
Если f(x) – нечетная,
то 
Итак:
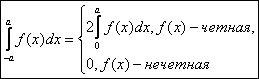
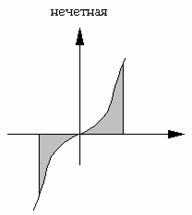 Геометрическая иллюстрация:
Геометрическая иллюстрация: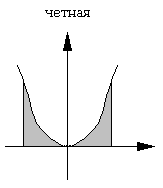
Лекция 8. Применения определенных интегралов.
Несобственные интегралы
1. Площадь плоской фигуры в декартовых, полярных координатах и в случае параметрического задания линии.
2. Длина дуги плоской кривой.
3. Объем тела по площади его поперечного сечения.
4. Объем тела вращения.
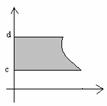
Вычисление площадей в прямоугольных координатах
Из ранее полученного:
|
|
|
|
|
|
|
|
|
Примеры: 1. Найти площадь фигуры, ограниченной линиями
y=cos x, y=0, x=0, x=p.
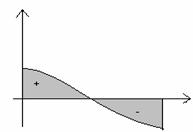
p/2
p
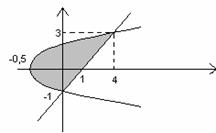 |
2. ![]()
![]()
![]()
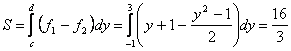
Вычисление площадей фигур, ограниченных параметрически
заданными кривыми
Пусть кривая задана параметрическими уравнениями: ![]()
![]() ,
, ![]() - непрерывные и дифференцируемые
функции.
- непрерывные и дифференцируемые
функции.
|
|
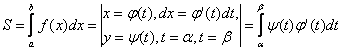 Þ
Þ
ПРИМЕР. Найти S эллипса. ![]()
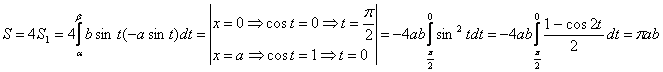
Вычисление площадей в полярных координатах
Пусть в полярной системе координат задана функция r=r(j). Она задает криволинейный сектор.
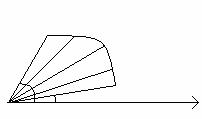 1) Разобьем угол (b-a) на n частей лучами с углами
1) Разобьем угол (b-a) на n частей лучами с углами ![]() …Обозначим углы между лучами через
…Обозначим углы между лучами через
![]()
2) Выберем в каждом из ![]() угол
угол ![]()
и вычислим длину r для этого угла:
![]()
b a
3) Заменим каждый элементарный сектор круговым сектором (на рисунке не показаны).
Его ![]() (использована формула
(использована формула ![]() ).
).
![]() -
интегральная сумма для r2.
-
интегральная сумма для r2.
![]() Þ
Þ 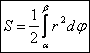
Вычисление длины дуги плоской кривой
В прямоугольных координатах
Длины измеряются масштабными мм, см,… - прямолинейными отрезками. Как измерить кривую линию, - ведь прямолинейный отрезок не совместим с дугой? Для этого вводится определение длины дуги.
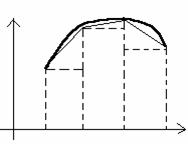 Длиной дуги АВ называется предел l, к которому стремится длина вписанной в нее ломанной при
стремлении к нулю ее звеньев (или n®¥):
Длиной дуги АВ называется предел l, к которому стремится длина вписанной в нее ломанной при
стремлении к нулю ее звеньев (или n®¥):
![]()
![]() Пусть кривая задана
непрерывной
Пусть кривая задана
непрерывной
![]() функцией
функцией ![]() . Длина ломаной:
. Длина ломаной: ![]()
![]()
А0 А1 А2
![]() Используя формулу конечных
приращений
Используя формулу конечных
приращений
(теорема Лагранжа) ![]() получим:
получим:
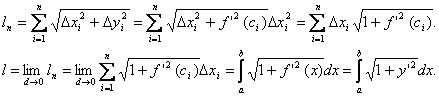
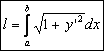
Вносим dx под знак корня:

В параметрической форме
Пусть кривая задана уравнениями ![]() .
.
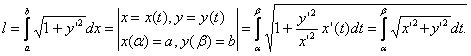

В полярных координатах
Пусть кривая задана уравнением ![]() . Воспользуемся формулами перехода
от полярных координат к прямоугольным:
. Воспользуемся формулами перехода
от полярных координат к прямоугольным:
![]() - параметрические уравнения,
- параметрические уравнения, ![]() .
.
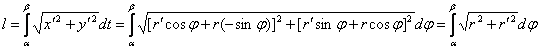

Несобственные интегралы
Несобственные интегралы первого рода (интегралы с бесконечными пределами).
При
определении интеграла 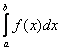 предполагалось, что:
предполагалось, что:
1) отрезок интегрирования [a;b] конечен;
2) f(x) определена и ограничена на [a;b].
Если нарушено условие 1), то интеграл называется несобственным интегралом первого рода или интегралом с бесконечными пределами.
Если нарушено условие 2), то интеграл называется несобственным интегралом второго рода или интегралом от неограниченной функции.
Пусть функция
y=f(x)
определена и ограничена при всех ![]() Рассмотрим интеграл
Рассмотрим интеграл 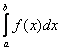 . При изменении
b
изменяется и интеграл, т.е. он является функцией от
b.
. При изменении
b
изменяется и интеграл, т.е. он является функцией от
b.
![]() Предел этого интеграла при
b
Предел этого интеграла при
b
![]() называется
несобственным интегралом первого рода и обозначается
называется
несобственным интегралом первого рода и обозначается 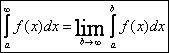
В случае если этот предел конечен, то говорят, что несобственный интеграл
сходится, а функция ![]() интегрируема на бесконечном промежутке [a;
интегрируема на бесконечном промежутке [a;![]() ).
).
Если же указанный предел не существует, то говорят, что несобственный интеграл расходится.
Аналогично вводятся интегралы:
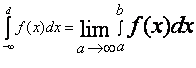
 Геометрически:
Геометрически:
![]() Пример 1.
Пример 1. 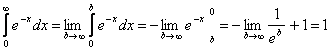 - интеграл сходится.
- интеграл сходится.
![]() Пример 2.
Пример 2. 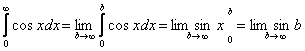 - не
существует.
- не
существует.
При вычислении несобственных интегралов можно применять сокращённый вариант записи. Пусть F(x) – первообразная для f(x). Тогда
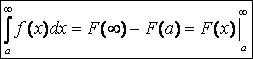
Пример
3. 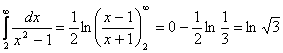 .
.
Несобственные интегралы второго рода
Если функция ![]() имеет
конечный разрыв первого рода на интервале [a;b],
то определённый интеграл существует и он равен
имеет
конечный разрыв первого рода на интервале [a;b],
то определённый интеграл существует и он равен
 |
 (рис.)
(рис.)
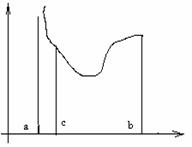
Пусть в точке а левого конца отрезка [a;b] функция
![]() имеет
разрыв второго рода
имеет
разрыв второго рода ![]() при
при
![]() . Возьмём
точку с правее точки а. На отрезке [c;b] функция
. Возьмём
точку с правее точки а. На отрезке [c;b] функция ![]() непрерывна и имеет
интеграл
непрерывна и имеет
интеграл 
 Определение.
Определение.  Предел называется несобственным
интегралом второго рода и обозначается
Предел называется несобственным
интегралом второго рода и обозначается 
Разумеется, этот предел может не существовать.
В таких случаях говорят, что этот интеграл расходится.
Пример
1. 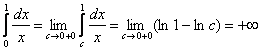
Пример
2. 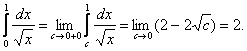
ПРИМЕЧАНИЯ. 1) Геометрический смысл несобственного интеграла второго рода тоже, что и у определённого интеграла – площадь соответствующей фигуры.
2)Вид обозначения у интеграла второго рода аналогичен виду определённого интеграла. В случае сходящегося интеграла это несовершенство обозначения к неприятностям не приводит, в противном случае можно получить неверный результат.
3) Несобственные интегралы второго рода ещё называются интегралами от неограниченных функций.
4) Аналогично выше сказанному определяются интегралы второго рода от функций с бесконечным разрывом в точке b и в любой промежуточной точке с интервала [a;b]:
-
в точке b:
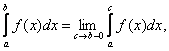
-
в точке c:
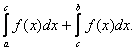
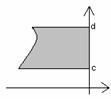
Если область D соответствует первому рисунку, то
Для построения тройного интеграла берётся функция трёх переменных и повторяется схема конструирования определенного и двойного интегралов.
Пусть функция ![]() определена в
ограниченной замкнутой пространственной области Т. Разобъём Т произвольным
образом на n элементарных областей
определена в
ограниченной замкнутой пространственной области Т. Разобъём Т произвольным
образом на n элементарных областей ![]() с диаметрами
с диаметрами ![]() и объёмами
и объёмами ![]() . В каждой области
возьмём произвольную точку
. В каждой области
возьмём произвольную точку ![]() и умножим значение функции в точке
и умножим значение функции в точке ![]() на объём этой области:
на объём этой области:
![]() . Выражение
. Выражение
![]() называется
интегральной суммой для функции
называется
интегральной суммой для функции ![]() по области Т.
по области Т.
Предел интегральной
суммы при стремлении к нулю наибольшего из диаметров элементарных областей
называется тройным интегралом от функции ![]() по области Т и обозначается:
по области Т и обозначается:
![]()
Основные свойства
тройных интегралов аналогичны свойствам
двойных интегралов. Если ![]() есть функция распределения плотности
вещества в области Т, то тройной интеграл численно равен массе всего вещества в
этой области (физический смысл тройного интеграла).
есть функция распределения плотности
вещества в области Т, то тройной интеграл численно равен массе всего вещества в
этой области (физический смысл тройного интеграла).
Вычисление тройного интеграла аналогично вычислению двойного через повторные интегралы:
 - формула для
вычисления тройного интеграла в прямоугольных координатах. На рисунке показаны
пределы интегрирования для повторных интегралов.
- формула для
вычисления тройного интеграла в прямоугольных координатах. На рисунке показаны
пределы интегрирования для повторных интегралов.
 Такого же типа
формулы записываются в случае изменения порядка интегрирования:
Такого же типа
формулы записываются в случае изменения порядка интегрирования:
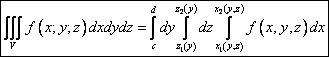 и др.
и др.
(всего шесть вариантов). В
некоторых случаях бывает удобно использовать разновидности этих формул: 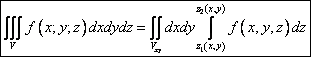 ,
,
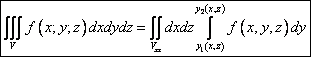 .
.
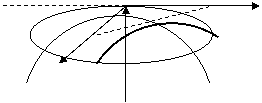
Пример. Вычислить тройной интеграл
![]() , где V – область, ограниченная
плоскостями
, где V – область, ограниченная
плоскостями ![]()
![]() (пирамида, рисунок).
(пирамида, рисунок).
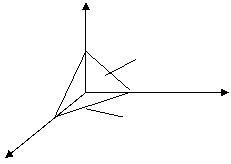 Если выбрать первую формулу
для вычисления, то интегрирование по х совершается от точки х = 0
до точки х = 1 (проекция пирамиды на ось Ох), интегрирование по у
производится от линии у = 0 до линии у = 1 – х (проекция пирамиды
на плоскость хОу), интегрирование по z совершается от поверхности z
= 0 до поверхности
Если выбрать первую формулу
для вычисления, то интегрирование по х совершается от точки х = 0
до точки х = 1 (проекция пирамиды на ось Ох), интегрирование по у
производится от линии у = 0 до линии у = 1 – х (проекция пирамиды
на плоскость хОу), интегрирование по z совершается от поверхности z
= 0 до поверхности
z = 1- x - y :
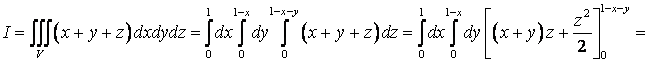
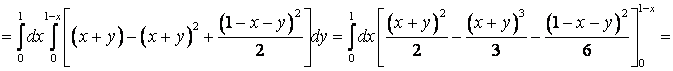
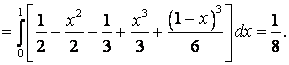
1. Тройной интеграл в криволинейных координатах
Пусть в тройном
интеграле ![]() прямоугольные
координаты x, y, z преобразуются к криволинейным координатам u,
v, w c помощью соотношений:
прямоугольные
координаты x, y, z преобразуются к криволинейным координатам u,
v, w c помощью соотношений:
 Если эти функции имеют непрерывные частные производные
Если эти функции имеют непрерывные частные производные
первого порядка и ![]() , то имеет место формула
, то имеет место формула
замены переменных:
 ,
,
где  - якобиан перехода к
новым координатам.
- якобиан перехода к
новым координатам.
 2. Тройной интеграл в
цилиндрических координатах
2. Тройной интеграл в
цилиндрических координатах
Цилиндрические
координаты r,
j ,z
связаны с прямоугольными x, y, я следующими
соотношениями: 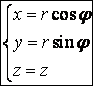 .
Формула замены переменных в этом случае принимает вид:
.
Формула замены переменных в этом случае принимает вид: 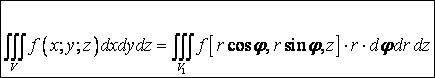 .
.
Пример. Вычислить интеграл ![]() , где область V ограничена снизу
параболоидом
, где область V ограничена снизу
параболоидом ![]() ,
а сверху сферой
,
а сверху сферой ![]() (рисунок).
(рисунок).
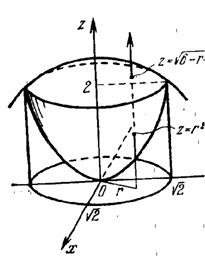 В
цилиндрических координатах эти уравнения имеют вид:
В
цилиндрических координатах эти уравнения имеют вид: ![]() - параболоид,
- параболоид, ![]() - сфера. Линия их пересечения –
окружность. Для получения радиуса окружности и уравнения плоскости, в которой
находится окружность, решается система уравнений
- сфера. Линия их пересечения –
окружность. Для получения радиуса окружности и уравнения плоскости, в которой
находится окружность, решается система уравнений  .
.
Отсюда: 
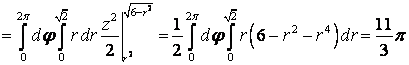
3. Тройной интеграл в сферических координатах
 Сферические
координаты
Сферические
координаты ![]() связаны
с прямоугольными x, y, z следующими формулами:
связаны
с прямоугольными x, y, z следующими формулами:
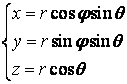 (
(
![]() )
)
Формула замены переменных:
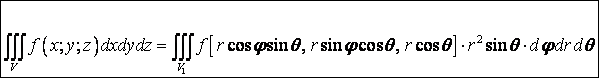
Замечание. К сферическим координатам переходить целесообразно в
тех случаях, когда подинтегральная функция содержит выражение ![]() , а областью
интегрирования является шар или его части.
, а областью
интегрирования является шар или его части.
Пример. Вычислить  , где V – шар
, где V – шар ![]() .
.
Граница области V – сфера, её
уравнение в сферических координатах ![]() . Новые переменные изменяются следующим
образом: r – от 0 до 1,
j - от 0 до 2p,
q - от 0 до
p. Таким образом,
. Новые переменные изменяются следующим
образом: r – от 0 до 1,
j - от 0 до 2p,
q - от 0 до
p. Таким образом, 
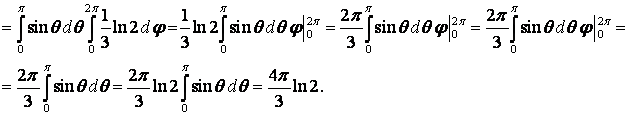
Обобщённые
сферические координаты r,j ,q
связаны с прямоугольными x, y, z следующими
формулами: 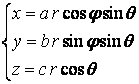 Тогда:
Тогда:
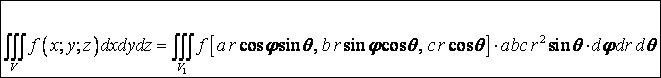 3. Приложения тройного
интеграла
3. Приложения тройного
интеграла
n Объём тела:
![]() n Масса
тела:
n Масса
тела: ![]()
n Статические моменты тела относительно
координатных плоскостей
![]() ,
, ![]() ,
, ![]() и др.
и др.
Лекция 11
Криволинейные интегралы
1. Кривые на плоскости и в пространстве.
2. Криволинейный интеграл первого рода.
3.
Криволинейный интеграл первого рода
К понятию криволинейного интеграла первого рода приводят многие физические задачи. Например, следующая задача о нахождении массы пространственной материальной кривой:
 требуется найти массу т кривой АВ, если
известна её плотность в каждой точке по формуле
требуется найти массу т кривой АВ, если
известна её плотность в каждой точке по формуле ![]() .
.
M2 В=Мn
Предположим, что на некоторой гладкой М1
кривой масса распределена непрерывно. А=М0
Mi
Средняя плотность дуги –
это отношение
её массы к длине. Плотность дуги в
точке – пре-
дел средней плотности дуги, стягивающейся в
данную точку.
Разобьём кривую АВ n точками М0, М1, … ,Мn на n дуг М0М1, … . Наибольшую из дуг обозначим d и назовём диаметром разбиения. Если
![]() , то число дуг
, то число дуг ![]() .
.
На
каждой дуге Mi-1Mi возьмём произвольную точку
Ni.
Плотность в этой точке равна ![]() .
.
Приближённо считая, что плотность соответствующей дуги во всех точках одинакова с точкой Ni, получим
![]() и
и ![]() (1)
(1)
Так как функция f непрерывна, то чем мельче разбиение кривой АВ, тем точнее равенство (1).
Массой кривой
АВ будет называться предел ![]() (2)
(2)
Таким образом,
полученный предел повторяет конструкцию определённого интеграла и является его
обобщением для пространственной функции ![]() , заданной на пространственной кривой АВ.
, заданной на пространственной кривой АВ.
Определение.
Если при стремлении ![]() интегральная
сумма
интегральная
сумма ![]() имеет
конечный предел I, не зависящий ни от способа разбиения кривой АВ, ни
от выбора точек Ni, то он называется криволинейным интегралом
первого рода (или по длине кривой) от функции
имеет
конечный предел I, не зависящий ни от способа разбиения кривой АВ, ни
от выбора точек Ni, то он называется криволинейным интегралом
первого рода (или по длине кривой) от функции ![]() , взятым по кривой АВ и обозначается
, взятым по кривой АВ и обозначается
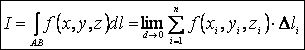
Свойства криволинейного интеграла первого рода
1)
Если кривая АВ лежит в плоскости,
то интеграл имеет вид ![]() .
.
2)
Криволинейный интеграл первого
рода не зависит от направления прохождения кривой, т.к. длина ![]() не зависит от выбора
начальной или конечной точки
не зависит от выбора
начальной или конечной точки ![]() или
или ![]() . Таким образом
. Таким образом ![]() .
.
3)
![]() - физический смысл интеграла.
- физический смысл интеграла.
Следующие свойства и их доказательства аналогичны свойствам определённого
интеграла.
4)
Аддитивность: ![]()
![]() .
.
5)
Линейность: ![]() .
.
6)
Оценка абсолютной величины: 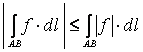 .
.
7)
Теорема о среднем значении: ![]() - на АВ найдётся
точка Q такая, что будет выполняться данное равенство,
L – длина
всей дуги.
- на АВ найдётся
точка Q такая, что будет выполняться данное равенство,
L – длина
всей дуги.
8)
Длина дуги: ![]() .
.
Вычисление криволинейного интеграла первого рода
Вычисление криволинейного интеграла сводится к вычислению определённого интеграла. Следующие три случая относятся к плоским кривым.
j Кривая АВ
задана явным уравнением ![]() . Тогда длина дуги
l
вычисляется (см. Определённый интеграл) по формуле
. Тогда длина дуги
l
вычисляется (см. Определённый интеграл) по формуле ![]() .
.
Дифференциал дуги: ![]() .Имеем:
.Имеем:
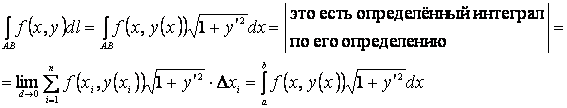
Итак, 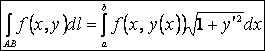
k Кривая АВ задана параметрическими
уравнениями ![]() .
.
Тогда 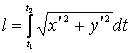 ,
, ![]() ,
, 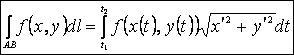
l Кривая АВ
задана на плоскости полярным уравнением ![]() .
.
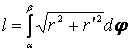 ,
,
![]() ,
, 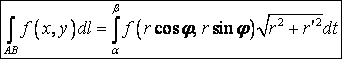
„ Случай пространственной кривой.
АВ задана параметрическими
уравнениями ![]() .
Тогда
.
Тогда 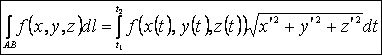
Пример.
1) Вычислить интеграл
![]() , АВ: прямая, соединяющая
точки (а;а) и (b;b).
, АВ: прямая, соединяющая
точки (а;а) и (b;b).
Уравнение АВ: ![]() . Данное уравнение
соответствует первой из формул:
. Данное уравнение
соответствует первой из формул: 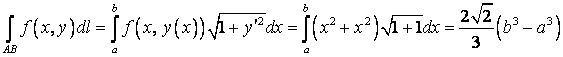 .
.
Криволинейные интегралы второго рода
Если точка М переходит из
положения А в положение В по вектору  и при этом на неё действует постоянная
сила
и при этом на неё действует постоянная
сила 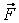 , то
работа W этой силы
, то
работа W этой силы
(из курса физики) равна скалярному
произведению ![]() .
.
Решим усложнённую задачу – вычислим работу переменной силы
![]() и
перемещение АВ возьмём криволинейным. Через координаты (проекции)
и
перемещение АВ возьмём криволинейным. Через координаты (проекции) ![]() может быть записана в
виде
может быть записана в
виде
![]() (1)
(1)
1) Разобъём кривую АВ на n дуг точками М0, М1, …,Мn и наибольшую из элементарных дуг обозначим через d.
2)
На каждой дуге выберем
произвольную точку Ni(xi,,
yi ,
zi) и найдём в
ней значение силы ![]() .
.
3) Временно предположим,
что сила ![]() по
элементарной дуге сохраняет постоянное значение и под её действием точка
перемещается не по дуге, а по хорде
по
элементарной дуге сохраняет постоянное значение и под её действием точка
перемещается не по дуге, а по хорде ![]() этой дуги. Тогда получим приближённое
значение работы этой силы на каждом элементарном участке (скалярное
произведение):
этой дуги. Тогда получим приближённое
значение работы этой силы на каждом элементарном участке (скалярное
произведение):
![]() ,
В
,
В
где ![]() -проекции (координаты)
i-ой
-проекции (координаты)
i-ой
![]()
хорды.
|
В |
 Суммируя
частичные работы
Суммируя
частичные работы ![]() :
:
![]()
За точное значение работы W
переменной
силы ![]() при перемещении
материальной
при перемещении
материальной
точки вдоль кривой АВ примем следующий
предел: ![]()
или ![]() .
.
Отвлекаясь от
физического содержания задачи, сконструируем аналогичный предел для функции ![]() вдоль кривой АВ:
вдоль кривой АВ:
Определение. Предел интегральной суммы ![]() (если он существует), называется
криволинейным интегралом второго рода (или по координате х) от функции
(если он существует), называется
криволинейным интегралом второго рода (или по координате х) от функции
![]() и обозначается
и обозначается
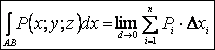 (частный вид
интеграла).
(частный вид
интеграла).
Аналогично
составляются интегралы ![]() и
и ![]() .
.
Сумма данных
интегралов называется общим интегралом второго рода и обозначается
![]() µ
µ
Свойства криволинейных интегралов второго рода
1) Отличие в конструкции
КИ-1 от КИ-2 заключается в умножении подинтегральной функции ![]() на длину элементарной
дуги dl для
интеграла первого рода и в умножении той же функции на проекцию
на длину элементарной
дуги dl для
интеграла первого рода и в умножении той же функции на проекцию ![]() дуги
dl
на ось Ох во
втором случае.
дуги
dl
на ось Ох во
втором случае.
2) Если P,
Q,
R –
проекции силы ![]() на
оси Ох, Оу, Оz, то
µ выражает работу этой силы на
пути АВ (физический смысл КИ-2):
на
оси Ох, Оу, Оz, то
µ выражает работу этой силы на
пути АВ (физический смысл КИ-2): ![]() .
.
3) Для плоской кривой АВ в
хОу µ примет вид ![]() .
.
4)
Если кривая АВ лежит в плоскости ![]() , то
, то ![]() и
и ![]() .
.
5)
Из интегральной суммы ![]() следует, что если
изменить направление кривой АВ на противоположное ВА, то изменится знак
проекции
следует, что если
изменить направление кривой АВ на противоположное ВА, то изменится знак
проекции ![]() и,
следовательно,
и,
следовательно, ![]() .
.
6) Остальные свойства КИ-2 совпадают со свойствами КИ-1.
Лекция 12. Вычисление криволинейных интегралов второго рода. Формула Грина.
Интеграл
вида ![]() называют
координатной формой записи КИ-2. Наряду с ней используется векторная
запись этого интеграла.
называют
координатной формой записи КИ-2. Наряду с ней используется векторная
запись этого интеграла.
Ранее
мы записывали: силу ![]() и
и
хорду ![]() . Переобозначим хорду:
. Переобозначим хорду: ![]() . Тогда
. Тогда ![]() и
и ![]() -векторная форма КИ-2.
-векторная форма КИ-2.
Вычисление КИ-2
Вычисление КИ-2 (как и КИ-1) сводится к вычислению определённых интегралов.
j Если АВ – плоская
кривая и задана явным уравнением ![]()
![]() , то:
, то: 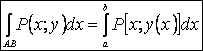 и
и
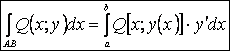 ²
²
Аналогичным образом можно КИ-2 приводить к определённому интегралу по переменной интегрирования у.
k Если АВ –
плоская кривая и задана параметрическими уравнениями
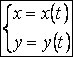 ,
причём изменению t от
,
причём изменению t от ![]() до
до ![]() соответствует движение по кривой от
точки А до точки В. Тогда
соответствует движение по кривой от
точки А до точки В. Тогда
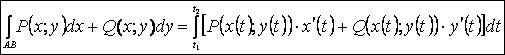
l Если АВ –пространственная кривая и задана параметрическими
уравнениями ![]() ,
то
,
то 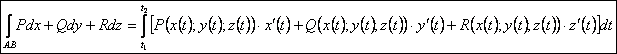
Пример 1. Вычислить
![]() , где кривая АВ представляет следующие линии: а)
отрезок прямой между точками А(0; 0) и В(1; 1);
, где кривая АВ представляет следующие линии: а)
отрезок прямой между точками А(0; 0) и В(1; 1);
б)
часть параболы ![]() (см.
рис.);
(см.
рис.);
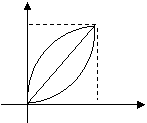 Решения.
а)
Решения.
а) 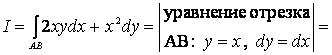
![]()
б) ![]()
В этом примере обратим внимание на тот факт, что интегрирование по различным путям привело к одинаковому результату. Случайно ли это?
Пример 2. Вычислить
![]() по
линиям а)-б) из Примера 1.
по
линиям а)-б) из Примера 1.
а) ![]()
б) ![]()
Здесь интегрирование по различным путям привело к разным результатам.
Пример 3. Вычислить
![]() вдоль
прямой АВ
вдоль
прямой АВ
от точки А(1; 1; 3) до точки В(3; 2; 1).
Составим параметрические
уравнения прямой АВ: 
Если ![]() , то
, то ![]() ,если
,если ![]() , то
, то ![]() .
.
![]() .
.
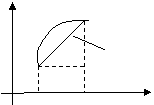
Связь между криволинейными интегралами первого и второго рода
Отличие КИ-1
![]() и КИ-2
и КИ-2
![]() состоит
в умножении подинтегральной функции
состоит
в умножении подинтегральной функции ![]() на длину элементарной дуги
на длину элементарной дуги ![]() в первом случае и в
умножении
в первом случае и в
умножении ![]() на
длину
на
длину ![]() проекции
на этой дуги во втором. Т.к. дуга
проекции
на этой дуги во втором. Т.к. дуга ![]() в пределе стремится к нулю, то её можно
считать прямолинейной, т.е. вектором
в пределе стремится к нулю, то её можно
считать прямолинейной, т.е. вектором ![]() с координатами-проекциями
с координатами-проекциями ![]() .
.
 Значит
Значит 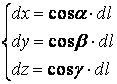 , где
, где ![]() -
углы,
»
dl
-
углы,
»
dl
образованные ![]() с осями координат.
Следовательно, dx
с осями координат.
Следовательно, dx
для общего вида КИ-2 имеем(левая часть - КИ-2, правая – КИ-1):
![]()
Формула Грина
Теорема. Если функции ![]() и
и ![]() непрерывны вместе со своими
непрерывны вместе со своими
частными производными в замкнутой ограниченной области D, то справедлива
формула Грина: 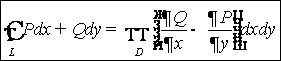
 Доказательство.
Рассмотрим область D (рисунок). Так как
Доказательство.
Рассмотрим область D (рисунок). Так как ![]() непрерывна, то
непрерывна, то
|
А D В
n
a b |
то существует двойной интеграл
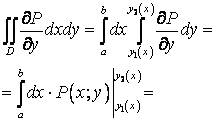
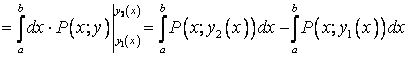 . Согласно формуле
. Согласно формуле
![]() (см. Вычисление КИ-2) определённый интеграл
можно представить через КИ-2:
(см. Вычисление КИ-2) определённый интеграл
можно представить через КИ-2: 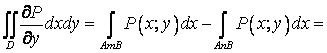
![]()
![]() .
.
Аналогично
выводится формула 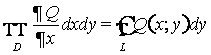 .
Если из этой формулы вычесть предыдущую, то получим формулу Грина.
.
Если из этой формулы вычесть предыдущую, то получим формулу Грина.
Условия
независимости КИ-2 от пути интегрирования
Если значения по всевозможным кривым
АВ одинаковы, то говорят, что КИ-2
не зависит от пути интегрирования. Это означает, что он зависит только
от начальной ![]() и
конечной
и
конечной ![]() точек.
Запись:
точек.
Запись:
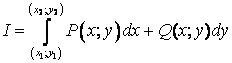 При каких же условиях I не
зависит от пути интегрирования?
При каких же условиях I не
зависит от пути интегрирования?
|
Для того, чтобы КИ-2 не
зависел от пути интегрирования |
Теорема 1.
Достаточность условия ![]() . Пусть выполнено
. Пусть выполнено ![]() и рассмотрим произвольный
замкнутый контур AmBnA. Для него справедлива формула Грина
и рассмотрим произвольный
замкнутый контур AmBnA. Для него справедлива формула Грина
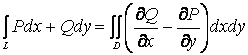 . С
учетом
. С
учетом ![]() Þ
Þ
![]() Þ
Þ ![]() , а это означает независимость
КИ-2 от пути интегрирования.
#
, а это означает независимость
КИ-2 от пути интегрирования.
#
По ходу доказательства теоремы было получено:
Следствие.  Верно и обратное утверждение (без доказательства).
Верно и обратное утверждение (без доказательства).
Теорема 2.
![]() Þ
Þ
![]() -
полный дифференциал некоторой функции.
-
полный дифференциал некоторой функции.
Доказательство. Рассмотрим
КИ-2 ![]() ,
где А0 (х0; у0)- фиксированная точка, В(х; у) – переменная.
По предыдущей теореме интеграл не зависит от пути интегрирования и при
фиксированной А0 зависит только от переменной конечной точки В. Это
записывается в виде
,
где А0 (х0; у0)- фиксированная точка, В(х; у) – переменная.
По предыдущей теореме интеграл не зависит от пути интегрирования и при
фиксированной А0 зависит только от переменной конечной точки В. Это
записывается в виде 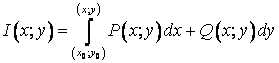 .
.
Отметим, что переменные х, у в верхнем пределе интегрирования и
в подинтегральной функции – разного происхождения и сейчас рассматриваются
только первые.
Докажем, что полный дифференциал функции I(x; y) равен
подинтегральной функции (аналог теоремы о производной определённого интеграла с
переменным верхним пределом). Вначале найдём ![]() .
.
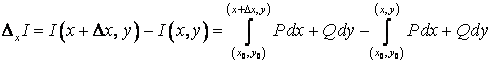 =
=
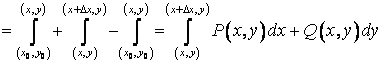 .
.
Последний интеграл
вычисляется по прямой![]() ,
,
поэтому ![]() и
и 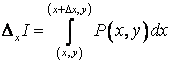 . Так как
. Так как
![]() , то можно записать
, то можно записать 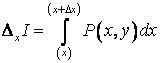 . Данный интеграл является
обыкновенным определённым и к нему применима теорема о среднем:
. Данный интеграл является
обыкновенным определённым и к нему применима теорема о среднем:
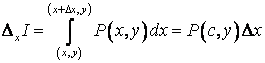 , где
, где ![]() . Отсюда
. Отсюда
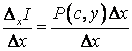
и 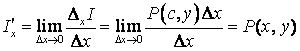 , так как
, так как ![]() при
при ![]() .
.
Аналогично: ![]() и тогда
и тогда ![]() .
#
.
#
Лекция 13. Формула Ньютона-Лейбница для криволинейных интегралов 2-го рода. Поверхностные интегралы
Из вышеизложенных лекций следует, что следующие четыре утверждения равносильны между собой:
1) ![]() .
.
2) ![]() не
зависит от линии интегрирования, соединяющей две точки.
не
зависит от линии интегрирования, соединяющей две точки.
3) Выражение ![]() есть полный
дифференциал.
есть полный
дифференциал.
4) Во всей области D
выполняется равенство ![]() .
.
Наиболее важную роль играет четвёртое утверждение. Оно обычно используется для проверки выполнения всех остальных.
Интегрирование полных дифференциалов (нахождение функции по её полному дифференциалу)
Случай 1. Точки ![]() являются фиксированными.
являются фиксированными.
Рассмотрим
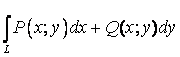 ,
считая выполненными все четыре предыдущих условия. Тогда КИ-2 может быть
записан в виде
,
считая выполненными все четыре предыдущих условия. Тогда КИ-2 может быть
записан в виде
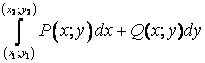 . Наиболее рациональным
. Наиболее рациональным
способом вычисления интеграла будет интегрирование
по отрезкам ломаной ![]() , звенья которой
, звенья которой
параллельны координатным осям (рисунок).
Так как на ![]() и на
и на ![]()
![]() , то
, то
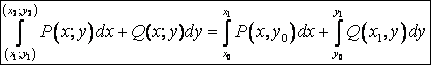 -
формула для вычисления КИ-2 от полного дифференциала для фиксированных точек
-
формула для вычисления КИ-2 от полного дифференциала для фиксированных точек ![]() (справа – определённые
интегралы).
(справа – определённые
интегралы).
Случай 2. Начальная точка М0 - фиксированная, конечная М(x; y) – переменная.
Тогда интеграл
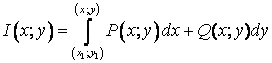 , как
не зависящий от пути интегрирования (упомянутые ранее четыре условия
выполнены), зависит только от конечной точки М(x; y), т.е. является функцией от
х, у.
, как
не зависящий от пути интегрирования (упомянутые ранее четыре условия
выполнены), зависит только от конечной точки М(x; y), т.е. является функцией от
х, у.
Подинтегральное
выражение ![]() при
этом является полным дифференциалом некоторой функции
при
этом является полным дифференциалом некоторой функции ![]() . Такая функция называется первообразной
для полного дифференциала
. Такая функция называется первообразной
для полного дифференциала ![]() .
.
Таких первообразных
бесчисленное множество и все они находятся в формуле ![]() .
. ![]() также является первообразной, поэтому она
принадлежит указанному множеству:
также является первообразной, поэтому она
принадлежит указанному множеству: ![]() . Так как
. Так как ![]() , то
, то![]() и
и ![]() . Поэтому
. Поэтому
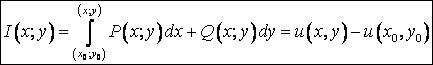
Полученная формула
называется формулой Ньютона-Лейбница для КИ-2 от полного дифференциала.
Её можно применять для вычислений КИ-2 от полных дифференциалов (случай 1) и
для нахождения первообразной ![]() :
:
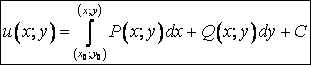 Если линии интегрирования -
вышеуказанные ломаные, то получим наиболее удобные (равносильные) формулы для нахождения
Если линии интегрирования -
вышеуказанные ломаные, то получим наиболее удобные (равносильные) формулы для нахождения
![]() сразу через
определённые интегралы:
сразу через
определённые интегралы:
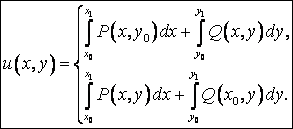
Примечание. Для пространственных кривых L общий вид КИ-2 запишется
в виде 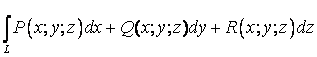 , а
условиями независимости от пути будут равенства
, а
условиями независимости от пути будут равенства ![]()
Поверхностные интегралы
Построим ещё один
вариант интегральной суммы для функции ![]() , заданной на поверхности S с уравнением
, заданной на поверхности S с уравнением
![]() .
.
 Разобьем
поверхность S на n частей Si с площадями
Разобьем
поверхность S на n частей Si с площадями
DSi
. В каждой части Si возьмем произвольную точку
![]() и составим
сумму
и составим
сумму 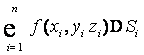 . Она
. Она
называется интегральной для функции
![]() по
по
поверхности S.
 - поверхностный интеграл 1 рода (или
по площади поверхности). Он является обобщением двойного интеграла и поэтому их
свойства аналогичны (см. свойства двойных интегралов).
- поверхностный интеграл 1 рода (или
по площади поверхности). Он является обобщением двойного интеграла и поэтому их
свойства аналогичны (см. свойства двойных интегралов).
Вычисление поверхностного интеграла 1 рода
Так же, как КИ-1 вычислялся через определенный интеграл, так же ПИ-1 вычисляется через двойной интеграл по сходственным формулам:
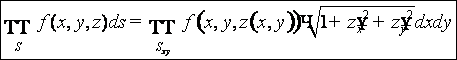 , где Sxy - проекция S на координатную
плоскость xOy. Если поверхность задана уравнением
, где Sxy - проекция S на координатную
плоскость xOy. Если поверхность задана уравнением
![]() , то
, то
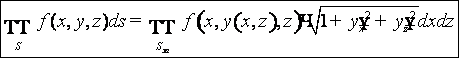
Физический смысл
ПИ-2: он равен массе поверхности S, если
![]() есть функция распределения плотности по
данной поверхности.
есть функция распределения плотности по
данной поверхности.
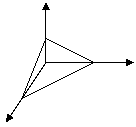 Пример 1. Вычислить
Пример 1. Вычислить ![]() , где
, где ![]() : часть плоскости
: часть плоскости ![]() , отсеченная
координатными плоскостями.
, отсеченная
координатными плоскостями.
Решение. 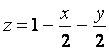 ,
, 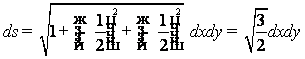 .
.
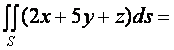
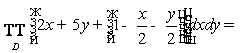
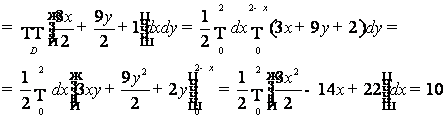
Поверхностный интеграл 2 рода
Отметим, что существуют двусторонние поверхности (плоскость, сфера, цилиндр и др.) и односторонние (лист Мёбиуса). Будем рассматривать наиболее распространённые двусторонние поверхности.
Как и в случае
криволинейных интегралов, отличие ПИ-2 от ПИ-1 состоит в умножении
подинтегральной функции ![]() не на площадь элементарной части ds поверхности
S, а на проекцию ds =dx× dy этой
части на плоскость xOy :
не на площадь элементарной части ds поверхности
S, а на проекцию ds =dx× dy этой
части на плоскость xOy :  - поверхностный интеграл 2 рода (по
координатам) от функции
- поверхностный интеграл 2 рода (по
координатам) от функции ![]() по переменным х и у по выбранной стороне
поверхности.
по переменным х и у по выбранной стороне
поверхности.
Если выбрана
верхняя сторона поверхности S (нормаль ![]() к выбранной стороне образует острый угол с
осью Oz острый угол), то интеграл берется со знаком «плюс» и «минус» для
нижней стороны. Другие свойства ПИ-2 аналогичны свойствам ПИ-1 и свойствам
двойных интегралов.
к выбранной стороне образует острый угол с
осью Oz острый угол), то интеграл берется со знаком «плюс» и «минус» для
нижней стороны. Другие свойства ПИ-2 аналогичны свойствам ПИ-1 и свойствам
двойных интегралов.
Соответственно определяется ПИ-2 по переменным y, z и x, z :
 Сумма этих частных случаев
ПИ-2 образует общий вид поверхностного интеграла 2 рода, который принято
записывать в виде (координатная форма):
Сумма этих частных случаев
ПИ-2 образует общий вид поверхностного интеграла 2 рода, который принято
записывать в виде (координатная форма):
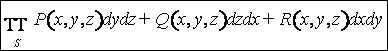
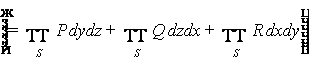
Вычисление ПИ-2
сводится к вычислению двойного интеграла. Например, 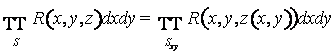
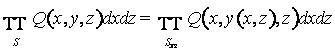 , где
, где
![]() - проекции
поверхности S на координатные плоскости xOy, xOz .
- проекции
поверхности S на координатные плоскости xOy, xOz .
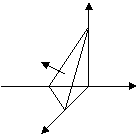 Пример.
Вычислить
Пример.
Вычислить ![]() по верхней стороне части плоскости
по верхней стороне части плоскости ![]() .
.
Нормаль ![]() образует с осями Ох
и Oz острые углы,
образует с осями Ох
и Oz острые углы,
а с осью Оу – тупой (это можно проверить, вычислив
направляющие косинусы нормального вектора).
Поэтому, ![]()

 .
.
Лекция 14. Связь между поверхностными интегралами 1-го и 2-го рода. Формулы Остроградского и Стокса
Так как площадь ds
в ПИ-1 связана со своими проекциями на координатные плоскости соотношениями ![]() ,
,![]() ,
,![]() , то
, то 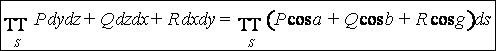 -
связь между поверхностными интегралами 1 и 2 рода.
-
связь между поверхностными интегралами 1 и 2 рода.
Если ввести обозначения новых векторов
![]() ,
, ![]() ,
то
,
то 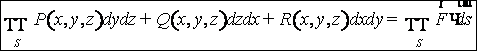
Справа – векторная запись поверхностного интеграла второго рода.
Так как ![]() , где
, где ![]() - единичный вектор
нормали к поверхности S, ds – дифференциал (элемент) площади
поверхности, причём
- единичный вектор
нормали к поверхности S, ds – дифференциал (элемент) площади
поверхности, причём
![]() , то
, то ![]() - ещё один вариант векторной записи ПИ-2.
- ещё один вариант векторной записи ПИ-2.
С учетом того, что ![]() , то
, то

Справа – сокращённая координатная запись ПИ-2.
Физический смысл ПИ-2 – его величина равна объёму жидкости, протекающей через поверхность S за единицу времени.
Формула Остроградского
Связь между ПИ-2 по замкнутой
поверхности S и тройным интегралом по объёму, ограниченному этой поверхностью
выражается формулой Остроградского: 
Формула Остроградского позволяет вычислять ПИ-2 через тройной интеграл и наоборот.
Пример. Вычислить
![]() ,
где S – внешняя сторона сферы
,
где S – внешняя сторона сферы ![]() .
.
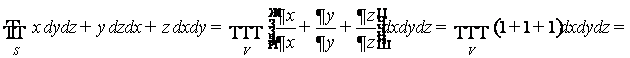
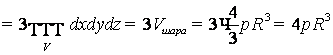 .
.
Формула Стокса
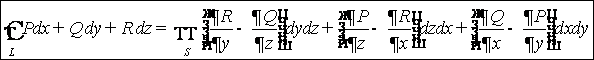
Формула Стокса является аналогом формулы Грина и связывает ПИ-2 по поверхности S с КИ-2 по контуру L, который ограничивает эту поверхность.
Пример. Вычислить ![]() , где L –
пересечение полусферы
, где L –
пересечение полусферы ![]() с плоскостью
с плоскостью ![]() .
.
По формуле Стокса:
![]()
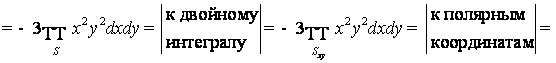

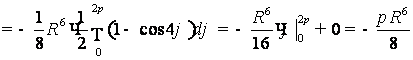 .
.
Приложения поверхностного интеграла 1 рода
1. ![]() - площадь поверхности П.
- площадь поверхности П.
2. ![]() - масса материальной
поверхности П, где
- масса материальной
поверхности П, где ![]() -
функция распределения плотности по поверхности П.
-
функция распределения плотности по поверхности П.
3. 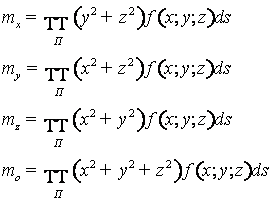 - моменты инерции поверхности
П.
- моменты инерции поверхности
П.
4.  - координаты центра тяжести
поверхности П.
- координаты центра тяжести
поверхности П.
5. ![]() - статические моменты
поверхности П относительно координатных плоскостей.
- статические моменты
поверхности П относительно координатных плоскостей.
6. ![]() - момент порядка к поверхности
П относительно координатных плоскостей или осей.
- момент порядка к поверхности
П относительно координатных плоскостей или осей.
r - расстояние от точки поверхности до координатных плоскостей или осей.
Масса – момент нулевого порядка ( к = 0 ).
Статический момент – момент первого порядка ( к = 1 ).
Момент инерции – момент второго порядка ( к = 2 ).
СПИСОК ЛИТЕРАТУРЫ
1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука,1973. – 720 с.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. - М.: Наука, 1980. - 432 с.
3. Письменный Д.Т. Конспект лекций по высшей математике. 2 часть. – М.: Айрис-пресс, 2003. – 256 с.
4. Натансон И.П. Краткий курс высшей математики. - СПб.: Издательство Лань, 1997. - 736 с.
5. Хасеинов К.А. Каноны математики. Учебник - Алматы, 2003. – 686 с.