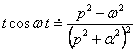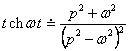АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС ИНСТИТУТЫ 

Жоғары математика кафедрасы   

 

Математика   3

Барлық мамандықтардың

барлық оқу түрінің студенттеріне арналған

дәрістер жинағы

 

 

 

Алматы 2008

ҚҰРАСТЫРУШЫЛАР: Жұматаева С.А., Темешева С.М. Математика 3. Барлық мамандықтардың барлық оқу түрінің студенттеріне арналған дәрістер жинағы. – Алматы: АЭжБИ, 2008. – 67 б.

 

Ұсынылып отырған дәрістер жинағына жоғары математика курсының “Математика 3” бөліміне енгізілген 17 дәрісі (“Өріс теориясы”, “Дифференциалдық теңдеулер”, “Қатарлар”, “Комплекс айнымалыдан тәуелді функция және амалдық есептеу”, “Ықтималдықтар теориясының элементтері” тараулары бойынша) кірген. Дәрістер жинағы Алматы энергетика және байланыс институтының барлық мамандықтарының барлық оқу түрінің бакалаврларын оқытудың оқу жоспарына сәйкес келеді.

Мазмұны 

1. Кіріспе сөз...………………………………………..…………………….......		4
2. 1 дәріс	Өріс теориясы…………………………...…………………...	5
3. 2 дәріс	Дифференциалдық теңдеулер. Жай дифференциалдық теңдеулер.....................…………....	9
4. 3 дәріс	Айнымалыларына қарағанда біртекті дифференциалдық теңдеулер. Сызықтық бірінші ретті дифференциалдық теңдеулер. Бернулли теңдеуі..........…………………………	13
5. 4 дәріс	Жоғары ретті дифференциалдық теңдеулер. Реті төмендейтін дифференциалдық теңдеулер. Жоғары ретті сызықтық дифференциалдық теңдеулер...…………………	17
6. 5 дәріс	Сызықтық біртекті дифференциалдық теңдеулер. Сызықтық біртекті емес дифференциалдық  теңдеудің шешімі. Сызықтық біртекті тұрақты коэффициентті дифференциалдық теңдеулер.........................………………	21
7. 6 дәріс	Сызықтық біртекті емес тұрақты коэффициентті дифференциалдық теңдеудің дербес шешімін таңдау әдісі. Анықталмаған коэффициенттер әдісі. Жай дифференциалдық теңдеулер жүйесі.....................................	25
8. 7 дәріс	Сандық қатарлар. Негізгі ұғымдар. Оң қатарлар ……….....	29
9. 8 дәріс	Айнымалы таңбалы және ауыспалы таңбалы қатарлар................................................................……………	33
10. 9 дәріс	Функциялық қатарлар, дәрежелік қатарлар. Тейлор қатары. Кейбір функциялардың Маклорен қатарына жіктелуі.......................................................................…..……	37
11. 10 дәріс	Фурье қатары………………………………………………...	41
12. 11 дәріс	Комплекс айнымалыдан тәуелді функция ұғымы...……….	43
13. 12 дәріс	Лаплас түрлендіруінің анықтамасы.....……………………..	47
14. 13 дәріс	Бейнесі бойынша түпнұсқаны табу. Амалдық есептеудің қолданылуы.........................…..……………………………...	51
15. 14 дәріс	Ықтималдықтар теориясының элементтері.……………….	53
16. 15 дәріс	Толық ықтималдық формуласы.……………………………	58
17. 16 дәріс	Кездейсоқ шамалар....………………………………………..	61
18. 17 дәріс	Дискретті кездейсоқ шаманың дисперсиясы.……………...	64
19. Әдебиеттер тізімі...………..……………………….....................................		67

 

Кіріспе сөз 

Ұсынылып отырған жинақта жоғары математика курсының “ Математика 3” бөліміне енгізілген 17 дәрісі кірген. Дәрістер жинағы Алматы энергетика және байланыс институтының барлық мамандықтарының барлық оқыту түрінің бакалаврларын оқытудың оқу жоспарына сәйкес келеді.

Дәрістер жинағы оқытушылар мен студенттерге пайдалы және жоғары математика курсының “Өріс теориясы”, “Дифференциалдық теңдеу-лер”, “Қатарлар”, “Комплекс айнымалыдан тәуелді функция және амалдық есептеу”, “Ықтималдықтар теориясының элементтері” тараулары бойынша аудиториялық сабақтар кезінде өзіндік жұмыстар өткізуге арналған.

Анықтамалар, теоремалар, формулалар нөмірлері екі саннан тұрады: олардың біріншісі дәріс нөмірін, ал екіншісі осы дәріс ішіндегі анықтаманың, теореманың, формуланың нөмірін білдіреді.

Оқу құралындағы материалды игеру студенттерге жоғары математика курсының аталып өткен тараулары бойынша жеткілікті жақсы білім алуға мүмкіндік береді.

№ 1 дәріс Өріс теориясы 

Мазмұны: Өріс анықтамасы, өрістер теориясының элементтері. Векторлық өрістердің түрлері. Векторлық өрістің ағыны мен циркуляциясын есептеу. Остроградский-Гаусс теоремасы. Стокс теоремасы.

Дәрістің мақсаты: Векторлық сызықтар жиынтығын анықтайтын диффе-ренциалдық теңдеулер жүйесін құра білу, векторлық өрістің дивергенциясы мен роторын табу. Векторлық өрістің ағынын есептеуге Остроградский-Гаусс және Стокс теоремаларын қолдана білу.

 

1.1 анықтама  облысының әрбір  нүктесінде  векторы анықталса,  облысында векторлық өріс берілді дейміз, басқаша айтқанда, векторлық өріс берілген болып есептеледі, егер әрбір  нүктесінде сәйкесінше  векторы берілсе векторлық өріс берілді дейміз (бұл жерде , ,  функциялары өздерінің дербес туындыларымен бірге үзіліссіз деп ұйғарамыз).

 

Векторлық өрістердің дербес жағдайлары

 

1. Егер  тұрақты вектор болса, яғни , ,  функциялары тұрақты болса, онда векторлық өріс біртекті болады.

2. Егер , ,  функциялары таңдап алынған координаттар жүйесінде екі айнымалыдан тәуелді функциялар және вектордың проекцияларының біреуі 0-ге тең болса, онда векторлық өріс жазық болады. Мысалы,  – жазық векторлық өріс.

3. Егер , ,  функциялары -дан тәуелсіз болса, онда өріс стационарлық болады.

 

1.2 анықтама Векторлық өрістің векторлық сызығы деп әрбір нүктесіндегі жанамасының бағыты осы нүктеге сәйкес келетін вектор бағытымен беттесетін сызықты айтады.

Айталық,  векторлық өрісі берілсін. Векторлық сызық параметрлік түрде берілсін: , , . Векторлық сызыққа  нүктесіндегі бағыттауыш векторы  болатын жанамасы 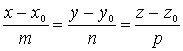 теңдеуімен беріледі. 1.2 анықтамасы бойынша  және  векторлары коллинеар болады, сондықтан, векторлардың коллинеар болу шартынан, 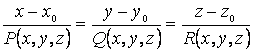  теңдеулерін аламыз.  шамасы  аргументінің өсімшесі болғандықтан,  теңдігін аламыз. Осыған ұқсас  және  болады.

Сонымен,

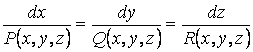.                                    (1.1)

(1.1) дифференциалдық теңдеулер жүйесі  векторлық өрісінің векторлық сызықтар жиынтығын анықтайды.

 Вектордың ағыны 

 векторлық өрісі берілсін. Осы өрісте кейбір  бетін алып, оның бір жағына тоқталайық.  беттің осы жағының кез келген нүктесіндегі бірлік нормаль векторы болсын. 

1.3 анықтама  векторының  беті арқылы ағыны деп өріс векторы мен беттің бірлік нормаль векторының скаляр көбейтіндісінің  беті бойынша интегралы аталады. Оны төмендегідей белгілейді

                                                 (1.2)

немесе

.               (1.3)

 

Дивергенция 

 векторлық өрісінің еркін  нүктесін қарастырамыз, оны толығымен өріске тиісті тұйық  бетімен қоршаймыз.

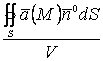 шамасын қарастырайық. Сұйықтың жылдамдықтар өрісінде бұл шама  облысындағы уақыттың бірлігіндегі көлем бірлігіне қатысты пайда болатын сұйық мөлшерін анықтайды, яғни жанар көзінің орташа көлемдік қуатын анықтайды. Егер ағын 0-ден кіші болса, онда ағын көзінің қуаты туралы айтады.

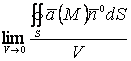 шегін есептейміз, анығырақ айтқанда  облысы  нүктесіне дейін сығылған жағдайдағы шекті есептейміз. Егер шек 0-ден артық болса, онда  нүктесі жанар көзі, ал егер 0-ден кіші болса, онда  ағын көзі болады. Шектің көзі жанар көзінің қуатын немесе ағын көзінің қуатын сипаттайды.

1.4 анықтама  векторлық өрісінің дивергенциясы немесе жинақсыздығы деп  нүктесін қоршайтын бет арқылы  векторының ағынының сол бетпен қоршалған дене көлеміне қатынасын (аталмыш бет  нүктесіне сығылған жағдайдағы) шегін айтады да, төмендегідей белгілейді

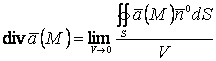.                                        (1.4)

 

Теорема.  векторлық өрісінің  нүктесіндегі дивергенциясы

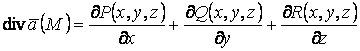                    (1.5)

формуласы бойынша табылады.

 

Остроградский-Гаусс теоремасы. Тұйық беттің ішінен шығатын вектордың ағыны өрістің дивергенциясынан осы бетпен қоршалған дене көлемі бойынша алынған үш еселі интегралға тең

немесе

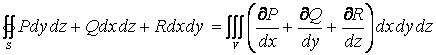.        (1.6)

 

Дивергенция қасиеттері

1. ;

2.  – векторлық өріс, ал  – скалярлық өріс болсын, онда

  .

 

Векторлық өрістің циркуляциясы

 

1.5 анықтама  векторының  тұйық контуры бойынша циркуляциясы деп  векторы мен осы контурды жанап өтетін  векторының скалярлық көбейтіндісінің  контуры бойынша қисық сызықты интегралы аталады

.           (1.7)

 

Векторлық өрістің роторы

 

1.6 анықтама  векторлық өрісінің роторы (құйыны) деп

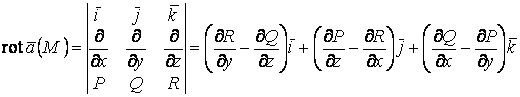     (1.8)

векторы аталады.

Стокс теоремасы.  беті арқылы -ның ағыны  векторының -тің шекарасы бойынша циркуляциясына тең

немесе

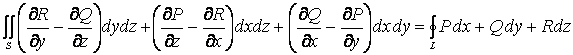.  (1.9)

Ротордың қасиеттері

1. ;

2. егер  – скалярлық функция, ал  – вектор болса, онда

.

 

Гамильтон операторы

 

Символдық  – набла-векторын енгізейік. 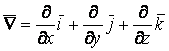 Гамильтон операторы деп аталады.

1. , .

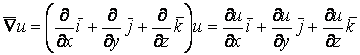2. , .

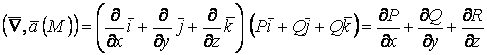3. , .

 

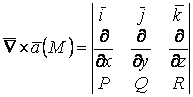Өрістердің типтері

 

1. Егер  болса, онда векторлық өрісі соленоидалдық немесе түтікшелік өріс болады.

2. Егер  болса, онда векторлық өрісі потенциалдық немесе құйынсыз өріс болады.

3. Егер векторлық өріс соленоидалдық та, потенциалдық та болса, онда ол гармониялық болады.

 

№ 2 дәріс Дифференциалдық теңдеулер.   Жай дифференциалдық теңдеулер 

Мазмұны: Негізгі анықтамалар және ұғымдар. Бірінші ретті дифференциалдық теңдеулердің түрлері, оларды шешу әдістері.

Дәрістің мақсаты: Дифференциалдық теңдеудің түрі мен ретін анықтауды, сәйкес ауыстыруларды қолдануды, дифференциалдық теңдеудің жалпы шешімін немесе жалпы интегралын табуды үйрету. 

Негізгі анықтамалар және ұғымдар 

2.1 анықтама Дифференциалдық теңдеу деп тәуелсіз айнымалы -ті, белгісіз функция -ті және оның әртүрлі ретті туындыларын немесе дифференциалдарын байланыстыратын теңдеуді атайды. 

2.2 анықтама Дифференциалдық теңдеуге кіретін туындының ең жоғары реті дифференциалдық теңдеудің реті деп аталады. 

Мысал 2.1 - . Берілген теңдеу дифференциалдық теңдеу болады, өйткені оның құрамында белгісіз функцияның бірінші және екінші ретті туындылары бар. Бұл екінші ретті дифференциалдық теңдеу, себебі теңдеуге енгізілген туындылардың ең жоғары реті 2-ге тең. 

Мысал 2.2 - . Бұл теңдеу дифференциалдық теңдеу болады, өйткені оның құрамында белгісіз функцияның бірінші ретті дифференциалдары бар. Берілген теңдеу бірінші ретті дифференциалдық теңдеу. 

2.3 анықтама Дифференциалдық теңдеуді тепе-теңдікке айналдыратын кез-келген  функциясы дифференциалдық теңдеудің шешімі немесе интегралы деп аталады. 

Бірінші ретті дифференциалдық теңдеулер

 

                                              (2.1)

түріндегі теңдеу – бірінші ретті дифференциалдық теңдеудің жалпы түрі.

Егер (2.1) теңдеуін бірінші ретті туындыға қарағанда шешуге болса, онда

,                                               (2.2)

түріндегі теңдеу бірінші ретті дифференциалдық теңдеудің нормалды формасы немесе бірінші ретті туындысына қарағанда шешілген дифференциалдық теңдеу деп аталады.  теңдігі орындалатынын ескеріп, (2.2)-ні келесі түрге келтіруге болады

.                                    (2.3)

2.4 анықтама Бірінші ретті дифференциалдық теңдеуді тепе-теңдікке айналдыратын,  анықталған  функциясы оның шешімі деп аталады.

Дифференциалдық теңдеудің шешімінің графигі интегралдық қисық деп аталады.

Мынадай сұрақ туындайды: қандай шарттар орындалғанда (2.2) теңдеуінің шешімі табылады? Бұл сұраққа (2.2) дифференциалдық теңдеудің шешімінің бар болуы және жалғыздығы туралы Коши теоремасы деп аталатын теорема жауап береді. 

Коши теоремасы. Егер  және оның  дербес туындысы  жазықтығының кейбір  облысында анықталған және үзіліссіз болса, онда  облысының қандай да бір ішкі  нүктесінің маңайында  теңдеуінің

“ болғанда  болады”                                      (2.4)

деген шарттарға қанағаттандыратын жалғыз шешімі бар болады.

(2.4) шарттары – бастапқы шарттар деп аталады да

                                                           (2.4’)

белгіленеді.

Егер де (2.2) теңдеуінің (2.4) бастапқы шарттарына қанағаттандыратын шешімін табу керек болса, Коши есебін шешу керек дейміз.

Геометриялық тұрғыдан Коши есебінің шешімін табу дегеніміз интегралдық қисықтар жиынынан  жазықтығының берілген  нүктесі арқылы өтетін қисықты алуды білдіреді.

Жазықтықтың кейбір нүктелерінен бірнеше интегралдық қисық өтетін немесе ешбір интегралдық қисық өтпейтін нүктелері теңдеудің ерекше нүктелері деп аталады. 

2.5 анықтама -тен және еркін тұрақты -дан тәуелді

                                                           (2.5)

функциясы

а) тұрақты -ның кез келген мәнінде (2.2) теңдеуіне қанағаттандырса,

б) (2.4) шарттары қандай болса да  теңдігі орындалатындай еркін тұрақтының  мәні табылса

(2.2) дифференциалдық теңдеуінің  жазықтығының кейбір  облысындағы жалпы шешімі деп аталады.

2.6 анықтама Дифференциалдық теңдеудің

       ,                                                  (2.6)

түрінде табылған шешімі (2.2)-нің жалпы интегралы деп аталады.

 

2.7 анықтама (2.2) теңдеуінің  облысындағы дербес шешімі деп теңдеудің жалпы шешімі (2.5)-тен еркін тұрақты -ның бекітілген  мәнінде алынған  функциясын айтамыз.

 

Бірінші ретті дифференциалдық теңдеудің геометриялық мағынасы

 

Айталық,  дифференциалдық теңдеуі берілсін және – оның шешімі болсын. Интегралдық қисықтың кез келген нүктесі арқылы жанама жүргізуге болады. Интегралдық қисыққа әрбір  нүктесінде жүргізілген жанаманың бұрыштық коэффициенті  осы нүктедегі  функциясының мәніне тең екені теңдеуден жеңіл байқалады. Демек,  теңдігі нүктенің координаттары мен осы нүктеде интегралдық қисықтың графигіне жүргізілген жанаманың бұрыштық коэффициенті  арасындағы тәуелділікті орнатады. Интегралдық қисықтың әрбір  нүктесіне бұрыштық коэффициенті  болатын бағытталған кесіндіні сәйкестендірейік, сонда берілген теңдеудің бағыттар өрісін аламыз.

Сонымен, геометриялық тұрғыдан  теңдеуі  жазықтығындағы бағыттар өрісін анықтайды, ал шешім – интегралдық қисық, оның әрбір нүктесінде жүргізілген жанаманың бағыты өрістің бағытымен беттеседі.

 

Теңдеулердің түрлері

 

I.

                                                     (2.7)

қарапайым дифференциалдық теңдеу деп аталады. Оны  түрінде де жазуға болады.

 белгісіз функциясы  формуласымен анықталады.

 

II.

                                          (2.8)

айнымалылары ажыратылған теңдеу деп аталады.

(2.8)-дің шешімі  формуласымен анықталады.

 

III.

                                (2.9)

айнымалылары ажыратылатын теңдеу деп аталады.

 және  деп есептеп, (2.9) теңдігінің екі жағын  көбейтіндісіне бөлеміз, онда  теңдеуін аламыз, яғни (2.9)-ды айнымалылары ажыратылған дифференциалдық теңдеуге келтіріп аламыз.

                                          (2.10)

айнымалылары ажыратылатын теңдеу, мұндағы  және  – үзіліссіз функциялар. (2.10)-ның шешімін табу үшін  теңдігін ескеріп, берілген теңдеуді

                                           (2.11)

түрінде жазып аламыз.

 деп ұйғарып, (2.11)-ді -ке бөлеміз, онда айнымалылары ажыратылған теңдеуді аламыз: 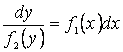. Соңғы теңдіктің екі жағын интегралдап, (2.10) теңдеуінің жалпы интегралын аламыз

.

 

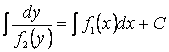Мысал 2.3 -  – бұл қарапайым бірінші ретті дифференциалдық теңдеу.

Интегралдаймыз

   .

 

Мысал 2.4 -  – бұл айнымалылары ажыратылатын дифференциалдық теңдеу.

Теңдеудің екі жағын  көбейтіндісіне бөлеміз, әрине алдын ала  деп ұйғарамыз, онда айнымалылары ажыратылған теңдеуді аламыз

.

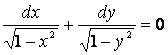Осы теңдеуді интегралдап  теңдігін табамыз.  формуласын пайдаланып, соңғы теңдікті

түрінде жазып аламыз. Бұл берілген дифференциалдық теңдеудің жалпы интегралы.

№ 3 дәріс Айнымалыларына қарағанда біртекті дифференциалдық

     теңдеулер. Біртекті теңдеулерге келтірілетін теңдеулер.

     І-ретті сызықтық дифференциалдық теңдеулер.

     Бернулли теңдеуі

 

Мазмұны: Функцияның біртектілік дәрежесін анықтау, ,  айнымалы-ларына қарағанда біртекті дифференциалдық теңдеулер. І-ретті сызықтық бір-текті және біртекті емес дифференциалдық теңдеулер. Еркін тұрақтыны вариациялау әдісі. Бернулли теңдеуі.

Дәрістің мақсаты: Функцияның біртектілік дәрежесін анықтауды, ,  айнымалыларына қарағанда біртекті дифференциалдық теңдеулерді және оларға келтірілетін теңдеулерді шешуді, І-ретті біртекті және біртекті емес дифференциалдық теңдеулерді шешуді, еркін тұрақтыны вариациялау әдісін қолдануды, Бернулли теңдеуін шешуді үйрету.

 

IV.  және  айнымалыларына қарағанда І-ретті біртекті дифференциал-дық теңдеулер.

3.1 анықтама  теңдігіне қанағаттандыратын функциясы өлшемі -ші ретті біртекті функция деп аталады.

Мысалы,  берілсін. Бұл функция үшін

,

яғни  – өлшемі -ші ретті біртекті функция.

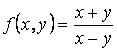 функциясы үшін 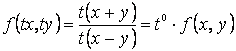, яғни  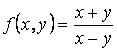– өлшемі -ші ретті біртекті функция.

3.2 анықтама  функциясы , айнымалыларына қарағанда өлшемі -ші ретті біртекті функция болса  теңдеуі І-ретті біртекті дифференциалдық теңдеу деп аталады.

3.3 анықтама  және  өлшем реттері бірдей функциялар болса  дифференциалдық теңдеуі , айнымалыларына қарағанда біртекті теңдеу болады.

 және  айнымалыларына қарағанда біртекті І-ретті дифференциалдық теңдеуді шешу үшін

            (3.1)

алмастыруын қолданып, III-ші түрдегі теңдеуге келтіру арқылы шешеді.

V.  және  айнымалыларына қарағанда І-ретті біртекті дифференциал-дық теңдеуге келтірілетін теңдеулерге

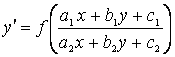                                          (3.2)

түріндегі теңдеулер жатады.

Шешуі: 1) егер 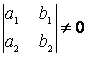 болса, онда 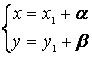 алмастыруын жасай-мыз, мұндағы  мен  сызықтық теңдеулер жүйесінен 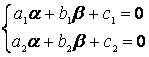 та-былады.

2) егер 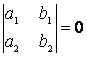 болса, онда  алмастыруын жасаймыз да, IV-ші түрдегі теңдеуге келтіреміз.

 

Сызықтық дифференциалдық теңдеулер 

3.4 анықтама VII

                                              (3.3)

І-ретті сызықтық дифференциалдық теңдеу деп аталады, мұндағы  және  – үзіліссіз функциялар. (3.3) теңдеуіне белгісіз функция  және оның туындысы  тек бірінші дәрежеде кіреді.

3.5 анықтама  болса, (3.3) І-ретті сызықтық біртекті дифференциалдық теңдеу болады да, VI-шы түрде жазылады

.                                                (3.4)

Егер  болса, онда (3.3) І-ретті сызықтық біртекті емес дифферен-циалдық теңдеу болады.

(3.4) теңдеуінің шешімін табамыз. Ол үшін алдымен (3.4)-ті айнымалы-лары ажыратылатын теңдеуге келтіреміз

  .

Енді айнымалыларын ажыратып алып, алынған теңдеуді интегралдаймыз

, .

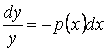Сонымен,

.                                                    (3.5)

(3.5) функциясы – (3.4)-тің жалпы шешімі.

(3.3) І-ретті сызықтық біртекті емес дифференциалдық теңдеудің шеші-мін табу алгоритмін келтірейік. (3.3)-ті шешу үшін еркін тұрақтыны вариация-лау әдісін пайдаланамыз. Оның мағынасы мынада:

а) алдымен сәйкес (3.4) түріндегі теңдеудің жалпы шешімін, яғни (3.5) түріндегі функцияны табамыз;

б) (3.5)-гі -ны -тен тәуелді белгісіз  функциясы деп есептейміз. Енді (3.3)-тің жалпы шешімін

                                              (3.6)

түрінде іздейміз.

Біздің ұйғаруымыз бойынша (3.6) (3.3)-тің шешімі болған соң, (3.6)-ны (3.3)-ке қойсақ, тепе-теңдік аламыз

осыдан  функциясын табамыз

    .

 үшін табылған өрнекті (3.6)-ға қоямыз да, (3.3) дифференциалдық тең-деуінің жалпы шешімін табамыз: , оны

                                    (3.7)

түрінде жазамыз.

(3.7) – (3.3)-тің жалпы шешімі, яғни (3.7) – І-ретті сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі.

 

І-ретті сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімінің құрамы 

І-ретті сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі сәйкес сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі мен біртекті емес дифференциалдық теңдеудің кейбір дербес шешімінен құра-лады, яғни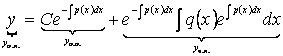, , мұндағы  – біртекті емес дифференциалдық теңдеудің жалпы шешімі, – біртекті диф-ференциалдық теңдеудің жалпы шешімі,  – біртекті емес дифференциал-дық теңдеудің дербес шешімі.

Мысал 3.1 -  теңдеуінің жалпы шешімін табу керек.

Шешуі: – бұл (3.3) түріндегі дифференци-алдық теңдеу. Сәйкес біртекті теңдеуді жазып аламыз: . Осыдан , , 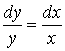, – бұл сызықтық біртекті теңдеудің жалпы шешімі, яғни . Онда сызықтық біртекті емес теңдеудің жалпы шешімін  түрінде іздейміз.  функциясын анықтаймыз:     

. Демек,  берілген теңдеудің жалпы шешімі болады.

 

Бернулли теңдеуі

 

VIII

                                    (3.8)

түріндегі теңдеу Бернулли теңдеуі деп аталады.

 алмастыруын орындағаннан кейін (, ) Бернулли теңдеуі VII-ші түрдегі теңдеуге келтіріледі.

Ескерту.

VII.  – белгісіз  функциясы үшін І-ретті сызықтық біртекті емес дифференциалдық теңдеу.

VI.  – белгісіз  функциясы үшін І-ретті сызықтық біртекті дифферен-циалдық теңдеу.

VIII.  – белгісіз  функциясы үшін Бернулли теңдеуі.

 

Толық дифференциалдардағы теңдеу 

3.5 анықтама

                                       (3.9)

түріндегі теңдеу

                                            (3.10)

шарты орындалғанда толық дифференциалдардағы теңдеу деп аталады.

(3.10) шарты орындалғанда (3.9)-дың сол жағы кейбір  функция-сының дифференциалы болатынын, яғни , дәлелдейміз.

Қажеттілік. (3.9)-дың сол жағы  үшін толық дифференциал болсын:  және , онда  және .  болғандықтан,  болады.

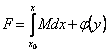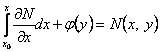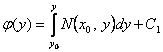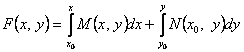Жеткіліктілік. (3.10) орындалсын, яғни , , онда  және . Басқа жағынан, , осыдан , онда . Сонымен, (3.9)-дың сол жағы  функциясының толық дифференциалы болады, ал (3.9) теңдеуінің жалпы шешімі 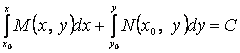 формуласымен анықталады.

№ 4 дәріс Жоғары ретті дифференциалдық теңдеулер.

      Реті төмендетілетін дифференциалдық теңдеулер.

      Жоғары ретті сызықтық дифференциалдық теңдеулер

Мазмұны: Негізгі ұғымдар мен анықтамалар. Екінші ретті сызықтық дифференциалдық теңдеулер. Біртекті сызықтық дифференциалдық теңдеудің шешімінің негізгі қасиеті. Сызықты тәуелді және сызықты тәуелсіз функциялар жүйесі, олардың вронскианы.

Дәрістің мақсаты: Жоғары ретті дифференциалдық теңдеудің анықтамасы. Реті төмендетілетін дифференциалдық теңдеулерді шешу тәсілдерін көрсету. Сызықтық біртекті және біртекті емес жоғары ретті дифференциалдық теңдеулер. Функциялар жүйесінің сызықтық тәуелділігі немесе тәуелсіздігін анықтауды үйрету. 

4.1 анықтама  теңдеуі екінші ретті дифференциалдық теңдеуі деп аталады, мұндағы – тәуелсіз айнымалы,  – белгісіз функция,  және  – оның туындылары.

Көп жағдайда -ке қарағанда шешілген теңдеу қарастырылады

.                                             (4.1)

(4.1) теңдеуінің шешімі деп -да анықталған, теңдеуге қойғанда оны тепе-теңдікке айналдыратын  функциясы аталады. Шешімнің графигі интегралдық қисық деп аталады.

Коши теоремасы. Егер  және оның ,  дербес туындылары  айнымалылар кеңістігінің кейбір  облысында анықталған және үзіліссіз болса, онда  облысының қандай да бір ішкі  нүктесінің маңайында  теңдеуінің

,       .                                       (4.2)

шарттарға қанағаттандыратын жалғыз шешімі бар болады. (4.2) – бастапқы шарттар.

Дифференциалдық теңдеудің бастапқы шарттарға қанағаттандыратын шешімін табу есебін Коши есебі дейміз.

Геометриялық тұрғыдан Коши есебінің шешімін табу дегеніміз интегралдық қисықтар жиынынан  жазықтығының берілген  нүктесі арқылы өтетін, осы нүктедегі жанамасының бұрыштық коэффициенті  болатын қисықты алуды білдіреді.

4.2 анықтама -тен және екі еркін тұрақты  мен -ден тәуелді  функциясы кейбір  облысында (4.1) теңдеуінің жалпы шешімі болады, егер ол: 1)  мен  тұрақтыларының кез келген мәндерінде шешім болса; 2) кез келген (4.2) бастапқы шарттары үшін ,  тұрақтыларының сәйкесінше ,  жалғыз ғана мәндері табылып,  функциясы бастапқы шарттарға қанағаттандырса.

4.3 анықтама Жалпы шешім –  функциясынан ,  мәндерінде шығатын кез келген  функциясы (4.1) теңдеуінің дербес шешімі деп аталады. 

Жоғары ретті дифференциалдық теңдеулер 

n-ретті дифференциалдық теңдеу деп

түріндегі теңдеу аталады. Егер де ол жоғары ретті туындысына қарағанда шешілген болса, онда n-ретті дифференциалдық теңдеу

                                        (4.3)

түрінде жазылады.

(4.3)-тің шешімі деп -да анықталған, (4.3)-ке қойғанда оны тепе-теңдікке айналдыратын  функциясы аталады.

(4.3)-тің жалпы шешімі х-тен және n еркін тұрақтыдан тәуелді болады: .

Жалпы шешімнен  тұрақтыларының бекітілген мәндерінде пайда болатын (4.3)-тің шешімі оның дербес шешімі деп аталады.

Жоғары ретті теңдеу үшін бастапқы шарттар

,     , …,                        (4.4)

түрінде жазылады.

(4.3) теңдеуінің (4.4) бастапқы шарттарына қанағаттандыратын шешімін табу есебін Коши есебін шешу дейміз. 

Реті төмендетілетін дифференциалдық теңдеулер 

 немесе

                                       (4.5)

дербес жағдайларын қарастырамыз.

1.  теңдеуі. Бұл теңдеуде  жоқ, оның шешімін бірте-бірте интегралдау көмегімен табамыз:

, ,     , …, .

2.  теңдеуі. Бұл теңдеуге  және оның -шы ретке дейінгі туындылары кірмеген. Алмастыру жасаймыз: , , …, ,  теңдеуін аламыз. Берілген теңдеудің ретті -ға төмендеді.

3.  теңдеуі. Бұл теңдеуде  айнымалысы айқын түрде жоқ. Алмастыру орындаймыз:. Енді -ті тәуелсіз айнымалы деп есептейміз, онда ,

,

т.с.с. Нәтижесінде -ші ретті теңдеуді аламыз. 

Жоғары ретті сызықтық дифференциалдық теңдеулер 

-ші ретті сызықтық дифференциалдық теңдеу деп

түріндегі теңдеуді айтамыз, мұндағы – ізделінді функция, – оның туындылары,  – аргумент, ,  – алдын ала берілген үзіліссіз функциялар.

Егер  болса, сызықтық дифференциалдық теңдеу біртекті емес, ал  болса, біртекті деп аталады.

Біз ІІ-ші ретті сызықтық дифференциалдық теңдеулерді қарастырамыз. Нәтижелері -ші ретті сызықтық дифференциалдық теңдеулерге үлестіріледі.

                                  (4.6)

түріндегі теңдеу – ІІ-ші ретті сызықтық біртекті емес дифференциалдық тең-деу болады. Ал

                                  (4.7)

(4.6)-ға сәйкес ІІ-ші ретті сызықтық біртекті дифференциалдық теңдеу.

 

ІІ-ші ретті сызықтық біртекті дифференциалдық теңдеулер.

Біртекті сызықтық дифференциалдық теңдеудің шешімінің негізгі қасиеті 

4.1 теорема Егер  мен  функциялары (4.7)-нің шешімдері бол-са, онда

                                             (4.8)

функциясы  және  тұрақтыларының кез келген мәндерінде (4.7) теңдеуі-нің шешімі болады.

Дәлелдеуі.  мен  функциялары (4.7)-нің шешімдері болғандықтан, ,  теңдіктері орындалады. (4.8) функциясын (4.7)-ге орнына қоямыз. Ол үшін  пен -ді табамыз:  ,   . Теорема дәлелденді.

Сонымен, (4.8) функциясы (4.7)-ші теңдеудің шешімі болды. Осы функция (4.7)-нің жалпы шешімі болады ма? Бұл сұраққа жауап беру үшін функциялар жүйесінің сызықтық тәуелді немесе сызықтық тәуелсіз болу ұғымын енгіземіз.

4.4 анықтама Барлығы бірдей нөлге тең емес, яғни ,  сандары табылып, -ның кез келген  үшін

                           (4.9)

теңдігі орындалса  функциялары  интервалында сызықтық тәуелді болады.

 үшін (4.9) теңдігі , , түріне келеді. Осы-дан  .

Егер (4.9) шарты орындалмаса, онда функциялар жүйесі сызықтық тәуел-сіз болады.

4.5 анықтама Вронский анықтауышы (вронскиан) деп

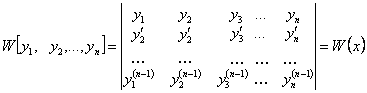         (4.10)

функциясы аталады.

4.2 теорема Егер  мен  функциялары -да сызықтық тәуелді болса, онда олардың вронскианы нөлге тең болады.

Дәлелдеуі.  мен  сызықтық тәуелді болған соң,  болады, сондықтан ,  болады да, анықтауыштардың қаси-еттері бойынша . Теорема дәлелденді.

4.3 теорема Егер (4.7) теңдеуінің шешімдері  мен  -да сызықтық тәуелсіз болса, онда олардың вронскианы -да нөлге тең болмайды.

Дәлелдеуі.  болатындай  нүктесі бар болсын деп ұйға-райық, яғни 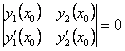 болсын.  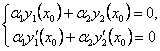жүйесін құрамыз, мұндағы  мен  – белгісіз сандар. Теңдеулер жүйесі біртекті болғандықтан, оның анықтауышы демек, жүйенің  мен -ге қарағанда нөлдік емес шешімі бар болады.  функциясын қарастырамыз, мұндағы  мен  – құрылған жүйенің нөлге тең емес шешімі, сонымен бірге  функциясы  және  бастапқы шарттарына қанағаттандырады. Бірақ осы шарттарға  функциясы да қанағаттандырады және де осы функция (4.7)-ге қанағаттандырады. Дифференциалдық теңдеудің шешімінің бар болуы және жалғыздығы туралы теорема бойынша бұл шешімдер беттеседі, яғни  аралығында , яғни  мен  сызықтық тәуелді болды. Қайшылыққа келдік. Сонымен, біздің ұйғаруымыз дұрыс емес. Егер  пен  – (4.7)-нің -ғы шешімі болса, онда

1) егер  мен  сызықтық тәуелсіз болса, онда , ;

2) егер  мен  сызықтық тәуелді болса, онда , .

№ 5 дәріс Сызықтық біртекті дифференциалдық теңдеулер.

      Сызықтық біртекті емес дифференциалдық теңдеудің  шешімі. Тұрақты коэффициентті сызықтық біртекті  дифференциалдық теңдеулер 

Мазмұны: Сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі. Еркін тұрақтыларды вариациялау әдісі. Тұрақты коэффициентті сызықтық біртекті дифференциалдық теңдеудің шешімі.

Дәрістің мақсаты: Сызықтық біртекті дифференциалдық теңдеудің жалпы шешімін, Остроградский-Лиувилль формуласы көмегімен дербес шешімді, еркін тұрақтыларды вариациялау әдісі көмегімен сызықтық біртекті емес дифференциалдық теңдеулердің шешімін, сипаттауыш теңдеу көмегімен сызықтық біртекті дифференциалдық теңдеулердің шешімін табуды үйрету. 

Қандай шарттар орындалғанда  функциясы сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі болатынын анықтап алайық.

5.1 теорема Егер  пен  –  аралығында

                                        (5.1)

теңдеуінің сызықтық тәуелсіз шешімдері болса, онда

                                         (5.2)

(5.1)-дің жалпы шешімі болады, мұндағы  мен  – еркін тұрақтылар.

Дәлелдеуі. 4.1-ші теорема бойынша  функциясы (5.1)-дің шешімі болады. Осы функция жалпы шешім болатынын дәлелдеу үшін оның құрамынан кез келген бастапқы шарттарға қанағаттандыратын дербес шешімді ажыратып алу керек. Айталық,  және ,  – кейбір бастапқы шарттар болсын. 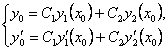 жүйесін құрамыз, мұндағы  мен  – белгісіз сандар.  – осы жүйенің анықтауышы.  мен  сызықтық тәуелсіз болғандықтан,  болады, сондықтан бұл жүйенің ,  жалғыз шешімі табылады, онда , яғни (5.2)-ден дербес шешімді ажыратып алдық. Сонымен, (5.2) функциясы (5.1) теңдеуінің жалпы шешімі болады.

Қорытынды. II-ші ретті сызықтық біртекті дифференциалдық теңдеудің жалпы шешімін табу үшін (5.1) теңдеуінің екі сызықтық тәуелсіз дербес шешімін тауып алып, (5.2) түріндегі функцияны жазып алған жеткілікті.

Остроградский-Лиувилль формуласы

(5.1)-дің тек қана бір дербес шешімі белгілі болса, осы теңдеудің жалпы шешімін қалай табуға болады?  – (5.1) теңдеуінің дербес шешімі болсын.  деп ұйғарып,  жаңа функциясын енгізейік.  пен -ті есептеп алайық: , . Енді (5.1)-де алмастырулар орындай-мыз:

 .

Келесі кезекте алынған дифференциалдық теңдеудің  алмасты-руы көмегімен ретін төмендету керек. Онда  болады да, сызықтық біртекті дифференциалдық теңдеуді аламыз

.

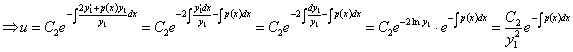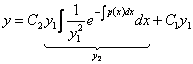Осыдан , сонымен, (5.1) теңдеуінің жалпы шешімі  функциясын анықтап алдық, мұндағы

.                                          (5.3)

(5.3) –Остроградский-Лиувилль формуласы. 

II-ші ретті сызықтық біртекті емес дифференциалдық теңдеулер  

II-ші ретті сызықтық біртекті емес дифференциалдық теңдеулерді қарастырамыз

  ,                                     (5.4)

.                                           (5.1)

5.2 теорема (5.4) сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі осы теңдеудің кез келген дербес шешімі мен (5.4)-ке сәйкес (5.1) біртекті теңдеудің жалпы шешімінің қосындысы болады

                                                 (5.5)

 – (5.4)-тің шешімі, – (5.1)-дің шешімі, – (5.4)-тің шешімі кейбір дербес шешімі.

Дәлелдеуі.  функциясын алайық. Осы функция (5.4)-тің шешімі болатынын көрсетейік. Ол үшін туындыларын есептейміз , . Туындыларды (5.4)-ке орнына қойып

,

яғни тепе-теңдікке келдік: .

 функциясы (5.4)-тің жалпы шешімі болатынын көрсетейік. (5.4)-тің кез келген  шешімін алайық, онда  біртекті теңдеудің жалпы шешімі болады, себебі төмендегі теңдік орындалады

.

 функциясы сызықтық біртекті теңдеудің шешімі болғандықтан, оны  түрінде жазуға болады, яғни  , демек, (5.5)-тен кейбір дербес шешімді ажыратып алдық. Олай болса, (5.5) – сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі. Теорема дәлелденді.

Еркін тұрақтыларды вариациялау көмегімен  табу жолын көрсетейік.  – (5.1) сызықтық біртекті теңдеудің жалпы шешімі болсын. Дербес шешімін табамыз. Жалпы шешімі

                                          (5.6)

түрінде жазылсын.

 туындысын есептейміз: .  және  функцияларын

                                                (5.7)

теңдігі орындалатындай етіп таңдаймыз. Онда . -ті есептейміз:, оны (7.1)-ге қойсақ, мынаны аламыз:

, яғни

.                                             (5.8)

Сонымен, егер де  мен  функциялары (5.7) мен (5.8)-ге, дәлірек айтқанда

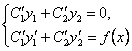                                           (5.9)

жүйесіне қанағаттандырса, онда (5.6) берілген теңдеудің шешімі болады

 мен  сызықтық тәуелсіз функциялар болған соң, жүйенің анықтауы-шы 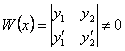 болады, сондықтан (5.9)-дың жалғыз ,  шешімі табылады. Осыдан , екенін таба-мыз. Табылған  мен  функцияларын (5.6)-ға қойсақ, (5.4) сызықтық біртекті емес теңдеудің жалпы шешімін анықтаймыз. 

Тұрақты коэффициентті II-ші ретті сызықтық біртекті дифференциалдық теңдеулер  

II-ші ретті сызықтық біртекті дифференциалдық теңдеулерді қарастыра-мыз

,                                             (5.10)

мұндағы  мен  – тұрақты шамалар.

                                              (5.11)

теңдеуі (5.10)-ға сәйкес келетін сипаттауыш теңдеу болады. 

5.3 теорема 1) Егер (5.11) теңдеуінің нақты  түбірі бар болса, онда  функциясы (5.10) теңдеуіне қанағаттандырады. 2) Егер (5.11)-дің комплекс  түбірлері бар болса, онда  және  функциялары (5.10)-ға қанағаттандырады.

Дәлелдеуі. 1)  – (5.11) теңдеуінің түбірі болсын.  функциясын жазып алып, оның туындыларын есептеп, (5.10)-ға орындарына қоямыз. Онда , , , , яғни  функциясы (5.10) теңдеуіне қанағаттандырады.

2) Дәлелдеуі теореманың бірінші бөлімінің дәлелдеуіне ұқсас.

5.4 теорема Егер (5.11) сипаттауыш теңдеудің түбірлері: а) нақты () және әртүрлі () болса, онда (5.10)-ның жалпы шешімі  болады; б) нақты () және өзара тең () болса, онда (5.10)-ның жалпы шешімі  функциясы болады; в) комплексті түйіндес (, ) болса, онда (5.10)-ның жалпы шешімі .

Дәлелдеуі. а)  болсын, онда ,  – (5.10)-ның дербес шешімдері болады. Оларды сызықтық тәуелділікке зерттейміз:  себебі , яғни  мен  сызықтық тәуелсіз, сондықтан .

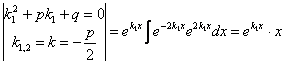б)  болсын, онда  – (5.10) теңдеуінің кейбір дербес шешімі болады. Остроградский-Лиувилль формуласы бойынша -ні есептейміз: , демек, .

в) ,  болсын, онда 5.3 теормасы бойынша ,  – дербес шешімдері болады. ,  функцияларын сызықтық тәуелділікке зерттейміз: , осы қатынастан  мен  сызықтық тәуелсіз екені көрінеді, онда

.

 теңдеуінің шешімін табу алгоритмі

1. (5.4)-ке сәйкес біртекті дифференциалдық теңдеуді жазамыз: ;

2. оның сипаттауыш  теңдеуін шешеміз;

3.  жалпы шешімін жазып аламыз;

4. еркін тұрақтыларды вариациялау әдісі көмегімен -ді табамыз, ол үшін (5.9) жүйесінен  функцияларын анықтап аламыз;

5.  теңдеудің шешімін жазамыз.

№ 6 дәріс Тұрақты коэффициентті сызықтық біртекті емес дифференциалдық теңдеудің дербес шешімін теру әдісі.       Анықталмаған коэффициенттер әдісі.  Жай дифференциалдық теңдеулер жүйесі 

Мазмұны: Тұрақты коэффициентті сызықтық біртекті емес дифференциалдық теңдеудің шешімі. Жай дифференциалдық теңдеулер жүйесі. Тұрақты коэффициентті сызықтық біртекті дифференциалдық теңдеулердің нормалды жүйесі.

Дәрістің мақсаты: Тұрақты коэффициентті сызықтық біртекті емес дифференциалдық теңдеуінің дербес шешімін табуға анықталмаған коэффициенттер әдісін пайдалануды үйрету. Жай дифференциалдық теңдеулер жүйесін бірте-бірте жою әдісі және сипаттауыш теңдеу көмегімен шешу. 

IІ-ші ретті тұрақты коэффициентті сызықтық біртекті емес дифференциалдық теңдеуді қарастырамыз

.                                         (6.1)

 екенін көрсеттік. Егер (6.1) теңдеуінде  функциясы

                      (6.2)

түрінде өрнектелетін болса, мұндағы ,  – көпмүшелер, онда

                        (6.3)

түрінде алуға болады, мұндағы ,  пен  – -дәрежелі көпмүшелер,  – сызықтық біртекті теңдеуге сәйкес сипаттауыш теңдеудің  түбірінің еселік реті (яғни  саны сипаттауыш теңдеудің -еселі түбірі болады).

Мысал 6.1 - .

,            ,            .

,       ,     .

, , ,

; , , .

, , ,

, .

.

 

,  

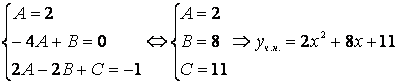
Мысал 6.2 - .

, , , .

, , .

, , , , .

, , , .

, .

.

 

Жай дифференциалдық теңдеулер жүйесі. Дифференциалдық теңдеулердің нормалды жүйесі 

6.1 анықтама Дифференциалдық теңдеулердің -ші ретті нормалды жүйесі деп

                                         (6.4)

І-ші ретті  дифференциалдық теңдеудің жиынтығын айтамыз, мұндағы  – тәуелсіз айнымалы,  – белгісіз функциялар, ,,  – олардың туындылары.

Түсініктеме. Нормалды жүйеде:

а) барлық теңдеулері , , туындыларына қарағанда шешілген;

б) белгісіз функциялардың туындылары тек І-ші ретті болады.

6.2 анықтама (6.4) жүйесінің жалпы шешімі деп  еркін тұрақты , , ,  шамаларынан тәуелді және  бойынша үзіліссіз туындылары бар

, , …,        (6.5)

 функциялардың жиынтығы аталады. Сонымен бірге төмендегі шарттар міндетті түрде орындалуы тиіс:

а) (6.5) теңдеулері , , ,  шамаларына қарағанда барлық () үшін, мұндағы  – Коши есебінің шешімінің жалғыз болу облысы, шешіледі, яғни

                                (6.6)

ә) (6.6)-дан барлық , , ,  мәндерінде шығатын (6.5) функциялар жиынтығы (6.4) жүйесінің шешімі болады.

Коши есебі деп (6.4) теңдеулер жүйесінің

                        (6.7)

бастапқы шарттарына қанағаттандыратын шешімін табу есебін айтамыз.

Бірте-бірте жою әдісі көмегімен -ші ретті нормалды жүйенің шешімін табу есебі -ші ретті бір дифференциалдық теңдеудің шешімін табу есебіне келтіріледі. Бұл әдістің мағынасы ізделінді функцияларды (6.4) жүйесінен бірте-бірте жоюда. Жүйенің бірінші теңдеуін  айнымалысы бойынша дифференциалдаймыз: . Жүйенің қалған теңдеулерін ескере отырып, алынған өрнекті мына түрде жазамыз

 немесе ,

 немесе , …,

, сонымен

                                (6.8)

жүйесін аламыз. Алғашқы  теңдеуден  шамаларын , , , …,  арқылы өрнектеп алуға болады, яғни .

 

Тұрақты коэффициентті сызықтық біртекті дифференциалдық теңдеулердің нормалды жүйесі  

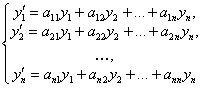                            (6.9)

түріндегі жүйе тұрақты коэффициентті сызықтық біртекті дифференциалдық теңдеулердің нормалды жүйесі деп аталады.

Белгілеулер енгіземіз: , , .

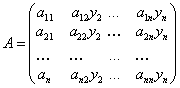Онда (6.9)-ды

                                       (6.10)

түрінде жазуға болады.

6.3 анықтама (6.10) жүйесінің , , …,  вектор-функциялар жиынтығы сызықтық тәуелді деп аталады, егер  теңдігі орындалса, мұндағы . Керсінше жағдайда, функциялар жүйесі сызықтық тәуелсіз деп аталады.

6.4 анықтама (6.10) жүйесінің  сызықтық тәуелсіз шешімдерінің жиынтығы шешімдердің фундаменталды жүйесі деп аталады.

Теорема (сызықтық біртекті дифференциалдық теңдеулердін нормалды жүйесінің шешімінің құрамы туралы). Егер , , …,  вектор-функциялар жиынтығы (6.10) жүйесі үшін шешімдердің фундаменталды жүйесі болса, онда теңдеулер жүйесінің жалпы шешімі   функциясы болады; мұндағы ,  – еркін тұрақтылар.

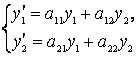                                        (6.11)

ІІ-ші ретті тұрақты коэффициентті сызықтық біртекті дифференциалдық тең-деулер жүйесін шешу жолын қарастырамыз.

Шешімді ,  түрінде іздейміз

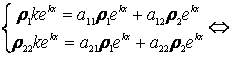
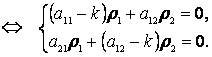                              (6.12)

(6.12)-нің нөлге тең емес шешімі бар болу үшін

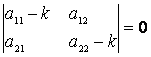                                   (6.13)

шарты орындалуы қажет.

(6.13) – (6.11)-ші теңдеудің сипаттауыш теңдеуі.

(6.13)-тің шешімдері – ,  сандары сипаттауыш теңдеудің меншікті мәндері деп, ал  меншікті векторы деп аталады. (6.11) жүйесінің шешімі

функциясы болады.

№ 7 дәріс Сандық қатарлар. Негізгі ұғымдар. Оң қатарлар  

Мазмұны: Сандық қатарлар, дербес қосындылар, сандық қатардың қалдығы, сандық қатардың жинақты болуының қажетті шарты, сандық қатардың жинақты болуының жеткілікті шарттары: салыстыру белгілері, шектік салыстыру белгісі, Д’Аламбер белгісі, Кошидың радикалдық белгісі, Кошидың интегралдық белгісі.

Дәрістің мақсаты: Студенттерді сандық қатар ұғымымен таныстыру, қатарды жинақтылыққа зерттеу мысалдарын келтіру. 

                               (7.1)

түріндегі өрнекті сандық қатар дейміз, мұндағы .  тізбегінің мүшелері қатардың мүшелері деп, ал  – сандық қатардың жалпы мүшесі деп аталады.

қосындылары дербес қосындылар деп, ал  – (7.1) сандық қатарының -ші дербес қосындысы деп аталады. Егер  бар болып әрі -ке тең болса, яғни , онда (7.1) қатары жинақты қатар болады, ал  – оның қосындысы.  табылмаса (дербес жағдайда шексіздік болса), онда (7.1) жинақсыз қатар деп аталады.

қосындысы (7.1)-дің қалдығы деп аталады.

Егер (7.1) жинақты қатар болса, онда

.

Мысал 7.1 -  қатары берілсін. Оның жинақтылығын анықтап, қосындысын табу керек.

Шешуі. Қатардың -ші дербес қосындысын жазып алып, оны ықшамдаймыз:

 болғандықтан, берілген қатар жинақты, ал қосындысы  болады.

 

Мысал 7.2 – Қатарды жинақтылыққа зерттеу

                               (7.2)

және мүмкін болған жағдайда қосындысын табу керек.

Шешуі. Дербес қосындысын жазып аламыз

.

Егер  болса, онда , яғни , демек, (7.2) жинақсыз қатар болады.

Енді  болсын, онда .  болсын деп ұйғарайық, онда , яғни . Ал егер  болса, онда  және  ақырлы шегі (конечный предел) табылмайды, демек, дербес қосындылар тізбегінің де шегі табылмайды. Егер  болса,  шегі тағы да табылмайды.

Сонымен, мүшелері (бірінші мұшесі , еселігі ) шексіз геометриялық прогрессия құрайтын  қатары  болғанда жинақты және оның қосындысы  болады, ал  болса жинақсыз болады.

(7.2) – геометриялық қатар деп аталады. 

7.1 теорема (қатардың жинақты болуының қажетті шарты). Егер (7.1) сандық қатары жинақты болса, онда .

Керісінше тұжырым дұрыс болмайды.  

Мысал 7.3 – Гармониялық қатар

 мүшелері 0-ге ұмтылса да, жинақсыз болатынын дәлелдеу керек.

Дәлелдеуі.  қатары жинақты, ал қосындысы  болады деп ұйғарайық.  айрмасын қарастырамыз. Біздің ұйғару бойынша  болады. Жоғарыдағы өрнекте әрбір қосылғышын  шамасымен ауыстыра отырып,

теңсіздігін аламыз.

Бұл теңсіздіктен  екені шығады, яғни біздің ұйғаруымыз дұрыс емес, демек, гармониялық қатар жинақсыз болады.

7.2 теорема (қатардың жинақсыз болуының жеткілікті шарты). Егер  болса, онда (7.1) жинақсыз қатар болады.

Мысал 7.4 - Қатарды жинақтылыққа зерттеу керек.

Шешуі. Берілген қатардың жалпы мүшесі  болады. Онда

,

яғни берілген қатар жинақсыз болады.

Қатардың кез келген ақырлы сан мүшесін қалдырып кеткеннен оның жинақтылығы немесе жинақсыздығы өзгермейді, ал егер оның қосындысы бар болса, онда ол өзгереді. 

Оң қатарлардың жинақты болуының кейбір жеткілікті шарттарын қарастырамыз.

7.3 теорема (салыстыру белгілері). Екі қатар берілсін

,                                             (7.3)

                                               (7.4)

және барлық  үшін  теңсіздіктері орындалсын, онда:

а) (7.4) қатары жинақты болса, (7.3) қатары да жинақты болады;

б) (7.3) қатары жинақсыз болса, (7.4) қатары да жинақсыз болады.

Салыстыру үшін көбіне  геометриялық қатарын және де гармониялық қатарды алады. 

7.4 теорема (салыстырудың шектік белгісі). Егер  ақырлы шегі бар болып, әрі  болса, онда (7.3) және (7.4) қатарлары екеуі де жинақты немесе екеуі де жинақсыз болады.

Мысал 7.5 -  қатары жинақты екенін біле отырып,  қатарын жинақтылыққа зерттеу керек.

Шешуі.  болғандықтан,  қатары да жинақты болады.

7.5 теорема (Д’Аламбер белгісі). (7.1) қатары үшін  болсын (кейбір  нөмірінен бастап) және  шегі бар болсын. Онда егер  болса, берілген қатар жинақталады, егер  болса, берілген қатар жинақсыз болады.  болғанда қосымша зерттеулер қажет етеді.

Мысал 7.6 - Қатарды жинақтылыққа зерттеу керек.

Шешуі. ,  болғандықтан, онда

.

Демек, берілген қатар жинақсыз болады.

7.6 теорема (Кошидың радикалдық белгісі). Егер кейбір  нөмірінен бастап  және  болса, онда  болғанда (7.1) жинақталады, ал  болғанда жинақсыз болады.  болғанда қосымша зерттеулер қажет етеді.

7.7 теорема (Кошидың интегралдық белгісі). (7.1) қатарының мүшелері монотонды кемімелі болсын, яғни

және  болғанда үзіліссіз  функциясы үшін  орындалсын. Онда (7.1) қатары мен 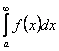 интегралы бір мезгілде жинақты немесе жинақсыз болады.

Мысал 7.7 - Қатарды жинақтылыққа зерттеу керек (Дирихле қатары) .

Шешуі.  меншіксіз интегралын жинақтылыққа зерттейміз,.

 болады. Соңғы теңдіктен  болғанда  меншіксіз интегралы жинақсыз, ал  болғанда жинақты болатыны көрінеді, әрі .  болғанда  жинақсыз интегралын аламыз. Сонымен, Дирихле қатары да осы интеграл секілді  болғанда жинақты, ал  болғанда жинақсыз болады.

Көптеген қатарлар жинақтылыққа сәйкес Дирихле қатарымен салыстыру арқылы зерттеледі.

№ 8 дәріс Айнымалы таңбалы және ауыспалы таңбалы қатарлар 

Мазмұны: Айнымалы таңбалы және ауыспалы таңбалы сандық қатарлар, Лейбниц белгісі, абсолютті жинақтылық, шартты жинақтылық.

Дәрістің мақсаты: Студенттерді айнымалы таңбалы және ауыспалы таңбалы қатарлар ұғымымен таныстыру, олардың негізгі қасиеттерін келтіру, қатарларды жинақтылыққа зерттеу мысалдарын келтіру, қатарлардың көбейтіндісін Коши бойынша табу. 

Мүшелерінің таңбасы әртүрлі болатын  сандық қатары берілсін. Мүшелерінің таңбалары кезектесіп отыратын сандық қатар

,           (8.1)

ауыспалы таңбалы сандық қатар деп аталады, бұл жерде – оң сандар. 

Лейбниц белгісі 

8.1 теорема (Лейбниц теоремасы). Егер

а)  – қатардың мүшелері кемімелі сандық тізбек құрайтын және

б)                                                                                                         (8.2)

болса, онда ауыспалы таңбалы  қатары жинақты болады.

Дәлелдеуі.  дербес қосын-дысын қарастырайық. Бұл қосындының әрбір қосылғышы а) шарты бойынша нөлден артық болған соң,  тізбегі өспелі болады. -де басқа жолмен топтастырулар орындайық  . Осыдан  екенін көреміз. Сонымен,  тізбегі өспелі және жоғарыдан шенелген тізбек болады, демек, оның ақырлы шегі бар: .

 дербес қосындысын қарастырамыз. Онда   болады ( теореманың б) шартынан шығады). Демек, -ші дербес қосындысының ақырлы шегі бар, сондықтан ауыспалы таңбалы қатар жинақты болады. Теорема дәлелденді.

Мысал 8.1 - Қатарды жинақтылыққа зерттеу керек

.

Шешуі. Лейбниц белгісін қолданамыз.

, , , ,

болғандықтан,  теңсіздіктері орындалады, яғни Лейбниц белгісінің а) шарты орындалады.

,

болады, яғни Лейбниц белгісінің б) шарты да орындалады. Сонымен, берілген қатар жинақталады.

Мысал 8.2 - Қатарды жинақтылыққа зерттеу керек

.

Шешуі. Лейбниц белгісінің а) шарты орындалады:

;

басқа жағынан, , 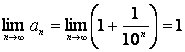.  болғандықтан, қатардың жинақтылығының қажетті шарты орындалмайды. Берілген қатар жинақсыз болады.

Мысал 8.3 - Қатарды жинақтылыққа зерттеу керек

.

Шешуі. Қатардың жинақтылығының қажетті шарты орындалмайды. Демек, берілген қатар жинақсыз болады.

Лейбниц белгісіне бағынатын жинақты ауыспалы таңбалы қатардың -ші дербес қосындысын алайық

.

 – қатардың -ші қалдығы болсын. -ді  түрінде жазуға болады.  болатыны жеңіл байқалады.

 шамасы  теңсіздігімен бағаланады.

Айнымалы таңбалы қатарлардың кейбір қасиеттеріне тоқталайық. 

Қатарлардың абсолютті және шартты жинақтылығы 

Айнымалы таңбалы қатар берілсін

.                    (8.3)

Мүшелерінің абсолют шамаларынан құрылған қатарды қарастырамыз

 .                           (8.4)

(8.4) – оң қатар.

8.2 теорема Егер абсолют шамалардан құрылған (8.4) қатары жинақты болса, онда айнымалы таңбалы (8.3) қатары да абсолютті жинақты болады.

Дәлелдеуі. Теорема шарты бойынша  жинақталады, сондықтан жинақты қатарлардың белгілі қасиеті бойынша  қатары да жинақталады. Салыстыру белгісі бойынша

(8.5)

теңсіздігі орындалады, онда  қатары жинақты болады. (8.3) қатарының мүшелері (8.5) және (8.4) жинақты қатарлардың мүшелерінің айырмасына тең, сондықтан (8.3) жинақты қатар болады. Теорема дәлелденді.

Мысал 8.4 - Қатарды жинақтылыққа зерттеу керек

.

Шешуі. Абсолют шамалардан қатар құрамыз:

.

Бұл қатар еселігі  болатын геометриялық қатар, сондықтан жинақты болады. Онымен бірге берілген қатар да жинақты болады. Берілген қатар абсолютті жинақты.

Жинақты  қатары шартты жинақты болады, егер қатардың өзі жинақты болып,  абсолют шамалардан құрылған қатар жинақсыз болса.

Мысал 8.5 - Қатарды жинақтылыққа зерттеу керек

.

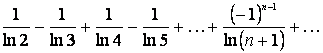Шешуі. Лейбниц белгісін қолданамыз.

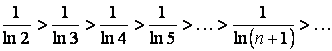
болғандықтан, а) шарты орындалады; б) шарты да орындалады, себебі

.

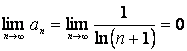Демек, берілген қатар жинақталады. Абсолют шамалардан қатар құрамыз:

.

Алынған қатардың мүшелері гармониялық қатардан шыққан

қатарының мүшелерінен артық болады, демек, бірінші салыстыру белгісі бойынша абсолют шамалардан құрылған қатар жинақсыз болады. Сонымен, берілген

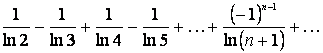
қатар шартты жинақты болады.

 

Егер  абсолютті жинақты болса, онда оның шексіз көп мүшелерінің орындарын алмастырғаннан кейін алынған қатар да абсолютті жинақты әрі оның қосындысы алғашқы қатардың қосындысына тең болады.

 

Егер  қатары шартты жинақты болса, оның шексіз көп мүшелерінің орындарын алмастырғаннан кейін оның қосындысы өзгеруі мүмкін. Дербес жағдайда мүшелерінің орындарын алмастырғаннан кейін шартты жинақты қатар жинақсыз қатарға айналуы мүмкін. 

Егер  және  қатарлары абсолютті жинақты, ал қосындылары сәйкесінше  және  болса, онда

 қатары да абсолютті жинақты болады. Бұл қатар қатарлардың Коши бойынша көбейтіндісі болады. Оның қосындысы -ке тең.

Мысал 8.6 – Абсолютті жинақты қатардың квадратын табу керек

.

Шешуі.

.

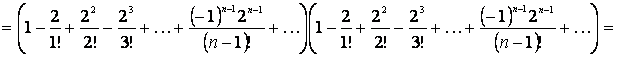
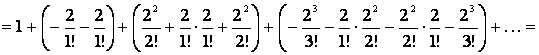
№ 9 дәріс Функциялық қатарлар, дәрежелік қатарлар.  Тейлор қатары. Кейбір функцияларды

      Маклорен қатарына жіктеу 

Мазмұны: функциялық қатардың жинақталу облысы, қатардың қосындысы, мажоранталанатын қатар, дәрежелік қатардың жинақталу облысы, дәрежелік қатардың жинақталу интервалы мен радиусы, Абель теоремасы, Тейлор және Маклорен формулалары мен қатарлары, функцияны дәрежелік қатарға жіктеу.

Дәрістің мақсаты: Студенттерді жуықтап есептеулерде жиі қолданылатын функциялық қатар, дәрежелік қатар ұғымдарымен таныстыру.

 

 () функциялары  облысында анықталған болсын. Онда

                            (9.1)

функциялық қатар деп аталады. Егер

.                         (9.2)

сандық қатары жинақталса, (9.1) қатары  нүктесінде жинақты деп аталады.

(9.1) қатары жинақты болатын  нүктелерінің жиыны функциялық қатардың жинақталу облысы деп аталады.

Жинақталу облысының әрбір  нүктесіне функциялық қатарға сандық қатардың қосындысы деп аталатын сан сәйкес келеді. Бұл сәйкестік (9.1) қатарының жинақталу облысындағы қосындысы  функциясын анықтайды.

Функциялық қатар кейбір  облысында мажоранталанатын қатар деп аталады, егер

                                               (9.3)

жинақты қатары табылып, әрбір  үшін

теңсіздіктері орындалатын болса.

(9.3) қатары (9.1)-ді мажоранталайтын (жоғарыдан шенейтін) қатар деп аталады.

Дәрежелік қатар деп

        (9.4)

түріндегі қатар аталады, мұндағы  – дәрежелік қатардың коэффициенттері деп аталатын тұрақты сандар,  – бекітілген сан. Егер  болса,

                                    (9.5)

түріндегі дәрежелік қатарды аламыз.

(9.5) үшін дұрыс болатын тұжырымдар мен теоремалар (9.4) қатары үшін де дұрыс болады.

 Дәрежелік қатардың жинақталу интервалы мен радиусы

 9.4 теорема (Абель теоремасы) 1. Егер (9.5) дәрежелік қатары кейбір  мәнінде жинақталса, онда  теңсіздігіне қанағаттандыратын барлық -тер үшін (9.5) абсолютті жинақты болады. 2. Егер (9.5) дәрежелік қатары  мәнінде жинақсыз болса, онда  теңсіздігіне қанағаттан-дыратын барлық -тер үшін (9.5)-ші қатар жинақсыз болады.

Барлық  теңсіздігіне қанағаттандыратын барлық -тер үшін (9.5) дәрежелік қатары жинақты, ал  теңсіздігіне қанағаттандыратын барлық -тер жинақсыз болсын. Бұндай теріс емес  саны дәрежелік қатардың жи-нақталу радиусы деп аталады.  аралығы (9.5)-ші қатардың жинақталу интервалы деп аталады.

Егер кейбір  нөмірінен бастап  шарты орындалса, онда (9.5) дәрежелік қатарының жинақталу радиусы

 немесе 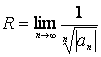                                  (9.6)

формулалары көмегімен есептеледі (бұл формулалардағы шектер бар немесе шексіз болады деп санаймыз). (9.6) формулалары сәйкесінше Д’Аламбер бел-гісімен немесе Кошидың радикалдық белгісімен қолданғанда пайда болады.

Егер (9.4) түріндегі қатар берілсе, оның да  жинақталу радиусы (9.6) формулалары көмегімен табылады, ал жинақталу интервалы центрі  болатын  интервалы болады.

Дәрежелік қатарды өзінің жинақталу интервалында мүшелеп интегралдауға және дифференциалдауға болады және де қатардың жинақталу радиусы өзгермейді.

 Тейлор және Маклорен формулалары мен қатарлары. Функцияны дәрежелік қатарға жіктеу

 Егер  функциясының  нүктесінің маңайында -ші ретке дейінгі туындылары бар болса, онда

(9.7)

мұндағы , болатындай   нүктесі табылады.

(9.7) –  функциясының  нүктесінің маңайындағы Тейлор формуласы, – Тейлор формуласының Лагранж формасындағы қалдық мүшесі.

көпмүшесі  функциясының Тейлор көпмүшесі деп аталады.

 болғанда (9.7) формуласының дербес жағдайына келеміз

                   (9.8)

мұндағы , .

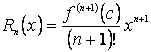(9.8) –  функциясының Маклорен формуласы.

Функцияның Тейлор қатарына жіктелуінің шартын келтіреміз. Егер  функциясы  нүктесінің маңайында шексіз көп рет дифференциалданатын болса және де осы нүктенің маңайында  немесе

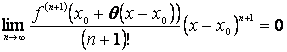                             (9.9)

шарты орындалса, онда

  (9.10)

Дербес жағдайда, егер  болса, онда

                (9.11)

болады. (9.10) – Тейлор қатары, ал (9.11) – Маклорен қатары деп аталады.

(9.9) шарты (9.10) немесе (9.11) сұлбасы бойынша құрылған қатардың кейбір  нүктесінің маңайында  функциясына жинақталуының қажеті және жеткілікті шарты болып табылады. Әрбір жеке алынған жағдайда қатардың берілген функцияға жинақталу облысын табу қажет.

Кейбір элементарлық функциялардың дәрежелік қатарға жіктелуін келтіреміз:

                                      (9.12)

                     (9.13)

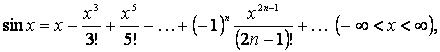                 (9.14)

                       (9.15)

 (9.16)

Жақша ішінде дәрежелік қатардың сәйкес функцияға жинақталу облысы белгіленген. (9.16) – биномиалдық қатар деп аталады, жинақталу интервалының шеткі нүктелерінде  шамасының мәніне байланысты жинақты немесе жинақсыз болады: егер  болса, онда (9.16)  нүктелерінде абсолютті жинақты болады; егер  болса, онда (9.16)  нүктесінде жинақсыз, ал  нүктесінде шартты жинақты болады; егер  болса, онда (9.16)  нүктелерінде жинақсыз болады.

Жалпы жағдайда дәрежелік қатарға жіктеу Тейлор немесе Маклорен қатарларын пайдалануға негізделген. Бірақ, практикада көптеген функциялар-дың дәрежелік қатарын (9.12) – (9.16) жіктеулерінің немесе геометриялық прогрессияның мүшелерінің қосындысын табу формуласының көмегімен алу-ға болады. Кейбір жағдайда қатарға жіктеуді белгілі қатарды мүшелеп диффе-ренциалдау немесе мүшелеп интегралдау көмегімен орындаған қолайлы бола-ды. Жинақталу интервалында қатарлар сәйкес функцияларға жинақталады.

 

Мысал 9.1 -  функциясын  дәрежелері бойынша қатарға жіктеп, жинақталу облысын табу керек.

Шешуі. Дәрежесін төмендету формуласы бойынша

болады. Енді (9.13)-ке -тің орнына -ті қоямыз, сонда

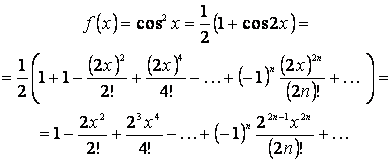
қатарын аламыз. Осы қатардың жинақталу радиусын табайық. 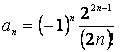 болғандықтан,  формуласы бойынша

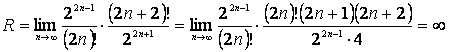
екенін аламыз. Сонымен, табылған қатар барлық  үшін жинақты болады.

№ 10 дәріс Фурье қатары 

Мазмұны: Функцияларды тригонометриялық Фурье қатарына жіктеу.

Дәрістің мақсаты: Серпіліс анализінде қолданылатын Фурье қатары ұғымын беру, функцияларды Фурье қатарына жіктеу мысалдарын келтіру.

                               (10.1)

түріндегі функциялық қатар  функциясының Фурье қатары деп аталады, мұндағы ,   коэффициенттері

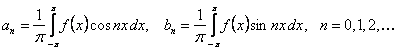                (10.2)

формулалары бойынша анықталады. Ескерте кететін жайт: әр уақытта да . (10.1) қатарының мүшелерін амплитудасы , жиілігі  және фазасы 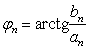 болатын,

гармоникалар түрінде жазуға болады.

-ны , , , ,  (ақырлы сан) интервалдарға бөлгенде, олардың әрқайсысында  монотонды болса,  функциясы  кесіндісінде үзінді-монотонды деп аталады.

10.1 теорема Егер  периодты (периоды ), үзінді-монотонды және  кесіндісінде шенелген болса, онда оны Фурье қатары кез келген  нүктесінде жинақты, ал қосындысы  болады.

Теоремадан  функциясының үзіліссіз болу нүктелерінде  теңдігі орындалатыны түсінікті. -тің бірінші текті үзіліс нүктелерінде Фурье қатарының қосындысы функцияның оң жақты және сол жақты шектерінің арифметикалық орташасына тең болады.

Егер  -периодты функция болса, оның Фурье қатары

                           (10.3)

түрінде жазылады, мұндағы

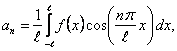
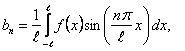
 . (10.4)

10.2 теорема Егер периоды  болатын периодты  функциясы  кесіндісінде үзінді-монотонды және шенелген болса, онда оның (10.3) түріндегі Фурье қатары кез келген  үшін

қосындысына жинақталады.

Егер периодты  функциясы жұп болса, онда ол Фурье қатарына тек косинустар бойынша жіктеледі, яғни , ал

.

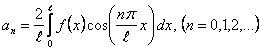Егер де периодты  – тақ функция болса, онда ол Фурье қатарына тек синустар бойынша жіктеледі, яғни , ал

.

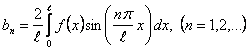Әрбір -периодты  функциясы және кез келген  саны үшін

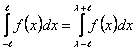
теңдігі орындалған соң, Фурье коэффициенттерін

,   ,

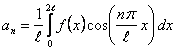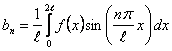мұндағы , формулалары бойынша есептеуге болады.

 функциясы  кесіндісінде үзінді-монотонды және шенелген болсын. Бұл функцияны Фурье қатарына жіктеу үшін оны  ин-тервалына, осы интервалда үзінді-монотонды және шенелген болатындай етіп, жалғастырамыз. Табылған функцияны -да берілген функцияға жинақтала-тын Фурье қатарына жіктейміз. Егер берілген функцияны  интервалына жұп түрінде жалғастырсақ, онда оның тек косинустар бойынша жіктелуін аламыз, ал егер тақ түрінде жалғастырсақ, онда -тың тек синустар бойынша жіктелуін аламыз.

Мысалы,  аралығында анықталған және -де

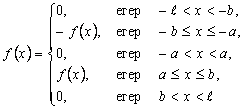
теңдіктеріне сәйкес жалғастырылған  функциясы тек синустар бойынша жіктеледі. Мұндай функцияның Фурье қатарының  қосындысы  ішінде -ке тең және 10.2 теоремасы бойынша ,  болады.

Фурье қатары -тің үзіліссіз болу нүктелерінде функцияның сәйкес мәндеріне жинақталған соң, Фурье қатарларын сандық қатарлардың қосындысын табу үшін пайдаланады. Мысалы, егер  функциясының -гі косинустар бойынша жіктелуің алсақ, төмендегі теңдікті аламыз

.

№ 11 дәріс Комплекс айнымалылы функция ұғымы

Мазмұны: Комплекс айнымалыдан тәуелді функция анықтамасы. Негізгі элементарлық функциялар. Дифференциалдау, Коши-Риман шарттары.

Дәрістің мақсаты: Негізгі элементарлық функциялардың анықтамасын білу, нақты және жорамал бөліктерін ажырата білу. Дифференциалдау ережесін қолдануды, Коши-Риман шарттарын тексеруді ұйрету.

11.1 анықтама  комплекс айнымалысының мәндерін суреттейтін кейбір  жиынында  функциясы анықталған дейміз, егер осы жиынның әрбір  нүктесіне бір немесе бірнеше  мәндері сәйкес қойылған болса.

Егер  функциясы  айнымалысынан тәуелді болса, онда  мен  айнымалыларының әрқайсысы  пен  нақты айнымалыларынан тәуелді функциялар, яғни  және  болады. Егер де  болса, мұндағы  және  – нақты  және  аргументті нақты функциялар, онда -ны  комплекс айнымалыдан тәуелді функция деп қарастыруға болады.

11.2 анықтама Кез келген  саны үшін  саны табылып, барлық  теңсіздігіне қанағаттандыратын  нүктелері үшін  теңсіздігі орындалса  саны бірмәнді  функциясының  шегі болады. Оны  түрінде жазады.

11.3 анықтама  функциясы  нүктесінде үзіліссіз болады, егер

 болса.

Комплекс айнымалыдан тәуелді негізгі элементарлық функциялар

1. Рационалдық функция .

2. Бөлшек-рационалдық функция .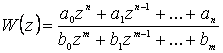

3. Көрсеткіштік функция комплекс жазықтығының барлық нүктелерінде абсолютті жинақты дәрежелік қатарлардың қосындысы ретінде анықталады

.

Көрсеткіштік функция қасиеттері: а) ; ә) , яғни  – -периодты функция.

4.  және  функцияларын Маклорен қатары түрінде анықтауға болады

,

.

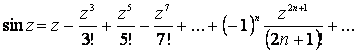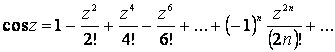Бұл қатарлар кез келген  үшін абсолютті жинақты. , ,  функциялары өзара Эйлер формуласымен байланыстырылады: , , , .

5. , .

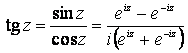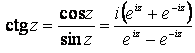6. Гиперболалық функциялар

,

,

,

.

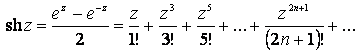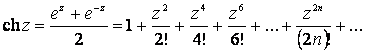Келесі қатынастар орындалады: , , , , , , , .

7.

Қасиеттері: , , , .

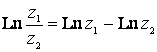8. Кері тригонометриялық функциялар

,

,

,

.

9. , мұндағы .

10.  мұндағы .

Комплекс айнымалыдан тәуелді функцияның туындысы

 функциясы комплекс айнымалы -тің кейбір  облысында анықталған болсын.  аргументіне  нүктесі  облысына тиісті болатындай етіп  өсімшесін береміз. Онда  функциясы  өсімшесін қабылдайды.

11.4 анықтама  функциясы  облысының  нүктесінде дифференциалданады дейміз, егер  еркін түрде ұмтылғанда  қатынасының шегі бар болса. Бұл шек -тің туындысы деп аталады да,

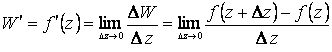                     (11.1)

белгіленеді.

11.5 анықтама Кейбір облыстың әрбір нүктесінде үзіліссіз туындысы бар  функциясы осы облыста аналитикалық болады.

Туынды қасиеттері:

1. ;

2. ;

3. 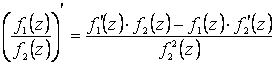, мұндағы .

4. Егер  – күрделі функция, мұндағы  – комплекс айнымалыдан тәуелді функция, және ,  туындылары бар болса, онда

формуласы орынды болады.

Туындылар кестесі нақты айнымалыдан тәуелді функциялардың туындылар кестесіне ұқсайды.

Коши-Риман шарттары

 болсын. -тің туындысы бар болсын, яғни

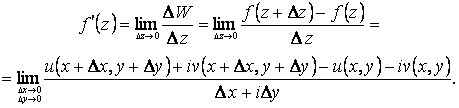
Анықтама бойынша бұл шек  пен -тің 0-ге қандай жолмен ұмтылуынан тәуелсіз болғандықтан, дербес жағдайларды қарастырамыз:

а)  болсын, онда

;

б)  болсын, онда

.

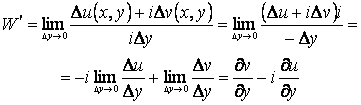Туындылар тең болған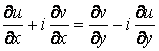дықтан,  теңдігі орындалады. Сондықтан,

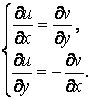                                               (11.2)

(11.2) –Коши-Риман шарттары.

Коши-Риман шарттары орындалғанда  функциясының туынды-сы  формуласы бойынша табылады.

11.6 анықтама  функциясы  облысында гармониялық болады, егер оның үшінші ретке дейінгі үзіліссіз дербес туындылары бар және -да  Лаплас теңдеуіне қанағаттандыратын болса

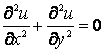.                                           (11.3)

(11.3) – Лаплас теңдеуі.

№ 12 дәріс Лаплас түрлендіруінің анықтамасы

Мазмұны: Лаплас түрлендіруінің анықтамасы, қасиеттері. Екі функцияның үйірткісі (свертка) және оның бейнесі. Бейнелер кестесі.

Дәрістің мақсаты: Лаплас түрлендіруінің анықтамасын білу. Функцияның бейнесін табуда түрлендірудің қасиеттерін пайдалануды үйрету. Бейнелердің негізгі кестесін білу.

12.1 анықтама Нақты айнымалыдан тәуелді  функциясының Лаплас түрлендіруі деп комплекс айнымалыдан тәуелді,

                                               (12.1)

формуласымен анықталатын  функциясы аталады.

(12.1)-дің оң жағындағы  комплекс параметрінен тәуелді меншіксіз интеграл Лаплас интегралы деп аталады.

Алдымен қандай  функцияларын қарастыратынымызды және (12.1) меншіксіз интегралы жинақты болу үшін -ға қандай шарттар қоятыны-мызды анықтап аламыз.

Төмендегі шарттар орындалсын деп ұйғарамыз:

1. егер  болса, онда;

2.  болғанда  үзінді-үзіліссіз болады, яғни  немесе үзіліссіз, немесе әрбір ақырлы кесіндіде санаулы бірінші текті үзіліс нүктелері бар функция;

3.  болғанда  функциясының модулі өсуі мүмкін, бірақ өсу жылдамдығы кейбір көрсеткіштік функциядан аспайды, яғни  және  тұрақты сандары табылып, кез келген  үшін

                                               (12.2)

теңсіздігі орындалады.

(12.2) теңсіздігі орындалатындай барлық  сандарының төменгі шекара-сы  функциясының өсу көрсеткіші деп аталады.

1, 2, 3 шарттарына қанағаттандыратын  функциясы түпнұсқа (ориги-нал) деп аталады.

(12.1) формуласы бойынша анықталатын  функциясы -ның бейнесі деп аталады да,  немесе  деп белгіленеді.

Хевисайдтың бірлік функциясын қарастырамыз. Ол мына түрде алынады

1                                    0                              t             1сурет

 функциясы түпнұсқа болатынын көрсетеміз.

Біріншіден,  болғанда ; екіншіден,  болғанда  үзіліс-сіз, өйткені ол тұрақты функция; үшіншіден, егер  болса , яғни  шенелген. Сонымен,  түпнұсқа болады.

 үшін бейнесін табамыз:

 егер  болса.

Сонымен, егер  болса  үшін  бейнесі табылады да, ол 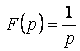 болады. Жазуды қысқарту үшін  деп жазамыз, онда

.                                                       (12.3)

Жалпы, егер кейбір  функциясы туралы айтатын болсақ, мысалы , ,  және т.с.с., онда   және т.с.с. функциялары туралы айтқанымыз деп келісеміз.

 функциясы көмегімен , , , т.с.с. түрінде жазуға болады, бірақ қысқаша , , , т.с.с. деп жазсақ жеткілікті.

12.1 теорема (бейне бар болу теоремасы). Кез келген  түпнұсқасы үшін  жартыжазықтығында анықталған  бейнесі табылады, мұндағы  – түпнұсқаның өсу көрсеткіші.  жартыжазықтығының әрбір нүктесінде  аналитикалық функция болады.

12.2 теорема (бейненің жалғыз болу теоремасы). Егер  функциясы  және  түпнұсқаларының бейнесі болса, онда бұл түпнұс-қалар өздерінің үзіліссіз болу нүктелерінде беттеседі.

  Лаплас түрлендіруінің қасиеттері

 Сызықтық теоремасы. Кез келген нақты немесе комплекс  және  тұрақтылары үшін  қатынасы орындалады, мұндағы , , яғни түпнұсқалардың сызықтық комбинациясына бейнелердің тап сондай сызықтық комбинациясы сәйкес келеді.

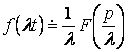Ұқсастық теоремасы. Кез келген тұрақты  үшін  қатынасы орындалады, мұндағы .

Ығысу теоремасы. Кез келген нақты немесе комплекс  саны үшін  қатынасы дұрыс болады, мұндағы .

Кешігу теоремасы. Кез келген тұрақты  үшін  болады, мұндағы .

Түпнұсқаны дифференциалдау теоремасы.  функциясы мен оның туындылары , , түпнұсқалар, ал  болсын, онда

                    ,

,

,

…,

.

Егер  болса, онда , , қатынастары дұрыс болады.

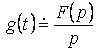Түпнұсқаны интегралдау теоремасы. Егер  және  , онда , яғни 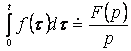, болады.

Бейнені дифференциалдау теоремасы. Егер , онда , , …, .

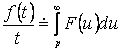Бейнені интегралдау теоремасы. Егер  және  функциясы түпнұсқа болса, онда  қатынасы орындалады, мұндағы 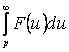 жинақталады.

 12.2 анықтама  пен  екі функцияның үйірткісі деп , , интегралы аталады.

 Функциялардың үйірткісінің қасиеттері

 1. Функциялардың үйірткісі коммутативті, яғни .

2. Егер  мен  түпнұсқалар болса, онда олардың  үйірткісі де түпнұсқа болады.

Бейнелерді көбейту теоремасы (Борель теоремасы). Егер  және  болса, онда  болады.

Дюамель формуласы

 бейнелерді көбейту теоремасының арнайы жағдайын қарастырамыз, мұндағы , , . Онда

.

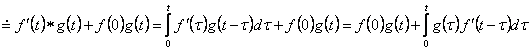Сонымен,

,

немесе

.                       (12.5)

Осыған ұқсас жолмен төмендегі формулаларды аламыз

,

.

(12.5) Дюамель интегралы немесе Дюамель формуласы деп аталады.

 Бейнелер кестесі

 

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.

№ 13 дәріс Түпнұсқаны бейнесі бойынша табу.  Амалдық есептеудің қолданылуы 

Мазмұны: Түпнұсқаны бейнесі бойынша табу. Амалдық есептеудің қолданылуы.

Дәрістің мақсаты: Белгілі бейнесі бойынша түпнұсқасын табуды, тұрақты коэффициентті сызықтық дифференциалдық теңдеу үшін Коши есебін шешуді, сызықтық дифференциалдық теңдеулер жүйесі үшін Коши есебін амалдық әдіспен шешуді үйрету. 

Егер 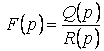 дұрыс рационалдық бөлшек болса, онда -ны элементарлық бөлшектердің қосындысына жіктейді де, олардың әрқайсысына сәйкес Лаплас түрлендіруінің қасиеттері және бейнелер кестесі көмегімен түпнұсқасын табады.

Мысал 13.1 – Бейне бойынша түпнұсқаны табу керек: .

Шешуі.

.

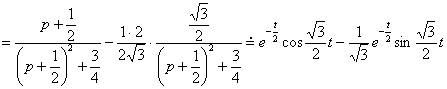Мысал 13.2 - Бейне бойынша түпнұсқаны табу керек:.

Шешуі. -ны элементарлық бөлшектерге жіктейміз:

.

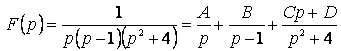 коэффициенттерін табамыз, онда .

 

Тұрақты коэффициентті сызықтық дифференциалдық теңдеу үшін Коши есебін шешу 

Коши есебін шешу жолын мысалмен көрсетеміз.

Мысал 13.3 – Коши есебін шешу керек: , .

Шешуі. болсын, онда  болады. Бейнелерге көшеміз: 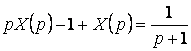. Бұл теңдеу қойылған Коши есебіне сәйкес амалдық (операторлық) теңдеу деп аталады. Бұдан -ны табамыз:

.

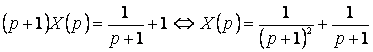Енді түпнұсқаларға көшеміз: . Сонымен,  функциясы Коши есебінің шешімі болады.

 

Сызықтық дифференциалдық теңдеулер жүйесі үшін Коши есебін амалдық әдіспен шешу 

Сызықтық дифференциалдық теңдеулер жүйесі үшін Коши есебін шешуді мысал үстінде көрсетеміз.

Мысал 13.4 – Біртекті емес екі сызықтық дифференциалдық теңдеу үшін Коши есебін шешу керек:  .

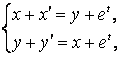
,  болсын, онда ,  болады. Амалдық теңдеулер жүйесіне көшеміз:

     

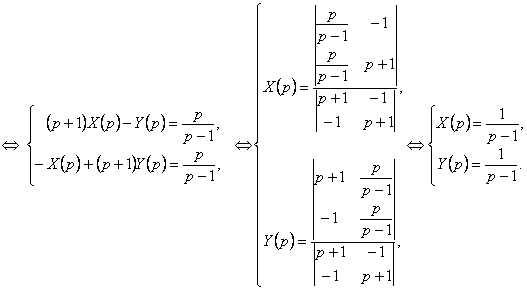
Түпнұсқаларды табамыз: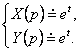 Демек, қойылған Коши есебінің шешімі 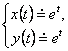 функциялар жиынтығы болады.

№ 14 дәріс Ықтималдықтар теориясының элементтері 

Мазмұны: Ықтималдықтар теориясының негізгі анықтамалары мен ұғымдары. Ықтималдықтың анықтамасы. Комбинаторика элементтері. Оқиғалар алгебрасы.

Дәрістің мақсаты: Студенттерді ықтималдықтар теориясының негізгі ұғымдарымен, ықтималдықты есептеудің кейбір әдістерімен таныстыру. 

Ықтималдықтар теориясы – кездейсоқ құбылыстардың заңдылықтарын зерттейтін математикалық ғылым. Зерттелетін құбылыстар олардың табиғатынан тәуелсіз қарастырылады, яғни ықтималдықтар теориясы кездейсоқ құбылыстардың математикалық модельдерін қарастырады. Бұл жерде кездейсоқ құбылыс деп ақырғы нәтижесі алдын ала болжауы мүмкін емес құбылыстарды түсінеміз. 

Кездейсоқ оқиғалар, олардың классификациясы 

Айталық, ақырғы нәтижесі алдын ала болжауы мүмкін емес кейбір тәжірибе (эксперимент, сынақ) жүргізілсін. Кездейсоқ оқиға деп тәжірибенің кейбір белгілі шарттар жиынтығы орындалу нәтижесінде пайда болуы да мүмкін, пайда болмауы да мүмкін кез келген нәтижесін айтамыз. Оқиғаларды латын , , , … әріптерімен белгілейміз. Тәжірибе нәтижелерін элементарлық оқиғалар дейміз де,  арқылы белгілейміз. Барлық элементарлық  оқиғаларының жиынын  арқылы белгілейміз. Табиғатта кездесетін оқиғаларды үш топқа бөлуге болады: ақиқат оқиғалар, мүмкін емес оқиғалар, кездейсоқ оқиғалар.

14.1 анықтама Егер  оқиғасы белгілі бір шарттар жиынтығы орындалғанда міндетті түрде пайда болса,  ақиқат оқиға деп аталады.

14.2 анықтама Егер  оқиғасы белгілі бір шарттар жиынтығы орындалғанда пайда болмаса,  мүмкін емес оқиға деп аталады.

14.3 анықтама Егер  оқиғасы белгілі бір шарттар орындалғанда пайда болуы да мүмкін, пайда болмауы да мүмкін оқиға болса,  кездейсоқ оқиға деп аталады.

Әрбір кездейсоқ шама көптеген кездейсоқ себептер әсерінің салдарынан болады. Ол себептердің әсер ету заңдылықтары белгісіз болғандықтан, олардың барлығының тәжірибе нәтижесіне әсер етуін ескеру мүмкін емес. Ал егер бірдей шарттар орындалғанда, сан рет жүргізілген бақылауларда пайда болатын кездейсоқ шамаларды қарастырсақ, мәселе өзгереді. Жеткілікті көп рет пайда болатын біртекті кездейсоқ оқиғалар өздерінің жаратылысынан тәуелсіз белгілі заңдылықтарға бағынады екен. Осы заңдылықтарды ықтималдықтар теориясы орнатады.

Сонымен, ықтималдықтар теориясы көптеген біртекті кездейсоқ оқиғалардың ықтимал заңдылықтарын зерттейді. 

Кездейсоқ оқиғалардың түрлері 

14.4 анықтама Егер бір тәжірибеде оқиғалардың біреуінің пайда болуы екіншісінің пайда болуына кедергі болса, оқиғалар үйлесімсіз деп аталады.

14.5 анықтама Егер  оқиғаларының кез келген екеуі үйлесімсіз болса, олар қос-қостан үйлесімсіз оқиғалар деп аталады.

14.6 анықтама Егер бірнеше оқиға қос-қостан үйлесімсіз және тәжірибе нәтижесінде олардың тек біреуі ғана пайда бола алатын болса, бұл оқиғалар толық топты құрайды.

14.7 анықтама Егер оқиғалардың еш біреуі қалғандарына қарағанда пайда болу мүмкіндігі жоғары болмаса, ондай оқиғаларды мүмкіндігі бірдей оқиғалар дейміз. 

Оқиғалар алгебрасы 

Оқиғаларға қолданылатын негізгі амалдар жиындарға қолданылатын амалдарға толық сәйкес келеді.

1.  және  оқиғаларының қосындысы деп олардың ең болмағанда біреуі пайда болуын (яғни немесе  пайда болады, немесе  пайда болады, немесе екеуі бірге пайда болады) білдіретін  оқиғасын айтамыз.

2.  және  оқиғаларының көбейтіндісі деп олардың екеуі бірдей пайда болу  оқиғасын айтамыз.

3.  және  оқиғаларының айырымы деп  оқиғасы пайда болып, бірақ  оқиғасы пайда болмайтынын білдіретін  оқиғасын айтамыз.

4.  оқиғасына қарама-қарсы оқиғасы деп тек  пайда болмағанда пайда болатын  оқиғасын айтамыз, яғни  оқиғасы -ның пайда болмағанын білдіреді.

5. Егер  оқиғасы пайда болуынан -ның пайда болуы шығатын болса, онда  оқиғасы -мен бірге пайда болады дейміз де,  деп жазамыз.

6. Егер  және  болса, онда  мен  – тең оқиғалар деп аталады да,  деп жазылады.

 Ықтималдықтың классикалық анықтамасы 

Бұл ұғымның бірнеше анықтамасы бар. Ықтималдықты анықтаудың қарапайым тәсілі саны ақырлы (конечное число) тәжірибелердің нәтижелерінің мүмкіндігі бірдей болуына негізделген. Мысал қарастырамыз. Урнада алты бірдей шар болсын. Олардың екеуі – қызыл шар, үшеуі – көк шар және біреуі ақ шар болсын. Урнадан қызыл немесе көк шарды алу мүмкіндігі ақ шар алу мүмкіндігіне қарағанда жоғары болатыны жеңіл байқалады. Осы мүмкіндікті сипаттайтын сан оқиғаның ықтималдығы болады.  оқиғасы пайда болуына келтіретін жағдай -ға қолайлы жағдай деп аталады.

14.4 анықтама  оқиғасының ықтималдығы деп осы оқиғаға қолайлы болатын жағдайлар саны -ның барлық элементарлық оқиғалар саны -ге қатынасын айтамыз, яғни

.                                                    (14.1)

Оқиға ықтималдығының қасиеттері

1. Ақиқат оқиғаның ықтималдығы 1-ге тең: .

2. Мүмкін емес оқиғаның ықтималдығы 0-ге тең: .

3. Кездейсоқ оқиғаның ықтималдығы 0 мен 1-дің арсындаға оң сан болады: .

 Оқиғаның салыстырмалы жиілігі 

14.5 анықтама  рет тәжірибе жүргізілгенде  оқиғасы  пайда болсын. Онда  бөлшегін  оқиғасының салыстырмалы жиілігі дейміз.

Оқиғаның салыстырмалы жиілігінің қасиеттері

1. Ақиқат оқиғаның салыстырмалы жиілігі 1-ге тең: .

2. Мүмкін емес оқиғаның салыстырмалы жиілігі 0-ге тең: .

3. Кездейсоқ оқиғаның салыстырмалы жиілігі 0 мен 1-дің арасындағы оң сан болады: .

4. Статистикалық орнықтылық қасиеті: тәжірибелердің қайталану саны мейлінше үлкен болғанда, салыстырмалы жиілік мәндері кейбір тұрақты санның маңайына топталады. Бұл заңдылық статистикалық тұрақтылық деп, ал осы тұрақты сан  оқиғасының ықтималдығы деп аталады. Бұл ықтималдықтың статистикалық тәсілмен анықталуы деп аталып, ықтималдықтың өмір шындығымен байланысын көрсетеді. 

Комбинаторика элементтері 

Комбинаторика – математика тарауларының бірі. Мұнда ақырлы жиының элементтерінің түрлі қосылыстары қарастырылып, олардың сандары саналады.  және  жиындарының әрқайсысынан бір-бірден элемент алынса, яғни  қосылыстарын парлар дейді. Бұл жағдайда элементтер парларының саны -ге тең

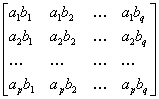
 элементтен  элемент бойынша жасалған теру деп  элементтен тұратын бірі бірінен тек қана құрамы бойынша ажыратылатын топтастырулардың санын айтамыз. Терулердің жалпы саны

                                           (14.2)

формуласымен есептеледі. Бұл жерде  (эн-факториал), , .

 элементтен  элемент бойынша жасалған орналасу деп әрқайсысы бірі бірінен құрамы және орналасу реті бойынша ажыратылатын топтастырулардың санын айтамыз. Орналасулардың жалпы саны

                                             (14.3)

формуласымен есептеледі.

 элементтен  элемент бойынша жасалған орналастыруларды алмастыру деп атайда. Алмастырудың жалпы саны

                                                  (14.4)

формуласымен есептеледі. 

Оқиғалар алгебрасы. Екі үйлесімсіз оқиғаның ықтималдықтарын қосу теоремасы 

14.1 теорема Егер  және  оқиғалары үйлесімсіз болса, онда

.                                     (14.5)

Салдар. Егер  оқиғалары қос-қостан үйлесімсіз болса, онда

.

 кездейсоқ оқиғалар тобы қос-қостан үйлесімсіз әрі  болса, онда олар толық топ құрайды.

14.2 теорема Толық топ құрайтын  оқиғалары үшін  теңдігі дұрыс болады.

14.3 теорема Қарама-қарсы оқиғалардың ықтималдықтарының қосындысы 1-ге тең

.                                               (14.6)

Егер  болса, онда  болады 

Тәуелді және тәуелсіз оқиғалар 

Егер екі оқиғаның біреуінің ықтималдығы екіншісінің пайда болу немесе пайда болмауына байланысты болмаса, онда оларды тәуелсіз оқиғалар деп атайды.

Егер  оқиғаларының кез келген екеуі тәуелсіз болса, онда осы оқиғаларды қос-қостан тәуелсіз оқиғалар дейміз. 

Тәуелсіз оқиғалардың ықтималдықтарын көбейту 

 және  оқиғаларының  көбейтіндісі деп  және  оқиғаларының бірге пайда болу оқиғасын айтамыз. Олай болса,  оқиғасы  оқиғаларының барлығының да пайда болу оқиғасы болып табылады.

14.4 теорема Егер  және  оқиғалары тәуелсіз болса, онда

.                                          (14.7)

Салдар. Егер  оқиғалары қос-қостан тәуелсіз оқиғалар болса, онда

.

14.5 теорема Ықтималдықтары белгілі, қос-қостан үйлесімсіз  оқиғаларының ең болмаса біреуі пайда болу оқиғасының ықтималдығы

,                                          (14.8)

формуласымен анықталады, мұндағы . 

Шартты ықтималдық 

 мен  тәуелді оқиғалар болсын.  деп  оқиғасы пайда болғаннан кейінгі  оқиғасының ықтималдығын айтамыз. 

Тәуелді оқиғалардың көбейтіндісі туралы теорема 

14.6 теорема Егер  мен  оқиғалары тәуелді болса, онда

.                  (14.9)

Салдар. Егер  оқиғалары тәуелді оқиғалар болса, онда

.            (14.10)

Салдар. (14.10) формуласынан шартты ықтималдықты табуға болады

.                                                 (14.11)

 Үйлесімді оқиғалардың ықтималдықтарын қосу туралы теорема 

Тәжірибе кезінде екі оқиғаның біреуінің пайда болуы екіншісінің пайда болуын жоққа шығармаса, ондай оқиғаларды үйлесімді оқиғалар дейміз.

14.7 теорема Егер  мен  оқиғалары үйлесімді болса, онда

.                     (14.12)

Ескерту. Егер  мен  тәуелді болса, онда (14.12) формуласын мына түрде қолданады

. 

№ 15 дәріс Толық ықтималдық формуласы 

Мазмұны: Толық ықтималдық формуласы, Байес формуласы, Бернулли формуласы, Лапластың локальдық теоремасы, Лапластың интегралдық теоремасы, Пуассон үлестіруі.

Дәрістің мақсаты: Сәйкес формулалар көмегімен ықтималдықты есептеу жолдарын түсіндіру. 

15.1 теорема Егер  оқиғасы қос-қостан үйлесімсіз, толық топ құрайтын  оқиғаларының (гипотезаларының) біреуімен бірге пайда болса, онда  оқиғасының ықтималдығы

.    (15.1)

формуласымен анықталады, мұндағы  – шартты ықтималдықтар әрі

(15.1) – толық ықтималдықтар формуласы деп аталады.

Дәлелдеуі. Теорема шартынан  оқиғасы үйлесімсіз , , …,  оқиғаларының қайсысы пайда болса да, пайда болатыны шығады, яғни

.                                 (15.2)

(15.2)-нің әр қосылғышын жеке есептеп аламыз

,

,

…,

.

Онда (15.2)-ні

түрінде жаза аламыз. Теорема дәлелденді. 

Байес формуласы 

 оқиғасы қос-қостан үйлесімсіз, толық топ құрайтын  оқиғаларының біреуімен бірге пайда болсын.  оқиғасының ықтималдығы (15.1) формуласымен анықталады.

Тәжірибе нәтижесінде  оқиғасы пайда болсын. Бұл жағдайда  оқиғасы пайда болғаннан кейінгі  гипотезаларының ықтималдықтары

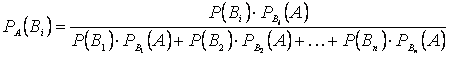         (15.3)

формуласымен анықталады.

(15.3) – Байес формуласы.

Байес формуласы  оқиғасы пайда болған тәжірибе нәтижесі белгілі болғаннан кейнгі гипотезалардың ықтималдықтарын қайта бағалауға мүмкіндік береді. 

Бернулли формуласы 

Нәтижесінде тәуелсіз оқиғалар пайда болатын тәжірибелерді тәуелсіз тәжірибелер деп атайды. Екі ғана нәтижесі бар тәуелсіз тәжірибелерді қарастырамыз. Мысалы, теңгені лақтыру, бұйымдардың стандартты болуын тексеру, бұйымның сапасын тексеру және т.б.

Жалпы жағдайда, екі нәтижені “ оқиғасы пайда болады” және “ оқиғасы пайда болмайды” деп атаймыз да, сәйкесінше ,  таңбаларын қолданамыз. Бұл оқиғалар қарама-қарсы оқиғалар болғандықтан, олардың ықтималдықтары  және  деп белгіленеді, мұндағы  – бір тәжірибеден екінші тәжірибеге көшкенде өзгермесін.

 тәуелсіз тәжірибелер кезінде ықтималдығы тұрақты болатын  оқиғасы  рет пайда болуының ықтималдығы  төмендегі формула бойынша анықталады

.                                        (15.4)

(15.4) – Бернулли формуласы.

Тәжірибелердің саны көп болса, онда Бернулли формуласымен ықтималдықты есептеу үлкен арифметикалық есептеулерге келтіреді. Сондықтан бұл жағдайда жуықтау формуласын қолданады. 

Лапластың локальдық теоремасы 

Егер  оқиғасының әрбір тәжірибе жүргізілгендегі ықтималдығы   тұрақты болса, онда  тәжірибеде  оқиғасының  рет пайда болу ықтималдығының жуық мәні

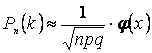                                     (15.5)

формуласымен анықталады, мұндағы 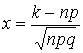,  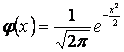– жұп функция және  үшін  функциясының мәндерінің кестесі кез келген ықтималдықтар теориясы бойынша оқулығында бар. 

Лапластың интегралдық теоремасы 

Егер  оқиғасының әрбір тәжірибе жүргізілгендегі ықтималдығы   тұрақты болса, онда  тәжірибеде  оқиғасы -ден кем емес және -ден артық емес рет пайда болу ықтималдығының жуық мәні

           (15.6)

формуласымен анықталады, мұндағы 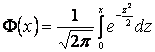 - Лаплас функциясы, ,  

Лаплас функциясы  тақ функция, яғни  және  үшін  функциясының мәндерінің кестесі кез келген ықтималдықтар теориясы бойынша оқулығында бар, ал  болғанда  деп есептеу керек. 

Пуассон үлестіруі 

Егер тәжірибелер саны  өте көп болып және әрбір тәжірибеде  оқиғасының пайда болуының ықтималдығы  өте аз болса,  ықтималдығының жуық мәнін

                                          (15.7)

формуласымен анықталады, мұндағы .

(15.7) – Пуассонның жуықтап есептеу формуласы деп аталады.

№ 16 дәріс Кездейсоқ шамалар 

Мазмұны: Дискретті және үзіліссіз кездейсоқ шамалар ұғымдары, үлестірім функциясы және оның қасиеттері, үлестірім тығыздығы және оның қасиеттері. Дискретті және үзіліссіз кездейсоқ шамалардың сандық сипаттамалары.

Дәрістің мақсаты: Кездейсоқ шаманың үлестірім заңын беруді, үлестірім функциясын және көпмүшесін құруды, дискретті және үзіліссіз кездейсоқ шамалардың сандық сипаттамаларын есептеуді үйрету. 

Кездейсоқ шама деп тәжірибе нәтижесінде алдын ала белгісіз және көптеген себептерге байланысты өзінің мүмкін сандық мәндерінің тек қана біреуін қабылдайтын шаманы айтамыз.

Кездейсоқ шамалар  бас әріптерімен, ал оның мүмкін мәндері  кіші әріптерімен белгіленеді. 

Дискретті және үзіліссіз кездейсоқ шамалар 

 кездейсоқ шамасының қабылдайтын мәндері бүтін сандар немесе тізбек түрінде жазылса, онда ол дискретті (үзілісті) кездейсоқ шама деп аталады.

 кездейсоқ шамасының қабылдайтын мәндері шенелген немесе шенелмеген аралықтардағы барлық мәндері болса, онда ол үзіліссіз кездейсоқ шама деп аталады. 

Дискретті кездейсоқ шаманың үлестіру заңдары 

 –  мәндерін сәйкесінше  ықтималдығымен қабылдайтын дискретті кездейсоқ шама болсын.

Дискретті кездейсоқ шаманың үлестіру заңы деп кездейсоқ шаманың  мәндері мен олардың сәйкес  ықтималдығының арасындағы байланысты айтады.

Үлестірім заңын кестемен, аналитикалық және графиктік тәсілдермен беруге болады. Кесте түрінде былай беріледі:

			…
			…

мұндағы , . 

Биномиалдық үлестірім

 

Егер  кездейсоқ шамасының мүмкін мәндері , , , …,  болып, оның сәйкес ықтималдығы

, ,

Бернулли формуласымен берілсе, онда  кездейсоқ шамасы Бернулли немесе бином үлестірім заңына бағынады.

Дәлелдеуі. Ньютон биномының жіктелуін қарастырамыз:

 .

 –  тәуелсіз тәжірибеде оқиғаның  рет пайда болу ықтималдығы,  –  тәуелсіз тәжірибеде оқиғаның  рет пайда болу ықтималдығы, …,  –  тәуелсіз тәжірибеде оқиғаның ешбір рет пайда болмау ықтималдығы. Онда

			…		…
			…		…

яғни  кездейсоқ шамасының үлестірім заңы кестемен берілді. Дәлелденді.

Графиктік түрде мына түрде беріледі: Декарт координаттар жүйесінде   … нүктелерін саламыз, мұндағы  – кездейсоқ шаманың мүмкін мәндері, ал  – сәйкес ықтималдықтары. Егер осы нүктелерді түзудің кесінділерімен қоссақ, пайда болған фигура үлестірім көпмүшесі деп аталады. 

Кездейсоқ шаманың үлестірім функциясы және оның қасиеттері 

 кездейсоқ шамасының үлестірім функциясы немесе интегралдық функциясы деп кездейсоқ шаманың -тен кіші мәндер қабылдау ықтималдығын айтады және оны былай белгілейді

.                                             (16.1)

Үлестірім функциясының қасиеттері:

1.  шенелген, яғни .

2.  – кемімейтін функция, яғни  болғанда .

3. , .

4.  кездейсоқ шамасының  аралығына түсу ықтималдығы

.                                     (16.2)

5.  сол жақты үзіліссіз, яғни .

Дискретті кездейсоқ шаманың үлестірім функциясы

                                                  (16.3)

түрде анықталады.

Дискретті  кездейсоқ шаманың үлестірім функциясы  нүктелерінде  секірісі бар болатын үзілісті функция болады. Оның графигі баспалдақ түрінде сызылады.

Кездейсоқ шаманың сандық сипаттамалары.

Дискретті кездейсоқ шаманың математикалық күтімі 

Үлестірім заңы кездейсоқ шаманы толық сипаттайды, бірақ көп жағдайларда үлестірім заңы белгілі бола бермейді, сондықтан көп жағдайларда кездейсоқ шаманың “сандық сипаттамасы” деген ұғым пайдаланылады. Оған математикалық күтім, дисперсия және орташа квадраттық ауытқу жатады.

Математикалық күтім кездейсоқ шаманың орта мәнін сипаттайды.

Дискретті  кездейсоқ шамасының математикалық күтімі деп олардың мүмкін мәндерінің сәйкес ықтималдықтарына көбейтінділерінің қосындысын айтады және оны былай белгілейді:

.                                  (16.4)

Берілген оқиға үшін  тұрақты шама болады.

Математикалық күтімнің ықтималдылық мағынасы

 тәжірибе жүргізілсін, олардың ішінде  кездейсоқ шамасы  рет  мәнін,  рет  мәнін, …,  рет  мәнін қабылдасын, мұндағы , онда кездейсоқ шаманың қабылдаған барлық мәндерінің қосындысы  болады.  –  кездейсоқ шамасының қабылдаған мәндерінің арифметикалық орташасы, оны  түрінде де жазуға болады, мұндағы  шамасы  мәнінің салыстырмалы жиілігі, яғни  . Айталық, тәжірибелер саны көп болсын, онда  және , яғни . Сонымен, математикалық күтім кездейсоқ шаманың қабылдаған мәндерінің арифметикалық орташасына жуық тең (тәжірибелер саны көбейген сайын жуық теңдіктің дәлдігі жоғарылай түседі).

Ескерту.  кездейсоқ шаманың қабылдайтын мүмкін мәндерінің ең кішісі мен ең үлкенінің арасындағы мәнге тең болатыны түсінікті, яғни сан осінде кездейсоқ шаманың мүмкін мәндері -тің сол және оң жақтарында орналасады. Сондықтан -ті үлестірудің орталығы деп те атайды.

Математикалық күтімнің қасиеттері

1. , мұндағы ;

2. .

Егер біреуінің үлестірім заңы екіншісінің қандай мәндер қабылдағанынан тәуелсіз болса, бұл екі кездейсоқ шама тәуелсіз болады.

Екі тәуелсіз  және  кездейсоқ шамаларының көбейтіндісі деп -тің әрбір мүмкін мәнінің -тің әрбір мәніне көбейтінділерін қабылдайтын кездейсоқ шаманы айтамыз.  шамасының мүмкін мәндерінің ықтималдықтары  пен -тің сәйкес ықтималдықтарының көбейтіндісіне тең.

3. .

4. .

№ 17 дәріс Дискретті кездейсоқ шаманың дисперсиясы

 Мазмұны: Дискретті кездейсоқ шаманың дисперсиясы мен орташа квадраттық ауытқуы. Үзіліссіз кездейсоқ шаманың сандық сипаттамасы.

Дәрістің мақсаты: Дискретті және үзіліссіз кездейсоқ шамалардың сандық сипаттамалар есептеу білу.

 Кездейсоқ шаманың математикалық күтімімен қатар оның математикалық күтімнен ауытқуын бағалайтын сипаттамалар – дисперсия және орташа квадраттық ауытқу.

 – кездейсоқ шама, ал  – оның математикалық күтімі болсын.  кездейсоқ шаманың өзінің математикалық күтімінен ауытқуы деп аталады.

кездейсоқ шамасының үлестірім заңы берілсін:

			…
			…

 кездейсоқ шамасының үлестірім заңын жазамыз:

			…
			…

17.1 теорема Кездейсоқ шаманың өзінің математикалық күтімінен ауытқуының математикалық күтімі 0-ге тең: .

Дәлелдеу. .

Дискретті кездейсоқ шамасының дисперсиясы (шашырауы) деп кездейсоқ шаманың өзінің математикалық күтімінен ауытқуының квадратының математикалық күтімін айтамыз да, оны төмендегідей белгілейміз

.                                      (17.1)

17.2 теорема Дисперсия кездейсоқ шаманың квадратының математикалық күтімі мен математикалық күтімнің квадратының айырымына тең

.                                     (17.2)

Дәлелдеу.

.

 Дисперсия қасиеттері

1. , мұндағы .

Дәлелдеу. .

2..

Дәлелдеу.

.

3. ,.

4. .

 

Тәуелсіз тәжірибелерде оқиғаның пайда болуының дисперсиясы 

17.3 теорема Биномдық үлестірім заңымен берілген кездейсоқ шаманың дисперсиясы

.                                             (17.8)

Дисперсияның ықтималдықтық мағынасы: дисперсия кездейсоқ шаманың өзінің орта мәнінің айналасында шашырау дәрежесін сипаттайды. 

 кездейсоқ шамасының орташа квадраттық ауытқуы

                                            (17.9)

шамасы болады, яғни -тің өлшеуі -тің өлшеуімен сәйкес келеді. 

Дискретті  кездейсоқ шамасының модасы деп кездейсоқ шаманың ең үлкен ықтималдықпен қабылдайтын  мәнін айтамыз. 

Үлестірім тығыздығы және оның қасиеттері 

Үзіліссіз кездейсоқ шама -тің үлестірім тығыздығы немесе дифференциалдық функциясы деп үлестірім функциясының бірінші ретті туындысын айтады да, оны төмендегідей белгілейді

.                                          (17.10)

 Дифференциалдық функцияның ықтималдылық мағынасы 

Туындының анықтамасы бойынша

.

Осыдан  екенін аламыз, яғни ықтималдықтың тығыздығы  шартына қанағаттандыратын үзіліссіз кездейсоқ шаманың функциясы түрінде анықталады.

-тің қасиеттері

1. .

2. .

3. Егер  үлестірім тығыздығы берілсе, онда үлестірім функциясы

                                       (17.11)

формуласымен табылады.

4. .

5.

 

Үзіліссіз кездейсоқ шаманың сандық сипаттамалары 

Үзіліссіз кездейсоқ шама -тің математикалық күтімі

                                     (17.12)

формуласымен анықталады. Егер -тің барлық мүмкін мәндері  аралығына тиісті болса, онда

.                                      (17.13)

Үзіліссіз кездейсоқ шама -тің дисперсиясы

,                           (17.14)

.                            (17.15)

Үзіліссіз кездейсоқ шама -тің орташа квадраттық ауытқуы

.                                          (17.16)

Үзіліссіз кездейсоқ шама үшін  модасы дегеніміз  функциясының максимум нүктесінің абсциссасы болады.

Үзіліссіз кездейсоқ шама -тің  медианасы дегеніміз  кездейсоқ шамасының

                              (17.17)

теңдігіне қанағаттандыратын  мүмкін мәні болады.

Үлестірім функциясы көмегімен медиананы

                                         (17.18)

формуласын пайдаланып табуға болады.

Әдебиеттер тізімі 

1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука, 1973. – 720 с.

2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисления. – М.: Наука, 1980. – 432 с.

3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. – М.: Высш. шк., 2003. – 479 с.

4. Натансон И.П. Краткий курс высшей математики. – СПб.: Издательство Лань, 1997. – 736 с.

5. Письменный Д.Т. Конспект лекций по высшей математике. – 2.– М.: Айрис-пресс, 2003. – 256 с.

6. Хасейнов К.А. Каноны математики: Учебник.– Алматы, 2003. – 686 с.