Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра  высшей математики

 

МАТЕМАТИКА  2

Конспект лекций
для студентов всех специальностей

 

 

Алматы 2013

 

СОСТАВИТЕЛИ: Нурпеисов С.А., Ултаракова Г.А. Математика 2: Конспект лекций. Для студентов всех специальностей. - Алматы: АУЭС, 2013 - 50 с.

 

Предлагаемый конспект лекций по Математике 2, написан в соответствии с типовой программой дисциплины и включает следующие основные разделы высшей математики: дифференциальное и интегральное исчисление функций нескольких переменных, обыкновенные дифференциальные уравнения, числовые и функциональные  ряды, элементы теории вероятностей. В целях активизации самостоятельной работы студентов теоретические вопросы изложены в основном в краткой форме и, в то же время, большое внимание уделено на возможности использования теории при решении практических задач.

 Ил.-13, библиогр.-6.

 

  Рецензент: канд. тех. наук, доц. Башкиров М.В.                     

 

           Печатается по плану издания некоммерческого акционерного общества   «Алматинский университет энергетики и связи» на 2013 г.

 

 

ã НАО «Алматинский университет энергетики и связи», 2013 г.

 

Сводный план 2013 г., поз.304

    

1 Лекция №1. Дифференциальное исчисление функции нескольких переменных

 

          Содержание лекции: частные производные и полный дифференциал. Касательная плоскость и нормаль к поверхности. Дифференцирование неяв-ной функции. Экстремум функции двух переменных. Условный экстремум.

         Цель лекции: развить логическое мышление, выработать умение самостоятельно изучать научную литературу по математике и её приложения.

 

         1.1 Область определения

 

         Определение. Совокупность всех точек , в которых определена функция нескольких переменных, называется областью определения функции.

    Для функции двух переменных областью определения является некоторая часть координатной плоскости, ограниченной одной или несколькими линиями (или вся плоскость), для функции трех переменных – часть пространства (или все пространство).

 

          1.2 Частные производные и полный дифференциал функции двух переменных

 

         Частные приращения

                                       ,                                              (1.2.1)

                                     .                                                (1.2.2)

    Полное приращение

                                      .                                                (1.2.3)

    Частные производные

                                               ,                                                (1.2.4)

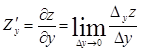                                              .                                                 (1.2.5)

    Частные дифференциалы

                                                ,                                                         (1.2.6)

                                              .                                                          (1.2.7)

    Полный дифференциал

                                              .                                                     (1.2.8)

    Приближенное вычисление значения функции с помощью дифференциала                                                                                                    (1.2.9)

    Так как частная производная по одной из переменных является производной по этой переменной, найденной при условии, что другая переменная есть постоянная величина, то все правила и формулы дифференцирования функций одной переменной применимы для нахождения частных производных функций любого числа переменных.

 

         1.3 Производная сложной функции

 

    Если  – дифференцируемая функция двух переменных  и , которые сами являются дифференцируемыми функциями независимой переменной t:

,,

то производная сложной функции  вычисляется по формуле

                                                  .                                            (1.3.1)

    Если  и , то

                                                 .                                                 (1.3.2)

     В этом случае  называется полной производной функции (в отличие от частной производной).

 

          1.4 Производные и дифференциалы высших порядков

 

     Частными производными второго порядка функции  называются частные производные от ее частных производных первого порядка:

         

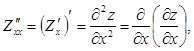
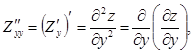                                                                                       (1.4.1)

.

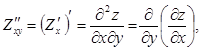
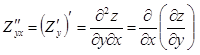    Дифференциал второго порядка

                                                                                (1.4.2)

 

         1.5 Полный дифференциал и его связь с частными производными  

 

         Для того, чтобы выражение   P(x,y)dx+Q(x,y)dy, где функции P(x,y) и Q(x,y) непрерывны в односвязной области D вместе со своими частными производными первого порядка, представляло собой в области D полный дифференциал некоторой функции U(x.y), необходимо и достаточно выполнение условия 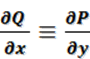   . Если выполняется данное условие, то функция U(x,y) находится по следующей формуле:

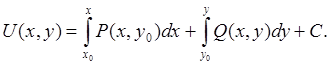                                                                   (1.5.1)

          Пример:  убедиться в том, что выражение   (2x+y)dx+(x+2y)dy есть полный дифференциал некоторой функции,  найти эту функцию.

         Решение: в данном случае P=2x+y, Q=x+2y. Поэтому 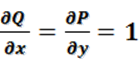, и, следовательно, dU=Pdx+Qdy. Пусть А(0;0) и В(x;y), тогда

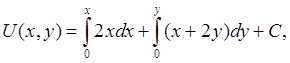                        т.е. U(x.y)=x²+xy+y²+C.

 

         1.6  Касательная плоскость и нормаль к поверхности

 

          Касательной плоскостью к поверхности в точке М (точка касания) называется плоскость, в которой лежат все касательные в точке М к различным кривым, проведенным на поверхности через эту точку. Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания.

          Если уравнение поверхности в декартовой системе координат задано в явной форме z=f(x;y), где f(x;y) – дифференцируемая функция, то уравнение касательная плоскости в точке М( x₀;y₀;z₀) поверхности есть

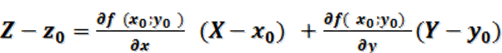              .                       (1.6.1)

          Здесь ,, a X, Y, Z – текущие координаты точки касательной плоскости.

          Уравнения нормали имеют вид 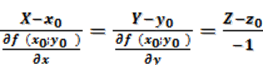    .          (1.6.2)

В том случае, когда уравнение гладкой поверхности задано в неявной форме  F(x,y,z)=0  и  F(x₀,y₀,z₀)=0 , соответствующие уравнения будут иметь вид:

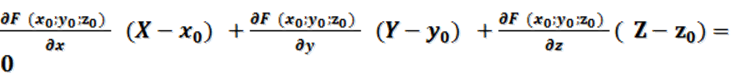(1.6.3)  - это уравнение касательной плоскости, и уравнение нормали:

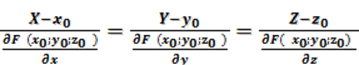                         .                                     (1.6.4)

 

 

         1.7 Дифференцирование неявной функции

 

         Функция z=f(x,y) называется неявной, если она задается уравнением                    F(x,y,z)=0  (*)  неразрешенным относительно z.  Найдем частные производные    и  неявной функции z, заданной уравнением (*). Для этого, подставив в уравнение вместо z функцию f(x;y), получим тождество   .

          Частные производные по х  и по у  функции, тождественно равной нулю, также равны нулю:

                       (у – считаем постоянным);

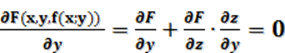                         (х - считаем постоянным).

          Откуда 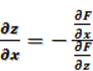           и     ,  (.                                 (1.7.1)

          Если неявная функция  y=f(x) одной переменной задается уравнением F(x,y)=0, то производная неявной функции находится по формуле                                , ().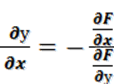

 

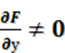          1.8 Экстремум функции двух переменных

 

     Определение. Точка называется точкой локального максимума (минимума) функции , если для всех точек , отличных от точки и принадлежащих достаточно малой ее окрестности выполняется неравенство

                                .

     Максимум или минимум функции называются ее экстремумами. Точка, в которой достигается экстремум функции, называется точкой экстремума.

    Необходимые условия экстремума.

    Если точка  является точкой экстремума функции , то  и  или хотя бы одна из этих производных не существует.

    Точки экстремума всегда являются критическими точками, однако критические точки не всегда могут быть точкой экстремума.

    Введем обозначения:

                         

                                           .    

    Достаточные условия экстремума.

    Пусть функция имеет непрерывные частные производные до третьего порядка включительно, в некоторой области содержащей критическую точку .

    Тогда:

    1) если , то  является точкой экстремума, причем при  точка  будет точкой максимума и при  точка  будет точкой минимума;

    2) если , то в точке экстремума нет;

          3) если , то экстремум может быть, а может и не быть. Для заключения об экстремуме в этой точке надо привлечь к рассмотрению частные производные выше второго порядка (этот случай в программу не входит и нами не рассматривается).

         Пример: исследовать на экстремум функцию

.

    Решение: находим частные производные и приравняем их к нулю,

                                        .

.

(Здесь комплексные корни не рассматриваются).

    Таким образом, имеем две критические точки:  и .

    Теперь найдем производные второго порядка

и вычислим их значения в критических точках:

          1) ,

    тогда D = 0×0-(-36)×(-36)<0,

    Поэтому в этой точке экстремума нет;

     2) ,

    тогда ,

         причем , поэтому .        

    Замечание 1. Из следует, что, , или , а это означает, что если функция имеет экстремум, то А и С имеют одинаковый знак.

     Замечание 2. В этом примере точка  является критической точкой, однако в этой точке экстремума нет, отсюда следует, что не все критические точки могут быть точками экстремума.

 

 

 

 

          1.9 Наибольшее и наименьшее значения функции двух переменных

 

          Функция непрерывная в ограниченной замкнутой области, достигает в ней наибольшего и наименьшего значений или в критических точках, или в точках, лежащих на границе области.

    Для нахождения наибольшего и наименьшего значений функции в замкнутой ограниченной области необходимо:

         1) найти критические точки функции и вычислить значение функции в этих точках;

         2) найти наибольшее и наименьшее значения функции на границе области;

         3) сравнить все полученные значения. Наибольшее (наименьшее) из них будет наибольшим (наименьшим) значением функции в замкнутой области.

    Замечание: если для функции  граница замкнутой области состоит из нескольких отрезков (дуг) уравнения которых , где  или , где , то на соответствующих отрезках (дугах) границы данная функция является функцией одной переменной

                                      

    или

                                   .

 

         1.10 Условный экстремум

 

    Функция  имеет условный максимум (минимум) в точке , если существует такая окрестность точки М₀ для всех точек
М (х,у) которой (М₀¹М), удовлетворяющих уравнениям связи

                                               ,          

выполняется неравенство .

     Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа:

                                       ,      

где – называется множителем Лагранжа.

    Необходимые условия условного экстремума функции трех переменных:

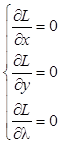                                              ,                                                               (1.10.1)

из которой находятся неизвестные , где  - координата точки, в которой возможен условный экстремум, – множитель Лагранжа.

    Достаточные условия:

    Пусть ,  – одно из решений системы (1.10.1) и

.

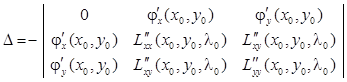    Тогда, если , то функция в точке  имеет условный максимум, если  - условный минимум.

 

          2 Лекция №2. Двойные интегралы

 

         Содержание лекции: основные свойства двойных интегралов. Вычисление двойных интегралов в декартовых координатах. Замена пере-менных в двойных интегрлах.

         Цель лекции: теория, изложенная в лекции, проиллюстрирована, что позволит студентам эффективно подготовиться к сдаче РГР, РК и экзаменов

        

         Пусть в замкнутой области D плоскости

Oxy задана непрерывная функция 

. Разобьем область D на n

элементарныхчастей D_i (i=1,n),

площади которых обозначим через ΔS_i,

а диаметры (наибольшее расстояние

 между точками области)-через d_i (см. рису-

нок 1). В каждой области  D_i выберем произ-              Рисунок 1

вольную точку М_i(x_i,y_i)_,умножим значение

f(x_i,y_i) функции в э той точке на ΔS_i и составим сумму всех таких произведений:       (2.1) 

          Эта сумма называется интегральной суммой функции  f(x,y)  в об-ласти D. Рассмотрим предел интегральной суммы (1), когда n стремится к бесконечности таким образом, что maxd_i→0. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x,y) по области D и обозначается 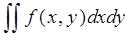  или .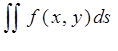  

         Таким образом, двойной интеграл определяется равенством

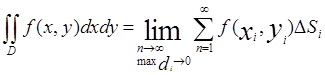              .                                        (2.2)                          

          В этом случае, функция f(x,y) называется интегрируемой в области D; D - область интегрирования; x и  y переменные интегрирования; dxdy или (ds) – элемент площади.

         Теорема 1. (достаточное условие интегрируемости функции).

         Если функция z=f(x,y) непрерывна в замкнутой области D, то она интегрируема в этой области.

         Определение. Конечный предел интегральной суммы (2.0.2) называется двойным интегралом.                                                                

         Таким образом, двойной интеграл пред-

ставляет собой: если  f(x,y)>0, то объем тела,

ограниченного сверху поверхностью z=f(x,y),        Z=f(x,y)                              

сбоку цилиндрической поверхностью,

образованной из прямых, скользящих по замкнутой

линии  в области D, снизу - самой областью D. Итак,       

величина двойного интеграла от неотрицательной

функции равна объему цилиндрического тела:                                      D    

                                                                                                        Рисунок 2

                                           .                         

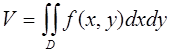          В этом состоит геометрический смысл двойного интеграла.

          Основные  свойства двойного интеграла:

          1) ;

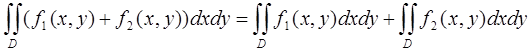          2) ;

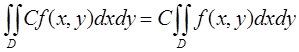          3) 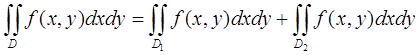, D=D₁+D₂

          4) если f(x,y)≥0, то ;

          5) если f(x,y)≥φ(x,y) , то ;

          6) , так как ;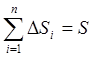

          7) если m≤f(x,y)≤M, то ,

где m и M–соответственно наименьшее и наибольшее значения подын-тегральной функции в области D.

          8)  Если функция f(x,y) непрерывна в замкнутой области D, площадь ко-торой S, то в этой области существует такая точка , что 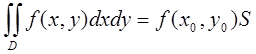, величину  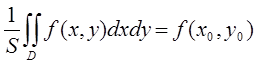называют средним значением функции f(x,y) в области D.

 

          2.1  Правила вычисления двойных интегралов

 

          Различают два основных вида области интегрирования.

          1) Область интегрирования D ограничена слева и справа прямыми  x=a и x=b (a<b), а снизу и сверху – непрерывными кривыми и y=φ(x) [φ₁(x)<φ ₂(x)] (см. рисунок 3).  Для такой области двойной интеграл вычисляется по формуле:

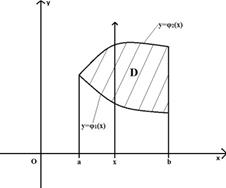
 (2.1.1)
     причем сначала вычисляется внутренний интеграл                
    в котором x считается постоянным.

 

   Рисунок 3 

               

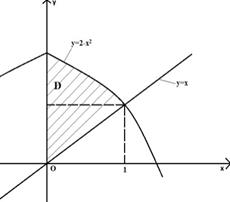Пример 1: вычислить двойной интеграл , если область интегрирования D ограничена линиями x=0, y=x, y=2-x².

Решение:

    Рисунок 4                   , 

             

          Из чертежа видно, что  ,  

           

              

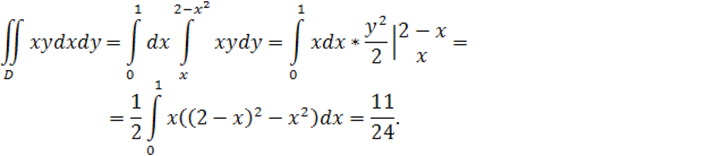
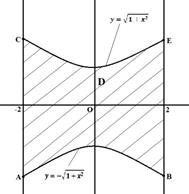
           Пример 2: определить пределы интегрирования  двойного интеграла, если область интегрирования D (см. рисунок 5) ограничена гиперболой     и двумя прямыми x=2 и x=-2 (имеется в виду область, содержащая начало координат).

          Решение: 

область интегрирования ABCE (см. рисунок 5) ограничена прямыми x=-2 и x=2 и двумя ветвями гиперболы:  и , т.е.

принадлежит к первому   виду.   

                     

               

      Имеем:
       

 

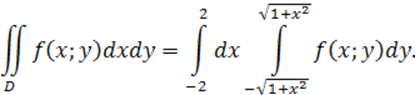
      Рисунок 5

 

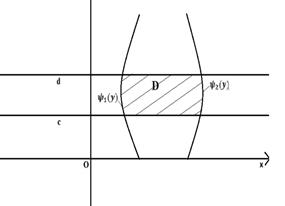          2) Область интегрирования D ограничена снизу и сверху прямыми y=c и y=d, а слева и справа – непрерывными кривыми x= и x= (c<d, . Для такой области двойной интеграл вычисляется по формуле

  

 

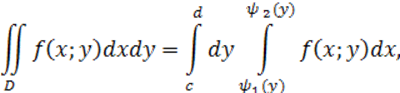
причем сначала вычисляется внутренний интеграл, в котором y считается постоянным.

    Рисунок 6                             Переход от одной формулы к другой называется

                                                  изменением порядка интегрирования:          
                                                                                             

 

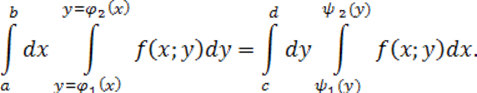
          2.2  Замена переменных в двойном интеграле

 

          Двойной интеграл в криволинейных координатах. Пусть в двойном интеграле  прямоугольные координаты x, y преобразуются к новым криволинейным координатам u, v, которые связаны с x, y соотношениями:                                        
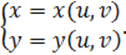                                                                                                     (2.2.1)

          Если  между областями D и D’, лежащими в плоскостях x0y и uOv, установлено взаимно однозначное соответствие формулами (1), имеют непрерывные частные производные первого порядка в области D’  и якобиан преобразования в   области D’ 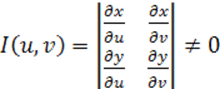 , то имеет место следующяя формула замены переменных в двойном интеграле:
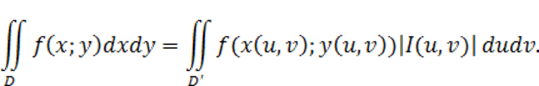                                        (2.2.2)

           В полярных координатах формулы (2.2.1) имеют вид:

                                                                                                                          (2.2.3)            

           Формула вычисления двойного интеграла в полярных координатах:

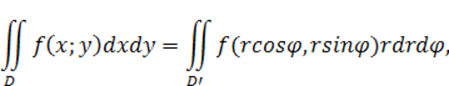                                                                  (2.2.4)

           где   

           Если область D соответствует рисунку 7, то
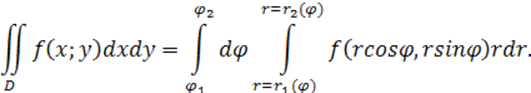                                              (2.2.5)

 

           

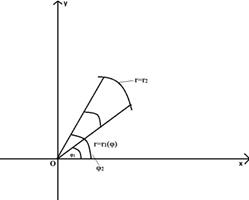
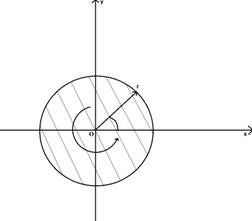
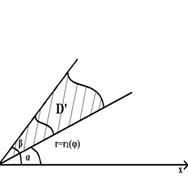
Рисунок 7                                    Рисунок 8                              Рисунок 9

 

           Если область D соответствует рисунку 8, то

                                      

Или

                               

    

           2.3  Применение двойного интеграла к задачам геометрии

 

           1. Площадь плоской фигуры:

;

.

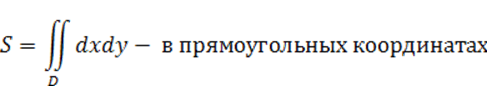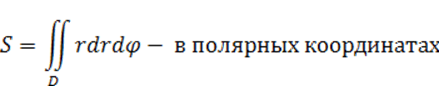            2. Объем тела:

            3. Площадь поверхности:  

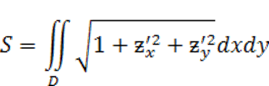
Пример 1:  вычислить площадь фигуры, ограниченной кривыми y²=2x, y=x.

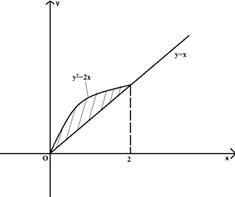
Решение:

  ,

.

 

 

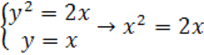   Рисунок 10

 

 

           

 

 

 

     3 Лекция №3.  Тройные интегралы

 

          Содержание лекции: Основные свойства тройных интегралов. Вычисление тройных интегралов в декартовых координатах. Замена переменных в тройных интегралах. Переход от декартовых координат к цилиндрическим и сферическим координатам. Применение кратных интегралов к задачам геометрии.

         Цель лекции: изучить некоторые приложения тройного интеграла.

 

         Пусть функция f(x;y;z) определена в ограниченной замкнутой пространственной области Т. Разобьем Т произвольным образом на n элементарных областей T₁, T₂, …, T_n с диаметрами d₁, d₂, d₃ …, d_n и объемами ∆V₁, ∆V₂, … , ∆V_n. В каждой элементарной области возьмем произвольную точку p_k(x_k, y_k, z_k), умножим значение функции в точке p_k на объем этой области:

Выражение
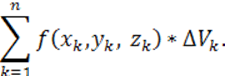                                                                                               (3.1)

называется интегральной суммой для функции f(x, y, z) по области Т.

         Предел интегральной суммы при стремлении к нулю наибольшего из диаметров элементарных областей называется тройным интегралом от функции f(x, y, z) по области Т и обозначается:

    

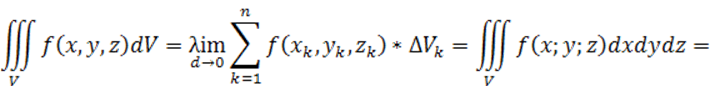
                                                                                               (3.2)                                                                                

формула для вычисления тройного интеграла в прямоугольных координатах.         Здесь   .

 

        3.1 Тройной интеграл в криволинейных координатах

 

          Пусть в тройном интеграле  прямоугольные координаты x, y, z преобразуются к криволинейным координатам     u, v, w   с помощью соотношений:

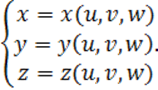                                                                                                                 (3.1.1)

              Если эти функции имеют непрерывные частные производные первого порядка и I(u,v,w)≠0, то имеет место формула замены переменных:

   

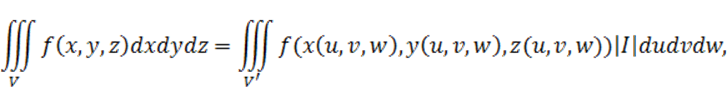
         где        

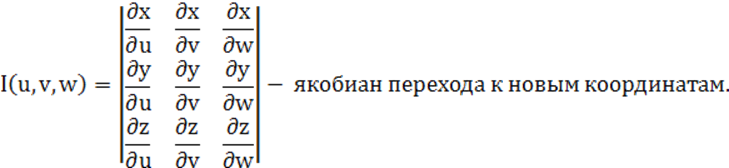
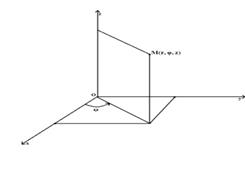
          a) Тройной интеграл в цилиндрических координатах.

          Цилиндрические координаты r,φ,z связаны с прямоугольными x, y,         z следующими соотношениями:

                                                                              

  

          Формула замены переменных в этом случае принимает вид:

 

     Рисунок 11

 

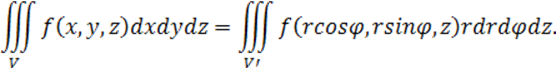
          б) Тройной интеграл в сферических координатах.

          Сферические координаты z, φ, θ связаны с прямоугольными x,y,z следующими формулами:

             ,

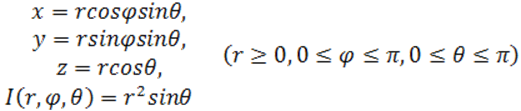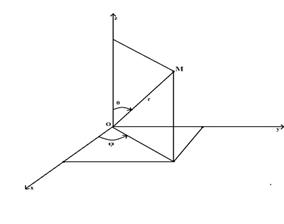
                                                         Рисунок 12      

    

          Формула замены переменных:                 

 

                  

          Пример 1:  вычислить    

где V – шар .  

          Решение: вычислим интеграл путем перехода к сферическим координатам: 

Тогда  dV=dxdydz=.

          Граница области V – сфера и ее уравнение имеет вид r=1, подынтегральная функция после замены переменных примет вид  . Новые переменные изменяются в следующих пределах: r – от 0 до 1, φ – от 0 до 2π, θ – от 0 до π. Таким образом, согласно формуле тройного интеграла в цилиндрических координатах:

    

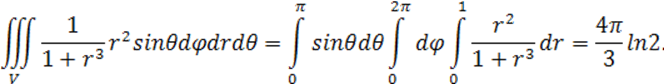
           Некоторые приложения тройного интеграла:

           Объем тела:

                             

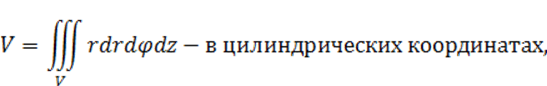
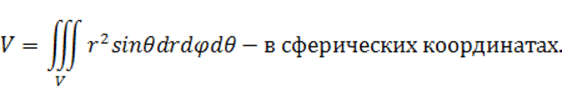
           Пример 2:  найти объем тела, ограниченного поверхностями z=x²+y² и z=1.

          Решение:

          Данное тело ограничено сверху плоскостью z=1, снизу  - параболоидом z=x²+y² (см. рисунок 14). Объем тела находим, используя цилиндрические координаты:

       

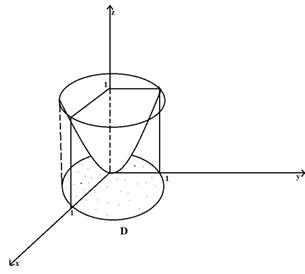
                                                    Рисунок 13

 

                 4 Лекция №4. Дифференциальные уравнения первого порядка

 

                 Содержание лекции: дифференциальные уравнения (ДУ) первого порядка. Задача Коши. Основные классы ДУ первого порядка.

                 Цель лекции: Уметь определять тип ДУ и его порядок, находить решение ДУ. При решении различных задач математики, физики, химии и других наук часто пользуются основные классы ДУ.

 

         4.1  Дифференциальные уравнения первого порядка

 

   Обыкновенное дифференциальное уравнение первого порядка имеет вид                                               .                                                                                        (4.1.1)

   Если его удается решить относительно производной, то оно запишется так:    .                                                                                         (4.1.2)

   Решением или интегралом уравнения (4.1.2) называется всякая дифференцируемая функция , удовлетворяющая этому уравнению, т.е. такая, что после подстановки этой функции в уравнение (4.1.2) оно обращается в тождество, т.е. является тождеством.

    Общим решением уравнения (4.1.1) или (4.1.2) называется соотношение вида                                                                           (4.1.3)

содержащее одну произвольную постоянную величину. Соотношение (4.1.3) также может быть записано в виде  .                                                               (4.1.4)

    Частным решением уравнения (4.1.2) называется такое его решение, которое получается из общего решения (4.1.4) при некотором частном значении произвольной постоянной.

    График решения дифференциального уравнения называется интегральной кривой.

    Задача Коши. Найти решение дифференциального уравнения (4.1.1), удовлетворяющее заданным начальным условиям:  при .

    Геометрический смысл частного решения: найти интегральную кривую уравнения (4.1.1), проходящую через данную точку .

    Методы решения дифференциальных уравнений, излагаемые ниже, применимы только к уравнениям определенных типов. Поэтому очень важно уметь по виду уравнения определить, относится ли оно к одному из изученных типов или нет.

 

         4.2 Дифференциальные уравнения с разделяющимися переменными

 

    Дифференциальным уравнением с разделяющимися переменными называется уравнение вида                      .                      (4.2.1)

    Уравнение (4.2.1) делением на  приводится к уравнению с разделенными переменными

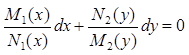                                         .                                                 (4.2.2)

    Общий интеграл уравнения (4.2.2)

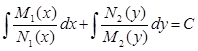                                        .                                                (4.2.3)

    Уравнение (4.2.1) может быть переписано так:

.

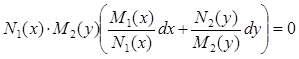    Поэтому, кроме найденного ранее решения (4.2.3), ему могут также удовлетворять решения, получаемые из уравнения

                                              .                                                  (4.2.4)

    Если эти решения не входят в общий интеграл (4.2.3), то они будут называться особыми решениями уравнения (4.2.1).

 

 

 

 

 

         4.3 Линейные уравнения первого порядка

 

    Если дифференциальное уравнение линейно относительно искомой функции  и  ее первой  производной, то оно называется линейным уравнением первого порядка. Его общий вид

                                  ,                                                           (4.3.1)

где  – заданные функции. Решение уравнения ищется методом Бернулли в виде произведения двух функций

                                        ,                                                          (4.3.2)

          где       ,                                                                             (4.3.3)

                                                                                    (4.3.4)

         Тогда

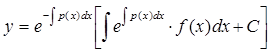                                 .                                          (4.3.5)

    1. Решить уравнение

.

    Решение: здесь . Тогда

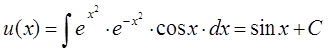
          Искомое решение запишется

          Уравнение Бернулли

     Уравнением Бернулли называется уравнение вида

                                     ,                                                     (4.3.6)

где a¹0, a¹1. При a=0 получим линейное уравнение, а при a=1 получится уравнение с разделяющимися переменными.

    Уравнение (4.3.6) решается, как и уравнение (4.3.1) путем выбора , причем  .

                              .                                          (4.3.7)

         Уравнение Бернулли также можно свести к линейному уравнению с помощью подстановки .

         2. Решить уравнение

.

    Решение: здесь . Поэтому используем подстановку

.

    Преобразуем данное уравнение

.

    Подставляя выражения  и  в исходное уравнение получим

.

    Получили линейное уравнение. Решение ищем в виде :

,

.

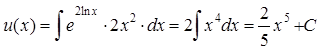    Тогда

.

          5 Лекция №5.  Дифференциальные уравнения второго порядка

 

          Содержание лекции: ДУ второго порядка. Задача Коши. ДУ, допускающие понижение порядка. Линейные однородные ДУ с постоянными коэффициентами.

          Цель лекции: дать определение ДУ второго порядка, показать способы решения ДУ, допускающих понижения порядка. Различать линейные однородные и неоднородные второго порядка ДУ, так как многие задачи математики, механики, электротехники и других технических наук приводятся к линейным ДУ.        

            

          5.1  Дифференциальные уравнения второго порядка. ДУ, допускающие понижение порядка

 

    Дифференциальные уравнения второго порядка имеют вид:

                                                                                             (5.1.1)

или                                                         .                                                                               (5.1.2)

    Общим решением уравнения (5.1.2) называется функция,

                                           ,                                                       (5.1.3)

cодержащая две произвольные постоянные .

    Задача Коши. Найти решение дифференциального уравнения (5.1.1), удовлетворяющее условиям:при .

    Постоянные  определяются из системы уравнений

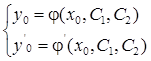                                             .                                                   (5.1.4)

         Ниже рассматриваются простейшие типы интегрируемых уравнений второго порядка и случаи понижения порядка дифференциальных уравнений.

    К простейшим типам интегрируемых уравнений второго порядка относятся уравнения, порядок которых может быть понижен с помощью каких-либо приемов. Рассмотрим три типа таких уравнений.

   Функция,  стоящая в правой части уравнения (5.1.2):

   а) зависит только от переменной 

                                                  ;                                                         (5.1.5)

   б) не содержит

                                                  ;                                                       (5.1.6)

   в) не содержит

                                                    .                                                       (5.1.7)

   а) Общее решение уравнения (5.1.5) находится путем двукратного интегрирования,

                                             .                                        (5.1.8)

         Пример: решите уравнение

.

   Решение: интегрируя дважды, находим

,

.

   б) Уравнение (5.1.6) интегрируется с помощью введения новой функции .

   Тогда  и уравнение (5.1.6) имеет вид

                                                        ,                                                     (5.1.9)

а это есть уравнение первого порядка относительно .

   в) Уравнение (5.1.7) интегрируется подстановкой  (введением новой независимой переменной  вместо переменной ), которая дает возможность свести ее к уравнению с разделяющимися переменными. Тогда

                                                                         (5.1.10)

т.е. .

         5.2 Линейные однородные уравнения второго порядка
с постоянными коэффициентами

 

   Дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

                                           .                                                 (5.2.1)

   Если , то уравнение (5.11) называется однородным дифференциальным уравнением второго порядка с постоянными коэффициентами

                                            .                                                  (5.2.2)

   Уравнение

                                                                                                       (5.2.3)

называется характеристическим уравнением для уравнения (5.2.2).

   В зависимости от корней и характеристического уравнения (5.2.3) получаем общее решение уравнения (5.2.2):

   1) и различные действительные числа

                                             ;                                                     (5.2.4)

   2) ,

                                              ;                                                   (5.2.5)

   3) – комплексные числа

                                         .                                  (5.2.6)

          

         6 Лекция №6. Линейные неоднородные уравнения второго порядка
с постоянными коэффициентами

 

         Содержание лекции:  линейные неоднородные ДУ с постоянными коэффициентами. Метод неопределенных коэффициентов. Метод вариации произвольных постоянных.

         Цель лекции: уметь находить общее решение линейного неоднородного ДУ, применяя метод вариации произвольных постоянных методом неопределенных коэффициентов. ЛНДУ применяется при изучении таких важных курсов, как «физика», «Теория электрических цепей» и других предметов.

 

    Если , то уравнение (5.2.1) называется неоднородным дифференциальным уравнением с постоянными коэффициентами.

    Общее решение уравнения (5.2.1) находится по формуле:

                                                    .                                                       (6.1)

          Где  – общее решение соответствующего однородного уравнения (5.2.2), а – частное решение уравнения (5.2.1).

    Рассмотрим методы нахождения общего решения уравнения (5.2.1). Пусть  имеет следующие два вида:

    а)a – постоянное число.

    В этом случае частное решение уравнения (5.2.1) в зависимости от значений числа  ищется в виде:

    1) Если ¹ к₁, ¹ к_{2 ,} где  и корни характеристического уравнения, то

                                                    .                                                     (6.2)

    2) Если  = к₁  либо  = к₂ , то

                                                    .                                                (6.3)

    3) Если  = к₁ = к₂ , то

                                                   ,                                               (6.4)

где – многочлен с  неопределенными коэффициентами.

    б) – постоянные числа.

    Тогда частное решение неоднородного уравнения ищется в виде:

    1. Если ±b не являются корнями характеристического уравнения, то

                                              .                                        (6.5)

    2. Если ±b = ±b являются корнями характеристического уравнения, то

                                             .                                  (6.6)

       

         Метод неопределенных коэффициентов

 

   Пример1: найти общее решение уравнения

.

    Решение: характеристическое уравнение

.

    Здесь  = 2, ¹ к₁, ¹ к₂. Поэтому общее решение однородного уравнения имеет вид , а частное решение неоднородного уравнения ищем в виде

                                                       .                                            (6.7)

т.к. , многочлен первой степени . Теперь необходимо определить коэффициенты А и В. С этой целью (6.0.7) подставим в данное уравнение, предварительно найдем

,

.

    Тогда имеем

4×(A+A+B) – 3×(2×A×+A+2B) – 4×(A+B) =+2.

    После сокращения на  и некоторых преобразований получим – 6A+A–6B = +2.

    Для того, чтобы это равенство было тождеством, достаточно совпадения коэффициентов при одинаковых степенях Х в обеих частях равенства, т.е.

 

  

 

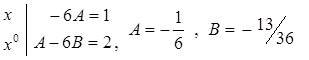
    Следовательно, функция

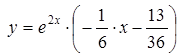
является частным решением неоднородного уравнения. Тогда общее решение уравнения запишется так:

.

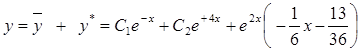   Замечание. Если неоднородное уравнение имеет вид

,

то частное решение этого уравнения может быть найдено в виде

 ,

где  есть частное решение уравнения

 ,

    а  есть частное решение уравнения

.

    Этот метод называется «принципом наложения».

    Выше показали метод решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами при определенных видах функции . Существует общий метод нахождения частного решения неоднородного уравнения. Этот метод называется методом вариации постоянных.

 

     6.1  Метод вариации произвольных постоянных

 

    Этот метод является общим методом для нахождения частного решения линейного неоднородного  уравнения второго порядка как с переменными, так и с постоянными коэффициентами, если известно общее решение соответствующего однородного уравнения.

    Пусть известно общее решение однородного уравнения

                                          .                                                  (6.1.1)

    Тогда частное решение неоднородного уравнения ищется в виде

                                      .                                             (6.1.2)

    Функции  определяются из системы

                                         .                                    (6.1.3)

    Определитель этой системы

называется определителем Вронского. Так как  и  линейно независимые решения однородного уравнения определитель , то система (6.1.3) всегда имеет решение и притом единственное.

    2. Решить уравнение

.

    Решение: общее решение однородного уравнения имеет вид

,

где  – частные решения.

    Теперь частное решение неоднородного уравнения найдем с помощью метода вариации произвольных постоянных

.

    Для определения  и  составим систему (6.10). Вначале находим:

.

    Тогда система (6.0.10) запишется так:

.

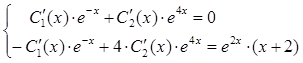    Из этой системы находим:

,

.

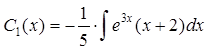    Используя метод интегрирования по частям получим выражения для

,

.

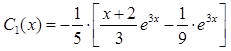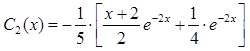    Подставив выражения  и  в выражение частного решения  получим

.

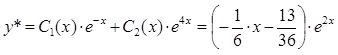    Этот пример (см. пример 1) был ранее решен методом неопределенных коэффициентов. Как видно, результаты совпадают.

 

          7 Лекция №7.  Системы дифференциальных уравнений

 

          Содержание лекции: системы ДУ. Задача Коши для нормальной системы ДУ. Решение систем ДУ методом исключения.

          Цель лекции: уметь решать системы ДУ методом исключений и с помощью характеристического уравнения.

 

          Рассмотрим систему дифференциальных уравнений первого порядка, разрешенных относительно производной, т.е.

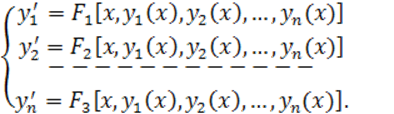                                                                                  (7.1)

Система (7.1) называется нормальной системой дифференциальных уравнений первого порядка.

         Решением системы (7.1) называется совокупность из n функций y₁, y₂, …, y_n, удовлетворяющих каждому из уравнений этой системы.

         Начальные условия для системы (7.1) имеют вид

                                 .                            (7.2)

         Задача Коши для системы (7.1) ставится следующим образом:

найти решение системы (7.1), удовлетворяющее начальным условиям (7.2).                              Метод  исключения.  (Структура общего решения).

        Нетрудно показать, что нормальная система n уравнений первого порядка приводится к одному уравнению n-го порядка относительно одной неизвестной функции.

        Продифференцируем по x первое уравнение системы (7.1), как сложную функцию (n+1) переменных:

                               .

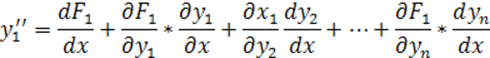        Подставим вместо производных  правые части системы  

c=1, 2, 3, …, n-1, тогда получим

                 

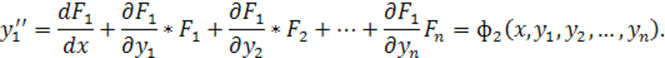
         Еще раз продифференцируя n раз и исключая y₂, y₃, …, y_n из получаемых уравнений, получим дифференциальное уравнение n-го порядка относительно одной функции:

                                                                    

                                                                 

          Пример:

.

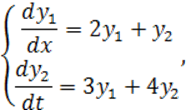
        Найдем y₁ из второго уравнения:

.

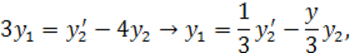
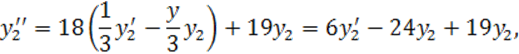
         Получили однородные ЛДУ второго порядка с постоянными коэффициентами, которое решается

,

,

.

 

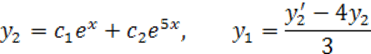          7.1 Система ЛДУ с постоянными коэффициентами

 

          Рассмотрим нормальную систему ЛДУ первого порядка с постоянными коэффициентами:

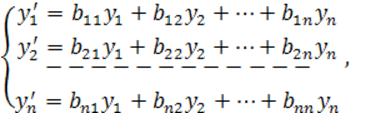                                                                                 (7.1.1)

         где a_ij, i; j=1, 2, …, n – постоянные числа. Требуется найти решение этой системы ДУ.

         Метод Эйлера. Будем искать решения в виде

                                                                   .                                                                             (7.1.2)

         Найдем их производные  

и подставим при i=1 в первое уравнение системы дифференциальных уравнений (7.1.1):

                                  .

         Сокращая на exp, получим:

                                          .

         Поступая аналогично с остальными уравнениями, получим систему однородных линейных алгебраических уравнений следующего вида:

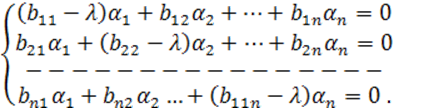                                                                     (7.1.3)

         Данная однообразная система линейных алгебраических уравнений имеет ненулевое решение тогда, когда главный определитель системы равен нулю, т.е.

                                                  

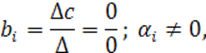
                                                                                         (7.1.4)

         Уравнение (7.1.4) называется характеристическим уравнением n-го порядка системы ЛДУ (7.1.1). Это уравнение имеет ровно n корней.

         Предположим, что характеристическое уравнение имеет n различных действительных корней λ₁, λ₂, … , λ_n.

         Для одного корня λ  получим соответствующую однородную систему алгебраических уравнений (7.1.3)

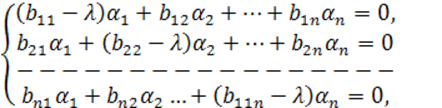                                                                    (7.1.5)

 

которая имеет ненулевое решение:

         Аналогично, для второго корня λ₂ имеем:

          Подставляя в однородную систему алгебраических уравнений (7.1.3) соответствующие решения характеристического уравнения (7.1.2) λ₁, λ₂, … , λ_n, будем получать n разных однородных систем алгебраических уравнений относительно неизвестных чисел λ₁, λ₂, … , λ_n.  Решая эти алгебраические системы, получим соответствующие решения системы дифференциальных уравнений. Тогда общее решение системы ЛДУ (7.1.1) определяется формулами:

                                   .

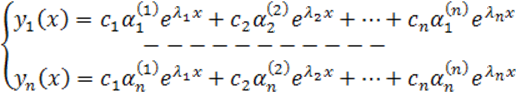           Пример 1: решить систему ЛДУ с постоянными коэффициентами:

.

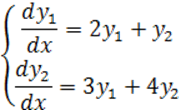          Составим характеристическое уравнение (7.1.4):

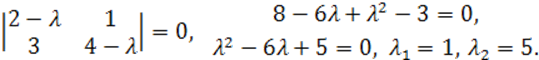
          Составим соответствующие однородные системы алгебраических уравнений:

.

          Тогда общее решение представляется по формуле (7.13) в виде:

.

 

          8 Лекция №8. Ряды

 

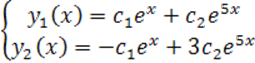          Содержание лекции: числовые ряды. Основные понятия. Знакоположительные ряды. Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.

         Цель лекции: ознакомить студентов с понятием числовых рядов, показать примеры исследования рядов на сходимость. Бесконечные числовые ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.

 

         8.1 Числовые ряды. Сходимость рядов

 

    Определение: Выражение вида

                                                                   (8.1.1)

называется числовым рядом, числа

                                           -                                                     (8.1.2)

членами ряда,  – общим членом.

    Обычно общий член ряда описывается как некоторая функция от своего номера, как общий член числовой последовательности

.

    Определение. Числовой ряд называется сходящимся, если последовательность

                                                                                                (8.1.3)

его частичных сумм имеет конечный предел

                                                                                                          (8.1.4)

    Определение. Числовой ряд называется расходящимся, если последовательность его частичных сумм не имеет предела (последовательность стремится к бесконечности или  колеблющаяся).

    Содержание теории числовых рядов состоит в установлении сходимости или расходимости числового ряда, а также в нахождении суммы ряда. Для этого каждый раз необходимо составлять аналитическое выражение для -ой частичной суммы ряда и находить его предел.

Пример1: исследовать сходимость ряда

                                           

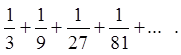
    Решение: в начале необходимо написать формулы общего члена и n-ой частичной суммы. Как видно, члены этого ряда являются членами бесконечно убывающей геометрической прогрессии ,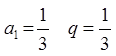

поэтому        .

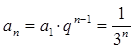n-ю частичную сумму находим, как сумму убывающей геометрической прогрессии

.

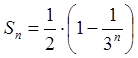   Следовательно, .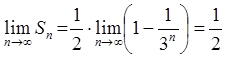

Этот ряд сходится, и его сумма равна .

 

         8.2 Признаки сходимости

      

   Исследование сходимости по определению весьма трудоемкий процесс, из-за необходимости нахождения суммы ряда. К тому же при решении практических задач сумма ряда нередко не представляет особого интереса. Поэтому достаточно установить сходимость или расходимость ряда без предварительного нахождения суммы ряда.

   Необходимый признак сходимости. Если ряд (8.1.1) сходится, то

                                                           .                                                      (8.2.1)

   Теперь укажем достаточные признаки сходимости. Пусть даны два числовых ряда 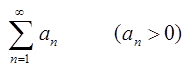                 ,                                                             (8.2.2)

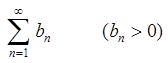                                           .                                                  (8.2.3)       Признак сравнения. Пусть для общих членов рядов (8.2.2) и (8.2.3) выполняется:

                                                            £.                                                  (8.2.4)

    Тогда:

    1) если ряд (8.2.3) сходится, то сходится и ряд (8.2.2);

    2) если ряд (8.2.2) расходится, то расходится и ряд (8.2.3).

    При использовании этого признака сходимость ряда (8.2.3) или расходимость ряда (8.2.2) предварительно должна быть установлена.

    Пример 1: рассмотрим ряд

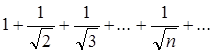
    покажем, что этот ряд является расходящимся.

    Решение: известно, что гармонический ряд расходящийся и его общий член имеет вид . Сравним общий член гармонического ряда с общим членом рассматриваемого ряда

.

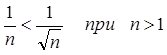    Поэтому, согласно признаку сравнения рассматриваемый ряд – расходящийся.

    Замечание. Признаки сравнения применимы и в том случае, когда условию (8.8) удовлетворяют члены рядов не при всех n, а лишь с некоторого номера n=m.

    Предельный признак сравнения.

    Если для рядов (8.2.2) и (8.2.3) выполняется

,

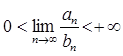то ряды (8.2.2) и (8.2.3) либо оба сходятся, либо оба расходятся.

    Признак Даламбера.

    Пусть для ряда (8.1.1) существует предел

                                                        .                                                (8.2.5)

    Тогда:

1)    при q<1 данный ряд сходится;

    2) при q>1 данный ряд расходится;

    3) в случае q=1 ответ на вопрос о сходимости или расходимости ряда признак не дает ответа.

    Интегральный признак Коши.

    Пусть члены ряда (8.2.2) монотонно убывают и функция непрерывная и . Тогда ряд (8.2.2) и несобственный интеграл 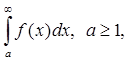 одновременно сходятся или расходятся.

    Пример 4: исследовать сходимость ряда

.

    Решение: при s=1получим гармонический ряд. Положим . Эта функция удовлетворяет условиям интегрального признака Коши. Тогда несобственный интеграл

.

1)  В случае s>1 имеем 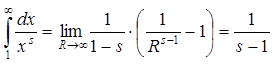, т.е. интеграл конечен, и, следовательно, ряд сходится.

2)  В случае s<1 имеем 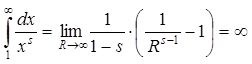, значит, ряд расходится.

     Поэтому, ряд

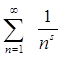
сходится при s>1 и расходится при s£1. Этот ряд называется обобщенно-гармоническим.

     Радикальный признак Коши.

     Если для ряда (8.2.2) выполняется   ,                                           (8.2.6)

то:

     1) при  ряд сходится;

          2) при  ряд расходится;

 

          8.3 Знакопеременные ряды

 

    Знакопеременным рядом называется ряд, членами которого являются числа произвольного знака.

    Пусть                                                                                          (8.3.1)

– знакопеременный ряд. Составим ряд из членов ряда (8.1.1) членами которого являются абсолютные величины

                                                                                  (8.3.2)

    Определение. Знакопеременный ряд (8.3.1) называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов (8.3.2).

    Теорема. Если сходится ряд (8.3.2), то сходится и ряд (8.3.1).

    Если сходится ряд (8.3.2), то ряд (8.3.1) называется абсолютно сходящимся. Если же расходится ряд (8.3.2), а ряд (8.3.1) сходится, то ряд (8.3.1)  называется  условно сходящимся.

          Признак сходимости Лейбница.

    Теорема. Если абсолютные величины членов знакочередующегося ряда

                                                                       (8.3.3)

образуют монотонно не возрастающую последовательность, стремящуюся к нулю, т.е. если

                                                                                    (8.3.4)

    и

                                                 ,                                                      (8.3.5)

то знакочередующийся ряд сходится.

    Следствие. Если знакочередующийся ряд  удовлет­воряет  признаку сходимости Лейбница, то остаток  ряда оценивается с помощью неравенства                               .                                                                         (8.3.6)

         Пример: исследовать на сходимость ряд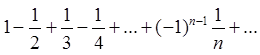

    Решение: этот ряд знакочередующийся. Проверим выполнение условий сходимости  по признаку Лейбница:

1) 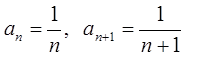    и ;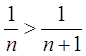

2)    .

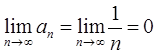    Оба условия признака Лейбница выполняются. Поэтому, ряд сходится.

 

          9 Лекция №9. Функциональные ряды. Степенные ряды

 

          Содержание лекции: область сходимости функционального ряда, сумма ряда, оьласть сходимости степенного ряда, интервал и радиус сходимости степенного ряда, теорема Абеля. Ряды Тейлора и  Маклорена, разложение функций в степенные ряды.

          Цель лекции: дать понятия часто применяемых в приближенных вычислениях определенного интеграла функциональных, степенных рядов.

 

    Выражение вида

                              ,                           (9.1)

где – последовательность функций от х, называется функциональным рядом.

    Степенным рядом называется ряд

                          ,                     (9.2)

члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням х, здесь – постоянные числа. При   x₀  получим, что

                           .                                             (9.3)

    Определение. Совокупность всех значений , для которых ряд (9.1) сходится, называется областью сходимости функционального ряда.

    Для степенного ряда (9.3) существует такое неотрицательное число R, что при  или  ряд расходится, при  – сходится, а поведение ряда при  подлежит дальнейшему анализу.

   Число  называется радиусом сходимости.

   Для ряда (9.2) интервал сходимости имеет вид .

   Если существует предел

                                             ,                                                          (9.4)                       или

                                                ,                                                     (9.5)                  то .

   Пример 1: найти область сходимости степенного ряда

    Решение: находим коэффициенты

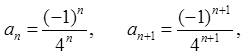
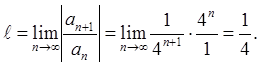
   Следовательно, 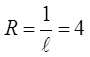. Значит,  интервал сходимости записывается в виде ; .

   Теперь исследуем сходимость ряда на концах интервала сходимости.

   1. При х = -1 имеем

.

  Общий член имеет постоянное значение. Поэтому этот ряд расходится.

   2. Пусть теперь х=7:

.

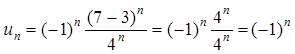   Это члены знакочередующегося ряда.

.

   Этот ряд расходящийся, поэтому область сходимости имеет вид
(-1;7).

   В случаях, когда ряд содержит только четные или нечетные степени,  радиусы интервалов сходимости определяются непосредственным применением либо признака Даламбера, либо признака Коши, т.е. из условий:

                        ,

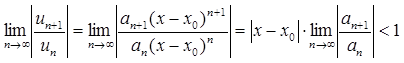   либо

.

 

          9.1 Разложение функций в ряды Тейлора и Маклорена

 

    Представление функции  в виде ряда

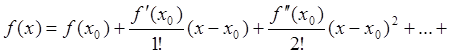                                          (9.1.1)

называется разложением этой функции в ряд Тейлора. При  разложение в ряд Тейлора называется разложением в ряд Маклорена

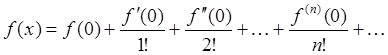                                               (9.1.2)

    Разложение заданной функции  в ряд Тейлора (Маклорена) в окрестности точки  (=0) распадается на два этапа:

    1) Сначала вычисляются значения функции и ее производных в точке  и составляется ряд Тейлора для функции. При этом предполагается, что функция  бесконечно дифференцируема.

    2) Находится интервал, в котором составленный ряд Тейлора сходится к функции , т.е. устанавливается, для каких значений  остаточный член ряда  будет стремится к нулю при .

    Теорема. Если функция  имеет производные сколь угодно высоких порядков и существует такая постоянная С, что при любых  и

,                                                                                                    (9.1.3)

то функция  разлагается в ряд Тейлора при любом .

    Разложение функций в ряд Маклорена:

         1) 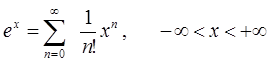                                                           (9.1.4)

         2) 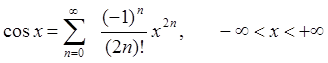                                                 (9.1.5)

         3)                                              (9.1.6)

    4)  

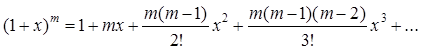
+,                                               (9.1.7)

     5) 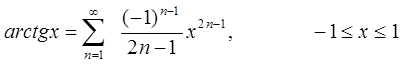                                   (9.1.8)

     6) 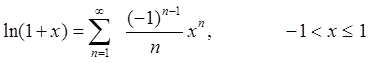                                         (9.1.9)

 

          9.2 Приближенное вычисление значений функции

 

    Пусть доказано, что функция разлагается в ряд Маклорена, тогда точное значение этой функции в любой точке в окрестности точки  можно вычислить по ряду Маклорена, а приближенное значение этой функции по частичной сумме ряда. Возникающую при этом ошибку можно оценить либо опираясь на теорему об оценке остаточного члена, либо непосредственно оценивая остаток ряда. Если же получающийся числовой ряд знакочередующийся, то это делается при помощи теоремы Лейбница; в случае знакоположительного ряда необходимо подобрать другой ряд (обычно ряд, составленный из членов бесконечно убывающей геометрической прогрессии), члены которого больше  членов остатка и сумму которого мы можем найти.

         Пример: вычислить  с точностью 0,001.

    Решение: для приближенного вычисления используем разложение (9.9), а для определения точности вычисления формулу (9.1.4). Точность определим путем подбора  так, чтобы выполнялось неравенство

.

   Пусть , тогда 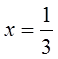и из (9.1.4) получим

.

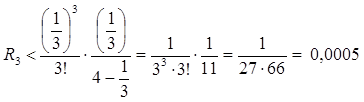   Следовательно, , т.е. если в разложении возьмем , то заданная точность обеспечивается:

 .

 

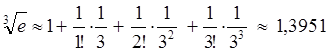       10 Лекция №10. Ряды Фурье

 

         Содержание лекции: разложение функций в тригонометрические ряды Фурье. Ряды Фурье в произвольном промежутке.

         Цель лекции: дать понятие ряда Фурье, применяемого при изучении разнообразных периодических процессов, привести примеры разложения функций в ряды Фурье.

 

         10.1 Тригонометрический ряд Фурье

 

         Тригонометрическим рядом называется функциональный ряд вида

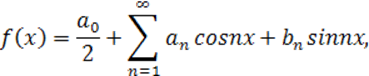                                                                           (10.1.1)

         где действительные числа a₀, a_n, b_n (n=1,2,…) называются коэффициентами ряда. Вычислим коэффициенты a_n и b_n. Для этого проинтегрируем обе части равенства (10.1) в пределах от –π до π:

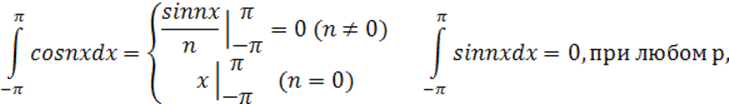
Отсюда
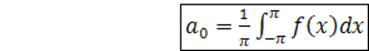                                                      (10.1.2)

         Умножив обе части равенства (10.1.1) на cosmx и проинтегрировав полученный ряд в пределах от-π до π, получим:   

 

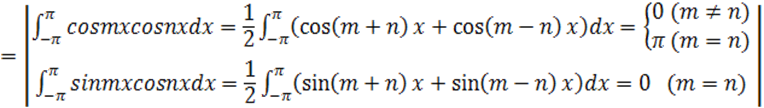
Отсюда 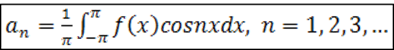    .                              (10.1.3)

         Аналогично, умножив равенство (10.1.1) на sinmx и проинтегрировав почленно на отрезке [-π;π], найдем:               
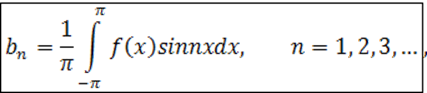                                                             (10.1.4)

  где
.

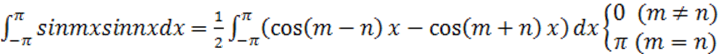         Семейство функций

обладает свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину 2π, равен нулю.

         Числа a₀, a_n, b_n, определяемые по формулам (10.1.1-10.1.3), называются коэффициентами Фурье функции f(x), а тригонометрический ряд (10.1.1) с такими коэффициентами – рядом Фурье функции f(x).

         Для интегрируемой на отрезке [-π;π] функции f(x) записывают

                                         ,

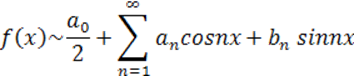и говорят: функции f(x) соответствует ее ряд Фурье. Если ряд сходится, то его сумму обозначим S(x).

          Будем рассматривать функции f(x), имеющие период Т=2π. Такие функции называют 2π-периодическими. Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.

         Теорема Дирихле. Пусть 2π-периодическая функция f(x) на отрезке [-π;π] удовлетворяет двум условиям:

1.              1) f(x) кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва 1 рода;

2.              2)f(x) кусочно-монотонна, т.е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.

          Тогда, соответствующий функции f(x) ряд Фурье сходится на этом отрезке и при этом:

1.               1) в точках непрерывности функции сумма ряда S(x) совпадает с самой функцией: S(x)=f(x);

2.               2) в каждой точке х₀ разрыва функции сумма ряда равна

                                                         

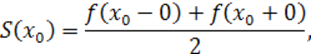
     арифметическому пределов функции f(x).                                                  

3.              В точках х=-π и х=π (на концах отрезка) сумма ряда равна:

                                                   .

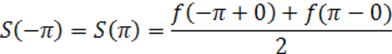          Таким образом, если функция f(x) удовлетворяет условиям 1 и 2 теоремы (условия Дирихле), то на отрезке [-π; π] имеет место разложение (10.1.1).

 

           10.2 Разложение в ряд Фурье четных и нечетных функций

 

           Если функция f(x) четная, то ее ряд Фурье  имеет вид

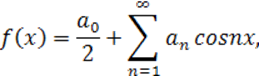                                                                                         (10.1.5)

           где  

             Если функция f(x) нечетная, то ее ряд Фурье имеет вид

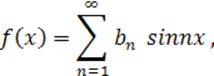                                                                                                (10.1.6)

            где                                                      
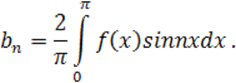                                                                            (10.1.7)

          Если функция f(x) – четная, то f(x)cosnx – четная функция: , а f(x)sinnx – нечетная функция: .

          Если же f(x) – нечетная функция, то очевидно, что функция f(x)cosnx – нечетная, а f(x)sinnx – четная.

                             .

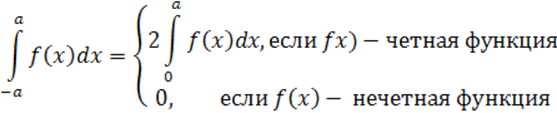          Ряды (10.1.5) и (10.1.6) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам, соответственно.

         Если функция f(x) – периодическая с периодом 2π, то справедлива следующая формула:

                                                       

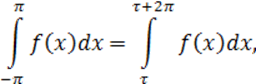
          где  – произвольное число.

 

         10.3 Ряд Фурье на произвольном промежутке

 

         Пусть дана функция f(x) – периодическая, с периодом 2λ. Требуется разложить эту функцию в ряд Фурье на отрезке [-λ;λ]. 

         Рассмотрим функцию . Эта функция является периодической с периодом 2π по аргументу t, т.к. t=π, то f(λ), t=-π, то f(-λ).

         Следовательно, ее можно разложить в ряд Фурье на отрезке [-π; π], т.е.

                                           

    где коэффициенты определяются формулами

                                                         ,

                                                       ,

                                                         .

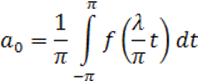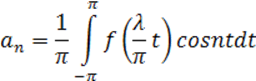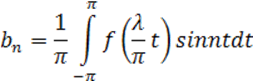         Перейдем в формулах коэффициентов к старой переменной x:

                                   

                                          

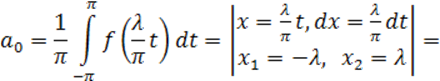
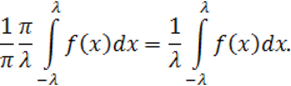
         Аналогично определяются коэффициенты

                      ,

                      .

         Таким образом, получили ряд Фурье для периодической функции на отрезке [-λ;λ]:

 .                             (10.1.8)

              

         11 Лекция №11. Элементы теории вероятностей. Случайные события

 

         Содержание лекции: основные понятия и определения теории вероятностей. Случайные события. Вероятность событий. Условная вероятность. Формула полной вероятности. Формула Байеса. Схема испытаний Бернулли.

         Цель лекции: ознакомить с основными понятиями теории вероятностей, методами и способами вычисления вероятности.

 

         11.1 Основные понятия. Виды событий

 

     Теория вероятностей–математическая наука, изучающая закономер-ности случайных явлений. В повседневной жизни вы оказываетесь свидетелями различных событий. Например, вы проходите тестирование по математике. В результате вы успешно сдали экзамен. Это-событие. Из ящика, содержащего одинакового размера шары белого и синего цветов наугад извлекается один шар. В результате может быть извлечен шар белого или синего цвета. Это также событие.

     Рассмотренные примеры показывают, что событие происходит в результате проведенного испытания. События обозначаются буквами А, В, С,...и т. д.

         Таким образом, результат испытания в теории вероятностей называется событием. 

         Случайное событие - это такое событие, которое в результате опыта может произойти  и не произойти (например, выпадение 3-х очков при бросании игрального кубика, выигрыш по лотерее, результат встречи двух футбольных команд равного рейтинга и др.).

         В общем случае с событиями связываются некоторые числа, характеризующие степень возможности появления события, называемые вероятностями. Вероятность события обозначают через Р(А).

         Для каждого опыта можно указать некоторую совокупность (множество) взаимно исключающих событий, причем в результате опыта должно обязательно появиться какое-нибудь одно из этих событий. Такая совокупность событий  называется пространством элементарных событий и обозначается буквой Ω, а элементы этого пространства- буквой , где   - элементарные события.

         Пространство Ω может быть конечным, бесконечным счетным или несчетным  множеством. Пространство элементарных событий Ω считается заданным, если указаны все  его элементы:  .

         Подмножества пространства элементарных событий Ω называются случайными событиями. Случайные события обозначаются буквами А, В, С, .... Таким образом, А . Элементарные события  входящие в состав случайного события А, называются благоприятствующими  появлению события А. Если  А=, то событие А называется достоверным, т.е. при проведении испытания достоверное событие А обязательно произойдет. Событие называется невозможным, если в результате испытания оно заведомо не произойдет.

        Если 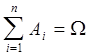, то группа событий A₁, A₂, ..., A_n  называется полной группой. Отсюда следует, что в результате опыта обязательно произойдет одно из событий, образующих полную группу.

        Два события, образующих полную группу называются противопо-ложными. Событие противоположное событию А обозначается буквой . Таким образом, A+=Ω.

         Суммой А+В двух событий А и В называется событие, состоящее в появлении хотя бы одного из этих событий.

         Произведением АВ двух событий А и В называется событие,  состоящее в совместном появлении этих событий.

         Аналогично определяется сумма и произведение конечного числа событий. Операции сложения и умножения событий обладают свойствами, присущими обычным операциям сложения и умножения.

         Если в результате  испытания появление или непоявление  события А не оказывает влияния  на появление или непоявление  события В, то эти два события называются независимыми. В противном случае, эти события называются зависимыми. Появление «герба» или «цифры» при бросании монеты являются примерами независимых событий.  Два события А и В называются несовместными, если появление одного из них исключает появление другого. Если для событий A₁, A₂, ..., A_n  выполняются P(A₁)= P(A₂)=...= P(A_n), то события A₁, A₂, ..., A_n  называются равновозможными.

         Множество В является подмножеством множества А , если все элементы множества В содержатся во множестве А.

        Объединением (суммой) множеств А и В называется множество С=А+В, состоящее из всех элементов А и всех элементов В.

         Пересечением (произведением) множеств  А и В называется множество D=A, состоящее из элементов входящих одновременно и в А и в В.

   Определение (классическое определение вероятности).

        Вероятностью события А называется отношение числа равно-возможных элементарных событий, благоприятствующих появлению события А, к общему числу равновозможных элементарных событий данного опыта:

                                                   P(A)=m/n.                                                (11.1.1)

        Из этого определения при m=n получим, что если А=Ω,то Р(А)=Р(Ω)=1, т.е. вероятность достоверного события равна 1, а при m=0 имеем Р(А)=0 следовательно– вероятность невозможного события равна 0. Таким образом, вероятность любого события заключена между нулем и единицей:

0 P(A)  1.

         Классическое определение вероятности применимо только в тех случаях, когда результаты испытания являются равновозможными элементарными событиями конечного числа. Обычно испытания, результаты которых являются равновозможными элементарными событиями, обладают симметрией. Так, например, игральная кость симметрична (имеет форму правильного многогранника). Однако в случаях, когда результаты испытаний нельзя представить в виде конечного числа элементарных событий, классическое определение вероятности не применимо.

     В таких случаях используют другое определение вероятности, а именно, статистическое определение вероятности.

    Определение. Статистической вероятностью события А называется   относительная частота появления этого события в n произведенных испытаниях.

     Статистическую вероятность обозначают через.Тогда  =W(А)=m/n, где W(А)- относительная частота события А, m – число испытаний, в которых появилось событие А в произведенных испытаниях, n – общее число произведенных испытаний.

     Статистическая вероятность обладает теми же свойствами, что и вероятность Р(А) события.

 

     11.2 Элементы комбинаторики

 

     Определение. Размещениями из n элементов по к элементов называются такие комбинации, каждая из  которых содержит к элементов, и отличаются друг от друга  либо составом, либо порядком расположения этих элементов.

    Общее число размещений из n  элементов по к элементов определяется по формуле

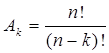                                                                                              (11.2.1)

Здесь  (читается “эн факториал”) также принято, что  0!=1

    Определение. Перестановками из данных n элементов называются такие комбинации, каждая из которых содержит все n данных элементов, и отличаются друг от друга только порядком расположения.

    Общее число перестановок определяется по формуле

                                                                    (11.2.2)

    Определение. Сочетаниями из n элементов по к элементов называются такие комбинации, каждая из которых содержит к элементов, и отличаются друг от друга только составом элементов.

    Общее число сочетаний определяется по формуле

                                                                                        (11.2.3)

    Подчеркнем, что число размещений, перестановок и сочетаний связано равенством

    Действительно,

                                 .

     При решении комбинаторных задач часто используются следующие два правила:

     Правило сложения. Если некоторый элемент  можно выбрать m способами, а другой элемент  – n способами, исключающими друг друга, то выбор какого-нибудь одного из этих элементов (либо a, либо b) можно осуществить  m+n  способами.

    Правило умножения. Если имеется m элементов одной группы и n элементов другой группы, то число различных упорядоченных пар, содержащих один элемент первой группы и один элемент второй группы, равно произведению m*n.

 

    11.3  Теорема умножения вероятностей

 

   Два события называются независимыми, если появление одного из них не изменяет вероятности другого. В противном случае события  А и В называются зависимыми. 

  Определение. Вероятность события В, найденная в предположении, что событие А наступило, называется условной вероятностью  события В. Условная вероятность события В обозначается через  .        

   Если  и , т.е. условная вероятность равна безусловной вероятности события, то события  А и В независимы.

   Найдем формулу для вычисления условной вероятности  .

   Пусть  общее число элементарных событий в данной серии испытаний. - число элементарных событий благоприятствующих событию А, - благоприятствующих событию В. Если пояление В зависимо от А, то число элементарных событий, благоприятствующих появлению события АВ равно . Таким образом, имеем , .

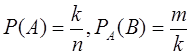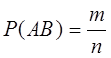   Теперь, преобразовав второе равенство, получим

.

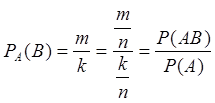   Тем самым доказали следующую теорему.

   Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого:

                                             .                                  (11.2.4)

   Теорема. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

.                                    (11.2.5)

    

    11.4 Теорема сложения вероятностей

 

    Если события А и В несовместные, то вероятность суммы равна сумме вероятностей этих событий:

                                   .                                 (11.4.1)          

    Если события  А и В совместные, то вероятность суммы равна сумме вероятностей этих событий без вероятности их совместного появления:

                            .                    (11.4.2)

     Теорема о вероятности появления хотя бы одного события.

     Если события   A₁, A₂, A₃, A₄,..., A_n независимые в совокупности и А событие, состоящее в появлении хотя бы одного из них, то вероятность события А равна

                            .                 (11.4.3)

     В частном случае, когда вероятности событий A₁, A₂, A₃,..., A_n  равны, т.е.

                               ,

     имеем                   .                                                       (11.4.4)

 

         11.5 Формула полной вероятности. Формула Байеса

 

         Если событие А может наступить вместе с одним из событий В₁, В₂,...,В_n несовместных, образующих полную группу событий, то вероятность события А находится по формуле полной вероятности:

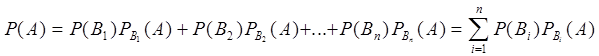.     (11.5.1)

Здесь условные вероятности события А. Если необходимо произвести количественную оценку априорных вероятностей событий  В₁, В₂,...,В_n    известных до испытания, т.е. найти апостериорные (получаемые после проведения испытания) условные вероятности , то используется формула Байеса

 ,                                (11.5.2)

где Р(А) находится по (11.5.1).

          Замечание. При использовании формул (11.5.1) и (11.5.2) необходима проверка несовместности гипотез В₁, B₂, ..., B_{n  ,}  а  также проверка, что В₁, B₂, ..., B_n  образуют полную группу.         

         

          11.6  Последовательность независимых испытаний

 

         Пусть производится n испытаний. Если вероятность появления события А в каждом испытании не зависит от  результатов предыдущих испытаний, то такие испытания называют независимыми испытаниями относительно события А.

         В общем случае событие А в каждом испытании может появиться с различной вероятностью. Ниже рассмотрим независимые испытания в результате которого может появиться либо событие А  с постоянной вероятностью P(A)=p , либо событие  с вероятностью  . Такая последовательность испытаний называется схемой Бернулли. К таким испытаниям относятся такие испытания как бросание монеты, проверка качества изделий и.т.д.

         Формула Бернулли.  В общем случае вероятность появления события А ровно k раз в nнезависимых испытаниях в схеме Бернулли находится по формуле Бернулли

          ,                                       (11.6.1)

где  p=P(A), q=1-p= , 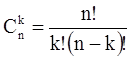– число сочетаний из n элементов по k элементов. В рассмотренном примере n=3, k=2 , т.е. из (11.6.1) получим              Р₃(2) = 3р²q.

         Число появлений раз события в n независимых испытаниях называется наивероятнейшим, если вероятность появления события   раз является наибольшей или по крайней мере не меньше каждого в остальных возможных появлениях события.

         Наивероятнейшее число появления события А в n независимых испытаниях находится из двойного неравенства

                                        ,                                             (11.6.2)

         если np-q равно целому числу, то  имеет два значения, если np-q равно дробному числу, то  имеет одно значение.

         Используя формулу Бернулли можно определить вероятность следующих  событий:

1.             1) вероятность появления события менее k раз

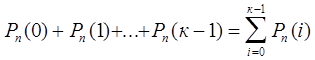                          ;                                   (11.6.3)

         2) вероятность появления события более k раз

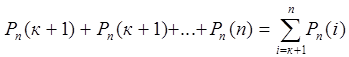                           ;                             (11.6.4)

         3) вероятность появления события  не менее k раз

                      ;                                (11.6.5)

         4) вероятность появления события  не более k раз

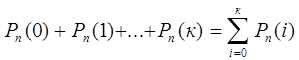                       .                                  (11.6.6)

         Вероятность появления события А хотя бы один раз в n независимых испытаниях в схеме Бернулли равна      P=1-qⁿ                                                           (11.6.7)

         Если число испытаний велико, то пользоваться формулой Бернулли достаточно трудно, так как в этих случаях она приводит к большим вычислениям. Поэтому в этих случаях используют формулы, которые позволяют приближенно найти вероятность появления события ровно k раз в n независимых испытаниях.

         Локальная теорема Муавра- Лапласа. Если вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится ровно k  раз в n независимых испытаниях приближенно находится по формуле

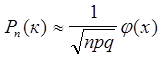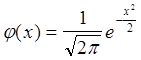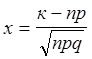   , , .                               (11.6.8)

Для функции φ(х) в конце книги дана таблица значений.

         Интегральная теорема Муавра-Лапласа. Если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность  того, что событие А появится в n независимых испытаниях от к₁  раз до к₂ раза приближенно находится по формуле

                          

                                                                     (11.6.9)

из формулы (11.6.8)  следует, что φ(х) четная функция, а из формулы (11.6.9) следует что Ф(х_i)  нечетная функция.

         Используя формулу (11.6.9) можно приближенно найти вероятность отклонения относительной частоты от постоянной вероятности P  события А в n независимых испытаниях:

                        .                                   

         Если же вероятность появления события А мала, а число испытаний велико, то используют формулу Пуассона:

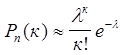                                     ,  λ=np.                                       

 

Список литературы

 

1 Хасеинов К.А. Каноны математики.-Алматы.: ММШ, 2003,- 683 с.

2. Натансон И.П. Краткий курс высшей математики. – М.: Наука, 1997.

3. Шипачев В.С. Высшая математика. – М.: Высшая школа, 1985. –369 с.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления ФНП для ВТУЗов. Т.2. – М.: Наука, 1985. – 432 с.

5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1985.

6. Гмурман В.Е. Руководство к решению. Задач по теории вероятностей и математической статистике.- М: Высшая школа, 1979,- 400 с.

 

Содержание

 

1 Лекция №1. Дифференциальное исчисление ФНП 

2 Лекция №2. Двойные интегралы 

3 Лекция №3. Тройные интегралы 

4 Лекция №4. Дифференциальные уравнения (ДУ) первого порядка. Задача Коши. Основные классы ДУ первого порядка

5 Лекция №5. ДУ второго порядка. Задача Коши. ДУ, допускающие понижение порядка.  ЛОДУ с постоянными коэффициентами 

6 Лекция №6. ЛНДУ с постоянными коэффициентами 

7 Лекция №7. Системы ДУ 

8 Лекция №8. Числовые ряды 

9 Лекция №9.  Функциональные ряды. Степенные ряды, теорема Абеля 

10 Лекция№ 10. Ряды Фурье 

11 Лекция №11.  Элементы теории вероятностей. Случайные события  

Список литературы
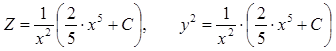