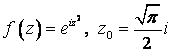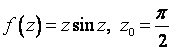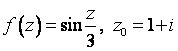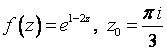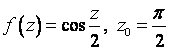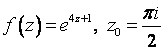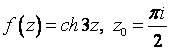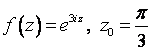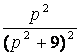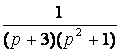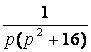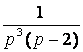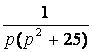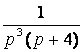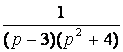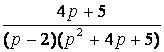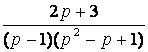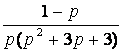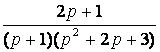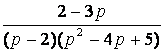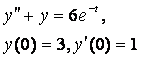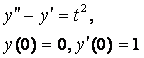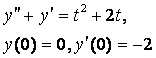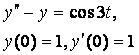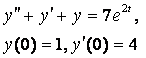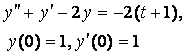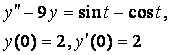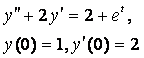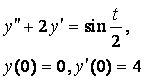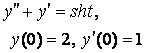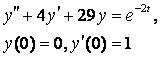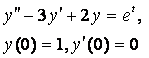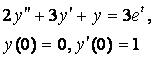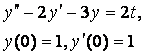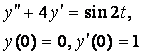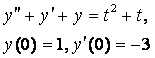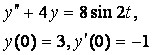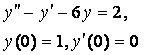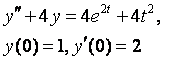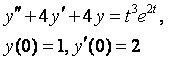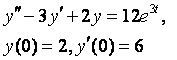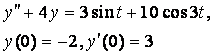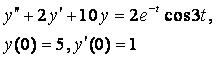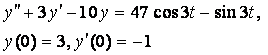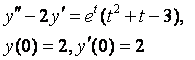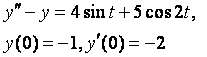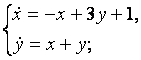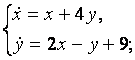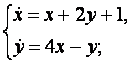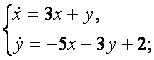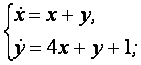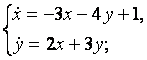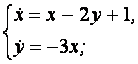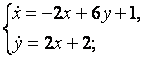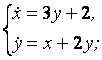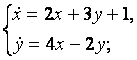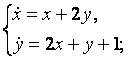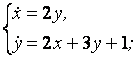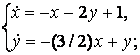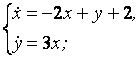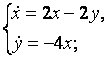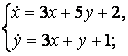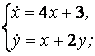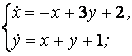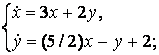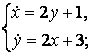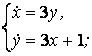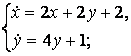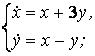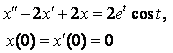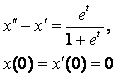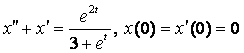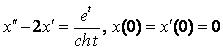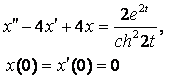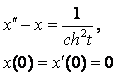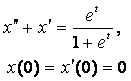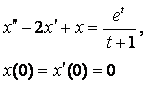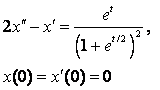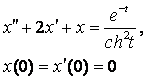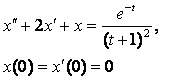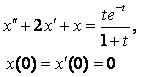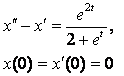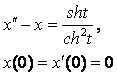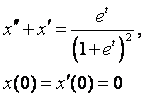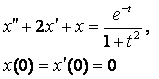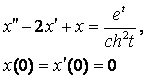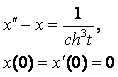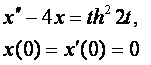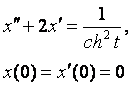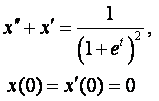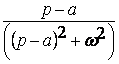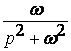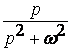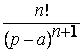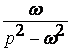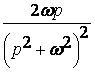Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

Математика 3

Методические указания и задания к выполнению расчетно-графической  работы для студентов  всех специальностей

Часть 4

 

Алматы 2010

         СОСТАВИТЕЛИ:  Л.Н.Ким.  Математика 3.  Методические указания и задания к выполнению расчетно-графических        работ для студентов  всех специальностей. Часть 4.-Алматы: АИЭС, 2010.-  30 с.

         Методические указания и задания к расчетно-графической работе содержат дополненное и переработанное издание типового расчета №8 программы второго семестра курса высшей математики для студентов всех специальностей дневного отделения АИЭС 2002 года. Приведены основные теоретические вопросы программы, варианты заданий и решение типового варианта. Расчетные задания разделены на два уровня сложности.

         Методические указания предназначены для студентов первого курса всех форм обучения всех специальностей.

       

Введение

         Методические указания представляют собой программу,  задания  к  модулю 4  «Ряды »  Математики 3 и решение типового варианта.  Задания состоят из  тридцати вариантов. Вторая цифра номера задания указывает вариант студента.

         Вариант задания  контрольной работы для студентов, обучающихся по заочной форме, определяется как остаток от деления номера зачетной книжки на 30. Например: номер зачетной книжки равен 080612. Это число представляется в виде: 080612=2687*30+2. Следовательно, студент должен выполнить задания варианта №2. Если остаток равен нулю, то студент выполняет вариант №30. 

         Контрольная работа должна быть решена в отдельной тетради, решение задач должно быть кратким и, в то же время, достаточно объяснено ссылками на теорию и сопровождено необходимыми рисунками. Примером для оформления контрольной работы может служить решение типового варианта, которое приведено в данном методическом указании.

 

         1  Типовой расчет  4.   Функции комплексного переменного.  Операционное исчисление

 

1.1    Теоретические вопросы

 

1        Функции комплексного переменного. Условия Коши-Римана.

         2   Преобразование Лапласа. Оригиналы и изображения.

         3   Теоремы линейности, подобия, смещения, запаздывания.

         4   Теоремы дифференцирования и интегрирования оригиналов и изображений.

         5   Свёртка функций. Теорема умножения. Формула Дюамеля.

         6 Теорема обращения. Нахождение оригинала по известному изображению.

         7   Применение преобразования Лапласа при решении дифференциальных уравнений и систем.

 

1.2              Расчетные задания первого уровня

 

         1.  Представить  заданную функцию   , где   , в виде      ;  проверить,  является ли она аналитической.  Если да, то найти значение её производной в заданной точке   .

Т а б л и ц а 1

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10

1.11

1.12

1.13

1.14

1.15

1.16

1.17

1.18

1.19

1.20

1.21

1.22

1.23

1.24

1.25

1.26

1.27

1.28

1.29

1.30

 

         2.  Является ли функция оригиналом или нет?   Если да,  то почему?

Т а б л и ц а 2

№

a) 

b) 

№

a)    

 b)  

2.1

2.2

2.3

2.4

2.5

2.6

2.7

 

2.8

2.9

2.10

2.11

 

2 12

2.13

 

2.14

2.15

2.16

2.17

2.18

2.19

 

2.20

2.21

2.22

2.23

 

2.24

2.25

2.26

2.27

 

2.28

2.29

 

2 30

 

         3. Найти изображение функции, пользуясь теоремами линейности, подобия, смещения, запаздывания.

Т а б л и ц а 3

№

 

 

 

 

3.1

 

3.2

 

3.3

 

3.4

 

3.5

 

3.6

 

3.7

 

3.8

 

3.9

 

3.10

 

3.11

 

3.12

 

3.13

 

3.14

 

3.15

 

3.16

 

3.17

 

3.18

 

3.19

 

3.20

 

3.21

 

3.22

 

3.23

3.24

 

3.25

 

3.26

 

3.27

 

3.28

 

3.29

 

3.30

 

         4 .  Найти изображение функции, пользуясь теоремами дифференцирования изображения, интегрирования оригинала и изображения.

Т а б л и ц а 4

№

a)

б)

в)

4.1

4.2

4.3

4.4

4.5

4.6

4.7

4.8

4.9

4.10

4.11

4.12

4.13

4.14

4.15

4.16

4.17

4.18

4.19

4.20

4.21

4.22

4.23

4.24

4.25

4.26

4.27

4.28

4.29

4.30

         5.  Найти свёртку функций   и  и её изображение.

Т а б л и ц а 5

№

 

 

№

 

 

5.1

 

5.2

5.3

 

5.4

5.5

 

5.6

5.7

 

5.8

5.9

 

1

5.10

5.11

 

1

5.12

1

5.13

 

5.14

5.15

 

5.16

5.17

 

5.18

5.19

 

5.20

5.21

 

5.22

5.23

5.24

 

5.25

 

1

5.26

5.27

 

1

5.28

5.29

 

5.30

         6.  Найти оригинал  функции  , применяя теорему умножения изображений.

Т а б л и ц а 6

№

№

 

№

 

 

6.1

6.2

6.3

6.4

6.5

6.6

6.7

6.8

6.9

6.10

6.11

6.12

6.13

6.14

6.15

6.16

6.17

6.18

6.19

6.20

6.21

6.22

6.23

6.24

6.25

6.26

6.27

6.28

6.29

6.30

 

 

         7.  Найти оригинал по заданному изображению.

Т а б л и ц а 7

№

 

№

 

7.1

 

 

7.2

7.3

 

 

7.4

7.5

 

 

7.6

7.7

 

 

7.8

7.9

 

 

7.10

7.11

 

 

7.12

7.13

 

 

7.14

7.15

 

 

7.16

7.17

 

 

7.18

7.19

 

 

7.20

7.21

 

 

7.22

7.23

 

 

7.24

7.25

 

 

7.26

7.27

 

 

7.28

7.29

 

 

7.30

 

         8.   Методом операционного исчисления решить задачу Коши.

Т а б л и ц а 8

8.1  

             

8.2      

               

8.3                                         

8.4               

8.5            

8.6         

8.7                                                 

8.8              

8.9       

             

8.10          

8.11      

8.12            

8.13  

             

8.14    

               

8.15    

              

8.16      

                 

8.17    

             

8.18      

                   

8.19      

                 

8.20   

                 

 

8.21   

                   

8.22      

              

8.23   

        

8.24

          

8.25  

        

8.26

           

8.27 

             

8.28     

           

8.29

             

8.30        

     

 

         9.    Решить систему уравнений операционным методом.

Т а б л и ц а 9

9.1                  

9.2           

9.3         

9.4          

9.5         

9.6          

9.7            

9.8        

9.9     

9.10          

9.11      

9.12          

9.13        

9.14         

9.15       

9.16       

9.17         

9.18   

9.19  

9.21     

9.20    

9.22

   

9.23     

9.24      

9.25 

9.26       

9.27       

9.29  

9.28         

9.30  

        

         10.   По графику оригинала найти изображение.

 

  10.1

 

 

 

 

 

10.2

 

 

 

 

 

 

  10.3

 

 

 

 

 

10.4

 

 

 

 

 

 

  10.5

 

 

 

 

 

10.6

 

 

 

 

 

 

  10.7

 

 

 

 

 

 

10.8

  10.9

 

 

 

 

10.10

10.11

 

 

 

 

 

 

10.12

10.13

 

 

 

 

10.14

 

 

 

 

 

 

10.15

 

 

 

 

 

10.16

10.17

 

 

 

 

 

10.18

10.19

 

 

 

 

10.20

10.21

 

 

 

 

 

 

10.22

10.23

 

 

 

 

 

10.24

10.25

 

 

 

 

 

10.26

10.27

 

 

 

 

 

10.28

10.29          f(t)

 

 

 

                                                        

 

 

10.30

 

         1.3   Расчётные задания второго уровня

         11.  Найти изображение  функции , пользуясь определением.

Т а б л и ц а 10

№

 

№

№

 

№

 

 

11.1

 

11.2

11.3

11.4

11.5

 

11.6

11.7

11.8

11.9

 

11.10

11.11

11.12

11.13

 

11.14

11.15

11.16

11.17

 

11.18

11.19

11.20

11.21

11.22

11.23

11.24

11.25

11.26

11.27

11.28

11.29

 

11.30

11.31

11.32

         12.  Найти изображение функции, применяя теорему о дифференцировании оригинала.

Т а б л и ц а 11

№

 

№

№

 

№

 

12.1

12.2

12.3

12.4

12.5

12.6

12.7

12.8

12.9

12.10

12.11

12.12

12.13

12.14

12.15

12.16

12.17

12.18

12.19

12.20

12.21

12.22

12.23

12.24

12.25

12.26

12.27

12.28

12.29

12.30

12.31

12.32

 

         13  Найти решение задачи Коши с помощью формулы Дюамеля.

Т а б л и ц а 12

13.1

 

13.2

13.3

13.4

13.5

13.6

13.7

13.8

13.9

 

13.10

13.11

 

13.12

13.13

13.14

 

13.15

13.16

 

13.17

13.18

13.19

13.20

 

13.21

13.22

 

13.23

13.24

13.25

13.26

 

13.27

13.28

 

13.29

13.30

 

 

         1.4   Решение типового варианта

 

         1.   Вычислить значение функции    сh ( 2-3i).

        

         Решение:

         ch (2-3i) = 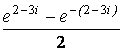=  [ e2(cos3-i sin3) – e-2( cos3 + i sin3)]=

=cos3 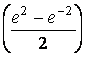 -i sin3  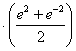 = cos3 sh2 - i sin3 ch2.                                                             

 

         2.  Проверить, является ли функция  аналитической. Если да, то найти ее производную в точке  

 

         Решение:

         Выделим действительную и мнимую части функции:

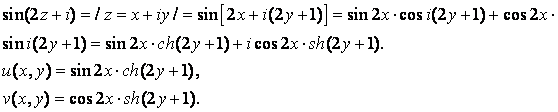           Проверим выполнение условий Коши-Римана:  

,       .

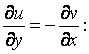
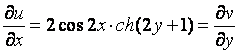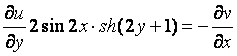Они выполняются для всех   следовательно, функция аналитическая на всей комплексной плоскости и ее можно дифференцировать по известным правилам дифференцирования функций действительного переменного:  

 

         3.  Является ли функция  оригиналом или нет, и почему?

         a);

         б) .

 

         Решение:

         Оригиналом называется комплекснозначная  функция   действительного аргумента , удовлетворяющая условиям:

         1)   - кусочно-непрерывна при ;

         2)    при  ;

         3)   , где М>0, -постоянные.

 

         а)  функция  является оригиналом, так как выполняются все три условия:

         1) она непрерывна по определению;

         2)  т.к. множитель   при ;

         3) , т.е. М=1, .

         б) функция  не является оригиналом, так как не

выполняются по крайней мере два условия:

         1) она имеет разрыв второго рода при ;

         2)  при t<0, т.е. отсутствует множитель .

 

         4.   Найти изображение    функции , пользуясь свойствами преобразования Лапласа:

         a) ;

         б) ;

         в) ;

         г) ;

         д) ;

         е) ;

         ж) .

         Решение:

         а) используя таблицу 13  и теорему линейности, имеем: ;

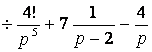         б) по таблице соответствия  Применяя далее теорему смещения, получим:  ;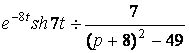

         в) по таблице 13 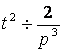   , а по теореме запаздывания  ;

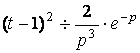         г) преобразуем данную функцию 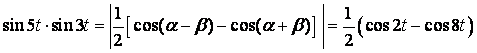. Применяя таблицу 13  и теорему линейности,  получим ;

         д)   по таблице соответствия 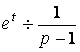  , а  по теореме о дифференцировании изображения ;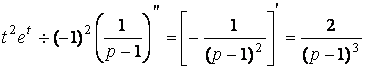

         е) 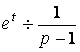  . По теореме об интегрировании оригинала ;

         ж) так как 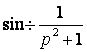 , то по теореме об интегрировании изображения  .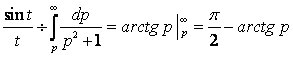

 

         5.    По заданному графику оригинала найти  изображение.

                   f(t)

 

                      2----------

 

                      1-----------

 

                      0             a          2a      3a                                            t

                                     

 

 

         Решение:

         Обозначим точки, в которых происходит разрыв или изменение функции через    ; скачок функции   в точке разрыва  - через   угловой коэффициент го  участка  - через  и  разность угловых коэффициентов через  Изображение такого вида функций можно найти по формуле:

         .

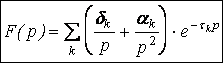         В нашей задаче:

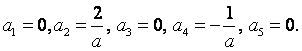
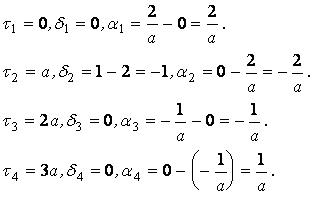
         Таким образом, 

         6.   Найти свёртку функций    и   и  её изображение.

 

         Решение:

         Свёртка функций  и   находится по формуле .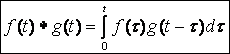

Поэтому 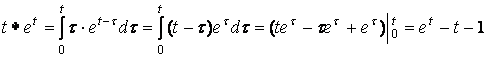. Изображение свёртки найдём по таблице 13  и теореме линейности .

         7.  Найти оригинал функц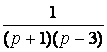ии, применяя теорему умножения изображений.

 

         Решение:

         Если  то по теореме умножения.

         Таким образом,

.

 

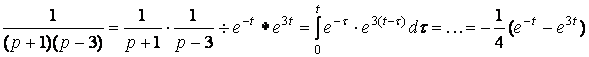         8.   Найти оригинал    по заданному изображению   .

 

         а)     

         б)    

 

         Решение:

 

         а) разложим дробно-рациональную функцию на сумму простых дробей:

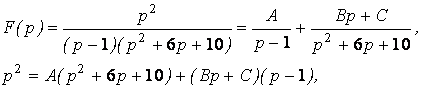
при     имеем:  

при      

при       

         Таким образом,    

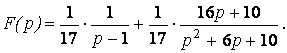
         По таблице 13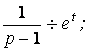        

 

=

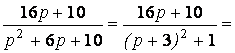
         Итак, искомый оригинал:  

         б)  по таблице 13 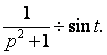        По теореме об интегрировании оригинала    

 

         9.  Операционным методом решить задачу Коши:

 

               

 

         Решение:

         Пусть    , тогда по теореме дифференцирования оригинала   По таблице 13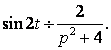 

Операторное уравнение имеет вид: 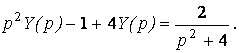                                            Откуда        

 

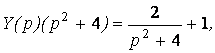
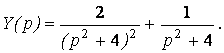
По таблице соответствия     Оригинал  изображения      

можно найти по теореме умножения: 

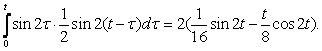
         Таким образом, искомое решение: 

 

         10.   Найти изображение функции , пользуясь определением.

 

         Решение:

         По определению изображением функции называется функция определяемая равенством 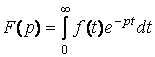. Поэтому .

 

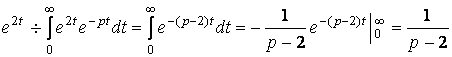         11.  Найти изображение функции  , применяя теорему дифференцирования оригинала.

 

         Решение:

         Так как , то . По теореме дифференцирования оригинала .

         Таким образом 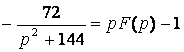  , откуда .

 

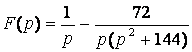         12.  Найти решение задачи Коши с помощью формулы Дюамеля:

         .

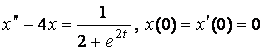         Решение:

         Составим вспомогательное уравнение   и решим его операторным методом. Операторное уравнение: 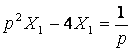 . Его решение  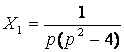. Известными методами найдём оригинал этого решения . Для определения решения данного уравнения воспользуемся формулой 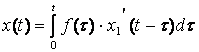 . Так как 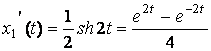,  то  =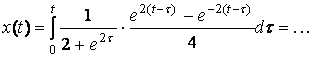

.

        

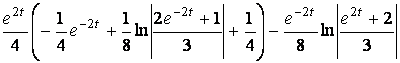         13.  Операционным методом решить систему дифференциальных уравнений.

 

        

        

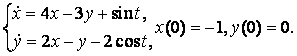
         Решение:

         Пусть x(t)=X(p),  y(t)=Y(p). Составим операторную систему, используя свойства преобразования Лапласа, таблицу 13  и начальные условия:

    

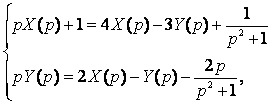
Решаем эту систему по правилу Крамера:

 

Для определения   и    разложим эти функции на сумму простых дробей:

Известным способом найдем A=-1, B=0, C=1, D=-1,A1=-2,B1=0,C1=2,D1=-2.

         Таким образом, 

                                      

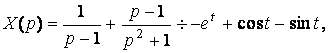
         Ответ: 

                      

 

 

         1.5   Справочный материал

 

         1.5.1  Свойства преобразования Лапласа

 

         Пусть     , 

 

         1   ,  (теорема линейности) .    

         2  ,     (теорема подобия ).              

         3   ,     (теорема смещения).             

         4  ,      ( теорема запаздывания).     

         5  ,…

     ,

 (теорема дифференцирования оригинала).                                                                                                

         6 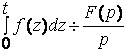   ,       (теорема интегрирования оригинала).  

         7      , ,   

(теорема дифференцирования изображения).

         8 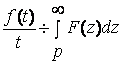   ,   ( теорема интегрирования изображения) . 

         9 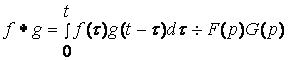    ,        (теорема умножения изображений) .                                                                                          

         10    ,

  (интеграл Дюамеля).                                                                                  

 

         1.5.2   Таблица оригинал-изображение

Т а б л и ц а  13

№

     

     

№

        

       

1

         1

      

7

   

2

        

     

8

  

3

          

    

9

     

4

  

10

  

5

   

  

11

 

6

   

  

12

          

 

Список литературы

1.                Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в    упражнениях и задачах: В 2 ч.-М.: Высш.шк., 1986.-Ч.1-352с.

2.     Сборник индивидуальных заданий по высшей математике: В 3ч.

/А.П.Рябушко, В.В.Бархатов , и др./ Под ред.А.П.Рябушко.-Минск:  Вышэйшая школа, 1991.-Ч.3.-351с.

         3.  Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики: Типовые расчеты.-М.: Высш.шк., 1983.-176с.

4.   Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. - М.:Наука,1971.-256 с.

         5. Хасеинов К.А. Каноны математики. Учебник – Алматы: 2003.-686 с.

         6. Математика 3. Конспект лекций для студентов всех форм обучения всех специальностей. Алматинский институт энергетики и связи: 2007.

 

Содержание 

Введение                                                                                                                

1  Типовой расчет 8.  Функции комплексного переменного и операционное исчисление      

1.1  Теоретические вопросы     

1.2   Расчетные задания первого уровня        

1.3 Расчетные задания второго уровня                              

1.4  Решение типового варианта                                                   

1.5  Справочный материал                 

1.5.1 Свойства преобразования Лапласа                                           

1.5.2 Таблица оригинал-изображение          

Список литературы