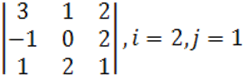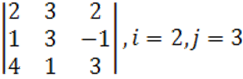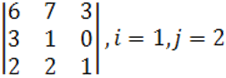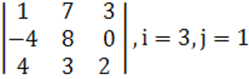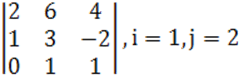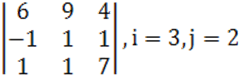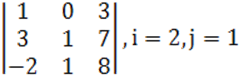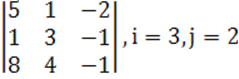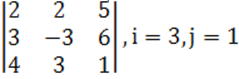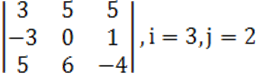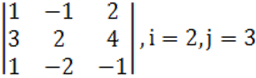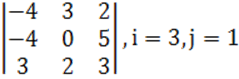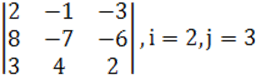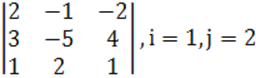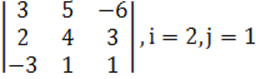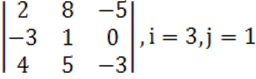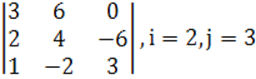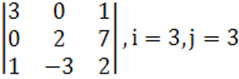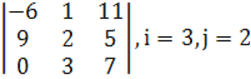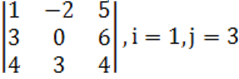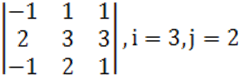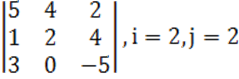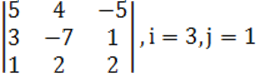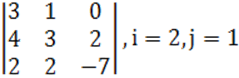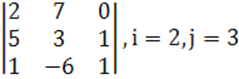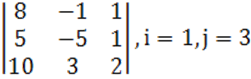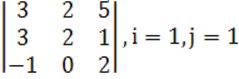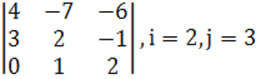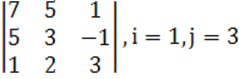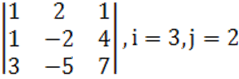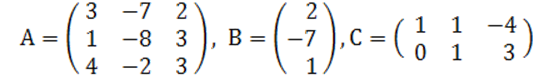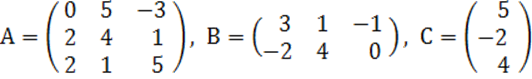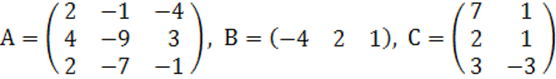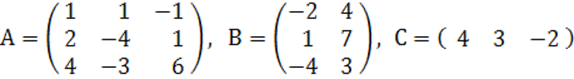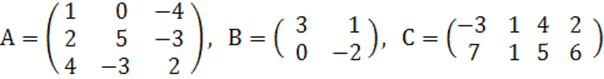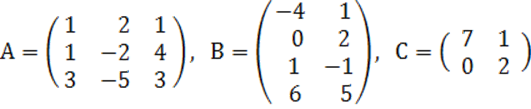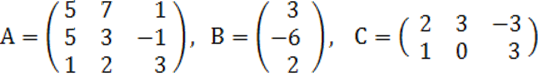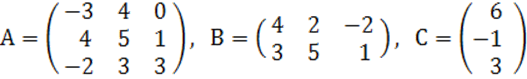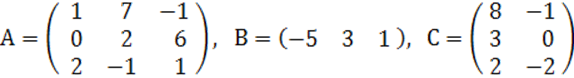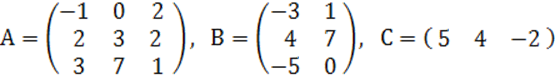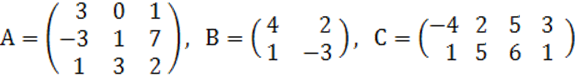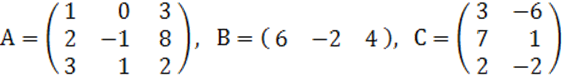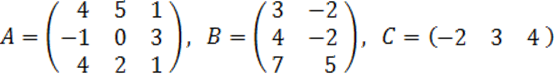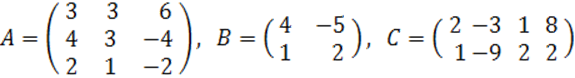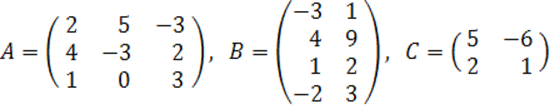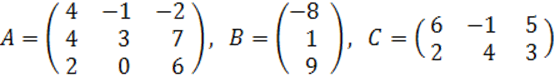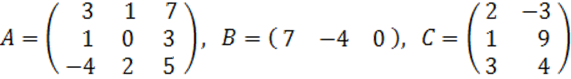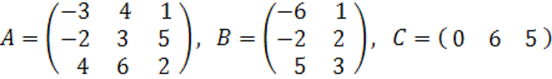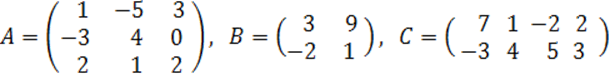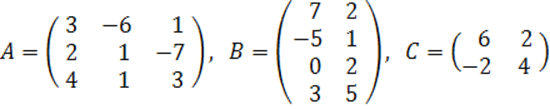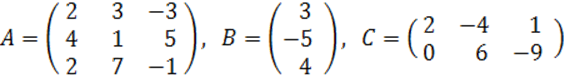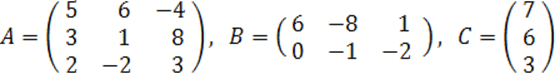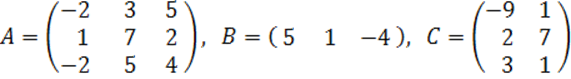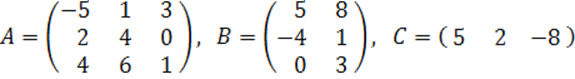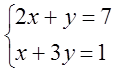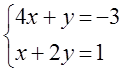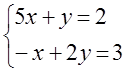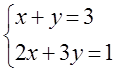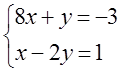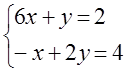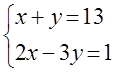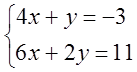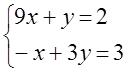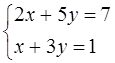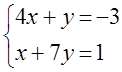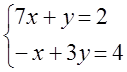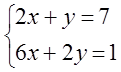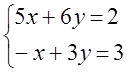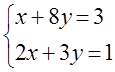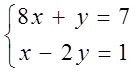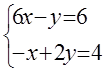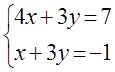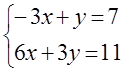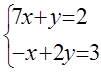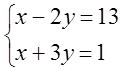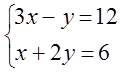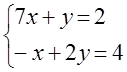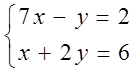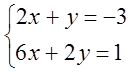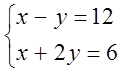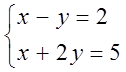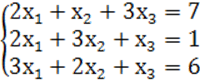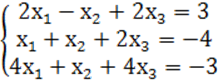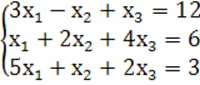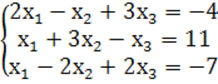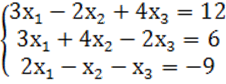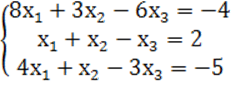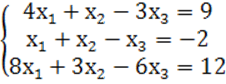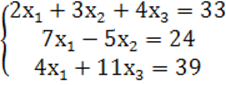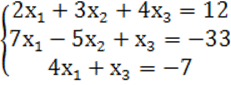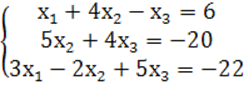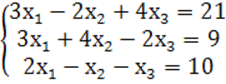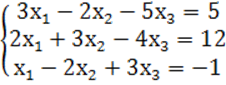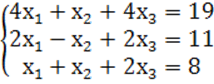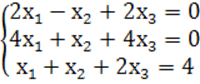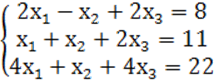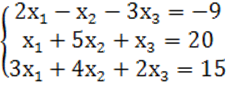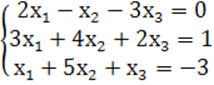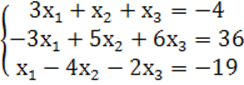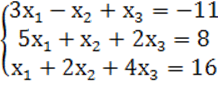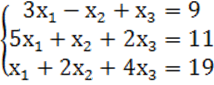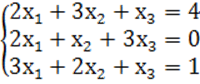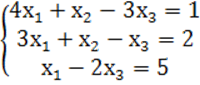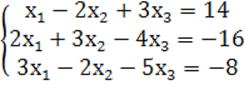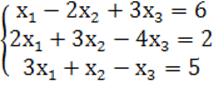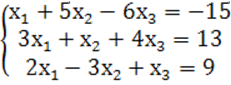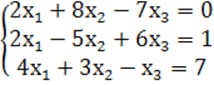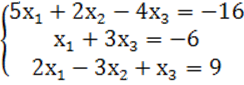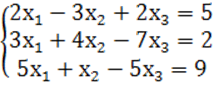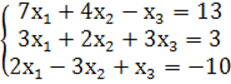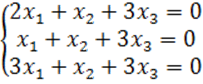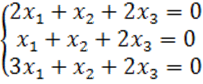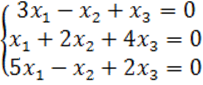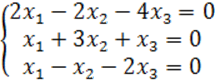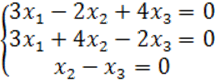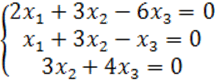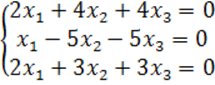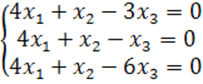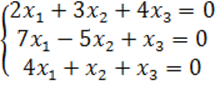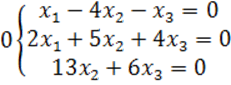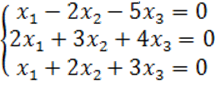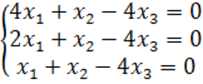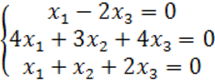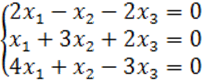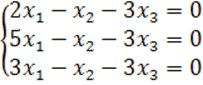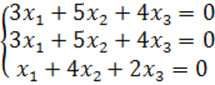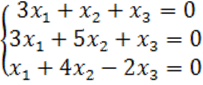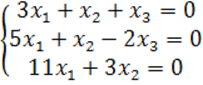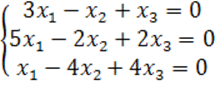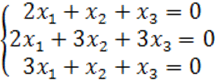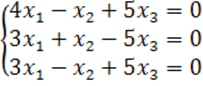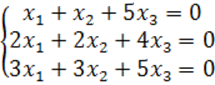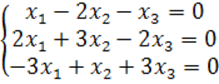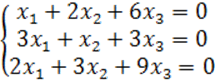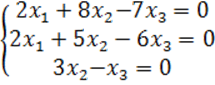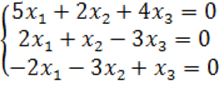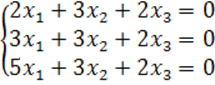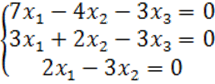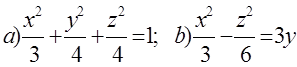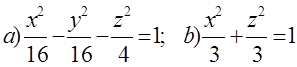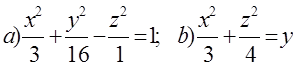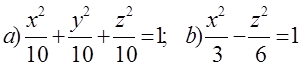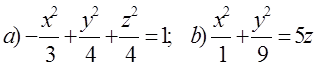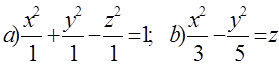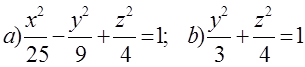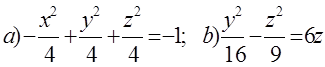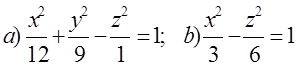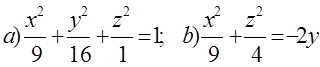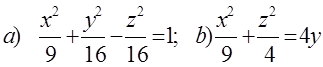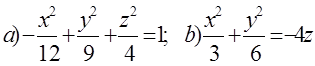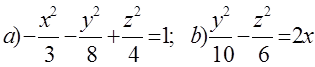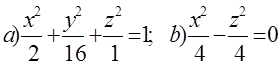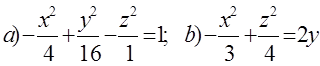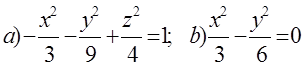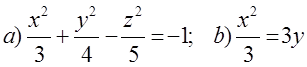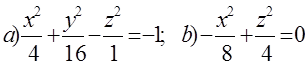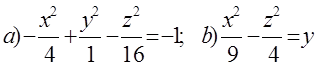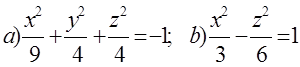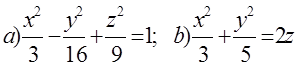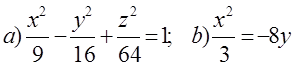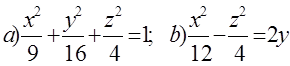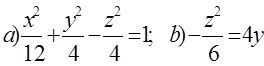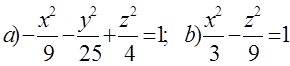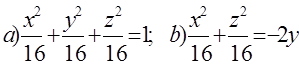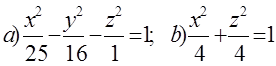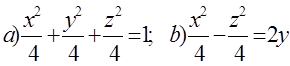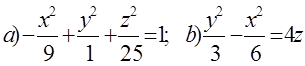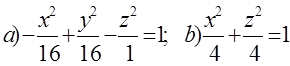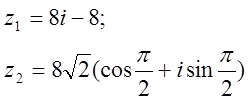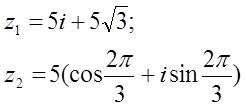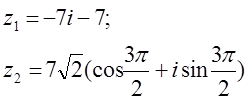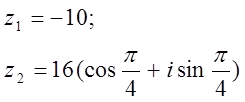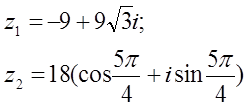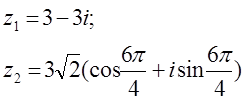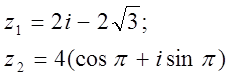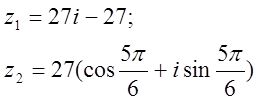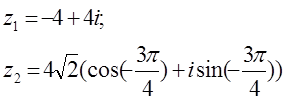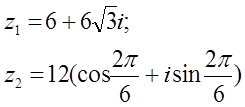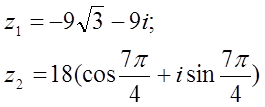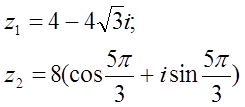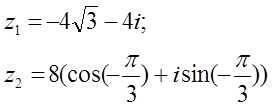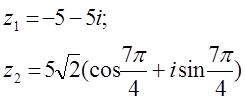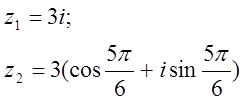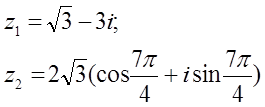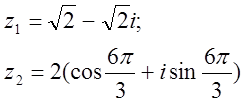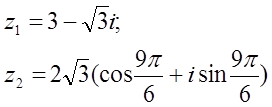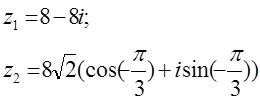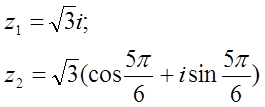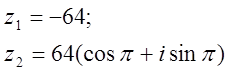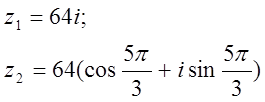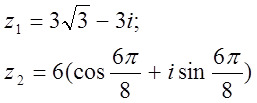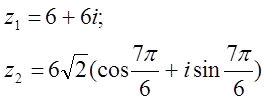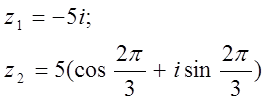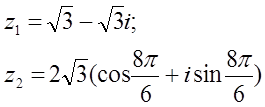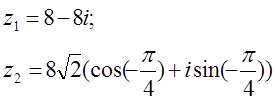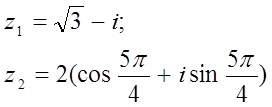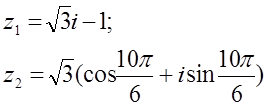Коммерциялық емес акционерлік қоғамы
АЛМАТЫ ЭНЕРГЕТИКА және БАЙЛАНЫС УНИВЕРСИТЕТІ
Жоғары математика кафедрасы
МАТЕМАТИКА 1
5В074600 « Ғарыштық техника
және технологиялар» мамандықтарында оқитын студенттер үшін
есептеу-сызбалық жұмыстарды орындауға арналған әдістемелік
нұсқаулар мен тапсырмалар 1-бөлім
Алматы 2013
ҚҰРАСТЫРУШЫЛАР: Масанова А.Ж., Ұлтарақова Г.А. Математика1 «Ғарыштық техника және технологиялар» мамандықтарында оқитын студенттер үшін есептеу-сызбалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар.1-бөлім. – Алматы: АЭжБУ, 2013. –34 б.
Бұл әдістемелік нұсқаулар мен тапсырмалар «Ғарыштық техника және технологиялар» мамандықтарында оқитын студенттер үшін «Математика 1» пәнінің №1 есептеу-сызбалық жұмыстарды орындауға арналған. Ұсынылған тақырып «Математика 1» пәнінің векторлық және сызықтық алгебра, аналитикалық геометрия бөлімдерін қамтиды. Мұнда бағдарламаның негізгі теориялық сұрақтары, тапсырмалардың нұсқалары және типтік нұсқаның шешуі берілген.
Суреттер-6, кестелер-13, Әдебиет көрсеткіші-4 атау.
Пікір беруші: физ.-мат. ғыл. канд., доц. Ибраева Л.Қ.
«Алматы энергетика және байланыс университеті» коммерциялық емес акционерлік қоғамының 2013 ж. жоспары бойынша басылып отыр.
ã «Алматы энергетика және байланыс университеті» КЕАҚ, 2013 ж.
2013ж. жиынтық жоспары, реті 182
1 Типтік есептер. Векторлық және сызықтық алгебра. Аналитика-лық геометрия
Кіріспе
Инженерлік-техникалық зерттеулерде математиканың алатын орны ерекше. Математика сандық есептеу аппараты ғана болып қоймай, сонымен қатар проблемалар мен ұғымдарды дәл жеткізу және зерттеу әдісі болып табылады. Математикалық әдістер – кез келген техникалық пәннің құрамындағы бөлігі. Осы айтылғандардың бәрі математика курсының қолдану бағытын күшейтудің қажеттілігіне және іргелі математикалық дайындықтың деңгейін көтеруге әкеледі.
Мақсаты: алгебра және геометрия теориясының іргелі ұғымдары мен әдістерін меңгеру. Теңдеулер жүйесін шешу барысында пайдаланылатын анықтауыштарды есептеу, матрицалар мен векторларға амалдар қолдануды үйрену, сонымен қатар, қисықтардың теңдеуінің түрі арқылы олардың геометриялық қасиеттерін, жазықтықта немесе кеңістікте өзара орналасуын анықтау. Комплекс сандармен барлық арифметикалық амалдарды орындау.
1.1 Теориялық сұрақтар
1. Анықтауыштар, олардың қасиеттері. Анықтауыштарды есептеу.
2. Матрицалар, оларға қолданылатын амалдар, кері матрица.
3. Векторлар, олардың ұзындығы. Векторларға қолданылатын сызықты амалдар. Векторлардың коллинеарлығы, компланарлығы және ортогональдығы. Векторлардың арасындағы бұрыш.
4. Векторлардың скалярлық, векторлық және аралас көбейтінділері, олардың қолданыстары.
5. Түзудің жазықтықтағы және кеңістіктегі теңдеулері.
6. Жазықтықтың теңдеулері.
7. Түзулердің және жазықтықтардың арасындағы бұрышы. Түзу мен жазықтықтың арасындағы бұрыш.
8. Нүктеден түзуге және жазықтыққа дейінгі арақашықтығы.
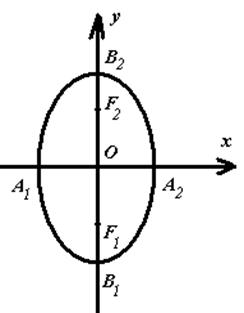
9. Эллипс, гипербола, парабола. Олардың канондық теңдеулері.
10. Екінші ретті беттер.
11. Екінші ретті беттердің жалпы теңдеулерін канондық түрге келтіру.
12. Матрицаның рангі және оны есептеу.
13. Сызықты теңдеулердің жүйелерін шешудің кейбір әдістері:
а) Крамер ережесі; б) Гаусс тәсілі; в) кері матрица арқылы шешу.
14. Сызықты теңдеулердің біртекті жүйелері.
15. Комплекс сандар. Оларға амалдар қолдану.
1.2 Есептердің тапсырмалары мен нұсқалары
1. Үшінші ретті анықтауыш берілген.
а) ![]() элементінің
миноры
элементінің
миноры ![]() мен оның
алгебралық толықтауышы
мен оның
алгебралық толықтауышы ![]() -ды табу керек.
-ды табу керек.
б) анықтауышты i-ші жатық жолы бойынша жіктеу керек.
в) анықтауышты j-ші тік жол бойынша жіктеп алып, есептеу керек.
г) анықтауышты үшбұрыш ережесі (Саррюс ережесі) бойынша есептеу керек.
1 к е с т е – 1 есепке берілген мәліметтер
|
1.1
|
1.2
|
1.3
|
|
1.4
|
1.5
|
1.6
|
|
1.7
|
1.8
|
1.9
|
|
1.10
|
1.11
|
1.12
|
|
1.13
|
1.14
|
1.15
|
|
1.16
|
1.17
|
1.18
|
|
1.19
|
1.20
|
1.21
|
|
1.22
|
1.23
|
1.24
|
|
1.25
|
1.26
|
1.27
|
|
1.28
|
1.29
|
1.30
|
2. A, B, C матрицалары берілген.
а) матрицалардың көбейтінділері АВ, ВС болулары мүмкін бе? Егер мүмкін болса, көбейтінділерді табу керек, егер мүмкін болмаса, неге мүмкін болмайтындығын түсіндіру керек.
б) кері матрица ![]() табу керек.
табу керек.
2 к е с т е – 2 есепке берілген мәліметтер
|
2.1 |
|
2.2
|
|
2.3
|
|
2.4
|
|
2.5
|
|
2.6
|
|
2.7
|
|
2.8
|
|
2.9
|
|
2.10
|
|
2.11
|
|
2.12
|
|
2.13
|
|
2.14
|
|
2.15
|
|
2.16
|
|
2.17
|
|
2.18 |
|
2.19
|
|
2.20
|
|
2.21
|
|
2.22
|
|
2.23
|
|
2.24 |
|
2.25
|
|
2.26
|
|
2.27 |
|
2.28
|
|
2.29 |
|
2.30 |
3. А, В
нүктелері, ![]()
![]() ,
, ![]() векторлары
берілген. Табу керек:
векторлары
берілген. Табу керек:
а) ![]() векторының
ұзындығын және АВ кесіндісінің ортасының
координаталарын;
векторының
ұзындығын және АВ кесіндісінің ортасының
координаталарын;
б) ![]() векторының
векторының
![]() векторына проекциясын;
векторына проекциясын;
в) ![]() ,
, ![]() векторларынан
құралған параллелограмның ауданын;
векторларынан
құралған параллелограмның ауданын;
г) ![]() ,
, ![]() векторларынан
құралған пирамиданың көлемін табу керек.
векторларынан
құралған пирамиданың көлемін табу керек.
3 к е с т е – 3 есепке берілген мәліметтер
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Жазықтықта ![]() нүктелері
және
нүктелері
және ![]() түзуінің теңдеуі
берілген. Келесі түзулердің теңдеулерін жазу керек:
түзуінің теңдеуі
берілген. Келесі түзулердің теңдеулерін жазу керек:
а) ![]() -
осы екі нүкте арқылы өтетін;
-
осы екі нүкте арқылы өтетін;
б) ![]() - жалпы
теңдеуін;
- жалпы
теңдеуін;
в) ![]() - бұрыштық
коэффициенті арқылы;
- бұрыштық
коэффициенті арқылы;
г) ![]() - кесіндідегі
теңдеуін;
- кесіндідегі
теңдеуін;
д) ![]() нүктесі
арқылы өтетін және
нүктесі
арқылы өтетін және ![]() түзуіне
перпендикуляр болатын
түзуіне
перпендикуляр болатын ![]() түзуінің теңдеуін
жазу керек.
түзуінің теңдеуін
жазу керек.
4 к е с т е – 4 есепке берілген мәліметтер
|
4.1 |
|
4.2 |
|
|
4.3 |
|
4.4 |
|
|
4.5 |
|
4.6 |
|
|
4.7 |
|
4.8 |
|
|
4.9 |
|
4.10 |
|
|
4.11 |
|
4.12 |
|
|
4.13 |
|
4.14 |
|
|
4.15 |
|
4.16 |
|
|
4.17 |
|
4.18 |
|
|
4.19 |
|
4.20 |
|
|
4.21 |
|
4.22 |
|
|
4.23 |
|
4.24 |
|
|
4.25 |
|
4.26 |
|
|
4.27 |
|
4.28 |
|
|
4.29 |
|
4.30 |
|
5. ![]() нүктелері берілген.
нүктелері берілген.
а) ![]() жазықтығының
теңдеуін жазу керек;
жазықтығының
теңдеуін жазу керек;
б) ![]() жазықтығының
жалпы теңдеуін жазу керек;
жазықтығының
жалпы теңдеуін жазу керек;
в) ![]() жазықтығының
кесіндідегі теңдеуін жазу керек;
жазықтығының
кесіндідегі теңдеуін жазу керек;
г) ![]() нүктесі
арқылы өтетін
нүктесі
арқылы өтетін ![]() жазықтығының жалпы
теңдеуін жазу керек;
жазықтығының жалпы
теңдеуін жазу керек;
д) ![]() түзуінің
канондық теңдеуін құру керек;
түзуінің
канондық теңдеуін құру керек;
е) ![]() түзуінің
параметрлік теңдеуін жазу керек;
түзуінің
параметрлік теңдеуін жазу керек;
ж)![]() жазықтығына
перпендикуляр болатын
жазықтығына
перпендикуляр болатын ![]() түзуінің теңдеуін
жазу керек.
түзуінің теңдеуін
жазу керек.
5 к е с т е – 5 есепке берілген мәліметтер
|
5.1 |
|
5.2 |
|
|
5.3 |
|
5.4 |
|
|
5.5 |
|
5.6 |
|
|
5.7 |
|
5.8 |
|
|
5.9 |
|
5.10 |
|
|
5.11 |
|
5.12 |
|
|
5.13 |
|
5.14 |
|
|
5.15 |
|
5.16 |
|
|
5.17 |
|
5.18 |
|
|
5.19 |
|
5.20 |
|
|
5.21 |
|
5.22 |
|
|
5.23 |
|
5.24 |
|
|
5.25 |
|
5.26 |
|
|
5.27 |
|
5.28 |
|
|
5.29 |
|
5.30 |
|
6. Жүйені шешіңіз:
а) Крамер ережесін қолданып;
б) матрицалық тәсіл бойынша (кері матрицаның көмегімен).
6 к е с т е – 6 есепке берілген мәліметтер
|
6.1 |
|
6.2 |
|
6.3 |
|
|
6.4 |
|
6.5 |
|
6.6 |
|
|
6.7 |
|
6.8 |
|
6.9 |
|
|
6.10 |
|
6.11 |
|
6.12 |
|
|
6.13 |
|
6.14 |
|
6.15 |
|
|
6.16 |
|
6.17 |
|
6.18 |
|
|
6.19 |
|
6.20 |
|
6.21 |
|
|
6.21 |
|
6.23 |
|
6.24 |
|
|
6.23 |
|
6.26 |
|
6.27 |
|
|
6.28 |
|
6.29 |
|
6.30 |
|
7. Жүйенің үйлесімділігін тексеріп, үйлесімді болған жағдайда Гаусс тәсілімен шығару керек.
7 к е с т е – 7 есепке берілген мәліметтер
|
7.1
|
7.2
|
7.3
|
|
7.4
|
7.5
|
7.6
|
|
7.7
|
7.8
|
7.9
|
|
7.10
|
7.11 |
7.12
|
|
7.13
|
7.14
|
7.15
|
|
7.16
|
7.17
|
7.18 |
|
7.19
|
7.20
|
7.21
|
|
7.22 |
7.23 |
7.24
|
|
7.25
|
7.26
|
7.27
|
|
7.28
|
7.29
|
7.30
|
8. Біртекті теңдеулер жүйесін шешу керек.
8 к е с т е – 8 есепке берілген мәліметтер
|
8.1
|
8.2
|
8.3
|
|
8.4
|
8.5
|
8.6
|
|
8.7
|
8.8
|
8.9
|
|
8.10
|
8.11 |
8.12 |
|
8.13
|
8.14 |
8.15
|
|
8.16
|
8.17
|
8.18 |
|
8.19
|
8.20
|
8.21 |
|
8.22
|
8.23
|
8.24 |
|
8.25
|
8.26
|
8.27 |
|
8.28
|
8.29
|
8.30 |
9. Берілгені: А- қисықта жатқан нүкте; R- шеңбердің радиусы; a,b –қисықтардың жарты осьтері; D – қисықтың директрисасы.
а) центрі А нүктесі және радиусы R болатын шеңбердің теңдеуін жазу керек;
б) жарты осьтері а, b болатын эллипстің теңдеуін құрастырып, эксцентриситетін және фокустарының координаталарын табу керек;
в) нақты жарты осі- а, жорамал жарты осі – b болатын гиперболаның теңдеуін құрастырып, эксцентриситетін, фокустарының координаталарын, асимптоталарының теңдеулерін табу керек;
г) симметрия осі Ох немесе Оу, төбесі координаталар басында, директрисасы D болатын параболаның теңдеуін құрастырып, фокусын табу керек;
д) эллипстің, гиперболаның, параболаның сызбасын сызу керек.
9 к е с т е – 9 есепке берілген мәліметтер
|
9.1 |
A(2,-4), R=4, a=1, b=3, D: x=-5 |
9.2 |
A(-8,2), R=1 , a=6, b=5, D: x=-5 |
|
9.3 |
A(1,-4), R=5, a=8 , b=3, D: y=-6 |
9.4 |
A(5,-4), R=2, a=6, b=4, D: y=-2 |
|
9.5 |
A(2,-5), R=7, a=3, b=2, D: x=4 |
9.6 |
A(1,8), R=5 , a=3, b=2, D: x=-3 |
|
9.7 |
A(3,-4), R=9, a=7, b=6, D: y=-2 |
9.8 |
A(10,1), R=8, a=1, b=6, D: y=-4 |
|
9.9 |
A(5,-4), R=1, a=6, b=4, D: x=-5 |
9.10 |
A(6,3), R=8 , a=2, b=3, D: x=-5 |
|
9.11 |
A(1,-3), R=5 , a=8, b=2, D: y=6 |
9.12 |
A(5,5), R=2, a=1, b=3, D: y=-7 |
|
9.13 |
A(2,-6), R=7, a=3, b=4, D: x=5 |
9.14 |
A(12,6), R=7, a=6, b=2, D: x=-5 |
|
9.15 |
A(3,4), R=9 , a=2, b=6, D: y=-8 |
9.16 |
A(0,5), R=4, a=6, b=4, D: y=8 |
|
9.17 |
A(2,-9), R=7, a=5, b=2, D: x=6 |
9.18 |
A(-5,0), R=7, a=4, b=5, D: x=1 |
|
9.19 |
A(8,4), R=6 , a=8, b=5, D: y=2 |
9.20 |
A(5,1), R=2, a=9, b=1, D: x=-1 |
|
9.21 |
A(5,-4), R=4, a=6, b=4, D: x=1 |
9.22 |
A(-3,2), R=4, a=8, b=4, D: y=1 |
|
9.23 |
A(1,8), R=5, a=9, b=4, D: y=-6 |
9.24 |
A(9,1), R=6, a=4, b=7, D: x=-3 |
|
9.25 |
A(2,-5), R=7, a=7, b=4, D: x=9 |
9.26 |
A(-9,2), R=7, a=1, b=8, D: y=7 |
|
9.27 |
A(7,4), R=5, a=1, b=7, D: y=8 |
9.28 |
A(11,-4), R=2, a=2, b=4, D: x=8 |
|
9.29 |
A(-2,5), R=5, a=7, b=1, D: x=8 |
9.30 |
A(12,-4), R=7, a=3,b=5, D: y=-9 |
10. Екінші ретті беттің түрін анықтап, сұлбалық сызбасын сызу керек.
10 к е с т е – 10 есепке берілген мәліметтер
|
10.1 |
|
9.2 |
|
|
10.3 |
|
10.4 |
|
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
|
10.9 |
|
10.10 |
|
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
|
10.15 |
|
10.16 |
|
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
|
10.21 |
|
10.22 |
|
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
|
10.27 |
|
10.28 |
|
|
10.29 |
|
10.30 |
|
11. Екінші ретті қисықтың теңдеуін канондық түрге келтіріп, сызбасын сызу керек.
11 к е с т е – 11 есепке берілген мәліметтер
|
11.1 |
|
11.2 |
|
|
11.3 |
|
11.4 |
|
|
11.5 |
|
11.6 |
|
|
11.7 |
|
11.8 |
|
|
11.9 |
|
11.10 |
|
|
11.11 |
|
11.12 |
|
|
11.13 |
|
11.14 |
|
|
11.15 |
|
11.16 |
|
|
11.17 |
|
11.18 |
|
|
11.19 |
|
11.20 |
|
|
11.21 |
|
11.22 |
|
|
11.23 |
|
11.24 |
|
|
11.25 |
|
11.26 |
|
|
11.27 |
|
11.28 |
|
|
11.29 |
|
11.30 |
|
12. z1 және z2 комплекс сандары берілген. Табу керек:
а) z1 комплекс санының модулін;
б) z1 комплекс санының аргументін;
в) z1 комплекс санын тригонометриялық және көрсеткіштік формада көрсету;
г) z1 және z2 комплекс сандарының қосындысын аналитикалық және графикалық түрде көрсету;
д) (z2)5;
е) z1 z2 көбейтіндісін тригонометриялық формада;
ж) ![]() (жұп
нұсқалар үшін) и
(жұп
нұсқалар үшін) и ![]() (тақ
нұсқалар үшін) барлық комплекс түбірлерін тауып,
шешімінің сызбасын сызу керек.
(тақ
нұсқалар үшін) барлық комплекс түбірлерін тауып,
шешімінің сызбасын сызу керек.
12 к е с т е – 12 есепке берілген мәліметтер
|
12.1 |
|
12.2 |
|
|
12.3 |
|
12.4 |
|
|
12.5 |
|
12.6 |
|
|
12.7 |
|
12.8 |
|
|
12.9 |
|
12.10 |
|
|
12.11 |
|
12.12 |
|
|
12.13 |
|
12.14 |
|
|
12.15 |
|
12.16 |
|
|
12.17 |
|
12.18 |
|
|
12.19 |
|
12.20 |
|
|
12.21 |
|
12.22 |
|
|
12.23 |
|
12.24 |
|
|
12.25 |
|
12.26 |
|
|
12.27 |
|
12.28 |
|
|
12.29 |
|
12.30 |
|
1.3 Типтік нұсқаның шешімі
1. Үшінші ретті анықтауыш
берілген: 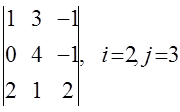 .
.
Табу керек:
а) ![]() элементінің
элементінің![]() минорын,
минорын, ![]() алгебралық
толықтауышын;
алгебралық
толықтауышын;
б) анықтауышты үшбұрыш ережесі бойынша (Саррюс ережесі) және j-ші тік жолы бойынша жіктеп, есептеу керек.
Шешуі:
a) a![]() элементінің
миноры M
элементінің
миноры M![]() берілген анықтауыштың i-ші
жатық жолы мен j-ші тік жолын сызып тастағанда қалған
анықтауышқа тең. Сондықтан берілген
анықтауыштың 2-ші жатық жолы мен 3-ші тік жолын сызып
тастаймыз. Сонда
берілген анықтауыштың i-ші
жатық жолы мен j-ші тік жолын сызып тастағанда қалған
анықтауышқа тең. Сондықтан берілген
анықтауыштың 2-ші жатық жолы мен 3-ші тік жолын сызып
тастаймыз. Сонда 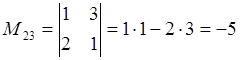 . a
. a![]() элементінің
алгебралық толықтауышын A
элементінің
алгебралық толықтауышын A![]() =(-1)
=(-1)![]() M
M![]() формуласы
бойынша табамыз. Сонда А
формуласы
бойынша табамыз. Сонда А![]() =(-1)
=(-1)![]() (-5)= 5;
(-5)= 5;
б) Үшбұрыш ережесі: Үшінші ретті
анықтауыш алты мүшенің қосын-дысына тең; таңбасы
оң болатын мүшелерін анықтауыштың үш мүшесін
мына сұлба бойынша көбейткенде 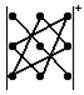 , ал таңбалары теріс
мүшелерін келесі сұлба бойынша көбейткенде табады
, ал таңбалары теріс
мүшелерін келесі сұлба бойынша көбейткенде табады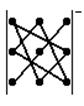 .
. 
Үшінші тік жол арқылы
жіктелістің формуласы: 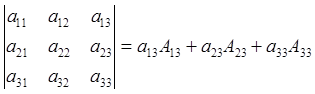 . Сондықтан
. Сондықтан
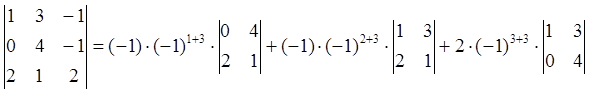 =8 – 5+8 =11.
=8 – 5+8 =11.
2. А, В, С матрицалары
берілген:
А=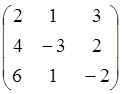 , В=
, В= , С=
, С=![]() .
.
а) АВ және ВС матрицаларының көбейтіндісін, мүмкін болған жағдайда, табу керек;
б) А матрицасының ![]() кері
матрицасын табу керек.
кері
матрицасын табу керек.
Шешуі:
а) егер А матрицасының
тік жолдарының саны В матрицасының жатық
жолдарының санына тең болса, онда АВ матрицаларының
көбейтіндісі бар болады. Матрицалардың
өлшемдері:
А![]() , В
, В![]() , С
, С![]() . Сондықтан А
. Сондықтан А![]() В
В![]() =
= ![]() – көбейтінді болуы
мүмкін емес.
В
– көбейтінді болуы
мүмкін емес.
В![]() С
С![]() =
= ![]() – көбейтіндісі болады. ВС
матрицаларының көбейтіндісі болатын Е матрицасының
жатық жолдарының саны В матрицасының жатық
жолдарының сандарына тең, тік жолдарының саны С
матрицасының тік жолдарының санына тең:
– көбейтіндісі болады. ВС
матрицаларының көбейтіндісі болатын Е матрицасының
жатық жолдарының саны В матрицасының жатық
жолдарының сандарына тең, тік жолдарының саны С
матрицасының тік жолдарының санына тең: ![]() . Е матрицасының
. Е матрицасының ![]() элементі
В матрицасының i–ші жатық жолының С матрицасының j–ші
тік жолының сәйкес элементтерінің
көбейтінділерінің қосындысына тең болады.
элементі
В матрицасының i–ші жатық жолының С матрицасының j–ші
тік жолының сәйкес элементтерінің
көбейтінділерінің қосындысына тең болады.
Сонымен ВС = 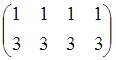
![]() =
= 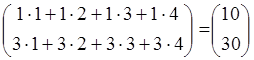 ,
,
мұндағы ![]() . Сонда
. Сонда ![]()
![]() ;
;
б) квадрат (шаршы)
матрицаның анықтауышы нөлге тең болмаса, ол
матрицаның кері матрицасы бар болады; егер анықтауышы нөлге
тең болса, кері матрица болмайды. А матрицасының кері матрицасы А![]() келесі
формула арқылы табылады: егер А=
келесі
формула арқылы табылады: егер А=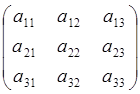 болса,
онда
болса,
онда 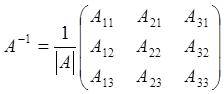 , мұндағы
, мұндағы ![]() – А
матрицасының анықтауышы;
– А
матрицасының анықтауышы; ![]() –
– ![]() элементтерінің
алгебралық толықтауыштары. А матрицасының анықтауышын
табайық:
элементтерінің
алгебралық толықтауыштары. А матрицасының анықтауышын
табайық: ![]() =
= 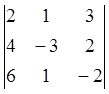 = 94
= 94![]() 0, яғни
А
0, яғни
А![]() бар. А-ның барлық элементтерінің
алгебралық толықтауыштарын анықтайық.
бар. А-ның барлық элементтерінің
алгебралық толықтауыштарын анықтайық.
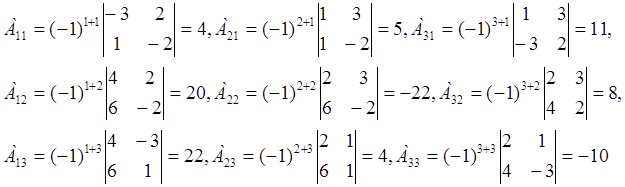
А![]() кері матрицаны жоғарыда
көрсетілген формула бойынша табамыз:
кері матрицаны жоғарыда
көрсетілген формула бойынша табамыз:
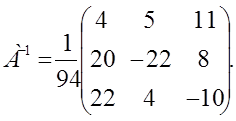
3. А(7,-9,3), В(1,0,-5)
нүктелері
және![]() векторлары
берілген.
Табу
керек:
векторлары
берілген.
Табу
керек:
а) ![]() векторының
ұзындығын және АВ кесіндісінің ортасын;
векторының
ұзындығын және АВ кесіндісінің ортасын;
б) ![]() векторының
векторының![]() векторына
проекциясын;
векторына
проекциясын;
в) ![]() және
және![]() векторларынан
құралған параллелограмның ауданын;
векторларынан
құралған параллелограмның ауданын;
г) ![]() векторларынан
құралған пирамиданың көлемін табу керек.
векторларынан
құралған пирамиданың көлемін табу керек.
Шешуі:
а) А(![]() ) және В(
) және В(![]() ) нүктелері
арқылы
) нүктелері
арқылы ![]() векторының координаталарын
векторының координаталарын ![]()
![]() = (
= (![]() )
формуласы бойынша табады. Сонда
)
формуласы бойынша табады. Сонда ![]() (1-7, 0-(-9),
-5-3) = (-6, 9, -8);
(1-7, 0-(-9),
-5-3) = (-6, 9, -8);
![]() векторының
ұзындығы:
векторының
ұзындығы: ![]() .
.
Олай болса ![]() =
=![]() =
= ![]() ;
;
АВ кесіндісінің ортасы
С-ның координаталары С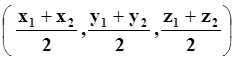 =
=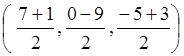 = С( 4, -9/2, -1 ).
= С( 4, -9/2, -1 ).
б) ![]() векторының
векторының
![]() векторына
проекциясы:
векторына
проекциясы:
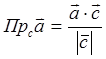 ; мұндағы
; мұндағы ![]() -
- ![]() векторларының
скаляр көбейтіндісі. Егер векторлар ортогональ болса, онда
векторларының
скаляр көбейтіндісі. Егер векторлар ортогональ болса, онда ![]() ;
; ![]() ,
, ![]() , олай
болса
, олай
болса
![]() және
және ![]() ортогональ
болмайды;
енді
вектордың проекциясын табамыз:
ортогональ
болмайды;
енді
вектордың проекциясын табамыз: 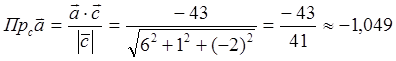 ;
;
в)![]() векторларынан құралған
параллело-грамның ауданы осы векторлардың векторлық
көбейтіндісінен шыққан век-тордың
ұзындығына тең болады:
векторларынан құралған
параллело-грамның ауданы осы векторлардың векторлық
көбейтіндісінен шыққан век-тордың
ұзындығына тең болады: ![]() ; алдымен
векторлық көбейтіндіні табамыз:
; алдымен
векторлық көбейтіндіні табамыз:
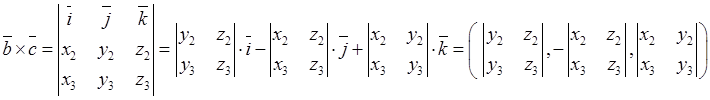 ;
;
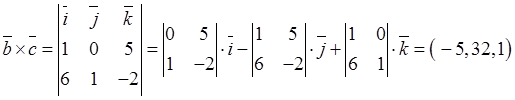 ; содан
кейін осы вектордың модулін есептейміз:
; содан
кейін осы вектордың модулін есептейміз: ![]() ;
г)
;
г) ![]() ,
, ![]() ,
, ![]() векторларынан
құралған пирамиданың көлемін табу үшін,
олардың аралас көбейтіндісінің модулінің алтыдан бір
бөлігін алу керек:
векторларынан
құралған пирамиданың көлемін табу үшін,
олардың аралас көбейтіндісінің модулінің алтыдан бір
бөлігін алу керек:

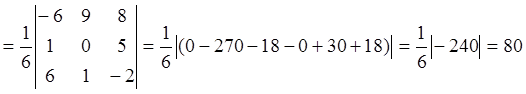 ,
,
![]() , онда бұл векторлар компланар
емес.
, онда бұл векторлар компланар
емес.
4.
Жазықтықта А![]() (4, -2), А
(4, -2), А![]() (8, 1) нүктелері
және L
(8, 1) нүктелері
және L![]() : -x + 4y + 5 = 0 түзуі
берілген. Келесі түзулердің теңдеулерін жазу керек:
: -x + 4y + 5 = 0 түзуі
берілген. Келесі түзулердің теңдеулерін жазу керек:
а) ![]() -
осы екі нүкте арқылы өтетін;
-
осы екі нүкте арқылы өтетін;
б) ![]() - жалпы теңдеуін;
- жалпы теңдеуін;
в) ![]() -
бұрыштық коэффициенті арқылы;
-
бұрыштық коэффициенті арқылы;
г) ![]() - кесіндідегі
теңдеуін;
- кесіндідегі
теңдеуін;
д) ![]() нүктесі
арқылы өтетін және
нүктесі
арқылы өтетін және ![]() түзуіне
перпендикуляр болатын
түзуіне
перпендикуляр болатын ![]() түзуінің теңдеуін
жазу керек.
түзуінің теңдеуін
жазу керек.
Шешуі:
a) (![]() )
және (
)
және (![]() ) нүктелері арқылы
өтетін түзудің теңдеуі:
) нүктелері арқылы
өтетін түзудің теңдеуі: 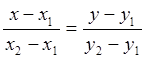 . Олай болса, L
. Олай болса, L![]() түзуінің
теңдеуі
түзуінің
теңдеуі 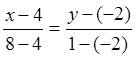 немесе
немесе 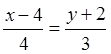 ;
;
б) L![]() түзуінің
теңдеуін Ax+By+C=0 жалпы түріне келтіреміз:
түзуінің
теңдеуін Ax+By+C=0 жалпы түріне келтіреміз: 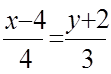
![]() ,( A=3,
B=-4, C=-20 ); А, В коэффициенттерінің геометриялық мағынасы
– ол түзудің нормаль (перпендикуляр) векторының
координаталары, яғни
,( A=3,
B=-4, C=-20 ); А, В коэффициенттерінің геометриялық мағынасы
– ол түзудің нормаль (перпендикуляр) векторының
координаталары, яғни ![]() ;
;
в) бұрыштық
коэффициент арқылы ![]() түзуінің теңдеуі y=kx+m:
түзуінің теңдеуі y=kx+m:
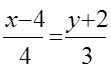
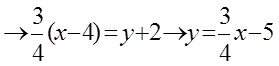 , ( k=
, ( k=![]() , m=-5
);
, m=-5
);
г) ![]() түзуінің
кесіндідегі теңдеуі x/a+y/b=1:
түзуінің
кесіндідегі теңдеуі x/a+y/b=1:
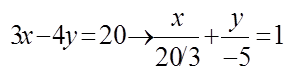 , ( a = 20/3, b
= -5 );
, ( a = 20/3, b
= -5 );
д) (![]() )
нүктесі арқылы өтетін және
)
нүктесі арқылы өтетін және![]() векторына
параллель болатын түзудің теңдеуі:
векторына
параллель болатын түзудің теңдеуі: 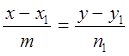 . Егер
. Егер ![]() түзуіне
перпендикуляр вектор
түзуіне
перпендикуляр вектор ![]() =(A;B)=(-1;4) болса, ал
=(A;B)=(-1;4) болса, ал ![]()
![]() -ге
де перпендикуляр болса, онда біздің жағдайда,
-ге
де перпендикуляр болса, онда біздің жағдайда, ![]() түзуінің
бағыттауыш векторы
түзуінің
бағыттауыш векторы ![]() болады,
сонда
болады,
сонда 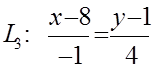 .
.
5. А![]() (1, 2, -1), А
(1, 2, -1), А![]() (3, 3, 2), А
(3, 3, 2), А![]() (2, -3, 7)
нүктелері берілген.
(2, -3, 7)
нүктелері берілген.
а) ![]() жазықтығының
теңдеуін жазу керек.
жазықтығының
теңдеуін жазу керек.
б) ![]() жазықтығының
жалпы теңдеуін жазу керек.
жазықтығының
жалпы теңдеуін жазу керек.
в) ![]() жазықтығының
кесіндідегі теңдеуін жазу керек.
жазықтығының
кесіндідегі теңдеуін жазу керек.
г) ![]() нүктесі
арқылы өтетін
нүктесі
арқылы өтетін ![]() жазықтығының жалпы
теңдеуін жазу керек.
жазықтығының жалпы
теңдеуін жазу керек.
д) ![]() түзуінің
канондық теңдеуін құру керек.
түзуінің
канондық теңдеуін құру керек.
е) ![]() түзуінің
параметрлік теңдеуін жазу керек.
түзуінің
параметрлік теңдеуін жазу керек.
ж) ![]() жазықтығына
перпендикуляр болатын
жазықтығына
перпендикуляр болатын ![]() түзуінің теңдеуін жазу
керек.
түзуінің теңдеуін жазу
керек.
Шешуі:
а) (![]() ), (
), (![]() ), (
), (![]() ) нүктелері
арқылы өтетін жазықтықтың теңдеуі:
) нүктелері
арқылы өтетін жазықтықтың теңдеуі: 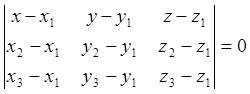 .
.
Біздің жағдайда Р![]() :
: 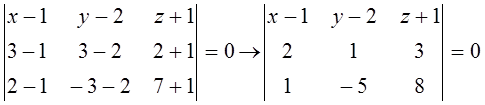 (*);
(*);
б) жоғарыдағы (*)
анықтауышын ашсақ, Р![]() жазықтығының
жалпы теңдеуін аламыз : Ax+By+Cz+D=0:
жазықтығының
жалпы теңдеуін аламыз : Ax+By+Cz+D=0:
23x – 13y – 11z – 8 = 0, (A=23, B=-13, C=-11, D=-8)
А, В, С коэффициенттерінің геометриялық
мағынасы – ол жазықтықтың нормаль векторының (перпендикуляр)
координаталары, яғни ![]() ;
;
в) жазықтықтың
теңдеуіндегі бос мүшені теңдіктің оң жағына
шығарып, теңдіктің екі жағын да бос мүшеге
бөлеміз. Сонда x/a+y/b+z/c=1 жазықтықтың кесіндідегі
теңдеуі шығады. Біздің жағдайда, 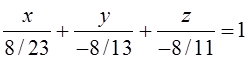 ,
мұндағы а=8/23, в=-8/13, с=-8/11 – бас нүктеден
бастағанда жазықтықтың сәйкес координата осьтерін
қиятын кесінділердің ұзындықтары;
,
мұндағы а=8/23, в=-8/13, с=-8/11 – бас нүктеден
бастағанда жазықтықтың сәйкес координата осьтерін
қиятын кесінділердің ұзындықтары;
г) (*) анықтауышын бірінші жатық жолының элементтері бойынша жіктеп, есептейміз:
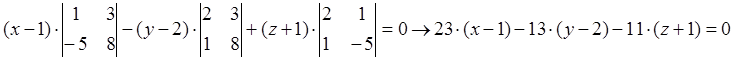 .
.
Сонда A(x-x![]() )+B(y-y
)+B(y-y![]() )+C(z-z
)+C(z-z![]() )=0 (
)=0 (![]() ) түріндегі
жазықтықтың теңдеуі шығады.
) түріндегі
жазықтықтың теңдеуі шығады.
д) (![]() ) және
(
) және
(![]() ) нүктелері арқылы
өтетін түзудің канондық теңдеуі:
) нүктелері арқылы
өтетін түзудің канондық теңдеуі: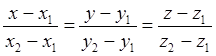 . Олай болса, L
. Олай болса, L![]() түзуінің теңдеуі
мынадай болады:
түзуінің теңдеуі
мынадай болады: 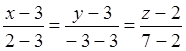 немесе
немесе 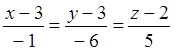 ;
;
е) 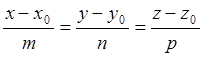 түріндегі
теңдеуді түзудің канондық теңдеуі деп атайды, мұндағы
түріндегі
теңдеуді түзудің канондық теңдеуі деп атайды, мұндағы
![]() (m,n,p) – түзудің
бағыттауыш векторы. Алдыңғы пунктте түзудің
канондық теңдеуін жазғанбыз. Енді түзудің мына
түрдегі
(m,n,p) – түзудің
бағыттауыш векторы. Алдыңғы пунктте түзудің
канондық теңдеуін жазғанбыз. Енді түзудің мына
түрдегі 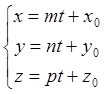 параметрлік теңдеуін жазу
үшін, түзудің канондық теңдеуін t параметріне
теңестіріп, табылған теңдіктерден x, y, z–терді
анықтаймыз. L
параметрлік теңдеуін жазу
үшін, түзудің канондық теңдеуін t параметріне
теңестіріп, табылған теңдіктерден x, y, z–терді
анықтаймыз. L![]() :
: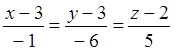 =
= 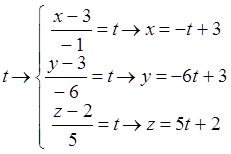 . Сонымен
түзудің параметрлік теңдеулері L
. Сонымен
түзудің параметрлік теңдеулері L![]() :
: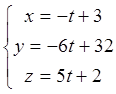 ;
;
ж) жазықтықтың жалпы
теңдеуінен ![]() және
және ![]()
![]() , түзуінің
бағыттауыш векторы болады, себебі
, түзуінің
бағыттауыш векторы болады, себебі ![]() . Онда
. Онда ![]() түзуінің
канондық теңдеуі келесідей болады:
түзуінің
канондық теңдеуі келесідей болады:
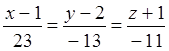
6. Жүйені шешу керек: 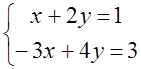
а) Крамер әдісімен;
б) матрицалық әдіспен (кері матрицаның көмегімен).
Шешуі:
а) 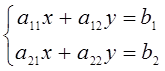 жүйесін
Крамер әдісімен шешу келесі формулаларға негізделген:
жүйесін
Крамер әдісімен шешу келесі формулаларға негізделген: 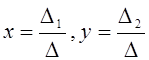 , мұндағы
, мұндағы
 - жүйенің анықтауышы,
- жүйенің анықтауышы, 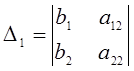 ,
, 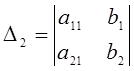 -
жүйенің анықтауышының, сәйкесінше, бірінші
және екінші тік жолдарының мүшелерін жүйенің бос
мүшелерімен ауыстыру арқылы алынған көмекші анықтауыштар.
-
жүйенің анықтауышының, сәйкесінше, бірінші
және екінші тік жолдарының мүшелерін жүйенің бос
мүшелерімен ауыстыру арқылы алынған көмекші анықтауыштар.
Бізде - 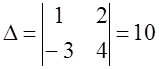 ,
, 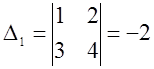 ,
, 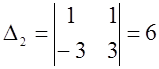 .
.
х = -1/5, у =3/5. Жауапты вектор түрінде беруге де болады: (-1/5; 3/5);
б)
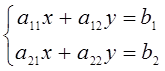 жүйесінің шешімі
матрицалар арқылы келесі түрде жазылады:
жүйесінің шешімі
матрицалар арқылы келесі түрде жазылады:![]() , мұнда
, мұнда 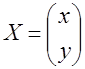 - белгісіздерден
құралған матрица –баған,
- белгісіздерден
құралған матрица –баған, 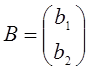 - бос мүшелердің матрица-бағаны,
- бос мүшелердің матрица-бағаны, ![]() - жүйенің
- жүйенің 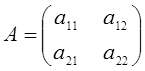 матрицасының кері матрицасы.
матрицасының кері матрицасы.
Енді 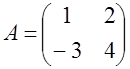 матрицасының
кері матрицасын табамыз,
матрицасының
кері матрицасын табамыз, ![]() болғандықтан,
бұл матрицаның кері матрицасы бар (2б есебін қараңыз)
болғандықтан,
бұл матрицаның кері матрицасы бар (2б есебін қараңыз)
және ол келесідей
болады: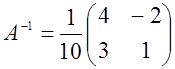 . Олай болса,
. Олай болса, 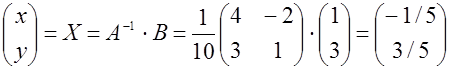 . Жауапты
мынадай қарапайым түрде берсе де болады: х=-1/5, у=3/5.
. Жауапты
мынадай қарапайым түрде берсе де болады: х=-1/5, у=3/5.
7.  жүйесі
берілген.
жүйесі
берілген.
а) жүйені Гаусс әдісі арқылы үйлесімділікке зерттеу керек;
б) жүйенің матрицасының және кеңейтілген матрицасының рангін табу керек.
в) жүйе үйлесімді болған жағдайда, оны шешу керек.
Шешуі:
а) Гаусс әдісі жәй
түрлендірулер арқылы белгісіздерді біртіндеп жойып, жүйені
трапеция түріне келтіруді талап етеді. Жүйелердің жәй
түрлендірулері матрицалардың жәй түрлендірулерімен
ұқсас болғандықтан, жүйелердің орнына
олардың кеңейтілген матрицаларының жатық жолдарына
жәй түрлендірулерді қолданамыз. Жүйенің
коэффициенттерінің матрицасы - 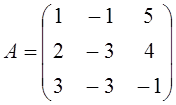 , ал
кеңейтілген матрицасы -
, ал
кеңейтілген матрицасы - 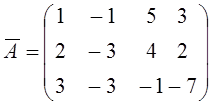 .
.
![]() кеңейтілген матрицасына келесі жәй
түрлендірулерді жүргіземіз:
кеңейтілген матрицасына келесі жәй
түрлендірулерді жүргіземіз: ![]() -ның бірінші жатық жолын -2-ге көбейтіп, екінші
жатық жолына қосамыз, бірінші жатық жолын -3-ке
көбейтіп, үшіншісіне қосамыз, сонда
-ның бірінші жатық жолын -2-ге көбейтіп, екінші
жатық жолына қосамыз, бірінші жатық жолын -3-ке
көбейтіп, үшіншісіне қосамыз, сонда 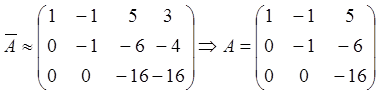 . Екі
матрица А мен
. Екі
матрица А мен ![]() нөлге
тең емес үш жатық жолы бар баспалдақ матрицаға
айналды.
нөлге
тең емес үш жатық жолы бар баспалдақ матрицаға
айналды.
Кронекер-Капелли теоремасы бойынша, егер
матрицаның рангі оның кеңейтілген матрицасының рангіне
тең болса ![]() , онда жүйе үйлесімді болады
(оның кемінде бір шешімі бар болады),
, онда жүйе үйлесімді болады
(оның кемінде бір шешімі бар болады), ![]() тең
болмаса, онда жүйе үйлесімсіз (оның шешімі болмайды).
тең
болмаса, онда жүйе үйлесімсіз (оның шешімі болмайды).
б) ![]() матрицаларының
рангі баспалдақты түрге келген матрицаның нөлге
тең емес жатық жолдарының санына тең болады. Яғни,
матрицаларының
рангі баспалдақты түрге келген матрицаның нөлге
тең емес жатық жолдарының санына тең болады. Яғни,
![]() , олай болса, жүйе үйлесімді.
Белгісіздердің саны n де 3-ке және ранг те 3-ке тең
болғандықтан (n=r), берілген жүйенің тек бір ғана
шешімі бар болады.
, олай болса, жүйе үйлесімді.
Белгісіздердің саны n де 3-ке және ранг те 3-ке тең
болғандықтан (n=r), берілген жүйенің тек бір ғана
шешімі бар болады.
в) Сонымен берілген жүйе
соңғы матрицаға сәйкес келетін жүйеге келтіріледі:
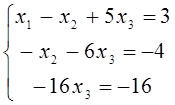 . Осы жүйе бойынша төменнен
жоғарыға көтері-ліп, соңғы теңдеуден
. Осы жүйе бойынша төменнен
жоғарыға көтері-ліп, соңғы теңдеуден ![]() ; оның
алдыңғысынан
; оның
алдыңғысынан ![]() ; ал біріншісінен
; ал біріншісінен ![]() табамыз.
Жауабы: (-4; -2; 1);
табамыз.
Жауабы: (-4; -2; 1);
8. Біртекті теңдеулер жүйесін
шешу керек: 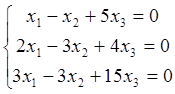 .
.
Шешуі:
Біртекті теңдеулер
жүйесі (![]() ) болғандықтан,
әр уақытта үйлесімді және нөлдік шешімі бар
) болғандықтан,
әр уақытта үйлесімді және нөлдік шешімі бар ![]() n белгісізі бар n теңдеуден
тұратын біртекті жүйенің нөлден өзгеше шешімі
болуы үшін белгісіздердің коэффициенттерінен
құралған анықтауыштың 0-ге тең болуы
қажетті және жеткілікті (rankA<n). Бізде
n белгісізі бар n теңдеуден
тұратын біртекті жүйенің нөлден өзгеше шешімі
болуы үшін белгісіздердің коэффициенттерінен
құралған анықтауыштың 0-ге тең болуы
қажетті және жеткілікті (rankA<n). Бізде 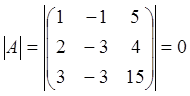 , яғни rankA<3. А матрицасы-ның
кез келген нөлден өзгеше 2-ші ретті минорын таңдап аламыз:
, яғни rankA<3. А матрицасы-ның
кез келген нөлден өзгеше 2-ші ретті минорын таңдап аламыз: 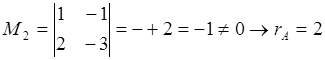 . Онда жүйенің шексіз
көп шешімі бар.
. Онда жүйенің шексіз
көп шешімі бар.
rankA=2
болғандықтан,
жүйенің
бір белгісізін ![]() деп аламыз да,
3-ші теңдеуді қалдырып кетеміз. Ары
қарай біртекті емес теңдеулер жүйесін Крамер
әдісімен шешеміз:
деп аламыз да,
3-ші теңдеуді қалдырып кетеміз. Ары
қарай біртекті емес теңдеулер жүйесін Крамер
әдісімен шешеміз:
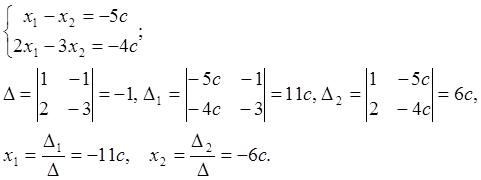
Осылайша біртекті теңдеулер жүйесін біртекті емес теңдеулер жүйесіне келтіріп, нөлден өзгеше шексіз көп шешімдері табылады:
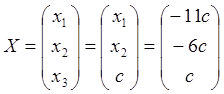 .
.
с=1 болса, бір
дербес шешімін аламыз: ![]() с=-2
болғанда, екінші
дербес шешімі шығады:
с=-2
болғанда, екінші
дербес шешімі шығады: ![]() және
т.с.с.
және
т.с.с.
9. А(3, -7)
нүктесі;
шеңбердің радиусы R=6; ![]() = 2,
= 2, ![]() = 3 – қисықтардың
жарты осьтері; Оу – төбесі бас нүктеде жататын параболаның
симметрия осі; D: у = -3 – параболаның директрисасының
теңдеуі берілген.
= 3 – қисықтардың
жарты осьтері; Оу – төбесі бас нүктеде жататын параболаның
симметрия осі; D: у = -3 – параболаның директрисасының
теңдеуі берілген.
а) центрі А нүктесі және радиусы R болатын шеңбердің теңдеуін жазу керек;
б) жарты осьтері а=2, b=3 болатын эллипстің теңдеуін құрастырып, эксцентриситетін және фокустарының координаталарын табу керек;
в) нақты жарты осі- а=2, жорамал жарты осі – b=3 болатын гипербола-ның теңдеуін құрастырып, эксцентриситетін, фокустарының координатала-рын, асимптоталарының теңдеулерін табу керек;
г) симметрия осі Оу, төбесі координаталар басында, директрисасы D болатын параболаның теңдеуін құрастырып, фокусын табу керек;
д) эллипстің, гиперболаның, параболаның сызбасын сызу керек
Шешуі:
а) Радиусы R-ге тең, центрі ![]() нүктесі болатын шеңбердің
теңдеуі
нүктесі болатын шеңбердің
теңдеуі ![]() , біздің
жағдайда:
, біздің
жағдайда: ![]() ;
;
б) Жарты осьтері ![]() және
және
![]() болатын эллипстің
канондық теңдеуі
болатын эллипстің
канондық теңдеуі 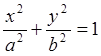 ; біздің
жағдайда:
; біздің
жағдайда: 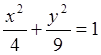 .
.
Эллипстің фокустары – ![]() болғанда,
болғанда,![]() ,
, ![]() нүктелері
немесе
нүктелері
немесе ![]() ,
, ![]() ,
,![]() нүктелері болады.
нүктелері болады.
Эллипстің эксцентриситеті 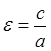 , Біздің
жағдайда
, Біздің
жағдайда ![]() болғандықтан,
эксцентриситет
болғандықтан,
эксцентриситет 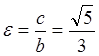 , (
, (![]() ) болады. Фокустары
Оу осінде жатады:
) болады. Фокустары
Оу осінде жатады: ![]() . Эллипстің координат
жазықтығындағы кескіні:
. Эллипстің координат
жазықтығындағы кескіні:
![]() -
эллипстің төбелері
-
эллипстің төбелері
1 сурет
в) Нақты жарты осі ![]() , жорамал жарты
осі
, жорамал жарты
осі ![]() болатын
гиперболаның канондық теңдеуі
болатын
гиперболаның канондық теңдеуі 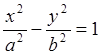 ; ал, керісінше,
нақты жарты осі
; ал, керісінше,
нақты жарты осі ![]() , жорамал жарты осі
, жорамал жарты осі ![]() болатын
гиперболаның канондық теңдеуі
болатын
гиперболаның канондық теңдеуі 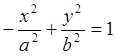 немесе
немесе 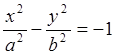 . Нақты
осі
. Нақты
осі ![]() болатын
гиперболаның эксцентриситеті
болатын
гиперболаның эксцентриситеті 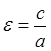 , мұндағы
, мұндағы ![]() ; гиперболаның
асимптоталары
; гиперболаның
асимптоталары 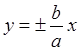 ; фокустары – нақты осьте
орналасатын
; фокустары – нақты осьте
орналасатын ![]() нүктелері.
нүктелері.
Есептің шарты бойынша ![]() =2,
=2, ![]() =3, сондықтан
нақты осі
=3, сондықтан
нақты осі ![]() болатын гиперболаның
канондық теңдеуі:
болатын гиперболаның
канондық теңдеуі: 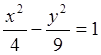 . Ол үшін
. Ол үшін ![]() ; эксцентриситет
; эксцентриситет
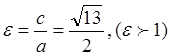 ; фокустары:
; фокустары:
![]() ;
асимптоталарының теңдеулері:
;
асимптоталарының теңдеулері: 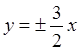 .
.
Гиперболаны келесі амалды пайдаланып, оңай сызуға болады: алдымен,
қабырғалары ![]() (бізде
(бізде ![]() ) тік
бұрышты төртбұрышты сызамыз. Тік
төртбұрыштың диагональдары гиперболаның асимптоталары
болады, қабырғаларының гиперболаның нақты осімен
қиылысатын нүктелері гиперболаның төбелері болады:
) тік
бұрышты төртбұрышты сызамыз. Тік
төртбұрыштың диагональдары гиперболаның асимптоталары
болады, қабырғаларының гиперболаның нақты осімен
қиылысатын нүктелері гиперболаның төбелері болады:
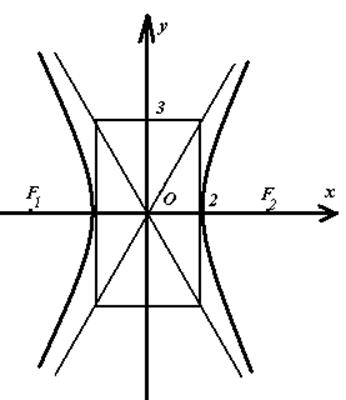
2 сурет
г) Есептің шарты бойынша,
төбесі бас нүктеде және симметрия осі Оу осі болатын
параболаның канондық теңдеуі: ![]() , ал директрисасы y=-p/2. Параболаның
директрисасының теңдеуі у = -3 болғандықтан,
, ал директрисасы y=-p/2. Параболаның
директрисасының теңдеуі у = -3 болғандықтан, 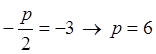 және
параболаның теңдеуі:
және
параболаның теңдеуі: ![]() . Параболаның фокусы –
симметрия осінде жататын
. Параболаның фокусы –
симметрия осінде жататын 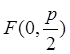 нүктесі. Біздің есебімізде
фокус -
нүктесі. Біздің есебімізде
фокус - ![]() . Енді параболаны саламыз:
. Енді параболаны саламыз:
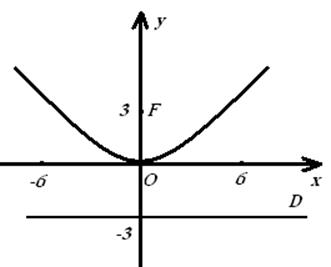
3 сурет
10. Екінші ретті беттің түрін (атын) анықтап, оның сұлбалық сызбасын сызу керек:
а) 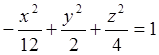 ; б)
; б) 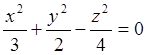 .
.
Шешуі:
а) 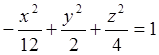 - бұл симметрия осі Ох болатын бірқуысты
гиперболоидтың канондық теңдеуі, оның сұлбалық
сызбасы мынадай:
- бұл симметрия осі Ох болатын бірқуысты
гиперболоидтың канондық теңдеуі, оның сұлбалық
сызбасы мынадай:
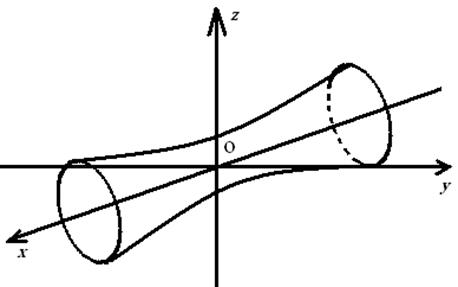
4 сурет
б) 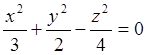 - симметрия осі
Оz және төбесі координата басында болатын екінші ретті
конустың канондық теңдеуі берілген. Оның сұлбалық
сызбасы:
- симметрия осі
Оz және төбесі координата басында болатын екінші ретті
конустың канондық теңдеуі берілген. Оның сұлбалық
сызбасы:
5 сурет
11. Екінші ретті
қисықтың жалпы теңдеуін канондық түрге
келтіріп, оның суретін салу керек: ![]() .
.
Шешуі:
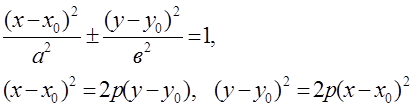 .
.
Жоғарыдағы
теңдеулер, сәйкесінше, симметрия центрі бар болатын эллипс пен
гиперболаның және төбесі ![]() нүктесі
болатын параболаның теңдеулерін береді. Екінші ретті
қисықтың жалпы теңдеуін осы теңдеулердің
біріне келтіру үшін, толық квадратты бөліп алу әдісін
қолданамыз:
нүктесі
болатын параболаның теңдеулерін береді. Екінші ретті
қисықтың жалпы теңдеуін осы теңдеулердің
біріне келтіру үшін, толық квадратты бөліп алу әдісін
қолданамыз:
![]()
x пен y кіретін
жақшалардың толық квадратын бөліп алатындай,
мүшелерін толықтаймыз: ![]() , сонда
, сонда
![]() ,
,
![]() ,
,
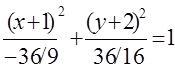 ,
, 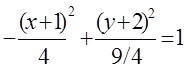 .
.
Біздің есебімізде центрі С(-1;-2) нүктесі, нақты осі b=6/4 (0y осі бойынша) және жорамал осі a=2 болатын гипербола шықты. Оның сызбасы мынадай болады:
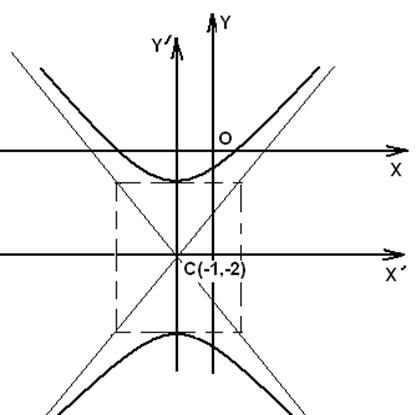
6 сурет
12. 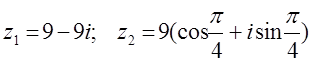 комплекс сандары берілген.
комплекс сандары берілген.
Табу керек:
а) z1 комплекс санының модулін;
б) z1 комплекс санының аргументін;
в) z1 комплекс санын тригонометриялық және көрсеткіштік формада көрсету;
г) z1 және z2 комплекс сандарының қосындысын аналитикалық және графикалық түрде көрсету;
д) (z2)5;
е) z1 z2 көбейтіндісін тригонометриялық формада;
ж) ![]() комплекс түбірлерін Муавр
формуласы арқылы табу керек.
комплекс түбірлерін Муавр
формуласы арқылы табу керек.
Шешуі:
а) Егер
комплекс санының алгебралық формасы келесідей болса: 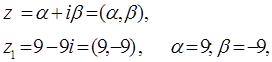
онда z1 комплекс санының модулі:
![]()
б) z1 комплекс санының аргументі:
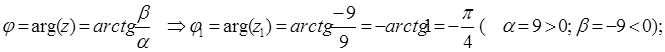
в) z1 комплекс санының тригонометриялық және көрсеткіштік формасы:
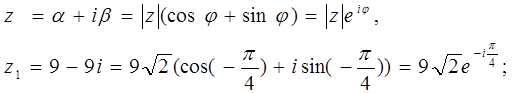
г) z1 және z2 сандарының қосындысы:
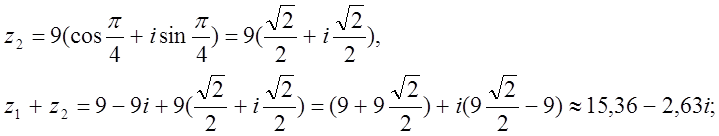
д) (z2)5 табу үшін Муавр формуласын қолданамыз:
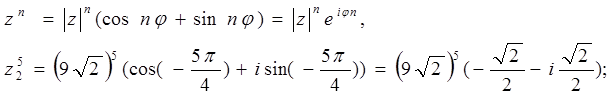
е) z1*z2 сандарының көбейтіндісін алгебралық формада тапсақ:
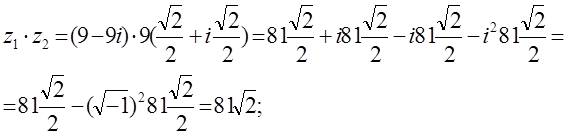
Ал тригонометриялық формада z1z2 көбейтіндісін табу есептеуді жеңілдетеді:
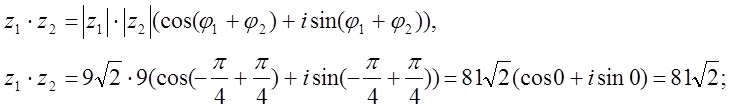
ж) ![]() , барлық n-ші
дәрежелі комплекс түбірлерді табу үшін Муавр
формуласы қолданылады:
, барлық n-ші
дәрежелі комплекс түбірлерді табу үшін Муавр
формуласы қолданылады:
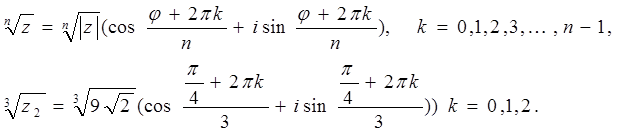
Барлық к үшін түбірлерді жазатын болсақ:
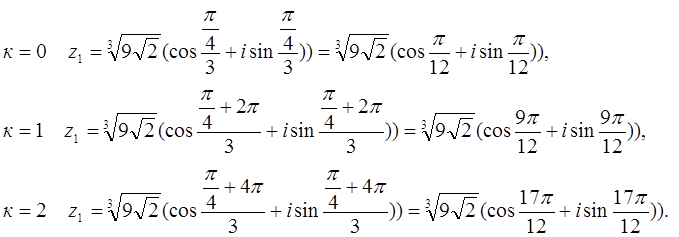
Әдебиеттер тізімі
1. Апатенок Р.Ф., Маркина А.М. Сборник задач по линейной алгебре. - Мн.: Высш. Школа, 1980. – 192 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2. - 352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000. - ч.1. - 396 с.
4. Хасеинов К.А. Математика канондары: Оқулық. – Алматы, 2003.- 686 б.
Маз м ұ н ы
1.1 Теориялық сұрақтар
1.2 Есептердің тапсырмалары
1.3 Типтік нұсқаның шешуі
Әдебиеттер тізімі