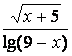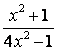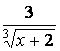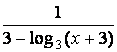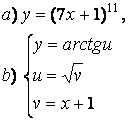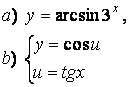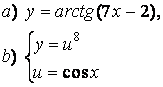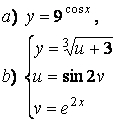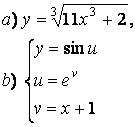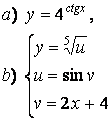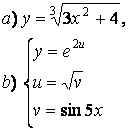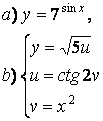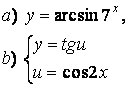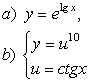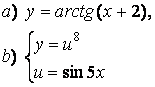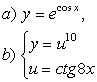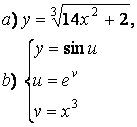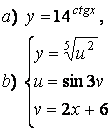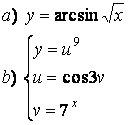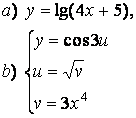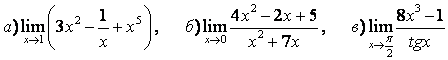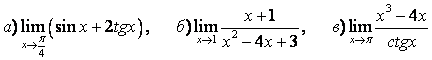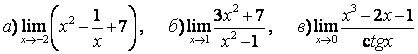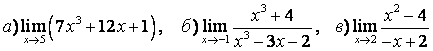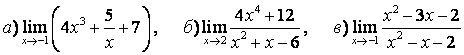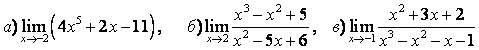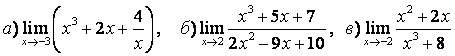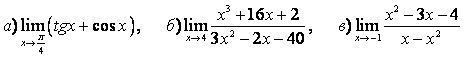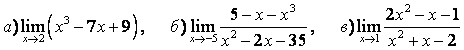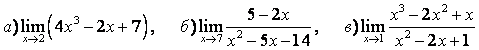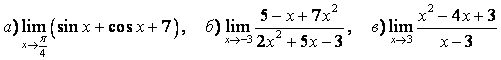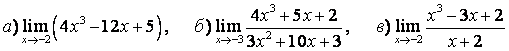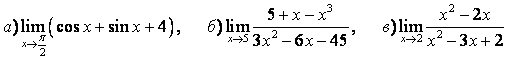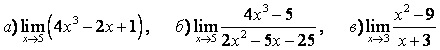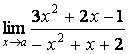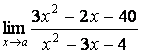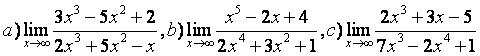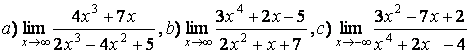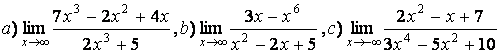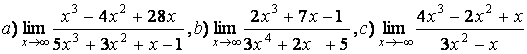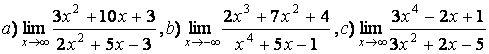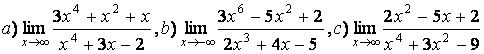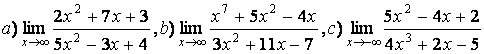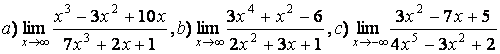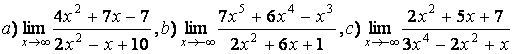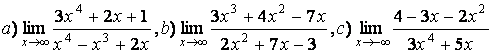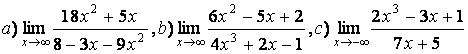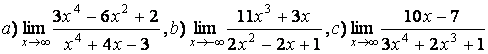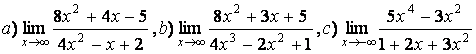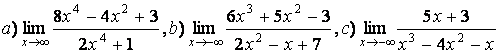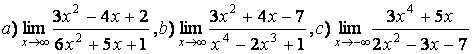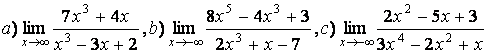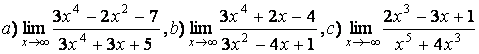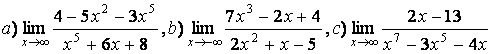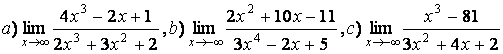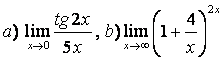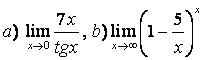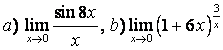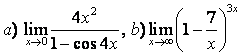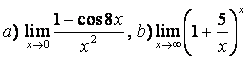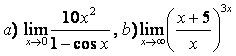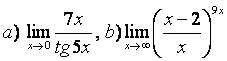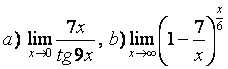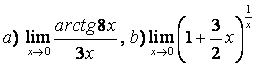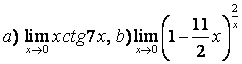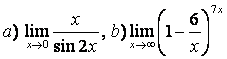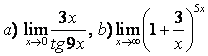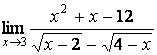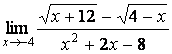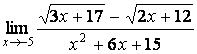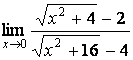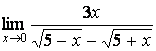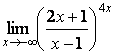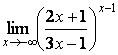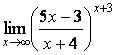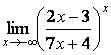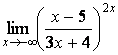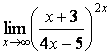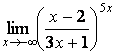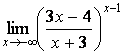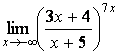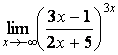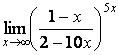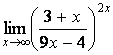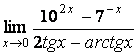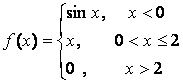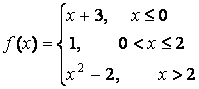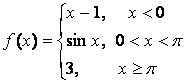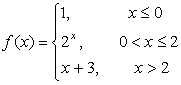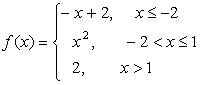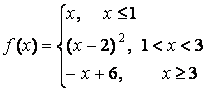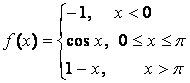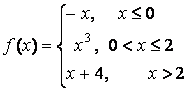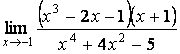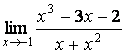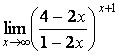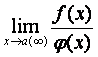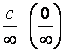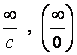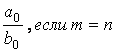Некоммерческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Математика 1
Методические указания и задания к выполнению расчетно-графической работы
для студентов всех форм обучения всех специальностей
Часть 2
Алматы 2009
СОСТАВИТЕЛИ: Л.Н.Ким,С.М.Темешева . Математика1. Методические указания и задания к выполнению расчетно-графических работ для студентов всех форм обучения всех специальностей. Часть 2.- Алматы: АИЭС, 2009.- 29 с.
Методические указания и задания к расчетно-графической работе содержат дополненное и переработанное издание типового расчета №2 программы первого семестра курса высшей математики для студентов всех специальностей дневного отделения АИЭС 2001 года. Приведены основные теоретические вопросы программы, варианты заданий и решение типового варианта. Расчетные задания разделены на два уровня сложности.
Методические указания предназначены для студентов первого курса всех форм обучения всех специальностей.
Введение
Методические указания представляют собой программу, справочный материал и задания к модулю 2 «Введение в математический анализ. Пределы. Непрерывность функций » Математики 1. Задания состоят из тридцати вариантов. Вторая цифра номера задания указывает вариант студента.
Вариант задания контрольной работы для студентов, обучающихся по заочной форме, определяется как остаток от деления номера зачетной книжки на 30. Например: номер зачетной книжки равен 080612. Это число представляется в виде: 080612=2687*30+2. Следовательно, студент должен выполнить задания варианта №2. Если остаток равен нулю, то студент выполняет вариант №30.
Контрольная работа должна быть решена в отдельной тетради, решение задач должно быть кратким и, в то же время, достаточно объяснено ссылками на теорию и сопровождено необходимыми рисунками. Примером для оформления контрольной работы может служить решение типового варианта, которое приведено в данном методическом указании.
1 Методические указания к модулю «Введение в математический
анализ. Пределы. Непрерывность функций»
1.1 Определение и способы задания функций
Если каждому элементу ![]() по
определенному правилу
по
определенному правилу ![]() поставлен в соответствие
единственный элемент
поставлен в соответствие
единственный элемент ![]() , то говорят, что задана функция
, то говорят, что задана функция
![]() , где
, где![]() –аргумент. Множество D-область
определения функции f(x)- ( D(f)=
–аргумент. Множество D-область
определения функции f(x)- ( D(f)= ![]() ) .
) .
При нахождении D(f) обращают внимание на следующие элементы формулы:
а) если есть радикалы чётной степени – функция будет определена только для тех значений x, при которых их подкоренные выражения будут неотрицательны;
б) если есть дробные выражения - функция будет определена только для тех значений x, при которых знаменатели отличны от нуля;
в) на трансцендентные функции log x, tg x, ctg x, arcsin x, arccos x, которые определены не всюду, а только при определённых значениях своего аргумента.
Чтобы определить, будет ли функция f(x) чётной или нечётной, нужно найти f(-x). Если f(-x)= f(x), то функция f(x) чётная; если f(-x)=-f(x), то функция f(x) нечётная; если оба последних равенства не выполняются, то функция общего вида (ни чётная, ни нечётная).
Функции вида ![]() называются явными.
называются явными.
![]() - неявное задание функции.
- неявное задание функции.
1.2
Пределы последовательностей и функций. Раскрытие простейших
неопределенностей вида 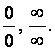
а) если функция является элементарной и предельное значение аргумента принадлежит её области определения, то вычисление предела сводится к простой подстановке предельного значения;
б) если аргумент стремится к бесконечности или к числу, которое не принадлежит области определения, то требуются специальные исследования. Эти исследования проводят, опираясь на свойства пределов, сравнение бесконечно малых, свойства эквивалентных бесконечно малых. Часто встречающиеся пределы сведены в таблицу 1.
При вычислении пределов применяется также таблица эквивалентных бесконечно малых.
1.3 Первый и второй замечательные пределы
1. 
![]() - следствие из первого замечательного предела;
- следствие из первого замечательного предела;
2. Если при указанном изменении аргумента функция представляет
неопределённость вида ![]() , то при раскрытии её применяется
второй замечательный предел (
, то при раскрытии её применяется
второй замечательный предел (  , или его следствие
, или его следствие ![]() ).
). 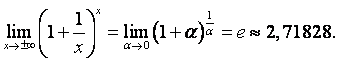
1.4 Сравнение бесконечно малых функций. Непрерывность
функций
Если 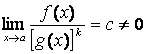 (с-константа, а f(x) и g(x)-бесконечно малые при
(с-константа, а f(x) и g(x)-бесконечно малые при ![]() ),
то f(x)- бесконечно малая к-го
порядка малости относительно g(x).
),
то f(x)- бесконечно малая к-го
порядка малости относительно g(x).
Если 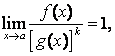 то бесконечно малые
эквивалентны.
то бесконечно малые
эквивалентны.
При отыскании точек разрыва следует иметь в виду следующее:
а) точками разрыва элементарной функции могут являться только те точки, в которых она не определена (при условии, что функция определена в некоторой окрестности рассматриваемой точки); Точками разрыва неэлементарной функции могут являться как точки, в которых она определена, так и точки, в которых она не определена; в частности, если функция задана несколькими различными аналитическими выражениями, то точками разрыва могут быть точки, в которых меняется аналитическое выражение функции.
б) если при вычислении предела ![]() рассматривать
только х<а
рассматривать
только х<а
(x>a), то получим понятие левого (правого) предела функции f(x) в точке а. Они обозначаются:
левый- ![]() ;
;
правый-![]() ;
;
в) если функция f(x) непрерывна в точке а, то выполняются равенствa
f(a) = f(a-0) = f(a+0); если а- точка разрыва, то её характер определяется
характером нарушения этих равенств. Если f(a-0) и f(a+0)
существуют, то а называется точкой разрыва первого рода; при этом, если f(a-0) ![]() f(a+0), то а называется точкой разрыва первого рода с конечным
скачком, а разность f(a+0) - f(f-0) – скачком функции f(x) в точке а; если f(a-0) = f(a+0), то а называется устранимой точкой разрыва первого рода.
Если хотя бы один из пределов f(a-0)
или f(a+0) не существует ( в
частности, “равен”
f(a+0), то а называется точкой разрыва первого рода с конечным
скачком, а разность f(a+0) - f(f-0) – скачком функции f(x) в точке а; если f(a-0) = f(a+0), то а называется устранимой точкой разрыва первого рода.
Если хотя бы один из пределов f(a-0)
или f(a+0) не существует ( в
частности, “равен”![]() или
или![]() ), то а называется точкой разрыва второго
рода.
), то а называется точкой разрыва второго
рода.
2 Типовой расчет 2 Введение в математический анализ. Пределы . Непрерывность функций
2.1 Теоретические вопросы
1 Функция одной переменной. Свойства.
2 Явные, неявные, обратные, сложные функции.
3 Классификация функций.
4 Числовая последовательность и предел.
5 Предел функции в точке.
6 Предел суммы, произведения, частного.
7 Замечательные пределы.
8 Бесконечно малые и бесконечно большие функции.![]()
9 Сравнение бесконечно малых функций.
10 Понятие непрерывности функции. Точки разрыва и их классификация.
2.2 Расчетные задания первого уровня
1 Дана функция ![]() Найти:
Найти:
а) найти область определения функции;
б) определить, четная или нечетная функция.
|
№ |
|
№ |
|
№ |
|
|
|
1.1 |
|
1.2 |
|
1.3 |
|
|
|
1.4 |
|
1.5 |
|
1.6 |
|
|
|
1.7 |
|
1.8 |
|
1.9 |
|
|
|
1.10 |
|
1.11 |
|
1.12 |
|
|
|
1.13 |
|
1.14 |
|
1.15 |
|
|
|
1.16 |
|
1.17 |
|
1.18 |
|
|
|
1.19 |
|
1.20 |
|
1.21 |
|
|
|
1.22 |
|
1.23 |
|
1.24 |
|
|
|
1.25 |
|
1.26 |
|
1.27 |
|
|
|
1.28 |
|
1.29 |
|
1.30 |
|
|
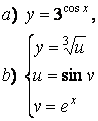
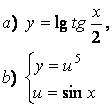
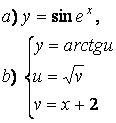
2 а) Сложную функцию разложить на последовательность основных
элементарных функций;
б) последовательность основных элементарных функций записать как одну сложную функцию.
|
2.1 |
|
2.2 |
|
2.3 |
|
|
2.4 |
|
2.5 |
|
2.6 |
|
|
2.7 |
|
2.8 |
|
2.9 |
|
|
2.10 |
|
2.11 |
|
2.12 |
|
|
2.13 |
|
2.14 |
|
2.15 |
|
|
2.16 |
|
2.17 |
|
2.18 |
|
|
2.19 |
|
2.20 |
|
2.21 |
|
|
2.22 |
|
2.23 |
|
2.24 |
|
|
2.25 |
|
2.26 |
|
2.27 |
|
|
2.28 |
|
2.29 |
|
2.30 |
|
3 Найти пределы.
|
3.1 |
|
|
3.2 |
|
|
3.3 |
|
|
3.4 |
|
|
3.5 |
|
|
3.6 |
|
|
3.7 |
|
|
3.8 |
|
|
3.9 |
|
|
3.10 |
|
|
3.11 |
|
|
3.12 |
|
|
3.13 |
|
|
3.14 |
|
|
3.15 |
|
|
3.16 |
|
|
3.17 |
|
|
3.18 |
|
|
3.19 |
|
|
3.20 |
|
|
3.21 |
|
|
3.22 |
|
|
3.23 |
|
|
3.24 |
|
|
3.25 |
|
|
3.26 |
|
|
3.27 |
|
|
3.28 |
|
|
3.29 |
|
|
3.30 |
|
4 Найти пределы.
|
№ |
|
при а= |
при а= |
№ |
|
при а= |
при а= |
|
4.1 |
|
2 |
1 |
4.2 |
|
0 |
1 |
|
4.3 |
|
3 |
2 |
4.4 |
|
1 |
-2 |
|
4.5 |
|
2 |
3 |
4.6 |
|
3 |
-3 |
|
4.7 |
|
1/3 |
4 |
4.8 |
|
-1 |
3 |
|
4.9 |
|
-1 |
-2 |
4.10 |
|
3 |
-2 |
|
4.11 |
|
2 |
-3 |
4.12 |
|
-1 |
4 |
|
4.13 |
|
4 |
3 |
4.14 |
|
-3 |
4 |
|
4.15 |
|
3 |
-2 |
4.16 |
|
-2 |
5 |
|
4.17 |
|
-1 |
2 |
4.18 |
|
-1 |
2 |
|
4.19 |
|
-1 |
2 |
4.20 |
|
4 |
-3 |
|
4.21 |
|
2 |
-3 |
4.22 |
|
1 |
-5 |
|
4.23 |
|
2 |
-2 |
4.24 |
|
7 |
-1 |
|
4.25 |
|
5 |
-3 |
4.26 |
|
-3 |
4 |
|
4.27 |
|
-5 |
4 |
4.28 |
|
-8 |
5 |
|
4.29 |
|
4 |
-2 |
4.30 |
|
-3 |
2 |
5 Найти пределы.
|
5.1 |
|
|
5.2 |
|
|
5.3 |
|
|
5.4 |
|
|
5.5 |
|
|
5.6 |
|
|
5.7 |
|
|
5.8 |
|
|
5.9 |
|
|
5.10 |
|
|
5.11 |
|
|
5.12 |
|
|
5.13 |
|
|
5.14 |
|
|
5.15 |
|
|
5.16 |
|
|
5.17 |
|
|
5.18 |
|
|
5.19 |
|
|
5.20 |
|
|
5.21 |
|
|
5.22 |
|
|
5.23 |
|
|
5.24 |
|
|
5.25 |
|
|
5.26 |
|
|
5.27 |
|
|
5.28 |
|
|
5.29 |
|
|
5.30 |
|
6 Найти пределы.
|
6.1 |
|
6.2 |
|
|
6.3 |
|
6.4 |
|
|
6.5 |
|
6.6 |
|
|
6.7 |
|
6.8 |
|
|
6.9 |
|
6.10 |
|
|
6.11 |
|
6.12 |
|
|
6.13 |
|
6.14 |
|
|
6.15 |
|
6.16 |
|
|
6.17 |
|
6.18 |
|
|
6.19 |
|
6.20 |
|
|
6.21 |
|
6.22 |
|
|
6.23 |
|
6.24 |
|
|
6.25 |
|
6.26 |
|
|
6.27 |
|
6.28 |
|
|
6.29 |
|
6.30 |
|
7 Найти пределы.
|
7.1 |
|
7.2 |
|
|
7.3 |
|
7.4 |
|
|
7.5 |
|
7.6 |
|
|
7.7 |
|
7.8 |
|
|
7.9 |
|
7.10 |
|
|
7.11 |
|
7.12 |
|
|
7.13 |
|
7.14 |
|
|
7.15 |
|
7.16 |
|
|
7.17 |
|
7.18 |
|
|
7.19 |
|
7.20 |
|
|
7.21 |
|
7.22 |
|
|
7.23 |
|
7.24 |
|
|
7.25 |
|
7.26 |
|
|
7.27 |
|
7.28 |
|
|
7.29 |
|
7.30 |
|
8 Определить порядок относительно ![]() указанных
указанных
бесконечно малых.
|
№ |
а) |
б) |
в) |
№ |
а) |
б) |
в) |
|
8.1 |
|
|
|
8.2 |
|
|
|
|
8.3 |
|
|
|
8.4 |
|
|
|
|
8.5 |
|
|
|
8.6 |
|
|
|
|
8.7 |
|
|
|
8.8 |
|
|
|
|
8.9 |
|
|
|
8.10 |
|
|
|
|
8.11 |
|
|
|
8.12 |
|
|
|
|
8.13 |
|
|
|
8.14 |
|
|
|
|
8.15 |
|
41 |
|
8.16 |
|
|
|
|
8.17 |
|
|
|
8.18 |
|
17 |
|
|
8.19 |
|
|
|
8.20 |
|
|
|
|
8.21 |
|
|
|
8.22 |
|
|
|
|
8.23 |
|
|
|
8.24 |
|
|
|
|
8.25 |
|
|
|
8.26 |
|
|
|
|
8.27 |
|
|
|
8.28 |
|
|
|
|
8.29 |
|
|
|
8.30 |
|
|
|
9 Чему эквивалентна сумма бесконечно малых (при![]() ?
?
|
9.1 |
|
9.2 |
|
|
9.3 |
|
9.4 |
|
|
9.5 |
|
9.6 |
|
|
9.7 |
|
9.8 |
|
|
9.9 |
|
9.10 |
|
|
9.11 |
|
9.12 |
|
|
9.13 |
|
9.14 |
|
|
9.15 |
|
9.16 |
|
|
9.17 |
|
9.18 |
|
|
9.19 |
|
9.20 |
|
|
9.21 |
|
9.22 |
|
|
9.23 |
|
9.24 |
|
|
9.25 |
|
9.26 |
|
|
9.27 |
|
9.28 |
|
|
9.29 |
|
9.30 |
|
10 Найти пределы, используя эквивалентные бесконечно малые.
|
10.1 |
|
10.2 |
|
10.3 |
|
|
10.4 |
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
10.9 |
|
|
10.10 |
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
10.15 |
|
|
10.16 |
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
10.21 |
|
|
10.22 |
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
10.27 |
|
|
10.28 |
|
10.29 |
|
10.30 |
|
11 Дана функция. Найти:
а) точку разрыва функции.
б) левый и правый пределы в точке разрыва.
Определить характер точки разрыва.
|
№ |
а)
|
в)
|
№ |
а)
|
в)
|
|
11.1 |
|
|
11.2 |
|
|
|
11.3 |
|
|
11.4 |
|
|
|
11.5 |
|
|
11.6 |
|
|
|
11.7 |
|
|
11.8 |
|
|
|
11.9 |
|
|
11.10 |
|
|
|
11.11 |
|
|
11.12 |
|
|
|
11.13 |
|
|
11.14 |
|
|
|
11.15 |
|
|
11.16 |
|
|
|
11.17 |
|
|
11.18 |
|
|
|
11.19 |
|
|
11.20 |
|
|
|
11.21 |
|
|
11.22 |
|
|
|
11.23 |
|
|
11.24 |
|
|
|
11.25 |
|
|
11.26 |
|
|
|
11.27 |
|
|
11.28 |
|
|
|
11.29 |
|
|
11.30 |
|
|
12 Найти пределы.
|
12.1 |
|
12.2 |
|
12.3 |
|
|
12.4 |
|
12.5 |
|
12.6 |
|
|
12.7 |
|
12.8 |
|
12.9 |
|
|
12.10 |
|
12.11 |
|
12.12 |
|
|
12.13 |
|
12.14 |
|
12.15 |
|
|
12.16 |
|
12.17 |
|
12.18 |
|
|
12.19 |
|
12.20 |
|
12.21 |
|
|
12.22 |
|
12.23 |
|
12.24 |
|
|
12.25 |
|
12.26 |
|
12.27 |
|
|
12.28 |
|
12.29 |
|
12.30 |
|
|
|
|||||
2.3 Расчетные задания второго уровня
13 Найти пределы, используя эквивалентные бесконечно малые.
|
13.1 |
|
13.2 |
|
|
13.3 |
|
13.4 |
|
|
13.5 |
|
13.6 |
|
|
13.7 |
|
13.8 |
|
|
13.9 |
|
13.10 |
|
|
13.11 |
|
13.12 |
|
|
13.13 |
|
13.14 |
|
|
13.15 |
|
13.16 |
|
|
13.17 |
|
13.18 |
|
|
13.19 |
|
13.20 |
|
|
13.21 |
|
13.22 |
|
|
13.23 |
|
13.24 |
|
|
13.25 |
|
13.26 |
|
|
13.27 |
|
13.28 |
|
|
13.29 |
|
13.30 |
|
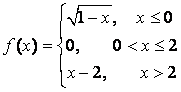
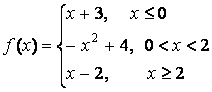
14 Исследовать функции на непрерывность и построить графики.
|
14.1 |
|
14.2 |
|
|
14.3 |
|
14.4 |
|
|
14.5 |
|
14.6 |
|
|
14.7 |
|
14.8 |
|
|
14.9 |
|
14.10 |
|
|
14.11 |
|
14.12 |
|
|
14.13 |
|
14.14 |
|
|
14.15 |
|
14.16 |
|
|
14.17 |
|
14.18 |
|
|
14.19 |
|
14.20 |
|
|
14.21 |
|
14.22 |
|
|
14.23 |
|
14.24 |
|
|
14.25 |
|
14.26 |
|
|
14.27 |
|
14.28 |
|
|
14.29 |
|
14.30 |
|
15 Найти указанные пределы, не применяя правило Лопиталя-Бернулли.
|
15.1 |
|
15.2 |
|
|
15.3 |
|
15.4 |
|
|
15.5 |
|
15.6 |
|
|
15.7 |
|
15.8 |
|
|
15.9 |
|
15.10 |
|
|
15.11 |
|
15.12 |
|
|
15.13 |
|
15.14 |
|
|
15.15 |
|
15.16 |
|
|
15.17 |
|
15.18 |
|
|
15.19 |
|
15.20 |
|
|
15.21 |
|
15.22 |
|
|
15.23 |
|
15.24 |
|
|
15.25 |
|
15.26 |
|
|
15.27 |
|
15.28 |
|
|
15.29 |
|
15.30 |
|
|
|
|
|
|
16 Найти пределы.
|
16.1 |
|
16.2 |
|
16.3 |
|
|
16.4 |
|
16.5 |
|
16.6 |
|
|
16.7 |
|
16.8 |
|
16.9 |
|
|
16.10 |
|
16.11 |
|
16.12 |
|
|
16.13 |
|
16.14 |
|
16.15 |
|
|
16.16 |
|
16.17 |
|
16.18 |
|
|
16.19 |
|
16.20 |
|
16.21 |
|
|
16.22 |
|
16.23 |
|
16.24 |
|
|
16.25 |
|
16.26 |
|
16.27 |
|
|
16.28 |
|
16.29 |
|
16.30 |
|
2.4 Решение типового варианта
1 Дана функция f(x)=![]() . Найти:
. Найти:
а) область определения D(f);
б) определить чётность или нечётность функции.
Решение:
а) поскольку x в данном примере
содержится под радикалом чётной степени, то f(x) будет иметь действительные значения только при тех
значениях х, при которых подкоренное выражение неотрицательно, т.е. ![]() . Решая неравенство, получим
. Решая неравенство, получим ![]() . Таким образом, D(f)=
. Таким образом, D(f)=![]() ;
;
б) для данной функции f(-x)= ![]() ,
,
значит функция общего вида.
2 а) сложную функцию ![]() разложить
на
разложить
на
последовательность основных элементарных функций;
б) последовательность основных элементарных функций
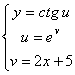
записать как одну сложную функцию.
Решение:
а) введём промежуточный аргумент, т.е. обозначим u=8x-1. Таким
образом, данная функция может быть представлена в виде следующей
последовательности основных элементарных функций![]() ;
;
б) поднимаясь снизу вверх, подставим сначала промежуточный
аргумент v в функцию u, а
затем значение u в функцию y.
Получим искомую сложную функцию ![]() .
.
3 Найти пределы:
а) ![]() ;
;
б) 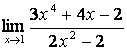 ;
;
в)
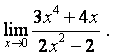
Решение:
а) данная функция определена в предельной точке x=0, поэтому просто
подставим это предельное значение в функцию:
![]() =
=![]() =
=![]() =2;
=2;
б) подставим предельную точку x=1 в данную функцию, получим:
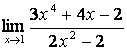 =
= , что
равно
, что
равно ![]() ( таблица 1,(1.3));
( таблица 1,(1.3));
в) подставим предельную точку x=0 в
данную функцию, получим: 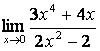 =
= , что равно 0 ( таблица1, (1.3)).
, что равно 0 ( таблица1, (1.3)).
4 Найти предел 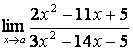 , при а=5.
, при а=5.
Решение:
Подставим предельную точку x=5 в данную функцию, получим
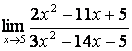 =
=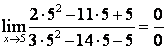 ,
т.е. неопределённость. Эту неопределённость можно раскрыть следующим способом.
Разложить числитель и знаменатель дроби на множители, а затем сократить дробь
на общий множитель (х-5):
,
т.е. неопределённость. Эту неопределённость можно раскрыть следующим способом.
Разложить числитель и знаменатель дроби на множители, а затем сократить дробь
на общий множитель (х-5):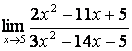 =
=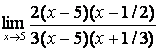 =
=![]() .
.
5 Найти пределы:
а)  ;
;
б)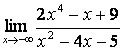 ;
;
в)  .
.
Решение:
При вычислении данных пределов используем правило 1.7
таблицы 1.
а) числитель и знаменатель имеют одинаковые степени m=n=2, поэтому предел равен отношению
коэффициентов старших степеней:

б) степень числителя больше степени знаменателя (4>2),
поэтому 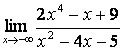 =
= ![]() ;
;
в) степень знаменателя больше степени числителя (6>2),
поэтому  =0.
=0.
6 Найти пределы: а) 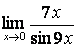 ;
;
б) 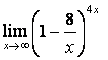 .
.
Решение:
а) данная функция не определена в предельной точке и в этой точке
представляет неопределённость вида ![]() . Для
раскрытия неопределённости можно применить различные способы: первый
замечательный предел
. Для
раскрытия неопределённости можно применить различные способы: первый
замечательный предел
(![]() ) и его следствия, сравнение бесконечно
малых (таблица эквивалентных бесконечно малых) и теоремы об эквивалентных бесконечно
малых . Используя следствие из первого замечательного предела
) и его следствия, сравнение бесконечно
малых (таблица эквивалентных бесконечно малых) и теоремы об эквивалентных бесконечно
малых . Используя следствие из первого замечательного предела 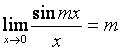 , имеем:
, имеем: 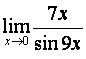 =
=  =
=![]() =
=![]() . Если же использовать бесконечно малые,
то, учитывая, что sin
. Если же использовать бесконечно малые,
то, учитывая, что sin![]() ~
~
![]() (
(![]()
![]() ), имеем:
), имеем: 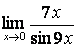 =
=![]() =
=![]() ;
;
б) можно убедиться, что при указанном изменении аргумента
функция представляет неопределённость вида ![]() , при
раскрытии которой применяется второй замечательный предел (
, при
раскрытии которой применяется второй замечательный предел (  , или его следствие
, или его следствие  ), или сравнение бесконечно малых и
теоремы об эквивалентных бесконечно малых. Преобразуем данный предел следующим
образом:
), или сравнение бесконечно малых и
теоремы об эквивалентных бесконечно малых. Преобразуем данный предел следующим
образом: 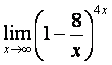 =
= =
=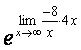 =
=![]() .
.
7 Найти предел  .
.
Решение:
При подстановке предельного значения получим неопределённость
вида ![]() , которую необходимо раскрыть,
умножая числитель и знаменатель на выражение, сопряжённое числителю:
, которую необходимо раскрыть,
умножая числитель и знаменатель на выражение, сопряжённое числителю: 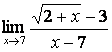 =
= =
= =
=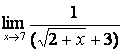 =1/6.
=1/6.
8 Определить порядок относительно х (![]() ) бесконечно малых:
) бесконечно малых:
а) ![]() ; б) 7х; в)
; б) 7х; в) ![]() .
.
Решение:
Если 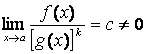 (с-константа, f(x) и g(x)
(с-константа, f(x) и g(x)
бесконечно малые при ![]() ), то f(x)- бесконечно малая к-го порядка
малости относительно g(x);
), то f(x)- бесконечно малая к-го порядка
малости относительно g(x);
а)  . Бесконечно малые
имеют первый порядок малости относительно х (эквивалентны x);
. Бесконечно малые
имеют первый порядок малости относительно х (эквивалентны x);
б) ![]() . Бесконечно малые
имеют первый порядок малости относительно х ;
. Бесконечно малые
имеют первый порядок малости относительно х ;
в) 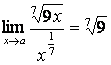 . Порядок малости
бесконечно малой равен 1/7.
. Порядок малости
бесконечно малой равен 1/7.
9 Чему эквивалентна сумма бесконечно малых ![]()
(при ![]() )?
)?
Решение:
Известно следующее свойство эквивалентных бесконечно малых:
алгебраическая сумма конечного числа бесконечно малых эквивалентна
слагаемому более низкого порядка малости. Для данной функции ![]() , значит, низший порядок имеет
, значит, низший порядок имеет ![]() и
и ![]() ~ (-
~ (-![]() ).
).
10 Найти предел 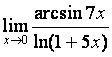 , используя
эквивалентные бесконечно малые.
, используя
эквивалентные бесконечно малые.
Решение:
Применяя таблицу и свойства эквивалентных бесконечно малых, имеем:
![]() ~
~ ![]() ,
,
![]() . Поэтому
. Поэтому
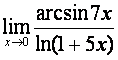 =
= 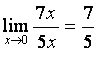 .
.
11 Дана функции ![]() .
.
Найти:
а) точку разрыва функции;
б) левый и правый пределы в точке разрыва;
в) определить характер точки разрыва.
Решение:
а) точка х=-6 не входит в область определения данной функции, но функция определена в окрестности этой точки, следовательно, х=-6 точка разрыва;
б)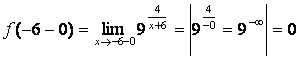 ,
,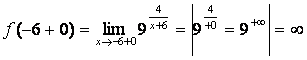 ;
;
в) так как один из односторонних пределов ![]() , то х=-6 будет точкой разрыва второго
рода.
, то х=-6 будет точкой разрыва второго
рода.
12 Дана функции

Найти:
а) точку разрыва функции;
б) левый и правый пределы в точке разрыва;
в) определить характер точки разрыва.
Решение:
а) точка х=3 не входит в область определения данной функции и функция определена в окрестности этой точки, значит х=3 точка разрыва;
б) 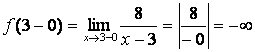 ,
,  ;
;
в) так как оба односторонних предела “равны”![]() и
и![]() , то
х=3 будет точкой разрыва второго рода.
, то
х=3 будет точкой разрыва второго рода.
Т а б л и ц а 1-Таблица неопределенностей
|
Виды пределов
|
Результат подстановки предельной точки |
Результат вычисления предела |
|
1.
|
1) |
неопределенности |
|
|
||
|
3)
|
|
|
|
4)
|
0 |
|
|
5) |
|
|
|
6)
|
0 |
|
|
7) |
|
|
|
0,если m<n |
||
|
|
||
|
2. |
|
неопределенность |
|
2)
|
|
|
|
3) |
0 |
|
|
3. |
|
неопределенность |
|
|
|
|
|
4. |
|
неопределенность |
|
|
||
|
|
||
|
|
0, если 0 |
|
|
|
0, если с>1,
|
Т а б л и ц а 2- Таблица эквивалентных бесконечно малых
|
|
|||
|
1 |
|
7 |
|
|
2 |
|
8 |
|
|
3 |
|
9 |
|
|
4 |
|
10 |
|
|
5 |
|
11 |
|
|
6 |
|
|
|
Список литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч.- М.: Высш. Шк., 1986. – Ч.1-352 с.
2. Сборник индивидуальных заданий по высшей математике: В 3 ч.
/А.П.Рябушко, В.В.Бархатов и др./ Под редакцией А.П.Рябушко.- Минск: Вышэйшая школа, 1991.-Ч.2-351 с.
3. Кузнецов А.А. Сборник заданий по высшей математике: Типовые расчеты.-М.: Высш.шк., 1983.-176 с.
4. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть.-М.: Айрис-пресс, 2003.-256 с.
5. Хасеинов К.А. Каноны математики. Учебник – Алматы: 2003.-686 с.
6. Математика 1. Конспект лекций для студентов всех форм обучения всех специальностей. Алматинский институт энергетики и связи: 2007.
Содержание
Введение…………………………………………………………………………….3
1 Методические указания к модулю «Введение в математический анализ. Пределы. Непрерывность.»…....3
1.1 Определение и способы задания функций…………………………………3
1.2
Пределы последовательностей и
функций. Раскрытие простейшихнеопределенностей вида
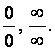 ….4
….4
1.3 Первый и второй замечательные пределы ……………………..…….........4
1.4 Сравнение бесконечно малых функций. Непрерывность функций ………………4
2 Типовой расчет 2. Введение в математический анализ. Пределы . Непрерывность функций ………5
2.1 Теоретические вопросы……………………………………………………….5
2.2 Расчетные задания первого уровня…………………………………………..5
2.3 Расчетные задания второго уровня…………………………………………17
2.4 Решение типового варианта…………………………………………………22
Таблица 1- Таблица неопределенностей………………………………………..26
Таблица 2- Таблица эквивалентных бесконечно малых……………………….27
Список литературы……………………………………………………………….28