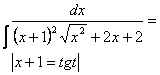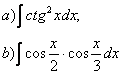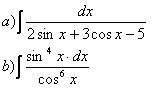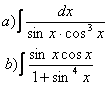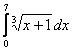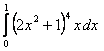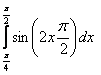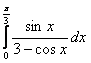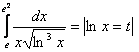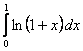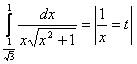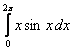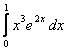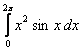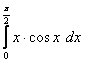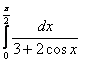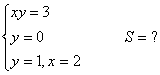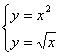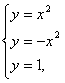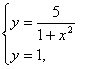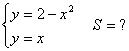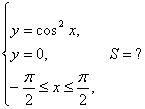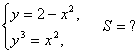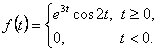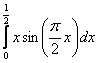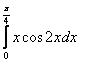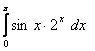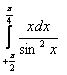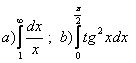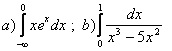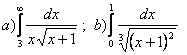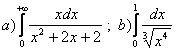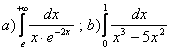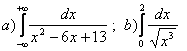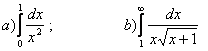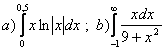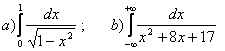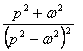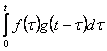Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
МАТЕМАТИКА 1
Методические указания к расчетно-графической работе
для студентов специальностей 5В071800- «Электроэнергетика», 5В071700- «Теплоэнергетика»,
5В071900- «Радиотехника, электроника и телекоммуникации»,
5В070200- «Автоматика и управление»
3-Часть
Алматы 2013
Составители: С.А. Нурпейсов, Ж.С. Абдулланова. Математика-1. Методические указания и задания к расчетно- графическим работам. Часть 3.-Алматы: АУЭС, 2013.-33 с.
Методическое указание подготовлено в соответствии с типовой программой по курсу «Математика-1» для специальностей 5В071700, 5В071800, 5В071900, 5В070200 дневного отделения АУЭС.
Методические указания и задания к РГР содержат задачи курса высшей математики: «Неопределенные и определенные интегралы. Операционные исчисления».
РГР содержит 2 уровня заданий. Даны основные теоретические вопросы программы и решение типового варианта.
Рецензент: доцент Туманов М.Е.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013 г.
© НАО «Алматинский университет энергетики и связи», 2013 г.
Сводный план 2013г., поз. 171
Введение
Это методическое указание представляет собой 3-ю часть расчетно-графической работы по курсу «Математика-1», который изучается студентами специальностей 5В071700, 5В071800, 5В071900, 5В070200 дневного отделения АУЭС на первом семестре.
Так как были изданы 1 и 2-е части этого курса, появилась необходимость выпуска 3-ей части.
Расчетно-графическая работа написана в соответствии с действующей программой по курсу «Математика-1» для студентов специальностей 5В071700, 5В071800, 5В071900, 5В070200. Настоящее методическое указание адресовано преподавателям и студентам и предназначено для проведения самостоятельной работы во время аудиторных занятий и выдачи индивидуальных домашних заданий. Здесь содержится материал по определенным и неопределенным интегралам, по операционным исчислениям.
Данный РГР состоит из 22 заданий (16 заданий 1-го уровня сложности и 6 заданий 2-го уровня сложности) по 30 вариантов каждый. В конце приведено решение типового варианта, где дано подробное решение каждого задания 1-го уровня сложности. Решение заданий 2-го уровня сложности предоставляется для самостоятельного решения студентам. Также приводятся основные теоретические вопросы, которые должны освоить студенты по этому разделу математики.
1Расчетно-графическая работа №3. Неопределенные и определенные интегралы. Некоторые элементы операционных исчислении
Цель: научить студентов применять теоретические знания для вычисления неопределенных и определенных интегралов по основным методам интегрирования: непосредственное интегрирование, интегрирование замены переменной и интегрирование по частям. Привить навыки исследования несобственных интегралов, а также ознакомить с основными элементами теории операционных исчислении.
1.1 Задания первого уровня
1. Вычислить интеграл.
|
1.1 |
|
1.16 |
|
|
1.2 |
|
1.17 |
|
|
1.3 |
|
1.18 |
|
|
1.4 |
|
1.19 |
|
|
1.5 |
|
1.20 |
|
|
1.6 |
|
1.21 |
|
|
1.7 |
|
1.22 |
|
|
1.8 |
|
1.23 |
|
|
1.9 |
|
1.24 |
|
|
1.10 |
|
1.25 |
|
|
1.11 |
|
1.26 |
|
|
1.12 |
|
1.27 |
|
|
1.13 |
|
1.28 |
|
|
1.14 |
|
1.29 |
|
|
1.15 |
|
1.30 |
|
2. Вычислить интегралы методом замены переменной.
|
2.1 |
|
2.16 |
|
|
2.2 |
|
2.17 |
|
|
2.3 |
|
2.18 |
|
|
2.4 |
|
2.19 |
|
|
2.5 |
|
2.20 |
|
|
2.6 |
|
2.21 |
|
|
2.7 |
|
2.22 |
|
|
2.8 |
|
2.23 |
|
|
2.9 |
|
2.24 |
|
|
2.10 |
|
2.25 |
|
|
2.11 |
|
2.26 |
|
|
2.12 |
|
2.27 |
|
|
2.13 |
|
2.28 |
|
|
2.14 |
|
2.29 |
|
|
2.15 |
|
2.30 |
|
3. Вычислить интегралы методом интегрирования по частям.
|
3.1 |
|
3.11 |
|
3.21 |
|
|
3.2 |
|
3.12 |
|
3.22 |
|
|
3.3 |
|
3.13 |
|
3.23 |
|
|
3.4 |
|
3.14 |
|
3.24 |
|
|
3.5 |
|
3.15 |
|
3.25 |
|
|
3.6 |
|
3.16 |
|
3.26 |
|
|
3.7 |
|
3.17 |
|
3.27 |
|
|
3.8 |
|
3.18 |
|
3.28 |
|
|
3.9 |
|
3.19 |
|
3.29 |
|
|
3.10 |
|
3.20 |
|
3.30 |
|
4. Вычислить интегралы.
|
4.1 |
|
4.11 |
|
4.21 |
|
|
4.2 |
|
4.12 |
|
4.22 |
|
|
4.3 |
|
4.13 |
|
4.23 |
|
|
4.4 |
|
4.14 |
|
4.24 |
|
|
4.5 |
|
4.15 |
|
4.25 |
|
|
4.6 |
|
4.16 |
|
4.26 |
|
|
4.7 |
|
4.17 |
|
4.27 |
|
|
4.8 |
|
4.18 |
|
4.28 |
|
|
4.9 |
|
4.19 |
|
4.29 |
|
|
4.10 |
|
4.20 |
|
4.30 |
|
5. Вычислить интегралы.
|
5.1 |
|
5.11 |
|
5.21 |
|
|
5.2 |
|
5.12 |
|
5.22 |
|
|
5.3 |
|
5.13 |
|
5.23 |
|
|
5.4 |
|
5.14 |
|
5.24 |
|
|
5.5 |
|
5.15 |
|
5.25 |
|
|
5.6 |
|
5.16 |
|
5.26 |
|
|
5.7 |
|
5.17 |
|
5.27 |
|
|
5.8 |
|
5.18 |
|
5.28 |
|
|
5.9 |
|
5.19 |
|
5.29 |
|
|
5.10 |
|
5.20 |
|
5.30 |
|
6. Вычислить интегралы от некоторых иррациональных функции.
|
6.1 |
|
6.11 |
|
6.21 |
|
|
6.2 |
|
6.12 |
|
6.22 |
|
|
6.3 |
|
6.13 |
|
6.23 |
|
|
6.4 |
|
6.14 |
|
6.24 |
|
|
6.5 |
|
6.15 |
|
6.25 |
|
|
6.6 |
|
6.16 |
|
6.26 |
|
|
6.7 |
|
6.17 |
|
6.27 |
|
|
6.8 |
|
6.18 |
|
6.28 |
|
|
6.9 |
|
6.19 |
|
6.29 |
|
|
6.10 |
|
6.20 |
|
6.30 |
|
7. Вычислить интегралы.
|
7.1 |
|
7.11 |
|
7.21 |
|
|
7.2 |
|
7.12 |
|
7.22 |
|
|
7.3 |
|
7.13 |
|
7.23 |
|
|
7.4 |
|
7.14 |
|
7.24 |
|
|
7.5 |
|
7.15 |
|
7.25 |
|
|
7.6 |
|
7.16 |
|
7.26 |
|
|
7.7 |
|
7.17 |
|
7.27 |
|
|
7.8 |
|
7.18 |
|
7.28 |
|
|
7.9 |
|
7.19 |
|
7.29 |
|
|
7.10 |
|
7.20 |
|
7.30 |
|
8. Вычислить определенные интегралы.
|
8.1 |
|
8.11 |
|
8.21 |
|
|
8.2 |
|
8.12 |
|
8.22 |
|
|
8.3 |
|
8.13 |
|
8.23 |
|
|
8.4 |
|
8.14 |
|
8.24 |
|
|
8.5 |
|
8.15 |
|
8.25 |
|
|
8.6 |
|
8.16 |
|
8.26 |
|
|
8.7 |
|
8.17 |
|
8.27 |
|
|
8.8 |
|
8.18 |
|
8.28 |
|
|
8.9 |
|
8.19 |
|
8.29 |
|
|
8.10 |
|
8.20 |
|
8.30 |
|
9. Вычислить интегралы.
|
9.1 |
|
9.11 |
|
9.21 |
|
|
9.2 |
|
9.12 |
|
9.22 |
|
|
9.3 |
|
9.13 |
|
9.23 |
|
|
9.4 |
|
9.14 |
|
9.24 |
|
|
9.5 |
|
9.15 |
|
9.25 |
|
|
9.6 |
|
9.16 |
|
9.26 |
|
|
9.7 |
|
9.17 |
|
9.27 |
|
|
9.8 |
|
9.18 |
|
9.28 |
|
|
9.9 |
|
9.19 |
|
9.29 |
|
|
9.10 |
|
9.20 |
|
9.30 |
|
10. Вычислить интегралы методом интегрирования по частям.
|
10.1 |
|
10.11 |
|
10.21 |
|
|
10.2 |
|
10.12 |
|
10.22 |
|
|
10.3 |
|
10.13 |
|
10.23 |
|
|
10.4 |
|
10.14 |
|
10.24 |
|
|
10.5 |
|
10.15 |
|
10.25 |
|
|
10.6 |
|
10.16 |
|
10.26 |
|
|
10.7 |
|
10.17 |
|
10.27 |
|
|
10.8 |
|
10.18 |
|
10.28 |
|
|
10.9 |
|
10.19 |
|
10.29 |
|
|
10.10 |
|
10.20 |
|
10.30 |
|
11. Вычислить несобственные интегралы.
|
11.1 |
|
11.11 |
|
11.21 |
|
|
11.2 |
|
11.12 |
|
11.22 |
|
|
11.3 |
|
11.13 |
|
11.23 |
|
|
11.4 |
|
11.14 |
|
11.24 |
|
|
11.5 |
|
11.15 |
|
11.25 |
|
|
11.6 |
|
11.16 |
|
11.26 |
|
|
11.7 |
|
11.17 |
|
11.27 |
|
|
11.8 |
|
11.18 |
|
11.28 |
|
|
11.9 |
|
11.19 |
|
11.29 |
|
|
11.10 |
|
11.20 |
|
11.30 |
|
12. Вычислить площади фигур, ограниченных графиками следующих функции.
|
12.1 |
|
12.16 |
|
|
12.2 |
|
12.17 |
|
|
12.3 |
|
12.18 |
|
|
12.4 |
|
12.19 |
|
|
12.5 |
|
12.20 |
|
|
12.6 |
|
12.21 |
|
|
12.7 |
|
12.22 |
|
|
12.8 |
|
12.23 |
|
|
12.9 |
|
12.24 |
|
|
12.10 |
|
12.25 |
|
|
12.11 |
|
12.26 |
|
|
12.12 |
|
12.27 |
|
|
12.13 |
|
12.28 |
|
|
12.14 |
|
12.29 |
|
|
12.15 |
|
12.30 |
|
13. Являются ли функции оригиналами, если да, то почему?
|
13.1 |
|
13.11 |
|
13.21 |
|
|
13.2 |
|
13.12 |
|
13.22 |
|
|
13.3 |
|
13.13 |
|
13.23 |
|
|
13.4 |
|
13.14 |
|
13.24 |
|
|
13.5 |
|
13.15 |
|
13.25 |
|
|
13.6 |
|
13.16 |
|
13.26 |
|
|
13.7 |
|
13.17 |
|
13.27 |
|
|
13.8 |
|
13.18 |
|
13.28 |
|
|
13.9 |
|
13.19 |
|
13.29 |
|
|
13.10 |
|
13.20 |
|
13.30 |
|
14. Найти изображения заданных функции.
|
14.1 |
|
14.11 |
|
14.21 |
|
|
14.2 |
|
14.12 |
|
14.22 |
|
|
14.3 |
|
14.13 |
|
14.23 |
|
|
14.4 |
|
14.14 |
|
14.24 |
|
|
14.5 |
|
14.15 |
|
14.25 |
|
|
14.6 |
|
14.16 |
|
14.26 |
|
|
14.7 |
|
14.17 |
|
14.27 |
|
|
14.8 |
|
14.18 |
|
14.28 |
|
|
14.9 |
|
14.19 |
|
14.29 |
|
|
14.10 |
|
14.20 |
|
14.30 |
|
15. Найти оригинал![]() функции F(p).
функции F(p).
|
15.1 |
|
15.11 |
|
15.21 |
|
|
15.2 |
|
15.12 |
|
15.22 |
|
|
15.3 |
|
15.13 |
|
15.23 |
|
|
15.4 |
|
15.14 |
|
15.24 |
|
|
15.5 |
|
15.15 |
|
15.25 |
|
|
15.6 |
|
15.16 |
|
15.26 |
|
|
15.7 |
|
15.17 |
|
15.27 |
|
|
15.8 |
|
15.18 |
|
15.28 |
|
|
15.9 |
|
15.19 |
|
15.29 |
|
|
15.10 |
|
15.20 |
|
15.30 |
|
16. Найти свертку функции![]() и
и ![]() , и их изображение.
, и их изображение.
|
№ |
|
|
№ |
|
|
№ |
|
|
|
|
16.1 |
|
|
16.11 |
|
|
16.21 |
|
|
|
|
16.2 |
|
|
16.12 |
|
|
16.22 |
1 |
|
|
|
16.3 |
|
|
16.13 |
|
|
16.23 |
1 |
|
|
|
16.4 |
|
|
16.14 |
|
|
16.24 |
|
|
|
|
16.5 |
|
|
16.15 |
|
|
16.25 |
|
|
|
|
16.6 |
|
|
16.16 |
1 |
|
16.26 |
|
|
|
|
16.7 |
|
|
16.17 |
1 |
|
16.27 |
|
|
|
|
16.8 |
|
|
16.18 |
|
|
16.28 |
|
|
|
|
16.9 |
|
|
16.19 |
|
|
16.29 |
|
|
|
|
16.10 |
1 |
|
16.20 |
|
|
16.30 |
1 |
|
1.2 Задания второго уровня
17. Вычислить интегралы.
|
17.1 |
|
17.16 |
|
|
17.2 |
|
17.17 |
|
|
17.3 |
|
17.18 |
|
|
17.4 |
|
17.19 |
|
|
17.5 |
|
17.20 |
|
|
17.6 |
|
17.21 |
|
|
17.7 |
|
17.22 |
|
|
17.8 |
|
17.23 |
|
|
17.9 |
|
17.24 |
|
|
17.10 |
|
17.25 |
|
|
17.11 |
|
17.26 |
|
|
17.12 |
|
17.27 |
|
|
17.13 |
|
17.28 |
|
|
17.14 |
|
17.29 |
|
|
17.15 |
|
17.30 |
|
18. Вычислить интегралы.
|
18.1 |
|
18.11 |
|
18.21 |
|
|
18.2 |
|
18.12 |
|
18.22 |
|
|
18.3 |
|
18.13 |
|
18.23 |
|
|
18.4 |
|
18.14 |
|
18.24 |
|
|
18.5 |
|
18.15 |
|
18.25 |
|
|
18.6 |
|
18.16 |
|
18.26 |
|
|
18.7 |
|
18.17 |
|
18.27 |
|
|
18.8 |
|
18.18 |
|
18.28 |
|
|
18.9 |
|
18.19 |
|
18.29 |
|
|
18.10 |
|
18.20 |
|
18.30 |
|
19. Вычислить интегралы.
|
19.1 |
|
19.11 |
|
19.21 |
|
|
19.2 |
|
19.12 |
|
19.22 |
|
|
19.3 |
|
19.13 |
|
19.23 |
|
|
19.4 |
|
19.14 |
|
19.24 |
|
|
19.5 |
|
19.15 |
|
19.25 |
|
|
19.6 |
|
19.16 |
|
19.26 |
|
|
19.7 |
|
19.17 |
|
19.27 |
|
|
19.8 |
|
19.18 |
|
19.28 |
|
|
19.9 |
|
19.19 |
|
19.29 |
|
|
19.10 |
|
19.20 |
|
19.30 |
|
20. Вычислить несобственные интегралы.
|
20.1 |
|
20.16 |
|
|
20.2 |
|
20.17 |
|
|
20.3 |
|
20.18 |
|
|
20.4 |
|
20.19 |
|
|
20.5 |
|
20.20 |
|
|
20.6 |
|
20.21 |
|
|
20.7 |
|
20.22 |
|
|
20.8 |
|
20.23 |
|
|
20.9 |
|
20.24 |
|
|
20.10 |
|
20.25 |
|
|
20.11 |
|
20.26 |
|
|
20.12 |
|
20.27 |
|
|
20.13 |
|
20.28 |
|
|
20.14 |
|
20.29 |
|
|
20.15 |
|
20.30 |
|
21. Найти изображение ![]() функции
функции![]() по определению.
по определению.
|
21.1 |
|
21.11 |
|
21.21 |
|
|
21.2 |
|
21.12 |
|
21.22 |
|
|
21.3 |
|
21.13 |
|
21.23 |
|
|
21.4 |
|
21.14 |
|
21.24 |
|
|
21.5 |
|
21.15 |
|
21.25 |
|
|
21.6 |
|
21.16 |
|
21.26 |
|
|
21.7 |
|
21.17 |
|
21.27 |
|
|
21.8 |
|
21.18 |
|
21.28 |
|
|
21.9 |
|
21.19 |
|
21.29 |
|
|
21.10 |
|
21.20 |
|
21.30 |
|
22. Найти изображения заданных функции, используя теорему дифференцирования оригинала.
|
22.1 |
|
22.11 |
|
22.21 |
|
|
22.2 |
|
22.12 |
|
22.22 |
|
|
22.3 |
|
22.13 |
|
22.23 |
|
|
22.4 |
|
22.14 |
|
22.24 |
|
|
22.5 |
|
22.15 |
|
22.25 |
|
|
22.6 |
|
22.16 |
|
22.26 |
|
|
22.7 |
|
22.17 |
|
22.27 |
|
|
22.8 |
|
22.18 |
|
22.28 |
|
|
22.9 |
|
22.19 |
|
22.29 |
|
|
22.10 |
|
22.20 |
|
22.30 |
|
Таблица основных интегралов.
|
1 |
|
11 |
|
|
2 |
|
12 |
|
|
3 |
|
13 |
|
|
4 |
|
14 |
|
|
5 |
|
15 |
|
|
6 |
|
16 |
|
|
7 |
|
17 |
|
|
8 |
|
18 |
|
|
9 |
|
19 |
|
|
10 |
|
Таблица оригинала-изображения.
|
№ |
|
|
№ |
|
|
|
1 |
1 |
|
17 |
|
|
|
2 |
|
|
18 |
|
|
|
3 |
|
|
19 |
|
|
|
4 |
|
|
20 |
|
|
|
5 |
|
|
21 |
|
|
|
6 |
|
|
22 |
|
|
|
7 |
|
|
23 |
|
|
|
8 |
|
|
24 |
|
|
|
9 |
|
|
25 |
|
|
|
10 |
|
|
26 |
|
|
|
11 |
|
|
27 |
|
|
|
12 |
|
|
28 |
|
|
|
13 |
|
|
29 |
|
|
|
14 |
|
|
30 |
|
|
|
15 |
|
|
31 |
|
|
|
16 |
|
|
32 |
|
|
1.3 Решение типового варианта
1. С помощью теоремы дифференцирования найти изображение
функции ![]() .
.
Решение. По теореме дифференцирования оригинала
получим: ![]() ;
;
![]()
Поэтому
![]()
2. Используя формулу преобразования Лапласа или нахождения
изображения функции ![]() , найти изображение функции
, найти изображение функции ![]() .
.
Решение. Формула  называется преобразованием Лапласа или
формулой нахождения изображения функции
называется преобразованием Лапласа или
формулой нахождения изображения функции ![]() .
.
Поэтому
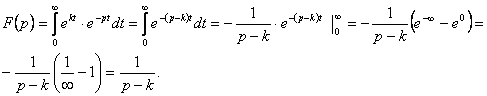
3. Используя формулу преобразования Лапласа или нахождения
изображения функции ![]() , найти изображение функции
, найти изображение функции ![]() .
.
Решение.
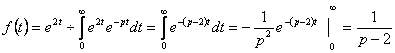 .
.
4.Найти оригинал функции![]() по заданному изображению
по заданному изображению ![]() .
.
Решение.
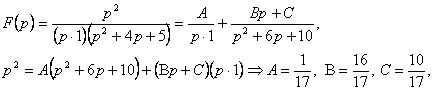
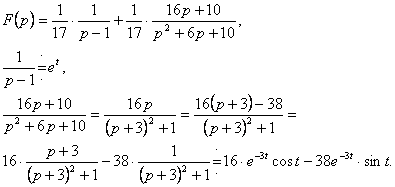
Поэтому
![]() .
.
5. Найти оригинал функции![]() по заданному изображению
по заданному изображению
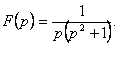
Решение.
Используя теорему интегрирования оригинала, получим:
![]()
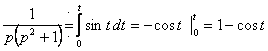 .
.
6. Найти изображение функции по заданному оригиналу ![]()
Решение.

Если 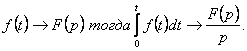
7. Найти изображение функции 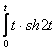 .
.
Решение.

8.Вычислить интеграл 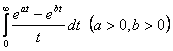 .
.
Решение.
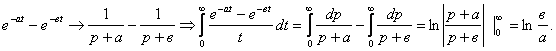
9. Используя теорему умножения изображении, найти свертку функции
![]() .
.
Решение.
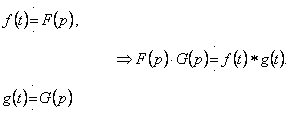
Тогда

10. Найти свертку и изображение функции ![]() .
.
Решение.
Решение будем искать по
формуле свертки функции ![]() и
и ![]() :
:
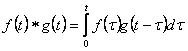 .
.
Тогда

11. Найти изображения ![]() заданных функции
заданных функции![]() , используя свойства преобразования Лапласа.
, используя свойства преобразования Лапласа.
![]()

Решение.
![]() так
как
так
как ![]()
![]() если
использовать теорему запаздывания
если
использовать теорему запаздывания
![]() то получим
то получим ![]() .
.

12. Будет ли оригиналом функция ![]() ,если
да, то почему?
,если
да, то почему?
![]()
Решение.
Функция ![]() называется функцией Хевисайда.
Это функция будет оригиналом.
называется функцией Хевисайда.
Это функция будет оригиналом.
Если:
а) при![]() функция
функция ![]() будет непрерывной или иметь разрыв первого рода;
будет непрерывной или иметь разрыв первого рода;
b) при ![]()
c) при ![]() где
где ![]() постоянная,
постоянная,
то функция![]() называется оригиналом.
называется оригиналом.
Покажем на примере, что следующая функция будет оригиналом.

При ![]() функция будет непрерывной;
функция будет непрерывной; ![]() так как
так как ![]() .
.
Все условия оригинала выполняются. Значит, данная функция будет оригиналом.
13. Будет ли оригиналом функция ![]() .
.
Решение. Эта функция не будет оригиналом, потому что:
1) точка ![]() является ее точкой разрыва второго рода;
является ее точкой разрыва второго рода;
2) при ![]() функция
функция ![]() так
как у нее нет множителя
так
как у нее нет множителя ![]() .
.
Интегрирование функции с помощью приведения к табличным интегралам
1. 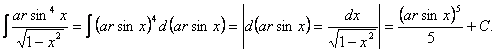
2.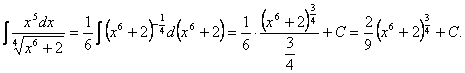
3. 
4.

5.

6.
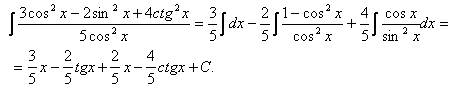
7.

8. ![]()
9.

10. 
11.
12.

13.![]()
14.
15.
16.

17.
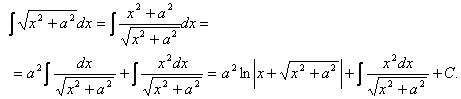
Теперь рассмотрим интеграл

Итак,
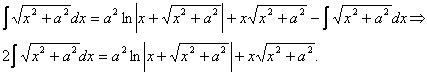
Окончательно:![]()
18.
19.

20.
21.![]()
22.![]()
23.
24.

Вычислить несобственные интегралы
1)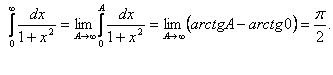
То
 сходится.
сходится.
2)![]() не
существует, тогда данный интеграл расходится.
не
существует, тогда данный интеграл расходится.
3)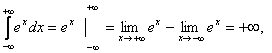 значит
интеграл расходится.
значит
интеграл расходится.
4)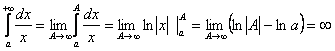 ,
то есть
,
то есть ![]() несобственный интеграл расходится.
несобственный интеграл расходится.
5) ![]() ,
если
,
если ![]() , то для
функции
, то для
функции ![]() точка
точка
![]() будет точкой
разрыва.
будет точкой
разрыва.
Поэтому
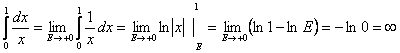 интеграл
расходится.
интеграл
расходится.

Итак, несобственный интеграл сходится.
7) 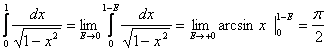 интеграл
сходится.
интеграл
сходится.
8) ![]() ,
,
то есть несобственный интеграл сходится.
9) 
10)![]()
11)

12)
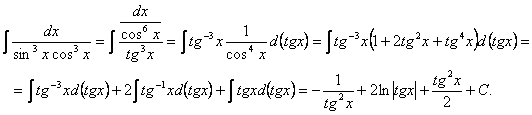
Вычисление площади фигур
1) Вычислить площадь фигуры, ограниченной осью абсцисс и
прямыми ![]() ,
,![]() и параболой
и параболой![]()
Решение.
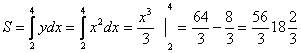 (кв.ед).
(кв.ед).
2) Вычислить площадь фигуры, ограниченной осью ординат и
кривой ![]()
Решение. Найдем точку пересечения кривой с осью ординат.
![]()
То есть кривая пересекает ось ординат в точках А(0,-2) и В(0, 1).
Поэтому искомая площадь будет равна:

3) Вычислить
площадь фигуры, ограниченной параболой ![]() и прямой
и прямой ![]() .
.
Решение. Точку пересечения параболы и прямой найдем из этой системы:

Получим: ![]() .
.
Таким образом, мы нашли пределы интегрирования.
Подставив эти значения в формулу вычислим искомую площадь:
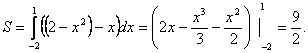
1.4 Теоретические вопросы
1. Неопределенный интеграл. Непосредственное интегрирование.
2. Метод замены переменной.
3. Метод интегрирования по частям в неопределенном интеграле.
4. Интегрирование простых рациональных функций.
5. Интегрирование квадратных трехчленов.
6. Интегрирование некоторых иррациональных функций.
7. Интегрирование некоторых тригонометрических функций.
8. Определенный интеграл.
9. Замена переменной в определенном интеграле.
10. Интегрирование по частям в определенном интеграле.
11. Несобственные интегралы.
12. Площадь плоской фигуры.
13.Определение изображения и оригинала в операционных исчислениях. Свойства преобразований Лапласа. Нахождение свертки функции и ее изображения.
Список литературы
1. Данко П.Е., Попов А.Т., Кожевникова Т.Я., Высшая математика в упражнениях и задача, В2ч.-М.: Высшая школа, 1986-4.1-352 с.
2. Сборник индивидуальных заданий по высшей математике: В 3ч.(А.П.Рябушко, В.В.Барахатов, и др./ Под ред. А.П.Рябушко.- Минск: Высшая школа, 1991.-4.2.-351 с.
3. Краснов М.Л., и др. Функции комплексного переменного. Операционное исчисление. Теория устройчивости- М.: Наука, 1971.- 256 с.
4. Письменный Д.Т. Сборник задач по курсу высшей математики.-М.: Айрис-пресс, 2010.-608 с.
Содержание
Введение 3
1 РГР №3 4
1.1 Задания первого уровня 4
1.2 Задания второго уровня 15
1.3 Решение типового варианта 21
1.4 Теоретические вопросы 32
Список литературы 33