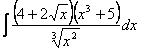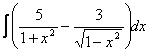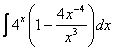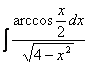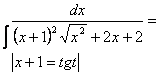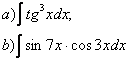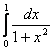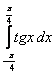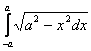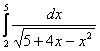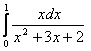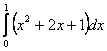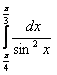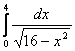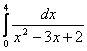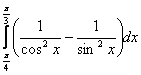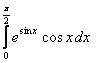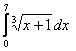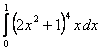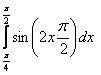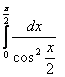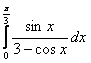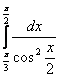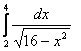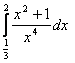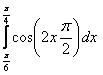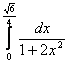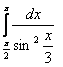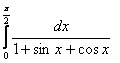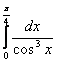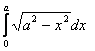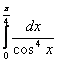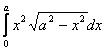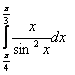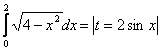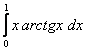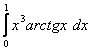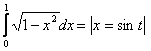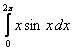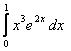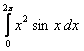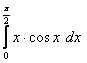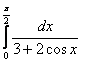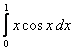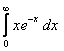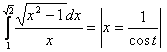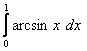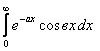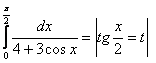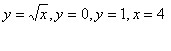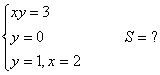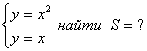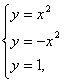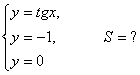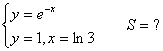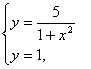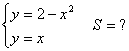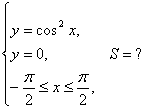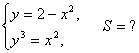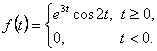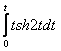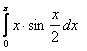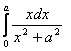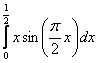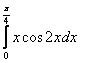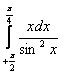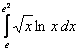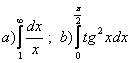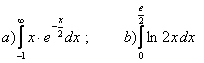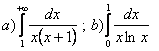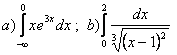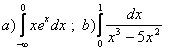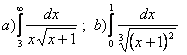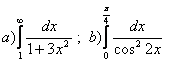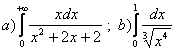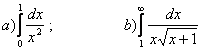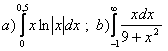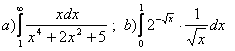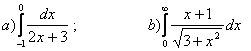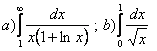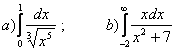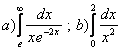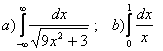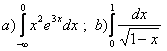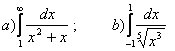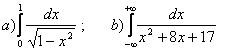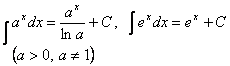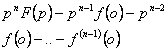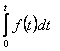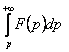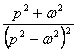МАТЕМАТИКА  1

Коммерциялық емес акционерлік қоғам

АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ

Жоғары математика кафедрасы

 

 

МАТЕМАТИКА  1 

5В071800 «Электр энергетикасы»,  5В071700 «Жылу энергетикасы», 5В071900 «Радиотехника, электроника және телекоммуникациялар», 5В070200 «Автоматтандыру және басқару» мамандықтарында оқитын студенттер үшін есептеу-сызбалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар 3-бөлім

 

 

Алматы 2013

Құрастырушылар: С.А. Нурпейсов, Ж.С.    Абдулланова.   Математика-1 Есептеу-сызбалық    жұмыстарға  арналған     әдістемелік нұсқаулар  мен тапсырмалар. 3- бөлім.-Алматы: АЭжБУ, 2013-32 б.

 

         Бұл әдістемелік  нұсқаулар және есептеу сызбалық  жұмыстарындағы тапсырмалар,  АЭжБУ күндізгі бөлімінің 5В071700, 5В071800, 5В071900, 5В070200 мамандықтарына арналған «Математика 1» бөлімі үшін 1 – семестр бағдарламасына сәйкес құрастырылған.

         Бұл әдістемелік құрал математика-1 пәнінің «Анықталмаған және анықталған интегралдар, меншіксіз интегралдар» және «Амалдық есептеулер теориясы» тарауларын қамтыған. Бағдарламаның негізгі теориялық сұрақтары берілген. Есептеу–сызбалық жұмыстар екі деңгейге бөлінген. Бірінші деңгей үшін типтік нұсқаудың шешімі талданып көрсетілген.

 

           Пікір беруші:  доцент  Туманов М.Е.

 

      «Алматы энергетика және байланыс университетінің» коммерциялық емес акционерлік қоғамының 2013ж. баспа жоспары бойынша басылды.

 

             © «Алматы энергетика және байланыс университеті» КЕАҚ, 2013 ж.

                                                                            Жиынтық жоспар 2013ж., реті 170

 

Кіріспе

 

           Бұл әдістемелік нұсқау 5В071700, 5В071800, 5В071900,  5В070200 мамандықтарының студенттеріне  бірінші семестрде оқытатын «Математика-1»  курсы бойынша есептеу-сызбалық жұмыстарының 3-ші бөлімі болып табылады.

          Аталған курстың  1 және 2-ші бөлімдері баспадан шығуына байланысты осы үшінші бөлімді дайындап шығару қажеттігі туындады.  

          Есептеу-сызбалық жұмыс «Математика-1» курсы бойынша 5В071700, 5В071800, 5В071900, 5В070200 мамандықтарының студенттеріне арналған типтік бағдарламаға сәйкес жазылған. Бұл ЕСЖ оқытушылар мен студенттерге қолдануға ұсынылады.

           Осы ЕСЖ көмегімен аудиториялық сабақтарда студенттердің өзіндік жұмыс жасауына және оқытушылардың студенттерге жеке үй тапсырмаларын беруіне ыңғайлы.

         Бұл әдістемелік нұсқауда анықталмаған және анықталған интегралдар, меншіксіз интегралдар, сонымен қатар амалдық есептеулер теориясының кейбір  сипаттамалары қамтылған.

         ЕСЖ  әрқайсысы 30 нұсқаудан 22 тапсырмадан  (16 тапсырма 1-ші деңгейлі, 6 тапсырма 2-ші деңгейлі қиындықта) тұрады. Соңында типтік нұсқаудың 1-ші деңгейлі тапсырмаларының толық шешімі көрсетілген. 2-ші деңгейлі тапсырмалардың шешуі студенттерге өздік ізденіс ретінде ұсынылады. Сонымен қатар, берілген курс  бойынша студенттердің меңгеруге тиісті негізгі теориялық сұрақтары берілген.

 

            1Есептеу-сызбалық жұмыс №3.   Анықталмаған және анықталған интегралдар. Амалдық есептеулер теориясының кейбір элементтері

           Мақсаты: cтуденттердің теориялық білімдерін анықталмаған және анықталған интегралдарды есептеудің негізгі есептеу әдістерін игеруге, меншіксіз интегралдарды зерттеуге және амалдық есептеу теориясының кейбір сипаттамаларын қолдана отырып есеп шығаруға  үйрету.

 

            1.1 Бірінші деңгейлі тапсырмалар

          1.Интегралды есептеу керек.

 

1.1

1.16

1.2

1.17

1.3

1.18

1.4

1.19

1.5

1.20

1.6

1.21

1.7

1.22

1.8

1.23

1.9

1.24

1.10

1.25

1.11

1.26

1.12

1.27

1.13

1.28

1.14

1.29

1.15

1.30

 

         2. Интегралды айнымалыны ауыстыру әдісі арқылы есептеу керек.

 

2.1

2.16

2.2

2.17

2.3

2.18

2.4

2.19

2.5

2.20

2.6

2.21

2.7

2.22

2.8

2.23

2.9

2.24

2.10

2.25

2.11

2.26

2.12

2.27

2.13

2.28

2.14

2.29

2.15

2.30

 

       3. Интегралды бөліктеп интегралдау әдісі арқылы есептеу керек.

 

3.1

3.11

3.21

3.2

3.12

3.22

3.3

3.13

3.23

3.4

3.14

3.24

3.5

3.15

3.25

3.6

3.16

3.26

3.7

3.17

3.27

3.8

3.18

3.28

3.9

3.19

3.29

3.10

3.20

3.30

 

       4.Интегралды есептеу керек.

 

4.1

4.11

4.21

4.2

4.12

4.22

4.3

4.13

4.23

4.4

4.14

4.24

4.5

4.15

4.25

4.6

4.16

4.26

4.7

4.17

4.27

4.8

4.18

4.28

4.9

4.19

4.29

4.10

4.20

4.30

 

        5. Интегралды есептеу керек.

 

5.1

5.11

5.21

5.2

5.12

5.22

5.3

5.13

5.23

5.4

5.14

5.24

5.5

5.15

5.25

5.6

5.16

5.26

5.7

5.17

5.27

5.8

5.18

5.28

5.9

5.19

5.29

5.10

5.20

5.30

 

        6.Кейбір  иррационал функциялардан тұратын интегралды есептеу керек.

 

6.1

6.11

6.21

6.2

6.12

6.22

6.3

6.13

6.23

6.4

6.14

6.24

6.5

6.15

6.25

6.6

6.16

6.26

6.7

6.17

6.27

6.8

6.18

6.28

6.9

6.19

6.29

6.10

6.20

6.30

 

          7. Интегралды есептеу керек.

 

7.1

7.11

7.21

7.2

7.12

7.22

7.3

7.13

7.23

7.4

7.14

7.24

7.5

7.15

7.25

7.6

7.16

7.26

7.7

7.17

7.27

7.8

7.18

7.28

7.9

7.19

7.29

7.10

7.20

7.30

 

     8. Анықталған интегралды есептеу керек.

 

8.1

8.11

8.21

8.2

8.12

8.22

8.3

8.13

8.23

8.4

8.14

8.24

8.5

8.15

8.25

8.6

8.16

8.26

8.7

8.17

8.27

8.8

8.18

8.28

8.9

8.19

8.29

8.10

8.20

8.30

          9. Интегралды есептеу керек.

 

9.1

9.11

9.21

9.2

9.12

9.22

9.3

9.13

9.23

9.4

9.14

9.24

9.5

9.15

9.25

9.6

9.16

9.26

9.7

9.17

9.27

9.8

9.18

9.28

9.9

9.19

9.29

9.10

9.20

9.30

 

         10. Анықталған интегралды айнымалыны ауыстыру әдісі арқылы есептеу керек.

 

10.1

10.11

10.21

10.2

10.12

10.22

10.3

10.13

10.23

10.4

10.14

10.24

10.5

10.15

10.25

10.6

10.16

10.26

10.7

10.17

10.27

10.8

10.18

10.28

10.9

10.19

10.29

10.10

10.20

10.30

 

        11. Меншіксіз интегралды есептеу керек.

 

11.1

11.11

11.21

11.2

11.12

11.22

11.3

11.13

11.23

11.4

11.14

11.24

11.5

11.15

11.25

11.6

11.16

11.26

11.7

11.17

11.27

11.8

11.18

11.28

11.9

11.19

11.29

11.10

11.20

11.30

 

          12. Берілген функциялардың графиктерімен шектелген  фигураның ауданын анықталған интеграл көмегімен есептеу керек.

 

12.1

12.16

12.2

12.17

12.3

12.18

12.4

12.19

12.5

12.20

12.6

12.21

12.7

12.22

12.8

12.23

12.9

12.24

12.10

12.25

12.11

12.26

12.12

12.27

12.13

12.28

12.14

12.29

12.15

12.30

 

    13. Келесі функциялар түпнұсқа бола ма, егер болса, онда неге?

 

13.1

13.11

13.21

13.2

13.12

13.22

13.3

13.13

13.23

13.4

13.14

13.24

13.5

13.15

13.25

13.6

13.16

13.26

13.7

13.17

13.27

13.8

13.18

13.28

13.9

13.19

13.29

13.10

13.20

13.30

 

        14. Берілген функциялардың бейнесін табу керек.

 

14.1

14.11

14.21

14.2

14.12

14.22

14.3

14.13

14.23

14.4

14.14

14.24

14.5

14.15

14.25

14.6

14.16

14.26

14.7

14.17

14.27

14.8

14.18

14.28

14.9

14.19

14.29

14.10

14.20

14.30

 

     15. Берілген F(p) функциясының  түпнұсқасын табу керек.

 

15.1

15.11

15.21

15.2

15.12

15.22

15.3

15.13

15.23

15.4

15.14

15.24

15.5

15.15

15.25

15.6

15.16

15.26

15.7

15.17

15.27

15.8

15.18

15.28

15.9

15.19

15.29

15.10

15.20

15.30

 

       16.және  функцияларының үйірткісі мен бейнесін табу керек.

 

№

№

№

16.1

16.11

16.21

16.2

16.12

16.22

1

 

16.3

16.13

16.23

1

16.4

16.14

16.24

16.5

16.15

16.25

16.6

16.16

1

16.26

16.7

16.17

1

16.27

16.8

16.18

16.28

16.9

16.19

16.29

16.10

1

16.20

16.30

1

 

           1.2 Екінші деңгейлі тапсырмалар

          17. Интегралды есептеу керек.

 

17.1

17.16

17.2

17.17

17.3

17.18

17.4

17.19

17.5

17.20

17.6

17.21

17.7

17.22

17.8

17.23

17.9

17.24

17.10

17.25

17.11

17.26

17.12

17.27

17.13

17.28

17.14

17.29

17.15

17.30

 

        18. Интегралды есептеу керек.

 

18.1

18.11

18.21

18.2

18.12

18.22

18.3

18.13

18.23

18.4

18.14

18.24

18.5

18.15

18.25

18.6

18.16

18.26

18.7

18.17

18.27

18.8

18.18

18.28

18.9

18.19

18.29

18.10

18.20

18.30

 

            19. Интегралды есептеу керек.

 

19.1

19.11

19.21

19.2

19.12

19.22

19.3

19.13

19.23

19.4

19.14

19.24

19.5

19.15

19.25

19.6

19.16

19.26

19.7

19.17

19.27

19.8

19.18

19.28

19.9

19.19

19.29

19.10

19.20

19.30

 

        20. Меншіксіз интегралды есептеу керек.

 

20.1

20.16

20.2

20.17

20.3

20.18

20.4

20.19

20.5

20.20

20.6

20.21

20.7

20.22

20.8

20.23

20.9

20.24

20.10

20.25

20.11

20.26

20.12

20.27

20.13

20.28

20.14

20.29

20.15

20.30

 

           21.функциясының бейнесі  функциясын анықтама бойынша есептеу керек.

 

21.1

21.11

21.21

21.2

21.12

21.22

21.3

21.13

21.23

21.4

21.14

21.24

21.5

21.15

21.25

21.6

21.16

21.26

21.7

21.17

21.27

21.8

21.18

21.28

21.9

21.19

21.29

21.10

21.20

21.30

        

 22.Түпнұсқаны  дифференциалдау теоремасын пайдалана отырып,  берілген функциялардың бейнесін табу керек.

 

22.1

22.11

22.21

22.2

22.12

22.22

22.3

22.13

22.23

22.4

22.14

22.24

22.5

22.15

22.25

22.6

22.16

22.26

22.7

22.17

22.27

22.8

22.18

22.28

22.9

22.19

22.29

22.10

22.20

22.30

   

          Негізгі интегралдар кестесі

 

1

11

2

12

3

13

4

14

5

15

6

16

7

17

8

18

9

19

10

 

              Түпнұсқа-бейне кестесі

 

№

№

1

1

17

2

18

3

19

4

20

5

21

6

22

7

23

8

24

9

25

10

26

11

27

12

28

13

29

14

30

15

31

16

32

 

         1.3 Типтік нұсқалардың кейбіреулерінің шешіміне талдау жасау

 

         1. функциясының бейнесін дифференциалдау теоремасын қолдану арқылы табу керек.

        Шешуі:

             .

        Түпнұсқаны дифференциалдау теоремасы бойынша

            

        Сондықтан

            

        2.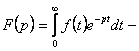бұл  функциясының бейнесін анықтайтын формула немесе Лаплас түрлендіруі деп аталады. Осы анықтаманы пайдаланып,  функцияның бейнесін табу керек.

           Шешуі:

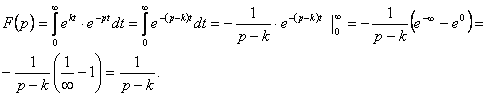
         3. функцияның бейнесін табу керек.

           Шешуі:

 .

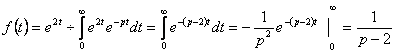         4.Берілген   бейнесі бойынша   түпнұсқасын табу керек.

           Шешуі:

           

                      

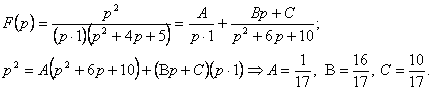
Демек,

                                 

         5. Берілген   бейнесі бойынша   түпнұсқасын табу керек

                                                        

         Шешуі: Түпнұсқаны интегралдау теоремасын пайдаланамыз:
                             .

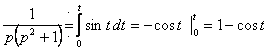         6. Дифференциалдау теоремасын пайдаланып, берілген функцияның бейнесін табу керек .

         Шешуі:

                    

Егер .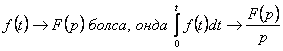

         7.  функциясының бейнесін табу керек.

         Шешуі:

            

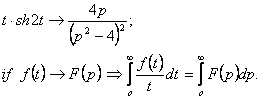
         8. 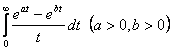 интегралын есептеу керек.

         Шешуі:

     

           9. Бейнелерді көбейту Th-сын қолданып,  функциясының үйіткісін табу керек.

           Шешуі:

           

          10.  функцияларының үйірткісін және оның бейнесін анықтау керек.

          Шешуі:

 және   формуласының үйірткісі 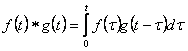  формуласымен табылады.

          Сондықтан

                    

         11. Лаплас түрлендіруінің қасиеттерін пайдалана отырып,  функцияларының  бейнелерін анықтау керек:

                         

                       

         Шешуі:                              себебі

егер кешігу теоремасын қолдансақ,    онда  .

 

            12. функциясы түпнұсқа бола ма, болмайды ма, болса, неге болады?

                                                  

          Шешуі:

функциясы Хевисайд  функциясы деп аталады.

           Бұл функция түпнұсқа болады.

           Егер:

a) болғанда - үзіліссіз немесе бірінші текті үзіліссіз болса,

b)

c) мұнда тұрақтылар, шарттары орындалса,

онда функциясы түпнұсқа деп аталады.

           Мысалы.

              

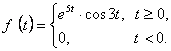
функциясының нұсқасының түпнұсқа болатындығын көрсетелік.

           Шешуі: Берілген функция  болғанда үзіліссіз функция,

                          шарттары орындалады.

           Сондықтан ол түпнұсқа болады.

          13.Берілген  функция түпнұсқа бола ма, тексер.

          Шешуі:  бұл функция түпнұсқа болмайды, себебі

1)  нүктесі оның екінші типті үзіліс нүктесі;

2)  болғанда  себебі  көбейткіші жоқ.

 

      Кестелік интегралдарға келтірілетін интегралдарды есептеуге мысал есептер

1.

 

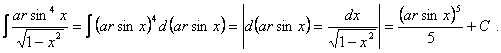
2.

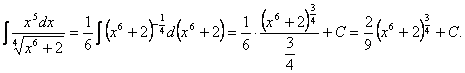
3.

4.

 

5.

6.

 

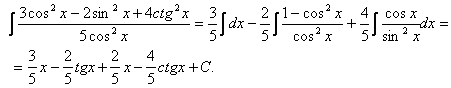
7.

 

8. 

9.

 

 

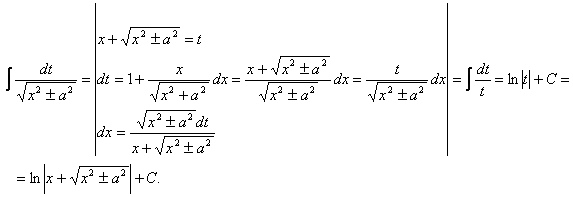
10.   

11.

12.

 

13.

14.

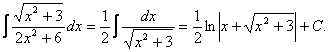
15.

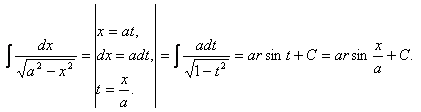
16.

 

17.

 

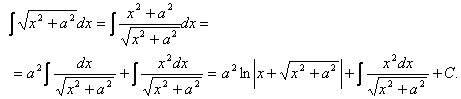
     Енді мынадай интегралды қарастырайық

.

Сонымен,

        

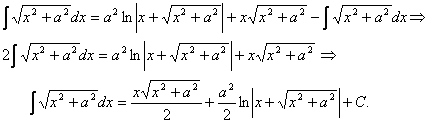
18.

 

19.

 

20.

21.

22.

23.

 

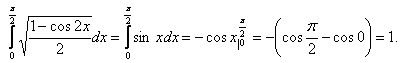
24.

 

         Меншіксіз интегралдарды есептеу

1.,

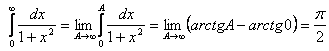онда 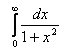жинақты.

2.табылмай

ды, сондықтан берілген интеграл жинақсыз.

3.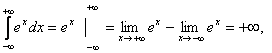яғни интеграл жинақсыз.

4.,

 онда  меншіксіз               интегралы жинақсыз.

5. , егер , онда  функциясы үшін  нүктесі үзіліс нүктесі болады.

       Сондықтан

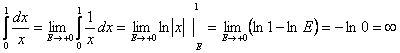 интеграл жинақсыз.

6.

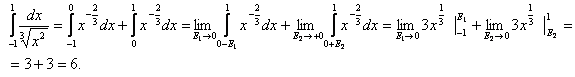
       Сонымен, берілген меншіксіз  интеграл жинақты.

 

7.

8. 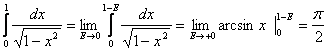   интеграл жинақты.

9. ,

яғни, берілген меншіксіз  интеграл жинақты.

10.

11.

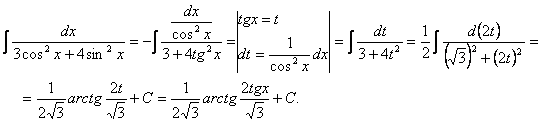
12.

 

             Жазық фигураның ауданы.

       1.Абсцисса осі , түзулері және  параболасымен шектелген ауданды есептеу керек.

            Шешуі:

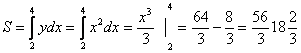                        (кв.бір).

      2.Ордината     осі және  қисығымен    шектелген       ауданды  

 есептеу керек.

           Шешуі: Қисықтың ордината осімен қиылысу нүктесін табалық,        яғни   

            Демек, берілген қисық А(0,-2), В(0, 1) нүктелерінде ордината өсін қиып өтеді.

           Сондықтан іздеген аудан мына

                       

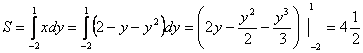
интегралы арқылы табылады.

          3.  параболасы мен  түзуімен шектелген ауданды табу керек.

          Шешуі:     Парабола мен  түзуінің     қиылысу      нүктесін        мына

                                                       

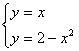
жүйені шешу арқылы табамыз.

          Сонда  интегралдау шектері табылады.

          Демек, іздеген аудан былай анықталады:

                       

 

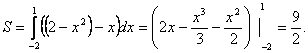
          1.4 Теориялық сұрақтар

1.     Анықталмаған интеграл. Тікелей интегралдау.

2.     Белгісізді ауыстыру әдісі.

3.     Анықтамаған интегралдағы бөліктеп интегралдау әдісі.

4.     Жай рационалдық  функцияларды интегралдау.

5.     Квадрат үш мүшелігі  бар кейбір интегралдар.

6.     Кейбір иррационалдық функцияларды интегралдау.

7.     Кейбір тригонометриялық функцияларды интегралдау.

8.     Анықталған интеграл.

9.     Анықталған интегралдағы айнымалыны ауыстыру

10. Анықталған интегралдағы бөліктеп интегралдау әдісі.

11. Меншіксіз интегралдар.

12. Жазық фигураның ауданы.

13. Амалдық есептеулердегі бейнелер мен тұпнұсқаларды анықтау. Лаплас түрлендіруінің қасиеттері. Функциялардың үйірткісі және оның бейнесі анықтау.

Әдебиеттер тізімі

1.     Данко П.Е., Попов А.Т., Кожевникова Т.Я.,  Высшая математика в упражнениях и задачах, В2ч.-М:Высшая школа, 1986-4.1-352 с.

2.     Сборник индивидуальных заданий по высшей математике: В 3ч.(А.П.Рябушко, В.В.Барахатов, и др./ Под ред. А.П.Рябушко.- Минск: Высшая школа, 1991.-351с.

3.     Краснов М.Л., и др. Функции комплексного переменного. Операционное исчисление.  Теория  устройчивости - М.: Наука,   1971. -     256 с.

4.   Письменный Д.Т.  Сборник    задач    по    курсу   высшей   математики.-   М.:Айрис-пресс, 2010.-608 с.

 

Мазмұны

Кіріспе   

1ЕСЖ №3                                                                                                             4

1.1 Бірінші деңгейдің тапсырмалары                                                                4

1.2 Екінші деңгейдің тапсырмалары                                                               15

1.3 Типтік нұсқаулардың шешімі                                                                    21

1.4 Теориялық сұрақтар                                                                                    31

Әдебиеттер тізімі                                                                                               32