Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Математика 1
Конспект лекций для студентов специальностей
5В071700 – “Теплоэнергетика”, 5В071800 –
“Электроэнергетика”,5В071900 – “Радиотехника, электроника и
телекоммуникации”
Алматы, 2013
Составители: Мустахишев К.М., Атабай Б.Ж. Математика 1. Конспект лекций для студентов специальностей 5В071700 – “Теплоэнергетика”, 5В071800 – “Электроэнергетика”, 5В071900 – “Радиотехника, электроника и телекоммуникации”. –Алматы, 2013. - 48 с.
Конспект лекций составлен в соответствии с программой, утвержденной МОН РК в 2012 г. Охватывает разделы: элементы линейной алгебры, аналитической геометрии и комплексные числа, дифференциальное и интегральное исчисления функций одной переменной, операционное исчисление (всего 11 лекций).
Ил. -17, библиогр. - 10 назв.
Рецензент: канд. физ.-мат. наук, доцент Дуйсек А.К.
Печатается по плану издания некоммерческого акционерного общества “Алматинский университет энергетики и связи” на 2013 г.
© НКАО “Алматинский университет энергетики и связи”, 2013 г.
Сводный план 2013., поз.302
Модуль 1. Элементы линейной алгебры, аналитической геометрии и комплексные числа
Лекция 1. Определители, матрицы и системы линейных уравнений
Цель лекции: ознакомить студентов с новыми для них понятиями определителя и матрицы, действиями над ними. Показать новые способы решения системы линейных уравнений: по правилу Крамера и матричным способом.
Прямоугольная таблица чисел
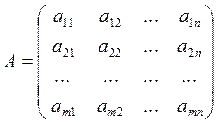 (1.1)
(1.1)
называется числовой матрицей
размера ![]() , содержащая
, содержащая
![]() строк и
строк и ![]() столбцов. При
столбцов. При ![]()
![]() называют квадратной матрицей
называют квадратной матрицей ![]() - порядка. Числа
- порядка. Числа ![]() называются элементами матрицы.
называются элементами матрицы.
Матрица, состоящая лишь из одной строки или из одного столбца, называется соответственно строчной или столбцевой матрицей.
Одной из основных
характеристик квадратной матрицы ![]() является число
является число
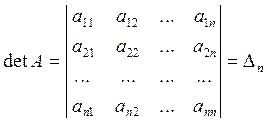 , (1.2)
, (1.2)
называемое определителем или
детерминантом матрицы. При ![]() имеем так называемую вырожденную, а при
имеем так называемую вырожденную, а при ![]() - невырожденную матрицу.
- невырожденную матрицу.
Вычисление определителей.
Отдельное число можно принимать за определитель первого порядка. Определитель второго порядка равен разности произведений элементов, лежащих на его диагоналях:
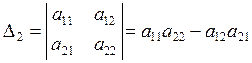 . (1.3)
. (1.3)
Определитель третьего порядка вычисляется с помощью так называемого правила Саррюса, которое также называют правилом диагоналей и треугольников (см. рисунок 1).
Иногда поступают так: две первые строки или столбца определителя путем параллельного переноса приписывают к концу определителя, далее по схеме (см. рисунок 1б):

Рисунок 1 – Схема вычисления определителя третьего порядка
Итак,
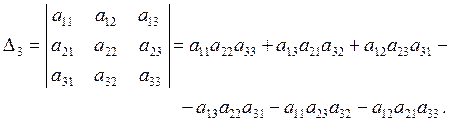 (1.4)
(1.4)
Свойства определителя.
Перемена местами строк и столбцов с одинаковыми номерами матрицы или определителя называется транспонированием.
1. При транспонировании матрицы ее определитель не меняет значения.
2. От перемены местами любых двух строк (столбцов) определитель меняет знак.
3. При умножении всех элементов какой-либо строки (столбца) на любое число, определитель умножается на это же число. Общий множитель элементов какой-либо строки или столбца можно вынести за знак определителя.
4. Определитель равен сумме двух определителей, если каждый элемент какой-либо строки (столбца) определителя представляет собой сумму двух чисел.
5. Определитель равен нулю, если:
1) все элементы какой-либо строки (столбца) равны нулю;
2) соответствующие элементы любых двух строк (столбцов) равны или пропорциональны между собой.
6. Определитель не изменится, если элементы какой-либо строки (столбца) его, умноженные на любое число, сложить с соответствующими элементами другой строки (столбца).
Определитель ![]() -
порядка
-
порядка ![]() ,
полученный вычёркиванием
,
полученный вычёркиванием ![]() -строки и
-строки и ![]() -столбца определителя
-столбца определителя ![]() , называется минором элемента
, называется минором элемента ![]() последнего.
Определитель
последнего.
Определитель ![]() называют
алгебраическим дополнением элемента
называют
алгебраическим дополнением элемента ![]() определителя
определителя ![]() .
.
7. Теорема Лапласа. Определитель равен сумме произведений элементов его какой-либо строки (столбца) и их алгебраических дополнений.
Последние представляют собой формулы раскрытия
определителя по элементам его соответственно ![]() -строки и
-строки и ![]() -столбца. С их помощью удобно вычислять
определители высших порядков.
-столбца. С их помощью удобно вычислять
определители высших порядков.
8. Сумма произведений элементов какой-либо строки (столбца) определителя и алгебраических дополнений соответствующих элементов любой другой строки (столбца) его равна нулю.
Действия над матрицами.
При умножении матрицы на число все ее элементы
умножаются на это число: ![]() . Складывать можно только матрицы
одинаковых размеров. При этом их соответствующие элементы складываются между
собой.
. Складывать можно только матрицы
одинаковых размеров. При этом их соответствующие элементы складываются между
собой.
Разностью матрицы называется матрица ![]() .
.
Матрицы одинаковых размеров равны тогда и только тогда, когда равны их соответствующие элементы и наоборот.
Произведение двух матриц
с размерами ![]() и
и
![]() (число
столбцов - ширина первого множителя равно числу строк - высоте второго
множителя) определяется по формуле:
(число
столбцов - ширина первого множителя равно числу строк - высоте второго
множителя) определяется по формуле:
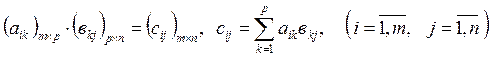 . (1.5)
. (1.5)
Действие сложения матриц
удовлетворяет переместительному (коммутативности) закону: ![]() , но не всегда
, но не всегда ![]() .
.
Задача 1. Даны две
матрицы А и В. Вычислить ![]() .
.

Решение.
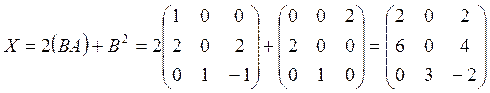 .
.
Ненулевая квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от диагонали, равны нулю. Квадратную матрицу называют диагональной, если у неё все элементы, кроме расположенных на главной диагонали, равны нулю. Если у диагональной матрицы все элементы главной диагонали равны единице, то она называется единичной:
 .
.
Обратная матрица.
Квадратные матрицы ![]() и
и ![]() , удовлетворяющие условию
, удовлетворяющие условию ![]() , называют взаимно
обратными. Только невырожденная матрица может иметь обратную матрицу, так как:
, называют взаимно
обратными. Только невырожденная матрица может иметь обратную матрицу, так как: ![]() .
.
Если для ![]() обратная матрица
существует, то она единственная, причём
обратная матрица
существует, то она единственная, причём
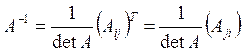 . (1.6)
. (1.6)
Матрица ![]() , составленная из
алгебраических дополнений элементов матрицы
, составленная из
алгебраических дополнений элементов матрицы ![]() и транспонированная, называется
присоединённой к
и транспонированная, называется
присоединённой к ![]() матрицей.
Поэтому нахождение обратной матрицы по формуле (1.6) носит название метода
присоединенной матрицы.
матрицей.
Поэтому нахождение обратной матрицы по формуле (1.6) носит название метода
присоединенной матрицы.
Системы линейных уравнений.
Система ![]() линейных уравнений с
линейных уравнений с ![]() неизвестными
неизвестными ![]() имеет общий вид:
имеет общий вид:
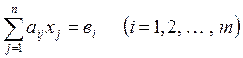 . (1.7)
. (1.7)
Коэффициенты ![]() и свободные члены
и свободные члены ![]() уравнений - заданные числа. Составленные
из них матрицы
уравнений - заданные числа. Составленные
из них матрицы ![]() и
и
![]() называются соответственно
матрицей и расширенной матрицей системы.
называются соответственно
матрицей и расширенной матрицей системы.
Систему, имеющую хотя бы
одно решение, называют совместной. В противном случае она является
несовместной. Система уравнений бывает определенной и неопределенной. В первом
случае она имеет единственное решение, а во втором – бесконечное множество
решений. Системы, обладающие одинаковым множеством решений, называются
эквивалентными. Если все ![]() , то (1.7) называют однородной, а в
противном случае, когда не все
, то (1.7) называют однородной, а в
противном случае, когда не все ![]() - неоднородной. Однородная система всегда
совместна, так как всегда имеет нулевое (тривиальное) решение
- неоднородной. Однородная система всегда
совместна, так как всегда имеет нулевое (тривиальное) решение ![]() .
.
Правило Крамера.
Пусть в (1.7) ![]() , т.е.
, т.е. ![]() - квадратная матрица
- квадратная матрица ![]() - порядка. Тогда
- порядка. Тогда ![]() будем называть
определителем системы.
будем называть
определителем системы.
Теорема. Если определитель системы ![]() , то система совместна и
имеет единственное решение, определяемое формулами
, то система совместна и
имеет единственное решение, определяемое формулами
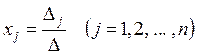 , (1.8)
, (1.8)
где ![]() - определитель, полученный заменой
- определитель, полученный заменой
![]() - столбца определителя
системы столбцом свободных членов уравнений (1.7).
- столбца определителя
системы столбцом свободных членов уравнений (1.7).
Равенства (1.8) называются формулами Крамера.
Проверка совместности
системы и нахождение её решения с помощью (1.8) называют правилом Крамера. Из
этого правила можно заключить, что однородная система с определителем ![]() имеет только нулевое
решение. При
имеет только нулевое
решение. При ![]() такая
система имеет бесконечное множество решений.
такая
система имеет бесконечное множество решений.
Задача 2. Решить систему:
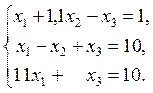
Решение. Система совместна, так как
 .
.

По формулам Крамера: ![]()
Матричные уравнения.
Произвольную систему линейных уравнений (1.7) можно представить в матричной форме
![]() , (1.9)
, (1.9)
где ![]() - заданные матрицы,
- заданные матрицы, ![]() - неизвестная
матрица-столбец. Тогда решение системы запишем в виде:
- неизвестная
матрица-столбец. Тогда решение системы запишем в виде:
![]() . (1.10)
. (1.10)
Задача 3. Решить
уравнение ![]() ,
,
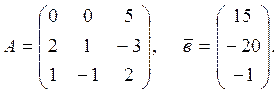
Решение. ![]() . Следовательно,
. Следовательно,
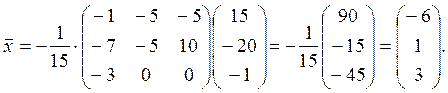
Лекция 2. Векторы в трехмерном пространстве. Прямая и плоскость
Цель лекции: восстановить в памяти студентов их знания о векторах, прямых и плоскости из школьного курса математики и сообщить им новые сведения о векторном и смешанном произведениях векторов, уравнения и задачи с участием линейных геометрических объектов.
Величина, характеризующаяся только числовым значением, называется скалярной величиной. Вектор, кроме числового значения (длины), характеризуется направлением, т.е. вектор есть направленный отрезок. Геометрически сложение двух векторов выполняется по известному правилу параллелограмма (треугольника, см. рисунок 2).
Повторно
применяя правило треугольника, можно сложить любое конечное число векторов ![]() (например,
(например, ![]() , см. рисунок 2б).
, см. рисунок 2б).

Рисунок 2 – Сложение векторов
Произведения векторов.
В
прямоугольной декартовой системе координат единичные векторы (орты) ![]() указывают направления
осей координат и составляют так называемый декартов базис. Любой вектор
указывают направления
осей координат и составляют так называемый декартов базис. Любой вектор ![]() можно разложить по
базису в виде
можно разложить по
базису в виде ![]() , где
, где ![]() - координаты вектора или точки
- координаты вектора или точки ![]() .
.
Рассмотрим векторы
![]() . (1.11)
. (1.11)
1. Скалярное произведение.
Число ![]() , равное произведению модулей
двух векторов и косинуса угла между ними, называют их скалярным произведением:
, равное произведению модулей
двух векторов и косинуса угла между ними, называют их скалярным произведением:
![]() (1.12)
(1.12)
или
![]() . (1.13)
. (1.13)
Для скалярного произведения справедливы равенства:
![]() . (1.14)
. (1.14)
Длина вектора:
![]() .
.
Из (1.12) можно найти угол между векторами:
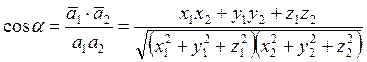 . (1.15)
. (1.15)
Отсюда условие перпендикулярности двух векторов имеет вид:
![]() . (1.16)
. (1.16)
2. Векторное произведение.
Если при
наблюдении с конца ![]() кратчайший
поворот от
кратчайший
поворот от ![]() к
к ![]() (см. рисунок 3) совершается
против хода часовой стрелки, то говорят, что декартов базис
(см. рисунок 3) совершается
против хода часовой стрелки, то говорят, что декартов базис ![]() составляет правую
тройку. В противном случае и тройка
векторов, и соответствующая ей система координат левая.
составляет правую
тройку. В противном случае и тройка
векторов, и соответствующая ей система координат левая.
Векторным
произведением векторов ![]() и
и ![]() называется вектор
называется вектор ![]() или
или ![]() ,
перпендикулярный к ним обоим, составляющий с векторами или
,
перпендикулярный к ним обоим, составляющий с векторами или ![]() , перпендикулярный к ним обоим,
составляющий с векторами
, перпендикулярный к ним обоим,
составляющий с векторами ![]() и
и ![]() правую тройку, модуль которого
равен произведению модулей умножаемых
правую тройку, модуль которого
равен произведению модулей умножаемых
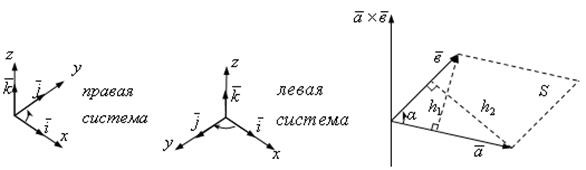
Рисунок 3 – Векторное произведение двух векторов
векторов и синуса угла между ними:
![]() . (1.17)
. (1.17)
Геометрически (1.17) выражает площадь параллелограмма, построенного на векторах-сомножителях:
![]() . (1.18)
. (1.18)
Векторные произведения базисных векторов:
![]() ,
, ![]() .
.
Итак,
![]() , (1.19)
, (1.19)
или
 . (1.20)
. (1.20)
Последнее выражение можно рассматривать как определитель, раскрытый по элементам первой строки:
 . (1.21)
. (1.21)
Теперь основные свойства векторного произведения могут быть установлены с помощью свойств определителей:
1) ![]() ,
,
2) ![]() ,
,
3)![]() ,
,
4)![]() ,
, ![]() .
.
Условия коллинеарности двух векторов:
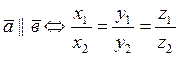 . (1.22)
. (1.22)
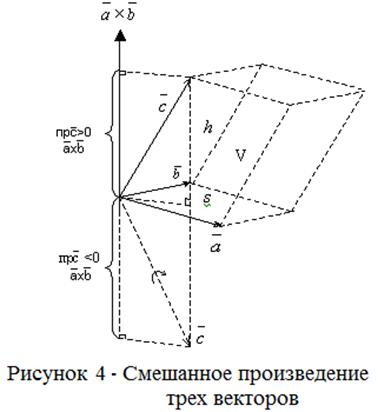
3. Смешанное произведение векторов.
Число ![]() , равное скалярному произведению
любого (см. рисунок 4) из трех заданных векторов и векторного произведения двух
остальных, называют смешанным произведением этих векторов.
, равное скалярному произведению
любого (см. рисунок 4) из трех заданных векторов и векторного произведения двух
остальных, называют смешанным произведением этих векторов.
Таким образом,
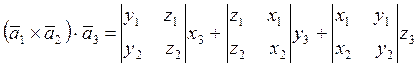
или
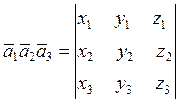 .
(1.23)
.
(1.23)
На основе свойств определителя можем утверждать, что
 1)
1) ![]() ;2)
;2) ![]() .
.
Смешанное произведение равно нулю, если любые два сомножителя в нём коллинеарны (в частности, равны).
Условие компланарности трех векторов теперь можно
представить в виде: ![]() . При невыполнении
этого условия на данных векторах можно построить параллелепипед. Найдем объем этого параллелепипеда, ползуясь
геометрическим смыслом векторного произведения:
. При невыполнении
этого условия на данных векторах можно построить параллелепипед. Найдем объем этого параллелепипеда, ползуясь
геометрическим смыслом векторного произведения:
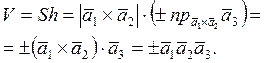
Вообще, ![]() .
.
Прямая и плоскость в ![]() .
.
Деление отрезка в данном отношении.
Рассмотрим точки ![]() ,
, ![]() , расположенные на одной прямой
, расположенные на одной прямой ![]() в плоскости или в пространстве. Пусть
в плоскости или в пространстве. Пусть ![]() - фиксированные точки, а
- фиксированные точки, а ![]() - любая точка прямой
- любая точка прямой ![]() , не совпадающая с
точкой
, не совпадающая с
точкой ![]() . Тогда
координаты точки
. Тогда
координаты точки ![]() ,
делящей заданный отрезок
,
делящей заданный отрезок ![]() в отношении
в отношении ![]() :
:
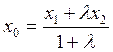 ,
, 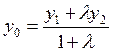 ,
, 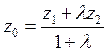 .
.
Координаты средины отрезка:
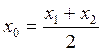 ,
, 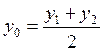 ,
, 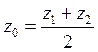 . (1.24)
. (1.24)
Плоскость в пространстве.
Линейное уравнение
![]()
![]()
![]() . (1.25)
. (1.25)
в системе координат ![]() определяет плоскость и (1.28) есть общее
уравнение
определяет плоскость и (1.28) есть общее
уравнение
плоскости. Первые три коэффициента одновременно обратиться в нуль
не могут. Если свободный член ![]() , то
плоскость отсекает на осях координат
, то
плоскость отсекает на осях координат
отрезки 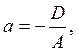
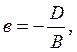
 , и придем к
уравнению плоскости в отрезках:
, и придем к
уравнению плоскости в отрезках:
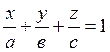 . (1.26)
. (1.26)
При ![]() плоскость проходит через начало координат
плоскость проходит через начало координат ![]() .
.
Вектор ![]() называют нормальным
вектором плоскости. С его помощью общее уравнение плоскости можно представить в
векторной форме
называют нормальным
вектором плоскости. С его помощью общее уравнение плоскости можно представить в
векторной форме
![]() .
.
Составим уравнения плоскостей с нормальным вектором ![]() ,
проходящих через заданные точки:
,
проходящих через заданные точки:
![]() . (1.27)
. (1.27)
Теперь возьмем три точки ![]() в
пространстве, не лежащие на одной прямой. Через них проходит единственная
плоскость
в
пространстве, не лежащие на одной прямой. Через них проходит единственная
плоскость ![]() .
Пусть
.
Пусть ![]() - текущая точка плоскости. Тогда условие компланарности векторов
- текущая точка плоскости. Тогда условие компланарности векторов ![]()
![]() ,
, ![]() дает уравнение
плоскости, проходящей через заданные три точки:
дает уравнение
плоскости, проходящей через заданные три точки:
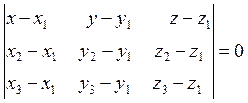 . (1.28)
. (1.28)
Найдем двугранный угол между плоскостями ![]()
![]() :
:
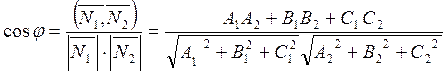 .
(1.29)
.
(1.29)
Условия параллельности и перпендикулярности двух плоскостей аналогичны соответствующим условиям для векторов:
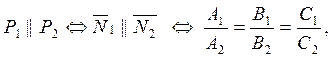
![]() .
.
Условия равенства векторов:
 (1.30)
(1.30)
представляют собой так называемые параметрические уравнения прямой в векторной и координатной формах. Условия коллинеарности векторов в координатной форме:
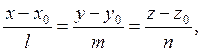
![]() (1.31)
(1.31)
называются каноническими уравнениями прямой в пространстве.
Уравнение прямой, проходящей через две заданные точки:
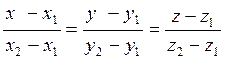 . (1.32)
. (1.32)
Система общих уравнений пересекающихся плоскостей
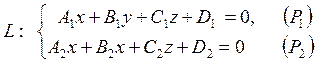 (1.33)
(1.33)
называется общим уравнением прямой.
Взаимное расположение двух прямых в пространстве соответствует расположению их направляющих векторов. Угол между ними в пространстве:
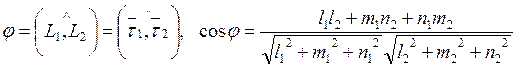 . (1.34)
. (1.34)
Условия параллельности и перпендикулярности прямых:
 (1.35)
(1.35)
![]() . (1.36)
. (1.36)
Считая, что заданные прямая и плоскость:
 (1.37)
(1.37)
пересекаются, найдем угол между ними:
 . (1.38)
. (1.38)
Условия параллельности и перпендикулярности прямой и плоскости:
![]() ,
,
 .
.
Прямая в ![]() .
.
 Если в общем уравнении
Если в общем уравнении ![]()
![]() , то полученное из него равенство
, то полученное из него равенство ![]() представляет собой
уравнение прямой с угловым коэффициентом
представляет собой
уравнение прямой с угловым коэффициентом 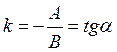 .
.
Уравнение прямой, проходящей через заданную точку ![]() , имеет вид:
, имеет вид:
![]() . (1.39)
. (1.39)
Угол 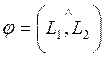 между прямыми с заданными угловыми
коэффициентами определяется как
разность углов наклона прямых к оси абсцисс (см. рисунок 5):
между прямыми с заданными угловыми
коэффициентами определяется как
разность углов наклона прямых к оси абсцисс (см. рисунок 5):
![]()
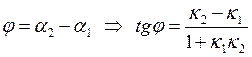 .
.
Угловой коэффициент определяет направление прямой в плоскости:
![]() ,
,
![]() .
.
Лекция 3. Кривые и поверхности второго порядка. Комплексные числа
Цель лекции: изложить способы приведения общих уравнений кривых и поверхностей второго порядка к их каноническим уравнениям, методы исследования их свойств. Ввести новые для студентов понятие комплексного числа (к.ч.), показать различные формы к.ч. и действия над ними.
Алгебраическое уравнение второй степени
![]() (1.40)
(1.40)
в системе координат ![]() определяет плоскую линию, называемую
кривой второго порядка. В зависимости от значений коэффициентов (1.40) могут
определять эллипс, окружность, гиперболу или параболу.
определяет плоскую линию, называемую
кривой второго порядка. В зависимости от значений коэффициентов (1.40) могут
определять эллипс, окружность, гиперболу или параболу.
Сохраняя прежние обозначения перменных, заданное уравнение можем представить в виде:
1) 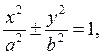 - эллипс (при
- эллипс (при ![]() окружность
окружность ![]() ) и гипербола.
) и гипербола.

(1.41)
5) 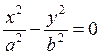 - пара прямых, проходящих через начало
координат.
- пара прямых, проходящих через начало
координат.
В канонических уравнениях эллипса
и гиперболы (1.41.1, см. рисунок 6 а,б) для определенности положим ![]() . Гипербола не пересекается с осью ординат.
Поэтому оси абсцисс и ординат, также откладываемые на них величины
. Гипербола не пересекается с осью ординат.
Поэтому оси абсцисс и ординат, также откладываемые на них величины ![]() и
и ![]() , называются соответственно
действительной и мнимой осями гиперболы. У эллипса
числа
, называются соответственно
действительной и мнимой осями гиперболы. У эллипса
числа ![]() и
и ![]() называют большой и
малой осями,
называют большой и
малой осями, ![]() и
и
![]() -
соответствующими полуосями. Точки
-
соответствующими полуосями. Точки ![]() ,
, ![]() называются вершинами кривых. Гипербола
состоит из двух частей (левой и правой ветвей), расположенных симметрично
относительно ее мнимой оси.
называются вершинами кривых. Гипербола
состоит из двух частей (левой и правой ветвей), расположенных симметрично
относительно ее мнимой оси.
Эллипс и гипербола имеют по две директрисы ![]() и
и ![]() , по два фокуса
, по два фокуса ![]() и
и ![]() с фокусным расстоянием
с фокусным расстоянием ![]() .
.
Число

называемое эксцентриситетом кривой, характеризует степень
вытянутости кривой вдоль оси абсцисс. В эллипсе ![]() ,
следовательно,
,
следовательно, ![]() ;
для гиперболы
;
для гиперболы ![]() .
В частных случаях: для окружности
.
В частных случаях: для окружности ![]() , для равнобочной
, для равнобочной ![]() гиперболы
гиперболы ![]() .
.
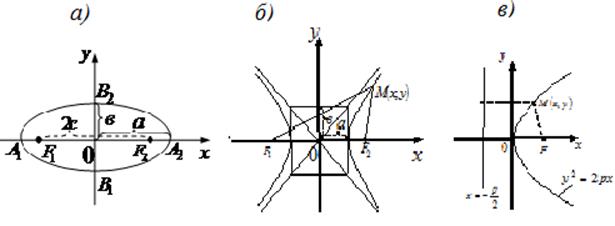
Рисунок 6 – Эллипс, гипербола и парабола
Парабола имеет одну директрису,
перпендикулярную оси симметрии, и соответственно один фокус, расположенный на
оси симметрии параболы. Точка ![]() - вершина параболы,
- вершина параболы, ![]() - ее фокусное расстояние (1.41.2, см. рисунок 6 в). Тогда
- ее фокусное расстояние (1.41.2, см. рисунок 6 в). Тогда  . Величину
. Величину ![]() называют фокальным
параметром кривых второго порядка. По определению
называют фокальным
параметром кривых второго порядка. По определению 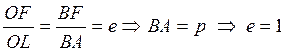 .
.
Расстояния ![]() (см. рисунок 6а,б) называются фокальными
радиусами текущей точки
(см. рисунок 6а,б) называются фокальными
радиусами текущей точки ![]() кривых. Для эллипса
кривых. Для эллипса ![]() , для гиперболы
, для гиперболы ![]() . Двойной знак соответствует правой и левой ветвям
гиперболы. Прямые
. Двойной знак соответствует правой и левой ветвям
гиперболы. Прямые 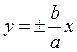 служат асимптотами гиперболы.
служат асимптотами гиперболы.
Кривые второго порядка в полярной системе координат.
Кривая
второго порядка ![]() есть
геометрическое место точек плоскости, отношение расстояний которых от
фиксириванных точки
есть
геометрическое место точек плоскости, отношение расстояний которых от
фиксириванных точки ![]() , называемой фокусом, и прямой
, называемой фокусом, и прямой ![]() , называемой директрисой, равно
постоянной
, называемой директрисой, равно
постоянной ![]() :
:
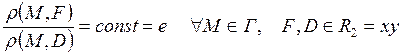 . (1.42)
. (1.42)
Из (1.42) можно найти уравнения директрис эллипса и гиперболы:
 .
.
Связь между декартовыми и полярными координатами точки выражается равенствами:
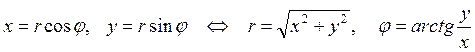 . (1.43)
. (1.43)
Для вывода общего
уравнения кривых второго порядка в полярных координатах фокус ![]() (см. рисунок 6в) примем за полюс, а
полярную ось направим перпендикулярно
(см. рисунок 6в) примем за полюс, а
полярную ось направим перпендикулярно ![]() в противоположную от нее сторону. Тогда из
(1.42):
в противоположную от нее сторону. Тогда из
(1.42):
 ;
; 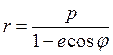 . (1.44)
. (1.44)
Поверхности второго порядка.
Общее уравнение поверхностей второго порядка в координатной форме:
![]() . (1.45)
. (1.45)
После приведения к каноническому виду с помощью линейных преобразований можно установить, какие геометрические образы в пространстве определяются этими уравнениями:
1)
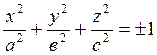 - эллипсоид с центром в
начале координат
- эллипсоид с центром в
начале координат ![]() или
мнимая поверхность;
или
мнимая поверхность;

(1.46)
4) 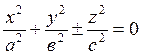 - отдельная точка - начало новой системы
координат или конус с вершиной в этой точке.
- отдельная точка - начало новой системы
координат или конус с вершиной в этой точке.
Равенства (1.46) представляют собой канонические уравнения поверхностей второго порядка в преобразованной системе координат.
В каконических уравнениях
эллипсоида и гиперболоидов ![]() есть полуоси поверхности. Если они
различны и в правой части (1.46) взят положительный знак, то уравнение
определяет трехосний эллипсоид с шестью вершинами (см. рисунок 7а):
есть полуоси поверхности. Если они
различны и в правой части (1.46) взят положительный знак, то уравнение
определяет трехосний эллипсоид с шестью вершинами (см. рисунок 7а): ![]() . Все ортогональные сечения трехоснего эллипсоида есть эллипсы. Если
две полуоси
. Все ортогональные сечения трехоснего эллипсоида есть эллипсы. Если
две полуоси
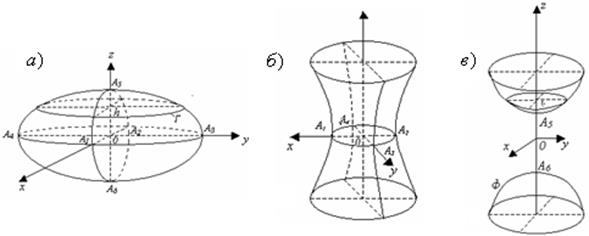
Рисунок 7 – Эллипсоид и гиперболоиды
эллипсоида равны, например, ![]() , то получим эллипсоид вращения:
, то получим эллипсоид вращения:
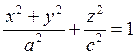 ,
,
образованный вращением эллипса вокруг оси ![]() . При
. При
![]() эллипсоид превращается в сферу радиуса
эллипсоид превращается в сферу радиуса ![]() с каноническим
уравнением:
с каноническим
уравнением:
![]() .
.
Если в правой части (1.46.2)) взята ![]() , то уравнение определяет
однополостный гиперболоид (см. рисунок 7б) с вершинами
, то уравнение определяет
однополостный гиперболоид (см. рисунок 7б) с вершинами ![]() . Указанное уравнение с
. Указанное уравнение с ![]() в правой части
определяет двуполостный гиперболоид, вершины
в правой части
определяет двуполостный гиперболоид, вершины ![]() которого лежат на оси аппликат. Ортогональные
сечения гиперболоида в плоскостях, перпендикулярных
которого лежат на оси аппликат. Ортогональные
сечения гиперболоида в плоскостях, перпендикулярных ![]() (
(![]() , для двуполостного гиперболоида
, для двуполостного гиперболоида ![]() ), есть эллипсы (при
), есть эллипсы (при ![]() - окружности), а другие
ортогональные сечения – гиперболы. При
- окружности), а другие
ортогональные сечения – гиперболы. При ![]() , например, имеем гиперболоиды вращения
, например, имеем гиперболоиды вращения
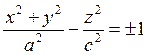 ,
,
полученные вращением ветвей гипербол вокруг оси аппликат.

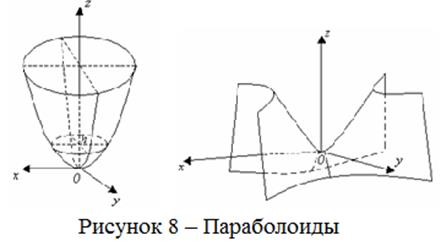 В зависимости от того, какой из двойного знака
берется уравнения (1.46.3) определяют эллиптический и гиперболический
параболоиды (см. рисунок 8). Они имеют единственную вершину, совпадающую с
началом координат. Ортогональные сечения плоскостями
В зависимости от того, какой из двойного знака
берется уравнения (1.46.3) определяют эллиптический и гиперболический
параболоиды (см. рисунок 8). Они имеют единственную вершину, совпадающую с
началом координат. Ортогональные сечения плоскостями ![]() (для эллиптического параболоида
(для эллиптического параболоида ![]() ) соответственно эллипсы
(при
) соответственно эллипсы
(при ![]() окружности) и гиперболы (при
окружности) и гиперболы (при ![]() равнобочные). Другие
ортогональные сечения параболы. Их ветви в плоскостях
равнобочные). Другие
ортогональные сечения параболы. Их ветви в плоскостях ![]() направлены для
эллиптического параболоида вверх, а для гиперболического параболоида (седла) –
вниз. Для последнего действительная ось гиперболы в плоскости
направлены для
эллиптического параболоида вверх, а для гиперболического параболоида (седла) –
вниз. Для последнего действительная ось гиперболы в плоскости ![]() параллельна при
параллельна при ![]() оси абсцисс, а при
оси абсцисс, а при ![]() - оси ординат. Эта
гипербола при
- оси ординат. Эта
гипербола при ![]() превращается
в пару прямых, проходящих через начало координат. Эллиптический параболоид при
превращается
в пару прямых, проходящих через начало координат. Эллиптический параболоид при ![]() превращается в
параболоид вращения
превращается в
параболоид вращения
![]() ,
,
образованный вращением параболы вокруг оси ![]() .
.
Уравнение (1.46.4)), где взят второй знак, определяет
прямой конус (см. рисунок 9). Его сечения плоскоcтями ![]() (направляющие) есть эллипсы, при
(направляющие) есть эллипсы, при ![]() - окружности. В последнем случае имеем
обычный прямой круглый конус. Остальные -ортогональные сечения гиперболы. В
координатных плоскостях
- окружности. В последнем случае имеем
обычный прямой круглый конус. Остальные -ортогональные сечения гиперболы. В
координатных плоскостях ![]() они превращаются в пару прямых, проходящих
через начало координат.
они превращаются в пару прямых, проходящих
через начало координат.
На рисунке 10 изображены прямые эллиптический,
гиперболический и параболический цилиндры. При ![]() эллиптический цилиндр превращается в
прямой круглый цилиндр. Заменив переменную
эллиптический цилиндр превращается в
прямой круглый цилиндр. Заменив переменную ![]() или
или ![]() в уравнении на
в уравнении на ![]() ,
можно получить цилиндрическую поверхность с образующими, параллельными оси абсцисс
или оси ординат.
,
можно получить цилиндрическую поверхность с образующими, параллельными оси абсцисс
или оси ординат.
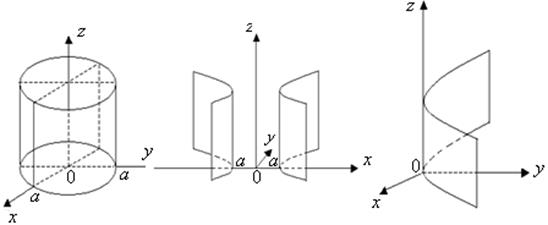
Рисунок 10 – Цилиндры
Комплексные числа.
I Алгебраическая форма комплексных чисел.
Комплексным числом (к.ч.) в алгебраической форме
называется выражение ![]()
![]() ,
, ![]() – так называемая мнимая единица.
Числа
– так называемая мнимая единица.
Числа ![]() и
и ![]() - соответственно
действительной частью и коэффициентом при мнимой части к.ч. К.ч.
- соответственно
действительной частью и коэффициентом при мнимой части к.ч. К.ч. ![]() и
и ![]() называются взаимно сопряженными.
называются взаимно сопряженными.
При сравнении, сложении и вычитании с к.ч. можно обращаться как с числовыми векторами:
1) ![]()
![]() ;
; ![]() ;
;
2) ![]() ;
;
3) ![]()
![]() ;
;
4) 
![]() .
.
II Тригонометрическая форма комплексных чисел.
Комплексная переменная ![]() может быть изображена и в полярных
координатах точки
может быть изображена и в полярных
координатах точки ![]() .
Пользуясь формулами (1.43), получим к.ч. в тригонометрической форме:
.
Пользуясь формулами (1.43), получим к.ч. в тригонометрической форме:
![]() , (1.47)
, (1.47)
где ![]() -
модуль,
-
модуль,  -
аргумент (главное значение полярного угла:
-
аргумент (главное значение полярного угла: ![]() ) к.ч..
) к.ч..
Действия умножения, деления, возведения в степень и извлечения корня удобно выполнять над к.ч. в тригонометрической форме. Возьмем к.ч.
![]()
![]() .
.
1. Пользуясь формулами синуса и косинуса суммы двух углов, произведение к.ч. можно представить в виде:
![]() , (1.48)
, (1.48)
т.е. при умножении к.ч. их модули перемножаются, а аргументы складываются.
2. При делении к.ч. их модули делятся друг на друга, а аргументы вычитаются:
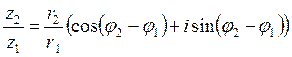 .
.
3. Выполняя возведение в ![]() -степень к.ч. (1.47) как последовательное
умножение
-степень к.ч. (1.47) как последовательное
умножение ![]() раз
числа само на себя, придем к формуле Муавра:
раз
числа само на себя, придем к формуле Муавра:
![]() , (1.49)
, (1.49)
т.е. при возведении к.ч. в ![]() -степень его модуль возводится в ту же
степень, а
-степень его модуль возводится в ту же
степень, а
 аргумент умножается на
аргумент умножается на ![]() . Формула (1.49) применима и для целых
отрицательных показателей
. Формула (1.49) применима и для целых
отрицательных показателей ![]() .
.
4. Корень ![]() -степени из к.ч. (1.47) есть к.ч.
-степени из к.ч. (1.47) есть к.ч. ![]() такое,
что
такое,
что
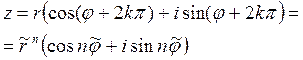 .
.
При извлечении корня ![]() - степени из к.ч. из его
модуля извлекается корень той же степени,
а общее значение аргумента делится на
- степени из к.ч. из его
модуля извлекается корень той же степени,
а общее значение аргумента делится на ![]() :
:
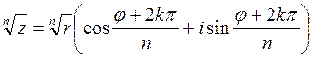 ,
, ![]() .
.
Корень ![]() -степени из к.ч. имеет
-степени из к.ч. имеет ![]() значений (комплексных). Эти
значения – точки
значений (комплексных). Эти
значения – точки ![]() в
комплексной плоскости располагаются в вершинах правильного
в
комплексной плоскости располагаются в вершинах правильного ![]() -угольника, вписанного в
окружность радиуса
-угольника, вписанного в
окружность радиуса ![]() (см. рисунок 11,
(см. рисунок 11, ![]() ).
).
III Показательная форма комплексных чисел.
Исследуя показательную функцию с чисто мнимым аргументом, А. Эйлер установил:
![]() . (1.50)
. (1.50)
Формула Эйлера дает возможность представить
к.ч. (1.47) в показательной форме ![]() , удобной для выполнения алгебраических
действий над к.ч.. Например:
, удобной для выполнения алгебраических
действий над к.ч.. Например:
![]() ,
, 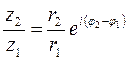 ,
, ![]() ,
, ![]() ,
,
![]() .
.
Модуль 2. Дифференциальное исчисление функций одной переменной
Лекция 4. Предел функции
Цель лекции: учитывая сопоставительные содержания программ по математике в средней школе и в технических вузах, дать понятия, свойства и графики гиперболических функций, предела функции, бесконечно малой и бесконечно большой функций, неопределенностей, замечательных пределов.
Функция и ее предел.
Определение. Если каждому
значению переменной ![]() из
множества
из
множества ![]() по
некоторому закону или правилу поставлено в соответствие определенное значение
переменной
по
некоторому закону или правилу поставлено в соответствие определенное значение
переменной ![]() из
другого множества
из
другого множества ![]() ,
то
,
то ![]() называют
функцией
называют
функцией ![]() и
записывают
и
записывают ![]() .
.
Здесь ![]() -независимая переменная или
аргумент,
-независимая переменная или
аргумент, ![]() -зависимая
переменная. Множество
-зависимая
переменная. Множество ![]() значений независимой переменной называется
областью определения функции. Множество
значений независимой переменной называется
областью определения функции. Множество ![]() соответствующих значений функции называют
областью изменения или областью значений функции.
соответствующих значений функции называют
областью изменения или областью значений функции.
Аргумент в свою очередь может являться функцией другой переменной:
![]() ,
, ![]() . (2.1)
. (2.1)
Если ![]() , то
говорят, что на множестве
, то
говорят, что на множестве ![]() определена сложная функция
определена сложная функция
![]() . (2.1/)
. (2.1/)
Исключив ![]() из (2/),
получаем сложную функцию.
из (2/),
получаем сложную функцию.
Основные элементарные функции содержатся в школьном курсе математики.
Гиперболические
функции. Полуразность и полусумма экспонент ![]() и
и ![]()
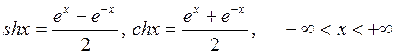 (2.2)
(2.2)
называются соответственно гиперболическим синусом и гиперболическим косинусом. Аналогично тригонометрическим функциям вводятся функции гиперболического тангенса и гиперболического котангенса:
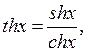

![]() .
.
Рассмотрим
функцию ![]() ,
определенную в некоторой окрестности
,
определенную в некоторой окрестности ![]() точки
точки ![]() за исключением, быть может, самой точки.
за исключением, быть может, самой точки.
Определение 1. Если
для любого заданного ![]() найдется
число
найдется
число ![]() такое,
что
такое,
что
![]()
![]()
![]()
![]() , (2.3)
, (2.3)
то число ![]() называют пределом функции
называют пределом функции ![]() в точке
в точке ![]() (при
(при ![]() ) и записывают:
) и записывают:
![]()
![]()
![]() . (2.4)
. (2.4)
Для функций ![]() и
и ![]() ,
имеющих конечный предел при
,
имеющих конечный предел при ![]() :
:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
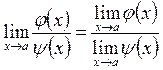 ,
, ![]() . (2.7)
. (2.7)
Предел функции также имеет свойства, выражаемые неравенствами:
1) ![]()
![]()
![]()
![]()
![]() ,
,
2) ![]()
![]()
![]()
![]() , 3)
, 3)![]()
![]()
![]() .
.
Функцию ![]() называют ограниченной в области
называют ограниченной в области ![]() , если найдется число
, если найдется число ![]() такое, что
такое, что
![]()
![]() . (2.8)
. (2.8)
Если при ![]() функция
функция ![]() имеет конечный предел
имеет конечный предел ![]() , то существует некоторая окрестность
, то существует некоторая окрестность ![]() точки
точки ![]() , где функция сохраняет знак своего
предела:
, где функция сохраняет знак своего
предела: ![]() .
.
Теорема (о пределе сложной функции). Если в
сложной функции (2.1) ![]() , то
, то
![]() . (2.9)
. (2.9)
Если в (2.4) потребовать, чтобы ![]() стремился к
стремился к ![]() , оставаясь: меньше
, оставаясь: меньше ![]() (слева) или больше
(слева) или больше ![]() (справа), то придем к понятиям
односторонних пределов функции в точке:
(справа), то придем к понятиям
односторонних пределов функции в точке:
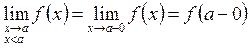

 .
.
Для того чтобы функция ![]() в точке
в точке ![]() имела конечный предел,
необходимо и достаточно, чтобы:
имела конечный предел,
необходимо и достаточно, чтобы: ![]() .
.
Бесконечно малая и бесконечно большая функции.
Функция ![]() называется бесконечно
малой при
называется бесконечно
малой при ![]() ,
если
,
если ![]() .
.
Для функции, имеющей конечный предел (2.4), выполняется
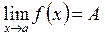

 ,
, 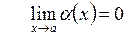 . (2.10)
. (2.10)
Если
![]() , (2.11)
, (2.11)
то функцию ![]() называют бесконечно
большой при
называют бесконечно
большой при ![]() .
.
Теорема 1. Если ![]()
![]() и при
и при ![]() функция
функция ![]() бесконечно малая, то функция
бесконечно малая, то функция ![]() бесконечно большая,
наоборот, функция
бесконечно большая,
наоборот, функция ![]() бесконечно
бесконечно
малая, когда ![]() бесконечно большая.
бесконечно большая.
Теорема 2. Произведение любого конечного
числа функций, бесконечно малых или бесконечно больших при ![]() есть функция соответственно
бесконечно малая и бесконечно большая при
есть функция соответственно
бесконечно малая и бесконечно большая при ![]() .
.
Теорема 3. Сумма любого конечного числа
бесконечно малых при ![]() функций
есть функция бесконечно малая при
функций
есть функция бесконечно малая при ![]() .
.
Теорема 4. Произведение функции,
ограниченной в окрестности ![]() точки
точки ![]() , и функции, бесконечно малой при
, и функции, бесконечно малой при ![]() , есть функция
бесконечно малая при
, есть функция
бесконечно малая при ![]() .
.
Функции ![]() и
и ![]() , удовлетворяющие условию
, удовлетворяющие условию

![]()
![]() ,
, ![]() , (2.12)
, (2.12)
называются
эквивалентными (асимптотически равными) при ![]() .
.
(2.12) по-другому записывается так:
![]() . (2.12.1)
. (2.12.1)
Здесь ![]() - главная часть суммы в
- главная часть суммы в ![]() , а вторая слагаемая
представляет собой бесконечно малую при
, а вторая слагаемая
представляет собой бесконечно малую при ![]() .
.
Применение действий над
бесконечно малыми и бесконечно большими функциями иногда приводит к
соотношениям, называемым неопределённостями. Непосредственный переход к пределу
может привести к неопределённостям вида: ![]() ,
, ![]() ,
, ![]() и
и ![]() . Степенные неопределённости
. Степенные неопределённости ![]() ,
, ![]() и
и ![]() путём логарифмирования переходит к неопределённостям
вида
путём логарифмирования переходит к неопределённостям
вида ![]() .
.
Замечательные пределы.
Предел
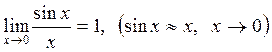 . (2.14)
. (2.14)
называется первым замечательным пределом.
Справедливы формулы:
![]()
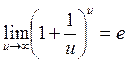 ,
, ![]() , (2.15)
, (2.15)
определяющие число ![]() и называемые вторым замечательным
пределом.
и называемые вторым замечательным
пределом.
Эквивалентность
функции при ![]() :
:
![]()
![]()
![]() ;
; ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() . (2.16)
. (2.16)
Задачу о нахождении
предела рациональной дроби при ![]() можно рассматривать как
сравнение старших членов двух многочленов
можно рассматривать как
сравнение старших членов двух многочленов ![]() и
и ![]() :
:
![]()
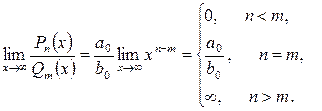
Задача 4. Найти предел функции:
![]()
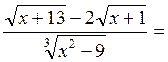
![]()
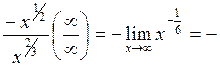
![]()
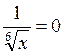 .
.
При ![]() для раскрытия
неопределенности вида
для раскрытия
неопределенности вида ![]() следует
следует
предварительно освободиться от иррациональности и упростить выражение:
![]()

![]() .
.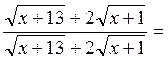
![]()
![]()

![]()

![]()
![]() .
.
Лекция 5. Непрерывность функции
Цель лекции: дать определение непрерывности функции в точке и классификацию точек разрыва. Изложить свойства (теоремы) функций, непрерывных на отрезке, и монотонных функций. Ввести понятие равномерной непрерывности функции на отрезке.
Функция ![]() , определенная в точке
, определенная в точке ![]() и в некоторой ее окрестности
и в некоторой ее окрестности ![]() , называется непрерывной в этой
точке, если она имеет предел при
, называется непрерывной в этой
точке, если она имеет предел при ![]() :
:
![]()
![]()
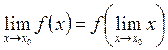 . (2.17)
. (2.17)
Если в
точке ![]() не
выполняется условие (2.17), то функцию
не
выполняется условие (2.17), то функцию ![]() называют разрывной в данной точке, а
называют разрывной в данной точке, а ![]() - точкой разрыва
функции. Если
- точкой разрыва
функции. Если ![]() непрерывна
в точке
непрерывна
в точке ![]() и
и ![]() , то существует
некоторая окрестность точки
, то существует
некоторая окрестность точки ![]() , где функция сохраняет свой знак:
, где функция сохраняет свой знак: ![]()
![]() .
.
Разность ![]() ,
, ![]() называют
приращением аргумента в точке
называют
приращением аргумента в точке ![]() . Тогда разность
. Тогда разность
![]() (2.17.1)
(2.17.1)
будет представлять собой приращение функции в точке ![]() , соответствующее
, соответствующее ![]() . Так
как
. Так
как ![]() и
и ![]() , то
первое из равенств (2.17) можно записать в виде:
, то
первое из равенств (2.17) можно записать в виде:
![]() . (2.18)
. (2.18)
Итак, для того чтобы функция была непрерывна в точке необходимо и достаточно, чтобы любому бесконечно малому приращению аргумента соответствовало бесконечно малое приращение функции.
Если для функции ![]() , определенной в самой точке
, определенной в самой точке ![]() и в некоторой ее левой
или правой полуокрестности, выполняется условие
и в некоторой ее левой
или правой полуокрестности, выполняется условие
![]()
![]()
![]() , (2.19)
, (2.19)
то функция называется непрерывной в точке ![]() соответственно слева или справа. Для того чтобы
функция была непрерывна в точке
соответственно слева или справа. Для того чтобы
функция была непрерывна в точке ![]() необходимо и достаточно, чтобы функция
была непрерывна в точке
необходимо и достаточно, чтобы функция
была непрерывна в точке ![]() как слева, так и справа:
как слева, так и справа: ![]() . Если
. Если ![]() , т.е. в точке
, т.е. в точке ![]() функция непрерывна
только слева, то
функция непрерывна
только слева, то ![]() -
точка разрыва функции.
-
точка разрыва функции.
Теорема 1. Алгебраическая сумма и произведение любого конечного числа, непрерывных в точке функций есть функция, непрерывная в этой точке.
Теорема 2. Частное от деления двух непрерывных в точке функций есть функция, непрерывная в этой точке (в предположении, что делитель неравен нулю).
Теорема 3 (о непрерывности сложной
функции). Если в (2.1) функция ![]() непрерывна в точке
непрерывна в точке ![]() , а функция
, а функция ![]() непрерывна в точке
непрерывна в точке ![]() , то сложная функция
, то сложная функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Функция, непрерывная
во всех точках интервала, называется непрерывной в этом интервале. Функцию, непрерывную в интервале ![]() и непрерывную в точке
и непрерывную в точке ![]() и
и ![]() соответственно справа и слева,
называют непрерывной на отрезке
соответственно справа и слева,
называют непрерывной на отрезке ![]() .
.
Классификация точек разрыва.
Если функция ![]() , определенная в некоторой окрестности
, определенная в некоторой окрестности ![]() точки
точки ![]() за исключением, быть
может, самой точки, совершает конечный скачок в этой точке, т.е. функция имеет
оба односторонние пределы в точке, но они не равны между собой:
за исключением, быть
может, самой точки, совершает конечный скачок в этой точке, т.е. функция имеет
оба односторонние пределы в точке, но они не равны между собой: ![]() , то
, то ![]() называется точкой
разрыва первого рода функции.
называется точкой
разрыва первого рода функции.
Если ![]() , но функция
, но функция ![]() не определена в точке
не определена в точке ![]() , то
, то ![]() называют устранимой точкой
разрыва функции.
называют устранимой точкой
разрыва функции.
Если хотя бы один из односторонних пределов
![]() не существует
или равен
не существует
или равен ![]() , то
, то
![]() называется
точкой разрыва второго рода функции
называется
точкой разрыва второго рода функции ![]() .
.
Для функции 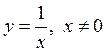 ,
описывающей равностороннюю гиперболу, начало координат является точкой разрыва
второго рода, так как
,
описывающей равностороннюю гиперболу, начало координат является точкой разрыва
второго рода, так как ![]() .
.
Функции, непрерывные на отрезке.
Функция ![]() , непрерывная на отрезке
, непрерывная на отрезке
![]() , имеет
конечный предел в каждой точке
, имеет
конечный предел в каждой точке ![]() и односторонние пределы
и односторонние пределы ![]() . Следовательно,
имеются окрестность
. Следовательно,
имеются окрестность ![]() и
полуокрестности
и
полуокрестности ![]() ,
где функция ограничена. Сказанное доказывает следующую теорему.
,
где функция ограничена. Сказанное доказывает следующую теорему.
Теорема 1. Функция ![]() , непрерывная на отрезке
, непрерывная на отрезке ![]() , ограничена на этом
отрезке, т.е. найдется число
, ограничена на этом
отрезке, т.е. найдется число ![]() такое, что
такое, что
![]()
![]()
![]() .
.
Теорема 2 (Вейерштрасса). Функция ![]() , непрерывная на отрезке
, непрерывная на отрезке
![]() , на этом отрезке
принимает свои наименьшее и наибольшее значения, т.е.
, на этом отрезке
принимает свои наименьшее и наибольшее значения, т.е.
существуют точки ![]() такие, что
такие, что
![]() .
.
Теорема 3. Функция ![]() , непрерывная на отрезке
, непрерывная на отрезке ![]() , принимает все значения
между своими любыми двумя значениями на этом отрезке:
, принимает все значения
между своими любыми двумя значениями на этом отрезке: ![]()
![]()
![]() ,
, ![]() , т.е. для любого числа
, т.е. для любого числа ![]() найдется число
найдется число ![]()
![]() такое, что
такое, что ![]()
![]() .
.
Следствие 1. Функция, непрерывная на
отрезке, принимает все значения между своими наименьшим ![]() и наибольшим
и наибольшим ![]() значениями на этом
отрезке, т.е. множество значений функции есть отрезок
значениями на этом
отрезке, т.е. множество значений функции есть отрезок ![]() оси ординат.
оси ординат.
Следствие 2. Если ![]() непрерывна на
непрерывна на ![]() и
и ![]() , то найдется хотя бы одна точка
, то найдется хотя бы одна точка ![]()
![]() такая, что
такая, что ![]() .
.
Монотонные функции.
Функция ![]() , определенная на
, определенная на ![]() ,
называется монотонной на отрезке, если для любых
,
называется монотонной на отрезке, если для любых ![]()
![]() ,
, ![]() она удовлетворяет одному из указанных ниже
условий. Функцию называют монотонной:
она удовлетворяет одному из указанных ниже
условий. Функцию называют монотонной:
1) возрастающей при ![]()
![]() ;
;
2) неубывающей, если ![]()
![]() ;
;
3) убывающей, когда ![]()
![]() ;
;
4) невозрастающей при ![]()
![]() .
.
Теорема. Для непрерывной, монотонно
возрастающей или убывающей на отрезке ![]() функции
функции ![]() существует непрерывная, соответственно
монотонно возрастающая или убывающая на отрезке
существует непрерывная, соответственно
монотонно возрастающая или убывающая на отрезке ![]() ,
, ![]() обратная функция
обратная функция ![]() .
.
Если для любых заданного числа ![]() и
и ![]()
![]() существует число
существует число ![]() такое, что
такое, что
![]()
![]() , (2.20)
, (2.20)
то функция ![]() называется равномерно непрерывной на
отрезке
называется равномерно непрерывной на
отрезке ![]() .
.
Лекция 6. Производные и дифференциалы функций
Цель лекции: обращать внимание на геометрические и механические смыслы производных начальных порядков и дифференциала, на их приложения в приближенных вычислениях. Изложить производные и дифференциалы высших порядков геометрические толкования теорем о среднем и применения правил Лопиталя.
Производная функции.
Из области определения функции ![]() возьмем точки
возьмем точки ![]() . Тогда приращению
независимой переменной
. Тогда приращению
независимой переменной ![]() будет соответствовать приращение функции
будет соответствовать приращение функции ![]() .
.
Определение. Если при ![]() отношение приращения функции
отношение приращения функции ![]() к соответствующему
приращению аргумента
к соответствующему
приращению аргумента ![]() имеет
конечный предел, то это число называют производной функции
имеет
конечный предел, то это число называют производной функции ![]() в точке
в точке ![]() и обозначают символами:
и обозначают символами: ![]()
![]()
 .
.
Итак,
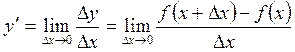 . (2.21)
. (2.21)
Угловой коэффициент касательной
кривой ![]() в
точке
в
точке ![]()
![]() . (2.22)
. (2.22)
Нормаль ![]() к касательной называют нормалью и к
кривой
к касательной называют нормалью и к
кривой ![]() . Для
. Для ![]() уравнения касательной и
нормали к кривой в точке
уравнения касательной и
нормали к кривой в точке ![]() имеют вид:
имеют вид:
![]() , (2.23)
, (2.23)
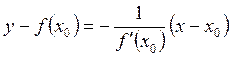 . (2.24)
. (2.24)
Операцию нахождения производной функции называют
дифференцированием функции. К графику
дифференцируемой в точке ![]() функции
функции ![]() в точке
в точке ![]() можно провести единственную касательную с
угловым коэффициентом, равным производной функции в точке
можно провести единственную касательную с
угловым коэффициентом, равным производной функции в точке ![]() . Это утверждение определяет геометрический смысл производной функции.
. Это утверждение определяет геометрический смысл производной функции.
Непрерывность функции в точке является необходимым условием ее дифференцируемости в данной точке. В соответствии с понятиями односторонней непрерывности функции в точке рассматриваются односторонние: левая и правая производные функции в точке:
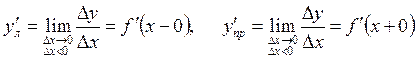 . (2.25)
. (2.25)
Для дифференцируемости функции в точке необходимо и
достаточно, чтобы она имела обе конечные и равные между собой односторонние производные в этой точке: ![]() . Если функция
. Если функция ![]() в точке
в точке ![]() имеет обе
односторонние производные, но они неравны между собой:
имеет обе
односторонние производные, но они неравны между собой: ![]() , то
, то ![]() - функция, недифференцируемая в
этой точке;
- функция, недифференцируемая в
этой точке; ![]() есть
точка возврата графика функции.
есть
точка возврата графика функции.
Если в (2.21) 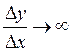 ,
, ![]() , то функция
, то функция ![]() не является дифференцируемой в точке
не является дифференцируемой в точке ![]() . Но, производная имеет
геометрический смысл: касательная к кривой
. Но, производная имеет
геометрический смысл: касательная к кривой ![]() в точке
в точке ![]() перпендикулярна оси абсцисс.
перпендикулярна оси абсцисс.
Механический
смысл производной функции: путь ![]() точки, движущейся по своей траектории
есть дифференцируемая функция времени. Пусть в моменты времени
точки, движущейся по своей траектории
есть дифференцируемая функция времени. Пусть в моменты времени ![]() и
и ![]() точка занимала положения
точка занимала положения ![]() и
и ![]() (см. рисунок 12) на траектории,
т.е. за время
(см. рисунок 12) на траектории,
т.е. за время ![]() точка
прошла путь
точка
прошла путь ![]() .
.
Отношение ![]() есть средняя скорость
точки за промежуток времени
есть средняя скорость
точки за промежуток времени ![]() .
.
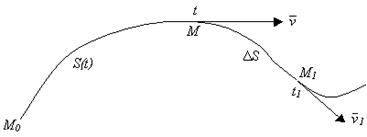
Рисунок 12 – Механический смысл производной
Ее предел
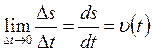 (2.26)
(2.26)
называют алгебраической скоростью
движущейся точки в момент времени ![]() . Вообще, скорость точки есть вектор,
направленный по касательной к траектории.
. Вообще, скорость точки есть вектор,
направленный по касательной к траектории.
Производная любой дифференцируемой функции характеризует скорость изменения функции с изменением аргумента.
Правила дифференцирования.
Основное
правило дифференцирования функции вытекает из определения производной (2.21):
аргументу ![]() сообщают
произвольное приращение
сообщают
произвольное приращение ![]() , находят соответствующее ему приращение
функции
, находят соответствующее ему приращение
функции ![]() ,
находят предел отношения второго из этих приращений к первому при
,
находят предел отношения второго из этих приращений к первому при ![]() .
.
Функция называется дифференцируемой на интервале, если
она имеет конечную производную в каждой
точке интервала. Функцию, дифференцируемую на интервале ![]() и имеющую в концах
интервала конечные односторонние: правую
и имеющую в концах
интервала конечные односторонние: правую ![]() и левую
и левую ![]() производные - называют
дифференцируемой на отрезке
производные - называют
дифференцируемой на отрезке ![]() . Например, функция
. Например, функция ![]() ,
, ![]() дифференцируема
на всей числовой оси. Ее приращение:
дифференцируема
на всей числовой оси. Ее приращение:
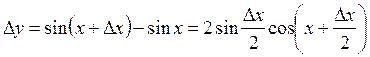 . (2.27)
. (2.27)
Поскольку 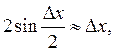
![]() , то
имеем
, то
имеем
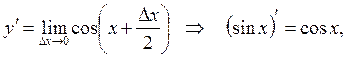
![]() .
.
Правила дифференцирования функций.
1. Постоянный множитель можно выносить за знак производной.
2. Производная суммы (разности) дифференцируемых функций равна сумме (разности) их производных:
![]() . (2.28)
. (2.28)
Так как это свойство справедливо для алгебраической суммы любого конечного числа дифференцируемых функций, то:
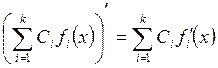 ,
, ![]() ,
, ![]() . (2.29)
. (2.29)
3. ![]()
![]() . (2.30)
. (2.30)
4. 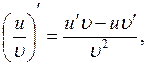
![]() (2.31)
(2.31)
5. Тероема (о производной сложной функции). Если в
(2.1) функции ![]() и
и
![]() дифференцируемы
в точках соответственно
дифференцируемы
в точках соответственно ![]() и
и ![]() , то сложная функция
, то сложная функция ![]() имеет конечную производную в
точке
имеет конечную производную в
точке ![]() ,
причем
,
причем
![]() (2.32)
(2.32)
6. Теорема (о производной обратной функции). Если
монотонно возрастающая ( убывающая) на отрезке ![]() функция
функция ![]() в точке
в точке ![]() имеет отличную от нуля конечную
производную
имеет отличную от нуля конечную
производную ![]() ,
то обратная ей функция
,
то обратная ей функция ![]() дифференцируема в соответствующей точке
дифференцируема в соответствующей точке ![]() , причем
, причем
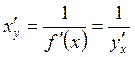 . (2.33)
. (2.33)
Производные основных (сложных) элементарных функций
1. ![]() 8.
8. 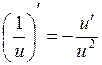 14.
14. 
2. ![]() ,
, ![]() 9.
9. ![]() 15.
15.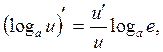
![]() ,
, ![]()
3. 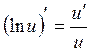 10.
10. ![]() 16.
16. ![]()
4. 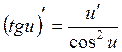 11.
11. 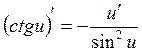 17.
17. 
5. ![]()
 12.
12. 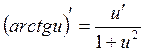 18.
18. 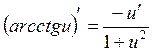
6. ![]() 13.
13. ![]() 19.
19. 
7. 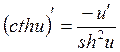 ,
, ![]() .
.
Дифференциал функции.
Пусть функция ![]() дифференцируема на
интервале
дифференцируема на
интервале ![]() и в
точке
и в
точке ![]() имеет
производную
имеет
производную ![]()
![]() . Из определения
производной следует, что соответствующие приращения независимой переменной и
функции величины, сравнимые при
. Из определения
производной следует, что соответствующие приращения независимой переменной и
функции величины, сравнимые при ![]() , и, пользуясь формой записи (2.12), имеем:
, и, пользуясь формой записи (2.12), имеем:
![]() . (2.34)
. (2.34)
Определение. Главную, линейную относительно ![]() часть приращения
функции
часть приращения
функции ![]() называют
дифференциалом функции в точке
называют
дифференциалом функции в точке ![]() , соответствующим приращению независимой
переменной
, соответствующим приращению независимой
переменной ![]() , и
обозначают символом
, и
обозначают символом ![]() или
или
![]() :
: ![]()
Положив ![]() , получим
, получим ![]() . Значит,
. Значит,
![]() , (2.35)
, (2.35)
т.е. дифференциал функции равен произведению производной функции и
дифференциала аргумента. При ![]() приращение и дифференциал функции величины
эквивалентные:
приращение и дифференциал функции величины
эквивалентные: ![]() ,
,
![]() . Этот факт
широко применяется в приближенных вычислениях. Формула нахождения приближенного
значения функции в любой точке
. Этот факт
широко применяется в приближенных вычислениях. Формула нахождения приближенного
значения функции в любой точке ![]() записывается в виде:
записывается в виде:
![]() . (2.36)
. (2.36)
Обозначение производной ![]() теперь можно рассматривать как отношение
дифференциалов функции и аргумента.
теперь можно рассматривать как отношение
дифференциалов функции и аргумента.
Правила нахождения дифференциалов:
![]()
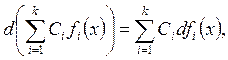
![]() ,
, ![]() ;
;
![]()
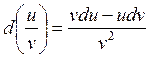 ,
, ![]() ;
; ![]() (2.37)
(2.37)
Геометрический смысл дифференциала:
дифференциал функции ![]() равен
приращению ординаты касательной к графику функции в точке
равен
приращению ординаты касательной к графику функции в точке ![]() , соответствующему приращению
, соответствующему приращению ![]() независимой переменной.
независимой переменной.
Для дифференцируемых на заданном промежутке
функций ![]() ,
, ![]() ,
, ![]() производная
производная ![]() равна отношению их
дифференциалов:
равна отношению их
дифференциалов:
![]()
![]() ,
,
т.е.
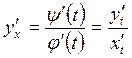 . (2.38)
. (2.38)
Эта операция известна как параметрическое дифференцирование.
Задача 5. Найти производную ![]() :
:
![]()
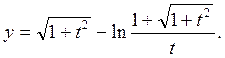
Решение: 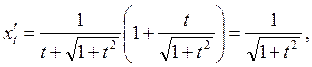
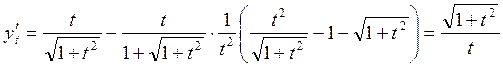 ;
;

Уравнения касательной и нормали к кривой (2.23,24) в
точке ![]()
теперь удобно записывать в виде:
![]() ;
; ![]() .
.
Производные и дифференциалы высших порядков.
Рассмотрим функцию ![]() , дифференцируемую в некоторой области
, дифференцируемую в некоторой области ![]() . Пусть ее производная
. Пусть ее производная ![]() есть функция,
дифференцируемая в области
есть функция,
дифференцируемая в области ![]() или в какой-либо ее части. Далее
или в какой-либо ее части. Далее ![]() будем называть
производной первого порядка или первой производной функции
будем называть
производной первого порядка или первой производной функции ![]() , найденная от нее производная
будет называться производной второго порядка или второй производной функции. Ее
обозначают через:
, найденная от нее производная
будет называться производной второго порядка или второй производной функции. Ее
обозначают через:
![]() ,
, ![]() ,
, 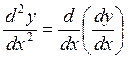 ,
, 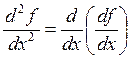 .
.
Допустим, процесс нахождения последующих производных
продолжен и найдена производная ![]() - порядка, обозначаемая одним из символов
- порядка, обозначаемая одним из символов
![]() ,
, ![]() ,
, 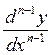 ,
, 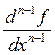 .
.
Если она окажется функцией, дифференцируемой в
области ![]() или в
некоторой ее части, то производную от нее:
или в
некоторой ее части, то производную от нее:
![]() ,
,
![]() ,
, 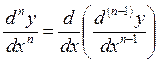 ,
, 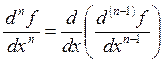 ,
, ![]()
будем называть ![]() - производной функции
- производной функции ![]() .
.
Рассмотрим функции ![]() и
и ![]() , имеющие производные
, имеющие производные ![]() -порядка в некоторой области. Производные
высших порядков их произведения:
-порядка в некоторой области. Производные
высших порядков их произведения:
![]()
![]()
![]()
![]()
![]() .
.
Производные ![]() - порядка:
- порядка:
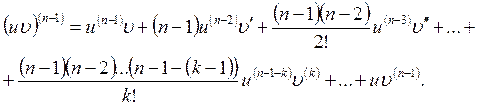
Взяв производные от обеих частей равенства и упростив, результат представим в виде
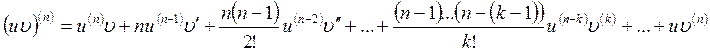 . (2.39)
. (2.39)
Это есть так называемая формула Лейбница для
производной ![]() -порядка
-порядка
произведения двух функций.
Задача 6. Найти производную четвертого порядка функции
![]() .
.
Решение. Для ![]() формула Лейбница выглядит так:
формула Лейбница выглядит так:
![]() .
.
По условию: ![]()
![]()
![]()
![]() ;
;
![]()
![]()
Пусть функция ![]() имеет производную
имеет производную ![]() -порядка в области
-порядка в области ![]() .
.
Дифференциал ![]() или
или ![]() называется дифференциалом второго порядка
или вторым дифференциалом функции
называется дифференциалом второго порядка
или вторым дифференциалом функции ![]() в точке
в точке ![]() . Дифференциал
. Дифференциал ![]() -порядка функции
-порядка функции ![]() определяют как
дифференциал от ее дифференциала
определяют как
дифференциал от ее дифференциала ![]() -порядка
-порядка ![]() . Итак, дифференциалы функции:
. Итак, дифференциалы функции:
![]()
![]() (2.40)
(2.40)
Последнее равенство
показывает, что обозначение ![]() - производной
- производной ![]() есть нечто иное, как отношение
есть нечто иное, как отношение ![]() -дифференциала функции к
-дифференциала функции к
![]() -степени
дифференциала независимой переменной. Для сложной функции такое суждение
невсегда верно. В самом деле, дифференциал имеет вид:
-степени
дифференциала независимой переменной. Для сложной функции такое суждение
невсегда верно. В самом деле, дифференциал имеет вид:
![]()
Из (2.38) производную ![]() следует найти путем параметрического
дифференцирования:
следует найти путем параметрического
дифференцирования:
 . (2.41)
. (2.41)
Задача 7. Найти производную второго порядка ![]() , если:
, если: ![]()
![]() .
.
Решение: 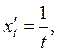
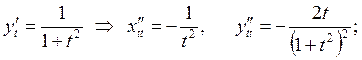
 .
.
Теоремы о среднем. Правило Лопиталя.
Если для функции ![]() , непрерывной на интервале (
, непрерывной на интервале (![]() ), существует некоторая окрестность
), существует некоторая окрестность ![]() точки
точки ![]() такая, что
такая, что
![]() , (2.42)
, (2.42)
то ![]() называется
точкой соответственно локального максимума или локального минимума функции.
Неравенства (2.42) через приращение функции можно представить в виде:
называется
точкой соответственно локального максимума или локального минимума функции.
Неравенства (2.42) через приращение функции можно представить в виде:
![]() . (2.43)
. (2.43)
При выполнении этого условия число ![]() называют локальным максимумом
или локальным минимумом функции. Вместе они называются локальными экстремумами
функции. На интервале
называют локальным максимумом
или локальным минимумом функции. Вместе они называются локальными экстремумами
функции. На интервале ![]() функция
может иметь несколько экстремумов. Если в соотношениях (2.42,43) знаки
равенства отсутствуют, то говорят о строгих экстремумах функции.
функция
может иметь несколько экстремумов. Если в соотношениях (2.42,43) знаки
равенства отсутствуют, то говорят о строгих экстремумах функции.
Теорема Ролля. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , дифференцируема на интервале (
, дифференцируема на интервале (![]() )
и
)
и ![]() , то
найдется по крайней
, то
найдется по крайней
мере одна точка ![]() такая, что
такая, что ![]() .
.
По теореме Вейерштрасса на ![]() функция принимает свои
наименьшее
функция принимает свои
наименьшее ![]() и
наибольшее
и
наибольшее ![]() значения.
Если хотя бы одно из этих значений достигается во внутренней точке отрезка, то
это есть точка
значения.
Если хотя бы одно из этих значений достигается во внутренней точке отрезка, то
это есть точка ![]() ,
удовлетворяющая теореме Ролля и касательная к графику функции в точке
,
удовлетворяющая теореме Ролля и касательная к графику функции в точке ![]() параллельна оси
абсцисс. Таких точек на интервале может быть несколько. В противном случае
любую точку
параллельна оси
абсцисс. Таких точек на интервале может быть несколько. В противном случае
любую точку ![]() можно
принять за
можно
принять за ![]() ,
так как
,
так как ![]() ,
, ![]() и всюду на промежутке
и всюду на промежутке
![]() . (2.44)
. (2.44)
(2.44) является только необходимым условием
существования экстремума функции в точке. И при выполнении (2.44) функция может
не иметь экстремума в точке ![]() .
.
Теорема Лагранжа. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и дифференцируема на интервале (
и дифференцируема на интервале (![]() ),
то существует хотя бы одна точка
),
то существует хотя бы одна точка ![]() такая, что
такая, что
 . (2.45)
. (2.45)
Теорема 1. Если дифференцируемые в некоторой
окрестности ![]() точки
точки ![]() функции
функции ![]() и
и ![]() бесконечно малы при
бесконечно малы при ![]() ,
, ![]() , отношение их производных при
, отношение их производных при ![]() имеет предел, то
отношение самих функций при
имеет предел, то
отношение самих функций при ![]() также имеет предел, причем
также имеет предел, причем
 .
(2.46)
.
(2.46)
Теорема 2. Если дифференцируемые в некоторой
окрестности ![]() точки
точки ![]() функции
функции ![]() и
и ![]() бесконечно большие при
бесконечно большие при ![]() ,
, ![]() , отношение их производных при
, отношение их производных при ![]() имеет предел, то
отношение самих функций при
имеет предел, то
отношение самих функций при ![]() имеет тот же предел, т.е. выполняется
(2.46).
имеет тот же предел, т.е. выполняется
(2.46).
Эти теоремы составляют основу так называемого правила
Лопиталя, применяемого для раскрытия неопределенностей вида ![]() и
и ![]() . Для
применения правила Лопиталя к раскрытию других неопределенностей их преобразуют
к неопределенностям указанных видов. Правило Лопиталя можно применять повторно:
. Для
применения правила Лопиталя к раскрытию других неопределенностей их преобразуют
к неопределенностям указанных видов. Правило Лопиталя можно применять повторно:
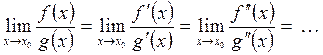 . (2.47)
. (2.47)
Задача 8. Найти предел функции
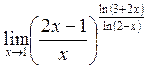
![]() .
.
Решение. После логарифмирования:

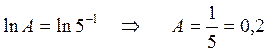 .
.
Лекция 7. Исследование функций с помщью производных
Цель лекции: изложить методы выяснения свойств дифференцируемой функции и особенностей ее графика с помощью производных. Дать образцы составления таблицы результатов исследований и построения с ее помощью эскиза графика функции на конкретном примере.
Экстремумы функции.
1. Интервалы монотонности функции.
Пусть функция ![]() непрерывна на
непрерывна на ![]() и
и ![]() произвольные точки интервала
произвольные точки интервала ![]() (см. рисунок 13). Из
определения монотонности
(см. рисунок 13). Из
определения монотонности

Рисунок 13 – К монотонности функции
функции на отрезке можно заключить, что если знаки соответствующих
приращений аргумента ![]() и функции
и функции ![]() одинаковы, то функция
возрастает, а если противоположны, то убывает на
одинаковы, то функция
возрастает, а если противоположны, то убывает на ![]() . Верно и обратное: для возрастающей
(убывающей) на
. Верно и обратное: для возрастающей
(убывающей) на ![]() функции
функции
![]() :
:
![]() . (2.48)
. (2.48)
Теорема 1. Для того чтобы функция ![]() , непрерывная на
, непрерывная на ![]() и дифференцируемая на
и дифференцируемая на ![]() , была возрастающей
(убывающей) на данном отрезке, необходимо и достаточно, чтобы
, была возрастающей
(убывающей) на данном отрезке, необходимо и достаточно, чтобы
![]()
![]()
![]() .
.
Промежутки, где производная функции имеет постоянный знак, представляют собой интервалы монотонности функции.
Теорема 2. Для того чтобы дифференцируемая
на ![]() функция
функция ![]() была постоянной на этом
интервале, необходимо и достаточно, чтобы
была постоянной на этом
интервале, необходимо и достаточно, чтобы ![]()
![]() .
.
Корни уравнения (2.48)
![]() , (2.49)
, (2.49)
т.е. нули производной дифференцируемой на ![]() функции
функции ![]() называются точками
стационарности функции. Точки стационарности и точки
называются точками
стационарности функции. Точки стационарности и точки ![]() , где функция не имеет конечной
производной, называют также критическими точками функции. Функция может иметь
экстремумы только в критических точках.
, где функция не имеет конечной
производной, называют также критическими точками функции. Функция может иметь
экстремумы только в критических точках.
2. Локальные экстремумы функции.
При исследовании поведения функции в
окрестности ![]() критической
точки
критической
точки ![]() предполагают, что в данной окрестности
содержится единственная критическая точка. Если в левой и правой
полуокрестностях точки
предполагают, что в данной окрестности
содержится единственная критическая точка. Если в левой и правой
полуокрестностях точки ![]() функция имеет противоположные знаки, то
говорят, что функция при переходе через точку
функция имеет противоположные знаки, то
говорят, что функция при переходе через точку ![]() меняет знак.
меняет знак.
Теорема 3. Если производная функции ![]() при переходе через критическую точку
при переходе через критическую точку ![]() меняет знак, то в точке
меняет знак, то в точке
![]() функция имеет
экстремум, причем минимум, когда знак производной меняется с минуса на плюс и
максимум, если
функция имеет
экстремум, причем минимум, когда знак производной меняется с минуса на плюс и
максимум, если ![]() меняет
знак с плюса на минус.
меняет
знак с плюса на минус.
Теорема
4. Если функция ![]() в
окрестности
в
окрестности ![]() точки
стационарности
точки
стационарности ![]() имеет
непрерывную отличную от нуля вторую производную, то
имеет
непрерывную отличную от нуля вторую производную, то ![]() является точкой экстремума
функции, и в ней функция имеет максимум
при
является точкой экстремума
функции, и в ней функция имеет максимум
при ![]() , а при
, а при ![]() - минимум.
- минимум.
На последних двух теоремах основываются два способа исследования функции на локальные экстремумы: І- с помощью первой производной дифференцируемой функции, ІІ- с помощью производной второго порядка. В обоих способах сперва находят корни уравнения (2.49) – точки стационарности функции. Присоединив к ним точки, где функция не имеет конечной производной, определяют множество критических точек функции. Далее, исследуя каждую критическую точку отдельно, выясняют наличие или отсутствие в ней экстремума функции.
3. Наименьшее и наибольшее значения функции на отрезке.
По теореме
Вейерштрасса непрерывная на отрезке ![]() функция
функция ![]() принимает на этом отрезке свои наименьшее
и наибольшее значения:
принимает на этом отрезке свои наименьшее
и наибольшее значения:
![]() ,
, ![]() , (2.50)
, (2.50)
называемые иногда глобальными экстремумами функции. Они могут быть
приняты либо в критических точках
функции ![]() ,
либо в концах отрезка. Поэтому для нахождения значений (2.50) определяют
значения функции в точках
,
либо в концах отрезка. Поэтому для нахождения значений (2.50) определяют
значения функции в точках ![]()
![]() и выбирают наименьшее и наибольшее из них:
и выбирают наименьшее и наибольшее из них:
![]()
![]() . (2.51)
. (2.51)
Задача 9. Найти
наименьшее и наибольшее значения на отрезке ![]() функци
функци
 .
.
Решение: 
![]() ;
;
![]()
![]()
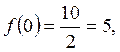
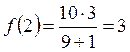 ,
,![]() .
.
1. Выпуклость и вогнутость кривой.
График функции ![]() , имеющей производную (конечную или не
ограниченную) на интервале
, имеющей производную (конечную или не
ограниченную) на интервале ![]() , рассмотрим в системе
координат
, рассмотрим в системе
координат ![]() , предполагая, что ось ординат направлена вертикально
вверх (см. рисунок 14).
, предполагая, что ось ординат направлена вертикально
вверх (см. рисунок 14).
 Если существует любая окрестность
Если существует любая окрестность ![]() точки
точки ![]() , где касательная к кривой
, где касательная к кривой ![]() в
точке
в
точке ![]() расположена выше (ниже), то
кривую называют выпуклой (вогнутой) в точке
расположена выше (ниже), то
кривую называют выпуклой (вогнутой) в точке ![]() .
.
Точка, где выпуклость меняется на
вогнутость или наоборот, называется точкой перегиба кривой. На рисунке 14 ![]() и
и ![]() точки
соответственно выпуклости и вогнутости кривой
точки
соответственно выпуклости и вогнутости кривой ![]() , а
, а ![]() - ее точка перегиба.
- ее точка перегиба.
Теорема 5. Если функция ![]() в точке
в точке ![]() и в некоторой ее окрестности
и в некоторой ее окрестности ![]() имеет непрерывную
вторую производную и
имеет непрерывную
вторую производную и ![]() ,
то для того чтобы график функции в точке
,
то для того чтобы график функции в точке ![]() был выпуклым (вогнутым), необходимо и
достаточно, чтобы
был выпуклым (вогнутым), необходимо и
достаточно, чтобы
![]()
![]() . (2.52)
. (2.52)
Следствие 1. Если функция ![]() имеет вторую
производную на
имеет вторую
производную на ![]() , то части интервала, где
, то части интервала, где ![]() имеет постоянный знак, представляют собой
промежутки выпуклости и вогнутости графика функции.
имеет постоянный знак, представляют собой
промежутки выпуклости и вогнутости графика функции.
Следствие 2. Если
функция ![]() имеет
непрерывную вторую производную
в некоторой окрестности
имеет
непрерывную вторую производную
в некоторой окрестности ![]() точки
точки ![]() за исключением, быть может, самой точки,
то для того чтобы
за исключением, быть может, самой точки,
то для того чтобы ![]() была
точкой перегиба графика функции, необходимо и достаточно, чтобы при переходе
через
была
точкой перегиба графика функции, необходимо и достаточно, чтобы при переходе
через ![]()
![]() меняла знак.
меняла знак.
Теорема 6. Если функция ![]() в точке
в точке ![]() имеет непрерывную отличную
имеет непрерывную отличную
от нуля третью производную и ![]() , то
, то ![]() является точкой перегиба графика
функции.
является точкой перегиба графика
функции.
Для определения промежутков выпуклости и
вогнутости, точек перегиба кривой ![]() необходимо найти все корни уравнения:
необходимо найти все корни уравнения:
![]() (2.53)
(2.53)
и точки, где функция не имеет конечной производной
второго порядка. Эти точки служат границами интервалов выпуклости и вогнутости
графика функции. Если при переходе через критическую точку по второй
производной ![]() не
меняет знака, то это есть точка возврата графика функции
не
меняет знака, то это есть точка возврата графика функции ![]() , а если меняет знак, то – точка перегиба
его.
, а если меняет знак, то – точка перегиба
его.
2. Асимптоты графика функции.
Все асимптоты кривой  , кроме вертикальных:
, кроме вертикальных: 
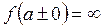 , определяются
уравнением
, определяются
уравнением
![]() .
.
Теорема 7. Для того, чтобы прямая ![]() была
асимптотой кривой
была
асимптотой кривой ![]() , необходимо и
достаточно, чтобы существовали конечные пределы:
, необходимо и
достаточно, чтобы существовали конечные пределы:
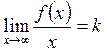 ,
,
![]() . (2.54)
. (2.54)
При ![]() кривая имеет наклонную асимптоту.
кривая имеет наклонную асимптоту.
Только при ![]() горизонтальная прямая
горизонтальная прямая ![]() может быть асимптотой кривой. Если в (2.54)
может быть асимптотой кривой. Если в (2.54) ![]() , то кривая асимптоты не имеет.
, то кривая асимптоты не имеет.
При решении задач по результатам исследований составляют таблицу, характеризующую свойства функции, особенности ее графика и строят эскиз графика функции.
Модуль 3. Интегральное исчисление функций одной переменной
Лекция 8. Первообразная функция – неопределенный интеграл
Цель лекции: подчеркнуть связь дифференцирования и интегрирования, как взаимно обратных операций, дающую возможность проверки правильности результата. Изложить основные методы интегрирования, демонстрируя их применение решением примеров.
Если дифференцируемая на промежутке ![]() функция
функция ![]() имеет производную
имеет производную
![]()
![]() , (3.1)
, (3.1)
то ![]() называется первообразной функцией для функции
называется первообразной функцией для функции ![]() на
на
![]() .
Если в (3.1)
.
Если в (3.1) ![]() , то
, то ![]()
![]() . При выполнении (3.1)
. При выполнении (3.1) ![]()
![]() , т.е.
, т.е. ![]()
![]() , также является первообразной функцией
, также является первообразной функцией ![]() на интервале
на интервале ![]() . Итак, функция, имеющая одну первообразную
на данном промежутке, имеет их бесконечное множество на этом промежутке.
. Итак, функция, имеющая одну первообразную
на данном промежутке, имеет их бесконечное множество на этом промежутке.
Теорема. Любые две первообразные функции ![]() на
интервале
на
интервале ![]() различаются на постоянную
слагаемую.
различаются на постоянную
слагаемую.
Определение. Произвольная перовобразная функция ![]() функции
функции
![]() на
промежутке
на
промежутке ![]() называется неопределенным
интегралом от функции
называется неопределенным
интегралом от функции ![]() на
на ![]() и обозначается символом
и обозначается символом ![]() .
.
По определению
![]()
![]()
![]()
![]() , (3.2)
, (3.2)
где:
![]() -
знак интеграла;
-
знак интеграла;
![]() -
подынтегральная функция;
-
подынтегральная функция;
![]() -
подынтегральное выражение.
-
подынтегральное выражение.
Теорема. Непрерывная на промежутке функция интегрируема на этом промежутке.
Если (3.1) выполняется, то
![]() , (3.3)
, (3.3)
т.е. подынтегральное выражение равно дифференциалу
первообразной функции. Например, ![]() , поэтому
, поэтому ![]() .
.
Свойства неопределенного интеграла.
1.
Производная
неопределенного интеграла равна подынтегральной функции: (![]() .
.
2.
Дифференциал
неопределенного интеграла равен подынтегральному выражению: ![]()
![]() .
.
3.
![]()
4. Постоянный множитель можно выносить за знак интеграла.
5.
Если функции ![]() и
и ![]() интегрируемы на
интегрируемы на ![]() , то
, то
![]() ; (3.4)
; (3.4)
![]()

![]() ,
, ![]() . (3.5)
. (3.5)
Таблица первообразных функций.
1. ![]() , 10.
, 10.
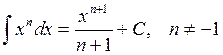 ,
,
2.  , 11.
, 11. 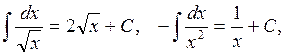
3. 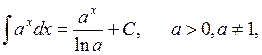 12.
12. ![]() ,
,
4. ![]() , 13.
, 13. ![]() ,
,
5. 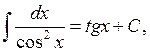 14.
14. 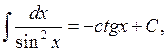
6. 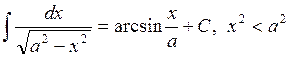 15.
15. 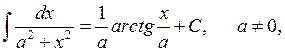
7. 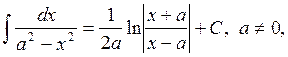
8. 
9. 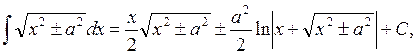
16. 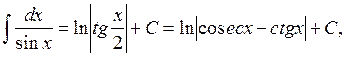
17. 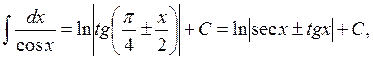 18.
18. ![]() , 19.
, 19. ![]() 20.
20. 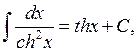 21.
21. 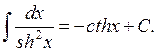
Примечание. Правильность формул можно проверять дифференцированием правых частей равенства.
Методы интегрирования.
Способ нахождения неопределенного интеграла с помощью его свойств и таблицы первообразных функций носит название непосредственного интегрирования. В случаях, когда этот способ “не работает”, применяются так называемые методы замены переменной и интегрирования по частям в неопределенном интеграле.
I. Метод подстановок.
Если подынтегральная
функция ![]() непрерывна
на
непрерывна
на ![]() , то,
подобрав непрерывно дифференцируемую на соответствующем промежутке
, то,
подобрав непрерывно дифференцируемую на соответствующем промежутке ![]() функцию
функцию ![]() и учитывая, что
и учитывая, что ![]() , по схеме
, по схеме
![]()
осуществляем замену переменной интегрирования в заданном интеграле:
![]() .
(3.6)
.
(3.6)
Если первоначально задан интеграл такой же структуры, как правая часть (3.6), то выгодно делать подстановку по схеме:
![]() ,
, ![]() .
.
Она приводит к формуле
![]() (3.7)
(3.7)
замены переменной в неопределенном интеграле, так как
![]() .
.
Результат не зависит
от обозначения переменной интегрирования. В полученной первообразной функции с
помощью обратной замены переходят к старой переменной ![]() .
.
Представление левой
части (3.7) в виде ![]() без
замены переменной интегрирования называется подведением функции
без
замены переменной интегрирования называется подведением функции ![]() под знак дифференциала:
под знак дифференциала:
![]()
![]() . (3.8)
. (3.8)
Примеры 1. Пусть аргументом подынтегральной функции служит линейный
двучлен ![]() и функция удовлетворяет (3.1). Тогда
и функция удовлетворяет (3.1). Тогда

2. Для непрерывно
дифференцируемой на ![]() функции
функции ![]()
![]() имеет место формула
имеет место формула
 , (3.9)
, (3.9)
называемая логарифмическим интегралом.
II. Интегрирование по частям.
Рассмотрим функции ![]() и
и ![]() , непрерывно дифференцируемые в
некоторой области. Дифференциал их произведения
, непрерывно дифференцируемые в
некоторой области. Дифференциал их произведения
![]() . (3.10)
. (3.10)
Взяв интеграл от обеих частей равенства, имеем
![]() . (3.11)
. (3.11)
Равенство (3.11)
носит название формулы интегрирования по частям. Левая часть его представляет
собой заданный интеграл, который требуется найти. В нем один из множителей
подынтегрального выражения обозначаем через ![]() , остальное выражение вместе с
, остальное выражение вместе с ![]() принимаем за
принимаем за ![]() . За
. За ![]() в первую очередь принимаются функции,
первообразные которых не являются табличными, например, логарифмические и
обратные тригонометрические функции. При их отсутствии через
в первую очередь принимаются функции,
первообразные которых не являются табличными, например, логарифмические и
обратные тригонометрические функции. При их отсутствии через ![]() выгодно обозначать
степенные функции. Далее составляем правую часть (3.11). Формулу интегрирования
по частям можно применять повторно.
выгодно обозначать
степенные функции. Далее составляем правую часть (3.11). Формулу интегрирования
по частям можно применять повторно.
Задача 10. Найти неопределенный интеграл
![]() .
.
Решение: 
![]() .
.
Лекция 9. Интегрирование рациональных функций
Цель лекции: научить студентов выбору подходящих замен переменной интегрирования, разложению подынтегральной функции на сумму простейших дробей, «рационализации» интеграла, применению необходимых тригонометрических формул из их школьных знаний.
Пусть требуется найти неопределенный
интеграл от правильной рациональной дроби. Последнюю разлагаем на сумму
простейших дробей так называемым методом неопределенных коэффициентов. Интеграл
от простейшей дроби, знаменателем которой служит та или иная степень линейного
двучлена приводится к табличным путем подведения двучлена под знак
дифференциала. Этот же прием применяется и для интегрирования простейшей дроби,
имеющей в знаменателе некоторую степень ![]() , неприводимого – не имеющего
действительных корней квадратного трехчлена. Если в числителе дроби имеем
постоянное число, то из знаменателя следует выделить полный квадрат суммы или
разности двух чисел:
, неприводимого – не имеющего
действительных корней квадратного трехчлена. Если в числителе дроби имеем
постоянное число, то из знаменателя следует выделить полный квадрат суммы или
разности двух чисел:
 . (3.12)
. (3.12)
Случай ![]() приводит к табличному интегралу. При
приводит к табличному интегралу. При ![]() после предварительного
преобразования применяем формулу интегрирования по частям:
после предварительного
преобразования применяем формулу интегрирования по частям:

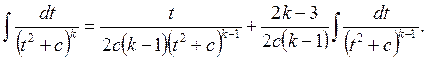 (3.13)
(3.13)
Последовательно применяя (3.13), можно придти к табличному интегралу.
Многочлен ![]() -степени с действительными
коэффициентами единственным
способом разлагается на простые множители:
-степени с действительными
коэффициентами единственным
способом разлагается на простые множители:
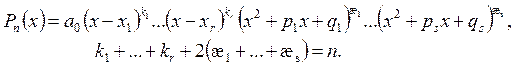 (3.14)
(3.14)
Правильная рациональная дробь, знаменатель которой есть некоторая степень неприводимого многочлена, называется простейшей дробью.
Теорема. Всякая правильная рациональная дробь обладает единственным разложением в сумму простейших дробей.
Метод неопределенных коэффициентов.
Для разложения правильной рациональной дроби на сумму простейших дробей применяется метод неопределенных коэффициентов, который состоит в следующем:
1) Знаменатель заданной дроби разлагают на простые множители в виде (3.14), находя все его корни.
2) Рациональную дробь представляют в виде суммы
простейших дробей, знаментаелями которых служат простые множители в разложении
(3.14), взятые столько раз, какова их кратность ![]() или
или ![]() в
степенях от 1 до
в
степенях от 1 до ![]() или
или
![]() соответственно.
соответственно.
3) За числители слагаемых простейших дробей берут пока неизвестные постоянные для линейных множителей из (3.14) или линейный двучлен с неизвестными коэффициентами для множителей вида (3.14).
4) Составленную сумму дробей приводят к общему
знаменателю ![]() ,
приравнивают числители заданной и полученной правильных рациональных дробей.
,
приравнивают числители заданной и полученной правильных рациональных дробей.
5) Приравнивая коэффициенты при одинаковых степенях ![]() в обоих многочленах,
составляют систему
в обоих многочленах,
составляют систему ![]() линейных
уравнений с
линейных
уравнений с ![]() неизвестными.
Она всегда совместна и имеет единственное решение.
неизвестными.
Она всегда совместна и имеет единственное решение.
6) Решая составленную систему линейных уравнений, находят неизвестные коэффициенты. Подставив их на места, получим требуемое разложение.
Интегрирование тригонометрических выражений.
Если рациональная функция ![]() является нечетной относительно хотя бы одного из своих аргументов:
является нечетной относительно хотя бы одного из своих аргументов:
![]()
![]()
![]()
то с помощью замены соответственно:
![]() (3.15)
(3.15)
можно притти к рациональной относительно промежуточной
переменной ![]() функции
функции
![]() . В достаточно
простых случаях неопределенный интеграл от функции
. В достаточно
простых случаях неопределенный интеграл от функции ![]() можно найти подведением под знак
дифференциала одной из функций (3.15), в явном виде не осуществляя замену.
можно найти подведением под знак
дифференциала одной из функций (3.15), в явном виде не осуществляя замену.
Если функция ![]() является четной относительно обоих
аргументов:
является четной относительно обоих
аргументов:
![]()
![]() ,
,
то ее можно интегрировать с помощью замены:
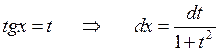 . (3.16)
. (3.16)
Пример: 
Если функция ![]() не
обладает свойствами четности или нечетности относительно своих аргументов, то
для интегрирования применяется так называемая универсальная тригонометрическая
подстановка:
не
обладает свойствами четности или нечетности относительно своих аргументов, то
для интегрирования применяется так называемая универсальная тригонометрическая
подстановка:
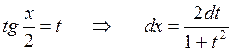 ;
; 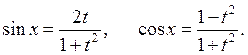 (3.17)
(3.17)
Пример: 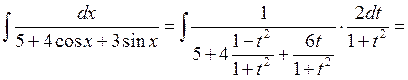
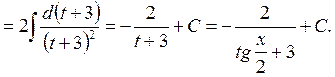
Интегрирование иррациональных функций.
Рассмотрим два основные вида иррациональности: дробно-линейную и
квадратичную. Операцию освобождения от иррациональности в подынтегральной функции называют “рационализацией” интеграла.
1. Для освобождения от дробно-линейной иррациональности применяют подстановку:
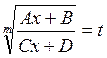
![]()
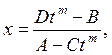

![]() . (3.18)
. (3.18)
Для рационализации
интегралов, содержащих в подынтегральной функции иррациональности вида ![]()
![]()
![]() , применяются тригонометрические
подстановки:
, применяются тригонометрические
подстановки:
1) ![]()
![]()
![]()
![]()
![]()
![]()
![]() ; (3.19)
; (3.19)
2) ![]()
![]()
![]()
![]()
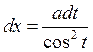
![]()
 (3.20)
(3.20)
3) ![]()
![]()
![]()
![]()
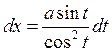
![]()
 (3.21)
(3.21)
Пример: 1. 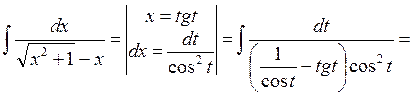
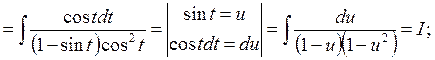
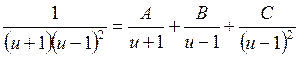
![]()
![]()
![]() .
.
Теперь последовательно найдем:
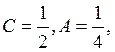
![]()
![]()
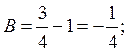

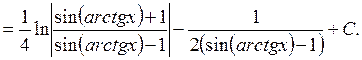
Лекция 10. Определенный интеграл
Цель лекции: обратить внимание на различие определенного интеграла от неопределенного, на геометрический и механический смыслы его, на некоторые отличительные свойства, включая теорему о среднем. Изложить методы вычисления определенного интеграла, его обощения в виде несобственных интегралов.
Определение и свойства интеграла.
Рассмотрим функцию ![]() ,
определенную на отрезке
,
определенную на отрезке ![]() . Точками
. Точками ![]() (см. рисунок 15) отрезок произвольно разобьем
на
(см. рисунок 15) отрезок произвольно разобьем
на ![]() частей. Из
каждой части произвольно выберем точку
частей. Из
каждой части произвольно выберем точку ![]() ,
найдем значения функции в этих точках. Умножив найденные значения на длины
,
найдем значения функции в этих точках. Умножив найденные значения на длины ![]() соответствующих
частей, сложим. Полученное таким образом выражение
соответствующих
частей, сложим. Полученное таким образом выражение
 (3.23)
(3.23)
называется
интегральной суммой для функции ![]() по отрезку
по отрезку ![]() .
Наибольшая из длин частичных отрезков
.
Наибольшая из длин частичных отрезков ![]() называется шагом разбиения
отрезка
называется шагом разбиения
отрезка ![]() на
части. При
на
части. При ![]()
![]() ,
, ![]() .
.
Определение. Если при ![]() интегральная сумма (3.23)
имеет конечный предел, то это
число называется определенным интегралом от функции
интегральная сумма (3.23)
имеет конечный предел, то это
число называется определенным интегралом от функции ![]() по
отрезку
по
отрезку ![]() и обозначается символом
и обозначается символом  .
.
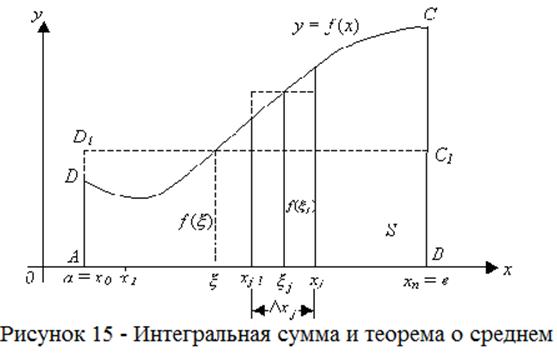
По определению
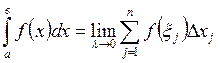 . (3.24)
. (3.24)
Нижний ![]() и верхний
и верхний ![]() пределы интеграла определяют промежуток (область – отрезок)
интегрирования
пределы интеграла определяют промежуток (область – отрезок)
интегрирования ![]() .
.
Плоская фигура ![]() (см.
рисунорк 15), ограниченная сверху кривой
(см.
рисунорк 15), ограниченная сверху кривой ![]() - графиком подынтегральной функции, снизу
осью абсцисс, по бокам прямыми
- графиком подынтегральной функции, снизу
осью абсцисс, по бокам прямыми ![]() и
и ![]() , называется криволинейной трапецией с
основанием
, называется криволинейной трапецией с
основанием ![]() . Ее площадь
. Ее площадь ![]() приближенно
определяется интегральной суммой (3.24). После предельного перехода при
приближенно
определяется интегральной суммой (3.24). После предельного перехода при ![]() получим точное значение площади
фигуры:
получим точное значение площади
фигуры:
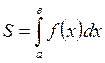 . (3.25)
. (3.25)
Итак, если существует
определенный интеграл от неотрицательной на ![]() функции, то он численно равен площади
криволинейной трапеции с основанием
функции, то он численно равен площади
криволинейной трапеции с основанием ![]() и ограниченной сверху графиком
подынтегральной функции. В этом и заключается геометрический смысл
определенного интеграла.
и ограниченной сверху графиком
подынтегральной функции. В этом и заключается геометрический смысл
определенного интеграла.
Свойства 4-5 неопределенного интеграла присущи и определенному интегралу.
Для определенного интеграла, условно можно записать так:
 .
(3.26)
.
(3.26)
Последнее называют свойством аддитивности интеграла по области.
Определенный интеграл имеет свойства, выражаемые и неравенствами:
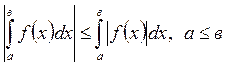 .
.
На основе свойств предела функции можно
утверждать, что (![]() ):
):

Теорема. Если
функция ![]() непрерывна
на
непрерывна
на ![]() , то на этом отрезке найдется, по крайней мере, одна точка
, то на этом отрезке найдется, по крайней мере, одна точка ![]() такая, что
такая, что
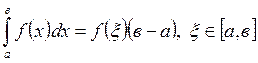 . (3.27)
. (3.27)
Для неотрицательной
на отрезке функции теорема о среднем допускает геометрическое истолкование:
если функция ![]() непрерывна
на отрезке, то существует прямоугольник
непрерывна
на отрезке, то существует прямоугольник ![]() (см. рисунок 15) с основанием
(см. рисунок 15) с основанием ![]() и
высотой
и
высотой
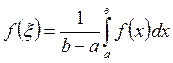 , (3.28)
, (3.28)
равновеликий с криволинейной трапецией ![]() с тем же основанием и ограниченной
сверху графиком подынтегральной функции. Число (3.28) называется средним
значением функции
с тем же основанием и ограниченной
сверху графиком подынтегральной функции. Число (3.28) называется средним
значением функции ![]() на
отрезке
на
отрезке ![]() .
.
Методы вычиления определенного интеграла.
1. Формула Ньютона – Лейбница.
Из геометрических истолкований определенного интеграла
и теоремы о среднем можем заключить, что определенный интеграл от непрерывной
на ![]() функции по этому отрезку существует и (см. рисунок 16)
функции по этому отрезку существует и (см. рисунок 16)
![]() .
.
Последняя (площадь) выражается с помощью определенного интеграла с переменным верхним пределом:
 .
.
Эта функция не зависит от обозначения
переменной интегрирования и непрерывно
дифференцируема на интервале ![]() . По определению производной и теореме о
среднем для отрезка
. По определению производной и теореме о
среднем для отрезка ![]() :
:
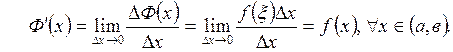
 т.е.
т.е. ![]() есть первообразная подынтегральной функции на
есть первообразная подынтегральной функции на ![]() . Это дает право
записать:
. Это дает право
записать:
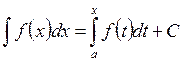 . (3.29)
. (3.29)
Равенство (3.29) выражает связь между неопределенным и определенным интегралами и доказывает ранее сформулированную теорему об интегрируемости функции.
Сравнивая (3.3) и (3.29), получим
 . (3.30)
. (3.30)
Здесь ![]() -
любая первообразная подынтегральной функции на
-
любая первообразная подынтегральной функции на ![]() . Равенство справедливо и в концах отрезка:
. Равенство справедливо и в концах отрезка: ![]() . Поочерёдно подставляя эти
значения в (3.30), сперва найдем постоянную интегрирования:
. Поочерёдно подставляя эти
значения в (3.30), сперва найдем постоянную интегрирования: ![]() - и придем к равенству:
- и придем к равенству:
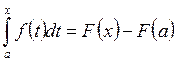 .
.
Далее, получим основную для вычисления определенных интегралов формулу Ньютона-Лейбница:
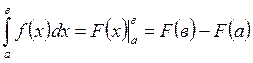 . (3.39)
. (3.39)
2. Методы вычисления.
Относительно функций![]() и отрезков
и отрезков ![]() имеет место формулы
замены переменной в определенном интеграле:
имеет место формулы
замены переменной в определенном интеграле:
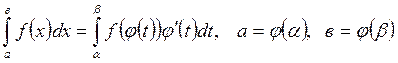 ; (3.40)
; (3.40)
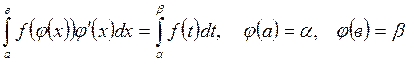 . (3.41)
. (3.41)
Теперь для непрерывно дифференцируемых на ![]() функций
функций ![]() составим
равенство (3.12) и от обеих частей его возьмем определенные интегралы по
отрезку
составим
равенство (3.12) и от обеих частей его возьмем определенные интегралы по
отрезку ![]() .
Записанный в виде:
.
Записанный в виде:
 (3.42)
(3.42)
результат представляет собой формулу интегрирования по частям в определенном интеграле.
Задача 11. Вычислить определенный интеграл  .
.
Решение:
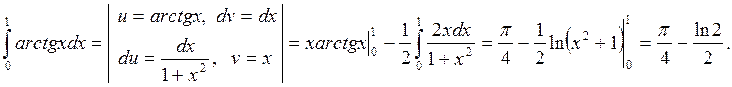
Несобственные интегралы.
Основу понятия определенного интеграла составляют предположения: 1) промежуток интегрирования конечен, 2) подынтегральная функция ограничена на данном промежутке. Если хотя бы одно из этих условий нарушается, то определенный интеграл теряет свой собственный смысл, и его называют несобственным интегралом. В зависимости от того, какие из указанных условий нарушаются, различают два вида несобственных интегралов.
І. Несобственные интегралы первого рода.
Рассматривается функция ![]() , непрерывная на одном из бесконечных
промежутков:
, непрерывная на одном из бесконечных
промежутков: ![]()
![]() и
и ![]() . В первых двух случаях существуют
определенные интегралы с переменными верхним и нижним пределами соответственно:
. В первых двух случаях существуют
определенные интегралы с переменными верхним и нижним пределами соответственно:
 . (3.43)
. (3.43)
Их пределы:
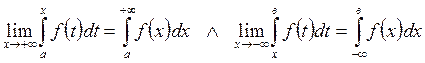 (3.44)
(3.44)
называются несобственными интегралами І-рода
от функции ![]() .
.
Если пределы (3.44) существуют и конечны, то равные им несобственные интегралы тоже существуют и называются сходящимися. В противном случае определяемые (3.44) несобственные интегралы называются расходящимися.
Для функции ![]() , непрерывной на всей числовой оси,
рассматривают несобственный интеграл с обоими бесконечными пределами:
, непрерывной на всей числовой оси,
рассматривают несобственный интеграл с обоими бесконечными пределами:
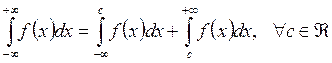 . (3.45)
. (3.45)
Если в правой части (3.45) оба
несобственные интегралы сходятся, то интеграл в левой части также сходящийся.
Если хотя бы один из слагаемых несобственных интегралов расходится, то является
расходящимся и несобственный интеграл по всей числовой оси ![]() .
.
Если ![]() является первообразной подынтегральной
функции в (3.45) на соответствующих бесконечных промежутках
является первообразной подынтегральной
функции в (3.45) на соответствующих бесконечных промежутках ![]() , то
, то
 . (3.46)
. (3.46)
Обобщенную формулу Ньютона-Лейбница записывают в обычной форме:
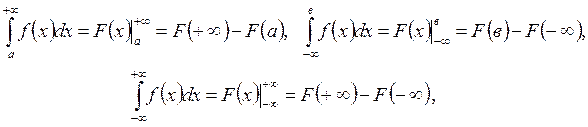 (3.47)
(3.47)
подразумевая под ![]() соответствующие пределы в (3.46).
соответствующие пределы в (3.46).
ІІ. Несобственные интегралы второго рода.
Точка, где функция не
ограничена (имеет разрыв второго рода), называется ее особой точкой.
Рассмотрим случаи, когда особой точкой подынтегральной функции являются
начальная ![]() ,
конечная
,
конечная ![]() или
внутренняя
или
внутренняя ![]() точки
промежутка интегрирования. Когда функция
точки
промежутка интегрирования. Когда функция ![]() не ограничена только в одном из концов
отрезка
не ограничена только в одном из концов
отрезка ![]() , то существует определенный интеграл:
, то существует определенный интеграл:
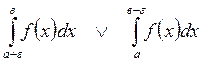 , (3.48)
, (3.48)
где ![]() достаточно малое число
такое, что
достаточно малое число
такое, что ![]() . Пределы выражений
(3.48)
. Пределы выражений
(3.48)
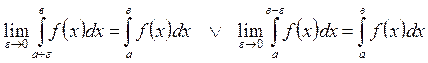 (3.49)
(3.49)
называются несобственными интегралами ІІ-рода от
функции ![]() .
.
Если функция ![]() на рассматриваемом
промежутке имеет единственную особую точку
на рассматриваемом
промежутке имеет единственную особую точку ![]() , то по свойству аддитивности интеграла по
области:
, то по свойству аддитивности интеграла по
области:
 . (3.50)
. (3.50)
Сходящийся несобственный интеграл от неотрицательной на соответствующем промежутке функции имеет геометрический смысл.
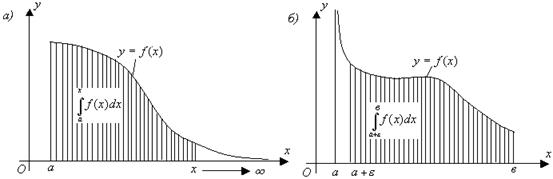
Рисунок 17 – Геометрический смысл несобственных интегралов
Например, если первые из интегралов (3.44) и (3.49) сходящиеся, то они численно равны площади неограниченных, но квадрируемых плоских фигур (см. рисунок 17 а), б)).
Если подынтегральная функция ![]() имеет конечное число
имеет конечное число ![]() особых точек
особых точек ![]() , но ее первообразная
функция
, но ее первообразная
функция ![]() непрерывна
на всем отрезке
непрерывна
на всем отрезке ![]() ,
то для вычисления несобственного интеграла ІІ-рода формулу Ньютона-Лейбница
можно применять в виде (3.39).
,
то для вычисления несобственного интеграла ІІ-рода формулу Ньютона-Лейбница
можно применять в виде (3.39).
Лекция 11. Операторное исчисление
Цель лекции: дать основы математической науки «Операторное (операционное) исчисление», имеющей приложения в инженерной практике. Изложить основные требования к оригиналу и изображению, теоремы – свойства оператора Лапласа и обратить внимание на прикладной характер раздела.
Оригинал и изображение.
Оригиналом называется функция ![]() , удовлетворяющая следующим
условиям: 1)
, удовлетворяющая следующим
условиям: 1) ![]() при
при
![]() и
и ![]() ; 2) на
любом отрезке
; 2) на
любом отрезке ![]() функция
функция
![]() непрерывна
или имеет конечное число точек разрыва I-рода; 3)
непрерывна
или имеет конечное число точек разрыва I-рода; 3) ![]() ограничена экспонентой, т.е. существуют
числа
ограничена экспонентой, т.е. существуют
числа ![]() и
и ![]() такие, что
такие, что
![]() . (3.51)
. (3.51)
Условие (3.51) означает, что при ![]() оригинал по модулю может расти
не быстрее чем экспонента
оригинал по модулю может расти
не быстрее чем экспонента ![]() . Число
. Число ![]() называется показателем роста функции
называется показателем роста функции ![]() .
.
Аргументом функции
![]() служит
время
служит
время ![]() .
Поэтому считается, что оригинал содержит множитель
.
Поэтому считается, что оригинал содержит множитель
 (3.52)
(3.52)
называемый функцией Хэвисайда.
Если указанные условия выполняются, то несобственный интеграл
 , (3.53)
, (3.53)
называемый изображением функции ![]() , сходится абсолютно и равномерно на
полуплоскости
, сходится абсолютно и равномерно на
полуплоскости ![]() .
В этой области
.
В этой области ![]() есть
аналитическая функция и представляет собой образ оригинала
есть
аналитическая функция и представляет собой образ оригинала ![]() с помощью оператора
(преобразования) Лапласа (3.53). Этот факт условно записывают так:
с помощью оператора
(преобразования) Лапласа (3.53). Этот факт условно записывают так:
![]() . (3.54)
. (3.54)
Вообще, нтеграл Лапласа (3.53) зависит от комплексного
параметра ![]() .
Подынтегральная функция в нем при
.
Подынтегральная функция в нем при ![]() и
и ![]() убывает быстрее затухающей экспоненты:
убывает быстрее затухающей экспоненты: ![]()
Свойства преобразования Лапласа.
1. Линейные свойства:
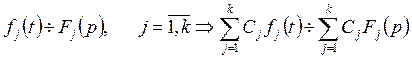 , (3.55)
, (3.55)
![]()
2. Теорема подобия:
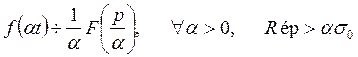 . (3.56)
. (3.56)
3. Теорема смещения:
![]() (3.57)
(3.57)
4. Теорема запаздывания:
![]() (3.58)
(3.58)
5.
Дифференцирование
оригинала. Если производные оригинала ![]() также являются оригиналами, то:
также являются оригиналами, то:
![]()
![]() (3.59)
(3.59)
![]()
6. Дифференцирование изображения:
![]() (3.60)
(3.60)
7. Интегрирование оригинала:
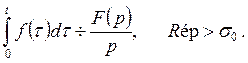 (3.61)
(3.61)
8.
Интегрирование
изображения. Если ![]() является
оригиналом, то
является
оригиналом, то
 (3.62)
(3.62)
Если ![]() и
и
![]() являются оригиналами,
то выражение
являются оригиналами,
то выражение
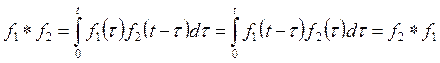 (3.63)
(3.63)
называется сверткой этих функций.
9. Теорема умножения изображений:
![]() . (3.64)
. (3.64)
Список литературы
1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (полный курс). - Алматы: “TST-Company”, 2009. -429 с.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М.: Наука, 2000.
3. Сборник задач по математике для ВТУЗов. Ч.1 Линейная алгебра и основы математического анализа. Под. Ред. А.В. Ефимова, Б.П. Демидовича. - М.: Наука, 2002.
4. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). - М.: Высшая школа, 2003.
5. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М.: Наука, 2001.
6. Курош А.Г. Курс высшей алгебры. - М.: Наука, 1962.
7. Письменный Д.Т. Конспект лекций по высшей математике (полный курс). - М.: Айрис пресс, 2004.
8. Рябушко А.П. и др. Индивидуальные задания по высшей математике. - Минск-Алматы, 2002. чч 1,2,3
9. Лунгу К.Н. и др. Сборник задач по высшей математике (с контрольными работами). – М.: Айрис пресс, 2005. 1,2-курсы.
10. Kazbek Khasseinov Canons of matematics. - Moscow: Nauka, 2007.
Содержание
|
Модуль 1. Элементы линейной алгебры, аналитической геометрии и комплексные числа |
3 |
|
Лекция 1. Определители, матрицы и системы линейных уравнений |
3 |
|
Лекция 2. Векторы в трехмерном пространстве |
7 |
|
Лекция 3. Кривые и поверхности второго порядка. Комплексные числа |
13 |
|
Модуль 2. Дифференциальное исчисление функций одной переменной |
19 |
|
Лекция 4. Предел функции |
19 |
|
Лекция 5. Непрерывность функции |
22 |
|
Лекция 6. Производые и дифференциалы функции |
24 |
|
Лекция 7. Исследование функций с помощью производных |
32 |
|
Модуль 3. Интегральное исчисление функций одной переменной |
35 |
|
Лекция 8. Первообразная функция – неопределенный интеграл |
35 |
|
Лекция 9. Интегрирование рациональных функций |
38 |
|
Лекция 10. Определенный интеграл |
41 |
|
Лекция 11. Операторное исчисление |
47 |
|
Список литературы |
50 |