Некомерцеское акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Математика 1,2
Методические указания к решению задач
повышенной трудности на практических занятиях
Алматы 2011
СОСТАВИТЕЛИ: К.М. Мұстахишев, Б.Ж. Атабай. Математика 1,2 Методические указания к решению задач повышенной трудности на практических занятиях. – Алматы: АЭжБУ, 2011, 21 с.
С методическими указаниями решены 30-ые варианты восьми заданий к СРСП (контрольных работ-коллоквиумов) из учебного пособия А.П. Рябушко и др. Сборник индивидуальных заданий по высшей математике. –Минск: Вышэйшая школа, 2000, чч 1,2,3.
Рецензент: канд.физ.-мат. наук, доцент Т.К. Каирбеков
Печатается по плану издания НАО “Алматинского университета энергетики и связи” на 2011 г.
©НАО “Алматинский университет энергетики и связи”, 2011 г.
Учебное пособие А.П. Рябушко и др. Индвидуальные задания по высшей математике. –Минск: Вышэйшая школа, 2000, чч 1,2,3. несомненно закрепилось в списке основной литературы для инженерно-технических специальностей вузов. В нем в качестве приложений приведены задания для восьми коллоквиумов-контрольных работ по разделам: «Векторная алгебра», «Аналитическая геометрия», «Пределы», «Производные и их приложения», «Неопределенные интегралы», «Определенный интеграл и его приложения», «Дифференциальные уравнения», «Кратные и криволинейные интегралы». Они могут быть использованы и как задания для СРСП по соответствующим темам курса “Математика 1,2”.
Для заданий, приведенных в основной части учебного пособия, решены так называемые типовые варианты. Аналогичная методическая помощь студентам не будет лишней и по упомянутым выше заданиям.
В предлегаемом руководстве с методическими указаниями решены 30-ые варианты всех восьми заданий. Приведены необходимые формулы. Некоторые задачи решены двумя способами.
1 Векторная алгебра
1.30 Дан тетраэдр ![]() (см. рисунок 1). Положив
(см. рисунок 1). Положив ![]() и
и ![]() ,
выразить через
,
выразить через ![]() и
и ![]() векторы
векторы ![]() и
и ![]() (точки
(точки ![]() и
и ![]() - середины ребер
- середины ребер ![]() и
и ![]() ,
а
,
а ![]() - середина
- середина ![]() ).
).
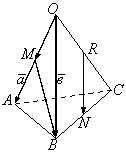 |
Решение. По свойству средней линии треугольника
Рисунок 1
2.30 Найти ![]() , если
, если ![]() .
.
Решение. Так как скалярное произведение
![]() ,
,
то
 .
.
Поэтому
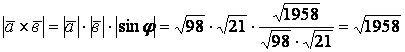 .
.
3.30 Найти координаты вектора ![]() , перпендикулярного векторам
, перпендикулярного векторам ![]() и
и ![]() и
образующего с осью
и
образующего с осью ![]() тупой
угол, если
тупой
угол, если ![]() .
.
Решение. Условия перпендикулярности векторов ![]() и
и ![]() ,
, ![]() и
и ![]() и формула скалярного квадрата для вектора
и формула скалярного квадрата для вектора ![]() приводит к системе
уравнений
приводит к системе
уравнений
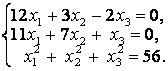 (1)
(1)
Решим отдельно первые два линейные уравнения системы:
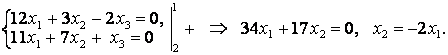
Из второго уравнения получим:
![]()
По условию ![]() ,
следовательно,
,
следовательно, ![]() и
и
![]() .
.
Из третьего уравнения системы (1) найдем:
![]() .
.
Требуемый вектор
![]() .
.
4.30 Выяснить, для каких векторов ![]() и
и ![]() выполняется условие
выполняется условие
![]() .
.
Решение. Левая часть заданного равенства представляет собой скалярный квадрат разности двух векторов:
![]() .
.
Требуемое условие выполняется лишь когда ![]() , т.е.
когда заданные векторы взаимно перпендикулярны:
, т.е.
когда заданные векторы взаимно перпендикулярны: ![]() .
.
5.30 Вычислить высоту параллелепипеда, построенного на
векторах ![]() и
и ![]() , если за основание взят
параллелограмм, построенный на векторах
, если за основание взят
параллелограмм, построенный на векторах ![]() и
и ![]() .
.
Решение. Используем геометрический смысл смешанного и векторного произведений соответственно трех и двух векторов.
Объем параллелепипеда (см. рисунок 2)
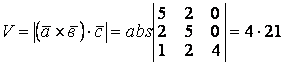 .
.
Площадь основания
![]() .
.
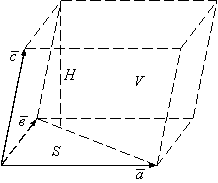 |
Рисунок 2
Высота параллелепипеда
![]() .
.
2 Аналитическая геометрия
 |
1.30 Даны уравнения двух сторон треугольника:
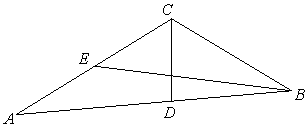
Решение. Найдем координаты вершин
![]()
![]() (см. рисунок 3),
считая,
(см. рисунок 3),
считая,
Рисунок 3
что заданы уравнения сторон ![]() и
и ![]() :
:
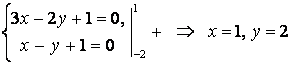 .
.
Подставив эти значения в уравнение медианы,
убеждаемся, что точка ![]() не
лежит на заданной медиане.
не
лежит на заданной медиане.
Рассмотрим два возможные случаи.
I. Пусть медиана опущена из вершины ![]() .
Найдем координаты точек
.
Найдем координаты точек ![]() и
и ![]() :
:
 ;
;
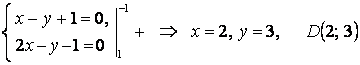 .
.
Точка ![]() делит
отрезок
делит
отрезок ![]() пополам:
пополам:
![]() . Поэтому
. Поэтому
![]() .
.
Уравнение третьей стороны ![]() , как прямой, проходящей через две заданные
точки:
, как прямой, проходящей через две заданные
точки:
![]() .
.
II. Предположим, что заданная медиана опущена из
вершины ![]() .
Поступая как в предыдущем случае, найдем:
.
Поступая как в предыдущем случае, найдем: ![]() . Так как
. Так как ![]() , то
, то
![]() .
.
Уравнение стороны ![]() :
:
![]() .
.
2.30 Составить уравнение параболы, фокус которой
находится в точке ![]() ,
а вершина – в начале координат.
,
а вершина – в начале координат.
Решение. Каноническое уравнение заданной параболы в
системе координат ![]() (см.
рисунок 4), повернутой на
(см.
рисунок 4), повернутой на ![]() относительно
относительно ![]() , имеет вид:
, имеет вид:
![]() ,
,
так как фокальный параметр определяется из условия
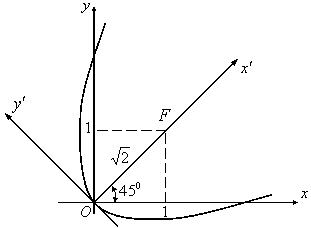 |
Рисунок 4
Осуществим поворот ![]() на угол
на угол ![]() по формулам:
по формулам:
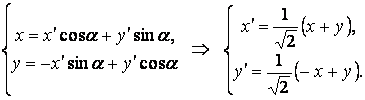
После замены переменных уравнение параболы запишется в виде:
![]()
или
![]() .
.
3.30 Найти координаты точки ![]() , лежащей внутри треугольника,
высекаемого на плоскоти
, лежащей внутри треугольника,
высекаемого на плоскоти ![]() плоскостями:
плоскостями:
![]()
![]() ,
, ![]() ,
,
и равноудаленной от этих плоскостей.
Решение. Согласно условию приравниваем расстояния
точки ![]() от трех
заданных плоскостей:
от трех
заданных плоскостей:
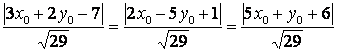 . (2)
. (2)
В точках открытого ![]() (см. рисунок 5), образованного прямыми
(см. рисунок 5), образованного прямыми
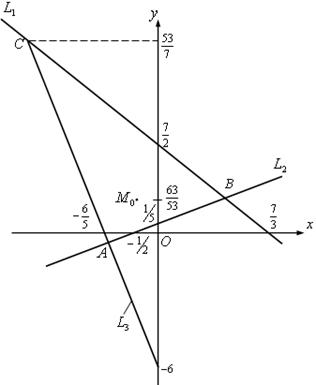 |
Рисунок 5
левые части первых двух уравнений отрицательны, а третьего уравнения положительна. Поэтому из соотношений (2) можно образовать систему уравнений
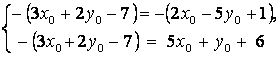
или
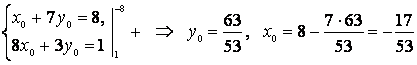 ,
,
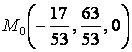 .
.
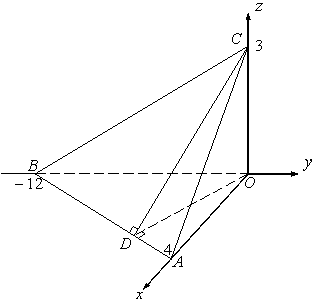 |
4.30 Треугольник
Решение.
Рисунок 6
Вершины треугольника имеют координаты ![]() ,
, ![]() , а вектор
, а вектор ![]() .
.
Заметим, что ![]() , кроме того, по условию
, кроме того, по условию ![]() , следовательно,
, следовательно, ![]() . Поэтому
. Поэтому ![]() служит нормальным
вектором плоскости
служит нормальным
вектором плоскости ![]() .
Уравнение этой плоскости, проходящей через ось
.
Уравнение этой плоскости, проходящей через ось ![]() , имеет вид
, имеет вид
![]() .
.
Как линия пересения плоскостей треуголиников ![]() и
и ![]() прямая
прямая ![]() имеет общие уравнения
имеет общие уравнения

и канонические уравнения

Далее,
![]() ;
;
![]() .
.
По-другому

3 Пределы
Найти пределы
1.30 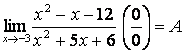 .
.
После разложения квадратных трехчленов на простые множители:
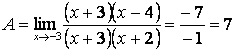 .
.
2.30 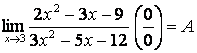 .
.
И здесь применим формулу ![]() :
:
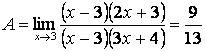 .
.
3.30 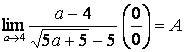 .
.
Числитель и знаменатель дроби умножим на сопряженное знаменателя:
 ,
,
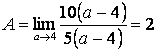 .
.
4.30 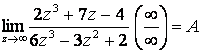 .
.
Разделим числитель и знаменатель рациональной дроби на старшую степень переменной и перейдем к пределу:
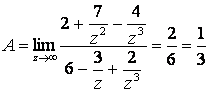 .
.
5.30 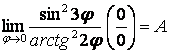 .
.
Так как при ![]() ,
, ![]() и
и ![]() , то:
, то:
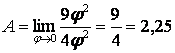 .
.
6.30 ![]() .
.
1. Приведем функцию к виду, удобному для применения формулы второго замечательного предела
![]() :
:
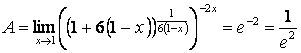 .
.
2. Прологарифмируем обе части заданного равенства:
![]() ,
,
и учтем, что при ![]()
![]() :
:
![]() .
.
4 Производные и их приложения
Для решения задач 1-4.30 достаточно применять таблицу производных, правила дифференцирования и формулу производной сложной функции:
![]()
![]()
Найти производные первого порядка ![]()
1.30 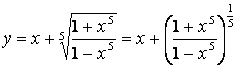 .
.
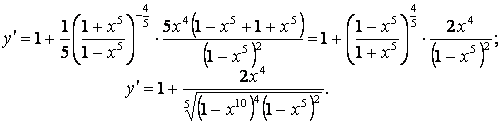
2.30 ![]() .
.
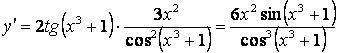 .
.
3.30 Найти ![]() и
и ![]() , если
, если ![]() .
.
Решение: 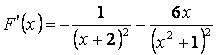 ;
;
![]() .
.
Найти вторые производные 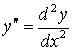 .
.
4.30 ![]() .
.
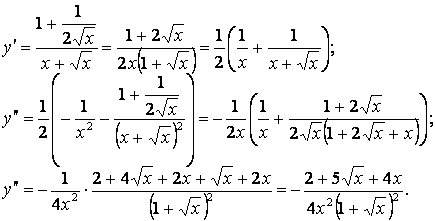
5.30 ![]() .
.
Решение. Считая, что ![]() , используем формулу параметрического
дифференцирования
, используем формулу параметрического
дифференцирования
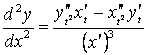
![]() ;
;
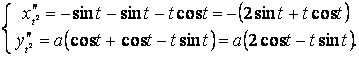
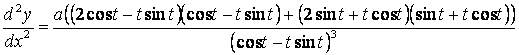 ,
,
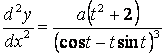 .
.
Решить следующие задачи
6.30 При каком
значении параметра ![]() парабола
парабола ![]() касается кривой
касается кривой ![]() ?
?
 |
Решение. При
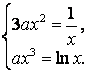
Из первого уравнения найдем ![]() . Подставив найденное значение во второе
уравнение, получим:
. Подставив найденное значение во второе
уравнение, получим:
![]() .
.
Освобождаясь от логарифма, найдем требуемое значение параметра
![]() .
.
7.30 Точка движется прямолинейно по закону ![]() . Через какой промежуток
времени после начала движения точка остановится? Найти путь, пройденный точкой
за это время?
. Через какой промежуток
времени после начала движения точка остановится? Найти путь, пройденный точкой
за это время?
Решение. Точка остановится, когда ее скорость
![]() ,
,
т.е. по истечении времени ![]() после начала движения. За это время точка
пройдет путь
после начала движения. За это время точка
пройдет путь
![]() ед. длины.
ед. длины.
5 Неопределенный интеграл
Найти неопределенные интегралы
С помощью простых преобразований приходим к «табличным» интегралам:
1.30  .
.
2.30 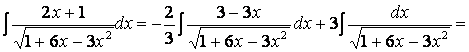
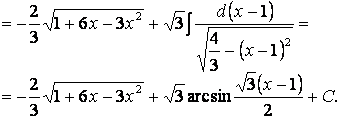
3.30 Для освобождения от линейной иррациональности заменяем переменную интегрирования
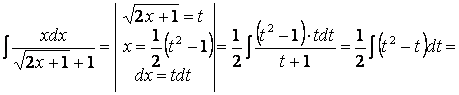
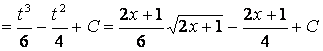 .
.
4.30 Применяем формулу интегрирования по частям
![]() .
.

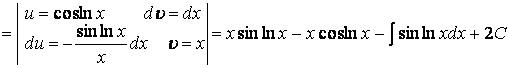 .
.
Рассматривая полученное равенство как уравнение, где неизвестным является заданный интеграл, найдем:
![]() .
.
5.30  .
.
Рациональную дробь под интегралом разложим в сумму простейших дробей, применяя метод неопределенных коэффициентов (произвольных значений):


Подведя числа ![]() и
и
![]() под знак
дифференциала, получим
под знак
дифференциала, получим
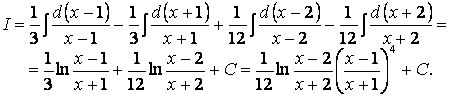
6.30 Применяем универсальную тригонометрическую подстановку:

6 Определенный интеграл и его приложения
1.30 Вычислить определенный интеграл:
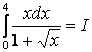 .
.
Для «рационализации» интеграла делаем замену переменной интегрирования:
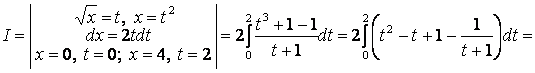
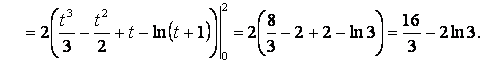
2.30 Вычислить несобственный интеграл или доказать его расходимость:
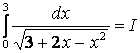 .
.
Решение. Имеем несобственный интеграл ![]() -рода, так как в точке
-рода, так как в точке ![]() подынтегральная функция
не ограничена. Поэтому
подынтегральная функция
не ограничена. Поэтому
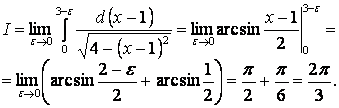
Заданный интеграл сходящийся.
3.30 Найти длину одной арки циклоиды ![]() .
.
Решение. Длина дуги плоской кривой, заданной своими параметрическими уравнениями, равна
 .
.
По условию: ![]() .
Поэтому
.
Поэтому

4.30 Какую работу нужно затратить, чтобы растянуть
пружину на ![]() ,
если сила в
,
если сила в ![]() растягивает
ее на
растягивает
ее на ![]() ?
Известно (закон Гука), что упругая сила пружины
?
Известно (закон Гука), что упругая сила пружины ![]() , где
, где ![]() - величина растяжения,
- величина растяжения, ![]() - постоянный коэффициент,
определяемый из условия задачи.
- постоянный коэффициент,
определяемый из условия задачи.
Решение. По условию ![]() , следовательно,
, следовательно, ![]() .
.
 |
В прямолинейном движении (см. рисунок 8) работа
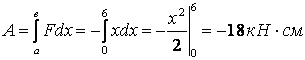 .
.
7 Дифференциальные уравнения
Решить данные дифференциальные уравнения (ДТ)
1.30 ![]() .
.
Решение. Общее решение линейного неоднородного ДУ 1-порядка
![]()
определяется по формуле
![]() .
.
По условию ![]() ,
поэтому:
,
поэтому:
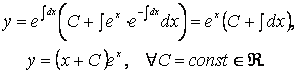
2.30 ![]() .
.
Решение. Имеем ДУ 1-порядка с разделяющимися переменными. После простых преобразований придем к уравнению с разделенными перменными:
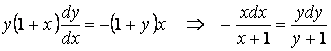
или
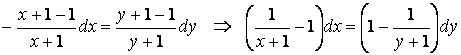 .
.
Взяв неопределенные интегралы от обеих частей равенства соответственно
по переменным ![]() и
и
![]() , общий
интеграл заданного ДУ представим в виде:
, общий
интеграл заданного ДУ представим в виде:
![]()
или
![]() .
.
3.30 ![]() (1)
(1)
Решение. Уравнение можно решить двумя способами: 1) путем понижения порядка и 2) как линейное неоднородное ДУ 2-порядка с постоянными коэффициентами.
1. В уравнении вместо отсутствующей независимой
переменной ![]() примем
примем
![]() и введем
новую неивестную функцию
и введем
новую неивестную функцию ![]() . Тогда
. Тогда
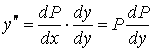 .
.
Тем самым, понизив порядок заданного ДУ, придем к уравнению с разделяющимися перменными:
 .
.
Его общее решение:
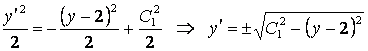 .
.
Это есть ДУ рассмотренного типа:
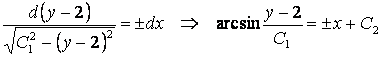 ,
,
![]() .
.
Заменив постоянные интегрирования на новые: ![]() , общее решение
заданного ДУ можно записать в виде закона гармонических колебаний:
, общее решение
заданного ДУ можно записать в виде закона гармонических колебаний:
![]() . (2)
. (2)
2. Составим и решим характеристическое уравнение
соответствующего (1) однородного уравнения ![]() :
:
![]() .
.
Общее решение однородного уравнения:
![]() . (3)
. (3)
Ввиду отсутствия резонанса: ![]() за частное решение (1) возьмем
за частное решение (1) возьмем ![]() и составим общее
решение заданного неоднородного ДУ:
и составим общее
решение заданного неоднородного ДУ:
![]() .
.
Заменив произвольные постоянные по схеме
![]() ,
,
полученное решение можно представить в виде (2).
4.30 ![]() .
(4)
.
(4)
Решение. Дана задача Коши. Поступая как в предыдущей
задаче, найдем общее решение (3), соответствующего (4) однородного ДУ. Ввиду
отсутствия резонанса: ![]() частное
решение неоднородного уравнения (4) будем искать в виде его правой части:
частное
решение неоднородного уравнения (4) будем искать в виде его правой части:
![]() .
.
Подставив эти выражения в уравнение (4) и приравняв коэффициенты перед ![]() и
и ![]() в обеих частях полученного
тождества, найдем:
в обеих частях полученного
тождества, найдем:
![]() .
.
Общее решение заданного ДУ и его производная:
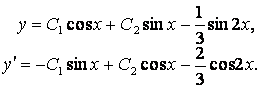
Удовлетворив заданным начальным условиям, найдем: ![]() и решение задачи Коши
и решение задачи Коши
![]() .
.
5.30 ![]() .
(5)
.
(5)
Решение. Применяем метод вариации произвольных постоянных. Для этого составим характеристическое уравнение соответствующего (5) однородного уравнения и фундаментальную систему решений последнего:
![]() ,
,![]() .
.
Общее решение заданного неоднородного уравнения ищем в виде
![]() . (6)
. (6)
Для нахождения неизвестных функций составим систему двух линейных уравнений
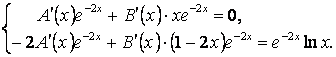
Так как ![]() ,
то
,
то

После интегрирования:

![]() ,
,
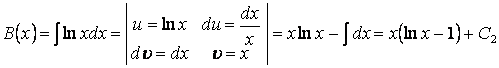 .
.
Подставив найденные функции в (6), получим искомое решение
![]() .
.
8 Кратные и криволинейные интегралы
1.30 Изменить порядок интегрирования в повторном интеграле
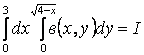 .
.
Решение. Область интегрирования ![]() (см. рисунок 9) ограничена
линиями:
(см. рисунок 9) ограничена
линиями: ![]() ,
, ![]() .
.
Парабола ![]() и прямая
и прямая ![]() пересекаются в точке
пересекаются в точке ![]() . Прямая
. Прямая ![]() делит область
делит область ![]() на две части, поэтому
на две части, поэтому
 |
Рисунок 9
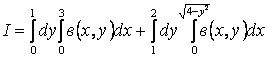 .
.
2.30 Вычислить тройной интеграл по области ![]() , ограниченной заданными
поверхностями:
, ограниченной заданными
поверхностями:
![]() .
.
Решение. Первые две поверхности представляют собой прямые, круглые конус и цилиндр:

с осями, параллельными оси ![]() (см. рисунок 10). На плоскости
(см. рисунок 10). На плоскости ![]() они пересекаются по
окружности
они пересекаются по
окружности ![]() .
Значит,
.
Значит,
![]() (круг).
(круг).
Область ![]() представляет
собой «чернилицу» (см. рисунок 10).
представляет
собой «чернилицу» (см. рисунок 10).
![]() Переходя к цилиндрической системе координат и
считая, что в «обычном» расположении осей координат произведена круговая
перестановка: , получим:
Переходя к цилиндрической системе координат и
считая, что в «обычном» расположении осей координат произведена круговая
перестановка: , получим:
![]() . (1)
. (1)
Подставив значения ![]() и
и ![]() из (1) в уравнение конуса, найдем:
из (1) в уравнение конуса, найдем: ![]() . Итак,
. Итак, ![]() . Это приводит к
трехкратному интегралу
. Это приводит к
трехкратному интегралу
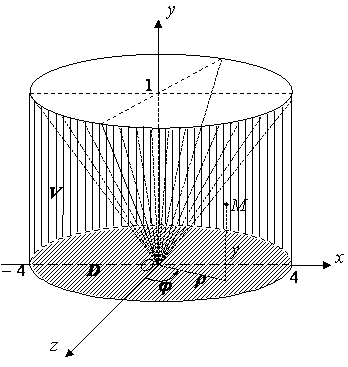 |
Рисунок 10
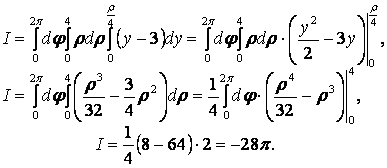
3.30 Проверить, является ли данное выражение полным
дифференциалом функции ![]() . Если да, то найти эту функцию:
. Если да, то найти эту функцию:
![]() (2)
(2)
где
 .
.
Решение. Найдем частные производные:

Так как 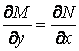 ,
то
,
то ![]() . По
формуле дифференциала функции двух переменных
. По
формуле дифференциала функции двух переменных
 . (3)
. (3)
Сравнивая выражения (2) и (3), заключаем, что
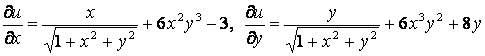 . (4)
. (4)
Найдем неопределенный интеграл по переменной ![]() от обеих частей первого из
равенств (4):
от обеих частей первого из
равенств (4):
![]() . (5)
. (5)
Для нахождения «постоянной» интегрирования ![]() приравняем частную производную
по
приравняем частную производную
по ![]() функции (5)
и второе из выражений (4):
функции (5)
и второе из выражений (4):
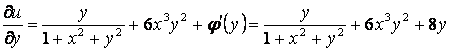 .
.
Отсюда
![]() .
.
Окончательно,
![]() .
.
4.30 Вычислить криволинейный интеграл вдоль заданной дуги ![]() :
:
![]() ,
, ![]() - отрезок прямой, заключенный между
точками
- отрезок прямой, заключенный между
точками ![]() и
и ![]() .
.
Решение. Линия интегрирования есть прямая, проходящая через две заданные точки:
![]() .
.
Элемент длины отрезка интегрирования
![]() .
.
Заданный криволинейный интеграл I-рода приводится к определенному интегралу:
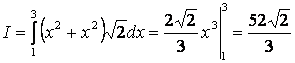 .
.
Список литературы
1. Я.С. Бугров, С.М. Никольский. Элементы линейной алгебры и аналитической геометрии. –Москва: Наука 2000.
2. Я.С. Бугров, С.М. Никольский. Дифференциальное и интегральное исчисление. –Москва: Наука, 2001.
3. Я.С. Бугров, С.М. Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. –Москва: Наука, 2002.
4. А.П. Рябушко и др. Индивидуальные задания по высшей математике. –Минск: Вышэйшая школа, 2000, чч 1,2,3.
Содержание
|
1 Векторная алгебра |
2 |
|
2 Аналитическая геометрия |
4 |
|
3 Пределы |
8 |
|
4 Производные и их приложения |
9 |
|
5 Неопределенный интеграл |
12 |
|
6 Определенный интеграл и его приложения |
13 |
|
7 Дифференциальные уравнения |
15 |
|
8 Кратные и криволинейные интегралы |
17 |
|
Список литературы |
21 |