Коммерциялық емес акционерлік қоғам
Алматы энергетика және байланыс Университеті
Жоғары математика кафедрасы
МАТЕМАТИКА 1,2
Күрделі есептерді шешуге арналған әдістемелік нұсқаулар
Практикалық сабақтар үшін
Алматы 2011
Құрастырғандар: К.М. Мұстахишев, Б.Ж. Атабай. Математика 1,2 Барлық мамандықтар мен оқу түрінің студенттері үшін практикалық сабақтарда күрделі есептерді шығаруға арналған әдістемелік құрал – Алматы: АЭжБУ, 2011, 21б.
А.П. Рябушко және басқ. Жоғары математика бойынша жеке тапсырмалар жинағы. -Минск; Жоғары мектеп, 2000, 1,2,3 б.б. оқу құралынан СӨЖ-ге (бақылау жұмыстары мен коллоквиумдарға) арналған сегіз тапсырманың 30-нұсқалары шығарылып, әдістемелік нұсқаулармен жабдықталған. Қажетті формулалар келтірілген.
Пікір беруші: м.-ф. ғыл. канд. доцент Т.К. Каирбеков
“Алматы энергетика және байланыс университеті” коммерциялық емес акционерлік қоғамының 2011 ж. баспа жоспары бойынша басылды
© “Алматы энергетика және байланыс университеті” КЕАҚ, 2011 ж.
А.П. Рябушко және басқ. Жоғары математика бойынша жеке тапсырмалар жинағы. -Минск; Жоғары мектеп, 2000, 1,2,3 б.б. оқу құралы жоғары техникалық оқу орындарының студенттері үшін математикадан негізгі әдебиеттер тізімінде тұрақты орын алып келеді. Онда қосымшалар ретінде сегіз тақырып: «Векторлық алгебра», «Талдама геометрия», «Шектер», «Туындылар және олардың қолданылулары», «Анықталмаған интеграл», «Анықталған интеграл және оның қолданылулары», «Дифференциалдық теңдеулер», «Еселі және қисықсызықты интегралдар» бойынша бақылау жұмыстары мен коллоквиумдарға арналған тапсырмалар келтірілген. Оларды Математика 1,2 курсының сәйкес тараулары бойынша СӨЖ үшін тапсырмалар ретінде де пайдалануға болады.
Оқу құралының негізгі бөліктерінде келтірілген тапсырмалар үшін «типтік варианттардағы» есептер шығарылып көрсетілген. Студенттер үшін осындай әдістемелік көмек «қосымшалардағы» тапсырмалар бойынша да артық болмасы белгілі.
Ұсынылып отырған құралда барлық сегіз тапсырманың 30-варианттары шығарылып, әдістемелік нұсқаулармен жабдықталған. Қажетті формулалар келтірілген. Кейбір есептер екі әдіспен шығарылған.
1 Векторлық алгебра
1.30 ![]() тетраэдрі (1 суретті қара) берілген;
тетраэдрі (1 суретті қара) берілген;
![]() деп алып,
деп алып, ![]() және
және ![]() векторларын (
векторларын (![]() және
және ![]() сәйкес
сәйкес ![]() және
және ![]() қырларының
ортаңғы нүктелері)
қырларының
ортаңғы нүктелері) ![]() және
және ![]() арқылы өрнектеңіз.
арқылы өрнектеңіз.
Шешу. Үшбұрыштың орта
сызығының қасиеттері бойынша ![]() , ал шарт бойынша
, ал шарт бойынша ![]() . Олай болса,
. Олай болса, ![]() .
.
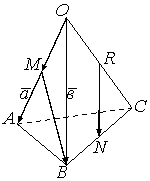 |
1 сурет
2.30 Егер ![]() болса, онда
болса, онда ![]() неге тең?
неге тең?
Шешу. Скалярлық көбейтінді
![]()
болғандықтан
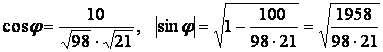 .
.
Олай болса,
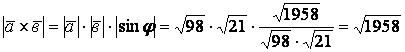 .
.
3.30 Модулі ![]() және
және ![]() векторларына перпендикуляр,
векторларына перпендикуляр, ![]() осімен доғал
бұрыш жасайтын
осімен доғал
бұрыш жасайтын ![]() векторынынң
координаталарын табыңыз.
векторынынң
координаталарын табыңыз.
Шешу. Векторлардың (![]() мен
мен ![]() және
және ![]() мен
мен ![]() ) перпендикулярлық
шарттары,
) перпендикулярлық
шарттары, ![]() векторы
үшін скалярлық квадраттың формуласы
векторы
үшін скалярлық квадраттың формуласы
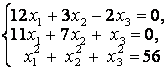 (1)
(1)
теңдеулерінің жүйесіне келтіреді.
Алғашқы екі сызықтық теңдеулер жүйесін бөлек шешелік:
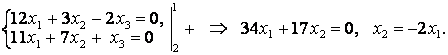
Екінші теңдеуден:
![]()
Шарт бойынша ![]() ,
демек,
,
демек, ![]() және
және
![]() . Табылған
белгісіздерді (1) жүйенің соңғы теңдеуіне
қойсақ:
. Табылған
белгісіздерді (1) жүйенің соңғы теңдеуіне
қойсақ:
![]() .
.
Ізделініп отырған вектор
![]() .
.
4.30 Қандай ![]() және
және ![]() векторлары үшін
векторлары үшін
![]()
шарты орындалады?
Шешу. Берілген теңдіктің сол жағы екі вектордың айырымының скалярлық квадраты болып табылады:
![]() .
.
Бұдан берілген шарт ![]() болғанда ғана, яғни
болғанда ғана, яғни ![]() және
және ![]() векторлары өзара
перпендикуляр:
векторлары өзара
перпендикуляр: ![]() болғанда
ғана орындалатынын көреміз.
болғанда
ғана орындалатынын көреміз.
5.30 Егер табанында ![]() және
және ![]() векторларына тұрғызылған
параллелограмм жатса, онда
векторларына тұрғызылған
параллелограмм жатса, онда ![]() және
және ![]() векторларына тұрғызылған
параллелепипедтің биіктігі неге тең?
векторларына тұрғызылған
параллелепипедтің биіктігі неге тең?
Шешу. Үш және екі вектордың сәйкес аралас және векторлық көбейтінділерінің геометриялық мағыналарын пайдаланайық.
Параллелепипедтің (2 суретті қара) көлемі
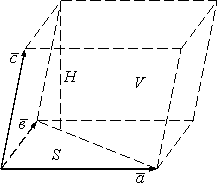 |
2 сурет
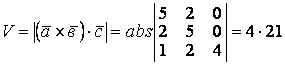 ,
,
табанының ауданы
![]() .
.
Параллелепипедтің биіктігі
![]() .
.
2 Талдама геометрия
1.30 Үшбұрыштың екі
қабырғасының: ![]() және бір медианасының:
және бір медианасының: ![]() теңдеулері
берілген. Оның үшінші қабырғасының теңдеуін
жазыңыз.
теңдеулері
берілген. Оның үшінші қабырғасының теңдеуін
жазыңыз.
Шешу. Үшбұрыштың (3 суретті
қара) ![]() және
және
![]() қабырғаларының
теңдеулері берілген деп есептеп. Оның
қабырғаларының
теңдеулері берілген деп есептеп. Оның ![]() төбесінің координаталарын
табайық:
төбесінің координаталарын
табайық:
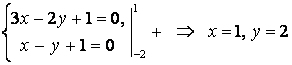 .
.
 Табылған мәндерді медиананың
теңдеуіне қойсақ,
Табылған мәндерді медиананың
теңдеуіне қойсақ, ![]() нүктесі берілген медиананың
бойында жатпайтынын көреміз.
нүктесі берілген медиананың
бойында жатпайтынын көреміз.
Екі мүмкін жағдайды қарастыралық.
I. Медиана ![]() төбесінен түсірілген деп,
төбесінен түсірілген деп, ![]() және
және
![]() нүктелерінің
координаталарын табайық:
нүктелерінің
координаталарын табайық:
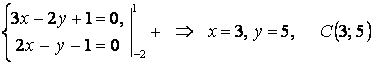 ;
;
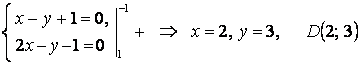 .
.
![]() нүктесі
нүктесі
![]() табанын
қақ бөледі:
табанын
қақ бөледі: ![]() . Сондықтан:
. Сондықтан:
![]() .
.
Берілген екі нүкте арқылы өтетін түзу ретінде
үшінші ![]() қабырғасының
теңдеуі:
қабырғасының
теңдеуі:
![]() .
.
II. Енді берілген медиана ![]() төбесінен түсірілген
делік. Алдыңғы жағдайдағыша медиананың екі
ұшының координаталарын табамыз:
төбесінен түсірілген
делік. Алдыңғы жағдайдағыша медиананың екі
ұшының координаталарын табамыз: ![]() . Ал,
. Ал, ![]() болғандықтан:
болғандықтан:
![]() .
.
Олай болса, ![]() қабырғасының
теңдеуі:
қабырғасының
теңдеуі:
![]() .
.
2.30 Төбесі координаталардың бас
нүктесінде, ал, фокусы ![]() нүктесінде орналасқан
параболаның теңдеуін жазыңыз.
нүктесінде орналасқан
параболаның теңдеуін жазыңыз.
Шешу. Парабола берілген ![]() координаталар жүйесін (4 суретті
қара) бас нүктеден айналдыра
координаталар жүйесін (4 суретті
қара) бас нүктеден айналдыра ![]() -қа бұрудан пайда болған
-қа бұрудан пайда болған ![]() системасында сол параболаның
канондық теңдеуі
системасында сол параболаның
канондық теңдеуі
![]()
түрінде жазылады. Өйткені фокальдық параметр ![]()
![]()
теңдігінен табылады.
Координаталар осьтерін белгілі бір бұрышқа
бұру формулаларын пайдаланып, ![]() жүйесін бас нүктеден айналдыра
жүйесін бас нүктеден айналдыра
![]() бұрышына
бұралық:
бұрышына
бұралық:
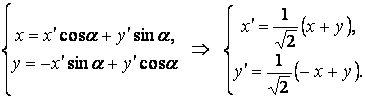
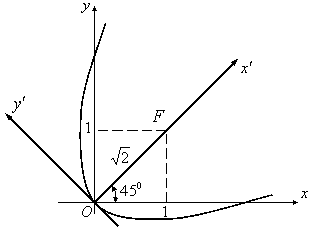 |
4 сурет
Айнымалыларды алмастырғаннан кейін параболаның теңдеуі
![]()
немесе
![]()
түрінде жазылады.
3.30 ![]() жазықтығының
жазықтығының
![]()
![]() ,
, ![]()
жазықтықтарымен қиылысуынан пайда болған
үшбұрыштың ішінде орналасқан және сол
жазықтықтардан бірдей қашықтықта жатқан ![]() нүктесінің
координаталарын табыңыз.
нүктесінің
координаталарын табыңыз.
Шешу. Шартқа сәйкес ![]() нүктесінің берілген
үш жазықтықтан қашықтықтарын
теңестірейік:
нүктесінің берілген
үш жазықтықтан қашықтықтарын
теңестірейік:
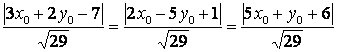 . (2)
. (2)
![]() түзулерімен шектелген ашық
түзулерімен шектелген ашық ![]() үшбұрышының
(5 суретті қара) нүктелерінде алғашқы екі
теңдеудің сол жақтары теріс, ал үшінші
теңдеудің сол жағы оң таңба қабылдайды.
Сондықтан (2) қатынастардан
үшбұрышының
(5 суретті қара) нүктелерінде алғашқы екі
теңдеудің сол жақтары теріс, ал үшінші
теңдеудің сол жағы оң таңба қабылдайды.
Сондықтан (2) қатынастардан
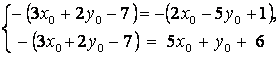
теңдеулер жүйесін құруға болады. Одан:
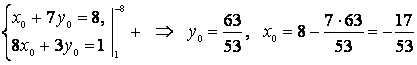 ,
,
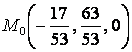 .
.
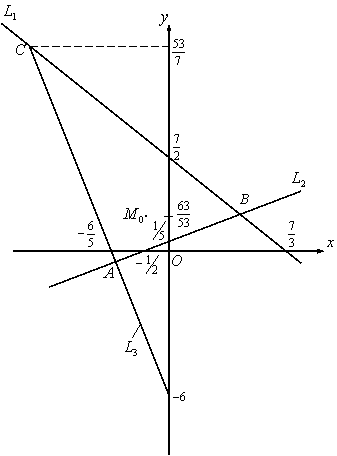 |
5 сурет
4.30 Координаталар жазықтықтарының ![]() жазықтығымен
қиылысуынан пайда болған
жазықтығымен
қиылысуынан пайда болған ![]() үшбұрышының (6 суретті
қара)
үшбұрышының (6 суретті
қара) ![]() биіктігін
тауып, оның канондық теңдеулерін жазыңыз.
биіктігін
тауып, оның канондық теңдеулерін жазыңыз.
Шешу. Аталмыш үшбұрыштың
төбелері мен оларды қосатын векторлардың координаталары
оңай табылады: ![]()
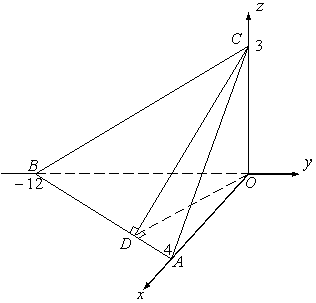 |
6 сурет
және, мысалы, ![]() .
.
Шарт бойынша ![]() . Одан басқа,
. Одан басқа, ![]() болғандықтан
болғандықтан ![]() . Сондықтан
. Сондықтан ![]() үшбұрышының
жазықтығы үшін
үшбұрышының
жазықтығы үшін ![]() нормальдық вектор бола алады;
нормальдық вектор бола алады; ![]() осі арқылы
өтетін бұл жазықтықтың теңдеуі
осі арқылы
өтетін бұл жазықтықтың теңдеуі
![]()
түрінде жазылады. Енді ![]() және
және ![]() үшбұрыштары
жазықтықтарының қиылысу сызығы ретінде
үшбұрыштары
жазықтықтарының қиылысу сызығы ретінде ![]() түзуінің
жалпы теңдеулерін құрастырайық:
түзуінің
жалпы теңдеулерін құрастырайық:
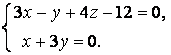
Бұдан түзудің ![]() нүктесі арқылы өтетінін
ескеріп, канондық теңдеулерге көшсек:
нүктесі арқылы өтетінін
ескеріп, канондық теңдеулерге көшсек:

Әрі қарай:
![]() ;
;
![]() .
.
Басқаша қарасақ:
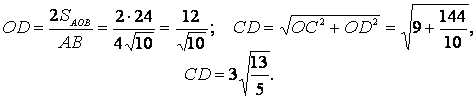
3 Шектер
Шектерді табыңыз
1.30 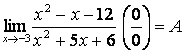 .
.
Квадрат үшмүшеліктерді жәй көбейткіштерге жіктегеннен кейін:
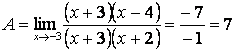 .
.
2.30 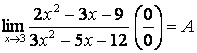 .
.
Мұнда да ![]() формуласын қолданайық:
формуласын қолданайық:
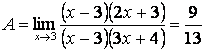 .
.
3.30 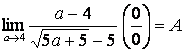 .
.
Бөлшектің алымын да, бөлімін де бөлімінінің түйіндесіне көбейтелік:
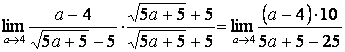 ,
,
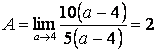 .
.
4.30 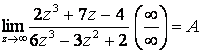 .
.
Рационал бөлшектің алымын да, бөлімін де айнымалының ең үлкен дәрежесіне мүшелеп бөліп, шекке көшелік:
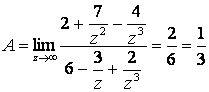 .
.
5.30 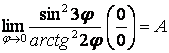 .
.
Аргумент ![]() -да
-да ![]() және
және ![]() болғандықтан:
болғандықтан:
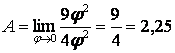 .
.
6.30 ![]() .
.
1 Функцияны екінші тамаша шектің формуласын
![]()
қолдануға ыңғайлы түрге келтірейік:
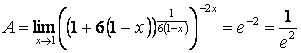 .
.
2 Берілген теңдіктің екі жағын да логарифмдеп:
![]() ,
,
![]() - да
- да ![]() екенін ескерсек:
екенін ескерсек:
![]() .
.
4 Туындылар және олардың қолданылулары
1-4.30 есептерді шешу үшін туындылар кестесін, дифференциалдау ережелерін және күрделі функция:
![]()
туындысының формуласын
![]()
қолдану жеткілікті.
Бірінші ретті туындыларды ![]() табыңыз
табыңыз
1.30 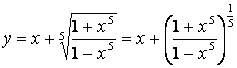 .
.
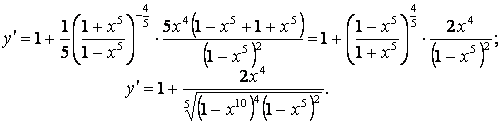
2.30 ![]() .
.
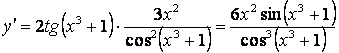 .
.
3.30 ![]() деп,
деп, ![]() мен
мен ![]() -ді табыңыз.
-ді табыңыз.
Шешу: 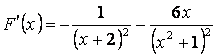 ;
;
![]() .
.
Екінші ретті туындыларды 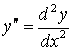 табыңыз
табыңыз
4.30 ![]() .
.
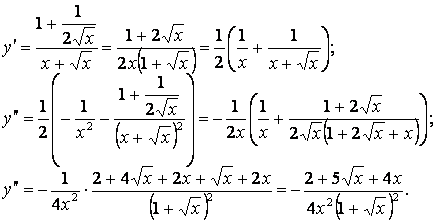
5.30 ![]() .
.
Шешу. Берілуінде ![]() деп, параметрлік дифференциалдау
формуласын
деп, параметрлік дифференциалдау
формуласын
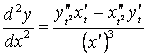
қолданайық:
![]() ;
;
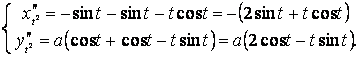
 ,
,
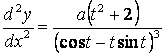 .
.
Төмендегі есептерді шешіңіз
6.30 Параметрдің ![]() қандай мәнінде
қандай мәнінде ![]() параболасы
параболасы ![]() қисығымен
жанасады?
қисығымен
жанасады?
Шешу. Берілген қисықтар ![]() болғанда
өзара қиылысады (7 суретті қара), ал,
болғанда
өзара қиылысады (7 суретті қара), ал, ![]() болғанда жанаса алады.
Олардың
болғанда жанаса алады.
Олардың ![]() жанасу
нүктесінде ортақ жанамалары
жанасу
нүктесінде ортақ жанамалары ![]() болады. Демек,
болады. Демек, ![]() нүктесінде
нүктесінде ![]() және
және ![]() функцияларының
ортақ мәндері
функцияларының
ортақ мәндері ![]() және тең туындылары бар.
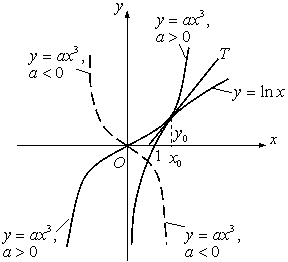
Яғни
және тең туындылары бар.
Яғни
 |
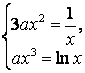
7 сурет
теңдеулер жүйесі орын алады. Бірінші теңдеуден ![]() . Мұны екінші
теңдеуге қойсақ:
. Мұны екінші
теңдеуге қойсақ:
![]() .
.
Логарифмнен құтылып, параметрдің ізделініп отырған мәнін табамыз:
![]() .
.
7.30 Түзу сызық бойымен ![]() заңына сай
қозғалыстағы нүктенің бастапқы сәттен
тоқтағанға дейінгі қозғалыс уақытын
және жолын табыңыз.
заңына сай
қозғалыстағы нүктенің бастапқы сәттен
тоқтағанға дейінгі қозғалыс уақытын
және жолын табыңыз.
Шешу. Нүкте жылдамдығы
![]()
болғанда, яғни қозғалыс басталған
соң ![]() уақыттан
кейін тоқтайды. Осы уақыт аралығында нүктенің
жүрген жолы
уақыттан
кейін тоқтайды. Осы уақыт аралығында нүктенің
жүрген жолы
![]() ұз. бірлігі.
ұз. бірлігі.
5 Анықталмаған интегралдар
Анықталмаған интегралды табыңыз
Қарапайым түрлендірулердің көмегімен «кестелік» интегралдарға келеміз:
1.30 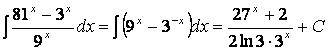 .
.
2.30 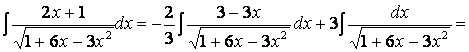
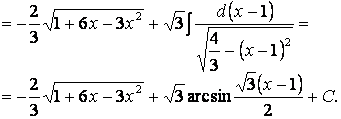
3.30 Сызықтық иррационалдықтан құтылу үшін интегралдау айнымалысын алмастырамыз:
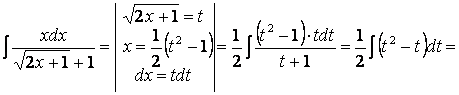
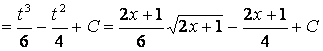 .
.
4.30 Бөліктеп интегралдау формуласын
![]()
қолданайық.
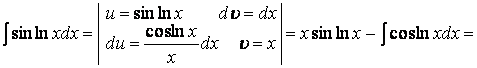
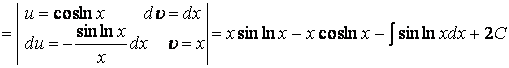 .
.
Бастапқы берілген интегралды белгісіз деп қарап, табылған қатынасты теңдеу ретінде шешсек:
![]() .
.
5.30 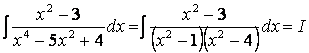 .
.
Анықталмаған коэффициенттер (ырықты мәндер) әдісін пайдаланып, интегралданушы рационал бөлшекті қарапайым бөлшектер қосындысына жіктейік:
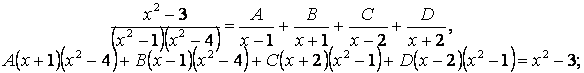
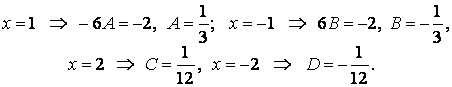
Табылған мәндерді орындарына қойып, ![]() және
және ![]() сандарын дифференциал
белгісінің астына енгізелік:
сандарын дифференциал
белгісінің астына енгізелік:
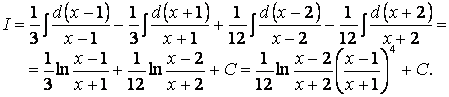
6.30 Универсал (шәміл) тригонометриялық алмастыруды қолданайық:
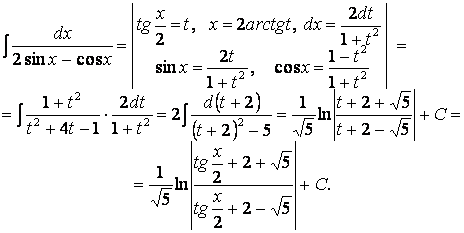
6 Анықталған интеграл және оның қолданылулары
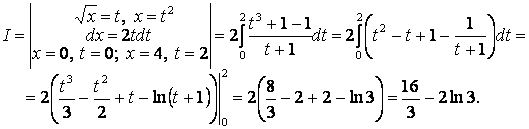
1.30 Анықталған интегралды
есептеңіз: 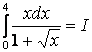 .
.
Интегралды «рационалдау» үшін интегралдау айнымалысын алмастырамыз:
2.30 Меншіксіз интегралды есептеңіз немесе оның жинақсыз екенін дәлелдеңіз:
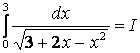 .
.
Шешу. Берілгені ![]() -текті меншіксіз интеграл, өйткені
интегралданушы функция
-текті меншіксіз интеграл, өйткені
интегралданушы функция ![]() нүктесінде шектелмеген.
Сондықтан
нүктесінде шектелмеген.
Сондықтан
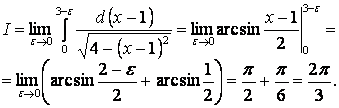
Берілген интеграл жинақты.
3.30 Циклоиданың: ![]() бір аркасының ұзындығын
табыңыз.
бір аркасының ұзындығын
табыңыз.
Шешу. Параметрлік теңдеулермен берілген жазық қисық доғасының ұзындығы
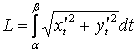 .
.
Шарт бойынша: ![]() . Олай болса,
. Олай болса,

4.30 Егер ![]() күштің әсерінен серіппе
күштің әсерінен серіппе ![]() -ге созылатын болса, оны
-ге созылатын болса, оны
![]() -ге созу
үшін қанша жұмыс шығындау қажет?
-ге созу
үшін қанша жұмыс шығындау қажет?
Ескерту. Гук заңы бойынша серіппенің
қарсылық күші ![]() . Мұнда
. Мұнда ![]() - серіппенің созылу
ұзындығы,
- серіппенің созылу
ұзындығы, ![]() -
есептің шартынан анықталатын тұрақты коэффициент.
-
есептің шартынан анықталатын тұрақты коэффициент.
Шешу. Шарт бойынша ![]() , демек,
, демек, ![]() . Түзусызықты
қозғалыс (8 суретті қара) үшін жұмыс
. Түзусызықты
қозғалыс (8 суретті қара) үшін жұмыс
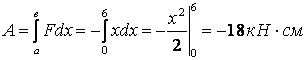 .
.
8 сурет
7 Дифференциалдық теңдеулер
Берілген дифференциалдық теңдеулерді (ДТ) шешіңіз.
1.30 ![]() .
.
Бірінші ретті сызықтық ДТ-ның
![]()
жалпы шешуі
![]()
Шарт бойынша ![]() болғандықтан
болғандықтан
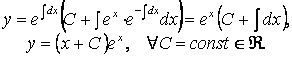
2.30 ![]() .
.
Шешу. Бірінші ретті айнымалылары ажыратылатын ДТ берілген. Қарапайым түрлендіруден кейін айнымалылары ажыратылған теңдеуге келеміз:
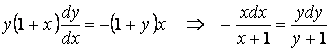
немесе
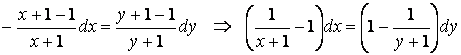 .
.
Теңдіктің екі жағынан сәйкес ![]() және
және ![]() айнымалылары бойынша
анықталмаған интегралдар алып, берілген ДТ-ның жалпы
интегралын табамыз:
айнымалылары бойынша
анықталмаған интегралдар алып, берілген ДТ-ның жалпы
интегралын табамыз:
![]()
немесе
![]() .
.
3.30 ![]() .
(1)
.
(1)
Теңдеуді шешудің екі тәсілін қарастыралық: 1) ретін төмендету, 2) коэффициенттері тұрақты екінші ретті біртексіз сызықтық ДТ ретінде қарау арқылы.
1) Теңдеуге енбеген ![]() тәуелсіз
айнымалысының орнына
тәуелсіз
айнымалысының орнына ![]() -ті қабылдап, жаңа
-ті қабылдап, жаңа ![]() белгісіз функциясын
енгізейік. Екінші туынды
белгісіз функциясын
енгізейік. Екінші туынды
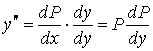
екенін ескеріп, бірінші ретті айнымалылары ажыратылатын теңдеуге келеміз:
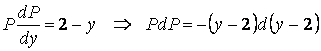 .
.
Оның жалпы шешуі
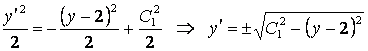 .
.
Бұл да айнымалылары ажыратылатын ДТ:
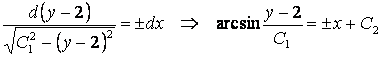 ,
,
![]() .
.
Интегралдау тұрақтыларын алмастырып: ![]() , табылған жалпы
шешуді гармониялық тербелістер заңы түрінде жазуға
болады:
, табылған жалпы
шешуді гармониялық тербелістер заңы түрінде жазуға
болады:
![]() . (2)
. (2)
2) Берілген (1) теңдеуге сәйкес біртекті ДТ-ның мінездеме теңдеуін құрып, оның түбірлерін табалық:
![]() .
.
Біртекті теңдеудің жалпы шешуі
![]() . (3)
. (3)
Резонанс жоқ: ![]() болғандықтан (1)
теңдеудің дербес шешуін
болғандықтан (1)
теңдеудің дербес шешуін ![]() деп алып, оның жалпы шешуін
деп алып, оның жалпы шешуін
![]()
түрінде жаза аламыз. Ырықты тұрақтыларды
![]()
жүйесі бойынша алмастырып, табылған жалпы шешуді (2) түрге келтіруге болады.
4.30 ![]() .
(4)
.
(4)
Шешу. Бұл Коши есебі. Алдыңғы
есептегідей жолмен (4)-ге сәйкес біртекті теңдеудің жалпы
шешуі (3) түрде табылады. Мұнда да резонанс жоқ: ![]() . Біртексіз (4)
теңдеудің дербес шешуін оның оң жағына
ұқсас түрде іздейміз:
. Біртексіз (4)
теңдеудің дербес шешуін оның оң жағына
ұқсас түрде іздейміз:
![]() .
.
Бұл өрнектерді (4) теңдеуге қойып,
алынған тепе-теңдіктің екі жағындағы ![]() пен
пен ![]() -тің коэффициенттерін теңестірсек:
-тің коэффициенттерін теңестірсек:
![]() .
.
Берілген ДТ-ның жалпы шешуі мен оның туындысы:
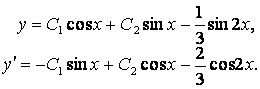
Бастапқы шарттарға қанағаттандыратын
интегралдау тұрақтыларының мәндері: ![]() болғандықтан
Коши есебінің шешуі
болғандықтан
Коши есебінің шешуі
![]() .
.
5.30 ![]() .
(5)
.
(5)
Шешу. Ырықты тұрақтыларды вариациялау әдісін қолданайық. Ол үшін (5)-ге сәйкес біртекті ДТ-ның мінездеме теңдеуін құрып, оның түбірлерін табамыз:
![]() .
.
Біртекті ДТ-ның іргелік шешулер жүйесі:
![]() .
.
Берілген біртексіз ДТ-ның жалпы шешуі
![]() (6)
(6)
түрінде ізделінеді. Мұндағы белгісіз функциялардың туындылары
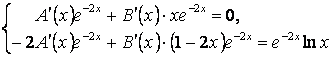
жүйесінен табылады. Бұдан ![]() болғандықтан:
болғандықтан:

Интегралданғаннан кейін:

![]() ,
,
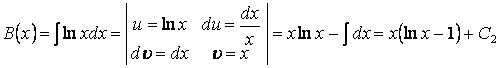 .
.
Табылған функцияларды (6)-ға қойып, ізделініп отырған шешуді табамыз:
![]() .
.
8 Еселі және қисықсызықты интегралдар
1.30 Қайталама интегралда интегралдау ретін өзгертіңіз
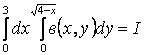 .
.
 |
Шешу. Интегралдау аймағы
9 сурет
Сондықтан
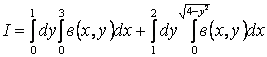 .
.
2.30 Үшқабат интегралды берілген беттермен
шектелген ![]() аймағы
бойынша есептеңіз:
аймағы
бойынша есептеңіз:
![]() .
.
Шешу. Алғашқы екі теңдеу осьтері ![]() осіне параллель тік
дөңгелек конус пен цилиндрді (10 суретті қара)
анықтайды:
осіне параллель тік
дөңгелек конус пен цилиндрді (10 суретті қара)
анықтайды:
 .
.
Олар ![]() жазықтығында
жазықтығында
![]() шеңбері
бойымен қиылысады, яғни
шеңбері
бойымен қиылысады, яғни
![]() (дөңгелек).
(дөңгелек).
Сонымен, интегралдау аймағы ![]() сиясауыт тәріздес.
сиясауыт тәріздес.
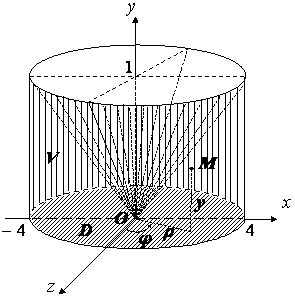 |
10 сурет
![]() Цилиндрлік координаталар жүйесіне
көшіп және координаталар осьтерінің «әдеттегі»
орналасуларында қума орыналмастыру: орын алған
десек:
Цилиндрлік координаталар жүйесіне
көшіп және координаталар осьтерінің «әдеттегі»
орналасуларында қума орыналмастыру: орын алған
десек:
![]() . (1)
. (1)
Конустың теңдеуіне (1)-ден ![]() пен
пен ![]() -тің мәндерін
қойсақ:
-тің мәндерін
қойсақ: ![]() .
Ақырында:
.
Ақырында: ![]() деп,
үшеселі интегралға келеміз:
деп,
үшеселі интегралға келеміз:
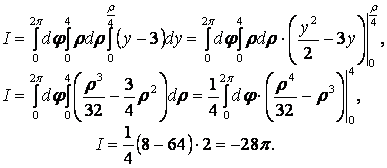
3.30 Берілген өрнек:
![]() (2)
(2)
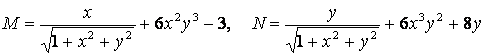
белгілі бір ![]() функциясының
толық дифференциалы бола ма? Болса, сол функцияны табыңыз.
функциясының
толық дифференциалы бола ма? Болса, сол функцияны табыңыз.
Шешу. Дербес туындыларды табайық:
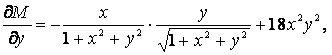
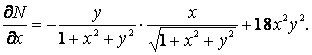
Мұнда 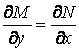 болғандықтан
болғандықтан
![]() . Екі
айнымалы функциясының толық дифференциалы
. Екі
айнымалы функциясының толық дифференциалы
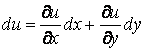 (3)
(3)
болғандықтан (2) және (3) өрнектерді салыстыра келіп:
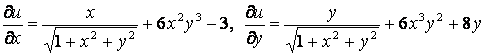 (4)
(4)
дей аламыз. Бұл теңдіктердің біріншісінің екі
жағынан да ![]() бойынша
анықталмаған интеграл алайық:
бойынша
анықталмаған интеграл алайық:
![]() . (5)
. (5)
Интегралдау «тұрақтысын» ![]() табу үшін (5)-нің
табу үшін (5)-нің ![]() бойынша алынған
дербес туындысын (4) өрнектердің екіншісімен теңестірейік:
бойынша алынған
дербес туындысын (4) өрнектердің екіншісімен теңестірейік:
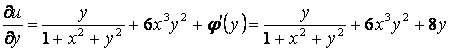 .
.
Бұдан:
![]() .
.
Талап етілген функция
![]() .
.
4.30 Қисықсызықты интегралды
![]()
![]() және
және
![]() нүктелерін
қосатын түзу кесіндісі
нүктелерін
қосатын түзу кесіндісі ![]() бойынша есептеңіз.
бойынша есептеңіз.
Шешу. Берілген екі нүкте арқылы өтетін түзудің теңдеуі
![]()
болғандықтан интегралдау «қисығы» доғасының элементі
![]() .
.
Берілген I-текті қисықсызықты интеграл анықталған интегралға келтіріледі:
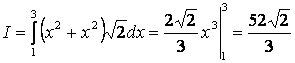 .
.
Қолданылған әдебиеттер
1. Я.С. Бугров, С.М. Никольский. Сызықтық алгебра және аналитикалық геометрия элементтері. –Москва: Ғылым, 2000.
2. Я.С. Бугров, С.М. Никольский. Дифференциалдық және интегралдық есептеу. –Москва: Ғылым, 2001.
3. Я.С. Бугров, С.М. Никольский. Дифференциалдық теңдеулер. Еселі интегралдар. Қатарлар. Комплекс айнымалының функциялары. –Москва: Ғылым, 2002.
4. А.П. Рябушко және басқ. Жоғары математика бойынша жеке тапсырмалар жинағы. –Минск: Жоғары мектеп, 2000, 1,2,3, б.б.
Мазмұны
|
1 Векторлық алгебра |
2 |
|
2 Талдама геометрия |
4 |
|
3 Шектер |
8 |
|
4 Туындылар және олардың қолданылулары |
9 |
|
5 Анықталмаған интегралдар |
12 |
|
6 Анықталған интеграл және оның қолданылулары |
13 |
|
7 Дифференциалдық теңдеулер |
15 |
|
8 Еселі және қисықсызықты интегралдар |
17 |
|
Қолданылған әдебиет |
21 |