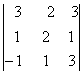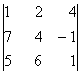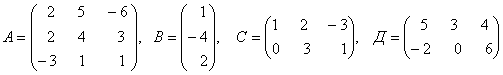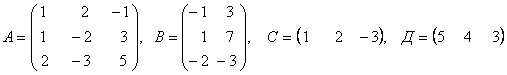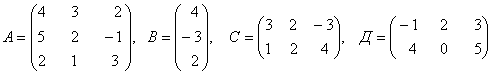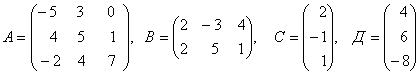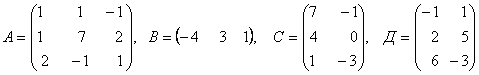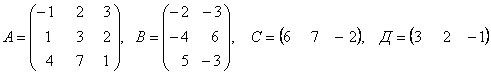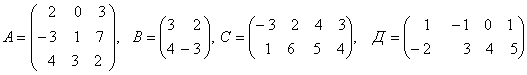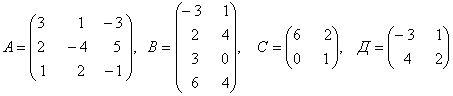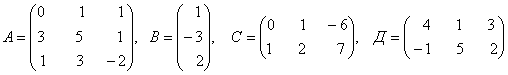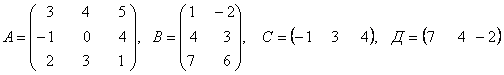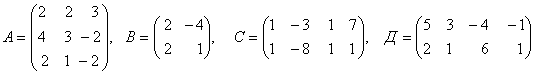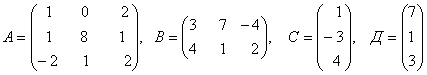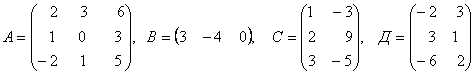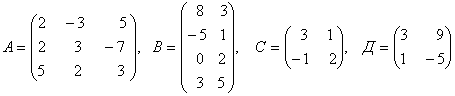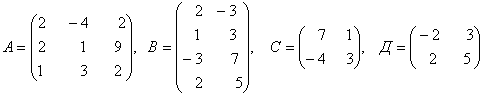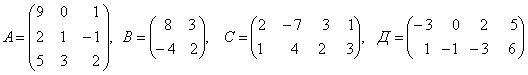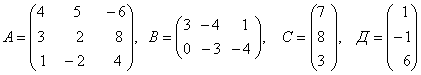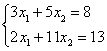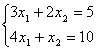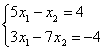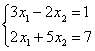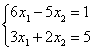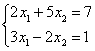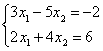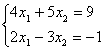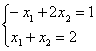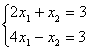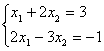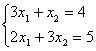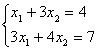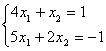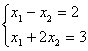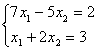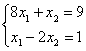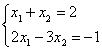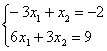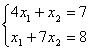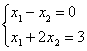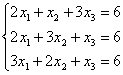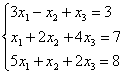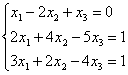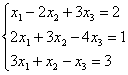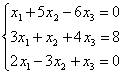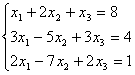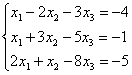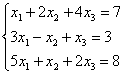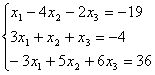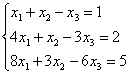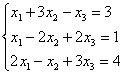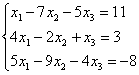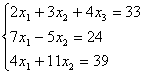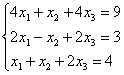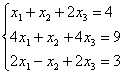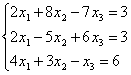Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

  

МАТЕМАТИКА В ЭКОНОМИКЕ

Методические указания и задания к расчетно-графическим работам

для студентов специальности 5В050600-«Экономика»

Часть 1

 

 

                                                      Алматы 2011                                                                

         Составители:  С.А. Нурпеисов,  Ж.С. Абдулланова.   Математика в экономике. Методические указания и задания к расчетно-графическим работам. Часть 1.-Алматы: АУЭС, 2011-28с.

 

        Методическое указание подготовлено в соответствии с типовой программой по курсу «Математика для экономистов» по всем направлениям экономических специальностей.

         Методические указания  и задания к РГР содержат задачи курса матема- тики для экономических специальностей дневного отделения АУЭС:«Элемен- ты линейной алгебры и аналитической  геометрии».  Даны основные теорети- ческие вопросы программы и решение типового варианта. 

 

        Рецензент: канд. физ.-мат. наук, проф. С.Е. Базарбаева.

 

          Печатается по плану издания некоммерческого акционерного общества  «Алматинский университет энергетики и связи» на 2011 г.

 

             ã НАО «Алматинский университет энергетики и связи», 2011 г.

 

                                                                                         Сводный план 2011г., поз

 

 

Типовой расчет 1

        Элементы линейной алгебры и аналитической геометрии

Теоретические вопросы

1.   Определители, их свойства, вычисление.

2.   Матрицы, действия над ними, обратная матрица.

3.   Ранг матрицы и его вычисление.

4.   Различные методы решения системы линейных уравнений:

а) правило Крамера;

б) метод Гаусса;

в) с помощью вычисления обратной матрицы;

г) с помощью теоремы Кронеккера-Капелли.

5. Однородные системы линейных уравнений.

6. Скалярное  произведение векторов, их приложения. Собственные значения и собственные   векторы матрицы.

7. Системы линейных неравенств.

8. Векторы, их длина, линейные операций над векторами.  Коллениарность,  компланарность, ортогональность векторов, угол между векторами. Системы n-мерных векторов.

9. Скалярное, векторное, смешанное произведения векторов, их приложения.

10. Точка и прямая на плоскости.

11.Уравнение прямой линии на плоскости.

12. Взаимное расположение двух прямых на плоскости.

13. Различные  уравнения  прямой  на плоскости.

14. Расстояние от точки до прямой.

15. Преобразование координат. Преобразование параллельного переноса.

16. а) гипербола - как график обратной пропорциональной зависимости;

б) гипербола как график дробно - линейной  функций;

в) парабола как график квадратного трехчлена.

 

 

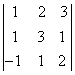
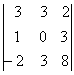
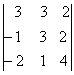
     1.   Вычислить определитель второго порядка

1.1

 

1.2  

 

 

1.3

     

1.4

 

1.5

 

 1.6

1.7

      

1.8

 

1.9

 

1.10

1.11

   

1.12

  

1.13

1.14

 

1.15

1.16

 

1.17

1.18

1.19

 

1.20

 

1.21

 

1.22

   

1.23

 

1.24

 

1.25

 

1.26

 

1.27

1.28

 

1.29

1.30

 

 

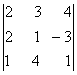
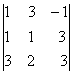
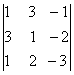
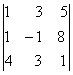
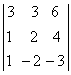
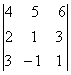
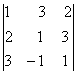
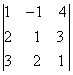
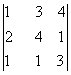
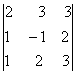
  2.  Дан определитель третьего порядка:

а) найти минор  Мij  и алгебраичеcкое дополнение Аij  элемента аij;

б) разложить определитель по i-ой строке;

в) вычислить определитель, разложив его по j-му столбцу;

г) вычислить по правилу треугольника ( правило Саррюса).

 

2.1

,

i=2; j=1

     

2.2

 ,

i=2; j=3

 

2.3

  ,  i=1;j=2                                     

 

2.4

 i=3; j=1

     

2.5

, i=3;j=2

 

2.6

  , i=3; j=2

 

2.7

, i=2;j=1

 

2.8

, i=3;j=2

 

2.9

            ,i=3;j=1

 

2.10

, i=3; j=2

 

2 .11

, i=2; j=3

 

2.12

 , i=3; j=1

 

2.13

, i=2; j=3

   

2.14

, i=2; j=2

 

2.15

, i=2; j=1 

 

2.16

, i=3; j=1   

 

2.17

, i=3; j=1

 

2.18

, i=2;j=3

 

2.19

, i=3; j=3

 

2.20

, i=3; j=2 

 

2.21

, i=1; j=3

 

2.22

, i=3; j=2

 

2.23

, i=2; j=2

 

2.24

, i=3;j=1

 

2.25

, i=2; j=1

 

2.26

, i=2;j=3  

 

2.27

, i=1; j=3

 

2.28

, i=1; j=1

  

2.29

, i=2; j=3

 

2.30

, i=1;j=3

 

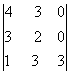
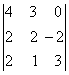
3. Даны матрицы А, В, С, Д:

 а) найти матрицы 4С+3Д, С-2Д;

 б) найти матрицу  В, транспонированную матрице В.

 

3.1

,  ,  ,   

3.2

3.3 

3.4 

3.5

3.6

3.7

3.8 

3.9

3.10

3.11

3.12

3.13

3.14

3.15

3.16

3.17

3.18

3.19

3.20

3.21

3.22

3.23

3.24

3.25

3.26

3.27

3.28

3.29

3.30

 

4. Даны матрицы А ,  В,  С (в заданий 3):

а) возможно ли произведение матриц АВ, ВС?

Обьяснить почему, если невозможно и  найти произведение , если возможно; 

б) найти матрицу , обратную матрице А.

5. Даны точки      на плоскости и уравнение прямой  :

а) составить уравнение прямой  , проходящей через  эти точки;

б) записать уравнение прямой  в виде :

  Сделать чертеж и на нем указать геометрический смысл      

в) найти угол между прямыми   . Будут ли эти прямые параллельны, перпендикулярны? 

5.1  

5.2  

5.3  

5.4 

5.5 

5.6  

5.7 

5.8  

5.9  

5. 10 

5.11 

5.12 

5.13 

5.14 

5.15 

5.16 

5.17 

5.18 

5.19 

5.20 

5.21 

5.22 

5.23 

5.24 

5.25 

5.26 

5.27 

5.28 

5.29 

5.30 

 

   6. Решить систему уравнений:

  а) по правилу Крамера;

  б) матричным методом  (с помощью обратной матрицы).

 

  6.1  

 

  6.2  

 

  6.3  

 

  6.4  

 

 

  6.5

 

  6.6  

 

  6.7

 

  6.8   

 

  6.9   

 

 6.10  

                                                   6.11  

 

  6.12  

 

 6.13   

  

  6.14  

 

  6.15 

 

 6.16

 

  6.17  

 

  6.18 

 

 6.19   

 

  6.20

 

  6.21 

 

 6.22

 

  6.23

 

  6.24 

 

 6.25   

 

  6.26  

 

  6.27 

 

 6.28   

 

  6.29  

 

  6.30 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7. Проверить совместность систем уравнений  и в случае совместности решить методом Гаусса.

 

7.1

 

7.2

 

7.3

 

 

7.4

 

7.5

 

7.6

 

 

7.7

 

7.8

 

7.9

 

7.10

 

7.11

 

7.12

  

 

7.13

 

7.14

 

7.15

 

7.16

 

7.17

 

7.18

 

7.19

 

7.20

 

7.21

 

7.22

 

7.23

 

7.24

 

7.25

 

7.26

 

7.27

 

7.28

 

7.29

                   

7.30

 

8.  Даны вершины треугольника: А, В, С.    

1) Найти систему неравенств, определяющую множество точек треугольника АВС.

2) Найти длину стороны АВ.

3) Найти косинус внутреннего угла при вершине А.

4) Найти уравнение медианы, проведенной из вершины С. 

5) Найти уравнение высоты , опущенной из вершины С.

6) Найти длину этой высоты.

7) Найти точку пересечения высот.

 

8.1  

8.2  

8.3   

8.4   

8.5      

8.6    

8.7     

8.8    

8.9

8.10   

8.11    

8.12

8.13

8.14

8.15    

8.16     

8.17    

8.18

8.19    

8.20   

8.21   

8.22

8.23   

8.24    

8.25  

8.26     

8.27  

8.28    

8.29  

8.30   

                         

9. Даны уравнения: а) параболы;  б) гиперболы.

Требуется  путем параллельного переноса системы координат найти:

а) координаты вершины параболы и привести ее уравнение к виду;

б) асимптоты гиперболы и привести ее уравнение к виду .

Построить обе системы  координат, параболу и гиперболу.

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8 

9.9

9.10

9.11

9.12

9.13

9.14

9.15

9.16

9.17

 9.18

9.19

9.20

9.21

9.22

9.23

9.24

9.25

9.26

9.27

9.28

9.29

9.30

 

                                   Решение типового варианта

1. Вычислить определитель второго порядка .

Решение. По формуле   имеем .

1.     Дан определитель третьего порядка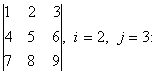    

а) найти минор  и алгебраическое дополнение  элемента ;

б) разложить определитель по i-ой строке;

в) вычислить определитель, разложив его по j-му столбцу;

г) вычислить по правилу треугольника  (правилу Саррюса).

Решение:

а) минор   элемента  равен поределителю,  полученному из данного определителя после вычеркивания i-ой строки и j-го столбца.  Таким образом, вычеркиваем в нашем определителе вторую строку и третий столбец, получаем

Алгебраическое дополнение  элемента  вычисляем по формуле  .  Значит   ;

б) формула разложения определителя по i-ой строке для определителя n-го порядка имеет вид:

,             

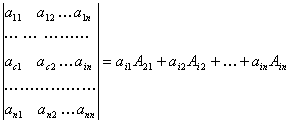где  алгебраическое дополнение  элемента . Так как , то формула перепишется так

.

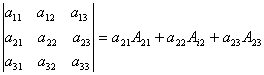Искомое разложение имеет вид

в) вычислить определитель, разложив его по j-му столбцу.

Формула разложения по третьему столбцу имеет вид     .

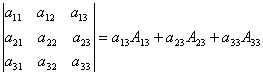Таким образом,

г) по правилу треугольника определитель третьего порядка равен сумме шести членов: члены со знаком плюс получают при перемножении по три   элемента определителя, взятых по схеме

 

, члены со знаком минус – по схеме   .

 Поэтому

3-4 . Даны матрицы:

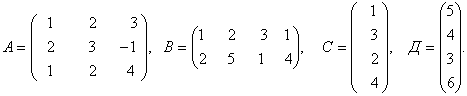
а) найти матрицы 4С+3Д, С-2Д;

б) найти матрицу  В, транспонированную матрице В;

в) возможно ли произведение матриц АВ, ВС?

Обьяснить, почему, если невозможно, и  найти произведение, если возможно; 

г) найти матрицу , обратную матрице А.

Решение : а)

.

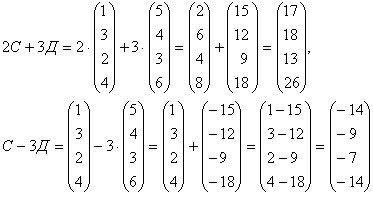б) матрица  В , транспонированная матрице В, получается заменой строк  матрицы  В  с ее столбцами с теми же номерами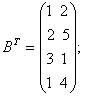   

в) произведение матриц АВ возможно, если число столбцов матрицы  А  равно числу строк матрицы В. Размеры матриц: .

Таким образом, - произведение невозможно.

- произведение   возможно.

Итак,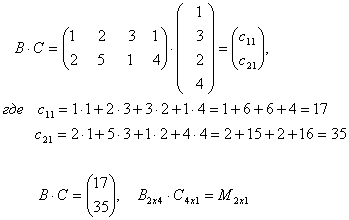

г) 

Найдем определитель матрицы А:

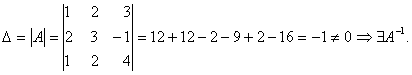
Далее найдем    

                   

               

тогда

5. Даны точки      на плоскости и уравнение прямой 

а) составить уравнение прямой  , проходящей через  эти точки;

Уравнение прямой , проходящие через точки  находится по формуле .   Значит, уравнение прямой    

имеет вид  

б) запишем уравнение  прямой                                                           

в виде 1)

2) .

3)   .

Построим прямую по двум точкам 

Укажем геометрический смысл коэффициентов:

     -это угловой коэффициент прямой ,

-величина  отрезка, отсекаемого прямой  на оси ОУ, считая от начала координат,

А=1,   В=-1  - координаты нормального вектора прямой , т.е. .

        Уравнение  называют уравнением прямой с угловым коэффициентом;

 - общим уравнением прямой;

 - уравнением прямой в отрезках.

 

в) угол  между  прямыми  можно найти по одной из двух формул. Если уравнения прямых заданы в общем виде     , то находим 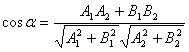. Если заданы уравнения  с угловыми коэффициентами ,  то находим

Так как по условию уравнение задано  в общем виде , то возьмем  уравнение тоже в общем виде и воспользуемся первой формулой:     

Ввиду того, что то прямые

не параллельны и не  перпендикулярны;

г) найти точку, симметрическую  точке относительно плоскости :. Сделать чертеж.

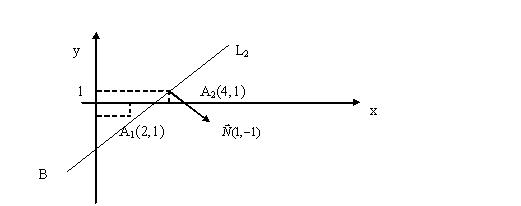
Решение. Для большей наглядности решение задачи начнем с построения чертежа (см.рисунок 1)

                     

 

                                             Рисунок 1

 

Прежде всего построим в пространстве точку , а затем плоскость  Для построения данной плоскости достаточно найти точки ее пересечения с осями координат. Полагая  в  уравнении  плоскости у=0,z=0, получим х=2. Это значит, что плоскость пересекает ось Ох в точке . Аналогично устанавливаем, что данная плоскость пересекает ось Оу в точке и ось Оz – в точке. Соединяя точки А, В, С прямыми, полу- чим треугольник АВС, через который  проходит данная плоскостьПо опре- делению точки М и N симметричны относительно плоскости, если они распо- ложены на одинаковом расстояний, но по разные стороны плоскости. Следо- вательно, точки М и N лежат на общем перпендикуляре МN и отрезки МР и РN равны по длине, если Р есть точка пересечения прямой МN с плоскостью . Исходя из вида уравнения плоскости, определим ее нормальный вектор . Составим теперь каноническое уравнение прямой МN , взяв  в качестве ее направляющего вектора:.

Далее, так как Р является точкой пересечения прямых МN с плоскостью ,то ее координаты удовлетворяют одновременно уравнениям прямой и плоскости, т. е.системе  

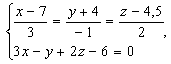
для решения которой лучше записать уравнение прямой в параметрической форме:.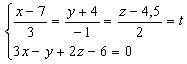

 Откуда следует, что .

 

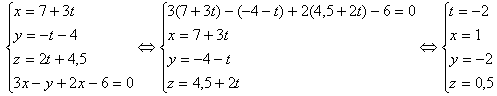Таким образом, координаты точки Р найдены:

 С  другой стороны, точка Р является серединой отрезка МN и ее координаты определяются через координаты точки М и N по формулам деления отрезка пополам:                 .

Выражая координаты искомой точки N  через координаты известных точек М и Р, подставляя их, получим:

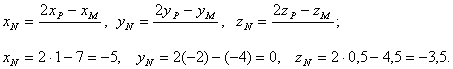
Следовательно, - искомая точка.

6.Решить систему 

а) по правилу Крамера;

б) матричным методом (т.е.  с помощью обратной матрицы).

Решение:а) решение системы   по правилу Крамера имеет вид - определитель системы, 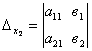      - вспомогательные определители, полученные из определителя системы заменой первого и второго столбцов столбцами свободных членов в нашем случае                     .

ответ: х=-7,  х.

б) решение системы в матричном виде записывается так: - матрица–столбец неизвестных,

- матрица- столбец свободных членов,

- матрица обратная для матрицы системы.    Если

 Найдем обратную матрицу для матрицы системы  . Так как определитель системы  то обратная матрица существует и 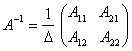. Алгебраические дополнения элементов матрицы:                      обратная матрица: ,

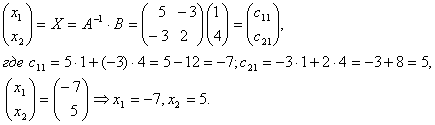
7. Проверить совместность системы уравнений и в случае совместности решить методом Гаусса.

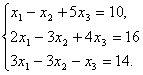
Решение: по теореме Кронекера-Капелли система совместна(т.е. имеет хотя бы одно решение), если ранг матрицы системы равен рангу расширенной матрицы системы ; система не совместна (т.е. не имеет решений), если .

Матрица системы ,   расширенная матрица системы . Будем определять ранг матрицы методом элементарных преобразований, т.е. элементарными преобразованиями над строками матриц приведем их к ступенчатому виду. Так как матрица А содержится в матрице , то достаточно преобразовать только :умножим первую строку на  -2 и прибавим ко второй, затем умножим первую на  -3 и прибавим к третьей, получим:  .

Обе матрицы преобразовались к ступенчатой матрице, имеющей три ненулевые строки, следовательно,   и система совместна. Кроме того, так как число неизвестных равно трем и равно рангу, то система имеет единственное решение.

Метод Гаусса заключается в последовательном исключений неизвестных из уравнений системы с помощью элементарных преобразований  и приведении системы к ступенчатому виду. Так как элементарные преобразования систе- мы аналогичны элементарным преобразованиям матриц, то на практике заме- няем первые вторыми, проводимыми над строками расширенной матрицы системы. Выше эти преобразования были приведены.  Таким образом, данная система сводится к системе, соответствующей последней матрице:

  .

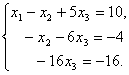Поднимаясь по этой системе снизу вверх, найдем из последнего уравнения , из последнего   ,     из первого: .  Ответ :.

8. Даны вершины треугольника: А(3;  0),  В(-5;   6),   С(-4;   1).

Найти: 1) Длину стороны АВ.

При нахождении  длины стороны АВ воспользуемся формулой для вычисления расстояния между двумя точками или, что то же самое, длины вектора АВ:.

2) Косинус внутреннего угла А.

Внутренний угол при вершине А есть угол, образованный векторами , совпадающими со сторонами треугольника АВС. Поэтому , исходя из опре- деления скалярного произведения векторов, можно сначала вычислить , а затем, пользуясь таблицей для значений тригонометрических функций, най- ти величину угла А в радианах. При этом косинус внутреннего угла вычисля- ется по формуле: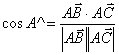. Определим координаты и длины векторов, входящих в последнюю формулу. Имеем:  .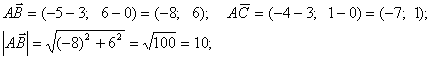

Тогда       .

3) Медиана СD делит сторону АВ или вектор  пополам. Поэтому сначала найдем координаты точки D:  .

Медиана проходит через точки С(-4,1) и D(-1,3), 2(х+4)=3(у-1), откуда окон- чательно  2х-3у+11=0  есть уравнение медианы СD.

4) Высота  , а поэтому векторы  и  ортогональны. Обозначим через х, у координаты точки  Е, найдем координаты векторов  и теперь, пользуясь условием ортогональности двух векторов, т.е. что их скалярное произведение равно нулю, получим уравнение высоты: .

5) Длину высоты СЕ можно вычислить как длину вектора , для чего пред- варительно надо определить координаты точки Е,одновременно принадлежа- щей прямым СЕ и АВ, а также координаты вектора . Но можно восполь- зоваться формулой для вычисления расстояния от точки до прямой, согласно которой надо координаты точки  С подставить вместо х и у в нормированное уравнение прямой АВ и взять модуль полученного значения. Как было пока- зано в предыдущей задаче, сторона АВ определяется уравнением 3х+4у-9=0, координаты точки С известны:

Поэтому длина  высоты  СЕ равна:

.

6) Для нахождения точки пересечения высот достаточно знать уравнение двух высот. Уравнение СЕ определено. Найдем теперь уравнение, например, высоты ВF.Обозначим координаты точки F через х,у. Выразим координаты векторов  и, пользуясь условием их ортогональности, будем иметь: есть уравнение высоты ВF. Тогда координаты точки Н пересечения высот ВF и СЕ находятся из условия при- надлежности Н обеим прямым ВF и СЕ, т.е. из системы

 Решая которую, получим  .

Следовательно,  Н(- точка пересечения высот.

9. Заданы уравнения параболы и гиперболы: .

Требуется: а) путем параллельного переноса системы координат найти коор- динаты вершины параболы и привести ее уравнение к виду ;

б) путем параллельного переноса системы координат найти асимптоты ги- перболы и привести ее уравнение к виду , построить обе системы координат и гиперболу.

Решение: используем формулы параллельного переноса системы координат

 ,  где а  и в   - координаты нового начала координат, а  - новые координаты. Тогда исходное уравнение примет вид:

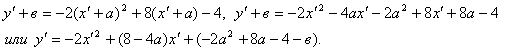
Найдем а и в, при  которых  коэффициент при  и свободный член обратятся в нуль: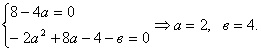

Следовательно, каноническое уравнение параболы . Вершина пара- болы находится в точке . График пара- болы дан на рисунке 1. Уравнение параболы  относительно новой системы координат  имеет простой вид , и ее легко построить. Так как , то ветви параболы направлены вниз. Тогда уравнение параболы отно- сительно новой системы координаты имеет простой вид  и ее легко построить. Так как -‹0, то ветви параболы направлены вниз. 

См. рисунок 2.

 

        

                                              Рисунок 2   

в)   .

Решение: путем параллельного переноса осей координат  преобразуем данные уравнения к виду:  или  

.

Найдем а и в из условий:  Тогда урав- нение гиперболы в новой системе координат примет вид

, ,

, координаты  относительно старой сис- темы координат, т.е. .  В новой системе координат уравнение ги- перболы примет вид:, причем новые оси координат являются асимп- тотами гиперболы. Уравнения этих асимптот относительно старой системы координат имеют вид: .  Так как  то ветви гиперболы будут расположены во второй и четвертой четвертях системы координат . Можно построить кривую во второй четверти, а затем отобразить от-

носительно начала координат и получить кривую в четвертой четверти.

 

 Канонические уравнения некоторых кривых второго порядка.

Задание гиперболы как график обратной пропорциональности .

Задание гиперболы как график дробно-линейной функции .

Если к этому уравнению применить формулу параллельного переноса системы координат, то оно примет вид .

 Уравнение параболы

Задание параболы как график квадратного трехчлена.

Если к этому уравнению применить формулу параллельного переноса сис- темы координат, то оно примет вид

Пример 1.  Дано уравнение параболы . С помощью параллель- ного переноса системы привести  к виду

Решение: используем формулы параллельного переноса системы координат .  Тогда исходное уравнение примет вид: .

Таким образом - вершина параболы.

Построим график параболы

 

 

 

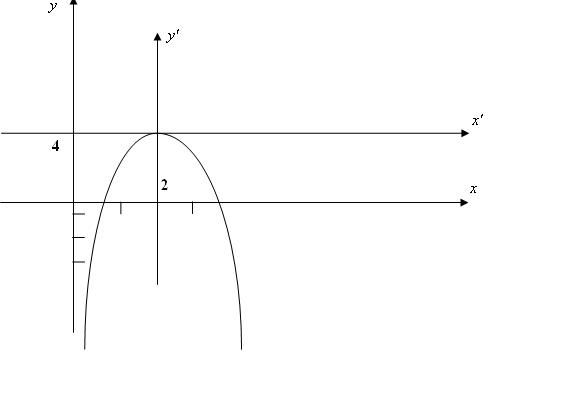
 Пример 2. Дано уравнение гиперболы . С помощью параллельного пере носа системы координат привести к виду

Решение: в начале определим координаты начала новой системы координат

.

Тогда исходное уравнение примет вид

 

 

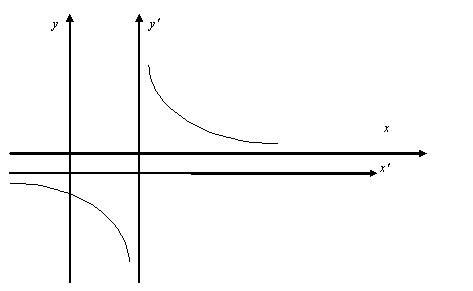
Пример 3. Для некоторого производства функция цены от спроса задана в виде ,а функция цены от предложения – в виде  .

1. Найти равновесную цену и соответствующие ей значения спроса и предложения.

2. При каких из значений наблюдается дефицит товара?

Решение. Для того чтобы найти равновесную цену приравниваем данные функции . Отсюда находим равновесную цену р=4. Известно, что дефицит товара наблюдается при уменьшении цены. Поэтому  при  имеем  ,   а при  имеем , т.е. при дефицит .

 

 

 

                                        Список литературы

 

1.        А.К Казешев, С.А. Нурпеисов «Математика для экономистов» учебное  пособие ./-Алматы:«Экономика» баспасы.2009.-450 с.

2.       Данко П.Е., Попов А.Г. и др.  «Высшая математика в упражнениях и  задачах» : В24.-М.:Высш.шк. 1986.-ч.1-352 с.

3.        Л.Н. Астраханцева, Л.Н. Ким, Ш.К. Айтчанова. Высшая математика. Методические указания и задания к расчетно-графической работе. ч.1.-Алматы:АИЭС,2001-48 с.

 

  

 

 

                                                 Содержание

 

Типовой расчет 1                                                                                    3

Теоретические вопросы                                                                          3  

Расчетные задания                                                                                  3  

Решение типового варианта                                                                  13 

Список литературы                                                                               28